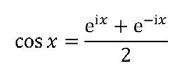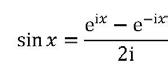VECTOR
FEBRUARI 2024 - nummer 19
TIJDSCHRIFT voor wiskundeonderwijs

IN DE WEER MET DE HOEPELSFEER 3
TWEE VERWEVEN LAGEN OPROLLEN 12
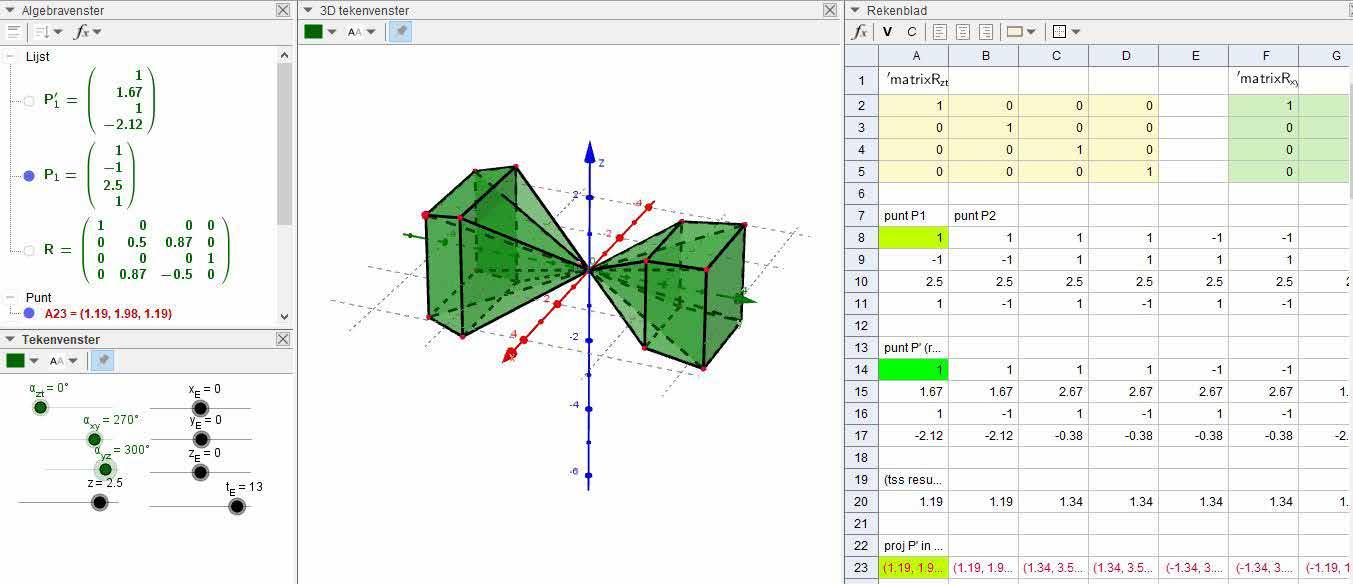
ROTEREN IN 4D 29
Met medewerking van Uitwiskeling, VVWL (Vlaamse Vereniging van Wiskundeleraars), GeoGebra Instituut, Vlaamse Wiskunde Olympiade, Ars et Mathesis en Pythagoras
VECTOR
3 IN DE WEER MET EEN HOEPELSFEER
TRAPGETALLEN 9
12 TWEE VERWEVEN LAGEN OPROLLEN
BOEKBESPREKINGEN 18
21 START- EN IJKINGSTOETSEN, DÉ SLEUTEL TOT STUDIESUCCES
OPPERVLAKTES VERGELIJKEN OP ZIJN GRIEKS 23
29 ROTEREN IN 4D
VAKANTIECURSUS 2024
BANACH-TARSKI: HOE GROEPENTHEORIE
VAN ÉÉN MELOEN ER TWEE MAAKT 34
DE MOOISTE FORMULE OOIT, EN HOE
36 LEONHARD EULER ZIJN FORMULE AFLEIDDE
VECTOR
6e jaargang - nummer 19
REDACTIE Nicolas Ruys, Tom Harteel, Anke Oderij, Karel Sierens - die Keure, Kleine Pathoekeweg 3, 8000 Brugge, educatief@diekeure.be
EXTERNE AUTEURS die occasioneel of op geregelde basis een bijdrage willen leveren, kunnen contact opnemen met educatief@diekeure.be.
VECTOR is gratis voor alle leerkrachten wiskunde in België.
VERANTWOORDELIJKE UITGEVER die Keure, Kleine Pathoekeweg 3, 8000 Brugge
VORMGEVING EN DRUK Isabelle Tilleman - die Keure, Brugge
REACTIES Al je reacties, suggesties en opmerkingen zijn welkom op educatief@diekeure.be
2
INHOUD
IN DE WEER MET EEN HOEPELSFEER
EEN ZONNEWIJZER LEER JE HET BESTE BEGRIJPEN DOOR ER MET JE
HANDEN AAN TE WERKEN. DAN ONTDEK JE DAT HET INTERESSANTE WISKUNDIGE PUZZELS ZIJN. EN JE MAAKT KENNIS MET HET VERBAND
TUSSEN TIJD EN DE BEWEGING VAN DE ZON AAN DE HEMELKOEPEL.
LEES OVER HANS’ EERSTE SCHREDEN OP HET PAD VAN DE ZONNEWIJZERKUNDE.
HANS SCHIPPER, HENK HIETBRINK
Jaren geleden kreeg Hans een oude zonnewijzer - met achterstallig onderhoud er gratis bij. Het metaal was gaan roesten en van de sokkel bladderde de verf af. Vergezeld door een filosofische tuinkabouter stond deze zogenaamde hoepelsfeer jarenlang scheefgezakt op een rustig plekje in de tuin: figuur 1.
De juiste tijd aangeven – ho maar.
Toen Hans het niet langer meer kon aanzien dat zo’n leuk instrument er zó bij stond, besloot hij zich in de zonnewijzerkunde te gaan verdiepen. Wat was de goede opstelling? Recht zetten leek Hans een eerste vereiste��, maar dat kon op allerlei manieren. Wat was de beste? In een voortvarend aangeschaft zonnewijzerboek las Hans: “de pijl moet naar het noorden gericht staan, onder een hoek die even groot is als
de breedtegraad van de plaats waar de hoepelsfeer staat”.
Huh? Wat staat er in die laatste zin?
Om dat te begrijpen, leek het Hans verstandig een schets te maken: figuur 2. De grootste cirkel stelt de Aarde voor. Zutphen, Hans’ woonplaats, is aangegeven op de 52e breedtegraad.
De pijl van de zonnewijzer, niet op schaal getekend, wijst in noordelijke richting. In noordelijke richting, maar niet naar de Noordpool!
OPGAVE 1
Met welke denkbeeldige lijn is de pijl evenwijdig?
Het antwoord op opgave 1 was een eerste resultaat, maar helemaal duidelijk was het allemaal nog

PYTHAGORAS
3
Figuur 1

Figuur 2

niet. Daarom maakte Hans een tweede schets: figuur 3. Voor het gemak is de aarde “rechtop gezet”. De aarde is rond, maar bij Zutphen lijkt hij gewoon plat. Dat heet het horizontale vlak. Bij Zutphen is dan ook een raaklijntje aan de aardecirkel getekend, zeg maar het zijaanzicht van het horizontale vlak van Hans’ tuin. Dat raaklijntje staat loodrecht op de bijbehorende straal van de cirkel.
Van de zonnewijzer is alleen nog maar de pijl getekend, waarvan we dankzij vraag 1 weten waar hij evenwijdig mee is.
OPGAVE 2
In de hoek, die de pijl met het horizontale vlak maakt, is een stip getekend.
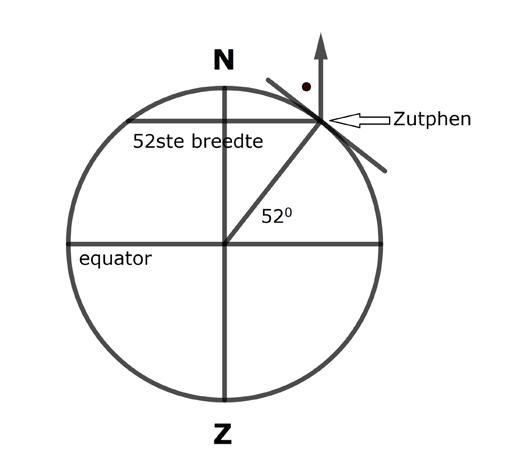
Kun je laten zien dat deze hoek 52° is?
Bij dit type zonnewijzer moet overal op aarde de pijl evenwijdig zijn met de aardas. De aardas is de verbindingslijn tussen de polen. Daarom heet de pijl een poolstijl. Waar je ook op aarde bent, de constructie van hoepel en poolstijl is vergelijkbaar, maar … op verschillende breedtegraden moet die hoepel met die poolstijl anders op zijn sokkel bevestigd worden.
OPGAVE 3
Welke richting ten opzichte van het aardoppervlak heeft de poolstijl, als de hoepelsfeer zich op de evenaar bevindt?
OPGAVE 4
Welke richting ten opzichte van het aardoppervlak heeft de poolstijl, als de hoepelsfeer op de noordpool staat?
Na schuren en schilderen, na vijlen en verven, na prutsen en poetsen stond er uiteindelijk een hoepelsfeer die ermee door kon: figuur 4. Je ziet de poolstijl, twee banden van noord naar zuid en een uurschaal rondom de poolstijl.
OPGAVE 5
Met welke denkbeeldige aardrijkskundige lijn is de uurschaal, bij een juiste opstelling, evenwijdig?
De uurschaal die loopt van VI via XII tot VI is een halve cirkel. Als de zon van zes uur ’s ochtends tot zes
4
Figuur 3

uur ’s avonds om de poolstijl draait, glijdt de schaduw van de poolstijl langs de uren op de uurschaal. De zon is dan over een hoek van 180° gedraaid.
OPGAVE 6
Hoeveel graden is dat per uur?
Je weet ook wel dat eigenlijk de aarde om de zon heen draait: het heliocentrisch model. In de zonnewijzerkunde gebruiken we soms dit model, maar vaker het geocentrisch model. Dat komt overeen met onze dagelijkse ervaring: de zon draait rond de aarde.
Om de hoepelsfeer te begrijpen gebruiken we het geocentrisch model. Als de zon om de aarde
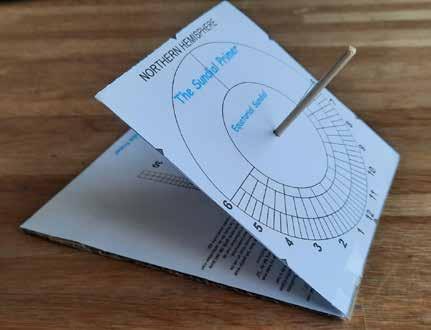
INSTRUCTIES
In figuur 6 zie je een afbeelding van een kartonnen zonnewijzer. Aan de regelmatige urenverdeling te oordelen is dit weer een equatoriale.
STAP 1
Download bouwplaten 01a en 01b op pyth.eu en voer de instructies uit.
OPGAVE 9
Welke hoek maakt de wijzerplaat van een equatoriale zonnewijzer met het horizontale vlak? (Hint: teken een zijaanzicht)
draait, draait hij meteen ook om de hoepelsfeer. Niet helemaal precies natuurlijk, want er is een zekere afstand tussen de poolstijl en de aardas. Die afstand is zo verwaarloosbaar klein vergeleken met de afstand tussen aarde en zon, dat we ervan uit kunnen gaan dat de zon om de poolstijl draait, net zo als om de aardas.
OPGAVE 7
De zon draait in 24 uur rond de aarde. Hoeveel graden draait de zon per uur?
Je antwoorden op de vorige twee vragen stemmen precies overeen. Eigenlijk is een hoepelsfeer een aarde in het klein, met een eigen aardas en een eigen equator.
Er zijn ook andere zonnewijzers, waarvan de uurschaal níet evenwijdig is met de evenaar, bijvoorbeeld de horizontale zonnewijzer. Daarvan ligt de wijzerplaat vlak op de grond. Je gaat zo’n horizontale zonnewijzer construeren uitgaande van een equatoriale zonnewijzer.
STAP 2
Download bouwplaten 02a en 02b Knip de rechthoekige bodemplaat uit. Knip “Southern Hemisphere” uit.
STAP 3
Leg de twee rechthoeken tegen elkaar zoals in figuur 7.
Figuur 4 Gerestaureerde hoepelsfeer, bewaakt door filosofische tuinkabouter.
5
Figuur 6
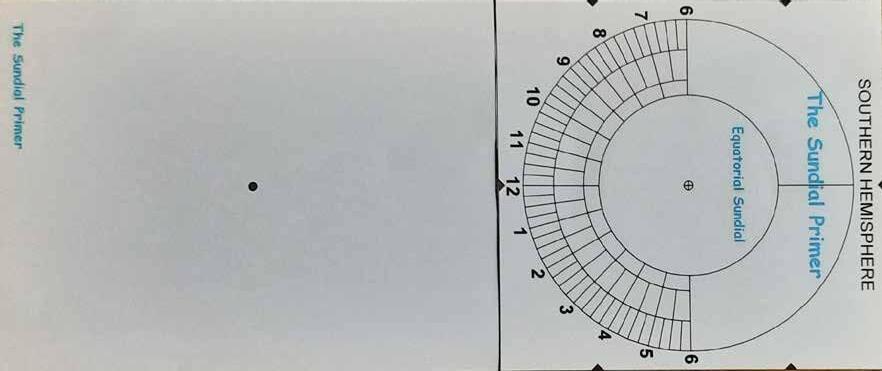

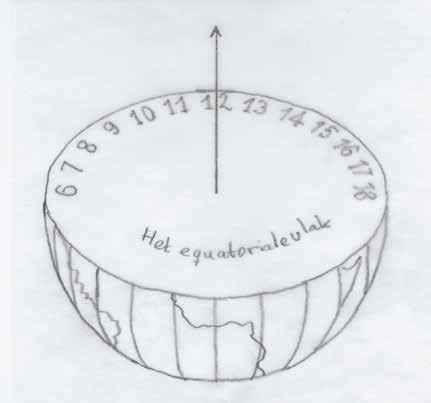
Als we de aarde op de evenaar zouden kunnen openknippen en de bovenste helft zouden verwijderen, konden we een tijdschaal aanbrengen als in figuur 5. Het vlak door de equator heet het equatoriale vlak. Terwijl de zon van oost naar west draait, glijdt de schaduw over de uurschaal van 6 naar 18. Op die manier beschouwd is de aarde een
Verleng nu eerst de uurlijnen in de rechter rechthoek tot ze de raaklijn van de twee rechthoeken snijden. Teken vervolgens vanuit de stip op de bodemplaat lijnen naar de snijpunten op de raaklijn. (zie figuur 8)
hoepelsfeer in het groot, zoals een hoepelsfeer een aarde in het klein is.
OPGAVE 8
Kun je bedenken naar welke ster de poolstijl 24 uur per dag wijst, als de poolstijl de goede richting heeft?
Omdat de uurschaal evenwijdig is met de evenaar (=equator)
Figuur 5
Figuur 7
Figuur 8
noemen we de hoepelsfeer ook wel equatoriale zonnewijzer. 6
STAP 4
Bouw met behulp van deze twee rechthoeken en de “Northern Hemisphere” een zonnewijzer op dezelfde manier als bij STAP 1.
Je zonnewijzer ziet er nu zó uit: een combinatie van een equatoriale en een horizontale zonnewijzer. Door op een ondergeschoven papier de raaklijn van de twee vlakken te verlengen kunnen ook de andere uurhoeken worden geconstrueerd.
OPGAVE 10
Wat valt je op aan de uurhoeken van de horizontale zonnewijzer?
OPGAVE 11
Als je de stip dichter bij de raaklijn van de vlakken tekent, wat verandert er dan aan de uurhoeken? Is dat bij een grotere of een kleinere breedtegraad?
Waarom is het interessant om meer te weten over zonnewijzers?
Als je regelmatig zonnewijzers bekijkt, zul je merken dat ieder nieuw type zonnewijzer nieuwe vragen oproept. Het zijn daarom echte onderzoeksobjecten. In deze aflevering werd de “makkelijkste” zonnewijzer behandeld. Voor vlakke zonnewijzers heb je iets meer wiskunde nodig. Je hebt verticale zonnewijzers, bijvoorbeeld op een kerkmuur, meestal georiënteerd op
OPGAVE 12
Als je de stip verder van de raaklijn van de vlakken weg tekent, wat verandert er dan aan de uurhoeken. Is dat bij een grotere of een kleinere breedtegraad?
Je zou natuurlijk graag de horizontale zonnewijzer willen gebruiken zonder de equatoriale zonnewijzer erop, maar dan valt de schaduwwerper omver. Daar is wat op verzonnen.
STAP 5
Download bouwplaat nr. 03 (figuur 9) en voer de instructies uit om een horizontale zonnewijzer te construeren. De rechthoek leg je plat op de grond en stelt de wijzerplaat voor. De driehoek is de schaduwvanger. Hij werpt zijn schaduw op de wijzerplaat. Deze bouwplaat is voor de 52e breedtegraad gemaakt.
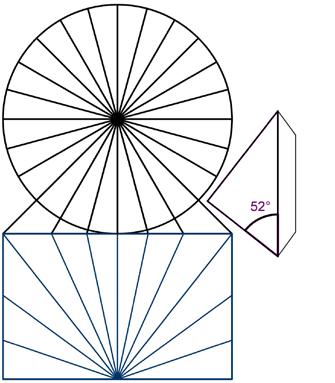
Schrijf op de rechthoekige wijzerplaat de uren erbij en je horizontale zonnewijzer is klaar!.
het zuiden, maar wat dacht je van een zonnewijzer die op een muur staat die op het noorden is gericht? Nog exotischer zijn zonnewijzers waarvan de schaduw niet door een poolstijl op de uurschaal wordt geworpen, maar door twee horizontale draden.
Zonnewijzers zijn al heel lang in gebruik. Je leert over de maatschappijen waarin ze ontstonden, maar je ziet ook dat
hun stijl past bij de tijd waarin ze gemaakt zijn. Architecten gebruiken ze vaak om gebouwen of tuinen te verfraaien. Veel zonnewijzers zijn heel kunstzinnig.
Zonnewijzers zijn echt wiskundige apparaten. Vind je wiskunde een leuk vak dan beleef je veel plezier aan dit vakgebied. Maar niet alleen wiskundig plezier.
Figuur 9
7

Het zijn ook astronomische apparaten. Je gaat het Aarde –Zon systeem beter begrijpen. En daarmee zijn het ook meteen aardrijkskundige apparaten.

Om zonnewijzers echt te begrijpen moet je inzicht ontwikkelen in de dagelijkse baan van de zon.
1
1. ChefGusteaumixtsoepineenrondekookpotvolgenseenvast systeem:demixerbeweegtinwijzerzinlangseenzesdevanderand ensteektdaarnadepotover.Hoeziethetuiteindelijkepatroon eruitalsGusteaudiestappenzoblijftherhalen? A B C D E
Bezoek eens op internet
https://www.zonnewijzer.nl/soort/ bouwplaten of https://www.mysundial.ca/sdu/ sdu_sundial_kits.html

vzwEerste Ronde JWO 2024 vraag 1
OEFENING 1
1. ChefGusteaumixtsoepineenrondekookpotvolgenseenvast systeem:demixerbeweegtinwijzerzinlangseenzesdevanderand ensteektdaarnadepotover.Hoeziethetuiteindelijkepatroon eruitalsGusteaudiestappenzoblijftherhalen?


Chef Gusteau mixt soep in een ronde kookpot volgens een vast systeem: de mixer beweegt in wijzerzin langs een zesde van de rand en steekt daarna de pot over. Hoe ziet het uiteindelijke patroon eruit als Gusteau die stappen zo blijft herhalen?



1Op bovengenoemde websites vind je bouwplaten voor verschillende zonnewijzers. Als je het écht serieus wilt aanpakken, word dan lid van de Zonnewijzerkring en doe de cursus. In dertien lessen leer je over de achtergronden van al die verschillende zonnewijzers. De cursus is gratis voor leden. www.dezonnewijzerkring.nl
ChefGusteaumixtsoepineenrondekookpotvolgenseenvast systeem:demixerbeweegtinwijzerzinlangseenzesdevanderand ensteektdaarnadepotover.Hoeziethetuiteindelijkepatroon eruitalsGusteaudiestappenzoblijftherhalen?
ChefGusteaumixtsoepineenrondekookpotvolgenseenvast systeem:demixerbeweegtinwijzerzinlangseenzesdevanderand ensteektdaarnadepotover.Hoeziethetuiteindelijkepatroon eruitalsGusteaudiestappenzoblijftherhalen?
1. ChefGusteaumixtsoepineenrondekookpotvolgenseenvast systeem:demixerbeweegtinwijzerzinlangseenzesdevanderand ensteektdaarnadepotover.Hoeziethetuiteindelijkepatroon eruitalsGusteaudiestappenzoblijftherhalen?
1. ChefGusteaumixtsoepineenrondekookpotvolgenseenvast systeem:demixerbeweegtinwijzerzinlangseenzesdevanderand ensteektdaarnadepotover.Hoeziethetuiteindelijkepatroon eruitalsGusteaudiestappenzoblijftherhalen?
1. ChefGusteaumixtsoepineenrondekookpotvolgenseenvast systeem:demixerbeweegtinwijzerzinlangseenzesdevanderand ensteektdaarnadepotover.Hoeziethetuiteindelijkepatroon eruitalsGusteaudiestappenzoblijftherhalen?
2. Als 1 a + 1 b = 1 3 ,danis a + b ab gelijkaan
2.
2. Als 1 a + 1 b = 1 3 ,danis a + b ab gelijkaan
OEFENING 2
Rana wandelt van haar huis naar de school. Elke straat heeft langs beide zijden een voetpad.
3. Ranawandeltvanhaarhuisnaardeschool. Elkestraatheeftlangsbeidezijdeneenvoetpad. Wanneerzeeenstraatoversteekt,doetzedat loodrecht.Zestaptookaltijdophetvoetpad tenzijzeoversteekt.
3. Ranawandeltvanhaarhuisnaardeschool. Elkestraatheeftlangsbeidezijdeneenvoetpad. Wanneerzeeenstraatoversteekt,doetzedat loodrecht.Zestaptookaltijdophetvoetpad tenzijzeoversteekt.
3. Ranawandeltvanhaarhuisnaardeschool. Elkestraatheeftlangsbeidezijdeneenvoetpad. Wanneerzeeenstraatoversteekt,doetzedat loodrecht.Zestaptookaltijdophetvoetpad tenzijzeoversteekt.
3. Ranawandeltvanhaarhuisnaardeschool. Elkestraatheeftlangsbeidezijdeneenvoetpad. Wanneerzeeenstraatoversteekt,doetzedat loodrecht.Zestaptookaltijdophetvoetpad tenzijzeoversteekt.
3. Ranawandeltvanhaarhuisnaardeschool. Elkestraatheeftlangsbeidezijdeneenvoetpad. Wanneerzeeenstraatoversteekt,doetzedat loodrecht.Zestaptookaltijdophetvoetpad tenzijzeoversteekt.
3. Ranawandeltvanhaarhuisnaardeschool. Elkestraatheeftlangsbeidezijdeneenvoetpad. Wanneerzeeenstraatoversteekt,doetzedat loodrecht.Zestaptookaltijdophetvoetpad tenzijzeoversteekt.
3. Ranawandeltvanhaarhuisnaardeschool.
Ranakiestvooreenroutewaarbijzezoweinig mogelijkoversteekt.HoeveelkeersteektRana eenstraatoverophaarroute?
Wanneer ze een straat oversteekt, doet ze dat loodrecht. Ze stapt ook altijd op het voetpad tenzij ze oversteekt.
Ranakiestvooreenroutewaarbijzezoweinig mogelijkoversteekt.HoeveelkeersteektRana eenstraatoverophaarroute?
Ranakiestvooreenroutewaarbijzezoweinig mogelijkoversteekt.HoeveelkeersteektRana eenstraatoverophaarroute?
Ranakiestvooreenroutewaarbijzezoweinig mogelijkoversteekt.HoeveelkeersteektRana eenstraatoverophaarroute?
Ranakiestvooreenroutewaarbijzezoweinig mogelijkoversteekt.HoeveelkeersteektRana eenstraatoverophaarroute?
Elkestraatheeftlangsbeidezijdeneenvoetpad. Wanneerzeeenstraatoversteekt,doetzedat loodrecht.Zestaptookaltijdophetvoetpad tenzijzeoversteekt.
Ranakiestvooreenroutewaarbijzezoweinig mogelijkoversteekt.HoeveelkeersteektRana eenstraatoverophaarroute?
Rana kiest voor een route waarbij ze zo weinig mogelijk oversteekt. Hoeveel keer steekt Rana een straat over op haar route?
Ranakiestvooreenroutewaarbijzezoweinig mogelijkoversteekt.HoeveelkeersteektRana eenstraatoverophaarroute?
huis school
4. Eenrechthoekigtabletchocoladebestaatuitvierkanteblokjes,allemaalevengroot. Liesbreekt´e´enrijblokjesafvolgensdelangezijdevanhettablet.Vervolgensdoet zehetzelfdevolgensdekortezijdevanhetovergebleventablet.Totslotbreekt zenog´e´enrijafvolgensdelangezijdevanhetovergebleventablet.Erblijven 7blokjesover.HoeveelblokjesheeftLiesintotaalafgebroken?
4. Eenrechthoekigtabletchocoladebestaatuitvierkanteblokjes,allemaalevengroot. Liesbreekt´e´enrijblokjesafvolgensdelangezijdevanhettablet.Vervolgensdoet zehetzelfdevolgensdekortezijdevanhetovergebleventablet.Totslotbreekt zenog´e´enrijafvolgensdelangezijdevanhetovergebleventablet.Erblijven 7blokjesover.HoeveelblokjesheeftLiesintotaalafgebroken?
school
4. Eenrechthoekigtabletchocoladebestaatuitvierkanteblokjes,allemaalevengroot. Liesbreekt´e´enrijblokjesafvolgensdelangezijdevanhettablet.Vervolgensdoet zehetzelfdevolgensdekortezijdevanhetovergebleventablet.Totslotbreekt zenog´e´enrijafvolgensdelangezijdevanhetovergebleventablet.Erblijven 7blokjesover.HoeveelblokjesheeftLiesintotaalafgebroken?
4. Eenrechthoekigtabletchocoladebestaatuitvierkanteblokjes,allemaalevengroot. Liesbreekt´e´enrijblokjesafvolgensdelangezijdevanhettablet.Vervolgensdoet zehetzelfdevolgensdekortezijdevanhetovergebleventablet.Totslotbreekt zenog´e´enrijafvolgensdelangezijdevanhetovergebleventablet.Erblijven 7blokjesover.HoeveelblokjesheeftLiesintotaalafgebroken?
4. Eenrechthoekigtabletchocoladebestaatuitvierkanteblokjes,allemaalevengroot. Liesbreekt´e´enrijblokjesafvolgensdelangezijdevanhettablet.Vervolgensdoet zehetzelfdevolgensdekortezijdevanhetovergebleventablet.Totslotbreekt zenog´e´enrijafvolgensdelangezijdevanhetovergebleventablet.Erblijven 7blokjesover.HoeveelblokjesheeftLiesintotaalafgebroken?
huis school
4. Eenrechthoekigtabletchocoladebestaatuitvierkanteblokjes,allemaalevengroot. Liesbreekt´e´enrijblokjesafvolgensdelangezijdevanhettablet.Vervolgensdoet zehetzelfdevolgensdekortezijdevanhetovergebleventablet.Totslotbreekt zenog´e´enrijafvolgensdelangezijdevanhetovergebleventablet.Erblijven 7blokjesover.HoeveelblokjesheeftLiesintotaalafgebroken?
5. Ineenrechthoekmetlengte11enbreedte7zijnvier vierkanteningekleurdzoalsindefiguur.Erblijfteen rechthoekiggebiedoverdatnietingekleurdis. Watisdeverhoudingtussendeoppervlaktevandat gebiedendievandeoorspronkelijkerechthoek?
5. Ineenrechthoekmetlengte11enbreedte7zijnvier vierkanteningekleurdzoalsindefiguur.Erblijfteen rechthoekiggebiedoverdatnietingekleurdis. Watisdeverhoudingtussendeoppervlaktevandat gebiedendievandeoorspronkelijkerechthoek?
5. Ineenrechthoekmetlengte11enbreedte7zijnvier vierkanteningekleurdzoalsindefiguur.Erblijfteen rechthoekiggebiedoverdatnietingekleurdis. Watisdeverhoudingtussendeoppervlaktevandat gebiedendievandeoorspronkelijkerechthoek?
5. Ineenrechthoekmetlengte11enbreedte7zijnvier vierkanteningekleurdzoalsindefiguur.Erblijfteen rechthoekiggebiedoverdatnietingekleurdis. Watisdeverhoudingtussendeoppervlaktevandat gebiedendievandeoorspronkelijkerechthoek?
5. Ineenrechthoekmetlengte11enbreedte7zijnvier vierkanteningekleurdzoalsindefiguur.Erblijfteen rechthoekiggebiedoverdatnietingekleurdis. Watisdeverhoudingtussendeoppervlaktevandat gebiedendievandeoorspronkelijkerechthoek?
4. Eenrechthoekigtabletchocoladebestaatuitvierkanteblokjes,allemaalevengroot. Liesbreekt´e´enrijblokjesafvolgensdelangezijdevanhettablet.Vervolgensdoet zehetzelfdevolgensdekortezijdevanhetovergebleventablet.Totslotbreekt
© Junior Wiskunde Olympiade
A B C D E 1
A B C D E 2. Als 1 a + 1 b = 1 3 ,danis a + b ab gelijkaan A 1 3 B 2 3 C 1 D 3 E 6
A 2 B 3 C 4 D 5 E 6
huis school
A 13 B 15 C 16 D 17 E 19
A 1 B 1 C 3 D 2 E 1 1
A B C D E 2. Als 1 a + 1 b = 1 3 ,danis a + b ab gelijkaan A 1 3 B 2 3 C 1 D 3 E 6
A 2 B 3 C 4 D 5 E 6
A 13 B 15 C 16 D 17 E 19
A 1 B 1 C 3 D 2 E 1 1
B C D E
A
Als 1 a + 1 b = 1 3
a + b ab
A 1 3 B 2 3 C 1 D 3 E 6
,danis
gelijkaan
huis school A 2 B 3 C 4 D 5 E 6
A 13 B 15 C 16 D 17 E 19
A 1 B 1 C 3 D 2 E 1
A B C D E 2. Als 1 a + 1 b = 1 3 ,danis a + b ab gelijkaan A 1 3 B 2 3 C 1 D 3 E 6
A 2 B 3 C 4 D 5 E 6
huis school
A 13 B 15 C 16 D 17 E 19
A 1 B 1 C 3 D 2 E 1
1
A B C D E 2. Als 1 a + 1 b = 1 3 ,danis a + b ab gelijkaan A 1 3 B 2 3 C 1 D 3 E 6
huis
A 2 B 3 C 4 D 5 E 6
A 13 B 15 C 16 D 17 E 19
A 1 B 1 C 3 D 2 E 1
1
A
B C D E
C 1 D 3 E 6
A 1 3 B 2 3
A 2 B 3 C 4 D 5 E 6
D
E 6
A 1 3 B 2 3 C 1
3
A 2 B 3 C 4 D 5 E 6
huis school
13 B 15 C 16 D 17 E 19
A B C D E 2 3 4 5 6 8
A
© Junior Wiskunde Olympiade vzwEerste Ronde JWO 2024 vraag 3
TRAPGETALLEN
ANTONELLA PERUCCA, VOOR UITWISKELING
Trapgetallen
Trapgetallen
Trapgetallen
Trapgetallen
Trapgetallen
Trapgetallen
Trapgetallen
Trapgetallen
AntonellaPerucca,voorUitwiskeling
AntonellaPerucca,voorUitwiskeling
AntonellaPerucca,voorUitwiskeling
AntonellaPerucca,voorUitwiskeling
AntonellaPerucca,voorUitwiskeling
AntonellaPerucca,voorUitwiskeling
AntonellaPerucca,voorUitwiskeling
AntonellaPerucca,voorUitwiskeling
Wenoemeneennatuurlijkgetaleen trapgetal (Enstaircasenumber of politenumber)alshetkan geschrevenwordenalsdesomvanminstenstwee opeenvolgendenatuurlijkegetallen.Zovindenwe bijvoorbeelddat12,13,14en15trapgetallenzijn:
Wenoemeneennatuurlijkgetaleen trapgetal (Enof politenumber)alshetkan geschrevenwordenalsdesomvanminstenstwee opeenvolgendenatuurlijkegetallen.Zovindenwe bijvoorbeelddat12,13,14en15trapgetallenzijn:
We noemen een natuurlijk getal een trapgetal (Engels: staircase number of polite number) als het kan geschreven worden als de som van minstens twee opeenvolgende natuurlijke getallen. Zo vinden we bijvoorbeeld dat 12 13, 14 en 15 trap getallen zijn:
Wenoemeneennatuurlijkgetaleen trapgetal (Engels: staircasenumber of politenumber)alshetkan geschrevenwordenalsdesomvanminstenstwee opeenvolgendenatuurlijkegetallen.Zovindenwe bijvoorbeelddat12,13,14en15trapgetallenzijn:
Wenoemeneennatuurlijkgetaleen trapgetal (Engels: staircasenumber of politenumber)alshetkan geschrevenwordenalsdesomvanminstenstwee opeenvolgendenatuurlijkegetallen.Zovindenwe bijvoorbeelddat12,13,14en15trapgetallenzijn:
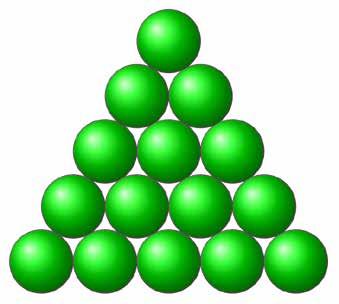
getallen is de kleinste term van de som gelijk aan 1. Een klassieke visualisering van driehoeksgetallen is die met een stapeling van stippen of van cirkels in een driehoeksverband.
Wenoemeneennatuurlijkgetaleen trapgetal (Engels: staircasenumber of politenumber)alshetkan geschrevenwordenalsdesomvanminstenstwee opeenvolgendenatuurlijkegetallen.Zovindenwe bijvoorbeelddat12,13,14en15trapgetallenzijn:
Wenoemeneennatuurlijkgetaleen trapgetal (Engels: staircasenumber of politenumber geschrevenwordenalsdesomvanminstenstwee opeenvolgendenatuurlijkegetallen.Zovindenwe bijvoorbeelddat12,13,14en15trapgetallenzijn:
Wenoemeneennatuurlijkgetaleen trapgetal (Engels: staircasenumber of politenumber)alshetkan geschrevenwordenalsdesomvanminstenstwee opeenvolgendenatuurlijkegetallen.Zovindenwe bijvoorbeelddat12,13,14en15trapgetallenzijn:
12 = 3 + 4 + 5;13 = 6 + 7;14
12 = 3 + 4 + 5;13
+ 4 + 5;13 = 6 + 7;14 = 2 + 3 + 4 + 5; = 7 + 8 = 4 + 5 + 6 = 1 + 2 + 3 + 4 + 5.
Wenoemeneennatuurlijkgetaleen gels: staircasenumber geschrevenwordenalsdesomvanminstenstwee opeenvolgendenatuurlijkegetallen.Zovindenwe bijvoorbeelddat12,13,14en15trapgetallenzijn:
15 = 7 + 8 = 4 + 5 + 6 = 1 + 2 +
15 = 7 +
12 = 3 + 4 + 5;13 = 6 + 7;14 = 2 +
12 = 3 + 4 + 5;13 = 6 + 7;14
= 6 + 7;14 = 2 + 3 + 4 + 5; + 6 = 1 + 2 + 3 + 4 + 5.
12 = 3 + 4 + 5;13
12 = 3 15
15 = 7 + 8 = 4 + 5 + 6 =
15 = 7 + 8 = 4 + 5 + 6 = 1 + 2 + 3 + 4
Hetgetal16echterkannietalseensomvanopeenvolgendenatuurlijkegetallengeschrevenworden.
Hetgetal16echterkannietalseensomvanopeenvolgendenatuurlijkegetallengeschrevenworden. Trapgetallendankenhunnaamaaneenvisuele voorstellingmetvierkantjesineentrapverband.



Hetgetal16echterkannietalseensomvanopeenvolgendenatuurlijkegetallengeschrevenworden. Trapgetallendankenhunnaamaaneenvisuele voorstellingmetvierkantjesineentrapverband.
Trapgetallendankenhunnaamaaneenvisuele voorstellingmetvierkantjesineentrapverband.
15 = 7 + 8 = 4 + 5 + 6 =
Hetgetal16echterkannietalseensomvanopeenvolgendenatuurlijkegetallengeschrevenworden. Trapgetallendankenhunnaamaaneenvisuele voorstellingmetvierkantjesineentrapverband.
Hetgetal16echterkannietalseensomvanopeenvolgendenatuurlijkegetallengeschrevenworden. Trapgetallendankenhunnaamaaneenvisuele voorstellingmetvierkantjesineentrapverband.


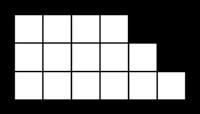
Figuur3Hetgetal12iseentrapeziumgetal.
Hetgetal16echterkannietalseensomvanopeenvolgendenatuurlijkegetallengeschrevenworden. Trapgetallendankenhunnaamaaneenvisuele voorstellingmetvierkantjesineentrapverband.

Hetgetal16echterkannietalseensomvanopeenvolgendenatuurlijkegetallengeschrevenworden. Trapgetallendankenhunnaamaaneenvisuele voorstellingmetvierkantjesineentrapverband.
Het getal 16 echter kan niet als een som van opeenvolgende natuurlijke getallen geschreven worden. Trap getallen danken hun naam aan een visuele voorstelling met vierkantjes in een trapverband.


Figuur3Hetgetal12iseentrapeziumgetal.
Figuur3Hetgetal12iseentrapeziumgetal.
Hetgetal16echterkannietalseensomvanopeenvolgendenatuurlijkegetallengeschrevenworden. Trapgetallendankenhunnaamaaneenvisuele voorstellingmetvierkantjesineentrapverband.

Hoeschrijvenweeentrapgetalalseensomvan opeenvolgendenatuurlijkegetallen?
Hoeschrijvenweeentrapgetalalseensomvan opeenvolgendenatuurlijkegetallen?


Hoeschrijvenweeentrapgetalalseensomvan opeenvolgendenatuurlijkegetallen?
Hoeschrijvenweeentrapgetalalseensomvan opeenvolgendenatuurlijkegetallen?
Hoeschrijvenweeentrapgetalalseensomvan opeenvolgendenatuurlijkegetallen?

Hoeschrijvenweeentrapgetalalseensomvan opeenvolgendenatuurlijkegetallen?
Hoeschrijvenweeentrapgetalalseensomvan opeenvolgendenatuurlijkegetallen?
Alsopwarmertjetonenweaandatelkonevengetaleentrapgetalis.Hetkanimmersgeschreven wordenalsdesomvandetweeopeenvolgende gehelegetallendielinksenrechtsvandehelftvan ditgetalliggen.Bijvoorbeeld: 21 = 10 + 11
Alsopwarmertjetonenweaandatelkonevengetaleentrapgetalis.Hetkanimmersgeschreven wordenalsdesomvandetweeopeenvolgende gehelegetallendielinksenrechtsvandehelftvan ditgetalliggen.Bijvoorbeeld: 21 = 10 + 11.
Figuur1Hetgetal15iseentrapgetal.



Alsopwarmertjetonenweaandatelkonevengetaleentrapgetalis.Hetkanimmersgeschreven wordenalsdesomvandetweeopeenvolgende gehelegetallendielinksenrechtsvandehelftvan ditgetalliggen.Bijvoorbeeld: 21 = 10 + 11.
Hoeschrijvenweeentrapgetalalseensomvan opeenvolgendenatuurlijkegetallen?
Alsopwarmertjetonenweaandatelkonevengetaleentrapgetalis.Hetkanimmersgeschreven wordenalsdesomvandetweeopeenvolgende gehelegetallendielinksenrechtsvandehelftvan ditgetalliggen.Bijvoorbeeld: 21 = 10 + 11
Alsopwarmertjetonenweaandatelkonevengetaleentrapgetalis.Hetkanimmersgeschreven wordenalsdesomvandetweeopeenvolgende gehelegetallendielinksenrechtsvandehelftvan ditgetalliggen.Bijvoorbeeld: 21 = 10 + 11
Merkbovendienopdatelkdrievoudeentrapgetal is.Hetgetal3isgelijkaan1+2.Alseendriegroterdandrieis,kunnenwehetalsvolgt
Driehoeksgetallen triangularnumbers)vormeneenspecialeklassevantrapgetallen.Bijdriehoeksgetallenisdekleinstetermvandesomgelijk aan1.Eenklassiekevisualiseringvandriehoeksgetallenisdiemeteenstapelingvanstippenof vancirkelsineendriehoeksverband.
Driehoeksgetallen (Engels: meneenspecialeklassevantrapgetallen.Bijdriehoeksgetallenisdekleinstetermvandesomgelijk aan1.Eenklassiekevisualiseringvandriehoeksgetallenisdiemeteenstapelingvanstippenof vancirkelsineendriehoeksverband.
(Engels: triangularnumbers meneenspecialeklassevantrapgetallen.Bijdriehoeksgetallenisdekleinstetermvandesomgelijk aan1.Eenklassiekevisualiseringvandriehoeksgetallenisdiemeteenstapelingvanstippenof vancirkelsineendriehoeksverband.
Alsopwarmertjetonenweaandatelkonevengetaleentrapgetalis.Hetkanimmersgeschreven wordenalsdesomvandetweeopeenvolgende gehelegetallendielinksenrechtsvandehelftvan ditgetalliggen.Bijvoorbeeld: 21 = 10 + 11
Het kan immers geschreven worden als de som van de twee opeenvolgende gehele getallen die links en rechts van de helft van dit getal liggen. Bijvoorbeeld:
Alsopwarmertjetonenweaandatelkonevengetaleentrapgetalis.Hetkanimmersgeschreven wordenalsdesomvandetweeopeenvolgende gehelegetallendielinksenrechtsvandehelftvan ditgetalliggen.Bijvoorbeeld: 21 = 10 + 11
Alsopwarmertjetonenweaandatelkonevengetaleentrapgetalis.Hetkanimmersgeschreven wordenalsdesomvandetweeopeenvolgende gehelegetallendielinksenrechtsvandehelftvan ditgetalliggen.Bijvoorbeeld: 21 = 10 + 11.
Merkbovendienopdatelkdrievoudeentrapgetal is.Hetgetal3isgelijkaan1+2.Alseendrievoud n groterdandrieis,kunnenwehetalsvolgt opsplitsen:
Driehoeksgetallen (Engels: triangularnumbers)vormeneenspecialeklassevantrapgetallen.Bijdriehoeksgetallenisdekleinstetermvandesomgelijk aan1.Eenklassiekevisualiseringvandriehoeksgetallenisdiemeteenstapelingvanstippenof vancirkelsineendriehoeksverband.
Driehoeksgetallen triangularnumbers)vormeneenspecialeklassevantrapgetallen.Bijdriehoeksgetallenisdekleinstetermvandesomgelijk aan1.Eenklassiekevisualiseringvandriehoeksgetallenisdiemeteenstapelingvanstippenof vancirkelsineendriehoeksverband.

Merkbovendienopdatelkdrievoudeentrapgetal is.Hetgetal3isgelijkaan1+2.Alseendrievoud n groterdandrieis,kunnenwehetalsvolgt opsplitsen:
(Engels: trapezoidal numbers) zijn trapgetallen die geen driehoeksgetallen zijn. We verkrijgen ze door in een driehoekige stapeling van cirkels een top weg te nemen. De configuratie die zo ontstaat, heeft de vorm van een gelijkbenig trapezium.
Merkbovendienopdatelkdrievoudeentrapgetal is.Hetgetal3isgelijkaan1+2.Alseendrievoud n groterdandrieis,kunnenwehetalsvolgt opsplitsen:
triangularnumbers)vormeneenspecialeklassevantrapgetallen.Bijdriehoeksgetallenisdekleinstetermvandesomgelijk aan1.Eenklassiekevisualiseringvandriehoeksgetallenisdiemeteenstapelingvanstippenof vancirkelsineendriehoeksverband.
Merkbovendienopdatelkdrievoudeentrapgetal is.Hetgetal3isgelijkaan1+2.Alseendrievoud n groterdandrieis,kunnenwehetalsvolgt opsplitsen:
Driehoeksgetallen (Engels: triangularnumbers)vormeneenspecialeklassevantrapgetallen.Bijdriehoeksgetallenisdekleinstetermvandesomgelijk aan1.Eenklassiekevisualiseringvandriehoeksgetallenisdiemeteenstapelingvanstippenof vancirkelsineendriehoeksverband.
(Engels: triangularnumbers)vormeneenspecialeklassevantrapgetallen.Bijdriehoeksgetallenisdekleinstetermvandesomgelijk aan1.Eenklassiekevisualiseringvandriehoeksgetallenisdiemeteenstapelingvanstippenof vancirkelsineendriehoeksverband.

Merkbovendienopdatelkdrievoudeentrapgetal is.Hetgetal3isgelijkaan1+2.Alseendrievoud n groterdandrieis,kunnenwehetalsvolgt opsplitsen:
Merk bovendien op dat elk drievoud een trapgetal is. Het getal 3 is gelijk aan
Merkbovendienopdatelkdrievoudeentrapgetal is.Hetgetal3isgelijkaan1+2.Alseendrievoud n groterdandrieis,kunnenwehetalsvolgt opsplitsen:
Merkbovendienopdatelkdrievoudeentrapgetal is.Hetgetal3isgelijkaan1+2.Alseendrievoud n groterdandrieis,kunnenwehetalsvolgt opsplitsen:
. Als een drievoud n groter dan drie is, kunnen we het als volgt opsplitsen:
Dedrietermenvandesomzijnopeenvolgendenatuurlijkegetallen.Eenvoorbeeld: 30 = 9 + 10 + 11
Dedrietermenvandesomzijnopeenvolgendenatuurlijkegetallen.Eenvoorbeeld: 30 = 9 + 10 + 11.

Dedrietermenvandesomzijnopeenvolgendenatuurlijkegetallen.Eenvoorbeeld: 30 = 9 + 10 + 11.
Driehoeksgetallen (Engels: triangular numbers) vormen een speciale klas se van trapgetallen. Bij driehoeks
Dedrietermenvandesomzijnopeenvolgendenatuurlijkegetallen.Eenvoorbeeld: 30 = 9 + 10 + 11


HOE SCHRIJVEN WE EEN TRAPGETAL ALS EEN SOM VAN OPEENVOLGENDE NATUURLIJKE GETALLEN? Als opwarmertje tonen we aan dat elk oneven getal een trapgetal is.
Dedrietermenvandesomzijnopeenvolgendenatuurlijkegetallen.Eenvoorbeeld: 30 = 9 + 10 + 11
Dedrietermenvandesomzijnopeenvolgendenatuurlijkegetallen.Eenvoorbeeld: 30 = 9 + 10 + 11.

Dedrietermenvandesomzijnopeenvolgendenatuurlijkegetallen.Eenvoorbeeld: 30 = 9 + 10 + 11.
eennatuurlijkgetalisen eenonevendelervan n is.Dankunnen schrijvenalseensomvan d gehelegetallen diestukvoorstukgelijkzijnaan n d .Vervolgens trekkenwevandezeidentiekegetalleneenheden afentellenwezeerweerbijomeenrijmetopeenvolgendenatuurlijkegetallentekrijgendie n

Algemener:steldat n eennatuurlijkgetalisen eenonevendelervan n is.Dankunnen schrijvenalseensomvan d gehelegetallen diestukvoorstukgelijkzijnaan n d .Vervolgens trekkenwevandezeidentiekegetalleneenheden afentellenwezeerweerbijomeenrijmetopeenvolgendenatuurlijkegetallentekrijgendie n alssomheeft:
Dedrietermenvandesomzijnopeenvolgendenatuurlijkegetallen.Eenvoorbeeld: 30 = 9 + 10 + 11.
De drie termen van de som zijn opeenvolgende natuurlijke getallen. Een voorbeeld:
Algemener:steldat n eennatuurlijkgetalisen eenonevendelervan n is.Dankunnen schrijvenalseensomvan d gehelegetallen diestukvoorstukgelijkzijnaan n d .Vervolgens trekkenwevandezeidentiekegetalleneenheden afentellenwezeerweerbijomeenrijmetopeenvolgendenatuurlijkegetallentekrijgendie n alssomheeft:
Algemener:steldat n eennatuurlijkgetalisen dat d > 1 eenonevendelervan n is.Dankunnen we n schrijvenalseensomvan d gehelegetallen diestukvoorstukgelijkzijnaan n d .Vervolgens trekkenwevandezeidentiekegetalleneenheden afentellenwezeerweerbijomeenrijmetopeenvolgendenatuurlijkegetallentekrijgendie n alssomheeft:
Algemener:steldat n eennatuurlijkgetalisen dat d > 1 eenonevendelervan n is.Dankunnen we n schrijvenalseensomvan d gehelegetallen diestukvoorstukgelijkzijnaan n d .Vervolgens trekkenwevandezeidentiekegetalleneenheden afentellenwezeerweerbijomeenrijmetopeenvolgendenatuurlijkegetallentekrijgendie n alssomheeft:

Algemener:steldat n eennatuurlijkgetalisen dat d > 1 eenonevendelervan n is.Dankunnen we n schrijvenalseensomvan d gehelegetallen diestukvoorstukgelijkzijnaan n d .Vervolgens trekkenwevandezeidentiekegetalleneenheden afentellenwezeerweerbijomeenrijmetopeenvolgendenatuurlijkegetallentekrijgendie n alssomheeft:
Algemener:steldat n eennatuurlijkgetalisen dat d > 1 eenonevendelervan n is.Dankunnen we n schrijvenalseensomvan d gehelegetallen diestukvoorstukgelijkzijnaan n d .Vervolgens trekkenwevandezeidentiekegetalleneenheden afentellenwezeerweerbijomeenrijmetopeenvolgendenatuurlijkegetallentekrijgendie n alssomheeft:
Algemener:steldat n eennatuurlijkgetalisen dat d > 1 eenonevendelervan n is.Dankunnen we n schrijvenalseensomvan d gehelegetallen diestukvoorstukgelijkzijnaan n d .Vervolgens trekkenwevandezeidentiekegetalleneenheden afentellenwezeerweerbijomeenrijmetopeenvolgendenatuurlijkegetallentekrijgendie n alssomheeft:
Figuur1Hetgetal15iseentrapgetal.
Figuur2Hetgetal15iseendriehoeksgetal.
n = n 3 + n 3 + n 3 = n 3 1 + n 3 + n 3 + 1 .
n = n d + ··· + n d + n d + n d + ··· + n d =
Figuur1Hetgetal15iseentrapgetal.
Figuur2Hetgetal15iseendriehoeksgetal.
Figuur3Hetgetal12iseentrapeziumgetal.
n = n 3 + n 3 + n 3 = n 3 1 + n 3 + n 3 + 1
n n n n n
n = n 3 + n 3 + n 3 = n 3 1 + n 3 + n 3 + 1 .
Figuur1Hetgetal15iseentrapgetal.
Figuur2Hetgetal15iseendriehoeksgetal.
Figuur3Hetgetal12iseentrapeziumgetal.
n = n 3 + n 3 + n 3 = n 3 1 + n 3 + n 3 + 1
n = n d + + n d + n d + n d + + n d =
Figuur2Hetgetal15iseendriehoeksgetal.
Figuur3Hetgetal12iseentrapeziumgetal.
n = n 3 + n 3 + n 3 = n 3 1 + n 3 + n 3 + 1
Figuur1Hetgetal15iseentrapgetal.
Figuur2Hetgetal15iseendriehoeksgetal.
Figuur3Hetgetal12iseentrapeziumgetal.
n = n 3 + n 3 + n 3 = n 3 1 + n 3 + n 3 + 1 .
n n n n n
Figuur1Hetgetal15iseentrapgetal.
Figuur3Hetgetal12iseentrapeziumgetal.
n = n 3 + n 3 + n 3 = n 3 1 + n 3 + n 3 + 1
UITWISKELING
Figuur1Hetgetal15iseentrapgetal.
n = 3 + 3 + n 3 = n 3 1 + n 3 + n 3 + 1
Figuur 1 Het getal 15 is een trapgetal.
Figuur 2 Het getal 15 is een driehoeksgetal.
Figuur 3 Het getal 12 is een trapeziumgetal.
9
TWEE VERWEVEN LAGEN OPROLLEN
KLAAS LAKEMAN, ARS ET MATHESIS

Bij het vijftigjarig bestaan van de Universiteit Twente te Enschede werden in 2011 vier beelden van de Nederlandse kunstenaar Rinus Roelofs op de campus geplaatst. Twee daarvan komen voort uit het oprollen van dezelfde set van twee met elkaar verweven lagen. Ze zijn ontworpen op de computer, daarna met een gigantische 3D-betonprinter uitgeprint en naar hun standplaats getransporteerd.
TWEE METHODEN
Figuur 1 bevat de set van twee met elkaar verweven lagen. Die kunnen op twee manieren tot een cilinder worden opgerold. Daarbij worden de uiteinden van de ene laag verbonden met die van de andere. De eerste manier wordt weergegeven in figuur 2. De rode laag aan de voorste doorsnijding wordt verbonden met de rode laag van de achterste doorsnijding. Ga na dat zo
ARS ET MATHESIS 12



inderdaad twee verschillende lagen met elkaar worden verbonden. De laag met de gele stippen aan de voorste doorsnijding wordt verbonden met de laag met de gele stippen van de achterste doorsnijding. Het resultaat is een cilinder die bestaat uit één aaneengesloten verweven laag of oppervlak (figuren 3 en 4). Bij de tweede manier (figuur 5) wordt het rode uiteinde
van de ene laag links verbonden met het rode uiteinde van de andere laag rechts. En het ongekleurde uiteinde aan de rechterkant wordt verbonden met dat aan de linkerkant. In figuur 5 is dat uiteinde niet zichtbaar omdat het onder het rode uiteinde ligt. Ook nu leidt dit weer tot een cilinder die bestaat uit één aaneengesloten verweven laag of oppervlak (figuur 6).
Figuur 1 De twee met elkaar verweven lagen
Figuur 2 Oprolmethode 1
Figuur 3 3D-print van oprolmethode 1
13
Figuur 4 Ontwerp van oprolmethode 1



 Figuur 5 Oprolmethode 2
Figuur 6 3D-print en ontwerp van methode 2
Figuur 5 Oprolmethode 2
Figuur 6 3D-print en ontwerp van methode 2
14
Figuur 7 De 3D-betonprinter produceert het ontwerp van oprolmethode 2 (horizontaal liggend).

DE BEELDEN
De ontwerpen uit de figuren 4 en 6 werden vervolgens met een grote 3D-betonprinter van de Italiaan Enrico Dini’s bedrijf D-Shape geprint (figuur 7). Die printer heeft een grondoppervlakte van 5 X 5 meter en een hoogte van 3 meter.
Via de printkoppen wordt de juiste hoeveelheid water – van belang om de juiste doorsnede te verkrijgen – op een dun laagje van een poedervormig mengsel van zand en cement gespoten. Vervolgens wordt een nieuw laagje poeder gelegd en bespoten, enzovoorts. Als het totale beeld droog is, worden de losse poederdeeltjes voor hergebruik weggezogen. Op foto’s van de uiteindelijke beelden (figuren 8 en 9) is die laagstructuur nog duidelijk herkennen aan de verticale strepen, de beelden lagen namelijk horizontaal in de betonprinter. Dat is met opzet zo gelaten om nog iets van het bijzondere productieproces terug te zien (figuur 10).

 Figuur 8 Resultaat van oprolmethode 1
Figuur 9 Resultaat van oprolmethode 2
Figuur 10 Oprol resultaat 2 uitvergroot
Figuur 8 Resultaat van oprolmethode 1
Figuur 9 Resultaat van oprolmethode 2
Figuur 10 Oprol resultaat 2 uitvergroot
15



TER VERDUIDELIJKING
Leg om zelf te ervaren hoe het oprollen werkt, twee (gekleurde) stroken papier op elkaar zoals in figuur 11A. Rol het rechter uiteinde van de blauwe strook naar het linker uiteinde van de gele strook. Lijm die uiteinden aan elkaar (figuur 11B). Rol daarna het rechter uiteinde van de gele strook naar het linker uiteinde van de blauwe en lijm die uiteinden ook aan elkaar. Hoewel de twee stroken niet met elkaar verweven zijn, levert het resultaat (figuur 11C) een redelijke indruk van het oprol-proces en de structuur van de beelden.
DE GOEDE DOORSNIJDING
Nog even terug naar de twee op elkaar liggende verweven lagen van figuur 1. Stel dat er een doorsnijding was gemaakt volgens de rode lijn in figuur 12. Dan ben je bij het oprollen volgens methode 2 gedwongen om het rode uiteinde met het gele uiteinde aan de rechter kant te verbinden en het groene uiteinde met het uiteinde dat onder het rode ligt. Immers als het groene uiteinde met het rode wordt verbonden, zit het gele uiteinde
opgesloten en kan niet met het uiteinde dat onder rood ligt worden verbonden. Het rode en het gele uiteinde behoren tot dezelfde laag. Ook het groene en het uiteinde onder het rode behoren tot eenzelfde laag. Dat resulteert dan in twee door elkaar zittende kolommen. Uitgaande van de twee met elkaar verweven lagen is het zaak om erop te letten dat ze op de juiste manier worden afgesneden om door oprollen een cilinder die bestaat uit één aaneengesloten verweven laag te krijgen, en uiteindelijk de beelden van figuur 8 en 9. In figuur 1 was dat zonder meer al goed gedaan.
NOG TWEE BEELDEN
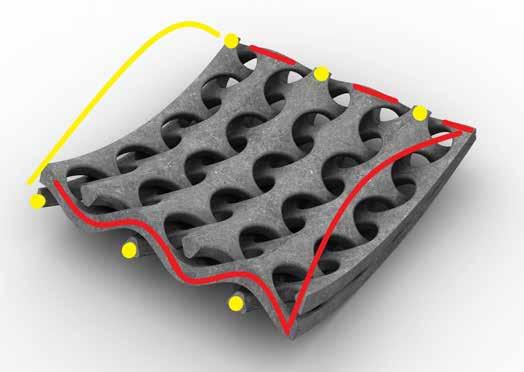
Zoals te zien in de foto aan het begin en in de inleiding terloops aangeduid, werden in 2011 nog twee beelden geplaatst op de campus van de Universiteit Twente. Dat zijn Spiraalvormige gaten – vierkant (figuur 13) en Spiraalvormige gaten – zeshoekig (figuur 14). Ze zijn eveneens met de 3D-betonprinter geprint. Wellicht kun je aan de hand van de figuren 13, 14 en 15 uitzoeken hoe ze in elkaar zitten en hun naam verklaren.
Figuur 11
16




FOTO’S EN ILLUSTRATIES
Figuur 12
Figuur 13 Spiraalvormige gaten – vierkant
17
Figuur 14 Spiraalvormige gaten – zeshoekig
Figuur 15 Spiraalvormige gaten – vierkant vanuit een andere hoek gefotografeerd
Figuur 11 Klaas Lakeman; alle andere foto’s Rinus Roelofs.
PAUL LEVRIE
BOEKBESPREKINGEN

KEIZER BEULMANS EN DE GEVANGEN KABOUTERS
Bespreking van: Alex van den Brandhof. De kabouterformule. Logische raadsels over gekleurde mutsen.
Wiskundedocent en auteur Alex van den Brandhof was jarenlang actief als eindredacteur van het tijdschrift Pythagoras, en nu en dan verscheen er in dat tijdschrift een bijdrage van zijn hand die over kabouters met gekleurde mutsen ging. Van den Brandhof is ook wetenschapsjournalist – hij schrijft o.a. voor NRC handelsblad – en ook in die hoedanigheid schreef hij wel eens over gekleurd gemutste kabouters.
Nu is er dus dit boek, dat volledig gewijd is aan kabouters die door een eerder wrede keizer, keizer Beulmans, gevangen worden gehouden en op de proef gesteld: de keizer zet gekleurde mutsen op hun hoofd en ze kunnen vrijkomen als ze aan bepaalde voorwaarden die verband houden met de kleur van die mutsen, voldoen. Het bekendste kaboutermutsenraadsel is wellicht het volgende.
Drie kabouters krijgen elk een rode of een gele muts op hun hoofd, uit een voorraad van twee gele en drie rode. Ze worden achter elkaar geplaatst zodat ze enkel de muts(en) kunnen zien van de kabouters voor hen:

Als ze de kleur van hun eigen muts kunnen zeggen, dan komen ze vrij. Eerst wordt aan de achterste van de rij gevraagd of hij de kleur weet, en het antwoord is neen. Dan krijgt de middelste dezelfde vraag, en ook hij moet het antwoord schuldig blijven. Maar als de vraag dan aan de voorste wordt gesteld, dan heeft die het goed, en wordt dan ook vrijgelaten. Wat was de kleur van zijn muts, en hoe wist de kabouter dat?
Hierbij is het belangrijk om te weten dat kabouters op alle gebieden perfect functioneren, zeker wat logisch redeneren betreft. Zie jij de oplossing?
18
Vind je zo’n raadsels leuk, en ben je ook wel goed in het logisch denken, dan is dit boek zeker een aanrader. Alex van den Brandhof heeft het hier anders aangepakt dan bij andere puzzelboeken: de lezer mag natuurlijk wel eens nadenken over de beste oplossing voor de kabouters, maar het is vooral de bedoeling van de auteur om de vaak ingenieuze tactiek die de kabouters kunnen gebruiken, uit te leggen aan de lezer. Dus elk hoofdstuk start met een raadsel dat wordt opgelost in dat hoofdstuk. Daarbij worden verschillende takken van de wiskunde aangeraakt, zo lees je over binaire getallen, foutencorrigerende codes en Motzkinpaden

en heb je ook kans- en differentiaalrekening nodig. De wiskunde in dit boek is lang niet altijd eenvoudig, zegt de auteur terecht in de inleiding, maar hij doet zijn uiterste best om die wiskunde duidelijk te brengen, en slaagt daar ook in. Achter in het boek vind je wat extra achtergrond i.v.m. de gebruikte methodes, bijvoorbeeld over modulorekenen en het keuzeaxioma (voor het raadsel met oneindig veel kabouters!).
Veel van de problemen die de kabouters voorgeschoteld krijgen, lijken (op het eerste zicht) onmogelijk. Maar als je dan leest dat het toch kan, en ziet hoe, dan heb je eventjes
WISKUNDE AAN DE HAND VAN METAFOREN?
Bespreking van: David Eelbode. Wiskunde. Oneindig veelzijdig.
Uitgeverij Academie Press is in 2019 gestart met de reeks Vizier: wetenschap in zakformaat, kleine boekjes waarin vakspecialisten ons een blik gunnen in hun onderzoeksveld. De onderwerpen in de reeks gaan van Klimaatbewust consumeren via Democratie naar Big data en AI. Sinds kort is er nu ook eentje over Wiskunde, van de hand van (mijn collega aan de UAntwerpen) David Eelbode.
In ons taalgebied zijn er weinig wiskundige auteurs die schrijven zoals David Eelbode. Hij doet dat namelijk
dat wow-gevoel dat wiskundigen wel vaker hebben als ze na dagen denken, proberen, zwoegen, rekenen tot een oplossing komen die prachtig is in haar eenvoud.
20 hoofdstukken, evenveel raadsels. Concentratie vereist!
Alex van den Brandhof publiceerde eerder bij dezelfde uitgeverij Priemwoestijnen (over zeventien hoogtepunten uit de eenentwintigste-eeuwse wiskunde), en samen met Roland van der Veen, Jan van de Craats, Barry Koren De zeven grootste raadsels van de wiskunde (over de millenniumproblemen).
met erg veel (gevoel voor) humor, en dat is spijtig genoeg in deze branche – populariserende boeken met wiskunde als onderwerp – nog steeds zeldzaam. Eerder verscheen van hem bij dezelfde uitgever het boek FUNdamental Mathematics. A voyage into the quirky universe of maths & jokes, geschreven in het Engels. Het is niet eenvoudig om te beschrijven waar dit boek precies over gaat, maar gelukkig hoeft dat hier niet te gebeuren.
Hoe begin je aan een boek over wiskunde dat bedoeld is voor de leek en een beeld moet geven van `de wiskunde’ maar dan wel in zakformaat? Nu, Johann Wolfgang Goethe zei het al (in 1802): In der Beschränkung zeigt sich erst der Meister. David Eelbode heeft hier zijn doel bereikt, denk ik: het boek geeft
19
een korte inleiding op de wiskunde op een manier die best te omschrijven is als succulent. Hij doet dit in 3 delen: Wiskunde als creatieve wetenschap, Wiskunde als classificerende wetenschap en Wiskunde als benaderende wetenschap.
In het eerste deel wordt het verhaal geschetst van de invoering van de complexe eenheid i (je weet wel, dat `getal’ waarvan het kwadraat gelijk is aan -1) en waar dit allemaal toe heeft geleid, meer bepaald bij het oplossen van veeltermvergelijkingen. Deel

twee werkt daarop door en laat zien hoe je vertrekkend van de veeltermvergelijking x2 = 1 in hogere dimensies kan belanden om tenslotte uit te komen bij de groepentheorie. Deel drie gaat dan over wat ik zou durven noemen de wiskunde voor de ingenieurs, meer bepaald de analyse van de verandering en de praktische toepassingen ervan.
Als je zelf wiskundige bent, dan denk je nu misschien dat je dit allemaal al wel weet, en waarschijnlijk is dat grotendeels ook zo. Maar je hebt het in
EEN PRACHTIG GESCHENK
Bespreking van:
Colin Stuart. Getallen - 10 feiten die je zou moeten kennen. Van nul tot oneindigvoormensen metweinig tijd.
We willen ook nog even dit boek vermelden van Colin Stuart, die vooral bekend is door zijn boeken over astronomie en aanverwante onderwerpen, en als journalist bijvoorbeeld ook publiceert in The Guardian en New Scientist. Bij dezelfde uitgever, in dezelfde reeks, verscheen recent van hem ook het boek Tijd. Een reis door het grootste mysterie van ons heelal.
Getallen bestaat uit 10 korte hoofdstukken over allerlei onderwerpen die verband houden met de titel. Wist je bijvoorbeeld dat er een volk is in Nieuw-Guinea dat een 27-tallig stelsel gebruikt (het eerste hoofdstuk gaat over talstelsels)? En dat onze (christelijke) jaartelling in de
elk geval nog nooit gelezen zoals het beschreven staat in dit boek. Dit boek zet je aan tot nadenken, en deze keer niet omdat het over wiskunde gaat, maar door de manier waarop het geschreven is, met veel metaforen en dubbele bodems. Dat zorgde ervoor dat het lezen van dit boek voor mij, nog meer dan bij andere wiskundeboeken, echt genieten was. Spijtig dat het zo dun is…
zesde eeuw werd geïntroduceerd door Dennis de Korte (Dionysius Exiguus)? Hij was wellicht ook de eerste die in deze streken het getal nul gebruikte (het tweede hoofdstuk gaat over nul). Ook priemgetallen, het getal π, niet-euclidische meetkunde, grafentheorie, de rij getallen van de luie traiteur (!), Monty Hall, het dubbelvouwen van papier, en de verschillende soorten oneindigheden passeren de revue.
Dit is een erg luchtig geschreven en leuk boek. Ook als je veel gelezen hebt over wiskunde, dan nog leer je wel iets bij in dit boek. Het is een ideaal geschenk voor de wiskundeminnende medemens. Zoals Ian Stewart zegt op de cover: Een gezellige, amusante en uiterst toegankelijke verkenningstocht van een aantal van de boeiende eigenschappen van getallen.
20
START- EN IJKINGSTOETSEN, DÉ SLEUTEL TOT STUDIESUCCES
CONTEXT
Voor onze studiekiezers is de ijkingstoets een grote hulp bij de overgang naar het academisch onderwijs. Deze positioneringstoets stelt onze toekomstige studenten in staat om zichzelf te 'ijken'. Aan de hand van meerkeuzevragen krijgen de laatstejaars in spe een beeld van hun wiskundige en wetenschappelijke vaardigheden en kennis in verhouding tot het verwachte instapniveau van de bacheloropleiding.
Het aanbod aan ijkingstoetsen is door de jaren heen enorm gegroeid, omdat ondertussen een brede waaier STEM en economische opleidingen deze al dan niet verplicht aanbieden. Voor sommige opleidingen is deelname aan een ijkingstoets verplicht, een voorwaarde tot inschrijving, maar niet-bindend. Wel zijn de deelnemers sinds dit jaar genoodzaakt om verplichte remediëring te volgen bij het niet-slagen van deze zogenaamde ‘starttoetsen’.
MEERWAARDE
De ijkingstoetsen vormen een belangrijke peiler in het studiekeuzeproces. Op basis van het resultaat
en de feedback na deelname weten de leerlingen of ze goed voorbereid aan de start komen, of ze hun kennis en vaardigheden best bijspijkeren, of dat mogelijk een andere studiekeuze aangewezen is. Met de invoering van de verplichte remediëring kunnen de leerlingen beter voorbereid aan de start komen. De universiteiten engageren zich om studenten te ondersteunen bij het wegwerken van remedieerbare tekorten. Remediëring is verplicht voor deelnemers die de minimumscore/cesuur niet halen, maar is ook toegankelijk voor hen die wel een voldoende haalden. De student kan hierbij kiezen tussen het volgen van een verplichte remediëring op de campus of remediëren via een online remediëringspakket. Het ultieme doel is om het studieen studentensucces te verhogen.
JOUW ROL ALS LEERKRACHT
Leerkrachten spelen vaak een belangrijke rol in de studiekeuze van hun leerlingen. De kans is groot dat jij als eerste de leerlingen informeert over de start- of ijkingstoets. De juiste informatie hiervoor vind je snel op www.ijkingstoets.be
Het kan zinvol zijn om je leerlingen te helpen om zich voor te bereiden op de ijkingstoetsen. De toetsen zijn gebaseerd op de leerstof van het hele secundair onderwijs. De focus ligt niet enkel op de leerinhouden van de derde graad. Hen aanmoedigen om de leerstof van de tweede graad even vanonder het stof te halen is geen overbodige luxe. Bovendien bevragen de ijkingstoetsen verschillende leerinhouden. Zo komt er in sommige ijkingstoetsen naast wiskunde ook chemie aan bod.
Elke opleiding legt eigen accenten en probeert de toets zo goed mogelijk af te stemmen op de verwachtingen. Daarnaast proberen de instellingen vaak ook een glimp van de opleiding mee te geven in de toets, zodat een deelnemer zich kan identificeren met een toekomstige opleiding. Wel is er natuurlijk een gedeelde basis: deelnemers aan verschillende toetsen komen uit dezelfde vooropleidingen en er is een gemeenschappelijke noemer in de startcompetenties van veel opleidingen. Daarom is het logisch dat er ook jaarlijks gedeelde vragen zijn die in verschillende ijkingstoetsen
21

1
terugkomen. Zo proberen de universiteiten een goed evenwicht te vinden tussen die gemeenschappelijke basis enerzijds en de eigenheid van de opleidingen anderzijds.
Op de website ‘ijkingstoets.be’ vind je de meest actuele informatie over de start- en ijkingstoetsen, een direct inzetbare powerpointpresentatie met de belangrijkste highlights, alsook een overzicht van de leerinhouden per toets.
samenstellen met het gewenste aantal oefeningen. Elke oude ijkingstoetsvraag is in usolv-it van een kwaliteitsvolle uitwerking voorzien. Daarnaast zijn oude ijkingstoetsen ook in hun geheel te raadplegen op de website.
als analytisch. Of je zou een ijkingstoetsvraag kunnen integreren binnen evaluaties. Maar het is geenszins de bedoeling om oude ijkingstoetsvragen nog eens als iets extra aan bod te laten komen tijdens de vaak al goedgevulde lessen.
6. Innevenstaandesomstellen X , Y en Z cijfersvoor. Waaraanis X + Y + Z dangelijk? XY ZZZ + ZZZ 2024 A
VOORBEREIDING
Om zich voor te bereiden kunnen leerlingen waar en wanneer ze maar willen oefeningen maken. Er is een grote hoeveelheid oude ijkingstoetsvragen beschikbaar in het online oefenplatform ‘usolv-it’. Per ijkingstoets is hiervoor een link voorzien op de ijkingstoetswebsite. Zo kunnen leerlingen een oefentoets op maat
7. Ineenregelmatigezeshoekmetoppervlakte12tekent Janneszescongruentetrapeziazoalsindefiguur.Elk trapeziumheefttweehoekpuntendiesamenvallenmet hetmiddenvaneenzijdevandezeshoek.
Watisdeoppervlaktevanzo’ntrapezium?
Om leerlingen inhoudelijk voor te bereiden zou je ook oude ijkingstoetsvragen kunnen integreren in je lessen. Uit bijscholingen en gesprekken met leerkrachten weten we dat jullie weten we dat deze vragen binnen verschillende lesfasen worden aangewend. Een uitdagende vraag kan bijvoorbeeld als teaser worden gebruikt om een nieuw onderwerp aan te snijden, of het onderwerp van een onderwijsleergesprek vormen. Bij het opstellen van ijkingstoetsvragen denken de opleidingen immers bewust na over verschillende oplossingsmethodes, zowel meetkundig
Gebruik de vragensets als een tool waaruit je extra info kan putten, waar en wanneer het voor jou past.
MEER INFO: www.ijkingstoets.be VRAGEN? info@ijkingstoets.be

OEFENING 5
8. DemierScottkruiptvanuithetpunt S opnevenstaandekubusoverachtribben.Hijgaatdaarbij nooittweekeeroverdezelfderibbe.
De mier Scott kruipt vanuit het punt S op nevenstaande kubus over acht ribben. Hij gaat daarbij nooit twee keer over dezelfde ribbe.
In welk van de andere aangeduide punten kan Scott eindigen met zijn traject?
Inwelkvandeandereaangeduidepuntenkan Scotteindigenmetzijntraject?
22
15 B 16 C 17 D 18 E 19
A 7 6 B 6 5 C 5 4 D 4 3 E 3 2
S D E A B C A A B B C C D D E E 9. Zo¨eschrijftdeafkortingvoor“zieommezijde”opeendoorzichtigbladpapier.Door © Junior Wiskunde Olympiade vzwEerste Ronde JWO 2024 vraag 8 A B C D E A B C D E
OPPERVLAKTES VERGELIJKEN OP ZIJN GRIEKS
IN DE OUDHEID KENDEN DE GRIEKEN NOG GEEN WORTELS VAN WILLEKEURIGE GETALLEN. DAARDOOR KONDEN ZE DE LENGTES EN OPPERVLAKTES VAN MEETKUNDIGE FIGUREN DIE ZE BESTUDEERDEN LANG NIET ALTIJD EXACT BEPALEN. ZE OMZEILDEN HET PROBLEEM DOOR FIGUREN TE VERGELIJKEN. DOOR OPTELLEN VAN DEELLENGTES OF OPPERVLAKTES KONDEN ZE VEELHOEKEN VOLGENS HUN LENGTE OF OPPERVLAKTE RANGSCHIKKEN. OPTELLEN VAN LENGTES IS SIMPEL: JE KUNT LIJNSTUKKEN
OppervlaktesvergelijkenopzijnGrieks
GeertjeHek
TEGEN ELKAAR LEGGEN EN ZO EEN TOTALE LENGTE BEPALEN. OPTELLEN EN VERGELIJKEN VAN OPPERVLAKTES IS LASTIGER. IN DIT ARTIKEL BEKIJKEN WE HOE DE GRIEKEN SLIM GEBRUIK MAAKTEN VAN VIERKANTEN OM DIT VOOR ELKAAR TE KRIJGEN.
GEERTJE HEK
IndeoudheidkendendeGriekennoggeenwortelsvanwillekeurigegetallen.Daardoor kondenzedelengtesenoppervlaktesvanmeetkundigefigurendiezebestudeerdenlangniet altijdexactbepalen.Zeomzeildenhetprobleemdoorfigurentevergelijken.Dooroptellen vandeel-lengtesofoppervlakteskondenzeveelhoekenvolgenshunlengteofoppervlakte rangschikken.Optellenvanlengtesissimpel:jekuntlijnstukkentegenelkaarleggenen zoeentotalelengtebepalen.Optellenenvergelijkenvanoppervlaktesislastiger.Indit artikelbekijkenwehoedeGriekenslimgebruikmaaktenvanvierkantenomditvoorelkaar tekrijgen.
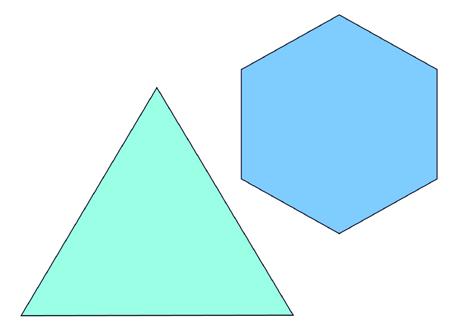
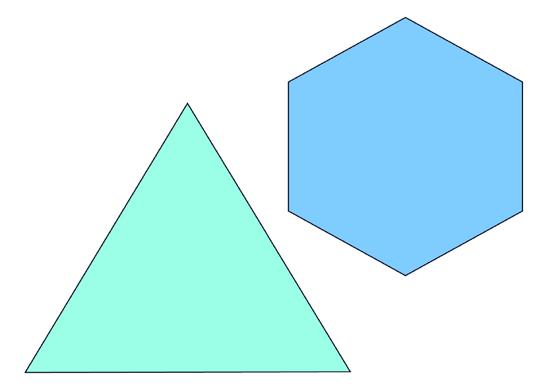
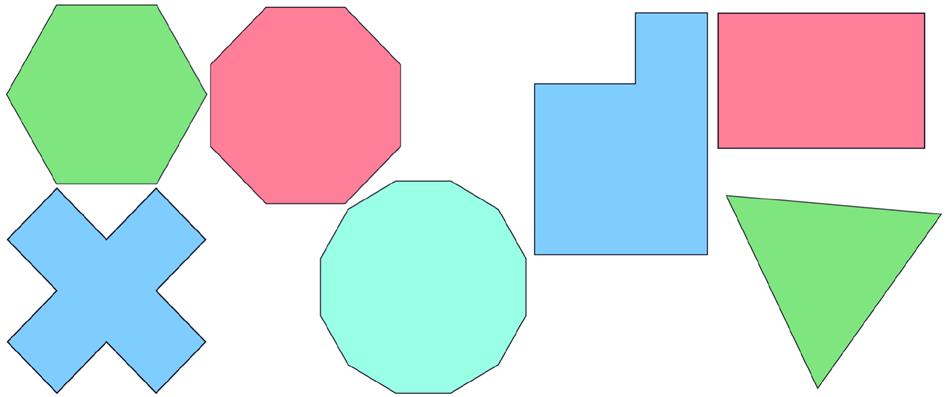
Stel dat je wilt bepalen welke van de twee regelmatige veelhoeken in figuur 1 de grootste oppervlakte heeft. Hoe zou je dat doen? Grote kans dat je de lengte van de zijden zou meten, wellicht de zeshoek in twee trapeziums zou verdelen, de lengte van hoogtelijnen zou meten om vervolgens de oppervlakte uit te rekenen. Maar als de oppervlaktes vrijwel gelijk zijn, mis je hiermee misschien de nodige precisie. Je kunt ook goniometrie of een verdeling in rechthoekige driehoeken en de Stelling van Pythagoras proberen te gebruiken, maar met beide zul je op het getal
stuiten. Een lastig getal voor de Grieken1. Wat je methode ook is, als je het goed gedaan hebt, vind je dat de zeshoek een iets grotere oppervlakte heeft dan de driehoek.
Steldatjewiltbepalenwelkevandetweeregelmatigeveelhoekeninfiguur1degrootste oppervlakteheeft.Hoezoujedatdoen?Grotekansdatjedelengtevandezijdenzou meten,wellichtdezeshoekintweetrapeziumszouverdelen,delengtevanhoogtelijnenzou metenomvervolgensdeoppervlakteuitterekenen.Maaralsdeoppervlaktesvrijwelgelijk zijnmisjehiermeemisschiendenodigeprecisie.Jekuntookgoniometrieofeenverdeling inrechthoekigedriehoekenendestellingvanPythagorasproberentegebruiken,maarmet beidezuljeophetgetal √3stuiten.EenlastiggetalvoordeGrieken. ookis,alsjehetgoedgedaanhebt,vindjedatdezeshoekeenietsgrotereoppervlakte heeftdandedriehoek.
PYTHAGORAS
23
Figuur 1
INGEWIKKELDER FIGUREN VERGELIJKEN
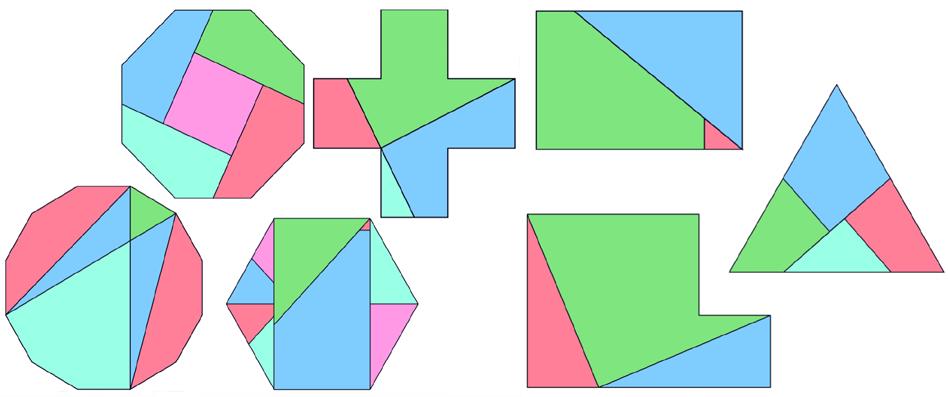
Probeer voordat je verder leest over de Griekse methode de veelhoeken in figuur 2 op basis van hun oppervlakte te rangschikken.
Omdat deze figuren niet allemaal regelmatig en niet allemaal convex zijn, wordt het ordenen op basis van oppervlakte lastiger. Zeker op het oog, zonder berekeningen, is het niet makkelijk om dit voor elkaar te krijgen. In stukken knippen, en de stukken aan elkaar passen om figuren te vormen die je wel makkelijk kunt vergelijken is een alternatief idee dat de Grieken hadden:
‘Als je een willekeurige veelhoek kunt ontbinden in stukken die daarna samen een vierkant vormen, kun je hun oppervlaktes vervolgens gemakkelijk vergelijken.’
Dit verklaart de vijfde betekenis die Van Dale geeft aan het woord ‘oppervlakte’: in ’t bijzonder de grootte, de afmeting van iets in het vierkant. Het heeft ook te maken met het streven van de Grieken om de kwadratuur van de cirkel te bepalen. Ze wilden de oppervlakte van een cirkel bepalen, met andere woorden, vinden welk vierkant dezelfde oppervlakte had als die cirkel, ofwel, welk getal in het kwadraat de oppervlakte zou geven.
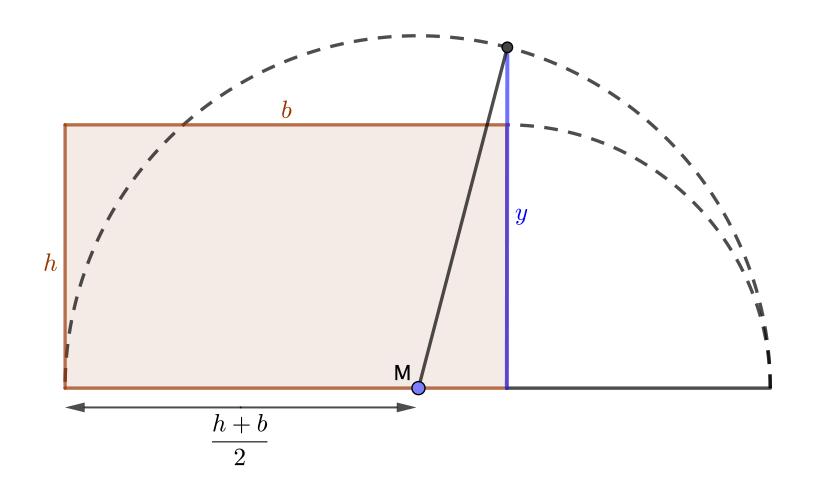
Figuur 3 toont dezelfde figuren als figuur 2, maar nu zijn het allemaal afzonderlijke puzzels.2 Iedere veelhoek is verdeeld in stukken en de opdracht is om deze zodanig te schuiven of (al dan niet op de kop) te draaien dat ze samen een vierkant vormen. Op https://pyth.eu/uploads/ default/d/e/de-7-figuren.pdf vind je een versie die je kunt printen
en uitknippen om dit te proberen. Rangschik vervolgens de figuren weer op grootte. Kom je op dezelfde volgorde uit als de eerste keer?
Tussen deze puzzels zitten een paar standaard voorbeelden. Allereerst de methode om een rechthoek om te vormen tot een vierkant. Euclides toonde in zijn Propositie 14 in boek II van De Elementen al aan dat je voor iedere rechthoek een vierkant kunt construeren met exact dezelfde oppervlakte. Je kunt natuurlijk het bewijs van Euclides nalopen en zo een vierkant maken maar dat is niet altijd de snelste manier. Het kan vaak mooier en efficiënter. De opdeling van de rechthoek die je hier ziet is zo’n efficiënt voorbeeld: de rechthoek is verdeeld in een vijfhoek, een grote driehoek en een klein driehoekje, die vervolgens samen een vierkant
24
Figuur 2





.Dedecompositiekunjevindendooropdelangstezijde aantegeven,vervolgensdediagonalelijntetrekkenentotslothetkleine driehoekjetetekenenm.b.v.eenverticaallijnstukje.Probeerditbijvoorbeeldvooreen rechthoekmetbasis16cmenhoogte9cm.
DezeconstructielijktvoordeoudeGriekenwellichtookonoverkomelijk,omdatjebij mindergoedgekozenhoogteenbreedteweereenwortelnodighebt.Maarjekunt alsvolgtmetpasserenlineaalbepalen.Verlengeerst

.BepaaldanhetmiddelpuntMvandenieuwezijdemetlengte kanm.b.v.eenmiddelloodlijnconstructie.VanuitMtekenjeeenhalvecirkelmetstraal
aantegeven,vervolgensdediagonalelijntetrekkenentotslothetkleine driehoekjetetekenenm.b.v.eenverticaallijnstukje.Probeerditbijvoorbeeldvooreen
Figure3:
).Verlengvervolgensdeoorspronkelijkezijdevanlengte waarvoorgebruikmakendvandeStellingvanPythagorasgeldtdat
y + 2 (h b) = 2 (h + b) 2 ,ofwel y = √hb

b waarvoor b 4 ≤ h ≤ b.Dedecompositiekunjevindendooropdelangstezijde b een lengtevan √hb aantegeven,vervolgensdediagonalelijntetrekkenentotslothetkleine driehoekjetetekenenm.b.v.eenverticaallijnstukje.Probeerditbijvoorbeeldvooreen rechthoekmetbasis16cmenhoogte9cm.
teken je een halve cirkel met straal
. Verleng vervolgens de oorspronkelijke zijde van lengte h tot aan deze halve cirkel.

DezeconstructielijktvoordeoudeGriekenwellichtookonoverkomelijk,omdatjebij mindergoedgekozenhoogteenbreedteweereenwortelnodighebt.Maarjekunt alsvolgtmetpasserenlineaalbepalen.Verlengeerst b metbehulpvaneenpassermet eenafstand h.BepaaldanhetmiddelpuntMvandenieuwezijdemetlengte kanm.b.v.eenmiddelloodlijnconstructie.VanuitMtekenjeeenhalvecirkelmetstraal 1 2 (h + b).Verlengvervolgensdeoorspronkelijkezijdevanlengte h totaandezehalvecirkel.
b waarvoor b 4 ≤ h ≤ b.Dedecompositiekunjevindendooropdelangstezijde lengtevan √hb aantegeven,vervolgensdediagonalelijntetrekkenentotslothetkleine driehoekjetetekenenm.b.v.eenverticaallijnstukje.Probeerditbijvoorbeeldvooreen rechthoekmetbasis16cmenhoogte9cm.
Optellenvanvierkanten Hetlaatsteplaatjeinfiguur3ishettweedestandaardvoorbeeld:een‘som’vantwee vierkantenmetalsresultaateenderdevierkant.DitiseigenlijkeenbewijsvandeStelling vanPythagoras:legtweevierkantenmetzijden Markeereenafstand b opdebasisvanhetgrootstevierkantentekendediagonalelijnen
Ditleverteenlengte y waarvoorgebruikmakendvandeStellingvanPythagorasgeldtdat y 2 + 1 2 (h b) 2 = 1 2 (h + b) 2 ,ofwel y = √hb.Ziefiguur4.
driehoekjetetekenenm.b.v.eenverticaallijnstukje.Probeerditbijvoorbeeldvooreen
Optellenvanvierkanten
lengtevan aantegeven,vervolgensdediagonalelijntetrekkenentotslothetkleine driehoekjetetekenenm.b.v.eenverticaallijnstukje.Probeerditbijvoorbeeldvooreen
DezeconstructielijktvoordeoudeGriekenwellichtookonoverkomelijk,omdatjebij mindergoedgekozenhoogteenbreedteweereenwortelnodighebt.Maarjekunt √hb alsvolgtmetpasserenlineaalbepalen.Verlengeerst b metbehulpvaneenpassermet eenafstand h.BepaaldanhetmiddelpuntMvandenieuwezijdemetlengte h + b;dit kanm.b.v.eenmiddelloodlijnconstructie.VanuitMtekenjeeenhalvecirkelmetstraal 1 2 (h + b).Verlengvervolgensdeoorspronkelijkezijdevanlengte h totaandezehalvecirkel. Ditleverteenlengte y waarvoorgebruikmakendvandeStellingvanPythagorasgeldtdat y 2 + 1 2 (h b) 2 = 1 2 (h + b) 2 ,ofwel y = √hb.Ziefiguur4.
Deze constructie lijkt voor de oude Grieken wellicht ook onoverkomelijk, omdat je bij minder goed gekozen hoogte en breedte weer een wortel nodig hebt. Maar je kunt
Optellenvanvierkanten
Dit levert een lengte y waarvoor gebruikmakend van de Stelling van Pythagoras geldt dat
te verbinden met de hoeken zoals in figuur 5. Als je de puzzel oplost vind je een vierkant met zijden c en oppervlakte gelijk aan de som van de oorspronkelijke twee oppervlaktes. Ofwel,
DezeconstructielijktvoordeoudeGriekenwellichtookonoverkomelijk,omdatjebij mindergoedgekozenhoogteenbreedteweereenwortelnodighebt.Maarjekunt √ metbehulpvaneenpassermet .BepaaldanhetmiddelpuntMvandenieuwezijdemetlengte h + b;dit kanm.b.v.eenmiddelloodlijnconstructie.VanuitMtekenjeeenhalvecirkelmetstraal 1 2 (h + b).Verlengvervolgensdeoorspronkelijkezijdevanlengte h totaandezehalvecirkel. Ditleverteenlengte y waarvoorgebruikmakendvandeStellingvanPythagorasgeldtdat y 2 + 1 2 (h b) 2 = 1 2 (h + b) 2 ,ofwel y = √hb.Ziefiguur4.
DezeconstructielijktvoordeoudeGriekenwellichtookonoverkomelijk,omdatjebij mindergoedgekozenhoogteenbreedteweereenwortelnodighebt.Maarjekunt alsvolgtmetpasserenlineaalbepalen.Verlengeerst b metbehulpvaneenpassermet eenafstand h.BepaaldanhetmiddelpuntMvandenieuwezijdemetlengte kanm.b.v.eenmiddelloodlijnconstructie.VanuitMtekenjeeenhalvecirkelmetstraal 1 2 (h + b).Verlengvervolgensdeoorspronkelijkezijdevanlengte h totaandezehalvecirkel.
doorditpuntteverbindenmetdehoekenzoalsinfiguur5.Alsjedepuzzeloplostvind jeeenvierkantmetzijden c enoppervlaktegelijkaandesomvandeoorspronkelijketwee oppervlaktes.Ofwel, c2 = a2 + b2 .
DE LAPJESPUZZEL VAN DUDENEY
DezeconstructielijktvoordeoudeGriekenwellichtookonoverkomelijk,omdatjebij alsvolgtmetpasserenlineaalbepalen.Verlengeerst eenafstand h.BepaaldanhetmiddelpuntMvandenieuwezijdemetlengte h + b;dit kanm.b.v.eenmiddelloodlijnconstructie.VanuitMtekenjeeenhalvecirkelmetstraal (h + b).Verlengvervolgensdeoorspronkelijkezijdevanlengte h totaandezehalvecirkel. Ditleverteenlengte y waarvoorgebruikmakendvandeStellingvanPythagorasgeldtdat + 1 2 (h b) 2 = 1 2 (h + b) 2 ,ofwel y = √hb.Ziefiguur4.
Optellenvanvierkanten
, ofwel
Figure3:
Optellenvanvierkanten
OPTELLEN VAN VIERKANTEN
b waarvoor b 4 ≤ h ≤ b.Dedecompositiekunjevindendooropdelangstezijde b een lengtevan √hb aantegeven,vervolgensdediagonalelijntetrekkenentotslothetkleine driehoekjetetekenenm.b.v.eenverticaallijnstukje.Probeerditbijvoorbeeldvooreen rechthoekmetbasis16cmenhoogte9cm.
Optellenvanvierkanten
als volgt met passer en lineaal bepalen. Verleng eerst b met behulp van een passer met een afstand h. Bepaal dan het middelpunt M van de nieuwe zijde met lengte
Hetlaatsteplaatjeinfiguur3ishettweedestandaardvoorbeeld:een‘som’vantwee vierkantenmetalsresultaateenderdevierkant.DitiseigenlijkeenbewijsvandeStelling vanPythagoras:legtweevierkantenmetzijden a en b,waarbij a>b,tegenelkaaraan. Markeereenafstand b opdebasisvanhetgrootstevierkantentekendediagonalelijnen doorditpuntteverbindenmetdehoekenzoalsinfiguur5.Alsjedepuzzeloplostvind jeeenvierkantmetzijden c enoppervlaktegelijkaandesomvandeoorspronkelijketwee oppervlaktes.Ofwel, c2 = a2 + b2
Ditleverteenlengte y waarvoorgebruikmakendvandeStellingvanPythagorasgeldtdat y 2 + 1 2 (h b) 2 = 1 2 (h + b) 2 ,ofwel y = √hb.Ziefiguur4.
Figure3: waarvoor b 4 ≤ h ≤ b.Dedecompositiekunjevindendooropdelangstezijde b een lengtevan √hb aantegeven,vervolgensdediagonalelijntetrekkenentotslothetkleine driehoekjetetekenenm.b.v.eenverticaallijnstukje.Probeerditbijvoorbeeldvooreen rechthoekmetbasis16cmenhoogte9cm.
DelapjespuzzelvanDudeney
DelapjespuzzelvanDudeney DavidHilberthadalbewezendateenwillekeurigeveelhoekkanwordengetransformeerd toteenandereveelhoekvandezelfdeoppervlaktedoorhemineeneindigaantalstukjesop tedelen.Hetbewijsislangmaarnietmoeilijk.Hetisgebaseerdoptweefeiten:(1)ieder polygonkanlangsdiagonalenwordenopgedeeldineeneindigaantaldriehoeken,(2)iedere driehoekkanwordenopgedeeldineeneindigaantalstukkendieherschiktkunnenworden toteenrechthoek.DitislaterveralgemeniseerddoorWallace,BolyaienGerwien.Deversie vandestellingdiewehiergebruikenis:
Hetlaatsteplaatjeinfiguur3ishettweedestandaardvoorbeeld:een‘som’vantwee vierkantenmetalsresultaateenderdevierkant.DitiseigenlijkeenbewijsvandeStelling vanPythagoras:legtweevierkantenmetzijden a en b,waarbij a>b,tegenelkaaraan. Markeereenafstand b opdebasisvanhetgrootstevierkantentekendediagonalelijnen doorditpuntteverbindenmetdehoekenzoalsinfiguur5.Alsjedepuzzeloplostvind jeeenvierkantmetzijden c enoppervlaktegelijkaandesomvandeoorspronkelijketwee oppervlaktes.Ofwel, c2 = a2 + b2
; dit kan m.b.v. een middelloodlijn constructie. Vanuit M
DelapjespuzzelvanDudeney
DezeconstructielijktvoordeoudeGriekenwellichtookonoverkomelijk,omdatjebij mindergoedgekozenhoogteenbreedteweereenwortelnodighebt.Maarjekunt √hb alsvolgtmetpasserenlineaalbepalen.Verlengeerst b metbehulpvaneenpassermet eenafstand h.BepaaldanhetmiddelpuntMvandenieuwezijdemetlengte h + b;dit kanm.b.v.eenmiddelloodlijnconstructie.VanuitMtekenjeeenhalvecirkelmetstraal 1 2 (h + b).Verlengvervolgensdeoorspronkelijkezijdevanlengte h totaandezehalvecirkel. Ditleverteenlengte y waarvoorgebruikmakendvandeStellingvanPythagorasgeldtdat y 2 + 1 2 (h b) 2 = 1 2 (h + b) 2 ,ofwel y = √hb.Ziefiguur4.
DelapjespuzzelvanDudeney
Hetlaatsteplaatjeinfiguur3ishettweedestandaardvoorbeeld:een‘som’vantwee vierkantenmetalsresultaateenderdevierkant.DitiseigenlijkeenbewijsvandeStelling vanPythagoras:legtweevierkantenmetzijden a en b,waarbij a>b,tegenelkaaraan. Markeereenafstand b opdebasisvanhetgrootstevierkantentekendediagonalelijnen doorditpuntteverbindenmetdehoekenzoalsinfiguur5.Alsjedepuzzeloplostvind jeeenvierkantmetzijden c enoppervlaktegelijkaandesomvandeoorspronkelijketwee oppervlaktes.Ofwel, c2 = a2 + b2 .
Hetlaatsteplaatjeinfiguur3ishettweedestandaardvoorbeeld:een‘som’vantwee vierkantenmetalsresultaateenderdevierkant.DitiseigenlijkeenbewijsvandeStelling vanPythagoras:legtweevierkantenmetzijden a en b,waarbij a>b,tegenelkaaraan. Markeereenafstand b opdebasisvanhetgrootstevierkantentekendediagonalelijnen doorditpuntteverbindenmetdehoekenzoalsinfiguur5.Alsjedepuzzeloplostvind jeeenvierkantmetzijden c enoppervlaktegelijkaandesomvandeoorspronkelijketwee oppervlaktes.Ofwel, c2 = a2 + b2
Het laatste plaatje in figuur 3 is het tweede standaard voorbeeld: een ‘som’ van twee vierkanten met als resultaat een derde vierkant. Dit is eigenlijk een bewijs van de Stelling van Pythagoras: leg twee vierkanten met zijden a en b, waarbij a > b, tegen elkaar aan. Markeer een afstand b op de basis van het grootste vierkant en teken de diagonale lijnen door dit punt
Hetlaatsteplaatjeinfiguur3ishettweedestandaardvoorbeeld:een‘som’vantwee vierkantenmetalsresultaateenderdevierkant.DitiseigenlijkeenbewijsvandeStelling vanPythagoras:legtweevierkantenmetzijden a en b,waarbij a>b,tegenelkaaraan. Markeereenafstand b opdebasisvanhetgrootstevierkantentekendediagonalelijnen doorditpuntteverbindenmetdehoekenzoalsinfiguur5.Alsjedepuzzeloplostvind jeeenvierkantmetzijden c enoppervlaktegelijkaandesomvandeoorspronkelijketwee oppervlaktes.Ofwel, c2 = a2 + b2
David Hilbert had al bewezen dat een willekeurige veelhoek kan worden getransformeerd tot een andere veelhoek van dezelfde oppervlakte door hem in een eindig aantal stukjes op te delen. Het bewijs is lang maar niet moeilijk. Het is gebaseerd op twee feiten: (1) ieder polygoon kan langs diagonalen worden opgedeeld in een eindig aantal driehoeken, (2) iedere driehoek kan worden opgedeeld in een eindig aantal stukken die herschikt kunnen worden tot een rechthoek. Dit is later
DezeconstructielijktvoordeoudeGriekenwellichtookonoverkomelijk,omdatjebij mindergoedgekozenhoogteenbreedteweereenwortelnodighebt.Maarjekunt √hb alsvolgtmetpasserenlineaalbepalen.Verlengeerst b metbehulpvaneenpassermet eenafstand h.BepaaldanhetmiddelpuntMvandenieuwezijdemetlengte h + b;dit kanm.b.v.eenmiddelloodlijnconstructie.VanuitMtekenjeeenhalvecirkelmetstraal (h + b).Verlengvervolgensdeoorspronkelijkezijdevanlengte h totaandezehalvecirkel. Ditleverteenlengte y waarvoorgebruikmakendvandeStellingvanPythagorasgeldtdat + 1 2 (h b) 2 = 1 2 (h + b) 2 ,ofwel y = √hb.Ziefiguur4.
DavidHilberthadalbewezendateenwillekeurigeveelhoekkanwordengetransformeerd toteenandereveelhoekvandezelfdeoppervlaktedoorhemineeneindigaantalstukjesop tedelen.Hetbewijsislangmaarnietmoeilijk.Hetisgebaseerdoptweefeiten:(1)ieder polygonkanlangsdiagonalenwordenopgedeeldineeneindigaantaldriehoeken,(2)iedere driehoekkanwordenopgedeeldineeneindigaantalstukkendieherschiktkunnenworden toteenrechthoek.DitislaterveralgemeniseerddoorWallace,BolyaienGerwien.Deversie vandestellingdiewehiergebruikenis:
‘Tweeveelhoekenhebbendezelfdeoppervlaktedanenslechtsdanalszeontbonden
DelapjespuzzelvanDudeney
Optellenvanvierkanten
DelapjespuzzelvanDudeney
DavidHilberthadalbewezendateenwillekeurigeveelhoekkanwordengetransformeerd toteenandereveelhoekvandezelfdeoppervlaktedoorhemineeneindigaantalstukjesop tedelen.Hetbewijsislangmaarnietmoeilijk.Hetisgebaseerdoptweefeiten:(1)ieder polygonkanlangsdiagonalenwordenopgedeeldineeneindigaantaldriehoeken,(2)iedere driehoekkanwordenopgedeeldineeneindigaantalstukkendieherschiktkunnenworden toteenrechthoek.DitislaterveralgemeniseerddoorWallace,BolyaienGerwien.Deversie vandestellingdiewehiergebruikenis:
DavidHilberthadalbewezendateenwillekeurigeveelhoekkanwordengetransformeerd
DavidHilberthadalbewezendateenwillekeurigeveelhoekkanwordengetransformeerd toteenandereveelhoekvandezelfdeoppervlaktedoorhemineeneindigaantalstukjesop tedelen.Hetbewijsislangmaarnietmoeilijk.Hetisgebaseerdoptweefeiten:(1)ieder polygonkanlangsdiagonalenwordenopgedeeldineeneindigaantaldriehoeken,(2)iedere driehoekkanwordenopgedeeldineeneindigaantalstukkendieherschiktkunnenworden toteenrechthoek.DitislaterveralgemeniseerddoorWallace,BolyaienGerwien.Deversie vandestellingdiewehiergebruikenis:
‘Tweeveelhoekenhebbendezelfdeoppervlaktedanenslechtsdanalszeontbonden
DavidHilberthadalbewezendateenwillekeurigeveelhoekkanwordengetransformeerd toteenandereveelhoekvandezelfdeoppervlaktedoorhemineeneindigaantalstukjesop tedelen.Hetbewijsislangmaarnietmoeilijk.Hetisgebaseerdoptweefeiten:(1)ieder
Hetlaatsteplaatjeinfiguur3ishettweedestandaardvoorbeeld:een‘som’vantwee vierkantenmetalsresultaateenderdevierkant.DitiseigenlijkeenbewijsvandeStelling
vanPythagoras:legtweevierkantenmetzijden
b,waarbij a>b,tegenelkaaraan.
3
‘Tweeveelhoekenhebbendezelfdeoppervlaktedanenslechtsdanalszeontbonden
. Zie figuur 4.
Figure3:
3
25
Figuur 3
veralgemeniseerd door Wallace, Bolyai en Gerwien. De versie van de stelling die we hier gebruiken is:
‘Twee veelhoeken hebben dezelfde oppervlakte dan en slechts dan als ze ontbonden kunnen worden in dezelfde eindige verzameling van driehoeken.’ Ze heten dan ‘equivalent door decompositie’.
Zoals we al zagen kun je rechthoeken omvormen tot een vierkant, zo nodig door er eerst een rechthoek van een geschikter formaat van te maken. Dus volgens de stelling van Hilbert kun je ieder polygoon opdelen in stukjes die je kunt herschikken tot een vierkant. Het vinden van een eenvoudige opdeling in stukken die samen ook een vierkant vormen is in het algemeen echter niet zo simpel. Iemand die hier heel goed in was,
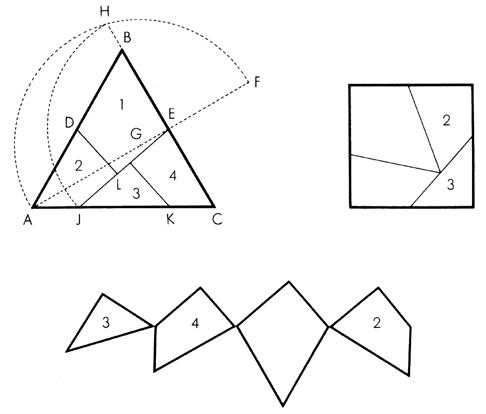
was Henry E. Dudeney. In 1907 publiceerde hij ‘The Canterbury puzzles’ waarin onder andere allerlei opdelingspuzzels stonden. De bekendste hiervan is het haberdasher’s problem ofwel de lapjespuzzel. Dudeney vond een heel elegante verdeling van een gelijkzijdige driehoek in stukken die aan elkaar genaaid konden worden tot een vierkant. In 1905 had hij zijn vondst al gepresenteerd voor de Royal Society
of London in de vorm van een mahoniehouten model met scharnieren.3 Dit is het meest rechtse plaatje in figuur 3. In figuur 6 zie je hoe je de vier stukken met scharnieren kunt verbinden zodat de driehoek gedraaid kan worden tot een vierkant.
TERUG NAAR DE STELLING
De voorbeelden hebben je waarschijnlijk overtuigd van het feit dat je iedere veelhoek door decompositie kunt omvormen tot een vierkant: iedere veelhoek kun je opdelen in een eindig aantal, zeg n driehoeken. Iedere driehoek kun je daarna verdelen in twee rechthoekige driehoeken, die je weer gemakkelijk in tweeën kunt snijden om ze zo tot een rechthoek om te vormen. Op zijn slechtst heb je nu 2n rechthoeken die ieder uit twee stukjes bestaan. Van iedere
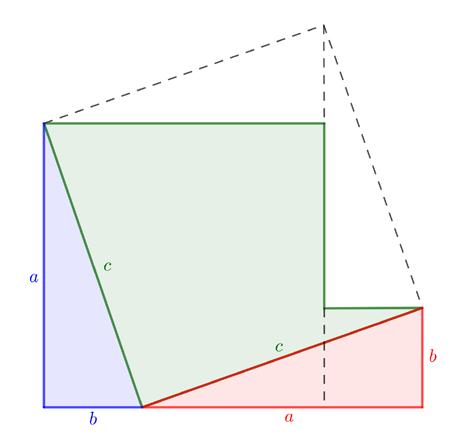 Figuur 4
Figuur 4
26
Figuur 5
© Junior Wiskunde Olympiade vzwEerste Ronde JWO 2024 vraag 4
OEFENING 6
Een rechthoekig tablet chocolade bestaat uit vierkante blokjes, allemaal even groot. Lies breekt één rij blokjes af volgens de lange zijde van het tablet. Vervolgens doet ze hetzelfde volgens de korte zijde van het overgebleven tablet. Tot slot breekt ze nog één rij af volgens de lange zijde van het overgebleven tablet. Er blijven 7 blokjes over. Hoeveel blokjes heeft Lies in totaal afgebroken?
rechthoek kun je zo nodig een rechthoek met de juiste verhouding b : h maken om hem vervolgens in drie stukjes te verdelen die samen een vierkant vormen. De vierkanten kun je m.b.v. de Stelling van Pythagoras in figuur 5 allemaal bij elkaar optellen tot een groot vierkant. Het moge duidelijk zijn dat deze ’bewijsconstructie’ leidt tot een opdeling in heel veel stukjes en dus vooral een gedachtenexperiment is dat aantoont dat er voor iedere veelhoek een vierkant bestaat zodanig dat de veelhoek en het vierkant equivalent zijn door decompositie. Net als Euclides’ bewijs van zijn Propositie 14 levert deze constructie helaas niet echt een praktisch uitvoerbare methode op. Het vinden van mooie opdelingen in weinig stukjes is een lastige puzzel die door mensen als Dudeney tot een ware kunst was verheven.
BRONNEN
1 Zie bijvoorbeeld Paul Tempelaar, Wortel drie bij Archimedes, https://www.promath.nl/Wortel_3/ Wortel3.pdf
2 Bron: Mathscope van de Université de Genève. De decompositie van de zeshoek is bedacht door Juraj Rosinsky. 3 M. Gardner The second Scientific American Book of Mathematical Puzzles & Diversions 1961, p.35
© Junior Wiskunde Olympiade vzwEerste Ronde JWO 2024 vraag 16
OEFENING 7
Hoeveel van deze vier uitspraken zijn waar?
• Als x deelbaar is door 3 en y deelbaar door 6, dan is x + y deelbaar door 6.
• Als x deelbaar is door 3 en y deelbaar door 6, dan is x + y deelbaar door 9.
• Als x deelbaar is door 3 en y deelbaar door 6, dan is xy deelbaar door 6.
• Als x deelbaar is door 3 en y deelbaar door 6, dan is xy deelbaar door 18.
A B C 13 15 16 D E 17 19
A B C 0 1 2 D E 3 4 1 1 4
27
Figuur 6. Illustratie van Dudeney’s haberdasher’s problem door Martin Gardner. De punten D en E zijn middens van de zijden AB en BC, en AJ + KC = JK.


2. Ineenrechthoekmetlengte11enbreedte7zijnvier vierkanteningekleurdzoalsindefiguur.Erblijfteen rechthoekiggebiedoverdatnietingekleurdis. Watisdeverhoudingtussendeoppervlaktevandat gebiedendievandeoorspronkelijkerechthoek?
3. EenmanwiloprestauranteenbedragbetalenmetPayconiq,maarvergeetde komma.Daardoorbetaalthij e 2346,30teveel. Welkvandevolgendebedragenmoesthijbetalen?
4. Indezeoptellingstaandeletters V , W en O elk vooreencijferverschillendvannul.Voorwelk cijferstaatdeletter W ?
OEFENING 8
5. Detotalelengtevanderandvandeblauwefiguuris gelijkaan24meter.Watisdeoppervlakteervan?
De totale lengte van de rand van de blauwe figuur is gelijk aan 24 meter. Wat is de oppervlakte ervan?
6. Colettekoopteenaantalstripverhalen,dieelkofwel e 7ofwel e 9kosten.Welk vanonderstaandebedragenkan geen eindtotaalzijnvanhaaraankoop?
Figuur 6. Het GeoGebradocument van Gawein
1 A B C D E
A 1 49 B 1 44 C 3 121 D 2 77 E 1 33
A e 23,50 B e 23,60 C e 23,70 D e 23,75 E e 23,80
VWO VWO + VWO OOO A 1 B 3 C 5 D 7 E 8
A 5m2 B 6m2 C 7m2 D 8m2 E 9m2
A e 44 B e 45 C e 46 D e 47 E e 48 © Vlaamse Wiskunde Olympiade vzwEerste Ronde VWO 2024 vraag 5 A B C D E 5 m2 6 m2 7 m2 8 m2 9 m2 33
VAKANTIECURSUS 2024 BANACH-TARSKI:
HOE GROEPENTHEORIE VAN ÉÉN MELOEN ER TWEE MAAKT
23/24 AUGUSTUS 2024 IN AMSTERDAM EN 6/7 SEPTEMBER 2024 IN ANTWERPEN
HOOFDSPREKERS: PROF. DR. STEFAAN VAES EN DR. HABIL. JEROEN SPANDAW

De Vakantiecursus voor Wiskundeleraren wordt vanaf 1946 jaarlijks georganiseerd. Sinds 2010 ligt de organisatie in handen van Platform Wiskunde Nederland en sinds vorig jaar wordt ook samengewerkt met Platform Wiskunde Vlaanderen. De cursus
richt zich in Nederland vooral op docenten in de bovenbouw vwo. De stof is bij uitstek geschikt voor wiskunde D: uitdagend, fascinerend en toch concreet en toegankelijk. Voor Vlaanderen richt de cursus zich in het bijzonder op leraren die lesgeven in sterk wiskundige
richtingen in de derde graad. De leerstof is bij uitstek geschikt voor 6 uur wiskunde of meer. Andere belangstellenden zijn natuurlijk ook van harte welkom!
Groepentheorie, dat wil zeggen de wiskundige studie van symmetrieën,
34

7. Zo¨eschrijftdeafkortingvoor“zieommezijde”opeendoorzichtigbladpapier.Door hetbladinverschillenderichtingenomtekeren,kanzeviervandeonderstaande figurenzien.WelkefiguurkanZo¨e niet zien? A B C D E
is een toegankelijk domein van de wiskunde, dat zowel theoretisch als praktisch geïnteresseerden veel te bieden heeft. In de scheikunde spelen symmetrieën van moleculen en kristallen een belangrijke rol. Natuurkundigen gebruiken groepentheorie in de relativiteitstheorie, kwantumtheorie, deeltjesfysica en om behoudswetten af te leiden. Groepentheorie wordt gebruikt in beeldverwerking, codering, cryptografie, …
OEFENING 9 1
8. Wenoteren n !voorhetproductvandegetallen1totenmet n .Zoisbijvoorbeeld 3!=1 · 2 · 3=6.
Watisderestvan1!+2!+3!+4!+ ··· +12!bijdelingdoor12?
9. Petrazaagtvaneenregelmatigviervlak(tetra¨eder)met ribbe10eenstukjeafaanelkvandevierhoekpunten. Devierafgezaagdestukjeszijnzelfregelmatigeviervlakkenmetribbe2.
In deze cursus richten we ons echter op een wiskundigtheoretische toepassing: de stelling van Banach en Tarski. Deze verbluffende stelling zegt dat een massieve driedimensionale bol van straal 1 opgedeeld kan worden in 5 niet-overlappende delen die vervolgens opnieuw kunnen worden samengevoegd tot twee bollen van straal 1. Bij het samenvoegen worden de 5 delen alleen maar geroteerd en getransleerd, maar niet vervormd. Deze stelling wordt vanwege haar contra-intuïtieve karakter meestal de Banach-Tarski-paradox genoemd.
Hoeveelribbenheefthetresterendelichaam?
9 Petra zaagt van een regelmatig viervlak (tetraëder) met ribbe 10 een stukje af aan elk van de vier hoekpunten. De vier afgezaagde stukjes zijn zelf regelmatige viervlakken met ribbe 2. Hoeveel ribben heeft het resterende lichaam?
10. OorspronkelijkverkochtpastaproducentPestoPrestospaghettiinverpakkingenvan 1kilogramvoor x euro.Doordestijgendeproductiekostenwerddespaghetti daarnaaangebodeninverpakkingenvandezelfdeprijsvan x euro,maarmet20% mindergewicht.Noglaterwerddeprijsmet20%verhoogd.
In de vakantiecursus van 2024 wordt eerst een laagdrempelige introductie in de groepentheorie gegeven, met een focus op eenvoudige voorbeelden en op de concepten die nodig zijn voor het bewijs van de stelling van Banach en Tarski. Hierbij krijgen de deelnemers de gelegenheid om vertrouwd te raken met die concepten door enkele goed gekozen voorbeelden concreet door te rekenen. Vervolgens zal Stefaan Vaes laten zien hoe deze groepentheorie gebruikt kan worden om de stelling van Banach en Tarski te bewijzen, hoe onmogelijk die stelling ook mag lijken…
Datbetekentdatdenieuweprijsperkilogramspaghettitenopzichtevande oorspronkelijkeprijsperkilogramverhoogdwerdmet
11. Ineenbokaalzittentweesoortensnoepjes:zurebollenenchocoladetoffees. Zackneemtdehelftvandezurebollen.VervolgensneemtCodyeenkwartvande overgeblevenzurebolleneneenderdevandechocoladetoffees.Erblijvendannog 15zurebollenen18chocoladetoffeesindebokaalover.
Hoeveelsnoepjeszateneroorspronkelijkindebokaal?
De cursus sluit aan op de wens van overheden om meer abstracte onderwerpen aan bod te laten komen in het curriculum. De nieuwe eindtermen in Vlaanderen verplichten de behandeling van een algebraïsche structuur, zoals groepen, in richtingen met 6 uur wiskunde. Het aangereikte materiaal biedt inspiratie en de broodnodige achtergrond aan leraren bij het invullen van hun lessen rond die abstracte structuren.
12. Jasperheefteenrode,eenoranje,eengele,eengroeneeneenblauwestift.Hijwil diezoopeenrijleggendat
• rood niet delaatstestiftinderijis, • geelaltijdjuistvoorgroenkomt, • enoranje niet juistnaastblauwligt.
11 In een bokaal zitten twee soorten snoepjes: zure bollen en chocoladetoffees. Zack neemt de helft van de zure bollen. Vervolgens neemt Cody een kwart van de overgebleven zure bollen en een derde van de chocoladetoffees. Er blijven dan nog 15 zure bollen en 18 chocoladetoffees in de bokaal over. Hoeveel snoepjes zaten er oorspronkelijk in de bokaal?
OphoeveelmanierenkanJasperdatdoen?
Binnenkort verschijnt een brochure met meer informatie. Om op de hoogte te blijven, zie https://www. platformwiskundenederland.nl/vakantiecursus
35
©
Vlaamse Wiskunde Olympiade vzwEerste Ronde VWO 2024 vraag
A B C 8 12 16 D E 18 24
© Vlaamse Wiskunde Olympiade vzwEerste Ronde VWO 2024 vraag
A B C 58 67 87 D E 114 174
OEFENING 10
B 3 C 5 D 7 E 9
A 1
A 8 B 12 C 16 D 18 E 24
A 20% B 30% C 40% D 44% E 50%
A 58 B 67 C 87 D 114 E 174
A 7 B 8 C 9 D 10 E 11

e is een speciaal geval van de volgende formule van Euler:

is een speciaal geval van de volgende formule van Euler: ei# = cos ���� + i sin ����
is een speciaal geval van de volgende formule van Euler:
e # = cos ���� + i sin ����
ei# = cos ���� + i sin ����
Als je hier
1 = 0 is een speciaal geval van de volgende formule van Euler:
Het getal e
is een speciaal geval van de volgende formule van Euler:
Als je hier ���� = ���� invult, krijg je ei" = cos ���� + i sin
Als je hier
Als je hier ���� = ���� invult, krijg je ei" = cos ���� + i sin
is een speciaal geval van de volgende formule van Euler:
invult, krijg je
Als je hier ���� = ���� invult, krijg je ei" = cos ���� + i sin
ei# = cos ���� + i sin ����
invult, krijg je ei" = cos ���� + i sin ���� = 1
is een speciaal geval van de volgende formule van Euler:
is een speciaal geval van de volgende formule van Euler:

We zetten eerst enkele vertrekpunten op een rijtje:
We zullen hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschil lende bewijzen voor gegeven heeft (zie [1]).
ei" + 1 = 0 is een speciaal geval van de volgende formule van Euler: sin ����


hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschillende bewijzen voor gegeven heeft (zie [1]).
hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschillende bewijzen voor gegeven heeft (zie [1]).
hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschillende bewijzen voor gegeven heeft (zie [1]).
���� + i sin ���� cos ���� + i sin ���� = 1
+ i sin ���� cos ���� + i sin ���� = 1
We zetten eerst enkele vertrekpunten op een rijtje:
We zetten eerst enkele vertrekpunten op een rijtje:
hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschillende bewijzen voor gegeven heeft (zie [1]).
We zetten eerst enkele vertrekpunten op een rijtje:
Als je hier ���� = ���� invult, krijg je ���� + i sin ���� = 1
We zetten eerst enkele vertrekpunten op een rijtje:
a. Het getal i heeft de eigenschap dat
zullen hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschillende bewijzen voor gegeven heeft (zie [1]).
hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschillende bewijzen voor gegeven heeft (zie [1]).
We zetten eerst enkele vertrekpunten op een rijtje:


a. Het getal i heeft de eigenschap dat , voor de rest kunnen we rekenen met het getal i alsof het een gewoon getal is.
a. Het getal i heeft de eigenschap dat , voor de rest kunnen we rekenen met het getal i alsof het een gewoon getal is.
a. Het getal i heeft de eigenschap dat , voor de rest kunnen we rekenen met het getal i alsof het een gewoon getal is.
b. Het getal e is wat we vinden als we in de uitdrukking
b. Het getal e is wat we vinden als we in de uitdrukking
, voor de rest kunnen we rekenen met het getal "i" alsof het een gewoon getal is.
b. Het getal e is wat we vinden als we in de uitdrukking
We zullen hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschillende bewijzen voor gegeven heeft (zie [1]).
hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschillende bewijzen voor gegeven heeft (zie [1]).
hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschillende bewijzen voor gegeven heeft (zie [1]).
41 + $
41 + $ %5% het natuurlijk getal
heeft de eigenschap dat i! = 1, voor de rest kunnen we rekenen met het alsof het een gewoon getal is.
b. Het getal e is wat we vinden als we in de uitdrukking
We zetten eerst enkele vertrekpunten op een rijtje:
Het getal i , voor de rest kunnen we rekenen met het getal i alsof het een gewoon getal is.
41 + $ %5 heel groot nemen. (Probeer het maar eens op je rekentoestel, bijv. voor Meer nog, voor een getal ���� hebben we dat
We zetten eerst enkele vertrekpunten op een rijtje:
We zetten eerst enkele vertrekpunten op een rijtje:
, voor de rest kunnen we rekenen met het is wat we vinden als we in de uitdrukking 41 + $ %5% het natuurlijk getal ���� Probeer het maar eens op je rekentoestel, bijv. voor ���� = 10$& .) heel groot.
heel groot nemen. (Probeer het maar eens op je rekentoestel, bijv. voor Meer nog, voor een getal ���� hebben we dat
heel groot nemen. (Probeer het maar eens op je rekentoestel, bijv. voor Meer nog, voor een getal ���� hebben we dat
het natuurlijk getal n heel groot nemen.
het natuurlijk getal ���� heel groot nemen. (Probeer het maar eens op je rekentoestel, bijv. voor ���� = 10$& .) Meer nog, voor een getal
heeft de eigenschap dat i! = 1, voor de rest kunnen we rekenen met het alsof het een gewoon getal is.
heeft de eigenschap dat i! = 1, voor de rest kunnen we rekenen met het alsof het een gewoon getal is.
is wat we vinden als we in de uitdrukking 41 + $ %5% het natuurlijk getal ���� heel groot nemen. (Probeer het maar eens op je rekentoestel, bijv. voor ���� = 10$& ) Meer nog, voor een getal ���� hebben we dat
a. Het getal i heeft de eigenschap dat i! = 1, voor de rest kunnen we rekenen met het getal i alsof het een gewoon getal is.
(Probeer het maar eens op je rekentoestel, bijv. voor
41 + ���� ����5% = e' voor ���� heel groot.
41 + ���� ����5% = e' voor ���� heel groot.
41 + ���� ����5% = e' voor ���� heel groot.

is wat we vinden als we in de uitdrukking 41 + $ %5% het natuurlijk getal ���� Probeer het maar eens op je rekentoestel, bijv. voor ���� = 10$& ) hebben we dat
is wat we vinden als we in de uitdrukking 41 + $ %5% het natuurlijk getal ���� Probeer het maar eens op je rekentoestel, bijv. voor ���� = 10$& ) hebben we dat
.) Meer nog, voor een getal z hebben we dat
c. Verbanden tussen hoeken en zijden in een rechthoekige driehoek zijn gekend.
c. Verbanden tussen hoeken en zijden in een rechthoekige driehoek zijn gekend.
c. Verbanden tussen hoeken en zijden in een rechthoekige driehoek zijn gekend.
41 + ���� ����5% = e' voor ���� heel groot.
b. Het getal e is wat we vinden als we in de uitdrukking heel groot nemen. (Probeer het maar eens op je rekentoestel, bijv. voor Meer nog, voor een getal ���� hebben we dat
voor n heel groot.
Verbanden tussen hoeken en zijden in een rechthoekige driehoek zijn gekend.
Verbanden tussen hoeken en zijden in een rechthoekige driehoek zijn gekend.
Verbanden tussen hoeken en zijden in een rechthoekige driehoek zijn gekend.
5% = e' voor ���� heel groot.
% = e' voor ���� heel groot.

c. Verbanden tussen hoeken en zijden in een rechthoekige driehoek zijn gekend.

Op de figuur kan je eveneens zien dat
41 + ���� ����5% = e' voor ���� heel groot.

c. Verbanden tussen hoeken en zijden in een rechthoekige driehoek zijn gekend.



Verbanden tussen hoeken en zijden in een rechthoekige driehoek zijn gekend.
Verbanden tussen hoeken en zijden in een rechthoekige driehoek zijn gekend.


Uit de bovenstaande grafieken van cosinus en sinus kunnen vervangen door 1 en sin ���� door ���� als ���� heel klein is. (Ook dit kan je checken met je rekentoestel, kies bijv. ���� = 10 $& )


Ook dit kan je checken met
is een speciaal geval van de volgende formule van Euler: is een speciaal geval van de volgende formule van Euler:
d. Uit de bovenstaande grafieken van cosinus en sinus kunnen we afleiden dat we cos ���� kunnen vervangen door 1 en sin ���� door ���� als ���� heel klein is. (Ook dit kan je checken met je rekentoestel, kies bijv. ���� = 10 $& .)
Op de figuur kan je eveneens zien dat cos( ���� ) = cos ���� en dat sin( ����) = sin ���� .
beginnen. We zullen gebruik maken van de formule van De Moivre, en om die aan te tonen hebben we de somformules van cos en sin nodig. Gelukkig is er hiervoor een grafisch bewijs (zie [2]) Zie de volgende figuur.
Uit de bovenstaande grafieken van cosinus en sinus kunnen we afleiden dat we cos x kunnen vervangen door 1 en sin x door x als x heel klein is. (Ook dit kan je checken met je rekentoestel, kies bijv.
ei" + 1 = 0 is een speciaal geval van de volgende formule van Euler:
Nu kunnen we beginnen. We zullen gebruik maken van de formule van De Moivre, en om die aan te tonen hebben we de somformules van cos en sin nodig. Gelukkig is er hiervoor een grafisch bewijs (zie [2]) Zie de volgende figuur.
d. Uit de bovenstaande grafieken van cosinus en sinus kunnen we afleiden dat we cos ���� kunnen vervangen door 1 en sin ���� door ���� als ���� heel klein is. (Ook dit kan je checken met je rekentoestel, kies bijv. ���� = 10 $& .)
ei# = cos ���� + i sin ����
ei# = cos ���� + i sin ���� invult, krijg je ei" = cos ���� + i sin ���� = 1
Hier ergens kan tekstkader 2
Op de figuur kan je eveneens zien dat cos( ���� ) = cos ���� en dat sin( ����) = sin ���� Nu kunnen we beginnen. We zullen gebruik maken van de formule van De Moivre, en om die aan te tonen hebben we de somformules van cos en sin nodig. Gelukkig is er hiervoor een grafisch bewijs (zie [2]) Zie de volgende figuur.
Hier ergens kan tekstkader 2
Uit de figuur kan je afleiden dat:
beginnen. We zullen gebruik maken van de formule van De Moivre, en om die aan te tonen hebben we de somformules van cos en sin nodig. Gelukkig is er hiervoor een grafisch bewijs (zie [2]) Zie de volgende figuur.
grafieken van cosinus en sinus kunnen vervangen door 1 en sin ���� door ���� als ���� heel klein is. ( je rekentoestel, kies bijv. ���� = 10 $& )
beginnen. We zullen gebruik maken van de formule van De Moivre, en om die aan te tonen hebben we de somformules van cos en sin nodig. Gelukkig is er hiervoor een grafisch bewijs (zie [2]) Zie de volgende figuur.
.)
Hier ergens kan tekstkader 2
Hier ergens kan tekstkader 2
Hier ergens kan tekstkader 2
Op de figuur kan je eveneens zien dat
Als je hier ���� = ���� invult, krijg je ei" = cos ���� + i sin
Op de figuur kan je eveneens zien dat cos( ���� ) = cos
Nu kunnen we beginnen. We zullen gebruik maken van de formule van De Moivre, en om die aan te tonen hebben we de somformules van cos en sin nodig. Gelukkig is er hiervoor een grafisch bewijs (zie [2]). Zie de volgende figuur.

Uit de figuur kan je afleiden dat:
Hier ergens kan tekstkader 2
en dat
Op de figuur kan je eveneens zien dat cos( ���� ) = cos ���� en dat sin( ����) = sin ���� .
Op de figuur kan je eveneens zien dat cos( ���� ) = cos ���� en dat sin( ����) = sin ���� .
Uit de figuur kan je afleiden dat:
Uit de figuur kan je afleiden dat:
Uit de figuur kan je afleiden dat: cos(���� + ����) = cos ���� cos ���� sin ���� sin �������� en ook sin(���� + ����) = cos ���� cos ���� + sin ���� sin ��������.
Nu kunnen we beginnen. We zullen gebruik maken van de formule van De Moivre, en om die aan te tonen hebben we de somformules van cos en sin nodig. Gelukkig is er hiervoor een grafisch bewijs (zie [2]). Zie de volgende figuur.
Hier ergens kan tekstkader 2
Nu kunnen we beginnen. We zullen gebruik maken van de formule van De Moivre, en om die aan te tonen hebben we de somformules van cos en sin nodig. Gelukkig is er hiervoor een grafisch bewijs (zie [2]). Zie de volgende figuur. Hier ergens kan tekstkader 2

cos(���� + ����) = cos ���� cos ���� sin ���� sin �������� en ook sin(���� + ���� ) = cos ���� cos
cos(���� + ����) = cos ���� cos ���� sin ���� sin �������� en ook sin(���� + ���� ) = cos
cos(���� + ����) = cos ���� cos ���� sin ���� sin �������� en ook sin(���� + ���� ) = cos ����
Uit de figuur kan je afleiden dat: cos(���� + ����) = cos ���� cos ���� sin ���� sin �������� en ook sin(���� + ���� ) = cos ���� cos ���� + sin ���� sin ��������
We zullen hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschillende bewijzen voor gegeven heeft (zie [1]).
Hiermee kunnen we het volgende product eenvoudiger schrijven. We werken eerst de haakjes uit:
hieronder deze prachtige formule afleiden, waarvoor we te rade gaan bij Euler zelf, die er verschillende bewijzen voor gegeven heeft (zie [1]).
Nu kunnen we beginnen. We zullen gebruik maken van de formule van De Moivre, en om die aan te tonen hebben we de somformules van cos en sin nodig. Gelukkig is er hiervoor een grafisch bewijs (zie [2]). Zie de volgende figuur. Hier ergens kan tekstkader 2
Hiermee kunnen we het volgende product eenvoudiger schrijven. We werken eerst de haakjes uit:
Hiermee kunnen we het volgende product eenvoudiger schrijven. We werken eerst de haakjes uit:
Hiermee kunnen we het volgende product eenvoudiger schrijven. We werken eerst de haakjes uit:
(cos ���� + i sin ���� ) ⋅ (cos ���� + i sin
(cos ���� + i sin ���� ) (cos ���� + i sin ����) =
Uit de figuur kan je afleiden dat:
(cos ���� + i sin ���� ) (cos ���� + i sin ����) = cos ���� cos
Hiermee kunnen we het volgende product eenvoudiger schrijven. We werken eerst de
We zetten eerst enkele vertrekpunten op een rijtje:
%5%
���� + i sin ���� cos ���� + i cos ����
���� + i sin ���� cos ���� + i cos
cos ���� cos
cos ���� cos ���� + i sin ���� cos ���� + i cos ���� sin
����) =
(cos ���� + i sin ����) (cos ���� + i sin ����) = cos ���� cos ���� + i sin ���� cos ���� + i cos ���� sin ���� + i! sin ���� sin ����
����
���� =
���� + ����) = cos ���� cos ���� sin ���� sin �������� en ook sin(���� + ���� ) = cos ���� cos ���� + sin ���� sin �������� .
Uit de figuur kan je afleiden dat:
Uit de figuur kan je afleiden dat: 37
Op precies dezelfde manier als boven volgt nu

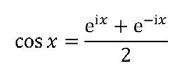
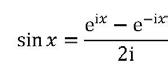
We zetten beide resultaten even naast elkaar: en Je ziet dan dat als je bij de eerste vergelijking i keer de tweede optelt, dat deze formule volgt:
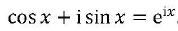
En dit was de formule die we wilden bewijzen. Euler deed het precies op dezelfde manier. Hier zie je een stukje uit het boek waarin hij het schreef.

Een Engelse vertaling van dit boek uit 1748 vind je in [3].
REFERENTIES
[1] Dunham W. Euler, The Master Of Us All. Mathematical Association of America, Dolciani Mathematical Expositions No. 22, 1999.
[2] Nelsen, R., Proofs without Words II: More Exercises in Visual Thinking Association of America, 2000.
[2] Nelsen, R., Proofs without Words II: More Exercises in Visual Thinking Association of America, 2000.
[2] Nelsen, R., Proofs without Words II: More Exercises in Visual Thinking Mathematical Association of America, 2000.
[3] Euler, L., Introduction to analysis of the infinite (transl. John D. Blanton), Springer New York, 1988.
[3] Euler L. Introduction to analysis of the infinite (transl. John D. Blanton) Springer-Verlag New York, 1988.
[3] Euler, L., Introduction to analysis of the infinite (transl. John D. Blanton), Springer New York, 1988.
Tekstkader 1
De notatie voor het getal π werd voor het eerst gebruikt in het boek Clavis Mathematicae van William Oughtred (1647).
Tekstkader 1
De notatie voor het getal ���� werd voor het eerst gebruikt in het boek Clavis Mathematicae van William Oughtred (1647).
De notatie voor het getal ���� werd voor het eerst gebruikt in het boek van William Oughtred (1647).
Het getal e wordt ook wel het getal van Euler genoemd. Euler heeft inderdaad het symbool e ingevoerd (in 1731) voor het getal 2, 718281828…. Maar hij heeft bij de keuze van die letter zeker niet gedacht aan de eerste letter van zijn naam, daar was hij veel te bescheiden voor. Ook de notatie i voor de complexe eenheid danken we aan Leonhard Euler (1777)..
Het getal e wordt ook wel het getal van Euler genoemd. Euler heeft inderdaad het symbool e ingevoerd (in 1731) voor het getal
2,718281828
Het getal e wordt ook wel het getal van Euler genoemd. Euler heeft inderdaad het symbool e ingevoerd (in 1731) voor het getal 2,718281828 …. Maar hij heeft bij de keuze van die letter zeker niet gedacht aan de eerste letter van zijn naam, daar was hij veel te bescheiden voor.
Ook de notatie i voor de complexe eenheid danken we aan Leonhard Euler (1777).
Tekstkader 2
van die letter zeker niet gedacht aan de eerste letter van zijn bescheiden voor.
Ook de notatie i voor de complexe eenheid danken we aan Leonhar
Tekstkader 2
De formule van De Moivre (Abraham De Moivre, 1667-1754) zegt dat
De formule van De Moivre (Abraham De Moivre, 1667-1754) zegt dat (cos ���� + i sin ���� )% = cos �������� + i sin ��������
De formule van De Moivre (Abraham De Moivre, 1667 (cos ���� + i sin ���� )% = cos �������� + i sin ��������
voor elk geheel getal ����. De formule van Euler die we willen bewijzen lijkt een verklar te geven voor die van De Moivre. Inderdaad: wat tussen de haakjes staat in het linkerlid is volgens Euler gelijk aan ei# , en het rechterlid is om dezelfde reden gelijk aan kunnen dus de formule van De Moivre ook zo schrijven: (ei# )% = ei%# wat lijkt te volgen uit eigenschappen van machten.
voor elk geheel getal n. De formule van Euler die we willen bewijzen lijkt een verklaring te geven voor die van De Moivre. Inderdaad: wat tussen de haakjes staat in het linkerlid is volgens Euler gelijk aan eix, en het rechterlid is om dezelfde reden gelijk aan einx. We kunnen dus de formule van De Moivre ook zo schrijven:
voor elk geheel getal ����. De formule van Euler die we willen bewijzen lijkt een verklar te geven voor die van De Moivre. Inderdaad: wat tussen de haakjes staat in het linkerlid is volgens Euler gelijk aan ei# , en het rechterlid is om dezelfde reden gelijk aan kunnen dus de formule van De Moivre ook zo schrijven: (ei# )% = ei%# wat lijkt te volgen uit eigenschappen van machten. wat lijkt te volgen uit eigenschappen van machten.
.
.
39








Taal Wiskunde






6 maart maart
20


13



Wetenschappen, geschiedenis en ICT
KEURIEUSDAGEN AUDACE! CE!




























 Figuur 5 Oprolmethode 2
Figuur 6 3D-print en ontwerp van methode 2
Figuur 5 Oprolmethode 2
Figuur 6 3D-print en ontwerp van methode 2


 Figuur 8 Resultaat van oprolmethode 1
Figuur 9 Resultaat van oprolmethode 2
Figuur 10 Oprol resultaat 2 uitvergroot
Figuur 8 Resultaat van oprolmethode 1
Figuur 9 Resultaat van oprolmethode 2
Figuur 10 Oprol resultaat 2 uitvergroot


















 Figuur 4
Figuur 4