VECTOR
MEI 2024 - nummer 20
TIJDSCHRIFT voor wiskundeonderwijs

TEKENEN IN BILDTSE GRAANAKKERS 3
HET
SCHATGRAVERSPROBLEEM 14
HET PRINCIPE VAN MAMIKON 34
Met medewerking van Uitwiskeling, VVWL (Vlaamse Vereniging van Wiskundeleraars), GeoGebra Instituut, Vlaamse Wiskunde Olympiade, Ars et Mathesis en Pythagoras
3 TEKENEN IN BILDTSE GRAANAKKERS DEEL 1
DE OPLOPENDE DUBBELE KEGEL 9
14 HET SCHATGRAVERSPROBLEEM
VAKANTIECURSUS VOOR LERAREN 17
22 CYCLISCH LIJNSPIEGELEN
GO SPELEN: OP JE TELLEN PASSEN 28
34 HET PRINCIPE VAN MAMIKON
TEKENEN IN BILDTSE GRAANAKKERS DEEL 2 41
44 HET INTERESSANTE GETAL
VECTOR
6e jaargang - nummer 20
REDACTIE Nicolas Ruys, Tom Harteel, Anke Oderij, Karel Sierens - die Keure, Kleine Pathoekeweg 3, 8000 Brugge, educatief@diekeure.be
EXTERNE AUTEURS die occasioneel of op geregelde basis een bijdrage willen leveren, kunnen contact opnemen met educatief@diekeure.be.
VECTOR is gratis voor alle leerkrachten wiskunde in België.
VERANTWOORDELIJKE UITGEVER die Keure, Kleine Pathoekeweg 3, 8000 Brugge
VORMGEVING EN DRUK Isabelle Tilleman - die Keure, Brugge
REACTIES Al je reacties, suggesties en opmerkingen zijn welkom op educatief@diekeure.be
2 VECTOR
INHOUD
TEKENEN IN BILDTSE GRAANAKKERS
DEEL 1 HET CONFORME SCHAAKBORD
IN 2018 WAS LEEUWARDEN, DE
HOOFDSTAD VAN DE NEDERLANDSE
PROVINCIE FRIESLAND, CULTURELE
HOOFDSTAD VAN EUROPA. LEEUWARDEN IS OOK DE GEBOORTESTAD
VAN M.C. ESCHER. AANLEIDING
GENOEG VOOR EEN TENTOONSTEL-
LING MET WERK VAN HEM IN HET
FRIES MUSEUM IN LEEUWARDEN
MET DE TITEL ESCHER OP REIS.
TEGELIJK WERD IN HET NOORDEN
VAN FRIESLAND OP INITIATIEF VAN

BEELDEND KUNSTENAAR HENK RUSMAN MET ACHT GROOTSCHALIGE
GRAANTEKENINGEN EEN EERBETOON AAN ESCHER GEBRACHT. DAT
DROEG DE TITEL ODE AAN M.C. ESCHER OP ’T BILDT. HIERVOOR HAD RUSMAN
KUNSTENAARS OPGEROEPEN OM EEN ONTWERP TE MAKEN. ER WERDEN
ZES VOORSTELLEN GEACCEPTEERD. DAARNAAST VERZORGDE RUSMAN
ZELF OOK TWEE ONTWERPEN ALS THEMA VOOR LEEUWARDEN-FRYSLÂN
2018 GOLD "MIENSKIP". DAT IS FRIES VOOR EEN GROEP PERSONEN DIE IN EEN BEPAALD OPZICHT EEN BAND MET ELKAAR HEBBEN. DAT GOLD ZEKER
VOOR DE KUNSTENAARS DIE MEEDEDEN AAN HET GRAANAKKERPROJECT.
ZIJ STONDEN ELKAAR DIKWIJLS MET RAAD EN DAAD BIJ.
KLAAS LAKEMAN, ARS ET MATHESIS
PYTHAGORAS
3

Figuur 1 Kuipers Conform Schaakbord, het ontwerp voor zijn graantekening
ZONDER WISKUNDE
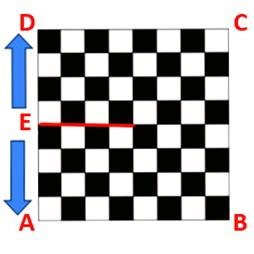
Toen Hans Kuiper de oproep van Henk Rusman zag, dacht hij meteen aan zijn Conform Schaakbord (figuur 1). In een ver verleden was hij daartoe gekomen door de afbeeldingen in een boek over fractals uit te proberen en daarmee verder te experimenteren. Zonder wiskunde is met een paar ruwe gedachtesprongen enig inzicht te krijgen in de vervorming van een normaal schaakbord tot het ontwerp. Ga uit van een normaal schaakbord met 64 velden, 8 bij 8 en 81 hoekpunten (figuur 2). Neem aan dat het van een materiaal is dat gemakkelijk in elkaar gedrukt en uitgerekt kan worden. Verbind het midden E van de zijde AD met het midden M van het bord. Knip dat bord langs de lijn EM open (de rode lijn in figuur 3). In plaats van één punt E zijn er dan twee punten E1 en E2. Trek dan de twee punten E1 en E2 zover uit elkaar dat E1, M en E2 op één rechte lijn komen waarbij het middelpunt M op zijn plaats blijft.

Het resultaat wordt dan figuur 4.
De meeste velden worden richting het oorspronkelijke middelpunt M wat in elkaar gedrukt. Slechts de vier velden rond het middelpunt M worden uitgerekt en het meest vervormd. Het vervormde bord heeft nog steeds 64 velden, maar geen enkel veld is meer precies vierkant. Veel van de oorspronkelijk rechte randen van de velden zijn een beetje gebogen. Op die van de vier velden met gemeenschappelijk hoekpunt M na zijn alle hoeken nog wel 90 graden gebleven. Door het knippen zijn er vier hoekpunten bij gekomen. Het aantal hoekpunten is nu dus 85 (81 + 4).
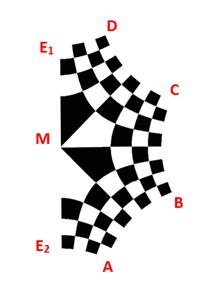
Doe hetzelfde met een tweede schaakbord, draai het resultaat over 180 graden en plaats het tegen het eerste vervormde bord (figuur 5). Het resultaat is een vervormd achthoekig schaakbord met 128 velden en 161 hoekpunten (85 + 85 – 9), het Conform Schaakbord en ontwerp voor de graantekening van Hans Kuiper (figuur 1).
SCHAALVERGROTING
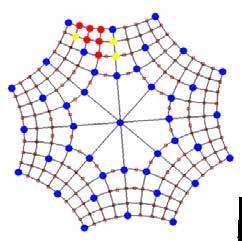
Als het ontwerp eenmaal is geprint, wordt het zaak daar een enorme schaalvergroting op toe te passen: van papierformaat A3 tot ongeveer twee voetbalvelden groot. Eerst wordt een aantal hoekpunten bepaald van waaruit de rest verder geconstrueerd kan worden. Dat zijn de 41 blauwe stippen in figuur 6. Als die eenmaal in de akker zijn vastgelegd, is de positie van de andere 120 hoekpunten van daaruit met bijvoorbeeld een meetlint vast te leggen.
Om de blauwe stippen in de akker uit te zetten, werd een techniek gebruikt die ook in de bouwwereld wordt toegepast om de exacte plaats van heipalen vast te leggen. Met een computer werd het ontwerp op een Google Maps-weergave van de betreffende akker geprojecteerd. Zo kon nauwkeurig een plek voor het ontwerp op de akker worden bepaald. Tegelijk konden de afmetingen zo worden gekozen dat het geheel daar netjes oppaste. Toen
Figuur 2 Normaal schaakbord
4
Figuur 3 Openknippen bij E
Figuur 4 Vervormd schaakbord met 64 velden en 85 hoekpunten
dat eenmaal naar tevredenheid was, werden van de 41 blauwe stippen uit het ontwerp de GPS-coördinaten bepaald. Met een GPS-ontvanger werden die coördinaten vervolgens in het voorjaar, voordat het graan opkwam, door een landmeetkundig bureau met paaltjes op de akker gemarkeerd (figuur 7). Daarna konden de 120 tussenliggende hoekpunten (de rode en gele stippen in figuur 6) met een meetlint door de kunstenaar zelf worden bepaald en ook met paaltjes gemarkeerd (figuur 8). Vaak kwam daarbij de hulp van enkele andere deelnemende kunstenaars goed van pas ('mienskip').
MAAIEN IS TEKENEN, OOGSTEN IS GUMMEN
Wat je het echte tekenen zou kunnen noemen, kon worden uitgevoerd toen het graan voldoende was opgekomen. Tussen de paaltjes werden markeringstouwen gespannen en in de tussenliggende vlakken werd het graan weggemaaid

(figuur 9). Dat zijn in het ontwerp de witte velden. Met twaalf vrijwilligers klaarde Kuiper voor zijn ontwerp die klus in één lange dag van tien uur aanpoten. Het resultaat was een graantekening die precies past in een cirkel met een middellijn van 142 m, in een vierkant met zijden
van 131 m en in een regelmatige achthoek met zijden van 54 m. De totale oppervlakte was 12 300 m2 waarvan de helft, 6150 m2 was gemaaid. Helaas was deze graantekening net als de andere zeven geen lang leven beschoren, want aan het einde van de zomer
 Figuur 5 Ontstaan van het conforme schaakbord met 128 velden en 161 hoekpunten
Figuur 6 De 41 (van de 161) met GPS uit te zetten blauwe hoekpunten
Figuur 5 Ontstaan van het conforme schaakbord met 128 velden en 161 hoekpunten
Figuur 6 De 41 (van de 161) met GPS uit te zetten blauwe hoekpunten
5
Figuur 7



werden ze met de oogst allemaal als het ware uitgegumd (figuur 10). Wat resteert zijn luchtfoto’s en filmpjes gemaakt met drones en vanuit vliegtuigjes.
WAAROM CONFORM SCHAAKBORD?
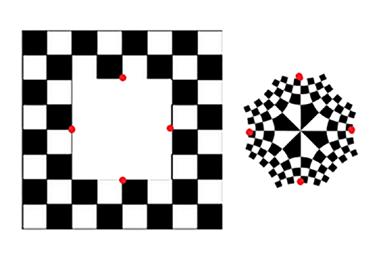
Waarom noemde Kuiper zijn ontwerp niet gewoon Vervormd Schaakbord? Dat heeft alles te maken met de wiskundige afbeelding of transformatie waaraan een normaal schaakbord wordt onderworpen om naar het uiteindelijke ontwerp te komen. Het normale schaakbord kan na openknippen op verschillende manieren zo vervormd worden dat de punten E1, M en E2 op één rechte lijn komen. Bijvoorbeeld door alle hoeken van de lijnen die door het middelpunt M gaan te halveren, zoals in een waaier (figuur 11B). Dat levert Kuipers ontwerp nog niet op, maar komt al een eind in de goede richting. Ook in zijn ontwerp zijn immers de hoeken van de lijnen die door het middelpunt M gaan gehalveerd (figuur 11C). Vergelijk de doorgetrokken rode en blauwe lijn in 11A met de overeenkomstig gekleurde stippellijnen in de figuren 11B en 11C. Merk op dat de rode lijn in 11A twee kanten op gaat vanwege het openknippen!
De naam Conform Schaakbord is afgeleid van de naam voor het soort afbeelding waarmee een normaal schaakbord kan worden overgevoerd in de rechterhelft van Kuipers ontwerp. Een conforme afbeelding of transformatie is een afbeelding waarbij alle hoeken
Figuur 8
Figuur 9
Figuur 10
6
gelijk blijven. Bij de waaier van figuur 11B is dat overduidelijk niet het geval. Zoals in het begin bij het gedachtenproces al terloops werd vermeld, zijn in het ontwerp van Kuiper op de vier velden met gemeenschappelijk hoekpunt M na, alle hoeken 90 graden gebleven.
AANZET TOT WISKUNDE
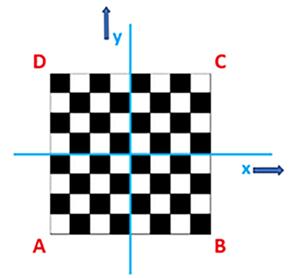
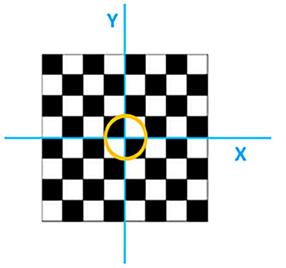
Leg het schaakbord in een normaal cartesisch (x,y)-assenstelsel zó dat het middelpunt M van het bord samenvalt met de oorsprong O. Als roostereenheid wordt de afmeting van een veld van het schaakbord gekozen. Daarmee vallen alle hoekpunten samen met de roosterpunten van het assenstelsel. Dan hebben de vier uiterste hoekpunten A, B, C en D achtereenvolgens de coördinaten (-4,-4), (4,-4), (4,4) en (-4,4) (figuur 12). In plaats van een punt vast te leggen met zijn (x,y)-coördinaten kan dat ook met poolcoördinaten (r,ϑϑ
).
Daarbij is r de lengte van het lijnstuk van het punt tot de oorsprong en ϑ
de hoek tussen dat lijnstuk en
de positieve x-as. Die hoek
ϑ
ϑ) → (√r,½ϑ + π) wordt uitgedrukt in radialen en loopt van -π tot π, positief boven de x-as en negatief onder de x-as (figuur 13). De vier uiterste hoekpunten A, B, C en D hebben daarmee achtereenvolgens de coördinaten (4√2,-¾π), (4√2,-¼π), (4√2,¼π) en (4√2,¾π). Met poolcoördinaten is de transformatie van figuur 11A naar de waaier van figuur 11B eenvoudig te schrijven als: (r,ϑϑ
onderworpen, namelijk: (r,ϑϑϑ
(√r,½
BEVINDINGEN
) > (r,½ ϑ
Zoals gezegd is die niet conform want niet alle hoeken zijn gelijk gebleven. Een geringe aanpassing levert wel de conforme afbeelding van figuur 11A naar 11C: (r,ϑ
ϑ
) > (√r,½
ϑ
)
ϑ) → (r,½ϑ
+ π)
daarmee achtereenvolgens de coördinaten
daarmee achtereenvolgens de coördinaten (4√2, ¾���� ), (4√2, ϑ) → (r,½ϑ ϑ) → (√r,½ϑ
Het middelpunt M, ofwel de oorsprong, blijft op zijn plaats, immers daar zijn r en ϑ daarmee achtereenvolgens
daarmee achtereenvolgens de coördinaten
gelijk aan nul. Voor punten met r = 1, dat zijn punten op de zogenoemde eenheidscirkel, is de wortel uit r ook 1. Deze punten hebben hun beeldpunt dus op de eenheidscirkel (oranje cirkel in figuur 14). Vanwege de halvering van hoek ϑ
daarmee achtereenvolgens de coördinaten (4√2, ¾���� ), (4√2, ¼���� ), (4√2,¼���� ) en (4√2,
ϑ) → (r,½ϑ
We halveren de hoek en trekken de wortel uit de afstand van een punt tot M.
daarmee achtereenvolgens de coördinaten (4√2, ¾���� ), (4√2, ¼���� ), (4√2,¼
daarmee achtereenvolgens de coördinaten
ϑ) → (√r,½ϑ
ϑ) → (√r,½ϑ
De tweede helft van het graanpatroon is dan te verkrijgen door het resultaat een halve slag of 180 graden te draaien zoals uit figuur 5 bleek. In feite komt het erop neer dat het oorspronkelijke bord aan een tweede transformatie wordt
ϑ) → (r,½ϑ
ϑ) → (r,½ϑ
daarmee achtereenvolgens de coördinaten (4√2, ), (4√2,¼���� ) en (4√2,
daarmee achtereenvolgens de coördinaten (4√2, ¼���� ), (4√2,¼
tot π, positief
ϑ) → (√r,½ϑ + π)
ϑ) → (√r,½ϑ
ϑ) → (√r,½ϑ + π)

→ (√r,½ + π)
ϑ) → (√r,½ϑ ) → (√r,½ϑ + π)
π tot π, positief
daarmee achtereenvolgens de coördinaten (4√2, ���� ) en (4√2,¾����
(√r,½ϑ + π) bewegen ze dus over de
daarmee achtereenvolgens de coördinaten (4√2, ¾���� ), (4√2, ¼���� ), (4√2,¼���� ) en (4√2,¾����

ϑ π
ϑ ϑ
)
ϑ ϑ
ϑ)
ϑ
→ (√r,½ϑ
6
ϑ
ϑ ϑ
ϑ
ϑ
ϑ)
6
ϑ ϑ
ϑ
6
ϑ
ϑ
ϑ) →
ϑ) →
) >
ϑ) →
ϑ) → (√r,½ϑ ϑ + π) + π)
(r,½ϑ
(√r,½ϑ
ϑ
(r,½ϑ
ϑ) → (r,½ϑ ) → (√r,½ϑ ) →
ϑ
ϑ
ϑ) →
(√r,½ϑ + π)
Figuur 11
Figuur 13 Poolcoördinaten
7
Figuur 12
eenheidscirkel in de richting van de positieve X-as.
Punten buiten de eenheidscirkel gaan – afgezien van de draaiing –richting de eenheidscirkel, maar blijven erbuiten. Daardoor worden delen van het bord buiten de eenheidscirkel samengedrukt, immers voor die punten is de wortel uit r kleiner dan r: √r < r.
Voor punten binnen de eenheidscirkel is r < 1 en zal r kleiner zijn dan de wortel uit r: r < √r. De beeldpunten van deze punten blijven binnen de eenheidscirkel maar komen verder van de oorsprong af. Dat is te zien aan de grote blokken binnen de eenheidscirkel.
Kijk in figuur 14 in het bijzonder naar de vier velden rondom en met gemeenschappelijk hoekpunt het middelpunt. Ze vallen grotendeels binnen de oranje eenheidscirkel en voor een klein deel erbuiten. Het deel binnen de cirkel wordt dus uitgerekt, terwijl het kleine deel daarbuiten samengedrukt wordt. In beide gevallen richting de eenheidscirkel.
Voor punten op de positieve x-as geldt
ϑ
= 0. Die punten hebben hun beeldpunt ook op de positieve x-as, want 0/2 = 0. In het bijzonder geldt dat punt (1,0) op zijn plek blijft en dat (4,0) aan de rand van het oorspronkelijke bord op (2,0) wordt afgebeeld. Dat betekent dat in de afbeelding de zijden van de vierkanten rondom de oorsprong net zo groot worden afgebeeld als de zijden van de drie volgende vierkanten gezamenlijk.
daarmee achtereenvolgens de coördinaten (4√2, ¾���� ), (4√2, ¼���� ), (4√2,¼���� ) en (4√2,
→ (r,½ϑ
→ (√r,½ϑ
In figuur 15 zijn het originele
→ (√r,½ϑ + π)
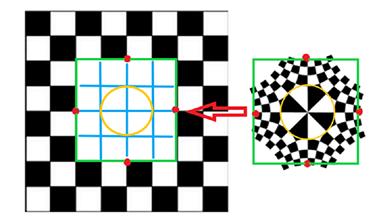
schaakbord en het conforme bord min of meer op vergelijkbare schaal weergegeven. Daar past het conforme bord bijna geheel binnen het uitgesneden 4 bij 4 vierkant van het normale bord waarbij de rode stippen in beide figuren op elkaar moeten komen. Zo is duidelijk dat het oorspronkelijke bord buiten de eenheidscirkel behoorlijk samengedrukt is (vergelijk dat met figuur 14)! De 128 velden van het conforme bord passen bijna binnen die 16 velden van het oorspronkelijke bord. Sterker nog, de 120 velden van het conforme bord buiten de oranje eenheidscirkel passen op de twaalf velden rondom de eenheidscirkel in het normale bord! In figuur 16 als uitbreiding van figuur 15 wordt dat nog eens duidelijk weergegeven.
6
ϑ ϑ
ϑ)
ϑ)
ϑ)
ϑ
Figuur 14
Figuur 15
8
Figuur 16
oplopende dubbele kegel
De oplopende dubbele
Leon Lenders, voor Uitwiskeling
DE OPLOPENDE DUBBELE KEGEL
Lenders, voor Uitwiskeling experiment van de ʼbergop lopende bestaat enerzijds uit een helling in met de scherpe hoek aan de kant en anderzijds uit twee kegels hun grondvlakken aan elkaar zijn tot een dubbele kegel. de dubbele kegel op de lage kant helling geplaatst wordt, zal hij – als bepaalde voorwaarden voldaan is –bergop lopen. Hoewel de kegel schijnbaar bergop loopt, zal door de breder wordende V-vorm het zwaartepunt toch dalen.
Het experiment van de 'bergop lopende kegel' bestaat enerzijds uit een helling in V-vorm met de scherpe hoek aan de laagste kant en anderzijds uit twee kegels die met hun grondvlakken aan elkaar gemaakt zijn tot een dubbele kegel. Wanneer de dubbele kegel op de lage kant van de helling geplaatst wordt, zal hij – als er aan bepaalde voorwaarden voldaan is – spontaan bergop lopen. Hoewel de dubbele kegel schijnbaar bergop loopt, zal door de breder wordende V-vorm het zwaartepunt toch dalen.
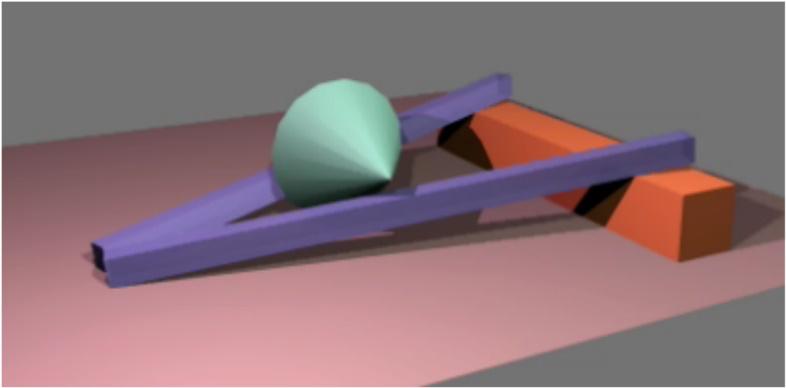
Het experiment van de ʼbergop lopende kegelʼ bestaat enerzijds uit een helling in V-vorm met de scherpe hoek aan de laagste kant en anderzijds uit twee kegels die met hun grondvlakken aan elkaar gemaakt zijn tot een dubbele kegel. Wanneer de dubbele kegel op de lage kant van de helling geplaatst wordt, zal hij – als er aan bepaalde voorwaarden voldaan is –spontaan bergop lopen. Hoewel de dubbele kegel schijnbaar bergop loopt, zal door
De voorwaarden waaraan moet voldaan zijn Hiervoor is een goed ruimtelijk inzicht nodig. beperkt: driehoeksmeting in rechthoekige driehoeken
Op Youtube worden verschillende animaties het trefwoord ʼUphill Rollerʼ, zie bijvoorbeeld
voorwaarden waaraan moet voldaan zijn voor het bergop lopen, worden in deze tekst onderzocht. is een goed ruimtelijk inzicht nodig. De wiskundige kennis die gebruikt wordt, is eerder driehoeksmeting in rechthoekige driehoeken en gelijkvormige driehoeken.
De voorwaarden waaraan moet voldaan zijn voor het bergop lopen, worden in deze tekst onderzocht. Hiervoor is een goed ruimtelijk inzicht nodig. De wiskundige kennis die gebruikt wordt, is eerder beperkt: driehoeksmeting in rechthoekige driehoeken en gelijkvormige driehoeken.
De dubbele kegel kan gemaakt worden door twee halve cirkels met straal R uit te knippen en ze op te rollen tot twee kegels. Als je ze in karton maakt, zal je ze bijvoorbeeld met rijstkorrels moeten vullen om voor het nodige gewicht te zorgen. Daarna plak je de twee kegels met de basissen aan elkaar.
Youtube worden verschillende animaties van dit experiment getoond. Je vindt ze door te zoeken op trefwoord ʼUphill Rollerʼ, zie bijvoorbeeld [1].
proefopstelling
Op Youtube worden verschillende animaties van dit experiment getoond. Je vindt ze door te zoeken op het trefwoord 'Uphill Roller', zie bijvoorbeeld [1].



De lengte van de boog van de halve cirkel (π R) wordt de omtrek van het grondvlak van de kegel (2π r). Hieruit kun je afleiden dat . De hoogte van de kegel is dan en de halve tophoek is Uiteraard kun je bij de constructie van de kegel ook uitgaan van een cirkelsector die kleiner (of groter) is
De dubbele kegel kan gemaakt worden door twee halve cirkels met straal R uit te knippen en ze op te rollen tot twee kegels. Als je ze in karton maakt, zal je ze bijvoorbeeld met rijstkorrels moeten vullen om voor het nodige gewicht te zorgen. Daarna plak je de twee kegels met de basissen aan elkaar.
De lengte van de boog van de halve cirkel ( ) wordt de omtrek van het grondvlak van de kegel ( ). Hieruit kun
De met
Als moeten plak
De omtrek afleiden en constructie kleiner scherper
UITWISKELING
je p R 2pr
9
LEON LENDERS
dan een halve cirkel. De kegel zal dan scherper (of stomper) zijn dan in het voorstel hierboven.
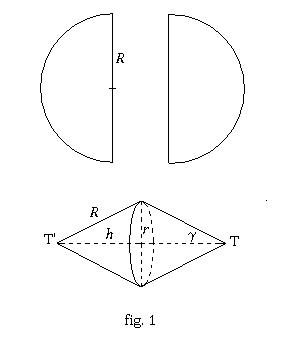
Vervolgens beschrijven we het hellend vlak (zie figuur 1). De twee rails AC en AE waarover de dubbele kegel rolt, komen samen in het punt A op een hoogte boven het tafelblad. De helling van het hellend vlak wordt gemeten in het bissectricevlak van de twee rails. De grootte van de hellingshoek DAB noemen we . De opening tussen de rails wordt gemeten in een horizontaal vlak. Om praktische redenen gaan we hier over op de halve openingshoek. De grootte van de hoek MOL noemen we


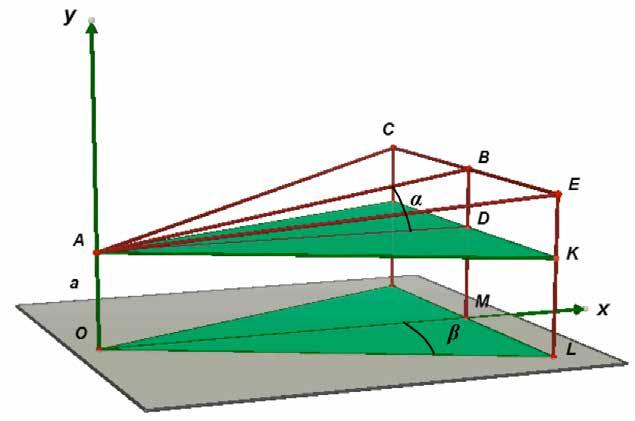
Hiermee ligt de hele helling vast. We definiëren nu een tweedimensionaal assenstelsel in het bissectricevlak van de twee rails. De y-as is de verticale rechte OA door het laagste punt van de rails. De x-as is de horizontale rechte OM loodrecht op OA in het bissectricevlak.
BEREKENING VAN DE ZWAARTEPUNTSHOOGTE
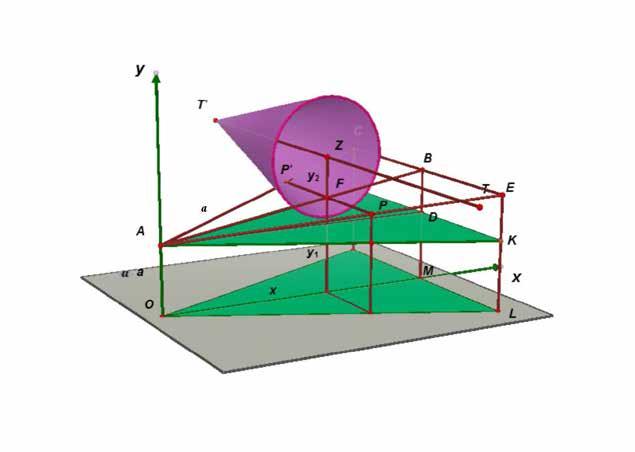
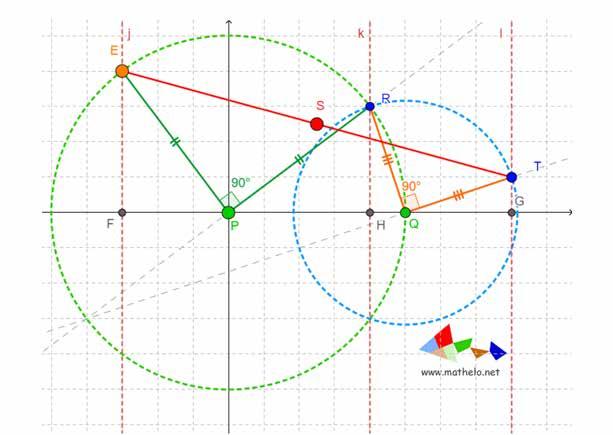
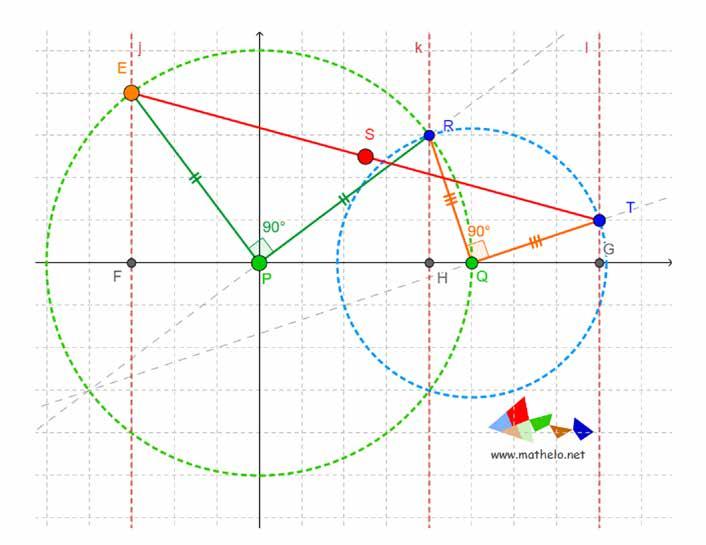
Nu voegen we de kegels toe (zie figuur 2). Om de figuur niet nodeloos te verzwaren, tekenen we slechts één van beide kegels. Het zwaartepunt Z van de dubbele kegel ligt in het midden van het horizontale lijnstuk [TT '] door de twee toppen. Dit lijnstuk is afgebeeld op de figuur hiernaast. Je ziet ook duidelijk de twee contactpunten van de dubbele kegel met de rails. Ze vormen het lijnstuk [PP '].
We onderzoeken nu de hoogte y van het zwaartepunt in functie van
1
2
Figuur
10
Figuur
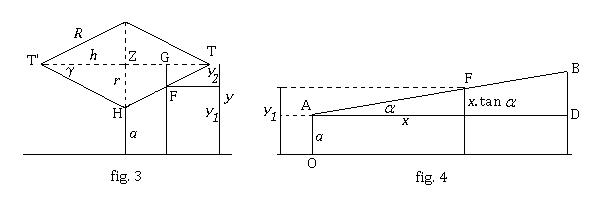
de x-waarde. Deze hoogte is de som van twee afstanden: de hoogte y1 van de contactpunten boven het tafelblad en de hoogte y2 van het zwaartepunt boven de verbindingsdwarsdoorsnede van het hellend vlak hierboven zie je hoe je y1 kunt uitdrukken in functie van x:

Hieronder zie je een andere dwarsdoorsnede, die van de dubbele kegel. Ze heeft de vorm van een ruit. Op deze tweedimensionale figuur kun je ook de hoogte y1 aflezen van de contactpunten boven het tafelblad en de hoogte y2 van het zwaartepunt Z boven de verbindingslijn van de contactpunten. Er zijn twee gelijkvormige driehoeken met een tophoek afgebeeld, de kleine driehoek TQP en de grote TZH

Alleen y2 moet nog berekend worden. Je kan dit doen met evenredigheden tussen overeenkomstige zijden van gelijkvormige
driehoeken. Maar het kan ook met de definitie van de tangens in de kleine rechthoekige driehoek TQP Deze driehoek heeft een korte rechthoekszijde y en een lange rechthoekszijde gelijk aan






. Deze laatste term vind je onmiddellijk op de driedimensionale figuur: . Hieruit volgt dat:

. Omdat in driehoek TZH geldt dat vinden we:

In een klasdiscussie zou je aan de leerlingen kunnen vragen om een concrete situatie (waarden voor , en ) te bedenken waarin de kegel niet omhoogloopt. En wat zou er gebeuren als je i.p.v. een dubbele kegel een cilinder zou gebruiken? Of als de rails evenwijdig zouden lopen? In deze laatste twee speciale gevallen (respectievelijk en ) kan het voorwerp nooit omhooglopen, hoe klein de helling ook is.



Samengevat geven deze formules een zwaartepuntshoogte





Het zwaartepunt van de kegels beweegt dus op een rechte die de y-as snijdt in het punt met als richtingscoëfficiënt

INTERPRETATIE VAN DE ZWAARTEPUNTSFORMULE

Als dan balanceert de dubbele kegel precies boven het punt A Het is dan duidelijk dat de zwaartepuntshoogte gelijk is aan




De rechte waarop het zwaartepunt zich beweegt is dalend als . Dat is bijvoorbeeld het geval indien , en . De richtingscoëfficiënt van de rechte waarop het zwaartepunt beweegt, is nu gelijk aan -0,093 terwijl de dubbele kegel schijnbaar 10° bergop loopt.

Ten slotte nog dit. Doordat het hellend vlak steeds breder wordt, zal de dubbele kegel na een bepaalde afstand x tussen de rails door vallen. Dit is het geval als Met de waarden , en en de hoogte h = 4,5 cm zal de dubbele kegel na 9,65 cm tussen de rails vallen. Daarom moet er op deze afstand een stootblok gelegd worden.
Op de site [2] vind je een applet waarop de hoeken , en kunnen ingesteld worden. De bijbehorende baan van het zwaartepunt en het hellend vlak worden hier visueel voorgesteld. Als je overtuigd bent van de juistheid van de berekeningen hierboven en je hebt niet direct zin om een hellend vlak en een dubbele kegel te knutselen, kan dit een mogelijk alternatief zijn
WEBSITES



[1] Uphill Roller, http://www.youtube.com/ watch?v=zkt1eScOCEI
[2] Applet dubbele kegel, https:// lkwadraat.com/content/toepass/ oplopende%20kegel.html
Dit artikel verscheen in Uitwiskeling 28/4. Op www.uitwiskeling.be vind je alle info.
...
a a 11
(D)4
OEFENING 1
(E)afhankelijkvandehoogtevanhettrapezium
In klas 4D zitten 30 leerlingen: 12 jongens en 18 meisjes. Mevrouw Deschamps merkt na een toets het volgende op: “In vergelijking met de vorige toets is het gemiddelde van de jongens met 2 punten gedaald en dat van de meisjes met 2 punten gestegen.” Dan is het gemiddelde van de volledige klas in vergelijking met de vorige toets
14. CarmenenXavierpoetsenelkedagtweekeerhuntanden.Carmenkomtjuist20dagen toemeteenvolletubetandpasta.Xavierisietszuinigerenkomtjuist30dagentoemet eenvolletube.AlsCarmenenXaviereentubedelen,hoelangduurthetdanvooraleer eenvolletubeleegis?
Eenrechthoekigtrapeziummetkleinebasis4engrote basis8wordtdooreendiagonaalintweeverdeeld.De verhoudingtussendeoppervlaktevanhetgrootstedeel endievanhetkleinstedeelis
Eenrechthoekigtrapeziummetkleinebasis4engrote basis8wordtdooreendiagonaalintweeverdeeld.De verhoudingtussendeoppervlaktevanhetgrootstedeel endievanhetkleinstedeelis
13. Eenrechthoekigtrapeziummetkleinebasis4engrote basis8wordtdooreendiagonaalintweeverdeeld.De verhoudingtussendeoppervlaktevanhetgrootstedeel endievanhetkleinstedeelis
13. Eenrechthoekigtrapeziummetkleinebasis4engrote basis8wordtdooreendiagonaalintweeverdeeld.De verhoudingtussendeoppervlaktevanhetgrootstedeel endievanhetkleinstedeelis
13. Eenrechthoekigtrapeziummetkleinebasis4engrote basis8wordtdooreendiagonaalintweeverdeeld.De verhoudingtussendeoppervlaktevanhetgrootstedeel endievanhetkleinstedeelis
gelijk gebleven met 0,4 punten gestegen met 0,5 punten gestegen met 0,6 punten gestegen met 1 punt gestegen
(A)10dagen(B)11dagen(C)12dagen(D)14dagen(E)18dagen
(B)1,5 (C)2 (D)4 (E)afhankelijkvandehoogtevanhettrapezium
(E)afhankelijkvandehoogtevanhettrapezium
15. Ineencirkelschijfmetstraal1iseenvierkantingeschreven.Akiravouwtvierstukjes vandeschijfnaarbinnenoverdezijdenvanhetvierkantzoalsindefiguur.Watisde oppervlaktevanhetzichtbaregekleurdedeelnahetvouwen?
OEFENING 2
CarmenenXavierpoetsenelkedagtweekeerhuntanden.Carmenkomtjuist20dagen toemeteenvolletubetandpasta.Xavierisietszuinigerenkomtjuist30dagentoemet eenvolletube.AlsCarmenenXaviereentubedelen,hoelangduurthetdanvooraleer eenvolletubeleegis?
14. CarmenenXavierpoetsenelkedagtweekeerhuntanden.Carmenkomtjuist20dagen toemeteenvolletubetandpasta.Xavierisietszuinigerenkomtjuist30dagentoemet eenvolletube.AlsCarmenenXaviereentubedelen,hoelangduurthetdanvooraleer eenvolletubeleegis?
CarmenenXavierpoetsenelkedagtweekeerhuntanden.Carmenkomtjuist20dagen toemeteenvolletubetandpasta.Xavierisietszuinigerenkomtjuist30dagentoemet eenvolletube.AlsCarmenenXaviereentubedelen,hoelangduurthetdanvooraleer eenvolletubeleegis?
14. CarmenenXavierpoetsenelkedagtweekeerhuntanden.Carmenkomtjuist20dagen toemeteenvolletubetandpasta.Xavierisietszuinigerenkomtjuist30dagentoemet eenvolletube.AlsCarmenenXaviereentubedelen,hoelangduurthetdanvooraleer eenvolletubeleegis?
14. CarmenenXavierpoetsenelkedagtweekeerhuntanden.Carmenkomtjuist20dagen toemeteenvolletubetandpasta.Xavierisietszuinigerenkomtjuist30dagentoemet eenvolletube.AlsCarmenenXaviereentubedelen,hoelangduurthetdanvooraleer eenvolletubeleegis?
(A)10dagen(B)11dagen(C)12dagen(D)14dagen(E)18dagen
(A)10dagen(B)11dagen(C)12dagen(D)14dagen(E)18dagen
(A)10dagen(B)11dagen(C)12dagen(D)14dagen(E)18dagen
(A)10dagen(B)11dagen(C)12dagen(D)14dagen(E)18dagen
(A)10dagen(B)11dagen(C)12dagen(D)14dagen(E)18dagen
Ineencirkelschijfmetstraal1iseenvierkantingeschreven.Akiravouwtvierstukjes vandeschijfnaarbinnenoverdezijdenvanhetvierkantzoalsindefiguur.Watisde oppervlaktevanhetzichtbaregekleurdedeelnahetvouwen?
Ineencirkelschijfmetstraal1iseenvierkantingeschreven.Akiravouwtvierstukjes vandeschijfnaarbinnenoverdezijdenvanhetvierkantzoalsindefiguur.Watisde oppervlaktevanhetzichtbaregekleurdedeelnahetvouwen?
15. Ineencirkelschijfmetstraal1iseenvierkantingeschreven.Akiravouwtvierstukjes vandeschijfnaarbinnenoverdezijdenvanhetvierkantzoalsindefiguur.Watisde oppervlaktevanhetzichtbaregekleurdedeelnahetvouwen?
15. Ineencirkelschijfmetstraal1iseenvierkantingeschreven.Akiravouwtvierstukjes vandeschijfnaarbinnenoverdezijdenvanhetvierkantzoalsindefiguur.Watisde oppervlaktevanhetzichtbaregekleurdedeelnahetvouwen?
15. Ineencirkelschijfmetstraal1iseenvierkantingeschreven.Akiravouwtvierstukjes vandeschijfnaarbinnenoverdezijdenvanhetvierkantzoalsindefiguur.Watisde oppervlaktevanhetzichtbaregekleurdedeelnahetvouwen?
In een cirkelschijf met straal 1 is een vierkant ingeschreven. Akira vouwt vier stukjes van de schijf naar binnen over de zijden van het vierkant zoals in de figuur. Wat is de oppervlakte van het zichtbare gekleurde deel na het vouwen?
π 1(B) π 2(C)4 π (D)8
16. Welkevandevolgendesommeniskleinerdan15?
Welkevandevolgendesommeniskleinerdan15?
16. Welkevandevolgendesommeniskleinerdan15?
Welkevandevolgendesommeniskleinerdan15?
16. Welkevandevolgendesommeniskleinerdan15?
16. Welkevandevolgendesommeniskleinerdan15?
17. Deviervlakkenvaneenregelmatigviervlak(tetra¨eder)zijngelabeld metdesymbolen , , en .Indefiguurziejeeenaanzicht
17. Deviervlakkenvaneenregelmatigviervlak(tetra¨eder)zijngelabeld metdesymbolen , , en .Indefiguurziejeeenaanzicht
17. Deviervlakkenvaneenregelmatigviervlak(tetra¨eder)zijngelabeld
© Junior Wiskunde Olympiade vzwTweede Ronde JWO 2023-2024, vraag 3
A B C D E
verhoudingtussendeoppervlaktevanhetgrootstedeel endievanhetkleinstedeelis 8
(A)1 (B)1,5 (C)2
(A) π 1(B) π 2(C)4 π (D)8 π (E)8
(A) √17+ √122(B) √26+ √102(C) √37+ √83(D) √40+ √65(E) √
© Junior Wiskunde Olympiade vzwTweede Ronde JWO 2023-2024, vraag 15
A B C D E
4 8 (A)1 (B)1,5 (C)2 (D)4
(A)
π (E)8 2π
(A) √17+ √122(B) √26+ √102(C) √37+ √83(D) √40+ √65(E) √50+ √64
4 8 (A)1 (B)1,5 (C)2 (D)4
(E)afhankelijkvandehoogtevanhettrapezium
(A) π 1(B) π 2(C)4 π (D)8 π (E)8 2π
(A) √17+ √122(B) √26+ √102(C) √37+ √83(D) √40+ √65(E) √50+ √64 17. Deviervlakkenvaneenregelmatigviervlak(tetra¨eder)zijngelabeld metdesymbolen
en
, ,
.Indefiguurziejeeenaanzicht
4 8 (A)1 (B)1,5 (C)2 (D)4
(E)afhankelijkvandehoogtevanhettrapezium
(A) π 1(B) π 2(C)4 π (D)8 π (E)8 2π
(A) √17+ √122(B) √26+ √102(C) √37+ √83(D) √40+ √65(E) √50+ √64
4 8 (A)1
(A) π 1(B) π 2(C)4 π (D)8 π (E)8 2π
(A) √17+ √122(B) √26+ √102(C) √37+ √83(D) √40+ √65(E) √50+ √64 Deviervlakkenvaneenregelmatigviervlak(tetra¨eder)zijngelabeld metdesymbolen , , en .Indefiguurziejeeenaanzicht
4 8 (B)1,5 (C)2
(E)afhankelijkvandehoogtevanhettrapezium
1(B) 2(C)4 π (D)8 π (E)8 2π
17+ √122(B) 26+ √37+ √83(D) √40+ √65(E) √50+ √64 Deviervlakkenvaneenregelmatigviervlak(tetra¨eder)zijngelabeld metdesymbolen , , en .Indefiguurziejeeenaanzicht 12
Degetallen r en s zijngeheel.Wanneerishetgetal
(A)als r + s ⩽ 0
(B)als s ⩽ 0
(C)als r ⩽ 0
(D)als r ⩾ s (E)voorallewaardenvan r en s
OEFENING 3
Twee punten verdelen een straal van een cirkel in drie even lange lijnstukken. Door elk van die punten wordt loodrecht op die straal een koorde getekend. Beide koorden zijn de zijde van een vierkant zoals in de figuur. Wat is de verhouding tussen de oppervlakte van het grote en die van het kleine vierkant?
Tweepuntenverdeleneenstraalvaneencirkelindrieeven langelijnstukken.Doorelkvandiepuntenwordtloodrecht opdiestraaleenkoordegetekend.Beidekoordenzijn dezijdevaneenvierkantzoalsindefiguur.Watisde verhoudingtussendeoppervlaktevanhetgroteendie vanhetkleinevierkant?
Opeenschoolbordstaandegehelegetallenvan1totenmet16.Duaveegteengetal ophetbordwegwaarvanhetdubbelnogophetbordstaat.Datherhaaltzetotzezo geengetallenmeerkanwegvegen.Hoeveelgetallenkunnenermaximaalophetbord
(A)1,25(B)1,33 ... (C)1,5(D)1,6(E)1,66 ...
OEFENING 4
Watisderestnadelingvan2+22 +23 +24 + ··· +22024 door6? (A)0 (B)1 (C)2 (D)3(E)4
(C)10(D)11(E)12
Op de vlakken van een dobbelsteen staan zes ogen tegenover één oog, vijf ogen tegenover twee ogen en vier ogen tegenover drie ogen.
Hetgetal
Opdevlakkenvaneendobbelsteenstaanzesogentegenover´e´enoog,vijfogentegenovertweeogenenvierogen tegenoverdrieogen.
Op tafel zijn zes dobbelstenen op elkaar gestapeld zoals in de figuur. Wat is het kleinst mogelijke totale aantal ogen op de 21 zichtbare vlakken?
isgelijkaan
Optafelzijnzesdobbelstenenopelkaargestapeldzoalsin defiguur.Watishetkleinstmogelijketotaleaantalogen opde21zichtbarevlakken?
(A) 8(B)4 (C)8 (D)16(E)4√6
Ikmaakeenaapgelukkigdoorhemdrievruchtenvaneenverschillendefruitsoortte geven.Watishetgrootsteaantalapendatikgelukkigkanmakenalsikbeschikover50 appels,40peren,30bananenen20perziken?
(A)56(B)57(C)58(D)59(E)60
(A)20(B)30(C)40(D)45(E)50
© Junior Wiskunde Olympiade vzwTweede Ronde JWO 2023-2024, vraag 21
(B)9
bondenmetdemiddensvandezeszijden.Zoont© Junior Wiskunde Olympiade vzwTweede Ronde JWO 2023-2024, vraag 26 A B C D E 1,25 1,33 … 1,5 1,6 1,66 … (A)2 (B)2 5(C)3 (D)3 5(E)4
Eenpuntbinneneenregelmatigezeshoekwordtver-
6r +s · 12r s 8r · 9r +2s geheel?
√3+ √2+1 √3 √2+1 √3+ √2 1 √3 √2 1
A B C D E 56 57 58 59 60 13
VVWL
HET SCHATGRAVERSPROBLEEM
DE OVERSTAP VAN HET GRAFISCH REKENTOESTEL NAAR HET GEBRUIK VAN WISKUNDESOFTWARE OP LAPTOPS OF CHROMEBOOKS BETEKENT VOOR
LERAREN EEN NIEUWE DIDACTISCHE UITDAGING. IN DIT ARTIKEL GAAN WE
MET EEN UITDAGENDE PROBLEEMSTELLING VIA GEOGEBRA AAN DE SLAG.
IVAN DE WINNE IS GEPENSIONEERD LERAAR WISKUNDE, VOORZITTER VAN DE VVWL EN LID VAN DE GEOGEBRA WERKGROEP VAN DE VVWL. DAARNAAST BIEDT HIJ VIA HET LEERPLATFORM MATHELO WEBCURSUSSEN TER ONDERSTEUNING VAN DE INTEGRATIE VAN ICT IN DE LESPRAKTIJK.
DIDACTISCH AAN DE SLAG
MET GEOGEBRA
Het is de bedoeling van de Vlaamse overheid om via subsidies in de loop van twee schooljaren de Digisprong in de klas te realiseren. Dit betekent dat elke leerling van het secundair onderwijs over een ICT-toestel van de school zal kunnen beschikken. Na het beschikbaar stellen van hardware is er ook grote nood aan goede praktijkvoorbeelden bij de overstap van een grafische rekentoestel naar wiskundesoftware op laptops. Het programma GeoGebra is een gereedschap waarmee het merendeel van de wiskundeleraars ondertussen vertrouwd is. Ook voor leerlingen kunnen met GeoGebra ICT-doelstellingen bereikt worden.
Ter illustratie een voorbeeld waarbij in het eerste deel leerlingen uit de eerste graad op een speelse manier de mogelijkheden van het gebruik van GeoGebra voor meetkundige
constructies ontdekken en waarbij in het tweede deel voor leerlingen uit
de tweede graad het bewijs via analytische meetkunde wordt gegeven.
Op een eiland werd een schat verborgen. Om de schat te vinden moet je de volgende aanwijzingen volgen.
1° Loop in een rechte lijn van de oude eik naar de grote zwerfkei P.
2° Loop vervolgens dezelfde afstand in tegenwijzerzin volgens een rechte lijn die loodrecht op de vorige richting staat.
3° Loop vervolgens in een rechte lijn naar de tweede kleine zwerfkei Q die op het eiland te vinden is.
4° Leg vervolgens opnieuw de laatste afstand af in tegenwijzerzin volgens de richting die loodrecht op het laatst afgelegde stuk staat. Noem T het punt waar je dan staat.
5° Ga ten slotte in een rechte lijn opnieuw naar de oude eik. De schat ligt precies in het midden van het lijnstuk begrensd door het punt T en door de oude eik.
Maar … bij het op zoek gaan naar de schat blijkt dat er op het hele eiland geen enkele eik meer te vinden is. Alleen de twee zwerfkeien P en Q liggen er nog.
Vind de schat door slechts één keer te graven!

14
OPDRACHT 1: MEETKUNDIGE
CONSTRUCTIE MET GEOGEBRA
Maak met GeoGebra een meetkundige constructie om dit probleem te visualiseren.
Maak hierbij gebruik van de webversie van GeoGebra SUITE. Dat is de recentste versie van het programma. Je kan deze app openen via de link www.geogebra.org/calculator.
Activeer de app “Meetkunde” van GeoGebra SUITE. De interface is opgesplitst in drie onderdelen met links de twee knoppen om te schakelen tussen het algebravenster en het tekenvenster, in het middengedeelte het knoppenvenster en rechts het tekenvenster. (zie figuur 1)
Maak nu een schets van de situatie.
De positie van de twee zwerfkeien is gekend en vast. Noem deze punten P en Q.
De positie van de oude eik is niet gekend. Teken daarom ergens een willekeurig punt E.
• Teken drie punten P (grote zwerfkei) en Q (kleine zwerfkei) en een denkbeeldige plaats voor de eik E.
• Teken een lijnstuk [EP] en vervolgens de loodlijn a in P op dit lijnstuk.
• Teken een cirkel c met middelpunt P en gaande door E.
• Bepaal het snijpunt R van de loodlijn met deze cirkel en hou rekening met de richting.
• Teken lijnstuk [RQ] en de loodlijn b in Q op dit lijnstuk.
• Teken een cirkel d met middelpunt Q en gaande door R.
• Bepaal het snijpunt T van de loodlijn met de cirkel en hou rekening met de richting.
• Teken het lijnstuk [QT] en het lijnstuk [TE].
• Bepaal het midden S van het lijnstuk [TE].
• Versleep nu het punt E.
Welk merkwaardig resultaat constateer je bij het verslepen van het punt E ? Uitgewerkt interactief GeoGebra bestand: https://www.geogebra.org/ m/w5gvhayu
15
Figuur 1
Figuur 2
OPDRACHT 2: ANALYTISCH BEWIJS
Geef ook een bewijs voor de gevonden oplossing door gebruik te maken van cartesiaanse coördinaten.
Gegeven
Uit de tekening volgt dat |EP| = |PR| en |RQ| = |QT|. De hoeken EPR en RQT zijn recht.
Te bewijzen
Het midden S van het lijnstuk [ET] kan niet van plaats veranderen indien het punt E van plaats verandert. De positie van het punt S is enkel afhankelijk van de positie van de punten P en Q (vaste punten) en is niet afhankelijk van de positie van het punt E.
Bewijs
Om de berekeningen zo eenvoudig mogelijk te houden, kiezen wij voor P de oorsprong en de x-as door het lijnstuk [PQ]. Daarvoor moet men in GeoGebra eerst de assen en het rooster aanzetten.
Teken de loodlijnen vanuit E, R en T op de x-as en bepaal de snijpunten F, H en G. (zie figuur 3)
Uitgewerkt GeoGebra bestand: https://www.geogebra.org/m/ scy5yh4r
Teken ook de driehoeken ∆EFP, ∆PHR, ∆RHQ en ∆QGT. (zie figuur 4)
Je ziet in de figuur de congruente driehoeken ∆EFP en ∆PHR. De driehoeken ∆RHQ en ∆QGT zijn eveneens congruent. Noem k de lengte van het lijnstuk [PQ]. Noem (-x,y) de coördinaat van E. Bepaal de coördinaatgetallen van T in functie van k, x en y.
3
Omdat de driehoeken ∆EFP en ∆PHR congruent zijn, is |PH| =|EF|= y. Omdat ook de driehoeken ∆RHQ en ∆QGT congruent zijn, is: |HQ| =|GT| = k – y. Bovendien is |FP|= x = |RH| en dus ook |QG| = x. Dus is de coördinaat van het punt T (k + x, k – y). De coördinaat van het midden S van [ET] is .
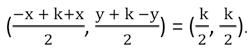
Het resultaat is onafhankelijk van E! Het is enkel afhankelijk van de afstand tussen P en Q. Uitgewerkt GeoGebra bestand: https://www.geogebra.org/m/ kfaxsppn

4
Figuur
16
Figuur
DE VAKANTIECURSUS VOOR LERAREN WISKUNDE
AL SINDS 1946 ORGANISEERT PLATFORM WISKUNDE NEDERLAND AAN HET EINDE VAN DE ZOMERVAKANTIE EEN VAKANTIECURSUS VOOR LERAREN WISKUNDE, ZO OOK KOMENDE ZOMERVAKANTIE. TRADITIONEEL WERD DE CURSUS IN AMSTERDAM EN EEN WEEK EERDER OF LATER OOK IN EINDHOVEN GEGEVEN. SINDS VORIG JAAR WORDT DE CURSUS ECHTER GEGEVEN IN AMSTERDAM EN ANTWERPEN, DIT JAAR OP 23 EN 24 AUGUSTUS IN AMSTERDAM EN OP 6 EN 7 SEPTEMBER IN ANTWERPEN. DE EDITIE IN ANTWERPEN IS EEN SAMENWERKING MET HET PLATFORM WISKUNDE VLAANDEREN. DOOR DIE SAMENWERKING KAN NU OOK VLAANDEREN GENIETEN VAN HET FENOMEEN ‘VAKANTIECURSUS’! HET THEMA VAN DIT
JAAR IS ‘BANACH-TARSKI EN GROEPENTHEORIE’. HOOFDSPREKERS ZIJN PROF. DR. STEFAAN VAES UIT LEUVEN EN DR. HABIL. JEROEN SPANDAW UIT DELFT.
JEROEN SPANDAW EN ELS VANLOMMEL
JEROEN SPANDAW IS GEPROMOVEERD EN GEHABILITEERD IN DE ALGEBRAÏSCHE MEETKUNDE. HIJ WAS DOCENT WISKUNDE EN NATUURWETENSCHAPPEN EN SINDS 2007 IS HIJ IS UNIVERSITAIR DOCENT EN LERARENOPLEIDER WISKUNDE AAN DE TU DELFT.
ELS VANLOMMEL IS LEERKRACHT WISKUNDE IN HET HEILIG HART VAN MARIA, BERLAAR. DAARNAAST IS ZIJ REDACTIELID BIJ HET TIJDSCHRIFT UITWISKELING EN BESTUURSLID VAN HET PLATFORM WISKUNDE VLAANDEREN.
In dit artikel vertellen we je iets over deze prachtige cursus. Voor gedetailleerde informatie en inschrijving verwijzen we graag naar de websites van Platform Wiskunde Nederland (https://platformwiskunde.nl/) en Platform Wiskunde Vlaanderen (https://platformwiskunde.be/).
In de vakantiecursus wordt pittige wiskunde op een toegankelijke wijze gepresenteerd door wiskundig onderzoekers. Deelnemers aan de cursus ontvangen
een syllabus in boekvorm die speciaal voor de cursus is geschreven door de hoofdspreker(s). De cursus richt zich op leraren wiskunde uit de derde graad ... met component wiskunde, maar uiteraard zijn ook andere geïnteresseerden welkom.
De thema’s van de afgelopen jaren waren priemgetallen, stochastische netwerken, meetkunde van stangconstructies, speltheorie, deep learning
17
en cryptografie. Om je een indruk te geven van de vakantiecursus, kijken we eerst vooruit naar de komende editie en geven we mee wat de meerwaarde is voor je lespraktijk door o.a. terug te blikken op de vorige editie.
VOORUITBLIK OP DE CURSUS VAN 2024
De vakantiecursus 2024 heeft als thema groepentheorie, met als toepassing de Banach-Tarski-paradox. Op vrijdag geeft dr. Jeroen Spandaw (TU Delft) een inleiding in de groepentheorie. Hierbij zullen we veel eenvoudige, maar inzicht verschaffende, concrete voorbeelden ‘doorrekenen’ om de abstracte begrippen uit de theorie betekenis te geven. De deelnemers zullen ook zelf aan de slag gaan met opgaven die hen zullen helpen om vertrouwd te raken met die begrippen. We maken daarbij gebruik van het computerprogramma GAP, waarmee snel gerekend kan worden in groepen. Op zaterdag zal prof. dr. Stefaan Vaes (KU Leuven) ons in een prettig rustig tempo door het bewijs van de verbluffende Banach-Tarski-paradox leiden. Gebruikmakend van de groepentheorie die we ons op vrijdag eigen hebben gemaakt, zal hij laten zien dat
een eenheidsbol in enkele disjuncte delen kan worden opgedeeld, die vervolgens via rotaties en translaties weer kunnen worden samengevoegd op zo’n manier dat er twee eenheidsbollen ontstaan! Het zou niet moeten mogen...
Vrijdagavond kunnen de deelnemers ontspannen en luisteren naar een lezing door prof. dr. David Eelbode (UAntwerpen) over het merkwaardige fenomeen dat rotaties over 360° niet altijd terugleiden naar de beginpositie: soms is daar een rotatie over 720° voor nodig! Dit kunnen we begrijpen door te kijken naar de vorm van de groep van rotaties in 3 dimensies.
ERVARINGEN EN VERWACHTINGEN VAN EEN LEERKRACHT
Als leraar ben ik (E.V.) al heel wat jaren trouwe bezoeker (er waren steeds wel enkele Vlamingen in Eindhoven) en het moet gezegd: je wordt serieus uitgedaagd in de vakantiecursus. Daartegenover staat dat je enorm veel bijleert op korte tijd. De workshops van de eerste dag zijn erg belangrijk om de basis in de vingers te krijgen.

18
Je kunt vragen stellen aan de lesgever, overleggen met medecursisten en je hebt de gelegenheid om de geziene theorie te laten bezinken. Op die manier doe je veel nieuwe kennis op. De tweede dag komen er meestal toepassingen aan bod en ga je een stuk dieper in op de theorie. Dan wordt het soms echt pittig. Af en toe gebeurde het al wel dat ik niet direct mee was, maar zeker de grote lijnen blijf je goed kunnen volgen doordat de lesgevers interactie voorzien met de cursisten. Bovendien: zelfs als je niet alle details onmiddellijk begrijpt, blijft het enorm boeiend om de toepassingen van de theorie te behandelen. Vrijwel altijd besteed ik op zaterdagnamiddag of zondag na de vakantiecursus wel wat tijd aan verdere verdieping in het topic. Dat is niet alleen plezierig, het leidt er ook toe dat ik in klassen met veel wiskunde beter gewapend ben en over meer achtergrond beschik om mijn lessen te verrijken. Ik verwacht dat dat met de vakantiecursus 2024 niet anders zal zijn!
Sedert de nieuwe eindtermen moeten we in de derde graad een algebraïsche structuur behandelen in de richtingen met component wiskunde. In mijn 8-uursklas zal ik zeker reële vectorruimten behandelen en daarnaast bestudeer ik er ook groepentheorie. Reële vectorruimten omdat vrijwel iedereen daarmee te maken krijgt in het hoger onderwijs, groepentheorie omdat dat heel snel leidt tot echt mooie wiskunde waarvan een wiskundehart sneller gaat kloppen. De vakantiecursus groepentheorie zal mij ineens klaarstomen om de nieuwe eindterm in mijn lessen te implementeren en daar direct veel achtergrond bij te hebben. Ik zou zelf nooit aan de stelling van Banach-Tarski beginnen, laat staan dat ik er aan mijn leerlingen iets gefundeerd over zou kunnen vertellen. Dankzij de vakantiecursus zal dat anders zijn. Ik kijk ernaar uit!
In wat volgt, tonen we concreet wat we bedoelen met ‘achtergrond en inspiratie opdoen voor je lessen’ door kort terug te blikken op de cursus van vorig jaar. Hierbij diepen we het concept van genererende functies iets verder uit.
TERUGBLIK OP DE CURSUS ‘PRIEMGETALLEN’ VAN 2023
De cursus over priemgetallen begon met Euclides’ beroemde bewijs dat er oneindig veel priemgetallen bestaan, waarna we leerden dat voor grote waarden van x ongeveer 1 op de lnx natuurlijke getallen kleiner dan of gelijk aan x een priemgetal is. De formulering van deze stelling van Hadamard en de la Vallée Poussin is goed te begrijpen voor iedereen die logaritmes kent. Het bewijs werd door de spreker, Frits Beukers, wijselijk achterwege gelaten vanwege de complexiteit ervan. In de andere lezingen van Beukers werd vooral gefocust op priemtesten: hoe test je of een gegeven groot getal, bijvoorbeeld priem is? Als we dit op de naïeve manier aanpakken door deelbaarheid te testen door 2, 3, 5… tot en als iedere deelbaarheidstest met een computer één miljardste seconde duurt, dan zijn we tientallen miljoenen jaren aan het rekenen. Gelukkig zijn er slimme methoden die de klus klaren in enkele seconden en die we bovendien nog kunnen begrijpen! Grote priemgetallen en priemtests zijn essentieel voor cryptografie die bijvoorbeeld wordt gebruikt in online transacties.
Gastspreker Benne de Weger leerde hoe je met deze kennis een plausibele schatting kunt maken van onder andere het aantal priemtweelingen kleiner dan of gelijk aan x. Een priemtweeling is een paar getallen (p, p + 2) waarbij zowel p als p + 2 priem zijn. In de praktijk blijken dergelijke schattingen goed te werken, hoewel de heuristische aanpak – waarbij deterministische priemgetallen als toevalsvariabelen worden behandeld! –niets bewijst. Zo weten we nog steeds niet of er oneindig veel priemtweelingen bestaan!
Professor Roland van der Veen vertelde over een belangrijke methode, die de discrete, grillige wereld van de (priem)getallen verbindt met de gladdere continue wereld van functies. Omdat het zo verrassend is, gaan we er in dit artikel iets dieper op in.
19
Telkens als we een rij getallen willen bestuderen, zoeken we daar een geschikte functie bij waar de hele rij op een mooie manier in verstopt zit. We noemen deze functie een genererende functie voor die rij. Door krachtige methoden als integreren en differentiëren toe te passen op die functies, kun je interessante uitspraken doen over de (priem)getallen waarom het ons uiteindelijk te doen is.
Neem bijvoorbeeld de Fibonacci-getallen 0, 1, 1, 2, 3, 5, 8, 13, ... Na de startgetallen 0 en 1 is ieder getal in deze rij de som van de vorige twee. Bij deze rij getallen definiëren we de machtreeks
Je ziet hoe de rij van Fibonacci vertaald is naar coëfficiënten van deze machtreeks. Vermenigvuldigen we G (x) nu met x en met x2 dan schuiven de coëfficiënten gewoon op:
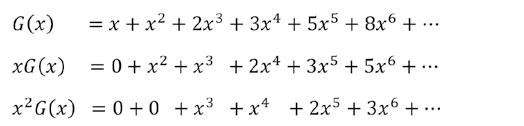

Bijgevolg is . Dus:
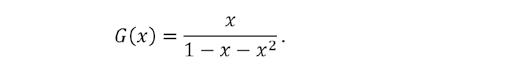
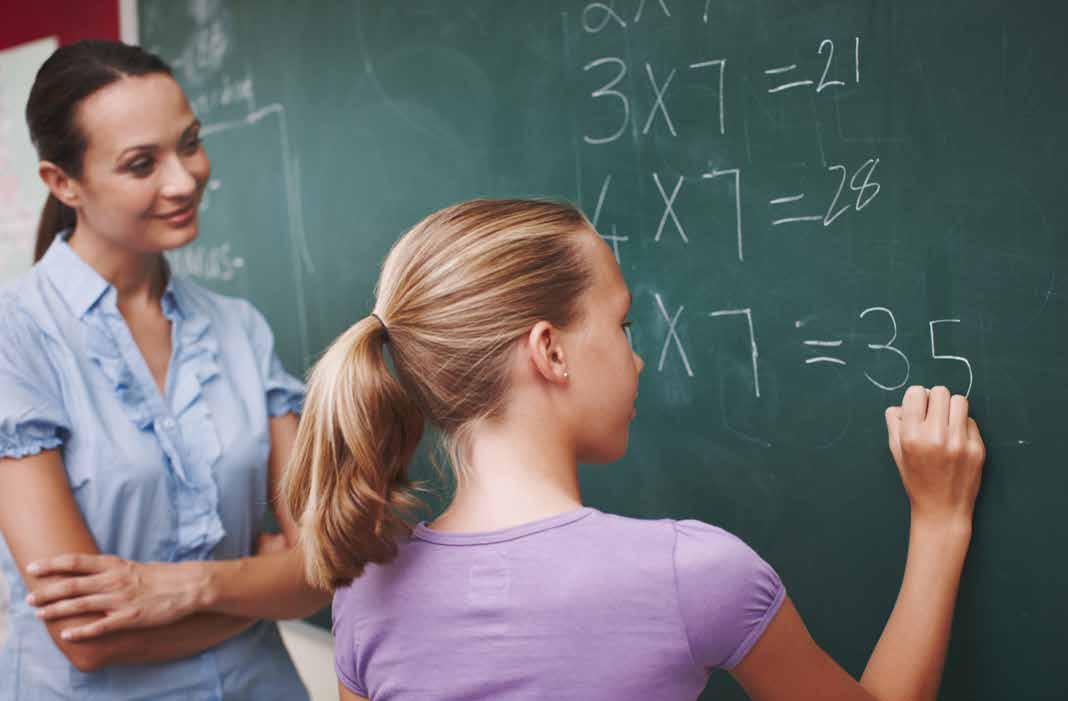
20
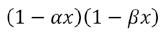
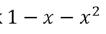
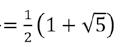


De vakantiecursus voor leraren wiskunde
Splitsen in partieelbreuken levert
In deze eenvoudige rationale functie zit alle info over de rij van Fibonacci verstopt! Door te ontbinden in factoren kun je met wat rekenwerk schrijven als met en , de gekende gulden getallen.
De vakantiecursus voor leraren wiskunde
Jeroen Spandaw en Els Vanlommel

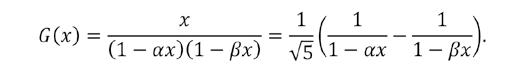
Sommigen herkennen hierin misschien de som van twee meetkundige reeksen. Immers, voor de meetkundige reeks met quotiënt x met | x | < 1 geldt:
Jeroen Spandaw en Els Vanlommel
In de recente edities van de vakantiecursus wordt telkens een deel van de tijd besteed aan een practicum, waarbij de deelnemers opgaven maken om zich de leerstof beter eigen te maken. In de cursus over priemgetallen werkten we met de gratis software PARI om efficiënt te kunnen rekenen met grote (priem)getallen en zo concreet aan de slag te gaan met bijvoorbeeld een toepassing van priemgetallen in de cryptografie.
Al sinds 1946 organiseert Platform Wiskunde Nederland aan het einde van de zomervakantie een vakantiecursus voor leraren wiskunde. Zo ook komende zomervakantie. Traditioneel gaat de cursus eerst door in Amsterdam, dit jaar op 23 en 24 augustus, om enkele weken later herhaald te worden in Eindhoven. Sinds vorig jaar echter gaat die herhaling niet meer door in Eindhoven, maar wel in Antwerpen en dit op 6 en 7 september. De editie in Antwerpen is een samenwerking met het Platform Wiskunde Vlaanderen. Door die samenwerking kan nu ook Vlaanderen genieten van het fenomeen 'vakantiecursus'! Het thema van dit jaar is ‘Banach-Tarski en groepentheorie’. Hoofdsprekers zijn prof. dr. Stefaan Vaes uit Leuven en dr. habil. Jeroen Spandaw uit Delft.
We kunnen G dus als volgt herschrijven:
Al sinds 1946 organiseert Platform Wiskunde Nederland aan het einde van een vakantiecursus voor leraren wiskunde. Zo ook komende zomervakantie. cursus eerst door in Amsterdam, dit jaar op 23 en 24 augustus, om enkele te worden in Eindhoven. Sinds vorig jaar echter gaat die herhaling niet meer maar wel in Antwerpen en dit op 6 en 7 september. De editie in Antwerpen met het Platform Wiskunde Vlaanderen. Door die samenwerking kan nu ook genieten van het fenomeen 'vakantiecursus'! Het thema van dit jaar is ‘Banach groepentheorie’. Hoofdsprekers zijn prof. dr. Stefaan Vaes uit Leuven en dr. Spandaw uit Delft.
In dit artikel vertellen we je iets over deze prachtige cursus. Voor gedetailleerde informatie en inschrijving verwijzen we graag naar de websites van Platform Wiskunde Nederland (https://platformwiskunde.nl/) en Platform Wiskunde Vlaanderen (https://platformwiskunde.be/).
In dit artikel vertellen we je iets over deze prachtige cursus. Voor gedetailleerde inschrijving verwijzen we graag naar de websites van Platform Wiskunde Nederland (https://platformwiskunde.nl/) en Platform Wiskunde Vlaanderen (https://platformwiskunde.be/).
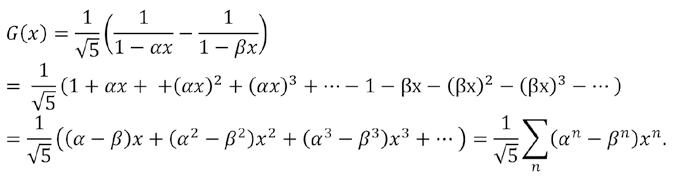
In de vakantiecursus wordt pittige wiskunde op een toegankelijke wijze gepresenteerd door wiskundig onderzoekers. Deelnemers aan de cursus ontvangen een syllabus in boekvorm die speciaal voor de cursus is geschreven door de hoofdspreker(s). De cursus richt zich op leraren wiskunde uit de derde graad met component wiskunde.
In de vakantiecursus wordt pittige wiskunde op een toegankelijke wijze gepresenteerd wiskundig onderzoekers. Deelnemers aan de cursus ontvangen een syllabus speciaal voor de cursus is geschreven door de hoofdspreker(s). De cursus wiskunde uit de derde graad met component wiskunde.
De thema’s van de afgelopen jaren waren priemgetallen, stochastische netwerken, meetkunde van stangconstructies, speltheorie, deep learning en cryptografie. Om je een indruk te geven van de vakantiecursus, kijken we eerst vooruit naar de komende editie en geven we mee wat de meerwaarde is voor je lespraktijk door o.a. terug te blikken op de vorige editie.
Omdat de coëfficiënten in de machtreeks overeenkomen met de termen in de rij van Fibonacci, levert dit een expliciete formule voor het n-de Fibonacci-getal, namelijk
Vooruitblik op de cursus van 2024
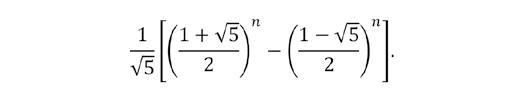
Een ‘vergelijkbare’ aanpak, toegepast op de rij van priemgetallen leidt tot de fameuze Riemann-zetafunctie
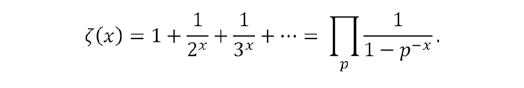
We leerden hoe de ligging van de complexe nulpunten van deze functie informatie geeft over het verschil tussen het aantal priemgetallen kleiner dan of gelijk aan x en de eerdergenoemde schatting
De thema’s van de afgelopen jaren waren priemgetallen, stochastische netwerken, van stangconstructies, speltheorie, deep learning en cryptografie. Om je een de vakantiecursus, kijken we eerst vooruit naar de komende editie en geven meerwaarde is voor je lespraktijk door o.a. terug te blikken op de vorige editie.
Vooruitblik op de cursus van 2024
Dit voorbeeld laat zien wat je kunt verwachten op een vakantiecursus: uitdagende en mooie wiskunde in de vorm van een zorgvuldig opgebouwde cursus van ongeveer 6 voordrachten in 2 dagen. Niet alleen krijg je een uitgebreide syllabus mee naar huis, maar ook een lijst met bronnen (bijvoorbeeld simulaties op internet) en vooral: een hoofd vol ideeën waarvan je er zeker enkele in de klas kunt toepassen. Een eenvoudige priemtest uit de cursus kan bijvoorbeeld een groot natuurlijk getal snel ‘ontmaskeren’ als nietpriemgetal, zonder dat we moeizaam naar een deler hebben moeten zoeken en zelfs zonder dat we er een deler van kennen! Je kunt hierbij gebruikmaken van ICT. Verder kun je laten zien hoe dit soort wiskunde in het dagelijks internetverkeer wordt gebruikt.
De vakantiecursus 2024 heeft als thema groepentheorie, met als toepassing de Banach-Tarskiparadox. Op vrijdag geeft dr. Jeroen Spandaw (TU Delft) een inleiding in de groepentheorie. Hierbij zullen we veel eenvoudige, maar inzicht verscha`ende, concrete voorbeelden ‘doorrekenen’ om de abstracte begrippen uit de theorie betekenis te geven. De deelnemers zullen ook zelf aan de slag gaan met opgaven die hen zullen helpen om vertrouwd te raken met die begrippen. We maken daarbij gebruik van het computerprogramma GAP, waarmee snel gerekend kan worden in groepen. Op zaterdag zal prof. dr. Stefaan Vaes (KU Leuven) ons in een prettig rustig tempo door het bewijs van de verblu`ende Banach-Tarski-paradox leiden. Gebruikmakend van de groepentheorie die we ons op vrijdag eigen hebben gemaakt, zal hij laten zien dat een eenheidsbol in 5 disjuncte delen kan worden opgedeeld, die vervolgens via rotaties
De vakantiecursus 2024 heeft als thema groepentheorie, met als toepassing paradox. Op vrijdag geeft dr. Jeroen Spandaw (TU Delft) een inleiding in de Hierbij zullen we veel eenvoudige, maar inzicht verscha`ende, concrete voorbeelden ‘doorrekenen’ om de abstracte begrippen uit de theorie betekenis te geven. zullen ook zelf aan de slag gaan met opgaven die hen zullen helpen om vertrouwd die begrippen. We maken daarbij gebruik van het computerprogramma GAP, gerekend kan worden in groepen. Op zaterdag zal prof. dr. Stefaan Vaes (KU prettig rustig tempo door het bewijs van de verblu`ende Banach-Tarski-paradox Gebruikmakend van de groepentheorie die we ons op vrijdag eigen hebben zien dat een eenheidsbol in 5 disjuncte delen kan worden opgedeeld, die
Je vindt trouwens al het lesmateriaal (presentaties en syllabus) van de vorige edities, dus ook het materiaal dat in dit artikel besproken werd, op de website van Platform Wiskunde Nederland. Een schat aan interessante wiskunde! Voor wie dus niet kan wachten tot 6 en 7 september in Antwerpen: ga zeker kijken op https:// platformwiskunde.nl/vakantiecursus/
Inschrijven kan tot 31 juli 2024 via https:// platformwiskunde.be/evenementen/
21
CYCLISCH LIJNSPIEGELEN
STEL DAT JE DE HOEKPUNTEN VAN EEN DRIEHOEK ∆ ABC ALS VOLGT (LIJN)
SPIEGELT: WE SPIEGELEN A OM DE RECHTE BC, B OM DE RECHTE AC EN C
OM DE RECHTE AB. DE BEELDPUNTEN NOEMEN WE ACHTEREENVOLGENS
A', B' EN C'. HOE KAN JE, GEGEVEN DRIEHOEK ∆ A'B'C', DE DRIEHOEK ∆ ABC TERUGVINDEN?
ILSE DE BOECK IS LERARENOPLEIDER AAN DE THOMAS MORE HOGESCHOOL TE VORSELAAR.
EEN MERKWAARDIGE FIGUUR
In Wiskunde en Onderwijs 167 verscheen een artikel van L. Gheysens en D. Tant rond een puntspiegelprobleem (Gheysens, Een driehoeksprobleem, 2016). Het probleem gaat als volgt. Gegeven een driehoek ∆ ABC Je spiegelt A om B, B om C en C om A. Het resultaat is de driehoek ∆ A'B'C' Hoe kan je, gegeven de driehoek ∆ A'B'C' de oorspronkelijke driehoek ∆ ABC terugvinden?
L. Gheysens en D. Tant beschrijven in hun artikel verschillende oplossingswijzen. De oplossing is uniek bepaald. Je zou je dan de vraag kunnen stellen of dit ook voor andere transformaties geldt. Wat zou er bijvoorbeeld gebeuren indien je het puntspiegelen zou vervangen door lijnspiegelen? Dat geeft de bovenstaande probleemstelling.
Ik zal deze manier van spiegelen in het vervolg cyclisch lijnspiegelen noemen.
EEN EIGENAARDIGE VASTSTELLING
Een beetje experimenteren met GeoGebra leert dat de oplossing niet eenduidig bepaald is. Zelfs in het eenvoudige geval van een gelijkzijdige beelddriehoek ∆ A'B'C' zijn er meerdere oplossingen mogelijk. Je zou in eerste instantie verwachten dat de oorspronkelijke driehoek ∆ ABC dan de driehoek is, gevormd door de middens van de zijden van driehoek ∆ A'B'C'. Figuur 1 laat echter zien dat er minstens zeven verschillende driehoeken zijn die je cyclisch kan lijnspiegelen op de driehoek ∆ A'B'C'
De blauwe driehoek ∆ ABC is de gelijkzijdige driehoek waarvan vertrokken werd. De rode driehoek ∆ A'B'C' is het beeld van driehoek ∆ ABC door een cyclische lijnspiegeling. Maar deze driehoek is eveneens het beeld van de geel gearceerde en van de geel gekleurde gelijkbenige driehoeken ∆ IJF, ∆ DJK, ∆ KGI, ∆ IFG, ∆ FJD en ∆ GDK
Het kan een mooie opdracht zijn om uit te vissen hoe deze figuur in elkaar zit … een sangaku als het ware. We geven hierna de hoofdlijnen van de redenering weer. We starten met uit te leggen hoe de constructie in elkaar zit. (zie figuur 1)
CONSTRUCTIE VAN DE 7 DRIEHOEKEN
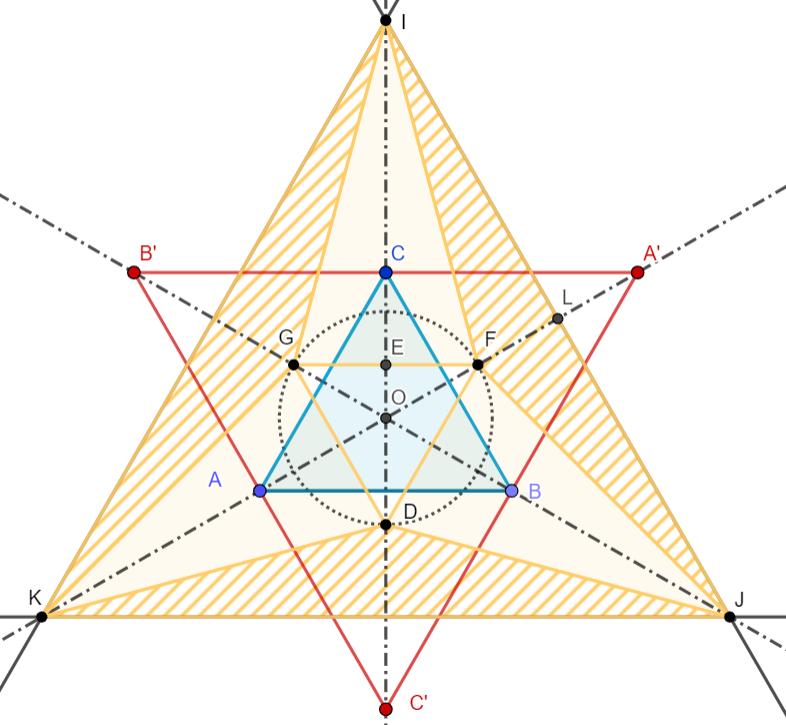
Veronderstel dat je start vanuit de gelijkzijdige driehoek ∆ A'B'C' met zijde Z en hoogte H. Driehoek ∆ ABC is dan de driehoek gevormd door de middens van de zijden van driehoek ∆ A'B'C'. Het is eenvoudig om in te zien dat driehoek ∆ ABC opnieuw gelijkzijdig is met zijde en hoogte . Bovendien is het spiegelbeeld van A om de rechte BC gelijk aan A', het spiegelbeeld van B om de rechte AC gelijk aan B' en het spiegelbeeld van C om de rechte AB gelijk aan C'. Dat betekent dat driehoek ∆ ABC cyclisch gelijnspiegeld wordt op driehoek ∆ A'B'C'
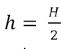
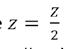
VVWL 22
Figuur 1: de zeven mogelijke driehoeken die via cyclisch lijnspiegelen afgebeeld worden op driehoek
Figuur 1 De zeven mogelijke driehoeken die via cyclisch lijnspiegelen afgebeeld worden op driehoek ∆ A'B'C'.
∆����′����′����′
Er zijn echter nog meer verbanden tussen beide driehoeken. Aangezien de hoogtelijnen van beide driehoeken samenvallen, hebben driehoek ∆ ABC en ∆ A'B'C' hetzelfde hoogtepunt O. De stelling van Pythagoras leert ons dat de hoogte h van een gelijkzijdige driehoek met zijde z gelijk is aan . Bovendien weten we dat in gelijkzijdige driehoeken het hoogtepunt eveneens zwaartepunt en middelpunt is van de in- en
Constructie van de 7 driehoeken
hoek, driehoek ∆ DGF en driehoek ∆ IJK. Beide driehoeken zijn gelijkzijdig.
Veronderstel dat je start vanuit de gelijkzijdige driehoek ∆����′����′����′ met zijde ���� en hoogte ���� . Driehoek
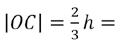
∆������������ is dan de driehoek gevormd door de middens van de zijden van driehoek ∆����′����′����′. Het is eenvoudig om in te zien dat driehoek ∆������������ opnieuw gelijkzijdig is met zijde ���� = " # en hoogte ℎ = $ # .
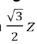
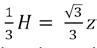
omgeschreven cirkels van de driehoek. Het verdeelt dus elke hoogtelijn in twee lijnstukken waarvan het ene dubbel zo lang is als het andere. Dat betekent dat bv. , waarbij we O zowel als hoogtepunt van driehoek ∆ ABC als van driehoek ∆ A'B'C' beschouwd hebben.
Bovendien is het spiegelbeeld van ���� om de rechte �������� gelijk aan ����! , het spiegelbeeld van ���� om de rechte �������� gelijk aan ����! en het spiegelbeeld van ���� om de rechte �������� gelijk aan ���� ! Dat betekent dat driehoek ∆������������ cyclisch gelijnspiegeld wordt op driehoek ∆����′����′����′.
We beschrijven nu de constructie van de kleine en de grote gele drie-
Er zijn echter nog meer verbanden tussen beide driehoeken. Aangezien de hoogtelijnen van beide driehoeken samenvallen, hebben driehoek ∆������������ en ∆����′����′����′ hetzelfde hoogtepunt ���� . De stelling van Pythagoras leert ons dat de hoogte ℎ van een gelijkzijdige driehoek met zijde ���� gelijk is aan √& # ���� .
De zijde van de kleine gelijkzijdige driehoek ∆ DGF noemen we z' en de hoogte h'. Deze driehoek heeft eveneens O als hoogtepunt. We kunnen de zijde z' van deze driehoek als volgt vinden. Omdat het beeld van F door de spiegeling om de rechte DJ gelijk is aan C', is |DC'| = |DF| = z'. Dan is enerzijds |CC'| = H =
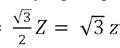
Bovendien weten we dat in gelijkzijdige driehoeken het hoogtepunt eveneens zwaartepunt en middelpunt is van de in- en omgeschreven cirkels van de driehoek. Het verdeelt dus elke hoogtelijn in twee lijnstukken waarvan het ene dubbel zo lang is als het andere. Dat betekent dat bv. |�������� | = # & ℎ =
23
En anderzijds is |CC'| = |CO| + |OD| + |DC'| =

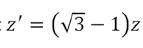
Gelijkstellen en oplossen naar z' levert . De bijbehorende hoogte h' is dan , wat ook gelijk is aan


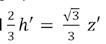
Omdat de hoogte z' is en O het hoogtepunt, kunnen we D bepalen door het snijpunt te nemen van de cirkel met middelpunt O en straal met de rechte CO. De snijpunten van de cirkel met de twee andere hoogtelijnen leveren de punten G en F
Op analoge manier construeren we de gelijkzijdige driehoek ∆ IJK met hoogtepunt O en zijde
|A'L| = |LF| omdat (1)
De verklaring waarom SIF(J) = C' is analoog aan die waarom SJF(I) = B' We tonen daarom enkel de eerste gelijkheid aan.
Voor SIF(J) = C' tonen we eerst aan dat en I en F beide op de middelloodlijn van het lijnstuk [EL] liggen.
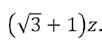
Z' = . De hoogte H' is dan of ook
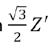
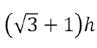
VERKLARING WAAROM DE GEEL
GEARCEERDE DRIEHOEKEN VOLDOEN
We leggen nu uit waarom de drie geel gearceerde driehoeken ∆ IJF, ∆ JDK en ∆ KIG cyclisch gelijnspiegeld worden op de driehoek ∆ A'B'C' Omwille van de symmetrie is het voldoende om dit voor één van de drie te doen, bijvoorbeeld driehoek ∆ IJF.
We merken eerst op dat deze driehoek gelijkbenig is. Punt F ligt immers op de rechte OK die hoogtelijn is in driehoek ∆ IJK en dus ook middelloodlijn van de zijde [IJ].
Dan is: SIJ(F) = A' want de rechte A'F staat loodrecht op de rechte IJ en
Uit (zie (1)) volgt dat |EF| = |LF| (2) en dus
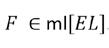
Uit (3) en volgt dat
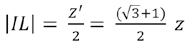
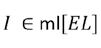
Dus is EF = ml [EL] en bijgevolg ook bissectrice van EÎL, de tophoek van de gelijkbenige driehoek ∆ EIL
Omdat is driehoek C'IJ gelijkbenig met top I. De rechte IF, de bissectrice van de tophoek EÎL, is dan ook middelloodlijn van de basis [C'J]. En dus geldt dat SIF(J) = C'
24
VERKLARING WAAROM DE GEEL
GEKLEURDE DRIEHOEKEN VOLDOEN
Ook hier volstaat het om de bewering aan te tonen voor één van de driehoeken, bijvoorbeeld driehoek ∆ IFG. Uit de symmetrie volgt dat deze driehoek gelijkbenig is.
Omdat de rechte IE loodrecht staat op de rechte GF, (zie (3)) en
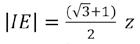
volgt dat SGF(I) = C'.
Aantonen dat SIF(G) = A' en SIG(F) = B' verloopt opnieuw analoog.
Omdat SIJ(F) = A', is IJ = ml [A'F] en dus |A'I| = |FI| = |GI|. Dat betekent dat I op de middelloodlijn van [A'G] ligt.
Bovendien is |GF| = 2|EF| = 2|FL| (zie (2)) zodat |GF| = |FA'| en ook F op de middelloodlijn van [A'G] ligt.
REFERENTIES
Gheysens, L. T. (2016). Een driehoeksprobleem. Wiskunde & Onderwijs 167, pp. 229-230. Gheysens, L. T. (2017). Reacties op een driehoeksprobleem. Wiskunde & Onderwijs 169, pp. 65-67.
Dit artikel komt uit Wiskunde en Onderwijs - VVWL.
L. T. (2016). Een driehoeksprobleem. Wiskunde & Onderwijs 167, pp. 229-230. Gheysens, L. T. (2017). Reacties op een driehoeksprobleem.

OEFENING 5
VlaamseWiskundeOlympiade2023–2024:tweederonde
Bijgevolg is IF = ml [A'G] waardoor SIF(G) = A'
CONCLUSIE
1. DewoonkamervanRogerPersoneisbetegeldmetkleine regelmatigezeshoekigetegels.Rogerlegtereennieuwe vloeropmetgrotezeshoekigetegels.Elkhoekpuntvan eengrotetegelvaltnusamenmethetmiddelpuntvan eenkleinetegelzoalsindefiguur.Watisdeverhouding tussendeoppervlaktevaneenkleinetegelendievaneen grotetegel?
Er blijken dus minstens 7 driehoeken te zijn die cyclisch gelijnspiegeld kunnen worden op een gegeven gelijkzijdige driehoek. De vraag blijft of dit de enige zijn. En wat gebeurt er bij gelijkbenige driehoeken? Of bij rechthoekige driehoeken?
Uit de vorige paragrafen volgt in elk geval al dat, als je vertrekt van een gelijkbenige driehoek met basishoeken van 75° of 15°, er ook minstens 6 driehoeken zijn met hetzelfde beeld. Geldt dat ook bij andere gelijkbenige driehoeken? Hoeveel mogelijkheden zijn er dan? Misschien iets om verder over na te denken?
VlaamseWiskundeOlympiade2023–2024:tweederonde
VlaamseWiskundeOlympiade2023–2024:tweederonde
VlaamseWiskundeOlympiade2023–2024:tweederonde
VlaamseWiskundeOlympiade2023–2024:tweederonde
1. DewoonkamervanRogerPersoneisbetegeldmetkleine regelmatigezeshoekigetegels.Rogerlegtereennieuwe vloeropmetgrotezeshoekigetegels.Elkhoekpuntvan eengrotetegelvaltnusamenmethetmiddelpuntvan eenkleinetegelzoalsindefiguur.Watisdeverhouding tussendeoppervlaktevaneenkleinetegelendievaneen grotetegel?
1. DewoonkamervanRogerPersoneisbetegeldmetkleine regelmatigezeshoekigetegels.Rogerlegtereennieuwe vloeropmetgrotezeshoekigetegels.Elkhoekpuntvan eengrotetegelvaltnusamenmethetmiddelpuntvan eenkleinetegelzoalsindefiguur.Watisdeverhouding tussendeoppervlaktevaneenkleinetegelendievaneen grotetegel?
1. DewoonkamervanRogerPersoneisbetegeldmetkleine regelmatigezeshoekigetegels.Rogerlegtereennieuwe vloeropmetgrotezeshoekigetegels.Elkhoekpuntvan eengrotetegelvaltnusamenmethetmiddelpuntvan eenkleinetegelzoalsindefiguur.Watisdeverhouding tussendeoppervlaktevaneenkleinetegelendievaneen grotetegel?
Vlaamse Wiskunde Olympiade vzwTweede Ronde VWO 2023-2024, vraag 3
VlaamseWiskundeOlympiade2023–2024:tweederonde
1. DewoonkamervanRogerPersoneisbetegeldmetkleine regelmatigezeshoekigetegels.Rogerlegtereennieuwe vloeropmetgrotezeshoekigetegels.Elkhoekpuntvan eengrotetegelvaltnusamenmethetmiddelpuntvan eenkleinetegelzoalsindefiguur.Watisdeverhouding tussendeoppervlaktevaneenkleinetegelendievaneen grotetegel?
De woonkamer van Roger Persone is betegeld met kleine regelmatige zeshoekige tegels. Roger legt er een nieuwe vloer op met grote zeshoekige tegels. Elk hoekpunt van een grote tegel valt nu samen met het middelpunt van een kleine tegel zoals in de figuur. Wat is de verhouding tussen de oppervlakte van een kleine tegel en die van een grote tegel?
1. DewoonkamervanRogerPersoneisbetegeldmetkleine regelmatigezeshoekigetegels.Rogerlegtereennieuwe vloeropmetgrotezeshoekigetegels.Elkhoekpuntvan eengrotetegelvaltnusamenmethetmiddelpuntvan eenkleinetegelzoalsindefiguur.Watisdeverhouding tussendeoppervlaktevaneenkleinetegelendievaneen grotetegel?
2. Eencirkelmetstraal2eneencirkelmetstraal3hebben hetzelfdemiddelpunt M zoalsindefiguur.Detweegekleurdegebiedenhebbendezelfdeoppervlakte.Hoegroot isdehoek α?
2. Eencirkelmetstraal2eneencirkelmetstraal3hebben hetzelfdemiddelpunt M zoalsindefiguur.Detweegekleurdegebiedenhebbendezelfdeoppervlakte.Hoegroot isdehoek α?
2. Eencirkelmetstraal2eneencirkelmetstraal3hebben hetzelfdemiddelpunt M zoalsindefiguur.Detweegekleurdegebiedenhebbendezelfdeoppervlakte.Hoegroot isdehoek α?
2. Eencirkelmetstraal2eneencirkelmetstraal3hebben hetzelfdemiddelpunt M zoalsindefiguur.Detweegekleurdegebiedenhebbendezelfdeoppervlakte.Hoegroot isdehoek α?
2. Eencirkelmetstraal2eneencirkelmetstraal3hebben hetzelfdemiddelpunt M zoalsindefiguur.Detweegekleurdegebiedenhebbendezelfdeoppervlakte.Hoegroot isdehoek α?
2. Eencirkelmetstraal2eneencirkelmetstraal3hebben hetzelfdemiddelpunt M zoalsindefiguur.Detweegekleurdegebiedenhebbendezelfdeoppervlakte.Hoegroot isdehoek α?
25
|�������� | = |��������| + |�������� | = ' & ℎ + # & ���� = ' & ;√3 1>ℎ + * & ℎ = √&0') # ���� = |�������� , volgt dat ����1+ (����) = ����′ Aantonen dat ����(+(����) ����′ en ����(1(����) ���� verloopt opnieuw analoog. Omdat ����()(����) = ���� is �������� = ml [���� ����] en dus |���� ����| = |��������| = |��������| Dat betekent dat ���� op de middelloodlijn van [���� ����] ligt. Bovendien is |��������| 2|��������| 2|��������| (zie (2) zodat |��������| |�������� | en ook ���� op de middelloodlijn van [���� ����] ligt. Bijgevolg is �������� ml [����!����] waardoor ����(+(����) ���� Conclusie Er blijken dus minstens 7 driehoeken te zijn die cyclisch gelijnspiegeld kunnen worden op een gegeven gelijkzijdige driehoek. De vraag blijft of dit de enige zijn. En wat gebeurt er bij gelijkbenige driehoeken? Of bij rechthoekige driehoeken? Uit de vorige paragrafen volgt in elk geval al dat, als je vertrekt van een gelijkbenige driehoek met basishoeken van 75° of 15° er ook minstens 6 driehoeken zijn met hetzelfde beeld. Geldt dat ook bij andere gelijkbenige driehoeken? Hoeveel mogelijkheden zijn er dan? Misschien iets om verder over na te denken? Referenties Gheysens,
Wiskunde & Onderwijs 169, pp. 65-67.
©
(A) 1 6 (B) 1 5 (C) 1 4 (D) 1 3 (E) 1 2
M α A B C D E
(A)
6 (B) 1 5 (C) 1 4 (D) 1 3 (E)
1
M
(A)
6 (B) 1 5 (C) 1 4 (D) 1 3 (E) 1 2
1
M α
(A) 1 6 (B) 1 5 (C) 1 4 (D) 1 3 (E) 1 2
M α
(A) 1 6 (B) 1 5 (C) 1 4 (D) 1 3 (E) 1 2
M α
(A)
(C)
(D)
(E)
1 6 (B) 1 5
1 4
1 3
1 2
M α
JuniorWiskundeOlympiade2023–2024:tweederonde
OEFENING 6
Viervierkantenzijnmetdehoekpuntenaanelkaarbevestigd zoalsindefiguur.Hoegrootisdesomvandeaangeduide
Vier vierkanten zijn met de hoekpunten aan elkaar bevestigd zoals in de figuur. Hoe groot is de som van de aangeduide hoeken?
OEFENING 7
OEFENING 8
Eeneersterechthoekheeftbreedte3enlengte4.Eentweede,gelijkvormigerechthoek heefteendiagonaalmetlengte15.Watisdeomtrekvandietweederechthoek?
Kleurenblinde Klaas bezoekt een eiland met elf bewoners: rode raven en groene gaaien. De rode raven liegen altijd en de groene gaaien spreken altijd de waarheid. Klaas vraagt aan elk van de elf bewoners: “Hoeveel groene gaaien wonen er op dit eiland?” De antwoorden zijn: drie, twee, vijf, zeven, drie, vier, vier, drie, vijf, nul en acht. Hoeveel rode raven wonen er op het eiland?
(A)14(B)21(C)28(D)42(E)48
Mieke en Dennis lopen rondjes op een looppiste aan constante snelheid, maar in tegengestelde zin. Ze doen elk exact één minuut over een rondje. Naast de piste staat een klok. De secondewijzer wijst 18 seconden aan telkens als Mieke de klok passeert en 32 seconden telkens als Dennis de klok passeert. Hoeveel seconden wijst de secondewijzer aan telkens als Mieke en Dennis elkaar passeren?
Inklas4Dzitten30leerlingen:12jongensen18meisjes.MevrouwDeschampsmerkt naeentoetshetvolgendeop:“Invergelijkingmetdevorigetoetsishetgemiddeldevan dejongensmet2puntengedaaldendatvandemeisjesmet2puntengestegen.”Dan ishetgemiddeldevandevolledigeklasinvergelijkingmetdevorigetoets
(A)gelijkgebleven
(C)met0,5puntengestegen
(E)met1puntgestegen
(B)met0,4puntengestegen
altijd 50 ofwel 20, ofwel 50 altijd 25 D E
ofwel 25, ofwel 55 ofwel 7, ofwel 37
(D)met0,6puntengestegen
© Junior Wiskunde Olympiade vzwTweede Ronde JWO 2023-2024, vraag 28 A B C
© Junior Wiskunde Olympiade vzwTweede Ronde JWO 2023-2024, vraag 1
(B)270° (C)300° (D)360° (E)450°
7+ a © Junior Wiskunde Olympiade vzwTweede Ronde JWO 2023-2024, vraag
A B C D E 180° 270° 300° 360° 450° A B C 6 7 8 D E 9 10
18
26
ishetgemiddeldevandevolledigeklasinvergelijkingmetdevorigetoets
(A)gelijkgebleven
(C)met0,5puntengestegen
(E)met1puntgestegen
OEFENING 9
(B)met0,4puntengestegen
(D)met0,6puntengestegen
4. Eenrechthoekigtrapeziummetkleinebasis4engrote basis8wordtdooreendiagonaalintweeverdeeld.De verhoudingtussendeoppervlaktevanhetgrootstedeel endievanhetkleinstedeelis
Een rechthoekig trapezium met kleine basis 4 en grote basis 8 wordt door een diagonaal in twee verdeeld. De verhouding tussen de oppervlakte van het grootste deel en die van het kleinste deel is.
afhankelijk van de hoogte van het trapezium
(D)4 (E)afhankelijkvandehoogtevanhettrapezium
OEFENING 10
© VlaamseWiskundeOlympiadevzw
Met a en b uit {1, 2, 3, 4, 5, 6, 7, 8, 9} construeren we twee getallen: de breuk a b en het decimale getal b,a.
Zo is bijvoorbeeld voor a = 3 en b = 4 het ene getal 3 4 en het andere getal 4,3.
In hoeveel gevallen is de breuk a b gelijk aan het decimale getal b,a ?
Voor een groot feest met 2024 genodigden bakt oma Arlette vier soorten taartjes. Omdat ze de voorkeur van de genodigden niet kent, bakt ze er van elke soort evenveel. Iedere genodigde mag één taartje nemen. Oma Arlette wil ervoor zorgen dat iedereen uit minstens twee soorten taartjes kan kiezen, zelfs de genodigde die als laatste kiest. Hoeveel taartjes moet ze dan minstens van elke soort bakken? OEFENING 11
© Vlaamse Wiskunde Olympiade vzwTweede Ronde VWO 2023-2024, vraag 4
© Vlaamse Wiskunde Olympiade vzwTweede Ronde VWO 2023-2024, vraag 11 A B C D 1 1,5 2 4 E
(A)1
(C)2
4 8
(B)1,5
A B C D E 0 1 2 3 4
© Vlaamse Wiskunde Olympiade vzwTweede Ronde VWO 2023-2024, vraag 30 A B C D E 506 507 674 675 1012 27
PYTHAGORAS
GO SPELEN:
OP JE TELLEN PASSEN
GO IS EEN VAN ORIGINE OOSTERS BORDSPEL. HET IS AL HEEL OUD, EN TOCH IS IEDERE PARTIJ DIE JE SPEELT NIEUW EN OPWINDEND. GO IS MINSTENS
ZO DIEP ALS SCHAKEN – SINDS KORT (MEDIO 2016) KUNNEN ALLEEN
COMPUTERPROGRAMMA’S ZOALS ALPHAGO ONS MENSEN VERTELLEN HOE HET EIGENLIJK GESPEELD ZOU MOETEN WORDEN. MAAR OOK ZONDER ZELF
EEN COMPUTER TE ZIJN KAN JE ER VEEL PLEZIER AAN BELEVEN.
LEO DORST
De regels van go zijn zo simpel dat er interessante wiskundige structuren in naar voren komen.
1. Go wordt gespeeld op een vierkant bord, met doorgaans 19 × 19 kruispunten in een raster. Maar kleiner is voor beginners misschien wel prettiger.
2. Om beurten plaatsen de twee spelers (zwart en wit) een go-steen op een kruispunt; die steen blijft daar verder staan (tenzij hij geslagen wordt, zie regel 4). De go-stenen zien er uit als Mentos, in diagrammen worden ze getekend als zwarte en witte cirkels.
3. Wie de meeste stenen kan neerzetten wint. (In de praktijk zijn er wat manieren om overeen te komen eerder te stoppen als de eindstand wel duidelijk is en dan de uitkomst te tellen.)
4. Maar: stenen van dezelfde kleur vormen ketens, verbonden via de lijntjes van het raster; zo’n
keten vormt één geheel. Een keten zonder vrije naastliggende kruispunten (dat heten vrijheden) mag niet op het bord blijven liggen. Als je een zet doet die de laatste vrijheid van een keten (van de tegenstander) wegneemt, dan moet je die keten van het bord verwijderen. Stenen zonder vrijheden mogen niet op het bord staan (behalve dus heel even tijdens het ‘slaan’ van stenen van de tegenstander).
5. Een bordpositie mag tijdens een partij niet herhaald worden.
Hoewel je dus individuele stenen plaatst, zijn de ontstane ketens en hun vrijheden eigenlijk de basiseenheden van het spel. Laten we een voorbeeld doen, op een klein stukje bord (voor een kleine partij, zie rrehm.home.xs4all.nl/ dropjes.pdf).




De witte keten van twee stenen in 1a heeft nog twee vrijheden. Zwart en wit spelen nu wat zetten 1 , 2 , 3 in 1b. Oeps! De witte keten van twee stenen wordt geslagen door zwart, door 3 . Daardoor ontstaat de positie in 1c
Wit heeft nu minder stenen op het bord, dus dat kost punten! Wit had er wel iets tegen kunnen doen, zet 2
28
in 1b was niet zo handig. Liever 2 in 1d, daarmee krijgt wit twee vrijheden en dreigt zelfs een zwarte steen te slaan (door op het punt van 3 te spelen). Zwart heeft dat verdedigd door met 3 die steen te verlengen tot een keten van twee stenen (met drie vrijheden).
Voor de duidelijkheid: een keten met maar één vrijheid (we zeggen dat die ‘atari staat’) kan bij de volgende zet geslagen worden (als regel 5 dat toestaat), zelfs als je daarvoor zelf even een keten zonder vrijheden op het bord krijgt tijdens het zetten.




Dus in stelling 2a mag zwart op het middenpunt spelen 2b en slaat dan de witte groep 2c. Maar in 2d mag dat niet, zwart moet eerst de zet van buitenaf spelen zodat wit echt nog maar één vrijheid heeft.
Dat is genoeg over de regels, we gaan nu vechten! Een lokaal gevecht ontstaat als twee groepen elkaar aan het omsingelen zijn. Wie is er eerder bij en kan de andere slaan? Dat blijkt nog behoorlijk subtiel te kunnen worden: een keten kan veel meer vrijheden hebben dan op het eerste gezicht lijkt. Zelfs ‘kwadratisch veel meer’! Dat afleiden is het doel van dit artikel.1
Bij het oplossen van dit soort wiskundige telproblemen is het gebruikelijk om ‘recursie’ te gebruiken. Je beziet of je een ingewikkelder situatie kan reduceren tot iets eenvoudigers, en die tot nog eenvoudiger, totdat je hem kunt oplossen. En je houdt bij hoeveel zetten je steeds moet doen voor die reductie; aan het eind tel je alles op. Bijvoorbeeld, als zwart een witte keten met drie interne vrijheden helemaal heeft omsingeld, heeft hij dan ook drie zetten nodig om hem van het bord te halen? In ieder geval op zijn minst drie, zoals de diagrammen 3a-c laten zien:



Wit heeft intussen op drie plaatsen elders op het bord kunnen spelen met 2 , 4 , 6 (totdat zwart weer aan zet is) en misschien waren dat wel heel nuttige zetten voor haar. Het nemen van de witte keten houdt zwart dus in feite drie zetten bezig. Maar misschien had wit zich nog beter kunnen verweren, bijvoorbeeld na zwart 3 ?


29





Je begint met zwart 1 in 4b; als wit nu een eigen vrijheid bezet met 2 dan kan je de keten pakken met 3 ; dus wit kan zet 2 beter ergens anders op het bord spelen. Dan zet je zwart 3 , en nu zou je met de volgende zet de witte keten kunnen slaan, want zij heeft nog maar één vrijheid. Wit voorkomt dat door jou
te slaan met 4 in 4b, zo ontstaat 4c Daarna kom je terug met 5 in 4d, weer staat wit ‘atari’. In de volgende zet kan zwart wit pakken; zelfs als wit nog even met 6 slaat in 4d, dan nog is zwart 7 in 4f de doodsklap. Maar je ziet dat wit nu maar twee keer elders op het bord heeft kunnen spelen, met 2 en 4 , dus dit is een minder goede mogelijkheid voor wit dan wat er in 3a-c gebeurde. Overigens: je kunt het als zwart ook goed fout doen! Dat zie je in 5a-c:



Als zwart begint 1 in 5b, dan slaat wit 2 de zwarte steen. Nu ontstaat een stelling in 5c waarin zwart niet op de twee laatste vrijheden kan (of mag) spelen: hij zou dan een steen op het bord zetten die geen vrijheden heeft, en zonder dat hij daarmee de laatste vrijheid van een witte keten wegneemt. De witte keten die is ontstaan in 5c kan
niet geslagen worden: we zeggen dat een keten met twee ogen ‘leeft’. Dat soort levende ketens worden eigenlijk de eenheden waarin je denkt als je go speelt; het zijn als het ware je (schaak)stukken, maar je maakt ze zelf en ze zijn iedere keer weer anders. Het is esthetisch wel bevredigend om te zien dat deze grotere denkeenheden vanzelf ontstaan uit de spelregels op het niveau van ketens en vrijheden...
Bij drie binnenvrijheden zijn er dus drie zetten nodig, dat lijkt logisch, want terloops zagen we in 4c-g dat bij twee vrijheden twee zetten nodig zijn, en in 4e-g dan één vrijheid ook één zet kost. Voor vier binnenvrijheden dus vier zetten?
Laten we eens kijken naar 6a, zo’n keten met vier binnenvrijheden.



We beginnen met volzetten met zetten 1 , 3 , 5 (terwijl wit dus
30
twee zetten ergens anders speelt). Nu staat wit atari en moet wit dus reageren met 6 . Daardoor slaat wit zwart en ontstaat 6c. Hee, dit herkennen we, dat is precies wat we eerder hebben gezien: drie binnenvrijheden, dus drie zetten. In totaal heeft wit vijf zetten ergens anders kunnen spelen voordat hij werd geslagen, dus om vier binnenvrijheden op te vullen heb je vijf zetten nodig.
Hoe gaat dit verder? Je kunt het spelenderwijs ontdekken, maar je kunt ook wiskundig gaan denken. En dat doen we in Vector natuurlijk!
Bij een aantal van n vrijheden zijn er steeds n − 1 zetten nodig om atari te zetten, waar wit dan meteen op reageert door te slaan; dus heeft wit n − 2 zetten elders kunnen doen. Vervolgens ontstaat een keten met n − 1 binnenvrijheden. Het proces herhaalt zich dan: dat is nou recursie Dus als we met Z n aangeven ‘het aantal zetten dat zwart nodig heeft om een keten met n binnenvrijheden te slaan’, dan hebben we de recursieve formule:
Z n = (n − 2) + Zn−1
En bovendien weten we dat Z3 = 3, want zo waren we begonnen.2
Iets wat lineair groeit (want de verandering Z n − Zn−1 = n − 2 hangt gestaag af van n) moet zelf kwadratisch zijn. We stellen daarom Z n = an2 + bn + c, en met wat rekenwerk krijgen we:
Z n − Zn−1 = (an2 + bn + c) − a(n − 1) 2 + b(n − 1) + c = 2 an − a + b.
Dat moet gelijk zijn aan n − 2, dus a = , b = − . Als we dan
invullen dat Z3 gelijk aan 3 moet zijn, dan leren we wat c is. We vinden uiteindelijk:
Z n = n2 − n + 3.
In de tabel staat wat de formule geeft voor een opeenvolging van waarden van n:

Voor Z3 en Z4 klopt de formule alvast met wat we boven deden, en we leren nu ook dat Z5 = 8 zonder stellingen te hoeven uitspelen. Maar volgens de formule zou je Z1 = 2 zetten nodig hebben om een keten met 1 vrijheid te slaan – en dat is niet waar?! De reden is dat het echte patroon van atari zetten en terugslaan (waarop we de formule baseerden) zich daar nog niet echt heeft gevormd, dat is pas vanaf n = 2 (zie bijvoorbeeld 4c-e). Dat Z0 = 3 is natuurlijk helemaal onzin. De formule heeft dus een beperkte geldigheid, dat is wel vaker zo met dit soort telformules.
En volgens de tabel zou je Z7 = 17 zetten nodig hebben om een keten met 7 vrijheden te slaan; maar als je meer go speelt merk je wel dat zo’n keten ‘te groot’ is om te slaan. Meestal leeft de keten gewoon omdat je twee ogen kunt maken (zoals in figuur 7a,b).

Toch kan er ook nog net een seki ontstaan, dat is een stelling waarbij geen van beide spelers de andere kan slaan. Het is een stelling die niet levend is, maar ook niet dood! Dat gebeurt met de witte keten in 8a, die een nogal rond pleintje van 7 binnenvrijheden heeft. Als wit speelt op dat punt in het midden, dan heeft hij twee ogen en leeft dus. Maar dat hoeft eigenlijk niet, want zwart kan de witte stelling toch niet doden.


n
Z
1 2 3 4 5 6 7
n 2? 2 3 5 8 12 17?
31




We zien 8b hoe wit de sterkste zwarte aanval pareert. De situatie na 8c is stabiel en heeft geen vervolgzet nodig. Zwart kan niet zetten zonder geslagen te worden in 8d; dan ontstaat 8e, een groep met 4 binnenvrijheden op een rij, en die kan altijd leven zoals 8f laat zien.3 Dus kan zwart beter niet aanvallen. Maar aan de andere kant, wit kan in 8c de zwarte stenen niet gaan slaan zonder zichzelf atari te zetten, dus zet ook liever ergens anders. De stelling van 8c is daarmee een soort lokale patstelling, en die zal zo op het bord blijven staan tot het einde van de partij, en dan tel je de stenen die mogen blijven staan (in onze simpele wiskundige variant van de regels, in Japan telt men dit anders). Net als bij ‘twee ogen leeft’ zien we dat de eenvoudige regels van go tot wat verrassingen leiden voor ketens. Het blijkt dus dat de formule voor Z n spaak loopt bij n = 7: er is geen vorm van 7 binnenvrijheden die echt in 17 zetten geslagen kan worden, bij de juiste verdediging. (Tenzij je twee zetten achter elkaar kunt doen, en dat kan voorkomen als er een ‘ko’ op het bord komt – maar dat is een ander verhaal...).
Deze simpele en nette situaties zijn nog wel uit te rekenen. Maar feitelijk omsingelen van de minder strak geformeerde groepjes stenen die in natuurlijke partijen voorkomen is niet makkelijk. Het totale go-spelen vergt heel wat meer, en de ‘vage’ fase van het spel met het plannen waar je jouw groepjes begint om uiteindelijk zo veel mogelijk stenen te mogen plaatsen, is knap lastig. En dus leuk en uitdagend, als je zo in elkaar zit...
Er zijn veel bronnen op het internet om een gevoel te krijgen voor de rijkdom van go, van beginnerscursussen tot becommentarieerde profpartijen, bijvoorbeeld op senseis.xmp.net.
De Nederlandstalige website 312go.org/home heeft een gratis online cursus, omsingelpuzzeltjes (dat heet ‘tsumego’) en voorbeeldpartijen. Speel er eens mee!
Puzzeltje:

Oplossing:


32

OEFENING 12
5. Voorelke r ∈ R noterenwe ⌊r ⌋ voorhetgrootstegehelegetalkleinerdanofgelijkaan r .Zoisbijvoorbeeld ⌊π ⌋ =3.
Defunctie f heeftvoorschrift


r .Zoisbijvoorbeeld ⌊π ⌋ =3.
VOETNOTEN
1 We doen dat aan de rand van het bord (aangeven door de dikke lijn) om ruimte te besparen voor onze diagrammen; het aantal vrijheden voor een punt aan de rand is 3 (want er zijn drie bordpunten via de lijntjes verbonden); maar je kunt de principes die we ontdekken makkelijk overdragen naar een stelling midden op het bord.
Voor elke r 5. Voorelke r ∈ R noterenwe ⌊r ⌋ voorhetgrootstegehelegetalkleinerdanofgelijkaan
r .Zoisbijvoorbeeld ⌊π ⌋ =3.
0 als [2x] even is, 1 als [2x] oneven is.
f (x )= 0als ⌊2x ⌋ evenis, 1als ⌊2x ⌋ onevenis.
5. Voorelke r ∈ R noterenwe ⌊r ⌋ voorhetgrootstegehelegetalkleinerdanofgelijkaan r .Zoisbijvoorbeeld ⌊π ⌋ =3.
Defunctie f heeftvoorschrift f (x )= 0als ⌊2x ⌋ evenis, 1als ⌊2x ⌋ onevenis.
Welkevandevolgendegrafiekenisdievandefunctie f ?
noteren we [r] voor het grootste gehele getal kleiner dan of gelijk aan r . Zo is bijvoorbeeld [π] = 3. De functie f heeft voorschrift f (x) = Welke van de volgende grafieken is die van de functie f ?
Defunctie f heeftvoorschrift f (x )= 0als ⌊2x ⌋ evenis, 1als ⌊2x ⌋ onevenis.
Welkevandevolgendegrafiekenisdievandefunctie f ?
Welkevandevolgendegrafiekenisdievandefunctie f ?
5. Voorelke r ∈ R noterenwe ⌊r ⌋ voorhetgrootstegehelegetalkleinerdanofgelijkaan
Defunctie f heeftvoorschrift f (x )= 0als ⌊2x ⌋ evenis, 1als ⌊2x ⌋ onevenis.
Welkevandevolgendegrafiekenisdievandefunctie f ?
2 Ja, ook dat Z1 = 1, maar er is zo meteen een verrassing.
3 En we vinden dus dat de formule nog subtieler is, want Z4 = 5 geldt niet voor deze keten! Alleen binnenvrijheden tellen is niet voldoende, de ‘vorm’ van de keten doet er ook toe!
6. Degetallen a =44 44 30cijfers en b =33 33 30cijfers bestaanelkuit30keerhetzelfdecijfer.
7. PitunaatverveeltzichenbegintopzijnpapierregelmatigeveelA
6. Degetallen a =44 44 30cijfers en b =33 33 30cijfers bestaanelkuit30keerhetzelfdecijfer.
6. Degetallen a =44 44 30cijfers en b =33 33 30cijfers bestaanelkuit30keerhetzelfdecijfer.
Welkevandeonderstaandeuitsprakeniswaar?
Welkevandeonderstaandeuitsprakeniswaar?
Welkevandeonderstaandeuitsprakeniswaar?
(A)Hetgetal a isdeelbaardoor18.
(A)Hetgetal a isdeelbaardoor18.
(A)Hetgetal a isdeelbaardoor18.
(B)Hetgetal b isdeelbaardoor3,maarnietdoor9.
(B)Hetgetal b isdeelbaardoor3,maarnietdoor9.
(B)Hetgetal b isdeelbaardoor3,maarnietdoor9.
(C)Degetallen a en b zijnbeidedeelbaardoor9.
(C)Degetallen a en b zijnbeidedeelbaardoor9.
(C)Degetallen a en b zijnbeidedeelbaardoor9.
(D)Hetproductvan a en b isdeelbaardoor27.
(D)Hetproductvan a en b isdeelbaardoor27.
(D)Hetproductvan a en b isdeelbaardoor27.
(E)Desomvan a en b isdeelbaardoor9.
(E)Desomvan a en b isdeelbaardoor9.
(E)Desomvan a en b isdeelbaardoor9.
33
(A) 1 2 3 4 1 (B) 1 2 3 1 (C) 1 2 3 4 1 (D) 1 2 3 1 (E) 1 2 3 4 1
© Vlaamse Wiskunde Olympiade vzwTweede Ronde VWO 2023-2024, vraag 3
(A) 1 2 3 4 1 (B) 1 2 3 4 1 (C) 1 2 3 4 1 (D) 1 2 3 4 1 (E) 1 2 3 4 1
(A) 1 2 3 4 1 (B) 1 2 1 (C) 1 2 3 4 1 (D) 1 2 1 (E) 1 2 3 4 1
(A) 1 2 3 4 1 (B) 1 2 3 4 1 (C) 1 2 3 4 1 (D) 1 2 3 4 1 (E) 1 2 3 4 1 B C D E
UITWISKELING
HET PRINCIPE VAN MAMIKON
Het principe van Mamikon
Luc Van den Broeck, redactie Uitwiskeling
IN UITWISKELING 27/3 BESPRAKEN WE HET BOEK ‘THE MATHEMATICAL MECHANIC’ VAN MARK LEVI, WAARIN WE EEN VARIANT VOORSTELDEN VAN HET PRINCIPE VAN CAVALIERI VOOR DE INHOUDSBEREKENING VAN BEPAALDE LICHAMEN, ZOALS DIE VAN EEN TROUWRING. TOEN IK DEZE BIZARRE REDENEERWIJZE VOOR HET EERST ONDER OGEN KREEG, VIEL MIJN MOND WIJD OPEN VAN VERBAZING. DE VOORGESTELDE TECHNIEK WAS INTUÏTIEF ZEER AANNEMELIJK, MAAR TOCH UITTE IK IN DE BIBWIJZERBIJDRAGE EEN VOORZICHTIG WANTROUWEN. DE VISUELE SCHOONHEID VAN DE THEORIE VOND IK ECHTER ONOVERTROFFEN.
LUC VAN DEN BROECK , REDACTIE UITWISKELING
In Uitwiskeling 27/3 bespraken we het boek ‘The mathematical mechanic’ van Mark Levi, waarin we een variant voorstelden van het principe van Cavalieri voor de inhoudsberekening van bepaalde lichamen, zoals die van een trouwring. Toen ik deze bizarre redeneerwijze voor het eerst onder ogen kreeg, viel mijn mond wijd open van verbazing. De voorgestelde techniek was intuïtief zeer aannemelijk, maar toch uitte ik in de bibwijzerbijdrage een voorzichtig wantrouwen. De visuele schoonheid van de theorie vond ik echter onovertroffen.

Een artikel in het tijdschrift Losanges heeft mijn wantrouwen totaal weggenomen. Het principe achter deze inhoudberekening blijkt een naam en een officieel bewijs te hebben. Het brein achter dit principe is de Armeniër Mamikon Mnatsakanian (1942-2021). De uitspraak van de familienaam is een tongtwister. Daarom wordt deze wiskundige meestal bij de voornaam genoemd en spreken we van het principe van Mamikon. Mamikon zette zijn belangrijkste ideeën op punt tijdens zijn vroege jaren aan de universiteit van Jerevan, de hoofdstad van Armenië (1959). Er werd toen geen openbaarheid aan gegeven omdat zijn professoren niet overtuigd waren van de grondige fundering van deze intuïtieve manier om oppervlakten en inhouden te berekenen. Pas in 1981 publiceerde Mamikon een exact bewijs, dat ook lange tijd onopgemerkt is gebleven. Het artikel was immers in het Russisch ge-
Een artikel in het tijdschrift Losanges heeft mijn wantrouwen totaal weggenomen. Het principe achter deze inhoudberekening blijkt een naam en een officieel bewijs te hebben. Het brein achter dit principe is de Armeniër Mamikon Mnatsakanian (1942-2021). De uitspraak van de familienaam is een tongtwister. Daarom wordt deze wiskundige meestal bij de voornaam genoemd en spreken we van het principe van Mamikon. Mamikon zette zijn belangrijkste ideeën op punt tijdens zijn vroege jaren aan de universiteit van Jerevan, de hoofdstad van Armenië (1959). Er werd toen geen openbaarheid aan gegeven omdat zijn professoren niet overtuigd waren van de grondige fundering van deze intuïtieve manier om oppervlakten en inhouden te berekenen. Pas in 1981 publiceerde Mamikon een exact bewijs, dat ook lange tijd onopgemerkt is gebleven. Het artikel was immers in het Russisch geschreven en was uitgegeven door de op wereldvlak minder bekende ‘Armeense academie voor wetenschappen’. In de jaren negentig werden de geschriften van Mamikon ontdekt door Tom Apostol. Dit was het begin van een lange samenwerking tussen de twee wetenschappers, die elkaar sinds 1997 vonden aan het Caltech (California Institute of Technology). Het resultaat van deze jarenlange samenwerking kun je lezen in het boek ‘New Horizons in Geometry’. De visuele methode waarvan Mamikon de uitvinder was, wordt ‘Visual Calculus’ genoemd. Waar gaat het nu over? Wel, Mamikon ontwikkelde een theorie die het in sommige gevallen mogelijk maakt de oppervlakte te berekenen tussen twee krommen zonder gebruik te maken van integralen. Er wordt enkel gesteund op het begrip raaklijn, dat meetkundig gedefinieerd wordt of analytisch door middel van afgeleiden. Stel je voor dat je met een tractor over één van beide krommen rijdt en dat je een maaimachine achter je aan sleept (zie figuur 1). De rechte maaiarm van de maaimachine raakt op elk ogenblik aan de kromme baan die de tractor volgt. Door een technologisch snufje kun je de maaiarm continu verlengen of inkorten tot aan de tweede kromme. Als je de lijnstukken die zo ontstaan allemaal laat vertrekken uit één punt krijg je het ‘gecentreerde veld’ (Eng: tangent cluster). De oppervlakte van het gecentreerde veld is dan gelijk aan de oppervlakte van het ‘afgemaaide veld’ (Eng: tangent sweep).
schreven en was uitgegeven door de op wereldvlak minder bekende ‘Armeense academie voor wetenschappen’. In de jaren negentig werden de geschriften van Mamikon ontdekt door Tom Apostol. Dit was het begin van een lange samenwerking tussen de twee wetenschappers, die elkaar sinds 1997 vonden aan het Caltech (California Institute of Technology). Het resultaat van deze jarenlange samenwerking kun je lezen in het boek ‘New Horizons in Geometry’. De visuele methode waarvan Mamikon de uitvinder was, wordt ‘Visual Calculus’ genoemd.
Waar gaat het nu over? Wel, Mamikon ontwikkelde een theorie die het in sommige gevallen mogelijk maakt de oppervlakte te berekenen tussen twee krommen zonder gebruik te maken van integralen. Er wordt enkel gesteund op het begrip raaklijn, dat meetkundig gedefinieerd wordt of analytisch door middel van afgeleiden. Stel je voor dat je met een tractor over één van beide krommen rijdt en dat je een maaimachine achter je aan sleept (zie figuur 1). De rechte maaiarm van de maaimachine raakt op elk ogenblik aan de kromme baan die de tractor
De kunst bestaat er nu in om ingewikkelde maaivelden (zoals het inwendige van een hartlijn, de
34
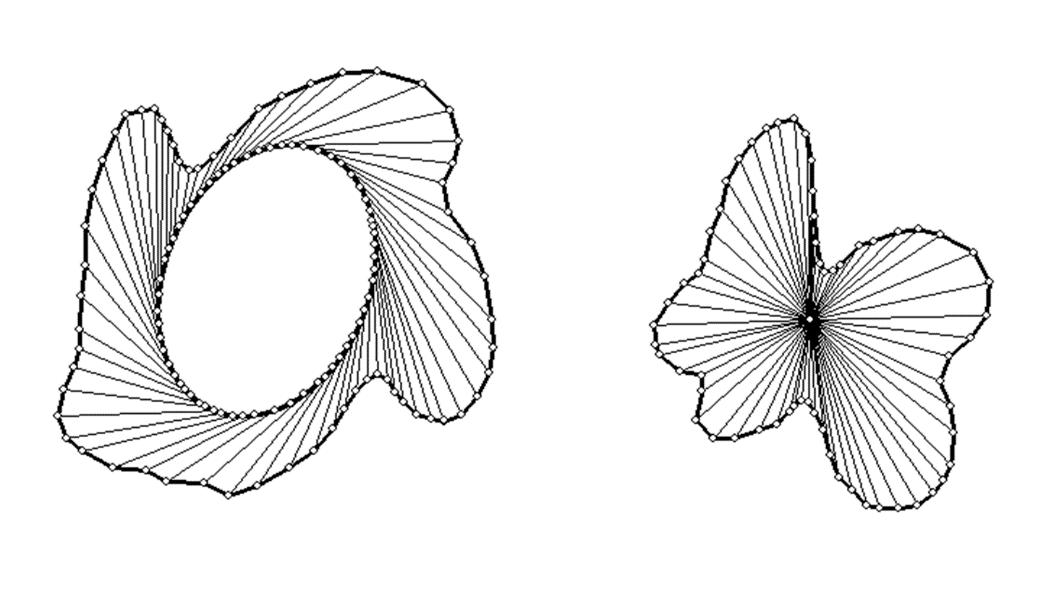
maaiveld tussen twee gesloten krommen

maaiveld tussen twee gesloten krommen gecentreerd maaiveld
Figuur 1
Figuur 1

In figuur 2 tonen we dit principe voor de oppervlakte tussen twee ellipsen, de donkerblauwe en de lichtblauwe ellips op de figuur. Neem een willekeurig punt ���� op de donkerblauwe ellips. De raaklijn aan die ellips in ���� snijdt de andere (lichtblauwe) ellips in ���� . Neem nu een vast punt ���� en verschuif het lijnstuk [�������� ] naar [��������]. Het punt ���� zal dan de groene kromme beschrijven. De oppervlakte tussen de twee ellipsen (links) is dan gelijk aan de oppervlakte binnen de groene kromme (rechts).
Figuur 1. Maaiveld tussen twee gesloten krommen

In figuur 2 tonen we dit principe voor de oppervlakte tussen twee ellipsen, de donkerblauwe en de lichtblauwe ellips op de figuur. Neem een willekeurig punt ���� op de donkerblauwe ellips. De raaklijn aan die ellips in ���� snijdt de andere (lichtblauwe) ellips in ���� . Neem nu een vast punt ���� en verschuif het lijnstuk [�������� ] naar [��������]. Het punt ���� zal dan de groene kromme beschrijven. De oppervlakte tussen de twee ellipsen (links) is dan gelijk aan de oppervlakte binnen de groene kromme (rechts).
In figuur 2 tonen we dit principe voor de oppervlakte tussen twee ellipsen, de donkerblauwe en de lichtblauwe ellips op de figuur. Neem een willekeurig punt op de donkerblauwe ellips. De raaklijn aan die ellips in en verschuif het lijnstuk [ zal dan de groene kromme beschrijven. De oppervlakte tussen de twee ellipsen (links) is dan gelijk aan de oppervlakte binnen de groene kromme (rechts). maaiveld tussen twee gesloten krommen gecentreerd maaiveld
maaiveld tussen twee gesloten krommen gecentreerd maaiveld
Figuur 1
Figuur 1
Figuur 2

Figuur 2
Figuur 2
De oppervlakte onder de sleepkromme
De oppervlakte onder de sleepkromme

In figuur 2 tonen we dit principe voor de oppervlakte tussen twee ellipsen, de donkerblauwe en de lichtblauwe ellips op de figuur. Neem een willekeurig punt op de donkerblauwe ellips. De raaklijn aan die ellips in en verschuif het lijnstuk [�������� ] naar zal dan de groene kromme beschrijven. De oppervlakte tussen de twee ellipsen (links) is dan gelijk aan de oppervlakte binnen de groene kromme


Figuur 2 gecentreerd maaiveld
volgt. Door een technologisch snufje kun je de maaiarm continu verlengen of inkorten tot aan de tweede kromme. Als je de lijnstukken die zo ontstaan allemaal laat ver trekken uit één punt krijg je het ‘gecentreerde veld’ (Eng: tangent cluster). De oppervlakte van het gecentreerde veld is dan gelijk aan de oppervlakte van het ‘afgemaaide veld’ (Eng: tangent sweep). De kunst bestaat er nu in om ingewikkelde maaivelden (zoals het inwendige van een hartlijn, de oppervlakte onder de grafiek van een exponentiële functie …) te herleiden tot overzichtelijke gecentreerde maaivelden (zoals een cirkel, een rechthoek …). We illustreren dit principe met vier voorbeelden. Het zijn
De meest eenvoudige kromme waarop je het principe van Mamikon kan toepassen is de sleepkromme. Stel dat je op een rechte lijn loopt en dat je een zwaar gewicht aan een strak touw met vaste lengte a achter je aansleept. Bij de start kies je de looprichting loodrecht op de richting van het aangespannen touw. Maar stelselmatig zal de hoek tussen het touw en de looprichting groter worden terwijl je nochtans in dezelfde richting blijft lopen. In de limiet wordt deze hoek de gestrekte hoek. De baan die het (puntvormige)
Figuur 2
De meest eenvoudige kromme waarop je het principe van Mamikon kan toepassen is de sleepkromme. Stel dat je op een rechte lijn loopt en dat je een zwaar gewicht aan een strak touw met vaste lengte a achter je aansleept. Bij de start kies je de looprichting loodrecht op de richting van het aangespannen touw. Maar stelselmatig zal de hoek tussen het touw en de looprichting groter worden terwijl je nochtans in dezelfde richting blijft lopen. In de limiet wordt deze hoek de gestrekte hoek. De baan die het
35
gewicht beschrijft, noemen we een sleepkromme (zie links in figuur 3). In deze
(puntvormige) gewicht beschrijft, noemen we een sleepkromme (zie links in figuur 3). In deze
relatief eenvoudige voorbeelden. Mamikon en Apostol hebben ook moeilijkere toepassingen op dit principe uitgedokterd, soms in drie dimensies, maar telkens uitblinkend door inspiratie en spitsvondigheid.
In figuur 2 tonen we dit principe voor de oppervlakte tussen twee ellipsen, de donkerblauwe en de lichtblauwe ellips op de figuur. Neem een willekeurig punt P op de donkerblauwe ellips. De raaklijn aan die ellips in P snijdt de andere (lichtblauwe) ellips in Q. Neem nu een vast punt R en verschuif het lijnstuk [PQ] naar [RS]. Het punt S zal dan de groene kromme beschrijven. De oppervlakte tussen de twee ellipsen (links) is dan gelijk aan de oppervlakte binnen de groene kromme (rechts).
DE OPPERVLAKTE ONDER DE SLEEPKROMME
De meest eenvoudige kromme waarop je het principe van Mamikon kan toepassen is de sleepkromme. Stel dat je op een rechte lijn loopt en dat je een zwaar gewicht aan een strak touw met vaste lengte a achter je aansleept. Bij de start kies je de looprichting loodrecht op de richting van het aangespannen touw. Maar stelselmatig zal de hoek tussen het touw en de looprichting groter worden terwijl je nochtans in dezelfde richting blijft lopen. In de limiet wordt deze hoek de gestrekte hoek. De baan die het (puntvormige) gewicht beschrijft, noemen we een sleepkromme (zie links in figuur 3). In deze toepassing berekenen we de oppervlakte tussen het looptraject en de sleepkromme.
We kunnen het principe van Mamikon toepassen door met een tractor over de sleepkromme te rijden. De ‘maaiarm’ die achteraan sleept, blijft nu steeds even lang. Het gecentreerde maaigebied zal bijgevolg een cirkelsector zijn. Indien je onder een rechte hoek begint te slepen, zal de oppervlakte onder de sleepkromme gelijk zijn aan de oppervlakte van een kwartcirkel met straal a (zie rechts in figuur 3). Als variant op deze klassieke sleepkromme zou je ook onder een stompe hoek kunnen beginnen te slepen. Het eerste segment onder de sleepkromme valt dan bijvoorbeeld weg. De oppervlakte onder de sleepkromme is dan één segmentje kleiner dan de kwartcirkel uit figuur 3.
OPPERVLAKTE ONDER DE CYCLOÏDENBOOG
Een andere klasse van krommen waarvan de oppervlakte te berekenen is met de techniek van Mamikon is de familie van de cycloïden. Je hoeft de vergelijking van deze krommen niet te kennen: de constructie als meetkundige plaats van een punt dat bevestigd is aan een rollende cirkel geeft hier accuratere informatie om de oppervlakte te berekenen. Als je een cirkel met straal a laat rollen over een rechte en je zet je tekenpen precies op een punt op de omtrek van de cirkel, dan verkrijg je een cycloïde. In figuur 4 is één boog van deze cycloïde getekend.
3
Het eerste segment onder de sleepkromme valt dan bijvoorbeeld weg. De oppervlakte onder de sleepkromme is dan één segmentje kleiner dan de kwartcirkel op de volgende pagina.
Rond deze cycloïdenboog past een rechthoek PQRS, waarvan de oppervlakte makkelijk te berekenen is. De
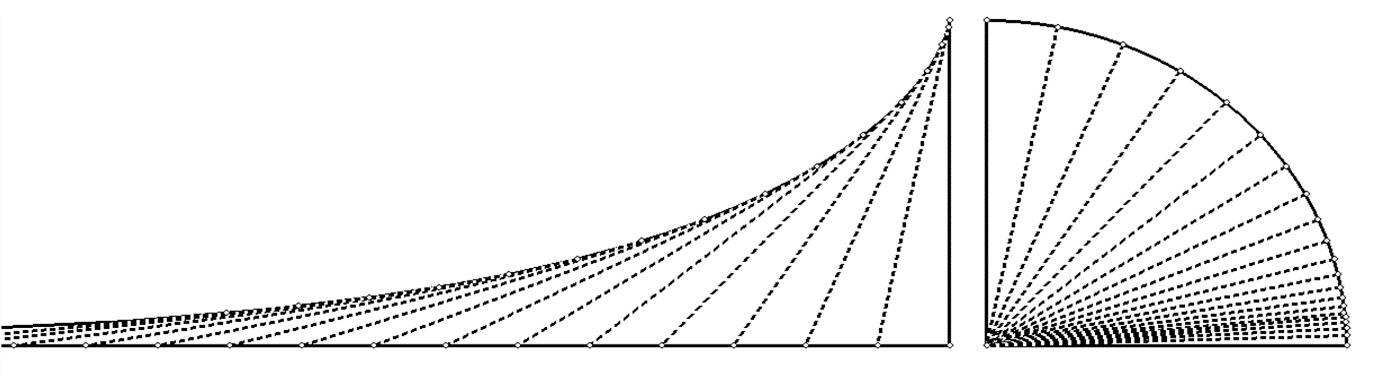
looprichting
a
36
Figuur
hoogte van deze rechthoek is de diameter van de cirkel, de breedte van de rechthoek is de omtrek van de cirkel.
Zo komen we op een oppervlakte van 4a2 ∏, die gelijk is aan vier keer de oppervlakte van de rollende cirkel. We zijn geïnteresseerd in de oppervlakte onder de cycloïdenboog maar berekenen eerst de oppervlakte boven deze boog.
Stel dat de cirkel (zonder slippen) gerold is over de rechte tot in het punt A en dat we de meetkundige plaats bekijken van het punt B dat vast aan de rolcirkel is bevestigd.
Als A het steunpunt van de cirkel is, zal B een rotatiebeweging rond A ondergaan. Het punt B beweegt zich met andere woorden in de richting loodrecht op [AB]. Deze
bewegingsrichting is in streepjeslijn getekend op figuur 4. De streepjeslijn is de raaklijn aan de cycloïdenboog in B. Ze snijdt de cirkel in C, het punt op de rolcirkel dat loodrecht boven het steunpunt A gelegen is. De verklaring voor deze vaststelling: in een cirkel ondersteunt elke rechte omtrekshoek een middellijn. (zie figuur 4)
Meer meetkundige inzichten zijn er niet nodig om de oppervlakte boven de cycloïdenboog te berekenen. Vul de volledige ruimte boven de boog op met deze raaklijnstukjes en cluster al deze lijnstukken in de noordpool van een vaste cirkel, die congruent is met de rolcirkel. Uiteindelijk zal heel deze vaste cirkel opgevuld worden.

Figuur 4
Meer meetkundige inzichten zijn er niet nodig om de oppervlakte boven de cycloïdenboog te berekenen. Vul de volledige ruimte boven de boog op met deze raaklijnstukjes en cluster al deze lijnstukken in de noordpool van een vaste cirkel, die congruent is met de rolcirkel. Uiteindelijk zal heel deze vaste cirkel opgevuld worden.
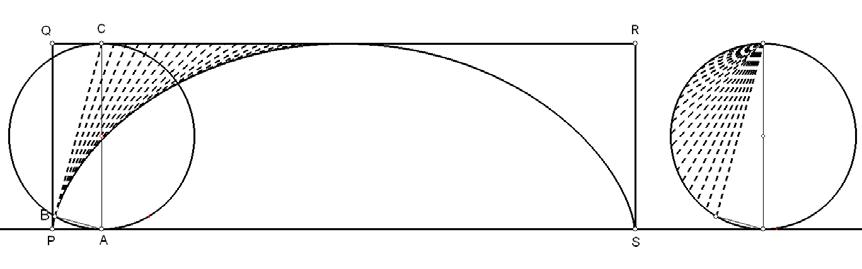
p 2 a
Figuur 5
2 3a p
De oppervlakte boven de cycloïdenboog is dus gelijk aan . De oppervlakte eronder is dan . Zou er voor de berekening van de booglengte van de cycloïdenboog ook zulke sluipweg bestaan?
37
De oppervlakte boven de cycloïdenboog is dus gelijk aan a2 ∏ . De oppervlakte eronder is dan 3a2 ∏ . Zou er voor de berekening van de booglengte van de cycloïdenboog ook zulke sluipweg bestaan?
OPPERVLAKTE ONDER DE GRAFIEK VAN EEN EXPONENTIËLE FUNCTIE
Op de tekening hieronder zijn de lijnstukken [ [EF] subraaklijnen aan de grafiek van een exponentiële functie. Het zijn de projecties op de ken aan de grafiek met één uiteinde op de grafiek en een ander uiteinde op de van alle exponentiële functies is dat de hellingsgraad evenredig is met de hoogte van de grafiek. Grafisch ver taalt dit zich in het feit dat in alle punten van de grafiek de subraaklijnen (Eng: subtangents) even lang zijn.

We berekenen eerst de oppervlakte onder de grafiek van de exponentiële functie, boven de x-as en links van het raaklijnstuk [EG] in figuur 7. Het maaiveld, gevuld met raaklijnstukken, zie je links in die figuur. Deze raaklijnstukken kunnen geclusterd worden door hun raakpunten te bundelen. Maar inzichtelijk is het beter de andere uiteinden te bundelen. Alle raaklijnstukken hebben een subraaklijn, die even lang is als de subraaklijn [EF]. Daarom passen ze, na verschuiving, precies in de driehoek KLM die congruent is met driehoek EFG
Oppervlakten onder grafieken van functies worden traditioneel berekend met verticale afbakening aan de zijkant. De rechtergrens [EG] moet dus verlegd worden naar [FG]. Het is duidelijk dat hierdoor de oppervlakte verdubbelt. De oppervlakte onder de kromme is bijgevolg gelijk aan
INHOUD VAN EEN EENBLADIGE HYPERBOLOÏDE
We passen hetzelfde principe nu toe om de inhoud te
6
De oppervlakte boven de cycloïdenboog is dus gelijk aan . De oppervlakte eronder is dan . Zou er voor de berekening van de booglengte van de cycloïdenboog ook zulke sluipweg bestaan?
Dit is het ruimtelichaam dat ontstaat door een (orthogonale) hyperbool te wentelen om één van zijn assen, namelijk de symmetrieas die de hyperbool niet snijdt. Een andere manier om dit lichaam te bekijken, is als een regeloppervlak. Op twee parallelle, congruente cirkels bewegen twee punten (één punt op elke cirkel) met dezelfde snelheid. Ze worden verbonden met lijnstukken. Zo ontstaat het koeltorenachtige ruimtelichaam dat eveneens een eenbladige hyperboloïde mag genoemd worden. Stel de hoogte van deze koeltoren gelijk aan h, de straal van de twee gegeven cirkels r en de straal van de cirkel rond het middel van de koeltoren s. Deze gegevens volstaan voor een snelle inhoudsberekening volgens Mamikon.
We berekenen eerst de oppervlakte onder de grafiek van de exponentiële functie, boven de x-as en links van het raaklijnstuk [EG] in figuur 7. Het maaiveld, gevuld met raaklijnstukken, zie je links in die figuur. Deze raaklijnstukken kunnen geclusterd worden door hun raakpunten te bundelen. Maar inzichtelijk is het beter de andere uiteinden te bundelen. Alle raaklijnstukken hebben een subraaklijn, die even lang is als de subraaklijn [EF]. Daarom passen ze, na verschuiving, precies in de driehoek KLM die congruent is met driehoek EFG p 2 a 2 3a p
 Figuur
Figuur
38
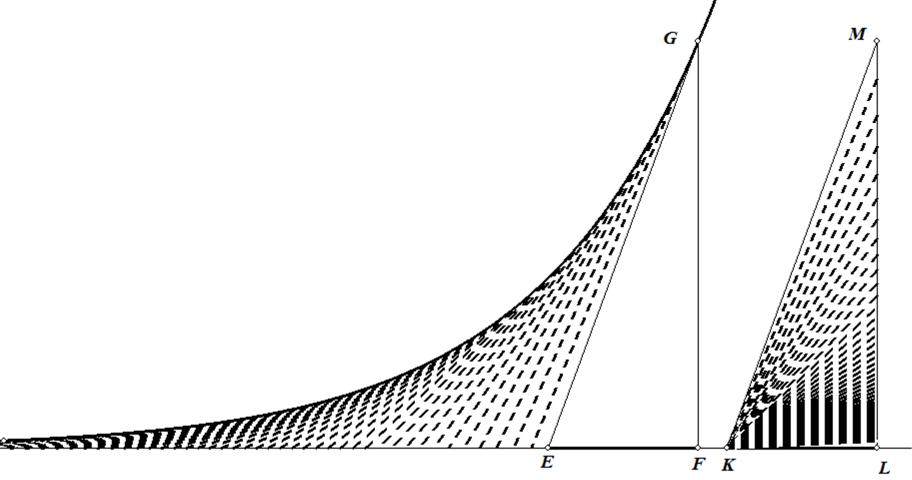

Omdat dit inhoudsprincipe gaat over een inhoud begrepen tussen twee afbakeningen, voegen we een ruimtelichaam toe: de opstaande cilinder die net in de koeltoren past. De inhoud hiervan is s2∏h. Er rest nu nog de inhoud te berekenen van het rotatiesymmetrische gebied, begrepen tussen de cilinder en de koeltoren.

Dit gebied moet ‘driedimensionaal gemaaid’ worden. Met dit doel voor ogen, snijden we de koeltoren met een oneindig aantal verticale vlakken, die raken aan de inwendige cilinder. Zoals je ziet op figuur 9, snijden deze vlakken van de koeltoren gelijkbenige driehoeken af, die met de toppen naar elkaar gericht zijn. Aanvankelijk

Omdat dit inhoudsprincipe gaat over een inhoud begrepen tussen twee afbakeningen, voegen we een ruimtelichaam toe: de opstaande cilinder die net in de koeltoren past. De inhoud hiervan is . Er rest nu nog de inhoud te berekenen van het rotatiesymmetrische gebied, begrepen tussen de cilinder en
Figuur 7
2 p
h r s
sh
Figuur 8
voorgevoel
voorgevoel blijkt niet te kloppen: de benen van de driehoeken liggen op de regels van het regeloppervlak. De dubbele gelijkbenige driehoeken met de punten naar elkaar toe raken aan het cilindrische oppervlak en vullen de hele ruimte tussen de cilinder en de koeltoren … precies wat Mamikon voor ogen had (zie links in figuur 9).
regeloppervlak. De dubbele gelijkbenige driehoeken met de punten naar elkaar toe raken
regeloppervlak. De dubbele gelijkbenige driehoeken cilindrische oppervlak en vullen de hele ruimte tussen Mamikon voor ogen had (zie links in figuur 9).
cilindrische oppervlak en vullen de hele ruimte tussen de cilinder en de koeltoren … precies Mamikon voor ogen had (zie links in figuur 9).
Er duikt toch nog een kleine complicatie op. Als we de dubbele gelijkbenige driehoek over een volledige omwenteling rond de symmetrieas laten rondtollen, wordt elk punt twee keer weggemaaid. Dat is niet de bedoeling. Daarom halveren we de driehoekige maaimessen (zie rechts in figuur 9). Nu blijkt het maaiproces helemaal in orde te zijn. Probeer je maar eens in te beelden wat er gebeurt als de twee rechthoekige driehoeken rond de symmetrieas van de ruimtefiguur geslingerd worden. Kan je je ook inbeelden hoe het gecentreerde maaiveld eruit ziet?
zou je misschien kromme benen verwachten bij deze driehoeken maar dat voorgevoel blijkt niet te kloppen: de benen van de driehoeken liggen op de regels van het regeloppervlak. De dubbele gelijkbenige driehoeken met de punten naar elkaar toe raken aan het cilindrische oppervlak en vullen de hele ruimte tussen de cilinder en de koeltoren … precies wat Mamikon voor ogen had (zie links in figuur 9).
Bronnen
Er duikt toch nog een kleine complicatie op. Als we de dubbele gelijkbenige driehoek over een volledige omwenteling rond de symmetrieas laten rondtollen, wordt elk punt twee keer weggemaaid. Dat is de bedoeling. Daarom halveren we de driehoekige maaimessen (zie rechts in figuur 9). Nu blijkt maaiproces helemaal in orde te zijn. Probeer je maar eens in te beelden wat er gebeurt als de twee rechthoekige driehoeken rond de symmetrieas van de ruimtefiguur geslingerd worden. Kan je je inbeelden hoe het gecentreerde maaiveld eruit ziet?
Inderdaad. We tekenen het hier niet maar indien je alle maaimessen met de rechtopstaande zijde samenclustert, ontstaat er een dubbele kegel die gelijkt op een zandloper. De totale hoogte van deze zandloperfiguur is h. En de straal van het grondvlak is . De inhoud van het geclusterde maaiveld is dus . Door optellen van de twee berekende inhouden vinden we een compacte formule voor de inhoud van de koeltoren: .
zandloper. De totale hoogte van deze zandloperfiguur is h. En de straal van het grondvlak is
Inderdaad. We tekenen het hier niet maar indien je alle maaimessen met de rechtopstaande zijde samenclustert, ontstaat er een dubbele kegel die gelijkt op een zandloper. De totale hoogte van deze zandloperfiguur is h. En de straal van het grondvlak is . De inhoud van het geclusterde maaiveld is dus . Door optellen van de twee berekende inhouden vinden we een compacte
formule voor de inhoud van de koeltoren: .
Bronnen
Er duikt toch nog een kleine complicatie op. Als we de dubbele gelijkbenige driehoek over een volledige omwenteling rond de symmetrieas laten rondtollen, wordt elk punt twee keer weggemaaid. Dat is niet de bedoeling. Daarom halveren we de driehoekige maaimessen (zie rechts in figuur 9). Nu blijkt het maaiproces helemaal in orde te zijn. Probeer je maar eens in te beelden wat er gebeurt als de twee rechthoekige driehoeken rond de symmetrieas van de ruimtefiguur geslingerd worden. Kan je je ook inbeelden hoe het gecentreerde maaiveld eruit ziet?
22 rs( ) 22 3 h rs p( ) 22 2 3 h rs p + . De inhoud van het geclusterde maaiveld is dus
Er duikt toch nog een kleine complicatie op. Als we de omwenteling rond de symmetrieas laten rondtollen, de bedoeling. Daarom halveren we de driehoekige maaiproces helemaal in orde te zijn. Probeer je maar rechthoekige driehoeken rond de symmetrieas van inbeelden hoe het gecentreerde maaiveld eruit ziet? Inderdaad. We tekenen het hier niet maar indien samenclustert, ontstaat er een dubbele kegel die gelijkt zandloperfiguur is h. En de straal van het grondvlak maaiveld is dus . Door optellen van de formule voor de inhoud van de koeltoren:
Bronnen
T.Apostol, & M. Mnatsakanian. (2017). New Horizons in Geometry. MAA Press
Figuur 9
optellen van de twee berekende inhouden vinden we een compacte formule voor de inhoud van de koeltoren:
T.Apostol, & M. Mnatsakanian. (2017). New Horizons in Geometry. MAA Press
BRONNEN
T.Apostol (2000). A Visual Approach to Calculus Problems Engineering and Science, 3(2000), 22-31. https://calteches.library.caltech.edu/4007/1/Calculus.pdf
Dit artikel verscheen in Uitwiskeling 27/4. Op www.uitwiskeling.be vind je alle info 22 rs( ) 22 3 h rs p( ) 22 2 3 h rs p +
T. Apostol, & M. Mnatsakanian. (2017). New Horizons in Geometry MAA Press.
J Bair, & V Henry (2011). Sur le théorème de Mamikon Losanges, 12, 10-15 (2010, 30 november). Mamikon Mnatsakanian. Wikipedia. https://en.wikipedia.org/wiki/Mamikon_Mnatsakanian
J Bair, & V Henry (2011). Sur le théorème de Mamikon Losanges, 12, 10-15 (2010, 30 november). Mamikon Mnatsakanian. Wikipedia. https://en.wikipedia.org/wiki/Mamikon_Mnatsakanian
T. Apostol. (2000). A Visual Approach to Calculus Problems. Engineering and Science, 3(2000), 22-31. https://calteches. library.caltech.edu/4007/1/Calculus.pdf
T.Apostol, & M. Mnatsakanian. (2017). New Horizons in Geometry T.Apostol (2000). A Visual Approach to Calculus https://calteches.library.caltech.edu/4007/1/Calculus.pdf J Bair, & V Henry (2011). Sur le théorème de Mamikon Losanges (2010, 30 november). Mamikon Mnatsakanian. Wikipedia. https://en.wikipedia.org/wiki/Mamikon_Mnatsakanian
T.Apostol (2000). A Visual Approach to Calculus Problems Engineering and Science, 3(2000), 22 https://calteches.library.caltech.edu/4007/1/Calculus.pdf
Dit artikel verscheen in Uitwiskeling 27/4. Op ( ) 22 3 h rs p( 22 2 rs + . Door
Dit artikel verscheen in Uitwiskeling 27/4. Op www.uitwiskeling.be vind je alle info
Inderdaad. We tekenen het hier niet maar indien je alle maaimessen met de rechtopstaande zijde samenclustert, ontstaat er een dubbele kegel die gelijkt op een
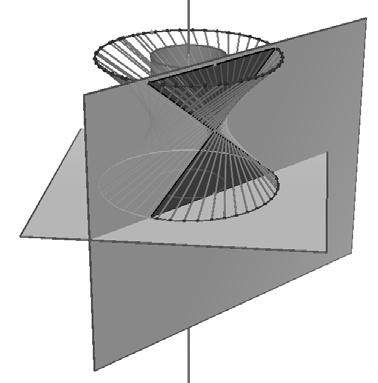
J. Bair, & V. Henry. (2011). Sur le théorème de Mamikon. Losanges, 12, 10-15. (2010, 30 november). Mamikon Mnatsakanian. Wikipedia. https://en.wikipedia.org/wiki/Mamikon_Mnatsakanian
Dit artikel verscheen in Uitwiskeling 27/4. Op www.uitwiskeling.be vind je alle info.
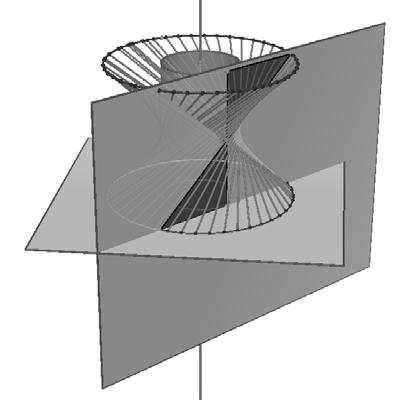
Dit gebied moet ‘driedimensionaal gemaaid’ worden. Met dit doel voor ogen, snijden we de koeltoren met een oneindig aantal verticale vlakken, die raken aan de inwendige cilinder. Zoals je ziet op figuur 9, snijden deze vlakken van de koeltoren gelijkbenige driehoeken af, die met de toppen naar elkaar gericht zijn. Aanvankelijk zou je misschien kromme benen verwachten bij deze driehoeken maar dat voorgevoel blijkt niet te kloppen: de benen van de driehoeken liggen op de regels van het
blijkt niet te kloppen: de benen van de driehoeken liggen op de regels van
aan
40
TEKENEN IN BILDTSE GRAANAKKERS
DEEL 2
DE ANDERE ONTWERPEN
NAAST DAT VAN HANS KUIPER WERDEN ER NOG ZEVEN ANDERE ONTWERPEN ALS GROOTSCHALIGE LANDART KUNSTWERKEN GEREALISEERD IN DE BILDTSE GRAANAKKERS. IN TOTAAL WAREN ER ZEVEN KUNSTENAARS BIJ BETROKKEN (HENK RUSMAN MAAKTE TWEE TEKENINGEN), EN ZES AKKERBOUWERS. HIER EEN OVERZICHT MET BIJ ELK ONTWERP EEN KORTE TOELICHTING.
KLAAS LAKEMAN, ARS ET MATHESIS


41
PYTHAGORAS
Allereerst een ontwerp van initiatiefnemer Henk Rusman (figuur 1). Dit paste in een cirkel van 61 meter. Voor wie bekend is met symmetriepatronen: het is systeem P3.
Het ontwerp van figuur 2 is van Marco Goldenbeld. Het zijn twee driehoekige objecten die in elkaar grijpen. Gezien vanuit verschillende richtingen veranderen de horizontale en de verticale richtingen en daarmee de plaats van de objecten onder of boven. Vergelijk de foto’s aan het begin. Deze graantekening paste in een rechthoek van 115 bij 81 meter.
De bijdrage van Rinus Roelofs bestond uit het ontwerp van figuur 3. Het is een vlakke projectie van een 3D-object met verschillende lagen. In het graan nam het een ruimte in van een rechthoek met afmetingen van 127 bij 104 meter.
Roland de Jong Orlando ontwierp een patroon van lemniscaten met symmetriesysteem PG (figuur 4). De uitvoering paste in een rechthoek van 65 bij 80 meter.
Het ontwerp van Ria Groenhof kreeg de titel Ingang tot de Aarde (figuur 5). Het bestond uit roterende en steeds kleiner wordende vierkanten en ruiten en paste in een vierkant van 50 bij 50 meter.
Het tweede ontwerp van Henk Rusman was even als zijn andere bijdrage een symmetriepatroon met symmetriesysteem P3 (figuur 6). Deze graantekening paste in een cirkel van 74 meter.
Tenslotte het spoor van een enorme tractorband dat afkomstig is van Bowe Roodbergen dat paste in een rechthoek van 182 bij 50 meter (figuur 7).
Gedurende de zomer veranderden de tekeningen – afhankelijk van lichtval en rijping van het graan – van kleur (vergelijk ook wat dat betreft de beide opnamen van de tekening van Marco Goldenbeld aan het begin) .
Bovendien vertoonden ze een meer of minder duidelijke reliëfomkering (optische illusie) zoals prachtig naar voren komt bij een van de vele opnamen van het in deel 1 beschreven Conforme Schaakbord van Hans Kuiper (figuur 8).


 Figuur 1
Figuur 2
Figuur 1
Figuur 2
42
Figuur 3




 Figuur 4
Figuur 5
Figuur 6
Figuur 7
Figuur 4
Figuur 5
Figuur 6
Figuur 7
43
Figuur 8 Reliëfomkering.
HET INTERESSANTE GETAL
 PaulLevrie
PAUL LEVRIE
PaulLevrie
PAUL LEVRIE
...ofhoezowelderijvanFibonaccialsdemachtenvan11gecodeerdzittenin´e´enenhetzelfde getal:
... of hoe zowel de rij van Fibonacci als de machten van 11 gecodeerd zitten in één en hetzelfde getal:
Hierbijis
Hierbij is
0,01123595505 = 1 89

PaulLevrie ...ofhoezowelderijvanFibonaccialsdemachtenvan11gecodeerdzittenin´e´enenhetzelfde getal:
Hetinteressantegetal 1 89
+ + Hierbijis
0,01123595505 = 1 89 Hetinteressantegetal 1 89
+ +
44
(B)Hetgetal
(C)Degetallen a en b zijnbeidedeelbaardoor9.
(D)Hetproductvan a en b isdeelbaardoor27.
(E)Desomvan a en b isdeelbaardoor9.
OEFENING 13
7. Pitunaatverveeltzichenbegintopzijnpapierregelmatigeveelhoekentetekenen.Hijbegintmeteenvierkantentekentdan eengelijkzijdigedriehoekdiedaarmeeeenzijdegemeenschappelijk heeft.Vervolgenswisselthijtelkenseenvierkanteneendriehoek afzoalsindefiguur,telkensinwijzerzinaansluitendopdevorige.
Pitunaat verveelt zich en begint op zijn papier regelmatige veelhoeken te tekenen. Hij begint met een vierkant en tekent dan een gelijkzijdige driehoek die daarmee een zijde gemeenschappelijk heeft. Vervolgens wisselt hij telkens een vierkant en een driehoek af zoals in de figuur, telkens in wijzerzin aansluitend op de vorige. Vanaf de vijfde veelhoek beginnen de regelmatige veelhoeken elkaar te overlappen. Het hoeveelste vierkant komt exact op de plaats van het eerste vierkant?
Vanafdevijfdeveelhoekbeginnenderegelmatigeveelhoekenelkaar teoverlappen.Hethoeveelstevierkantkomtexactopdeplaatsvan heteerstevierkant?
8. Als(x +22)2 =2024,danis(x +20)(x +24)gelijkaan
(A)2016(B)2020(C)2022(D)2024(E)2028
OEFENING 14
9. Dezijden[AB ],[BC ]en[CD ]vandrievierkantenliggenopeenrechtezoalsindefiguur. Ookdehoekpunten E , F en G liggenopeenrechte.Deoppervlaktevanhetkleinste vierkantis9endeoppervlaktevanhetgrootstevierkantis25.Watisdeoppervlakte vanhetmiddelstevierkant?
De zijden [AB], [BC] en [CD] van drie vierkanten liggen op een rechte zoals in de figuur. Ook de hoekpunten E, F en G liggen op een rechte. De oppervlakte van het kleinste vierkant is 9 en de oppervlakte van het grootste vierkant is 25. Wat is de oppervlakte van het middelste vierkant?
10. Desomvandecijfersvaneennatuurlijkgetal n noterenweals S (n ).Zoisbijvoorbeeld S (2024)=8.Welkevandeonderstaandegetallenis geen mogelijkewaardevan S (n +1)?
© Vlaamse Wiskunde Olympiade vzwTweede Ronde VWO 2023-2024, vraag 7
© Vlaamse Wiskunde Olympiade vzwTweede Ronde VWO 2023-2024, vraag 9 A B C D E 7 9 11 13 15
b isdeelbaardoor3,maarnietdoor9.
(A)7 (B)9 (C)11(D)13(E)15
A
B
C 25 D E F G
9
?
(A)15(B)16(C)17(D)18(E)20
(A) 1(B)8 (C)16(D)26(E)35 A B C D E 15 16 17 18 20 45
Beste vrienden van de wiskunde


Op 22 september 2024 vieren we de tweede editie van MathFest, het wiskundefestival voor jong en oud, dat nu reeds in ons collectief geheugen is gegrift. Net zoals vorig jaar kiezen we als locatie het mooie bezoekerscentrum van de volkssterrenwacht van Brugge, in het natuurdomein Beisbroek. Tijdens onze eerste editie ontvingen we talloze enthousiaste reacties op de lezingen en workshops, en braken we het wereldrecord aperiodieke betegeling door een zo groot mogelijk aantal einsteintegels aan elkaar te puzzelen.
Wil jij dit jaar ook jouw steentje bijdragen aan dit geweldige evenement?
We mikken op mensen die een band hebben met wiskunde, of er ooit mee in aanraking kwamen, of gewoon nieuwsgierig zijn. Jong en oud, leerlingen en ouders, gezinnen met kinderen, puzzelaars en knutselaars, ...
Bij deze vinden jullie een oproep voor activiteiten om die dag vorm te geven: workshops, kampioenschappen,
46



een recordverbreking, speelse experimenten, theater, dans, kunst, presentaties, … die jullie kunnen/willen aanbieden aan een breed publiek. Stuur deze oproep gerust ook door naar personen, groepen, organisaties waarvan je weet dat ze iets te bieden hebben dat in het kader past.
De voorstellen worden verwacht ten laatste op zondag 16 juni om 23u59 via bovenstaande QR-code of via onderstaande url.
Volg alle updates en ander festivalnieuws op www.platformwiskunde.be/ mathfest-2024/
MATHFEST 47
wiskunde vakantieboekjes
1> 2 2> 3 van het 1e naar het 2e jaar van het 2e naar het 3e jaar




Herhaal de leerstof wiskunde op een speelse en creatieve manier tijdens de zomervakantie! Scan de QR-code bij het boekje en bestel jouw vakantieboekje via onze webshop!
De vakantieboekjes zijn ideaal voor leerlingen die tijdens de vakantie de leerstof van het voorbije jaar willen onderhouden en die goed voorbereid aan volgend schooljaar willen beginnen.

helpen. controleren. speelse onderwijs. Die Keure wil het milieu beschermen. Daarom kiezen wij bewust voor papier dat het keurmerk van de Forest Stewardship Council® (FSC®) draagt. Dit product is gemaakt van materiaal afkomstig uit goed beheerde, FSC®- gecertificeerde bossen en andere gecon9 789048 638314 by die Keure, Brugge Verantwoordelijke uitgever N.V. die Keure, Pathoekeweg - 8000 Brugge België RPR 0405 108 325 1> 2 wiskunde Vakantieboek 1> 2 Aangepast aan de hervorming van de eerste graad secundair onderwijs. 17/08/2022 07:37 2> 3 wiskunde Vakantieboek Aangepast aan de hervorming van de eerste graad secundair onderwijs. 22/02/2023 08:50 Kleine Pathoekeweg 3, B-8000 Brugge – 050 47 12 62 – so@diekeure.be – diekeure.be/educatief diekeure.be/educatief Laat je inspireren! @DieKeureEducatief / @DieKeureEducatief / @ DieKeure / @UitgeverijDieKeure
850001318









 Figuur 5 Ontstaan van het conforme schaakbord met 128 velden en 161 hoekpunten
Figuur 6 De 41 (van de 161) met GPS uit te zetten blauwe hoekpunten
Figuur 5 Ontstaan van het conforme schaakbord met 128 velden en 161 hoekpunten
Figuur 6 De 41 (van de 161) met GPS uit te zetten blauwe hoekpunten




















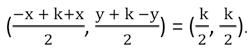


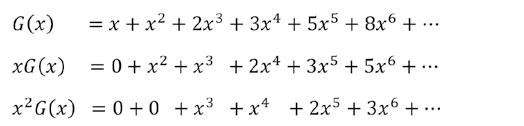
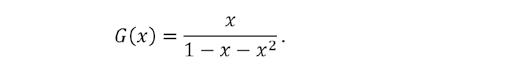


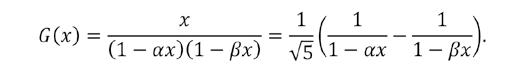
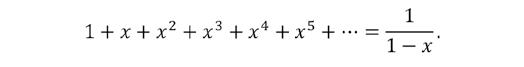
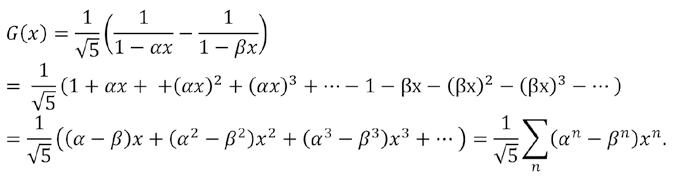
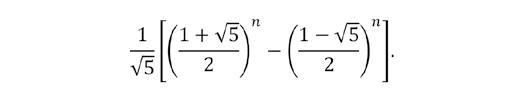
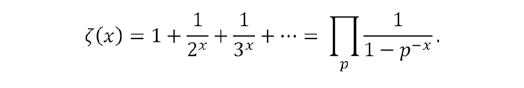






















 Figuur
Figuur









 Figuur 1
Figuur 2
Figuur 1
Figuur 2




 Figuur 4
Figuur 5
Figuur 6
Figuur 7
Figuur 4
Figuur 5
Figuur 6
Figuur 7
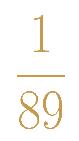 PaulLevrie
PAUL LEVRIE
PaulLevrie
PAUL LEVRIE










