A Conquista - Matemática - Volume 2

RECURSO EDUCACIONAL DIGITAL

Ensino Fundamental - Anos Iniciais

Área: Matemática

MATEMÁTICA 2

Componente: Matemática

JOSÉ RUY GIOVANNI JÚNIOR

Licenciado em Matemática pela Universidade de São Paulo (USP). Professor e assessor de Matemática em escolas de Ensino Fundamental e Ensino Médio desde 1985.

A conquista – Matemática – Recurso Educacional Digital – 2o ano (Ensino Fundamental – Anos Iniciais)

Copyright © José Ruy Giovanni Júnior, 2021

Direção-geral Ricardo Tavares de Oliveira

Direção de Conteúdo e Negócios Cayube Galas

Direção editorial adjunta Luiz Tonolli

Gerência editorial Natalia Taccetti

Edição Nubia de Cassia de Moraes Andrade e Silva (coord.)

Leticia Mancini Martins, João Alves de Souza Neto

Preparação e revisão de textos Viviam Moreira (sup.)

Adriana Périco, Caline Devèze, Camila Cipoloni, Carina Luca, Fernanda Marcelino, Fernando Cardoso, Graziele Ribeiro, Paulo José Andrade

Gerência de produção e arte Ricardo Borges

Design Daniela Máximo (coord.)

Arte e produção Isabel Cristina Corandin Marques (coord.)

Coordenação de imagens e textos Elaine Bueno Koga

Licenciamento de textos Erica Brambilla

Iconografia Jonathan Santos

Coordenação de audiovisuais Diego Vieira Cury Morgado de Oliveira

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil)

Giovanni Júnior, José Ruy

A conquista [livro eletrônico] : matemática : 2o ano : ensino fundamental : anos iniciais / José Ruy Giovanni Júnior. – 1. ed. – São Paulo : FTD, 2021.

PDF

Área: Matemática.

Componente: Matemática.

ISBN 978-85-96-03237-7 (recurso educacional digital professor – coleção)

1. Matemática (Ensino fundamental) I. Título. 21-90871 CDD-372.7

Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Cibele Maria Dias - Bibliotecária - CRB-8/9427

EDITORA FTD

Rua Rui Barbosa, 156 – Bela Vista – São Paulo-SP CEP 01326-010 – Tel. 0800 772 2300 Caixa Postal 65149 – CEP da Caixa Postal 01390-970 www.ftd.com.br central.relacionamento@ftd.com.br

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Carta ao professor

Olá, professor! Seja bem-vindo ao Recurso Educacional Digital!

O Recurso Educacional Digital é um material que tem como objetivo auxiliar o seu trabalho e ampliar as possibilidades de planejamento das aulas de Matemática nos Anos Iniciais do Ensino Fundamental O Recurso Educacional Digital em PDF apresenta subsídios para enriquecer o dia a dia em sala de aula, com propostas de abordagens que complementam os materiais já utilizados em sala de aula e que contribuem para a atualização contínua do professor.

Os conteúdos do Recurso Educacional Digital foram formulados com base nos componentes de Literacia e Numeracia da Política Nacional de Alfabetização (PNA), nas competências gerais da Educação Básica, nas competências específicas de Matemática para o Ensino Fundamental, nos objetivos de aprendizagem e nas habilidades correspondentes aos Anos Iniciais do Ensino Fundamental, presentes na Base Nacional Comum Curricular (BNCC)

É importante enfatizar que todas as propostas deste material são sugestões Portanto, o professor tem total liberdade para adequar cada material à sua realidade escolar.

O conteúdo em PDF deste material digital apresenta quatro recursos pedagógicos. São eles:

• Plano de desenvolvimento anual: contém uma proposta de planejamento de conteúdos, de habilidades e de componentes essenciais para a alfabetização, elaborada em formato de um quadro organizado em bimestre, trimestre e semestre A ordem e os conteúdos listados são sugestões elaboradas com o objetivo de fornecer subsídios complementares a outros materiais didáticos. Nesse sentido, este plano pode ser adaptado à realidade da escola ou da turma a critério do professor. O plano, também, contém sugestões de práticas de ensino em sala de aula e texto formativo sobre avaliação.

• Sequências didáticas: contempla duas sequências por bimestre, que consistem em uma proposta de conteúdo para desenvolver competências gerais, competências específicas da área da Matemática e suas Tecnologias, as habilidades dessa mesma área e os componentes essenciais para a alfabetização Cada sequência é composta de um descritivo, uma listagem de objetivos de aprendizagem, um plano de aula - que contém uma listagem das aulas, dos materiais e dos recursos que serão utilizados nas aulas, bem como dos componentes e das habilidades trabalhadas - e a descrição aula a aula do encaminhamento a ser trabalhado, das atitudes e dos procedimentos que os alunos devem realizar sob mediação do professor, de sugestões de atividades.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

• Relatórios e indicadores do acompanhamento da aprendizagem: traz subsídios para auxiliar o professor na produção de relatórios e de indicadores do acompanhamento da aprendizagem Os indicadores do acompanhamento da aprendizagem são apresentados em modelos de fichas avaliativas que servem como sugestões para que o professor possa aplicar conforme a realidade da escola e da turma para auxiliá-lo no processo de avaliação coletiva e individual dos alunos. São elas: ficha de avaliação diagnóstica (usada para obter um diagnóstico dos conhecimentos prévios dos alunos), ficha de acompanhamento das aprendizagens (permite observar a evolução de aprendizados ao longo do processo de ensino e aprendizagem), ficha de verificação de resultados (permite observar quais objetivos de aprendizagem foram atingidos ao final do ano letivo) e a ficha de acompanhamento do desenvolvimento de competências socioemocionais (permite observar quais habilidades socioemocionais foram atingidas ao final do ano letivo). Além disso, nesta seção, são apresentadas informações sobre como trabalhar com os dados obtidos, bem como apresentar esses dados para gestores escolares, professores e responsáveis pelos alunos

• Catálogo de audiovisuais: apresenta informações a respeito do conjunto de materiais audiovisuais que acompanha este material. O catálogo tem como objetivo complementar e aprofundar a prática pedagógica e pode ser utilizado de acordo com as características da turma e do planejamento do professor. Para cada audiovisual são apresentadas orientações introdutórias, bem como propostas de atividades que explorem o uso de cada recurso em sala de aula.

A seguir estão listados os principais temas trabalhados neste volume:

• noções de quantidade e contagem até 1 000 (mil unidades);

• adição e subtração até três ordens;

• sistema monetário brasileiro;

• noções de localização e de movimentação;

• figuras geométricas planas e sólidos geométricos;

• multiplicação com ideia de adição;

• dobro, metade, triplo e terça parte;

• medidas de comprimento, de massa e de capacidade;

• classificações e sequências;

• noções de probabilidade e de estatística.

Esperamos que este material possa ser usado para enriquecer o dia a dia em sala de aula, auxiliando na sua prática docente e contribuindo para a formação de seus alunos.

Bom trabalho!

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Instrumentos pedagógicos

Plano de desenvolvimento anual

O Plano de desenvolvimento anual é uma proposta de planejamento elaborada em formato de um quadro organizado em bimestre, trimestre e semestre. Nele, são indicados os conteúdos, as habilidades da Base Nacional Comum Curricular (BNCC) e os componentes essenciais para a alfabetização a serem desenvolvidos em cada período. É importante enfatizar que a organização proposta é uma sugestão e que o professor pode adaptá-la de acordo com a realidade da turma com a qual está trabalhando.

Além do quadro, este plano também contém as seguintes seções:

• Práticas de ensino na sala de aula: são apresentadas sugestões gerais de estratégias e de atitudes que podem ser incorporadas pelo professor para alcançar os objetivos de aprendizagem pretendidos;

• Avaliação: composta de um texto formativo para o professor no qual são apresentadas possibilidades para avaliação diagnóstica, processual e formativa;

• Para saber mais: lista de sugestões complementares de sites , vídeos, livros, artigos, séries, revistas ou filmes que podem ajudar o professor a desenvolver o trabalho em sala de aula.

Freepik.com

O planejamento é uma etapa muito importante das atividades docentes.

º semestre

1º trimestre 1º bimestre

Aprendizagens desenvolvidas no 2º ano

Números naturais e sistema monetário

• Compor e decompor números naturais até a ordem das centenas.

• Compreender características do Sistema de Numeração Decimal.

• Comparar e ordenar números naturais até a ordem das centenas.

• Fazer estimativas, comparar e registrar a quantidade de objetos (até 1 000 unidades) por meio de estratégias diversas de contagem.

• Reconhecer ideias de adição e subtração

• Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro

• Explorar situações-problema envolvendo atividades de compra e venda.

Localização e movimentação

• Localizar pessoas e objetos no espaço segundo um ponto de referência.

• Descrever a localização de pessoas e objetos no espaço segundo um ponto de referência.

• Identificar e descrever deslocamentos no espaço

• Esboçar roteiros e plantas simples.

Adição e subtração

• Construir fatos básicos da adição e da subtração

• Explorar fatos básicos da adição e da subtração por meio de material manipulativo.

• Resolver problemas de adição e subtração com números de até três ordens.

• Elaborar problemas de adição e subtração com números de até três ordens.

2º bimestre

Figuras geométricas e sequências

• Reconhecer, nomear e comparar sólidos geométricos (cubo, bloco retangular, pirâmide, esfera, cone e cilindro) e associá-los a objetos do dia a dia.

• Reconhecer, nomear e comparar figuras geométricas planas (quadrado, retângulo, triângulo, círculo) e identificá-las em sólidos geométricos.

• Identificar e descrever regularidades de sequências de números, figuras ou objetos.

• Identificar e descrever elementos ausentes de sequências de números, figuras ou objetos.

• Construir sequências com base em regularidades estabelecidas.

BNCC

EF02MA01

EF02MA02

EF02MA03

EF02MA04

EF02MA05

EF02MA06

EF02MA12

EF02MA13

EF02MA20

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Compreensão de textos.

• Produção de escrita.

BNCC

EF02MA01

EF02MA05

EF02MA06

EF02MA09

EF02MA10

EF02MA11

EF02MA14

EF02MA15

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento do vocabulário.

• Produção de escrita.

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra de rivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

Material disponibilizado em licença aberta do tipo Creative Commons

2 º trimestre

3 º bimestre

Intervalos de tempo e probabilidade

• Ler e escrever as horas em um relógio digital.

• Calcular a duração de atividades cotidianas.

• Organizar agenda envolvendo datas (dias da semana, meses do ano).

• Resolver problemas relacionados a horários e duração de atividades.

• Reconhecer os termos "pouco prováveis", "muito prováveis", "improváveis" e "impossíveis" como possíveis classificações de eventos aleatórios.

• Realizar pesquisa.

• Apresentar dados em tabela de dupla entrada e em gráfico de colunas.

Multiplicação com ideia de adição

BNCC

EF02MA16

EF02MA17

EF02MA18

EF02MA19

EF02MA21

EF02MA22

EF02MA23

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento do vocabulário.

• Compreensão de textos.

• Compreender a multiplicação (por 2, 3, 4 e 5) como ideia de adição de parcelas iguais.

• Resolver problemas de multiplicação (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais.

• Elaborar problemas de multiplicação (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais, representados por meio de desenhos, esquemas ou material de contagem.

Dobro, metade, triplo e terça parte

• Compreender a ideia de dobro, triplo, metade e terça parte.

• Compreender a relação entre dobro e metade.

• Compreender a relação entre triplo e terça parte.

• Elaborar e resolver problemas envolvendo dobro, metade, triplo e terça parte.

Grandeza e medidas

• Estimar, medir e comparar comprimentos utilizando unidades de medida não convencionais e convencionais.

• Estimar medidas de capacidade e massa utilizando estratégias diversas de comparação.

• Estimar, medir e comparar medidas de capacidade e massa utilizando unidades de medida não convencionais e convencionais.

BNCC

EF02MA06

EF02MA07

EF02MA08

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento do vocabulário.

• Produção de escrita.

• Produção de escrita. 3

Práticas de ensino na sala de aula

Nesta seção, serão apresentadas algumas sugestões gerais de estratégias de ensino e de atitudes que contribuem para a aprendizagem dos alunos e promovem o alcance dos objetivos de aprendizagem, das habilidades e das competências desta etapa do Ensino Básico

Oralidade

Nos Anos Iniciais do Ensino Fundamental, é importante que a oralidade seja desenvolvida por meio de atividades que incentivem, por exemplo, a troca de ideias entre os próprios alunos, a explicação ou a justificativa de raciocínios ou resoluções e a socialização de opiniões e reflexões.

Saber se comunicar efetivamente, com objetividade e coerência, é uma habilidade importante não apenas no ambiente escolar, mas, também, para a vida cotidiana e para o exercício pleno da cidadania.

A prática da oralidade deve perpassar por diversos atributos: desenvolver a capacidade de ouvir e prestar atenção à fala do colega; respeitar os turnos de fala; identificar e usar corretamente os momentos de interrupção ou de resposta em uma conversa ou discussão; desenvolver a capacidade de recontar histórias ou argumentos, como interagir e reagir a diferentes tipos de situações que envolvam a oralidade (conversar com colegas, fazer apresentação na sala de aula, discutir um assunto sério, fazer uma dramatização e uma exposição para outras turmas ou para os responsáveis).

Sempre que possível, ao realizar discussões, incentivar a manutenção de um ambiente descontraído e agradável, organizando os alunos em uma roda, por exemplo. O uso de roda de conversas é importante para que os alunos possam ser vistos pelos colegas quando exercem sua oralidade. Atividades em que o aluno se levanta e vai até a frente da turma para falar devem ser introduzidas aos poucos até que se tornem parte da rotina da sala de aula.

rawpixel.com/Freepik.com

É importante que a oralidade não seja associada apenas a ir até a frente da turma para falar, mas, também, seja incentivada em atividades lúdicas e em situações de socialização de maneira a favorecer a troca de ideias.

Rotina de sala de aula

Além dos conteúdos exigidos pelos documentos norteadores e pelos currículos escolares, os alunos deverão aprender, ainda no Ensino Fundamental, a organizar seus estudos e suas rotinas diárias. Essa prática é, também, chamada de "aprender a aprender", significando o aprendizado de estratégias de organização e de estratégias de estudo que auxiliam diretamente no aprendizado não só do conteúdo de uma área do conhecimento, mas de todas as áreas.

Há diversas atitudes que podem ser tomadas em sala de aula para auxiliar os alunos nessa prática. Por exemplo, apresentar a agenda ou a rotina do dia no início da primeira aula contribui para que os alunos tenham um panorama do que estudarão no dia, entendam como priorizar tarefas e qual é a importância da organização do tempo. Além disso, abre espaço para um diálogo em que os próprios alunos possam fornecer sugestões para o professor, como a troca na ordem de atividades do dia.

Esta proposta, também, ajuda a garantir que a participação dos alunos em sala de aula ocorra de maneira efetiva, pois a rotina da turma deixa de ser algo de responsabilidade apenas do professor e passa a ser uma construção colaborativa de todos os integrantes desse processo: alunos e professores.

A agenda ou rotina da turma pode consistir em uma listagem numerada das atividades programadas para o dia, escrita na lousa ou em outro suporte que permita a visualização por todos. É importante incluir, nessa listagem, os momentos de alimentação e diversão (hora do lanche, visita a um parque, hora da brincadeira ou atividade envolvendo jogos etc.) para que os alunos compreendam a separação entre as situações e as posturas que devem adotar de acordo com cada contexto.

Ao seguir esta proposta, é importante que o tempo reservado para checar a agenda do dia e discuti-la no começo da primeira aula seja breve e objetivo. Ao completar cada aula ou atividade listada, marcar na agenda do dia com um símbolo, que pode ser, por exemplo, o símbolo de checado (✓) para indicar que a atividade foi concluída. Essa atitude fortalece o senso de realização e permite que os alunos ampliem suas noções da passagem do tempo pela observação da sequência de atividades ou aulas realizadas.

A agenda do dia, também, fornece um aprendizado importante sobre rotinas e planejamento: como lidar com mudanças de planos e eventos imprevisíveis. É importante que os alunos entendam que o planejamento da rotina é algo que deve ser usado em favor deles, mas que não deve ser algo imutável. Imprevistos acontecem e eles devem aprender a lidar com isso. Por exemplo, é possível que uma atividade ao ar livre seja programada e chova, impedindo que a atividade seja realizada com segurança naquele dia.

Para lidar com eventualidades, é importante ter um acervo de atividades diversas, individuais ou em grupos, que podem ser utilizadas para ocupar tempos ociosos ou ocupar os alunos que finalizam atividades mais rapidamente, permitindo que os outros alunos tenham tempo para realizar as atividades no tempo deles.

Glossário ou dicionário ilustrado

Para garantir que os alunos se apropriem de nomes e de termos adequados na Matemática é imprescindível usar o vocabulário correto. Nos Anos Iniciais do Ensino Fundamental, ainda, é comum que alguns alunos chamem tudo o que é redondo de círculo ou chamem o cubo de quadrado. Em situações assim, é fundamental corrigir a fala dos alunos com os termos corretos; por exemplo, dizer "cubo" quando algum aluno chamar um cubo de quadrado, até que eles se apropriem do nome e passem a usá-lo de modo correto. Uma proposta para consolidar esse aprendizado e favorecer o desenvolvimento do vocabulário dos alunos é a criação de um glossário ou dicionário ilustrado da turma. Para isso, pode-se usar uma pasta, um cartaz ou um varal em que o professor escreve a palavra aprendida e um aluno é sorteado para ilustrar o significado da palavra. Sempre que um aluno utilizar o termo incorreto, o glossário pode ser retomado.

KamranAydinov/Freepik.com

Atividades envolvendo criatividade e materiais artísticos enriquecem o repertório dos alunos e favorecem o desenvolvimento de habilidades motoras

Grupos de estudo ou de revisão

Para ter condições de intervir no processo de formação dos alunos de maneira eficaz, é imprescindível acompanhar de modo contínuo as aprendizagens deles, percebendo rapidamente suas dificuldades e seus avanços. No momento em que constatar quais são os alunos que necessitam de maior investimento para alcançar as aprendizagens esperadas, iniciar um trabalho com abordagem diferenciada, para que todos tenham condições de avançar em suas aprendizagens.

Uma estratégia de sala de aula que se mostra bastante eficaz é agrupar os alunos de acordo com as suas necessidades de revisão, em um momento específico da aula, pelo menos uma vez na semana. O intuito disso é retomar o assunto por meio de jogos, de atividades lúdicas ou de situações-problema que tenham como objetivo auxiliar grupos de alunos em suas dificuldades específicas.

Embora essa estratégia exija mais desenvoltura da sua parte, traz resultados nas aprendizagens dos alunos que compensam o investimento de tempo por potencializar o sucesso de todos os envolvidos no processo de ensino-aprendizagem.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra de rivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Avaliação

O processo de avaliação deve estar presente em todo e qualquer momento em que a aprendizagem escolar estiver envolvida. Antigamente, o processo avaliativo era considerado um procedimento de medida da aprendizagem em que se verificava apenas se o aluno atingiu os requisitos mínimos para progredir com os estudos.

Ao longo do tempo, as avaliações passaram por um processo de ressignificação em que assumiram o papel de verificar o progresso do aluno, ao mesmo tempo que sinalizam a necessidade de novas estratégias para o sucesso do processo de ensino e aprendizagem

Atualmente, é quase consenso a compreensão de que a avaliação escolar não deve apenas verificar se o aluno atingiu os requisitos mínimos para seguir para o próximo ciclo ou se atingiu os objetivos mínimos definidos pelo currículo. Os resultados do processo avaliativo não só representam o panorama da aprendizagem individual dos alunos, como também podem servir como fonte de dados a respeito do trabalho desenvolvido pelos profissionais da escola. Tais dados podem dar direcionamento para a autorregulação do processo de ensino, possibilitando ao professor e demais profissionais da escola refletir sobre suas práticas e procurar estratégias para desenvolvê-las e ampliá-las.

Para que haja um ensino de qualidade, é essencial compreender como os alunos lidam com o conhecimento e quais são as habilidades e necessidades individuais que apresentam, sendo importante que o professor reveja os processos de modo a permitir que os alunos possam superar eventuais dificuldades.

A avaliação não pode se resumir a uma prova isolada no processo de ensino e aprendizagem. É preciso utilizar instrumentos avaliativos diversificados que sejam aplicados ao longo do ano letivo. Além disso, fazer o registro periódico de observações o ajudará a acompanhar o desenvolvimento dos alunos.

Sendo assim, é importante que o processo avaliativo seja, de fato, um processo com diversos e variados momentos passando por: avaliações iniciais que permitam obter um diagnóstico dos conhecimentos prévios; avaliações recorrentes de processo que permitam observar a evolução de aprendizados, bem como identificar pontos de ampliação de conhecimento ou pontos que precisam ser retomados e reforçados; e, por fim, avaliações de resultado que permitam observar o desenvolvimento do aluno fornecendo condições de elaborar estratégias para o ano seguinte.

No processo de avaliação, também, é importante que o aluno conheça os resultados obtidos em seu desenvolvimento individual, ciente do que já é capaz de realizar sozinho e como pode melhorar para avançar, assumindo o papel de protagonista. Nesse sentido, o processo de avaliação inclui, ainda, a autoavaliação do aluno e a participação dos familiares.

A inclusão dos familiares no conhecimento dos resultados do processo avaliativo permite que estejam cientes dos avanços e até mesmo das dificuldades dos alunos, e

poderão cooperar com a escola apoiando adoções de estratégias que favoreçam melhores resultados.

Para auxiliar no processo de avaliação, este material apresenta sugestões de fichas e outros materiais de acompanhamento de aprendizagens na seção Relatórios e indicadores do acompanhamento da aprendizagem

Para saber mais

• ALRØ, Helle; SKOVSMOSE, Ole. Diálogo e aprendizagem em educação matemática Belo Horizonte: Autêntica, 2006. O livro trata da importância do diálogo entre professores e alunos como modo de elevar a qualidade das aprendizagens nas aulas de Matemática.

• BACICH, Lilian; MORAN, José (org.). Metodologias ativas para uma educação inovadora: uma abordagem teórico-prática Porto Alegre: Penso, 2018. Obra de referência para aprofundar a compreensão do que são as metodologias ativas, do porquê a utilização delas na educação se faz necessária e de como a incorporação delas nas aulas de Matemática é favorável a experiências de experimentação e compartilhamento.

• CARNEIRO, Reginaldo Fernando; SOUZA, Antonio Carlos de; BERTINI, Luciane de Fatima (org.) A Matemática nos anos iniciais do ensino fundamental [livro eletrônico]: práticas de sala de aula e de formação de professores. Brasília, DF: SBEM, 2018. (Coleção SBEM, 11). Disponível em: http://www.sbembrasil.org.br/files/ebook_matematica_iniciais.pdf

Acesso em: 5 dez. 2021.

A publicação, que faz parte da biblioteca do educador matemático da Sociedade Brasileira de Educação Matemática, traz comentários sobre práticas de sala de aula e formação de professores. O diferencial da obra é que, a esses comentários, já constam incorporadas características recomendadas na BNCC.

• CORSO, Luciana Vellinho; DORNELES, Beatriz Vargas. Memória de trabalho, raciocínio lógico e desempenho em aritmética e leitura. Ciências & Cognição, Rio de Janeiro, v 20, n. 2, p. 293-300, 2015.

No artigo, é retratada uma pesquisa cujos resultados indicaram conexões entre raciocínio lógico, leitura e memória de trabalho.

• MALUF, Maria Regina; CARDOSO-MARTINS, Cláudia (org.). Alfabetização no século XXI: como se aprende a ler e a escrever Porto Alegre: Penso, 2013. O texto auxilia a entender como se dá a aprendizagem dos processos de leitura e escrita, sendo uma das obras que embasaram a Política Nacional de Alfabetização (PNA).

• MATEMÁTICA multimídia. Áudios da coleção M3 Podcast Disponível em: https://anchor.fm/matematica-multimidia Acesso em: 5 dez. 2021.

Mate rial disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciada s sob os mesmos

A coleção de podcastsMatemática Multimídia, produzida pelo Instituto de Matemática, Estatística e Computação Científica (IME) da Unicamp, apresenta diversos recursos educacionais para auxiliar professores.

• MATEMATIZOOM. Podcast Disponível em: https://www.youtube.com/channel/UCY4_E6YSgzjEpyLyJQMFGxQ Acesso em: 5 dez. 2021.

A coleção de podcastsMatematizoom, da Universidade do Estado de Santa Catarina (Udesc), utiliza a cientificidade lúdica para explicar conceitos variados envolvendo situações cotidianas atuais.

• NACARATO, Adair Mendes; CUSTÓDIO, Iris Aparecida (org.). O desenvolvimento do pensamento algébrico na educação básica [livro eletrônico]: compartilhando propostas de sala de aula com o professor que ensina (ensinará) matemática. Brasília, DF: Sociedade Brasileira de Educação Matemática, 2018. (Coleção SBEM, 12) Disponível em: http://www.sbembrasil.org.br/files/ebook_desenv.pdf. Acesso em: 5 dez. 2021. A publicação faz parte da Biblioteca do Educador Matemático da Sociedade Brasileira de Educação Matemática. Trata prioritariamente do desenvolvimento do trabalho com as habilidades relacionadas à unidade temática Álgebra da BNCC nos Anos Iniciais do Ensino Fundamental, visto que esse trabalho constitui um desafio para ser efetivado com adequação à faixa etária.

• NEVES, Iara Conceição B. etal.(org.). Ler e escrever: compromisso de todas as áreas. 9. ed. Porto Alegre: Editora da UFRGS, 2011. O livro esclarece como as atividades, em todas as áreas de conhecimento, podem favorecer de modo integrado a construção da competência leitora e a escrita dos alunos.

• SKOVSMOSE, Ole. Educação crítica: incerteza, matemática, responsabilidade Tradução: Maria Aparecida Viggiani Bicudo. São Paulo: Cortez, 2007. No livro, o autor defende o aspecto de criticidade existente no reconhecimento da potencialidade social que há na Educação Matemática.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Sequências didáticas

Sequência didática 1 • Números, operações e sistema monetário

Nesta sequência didática, serão abordadas a composição e a decomposição de números naturais até a ordem das centenas e também a comparação e a ordenação desses números, tendo materiais manipuláveis como apoio. Além disso, serão exploradas situações-problema envolvendo adições e subtrações em contextos que envolvem o sistema monetário brasileiro.

Objetivos de aprendizagem

• Comparar e ordenar números naturais até a ordem das centenas.

• Compreender características do Sistema de Numeração Decimal

• Compor e decompor números naturais até a ordem das centenas.

• Resolver e elaborar problemas de adição e subtração.

• Reconhecer ideias da adição e ideias da subtração.

• Utilizar diferentes estratégias de cálculo na resolução de problemas.

• Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro.

Plano de aulas

Aula 1: Compor números naturais usando ábaco.

Aula 2: Decompor números naturais usando material dourado.

Aula 3: Comparar e ordenar números naturais usando ábaco e material dourado.

Aula 4: Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro.

Aulas 5 e 6: Resolver situações-problema envolvendo ideias da adição e ideias da subtração.

Aula 7: Elaborar situações-problema envolvendo adição e subtração.

Aulas 8 e 9: Reconhecer e utilizar diferentes estratégias de cálculo na resolução de problemas.

Componentes essenciais para a alfabetização: compreensão de textos e produção de escrita

Competência geral da Educação Básica: 2.

Competências específicas de Matemática: 2, 3, 5 e 6

Habilidades: EF02MA01, EF02MA04, EF02MA05, EF02MA06 e EF02MA20

Materiais necessários: ábaco, material dourado, reprodução de moedas e cédulas do sistema monetário brasileiro, folha avulsa, lápis e borracha

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Aula 1

Iniciar a aula mostrando aos alunos um modelo de ábaco de pinos que represente números até a ordem das centenas. Ainda que muitos alunos já tenham visto esse material, é importante explicar como ele é utilizado, para certificar-se de que todos reconheçam sua finalidade e para que possíveis dúvidas sejam sanadas.

Lembrar-se de salientar as regras do Sistema de Numeração Decimal que podem ser associadas ao ábaco. Explicar que:

• cada pino corresponde a uma ordem numérica;

• a mesma quantidade de argolas assume um valor diferente de acordo com o pino em que são posicionadas;

• a ausência de argolas corresponde ao zero;

• são feitos agrupamentos de 10, portanto o máximo de argolas que podem ser postas em cada pino é igual a 9.

Se for necessário, construir antecipadamente com os alunos modelos de ábacos de pino reutilizando materiais como caixa de ovos, varetas e argolas de papelão.

Para iniciar a proposta de composição de números utilizando o ábaco, organizar os alunos em duplas ou trios para cada ábaco.

Dar então diferentes exemplos de números para que os alunos os representem com o ábaco. Pode-se iniciar pedindo que cada membro do grupo componha números livremente para os colegas descobrirem que números foram compostos. O aluno que compôs explica como pensou para formar seus números. Oriente os alunos a realizarem composições de números com 3 centenas, com 9 dezenas exatas, entre outros.

Para contribuir com o desenvolvimento da linguagem matemática, os alunos podem registrar no caderno cada uma de suas composições numéricas. Com isso, eles desenvolvem a competência específica 6 da área da Matemática e suas Tecnologias. Dar exemplos explicitando e escrevendo na lousa, por exemplo: ao trabalhar com o número 728, a composição pode ser representada assim:

7 centenas, 2 dezenas e 8 unidades é igual a 728 ou

7 centenas + 2 dezenas + 8 unidades = 728

Se houver oportunidade, aprofundar a exploração e abordar também o valor posicional que os algarismos assumem nos números, de acordo com a ordem que ocupam. No exemplo citado, mostrar que:

7 centenas + 2 dezenas + 8 unidades = 700 + 20 + 8 = 728

O uso do ábaco nas aulas permite desenvolver a competência geral 2 e a competência específica 5 da área da Matemática e suas Tecnologias.

Retomar com os alunos como eles fizeram para compor números com os ábacos, ressaltando as regras do Sistema de Numeração Decimal. Depois, explicar a eles que vão explorar o material dourado, fazendo a decomposição de números até a ordem das centenas.

Novamente, mostrar aos alunos o recurso que será utilizado e explicar seu funcionamento, certificando-se de que todos o entenderam. Explicitar que o material dourado contribui para a compreensão do Sistema de Numeração Decimal, pois permite a realização de agrupamentos de 10. Reforçar então o que cada peça representa e como elas podem ser trocadas por outras peças quando formam grupos de 10

No caso de não dispor do material, pode-se reproduzir antecipadamente as peças do material dourado usando malhas quadriculadas e reforçar o objeto colando um papel resistente no verso dele, como cartolina ou papel cartão ou papelão.

Para explorar decomposições de números utilizando o material dourado, mostrar um exemplo aos alunos, como o representado a seguir.

Explicar que o número composto é 325. Se julgar necessário, fazer a representação desse número em um Quadro de ordens para facilitar a identificação da ordem numérica que cada algarismo ocupa e a associação com as peças do material dourado.

Depois, oferecer fichas com números para os alunos sortearem e representarem com o material dourado. Para explorar as decomposições, pedir aos alunos que expliquem quantas centenas, dezenas e unidades cada número representado tem.

Favorecer o desenvolvimento da linguagem matemática na realização dessa atividade, orientando os alunos a registrar as decomposições que fizeram. Então, usando o número do exemplo acima, mostrar como é possível fazer esse registro:

325 é igual a 3 centenas, 2 dezenas e 5 unidades, ou

325 = 3 centenas + 2 dezenas + 5 unidades

Observar se os alunos fazem diferentes decomposições e mostrar como as peças podem ser trocadas por outras, obedecendo às regras do Sistema de Numeração Decimal Exemplo de como orientar os alunos sobre uma decomposição do número 116.

Editoria de arte

Mostrar aos alunos que essa decomposição pode ser representada por:

1 centena e 16 unidades

Explicar então que o número 16 pode ser decomposto em:

1 dezena e 6 unidades

Verificar se os alunos percebem que é possível agrupar 10 unidades em uma dezena. Mostrar como esse agrupamento pode ser feito trocando dez cubinhos do material dourado por uma barra.

Aula 3

Depois de os alunos explorarem a composição e decomposição de números utilizando o ábaco e/ou material dourado, explicar que vão realizar comparações de números até a ordem das centenas.

Antes de iniciar as comparações, esclarecer a importância de seguir as regras do Sistema de Numeração Decimal ao usar o ábaco ou o material dourado, representando agora os números que serão comparados pela colocação do menor número possível de argolas em cada pino e utilizando o menor número de peças possíveis do material dourado. Dessa maneira se assegura que os alunos farão todos os reagrupamentos possíveis sem que ocorram representações diferentes para um mesmo número.

Para iniciar a atividade de comparação, organizar os alunos em grupos, de modo que cada grupo tenha de maneira suficiente dois ábacos ou um material dourado para representar os números, que podem ser disponibilizados antecipadamente para uma melhor exploração pelos alunos. Ditar dois números para serem representados pelos grupos usando o recurso de que cada grupo dispõe. Em seguida, escolher um grupo que usou o ábaco para dizer qual dos números ditados é o maior, por que e como o grupo chegou a essa conclusão. Depois, dar a oportunidade para outro grupo, que usou o material dourado, se manifestar da mesma maneira.

Se perceber que os alunos estão com dificuldade para comparar os números, dar exemplos de como proceder Explicar que com o ábaco é possível analisar, primeiro, o pino das centenas para comparar quantas argolas há nele. Se houver o mesmo número de argolas para os dois números, pedir que comparem a quantidade de argolas do pino das dezenas e, depois, das unidades. De maneira análoga, para quem estiver usando o material dourado, explicar que se compara primeiro a quantidade de placas, depois a de barras e, por fim, a de cubinhos.

Aula 4

Como os alunos já trabalharam com a comparação de números até as centenas utilizando diferentes recursos, fazer uma analogia entre o Sistema de Numeração Decimal e o sistema monetário brasileiro, para que eles estabeleçam a equivalência de valores.

Apresentar aos alunos as seguintes reproduções de moedas e cédulas do real:

• uma moeda de 10 centavos;

• uma moeda de 1 real;

• uma cédula de 10 reais;

• uma cédula de 100 reais.

Relembrar que essas não são as únicas moedas e cédulas do real, mas que o estudo realizado nesta aula utiliza apenas essas reproduções.

Incentivar os alunos a verbalizar o que sabem sobre o valor dessas moedas e cédulas, procurando utilizar as informações trazidas por eles para explicar algumas equivalências de valores. Em seguida, pedir que verbalizem as equivalências a seguir:

• 10 moedas de 10 centavos podem ser trocadas por 1 moeda de um real;

• 10 moedas de 1 real podem ser trocadas por 1 cédula de 10 reais;

• 10 cédulas de 10 reais podem ser trocadas por 1 cédula de 100 reais

Depois, disponibilizar reproduções de cédulas e moedas para que os alunos representem algumas quantias. Trabalhar a composição e a decomposição das quantias e também as trocas entre moedas e cédulas para evidenciar as equivalências e a relação que pode ser estabelecida entre o sistema monetário brasileiro e o Sistema de Numeração

Decimal

Por fim, propor aos alunos que representem quantias usando a menor quantidade possível de cédulas e moedas e, depois, que realizem a comparação dessas quantias.

Aulas 5 e 6

Continuar a contextualização do sistema monetário brasileiro para resolver com os alunos problemas envolvendo ideias da adição e da subtração e progredir na aprendizagem

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

de composição e decomposição de valores. Comentar com eles que vão estudar algumas situações do dia a dia usando reproduções de moedas e cédulas para realizar os cálculos necessários. Seguem alguns exemplos, mas é possível explorar diversas outras situações com os alunos.

1. As irmãs Lívia e Catarina querem juntar algumas moedas para comprar um pacote de figurinhas que custa 1 real. Lívia tem 5 moedas de 10 centavos, e Catarina tem 3 moedas de 10 centavos. O valor que as duas irmãs têm juntas é suficiente para comprar o pacote de figurinhas?

Para resolver essa situação, que envolve a ideia de juntar da adição, verificar se os alunos representam a quantia que cada irmã tem e, depois, se juntam essas quantias para calcular o total de moedas que elas têm. Após a realização dos cálculos utilizando as reproduções de moedas, solicitar aos alunos que façam o registro no caderno. Espera-se que eles utilizem linguagem matemática e registrem:

50 + 30 = 80

Contudo, é possível que façam outros registros, como:

10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = 80

Ao final, espera-se que os alunos percebam que 80 centavos não são suficientes para comprar o pacote de figurinhas que custa 1 real, pois a quantia de 1 real equivale a 100 centavos.

2. Vítor economizou 120 reais para comprar uma bicicleta nova. Como essa quantia não era suficiente, sua mãe contribuiu com 175 reais. Agora, quantos reais Vítor tem para comprar a bicicleta?

Para resolver essa situação, que envolve a ideia de acrescentar da adição, verificar se os alunos representam a quantia que Vítor economizou e, depois, se acrescentam a ela a quantia dada pela mãe. Espera-se que eles concluam que agora Vítor tem 295 reais para comprar a bicicleta.

Se julgar oportuno, neste momento, é possível trabalhar com os alunos outras equivalências de valores monetários e utilizar reproduções das outras cédulas do real. Explore, por exemplo, que 2 cédulas de 10 reais equivalem a 1 cédula de 20 reais, que 5 cédulas de 20 reais equivalem a 1 cédula de 100 reais etc.

3. Um cliente gastou 75 reais em uma compra no supermercado e usou uma cédula de 100 reais para pagar por essa compra. Quantos reais ele recebeu de troco?

Para resolver essa situação, que envolve a ideia de retirar da subtração, verificar se os alunos reconhecem que para obter o troco é necessário retirar o valor gasto pelo cliente daquele que ele entregou ao caixa, ou seja, deve-se calcular 100

75. Mesmo sem estarem familiarizados com subtrações envolvendo trocas, os alunos podem realizar essa operação explorando o que conhecem sobre equivalências entre valores monetários, como trocar a

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

cédula de 100 reais por outras cédulas. Por exemplo, eles podem trocar por 10 cédulas de 10 reais. Nesse caso, eles tiram 7 cédulas de 10 reais e verificam que é necessário fazer uma nova troca, substituindo, por exemplo, 1 cédula de 10 reais por 2 cédulas de 5 reais. Para finalizar os cálculos, retiram 1 cédula de 5 reais e encontram o troco, que é 25 reais.

4. Em suas economias, Ana tem 68 reais. Desse valor, ela vai separar 25 reais para comprar itens de papelaria e guardar o restante. Quantos reais Ana vai manter guardados?

Para resolver essa situação, que envolve a ideia de separar da subtração, verifique se os alunos reconhecem que para saber quantos reais Ana vai manter guardados é necessário separar o que ela vai gastar do total, ou seja, calcular 68 – 25. Os alunos podem representar os valores monetários de diferentes maneiras. É oportuno compartilhar entre os alunos as estratégias apresentadas, solicitando que expliquem como procederam com os cálculos.

Aula 7

Organizar grupos de três alunos e pedir que cada grupo crie três situações-problema. Orientar que os temas devem ser situações do dia a dia em que se utiliza dinheiro. Como suporte para a realização dos cálculos, disponibilizar para cada grupo reproduções de moedas e cédulas. Entregar também para cada grupo três fichas para o registro de cada problema. Cada aluno deve estar munido de lápis e borracha, já que todos devem participar da elaboração da tarefa.

Pode ser interessante pedir aos alunos que, depois de criada cada situação, eles a representem para validar a ideia que tiveram. Nesse caso, um aluno pode ser o comprador, o outro, o vendedor e o terceiro participa como observador para ajudar a conferir se a situação-problema criada tem lógica suficiente para ser resolvida.

As situações devem envolver diferentes ideias da adição e da subtração.

Explicar aos alunos que dois fatores são essenciais na situação-problema: os dados necessários para a resolução e o enunciado desses dados. Explicitar também a importância de, nesse momento, evitar informações desnecessárias no enunciado da situação.

Se julgar necessário, criar exemplos de situações para que os alunos possam se inspirar neles antes de elaborar os próprios problemas e estimular que eles usem a criatividade e proponham problemas diferentes. Pode-se sugerir que usem o próprio nome ou os nomes dos colegas nas simulações. Apresentar situações de compra e venda em diferentes ambientes comerciais, como supermercado, papelaria, lanchonete, padaria, feira etc. Exemplo:

1. Caio foi a uma papelaria e levou 50 reais. Ele pensou em comprar os seguintes itens:

• calculadora: preço 25 reais;

• caixa de canetas coloridas: preço 17 reais;

• caderno de desenho: preço 12 reais

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

2. Logo Caio percebeu que o valor em dinheiro que ele tinha não seria suficiente para essa compra.

a) Qual valor Caio precisaria ter para pagar pelos três itens?

Espera-se que os alunos respondam: 54 reais.

b) Quanto falta para que Caio possa comprar os três itens?

Espera-se que os alunos respondam: 4 reais.

c) Se Caio comprar apenas a calculadora e as canetas coloridas, quanto ele receberá de troco?

Espera-se que os alunos respondam: 8 reais.

Circular pela sala de aula durante a elaboração e a resolução dos problemas, identificando dificuldades e dúvidas que possam ser resolvidas nesse momento.

Informar que na próxima aula as fichas serão trocadas entre os grupos, para que um grupo resolva o problema criado por outro grupo. A avaliação será feita pelo grupo que propôs o problema. Portanto, cada grupo deverá estar de posse da resolução de seus problemas antes da próxima aula, para sua devida avaliação.

Finalizar a aula pedindo que cada dupla identifique suas três fichas com uma mesma letra do alfabeto determinada pelo professor. Recolher então as fichas.

Essa aula colabora para o desenvolvimento da competência específica 3 da área da Matemática e suas Tecnologias, bem como desenvolve a compreensão de textos e a produção de escrita, consideradas componentes essenciais para a alfabetização.

Aulas 8 e 9

Distribuir as três fichas de cada grupo para outro grupo resolver as situações-problema criadas pelos colegas. Explicar que eles podem utilizar diferentes estratégias na resolução. Disponibilizar o ábaco, o material dourado e as reproduções de moedas e cédulas já utilizadas em aulas anteriores, para os alunos manipularem durante as resoluções. Mencionar também que eles podem recorrer a registros pessoais usando o caderno.

Mostrar aos alunos alguns exemplos de resolução usando os materiais que foram disponibilizados, relacionando-os ao algoritmo da decomposição ou ao algoritmo usual.

Depois, permitir que os grupos resolvam as situações-problema que receberam. É possível que algumas situações elaboradas apresentem falhas, como dados insuficientes.

Nesse caso, pedir que o grupo indique os dados que faltam e que tente corrigir as falhas sem alterar o contexto original do problema. Essa experiência pode ser enriquecedora para os alunos, uma vez que terão o desafio de identificar falhas e propor soluções, dando a eles a oportunidade de exercitar pensamento crítico e colaborativo. Caso os alunos não consigam

corrigir a proposição do problema, a resposta deve ser: problema sem solução por falta de dados.

É importante verificar se cada grupo está empregando diferentes estratégias de resolução e se o fazem de acordo com a conveniência, pois determinados problemas podem ser mais facilmente resolvidos usando-se um recurso ou outro.

Fazer o monitoramento da aprendizagem acompanhando os alunos nas resoluções. Convém fazer registros, como anotações na lousa, que reforcem as conclusões corretas a que chegaram.

Para finalizar a aula, escolher algumas resoluções para que sejam verificadas coletivamente e aproveitar para mostrar o emprego de estratégias variadas.

Sugestões

• LIMA, Roberta Lígia de etal O uso do ábaco no ensino da operação adição: mediação pedagógica realizada na sala de aula do 3º ano do ensino fundamental. Disponível em: http://repositorio.ufc.br/bitstream/riufc/48253/1/2019_capliv_rllimamjcsantos.pdf

Acesso em: 4 jun. 2021.

• VIEGAS, Elis Regina dos Santos; SERRA, Hiraldo Usando algoritmos e ábaco no estudo do sistema de numeração decimal em um curso de Pedagogia. Disponível em: http://www.reveduc.ufscar.br/index.php/reveduc/article/viewFile/987/388 Acesso em: 4 jun. 2021.

Sequência didática 2 • Localização e movimentação

Nesta sequência didática, será retomada a noção de direita e esquerda, serão trabalhadas as ideias de trajeto e de mudanças de direção em um percurso e, ainda, será proposto aos alunos que esbocem a planta baixa da escola.

Objetivos de aprendizagem

• Identificar e registrar localização ou deslocamentos no espaço.

• Compreender a importância de considerar o ponto de referência ao dar instruções de deslocamento ou ao indicar mudanças de direção e de sentido.

• Esboçar roteiros a serem seguidos ou plantas de ambientes familiares.

Plano de aulas

Aula 1: Identificar a mão esquerda e a mão direita por meio de uma atividade de desenho do contorno das mãos.

Aulas 2 e 3: Compor um tabuleiro para realizar deslocamentos nele.

Aulas 4 e 5: Analisar e explorar a planta baixa de um local fictício para indicar os deslocamentos de acordo com um referencial.

Aula 6: Realizar um itinerário pela escola.

Aulas 7 e 8: Obter o esboço da planta baixa da escola.

Aulas 9 e 10: Retomar os conceitos trabalhados por meio de um jogo de tabuleiro.

Componentes essenciais para a alfabetização: produção de escrita, desenvolvimento do vocabulário e fluência em leitura oral.

Competência geral da Educação Básica: 4.

Competências específicas de Matemática: 2, 6 e 8.

Habilidades: EF02MA12 e EF02MA13.

Materiais necessários: régua, cartolina, projetor multimídia e computador, tesoura com pontas arredondadas, lápis de cor, folhas de papel sulfite, dados de seis faces, tampinhas de garrafa e fita adesiva ou etiquetas autoadesivas.

Aula 1

Para iniciar a aula, organizar os alunos em grupos de dois ou três integrantes. É importante que os alunos não estejam em fileiras e que fiquem virados para diferentes direções da sala de aula, de maneira que haja, por exemplo, alunos de frente para a lousa e alunos de costas para a lousa.

Disponibilizar folha de papel sulfite, lápis de cor e tesoura de pontas arredondadas para cada aluno. Propor a eles que expliquem se algum elemento da sala de aula, por exemplo, a porta, está à direita ou à esquerda e estimulá-los a revisar a ideia de esquerda e direita.

Em seguida, propor que cada aluno fixe a mão esquerda na folha de papel sulfite e faça o contorno dessa mão, escrevendo ESQUERDA no interior do contorno feito Analogamente, oriente-os a fazer o contorno da mão direita e, no interior do contorno, escrever DIREITA.

Após os alunos finalizarem, questioná-los sobre qual mão foi mais fácil desenhar, ou qual contorno de mão ficou mais bem desenhado, estimulando-os a perceber se são destros, ambidestros ou canhotos. É interessante registrar essas possibilidades na lousa e explicar o significado dessas palavras.

Pedir aos alunos que desenhem outros elementos da mão, como as unhas ou as marcas da dobra dos dedos e que pintem o interior do contorno desse desenho. É importante que as palavras DIREITA e ESQUERDA fiquem visíveis após eles colorirem o desenho. Em seguida, pedir que recortem o desenho de ambas as mãos e ensine-os a distinguir a mão direita da mão esquerda, por meio desses desenhos. Para isso, pode-se propor que segurem na mão direita o desenho relacionado a ela e na mão esquerda o desenho que a representa.

Para finalizar a aula, fazer uma dinâmica: sortear um aluno e pedir que os demais indiquem alguns objetos, pessoas ou outros elementos que estejam à direita e outros que estejam à esquerda do aluno sorteado. Questioná-los também se, por exemplo, a porta está

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

sempre à direita de um aluno, motivando-os a perceberem e justificarem que é necessário sempre ter um referencial.

Propor aos alunos que realizem uma pesquisa com as pessoas com quem moram e verifiquem se elas são destras, ambidestras ou canhotas.

Caso os alunos ainda apresentem alguma dificuldade para discernir a própria esquerda ou direita, orientar que guardem os desenhos das mãos para utilizar como auxílio no desenvolvimento das demais aulas dessa sequência didática.

Esta aula contribui para o desenvolvimento da competência geral 4 da área da Matemática e suas Tecnologias.

Aulas 2 e 3

Com base na pesquisa proposta aos alunos, retomar a ideia de esquerda e direita. Possibilitar a eles que compartilhem o resultado da pesquisa realizada e incentivá-los a decidir se, no total de pessoas entrevistadas, há mais destros, canhotos ou ambidestros. Para isso, auxiliá-los a registrar as quantidades, por exemplo, representando um quadro de três colunas na lousa e, em cada coluna, o total de pessoas que cada aluno indicar.

Essa atividade contribui para o desenvolvimento da competência específica 6 da área da Matemática e suas Tecnologias.

Em seguida, organizar os alunos em grupos de até quatro integrantes e fornecer uma folha de papel quadriculado, uma cartolina e uma régua para que construam um tabuleiro, composto de uma malha quadriculada de 10 fileiras de 10 quadrinhos cada uma, conforme modelo representado mais adiante. Orientá-los na construção desse tabuleiro ou pode-se também construir esses tabuleiros antecipadamente e distribuí-los prontos aos alunos. Isso fica a critério do professor.

Pedir a cada grupo que crie uma peça que será usada para se movimentar pelo tabuleiro. Para isso, cada grupo deve cortar um pequeno pedaço de cartolina, no mesmo formato e tamanho de um quadrinho da malha, e deve pintá-lo de vermelho. Explicar

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

detalhadamente que essa peça poderá ser situada em qualquer posição da malha quadriculada e movimentada nas direções para a frente, para trás, para a direita ou para a esquerda. Ajudá-los na identificação dos termos "em frente", "atrás", "à direita" e "à esquerda" Para isso, pode-se desenhar na lousa o esquema de setas indicando essas direções, conforme exemplo a seguir.

Editoria de arte

Setas indicando direções.

Inicialmente, pedir aos alunos que coloquem a peça vermelha na posição localizada na terceira linha e quarta coluna do tabuleiro, conforme referência a seguir. Além disso, pedir que pintem de verde o quadrinho da quarta linha e sétima coluna e de azul o quadrinho da sétima linha e sexta coluna. É interessante representar na lousa a escrita, com algarismos e por extenso, dos números ordinais que forem explorados.

Editoria de arte

Modelo de tabuleiro

Após a confecção do tabuleiro e com a peça vermelha na localização inicial indicada, solicitar aos alunos que marquem o quadrinho em que a peça estará localizada, de acordo com cada comando de movimentação, como os sugeridos a seguir, em que D, E, F e T indicam, respectivamente, à direita, à esquerda, em frente, atrás e os números que antecedem as letras indicam o total de quadrinhos na direção proposta pela letra.

1. Partindo da posição inicial, movimente a peça 2T, 2E, 2T e 4D.

2. Partindo da posição inicial, movimente a peça 2T, 5D, 1F e 2E.

3. Descreva o caminho mais curto para movimentar a peça a partir do quadrinho azul até o verde.

Espera-se que os alunos indiquem o seguinte comando: 1D e 3F ou 3F e 1D.

Após a explicação dessas movimentações, propor que um aluno de cada grupo faça comandos para que os demais integrantes movimentem a peça seguindo os comandos dados. Orientar que o aluno troque a função com outro colega do grupo, de maneira que todos os alunos deem instruções de movimentações da peça e que todos realizem movimentações dela. Circular pela sala de aula, a fim de verificar se os alunos conseguem dar e seguir adequadamente as orientações de movimentação.

Orientar os alunos a guardar os materiais construídos nesta aula, pois serão utilizados novamente na última aula desta sequência didática.

Esta aula contribui para o desenvolvimento da competência específica 8 da área da Matemática e suas Tecnologias.

Aulas 4 e 5

Retomar com os alunos a atividade realizada na aula anterior, referente aos deslocamentos da peça no tabuleiro. Questioná-los sobre os comandos dados e sobre as possibilidades de direção. Em seguida, organizar os alunos em pequenos grupos e disponibilizar uma imagem como a sugerida a seguir, impressa ou projetada.

Mapa fictício.

Em um primeiro momento, estimule-os a explorar o mapa identificando os pontos de referência. Depois, discutir oralmente algumas possibilidades de trajetos pedindo aos alunos que apresentem sugestões. Deixe-os se expressarem livremente. Indicar então na lousa alguns outros exemplos de trajetos, como:

• Qual trajeto deve fazer alguém que mora na casa 1 e deseja ir até a escola?

Resposta: Ao sair da casa, virar à direita e, depois, virar à esquerda na Avenida A.

• Qual trajeto deve fazer alguém que está na escola e deseja chegar à livraria?

Resposta: Ao sair da escola, virar à direita e, depois, virar à esquerda na Rua 2 Em seguida, virar à direita na Avenida B.

Em seguida, pedir que os alunos descrevam as orientações de movimentação. Pode-se discutir oralmente possibilitando aos alunos compartilhar estratégias e identificar pontos de referência. Depois, escolher algumas das descrições apresentadas e escrevê-las na lousa, pedindo aos alunos que as leiam em voz alta, contribuindo assim para o desenvolvimento da fluência em leitura oral, um dos componentes essenciais da alfabetização.

Caso os alunos demonstrem dificuldade em descrever corretamente os trajetos, utilizar algumas carteiras da sala de aula para representar os quarteirões da figura e pedir a alunos voluntários que representem os pontos de referência. Deixar que os alunos realizem os trajetos que desejarem, indo de um ponto de referência a outro.

Após os alunos discutirem oralmente alguns trajetos possíveis, por meio da figura apresentada a eles e da representação com as carteiras, propor-lhes que registrem no caderno outros trajetos. Circular pela sala de aula a fim de verificar se eles conseguem descrever corretamente os itinerários.

Aula 6

Retomar com os alunos a importância de perceber o referencial para descrever localização ou trajetos. Em seguida, explicar que realizarão uma excursão pela escola, a fim de passar por algumas dependências como quadra de esportes, biblioteca, pátio, lanchonete e outros ambientes para assim reconhecer a posição desses locais em relação ao percurso que realizarão.

Antes de iniciar a excursão, escrever na lousa ou ditar para que os alunos registrem no caderno os ambientes que visitarão.

Começar a excursão pela entrada da escola ou outro ponto de partida. Com os alunos, destacar o caminho percorrido e a localização de cada lugar a partir do ponto de partida, observando indicações como "à frente", "atrás", 'à direita", "à esquerda". Se possível, tirar fotos dos locais para auxiliar no desenvolvimento das aulas 7 e 8.

Ao retornar para a sala de aula, oralmente, explorar com alunos sobre o percurso realizado, os locais visitados e a posição deles, com base no ponto de partida e em perguntas como:

• Na entrada, viramos no corredor à direita ou à esquerda?

• Após isso, no corredor, a primeira sala à direita é a secretaria da escola?

• Qual é a segunda sala à direita nesse corredor?

• O que há em frente à sala dos professores?

• No fim do corredor, viramos à direita e entramos no pátio da escola; nesse momento, o que havia à nossa esquerda?

• Para finalizar, propor aos alunos que registrem no caderno algumas informações discutidas oralmente. Se necessário, escrevê-las na lousa ou ditá-las

Aulas 7 e 8

Retomar a discussão do itinerário realizado na aula anterior. Se possível, apresentar as fotos registradas no percurso, a fim de que os alunos discutam sobre a posição de pessoas e de objetos presentes nas fotos, de acordo com diferentes referenciais.

Em seguida, propor aos alunos que se reúnam em pequenos grupos, de até quatro integrantes, e disponibilizar régua, cartolina e um lápis de cor para cada grupo.

Com o auxílio das anotações feitas na excursão, realizada na aula anterior, solicitar aos alunos que produzam, na cartolina fornecida, um esboço da planta baixa da escola (ou de uma parte dela).

É interessante, se possível, disponibilizar as fotografias registradas durante a excursão em um projetor multimídia ou impressas deixando-as em uma mesa para consulta dos alunos. Lembrá-los de que devem escrever o nome de cada dependência representada.

Neste momento, os alunos estão desenvolvendo a habilidade de identificar e registrar a localização de objetos no espaço. Assim, todo tipo de representação é válida e deve ser valorizada. Isto é, neste momento o foco não deve ser a precisão ou a proporção das medidas. O objetivo é que os alunos indiquem os lugares visitados relembrando a localização deles de acordo com os deslocamentos realizados no percurso.

Ao final da atividade, propor que compartilhem as produções com os demais colegas da turma pedindo que o aluno explique o que quer representar. É importante valorizar a produção dos alunos e explicar que, por ser uma atividade que requer memorização dos trajetos, podem ser obtidas diferentes representações. Se possível, refazer o itinerário com os alunos levando consigo o esboço que fizeram da planta baixa da escola, a fim de verificar se é necessário fazer ajustes ou correções.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Aulas 9 e 10

Relembrar os alunos sobre o percurso feito na excursão pela escola e verificar se eles utilizam adequadamente os termos para indicar os deslocamentos realizados. Questione-os também, a fim de revisar o significado das palavras, quais deles são destros, ambidestros ou canhotos.

Em seguida, explicar aos alunos que utilizarão o tabuleiro produzido nas aulas 2 e 3 em uma brincadeira. Organize-os em grupos de maneira que cada grupo possua um tabuleiro. Para cada integrante do grupo, disponibilizar um objeto que possa servir como peão (como tampinhas de garrafa, peças de papel) e dois dados, um numerado de 1 a 6 e outro com as indicações "à direita", "à esquerda", "em frente", "atrás", "pule a vez", "jogue de novo". Essas indicações podem ser escritas em etiquetas e coladas sobre as faces de um dado comum.

Explicar que todos os peões devem começar posicionados no quadrinho verde e que o primeiro que chegar ao quadrinho azul será o vencedor. E que, para realizar os deslocamentos, os alunos devem jogar o dado com as indicações de deslocamentos e o dado numerado, andando o total de quadrinhos obtido neste e a direção registrada no dado com indicações de deslocamentos. Caso o dado com essas indicações caia com a face "pule a vez " , o jogador não realiza nenhum deslocamento e, se cair em "jogue de novo", o jogador tem uma nova chance para realizar o lançamento dos dados.

Como regra, explicar que os peões apenas podem se deslocar se for possível realizar o deslocamento indicado nos dados movimentando o peão apenas pelos quadrinhos do tabuleiro. Por exemplo, se o peão estiver na posição indicada pelo quadrinho verde, na figura a seguir, e o deslocamento obtido for 4 quadrinhos para a direita, o jogador não realizará nenhum movimento e passará a vez para o próximo aluno jogar.

Como alternativa para que haja mais rodadas da brincadeira, reduzir o tamanho do tabuleiro, delimitando, por exemplo, um tabuleiro de 6 quadrinhos por 6 quadrinhos ou um de 6 quadrinhos por 4 quadrinhos (contendo o azul e o verde, sempre).

Reservar cerca de 10 minutos do final da aula para propor aos alunos que representem no caderno o tabuleiro e o peão em determinado quadrinho. Então, pedir que indiquem um trajeto possível para que esse peão chegue ao quadrinho azul.

Esta aula contribui para o desenvolvimento das competências específicas 2 e 8 da área da Matemática e suas Tecnologias.

Sugestões

• AGUIAR, Maria Cecília Antunes de; PEDROSA, Maria Isabel Patrício de Carvalho. Desenvolvimento do conceito de espaço em crianças e a educação infantil. Psicologia USP, v. 20, n. 3, p. 389- 415, set. 2009. Disponível em: https://doi.org/10.1590/S0103-65642009000300006. Acesso em: 13 dez. 2021.

• AGUIAR, M. C. A. de O desenvolvimento do conceito de espaço da criança e a educação infantil: esquemas e interações socioafetivas em situações problemas. Tese (Doutorado em Educação) – Universidade Federal de Pernambuco, Recife, Pernambuco, 2006.

• PLANO de aula: diferentes espaços e direções. Nova Escola. Disponível em: https://novaescola.org.br/plano-de-aula/57/diferentes-espacos-e-direcoes. Acesso em: 13 dez. 2021.

• SAIZ, Irma Elena. A direita de quem? Localização espacial na Educação Inicial e nas séries iniciais. In : PANIZZA, Mabel etal Ensinar Matemática na Educação infantil e nas séries iniciais: análise e propostas. Tradução: Antônio Feltrin. Porto Alegre: Artmed, 2006.

• SMOLE, Kátia Cristina Stocco; DINIZ, Maria Ignez; CÂNDIDO, Patrícia Geometria: percebendo espaços, figuras e formas In : SMOLE, Kátia Cristina Stocco; DINIZ, Maria Ignez; CÂNDIDO, Patrícia (org.). Figuras e formas Porto Alegre: Artmed, 2003. (Matemática de 0 a 6).

Sequência didática 3 • Adição e subtração com a escala de Cuisenaire

Nesta sequência didática, serão propostas atividades com o objetivo de construir os fatos básicos da adição e da subtração por meio da manipulação da escala de Cuisenaire Esta escala – também conhecida como "material Cuisenaire" ou "barrinhas" – é um material didático de apoio ao trabalho com a contagem e com as operações.

A elaboração e a resolução de problemas variados também serão propostas nesta sequência didática, com o objetivo de ampliar o repertório de estratégias dos alunos e o estudo das operações de adição e de subtração com números de até três ordens.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Objetivos de aprendizagem

• Construir fatos básicos da adição e da subtração.

• Resolver problemas de adição e de subtração com números de até três ordens

• Elaborar problemas de adição e de subtração com números de até três ordens

Plano de aulas

Aula 1: Explorar a escala Cuisenaire e associar os números de 1 a 10 para as peças desse material.

Aula 2: Utilizar a escala Cuisenaire para compreender fatos básicos da adição.

Aulas 3 e 4: Representar numericamente os fatos básicos da adição e resolver problemas de adição.

Aula 5: Relacionar a adição e a subtração apresentando a ideia de operações inversas e explorar fatos básicos da subtração por meio da manipulação da escala Cuisenaire.

Aula 6: Resolver problemas de subtração.

Aulas 7 e 8: Elaborar e resolver problemas de adição e de subtração.

Aulas 9 e 10: Elaborar e resolver problemas de adição e de subtração com números de até três ordens.

Componentes essenciais para a alfabetização: produção de escrita e desenvolvimento de vocabulário

Competências gerais da Educação Básica: 1, 2 e 4.

Competências específicas de Matemática: 2, 5 e 6

Habilidades: EF02MA01, EF02MA05 e EF02MA06

Materiais necessários: escala Cuisenaire ou material para construir a escala com os alunos (como cartolina, papel cartão, EVA e régua), malha quadriculada de 1 cm por 1 cm de lado, lápis de cor, tesoura de ponta arredondada, material dourado e folhetos de propaganda de produtos diversos.

Aula 1

Nesta aula, os alunos podem estar organizados em grupos de até 4 alunos na sala de aula. Iniciar a aula explicando aos alunos que nesta aula eles vão manipular um material chamado "escala Cuisenaire", a fim de explorar adições. Se achar conveniente, explicar a origem desse material para que os alunos saibam que utilizarão um material construído e pesquisado nos últimos 100 anos por alunos do mundo todo. Esse tipo de reflexão favorece o desenvolvimento da competência geral 1

Se a escola não dispõe desse material, é possível confeccioná-lo como atividade com os alunos na aula de Arte ou como parte desta aula. Nesse caso, sugerimos que cada aluno confeccione sua escala Nesse caso pode-se distribuir folhas de papel quadriculado com quadros de 1 cm² e orientar os alunos a colorir os retângulos seguindo o esquema de cores da escala Cuisenaire, como indicado a seguir.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Se for conveniente, as escalas podem ser confeccionadas antecipadamente pelo professor. No caso dessa confecção, convém utilizar materiais como cartolina, papel-cartão, EVA ou outro material que permita o manuseio sem ser destruído facilmente.

A seguir são apresentados um quadro e um esquema com as cores da escala Cuisenaire e o comprimento de cada cor.

Editoria de arte.

Cor da peça Número representado

Branco 1

Vermelho 2

Verde-claro 3

Rosa ou lilás 4

Amarelo 5

Verde-escuro 6

Preto 7

Marrom 8

Azul 9

Laranja 10

Esquema de cores das peças da escala de Cuisenaire.

Neste momento não é necessário apresentar esse quadro, pois nesta aula os alunos vão montar um esquema similar Organizar a turma em grupos de até quatro alunos e distribuir a escala para cada grupo ou pedir que cada um pegue a sua, caso eles a tenham produzido Incentivar os alunos a manipular e explorar livremente as peças do material. Em seguida, fazer perguntas exploratórias como as sugeridas a seguir.

1. Qual é a maior peça?

A maior peça é a peça de cor laranja, que representa 10 unidades.

2. Qual é a menor peça?

A menor peça é a peça branca, que representa 1 unidade.

3. Quantas peças amarelas é preciso juntar para obter o mesmo comprimento de uma peça laranja?

É preciso juntar 5 peças.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição

comercial (CC BY

–

não

NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

4. É possível agrupar apenas peças vermelhas para obter exatamente o comprimento de uma peça azul?

Não é possível, pois o comprimento de 4 peças vermelhas alinhadas é menor do que o comprimento da peça azul e o comprimento de 5 peças vermelhas alinhadas é maior do que o comprimento da peça azul.

Com base em questões como essas, direcionar os alunos a explorar e a refletir sobre noções de adição associadas à ideia de juntar.

Pedir aos alunos que, em uma malha quadriculada, representem um retângulo para cada tipo de peça da escala Cuisenaire. Orientá-los a separar as peças antes de representá-las, estimulando-os a determinar uma maneira de organizá-las, que pode ser em ordem crescente ou decrescente de acordo com o comprimento, mas também de outras maneiras, por exemplo, por meio das cores.

Enquanto os alunos desenvolvem essa tarefa, é importante circular pela sala de aula retomando algumas perguntas que estimulem a reflexão e a compreensão de como associar cada peça aos respectivos números de 1 a 10.

Para finalizar a aula, pedir aos alunos que colem no caderno a malha com a representação das peças da escala Cuisenaire e, na frente da representação, indiquem o número que cada peça representa, sabendo que os números vão de 1 a 10. Espera-se que o resultado seja um esquema similar ao quadro apresentado anteriormente nesta sequência didática.

As propostas dessa aula favorecem o desenvolvimento da competência geral 2, da competência específica 2 da área de Matemática e suas Tecnologias e da habilidade

EF02MA01

Aula 2

Iniciar a aula revisando com os alunos a atividade realizada na aula anterior, retomando o número que representa cada peça da escala Cuisenaire. Sugere-se, novamente, que os alunos sejam reunidos em grupos de até quatro integrantes para o desenvolvimento desta aula.

Após relembrar o número de cada peça da escala Cuisenaire, orientar os alunos a posicionar, lado a lado, a peça verde-claro e a peça amarela, por exemplo.

Perguntar quais são os números que cada peça representa (3 e 5) e como se pode representar, com números e símbolos, a junção delas (3 + 5 = 8). Conduza a conversa de maneira que os alunos compreendam que a representação pode ser feita por meio de 3 + 5 ou, ainda, 3 + 5 = 8

Em seguida, orientar os alunos a juntar outras peças da escala Cuisenaire para obter o mesmo comprimento das peças amarela e verde-clara juntas. Após realizar essa atividade, possibilitar aos grupos que compartilhem e verifiquem as possibilidades de construção, auxiliando-os a escrever a expressão numérica para cada caso.

As possibilidades estão descritas no esquema a seguir.

1 + 7 = 8

2 + 6 = 8

3 + 5 = 8

4 + 4 = 8

5 + 3 = 8

6 + 2 = 8

7 + 1 = 8

Solicitar aos alunos que, usando no máximo duas peças da escala Cuisenaire, registrem em uma malha quadriculada todas as possibilidades de representar cada um dos números de 1 a 10. Para orientá-los, pode-se retomar o exemplo do número 8 e explorar verbalmente as palavras relacionadas à adição, como ADICIONAR e JUNTAR, que em Matemática significam "realizar a adição" É importante explicar o significado dessas palavras e estimular os alunos a falar outras que considerem ter o mesmo significado, podendo surgir expressões como acrescentar (alguma coisa à outra), somar, ajuntar, prender. Depois de escrevê-las na lousa, pedir aos alunos que as registrem no caderno. Explicar a eles que usualmente utilizamos os termos "adicionar", "juntar" e "acrescentar" e que os demais são termos informais. Esse tipo de proposta favorece o desenvolvimento de componentes essenciais da alfabetização como o desenvolvimento de vocabulário e a produção de escrita.

Para finalizar a aula, solicitar que usem números e símbolos matemáticos para registrar no caderno as adições representadas na malha quadriculada. Por exemplo, é possível representar o número 3 com a peça verde-clara ou com a peça branca junto da vermelha ou, ainda, com a peça vermelha junto da branca. Respectivamente, as adições representadas são: 3 + 0 = 3 (ou 0 + 3 = 3); 1 + 2 = 3; 2 + 1 = 3

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Representação das peças da escala de Cuisenaire para adições cuja soma é 8 e da peça que representa 8.

As propostas desta aula favorecem o desenvolvimento da competência geral 2, da competência específica 2 da área de Matemática e suas Tecnologias e das habilidades

EF02MA01 e EF02MA05

Aulas 3 e 4

Nestas aulas, os alunos vão resolver as propostas individualmente na sala de aula. Relembrá-los dos fatos básicos da adição explorados na aula anterior e solicitar que analisem a representação das adições na malha quadriculada que elaboraram. Instruí-los a organizar as adições usando símbolos e números de maneira ordenada em um quadro Se achar conveniente, fazer um modelo na lousa, ilustrando algumas colunas do quadro, como o exemplo a seguir

Os alunos podem precisar de duas páginas do caderno para escrever todas as adições. Nesse caso, orientá-los a fazer metade em uma página e metade na outra. Para se organizar, eles podem colocar um título para cada coluna do quadro, por exemplo, "Soma 1", "Soma 2", "Soma 3" e assim por diante.

Após isso, explorar algumas regularidades das adições do quadro com os alunos, a fim de que percebam intuitivamente certas propriedades da adição, por exemplo:

• Qualquer número adicionado a zero resulta no próprio número.

• Ao inverter a ordem das parcelas, a soma (ou resultado da adição) não se altera. Caso os alunos apresentem dificuldade para chegar a essas conclusões, questionar:

2. O que acontece quando adicionamos um valor a zero?

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Espera-se que os alunos percebam que o resultado da adição (ou soma) é o mesmo número que foi adicionado inicialmente ao zero. É provável que os alunos expliquem essa propriedade usando termos próprios como "nada acontece", ou "não saímos do lugar". Sempre que possível, orientá-los a se expressarem usando os termos matemáticos aprendidos.

3. Quanto é 1 mais 9? E 9 mais 1?

1 + 9 = 10; 9 + 1 = 10

4. Quanto é 2 mais 7? E 7 mais 2?

2 + 7 = 9; 7 + 2 = 9

5. A soma se altera quando mudamos a posição dos números na adição?

Espera-se que os alunos percebam que a soma não se altera.

Após essa discussão, propor aos alunos que façam algumas adições cujas parcelas não sejam as mesmas, mas a soma seja igual; por exemplo: 5 + 4 e 1 + 8; 7 + 1 e 8 + 0; 3 + 2 e 1 + 4 É importante que os alunos utilizem diferentes estratégias para comparar operações e seus resultados, como contar peças do material dourado, contar nos dedos; e que manipulem as peças da escala Cuisenaire para atribuir significados às adições. Para sistematizar essa manipulação, propor que, sempre que possível, representem cada adição e o resultado por meio de desenhos das peças da escala Cuisenaire.

Após os alunos concluírem essa tarefa, explorar com eles algumas situações-problema que envolvam a adição, destacando a utilização dos termos JUNTAR e ACRESCENTAR tanto verbalmente como nos enunciados escritos. A ideia é verificar se eles relacionam os termos utilizados com a operação de adição. A seguir, são apresentadas algumas sugestões de situações-problema que podem ser trabalhadas nesse momento:

1. João, Pedro e Mariana têm juntos 5 carrinhos. Quando encontraram Caio, juntaram seus carrinhos aos 2 carrinhos de Caio. Quantos carrinhos os quatro amigos possuem juntos?

5 + 2 = 7 (7 carrinhos.)

2. Roberto tem 4 reais e quer comprar um lanche, mas não tem dinheiro suficiente. Sua mãe acrescentou a esse valor 5 reais, o que fez com que Roberto tivesse o valor exato do lanche. Qual é o preço do lanche que Roberto deseja comprar?

4 + 5 = 9 (9 reais.)

3. Sueli é dona de uma loja e tem em seu estoque 3 bermudas. Ela recebeu outras 3 bermudas, que acrescentou ao estoque. Quantas peças de bermuda há no estoque?

3 + 3 = 6 (6 bermudas.)

4. Marcelo tem 4 galinhas em seu sítio. Juntou a elas outras 6 galinhas que um amigo deu a ele. Com quantas galinhas Marcelo ficou?

4 + 6 = 10 (10 galinhas )

4 + 6 = 10 (10 galinhas )

Os alunos podem ser organizados em duplas ou pequenos grupos para resolver as situações-problema. É importante disponibilizar diferentes materiais de contagem, inclusive a escala Cuisenaire, para que utilizem as estratégias que acharem mais apropriadas.

Circular pela sala de aula, a fim de orientar cada grupo quanto às estratégias adotadas e maneiras de registrá-las, tanto com desenhos ou esquemas como com símbolos matemáticos. Após a conclusão das atividades, realizar a correção e pedir aos grupos que compartilhem com os colegas as estratégias e os registros que utilizaram.

As propostas destas aulas favorecem o desenvolvimento da competência geral 4, da competência específica 6 da área de Matemática e suas Tecnologias e das habilidades EF02MA05 e EF02MA06

Aula 5

Nesta aula, os alunos vão explorar os fatos básicos da subtração. Organizar os alunos em grupos de até 4 integrantes e distribuir a cada grupo as peças da escala Cuisenaire

Se achar conveniente, revisar com os alunos o que foi trabalhado nas aulas anteriores, relembrando-os de como registraram as adições por meio de desenhos e pela representação com as peças da escala Cuisenaire.

Em seguida, explorar a ideia de subtração, com questionamentos como: quanto falta para de 2 obter 5? Registre na lousa uma expressão com lacuna, como 2 + ___ = 5. Espera-se que os alunos indiquem que faltam 3 unidades. Perguntar: qual peça da escala Cuisenaire pode ser juntada à peça que representa o número 2 para obter 5? Após as respostas, orientar a representação do número 5 com as peças do 2 e do 3 como representado a seguir.

Editoria de arte.

Representação da escala de Cuisenaire para 2 + 3.

Questionar em seguida sobre o valor de 5 quando se retira 2. Conduzir a percepção de que como se representa 5 como 2 + 3, ao retirar 2 restam 3. Pode-se também questioná-los sobre quanto é 5 menos 3, conduzindo-os a perceber, com a manipulação da escala Cuisenaire, que o resultado equivale a 2. Explorar outros fatos básicos da subtração e, sempre que necessário, estabelecer a relação entre adição e subtração com a ideia de "quanto falta"

É importante propor e orientar os alunos a registrar os fatos básicos da subtração sistematicamente. Por exemplo, sugere-se pedir a eles que elaborem um quadro no caderno como fizeram com os fatos básicos da adição, como o quadro indicado a seguir.

As propostas desta aula favorecem o desenvolvimento da competência geral 4, da competência específica 2 da área de Matemática e suas Tecnologias e da habilidade

Aula 6

Com os alunos sentados individualmente na sala de aula, revisar com eles o quadro elaborado na aula anterior com os fatos básicos da subtração. Relembrar a relação entre adição e subtração e como podem manipular as peças da escala Cuisenaire para resolver subtrações. Após essa conversa inicial, organizar os alunos em duplas ou trios e propor algumas situações-problema envolvendo subtração, como as sugeridas a seguir.

1. Bruna tinha 7 reais em seu cofrinho e retirou 4 reais. Quantos reais ficaram no cofrinho de Bruna após essa retirada?

7 – 4 = 3 (3 reais.)

2. Alexandre tem 7 camisetas no estoque de sua loja. Ele separou 5 camisetas para fazer uma promoção. Quantas camisetas não foram para a promoção?

7 – 5 = 2 (2 camisetas.)

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações se jam licenciadas sob os mesmos

3. José fornece laranjas para o comércio de Daniel e para o comércio de Renata. Em um mês, José tinha 10 quilogramas de laranjas, separou 4 quilogramas para Daniel e o restante enviou para Renata. Quantos quilogramas de laranja Renata recebeu?

10 – 4 = 6 (6 quilogramas.)

4. Uma empresa de transporte foi retirar caixas em um mercado. Para isso precisou levar 2 caminhões. Eram 8 caixas no total. Um dos caminhões levou 4 caixas. Quantas caixas o outro caminhão levou?

8 – 4 = 4 (4 caixas.)

Enquanto os alunos resolvem os problemas, circular pela sala de aula a fim de verificar as estratégias que estão sendo utilizadas para resolver cada problema, orientando-os nas dificuldades que possam surgir. Se necessário, relembrá-los de que podem usar a escala Cuisenaire, assim como outros materiais de contagem, para auxiliar na resolução dos problemas. Finalizada a atividade, propor o compartilhamento das resoluções. Como tarefa de casa, pedir aos alunos que elaborem no caderno dois problemas com números de 0 a 10: um problema envolvendo adição e outro envolvendo subtração. Orientá-los a conversar com as pessoas que moram com eles para explorar contextos próximos da realidade de cada aluno.

Eles também podem pedir ajuda a essas pessoas para escrever os enunciados, mas devem resolver sozinhos os problemas. Informar que a solução de cada problema deve estar separada do enunciado, pois na próxima aula vão trocar a tarefa entre si: um aluno vai resolver o problema elaborado por outro aluno, por isso não poderão ver a resposta. Esse tipo de proposta favorece o desenvolvimento de componentes essenciais da alfabetização, como a produção de escrita.

As propostas desta aula favorecem o desenvolvimento da competência geral 4, da competência específica 6 da área de Matemática e suas Tecnologias e das habilidades

EF02MA05 e EF02MA06

Aulas 7 e 8

Organizar os alunos em duplas ou trios orientando-os a trocar entre si os problemas elaborados em casa. Cada aluno resolve os problemas de um colega e, ao devolvê-los, o elaborador avalia se o problema foi resolvido corretamente Assim, ao final, cada aluno deve ter elaborado e resolvido dois problemas em casa, e em sala de aula deve ter resolvido dois outros problemas elaborados pelos colegas e corrigido as resoluções de dois problemas.

Durante a atividade, circular pela sala de aula e verificar os enunciados e as respostas elaboradas como tarefa de casa e as estratégias de resolução que os alunos adotam nesse momento. É necessário sempre ressaltar a importância de registrar as estratégias, por meio de desenhos que representem as peças da escala Cuisenaire ou por outros recursos.

Sugere-se utilizar esta proposta para avaliar o aprendizado dos alunos e sanar dúvidas eventuais apresentando problemas na lousa e resolvendo-os juntos. Se necessário, trocar as duplas e os trios e repetir a proposta de maneira que os alunos resolvam e corrijam os problemas.

Reservar cerca de 25 minutos antes de finalizar a aula, possibilitando aos grupos o compartilhamento de algumas estratégias de resolução e de registro das operações. Nesse momento, é adequado possibilitar uma troca de ideias entre os alunos sobre os contextos utilizados na elaboração dos problemas, para que percebam as situações que se repetem e as que menos aparecem.

As propostas destas aulas favorecem o desenvolvimento das competências gerais 2 e 4, das competências específicas 5 e 6 da área de Matemática e suas Tecnologias e das habilidades EF02MA05 e EF02MA06

Aulas 9 e 10

Para iniciar as explorações dos conceitos sobre adição e subtração com números naturais, envolvendo números de até dois algarismos, levar para a sala de aula diferentes materiais manipuláveis, por exemplo, peças do material dourado, tampinhas de garrafa, botões etc. Se possível, a coleção deve ter 100 elementos e ficar disponível para que os alunos utilizem quando acharem necessário.

Organizar os alunos em duplas e distribuir entre elas folhetos de propagandas de produtos diversos mostrando preços com um e com dois algarismos. O professor pode criar folhetos com recortes de figuras, caso não consiga em lojas comerciais folhetos adequados para a atividade. Por exemplo: bola, 8 reais; caixa de lápis de cor, 12 reais; estojo, 11 reais; quebra-cabeça, 22 reais; mochila, 44 reais; camiseta, 32 reais; boné, 22 reais; tênis, 54 reais. Apresentar aos alunos alguns problemas que envolvam adição e/ou subtração com os valores que aparecem nos folhetos. Observar as estratégias utilizadas e depois solicitar o compartilhamento das diferentes maneiras de resolução. A seguir são sugeridas algumas situações-problema envolvendo os objetos exemplificados anteriormente

1. Cite três valores possíveis para a compra de 1 bola e de 1 caixa de lápis de cor.

A resposta depende dos folhetos disponibilizados. Espera-se que os alunos combinem os produtos e descubram as opções de compra possíveis utilizando adições. Por exemplo, usando os valores citados anteriormente, uma possibilidade seria: 8 reais (preço da bola) mais 12 reais (preço da caixa de lápis de cor) é igual a 20 reais (valor total)

2. Qual é a diferença entre o preço de um tênis e o de uma camiseta?

A resposta depende dos folhetos disponibilizados. Por exemplo, usando os valores citados anteriormente, uma possibilidade seria: 54 – 32 = 22 (22 reais)

Propor aos alunos que elaborem e resolvam outros problemas utilizando os valores apresentados para os itens dos folhetos. Pode-se solicitar aos grupos que desenhem

folhetos com produtos de sua escolha e lhes atribuam preços para utilizar na elaboração dos problemas.

Circular pela sala de aula a fim de orientá-los quanto às estratégias que podem ser adotadas

É importante disponibilizar diferentes materiais, como a escala Cuisenaire e o material dourado, para que os alunos os utilizem como apoio para as resoluções. Além disso, é preciso avançar nessa aprendizagem, auxiliando os alunos a entender como utilizar os fatos básicos da adição e da subtração para resolver operações com números de até três ordens. Por exemplo, para resolver 125 – 12, oriente-os a perceber que podem subtrair, de 5 unidades, 2 unidades e, depois, de 2 dezenas, 1 dezena.

As propostas destas aulas favorecem o desenvolvimento das competências gerais 2 e 4, das competências específicas 5 e 6 da área de Matemática e suas Tecnologias e das habilidades EF02MA05 e EF02MA06

Sugestões

• PLANO de aula: jogo dos fatos básicos da adição e subtração. Nova Escola Disponível em:

https://planosdeaula.novaescola.org.br/fundamental/2ano/matematica/jogo-dos-fatosbasicos-da-adicao-e-subtracao/504?gclid=CjwKCAjwj6SEBhAOEiwAvFRuKKOvFvugav-K dDnqzf-zgM7VzmoVXngEKxPqAP9YMnWxsJJWxIjKkBoCDxQQAvD_BwE Acesso em: 7 dez. 2021.

• SANTOS, D M.; SANTOS-WAGNER, V M Jogo Soma 10: fatos fundamentais e cálculo mental Em teia: revista de Educação Matemática e Tecnológica Iberoamericana, v. 4, n. 2, 2013. Disponível em: https://periodicos.ufpe.br/revistas/emteia/article/viewFile/2232/1804 Acesso em: 7 dez. 2021.

Sequência didática 4 • Figuras geométricas e sequências

Esta sequência didática analisa objetos do mundo físico, associando-os com sólidos geométricos e, partindo de alguns modelos, são feitos carimbos para o reconhecimento de figuras geométricas. Além disso, serão estudadas sequências numéricas e de figuras geométricas para a identificação de regularidades e de elementos ausentes

Objetivos de aprendizagem

• Relacionar objetos do mundo físico a figuras geométricas.

• Reconhecer figuras geométricas planas a partir de sólidos geométricos

• Nomear e comparar figuras geométricas planas

• Descrever regularidades de sequências.

• Descrever elementos ausentes de sequências.

• Construir sequências a partir de regularidades estabelecidas.

Plano de aulas

Aulas 1 e 2: Relacionar o formato de objetos do mundo físico com o formato de sólidos geométricos, nomeando esses sólidos e os comparando.

Aulas 3 e 4: Utilizar embalagens e objetos cujo formato se parece com o formato de sólidos geométricos para fazer carimbos e relacionar os resultados dos carimbos com o formato de figuras geométricas planas, nomeando-as e comparando-as.

Aulas 5 e 6: Analisar e compor sequências de figuras geométricas planas com padrão ou recursão.

Aulas 7 e 8: Explorar, analisar e construir diferentes sequências com figuras geométricas planas.

Componentes essenciais para a alfabetização: fluência em leitura oral e desenvolvimento de vocabulário

Competências gerais da Educação Básica: 1 e 2.

Competências específicas de Matemática: 1, 2 e 3.

Habilidades: EF02MA10, EF02MA11, EF02MA14 e EF02MA15.

Materiais necessários: coleção de várias embalagens ou objetos que se parecem com os seguintes sólidos geométricos: cubo, paralelepípedo, pirâmide e cilindro, várias fichas com representações dos seguintes sólidos geométricos: cubo, paralelepípedo, pirâmide, cilindro e esfera, várias fichas com representações das seguintes figuras geométricas planas: quadrado, retângulo, triângulo, círculo, várias sequências recursivas de figuras geométricas planas associadas a sequências numéricas, tinta guache e pincel, papel pardo, fichas com representações de sequências, folhas de papel avulsas, lápis e borracha.

Aulas 1 e 2

Para as atividades desta aula, é necessário preparar previamente, com a ajuda dos alunos, uma coleção de embalagens e objetos diversos. Certificar-se de que nessa coleção existam itens que sejam parecidos com os sólidos geométricos que serão estudados: cubo, bloco retangular, pirâmide, cone, cilindro e esfera.

As duas aulas podem ser realizadas na sala de aula com as carteiras organizadas para formar duas mesas grandes e separadas com espaço para os alunos circularem entre elas, com uma roda de cadeiras ao redor das mesas.

Iniciar a aula organizando os itens da coleção formada sobre as duas mesas aleatoriamente, de modo que os alunos possam acessá-los e escolher um deles para manusear. Explicar a eles que os itens expostos são parecidos com os sólidos geométricos

Material disponibilizado em licença aberta do tipo

e que devem escolher um dos itens para explorar e, depois, compartilhar com os colegas o que observaram e como relacionam esse item com um sólido geométrico

Permitir aos alunos que escolham livremente o item da coleção que desejam observar. Quando todos tiverem escolhido seu item, orientar como analisá-lo, explicando que se pode verificar, por exemplo, se tem "pontas", "cantos", partes arredondadas, partes planas. Incentivar os alunos a contar quantas partes do item escolhido são iguais. Com essas observações, os alunos desenvolvem, mesmo intuitivamente, noções sobre vértices, arestas e faces, o que contribui para desenvolver a competência geral 2 e a competência específica 2 da área de Matemática e suas Tecnologias

Conversar com os alunos sobre as características práticas que esses itens podem ter no cotidiano. Perguntar, por exemplo: para que servem as embalagens? Façam um empilhamento das embalagens. O que vocês notaram? Por que a maioria das embalagens não tem partes arredondadas?, entre outras. Encaminhar a reflexão de que as embalagens servem para proteger os produtos; o fato de a maioria delas não ter partes arredondadas integra essa proteção e serve para empilhar sem sobrar espaço e dar estabilidade na posição em que foi colocada. Fazer também perguntas específicas sobre os outros objetos da coleção, como brinquedos, estojos etc. e relacionar o formato com sua função, por exemplo: faria sentido que um estojo de lápis de cor tivesse formato parecido com o de uma esfera? Debates como esse contribuem para desenvolver a competência geral 1 e a competência específica 1 da área de Matemática e suas Tecnologias

Depois de analisar os itens com os alunos, afixar uma ficha ou cartaz com representações de sólidos geométricos e o nome deles (cubo, bloco retangular, pirâmide, cone, cilindro e esfera) ou desenhar essas representações na lousa e escrever os nomes dos sólidos embaixo de cada representação.

Colocar uma carteira embaixo ou próximo de cada representação dos sólidos. Pedir que cada aluno verifique com qual sólido geométrico o item que ele escolheu se parece mais e colocar o item na carteira correspondente.

Pode-se começar com a apresentação de alunos voluntários, chamando ao final os que ainda não se apresentaram. Se achar conveniente, pedir aos alunos que justifiquem a classificação feita, falando as características comuns entre o item e o sólido. Para tornar a aula ainda mais dinâmica, pedir aos alunos cujos itens são diferentes do que está sendo apresentado, mas têm semelhanças com a figura geométrica tratada, que se manifestem e se for o caso complementem as explicações do colega.

A avaliação das atividades desta aula deve acontecer de maneira progressiva durante as atividades, identificando não apenas se os alunos entenderam o conteúdo estudado, mas também atitudes e como agem em relação aos colegas.

Além das competências citadas anteriormente, as atividades desta aula favorecem o desenvolvimento da habilidade EF02MA14.

Aulas 3 e 4

Nestas aulas, prosseguir com o estudo sobre sólidos geométricos, usando os itens ou as embalagens da coleção formada anteriormente. Como as aulas envolverão pintura com tinta guache ou similar, sugere-se que sejam realizadas em um ambiente favorável a esse tipo de atividade.

Reescrever na lousa os nomes dos sólidos geométricos: cubo, bloco retangular, pirâmide, cone, cilindro e esfera Pedir aos alunos que leiam em conjunto e em voz alta o nome de cada sólido e que depois os copiem no caderno. Esta proposta favorece o desenvolvimento em componentes essenciais para a alfabetização, como a produção de escrita e a fluência em leitura oral.

Continuar a aula selecionando itens da coleção e mostrando-os para os alunos. Solicitar que nomeiem, de acordo com o que aprenderam na aula anterior, o sólido geométrico com que cada item se parece e verbalizem as características desse sólido Essa retomada pode servir para avaliar a aprendizagem do reconhecimento e da nomeação dos sólidos geométricos e a associação deles com objetos do dia a dia.

Entre os itens da coleção, separar os que se parecem com esferas e cone e colocá-los em uma caixa separadamente. Comentar que, na próxima atividade, os alunos não usarão esses itens. Caso haja algum objeto na coleção que não pode ser pintado com tinta nem danificado, separar esse item também, pois na próxima atividade os alunos usarão os itens da coleção como moldes de carimbos com tinta. É importante se certificar de que há mais itens na coleção do que alunos na turma para que todos tenham a oportunidade de fazer pelo menos um carimbo.

Informar aos alunos que os itens restantes serão utilizados como modelos para a feitura de carimbos no papel pardo.

Antes de produzir os carimbos, organizar o papel pardo sobre um conjunto de mesas ou no chão, para seu uso coletivo pelos alunos. Deixar as tintas guache e os pincéis acessíveis a todos.

Iniciar a produção dos carimbos mostrando o procedimento com um dos itens: pintar de preferência a base do cilindro para obter uma figura com formato de círculo. Evidenciar a necessidade de pintar apenas uma parte ou um lado de cada modelo pressionando-o depois sobre o papel, para que essa parte seja carimbada.

Propor aos alunos que façam carimbos livremente com o restante dos itens da coleção, verificando se durante a atividade eles levantam hipóteses de como obter as diferentes figuras geométricas planas com o carimbo dos itens que parecem sólidos geométricos. Fazer questionamentos durante a produção que levem a essa descoberta, como os sugeridos a seguir.

1. Quem está carimbando um lado de uma embalagem cujo formato se parece com o formato de um cubo levanta a mão.

2. Quem está carimbando a base plana de um cilindro levanta a mão.

3. Quem está carimbando um dos lados compridos de uma embalagem que se parece com o formato de um bloco retangular levanta a mão.

4. Quem está carimbando um lado de embalagem que tem uma "ponta" levanta a mão. Quando os alunos terminarem de fazer os carimbos, desenhar na lousa representações das figuras geométricas obtidas: quadrado (do cubo); retângulo (do paralelepípedo); triângulo (da pirâmide); círculo (da base do cilindro). Escrever embaixo de cada representação o nome da figura. Solicitar aos alunos que indiquem os carimbos que se parecem com essas figuras. Aproveitar o momento para nomear na lousa essas figuras geométricas planas. Finalizar apontando para uma figura plana de cada vez e solicitando aos alunos que indiquem um item da coleção que pode ser usado para fazer um carimbo parecido com a figura mostrada. A cada indicação dos alunos, enfatizar a relação entre as figuras planas e os sólidos geométricos, dizendo, por exemplo: esse item se parece com um cubo e com ele podemos fazer um carimbo cujo formato é parecido com o formato de um quadrado.

Ao final das aulas, orientar os alunos a ajudar a guardar os materiais utilizados, identificando se algum estragou e precisa ser jogado fora. Os itens restantes da coleção (ou um novo conjunto de itens) serão necessários para dar continuidade à aprendizagem dos alunos nas próximas aulas

As propostas destas aulas favorecem o desenvolvimento da competência geral 2, das competências específicas 1 e 2 da área de Matemática e suas Tecnologias e da habilidade

EF02MA15

Aulas 5 e 6

Estas aulas podem ser realizadas com os alunos organizados em duplas na sala de aula. Produzir antecipadamente algumas peças de papel para eles usarem para formar sequências, podendo ser desenhadas, pintadas e recortadas de cartolina ou recortadas de revistas e jornais pelo próprio professor. Serão necessários vários quadrados, círculos, triângulos e retângulos. Nesse momento, apenas o formato será analisado, por isso as peças cortadas de mesmo tipo precisam ter o mesmo tamanho, mas não precisam ter a mesma cor.

Explicar aos alunos que eles vão estudar sequências de figuras geométricas planas utilizando as estudadas nas aulas anteriores. Desenhar na lousa uma sequência de figuras como a sugerida a seguir, sem dizer os nomes das figuras e depois fazer questionamentos como os sugeridos a seguir.

Editoria de arte.

1. As figuras dessa sequência se parecem com quais figuras geométricas planas?

Com o quadrado, o círculo e o triângulo.

2. Nessa sequência, que figura está representada logo depois do primeiro círculo? E do segundo círculo?

Espera-se que os alunos percebam que depois de cada círculo está representado um triângulo.

3. Que figura sempre está entre o quadrado e o triângulo nessa sequência?

Espera-se que os alunos percebam que entre o quadrado e o triângulo sempre está o círculo.

4. Qual é a última figura da sequência? Para dar a continuidade correta a essa sequência, que figura deve ser colocada em seguida?

O quadrado. O círculo.

Se os alunos tiverem dificuldade em identificar o círculo como a figura que continua a sequência, verbalizar os nomes das figuras da sequência, depois verbalizar novamente pedindo aos alunos para repetir, e que repitam sozinhos mais uma vez, enquanto o professor aponta as figuras em sequência.

Após essas investigações, explicitar que essa sequência tem uma regularidade, também chamada de padrão. Escrever na lousa REGULARIDADE e PADRÃO, ler cada palavra e repetir com os alunos para favorecer o desenvolvimento de competências essenciais para a alfabetização, como a fluência em leitura oral e o desenvolvimento de vocabulário Essa regularidade ou padrão é um trecho da sequência que se repete várias vezes.

Entregar a cada dupla uma folha avulsa, um conjunto de peças de papel de figuras geométricas e cola para os alunos reproduzirem a sequência e colarem os próximos elementos da sequência, que são o círculo e o triângulo. Certificar-se de que cada dupla receba pelo menos 4 quadrados, 4 círculos e 4 triângulos e algumas peças a mais.

Após essa primeira exploração dirigida, organizar os alunos em pequenos grupos para que criem outras sequências utilizando a repetição de um padrão de figuras geométricas planas. Para isso, disponibilizar para cada grupo peças variadas, cola e folhas avulsas. Incentivar a criatividade da turma pedindo que elaborem sequências diferentes da que trabalharam antes e diferentes das elaboradas pelos colegas

Circular pela sala de aula, verificando as sequências elaboradas pelos alunos e avaliando o desempenho e atitude deles. Se identificar algum erro, fazer questionamentos ao aluno a respeito da sequência para que o próprio aluno identifique o erro e corrija-o.

Finalizar a aula pedindo aos grupos que apresentem à turma as sequências de figuras que criaram, descrevendo a regularidade de cada uma delas

As atividades destas aulas favorecem o desenvolvimento das competências gerais 1 e 2, das competências específicas 2 e 3 da área de Matemática e suas Tecnologias e das habilidades EF02MA10 e EF02MA11

Aulas 7 e 8

Estas aulas podem ser realizadas na sala de aula com os alunos sentados individualmente. Como os alunos estão mais familiarizados com a análise de sequências, pode-se aprofundar esse estudo. Para isso, providenciar antecipadamente cópias de sequências recursivas de figuras geométricas e de figuras geométricas que podem ser associadas a sequências numéricas. A seguir há dois exemplos de sequências e propostas de atividades de exploração das características delas.

Iniciar a aula explicando aos alunos que as novas sequências têm regularidades ou padrões diferentes das sequências observadas na aula anterior, e que eles deverão investigar para descobrir as novas regularidades. Atividades como essa contribuem para desenvolver a competência geral 2 e a competência específica 2 da área de Matemática e suas Tecnologias. Propor algumas observações de maneira dirigida e coletiva, mostrando sequências recursivas de figuras previamente preparadas como a sugerida a seguir. Editoria de arte.

Fazer questionamentos para conduzir os alunos nas investigações. Perguntar, por exemplo:

1. O que é parecido entre a primeira e a segunda figuras?

Espera-se que os alunos respondam que as figuras têm o mesmo formato quadrado, que estão divididas na mesma quantidade de partes e que têm as mesmas cores.

2. O que é diferente entre a primeira e a segunda figuras?

Espera-se que os alunos respondam que as partes pintadas de amarelo estão em posições diferentes em cada figura.

3. É possível obter a segunda figura a partir da primeira?

Espera-se que os alunos respondam que sim, pois, girando a primeira figura para a direita, obtém-se a segunda.

4. O mesmo acontece com as demais figuras da sequência?

Espera-se que alunos respondam que girando uma figura para a direita é possível obter a seguinte.

Outra possibilidade de resposta para as atividades 3 e 4 é dizer que, na próxima figura da sequência, o amarelo terá "andado" um quadrado em sentido horário. Espera-se que os alunos usem termos próprios para descrever o que acontece, socializem as respostas e apresentem termos matemáticos corretos, quando necessário.

Como provavelmente os alunos não dominam o conceito de ângulos, não se espera que eles indiquem que foi efetuado um giro de 90 graus para a direita de uma figura para outra. Eles podem se referir aos giros dizendo que de uma figura para a outra é preciso girar uma vez, ou podem descrever a regularidade apontando com o dedo como esse giro deve ser feito.

Explorar também, coletivamente, exemplos de sequências recursivas de figuras geométricas que podem ser associadas a sequências numéricas, conforme o exemplo a seguir

Editoria de arte.

Começar a observação pedindo aos alunos que realizem uma contagem e anotem o número de quadrinhos em cada figura. Espera-se que eles obtenham a sequência: 1, 3, 5, 7.

Prosseguir com questionamentos que os ajudem a analisar a regularidade apresentada, como os sugeridos a seguir

5. Esta sequência é formada por figuras com quadrinhos. Há quantas figuras desse tipo nessa sequência?

Espera-se que os alunos respondam que n a sequência há 4 figuras formadas por quadrinhos

6. De uma figura para a outra, o número de quadrinhos aumenta ou diminui?

Aumenta.

7. De uma figura para a seguinte, quantos quadrinhos são adicionados?

São adicionados 2 quadrinhos.

8. A diferença entre a quantidade de quadrinhos de uma figura e a quantidade de quadrinhos da próxima sequência é sempre a mesma ou se altera?

Espera-se que os alunos respondam que é sempre a mesma, já de uma figura para a seguinte são adicionados 2 quadrinhos.

Para finalizar, solicitar aos alunos que desenhem individualmente no caderno ou em uma malha quadriculada a próxima figura da sequência de figuras formadas por quadrinhos,

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

mantendo a regularidade apresentada A figura formada deve ser a figura representada a seguir.

Organizar os alunos em grupos para que analisem outras sequências de figuras recursivas, associadas ou não a sequências numéricas Disponibilizar aos grupos as sequências e os materiais necessários para que possam representar com desenhos as próximas figuras das sequências seguindo as regularidades estabelecidas.

Para finalizar a aula, um representante de cada grupo pode apresentar aos colegas as sequências que receberam e as próximas figuras desenhadas, descrevendo a regularidade identificada.

As atividades destas aulas favorecem o desenvolvimento das competências gerais 1 e 2, das competências específicas 2 e 3 da área de Matemática e suas Tecnologias e das habilidades EF02MA10 e EF02MA11.

Sugestões

• COLETTI, Selene. Como desenvolver o pensamento lógico no Fundamental 1. Revista

Nova Escola, 5 jul. 2021. Disponível em:

https://novaescola.org.br/conteudo/20482/como-desenvolver-o-pensamento-logico-nofundamental-1 Acesso em: 6 dez. 2021.

• HABILIDADE EF02MA11: Unidade Temática: Álgebra: 2º ano do Ensino Fundamental.

Vídeo (ca. 3 min). Publicado por: Márcio Urel Rodrigues. Disponível em:

https://www.youtube.com/watch?v=sio0hhfcN6U Acesso em: 6 dez. 2021.

• HABILIDADE EF02MA10: Unidade Temática: Álgebra: 2º Ano do Ensino Fundamental.

Vídeo (ca. 5 min). Publicado por: Márcio Urel Rodrigues. Disponível em:

https://www.youtube.com/watch?v=LNG7E6n-CIc Acesso em: 6 dez. 2021.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Sequência didática 5 • Duração e ocorrência de eventos cotidianos

Esta sequência didática aborda a leitura de horas em relógios digitais, a duração de atividades cotidianas e a classificação de eventos aleatórios.

O estudo de noções de tempo, de leitura de horas e de intepretação de situações que envolvam a duração de eventos ou rotina é muito importante desde os Anos Iniciais do Ensino Fundamental, não só do ponto de vista matemático, mas também por permear atividades do dia a dia do aluno até a vida adulta. Para trazer esse conteúdo para o cotidiano do aluno, será apresentada uma proposta de organização de uma agenda semanal.

Por fim, será explorado o significado dos termos "impossível", "improvável", " pouco provável" e "muito improvável", para que os alunos discutam sobre a probabilidade de ocorrência de alguns eventos cotidianos e desenvolvam conhecimentos relacionados com noções de probabilidades e de eventos relacionados ao acaso.

Objetivos de aprendizagem

• Ler e escrever as horas em um relógio digital.

• Calcular a duração de atividades cotidianas.

• Resolver problemas relacionados com horários e duração de atividades.

• Reconhecer os termos " pouco provável", "muito provável", "improvável" e "impossível" como classificação de eventos aleatórios.

• Realizar pesquisa.

• Apresentar dados em tabela de dupla entrada.

Plano de aulas

Aula 1: Reconhecer horário de atividades cotidianas e escrever horas em diversos formatos

Aula 2: Calcular a duração de atividades cotidianas e determinar o horário de término de atividades de acordo com intervalo de duração e horário de início.

Aula 3: Organizar uma agenda semanal.

Aula 4: Organizar uma agenda semanal.

Aulas 5 e 6: Explorar noções de probabilidade em relação a eventos do cotidiano.

Aulas 7 e 8: Realizar uma atividade para verificar ocorrência de eventos aleatórios.

Componentes essenciais para a alfabetização: desenvolvimento de vocabulário, produção de escrita e fluência em leitura oral

Competências gerais da Educação Básica: 4 e 6.

Competências específicas de Matemática: 1 e 3

Habilidades: EF02MA19 e EF02MA22

Materiais necessários: cola, dados ou cubos menores do material dourado, folha de papel quadriculado ou malha quadriculada, relógio digital, tampa de caixa de calçado ou papelão.

Aula 1

Para iniciar a aula, explicar aos alunos que eles vão aprender como ler horas em relógios digitais. Propor uma atividade para verificar a familiaridade dos alunos com a leitura de horas em relógios desse tipo. É comum que os alunos já tenham certo conhecimento das horas e familiaridade com algumas maneiras de falar as horas. Esse conhecimento será consolidado e ampliado nesta aula e na próxima.

Para verificar o conhecimento prévio dos alunos, sugere-se apresentar diferentes imagens e possibilitar que discutam e determinem um horário em que cada cena apresentada pode ter ocorrido. É importante que as cenas tenham relação com a rotina dos alunos e do contexto ao qual estão inseridos.

Sugere-se o uso de projetor multimídia para apresentar as imagens, ou pode-se imprimir uma cópia de cada uma delas e estipular alguns minutos para que sejam compartilhadas entre os alunos. Também podem ser utilizadas imagens de jornais e revistas pré-escolhidas pelo professor e distribuídas aos alunos.

À medida que os alunos falam um horário, por exemplo, "sete e meia da manhã", registrar na lousa cada horário, no formato digital "7:30" Oralmente, apresentar outras maneiras de expressar as horas, quando for pertinente, como "sete horas e trinta minutos"

Explicar aos alunos a diferença entre, por exemplo, "17:00", " 17h00min" e "5:00 da tarde" e verificar com qual desses tipos de escrita das horas eles estão mais familiarizados. Para consolidar as diferentes maneiras de ler e escrever as horas, sugere-se fazer um ditado, propondo aos alunos que escrevam as horas ditadas. Após finalizar o ditado, corrija-o registrando as horas na lousa. Esse tipo de proposta favorece o desenvolvimento de um dos componentes essenciais para a alfabetização, a produção de escrita. A seguir são apresentados exemplos de alguns horários que podem ser ditados e suas diferentes escritas.

• Dez horas e quinze minutos: 10:15; 10h15min

• Quinze horas e quarenta e cinco minutos: 15:45; 15h45min; três horas da tarde e quarenta e cinco minutos

• Seis horas e trinta minutos: 06:30; 06h30min; seis e meia.

• Vinte e uma horas e vinte minutos: 21:20; 21h20min; nove horas da noite e vinte minutos.

As propostas desta aula favorecem o desenvolvimento da Competência geral 6 e da Competência específica 1 da área de Matemática e suas Tecnologias

Para finalizar a aula, propor aos alunos que escrevam algumas atividades que eles fazem diariamente, em um mesmo horário. Para orientá-los, pode-se propor que pensem, por

exemplo, sobre o horário em que acordam, em que tomam café da manhã, em que vão à escola, em que jantam ou em que vão dormir. Como tarefa de casa, propor que conversem com as pessoas com quem residem para listarem outras atividades da rotina de cada família.

Aula 2

No início da aula, organizar os alunos em uma roda de conversa e pedir a eles que socializem o resultado da tarefa de casa, a fim de compararem os diferentes horários em que realizam atividades comuns. Em seguida, explicar que, nesta aula, eles vão determinar os horários de início e de término de atividades, com base no intervalo de duração de cada uma.

Escrever na lousa o horário de início de algumas atividades cotidianas dos alunos e o tempo de duração delas, propondo a eles que determinem o horário de término. Orientar que registrem no caderno as respostas.

Iniciar com exemplos de atividades que começam e terminam dentro da mesma hora; por exemplo, uma atividade que dura 30 minutos e se inicia às 8h10min da manhã. Destacar, oralmente, a contagem de 10 minutos com 30 minutos e o resultado "oito horas e quarenta minutos". Explorar diferentes situações e, em seguida, auxiliar os alunos a determinar o horário de término de atividades que se iniciam em uma hora e termina na seguinte, por exemplo, uma atividade que começa às 8h50min e tem duração de 30 minutos.

Para auxiliar na compreensão do fato de que um minuto após 8h59min corresponde às 9h00min, pode-se disponibilizar um relógio digital e ajustar o horário para 8h50min e, depois, ir ajustando o horário, minuto a minuto, até chegar a 9h20min. Fazer outros exemplos, sempre utilizando o relógio digital como recurso e ajustando a hora, minuto a minuto.

Alguns exemplos de atividades cotidianas e horários que podem ser usados para a atividade ou servir de inspiração estão listados a seguir.

Aula de inglês

Horário de início: 8h30

Duração: 40 minutos

Horário do fim: 9h10

Natação

Horário de início: 14h10

Duração: 50 minutos

Horário do fim: 15h00

Culinária

Horário de início: 9h30

Duração: 2 horas e 30 minutos

Horário do fim: 12h00

Momento de leitura

Horário de início: 19h15

Duração: 1 hora e 20 minutos

Horário do fim: 20h35

Ao final, solicitar aos alunos que socializem as respostas e conversem sobre as atividades que fazem no dia a dia, com os horários de início e de término, para que discutam sobre a duração destas atividades.

É importante verificar a compreensão de cada aluno nas atividades propostas. Observar se eles conseguem realizar o registro de horas e minutos em relógios digitais e se perceberam que a numeração das horas no relógio digital é de 0 até 23, a numeração dos minutos é de 0 até 59 e que existem dois pontos para separar as horas e os minutos nesse tipo de relógio

Outro ponto a ser avaliado é a compreensão da maneira de analisar intervalos de tempo, observando o horário de início e a duração de uma atividade para determinar o horário de término.

A fim de ampliar a abordagem da habilidade a ser desenvolvida nesta sequência didática, sugere-se disponibilizar aos alunos folhas com figuras de relógios digitais para que eles insiram os horários de início e de término de uma atividade de que eles gostam de fazer. Pedir a eles que troquem esses horários com um colega, que deverá determinar o tempo de duração desta atividade.

As propostas desta aula favorecem o desenvolvimento da competência geral 6 e da competência específica 1 da área de Matemática e suas Tecnologias e da habilidade EF02MA19

Aulas 3 e 4

Retomar com os alunos a maneira de registrar horas em relógios digitais e como determinar a duração de eventos cotidianos com base em horários de início e de fim Fazer alguns exemplos na lousa possibilitando aos alunos relembrar o que foi trabalhado na aula anterior.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra der ivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Em seguida, propor aos alunos que elaborem, coletivamente, uma agenda semanal das atividades em comum que realizam. Explicar que a finalidade disso é reconhecer uma ferramenta para organizar o tempo de cada atividade e perceber momentos que podem utilizar para brincar, fazer tarefas de casa ou descansar, por exemplo.

Durante a produção da agenda, verificar se os alunos esperam a vez de o colega falar, se eles fazem anotações e se essas anotações estão escritas corretamente, se eles fazem a leitura correta de informações da lousa ou do caderno, se eles utilizam argumentos pertinentes, entre outros. Esse tipo de proposta e as atividades descritas a seguir favorecem o desenvolvimento e a subsequente avaliação de componentes essenciais para a alfabetização, como a fluência em leitura oral, a compreensão de textos e a produção de escrita

Para iniciar, perguntar aos alunos qual a ordem dos dias da semana e incentivá-los a registrar os nomes dos dias da semana no caderno. Se julgar oportuno, pode-se associar nesse momento a escrita de "Segunda-feira" a "2ª feira", relembrando a representação e a escrita de números ordinais

Na lousa, elaborar um quadro como o indicado a seguir e orientar os alunos a reproduzi-lo no caderno ou em uma folha de papel quadriculado. Se possível, sugere-se imprimir uma cópia do quadro para cada aluno.

Ao elaborar o quadro, ajustar os horários de acordo com aqueles mais próximos da realidade de cada turma. Para isso, pode-se, por exemplo, questionar o horário em que costumam ir dormir e o horário em que costumam acordar. No exemplo a seguir, o quadro contém apenas dois horários, mas é esperado que o quadro completo tenha os horários entre a hora inicial e a final acordadas com os alunos

Explicar aos alunos que a primeira coluna apresenta horários do dia, e as demais colunas representam os dias da semana. É importante que no quadro construído cada horário esteja dividido em quatro partes iguais, pois o quadro será utilizado, posteriormente, para explorar ideias associadas à probabilidade. Além disso, explorar com os alunos que cada uma dessas partes equivale a 15 minutos. Aproveitar para retomar o fato de que 1 hora tem 60 minutos, meia hora equivale a 30 minutos, e metade de meia hora, a 15 minutos.

Em seguida, orientar os alunos a preencher o quadro com os horários que são comuns a todos; por exemplo, o início da primeira aula na segunda-feira e o horário de término da última aula desse mesmo dia. Repetir o procedimento para os demais dias da semana.

Em seguida, questionar sobre atividades de rotina, como almoçar, acordar, dormir, tomar banho, escovar os dentes e jantar. Propor que decidam horários aproximados para cada uma dessas atividades e os registrem no quadro. É interessante orientá-los quanto à possibilidade de aproximar esses horários para horas, como 8h00min, 8h15min, 8h30min ou 8h45min, sempre considerando um quarto de hora como referência. Relembrar que eles podem escrever, também, no formato digital como 08:15. Não é necessário preencher todos os horários da agenda, mas é importante registrar atividades que tenham duração maior que 1 hora ou que sejam importantes para a vida diária dos alunos

Após os alunos se familiarizarem com a escrita e identificação dos horários, propor novas atividades, orientando-os a indicar outras atividades que gostariam de fazer na semana, por exemplo, ir ao parque, brincar com os amigos, jogar videogame e assistir a desenhos animados, e relembrá-los de suas responsabilidades, como fazer tarefa, estudar e ajudar a organizar a casa ou outras tarefas que façam rotineiramente. Auxiliar os alunos a organizar a agenda semanal inserindo essas atividades. Ressaltar a importância de momentos para a prática de atividades físicas e para descanso, por exemplo.

Se achar conveniente, após definirem as atividades e preencherem a agenda, orientá-los a colorir os espaços de início e término de cada atividade, preferencialmente com cores diferentes para atividades distintas.

Após finalizarem os registros e a organização da agenda semanal, utilizá-la para conduzir os alunos a analisar as atividades indicadas e a duração de cada uma delas. Pedir aos alunos que colem a agenda semanal no interior da tampa de uma caixa de calçado para usar nas demais aulas desta sequência didática. Se isso não for possível, pode-se utilizar um pedaço de papelão, papel-cartão ou cartolina para compor um objeto semelhante à tampa da caixa de calçado. É importante que a agenda ocupe todo o fundo da tampa.

As propostas destas aulas favorecem o desenvolvimento da competência geral 6 e da competência específica 1 da área de Matemática e suas Tecnologias, da habilidade EF02MA19 e de um dos componentes essenciais para a alfabetização, a produção de escrita.

Aulas 5 e 6

Retomar com os alunos o que foi feito na aula anterior, explicando como uma agenda, programação semanal ou outro tipo de planejamento similar pode ser útil para o dia a dia deles. Em seguida, com base na agenda semanal construída coletivamente na aula anterior, questioná-los sobre quais atividades têm a maior duração, quais têm a mesma duração e quais têm a menor duração.

Em seguida, explorar a ideia de eventos aleatórios sorteando ao acaso um dia da semana e um horário do dia, e perguntar aos alunos qual é a atividade que tem a maior chance de ser sorteada. Conduzi-los na discussão a utilizar os termos " pouco provável", "muito provável", "improvável" e "impossível". Nesse momento, sugere-se explicar oralmente o significado das palavras "provável", "improvável" e "impossível", registrar a escrita dessas palavras na lousa e orientá-los a escrever as palavras e os significados delas no caderno.

Espera-se que os alunos percebam que os eventos que ocorrem mais vezes na agenda da semana, como "estar em aula na escola" ou "almoçar", são os mais prováveis, enquanto eventos que acontecem, por exemplo, apenas uma vez na semana são os mais improváveis. Para explorar a ideia de "impossível", questioná-los sobre atividades que não foram registradas na agenda semanal e que os alunos não costumam fazer, como "ir trabalhar"

Para finalizar a aula, pedir aos alunos que escrevam algumas frases utilizando os termos relacionados à chance de ocorrer um evento, classificando-os como " pouco prováveis", "muito prováveis", "improváveis" e "impossíveis"

As propostas de atividade desta aula favorecem o desenvolvimento de componentes essenciais para a alfabetização, como a produção de escrita e o desenvolvimento de vocabulário Além disso, estas propostas também favorecem o desenvolvimento das competências gerais 4 e 6 e das competências específicas 1 e 3 da área de Matemática e suas Tecnologias e da habilidade EF02MA21

Aulas 7 e 8

Relembrar os alunos sobre os termos utilizados para classificar eventos aleatórios cotidianos explorados anteriormente. Solicitar que compartilhem algumas frases que foram produzidas no final da aula anterior e, oralmente, decidam sobre a validade de cada uma.

Em seguida, organizar os alunos em grupos de três ou quatro integrantes e distribuir a cada grupo um cubo pequeno do material dourado ou um dado de tamanho similar. Orientá-los a lançar o cubo sobre a tampa na qual foi colada a agenda. As laterais da tampa servirão como barreira para evitar que o cubo saia do limite da tampa.

Explicar que eles devem lançar o cubo 20 vezes sobre a tampa, verificar sobre qual atividade da agenda o dado parou e anotar no caderno. Orientá-los também que, no caso de

ficarem em dúvida de qual atividade foi sorteada (se o dado ficar sobre duas atividades ou sobre nenhuma, por exemplo), façam um novo lançamento.

Durante a realização desta atividade, circular pela sala de aula a fim de verificar como os alunos registram os resultados e se os organizam de maneira adequada. Pode-se sugerir, por exemplo, que registrem a atividade sorteada e, em frente a esse registro, indiquem a quantidade de vezes que ela for sorteada em vez de registrar várias vezes cada atividade sorteada.

Após os alunos finalizarem a atividade, fazer questionamentos para cada grupo como os sugeridos a seguir:

• Qual foi a atividade mais sorteada no seu grupo?

• Alguma atividade da agenda não foi sorteada?

Na exploração oral, retomar, também, o uso dos termos " pouco provável", "muito provável", "improvável" e "impossível".

Para finalizar a aula, orientar os alunos a registrar a ocorrência de sorteios das atividades de toda a turma em uma tabela e construir um gráfico de barras com os dados Se possível, disponibilizar folhas de papel quadriculado para auxiliar na construção dos gráficos. Por fim, promover uma análise desses dados por meio de questionamentos como:

• Qual foi a atividade mais sorteada na turma?

• Alguma atividade da agenda não foi sorteada pela turma?

Em seguida, perguntar aos alunos se as respostas foram iguais às respostas de cada grupo. É possível que um grupo tenha sorteado mais uma atividade que não foi a mais sorteada pela turma. Nesse caso, questioná-los sobre isso.

As propostas de atividade desta aula favorecem o desenvolvimento de componentes essenciais para a alfabetização, como a produção de escrita e o desenvolvimento de vocabulário. Além disso, essas propostas também favorecem o desenvolvimento das competências gerais 4 e 6 e das competências específicas 1 e 3 da área de Matemática e suas Tecnologias e das habilidades EF02MA21 e EF02MA22

Sugestões

• CAMPOS, Tânia M. M.; CARVALHO, José Ivanildo Felisberto. Probabilidade nos anos iniciais da educação básica: contribuições de um programa de ensino. Em teia: revista de Educação Matemática e Tecnológica Iberoamericana, v. 7, n. 1, 2016. Disponível em: https://periodicos.ufpe.br/revistas/emteia/article/download/3884/pdf Acesso em: 11 dez. 2021

• WINKEL, Sophia. O certo, o provável e o impossível. Nova Escola Disponível em: https:// novaescola.org.br/conteudo/10540/matematica-probabilidade-estatistica-funda mental-1 Acesso em: 11 dez. 2021

Sequência didática 6 • Multiplicação com ideia de adição e o dominó das multiplicações

Esta sequência didática aborda a resolução de problemas que envolvem a multiplicação com a ideia de adição de parcelas iguais (por exemplo: 2 + 2 + 2 = 3 x 2)

A sequência se inicia com a retomada da adição com múltiplas parcelas com números de até dois algarismos por meio da resolução de problemas. Nas aulas seguintes, serão estudados conceitos de multiplicação com a resolução de problemas diversos e a representação matemática e por desenhos e esquemas de multiplicações. Por fim, é proposta uma avaliação por meio de uma atividade lúdica que envolve um dominó de multiplicações produzido pela turma com o auxílio do professor.

Objetivos de aprendizagem

• Resolver problemas de multiplicação (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais

• Elaborar problemas de multiplicação (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais, representados por meio de desenhos, esquemas ou material de contagem.

• Consolidar conhecimentos de multiplicação (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais por meio de atividade lúdica (dominó da multiplicação).

Plano de aulas

Aula 1: Relembrar conceitos de adição com números de até dois algarismos por meio da resolução de problemas.

Aula 2: Relembrar conceitos de adição com números de até dois algarismos por meio da resolução de problemas.

Aulas 3 e 4: Estudar a multiplicação (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais por meio da resolução de problemas.

Aulas 5 e 6: Elaborar problemas de multiplicação com a ideia de adição de parcelas iguais, representando-os com desenhos, esquemas ou material de contagem.

Aulas 7 e 8: Criar um jogo de dominó da turma formado por multiplicações (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais e jogar uma partida do jogo de dominó da turma.

Componentes essenciais para a alfabetização: produção de escrita e fluência em leitura oral.

Competências gerais da Educação Básica: 2, 4 e 7.

Competências específicas de Matemática: 2, 5, 6 e 8.

Habilidades: EF02MA06 e EF02MA07.

Materiais necessários: folhas de papel sulfite, material de contagem, 80 pedaços de papel-cartão, cartolina ou papelão com formato de um retângulo de 10 cm por 5 cm, lápis de cor, canetinhas ou outros materiais de pintura, tesoura com pontas arredondadas, lápis e borracha.

Aulas 1 e 2

As atividades propostas para estas aulas têm o objetivo de relembrar conceitos de adição com números de até dois algarismos. Esses conceitos serão necessários, posteriormente, para o estudo da multiplicação com ideia de adição de parcelas iguais Sugere-se que elas sejam feitas individualmente na própria sala de aula e que a avaliação delas seja realizada em duplas de maneira que um aluno corrige a atividade do outro e, depois, cada um retoma seu trabalho para validar ou não a avaliação feita pelo colega, o que colabora com o desenvolvimento da competência geral 2

Avisar os alunos de que, para resolver as atividades, eles podem utilizar as estratégias estudadas anteriormente como: reta numerada, peças do material dourado e desenhos. Se achar necessário, retomar as estratégias

Para iniciar, apresentar a seguinte situação oralmente: Diana precisa arrumar a gaveta onde ficam guardadas as camisetas dela. Para isso, ela espalhou sobre a cama as peças que estavam na gaveta

Nesse momento, desenhar na lousa 9 camisetas, ou representações de camiseta, de maneira que sejam 3 brancas, 2 rosa, 1 vermelha, 2 listradas e 1 de bolinhas. Uma outra possibilidade é reservar uma aula a mais para confeccionar representações das roupas com os alunos, usando tesoura com pontas arredondadas, folhas de papel sulfite e lápis de cor.

Orientar os alunos a resolver as atividades sugeridas a seguir no caderno ou propor atividades similares para explorar a situação envolvendo adições.

1. Complete o quadro com a quantidade de camisetas de Diana, de acordo com a cor ou a estampa.

a) Quantas camisetas brancas e rosa Diana tinha na gaveta?

3 + 2 = 5 (5 camisetas.)

b) Quantas camisetas listradas, de bolinha e vermelhas Diana tinha na gaveta?

2 + 1 + 1 = 4 (4 camisetas.)

c) Quantas camisetas ao todo Diana tinha na gaveta? 3 + 2 + 2 + 1 + 1 = 9 (9 camisetas.)

2. Diana tem mais 2 camisetas secando no varal. Marque um X na quantidade de camisetas que Diana tem no total.

( ) 9 camisetas. ( ) 10 camisetas. ( ) 11 camisetas. ( ) 13 camisetas.

9 + 2 = 11 (11 camisetas).

3. Depois de guardar as camisetas, Diana decidiu organizar outra gaveta. Nela, Diana encontrou 6 calças, 5 bermudas e 2 saias.

a) Quantas calças e bermudas Diana tinha na gaveta?

6 + 5 = 11 (11 c alças e bermudas.)

b) Quantas calças e camisetas Diana tem?

6 + 11 = 17 (17 calças e camisetas.)

c) Quantas camisetas, saias e bermudas Diana tem?

11 + 5 + 2 = 18 (18 camisetas, saias e bermudas.)

d) Quantas peças de roupa Diana tem ao todo?

11 + 6 + 5 + 2 = 24 (24 peças de roupas.)

Após os alunos resolverem as atividades, pedir que troquem o caderno com um colega e orientar cada um a corrigir as atividades do outro. Em seguida, destrocar e orientar os alunos a validar a correção. Circular pela sala de aula, tirando dúvidas e, se necessário, corrigir as atividades na lousa.

Ao final, fazer uma conversa e pedir para contarem as estratégias que utilizaram para fazer os cálculos e se encontraram alguma estratégia diferente ao corrigir as atividades dos colegas. Caso alguém tenha utilizado uma estratégia diferente das que foram trabalhadas anteriormente, explorá-la com a turma, enriquecendo o aprendizado dos alunos

As atividades propostas nestas aulas favorecem o desenvolvimento da competência geral 2, da competência específica 6 da área de Matemática e suas Tecnologias e da habilidade EF02MA06.

Aulas 3 e 4

Nesta aula, os alunos podem ser organizados individualmente na sala de aula. Iniciar a aula propondo um problema como o sugerido a seguir para que os alunos recorram a seus conhecimentos prévios de multiplicação com ideia de adição de parcelas iguais. Orientar os alunos a tentar solucionar o problema sozinhos

Se achar conveniente, ditar o problema lendo-o pausadamente para os alunos. Em seguida, escrever o problema na lousa e pedir a eles que acompanhem lendo oralmente cada palavra. Por fim, pedir também que comparem o enunciado da lousa com a própria escrita

no caderno e corrijam erros em conjunto com os colegas. Esse tipo de proposta favorece o desenvolvimento de componentes essenciais para a alfabetização, como a produção de escrita e a fluência em leitura oral.

1. Sofia toma 4 copos de água por dia, todos os dias. Quantos copos Sofia toma em uma semana?

Espera-se que os alunos respondam que Sofia toma, ao todo, 28 copos de água em uma semana. Explicar brevemente o problema, sem detalhar muito, de maneira que a explicação inclua o nome dos sete dias da semana ou relembrar os alunos de que uma semana tem 7 dias.

Pedir aos alunos que expliquem o que entenderam do problema e socializem com os colegas como eles fariam para resolvê-lo. Em seguida, reservar alguns minutos para que eles tentem resolver o problema individualmente usando a estratégia levantada. Nesse momento, caso não surjam estratégias variadas de resolução, propor algumas como a utilização de desenhos ou de esquemas.

Em seguida, fazer um levantamento rápido sobre o resultado obtido por eles e mostrar uma possível resolução usando um recurso visual que envolve a adição de parcelas iguais como o sugerido a seguir.

Domingo Segunda-feira Terça-feira Quarta-feira

Mostrar que, como uma semana tem 7 dias, o problema pode ser entendido como a adição de 7 parcelas iguais do número 4: 4 + 4 + 4 + 4 + 4 + 4 + 4 = 28.

Contar juntamente com a turma, em voz alta, unidade por unidade até que alcancem as 28 unidades. Em seguida, adicionar de 4 em 4 até que alcancem as 28 unidades. Destacar que há 7 parcelas de 4 unidades e para finalizar esse primeiro momento, introduzir a notação de multiplicação para o mesmo problema: 7 x 4 = 28, identificando que o 7 representa a quantidade de parcelas e 4 a quantidade em cada parcela.

Em seguida, propor problemas como os sugeridos a seguir que envolvam a adição de parcelas iguais e orientar os alunos a tentar resolvê-los usando as diversas estratégias socializadas anteriormente.

2. Gustavo ganhou 5 pacotes de figurinhas. Cada pacote tem 6 figurinhas. Quantas figuras Gustavo ganhou ao todo?

5 x 6 = 30 (30 figurinhas.)

3. Em cada rodada do jogo de que Enzo está participando, ele pode ganhar 8 pontos. Enzo jogou 2 rodadas e ganhou 8 pontos em todas as rodadas. Quantos pontos ele ganhou?

2 x 8 = 16 (16 pontos.)

4. Laura vai fazer bolinhos para seus amigos. Ela tem 3 amigos e vai fazer 9 bolinhos para cada um. Quantos bolinhos Laura vai fazer?

3 x 9 = 27 (27 bolinhos.)

Corrigir na lousa o primeiro problema sugerido, dando assim a chance para que os alunos façam uma autocorreção nos problemas seguintes caso tenham percebido que repetiram algum tipo de raciocínio errado. Dessa maneira, dar mais algum tempo para que ajustes sejam feitos no segundo e no terceiro problemas. Depois, corrigir, também, os dois últimos problemas reforçando mais uma vez a ideia inicial da aula.

As propostas destas aulas favorecem o desenvolvimento das competências gerais 2 e 4, da competência específica 5 da área de Matemática e suas Tecnologias e da habilidade

EF02MA07

Aulas 5 e 6

Nestas aulas, os alunos podem ser organizados em duplas na sala de aula. Começar a aula com um resumo do que foi abordado na aula anterior. Enfatizar a ideia utilizada para obter o conceito de multiplicação. Reforçar que ela torna mais fácil a resolução da adição de parcelas iguais, e que, na nova maneira de representar, os dois números utilizados à esquerda da igualdade têm um significado. Dizer que o primeiro número indica quantas vezes o segundo número será adicionado

Se achar conveniente, escrever na lousa um exemplo visual da resolução de um dos problemas da aula anterior à medida que o resumo é apresentado Verificar se os alunos entendem que a multiplicação, nesse caso, pode ser descrita como "a quantidade de parcelas vezes a quantidade de itens em cada parcela, que é igual ao resultado que procuramos", e se eles usam o sinal de vezes e de igual adequadamente para representar a multiplicação.

Pedir às duplas de alunos que elaborem um desenho ou esquema que represente uma situação envolvendo a multiplicação com ideia de adição de parcelas iguais até que cheguem à representação da multiplicação usando o sinal de vezes e de igual, conforme o que foi revisado. Nesse momento, a criatividade pode ser incentivada por meio da distribuição de revistas para o recorte de figuras, de material de contagem, como palitos, sementes, entre outros. Dependendo do desenvolvimento dos alunos, pode-se, em algum momento, desafiar os alunos a criar problemas que não envolvam nenhum objeto, apenas uma situação imaginada

Acompanhar as duplas no andamento da elaboração, de modo que estímulos adicionais possam ser dados àquelas que tenham mais dificuldade. Quando notar que a maior parte das duplas já tenha terminado, pedir que cada uma delas vá à frente da sala de aula para narrar os problemas criados e, se possível, utilizar algum recurso visual (como o material de contagem, os desenhos ou, até mesmo, escrever ou desenhar na lousa) para explicar sua situação-problema, demonstrando para a turma como a dupla fez para

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

representar a multiplicação usando o sinal de vezes e de igual. Nesse momento, pedir que as duplas não escrevam o produto na lousa, apenas a multiplicação

O registro da multiplicação elaborada por cada dupla formará uma lista de multiplicações. Se necessário, reescrever a listagem em um canto da lousa.

Para a discussão sugerida a seguir, é importante que a listagem contenha multiplicações das quais um dos fatores seja o mesmo de outras multiplicações. Se isso não ocorrer naturalmente, contribuir com alguma situação-problema que possa ser resolvida por uma multiplicação que tenha um dos fatores idênticos ao fator da multiplicação de alguma(s) dupla(s)

Organizar os alunos em uma roda de conversa e propor questionamentos como os sugeridos a seguir:

1. Entre as multiplicações listadas na lousa, quais têm um número em comum?

A resposta depende das multiplicações listadas na lousa.

2. Entre as multiplicações que possuem um número em comum, qual terá o maior resultado? Como vocês chegaram a essa conclusão?

A resposta depende das multiplicações listadas na lousa.

Espera-se que os alunos justifiquem o raciocínio deles de maneiras diversas; alguns deles podem não apresentar uma lógica correta, assim, direcionar a conversa de maneira a corrigir esses raciocínios. Para isso, comparar duas multiplicações em que um dos fatores é o mesmo número, representando cada uma delas como adições de parcelas iguais. Acompanhar os exemplos a seguir e a descrição do raciocínio esperado ao final da explicação.

• 2 x 4 e 2 x 5

• 2 x 4 = 4 + 4

• 2 x 5 = 5 + 5

• Nesse caso, a quantidade de parcelas é igual (2 parcelas) e a quantidade em cada parcela é diferente. Como 5 é maior que 4, então o produto de 2 x 5 é maior que o produto de 2 x 4.

• 4 x 3 e 2 x 3

• 4 x 3 = 3 + 3 + 3 + 3

• 2 x 3 = 3 + 3

• Já nesse caso, a quantidade de parcelas é diferente e a quantidade em cada parcela é igual (3). Como 4 é maior que 2, então o produto de 4 x 3 é maior que o produto de 2 x 3.

A avaliação do desenvolvimento da aprendizagem dos alunos nesta aula deve ser feita continuamente medindo: a participação dos indivíduos da dupla; as contribuições nas discussões realizadas na roda de conversa; e como cada aluno se comporta durante as atividades e se respeita a hora de falar do colega

Ao promover a justificativa dos raciocínios dos alunos e a reflexão sobre as justificativas dos colegas, as propostas destas aulas favorecem o desenvolvimento da competência geral 7. A resolução de problemas, utilizando tanto as notações matemáticas como desenhos e esquemas, favorece o desenvolvimento das competências gerais 2 e 4 Além disso, as propostas destas aulas favorecem o desenvolvimento das competências específicas 2 e 5 da área de Matemática e suas Tecnologias e da habilidade EF02MA07

Aulas 7 e 8

A primeira aula pode ser realizada com os alunos organizados em grupos de até 4 integrantes, na sala de aula ou em outro espaço que possibilite desenhar, colorir e usar outros materiais artísticos. Sugere-se realizar a segunda aula em um espaço aberto que permita aos alunos se sentarem no chão em roda para jogar Dominó.

Nesta aula, os alunos vão construir em conjunto um jogo de dominó da multiplicação com ideia de adição de parcelas iguais. Para isso, será necessário preparar previamente 80 pedaços de cartolina, papel-cartão ou papéis cortados com formato de retângulos de 10 cm por 5 cm, divididos ao meio, conforme modelo a seguir. Para o caso de algum aluno errar ou perder um papel, sugere-se que sejam feitos alguns papéis a mais.

Editoria de arte

A produção do dominó será dividida em duas etapas:

• Etapa 1: fazer uma lista na lousa de todas as multiplicações por 2, 3, 4 e 5 (de 0 a 10), sem os produtos. Cada aluno deverá levantar uma vez, escolher uma multiplicação da lousa e riscá-la. Dar um papel para o aluno e orientá-lo a escrever em uma das partes a multiplicação escolhida. Repetir até que todos os papéis tenham uma multiplicação escrita. Em seguida, recolher os papéis.

• Etapa 2: chamar os alunos novamente um a um; cada aluno deverá escolher uma outra multiplicação da lousa e contorná-la. Dar para o aluno um papel que contenha uma multiplicação diferente da que ele acabou de escolher. Orientar o aluno a desenhar na parte em branco uma representação da multiplicação escolhida, de

maneira que seja possível identificar quantas parcelas e quantos itens há em cada parcela. Repetir até que todos os papéis tenham um desenho. Em seguida, recolher os papéis.

A seguir são apresentados alguns exemplos de como as peças podem ficar.

Editoria de arte

Exemplos de peças possíveis para o jogo de dominó da multiplicação.

Após a confecção das peças, levar os alunos para um espaço aberto onde possam se sentar confortavelmente em roda para jogar Dominó. Caso os alunos nunca tenham jogado dominó antes, apresentar o jogo e as regras, conforme descrito a seguir.

• A turma será separada em 4 times.

• Cada time receberá 20 peças, as quais não devem ser mostradas aos outros times

• Organizar-se em roda de maneira que os times estejam suficientemente separados.

• O primeiro time escolhe uma carta para jogar e a coloca no meio da roda, de maneira que todos possam vê-la.

• Na sua vez, cada time precisa colocar uma carta de maneira que um desenho seja alinhado com a multiplicação que o representa. Caso o time não tenha nenhuma carta que possa ser jogada, o time passa a vez.

• Vence a partida, o primeiro time a jogar todas as suas 20 cartas.

Além de ser uma atividade lúdica, esta proposta serve de avaliação do que foi aprendido nas aulas anteriores. Mediar as jogadas, verificando se os alunos fizeram as associações corretamente e tirando potenciais dúvidas. Durante as jogadas, avaliar também a participação dos alunos, a interação com os colegas e se há trocas de estratégias entre os alunos de um mesmo time, entre outros aspectos relevantes.

As propostas desta aula favorecem o desenvolvimento de um dos componentes essenciais para a alfabetização, a produção de escrita, da competência geral 4 e das competências específicas 2 e 8 da área de Matemática e suas Tecnologias.

Sugestões

• KUHN, M. C.; PEREIRA, J de F A multiplicação nos anos iniciais do Ensino Fundamental: da teoria para a prática. Revista Thema, v. 17, n. 2, p. 464-482, 2020 Disponível em: https://doi.org/10.15536/thema.V17.2020.464-482.1753 Acesso em: 14 dez. 2021

• PRÁTICAS para o Ensino de Matemática III: aula 2: jogos didáticos Vídeo (ca. 21 min). Publicado por: canal Univesp Disponível em: https://www.youtube.com/watch?v=wXW99tH71ek Acesso em: 4 dez. 2021

Sequência didática 7 • Dobro, metade, triplo e terça parte

Nesta sequência didática, serão trabalhadas atividades para desenvolver o significado de dobro, metade, triplo e terça parte, com suporte de material manipulável e com outras estratégias.

Objetivos de aprendizagem

• Compreender a ideia de dobro, triplo, metade e terça parte.

• Compreender a relação entre dobro e metade.

• Compreender a relação entre triplo e terça parte.

• Elaborar e resolver problemas envolvendo dobro, metade, triplo e terça parte.

Plano de aulas

Aulas 1 e 2: Explorar a ideia de dobro e de triplo por meio de figuras retangulares em malhas quadriculadas.

Aulas 3 e 4: Determinar o dobro e o triplo de quantidades com suporte de materiais manipuláveis e resolver problemas que envolvam o dobro e o triplo de quantidades.

Aulas 5 e 6: Explorar imagens para atribuir significado à ideia de metade e trabalhar estratégias para determinar a metade e a terça parte de quantidades com suporte de materiais manipuláveis e de diferentes registros.

Aulas 7 e 8: Elaborar e resolver problemas que envolvam a ideia de metade e de terça parte.

Aulas 9 e 10: Aplicar a ideia de dobro, triplo, metade e terça parte em diferentes atividades com ou sem suporte de material manipulável.

Componentes essenciais para a alfabetização: compreensão de textos, desenvolvimento de vocabulário, produção de escrita e fluência em leitura oral

Competências gerais da Educação Básica: 2 e 7

Competências específicas de Matemática: 2, 6 e 8.

Habilidade: EF02MA08.

Materiais necessários: material dourado, lápis de cor, folhas de papel quadriculado e copos descartáveis.

Aulas 1 e 2

Para iniciar a aula, explicar aos alunos que eles farão uma atividade para descobrir o significado das palavras "dobro" e "triplo". Dividir a lousa em duas colunas e escrever "dobro" na coluna à direita e "triplo" na coluna à esquerda.

Em seguida, organizar os alunos em duplas ou trios e disponibilizar folhas de papel quadriculado e lápis de cor para cada um. Primeiro, orientá-los a colorir uma sequência de quadrinhos na cor verde, de maneira a formar figuras com 1 quadrinho, 2 quadrinhos, 3 quadrinhos, 4 quadrinhos e 5 quadrinhos, como representado a seguir.

Editoria de arte

Sequência de quadrinhos a serem coloridos na cor verde.

Após colorir os quadrinhos verdes, orientá-los a formar uma nova sequência de figuras, formadas por quadrinhos coloridos em azul, mas de modo que para cada quadrinho verde haja dois quadrinhos azuis, conforme indicado a seguir.

Editoria de arte

Sequência de quadrinhos a serem coloridos na cor azul.

Auxiliar os alunos quanto à composição das primeiras quatro figuras azuis da nova sequência e, após deixar que façam sozinhos a quinta figura, questioná-los sobre qual seria a sexta figura azul dessa sequência. Verificar se eles formam uma figura com 12 quadrinhos azuis e se eles percebem que as figuras azuis correspondem ao dobro das figuras verdes da primeira sequência, observando como expressam esse fato. Utilizar oralmente a palavra "dobro" associada a seu significado. Isso pode ser feito por meio de expressões como "o total de quadrinhos azuis é o dobro do total de quadrinhos verdes, pois para cada quadrinho verde temos dois quadrinhos azuis".

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra der ivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas

Em seguida, propor aos alunos que representem a sétima figura da sequência de figuras verdes e, depois, que registrem uma figura azul com o dobro de quadrinhos da sétima figura verde. Verificar se eles conseguem utilizar estratégias pessoais para resolver a situação e se compreendem que a sétima figura azul deverá ter 14 quadrinhos. Para isso, eles podem, por exemplo, colorir dois quadrinhos azuis para cada quadrinho verde e, após isso, contar o total de quadrinhos azuis obtidos.

Se necessário, pode-se propor aos alunos que representem mais figuras das sequências, sempre utilizando expressões que atribuam significado à palavra "dobro"

De forma semelhante, questionar os alunos sobre qual seria a sequência de figuras vermelhas obtidas com o triplo de quadrinhos da sequência de figuras verdes. Utilizar oralmente a palavra "triplo" e, depois, fazer alguns exemplos com os alunos associando à ideia "para cada quadrinho verde, três vermelhos". Junto deles, fazer as cinco primeiras figuras da sequência e propor-lhes que determinem a formação da sexta e da sétima figuras verdes, azuis e vermelhas, conforme representado a seguir

Após a realização desta atividade exploratória, orientar os alunos a registrar na folha de papel quadriculado algumas figuras com determinadas quantidades de quadrinhos, envolvendo a ideia de dobro e triplo. Por exemplo, oralmente solicitar que façam:

a) uma figura alaranjada com o dobro de 8 quadrinhos.

b) uma figura lilás com o triplo de 9 quadrinhos.

c) uma figura amarela com o triplo de 10 quadrinhos.

d) uma figura verde-clara com o dobro de 15 quadrinhos.

Sempre que necessário, retomar oralmente a associação entre o significado de dobro e de triplo de uma quantidade.

Para finalizar a aula, solicitar aos alunos que registrem no caderno, por meio de desenhos, palavras ou esquemas, o significado de dobro e de triplo e que discutam com os responsáveis sobre esses termos, verificando situações em que eles se aplicam.

Sequência de quadrinhos a serem coloridos na cor vermelha.

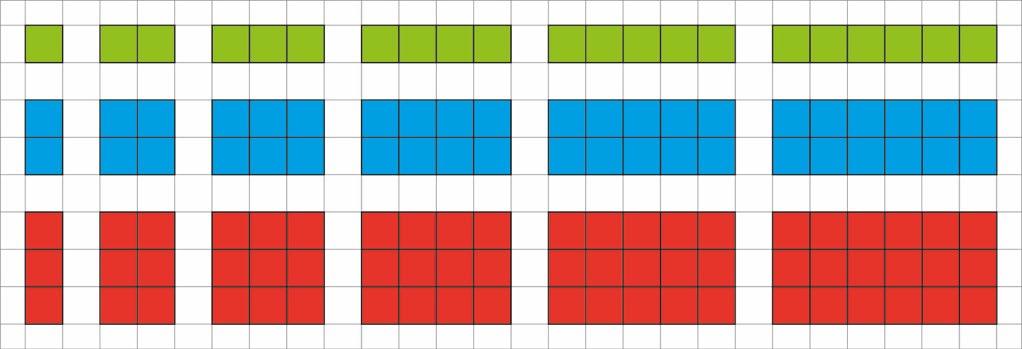
Esta atividade contribui para o desenvolvimento das competências específicas 6 e 8 da área da Matemática e suas Tecnologias.

Aulas 3 e 4

Retomar com os alunos a ideia de dobro e de triplo de uma quantidade. Possibilitar que eles se expressem oralmente sobre o significado de dobro e de triplo e solicitar que deem alguns exemplos, seja por meio de esquemas apresentados na lousa, seja por meio da manipulação de objetos.

Distribuir, para cada aluno, dois copos descartáveis e cubos menores do material dourado. Explicar que para determinar o dobro de uma quantidade é preciso repeti-la duas vezes e orientá-los a determinar o dobro de algumas quantidades. Por exemplo, explicar que para saber o dobro de 4 cubos, devem-se colocar 4 cubos do material dourado em cada um dos dois copos e, depois, determinar o total de cubos utilizados. Fazer alguns exemplos com os alunos até que eles compreendam o procedimento e, em seguida, propor que determinem o dobro de algumas quantidades.

É importante continuar associando a palavra "dobro" ao seu significado, explorando oralmente diferentes maneiras de expressá-lo.

Depois, distribuir mais um copo descartável para cada aluno e questioná-los como poderiam determinar o triplo de 5 cubos do material dourado. Verificar se eles associam a ideia de que é necessário colocar 5 cubos em cada um dos três copos e contar o total de cubos utilizados. Fazer alguns exemplos e, depois, propor algumas quantidades para os alunos determinarem o triplo delas.

Em seguida, orientar os alunos a fazer no caderno um quadro como o indicado a seguir. Explicar aos alunos que, na primeira coluna, eles devem registrar uma quantidade, na segunda o dobro dessa quantidade e na terceira coluna, o triplo. Fazer alguns exemplos para os alunos se familiarizarem com o preenchimento do quadro. Depois, propor algumas quantidades para que determinem o dobro e o triplo.

Durante a realização da atividade, verificar se os alunos utilizam estratégias pessoais para determinar o dobro e o triplo das quantidades. Caso prefiram, é importante que tenham à disposição, por exemplo, folhas de papel quadriculado para utilizarem a estratégia

apresentada nas aulas 1 e 2. É essencial, também, que eles consigam representar outros esquemas e, de preferência, sem o apoio de materiais manipulativos.

Permitir que os alunos compartilhem com os colegas diferentes estratégias que utilizaram para determinar o dobro e o triplo das quantidades. Na correção, oralmente, associar a adição de parcelas iguais à multiplicação e aos termos "dobro" e "triplo". Por exemplo, para o dobro de 7, explicar aos alunos que é preciso determinar "duas vezes 7, ou seja, 7 mais 7"

Propor aos alunos alguns problemas, como os sugeridos a seguir.

1. Em um pacote de figurinhas há 5 figurinhas. Theo comprou 3 pacotes. Quantas figurinhas ele comprou?

Espera-se que os alunos respondam 15 figurinhas.

2. Ana Paula ganhou 15 reais e Beatriz ganhou o dobro dessa quantia. Quantos reais Beatriz ganhou?

Espera-se que os alunos respondam 30 reais.

3. O tio de Bruno trabalhou 4 horas na segunda-feira. Na terça-feira, ele trabalhou o triplo. Quantas horas o tio de Bruno trabalhou na terça-feira?

Espera-se que os alunos respondam 12 horas.

4. Helena foi ao mercado e comprou 5 quilogramas de arroz. Gláucia comprou o dobro dessa quantidade. Quantos quilogramas Gláucia comprou? Ao todo, quantos quilogramas de arroz as duas amigas compraram?

Espera-se que os alunos respondam 10 quilogramas e 15 quilogramas, respectivamente.

5. Mariana pedala com sua bicicleta, todo dia, 3 voltas completas na ciclovia que existe em um parque próximo a sua casa. A ciclovia tem 4 quilômetros de extensão. Nessas condições, quantos quilômetros ela percorre por dia?

Espera-se que os alunos respondam 12 quilômetros.

Circular pela sala de aula a fim de verificar se os alunos desenvolvem estratégias adequadas para resolver os problemas e se compreenderam a ideia de dobro e de triplo, utilizando o material dourado ou outras estratégias. Finalizar a aula corrigindo os problemas.

Estas aulas contribuem para o desenvolvimento das competências específicas 2 e 6 da área de Matemática e suas Tecnologias

Aulas 5 e 6

Iniciar a aula revisando com os alunos o significado de dobro e de triplo. Perguntar se algum aluno gostaria de contar alguma situação que ele tenha vivido e que envolveu as ideias de dobro e de triplo. Solicitar aos alunos que se reúnam em duplas ou trios e que

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribu ído crédito autoral e as criações sejam licenciadas sob os mesmos

representem, por meio de figuras ou materiais manipuláveis, o dobro e o triplo de algumas quantidades. Por exemplo, pedir que determinem o dobro e o triplo de 13 com o apoio do material dourado e dos copos descartáveis utilizados anteriormente.

Após essa revisão inicial, propor aos alunos que analisem algumas imagens que envolvam a ideia de metade e, em seguida, de terça parte. Por exemplo, apresentar algumas imagens de frutas cortadas em duas partes, como as sugeridas a seguir, e pedir aos alunos que descrevam oralmente cada imagem e que identifiquem similaridades entre elas.

Shutterbug75/Pixabay.com

fernandozhiminaicela/Pixabay.com

Incentivar os alunos a descrever essas imagens e a falar como as frutas estão cortadas. Verificar se eles já utilizam a palavra "metade" e se compreendem o significado dela. Ressaltar que, nessa situação, utiliza-se a ideia de metade de maneira imprecisa, pois não significa que há exatamente metade da fruta em cada parte cortada. Em seguida, propor a cada grupo que separe 12 cubos pequenos do material dourado e que distribua metade desses cubos em cada copo. Auxiliá-los, se necessário, e incentivá-los a compartilhar as

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribu ído crédito autoral e as criações sejam licenciadas sob os mesmos

Utilizar imagens de frutas repartidas ao meio pode ajudar os alunos a fixar o conceito matemático de "metade"

A expressão "metade da laranja" pode ajudar os alunos a fixar o conceito matemático de "metade".

estratégias que utilizaram. Perguntar quantos cubos eles colocaram em cada copo e conduzi-los a perceber que 6 é a metade de 12.

Registrar na lousa a frase: 6 é a metade de 12 porque o dobro de 6 é 12. Explorar essa ideia por meio dos copos descartáveis com os cubos do material dourado, de maneira que os alunos percebam que 2 copos com 6 cubos em cada um resultam em 12 cubos, ou que distribuir igualmente 12 cubos em dois copos equivale a colocar metade deles em um copo e a outra metade no outro copo. Fazer mais alguns exemplos com os alunos e, depois, propor que determinem a metade de algumas quantidades.

Em seguida, pedir aos alunos que utilizem três copos descartáveis para distribuir igualmente 12 cubos do material dourado entre eles. Verificar se os alunos se apropriam das estratégias utilizadas para determinar a metade, por exemplo, distribuindo ordenadamente um cubo por vez em cada copo até que todos tenham sido distribuídos e os copos tenham recebido a mesma quantidade de cubos. Incentivá-los a contar o total de cubos em cada copo e a certificar-se de que todos possuem a mesma quantidade. Explicar que 4 é a terça parte de 12, porque o triplo de 4 é 12 e, depois, fazer mais alguns exemplos para explorar o que é terça parte e como determiná-la.

Incentivar os alunos a compartilhar outras estratégias de resolução que não dependam de materiais manipuláveis. Eles podem, por exemplo, representar a quantidade em três grupos, inserindo uma marcação (bolinha, tracinho, quadrinho, triângulo, entre outros) em cada grupo até obter o total de marcas relacionadas à quantidade que se deseja saber a terça parte. Por exemplo, para determinar a terça parte de 15, auxiliá-los a perceber que podem distribuir entre os três conjuntos, um a um, 15 triângulos como indicado a seguir.

Editoria de arte

Reforçar a ideia de que a terça parte, nesse caso, é determinada pelo total de marcações feitas em um desses conjuntos.

Representação da terça parte de 15: o total de triângulos foi dividido em 3 grupos de 5 triângulos.

Propor aos alunos que determinem a terça parte de outras quantidades, utilizando diferentes estratégias.

Para finalizar a aula, na lousa, registrar as palavras "metade" e "terça parte" Sempre que possível, pedir que os alunos leiam em voz alta as palavras escritas na lousa, o que contribui para a fluência em leitura oral, um dos componentes essenciais para a alfabetização. Depois, solicitar aos alunos que façam um esquema, desenho ou outro tipo de registro para explicar o significado dessas palavras.

Estas aulas contribuem para o desenvolvimento da competência geral 2 da área de Matemática e suas Tecnologias

Aulas 7 e 8

Iniciar a aula retomando o significado das palavras "metade" e "terça parte". Em seguida, relembrar os alunos sobre o significado de metade e de dobro. Verificar se eles fazem associações como "5 é a metade de 10, porque o dobro de 5 é 10"

É importante retomar o uso dos materiais manipuláveis para representar essas situações, por exemplo, colocando 5 cubos do material dourado em 2 copos descartáveis para afirmar que "10 é o dobro de 5" e demonstrar que 2 copos com 5 cubos cada resulta em 10 cubos; e afirmar que "5 é a metade de 10", demonstrando que, ao distribuir igualmente 10 cubos em 2 copos, cada um fica com 5 cubos.

Demonstrar um exemplo como esse e, depois, propor aos alunos que repitam e experimentem outras associações entre dobro e metade e entre triplo e terça parte.

Em seguida, propor aos alunos que elaborem e resolvam alguns problemas, como os sugeridos a seguir.

1. Cristina tem a metade da quantia de Valdir. Se Valdir tem 12 reais, quanto tem Cristina?

Espera-se que os alunos respondam 6 reais.

2. Quantas laranjas representam a terça parte de 18 laranjas?

Espera-se que os alunos respondam 6 laranjas.

Estimular os alunos a utilizar diferentes estratégias para a resolução dos problemas. Para finalizar a aula, socializar as estratégias utilizadas pelos alunos em cada problema que for proposto e corrigir as atividades.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra der ivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Aulas 9 e 10

Nestas aulas, propor atividades para que os alunos apliquem a ideia de dobro, triplo, metade e terça parte, utilizando diferentes registros. Iniciar com atividades em que eles possam utilizar recursos visuais, como a representação por meio de desenhos, como nos exemplos a seguir.

1. Para cada figura azul da malha quadriculada a seguir, desenhe uma nova figura que tenha o dobro de quadrinhos.

Editoria de arte

Exemplo de figuras a serem apresentadas (azul) e repostas possíveis (magenta).

2. Para cada figura verde da malha quadriculada a seguir, desenhe uma nova figura que tenha o triplo de quadrinhos.

Editoria de arte

Exemplo de figuras a serem representadas (em verde) e respostas possíveis (em magenta).

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra der ivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

3. Observar as figuras a seguir formadas por quadrinhos. Em cada uma, pinte a metade dos quadrinhos.

Editoria de arte

Exemplo de figuras a serem coloridas.

Sugestões de resposta:

4. Pinte a terça parte dos quadrinhos de cada figura a seguir.

Editoria de arte

Sugestões de resposta:

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra der ivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

É interessante corrigir estas atividades e demonstrar aos alunos que há diferentes possibilidades de resposta. Explorar estratégias de contagem, retomando a ideia de dobro, triplo, metade e terça parte. Por exemplo, na atividade 4, para determinar a terça parte dos quadrinhos do retângulo formado por 9 colunas de 11 quadrinhos cada, em cada linha eles podem colorir 1 quadrinho a cada 2 que deixarem em branco.

Após discutir diferentes estratégias de resolução de atividades como essas sugeridas anteriormente, propor atividades para os alunos determinarem numericamente o dobro, triplo, metade e terça parte, como as sugeridas a seguir.

1. Determine o dobro de cada número do quadro a seguir.

• Agora, determine o triplo dos números do quadro a seguir

2. Qual é a metade de cada número indicado a seguir? a) 36

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra der ivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

3. Determine a terça parte das quantidades registradas no quadro a seguir

Enquanto os alunos resolvem cada atividade, circular pela sala de aula a fim de verificar se utilizam estratégias de resolução adequadas. É importante disponibilizar materiais manipuláveis, como o material dourado.

Corrigir as atividades possibilitando aos alunos discutirem as diferentes estratégias de resolução utilizadas.

Sugestões

• CAPOVILLA, Renata Ariane. Plano de aula: dobro e triplo. Nova Escola Disponível em: https://novaescola.org.br/plano-de-aula/1075/dobro-e-triplo. Acesso em: 6 dez. 2021.

• CAPOVILLA, Renata Ariane. Plano de aula: o que é terça parte. Nova Escola Disponível em:

https://planosdeaula.novaescola.org.br/fundamental/2ano/matematica/o-que-e-terca-p arte/532?gclid=Cj0KCQjwytOEBhD5ARIsANnRjViLhQYpI4iynfnG4lTfdMXvJDzut0Jv38clO VNm9SuWnAp03kpKJXkaAiRoEALw_wcB Acesso em: 6 dez. 2021.

• CURI, Edda Resolução de problemas nos Anos Iniciais do Ensino Fundamental: mitos, práticas e desafios Rematec, v. 11, n 21, p. 64-78, 2016. Disponível em: http://www.rematec.net.br/index.php/rematec/article/view/60 Acesso em: 7 dez. 2021.

Sequência didática 8 • Medidas e receitas

Nesta sequência didática, serão abordadas medidas de comprimento, de massa e de capacidade padronizadas e não padronizadas por meio da resolução de problemas práticos de medição. Ao final, será proposta a realização de uma receita, aproximando conteúdos relacionados a medidas com o cotidiano dos alunos

Objetivos de aprendizagem

• Consolidar o conhecimento sobre unidade de medida não padronizada a fim de entender o sentido prático de medir.

• Identificar a unidade de medida adequada a cada situação.

• Expressar medidas de diferentes maneiras, utilizando diferentes unidades de medida

• Conhecer e mensurar medidas de capacidade, de massa e de comprimento

Plano de aulas

Aulas 1 e 2: Estimar e comparar comprimentos utilizando unidades de medidas não padronizadas por meio de atividades investigativas.

Aulas 3 e 4: Fazer a transição para a medida de comprimento padronizada, verificando a importância da padronização na unidade de medida.

Aulas 5 e 6: Estimar e comparar medidas de massa maiores, menores e iguais a 1 kg por meio da medição de objetos.

Aulas 7 e 8: Estimar e comparar medidas no preparo de uma receita.

Componentes essenciais para a alfabetização: compreensão de textos, desenvolvimento de vocabulário e fluência em leitura oral

Competências gerais da Educação Básica: 1 e 2.

Competências específicas de Matemática: 1, 2 e 3

Habilidades: EF02MA16 e EF02MA17.

Materiais necessários: fita crepe, régua, trena, fita métrica, um pacote de 1 kg de alimento (como açúcar, arroz ou feijão), uma balança de cozinha, ingredientes para uma receita, pratos, guardanapos e toucas de culinária para os alunos

Aulas 1 e 2

Antes de começar a aula, eleger um local aberto da escola que sofra pouca interferência externa durante o horário de aula. Medir com a trena, em linha reta no chão, a distância de dois metros e marcar o início e o fim da medida com a fita crepe, sem exibir o valor da medida.

Iniciar a atividade na sala de aula de maneira expositiva trazendo o contexto histórico das medidas. Convidar os alunos para a reflexão de que a Matemática está inserida na evolução dos povos antigos como um agente modificador na medida em que sua utilização teve papel fundamental na arquitetura, nas navegações, no comércio, entre outras relações. E, para que tudo isso acontecesse, foi preciso utilizar parâmetros que medissem grandezas necessárias nesses diferentes campos. Se achar conveniente, nesse momento, comentar, também, que no dia a dia de variadas profissões as medidas e os instrumentos de medidas estão presentes. Esse tipo de discussão favorece o desenvolvimento da competência geral

Conduzir os alunos para o local escolhido munido de um caderno para anotação. Em seguida, falar que a turma toda medirá a distância entre as duas marcas por meio da utilização dos passos, ou seja, utilizando seus próprios pés como instrumento de medição Instruir os alunos nas medições: posicionar o calcanhar de um dos pés na marca inicial, e em seguida ajustar o calcanhar do outro pé exatamente na ponta do primeiro, sem sobrar

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra der ivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

espaço, e assim por diante, até medir toda a distância entre as duas marcações. Então, anunciar à turma quantos pés couberam na distância estabelecida.

Enfileirar os alunos, um a um, para que eles repitam o procedimento e falem em voz alta quantos pés, mas desta vez os deles, couberam na mesma demarcação. Anotar o que foi falado por cada aluno e montar com a turma uma tabela.

Retornar com os alunos para a sala de aula e desenhar na lousa uma tabela contendo a quantidade de passos que coube na medida estipulada no chão, de cada aluno. Então, instigar uma reflexão sobre o motivo pelo qual o resultado obtido varia para cada medição, orientando a conversa até que os alunos concluam que é devido à diferença de tamanho de cada pé. O comprimento do pé de cada aluno é diferente e, consequentemente, cabe, ao longo de uma mesma medida de comprimento, uma quantidade diferente de passos

Em seguida, sugere-se explicar aos alunos, por conta dessa característica, que o passo é uma unidade não padronizada de medida

Sugere-se a proposta de atividades como as indicadas a seguir para os alunos resolverem individualmente e se inspirarem para o desafio que será dado ao final da aula.

1. Escolher dois materiais diferentes disponíveis em seu estojo.

a) Quais materiais foram escolhidos?

b) Meça o comprimento da sua carteira utilizando como unidade de medida o material 1 e o material 2

c) Quantas vezes o material 1 coube no comprimento da carteira? E o material 2?

As respostas dos itens desta atividade dependem dos materiais escolhidos.

2. De que maneira podemos representar o comprimento da carteira tendo como unidade de medida o material 1?

A resposta das atividades 2 e 3 depende dos materiais escolhidos. Espera-se que os alunos indiquem, por exemplo, algo como "o comprimento da carteira é de 6 lápis", indicando um número e o nome do objeto como unidade de medida.

3. De que maneira podemos representar o comprimento da carteira tendo como unidade de medida o material 2?

4. Por que a carteira tem um número diferente na representação de sua medida de acordo com os materiais 1 ou 2?

Espera-se que os alunos indiquem que isso ocorre porque os objetos têm comprimentos diferentes e que quanto maior o objeto menor será a quantidade de vezes que usamos para medir algo, se comparado com outro objeto menor

Para finalizar a aula, reunir os alunos em duplas e lançar o desafio proposto a seguir

5. Qual outro instrumento de medição não padronizado vocês poderiam utilizar para medir a demarcação feita no pátio? Justifique.

Cada dupla deve pensar em uma estratégia para, na próxima aula, realizar a medição utilizando um instrumento diferente e apresentando o resultado à turma, se julgar conveniente. Mas, nesse primeiro momento, ambos da dupla devem apenas registrar as ideias e a estratégia nos seus respectivos cadernos, por meio de frases, desenhos ou esquemas Esta proposta favorece o desenvolvimento de componentes para a alfabetização, como a produção de escrita e o desenvolvimento de vocabulário. Passar pelas duplas verificando as estratégias. Se alguma estratégia de medição necessitar de material auxiliar, como um objeto que será utilizado como instrumento de medição, tomar nota e se organizar para trazê-lo no próximo encontro.

As propostas destas aulas favorecem o desenvolvimento da competência geral 2 e da competência específica 1 da área de Matemática e suas Tecnologias e da habilidade

EF02MA16

Aulas 3 e 4

Como forma de retomada do que foi trabalhado anteriormente, pedir que um integrante de cada dupla formada na última aula conte ou leia a estratégia pensada à turma Em seguida, escolher algumas estratégias criadas pelos alunos para, também, medir a marca feita no pátio na aula anterior. Levar os alunos até o pátio novamente e orientá-los na medição usando as estratégias escolhidas. Pedir aos alunos que façam anotações indicando os resultados das medições. Em seguida, voltar para a sala de aula e fazer questionamentos sobres os resultados obtidos, como os sugeridos a seguir.

1. Como é possível que o mesmo comprimento marcado no chão do pátio possa ser representado por vários números diferentes? O que isso quer dizer?

Espera-se que os alunos cheguem à conclusão de que os números dependem dos objetos utilizados para realizar a medição, reforçando a ideia de medida não padronizada, conforme as atividades realizadas no final da última aula.

2. Faz sentido representar a medida daquele comprimento somente com o valor numérico?

Por quê?

Espera-se que os alunos respondam que não, pois o número nada significa, nesse contexto, sem a unidade de medida.

Durante a resolução da questão 2, deve-se provocar os alunos para que percebam que o valor numérico deve vir acompanhado da unidade referente ao instrumento de medida utilizado, pois se trata de estimar uma medida com base na verificação de quantas vezes o instrumento, objeto ou parte do corpo cabe dentro da distância em questão. Uma vez realizada essa reflexão e respondidas essas perguntas de retomada, sugere-se propor algumas situações-problema para os alunos responderem, como a sugerida a seguir.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra der ivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

3. Imagine que você convide seu amigo para sua festa de aniversário. Como você precisa de barbante para prender algumas decorações na parede, você pede a ele a gentileza de levar o barbante para a festa. Pelo telefone você diz a ele: "Preciso de 20 palmos de comprimento de barbante". Na hora de medir, seu amigo utiliza a mesma estratégia e mede o barbante com a palma da mão dele, no entanto, quando ele lhe dá o barbante, você percebe que o tamanho é menor do que aquele de que você precisava e não conseguirá prender todas as decorações

Refletir com os alunos que, por essa e outras situações, ao longo do tempo surgiu a necessidade de padronizar algumas unidades de medida em nosso cotidiano. Em se tratando de comprimento, apresentar para a turma o tamanho de 1 metro na trena ou na fita métrica. Mostrar que dentro de um metro cabem diversas outras medidas e subdivisões, mas especificar a subdivisão centímetro, mostrando ser idêntica à mesma subdivisão da régua, comumente presente na lista de material escolar dos alunos

Explicar que, desta vez, ao medir um mesmo comprimento com um instrumento de unidade de medida padronizado, o resultado sempre será o mesmo valor numérico, já que quem o acompanhará também será a mesma unidade de medida.

Por isso, retomar a atividade iniciada no encontro passado: a turma deve se dirigir, novamente, ao local onde foi feita a marcação da primeira atividade. Porém, desta vez, cada dupla aprenderá a manejar a trena ou a fita métrica para que obtenham com exatidão e com uma unidade de medida padronizada o tamanho do comprimento do local que, em outro momento, foi medido pelos pés deles. Espera-se que todas as duplas registrem 2 metros como resposta.

Voltar à sala de aula e orientar as duplas que se sentem juntas e sugerir algumas atividades, como as indicadas a seguir.

4. Escreva um breve texto (de 5 a 10 linhas) sobre como o problema do barbante da festa de aniversário, proposto no início da aula, poderia ter sido evitado.

Espera-se que os alunos concluam que o problema poderia ter sido evitado se fossem utilizadas unidades de medida padronizadas, como o metro, e um instrumento de medição, como a trena ou a fita métrica, para medir o barbante.

Estimular a colaboração mútua entre os pares e ir até as duplas para sondar o raciocínio dos alunos. Em seguida, individualmente, propor as seguintes questões.

5. Quais unidades de medida padronizadas você conheceu ou sobre quais conversou hoje?

Espera-se que os alunos respondam o metro e o centímetro.

6. Após as duplas medirem com a trena a distância entre as marcas e obterem o mesmo resultado, é correto afirmar que a medida realizada anteriormente com os pés estava errada? Por quê?

Espera-se que os alunos respondam que a medida com os pés não estava errada, mas foi feita utilizando-se instrumentos de medição diferentes

7. Escreva a seguir, para cada caso, se é mais adequado utilizar como unidade de medida o metro ou o centímetro

a) Para medir o tamanho de um lápis Centímetro.

b) Para medir um fio de cabelo Centímetro.

c) Para medir o tamanho da lousa Metro

d) Para medir a distância entre as traves na quadra Metro

e) Para medir o tamanho da palma da sua mão. Centímetro.

As propostas destas aulas favorecem o desenvolvimento das competências gerais 1 e 2 e das competências específicas 1 e 2 da área de Matemática e suas Tecnologias e da habilidade EF02MA16.

Aulas 5 e 6

Contextualizar esta aula com as anteriores, fazendo uma breve revisão das atividades realizadas nos últimos encontros e ressaltar que não são somente as medidas de comprimento que necessitam de unidades de medida padronizadas Perguntar quais outras medidas eles conhecem e quais são as unidades de medidas

Guiar a conversa em torno das medidas de capacidade e de massa. Quando essa introdução já estiver no contexto, mostrar aos alunos um pacote de açúcar (ou de outro alimento) de 1 quilograma e perguntar se eles já conhecem a unidade de medida pela qual o conteúdo do pacote é mensurado e em quais outras situações pode ser utilizada essa mesma unidade de medida.

Em seguida, propor a estimativa da medida de massa de objetos encontrados dentro da sala de aula com base na medida de massa conhecida do pacote de açúcar (1 quilograma). Selecionar dois ou três objetos da sala de aula e pedir à turma que estime se eles têm menos, mais ou igual medida de massa em relação à medida de massa do pacote de açúcar

As comparações podem ser feitas passando os objetos pela turma ou por meio de um aluno que se voluntariará a segurar os itens para comparação. Observação: evidentemente que alguns desses itens não trarão dúvidas, como a comparação entre um

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra der ivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

apontador e o pacote de açúcar No entanto, é importante trabalhar o sensorial para que sirva de ajuste fino na tentativa de obter uma percepção mais aguçada para algo que tenha a medida de massa parecida com a do pacote de açúcar (por exemplo: uma mochila, uma apostila, entre outros). Espera-se que os alunos saibam estimar o que é mais ou menos pesado utilizando uma medida de massa já conhecida.

Depois desta dinâmica, propor questionamentos como os sugeridos a seguir. Orientar os alunos a registrar as respostas em seus cadernos

1. Em que outras situações precisamos medir massa?

Sugestões de resposta: quando vamos ao médico ou levamos nosso animal de estimação ao veterinário, quando compramos frutas, verduras e legumes, quando separamos ingredientes para receitas, entre outras

2. Você conhece algum instrumento que auxilia nesta medição?

Espera-se que os alunos respondam que sim, pois devem conhecer a balança.

3. Você consegue pensar em algum produto que é vendido por massa?

Espera-se que os alunos respondam que sim, pois devem saber que frutas, verduras, macarrão, arroz, feijão, farinha, entre outros, são vendidos por massa

Após respondidas as perguntas, fazer um levantamento, sobre as respostas, discutindo os pontos cabíveis sobre o assunto. Em seguida, mostrar uma balança de culinária para os alunos. Caminhar entre as fileiras da sala de aula e se aproximar deles para que enxerguem as subdivisões das marcações de quilogramas e de gramas. Depois, medir a massa do pacote de açúcar para que verifiquem o valor descrito na embalagem. Então, medir os outros itens selecionados anteriormente para verificar a assertividade da atividade inicial da aula. Dar foco às medidas que ficam entre os valores inteiros em quilograma, dando a entender que a unidade de medida quilograma se subdivide em gramas, podendo ser utilizada em situações mais específicas, como a compra de frios no mercado ou em pequenas embalagens de temperos.

Depois, propor atividades de fixação e de ampliação como as sugeridas a seguir.

4. Quais unidades de medida de massa foram apresentadas hoje?

Quilograma e grama.

5. Complete com "grama" e "quilograma": O _____________ é subdivido em _____________.

Quilograma e grama, respectivamente.

6. Escreva a seguir, para cada caso, se é mais adequado utilizar como unidade de medida de massa o grama (g) ou o quilograma (kg) a) Para medir a massa de um lápis Grama.

b) Para medir a massa de um copo contendo açúcar Grama.

c) Para medir a massa de uma pessoa Quilograma.

d) Para medir a massa de um saco de feijão Quilograma.

e) Para medir a massa de um saco de cimento. Quilograma.

Encerrar a aula explicando aos alunos que, na próxima aula, eles farão uma atividade diferente que envolve prática culinária. Caso haja preparativos ou orientações que os alunos deverão seguir, orientá-los nesse momento.

As propostas destas aulas favorecem o desenvolvimento das competências gerais 1 e 2 e das competências específicas 1 e 2 da área de Matemática e suas Tecnologias e da habilidade EF02MA17

Aulas 7 e 8

Nestas aulas, os alunos realizarão uma atividade prática de culinária. Sugere-se o uso de uma receita que possa ser realizada com segurança na escola pelos próprios alunos, e, para isso, é importante que não necessite de materiais de cozinha como faca, micro-ondas, batedeira, fogão e forno. Previamente, pedir que os pais ou responsáveis dos alunos providenciem os ingredientes da receita escolhida. Além disso, se possível, providenciar toucas culinárias para os alunos.

A seguir, sugerimos algumas receitas que seguem esses requisitos.

Salada de frutas

Ingredientes

• 200 g de morango (cerca de 12 morangos médios) cortados em fatias;

• 100 g de maçã ou pera (cerca de uma maçã pequena) cortada em fatias;

• 100 g de laranja (cerca de uma laranja pequena), ou mexerica ou tangerina, cortada em pedaços pequenos;

• 100 g de banana (cerca de uma banana média), ou manga ou mamão ou abacaxi, cortada em fatias;

• 15 g de suco de limão (ou 15 mL ou 1 colher de sopa, cerca de 1/2 limão);

• 125 g de suco de laranja (cerca de 1 laranja grande) coado e sem açúcar;

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra der ivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

• 18 g de mel (1 colher de sopa);

• 3 folhas de hortelã (opcional)

Modo de preparo

Em uma tigela grande, misturar todos os ingredientes. Servir em copinhos

Lanche de maionese de atum e vegetais

Ingredientes

• 200 g de atum em conserva;

• 500 g de maionese;

• 100 g de ervilha e milho em conserva;

• 100 g de legumes em conserva;

• Pães ou torradas.

Modo de preparo

Retirar a água, previamente, dos produtos enlatados. Em uma tigela grande, misturar todos os ingredientes. Passar o patê nos pães ou torradas e servir.

Iniciar a atividade enfileirando os alunos para que lavem as mãos e coloquem a touca, conforme o recomendado. Em seguida, ler a receita escolhida com os alunos, permitindo que eles, também, leiam trechos em voz alta, a fim de favorecer o desenvolvimento de componentes para a alfabetização, como a fluência em leitura oral, o desenvolvimento de vocabulário e a compreensão de textos. Durante a leitura, deixar claro que algumas medidas dentro da mesma receita podem vir seguidas de unidades padronizadas e não padronizadas. Pedir que digam quais são as medidas padronizadas e quais são as medidas não padronizadas da receita.

Aproveitar a oportunidade para ressaltar quais medidas de capacidade podem ser mensuradas em subdivisões análogas ao grama. Por exemplo, o mililitro é uma subdivisão do litro.

Durante o preparo, pedir a diferentes alunos que façam diferentes tarefas, como medir a quantidade de um ingrediente. No caso de uma receita que indique um líquido em copos, pedir que dois alunos meçam os copos de um mesmo ingrediente. Utilizar essa prática para enfatizar a incerteza associada a uma medida não padronizada, uma vez que a capacidade do copo pode ser exata, mas até onde o nível do copo será cheio determinará uma quantidade diferente de líquido, dependendo do critério de cada pessoa que opera a medição, podendo, consequentemente, alterar a receita.

Depois que os copos forem cheios, comparar as medições entre si, mas desta vez utilizando o copo medidor de capacidade graduado em mililitros (mL) e mostrar à turma a

diferença entre eles. Fica a critério do professor realizar a comparação também com os ingredientes medidos em gramas.

Caso a receita escolhida contenha ingredientes medidos em litros ou mililitros, sugere-se realizar uma atividade análoga à atividade das aulas anteriores, para que os alunos identifiquem em quais situações utilizar essas medidas, conforme sugerido a seguir.

1. Quais medidas de capacidade você aprendeu hoje? Mililitros e litros.

2. Escreva a seguir, para cada caso, se é mais adequado utilizar como unidade de medida de capacidade o mililitro (mL) ou o litro (L)

a) Para medir a capacidade de um copo Mililitros.

b) Para medir a capacidade de uma piscina Litros.

c) Para medir a capacidade de um lago. Litros.

Para finalizar, terminar a receita e separar um tempo para que os alunos possam comer o que prepararam

A avaliação dos alunos acontece a todo momento durante as aulas e os trabalhos em grupo, avaliando não somente os conteúdos, mas também a interação dos alunos com os colegas, as atitudes e as conversas. Outro modo de avaliar é utilizar as atividades sugeridas ao longo das aulas. Levar em consideração os diferentes níveis de aprendizagem de cada aluno ao estabelecer os critérios de avaliação.

As propostas destas aulas favorecem o desenvolvimento das competências gerais 1 e 2 e das competências específicas 1 e 3 da área de Matemática e suas Tecnologias e da habilidade EF02MA17

Sugestões

• 3 RECEITAS para fazer com as crianças: fáceis e divertidas 2020. Vídeo (ca. 6 min).

Publicado por: canal Cozinha do Bom Gosto. Disponível em:

https://www.youtube.com/watch?v=U6tGnd5n1_A Acesso em: 11 dez. 2021.

• 4 RECEITAS para crianças fazerem: especial de férias de julho 2019. Vídeo (ca 10 min).

Publicado por: canal Cozinha do Bom Gosto Disponível em:

https://www.youtube.com/watch?v=oSymiPUVuf8. Acesso em: 11 dez. 2021.

• PERES, Paula; MEIRELLES, Elisa. Receitas e desafios na medida certa Nova Escola Disponível em:

https://novaescola.org.br/conteudo/8915/receitas-e-desafios-na-medida-certa Acesso em: 11 dez. 2021.

• SÃO PAULO (Estado). Secretaria da Educação. Culinária é utilizada por educadora dos Anos Iniciais para ensinar Matemática: iniciativa instigou interesse dos alunos pela disciplina e melhorou rendimento escolar São Paulo, 10 mar. 2015. Disponível em: https://www.educacao.sp.gov.br/culinaria-e-utilizada-por-educadora-dos-anos-iniciais-pa ra-ensinar-matematica/ Acesso em: 11 dez. 2021.

Relatórios e indicadores do acompanhamento da aprendizagem

Nesta seção, são apresentados subsídios que auxiliam a produção de relatórios e indicadores do acompanhamento da aprendizagem, itens indispensáveis para o processo de ensino-aprendizagem e supervisão sistemática e contínua do desenvolvimento dos alunos São sugestões que podem ser adaptadas à rotina da turma e à realidade escolar do professor.

Produção de relatórios

Os relatórios escolares são importantes ferramentas para fornecer a professores, coordenadores e familiares uma visão global do desenvolvimento e do desempenho dos alunos em sala de aula. Além de aspectos relacionados à aprendizagem de objetos de conhecimento, de habilidades e de competências, os relatórios podem apresentar informações sobre a participação dos alunos nas aulas, a interação deles com os colegas, seu desenvolvimento motor, interesses pessoais, entre outros aspectos.

Esses documentos devem ser produzidos periodicamente, de forma anual, semestral ou bimestral, por exemplo. Dessa maneira, além de monitorar o processo de ensino-aprendizagem, os relatórios podem ser utilizados pela gestão escolar para formular práticas e estratégias, além de promover mudanças nos ambientes e espaços, que contribuam para a melhoria dos níveis de aprendizagem.

Para elaborar um relatório, pode-se usar como apoio as fichas apresentadas na seção Indicadores do acompanhamento da aprendizagem. Nessas fichas, são listados conceitos, habilidades, objetos de conhecimento e competências que podem ser diagnosticados e aferidos ao longo do ano letivo. São sugestões às quais o professor pode acrescentar os dados e as informações que julgar convenientes tirachardz/Freepik.com

O trabalho com os dados de indicadores e as análises com base neles trazem reflexões que auxiliam na tomada de decisões para o aprimoramento de estratégias de ensino e aprendizagem.

Os relatórios devem ser redigidos em linguagem adequada e de fácil compreensão, para que sejam compreendidos por familiares, outros professores que acompanham o processo educacional e gestores. Estes podem ser estruturados da seguinte maneira:

• Apresentação dos objetivos da disciplina e como esses objetivos foram trabalhados em sala de aula, ao longo do período;

• Apresentação do acompanhamento de aspectos cognitivos, comportamentais e socioemocionais dos alunos, ao longo do período.

Esses relatórios podem ser acompanhados de apresentações visuais e gráficas que visam facilitar a compreensão das informações. Os dados compilados nas fichas da seção Indicadores do acompanhamento da aprendizagem, por exemplo, possibilitam obter uma boa visão global do desenvolvimento dos alunos, ressaltando os pontos positivos e estabelecendo pontos de atenção em caso de defasagem nas aprendizagens. Pode ser feita, por exemplo, a distribuição percentual dos conceitos atribuídos aos alunos a cada uma das competências gerais, competências específicas e habilidades trabalhadas no período.

Porcentagem de alunos da turma A de acordo com os conceitos atribuídos a eles em relação às competências gerais trabalhadas no período

Necessita ser consolidado (NC) Em processo de consolidação (PC) Consolidado (C)

Exemplo: Fonte: dados fictícios.

É importante ressaltar que os relatórios e os indicadores do acompanhamento da aprendizagem devem ser analisados e utilizados de forma contextualizada, ou seja, em conjunto com as características tanto individuais dos alunos quanto coletivas da turma, tornando-os uma ferramenta eficaz e adequada a cada realidade escolar.

Indicadores do acompanhamento da aprendizagem

Os indicadores de aprendizagem auxiliam no acompanhamento da turma, assim como na investigação das possíveis causas de defasagem nas aprendizagens, favorecendo a revisão de decisões pedagógicas, com o propósito de potencializar o desenvolvimento dos alunos

Os indicadores a seguir foram elaborados com base na BNCC e na PNA e são apresentados na forma de fichas que podem ser aplicadas em diferentes etapas do processo educacional, de modo a diagnosticar e monitorar o desenvolvimento de aprendizagens individuais e coletivas

São apresentadas sugestões de quatro tipos de fichas:

• Ficha de avaliação diagnóstica: permite obter um diagnóstico dos conhecimentos prévios dos alunos.

• Ficha de acompanhamento das aprendizagens: permite observar o desenvolvimento de diferentes aprendizagens ao longo do processo educacional, identificando pontos de sucesso ou que necessitam de novas intervenções para a consolidação das aprendizagens pretendidas

• Ficha de verificação de resultados: permite avaliar o atingimento de objetivos de aprendizagem ao final do ano letivo, podendo também servir de fonte de dados para a elaboração de estratégias para o ano escolar seguinte.

• Ficha de acompanhamento do desenvolvimento de competências socioemocionais: permite acompanhar de forma planejada o desenvolvimento de competências socioemocionais.

wayhomestudio/Freepik.com

gpointstudio/Freepik.com

freepik/Freepik.com

O compartilhamento de informações sobre o andamento e os resultados do desenvolvimento dos alunos é do interesse de gestores escolares, de professores, de pais ou responsáveis e de alunos, e promove momentos de debate e reflexão sobre a prática docente.

Ficha de avaliação diagnóstica

Professor(a):

Turma:

Sugestão de critérios de avaliação

C = consolidado (estudante faz sozinho); PC = em processo de consolidação (estudante precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (estudante não consegue realizar a atividade proposta)

Ficha de avaliação diagnóstica

Resolver e elaborar problemas de adição e de subtração com números de até dois algarismos utilizando o suporte de imagens, material manipulável ou estratégias pessoais.

Reconhecer regularidades e padrões em sequências, inclusive identificando elementos faltantes.

Descrever a localização de pessoas e de objetos no espaço em relação a si mesmo e em relação a um referencial dado utilizando termos próprios da Matemática.

Identificar e nomear figuras planas (círculo, quadrado, retângulo e triângulo) como faces de sólidos geométricos apresentados em diferentes posições.

Reconhecer períodos do dia (manhã, tarde e noite), dias da semana e meses do ano e conseguir utilizar o calendário, quando necessário.

Utilizar medidas não convencionais para medir e comparar comprimentos, capacidades ou massas de objetos do cotidiano.

Números Álgebra Geometria Grandezas e medidas Estatística Aluno Contar, comparar e ordenar números (até 100 unidades) e expressar quantidades de forma verbal ou simbólica.

Ler e interpretar dados apresentados em tabelas e em gráficos de colunas simples.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribui çã o n ã o comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de acompanhamento das aprendizagens

Professor(a):

Turma:

Aluno:

Sugestão de critérios de avaliação

C = consolidado (estudante faz sozinho);

PC = em processo de consolidação (estudante precisa de apoio de um mediador);

NC = necessita de novas oportunidades de consolidação (estudante não consegue realizar a atividade proposta)

Ficha de acompanhamento das aprendizagens (Matemática)

Habilidades C PC NC Observações

(EF02MA01) Comparar e ordenar números naturais (até a ordem de centenas) pela compreensão de características do sistema de numeração decimal (valor posicional e função do zero).

(EF02MA02) Fazer estimativas por meio de estratégias diversas a respeito da quantidade de objetos de coleções e registrar o resultado da contagem desses objetos (até 1000 unidades).

(EF02MA03) Comparar quantidades de objetos de dois conjuntos, por estimativa e/ou por correspondência (um a um, dois a dois, entre outros), para indicar "tem mais" , "tem menos" ou "tem a mesma quantidade", indicando, quando for o caso, quantos a mais e quantos a menos.

(EF02MA04) Compor e decompor números naturais de até três ordens, com suporte de material manipulável, por meio de diferentes adições.

(EF02MA05) Construir fatos básicos da adição e subtração e utilizá-los no cálculo mental ou escrito.

(EF02MA06) Resolver e elaborar problemas de adição e de subtração, envolvendo números de até três ordens, com os significados de juntar, acrescentar, separar, retirar, utilizando estratégias pessoais.

(EF02MA07) Resolver e elaborar problemas de multiplicação (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais por meio de estratégias e formas de registro pessoais, utilizando ou não suporte de imagens e/ou material manipulável.

(EF02MA08) Resolver e elaborar problemas envolvendo dobro, metade, triplo e terça parte, com o suporte de imagens ou material manipulável, utilizando estratégias pessoais.

(EF02MA09) Construir sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.

(EF02MA10) Descrever um padrão (ou regularidade) de sequências repetitivas e de sequências recursivas, por meio de palavras, símbolos ou desenhos.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribui çã o n ã o comercial (CC BY NC

4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

(EF02MA11) Descrever os elementos ausentes em sequências repetitivas e em sequências recursivas de números naturais, objetos ou figuras.

(EF02MA12) Identificar e registrar, em linguagem verbal ou não verbal, a localização e os deslocamentos de pessoas e de objetos no espaço, considerando mais de um ponto de referência, e indicar as mudanças de direção e de sentido.

(EF02MA13) Esboçar roteiros a ser seguidos ou plantas de ambientes familiares, assinalando entradas, saídas e alguns pontos de referência.

(EF02MA14) Reconhecer, nomear e comparar figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone, cilindro e esfera), relacionando-as com objetos do mundo físico.

(EF02MA15) Reconhecer, comparar e nomear figuras planas (círculo, quadrado, retângulo e triângulo), por meio de características comuns, em desenhos apresentados em diferentes disposições ou em sólidos geométricos.

(EF02MA16) Estimar, medir e comparar comprimentos de lados de salas (incluindo contorno) e de polígonos, utilizando unidades de medida não padronizadas e padronizadas (metro, centímetro e milímetro) e instrumentos adequados.

(EF02MA17) Estimar, medir e comparar capacidade e massa, utilizando estratégias pessoais e unidades de medida não padronizadas ou padronizadas (litro, mililitro, grama e quilograma).

(EF02MA18) Indicar a duração de intervalos de tempo entre duas datas, como dias da semana e meses do ano, utilizando calendário, para planejamentos e organização de agenda.

(EF02MA19) Medir a duração de um intervalo de tempo por meio de relógio digital e registrar o horário do início e do fim do intervalo.

(EF02MA20) Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro para resolver situações cotidianas.

(EF02MA21) Classificar resultados de eventos cotidianos aleatórios como "pouco prováveis" , "muito prováveis", "improváveis" e "impossíveis"

(EF02MA22) Comparar informações de pesquisas apresentadas por meio de tabelas de dupla entrada e em gráficos de colunas simples ou barras, para melhor compreender aspectos da realidade próxima.

(EF02MA23) Realizar pesquisa em universo de até 30 elementos, escolhendo até três variáveis categóricas de seu interesse, organizando os dados coletados em listas, tabelas e gráficos de colunas simples.

Competências específicas de Matemática para o Ensino Fundamental C PC NC Observações

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial

(CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Competências gerais da Educação Básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

C PC NC Observações

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Componentes essenciais para a alfabetização

Fluência em leitura oral

Desenvolvimento de vocabulário

Compreensão de textos

Produção de escrita

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de verificação de resultados

Professor(a):

Turma:

Sugestão de critérios de avaliação

C = consolidado (estudante faz sozinho); PC = em processo de consolidação (estudante precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (estudante não consegue realizar a atividade proposta)

Ficha de verificação de resultados

Principais objetivos de aprendizagem

Aluno Comparar e ordenar números naturais até a ordem das centenas por meio da compreensão do sistema de numeração decimal.

Descrever e registrar a localização e/ou deslocamentos no espaço por meio de esboços ou desenhos de plantas baixas.

Resolver e elaborar problemas de adição e de subtração com números até a ordem das centenas

Identificar e descrever regularidades e padrões em sequências, inclusive identificando elementos faltantes.

Realizar a leitura e a escrita das horas observadas em um relógio digital.

Resolver e elaborar problemas de multiplicação (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais.

Elaborar e resolver problemas envolvendo dobro, metade, triplo e terça parte.

Medir e comparar comprimentos, capacidades e massas por meio de unidades de medida convencionais.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribui çã o n ã o comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Professor:

Turma:

Período:

Competências socioemocionais Sempre Frequentemente Raramente Nunca

Determinação

Foco

Organização

Persistência

Responsabilidade

Empatia

Respeito

Confiança

Tolerância ao estresse

Autoconfiança

Tolerância à frustração

Iniciativa social

Assertividade

Entusiasmo

Curiosidade para aprender

Imaginação criativa

Interesse artístico

Material disponibilizado em licença aberta do tipo Creative Commons – Atribui çã o n ã o comercial (CC BY NC

4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Catálogo dos audiovisuais

Esta seção apresenta informações a respeito do conjunto de materiais audiovisuais que compõem a coleção. O material aqui apresentado tem por objetivo complementar e aprofundar a prática pedagógica e pode ser utilizado de acordo com as características da turma e do planejamento do professor. Cada audiovisual apresenta orientações introdutórias, bem como propostas de atividades que explorem o uso de cada recurso em sala de aula. Ressalta-se aqui a necessidade de sempre orientar os alunos quanto aos procedimentos de segurança ao se realizarem alguns dos experimentos propostos.

Audiovisuais da coletânea

Relação de audiovisuais da coletânea

Título do audiovisual Descrição Objetivos de aprendizagem Conteúdos abordados

Geometria no dia a dia

Neste audiovisual, são apresentados objetos ou partes de objetos do mundo físico que se parecem com algumas figuras geométricas espaciais (cubo, bloco retangular, pirâmide, esfera, cone e cilindro). Além disso, são apresentadas, também, algumas características dessas figuras geométricas.

• Relacionar figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone, cilindro e esfera) com objetos ou parte de objetos do mundo físico.

• Reconhecer e nomear figuras geométricas espaciais.

• Comparar figuras geométricas espaciais

• Sólidos geométricos (cubo, bloco retangular e pirâmide)

• Corpos redondos (cone, cilindro e esfera)

Quanto açúcar tem no meu copo?

Este audiovisual problematiza a quantidade excessiva de açúcar em alimentos industrializados como mote para o estudo de medidas de capacidade e de massa.

• Realizar experimento para descobrir a quantidade de açúcar em alimentos do cotidiano.

• Medir massa usando balança de cozinha.

• Comparar unidades de medida de massa e de capacidade.

• Medidas de capacidade: mililitro e litro

• Medidas de massa: grama e quilograma

De um lugar a outro

Com o objetivo de trabalhar noções de localização e de deslocamento no espaço, este audiovisual apresenta diferentes meios de transporte, indicando a importância deles na movimentação e na conexão entre pessoas e lugares.

• Descrever a localização e a movimentação de pessoas, indicando mudanças de direção e de sentido.

• Esboçar roteiros a serem seguidos indicando instruções.

• Noções de localização e de deslocamento.

• Descrição de trajetos (ou caminhos).

• Esboço de trajetos (ou caminhos).

• Elaborar a descrição de instruções de trajetos (ou caminhos) a serem seguidos.

Vamos pesquisar!

Neste recurso educacional, são apresentadas as etapas de realização de uma pesquisa estatística por meio de uma linguagem simples e acessível

• Coletar e organizar dados.

• Ler dados em tabelas e em gráficos de colunas simples.

• Noções de estatística.

• Pesquisa estatística.

• Tabelas.

Neste audiovisual, é apresentado o passo a passo para a criação de uma ampulheta de areia. Esse instrumento pode ser utilizado para explorar noções de medidas de tempo

• Representar dados em tabelas simples.

• Organizar dados em gráfico de colunas.

• Realizar pesquisa.

• Construir ampulheta de areia com materiais cotidianos

• Comparar as ampulhetas construídas.

• Identificar que ampulhetas de areia são instrumentos de medida não padronizada de tempo.

• Noção de tempo.

• Ampulheta de areia.

• Gráficos de colunas. Ampulhetas e intervalos de tempo

• Unidade não padronizada de medida de tempo.

Orientações para o uso dos audiovisuais

Geometria no dia a dia

Este audiovisual pode ser apresentado de maneira introdutória ao estudo de figuras geométricas espaciais ou como retomada desse estudo. Nele, são apresentados objetos ou partes de objetos do mundo físico que se parecem com algumas figuras geométricas espaciais (cubo, bloco retangular, pirâmide, esfera, cone e cilindro) e são apresentadas, também, algumas características dessas figuras geométricas.

Caso o vídeo seja apresentado como introdução ao conteúdo, sugere-se que a aula seja iniciada com o vídeo. Em seguida, perguntar aos alunos o que eles entenderam e o que acharam mais interessante. Retomar o que foi explicado, solicitando que os alunos indiquem algumas características das figuras geométricas espaciais estudadas. Perguntar a eles sobre algumas características de cada figura geométrica espacial apresentada no vídeo e solicitar que indiquem, na sala de aula, objetos cuja forma lembra a de alguma dessas figuras geométricas. Se for possível, selecionar previamente alguns objetos que tenham o formato parecido com o das figuras geométricas que serão estudadas, para serem explorados nesse momento. Em seguida, sugere-se a resolução das atividades propostas a seguir ou de atividades semelhantes

Se a opção for apresentar o vídeo como retomada, sugere-se exibi-lo para a turma e promover uma conversa sobre o conteúdo apresentado e sobre as dúvidas que os alunos têm sobre o conteúdo ou dúvidas que tiveram durante o vídeo. Caso seja possível, selecionar previamente objetos que têm a forma das figuras geométricas espaciais estudadas e propor uma brincadeira em que um aluno escolhe um dos objetos e descreve suas características para os colegas. Em seguida, eles precisam descobrir qual é o objeto que está sendo descrito. Após a brincadeira, sugere-se a resolução das atividades propostas a seguir.

Sugestões de atividades

1. A seguir estão representados alguns cubos e alguns blocos retangulares. cubos blocos retangulares

a) O que o cubo e o bloco retangular têm de parecido?

Espera-se que os alunos citem características como: a quantidade de faces, a quantidade de arestas ou a quantidade de vértices

b) O que eles têm de diferente?

Espera-se que os alunos indiquem que todas as faces do cubo são quadradas enquanto as faces do bloco retangular são retângulos.

2. Laura contornou todas as faces do objeto a seguir Editoria de arte

a) Marque um X nas figuras que ela obteve.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

A primeira opção é a resposta correta.

b) Esse objeto lembra qual figura geométrica?

( ) cilindro ( ) cone ( ) pirâmide ( ) esfera Pirâmide.

3. Liste o nome de três objetos, alimentos ou outros elementos do seu cotidiano que lembram o formato do cilindro e da esfera.

Sugestões de resposta:

• cilindro: lata de milho, rolo de papel higiênico, rocambole;

• esfera: bola, laranja

Quanto açúcar tem no meu copo?

Neste audiovisual, são apresentadas informações a respeito da quantidade de açúcar em alimentos diversos, em especial os industrializados, com comparações usando medidas de capacidade e de massa. Também, é mencionado que o consumo excessivo dessa substância pode causar danos aos seres humanos.

Este audiovisual pode ser trabalhado após o estudo formal do conteúdo de grandezas e medidas relacionado com as unidades de medida capacidade e massa, com a medição e com a comparação dessas medidas. Para isso, propor que seja realizado um experimento utilizando as informações fornecidas pelo vídeo e, se achar necessário, outras informações pesquisadas pelos alunos (com o auxílio de adultos) a respeito da quantidade de açúcar em alimentos industrializados. Dar preferência para exemplos de alimentos que sejam comuns no dia a dia dos alunos, adaptando a aula conforme a realidade da turma e da região. Sugere-se que, pelo menos, um dos alimentos escolhidos seja salgado, como molho de tomate ou ketchup

Nesse experimento, os alunos, com a ajuda do professor, vão medir as quantidades de alimentos e de açúcar indicados nos vídeos e na pesquisa para formar um mural interativo, que pode ser aproveitado e observado por outras turmas. Inicialmente, propor aos alunos que realizem uma listagem dos alimentos que farão parte do experimento. Em seguida, solicitar aos alunos que peçam embalagens vazias desses alimentos para os pais ou responsáveis Orientá-los a levar as embalagens, aos poucos, para a sala de aula e verificar se todos os alimentos têm pelo menos uma embalagem, que deve estar vazia e limpa.

No dia acordado previamente com os alunos, disponibilizar açúcar, uma balança de cozinha (que seja capaz de medir em grama), saquinhos limpos de plástico (como os de geladinho) ou pequenas embalagens limpas, grampeadores ou seladores para fechar os saquinhos, barbante ou fita adesiva (para prender as embalagens e os saquinhos), além de papel-paraná, cartolina ou papel-cartão para servir de apoio para o mural.

Com os dados do vídeo e com outros pesquisados pelos alunos, explorar a quantidade de açúcar em cada alimento listado. Por exemplo, mostrar uma lata de refrigerante, perguntar quem da turma consome esse tipo de bebida e identificar com os alunos quantos gramas de açúcar tem no produto. Depois, auxiliar os alunos na medição dessa quantidade na balança e no armazenamento do açúcar em um saquinho selado. Comparar com o saquinho de outros alimentos, como uma lata de suco de mesma capacidade

Após feitas as comparações, auxiliar os alunos a prender a embalagem e o saquinho de açúcar no mural, um embaixo do outro. Orientar os alunos a anotar no mural a quantidade de açúcar em grama, embaixo do saquinho, e a quantidade em mililitro ou em grama do alimento que está sendo considerado

Continuar esse procedimento até que todas as embalagens estejam no mural. Nesse momento, permitir que os alunos observem o mural e deem suas opiniões sobre o experimento que fizeram. Incentivá-los a perceber, por exemplo, que um copo de suco e um copo de refrigerante têm quantidades diferentes de açúcar. Se achar conveniente, promover uma conversa sobre atenção e cuidado à saúde, realizando um trabalho interdisciplinar com a área de Ciências da Natureza e suas Tecnologias.

Por fim, sugerir aos alunos que realizem atividades sobre o mural e sobre as comparações que podem ser feitas em relação à quantidade de açúcar nos alimentos.

Sugestões de atividades

1. Escreva o que mais te surpreendeu em relação à quantidade de açúcar nos alimentos.

A resposta depende das impressões dos alunos. Espera-se que os alunos indiquem, pelo menos, que ficaram surpresos ao saber que alimentos salgados (caso algum tenha sido apresentado), também, contêm açúcar.

2. Observe o mural que você fez com a turma.

a) Liste o nome dos alimentos do mural que você consome com frequência.

Resposta pessoal.

b) Imagine que você vai tomar um lanche. Selecione alguns alimentos do mural para compor o seu lanche. Adicione a quantidade de açúcar, em grama, de cada alimento que você escolheu e descubra a quantidade de açúcar total

A resposta depende dos alimentos disponíveis no mural e dos alimentos escolhidos pelos alunos.

3. Em uma folha avulsa, faça um desenho e escreva frases para explicar para um de seus responsáveis o que você aprendeu sobre o açúcar nos alimentos.

Produção pessoal

De um lugar a outro

Neste audiovisual, diferentes meios de transporte são apresentados indicando sua importância na movimentação e na conexão entre pessoas e lugares.

Esse é um tema que, sob o aspecto da Matemática, envolve conhecimentos de como localizar-se e orientar-se no espaço de acordo com a indicação de pontos de referência, bem como mudanças de direção e sentido, favorecendo o desenvolvimento das habilidades EF02MA12 e EF02MA13. Desse modo, este audiovisual pode ser utilizado como recurso de retomada e revisão de conteúdos relacionados a essas habilidades.

Para ampliar essa temática, favorecendo interdisciplinaridade com Geografia, após a exibição do audiovisual, sugere-se conversar com os alunos sobre o uso responsável desses meios de transporte já que a utilização deles, quando desnecessária, pode acarretar riscos ao meio ambiente e, consequentemente, para a vida dos seres humanos por causa da poluição que certos tipos de veículo lançam no ar.

Explorar com os alunos exemplos em que trajetos (ou caminhos) não tão distantes poderiam ser feitos a pé ou de bicicleta como atitude de uso responsável dos meios de transporte para locomoção. Esses são aspectos da Matemática e da Geografia que os alunos mobilizam na tomada de decisão em situações pertencentes ao cotidiano deles.

As atividades a seguir são sugeridas para complementar o objetivo de apoio pedagógico deste recurso e, se achar necessário, podem ser adaptadas à realidade da turma Providenciar (ou pedir aos alunos que providenciem), previamente, folhas de papel quadriculado para que sejam utilizadas na realização das atividades.

Sugestões de atividades

1. Leia o trajeto descrito a seguir e, em seguida, em uma malha quadriculada, traçando setas de acordo com a descrição, represente esse trajeto.

Sobre as linhas da malha, repita os passos abaixo quatro vezes seguidas:

• 1 lado de quadrinho para a direita e vire à esquerda;

• 1 lado de quadrinho para a frente;

• 1 lado de quadrinho para a direita e vire à direita;

• 1 lado de quadrinho para a frente

2. Elabore, usando desenhos de setas, instruções para descrever um trajeto a ser seguido na malha quadriculada. Em seguida, em dupla, troque com um colega as instruções elaboradas. Enquanto você traça, em uma folha de papel quadriculado, o trajeto descrito pelo colega, ele traça o trajeto descrito por você.

A resposta depende da descrição elaboração pelo aluno.

Sugestão de resposta:

3. Em uma folha de papel avulsa, desenhe o trajeto que você faz para ir de sua casa até o local que você mais gosta de visitar com sua família. Não deixe de incluir pontos de referência pelos quais vocês passam para chegar até esse local.

Produção pessoal.

4. Vamos brincar de robô? Para isso, siga as orientações descritas a seguir.

a) Cada aluno, na sua vez, vai ser o robô.

b) O professor vai vendar os olhos do aluno e vai acompanhar lado a lado o aluno-robô de modo que não ocorra risco de ele tropeçar e se machucar.

c) Os outros colegas da turma, um a um, vão dar instruções ao robô, como indicar ir para a frente ou para trás, virar para a direita ou para a esquerda, e indicar também a quantidade de passos a serem dados de modo que o robô siga um trajeto de um ponto de referência até o outro na sala de aula, por exemplo, ir da porta até a lousa.

Atividade lúdica e oral.

Vamos pesquisar!

Com base neste recurso educacional, os alunos entram em contato com uma explicação a respeito das etapas de realização de uma pesquisa estatística.

Por meio de uma linguagem simples e acessível, a narração visa estabelecer um diálogo agradável e envolvente com o interlocutor, que é o aluno do 2º ano, tornando a explicação adequada à faixa etária a qual se destina.

No 2º ano, os alunos ainda estão ampliando conceitos básicos de tabelas e gráficos, que começaram a ser explorados no 1º ano, por isso este recurso pode ser utilizado introdutoriamente a propostas de atividades que envolvam a realização de pesquisa em conformidade com a habilidade EF02MA23.

Sugere-se que os alunos tenham contato pelo menos duas vezes com este recurso de modo que, na primeira, sejam acompanhados do começo ao fim e, na segunda, coletivamente, a turma sistematize as etapas a serem seguidas, organizando por escrito uma lista delas.

Após o contato com o recurso e com essa sistematização, espera-se que a proposição das atividades sugeridas a seguir torne-se mais fluida e produtiva.

Sugestões de atividades

1. Na turma do 2º ano em que Fernanda estuda, a professora fez uma pesquisa sobre as tarefas domésticas as quais os alunos ajudam a realizar em casa. A professora orientou que cada aluno deveria votar apenas uma única vez em uma tarefa e distribuiu, a cada aluno, uma ficha de votação, conforme modelo representado a seguir.

Editoria de arte

Ficha de votação

( ) Arrumar a cama

( ) Retirar da mesa a louça usada na refeição

( ) Organizar o quarto

( ) Tirar o lixo

A quantidade de alunos que votaram em cada tarefa foi organizada na tabela a seguir.

Fonte: Alunos da turma do 2º ano.

Explorar com os alunos todos os elementos da tabela, como: título, colunas, linhas e fonte.

Responda às questões de acordo com a tabela.

a) Qual foi a tarefa mais votada?

Organizar o quarto.

b) Qual foi a tarefa menos votada?

Tirar o lixo.

2. De acordo com a tabela da atividade anterior, para representar um voto de cada aluno, pinte um quadrinho no gráfico a seguir. Depois, responda às questões.

Editoria de arte

Tarefas domésticas as quais os alunos ajudam a realizar em casa

Fonte: Alunos da turma do 2º ano.

a) Quais tarefas receberam quantidades iguais de votos?

Arrumar a cama e retirar da mesa a louça usada na refeição.

b) Quantos alunos responderam a essa pesquisa?

29 alunos.

c) Quais tarefas domésticas vocês costumam fazer em casa?

Resposta pessoal. Conversar com os alunos sobre os hábitos que, em casa, possuem e estão relacionados à distribuição das tarefas domésticas entre todos que moram com eles. Orientá-los que é importante auxiliar na realização de tarefas domésticas com responsabilidade e, inclusive, demonstrar autonomia em relação a algumas, como organizar o próprio quarto e os materiais escolares, entre outras, pois, nesse caso, essa atividade é responsabilidade de cada um.

3. Agora, é a vez de sua turma fazer uma pesquisa Sigam as orientações com as quais tiveram contato no recurso educacional "Vamos pesquisar!" e as orientações do professor.

Produção da turma. Orientar os alunos com relação às etapas apresentadas no recurso fazendo as mediações necessárias para o encaminhamento da pesquisa de acordo com a realidade da turma.

Ampulhetas e intervalos de tempo

Este audiovisual pode ser apresentado de maneira introdutória ao estudo de medidas de tempo. Nele, são apresentados os materiais e o passo a passo da construção de uma ampulheta - também conhecida como relógio de areia - utilizando materiais recicláveis, fita adesiva e areia.

Para esta aula, sugere-se selecionar previamente os materiais apresentados no vídeo, necessários para a construção da ampulheta, para que os alunos possam construir esse instrumento. Sugere-se, também, que sejam formados grupos e que cada grupo construa uma ampulheta. Se achar necessário, pode-se confeccionar algumas ampulhetas previamente para que os alunos possam utilizá-las durante a aula.

Antes de começar a aula, fazer perguntas aos alunos relacionadas à medição de intervalos de tempo. Por exemplo, perguntar como fazemos para saber quanto tempo dura uma brincadeira, uma música e uma aula. Após o relógio surgir nas respostas de alguns alunos, perguntar se eles acham que os relógios usados atualmente sempre existiram e como essa medição poderia ser feita se não existissem os relógios. Deixar que os alunos pensem por um tempo e, depois, explicar a eles que vão conhecer um instrumento de medida de tempo que foi utilizado antes da criação dos relógios que eles conhecem atualmente

Iniciar a exibição do vídeo e, após seu término, perguntar aos alunos se eles já conheciam ou se já viram esse instrumento de medida de intervalo de tempo. Depois, propor a construção da ampulheta e perguntar a eles como esse instrumento pode ser utilizado para medir intervalos de tempo. Permitir que explorem o instrumento e meçam diferentes atividades. É importante que eles compreendam que a contagem do tempo inicia quando, ao ser virada a ampulheta, a areia começa a cair na parte inferior.

Após os alunos manipularem a ampulheta e entenderem como ela funciona, propor as atividades seguintes, ou atividades semelhantes, que envolvem o uso desse instrumento de medida de tempo. As atividades podem ser realizadas em grupo e oralmente.

As atividades sugeridas propõem aos alunos refletirem sobre algumas limitações desse instrumento de medida e a necessidade de o ser humano criar outros instrumentos de medidas de tempo, como os relógios analógicos e digitais, e estabelecer unidades de medida para intervalos de tempos curtos e longos. Sugere-se apresentar aos alunos outros instrumentos de medida que, também, foram utilizados ao longo tempo. Como sugestão, assistir ao vídeo Como era o primeiro relógio inventado? Quem inventou?, disponível em: https://youtu.be/AyN73O2MVfg (acesso em: 13 jan. 2022).

A atividade 1 envolve verificar o tempo de duração de uma música. Essa música, adequada para o 2º ano, deverá ser selecionada pelo professor para ser executada durante a realização da atividade.

Sugestões de atividades

1. Utilizando uma ampulheta, verifique o tempo de duração da música apresentada pelo professor.

a) Como essa duração poderia ser registrada de forma escrita?

Resposta pessoal.

b) Tente explicar a um colega, sem utilizar relógios, o tempo inicial e o tempo final da música?

Resposta pessoal.

2. Utilizando uma ampulheta, peça que um colega se dirija, devagar, até a porta da sala de aula e retorne para a carteira. Quanto tempo ele gastou?

Resposta pessoal.

3. Em que situações você acha que seria possível utilizar uma ampulheta para medir ou controlar a duração de uma atividade?

Resposta pessoal.

4. Em que situações você acha que não seria possível utilizar uma ampulheta para medir intervalos de tempo?

Resposta pessoal.

5. Por que você acha que esse instrumento de medida não é adotado nos dias de hoje?

Resposta pessoal.

BNCC

A Base Nacional Comum Curricular (BNCC) é um documento oficial, homologado em dezembro de 2018, que traz um conjunto de habilidades e competências considerados essenciais para o desenvolvimento dos alunos na Educação Básica (Ensino Infantil, Ensino Fundamental e Ensino Médio).

A BNCC tem por objetivo possibilitar ações escolares que desenvolvam competências e habilidades comuns, garantindo igualdade das aprendizagens a que todos os estudantes brasileiros têm direito.

A seguir, são apresentadas na íntegra as Competências gerais da Educação Básica, as Competências específicas da área de Matemática e suas Tecnologias para o Ensino Fundamental e as habilidades, os objetos de conhecimento e as respectivas unidades temáticas para o 2º Ano do Ensino Fundamental e que podem ser encontrados nas páginas 9, 10, 267, 282, 283, 284 e 285 no documento:

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília: SEB, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf

Acesso em: 2 dez. 2021.

Matemática

2º Ano

Unidades temáticas Objetos de conhecimento Habilidades

Números Leitura, escrita, comparação e ordenação de números de até três ordens pela compreensão de características do sistema de numeração decimal (valor posicional e papel do zero)

(EF02MA01) Comparar e ordenar números naturais (até a ordem de centenas) pela compreensão de características do sistema de numeração decimal (valor posicional e função do zero).

(EF02MA02) Fazer estimativas por meio de estratégias diversas a respeito da quantidade de objetos de coleções e registrar o resultado da contagem desses objetos (até 1000 unidades).

(EF02MA03) Comparar quantidades de objetos de dois conjuntos, por estimativa e/ou por correspondência (um a um, dois a dois, entre outros), para indicar “tem mais” , “tem menos” ou “tem a mesma quantidade” , indicando, quando for o caso, quantos a mais e quantos a menos.

Composição e decomposição de números naturais (até 1000)

Construção de fatos fundamentais da adição e da subtração

(EF02MA04) Compor e decompor números naturais de até três ordens, com suporte de material manipulável, por meio de diferentes adições.

(EF02MA05) Construir fatos básicos da adição e subtração e utilizá-los no cálculo mental ou escrito.

Problemas envolvendo diferentes significados da adição e da subtração (juntar, acrescentar, separar, retirar)

Problemas envolvendo adição de parcelas iguais (multiplicação)

(EF02MA06) Resolver e elaborar problemas de adição e de subtração, envolvendo números de até três ordens, com os significados de juntar, acrescentar, separar, retirar, utilizando estratégias pessoais.

(EF02MA07) Resolver e elaborar problemas de multiplicação (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais por meio de estratégias e formas de registro pessoais, utilizando ou não suporte de imagens e/ou material manipulável.

Problemas envolvendo significados de dobro, metade, triplo e terça parte

Álgebra Construção de sequências repetitivas e de sequências recursivas

Identificação de regularidade de sequências e determinação de elementos ausentes na sequência

(EF02MA08) Resolver e elaborar problemas envolvendo dobro, metade, triplo e terça parte, com o suporte de imagens ou material manipulável, utilizando estratégias pessoais.

(EF02MA09) Construir sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.

(EF02MA10) Descrever um padrão (ou regularidade) de sequências repetitivas e de sequências recursivas, por meio de palavras, símbolos ou desenhos.

(EF02MA11) Descrever os elementos ausentes em sequências repetitivas e em sequências recursivas de números naturais, objetos ou figuras.

Geometria Localização e movimentação de pessoas e objetos no espaço, segundo pontos de referência, e indicação de mudanças de direção e sentido

Esboço de roteiros e de plantas simples

Figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone, cilindro e esfera): reconhecimento e características

Figuras geométricas planas (círculo, quadrado, retângulo e triângulo): reconhecimento e características

Grandezas e medidas Medida de comprimento: unidades não padronizadas e padronizadas (metro, centímetro e milímetro)

Medida de capacidade e de massa: unidades de medida não

(EF02MA12) Identificar e registrar, em linguagem verbal ou não verbal, a localização e os deslocamentos de pessoas e de objetos no espaço, considerando mais de um ponto de referência, e indicar as mudanças de direção e de sentido.

(EF02MA13) Esboçar roteiros a ser seguidos ou plantas de ambientes familiares, assinalando entradas, saídas e alguns pontos de referência.

(EF02MA14) Reconhecer, nomear e comparar figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone, cilindro e esfera), relacionando-as com objetos do mundo físico.

(EF02MA15) Reconhecer, comparar e nomear figuras planas (círculo, quadrado, retângulo e triângulo), por meio de características comuns, em desenhos apresentados em diferentes disposições ou em sólidos geométricos.

(EF02MA16) Estimar, medir e comparar comprimentos de lados de salas (incluindo contorno) e de polígonos, utilizando unidades de medida não padronizadas e padronizadas (metro, centímetro e milímetro) e instrumentos adequados.

(EF02MA17) Estimar, medir e comparar capacidade e massa, utilizando estratégias pessoais e unidades de

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Probabilidade e estatística

convencionais e convencionais (litro, mililitro, cm³, grama e quilograma)

Medidas de tempo: intervalo de tempo, uso do calendário, leitura de horas em relógios digitais e ordenação de datas

medida não padronizadas ou padronizadas (litro, mililitro, grama e quilograma).

(EF02MA18) Indicar a duração de intervalos de tempo entre duas datas, como dias da semana e meses do ano, utilizando calendário, para planejamentos e organização de agenda.

(EF02MA19) Medir a duração de um intervalo de tempo por meio de relógio digital e registrar o horário do início e do fim do intervalo.

Sistema monetário brasileiro: reconhecimento de cédulas e moedas e equivalência de valores

Análise da ideia de aleatório em situações do cotidiano

Coleta, classificação e representação de dados em tabelas simples e de dupla entrada e em gráficos de colunas

(EF02MA20) Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro para resolver situações cotidianas.

(EF02MA21) Classificar resultados de eventos cotidianos aleatórios como “pouco prováveis” , “muito prováveis” , “improváveis” e “impossíveis”

(EF02MA22) Comparar informações de pesquisas apresentadas por meio de tabelas de dupla entrada e em gráficos de colunas simples ou barras, para melhor compreender aspectos da realidade próxima.

(EF02MA23) Realizar pesquisa em universo de até 30 elementos, escolhendo até três variáveis categóricas de seu interesse, organizando os dados coletados em listas, tabelas e gráficos de colunas simples.

Competências específicas de Matemática para o Ensino Fundamental

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Competências gerais da Educação básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital

, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Referências bibliográficas comentadas

• BORBA, Marcelo de Carvalho; SILVA, Ricardo Scucuglia Rodrigues da; GADANIDIS, George. Fases das tecnologias digitais em educação matemática: sala de aula e internet em movimento. Belo Horizonte: Autêntica Editora, 2014. (Tendências em Educação Matemática).

A obra apresenta uma síntese sobre a utilização de tecnologias e internet em favor da Educação Matemática, explorando exemplos de utilização do softwareGeoGebra®, entre outros recursos.

• CARRAHER, Terezinha Nunes (org.). Aprender pensando: contribuições da psicologia cognitiva para a educação. 20. ed. Petrópolis: Vozes, 2012. Nesse livro, é debatida a maneira de pensar das crianças, a fim de proporcionar a elas abordagens significativas das ideias matemáticas.

• COLL, César; TEBEROSKY, Ana. Aprendendo Matemática. São Paulo: Ática, 2006. Os autores, especialistas em didática e psicologia, tratam de assuntos sobre aprendizagem e ensino de Matemática nos Anos Iniciais.

• D’AMBROSIO, Ubiratan. Educação matemática: da teoria à prática. Campinas: Papirus, 1996.

O autor aborda questões relacionadas à cognição, bem como apresenta ponderações sobre práticas de ensino da Matemática.

• ETCHEVERRIA, Teresa Cristina. O ensino de conceitos aditivos: trajetórias e possibilidades. Curitiba: Appris, 2019. Professoras relatam, nesse livro, um processo de trabalho formativo com a resolução de problemas nos Anos Iniciais do Ensino Fundamental.

• HOFFMANN, Jussara. Avaliação mito & desafio: uma perspectiva construtivista. 44. ed. Porto Alegre: Mediação, 2014.

A autora relata exemplos da experiência dela com base na avaliação como acompanhamento constante e mediação do processo de ensino e aprendizagem.

• KAMII, Constance. A criança e o número. Tradução de Regina A. de Assis. Campinas: Papirus, 2007. O livro apresenta uma reflexão sobre as relações estabelecidas pelas crianças na compreensão do conceito de número.

• KISHIMOTO, Tizuko Morchida. Jogos tradicionais infantis: o jogo, a criança e a educação. 18. ed. Petrópolis: Vozes, 2014. Nesse livro, são descritos estudos acerca dos vínculos existentes entre o jogo, a criança e a educação.

• KRULIK, Stephen; REYS, Robert (org.). A resolução de problemas na Matemática escolar. Tradução de Hygino H. Domingues e Olga Corbo. São Paulo: Atual, 2012. Estão reunidos, nesse livro, artigos de Matemática sobre a resolução de problemas. Contribuem para o conhecimento de tendências que valorizam e atribuem valor a esse trabalho.

• PARRA, Cecilia; SAIZ, Irma (org.). Didática da Matemática: reflexões psicopedagógicas. Porto Alegre: Artmed, 1996.

Na obra, há reflexões sobre o ensino do Sistema de Numeração Decimal, o trabalho com cálculo mental e exploração de noções espaciais e Geometria, entre outros assuntos.

• ZUNINO, Delia Lerner de. A Matemática na escola: aqui e agora. 2. ed. Porto Alegre: Artes Médicas, 2007.

Nesse livro, é debatida a importância de os alunos pensarem os cálculos matemáticos que fazem nas aulas, de modo que os relacionem com a aplicação no cotidiano deles.

Documentos oficiais

• BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília: SEB, 2018. Disponível em:

http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pd f. Acesso em: 5 dez. 2021.

Documento normativo no qual está definido o conjunto de aprendizagens essenciais que os alunos precisam desenvolver durante a Educação Básica, assegurando direitos de aprendizagem e desenvolvimento.

• BRASIL. Ministério da Educação. PNA: Política Nacional de Alfabetização. Brasília: Sealf, 2019. Disponível em: http://alfabetizacao.mec.gov.br/images/pdf/caderdo_final_pna.pdf

Acesso em: 5 dez. 2021.

Política instituída pelo Decreto nº 9.765, de 11 de abril de 2019, com o objetivo de implementar ações a fim de melhorar a qualidade dos processos de alfabetização e combater o analfabetismo no Brasil.

• BRASIL. Ministério da Educação. Relatório Nacional de Alfabetização Baseada em Evidências (Renabe). Brasília: Sealf, 2020. Disponível em: https://www.gov.br/mec/pt-br/media/acesso_informacacao/pdf/RENABE_web.pdf

Acesso em: 5 dez. 2021.

Esse relatório originou-se da primeira Conferência Nacional de Alfabetização Baseada em Evidências (Conabe), que aconteceu em Brasília, em 2019. No Renabe, há uma síntese de pesquisas recentes de especialistas (nacionais e estrangeiros) sobre alfabetização, literacia e numeracia.

Leituras complementares para o professor

• CORSO, Luciana Vellinho; DORNELES, Beatriz Vargas. Qual o papel que a memória de trabalho exerce na aprendizagem da Matemática? Bolema, Rio Claro, v. 26, n. 42b, p. 627-647, abr. 2012.

Artigo sobre a função cognitiva da memória de trabalho no desenvolvimento de habilidades em cálculos aritméticos e leitura.

• MALUF, Maria Regina; CARDOSO-MARTINS, Cláudia (org.). Alfabetização no século XXI: como se aprende a ler e a escrever. Porto Alegre: Penso, 2013. É uma das obras que embasaram a Política Nacional de Alfabetização (PNA). Auxilia a compreender como se dá a aprendizagem dos processos de leitura e escrita.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas