Entrelaços - Matemática - Volume 1

ÁREA: MATEMÁTICA

COMPONENTE: MATEMÁTICA

JOAMIR SOUZA ANGÉLICA REGHIN 1

ENSINO FUNDAMENTAL ANOS INICIAIS

MATEMÁTICA

RECURSO

EDUCACIONAL DIGITAL

1o ANO ENSINO FUNDAMENTAL ANOS INICIAIS

MATEMÁTICA

Joamir Roberto de Souza

Mestre em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Especialista em Estatística pela Universidade Estadual de Londrina (UEL-PR).

Licenciado em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professor de Matemática da rede pública de ensino.

Autor de livros didáticos para o Ensino Fundamental e para o Ensino Médio.

Maria Angélica Reghin de Souza

Especialista em Gestão Escolar pela Universidade Norte do Paraná (Unopar).

Licenciada em Pedagogia pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora na Educação Infantil.

Autora de livros didáticos para o Ensino Fundamental.

ÁREA: MATEMÁTICA COMPONENTE: MATEMÁTICA

RECURSO EDUCACIONAL DIGITAL

Entrelaços – Matemática – Recurso Educacional Digital – 1o ano (Ensino Fundamental – Anos Iniciais)

Copyright © Joamir Roberto de Souza, Maria Angélica Reghin de Souza, 2021

Direção-geral Ricardo Tavares de Oliveira

Direção de Conteúdo e Negócios Cayube Galas

Direção editorial adjunta Luiz Tonolli

Gerência editorial Natalia Taccetti

Edição Nubia de Cassia de Moraes Andrade e Silva (coord.)

Leticia Mancini Martins, João Alves de Souza Neto

Preparação e revisão de textos Viviam Moreira (sup.)

Adriana Périco, Caline Devèze, Camila Cipoloni, Carina Luca, Fernanda Marcelino, Fernando Cardoso, Graziele Ribeiro, Paulo José Andrade

Gerência de produção e arte Ricardo Borges

Design Daniela Máximo (coord.)

Arte e produção Isabel Cristina Corandin Marques (coord.)

Coordenação de imagens e textos Elaine Bueno Koga

Licenciamento de textos Erica Brambilla

Iconografia Priscilla Narciso

Coordenação de audiovisuais Diego Vieira Cury Morgado de Oliveira

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil) Souza, Joamir Roberto de Entrelaços [livro eletrônico] : matemática : 1o ano : ensino fundamental : anos iniciais / Joamir Roberto de Souza, Maria Angélica Reghin de Souza. – 1. ed. – São Paulo : FTD, 2021.

PDF Área: Matemática.

Componente: Matemática.

ISBN 978-85-96-03227-8 (recurso educacional digital professor – coleção)

1. Matemática (Ensino fundamental) I. Souza, Maria Angélica Reghin de. II. Título. 21-90773

CDD-372.7

Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Cibele Maria Dias - Bibliotecária - CRB-8/9427

EDITORA FTD

Rua Rui Barbosa, 156 – Bela Vista – São Paulo-SP CEP 01326-010 – Tel. 0800 772 2300 Caixa Postal 65149 – CEP da Caixa Postal 01390-970 www.ftd.com.br central.relacionamento@ftd.com.br

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Carta ao professor

Olá, professor! Seja bem-vindo ao Recurso Educacional Digital!

Este Recurso Educacional Digital tem como objetivo fornecer subsídios e sugestões que apoiem o trabalho pedagógico e a ação educativa em sala de aula no ensino da Matemática para os Anos Iniciais do Ensino Fundamental. O material oferece diferentes instrumentos de ampliação e intervenção que propiciam um ambiente de trocas, comunicação e diálogo, estimulam o levantamento de hipóteses e promovem a construção gradativa de conceitos e procedimentos matemáticos.

Neste material, são propostas situações de ensino-aprendizagem que favorecem a investigação, a experimentação, a criação de registros, a manipulação de objetos e as brincadeiras, permitindo aos alunos compreender que a Matemática não é um conhecimento restrito à sala de aula.

Os conteúdos e propostas de atividades que compõem este material também possibilitam o desenvolvimento das habilidades da Base Nacional Comum Curricular (BNCC), das competências específicas da área de Matemática e suas Tecnologias para o Ensino Fundamental, das competências gerais da Educação Básica, dos objetivos de aprendizagem e dos componentes essenciais para a alfabetização propostos na Política Nacional de Alfabetização (PNA).

Este material digital está organizado em quatro recursos pedagógicos descritos a seguir.

Plano de desenvolvimento anual

O Plano de desenvolvimento anual apresenta um quadro com uma programação de como os conteúdos podem ser organizados e trabalhados durante o ano letivo, seja em bimestres, trimestres ou semestres. Também, apresenta as habilidades da BNCC e os componentes essenciais para a alfabetização que podem ser trabalhados no período. Esse quadro é uma sugestão de programação, tendo o professor autonomia para adaptá-lo à realidade e às necessidades da turma.

O Plano de desenvolvimento apresenta, ainda: textos sobre estratégias e atitudes docentes que podem contribuir para alcançar os objetivos de aprendizagem estabelecidos; uma reflexão sobre avaliação e como esse instrumento pode auxiliar o processo de ensino-aprendizagem; e sugestões de leitura e sitesque podem aprimorar o trabalho docente em sala de aula.

Sequências didáticas

As sequências didáticas são sugestões de planejamento aula a aula que têm como objetivos complementar e aprofundar os conteúdos contemplados em outros materiais

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

didáticos e, consequentemente, contribuir com o desenvolvimento das habilidades e das competências específicas da área de Matemática e suas Tecnologias, das competências gerais da Educação Básica e dos componentes essenciais para a alfabetização. Além disso, essas sequências também podem contribuir para a remediação de eventuais dificuldades de aprendizagem dos alunos.

Com relação a sua estrutura, cada sequência didática é composta de um texto de introdução, dos objetivos de aprendizagem, do planejamento das aulas, de um passo a passo descritivo com sugestões metodológicas de como desenvolver as aulas, de exemplos de atividades que podem ser propostas aos alunos e de orientações de como acompanhar o desenvolvimento das aprendizagens em diferentes momentos.

Relatórios e indicadores do acompanhamento da aprendizagem

Os relatórios e indicadores do acompanhamento da aprendizagem têm como objetivo oferecer ao professor subsídios para acompanhar a aprendizagem dos alunos de maneira individual e coletiva, bem como apresentar orientações sobre como sistematizar os dados e apresentá-los aos pares, aos gestores escolares e aos responsáveis pelos alunos.

Esse relatório é composto de quatro fichas:

• Ficha de avaliação diagnóstica: possibilita avaliar os conhecimentos prévios dos alunos sobre determinados conteúdos e verificar a proficiência em algumas habilidades e competências.

• Ficha de acompanhamento das aprendizagens: possibilita avaliar o aprendizado e o progresso do aluno durante o processo de ensino-aprendizagem e fornece dados que permitem ao professor avaliar esse processo e ajustar a prática docente.

• Ficha de verificação dos resultados: possibilita avaliar quais objetivos de aprendizagem estabelecidos foram alcançados ao final do ano letivo.

• Ficha de acompanhamento para o desenvolvimento de habilidades socioemocionais: possibilita avaliar a evolução dos alunos em relação às habilidades socioemocionais.

É importante destacar a autonomia do professor para avaliar como essas fichas devem ser aplicadas e adaptadas de acordo com a realidade dos seus alunos e da escola na qual leciona e como elas podem complementar os diferentes instrumentos de avaliação e de acompanhamento de aprendizagem já utilizados.

Catálogo de audiovisuais

O catálogo de audiovisuais apresenta um descritivo de cada um dos audiovisuais que acompanham o Recurso Educacional Digital e tem como objetivo complementar e aprofundar o trabalho com os conteúdos explorados nesse material.

Além disso, oferece encaminhamentos à autonomia do professor, permitindo que, por meio de uma reflexão sobre as características da sua turma e do seu planejamento, seja possível estabelecer a melhor maneira de utilizar os audiovisuais. Para isso, o catálogo

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenc iadas sob os mesmos

apresenta sugestões de como esses audiovisuais podem ser trabalhados, bem como propostas de atividades que possibilitam explorar o uso desses recursos com os alunos.

No volume do 1º ano, são trabalhados os seguintes temas:

• Noções de posição, direção e tempo;

• Classificações e sequências;

• Os números naturais até 100;

• Adição e subtração com números até 100;

• Localização e deslocamento;

• Figuras geométricas espaciais e figuras geométricas planas;

• Grandezas e medidas;

• Probabilidade e estatística.

Esperamos que este material contribua para o aprimoramento da sua prática docente e para a formação de alunos aptos a viver em sociedade, fazendo valer seus direitos e exercendo seus deveres individuais e coletivos.

Bom trabalho!

Instrumentos pedagógicos

Plano de desenvolvimento anual

Este Plano de desenvolvimento anual consiste em um instrumento pedagógico que tem como objetivo auxiliar o planejamento docente na gestão dos conteúdos a serem apresentados ao longo de um ano letivo.

Para isso, em um primeiro momento, são apresentadas propostas de organização semestral, trimestral e bimestral, ordenadas em um quadro.

No quadro, a fim de favorecer a visualização da progressão das aprendizagens, constam, em colunas:

• a descrição sequencial de distribuição dos conteúdos;

• a indicação dos códigos alfanuméricos das habilidades da Base Nacional Comum Curricular (BNCC);

• a nomeação dos componentes essenciais para a alfabetização, de acordo com a Política Nacional de Alfabetização (PNA).

É importante considerar que o plano de ação sugerido nesta proposta pode ser adaptado à realidade escolar interna (infraestrutura, características da turma, entre outros aspectos) e à realidade escolar externa (parceria com os responsáveis dos alunos) da instituição em que se atua.

Imediatamente após o quadro, para auxiliar na gestão do processo de ensino-aprendizagem, constam três seções que são descritas a seguir.

A seção Práticas de ensino na sala de aula apresenta a proposição de algumas estratégias e procedimentos que podem ser eficazes para a concretização dos objetivos de aprendizagem previstos.

Na seção Avaliação, a importância dessa ferramenta pedagógica é enfatizada como instrumento a ser empregado de modo contínuo e processual. Deve ser utilizada para aferir não só os conhecimentos curriculares disciplinares, mas também os conhecimentos da realidade do mundo que cerca os alunos.

Por fim, a seção Saiba mais apresenta sugestões de referências complementares para consulta (sites , vídeos etc.) relacionadas a temas de cunho de ampliação do repertório da formação docente continuada.

De modo articulado e vinculado, com base nas indicações do quadro e das seções, é possível planejar o desenvolvimento anual de sua atuação docente.

1 º semestre 1º trimestre 1º bimestre

Aprendizagens desenvolvidas no 1º ano

Primeiras noções matemáticas

• Compreender, classificar e estabelecer relações de direção e sentido: para frente, para trás, para a direita e para a esquerda

• Compreender, classificar e estabelecer relações de posição: perto, longe, aberto, fechado, fora e dentro.

• Identificar regularidades e acrescentar elementos em sequência de objetos.

• Organizar e ordenar objetos de acordo com alguns atributos como forma, tamanho, cor, entre outros.

Os números de 0 a 10

• Contar até 10.

• Representar quantidades utilizando algarismos.

• Estimar e comparar quantidades de elementos em coleções.

• Utilizar números para indicar quantidade e ordem.

• Comparar e ordenar números.

• Identificar sequências crescentes e decrescentes de números naturais.

• Números ordinais.

Adição e subtração com números até 10

• Ideias da adição

• Construir fatos básicos da adição.

• Resolver adições

• Compor e decompor números por meio de diferentes adições.

• Ideias da subtração

2º bimestre

• Resolver subtrações

As figuras geométricas

• Reconhecer figuras geométricas espaciais e planas

2º trimestre

• Relacionar figuras geométricas espaciais com objetos do mundo físico.

• Nomear figuras geométricas planas.

• Identificar e nomear figuras geométricas planas em contornos de faces de objetos que lembram figuras geométricas espaciais.

BNCC

EF01MA01

EF01MA02

EF01MA03

EF01MA04

EF01MA05

EF01MA09

EF01MA10

EF01MA11

EF01MA12

Componentes essenciais para a alfabetização

• Consciência fonológica e fonêmica.

• Conhecimento alfabético.

• Fluência em leitura oral.

• Desenvolvimento de vocabulário

• Compreensão de textos.

• Produção de escrita

BNCC

EF01MA06

EF01MA07

EF01MA08

EF01MA13

EF01MA14

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento de vocabulário.

• Compreensão de textos.

• Produção de escrita

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

2º semestre

3º trimestre

3º bimestre

Números até 100

• A dezena

• Os números até 100.

• Contar coleções de até 100 elementos de maneira exata ou aproximada.

• Estimar e comparar quantidades de elementos em coleções.

• Identificar, ler e escrever números naturais.

• Compor e decompor números naturais.

• Utilizar números para indicar quantidade, ordem ou código.

• Compreender relações do Sistema de Numeração Decimal.

• Comparar números até 100.

Grandezas e medidas

• Medir comprimento, massa e capacidade utilizando unidades de medidas não padronizadas.

• Reconhecer e comparar as cédulas e moedas do Sistema Monetário Brasileiro.

• Compor quantias com cédulas e moedas do Sistema Monetário Brasileiro.

• Reconhecer e estabelecer relações entre medidas de tempo em dias, semanas, meses e anos

• Relatar sequências de acontecimentos de um dia.

• Ler informações do calendário.

• Consultar um calendário para escrever datas.

Adição e subtração com números até 100

• Construir fatos básicos da adição.

• Resolver e elaborar problemas envolvendo adições.

• Compor e decompor números naturais por meio de diferentes adições.

• Resolver e elaborar problemas envolvendo subtrações.

4º bimestre

• Identificar e descrever regularidades em sequências numéricas.

Estatística e probabilidade

• Ler, interpretar e comparar informações apresentadas em tabelas simples e gráficos de colunas.

• Realizar pesquisa.

• Organizar dados em tabelas simples e gráficos de colunas.

• Analisar, identificar e classificar eventos que envolvem o acaso, utilizando expressões como: "acontecerá com certeza", "talvez aconteça" e "é impossível acontecer"

BNCC

EF01MA01

EF01MA02

EF01MA03

EF01MA04

EF01MA05

EF01MA07

EF01MA10

EF01MA15

EF01MA16

EF01MA17

EF01MA18

EF01MA19

Componentes essenciais para a alfabetização

• Consciência fonológica e fonêmica.

• Conhecimento alfabético.

• Fluência em leitura oral.

• Desenvolvimento de vocabulário.

• Compreensão de textos.

• Produção de escrita

BNCC

EF01MA06

EF01MA07

EF01MA08

EF01MA10

EF01MA20

EF01MA21

EF01MA22

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento de vocabulário.

• Compreensão de textos.

• Produção de escrita

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

Práticas de ensino na sala de aula

Para que o Plano de desenvolvimento anual possa efetivamente se consolidar de modo que sejam alcançados os objetivos de aprendizagem pretendidos para o ano letivo, é importante o docente ter atitudes e utilizar práticas que contribuam para o desenvolvimento dos componentes essenciais para a alfabetização e das competências e habilidades matemáticas nos alunos sob sua responsabilidade. Para isso, a seguir é apresentada uma visão geral de algumas abordagens possíveis.

É importante ressaltar, ainda, que o processo de ensino-aprendizagem já não se encontra mais intimamente vinculado apenas ao espaço físico da sala de aula e, em virtude das mudanças ocorridas socialmente, cenários de aprendizagem virtual passaram a fazer parte da dinâmica escolar, sendo necessário considerar essa perspectiva no planejamento, nas práticas, bem como na busca de atualização da formação docente.

Leitura inferencial

Para abordar situações significativas apresentadas em cada proposta didática, a leitura inferencial é uma prática importante a ser desenvolvida com os alunos. Essa prática envolve tanto estratégias de leitura de imagens quanto de leitura de textos.

A leitura de imagens, em Matemática, nos Anos Iniciais do Ensino Fundamental, é tão explorada quanto a leitura de textos, visto que o suporte de apoio visual na realização de contagens ou resolução de operações matemáticas é um recurso didático muito utilizado.

A reflexão sobre o processo de leitura inferencial pode ser promovida pelo docente por meio de perguntas ou solicitações propostas que permitam aos alunos demonstrarem respostas que não estejam apenas circunscritas aos textos, e sim possam ser inferidas considerando conhecimentos prévios e de mundo de modo geral.

Os enunciados dos problemas matemáticos são textos que requerem leitura analítica e inferencial por parte dos alunos para que possam desenvolver melhores estratégias de resolução.

Produzir inferências é uma ação que auxilia na compreensão de um texto. No caso das aulas de Matemática, de um texto matemático, por exemplo, o enunciado de um problema.

A compreensão de texto, em qualquer área de conhecimento, é uma habilidade que depende das inferências geradas pelo leitor, considerando que cada texto possui informações implícitas e explícitas.

A qualidade e a quantidade das inferências geradas por um leitor dependem, prioritariamente, das associações estabelecidas entre as informações explícitas no texto e os conhecimentos prévios e de mundo que o leitor possui.

Para auxiliar os alunos a lerem um texto de maneira analítica, a fim de que possam concluir, deduzir e formular novos sentidos, levantar hipóteses, bem como ressignificar informações, uma estratégia é sugerir que, ao fazer a leitura:

• dividam o texto em partes menores que forneçam informações principais;

• estabeleçam relações entre essas partes de modo a identificar como elas se inter-relacionam;

• identifiquem o panorama geral do que essas inter-relações indicam.

Destaca-se o fato de que a leitura de um texto matemático mobiliza o leitor para a interpretação de elementos textuais combinados a elementos matemáticos, como números, tabelas, gráficos, entre outros.

Nesse sentido, outra estratégia é fazer com que os alunos compreendam que ler um texto matemático não se resume a identificar palavras-chave.

Sugere-se, sempre que possível, incentivar os alunos a realizar uma leitura analítica e inferencial de:

• imagens que permeiam o material didático (imagens de aberturas de partes hierárquicas do livro, como unidades ou capítulos, por exemplo);

• textos (enunciados de problemas, textos instrucionais de jogos, entre outros).

Sugere-se, ainda, solicitar aos alunos que façam registros das compreensões, pois essa prática vai ajudá-los a melhorar o desempenho na resolução e condução das tarefas propostas.

Esses registros podem ser compartilhados em um mural da sala de aula ou da escola, em um mural on-line criado na rede social da escola ou, até mesmo, em uma folha de cartolina, na qual os alunos façam registros. O cartaz pode ser afixado em algum espaço da sala de aula ou da escola

Fazer diferentes registros

Na Competência específica 6 de Matemática e suas Tecnologias da BNCC (BRASIL, 2018, p. 267), é abordada a importância de expressar respostas e sintetizar conclusões utilizando diferentes registros e linguagens.

Desse modo, uma prática importante, ao longo do desenvolvimento das atividades propostas, é solicitar aos alunos que façam diferentes registros para expressar as justificativas de suas respostas, esquematizar a descrição de estratégias utilizadas no processo de resolução, representar um problema com uma organização visual etc.

Essa prática é importante de ser desenvolvida desde os primeiros anos de escolaridade já que é um processo que deve ser aprimorado durante toda a vida escolar e não escolar, pois fazer registros e interpretá-los é uma habilidade importante, por exemplo, no trabalho, assim como em diversas situações da vida cotidiana que requerem a

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

esquematização de sistemas, situações ou processos, com a finalidade de compreendê-los melhor

Como estratégia de aplicação dessa prática, explorar com os alunos algumas possibilidades, como:

• no processo de resolução de problemas que envolvam proporcionalidade, fazer registros organizados em quadros;

• em pesquisas estatísticas, fazer registros dos dados coletados em tabelas e gráficos;

• questões que abrangem características geométricas, fazer desenhos (esboços esquemáticos) que representem plantas baixas ou figuras (bidimensionais ou tridimensionais);

• no trabalho com sequências recursivas (numéricas ou figurais), fazer registros por escrito das regularidades identificadas na regra de formação do padrão de cada sequência;

• ao resolver problemas que envolvem multiplicação com a ideia de combinatória, fazer a organização da representação de uma árvore de possibilidades (ou de um quadro de possibilidades);

• na elaboração de problemas, solicitar que façam diagramas de fluxo ligando as etapas, a fim de representar a sequência que encadeou o raciocínio empregado no desenvolvimento da elaboração

Permitir aos alunos eleger de maneira autônoma os diferentes registros e linguagens é muito importante para valorizar o protagonismo deles no processo de ensino-aprendizagem.

Educação para a cidadania

Além dos conteúdos disciplinares, o processo de formação educacional abrange, também, a responsabilidade de formar indivíduos conscientes da importância que atitudes individuais exercem sobre a vida do outro e das responsabilidades que possuem em relação ao grupo social a que pertencem, entre outros aspectos.

Na BNCC (BRASIL, 2018), nas páginas 9 e 10, estão relacionadas dez competências gerais da Educação Básica e, nas páginas 19 e 20, são elencados os Temas Contemporâneos Transversais, os quais apontam para o desenvolvimento de capacidades a serem aperfeiçoadas, ao longo da vida, com base no exercício de práticas sociais inseridas em determinados contextos, como meio ambiente, saúde, educação financeira, entre outros.

Considerando essa perspectiva, a prática da educação para a cidadania prioriza envolver todos os alunos em vivências significativas consigo mesmos e com outras pessoas, por meio da percepção de que há direitos que são garantidos com base no cumprimento dos deveres, e vice-versa. Sendo assim, a educação para a cidadania vai além da transmissão de conteúdo e da assimilação dele

Uma estratégia que se pode utilizar, a cada semana, é escolher ou pedir que se voluntarie um ajudante da semana para auxiliar você em algumas tarefas. O objetivo é levar os alunos a assumirem uma postura cooperativa com você e os colegas.

É adequado, se possível, que cada aluno da turma, ao longo do ano letivo, seja o ajudante da semana, pois essa experiência ajudará a lidar com a indisciplina, caso exista no ambiente. Isso, também, favorecerá o desenvolvimento de sentimentos de pertencimento, autonomia, responsabilidade, resiliência, foco, cuidado consigo mesmo e com os outros, entre outros.

O ajudante da semana pode cuidar do compartilhamento de comunicados e lembretes de compromissos. Essa comunicação pode ser:

• on-line , por meio de aplicativos de mídia que compartilham vídeos curtos ou áudios;

• off-line , com base na escrita de recados diários no mural ou no quadro da sala de aula

É importante que seja incluída alguma atividade envolvendo tecnologia digital para que os alunos se apropriem de fazer uso cidadão e crítico no ambiente escolar.

Estímulo à criatividade

A criatividade (ou pensamento criativo) é um potencial que todos nós possuímos e pode ser desenvolvida no ambiente escolar com base em determinadas estratégias e em certos contextos apropriados.

Nas aulas de Matemática, estimular práticas que envolvam o potencial criativo é uma ação que pode ser associada a diferentes unidades temáticas dessa área de conhecimento.

Nas atividades relacionadas a conhecimentos geométricos, por exemplo, uma estratégia é propor aos alunos atividades em que eles sejam construtores de maquetes ou de outras elaborações relacionadas ao tema, de acordo com a criatividade deles.

Para realizar essas construções, os alunos devem mobilizar os conhecimentos desse tema para reconhecer em embalagens e objetos do mundo físico características de figuras geométricas espaciais estudadas para assim selecionar as melhores embalagens ou objetos a serem empregados nessas construções de acordo com as características identificadas, como superfícies arredondadas ou não.

Esse tipo de atividade, geralmente realizada em grupos, envolve a produção de ideias originais Sendo assim, além de estimular a criatividade para apresentar ideias, exercita a flexibilidade dos alunos em acolher as ideias dos colegas de grupo e a solucionar problemas de forma construtiva e respeitosa

A captura de retratos de construções arquitetônicas que se pareçam com figuras geométricas espaciais para elaborar uma apresentação de slides também é uma atividade que estimula a criatividade, além de utilizar tecnologia digital.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Outra estratégia são atividades de elaboração de problemas. Esse tipo de atividade também estimula a criatividade dos alunos. Além de empregarem conhecimentos matemáticos nessa elaboração, a criação do contexto do problema requer a originalidade na concepção de ideias novas e, para isso, o pensamento criativo é estimulado.

Avaliação

A avaliação exerce uma das principais funções em favor da promoção e da consolidação do processo de ensino-aprendizagem. Por isso, a avaliação não pode ser concebida somente como uma fase final desse processo, mas precisa ser integrada a todo o processo, de maneira contínua.

Para que a avaliação seja empregada com eficácia, é importante coletar informações sobre aspectos não desenvolvidos, os parcialmente desenvolvidos e os desenvolvidos pelos alunos. Com base nessas informações, oferecer feedbacka cada um deles, aos gestores escolares e aos responsáveis pelos alunos

A coleta dessas informações pode ser dirigida de maneira diversificada considerando diferentes possibilidades, como avaliação diagnóstica, avaliação de processo e avaliação formativa.

Com a avaliação diagnóstica, é possível mapear os diferentes perfis dos alunos em relação aos conhecimentos prévios que possuem. Assim, a observação e a reflexão do docente sobre as informações obtidas é uma importante ferramenta nesse tipo de avaliação. Embora, em um diagnóstico, muitas informações possam ser observadas, é indicado, além da sondagem de conhecimentos prévios, que se observem também:

• a linguagem corporal dos alunos durante suas explicações (se demonstram interesse ou não);

• o modo como se organizam no trabalho em duplas ou grupos para a prática de uma atividade;

• se manifestam ansiedade ou demonstram desinteresse quando questionados individualmente.

Na avaliação diagnóstica, a observação desses padrões de comportamento compõe dados relevantes a serem vinculados à análise do desempenho cognitivo de cada aluno nas atividades propostas.

Já a avaliação de processo produz uma experiência educacional que motiva os alunos, por ser contínua e se dar também por meio da utilização de instrumentos informais, como paradas para uma autoavaliação.

A fim de tornar a avaliação de processo um momento mais próximo de cada aluno:

• questionar a avaliação pessoal que cada um faz das próprias produções e atuações escolares No caso de trabalho em duplas ou em grupo, essa prática de autoavaliação pode ser incorporada de maneira reflexiva e compartilhada entre eles;

• solicitar relatórios concisos sobre atividades específicas, ou qualquer outro tipo de registro, para obter informações do processo de aprendizagem de cada aluno, a fim de rever o processo sempre que necessário.

Na avaliação formativa, a utilização de instrumentos formais, mantendo o formato de atividades diárias, se destaca, pois, nesse tipo de avaliação, critérios mais específicos são considerados, como o nível de apreensão dos alunos em relação aos conteúdos, a aplicação da linguagem matemática, entre outros que permitem a sistematização de informações.

Avaliar é um ato que dá origem a informações úteis para docentes e discentes, conforme a interpretação e a comunicação dialógica entre os atores do processo educacional.

Para auxiliar na geração de informações e interpretação dessas informações, consultar os Relatórios e Indicadores do Acompanhamento da Aprendizagem disponíveis neste material.

Para saber mais

• BARLOW, Michel Avaliação escolar: mitos e realidades. Porto Alegre: Artmed, 2006. Nessa obra, Michel Barlow discute práticas avaliativas em sala de aula.

• BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática. 6. ed. Belo Horizonte: Autêntica, 2019. (Tendências em Educação Matemática).

Nesse livro, os autores apresentam resultados de um trabalho sobre informática educativa, como questões pedagógicas sobre o uso do computador e da calculadora.

• BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base Brasília: SEB, 2018. Disponível em:

http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pd f. Acesso em: 8 dez. 2021.

Documento que regulamenta as aprendizagens essenciais na Educação Básica.

• BRASIL. Ministério da Educação. PNE: Plano Nacional de Educação. Brasília: Inep, 2014. Disponível em:

https://download.inep.gov.br/publicacoes/institucionais/plano_nacional_de_educacao/pl ano_nacional_de_educacao_pne_2014_2024_linha_de_base.pdf. Acesso em: 8 dez. 2021.

Nesse documento, são apresentadas as diretrizes, metas e estratégias para a educação brasileira de 2014 a 2024.

• COLL, César; TEBEROSKY, Ana. Aprendendo Matemática. São Paulo: Ática, 2000.

Nesse livro, é possível ter acesso a conceitos matemáticos de diversos campos, compreendendo estruturas e ideias fundamentais.

• GAUTHIER, C.; BISSONNETTE, S.; RICHARD, M. Ensino explícito e desempenho dos alunos: a gestão dos aprendizados. Petrópolis: Vozes, 2014.

Nesse livro, os autores discutem as principais características e os fundamentos do ensino explícito como uma proposta de ensino eficaz.

• HADJI, C. A avaliação, regras do jogo: das intenções aos instrumentos. Porto: Porto Editora, 1994.

Nesse livro, é apresentada uma proposta de abordagem de avaliação da aprendizagem escolar, incluindo reflexões e análises relacionadas aos tipos de avaliação.

• LORENZATO, S. Laboratório de ensino de Matemática e materiais didáticos manipuláveis. In : LORENZATO, S. O Laboratório de Ensino de Matemática na formação de professores. Campinas: Autores Associados, 2006. p. 3-38. (Coleção Formação de professores).

Nesse texto, é discutido o papel do Laboratório de Ensino de Matemática (LEM) no ensino e na aprendizagem de Matemática.

• LUCKESI, C. C. Verificação ou avaliação: o que pratica a escola. Ideias, São Paulo, n. 8, p. 71-80, 1998. (Série Ideias).

Nesse texto, o autor faz uma abordagem sobre aspectos que diferenciam as ações de verificar e avaliar no ensino escolar.

• MONTEIRO, Alexandrina; POMPEU JUNIOR, Geraldo. A Matemática e os temas transversais. São Paulo: Moderna, 2001.

Nesse livro, há reflexões sobre os temas transversais, com especial atenção às aulas de Matemática.

• NACARATO, Adair Mendes; MENGALI, Brenda Leme da Silva; PASSOS, Cármen Lúcia Brancaglion A Matemática nos anos iniciais do Ensino Fundamental. 2. ed. Belo Horizonte: Autêntica, 2015.

Nesse livro, os autores debatem sobre o ato de aprender e o ato de ensinar a Matemática, nos Anos Iniciais do Ensino Fundamental.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

• PAIS, L.

C. Ensinar e aprender

Matemática. Belo Horizonte: Autêntica, 2006.

Com essa obra, o autor propõe uma reflexão acerca de aspectos metodológicos do ensino da Matemática, incluindo uma análise do livro didático.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Sequências didáticas

Sequência

didática 1: Noções de posição, direção e tempo

Esta sequência didática aborda a localização de objetos e de pessoas no espaço em relação a sua própria posição ou em relação à posição de um referencial, utilizando termos como esquerda, direita, para a frente e para trás. Além disso, será abordada a localização de pessoas e de figuras geométricas espaciais do ponto de referência pessoal e de outro ponto de referência, por meio de atividades nas quais os alunos confeccionarão modelos de figuras geométricas espaciais com massa de modelar.

Objetivos de aprendizagem

• Identificar posições usando termos: esquerda, direita, para a frente, para trás, à frente, atrás, acima e abaixo

• Localizar objetos e pessoas a partir de um referencial e da sua própria posição.

• Reconhecer e saber descrever a localização de objetos e de pessoas no espaço com base em um ponto de referência próprio e a partir de outro ponto de referência.

• Relacionar figuras geométricas espaciais a objetos do dia a dia

Plano de aulas

Aulas 1 e 2: Identificar posições de objetos e de pessoas por meio de perguntas e atividades.

Aula 3: Brincadeira para aprimorar e/ou compreender comandos como "para a direita", " para a esquerda", " para a frente" e "para trás"

Aula 4: Brincadeira para aprimorar a ideia de sentido e de direção e a coordenação motora.

Aula 5: Jogo para ampliar os conceitos de direção.

Aula 6: Preparação de massa de modelar.

Aula 7: Construção de representações de figuras geométricas espaciais com massa de modelar e localização dessas construções de acordo com o referencial, que deve ser o próprio aluno.

Aula 8: Localizar representações de figuras geométricas espaciais de acordo com o referencial, que deve ser outra pessoa.

Componentes essenciais para a alfabetização: Produção de escrita e compreensão de textos

Competências gerais da Educação Básica: 4 e 9

Competências específicas de Matemática: 2 e 8.

Habilidades: EF01MA11, EF01MA12 e EF01MA13.

Materiais necessários: Lápis, borracha, barbante, massa de modelar colorida, folhas de atividades, jornal, sal, farinha, água, óleo, corante e vendas para os olhos.

Explicar, por meio de exemplos, as posições da localização de objetos e de pessoas em relação a um ponto referencial, utilizando os termos: direita, esquerda, para a frente e para trás.

Ressaltar a importância da referência. Por exemplo, ficar de frente para os alunos e dar um passo para a direita. Depois, fazer o seguinte questionamento: eu andei para qual direção? Espera-se que os alunos respondam que em relação à sua posição, você andou para a direita, e, em relação aos alunos, você andou para a esquerda.

Fazer outros questionamentos utilizando objetos localizados em pontos diferentes da sala de aula. A intenção é preparar a turma para as próximas atividades. Por exemplo, fazer perguntas de fácil resposta a ser dada verbalmente pela turma em conjunto, como: a lâmpada está acima ou abaixo das carteiras? Em relação à minha mesa, a lousa está à frente ou atrás dela?

É possível aumentar a dificuldade das perguntas, como: em relação às cadeiras que os alunos estão sentados, a porta está à direita ou à esquerda delas? O aluno "X" está sentado à direita ou à esquerda do aluno "Y"? O aluno "A" está sentado à frente ou atrás do aluno "B"? Aproveitar algum objeto que esteja na parede da sala de aula, por exemplo, um relógio, e trabalhar de frente para os alunos; mostrar que, se o objeto está à sua direita, ele está à esquerda dos alunos.

Chamar os alunos para trocarem de posição com você e perceber como eles lidam com essa mudança entre direita e esquerda, a depender do ponto de referência.

Após propor as perguntas, entregar, para cada aluno, a folha de atividade com imagens e questionamentos para que identifiquem as posições usando os termos: direita, esquerda e na frente, como exemplificado a seguir. Esta atividade será individual para promover a autonomia do aluno.

Como os alunos estão em fase de alfabetização, é importante ler toda a atividade com eles e pedir para que acompanhem a leitura, assegurando que todos entendam a proposta Por isso, é preciso explicar cada comando e pedir aos alunos que indiquem oralmente se estão entendendo o que está sendo pedido na atividade. Se necessário, repetir a leitura e explicá-la novamente. Ressaltar que a referência é em relação a quem está observando a imagem. Por exemplo, na imagem da atividade 1, se a referência é o observador, Tais está à esquerda de Pedro. No entanto, se a referência for Manu, Tais está à sua direita. Após a explicação, estipular um tempo de resolução, que pode ser de dez minutos. Durante esse período, é interessante andar pela sala de aula para observar o que os alunos estão produzindo e intervir caso seja necessário.

Propor uma discussão sobre as respostas colocadas na ficha, de modo que os alunos ampliem suas perspectivas e reflitam sobre o assunto.

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

ATIVIDADE 1: APRENDENDO SOBRE AS POSIÇÕES

OBSERVE A IMAGEM A SEGUIR E MARQUE UM X NA RESPOSTA CORRETA.

macrovector/Freepik.com

Sala de aula com professor e alunos

1. BRUNO ESTÁ À DIREITA, À ESQUERDA OU À FRENTE DE CLARA?

( ) DIREITA ( ) ESQUERDA ( ) À FRENTE

À esquerda.

2. MANU ESTÁ À FRENTE, ATRÁS OU À DIREITA DE BRUNO?

( ) DIREITA ( ) ATRÁS ( ) À FRENTE

À frente.

3. PEDRO ESTÁ À DIREITA, À ESQUERDA OU À FRENTE DE TAIS?

( ) DIREITA ( ) ESQUERDA ( ) À FRENTE

À direita.

Se alguns alunos apresentarem dificuldade para realizar a atividade, retomar o conteúdo e citar novos exemplos.

Uma dificuldade que os alunos podem apresentar é identificar as posições em relação a um ponto referencial. Uma sugestão de atividade complementar para sanar essa dificuldade será proposta na próxima aula.

Aula 2

Formar duplas com os alunos e apontar um referencial. Por exemplo, escolher seis objetos na sala de aula que estão à direita, à esquerda, à frente ou atrás dos alunos. Entregar uma folha de atividade complementar para que os alunos registrem a posição de cada objeto da sala de aula em relação ao professor. É importante realizar a leitura com os alunos, garantindo que todos entendam a proposta da atividade.

A seguir, há uma sugestão de atividade complementar. Orientá-los a responder a atividade 1 oralmente.

ATIVIDADE COMPLEMENTAR: APRENDENDO MAIS SOBRE AS POSIÇÕES

1. QUAL É O REFERENCIAL QUE SERÁ UTILIZADO?

Sugestão de resposta: O professor.

2. DESENHE OBJETOS NO QUADRO A SEGUIR E ESCREVA A POSIÇÃO DELES EM RELAÇÃO AO REFERENCIAL.

Resposta pessoal.

OBJETO POSIÇÃO EM RELAÇÃO AO REFERENCIAL ESCOLHIDO

( ) DIREITA ( ) ESQUERDA ( ) À FRENTE ( ) ATRÁS

( ) DIREITA ( ) ESQUERDA ( ) À FRENTE ( ) ATRÁS

( ) DIREITA ( ) ESQUERDA ( ) À FRENTE ( ) ATRÁS

( ) DIREITA ( ) ESQUERDA ( ) À FRENTE ( ) ATRÁS

( ) DIREITA ( ) ESQUERDA ( ) À FRENTE ( ) ATRÁS

( ) DIREITA ( ) ESQUERDA ( ) À FRENTE ( ) ATRÁS

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

Ao final, perguntar quais as posições que os alunos marcaram para cada objeto. Se alguma resposta não estiver correta, pedir para eles explicarem como pensaram para responder. Pode-se, para sanar as dúvidas, sugerir que um deles troque de lugar com você, a fim de analisar a posição dele em relação ao objeto em questão

Aula 3

Nesta aula, será proposta uma brincadeira para que os alunos consolidem o desenvolvimento das habilidades adquiridas na aula anterior. É importante conversar com eles sobre perder e ganhar em um jogo, para que não fiquem chateados ao sair da brincadeira, mesmo que momentaneamente.

Apresentar a atividade e explicar as regras da brincadeira para os alunos Retomar o que foi visto na aula anterior sobre as posições e levá-los para a quadra, o pátio ou outro lugar que seja adequado para realizar a atividade.

Organizar os alunos em duplas e pedir a cada uma que pegue um pedaço de barbante, de mais ou menos 1 metro de comprimento, e amarre uma extremidade na perna esquerda de um aluno e a outra extremidade na perna direita do outro aluno da dupla.

Quando todas as duplas estiverem prontas, citar comandos como: para a frente, para trás, para a esquerda e para a direita. Os alunos devem obedecer aos comandos; a dupla que errar a direção fornecida sairá da brincadeira naquele momento. Ganhará a dupla que ficar até o fim.

Repetir a brincadeira quantas vezes for possível ou necessário.

Caso algum aluno não tenha entendido a brincadeira, montar novas duplas, procurando unir aqueles que compreenderam com os que estão com dificuldade. Sem utilizar o barbante, posicioná-los um atrás do outro, em uma fila, colocando o aluno que compreendeu na frente, pedindo ao de trás que coloque a mão direita sobre o ombro direito do aluno da frente. Dar os comandos de forma que os que estão atrás possam identificar o movimento que estão errando e corrigi-lo. Depois que todos compreenderem, pedir às duplas que troquem a posição, para verificar se os alunos que apresentaram dificuldades aprenderam os comandos.

Aula 4

Nesta aula, é proposta a brincadeira Controle sua bolinha no pé. Para isso, providenciar, com antecedência, jornais para fazer duas bolinhas.

Realizar a brincadeira proposta no pátio da escola ou em algum lugar aberto no qual possam ser desenhadas as pistas no chão utilizando giz

No local escolhido, desenhar duas pistas com largura de 30 centímetros cada e indicar "PISTA 1" e "PISTA 2". Cada pista deve ser marcada com um sentido diferente, ou seja, uma pista deve ter o início começando da direita para a esquerda e a outra da esquerda para a

direita. Indicar no chão o início e o fim de cada uma. Depois, formar duas equipes enfileiradas no início de cada pista, conforme a representação a seguir. EDITORIA

Representação de pistas que devem ser desenhadas no chão

Um aluno de cada equipe receberá uma bolinha, e ambos deverão empurrar sua bolinha na ponta do pé direito ou dando pequenos chutes nela, pela pista determinada para a equipe. Assim que o aluno chegar na indicação "FIM", ele deve pegar a bolinha na mão, correr até o próximo da fila da sua equipe e entregar a bolinha para que esse último faça o percurso empurrando ou chutando a bolinha. Cada aluno que chegar deve entregar a bolinha e entrar no final da fila, para que quando chegar sua vez novamente, inicie mais uma rodada, mas dessa vez utilizando o pé esquerdo

O procedimento continuará até que todos os alunos tenham passado pela pista com o pé direito, primeiro, e, depois, com o pé esquerdo Vencerá a equipe que terminar primeiro.

Alertar os alunos de que, cada vez que a bolinha sair da pista, o participante deve voltar ao início. Esse tipo de brincadeira, que utiliza linguagem corporal, desenvolve aspectos da Competência geral 4 da BNCC.

Aula 5

Para ampliar os conceitos desenvolvidos nas aulas anteriores, propor o seguinte jogo.

Em algum espaço amplo, como o pátio ou a quadra, organizar os alunos em trios. Em cada trio, um aluno será o Guia, o outro, o Guiado e o terceiro, o Prêmio. O Guiado ficará de olhos vendados. O Prêmio se posicionará no local desejado. O Guia deve, então, conduzir o

Material disponibilizad o em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Guiado, dando ordens de comando com as posições para a frente, para trás, para a direita, para a esquerda, até encontrar o Prêmio.

Ao final do jogo, fazer uma roda de conversa e pedir para que os alunos relatem o que acharam do jogo, se os comandos ajudaram o colega a chegar no destino, entre outros questionamentos.

Para que os alunos sejam ainda mais estimulados a se familiarizar com as posições, pode ser interessante apresentar o jogo on-lineLabirinto animal. O objetivo é fazer com que o aluno, a partir de um referencial, consiga utilizar de maneira adequada as posições aprendidas para levar o animal até a sua comida. Esse jogo está disponível em: https://clubinho.xalingo.com.br/jogos/labirinto-animal#. Acesso em: 17 dez. 2021.

Aula 6

Para a realização das atividades propostas nas aulas seguintes, preparar massa de modelar caseira. Esse tipo de atividade desenvolve a motricidade e a atenção dos alunos.

Escolher um ambiente mais adequado para esta aula, como a quadra, a cozinha da escola ou a própria sala de aula (considerando os cuidados extras que a atividade exige, como um pano para secar o chão, caso seja necessário, etc.)

Receita de massa de modelar

Ingredientes

1 xícara de sal

4 xícaras de farinha de trigo

1,5 xícara de água

3 colheres (de sopa) de óleo vegetal

Corante alimentício ou pó para suco

Modo de preparo

1 Misturar o sal e a farinha, e depois, aos poucos, a água e o óleo.

2 Se a massa ficar seca, acrescentar mais água; se ficar muito úmida, acrescentar mais farinha.

3 Para dar cor, acrescentar os corantes alimentícios ou o pó para suco. As cores devem ser vermelha, azul clara, verde, amarela, branca, laranja e azul escura.

Dica: A massa vai durar mais tempo se for mantida na geladeira, em recipiente fechado.

Depois de pronta a massa de modelar, reservar na geladeira uma porção dela para ser utilizada nas duas aulas seguintes. A outra parte já pode ser utilizada pelos alunos

Nesta aula, são abordadas a construção de modelos de figuras geométricas espaciais, com massa de modelar, e a relação espacial delas na referência dos próprios alunos – isto é, sua localização em relação a um ponto de referência pessoal.

Para iniciar a aula, projetar para a turma imagens com as representações do cubo, do bloco retangular, da pirâmide, do cone, do cilindro e da esfera e de alguns objetos do dia a dia, como bola, chapéu de festa de aniversário, lata de leite em pó, caixa de sapato, cubo mágico e objetos cujo formato lembram uma pirâmide, como por exemplo, o dado tetraédrico. Na projeção, dispor as representações das figuras e as imagens dos objetos em duas colunas

Em seguida, com a colaboração dos alunos, relacionar os objetos às representações das figuras apresentadas, nomeando cada figura. Se julgar oportuno, levar alguns objetos ou embalagens com formatos que lembram as figuras geométricas espaciais para a sala de aula.

Posteriormente, organizar os alunos em duplas, sentados um ao lado do outro Entregar uma porção de massa de modelar a cada grupo para que moldem os objetos descritos a seguir, de acordo com a cor correspondente. É aconselhável que cada modelo tenha uma cor padronizada, a fim de facilitar a avaliação dos objetos moldados pelos grupos.

EDITORIA DE ARTE

Representação indicando a cor da massa de modelar que deve ser utilizada na construção dos modelos de figuras geométricas espaciais

As figuras espaciais representadas podem ter o tamanho de uma borracha plástica média, para agilizar a construção e permitir a disposição no espaço. Instigar os alunos, a fim de que interajam com seus pares de forma cooperativa, trabalhando coletivamente, de modo que sejam desenvolvidos aspectos da Competência específica 8 da área de Matemática e suas Tecnologias da BNCC.

Depois da modelagem das representações das figuras geométricas espaciais, fornecer as instruções a seguir, preferencialmente uma a uma, para que os alunos possam acompanhá-las:

1. coloquem o modelo do cubo na frente do modelo do cone;

2. o modelo do bloco retangular deve estar à esquerda do modelo do cubo;

3 o modelo do cilindro deve ser colocado à direita do modelo do cubo, com o modelo da pirâmide atrás dele;

4 o modelo da esfera deve estar à frente do modelo do cubo Circular pela sala de aula a fim de identificar se existem dúvidas quanto às orientações.

Se houver dúvida referente à localização dos objetos em relação à posição dos próprios alunos, esclarecer os termos pedidos nas orientações com os objetos construídos por eles.

Do ponto de vista dos alunos sentados lado a lado, o "modelo do cubo à frente do modelo do cone", por exemplo, significa que o modelo do cone, a partir da posição do aluno, deve estar atrás do modelo do cubo, e assim por diante.

Lembrar os alunos que as formas modeladas serão usadas na próxima aula. Por isso, elas devem ser manipuladas e guardadas com cuidado no fim da atividade.

Aula 8

Nesta aula, os alunos vão localizar as figuras geométricas espaciais, que eles moldaram, de acordo com o referencial de outra pessoa – isto é, sua localização vista por outra pessoa (e não pelo próprio aluno); por exemplo, por alguém que esteja perto da lousa ou por alguém que esteja junto à porta.

Manter a configuração anterior da turma, em duplas de alunos sentados lado a lado. Pedir a eles que sigam as instruções dadas pelo professor, uma de cada vez, como na aula anterior

Dizer a eles: imaginem que eu, que estou junto da lousa, quero ver em outra posição as figuras geométricas espaciais que vocês construíram. Então, para que eu veja desse jeito (e não do ponto de vista de vocês):

1. coloquem o modelo do cubo à frente do modelo do cone;

2. agora, quero ver o modelo do bloco retangular à esquerda do modelo do cubo;

3 o modelo do cilindro deve ser colocado à direita do modelo do cubo, com o modelo da pirâmide atrás dele;

4 o modelo da esfera deve ficar à frente do modelo do cubo

Trocar de posição com uma ou duas duplas de alunos, que irão para junto da lousa enquanto o professor toma o lugar deles nas mesas. Notar que, agora, eles estão à frente da turma e pedir que se aproximem um pouco para descrever o que veem na disposição das representações que fizeram. Eles devem comprovar, assim, a mudança de correspondência de posição.

Podem ser feitas várias outras experimentações para que os alunos percebam a relatividade de uma posição espacial, como pedir que um aluno se volte para a mesa do professor, de costas para a turma, e diga qual é a localização da mesa em relação a ele (Espera-se que os alunos respondam que a mesa está na frente do aluno e na frente deles) Agora, se o aluno ficar de costas para a mesa, esta estará localizada atrás dele. Do ponto de vista da turma, porém, a mesa continuará à frente.

Sequência didática 2: Classificações e sequências

Nesta sequência didática, serão trabalhadas as classificações de sequências usando padrões, ou seja, regularidades que serão organizadas por meio de uma característica, como cor, tamanho, forma, medida, entre outras.

Objetivos de aprendizagem

• Identificar e classificar sequências conforme um padrão.

• Compreender, classificar e estabelecer relações de dimensão, como tamanho, e de tempo, como o que vem antes e o que vem depois.

• Discutir relações de direção e de sentido com base em movimentos corporais.

• Organizar e ordenar objetos por meio de atributos, como forma, tamanho, cor, entre outros.

• Acrescentar elementos em sequências ordenadas de acordo com regras preestabelecidas.

Plano de aulas

Aula 1: Reconhecer e elaborar sequências utilizando tampinhas de garrafas.

Aula 2: Realizar movimentos corporais de acordo com uma sequência estabelecida.

Aula 3: Completar sequências com colagens de imagens.

Aula 4: Memorizar e descrever sequências.

Aula 5: Identificar padrões de sequência nas peças do jogo Dominó

Aula 6: Realizar classificações e padronizações de objetos e figuras.

Aula 7: Elaborar uma sequência de cores a partir da rotina do dia a dia.

Aula 8: Criar um padrão de sequência para uma peça de roupa.

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita

Competências gerais da Educação Básica: 4 e 9

Competências específicas de Matemática: 2 e 8

Habilidades: EF01MA09 e EF01MA10.

Materiais necessários: Lápis grafite, lápis de cor, borracha, folha de atividade com imagens de sequências para identificar padrões, cola, tesoura com pontas arredondadas, folha de resposta, jogos de dominó (imagem ou brinquedo), tampinhas coloridas, imagens em papel A4, fita crepe, blocos de montar, representações de figuras geométricas planas, folha de atividades e cartolina.

Aula 1

Iniciar a aula conversando com os alunos sobre o hábito de colecionar objetos ser uma atividade lúdica, bastante antiga. Depois, mostrar, desenhar na lousa ou projetar a imagem descrita a seguir.

"Um menino de 6 anos organizando uma coleção de tampinhas coloridas em cima de uma mesa de acordo com uma sequência em linha reta. Ilustrar uma tampinha vermelha, uma verde, uma azul, uma amarela e uma vermelha. Ilustrar, ao lado dessa sequência, uma caixa cheia de tampinhas coloridas. Inserir o nome ARTUR na imagem como legenda e um balão de pensamento com o seguinte texto: VOU MUDAR ESSA SEQUÊNCIA"

Agora, entregar para os alunos tampinhas das mesmas cores da imagem, para que eles respondam às questões a seguir utilizando as tampinhas

• Como Artur organizou a sequência e como essa sequência deve ser continuada depois da tampinha vermelha? Monte-a em sua carteira.

• Como você ajudaria Artur mudando a sequência dele? Elabore outra sequência em sua carteira.

Organizar os alunos em duplas e pedir para que elaborem sequências de diferentes tipos e que depois troquem de cadeira para o colega da dupla continuar a sequência. Finalizar a aula perguntando quem coleciona objetos (figurinhas, pedrinhas, bonecas, carrinhos, por exemplo). Pedir aos que colecionam para trazer suas coleções na próxima aula, com a autorização dos responsáveis, para mostrar aos colegas.

Aula 2

Organizar a turma em grupos com cinco integrantes e levá-los para a quadra, o pátio, ou outro lugar adequado para realizar a atividade, a qual consiste em: cada grupo fará uma sequência de movimentos usando um padrão e, depois, apresentará aos colegas, para que todos possam realizar a mesma sequência feita pelo grupo. Este tipo de atividade, que utiliza linguagem corporal e visual-motora, colabora com o desenvolvimento da Competência geral 4 da BNCC.

É interessante dar um exemplo de sequência utilizando um padrão, como por exemplo apertar a mão de um aluno qualquer e depois dar um pulo. Depois, seguir a sequência – nesse caso, o padrão dessa sequência é: após um aperto de mão sempre ocorre o pulo, que é seguido por outro aperto de mão, e assim por diante. Apresentar essa e outras sequências aos alunos. Estipular cerca de 15 minutos para a realização das sequências.

Exemplos de sequências:

• Levantar o braço direito e colocar a mão na testa.

• Pular com os dois pés para a frente e levantar o braço esquerdo.

• Girar, bater uma palma e levantar os dois braços.

• Dar um passo para a frente com o pé direito e outro com o pé esquerdo, bater duas palmas e dar um pulo.

As sequências podem ter dois, três ou mais movimentos. Durante a atividade, observar cada grupo e verificar se a proposta está sendo executada corretamente; em caso negativo, realizar a intervenção que julgar adequada.

Depois de cada apresentação, pedir aos alunos que se sentem em roda e propor uma discussão sobre o que foi realizado para que eles reflitam sobre a atividade. Caso algum aluno não tenha entendido a dinâmica, o professor deve fazê-la novamente e, se necessário, trocar os grupos.

Aula 3

Nesta aula, será realizada uma atividade individual. Como sugestão, pode ser mantida a configuração da sala de aula. Entregar para cada aluno a folha de resposta com instruções e uma folha com a imagem de sequências, para que cada um possa recortar e depois colar na folha de resposta.

Por estarem em fase inicial de alfabetização, é importante ler a atividade com os alunos, garantindo que todos entendam a proposta. Após a explicação, estipular um tempo de resolução, que pode ser de 30 minutos. Durante esse período, é interessante circular pela sala de aula para observar o que os alunos estão produzindo e, caso necessário, intervir.

Propor uma discussão sobre as respostas colocadas na ficha, de modo que o aluno amplie a sua perspectiva e reflita sobre o assunto. Como sugestão, podem ser utilizados o modelo de folha de resposta e a folha com a imagem da sequência a seguir.

EDITORIA DE ARTE

Representação de cartela com diferentes figuras para o aluno recortar.

COM BASE NA IMAGEM ANTERIOR, SIGA AS INSTRUÇÕES A SEGUIR.

1. RECORTE E COLE AQUI A PRIMEIRA SEQUÊNCIA. DEPOIS, RECORTE E COLE AS FIGURAS

QUE COMPLETAM A SEQUÊNCIA, SEGUINDO O PADRÃO.

A sequência se completa com as figuras de duas estrelas

2. RECORTE E COLE AQUI A SEGUNDA SEQUÊNCIA. DEPOIS, RECORTE E COLE AS FIGURAS

QUE COMPLETAM A SEQUÊNCIA, SEGUINDO O PADRÃO.

A sequência se completa com as figuras de dois triângulos

3. RECORTE E COLE AQUI A TERCEIRA SEQUÊNCIA. DEPOIS, RECORTE E COLE AS FIGURAS

QUE COMPLETAM A SEQUÊNCIA, SEGUINDO O PADRÃO.

A sequência se completa com as figuras de um hexágono e de um retângulo

4. RECORTE E COLE AQUI A QUARTA SEQUÊNCIA. DEPOIS, RECORTE E COLE AS FIGURAS

QUE COMPLETAM A SEQUÊNCIA, SEGUINDO O PADRÃO.

A sequência se completa com as figuras de um quadrado e de uma esfera

5. RECORTE E COLE AQUI A QUINTA SEQUÊNCIA. DEPOIS, RECORTE E COLE AS FIGURAS

QUE COMPLETAM A SEQUÊNCIA, SEGUINDO O PADRÃO.

A sequência se completa com as figuras de um pentágono e uma estrela

Se alguns alunos apresentarem dúvida após a atividade, é importante retomar o conteúdo e propor uma nova atividade, semelhante à anterior, para complementar o processo de ensino-aprendizagem. Realizar a nova atividade formando duplas compostas de alunos que entenderam o objetivo e de alunos que estão com dificuldade. Por estarem em fase de alfabetização inicial, é importante ler a atividade com os alunos, garantindo que todos entendam a proposta. Segue como sugestão um modelo de atividade complementar.

ATIVIDADE COMPLEMENTAR

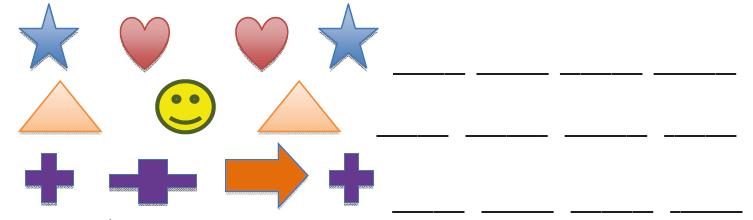
COMPLETE AS SEQUÊNCIAS COM DESENHOS SEGUINDO O PADRÃO.

EDITORIA DE ARTE

Material disponibilizad o em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Representação de sequências formadas por diferentes figuras

Primeira sequência: coração, coração, estrela, coração

Segunda sequência: carinha sorridente, triângulo, carinha sorridente, triângulo

Terceira sequência: cruz larga, seta, cruz estreita, cruz larga

Aula 4

Nesta aula, além dos alunos reconhecerem padrões de uma sequência, terão a oportunidade de estimular a memória.

Preparar, com antecedência, impressões em tamanho A3 ou A4 de algumas imagens como, por exemplo, uma flor, um foguete, um urso, um trem, uma nuvem, um laço de fita, um abacaxi, entre outras.

Com fita crepe, fixar três imagens quaisquer na lousa, uma ao lado da outra e deixar por aproximadamente 10 segundos para que os alunos as memorizem. Em seguida, retirar os cartazes e perguntar qual é a ordem das imagens e quais delas foram mostradas. Deixar que respondam em voz alta.

Esse tipo de dinâmica colabora com o desenvolvimento do raciocínio lógico e do espírito de investigação, que é abordado na Competência específica 2 de Matemática e suas Tecnologias da BNCC.

Repita esse processo por mais 3 ou 4 vezes, aumentando a dificuldade. Se for conveniente, inserir mais uma figura em cada sequência ou deixar um tempo mais curto para eles memorizarem.

Se verificar que nem todos os alunos estão participando com as respostas em voz alta, pedir para desenharem a sequência no caderno assim que forem retiradas as imagens da lousa. Dessa maneira, é possível acompanhar e verificar se os alunos estão acertando e participando.

Caso a escola tenha uma sala de informática, levar os alunos até ela e acessar o site disponível em: https://rachacuca.com.br/jogos/jogo-da-memoria/ (acesso em: 17 dez 2021), para que eles brinquem, individualmente, com um jogo parecido com o proposto nesta aula.

Aula 5

Para ampliar as habilidades desenvolvidas nas aulas anteriores, propor a seguinte atividade: organizar a sala em grupos com quatro integrantes e entregar um jogo de dominó para cada quarteto.

Em seguida, pedir a cada grupo que identifique o padrão da sequência do dominó e que registre no caderno. Esse registro pode ser feito por meio de desenhos, como representado a seguir

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4. 0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Durante o desenvolvimento da atividade, circular pela sala de aula, a fim de verificar se os alunos estão conseguindo entender o padrão.

No final, explicar as regras do jogo e deixar que brinquem algumas partidas.

Aula 6

Nesta aula, os alunos poderão perceber tipos de organização e realizar classificações. Para isso, sugere-se, nesse momento, projetar imagens ou distribuir cópias de imagens que mostrem espaços e coleções de itens organizados de diversas maneiras, como por cor, por tipo, por tamanho, entre outros. Por exemplo, lápis organizados de acordo com a cor ou roupas organizadas pelo tipo de peça Caso isso não seja possível, desenhar na lousa conjuntos de figuras simples, organizadas de diferentes maneiras, conforme representado a seguir.

Representação de peças do dominó

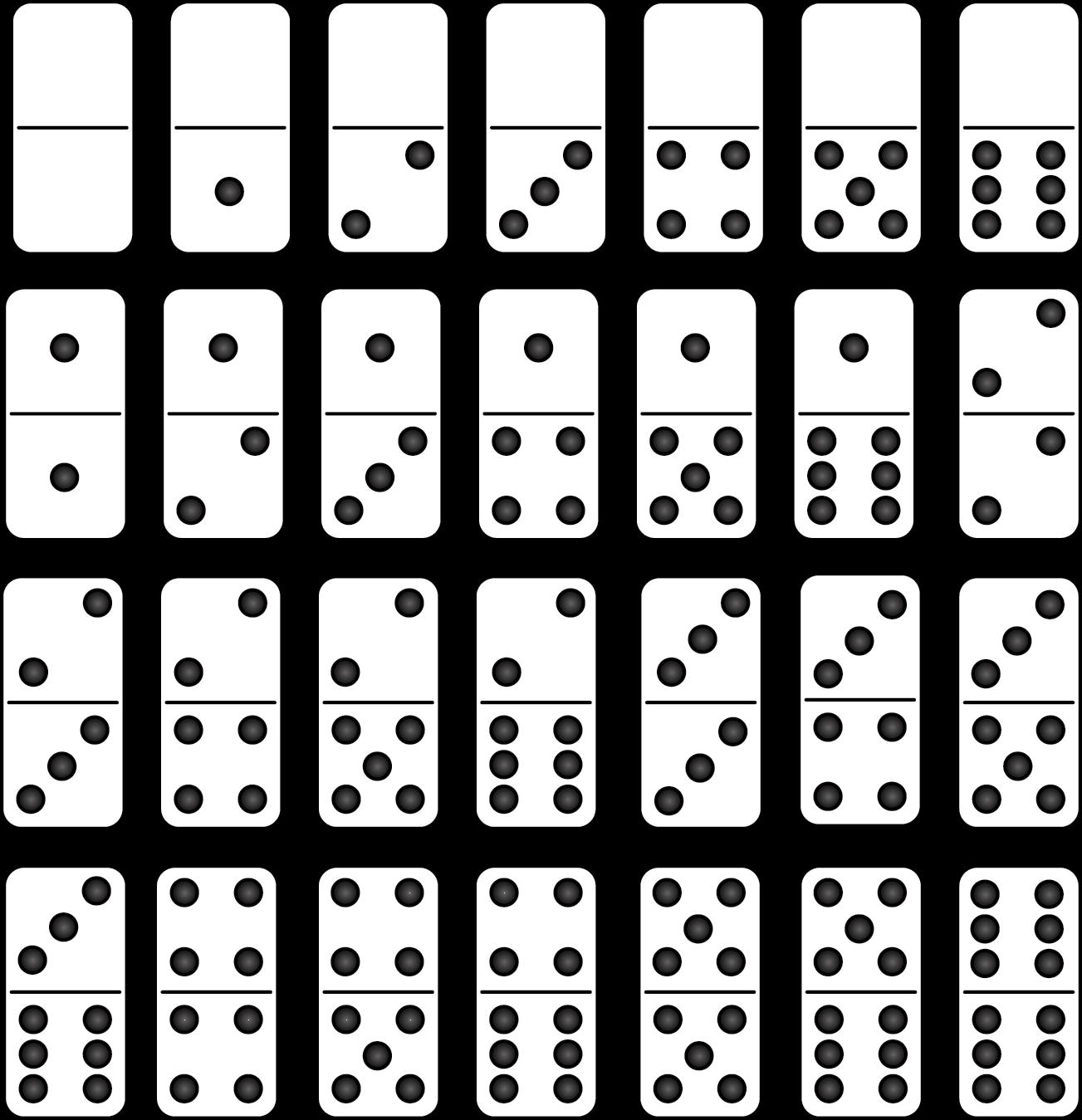
Representação de círculos em diferentes cores EDITORIA

Representação de corações em diferentes tamanhos.

Depois de os alunos interagirem dizendo quais os possíveis critérios utilizados para classificar os objetos dessas imagens, pedir para que formem duplas e que tirem os materiais do estojo. Em seguida, pedir que organizem esses materiais seguindo algum critério.

Circular pela sala de aula, perguntando às duplas quais os critérios que eles utilizaram. Se possível, providenciar blocos de montar coloridos e distribuir uma certa quantidade de peças para as duplas. A intenção é que eles organizem essas peças por cor, por tamanho ou por outro critério de livre escolha.

Outra ideia é levar imagens de figuras geométricas planas (como retângulos, triângulos e quadrados de diferentes tamanhos e cores) e pedir que organizem de alguma maneira. Depois de organizado, perguntar como eles classificaram as figuras e deixar que troquem as experiências.

Aula 7

Iniciar a aula conversando com os alunos sobre a rotina diária deles. Perguntar o que eles fazem de manhã, de tarde, de noite, se tomam banho antes do café da manhã, em que momento fazem as tarefas etc.

Projetar na lousa imagens de situações do dia a dia de uma mesma criança tomando banho, chegando à escola, escovando os dentes, tomando café da manhã, estudando, brincando, acordando, entre outras. As imagens devem estar identificadas com letras. Pedir

Material disponibilizado em licença aberta do tipo Creative Commons

aos alunos que transcrevam, no caderno, as letras das imagens, na ordem em que acontece a rotina diária deles.

Depois de resolver esta atividade, organizar os alunos em duplas para que conversem como é a sua rotina no domingo. Pedir para a dupla fazer um desenho que represente seu sentimento por esse dia da semana

Aula 8

Propor a seguinte atividade aos alunos, lendo e explicando como eles devem proceder

1. MARA E SEUS IRMÃOS PEDRO, GABRIELA E ARTUR GANHARAM ROUPAS NOVAS.

• O VESTIDO DE MARA É ESTAMPADO COM UMA SEQUÊNCIA DE CORAÇÕES.

• A BERMUDA DE PEDRO É ESTAMPADA COM UMA SEQUÊNCIA DE BICICLETAS.

• O VESTIDO DE GABRIELA É ESTAMPADO COM UMA SEQUÊNCIA DE BOLINHAS COLORIDAS.

• A BERMUDA DE ARTUR É ESTAMPADA COM UMA SEQUÊNCIA DE DESENHOS DE DINOSSAUROS.

2. AGORA É A SUA VEZ CRIE UM PADRÃO PARA O TECIDO DE UMA ROUPA NOVA.

Entregar uma cartolina para cada aluno desenhar.

Utilizar as imagens elaboradas por eles para expor na escola, fora da sala de aula.

Sendo assim, no início da atividade, informar que é interessante eles desenharem a peça de roupa, além do padrão que será estampado. Além disso, estimular os alunos a capricharem nos desenhos. Pode-se pedir que se lembrem das estampas de tecidos que preferem, não para fazer igual, mas para se inspirar nelas.

Sequência didática 3: Figuras geométricas espaciais e figuras geométricas planas

Nesta sequência didática, serão abordadas as figuras geométricas espaciais a partir de objetos do cotidiano dos alunos, isto é, eles desenvolverão a habilidade de relacionar tais figuras a imagens de elementos conhecidos.

Serão abordadas, também, as figuras geométricas planas e algumas noções de posição, direção e sentido.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Objetivos de aprendizagem

• Correlacionar objetos do dia a dia a figuras geométricas espaciais.

• Manipular e construir representações de figuras geométricas espaciais.

• Identificar características de figuras geométricas planas.

• Localizar objetos e pessoas no espaço, utilizando diversos pontos de referência e vocabulário apropriado.

Plano de aulas

Aula 1: Explorar a noção de localização na sala de aula.

Aula 2: Descrever a localização de pessoas ou de objetos e realizar trajetos em sala de aula e em atividades.

Aula 3: Relacionar figuras geométricas espaciais a objetos familiares do mundo físico, por meio de atividade de recorte de revistas e/ou de panfletos de lojas

Aula 4: Identificar e nomear figuras geométricas espaciais por meio de atividades com palitos.

Aula 5: Reconhecer figuras geométricas espaciais por meio de ilustração de cenário e criar cenário com objetos que lembram figuras geométricas espaciais

Aula 6: Reconhecer figuras geométricas planas a partir de ilustrações e participar da utilização das mesmas figuras, criando novas ilustrações.

Aula 7: Reconhecer figuras planas e não planas por meio de representações impressas.

Aula 8: Desenvolver a noção de localização e reconhecer figuras geométricas planas por meio de atividade lúdica.

Componentes essenciais para a alfabetização: Produção de escrita e compreensão de textos

Competências gerais da Educação Básica: 2, 4 e 7.

Competências específicas de Matemática: 2, 3 e 6.

Habilidades: EF01MA11, EF01MA12, EF01MA13 e EF01MA14.

Materiais necessários: Lápis, borracha, palitos de churrasco sem pontas, massa de modelar, folhas de atividades, revistas e panfletos de supermercados e de lojas de brinquedo, tesoura com pontas arredondadas e fita adesiva

Aula 1

Nesta aula, será desenvolvida a exploração do espaço pelos alunos a partir de seu próprio corpo. Para isso, serão utilizadas instruções de direção para localizar objetos. Eles descobrirão como é importante ter pontos de referência para indicação ou para a localização de pessoas ou de objetos.

A primeira atividade será chamada de "Quem está". Ela será realizada em grupos de nove alunos, que deverão posicionar-se em suas carteiras formando três fileiras e três linhas lado a lado, conforme o esquema representativo a seguir.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Representações de vista superior de sala de aula

Confeccionar fichas com os nomes dos alunos, que podem ser escritos em uma folha de papel sulfite A4 cortada em pedaços menores. Essas fichas deverão estar separadas conforme os grupos. Será necessário, também, confeccionar um conjunto de fichas para cada grupo (com as localizações: à direita, à esquerda, na frente e atrás).

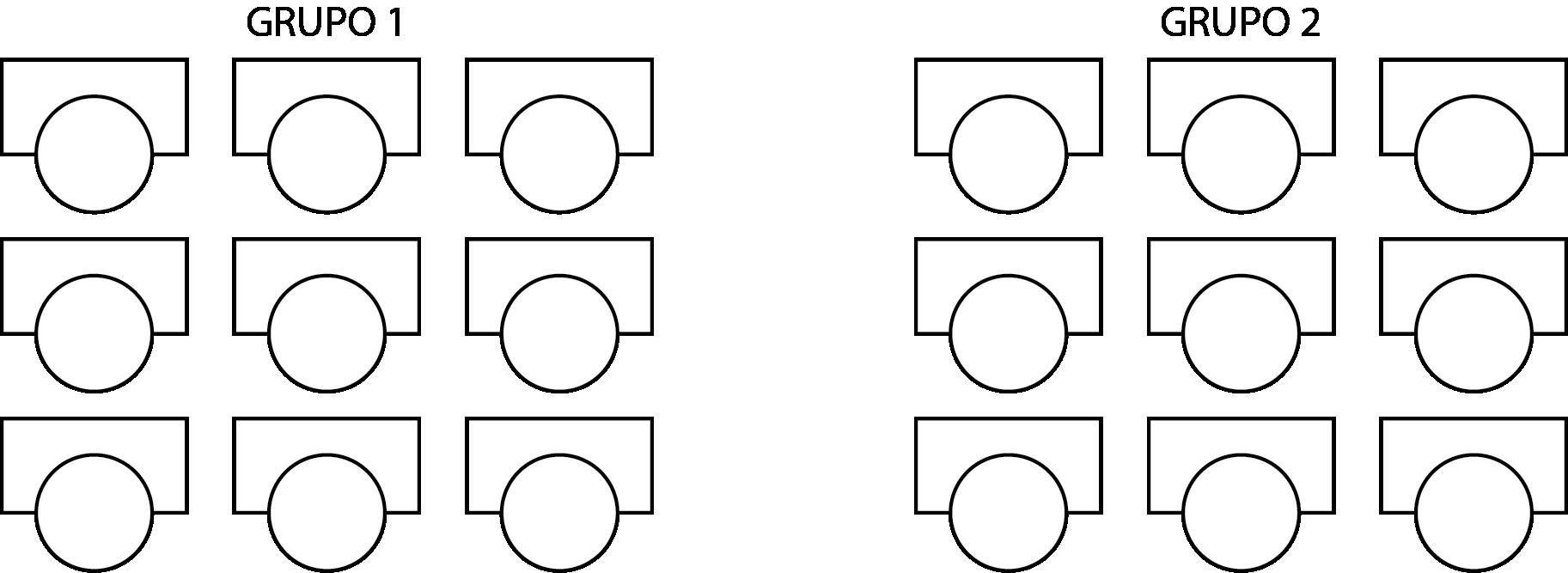
Assim que a organização for feita, um aluno sorteia um nome e uma localização. Por exemplo, Paulo sorteou "Fernanda" e a ficha "à direita". Paulo deverá perguntar à Fernanda: Fernanda, quem está à sua direita? Ela deverá responder: à minha direita está o Mário. Agora, Mário deverá fazer um novo sorteio excluindo a ficha com o nome de Fernanda. O jogo termina quando todos os alunos tiverem respondido uma pergunta, ou seja, quando as fichas de nomes acabarem O jogo pode ser reiniciado para que eles respondam mais perguntas.

Terminada a atividade, o professor pode questionar os alunos sobre as dificuldades encontradas como, por exemplo, o caso de não ter alguém na posição indicada e qual solução eles encontraram para resolver isso. O sorteio de outra posição pode ser a solução mais frequente para a dificuldade.

A segunda atividade será feita coletivamente, sendo que os alunos podem permanecer nos grupos já formados. O professor deverá pedir que os alunos guardem seus pertences e que deixem somente um objeto embaixo da mesa ou em cima dela.

Nesta atividade, o professor escolherá o aluno sem dizer o nome, somente dizendo entre quais alunos ele está. Por exemplo, "o aluno que está entre Paulo e Fernanda deverá dizer a posição do objeto", e João deverá dizer "coloquei meu estojo em cima da mesa"

A atividade deve ser feita até que todos os alunos respondam pelo menos uma vez. E, caso seja necessário, um aluno pode ser questionado mais de uma vez.

Aula 2

Nesta aula, os alunos realizarão trajetos pela escola e utilizarão o conhecimento adquirido sobre direita e esquerda. Para isso, pode ser utilizada a área da quadra com a colaboração do professor de Educação Física

Se for utilizar somente a área da sala de aula, será necessário organizar as carteiras para que fiquem alinhadas. E com isso, é possível realizar orientações para que alguns alunos as sigam, como, por exemplo:

• entre nas fileiras entre Paulo e Amanda;

• ande por duas carteiras e vire à esquerda;

• ande por duas carteiras e vire à direita;

• ande por uma carteira e vire à esquerda;

• ande por duas carteiras e responda: quem é o aluno ao seu lado direito?

Essas situações podem ser criadas no momento da aula ou previamente definidas e lidas para os alunos.

Posteriormente, organizar os alunos em duplas para realizar as atividades a seguir.

1. SIGA AS INSTRUÇÕES DAS SETAS E DESENHE O CAMINHO DO PONTO A AO PONTO B

2. SIGA AS INSTRUÇÕES DAS SETAS E DESCUBRA QUAL É A CASA DE RUI.

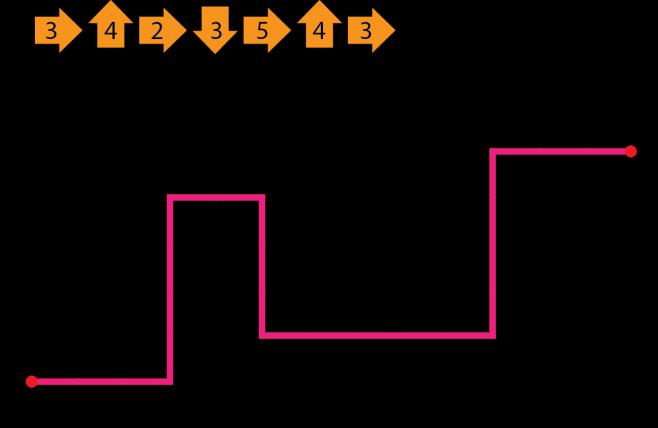
Depois do tempo previsto, uma dupla se reúne com outra dupla, para que uma verifique o trabalho da outra e cheque se os caminhos foram traçados corretamente.

Aula 3

Providenciar, antecipadamente, revistas diversas e panfletos de lojas como supermercados e lojas de brinquedos, para que os alunos possam realizar a atividade.

Lembrar os alunos de que os objetos que vemos e usamos todos os dias se parecem de algum modo com figuras geométricas tridimensionais (ou 3D, termo mais próximo do linguajar deles), cada uma com um nome especial, que eles podem já conhecer. Na própria sala de aula deve haver, para mostrar a eles, objetos comuns parecidos com figuras geométricas espaciais. A caixa de giz, por exemplo, costuma lembrar um bloco retangular.

Em seguida, desenhar na lousa as figuras geométricas espaciais que eles podem já conhecer: cubo, cilindro, esfera, pirâmide, bloco retangular e cone. Escrever os nomes ao lado de cada figura desenhada. Dividir a turma em duplas para realizar a atividade.

Explicar que o objetivo da atividade é selecionar e recortar, de revistas e de panfletos de lojas, a representação de objetos que lembrem figuras geométricas espaciais. Após a seleção e recorte, os alunos devem colar em uma folha avulsa, uma abaixo da outra, as figuras selecionadas, compará-las com os desenhos da lousa e nomear cada uma delas Estipular um tempo para a realização da atividade (20 minutos, por exemplo)

Pedir, então, à turma, que deem outros exemplos de objetos do cotidiano que lembrem figuras geométricas espaciais. Fazer os seguintes questionamentos orais: quais outros objetos do seu dia a dia se parecem com um cilindro? E com um cubo? E com uma esfera? E com um bloco retangular? E com uma pirâmide? É necessário que todos os alunos da turma tenham a oportunidade de expressar-se e sanar eventuais dúvidas ou equívocos.

Para finalizar a aula, explicar que as figuras geométricas espaciais podem ser divididas em dois grupos: o grupo das que possuem a superfície ou parte dela arredondada e o grupo daquelas que não possuem parte arredondada na superfície. Peça a eles que, oralmente, olhem para as figuras desenhadas na lousa e digam quais delas se encaixam em um ou outro grupo. Espera-se que eles respondam que o cilindro, o cone e a esfera se

encaixam no grupo das que tem superfície arredondada e que o cubo, o bloco retangular e a pirâmide pertencem ao grupo das que não possuem superfície arredondada.

Aula 4

Dividir a turma em grupos de quatro alunos. Propor a construção da representação de três figuras: um bloco retangular, um cubo e uma pirâmide, conforme referência a seguir.

Representação de estruturas que lembram figuras geométricas espaciais

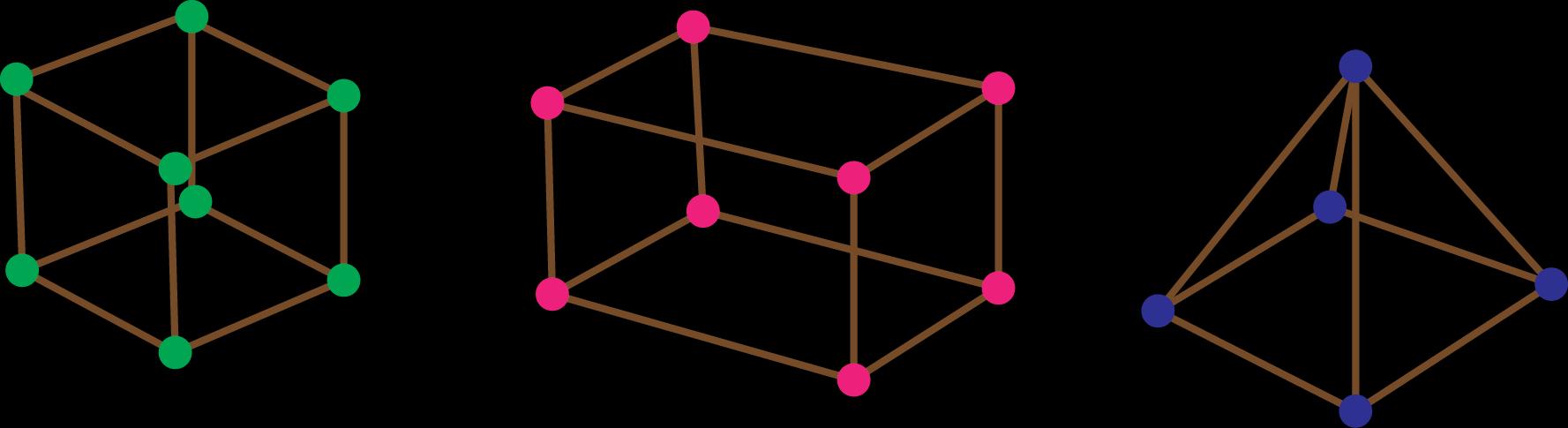
Entregar para cada grupo:

• 12 palitos de churrasco previamente cortados ao meio para construir a representação do cubo;

• 4 palitos inteiros e 8 palitos cortados ao meio para construir a representação do bloco retangular;

• 8 palitos cortados ao meio para construir a representação da pirâmide;

• massa de modelar para unir os palitos.

Conversar com os alunos sobre quais figuras geométricas espaciais eles representarão. Construir antecipadamente uma dessas figuras e mostrá-la aos alunos, para que vejam como devem realizar a construção.

Comentar que a modelagem fica mais ágil fazendo primeiro as bolinhas com a massa de modelar e, depois, construindo as partes com os palitos. Pedir a eles que planejem a atividade de montagem, ou seja, que desenhem as figuras geométricas propostas e decidam quantos palitos grandes e pequenos terão de usar em cada figura e quantas bolinhas de massa de modelar precisarão fazer para unir os palitos.

Após a explicação, estipular um tempo de resolução, que pode ser de 40 minutos. Durante a atividade, circular pela sala de aula para auxiliar na montagem, se necessário.

Quando terminarem as construções, entregar aos grupos uma folha de atividades, para que respondam perguntas relacionadas às figuras representadas. Como os alunos estão em fase de alfabetização, deve-se ler a atividade para eles, a fim de que todos

entendam a proposta. É melhor ler uma das questões a seguir, esperar que a resolvam, depois ler a outra, e assim sucessivamente.

1. NA CONSTRUÇÃO DA REPRESENTAÇÃO DO CUBO:

• QUANTOS PALITOS IGUAIS FORAM USADOS?

• QUANTAS BOLINHAS DE MASSA DE MODELAR FORAM USADAS?

12 palitos iguais e 8 bolinhas de massa de modelar.

2. NA CONSTRUÇÃO DA REPRESENTAÇÃO DO BLOCO RETANGULAR:

• QUANTOS PALITOS FORAM USADOS? QUANTOS SÃO GRANDES E QUANTOS SÃO PEQUENOS?

• QUANTAS BOLINHAS DE MASSA DE MODELAR FORAM USADAS?

4 palitos grandes, 8 palitos pequenos e 8 bolinhas de massa de modelar.

3. NA CONSTRUÇÃO DA REPRESENTAÇÃO DA PIRÂMIDE:

• QUANTOS PALITOS FORAM USADOS? TODOS TÊM O MESMO TAMANHO?

• QUANTAS BOLINHAS DE MASSA DE MODELAR FORAM USADAS?

8 palitos do mesmo tamanho e 5 bolinhas de massa de modelar.

4. QUE DIFERENÇA VOCÊ PERCEBEU ENTRE A CONSTRUÇÃO DAS REPRESENTAÇÕES DE FIGURAS DO CUBO E DO BLOCO RETANGULAR?

Espera-se que os alunos respondam que na figura do cubo todos os palitos são iguais, mas para construir a figura do bloco retangular é necessário palitos de tamanhos diferentes.

Aula 5

Nesta aula, os alunos trabalharão no reconhecimento de figuras geométricas espaciais por meio de representações de objetos. Para isso, imprimir previamente a folha de atividade a seguir e entregá-la a cada aluno – ou duplas, se preferir – para que identifiquem figuras geométricas espaciais parecidas com os objetos familiares presentes na ilustração de um quarto de dormir.

1. OBSERVE A FIGURA A SEGUIR

A) MARQUE UM X NOS OBJETOS QUE NÃO LEMBRAM AS FIGURAS GEOMÉTRICAS ESPACIAIS QUE VOCÊ ESTUDOU.

B) ESCREVA O NOME DAS FIGURAS ESPACIAIS COM AS QUAIS SE PARECEM OS OBJETOS QUE NÃO FORAM MARCADOS.

Representação de quarto infantil com personagens

Espera-se que os alunos marquem um X nas bandeirinhas, no relógio, no travesseiro, nos dinossauros, no tapete, no violão, no aspirador e que reconheçam que:

• a bola lembra uma esfera;

• os blocos coloridos lembram cubos;

• os livros, a mesa de cabeceira e o colchão lembram blocos retangulares

É mais difícil, porém, que os alunos abstraiam e reconheçam a cabeceira e o pé da cama como blocos retangulares.

A correção dessa atividade pode ser feita coletivamente, de forma que alguns alunos participem e compartilhem as figuras que identificaram.

2. AGORA, JUNTE-SE A UM COLEGA E CRIEM UMA CENA BEM BONITA, EM UMA FOLHA AVULSA, DE UMA FESTA DE ANIVERSÁRIO COM OBJETOS QUE LEMBREM AS FIGURAS

GEOMÉTRICAS ESPACIAIS QUE VOCÊS CONHECEM

Durante a realização da atividade 2, circular pela sala de aula e auxiliar os alunos que estiverem com dificuldade. Se necessário, lembrá-los de que os chapéus de aniversário se parecem com cones, os copos lembram cilindros, o bolo lembra um bloco retangular ou um cilindro (dependendo do formato), as caixas de presente em geral lembram blocos retangulares etc. Se julgar conveniente, expor os desenhos no mural da sala de aula

Aula 6

Nesta aula, os alunos reconhecerão figuras geométricas planas nas imagens ilustradas e, logo após, participarão da criação de um desenho que contenha essas mesmas figuras.

Reproduzir os desenhos a seguir, em uma folha avulsa, para que os alunos os pintem de acordo com a legenda.

1. PINTE OS DESENHOS A SEGUIR, FEITOS COM REPRESENTAÇÕES DE FIGURAS GEOMÉTRICAS PLANAS. SIGA AS CORES INDICADAS NA LEGENDA.

EDITORIA DE ARTE

Boneco e foguete formados com representações de figuras geométricas planas

2. AGORA, CRIE UM DESENHO, NO CADERNO, APENAS COM REPRESENTAÇÕES DAS SEGUINTES FIGURAS GEOMÉTRICAS PLANAS: RETÂNGULOS, QUADRADOS, CÍRCULOS E TRIÂNGULOS. ESCOLHA AS MESMAS CORES PARA PINTAR AS FORMAS PARECIDAS.

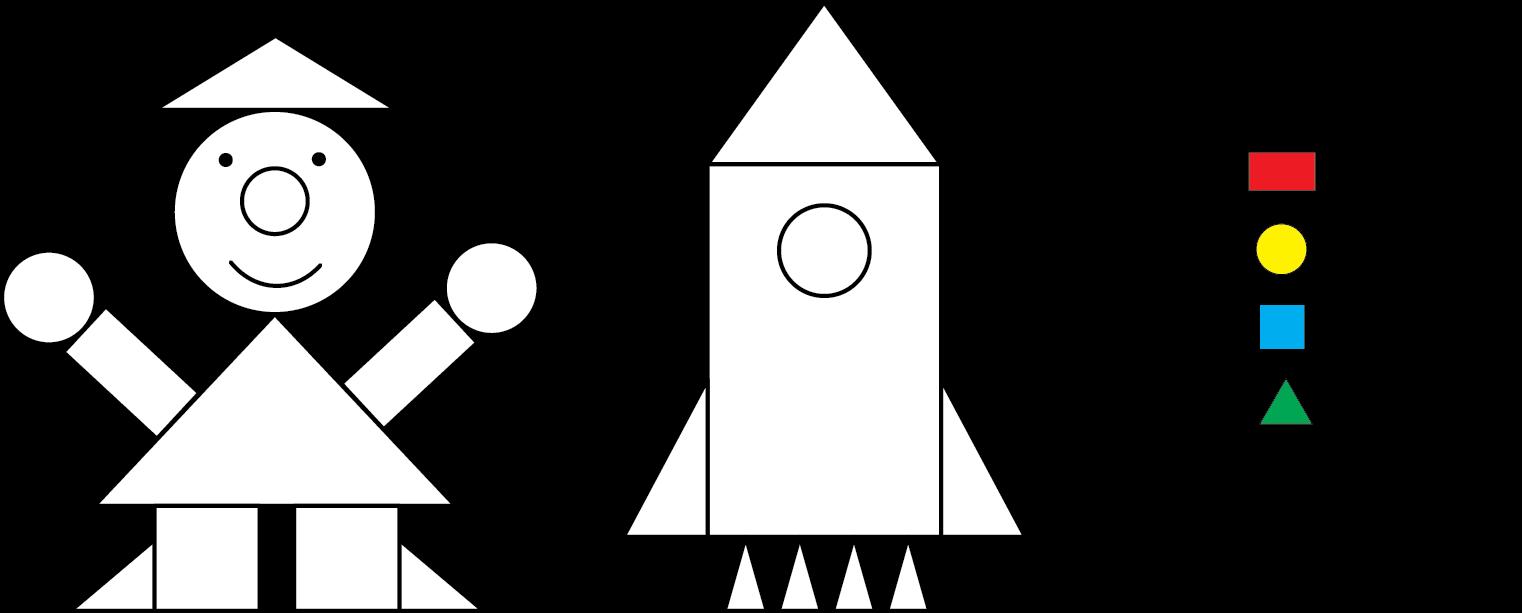
Conversar com os alunos sobre as ideias que eles tiveram para o desenho e solicitar que sejam desenhos diferentes da primeira atividade. Se necessário, fazer sugestões desafiadoras, como desenhar vários objetos de um cenário, como casa com árvores e animais, oceano e animais marinhos, ou céu com pássaros e montanhas ao fundo.

A correção da atividade pode ser feita pelos próprios alunos ao trocarem entre si os cadernos

Aula 7

Nestas atividades, os alunos trabalharão no reconhecimento de figuras geométricas planas e não planas por meio de ilustrações. Estas atividades requerem certa abstração para alunos dos Anos Iniciais do Ensino Fundamental na visualização das figuras não planas. Circular pela sala de aula e auxiliar os alunos, caso haja necessidade.

Entregar uma folha de atividade com imagens para cada aluno, que deverá recordar cada uma delas.

1. MOSTRE QUE VOCÊ SABE A DIFERENÇA ENTRE FIGURAS PLANAS E FIGURAS NÃO PLANAS. PARA ISSO, CONTORNE DE AZUL AS FIGURAS PLANAS E DE VERMELHO AS FIGURAS NÃO PLANAS.

2. AGORA, ESCOLHA DUAS FIGURAS NÃO PLANAS DA ATIVIDADE 1 E DESENHE AS FIGURAS PLANAS QUE FORMAM OS LADOS DAS FIGURAS NÃO PLANAS.

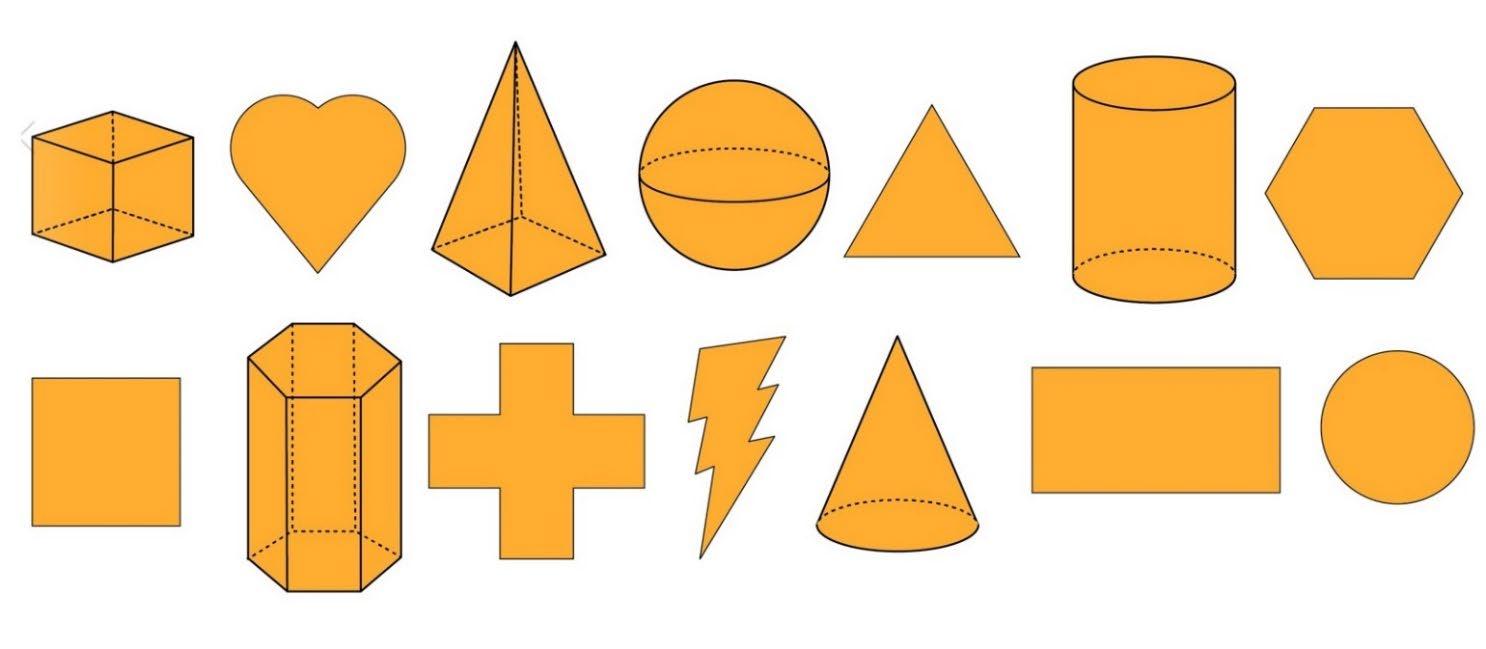
É importante, após os alunos terem feitos as atividades, discutir os principais erros. Caso haja formas planas ou não planas identificadas erroneamente, buscar entender a dificuldade nessa identificação e esclarecer as dúvidas.

Caso seja necessário, retomar a ideia de analogia das figuras não planas com objetos do dia a dia e a semelhança das figuras planas com sombras projetadas, por exemplo.

Aula 8

Nesta aula, são propostas atividades de localização utilizando figuras geométricas planas. Para isso, cada aluno terá um papel a desempenhar de acordo com um sorteio.

1. FAÇA UM X NA ALTERNATIVA CORRETA. EDITORIA DE ARTE

Representações de figuras geométricas planas com carinhas.

( ) SOU VERMELHO E ESTOU ACIMA DO MEU AMIGO AZUL.

( ) SOU AMARELO E ESTOU AO LADO DO MEU AMIGO VERDE

( ) SOU AZUL E ESTOU AO LADO DO MEU AMIGO AMARELO.

( ) SOU VERDE E ESTOU EMBAIXO DO MEU AMIGO AZUL.

Espera-se que os alunos assinalem a terceira alternativa.

2. MOSTRE QUE VOCÊ SABE O NOME DAS QUATRO FIGURAS REPRESENTADAS ANTERIORMENTE. PARA ISSO, LIGUE AS DUAS COLUNAS CORRETAMENTE.

FIGURA VERMELHA TRIÂNGULO

FIGURA AMARELA CÍRCULO

FIGURA VERDE RETÂNGULO

FIGURA AZUL QUADRADO

Retângulo – figura vermelha; triângulo – figura amarela; círculo – figura verde; quadrado – figura azul.

Após a resolução, organizar grupos com quatro alunos para criar verbalmente uma atividade de localização semelhante às atividades 1 e 2 referentes às figuras geométricas planas. É importante o professor deixar claro que as falas a serem criadas na atividade devem se referir à localização de cada um no espaço do grupo e da sala de aula, além de outras que o grupo quiser criar.

Cada aluno escolherá ou sorteará seu personagem, passando a ter o nome daquela figura: retângulo, círculo, triângulo e quadrado. Para isso, os alunos devem desenhar, pintar e recortar a figura que o representa, colando-a (com fita adesiva) em sua roupa posteriormente. Depois, cada grupo deve se posicionar na frente da sala de aula e se manter alinhado, como no desenho da atividade 1, virados de frente para a turma, para relatar seu nome e sua posição no grupo.

Dar um exemplo de como pode ser o começo da apresentação: cada grupo, na sua vez, se apresenta igualmente, explicando para os colegas: "somos quatro amigos. Temos cores e nomes diferentes" A partir daí, seguir com a criação do grupo. Por exemplo, o retângulo diz: "eu sou o retângulo vermelho. Do meu lado esquerdo, está meu amigo círculo verde". O círculo verde diz: " eu sou o círculo verde e do meu lado esquerdo não tem alguém" Nesse momento, fazer a intervenção: "não tem amigo do seu lado esquerdo, mas tem um colega que está atrás". O importante é que o aluno diga a localização de um colega e identifique a forma geométrica a qual este está representando

A atividade, então, deve se repetir até que todos tenham se apresentado e participado. Como mediador, identificar se os alunos estão utilizando as indicações de localizações corretamente Assim que for identificado algum erro, trabalhar e explorar essa dificuldade, a

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

fim de que compreendam as localizações. Caso haja necessidade, determinado aluno pode falar mais de uma localização de amigos.

Sugestões

• ALCY. Tô dentro, tô fora... São Paulo: Formato, 2005.

Sequência didática 4: Contar e adicionar números de 0 a 10

Esta sequência didática aborda rotinas de contagem, utilizando os números naturais como indicador de quantidade em diferentes situações. Além disso, será abordada a construção de sentenças da adição e o cálculo da adição usando materiais manipuláveis e diferentes estratégias.

Objetivos de aprendizagem

• Identificar e registrar os números naturais de 1 a 10.

• Contar quantidades de objetos de 1 a 10.

• Identificar quantidade de objetos em diferentes coleções.

• Estimar, contar e comparar quantidades de objetos em uma coleção.

• Contar e adicionar quantidades de objetos e de pessoas

• Construir sentenças de adição.

Plano de aulas

Aula 1: Contar e reconhecer números naturais de 1 a 10 por meio da criação de material de apoio de contagem

Aula 2: Contar quantidades de objetos em coleções

Aula 3: Resolver atividades envolvendo contagem e registro de quantidades.

Aula 4: Estimar, contar e comparar quantidade de objetos em uma coleção

Aula 5: Realizar contagem, escrever sentenças de adição e realizar o cálculo da adição com apoio de material manipulável.

Aula 6: Realizar cálculo de adição por meio de uma atividade lúdica com massa de modelar.

Aula 7: Escrever sentença da adição e realizar cálculo da adição com o apoio de material manipulável

Aula 8: Escrever sentenças de adição e realizar o cálculo da adição com o apoio de figuras.

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita.

Competências gerais da Educação Básica: 2, 4 e 8.

Competências específicas de Matemática: 2, 4, 6 e 8.

Habilidades: EF01MA01, EF01MA02, EF01MA03, EF01MA06 e EF01MA08

Materiais necessários: Papel-cartão, papel crepom de cores diferentes, palito de sorvete, lápis de cor, giz de lousa, giz de cera, massa de modelar, tampinhas de garrafa PET, caneta hidrográfica, cola, tesoura com pontas arredondadas, caixa de papelão e caixa de ovos vazia.

Aula 1

Nesta aula, os alunos vão construir um material de apoio de contagem, para organizar quantidades de 1 a 10 palitos. Para isso, sugere-se separar antecipadamente folhas de papel-cartão cortadas em quatro pedaços (quantidade suficiente para que cada aluno receba um pedaço), folha de papel crepom cortada em pedaços de sete por sete centímetros (quantidade suficiente para que cada aluno receba dez pedaços), cola e palitos de sorvete.

Se julgar oportuno, construir previamente um modelo do material de apoio de contagem ilustrado a seguir ou desenhá-lo na lousa e mostrá-lo aos alunos, para que observem como devem construir esse material de apoio e realizar a colagem do papel crepom

Em seguida, organizar a turma em duplas para confeccionar o material de apoio de contagem. Se julgar oportuno, antes de iniciar a atividade, estabelecer combinados para que todos possam aproveitar ao máximo essa situação de aprendizagem, sem distrações. Os

Representação de modelo de material de apoio para contagem

combinados são regras previamente estabelecidas e acordadas entre professor e alunos para garantir o bom andamento de uma atividade.

Após os alunos finalizarem a confecção do material de apoio, pedir que, utilizando uma caneta hidrográfica, escrevam em cada quadro de papel crepom os números de 1 até 10. Se julgar oportuno, faça um exemplo na lousa ou escreva os números no material de apoio confeccionado previamente. EDITORIA

Estipular um tempo de 15 minutos para os alunos confeccionarem o material de apoio para contagem. Durante esse período, sugere-se circular pela sala de aula para observar se há algum aluno com dúvidas no preparo do material de apoio de contagem e, se necessário, intervir auxiliando em alguma dificuldade.

Após a confecção do material de apoio para contagem, entregar palitos de sorvete para cada dupla e pedir que coloquem a quantidade de palitos adequada em cada quadro. Por exemplo, no quadro 1, colocar um palito; no quadro 2, colocar dois palitos; e assim sucessivamente. Durante a realização da atividade, auxiliar os alunos que tiverem mais dificuldade

Para ampliar o trabalho com contagem, sugere-se propor aos alunos que contem quantos objetos têm em sua mochila. Eles podem desenhar o objeto em seu caderno e escrever, ao lado, a quantidade de palitos de sorvete referente à quantidade de objetos. Por exemplo, um aluno pode desenhar um estojo, um caderno e dois lápis, e ao lado desenhar quatro palitos.

Representação de modelo de material de apoio para contagem numerado.

Aula 2

Para esta aula, sugere-se providenciar antecipadamente tampinhas de garrafa PET, botões, lápis de cor, entre outros objetos. Para iniciar, organizar duas mesas em um lugar da sala de aula que seja visível para todos os alunos e dispor os objetos na mesa, variando a quantidade de 1 a 10 unidades.

Em seguida, reproduzir na lousa o quadro a seguir para que os alunos copiem no caderno e o completem no decorrer da atividade. Pedir a cada aluno que pegue seu material de apoio de contagem

NOME DO OBJETO ESCOLHIDO PELO PROFESSOR E QUANTIDADE

NOME QUANTIDADE

Após todos os alunos copiarem o quadro, mostrar à turma uma quantidade de objetos e pedir que façam a contagem deles, juntos, em voz alta. Depois, propor a eles que completem o quadro com o nome do objeto e a quantidade. Os alunos podem utilizar o material de apoio de contagem ou outro material manipulável para auxiliá-los na contagem. Estipular um tempo para o desenvolvimento da atividade (por exemplo, 20 minutos) para os alunos realizarem a contagem e preencherem o quadro. Após essa dinâmica, sugere-se propor uma discussão sobre o que foi trabalhado na aula para que os alunos reflitam sobre a contagem de objetos e a representação numérica deles. Para isso, questioná-los sobre objetos diferentes, mas que estavam em mesma quantidade, para que percebam que a representação do número só está relacionada à quantidade e não à natureza do objeto em si.

Outro questionamento que pode ser feito é sobre as vantagens de se representar uma quantidade por um símbolo ou por palitos, a fim de que os alunos reconheçam a facilidade em relação ao uso dos números na representação de quantidades e na contagem. É possível que, nesse momento, eles prefiram a representação por palitos (correspondência um a um).

Caso alguns alunos apresentem dificuldade durante a atividade, é importante retomar o conteúdo e citar novos exemplos para que eles possam superar suas dúvidas.

Se julgar oportuno, para ampliar, levar os alunos ao laboratório de informática da escola e propor a realização do jogo Eu sei contar, disponível em: https://www.escolagames.com.br/jogos/euSeiContar/ (acesso em: 13 mar. 2023), que possibilita a contagem de 1 a 10.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

A primeira parte do jogo consiste em 5 fases de contar figuras. Como não existe tempo limite, o aluno pode contar tranquilamente, clicar no número correspondente à quantidade e em confirmar. A segunda parte consiste em controlar um personagem por meio das setas do teclado e, ao longo do caminho, coletar estrelas. Conforme os alunos conseguem coletá-las, poderão ouvir e fazer a contagem junto com o personagem.

Aula 3

Nesta aula, sugere-se organizar os alunos em duplas e disponibilizar um conjunto de fichas com números de 1 a 10 para cada dupla. Essas fichas podem ser produzidas com cartolina. Cada aluno deve sortear uma ficha e escolher um objeto para ser desenhado naquela quantidade, sem que o outro aluno da dupla veja.

Após desenhado, ele deve pedir para o colega contar e dizer a quantidade; durante a atividade os alunos podem inverter os papéis com outros colegas Se julgar necessário, para exemplificar, sortear um número e desenhar na lousa algo que indique qual foi a quantidade sorteada

A atividade terminará assim que as fichas acabarem, ou seja, quando cada aluno tiver desenhado 5 grupos de objetos. Se julgar oportuno, acompanhar os alunos durante a atividade, observando os cadernos para identificar possíveis dificuldades. Estas podem ser trabalhadas e complementadas ao final da atividade.

Aproveitar o momento para verificar se os alunos possuem dificuldade na contagem até 10; se for na contagem, pedir que contem novamente, ou se for no conhecimento do símbolo correto, fazer com que comparem com o símbolo utilizado por outro aluno, ou por cartazes com números, caso tenha na sala de aula.

Para finalizar, propor aos alunos a realização das atividades a seguir Elas podem ser escritas na lousa para os alunos copiarem ou entregue à turma em uma folha avulsa. É importante realizar a leitura da atividade e pedir aos alunos que a acompanhem, assegurando que todos entendam a proposta, pois nessa faixa etária eles estão em fase de alfabetização.

1. CONTE A QUANTIDADE DE FIGURAS A SEGUIR E ESCREVA O NÚMERO QUE INDICA ESSA QUANTIDADE.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

2 CONTE AS FIGURAS E COMPLETE O QUADRO

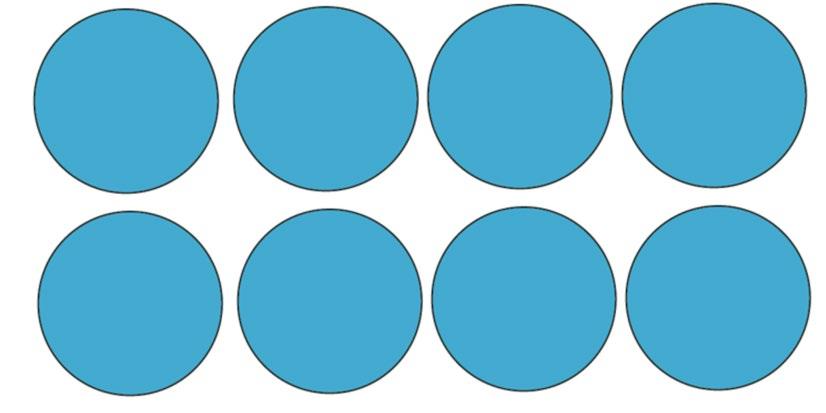
3. DESENHE A QUANTIDADE DE FIGURAS INDICADAS EM CADA ITEM:

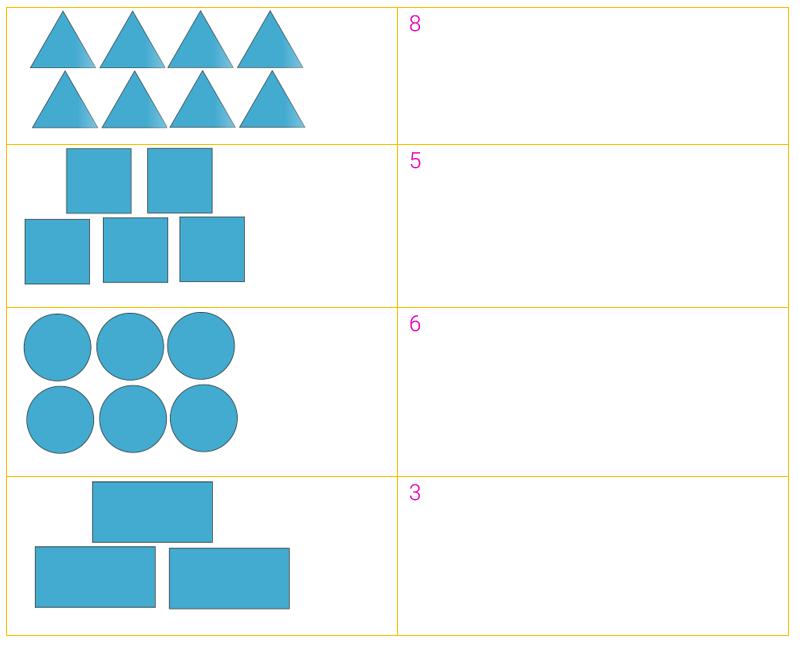
a) 8 QUADRADOS

b) 5 CÍRCULOS

c) 2 RETÂNGULOS

d) 10 TRIÂNGULOS

Resposta:

Material disponibilizado em licença aberta do tipo Creative Commons

Se julgar oportuno, antes de os alunos responderem a atividade 3, desenhar as figuras (quadrado, círculo, retângulo e triângulo) na lousa. Ao final, propor a eles que compartilhem com os colegas suas respostas e as comparem Nesse momento, um aluno que compreendeu o conteúdo pode auxiliar o colega que tem dúvidas, favorecendo a cooperação entre eles.

Aula 4

Nesta aula, os alunos vão estimar, contar e comparar quantidade de objetos em uma coleção. Para isso, se possível, providenciar antecipadamente palitos de sorvete ou outro material manipulável.

Para iniciar a aula, organizar os alunos em grupos de três integrantes e entregar a cada grupo 10 palitos de sorvete. Solicitar aos grupos que estimem a quantidade de palitos que receberam, sem realizar a contagem. Anotar na lousa as quantidades estimadas pelos alunos e, depois, propor que cada aluno conte os palitos, comparando a quantidade estimada com o valor encontrado.

Em seguida, propor aos alunos que separem os palitos de sorvete em dois grupos, um com 6 palitos e outro com 4 palitos e perguntar a eles: qual grupo tem mais palitos? Qual grupo tem menos palitos? Qual estratégia vocês utilizaram para comparar essas quantidades? Espera-se que os alunos respondam que o grupo com 6 palitos tem mais palitos e o grupo com 4 palitos tem menos palitos Verificar se, ao realizar a comparação, os alunos utilizam como estratégia a correspondência um a um; se julgar oportuno, explorar com a turma a comparação utilizando os números.

Para ampliar, sugere-se propor novos agrupamentos para que os alunos exercitem a contagem e comparem novas quantidades. Uma sugestão é propor que formem dois grupos com 5 palitos para explorar agrupamentos com a mesma quantidade.

Aula 5

Nesta aula, os alunos vão realizar uma atividade na qual será trabalhada a construção de fatos básicos da adição. Para isso, organizar os alunos em grupos de 8 a 10 integrantes.

Em seguida, explicar que a atividade será realizada ao ar livre (no pátio, na quadra ou em outro lugar da escola que seja adequado) e que durante a atividade cada grupo se dividirá em dois subgrupos menores, cuja quantidade de alunos o próprio grupo pode escolher.

Explicar que esses subgrupos vão representar as parcelas de uma adição

Após separados os subgrupos, os outros grupos devem observar a quantidade de integrantes de cada subgrupo e realizar a adição da quantidade de alunos nos dois subgrupos, registrando em uma folha avulsa a operação que realizou e a estratégia que utilizou para chegar no resultado.

Se julgar necessário, antes de iniciar a atividade, para elucidá-la, dividir um grupo em dois subgrupos, um com dois alunos e outro com quatro alunos e, em seguida, registrar a adição que representa a quantidade total de alunos desses dois subgrupos.

Deixar à disposição dos grupos materiais manipuláveis que auxiliem na representação dos subgrupos ou na adição, como material dourado, tampinhas, palitos, entre outros. Estabelecer um tempo para a realização de cada etapa da brincadeira, conforme o número de grupos formados.

Em seguida, levar a turma ao local escolhido. Pedir a cada grupo que escolha a quantidade de alunos dos dois subgrupos que representam as parcelas da adição Depois, o outro grupo deve determinar a soma da quantidade de alunos dos dois subgrupos, que no exemplo anterior é 6.

Sugere-se realizar, por exemplo, cinco rodadas, número relativamente baixo, o que agiliza a atividade e facilita na soma da pontuação final de cada grupo, que será feita na sala de aula. Em cada rodada, anotar os pontos dos grupos vencedores que fizeram a adição corretamente

Após finalizar a atividade, sugere-se voltar com os alunos para a sala de aula para debater a experiência e para que eles reflitam sobre o que aprenderam. Pedir aos grupos que:

• digam qual foi cada uma das adições que realizaram e quais foram os resultados;

• compartilhem qual estratégia usaram para chegar à soma;

• expliquem se tiveram mais dificuldade nas adições com um número específico, o que pode levar à conclusão de que um ou outro aluno ainda não consegue fazer a contagem corretamente.

Durante a conversa, fazer perguntas aos alunos que possam esclarecer quais foram as estratégias adotadas por eles e quais os eventuais erros obtidos nas adições, de modo que possam ser avaliadas as dificuldades e a evolução, esclarecendo possíveis dúvidas

Se julgar oportuno, para auxiliá-los com possíveis dúvidas, realizar a adição com material manipulável, mesmo que já tenha sido usado na mesma operação pelo aluno, pois a repetição pode ajudá-lo a perceber a solução do problema.

Aula 6

Nesta aula, os alunos vão realizar uma atividade para consolidar os conhecimentos sobre a operação de adição e realizar cálculos de adição por meio de uma atividade lúdica

Para esta atividade, sugere-se providenciar antecipadamente massa de modelar nas cores amarela, vermelha, verde e azul.

Para iniciar a aula, organizar a turma em duplas e disponibilizar a massa de modelar nas cores indicadas. Explicar aos alunos que eles vão representar objetos – bolinhas, cobrinhas, discos, dentre outros, utilizando as massas de modelar.

Em seguida, comentar com a turma que o objetivo da atividade é adicionar a quantidade de objetos criados por eles com as massas de modelar. Ressaltar que a diferença de cor dos objetos serve para agrupá-los e representar as parcelas da adição

Após a explicação, sugere-se escrever a atividade a seguir na lousa para os alunos copiarem ou entregar à turma em uma folha avulsa

FAÇA COM AS MASSAS DE MODELAR 7 OBJETOS AMARELOS, 5 OBJETOS VERMELHOS, 5 OBJETOS VERDES E 3 OBJETOS AZUIS. DEPOIS, ADICIONE AS QUANTIDADES DE OBJETOS DE ACORDO COM O QUE É INDICADO EM CADA ITEM:

• 5 OBJETOS VERMELHOS MAIS 4 OBJETOS AMARELOS. ______

• 1 OBJETO VERDE MAIS 3 OBJETOS AZUIS. ______

• 6 OBJETOS AMARELOS MAIS 2 OBJETOS VERDES. ______

• 5 OBJETOS VERDES MAIS 2 OBJETOS AZUIS. ______

• 3 OBJETOS AZUIS MAIS 7 OBJETOS AMARELOS. ______

9 objetos (5 + 4 = 9)

4 objetos (1 + 3 = 4)

8 objetos (6 + 2 = 8)

7 objetos (5 + 2 = 7)

10 objetos (3 + 7 = 10)

Após todos os alunos compreenderem a atividade, estipular um tempo para a realização dela, por exemplo, 40 minutos. Durante esse período, sugere-se circular pela sala de aula para acompanhar e observar o que os alunos estão produzindo e, se necessário, auxiliá-los com alguma dificuldade ou dúvida.

É importante verificar se todas as duplas produziram os objetos na quantidade e na cor prevista e orientá-las na produção dos objetos que eventualmente faltem.

Aula 7

Nesta aula, os alunos vão realizar atividades que os auxiliarão a sanar possíveis dúvidas nos conteúdos explorados até o momento Para isso, sugere-se providenciar antecipadamente tampinhas de garrafa PET de diferentes cores e caixas de sapato.

Em seguida, reproduzir na lousa o quadro a seguir para que os alunos o copiem no caderno ou em uma folha avulsa. Explicar à turma que serão mostradas tampinhas de diferentes cores e que os alunos devem completar o quadro indicando a quantidade de cada cor da tampinha que representa cada parcela da adição, escrever a sentença da adição e a soma, conforme exemplo apresentado.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Vermelho: 2 Azul: 3 2 + 3 = 5

Esta atividade possibilita aos alunos exercitar a escrita. Se julgar oportuno, escrever o nome das cores utilizadas na lousa, para que eles as copiem.

Para uma segunda atividade de reforço, sugere-se utilizar tampinhas de garrafa PET de diferentes cores e caixas de sapatos. Em duplas, cada aluno deve colocar uma quantidade de até cinco tampinhas dentro da caixa. Cada vez que colocarem determinada quantidade, eles devem registrá-la como uma parcela da sentença da adição; e, após os dois alunos terem colocado as tampinhas, devem realizar a soma das quantidades depositadas. Por fim, eles devem contar as tampinhas que ficaram na caixa para que confiram a resposta.

Se julgar oportuno, realizar de quatro a seis rodadas desta atividade. Após a utilização do material, sugere-se organizar uma roda de conversa e explicar para os alunos a importância de descartar corretamente materiais como plástico e papelão e sobre os impactos do descarte incorreto de alguns materiais para o meio ambiente. Essa discussão contribui para a formação de cidadãos que tomam decisões com base em princípios sustentáveis.

Aula 8

Nesta aula, os alunos vão realizar uma atividade lúdica para explorar a ideia de acrescentar da adição e escrever sentenças; e realizar o cálculo da adição com o apoio de figuras. Para isso, sugere-se providenciar antecipadamente caixas de ovos com espaço para dez unidades e massa de modelar.

Para iniciar a aula, pedir a cada dupla que modele dez ovos utilizando massa de modelar. Em seguida, escolher uma quantidade de ovos, por exemplo, seis, e propor aos alunos que coloquem essa quantidade de ovos na caixa; perguntar quantos ovos faltam para completar a caixa. Espera-se que eles respondam que faltam 4 ovos. Fazer essa mesma pergunta utilizando diferentes quantidades de 1 a 10. Dessa forma, é possível trabalhar com os alunos a ideia de acrescentar da adição.

Em seguida, sugere-se escrever a atividade a seguir na lousa para que os alunos a copiem ou entregar as atividades em uma folha avulsa

1. EM CADA ITEM, ADICIONE AS QUANTIDADES DE OVOS E DESENHE A QUANTIDADE TOTAL. DEPOIS, ESCREVA UMA SENTENÇA PARA REPRESENTAR A ADIÇÃO FEITA.

a)

EDITORIA DE ARTE

Imagens de ovos

3 + 3 = 6

b)

EDITORIA DE ARTE

Imagens de ovos

3 + 4 = 7

c)

EDITORIA DE ARTE

Imagens de ovos.

5 + 3 = 8

Após os alunos resolverem a atividade, pedir a eles que troquem a folha de atividade com as respostas com a de um colega para que um corrija a atividade do outro, mas sem apagar o que o colega respondeu; pedir que façam anotações na própria folha avulsa daquilo que consideraram incorreto O livro indicado na seção Sugestões aborda o processo de adição e subtração de números por meio do nascimento e da partida dos animais da floresta.

Sugestões

• NA, Eun Hee. Os filhotes do vovô coruja São Paulo: Callis, 1ª edição, 2010

Sequência didática 5: Números até 100

Nesta sequência didática, são abordados os números naturais até 100, explorando unidades e dezenas por meio de diferentes atividades lúdicas, assim como a comparação e o valor posicional deles Além disso, há atividades que possibilitam aos alunos reconhecerem e relacionarem valores de moedas e cédulas do Sistema Monetário Brasileiro.

Objetivos de aprendizagem

• Identificar unidade e dezena.

• Contar e reconhecer os números naturais até 100.

• Comparar números de até duas ordens.

• Reconhecer o valor posicional dos algarismos de números até a ordem das dezenas.

• Reconhecer e comparar cédulas e moedas do Sistema Monetário Brasileiro

Plano de aulas

Aula 1: Reconhecer e representar quantidades por meio do material dourado e do Quadro de ordens

Aula 2: Contar quantidades, relacionar e comparar cédulas e moedas do Sistema Monetário

Brasileiro em situações de compra e venda

Aula 3: Representar números utilizando material dourado e realizar a contagem de objetos em coleções, indicando a quantidade por meio de unidades e dezenas

Aulas 4 e 5: Compreender o valor posicional dos algarismos na ordem das unidades e das dezenas por meio de uma atividade lúdica

Aula 6: Explorar situações relacionadas ao valor posicional com o auxílio de pratos e de feijões.

Aula 7: Contar quantidades por meio de uma situação de compra e venda com troco e comparar cédulas do Sistema Monetário Brasileiro.

Aula 8: Reconhecer, comparar e compor quantias até 100 reais com cédulas do Sistema Monetário Brasileiro

Componentes essenciais para a alfabetização: Produção de escrita e compreensão de textos

Competências gerais da Educação Básica: 2, 4 e 7.

Competências específicas de Matemática: 2, 4 e 6.

Habilidades: EF01MA04 e EF01MA05.

Materiais necessários: Material dourado, feijões, prato descartável, caneta hidrográfica, embalagens recicláveis, frutas e legumes de brinquedo, representações de cédulas e moedas do Real, cartolina, tampinhas de garrafa PET, cola, tesoura de pontas arredondadas, revistas e panfletos de produtos.

Material disponibilizado em licença aberta do tipo Creative Commons

Aula 1

Nesta aula, os alunos vão representar números naturais e estabelecer uma relação entre uma quantidade e o número que a simboliza. Para isso, verificar se a escola dispõe de material dourado e se a quantidade é suficiente para trabalhar com todos os alunos. Caso a escola não o tenha disponível, pode-se produzi-lo com EVA. Ver na seção Sugestões o link para um vídeo que contém um passo a passo para fazer material dourado utilizando EVA. Organizar a turma em duplas e entregar a cada dupla um material dourado. Em seguida, pedir aos alunos que manuseiem esse material para que se familiarizem com ele. Escrever na lousa que cada cubinho corresponde a 1 unidade e orientá-los a verificar que uma barra corresponde a 10 cubinhos, ou 1 dezena. Para isso, propor que coloquem lado a lado quantidades equivalentes, por exemplo, 10 cubinhos e 1 barra.

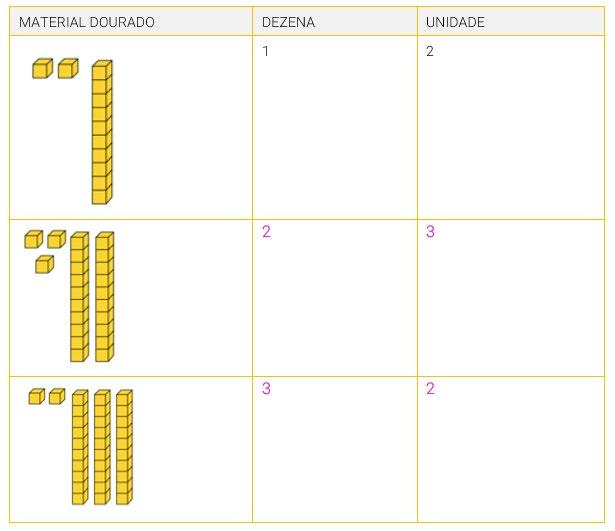
Se julgar oportuno, verificar se os alunos compreenderam a atividade, perguntando: para representar o número 2, qual peça deve ser utilizada? E para representar o número 10? Após realizar esses questionamentos, sugere-se escrever alguns números na lousa. Pedir aos alunos, então, que os representem com o material dourado e registrem essa representação no caderno, por meio de desenhos.

Em seguida, sugere-se reproduzir o quadro a seguir na lousa e pedir aos alunos que o copiem em uma folha avulsa, para depois completar as colunas da UNIDADE e da DEZENA.

EDITORIA DE ARTE

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribu ído crédito autoral e as criações sejam licenciadas sob os mesmos

Após explicar a atividade aos alunos, determinar um tempo para que a realizem. É importante acompanhá-los nesse momento para verificar se conseguem reconhecer e representar números naturais com o material dourado; se necessário, fazer intervenções de modo a auxiliá-los com as dúvidas. Para possibilitar um trabalho colaborativo, propor aos alunos que compreenderam a atividade anterior que ajudem os colegas com dificuldades

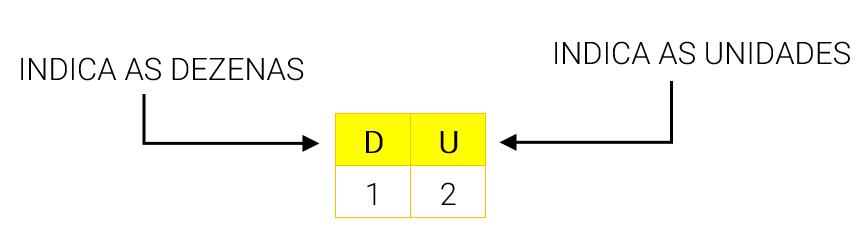
Se julgar oportuno, comentar com a turma outra maneira de representar os números, que é utilizando um Quadro de ordens, e escrever o exemplo a seguir na lousa.

Para finalizar, propor aos alunos que, no caderno, representem os números 23, 32, 46 e 69 utilizando um Quadro de ordens.

Aula 2

Nesta aula, os alunos vão realizar contagem, além de relacionar e comparar cédulas e moedas do Sistema Monetário Brasileiro em situações de compra e venda Para isso, sugere-se providenciar antecipadamente embalagens de diferentes produtos para que sejam vendidas pelos alunos Os produtos devem ter valores inferiores a 10 reais. Se possível, providenciar, também, representações de cédulas e moedas do Real

Inicialmente, organizar a turma em três grupos, os "vendedores", os "compradores" e os "banqueiros". Todos devem participar da confecção dos materiais, recortar as cédulas e os objetos dos folhetos e criar a identificação dos locais (mercados e bancos). Para isso, após organizar os grupos, distribuir as tarefas entre os alunos e ajudá-los, caso necessário.

EDITORIA DE ARTE

Auxiliar os alunos a definirem valores inteiros, em real, que possam ser trabalhados na venda. A intenção é que eles consigam realizar as compras sem precisar de troco. Se necessário, os "compradores" podem trocar cédulas de valores maiores no banco.

Uma vez preparados, os "compradores" devem ficar com cédulas de 2 reais e moedas de 1 real. Em um primeiro momento, devem fazer as compras nos mercados e depois os "vendedores" devem trocar, no banco, o dinheiro que receberam com as vendas por cédulas de 10 e 100 reais.

O professor deve ajudar os alunos a realizarem a atividade de forma organizada, estabelecer combinados para que não haja distrações e interrupções e para que no decorrer da atividade todos observem as situações criadas.

Os papéis devem ser trocados três vezes, de forma que todos os alunos façam parte de cada grupo. Durante a atividade, observar se tanto as vendas quanto as trocas de cédulas e moedas do Real estão sendo feitas corretamente.

Ao final, propor aos alunos que façam a atividade a seguir. Para isso, reproduzir o enunciado na lousa e pedir que o copiem no caderno. Disponibilizar as cédulas e as moedas para auxiliá-los a responder a atividade.

DESENHE COMBINAÇÕES DE CÉDULAS E MOEDAS QUE TENHAM VALOR EQUIVALENTE A UMA CÉDULA DE

10 REAIS.

Sugestões de resposta: 5 cédulas de 2 reais; 1 cédula de 5 reais e 5 moedas de 1 real; 2 cédulas de 2 reais, 1 cédula de 5 reais e 1 moeda de 1 real.

Após os alunos concluírem a atividade, propor que compartilhem com a turma os desenhos que fizeram das diferentes combinações. Nesse momento, pode-se realizar uma correção coletiva e esclarecer possíveis dúvidas.

Aula 3

Nesta aula, os alunos vão representar números utilizando material dourado e realizar a contagem de objetos em coleções representando-as por meio das unidades e das dezenas. Para isso, providenciar antecipadamente tampinhas de garrafa PET.

Inicialmente, organizar a turma em duplas e propor a seguinte atividade: um aluno da dupla deve representar um número natural com as peças do material dourado, e o outro deve escrever o número representado pelo colega com algarismos e indicar quantas unidades e dezenas formam esse número Depois, inverter os papéis para que ambos os alunos representem o número com material dourado e com algarismo.

Em seguida, propor às duplas que analisem quantas barras e quantos cubinhos foram utilizados para representar os algarismos dos números. Nesse momento, os alunos vão efetuar informalmente a adição de números (composição). Ao final da atividade, é importante que todos compreendam que, na escrita numérica, cada algarismo tem seu valor de acordo com a ordem que ocupa.

Em seguida, dispor na mesa coleções de tampinhas de garrafa PET com até 100 unidades e convidar alguns alunos para realizarem a contagem dos objetos das coleções e representarem essa quantidade no Quadro de ordens. Para finalizar, imprimir a atividade a seguir e entregá-la aos alunos ou reproduzi-la na lousa para que eles a copiem no caderno

CONTE AS FIGURAS DE CADA COLEÇÃO A SEGUIR E ESCREVA QUANTAS DEZENAS

E QUANTAS UNIDADES APARECEM EM CADA UMA

A)

EDITORIA DE ARTE

Representação de corações.

1 dezena e 5 unidades.

B)

EDITORIA DE ARTE

Representação de círculos.

2 dezenas e 8 unidades.

C)

EDITORIA DE ARTE

Representação de cruz.

3 dezenas e 2 unidades.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Como os alunos estão em fase inicial de alfabetização, é importante ler a atividade com eles e verificar se compreenderam o enunciado. Estipular um tempo de resolução e, durante esse período, caminhar pela sala de aula para observar se estão respondendo corretamente e auxiliá-los esclarecendo possíveis dúvidas Ao final, propor à turma uma discussão sobre o assunto, para que reflitam sobre o que aprenderam.

Aulas 4 e 5

Nestas aulas, os alunos vão compreender o valor posicional dos algarismos na ordem das unidades e das dezenas por meio de uma atividade lúdica. Para isso, sugere-se providenciar com antecedência pratos descartáveis e feijões.

Inicialmente, organizar a turma em duplas e disponibilizar para cada dupla um prato descartável e uma porção de grãos de feijão. Se julgar oportuno, estabelecer combinados com a turma para assegurar o bom andamento da atividade.

Em seguida, pedir aos alunos que tracem uma linha reta no meio do prato descartável e escrevam a letra D no lado esquerdo; e a letra U, no lado direito. Explicar que D significa "dezena" e U significa "unidade" Reproduzir o desenho a seguir na lousa para que eles visualizem o que deve ser feito.

Neste jogo, cada aluno vai pegar de 1 a 10 feijões e jogá-los no prato de maneira aleatória, observando quantos feijões caem na parte da dezena e quantos caem na parte da unidade. Em seguida, em uma folha avulsa, cada aluno deve anotar quantos feijões jogou, desenhar a representação do prato com os feijões e escrever o número formado, conforme exemplo a seguir Reproduzir o quadro a seguir na lousa para que os alunos o copiem e explicar a eles que, no exemplo apresentado, foram lançados sete feijões: dois caíram na dezena e 5 na unidade, formando o número 25.

Em um segundo momento, reproduzir na lousa o quadro a seguir e propor aos alunos que o copiem em uma folha avulsa Orientá-los a desenhar em cada linha da coluna da direita um prato igual ao utilizado anteriormente e preencher a dezena e a unidade com um algarismo de 0 a 9 cada. Depois, orientá-los a colocar um número de 1 a 99 na coluna da esquerda, mas somente nas linhas em que os pratos não foram preenchidos. Para exemplificar, reproduzir o quadro a seguir na lousa. Ressaltar para os alunos que este quadro é um exemplo e que eles devem elaborar seus quadros utilizando outros números.

EDITORIA DE ARTE

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribu ído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ao finalizarem a atividade, pedir que troquem a folha com o colega de dupla e propor que cada aluno realize a seguinte atividade na folha da sua dupla: nas linhas em que há número na coluna da esquerda, eles devem escrever nos pratos o algarismo referente à dezena e à unidade. Nas linhas em que os pratos estão preenchidos, devem colocar na coluna da esquerda o número formado.

Depois de preencherem o quadro, os alunos devem trocar novamente as folhas com o colega de dupla para que um corrija a resposta do outro

Após explicar esse procedimento aos alunos, definir um tempo para a realização da atividade. Entre uma etapa e outra, circular pela sala de aula e observar se todos executam corretamente a atividade. Em seguida, discutir com a turma sobre a importância do valor posicional de um número, levantando questionamentos e elucidando eventuais dúvidas.

Se alguns alunos apresentarem dificuldade para realizar a atividade, é importante retomar o conteúdo e citar novos exemplos. Se julgar oportuno, para finalizar, ditar números para a turma e pedir que registrem no caderno as unidades e as dezenas utilizando o modelo do prato.

Aula 6

Para ampliar o trabalho desenvolvido nas aulas anteriores, organizar a turma em duplas e propor a realização de uma atividade lúdica para explorar o valor posicional dos números e a sua ordenação

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribu ído crédito autoral e as criações sejam licenciadas

Para isso, entregar a cada grupo um prato descartável e grãos de feijão Pedir aos alunos que tracem uma linha reta no meio do prato e escrevam a letra D no lado esquerdo e a letra U no lado direito, como feito nas aulas anteriores (se os pratos e os feijões tiverem sido guardados, pode-se reutilizá-los). Perguntar a eles o que significa a letra D e a letra U Espera-se que respondam que significam dezenas e unidades, respectivamente.

Explicar aos alunos que, nesta atividade, um integrante da dupla vai ditar cinco números e o outro vai indicar a quantidade de dezenas e unidades do número ditado colocando no prato a quantidade de feijões que representam cada algarismo do número proposto pelo colega. Pedir a eles que escrevam os números ditados pelo colega no caderno Cada aluno deve ditar um número pelo menos uma vez.

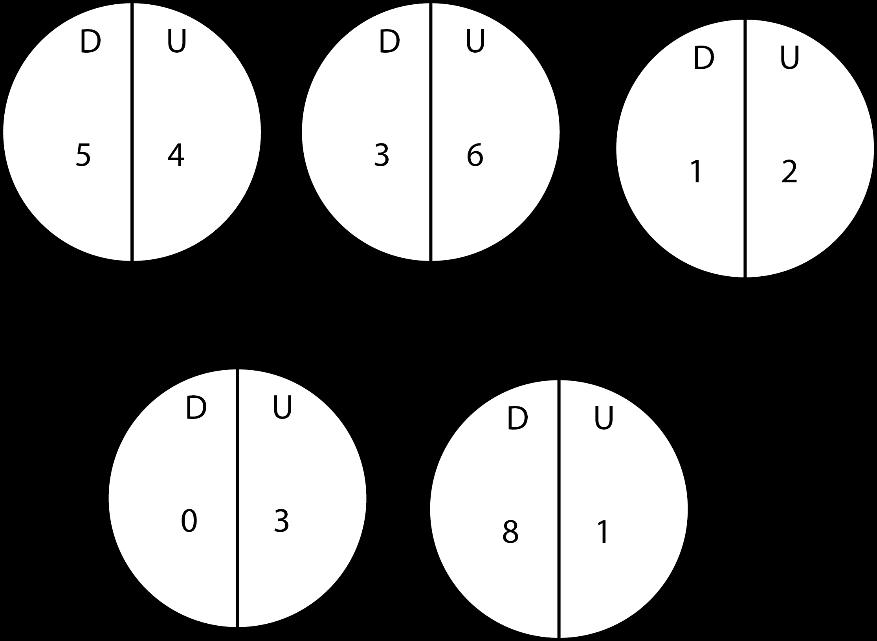
Depois, em uma folha avulsa, cada aluno deve desenhar cinco pratos indicando quantas dezenas e unidades cada número tem e ordenar os números em ordem crescente. Reproduzir o exemplo a seguir na lousa para que a turma possa visualizar o que deve ser feito na atividade proposta.

Definir os números:

1º número: 54

2º número: 36

3º número: 12

4º número: 3

5º número: 81

Representar os números no prato: EDITORIA

Escrever os números em ordem crescente:

3, 12, 36, 54 e 81, para este exemplo.

Para verificar se os alunos compreenderam o valor posicional dos algarismos, propor outras situações utilizando o prato descartável e os feijões Por exemplo, pedir a eles que coloquem 5 feijões nas unidades e, depois, movam os 5 feijões para as dezenas. Em seguida, perguntar: o número representado ainda é o mesmo? Qual é o valor posicional do algarismo 5 nas duas situações? Pedir que justifiquem as respostas. Espera-se que os alunos respondam que os números representados são diferentes – na primeira situação, há uma representação para o número 5; na segunda situação, há uma representação para o número 50. Além disso, o valor posicional do 5 na primeira situação é de 5 unidades, e na segunda situação é de 5 dezenas.

Aula 7

Nesta aula, os alunos vão realizar uma atividade de contagem e de representação de quantidades por meio de compra e venda. Para isso, sugere-se providenciar antecipadamente representações de cédulas e moedas de Real e pedir a eles que levem, para a sala de aula, embalagens recicláveis (caixa de leite, pacote de café, entre outras); brinquedos que simulem frutas e legumes (com autorização dos responsáveis).

Inicialmente, organizar a turma em grupos com seis integrantes e propor que cada grupo organize sua barraca de venda, dispondo os produtos em uma mesa e colocando preços, que podem variar de 2 a 99 reais.

Após a montagem das barracas, entregar a cada aluno 10 cédulas de cada valor (20, 10, 5 e 2 reais) e explicar a atividade a eles. Comentar que dois alunos devem ficar em cada barraca, enquanto os demais circulam pela sala de aula, visitando as outras barracas e comprando os produtos. Cada compra feita deve ser anotada em uma folha avulsa e, depois, esses dados devem ser copiados na folha que o grupo entregará ao professor, indicando os objetos comprados, o valor de cada um, as cédulas que foram utilizadas, se houve troco e o valor total que sobrou em dezenas e unidades, conforme descrito no quadro a seguir. Reproduzir esse quadro na lousa para os alunos copiarem.

OBJETO COMPRADO VALOR

CÉDULAS UTILIZADAS TROCO

VALOR TOTAL QUE SOBROU EM DEZENAS E UNIDADES:

Ao final da atividade, definir um tempo para que os alunos registrem o que compraram no quadro Nesse momento, verificar se eles estão preenchendo corretamente o quadro e elucidar possíveis dúvidas.

Para ampliar, atribuir valores monetários a outros objetos da sala de aula e pedir aos alunos que escrevam no caderno com quantas cédulas de 20, 10, 5 ou 2 reais podem ser comprados tais objetos Propor a eles que apresentem, quando possível, diferentes respostas para um mesmo valor; por exemplo, 1 cédula de 10 reais ou 5 cédulas de 2 reais.

Aula 8

Nesta aula, os alunos vão realizar uma atividade para reconhecer, comparar e compor quantias com cédulas do Sistema Monetário Brasileiro por meio da elaboração de um cartaz. Para isso, organizar a turma em grupos com quatro alunos e entregar a cada grupo cinco representações de cédulas de 50, 20, 10, 5 e 2 reais, uma cartolina e revistas.

Em seguida, pedir que cada grupo corte a cartolina em seis partes iguais e cole em cada parte a imagem de um objeto cujo valor monetário pode ser de até 100 reais

Após os grupos produzirem os cartazes, propor que os troquem entre si, de modo que nenhum deles fique com seu próprio cartaz. Pedir que cada aluno escreva em uma folha avulsa o nome do objeto, o valor do objeto em reais e a quantidade de cédulas (de 50, 20, 10, 5 e 2 reais) necessárias para comprá-lo

Realizar a troca de cartazes, até que todos os alunos tenham registrado os objetos escolhidos por todos os grupos, e indicar as cédulas que podem ser utilizadas para comprá-los. Determinar um tempo para a realização da atividade Acompanhar os alunos durante esse período, esclarecendo possíveis dúvidas.

Ao final, se julgar oportuno, organizar uma roda de conversa e propor à turma uma discussão sobre os cartazes, para que todos reflitam sobre o que aprenderam na atividade Para nortear a conversa, perguntar aos alunos: como foi feita a escolha dos valores dos objetos? Alguns desses objetos poderiam ser comprados com quantidades de cédulas diferentes das anotadas por vocês? Para qual objeto foi mais difícil escolher as cédulas? Por quê?

A primeira pergunta possibilita discutir com os alunos o valor de objetos, comparando-os a fim de identificar o maior e o menor valor. Se julgar oportuno, construa uma reta numérica na lousa e faça as comparações relacionando os preços de alguns produtos com pontos da reta numérica. Com a segunda pergunta, é possível mostrar aos alunos como um mesmo valor pode ser composto de diferentes agrupamentos de cédulas.

Por fim, por meio da terceira pergunta, é possível identificar situações em que os alunos apresentam mais dificuldade, sendo possível trabalhar de forma coletiva essas situações e resolver possíveis defasagens. Se alguns alunos apresentarem dificuldade na realização da atividade, é importante retomar o conteúdo e citar novos exemplos para que possam elucidar suas dúvidas.

Sugestões

• MATEMATICANDO: material dourado. 2013. Vídeo (7min37s). Publicado pelo canal Matematicando UFRGS. Disponível em: https://www.youtube.com/watch?v=gkuEOq4uZj0 Acesso em: 4 jan. 2022.

Sequência didática 6: Adição e subtração com números até 100

Nesta sequência didática, serão abordadas as operações de adição e de subtração de números naturais até 100 por meio de atividades lúdicas, da resolução de problemas e da utilização de materiais manipuláveis, como o material dourado.

Objetivos de aprendizagem

• Resolver problemas com diferentes ideias da adição.

• Resolver e elaborar problemas com diferentes ideias da subtração.

• Adicionar e subtrair números com o auxílio de materiais manipuláveis e da calculadora.

Plano de aulas

Aulas 1 e 2: Resolver adições utilizando material dourado e estratégias pessoais.

Aula 3: Resolver adições por meio de atividade lúdica.

Aula 4: Resolver subtrações utilizando o suporte de imagens e de materiais manipuláveis.

Aula 5: Elaborar e resolver problemas que envolvam a subtração.

Aula 6: Resolver problemas de adição utilizando diferentes estratégias por meio de atividade lúdica.

Aula 7: Elaborar um jogo que envolve o cálculo da adição e da subtração e participar dele.

Aula 8: Resolver adições e subtrações por meio de atividade lúdica e utilizar a calculadora para verificar os resultados dessas operações.

Componentes essenciais para a alfabetização: Produção de escrita e compreensão de textos

Competências gerais da Educação Básica: 5 e 9

Competências específicas de Matemática: 6 e 8

Habilidades: EF01MA07 e EF01MA08.

Materiais necessários: Lápis, borracha, folhas de atividades, papel, lápis de cor, cola, tesoura com pontas arredondadas, material dourado ou pedrinhas em saquinhos, fichas de cartolina, caneta hidrográfica, folha avulsa, calculadora, dado e tabuleiro do jogo Corrida dos números.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Aulas 1 e 2

Nestas aulas, os alunos vão resolver adições utilizando o material dourado ou outros objetos manipuláveis. Para isso, providenciar fichas com diferentes adições e verificar se a escola dispõe de material dourado (conferir se a quantidade é suficiente para trabalhar com todos os alunos). Caso a escola não o tenha disponível, pode-se produzi-lo com EVA. Ver na seção Sugestões o linkpara um vídeo que contém um passo a passo para fazer material dourado utilizando EVA.

Inicialmente, organizar a turma em grupos com três alunos e entregar um material dourado e cinco fichas com diferentes adições. Observar a seguir algumas fichas que podem ser confeccionadas em cartolina e entregues aos alunos. Nessas fichas, a soma das unidades não pode ultrapassar nove unidades e a soma das dezenas não pode ultrapassar nove dezenas, a fim de evitar reagrupamentos.

Em seguida, propor aos alunos que resolvam a adição das fichas com o auxílio do material dourado. Depois de eles resolverem a adição das cinco primeiras fichas, propor aos grupos que troquem as fichas, para que todos os grupos resolvam as adições de todas as fichas Acompanhar os alunos durante essa atividade para verificar se estão realizando as adições corretamente e esclarecer possíveis dúvidas.

Posteriormente, escrever as adições de algumas dessas fichas na lousa e propor aos alunos que, individualmente, as resolvam utilizando outra estratégia de cálculo. Se julgar oportuno, após o término, convidar alunos que tenham utilizado estratégias diferentes para apresentá-las aos colegas.

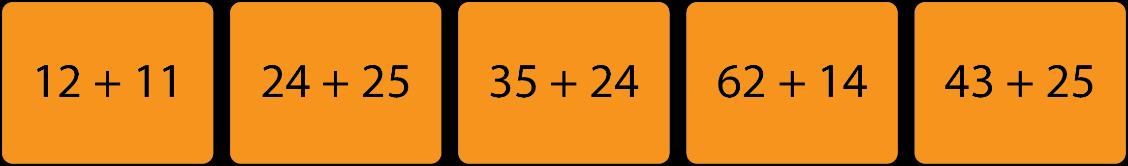
Para finalizar, escrever na lousa as atividades a seguir ou entregá-las, em folhas impressas, para cada aluno. O objetivo dessas atividades é possibilitar que os alunos consolidem seus conhecimentos sobre a operação de adição e ampliem seus repertórios de estratégias.

1. OBSERVE O PLACAR DE UMA PARTIDA DE BASQUETE. ESCREVA A SENTENÇA DE ADIÇÃO QUE REPRESENTA O TOTAL DE PONTOS DESSA PARTIDA.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

EDITORIA DE ARTE

EDITORIA DE ARTE

Representação de placar.

59 pontos 24 + 35 = 59

2. UMA PESSOA QUER COMPRAR DOIS LIVROS UM CUSTA 52 REAIS E O OUTRO CUSTA 36 REAIS QUAL VALOR ELA PAGARÁ PELOS DOIS LIVROS?

88 reais

52 + 36 = 8

3. O QUADRO A SEGUIR APRESENTA A QUANTIDADE DE PESSOAS QUE ASSISTIRAM A UMA PEÇA DE TEATRO NA SEXTA-FEIRA. AO TODO, QUANTAS PESSOAS ASSISTIRAM A ESSA PEÇA NA SEXTA-FEIRA?

PESSOAS QUE ASSISTIRAM A UMA PEÇA DE TEATRO NA SEXTA-FEIRA

1º HORÁRIO 52 PESSOAS

2º HORÁRIO 47 PESSOAS

99 pessoas.

52 + 47 = 99

Realizar a leitura dos enunciados com a turma e determinar um tempo para a resolução das atividades. Acompanhar os alunos durante a resolução, verificando se compreenderam os problemas e esclarecendo possíveis dúvidas na montagem das sentenças

Se alguns alunos apresentarem dificuldade durante a resolução das atividades, utilizar material de apoio (como o material dourado) nas adições, a fim de tornar concreto o processo de adicionar partes distintas para formar o todo.

Aula 3

Nesta aula, os alunos vão jogar o jogo Corrida dos números. Para isso, sugere-se providenciar antecipadamente dados e tampinhas de garrafa PET e imprimir o tabuleiro apresentado a seguir

Para iniciar aula, organizar a turma em grupos com quatro alunos e entregar um tabuleiro para cada grupo, quatro tampinhas de garrafa PET, que serão utilizadas como pino, e um dado.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Representação de tabuleiro de trilha.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Em seguida, explicar as seguintes regras do jogo para os alunos.

• Cada jogador movimentará o seu pino, alternadamente, iniciando na casa de número 1.

• Cada jogador, na sua vez, lançará o dado e fará uma adição do número da casa, em que o pino dele está localizado, com a pontuação do dado que foi lançado. Se houver o resultado dessa adição no tabuleiro, o jogador movimentará o pino direto para a casa em que ele aparece. Se não houver uma casa do tabuleiro com essa soma, o jogador deverá passar a vez.

• Vencerá o jogador que chegar primeiro à casa com a palavra CHEGADA. Verificar se todos os alunos compreenderam as regras e iniciar o jogo.

Se necessário, pedir que joguem mais de uma vez. Acompanhar os grupos durante a realização do jogo para conferir se estão realizando os cálculos corretamente e esclarecer possíveis dúvidas.

Aula 4

Nesta aula, os alunos vão realizar o cálculo de subtrações, utilizando o suporte de imagens e de materiais manipuláveis. Incialmente, sugere-se fazer a seguinte pergunta a eles: eu tenho seis gizes brancos na mão. Se eu tirar ou separar quatro gizes, com quantos gizes eu fico na mão? (dois gizes). Isso possibilita verificar os conhecimentos prévios da turma sobre subtração.

Para explorar com os alunos a operação de subtração, colocar dois livros lado a lado sobre a mesa e pedir a um aluno da turma que retire ou separe um dos livros; em seguida, perguntar à turma: quantos livros ficaram na mesa? Deixar que respondam livremente.

Representar essa situação na lousa escrevendo a sentença matemática correspondente: 2 – 1 = 1. Se julgar oportuno, fazer perguntas utilizando outros materiais (como lápis de cor) e outras quantidades.

Posteriormente, perguntar aos alunos o que eles entendem por "retirar" e " separar " um livro. Deixar que respondam oralmente para que expressem suas ideias e aprendam a comunicar-se de forma clara e objetiva.

Para dar continuidade ao trabalho com a operação de subtração, propor à turma a realização das atividades a seguir. Para isso, se possível, imprimir essas atividades e entregá-las aos alunos ou escrever na lousa para que eles as copiem.

Acompanhar a turma durante a resolução das atividades, observando quais estratégias eles estão utilizando – contagem nos dedos, material concreto etc. Orientá-los, se julgar necessário.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

1. OBSERVE AS IMAGENS E ESCREVA O RESULTADO DAS SUBTRAÇÕES. EDITORIA

6

2 = 4

8

5 = 3

6 – 3 = 3

3 – 1 = 2

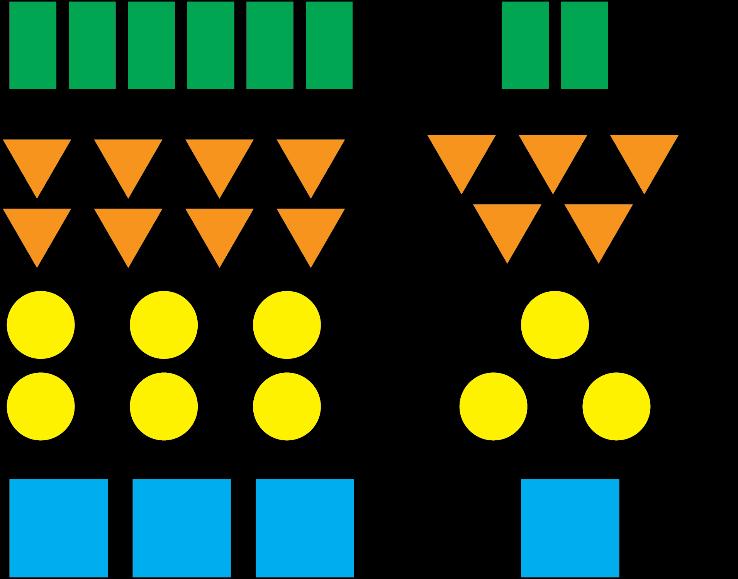
2. OBSERVE O EXEMPLO DA PRIMEIRA FIGURA DO QUADRO (NO ALTO E À ESQUERDA) E COMPLETE AS OUTRAS SENTENÇAS DE SUBTRAÇÃO.

Ficha de subtrações com apoio de figuras.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

4

3 = 1; 5

3 = 2

3 – 2 = 1; 5 – 2 = 3

4 – 1 = 3; 2

2

1 = 1; 3

2 = 0

1 = 2

Se julgar oportuno, propor aos alunos que, após resolverem as atividades, troquem as folhas com os colegas para que um corrija as atividades do outro e, depois, conversem sobre as estratégias que utilizaram. Isso contribui para que um ajude o outro a compreender o conceito da subtração e favorece o trabalho colaborativo entre eles

Aula 5

Nesta aula, os alunos vão elaborar e resolver problemas que envolvem subtração. Para isso, organizar a turma em duplas Em seguida, entregar a cada dupla uma folha avulsa e propor que elaborem um problema que envolva o cálculo da subtração.

Antes de os alunos iniciarem a atividade, apresentar alguns problemas na lousa, por exemplo: um vendedor tem 8 canetas e vendeu 3; quantas canetas ele ainda tem para vender? Acompanhar os alunos durante a elaboração dos problemas, verificando se estão fazendo de forma correta e intervir quando julgar necessário.

Ao final dessa etapa, cada dupla pode apresentar o seu problema à turma. Conversar com os alunos sobre a importância de prestar atenção e não interromper os colegas no momento da apresentação. Esta atividade possibilita o desenvolvimento da habilidade de falar de forma clara e objetiva, de ouvir com empatia e de cooperar com os demais

Após a apresentação dos problemas, propor às duplas que troquem o problema com outra dupla para que uma resolva o problema da outra. Orientá-los a utilizar diferentes estratégias de cálculo (como os dedos das mãos, os palitos ou outro material manipulável) ou o desenho de figuras, riscando a quantidade que deve ser subtraída.

Para ampliar, se julgar oportuno, propor à turma a resolução dos problemas a seguir. Para isso, escrever os problemas na lousa para que eles os copiem ou entregá-los em uma folha avulsa

Orientar os alunos a escreverem uma sentença para representar os problemas das atividades 1 e 2. Acompanhar a turma durante a resolução verificando se os alunos estão escrevendo corretamente as sentenças.

1. MARIA TINHA 6 MORANGOS E COMEU 2. COM QUANTOS MORANGOS ELA FICOU?

4 MORANGOS.

2. JOÃO TEM 10 FIGURINHAS. ELE DEU 4 FIGURINHAS REPETIDAS PARA SEU AMIGO DANIEL. QUANTAS FIGURINHAS JOÃO TEM AGORA?

6 FIGURINHAS.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Aula 6

Nesta aula, os alunos vão resolver subtrações utilizando diferentes estratégias e jogar o jogo O dominó das subtrações. Para isso, sugere-se imprimir com antecedência a ilustração do dominó apresentado a seguir. Se julgar oportuno, colar as peças impressas em EVA para que fiquem mais firmes.

Representação do dominó das subtrações.

Inicialmente, escrever na lousa algumas subtrações e pedir aos alunos que as copiem e as resolvam no caderno. Orientá-los a utilizarem diferentes estratégias de resolução, por exemplo, contagem com os dedos ("baixando" ou "retirando" os dedos), materiais manipuláveis, desenho de figuras, entre outras.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Para fazer a subtração de 4 2, por exemplo, os alunos podem levantar 4 dedos da mão e depois abaixar 2 dedos, ficando com 2 dedos levantados ou, ainda, desenhar 4 figuras e riscar duas, ficando com 2 figuras sem riscar

Caso os alunos utilizem materiais manipuláveis, eles podem dispor sobre a mesa 4 objetos e retirar a quantidade suficiente para chegar ao resto 2. No fim, terão retirado ou separado 2 objetos para obter o 2. Acompanhá-los durante a resolução das subtrações auxiliando-os e esclarecendo possíveis dúvidas.

Em seguida, propor à turma o jogo O dominó das subtrações, que estimula a realização de cálculos mentais. Para tanto, organizar grupos com quatro integrantes e disponibilizar um dominó para cada grupo

Explicar aos alunos como jogar o Dominó das subtrações Comentar que, em cada peça, a operação está de um lado e o resultado do outro. Antes de iniciar o jogo, eles devem embaralhar as peças viradas para baixo e distribuí-las entre os quatro jogadores, ficando cada um com sete peças.

Em seguida, o grupo deverá definir, por meio de um sorteio, quem começa jogando O jogador selecionado deverá escolher uma peça e colocá-la na mesa. O próximo jogador deverá escolher uma peça que tenha o resultado ou a operação correspondente em um dos lados da peça que está na mesa. Caso não tenha uma peça que se encaixe, ele perde a vez.

O jogo continuará até que todos os participantes tenham colocado todas as suas peças na mesa ou até que nenhum deles tenha uma peça que se encaixe. Vencerá a partida o jogador que ficar sem peças ou com um menor número delas na mão.

Aula 7

Nesta aula, os alunos vão construir e utilizar um jogo da memória que envolve as operações de adição e subtração. Para isso, sugere-se providenciar antecipadamente cartolinas de duas cores e recortá-las para que sejam entregues a cada grupo.

Inicialmente, organizar os alunos em grupos de quatro integrantes e entregar a cada grupo 20 pedaços de cartolina, sendo 10 de cada cor. Em seguida, propor que elaborem um jogo da memória. Comentar que, para isso, eles devem escrever em diferentes cartas operações de adição e de subtração e o resultado correspondente a essas operações.

Explicar que, antes de confeccionarem as cartas, eles devem escrever em folha avulsa (que será entregue no final da aula) cinco sentenças matemáticas de adição e cinco de subtração, usando sempre números de duas ordens cujos resultados das operações não se repetem – a intenção é diminuir a chance de um mesmo resultado ser tirado mais vezes no jogo da memória.

É importante verificar as sentenças escritas pelos alunos a fim de assegurar que não ocorra a necessidade de reagrupamentos de unidades ou dezenas e outras incorreções,

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

como mais sentenças de adição que de subtração, ou vice-versa; números que não tenham duas ordens; sinais de adição, subtração ou igualdade colocados em posição errada.

Em seguida, orientar os grupos a transcreverem as 10 sentenças nas cartas de cartolina de mesma cor que receberam Pedir que resolvam as sentenças em uma folha avulsa.

Após finalizar as resoluções, os grupos deverão escrever a resposta de cada sentença nas outras 10 cartolinas que restaram. É importante que as sentenças e o resultado sejam escritos em carolinas de cores diferentes.

Depois de finalizarem a confecção das cartas, conversar com a turma sobre ganhar ou perder em um jogo, a fim de que não fiquem magoados ou bravos se perderem. Em seguida, explicar as regras do jogo.

Se julgar oportuno, escrever as regras na lousa para que todos possam consultá-las em caso de dúvidas. Quando todos os alunos compreenderem as regras, o jogo poderá ser iniciado

Regras do jogo

• Antes de começar o jogo, misturar as cartas

• Dispor as cartas em uma mesa com as faces escritas voltadas para baixo

• Definir a ordem de jogada (os grupos podem alterar a ordem dos jogadores a cada rodada).

• O participante que iniciar o jogo deverá escolher duas cartas, uma com as sentenças e outra com os resultados, e verificar se são correspondentes. Se corresponderem, ele ficará com as cartas. Se não corresponderem, deverá colocar as cartas no mesmo lugar de onde as tirou, e passará a vez ao próximo jogador

• Vencerá o jogador que obtiver o maior número de cartas.

Definir um tempo para a preparação das cartas, que pode ser de aproximadamente 20 minutos, e um tempo para a realização do jogo, que pode ser de 30 minutos. Se julgar necessário para a aprendizagem dos alunos, repetir o jogo outras vezes.

Aula

8

Nesta aula, a turma vai utilizar o jogo Bingo das adições e das subtrações e conferir o resultado dos cálculos dessas operações utilizando uma calculadora. Para isso, sugere-se imprimir antecipadamente as cartelas de bingo representadas a seguir e providenciar calculadoras. Se julgar necessário, explicar aos alunos o funcionamento da calculadora e a forma como utilizá-la para efetuar adições e subtrações.

Representação de cartelas de bingo.

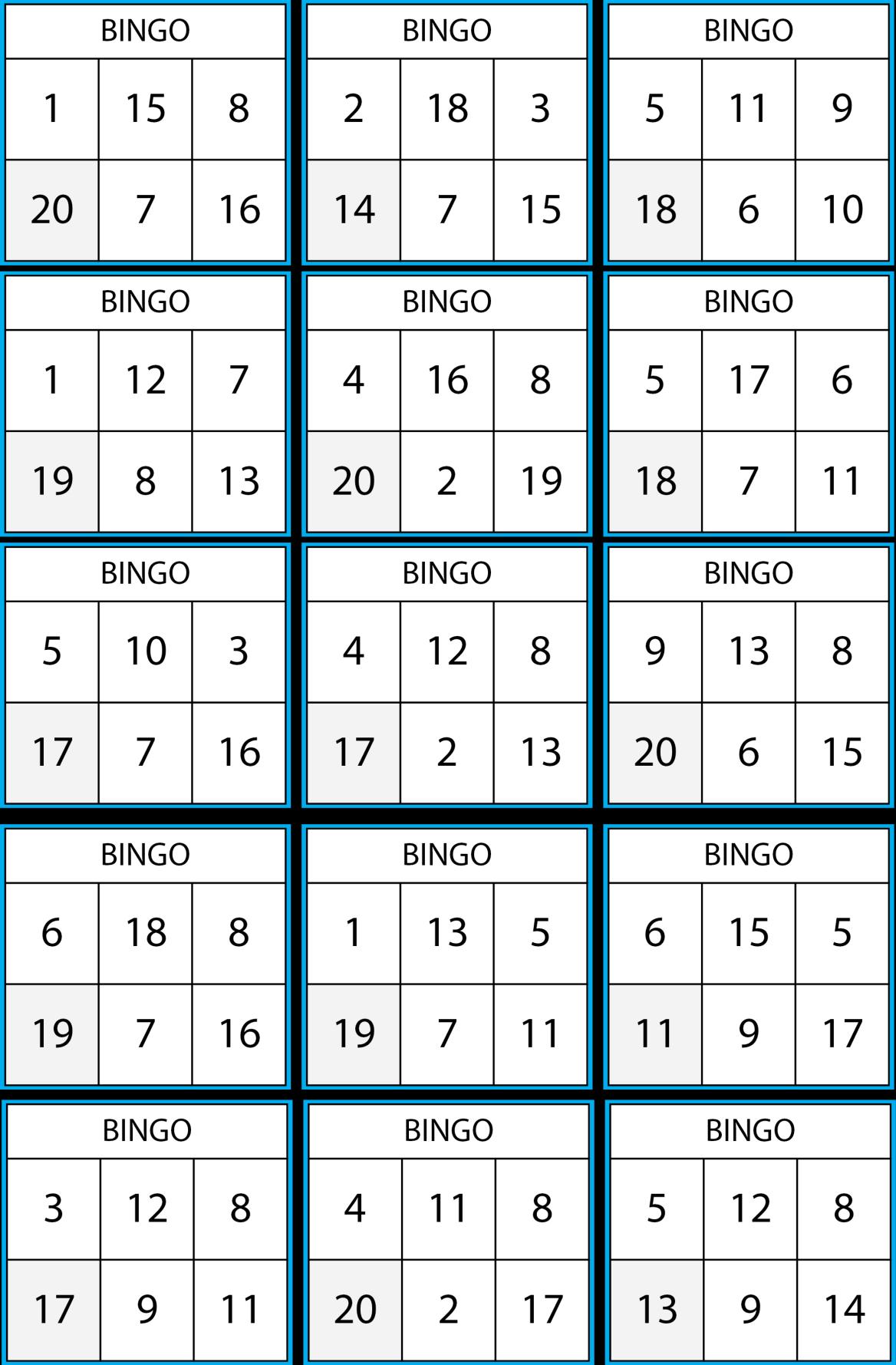
Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Entregar uma cartela para cada aluno e explicar como jogar O bingo das adições e das subtrações. Escrever algumas operações de adição e de subtração na lousa e explicar aos alunos que eles precisam calcular o valor dessas operações e verificar se o número do resultado está na cartela que receberam. Se sim, devem marcar esse número na cartela. As operações de adição e de subtração devem ter como resultado números entre 1 e 20 e não ter reagrupamentos e trocas. O aluno que marcar todos os números na cartela primeiro vencerá o jogo. Depois que todos compreenderam como jogar, iniciar o bingo.

Ao final do jogo, propor à turma que refaçam os cálculos das adições e das subtrações da lousa utilizando uma calculadora. Dessa maneira, os alunos podem verificar se marcaram algum número errado na cartela ou se deixaram de marcar algum número. Podem, ainda, conferir se o ganhador efetuou corretamente todas as operações e se marcou os números corretamente Esta atividade possibilita realizar os cálculos das adições e das subtrações por meio de uma atividade lúdica e a se familiarizar com o uso da calculadora.

Sugestões

• MATEMATICANDO: material dourado. 2013. Vídeo (7min37s). Publicado pelo canal Matematicando UFRGS. Disponível em: https://www.youtube.com/watch?v=gkuEOq4uZj0. Acesso em: 4 jan. 2022.

Sequência didática 7: Grandezas e medidas

Esta sequência didática aborda noções básicas de grandezas e medidas, utilizando instrumentos de medida como balança, blocos lógicos e garrafas. Além disso, possibilita comparar comprimentos, massas e capacidades mediante o uso de termos e expressões do dia a dia do aluno, como maior, menor, mais pesado, mais leve, quanto cabe, entre outros.

Objetivos de aprendizagem

• Medir comprimentos, massas e capacidades

• Reconhecer a balança como principal instrumento para medir massas.

• Identificar e comparar grandezas de comprimento, massa, capacidade e tempo.

Plano de aulas

Aula 1: Utilizar medidas de massa e de comprimento, em linguagem adequada, para comparar características de animais.

Aula 2: Explorar o conceito de medida de comprimento com base na comparação entre estaturas.

Aula 3: Comparar massas de objetos utilizando uma balança de dois pratos.

Aula 4: Explorar as diferentes possibilidades de comparação utilizando o material manipulativo blocos lógicos.

Aula 5: Refletir sobre a capacidade de recipientes de armazenamento de líquidos.

Aula 6: Utilizar unidades de medida não padronizadas para medir objetos na sala de aula.

Aula 7: Comparar medidas de comprimento, capacidade e massa.

Aula 8: Discutir sobre medidas de tempo.

Componentes essenciais para a alfabetização: Produção de escrita e compreensão de textos

Competências gerais da Educação Básica: 2, 3, 6 e 10

Competências específicas de Matemática: 2 e 8 Habilidades: EF01MA15, EF01MA16 e EF01MA17.

Materiais necessários: Blocos lógicos, folhas impressas com imagens de cachorro, girafa, formiga e pássaro, urna ou sacola não transparente com papéis com números naturais associados aos alunos, balança de dois pratos, calendário e objetos para comparação de massa, espessura e comprimento

Aula 1

O objetivo desta aula é utilizar os conceitos de massa e de comprimento, em linguagem adequada para a faixa etária, para comparar características de animais.

Para isso, organizar a turma em uma roda de conversa e iniciar uma discussão que resgate algumas de suas experiências. Inicialmente, pedir aos alunos que têm ou que tiveram animais de estimação que os descrevam.

Comentar com os alunos que os cachorros, embora sejam de uma mesma espécie de animal, podem possuir características distintas. Isso vale, também, para gatos e outros animais.

Após essa discussão, apresentar à turma as imagens a seguir.

Racool_studio/Freepik.com

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribu ído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Imagem de cachorro.

wirestock/Freepik.com

Imagem de pássaro. master1305/Freepik.com

Imagem de girafa

jcomp/Freepik.com

Imagem de formiga.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribu ído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Reservar um tempo para que os alunos apresentem suas considerações a respeito das imagens. Depois, pedir que reconheçam os animais representados. Espera-se que eles digam cachorro, pássaro, girafa e formiga.

Em seguida, propor alguns questionamentos:

• Qual desses animais é o mais alto?

• Qual desses animais é o mais leve?

• O cachorro é mais leve que a formiga?

• O cachorro é menor que a girafa?

Deixar que os alunos discutam as respostas antes da correção. Essa é uma maneira de incentivá-los a exercitarem a comunicação oral.

Aula 2

O objetivo desta aula é explorar o conceito de medida de comprimento comparando estaturas. Para isso, em uma discussão com a turma, associar os primeiros números naturais a cada aluno. Por exemplo, número 1 – nome do aluno, número 2 – nome do aluno, número 3 – nome do aluno etc.

Registrar essa organização na lousa e solicitar a ajuda dos alunos para fazer esse registro, perguntando: qual é o próximo número da sequência? Qual é o próximo aluno? Essa discussão inicial é importante para estabelecer uma relação biunívoca entre o conjunto de alunos e um subconjunto dos números naturais.

Em seguida, escrever cada número em pedaços de papéis idênticos e colocá-los em uma urna ou sacola não transparente para a realização de um sorteio. Solicitar que o aluno relativo ao número sorteado vá até o centro da sala. Da mesma maneira, sortear outro número e convidar o aluno sorteado a ir ao centro da sala. Nesse momento, perguntar aos alunos: qual dos dois alunos é o mais alto? De acordo com a resposta dos alunos, solicitar ao aluno mais alto que se posicione ao lado do que tem menor estatura. Realizar o mesmo procedimento até que todos os alunos estejam em uma mesma fila, organizada de acordo com a estatura.

Ao final da aula, organizar os alunos na disposição original da turma e discutir com eles que é possível seguir vários critérios para organizar um conjunto de elementos. Um deles é a estatura.

Comentar com a turma que a massa é outro critério usado para organizar um conjunto de elementos Solicitar, então, que os alunos respondam às seguintes perguntas, no caderno, para a próxima aula.

• Quem é a pessoa mais alta da sua casa?

• Quem é a pessoa mais baixa da sua casa?

disponibilizado

licença aberta do tipo

Material

em

Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribu ído crédito autoral e as criações sejam licenciadas sob os mesmos

• Quem é a pessoa mais alta que você conhece?

• Quem é a pessoa mais baixa que você conhece?

• Quem é a pessoa mais pesada da sua casa?

• Quem é a pessoa mais leve da sua casa?

Aula 3

O objetivo desta aula é comparar massas de objetos utilizando uma balança de dois pratos. Para isso, realizar inicialmente uma roda de conversa para discutir a respeito da tarefa proposta na aula anterior. Solicitar que os alunos apresentem suas respostas.

A seguir, destacar as pessoas mais leves e as mais pesadas elencadas por eles e comentar que a massa de uma pessoa envolve características fisiológicas. Argumentar que o fato de uma pessoa ter maior massa não significa ter mais ou menos saúde que uma pessoa que tem menor massa e vice-versa. Aproveitar esse momento para discutir com os alunos que respeitar as pessoas por suas características físicas é essencial. Ou seja, ninguém deve ser julgado por ser mais leve ou mais pesado que o outro

Ao realizar essa discussão sobre a massa, apresentar a balança de dois pratos. Comentar que esse instrumento faz parte da cultura popular brasileira e, até hoje, é utilizado por muitas pessoas.

Nesse momento, explicar aos alunos o funcionamento da balança de dois pratos. Comentar que os objetos são colocados nos pratos para que suas massas sejam comparadas. Quando os objetos colocados em um prato possuem, juntos, a mesma massa que os objetos colocados no outro prato, os pratos ficam alinhados. Quando possuem massas diferentes, os pratos não ficam alinhados. O lado que pende para cima é aquele com menor massa.

Caso a escola não possua uma balança de dois pratos, é possível construir uma com os alunos, utilizando um modelo simples, cujo passo a passo de montagem está disponível em: https://www.laboratoriosustentaveldematematica.com/2014/05/faca-uma-balanca-depratos-ensine-algebra-garrafas-pet.html (acesso em: 13 mar. 2023)

Com a balança disponível, selecionar dois objetos para serem comparados em relação à massa. Perguntar aos alunos qual deles é mais pesado, ou seja, qual deles possui maior massa. Após os alunos apresentarem suas expectativas, comparar os dois objetos na balança. Os objetos podem ser do próprio contexto da sala de aula, como caixas de giz, mochilas, estojos etc. Realizar mais algumas comparações, sempre permitindo que os alunos estimem qual é o objeto mais leve e qual é o mais pesado, antes de colocá-los na balança.

Aula 4

O objetivo desta aula é explorar as diferentes possibilidades de comparação por meio do material manipulativo blocos lógicos. Inicialmente, apresentar aos alunos esse material. Perguntar a eles se o conhecem, se já ouviram falar dele, se já o manipularam. Organizar, então, a turma em grupos de quatro alunos e entregar para cada grupo um kit de blocos lógicos. Deixar um tempo para que eles manipulem o kit

Em seguida, solicitar aos alunos que disponham, livremente, algumas peças dos blocos lógicos em grupos que tenham características em comum. Cada grupo deverá organizar, pelo menos, um grupo de blocos. Nesse momento, acompanhar as discussões e realizar intervenções se necessário.

Após trabalharem coletivamente, solicitar que cada grupo apresente à turma como organizaram as peças. Seguem alguns agrupamentos possíveis:

• peças de mesma cor;

• peças de mesmo tamanho;

• peças de mesmo formato;

• peças de mesma espessura.

Após a apresentação dos alunos, focar nos grupos de peças propostos por eles, e comparar com as demais peças dos blocos lógicos. Por exemplo, as peças que possuem uma mesma espessura são mais finas ou mais grossas que outras peças? As peças que possuem um mesmo tamanho são maiores ou menores que outras peças?

Aula 5

O objetivo desta aula é discutir sobre a capacidade que recipientes têm de armazenar líquidos. Para isso, mostrar dois recipientes vazios transparentes, com mesma capacidade e formato. Comentar com os alunos que nesses dois recipientes cabe a mesma quantidade de líquido. É importante que esses recipientes tenham um tamanho que permita aos alunos comparar quantidades de líquido que serão colocadas neles.

Em seguida, mostrar vários recipientes menores, com diferentes formatos, cheios de água. Realizar uma discussão com os alunos comparando sempre duas garrafas. Para isso, perguntar para a eles: qual das duas garrafas possui maior quantidade de líquido? Deixar que eles debatam sobre suas justificativas. Em seguida, transferir os líquidos de cada garrafa para cada um dos dois recipientes maiores. Comentar que, como nos dois recipientes cabe a mesma quantidade de líquido e eles têm o mesmo formato, é possível verificar qual garrafa possui maior quantidade de líquido, comparando o nível da água nesses recipientes. Após uma primeira rodada dessa dinâmica, descartar todo o líquido dos dois recipientes em um recipiente maior como um balde, por exemplo, que não será utilizado. Essa água não deve

ser desperdiçada, podendo, por exemplo, ser usada para regar plantas. Se julgar conveniente, realizar essa dinâmica na quadra da escola.

Buscar diversificar o formato das garrafas que serão comparadas em relação à capacidade. Por exemplo, uma garrafa mais alta e estreita com uma garrafa mais baixa e menos estreita. Se julgar conveniente, discutir com os alunos que não apenas a altura determina se uma garrafa terá uma maior capacidade de armazenar líquidos que outra.

Aproveitar esse momento para conversar com a turma sobre a importância da economia de água, mostrando a eles o vídeo sobre uso racional da água da seção Sugestões

Aula 6

O objetivo desta aula é medir comprimentos utilizando medidas de comprimento não convencionais.

Explicar aos alunos que, antes de surgirem as unidades de medida de comprimento que utilizamos hoje, muitos povos utilizavam partes do corpo para medir e comparar comprimentos, como o pé, a polegada, o passo e o palmo.

Organizar a turma em duplas e explicar que cada dupla deve utilizar partes do corpo para medir objetos e comprimentos na sala de aula.

Escrever na lousa um quadro com os objetos ou distâncias que serão medidos e pedir aos alunos que reproduzam o quadro no caderno para que anotem as partes do corpo utilizadas e as medidas obtidas. Observe, a seguir, um exemplo de quadro que poderá ser usado.

Objeto ou comprimento Parte do corpo utilizada Medida obtida

Largura da carteira

Altura da mesa do professor

Comprimento do estojo

Comprimento do caderno

Espessura do caderno

Largura da porta

Comprimento da sala

Depois de feitas as medições, preencher o quadro com os resultados obtidos pelas duplas. Discutir com a turma quais partes do corpo eles utilizaram para fazer as medições, levando-os a concluírem que nem todas são adequadas para uma medida específica. Por exemplo, não é adequado medir o comprimento da sala utilizando o palmo ou a polegada, tampouco é possível usar o passo para medir o comprimento da mesa do professor.

Discutir, também, as eventuais diferenças nas medições, levando a turma a concluir que elas ocorrem devido às variações no tamanho das partes do corpo de cada aluno.

Aula 7

Nesta aula, os alunos farão comparações de medidas de comprimento, massa e capacidade, utilizando termos como mais alto, mais baixo, mais comprido, mais curto, mais grosso, mais fino, mais largo, mais pesado, mais leve, cabe mais, cabe menos, cheio, vazio, quase cheio, quase vazio.

Para isso, disponibilizar recipientes de diversas capacidades, além de objetos variados, para que os alunos possam responder a determinadas perguntas, como as sugeridas a seguir.

• Segurar um lápis e um marcador de texto e perguntar: qual é o mais grosso? Em seguida, perguntar: qual é o mais comprido?

• Pegar um abacaxi e uma maçã e perguntar: qual é a fruta mais pesada?

• Pedir aos alunos que comparem uma carteira escolar e a mesa do professor, perguntando: qual é a mais larga?

• Segurar uma garrafa PET de 1,5 L e uma de 500 mL, ambas vazias, e perguntar: em qual delas cabe mais água?

• Encher uma garrafa e manter a outra vazia e perguntar: Qual está cheia?

• Pegar quatro garrafas: uma totalmente cheia, uma totalmente vazia, uma quase cheia e a outra quase vazia. Questionar: qual está quase cheia, qual está quase vazia?

• Chamar um aluno de cabelos longos e um de cabelos curtos e perguntar: quem tem cabelo mais comprido?

Se achar conveniente, pedir aos alunos que formulem perguntas para os colegas responderem e verificar se todos estão à vontade para formular e responder perguntas de comparação de medidas em geral.

Aula 8

O objetivo desta aula é discutir medidas de tempo. Para isso, realizar uma conversa inicial com a turma, perguntando:

• Quais são os períodos do dia? Espera-se que os alunos respondam: manhã, tarde e noite

• Vocês frequentam a escola em qual período do dia?

• Vocês dormem em qual período do dia?

• Vocês acordam em qual período do dia?

Após essa discussão, perguntar aos alunos:

• Que dia da semana é hoje?

• Que dia da semana será amanhã?

• Que dia da semana foi ontem?

• Vocês sabem todos os dias da semana? Quais são? Espera-se que os alunos respondam: domingo, segunda-feira, terça-feira, quarta-feira, quinta-feira, sexta-feira e sábado.

• Qual é o primeiro dia da semana? Espera-se que eles respondam domingo.

• Qual é o último dia da semana? Espera-se que eles respondam sábado.

Após essa discussão, sistematizar com os alunos os dias da semana e os períodos do dia na lousa. Comentar que essas são maneiras de organizar o tempo. Por meio delas, as ações humanas tendem a ser mais organizadas.

Em seguida, propor aos alunos mais algumas reflexões, como:

• Quantos meses há em 1 ano?

• Quais são os meses do ano?

• O Natal é comemorado em qual dia e mês do ano?

• O Dia das Crianças é comemorado em qual dia e mês do ano?

Comentar com os alunos que os dias e os meses de um ano são organizados em um calendário. Se possível, mostrar aos alunos um calendário do ano vigente e chamar a atenção deles para alguns fatos:

• alguns meses possuem 30 dias, outros 31;

• fevereiro possui 28 dias ou 29 dias;

• as datas comemorativas, os feriados e os domingos, geralmente, são destacados em um calendário.

Por fim, solicitar aos alunos que façam um desenho, em folha avulsa, que remeta a algum dia ou época do ano. Por exemplo, uma árvore de Natal, uma alegoria de carnaval, folhas caindo de uma árvore (outono), crianças brincando (Dia das Crianças) etc.

Se julgar interessante, expor os desenhos no mural da sala de aula

Sugestões

• O USO racional da água. 2015. Vídeo (4min49s). Publicado pelo canal anagovbr. Disponível em: https://youtu.be/JtshF-n-mis Acesso em: 4 jan 2022.

Sequência didática 8: Probabilidade e estatística

Nesta sequência didática, são abordadas situações do dia a dia do aluno, em que ele poderá identificar e classificar se a situação é um evento envolvendo o acaso, e usando termos como: acontecerá com certeza, talvez aconteça ou é impossível acontecer.

Além disso, será abordada a coleta de dados envolvendo situações do dia a dia dos alunos e a organização dos dados coletados em tabelas e gráficos de coluna simples.

Objetivos de aprendizagem

• Identificar e classificar acontecimentos cotidianos que dependem do acaso.

• Coletar dados e organizá-los em tabelas e gráficos de coluna simples.

• Identificar, ler e interpretar dados em tabelas e gráficos de colunas simples.

Plano de aulas

Aula 1: Introduzir a discussão sobre classificação de eventos.

Aula 2: Ampliar as discussões sobre classificações de eventos.

Aula 3: Desenvolver uma atividade individual sobre classificação de eventos.

Aula 4: Associar e classificar eventos relacionados a obras de ficção.

Aula 5: Iniciar o processo de realização de uma pesquisa estatística.

Aula 6: Introduzir o conceito de tabela como um recurso para representar dados.

Aula 7: Introduzir o conceito de gráfico de colunas como um recurso para representar dados.

Aula 8: Apresentar os resultados de uma pesquisa estatística.

Componentes essenciais para a alfabetização: Produção de escrita e compreensão de textos

Competências gerais da Educação Básica: 1, 2, 3 e 4

Competências específicas de Matemática: 2 e 8

Habilidades: EF01MA20, EF01MA21 e EF01MA22

Materiais necessários: Lápis, lápis de cor, borracha, urna ou saquinho de pano, tiras de papel, cartolina, cola, tesoura com pontas arredondadas e projetor multimídia.

Aula 1

O objetivo desta aula é introduzir a discussão sobre classificação de eventos. Para isso, pedir aos alunos que organizem as carteiras em formato de U.

Em seguida, escrever na lousa três situações cotidianas e casuais que eles possam classificar como "acontecerá com certeza", "talvez aconteça" e "é impossível acontecer".

Exemplos de situações:

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

1. HOJE VAI

ANOITECER?

Para essa situação, ouvir as respostas dos alunos. Espera-se que digam "claro que vai!" ou algo parecido. É importante que eles concluam que, entre as três classificações anteriormente citadas, anoitecer é um fato que "acontecerá com certeza"

2. SERÁ QUE HOJE VAI CHOVER?

A provável resposta a isso será "não sei", ou "vai, porque ouvi no rádio". Lembrar, porém, que essa ocorrência depende de condições meteorológicas – vento, formação de nuvens, frio, calor etc. – e que não há como ter certeza absoluta de que choverá (mesmo ouvindo a previsão do tempo), ou seja, esse é um evento que "talvez aconteça"

3.

VAI CHOVER CAFÉ HOJE?

Esta é uma situação que nunca ocorrerá – e é muito provável que todos os alunos concordem. Portanto, "é impossível acontecer" esse evento.

Depois dessa breve conversa, verificar se os alunos compreenderam as classificações que envolvem o acaso. Porém, nessa faixa etária muitas vezes uma fantasia pode ser confundida com realidade (Papai Noel, fada do dente etc.), e essa crença precisa ser tratada com cautela.

Em seguida, perguntar à turma quem consegue dar um exemplo de evento que "acontecerá com certeza". Após darem um exemplo, solicitar que façam o mesmo para "talvez aconteça" e "é impossível acontecer". Realizar uma discussão avaliando os exemplos dados por eles. Por fim, entregar uma folha impressa com as seguintes situações.

1 AMANHÃ NO PROGRAMA DE CULINÁRIA, VAMOS SENTIR O CHEIRO DA RECEITA PELA TELEVISÃO.

2 NESTA SEMANA, O BEBÊ DE FÁTIMA NASCERÁ.

3 JOÃO FARÁ ANIVERSÁRIO NO DIA 31 DE FEVEREIRO.

4 HOJE, CARLOS ASSISTIRÁ A UM FILME.

5. AMANHÃ, O SOL VAI SE PÔR.

6. HOJE, O DIA TERÁ 24 HORAS.

Pedir aos alunos que classifiquem essas situações em "acontecerá com certeza", "talvez aconteça" e "é impossível acontecer" Espera-se que eles respondam que "acontecerá com certeza": 5 e 6; "talvez aconteça": 2 e 4; "é impossível acontecer":1 e 3

Para finalizar a aula, realizar uma discussão coletiva e sanar eventuais dúvidas.

Aula 2

O objetivo desta aula é ampliar as discussões sobre classificações de eventos. Para isso, preparar antecipadamente uma urna ou um saquinho de pano contendo 18 papéis

idênticos – escrever em seis deles "acontecerá com certeza"; em outros seis, "talvez aconteça"; e nos seis restantes, "é impossível acontecer"

Explicar à turma como será a atividade. Cada aluno deverá tirar um papel com a classificação do evento, anotá-la em uma folha avulsa e colocar o papel de volta na urna ou no saquinho. É importante que, ao sortear a classificação, o aluno não a conte aos colegas.

Esperar que todos os alunos tirem e devolvam o papel para iniciar a segunda parte da atividade. A partir daí, eles deverão criar uma situação cotidiana que combine com a frase sorteada. Por exemplo, quem tirar a classificação "acontecerá com certeza" poderá criar uma situação-problema como: hoje eu vou embora da escola ao final das aulas? Esse evento "acontecerá com certeza", pois, quando acabar o período de aula, os alunos vão embora. Estipular um tempo para a criação das situações, que pode ser de 15 minutos. Durante a criação da situação do dia a dia, é importante circular pela sala de aula para observar como os alunos estão procedendo. Possíveis enganos – como uma situação impossível ser classificada de "talvez aconteça" – serão corrigidos depois. Nesse momento, selecionar as produções dos alunos que serão apresentadas por eles na próxima etapa da aula.

Retomar as situações e suas classificações, realizando uma discussão coletiva por meio da apresentação dos eventos criados pelos alunos. A ordem das apresentações pode ser estabelecida por tipo de evento. Por exemplo, primeiro se discutem situações criadas pelos alunos para "acontecerá com certeza". Depois, se discutem as demais. Mais uma vez, estar atento com o que pode ser realidade para certas crianças e é tido como fantasia pelos adultos.

Se achar conveniente, repetir a brincadeira, não só para que os alunos com dificuldade desenvolvam essa habilidade de diferenciar probabilidades como, também, para avaliar o progresso deles. Nesse momento, é possível, ao invés de trabalhar individualmente, solicitar aos alunos que se reúnam em grupos.

Aula 3

O objetivo desta aula é desenvolver uma atividade individual sobre classificação de eventos. Para isso, entregar para cada aluno uma folha avulsa contendo a descrição de situações do dia a dia, como as descritas a seguir, de maneira que o aluno classifique cada acontecimento descrito e escolha uma das opções disponíveis.

Como os alunos estão em fase de alfabetização, escrever na lousa um exemplo de evento e as três opções abordadas, ou seja, ACONTECERÁ COM CERTEZA, TALVEZ

ACONTEÇA e É IMPOSSÍVEL ACONTECER

Explicar aos alunos que eles deverão marcar um X dentro dos parênteses da opção escolhida. Nesse momento, ler, pausadamente, cada uma das questões propostas e aguardar que eles respondam às perguntas.

Material disponibilizado em licença aberta do tipo Creative Commons

CLASSIFICANDO EVENTOS ENVOLVENDO O ACASO.

LEIA AS SITUAÇÕES A SEGUIR. DEPOIS, CLASSIFIQUE O EVENTO MARCANDO UM X DENTRO DOS PARÊNTESES.

1. AMANHÃ O SOL VAI NASCER.

( ) ACONTECERÁ COM CERTEZA

( ) TALVEZ ACONTEÇA

( ) É IMPOSSÍVEL ACONTECER

Acontecerá com certeza, pois todos os dias o Sol nasce.

2. HOJE O DIA SERÁ ENSOLARADO.

( ) ACONTECERÁ COM CERTEZA

( ) TALVEZ ACONTEÇA

( ) É IMPOSSÍVEL ACONTECER

Talvez aconteça, se não tiver nuvens no céu.

3. UM DIA OS CACHORROS VÃO FALAR.

( ) ACONTECERÁ COM CERTEZA

( ) TALVEZ ACONTEÇA

( ) É IMPOSSÍVEL ACONTECER

É impossível acontecer, porque animais não falam.

4. AMANHÃ UM ELEFANTE VAI PASSAR PELO BURACO DE UMA FECHADURA.

( ) ACONTECERÁ COM CERTEZA

( ) TALVEZ ACONTEÇA

( ) É IMPOSSÍVEL ACONTECER

É impossível acontecer, porque o elefante é grande demais para passar por um buraco tão pequeno.

5. A TURMA IRÁ AO PARQUINHO HOJE.

( ) ACONTECERÁ COM CERTEZA

( ) TALVEZ ACONTEÇA

( ) É IMPOSSÍVEL ACONTECER

Talvez aconteça, pois isso depende do que foi combinado com a turma.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

6. NO HORÁRIO DO LANCHE, VAI CHOVER SANDUÍCHE.

( ) ACONTECERÁ COM CERTEZA

( ) TALVEZ ACONTEÇA

( ) É IMPOSSÍVEL ACONTECER

É impossível acontecer, porque não chove sanduíche.

7. MINHA AVÓ FAZ ANIVERSÁRIO AMANHÃ.

( ) ACONTECERÁ COM CERTEZA

( ) TALVEZ ACONTEÇA

( ) É IMPOSSÍVEL ACONTECER

Acontecerá com certeza para uns, e é impossível acontecer para outros.

8. QUANDO AMANHECER, HAVERÁ DOIS SÓIS NO CÉU.

( ) ACONTECERÁ COM CERTEZA

( ) TALVEZ ACONTEÇA

( ) É IMPOSSÍVEL ACONTECER

É impossível acontecer, pois a Terra não tem dois sóis.

9. HOJE À NOITE VEREMOS VÁRIAS ESTRELAS NO CÉU.

( ) ACONTECERÁ COM CERTEZA

( ) TALVEZ ACONTEÇA

( ) É IMPOSSÍVEL ACONTECER

Talvez aconteça, se o céu estiver limpo para vermos as estrelas.

10. AS PESSOAS NÃO PRECISAM DE PORTAS PARA ATRAVESSAR AS PAREDES.

( ) ACONTECERÁ COM CERTEZA

( ) TALVEZ ACONTEÇA

( ) É IMPOSSÍVEL ACONTECER

É impossível acontecer, pois não conseguimos atravessar paredes.

Depois de respondidas as dez situações propostas, pedir a dez alunos que leiam em voz alta, um de cada vez, uma situação e digam a resposta que escolheram. Ao final de cada situação e resposta lidas, perguntar à turma se alguém discorda de alguma resposta. Caso

haja discordâncias, explicar o motivo, de maneira parecida com a apresentada nas respostas anteriores

Como tarefa para a próxima aula, solicitar aos alunos que assistam a um filme ou leiam um livro sobre ficção científica – por exemplo, sobre viagens espaciais, viagens no tempo, pessoas com superpoderes etc.

Mostrar aos alunos algumas histórias de ficção científica presentes no programa Conta para mim. Essas histórias estão registradas em áudio e podem ser acessadas no site indicado na seção Sugestões

Aula 4

O objetivo desta aula é associar a classificação de eventos a obras de ficção científica Para isso, inicialmente, retomar a tarefa proposta na aula anterior. Convidar os alunos a comentarem sobre o filme ou o livro que escolheram, trazendo elementos gerais dos enredos.

Em seguida, pedir aos alunos que pensem em cenas do filme ou trechos do livro que representam eventos que:

• aconteceram ou acontecerão com certeza;

• que talvez possam acontecer;

• que são impossíveis de acontecer na realidade.

Destinar 15 minutos para que os alunos façam esse registro. Em seguida, escolher alguns deles para relatarem os trechos escolhidos ou as cenas e explicarem por que deram determinada classificação.

Após essa discussão, abrir o debate para a turma sobre as situações presentes em obras de ficção científica. Esse tipo de debate é importante para que os alunos reconheçam essas situações, desenvolvam a noção do que é real, do que é possível e do que é fantasia, e percebam que existe grande liberdade de criação nas obras audiovisuais e na literatura. Por fim, solicitar aos alunos que façam um desenho que ilustre algum evento do filme ou do livro que escolheram que é impossível de acontecer na realidade.

Aula 5

O objetivo desta aula é iniciar o processo de realização de uma pesquisa estatística. Para isso, dividir a turma em grupos de cinco alunos e pedir que elaborem uma proposta de pesquisa a ser feita com os colegas da turma – por exemplo, qual é a comida, a brincadeira ou o esporte preferido etc. Solicitar que, em cada categoria, estipulem quatro opções, para que a pesquisa não seja longa demais. Se o tema escolhido for comida preferida, por exemplo, podem ser apresentadas opções de escolha como carne, feijão, verdura, fruta, entre outras.

Estipular um tempo para os grupos escolherem o tema da pesquisa. Em seguida, pedir que um grupo de cada vez vá à frente da sala de aula, apresente o tema da pesquisa e diga quais são as 4 opções de resposta. Anotar na lousa essas informações, para que todos possam vê-la. O grupo passa, então, a perguntar aos colegas, ordenadamente, qual é a preferência deles naquela categoria escolhida, e vai anotando as respostas no caderno. Em seguida, os próprios alunos do grupo escolhem sua preferência e a anotam.

A anotação das respostas pelos alunos pode ser feita por meio do método que preferirem: fazendo um risquinho para cada voto ao lado das opções escolhidas; com uma sequência numérica; com bolinhas etc. No exemplo apresentado anteriormente, os alunos podem fazer a anotação a seguir.

QUAL É A SUA COMIDA PREFERIDA?

CARNE | | | | | | | | | |

FEIJÃO | | | | |

VERDURA | | | |

FRUTA | | | | | |

Se necessário, orientar algumas possíveis anotações ou, se preferir, apresentar um exemplo.

Após os alunos anotarem as informações, apresentar uma proposta de pesquisa. Essa pesquisa será importante para as próximas aulas.

Após apresentar aos alunos a pesquisa a ser realizada, anotar os resultados da pesquisa no quadro. A seguir, há um possível exemplo de pesquisa e de anotação

QUAL É O SEU ESTILO DE MÚSICA FAVORITO?

POP | | | | | | |

ROCK | | | | | | | | |

SERTANEJO | | | | |

HIP HOP | | | |

Finalizar a aula solicitando aos alunos que guardem as anotações realizadas.

Aula 6

O objetivo desta aula é introduzir a tabela como uma maneira de representar informações. Para isso, organizar os alunos nos mesmos grupos da aula anterior e solicitar que resgatem as informações anotadas. Dar um tempo para que eles se organizem.

Em seguida, retomar com eles a pesquisa feita, apresentando, novamente, o esquema a seguir.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

QUAL É O SEU ESTILO DE MÚSICA FAVORITO?

POP | | |

ROCK

SERTANEJO | | | | |

HIP HOP | | | |

A seguir, perguntar aos alunos qual é a quantidade de alunos que possuem pop como estilo de música favorito. Espera-se que eles respondam 7 alunos.

Em seguida, fazer isso para os demais estilos musicais. Espera-se que os alunos respondam: rock= 9 alunos; sertanejo = 5 alunos; hiphop= 4 alunos.

Registrar os resultados das contagens na lousa, conforme a distribuição a seguir:

Qual é o seu estilo de música favorito?

• Pop: 7 alunos

• Rock : 9 alunos

• Sertanejo: 5 alunos

• Hiphop: 4 alunos

Após registrar essa distribuição, comentar que a tabela é um recurso eficaz para representar dados de uma pesquisa como essa. Em seguida, propor na lousa o seguinte modelo de tabela e preenchê-la com a turma ESTILO DE MÚSICA FAVORITO DOS ALUNOS

ESTILO QUANTIDADE DE ALUNOS

POP 7

ROCK 9

SERTANEJO 5

HIP HOP 4

Ao preencher a tabela com os alunos, compor com eles o título e a fonte.

Por fim, solicitar aos grupos que tentem preencher uma tabela de acordo com esse modelo. Nesse momento, acompanhar as discussões e intervir, de maneira que eles associem a sua pesquisa com a que realizaram em grupo.

Aula 7

O objetivo desta aula é introduzir o trabalho com gráfico de colunas como um recurso para representar informações. Para isso, organizar a turma nos mesmos grupos das aulas

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

FONTE: PESQUISA DO PROFESSOR.

anteriores e retomar a temática da pesquisa desenvolvida pelo professor. Com isso, apresentar novamente o esquema para contagem de respostas e a tabela elaborada na aula anterior.

QUAL É O SEU ESTILO DE MÚSICA FAVORITO?

POP | | | | | | |

ROCK | | | | | | | | |

SERTANEJO | | | | |

HIP HOP | | | |

ESTILO DE MÚSICA FAVORITO DOS ALUNOS

ESTILO QUANTIDADE DE ALUNOS

POP 7

ROCK 9

SERTANEJO 5

HIP HOP 4

Em seguida, comentar com os alunos que existe outro recurso para representar essas informações chamado gráfico de colunas. Para montar o gráfico de colunas com os alunos, desenhar o seguinte esquema na lousa.

Comentar com os alunos que o gráfico será composto a partir desse "molde". Em seguida, preencher com os alunos algumas informações da pesquisa, conforme a imagem a seguir.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

FONTE: PESQUISA DO PROFESSOR.

FONTE: PESQUISA DO PROFESSOR

Essas informações precisam ser preenchidas com cautela e paciência. Os alunos devem associar essas informações com o esquema e com a tabela elaborados nas aulas anteriores. Comentar que para terminar a composição do gráfico de colunas, basta pintar a quantidade de retângulos relativa a cada estilo. Nesse momento, recorrer às informações da tabela e pintar as quantidades relativas a cada estilo, explicitando a versão final do gráfico.

FONTE: PESQUISA DO PROFESSOR

Por fim, propor aos grupos que componham um gráfico de barras da pesquisa realizada por eles, como no exemplo da pesquisa do professor. Para isso, disponibilizar um "molde" impresso para cada grupo, conforme a figura a seguir.

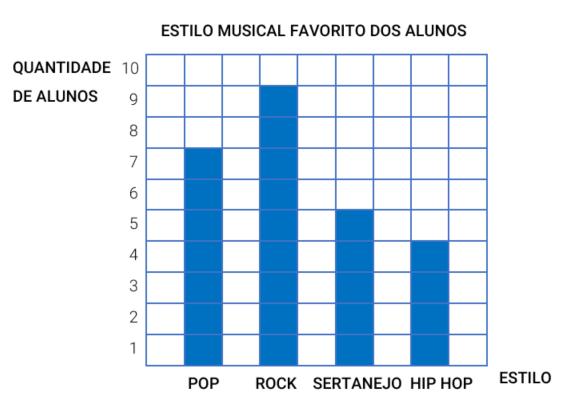
Caso algum grupo tenha a quantidade de alguma categoria maior que 10, adaptar esse "molde" aumentando-o. Se julgar complexa a ideia de os alunos preencherem as informações da pesquisa, trazê-las já preenchidas no molde e pedir a eles que apenas pintem os retângulos.

Nesse momento, conforme os alunos forem compondo os gráficos, acompanhar as discussões e realizar as intervenções necessárias

Ao final, recolher todas as produções de cada grupo para a próxima aula.

Aula 8

O objetivo desta aula é apresentar os resultados de uma pesquisa estatística.

Antes da aula, compor para cada grupo um documento de texto com imagens dos esquemas, tabelas e gráficos de colunas desenvolvidos por eles.

Com o auxílio de um projetor multimídia, solicitar que grupo por grupo apresente os resultados obtidos da pesquisa e as representações (esquema, tabela e gráfico). Nesse momento, auxiliá-los em caso de dúvidas. Se preferir, eles podem apresentar os resultados das próprias mesas, enquanto as informações são mostradas no projetor.

Por fim, devolver as produções aos alunos e solicitar que colem os esquemas, gráficos de coluna e tabelas em uma cartolina, de maneira que possam ser expostas no mural da escola. Se julgar conveniente, imprimir as imagens das produções dos alunos em tamanho maior.

Sugestões

• BRASIL. Ministério da Educação. Conta pra mim. Brasília: Sealf, 2019. Disponível em: http://alfabetizacao.mec.gov.br/contapramim. Acesso em: 4 jan. 2022.

Relatórios e indicadores do acompanhamento da aprendizagem

O processo avaliativo exige do professor um olhar reflexivo permanente sobre o desenvolvimento da aprendizagem dos alunos e, consequentemente, sobre a sua própria prática pedagógica. Dessa forma, instrumentos de avaliação, como provas, testes, questionários, redações, trabalhos, seminários, entre outros, não devem ser encarados como instrumentos pontuais de avaliação, mas, sim, como ferramentas de coleta de indicadores que descrevem o desempenho dos alunos e possibilitam uma análise coletiva e individual dos avanços e dos pontos de melhoria da aprendizagem.

Os indicadores de aprendizagem devem auxiliar o professor no acompanhamento do desenvolvimento das aprendizagens dos alunos, apontando se os objetivos, as competências, as habilidades e os conteúdos previstos em seu plano de trabalho estão sendo alcançados ou se há necessidade de intervenção no processo de aprendizagem para que possam ser atingidos.

Esses indicadores de aprendizagem, isoladamente nada apontam, uma vez que os resultados são fruto da análise do professor com base em objetivos, competências e habilidades desenvolvidos em determinado contexto educacional. Assim, com o apoio da avaliação dos indicadores de aprendizagem, é necessário que sejam produzidos relatórios descritivos das análises, considerações e observações a respeito do processo de aprendizado e desenvolvimento dos alunos e de sua prática pedagógica em sala de aula.

Produção de relatórios

Os relatórios escolares são registros que devem ser realizados periodicamente (a cada bimestre, trimestre ou semestre) a respeito do desenvolvimento de diferentes aprendizagens dos alunos ao longo do processo de ensino-aprendizagem.

Dentro do processo de aprendizagem escolar, os relatórios, entre outras finalidades, deverão:

• Possibilitar ao educador compreender de forma significativa o processo de aprendizagem dos alunos, respeitando suas individualidades, particularidades e diferenças.

• Produzir informações e dados significativos sobre o processo de aprendizagem de modo a planejar intervenções pedagógicas com base em objetivos, conteúdos, competências e habilidades a serem desenvolvidos.

• Fornecer subsídios teóricos para as reuniões de conselho de classe para que professores, coordenadores pedagógicos e diretores da escola possam analisar o desempenho individual e coletivo dos alunos e, consequentemente, discutir formas,

ações, intervenções, estratégias e métodos de melhoria do processo de ensino-aprendizagem com base no Projeto Político Pedagógico da escola

• Realizar uma comunicação orientada, assertiva e planejada com pais ou responsáveis de modo a engajá-los no processo de aprendizagem, contribuindo desse modo para o desenvolvimento dos alunos e a efetividade do ensino.

• Proporcionar ao aluno o direito de acompanhar o próprio processo de aprendizagem, de modo a oportunizar a superação de suas dificuldades.

Apesar de não existir um modelo fixo de relatório a ser seguido, alguns pontos importantes podem ser considerados na elaboração desse material. O texto do relatório deverá ser escrito de forma clara, concisa e objetiva, de modo que o leitor o compreenda Devem ser registrados os conteúdos trabalhados e como foram avaliados, assim como todas as considerações julgadas pertinentes ao processo de ensino-aprendizagem É importante, também, descrever quais foram os encaminhamentos adotados em caso de dificuldade dos alunos.

Se possível, os relatórios devem ainda captar as diferentes dimensões envolvidas nas experiências dos alunos no grupo, ou seja, devem trazer aspectos relacionados a sentimentos, afetos, emoções, movimentos e cognição.

Os relatórios podem conter apresentações visuais e gráficas dos dados coletados, de modo a facilitar a compreensão das informações que estão sendo transmitidas. Pode-se elaborar um gráfico de barras comparando a distribuição percentual dos resultados quantitativos da aprendizagem dos alunos a respeito de competências gerais, de competências específicas e de habilidades em um período, como no exemplo a seguir

Fonte: Dados fictícios.

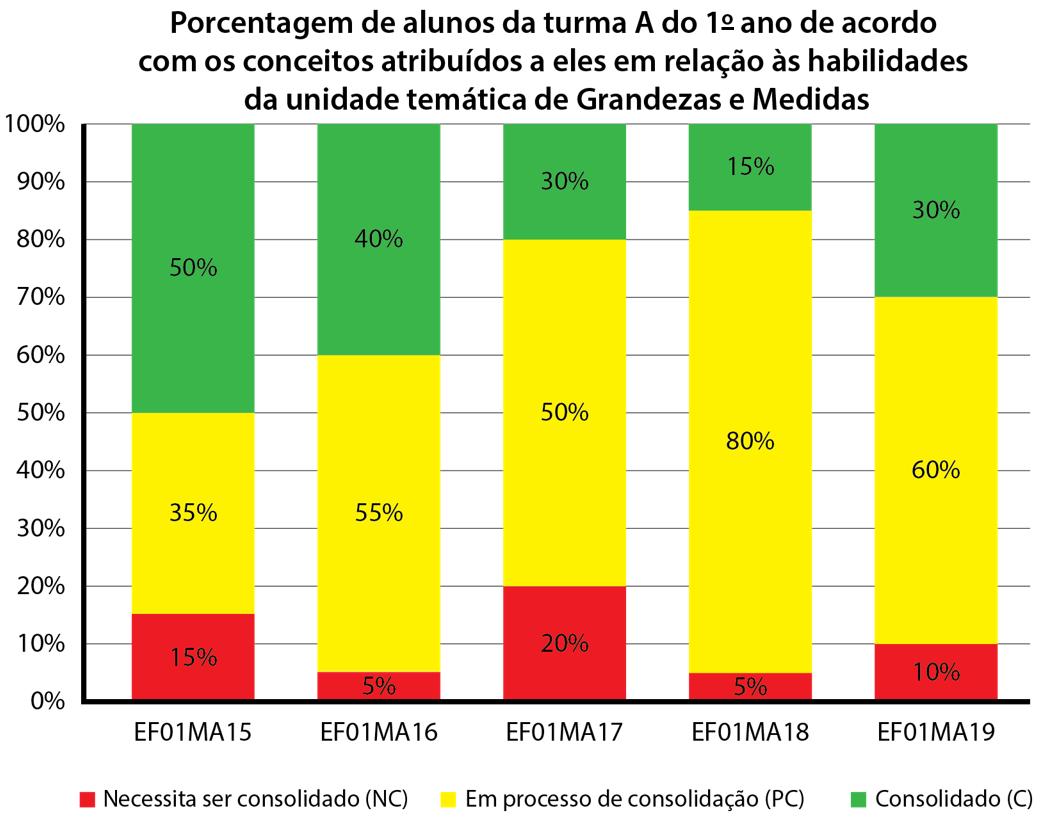
Gráficos e tabelas podem ser elaborados por meio de um editor de planilhas eletrônicas, como o LibreOffice, que é um software livre e gratuito, disponível em: https://pt-br.libreoffice.org/ (acesso em: 10 dez. 2021).

Indicadores do acompanhamento da aprendizagem

De modo geral, o termo "indicadores" é usado para apontar parâmetros que avaliam certa realidade em determinado intervalo de tempo. Um médico, por exemplo, examina vários indicadores antes de oferecer um diagnóstico a um paciente. Um economista, também, se utiliza de indicadores para analisar se a inflação de um país aumentou ou diminuiu. Já no contexto escolar, os indicadores do acompanhamento da aprendizagem têm como objetivo mapear os diferentes níveis de desenvolvimento das aprendizagens dos alunos.

Uma vez que o processo de aprendizagem ocorre simultânea e interativamente nas dimensões cognitiva, afetiva e psicomotora, os indicadores de aprendizagem a serem observados e avaliados deverão abarcar aspectos tanto quantitativos quanto qualitativos do processo de aprendizagem dos alunos, garantindo, assim, uma visão ampla e significativa desse processo.

Os aspectos qualitativos dos indicadores de aprendizagem, geralmente, são aqueles ligados às competências gerais e socioemocionais que expressam a voz, as percepções, as crenças, os sentimentos, os pensamentos, as emoções, as atitudes e os modos de agir dos educandos. São eles que possibilitam ao educador avaliar se os alunos alcançaram a construção e a formação de atitudes e valores, como autonomia, responsabilidade, empatia, resiliência, determinação, criticidade e capacidade de ouvir, ser ouvido e dialogar.

Já os aspectos quantitativos dos indicadores de aprendizagem são aqueles que descrevem quantidades ou percentuais da consecução do processo de ensino-aprendizagem. São esses aspectos quantitativos que permitem ao professor fazer uma avaliação do quanto os alunos estão avançando em relação aos objetivos, competências, habilidades e conteúdos, gerais ou específicos, de determinada área do conhecimento, previstos em seu plano de trabalho.

São apresentados, a seguir, quatro modelos de fichas com sugestões de indicadores que podem ser obtidos por meio do processo avaliativo que julgar mais conveniente Esses modelos podem ser impressos e preenchidos com os dados dos alunos ou da turma

O primeiro modelo é o de Ficha de avaliação diagnóstica Nela, estão presentes alguns indicadores que poderão servir de subsídio para que seja reconhecido o domínio dos alunos a respeito de alguns conteúdos, no início do ano letivo.

O segundo modelo é o de Ficha de acompanhamento das aprendizagens, na qual são apresentadas as habilidades da BNCC indicadas para o ano de escolaridade, as Competências específicas de Matemática para o Ensino Fundamental, as Competências gerais da Educação Básica e os componentes essenciais para a alfabetização. Nela, há uma coluna para preenchimento de observações mais detalhadas

O terceiro modelo é o de Ficha de verificação de resultados, em que estão indicados, a cada ano de escolaridade, alguns objetivos de aprendizagem categorizados como focais, por influenciarem de modo mais evidente o desenvolvimento vinculado às Competências gerais e às Competências específicas da área de Matemática para o Ensino Fundamental.

Por fim, considerando a ideia de educação integral, também é preciso avaliar o desenvolvimento das dimensões sociais e emocionais dos alunos. Para tanto, o quarto modelo é o de Ficha de acompanhamento do desenvolvimento de competências socioemocionais, que apresenta indicadores para que seja apontada a frequência com que essas competências são reconhecidas nas atitudes dos alunos

Os modelos de fichas aqui apresentados são apenas proposições para apoiar o processo de ensino-aprendizagem. É fundamental que o trabalho pedagógico seja planejado com intencionalidade para explorar todos os potenciais de aprendizagem e garantir as condições de desenvolvimento pleno e integral de cada aluno. Essa tarefa requer a participação de toda a comunidade escolar, envolvendo professores, gestores e os responsáveis pelos alunos

RECURSO EDUCACIONAL DIGITAL

Ficha de avaliação diagnóstica

Professor:

Turma:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de avaliação diagnóstica (Numeracia)

Números e quantidades Resolução de problemas verbais

Aluno Identificar quantidades por meio de diferentes formas de representação (contagens, desenhos, símbolos, escrita de números, organização de gráficos básicos etc.).

Registrar quantidades por meio de diferentes formas de representação (contagens, desenhos, símbolos, escrita de números, organização de gráficos básicos etc.).

Identificar, nomear adequadamente e comparar as propriedades dos objetos, estabelecendo relações entre eles.

Utilizar vocabulário relativo às noções de grandeza (maior, menor, igual etc.) e de medidas (comprido, curto, grosso, fino) como meio de comunicação de suas experiências.

Utilizar vocabulário relativo às noções de espaço (dentro e fora) como meio de comunicação de suas experiências.

Utilizar unidades de medida (dia e noite, dias, semanas, meses e ano) e de noções de tempo (presente, passado e futuro; antes, agora e depois), para responder a necessidades e questões do cotidiano.

Argumentar e relatar fatos oralmente, em sequência temporal e causal, organizando e adequando sua fala ao contexto em que é produzida.

Reconhecer ideias de regularidade em sequências para generalizar a regra de formação de padrões simples.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de acompanhamento das aprendizagens

Professor(a):

Turma:

Aluno:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de acompanhamento das aprendizagens (Matemática)

Habilidades C PC NC Observações

(EF01MA01) Utilizar números naturais como indicador de quantidade ou de ordem em diferentes situações cotidianas e reconhecer situações em que os números não indicam contagem nem ordem, mas sim código de identificação.

(EF01MA02) Contar de maneira exata ou aproximada, utilizando diferentes estratégias como o pareamento e outros agrupamentos.

(EF01MA03) Estimar e comparar quantidades de objetos de dois conjuntos (em torno de 20 elementos), por estimativa e/ou por correspondência (um a um, dois a dois) para indicar "tem mais", "tem menos" ou "tem a mesma quantidade".

(EF01MA04) Contar a quantidade de objetos de coleções até 100 unidades e apresentar o resultado por registros verbais e simbólicos, em situações de seu interesse, como jogos, brincadeiras, materiais da sala de aula, entre outros.

(EF01MA05) Comparar números naturais de até duas ordens em situações cotidianas, com e sem suporte da reta numérica.

(EF01MA06) Construir fatos básicos da adição e utilizá-los em procedimentos de cálculo para resolver problemas.

(EF01MA07) Compor e decompor número de até duas ordens, por meio de diferentes adições, com o suporte de material manipulável, contribuindo para a compreensão de características do sistema de numeração decimal e o desenvolvimento de estratégias de cálculo.

(EF01MA08) Resolver e elaborar problemas de adição e de subtração, envolvendo números de até dois algarismos, com os significados de juntar, acrescentar, separar e retirar, com o suporte de imagens e/ou material manipulável, utilizando estratégias e formas de registro pessoais.

(EF01MA09) Organizar e ordenar objetos familiares ou representações por figuras, por meio de atributos, tais como cor, forma e medida.

(EF01MA10) Descrever, após o reconhecimento e a explicitação de um padrão (ou regularidade), os elementos ausentes em sequências recursivas de números naturais, objetos ou figuras.

(EF01MA11) Descrever a localização de pessoas e de objetos no espaço em relação à sua própria posição, utilizando termos como à direita, à esquerda, em frente, atrás.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial

(CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

(EF01MA12) Descrever a localização de pessoas e de objetos no espaço segundo um dado ponto de referência, compreendendo que, para a utilização de termos que se referem à posição, como direita, esquerda, em cima, em baixo, é necessário explicitar-se o referencial.

(EF01MA13) Relacionar figuras geométricas espaciais (cones, cilindros, esferas e blocos retangulares) a objetos familiares do mundo físico.

(EF01MA14) Identificar e nomear figuras planas (círculo, quadrado, retângulo e triângulo) em desenhos apresentados em diferentes disposições ou em contornos de faces de sólidos geométricos.

(EF01MA15) Comparar comprimentos, capacidades ou massas, utilizando termos como mais alto, mais baixo, mais comprido, mais curto, mais grosso, mais fino, mais largo, mais pesado, mais leve, cabe mais, cabe menos, entre outros, para ordenar objetos de uso cotidiano.

(EF01MA16) Relatar em linguagem verbal ou não verbal sequência de acontecimentos relativos a um dia, utilizando, quando possível, os horários dos eventos.

(EF01MA17) Reconhecer e relacionar períodos do dia, dias da semana e meses do ano, utilizando calendário, quando necessário.

(EF01MA18) Produzir a escrita de uma data, apresentando o dia, o mês e o ano, e indicar o dia da semana de uma data, consultando calendários.

(EF01MA19) Reconhecer e relacionar valores de moedas e cédulas do sistema monetário brasileiro para resolver situações simples do cotidiano do estudante.

(EF01MA20) Classificar eventos envolvendo o acaso, tais como “acontecerá com certeza” , “talvez aconteça” e “é impossível acontecer” , em situações do cotidiano.

(EF01MA21) Ler dados expressos em tabelas e em gráficos de colunas simples.

(EF01MA22) Realizar pesquisa, envolvendo até duas variáveis categóricas de seu interesse e universo de até 30 elementos, e organizar dados por meio de representações pessoais.

Competências específicas de Matemática para o Ensino Fundamental C PC NC Observações

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Competências gerais da Educação Básica C PC NC Observações

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Componentes essenciais para a alfabetização

Consciência fonológica e fonêmica

Conhecimento alfabético

Fluência em leitura oral

Desenvolvimento de vocabulário

Compreensão de textos

Produção de escrita

Ficha de verificação de resultados

Professor:

Turma:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de verificação de resultados

Principais objetivos de aprendizagem

Aluno Reconhecer e descrever a localização de objetos e pessoas no espaço com base em um ponto de referência próprio e a partir de outro ponto de referência.

Acrescentar elementos em sequências ordenadas de acordo com regras preestabelecidas.

Correlacionar objetos do dia a dia a figuras geométricas espaciais

Contar e reconhecer os números naturais até 100.

Adicionar e subtrair quantidade de objetos e de pessoas.

Identificar e comparar grandezas de comprimento, massa, capacidade e tempo, usando termos do dia a dia do aluno, como maior, menor, mais pesado, mais leve, quanto cabe, entre outros.

Identificar e classificar acontecimentos cotidianos que dependem do acaso

Identificar, ler e interpretar dados em tabelas e gráficos de colunas simples.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Professor(a):

Turma:

Aluno:

Competências socioemocionais Sempre Frequentemente Raramente Nunca

Determinação

Foco

Organização

Persistência

Responsabilidade

Empatia

Respeito

Confiança

Tolerância ao estresse

Autoconfiança

Tolerância à frustração

Iniciativa social

Assertividade

Entusiasmo

Curiosidade para aprender

Imaginação criativa

Interesse artístico

Material disponibilizado em licença aberta do tipo Creative Commons – Atribui çã o n ã o comercial (CC BY NC – 4.0 International). Permitida a cria çã o de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam lice nciadas sob os mesmos

Catálogo dos audiovisuais

Nesta seção, são disponibilizados detalhamentos, como objetivos de aprendizagem e conteúdos abordados, entre outros aspectos, acerca de cada um dos audiovisuais que compõem a coletânea desta coleção. Também, para cada audiovisual, são descritas sugestões de utilização e são sugeridas propostas de atividades, a fim de apoiar pedagogicamente o uso desses recursos digitais audiovisuais. Tais informações visam trazer insumos para favorecer o planejamento de aplicação deles de acordo com a realidade da comunidade escolar e da turma com que forem trabalhados.

Audiovisuais da coletânea

Relação de audiovisuais da coletânea

Título do audiovisual Descrição Objetivos de aprendizagem Conteúdos abordados

O aniversário de Luma Neste vídeo, serão apresentadas as funções dos números, situações de contagem e de comparação de números até 100.

• Identificar a função de um número.

• Realizar contagem de 1 a 100.

• Realizar estimativa.

• Comparar dois números identificando o maior e o menor.

• Função dos números (quantidade, ordem e código).

• Contagem até 100.

• Comparação de números.

• Representação de números com material dourado.

Maneiras de medir o tempo

Este recurso educacional apresenta ideias introdutórias sobre medidas de tempo, abrangendo a importância da medição do tempo e os instrumentos utilizados ao longo da história.

Katherine Johnson Este vídeo apresenta uma breve história da norte-americana Katherine Johnson que, com sua extraordinária habilidade de contar, se tornou uma importante matemática da NASA. O vídeo traz, também, pontos de reflexão sobre a

• Relatar de maneira verbal ou não verbal acontecimentos do dia

• Reconhecer períodos do dia (manhã, tarde, noite)

• Ler e escrever horas em um relógio digital.

• Identificar os dias da semana e os meses do ano.

• Usar calendário para identificar e escrever datas.

• Produzir a escrita de uma data

• Consultar calendários para indicar o dia da semana de uma data

• Compreender o papel da mulher na área das Ciências Exatas

• Medidas de tempo.

• Leitura e escrita de horas.

• Utilização de calendário.

• Medidas de tempo

• Utilização de calendário.

• Escrita de datas.

substituição do trabalho humano por trabalho com computadores ou máquinas e aborda questões transversais como preconceito racial, reconhecimento do papel das mulheres na área das ciências exatas e a necessidade de fazer questionamentos na luta por um mundo mais justo

Os animais do zoológico Este recurso educacional explora o contexto de um passeio no zoológico para estimular a observação de diferenças entre diversos animais, de modo que se possa fazer comparações de algumas de suas características, como tamanho ou ambiente em que ficam.

Meu lugar: moradia e escola

Neste vídeo, os alunos serão convidados a refletirem sobre os lugares de vivência, os objetos que nele estão e a rotina que cada um tem nesses lugares. Em especial, serão trabalhadas a residência do aluno e a escola. Os alunos, também, serão convidados a participarem de outras reflexões como: quais atividades fazem em casa e quais fazem na escola, quem são as pessoas que trabalham na escola além do professor, quais são os espaços da escola e o que se faz em cada um deles.

• Refletir sobre a associação homem-máquina e sobre suas relações de trabalho

• Refletir sobre as barreiras impostas pelo preconceito e discriminação racial no desenvolvimento profissional e pessoal de um indivíduo.

• Comparar comprimentos

• Comparar capacidades.

• Utilizar termos como "mais alto", "mais baixo, "mais comprido", "mais curto", "mais cheio", "mais vazio", entre outros.

• Medidas de comprimento e capacidade.

• Comparação de comprimento e capacidade utilizando medidas não convencionais.

• Identificar características próprias de diferentes lugares de vivência dos alunos.

• Descrever seus lugares de vivência e elementos desses lugares, usando termos como em cima, embaixo, entre, ao lado, atrás, na frente, entre outros.

• Refletir sobre a escola como espaço de convivência.

• Conhecer diferentes tipos de moradia e escola.

• Explorar situações sobre localização de pessoas e de objetos no espaço segundo um ponto de referência.

• Noções de localização no espaço.

• Noções de rotina.

• Noções de tempo e horário.

Orientações para o uso dos audiovisuais

O aniversário de Luma

Este audiovisual pode ser apresentado de maneira introdutória ao estudo do campo numérico até 100 ou como uma retomada desse conteúdo. Nele, serão exploradas, inicialmente, algumas situações em que os números são utilizados para contagem por meio de um contexto familiar ao aluno, que é uma festa de aniversário. Serão apresentadas,

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

também, a decomposição de alguns números naturais em dezenas e unidades, utilizando o material dourado como apoio.

Caso o vídeo seja utilizado como introdução ao conteúdo, sugere-se, antes de exibi-lo, propor aos alunos que relatem oralmente algumas situações do dia a dia deles em que é necessário realizar contagem. Sugere-se, também, pausar o vídeo logo após a introdução do conceito dezena e perguntar aos alunos quantas unidades há em uma dezena para verificar se compreenderam o que foi explicado. Caso eles não tenham compreendido, retomar na lousa a explicação proposta no vídeo, uma vez que o conceito dezena será utilizado nos exemplos seguintes.

Fazer outra pausa logo após a apresentação da decomposição do número 12, com o apoio do material dourado. Pedir aos alunos que expliquem por que 12 equivale a 1 dezena e 2 unidades. Espera-se que eles percebam que, conforme apresentado no vídeo, se deve ao fato de 12 ser formado por 10 unidades (1 barra) e 2 dezenas (2 cubinhos). A compreensão dessa primeira decomposição será importante para o aluno entender os próximos exemplos.

Se a opção for apresentar o vídeo como retomada, sugere-se exibir o audiovisual para a turma e promover uma conversa sobre a relação entre as situações apresentadas e os conteúdos que eles estudaram. Ao final da apresentação do vídeo, sugere-se perguntar aos alunos sobre outras situações do dia a dia que envolvem contagem. Em seguida, escrever alguns números na lousa para os alunos fazerem a leitura e a decomposição.

Após a exibição do vídeo, sugere-se a resolução das atividades propostas a seguir ou de atividades semelhantes.

Sugestões de atividades

1. Marque um X na resposta correta de acordo com o vídeo a qual você assistiu.

a) Luma estava comemorando seu aniversário de quantos anos?

( ) 4 ( ) 5 ( ) 6

5 anos

b) Quantos irmãos Luma tem?

( ) 4 ( ) 2

c) Qual é o número da casa onde Luma mora?

Nenhum

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

2. Responda:

a) O seu nome é formado por quantas letras?

A resposta depende do nome do aluno

b) Quantos irmãos você tem?

A resposta depende da quantidade de irmãos que o aluno tem

c) Quantas pessoas moram na sua casa?

A resposta depende da quantidade de pessoas que moram com o aluno.

d) Na sua turma, há mais de 10 alunos ou menos?

Mais de 10 alunos.

3. Contorne 2 dezenas de maçãs. EDITORIA

O aluno deve contornar 20 maçãs.

4 Complete as lacunas conforme os exemplos.

a) 21 = 20 + 1

b) 33 = 30 + 3

c) 46 = 40 + _____ 6

d) 55 = 50 + _____ 5

e) 61 = _____ + 1

f) 84 = _____ + 4

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

DE ARTE

Maneiras de medir o tempo

Este recurso educacional pode ser apresentado de maneira introdutória ao estudo sobre medidas de tempo. Nele, é explorada a importância da medição do tempo e os instrumentos utilizados ao longo da história. Depois, é apresentado o conceito de tempo cronológico e os instrumentos que medem o tempo cronológico ressaltando que, apesar de relógios e calendários serem comuns em nosso dia a dia, alguns povos indígenas utilizam como referência a natureza para medir o tempo e organizar suas atividades. Se possível, levar para sala de aula um calendário com todos os meses do ano e um relógio digital para serem mostrados aos alunos durante a aula.

Caso este recurso educacional seja utilizado como introdução ao estudo de medidas de tempo, sugere-se iniciar a aula com a seguinte pergunta: por que medimos o tempo? Após as respostas dos alunos sobre essa pergunta, pedir a eles que relatem oralmente como eles combinariam uma atividade com um colega, o que fariam para saber o tempo de início e de fim de uma aula ou como eles explicariam quando nasceram se não existissem relógios ou calendários (esses relatos possibilitam aos alunos refletirem sobre a importância da medição do tempo em nosso dia a dia). Após as reflexões dos alunos, iniciar o áudio.

Depois de apresentar o áudio, retomar a pergunta inicial: por que medimos o tempo? Pedir aos alunos que a respondam com base no que aprenderam com o recurso educacional. Nesse momento, outras perguntas podem ser feitas, por exemplo: como as pessoas mediam o tempo antigamente? Como medimos o tempo hoje em dia? Em relação à segunda pergunta, os alunos podem respondê-la tanto mencionando as divisões de tempo que eles conhecem quanto os instrumentos utilizados. É importante que eles compreendam que o tempo cronológico pode ser dividido de diferentes formas (hora, minuto, dia, semana, mês, ano etc.).

Em seguida, perguntar aos alunos sobre a rotina deles (por exemplo, as atividades realizadas no período da manhã, da tarde e da noite, e quanto tempo duram essas atividades). Depois, propor a resolução das atividades a seguir ou de atividades semelhantes.

Sugestões de atividades

1. Registre com desenho a atividade que você mais gosta de fazer em cada período do dia.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Resposta pessoal.

2. Registre em cada relógio digital a hora em que sua aula na escola começa e a hora em que ela termina.

EDITORIA DE ARTE

Resposta pessoal.

3. Complete o calendário com os dias e o nome do mês em que estamos. Em seguida, responda às questões.

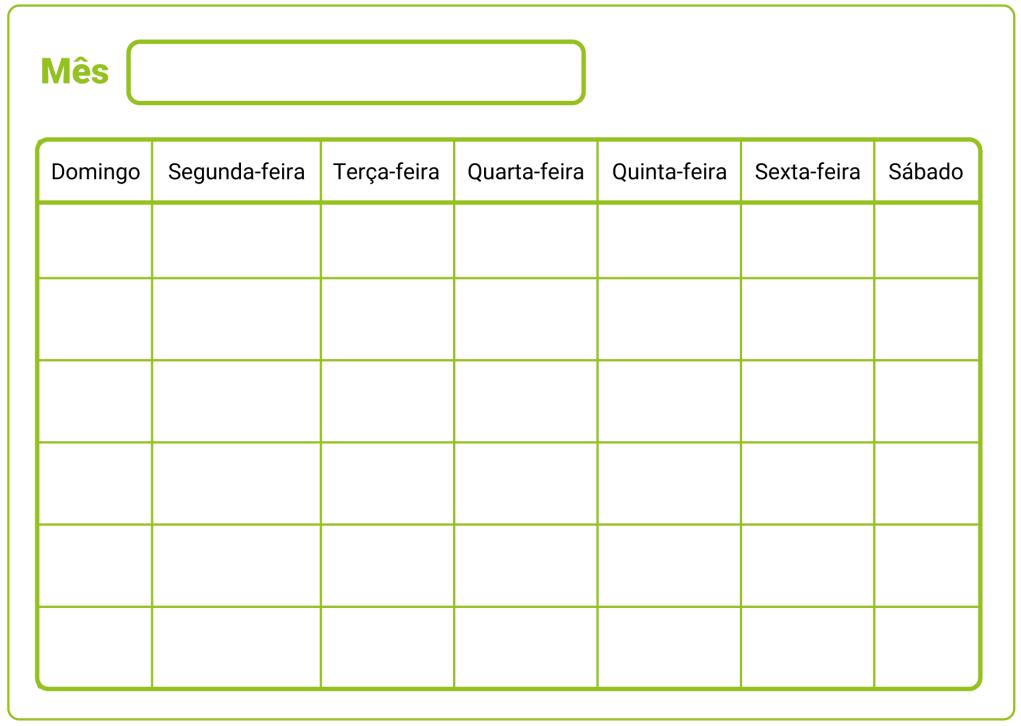
EDITORIA DE ARTE

a) Em que mês estamos?

A resposta dependerá do mês em que a atividade for realizada.

b) Que dia da semana é hoje?

A resposta dependerá do dia da semana em que a atividade for realizada.

c) Que dia do mês é hoje?

A resposta dependerá do dia do mês em que a atividade for realizada.

d) Quantos dias têm esse mês?

A resposta dependerá do mês em que a atividade for realizada.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

e) Qual é o primeiro dia da semana?

Domingo.

f) Qual é o último dia da semana?

Sábado.

g) Quantos dias têm em uma semana?

Sete dias

Katherine Johnson

Este audiovisual possibilita trabalhar a produção de escrita de uma data e a utilização de calendário para indicar o dia da semana de uma data. Além disso, abrange pontos de reflexão sobre a substituição do trabalho humano por trabalho com computadores ou máquinas. O conteúdo do vídeo também atinge questões transversais como preconceito racial, reconhecimento do papel das mulheres na área das ciências exatas e a necessidade de fazer questionamentos a fim de promover um mundo mais justo.

Para iniciar a aula, antes de exibir o vídeo, perguntar aos alunos se eles costumam utilizar o calendário para saber o dia da semana que determinada data ocorreu ou ocorrerá Depois, comentar que eles vão assistir a um vídeo que trata da história de Katherine Johnson, uma mulher que possuía extraordinária habilidade de contar, e que, por isso, se tornou uma importante matemática que trabalhou para a NASA (National Aeronautics and Space Administration). É importante, nesse momento, escrever o nome Katherine Johnson na lousa e comentar com os alunos que, durante o vídeo, algumas datas serão mencionadas.

Após o término do vídeo, organizar uma roda de conversa e perguntar aos alunos: o que vocês acharam do vídeo? Deixar que se expressem livremente e, em seguida, direcionar o debate a respeito de questões apresentadas por eles. Pode-se perguntar a eles se acreditam que um dia as máquinas poderão superar os seres humanos na habilidade de pensar criticamente. Perguntar se acham justo que algumas pessoas recebam um salário menor que outras mesmo realizando o mesmo trabalho.

Após a exibição do vídeo e das discussões levantadas pelos alunos, sugere-se a resolução das atividades propostas a seguir ou de atividades semelhantes.

Sugestões de atividades

1. Marque um X na resposta correta de acordo com o vídeo a que você assistiu.

a) Onde Katherine Johnson nasceu?

( ) Inglaterra ( ) Canadá ( ) Estados Unidos

Estados Unidos

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

b) Com quantos anos Katherine Johnson entrou na faculdade?

( ) 15 ( ) 20 ( ) 30 15

c) Quantos anos Katherine Johnson fez em 2018?

( ) 40 ( ) 70 ( ) 100 100

2 Escreva as datas destacadas utilizando as notações de marcação de datas

a) Katherine Johnson nasceu em 26 de agosto de 1918 26/8/1918

b) Katherine Johnson faleceu aos 101 anos, no dia 24 de fevereiro de 2020 24/2/2020

c) Em 21 de julho de 1969, o homem pisou na Lua pela primeira vez 21/7/1969

3 Analise o calendário do mês de agosto de 1918.

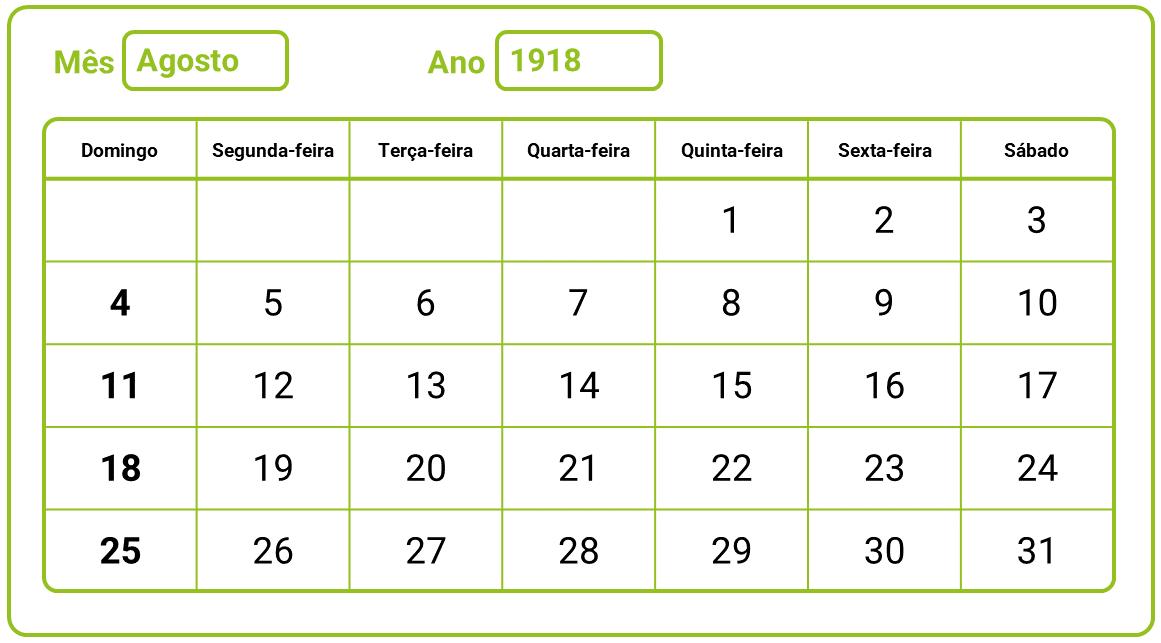
a) De acordo com o vídeo que você assistiu, indique no calendário de agosto de 1918 o dia que Katherine Johnson nasceu. O aluno deve contornar o dia 26.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

b) Qual foi o dia da semana que Katherine Johnson nasceu?

Segunda-feira.

c) Que dia da semana foi o primeiro dia de agosto de 1918?

Quinta-feira

d) Que dia da semana foi o último dia de agosto de 1918? Sábado.

Os animais do zoológico

Este recurso educacional pode ser apresentado de maneira introdutória ao estudo de noções de medidas. Nele, é explorado o contexto de um passeio no zoológico, situação que favorece a observação de diferenças entre diversos animais, de modo que se possa fazer comparação de algumas de suas características, como tamanho ou ambiente em que ficam.

Antes de iniciar o recurso educacional, perguntar aos alunos: vocês já foram ao zoológico? Estimule-os a compartilhar com os colegas as experiências que tiveram. Em seguida, fazer as seguintes perguntas à turma: qual animal vocês mais gostaram de ver no zoológico? Porquê? Qual é o animal preferido de vocês? Existe algum animal que vocês gostariam de ver e nunca viram? Depois, comentar que eles vão escutar um áudio sobre um passeio no zoológico.

Após a exibição do recurso educacional, escrever na lousa termos como "mais longe", "mais perto" "mais alto", "mais baixo", "mais curto", "mais comprido", entre outros. Depois, pedir aos alunos que deem exemplos de comparações, como:

• O elefante é mais alto que o macaco.

• A tartaruga é mais baixa que a girafa.

As situações podem se referir aos animais do zoológico, mas também expandir para outros contextos próximos dos alunos, como:

• A mesa do professor está mais perto que a porta da sala de aula.

• A biblioteca da escola está mais longe que a cantina da escola.

Estimular os alunos a citarem em voz alta tais exemplos. Comentar que não é necessário que eles se lembrem exatamente quais foram as situações apresentadas no recurso educacional, mas que eles podem se basear no que já conhecem de animais que já viram pessoalmente ou por imagens.

Após explorar com os alunos os exemplos apresentados, sugere-se a resolução das atividades propostas a seguir ou de atividades semelhantes.

Sugestões de atividades

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

1. Marque um X no animal que é mais alto

EDITORIA DE ARTE

Espera-se que os alunos marquem um X no segundo elefante.

2. Marque um X no animal que é mais baixo

EDITORIA DE ARTE

Espera-se que os alunos marquem um X no terceiro gato.

3. Marque um X nos dois animais que possuem o mesmo comprimento.

EDITORIA DE ARTE

Espera-se que os alunos marquem um X na primeira e na terceira imagens

4. Marque um X nas duas árvores que têm a mesma altura.

EDITORIA DE ARTE

Espera-se que os alunos marquem um X na segunda e na terceira imagens

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído cr édito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Meu lugar: moradia e escola

Neste vídeo, serão apresentados conceitos a respeito de moradia e locais de vivência. Antes de exibir o audiovisual, organizar uma roda de conversa e perguntar aos alunos: quais lugares vocês costumam frequentar? Já visitaram a residência de outras pessoas? Já visitaram outras escolas? Quais semelhanças e diferenças esses locais têm em relação à residência e à escola de vocês? Deixar que os alunos se expressem livremente.

Durante a exibição do vídeo, se julgar oportuno, realizar pausas nos momentos em que são feitas perguntas e propor aos alunos que reflitam individualmente sobre elas. Depois, pedir que compartilhem com os colegas o que pensaram para formular as respostas.

Após a exibição do vídeo, sugere-se a resolução das atividades propostas a seguir ou de atividades semelhantes.

Sugestões de atividades

1. Observe ao seu redor e identifique quem está sentado em cada carteira próximo à sua. No esquema a seguir, escreva seu nome na carteira cinza e o nome dos seus colegas nas carteiras conforme eles estão sentados.

EDITORIA DE ARTE

A resposta dependerá do local em que o aluno está sentado e dos colegas que estão sentados ao redor dele. Verificar qual estratégia os alunos, que estão sentados na primeira carteira, na última carteira ou nas carteiras laterais, estão utilizando. Espera-se que eles deixem as carteiras do esquema em branco ou que escrevam NINGUÉM.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

2. Complete cada frase com o nome de um colega.

a) _______________________ está sentado à minha direita.

b) _______________________ está sentado à minha esquerda.

c) está sentado à minha frente.

d) está sentado atrás de mim.

A resposta dependerá do local em que o aluno está sentado e dos colegas que estão sentados ao redor dele.

3. Pense na sua rotina diária e ordene as atividades de acordo com a ordem com a qual você as faz.

( ) Almoçar.

( ) Ir para a escola.

( ) Fazer tarefa.

( ) Brincar.

A resposta dependerá da rotina do aluno

4. No vídeo a que você assistiu, você aprendeu algumas palavras novas. Ligue cada palavra ao seu significado.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

BNCC

A Base Nacional Comum Curricular (BNCC), homologada em 2018, é um documento oficial e normativo sobre as aprendizagens (e suas progressões) da Educação Básica (Ensino Infantil, Ensino Fundamental e Ensino Médio). A BNCC estrutura as etapas de aprendizagens em competências, mais abrangentes, e habilidades, mais específicas; e, dessa forma, objetiva garantir a progressão das aprendizagens entre os diferentes anos/ciclos da Educação Básica

A BNCC tem como objetivo assegurar o direito de uma aprendizagem de qualidade a todos os alunos, buscando colaborar com a formação de uma sociedade mais justa, democrática e inclusiva. Seu caráter normativo colabora com esse objetivo, ao ser um documento que orienta a elaboração e a revisão de currículos, a formação inicial e continuada de professores e as avaliações e exames nacionais.

A seguir, são apresentadas na íntegra as Competências gerais da Educação Básica, as Competências específicas da área de Matemática e suas Tecnologias para o Ensino Fundamental e as cinco unidades temáticas com os respectivos objetos de conhecimento e habilidades para o 1º ano do Ensino Fundamental, que podem ser encontrados nas páginas 9, 10, 267, 278, 279, 280 e 281 da BNCC (BRASIL, 2018).

Competências gerais da Educação Básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Competências específicas de Matemática para o Ensino Fundamental

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Matemática

– 1º ano

Unidades temáticas Objetos de conhecimento Habilidades

Números Contagem de rotina Contagem ascendente e descendente (EF01MA01) Utilizar números naturais como indicador de quantidade ou de ordem em diferentes situações cotidianas e reconhecer situações em que os números

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações se jam licenciadas sob os mesmos parâmetros.

Reconhecimento de números no contexto diário: indicação de quantidades, indicação de ordem ou indicação de código para a organização de informações

Quantificação de elementos de uma coleção: estimativas, contagem um a um, pareamento ou outros agrupamentos e comparação

não indicam contagem nem ordem, mas sim código de identificação.

(EF01MA02) Contar de maneira exata ou aproximada, utilizando diferentes estratégias como o pareamento e outros agrupamentos.

(EF01MA03) Estimar e comparar quantidades de objetos de dois conjuntos (em torno de 20 elementos), por estimativa e/ou por correspondência (um a um, dois a dois) para indicar "tem mais", "tem menos" ou "tem a mesma quantidade".

Leitura, escrita e comparação de números naturais (até 100)

Reta numérica

(EF01MA04) Contar a quantidade de objetos de coleções até 100 unidades e apresentar o resultado por registros verbais e simbólicos, em situações de seu interesse, como jogos, brincadeiras, materiais da sala de aula, entre outros.

(EF01MA05) Comparar números naturais de até duas ordens em situações cotidianas, com e sem suporte da reta numérica.

Construção de fatos básicos da adição

Composição e decomposição de números naturais

(EF01MA06) Construir fatos básicos da adição e utilizá-los em procedimentos de cálculo para resolver problemas.

(EF01MA07) Compor e decompor número de até duas ordens, por meio de diferentes adições, com o suporte de material manipulável, contribuindo para a compreensão de características do sistema de numeração decimal e o desenvolvimento de estratégias de cálculo.

Problemas envolvendo diferentes significados da adição e da subtração (juntar, acrescentar, separar, retirar)

Álgebra Padrões figurais e numéricos: investigação de regularidades ou padrões em sequências

Sequências recursivas: observação de regras usadas utilizadas em seriações numéricas (mais 1, mais 2, menos 1, menos 2, por exemplo)

Geometria Localização de objetos e de pessoas no espaço, utilizando diversos pontos de referência e vocabulário apropriado

(EF01MA08) Resolver e elaborar problemas de adição e de subtração, envolvendo números de até dois algarismos, com os significados de juntar, acrescentar, separar e retirar, com o suporte de imagens e/ou material manipulável, utilizando estratégias e formas de registro pessoais.

(EF01MA09) Organizar e ordenar objetos familiares ou representações por figuras, por meio de atributos, tais como cor, forma e medida.

(EF01MA10) Descrever, após o reconhecimento e a explicitação de um padrão (ou regularidade), os elementos ausentes em sequências recursivas de números naturais, objetos ou figuras.

(EF01MA11) Descrever a localização de pessoas e de objetos no espaço em relação à sua própria posição, utilizando termos como à direita, à esquerda, em frente, atrás.

(EF01MA12) Descrever a localização de pessoas e de objetos no espaço segundo um dado ponto de

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações se jam licenciadas sob os mesmos parâmetros.

Figuras geométricas espaciais: reconhecimento e relações com objetos familiares do mundo físico

Figuras geométricas planas: reconhecimento do formato das faces de figuras geométricas espaciais

Grandezas e medidas Medidas de comprimento, massa e capacidade: comparações e unidades de medida não convencionais

referência, compreendendo que, para a utilização de termos que se referem à posição, como direita, esquerda, em cima, em baixo, é necessário explicitar-se o referencial.

(EF01MA13) Relacionar figuras geométricas espaciais (cones, cilindros, esferas e blocos retangulares) a objetos familiares do mundo físico.

(EF01MA14) Identificar e nomear figuras planas (círculo, quadrado, retângulo e triângulo) em desenhos apresentados em diferentes disposições ou em contornos de faces de sólidos geométricos.

(EF01MA15) Comparar comprimentos, capacidades ou massas, utilizando termos como mais alto, mais baixo, mais comprido, mais curto, mais grosso, mais fino, mais largo, mais pesado, mais leve, cabe mais, cabe menos, entre outros, para ordenar objetos de uso cotidiano.

Medidas de tempo: unidades de medida de tempo, suas relações e o uso do calendário

(EF01MA16) Relatar em linguagem verbal ou não verbal sequência de acontecimentos relativos a um dia, utilizando, quando possível, os horários dos eventos.

(EF01MA17) Reconhecer e relacionar períodos do dia, dias da semana e meses do ano, utilizando calendário, quando necessário.

(EF01MA18) Produzir a escrita de uma data, apresentando o dia, o mês e o ano, e indicar o dia da semana de uma data, consultando calendários.

Sistema monetário brasileiro: reconhecimento de cédulas e moedas

Probabilidade e estatística Noção de acaso

(EF01MA19) Reconhecer e relacionar valores de moedas e cédulas do sistema monetário brasileiro para resolver situações simples do cotidiano do estudante.

(EF01MA20) Classificar eventos envolvendo o acaso, tais como "acontecerá com certeza", "talvez aconteça" e "é impossível acontecer", em situações do cotidiano. Leitura de tabelas e de gráficos de colunas simples

Coleta e organização de informações Registros pessoais para comunicação de informações coletadas

(EF01MA21) Ler dados expressos em tabelas e em gráficos de colunas simples.

(EF01MA22) Realizar pesquisa, envolvendo até duas variáveis categóricas de seu interesse e universo de até 30 elementos, e organizar dados por meio de representações pessoais.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações se jam licenciadas sob os mesmos parâmetros.

Referências bibliográficas comentadas

• AMANCIO, Daniel de Traglia; SANZOVO, Daniel Trevisan. Ensino de Matemática por meio das tecnologias digitais. Revista Educação Pública, v. 20, n. 47, 8 dez. 2020. Disponível em:

https://educacaopublica.cecierj.edu.br/artigos/20/47/ensino-de-matematica-por-meio-d as-tecnologias-digitais. Acesso em: 5 jan. 2022.

No artigo, é apresentada uma discussão sobre as contribuições da utilização das tecnologias digitais no ensino-aprendizagem de Matemática.

• BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática. 6. ed. Belo Horizonte: Autêntica, 2019. (Coleção Tendências em educação matemática).

No livro, os autores apresentam resultados de um trabalho sobre informática educativa, como questões pedagógicas sobre o uso do computador e da calculadora.

• CARAÇA, Bento de Jesus. Conceitos fundamentais da Matemática Lisboa: Gradiva, 1991.

O livro oportuniza ao leitor entrar em contato com ideias e práticas para o desenvolvimento de aulas de Matemática.

• COLL, César; TEBEROSKY, Ana. Aprendendo Matemática São Paulo: Ática, 2000.

No livro, são apresentados conceitos matemáticos de diversos campos, compreendendo estruturas e ideias fundamentais.

• EVES, Howard. Introdução à história da Matemática Tradução de Hygino H Domingues. Campinas: Editora da Unicamp, 2004.

Na obra, são apresentados tópicos importantes da história da Matemática

• GAUTHIER, Clermont; BISSONNETTE, Steve; RICHARD, Mario. Ensino explícito e desempenho dos alunos Tradução de Stephania Matousek. Petrópolis: Vozes, 2014.

Os autores do livro se propõem a oferecer aos leitores detalhamento da prática docente por meio das ideias do ensino explícito.

• IFRAH, Georges. História universal dos algarismos: a inteligência dos homens contada pelos números e pelo cálculo. Tradução de Alberto Muñoz e Ana Beatriz Katinsky. Rio de Janeiro: Nova Fronteira, 1997. v. 1

O livro tem enfoque no desenvolvimento de sistemas de numeração ao longo do tempo, em particular o Sistema de Numeração Decimal

• LOPES, Maria Laura M Leite. Tratamento da informação: explorando dados estatísticos e noções de probabilidade a partir de séries iniciais. Rio de Janeiro: Instituto de Matemática/UFRJ-Projeto Fundão, 2005.

No livro, a autora propõe a apoiar o professor no ensino de conceitos relacionados à estatística e à probabilidade nos Anos Iniciais do Ensino Fundamental

• LUCKESI, Cipriano C Avaliação da aprendizagem escolar: estudos e proposições. 22. ed. São Paulo: Cortez, 2011.

No livro, são apresentados estudos críticos sobre avaliação escolar, possibilitando ao educador refletir sobre sua prática avaliativa.

• MACHADO, Nílson José. Matemática e língua materna: análise de uma impregnação mútua. 5. ed. São Paulo: Cortez, 2001.

O autor apresenta uma reflexão sobre a relação entre o alfabeto e o Sistema de Numeração Decimal, com o objetivo de contribuir com o ensino da Matemática.

• MORAN, José Manuel; MASETTO, Marcos Tarciso; BEHRENS, Marilda Aparecida. Novas tecnologias e mediação pedagógica. 21. ed. Campinas: Papirus, 2013. (Coleção Papirus Educação)

No livro, é abordada uma reflexão sobre a inserção da informática e da telemática na educação.

• NEVES, Iara Conceição Bitencourt etal Ler e escrever: compromisso de todas as áreas. 9.ed. Porto Alegre: Editora da UFRGS, 2011.

No livro, são discutidas questões relacionadas à leitura e à escrita nos textos dos diferentes componentes curriculares, inclusive na Matemática

• POLYA, George. A arte de resolver problemas: um novo aspecto do método matemático. Tradução de Heitor Lisboa de Araújo. Rio de Janeiro: Interciência, 1995.

O autor apresenta reflexões sobre a resolução de problemas e propostas didáticas práticas para o trabalho com problemas em sala de aula.

• SANT'ANA, Claudinei de Camargo; AMARAL, Rúbia Barcelos; BORBA, Marcelo de Carvalho O uso desoftwaresna prática profissional do professor de Matemática

Revista Ciência & Educação, Bauru, v. 18, n 3, p. 527-542, 2012 Disponível em: https://doi.org/10.1590/S1516-73132012000300003 Acesso em: 10 dez. 2021.

Os autores apresentam uma discussão sobre a incorporação de softwaresna prática docente.

• TOLEDO, Marília; TOLEDO, Mauro. Teoria e prática de Matemática: como dois e dois. São Paulo: FTD, 2010.

Os autores apresentam informações relevantes sobre o processo de ensino-aprendizagem da Matemática, como reflexões com base em práticas de sala de aula.

Documentos oficiais

• BRASIL Ministério da Educação Base Nacional Comum Curricular: educação é a base. Brasília: SEB, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pd f. Acesso em: 5 jan. 2022.

Documento de caráter normativo que define o conjunto de aprendizagens essenciais que os alunos devem desenvolver ao longo das etapas e modalidades da educação básica, de modo que tenham assegurados seus direitos de aprendizagem e desenvolvimento

• BRASIL Ministério da Educação PNA: Política Nacional de Alfabetização. Brasília: Sealf, 2019. Disponível em: http://alfabetizacao.mec.gov.br/images/pdf/caderdo_final_pna.pdf Acesso em: 5 jan. 2022

O documento instituído pelo Ministério da Educação, por meio da Secretaria de Alfabetização (Sealf), apresenta políticas que visam melhorar os processos de alfabetização e combater o analfabetismo no Brasil

• BRASIL. Ministério da Educação. Relatório Nacional de Alfabetização Baseada em Evidências (Renabe) Brasília: Sealf, 2020. Disponível em: http://alfabetizacao.mec.gov.br/images/pdf/renabe_web.pdf Acesso em: 5 jan 2022.

Relatório que apresenta pesquisas recentes sobre alfabetização, literacia e numeracia e cujo objetivo é contribuir para a melhoria nas políticas públicas e nas práticas de ensino no Brasil.

Leituras complementares para o professor

• FERREIRA, Mariana K Leal. Ideias matemáticas de povos culturalmente distintos São Paulo: Global, 2002. (Série antropologia e educação).

No livro, são reunidos relatos de atividades matemáticas aplicadas em diversos países, possibilitando ao leitor refletir sobre sua prática docente.

• LINDQUIST, Mary Montgomery; SHULTE, Albert P. (org.). Aprendendo e ensinando Geometria Tradução de Hygino H Domingues. São Paulo: Atual, 1994.

A obra contém artigos relevantes sobre o ensino-aprendizagem da Geometria em diferentes faixas etárias.

• MONTEIRO, Alexandrina; POMPEU JUNIOR, Geraldo. A Matemática e os temas transversais São Paulo: Moderna, 2001.

Os autores propõem reflexões sobre os temas transversais, com especial atenção às aulas de Matemática.

• SOUZA, Eliane R. de etal . A Matemática das sete peças do tangram. 2. ed. São Paulo: Caem/IME-USP, 1997.

No livro, há textos e atividades para serem desenvolvidas com o tangram nas aulas de Matemática.

Material disponibilizado em licença aberta do tipo