Entrelaços - Matemática - Volume 2

ÁREA: MATEMÁTICA

COMPONENTE: MATEMÁTICA

JOAMIR SOUZA ANGÉLICA REGHIN 2

ENSINO FUNDAMENTAL ANOS INICIAIS

MATEMÁTICA

RECURSO

EDUCACIONAL DIGITAL

2o ANO ENSINO FUNDAMENTAL ANOS INICIAIS

MATEMÁTICA

Joamir Roberto de Souza

Mestre em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Especialista em Estatística pela Universidade Estadual de Londrina (UEL-PR).

Licenciado em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professor de Matemática da rede pública de ensino.

Autor de livros didáticos para o Ensino Fundamental e para o Ensino Médio.

Maria Angélica Reghin de Souza

Especialista em Gestão Escolar pela Universidade Norte do Paraná (Unopar).

Licenciada em Pedagogia pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora na Educação Infantil.

Autora de livros didáticos para o Ensino Fundamental.

ÁREA: MATEMÁTICA COMPONENTE: MATEMÁTICA

RECURSO EDUCACIONAL DIGITAL

Entrelaços – Matemática – Recurso Educacional Digital – 2o ano (Ensino Fundamental – Anos Iniciais)

Copyright © Joamir Roberto de Souza, Maria Angélica Reghin de Souza, 2021

Direção-geral Ricardo Tavares de Oliveira

Direção de Conteúdo e Negócios Cayube Galas

Direção editorial adjunta Luiz Tonolli

Gerência editorial Natalia Taccetti

Edição Nubia de Cassia de Moraes Andrade e Silva (coord.)

Leticia Mancini Martins, João Alves de Souza Neto

Preparação e revisão de textos Viviam Moreira (sup.)

Adriana Périco, Caline Devèze, Camila Cipoloni, Carina Luca, Fernanda Marcelino, Fernando Cardoso, Graziele Ribeiro, Paulo José Andrade

Gerência de produção e arte Ricardo Borges

Design Daniela Máximo (coord.)

Arte e produção Isabel Cristina Corandin Marques (coord.)

Coordenação de imagens e textos Elaine Bueno Koga

Licenciamento de textos Erica Brambilla

Iconografia Priscilla Narciso

Coordenação de audiovisuais Diego Vieira Cury Morgado de Oliveira

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil) Souza, Joamir Roberto de Entrelaços [livro eletrônico] : matemática : 2o ano : ensino fundamental : anos iniciais / Joamir Roberto de Souza, Maria Angélica Reghin de Souza. – 1. ed. – São Paulo : FTD, 2021.

PDF

Área: Matemática.

Componente: Matemática.

ISBN 978-85-96-03227-8 (recurso educacional digital professor – coleção)

1. Matemática (Ensino fundamental) I. Souza, Maria Angélica Reghin de. II. Título. 21-90776 CDD-372.7

Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Cibele Maria Dias - Bibliotecária - CRB-8/9427

EDITORA FTD

Rua Rui Barbosa, 156 – Bela Vista – São Paulo-SP CEP 01326-010 – Tel. 0800 772 2300 Caixa Postal 65149 – CEP da Caixa Postal 01390-970 www.ftd.com.br central.relacionamento@ftd.com.br

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Carta ao professor

Olá, professor! Seja bem-vindo ao Recurso Educacional Digital!

Este Recurso Educacional Digital tem como objetivo fornecer subsídios e sugestões que apoiem o trabalho pedagógico e a ação educativa em sala de aula no ensino da Matemática para os Anos Iniciais do Ensino Fundamental. O material oferece diferentes instrumentos de ampliação e intervenção que propiciam um ambiente de trocas, comunicação e diálogo, estimulam o levantamento de hipóteses e promovem a construção gradativa de conceitos e procedimentos matemáticos.

Neste material, são propostas situações de ensino-aprendizagem que favorecem a investigação, a experimentação, a criação de registros, a manipulação de objetos e as brincadeiras, permitindo aos alunos compreender que a Matemática não é um conhecimento restrito à sala de aula.

Os conteúdos e propostas de atividades que compõem este material também possibilitam o desenvolvimento das habilidades da Base Nacional Comum Curricular (BNCC), das competências específicas da área de Matemática e suas Tecnologias para o Ensino Fundamental, das competências gerais da Educação Básica, dos objetivos de aprendizagem e dos componentes essenciais para a alfabetização propostos na Política Nacional de Alfabetização (PNA).

Este material digital está organizado em quatro recursos pedagógicos descritos a seguir.

Plano de desenvolvimento anual

O Plano de desenvolvimento anual apresenta um quadro com uma programação de como os conteúdos podem ser organizados e trabalhados durante o ano letivo, seja em bimestres, trimestres ou semestres. Também, apresenta as habilidades da BNCC e os componentes essenciais para a alfabetização que podem ser trabalhados no período. Esse quadro é uma sugestão de programação, tendo o professor autonomia para adaptá-lo à realidade e às necessidades da turma.

O Plano de desenvolvimento apresenta, ainda: textos sobre estratégias e atitudes docentes que podem contribuir para alcançar os objetivos de aprendizagem estabelecidos; uma reflexão sobre avaliação e como esse instrumento pode auxiliar o processo de ensino-aprendizagem; e sugestões de leitura e sitesque podem aprimorar o trabalho docente em sala de aula.

Sequências didáticas

As sequências didáticas são sugestões de planejamento aula a aula que têm como objetivos complementar e aprofundar os conteúdos contemplados em outros materiais

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

didáticos e, consequentemente, contribuir com o desenvolvimento das habilidades e das competências específicas da área de Matemática e suas Tecnologias, das competências gerais da Educação Básica e dos componentes essenciais para a alfabetização. Além disso, essas sequências também podem contribuir para a remediação de eventuais dificuldades de aprendizagem dos alunos.

Com relação a sua estrutura, cada sequência didática é composta de um texto de introdução, dos objetivos de aprendizagem, do planejamento das aulas, de um passo a passo descritivo com sugestões metodológicas de como desenvolver as aulas, de exemplos de atividades que podem ser propostas aos alunos e de orientações de como acompanhar o desenvolvimento das aprendizagens em diferentes momentos.

Relatórios e indicadores do acompanhamento da aprendizagem

Os relatórios e indicadores do acompanhamento da aprendizagem têm como objetivo oferecer ao professor subsídios para acompanhar a aprendizagem dos alunos de maneira individual e coletiva, bem como apresentar orientações sobre como sistematizar os dados e apresentá-los aos pares, aos gestores escolares e aos responsáveis pelos alunos.

Esse relatório é composto de quatro fichas:

• Ficha de avaliação diagnóstica: possibilita avaliar os conhecimentos prévios dos alunos sobre determinados conteúdos e verificar a proficiência em algumas habilidades e competências.

• Ficha de acompanhamento das aprendizagens: possibilita avaliar o aprendizado e o progresso do aluno durante o processo de ensino-aprendizagem e fornece dados que permitem ao professor avaliar esse processo e ajustar a prática docente.

• Ficha de verificação dos resultados: possibilita avaliar quais objetivos de aprendizagem estabelecidos foram alcançados ao final do ano letivo.

• Ficha de acompanhamento para o desenvolvimento de habilidades socioemocionais: possibilita avaliar a evolução dos alunos em relação às habilidades socioemocionais.

É importante destacar a autonomia do professor para avaliar como essas fichas devem ser aplicadas e adaptadas de acordo com a realidade dos seus alunos e da escola na qual leciona e como elas podem complementar os diferentes instrumentos de avaliação e de acompanhamento de aprendizagem já utilizados.

Catálogo de audiovisuais

O catálogo de audiovisuais apresenta um descritivo de cada um dos audiovisuais que acompanham o Recurso Educacional Digital e tem como objetivo complementar e aprofundar o trabalho com os conteúdos explorados nesse material.

Além disso, oferece encaminhamentos à autonomia do professor, permitindo que, por meio de uma reflexão sobre as características da sua turma e do seu planejamento, seja possível estabelecer a melhor maneira de utilizar os audiovisuais. Para isso, o catálogo

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

apresenta sugestões de como esses audiovisuais podem ser trabalhados, bem como propostas de atividades que possibilitam explorar o uso desses recursos com os alunos.

No volume do 2º ano, são trabalhados os seguintes temas:

• Os números naturais de até três ordens;

• Adição e subtração;

• Figuras geométricas espaciais e planas;

• Localização e deslocamento;

• Grandezas e medidas;

• Multiplicação e divisão;

• Sequências numéricas recursivas;

• Probabilidade e estatística;

• Sistema monetário brasileiro.

Esperamos que este material contribua para o aprimoramento da sua prática docente e para a formação de alunos aptos a viver em sociedade, fazendo valer seus direitos e exercendo seus deveres individuais e coletivos.

Bom trabalho!

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC

BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Instrumentos pedagógicos

Plano de desenvolvimento anual

Este Plano de desenvolvimento anual consiste em um instrumento pedagógico que tem como objetivo auxiliar o planejamento docente na gestão dos conteúdos a serem apresentados ao longo de um ano letivo.

Para isso, em um primeiro momento, são apresentadas propostas de organização semestral, trimestral e bimestral, ordenadas em um quadro.

No quadro, a fim de favorecer a visualização da progressão das aprendizagens, constam, em colunas:

• a descrição sequencial de distribuição dos conteúdos;

• a indicação dos códigos alfanuméricos das habilidades da Base Nacional Comum Curricular (BNCC);

• a nomeação dos componentes essenciais para a alfabetização, de acordo com a Política Nacional de Alfabetização (PNA).

É importante considerar que o plano de ação sugerido nesta proposta pode ser adaptado à realidade escolar interna (infraestrutura, características da turma, entre outros aspectos) e à realidade escolar externa (parceria com os responsáveis dos alunos) da instituição em que se atua.

Imediatamente após o quadro, para auxiliar na gestão do processo de ensino-aprendizagem, constam três seções que são descritas a seguir.

A seção Práticas de ensino na sala de aula apresenta a proposição de algumas estratégias e procedimentos que podem ser eficazes para a concretização dos objetivos de aprendizagem previstos.

Na seção Avaliação, a importância dessa ferramenta pedagógica é enfatizada como instrumento a ser empregado de modo contínuo e processual. Deve ser utilizada para aferir não só os conhecimentos curriculares disciplinares, mas também os conhecimentos da realidade do mundo que cerca os alunos.

Por fim, a seção Saiba mais apresenta sugestões de referências complementares para consulta (sites , vídeos etc.) relacionadas a temas de cunho de ampliação do repertório da formação docente continuada.

De modo articulado e vinculado, com base nas indicações do quadro e das seções, é possível planejar o desenvolvimento anual de sua atuação docente.

1 º semestre 1º trimestre 1º bimestre

Aprendizagens desenvolvidas no 2º ano

Relembrando os números

• Os números até 10

• Identificar ou representar a escrita de números até 10 em algarismos

• Contar coleções com até 10 objetos

• Comparar quantidades de elementos em dois conjuntos

• Identificar e escrever dezenas inteiras

• Os números até 100

• Fazer contagem até 100

• Compor, identificar, ler e escrever números naturais até 100

• Comparar e ordenar números naturais até 100

• Classificar um número natural em par ou ímpar.

• Resolver problemas envolvendo as ideias de juntar e acrescentar da adição, sem reagrupamentos

• Resolver problemas envolvendo as ideias de completar, retirar e comparar da subtração, sem reagrupamentos.

• Estabelecer relações de equivalência entre valores de cédulas e moedas do sistema monetário brasileiro.

• Resolver problemas envolvendo valores monetários em situações de compra e venda.

Figuras geométricas espaciais, localização e deslocamento

• Reconhecer e nomear figuras geométricas espaciais

• Relacionar figuras geométricas espaciais com objetos do dia a dia

• Utilizar noções de posição para identificar e indicar a localização de pessoas e objetos no espaço, de acordo com um ponto de referência

• Esboçar um caminho a ser seguido, indicando comandos de deslocamento e pontos de referência

• Esboçar planta simples de ambientes familiares

Grandezas e medidas

• Reconhecer unidades de medida não padronizadas

2º bimestre

• Estimar, medir e comparar medidas de comprimento

• Reconhecer o metro, o centímetro e o milímetro como unidades de medida de comprimento padronizadas

• Medir contornos de figuras e de ambientes familiares para desenvolver a ideia intuitiva de perímetro

BNCC

EF02MA01

EF02MA03

EF02MA04

EF02MA05

EF02MA06

EF02MA12

EF02MA13

EF02MA14

EF02MA20

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento de vocabulário

• Compreensão de textos.

• Produção de escrita

BNCC

EF02MA01

EF02MA02

EF02MA03

EF02MA04

EF02MA05

EF02MA06

EF02MA16

EF02MA17

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

2º trimestre

• Comparar medidas de massa

• Reconhecer o quilograma e o grama como unidades de medida de massa padronizadas

• Estimar, medir e comparar medidas de capacidade

• Reconhecer o litro e o mililitro como unidades de medida de capacidade padronizadas

• Identificar medidas de tempo, como dias da semana, mês e ano, consultando o calendário

• Identificar e determinar intervalos de tempo, em dias ou meses, consultando o calendário

• Organizar eventos em agendas utilizando datas (dias da semana, meses do ano)

• Ler e registrar medidas de tempo, em horas, consultando relógios digitais e de ponteiros

• Determinar intervalos de tempo, em horas, consultando relógios digitais e de ponteiros

Os números até 1 000

• Relembrar os números estudados

• Estimar, contar e comparar as quantidades de objetos de uma coleção até 1 000

• Ler e escrever números naturais até 1 000 com algarismos e por extenso

• Compor e decompor números naturais até 1 000

• Classificar um número natural em par ou ímpar

• Resolver problemas envolvendo as ideias de juntar e acrescentar da adição, sem reagrupamentos

• Resolver adições com três números de diferentes maneiras e observar que o resultado é sempre o mesmo

• Resolver problemas envolvendo as ideias de completar, retirar e comparar da subtração, sem reagrupamentos.

• Calcular adições e subtrações utilizando calculadora e arredondamentos para obter resultados aproximados

• Estabelecer relações de equivalência entre valores de cédulas e moedas do sistema monetário brasileiro.

• Resolver problemas envolvendo valores monetários em situações de compra e venda

EF02MA18

EF02MA19

EF02MA20

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento de vocabulário.

• Compreensão de textos.

• Produção de escrita

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

2º semestre

3º bimestre

Sequências

• Identificar e descrever regularidades em sequências de números naturais, figuras e objetos

• Identificar e descrever elementos ausentes em sequências de números naturais, figuras e objetos

• Escrever os próximos elementos de uma sequência de números naturais, figuras e objetos

• Construir sequências a partir de regularidades estabelecidas

Multiplicação e divisão

• Resolver problemas envolvendo a ideia de adição de parcelas iguais da multiplicação

• Resolver problemas envolvendo a ideia de disposição retangular da multiplicação

• Compreender de maneira intuitiva a ideia da propriedade comutativa da multiplicação

• Resolver problemas envolvendo a ideia de dobro e de triplo

• Resolver problemas envolvendo as ideias de metade (divisão por 2) e de terça parte (divisão por 3)

• Resolver problemas de divisão em partes iguais, com resto zero

3º trimestre

4º bimestre

Estatística e probabilidade

• Ler, interpretar, comparar e organizar informações apresentadas em tabelas simples e de dupla entrada

• Ler, interpretar, comparar e organizar informações em gráficos de colunas e de barras

• Realizar pesquisa, organizar e representar dados coletados utilizando tabelas e gráficos

• Identificar e classificar resultados de eventos aleatórios em possível, impossível, mais provável ou menos provável de ocorrer

Figuras geométricas planas

• Identificar, comparar e desenhar figuras geométricas planas analisando características de seu contorno

• Reconhecer e identificar figuras geométricas planas (quadrado, retângulo, triângulo, círculo) em figuras geométricas espaciais

BNCC

EF02MA07

EF02MA08

EF02MA09

EF02MA10

EF02MA11 Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Compreensão de textos.

• Produção de escrita

BNCC

EF02MA15

EF02MA21

EF02MA22

EF02MA23

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Compreensão de textos.

• Produção de escrita

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

Práticas de ensino na sala de aula

Para que o Plano de desenvolvimento anual possa efetivamente se consolidar de modo que sejam alcançados os objetivos de aprendizagem pretendidos para o ano letivo, é importante o docente ter atitudes e utilizar práticas que contribuam para o desenvolvimento dos componentes essenciais para a alfabetização e das competências e habilidades matemáticas nos alunos sob sua responsabilidade. Para isso, a seguir é apresentada uma visão geral de algumas abordagens possíveis.

É importante ressaltar, ainda, que o processo de ensino-aprendizagem já não se encontra mais intimamente vinculado apenas ao espaço físico da sala de aula e, em virtude das mudanças ocorridas socialmente, cenários de aprendizagem virtual passaram a fazer parte da dinâmica escolar, sendo necessário considerar essa perspectiva no planejamento, nas práticas, bem como na busca de atualização da formação docente.

Leitura inferencial

Para abordar situações significativas apresentadas em cada proposta didática, a leitura inferencial é uma prática importante a ser desenvolvida com os alunos. Essa prática envolve tanto estratégias de leitura de imagens quanto de leitura de textos.

A leitura de imagens, em Matemática, nos Anos Iniciais do Ensino Fundamental, é tão explorada quanto a leitura de textos, visto que o suporte de apoio visual na realização de contagens ou resolução de operações matemáticas é um recurso didático muito utilizado.

A reflexão sobre o processo de leitura inferencial pode ser promovida pelo docente por meio de perguntas ou solicitações propostas que permitam aos alunos demonstrarem respostas que não estejam apenas circunscritas aos textos, e sim possam ser inferidas considerando conhecimentos prévios e de mundo de modo geral.

Os enunciados dos problemas matemáticos são textos que requerem leitura analítica e inferencial por parte dos alunos para que possam desenvolver melhores estratégias de resolução.

Produzir inferências é uma ação que auxilia na compreensão de um texto. No caso das aulas de Matemática, de um texto matemático, por exemplo, o enunciado de um problema.

A compreensão de texto, em qualquer área de conhecimento, é uma habilidade que depende das inferências geradas pelo leitor, considerando que cada texto possui informações implícitas e explícitas.

A qualidade e a quantidade das inferências geradas por um leitor dependem, prioritariamente, das associações estabelecidas entre as informações explícitas no texto e os conhecimentos prévios e de mundo que o leitor possui.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Para auxiliar os alunos a lerem um texto de maneira analítica, a fim de que possam concluir, deduzir e formular novos sentidos, levantar hipóteses, bem como ressignificar informações, uma estratégia é sugerir que, ao fazer a leitura:

• dividam o texto em partes menores que forneçam informações principais;

• estabeleçam relações entre essas partes de modo a identificar como elas se inter-relacionam;

• identifiquem o panorama geral do que essas inter-relações indicam.

Destaca-se o fato de que a leitura de um texto matemático mobiliza o leitor para a interpretação de elementos textuais combinados a elementos matemáticos, como números, tabelas, gráficos, entre outros.

Nesse sentido, outra estratégia é fazer com que os alunos compreendam que ler um texto matemático não se resume a identificar palavras-chave.

Sugere-se, sempre que possível, incentivar os alunos a realizar uma leitura analítica e inferencial de:

• imagens que permeiam o material didático (imagens de aberturas de partes hierárquicas do livro, como unidades ou capítulos, por exemplo);

• textos (enunciados de problemas, textos instrucionais de jogos, entre outros).

Sugere-se, ainda, solicitar aos alunos que façam registros das compreensões, pois essa prática vai ajudá-los a melhorar o desempenho na resolução e condução das tarefas propostas.

Esses registros podem ser compartilhados em um mural da sala de aula ou da escola, em um mural on-line criado na rede social da escola ou, até mesmo, em uma folha de cartolina, na qual os alunos façam registros. O cartaz pode ser afixado em algum espaço da sala de aula ou da escola

Fazer diferentes registros

Na Competência específica 6 de Matemática e suas Tecnologias da BNCC (BRASIL, 2018, p. 267), é abordada a importância de expressar respostas e sintetizar conclusões utilizando diferentes registros e linguagens.

Desse modo, uma prática importante, ao longo do desenvolvimento das atividades propostas, é solicitar aos alunos que façam diferentes registros para expressar as justificativas de suas respostas, esquematizar a descrição de estratégias utilizadas no processo de resolução, representar um problema com uma organização visual etc.

Essa prática é importante de ser desenvolvida desde os primeiros anos de escolaridade já que é um processo que deve ser aprimorado durante toda a vida escolar e não escolar, pois fazer registros e interpretá-los é uma habilidade importante, por exemplo, no trabalho, assim como em diversas situações da vida cotidiana que requerem a

Material disponibilizado em licença aberta do tipo Creative Commons

não comercial

esquematização de sistemas, situações ou processos, com a finalidade de compreendê-los melhor

Como estratégia de aplicação dessa prática, explorar com os alunos algumas possibilidades, como:

• no processo de resolução de problemas que envolvam proporcionalidade, fazer registros organizados em quadros;

• em pesquisas estatísticas, fazer registros dos dados coletados em tabelas e gráficos;

• questões que abrangem características geométricas, fazer desenhos (esboços esquemáticos) que representem plantas baixas ou figuras (bidimensionais ou tridimensionais);

• no trabalho com sequências recursivas (numéricas ou figurais), fazer registros por escrito das regularidades identificadas na regra de formação do padrão de cada sequência;

• ao resolver problemas que envolvem multiplicação com a ideia de combinatória, fazer a organização da representação de uma árvore de possibilidades (ou de um quadro de possibilidades);

• na elaboração de problemas, solicitar que façam diagramas de fluxo ligando as etapas, a fim de representar a sequência que encadeou o raciocínio empregado no desenvolvimento da elaboração.

Permitir aos alunos eleger de maneira autônoma os diferentes registros e linguagens é muito importante para valorizar o protagonismo deles no processo de ensino-aprendizagem.

Educação para a cidadania

Além dos conteúdos disciplinares, o processo de formação educacional abrange, também, a responsabilidade de formar indivíduos conscientes da importância que atitudes individuais exercem sobre a vida do outro e das responsabilidades que possuem em relação ao grupo social a que pertencem, entre outros aspectos.

Na BNCC (BRASIL, 2018), nas páginas 9 e 10, estão relacionadas dez competências gerais da Educação Básica e, nas páginas 19 e 20, são elencados os Temas Contemporâneos Transversais, os quais apontam para o desenvolvimento de capacidades a serem aperfeiçoadas, ao longo da vida, com base no exercício de práticas sociais inseridas em determinados contextos, como meio ambiente, saúde, educação financeira, entre outros.

Considerando essa perspectiva, a prática da educação para a cidadania prioriza envolver todos os alunos em vivências significativas consigo mesmos e com outras pessoas, por meio da percepção de que há direitos que são garantidos com base no cumprimento dos deveres, e vice-versa. Sendo assim, a educação para a cidadania vai além da transmissão de conteúdo e da assimilação dele

Uma estratégia que se pode utilizar, a cada semana, é escolher ou pedir que se voluntarie um ajudante da semana para auxiliar você em algumas tarefas. O objetivo é levar os alunos a assumirem uma postura cooperativa com você e os colegas.

É adequado, se possível, que cada aluno da turma, ao longo do ano letivo, seja o ajudante da semana, pois essa experiência ajudará a lidar com a indisciplina, caso exista no ambiente. Isso, também, favorecerá o desenvolvimento de sentimentos de pertencimento, autonomia, responsabilidade, resiliência, foco, cuidado consigo mesmo e com os outros, entre outros.

O ajudante da semana pode cuidar do compartilhamento de comunicados e lembretes de compromissos. Essa comunicação pode ser:

• on-line , por meio de aplicativos de mídia que compartilham vídeos curtos ou áudios;

• off-line , com base na escrita de recados diários no mural ou no quadro da sala de aula

É importante que seja incluída alguma atividade envolvendo tecnologia digital para que os alunos se apropriem de fazer uso cidadão e crítico no ambiente escolar.

Estímulo à criatividade

A criatividade (ou pensamento criativo) é um potencial que todos nós possuímos e pode ser desenvolvida no ambiente escolar com base em determinadas estratégias e em certos contextos apropriados.

Nas aulas de Matemática, estimular práticas que envolvam o potencial criativo é uma ação que pode ser associada a diferentes unidades temáticas dessa área de conhecimento.

Nas atividades relacionadas a conhecimentos geométricos, por exemplo, uma estratégia é propor aos alunos atividades em que eles sejam construtores de maquetes ou de outras elaborações relacionadas ao tema, de acordo com a criatividade deles.

Para realizar essas construções, os alunos devem mobilizar os conhecimentos desse tema para reconhecer em embalagens e objetos do mundo físico características de figuras geométricas espaciais estudadas para assim selecionar as melhores embalagens ou objetos a serem empregados nessas construções de acordo com as características identificadas, como superfícies arredondadas ou não.

Esse tipo de atividade, geralmente realizada em grupos, envolve a produção de ideias originais Sendo assim, além de estimular a criatividade para apresentar ideias, exercita a flexibilidade dos alunos em acolher as ideias dos colegas de grupo e a solucionar problemas de forma construtiva e respeitosa

A captura de retratos de construções arquitetônicas que se pareçam com figuras geométricas espaciais para elaborar uma apresentação de slidestambém é uma atividade que estimula a criatividade, além de utilizar tecnologia digital.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Outra estratégia são atividades de elaboração de problemas. Esse tipo de atividade também estimula a criatividade dos alunos. Além de empregarem conhecimentos matemáticos nessa elaboração, a criação do contexto do problema requer a originalidade na concepção de ideias novas e, para isso, o pensamento criativo é estimulado.

Avaliação

A avaliação exerce uma das principais funções em favor da promoção e da consolidação do processo de ensino-aprendizagem. Por isso, a avaliação não pode ser concebida somente como uma fase final desse processo, mas precisa ser integrada a todo o processo, de maneira contínua.

Para que a avaliação seja empregada com eficácia, é importante coletar informações sobre aspectos não desenvolvidos, os parcialmente desenvolvidos e os desenvolvidos pelos alunos. Com base nessas informações, oferecer feedbacka cada um deles, aos gestores escolares e aos responsáveis pelos alunos

A coleta dessas informações pode ser dirigida de maneira diversificada considerando diferentes possibilidades, como avaliação diagnóstica, avaliação de processo e avaliação formativa.

Com a avaliação diagnóstica, é possível mapear os diferentes perfis dos alunos em relação aos conhecimentos prévios que possuem. Assim, a observação e a reflexão do docente sobre as informações obtidas é uma importante ferramenta nesse tipo de avaliação. Embora, em um diagnóstico, muitas informações possam ser observadas, é indicado, além da sondagem de conhecimentos prévios, que se observem também:

• a linguagem corporal dos alunos durante suas explicações (se demonstram interesse ou não);

• o modo como se organizam no trabalho em duplas ou grupos para a prática de uma atividade;

• se manifestam ansiedade ou demonstram desinteresse quando questionados individualmente.

Na avaliação diagnóstica, a observação desses padrões de comportamento compõe dados relevantes a serem vinculados à análise do desempenho cognitivo de cada aluno nas atividades propostas.

Já a avaliação de processo produz uma experiência educacional que motiva os alunos, por ser contínua e se dar também por meio da utilização de instrumentos informais, como paradas para uma autoavaliação.

A fim de tornar a avaliação de processo um momento mais próximo de cada aluno:

• questionar a avaliação pessoal que cada um faz das próprias produções e atuações escolares No caso de trabalho em duplas ou em grupo, essa prática de autoavaliação pode ser incorporada de maneira reflexiva e compartilhada entre eles;

• solicitar relatórios concisos sobre atividades específicas, ou qualquer outro tipo de registro, para obter informações do processo de aprendizagem de cada aluno, a fim de rever o processo sempre que necessário.

Na avaliação formativa, a utilização de instrumentos formais, mantendo o formato de atividades diárias, se destaca, pois, nesse tipo de avaliação, critérios mais específicos são considerados, como o nível de apreensão dos alunos em relação aos conteúdos, a aplicação da linguagem matemática, entre outros que permitem a sistematização de informações.

Avaliar é um ato que dá origem a informações úteis para docentes e discentes, conforme a interpretação e a comunicação dialógica entre os atores do processo educacional.

Para auxiliar na geração de informações e interpretação dessas informações, consultar os Relatórios e Indicadores do Acompanhamento da Aprendizagem disponíveis neste material.

Para saber mais

• BARLOW, Michel Avaliação escolar: mitos e realidades. Porto Alegre: Artmed, 2006. Nessa obra, Michel Barlow discute práticas avaliativas em sala de aula.

• BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática. 6. ed. Belo Horizonte: Autêntica, 2019. (Tendências em Educação Matemática).

Nesse livro, os autores apresentam resultados de um trabalho sobre informática educativa, como questões pedagógicas sobre o uso do computador e da calculadora.

• BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília: SEB, 2018. Disponível em:

http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pd

f. Acesso em: 8 dez. 2021.

Documento que regulamenta as aprendizagens essenciais na Educação Básica.

• BRASIL. Ministério da Educação. PNE: Plano Nacional de Educação. Brasília: Inep, 2014. Disponível em:

https://download.inep.gov.br/publicacoes/institucionais/plano_nacional_de_educacao/pl ano_nacional_de_educacao_pne_2014_2024_linha_de_base.pdf. Acesso em: 8 dez. 2021.

Nesse documento, são apresentadas as diretrizes, metas e estratégias para a educação brasileira de 2014 a 2024.

• COLL, César; TEBEROSKY, Ana. Aprendendo Matemática. São Paulo: Ática, 2000.

Nesse livro, é possível ter acesso a conceitos matemáticos de diversos campos, compreendendo estruturas e ideias fundamentais.

• GAUTHIER, C.; BISSONNETTE, S.; RICHARD, M. Ensino explícito e desempenho dos alunos: a gestão dos aprendizados. Petrópolis: Vozes, 2014.

Nesse livro, os autores discutem as principais características e os fundamentos do ensino explícito como uma proposta de ensino eficaz.

• HADJI, C. A avaliação, regras do jogo: das intenções aos instrumentos Porto: Porto Editora, 1994.

Nesse livro, é apresentada uma proposta de abordagem de avaliação da aprendizagem escolar, incluindo reflexões e análises relacionadas aos tipos de avaliação.

• LORENZATO, S Laboratório de ensino de Matemática e materiais didáticos manipuláveis In : LORENZATO, S. O Laboratório de Ensino de Matemática na formação de professores Campinas: Autores Associados, 2006. p. 3-38. (Coleção Formação de professores).

Nesse texto, é discutido o papel do Laboratório de Ensino de Matemática (LEM) no ensino e na aprendizagem de Matemática.

• LUCKESI, C. C. Verificação ou avaliação: o que pratica a escola. Ideias, São Paulo, n. 8, p. 71-80, 1998. (Série Ideias).

Nesse texto, o autor faz uma abordagem sobre aspectos que diferenciam as ações de verificar e avaliar no ensino escolar.

• MONTEIRO, Alexandrina; POMPEU JUNIOR, Geraldo. A Matemática e os temas transversais. São Paulo: Moderna, 2001.

Nesse livro, há reflexões sobre os temas transversais, com especial atenção às aulas de Matemática.

• NACARATO, Adair Mendes; MENGALI, Brenda Leme da Silva; PASSOS, Cármen Lúcia

Brancaglion A Matemática nos anos iniciais do Ensino Fundamental. 2. ed. Belo

Horizonte: Autêntica, 2015.

Nesse livro, os autores debatem sobre o ato de aprender e o ato de ensinar a Matemática, nos Anos Iniciais do Ensino Fundamental.

• PAIS, L. C. Ensinar e aprender Matemática. Belo Horizonte: Autêntica, 2006.

Com essa obra, o autor propõe uma reflexão acerca de aspectos metodológicos do ensino da Matemática, incluindo uma análise do livro didático.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Sequências didáticas

Sequência didática 1: Os números naturais

Nesta sequência didática, serão explorados algumas propriedades e regularidades do sistema de numeração decimal, os números ordinais, a ordem crescente e decrescente, a apresentação de informações em tabelas, as ideias que envolvem adição, subtração e multiplicação (a partir de um jogo de boliche) e as possibilidades de cálculo escrito e mental para resolver essas situações-problema.

Objetivos de aprendizagem

• Compreender a composição dos números.

• Perceber regularidades existentes na ordem numérica.

• Comparar e ordenar números naturais.

• Perceber e compreender o valor posicional e a função do zero.

• Compreender a ordem numérica com números menores e maiores que 100.

• Perceber a utilização dos números ordinais.

• Comparar medidas.

• Apresentar informações em tabelas.

• Construção de fatos fundamentais da adição e da subtração.

• Problemas envolvendo diferentes significados da adição e da subtração (juntar, acrescentar, separar, retirar).

• Problemas envolvendo adição de parcelas iguais (multiplicação).

Plano de aulas

Aula 1: Realizar estimativas e contagens por meio de um jogo.

Aula 2: Perceber regularidades existentes na ordem numérica por meio de dinâmicas.

Aula 3: Comparar e ordenar números utilizando uma dinâmica com varal e cartelas com números.

Aula 4: Conhecer sequência numérica apresentada em instrumentos de medida como a fita métrica.

Aula 5: Ordenar de maneira crescente e decrescente medidas em centímetro com base na dinâmica de medições com barbantes.

Aula 6: Construir fatos básicos da adição e realizar trocas com material dourado após o jogo com boliche.

Aula 7: Realizar multiplicações e trocas com material dourado após o jogo com boliche.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito

autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Aula 8: Construir fatos básicos da subtração e realizar trocas com material dourado após o jogo com boliche.

Componentes essenciais para a alfabetização: Consciência fonológica e fonêmica e produção de escrita.

Competências gerais da Educação Básica: 2 e 9 Competências específicas de Matemática: 2 e 8 Habilidades: EF02MA01, EF02MA02, EF02MA04, EF02MA05, EF02MA06, EF02MA07 e EF02MA09.

Materiais necessários: Material dourado, fichas sobrepostas, barbante, tesoura com pontas arredondadas, pregadores, fita adesiva, folhas avulsas, dado, folhas com uma tabela impressa (1 coluna e várias linhas), fita métrica graduada em centímetro, folha de papel A3, cola, garrafas plásticas, bolas pequenas, triângulo para marcar a posição das garrafas, tabela para anotar os pontos em cada rodada, lápis e ábaco.

Aula 1

Antes de iniciar as explorações desta aula, promover uma roda de conversa para que os alunos possam expressar os conhecimentos que possuem acerca dos numerais utilizados no cotidiano e a função deles em cada situação.

Estimular os alunos a compartilharem, por exemplo, a idade; a data de nascimento; o número dos sapatos e da roupa; se tiverem irmãos, a ordem de nascimento em relação a eles (primeiro a nascer, segundo a nascer etc.) e o número da casa onde moram. Ajudá-los a perceber que em cada uma dessas situações os números assumem uma finalidade: quantificar, medir, codificar e ordenar.

Perguntar aos alunos se eles conhecem a ordem numérica e incentivar que compartilhem as informações que têm acerca do tema. Verificar se conseguem recitar os números até 20, propondo algumas explorações concretas, como cantar cantigas ou parlendas que envolvam a ordem numérica, por exemplo, "A galinha do vizinho"

Em seguida, dividir a turma em grupos de três alunos e entregar, para cada grupo, alguns cubinhos do material dourado e um dado.

Orientar os alunos a realizarem o jogo Quem tem mais. Comentar que, antes do início da partida, eles deverão estimar a quantidade de cubinhos recebida e, em seguida, contá-la para que possam averiguar se as hipóteses apresentadas anteriormente se aproximam da quantidade real de cubinhos. Sempre que possível, realizar atividades que permitam o uso de estimativas.

No jogo Quem tem mais, a turma deverá decidir quem começará lançando o dado. O jogador deve então pegar a quantidade de cubinhos equivalente ao valor tirado na face superior do dado, ou seja, na face que ficou virada para cima. Entregar a cada aluno uma tabela para que seja possível registrar a quantidade de cubinhos sorteada em cada rodada –assim, pode-se observar a maneira como os alunos representam quantidades.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Com os alunos, estipular a quantidade de rodadas e, ao final, desafiá-los a descobrir a quantidade total de cubinhos de cada jogador. O jogador que conseguir o maior número de cubinhos será o vencedor.

Se julgar conveniente, propor uma nova maneira de jogar. Dessa vez, cada jogador pode iniciar o jogo com 20 cubinhos e, a cada jogada, deverá retirar de seus cubinhos a quantidade sorteada. Vencerá o jogo aquele que ficar sem cubinhos primeiro

Aula 2

Relembrar o jogo da aula anterior e incentivar os alunos a expressar sensações despertadas ao longo do jogo e resgatar os registros por eles elaborados durante a partida. Nesse momento, retomar a ordem numérica construindo com os alunos cartelas numeradas na mesma quantidade de alunos da turma (se o número de alunos da turma for maior que 20) ou apenas 20 cartelas (caso haja menos de 20 alunos).

Para a confecção das cartelas, convidar um aluno de cada vez, entregar a ele uma folha em branco e pedir que escreva, usando algarismos, o número ditado (entre 1 e o número de alunos da turma ou entre 1 e 20). Em seguida, cada aluno deve desenhar no verso da cartela um objeto de sua escolha (podem ser bolinhas, cubos, estrelas etc.) na quantidade do valor representado numericamente.

Aproveitar a oportunidade para construir com o grupo um "trem" com os cubinhos do material dourado. Comentar que cada vagão deverá ter uma unidade a mais que a quantidade de cubinhos do vagão anterior. Uma sugestão para elaborar esse trem é utilizando copinhos plásticos transparentes.

Cada vagão poderá ser associado a uma cartela numérica. Dessa forma, os alunos serão estimulados a perceberem diferentes registros de representação dos números.

Estimular os alunos a observarem a regularidade existente na constituição do trem e das cartelas numeradas. Verificar se percebem a inclusão de mais uma unidade a cada número imediatamente posterior

Ao final da proposta, orientar os alunos a guardar as cartelas para a exploração que será realizada na próxima aula.

Caso algum aluno apresente dificuldade durante as explorações, retomar o trabalho com a ordem numérica, inicialmente propondo brincadeiras que envolvam a recitação numérica, como a parlenda "Um, dois, feijão com arroz" ou com as cantigas "A galinha do vizinho", "Um, dois, três indiozinhos" etc.

Em seguida, propor explorações relacionadas à quantificação de objetos utilizando, por exemplo, tampinhas de garrafa PET, pequenos objetos e, caso haja alguma coleção da turma, os elementos dessa coleção.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Nesta aula, apresentar as cartelas numeradas construídas anteriormente e perguntar aos alunos quais lembranças eles têm acerca das explorações realizadas antes e durante a confecção de cada cartela.

Escolher um ambiente da sala de aula para esticar um barbante e, assim, construir um varal. O tamanho do barbante dependerá da quantidade de alunos existentes na sala de aula, pois as cartelas numeradas construídas anteriormente serão penduradas no fio.

Após pendurar o varal, incentivar os alunos a levantar hipóteses acerca da atividade que será realizada. Em seguida, mostrar os pregadores e verificar se associam o barbante a um varal, no qual são penduradas roupas molhadas para secar.

Colocar as cartelas em um saco não transparente ou em uma caixa e pedir que cada aluno sorteie uma cartela e pegue um pregador.

Há duas possibilidades de exploração: na primeira, o aluno que sorteou o número 1 inicia a atividade pendurando no varal sua cartela; em seguida, o aluno que sorteou o número 2 é convidado a pendurar sua cartela, e assim sucessivamente.

Outra possibilidade é convidar um aluno para iniciar a brincadeira, independentemente do número que sorteou. Nessa exploração, os próximos alunos deverão observar o número pendurado para, assim, decidir o local onde deverá ser pendurada a sua cartela. Nessa segunda possibilidade, é necessário ter uma percepção maior da ordem numérica e da posição dos números na reta numérica.

O varal de cartelas permitirá inúmeras explorações, como a ordem numérica, ordem crescente, antes e depois, sucessor e antecessor, maior e menor, número entre outros etc. A reta numérica poderá ser retomada e ampliada. Para isso, criar diferentes indagações, por exemplo: qual é o primeiro número do varal? E o último? Qual é o menor número? E o maior?

Qual número está entre os números 8 e 10? Quais números são maiores que o número 12?

Qual número vem imediatamente antes do número 14?

Se julgar conveniente, deixar o varal exposto para que possa ser consultado sempre que necessário e ampliado no decorrer do bimestre.

A partir desta aula, é possível realizar diferentes ampliações, como apresentar aos alunos o quadro numérico, fazendo-os perceber diferentes regularidades existentes em cada linha e em cada coluna. Também, é possível explorar os princípios da adição e da subtração com base no varal numérico, fazendo-os observar quantos números são colocados ou retirados para chegar a outro número existente no varal.

Outra possibilidade é elaborar outras cartelas com números maiores (de 0 a 1 000) e aleatórios, sendo um número para cada aluno. Por exemplo, 2, 40, 79, 103, 278, 300, 469, 552, 667, 668, 708, 715, 718, 800, 802, 820, 964, 990.

Inicialmente, propor uma roda de conversa para que os alunos possam compartilhar informações acerca da altura de cada um. Perguntar à turma se já tiveram a oportunidade de realizar alguma medição e, em caso afirmativo, estimular o compartilhamento de experiências e vivências relacionadas ao tema. Em seguida, fazê-los refletir sobre a importância de respeitar as diferenças, como alguma característica física de um amigo ou um hábito diferente do dele. Essas reflexões exercitam a empatia, o diálogo, a resolução de conflitos e a cooperação, promovendo o respeito aos outros e aos direitos humanos, o que desenvolve a Competência geral 9 da BNCC.

Comentar com os alunos que eles deverão descobrir a altura de cada colega e verificar as estratégias apresentadas para cumprir o desafio. Explicar que será possível utilizar barbante e fita métrica. Apresentar a fita métrica aos alunos, verificar se já conhecem esse instrumento de medição e questionar sobre o seu uso. Caso algum aluno conheça, entre familiares e conhecidos, alguma costureira ou costureiro, provavelmente já terá visto a fita métrica sendo utilizada e poderá compartilhar com os colegas as informações prévias acerca desse instrumento.

Nesse momento, não há necessidade de explorar as diferentes unidades de medida como o centímetro e o metro, tampouco a relação entre elas, pois a ideia inicial é de fazê-los perceber a sequência numérica apresentada nesse instrumento de medição

Pedir aos alunos que se reúnam em duplas para realizar a medição de seus parceiros. Observar as estratégias utilizadas ao receberem a fita métrica e um barbante de tamanho superior ao tamanho da fita. Comentar que, ao final da medição, deverão saber o número contido na fita métrica que representa a altura do colega e recortar um pedaço de barbante com a altura exata dele, ou seja, o barbante deverá ter o mesmo comprimento do que foi identificado e marcado na fita métrica ao medi-lo

Após essa exploração, reunir a turma para que todos possam compartilhar as estratégias utilizadas e possíveis dificuldades encontradas para realizar o desafio. Verificar se todos estão com um barbante com a altura do colega e, caso perceba alguma inadequação, auxiliá-los a realizar uma nova medição. Ao final, cada aluno deverá entregar ao colega o barbante que representa a altura dele. Pedir aos alunos que identifiquem o barbante escrevendo em uma fita adesiva o nome do colega.

Aula 5

Retomar as explorações de medição realizadas na aula anterior. Pedir aos alunos que peguem o barbante que representa a altura de cada um, ou seja, o barbante com o nome dele. Incentivá-los a realizar diferentes experimentações como comparar os barbantes para localizar algum que tenha o mesmo comprimento que o dele, um barbante mais curto e outro mais comprido. Em seguida, criar um painel que deverá ter uma marcação inicial (todos os barbantes deverão ser ajustados com base nela) e orientar os alunos a colocar os barbantes

respeitando essa marcação. Assim, será possível visualizar e comparar o comprimento dos barbantes.

Posteriormente, criar algumas indagações que levem a reflexões acerca do comprimento dos barbantes e diferentes possibilidades de organizá-los. Verificar se os alunos são capazes de ordenar os barbantes do mais curto ao mais comprido. Para isso, poderão trocar os barbantes de posição. Incentivar a turma a identificar o aluno que, segundo esse critério, se encontra em primeiro lugar e em último lugar; cada aluno poderá tentar identificar sua posição nessa organização.

Desafiar a turma a inverter a ordem iniciando a sequência do barbante mais comprido para o mais curto, percebendo, assim, que o último se torna o primeiro e vice-versa. Para finalizar a atividade, entregar aos alunos uma folha avulsa e pedir que representem uma das descobertas obtidas, por meio da exploração com barbantes, e uma das ordens identificadas.

Caso algum aluno apresente dificuldade durante as atividades, retomar explorações envolvendo medições com a fita métrica, fazendo-os perceber a sequência numérica nela representada. Se necessário, utilizar o quadro numérico para que possam observar a sequência numérica e relacioná-la à apresentada na fita métrica Ao perceber dificuldade em ordenar os barbantes, segundo os critérios selecionados pela turma, criar algumas explorações por meio das quais sejam convidados a dizer sua posição em relação à dos colegas, utilizando-se dos números ordinais, que poderão ser representados em um painel a ser consultado sempre que necessário.

É possível ampliar essas explorações pedindo aos alunos que representem, em cartelas, os números obtidos na fita métrica referentes à altura de cada aluno. Nesse caso, deverão utilizar apenas os centímetros que mais se aproximam da altura de cada um, desconsiderando os milímetros. As cartelas poderão ser ordenadas segundo critérios estabelecidos pela turma, como em ordem crescente ou decrescente.

Aula 6

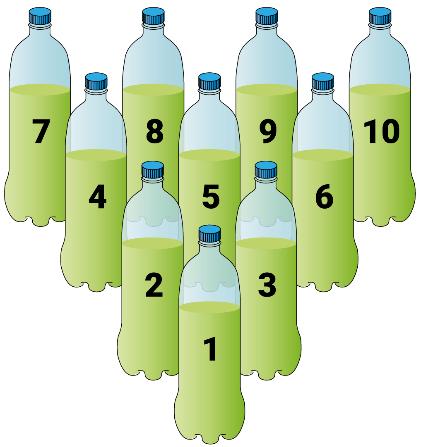
Organizar a turma em equipes com cinco alunos e entregar, a cada duas equipes, nove garrafas de plástico, todas de mesmo tamanho e de mesma massa, e uma bola. As garrafas de plástico devem ser numeradas com valores de 10 a 19 (ou outros valores adequados para a turma). Desenhar no chão um triângulo para arrumar as garrafas sempre na mesma posição (nem muito próximas nem muito distantes umas das outras). Providenciar o material dourado ou o ábaco para auxiliar no cálculo da soma dos pontos e explicar o jogo Boliche da soma aos alunos.

Representação de jogo de boliche com garrafas PET

Os alunos deverão organizar as garrafas de plástico para o jogo de boliche. Cada aluno, então, jogará a bola para derrubar a maior quantidade de garrafas. Em seguida, calculará e marcará os pontos e, com a ajuda dos colegas de equipe, deve separar o material dourado na quantidade correspondente a essa pontuação. A equipe anotará, então, o resultado em uma tabela.

Posteriormente, um jogador da outra equipe procederá do mesmo modo, e assim sucessivamente. O jogo continuará até que todos tenham feito 5 rodadas. Ao final, os jogadores devem verificar a tabela, somar os pontos e constatar qual foi a equipe vencedora.

A cada jogada, reservar um tempo para que os alunos possam calcular os pontos, separar o material dourado e fazer a anotação na tabela. Nesse momento, é importante perceber a representação dos alunos que conseguiram fazer as trocas das dezenas com o material dourado. Verificar se, ao registrar a quantidade de pontos adquiridos na jogada, o aluno representa o valor de maneira adequada e no local correto da tabela. A contagem de pontos desse jogo desenvolve o raciocínio lógico, recorrendo a conhecimentos matemáticos como as trocas realizadas com o material dourado, o que explora a Competência específica 2 de Matemática e suas Tecnologias da BNCC.

Quando todos os grupos terminarem o jogo, pedir que retornem ao seu lugar e que registrem no caderno o resultado das partidas anotado na tabela. Em seguida, incentivá-los a escrever suas observações sobre as regras e o desenvolvimento do jogo.

Aula 7

Nesta aula, os alunos vão brincar com o jogo Boliche da multiplicação. Propor a atividade de modo semelhante ao da brincadeira da aula anterior. No entanto, explicar que cada garrafa derrubada terá o valor que ela representa multiplicado por 3, por exemplo. Ressaltar que o multiplicador 2, 3, 4 ou 5 deve ser escolhido conforme a fase.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

Explicar que a multiplicação pode representar uma adição de parcelas iguais: multiplicar um número por três é o mesmo que adicionar três vezes esse mesmo número. Assim, se caírem as garrafas 2 e 4, o aluno tomará nota desses números, multiplicará cada um por 3 e somará os resultados:

3 × 2 = 6

3 × 4 = 12

6 + 12 = 18

O resultado será o mesmo se usarmos a adição:

2 + 2 + 2 = 6

4 + 4 + 4 = 12

6 + 12 = 18

Assim, o jogador terá marcado para a sua equipe, nessa rodada, 18 pontos. Reservar um tempo para a separação do material dourado, o cálculo dos pontos e a anotação na tabela. Observar a representação feita pelos alunos que conseguiram fazer as trocas das dezenas com o material dourado. Oferecer ajuda na separação do material dourado para representar os pontos de cada equipe, se necessário, e verificar se a representação dos valores e a transferência deles para a tabela foram feitas corretamente, já que agora as somas podem envolver valores maiores.

Pedir aos grupos que voltem ao seu lugar no término do jogo. Solicitar que transfiram para o caderno os resultados das partidas registrados na tabela e, então, que escrevam suas observações sobre as regras e o desenvolvimento do jogo.

Representação de jogo de boliche com garrafas PET.

Propor novamente o jogo de boliche, agora voltado para a subtração, utilizando as mesmas garrafas da aula anterior.

Explicar que as equipes vão começar o jogo com 200 pontos. Entregar-lhes o material dourado, incluindo duas placas de centena.

Na primeira jogada, a equipe soma os pontos das garrafas que derrubou e os subtrai dos 200 pontos iniciais. Propor que façam as trocas com o material dourado. Por exemplo:

Adição do valor das garrafas derrubadas: 1 + 3 + 5 + 6 + 9 + 10 = 34

Subtração do valor obtido dos pontos iniciais: 200 - 34 = 166

Assim, 166 é o saldo dos pontos dessa equipe, que deverá ser lançado na tabela. Na segunda rodada, a soma dos pontos obtidos pela adição do valor de cada garrafa derrubada será subtraída do saldo obtido na jogada anterior, nesse caso, 166. Por exemplo:

Fonte: Dados

Os alunos devem continuar a jogar e anotar dessa maneira até que uma equipe obtenha em uma rodada uma pontuação maior que o saldo de pontos dela – ou seja, quando não for possível fazer a subtração e obter um resultado natural. Por exemplo:

Resultados do jogo de boliche Equipe B Pontos Saldo

Fonte: Dados fictícios.

Ao final da partida, os alunos devem transpor a tabela de resultados do jogo para o caderno e, em seguida, produzir um texto para explicar as regras do jogo.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Sequência didática 2: Matemática e o evento Caminhada colaborativa

Nesta sequência didática, serão estudados o corpo humano e a sua movimentação, assim como importantes aspectos para alcançar uma vida saudável. Conscientizar os alunos, com base nessa pesquisa, da importância de manter-se em movimento, de praticar exercícios regularmente e de ter uma alimentação balanceada.

Os alunos produzirão cartazes e panfletos convidando os pais e/ou responsáveis e a comunidade escolar a participarem de uma caminhada colaborativa pela saúde. Durante todo o processo de organização desse evento, será possível rever e praticar atividades envolvendo conteúdos matemáticos de diferentes campos (Números, Álgebra, Geometria, Grandezas e medidas, Probabilidade e estatística), que desenvolvem a Competência específica 3 de Matemática e suas Tecnologias da BNCC, como estimativa, pesquisa, elaboração de tabelas e gráficos, medir a duração de intervalos de tempo, construir sequências de números naturais, utilizar calendário para agendamentos, registrar localização e deslocamentos de pessoas, esboçar roteiros e classificar eventos aleatórios.

Objetivos de aprendizagem

• Reconhecer a importância do movimento para a saúde corporal.

• Realizar pesquisa.

• Organizar, sintetizar e classificar as informações pesquisadas.

• Planejar e organizar roteiros.

• Elaborar e produzir panfletos e cartazes informativos para a comunidade escolar.

• Organizar um evento de caminhada para a comunidade escolar.

• Realizar estimativa.

• Medir a duração de intervalos de tempo.

• Utilizar calendário para agendamento da caminhada.

• Registrar deslocamento das pessoas durante a caminhada.

• Esboçar percurso da caminhada.

Plano de aulas

Aula 1: Refletir e reconhecer a importância dos movimentos para a saúde corporal e conhecer o evento Caminhada colaborativa.

Aula 2: Preparar as etapas que antecedem a pesquisa sobre atividade física e o evento Caminhada colaborativa.

Aula 3: Analisar resultados da pesquisa e decidir a fala para o evento Caminhada colaborativa

Aula 4: Planejar o trajeto para o evento Caminhada colaborativa

Aula 5: Produzir panfletos para a divulgação do evento Caminhada colaborativa

Aulas 6 e 7: Organizar o evento Caminhada colaborativa e a confraternização pós-evento.

Aula 8: Relatar o evento Caminhada colaborativa por meio de desenhos e textos.

Componentes essenciais para a alfabetização: Desenvolvimento de vocabulário e produção de escrita.

Competências gerais da Educação Básica: 4, 8 e 9.

Competências específicas de Matemática: 3 e 8

Habilidades: EF02MA02, EF02MA09, EF02MA12, EF02MA13, EF02MA18, EF02MA19, EF02MA21, EF02MA22 e EF02MA23.

Materiais necessários: Lápis de cor, lápis grafite, caneta preta, canetas hidrocor, cartolinas, papel sulfite, computadores ou tabletscom acesso à internet, questionário para a pesquisa, calendário, régua e mapa do bairro.

Aula 1

Incentivar os alunos a descreverem como é o início do dia de cada um: como se levanta da cama? Você se espreguiça antes de se levantar? Depois de se levantar, qual é a primeira atividade do dia? Você tem dificuldade para acordar no horário desejado? A que horas foi dormir e como se alimentou antes de se deitar? Você toma café da manhã? O que normalmente consome nessa refeição?

A conversa, também, pode refletir com quanto tempo de antecedência os alunos se levantam para se aprontarem; se tomam café da manhã ou não; se fazem algum planejamento para o dia; se cumprem os horários de alimentação; se praticam atividades físicas. Perguntar a eles se fazem atividades porque gostam; se são encorajados pelos pais ou responsáveis; ou se apenas as praticam na escola. Nesse momento, diferentes rotinas serão apresentadas e poderá surgir a ausência de rotina na vida de alguns alunos; portanto, é preciso estar preparado para lidar com situações diversas.

Conhecer em quais atividades de manutenção da casa os alunos estão envolvidos. Se arrumam a própria cama; se colocam comida para os animais; se guardam as próprias roupas etc. Todas essas atividades requerem a movimentação do corpo, com gasto de energia, sendo consideradas atividades físicas.

Investigar quais tipos de motivação levam os alunos a praticarem uma rotina de alimentação, atividades físicas e auxílio nos afazeres domésticos. Mencionar os cuidados necessários à prevenção de acidentes em casa, por exemplo, precauções com objetos cortantes e inflamáveis, com eletricidade, com produtos de limpeza, com medicamentos etc.

Propor à turma o evento Caminhada colaborativa, explicando aos alunos que eles produzirão panfletos e cartazes convidando seus pais ou responsáveis e a comunidade para uma caminhada, em data predeterminada pela turma. Esse é o primeiro momento de conversa a respeito das próximas atividades.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Discutir com os alunos, em sala de aula, o conceito de autonomia. Escrever essa palavra na lousa e perguntar à turma se alguém já a conhece, ou gostaria de explicar o significado dela. Posteriormente, sugerir que busquem a palavra no dicionário.

Com o significado em mãos, explicar aos alunos e incentivar indagações acerca das atividades praticadas por eles e as praticadas por seus familiares ou responsáveis. Procurar relacionar adequadamente idade, força e capacidade para a realização das tarefas, perceber estereótipos de certas atividades físicas e explicar por que algumas delas são praticadas por pessoas idosas e outras por jovens. Indagar se eles se acham capazes de praticar todos os tipos de atividade e quais.

Pedir aos alunos que pesquisem sobre o estilo de vida e a prática de atividades físicas por familiares ou responsáveis, fazendo as seguintes perguntas: qual é a sua idade? Você pratica atividades físicas? Qual atividade você pratica? Com qual frequência? A intenção é trabalhar com pesquisas e organização de dados em tabelas ou, até mesmo, em gráficos, além de serem informações relevantes para estabelecer a necessidade da prática, adequação das atividades e o estilo de vida dos entrevistados.

A pesquisa pode ser ampliada a fim de verificar quantas pessoas teriam interesse em participar do evento Caminhada colaborativa e qual data elas preferem.

Para isso, distribuir o calendário do mês que estiverem (ou do próximo mês, caso estejam nos últimos dias), um para cada aluno, e questionar as datas que seriam adequadas para a realização desse evento Lembrar de que são necessárias, pelo menos, mais três aulas para a discussão dos resultados das pesquisas, alinhamento do trajeto da caminhada e produção e distribuição dos panfletos.

Escolher três datas possíveis para a caminhada e realizar questionamentos como: daqui quantos dias será a caminhada se escolhermos a primeira data? E a segunda? E a terceira? Teremos tempo para as três aulas que antecipam a data da caminhada? Em qual dia da semana são as possíveis datas escolhidas?

Depois, verificar com a equipe pedagógica da escola se as datas sugeridas estão de acordo com o calendário escolar e se não influenciaria em outras situações ou eventos da escola.

Por fim, preencher a ficha a seguir com as datas escolhidas, fazer cópias para os alunos e entregá-las. Os alunos terão que realizar a pesquisa com seus amigos e familiares, em torno de 5 a 30 pessoas.

Orientar os alunos quanto às perguntas e opções da ficha e pedir que realizem essa pesquisa com a ajuda dos familiares, promovendo assim uma educação continuada em casa. Os itens C, D e E podem ser respondidos com um risquinho para cada voto do entrevistado.

Pedir aos alunos que tragam essa ficha preenchida na próxima aula.

Aula 3

Apresentar aos alunos novos dados sobre a importância da atividade física, por meio da opinião de médicos, esportistas e psicólogos. Pesquisar sobre autonomia,

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

desenvolvimento psicológico e dados sobre alimentação balanceada. Incentivar a observação em relação às atividades praticadas pelos alunos durante os intervalos das aulas e nos momentos de brincadeira no pátio da escola, mostrando a eles que essas atividades também fazem parte das boas práticas para a manutenção da saúde. Pesquisas como essas colaboram para que os alunos conheçam, apreciem e cuidem de sua saúde física e emocional, desenvolvendo aspectos da Competência geral 8 da BNCC.

Em seguida, analisar com os alunos os dados levantados por eles de acordo com a pesquisa. Para isso, formar grupos com 4 ou 5 alunos e pedir que organizem os dados obtidos por eles, em tabelas e gráficos, utilizando o caderno. Circular pela sala de aula, a fim de verificar se eles estão tendo dificuldade em elaborar a tabela ou o gráfico. Esboçar na lousa alguns modelos de tabelas e gráficos

Idade dos entrevistados

a 65

Fonte: Dados coletados pela turma.

Com base na tabela acima, desenhar na lousa os eixos de um gráfico de barras apenas com as indicações dos dados. Deve-se compor o eixo da vertical com o nome "Quantidade" e o eixo da horizontal com o nome "Idade (em anos)". Além disso, indicar os dados no eixo da horizontal: Menos de 15, 15 a 25, 26 a 35, 36 a 45, 46 a 65, 66 ou mais. Título do gráfico: Idade dos entrevistados; Fonte: Dados coletados pela turma.

Frequência com que os entrevistados praticam atividade física

Fonte: Dados coletados pela turma.

Com base na tabela acima, desenhar na lousa os eixos de um gráfico de barras apenas com as indicações dos dados. Deve-se compor o eixo da vertical com o nome

"Quantidade" e o eixo da horizontal com o nome "Frequência (por semana)". Indicar os dados no eixo da horizontal: 1 vez, 2 vezes, 3 vezes ou mais. Título do gráfico: Frequência com que os entrevistados praticam atividade física; Fonte: Dados coletados pela turma.

Data preferida pelos entrevistados para a caminhada

Data Quantidade

Após a atividade em grupo, reunir os dados da turma por meio de gráficos e/ou tabelas feitos na lousa. Fazer algumas perguntas como: das pessoas entrevistadas, quantas praticam esportes? E quantas não praticam? Qual é o esporte mais citado nas pesquisas? (com essa pergunta, é possível elaborar um ranking para saber quais são os mais praticados) Quantas pessoas gostariam de participar da caminhada? E quantas não gostariam? A quantidade de pessoas que gostaria de participar é maior ou menor que a quantidade que não gostaria de participar? Qual data foi a mais votada?

Depois de respondidas às questões, determinar a data para o evento Levar em consideração não só a data mais votada, mas também a previsão do tempo. Para isso, verificar a possibilidade de levar os alunos ao laboratório de informática para acessar sites de previsão do tempo no computador ou utilizar smartphones

Questionar os alunos a fim de classificarem os eventos como pouco provável, muito provável, improvável ou impossível de acontecer. A intenção é que eles escolham a data do evento em um dia que seja mais provável de ter sol do que chuva. Supondo que a previsão do tempo para as três datas fosse sol (dia 1), nublado (dia 2), chuva (dia 3), perguntar a eles: em qual desses três dias é mais provável que chova? Em qual desses dias é pouco provável que chova? Em algum dia desses é impossível chover? Para finalizar a aula, definir a data da caminhada e um horário de início.

Aula 4

Iniciar a aula dizendo como funcionará o evento. Os alunos deverão, nesta aula, pensar em um trajeto para a caminhada e, na aula seguinte, produzir e distribuir panfletos para convidar familiares e amigos. No dia do evento, os participantes deverão levar lanche para a confraternização no final da caminhada. Esse lanche, também, pode ser providenciado pela escola.

Realizar uma caminhada de teste nas redondezas da escola com os alunos a fim de que percebam quanto tempo a turma levou para caminhar de uma quadra até outra (ou usar

Fonte: Dados coletados pela turma.

outros pontos de referência). Levar um relógio digital para marcar o início e o fim da caminhada ou marcar o intervalo de tempo de uma quadra a outra, o que achar mais conveniente. Pedir a alguns alunos que anotem os intervalos de tempo utilizando papel e lápis.

Providenciar antecipadamente o mapa do local escolhido para a caminhada, que pode ser obtido em sitesou aplicativos de mapas digitais interativos. Organizar os alunos em grupos e entregar uma cópia desse mapa por grupo. Deixar que escolham o ponto de partida e o ponto de chegada. Deve-se levar em consideração que, após a caminhada, ocorrerá o lanche de confraternização. Assim, é interessante que o ponto de chegada seja um local seguro para se acomodarem (como a escola, por exemplo). Pedir que tracem no mapa o caminho que eles consideram o melhor trajeto para a caminhada, observando quais são as ruas movimentadas, a distância e o tempo de percurso

Promover uma roda de conversa com os alunos para que eles exponham suas ideias e para que a turma chegue em uma conclusão para esse trajeto.

Aula 5

Organizar os alunos em pequenos grupos e explicar-lhes que deverão elaborar e confeccionar um panfleto que será, também, o convite para o dia da Caminhada colaborativa. Pedir que elaborem textos curtos e chamativos que atraiam a atenção do leitor e o incentive a participar. Eles devem ilustrar o panfleto como desejarem, lembrando de fornecer informações importantes, como data, hora, local do encontro, e pedindo aos participantes que tragam algum alimento para um lanche coletivo que acontecerá no encerramento da atividade. Assim, o panfleto terá o seguinte formato: título (Caminhada colaborativa); ilustração; informações de data, horário e local de saída. Esse trabalho explora e reconhece elementos constitutivos das artes visuais, relacionados ao componente curricular Arte e colabora com o desenvolvimento da habilidade EF15AR02 da BNCC.

Os panfletos confeccionados pelos alunos serão utilizados para divulgar a caminhada que acontecerá uma aula depois desta, e serão distribuídos a toda comunidade escolar e aos participantes. Alguns cartazes serão afixados pela escola para melhor divulgação interna do evento. É importante que os alunos divulguem a caminhada, evidenciando o papel das atividades físicas como um momento importante de socialização e busca de uma vida mais saudável.

No final da aula, organizar os alunos em grupos de trabalho para a divulgação do evento. Distribuir pela escola os panfletos produzidos. Orientar os alunos a escolher locais de maior visibilidade, para que a exposição desses panfletos atinja a maior parte da comunidade escolar. Para divulgar o evento, os alunos podem, ainda, distribuir os panfletos na saída das aulas. Essa ação é necessária para o sucesso do evento e familiariza os alunos com a produção de textos de divulgação, organização, autogestão e realização de outros eventos que sejam importantes para o grupo.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Aula 6

Antes do evento, reunir os alunos e perguntar quantas pessoas eles estimam que comparecerão na caminhada. Depois, entregar para eles cartões de folha de papel sulfite (recorte-as previamente do tamanho que caibam no bolso), a fim de enumerarem sequencialmente os participantes, em ordem crescente, a partir do número 1. Assim, é possível controlar o número de pessoas que completarão a caminhada.

No dia da caminhada, sugere-se receber os alimentos para o lanche coletivo (sucos, água, frutas, pães, bolos etc.), que podem ser dispostos em uma mesa, com o auxílio dos pais e/ou responsáveis dos alunos e da equipe da escola

Na hora prevista para a caminhada, decidir quem será o aluno escolhido pela turma que vai falar aos participantes sobre a conscientização promovida entre os alunos e sobre uma vida mais saudável entre todos da comunidade escolar. Expor o percurso da caminhada e agradecer a participação de todos, lembrando que haverá um lanche para encerrar o evento.

Aula 7

Esta aula deverá ser continuação da aula anterior, pois são necessárias duas aulas para a organização do evento, para a realização da caminhada e para a confraternização ao final.

Depois da explicação do aluno escolhido, iniciar a caminhada, marcando o horário exato de início. Durante todo o percurso, ficar atento para que todos estejam acompanhando e se estão todos bem.

Ao chegar, realizar a confraternização e conversar com os participantes.

Aula 8

Nesta aula, os alunos deverão descrever o que acharam de mais interessante em todo o processo de organização do evento e da caminhada em si. Pedir que relatem o que eles sentiram, onde ocorreu o evento, que horas eles iniciaram, que horas eles retornaram, qual o dia em que ocorreu e pedir que desenhem o trajeto percorrido, ou se preferirem, que escrevam qual foi o trajeto, podendo utilizar termos como "viramos à direita", "passamos na frente de um mercado" etc.

Caso considerar necessário, esse relato pode ser feito em cartolina, para que os alunos tenham mais espaço para desenhar e escrever. Ao final, os cartazes podem ser expostos fora da sala de aula para que outros alunos e a comunidade escolar vejam os resultados obtidos.

Sequência didática 3: Adição e subtração com números naturais

Nesta sequência didática, serão abordados conceitos relacionados ao sistema de numeração decimal e situações envolvendo cálculos da adição e da subtração com números naturais, explorando diferentes estratégias de cálculo.

Objetivos de aprendizagem

• Comparar e ordenar números naturais.

• Construir os fatos básicos da adição e da subtração.

• Resolver problemas envolvendo adição e subtração.

Plano de aulas

Aula 1: Comparar quantidade de objetos em duas coleções, utilizando termos como "tem mais", "tem menos" e "tem a mesma quantidade".

Aulas 2 e 3: Explorar as operações de adição e de subtração por meio de um jogo de tabuleiro.

Aulas 4 e 5: Comparar e ordenar números naturais, resolver adições e discutir diferentes estratégias de cálculo.

Aula 6: Resolver subtrações e discutir diferentes estratégias de cálculo.

Aulas 7 e 8: Explorar as operações de adição e de subtração por meio de um jogo com fichas.

Componentes essenciais para a alfabetização: Produção de escrita e compreensão de textos

Competências gerais da Educação Básica: 2 e 6.

Competências específicas de Matemática: 2 e 8.

Habilidades: EF02MA01, EF02MA03, EF02MA05 e EF02MA06

Materiais necessários: Papel, tesouras com pontas arredondadas, material dourado, tampinhas de garrafa, cartelas numeradas, dados e ábacos.

Aula 1

O objetivo desta aula é explorar a comparação de quantidades de objetos de duas coleções por meio de estimativas ou da correspondência (um a um, dois a dois etc.). Para isso, providenciar antecipadamente materiais manipuláveis, como tampinhas de garrafas PET, clipes, palitos de sorvete, botões, entre outros. Organizar esses materiais em diferentes coleções, de maneira que os alunos possam comparar as quantidades de objetos entre elas. É importante que ao menos um grupo receba duas coleções com a mesma quantidade de objetos.

Para iniciar a aula, sugere-se organizar os alunos em grupos e entregar pelo menos duas coleções diferentes a cada um. Determinar o número de grupos de acordo com a

quantidade de coleções disponíveis. Dessa forma, a quantidade de integrantes de cada grupo pode ser adaptada.

Destinar um tempo para que os alunos manipulem os materiais. Em seguida, propor aos grupos que discutam entre os integrantes e, utilizando a estratégia que preferirem, determinem qual coleção "tem mais", "tem menos" ou "tem a mesma quantidade" de objetos. Nesse momento, acompanhar as discussões e, se necessário, fazer intervenções. Propor aos grupos que compartilhem suas estratégias com os colegas.

Em seguida, se julgar oportuno, pedir que cada grupo determine o total de objetos das coleções que receberam e depois compartilhem com os colegas quais estratégias utilizaram para determinar essa quantidade.

Aulas 2 e 3

O objetivo dessas aulas é explorar a operação de adição e de subtração a partir de um jogo de tabuleiro. Para isso, sugere-se organizar os alunos em duplas e entregar duas folhas em branco e dois dados comuns para cada dupla.

Em seguida, propor aos alunos que desenhem um tabuleiro com os números de 2 a 12. Deixar que eles utilizem a criatividade para representar o tabuleiro, que pode ser desenhado, por exemplo, em forma de trilha ou ter apenas os números espalhados na folha.

Após todos finalizarem o desenho dos tabuleiros, explicar as regras do jogo para a turma. Comentar que, alternadamente, um aluno da dupla deve jogar os dados, observar os números das faces que caírem voltadas para cima, adicionar esses valores e marcar no tabuleiro o número que representa essa soma. Por exemplo, se os valores sorteados nos dados foram 3 e 4, a soma será igual a 7, portanto, o aluno deve marcar o número 7, pintá-lo ou fazer um X sobre ele. Explicar que, se um aluno jogar os dados e a soma dos números obtidos for um número que já foi marcado no tabuleiro, ele perde a vez. Ganha o jogo quem marcar primeiro todos os números do tabuleiro.

Se julgar conveniente, propor aos alunos que registrem em um quadro os números obtidos no lançamento dos dados e a soma. Se necessário, escrever um modelo de quadro na lousa para que eles o copiem no caderno.

Em um segundo momento, propor aos alunos que elaborem um novo tabuleiro com os números naturais de 0 a 12. Em seguida, explicar que nesta rodada eles podem utilizar a adição e a subtração para marcar um número no tabuleiro, ou seja, ao jogar os dados e observar os números que ainda não foram marcados, os alunos podem escolher a operação que é, naquele momento, mais conveniente. Por exemplo, ao sortear os valores 5 e 4, será possível obter o número 9, a partir da adição, ou o número 1, ao subtrair o menor número do maior (5

4 = 1). Suponhamos que o número 9 já tenha sido marcado: é mais conveniente dizer que será utilizada a subtração, para obter o número 1, caso ainda não tenha sido marcado.

Se julgar conveniente, entregar outra folha para que possam registrar as estratégias utilizadas ou, ainda, se julgar necessário, entregar o material dourado para que utilizem como material de apoio no momento da realização dos cálculos Propor aos alunos que compartilhem com os colegas possíveis dificuldades e estratégias utilizadas durante os jogos.

Para finalizar, sugere-se organizar uma roda de conversa e fazer algumas perguntas que possibilitem aos alunos refletirem sobre as atividades propostas, por exemplo, por que o primeiro tabuleiro não continha o número zero e o segundo, sim. Verificar se eles percebem que, de acordo com as regras do jogo, o número zero só poderia ser obtido a partir da subtração de valores iguais (um e um, dois e dois, e assim sucessivamente até o número seis).

Aulas 4 e 5

Nestas aulas, os alunos vão reconhecer a utilização dos números naturais em situações do cotidiano realizando a comparação e a ordenação de números naturais e a operação de adição para resolver problemas. Além disso, vão discutir diferentes estratégias para resolver adições. Para isso, levar para a sala de aula um cartaz com preços hipotéticos de alguns produtos vendidos em uma lanchonete. Por exemplo:

• café com leite: 2 reais;

• garrafa de suco: 11 reais;

• misto quente: 6 reais;

• pão de queijo: 3 reais;

• sanduíche natural: 9 reais;

• tapioca: 15 reais;

• torta de morangos: 13 reais;

• refeição completa (arroz integral, feijão, filé de frango grelhado e salada): 21 reais. Para iniciar a aula, propor aos alunos que realizem uma leitura compartilhada dos itens apresentados no cartaz. Em seguida, organizar a turma em duplas e pedir que comparem os valores apresentados e que os ordenem do maior valor para o menor valor, ou seja, em ordem decrescente. Para isso, sugere-se realizar as seguintes perguntas: qual é o produto mais caro? Qual é o produto mais barato? Qual é o produto mais barato: a garrafa de suco ou o pão de queijo?

Se julgar oportuno, para finalizar esse primeiro momento, conversar com os alunos da turma sobre como é possível compor quantias com cédulas e moedas do Real para comprar alguns dos itens indicados no cartaz. Para isso, pode-se levar para a sala de aula representações de cédulas e moedas do Real.

Em um segundo momento, organizar os alunos em duplas e escrever o problema a seguir na lousa para que o copiem no caderno.

• Pablo realizou uma compra de uma refeição completa e de uma tapioca nessa lanchonete. Qual valor, no total, Pablo pagou nessa compra?

Após todos os alunos copiarem o problema, verificar se possuem alguma dúvida sobre o enunciado da questão. Em seguida, se possível, entregar a cada grupo peças do material dourado, ábaco e folhas avulsas para auxiliá-los na resolução do problema. Propor aos alunos que resolvam o problema utilizando duas estratégias diferentes.

Acompanhar os alunos durante a resolução e realizar intervenções se julgar necessário. Em seguida, selecionar três resoluções distintas para serem apresentadas pelos alunos na lousa. Se julgar oportuno, utilizando os materiais disponíveis, fazer as resoluções a seguir com a colaboração da turma.

Resolução 1

Utilizando um ábaco, representar o número 21 (preço da refeição completa) e, em seguida, colocar argolas referentes ao número 15 (preço da tapioca). Ao final, com a ajuda dos alunos contar as argolas das dezenas e das unidades, obtendo assim 3 argolas na dezena e 6 na unidade.

Resolução 2

Com o material dourado, representar o número 21 (preço da refeição completa) utilizando 2 barras e 1 cubinho o e o número 15 (preço da tapioca) utilizando 1 barra e 5 cubinhos. Em seguida, juntar as peças para representar o total, obtendo assim 3 barras e 6 cubinhos

Resolução 3

Podemos decompor cada um dos números e depois adicionar as unidades e as dezenas.

21 = 20 + 1

15 = 10 + 5

Dezenas: 20 + 10 = 30

Unidades: 1 + 5 = 6

Adição: 30 + 6 = 36

Para ampliar, escrever na lousa a atividade a seguir e propor aos alunos que a resolvam utilizando a estratégia que preferirem

• Quantos reais Pablo gastaria se comprasse nessa lanchonete uma garrafa de suco, uma tapioca e uma torta de morangos?

Verificar se os alunos percebem que é possível realizar essa adição de diferentes maneiras, por exemplo, por decomposição:

11 = 10 + 1

15 = 10 + 5

13 = 10 + 3

Dezenas: 10 + 10 + 10 = 30

Unidades: 1 + 5 + 3 = 9

Adição: 30 + 9 = 39

Propor aos alunos que compartilhem com os colegas quais estratégias utilizaram para realizar a adição com três parcelas. Finalizar a aula comparando as três resoluções e indicando que elas representam estratégias para resolver adições. Caso ainda haja tempo disponível, selecionar outros pares e trios de itens para que os alunos calculem o preço total utilizando diferentes estratégias.

Aula 6

O objetivo desta aula é discutir diferentes estratégias para resolver subtrações. Para isso, retomar com os alunos o cartaz e o primeiro problema apresentado na aula anterior. Em seguida, organizar os alunos em grupos e escrever na lousa o problema a seguir para que eles o copiem no caderno.

• Pablo possui 48 reais para pagar a compra (de uma refeição completa e de uma tapioca) nessa lanchonete. Qual é o valor do troco que a lanchonete deve entregar para Pablo?

Após apresentar o problema aos alunos, verificar se eles possuem alguma dúvida sobre o enunciado da questão. Em seguida, entregar à cada grupo peças do material dourado, ábaco e folhas avulsas para auxiliá-los na resolução. Comentar com a turma que eles devem resolver esse problema utilizando diferentes estratégias.

Acompanhar os alunos durante a resolução e realizar intervenções se julgar necessário. Em seguida, selecionar três resoluções distintas para serem apresentadas pelos alunos na lousa. Para finalizar, se julgar oportuno, explorar com os alunos as três possíveis resoluções apresentadas a seguir.

Resolução 1

Com o ábaco, representar o número 48 (valor que Pablo tem), depois retirar as argolas referentes ao número 36 (valor total da compra). Contar as argolas das dezenas e das unidades que ficaram, após retirar as argolas referentes ao número 36, obtendo 1 argola na dezena e duas argolas na unidade.

Resolução 2

Com o material dourado, representar o número 48 (4 barras e 8 cubinhos), depois retirar as barras e os cubinhos referentes ao número 36 (3 barras e 6 cubinhos). Contar as barras e os cubinhos que sobraram, obtendo assim 1 barra e 2 cubinhos

Resolução 3

Podemos decompor cada um dos números e depois subtrair as unidades e as dezenas.

48 = 40 + 8

36 = 30 + 6

Dezenas: 40 – 30 = 10

Unidades: 8 – 6 = 2

Subtração: 48 – 36 = 12

Finalizar a aula comparando as três resoluções e indicando que elas representam estratégias para resolver subtrações. É possível complementar a aula simulando outras compras de itens nessa lanchonete, de maneira que os alunos devam calcular o troco. Nesse caso, atenção para evitar reagrupamentos nos cálculos.

Aulas 7 e 8

O objetivo destas aulas é explorar a operação de adição e de subtração a partir de um jogo com fichas. Para isso, confeccionar antecipadamente fichas com números entre 0 e 99. Distribuir as fichas aos grupos de forma a evitar que haja adições com reagrupamentos.

Para iniciar a aula, sugere-se organizar a turma em grupos com três integrantes e entregar 18 fichas para cada grupo. Em seguida, explicar aos alunos que eles devem embaralhar as fichas e distribuí-las entre os integrantes dos grupos. Cada aluno ficará com seis fichas. Orientá-los a deixar a face, onde está escrito o número, voltada para baixo.

Depois, explicar aos alunos que em cada rodada, cada integrante desvirará uma das fichas e, em seguida, todos realizarão a adição dos números que aparecem nas três fichas. Pedir aos alunos que registrem as operações de adição e as resolva em uma folha avulsa. O aluno que determinar primeiro o resultado correto da adição dos números das três fichas viradas ganha a rodada. Vencerá o jogo o aluno que ganhar mais rodadas.

Acompanhar a turma durante a realização do jogo verificando as estratégias que estão utilizando para determinar a soma das adições Eles podem fazer o cálculo da adição por meio da decomposição, do cálculo mental, entre outras estratégias. Caso algum aluno apresente dificuldade em realizar as adições com três parcelas, fazer algumas adições na lousa utilizando diferentes estratégias, por exemplo, decomposição.

Material disponibilizado em licença aberta do tipo Creative Commons

Em um segundo momento, sugere-se propor aos alunos que realizem o mesmo jogo fazendo a subtração dos números que aparecem nas fichas. Para isso, organizar a turma em duplas, recolher as fichas entregues aos alunos, embaralhá-las e redistribui-las entregando 12 cartas para cada dupla. Distribuir as fichas de forma a evitar que resultem em subtrações com reagrupamentos.

Os alunos devem realizar os mesmos procedimentos do jogo anterior, ou seja, em cada rodada um integrante desvirará uma das suas fichas, depois, eles realizarão as subtrações dos números que aparecem nas duas cartas. O aluno que determinar primeiro o resultado correto da subtração dos números das duas fichas viradas ganha a rodada. Vencerá o jogo o aluno que ganhar mais rodadas. Pedir aos alunos que registrem a operação de subtração e as resolva em uma folha avulsa

Se possível, propor aos alunos que utilizem uma calculadora para verificar o cálculo das adições e das subtrações feito durante os jogos. Ao final, organizar uma roda de conversa para que os alunos compartilhem o que acharam da aula, expondo as estratégias que utilizaram, as dificuldades, dentre outras percepções que julgarem necessárias.

Sequência didática 4: Figuras geométricas

Nesta sequência didática, serão abordadas características comuns e diferentes entre figuras geométricas espaciais e entre figuras geométricas planas. Também, será abordada a planificação de sólidos geométricos, bem como a construção de representações deles e sua representação no geoplano.

Objetivos de aprendizagem

• Representar figuras geométricas planas e reconhecê-las nas construções, desenhos de objetos ou imagens encontradas no dia a dia.

• Classificar figuras geométricas espaciais e figuras geométricas planas segundo diferentes critérios.

• Perceber e reconhecer a composição de figuras geométricas planas (círculo, quadrado, retângulo e triângulo) e apontar suas características.

• Reconhecer características de figuras geométricas planas, como círculo, quadrado, retângulo e triângulo.

• Desenvolver a percepção e o reconhecimento da posição de objetos no espaço.

• Representar figuras geométricas espaciais no plano.

• Observar, experimentar e representar posições de objetos em diferentes perspectivas.

Planos de aula

Aulas 1 e 2: Explorar ideias iniciais a respeito de figuras geométricas planas.

Aula 3: Discutir características de figuras geométricas planas e espaciais a partir da confecção e exploração de um jogo.

Aulas 4 e 5: Discutir características de linhas retas e de linhas curvas.

Aula 6: Explorar características de figuras geométricas planas.

Aula 7: Explorar características de figuras geométricas planas por meio de materiais manipulativos.

Aula 8: Associar figuras geométricas planas e figuras geométricas espaciais.

Componentes essenciais para a alfabetização: Produção de escrita e desenvolvimento de vocabulário.

Competências gerais da Educação Básica: 2 e 3.

Competências específicas de Matemática: 2 e 8.

Habilidades: EF02MA14 e EF02MA15.

Materiais necessários: Folha avulsa, régua, lápis preto, lápis coloridos, canetas hidrográficas, cola, barbante, elástico, papel quadriculado, geoplano, embalagens de produtos de uso diário, imagens de pinturas, plantas baixas, mosaicos, moldes de planificação de sólidos geométricos, tesoura com pontas arredondadas, revistas, tinta guache, marcador, pino ou peão.

Aula 1

O objetivo desta aula é explorar ideias iniciais a respeito de figuras geométricas planas. Distribuir uma folha avulsa aos alunos e pedir que cada um escreva seu nome para identificação. Registrar na lousa o título FIGURAS GEOMÉTRICAS PLANAS. Em seguida, incentivá-los a desenhar as figuras geométricas planas que conhecem. Nesse momento, permitir a livre expressão dos conhecimentos que possuem acerca do tema.

Reservar um tempo para que possam representar as figuras e, em seguida, solicitar que troquem de folha com um colega para que ele possa nomear os desenhos das figuras geométricas ilustradas no papel que recebeu. Ao final, orientá-los a guardar seus desenhos, pois serão retomados posteriormente. É importante perceber que os desenhos, nesse caso, são uma representação dos conhecimentos prévios dos alunos, assim como a interpretação das figuras ilustradas pelo colega.

EDITORIA DE ARTE

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Em seguida, organizar os alunos em duplas para que possam refletir sobre a pergunta: como podemos construir ou obter representações de figuras geométricas planas?

Existem diferentes estratégias que podem permitir a representação de figuras geométricas planas, como, contornando objetos, desenhando no papel quadriculado com régua, construindo no geoplano com linha ou elástico e utilizando dobraduras. Verificar e anotar as informações e sugestões apresentadas por eles. Os alunos podem, inclusive, responder que basta fazer um desenho

Para incentivar a discussão acerca da representação de figuras geométricas planas, disponibilizar objetos de diferentes formas (embalagem de produtos), régua, lápis, papel quadriculado, tabuleiro com pinos (geoplano), linha e elásticos. Comentar com a turma que eles deverão pegar a folha avulsa utilizada anteriormente e, na parte de trás, com seu colega de dupla, elaborar uma lista com as estratégias para representar as figuras geométricas planas que foram apresentadas durante a discussão.

Avisar a turma que, na próxima aula, serão disponibilizados os materiais para a realização das construções propostas por eles. Se julgar pertinente, comentar com o grupo que, também, poderão contribuir trazendo de casa embalagens de produtos com diferentes formatos. A partir das listas elaboradas pelos alunos, providenciar os materiais e levá-los na segunda aula.

Aula 2

O objetivo desta aula é explorar ideias iniciais a respeito de figuras geométricas planas. Para isso, distribuir aos alunos os materiais listados anteriormente e a folha em que se encontra o desenho feito na primeira aula, juntamente com a lista de possíveis estratégias que permitam a representação de figuras geométricas planas. A seguir, pedir que se organizem em duplas e utilizem os materiais para representar algumas dessas figuras.

Enquanto os alunos produzem, circular por entre as mesas para verificar se as duplas necessitam de algum auxílio e aproveitar para identificar as estratégias utilizadas por eles. Se julgar necessário, realizar intervenções.

Conforme as duplas forem terminando suas produções, dar uma nova folha para que possam registrar qual material ou procedimento foram utilizados por elas na produção de cada figura e se, de fato, a estratégia escolhida permitiu ou não a obtenção de uma representação de figura geométrica plana. Assim que todas as duplas terminarem, organizar os alunos em um semicírculo para a socialização das respostas e apresentação das suas produções.

Para elaborar uma conclusão final, registrar na lousa as principais ideias citadas pelos alunos, inclusive os materiais utilizados na construção das representações de figuras geométricas planas. Para finalizar, verificar se os alunos conhecem os nomes das figuras representadas pelas diferentes duplas e, caso necessário, auxiliá-los nessa demanda explorando, inclusive, o que há em comum e de diferente entre as figuras representadas.

O objetivo desta aula é discutir características de figuras geométricas planas e espaciais a partir da confecção e exploração de um jogo. Para isso, inicialmente, levar para a sala de aula um conjunto de representações de sólidos geométricos já montados e pedir que os alunos os classifiquem utilizando critérios por eles selecionados, como, os que possuem pontas, os que rolam com mais facilidade ou que possuem partes arredondadas, de modo que percebam propriedades comuns e diferentes entre eles. Em seguida, solicitar que os alunos se organizem em duplas.

Posteriormente, entregar um modelo de planificação de um cubo para cada dupla da turma. Em cada face do cubo, pedir que escrevam um dos seis nomes de figuras geométricas espaciais: cubo, bloco retangular, esfera, cilindro, cone e pirâmide. Em duplas, os alunos deverão recortar, dobrar, colar e montar a representação de cubo (dado) para um jogo, deixando os nomes das figuras geométricas espaciais para o lado de fora do cubo. Nas mesmas duplas, os alunos explorarão um jogo que possui as seguintes regras.

• Um aluno jogará o dado e deverá ler a identificação escrita na face sorteada; em seguida, sua dupla repetirá o procedimento, de modo que cada aluno da dupla tenha sorteado uma figura geométrica espacial.

• Em seguida, simultaneamente, cada jogador escreverá na folha avulsa itens relacionados à figura geométrica espacial que sorteou. Tais itens podem ser: o nome de um ou de mais objetos do cotidiano que lembre essa figura; quantidade de figuras geométricas planas que compõem a figura geométrica espacial (faces); características das figuras geométricas planas identificadas (nome, número de lados).

• Após o tempo estabelecido, todos devem parar de realizar os registros.

• Vencerá o jogador que descrever mais elementos observados na figura geométrica espacial que sorteou.

Caso algum aluno apresente dificuldade na identificação das características das figuras geométricas planas representadas, solicitar a contagem e comparação entre elementos, como os lados. Outra possibilidade é pedir que observem e identifiquem o que há em comum ou de diferente entre as figuras geométricas planas e as figuras geométricas espaciais estudadas.

Apresentar, se possível, a imagem de uma obra de arte retratando uma paisagem com representações geométricas espaciais ou planas. Pedir aos alunos para que, individualmente, identifiquem as figuras geométricas planas que podem ser percebidas nessa pintura. Para ampliar essas explorações, solicitar aos alunos que procurem elementos que lembrem figuras geométricas planas e figuras geométricas espaciais e criem um desenho com os elementos identificados. As criações poderão ser expostas para apreciação de todos.

Desenhar na lousa linhas retas em diferentes posições (horizontal, vertical, diagonal, linhas poligonais). Pedir que os alunos observem as linhas apresentadas e, posteriormente, apresentar o desenho de algumas linhas curvas (incluir linhas abertas e fechadas, círculos, semicírculos, formas onduladas, entre outros). Depois, perguntar aos alunos quais diferenças eles observam entre as primeiras linhas desenhadas (retas) e entre as segundas (curvas). Deixar que eles se expressem livremente na descrição. Por fim, sistematizar esses elementos, estabelecendo diferenças entre linhas retas e linhas curvas.

Após a abordagem inicial, distribuir aos alunos, em duplas, pedaços pequenos de barbante e pedir que identifiquem qual é o mais comprido e qual é o mais curto, apenas pela avaliação visual. Após a elaboração das estimativas, solicitar que reorganizem os mesmos barbantes em linha reta e em ordem crescente de comprimento. Orientá-los a colar os barbantes em uma folha compondo diferentes imagens e formas.

Reservar um tempo para que os alunos possam argumentar, decidir e executar a tarefa. Propor uma roda de conversa e estimulá-los a contar percepções visuais em relação a linhas retas e linhas curvas que podem ser identificadas em suas produções.

Por fim, apresentar aos alunos quadros, gravuras e ilustrações com motivos formados por linha retas e linhas curvas e mediar as explorações com questionamentos como:

• Quais elementos são parecidos nas imagens?

• Quais são as diferenças apresentadas nas imagens?

Esta atividade pode ser ampliada nas aulas de Arte. Para isso, apresentar aos alunos imagens diversas em que se possa explorar a observação de linhas retas e de linhas curvas. Em seguida, pedir que compartilhem suas observações e impressões acerca das estratégias utilizadas pelos autores.

Aula 5

O objetivo desta aula é explorar características de linhas retas e de linhas curvas com foco em seus comprimentos. Para isso, propor um jogo de percurso em que cada jogador avança de acordo com o comprimento de um barbante. Organizar os alunos em grupos de seis. Propor que construam uma pista com cerca de 60 centímetros de comprimento (o comprimento de duas réguas, por exemplo).

Entregar a cada grupo uma caixinha com pedaços de barbante de comprimentos variados, os quais, no entanto, não devem ultrapassar 5 centímetros, para que o jogo tenha certa duração.

Cada jogador do grupo deve ter uma folha avulsa, um lápis e uma régua para marcar o comprimento do barbante sorteado. Cada um deles deve pegar um pedaço de barbante na caixinha, sem escolher, esticar o barbante na pista e avançar com seu marcador, pino ou

peão, até a extremidade do barbante. A cada rodada, o aluno marcará no papel o comprimento dos barbantes que sorteou – um traço em uma ponta, outro traço na outra ponta – e devolverá o barbante para a caixinha. O próximo jogador procederá da mesma maneira. Ganhará o jogo quem chegar primeiro ao final da pista. No final, convidar os alunos a observar a marcação que fizeram dos barbantes sorteados e a responder a algumas perguntas, como:

• Quem tirou o barbante mais longo mais vezes? Resposta pessoal.

• O vencedor foi o jogador que tirou o barbante mais longo? Resposta pessoal.

• Existe alguma chance de um jogador tirar o barbante mais longo e não vencer o jogo?

Sugestão de resposta: Sim, pois o jogador depende de vários sorteios para ganhar o jogo.

• Há possibilidade de vencer o jogo mesmo sem tirar o barbante mais longo?

Sugestão de resposta: Sim, pois o jogador depende de vários sorteios para ganhar o jogo.

Ao final da aula, retomar as características de linhas curvas e de linhas retas. Realizar uma comparação entre esses dois conceitos, associando-os aos elementos do jogo.

Aula 6

O objetivo desta aula é explorar características de figuras geométricas planas. Para isso, disponibilizar gravuras de quadros, figuras de fachadas de prédio, fotografias que ressaltem figuras geométricas planas (retângulo, quadrado, círculo, triângulo). Pode-se apresentar mosaicos ou imagens de planta baixa de espaços delimitados.

Promover uma roda de conversa para que os alunos comentem as imagens apresentadas e mencionem outras que lembram figuras geométricas planas, sempre chamando a atenção deles para figuras não percebidas.

Entregar à cada aluno uma folha quadriculada com desenhos de figuras geométricas planas variadas e pedir que identifiquem e pintem os triângulos. Circular pela sala de aula enquanto os alunos desenvolvem as atividades para identificar as dúvidas e possíveis dificuldades.

Disponibilizar papéis coloridos recortados em forma de quadrado, retângulo, círculo e triângulo. Organizar grupos de três alunos e propor que elaborem quadros ou painéis decorativos com uma colagem desses recortes.

Em seguida, solicitar aos alunos que façam um mosaico com figuras geométricas planas. Orientá-los a não sobrepor as figuras nessa composição. A intenção é que o mosaico de figuras preencha a folha avulsa. Acompanhar a produção dos mosaicos para conhecer as dificuldades dos alunos, as hipóteses e as soluções encontradas.

Quando os alunos terminarem a atividade, expor os trabalhos e propor uma roda de conversa para que eles compartilhem impressões sobre as possibilidades de composição em cada situação. Ao final da aula, comentar com os alunos que não sobrepor as representações de figuras planas indica uma característica do mosaico.

Aula 7

O objetivo desta aula é explorar características de figuras geométricas planas por meio de materiais manipulativos. Para isso, disponibilizar geoplanos, de modo que os alunos possam criar, com elásticos, diferentes representações de figuras geométricas planas. Caso não seja possível trabalhar com geoplanos, substituí-los por malha pontilhada ou papel quadriculado. Perguntar aos alunos:

• Quais são as possibilidades de criar figuras no geoplano ou na malha quadriculada? Quais são as dificuldades?

• O que é possível representar no geoplano ou na malha quadriculada?

• Faça o contorno da figura de um quadrado com três unidades de lado.

• Represente o contorno de um triângulo com quatro unidades em um dos lados. Respostas pessoais.

Após a exploração dessas perguntas, solicitar que os alunos se reúnam em duplas. Em seguida, propor a seguinte problematização.

• Compare suas produções com as de um colega. Os quadrados representados ficaram iguais? Os triângulos representados ficaram iguais?

Sugestão de resposta: os triângulos possuem os outros dois lados correspondentes distintos.

Desafiá-los a representar, em duplas, figuras diferentes, como um círculo, na malha quadriculada ou no geoplano. Enquanto os alunos trabalham, andar entre as mesas para verificar se as duplas descobrem outras possibilidades para o triângulo e se percebem que não é possível um traçado diferente de um quadrado. Socializar as conclusões.

Para elaborar a conclusão, registrar na lousa as principais ideias citadas pelos alunos e mediar para que tirem conclusões sobre as características dessas figuras geométricas.

Para ampliar as explorações, utilizar dobraduras para fazer e transformar representações de figuras geométricas planas. Por exemplo, perguntar aos alunos como compor com dobradura a figura de um quadrado – ou, também, de um triângulo – com uma folha de papel retangular (sulfite, por exemplo). Uma maneira de resolver essa questão é (1) pegar uma das pontas do papel (ou um dos vértices do retângulo) e levá-lo à margem contrária, compondo uma diagonal. Depois, para marcar o papel, (2) dobrar o retângulo estreito por cima do triângulo feito na primeira dobra, (3) criando uma composição

geométrica. (4) Então, levar à posição inicial a ponta que havia sido dobrada. (5) Cortar ou dobrar para trás o retângulo estreito superior para chegar ao quadrado (6).

EDITORIA DE ARTE

Composição de quadrado por meio de dobradura.

Aula 8

O objetivo desta aula é associar figuras geométricas planas e figuras geométricas espaciais. Para isso, organizar grupos de três alunos e levá-los em um local em que seja possível trabalhar com tinta (o pátio da escola, por exemplo). Em seguida, entregar objetos variados a cada grupo e propor que pintem uma das faces dos objetos e a imprimam em um papel, como se fosse um carimbo. Os objetos podem ser embalagens que lembrem bloco retangular, prismas, cubos, cilindros ou pirâmides. Providenciar, também, objetos irregulares, como batatas cortadas, e outros com superfícies em diferentes planos, como montagens de cubos e paralelepípedos.

Quando finalizarem o trabalho, pedir que observem as regiões pintadas e tentem identificar o nome da figura representada (quadrado, triângulo, retângulo, círculo) e o formato do objeto que a produziu (cubo, pirâmide, bloco, cone). Convidar os alunos de um grupo a ver otrabalho das outras equipes. Reservar um tempo para essa observação e depois trocar ideias a respeito. Por fim, solicitar que os alunos apresentem, já na sala de aula, suas produções e sistematizar as associações entre figuras geométricas espaciais e figuras geométricas planas.

Sugestões

• ALAGOAS. Prefeitura de Marechal Deodoro. Exposição de arte com mosaico apresenta obras feitas por estudantes deodorenses. Marechal Deodoro, 26 jan. 2017. Disponível em: www.marechaldeodoro.al.gov.br/2017/01/exposicao-de-arte-com-mosaicoapresenta-obras-feitas-por-estudantes-deodorenses/. Acesso em: 17 jan. 2022.

Material disponibilizado em licença aberta do tipo Creative Commons

Sequência didática 5: Multiplicação e divisão

Nesta sequência didática, serão abordadas atividades lúdicas e situações-problema envolvendo a multiplicação, com a ideia de adição de parcelas iguais.

Objetivos de aprendizagem

• Comparar quantidades.

• Explorar e resolver situações-problema envolvendo adição de parcelas iguais.

• Compreender e utilizar diferentes estratégias para o cálculo de multiplicação.

Plano de aulas

Aula 1: Compreender a igualdade de adições de parcelas iguais e respectivas multiplicações por meio de atividade lúdica.

Aula 2: Resolver problemas utilizando multiplicações com a ideia de adição de parcelas iguais.

Aula 3: Resolver e elaborar situações-problema que envolvam multiplicação.

Aula 4: Relacionar adições de parcelas iguais à respectiva multiplicação por meio de atividade lúdica.

Aula 5: Calcular metade, dobro ou triplo de uma quantidade por meio de atividade lúdica.

Aula 6: Compreender e calcular terça parte de uma quantidade por meio de situação-problema.

Aula 7: Calcular dobro e triplo de uma quantidade e investigar a relação com metade e terça parte.

Aula 8: Revisar os conteúdos de multiplicação por meio de um jogo da memória.

Componentes essenciais para a alfabetização: Produção de escrita e compreensão de textos Competências gerais da Educação Básica: 2, 4 e 6 Competências específicas de Matemática: 2 e 4

Habilidades: EF02MA07 e EF02MA08.

Materiais necessários: Material dourado, botões, bolinhas de papel, folhas avulsas, canetas hidrográficas coloridas ou lápis de cor, cartolina ou papel pardo, cola, papel para dobradura (16 cm × 16 cm), papel quadriculado, fichas com situações-problema de multiplicação, aparelho de som, tesoura com pontas arredondadas, folha impressa do Jogo da memória e folha impressa com dados da Caça ao tesouro

Aula 1

Inicialmente, desenhar no chão, com giz, círculos grandes, de maneira que caiba dentro deles um grupo com cinco integrantes Em seguida, dividir a turma em grupos com cinco alunos. O número de figuras de círculos será igual ao número de grupos. Caso a turma não seja formada por uma quantidade de alunos múltipla de 5, os alunos que sobrarem poderão realizar tarefas auxiliares, ou mesmo trocar de lugar com os colegas de um grupo.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Se não for possível realizar a brincadeira Só vale 2, 3, 4, 5, na sala de aula, procurar um espaço adequado na escola.

Explicar as seguintes regras da brincadeira Os alunos deverão caminhar pelo espaço enquanto toca uma música. De repente, parar a música e dar um comando: "Só vale 2". Duas crianças de cada grupo deverão entrar nas figuras de círculos e registrar, em uma folha de papel sulfite, uma operação com o resultado correspondente à quantidade total de alunos no interior das figuras de círculos. Supondo que sejam 20 alunos na turma e, portanto, quatro figuras de círculos, a operação registrada será:

2 + 2 + 2 + 2 = 8 (notar que são quatro parcelas, pois inicialmente a quantidade de 20 alunos foi dividida de cinco em cinco, resultando em quatro grupos).

Repetir, então, a situação anterior. Tocar a música e dizer o comando "Só vale 3" Três alunos de cada grupo entrarão nas figuras de círculos, e assim sucessivamente até o comando "Só vale 5" ser dado. Ao final de cada rodada, os grupos devem anotar as operações. Observar como é feito esse registro e como são efetuados os cálculos correspondentes. Essa prática permitirá verificar os conhecimentos prévios sobre adição de parcelas iguais e a noção da multiplicação dos alunos.

No final da brincadeira, os registros devem estar assim:

2 + 2 + 2 + 2 = 8

3 + 3 + 3 + 3 = 12

4 + 4 + 4 + 4 = 16

5 + 5 + 5 + 5 = 20

Em seguida, elaborar e propor as seguintes questões aos grupos, com a intenção de que reflitam sobre a ideia da multiplicação como adição de parcelas iguais

• Quantas vezes tem-se a mesma quantidade?

Quatro vezes.

• Qual modificação deveria ser feita no jogo para que as quantidades se repetissem mais uma vez?

Desenhar mais um círculo no chão e criar um grupo.

• Criando mais um círculo no chão, quantos alunos seriam necessários para preencher os cinco círculos existentes com cinco alunos?

A quantidade de alunos que estiver jogando mais cinco. No exemplo acima, 5 + 5 + 5 + 5 + 5 = 25.

Após a brincadeira, na sala de aula, organizar quatro grupos e entregar a eles cubinhos do material dourado, botões ou bolinhas de papel. Propor construções em que haja a adição de parcelas iguais com 2, 3, 4 e 5 objetos, em cada adição, com total até 10, 15, 20 e 25, respectivamente.

Por exemplo:

Adição de 2 parcelas iguais, com resultado até 10

2 + 2 = 2 × 2 = 4

2 + 2 + 2 = 3 × 2 = 6

2 + 2 + 2 + 2 = 4 × 2 = 8

2 + 2 + 2 + 2 + 2 = 5 × 2 = 10

Ao final, orientá-los a guardar os registros, pois serão retomados posteriormente.

Avaliar a compreensão dos alunos a respeito da correspondência entre os agrupamentos de números iguais adicionados e a quantidade de vezes que esses números aparecem na sentença matemática, o que leva a representar a adição pela multiplicação. Nessa fase, os alunos já devem estar familiarizados com a adição de parcelas iguais. Caso ainda haja dificuldade, retomar a questão da adição com os alunos que precisarem desse reforço, pois esse processo auxiliará na compreensão do conceito de multiplicação.

Aula 2

Começar a aula relembrando o que foi estudado na aula anterior. Caso seja necessário, sanar possíveis dúvidas.

Em seguida, pedir aos alunos que formem duplas. Entregar a cada dupla folhas quadriculadas e a seguinte atividade impressa.

Observe as figuras e resolva as questões.

brgfx/Freepik.com

Imagem de peras.

azerbaijan_stockers/Freepik.com

Imagem de bananas. freepik/Freepik.com

Imagem de maçãs.

1. Conte a quantidade de peras na embalagem e calcule a quantidade de peras em:

a) 2 embalagens iguais a essa

4 + 4 = 8; 8 peras

b) 3 embalagens iguais a essa

4 + 4 + 4 = 12; 12 peras

c) 4 embalagens iguais a essa

4 + 4 + 4 + 4 = 16; 16 peras

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

d) 5 embalagens iguais a essa

4 + 4 + 4 + 4 + 4 = 20; 20 peras

2. Conte a quantidade de bananas na caixa e calcule a quantidade de bananas em:

a) 2 caixas iguais a essa

3 + 3 = 6; 6 bananas

b) 3 caixas iguais a essa

3 + 3 + 3 = 9; 9 bananas.

c) 4 caixas iguais a essa

3 + 3 + 3 + 3 = 12; 12 bananas.

d) 5 caixas iguais a essa

3 + 3 + 3 + 3 + 3 = 15; 15 bananas.

3. Conte a quantidade de maçãs que há no prato e calcule a quantidade de maçãs em:

a) 2 pratos iguais a esse

2 + 2 = 4; 4 maçãs.

b) 3 pratos iguais a esse

2 + 2 + 2 = 6; 6 maçãs.

c) 4 pratos iguais a esse

2 + 2 + 2 + 2 = 8; 8 maçãs.

d) 5 pratos iguais a esse

2 + 2 + 2 + 2 + 2 = 10; 10 maçãs.

Verificar se os alunos perceberam que primeiro é questionada a quantidade de peras, que são quatro; depois de bananas, que são três; e por último maçãs, que são duas. Feito isso, eles deverão preencher os resultados no papel quadriculado, formando o seguinte quadro.

Material disponibilizado em licença aberta do tipo Creative Commons

4.0 International).

Atribuição

comercial (CC BY NC

não

–

Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Reforçar com a turma essa ideia dizendo que, à medida que forem preenchendo o quadro com os resultados das situações-problema, perceberão um padrão que pode ser associado por eles com sequências numéricas.

Solicitar que observem o quadro e tentem completar os valores que estão faltando somente pela regularidade encontrada.

Reproduzir o quadro na lousa fazendo com que os alunos notem a progressão que existe, por exemplo, na linha do número três: da esquerda para a direita, há uma adição constante de três unidades, e da direita para a esquerda, sempre uma subtração constante de três unidades. Mostrar, ainda, que na coluna do número três ocorre o mesmo fenômeno: uma adição de cima para baixo e uma subtração de baixo para cima. E o mesmo ocorre de maneira parecida com todas as outras linhas e colunas.

Para finalizar a aula, entregar uma folha avulsa ou uma ficha em branco e pedir que cada dupla elabore um problema envolvendo adição de parcelas iguais ou mesmo a multiplicação.

Observar como cada dupla conduz esse registro e propor a troca entre as duplas dos papéis ou das fichas com o problema, para que conversem a respeito de suas conclusões e transfiram os resultados para o papel quadriculado. Nesse momento, é importante caminhar entre as duplas para verificar as resoluções e a coerência dos argumentos de cada aluno.

Verificar se as duplas conseguiram resolver os problemas apresentados e registraram corretamente os resultados. Analisar se os alunos perceberam a relação entre a adição de parcelas iguais e a multiplicação e se lançaram os resultados no lugar correto no papel quadriculado.

Deixar disponível o material dourado e caixas com sucata (tampinhas, palitos, bolinhas, botões etc.) a fim de retomar a questão da adição de parcelas e levar o aluno a dominar a habilidade com a multiplicação. Rever com a turma a questão das sequências numéricas, que podem ser identificadas no papel quadriculado com as multiplicações, e relacioná-las com a repetição e a adição de uma mesma parcela para obter um resultado crescente, propiciando a correspondência com a multiplicação. Outra possibilidade é entregar resoluções de situações-problema escritas em tiras de papel.

Pedir aos alunos que leiam a informação apresentada, criem o enunciado do problema e, depois, procedam da mesma maneira que antes, preenchendo o quadro da tabuada. É possível, também, que os alunos consigam se organizar melhor se destacarem as informações relevantes e representá-las com material manipulável.

Aula 3

Nesta aula, os alunos trabalharão a operação de multiplicação por meio de situações-problema, descritas a seguir. As atividades, no primeiro momento, serão expostas na lousa, e deverá ser solicitado que os alunos as resolvam individualmente em seus

cadernos. No segundo momento, os alunos farão parte da criação e resolução de situações-problema.

1. Marcela foi ao médico e recebeu uma receita para tomar medicamentos. Ela deveria tomar dois comprimidos no café da manhã, mais dois no almoço e mais dois no jantar, todos os dias por três semanas. Ajude Marcela a calcular as quantidades em cada situação.

a) Quantos comprimidos ela precisa tomar por dia? Faça um esquema e calcule.

2

2

2

2 + 2 + 2 = 3 × 2 = 6; 6 comprimidos por dia.

b) Quantos comprimidos ela precisa tomar por semana? Faça um esquema e calcule.

6 + 6 + 6 + 6 + 6 + 6 + 6 = 7 × 6 = 42; 42 comprimidos por semana.

c) Quantos comprimidos ao todo ela precisa tomar para completar o tratamento?

42 + 42 + 42 = 3 × 42 = 126; 126 comprimidos nas três semanas de tratamento

d) Ao chegar em casa, sua mãe tinha comprado 6 caixas que continham 21 comprimidos cada. Eles serão suficientes para completar o tratamento?

21 + 21 + 21 + 21 + 21 + 21 = 6 × 21 = 126; sim, eles serão suficientes para completar o tratamento

Ao solicitar que os alunos resolvam de diferentes maneiras a atividade, levantar conhecimentos prévios fazendo questionamentos. Perguntar se o problema pode ser resolvido pela adição ou pela multiplicação e como fariam. Estimular diferentes resoluções e disponibilizar material dourado para que possam representar a atividade. Após a primeira situação ser resolvida, propor verbalmente uma segunda atividade, e solicitar ajuda deles para criar uma história que envolva uma situação que exija o cálculo de uma multiplicação. A questão anterior pode ser colocada como exemplo, porém essa nova história tem que ter mais elementos. Por exemplo:

"João adora ler quadrinhos de super-heróis. Ele tem 26 revistas e 85 bonecos de diferentes personagens em sua coleção. Ele guarda esses itens com muito cuidado. Sempre

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

que inicia uma nova coleção ele brinca, ou lê, e guarda tudo em caixas. Ao navegar pela internet, João descobriu um plano de assinatura mensal em que o assinante recebe 3 bonecos e 7 revistas todo mês. Ele gostaria de saber quantos bonecos e revistas novas ele teria se assinasse esse plano por 6 meses"

No exemplo dado, as informações iniciais não foram necessárias para a resolução do problema criado. Encaminhar os alunos para que o mesmo aconteça nessa história contada e, no final, questionar o porquê de não usarem essas informações para a resolução.

Para desenvolver a história, o professor pode fazer perguntas divertidas, solicitar nomes, ações, motivos e quantidades, além de parar a história para avaliar e questionar se é possível desenvolver alguma situação de multiplicação, para que a história tenha uma conclusão. Caso seja necessário, mais de uma história pode ser desenvolvida, ou alguns alunos podem desenvolver suas histórias para que os colegas façam a resolução dela no caderno.

Aula 4

Nesta aula, é proposta uma competição na qual os alunos utilizarão a igualdade entre adições de parcelas iguais e multiplicações. Para isso, os alunos, que serão divididos em dois grupos, deverão escolher um nome para o grupo. O professor pode ajudar propondo temas, como super-heróis, animais, adjetivos, frutas, personagens de desenhos.

Assim que os dois grupos tiverem nomes, atribuir um tema a cada um: multiplicação ou adição. Por exemplo, o Grupo A deverá escrever adições na lousa e o Grupo B deverá escrever multiplicações. A competição consiste em um grupo responder por multiplicação uma adição apresentada pelo outro grupo, e vice-versa.

Cada grupo deverá ser subdividido em cinco grupos menores e cada grupo menor deverá escrever duas igualdades de adições de parcelas iguais e multiplicação correspondentes com resposta, para conferência dos pontos. Por exemplo, o grupo de tema adição apresenta 5 + 5 + 5 + 5 já sabendo que a resposta é 4 × 5. O grupo desafiado deve responder 4 × 5 e já apresentar a sua multiplicação, devolvendo uma tarefa para o outro grupo Por exemplo: para a multiplicação 3 × 3, o outro grupo deve responder 3 + 3 + 3. Ou seja, o grupo da adição só responde com adições de parcelas iguais e propõe adições de parcelas iguais para que o outro grupo responda, enquanto o outro grupo responde com multiplicação.

O professor deve participar ativamente da organização dos subgrupos, verificar as igualdades escolhidas por eles e acompanhar a atividade de perto. Vencerá o grupo que acertar mais perguntas. Para isso, a pontuação pode ser marcada na lousa, conforme cada etapa é cumprida. Porém, a atividade pode ser retomada trocando o tema dos grupos e solicitando que os subgrupos elaborem novamente as igualdades, gerando uma nova pontuação ao término do jogo.

Aula 5

Nesta aula, os alunos farão uma caça ao tesouro utilizando os termos dobro, triplo ou metade. O professor deverá dividir a turma em grupos de quatro alunos, entregar uma folha avulsa para cada grupo e solicitar que montem os dados, conforme os moldes a seguir.

Cada aluno, em sua vez, deverá jogar os dois dados: primeiro o dado de moedas e, depois, o outro dado. Quando souber o resultado, anotar no caderno e calcular quantas moedas ganhou nos lançamentos. Por exemplo, se o aluno obtiver os resultados "METADE" e "16 moedas", então ele recebe a pontuação correspondente a 8 moedas, pois 2 × 8 = 16. Um dos alunos deverá fazer um placar com os resultados, pois serão 6 rodadas.

No grupo, vencerá quem conseguir o maior resultado. Porém, após as 6 rodadas, o professor deve solicitar que cada grupo adicione a pontuação de todos os participantes do grupo. Feito isso, transpor os resultados para a lousa e finalizar com uma competição entre os grupos.

EDITORIA DE ARTE

Molde de planificações de dados.

O aluno que ficou com a maior pontuação do grupo deverá lançar uma última vez o dado com os termos dobro, metade e triplo, podendo modificar a pontuação do grupo. Ganhará o grupo que ficar com a maior pontuação. É importante observar os cálculos feitos no caderno de cada aluno, a fim de verificar as dificuldades e auxiliá-los.

Novas rodadas podem ser feitas, para que os alunos trabalhem mais com as ideias de dobro, triplo e metade. É possível sugerir que eles criem novas faces para os dados, como mais moedas, ou trocar uma face de moeda por regras como "dobre a pontuação obtida pelo aluno anterior" ou " perca a vez". Caso haja mudança nos dados, não fazer a competição final de grupos por ficarem desiguais as possibilidades. Essa questão pode ser levantada ou observar as modificações que foram feitas e como elas interferiram nos resultados.

Aula 6

Nesta aula, o professor deverá resgatar os conhecimentos prévios dos alunos, como as noções de dividir objetos (ou conjunto de itens) em partes iguais para que aprendam sobre a terça parte. Para isso, reunir os alunos em torno do material dourado, separar algumas quantidades e fazer os questionamentos:

• Quantos cubinhos nós temos separados?

• Como fazemos para dividir igualmente entre dois alunos essa quantidade?

• Quem pode explicar o que é a terça parte? Como obtenho a terça parte de alguma quantidade?

• Como fazemos para dividir essa quantidade igualmente entre três alunos?

Para essas perguntas, separar uma quantidade que seja par e múltiplo de três, como, por exemplo, 18 cubinhos. Só definir o conceito caso nenhum aluno saiba, pois é importante explorar os saberes deles.

Após compreenderem a ideia da terça parte, questionar o que seriam duas terças partes, três terças partes e quatro terças partes. Feito isso, propor as seguintes atividades para que sejam feitas individualmente, no caderno

1 Desenhe e contorne a terça parte dos seguintes conjuntos de frutas.

a) 3 maçãs.

b) 6 abacaxis.

c) 9 morangos.

d) 12 laranjas.

e) 15 peras.

f) 18 goiabas

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Espera-se que os alunos contornem: 1 maçã; 2 abacaxis; 3 morangos; 4 laranjas; 5 peras, 6 goiabas

2 Observe a atividade anterior e calcule:

a) Três vezes um terço de 6 abacaxis.

3 × 2 = 6; 6 abacaxis.

b) Três vezes um terço de 12 laranjas.

3 × 4 = 12; 12 laranjas.

c)Três vezes um terço de 15 peras.

3 × 5 = 15; 15 peras.

d) Qual regularidade você pode observar ao multiplicar por três uma terça parte?

Espera-se que os alunos respondam que, quando fazemos três vezes a terça parte de uma quantidade, obtemos como resultado a quantidade inicial.

3 Na embalagem de um brinquedo, é informado que sua bateria recarregável dura 45 minutos de uso contínuo e que leva a terça parte desse tempo para recarregar totalmente. Quanto tempo demora para recarregar totalmente a bateria deste brinquedo?

15 minutos (3 × 15 = 45).

4 Ana e seus dois colegas farão uma apresentação de 21 minutos na aula de Matemática. Eles repartiram igualmente esse tempo, ou seja, cada um tem a terça parte do tempo total para apresentar. Quanto tempo cada um terá para apresentar?

7 minutos (3 × 7 = 21).

Para as atividades, deixar disponível material dourado para que manipulem, como foi feito no início da aula. Sugerir que confiram as respostas realizando multiplicações (por 3). Caso apresentem dificuldade com o terceiro problema, solicitar que façam o desenho de um relógio e observem quanto é 45 minutos e separem a terça parte para que compreendam quantos minutos são. Para complementar a aula, novas quantidades de minutos podem ser colocadas a fim de que calculem a terça parte.

Aula 7

Na aula anterior, os alunos aprenderam sobre terça parte e foram levados a descobrir como determinar a terça parte de uma quantidade. Nesta aula, eles recordarão a relação entre terça parte e triplo e entre dobro e metade. Os alunos trabalharão em duplas e deverão responder em uma folha avulsa impressa com os seguintes problemas:

1 Giovana e Paulo resolveram preparar uma salada de frutas para seus amigos. Porém, a receita que encontraram não será suficiente para os convidados. Ajude-os a fazer duas ou três receitas dessas.

Ingredientes

• 1 laranja

• 2 mamões

• 3 maçãs

• 4 bananas

• 8 morangos

Preparo

Lave bem todas as frutas. Pique os mamões (retire sua casca e sementes), as maçãs (retirando apenas seu miolo), as bananas e os morangos. Esprema a laranja e coe para retirar as sementes. Misture em uma tigela as frutas picadas e o suco da laranja.

Construir na lousa um quadro para que os alunos copiem na folha de atividade e o preencham.

Feito isso, observe as quantidades preenchidas e responda:

a) Qual é a metade de 2, 4, 6, 8 e 16? 1; 2; 3; 4; 8

b) Ao calcular a metade do dobro, o que puderam perceber?

Espera-se que os alunos respondam que as quantidades obtidas foram as iniciais.

c) Qual é a terça parte de 3, de 6, de 9, de 12 e de 24? 1; 2; 3; 4; 8

d) Ao calcular o triplo e depois a terça parte, o que puderam perceber?

Espera-se que os alunos respondam que as quantidades obtidas foram as iniciais.

Se os alunos tiverem dificuldade ao calcular a metade ou o triplo das quantidades, estimular que usem as adições de parcelas iguais e que manipulem o material dourado. Ao calcular a metade ou a terça parte, podem desenhar as frutas para que possam circular as

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

quantidades necessárias. É importante que todos percebam que, ao calcular o dobro e, depois, a metade, eles obtêm a quantidade inicial.

Feito isso, solicitar que as duplas escrevam uma receita que elas souberem e que gostariam de fazer em dobro ou triplo. Eles poderão pesquisar na internet ou em livros de receitas que forem disponibilizados ou que estejam disponíveis na biblioteca.

O processo deverá ser o mesmo, de criar um quadro semelhante ao do problema anterior, calculando dobro e triplo das quantidades de cada ingrediente.

Aula 8

Uma vez que os alunos compreenderam as situações de dobro, triplo, metade, terça parte, adições de parcelas iguais e suas correspondentes multiplicações, assuntos tratados nas aulas anteriores, a proposta para esta aula é a realização de um Jogo da memória. Para isso, os alunos devem estar organizados em duplas e receber a seguinte folha com fichas para recortar.

EDITORIA DE ARTE

Cartas de jogo da memória para serem recortadas.

Cartas de jogo da memória para serem recortadas.

Após os alunos recortarem todas as fichas, elas devem ter suas faces viradas para baixo e devem ser misturadas. Cada aluno da dupla, na sua vez, virará duas fichas; se elas forem correspondentes, ele deverá recolhê-las e terá direito a uma nova tentativa. Por exemplo, se uma ficha for a multiplicação e a outra for a adição de parcelas iguais correspondentes, ele poderá ficar com as fichas e terá o direito de jogar novamente, até que não encontre mais fichas correspondentes, passando assim a vez para o colega. Vencerá o jogo quem obtiver maior número de cartas ao final.

Novas partidas podem ser realizadas, assim como a troca entre alunos nos grupos.

Observar os alunos que costumam ficar com menos peças e verificar se possuem alguma dificuldade na identificação das fichas correspondentes.

Sugestões

• LIMA, Gisele Ferreira; LIMA, Ingridy Lilith F. A tabuada de Inês Londrina: Eduel, 2009.

Sequência didática 6: Sequências

Nesta sequência didática, serão abordados os conceitos do sistema de numeração decimal, bem como o uso dos números em sequências numéricas recursivas. Além disso, serão propostos jogos envolvendo adição e subtração para desenvolver o conceito de sequências repetitivas.

Objetivos de aprendizagem

• Construir sequências de números e figuras.

• Identificar a regularidade de sequências e determinar elementos ausentes na sequência.

• Fazer estimativas.

• Comparar quantidades.

• Entender e utilizar técnicas operatórias para adição e subtração.

• Compreender sequências.

Plano de aulas

Aula 1: Compreender sequências numéricas com auxílio de figuras.

Aula 2: Explorar novas sequências, crescentes e decrescentes, por meio de situações-problema e elaboração de trabalho expositivo.

Aula 3: Criar sequências a partir de adições e subtrações.

Aula 4: Identificar padrão de sequências e descobrir elementos ausentes.

Aula 5: Reconhecer sequências que possuem mais de uma característica de distinção.

Aula 6: Interagir com os colegas a fim de formar sequências em atividade lúdica.

Aula 7: Trabalhar sequências em diferentes contextos, como em reta numérica, quadros, relógios e material dourado.

Aula 8: Criar sequências e propor atividades para os colegas por meio de atividade com fichas.

Componentes essenciais para a alfabetização: Fluência em leitura oral, produção de escrita e desenvolvimento de vocabulário.

Competências gerais da Educação Básica: 2 e 4

Competências específicas de Matemática: 2, 3 e 6.

Habilidades: EF02MA01, EF02MA09, EF02MA10 e EF02MA11.

Materiais necessários: Papel, lápis, papéis coloridos, tampinhas plásticas, canudinhos coloridos de papel, material dourado, tesoura com pontas arredondadas

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Aula 1

Iniciar a aula distribuindo aos alunos cartões coloridos com formatos diferentes. Organizar uma sequência de cartões, como a representada a seguir, e perguntar se alguém descobre o segredo da colocação das próximas figuras, ou seja, o padrão utilizado na sequência sugerida. EDITORIA

Em seguida, desafiá-los a criar uma sequência para que o colega descubra a regularidade e complete. Expor os trabalhos. Escrever na lousa uma sequência de números e pedir aos alunos que a completem com os números seguintes. Por exemplo:

1 2 3 4 5 __ __ __ __ __

Quando completarem a sequência, orientá-los para que conversem com o colega que está ao lado e escrevam a regra. Propor novos desafios, alertando-os que as sequências são crescentes:

• 10 20 30 40 __ __ __ __ __ __ •

__ __ __ __ __ __ __ __ __ __

•

7 9 __ __ __ __ __ __ __ __

Reservar um tempo para que os alunos possam observar e descobrir a regularidade e pedir que a escrevam. O exercício de observar e verbalizar deverá ampliar a compreensão dos fatos.

Em seguida, entregar a cada grupo um quadro, como o representado a seguir, com linhas numeradas de 1 a 5 e colunas numeradas de 1 a 10, com apenas alguns espaços preenchidos, e pedir que descubram a regularidade e completem os espaços em branco. Desafiá-los a indicar a regularidade na horizontal e na vertical. Isso vai levá-los a encontrar alguns resultados das tabuadas da multiplicação de números naturais.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Caminhar pela sala de aula e questionar os alunos sobre a regularidade dos números presentes em uma única coluna do quadro ou, também, os números pertencentes a uma única linha. Abrir uma roda de conversa para que possam compartilhar suas hipóteses e descobertas.

A troca de informações com os colegas é essencial para resolver possíveis dificuldades. Por isso, é importante incentivar a comunicação, os registros e a exposição das descobertas, a fim de promover uma compreensão mais ampla do tema tratado.

Outra possibilidade para reforçar a aprendizagem é transmitir aos alunos uma regra escrita e pedir que criem um exemplo que a atenda, por exemplo, "a regularidade é subtrair 2 do número anterior"

Aula 2

No início da aula, apresentar uma sequência numérica que não se inicia em 1 e pedir que a completem com acréscimo de 1 ao número anterior.

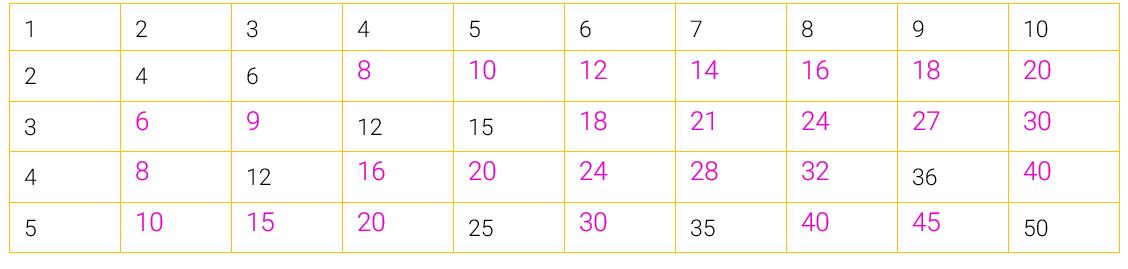
5 6 7 8 __ __ __ __

Depois que discutirem a regularidade e concluírem a atividade, propor novas sequências. Durante essa exploração, é importante solicitar aos alunos que observem e expressem verbalmente as regularidades que identificaram. Também, é interessante trabalhar com sequências que repitam símbolos, por exemplo:

1. Observe as sequências e preencha os espaços com os termos faltantes.

Material disponibilizado em licença aberta do tipo Creative Commons

Respostas:

1.

a) 0 00 000 0000 00000 000000

b) J JJ JJJ JJJJ JJJJJ JJJJJJ

Em seguida, organizar os alunos em duplas para que elaborem algumas sequências de figuras e números, alertando-os sobre o objetivo em cada caso. Incentivá-los a fazer um trabalho harmonioso e colorido para ser exposto. Para isso, deixar à disposição dos alunos, na sala de aula, canudinhos coloridos de papel, tampinhas de garrafa, papéis coloridos e outros materiais incitando a criatividade na elaboração de sequências.

Enquanto os alunos trabalham, caminhar por entre as mesas para verificar se as duplas precisam de algum auxílio e aproveitar para identificar as estratégias utilizadas por elas.

Assim que todas as duplas concluírem a atividade, organizar a exposição dos trabalhos e proporcionar aos alunos um ambiente favorável para que compartilhem sua produção.

Criar novas sequências para que os alunos identifiquem a regularidade e, portanto, entendam como completá-la. Os alunos poderão ser incentivados a criar sequências e a escrever no caderno a regularidade utilizada em cada uma – se é uma sequência crescente ou decrescente, qual é a adição ou a subtração que se deve fazer em relação ao número anterior para determinar o próximo, se é uma sequência repetitiva etc.

Aula 3

Para esta aula, providenciar previamente 16 fichas de papel-cartão ou cartolina de tamanho suficiente para apresentar à turma. Em cada uma delas deve ser escrito um número de uma ou duas ordens, sem necessidade de que formem uma sequência. O objetivo é tirar duas fichas de cada vez e apresentá-las aos alunos, dizendo ao mesmo tempo que operação realizar com esses números – adição ou subtração.

Por exemplo, mostrar as fichas que têm os números 13 e 9 e anunciar a operação adição. Os alunos deverão anotar no caderno os números apresentados, escrever as sentenças matemáticas com a operação indicada, realizar os cálculos, obter o resultado e lançar as parcelas e os resultados em um quadro. Lembrar aos alunos que o material dourado ou outro material manipulável está à disposição deles para auxiliar nos cálculos.

Repetir o procedimento mais cinco vezes, anunciando a operação a ser realizada. Contudo, se saírem, por exemplo, os números 11 e 39, nessa ordem, e a operação anunciada

for subtração, os alunos terão de perceber que o cálculo deverá ser feito subtraindo o menor número do maior.

Ao final das rodadas, os alunos deverão ter montado um quadro como este:

Ao final dos cálculos com os números sorteados, espera-se que os alunos cheguem a resultados em certa ordem de ocorrência no tempo, do primeiro ao sexto sorteio:

22 13 9 28 33 15

Pedir aos alunos que efetuem cálculos com números diferentes, escolhidos por eles, por meio de adições ou subtrações, para reproduzir mais duas vezes a mesma ordem de resultados obtidos anteriormente. Esse é um momento importante para reavaliar os conhecimentos prévios da turma a respeito de adição e de subtração.

Com o objetivo de repetir mais duas vezes os resultados na mesma ordem em que ocorreram, um aluno pode chegar, por exemplo, a quadros como estes:

Em seguida, eles devem transcrever no caderno as três sequências de resultados a que chegaram – aquela motivada pelo sorteio realizado e as duas que construíram. A sequência de números deve ser anotada necessariamente na mesma linha:

22 13 9 28 33 15 22 13 9 28 33 15 22 13 9 28 33 15

Mostrar aos alunos que eles criaram uma sequência numérica em que 22, 13, 9, 28, 33 e 15 se repetem sempre na mesma ordem e sem outros elementos que não pertençam a esse grupo de números. Explicar à turma que sequências como essas são denominadas sequências repetitivas.

Pedir à turma que desenhe no caderno um grupo de seis símbolos ou objetos simples que se repitam em sequência, como representado a seguir.

Esse exercício servirá para ampliar a percepção dos alunos sobre a formação das sequências repetitivas.

É possível encontrar erros comuns nas adições e, principalmente, nas subtrações, que costumam causar maior dificuldade para alguns alunos. A obrigatoriedade do resultado pode também confundir certos alunos, por terem de fazer cálculo com um resultado já estabelecido, levando-os a errar. Nesse caso, verificar que estratégia eles utilizaram na contagem e pedir que refaçam os cálculos ao lado de colegas que já dominam essas operações. Sugerir, também, a troca de estratégias: se usaram tracinhos no caderno, por exemplo, sugerir que experimentem fazer uso de material manipulável, que dá uma visão mais concreta dos conceitos de juntar, de separar ou de retirar.

Aula 4

O objetivo desta aula é que os alunos adquiram a habilidade de identificar sequências e reconhecer que podem faltar componentes ou elementos necessários para completar sequências.

Retomar a sequência abordada na aula anterior. Escrevê-la na lousa ampliando o padrão com mais um grupo de números:

Perguntar aos alunos qual é a diferença entre essa sequência e a sequência que anotaram no caderno na aula anterior. Muito provavelmente eles reconhecerão que a diferença é que existe mais um grupo de números que repete o padrão anterior, formando uma sequência repetitiva, que não se alterou.

Apagar números da sequência escrita na lousa. Por exemplo:

Material disponibilizado em licença aberta do tipo Creative Commons

Pedir à turma que identifique o que aconteceu com a sequência – alguns dirão que ela tem menos números. Perguntar o que está faltando no primeiro grupo de números. A resposta correta é que falta o 13. Solicitar a cada aluno que reproduza essa sequência repetitiva no caderno e indique quais demais elementos faltam para que a sequência fique correta.

Caso restem dúvidas desse tipo, pedir aos alunos que construam mais sequências usando lápis, borrachas, números, tampinhas, bolinhas, material dourado, bloquinhos de construção, permitindo que misturem as categorias. Pedir que retirem elementos dessas sequências criadas e misturem os que foram tirados. Depois, solicitar que reconheçam o que falta e em qual lugar da sequência, acrescentando o elemento faltante.

Aula 5

Nesta aula, os alunos serão envolvidos com sequências que possuem mais de uma característica na distinção. Desse modo, além de observarem que a sequência é composta de figuras, deverão observar também as cores nas quais elas estão sendo apresentadas.

Propor uma sequência envolvendo na regra de formação do padrão, além da característica de formas diferentes, a característica cores diferentes. Por exemplo: EDITORIA

Perguntar aos alunos o que há de novo nessa sequência. Espera-se que eles percebam que agora há figuras com formas iguais, porém cores diferentes, como o triângulo que se repete, sendo um deles na cor laranja e o outro na cor roxa.

Reproduzir o grupo de figuras na lousa mais uma vez, porém contendo mais alguns elementos da sequência. Por exemplo:

Pedir aos alunos que observem e, após isso, digam quais as próximas três figuras que completam a sequência dada. Espera-se que eles respondam que os próximos três elementos da sequência são, nessa ordem, o triângulo verde, o retângulo amarelo e o triângulo roxo.

Após essa exploração, pedir aos alunos que se organizem em duplas e criem uma sequência em que grupos de cinco figuras coloridas se repitam quatro vezes seguindo determinada regra na formação de um padrão.

Solicitar que após a criação eles troquem com outra dupla a sequência elaborada, porém sem as três últimas figuras exibidas para que a outra dupla complete a sequência formada identificando o padrão que foi criado.

É importante a socialização nesse momento, visto que a atividade é de completar a sequência com as figuras que estão faltando. Porém, alguns dos alunos podem completá-la incorretamente, gerando uma atividade de correção.

Aula 6

Esta aula poderá ser desenvolvida tanto em sala de aula quanto na quadra poliesportiva ou no pátio da escola. O professor poderá verificar a possibilidade de os alunos construírem pompons de 5 cores, por exemplo: azul, vermelho, amarelo, rosa e verde. Caso não seja possível, a atividade poderá ser feita com fitas ou tiras de papel previamente providenciadas.

Distribuir entre os alunos as fitas ou tiras de papel de cinco cores. Inicialmente, os alunos se movimentam livremente pelo ambiente, agitando sua fita no ar (com cuidado para evitar tumulto). A um sinal combinado, todos param seu movimento e formam uma roda (independentemente da cor da fita); então, cada aluno deve dizer o nome da cor da sua fita. No segundo momento da brincadeira, o professor diz que, ao próximo sinal, os alunos devem formar a roda organizando-se pelo padrão das cores, quer dizer, na roda formam-se subgrupos de cores. Pedir aos alunos que observem como a roda ficou organizada e que contem quantos grupos se formaram de cada cor, quantos alunos há em cada grupo e quantos alunos há no total.

No terceiro momento da brincadeira, combinar que, a um sinal, os alunos formem uma roda de maneira intercalada, conforme a seguinte sequência de cores: grupo azul, grupo vermelho, grupo amarelo, grupo rosa e grupo verde. Pedir que observem novamente como a roda ficou organizada e que verbalizem o nome da sequência de cores que se formou.

No quarto momento da brincadeira, variar a sequência, combinando que os alunos não se organizem mais em grupos de cores, mas sim individualmente da seguinte forma: um aluno com fita azul, um aluno com fita vermelha, um aluno com fita amarela, um aluno com fita rosa, um aluno com fita verde, um aluno com fita azul e um aluno com fita vermelha. Pedir que voltem a observar a sequência que se formou na roda.

Essa brincadeira pode ter várias formações: um aluno com fita vermelha, dois alunos com fitas amarelas, um aluno com fita azul, dois alunos com fitas rosa, um aluno com fita vermelha, dois alunos com fitas amarela etc.

Pode-se, ainda, tirar algumas cores da sequência para os alunos identificarem e corrigirem. O importante é que a cada formação os alunos sejam chamados a observá-la e a verbalizar a sequência formada.

Para finalizar a brincadeira, pedir que relatem verbalmente qual foi a sequência da brincadeira, do primeiro ao último momento: primeiro, aleatoriamente; em seguida, por grupos de cores; depois, individualmente, na sequência de cores estipulada pelo professor. Acalmar a turma e pedir aos alunos que desenhem uma sequência em segredo, individualmente, deixando faltar um ou mais elementos que só eles sabem qual é. Depois, organizar os alunos em duplas para um aluno resolver a sequência que o colega construiu.

Aula 7

Nesta aula, os alunos trabalharão com sequências em diferentes contextos, como em reta numérica, quadros e material dourado.

Distribuir, projetar ou escrever na lousa as atividades a seguir, para serem realizadas em duplas de alunos.

1. Na reta numérica a seguir, qual é o valor M? Para descobrir, continue o registro dos números contando de 2 em 2.

6; 8; 10; 12; M = 14; 16; 18, 20.

2. Pinte esta sequência numérica contando de 5 em 5 e começando pelo número 5. Escolha duas cores diferentes para pintar alternadamente. É possível observar algum padrão na sequência colorida com cada cor?

Serão coloridos múltiplos de 5, de maneira que os terminados em 5 ficarão de uma cor e terminados em 0 de outra cor.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

3. Complete a sequência numérica.

Resposta:

4. O material dourado deveria formar e representar uma sequência numérica que se repete 3 vezes. Descubra qual número está faltando em cada sequência. a)

EDITORIA DE ARTE

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Respostas:

a) 22; b) 4

Posteriormente, cada dupla deve trocar seu trabalho com outra dupla, observando se as soluções se equivalem. Para isso, formar grupos com duas duplas

As dúvidas frequentes podem ser compartilhadas coletivamente na lousa após as duplas terem socializado as respostas no grupo maior.

Aula 8

Nesta aula, os alunos participarão da criação de sequências repetitivas, nas quais deverão identificar a quantidade e quais elementos estão faltando. Para isso, propor a eles que respondam coletivamente e entendam o funcionamento da atividade.

Nesta atividade, serão utilizadas as seguintes fichas, que podem ser impressas para que os alunos as recortem.

Fichas com nome de animais e objetos para recortar.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

EDITORIA DE ARTE

Posteriormente, reunir os alunos próximos à mesa e formar em uma linha a primeira sequência de 6 fichas. Por exemplo: sapo, bola, galo, pena, bota e foca. Depois, repetir a mesma sequência, porém com duas fichas faltando, e novamente, pela terceira vez, repeti-la com duas fichas faltando.

Questionar os alunos:

• Quantos elementos estão faltando para formar a sequência?

• Quais são os elementos que estão faltando?

Os alunos deverão responder a essas questões de acordo com as fichas que o professor escolheu retirar, podendo variar as figuras e as quantidades. Posteriormente, organizar as fichas iguais, uma sobre as outras, semelhante ao exemplo a seguir, e questionar se assim fica mais fácil identificar as fichas que faltam.

Fichas com nomes de animais e objetos recortadas e organizadas.

Repetir o processo feito anteriormente, dispondo as fichas em linhas e em colunas, retirando mais fichas e criando uma quarta linha. Os questionamentos deverão ser os mesmos.

Feita essa primeira parte, em duplas, os alunos deverão criar sequências semelhantes às que foram propostas. Primeiramente, eles deverão testar sequências em uma única linha, de forma que, quando o colega acertar, ele propõe de volta uma sequência para o colega que o havia desafiado. Eles deverão responder às mesmas perguntas feitas para o grupo no início da aula, sobre quantidade e quais elementos estão faltando.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Depois de testar sequências em linhas, deverão propor sequências de figuras organizadas em linhas e colunas, e mostrar novamente ao colega para que ele descubra quantas e quais fichas estão faltando.

É importante que percebam que em diferentes maneiras de organizar é possível identificar padrões de repetição dos elementos, e que algumas maneiras de organizar, como em linhas e colunas, podem ajudar na identificação dos elementos da repetição, inclusive os faltantes.

Sugestões

• WELTMAN, Anna. Isto não é um livro de Matemática: arte inteligente, criada a partir de padrões matemáticos. São Paulo: Publifolhinha, 2016.

Sequência didática 7: Probabilidade e Estatística

Nesta sequência didática, será explorada a probabilidade por meio da análise de resultados de eventos aleatórios e da classificação desses eventos em "possível", "impossível", "mais provável" ou "menos provável". Além disso, os alunos vão realizar pesquisas, organizar dados em tabelas simples e de dupla entrada, organizar dados em gráficos de colunas simples e elaborar um texto para apresentar as conclusões obtidas a partir da análise de dados coletados em uma pesquisa.

Objetivos de aprendizagem

• Identificar e classificar resultados de eventos aleatórios em "possível", "impossível", "mais provável" ou "menos provável".

• Realizar pesquisa e organizar os dados coletados em tabelas simples.

• Organizar dados coletados em gráficos de colunas simples.

• Elaborar texto para apresentar conclusões.

• Organizar dados em tabelas de dupla entrada.

Plano de aulas

Aula 1: Identificar e classificar eventos cotidianos aleatórios em "possível", "impossível", "mais provável" ou "menos provável" de ocorrer.

Aula 2: Classificar os resultados de eventos aleatórios como "possível", "impossível", "mais provável" ou "menos provável" de ocorrer por meio da participação em atividades práticas

Aulas 3 e 4: Classificar os resultados de um experimento aleatório e resolver atividades classificando eventos aleatórios em "possível", "impossível", "mais provável" ou "menos provável".

Aulas 5 e 6: Realizar uma pesquisa e organizar dados em tabelas.

Aula 7: Organizar dados em um gráfico de colunas simples

Aula 8: Ler e interpretar dados apresentados em tabelas simples e organizar esses dados em uma tabela de dupla entrada

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita.

Competências gerais da Educação Básica: 2 e 4.

Competências específicas de Matemática: 2, 4 e 6

Habilidades: EF02MA21, EF02MA22 e EF02MA23.

Materiais necessários: Papel quadriculado, dados, bolinhas brancas e azuis, saco não transparente e retroprojetor

Aula 1

Nesta aula, serão exploradas algumas noções de probabilidade. Para iniciar a aula, organizar uma roda de conversa para discutir com os alunos acontecimentos do cotidiano que podem ser classificados como "possível", "impossível", "mais provável" ou "' menos provável" de ocorrer. Para isso, sugere-se fazer as seguintes perguntas para a turma: em um dia de sol e sem nuvens, é mais provável ou menos provável que chova? Ao jogar um dado, é possível ou impossível que o número da face voltada para cima seja 7?

Aproveitar a conversa sobre os acontecimentos do cotidiano que podem ser classificados em "possível", "impossível", "mais provável" ou "menos provável" de ocorrer para explorar com os alunos a ideia de aleatoriedade em situações cotidianas e para esclarecer possíveis dúvidas. Em seguida, organizar a turma em grupos de quatro integrantes e reproduzir o quadro a seguir na lousa para que os alunos o copiem em uma folha avulsa.

Evento Possível Impossível Justificativa

Explicar à turma que cada aluno do grupo deve escrever um evento diferente dos que foram citados no início da aula, totalizando quatro eventos por folha de atividade Em seguida, eles devem trocar essa folha com outro grupo para que um complete o quadro do outro. Por fim, os grupos trocam novamente as folhas para que os alunos possam corrigir as respostas dos colegas.

Posteriormente, reproduzir o quadro a seguir na lousa para que os alunos o copiem em uma folha avulsa e propor que façam o mesmo processo da atividade anterior, analisando agora os eventos mais prováveis e menos prováveis de ocorrer.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

No final da aula, se julgar oportuno, propor que os grupos compartilhem ao menos um dos exemplos presentes nos quadros e, em seguida, perguntar: quais eventos foram mais difíceis de serem classificados? Quais foram mais fáceis? Aproveitar o momento para identificar e sanar possíveis dúvidas dos alunos em relação ao conteúdo estudado nesta aula.

Aula 2

Nesta aula, os alunos vão classificar os resultados de eventos aleatórios como "possível", "impossível", "mais provável" ou "menos provável" de ocorrer por meio da participação em atividades práticas. Para isso, providenciar antecipadamente um dado, um saquinho que não seja transparente e bolinhas brancas e azuis.

Para iniciar a aula, mostrar um dado comum aos alunos e conversar com eles sobre os possíveis resultados que podem ser obtidos no lançamento de um dado Para isso, sugere-se fazer as seguintes perguntas aos alunos: é possível ou impossível obter o número 4 ao lançar o dado? E o número 7? É mais provável obter o número 5 ou um número menor que 4?

Para ampliar, sugere-se organizar os alunos em grupos e entregar um dado a cada um. Propor que lancem os dados e registrem os resultados obtidos em uma folha avulsa Depois, organizar uma roda de conversa para que eles compartilhem com os colegas os resultados obtidos e perguntar: qual resultado ocorreu mais vezes? Há mais chances de ocorrer um ou outro resultado? Repetir o jogo algumas vezes e incentivar que os alunos percebam que as chances de ocorrer todos os resultados é a mesma.

Em um segundo momento, organizar a turma em grupos e entregar a cada grupo um saquinho que não seja transparente, cinco bolinhas brancas e cinco bolinhas azuis, todas de mesma massa e tamanho. Em seguida, propor aos alunos que coloquem todas as bolinhas no saquinho e perguntar: é mais provável retirar do saquinho uma bolinha branca ou uma bolinha azul? Propor que façam algumas retiradas e anotem os resultados. A cada retirada, o aluno deve devolver a bolinha para o saquinho. Por exemplo, um aluno tira uma bolinha, anota a cor, recoloca a bolinha no saquinho e passa para o próximo aluno do grupo; este retira uma bolinha e anota em seus registros a cor. Propor que repitam a operação até que cada aluno do grupo tenha completado 5 retiradas. Ao final, solicitar que observem os

registros de cada um na dinâmica e respondam à pergunta feita anteriormente, justificando a resposta

Dessa maneira, é possível que os alunos percebam que, como há cinco bolinhas brancas e cinco bolinhas azuis, a chance de retirar uma bolinha branca ou uma bolinha azul é a mesma.

Aulas 3 e 4

Nestas aulas, os alunos vão continuar a explorar o estudo da probabilidade por meio de um experimento aleatório e resolver atividades classificando eventos aleatórios em "possível", "impossível", "mais provável" ou "menos provável". Para isso, providenciar com antecedência as bolinhas brancas e azuis utilizadas nas aulas anteriores.

Para iniciar a aula, propor aos alunos que façam um experimento semelhante ao realizado na aula 2, agora, sem devolver as bolinhas retiradas ao saquinho e utilizando cinco bolinhas brancas e três bolinhas azuis. Orientá-los a registrar a cor das bolinhas a cada retirada e pedir que, ao final, analisem os registros do grupo. Para auxiliar os grupos na análise, sugere-se fazer as seguintes perguntas à turma: qual bolinha é mais provável de ser retirada do saquinho: a branca ou a azul? Espera-se que os alunos percebam que quanto maior é a quantidade de bolinhas de determinada cor, maior é a chance dessa determinada bolinha ser tirada, e que no decorrer da atividade as chances vão mudando com a retirada das bolinhas

Em seguida, perguntar aos alunos: ao retirar uma bolinha do saquinho, é possível ou impossível retirar uma bolinha verde? Espera-se que eles percebam que, como a bolinha verde não faz parte das opções de bolinhas que estão no saquinho, é impossível retirar uma bolinha dessa cor.

Se julgar necessário, ao final, fazer mais retiradas de bolinhas para que os alunos acompanhem e percebam que as chances de retirar bolinhas brancas ou azuis mudam sempre que retiramos uma bolinha do saquinho.

Se necessário, auxiliar os alunos que tiverem dificuldade para identificar as cores das bolinhas que já saíram e das bolinhas que ainda estão no saquinho. Caso seja necessário, para facilitar o processo, sugerir aos alunos que desenhem e risquem as bolinhas que forem aparecendo.

Para finalizar o trabalho com o conteúdo de probabilidade, sugere-se entregar uma folha avulsa impressa ou apresentar em um projetor os problemas a seguir e propor aos alunos que respondam no caderno.

1. Duas crianças estão sorteando fichas coloridas de um saquinho em que foram colocadas 5 fichas vermelhas e 5 fichas azuis (de mesmo tamanho):

a) É mais provável uma criança sortear uma ficha vermelha ou uma azul?

As fichas têm chances iguais de serem sorteadas.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

b) Se o jogo for sem reposição das fichas, depois de retirada uma ficha vermelha, é mais provável que a segunda ficha retirada seja vermelha ou azul?

É mais provável que seja azul.

2) Marcos guardou em uma caixa 10 blocos de montar, de mesmo formato e massa, sendo 7 azuis, 2 vermelhos e 1 verde.

a) Quantos blocos há na caixa? 10 blocos.

b) Ao retirar um bloco sem ver, qual cor é mais provável de ser retirada? Azul.

c) Ao retirar um bloco sem ver, qual cor é menos provável de ser retirada? Verde.

d) Como você classificaria a chance de sortear aleatoriamente um bloco azul: muito provável, pouco provável ou impossível?

Muito provável.

e) Como você classificaria a chance de sortear aleatoriamente um bloco verde: muito provável, pouco provável ou impossível?

Pouco provável.

f) Como você classificaria a chance de sortear aleatoriamente um bloco amarelo: muito provável, pouco provável ou impossível?

Impossível.

3) Ao arremessar um dado honesto de 6 faces:

a) é mais provável que saia um número par ou o número 1? Justifique.

É mais provável que saia um número par, pois há três números pares e somente um número 1.

b) é menos provável que saia um número ímpar ou o número 6? Justifique.

É menos provável que saia o número 6, pois há somente um número 6 e três números ímpares.

Acompanhar os alunos durante a resolução e sanar possíveis dúvidas. Se julgar oportuno, para auxiliar os alunos com dificuldade, fazer alguns questionamentos para que eles reflitam sobre o problema e possam encontrar a resposta.

Para finalizar, sugere-se fazer a correção das questões com a turma. Se julgar oportuno, convidar alguns alunos a resolverem questões na lousa, compartilhando como pensaram para resolvê-las

Material disponibilizado em licença aberta do tipo Creative Commons

comercial (CC

Atribuição não

BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Aulas 5 e 6

Nestas aulas, os alunos vão fazer uma pesquisa e organizar os dados coletados em uma tabela. Para iniciar a aula, organizar uma roda de conversa e fazer algumas perguntas à turma, por exemplo: o que é uma pesquisa? Você já participou de alguma pesquisa? Incentivar os alunos a expressarem suas opiniões e aproveitar o momento para verificar os conhecimentos prévios da turma sobre esse tema e para conversar sobre a importância da pesquisa e da estatística para a sociedade.

Depois, perguntar aos alunos se eles sabem quais são as etapas de uma pesquisa e, com o auxílio da turma, escrever essas etapas na lousa.

• Elaborar perguntas sobre o tema que se deseja investigar.

• Escolher o grupo de pessoas que vão participar da pesquisa.

• Realizar as entrevistas.

• Representar os dados coletados em tabelas ou gráficos.

Organizar os alunos em duplas e propor que elaborem uma pergunta sobre algum tema de interesse deles, por exemplo, animal, cor, gênero musical ou esporte preferido dos colegas. Comentar que é importante que a pergunta elaborada apresente algumas opções de resposta para que o entrevistado possa escolher entre uma delas. Orientá-los a elaborar, no máximo, quatro opções.

Em seguida, pedir às duplas que realizem uma pesquisa com os colegas. Antes de os alunos realizarem as entrevistas é importante ler a questão elaborada por cada dupla e verificar se estão coerentes e se permitem a coleta de dados estatísticos. Comentar com a turma sobre a importância de registrar de forma organizada as respostas obtidas na entrevista.

Para finalizar, propor aos alunos que organizem os dados coletados em uma tabela. Os alunos podem pesquisar exemplos de tabelas caso tenham dúvidas na construção. Comentar com os alunos sobre os elementos obrigatórios de uma tabela, título e fonte. Acompanhar a turma durante a construção da tabela e sanar possíveis dúvidas.

Aula

7

Nesta aula, os alunos vão organizar os dados coletados e apresentados na aula anterior em uma tabela em um gráfico de colunas simples. Além disso, vão elaborar um texto apresentando as conclusões que chegaram a partir da análise dos dados coletados. Para isso, se possível, entregar a cada dupla uma folha de papel quadriculada e uma folha avulsa.

Para iniciar a aula, sugere-se apresentar alguns gráficos de colunas simples aos alunos, que podem ser representados na lousa ou apresentados utilizando um retroprojetor. Aproveitar o momento para conversar com os alunos sobre os elementos obrigatórios de um gráfico: títulos dos eixos, valores dos eixos, título do gráfico e fonte.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

Em seguida, determinar um tempo para as duplas construírem o gráfico e elaborarem um texto. Acompanhar a turma durante a atividade e verificar se estão construindo o gráfico corretamente; se necessário, realizar intervenções e sanar possíveis dúvidas. Ao final da aula, propor aos alunos que apresentem o texto aos colegas, compartilhando com a turma as conclusões que obtiveram.

Aula 8

Nesta aula, será explorada uma situação que vai possibilitar aos alunos ler e interpretar dados apresentados em tabelas simples e organizar esses dados em uma tabela de dupla entrada. Para iniciar, reproduzir a situação a seguir na lousa ou apresentá-la aos alunos utilizando um retroprojetor.

• A escola em que Joana é professora está organizando uma gincana. Para definir as modalidades esportivas da gincana, ela fez uma pesquisa com os alunos do 2º ano. Cada aluno escolheu apenas um esporte. Observe os dados coletados e organizados por Joana nas tabelas a seguir

Modalidades esportivas preferidas das alunas do 2º ano

Fonte: Dados obtidos pela professora do 2º ano, em janeiro de 2022.

Modalidades esportivas preferidas dos alunos do 2º ano

Fonte: Dados obtidos pela professora do 2º ano, em janeiro de 2022.

Em seguida, conversar com a turma sobre os dados apresentados nas tabelas. Para isso, podem-se fazer algumas perguntas como: o que o número 15 representa na tabela? Quais números nas tabelas indicam a quantidade de alunas e de alunos que preferem basquete? Aproveitar o momento para verificar se os alunos possuem alguma dificuldade para ler e interpretar os dados apresentados em tabelas simples.

Se julgar oportuno, retomar com a turma que os títulos das tabelas expressam a informação principal transmitida pelos dados e que as fontes indicam onde ou de quem esses dados foram obtidos.

Depois, explorar com os alunos a utilização de uma tabela de dupla entrada como maneira de representar os dados apresentados nas tabelas anteriores. Para isso, escrever a tabela a seguir na lousa ou apresentá-la com o auxílio de um retroprojetor. Pedir aos alunos que copiem a tabela no caderno.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Número de alunas 14

Número de alunos 12

Total 26

Fonte: Dados obtidos pela professora do 2º ano, em janeiro de 2022.

Conversar com a turma sobre o que representa as linhas e as colunas na tabela de dupla entrada anterior. Explicar que a leitura dos dados apresentados na célula é feita cruzando as informações das linhas e das colunas; por exemplo, o número 14 indica a quantidade de alunas que preferem vôlei, o número 12 a quantidade de alunos que preferem vôlei e o número 26 representa a quantidade total de alunos da turma que preferem vôlei. Explicar aos alunos que o cruzamento da última linha com a última coluna deve apresentar a quantidade total de alunos da turma que participaram da pesquisa.

Em seguida, propor aos alunos que completem a tabela anterior de acordo com os dados das duas primeiras tabelas apresentadas. Acompanhar os alunos durante a atividade para verificar se estão fazendo corretamente e sanar possíveis dúvidas. Se julgar oportuno, com o auxílio dos alunos, preencher a tabela na lousa, conforme o exemplo a seguir.

Modalidades esportivas preferidas da turma do 2º ano

Sequência didática 8: Unidades de medida de massa, de comprimento e de tempo

Serão abordadas as unidades de medida de massa (quilograma e grama) e exploradas comparações entre a massa de diferentes produtos, além de alguns conceitos relacionados à educação financeira. O sistema monetário brasileiro será observado com base na comparação de preços entre produtos diferentes e entre produtos iguais vendidos em embalagens diferentes, de acordo com a massa. Também, serão tratadas as unidades de medida de comprimento e suas inter-relações e as medidas de tempo. As medições e

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas

Fonte: Dados obtidos pela professora do 2º ano, em janeiro de 2022.

comparações entre os resultados obtidos serão estimuladas, assim como o uso dos diferentes registros de representação de uma medida.

Objetivos de aprendizagem

• Identificar diferentes instrumentos de medição de massa.

• Construir uma balança de dois pratos.

• Estimar e comparar a massa de diferentes produtos.

• Perceber a importância da pesquisa de preços.

• Localizar, em panfletos de propaganda, produtos vendidos por quilograma ou grama.

• Resolver problemas envolvendo medidas de massa, incluindo-se problemas não rotineiros.

• Explorar os conceitos de metade, metade da metade etc., utilizando as unidades de medida de comprimento.

• Relacionar o metro com o centímetro e o milímetro.

• Realizar diferentes medições de tempo

Plano de aulas

Aula 1: Compreender as relações entre unidades de medidas de comprimento.

Aula 2: Medir e comparar comprimentos de formas e polígonos por meio de dobradura.

Aula 3: Confeccionar uma balança caseira, a fim de comparar medidas de massa de objetos.

Aula 4: Estimar e comparar a massa de objetos especificados em panfletos.

Aula 5: Exemplificar e resolver situações de pesagens.

Aula 6: Reconhecer medidas de massa padronizadas em embalagens.

Aula 7: Estimar medidas e criar estratégias de medição.

Aula 8: Resolver situações-problema envolvendo calendários e relógios.

Componentes essenciais para a alfabetização: Produção de escrita.

Competências gerais da Educação Básica: 2, 6 e 7

Competências específicas de Matemática: 2, 6 e 8

Habilidades: EF02MA16, EF02MA17, EF02MA18 e EF02MA19.

Materiais necessários: Garrafas PET, barbante ou fio de nylon , palito de churrasco ou vareta de madeira, massa de modelar, embalagens vazias, panfletos com propaganda de venda de mercadorias, papéis de diferentes tamanhos, régua, fita métrica, tesouras com pontas arredondadas, material dourado, folhas impressas com atividades e folhas avulsas para dobradura.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Aula 1

Para esta aula, organizar os alunos em grupos com até quatro integrantes e providenciar um kitdo material dourado contendo a placa da centena, as barras das dezenas e os cubinhos das unidades. Apresentar para a turma a fita métrica, fazendo-os perceber a presença dos cem centímetros associados a um metro. Em seguida, apresentar a placa da centena e perguntar à turma quantos cubinhos e quantas barras são necessários para construir uma placa da centena. Anotar as informações apresentadas pelos alunos.

Em seguida, comentar que a placa da centena, assim como o metro, está dividida em 10 partes (10 barras) e cada uma dessas partes (1 barra) foi novamente dividida em 10 partes (10 cubinhos). Mostrar as divisões utilizando o material dourado para que os alunos façam essas associações.

Registrar na lousa as seguintes informações:

• 1 metro = 10 partes de 10 cm cada

• 1 placa = 10 barras com 10 cubinhos em cada

• 10 cm = 10 partes de 1 cm

• 1 barra = 10 cubinhos

• 1 metro = 100 cm

• 1 placa = 100 cubinhos

Assim que alunos compreenderem a relação entre os centímetros e as placas, o material dourado poderá ser manipulado por eles para que façam algumas experiências.

Promover as seguintes explorações:

1 50 cm representa a metade do metro (assim como 5 barras representam metade da placa do material dourado);

2 50 cm pode ser representado por 5 tiras de 10 cm ou 50 partes de 1 cm (assim como 50 cubinhos, ou 5 barras, representam metade da placa);

3 Medir o comprimento de materiais escolares com o material dourado (caneta, caderno, estojo).

4 Medir comprimentos que envolvam a medida de dezenas de cubinhos, de forma que percebam que podem utilizar primeiro barras e, depois, cubinhos para completar.

Após utilizarem o material dourado como instrumento de medida, promover a discussão de como o agrupamento das unidades em uma barra facilitou as medições. Feito isso, questionar sobre as unidades de medida de comprimento padronizadas que eles conhecem e como esses agrupamentos são feitos. A intenção é que se recordem das unidades de medida milímetro, centímetro e metro, e como pode ser representada uma mesma medida em diferentes unidades.

Para complementar, alguns dos mesmos objetos podem ser medidos com uma fita métrica, de forma que eles escrevam as medidas em milímetros e em centímetros.

Aula 2

Nesta aula, retomar algumas explorações que envolvam o uso de dobraduras e, principalmente, a sobreposição das partes obtidas a partir das dobras. Muitas vezes, as medições realizadas com a régua e a fita métrica exigem uma habilidade manual adquirida por meio de repetidas situações envolvendo seu uso, portanto, sempre que possível, propor atividades com a régua ou com a fita métrica. Retomar com os alunos a importância de iniciar a medição a partir do número zero e de posicionar corretamente a régua no objeto que será medido.

Para isso, os alunos devem desenvolver um passo a passo de dobradura em folha de papel sulfite e anotar as medidas das figuras em cada etapa.

A atividade pode ser realizada em grupos com até quatro alunos, para que as réguas ou as fitas métricas possam ser compartilhadas; porém, cada um deverá desenvolver uma dobradura própria

Conforme exemplificado a seguir, assim que os alunos finalizarem cada etapa, o perímetro da dobradura deverá ser medido e anotado no caderno.

Representação de passo a passo da dobradura com folha de papel sulfite.

Ao terminar a dobradura, os alunos poderão desenhar um animal que preferirem e pintá-lo.

Durante a utilização da fita métrica e nos momentos de exploração das regularidades existentes entre esse instrumento e as peças do material dourado, oferecer diferentes registros de representação, como, por exemplo, desenhos, pequenos textos e informações numéricas, para que os alunos possam visualizar as relações entre diferentes maneiras.

Para ampliar as explorações realizadas anteriormente, propor aos alunos diferentes medições e transformações de unidades de medida. Por exemplo, medir a etapa 1 em centímetros e medir a etapa 2 em milímetros. Para complementar, em uma folha de papel sulfite maior, como a de tamanho A3, o grupo pode repetir o processo anotando as medições.

Aula 3

Nesta aula, os alunos participarão da confecção de uma balança caseira, feita com materiais simples, a fim de estimarem e compararem as medidas de massa de determinados objetos. Além disso, deverão observar o funcionamento de diferentes tipos de balanças.

Providenciar, antecipadamente, o material necessário para a construção de uma balança de dois pratos, de acordo com o tutorial disponível em: https://www.laboratoriosustentaveldematematica.com/2014/05/faca-uma-balanca-depratos-ensine-algebra-garrafas-pet.html (acesso em: 13 mar. 2023).

Se julgar conveniente, elaborar com os alunos um bilhete convidando os familiares e a comunidade a participarem do projeto

Depois de construída a balança, promover uma roda de conversa para que os alunos possam compartilhar as informações que possuem acerca dos instrumentos de medição. Para isso, mostrar imagens de diferentes tipos de balança e estimular a socialização do conhecimento ou experiência que possuem na utilização desses instrumentos.

Solicitar aos alunos que providenciem embalagens vazias ou materiais que possam ser pesados, como bolas pequenas, alguns materiais escolares de pequeno porte, como borrachas, lápis, apontadores etc. É importante lembrar que os objetos não podem ter medida de massa além do que os pratos da balança possam suportar. Disponibilizar aos alunos massa de modelar e pedir que confeccionem peças com quantidades diferentes de massinha. Antes de solicitar que coloquem os objetos selecionados na balança, incentivar os alunos a estimar quais são os objetos mais pesados e quais são os mais leves. Retomar com a turma o conceito de massa, fazendo-os perceber que, cotidianamente, utiliza-se erroneamente a palavra " peso". Os alunos deverão anotar suas estimativas para, em seguida, conferi-las na balança de dois pratos.

Depois, organizar os alunos em duplas e solicitar que façam algumas experiências e anotem os resultados.

Inicialmente, um aluno da dupla deve escolher dois objetos e colocá-los na balança. Os dois alunos da dupla deverão anotar em seus cadernos, sem que o outro veja, uma frase que explique a comparação entre as massas, verificando depois se ambas são iguais e se estão corretas; por exemplo: um pode anotar que a borracha possui maior massa que o

apontador, e o outro pode anotar que o apontador possui menor massa que a borracha. Ao verificarem as anotações, eles observarão que as duas respostas estão corretas.

Posteriormente, os alunos das duplas devem inverter os papéis nessa atividade e repetir o processo.

Cada etapa da atividade deve ser repetida de 4 a 6 vezes e os objetos de massinha podem ser utilizados para isso.

Ao final da atividade, solicitar que os alunos socializem as conclusões que obtiveram. É esperado que respondam que, quando corretas, as frases eram parecidas ou que, se o objeto da direita possuir maior massa que o da esquerda, o da esquerda deve possuir menor massa que o da direita.

Aula 4

Providenciar, antecipadamente, panfletos contendo propaganda de produtos, como, por exemplo, panfletos de mercado que informam as ofertas. O importante é que haja a representação dos valores cobrados pelos produtos e sua massa em quilograma ou grama. Se possível, providenciar panfletos de diferentes estabelecimentos.

Organizar os alunos em grupos com até quatro integrantes, entregar os panfletos para cada grupo e pedir que analisem os produtos verificando a massa do produto em cada embalagem e o respectivo preço.

Após a análise, questionar os alunos a respeito da pesquisa de preços e verificar se os familiares e pessoas que moram com eles têm o hábito de pesquisar preços, e os motivos que levam alguém a desenvolver esse hábito. Ampliar a conversa apresentando aos alunos diferentes situações em que a pesquisa de preço poderá favorecer uma importante economia financeira. Observar se levam em consideração o gasto com o deslocamento até esses locais. Por exemplo, um produto poderá estar mais barato em uma loja que fica muito distante do local onde o aluno se encontra e, portanto, haverá um gasto de tempo e de dinheiro com deslocamento.

Se possível, providenciar uma balança digital e um produto que contenha exatamente 1 kg ou 500 g para servir de parâmetro de comparação. Esse produto ficará na balança e os alunos deverão reconhecer alguns produtos do folheto que tenham menos ou mais de 1 kg, ou menos ou mais de 500 g.

Posteriormente, pedir aos alunos que recortem 10 produtos representados no folheto e os organizem em ordem crescente de medidas de massa Os produtos com medidas de massa iguais deverão ser organizados em ordem crescente de preço.

Após os alunos terem colado os produtos numa folha avulsa, em ordem crescente de massa e/ou de preço, eles deverão trocar a folha com outro grupo para que ambos verifiquem se a ordem está correta

Nesta aula, os alunos serão envolvidos em alguns desafios e utilizarão os conhecimentos que possuem para resolvê-los. Dividir a turma em duplas.

O professor deverá desenhar na lousa duas balanças contendo objetos em seus pratos e formular questões para os alunos descobrirem a massa de determinado objeto a partir das informações fornecidas. Pode-se, por exemplo, desenhar uma balança com os pratos equilibrados no qual o prato da esquerda contém uma bola vermelha e, no da direita, três bolas azuis de tamanhos iguais, mas menores que a bola vermelha

Fazer a seguinte afirmação: a bola vermelha tem massa de 300 gramas. Perguntar: qual é a massa de uma bola verde? Espera-se que as duplas concluam que uma bola verde tem um terço da massa da bola vermelha, ou seja, 100 gramas.

Outro exemplo: desenhar uma balança equilibrada contendo uma caixa vermelha e uma caixa verde uma sobre a outra no prato esquerdo da balança e duas caixas azuis e uma vermelha empilhadas no prato direito da balança. As caixas devem ser todas do mesmo tamanho. Perguntar:

1. Sabendo que as caixas vermelhas têm a mesma massa, se as caixas vermelhas forem retiradas dos dois pratos da balança o que acontecerá com a balança? Continuará equilibrada? Espera-se que os alunos respondam que sim, já que foi retirada a mesma massa dos dois lados da balança.

2. O que é possível concluir sobre as massas das caixas azul e verde? Espera-se que os alunos respondam que a caixa verde possui a mesma massa de duas caixas azuis, ou seja, que a caixa verde tem o dobro da massa da caixa azul.

3. Se eu retirar uma caixa azul do prato direito da balança, o que acontecerá? A balança vai continuar equilibrada? Um lado vai ficar mais baixo? Qual lado vai ficar mais baixo? Espera-se que os alunos concluam que o prato esquerdo da balança vai ficar mais baixo.

Concluída a atividade, algumas duplas poderão sugerir situações semelhantes às expostas anteriormente para que os demais alunos as representem, seguindo o mesmo processo.

É importante observar cada uma das etapas para sanar possíveis dúvidas. Estimular os alunos a tentar localizar procedimentos ou conceitos que foram realizados com tranquilidade e outros que foram mais desafiadores.

Aula 6

Nesta aula, solicitar que os alunos providenciem pelo menos 3 embalagens vazias de produtos. Eles manipularão as embalagens, reconhecerão informações importantes e farão o descarte correto dos materiais ao término da atividade

Os alunos poderão trabalhar em grupos com quatro integrantes e deverão anotar as seguintes informações em um quadro

Essas informações referem-se a todos os produtos que foram levados pelo grupo. Caso falte alguma informação, como data de validade, deixar a referida célula do quadro em branco.

A primeira discussão que deverá ser feita é sobre a diferença entre produtos e marcas. Questionar os alunos se eles costumam utilizar mais o nome da marca ou do produto no dia a dia. Conversar sobre a importância da especificação de produtos feita pela ANVISA (Agência Nacional de Vigilância Sanitária) e tentar mostrar produtos que parecem ser iguais, porém são diferentes em sua composição e, por isso, precisam ser classificados de maneiras distintas, como margarina e creme vegetal; requeijão e produto cremoso sabor requeijão; leite em pó e composto lácteo; creme de leite e creme de leite leve; entre outros

Outra discussão que deve ser estimulada é sobre a validade dos produtos Solicitar aos alunos que anotem quais produtos estão vencidos e quais estariam na validade caso fossem ser consumidos no dia da aula.

Os alunos deverão, também, organizar os produtos pelas massas em ordem crescente. Se algum aluno tiver dúvida na unidade de medida de algum produto, outros grupos podem ser consultados Se necessário, relembrar as unidades já estudadas.

Após organizar as embalagens, solicitar aos alunos que elaborem duas situações-problema com algumas delas, cujas informações deverão ser anotadas em uma folha avulsa para que seja trocada entre os grupos. Após resolvê-las, as folhas deverão ser destrocadas para que sejam feitas as correções.

Aula 7

Providenciar, antecipadamente, folhas de papel de diferentes tamanhos, réguas e fitas métricas. Orientar os alunos a se sentarem em círculo e, em seguida, apresentar cada um dos papéis solicitando que identifiquem as semelhanças e as diferenças entre eles, inclusive comparando o tamanho dos lados. Solicitar que estimem o valor aproximado, em centímetro,

Produto Marca Validade Massa

de cada um dos lados das folhas. Incentivá-los a confirmar as medidas estimadas utilizando a régua ou a fita métrica.

As estimativas e os valores obtidos na medição deverão ser registrados no caderno para que os alunos possam averiguar a razoabilidade dos valores estimados e medidos. Desafiar a turma a encontrar estratégias para obter, a partir da dobradura e do recorte de cada uma das folhas, uma que contenha medidas diferentes das originais, inclusive as que tenham como medida dos lados a metade do valor registrado inicialmente. Por exemplo, se uma folha tinha como medida de lados 20 cm e 10 cm, os alunos deverão conseguir folhas que tenham como medida 10 cm e 5 cm, e assim sucessivamente. Observar as estratégias utilizadas por eles e verificar se são capazes de identificar a possibilidade de dobrar a folha ao meio.

Além das explorações relacionadas à medida dos lados das folhas, é possível explorar figuras geométricas planas. Estimular a turma a realizar diferentes dobras para obter representações de figuras geométricas planas com variadas medidas de lado. Ao final, deverão representar as etapas realizadas e as descobertas obtidas por meio de um desenho ou de um pequeno texto.

Aula 8

Nesta aula, os alunos trabalharão com instrumentos de medida de tempo Vão criar um calendário e utilizá-lo para anotar tarefas do dia a dia, além de trabalhar com relógios de ponteiro

Inicialmente, perguntar aos alunos: como podemos medir o tempo para organizar as atividades diárias? Existem vários instrumentos para medir o tempo: relógios digital e analógico, calendário, ampulheta, entre outros. Os alunos podem, até mesmo, responder que basta anotar na agenda. Para continuar as explorações acerca dos instrumentos utilizados para medir o tempo, apresentar imagens de diferentes tipos de relógios e curiosidades acerca da evolução dos instrumentos de medição do tempo no decorrer da história

Os alunos trabalharão individualmente a folha impressa entregue por você com as seguintes situações-problema.

1 Fernanda costuma fazer anotações que facilitam a organização. Porém, ela perdeu a folha de um dos meses e precisa anotar novamente suas tarefas. Ajude-a a criar o calendário do mês de acordo com as informações que ela se lembra, e responda às questões a seguir.

• Era um mês que começava em uma terça-feira;

• Era um mês com 31 dias;

• Ela circulou as terças-feiras e as quintas-feiras em vermelho, pois tem aula de basquete nesses dias;

Material disponibilizado em licença aberta do tipo Creative Commons

• Ela circulou o primeiro domingo em azul, pois é aniversário de seu amigo Paulo;

• Ela circulou o dia 25 em amarelo, pois é o dia de buscar a bicicleta no conserto.

a) Há quantos dias de intervalo entre o dia do aniversário de Paulo e o dia de buscar a bicicleta no conserto?

19 dias; 25

6 = 19

b) Se esse fosse o quinto mês do ano, seria o calendário de qual mês? Maio.

c) Se Fernanda mudasse as aulas de basquete para as segundas-feiras e para as quintas-feiras, ela teria mais ou menos aulas nesse mês? Justifique fazendo novas marcações no calendário.

Menos aulas.

Caso os alunos tenham dificuldade de criar o calendário, um calendário do ano pode ser disponibilizado, a fim de identificarem um mês com as características enunciadas. Outra possibilidade é disponibilizar o quadro a seguir.

Após terem concluído a atividade, socializar o conhecimento e fazer a correção coletivamente. Para isso, pedir que alguns alunos expliquem como preencheram o quadro.

Posteriormente, propor um segundo problema que usa o relógio como instrumento de medição de tempo.

2 Marque nos relógios a seguir as horas indicadas

EDITORIA DE ARTE

Material disponibilizado em licença aberta do tipo Creative Commons

Representação de relógios sem ponteiros

3. Agora, são 10 horas. Faz exatamente 2 horas que a mãe de Lucas saiu de casa para ir ao mercado.

a) Que horas a mãe de Lucas saiu para ir ao mercado?

Ela saiu às 8 horas

b) Desenhe os ponteiros do relógio para indicar o horário que a mãe de Lucas foi ao mercado.

EDITORIA DE ARTE

Representação de relógio sem ponteiros.

Estas atividades poderão ser corrigidas coletivamente Identificar e sanar possíveis dificuldades dos alunos.

Complementar a atividade com algumas situações de horários com quantidades maiores que 12 horas, como 13 horas ou 14 horas, a fim de que os alunos identifiquem os três períodos (manhã, tarde e noite), ou situações com horário de início e de fim para que descubram a duração do intervalo de tempo.

Em seguida, fazer perguntas mediadoras que levem os alunos a refletirem sobre a numeração até 12 e a relação com a divisão do dia em 24 horas. Verificar se são capazes de perceberem, por exemplo, a diferença entre os ponteiros e que, ao longo do dia, o ponteiro menor dá duas voltas completas no relógio.

Sugestões

• HORE, Rosie etal Vamos pesar e medir?: brinque e aprenda. Cotia: Usborne, 2018.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e

as criações sejam licenciadas sob os mesmos parâmetros.

Relatórios e indicadores do acompanhamento da aprendizagem

O processo avaliativo exige do professor um olhar reflexivo permanente sobre o desenvolvimento da aprendizagem dos alunos e, consequentemente, sobre a sua própria prática pedagógica. Dessa forma, instrumentos de avaliação, como provas, testes, questionários, redações, trabalhos, seminários, entre outros, não devem ser encarados como instrumentos pontuais de avaliação, mas, sim, como ferramentas de coleta de indicadores que descrevem o desempenho dos alunos e possibilitam uma análise coletiva e individual dos avanços e dos pontos de melhoria da aprendizagem.

Os indicadores de aprendizagem devem auxiliar o professor no acompanhamento do desenvolvimento das aprendizagens dos alunos, apontando se os objetivos, as competências, as habilidades e os conteúdos previstos em seu plano de trabalho estão sendo alcançados ou se há necessidade de intervenção no processo de aprendizagem para que possam ser atingidos

Esses indicadores de aprendizagem, isoladamente nada apontam, uma vez que os resultados são fruto da análise do professor com base em objetivos, competências e habilidades desenvolvidos em determinado contexto educacional. Assim, com o apoio da avaliação dos indicadores de aprendizagem, é necessário que sejam produzidos relatórios descritivos das análises, considerações e observações a respeito do processo de aprendizado e desenvolvimento dos alunos e de sua prática pedagógica em sala de aula

Produção de relatórios

Os relatórios escolares são registros que devem ser realizados periodicamente (a cada bimestre, trimestre ou semestre) a respeito do desenvolvimento de diferentes aprendizagens dos alunos ao longo do processo de ensino-aprendizagem.

Dentro do processo de aprendizagem escolar, os relatórios, entre outras finalidades, deverão:

• Possibilitar ao educador compreender de forma significativa o processo de aprendizagem dos alunos, respeitando suas individualidades, particularidades e diferenças.

• Produzir informações e dados significativos sobre o processo de aprendizagem de modo a planejar intervenções pedagógicas com base em objetivos, conteúdos, competências e habilidades a serem desenvolvidos.

• Fornecer subsídios teóricos para as reuniões de conselho de classe para que professores, coordenadores pedagógicos e diretores da escola possam analisar o desempenho individual e coletivo dos alunos e, consequentemente, discutir formas,

ações, intervenções, estratégias e métodos de melhoria do processo de ensino-aprendizagem com base no Projeto Político Pedagógico da escola.

• Realizar uma comunicação orientada, assertiva e planejada com pais ou responsáveis de modo a engajá-los no processo de aprendizagem, contribuindo desse modo para o desenvolvimento dos alunos e a efetividade do ensino.

• Proporcionar ao aluno o direito de acompanhar o próprio processo de aprendizagem, de modo a oportunizar a superação de suas dificuldades.

Apesar de não existir um modelo fixo de relatório a ser seguido, alguns pontos importantes podem ser considerados na elaboração desse material. O texto do relatório deverá ser escrito de forma clara, concisa e objetiva, de modo que o leitor o compreenda. Devem ser registrados os conteúdos trabalhados e como foram avaliados, assim como todas as considerações julgadas pertinentes ao processo de ensino-aprendizagem. É importante, também, descrever quais foram os encaminhamentos adotados em caso de dificuldade dos alunos.

Se possível, os relatórios devem ainda captar as diferentes dimensões envolvidas nas experiências dos alunos no grupo, ou seja, devem trazer aspectos relacionados a sentimentos, afetos, emoções, movimentos e cognição.

Os relatórios podem conter apresentações visuais e gráficas dos dados coletados, de modo a facilitar a compreensão das informações que estão sendo transmitidas. Pode-se elaborar um gráfico de barras comparando a distribuição percentual dos resultados quantitativos da aprendizagem dos alunos a respeito de competências gerais, de competências específicas e de habilidades em um período, como no exemplo a seguir.

Fonte: Dados fictícios.

Gráficos e tabelas podem ser elaborados por meio de um editor de planilhas eletrônicas, como o LibreOffice, que é um software livre e gratuito, disponível em: https://www.libreoffice.org/discover/libreoffice/ (acesso em: 10 dez. 2021).

Indicadores do acompanhamento da aprendizagem

De modo geral, o termo "indicadores" é usado para apontar parâmetros que avaliam certa realidade em determinado intervalo de tempo. Um médico, por exemplo, examina vários indicadores antes de oferecer um diagnóstico a um paciente. Um economista, também, se utiliza de indicadores para analisar se a inflação de um país aumentou ou diminuiu. Já no contexto escolar, os indicadores do acompanhamento da aprendizagem têm como objetivo mapear os diferentes níveis de desenvolvimento das aprendizagens dos alunos.

Uma vez que o processo de aprendizagem ocorre simultânea e interativamente nas dimensões cognitiva, afetiva e psicomotora, os indicadores de aprendizagem a serem observados e avaliados deverão abarcar aspectos tanto quantitativos quanto qualitativos do processo de aprendizagem dos alunos, garantindo, assim, uma visão ampla e significativa desse processo.

Os aspectos qualitativos dos indicadores de aprendizagem, geralmente, são aqueles ligados às competências gerais e socioemocionais que expressam a voz, as percepções, as crenças, os sentimentos, os pensamentos, as emoções, as atitudes e os modos de agir dos educandos. São eles que possibilitam ao educador avaliar se os alunos alcançaram a construção e a formação de atitudes e valores, como autonomia, responsabilidade, empatia, resiliência, determinação, criticidade e capacidade de ouvir, ser ouvido e dialogar.

Já os aspectos quantitativos dos indicadores de aprendizagem são aqueles que descrevem quantidades ou percentuais da consecução do processo de ensino-aprendizagem. São esses aspectos quantitativos que permitem ao professor fazer uma avaliação do quanto os alunos estão avançando em relação aos objetivos, competências, habilidades e conteúdos, gerais ou específicos, de determinada área do conhecimento, previstos em seu plano de trabalho.

São apresentados, a seguir, quatro modelos de fichas com sugestões de indicadores que podem ser obtidos por meio do processo avaliativo que julgar mais conveniente. Esses modelos podem ser impressos e preenchidos com os dados dos alunos ou da turma.

O primeiro modelo é o de Ficha de avaliação diagnóstica Nela, estão presentes alguns indicadores que poderão servir de subsídio para que seja reconhecido o domínio dos alunos a respeito de alguns conteúdos, no início do ano letivo.

O segundo modelo é o de Ficha de acompanhamento das aprendizagens, na qual são apresentadas as habilidades da BNCC indicadas para o ano de escolaridade, as Competências específicas de Matemática para o Ensino Fundamental, as Competências gerais da Educação Básica e os componentes essenciais para a alfabetização. Nela, há uma coluna para preenchimento de observações mais detalhadas.

O terceiro modelo é o de Ficha de verificação de resultados, em que estão indicados, a cada ano de escolaridade, alguns objetivos de aprendizagem categorizados como focais, por influenciarem de modo mais evidente o desenvolvimento vinculado às Competências gerais e às Competências específicas da área de Matemática para o Ensino Fundamental.

Por fim, considerando a ideia de educação integral, também é preciso avaliar o desenvolvimento das dimensões sociais e emocionais dos alunos. Para tanto, o quarto modelo é o de Ficha de acompanhamento do desenvolvimento de competências socioemocionais, que apresenta indicadores para que seja apontada a frequência com que essas competências são reconhecidas nas atitudes dos alunos.

Os modelos de fichas aqui apresentados são apenas proposições para apoiar o processo de ensino-aprendizagem. É fundamental que o trabalho pedagógico seja planejado com intencionalidade para explorar todos os potenciais de aprendizagem e garantir as condições de desenvolvimento pleno e integral de cada aluno. Essa tarefa requer a participação de toda a comunidade escolar, envolvendo professores, gestores e os responsáveis pelos alunos

RECURSO EDUCACIONAL DIGITAL

Ficha de avaliação diagnóstica

Professor:

Turma:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de avaliação diagnóstica

Números Álgebra Geometria Grandezas e medidas Estatística

Aluno Ler, escrever, comparar, compor e decompor números naturais até 100.

Problemas envolvendo diferentes significados da adição (juntar e acrescentar) e da subtração (separar e retirar).

Investigar regularidades ou padrões em sequências.

Utilizar diferentes pontos de referência, bem como vocabulário apropriado, para indicar a localização de objetos e de pessoas no espaço

Identificar e nomear as figuras geométricas planas (círculo, quadrado, retângulo e triângulo).

Medidas de comprimento, massa e capacidade: fazer comparações usando unidades de medida não convencionais.

Explorar unidades de medida de tempo (períodos do dia, dias da semana e meses do ano), suas relações e o uso do calendário.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ler tabelas e gráficos de colunas simples.

Ficha de acompanhamento das aprendizagens

Professor:

Turma:

Aluno:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de acompanhamento das aprendizagens (Matemática)

Habilidades C PC NC Observações

(EF02MA01) Comparar e ordenar números naturais (até a ordem de centenas) pela compreensão de características do sistema de numeração decimal (valor posicional e função do zero).

(EF02MA02) Fazer estimativas por meio de estratégias diversas a respeito da quantidade de objetos de coleções e registrar o resultado da contagem desses objetos (até 1000 unidades).

(EF02MA03) Comparar quantidades de objetos de dois conjuntos, por estimativa e/ou por correspondência (um a um, dois a dois, entre outros), para indicar “tem mais” , “tem menos” ou “tem a mesma quantidade”, indicando, quando for o caso, quantos a mais e quantos a menos.

(EF02MA04) Compor e decompor números naturais de até três ordens, com suporte de material manipulável, por meio de diferentes adições.

(EF02MA05) Construir fatos básicos da adição e subtração e utilizá-los no cálculo mental ou escrito.

(EF02MA06) Resolver e elaborar problemas de adição e de subtração, envolvendo números de até três ordens, com os significados de juntar, acrescentar, separar, retirar, utilizando estratégias pessoais.

(EF02MA07) Resolver e elaborar problemas de multiplicação (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais por meio de estratégias e formas de registro pessoais, utilizando ou não suporte de imagens e/ou material manipulável.

(EF02MA08) Resolver e elaborar problemas envolvendo dobro, metade, triplo e terça parte, com o suporte de imagens ou material manipulável, utilizando estratégias pessoais.

(EF02MA09) Construir sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.

(EF02MA10) Descrever um padrão (ou regularidade) de sequências repetitivas e de sequências recursivas, por meio de palavras, símbolos ou desenhos.

(EF02MA11) Descrever os elementos ausentes em sequências repetitivas e em sequências recursivas de números naturais, objetos ou figuras.

Material disponibilizado em licença aberta do tipo Creative Commons

(EF02MA12) Identificar e registrar, em linguagem verbal ou não verbal, a localização e os deslocamentos de pessoas e de objetos no espaço, considerando mais de um ponto de referência, e indicar as mudanças de direção e de sentido.

(EF02MA13) Esboçar roteiros a ser seguidos ou plantas de ambientes familiares, assinalando entradas, saídas e alguns pontos de referência.

(EF02MA14) Reconhecer, nomear e comparar figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone, cilindro e esfera), relacionando-as com objetos do mundo físico.

(EF02MA15) Reconhecer, comparar e nomear figuras planas (círculo, quadrado, retângulo e triângulo), por meio de características comuns, em desenhos apresentados em diferentes disposições ou em sólidos geométricos.

(EF02MA16) Estimar, medir e comparar comprimentos de lados de salas (incluindo contorno) e de polígonos, utilizando unidades de medida não padronizadas e padronizadas (metro, centímetro e milímetro) e instrumentos adequados.

(EF02MA17) Estimar, medir e comparar capacidade e massa, utilizando estratégias pessoais e unidades de medida não padronizadas ou padronizadas (litro, mililitro, grama e quilograma).

(EF02MA18) Indicar a duração de intervalos de tempo entre duas datas, como dias da semana e meses do ano, utilizando calendário, para planejamentos e organização de agenda.

(EF02MA19) Medir a duração de um intervalo de tempo por meio de relógio digital e registrar o horário do início e do fim do intervalo.

(EF02MA20) Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro para resolver situações cotidianas.

(EF02MA21) Classificar resultados de eventos cotidianos aleatórios como “pouco prováveis” , “muito prováveis” , “improváveis” e “impossíveis”

(EF02MA22) Comparar informações de pesquisas apresentadas por meio de tabelas de dupla entrada e em gráficos de colunas simples ou barras, para melhor compreender aspectos da realidade próxima.

(EF02MA23) Realizar pesquisa em universo de até 30 elementos, escolhendo até três variáveis categóricas de seu interesse, organizando os dados coletados em listas, tabelas e gráficos de colunas simples.

Competências específicas de Matemática para o Ensino Fundamental C PC NC Observações

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Competências gerais da Educação Básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

C PC NC Observações

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Componentes essenciais para a alfabetização

Consciência fonológica e fonêmica

Conhecimento alfabético

Fluência em leitura oral

Desenvolvimento de vocabulário

Compreensão de textos

Produção de escrita

Ficha de verificação de resultados

Professor:

Turma:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de verificação de resultados

Principais objetivos de aprendizagem

Aluno(a) Ler, escrever, comparar, compor e decompor números naturais até 999.

Construir fatos fundamentais da adição e da subtração.

Problemas envolvendo significados de dobro, metade, triplo e terça parte.

Construir sequências repetitivas e sequências recursivas.

Sistema monetário brasileiro: reconhecer cédulas e moedas, bem como estabelecer equivalência de valores entre elas.

Medida de comprimento: unidades padronizadas (metro, centímetro e milímetro).

Medidas de tempo: intervalo de tempo, uso do calendário, leitura de horas em relógios digitais e ordenação de datas.

Coletar, classificar e representar dados em tabelas e em gráficos.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Professor:

Turma:

Aluno:

Competências socioemocionais Sempre Frequentemente Raramente Nunca

Determinação

Foco

Organização

Persistência

Responsabilidade

Empatia

Respeito

Confiança

Tolerância ao estresse

Autoconfiança

Tolerância à frustração

Iniciativa social

Assertividade

Entusiasmo

Curiosidade para aprender

Imaginação criativa

Interesse artístico

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Catálogo dos audiovisuais

Nesta seção, são disponibilizados detalhamentos, como objetivos de aprendizagem e conteúdos abordados, entre outros aspectos, acerca de cada um dos audiovisuais que compõem a coletânea desta coleção. Também, para cada audiovisual, são descritas sugestões de utilização e são sugeridas propostas de atividades, a fim de apoiar pedagogicamente o uso desses recursos digitais audiovisuais. Tais informações visam trazer insumos para favorecer o planejamento de aplicação deles de acordo com a realidade da comunidade escolar e da turma com que forem trabalhados.

Audiovisuais da coletânea

Relação de audiovisuais da coletânea

Título do

Grandezas e medidas As medidas estão vinculadas a muitas atividades cotidianas das pessoas. Neste audiovisual, os alunos são levados a essa reflexão por meio de exemplos de situações do dia a dia em que medições de comprimento, capacidade e massa são realizadas considerando unidades de medidas não padronizadas e unidades de medidas padronizadas

• Medir comprimentos utilizando unidades de medida não padronizadas: o palmo.

• Medir comprimentos utilizando unidades de medida padronizadas por meio de instrumentos adequados.

• Estimar medidas de comprimento utilizando unidades de medida não padronizadas e unidades de medida padronizadas

• Estimar medidas de capacidade e medidas de massa utilizando unidades de medida não padronizadas e unidades de medida padronizadas

• Unidade de medida de comprimento não padronizada: o palmo.

• Unidades de medida de comprimento padronizadas: metro, centímetro e milímetro.

• Unidades de medida de capacidade padronizadas: litro e mililitro

• Unidades de medida de massa padronizadas: grama e quilograma

O corpo humano e as medidas de comprimento não padronizadas

Para medir comprimentos, partes do corpo eram usadas como unidades não padronizadas antes de surgirem as unidades padronizadas de medida. Neste audiovisual, os alunos refletem sobre as relações entre as medidas de

• Medir comprimentos utilizando unidades de medida não padronizadas: o palmo, o polegar e o pé

• Unidades de medida não padronizadas de comprimento.

Bioconstrução: um jeito diferente e sustentável de construir

comprimento de algumas partes do corpo

Considerando o Tema Contemporâneo Transversal "Meio ambiente", neste audiovisual, bioconstruções são apresentadas como possibilidade de esse tema vincular a Matemática por meio do reconhecimento de figuras geométricas espaciais associadas a construções do mundo físico

• Reconhecer representações de figuras geométricas espaciais relacionando-as a construções arquitetônicas do mundo físico.

• Figuras geométricas espaciais: reconhecimento e características.

Triângulos por toda parte

A importância da figura geométrica plana triângulo para tornar mais fortes e firmes estruturas de construções é o foco deste audiovisual.

• Reconhecer representações da figura geométrica plana triângulo relacionando-as a objetos e a estruturas do mundo físico.

• Figura geométrica plana (triângulo): reconhecimento e características.

Mudanças que ocorrem com o passar do tempo

Neste audiovisual, a importância do uso das unidades padronizadas de medida de tempo (dia, mês e ano) para registrar intervalos de tempo é exibida

• Medidas de tempo: reconhecer a importância do uso do calendário e da ordenação de datas em dias, meses e anos.

• Utilizar calendário para indicar a duração de intervalos de tempo entre duas datas

Orientações para o uso dos audiovisuais

Grandezas e medidas

Com base em situações familiares aos alunos no cotidiano, o audiovisual comenta a importância das unidades de medida, não padronizadas e padronizadas, e apresenta também alguns instrumentos adequados a serem utilizados em determinadas medições

Sugere-se que este audiovisual seja exibido como recurso introdutório ao trabalho com os conteúdos relacionados à unidade temática Grandezas e medidas

Se o audiovisual for utilizado antes da exploração dos conteúdos, pode-se fazer:

• uma pausa logo após a narração e mencionar que 1 centímetro corresponde a 10 milímetros. Nesse momento, apresente uma régua para demostrar aos alunos essa afirmação.

• outra pausa quando a narração mencionar que 1 metro corresponde a 100 centímetros. Nesse momento, apresente uma fita métrica para demonstrar aos alunos essa outra afirmação

Ao término da exibição do audiovisual, perguntar aos alunos quais informações eles compreenderam com mais facilidade e do que mais gostaram daquilo que foi apresentado. Perguntar-lhes sobre a importância de medir comprimentos, massas e capacidade no dia a dia e pedir a eles que deem alguns exemplos diferentes dos que aparecem no audiovisual

Em seguida, sugere-se a proposição das atividades como as indicadas a seguir.

Sugestões de atividades

1. Meça a altura de uma das " pernas " da mesa em que você estuda utilizando seu palmo e registre a medida obtida em palmo.

A resposta depende das medidas do palmo e da " perna " da mesa que o aluno medir.

• Se você comparar a medida registrada por você com a medida, por exemplo, feita com o palmo do professor, é possível que sejam obtidas medidas diferentes? Justifique sua resposta

Espera-se que os alunos respondam que sim. Sugestão de resposta: a medida do palmo do professor, que é uma pessoa adulta, é maior que a medida do palmo de uma criança, razão pela qual as medidas obtidas em palmos são diferentes.

2. Em cada item, de acordo com a unidade padronizada de medida, marque CO se for utilizada para indicar medida de comprimento, MA se for utilizada para indicar medida de massa ou CA se for utilizada para indicar medida de capacidade.

a) milímetro d) mililitro

CO CA

b) litro e) centímetro

CA CO

c) grama

MA CO

f) metro

3 Faça uma estimativa e marque um X em cada um dos itens em que a medida indicada é maior que 1 metro.

a) Comprimento de uma cama de casal.

b) Altura de uma cama de solteiro

c) Largura de uma rua

d) Altura de um caminhão.

Espera-se que os alunos marquem um X nos itens a, c e d

4 Com o auxílio de um responsável, pesquise três produtos que são vendidos em quilograma e registre o nome do produto e a massa, em quilograma, que consta na embalagem de cada um.

A resposta depende das embalagens dos produtos pesquisados pelos alunos Sugestões de resposta: arroz (pacote com 5 quilogramas); açúcar (pacote com 1 quilograma); feijão (pacote com 1 quilograma)

• Qual dos produtos pesquisados é mais pesado?

A resposta depende das embalagens dos produtos pesquisados pelos alunos Espera-se que os alunos respondam que o produto que é mais pesado é o produto cuja massa, em quilograma, é maior e está indicada pelo número maior.

5 Com o auxílio de um responsável, pesquise três produtos que são vendidos em recipientes cuja capacidade é indicada em litro e registre o nome do produto e a capacidade, em litro, de cada recipiente.

A resposta depende dos recipientes dos produtos pesquisados pelos alunos Sugestões de resposta: leite (caixa com 1 litro); água (garrafão com 20 litros).

• Em qual dos recipientes pesquisados cabe mais líquido?

A resposta depende dos recipientes dos produtos pesquisados pelos alunos Espera-se que os alunos respondam que o recipiente em que cabe mais líquido é o recipiente cuja capacidade, em litro, é maior e está indicada pelo número maior

Este audiovisual pode ser apresentado como retomada ou revisão do estudo de unidades de medida não padronizadas de comprimento, pois nele são apresentadas algumas relações entre a medida do comprimento de algumas partes do corpo humano

Sugere-se, após o término da exibição deste audiovisual, perguntar aos alunos o que eles acharam mais interessante e propor que, assim como no audiovisual, verifiquem no próprio corpo algumas das relações apresentadas. Por exemplo, os alunos podem verificar se as medidas do comprimento do pé e do antebraço são próximas.

Para realizar essa verificação, os alunos podem utilizar unidades de medida não padronizadas, como o palmo para medir o comprimento do pé em palmos e, em seguida, o antebraço, comparando as medidas

Conversar com os alunos que, além do palmo, outras partes do corpo podem ser utilizadas para fazer medições, por exemplo, o polegar e o pé.

Propor algumas situações em sala de aula para que os alunos realizem medições utilizando essas partes do corpo como unidades não padronizadas de medida e debater com eles as diferenças obtidas nos resultados dessas medições, já que as pessoas são diferentes e cada um tem partes do corpo com medidas diferentes Explicar aos alunos que medir

O corpo humano e as medidas de comprimento não padronizadas

comprimentos corresponde a uma ação de comparar o que se quer medir com uma unidade de medida escolhida para verificar quantas vezes essa unidade de medida escolhida "cabe" no comprimento do que se quer medir

Após essa abordagem, a fim de complementar o trabalho e favorecer o desenvolvimento da habilidade EF02MA16, propor as seguintes atividades

Sugestões de atividades

1 Cada aluno da turma do 2º ano, em que Ana estuda, mediu, usando o palmo, o comprimento do tampo da mesa do professor. Observe a medida aproximada, em palmos, encontrada por quatro alunos e o professor.

Nome Medida aproximada (em palmos)

Ana 13 palmos

Caio 10 palmos

Júlio 11 palmos

Flávia 12 palmos

Professor César 6 palmos

a) Escreva uma justificativa possível para que as medidas obtidas sejam diferentes

Sugestão de resposta: as medidas obtidas são diferentes porque a medida do palmo de cada um era diferente da medida do outro

b) De acordo com essas medidas indicadas no quadro, é possível estimar quem tem o palmo com a medida maior? Se sim, escreva o nome.

Espera-se que os alunos respondam que é possível e escrevam o nome do professor César.

c) Como você pensou para responder à questão do item anterior? Descreva por escrito a seguir.

Espera-se que os alunos respondam que, quanto maior for a medida do palmo, menor será a quantidade de vezes que ele cabe no tampo da mesa que está sendo medido e, sendo assim, de acordo com o quadro, a menor medida obtida é a do professor César, razão pela qual ele possui o palmo com medida maior.

2 Qual é a unidade não padronizada de medida que você acha mais adequada para medir o contorno da sala de aula: o pé, o passo ou o palmo? Justifique sua resposta.

Espera-se que os alunos respondam que o passo é a unidade de medida mais adequada para medir o contorno da sala de aula. Sugestão de resposta: é a maneira mais prática de realizar a medição.

3 Realize as medições indicadas em cada item e registre as medidas obtidas

As respostas desta atividade dependem das medições realizadas.

a) Medida, em polegada, do comprimento de seu lápis.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

b) Medida, em palmo, da altura de um colega da turma

c) Medida, em passo, da largura de uma porta

d) Medida, em palmo, do comprimento da lousa.

Bioconstrução: um jeito diferente e sustentável de construir

Neste audiovisual, a contextualização ocorre com base no Tema Contemporâneo Transversal "Meio ambiente" sob o recorte da temática da bioconstrução, que é um tipo de construção na qual são utilizados materiais que simultaneamente:

• são adequados às necessidades da arquitetura;

• geram baixo impacto no ambiente por não agredirem a natureza.

Esse recorte de temática visa direcionar a reflexão dos alunos por se tratar de um contexto que reflete uma problematização da realidade Assim, uma situação de aprendizagem é favorecida com a intencionalidade prioritária de promover a educação ambiental

Caso queira saber mais sobre bioconstrução para compartilhar com os alunos, sugere-se a leitura da referência a seguir.

• BRASIL. Ministério do Meio Ambiente. Secretaria de Extrativismo e Desenvolvimento Rural Sustentável. Curso de Bioconstrução. Texto elaborado por: Cecília Prompt.

Brasília: MMA, 2008. Disponível em: https://comosereformaumplaneta.files.wordpress.com/2013/09/curso-debioconstruc3a7c3a3o.pdf. Acesso em: 11 jan. 2022.

Dado esse aspecto do contexto, este audiovisual pode ser usado tanto na introdução aos estudos de figuras geométricas espaciais como na retomada ou revisão desse conteúdo Após a exibição deste audiovisual, sugere-se a aplicação das seguintes atividades, que têm como objetivo explorar o reconhecimento de características de figuras geométricas espaciais em objetos ou construções arquitetônicas do mundo físico favorecendo o desenvolvimento da habilidade EF02MA14.

Sugestões de atividades

1. Qual material de construção usado em construções se parece com um bloco retangular?

Sugestão de resposta: tijolo. Espera-se que os alunos se recordem do que assistiram no audiovisual.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

2. Nas bioconstruções, recursos do meio ambiente tornam-se materiais utilizados nas construções. Escreva um exemplo de um material utilizado nesse tipo de construção, o qual se pareça com um cilindro.

Sugestão de resposta: bambu. Espera-se que os alunos se recordem do que assistiram no audiovisual.

3. No local onde você mora, quais figuras geométricas espaciais você reconhece nas construções ao redor?

A resposta vai depender do local em que o aluno mora. Sugestões de resposta: prédios que se parecem com blocos retangulares; casas que se parecem com cubos; telhados de casas que se parecem com pirâmides Espera-se que os alunos se recordem de algumas imagens apresentadas no audiovisual a que assistiram e as associem com as construções do mundo físico que observam no trajeto da casa deles até a escola

4. O cone é uma figura geométrica espacial pouco identificada em construções. Em qual tipo de moradia podemos identificar essa forma? Escreva um exemplo

Sugestão de resposta: ocas indígenas

5 Em cada item a seguir, leia o nome de uma figura geométrica espacial e pense nela, em como ela é e nas características dela. Em seguida, escreva um exemplo de um objeto que se parece com cada figura.

a) bloco retangular

Sugestão de resposta: caixa de leite

b) cubo

Sugestão de resposta: dado.

c) cilindro

Sugestão de resposta: lata de ervilha

d) esfera

Sugestão de resposta: bola de basquete

e) pirâmide

Sugestão de resposta: enfeite que representa a pirâmide do Egito

f) cone

Sugestão de resposta: vela cônica usada para enfeite

Triângulos por toda parte

Neste audiovisual, a simulação da construção da estrutura de um prédio é apresentada com palitos de madeira e balas de goma para demonstrar aos alunos como

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

uma estrutura que representa o contorno da figura geométrica plana triângulo é mais rígida (firme e resistente) que uma estrutura que representa o contorno da figura geométrica plana quadrado e, por isso, está em toda parte e em muitas construções do mundo físico.

Este audiovisual pode ser usado tanto na introdução aos estudos de figuras geométricas planas quanto na retomada ou revisão desse conteúdo

Sugere-se que, se possível, este audiovisual seja trabalhado em momento posterior à exploração do audiovisual "Bioconstrução: um jeito diferente e sustentável de construir" (que, também, faz parte da coletânea deste volume da coleção). Isso porque o reconhecimento das figuras geométricas espaciais em bioconstruções é um trabalho que se complementa ao ser vinculado a este audiovisual, em que a importância da rigidez dos triângulos é demonstrada para manter firmes e resistentes muitas construções arquitetônicas.

Desse modo, os alunos são levados a reconhecer figuras geométricas planas em construções que se parecem com figuras geométricas espaciais.

Neste audiovisual, as características das figuras geométricas planas (triângulo e quadrado) demonstradas visam favorecer nos alunos o desenvolvimento da habilidade

EF02MA15

Após os alunos assistirem ao audiovisual, sugere-se que as seguintes atividades sejam propostas.

Sugestões de atividades

1. Escreva uma adição para indicar quantos lados tem um triângulo.

Sugestões de resposta: 2 + 1 = 3; 1 + 1 + 1 = 3; há outras respostas possíveis. O objetivo desta atividade é apresentar aos alunos o questionamento sobre a característica de quantos lados a figura geométrica plana triângulo tem, de modo que os alunos mobilizem habilidades de cálculos de adição para fazer o registro da resposta.

2. Escreva uma adição para indicar quantos lados tem um quadrado.

Sugestões de resposta: 2 + 2 = 4; 1 + 1 + 1 + 1 = 4; há outras respostas possíveis. O objetivo desta atividade é apresentar aos alunos o questionamento sobre a característica de quantos lados a figura geométrica plana quadrado tem de modo que os alunos mobilizem habilidades de cálculos de adição para fazer o registro da resposta.

3. Escreva uma adição para indicar quantos lados tem um retângulo.

Sugestões de resposta: 3 + 1 = 4; 2 + 1 + 1 = 4; há outras respostas possíveis.

O objetivo desta atividade é apresentar aos alunos o questionamento sobre a característica de quantos lados a figura geométrica plana retângulo tem, de modo que os alunos mobilizem habilidades de cálculos de adição para fazer o registro da resposta.

4. Marque um X em cada um dos itens em que a frase apresenta uma afirmação verdadeira

a) A quantidade de lados de um triângulo é menor que a quantidade de lados de um retângulo.

b) A quantidade de lados de um quadrado é maior que a quantidade de lados de um triângulo.

c) O círculo não tem lados

d) A quantidade de lados de um triângulo é igual à quantidade de lados de um retângulo. Espera-se que os alunos marquem um X nos itens a, b e c

5. É possível desenhar representações de figuras geométricas planas, como de um círculo, um quadrado, um retângulo e um triângulo, contornando objetos e, depois, colorindo a parte interior do contorno. Em cada item a seguir, escreva o nome de um objeto que pode ser utilizado para desenhar a representação da figura

a) círculo

Sugestão de resposta: moeda

b) retângulo

Sugestão de resposta: livro.

Mudanças que ocorrem com o passar do tempo

Neste audiovisual, é refletida a importância dos registros de intervalos de tempo entre duas datas com base em exemplos que ocorrem no dia a dia, como saber quantos dias faltam para celebrar o aniversário Também, é foco dessa reflexão como esses registros são necessários para marcar datas em que mudanças ocorrem com o passar do tempo

Por isso, este audiovisual pode ser utilizado de maneira introdutória ao estudo das unidades de medida de tempo: dia, mês e ano.

Uma possibilidade de encaminhamento para o trabalho com este recurso é, ao término da exibição, pedir aos alunos que respondam ao questionamento apresentado na cena final acerca de mudanças ocorridas entre ontem e hoje, as quais foram percebidas pelos alunos

Em seguida, sugere-se apresentar calendários de diversos tipos, como diário, semanal, mensal e anual, providenciados previamente para que os alunos os observem e, coletivamente, comentem:

• a estrutura de cada um deles;

• quantos e quais são os dias da semana;

• quantos e quais são os meses do ano;

• como o uso de cada tipo de calendário favorece planejar atividades e organizar compromissos de agenda.

Neste último item, pode-se questionar aos alunos qual tipo de calendário é mais adequado para esse planejamento Por exemplo, em um calendário anual, não é possível registrar as atividades da semana, pois não há espaço para esse tipo de anotação.

Neste momento, pode-se organizar com os alunos uma agenda das atividades da semana caso os alunos ainda não tenham feito essa organização. Comentar a importância desse tipo de atitude em favor dos estudos. Após essa conversa, propor as atividades sugeridas a seguir que envolvem aspectos da habilidade EF02MA18

Na atividade 2, a proposição da observação da germinação de grãos de feijão favorece um trabalho interdisciplinar com Ciências. Previamente, providenciar (ou pedir aos alunos que providenciem) os materiais necessários para realizar esta atividade: pedaço de algodão, aproximadamente, com 5 gramas; um copo descartável; dois grãos de feijão

A fim de favorecer a literacia familiar, incentivar os alunos a lerem com os responsáveis, a história "João e o pé de feijão", conforme sugerido a seguir.

• JOÃO e o pé de feijão [recurso eletrônico]. Brasília: MEC; Sealf, 2020. (Coleção Conta pra Mim). Disponível em:

http://alfabetizacao.mec.gov.br/images/conta-pramim/livros/versao_digital/joao_pe_de_feijao_versao_digital.pdf Acesso em: 11 jan. 2022

Esse material e outros, bem como informações a respeito da prática de literacia familiar, podem ser encontrados em:

• BRASIL. Ministério da Educação. Conta pra mim Brasília: Sealf, 2020 Disponível em: http://alfabetizacao.mec.gov.br/contapramim. Acesso em: 11 jan. 2022.

Sugestões de atividades

1. No caderno, desenhe um quadro para representar um calendário mensal e preencha o nome do mês e o ano em que está realizando esta atividade. Depois, complete as colunas com os nomes dos dias da semana e os números que indicam os dias. Em seguida, responda às questões.

O preenchimento do quadro depende do mês e do ano em que a atividade for realizada.

a) Indique a duração, em dias, do intervalo de tempo compreendido entre uma segunda-feira até a segunda-feira seguinte.

7 dias.

b) Que dia do mês é hoje?

A resposta depende do dia em que esta atividade for realizada.

c) Que dia da semana é hoje?

A resposta depende do dia em que esta atividade for realizada.

d) Quantos dias já se passaram desde o início deste mês?

A resposta depende do dia e do mês em que esta atividade for realizada.

e) Quantos dias faltam para terminar este mês?

A resposta depende do dia e do mês em que esta atividade for realizada.

2 Com a ajuda de um responsável, plante dois grãos de feijão e observe-os durante uma semana. Para isso, faça o que se pede em cada item.

a) Umedeça um pedaço de algodão, aproximadamente, com 5 gramas

b) Forre o fundo de um copo descartável biodegradável com esse algodão umedecido.

c) Depois, coloque dois grãos de feijão sobre o algodão.

d) Coloque o copo em um local iluminado e arejado.

e) Observe o que ocorre com esses grãos durante 7 dias de germinação.

f) Registre, no caderno, ao longo desses 7 dias, suas observações sobre as mudanças que ocorrem com o tempo nesses grãos

Atenção: não deixe o algodão ficar seco. Coloque um pouco de água sempre que necessário. Atividade de produção de escrita.

BNCC

A Base Nacional Comum Curricular (BNCC), homologada em 2018, é um documento oficial e normativo sobre as aprendizagens (e suas progressões) da Educação Básica (Ensino Infantil, Ensino Fundamental e Ensino Médio). A BNCC estrutura as etapas de aprendizagens em competências, mais abrangentes, e habilidades, mais específicas; e, dessa forma, objetiva garantir a progressão das aprendizagens entre os diferentes anos/ciclos da Educação Básica.

A BNCC tem como objetivo assegurar o direito de uma aprendizagem de qualidade a todos os alunos, buscando colaborar com a formação de uma sociedade mais justa, democrática e inclusiva. Seu caráter normativo colabora com esse objetivo, ao ser um documento que orienta a elaboração e a revisão de currículos, a formação inicial e continuada de professores e as avaliações e exames nacionais.

A seguir, são apresentadas na íntegra as Competências gerais da Educação Básica, as Competências específicas da área de Matemática e suas Tecnologias para o Ensino Fundamental e as cinco unidades temáticas com os respectivos objetos de conhecimento e habilidades para o 2º ano do Ensino Fundamental, que podem ser encontrados nas páginas 9, 10, 267, 282, 283, 284 e 285 da BNCC (BRASIL, 2018).

Competências gerais da Educação Básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Competências específicas de Matemática para o Ensino Fundamental

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Matemática – 2º ano

Unidades temáticas Objetos de conhecimento Habilidades

Números Leitura, escrita, comparação e ordenação de números de até três ordens pela compreensão de características do sistema de

(EF02MA01) Comparar e ordenar números naturais (até a ordem de centenas) pela compreensão de características do sistema de numeração decimal (valor posicional e função do zero).

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

numeração decimal (valor posicional e papel do zero)

(EF02MA02) Fazer estimativas por meio de estratégias diversas a respeito da quantidade de objetos de coleções e registrar o resultado da contagem desses objetos (até 1000 unidades).

(EF02MA03) Comparar quantidades de objetos de dois conjuntos, por estimativa e/ou por correspondência (um a um, dois a dois, entre outros), para indicar tem mais", "tem menos" ou "tem a mesma quantidade", indicando, quando for o caso, quantos a mais e quantos a menos.

Composição e decomposição de números naturais (até 1000)

Construção de fatos fundamentais da adição e da subtração

Problemas envolvendo diferentes significados da adição e da subtração (juntar, acrescentar, separar, retirar)

Problemas envolvendo adição de parcelas iguais (multiplicação)

(EF02MA04) Compor e decompor números naturais de até três ordens, com suporte de material manipulável, por meio de diferentes adições.

(EF02MA05) Construir fatos básicos da adição e subtração e utilizá-los no cálculo mental ou escrito.

(EF02MA06) Resolver e elaborar problemas de adição e de subtração, envolvendo números de até três ordens, com os significados de juntar, acrescentar, separar, retirar, utilizando estratégias pessoais.

(EF02MA07) Resolver e elaborar problemas de multiplicação (por 2, 3, 4 e 5) com a ideia de adição de parcelas iguais por meio de estratégias e formas de registro pessoais, utilizando ou não suporte de imagens e/ou material manipulável.

Problemas envolvendo significados de dobro, metade, triplo e terça parte

Álgebra Construção de sequências repetitivas e de sequências recursivas

Identificação de regularidade de sequências e determinação de elementos ausentes na sequência

(EF02MA08) Resolver e elaborar problemas envolvendo dobro, metade, triplo e terça parte, com o suporte de imagens ou material manipulável, utilizando estratégias pessoais.

(EF02MA09) Construir sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.

(EF02MA10) Descrever um padrão (ou regularidade) de sequências repetitivas e de sequências recursivas, por meio de palavras, símbolos ou desenhos.

(EF02MA11) Descrever os elementos ausentes em sequências repetitivas e em sequências recursivas de números naturais, objetos ou figuras.

Geometria Localização e movimentação de pessoas e objetos no espaço, segundo pontos de referência, e indicação de mudanças de direção e sentido

Esboço de roteiros e de plantas simples

Figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone,

(EF02MA12) Identificar e registrar, em linguagem verbal ou não verbal, a localização e os deslocamentos de pessoas e de objetos no espaço, considerando mais de um ponto de referência, e indicar as mudanças de direção e de sentido.

(EF02MA13) Esboçar roteiros a ser seguidos ou plantas de ambientes familiares, assinalando entradas, saídas e alguns pontos de referência.

(EF02MA14) Reconhecer, nomear e comparar figuras geométricas espaciais (cubo, bloco retangular,

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Grandezas e medidas

cilindro e esfera): reconhecimento e características

Figuras geométricas planas (círculo, quadrado, retângulo e triângulo): reconhecimento e características

Medida de comprimento: unidades não padronizadas e padronizadas (metro, centímetro e milímetro)

Medida de capacidade e de massa: unidades de medida não convencionais e convencionais (litro, mililitro, cm³, grama e quilograma)

Medidas de tempo: intervalo de tempo, uso do calendário, leitura de horas em relógios digitais e ordenação de datas

pirâmide, cone, cilindro e esfera), relacionando-as com objetos do mundo físico.

(EF02MA15) Reconhecer, comparar e nomear figuras planas (círculo, quadrado, retângulo e triângulo), por meio de características comuns, em desenhos apresentados em diferentes disposições ou em sólidos geométricos.

(EF02MA16) Estimar, medir e comparar comprimentos de lados de salas (incluindo contorno) e de polígonos, utilizando unidades de medida não padronizadas e padronizadas (metro, centímetro e milímetro) e instrumentos adequados.

(EF02MA17) Estimar, medir e comparar capacidade e massa, utilizando estratégias pessoais e unidades de medida não padronizadas ou padronizadas (litro, mililitro, grama e quilograma).

(EF02MA18) Indicar a duração de intervalos de tempo entre duas datas, como dias da semana e meses do ano, utilizando calendário, para planejamentos e organização de agenda.

(EF02MA19) Medir a duração de um intervalo de tempo por meio de relógio digital e registrar o horário do início e do fim do intervalo.

Probabilidade e estatística

Sistema monetário brasileiro: reconhecimento de cédulas e moedas e equivalência de valores

Análise da ideia de aleatório em situações do cotidiano

Coleta, classificação e representação de dados em tabelas simples e de dupla entrada e em gráficos de colunas

(EF02MA20) Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro para resolver situações cotidianas.

(EF02MA21) Classificar resultados de eventos cotidianos aleatórios como " pouco prováveis", "muito prováveis", "improváveis" e "impossíveis"

(EF02MA22) Comparar informações de pesquisas apresentadas por meio de tabelas de dupla entrada e em gráficos de colunas simples ou barras, para melhor compreender aspectos da realidade próxima.

(EF02MA23) Realizar pesquisa em universo de até 30 elementos, escolhendo até três variáveis categóricas de seu interesse, organizando os dados coletados em listas, tabelas e gráficos de colunas simples.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial

(CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Referências bibliográficas comentadas

• AMANCIO, Daniel de Traglia; SANZOVO, Daniel Trevisan. Ensino de Matemática por meio das tecnologias digitais. Revista Educação Pública, v. 20, n. 47, 8 dez. 2020. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/20/47/ensino-de-matematica-pormeio-das-tecnologias-digitais. Acesso em: 5 jan. 2022.

No artigo, é apresentada uma discussão sobre as contribuições da utilização das tecnologias digitais no ensino-aprendizagem de Matemática.

• BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática. 6. ed. Belo Horizonte: Autêntica, 2019. (Coleção Tendências em educação matemática).

No livro, os autores apresentam resultados de um trabalho sobre informática educativa, como questões pedagógicas sobre o uso do computador e da calculadora.

• CARAÇA, Bento de Jesus. Conceitos fundamentais da Matemática Lisboa: Gradiva, 1991.

O livro oportuniza ao leitor entrar em contato com ideias e práticas para o desenvolvimento de aulas de Matemática.

• COLL, César; TEBEROSKY, Ana. Aprendendo Matemática São Paulo: Ática, 2000.

No livro, são apresentados conceitos matemáticos de diversos campos, compreendendo estruturas e ideias fundamentais.

• EVES, Howard. Introdução à história da Matemática Tradução de Hygino H Domingues. Campinas: Editora da Unicamp, 2004.

Na obra, são apresentados tópicos importantes da história da Matemática.

• GAUTHIER, Clermont; BISSONNETTE, Steve; RICHARD, Mario. Ensino explícito e desempenho dos alunos Tradução de Stephania Matousek. Petrópolis: Vozes, 2014.

Os autores do livro se propõem a oferecer aos leitores detalhamento da prática docente por meio das ideias do ensino explícito.

• IFRAH, Georges. História universal dos algarismos: a inteligência dos homens contada pelos números e pelo cálculo. Tradução de Alberto Muñoz e Ana Beatriz Katinsky. Rio de Janeiro: Nova Fronteira, 1997. v. 1

O livro tem enfoque no desenvolvimento de sistemas de numeração ao longo do tempo, em particular o Sistema de Numeração Decimal.

• LOPES, Maria Laura M Leite. Tratamento da informação: explorando dados estatísticos e noções de probabilidade a partir de séries iniciais. Rio de Janeiro: Instituto de Matemática/UFRJ-Projeto Fundão, 2005.

No livro, a autora propõe apoiar o professor no ensino de conceitos relacionados à estatística e à probabilidade nos Anos Iniciais do Ensino Fundamental.

• LUCKESI, Cipriano C Avaliação da aprendizagem escolar: estudos e proposições. 22. ed. São Paulo: Cortez, 2011.

No livro, são apresentados estudos críticos sobre avaliação escolar, possibilitando ao educador refletir sobre sua prática avaliativa.

• MACHADO, Nílson José. Matemática e língua materna: análise de uma impregnação mútua. 5. ed. São Paulo: Cortez, 2001.

O autor apresenta uma reflexão sobre a relação entre o alfabeto e o Sistema de Numeração Decimal, com o objetivo de contribuir com o ensino da Matemática.

• MORAN, José Manuel; MASETTO, Marcos Tarciso; BEHRENS, Marilda Aparecida. Novas tecnologias e mediação pedagógica. 21. ed. Campinas: Papirus, 2013. (Coleção Papirus Educação)

No livro, é abordada uma reflexão sobre a inserção da informática e da telemática na educação.

• NEVES, Iara Conceição Bitencourt etal Ler e escrever: compromisso de todas as áreas. 9.ed. Porto Alegre: Editora da UFRGS, 2011.

No livro, são discutidas questões relacionadas à leitura e à escrita nos textos dos diferentes componentes curriculares, inclusive na Matemática.

• POLYA, George. A arte de resolver problemas: um novo aspecto do método matemático. Tradução de Heitor Lisboa de Araújo. Rio de Janeiro: Interciência, 1995.

O autor apresenta reflexões sobre a resolução de problemas e propostas didáticas práticas para o trabalho com problemas em sala de aula.

• SANT'ANA, Claudinei de Camargo; AMARAL, Rúbia Barcelos; BORBA, Marcelo de Carvalho. O uso de softwaresna prática profissional do professor de Matemática.

Revista Ciência & Educação, Bauru, v. 18, n. 3, p. 527-542, 2012. Disponível em: https:// www.scielo.br/j/ciedu/a/ZHkPf6xCR57XCR5tW736FYB/?lang=pt. Acesso em: 10 dez. 2021.

Os autores apresentam uma discussão sobre a incorporação de softwaresna prática docente.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

• TOLEDO, Marília; TOLEDO, Mauro. Teoria e prática de Matemática: como dois e dois. São Paulo: FTD, 2010.

Os autores apresentam informações relevantes sobre o processo de ensino-aprendizagem da Matemática, como reflexões com base em práticas de sala de aula.

Documentos oficiais

• BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília: SEB, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pd f. Acesso em: 5 jan. 2022.

Documento de caráter normativo que define o conjunto de aprendizagens essenciais que os alunos devem desenvolver ao longo das etapas e modalidades da educação básica, de modo que tenham assegurados seus direitos de aprendizagem e desenvolvimento

• BRASIL. Ministério da Educação. PNA: Política Nacional de Alfabetização. Brasília: Sealf, 2019. Disponível em: http://alfabetizacao.mec.gov.br/images/pdf/caderdo_final_pna.pdf. Acesso em: 5 jan. 2022.

O documento instituído pelo Ministério da Educação, por meio da Secretaria de Alfabetização (Sealf), apresenta políticas que visam melhorar os processos de alfabetização e combater o analfabetismo no Brasil

• BRASIL. Ministério da Educação. Relatório Nacional de Alfabetização Baseada em Evidências (Renabe). Brasília: Sealf, 2020. Disponível em: http://alfabetizacao.mec.gov.br/images/pdf/renabe_web.pdf. Acesso em: 5 jan. 2022.

Relatório que apresenta pesquisas recentes sobre alfabetização, literacia e numeracia e cujo objetivo é contribuir para a melhoria nas políticas públicas e nas práticas de ensino no Brasil.

Leituras complementares para o professor

• FERREIRA, Mariana K Leal. Ideias matemáticas de povos culturalmente distintos São Paulo: Global, 2002. (Série antropologia e educação).

No livro, são reunidos relatos de atividades matemáticas aplicadas em diversos países, possibilitando ao leitor refletir sobre sua prática docente.

• LINDQUIST, Mary Montgomery; SHULTE, Albert P. (org.). Aprendendo e ensinando Geometria Tradução de Hygino H Domingues. São Paulo: Atual, 1994.

A obra contém artigos relevantes sobre o ensino-aprendizagem da Geometria em diferentes faixas etárias.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

• MONTEIRO, Alexandrina; POMPEU JUNIOR, Geraldo. A Matemática e os temas transversais São Paulo: Moderna, 2001.

Os autores propõem reflexões sobre os temas transversais, com especial atenção às aulas de Matemática

• SOUZA, Eliane R. de etal A Matemática das sete peças do tangram. 2. ed. São Paulo: Caem/IME-USP, 1997.

No livro, há textos e atividades para serem desenvolvidas com o tangramnas aulas de Matemática.