Entrelaços - Matemática - Volume 3

ÁREA: MATEMÁTICA

COMPONENTE: MATEMÁTICA

JOAMIR SOUZA ANGÉLICA REGHIN 3

ENSINO FUNDAMENTAL ANOS INICIAIS

MATEMÁTICA

RECURSO

EDUCACIONAL DIGITAL

3o ANO ENSINO FUNDAMENTAL ANOS INICIAIS

MATEMÁTICA

Joamir Roberto de Souza

Mestre em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Especialista em Estatística pela Universidade Estadual de Londrina (UEL-PR).

Licenciado em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professor de Matemática da rede pública de ensino.

Autor de livros didáticos para o Ensino Fundamental e para o Ensino Médio.

Maria Angélica Reghin de Souza

Especialista em Gestão Escolar pela Universidade Norte do Paraná (Unopar).

Licenciada em Pedagogia pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora na Educação Infantil.

Autora de livros didáticos para o Ensino Fundamental.

RECURSO EDUCACIONAL DIGITAL

Entrelaços – Matemática – Recurso Educacional Digital – 3o ano (Ensino Fundamental – Anos Iniciais)

Copyright © Joamir Roberto de Souza, Maria Angélica Reghin de Souza, 2021

Direção-geral Ricardo Tavares de Oliveira

Direção de Conteúdo e Negócios Cayube Galas

Direção editorial adjunta Luiz Tonolli

Gerência editorial Natalia Taccetti

Edição Nubia de Cassia de Moraes Andrade e Silva (coord.)

Leticia Mancini Martins, João Alves de Souza Neto

Preparação e revisão de textos Viviam Moreira (sup.)

Adriana Périco, Caline Devèze, Camila Cipoloni, Carina Luca, Fernanda Marcelino, Fernando Cardoso, Graziele Ribeiro, Paulo José Andrade

Gerência de produção e arte Ricardo Borges

Design Daniela Máximo (coord.)

Arte e produção Isabel Cristina Corandin Marques (coord.)

Coordenação de imagens e textos Elaine Bueno Koga

Licenciamento de textos Erica Brambilla

Iconografia Priscilla Narciso

Coordenação de audiovisuais Diego Vieira Cury Morgado de Oliveira

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil) Souza, Joamir Roberto de Entrelaços [livro eletrônico] : matemática : 3o ano : ensino fundamental : anos iniciais / Joamir Roberto de Souza, Maria Angélica Reghin de Souza. – 1. ed. – São Paulo : FTD, 2021.

PDF

Área: Matemática.

Componente: Matemática.

ISBN 978-85-96-03227-8 (recurso educacional digital professor – coleção)

1. Matemática (Ensino fundamental) I. Souza, Maria Angélica Reghin de. II. Título. 21-90777 CDD-372.7

Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Cibele Maria Dias - Bibliotecária - CRB-8/9427

EDITORA FTD

Rua Rui Barbosa, 156 – Bela Vista – São Paulo-SP CEP 01326-010 – Tel. 0800 772 2300 Caixa Postal 65149 – CEP da Caixa Postal 01390-970 www.ftd.com.br central.relacionamento@ftd.com.br

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Carta ao professor

Olá, professor! Seja bem-vindo ao Recurso Educacional Digital!

Este Recurso Educacional Digital tem como objetivo fornecer subsídios e sugestões que apoiem o trabalho pedagógico e a ação educativa em sala de aula no ensino da Matemática para os Anos Iniciais do Ensino Fundamental. O material oferece diferentes instrumentos de ampliação e intervenção que propiciam um ambiente de trocas, comunicação e diálogo, estimulam o levantamento de hipóteses e promovem a construção gradativa de conceitos e procedimentos matemáticos.

Neste material, são propostas situações de ensino-aprendizagem que favorecem a investigação, a experimentação, a criação de registros, a manipulação de objetos e as brincadeiras, permitindo aos alunos compreender que a Matemática não é um conhecimento restrito à sala de aula.

Os conteúdos e propostas de atividades que compõem este material também possibilitam o desenvolvimento das habilidades da Base Nacional Comum Curricular (BNCC), das competências específicas da área de Matemática e suas Tecnologias para o Ensino Fundamental, das competências gerais da Educação Básica, dos objetivos de aprendizagem e dos componentes essenciais para a alfabetização propostos na Política Nacional de Alfabetização (PNA).

Este material digital está organizado em quatro recursos pedagógicos descritos a seguir.

Plano de desenvolvimento anual

O Plano de desenvolvimento anual apresenta um quadro com uma programação de como os conteúdos podem ser organizados e trabalhados durante o ano letivo, seja em bimestres, trimestres ou semestres. Também, apresenta as habilidades da BNCC e os componentes essenciais para a alfabetização que podem ser trabalhados no período. Esse quadro é uma sugestão de programação, tendo o professor autonomia para adaptá-lo à realidade e às necessidades da turma.

O Plano de desenvolvimento apresenta, ainda: textos sobre estratégias e atitudes docentes que podem contribuir para alcançar os objetivos de aprendizagem estabelecidos; uma reflexão sobre avaliação e como esse instrumento pode auxiliar o processo de ensino-aprendizagem; e sugestões de leitura e sitesque podem aprimorar o trabalho docente em sala de aula.

Sequências didáticas

As sequências didáticas são sugestões de planejamento aula a aula que têm como objetivos complementar e aprofundar os conteúdos contemplados em outros materiais

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

didáticos e, consequentemente, contribuir com o desenvolvimento das habilidades e das competências específicas da área de Matemática e suas Tecnologias, das competências gerais da Educação Básica e dos componentes essenciais para a alfabetização. Além disso, essas sequências também podem contribuir para a remediação de eventuais dificuldades de aprendizagem dos alunos.

Com relação a sua estrutura, cada sequência didática é composta de um texto de introdução, dos objetivos de aprendizagem, do planejamento das aulas, de um passo a passo descritivo com sugestões metodológicas de como desenvolver as aulas, de exemplos de atividades que podem ser propostas aos alunos e de orientações de como acompanhar o desenvolvimento das aprendizagens em diferentes momentos.

Relatórios e indicadores do acompanhamento da aprendizagem

Os relatórios e indicadores do acompanhamento da aprendizagem têm como objetivo oferecer ao professor subsídios para acompanhar a aprendizagem dos alunos de maneira individual e coletiva, bem como apresentar orientações sobre como sistematizar os dados e apresentá-los aos pares, aos gestores escolares e aos responsáveis pelos alunos.

Esse relatório é composto de quatro fichas:

• Ficha de avaliação diagnóstica: possibilita avaliar os conhecimentos prévios dos alunos sobre determinados conteúdos e verificar a proficiência em algumas habilidades e competências.

• Ficha de acompanhamento das aprendizagens: possibilita avaliar o aprendizado e o progresso do aluno durante o processo de ensino-aprendizagem e fornece dados que permitem ao professor avaliar esse processo e ajustar a prática docente.

• Ficha de verificação dos resultados: possibilita avaliar quais objetivos de aprendizagem estabelecidos foram alcançados ao final do ano letivo.

• Ficha de acompanhamento para o desenvolvimento de habilidades socioemocionais: possibilita avaliar a evolução dos alunos em relação às habilidades socioemocionais.

É importante destacar a autonomia do professor para avaliar como essas fichas devem ser aplicadas e adaptadas de acordo com a realidade dos seus alunos e da escola na qual leciona e como elas podem complementar os diferentes instrumentos de avaliação e de acompanhamento de aprendizagem já utilizados.

Catálogo de audiovisuais

O catálogo de audiovisuais apresenta um descritivo de cada um dos audiovisuais que acompanham o Recurso Educacional Digital e tem como objetivo complementar e aprofundar o trabalho com os conteúdos explorados nesse material.

Além disso, oferece encaminhamentos à autonomia do professor, permitindo que, por meio de uma reflexão sobre as características da sua turma e do seu planejamento, seja possível estabelecer a melhor maneira de utilizar os audiovisuais. Para isso, o catálogo

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

apresenta sugestões de como esses audiovisuais podem ser trabalhados, bem como propostas de atividades que possibilitam explorar o uso desses recursos com os alunos.

No volume do 3º ano, são trabalhados os seguintes temas:

• Os números naturais até a 4ª ordem;

• Adição e subtração com números naturais;

• Multiplicação e divisão com números naturais;

• Figuras geométricas planas e espaciais;

• Grandezas e medidas;

• Probabilidade e estatística.

Esperamos que este material contribua para o aprimoramento da sua prática docente e para a formação de alunos aptos a viver em sociedade, fazendo valer seus direitos e exercendo seus deveres individuais e coletivos.

Bom trabalho!

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Instrumentos pedagógicos

Plano de desenvolvimento anual

Este Plano de desenvolvimento anual consiste em um instrumento pedagógico que tem como objetivo auxiliar o planejamento docente na gestão dos conteúdos a serem apresentados ao longo de um ano letivo.

Para isso, em um primeiro momento, são apresentadas propostas de organização semestral, trimestral e bimestral, ordenadas em um quadro.

No quadro, a fim de favorecer a visualização da progressão das aprendizagens, constam, em colunas:

• a descrição sequencial de distribuição dos conteúdos;

• a indicação dos códigos alfanuméricos das habilidades da Base Nacional Comum Curricular (BNCC);

• a nomeação dos componentes essenciais para a alfabetização, de acordo com a Política Nacional de Alfabetização (PNA).

É importante considerar que o plano de ação sugerido nesta proposta pode ser adaptado à realidade escolar interna (infraestrutura, características da turma, entre outros aspectos) e à realidade escolar externa (parceria com os responsáveis dos alunos) da instituição em que se atua.

Imediatamente após o quadro, para auxiliar na gestão do processo de ensino-aprendizagem, constam três seções que são descritas a seguir.

A seção Práticas de ensino na sala de aula apresenta a proposição de algumas estratégias e procedimentos que podem ser eficazes para a concretização dos objetivos de aprendizagem previstos.

Na seção Avaliação, a importância dessa ferramenta pedagógica é enfatizada como instrumento a ser empregado de modo contínuo e processual. Deve ser utilizada para aferir não só os conhecimentos curriculares disciplinares, mas também os conhecimentos da realidade do mundo que cerca os alunos.

Por fim, a seção Saiba mais apresenta sugestões de referências complementares para consulta (sites , vídeos etc.) relacionadas a temas de cunho de ampliação do repertório da formação docente continuada.

De modo articulado e vinculado, com base nas indicações do quadro e das seções, é possível planejar o desenvolvimento anual de sua atuação docente.

Aprendizagens desenvolvidas no 3º ano

Os números

• Reconhecer situações cotidianas em que os números indicam quantidade, medida, ordem e código.

• Ler e escrever números naturais até a 4ª ordem com algarismos e por extenso

• Compor e decompor números naturais até a 4ª ordem

• Comparar e ordenar números naturais até a 4ª ordem.

• Relacionar números naturais a pontos da reta numérica.

• Reconhecer e determinar o antecessor e o sucessor de um número natural

• Classificar um número natural em par ou ímpar.

1 º semestre 1º trimestre 1º bimestre

Figuras geométricas espaciais

• Reconhecer e nomear figuras geométricas espaciais

• Associar figuras geométricas espaciais a objetos do dia a dia

• Identificar se uma figura geométrica espacial possui partes planas ou arredondadas na superfície

• Identificar figuras geométricas planas na superfície de figuras geométricas espaciais.

• Associar as figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone e cilindro) às suas planificações.

• Identificar faces, vértices e arestas de figuras geométricas espaciais (cubo, bloco retangular e pirâmides)

• Identificar vértices, base e superfícies arredondadas do cone.

Adição e subtração

• Construir fatos básicos da adição.

2º bimestre

• Resolver e elaborar problemas envolvendo as ideias da adição sem e com reagrupamentos

• Resolver e elaborar problemas envolvendo as ideias da subtração sem e com reagrupamentos.

• Compreender a ideia de propriedade associativa da adição.

• Reconhecer que diferentes adições de duas parcelas podem ter somas iguais.

BNCC

EF03MA01

EF03MA02

EF03MA04

EF03MA13

EF03MA14

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento de vocabulário

• Compreensão de textos.

• Produção de escrita

BNCC

EF03MA03

EF03MA04

EF03MA05

EF03MA06

EF03MA10

EF03MA11

EF03MA12

EF03MA15

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Material disponibilizado em licença aberta do tipo Creative Commons

• Reconhecer que diferentes subtrações de duas parcelas podem ter um mesmo resultado.

• Resolver e elaborar problemas envolvendo adição e subtração.

• Resolver problemas que envolvam a comparação de valores monetários em situações de compra, venda ou troca.

• Identificar regularidades em sequências ordenadas de números naturais obtidas por adições e subtrações sucessivas.

EF03MA16

EF03MA21

EF03MA24

Componentes essenciais para a alfabetização

• Desenvolvimento de vocabulário.

• Compreensão de textos.

2º trimestre

• Escrever os próximos números de sequências ordenadas de números naturais obtidas por adições e subtrações sucessivas.

Figuras geométricas planas, localização e deslocamento

• Identificar e comparar figuras geométricas planas (quadrado, retângulo, triângulo, trapézio, paralelogramo e círculo) analisando características do seu contorno.

• Identificar lados e vértices de figuras geométricas planas.

• Determinar a medida do contorno de uma figura geométrica plana.

• Reconhecer figuras congruentes, usando sobreposição e desenhos em malhas quadriculadas ou triangulares, incluindo o uso de tecnologias digitais.

• Comparar figuras geométricas planas por sobreposição, explorando a ideia de área.

• Utilizar noções de posição para localizar objetos no espaço com base em pontos de referência.

• Utilizar noções de posição para descrever deslocamentos no espaço com base em pontos de referência.

Multiplicação

• Resolver e elaborar problemas envolvendo a ideia de adição de parcelas iguais da multiplicação.

• Resolver e elaborar problemas envolvendo a ideia de disposição retangular da multiplicação.

• Identificar e relacionar as ideias de dobro e triplo às multiplicações por 2 e 3.

• Identificar regularidades em multiplicações por 0 e 1.

• Identificar regularidades em sequências de números naturais e determinar os próximos elementos ou elementos ausentes

BNCC

EF03MA03

EF03MA04

EF03MA07

EF03MA08

EF03MA09

EF03MA10

EF03MA24

• Produção de escrita 2º semestre 3º bimestre

Componentes essenciais para a alfabetização

• Compreensão de textos.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

• Resolver e elaborar problemas envolvendo multiplicação sem e com reagrupamento.

• Identificar equivalência de valores monetários.

Divisão

• Resolver e elaborar problemas de divisão em partes iguais, com restos iguais ou diferentes de zero.

• Resolver e elaborar problemas de divisão com a ideia de medir.

• Resolver e elaborar problemas de divisão envolvendo as ideias de metade, terça, quarta, quinta e décima partes

3º trimestre

4º bimestre

Grandezas e medidas

• Estimar, medir e comparar comprimento, massa e capacidade utilizando unidades de medida padronizadas e não padronizadas.

• Estimar, medir e comparar comprimentos utilizando metro, centímetro e milímetro como unidades de medida.

• Identificar o instrumento mais apropriado para medições de comprimento.

• Relacionar e converter as unidades de medida de comprimento metro, centímetro e milímetro.

• Resolver problemas envolvendo medidas de capacidade.

• Estimar e comparar massa utilizando quilograma, grama e miligrama.

• Resolver problemas envolvendo medidas de massa.

• Identificar litro e mililitro como unidades de medida de capacidade padronizada

• Escolher o instrumento mais apropriado para medir capacidade.

• Resolver problemas envolvendo medidas de capacidade.

• Ler, medir e registrar medidas de tempo utilizando relógios digitais e de ponteiro.

• Determinar a duração de um evento de acordo com seus horários de início ou término.

• Identificar as relações entre as medidas de tempo horas e minutos e minutos e segundos.

Estatística e probabilidade

• Ler, interpretar, comparar e organizar dados em tabelas simples e de dupla entrada.

• Ler, interpretar, comparar e organizar dados em gráficos de colunas e barras

• Desenvolvimento de vocabulário.

• Produção de escrita

BNCC

EF03MA17

EF03MA18

EF03MA19

EF03MA20

EF03MA22

EF03MA23

EF03MA25

EF03MA26

EF03MA27

EF03MA28

Componentes essenciais para a alfabetização

• Compreensão de textos.

• Desenvolvimento de vocabulário.

• Produção de escrita

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

• Construir gráficos de colunas e barras utilizando malha quadriculada e planilhas eletrônicas

• Realizar pesquisa.

• Organizar dados coletados em uma pesquisa em listas e tabelas.

• Representar dados coletados em uma pesquisa em gráficos.

• Reconhecer e determinar todos os resultados possíveis de um experimento aleatório.

• Analisar resultados de um experimento aleatório indicando qual deles é mais provável de ocorrer

Práticas de ensino na sala de aula

Para que o Plano de desenvolvimento anual possa efetivamente se consolidar de modo que sejam alcançados os objetivos de aprendizagem pretendidos para o ano letivo, é importante o docente ter atitudes e utilizar práticas que contribuam para o desenvolvimento dos componentes essenciais para a alfabetização e das competências e habilidades matemáticas nos alunos sob sua responsabilidade. Para isso, a seguir é apresentada uma visão geral de algumas abordagens possíveis.

É importante ressaltar, ainda, que o processo de ensino-aprendizagem já não se encontra mais intimamente vinculado apenas ao espaço físico da sala de aula e, em virtude das mudanças ocorridas socialmente, cenários de aprendizagem virtual passaram a fazer parte da dinâmica escolar, sendo necessário considerar essa perspectiva no planejamento, nas práticas, bem como na busca de atualização da formação docente.

Leitura inferencial

Para abordar situações significativas apresentadas em cada proposta didática, a leitura inferencial é uma prática importante a ser desenvolvida com os alunos. Essa prática envolve tanto estratégias de leitura de imagens quanto de leitura de textos.

A leitura de imagens, em Matemática, nos Anos Iniciais do Ensino Fundamental, é tão explorada quanto a leitura de textos, visto que o suporte de apoio visual na realização de contagens ou resolução de operações matemáticas é um recurso didático muito utilizado.

A reflexão sobre o processo de leitura inferencial pode ser promovida pelo docente por meio de perguntas ou solicitações propostas que permitam aos alunos demonstrarem respostas que não estejam apenas circunscritas aos textos, e sim possam ser inferidas considerando conhecimentos prévios e de mundo de modo geral.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Os enunciados dos problemas matemáticos são textos que requerem leitura analítica e inferencial por parte dos alunos para que possam desenvolver melhores estratégias de resolução.

Produzir inferências é uma ação que auxilia na compreensão de um texto. No caso das aulas de Matemática, de um texto matemático, por exemplo, o enunciado de um problema.

A compreensão de texto, em qualquer área de conhecimento, é uma habilidade que depende das inferências geradas pelo leitor, considerando que cada texto possui informações implícitas e explícitas.

A qualidade e a quantidade das inferências geradas por um leitor dependem, prioritariamente, das associações estabelecidas entre as informações explícitas no texto e os conhecimentos prévios e de mundo que o leitor possui.

Para auxiliar os alunos a lerem um texto de maneira analítica, a fim de que possam concluir, deduzir e formular novos sentidos, levantar hipóteses, bem como ressignificar informações, uma estratégia é sugerir que, ao fazer a leitura:

• dividam o texto em partes menores que forneçam informações principais;

• estabeleçam relações entre essas partes de modo a identificar como elas se inter-relacionam;

• identifiquem o panorama geral do que essas inter-relações indicam.

Destaca-se o fato de que a leitura de um texto matemático mobiliza o leitor para a interpretação de elementos textuais combinados a elementos matemáticos, como números, tabelas, gráficos, entre outros.

Nesse sentido, outra estratégia é fazer com que os alunos compreendam que ler um texto matemático não se resume a identificar palavras-chave.

Sugere-se, sempre que possível, incentivar os alunos a realizar uma leitura analítica e inferencial de:

• imagens que permeiam o material didático (imagens de aberturas de partes hierárquicas do livro, como unidades ou capítulos, por exemplo);

• textos (enunciados de problemas, textos instrucionais de jogos, entre outros).

Sugere-se, ainda, solicitar aos alunos que façam registros das compreensões, pois essa prática vai ajudá-los a melhorar o desempenho na resolução e condução das tarefas propostas.

Esses registros podem ser compartilhados em um mural da sala de aula ou da escola, em um mural on-line criado na rede social da escola ou, até mesmo, em uma folha de cartolina, na qual os alunos façam registros. O cartaz pode ser afixado em algum espaço da sala de aula ou da escola

Fazer diferentes registros

Na Competência específica 6 de Matemática e suas Tecnologias da BNCC (BRASIL, 2018, p. 267), é abordada a importância de expressar respostas e sintetizar conclusões utilizando diferentes registros e linguagens.

Desse modo, uma prática importante, ao longo do desenvolvimento das atividades propostas, é solicitar aos alunos que façam diferentes registros para expressar as justificativas de suas respostas, esquematizar a descrição de estratégias utilizadas no processo de resolução, representar um problema com uma organização visual etc.

Essa prática é importante de ser desenvolvida desde os primeiros anos de escolaridade já que é um processo que deve ser aprimorado durante toda a vida escolar e não escolar, pois fazer registros e interpretá-los é uma habilidade importante, por exemplo, no trabalho, assim como em diversas situações da vida cotidiana que requerem a esquematização de sistemas, situações ou processos, com a finalidade de compreendê-los melhor

Como estratégia de aplicação dessa prática, explorar com os alunos algumas possibilidades, como:

• no processo de resolução de problemas que envolvam proporcionalidade, fazer registros organizados em quadros;

• em pesquisas estatísticas, fazer registros dos dados coletados em tabelas e gráficos;

• questões que abrangem características geométricas, fazer desenhos (esboços esquemáticos) que representem plantas baixas ou figuras (bidimensionais ou tridimensionais);

• no trabalho com sequências recursivas (numéricas ou figurais), fazer registros por escrito das regularidades identificadas na regra de formação do padrão de cada sequência;

• ao resolver problemas que envolvem multiplicação com a ideia de combinatória, fazer a organização da representação de uma árvore de possibilidades (ou de um quadro de possibilidades);

• na elaboração de problemas, solicitar que façam diagramas de fluxo ligando as etapas, a fim de representar a sequência que encadeou o raciocínio empregado no desenvolvimento da elaboração

Permitir aos alunos eleger de maneira autônoma os diferentes registros e linguagens é muito importante para valorizar o protagonismo deles no processo de ensino-aprendizagem.

Educação para a cidadania

Além dos conteúdos disciplinares, o processo de formação educacional abrange, também, a responsabilidade de formar indivíduos conscientes da importância que atitudes individuais exercem sobre a vida do outro e das responsabilidades que possuem em relação ao grupo social a que pertencem, entre outros aspectos.

Na BNCC (BRASIL, 2018), nas páginas 9 e 10, estão relacionadas dez competências gerais da Educação Básica e, nas páginas 19 e 20, são elencados os Temas Contemporâneos Transversais, os quais apontam para o desenvolvimento de capacidades a serem aperfeiçoadas, ao longo da vida, com base no exercício de práticas sociais inseridas em determinados contextos, como meio ambiente, saúde, educação financeira, entre outros.

Considerando essa perspectiva, a prática da educação para a cidadania prioriza envolver todos os alunos em vivências significativas consigo mesmo e com outras pessoas, por meio da percepção de que há direitos que são garantidos com base no cumprimento dos deveres, e vice-versa. Sendo assim, a educação para a cidadania vai além da transmissão de conteúdo e da assimilação dele

Uma estratégia que se pode utilizar, a cada semana, é escolher ou pedir que se voluntarie um ajudante da semana para auxiliar você em algumas tarefas. O objetivo é levar os alunos a assumirem uma postura cooperativa com você e os colegas.

É adequado, se possível, que cada aluno da turma, ao longo do ano letivo, seja o ajudante da semana, pois essa experiência ajudará a lidar com a indisciplina, caso exista no ambiente. Isso, também, favorecerá o desenvolvimento de sentimentos de pertencimento, autonomia, responsabilidade, resiliência, foco, cuidado consigo mesmos e com os outros, entre outros.

O ajudante da semana pode cuidar do compartilhamento de comunicados e lembretes de compromissos. Essa comunicação pode ser:

• on-line , por meio de aplicativos de mídia que compartilham vídeos curtos ou áudios;

• off-line , com base na escrita de recados diários no mural ou no quadro da sala de aula

É importante que seja incluída alguma atividade envolvendo tecnologia digital para que os alunos se apropriem de fazer uso cidadão e crítico no ambiente escolar.

Estímulo à criatividade

A criatividade (ou pensamento criativo) é um potencial que todos nós possuímos e pode ser desenvolvida no ambiente escolar com base em determinadas estratégias e em certos contextos apropriados.

Nas aulas de Matemática, estimular práticas que envolvam o potencial criativo é uma ação que pode ser associada a diferentes unidades temáticas dessa área de conhecimento.

Nas atividades relacionadas a conhecimentos geométricos, por exemplo, uma estratégia é propor aos alunos atividades em que eles sejam construtores de maquetes ou de outras elaborações relacionadas ao tema, de acordo com a criatividade deles.

Para realizar essas construções, os alunos devem mobilizar os conhecimentos desse tema para reconhecer em embalagens e objetos do mundo físico características de figuras geométricas espaciais estudadas para assim selecionar as melhores embalagens ou objetos a serem empregados nessas construções de acordo com as características identificadas, como superfícies arredondadas ou não.

Esse tipo de atividade, geralmente realizada em grupos, envolve a produção de ideias originais Sendo assim, além de estimular a criatividade para apresentar ideias, exercita a flexibilidade dos alunos em acolher as ideias dos colegas de grupo e a solucionar problemas de forma construtiva e respeitosa

A captura de retratos de construções arquitetônicas que se pareçam com figuras geométricas espaciais para elaborar uma apresentação de slidestambém é uma atividade que estimula a criatividade, além de utilizar tecnologia digital.

Outra estratégia são atividades de elaboração de problemas. Esse tipo de atividade também estimula a criatividade dos alunos. Além de empregarem conhecimentos matemáticos nessa elaboração, a criação do contexto do problema requer a originalidade na concepção de ideias novas e, para isso, o pensamento criativo é estimulado.

Avaliação

A avaliação exerce uma das principais funções em favor da promoção e da consolidação do processo de ensino-aprendizagem. Por isso, a avaliação não pode ser concebida somente como uma fase final desse processo, mas precisa ser integrada a todo o processo, de maneira contínua.

Para que a avaliação seja empregada com eficácia, é importante coletar informações sobre aspectos não desenvolvidos, os parcialmente desenvolvidos e os desenvolvidos pelos alunos. Com base nessas informações, oferecer feedbacka cada um deles, aos gestores escolares e aos responsáveis pelos alunos

A coleta dessas informações pode ser dirigida de maneira diversificada considerando diferentes possibilidades, como avaliação diagnóstica, avaliação de processo e avaliação formativa.

Com a avaliação diagnóstica, é possível mapear os diferentes perfis dos alunos em relação aos conhecimentos prévios que possuem. Assim, a observação e a reflexão do docente sobre as informações obtidas é uma importante ferramenta nesse tipo de avaliação.

Embora, em um diagnóstico, muitas informações possam ser observadas, é indicado, além da sondagem de conhecimentos prévios, que se observem também:

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

• a linguagem corporal dos alunos durante suas explicações (se demonstram interesse ou não);

• o modo como se organizam no trabalho em duplas ou grupos para a prática de uma atividade;

• se manifestam ansiedade ou demonstram desinteresse quando questionados individualmente.

Na avaliação diagnóstica, a observação desses padrões de comportamento compõe dados relevantes a serem vinculados à análise do desempenho cognitivo de cada aluno nas atividades propostas.

Já a avaliação de processo produz uma experiência educacional que motiva os alunos, por ser contínua e se dar também por meio da utilização de instrumentos informais, como paradas para uma autoavaliação.

A fim de tornar a avaliação de processo um momento mais próximo de cada aluno:

• questionar a avaliação pessoal que cada um faz das próprias produções e atuações escolares No caso de trabalho em duplas ou em grupo, essa prática de autoavaliação pode ser incorporada de maneira reflexiva e compartilhada entre eles;

• solicitar relatórios concisos sobre atividades específicas, ou qualquer outro tipo de registro, para obter informações do processo de aprendizagem de cada aluno, a fim de rever o processo sempre que necessário.

Na avaliação formativa, a utilização de instrumentos formais, mantendo o formato de atividades diárias, se destaca, pois, nesse tipo de avaliação, critérios mais específicos são considerados, como o nível de apreensão dos alunos em relação aos conteúdos, a aplicação da linguagem matemática, entre outros que permitem a sistematização de informações.

Avaliar é um ato que dá origem a informações úteis para docentes e discentes, conforme a interpretação e a comunicação dialógica entre os atores do processo educacional.

Para auxiliar na geração de informações e interpretação dessas informações, consultar os Relatórios e Indicadores do Acompanhamento da Aprendizagem disponíveis neste material.

Para saber mais

• BARLOW, Michel. Avaliação escolar: mitos e realidades. Porto Alegre: Artmed, 2006. Nessa obra, Michel Barlow discute práticas avaliativas em sala de aula.

• BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática. 6. ed. Belo Horizonte: Autêntica, 2019. (Tendências em Educação Matemática).

Nesse livro, os autores apresentam resultados de um trabalho sobre informática educativa, como questões pedagógicas sobre o uso do computador e da calculadora.

• BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília: SEB, 2018. Disponível em:

http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pd f. Acesso em: 8 dez. 2021.

Documento que regulamenta as aprendizagens essenciais na Educação Básica.

• BRASIL. Ministério da Educação. PNE: Plano Nacional de Educação. Brasília: Inep, 2014. Disponível em:

https://download.inep.gov.br/publicacoes/institucionais/plano_nacional_de_educacao/pl ano_nacional_de_educacao_pne_2014_2024_linha_de_base.pdf. Acesso em: 8 dez. 2021.

Nesse documento, são apresentadas as diretrizes, metas e estratégias para a educação brasileira de 2014 a 2024.

• COLL, César; TEBEROSKY, Ana. Aprendendo Matemática. São Paulo: Ática, 2000.

Nesse livro, é possível ter acesso a conceitos matemáticos de diversos campos, compreendendo estruturas e ideias fundamentais.

• GAUTHIER, C.; BISSONNETTE, S.; RICHARD, M. Ensino explícito e desempenho dos alunos: a gestão dos aprendizados. Petrópolis: Vozes, 2014.

Nesse livro, os autores discutem as principais características e os fundamentos do ensino explícito como uma proposta de ensino eficaz.

• HADJI, C. A avaliação, regras do jogo: das intenções aos instrumentos. Porto: Porto Editora, 1994.

Nesse livro, é apresentada uma proposta de abordagem de avaliação da aprendizagem escolar, incluindo reflexões e análises relacionadas aos tipos de avaliação.

• LORENZATO, S. Laboratório de ensino de Matemática e materiais didáticos manipuláveis. In : LORENZATO, S. O Laboratório de Ensino de Matemática na formação de professores. Campinas: Autores Associados, 2006. p. 3-38. (Coleção Formação de professores).

Nesse texto, é discutido o papel do Laboratório de Ensino de Matemática (LEM) no ensino e na aprendizagem de Matemática.

• LUCKESI, C. C. Verificação ou avaliação: o que pratica a escola. Ideias, São Paulo, n. 8, p. 71-80, 1998. (Série Ideias).

Nesse texto, o autor faz uma abordagem sobre aspectos que diferenciam as ações de verificar e avaliar no ensino escolar.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

• MONTEIRO, Alexandrina; POMPEU JUNIOR, Geraldo. A Matemática e os temas transversais. São Paulo: Moderna, 2001.

Nesse livro, há reflexões sobre os temas transversais, com especial atenção às aulas de Matemática.

• NACARATO, Adair Mendes; MENGALI, Brenda Leme da Silva; PASSOS, Cármen Lúcia Brancaglion A Matemática nos anos iniciais do Ensino Fundamental. 2. ed. Belo Horizonte: Autêntica, 2015.

Nesse livro, os autores debatem sobre o ato de aprender e o ato de ensinar a Matemática, nos Anos Iniciais do Ensino Fundamental.

• PAIS, L. C. Ensinar e aprender Matemática. Belo Horizonte: Autêntica, 2006.

Com essa obra, o autor propõe uma reflexão acerca de aspectos metodológicos do ensino da Matemática, incluindo uma análise do livro didático.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Sequências didáticas

Sequência

ordem

didática 1: Os números naturais até a 4ª

Serão trabalhados nesta sequência didática a escrita e o valor posicional dos números naturais de até quatro ordens, visando à compreensão das relações entre as ordens, sua composição e decomposição. Esses fatores são muito importantes para o entendimento do sistema de numeração decimal.

Objetivos de aprendizagem

• Representar com material dourado e ábaco os números naturais até a 4ª ordem.

• Compor e decompor números naturais.

• Comparar números naturais.

• Reconhecer o valor posicional dos algarismos na escrita de números naturais.

• Entender o conceito de antecessor e sucessor de um número natural.

• Realizar a leitura e a escrita de números naturais, entendendo o significado de unidade de milhar, centena, dezena e unidade.

• Realizar cálculos por meio de diferentes estratégias.

Plano de aulas

Aula 1: Representar números com o material dourado.

Aula 2: Discutir características do sistema de numeração decimal com o auxílio do material dourado.

Aula 3: Compreender as representações de números naturais com o material dourado.

Aula 4: Explorar os conhecimentos dos alunos sobre números naturais até a 4ª ordem.

Aula 5: Introduzir o ábaco como instrumento de representação de números no sistema de numeração decimal.

Aula 6: Confeccionar o Jogo da memória sobre o sistema de numeração decimal.

Aula 7: Explorar o Jogo da memória sobre o sistema de numeração decimal.

Aula 8: Relacionar três representações de um mesmo número natural: material dourado, escrita por extenso e ábaco.

Componentes essenciais para a alfabetização: Produção de escrita e compreensão de textos

Competências gerais da Educação Básica: 2 e 10.

Competências específicas de Matemática: 2 e 8

Habilidades: EF03MA01 e EF03MA02.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Materiais necessários: Material dourado, ábaco, caderno, folhas avulsas, tabelas impressas e cartas em branco

Aula 1

O objetivo desta aula é representar números com o material dourado, de acordo com os conhecimentos prévios dos alunos. Para isso, organizar a turma em duplas e, em seguida, apresentar aos alunos o material dourado. Comentar que esse material é um importante recurso que contribui para a compreensão de características do sistema de numeração decimal.

Após essa abordagem inicial, distribuir para cada dupla caixas com o material dourado, em quantidade suficiente para que representem qualquer número natural até 1 300. Caso não haja essa quantidade de peças, aumentar a quantidade de integrantes dos grupos.

Pedir aos alunos que manuseiem o material, como desejarem. Comentar que, nesse momento, eles estarão livres para manusear os objetos, mas que essa ação exige responsabilidade deles, uma vez que esse material será usado, também, por outros alunos.

Em seguida, solicitar que escolham um número qualquer até 1 300 e registrem-no. Pedir, então, que a dupla represente, com as peças do material dourado, o número escolhido.

Na sequência, compor grupos de duas duplas, de maneira que uma dupla indique um número (até 1 300) e a outra dupla tente representar esse número com o material dourado. Nesse momento, acompanhar a turma e avaliar se as respostas apresentadas estão corretas. Alternar as funções das duplas nesta atividade.

Ao final da aula, solicitar aos alunos que produzam um relatório descrevendo a experiência desenvolvida. Comentar que essa produção será retomada na próxima aula.

Aula 2

O objetivo desta aula é discutir características do sistema de numeração decimal com o auxílio do material dourado. Inicialmente, retomar a atividade desenvolvida na aula anterior. Para isso, propor a alguns alunos que apresentem os relatórios produzidos Disponibilizar o material dourado, conversar com os alunos sobre o que acharam desse recurso e propor as seguintes perguntas:

1. Quantos cubinhos formam uma barra?

10 cubinhos.

2. Quantas barras formam uma placa?

10 barras.

3. Quantas placas são necessárias para formar um cubo?

10 placas.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Permitir que os alunos manuseiem o material dourado para efetuarem a contagem, se sentirem necessidade. Apresentar, em seguida, novas questões

4. Quantos cubinhos são necessários para formar uma placa?

100 cubinhos.

5. E quantos cubinhos formam um cubo?

1 000 cubinhos.

Pedir aos alunos que justifiquem a resposta. Espera-se que tenham percebido que, como a placa é formada por 10 barras e cada barra é composta de 10 cubinhos, ela tem 100 cubinhos (10 × 10 = 100), e que, como 10 placas, de 100 cubinhos, formam o cubo do material dourado, tem-se, então, um total de 1 000 cubinhos (10 × 100 = 1 000).

Explicar aos alunos que essa constatação se trata de uma observação feita com base 10: unidade, dezena, centena, unidade de milhar. Comentar que os números são organizados de acordo com essa base e que, por esse motivo, chamamos nosso sistema de numeração de sistema de numeração decimal. Mostrar em um cartaz a representação do número 1 235 com o material dourado.

Indicar cada figura do material dourado, relacioná-la com a ordem correspondente e explicar que essa decomposição tem correspondência na sentença matemática da coluna à direita, cuja soma é o número representado no início, 1 235.

Solicitar à turma que se reorganize nas mesmas duplas da aula anterior. Em seguida, entregar para cada dupla o material dourado e solicitar que façam um cartaz análogo ao apresentado.

Comentar que, para compor o desenho da representação do número com o material dourado, os alunos podem recorrer a imagens disponíveis na internet. Eles podem imprimir, cortar e colar imagens dos cubinhos, das barras, das placas e dos cubos no cartaz. Outra

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

sugestão é trazer cópias de imagens do material dourado para os alunos. Por fim, se julgar conveniente, expor os cartazes produzidos pelos alunos no mural da escola.

Aula 3

O objetivo desta aula é compreender as representações de números naturais com o material dourado. Para isso, solicitar aos alunos que relatem tudo o que foi feito nas aulas anteriores com o material dourado. É importante promover essa discussão inicial, de maneira a identificar como os alunos compreenderam esse recurso. Caso eles apresentem alguma informação que não esteja correta, realizar a correção.

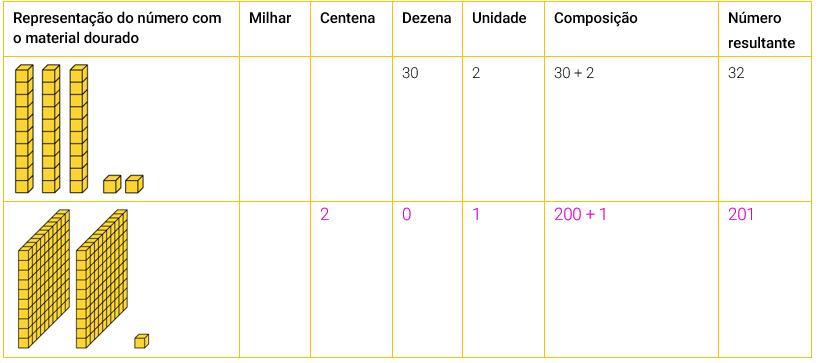
Em seguida, fazer cópias do quadro a seguir e entregar aos alunos para que o completem individualmente. Destinar um tempo para a atividade. Desta vez, os alunos partirão da representação de determinados números com material dourado e deverão determinar, por meio da composição, cada número.

1. Complete o quadro de acordo com o material dourado. EDITORIA DE ARTE

Respostas: EDITORIA DE ARTE

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Após os alunos realizarem essa tarefa, entregar uma versão impressa do quadro completo e solicitar que observem se acertaram ou se erraram os itens. Se julgar conveniente, pedir que eles próprios avaliem suas produções, atribuindo uma pontuação de 0 a 5 (um ponto para cada linha incompleta do quadro). É importante que, nesse processo de autoavaliação, os possíveis erros sejam interpretados como oportunidade de aprendizagem. Posteriormente, discutir todas as linhas do quadro, problematizando os possíveis erros dos alunos e corrigindo-os.

Aula 4

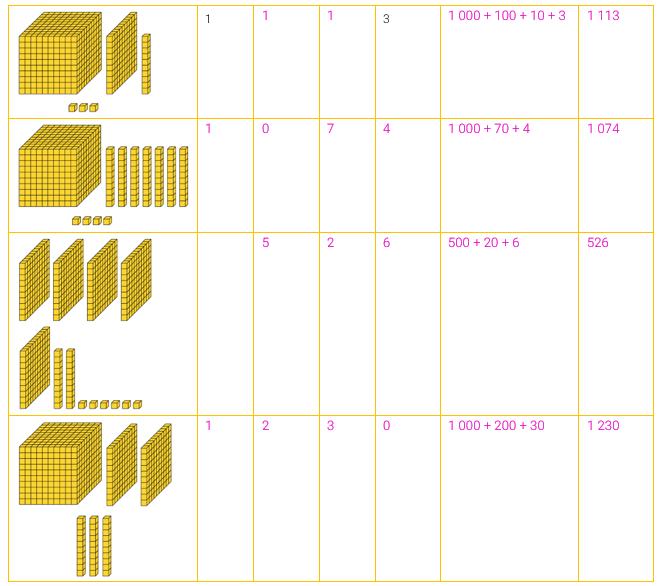
O objetivo desta aula é explorar o conhecimento dos alunos sobre números naturais até a 4ª ordem. Para isso, propor aos alunos o desafio "Em que número estou pensando?".

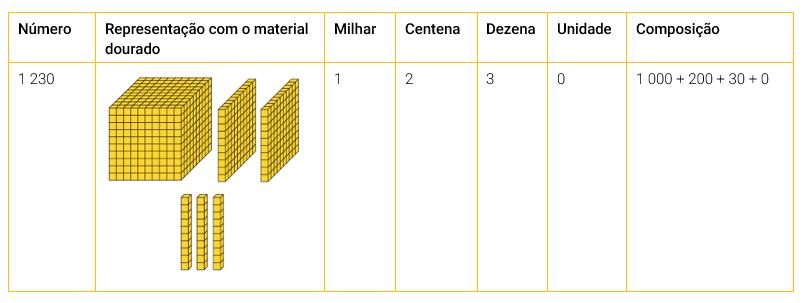
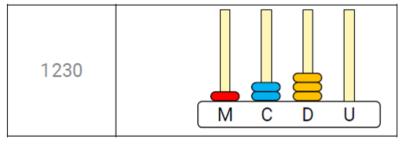
Organizar a turma em duplas e entregar a elas um quadro com informações a respeito de um número entre 1 100 e 1 300. Observar a seguir uma sugestão de organização desse quadro para o número 1 230.

Material disponibilizado em licença aberta do tipo Creative Commons

Após entregar o quadro para os alunos, destinar um tempo para que eles o observem. Explicar que cada dupla terá sua vez de ir à frente da turma, e que os demais alunos deverão utilizar seus conhecimentos para fazer perguntas com o objetivo de adivinhar o número do quadro que está com essa dupla. Explicar aos alunos qual será a ordem da dupla. Ressaltar que a dupla poderá responder apenas "sim" ou "não" para as perguntas.

Para ajudá-los a ampliar o repertório de perguntas, lembrar que devem usar todo o conhecimento que possuem – ordens, números pares e ímpares, representação por material dourado etc. Explicar que um número pode ser, conforme a sua posição em relação a outro número natural, antecessor ou sucessor dele. Por exemplo, 1 101 é sucessor de 1 100 e antecessor de 1 102. Caso seja conveniente, retomar outros conceitos ou dar dicas. Por exemplo, não há como ter qualquer valor diferente de 1 na 4ª ordem, pois o desafio foi pensado para números entre 1 100 e 1 300. Já para terceira ordem, podemos ter os algarismos 1, 2 ou 3.

A seguir, há algumas perguntas que se espera ouvir dos alunos no desafio, a fim de determinar com mais precisão o número escolhido.

• A representação do número no material dourado tem barra?

• O número tem unidade maior que 0?

• O número tem duas centenas?

• O algarismo na ordem das dezenas tem valor maior que 50?

Quanto mais precisas forem as perguntas, mais o professor saberá se o aluno compreendeu o conceito das ordens ou se ainda precisa desenvolver essa habilidade. Se julgar conveniente, apresentar outros exemplos além dos utilizados pelas duplas. Caso os alunos não consigam determinar a resposta, analisar com a turma o que faltou perguntar para se aproximarem mais da resposta certa e se foi utilizado o vocabulário matemático adequado.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

Aula 5

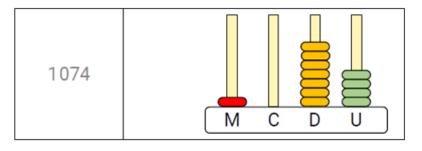
O objetivo desta aula é introduzir o ábaco como instrumento de representação do sistema de numeração decimal. O ábaco é um importante instrumento para que os alunos percebam com mais detalhes as ordens e o valor posicional de determinado número. Se o professor não dispuser de ábaco, ele pode ser feito, por exemplo, com palitos fincados lado a lado em um bloquinho de massa de modelar e contas de colar, que funcionarão como argolas de contagem.

Mostrar aos alunos a correspondência entre as representações de um número natural: com algarismos, com material dourado, com ábaco e escrito por extenso.

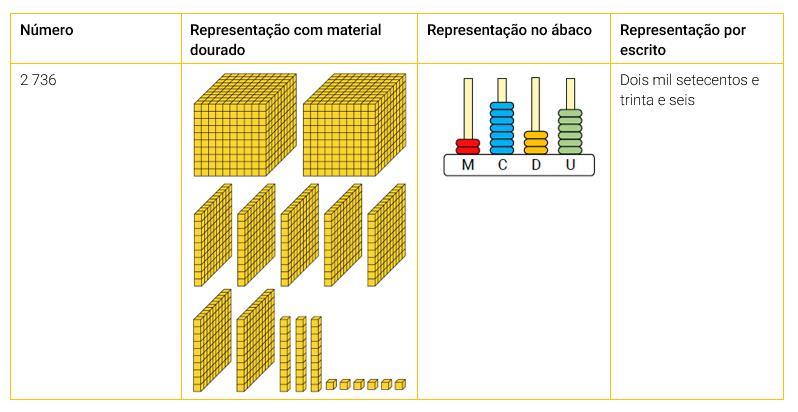EDITORIA DE ARTE

Verificar se os alunos compreendem que a leitura do número no ábaco contribui com a escrita desse número com algarismos e por extenso.

Se dispuser de ábacos suficientes, organizar a turma nas mesmas duplas do desafio da aula anterior. Em seguida, pedir às duplas que representem no ábaco os mesmos números utilizados por eles no desafio. Se não houver ábacos suficientes para distribuir, propor a eles que construam um, utilizando materiais alternativos, como palitos e massa de modelar.

Exemplos de representações no ábaco:

EDITORIA DE ARTE

Material disponibilizado em licença aberta do tipo Creative Commons

comercial

Atribuição não

(CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Ao final, solicitar que cada dupla apresente a disposição que realizou. Se necessário, realizar a correção.

Aula 6

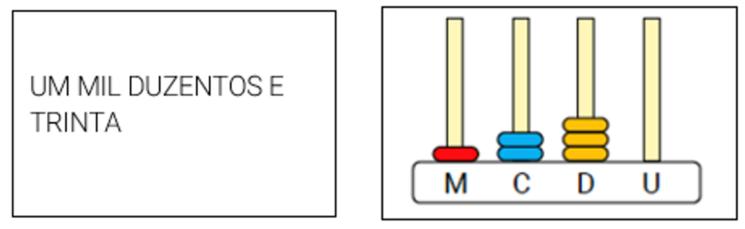
O objetivo desta aula é elaborar o Jogo da memória para exploração do ábaco. Para isso, organizar a turma em duplas e entregar um kitde 16 cartas em branco para cada dupla Em seguida, solicitar às duplas que organizem as cartas dos kitsem pares, de maneira a compor, em uma das cartas, um número de 1 000 a 5 000 por extenso, e, na outra, o desenho da representação desse número no ábaco. Observar a seguir um exemplo de par de cartas.

EDITORIA DE ARTE

Ao explicar a composição do jogo aos alunos, estabelecer algumas regras.

• Para os desenhos, deverão ser utilizados lápis de cor ou giz de cera.

• É importante que, nos desenhos, as peças utilizadas para unidade de milhar sejam vermelhas.

• De modo análogo, as peças utilizadas para centenas, dezenas e unidades deverão ser pintadas nas cores azul, amarela e verde, respectivamente.

Conforme os alunos produzirem os kits dos jogos, acompanhar as discussões e intervir, se necessário.

Aula 7

O objetivo desta aula é explorar o Jogo da memória do sistema de numeração decimal. Para isso, organizar a turma em duplas. Essas duplas não precisam, necessariamente, ser as mesmas da aula anterior.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas

Em seguida, entregar para cada dupla um kitde cartas e solicitar que embaralhem as cartas e as organizem em uma disposição retangular de 4 linhas por 4 colunas, de maneira que suas faces em branco estejam posicionadas para cima Nesse momento, comentar com os alunos que eles devem tomar cuidado com esse material, pois poderá ser utilizado em outra aula. Explicar, então, as regras do jogo.

Regras do jogo

• O Jogo da memória do sistema de numeração decimal relacionará cartas que representem um mesmo número de duas maneiras diferentes: escrita por extenso e com o ábaco.

• Cada integrante terá sua vez de jogar. Jogará primeiro o aluno que for mais novo.

• Cada integrante da dupla deverá, na sua vez, virar duas cartas e deixar que o outro integrante as veja.

• Se as cartas representarem um mesmo número, o participante da vez retirará o par de cartas da disposição. Os dois integrantes da dupla devem concordar que o par de cartas poderá ser retirado.

• Ganhará o participante que tiver a maior quantidade de cartas ao final da partida

• Os alunos que tiverem dúvidas se podem retirar os pares de cartas deverão pedir auxílio para esclarecê-las.

Após explicar as regras à turma, deixar que as duplas explorem o jogo. Ao final da aula, realizar uma breve discussão de maneira que os alunos manifestem suas impressões sobre o jogo.

Aula 8

O objetivo desta aula é relacionar três representações de um mesmo número: material dourado, escrita por extenso e ábaco. Para isso, organizar a turma, inicialmente, em grupos de 4 integrantes. Em seguida, entregar, para cada grupo, um ábaco e caixas com o material dourado, em quantidade suficiente para representar números naturais de 0 a 1 300.

Na sequência, pedir aos alunos que escolham e representem um número natural de 0 a 1 300, de três modos diferentes: no ábaco, pela escrita por extenso e no material dourado.

Solicitar que escrevam um relatório, também em grupos, mostrando o número que escolheram e comparando as três representações. Além disso, esse relatório deverá conter a resolução da atividade a seguir.

Sobre o número escolhido pelo grupo, resolvam os itens a seguir.

a) Qual é o seu sucessor?

b) Qual é o seu antecessor?

c)Ele é maior que 500?

d)Ele é menor que 1 253?

e)Realizem a decomposição desse número.

Ao final, realizar uma discussão em que os grupos mostrem, coletivamente, o número que escolheram e a atividade resolvida.

Sugestões

• MATERIAL dourado virtual. Atividade.Digital Disponível em: https://atividade.digital/ed/views/game_educativo.php?id=13&jogo=Material%20Dourad o%20Virtual. Acesso em: 11 jan. 2022.

Sequência didática 2: Figuras geométricas espaciais

Nesta sequência didática, serão estudadas e nomeadas as figuras geométricas espaciais, associadas a objetos do mundo físico, de modo que sejam reconhecidas características dessas figuras, relacionando-as com suas planificações e contornos.

Serão abordadas as semelhanças e as diferenças entre objetos no espaço, identificando figuras geométricas planas e não planas em descrições orais, construções e representações.

Objetivos de aprendizagem

• Classificar figuras como planas ou não planas.

• Descrever as figuras geométricas espaciais e relacioná-las com objetos do cotidiano.

• Associar, comparar e nomear as figuras geométricas espaciais: cubo, cilindro, cone, pirâmide, bloco retangular e esfera.

• Reconhecer figuras planas na superfície de figuras geométricas espaciais.

• Exercitar a visão geométrica tridimensional.

• Refletir sobre características de figuras geométricas espaciais.

Plano de aulas

Aula 1: Observar e desenhar representações de formas geométricas.

Aula 2: Desenhar contornos de embalagens, associar tais desenhos a figuras geométricas planas e explorar o conceito de planificação.

Aulas 3 e 4: Confeccionar o Jogo de dominó de figuras geométricas planas e espaciais.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Aula 5: Explorar o Jogo de dominó de figuras geométricas planas e espaciais.

Aula 6: Observar e classificar objetos que se parecem com figuras geométricas espaciais.

Aula 7: Explorar planificações de figuras geométricas espaciais.

Aula 8: Observar construções ou objetos e relacioná-los a figuras geométricas espaciais.

Componentes essenciais para a alfabetização: Produção de escrita e desenvolvimento de vocabulário.

Competências gerais da Educação Básica: 3 e 10.

Competências específicas de Matemática: 2 e 8.

Habilidades: EF03MA13 e EF03MA14.

Materiais necessários: Lápis de cor, jornais, revistas, folhas de papel sulfite, tinta guache, tesoura com pontas arredondadas, cola, embalagens de material reciclável de plástico e de papel, giz de cera, caderno, papel ou papelão, objetos do cotidiano que lembrem figuras geométricas espaciais (relógio de parede, lousa, mesa, gaveta, borracha, tubo de cola, lápis, copo etc.), embalagens de papelão com diferentes formatos (caixas de remédio, alimento, produtos de higiene e limpeza) e rolinhos de papelão (de papel higiênico, papel-toalha, filme de PVC) e malha quadriculada

Aula 1

O objetivo desta aula consiste em observar e desenhar representações de formas geométricas. Inicialmente, propor uma discussão perguntando aos alunos se é possível enxergar formas geométricas em elementos da natureza. Nesse momento, não tratar das figuras geométricas espaciais e das figuras geométricas planas pode ajudar a identificar conhecimentos que os alunos já possuem. Desafiá-los a olhar o formato dos objetos ao redor e observar que quase tudo pode ser associado a figuras geométricas, como cubos, cilindros, esferas, triângulos, retângulos etc. É importante que os próprios alunos comentem a respeito desses elementos.

Em seguida, explorar com os alunos os espaços da sala de aula e, posteriormente, os do restante da escola, chamando a atenção para as formas geométricas. Orientá-los a observar as paredes, as portas, as janelas, os objetos da sala de aula e do pátio da escola, além das formas da natureza, associando seus contornos às formas das figuras geométricas planas. Ressaltar que, nesse momento, os elementos identificados estão sendo associados a figuras geométricas planas.

Após essa exploração, solicitar aos alunos que, em uma folha de papel sulfite, façam desenhos das figuras geométricas planas que identificaram. Ao final, realizar uma discussão de maneira a organizar as representações de figuras geométricas planas em dois grupos:

• Figuras geométricas planas com contorno formado por linhas retas.

• Figuras geométricas planas com contorno formado por linhas curvas.

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

O objetivo desta aula é desenhar contornos de embalagens, associar tais desenhos a figuras geométricas planas e explorar o conceito de planificação. Para isso, trazer algumas embalagens vazias pequenas para que os alunos, em uma folha avulsa, façam o contorno dessas embalagens e de outros objetos pequenos disponíveis. Realizar com eles uma classificação das figuras planas obtidas com base nos contornos das embalagens.

Confeccionar um painel, orientando os alunos a organizarem as figuras representadas na folha avulsa, de acordo com a seguinte classificação: quadriláteros, triângulos, outros polígonos, circunferências e outras figuras com contornos formados por linhas curvas. Esse painel pode, também, ser organizado com uma classificação mais detalhada, na qual haja, por exemplo, quadrados, retângulos e losangos, além de outros quadriláteros.

Aproveitar a dinâmica para trabalhar o tema transversal meio ambiente e conversar com os alunos sobre a produção de lixo e o destino que se dá a ele. Comentar que trabalhar com essas embalagens em sala de aula permite que elas sejam utilizadas na aprendizagem, ressaltando que esse é o princípio da reciclagem. Problematizar que o descarte de resíduos sólidos é tema de discussão em cidades e a reciclagem surge como alternativa para diminuir o impacto ao meio ambiente. Enquanto os alunos realizam as atividades, circular pela sala de aula para acompanhá-los e orientá-los, quando necessário.

Para trabalhar a planificação de figuras geométricas espaciais (prismas retos, pirâmides, cilindros, cones), levar objetos que se parecem com essas figuras (embalagens vazias montadas, como caixas de papelão, chapéu de festa, latas, tubos cilíndricos com fundo e tampa). Inicialmente, pedir aos alunos que descrevam os objetos, procurando indicar se as linhas dos contornos são retas ou curvas, o número de partes planas e arredondadas na superfície, se há faces opostas etc. Para obter a representação da planificação de prismas e pirâmides, solicitar que, em uma folha avulsa, façam o contorno de cada parte da superfície, movendo o objeto sem levantá-lo do papel.

Comentar com os alunos que a planificação de objetos arredondados, como aqueles que se parecem com cones e cilindros, pode ser obtida por meio da técnica de carimbo com tinta guache sobre papel. Por exemplo, passar tinta na superfície e nas bases da embalagem (ou do objeto) de formato cilíndrico, fazê-lo deslizar sobre o papel e, depois, apoiar cada base, obtendo sua representação de planificação completa.

Aulas 3 e 4

O objetivo destas aulas é confeccionar um jogo de dominó sobre figuras geométricas espaciais e planas. Inicialmente, perguntar se eles já ouviram falar no Jogo de dominó Comentar que ele faz parte da cultura popular brasileira e que, ainda hoje, é muito praticado.

Em seguida, dizer aos alunos que, nestas aulas, eles confeccionarão um dominó das figuras geométricas planas e espaciais. Para isso, organizar a turma em duplas e distribuir, para cada dupla, 28 pedaços de cartão recortados do tamanho de peças de dominó (5 cm

de comprimento e 2,5 cm de largura, por exemplo), marcados ao meio com caneta, conforme o modelo a seguir EDITORIA

Instruir as duplas a construir o Jogo de dominó sobre figuras geométricas espaciais e planas como descrito a seguir.

• Em um dos lados da peça, deve ser colada a representação de uma figura geométrica plana ou a imagem de um objeto que se parece com uma figura geométrica espacial.

• Do outro lado de cada peça, deve ser escrito o nome de uma figura geométrica diferente da imagem que foi colada, conforme os exemplos a seguir. EDITORIA

Orientar os alunos a garantirem que as peças correspondentes sejam construídas. Por exemplo, se em uma das peças foi colada a figura de um triângulo, em outra peça deverá, necessariamente, estar escrita a palavra "triângulo". Sugerir que eles sigam esta ordem: cole a figura e, em seguida, componha a palavra correspondente em outra peça.

Se necessário, disponibilizar revistas ou jornais para os alunos recortarem as imagens. Para as representações de figuras planas, explicar que eles podem desenhá-las em outras folhas para recortar e colar. Se possível, solicitar (na aula anterior) que os próprios alunos coletem essas imagens em revistas ou na internet.

Garantir que todos os kitsde jogos estejam confeccionados para a próxima aula, para que possam ser explorados pela turma

Aula 5

O objetivo desta aula é explorar o Jogo de dominó das figuras geométricas planas e espaciais. Para isso, organizar a turma em duplas. Não há necessidade de que sejam as mesmas duplas organizadas na aula anterior, pois todas receberão um kitde jogo.

Com as duplas organizadas, distribuir os kits arbitrariamente para cada dupla e realizar a leitura das regras do jogo.

Regras do jogo

• Organizar todas as peças em um mesmo grupo, de maneira que sua face sem desenhos, colagens ou nomes de figuras esteja posicionada para cima.

• Cada jogador deverá resgatar 7 cartas desse grupo. As cartas que sobrarem ficam organizadas em um "monte"

• Cada jogo durará, no máximo, 10 minutos.

• A dupla jogará " par ou ímpar" para decidir quem começará o jogo

• O aluno que começará o jogo deverá selecionar uma das 7 peças que possui, posicionando-a sobre a mesa.

• O adversário deverá selecionar uma de suas peças, de maneira que uma de suas extremidades corresponda a uma das extremidades da peça que deu início ao jogo. Em seguida, ele deverá posicionar a peça escolhida de modo que as extremidades correspondentes fiquem, exatamente, uma do lado da outra, como na imagem a seguir.

• A cada jogada, a fileira aumentará

• Caso os adversários não tenham as peças necessárias para jogar, eles poderão retirar uma peça do monte até que tenham a peça desejada

• O primeiro jogador que não tiver mais peças vencerá o jogo

• Caso nenhum jogador tenha vencido até os primeiros 10 minutos, aquele que tiver menos peças ganhará o jogo.

Após a explicação das regras, solicitar às duplas que comecem o jogo. Conforme elas terminarem o jogo, reorganizar a turma variando os competidores. Para evitar desorganização, deixar os jogos fixos nas mesas e solicitar que um dos integrantes da dupla troque de lugar com um integrante de outra dupla. Ao final, realizar uma discussão com os alunos, a fim de refletirem sobre suas experiências com o dominó das figuras geométricas planas e espaciais.

Aula 6

O objetivo desta aula é observar e classificar objetos que se parecem com figuras geométricas espaciais. Para isso, solicitar previamente que os alunos tragam de casa caixas usadas ou descartadas de tamanhos e formatos diferentes – de remédio, alimento, produtos

Material disponibilizado em licença aberta do tipo Creative Commons

de higiene e de limpeza, sapatos etc. – e rolinhos de papelão (de papel higiênico, papel-toalha, filme de PVC).

Organizar a turma em roda e colocar, no centro dela, esse material para ser manuseado pelos alunos. Instigá-los a relacionar esses objetos com seu uso em casa, na escola ou em outros lugares que conhecem e, ainda, a se recordarem de alimentos e objetos cuja forma se pareça com um sólido geométrico (casquinha de sorvete; tablete de manteiga; bastão de cola; lápis sem estar apontado, cilíndrico ou sextavado). Reunir as características de cada objeto, questionando os alunos com perguntas como: quais desses objetos podem rolar com facilidade? Quais não podem rolar com facilidade? Por que eles não rolam com facilidade? Com quais figuras geométricas espaciais eles se parecem?

Após observarem os objetos, os alunos devem agrupar os que têm formato parecido. Para que não compreendam erroneamente o conceito de figura geométrica espacial, esclarecer que uma embalagem, ou os outros objetos que trouxeram, apenas se parecem com o formato de uma figura geométrica espacial.

Em seguida, organizar a turma em grupos de acordo com os formatos identificados, isto é, um grupo com cilindros, um com cubos, outro com cones etc. Os grupos vão registrar, em uma folha avulsa todas as descobertas sobre a figura geométrica estudada e as representarão com desenhos. Estipular o tempo para fazer o registro e propor uma discussão, de maneira que os alunos apresentem as descobertas à turma.

Os objetos e os materiais escritos deverão ser utilizados na próxima aula.

Ao final, solicitar que cada grupo tente, sem desmontar a caixa, fazer o desenho de como seria a embalagem aberta.

Aula 7

O objetivo desta aula é explorar planificações de figuras geométricas espaciais. Para isso, organizar a turma nos mesmos grupos estabelecidos na aula anterior. Em seguida, fazer uma breve discussão, problematizando os desenhos produzidos pelos grupos, em que tentaram registrar a representação de uma embalagem aberta (que se parece com uma figura geométrica espacial), sem desmontá-la.

Após essa retomada inicial, entregar novamente as embalagens específicas de cada grupo. Perguntar a eles se, alguma vez, já abriram uma embalagem de creme dental, por exemplo, desdobrando-a pelas emendas. Deixar que a turma comente a respeito do tema e perguntar o que descobriram com essa experiência.

Posteriormente, propor um desafio aos alunos: abrir cuidadosamente as emendas das embalagens que estão com eles e desdobrá-las para desenhá-las abertas

ou seja, planificá-las

em uma malha quadriculada, mantendo a proporção das faces. Fazer como no exemplo a seguir, que representa uma embalagem que, quando fechada, parece um bloco retangular

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Pedir aos alunos que marquem com giz de cera ou lápis de cor as dobras das caixas abertas e as reproduzam nos desenhos. Com isso, eles perceberão claramente as figuras geométricas planas que compõem a superfície do sólido geométrico. Nesse momento, eles devem manifestar o que acharam das descobertas. Complementar as ideias que surgirem durante essa troca de informações, dando novas explicações. Solicitar, então, que recortem os desenhos pelas bordas da figura, façam as dobras e montem sua representação de sólido.

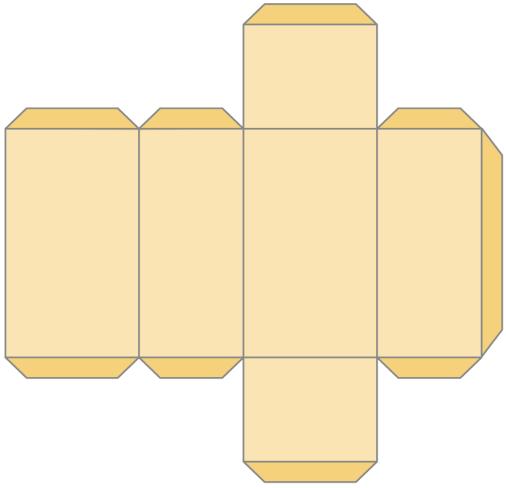
Em seguida, realizar o trabalho inverso, o de remontagem das embalagens que foram abertas. Essa é uma maneira de levar os alunos a perceberem que as figuras descritas como quadrado, retângulo, triângulo ou círculo são as partes que compõem um todo. Por exemplo, eles podem notar que com seis retângulos, ou quatro retângulos e dois quadrados, se monta a superfície de um bloco retangular, e, com uma base quadrada e quatro triângulos idênticos, monta-se a superfície de uma pirâmide. Recolher as embalagens abertas pela turma e redistribuí-las entre os grupos, de maneira que não recebam as que planificaram. Depois, solicitar que as remontem, fechando-as com cola e decorando-as como preferirem.

Deixar o material exposto na sala de aula e pedir aos alunos que o avaliem.

Aula 8

O objetivo desta aula é observar prédios ou objetos e relacioná-los a figuras geométricas espaciais. Para isso, disponibilizar imagens de prédios ou objetos cujo formato se pareça com figuras geométricas espaciais. Instigar os alunos, por meio dessas imagens, a observarem prédios históricos como Torre de Pisa (Itália), Museu de Arte de São Paulo (Masp), Catedral de Maringá, Elevador Lacerda de Salvador, Museu de Arte Contemporânea de Niterói, entre outros

Numerar as imagens levadas para que os alunos possam referir-se a elas pelo número. É importante que as imagens tenham legenda, com nome e localização. Se julgar conveniente, colocá-las na parede da sala de aula para que todos as vejam; do contrário,

dividir a turma em grupos e entregar a cada grupo poucas imagens – duas ou três

, numeradas sequencialmente.

Pedir que observem com atenção as imagens e anotem no caderno com quais figuras geométricas espaciais elas se parecem. Explicar que nem tudo se parece com um sólido geométrico perfeito, de faces polidas.

Em seguida, discutir com a turma os elementos identificados. Propor uma discussão, ressaltando que a maioria dos prédios ou objetos parece ter embutida figuras geométricas espaciais modificadas. Por exemplo, na imagem do Museu de Arte de São Paulo, o formato do prédio sugere um bloco retangular, ou paralelepípedo, mas sua fachada dianteira é cortada por barras e vidros longos, formando as janelas, algo que não acontece em um sólido geométrico com essas características. As colunas e a viga de sustentação, que passa por cima do conjunto, parecem blocos retangulares emendados, mas com uma das faces proporcionalmente mais fina que as do corpo principal do prédio.

No Elevador Lacerda, em Salvador, notam-se também estruturas que remetem a blocos retangulares nas torres dos elevadores e a outros blocos nos terraços e na passarela. A Torre de Pisa, sem dúvida, se parece com um cilindro, ainda que entrecortado em cada andar por pilares também cilíndricos e arcos, que remetem a outra figura geométrica, um círculo cortado ou semicírculo. Já a edificação principal (central) da catedral de Maringá se parece com um cone.

Comentar com os alunos que as figuras geométricas espaciais modificadas não representam defeitos. Muitas vezes, elas representam expressões artísticas e culturais ou movimentos específicos da arquitetura. É importante analisar com a turma as imagens, descrevendo características do contexto delas.

Perguntar aos alunos se conseguem mexer nessas figuras geométricas espaciais identificadas do mesmo modo que manusearam as caixas e outros objetos na aula anterior. Espera-se que respondam que não, e é até provável que alguém diga que não dá para mexer no que está em uma fotografia. Se não expressarem essa ideia, comentar com os alunos que identificaram figuras geométricas espaciais em fotografias, que, na verdade, elas são planas, ou seja, têm duas dimensões. Nesse momento, questioná-los, de maneira que percebam que as fotografias criam uma sensação de realidade porque captam luz e sombra, dando volume e profundidade ao que é retratado. Portanto, os prédios e os objetos observados realmente se parecem com figuras geométricas espaciais, embora estejam reproduzidas em um objeto plano, o papel fotográfico, que em si lembra um retângulo ou um quadrado.

Sugestões

• BRASIL. Ministério da Educação e Cultura. Dominós Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/EnsMed/expensmat_iicap4.pdf. Acesso em: 11 jan. 2022

Sequência didática 3: Adição e subtração

Nesta sequência didática, os alunos resolverão diversas situações-problema que envolvem as principais ideias da adição com o objetivo de identificar a operação envolvida, explorar a criação de estratégias pessoais de cálculo, reforçar o uso do símbolo da adição (+) e contribuir para a construção de um repertório básico de cálculo mental.

Além disso, serão trabalhadas as ideias básicas da subtração por meio de situações-problema, para a constituição de estratégias a serem utilizadas no cálculo escrito e mental. Também, serão abordadas questões referentes à decomposição, à leitura, à escrita e à resolução de problemas.

Objetivos de aprendizagem

• Sistematizar as ideias de acrescentar e juntar da adição.

• Identificar as situações em que se usa a adição.

• Sistematizar conhecimentos acerca da adição.

• Desenvolver o raciocínio lógico e a concentração.

• Utilizar fatos fundamentais no cálculo mental.

• Resolver situações-problema que envolvam a adição.

• Realizar operações de subtração utilizando o material dourado.

• Ler e interpretar enunciados de problemas matemáticos.

• Compreender a relação existente entre a pergunta e o restante do texto do enunciado de um problema.

• Resolver situações-problema de subtração com números naturais.

• Usar diferentes estratégias de cálculo mental relacionadas à subtração.

Plano de aulas

Aula 1: Explorar diferentes estratégias para a resolução de situações-problema envolvendo o conceito de adição.

Aula 2: Estabelecer e comparar diferentes estratégias para a resolução de situações-problema envolvendo o conceito de adição.

Aula 3: Utilizar recursos e materiais manipuláveis para explorar o conceito de adição.

Aula 4: Utilizar o material dourado para discutir o conceito de adição.

Aula 5: Introduzir a discussão a respeito das ideias da subtração.

Aula 6: Discutir o conceito de subtração com o auxílio do material dourado.

Aula 7: Elaborar problemas com as ideias da subtração.

Aula 8: Realizar uma competição colaborativa envolvendo os conceitos de adição e de subtração

Componentes essenciais para a alfabetização: Produção de escrita e compreensão de textos.

Competências gerais da Educação Básica: 2, 6 e 10.

Competências específicas de Matemática: 2 e 8.

Habilidades: EF03MA05 e EF03MA06.

Materiais necessários: Lápis, borracha, palitos de sorvete, elásticos de borracha, quadro da adição impresso para cada aluno, folha impressa com atividades propostas e material dourado

Aula 1

O objetivo desta aula é explorar diferentes estratégias para a resolução de situações-problema envolvendo o conceito de adição. Inicialmente, realizar uma discussão de maneira que os próprios alunos apresentem o que entendem por adição, e que as ideias de acrescentar e de juntar sejam mobilizadas e associadas à adição. Em seguida, a fim de observar se os alunos conseguem calcular algumas adições mentalmente, propor perguntas como as sugeridas a seguir

• Quanto é 2 + 6?

• Quanto é 5 + 4?

• Quanto é 7 + 10?

• Quanto é 6 + 6?

Em seguida, organizar os alunos em grupos e solicitar que resolvam a atividade a seguir

• Vocês já ouviram falar em catadores de materiais recicláveis? São pessoas que trabalham coletando materiais recicláveis em ruas, residências, restaurantes, bares, cafeterias, entre outros estabelecimentos. O trabalho dos catadores é muito importante, porque promove a reciclagem e ajuda na proteção ao meio ambiente. Ao final do dia, o gerente de uma lanchonete separa todas as latinhas de alumínio utilizadas pelos seus clientes para destiná-las a um catador de materiais recicláveis. Em determinado dia, no período da manhã, foram utilizadas, nessa lanchonete, 13 latinhas de alumínio. Já no período da tarde, foram utilizadas 17 latinhas. Ao todo, quantas latinhas de alumínio foram destinadas ao catador de materiais recicláveis?

Em um primeiro momento, ler o enunciado e esclarecer eventuais dúvidas dos alunos Se julgar conveniente, realizar uma discussão a respeito da importância da reciclagem para a sociedade. O sitedisponível na seção Sugestões trata de mais informações a respeito dos catadores de materiais recicláveis e sua importância.

Solicitar aos alunos que resolvam esta atividade em grupo. Durante a resolução, acompanhar as discussões e realizar as intervenções que julgar necessárias. Nesse momento, selecionar as diferentes estratégias utilizadas pelos alunos e solicitar que as apresentem na lousa. Eles podem utilizar várias estratégias, como desenho, contagem pelos dedos, realização de decomposições, utilização do Quadro de ordens etc. É importante,

nesse momento, mostrar essas diferentes estratégias e validá-las. Além disso, é essencial relacionar essas estratégias à ideia de adição.

Caso ainda tenha tempo disponível na aula, propor outros problemas, similares ao apresentado, para que os alunos os resolvam utilizando as estratégias que preferirem. Nesse caso, sempre que possível, promover o compartilhamento das resoluções, corrigindo o que for necessário.

Aula 2

O objetivo desta aula é estabelecer e comparar diferentes estratégias para a resolução de situações-problema envolvendo o conceito de adição. Para isso, organizar a turma em duplas e propor a seguinte situação.

• Durante um passeio ao parque florestal, Leonardo, Gabriel e Larissa souberam que, uma semana antes, foram plantados ali 43 jabuticabeiras e 25 abacateiros. Decidiram, então, que, ao chegarem em casa, calculariam quantas árvores foram plantadas e compartilhariam o resultado.

No dia seguinte, ao se encontrarem na escola, os três alunos mostraram como fizeram esse cálculo. Observe e confira se estão corretos.

Fazer a leitura com os alunos. Pedir que imaginem a situação-problema e encontrem, também, uma solução. Durante a execução da atividade, caminhar pela sala de aula observando os procedimentos utilizados pelas duplas. Após a resolução do problema, socializar na lousa todos os procedimentos utilizados pelos alunos, perguntando:

• Como a dupla se organizou para resolver o problema?

• Que operação foi utilizada?

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

• Quais foram as dificuldades encontradas para resolver a atividade?

Após a socialização das estratégias, realizar a parte seguinte da atividade coletivamente. Orientar os alunos a explorarem os procedimentos utilizados pelas três crianças na resolução do problema e pedir que comentem as estratégias, comparando com os procedimentos utilizados pela sua dupla. Em seguida, questionar:

1. Como Leonardo resolveu o problema?

Espera-se que os alunos respondam que pela decomposição do número em dezenas e unidades, adição de dezena com dezena e unidade com unidade para, ao final, compor o número com a dezena e a unidade calculadas anteriormente.

2. A estratégia de Gabriel é parecida com a de Leonardo? Por quê?

Espera-se que os alunos respondam que sim. Somente o processo de montagem da sentença é diferente.

3. Como Larissa procedeu para determinar a solução?

Espera-se que os alunos respondam que Larissa escreveu a sentença de adição organizando o cálculo da adição sem a necessidade de decomposição dos números.

4. Os procedimentos usados estão corretos? Os resultados estão corretos?

Sim, os procedimentos estão corretos, assim como os resultados.

5. Qual das estratégias você considera mais prática?

Resposta pessoal.

Explicar que todos os procedimentos estão corretos, mas explorar com atenção a resolução de Larissa, pois essa estratégia antecede o algoritmo convencional da adição.

Transcrever na lousa a situação-problema a seguir e pedir aos alunos que escolham um dos procedimentos utilizados pelas crianças na atividade anterior para resolvê-la

• Para reflorestar uma área de Mata Atlântica foram plantadas 36 mudas de araribás-amarelos e 22 mudas de embaúbas-vermelhas. Quantas mudas de árvores foram plantadas?

A estratégia utilizada é uma resposta pessoal e o resultado é 58 árvores.

Circular pela sala de aula observando os procedimentos utilizados pelos alunos. Em seguida, escolher duplas que utilizaram procedimentos diferentes e pedir que os socializem com a turma, justificando suas escolhas.

Aula 3

O objetivo desta aula é utilizar recursos e materiais manipuláveis para explorar o conceito de adição. Para isso, disponibilizar aos alunos 20 palitos de sorvete e um elástico. Colocar 8 palitos de sorvete na mesa e mostrá-los aos alunos. Em seguida, realizar uma discussão coletiva, apresentando a seguinte situação-problema

1. Eu coloquei 8 palitos de sorvete na mesa. Se eu adicionar 7 palitos a eles, quantos palitos terei na mesa? Expliquem como vocês fizeram.

Espera-se que os alunos respondam que, quando adicionamos, primeiro completamos uma dezena adicionando 2 palitos aos 8 iniciais. Então, adicionamos o que restou; nesse caso, adicionamos os outros 5 palitos. Como resultado, temos 10 palitos de sorvete mais 5, que totalizam 15 palitos.

Observar as hipóteses apresentadas pelos alunos. Se necessário, registrá-las na lousa. Em seguida, mostrar a operação de adição com os palitos de sorvete nas mãos. Quando aumentar os 8 palitos para 10, prendê-los com um elástico. Esse momento é importante para que a turma produza significados para a ideia de dezena. Mostrar que há um grupo de 10 e um de 5 palitos separados em suas mãos. Lembrar aos alunos que, no número 15, o algarismo 1 representa que há 1 dezena e o algarismo 5 representa que há 5 unidades.

Escrever na lousa a expressão que representa a situação:

8 + 7 = 8 + 2 + 5 = 10 + 5 = 15

Em seguida, entregar para cada aluno o quadro a seguir, impresso em folha de papel sulfite.

Posteriormente, explicar o seguinte procedimento para a realização da atividade.

• Esse quadro apresenta algumas operações de adição com números naturais no intervalo de 0 a 15. Cada célula desse quadro contém a soma que está na junção da parcela da primeira linha com a parcela da primeira coluna correspondentes.

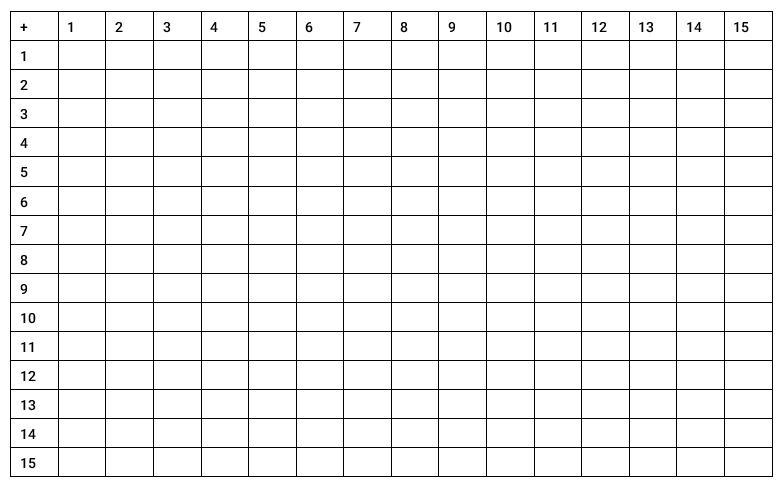
Pedir aos alunos que preencham o quadro que receberam e, enquanto estiverem trabalhando, preparar na lousa parte do quadro (por exemplo, o intervalo de 1 a 5). Depois que eles terminarem, preencher o quadro na lousa com eles, corrigindo item a item.

Ao terminar a correção, realizar uma discussão com os alunos e observar se eles acertaram a atividade. Perguntar se gostaram de preencher o quadro. Comentar que quadros, esquemas e tabelas correspondem a maneiras de representar e organizar ideias matemáticas.

Chamar a atenção dos alunos para o fato de existirem alguns padrões no quadro. Mostrar um deles e solicitar que tentem identificar mais alguns. Seguem algumas sugestões de padrões.

• Ao mover-se de uma célula para a imediatamente à direita ou abaixo, o número aumenta uma unidade.

• Ao mover-se na diagonal, passando de uma célula àquela imediatamente abaixo à direita, os números aumentam em duas unidades e, para cima à esquerda, os números diminuem em duas unidades.

• Ao mover-se na diagonal de uma célula para aquela imediatamente acima à direita ou abaixo à esquerda, os números permanecem os mesmos.

Aula 4

O objetivo desta aula é utilizar o material dourado para discutir o conceito de adição. Para isso, inicialmente, recordar com os alunos as diferenças entre unidade, dezena e centena utilizando as próprias peças do material dourado.

Em seguida, organizar a turma em grupos, entregar peças do material dourado para eles e apresentar situações para que resolvam com o suporte desse recurso.

1. Caio e Henrique colecionam selos. Caio tem 25 selos e Henrique tem 33. Quantos selos os dois possuem ao todo?

58 selos.

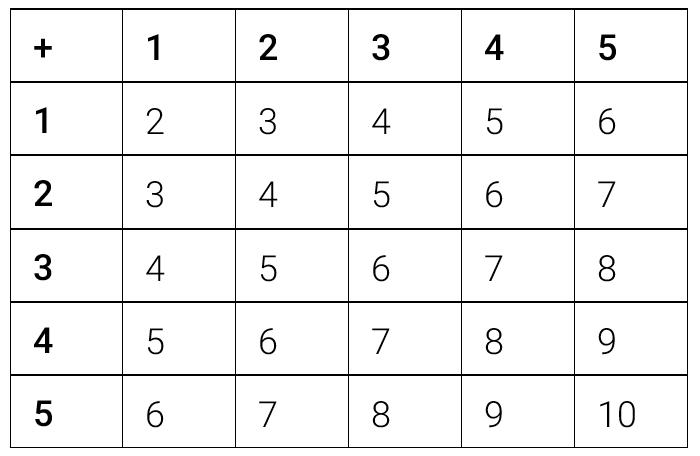
2. Débora foi à padaria comprar pães para uma festa de aniversário. Comprou 50 pães para fazer cachorro-quente e 45 pães doces. Quantos pães Débora comprou ao todo?

95 pães.

3. Na sala de aula de Flávia há 16 meninas e 13 meninos. Quantos alunos há na sala?

29 alunos.

4. Vivian e Vinícius juntaram suas mesadas para comprar livros de histórias. Vinícius tinha 27 reais e Vivian, 13 reais. Quantos reais os dois tinham ao todo para comprar os livros?

40 reais.

5. Luciana percorre 75 metros para ir de sua casa à padaria mais próxima. Quantos metros ela percorre no total para ir e voltar por esse caminho?

150 metros.

Ao final da aula, corrigir essas situações-problema coletivamente, mostrando como elas poderiam ser resolvidas com o uso do material dourado. Nesse momento, é essencial comparar as possíveis estratégias. Por exemplo, na resolução da situação-problema 3, poderíamos juntar 16 cubinhos com 13 cubinhos, totalizando 29 cubinhos ou poderíamos juntar 1 barra e 6 cubinhos com 1 barra e 3 cubinhos, totalizando 2 barras e 9 cubinhos.

Aula 5

O objetivo desta aula é introduzir a discussão a respeito da subtração. Para isso, inicialmente, realizar uma discussão de maneira que os próprios alunos apresentem o que entendem por subtração. Em seguida, propor algumas perguntas, observando se os alunos conseguem realizar subtrações mentalmente:

• Quanto é 6 – 2?

• Quanto é 5 – 4?

• Quanto é 10 – 7?

• Quanto é 6 – 6?

Após o trabalho com cálculos mentais, entregar a cada aluno uma folha avulsa para registro ou pedir que usem o caderno. Explicar aos alunos que, após ditar um número, deverão sempre subtrair 1 desse número e registrar o resultado do cálculo. Ditar um número de cada vez e esperar que registrem os resultados dos cálculos. Organizar a turma em duplas e solicitar que comparem suas resoluções.

Em seguida, solicitar às duplas que acrescentem 1 para todos os resultados encontrados e escrevam uma conclusão. Espera-se que os alunos escrevam que o novo resultado corresponde ao número ditado pelo professor.

Ao final, realizar uma discussão geral, permitindo que as duplas manifestem as conclusões a que chegaram, no sentido de evidenciar que o novo resultado corresponde ao

número ditado pelo professor. Ao final, ampliar a discussão, sistematizando que ao subtrair 1 dos números ditados, estamos obtendo os antecessores desses números. Por fim, apresentar alguns números para que os alunos determinem seus respectivos antecessores.

Aula 6

O objetivo desta aula é discutir o conceito de subtração com o auxílio do material dourado. Para isso, organizar a turma em grupos de três ou quatro alunos e distribuir o material dourado. Ressaltar que esse material também pode ser utilizado para compreender as operações de subtração. Comentar que, ao se fazer a subtração utilizando o material dourado, pode-se primeiro subtrair as placas, depois as barras e, então, os cubinhos Nesse momento, apresentar à turma uma operação em que o minuendo é formado por dois algarismos e o subtraendo por um algarismo, não sendo necessário o reagrupamento. Por exemplo: 18 – 5.

Solicitar aos alunos que façam os cálculos utilizando o material dourado e registrem a operação no caderno. Em seguida, apresentar outra operação de subtração em que não sejam necessários reagrupamentos, como o exemplo a seguir: 375 – 234.

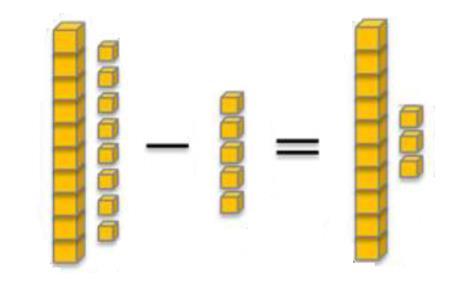
Comentar que, nesse caso, retiram-se 2 placas (2 centenas), 3 barras (3 centenas) e 4 cubinhos (4 unidades):

EDITORIA DE ARTE

EDITORIA DE ARTE

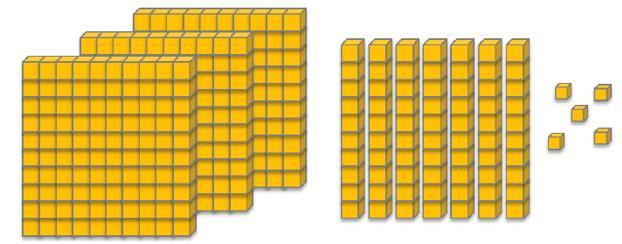
Observar as resoluções dos alunos e apresentar uma operação de subtração, agora com a necessidade de algum reagrupamento. Exemplo: 457 – 273.

Pedir aos alunos que representem com o material dourado o número 457

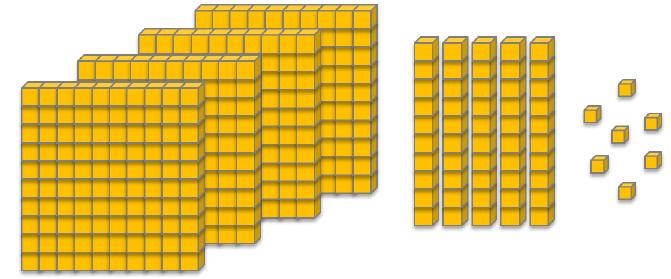
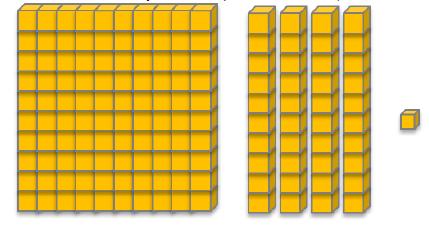
Depois de mostrar aos alunos que não é possível retirar, nesse contexto, 7 dezenas de 5 dezenas, explicar que é preciso decompor 1 centena em 10 dezenas, que serão acrescentadas às 5 dezenas que se tinha anteriormente. Assim, eles devem trocar 1 placa por 10 barras:

EDITORIA DE ARTE

Em seguida, orientar os alunos a retirarem 2 placas (2 centenas), 7 barras (7 dezenas) e 3 cubinhos (3 unidades), o que resulta em:

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais,

desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

EDITORIA DE ARTE

Espera-se que os alunos compreendam o sistema de numeração decimal de base 10, no qual 1 dezena equivale a 10 unidades, 1 centena equivale a 10 dezenas e assim por diante. Isso permite, por exemplo, "desagrupar" 1 centena e representá-la por meio de 10 dezenas e, consequentemente, "desagrupar" 1 dezena e representá-la por meio de 10 unidades. Se julgar conveniente, fixar um quadro posicional com fita adesiva colorida e fichas, indicando as centenas (C), as dezenas (D) e as unidades (U), na mesa dos alunos.

Aula 7

O objetivo desta aula é elaborar situações-problema com as ideias da subtração. Para isso, organizar a turma em grupos de três alunos e escrever na lousa a seguinte operação: 24 – 11 = 13

Em seguida, pedir aos grupos que formulem uma situação-problema para a operação indicada. Disponibilizar o material dourado para os alunos recorrerem a ele se desejarem. É importante incentivar a criatividade da turma na elaboração da situação-problema, comentando que é possível relacionar situações reais a essa operação. Aproveitar essa oportunidade para apresentar o seguinte exemplo, salientando que essa ideia não poderá ser aproveitada para a resolução da tarefa.

Pedro ganhou 24 figurinhas para colar no álbum, mas 11 delas eram repetidas. Quantas figurinhas puderam ser coladas?

Após a resolução, solicitar que socializem na lousa os diferentes procedimentos utilizados para criar e resolver a situação-problema, e questionar a turma sobre:

• Como pensaram para criar a situação-problema?

• Partiram da operação apresentada?

• Quais foram as dificuldades encontradas?

Após a resolução da operação pelos alunos, organizá-los individualmente e apresentar a seguinte proposta de atividade.

• O professor do 3º ano distribuiu várias subtrações e pediu aos alunos que formulassem situações-problema que pudessem ser resolvidas com essas operações. Pediu, também, que apresentassem o cálculo do jeito que soubessem.

Escrever na lousa as operações e solicitar que formulem, no caderno, situações-problema a partir das operações, bem como os cálculos com resultados.

a) 26 – 15

b) 55 – 40

c) 64 – 37

d) 82 – 69

a) 11; b) 15; c) 27; d) 13

Os alunos devem determinar os dados das situações-problema a partir das operações, tomando consciência dos elementos que os constituem e da relação que deve existir entre os dados. Ressaltar que, para formular o enunciado, eles precisam ter conhecimentos sobre as estruturas dos textos e sobre as partes que os compõem. Circular pela sala de aula observando os alunos e interferindo quando perceber que há dificuldades. Assim que terminarem a atividade, perguntar:

• Qual operação é contemplada em cada item?

• Quais foram os números utilizados para a elaboração da situação-problema?

• A operação é a mesma em todas as situações-problema elaboradas?

• O resultado é o mesmo?

Escolher algumas situações-problema elaboradas pelos alunos e pedir que socializem e expliquem como elas foram elaboradas. O objetivo é que a turma compreenda que uma mesma operação (e o mesmo resultado) pode gerar diferentes textos para a situação-problema.

Aula 8

O objetivo desta aula é realizar uma competição colaborativa envolvendo os conceitos de adição e de subtração. Para isso, organizar a turma em dois grupos e entregar a cada grupo uma folha avulsa com as adivinhas, a seguir, impressas.

• Francisco e seus amigos estavam brincando de adivinhar números. Veja se você consegue adivinhar alguns, sem usar lápis, papel e calculadora.

a) Pensei em um número, somei 20 e o resultado foi 70. Em qual número pensei?

b) Pensei em um número, somei 200 e o resultado foi 700. Em qual número pensei?

c) Pensei em um número, tirei 70 e o resultado foi 50. Em qual número pensei?

d)Pensei em um número, somei 400 e o resultado foi 800. Em qual número pensei?

400

e)Pensei em um número, tirei 600 e o resultado foi 300. Em qual número pensei?

900

Inicialmente, realizar a leitura das questões. Em seguida, explicar aos alunos as regras da competição. Comentar que a brincadeira consiste em um grupo ler a adivinha em voz alta e o outro responder; a cada duas questões, trocam-se os papéis. Se um grupo tiver dificuldade, o outro pode ajudar. O professor deve possuir o gabarito em mãos para validar se o grupo acertou ou errou. Se o grupo acertar a resposta, ele ganha 2 pontos. Se errar, não ganha pontos e o grupo adversário (que fez a leitura) ganha os dois pontos. Ao final, o grupo que tiver maior pontuação vence a competição.

Ao final, realizar uma discussão com a turma e verificar se os alunos percebem a seguinte regularidade:

• se 20 + 50 = 70, então 200 + 500 = 700; se há "um zero a mais" em cada parcela, o resultado também tem "um zero a mais"

Caso não percebam, explicar aos alunos a regularidade apresentando outros exemplos na lousa.

Repetir esta atividade usando outros números e incorporando-a à rotina.

Sugestões

• BRASIL. Ministério do Meio Ambiente. Coleta Seletiva. Disponível em: https://antigo.mma.gov.br/cidades-sustentaveis/residuos-solidos/catadores-demateriais-reciclaveis/reciclagem-e-reaproveitamento.html. Acesso em: 11 jan. 2022.

Sequência didática 4: Figuras geométricas planas

Nesta sequência didática serão trabalhadas, por meio de atividades que possibilitam a participação, a visualização, a investigação e a criatividade dos alunos, as figuras geométricas planas (triângulo, quadrado, retângulo, círculo, trapézio e paralelogramo), explorando suas características e reconhecendo algumas de suas propriedades, o que possibilitará aos alunos desenvolverem o pensamento geométrico.

Objetivos de aprendizagem

• Comparar e identificar figuras geométricas planas analisando características do seu contorno.

• Reconhecer, comparar e associar figuras geométricas planas às peças do tangram.

• Comparar e identificar figuras geométricas planas analisando suas características (lado e vértice).

• Compor figuras geométricas com peças do tangram

Plano de aulas

Aula 1: Explorar o reconhecimento de figuras geométricas planas em uma atividade lúdica.

Aulas 2 e 3: Explorar com os alunos o tangrame comparar suas peças a figuras geométricas planas.

Aula 4: Explorar as peças do tangrame suas relações com as figuras geométricas planas

Aulas 5 e 6: Sistematizar características de figuras geométricas planas e construir essas figuras utilizando um softwarede Geometria dinâmica.

Aulas 7 e 8: Retomar o que aprenderam sobre figuras geométricas planas ao explorar o material manipulativo blocos lógicos

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita Competências gerais da Educação Básica: 2 e 3.

Competências específicas de Matemática: 2 e 8.

Habilidade: EF03MA15.

Materiais necessários: Folha de papel sulfite, papel-cartão, tesoura com pontas arredondadas, tangram , blocos lógicos, lápis de cor

Aula 1

O objetivo desta aula é explorar o reconhecimento de figuras geométricas planas em uma atividade lúdica.

Inicialmente, perguntar aos alunos se conhecem a brincadeira Dança das cadeiras Realizar uma discussão, explorando o que os alunos sabem a respeito dela. Verificar se eles conhecem as regras e, se necessário, explicá-las à turma.

Em seguida, propor a brincadeira Dança das figuras e comentar com os alunos que, nessa adaptação da Dança das cadeiras, nenhum aluno sairá durante as rodadas

Levar os alunos para um espaço da escola no qual a brincadeira pode ser realizada com segurança, por exemplo, o pátio. Depois, com giz escolar, desenhar no chão as seguintes figuras geométricas planas: retângulos, quadrados, triângulos e círculos. Desenhar uma quantidade de figuras igual à quantidade de alunos.

Ao som de uma música bem animada, propor aos alunos que dancem livremente, movimentando-se em todas as direções, explorando todo o espaço. Explicar que, ao interromper a música, todos devem "entrar" em uma das representações das figuras geométricas planas desenhadas no chão e, depois, falar o nome dessa figura e algumas de suas características. Por exemplo, se possuem apenas linhas retas em seu contorno, se possuem apenas linhas curvas em seu contorno, se possuem todos os lados de mesmo comprimento etc.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Caso algum aluno tenha dificuldade em citar as características dessas figuras, sugere-se fazer perguntas como: todas essas figuras possuem linhas retas em seus contornos? Quem está em uma figura apenas com linhas retas em seu contorno? Quem está em uma figura apenas com linhas curvas em seu contorno? Quem está em uma figura que tem todos os lados de mesmo comprimento? Aproveitar esse momento para verificar os conhecimentos prévios dos alunos.

Realizar algumas rodadas desta brincadeira e sugerir aos alunos que "entrem" em figuras diferentes a cada rodada. Após finalizar a Dança das figuras, promover uma roda de conversa e propor aos alunos que compartilhem com os colegas suas percepções sobre esta brincadeira. Para isso, sugere-se realizar as perguntas a seguir:

• Como foi para vocês participarem da brincadeira? Como se sentiram?

• Do que mais gostaram? Do que não gostaram?

• Como se perceberam brincando: mais colaborativos ou mais competitivos?

• Qual foi a maior dificuldade que encontraram na brincadeira?

Aproveitar o momento para conversar com os alunos sobre a importância de cooperar com os colegas e de solucionar conflitos de forma respeitosa.

Aulas 2 e 3

O objetivo destas aulas é explorar com os alunos o tangrame comparar suas peças a figuras geométricas planas. Iniciar com uma roda de conversa para verificar o que os alunos conhecem sobre otangram. Para isso, sugere-se fazer as seguintes perguntas: vocês conhecem o tangram? Já brincaram com ele? Acharam interessante?

Após essa discussão, organizar a turma em grupos de três ou quatro integrantes e entregar jogos de tangrampara cada grupo. Se necessário, confeccionar jogos de tangram com EVA. Deixar os alunos explorarem as peças livremente e, em seguida, contar um pouco sobre a lenda da criação do tangram , um quebra-cabeça de origem chinesa muito antigo, constituído por sete peças com os seguintes formatos: cinco triângulos, um quadrado e um paralelogramo. Explicar que esse quebra-cabeça tem como objetivo desafiar o jogador a montar diferentes figuras usando as sete peças.

Em seguida, ainda em grupos, propor que confeccionem umtangramutilizando folhas de papel sulfite ou papel-cartão. Entregar a cada grupo uma folha de papel sulfite ou papel-cartão, uma tesoura de pontas arredondadas e lápis de cor. Explicar que devem confeccionar o tangramfazendo diferentes dobraduras e orientá-los com o passo a passo a seguir, com o auxílio de um retroprojetor. Caso não seja possível utilizar o retroprojetor, reproduzir as orientações na lousa ou imprimir e entregá-las aos grupos. Ao final, os alunos podem colorir as peças do tangramconfeccionadas.

Acompanhar os grupos durante a atividade e verificar se estão fazendo corretamente as dobraduras; se necessário, auxiliá-los. Ao identificar uma dificuldade comum a grande parte da turma, propor aos alunos que façam uma pausa para sanar a dúvida.

• Passo 1: Obter uma figura de quadrado na folha de papel sulfite retangular com as seguintes dobras e recortes

EDITORIA DE ARTE

• Passo 2: Dobrar a folha quadrada ao meio e recortá-la para obter as figuras A e B.

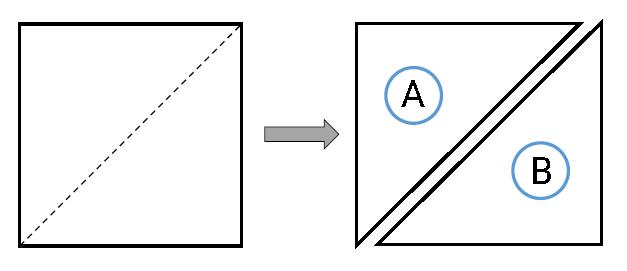
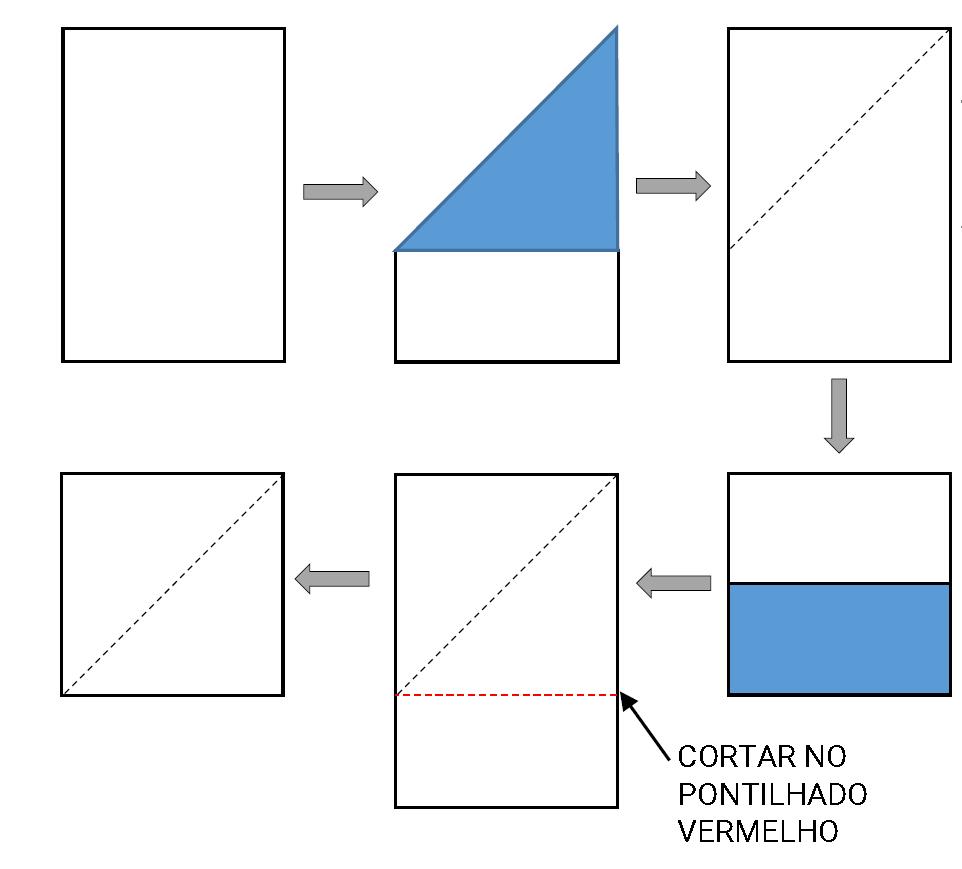
EDITORIA DE ARTE

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

• Passo 3: Dividir a figura do triângulo A em duas para obter os triângulos C e D

EDITORIA DE ARTE

• Passo 4: Na figura do triângulo B, marcar o meio do lado maior, dobrar o vértice oposto até essa marca e recortá-lo para obter o triângulo E e o trapézio F

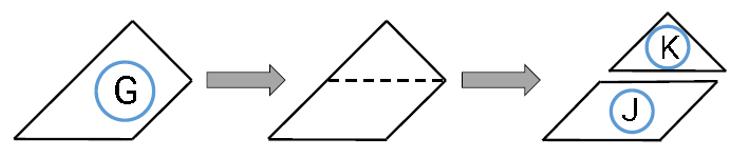
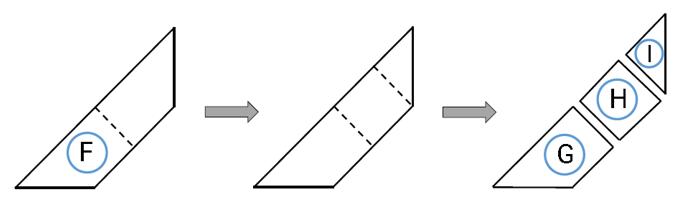
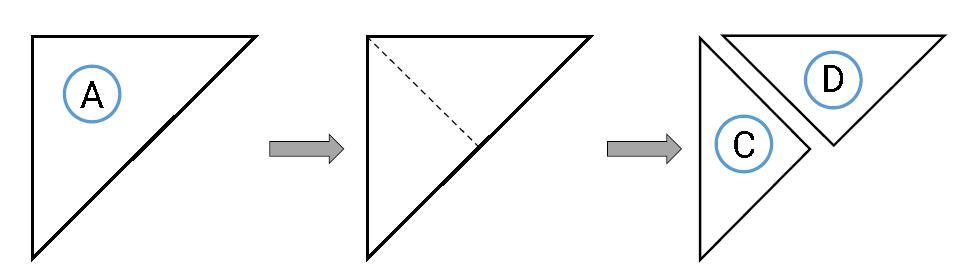
EDITORIA DE ARTE

• Passo 5: Dobrar a figura do trapézio ao meio, marcar e dobrar uma das pontas para dentro, fazendo outra marca. Recortar nas marcas para obter o trapézio G, o quadrado H e o triângulo I

EDITORIA DE ARTE

• Passo 6: Dobrar a figura do trapézio G e recortá-la para obter o paralelogramo J e o triângulo K.

EDITORIA DE ARTE

• Passo 7: Juntar as peças representadas a seguir para formar o tangram

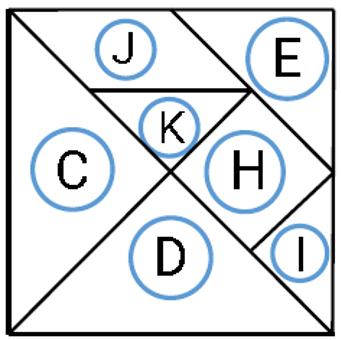
Ao final, perguntar aos alunos quais figuras geométricas planas são representadas nas peças do tangram. Espera-se que respondam triângulos, quadrados e paralelogramo.

Aula 4

Nesta aula, os alunos continuarão a explorar as peças do tangrame suas relações com as figuras geométricas planas. Propor aos grupos que construam, com as peças do tangramconfeccionadas nas aulas 2 e 3, figuras geométricas planas.

Em um primeiro momento, propor a todos os grupos que construam um triângulo e, depois, comparem os triângulos construídos com os dos colegas. Espera-se que percebam que é possível representar uma mesma figura com diferentes peças do tangram. Sugere-se fazer essa mesma atividade de construção e comparação das figuras para o quadrado, o retângulo, o trapézio e o paralelogramo.

Acompanhar os alunos durante a atividade e incentivá-los a observar as características das peças do tangram , identificando as diferenças e o que há em comum entre elas. Por exemplo, o triângulo possui três lados e o quadrado possui quatro lados, o retângulo e o quadrado possuem quatro lados

Para ampliar a atividade, propor aos alunos que construam outras figuras, por exemplo, animais (coelho, gato), objetos (barco, casa) e pessoas. Incentivá-los a utilizar a criatividade. Se for oportuno, apresentar aos alunos algumas silhuetas para que eles as utilizem como modelo. Na seção Sugestões, indicamos um siteno qual é possível encontrar a imagem de diferentes silhuetas.

Aulas 5 e 6

O objetivo destas aulas é sistematizar características de figuras geométricas planas, retomando as peças do tangram , e construir essas figuras utilizando um software de

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Geometria dinâmica Para iniciar a aula, mostrar um tangramaos alunos e perguntar a eles quais figuras geométricas planas formam esse quebra-cabeça. Espera-se que respondam triângulos, quadrados e paralelogramos.

Para começar o trabalho com as figuras geométricas planas, desenhar o triângulo representado a seguir na lousa e perguntar aos alunos: quais são as características do triângulo? Deixar que expressem seus conhecimentos Aproveitar o momento para sistematizar as características desta figura na lousa.

Triângulo

• Figura geométrica plana.

• Contorno formado apenas por linhas retas.

• Possui 3 lados.

• As medidas dos seus lados não necessariamente precisam ser iguais.

• Para construir um triângulo, podemos marcar três pontos, não alinhados, ligá-los por linhas retas e pintar o interior da figura.

Em seguida, desenhar o quadrado representado a seguir na lousa e perguntar aos alunos: quais são as características de um quadrado? Deixar que eles expressem seus conhecimentos Aproveitar o momento para sistematizar as características desta figura na lousa.

Quadrado

EDITORIA DE ARTE

• Figura geométrica plana.

• Assim como o triângulo, possui seu contorno formado apenas por linhas retas.

• Diferentemente do triângulo, o quadrado necessariamente possui 4 lados de mesma medida.

• Possui 4 vértices.

Desenhar na lousa a última figura geométrica plana destacada no tangram : o paralelogramo. Perguntar aos alunos: quais são as características desta figura geométrica plana? Deixar que expressem seus conhecimentos e sistematizar as características desta figura na lousa.

Paralelogramo EDITORIA

• O paralelogramo, também, possui seu contorno formado por linhas retas.

• Assim como o quadrado, o paralelogramo possui 4 lados.

• O paralelogramo, também, possui 4 vértices.

• Os 4 lados do paralelogramo não precisam, necessariamente, ter uma mesma medida. Porém, seus lados opostos devem, necessariamente, ter medidas iguais.

Em seguida, comentar que, embora o trapézio, o retângulo e o círculo não estejam representados no tangram , eles são figuras geométricas planas que serão exploradas na aula. Perguntar aos alunos: quais são as características dessas figuras geométricas planas? Depois, sistematizar as características na lousa.

Trapézio

EDITORIA DE ARTE

• Figura geométrica plana.

• Possui contorno formado por linhas retas.

• Assim como o paralelogramo, o trapézio possui 4 lados.

• Possui 4 vértices.

• 2 lados do trapézio precisam, necessariamente, ser paralelos.

Retângulo

EDITORIA DE ARTE

• Figura geométrica plana.

• Possui contorno formado apenas por linhas retas.

• Possui 4 lados, que não necessariamente precisam ter uma mesma medida. Porém, necessariamente, seus lados opostos devem ter medidas iguais.

Círculo

EDITORIA DE ARTE

• Figura geométrica plana.

• Possui contorno formado por linha curva.

• Para representar um círculo, pode-se utilizar uma moeda, contorná-la com um lápis e pintar o interior da figura.

Após explorar as características das figuras geométricas planas com a turma, propor a construção das figuras estudadas utilizando o software de Geometria dinâmica, o GeoGebra. Para isso, organizar a turma em duplas e levá-la à sala de informática da escola Para conhecer o GeoGebra, ler o tutorial indicado na seção Sugestões

Aulas 7 e 8

Nestas aulas, os alunos vão retomar o que aprenderam sobre figuras geométricas planas ao explorar o material manipulativo blocos lógicos e participar de um jogo utilizando esse material. Para isso, providenciar com antecedência alguns kitsde blocos lógicos para serem entregues a eles

Organizar a turma em grupos com três integrantes e entregar um kitde blocos lógicos para cada grupo. Deixar que eles manipulem livremente o material e, em seguida, propor que organizem as peças em grupos, de maneira que todas as peças de um grupo tenham alguma característica em comum. Os alunos podem organizar de acordo com as figuras geométricas planas (círculos, quadrados, triângulos e retângulos), com as cores (azuis, amarelas e vermelhas), com os tamanhos (grande e pequeno) e com as espessuras (fino ou grosso).

Caso nenhum grupo tenha organizado de acordo com as figuras geométricas planas, propor a eles que agrupem as peças do bloco lógico (círculos, quadrados, triângulos e

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

retângulos) utilizando seus conhecimentos sobre figuras geométricas planas. Ao final, pedir que compartilhem com os colegas como pensaram.

Em um segundo momento, propor à turma o jogo Desafio dos blocos lógicos e explicar as regras desse jogo. Se necessário, escrever as regras a seguir na lousa, para que os alunos leiam sempre que tiverem dúvidas.

Regras do jogo Desafio dos blocos lógicos

• Cada grupo terá sua vez de jogar. Essa ordem é estabelecida por sorteio realizado pelo professor.

• Em sua vez, cada grupo deverá escolher, sem que os outros vejam, uma peça dos blocos lógicos. Em seguida, deverá dizer ao professor qual peça escolheu. Um grupo não pode ver a peça escolhida pelo outro.

• Após escolhida a peça, o grupo da vez vai à frente da sala. Os outros grupos deverão fazer uma pergunta sobre a peça escolhida para adivinhá-la. As perguntas devem estar relacionadas com as características das figuras geométricas planas Sugestões de perguntas: a peça é formada apenas por linhas retas? A peça é formada apenas por linhas curvas? A peça tem quantos lados? Quantos vértices tem a peça? Todos os lados da peça têm a mesma medida de comprimento? A peça tem apenas dois lados com a mesma medida de comprimento?

• Os integrantes do grupo da vez, com o auxílio do professor, deverão responder apenas "sim" ou "não" para as perguntas.

• O grupo que adivinhar a peça escolhida ganhará a pontuação da rodada. Cada rodada vale 10 pontos.

Quando a turma compreender as regras, iniciar o jogo. Ao final da aula, perguntar aos alunos o que acharam do jogo: se gostaram, se acharam divertido, entre outras

Sugestões

• TANGRAM Chinês (Qí qiao ban). Espaço Ciência Viva, c2022. Disponível em:

http://cienciaviva.org.br/index.php/2019/07/07/tangram-chines-qiqiao-ban/. Acesso em: 11 jan. 2022

• TANGRAM. Racha Cuca, c2006-2022. Disponível em: https://rachacuca.com.br/raciocinio/tangram/. Acesso em: 11 jan. 2022.

• SIQUEIRA, Ruan de Freitasetal Tutorial para GeoGebra. Grupo PET-Tele/UFF, Rio de Janeiro, out. 2017. Disponível em:

http://www.telecom.uff.br/pet/petws/downloads/tutoriais/geogebra/Tutorial_GeoGebra. Acesso em: 7 jan. 2022.

Sequência didática 5: Multiplicação

Nesta sequência didática, os alunos resolverão problemas de multiplicação com o objetivo de levá-los a compreender a multiplicação como uma adição de parcelas iguais. Também, serão abordadas as multiplicações por 2, 3, 4, 5 e 10, explorando diferentes estratégias de cálculo.

Objetivos de aprendizagem

• Reconhecer a multiplicação como adição de parcelas iguais.

• Utilizar a multiplicação para realizar cálculos de quantidade de objetos dispostos em configuração retangular (linhas e colunas).

• Trabalhar com multiplicações por 2, 3, 4, 5 e 10.

• Utilizar cálculo mental como estratégia de resolução de problemas.

• Compreender a aplicação da multiplicação de dois fatores.

• Calcular multiplicações com os números 2, 3, 4, 5, 6, 7, 8, 9 e 10 utilizando diferentes estratégias de cálculos.

• Realizar multiplicações utilizando cálculo mental.

Plano de aulas

Aula 1: Confeccionar cartas para um jogo sobre multiplicação.

Aula 2: Explorar a multiplicação com o suporte de material manipulativo.

Aula 3: Ampliar a discussão sobre multiplicação, iniciada nas aulas anteriores.

Aula 4: Explorar um jogo de multiplicação.

Aula 5: Explorar um jogo de multiplicação e ampliar a ideia de multiplicação com base na elaboração de problemas.

Aula 6: Confeccionar o jogo Bingo da multiplicação.

Aula 7: Explorar o jogo Bingo da multiplicação.

Aula 8: Introduzir o contato dos alunos com a multiplicação por meio de números naturais maiores que 10.

Componentes essenciais para a alfabetização: Produção de escrita, desenvolvimento de vocabulário e compreensão de textos.

Competências gerais da Educação Básica: 2 e 9

Competências específicas de Matemática: 2, 6 e 8

Habilidades: EF03MA03 e EF03MA07.

Materiais necessários: Folha de papel sulfite, cartolina, lápis, caneta, tesoura com pontas arredondadas, régua, material dourado e lápis de cor

Aula 1

O objetivo desta aula é confeccionar as cartas para um desafio sobre multiplicação. Iniciar a aula organizando a turma em grupos com quatro alunos. É importante ter uma quantidade par de grupos. Portanto, modificar a quantidade de integrantes de cada grupo, se for necessário. Entregar cartolina, lápis, caneta, régua e tesoura com pontas arredondadas para que os alunos confeccionem cartas numeradas de acordo com as seguintes regras.

Regras para a confecção das cartas

Cada grupo confeccionará 15 cartas. As cartas deverão ser retangulares, com dimensões de 8 cm por 6 cm. Inicialmente, os alunos deverão desenhar as cartas na cartolina e, em seguida, recortá-las. Depois de recortadas, os alunos deverão escrever números, em cada uma das cartas, de acordo com a seguinte distribuição:

• uma carta com o número 1;

• duas cartas com o número 2;

• duas cartas com o número 3;

• duas cartas com o número 4;

• duas cartas com o número 5;

• uma carta com o número 6;

• uma carta com o número 7;

• uma carta com o número 8;

• uma carta com o número 9;

• duas cartas com o número 10.

Comentar com os alunos que as cartas deverão ser utilizadas na próxima aula. Recolher as cartas, identificadas por grupo, e guardá-las para a aula seguinte.

Aula 2

O objetivo desta aula é explorar a multiplicação com o suporte de material manipulativo. Para isso, inicialmente, organizar os alunos nos mesmos grupos definidos na aula anterior (grupo menor). Em seguida, agrupar de dois em dois grupos e formar equipes maiores (grupo maior). Depois, separar os kitsde cartas confeccionados na aula anterior e entregar um deles para cada grupo maior. Nesta aula, não serão usados todos os kits confeccionados, porém deve-se guardar todos, pois serão utilizados em uma aula posterior. Entregar, também, para cada grupo maior, cubinhos do material dourado. Caso não haja cubinhos, substituí-los por outras peças, como tampinhas de garrafa, clipes, botões etc.

Pedir que cada grupo maior reorganize o kit de cartas em dois conjuntos, A e B, conforme a distribuição a seguir.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Neste momento, comentar com os alunos que os conjuntos A e B serão dados, respectivamente, aos grupos menores. Esses grupos devem dispor as cartas, com o número voltado para baixo, sobre uma mesa, e embaralhá-las.

Cada grupo menor deverá escolher uma das cartas e mostrá-la a todos do grupo maior. Dessa forma, em cada rodada, dois números serão sorteados. Nesse momento, comentar com os alunos que os números sorteados deverão ser utilizados para compor fileiras com os cubinhos do material dourado. Por exemplo, se no conjunto A foi sorteada a carta de número 5, e, no conjunto B, a de número 4, podemos ter como resposta 5 fileiras com 4 cubinhos em cada uma. Os grupos menores podem entender fileira como coluna ou como linha. Portanto, a disposição pode ser diferente. Deixar que a montagem seja livre.

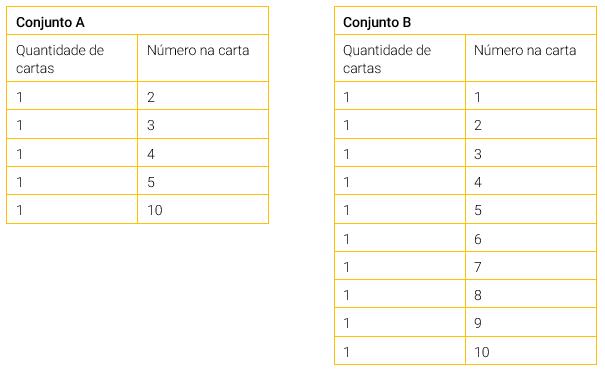
Depois que os grupos tiverem concluído as montagens, pedir que contem quantos cubinhos usaram para chegar ao resultado. Comentar que os alunos devem registrar de que maneira realizaram esse cálculo.

Em seguida, reorganizar os alunos em uma roda de conversa e propor uma discussão geral, perguntando quais foram as estratégias que utilizaram para contar todos os cubinhos. Nesse momento, diversas estratégias devem surgir, como contar fileiras e efetuar uma adição, multiplicar o número de cubinhos de cada fileira pela quantidade de fileiras, contar cubinho por cubinho etc.

Após os alunos apresentarem suas estratégias, fazer uma comparação entre as estratégias que foram mais rápidas e as mais demoradas. É importante que eles percebam que não há método certo ou errado, e, sim, métodos que podem ser considerados mais práticos.

Aula 3

O objetivo desta aula é ampliar a discussão sobre a multiplicação, iniciada nas aulas anteriores. Com isso, realizar um debate inicial de maneira que os alunos tenham a oportunidade de manifestar suas impressões sobre o trabalho com o material manipulativo. Alguns questionamentos são importantes nesse momento, como:

• O que vocês acharam da atividade?

• Como foi realizar uma atividade que vocês mesmos construíram?

• Quais foram as dificuldades que vocês tiveram com esta atividade?

Além disso, nesse debate inicial, fazer outros questionamentos, de maneira a explorar essas dificuldades. Por exemplo:

• Por que as cartas foram divididas em dois conjuntos?

• Por que decidiram dispor e contar os cubinhos de determinada maneira, se havia outro modo que pudesse tornar o cálculo mais prático?

Após essa discussão, organizar os alunos em grupos e propor a seguinte atividade.

Em uma quarta-feira, determinada escola realizou uma encomenda de vários produtos em uma loja. Para realizar a entrega desses produtos, o entregador deverá fazer 5 viagens da loja até a escola e, em cada uma, ele transportará 4 caixas de produtos. Ao todo, quantas caixas de produtos serão entregues à escola?

Assim que os alunos estiverem organizados em grupos, entregar cubinhos do material dourado para cada equipe. Em seguida, pedir que representem com as peças o número de viagens e o número de caixas de produtos em cada viagem. Levá-los a concluir que o raciocínio por trás dessa nova atividade é análogo ao utilizado com a atividade do sorteio das cartas: 5 viagens na escola, com 4 caixas de produtos em cada (5 × 4).

Por fim, questionar se os alunos conhecem alguma situação parecida, em que a multiplicação contribuiria para a determinação da quantidade total de objetos, elementos ou pessoas. Espera-se que comentem a respeito da disposição dos próprios alunos em fileiras na sala de aula ou em outras situações vivenciadas no dia a dia deles. Promover um momento para que os alunos compartilhem entre si essas experiências.

Aula 4

O objetivo desta aula é explorar um jogo de multiplicação. Para isso, serão utilizadas todas as cartas feitas na primeira aula desta sequência didática. Então, solicitar que os alunos se organizem nos mesmos grupos que confeccionaram as cartas e entregar-lhes os kitscorrespondentes.

Cada grupo deve separar as cartas da mesma maneira que nas aulas anteriores, formando os conjuntos de cartas A e B.

Após os alunos organizarem as cartas, mostrar-lhes as regras do jogo.

Regras do jogo

• Dispor as cartas sobre uma mesa, com o número voltado para baixo, e embaralhá-las.

• Cada aluno do grupo terá sua vez de jogar, que será estabelecida de acordo com a ordem alfabética.

• O aluno da vez sorteará uma carta de cada conjunto e a mostrará aos colegas do grupo.

• Esse mesmo aluno terá 30 segundos para determinar o resultado da multiplicação.

• Terminado o prazo, se o aluno acertar o resultado, ele ganhará 2 pontos. Se errar, todos os seus adversários ganharão 1 ponto. Os resultados poderão ser conferidos, ao final da rodada, com uma calculadora, que poderá ser utilizada apenas na etapa de conferência.

• Vencerá o aluno que fizer mais pontos ao final de uma quantidade estabelecida de rodadas.

Caso haja empate entre os alunos, fazer uma rodada de desempate, aumentando a dificuldade – por exemplo, reduzindo o tempo para resolver o cálculo.

Como nessa faixa etária os alunos ainda não estão acostumados com marcação de tempo no relógio, pode-se cronometrar o tempo para todos os grupos. Para tanto, é importante que todos comecem a jogar no mesmo momento. Isso ajudará, inclusive, no controle da turma.

Após a finalização do jogo, realizar uma discussão com os alunos, a fim de que comentem suas experiências. É provável que eles apontem que uma mesma operação tenha

aparecido mais de uma vez, com os fatores na mesma posição ou invertidos, por exemplo, 2 × 5 = 10 e 5 × 2 = 10. Se julgar que os alunos estão prontos para isto, chamar a atenção deles para esse fato – será uma abordagem inicial da propriedade comutativa da multiplicação.

Nesta aula, o ideal é que os alunos já tenham adquirido a habilidade da multiplicação sem o auxílio do material manipulável. Dessa forma, é fundamental avaliar as estratégias empregadas por eles nessa etapa.

Diferentemente da primeira aula, nesta aula, os alunos organizarão o jogo e trabalharão os cálculos individualmente. Assim, é possível observar como eles se comportam, se seguem a ordem de retirada das cartas, se fazem todas as anotações corretamente etc.

Aula 5

O objetivo desta aula é trabalhar o resultado de algumas multiplicações por meio do jogo Dominó. Para isso, organizar a turma em duplas e distribuir, para cada dupla, 28 peças relacionadas a seguir. Se julgar oportuno, criar outras peças, variando os kitsentre os alunos.

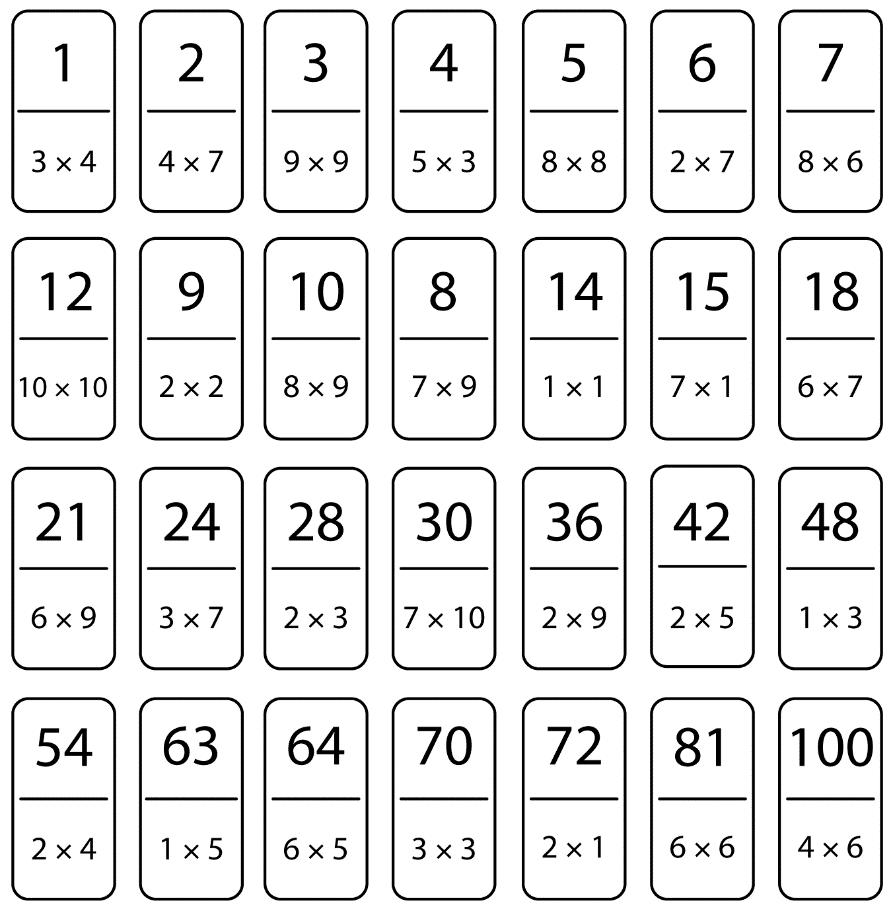
Representação de dominó da multiplicação.

Assim que as duplas estiverem organizadas e cada uma dispondo de seu kitde peças, realizar a leitura das regras do jogo.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Regras do jogo

• Dispor todas as peças sobre a mesa de modo que a face sem números esteja posicionada para cima.

• Cada jogador da dupla retirará 14 peças; isto é, o número de peças do jogo Dominó será dividido igualmente entre a dupla.

• A dupla jogará par ou ímpar para decidir quem começa.

• O aluno que começar o jogo deverá selecionar uma das 14 peças que possui, posicionando-a sobre a mesa.

• O adversário posicionará uma de suas peças, de maneira que uma de suas extremidades corresponda, com um número ou uma operação, a uma das extremidades da peça que deu início ao jogo, como no exemplo a seguir, em que 2 x 4 corresponde a 8:

Representação de peças do dominó da multiplicação.

• Caso o jogador da vez não tenha peça para posicionar, ele passará a vez para o adversário.

• Vencerá o jogador que primeiro conseguir colocar todas as peças no jogo

Após explicar as regras aos alunos, deixar que iniciem o jogo Conforme as duplas forem terminando os jogos, reorganizar os alunos, a fim de variar os competidores. Para evitar desorganização, deixar os jogos fixos nas mesas e solicitar que um dos integrantes da dupla troque de lugar com um integrante de outra dupla.

Para finalizar, com os alunos em dupla, pedir que cada uma indique uma operação de multiplicação que não esteja presente nas peças, por exemplo, 3 x 9. Em seguida, solicitar que cada dupla elabore uma situação-problema que envolva a operação que indicaram O objetivo desta atividade é ampliar a ideia da multiplicação por meio da elaboração de problemas.

Depois de elaborados os problemas, cada dupla deverá escrever o seu, sem solução, em uma folha avulsa. Em seguida, trocar entre as duplas os problemas elaborados para que os alunos resolvam os problemas recebidos.

Ao final, as resoluções realizadas pelos alunos deverão ser entregues às duplas que elaboraram os problemas. Cada dupla deverá avaliar as resoluções dos colegas, comparando com as resoluções iniciais registradas no caderno. Por fim, cada dupla deverá

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

atribuir uma nota de 0 a 10 para a resolução dos colegas, explicando como determinaram essa pontuação. Todos os problemas elaborados e as respectivas soluções corretas podem ser fixados em um mural na sala de aula para consultas.

Aula 6

O objetivo desta aula é confeccionar o jogo bingo da multiplicação. Iniciar a aula organizando a turma em duplas ou grupos com, no máximo, quatro alunos e explicar que, nesta aula, será construído um jogo que envolve multiplicação. Entregar cartolina, lápis, caneta, régua, lápis de cor e tesoura com pontas arredondadas para os alunos.

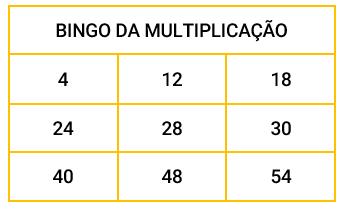
Para iniciar, pedir que confeccionem cartelas com os resultados das tabuadas de dois números diferentes (de 1 a 10). Por exemplo, a tabuada do número 4 e a do número 6. Explicar que essas cartelas serão usadas para o jogo Bingo da multiplicação. É importante que, primeiro, os alunos escrevam a tabuada dos números escolhidos e, depois, confeccionem as cartelas.

Ao escrever a tabuada dos números escolhidos, os alunos poderão utilizar diferentes estratégias para obter os resultados. Aproveitar para perguntar quais métodos utilizaram e pedir que façam comparações entre os métodos, indicando quais acharam mais eficazes. Conversar com eles sobre o fato de que não existe uma única maneira de realizar os cálculos. Alguns métodos podem ser considerados mais práticos que outros, ficando a critério de cada um utilizar o que julgar melhor. Feito isso, é hora de produzir as cartelas do jogo.

Explicar que cada cartela será formada por 9 números, que devem constar na tabuada dos dois números escolhidos. Solicitar aos alunos que coloquem os números em ordem crescente na cartela. Caso os números não estejam nessa ordem, isso não vai interferir no resultado do jogo; é apenas uma questão de organização. Porém, ao fazer isso, os alunos terão a oportunidade de mobilizar outras habilidades.

As cartelas podem ser retangulares com dimensões de 8 cm × 8 cm. Cada dupla/grupo deve ficar responsável pela confecção de uma cartela. Exemplo de cartela com números da tabuada do 4 e do 6:

EDITORIA DE ARTE

Representação de cartela de bingo da multiplicação.

Pedir às duplas ou aos grupos que confeccionem as fichas que serão usadas no sorteio do bingo. Devem ser confeccionadas fichas com a tabuada dos números escolhidos

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

e que tenham como resultado os números utilizados na cartela feita pelo grupo. Exemplo de ficha:

A avaliação deve ser constante em todo o processo de construção do jogo. Observar os métodos utilizados para realizar as multiplicações, o modo como dividiram as tarefas e a interação que tiveram não só no grupo, mas com os colegas de modo geral.

É importante verificar como os alunos escolheram as duas tabuadas que serão utilizadas e como definiram os números que constarão na cartela. Observar se todos os alunos estão participando de cada etapa e se estão conscientes de todas as instruções.

Caso alguma dupla ou algum grupo apresente dificuldade na elaboração das cartelas, auxiliar com ideias para que eles compreendam como devem construí-las. Os alunos podem escolher o método para fazer as multiplicações. Mas, se mesmo com essa flexibilidade eles tiverem dúvidas, retomar algumas estratégias de multiplicação.

É importante circular pela sala de aula e, ao observar que alguma dupla ou grupo está com dificuldade, ajudar os alunos por meio de questionamentos que os levem a refletir sobre a questão. É interessante ajudá-los a sanar as dúvidas, mas sem resolvê-las de imediato.

Aula 7

O objetivo desta aula é explorar o jogo Bingo da multiplicação. Para isso, retomar com os alunos o que foi construído na aula anterior, pedindo às duplas ou aos grupos que se juntem novamente para dar continuidade ao trabalho que estavam desenvolvendo. Distribuir as cartelas aos alunos e explicar como será o jogo. Todos devem estar atentos às regras para evitar contratempos. Explicar-lhes que será sorteada uma multiplicação e que cada dupla ou grupo deverá escrever a multiplicação no caderno, realizar os cálculos mentalmente, anotar o produto e verificar se há esse número na sua cartela. Se houver, marcar o quadradinho correspondente a esse número com lápis ou lápis de cor, para identificar que aquele número é o resultado de uma multiplicação que já foi sorteada. Ao fazer a marcação, é importante não cobrir completamente o número, pois, no final, antes de uma dupla (ou grupo) ser confirmada como vencedora, sua cartela precisará ser verificada.

Vencerá o jogo quem conseguir completar toda a cartela primeiro. É interessante deixar as fichas das multiplicações disponíveis para que seja possível verificar se os cálculos da dupla vencedora estão corretos. Caso a dupla tenha feito algum cálculo de maneira equivocada, continuar o sorteio até que outra dupla consiga marcar toda a cartela com os resultados corretos.

Avaliar se a turma foi participativa no desenvolvimento da atividade e como os alunos resolveram as multiplicações propostas, ou seja, verificar se os critérios pedidos foram adotados, evitando-se realizar os cálculos de outra maneira que não fosse mentalmente.

Espera-se que os alunos desenvolvam os cálculos sem muita dificuldade, uma vez que o conteúdo já foi estudado e por terem confeccionado o jogo.

Aula 8

O objetivo desta aula é introduzir o contato dos alunos com o cálculo de multiplicação com números naturais maiores que 10. Para isso, organizar os alunos em quatro grupos e entregar, para cada um deles, os seguintes quadros.

Cada grupo deverá completar, no quadro, os resultados das multiplicações (número indicado na linha pelo número indicado na coluna). Se julgar conveniente, antes de os alunos o resolverem, apresentar os exemplos a seguir.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Ao final da aula, solicitar que cada grupo apresente como resolveu a atividade. Se necessário, coletivamente, confirmar com calculadora os resultados obtidos.

Então, com os alunos, montar um cartaz com os quadros preenchidos corretamente e fixá-lo em um mural na sala de aula.

Sugestões

• QUAL é a origem do bingo? Superinteressante, 4 jul. 2018. Disponível em: https://super.abril.com.br/mundo-estranho/qual-e-a-origem-do-bingo/. Acesso em: 16 maio 2021.

Sequência didática 6: Divisão

Nesta sequência didática, será abordada a divisão de números naturais até 10, utilizando material manipulável e cálculo mental, além da comunicação de estratégias de cálculo por meio da fala, da escrita e de imagens.

Será abordada, também, a associação dos termos metade, terça parte, quarta parte, quinta parte e décima parte a quocientes de divisão, trabalhando com unidades de medida não padronizadas de massa e de capacidade.

Objetivos de aprendizagem

• Compreender a aplicação da divisão.

• Resolver situações-problema envolvendo divisão.

• Fazer estimativas.

• Compreender o significado dos termos metade, terça parte, quarta parte, quinta parte e décima parte.

• Associar cada um dos termos ao quociente de uma divisão de um número natural por 2, 3, 4, 5 e 10 com resto zero.

Plano de aulas

Aula 1: Explorar um jogo sobre divisões.

Aula 2: Ampliar as discussões sobre estratégias de divisão.

Aulas 3 e 4: Ampliar a discussão sobre divisão com o auxílio de material manipulativo.

Aula 5: Associar o conceito de divisão a uma situação de adaptação de receita de bolo.

Aula 6: Introduzir a ideia de divisão como medida.

Aula 7: Explorar o jogo dos Restos.

Aula 8: Elaborar e resolver problemas sobre divisão.

Componentes essenciais para a alfabetização: Produção de escrita e compreensão de textos.

Competências gerais da Educação Básica: 2 e 9

Competências específicas de Matemática: 2, 6 e 8

Habilidades: EF03MA03, EF03MA08 e EF03MA09.

Materiais necessários: Material dourado (ou outro material para manipulação e contagem), fichas com instruções, fichas numeradas de 1 até 10, cartões com receitas, folhas avulsas, tabuleiro com sequência de números, dados e pequenos objetos para marcação (carrinhos, anéis, clipes, botões etc.).

Aula 1

O objetivo desta aula é explorar um jogo sobre divisões. Nesse jogo, os alunos efetuarão divisões com o objetivo de ganhar pontos ou evitar perdê-los.

Para isso, disponibilizar fichas em quantidade suficiente para grupos com quatro ou cinco alunos: um conjunto com instruções da atividade e outro conjunto com fichas contendo números de 1 a 10.

Exemplos de instruções que podem estar nas fichas (uma instrução por ficha):

• Sorteie uma ficha numerada e escolha um número menor que o sorteado. Divida o número sorteado pelo escolhido. Subtraia o resto dessa divisão da sua pontuação. Se não tiver pontos, apenas passe a vez.

• Escolha dois números diferentes de 1 a 10. Divida o maior número pelo menor e adicione o resto dessa divisão à sua pontuação.

• Sorteie uma carta numerada, escolha um número menor ou igual ao número sorteado. Divida o número sorteado pelo número escolhido. Subtraia o resto dessa divisão da pontuação de um grupo a sua escolha.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Organizar a turma em grupos com quatro ou cinco alunos. Em seguida, comunicar as regras do jogo e pedir que anotem cada passo da atividade, bem como os cálculos realizados.

• Um aluno do grupo pegará uma carta de instrução, anotará os números tirados e executará o comando.

• Em seguida, descreverá sua estratégia para chegar ao resultado.

• Depois, devolverá as cartas para os respectivos montes.

• Na sequência, os montes serão embaralhados e o próximo aluno repetirá o processo. Ao final de algumas rodadas, vencerá o grupo que obtiver mais pontos. Nesse momento, avaliar o desempenho dos alunos durante o jogo, sua compreensão das instruções, a execução da divisão e a escolha dos melhores números para ganhar o jogo.

Todas as etapas devem ser avaliadas tendo em perspectiva a progressão das habilidades dos alunos, pois se espera que a cada rodada eles tenham mais facilidade do que na anterior.

A etapa de identificação de dúvidas, também, é muito importante, pois ajuda a direcionar os esforços de forma mais eficaz para saná-las. Como o jogo é organizado em partes bem definidas – leitura e interpretação da instrução, escolha de números apropriados e efetivação do cálculo –, pode-se solicitar aos alunos que narrem cada uma das etapas que forem executando, para que sejam feitas intervenções pontuais assim que aparecerem dúvidas. Se julgar necessário, realizar uma rodada de teste com os alunos, sem pontuação.

Aula 2

O objetivo desta aula é ampliar as discussões sobre estratégias de divisão utilizadas na aula anterior. Iniciar as produções solicitando aos alunos que relembrem as regras do jogo da primeira aula. Nesse momento, é importante que os alunos recorram às anotações que fizeram.

É importante orientá-los a descreverem as características das instruções, pois nelas estão os cálculos que eles precisariam fazer. Depois de retomar as regras, pedir aos alunos que conversem sobre a experiência do jogo: se o acharam desafiador, se sentiram diferença de uma rodada para outra etc.

Esse é um momento para que os alunos relembrem a aula anterior e se sintam novamente imersos no jogo. Quando perceber que já atingiram esse estágio, debater com eles as estratégias utilizadas durante o jogo. Separar essa etapa em duas partes: uma em que os alunos deverão revelar as estratégias que utilizaram para tentar ganhar o jogo, e outra em que deverão escrever na lousa um exemplo da estratégia utilizada – usar, de preferência, um caso que tenha ocorrido com eles no decorrer do jogo.

A estratégia utilizada pelos alunos não terá relação apenas com o cálculo da divisão, mas também com a escolha dos números. É importante que os alunos falem sobre o cálculo mental para a adição e para a subtração. Uma estratégia esperada quando, por exemplo, se deseja obter resto zero na divisão, é escolher sempre o número 2 como divisor se o número sorteado for par: 2, 4, 6, 8 ou 10. Caso essa estratégia não tenha sido mencionada, mostrar aos alunos as divisões desses números por 2, para que comecem a perceber que números pares são sempre divisíveis por 2.

Esta aula tem como objetivo verificar a habilidade dos alunos de criar estratégias para solucionar problemas, habilidade que será fundamental por toda a vida deles. Os alunos são levados a usar maneiras diferentes de comunicar estratégias – por meio da fala, da escrita e de imagens –, dando assim mais elementos para poder avaliá-los.

Para isso, é importante fazer perguntas durante a exposição das estratégias pelos alunos, tendo sempre o cuidado de deixá-los à vontade para responder, pois o questionamento costuma gerar certa tensão.

Aulas 3 e 4

O objetivo destas aulas é ampliar a discussão sobre divisão realizada nas aulas anteriores com o auxílio de material manipulativo. Para isso, iniciar a aula propondo um debate aos alunos, pedindo que comentem o que acharam de estudar as estratégias para conseguir vantagens no jogo. Nesse momento, dizer aos alunos que a Matemática pode nos ajudar a viver em sociedade, nos dando condições para lidar com situações que envolvem relações de interesse, como em jogos, financiamento, empréstimos, compras etc. Realizar essa discussão pode desmistificar algumas crenças internalizadas que os alunos já tenham. Em seguida, propor a seguinte questão: por que o número escolhido deve ser sempre menor ou igual ao número sorteado?

Registrar a pergunta na lousa e solicitar que os alunos a respondam coletivamente, anotando algumas respostas na lousa.

Em seguida, organizar os alunos em grupos com três integrantes e entregar, para cada grupo, cubinhos do material dourado ou outro material, como tampinhas e clipes. Depois, sugerir que os alunos tentem encontrar uma resposta para essa pergunta, manipulando os materiais. É importante deixar as respostas, indicadas anteriormente por eles, na lousa, pois isso pode motivá-los.

Acompanhar as discussões, fazendo intervenções quando julgar conveniente. Depois que os alunos responderem à pergunta, selecionar alguns deles para apresentarem o que realizaram. É importante que um representante do grupo vá à frente da sala de aula para mostrar como manipularam o material. Ao final, sistematizar com os alunos que é impossível dividir um número natural por outro maior de maneira a obter como quociente um número maior que 1.

Material disponibilizado em licença aberta do tipo Creative Commons

Na aula 4, pedir aos alunos que novamente formem grupos, desta vez dinâmicos, pois a quantidade de integrantes em cada grupo será diferente no decorrer da atividade. Caso necessário, fazer adaptações na quantidade de integrantes por grupo, dependendo da quantidade de alunos que há na sala de aula. O importante é que todos os grupos tenham a mesma quantidade de participantes (2, 3, 4, 5 ou 10). Incluir-se em um grupo, também, pode ajudar nessa dinâmica

Entregar uma quantidade de cubinhos do material dourado que seja múltipla do número de alunos que formam o grupo. Solicitar aos grupos que dividam o material igualmente entre todos os integrantes e que anotem em uma folha de papel sulfite os seguintes dados: quantos alunos formam o grupo; quantos cubinhos o grupo recebeu; e quantos cubinhos ficaram com cada aluno.

Solicitar à turma que se organize novamente em grupos, agora com outra quantidade de componentes por grupo, e repetir o processo.

Esta atividade deve ser feita preferencialmente com grupos de dois, três, quatro, cinco e dez integrantes.

Após essa conclusão, anotar na lousa os termos metade, terça parte, quarta parte, quinta parte e décima parte. Pedir aos alunos que relacionem esses termos às divisões que fizeram.

Conversar com os alunos sobre os termos utilizados e sobre o que esses termos lembram. Espera-se que façam a relação entre cada um dos termos e os números ordinais (exceto o termo metade). Por exemplo: quarta deve remetê-los ao ordinal 4ª, que os conduzirá ao número 4. Mostrar como o conhecimento da língua materna é importante para a compreensão de novos conhecimentos, inclusive da Matemática.

Avaliar se os alunos compreenderam corretamente o significado dos termos, como utilizaram a língua materna para desenvolver essa habilidade e como manipularam o material dourado, se fizeram a divisão dos cubinhos em uma única etapa, se entregaram um cubinho de cada vez etc.

É importante sempre circular entre os grupos para verificar o andamento do trabalho e a participação dos alunos, aproveitando para fazer indagações e intervenções quando julgar necessário.

Trabalhar as dúvidas dos alunos é fundamental para garantir que eles desenvolvam a habilidade da melhor maneira possível. Dessa forma, identificar onde está a dúvida deve ser a prioridade desta etapa. Fazer perguntas desde o início da atividade até seu objetivo final, ajuda nesse aspecto, pois é possível verificar em que momento o aluno não tem mais as respostas (ou tem a resposta incorreta), e onde está a dúvida.

Guiar os alunos por meio de exemplos, ou de perguntas direcionadas, os ajuda a desenvolver sozinhos a habilidade. Lembrar sempre que dar a resposta não é o foco desta etapa, mas, sim, fazer com que compreendam onde está a dificuldade e o que se pretende na aula.

Material disponibilizado em licença aberta do tipo Creative Commons

É importante que os termos utilizados sejam compreendidos pelos alunos, e não decorados. Para isso, utilizar dias da semana ou números ordinais para direcionar os alunos em caso de dúvida. A palavra "parte", também, deve ser compreendida como uma indicação de que algo foi partido, dividido, daí a compreensão da relação com a operação de divisão.

Aula 5

O objetivo desta aula é associar o conceito de divisão a uma situação de adaptação de receita de bolo. Para isso, organizar a turma em grupos de cinco alunos e explicar que, nesta aula, eles serão responsáveis pela adaptação de uma receita de bolo. Cada grupo receberá uma parte da receita do bolo e precisará adaptá-la de acordo com as instruções contidas na receita. É importante mostrar à turma que o sucesso da atividade dependerá do sucesso de todos os grupos, ou seja, mesmo que estejam trabalhando em grupos menores, é importante ficarem atentos às necessidades dos demais.

Elaborar previamente fichas com as partes de uma receita, que deverão ser entregues aos alunos. A ficha deverá ter o item, a quantidade disponível e uma instrução de como proceder para obter a quantidade correta para a receita. Por exemplo:

Item Quantidade disponível Instrução para a quantidade correta

Farinha de trigo 8 xícaras Usar a quarta parte da quantidade disponível

Ovos 8 unidades Usar a metade da quantidade disponível

Leite 10 copos Usar a décima parte da quantidade disponível

Fermento em pó 12 colheres Usar a quarta parte da quantidade disponível

Chocolate em pó 6 xícaras Usar a terça parte da quantidade disponível

Explicar que a atividade consiste em fazer as divisões necessárias para se obter a quantidade correta. Nesse momento, os alunos precisarão utilizar os termos metade, terça parte, quarta parte e décima parte para efetuar os cálculos. Observar que, em um primeiro momento, espera-se que eles não tenham dificuldades com os cálculos, por isso, a opção por utilizar valores pequenos na coluna "Quantidade disponível".

Também, é importante mostrar aos alunos que a unidade de medida se mantém mesmo após a divisão, ou seja, o resultado deve ter a mesma unidade de medida do item na coluna "Quantidade disponível".

Depois que os alunos completarem os cálculos, pedir que os escrevam na lousa, para que todos os confiram, pois somente após a conferência será possível declarar que o grupo atingiu sua meta.

Caso um grupo tenha sido o responsável pelo fato de a turma não alcançar o objetivo, é importante não permitir que esse grupo seja criticado por isso. Lembrar aos alunos que todos eram responsáveis pela atividade, e que os grupos poderiam ter trabalhado de forma colaborativa entre si, a fim de evitar o problema.

A avaliação da aula se dá em dois aspectos: o matemático e o colaborativo. No primeiro, avaliar se os alunos compreenderam corretamente o significado dos termos e quais estratégias de cálculo foram utilizadas, pois não haverá o uso do material dourado. O segundo aspecto deve ser avaliado ao observar como os alunos interagem entre si, assim como os grupos, pois, desde o início da atividade, fica claro aos alunos que o resultado será coletivo.

Parte da avaliação se dá pela observação dos alunos e dos grupos, por isso é importante sempre caminhar entre os alunos para verificar o andamento do trabalho e a participação deles. Durante esse momento, fazer perguntas avaliadoras para verificar quão comprometidos com a atividade eles estão, como essas: por que vocês dividiram esse item por três? Por que você ficou responsável por esse cálculo?

Aula 6

O objetivo desta aula é introduzir a ideia de divisão como medida. Para isso, apresentar à turma a seguinte situação-problema.

Para o encerramento do ano letivo, a professora de uma turma decidiu organizar uma competição com seus alunos. Para isso, os alunos foram organizados em equipes de 4 integrantes. Considerando que, nessa turma, há 36 alunos, quantas equipes foram formadas?

9 (36 ÷ 4 = 9).

Solicitar que os alunos resolvam esta atividade em grupos. Enquanto isso, acompanhar as discussões e selecionar pelo menos duas resoluções para a discussão. A seguir há duas resoluções que podem ser apresentadas.

a) 9 equipes, pois 36 ÷ 4 = 9, já que 9 × 4 = 36

b) usando subtrações sucessivas:

1 equipe formada. Alunos restantes: 36 – 4 = 32

2 equipes formadas. Alunos restantes: 32 – 4 = 28

3 equipes formadas. Alunos restantes: 28 – 4 = 24

4 equipes formadas. Alunos restantes: 24 – 4 = 20

5 equipes formadas. Alunos restantes: 20 – 4 = 16

6 equipes formadas. Alunos restantes: 16 – 4 = 12

7 equipes formadas. Alunos restantes: 12 – 4 = 8

8 equipes formadas. Alunos restantes: 8 – 4 = 4

9 equipes formadas. Alunos restantes: 4 – 4 = 0

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Caso os alunos não apresentem essas estratégias de resolução, apresentar cada uma delas à turma. Comentar que a resolução explicitada no item b envolve a ideia de subtrações sucessivas.

Comentar também que, nessa situação, nenhum aluno ficou sem grupo. Com isso, pode-se afirmar que o resto da divisão de 36 por 9 é igual a 0. Por esse motivo, essa divisão pode ser chamada exata. Aproveitar esse momento para informar que, quando o resto da divisão é diferente de 0, ela pode ser chamada não exata.

Explicar que a divisão realizada nesta aula, com base nessa situação-problema, corresponde a uma ideia específica: divisão como medida. Comentar com os alunos que essa ideia de divisão é utilizada quando se tem a quantidade total de elementos e é preciso organizá-los em grupos com uma quantidade específica de elementos. Fazer perguntas sobre a ideia de divisão como: quantos grupos podem ser formados? Quantos cabem?

Aula 7

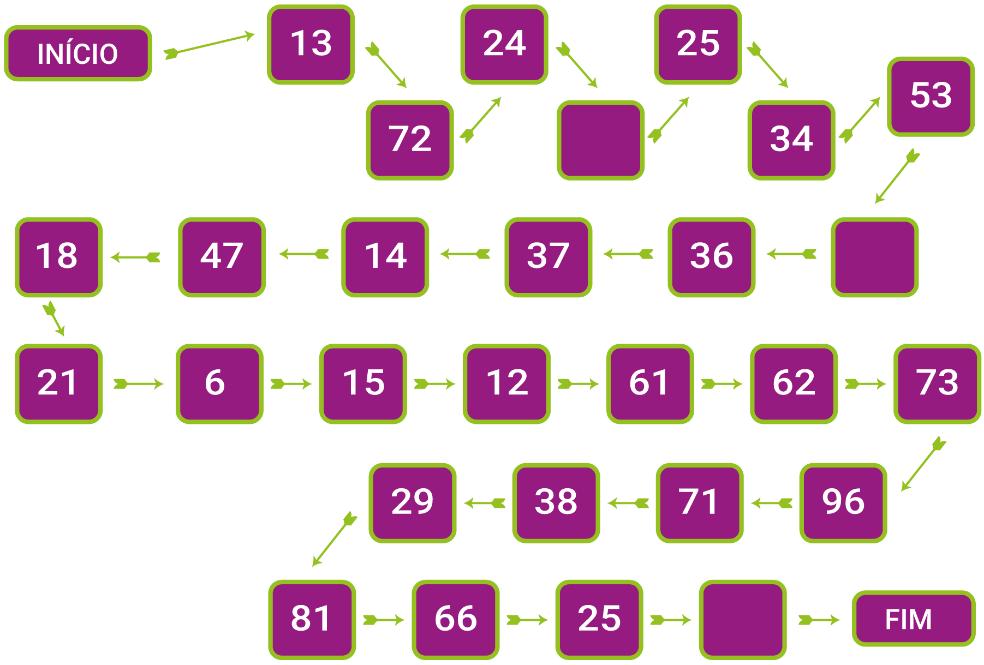
O objetivo desta aula é explorar o jogo dos Restos. Para esse jogo serão necessários alguns dados, pequenos objetos para marcação das casas (carrinhos, anéis, clipes, botões etc ) e um tabuleiro com uma sequência de números, de maneira que cada número esteja em uma casa e que os alunos consigam avançar de casa em casa. Segue uma sugestão de tabuleiro.

Iniciar a aula dizendo que os alunos vão conhecer o jogo dos Restos. Comentar que ele será realizado em equipes com cinco alunos. Destinar um tempo para que se organizem e, em seguida, apresentar as seguintes regras.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

EDITORIA DE ARTE

Regras do jogo dos Restos

• Cada grupo terá um tabuleiro e um dado.

• Em cada tabuleiro há um conjunto de casas e flechas.

• As flechas indicam o caminho que deverá ser percorrido por cada integrante do grupo.

• Cada integrante do grupo terá um peão (alguns possíveis objetos que podem ser utilizados: botões, clipes, anéis, carrinhos, tampinhas, entre outros).

• Inicialmente, todos se posicionam na casa "INÍCIO".

• Cada aluno terá sua vez. A ordem de jogadas dos alunos é estabelecida pela ordem alfabética (ou sorteio).

• Na primeira rodada, o aluno jogará o dado para definir em qual casa ele estará. Por exemplo, caso tenha sido sorteado o número 3 no dado, ele contará, a partir da casa "INÍCIO", três casas, na qual deverá posicionar o peão.

• Na primeira rodada, o aluno da vez vai jogar o dado. Em seguida, ele dividirá o número correspondente à casa que está posicionado pelo número sorteado no dado. O resto da divisão determinará a quantidade de casas que ele andará no tabuleiro.

• Caso se posicione em uma casa que não tenha número, o aluno deverá voltar para a casa "INÍCIO".

• O aluno que chegar à casa "FIM" primeiro, vencerá o jogo dos Restos

Ao final da aula, realizar uma roda de conversa com os alunos e discutir as impressões deles com a realização desta atividade. Comentar sobre as peculiaridades do jogo. Por exemplo, caso um aluno ficasse na casa com o número 12, ele só conseguiria avançar se sorteasse o número 5 no dado, uma vez que:

• 12 = 1 × 12 + 0

• 12 = 2 × 6 + 0

• 12 = 3 × 4 + 0

• 12 = 4 × 3 + 0

• 12 = 5 × 2 + 2

• 12 = 6 × 2 + 0

Aula 8

O objetivo desta aula é elaborar e resolver problemas envolvendo a divisão. Para isso, organizar os alunos em duplas e entregar uma folha avulsa a cada uma. Em seguida, solicitar que elaborem problemas envolvendo o conceito de divisão e que registrem seu enunciado na folha avulsa que foi entregue. Comentar que é essencial que esse problema tenha uma

associação com o mundo real. Além disso, dizer que é necessário que resolvam esse mesmo problema no caderno.

Nesse momento, acompanhar as produções dos grupos, observando as estratégias que utilizaram para elaborar os problemas.

Após cada dupla terminar de elaborar o problema, trocá-lo com o produzido por outra dupla. Orientar as duplas a resolverem, em outra folha avulsa, os problemas que receberam. Por fim, depois que as duplas resolverem o problema uma da outra, realizar novamente a troca, de maneira que a dupla que elaborou o problema agora receba a resolução produzida pela outra dupla. Solicitar, então, que os alunos comparem a resolução dos colegas com a registrada no caderno. Os problemas elaborados e as respectivas resoluções podem ser expostos em um painel na sala de aula, para a visualização de toda a turma.

Sugestões

• POR QUE resgatar o caderno de receitas da família pode fazer a diferença na sua alimentação e na sua vida. Saúde Brasil, 16 out. 2020. Disponível em: https://saudebrasil.saude.gov.br/eu-quero-me-alimentar-melhor/por-que-resgatar-ocaderno-de-receitas-da-familia-pode-fazer-a-diferenca-na-sua-alimentacao-e-na-sua-vida Acesso em: 7 jan. 2022.

Sequência didática 7: Grandezas e medidas

Nesta sequência didática, serão abordadas, por meio de atividades lúdicas, as medidas de comprimento, massa e capacidade. Além disso, será abordado o sistema monetário brasileiro, explorando a comparação e a equivalência entre cédulas e moedas do Real, por meio de uma atividade que simula compra, venda e troco.

Objetivos de aprendizagem

• Estimar e comparar medidas de massa.

• Estimar e comparar medidas de comprimento.

• Realizar medidas de comprimento.

• Estimar e comparar medidas de capacidade.

• Identificar cédulas e moedas do sistema monetário brasileiro.

• Comparar e estabelecer relações de equivalência entre cédulas e moedas.

Material disponibilizado em licença aberta do tipo Creative Commons

Plano de aulas

Aulas 1 e 2: Estimar a massa de diferentes produtos por meio de uma atividade lúdica.

Aula 3: Explorar unidades de medida de massa e a relação entre preços e medidas de massa.

Aula 4: Medir comprimento de pessoas utilizando, como instrumento de medida, a fita métrica.

Aula 5: Medir comprimento de diferentes objetos utilizando, como instrumento de medida, a régua e a fita métrica.

Aula 6: Estimar e medir medidas de capacidade por meio de uma atividade lúdica.

Aulas 7 e 8: Reconhecer características das cédulas e moedas do Real e realizar comparações e equivalências de valores monetários.

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita.

Competências gerais da Educação Básica: 1 e 2.

Competências específicas de Matemática: 2, 5 e 8.

Habilidades: EF03MA18, EF03MA19, EF03MA20 e EF03MA24.

Materiais necessários: Folhas avulsas, pacotes de itens vendidos por massa, tesoura com pontas arredondadas, fita adesiva opaca, encartes de mercados, garrafas (1 L e 500 mL), copos descartáveis (250 mL, 100 mL), conta-gotas, copinho de remédio, régua, fita métrica, trena, reproduções de modelos de cédulas e moedas do Real e imagens de objetos.

Aulas

1 e 2

O objetivo destas aulas é possibilitar aos alunos estimar a massa de diferentes produtos utilizados no cotidiano por meio de uma atividade lúdica que possibilita mais interatividade e torna a aula mais dinâmica. Para isso, sugere-se providenciar, com antecedência, pacotes de alguns produtos consumidos no dia a dia, por exemplo, arroz (1 kg), feijão (1 kg), milho de pipoca (500 g), macarrão (500 g), sabonete (90 g), algodão (200 g), sabão em pó (1 kg), gelatina (20 g) e encartes de diferentes mercados. Cubra as indicações de massa de todos os produtos utilizando fita adesiva opaca.

Para iniciar a aula, colocar sobre a mesa os diferentes produtos e mostrar cada um deles à turma. Comentar que esses produtos são vendidos de acordo com suas massas. Se julgar oportuno, antes de explorar a estimativa das massas com os alunos, comentar que as pessoas geralmente utilizam a palavra peso no lugar de massa, citar exemplos de situações nas quais isso pode acontecer.

Propor que realizem estimativas da massa dos produtos sobre a mesa. Para isso, sugere-se fazer algumas perguntas de acordo com os produtos selecionados, por exemplo: o que tem maior massa: um pacote de arroz ou um pacote de feijão? O que tem maior massa: um pacote de macarrão ou um pacote de pipoca? O que tem maior massa: um pacote de pipoca ou um pacote de algodão? Se julgar oportuno, convidar alguns alunos para segurarem alguns produtos e verificarem se acreditam que a estimativa feita pela turma está correta.

Espera-se que os alunos façam estimativas com base nas observações dos tamanhos e formato dos pacotes e, também, nos conhecimentos prévios advindos do que

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

apreenderam em anos anteriores e em situações do cotidiano. Aproveitar o momento em que a turma estiver respondendo às perguntas para verificar os conhecimentos prévios deles sobre medidas de massa.

Em seguida, ainda com as indicações de massa cobertas, fazer algumas perguntas para verificar os conhecimentos dos alunos sobre unidades de medida, por exemplo: qual é a unidade de medida utilizada para indicar a massa do pacote de arroz? E a massa do sabonete? Entre outras. Os alunos podem responder que a unidade de medida utilizada para indicar a massa do arroz é o quilograma; para indicar a massa do sabonete, utilizamos o grama.

Retirar a fita adesiva para que os alunos vejam as indicações de massas e verifiquem se a estimativa que fizeram estão corretas. É importante que percebam que pode haver uma embalagem grande que contenha um produto com massa menor que a de um produto com embalagem menor, como: uma embalagem de 200 gramas de algodão e outra de 1 quilograma de arroz.

Explorar com os alunos os rótulos com as informações nutricionais dos alimentos. Pedir que observem as unidades de medida de massa que aparecem nos rótulos. Espera-se que eles percebam que, além do grama (g), aparece outra unidade de medida, o miligrama (mg). Explicar que essa é outra unidade de medida de massa muito utilizada para indicar a quantidade de alguns nutrientes em alguns alimentos, por exemplo, a quantidade de sódio e de cálcio.

Para ampliar a discussão sobre medidas de massa, organizar os alunos em grupos de quatro integrantes e entregar a cada grupo encartes de diferentes mercados. Propor que observem nos encartes os produtos vendidos de acordo com a massa. Espera-se que os alunos identifiquem produtos vendidos em grama e quilograma e que percebam que alguns produtos indicam o peso bruto e o peso drenado ou líquido. Explicar que peso bruto significa a massa da embalagem e a massa do produto somadas, enquanto peso líquido e peso drenado indicam apenas a massa do produto, sem contar a da embalagem ou a do líquido que protege o produto.

Aula 3

O objetivo desta aula é ampliar o estudo sobre as unidades de medida de massa realizado nas aulas anteriores e explorar a relação entre preços e medidas de massa de produtos do cotidiano. Para isso, providenciar com antecedência encartes de mercados.

Propor aos alunos que façam uma pesquisa dos preços de diversos produtos, como açúcar, feijão, biscoitos, milho de pipoca, leite em pó, entre outros. É importante destacar que a unidade de medida do pacote deve ser em quilograma ou grama. Para isso, sugere-se disponibilizar à turma encartes de mercados, utilizados nas aulas anteriores, ou levá-los à sala de informática, a fim de pesquisarem sitesde diferentes mercados para realizarem a pesquisa de preço.

Pedir aos alunos que pesquisem o valor de produtos com diferentes massas, por exemplo, açúcar de 2 kg e 5 kg. Depois, reproduzir o quadro a seguir na lousa e propor que o copiem no caderno e o preencham com as informações encontradas na pesquisa.

Após registrarem no quadro as informações encontradas, pedir aos alunos que comparem a massa dos produtos pesquisados com o valor. Se julgar oportuno, propor aos grupos que também comparem seus valores com os de outros grupos. Em seguida, solicitar que apresentem uma situação vantajosa tendo em vista o objetivo de pagar menos e adquirir uma quantidade maior de produto. Realizar um debate fomentando discussões que possibilitam trabalhar a educação financeira com a turma.

Por fim, se julgar oportuno, entregar cartolinas aos grupos e propor que confeccionem cartazes para alertar as pessoas sobre a relação entre a massa e o preço dos produtos. Comentar que esse alerta deve indicar, de algum modo, que nem sempre o produto mais barato é o mais vantajoso quando realizamos compras. Ao final da aula, verificar a possibilidade de expor os cartazes no mural da escola.

Aula 4

O objetivo desta aula é explorar as medidas de comprimento e apresentar instrumentos que podem ser utilizados para realizar medições em metro e em centímetro. Para isso, providenciar, com antecedência, alguns instrumentos de medida de comprimento, como régua, trena e fita métrica.

Para iniciar a aula, perguntar aos alunos: vocês já observaram esses instrumentos sendo utilizados em alguma situação? Qual desses instrumentos é o mais adequado para medir a altura de uma pessoa: régua ou fita métrica? Deixar que eles compartilhem com os colegas suas vivências. Se julgar necessário, citar algumas situações em que se utilizam esses instrumentos para realizar medições. Depois, apresentar aos alunos as unidades de medida presentes nesse instrumento, milímetro, centímetro e metro, e explorar as correspondências entre elas.

Em seguida, organizar os alunos em duplas e propor que, utilizando uma fita métrica, meçam a altura um do outro e a registrem no caderno. Acompanhar a turma durante as medições, intervindo e ajudando, se necessário. Nesse momento, realizar uma discussão

Produto Medida de massa Preço em reais

sobre pluralidade de características do ser humano. Comentar que algumas pessoas são mais altas, outras mais baixas, e que todos devem ser respeitados.

Em seguida, com a colaboração dos alunos, registrar todas as estaturas no quadro e propor que, em duplas, as organizem em uma folha avulsa do maior comprimento para o menor.

As medidas indicadas na lousa podem ser expressas em centímetro, ou em metro e centímetro. Por exemplo, a estatura de 120 centímetros também pode ser expressa por 1 metro e 20 centímetros. Aproveitar esse momento para estabelecer equivalência entre as unidades de medida metro e centímetro e sanar possíveis dúvidas. Comentar, também, que as medidas obtidas são aproximadas, uma vez que há imprecisões na realização das medições.

Aula 5

O objetivo desta aula é ampliar o estudo das medidas de comprimento com base em medições de objetos, por exemplo: lápis, caderno, carteira, estojo, porta, mesa e sala de aula. Para isso, providenciar com antecedência régua e fita métrica.

Para iniciar a aula, organizar os alunos em grupos de três integrantes e entregar os instrumentos de medidas aos grupos. É importante que cada grupo tenha pelo menos um desses instrumentos e que, após realizar algumas medições, os grupos os troquem entre si. Em seguida, reproduzir na lousa um quadro e explicar que, em uma coluna, eles devem indicar os objetos que serão medidos, e, na outra, a medida do objeto Cada grupo deve preencher de acordo com as medidas realizadas. Observe o exemplo a seguir.

Objeto Medida

Comprimento de um lápis

Largura de um caderno

Comprimento de um estojo

Altura da porta da sala de aula

Largura da mesa do aluno

Depois que todos os alunos copiarem o quadro, propor que realizem as medições e que preencham esse quadro de acordo com as medições realizadas.

Na medição, é possível que os alunos encontrem valores não inteiros, em centímetro. Neste caso, explicar como se mede com a régua utilizando centímetro e milímetro: de um traço maior ao seguinte (1 cm) existem 10 milímetros; de um traço maior a um traço médio (e vice-versa) há 5 milímetros; e de um traço pequeno ao seguinte existe 1 milímetro. Desse modo, um objeto que tenha, por exemplo, 4,5 cm de comprimento pode ser expresso em milímetros, pois 4 cm = 40 milímetros, e que até o próximo traço médio são 5 milímetros.

Material disponibilizado em licença aberta do tipo Creative Commons

Dessa forma, basta adicionar os dois valores para chegar à medida do comprimento do objeto: 40 + 5 = 45; 45 milímetros.

Acompanhar a turma durante as medições e verificar se os alunos estão escolhendo o instrumento mais adequado para realizá-las e se medem corretamente. É interessante observar se todos os integrantes do grupo estão envolvidos na atividade, como se organizam para auxiliar um colega que precisa de ajuda e se percebem que a medição de um mesmo objeto pode ser expressa utilizando diferentes unidades de medida de comprimento, por exemplo, a altura de uma porta pode ser expressa em centímetro ou metro.

Se julgar oportuno, para ampliar, propor aos alunos que construam um quadro semelhante ao desta aula e que, em casa e com a ajuda de um adulto, realizem as medições de objetos e registrem os valores encontrados. Os alunos podem entregar a atividade na próxima aula para correção.

Aula 6

O objetivo desta aula é explorar com os alunos as medidas de capacidade. Para isso, providenciar com antecedência embalagens de diferentes produtos do cotidiano do aluno, por exemplo, xampu, condicionador, suco, iogurte, amaciante, entre outras. É importante que algumas dessas embalagens tenham capacidade maior e menor que 1 L. Cobrir a parte das embalagens que indica as capacidades com fita adesiva opaca. Além dessas embalagens, disponibilizar garrafas de diferentes capacidades (1 L e 500 mL) e copos descartáveis (250 mL e 100 mL).

Para iniciar a aula, organizar uma roda de conversa e perguntar aos alunos: vocês já escutaram algum adulto falar que precisava comprar 1 L de algum produto? Ou que em alguma embalagem tem meio litro de um algum produto? Deixar que compartilhem com os colegas o que sabem sobre o tema e aproveitar o momento para verificar os conhecimentos prévios da turma.

Em seguida, colocar sobre a mesa as diferentes embalagens e mostrá-las aos alunos. Comentar que esses produtos são vendidos de acordo com a capacidade. Ao mostrar cada embalagem, propor que as classifiquem de acordo com a capacidade: tem mais de 1 L, menos de 1 L ou exatamente 1 L. Depois, retirar a fita adesiva das partes que indicam a capacidade das embalagens, para que verifiquem suas estimativas. Explorar a unidade de medida de cada embalagem para que percebam a diferença entre elas e identifiquem o mililitro como outra unidade de medida de capacidade padronizada, utilizada em diferentes situações do cotidiano.

Para dar continuidade à aula, realizar alguns experimentos utilizando as garrafas e os copos descartáveis. Para isso, mostrar à turma uma garrafa com 1 litro de água e copos descartáveis de 250 mililitros e perguntar: quantos copos é possível encher com essa quantidade de água? Convidar algum aluno para verificar se a estimativa feita pelos colegas foi adequada. Depois, mostrar à turma a garrafa de 500 mililitros de água e copos

descartáveis de 250 mililitros e perguntar: quantos copos é possível encher com essa quantidade de água? Convidar outro aluno para verificar se a estimativa feita pelos colegas está correta. Se possível, realizar outros experimentos utilizando copos de 100 mL, conta-gotas e copinhos de remédios. Além de estimar e comparar medidas de capacidade, esse experimento possibilita que os alunos aprendam de forma intuitiva a ideia de proporcionalidade.

Aulas 7 e 8

O objetivo destas aulas é explorar com os alunos as cédulas e moedas do sistema monetário brasileiro, para que possam reconhecer suas características e utilização em situações do dia a dia. Além disso, por meio de simulações de situações de compra e venda, são exploradas a ideia de troco e a comparação e a equivalência de valores monetários. Dessa forma, providenciar com antecedência representações de cédulas e moedas do Real e encartes de mercado.

Para iniciar a aula, organizar os alunos em grupos com cinco integrantes e entregar a eles as representações das cédulas e moedas do Real. Propor que observem os símbolos e as características de cada uma. Espera-se que percebam que as cédulas e moedas têm tamanhos específicos e que no verso das cédulas é representado um animal da fauna brasileira.

Depois, sugere-se conversar com os alunos sobre a história do dinheiro. Na seção Sugestão indicamos sitescom textos que podem auxiliá-lo a conduzir essa conversa.

Em um segundo momento, entregar aos grupos os encartes de diferentes mercados e a tesoura com pontas arredondadas. Explicar a atividade de simulação de compra e venda e orientar que um aluno do grupo será o vendedor e os outros quatro os compradores. Pedir aos grupos que recortem os produtos que serão vendidos e precifiquem cada um. As imagens podem ficar dispostas na mesa do aluno vendedor com seus respectivos preços.

Depois, orientar os grupos a distribuírem as representações de cédulas e moedas entre os integrantes, de modo que os alunos compradores fiquem com os valores mais altos e o aluno vendedor, com as reproduções de cédulas e moedas de valores mais baixos, que vão ser utilizadas para troco.

Antes de iniciar a atividade, propor aos alunos que copiem em uma folha de papel sulfite as seguintes informações.

• A quantia que receberam no início da atividade.

• Quais e quantas cédulas e moedas receberam no início da atividade.

• Qual produto compraram e quanto ele custou.

• Quanto entregaram de dinheiro e quanto receberam de troco.

• Quanto sobrou de dinheiro ao final das compras e quais as cédulas e moedas que sobraram.

Pedir aos alunos vendedores que anotem as seguintes informações em uma folha avulsa

• A quantia que receberam no início da atividade.

• Quais e quantas cédulas e moedas receberam no início da atividade.

• Quais produtos venderam.

• Quanto receberam de dinheiro por produto, e quanto deram de troco.

• Quanto dinheiro restou após as vendas.

• Com quais cédulas e moedas eles ficaram no fim das vendas.

É importante que todos os alunos passem pelas funções de vendedor e comprador Dessa maneira, recomenda-se que se façam pelo menos cinco rodadas da atividade para que os alunos possam vivenciar situações variadas.

As informações das folhas de respostas produzidas pelos alunos podem ser conferidas pelo grupo, para verificar se os cálculos (valor final da compra, troco etc.) estão corretos.

Acompanhar os alunos durante a atividade e verificar se estão realizando corretamente as trocas. Avaliar, também, se todos estão participando das atividades, desenvolvendo as habilidades de cooperar com os demais e resolver problemas de forma construtiva e respeitosa.

Sugestões

• BANCO CENTRAL DO BRASIL. Caderno de Educação Financeira – Gestão de Finanças

Pessoais Brasília, DF. Disponível em:

https://www.bcb.gov.br/content/cidadaniafinanceira/documentos_cidadania/Cuidando_ do_seu_dinheiro_Gestao_de_Financas_Pessoais/caderno_cidadania_financeira.pdf

Acesso em: 13 mar. 2023

• CASA DA MOEDA BRASIL. Origem do dinheiro Brasília, DF, c2021. Disponível em:

https://www.casadamoeda.gov.br/portal/socioambiental/cultural/origem-dodinheiro.html. Aceso em: 8 jan. 2022.

• A HISTÓRIA do dinheiro. Conexão Escola/SME de Goiânia. Disponível em:

https://sme.goiania.go.gov.br/conexaoescola/ensino_fundamental/a-historia-dodinheiro/. Acesso em: 8 jan. 2022.

Sequência didática 8: Probabilidade e estatística

Nesta sequência didática, os alunos trabalharão com coleta de informações, por meio de pesquisa em periódicos e na internet, representarão essas informações em tabela e, com base nelas, construirão gráficos de colunas e de barras. Além disso, serão exploradas, também, ideias da probabilidade.

Objetivos de aprendizagem

• Compreender a construção de tabelas.

• Resolver situações-problemas.

• Compreender a construção de gráficos de colunas e de barras.

• Compreender eventos aleatórios e como sua frequência varia com a quantidade de possibilidades contidas no evento.

Plano de aulas

Aula 1: Refletir sobre temas importantes nacionais, estaduais ou municipais.

Aula 2: Representar informações de contextos reais por meio de tabelas.

Aula 3: Representar informações de contextos reais por meio de gráficos de coluna.

Aula 4: Representar informações de contextos reais por meio de gráficos de barras.

Aula 5: Sistematizar os diferentes modos de representação de informações utilizados pelos alunos para desenvolver uma pesquisa.

Aula 6: Explorar o conceito de tabelas e de gráficos, discutidos anteriormente, para introduzir a ideia de probabilidade.

Aula 7: Ampliar as discussões sobre probabilidade, iniciadas na aula anterior.

Aula 8: Interpretar informações em gráficos de colunas.

Componentes essenciais para a alfabetização: Compreensão de textos, produção de escrita e desenvolvimento de vocabulário.

Competências gerais da Educação Básica: 1, 2 e 6.

Competências específicas de Matemática: 2 e 8.

Habilidades: EF03MA25, EF03MA26, EF03MA27 e EF03MA28.

Materiais necessários: Folhas de papel quadriculado, jornais e revistas atuais, computador com acesso à internet, lápis de cor ou giz de cera, régua, borracha, um dado de seis faces para cada aluno e folhas para anotação.

Aula 1

O objetivo desta primeira aula é refletir sobre temas importantes nacionais, estaduais ou municipais. Para isso, orientar os alunos a pesquisarem temáticas de interesse em jornais, revistas e na internet. Nesse momento, destacar que eles não precisam ler reportagens inteiras, pois costumam ser muito extensas para essa faixa etária. A ideia é despertar a curiosidade sobre temas atuais, como internet, preços, vida animal, esporte, desemprego, segurança, vacina, economia etc.

A fim de motivá-los e orientá-los, ler com eles uma reportagem que contenha números passíveis de se representar em gráfico, de modo que tenham uma ideia do que procurar.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Pedir à turma que formem grupos com quatro alunos e que debatam a escolha de temas. Realizar uma roda de conversa para que exponham os temas selecionados e expliquem o motivo da escolha. A fim de nortear a conversa, fazer perguntas como: quais assuntos mais interessam a vocês? Onde vocês pretendem pesquisá-los?

Nesse momento, verificar se os temas escolhidos são apropriados para a faixa etária e, se não forem, orientá-los a escolher outros mais simples. É importante reforçar a ideia de que precisam buscar dados numéricos, ou seja, as informações precisam dar subsídio para a construção de gráficos e de tabelas. Em seguida, solicitar que os grupos escolham os temas e pesquisem sobre eles na escola ou em casa. Alertá-los sobre a importância de anotar todas as fontes de pesquisa: nome de jornais e revistas, data, título da matéria e endereço dos sites

Se tiverem dificuldade durante a pesquisa, porque ela se mostrou muito complicada ou demorada, verificar novamente o tema e as fontes pesquisadas e direcionar os alunos para um tema que propicie uma coleta de dados mais acessível e esteja de acordo com a realidade em que vivem.

Comentar com os alunos que eles precisarão trazer as informações coletadas na próxima aula.

Se surgirem dificuldades na pesquisa em si, fica a seu critério dar nova orientação ou conceder um prazo maior a esse grupo.

Aula 2

O objetivo desta aula é representar informações de contextos reais por meio de tabelas. Inicialmente, pedir que os alunos se reúnam nos mesmos grupos da aula anterior. Em seguida, solicitar que preparem uma tabela com as informações da pesquisa que realizaram, recordando que uma tabela deve ter um título e a(s) fonte(s) da pesquisa. É importante que o professor percorra a sala esclarecendo eventuais dúvidas.

Quando os alunos acabarem, solicitar que apresentem o modo com que representaram a tabela. Nesse momento, realizar uma discussão, corrigindo com a turma as informações que faltarem. Levantar algumas perguntas, questionando os alunos a respeito do motivo que os levaram a escolher esse tema.

Ao final, apresentar um tema investigado por você. Esse momento é importante para os alunos perceberem que o professor também realizou uma investigação, como a representada a seguir

• Pesquisa sobre espécies brasileiras que saíram da lista das ameaçadas de extinção. Baseada em dados divulgados, em 2014, pelo Instituto Chico Mendes (ICMBio), pertencente ao Ministério do Meio Ambiente, a respeito das classes de animais a que pertencem essas espécies. Com essas informações, é possível representar a tabela a seguir.

Espécies animais brasileiras que não estão mais ameaçadas de extinção (2014)

Fonte: BRASIL. Ministério do Meio Ambiente. ICMBio MMAeICMBiodivulgamnovas listasdeespéciesameaçadasdeextinção Brasília, DF, 17 dez. 2014. Disponível em: http://www.icmbio.gov.br/portal/ultimas-noticias/4-destaques/6658-mma-e-icmbio-divulganovas-listas-de-especies-ameacadas-de-extincao Acesso em: 8 jan. 2022.

Nesse momento, questionar os alunos a respeito da temática investigada pelo professor. Questionar o que entendem por extinção e realizar uma discussão sobre esse tema, problematizando os motivos sociais que levam determinadas espécies de animais a serem extintas.

Ao final, realizar a sistematização, comentando que a tabela permite que se representem informações de maneira organizada. Discutir que essa organização passa credibilidade ao pesquisador e possibilita que diferentes pessoas interpretem as informações com mais facilidade.

Aula 3

O objetivo desta aula é representar informações de contextos reais por meio de gráficos de coluna. Para isso, organizar os alunos nos mesmos grupos definidos nas aulas anteriores e destinar um tempo para que os alunos retomem a tabela elaborada. Se necessário, estabelecer um prazo para que os alunos corrijam eventuais erros com base na discussão anteriormente realizada. Ao final dessa retomada, resgatar algumas informações sobre tabelas.

Após esse momento inicial, entregar, a cada grupo, papel quadriculado e orientá-los a construírem um gráfico de colunas com régua e lápis, para a eventualidade de precisarem corrigi-lo. Depois de pronto o gráfico, os alunos poderão pintá-lo com lápis de cor ou giz de cera. Lembrá-los de que os gráficos também devem ter título, graduação em pelo menos um eixo, legenda e fonte. Se necessário, problematizar coletivamente essas características.

Mostrar à turma as características essenciais de um gráfico de colunas. Explicar que eles têm esse nome porque as quantidades coletadas determinam a altura das colunas, as quais, por estarem na vertical, lembram colunas de construções.

Por meio de desenhos na lousa, explicar aos alunos que esse tipo de gráfico tem um eixo horizontal, ocupado pelos elementos do tema pesquisado, e um eixo vertical, ao lado do

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

qual estão as quantidades, para que se possa medir o dado numérico e traçar cada coluna de acordo com ele.

Conforme os alunos esboçam o gráfico, apresentar o gráfico da investigação realizada por você. Caso tenha adotado o exemplo da aula anterior, mostrar que o gráfico a ser desenhado com base na tabela terá no eixo horizontal o nome das classes de animais cujas espécies foram poupadas; no eixo vertical haverá uma régua, dividida em intervalos de cinco unidades ou de dezenas. Demonstrar que a malha quadriculada auxilia na construção dos gráficos, porque ela tem linhas verticais e horizontais em espaços de medida constante, nos quais se podem traçar os eixos e as colunas com facilidade.

Com os dados da tabela de exemplo, constrói-se o seguinte gráfico.

Fonte dos dados: INSTITUTO CHICO MENDES DE CONSERVAÇÃO DA BIODIVERSIDADE. MMA e ICMBio divulgam novas listas de espécies ameaçadas de extinção. Disponível em: http://www.icmbio.gov.br/portal/ultimas-noticias/4-destaques/6658-mma-e-icmbio-divulga-novaslistas-de-especies-ameacadas-de-extincao. Acesso em: 8 jan. 2022.

No exemplo anterior, os números que constam na tabela foram escritos acima das colunas para indicar a quantidade exata de determinada categoria – nesse caso, as classes de animais cujas espécies deixaram de correr risco de extinção. Os números poderiam também estar dentro de cada coluna, no entanto, quando a coluna reflete uma quantidade pequena, como em anfíbios, mamíferos e répteis, o número pode não caber dentro da coluna e ficar fora dela.

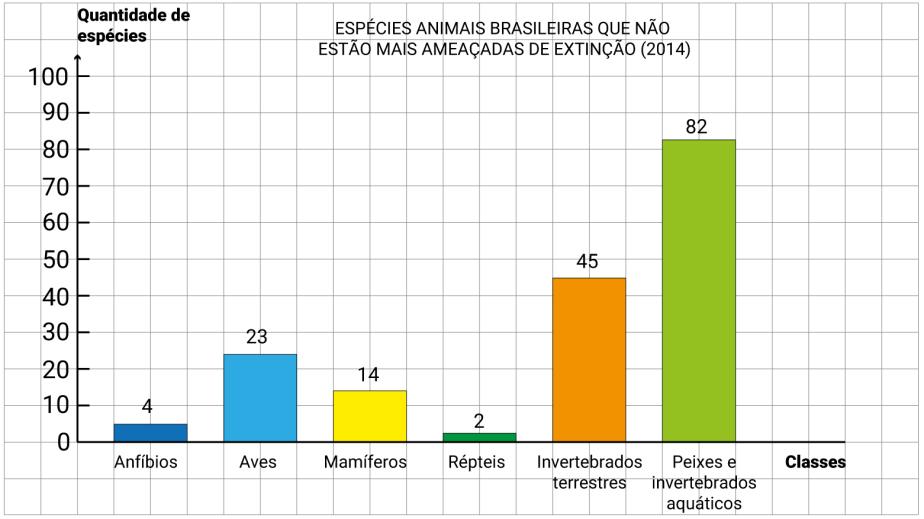
Entre outras apresentações, é possível ainda traçar uma linha horizontal de cada quantidade do eixo vertical, assim como dividir o eixo vertical em unidades, e não em dezenas. Quanto à fonte dos dados, são suficientes o endereço de internet ou o nome da publicação e data de acesso. Não se pode exigir de alunos dessa idade que façam anotações muito precisas conforme um padrão oficial.

Ao final da aula, criar uma roda de conversa, em que os alunos poderão falar sobre as experiências na composição do gráfico. Por fim, sistematizar com os alunos que os gráficos

de colunas ajudam na representação de informações de uma forma organizada. Além disso, graças à altura das colunas, é mais simples realizar comparações entre as informações.

Aula 4

O objetivo desta aula é representar informações de contextos reais por meio de gráficos de barras. Para isso, comentar que os alunos vão desenvolver um processo parecido com o das aulas anteriores. Pedir que se organizem nos mesmos grupos definidos nas três primeiras aulas. Em seguida, entregar, novamente, um papel quadriculado e propor que os alunos construam um gráfico de barras que represente as informações expressas na tabela de cada grupo. Explicar que, embora a disposição dos dados seja diferente, a construção do gráfico de barras se parece muito com a do gráfico de colunas, e devem ser mantidos o título, as legendas e a fonte.

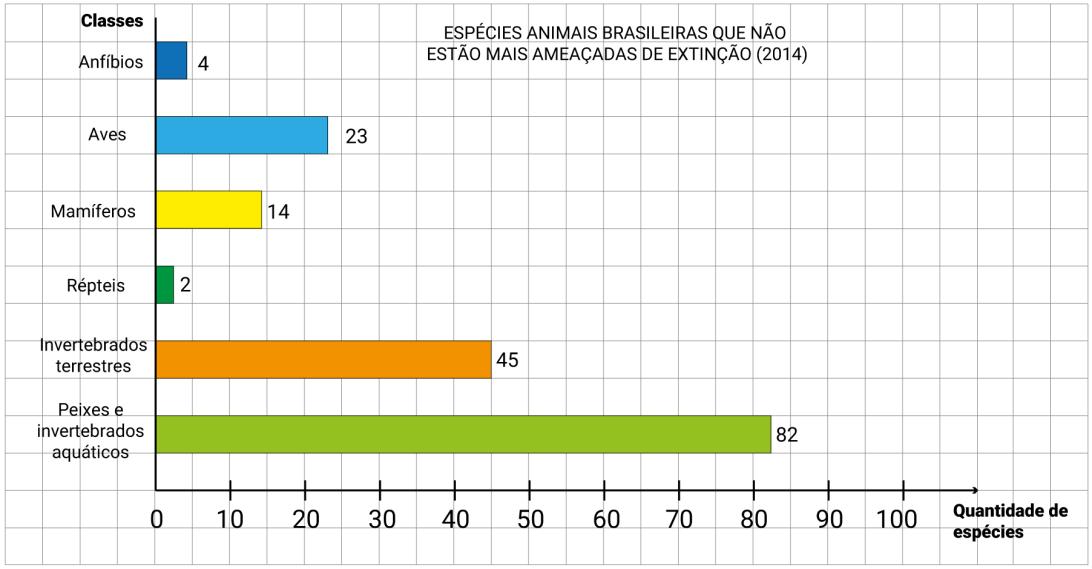
Comentar com os alunos que o gráfico de barras é definido de acordo com o comprimento das barras. Ou seja, as quantidades investigadas determinam o comprimento que cada barra terá. Além disso, explicar que, no gráfico de colunas, a disposição das informações acontece verticalmente, no de barras, as informações são representadas na horizontal. Enquanto os alunos tentam construir o gráfico, acompanhar as discussões e intervir, se for necessário.

Nesse momento, apresentar um gráfico de barras, feito com base na investigação realizada, conforme a imagem a seguir.

Fonte dos dados: INSTITUTO CHICO MENDES DE CONSERVAÇÃO DA BIODIVERSIDADE. MMA e ICMBio divulgam novas listas de espécies ameaçadas de extinção. Disponível em: http://www.icmbio.gov.br/portal/ultimas-noticias/4-destaques/6658-mma-e-icmbio-divulga-novaslistas-de-especies-ameacadas-de-extincao. Acesso em: 8 jan. 2022.

Depois que os alunos construírem o gráfico, realizar uma discussão coletiva sobre as características das três representações realizadas pelos alunos: tabela, gráfico de colunas e gráfico de barras. Se necessário, realizar correções de imprecisões que forem apresentadas

no decorrer das aulas. Pedir que os alunos registrem no caderno a comparação entre esses três tipos de representação de informações, pois ela será útil na próxima aula.

Aula 5

O objetivo desta aula é sistematizar os diferentes modos de representação de informações utilizados pelos alunos para desenvolver uma pesquisa. Para isso, solicitar que os alunos se organizem nos mesmos grupos trabalhados nas aulas anteriores. Em seguida, indicar que escrevam um relatório, contando toda a experiência desenvolvida até o momento É importante que esse relatório tenha as seguintes informações:

• os motivos que levaram os alunos a escolherem a temática;

• os gráficos e as tabelas produzidos;

• a experiência de representar informações por meio de tabelas, gráficos de colunas e gráficos de barras;

• conclusões gerais da pesquisa realizada.

Enquanto os alunos produzem o relatório, realizar intervenções, ajudando-os a organizar as ideias. Por fim, solicitar que cada grupo apresente seu relatório à turma, sistematizando as informações levantadas na pesquisa. Nesse momento, questionar os alunos se os resultados que obtiveram correspondem aos mesmos que esperavam quando estabeleceram essa temática.

Finalizar a atividade formalizando que o relatório é um instrumento muito utilizado por pesquisadores no mundo. Eles trazem a trajetória de uma pesquisa de forma detalhada e organizada. Sendo assim, os relatórios de pesquisas são fundamentais para a divulgação do conhecimento científico.

Aula 6

O objetivo desta aula é explorar o conceito de tabelas e gráficos, discutidos anteriormente, para introduzir a ideia de probabilidade. Para isso, separar a turma em grupos de quatro integrantes e entregar a cada um dos alunos um dado de seis faces. Explicar que cada grupo terá de representar, em uma única tabela, quantas vezes cada número foi sorteado nos dados.

Cada aluno deverá jogar o dado 20 vezes. Ao final dessa etapa, cada grupo terá 80 resultados. Essa quantidade "grande" de lançamentos é importante para tentar garantir que a frequência de cada resultado possível seja próxima uma da outra. Durante essa etapa, circular pela sala de aula para observar se os grupos estão anotando o resultado do lançamento dos dados corretamente e se estão preenchendo uma única tabela. Se necessário, apresentar para os alunos uma tabela de exemplo, como a representada a seguir.

Depois que todos os grupos completarem os lançamentos e preencherem a tabela, solicitar que, com o uso do papel quadriculado, construam um gráfico de colunas contendo os eventos possíveis, ou seja, as opções que podem ser tiradas no dado (1, 2, 3, 4, 5 e 6) e a quantidade de vezes que cada um desses eventos ocorreu. O gráfico ficará parecido com o representado a seguir.

É importante lembrar aos alunos que este é um experimento de probabilidade (destacar essa palavra). Então, a frequência não será exatamente a mesma para todos os eventos, e o gráfico não será o mesmo para todos os grupos.

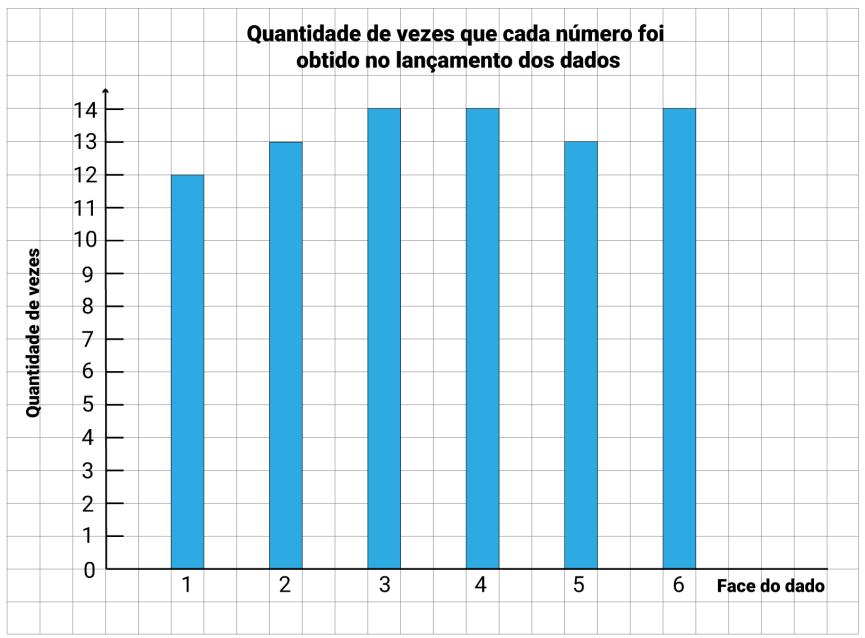
Após a montagem dos gráficos, solicitar que cada grupo indique qual face foi a mais obtida e qual a menos obtida. Em seguida, sugerir que um representante do grupo anote essas informações da lousa. Nesse momento, devem surgir respostas diferentes para cada um dos grupos. Perguntar aos alunos se os valores para cada um dos lançamentos são

Fonte: Dados fictícios.

Fonte: Dados fictícios

parecidos, que é o que se espera desse tipo de experimento, mas que também pode não ocorrer.

Guiar os alunos para que eles compreendam que, em um lançamento de dado (neste caso, aproximamos o dado real do dado honesto), cada uma das faces tem a mesma chance de ser obtida (destacar a palavra chance). Após essa atividade, recolher as folhas criadas pelos grupos, devidamente identificadas, pois elas serão utilizadas na próxima aula.

Aula 7

O objetivo desta aula é ampliar as discussões sobre probabilidade, iniciadas na aula anterior. Para isso, devolver as folhas para os grupos com o material produzido na aula anterior, certificando-se de que os grupos são os mesmos. A continuidade do trabalho de cada grupo é uma garantia de sequência de raciocínio. Caso algum aluno tenha faltado na atividade anterior, deve-se colocá-lo em algum grupo, para que ele possa, pelo menos, acompanhar o término da atividade.

Com todos os grupos em posse de seu material, entregar um dado a cada aluno e pedir que repitam o experimento da aula anterior, mas, desta vez, separando os resultados em dois eventos:

• Evento A: números menores que 3 (1 e 2);

• Evento B: números maiores ou iguais a 3 (3, 4, 5 e 6).

Lembrar aos alunos que cada um deles deve lançar o dado 20 vezes e que cada grupo deverá preencher uma única tabela. Após o preenchimento, solicitar que construam o gráfico dos dados obtidos. Tal gráfico deve ficar parecido com o representado a seguir.

Fonte: Dados fictícios.

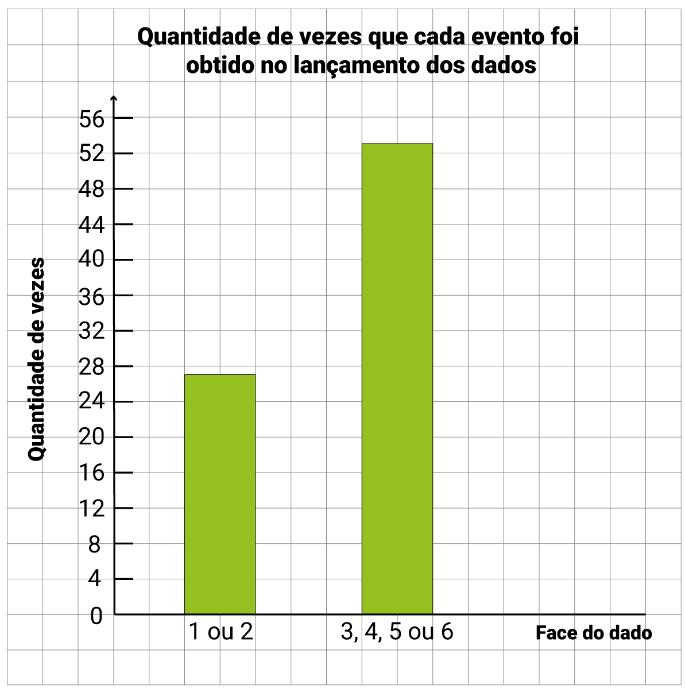
Como na aula anterior, é importante lembrar aos alunos que este é um experimento de probabilidade, então, a frequência não será exatamente a mesma para todos os eventos, e o gráfico não será o mesmo para todos os grupos.

Após a montagem dos gráficos, pedir aos alunos que comparem o gráfico da aula anterior com este gráfico. Devem surgir respostas como: a quantidade de colunas, o número máximo no eixo vertical, e, o mais importante, no primeiro gráfico as colunas eram quase da mesma altura, e, neste, as colunas têm alturas bem diferentes.

Mostrar aos alunos que o evento A tem duas possibilidades (1 ou 2), e que o evento B tem quatro possibilidades (3, 4, 5 ou 6), ou seja, há o dobro de possibilidades no evento B.

Pedir aos alunos que observem a frequência com que o evento A ocorreu, que dobrem esse valor e o comparem com a frequência com que o evento B ocorreu, e perguntar se esses valores são parecidos. Concluir esta parte da atividade com o seguinte questionamento: o evento B ocorreu aproximadamente o dobro de vezes que o evento A e o evento B tinha o dobro de possibilidades do evento A. Será que isso é uma coincidência?

Permitir aos alunos debater esse questionamento, observando, primeiro, se eles notaram a presença da palavra dobro nas duas afirmações e, em um segundo momento, as hipóteses levantadas.

Após a discussão, solicitar que façam o mesmo trabalho, mas com dois novos eventos:

• Evento C: números menores que 5 (1, 2, 3 ou 4);

• Evento D: números maiores que 4 (5 ou 6).

Guiar os alunos pelos mesmos questionamentos da situação anterior. Sempre usar o termo dobro quando se referir às quantidades, assim, os alunos terão a oportunidade de notar que a mesma proporção da situação anterior ocorreu nesta.

Para finalizar, fazer com os alunos o comparativo dos três gráficos construídos e mostrar como a chance de determinado evento aleatório acontecer depende de quantas opções possíveis compõem os eventos envolvidos e comparados.

Explicar que a questão da opção possível é fundamental mostrando a situação a seguir

1. Ao lançar um dado de seis faces numeradas de 1 a 6, o que ocorrerá com maior frequência: a face com o número 1 sair voltada para cima, ou tirar qualquer número natural maior que 6?

Um dos eventos só tem uma opção (obter o número 1); o segundo evento tem infinitas opções (qualquer número maior que 6) No entanto, não há opções possíveis no dado mencionado para números maiores que 6. Então, este é um evento impossível, independentemente da quantidade de opções que componham o evento. Logo, o evento "a face com o número 1 sair voltada para cima" terá mais chances de ocorrer, mesmo com uma única opção, pois é uma opção possível contra opções impossíveis.

O objetivo desta aula é interpretar informações em gráficos de colunas. Para isso, organizar os alunos em duplas e propor a resolução da seguinte atividade.

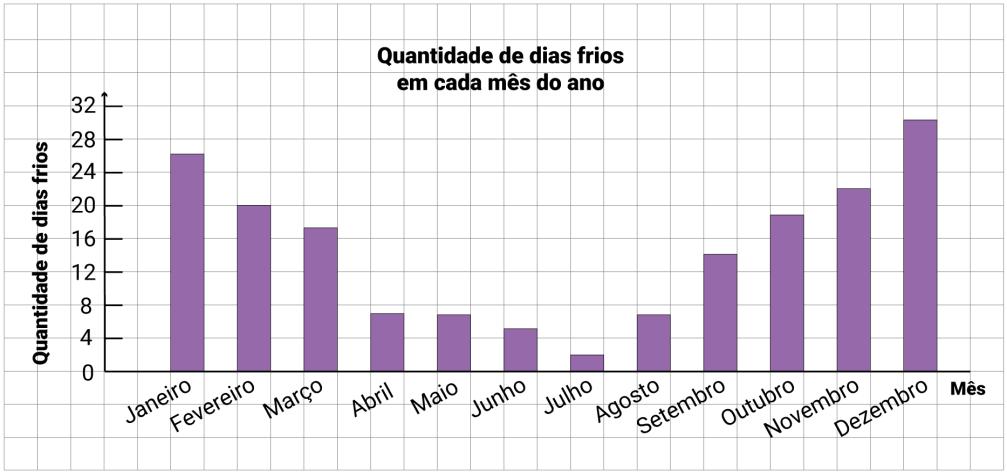
Sabe-se que as estações do ano ocorrem em períodos diferentes no hemisfério Norte e no hemisfério Sul. Por exemplo, o verão no hemisfério Sul ocorre, aproximadamente, entre dezembro e março, enquanto nessa mesma época, no hemisfério Norte, é inverno. Além disso, na primavera e no verão, há maior chance de um dia ser quente do que frio.

A seguir, estão apresentados dois gráficos: um referente a uma cidade localizada no hemisfério Sul, e outro de uma cidade localizada no hemisfério Norte.

Com base nessas informações, fazer a leitura dos gráficos e identificar qual deles tem dados da cidade localizada no hemisfério Sul e qual tem dados da cidade localizada no hemisfério Norte.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Fonte: Dados fictícios.

Fonte: Dados fictícios.

Espera-se que os alunos percebam que o primeiro gráfico representa uma cidade A, localizada no hemisfério Sul, e que o segundo gráfico representa uma cidade B, localizada no hemisfério Norte.

Para resolver esta atividade, o aluno precisará ler os títulos dos gráficos e o título do eixo vertical e lembrar-se de qual evento tem maior chance de acontecer (dias quentes ou dias frios) nas estações dos anos, e em quais meses as estações ocorrem nos dois hemisférios.

Depois que as duplas resolverem a atividade, compor grupos com duas duplas cada e solicitar que os alunos comparem suas resoluções. Ao final, realizar uma discussão coletiva, corrigindo a questão e interpretando, coletivamente, o gráfico.

Por fim, solicitar que os alunos comentem o que acharam de trabalhar com a Estatística. Dizer que esse tipo de conhecimento ajuda a interpretar diferentes situações na sociedade. Comentar, por exemplo, que em telejornais, revistas e na internet, sempre há gráficos de colunas ou tabelas. Dessa forma, ter a capacidade crítica de interpretar essas informações é essencial para uma atuação plena na sociedade.

Sugestões

• LEITE, Catalina. Ceará lidera alfabetização no Brasil e é o melhor no Nordeste em relação ao 9º ano. O Povo, 5 nov. 2020. Disponível em:

https://www.opovo.com.br/noticias/ceara/2020/11/05/ceara-lidera-alfabetizacao-brasilmelhor-nordeste-em-relacao-ao-9---ano.html. Acesso em: 19 maio 2021.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

Relatórios e indicadores do acompanhamento da aprendizagem

O processo avaliativo exige do professor um olhar reflexivo permanente sobre o desenvolvimento da aprendizagem dos alunos e, consequentemente, sobre a sua própria prática pedagógica. Dessa forma, instrumentos de avaliação, como provas, testes, questionários, redações, trabalhos, seminários, entre outros, não devem ser encarados como instrumentos pontuais de avaliação, mas, sim, como ferramentas de coleta de indicadores que descrevem o desempenho dos alunos e possibilitam uma análise coletiva e individual dos avanços e dos pontos de melhoria da aprendizagem.

Os indicadores de aprendizagem devem auxiliar o professor no acompanhamento do desenvolvimento das aprendizagens dos alunos, apontando se os objetivos, as competências, as habilidades e os conteúdos previstos em seu plano de trabalho estão sendo alcançados ou se há necessidade de intervenção no processo de aprendizagem para que possam ser atingidos

Esses indicadores de aprendizagem, isoladamente nada apontam, uma vez que os resultados são fruto da análise do professor com base em objetivos, competências e habilidades desenvolvidos em determinado contexto educacional. Assim, com o apoio da avaliação dos indicadores de aprendizagem, é necessário que sejam produzidos relatórios descritivos das análises, considerações e observações a respeito do processo de aprendizado e desenvolvimento dos alunos e de sua prática pedagógica em sala de aula

Produção de relatórios

Os relatórios escolares são registros que devem ser realizados periodicamente (a cada bimestre, trimestre ou semestre) a respeito do desenvolvimento de diferentes aprendizagens dos alunos ao longo do processo de ensino-aprendizagem.

Dentro do processo de aprendizagem escolar, os relatórios, entre outras finalidades, deverão:

• Possibilitar ao educador compreender de forma significativa o processo de aprendizagem dos alunos, respeitando suas individualidades, particularidades e diferenças.

• Produzir informações e dados significativos sobre o processo de aprendizagem de modo a planejar intervenções pedagógicas com base em objetivos, conteúdos, competências e habilidades a serem desenvolvidos.

• Fornecer subsídios teóricos para as reuniões de conselho de classe para que professores, coordenadores pedagógicos e diretores da escola possam analisar o desempenho individual e coletivo dos alunos e, consequentemente, discutir formas,

ações, intervenções, estratégias e métodos de melhoria do processo de ensino-aprendizagem com base no Projeto Político Pedagógico da escola.

• Realizar uma comunicação orientada, assertiva e planejada com pais ou responsáveis de modo a engajá-los no processo de aprendizagem, contribuindo desse modo para o desenvolvimento dos alunos e a efetividade do ensino.

• Proporcionar ao aluno o direito de acompanhar o próprio processo de aprendizagem, de modo a oportunizar a superação de suas dificuldades.

Apesar de não existir um modelo fixo de relatório a ser seguido, alguns pontos importantes podem ser considerados na elaboração desse material. O texto do relatório deverá ser escrito de forma clara, concisa e objetiva, de modo que o leitor o compreenda. Devem ser registrados os conteúdos trabalhados e como foram avaliados, assim como todas as considerações julgadas pertinentes ao processo de ensino-aprendizagem. É importante, também, descrever quais foram os encaminhamentos adotados em caso de dificuldade dos alunos.

Se possível, os relatórios devem ainda captar as diferentes dimensões envolvidas nas experiências dos alunos no grupo, ou seja, devem trazer aspectos relacionados a sentimentos, afetos, emoções, movimentos e cognição.

Os relatórios podem conter apresentações visuais e gráficas dos dados coletados, de modo a facilitar a compreensão das informações que estão sendo transmitidas. Pode-se elaborar um gráfico de barras comparando a distribuição percentual dos resultados quantitativos da aprendizagem dos alunos a respeito de competências gerais, de competências específicas e de habilidades em um período, como no exemplo a seguir.

Fonte: Dados fictícios.

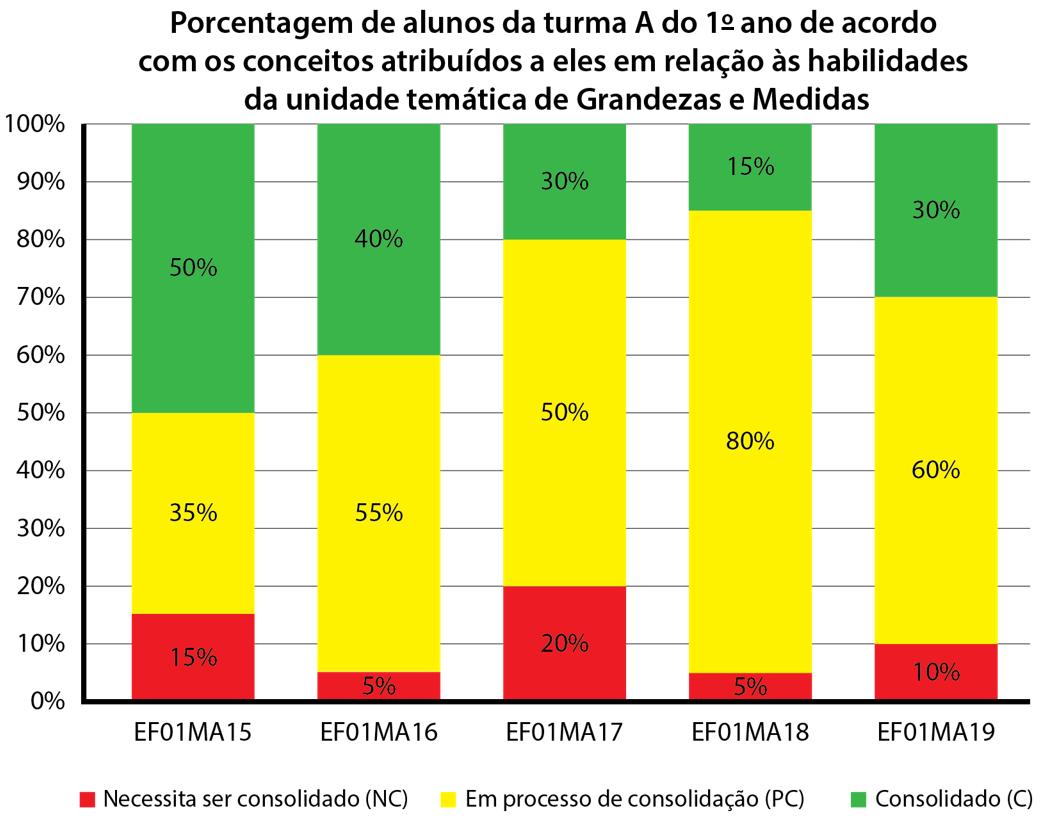
Gráficos e tabelas podem ser elaborados por meio de um editor de planilhas eletrônicas, como o LibreOffice, que é um software livre e gratuito, disponível em: https://www.libreoffice.org/discover/libreoffice/ (acesso em: 10 dez. 2021).

Indicadores do acompanhamento da aprendizagem

De modo geral, o termo "indicadores" é usado para apontar parâmetros que avaliam certa realidade em determinado intervalo de tempo. Um médico, por exemplo, examina vários indicadores antes de oferecer um diagnóstico a um paciente. Um economista, também, se utiliza de indicadores para analisar se a inflação de um país aumentou ou diminuiu. Já no contexto escolar, os indicadores do acompanhamento da aprendizagem têm como objetivo mapear os diferentes níveis de desenvolvimento das aprendizagens dos alunos.

Uma vez que o processo de aprendizagem ocorre simultânea e interativamente nas dimensões cognitiva, afetiva e psicomotora, os indicadores de aprendizagem a serem observados e avaliados deverão abarcar aspectos tanto quantitativos quanto qualitativos do processo de aprendizagem dos alunos, garantindo, assim, uma visão ampla e significativa desse processo.

Os aspectos qualitativos dos indicadores de aprendizagem, geralmente, são aqueles ligados às competências gerais e socioemocionais que expressam a voz, as percepções, as crenças, os sentimentos, os pensamentos, as emoções, as atitudes e os modos de agir dos educandos. São eles que possibilitam ao educador avaliar se os alunos alcançaram a construção e a formação de atitudes e valores, como autonomia, responsabilidade, empatia, resiliência, determinação, criticidade e capacidade de ouvir, ser ouvido e dialogar.

Já os aspectos quantitativos dos indicadores de aprendizagem são aqueles que descrevem quantidades ou percentuais da consecução do processo de ensino-aprendizagem. São esses aspectos quantitativos que permitem ao professor fazer uma avaliação do quanto os alunos estão avançando em relação aos objetivos, competências, habilidades e conteúdos, gerais ou específicos, de determinada área do conhecimento, previstos em seu plano de trabalho.

São apresentados, a seguir, quatro modelos de fichas com sugestões de indicadores que podem ser obtidos por meio do processo avaliativo que julgar mais conveniente. Esses modelos podem ser impressos e preenchidos com os dados dos alunos ou da turma.

O primeiro modelo é o de Ficha de avaliação diagnóstica Nela, estão presentes alguns indicadores que poderão servir de subsídio para que seja reconhecido o domínio dos alunos a respeito de alguns conteúdos, no início do ano letivo.

O segundo modelo é o de Fichadeacompanhamentodasaprendizagens, na qual são apresentadas as habilidades da BNCC indicadas para o ano de escolaridade, as Competências específicas de Matemática para o Ensino Fundamental, as Competências gerais da Educação Básica e os componentes essenciais para a alfabetização. Nela, há uma coluna para preenchimento de observações mais detalhadas.

O terceiro modelo é o de Ficha de verificação de resultados, em que estão indicados, a cada ano de escolaridade, alguns objetivos de aprendizagem categorizados como focais, por influenciarem de modo mais evidente o desenvolvimento vinculado às Competências gerais e às Competências específicas da área de Matemática para o Ensino Fundamental.

Por fim, considerando a ideia de educação integral, também é preciso avaliar o desenvolvimento das dimensões sociais e emocionais dos alunos. Para tanto, o quarto modelo é o de Ficha de acompanhamento do desenvolvimento de competências socioemocionais, que apresenta indicadores para que seja apontada a frequência com que essas competências são reconhecidas nas atitudes dos alunos.

Os modelos de fichas aqui apresentados são apenas proposições para apoiar o processo de ensino-aprendizagem. É fundamental que o trabalho pedagógico seja planejado com intencionalidade para explorar todos os potenciais de aprendizagem e garantir as condições de desenvolvimento pleno e integral de cada aluno. Essa tarefa requer a participação de toda a comunidade escolar, envolvendo professores, gestores e os responsáveis pelos alunos

RECURSO EDUCACIONAL DIGITAL

Ficha de avaliação diagnóstica

Professor:

Turma:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de avaliação diagnóstica

Números Álgebra Geometria Grandezas e medidas Estatística

Aluno Identificar características do Sistema de Numeração Decimal com base na composição e decomposição de números naturais até 999.

Utilizar fatos básicos da adição e da subtração no cálculo mental ou escrito e na resolução de problemas envolvendo números naturais até 999.

Identificar regularidades e elementos ausentes em sequências.

Reconhecer características de figuras geométricas planas (círculo, quadrado, retângulo e triângulo).

Reconhecer características de figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone, cilindro e esfera).

Estabelecer equivalência de valores entre moedas e cédulas do sistema monetário brasileiro para resolver situações do dia a dia.

Registrar, estimar e comparar medidas de comprimento, usando unidades não padronizadas e padronizadas.

Comparar informações de pesquisas apresentadas por meio de tabelas e gráficos.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de acompanhamento das aprendizagens

Professor:

Turma:

Aluno:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de acompanhamento das aprendizagens (Matemática)

Habilidades C PC NC Observações

(EF03MA01) Ler, escrever e comparar números naturais de até a ordem de unidade de milhar, estabelecendo relações entre os registros numéricos e em língua materna.

(EF03MA02) Identificar características do sistema de numeração decimal, utilizando a composição e a decomposição de número natural de até quatro ordens.

(EF03MA03) Construir e utilizar fatos básicos da adição e da multiplicação para o cálculo mental ou escrito.

(EF03MA04) Estabelecer a relação entre números naturais e pontos da reta numérica para utilizá-la na ordenação dos números naturais e também na construção de fatos da adição e da subtração, relacionando-os com deslocamentos para a direita ou para a esquerda.

(EF03MA05) Utilizar diferentes procedimentos de cálculo mental e escrito, inclusive os convencionais, para resolver problemas significativos envolvendo adição e subtração com números naturais.

(EF03MA06) Resolver e elaborar problemas de adição e subtração com os significados de juntar, acrescentar, separar, retirar, comparar e completar quantidades, utilizando diferentes estratégias de cálculo exato ou aproximado, incluindo cálculo mental.

(EF03MA07) Resolver e elaborar problemas de multiplicação (por 2, 3, 4, 5 e 10) com os significados de adição de parcelas iguais e elementos apresentados em disposição retangular, utilizando diferentes estratégias de cálculo e registros.

(EF03MA08) Resolver e elaborar problemas de divisão de um número natural por outro (até 10), com resto zero e com resto diferente de zero, com os significados de repartição equitativa e de medida, por meio de estratégias e registros pessoais.

(EF03MA09) Associar o quociente de uma divisão com resto zero de um número natural por 2, 3, 4, 5 e 10 às ideias de metade, terça, quarta, quinta e décima partes.

(EF03MA10) Identificar regularidades em sequências ordenadas de números naturais, resultantes da realização de adições ou subtrações sucessivas, por um mesmo número, descrever uma regra de formação da sequência e determinar elementos faltantes ou seguintes.

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

(EF03MA11) Compreender a ideia de igualdade para escrever diferentes sentenças de adições ou de subtrações de dois números naturais que resultem na mesma soma ou diferença.

(EF03MA12) Descrever e representar, por meio de esboços de trajetos ou utilizando croquis e maquetes, a movimentação de pessoas ou de objetos no espaço, incluindo mudanças de direção e sentido, com base em diferentes pontos de referência.

(EF03MA13) Associar figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone, cilindro e esfera) a objetos do mundo físico e nomear essas figuras.

(EF03MA14) Descrever características de algumas figuras geométricas espaciais (prismas retos, pirâmides, cilindros, cones), relacionando-as com suas planificações.

(EF03MA15) Classificar e comparar figuras planas (triângulo, quadrado, retângulo, trapézio e paralelogramo) em relação a seus lados (quantidade, posições relativas e comprimento) e vértices.

(EF03MA16) Reconhecer figuras congruentes, usando sobreposição e desenhos em malhas quadriculadas ou triangulares, incluindo o uso de tecnologias digitais.

(EF03MA17) Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.

(EF03MA18) Escolher a unidade de medida e o instrumento mais apropriado para medições de comprimento, tempo e capacidade.

(EF03MA19) Estimar, medir e comparar comprimentos, utilizando unidades de medida não padronizadas e padronizadas mais usuais (metro, centímetro e milímetro) e diversos instrumentos de medida.

(EF03MA20) Estimar e medir capacidade e massa, utilizando unidades de medida não padronizadas e padronizadas mais usuais (litro, mililitro, quilograma, grama e miligrama), reconhecendo-as em leitura de rótulos e embalagens, entre outros.

(EF03MA21) Comparar, visualmente ou por superposição, áreas de faces de objetos, de figuras planas ou de desenhos.

(EF03MA22) Ler e registrar medidas e intervalos de tempo, utilizando relógios (analógico e digital) para informar os horários de início e término de realização de uma atividade e sua duração.

(EF03MA23) Ler horas em relógios digitais e em relógios analógicos e reconhecer a relação entre hora e minutos e entre minuto e segundos.

(EF03MA24) Resolver e elaborar problemas que envolvam a comparação e a equivalência de valores monetários do sistema brasileiro em situações de compra, venda e troca.

(EF03MA25) Identificar, em eventos familiares aleatórios, todos os resultados possíveis, estimando os que têm maiores ou menores chances de ocorrência.

(EF03MA26) Resolver problemas cujos dados estão apresentados em tabelas de dupla entrada, gráficos de barras ou de colunas.

(EF03MA27) Ler, interpretar e comparar dados apresentados em tabelas de dupla entrada, gráficos de barras ou de colunas, envolvendo resultados de

pesquisas significativas, utilizando termos como maior e menor frequência, apropriando-se desse tipo de linguagem para compreender aspectos da realidade sociocultural significativos.

(EF03MA28) Realizar pesquisa envolvendo variáveis categóricas em um universo de até 50 elementos, organizar os dados coletados utilizando listas, tabelas simples ou de dupla entrada e representá-los em gráficos de colunas simples, com e sem uso de tecnologias digitais.

Competências específicas de Matemática para o Ensino Fundamental C PC NC Observações

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Competências gerais da Educação Básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Componentes essenciais para a alfabetização

Consciência fonológica e fonêmica

Conhecimento alfabético

Fluência em leitura oral

Desenvolvimento de vocabulário

Compreensão de textos

Produção de escrita

C PC NC Observações

Ficha de verificação de resultados

Professor:

Turma:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de verificação de resultados

Principais objetivos de aprendizagem

Aluno Analisar e descrever características de figuras geométricas espaciais, como cubo, bloco retangular, pirâmide, cone, cilindro e esfera.

Classificar e comparar figuras geométricas planas (triângulo, quadrado, retângulo, trapézio e paralelogramo) em relação a seus lados (quantidade, posições relativas e comprimento) e vértices.

Ler, escrever, comparar, compor e decompor números naturais até 9 999.

Resolver e elaborar problemas de adição e de subtração.

Problemas envolvendo diferentes significados da multiplicação (adição de parcelas iguais e configuração retangular) e da divisão (repartição em partes iguais e medida).

Construir fatos básicos da multiplicação para utilizar no cálculo mental ou escrito.

Medidas de capacidade e medidas de massa: registro, estimativas e comparações.

Ler, interpretar e representar dados em tabelas e gráficos de barras.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Professor:

Turma:

Aluno:

Competências socioemocionais Sempre Frequentemente Raramente Nunca

Determinação

Foco

Organização

Persistência

Responsabilidade

Empatia

Respeito

Confiança

Tolerância ao estresse

Autoconfiança

Tolerância à frustração

Iniciativa social

Assertividade

Entusiasmo

Curiosidade para aprender

Imaginação criativa

Interesse artístico

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Catálogo dos audiovisuais

Nesta seção, são disponibilizados detalhamentos, como objetivos de aprendizagem e conteúdos abordados, entre outros aspectos, acerca de cada um dos audiovisuais que compõem a coletânea desta coleção. Também, para cada audiovisual, são descritas sugestões de utilização e são sugeridas propostas de atividades, a fim de apoiar pedagogicamente o uso desses recursos digitais audiovisuais. Tais informações visam trazer insumos para favorecer o planejamento de aplicação deles de acordo com a realidade da comunidade escolar e da turma com que forem trabalhados.

Audiovisuais da coletânea

Relação de audiovisuais da coletânea

Figuras geométricas espaciais

Neste audiovisual, são apresentadas figuras geométricas espaciais, seus elementos e objetos do mundo físico que lembram essas figuras.

• Associar figuras geométricas espaciais a objetos do mundo físico.

• Nomear figuras geométricas espaciais.

• Identificar e analisar características de algumas figuras geométricas espaciais

Praticando a adição

Neste recurso educacional, é explorada a operação de adição. Nele, é resolvido um problema de adição utilizando o material dourado e o algoritmo da adição.

• Reconhecer a importância das operações matemáticas em situações do dia a dia.

• Identificar características do sistema de numeração decimal.

• Resolver problemas de adição com o apoio do material dourado.

• Resolver problemas de adição utilizando o algoritmo da adição.

• Sistema de numeração decimal.

• Adição

• Figuras geométricas espaciais

O litro e o decímetro cúbico Neste audiovisual, são exploradas as medidas de capacidade e as unidades de medida padronizadas (litro e mililitro). Além disso, é ampliado o trabalho ao explorar a unidade de medida de volume (decímetro cúbico), estabelecendo relações de equivalência entre litro e decímetro cúbico.

Estamparia geométrica

Neste audiovisual, são exploradas as figuras geométricas planas e a congruência entre figuras. São apresentadas, ainda, as tradições culturais de alguns povos do continente africano, como o símbolo Adinkra dos povos Acã, e as estampas Bogolan, um tipo de tingimento natural da região do Mali.

Nossas origens Neste recurso educacional, é abordada a realização de uma pesquisa. É apresentada uma situação em que uma criança faz uma entrevista para verificar suas origens familiares ao realizar um trabalho sobre as origens da população brasileira.

• Reconhecer a utilização da unidade de medida de capacidade em diferentes situações do dia a dia.

• Identificar equivalências entre as unidades de medida litro e decímetro cúbico.

• Medidas de capacidade

• Unidades de medidas de capacidade

• Reconhecer figuras geométricas planas em diferentes obras de arte.

• Reconhecer figuras congruentes.

• Figuras geométricas planas

• Congruência entre figuras geométricas planas

• Reconhecer os processos migratórios e seus impactos para a formação do Brasil.

• Reconhecer uma das etapas de uma pesquisa.

• Questões históricas referentes à formação do Brasil.

• Pesquisa.

Orientações para o uso dos audiovisuais

Figuras geométricas espaciais

Este audiovisual pode ser apresentado de maneira introdutória ao estudo de figuras geométricas espaciais. Nele, são apresentadas figuras geométricas espaciais, seus elementos e objetos do mundo físico que lembram essas figuras.

Sugere-se que este audiovisual seja exibido como introdução ao conteúdo. Se julgar oportuno, fazer pausas logo após o momento em que são apresentados os elementos de algumas dessas figuras, como as dimensões de uma caixa e as faces de figuras geométricas espaciais. Explicar aos alunos que a base da pirâmide pode ter diferentes formas: triangular, quadrada, entre outras

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Após o término da apresentação, sugere-se perguntar aos alunos o que aprenderam com o audiovisual e o que mais gostaram do que foi apresentado. Perguntar a eles sobre as características de cada figura geométrica espacial apresentada e, em seguida, solicitar que indiquem alguns objetos da sala de aula cuja forma lembra a de alguma dessas figuras geométricas.

Caso seja possível, pedir aos alunos para levarem para a aula, em um momento posterior, embalagens vazias cujas formas lembram as figuras geométricas estudadas. Nesta aula, explorar as características desses objetos, fazendo relação com as figuras geométricas espaciais. Perguntar a eles se alguma dessas embalagens lembra um corpo redondo e quais as características dele

Em seguida, sugere-se a resolução das atividades propostas a seguir ou de atividades semelhantes

Sugestões de atividades

1. Contorne as figuras geométricas espaciais a seguir que são chamadas corpos redondos.

EDITORIA DE ARTE

Esfera, cilindro e cone.

2. Escreva o nome de cada figura geométrica espacial a seguir.

EDITORIA DE ARTE

Bloco retangular

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

EDITORIA DE ARTE

Cubo.

EDITORIA DE ARTE

Cilindro

EDITORIA DE ARTE

Esfera

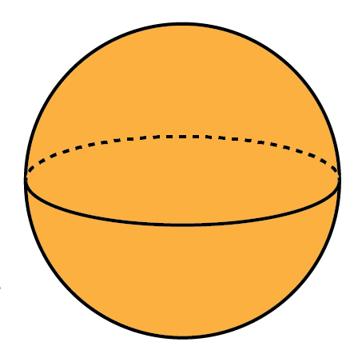
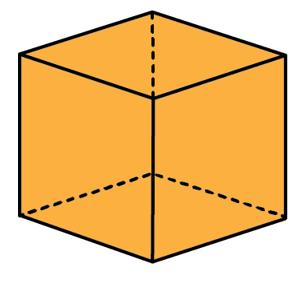
Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Cone

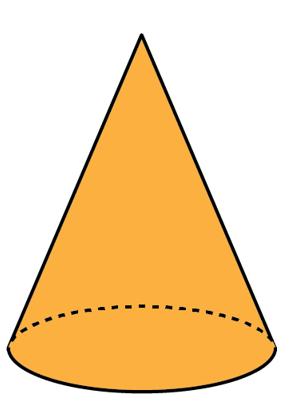
3. Desenhe um objeto que lembra cada figura geométrica espacial a seguir.

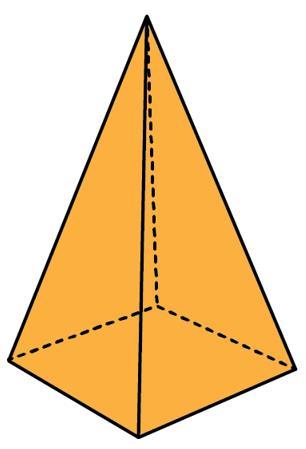
Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

4. Leia o texto a seguir e contorne a figura a qual o texto se refere

Sou uma figura geométrica espacial. Tenho 6 faces e todas as minhas faces são quadradas. Quem sou eu? EDITORIA

Cubo.

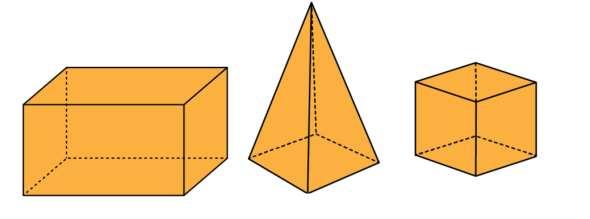
Praticando a adição

Este recurso educacional pode ser apresentado de maneira introdutória ao estudo da adição com reagrupamento. Nele, é resolvido um problema de adição utilizando o material dourado e o algoritmo da adição. Se for possível, levar o material dourado para ser explorado durante a aula.

Caso o recurso educacional seja utilizado como introdução ao estudo de adição com reagrupamento, fazer uma pausa logo após a representação dos valores com o material dourado Perguntar aos alunos o motivo pelo qual foram utilizadas aquelas quantidades de peças. Se for necessário, retomar a relação entre cada peça do material dourado com a centena, a dezena e a unidade. Em seguida, perguntar como seria a representação de outros números por meio do material dourado, por exemplo, 23, 57, 336 e 441.

Fazer outra pausa após a troca envolvendo dezenas e centenas. Perguntar aos alunos o motivo pelo qual foi utilizada aquela estratégia e, se julgar necessário, refazer a troca com o apoio do material dourado. Ainda utilizando o material dourado, mostrar aos alunos 3 dezenas (3 barras) e 15 unidades (15 cubinhos) e pedir a eles que representem essa quantidade numericamente. Observar que, nesse caso, eles precisarão fazer a troca de 10 unidades (10 cubinhos) por 1 dezena (1 barra), ficando com 4 dezenas e 5 unidades, ou seja, 45.

Apresentar outras situações semelhantes para o aluno se familiarizar com esse tipo de "troca" e, caso não seja possível levar o material dourado para a aula, utilizar a lousa para a explicação. É importante que, ao citar as peças do material dourado, seja utilizada a nomenclatura centenas, dezenas e unidades.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Depois, pausar logo após a resolução da operação com o algoritmo. Refazer, com os alunos, o passo a passo utilizado para verificar se compreenderam e, se julgar necessário, retomar o passo a passo da operação com o apoio do material dourado, relacionando as etapas das duas estratégias.

Em seguida, sugere-se a resolução das atividades propostas a seguir ou de atividades semelhantes. As atividades propostas exploram representação numérica, "trocas", adição utilizando o material dourado e adição utilizando o algoritmo.

Sugestões de atividades

1. Represente, utilizando algarismos, as quantidades indicadas a seguir

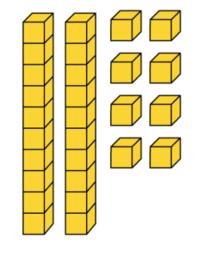
2. Calcule as adições a seguir com o apoio do material dourado.

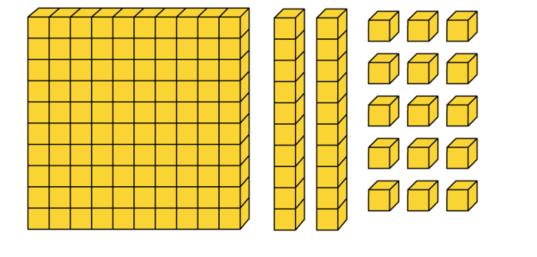
a) 237 + 121

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

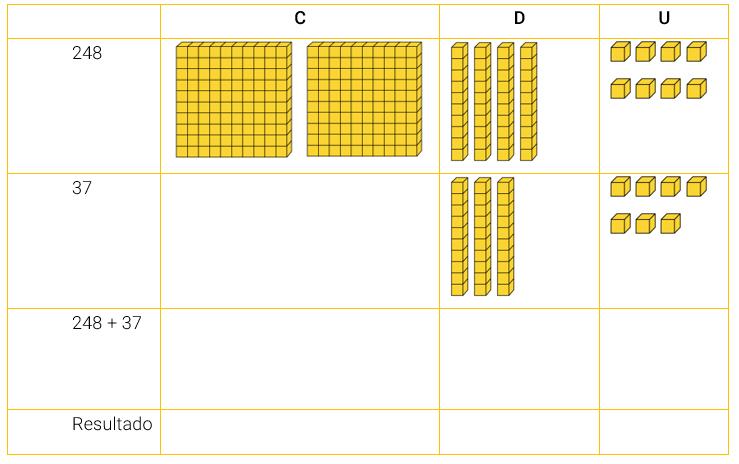
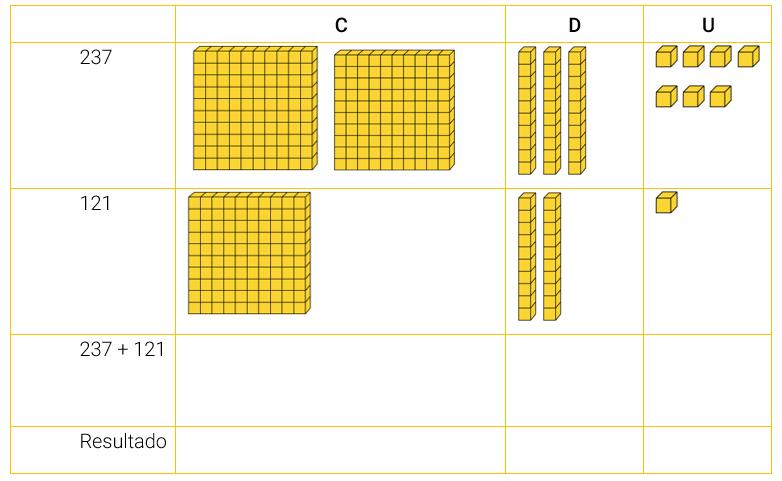
Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

3. Calcule as adições a seguir utilizando o algoritmo da adição.

a) 128 + 55

b) 337 + 149 486

O litro e o decímetro cúbico

Este audiovisual pode ser utilizado como revisão do estudo de medidas de capacidade e das unidades de medida padronizadas Nele, os alunos entrarão em contato com medidas de capacidade e as unidades de medida padronizadas (litro e mililitro). Além disso, é ampliado o trabalho ao explorar a medida de volume decímetro cúbico, estabelecendo relações de equivalência entre litro e decímetro cúbico.

Iniciar a aula apresentando o audiovisual aos alunos Logo após a narração "Você já deve ter comprado um refrigerante de dois litros, ou levou um suco de um litro num piquenique ou usou duzentos mililitros de leite numa receita de bolo.", fazer uma pausa e perguntar aos alunos:

• Quais produtos utilizados no dia a dia são vendidos em litro?

• Quais produtos utilizados no dia a dia são vendidos em mililitro?

Escrever na lousa os produtos que os alunos mencionarem, organizando-os em duas colunas, uma com os produtos vendidos em litro e outra com os vendidos em mililitro. Em seguida, com a ajuda da turma, verificar se algum produto foi classificado de forma incorreta e fazer as correções necessárias.

Se possível, mostrar para a turma imagens de embalagens de iogurte, remédio, água, detergente, entre outras, em que é apresentado o mililitro como medida de capacidade, para que os alunos reconheçam a utilização dessa medida e percebam a Matemática como uma ferramenta de compreensão do mundo físico.

Se julgar oportuno, propor aos alunos que assistam a um vídeo, disponível em: https://www.youtube.com/watch?v=3ojA2MKMoGA (acesso em: 12 jan. 2022), que aborda a importância da padronização das medidas para a sociedade. Posteriormente, dar continuidade àexibição do vídeo. Ao finalizar a exibição, sugere-se a resolução das atividades propostas a seguir ou de atividades semelhantes.

Sugestões de atividades

1. Complete as frases a seguir com litros ou mililitros.

a)Essa garrafa contém 350 de suco

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

b) Na piscina inflável que a mãe de Joana comprou cabem 1 400

c) Juliana precisa tomar 25 de xarope.

d) Camila quer comprar um copo de caldo de cana com 500 ______.

Resposta: a) mililitros, b) litros, c) mililitros, d) mililitros.

2. Para encher um aquário de 3 litros, Letícia vai utilizar um recipiente com capacidade para 600 mL. De quantos recipientes cheios ela vai precisar para encher completamente o aquário?

Espera-se que os alunos respondam que ela vai precisar de 5 recipientes cheios, pois 600 mL x 5 = 3 000 mL e 3 000 mL é equivalente a 3 L.

3. Catarina e Lívia foram ao mercado e compraram bebidas para levar ao piquenique da escola. Catarina comprou três garrafinhas de suco de 200 mL e Lívia comprou quatro garrafinhas de 120 mL. Qual delas comprou mais de meio litro de suco, ou seja, mais de 500 mL?

Espera-se que os alunos respondam que Catarina comprou mais de meio litro de suco, pois ela comprou 600 mL que é maior que 500 mL. Lívia comprou 480 mL que é menor que 500 mL.

200 mL x 3 = 600 mL

120 mL x 4 = 480 mL

Estamparia geométrica

Este audiovisual pode ser utilizado como revisão do estudo das figuras geométricas planas e da congruência entre figuras Nele, são apresentadas as tradições culturais de alguns povos do continente africano, como o símbolo Adinkra dos povos Acã e as estampas Bogolan, um tipo de tingimento natural da região do Mali.

Se julgar oportuno, para ampliar o trabalho com este audiovisual, sugere-se propor aos professores de Geografia e de História a realização de um projeto que tenha como objetivo possibilitar aos alunos conhecer o continente africano e sua cultura. Isso contribui para o conhecimento, também, da história e da cultura afro-brasileira, o que favorece o desenvolvimento de uma educação para a valorização do multiculturalismo nas matrizes históricas e culturais

Iniciar a aula apresentando o audiovisual aos alunos Após a citação das inspirações para a confecção das estampas Bogolan e das imagens demonstradas de tecidos com essas estampas, fazer uma pausa e perguntar aos alunos: com quais figuras geométricas alguns dos desenhos que formam a estampa do tecido se parecem? Nas imagens, há figuras com o mesmo formato e com o mesmo tamanho? Essas figuras são idênticas? Aproveitar o momento para explorar com os alunos a ideia de congruência entre figuras.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Após a exploração das figuras geométricas planas e da congruência de figuras, dar continuidade à exibição do vídeo. Ao finalizar a exibição, sugere-se a resolução das atividades propostas a seguir ou de atividades semelhantes.

Sugestões de atividades

1. Observe as figuras a seguir e faça o que se pede.

EDITORIA DE ARTE

a) Escreva o nome das figuras representadas anteriormente

A: quadrado, B: retângulo, C: círculo; D: triângulo.

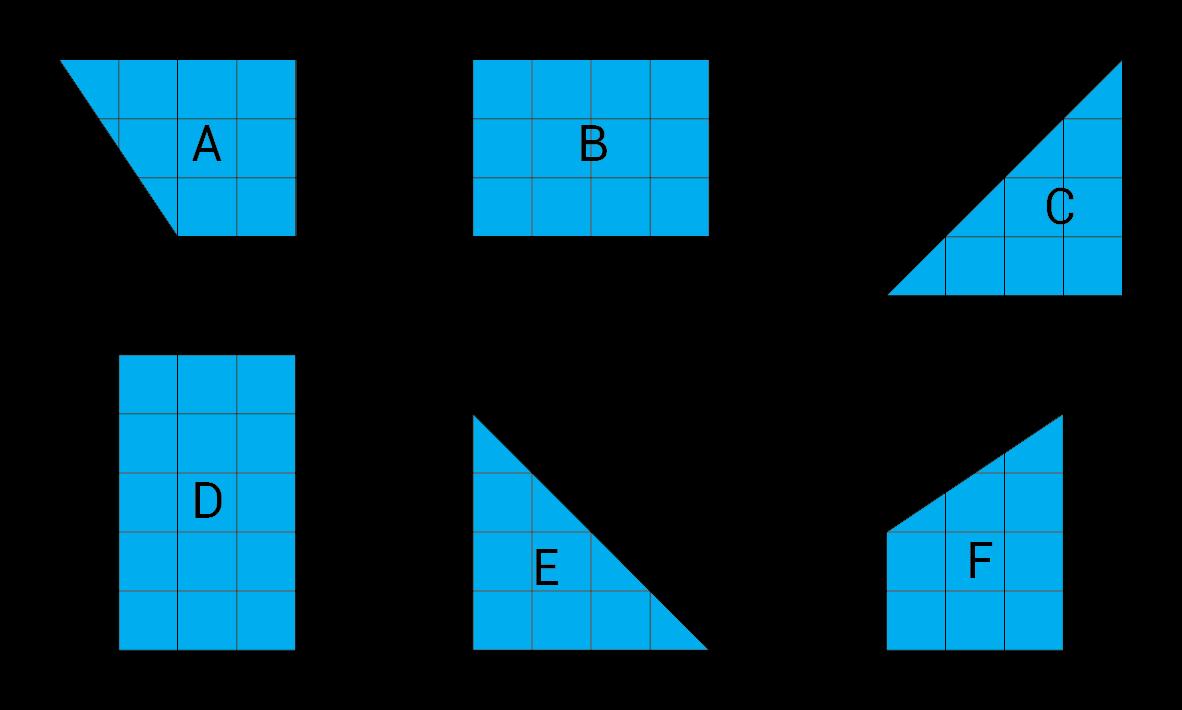
b) Escreva o número de lados e de vértices das figuras A, B e D.

A: 4 lados e 4 vértices; B: 4 lados e 4 vértices; C: 3 lados e 3 vértices

2. Observe as figuras representadas na malha quadriculada a seguir. EDITORIA DE ARTE

• Quais dessas figuras são idênticas? Justifique.

A e F; E e C. Espera-se que os alunos respondam que as figuras são idênticas, pois possuem o mesmo tamanho e forma, sendo diferentes apenas na posição.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

3. Em uma folha de papel quadriculada, construa pares de figuras geométricas planas idênticas e em posições diferentes. Em seguida, troque a folha com o colega para que ele identifique os pares de figuras idênticas que você desenhou e faça o mesmo com a que receber. Ao final, confiram juntos as respostas.

Resposta pessoal.

Nossas origens

Este recurso educacional pode ser utilizado como revisão do trabalho com a realização de pesquisa, organização de dados coletados utilizando tabelas e representação desses dados por meio de gráficos Nele, é apresentada uma situação em que uma criança faz uma entrevista para verificar suas origens familiares ao realizar um trabalho sobre as origens da população brasileira.

Se julgar oportuno, propor ao professor de História que amplie o trabalho com esse recurso educacional ao explorar a unidade temática "As pessoas e os grupos que compõem a cidade e o município".

Para iniciar a aula, conversar com os alunos sobre a importância das pesquisas estatísticas Comentar que os resultados dessas pesquisas estão presente em diferentes situações do cotidiano, influenciando na tomada de decisão. Em seguida, perguntar à turma: quais são as etapas de uma pesquisa? Como podemos organizar os dados coletados em uma pesquisa? Deixar que os alunos compartilhem o que sabem sobre o assunto e comentar sobre a importância do planejamento para a execução de uma pesquisa. Se julgar oportuno, escrever, com o auxílio dos alunos, as etapas de uma pesquisa na lousa, conforme exemplo a seguir.

• Elaborar perguntas sobre o tema que se deseja investigar.

• Escolher o grupo de pessoas que vai participar da pesquisa.

• Realizar as entrevistas.

• Organizar e representar os dados coletados em tabelas ou gráficos.

Posteriormente, dar continuidade à exibição do vídeo. Ao finalizar, sugere-se a resolução das atividades propostas a seguir ou de atividades semelhantes.

Sugestões de atividades

1 Uma professora de Língua Portuguesa das turmas do 3º ano fez uma pesquisa para saber quais os gêneros literários preferidos dos alunos e organizou os dados coletados no gráfico a seguir. Observe o gráfico em que cada quadradinho representa 5 alunos e responda às questões a seguir.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

a) O que cada coluna do gráfico representa?

A quantidade de alunos que preferem cada gênero literário

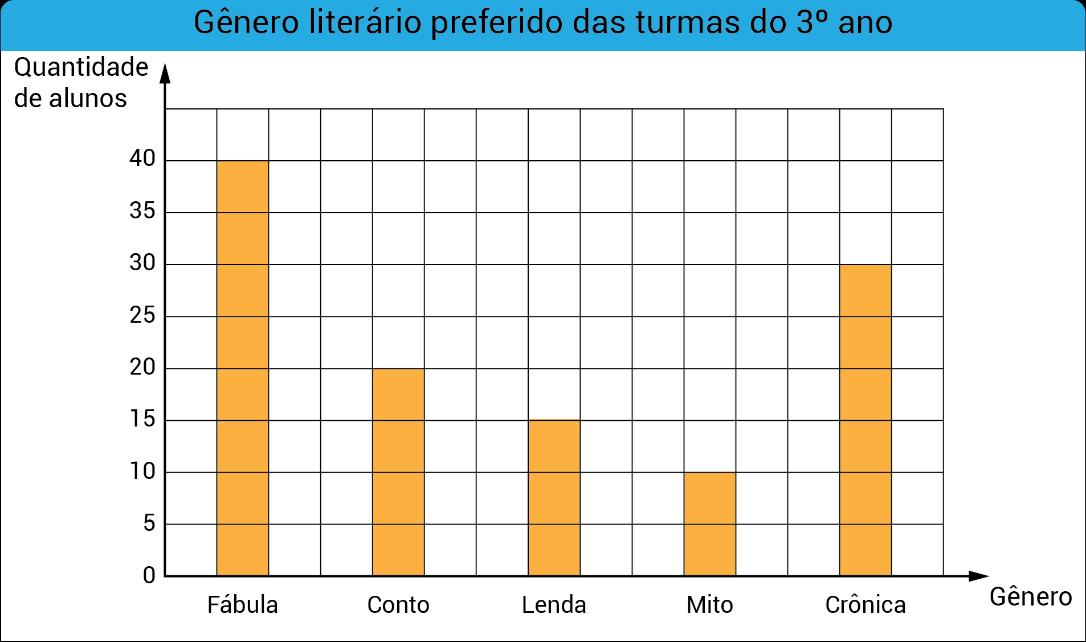
b) Qual é o gênero literário que foi escolhido com maior frequência? E qual foi o escolhido com menor frequência?

Fábula. Mito.

2. A escola em que Laura estuda está desenvolvendo um projeto chamado "Cantina Saudável", que busca promover uma alimentação balanceada e saudável para seus alunos. Para elaborar o cardápio, a nutricionista da escola fez uma pesquisa para saber quais as frutas preferidas dos alunos. Observe os resultados dessa pesquisa na tabela a seguir

Fonte: Alunos

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

Fonte: Turmas do 3º ano.

• Complete o gráfico de colunas a seguir para representar os dados apresentados na tabela anterior. Para cada 10 votos, pinte um quadradinho.

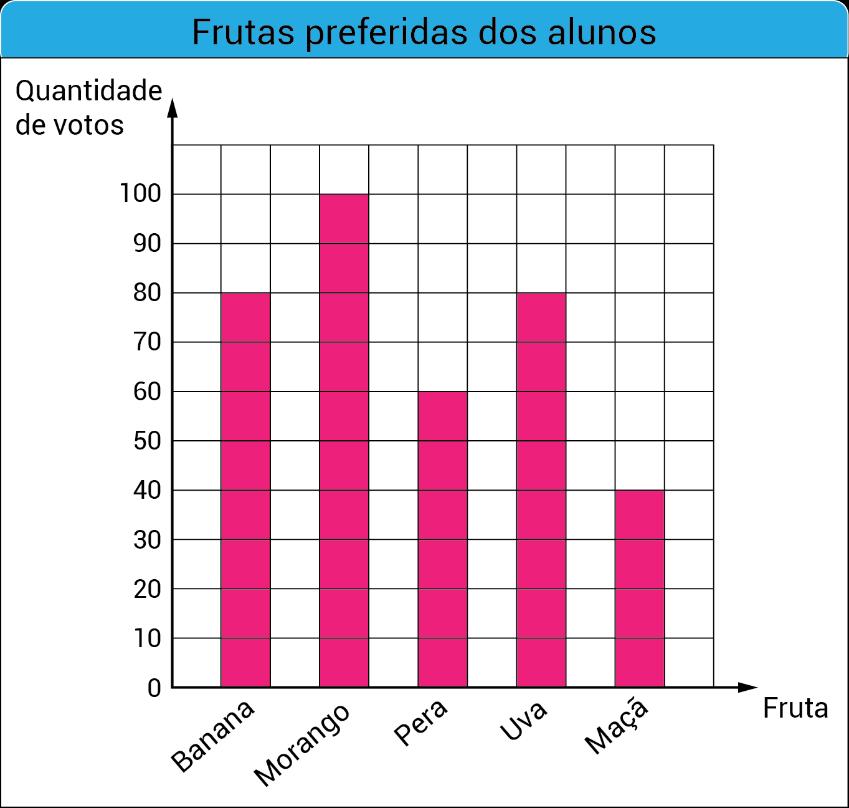
Resposta:

Fonte: Alunos da escola

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

Fonte: Alunos da escola

3. O funcionário de um museu fez um levantamento para saber a quantidade de visitantes na exposição "Biomas brasileiros" nos dois últimos meses de 2021. Observe os dados obtidos na tabela a seguir.

Visitantes da exposição "Biomas brasileiros" nos dois últimos meses de 2021

a) Em qual mês a quantidade de mulheres que visitaram essa exposição do museu foi maior que a de homens? Em qual mês foi menor?

Novembro. Dezembro

b) Em qual mês mais pessoas visitaram essa exposição do museu?

Dezembro.

Novembro 96 (34 + 62 = 96)

Dezembro 95 (53 + 45 = 98)

c) Qual é a quantidade total de pessoas que visitaram essa exposição do museu nos dois últimos meses?

194 pessoas (96 + 98 = 194).

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

BNCC

A Base Nacional Comum Curricular (BNCC), homologada em 2018, é um documento oficial e normativo sobre as aprendizagens (e suas progressões) da Educação Básica (Ensino Infantil, Ensino Fundamental e Ensino Médio). A BNCC estrutura as etapas de aprendizagens em competências, mais abrangentes, e habilidades, mais específicas; e, dessa forma, objetiva garantir a progressão das aprendizagens entre os diferentes anos/ciclos da Educação Básica.

A BNCC tem como objetivo assegurar o direito de uma aprendizagem de qualidade a todos os alunos, buscando colaborar com a formação de uma sociedade mais justa, democrática e inclusiva. Seu caráter normativo colabora com esse objetivo, ao ser um documento que orienta a elaboração e a revisão de currículos, a formação inicial e continuada de professores e as avaliações e exames nacionais.

A seguir, são apresentadas na íntegra as Competências gerais da Educação Básica, as Competências específicas da área de Matemática e suas Tecnologias para o Ensino Fundamental e as cinco unidades temáticas com os respectivos objetos de conhecimento e habilidades para o 3º ano do Ensino Fundamental, que podem ser encontrados nas páginas 9, 10, 267, 286, 287, 288 e 289 da BNCC (BRASIL, 2018).

Competências gerais da Educação Básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Competências específicas de Matemática para o Ensino Fundamental

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Matemática – 3º ano

Unidades temáticas Objetos de conhecimento Habilidades

Números Leitura, escrita, comparação e ordenação de números naturais de quatro ordens

(EF03MA01) Ler, escrever e comparar números naturais de até a ordem de unidade de milhar, estabelecendo relações entre os registros numéricos e em língua materna

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Composição e decomposição de números naturais

Construção de fatos fundamentais da adição, subtração e multiplicação Reta numérica

(EF03MA02) Identificar características do sistema de numeração decimal, utilizando a composição e a decomposição de número natural de até quatro ordens.

(EF03MA03) Construir e utilizar fatos básicos da adição e da multiplicação para o cálculo mental ou escrito.

(EF03MA04) Estabelecer a relação entre números naturais e pontos da reta numérica para utilizá-la na ordenação dos números naturais e também na construção de fatos da adição e da subtração, relacionando-os com deslocamentos para a direita ou para a esquerda.

Procedimentos de cálculo (mental e escrito) com números naturais: adição e subtração

Problemas envolvendo significados da adição e da subtração: juntar, acrescentar, separar, retirar, comparar e completar quantidades

Problemas envolvendo diferentes significados da multiplicação e da divisão: adição de parcelas iguais, configuração retangular, repartição em partes iguais e medida

(EF03MA05) Utilizar diferentes procedimentos de cálculo mental e escrito, inclusive os convencionais, para resolver problemas significativos envolvendo adição e subtração com números naturais.

(EF03MA06) Resolver e elaborar problemas de adição e subtração com os significados de juntar, acrescentar, separar, retirar, comparar e completar quantidades, utilizando diferentes estratégias de cálculo exato ou aproximado, incluindo cálculo mental.

(EF03MA07) Resolver e elaborar problemas de multiplicação (por 2, 3, 4, 5 e 10) com os significados de adição de parcelas iguais e elementos apresentados em disposição retangular, utilizando diferentes estratégias de cálculo e registros.

(EF03MA08) Resolver e elaborar problemas de divisão de um número natural por outro (até 10), com resto zero e com resto diferente de zero, com os significados de repartição equitativa e de medida, por meio de estratégias e registros pessoais.

Significados de metade, terça parte, quarta parte, quinta parte e décima parte

Álgebra Identificação e descrição de regularidades em sequências numéricas recursivas

Relação de igualdade

Geometria Localização e movimentação: representação de objetos e pontos de referência

(EF03MA09) Associar o quociente de uma divisão com resto zero de um número natural por 2, 3, 4, 5 e 10 às ideias de metade, terça, quarta, quinta e décima partes.

(EF03MA10) Identificar regularidades em sequências ordenadas de números naturais, resultantes da realização de adições ou subtrações sucessivas, por um mesmo número, descrever uma regra de formação da sequência e determinar elementos faltantes ou seguintes.

(EF03MA11) Compreender a ideia de igualdade para escrever diferentes sentenças de adições ou de subtrações de dois números naturais que resultem na mesma soma ou diferença.

(EF03MA12) Descrever e representar, por meio de esboços de trajetos ou utilizando croquis e maquetes, a movimentação de pessoas ou de objetos no espaço,

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone, cilindro e esfera): reconhecimento, análise de características e planificações

incluindo mudanças de direção e sentido, com base em diferentes pontos de referência.

(EF03MA13) Associar figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone, cilindro e esfera) a objetos do mundo físico e nomear essas figuras.

(EF03MA14) Descrever características de algumas figuras geométricas espaciais (prismas retos, pirâmides, cilindros, cones), relacionando-as com suas planificações.

Figuras geométricas planas (triângulo, quadrado, retângulo, trapézio e paralelogramo): reconhecimento e análise de características

Congruência de figuras geométricas planas

Grandezas e medidas Significado de medida e de unidade de medida

(EF03MA15) Classificar e comparar figuras planas (triângulo, quadrado, retângulo, trapézio e paralelogramo) em relação a seus lados (quantidade, posições relativas e comprimento) e vértices.

(EF03MA16) Reconhecer figuras congruentes, usando sobreposição e desenhos em malhas quadriculadas ou triangulares, incluindo o uso de tecnologias digitais.

(EF03MA17) Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.

(EF03MA18) Escolher a unidade de medida e o instrumento mais apropriado para medições de comprimento, tempo e capacidade.

Medidas de comprimento (unidades não convencionais e convencionais): registro, instrumentos de medida, estimativas e comparações

Medidas de capacidade e de massa (unidades não convencionais e convencionais): registro, estimativas e comparações

Comparação de áreas por superposição

Medidas de tempo: leitura de horas em relógios digitais e analógicos, duração de eventos e reconhecimento de relações entre unidades de medida de tempo

(EF03MA19) Estimar, medir e comparar comprimentos, utilizando unidades de medida não padronizadas e padronizadas mais usuais (metro, centímetro e milímetro) e diversos instrumentos de medida.

(EF03MA20) Estimar e medir capacidade e massa, utilizando unidades de medida não padronizadas e padronizadas mais usuais (litro, mililitro, quilograma, grama e miligrama), reconhecendo-as em leitura de rótulos e embalagens, entre outros.

(EF03MA21) Comparar, visualmente ou por superposição, áreas de faces de objetos, de figuras planas ou de desenhos.

(EF03MA22) Ler e registrar medidas e intervalos de tempo, utilizando relógios (analógico e digital) para informar os horários de início e término de realização de uma atividade e sua duração.

(EF03MA23) Ler horas em relógios digitais e em relógios analógicos e reconhecer a relação entre hora e minutos e entre minuto e segundos.

Sistema monetário brasileiro: estabelecimento de equivalências de um mesmo valor na utilização de diferentes cédulas e moedas

(EF03MA24) Resolver e elaborar problemas que envolvam a comparação e a equivalência de valores monetários do sistema brasileiro em situações de compra, venda e troca.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial

(CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Probabilidade e estatística

Análise da ideia de acaso em situações do cotidiano: espaço amostral

Leitura, interpretação e representação de dados em tabelas de dupla entrada e gráficos de barras

(EF03MA25) Identificar, em eventos familiares aleatórios, todos os resultados possíveis, estimando os que têm maiores ou menores chances de ocorrência.

(EF03MA26) Resolver problemas cujos dados estão apresentados em tabelas de dupla entrada, gráficos de barras ou de colunas.

(EF03MA27) Ler, interpretar e comparar dados apresentados em tabelas de dupla entrada, gráficos de barras ou de colunas, envolvendo resultados de pesquisas significativas, utilizando termos como maior e menor frequência, apropriando-se desse tipo de linguagem para compreender aspectos da realidade sociocultural significativos.

Coleta, classificação e representação de dados referentes a variáveis categóricas, por meio de tabelas e gráficos

(EF03MA28) Realizar pesquisa envolvendo variáveis categóricas em um universo de até 50 elementos, organizar os dados coletados utilizando listas, tabelas simples ou de dupla entrada e representá-los em gráficos de colunas simples, com e sem uso de tecnologias digitais.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial

(CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Referências bibliográficas comentadas

• AMANCIO, Daniel de Traglia; SANZOVO, Daniel Trevisan. Ensino de Matemática por meio das tecnologias digitais. Revista Educação Pública, v. 20, n. 47, 8 dez. 2020. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/20/47/ensino-de-matematica-pormeio-das-tecnologias-digitais. Acesso em: 5 jan. 2022.

No artigo, é apresentada uma discussão sobre as contribuições da utilização das tecnologias digitais no ensino-aprendizagem de Matemática.

• BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática. 6. ed. Belo Horizonte: Autêntica, 2019. (Coleção Tendências em educação matemática).

No livro, os autores apresentam resultados de um trabalho sobre informática educativa, como questões pedagógicas sobre o uso do computador e da calculadora.

• CARAÇA, Bento de Jesus. Conceitos fundamentais da Matemática Lisboa: Gradiva, 1991.

O livro oportuniza ao leitor entrar em contato com ideias e práticas para o desenvolvimento de aulas de Matemática.

• COLL, César; TEBEROSKY, Ana. Aprendendo Matemática São Paulo: Ática, 2000.

No livro, são apresentados conceitos matemáticos de diversos campos, compreendendo estruturas e ideias fundamentais.

• EVES, Howard. Introdução à história da Matemática Tradução de Hygino H Domingues. Campinas: Editora da Unicamp, 2004.

Na obra, são apresentados tópicos importantes da história da Matemática.

• GAUTHIER, Clermont; BISSONNETTE, Steve; RICHARD, Mario. Ensino explícito e desempenho dos alunos Tradução de Stephania Matousek. Petrópolis: Vozes, 2014.

Os autores do livro se propõem a oferecer aos leitores detalhamento da prática docente por meio das ideias do ensino explícito.

• IFRAH, Georges. História universal dos algarismos: a inteligência dos homens contada pelos números e pelo cálculo. Tradução de Alberto Muñoz e Ana Beatriz Katinsky. Rio de Janeiro: Nova Fronteira, 1997. v. 1

O livro tem enfoque no desenvolvimento de sistemas de numeração ao longo do tempo, em particular o Sistema de Numeração Decimal.

• LOPES, Maria Laura M Leite. Tratamento da informação: explorando dados estatísticos e noções de probabilidade a partir de séries iniciais. Rio de Janeiro: Instituto de Matemática/UFRJ-Projeto Fundão, 2005.

No livro, a autora propõe apoiar o professor no ensino de conceitos relacionados à estatística e à probabilidade nos Anos Iniciais do Ensino Fundamental.

• LUCKESI, Cipriano C Avaliação da aprendizagem escolar: estudos e proposições. 22. ed. São Paulo: Cortez, 2011.

No livro, são apresentados estudos críticos sobre avaliação escolar, possibilitando ao educador refletir sobre sua prática avaliativa.

• MACHADO, Nílson José. Matemática e língua materna: análise de uma impregnação mútua. 5. ed. São Paulo: Cortez, 2001.

O autor apresenta uma reflexão sobre a relação entre o alfabeto e o Sistema de Numeração Decimal, com o objetivo de contribuir com o ensino da Matemática.

• MORAN, José Manuel; MASETTO, Marcos Tarciso; BEHRENS, Marilda Aparecida. Novas tecnologias e mediação pedagógica. 21. ed. Campinas: Papirus, 2013. (Coleção Papirus Educação)

No livro, é abordada uma reflexão sobre a inserção da informática e da telemática na educação.

• NEVES, Iara Conceição Bitencourt etal Ler e escrever: compromisso de todas as áreas. 9.ed. Porto Alegre: Editora da UFRGS, 2011.

No livro, são discutidas questões relacionadas à leitura e à escrita nos textos dos diferentes componentes curriculares, inclusive na Matemática.

• POLYA, George. A arte de resolver problemas: um novo aspecto do método matemático. Tradução de Heitor Lisboa de Araújo. Rio de Janeiro: Interciência, 1995.

O autor apresenta reflexões sobre a resolução de problemas e propostas didáticas práticas para o trabalho com problemas em sala de aula.

• SANT'ANA, Claudinei de Camargo; AMARAL, Rúbia Barcelos; BORBA, Marcelo de Carvalho. O uso de softwaresna prática profissional do professor de Matemática.

Revista Ciência & Educação, Bauru, v. 18, n. 3, p. 527-542, 2012. Disponível em: https:// www.scielo.br/j/ciedu/a/ZHkPf6xCR57XCR5tW736FYB/?lang=pt. Acesso em: 10 dez. 2021.

Os autores apresentam uma discussão sobre a incorporação de softwaresna prática docente.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

• TOLEDO, Marília; TOLEDO, Mauro. Teoria e prática de Matemática: como dois e dois. São Paulo: FTD, 2010.

Os autores apresentam informações relevantes sobre o processo de ensino-aprendizagem da Matemática, como reflexões com base em práticas de sala de aula.

Documentos oficiais

• BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília: SEB, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pd f. Acesso em: 5 jan. 2022.

Documento de caráter normativo que define o conjunto de aprendizagens essenciais que os alunos devem desenvolver ao longo das etapas e modalidades da educação básica, de modo que tenham assegurados seus direitos de aprendizagem e desenvolvimento

• BRASIL. Ministério da Educação. PNA: Política Nacional de Alfabetização. Brasília: Sealf, 2019. Disponível em: http://alfabetizacao.mec.gov.br/images/pdf/caderdo_final_pna.pdf. Acesso em: 5 jan. 2022.

O documento instituído pelo Ministério da Educação, por meio da Secretaria de Alfabetização (Sealf), apresenta políticas que visam melhorar os processos de alfabetização e combater o analfabetismo no Brasil

• BRASIL. Ministério da Educação. Relatório Nacional de Alfabetização Baseada em Evidências (Renabe). Brasília: Sealf, 2020. Disponível em: http://alfabetizacao.mec.gov.br/images/pdf/renabe_web.pdf. Acesso em: 5 jan. 2022.

Relatório que apresenta pesquisas recentes sobre alfabetização, literacia e numeracia e cujo objetivo é contribuir para a melhoria nas políticas públicas e nas práticas de ensino no Brasil.

Leituras complementares para o professor

• FERREIRA, Mariana K Leal. Ideias matemáticas de povos culturalmente distintos São Paulo: Global, 2002. (Série antropologia e educação).

No livro, são reunidos relatos de atividades matemáticas aplicadas em diversos países, possibilitando ao leitor refletir sobre sua prática docente.

• LINDQUIST, Mary Montgomery; SHULTE, Albert P. (org.). Aprendendo e ensinando Geometria Tradução de Hygino H Domingues. São Paulo: Atual, 1994.

A obra contém artigos relevantes sobre o ensino-aprendizagem da Geometria em diferentes faixas etárias.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

• MONTEIRO, Alexandrina; POMPEU JUNIOR, Geraldo. A Matemática e os temas transversais São Paulo: Moderna, 2001.

Os autores propõem reflexões sobre os temas transversais, com especial atenção às aulas de Matemática

• SOUZA, Eliane R. de etal A Matemática das sete peças do tangram. 2. ed. São Paulo: Caem/IME-USP, 1997.

No livro, há textos e atividades para serem desenvolvidas com o tangramnas aulas de Matemática.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos