Entrelaços - Matemática - Volume 5

ÁREA: MATEMÁTICA

COMPONENTE: MATEMÁTICA

JOAMIR SOUZA ANGÉLICA REGHIN 5

ENSINO FUNDAMENTAL ANOS INICIAIS

MATEMÁTICA

RECURSO

EDUCACIONAL DIGITAL

5o ANO ENSINO FUNDAMENTAL ANOS INICIAIS

MATEMÁTICA

Joamir Roberto de Souza

Mestre em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Especialista em Estatística pela Universidade Estadual de Londrina (UEL-PR).

Licenciado em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professor de Matemática da rede pública de ensino.

Autor de livros didáticos para o Ensino Fundamental e para o Ensino Médio.

Maria Angélica Reghin de Souza

Especialista em Gestão Escolar pela Universidade Norte do Paraná (Unopar).

Licenciada em Pedagogia pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora na Educação Infantil.

Autora de livros didáticos para o Ensino Fundamental.

ÁREA: MATEMÁTICA COMPONENTE: MATEMÁTICA

RECURSO EDUCACIONAL DIGITAL

Entrelaços – Matemática – Recurso Educacional Digital – 5o ano (Ensino Fundamental – Anos Iniciais)

Copyright © Joamir Roberto de Souza, Maria Angélica Reghin de Souza, 2021

Direção-geral Ricardo Tavares de Oliveira

Direção de Conteúdo e Negócios Cayube Galas

Direção editorial adjunta Luiz Tonolli

Gerência editorial Natalia Taccetti

Edição Nubia de Cassia de Moraes Andrade e Silva (coord.)

Leticia Mancini Martins, João Alves de Souza Neto

Preparação e revisão de textos Viviam Moreira (sup.)

Adriana Périco, Caline Devèze, Camila Cipoloni, Carina Luca, Fernanda Marcelino, Fernando Cardoso, Graziele Ribeiro, Paulo José Andrade

Gerência de produção e arte Ricardo Borges

Design Daniela Máximo (coord.)

Arte e produção Isabel Cristina Corandin Marques (coord.)

Coordenação de imagens e textos Elaine Bueno Koga

Licenciamento de textos Erica Brambilla

Iconografia Priscilla Narciso

Coordenação de audiovisuais Diego Vieira Cury Morgado de Oliveira

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil) Souza, Joamir Roberto de Entrelaços [livro eletrônico] : matemática : 5o ano : ensino fundamental : anos iniciais / Joamir Roberto de Souza, Maria Angélica Reghin de Souza. – 1. ed. – São Paulo : FTD, 2021.

PDF

Área: Matemática.

Componente: Matemática.

ISBN 978-85-96-03227-8 (recurso educacional digital professor – coleção)

1. Matemática (Ensino fundamental) I. Souza, Maria Angélica Reghin de. II. Título. 21-90779 CDD-372.7

Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Cibele Maria Dias - Bibliotecária - CRB-8/9427

EDITORA FTD

Rua Rui Barbosa, 156 – Bela Vista – São Paulo-SP CEP 01326-010 – Tel. 0800 772 2300 Caixa Postal 65149 – CEP da Caixa Postal 01390-970 www.ftd.com.br central.relacionamento@ftd.com.br

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Carta ao professor

Olá, professor! Seja bem-vindo ao Recurso Educacional Digital!

Este Recurso Educacional Digital tem como objetivo fornecer subsídios e sugestões que apoiem o trabalho pedagógico e a ação educativa em sala de aula no ensino da Matemática para os Anos Iniciais do Ensino Fundamental. O material oferece diferentes instrumentos de ampliação e intervenção que propiciam um ambiente de trocas, comunicação e diálogo, estimulam o levantamento de hipóteses e promovem a construção gradativa de conceitos e procedimentos matemáticos.

Neste material, são propostas situações de ensino-aprendizagem que favorecem a investigação, a experimentação, a criação de registros, a manipulação de objetos e as brincadeiras, permitindo aos alunos compreender que a Matemática não é um conhecimento restrito à sala de aula.

Os conteúdos e propostas de atividades que compõem este material também possibilitam o desenvolvimento das habilidades da Base Nacional Comum Curricular (BNCC), das competências específicas da área de Matemática e suas Tecnologias para o Ensino Fundamental, das competências gerais da Educação Básica, dos objetivos de aprendizagem e dos componentes essenciais para a alfabetização propostos na Política Nacional de Alfabetização (PNA).

Este material digital está organizado em quatro recursos pedagógicos descritos a seguir.

Plano de desenvolvimento anual

O Plano de desenvolvimento anual apresenta um quadro com uma programação de como os conteúdos podem ser organizados e trabalhados durante o ano letivo, seja em bimestres, trimestres ou semestres. Também, apresenta as habilidades da BNCC e os componentes essenciais para a alfabetização que podem ser trabalhados no período. Esse quadro é uma sugestão de programação, tendo o professor autonomia para adaptá-lo à realidade e às necessidades da turma.

O Plano de desenvolvimento apresenta, ainda: textos sobre estratégias e atitudes docentes que podem contribuir para alcançar os objetivos de aprendizagem estabelecidos; uma reflexão sobre avaliação e como esse instrumento pode auxiliar o processo de ensino-aprendizagem; e sugestões de leitura e sitesque podem aprimorar o trabalho docente em sala de aula.

Sequências didáticas

As sequências didáticas são sugestões de planejamento aula a aula que têm como objetivos complementar e aprofundar os conteúdos contemplados em outros materiais

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

didáticos e, consequentemente, contribuir com o desenvolvimento das habilidades e das competências específicas da área de Matemática e suas Tecnologias, das competências gerais da Educação Básica e dos componentes essenciais para a alfabetização. Além disso, essas sequências também podem contribuir para a remediação de eventuais dificuldades de aprendizagem dos alunos.

Com relação a sua estrutura, cada sequência didática é composta de um texto de introdução, dos objetivos de aprendizagem, do planejamento das aulas, de um passo a passo descritivo com sugestões metodológicas de como desenvolver as aulas, de exemplos de atividades que podem ser propostas aos alunos e de orientações de como acompanhar o desenvolvimento das aprendizagens em diferentes momentos.

Relatórios e indicadores do acompanhamento da aprendizagem

Os relatórios e indicadores do acompanhamento da aprendizagem têm como objetivo oferecer ao professor subsídios para acompanhar a aprendizagem dos alunos de maneira individual e coletiva, bem como apresentar orientações sobre como sistematizar os dados e apresentá-los aos pares, aos gestores escolares e aos responsáveis pelos alunos.

Esse relatório é composto de quatro fichas:

• Ficha de avaliação diagnóstica: possibilita avaliar os conhecimentos prévios dos alunos sobre determinados conteúdos e verificar a proficiência em algumas habilidades e competências.

• Ficha de acompanhamento das aprendizagens: possibilita avaliar o aprendizado e o progresso do aluno durante o processo de ensino-aprendizagem e fornece dados que permitem ao professor avaliar esse processo e ajustar a prática docente.

• Ficha de verificação dos resultados: possibilita avaliar quais objetivos de aprendizagem estabelecidos foram alcançados ao final do ano letivo.

• Ficha de acompanhamento para o desenvolvimento de habilidades socioemocionais: possibilita avaliar a evolução dos alunos em relação às habilidades socioemocionais.

É importante destacar a autonomia do professor para avaliar como essas fichas devem ser aplicadas e adaptadas de acordo com a realidade dos seus alunos e da escola na qual leciona e como elas podem complementar os diferentes instrumentos de avaliação e de acompanhamento de aprendizagem já utilizados.

Catálogo de audiovisuais

O catálogo de audiovisuais apresenta um descritivo de cada um dos audiovisuais que acompanham o Recurso Educacional Digital e tem como objetivo complementar e aprofundar o trabalho com os conteúdos explorados nesse material.

Além disso, oferece encaminhamentos à autonomia do professor, permitindo que, por meio de uma reflexão sobre as características da sua turma e do seu planejamento, seja possível estabelecer a melhor maneira de utilizar os audiovisuais. Para isso, o catálogo

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

apresenta sugestões de como esses audiovisuais podem ser trabalhados, bem como propostas de atividades que possibilitam explorar o uso desses recursos com os alunos.

No volume do 5º ano, são trabalhados os seguintes temas:

• Os números naturais de até seis ordens;

• Números na forma de fração e na forma decimal;

• Adição e subtração com números naturais;

• Multiplicação e divisão com números naturais;

• Localização e deslocamento;

• Figuras geométricas planas e espaciais;

• Grandezas e medidas;

• Probabilidade e estatística.

Esperamos que este material contribua para o aprimoramento da sua prática docente e para a formação de alunos aptos a viver em sociedade, fazendo valer seus direitos e exercendo seus deveres individuais e coletivos.

Bom trabalho!

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Instrumentos pedagógicos

Plano de desenvolvimento anual

Este Plano de desenvolvimento anual consiste em um instrumento pedagógico que tem como objetivo auxiliar o planejamento docente na gestão dos conteúdos a serem apresentados ao longo de um ano letivo.

Para isso, em um primeiro momento, são apresentadas propostas de organização semestral, trimestral e bimestral, ordenadas em um quadro.

No quadro, a fim de favorecer a visualização da progressão das aprendizagens, constam, em colunas:

• a descrição sequencial de distribuição dos conteúdos;

• a indicação dos códigos alfanuméricos das habilidades da Base Nacional Comum Curricular (BNCC);

• a nomeação dos componentes essenciais para a alfabetização, de acordo com a Política Nacional de Alfabetização (PNA).

É importante considerar que o plano de ação sugerido nesta proposta pode ser adaptado à realidade escolar interna (infraestrutura, características da turma, entre outros aspectos) e à realidade escolar externa (parceria com os responsáveis dos alunos) da instituição em que se atua.

Imediatamente após o quadro, para auxiliar na gestão do processo de ensino-aprendizagem, constam três seções que são descritas a seguir.

A seção Práticas de ensino na sala de aula apresenta a proposição de algumas estratégias e procedimentos que podem ser eficazes para a concretização dos objetivos de aprendizagem previstos.

Na seção Avaliação, a importância dessa ferramenta pedagógica é enfatizada como instrumento a ser empregado de modo contínuo e processual. Deve ser utilizada para aferir não só os conhecimentos curriculares disciplinares, mas também os conhecimentos da realidade do mundo que cerca os alunos.

Por fim, a seção Saiba mais apresenta sugestões de referências complementares para consulta (sites , vídeos etc.) relacionadas a temas de cunho de ampliação do repertório da formação docente continuada.

De modo articulado e vinculado, com base nas indicações do quadro e das seções, é possível planejar o desenvolvimento anual de sua atuação docente.

1 º semestre 1º trimestre 1º bimestre

Aprendizagens desenvolvidas no 5º ano

Números, adição e subtração

• Os números e suas representações

• Nosso sistema de numeração

• A classe dos milhões

• Os números naturais

• Diferentes maneiras de adicionar.

• Propriedades da adição

• Diferentes maneiras de subtrair.

• Igualdade.

• Propriedade aditiva da igualdade.

Figuras geométricas planas, localização e deslocamento

• Retas, semirretas e segmentos de reta.

• Retas paralelas e retas concorrentes.

• Ângulos.

• Localização

• Pares ordenados.

• Deslocamento.

• Reconhecendo polígonos.

• Construindo polígonos.

• Ampliação e redução de polígonos.

Multiplicação e divisão

• Resolvendo multiplicações

• Propriedades da multiplicação

• Princípio multiplicativo

• Resolvendo divisões

• Repartir em partes desiguais

2º bimestre

• Expressões numéricas

• Algumas relações entre multiplicação e divisão

• Proporcionalidade

• Propriedade multiplicativa da igualdade

2º trimestre

Figuras geométricas espaciais e volume

• Poliedros e não poliedros

• Prismas e pirâmides

• Cilindro, cone e esfera

• Volume de uma figura geométrica espacial

BNCC

EF05MA01

EF05MA07

EF05MA10

EF05MA11

EF05MA14

EF05MA15

EF05MA17

EF05MA18

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento de vocabulário

• Compreensão de textos.

• Produção de escrita

BNCC

EF05MA08

EF05MA09

EF05MA10

EF05MA11

EF05MA12

EF05MA13

EF05MA16

EF05MA21

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento de vocabulário.

• Compreensão de textos.

• Produção de escrita.

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

2º semestre

3º bimestre

Números na forma de fração

• As frações.

• Leitura de frações.

• Fração de uma quantidade.

• Fração e divisão.

• Frações na reta numérica.

• Frações equivalentes.

• Simplificação de frações.

• Comparação e ordenação de frações.

Números na forma decimal

• Os números decimais

• O décimo, o centésimo e o milésimo

• Os números decimais e o nosso sistema de numeração.

• Comparação e ordenação de números decimais.

• Adição e subtração com números decimais.

• Multiplicação com números decimais.

• Divisão de números naturais com quociente decimal.

• Divisão de um número decimal por um número natural.

• Cálculo de porcentagem

Estatística

• Tabelas.

3º trimestre

4º bimestre

e probabilidade

• Gráfico de colunas.

• Gráfico de barras.

• Gráfico de segmentos.

• Realizando pesquisa.

• Experimentos aleatórios.

• Cálculo de probabilidade.

Grandezas e medidas

• Medidas de massa (grama, quilograma, tonelada e miligrama).

• Medidas de tempo (hora, minuto e segundo)

• Medidas de comprimento (decímetro, centímetro, milímetro, metro e quilômetro).

• Medidas de temperatura (escala Celsius).

• Medidas de capacidade (litro e mililitro).

• Medidas de área (centímetro quadrado, metro quadrado e quilômetro quadrado).

• Área do retângulo e do quadrado.

• Relações entre área e perímetro.

BNCC

EF05MA02

EF05MA03

EF05MA04

EF05MA05

EF05MA06

EF05MA07

EF05MA08

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento de vocabulário.

• Compreensão de textos.

• Produção de escrita.

BNCC

EF05MA19

EF05MA20

EF05MA22

EF05MA23

EF05MA24

EF05MA25

Componentes essenciais para a alfabetização

• Desenvolvimento de vocabulário.

• Compreensão de textos.

• Produção de escrita.

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Material disponibilizado em licença aberta do tipo Creative Commons

Práticas de ensino na sala de aula

Para que o Plano de desenvolvimento anual possa efetivamente se consolidar de modo que sejam alcançados os objetivos de aprendizagem pretendidos para o ano letivo, é importante o docente ter atitudes e utilizar práticas que contribuam para o desenvolvimento dos componentes essenciais para a alfabetização e das competências e habilidades matemáticas nos alunos sob sua responsabilidade. Para isso, a seguir é apresentada uma visão geral de algumas abordagens possíveis.

É importante ressaltar, ainda, que o processo de ensino-aprendizagem já não se encontra mais intimamente vinculado apenas ao espaço físico da sala de aula e, em virtude das mudanças ocorridas socialmente, cenários de aprendizagem virtual passaram a fazer parte da dinâmica escolar, sendo necessário considerar essa perspectiva no planejamento, nas práticas, bem como na busca de atualização da formação docente.

Leitura inferencial

Para abordar situações significativas apresentadas em cada proposta didática, a leitura inferencial é uma prática importante a ser desenvolvida com os alunos. Essa prática envolve tanto estratégias de leitura de imagens quanto de leitura de textos.

A leitura de imagens, em Matemática, nos Anos Iniciais do Ensino Fundamental, é tão explorada quanto a leitura de textos, visto que o suporte de apoio visual na realização de contagens ou resolução de operações matemáticas é um recurso didático muito utilizado.

A reflexão sobre o processo de leitura inferencial pode ser promovida pelo docente por meio de perguntas ou solicitações propostas que permitam aos alunos demonstrarem respostas que não estejam apenas circunscritas aos textos, e sim possam ser inferidas considerando conhecimentos prévios e de mundo de modo geral.

Os enunciados dos problemas matemáticos são textos que requerem leitura analítica e inferencial por parte dos alunos para que possam desenvolver melhores estratégias de resolução.

Produzir inferências é uma ação que auxilia na compreensão de um texto. No caso das aulas de Matemática, de um texto matemático, por exemplo, o enunciado de um problema.

A compreensão de texto, em qualquer área de conhecimento, é uma habilidade que depende das inferências geradas pelo leitor, considerando que cada texto possui informações implícitas e explícitas.

A qualidade e a quantidade das inferências geradas por um leitor dependem, prioritariamente, das associações estabelecidas entre as informações explícitas no texto e os conhecimentos prévios e de mundo que o leitor possui.

Para auxiliar os alunos a lerem um texto de maneira analítica, a fim de que possam concluir, deduzir e formular novos sentidos, levantar hipóteses, bem como ressignificar informações, uma estratégia é sugerir que, ao fazer a leitura:

• dividam o texto em partes menores que forneçam informações principais;

• estabeleçam relações entre essas partes de modo a identificar como elas se inter-relacionam;

• identifiquem o panorama geral do que essas inter-relações indicam.

Destaca-se o fato de que a leitura de um texto matemático mobiliza o leitor para a interpretação de elementos textuais combinados a elementos matemáticos, como números, tabelas, gráficos, entre outros.

Nesse sentido, outra estratégia é fazer com que os alunos compreendam que ler um texto matemático não se resume a identificar palavras-chave.

Sugere-se, sempre que possível, incentivar os alunos a realizar uma leitura analítica e inferencial de:

• imagens que permeiam o material didático (imagens de aberturas de partes hierárquicas do livro, como unidades ou capítulos, por exemplo);

• textos (enunciados de problemas, textos instrucionais de jogos, entre outros).

Sugere-se, ainda, solicitar aos alunos que façam registros das compreensões, pois essa prática vai ajudá-los a melhorar o desempenho na resolução e condução das tarefas propostas.

Esses registros podem ser compartilhados em um mural da sala de aula ou da escola, em um mural on-line criado na rede social da escola ou, até mesmo, em uma folha de cartolina, na qual os alunos façam registros. O cartaz pode ser afixado em algum espaço da sala de aula ou da escola

Fazer diferentes registros

Na Competência específica 6 de Matemática e suas Tecnologias da BNCC (BRASIL, 2018, p. 267), é abordada a importância de expressar respostas e sintetizar conclusões utilizando diferentes registros e linguagens.

Desse modo, uma prática importante, ao longo do desenvolvimento das atividades propostas, é solicitar aos alunos que façam diferentes registros para expressar as justificativas de suas respostas, esquematizar a descrição de estratégias utilizadas no processo de resolução, representar um problema com uma organização visual etc.

Essa prática é importante de ser desenvolvida desde os primeiros anos de escolaridade já que é um processo que deve ser aprimorado durante toda a vida escolar e não escolar, pois fazer registros e interpretá-los é uma habilidade importante, por exemplo, no trabalho, assim como em diversas situações da vida cotidiana que requerem a

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

esquematização de sistemas, situações ou processos, com a finalidade de compreendê-los melhor

Como estratégia de aplicação dessa prática, explorar com os alunos algumas possibilidades, como:

• no processo de resolução de problemas que envolvam proporcionalidade, fazer registros organizados em quadros;

• em pesquisas estatísticas, fazer registros dos dados coletados em tabelas e gráficos;

• questões que abrangem características geométricas, fazer desenhos (esboços esquemáticos) que representem plantas baixas ou figuras (bidimensionais ou tridimensionais);

• no trabalho com sequências recursivas (numéricas ou figurais), fazer registros por escrito das regularidades identificadas na regra de formação do padrão de cada sequência;

• ao resolver problemas que envolvem multiplicação com a ideia de combinatória, fazer a organização da representação de uma árvore de possibilidades (ou de um quadro de possibilidades);

• na elaboração de problemas, solicitar que façam diagramas de fluxo ligando as etapas, a fim de representar a sequência que encadeou o raciocínio empregado no desenvolvimento da elaboração.

Permitir aos alunos eleger de maneira autônoma os diferentes registros e linguagens é muito importante para valorizar o protagonismo deles no processo de ensino-aprendizagem.

Educação para a cidadania

Além dos conteúdos disciplinares, o processo de formação educacional abrange, também, a responsabilidade de formar indivíduos conscientes da importância que atitudes individuais exercem sobre a vida do outro e das responsabilidades que possuem em relação ao grupo social a que pertencem, entre outros aspectos.

Na BNCC (BRASIL, 2018), nas páginas 9 e 10, estão relacionadas dez competências gerais da Educação Básica e, nas páginas 19 e 20, são elencados os Temas Contemporâneos Transversais, os quais apontam para o desenvolvimento de capacidades a serem aperfeiçoadas, ao longo da vida, com base no exercício de práticas sociais inseridas em determinados contextos, como meio ambiente, saúde, educação financeira, entre outros.

Considerando essa perspectiva, a prática da educação para a cidadania prioriza envolver todos os alunos em vivências significativas consigo mesmos e com outras pessoas, por meio da percepção de que há direitos que são garantidos com base no cumprimento dos deveres, e vice-versa. Sendo assim, a educação para a cidadania vai além da transmissão de conteúdo e da assimilação dele

Uma estratégia que se pode utilizar, a cada semana, é escolher ou pedir que se voluntarie um ajudante da semana para auxiliar você em algumas tarefas. O objetivo é levar os alunos a assumirem uma postura cooperativa com você e os colegas.

É adequado, se possível, que cada aluno da turma, ao longo do ano letivo, seja o ajudante da semana, pois essa experiência ajudará a lidar com a indisciplina, caso exista no ambiente. Isso também favorecerá o desenvolvimento de sentimentos de pertencimento, autonomia, responsabilidade, resiliência, foco, cuidado consigo mesmo e com os outros, entre outros.

O ajudante da semana pode cuidar do compartilhamento de comunicados e lembretes de compromissos. Essa comunicação pode ser:

• on-line , por meio de aplicativos de mídia que compartilham vídeos curtos ou áudios;

• off-line , com base na escrita de recados diários no mural ou no quadro da sala de aula

É importante que seja incluída alguma atividade envolvendo tecnologia digital para que os alunos se apropriem de fazer uso cidadão e crítico no ambiente escolar.

Estímulo à criatividade

A criatividade (ou pensamento criativo) é um potencial que todos nós possuímos e pode ser desenvolvida no ambiente escolar com base em determinadas estratégias e em certos contextos apropriados.

Nas aulas de Matemática, estimular práticas que envolvam o potencial criativo é uma ação que pode ser associada a diferentes unidades temáticas dessa área de conhecimento.

Nas atividades relacionadas a conhecimentos geométricos, por exemplo, uma estratégia é propor aos alunos atividades em que eles sejam construtores de maquetes ou de outras elaborações relacionadas ao tema, de acordo com a criatividade deles.

Para realizar essas construções, os alunos devem mobilizar os conhecimentos desse tema para reconhecer em embalagens e objetos do mundo físico características de figuras geométricas espaciais estudadas para assim selecionar as melhores embalagens ou objetos a serem empregados nessas construções de acordo com as características identificadas, como superfícies arredondadas ou não.

Esse tipo de atividade, geralmente realizada em grupos, envolve a produção de ideias originais Sendo assim, além de estimular a criatividade para apresentar ideias, exercita a flexibilidade dos alunos em acolher as ideias dos colegas de grupo e a solucionar problemas de forma construtiva e respeitosa

A captura de retratos de construções arquitetônicas que se pareçam com figuras geométricas espaciais para elaborar uma apresentação de slides também é uma atividade que estimula a criatividade, além de utilizar tecnologia digital.

Outra estratégia são atividades de elaboração de problemas. Esse tipo de atividade também estimula a criatividade dos alunos. Além de empregarem conhecimentos matemáticos nessa elaboração, a criação do contexto do problema requer a originalidade na concepção de ideias novas e, para isso, o pensamento criativo é estimulado.

Avaliação

A avaliação exerce uma das principais funções em favor da promoção e da consolidação do processo de ensino-aprendizagem. Por isso, a avaliação não pode ser concebida somente como uma fase final desse processo, mas precisa ser integrada a todo o processo, de maneira contínua.

Para que a avaliação seja empregada com eficácia, é importante coletar informações sobre aspectos não desenvolvidos, os parcialmente desenvolvidos e os desenvolvidos pelos alunos. Com base nessas informações, oferecer feedbacka cada um deles, aos gestores escolares e aos responsáveis pelos alunos

A coleta dessas informações pode ser dirigida de maneira diversificada considerando diferentes possibilidades, como avaliação diagnóstica, avaliação de processo e avaliação formativa.

Com a avaliação diagnóstica, é possível mapear os diferentes perfis dos alunos em relação aos conhecimentos prévios que possuem. Assim, a observação e a reflexão do docente sobre as informações obtidas é uma importante ferramenta nesse tipo de avaliação. Embora, em um diagnóstico, muitas informações possam ser observadas, é indicado, além da sondagem de conhecimentos prévios, que se observem também:

• a linguagem corporal dos alunos durante suas explicações (se demonstram interesse ou não);

• o modo como se organizam no trabalho em duplas ou grupos para a prática de uma atividade;

• se manifestam ansiedade ou demonstram desinteresse quando questionados individualmente.

Na avaliação diagnóstica, a observação desses padrões de comportamento compõe dados relevantes a serem vinculados à análise do desempenho cognitivo de cada aluno nas atividades propostas.

Já a avaliação de processo produz uma experiência educacional que motiva os alunos, por ser contínua e se dar também por meio da utilização de instrumentos informais, como paradas para uma autoavaliação.

A fim de tornar a avaliação de processo um momento mais próximo de cada aluno:

• questionar a avaliação pessoal que cada um faz das próprias produções e atuações escolares No caso de trabalho em duplas ou em grupo, essa prática de autoavaliação pode ser incorporada de maneira reflexiva e compartilhada entre eles;

• solicitar relatórios concisos sobre atividades específicas, ou qualquer outro tipo de registro, para obter informações do processo de aprendizagem de cada aluno, a fim de rever o processo sempre que necessário.

Na avaliação formativa, a utilização de instrumentos formais, mantendo o formato de atividades diárias, se destaca, pois, nesse tipo de avaliação, critérios mais específicos são considerados, como o nível de apreensão dos alunos em relação aos conteúdos, a aplicação da linguagem matemática, entre outros que permitem a sistematização de informações.

Avaliar é um ato que dá origem a informações úteis para docentes e discentes, conforme a interpretação e a comunicação dialógica entre os atores do processo educacional.

Para auxiliar na geração de informações e interpretação dessas informações, consultar os Relatórios e Indicadores do Acompanhamento da Aprendizagem disponíveis neste material.

Para saber mais

• BARLOW, Michel Avaliação escolar: mitos e realidades. Porto Alegre: Artmed, 2006. Nessa obra, Michel Barlow discute práticas avaliativas em sala de aula.

• BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática. 6. ed. Belo Horizonte: Autêntica, 2019. (Tendências em Educação Matemática).

Nesse livro, os autores apresentam resultados de um trabalho sobre informática educativa, como questões pedagógicas sobre o uso do computador e da calculadora.

• BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base Brasília: SEB, 2018. Disponível em:

http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pd f. Acesso em: 8 dez. 2021.

Documento que regulamenta as aprendizagens essenciais na Educação Básica.

• BRASIL. Ministério da Educação. PNE: Plano Nacional de Educação. Brasília: Inep, 2014. Disponível em:

https://download.inep.gov.br/publicacoes/institucionais/plano_nacional_de_educacao/pl ano_nacional_de_educacao_pne_2014_2024_linha_de_base.pdf. Acesso em: 8 dez. 2021.

Nesse documento, são apresentadas as diretrizes, metas e estratégias para a educação brasileira de 2014 a 2024.

• COLL, César; TEBEROSKY, Ana. Aprendendo Matemática. São Paulo: Ática, 2000.

Nesse livro, é possível ter acesso a conceitos matemáticos de diversos campos, compreendendo estruturas e ideias fundamentais.

• GAUTHIER, C.; BISSONNETTE, S.; RICHARD, M. Ensino explícito e desempenho dos alunos: a gestão dos aprendizados. Petrópolis: Vozes, 2014.

Nesse livro, os autores discutem as principais características e os fundamentos do ensino explícito como uma proposta de ensino eficaz.

• HADJI, C. A avaliação, regras do jogo: das intenções aos instrumentos. Porto: Porto Editora, 1994.

Nesse livro, é apresentada uma proposta de abordagem de avaliação da aprendizagem escolar, incluindo reflexões e análises relacionadas aos tipos de avaliação.

• LORENZATO, S. Laboratório de ensino de Matemática e materiais didáticos manipuláveis. In : LORENZATO, S. O Laboratório de Ensino de Matemática na formação de professores. Campinas: Autores Associados, 2006. p. 3-38. (Coleção Formação de professores).

Nesse texto, é discutido o papel do Laboratório de Ensino de Matemática (LEM) no ensino e na aprendizagem de Matemática.

• LUCKESI, C. C. Verificação ou avaliação: o que pratica a escola. Ideias, São Paulo, n. 8, p. 71-80, 1998. (Série Ideias).

Nesse texto, o autor faz uma abordagem sobre aspectos que diferenciam as ações de verificar e avaliar no ensino escolar.

• MONTEIRO, Alexandrina; POMPEU JUNIOR, Geraldo. A Matemática e os temas transversais. São Paulo: Moderna, 2001.

Nesse livro, há reflexões sobre os temas transversais, com especial atenção às aulas de Matemática.

• NACARATO, Adair Mendes; MENGALI, Brenda Leme da Silva; PASSOS, Cármen Lúcia Brancaglion A Matemática nos anos iniciais do Ensino Fundamental. 2. ed. Belo Horizonte: Autêntica, 2015.

Nesse livro, os autores debatem sobre o ato de aprender e o ato de ensinar a Matemática, nos Anos Iniciais do Ensino Fundamental.

• PAIS, L. C. Ensinar e aprender Matemática. Belo Horizonte: Autêntica, 2006

Com essa obra, o autor propõe uma reflexão acerca de aspectos metodológicos do ensino da Matemática, incluindo uma análise do livro didático.

Sequências didáticas

Sequência didática 1: Os números naturais, adição e subtração

Esta sequência didática aborda a leitura de dados em tabelas e a construção de gráficos por meio de uma situação-problema que envolve a produção de energia. Serão exploradas a leitura de números, a operação de adição de números naturais, a construção de gráficos, a aproximação de números e a ordenação dos números naturais.

Além disso, explora por meio de situações-problema, as operações de adição e de subtração de números naturais. As situações são contextualizadas e apresentam dados referentes à extensão territorial das unidades federativas do Brasil e de alguns países, a fim de que os alunos comparem números naturais e usem números ordinais. Pretende-se, também, explorar a linguagem matemática dos números na classe dos milhões e a leitura de números ordinais.

Objetivos de aprendizagem

• Compreender relações no Sistema de Numeração Decimal.

• Ler e escrever números naturais com algarismos e por extenso.

• Representar números naturais no Quadro de ordens e classes.

• Comparar e ordenar números naturais.

• Arredondar números naturais.

• Identificar e resolver situações-problema envolvendo ideias da adição e da subtração.

• Compreender a representação gráfica como uma forma de comparar números naturais.

Plano de aulas

Aula 1: Realizar pesquisa sobre as principais fontes energéticas do Brasil e classificá-las em renováveis e não renováveis.

Aula 2: Interpretar dados em tabela, fazer comparação, ordenação e arredondamento de números naturais e resolver situações-problema envolvendo o cálculo de adição.

Aula 3: Interpretar dados em gráficos, fazer comparação e ordenação de números naturais e resolver situações-problema envolvendo o cálculo de adição e de subtração.

Aula 4: Fazer comparação e ordenação de números naturais e resolver situações-problema envolvendo o cálculo de adição e de subtração.

Aula 5: Compreender a distribuição das unidades da federação do Brasil em grandes regiões e identificar elementos cartográficos.

Aula 6: Interpretar dados em quadro, fazer comparação e ordenação de números naturais e resolver situações-problema envolvendo o cálculo de adição e de subtração.

Aula 7: Comparar e ordenar números naturais, e representar números no Quadro de ordens.

Aula 8: Interpretar dados em quadro e resolver situações-problema envolvendo o cálculo de adição e de subtração.

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita.

Competências gerais da Educação Básica: 2 e 7.

Competências específicas de Matemática: 3, 7 e 8.

Habilidades: EF05MA01, EF05MA07 e EF05MA24.

Materiais necessários: Régua, papel quadriculado, folha avulsa, lápis de cor, representação impressa do mapa do Brasil (de regiões e estados), representação impressa do mapa do Brasil (de estados) para colorir e computador com acesso à internet.

Aula 1

Inicialmente, promover uma atividade para identificar os conhecimentos prévios dos alunos sobre o assunto tratado nesta sequência didática. Para isso, entregar uma folha avulsa para cada um e fazer a seguinte pergunta:

• De onde vem a energia elétrica usada no dia a dia (seja em casa, na escola, no comércio, nas empresas, na iluminação pública etc.)?

Pedir aos alunos que reflitam sobre essa pergunta e que desenhem na folha avulsa como eles acreditam que a energia chega até as residências Reservar um tempo da aula para esta atividade, que pode ser de 15 a 20 minutos.

Ao término, promover uma roda de conversa e pedir aos alunos que exponham suas ideias. Anotar na lousa as informações que forem levantadas pela turma.

Espera-se que os alunos reconheçam que a energia utilizada no nosso dia a dia é proveniente de diversos recursos naturais ou artificiais, os quais são transformados em energia, por exemplo, a energia elétrica.

Explicar a eles que esses recursos são chamados fontes de energia. Perguntar quais fontes de energia eles acham que são abundantes no Brasil. No nosso país, as fontes de energia mais abundantes são: eólica, fóssil, hídrica e solar.

Em seguida, dividir os alunos em quatro grandes grupos e pedir a cada grupo que pesquise informações sobre essas fontes de energia. Essa pesquisa pode ser realizada na biblioteca ou no laboratório de informática. Sugere-se, para consulta, o site https://www.epe.gov.br/pt/abcdenergia/fontes-de-energia. Acesso em: 8 dez 2021.

Ao final da pesquisa, os grupos devem apresentar os resultados obtidos aos demais colegas da turma. Para terminar a aula, propor um debate com os alunos a partir da seguinte questão:

Material disponibilizado em licença aberta do tipo

• Das fontes de energia pesquisadas, quais são consideradas renováveis e quais são não renováveis?

Espera-se que eles respondam que a eólica, a hídrica e a solar são renováveis, enquanto a fóssil é não renovável.

Aula 2

Nos minutos iniciais desta aula, promover uma conversa com a turma com o objetivo de relembrar o que foi tratado na aula anterior, em especial sobre as principais fontes de energia no Brasil. Na atividade proposta nesta aula, foram utilizados dados da matriz energética brasileira, obtidos na Agência Nacional de Energia Elétrica (Aneel).

Em seguida, organizar os alunos em duplas e mostrar a eles a tabela a seguir, que apresenta os dados da matriz energética brasileira. Explicar-lhes que a unidade de medida referente à capacidade de energia é o quilowatt (kW) e que eles a estudarão com mais detalhes em anos posteriores. Se necessário, explicar que assim como utilizamos o quilograma para medida de massa e o litro para medida de capacidade, o quilowatt é utilizado para medida de energia.

Origem das fontes de energia Capacidade de energia transformada pelas usinas (em kW)

Pedir aos alunos que resolvam às questões a seguir.

1.Com base nos dados da tabela, colocar em ordem crescente as fontes que mais produzem energia elétrica no Brasil.

Outras (3 340 050 kW), solar (19 681 822), eólica (29 765 534 kW), fóssil (52 248 581 kW), hídrica (111 379 574 kW).

2.Qual é o total de energia elétrica produzido por essas fontes?

216 415 561 kW.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Matriz de energia elétrica brasileira, em 2/4/2021

3.Complete a tabela a seguir colocando em ordem decrescente as fontes de energia listadas anteriormente, de acordo com a capacidade de produção, e arredondando os números para a classe das centenas de milhar.

Matriz de energia elétrica brasileira, em 2/4/2021

Origem das fontes de energia Capacidade de energia transformada pelas usinas (em kW)

É importante assumir uma posição de mediador da atividade, deixando os alunos levantarem hipóteses e discutirem as possíveis conclusões. Levantar questões que possam encaminhar a discussão e chegar ao objetivo de comparar números naturais, adicionar números e realizar uma correta leitura de tabelas.

Ao término da aula, solicitar a eles que façam uma pesquisa sobre as usinas hidrelétricas de Itaipu (Brasil/Paraguai) e a Três Gargantas (China). Orientá-los a pesquisar a localização de cada uma delas e em que rios foram instaladas, suas capacidades de produção de energia e o ano em que foram inauguradas.

Se algum aluno permanecer com dúvidas em relação à comparação dos números naturais, propor a seguinte atividade: construir uma reta numérica para indicar números naturais na lousa e demonstrar a importância da posição dos números nessa reta. Utilizar os símbolos > (maior que) e < (menor que). Caso os alunos estejam com dúvidas no momento de adicionar os números naturais, tentar utilizar a estratégia de adicionar com o número decomposto e, depois, mostrar a mesma adição em um Quadro de ordens e classes.

Aula 3

Retomar os conceitos trabalhados nas atividades das aulas anteriores. Solicitar aos alunos que apresentem as informações levantadas na pesquisa sobre as usinas. Depois, anotar na lousa essas informações. Construir, com o auxílio deles, um gráfico de barras com esses dados. O gráfico a seguir apresenta a capacidade de produção de energia dessas usinas. Auxiliar os alunos na interpretação dos dados e verificar se percebem qual usina produz mais energia.

Material disponibilizado em licença aberta do tipo

(CC

Creative Commons – Atribuição não comercial

BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Fonte: ANEEL Disponível em: https://www.aneel.gov.br/siga Acesso em: 8 dez 2021.

Após esta atividade, solicitar aos alunos que se organizem novamente em duplas (a mesma formação da aula anterior) e que construam um gráfico com os dados da tabela que organizaram na atividade 3 da aula anterior. Essa construção pode ser realizada em uma planilha eletrônica ou em papel quadriculado. Informar aos alunos que o uso da fonte solar e eólica (vento) vem aumentando no Brasil nos últimos anos. Nesse sentido, propor a eles que respondam à questão a seguir em uma folha avulsa

• De acordo com o gráfico que vocês construíram, a partir de qual dessas duas fontes é gerada mais energia no Brasil? Quantos quilowatts a mais?

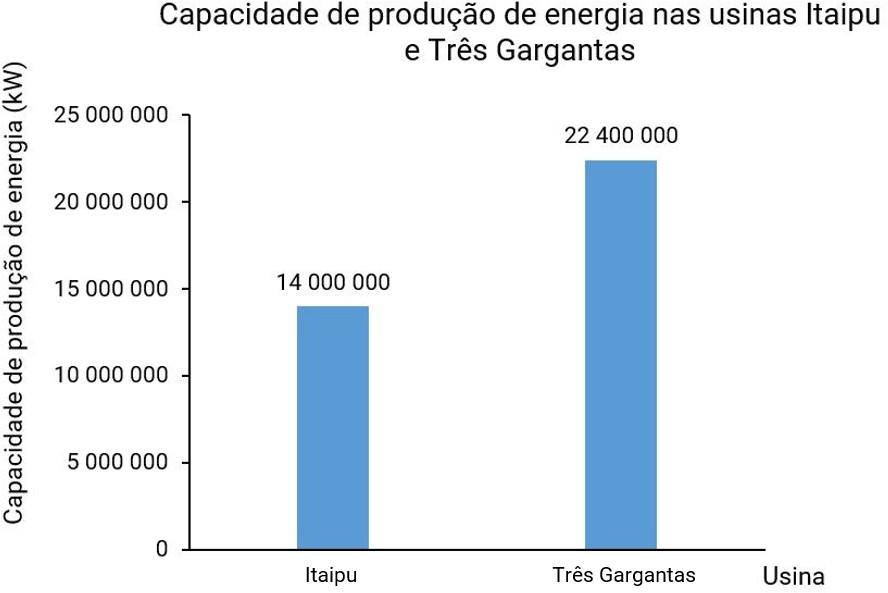
A energia eólica gera mais energia, cerca de 10 084 000 kW a mais do que a solar; 29 766 000 – 19 682 000 = = 10 084 000)

Cada dupla deve apresentar a estratégia utilizada e a diferença encontrada escrita por extenso (dez milhões e oitenta e quatro mil quilowatts). É importante que eles observem que oresultado obtido é um valor aproximado, uma vez que foi calculado a partir de dados arredondados.

Estipular um tempo de 10 minutos para os alunos refletirem sobre essa questão. No decorrer desse período, recolher os gráficos elaborados por eles e, ao término, apresentar a correta representação gráfica do que foi solicitado.

Para ampliar o trabalho com esse tema, propor às duplas que elaborem problemas de adição e de subtração envolvendo dados apresentados no gráfico e que os troquem com outras duplas.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Fonte: ITAIPU Binacional Comparações Disponível em: https://www.itaipu.gov.br/energia/comparacoes Acesso em: 10 jan 2022

Aula 4

Iniciar a aula explicando aos alunos que o uso de fontes geradoras de energia elétrica no Brasil não é uniforme nas diferentes regiões do país. Dizer que a escolha da fonte depende de características da região. Por exemplo, a exploração da fonte hídrica depende dos rios disponíveis e do comportamento das águas em seu curso. Assim, cada região tende a explorar de maneira mais intensa as fontes com maior disponibilidade local.

Em seguida, comentar que a energia eólica depende fundamentalmente da força do vento e que esse recurso ocorre de maneira desigual nas diversas regiões brasileiras. Na lousa, indicar a quantidade total de unidades geradoras de energia eólica, em 2/4/2021, escrevendo que no Brasil a quantidade total é de 1 034 unidades e nos estados o total é de: 317 unidades na Bahia; 103 unidades no Ceará; 116 unidades no Piauí; 294 unidades no Rio Grande do Norte.

Pedir aos alunos que calculem quantas unidades geradoras de energia eólica havia nos outros estados brasileiros. Para que resolvam a questão, permitir que utilizem a estratégia que preferirem. Duas das estratégias são:

• adicionar as quantidades de unidades geradoras nos estados apresentados e subtrair esse resultado do total de unidades geradoras no Brasil (317 + 103 + 116 + + 294 = 830; 1 034 – 830 = 204);

• subtrair do total de unidades geradoras do Brasil a quantidade em cada estado apresentado, a partir do resultado anterior (1 034 – 317 = 717; 717 – 103 = 614; 614 –– 116 = 498; 498 – 294 = 204).

Ao final do tempo estipulado para a resolução (de 5 a 10 minutos), propor um momento para que os alunos apresentem aos colegas as estratégias de cálculo utilizadas. Caso alguma das estratégias apresentadas anteriormente não tenham sido citadas pelos alunos, apresente-a na lousa. Perguntar aos alunos se esses estados correspondem a mais ou a menos da metade do total de unidade geradoras de energia eólica no Brasil. Espera-se que eles percebam que esses estados possuem juntos 830 unidades geradoras, o que corresponde a mais da metade do total no Brasil.

Em seguida, questionar os alunos se eles sabem onde se localizam esses estados no território brasileiro. Deixar que conversem sobre essa questão, compartilhando entre si experiências que possam ter sobre a localização geográfica dos estados da Bahia, do Ceará, do Piauí e do Rio Grande do Norte. Propor a eles que, para a próxima aula, tragam mais informações desses estados. Eles podem realizar pesquisas na internet ou conversar com pessoas da família sobre esse assunto.

Aula 5

Iniciar a aula retomando a discussão sobre a localização dos estados brasileiros com mais unidades geradoras de energia eólica. Permitir aos alunos que, em uma roda de

conversa, apresentem aos colegas os resultados de suas pesquisas. É possível que alguns alunos identifiquem que todos esses estados fazem parte da região Nordeste do Brasil. Em seguida, apresentar aos alunos um mapa do Brasil, dividido por regiões e por estados. Pedir aos alunos que observem o mapa. Perguntar a eles então quantos estados fazem parte da República Federativa do Brasil. Pela contagem das siglas inscritas no mapa, eles devem contar 27 estados, mas explicar que são 26 estados mais o Distrito Federal (DF). Depois, questionar em quantas regiões se divide o país. Se os alunos não conseguirem chegar a uma resposta, orientá-los a notar as cores diferentes no mapa do Brasil, que delimitam as cinco regiões (Norte, Nordeste, Centro-Oeste, Sudeste e Sul).

Apresentar a eles os outros elementos do mapa:

• a legenda (à esquerda), que mostra as cores utilizadas no mapa e o que elas representam;

• a rosa dos ventos (à direita), sempre presente nos mapas, e que pode apresentar desenhos variados, indica os pontos cardeais – Norte e Sul, na vertical; Oeste e Leste, na horizontal;

• a escala, normalmente definida em centímetros ou frações;

• as siglas das unidades da federação, os nomes dos oceanos, os trópicos e a linha do equador.

Em seguida, organizar a turma em grupos de três ou quatro alunos e entregar a cada grupo um mapa do Brasil com as subdivisões em estados, sem preenchimento. Escrever na lousa o nome de cada estado e do Distrito Federal e o nome da região a qual eles pertencem. Pedir aos alunos que pintem cada região de uma cor e que escrevam as legendas no mapa. As regiões e seus estados, com o Distrito Federal, são:

• Norte: Acre, Amapá, Amazonas, Pará, Rondônia, Roraima, Tocantins;

• Nordeste: Alagoas, Bahia, Ceará, Maranhão, Paraíba, Pernambuco, Piauí, Rio Grande do Norte, Sergipe;

• Centro-Oeste: Goiás, Mato Grosso, Mato Grosso do Sul, Distrito Federal;

• Sudeste: Espírito Santo, Minas Gerais, Rio de Janeiro, São Paulo;

• Sul: Paraná, Santa Catarina, Rio Grande do Sul.

Promover uma conversa sobre a localização dos estados com mais unidades geradoras de energia eólica: Bahia, Ceará, Piauí e Rio Grande do Norte. Nesse momento, caso não tenham percebido ainda, perguntar a eles: em qual região do Brasil ficam esses estados? Ao notarem que são todos estados da região Nordeste, explicar a eles que essa região do Brasil é a que recebe mais vento no país, vindo do Oceano Atlântico, o que potencializa a exploração da fonte eólica para a geração de energia elétrica. Ao final, solicitar aos alunos que guardem para usar na próxima aula o mapa que coloriram.

Aula 6

Retomar com os alunos o trabalho da aula anterior e pedir que peguem o mapa do Brasil com as regiões e estados que coloriram. Organizar a turma em grupos de três ou quatro alunos e entregar a cada grupo uma cópia impressa do quadro a seguir, que apresenta a área territorial brasileira aproximada por unidade da federação (estados e Distrito Federal).

Solicitar aos alunos que calculem a área total de cada região.

Fonte: IBGE. Áreaterritorialbrasileira. Disponível em: www.ibge.gov.br/home/geociencias/areaterritorial/principal.shtm. Acesso em:

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Estipular um tempo para a resolução da atividade, que pode ser de 25 a 35 minutos. Espera-se que os alunos determinem que a área total de cada região é: Norte: 3 853 841 km²; Nordeste: 1 554 290 km²; Centro-Oeste: 1 606 234 km²; Sudeste: 924 610 km²; Sul: 576 784 km².

É possível permitir que os alunos utilizem a calculadora para conferir as adições realizadas. Ao término, verificar se os alunos responderam corretamente e quais estratégias utilizaram. Se julgar necessário, orientá-los a fazer a adição de duas áreas por vez. Fazer com eles os cálculos e tirar as dúvidas que surgirem. O ábaco, também, pode ser utilizado na realização dos cálculos.

Em seguida, solicitar que calculem a área territorial do Brasil. Verificar se eles percebem que podem adicionar as áreas de todas as regiões. A resposta é 8 515 759 km². Pedir aos alunos que arredondem esse número na ordem das centenas de milhar. A resposta esperada é 8 500 000 km².

Aula 7

Retomar com os alunos o que foi trabalhado na aula anterior e relembrar que a área territorial do Brasil é de aproximadamente 8 500 000 km². Mostrar a eles um mapa-múndi e perguntar se consideram o Brasil um país de grande extensão territorial, comparando a área do Brasil com a de outros países por meio da observação do mapa.

Em seguida, apresentar a área territorial aproximada de alguns países, conforme a seguir, e pedir que comparem com a do Brasil.

• Rússia: 17 100 000 km ²

• Índia: 3 000 000 km²

• Argentina: 2 800 000 km².

• Inglaterra: 130 000 km².

• Portugal: 92 000 km²

Explicar que essa é uma lista parcial de países, com área decrescente. A Rússia ocupa o primeiro lugar em extensão territorial, e o Brasil está em sexto lugar.

Perguntar aos alunos qual é a colocação de Portugal na lista completa dos países segundo a sua área, sabendo que há 111 países com território maior que o de Portugal. Espera-se que eles respondam que Portugal é o 112º (centésimo décimo segundo) colocado na lista de países.

Levar os alunos a um laboratório de informática e propor que, organizados em trios, acessem o site do IBGE que apresenta informações sobre os países, disponível em: https://paises.ibge.gov.br/#/mapa (acesso em: 8 dez. 2021). No mapa interativo disponível nesse site , solicitar a cada grupo que escolham dois países e cliquem sobre sua respectiva

licença aberta do tipo

região. Na síntese de dados sobre o país que surgir na tela, pedir a eles que registrem a extensão territorial e a localização de cada país pesquisado.

De volta à sala de aula, pedir a cada grupo que registre na lousa os dados sobre os países pesquisados. Caso diferentes grupos tenham pesquisado sobre um mesmo país, pedir que o registro seja feito uma única vez. Em seguida, com os alunos organizados nos mesmos grupos, pedir a eles que anotem no caderno as informações sobre todos os países registrados na lousa, organizando-os em uma lista decrescente em relação à extensão territorial. Para finalizar a aula, fazer a conferência desta atividade na lousa com o auxílio dos alunos.

Assumir o papel de mediador nas atividades desta sequência didática, sempre propondo perguntas instigadoras, para que os alunos se sintam à vontade para procurar as respostas. É recomendável acompanhar de perto a realização das atividades. Sempre que necessário, incentivar a utilização do Quadro de ordens e classes.

Aula 8

Conversar com os alunos sobre o bioma Cerrado e sua vegetação típica. Explicar que oCerrado ocupa uma área de grande riqueza natural, estendendo-se pelos estados de Goiás, Tocantins, Mato Grosso, Mato Grosso do Sul, Minas Gerais, Bahia, Maranhão, Piauí, Rondônia, Paraná, São Paulo e Distrito Federal.

Perguntar aos alunos o que eles entendem por desmatamento, se essa prática é maléfica ou benéfica, quais são suas possíveis consequências, se é importante preservar florestas e por que se deve promover a preservação. Anotar na lousa as perguntas e as respostas, que podem ser pessoais. Com isso, procura-se provocar reflexão e diálogo entre os alunos sobre o tema, resultando em um levantamento do que eles pensam e sabem sobre oassunto sem ter base teórica.

Em seguida, apresentar a eles o quadro a seguir.

Área total do Cerrado (em km²) Área desmatada em km² (2002-2009)

2 039 386

983 347

Área desmatada em km² (2009-2011)

13 716

Fonte: IBAMA Monitoramento do Cerrado Disponível em: http://siscom.ibama.gov.br/monitora_biomas/PMDBBS%20-%20CERRADO.html Acesso em: 8 dez 2021

Perguntar o que os alunos entendem pelas expressões " no período de 2002 a 2009" e " no período de 2009 a 2011". Explicar que é o intervalo de tempo entre esses anos. Pedir a eles que calculem a área desmatada no período de 2002-2011 pela adição dos dados do quadro. Espera-se que eles calculem que a área desmatada, nesse período, foi de 997 063 km².

Neste momento, é interessante comparar a área total do Cerrado com a área territorial de países pesquisados na aula anterior. Verificar se os alunos compreendem que alguns desses países caberiam dentro do Cerrado. Ressaltar que a área desmatada no período, de 2002 a 2011, é maior que a de muitos países, como Portugal e Inglaterra.

Após a atividade de comparação, perguntar aos alunos se eles saberiam calcular a área ainda não desmatada do Cerrado. Uma forma de resolver esse problema é subtraindo, da área total, o que foi desmatado de 2002 a 2011 (1 042 323 km²; 2 039 386 – 997 063 = = 1 042 323). Perguntar aos alunos o que eles acham dos números do desmatamento, se são significativos, comparando-os com as áreas territoriais vistas até o momento e com a área total do Cerrado. Explicar aos alunos que esse número é mesmo significativo e indica que quase metade do Cerrado já foi desmatada.

Propor um desafio aos alunos: quantos anos demoraria, aproximadamente, para que orestante do Cerrado fosse totalmente arrasado e desaparecesse, considerando que em 10 anos foram desmatados 997 063 km²? Conceder um tempo para que pensem nas respostas. Depois, desenvolver o raciocínio na lousa. Se em 10 anos foram desmatados 997 063 km², supondo que esse ritmo de desmatamento se mantenha, em 20 anos terá sido desmatado odobro: 997 063 + 997 063 = 1 994 126, número próximo do que ainda resta do Cerrado.

Ao término da aula, deixar que os alunos reflitam sobre o que pode acontecer se o Cerrado acabar, por que se deve proteger uma área como essa e se o desmatamento pode ser bom para a sociedade.

Para obter mais informações sobre a energia eólica e sobre o cerrado brasileiro, pedir aos alunos que acessem os vídeos indicados na seção Sugestões

Sugestões

• CAMINHO da Energia Eólica. 2014. Vídeo (2min28s). Publicado pelo canal CanalFurnas.

Disponível em: https://www.youtube.com/watch?v=rPgjNdOqrKE. Acesso em: 8 dez. 2021.

• VOCÊ conhece o Cerrado? 2014. Vídeo (2min47s). Publicado pelo canal WWF-Brasil.

Disponível em: https://www.youtube.com/watch?v=orGhCBbK4Iw Acesso em: 8 dez 2021.

Sequência didática 2: Figuras geométricas planas, localização e deslocamento

Esta sequência didática tem como objetivo principal iniciar os estudos com a movimentação de objetos no plano cartesiano (1º quadrante) e o reconhecimento de figuras geométricas planas, em especial, de polígonos. Serão desenvolvidas atividades que possibilitam a compreensão da movimentação no plano em duas direções, vertical e

horizontal, e características e elementos de polígonos, como lados, vértices e ângulos internos.

Além disso, serão utilizados comandos que lembram códigos de programação. Dessa maneira, os alunos podem começar, também, a desenvolver o pensamento lógico que rege esse tipo de linguagem.

Objetivos de aprendizagem

• Identificar pontos no plano cartesiano (1º quadrante) por meio de pares ordenados.

• Movimentar objetos na horizontal e na vertical, indicando distância a ser percorrida e o ângulo de giro.

• Identificar figuras geométricas planas.

• Comparar figuras geométricas planas.

• Identificar as figuras geométricas planas de acordo com as suas características.

• Classificar triângulo retângulo de acordo com suas características.

Plano de aulas

Aula 1: Localizar, por meio de uma brincadeira, carteiras na sala de aula de acordo com sua posição, utilizando códigos de localização.

Aula 2: Identificar localização em malha quadriculada de acordo com coordenadas verticais e horizontais.

Aula 3: Descrever deslocamento em malha quadriculada de acordo com coordenadas verticais e horizontais.

Aula 4: Identificar a representação de polígonos em malha quadriculada e localizar seus vértices de acordo com coordenadas verticais e horizontais.

Aula 5: Compreender, por meio de um jogo, características e elementos de polígonos, como lados, vértices e ângulos internos.

Aula 6: Relacionar a quantidade de lados, vértices e ângulos internos de um polígono por meio de atividades de identificação e de construção de figuras.

Aula 7: Reconhecer triângulos em edificações da escola e identificar triângulo retângulo por meio de suas características.

Aula 8: Revisar os conhecimentos desenvolvidos de maneira a consolidar a compreensão de representações de polígonos em malha quadriculada, localizando seus vértices de acordo com coordenadas verticais e horizontais, e identificando características de triângulo retângulo.

Componentes essenciais para a alfabetização: Desenvolvimento de vocabulário e produção de escrita.

Competências gerais da Educação Básica: 5 e 9

Competências específicas de Matemática: 2 e 8.

Habilidades: EF05MA15 e EF05MA17.

Materiais necessários: Folhas de papel quadriculado (com malha de 1 cm por 1 cm), folhas avulsas, lápis grafite, régua, transferidor, cartões com representações de figuras geométricas planas e ficha com contornos de figuras geométricas planas.

Aula 1

Iniciar a aula conversando com os alunos sobre como as carteiras da sala de aula podem ser organizadas em fileiras, de maneira que cada fileira tenha a mesma quantidade de carteiras. Permitir que os alunos exponham suas ideias e verifiquem se é possível realizar essa organização com as carteiras disponíveis.

Em seguida, propor a eles que façam a organização das carteiras conforme indicado. Considerar o caso de algumas fileiras ficarem com uma carteira a menos que as demais. Depois, com os alunos, desenhar na lousa um esquema com a organização das carteiras na sala de aula. Observe um exemplo a seguir.

Representação de vista superior de sala de aula.

Notar que, nesse esquema, as duas primeiras fileiras da esquerda têm uma carteira a menos que as demais.

Marcar uma das carteiras e pedir aos alunos que descrevam a localização dela. Por exemplo, a carteira destacada a seguir poderia ser indicada de diferentes maneiras, como: 4ª carteira da 4ª fileira (da esquerda para a direita). Repetir esse procedimento com mais duas ou três carteiras.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Em seguida, propor a indicação de elementos que possam facilitar a localização das carteiras nesta sala de aula. Para isso, começando da carteira do canto inferior esquerdo, indicar, na horizontal, as letras do alfabeto de maneira ordenada e, na vertical, a sequência dos números naturais a partir do 1. Observe o exemplo a seguir.

EDITORIA DE ARTE

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Representação de vista superior de sala de aula.

Representação de vista superior de sala de aula com coordenadas para localização.

Em seguida, pedir a eles que indiquem a localização daquela carteira destacada anteriormente, usando para isso um código em que o primeiro dígito seja a letra da fileira vertical e, o segundo dígito, o número da fileira horizontal. Nesse caso, D4. Com os alunos, indicar mais algumas carteiras no esquema e pedir a eles que digam a localização correspondente.

Para finalizar a aula, propor uma brincadeira. Para isso, os alunos devem ficar sentados nas carteiras organizadas conforme o esquema na lousa. Você deve dizer um código de localização e, imediatamente, a turma tem de dizer o nome do aluno sentado na carteira correspondente. Fazer ao menos dez rodadas da brincadeira. Em seguida, pedir aos alunos que troquem de carteira entre si, mantendo a organização, e mudar a regra da brincadeira: você diz o nome do aluno e, imediatamente, eles devem dizer a localização da carteira correspondente.

Aula 2

Para iniciar esta aula, entregar aos alunos uma folha de papel quadriculado e pedir que marquem dois pontos, A e B, distantes um do outro, sempre nos vértices das figuras de quadrados.

A seguir, um exemplo de quadriculado com dois pontos marcados.

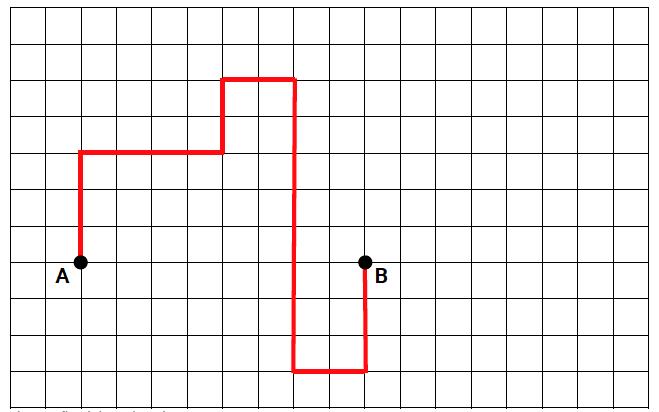
EDITORIA DE ARTE

A seguir, propor uma atividade em que os alunos tracem na malha um caminho que ligue o ponto A ao ponto B, seguindo sempre sobre as linhas verticais e horizontais do quadriculado. Pedir que evitem traçar poucas linhas, pois eles usarão esse caminho para a próxima atividade. Conceder alguns minutos para que façam o traçado e, durante a atividade, verificar se eles estão sendo criativos na elaboração dos caminhos.

A seguir, há um exemplo de caminho que liga os pontos A e B e que pode ser desenhado no quadriculado.

Após a composição, solicitar aos alunos que numerem as linhas horizontais e verticais da malha quadriculada, começando em 1 no canto inferior esquerdo da folha, até completar a numeração de todas as linhas. Ver a seguir um exemplo de como ficará.

Depois de todos terem finalizado a numeração das linhas, conversar com os alunos a respeito de como indicariam a localização dos pontos no quadriculado. Observar os apontamentos deles e orientá-los de tal modo que consigam escrever a localização dos pontos A e B utilizando a numeração das linhas.

No exemplo anterior, a localização dos pontos poderia ser indicada da seguinte maneira: A (4, 5) e B (12, 5). Nesse caso, a primeira coordenada indica a linha vertical; a segunda coordenada, a linha horizontal, de maneira parecida à que ocorre na localização de pontos no plano cartesiano.

No final da aula, solicitar aos alunos que coloquem o nome na folha de trabalho.

Recolher as folhas, pois serão utilizadas na aula seguinte.

Podem surgir dúvidas, principalmente, quanto à ideia de localização e à representação dos pares ordenados dos pontos A e B. Verificar se eles associam essa maneira de localizar pontos no quadriculado à brincadeira de localizar carteiras realizada na aula anterior.

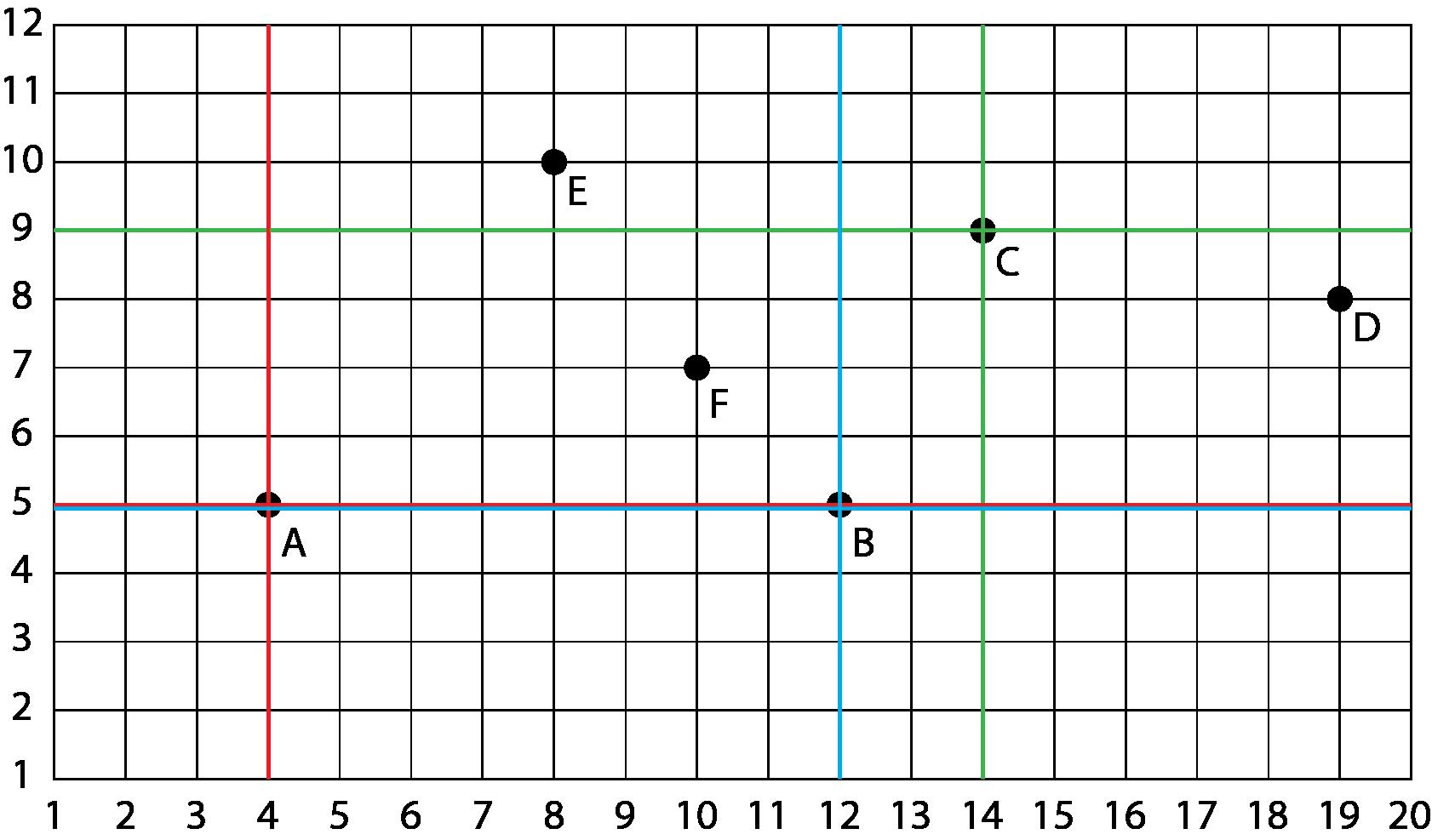
Para superar as dúvidas, mostrar em um quadriculado a intersecção das linhas que gerará o par ordenado dos pontos. Usar outros pontos como exemplos, determinando os primeiros pares ordenados e deixando que os alunos completem os demais. Por exemplo:

O par ordenado do ponto A (4, 5) está indicado pelas linhas vermelhas; o do ponto B (12, 5), pelas linhas azuis; o do ponto C (14, 9), pelas linhas verdes. Há mais pontos nesse exemplo com os quais os alunos poderão exercitar a habilidade de localização por meio do par ordenado.

Aula 3

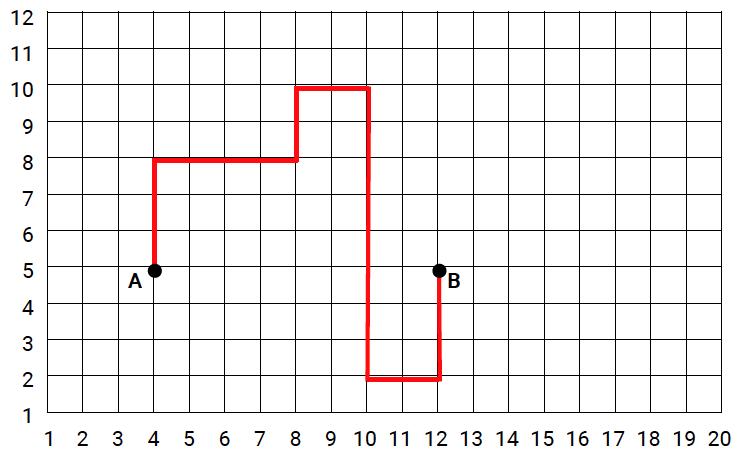
Devolver as folhas quadriculadas aos alunos e pedir que identifiquem todos os pontos em que o trajeto traçado por eles mudou de direção – ou seja, toda vez que o traço passou da vertical para a horizontal, e vice-versa. Retomando o exemplo da aula 2, os pontos em que há mudança de direção estão marcados aqui com circunferências azuis.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas

Depois de os alunos terem marcado os pontos, pedir que escrevam a localização de cada um deles por meio de pares ordenados e lhes deem um nome (utilizando uma letra maiúscula), buscando identificar a qual número eles correspondem na linha horizontal e na linha vertical.

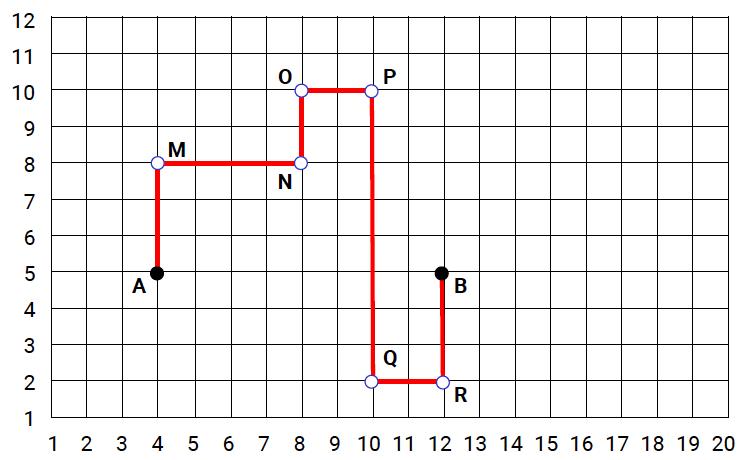
Pela ordem indicada no exemplo, seguindo o trajeto, temos os pontos de mudança de sentido (denominados de M a R) e novas coordenadas, que podem determinar o trajeto completo em pares ordenados: A (4, 5), M (4, 8), N (8, 8), O (8, 10), P (10, 10), Q (10, 2), R (12, 2), B (12, 5).

Feito isso, pedir aos alunos que realizem a atividade a seguir.

• Imagine que um objeto está sobre o ponto A e deve se mover até o ponto B pelo caminho que você traçou. Sabendo que o objeto só anda para a frente e que, pelo exemplo dado, há giros, dê comandos a ele para que chegue ao destino.

Lembrando que cada representação de quadrado tem 1 centímetro de lado, utilize uma lista de comandos parecida com esta:

• Siga em frente por centímetros.

• Você chegou ao ponto de par ordenado (____, ____)

• Vire graus à direita.

• Ande mais centímetros.

• Você chegou ao ponto de par ordenado (____, ____)

• Vire graus à

• Siga em frente por centímetros.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

• Você chegou ao ponto de par ordenado (____, ____)

• Vire graus à

• Siga em frente por _________ centímetros.

• Você chegou ao ponto do par ordenado ( , ).

• Vire ________ graus à direita.

• Siga em frente por _________ centímetros.

• Você chegou ao ponto de par ordenado (____, ____).

• Vire graus à esquerda

• Siga em frente por centímetros.

• Você chegou ao ponto de par ordenado (____, ____)

• Vire graus à

• Siga em frente por centímetros.

• Você chegou ao ponto de par ordenado (____, ____)

• Você chegou ao destino.

Se julgar pertinente, comentar com os alunos que essa lista de comandos se parece com códigos de programação de máquinas, como tornos e robôs industriais.

Pelo exemplo anterior, os comandos seriam:

• Siga em frente por 3 centímetros. • Você chegou ao ponto de par ordenado M(4, 8). • Vire 90 graus à direita. • Ande mais 4 centímetros. • Você chegou ao ponto de par ordenado N(8, 8). • Vire 90 graus à esquerda. • Siga em frente por 2 centímetros. • Você chegou ao ponto de par ordenado O(8, 10). • Vire 90 graus à direita. • Siga em frente por 2 centímetros. • Você chegou ao ponto de par ordenado P(10, 10). • Vire 90 graus à direita. • Siga em frente por 8 centímetros. • Você chegou ao ponto de par ordenado Q(10,2). • Vire 90 graus à esquerda. • Siga em frente por 2 centímetros. • Você chegou ao ponto de par ordenado R(12,2). • Vire 90 graus à esquerda. • Siga em frente por 3 centímetros. • Você chegou ao ponto de par ordenado B(12,5). • Você chegou ao destino.

Aula 4

Nesta aula, será retomado e expandido o trabalho com os conceitos de localização e de deslocamento em papel quadriculado, desenvolvendo as ideias iniciais de plano cartesiano (1º quadrante).

Para iniciar a aula e sanar possíveis dúvidas de aulas anteriores, elaborar um novo caminho no quadriculado para que os alunos redijam as instruções em grupo (formado por aqueles que dominaram a habilidade e por outros que ainda têm dificuldades). Desta vez, os alunos com dificuldade deverão narrar o comando e, caso esteja correto, os outros alunos o

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

executarão. Do contrário, o comando não será aceito e os alunos deverão dar mais dicas aos colegas.

Passado esse primeiro momento, pedir aos grupos que, em um novo papel quadriculado, façam as mesmas indicações de numeração nas linhas verticais e horizontais. Na lousa, represente um quadrado a partir de um ponto A, passando pelos pontos B, C e D, respectivamente, e retornando ao ponto A. Observe um exemplo. EDITORIA

Com base nesse desenho, propor à turma as questões a seguir.

• Descrevam o caminho traçado.

Marcar o ponto A(5,3) e seguir em frente na linha horizontal por 4 cm e marcar o ponto B(9,3). Virar 90 graus à esquerda e seguir em frente por 4 cm e marcar o ponto C(9,7). Virar 90 graus à esquerda e seguir em frente por 4 cm e marcar o ponto D(5,7). Virar 90 graus à esquerda e seguir em frente por 4 cm até retornar ao ponto A(5,3).

• Ao todo, de quantos centímetros foi o deslocamento?

16 cm (4 x 4 = 16).

• Após colorir o interior, qual figura geométrica plana foi obtida?

A figura geométrica obtida foi um quadrado. Em seguida, propor aos grupos a construção de uma trajetória, no papel quadriculado, com base nos comandos a seguir.

• Marcar o ponto A(4, 5) e seguir em frente na linha horizontal por 12 cm e marcar o ponto B(16, 5).

• Virar 90 graus à esquerda, seguir em frente por 5 cm e marcar o ponto C(16, 10).

• Virar 90 graus à esquerda, seguir em frente por 12 cm e marcar o ponto D(4, 10).

• Virar 90 graus à esquerda, seguir em frente por 5 cm até retornar ao ponto A(4, 5).

• Por fim, colorir o interior da figura obtida.

Observar a seguir a representação desta construção.

Permitir aos grupos que interajam entre si comparando os desenhos obtidos. Em seguida, propor novamente à turma as seguintes questões:

• Ao todo, de quantos centímetros foi o deslocamento?

34 cm (12 + 5 + 12 + 5 = 34).

• Qual figura geométrica plana foi obtida ao final?

A figura geométrica obtida foi um retângulo.

Para finalizar a aula, propor aos grupos que, no mesmo quadriculado, representem um outro quadrado e descrevam os deslocamentos realizados para obter o contorno dele. Os grupos, também, devem registrar a medida total do deslocamento, correspondente ao perímetro do quadrado.

Aula 5

No início da aula, lembrar os alunos das construções de quadrados e retângulo realizadas na aula anterior. Em seguida, promover uma atividade para identificar os conhecimentos prévios dos alunos sobre as características e as representações de figuras geométricas planas. Para isso, organizá-los em grupos de três ou quatro integrantes. É importante ter um número par de grupos, pois a atividade exige duplas de grupos.

Explicar que cada grupo será uma equipe de um jogo de adivinhação.

Providenciar, antecipadamente, fichas com contornos de figuras geométricas planas, uma para cada grupo, e cartões com as representações dessas figuras cujos contornos estão representados nas fichas.

Ver a sugestão a seguir. EDITORIA

Antes de entregar as fichas e os cartões aos alunos, explicar detalhadamente as regras do jogo.

Regras do jogo

• Cada grupo receberá uma ficha contendo contornos de nove figuras geométricas planas.

• Os integrantes de cada grupo deverão observar e analisar os contornos representados, utilizando uma régua e fazendo anotações, no caderno, das características de cada um dos contornos.

• Dois grupos (A e B) deverão se sentar frente a frente. Eles receberão uma caixa com cartões, cada um dos quais virá com a representação de uma figura geométrica plana.

• Os grupos decidirão qual deles começará sorteando um cartão.

• Um integrante do grupo A deverá sortear um cartão, sem deixar que os integrantes do grupo B o observem

• Os integrantes do grupo B começarão a fazer perguntas para tentar descobrir qual figura geométrica foi sorteada. Poderão ser feitas apenas três perguntas, que devem ser respondidas com "sim" ou "não"

• Se após as três perguntas o grupo B descobrir qual é a figura, seus integrantes deverão pintar o interior do contorno na ficha com a cor que preferirem. Se errarem a figura, quem pintará é o grupo A, que sorteou o cartão.

• O grupo só poderá tentar acertar a figura uma única vez. Se depois da primeira ou segunda pergunta os alunos disserem o nome da figura e errarem, não poderão fazer as demais perguntas; o outro grupo ganhará a rodada e deverá pintar a figura em sua ficha.

• Depois, será a vez de o grupo B sortear um cartão.

• O grupo vencedor será aquele que conseguir pintar cinco figuras primeiro.

Orientar os alunos a fazerem as perguntas sem dar nome às figuras, mas é permitido questionarem sobre as características delas. Alguns exemplos de perguntas:

• A figura tem quatro lados?

• A figura tem três ângulos internos?

• A figura tem um ângulo reto?

• A figura tem lados de mesma medida?

Determinar um tempo, que pode ser de 30 minutos, para os alunos jogarem. Durante o jogo, caminhar pela sala de aula e observar se eles estão seguindo as regras e quais são os tipos de perguntas mais comuns. Se julgar necessário, fazer intervenções pontuais, a fim de esclarecer possíveis dúvidas dos alunos.

Ao final do jogo, promover uma roda de conversa e pedir aos alunos que falem quais impressões tiveram a respeito do jogo, quais dificuldades enfrentaram e quais estratégias utilizaram.

Aula 6

Retomar com os alunos o que foi trabalhado na aula anterior. Realizar uma roda de conversa para relembrar as características das figuras geométricas planas que estavam presentes no jogo de adivinhação. Anotar na lousa o nome das figuras e classificá-las de acordo com suas características (lados, vértices, ângulos).

Em seguida, pedir aos alunos que se organizem em duplas. Escrever na lousa as atividades a seguir, ou entregá-las em folha impressa, e pedir que as resolvam.

• Observe os polígonos representados a seguir e escreva a quantidade de lados, vértices e ângulos internos de cada um.

Lados: _____

Resposta: 7

Vértices: _____

Resposta: 7

Ângulos internos: _____

Resposta: 7

Lados: _____

Resposta: 4

Vértices: _____

Resposta: 4

Ângulos internos: _____

Resposta: 4

Lados: _____

Resposta: 8

Vértices: _____

Resposta: 8

Ângulos internos: _____

Resposta: 8

Fazer a correção da atividade na lousa, com a participação dos alunos, e a contagem dos lados de cada figura, assim como, também, dos ângulos internos, indicando cada um desses ângulos. Verificar se eles perceberam que cada ângulo interno é determinado por dois lados, denominados lados adjacentes.

Em seguida, com as duplas ainda formadas, entregar uma folha avulsa para cada dupla e pedir a eles que desenhem, utilizando régua, figuras geométricas planas, com as seguintes características:

• polígono A de 3 lados;

• polígono B de 5 vértices;

• polígono C de 6 ângulos internos.

Lembrá-los de que é necessário colorir o interior das figuras desenhadas.

Pedir às duplas que indiquem na folha avulsa a quantidade de lados, vértices e ângulos internos de cada figura que construíram. Em seguida, pedir às duplas que troquem as folhas avulsas entre si, para que uma dupla faça a correção das construções realizadas pela outra dupla. Após elas serem devolvidas às duplas correspondentes, propor à turma a questão a seguir.

• As figuras que vocês construíram são iguais àquelas construídas pela outra dupla? E as quantidades de lados, vértices e ângulos internos das figuras correspondentes são iguais ou diferentes? Espera-se que os alunos digam que as figuras correspondentes são diferentes, porém possuem a mesma quantidade de lados, vértices e ângulos internos.

Para finalizar a aula, perguntar aos alunos: podemos afirmar que polígonos possuem sempre a mesma quantidade de lados, vértices e ângulos internos? Espera-se que os alunos concluam que sim.

Aula 7

Iniciar a aula conversando com os alunos sobre os polígonos construídos na aula anterior. Relembrar o que são lados, vértices e ângulos internos de um polígono. Fazer a seguinte pergunta: qual é o nome do polígono que tem 3 lados, 3 vértices e 3 ângulos internos?

Espera-se que os alunos respondam que esse polígono é o triângulo. Nesse momento, explicar a eles que a palavra triângulo tem origem grega, em que "tri" indica três e " gonos " , ângulos.

Propor aos alunos que se organizem em grupos de três integrantes. Os grupos devem percorrer ambientes da escola, como o pátio, por exemplo, e identificar triângulos em construções (estrutura do telhado, formato de rampa etc.). Após a identificação, os grupos devem fazer o registro com um desenho no caderno, indicando a qual construção se refere

e destacar a figura de triângulo observada. Ao final, permitir que os grupos troquem entre si os desenhos para que possam analisar as diferentes representações de triângulos identificadas pelos colegas.

Comentar com os alunos que o formato triangular é utilizado com frequência por uma importante característica do triângulo: sua rigidez. Dizer a eles que a rigidez do triângulo permite que as construções com estruturas triangulares sejam mais estáveis, tornando-as mais firmes e seguras.

A seguir, explicar aos alunos que os triângulos podem ser classificados de acordo com algumas de suas características, como a medida dos lados e dos ângulos internos. Dizer a eles que um tipo de triângulo é denominado triângulo retângulo. Para exemplificar, desenhar na lousa um retângulo e, com base nele, construir um triângulo retângulo, conforme o exemplo a seguir.

Pedir aos alunos que digam qual dos ângulos internos do triângulo construído é o coincidente ao do retângulo cujo contorno foi feito anteriormente. Em seguida, perguntar a eles uma característica desse ângulo. Espera-se que eles indiquem o ângulo interno inferior esquerdo e digam que esse é um ângulo reto, ou seja, de 90 graus de medida. Então, dizer aos alunos que denominamos triângulo retângulo todo triângulo em que um de seus ângulos internos é reto.

Em seguida, propor aos grupos as seguintes atividades, que podem ser entregues impressas a eles.

1. Quais dos triângulos representados a seguir são retângulos?

2. No caderno, desenhem dois triângulos retângulos. Destaquem o ângulo interno reto e não se esqueçam de colorir o interior da figura.

Após os alunos realizarem as atividades, corrigir e discutir as estratégias que eles utilizaram para resolver cada uma delas. Espera-se que eles tenham utilizado diferentes

estratégias, como o uso de transferidor ou de uma folha de papel retangular para justapor aos lados do triângulo, a fim de verificar se é um ângulo reto ou de construir um ângulo reto. Promover uma roda de conversa para que os grupos exponham tais estratégias aos colegas. Para finalizar a aula, pedir aos grupos que retomem o desenho que realizaram no início da aula e identifiquem se a figura triangular observada e reproduzida da construção lembra um triângulo retângulo.

Aula 8

Nesta última aula, serão propostas atividades que relacionam o estudo de localização e deslocamento no plano e polígonos, tratados nas aulas anteriores. Com isso, espera-se contribuir com o processo avaliativo dos alunos.

Formar duplas com os alunos e propor a eles que realizem as atividades a seguir. Se possível, entregar as atividades impressas aos alunos.

1. Observem o polígono representado na malha quadriculada a seguir. Considerem que cada quadrado da malha tenha 1 cm de lado. EDITORIA

a) Como é classificado o quadrilátero representado na malha? Retângulo.

b) Escrevam a localização de cada vértice desse quadrilátero. A(2,8), B(2,2), C(12,2), D(12,8).

c) O ponto de localização (12,5) está no contorno desse quadrilátero? E o ponto de localização (13,2)?

Sim; não

d) Qual é o perímetro desse quadrilátero?

32 cm (6 + 10 + 6 + 10)

2. Analisem o triângulo representado na malha quadriculada a seguir. Considerem que cada quadrado da malha tenha 1 cm de lado.

Agora, respondam às questões.

a) Escrevam a localização de cada vértice desse triângulo.

A(16,4), B(4,8), C(4,4).

b) O ponto de localização (8,5) está na região interna ou externa do triângulo? E o ponto de localização (10,7)?

(8,5): região interna; (10,7): região externa.

c) Nesse triângulo, qual é a medida do:

• lado AC?

12 cm

• lado BC?

4 cm

d) Qual é o lado mais comprido desse triângulo: lado AB, lado AC ou lado BC?

Lado AB.

e) Podemos afirmar que esse é um triângulo retângulo? Expliquem. Espera-se que os alunos respondam que sim, pois o lado AC e o lado BC determinam um ângulo interno reto no triângulo.

3. Na malha quadriculada a seguir, desenhem um triângulo retângulo. Mas, atenção: os vértices desse triângulo devem ser nomeados com letras maiúsculas e posicionados

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

sobre vértices de figuras de quadradinhos da malha. Em seguida, troquem o desenho de vocês com o de outra dupla, para que uma resolva as questões da outra. Considerem que cada figura de quadrado da malha tenha 1 cm de lado.

EDITORIA DE ARTE

a) Qual é a localização de cada vértice desse triângulo?

b) Indiquem a localização de dois pontos que estejam:

• sobre o contorno do triângulo.

• na região interna do triângulo.

• na região externa do triângulo.

c) Destaquem no desenho o ângulo interno reto.

As respostas dos itens a, b e c vão depender do triângulo desenhado pelas duplas.

Caso os alunos sintam dificuldade na realização das atividades, é importante retomar o conteúdo e incentivar aqueles que já dominam determinado assunto a auxiliar os colegas nas atividades. É importante que os alunos mais adiantados consigam resolver sozinhos as atividades, sem que o professor ou os colegas deem a resposta, estimulando a autonomia

Sequência didática 3: Multiplicação e divisão com números naturais

Esta sequência didática aborda a resolução de multiplicações de números naturais de 1 até 10 e de divisões exatas por números naturais de 1 até 10. Além disso, explora as ideias iniciais de proporcionalidade por meio da resolução de situações-problema.

Objetivos de aprendizagem

• Resolver situações-problema de multiplicação com as ideias de adição de parcelas iguais e disposição retangular.

• Resolver situações-problema de proporcionalidade com base em relações entre a multiplicação e a divisão.

• Resolver situações-problema que envolvam a ideia de proporcionalidade utilizando diversas estratégias de cálculo.

Plano de aulas

Aula 1: Relembrar e discutir as ideias de adição de parcelas iguais e disposição retangular da multiplicação por meio de diferentes tipos de registro.

Aula 2: Desenvolver as multiplicações de números naturais de 1 até 10 (tabuada da multiplicação) por meio de jogo.

Aula 3: Desenvolver as divisões exatas por números naturais de 1 até 10 (tabuada da divisão) por meio de jogo.

Aula 4: Discutir ideias iniciais de proporcionalidade resolvendo situações-problema com apoio de tabuada.

Aula 5: Compreender a relação de proporcionalidade na análise de receita culinária.

Aula 6: Aplicar o conhecimento sobre proporcionalidade para resolver uma situação-problema que envolve receitas culinárias.

Aula 7: Discutir e compreender ideias de proporcionalidade relacionadas à ampliação e à redução de fotografias.

Aula 8: Discutir e compreender ideias de proporcionalidade relacionadas à representação de linha do tempo.

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita.

Competências gerais da Educação Básica: 2 e 9.

Competências específicas de Matemática: 2, 3 e 8

Habilidades: EF05MA08 e EF05MA12.

Materiais necessários: Cartolinas ou papéis-cartões, folhas avulsas, régua, canetas hidrográficas, lápis grafite, lápis de cor, fotografias de diferentes tamanhos, e dados (um para cada grupo)

Aula 1

Iniciar a aula relembrando ideias relativas à multiplicação. Caso seja necessário, ajudar os alunos a lembrarem que uma delas é entender a multiplicação como uma adição de parcelas iguais. Perguntar em quais situações a multiplicação pode ser usada para facilitar os cálculos e a solução de problemas no dia a dia.

Por exemplo, propor a seguinte questão: Mônica coleciona figurinhas do campeonato de futebol. Cada pacote de figurinhas contém 5 unidades. Quantas figurinhas há em 9 pacotes desses?

Após apresentar o problema, sugerir a eles que tentem resolvê-lo utilizando apenas a adição. Após cerca de 3 minutos, verificar as estratégias utilizadas e fazer a correção na lousa: 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 45

Depois, escrever na lousa a seguinte multiplicação, que também pode ser usada para resolver esse problema:

EDITORIA DE ARTE

Nesse momento, é importante que os alunos compreendam a ideia da multiplicação como uma adição de parcelas iguais.

Em seguida, relembrar outra ideia da multiplicação: disposição retangular. Para isso, pedir a eles que calculem a quantidade de quadradinhos verdes que compõem o retângulo representado na malha quadriculada a seguir.

Após 5 minutos de atividade, verificar as estratégias de cálculo realizadas por eles (contagem, adição, multiplicação etc.). Destacar a estratégia da multiplicação. Para isso, compor na lousa o esquema representado a seguir.

EDITORIA DE ARTE

Após esclarecer possíveis dúvidas dos alunos em relação à ideia de disposição retangular da multiplicação, organizar a turma em grupos de três alunos e pedir que usem uma cartolina ou um papel-cartão para fazer um modelo de tabuada, que servirá de tabuleiro para o jogo das próximas aulas.

EDITORIA DE ARTE

Explicar aos alunos que eles devem preencher cada célula com o produto dos números indicados na linha e na coluna correspondentes. Para esse preenchimento, os alunos podem associar o resultado à ideia de disposição retangular da multiplicação. Por exemplo, o número 12, indicado a seguir, corresponde às multiplicações 2 × 6 = 12 ou 6 × 2 = 12 e pode ser compreendido com a quantidade de quadrinhos destacados em verde.

EDITORIA DE ARTE

Para finalizar a aula, pedir às duplas que troquem as cartelas entre seus integrantes para que um confira a cartela do outro. A seguir está representada a cartela preenchida.

Pedir aos alunos que guardem as cartelas, pois elas serão utilizadas em jogos nas próximas aulas.

Aula 2

Após uma conversa inicial, em que podem ser retomados os estudos da aula anterior, propor aos alunos um jogo de multiplicação. Organizar a turma nas mesmas duplas da aula anterior e pedir que peguem as cartelas confeccionadas por eles, que servirão de tabuleiro no jogo (uma cartela por partida). Para cada dupla, disponibilizar um dado comum.

Explicar que, inicialmente, os tabuleiros devem estar com a face voltada para baixo.

• Cada aluno da dupla escolhe um lápis de cor diferente, pois as cores identificarão os jogadores.

• Cada jogador lança o dado duas vezes.

• Os números sorteados nos lançamentos são multiplicados entre si, e o aluno que jogou fala o resultado em voz alta. Se o resultado estiver correto, ele deverá desvirar o tabuleiro, localizar a casa correspondente a esse produto e pintá-la com a cor de lápis que escolheu. O número sorteado na primeira jogada indica o número da linha no tabuleiro; o número sorteado na segunda jogada indica o número da coluna. Por exemplo:

• Primeira jogada: face 4 do dado; linha de número 4

• Segunda jogada: face 5 do dado; coluna de número 5 Como foram obtidos os números 4 e 5, respectivamente, deve-se pintar o número 20 que se encontra no cruzamento da linha 4 com a coluna 5

• Se o jogador errar o resultado da multiplicação, ele não pintará quadradinho algum.

• Nesse caso, o tabuleiro voltará a ser virado com a face para baixo e os outros jogadores prosseguirão o jogo.

• Se o resultado de uma multiplicação já estiver preenchido, o jogador deverá lançar o dado mais duas vezes para obter o novo resultado.

Cada jogador faz cinco jogadas de dois lançamentos cada uma. Pintados os quadradinhos, a dupla apura o resultado. Vence o jogo quem pintar mais quadradinhos. Pode ocorrer empate entre os jogadores

Após cada partida, propor aos alunos que troquem as duplas.

Como não foram trabalhadas as multiplicações por 7, 8 e 9, na parte final da aula, pedir aos alunos que guardem as cartelas, enunciar oralmente algumas multiplicações por 7, 8 e 9 e pedir a eles que registrem o resultado no caderno, sem dizer aos colegas o resultado. Em seguida, pedir que confiram na cartela se o resultado que eles indicaram estão corretos.

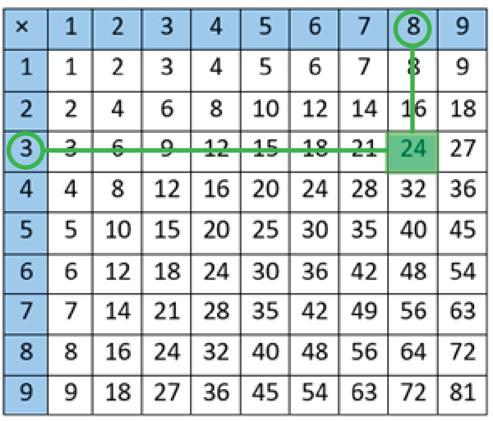
Pedir aos alunos que guardem os tabuleiros, pois serão utilizados em outro jogo na aula seguinte.

Caso os alunos ainda manifestem alguma dúvida sobre a multiplicação e as diferentes estratégias de cálculo, trabalhar com outros exemplos obtidos no próprio jogo e reforçar a inter-relação entre as linhas, as colunas e as diagonais no tabuleiro.

Aula 3

No início da aula, construir na lousa o tabuleiro que os alunos confeccionaram e usaram nas aulas anteriores. A ideia, agora, é que eles reconheçam relações entre a multiplicação e a divisão. Com o tabuleiro já construído, pedir a eles que determinem o resultado de 24 ÷ 3 observando o tabuleiro. Após 3 minutos, avaliar as respostas e as estratégias dos alunos. Então, destacar na cartela o número 24, o número 3 que indica a linha e o número 8 que indica a coluna, conforme representado a seguir

EDITORIA DE ARTE

Em seguida, compor na lousa o seguinte esquema:

3 × 8 = 24 ⟶ 24 ÷ 3 = 8

Com isso, espera-se que os alunos identifiquem características da relação inversa entre a multiplicação e a divisão. Para verificar a compreensão dos alunos, propor a eles mais cinco divisões, que eles devem resolver com o auxílio do tabuleiro.

Passado esse momento inicial da aula, pedir aos alunos que se organizem em trios para brincarem com um jogo da divisão. Em cada partida desse jogo, um aluno será o juiz e, os demais, competidores. Nas 6 rodadas que compõem uma partida, o juiz deve observar o tabuleiro, escolher um número e indicar aos competidores a divisão do número escolhido por aquele que indica sua linha. No caso do exemplo apresentado anteriormente, o juiz indicaria a divisão 24 ÷ 3. Então, sem observar os tabuleiros, os competidores devem obter o resultado e, quem disser primeiro o resultado correto ao juiz, marca 1 ponto. Mas, se disser o resultado incorreto, quem marca 1 ponto é o outro competidor. Ao final das 6 rodadas, vence o competidor com mais pontos; e pode haver empate.

A cada partida, os integrantes do grupo se alternam na função de juiz.

Caso os alunos ainda tenham dúvidas sobre a relação entre a multiplicação e a divisão estudadas nesta aula, trabalhar com outras situações do jogo, apresentando exemplos na lousa.

Aula 4

Iniciar a aula perguntando se restou alguma dúvida da aula anterior. Depois de resolvidas as pendências eventuais, perguntar aos alunos se conhecem algo sobre proporções e para que elas servem. Anotar na lousa as respostas. Nesse momento, é bom ouvir o que eles têm para dizer antes de apresentar o conceito de proporcionalidade. Abordar situações que despertem a curiosidade da turma e promover desafios. Para isso, propor o problema a seguir.

• Para fazer uma jarra de refresco, Marcos usou 4 copos de água para cada copo de suco concentrado. Quantos copos de água serão necessários para dissolver 2 copos de suco concentrado? E 3 copos de suco concentrado? E 6 copos de suco concentrado?

Os alunos podem utilizar estratégias variadas para resolver esse problema

Sugestão de resposta:

2 copos de suco concentrado: 2 × 4 = 8; 8 copos de água.

3 copos de suco concentrado: 3 × 4 = 12; 12 copos de água.

6 copos de suco concentrado: 6 × 4 = 24; 24 copos de água.

Os alunos podem, ainda, decidir montar um quadro como o da tabuada das aulas anteriores. Se isso ocorrer, explicar que, para este caso, essa solução é viável, mas ressaltar que existem situações em que se torna inviável montar um quadro. Pedir a eles que imaginem como seria se Marcos tivesse que usar a mesma quantidade de água para cada

copo de suco concentrado, mas decidisse misturar com água 18 copos de suco. Nesse caso, a montagem de um quadro pode ser longa e cansativa.

Se o aluno conhecer bem o funcionamento da multiplicação, explícito na tabuada de 1 a 9, terá mais facilidade para resolver situações desse tipo por meio de uma multiplicação: se 4 copos de água servem para diluir 1 copo de suco concentrado, então para 18 copos de suco concentrado são necessários 72 copos de água (18 × 4 = 72).

Por outro lado, recorrendo a um cálculo mental ou à tabuada (na qual não há multiplicações explícitas por 18), o aluno poderá primeiro encontrar a metade de 18, que é 9, multiplicá-la por 4 (o número de copos de água), repetir a multiplicação e adicionar os 2 resultados

já que antes ele dividiu 18 por 2. Assim, terá 9 × 4 = 36 e, outra vez, 9 × 4 = 36. Adicionando os 2 resultados terá 36 + 36 = 72. Portanto, são necessários 72 copos de água para diluir 18 copos de suco concentrado.

Depois de conversar com os alunos a respeito das estratégias para solucionar problemas com números que não recomendam a confecção de um quadro, propor a eles que resolvam as atividades a seguir.

1. O pai de Luís pretende fazer um churrasco para comemorar o aniversário do filho. Observe como ele fez os cálculos para saber quanto de carne deve comprar:

• Quantidade de carne para 1 pessoa: 350 g.

• Quantidade de carne para 2 pessoas: 700 g.

• Quantidade de carne para 3 pessoas: 1 050 g.

Sabendo que o pai de Luís convidou 15 pessoas, quantos gramas de carne ele deve comprar?

15 × 350 = 5 250. O pai de Luís deve comprar 5 250 g de carne, ou seja, 5 quilogramas e 250 gramas de carne.

2. Se o número de convidados fosse o triplo, quantos gramas de carne ele teria de comprar?

Espera-se que os alunos efetuem a multiplicação a seguir para obter o triplo da quantidade de carne anteriormente imaginada.

3 × 5 250 = 15 750. O pai de Luís deve comprar 15 750 g de carne, ou 15 quilogramas e 750 gramas.

3. Se o quilograma da carne escolhida custar 30 reais, quanto o pai de Luís gastará para comprar 6 quilogramas dessa carne?

EDITORIA DE ARTE

6 × 30 = 180. Ele gastará 180 reais.

Caso algum aluno demonstre ter dificuldade na resolução da atividade, é importante estimulá-lo a dizer exatamente o que não compreendeu. Se quiser evitar a exposição do aluno perguntando à turma a possível solução do problema, fale como se fosse uma possibilidade distante, usando frases como: e se alguém perguntasse quantos quilogramas de carne equivalem a 4 200 g? Como fazer esse cálculo?

Perguntar se alguém da turma se sente à vontade para explicar aos colegas essa conversão e tentar solucionar as dúvidas antes do fim da aula.

Aula 5

Para iniciar a aula, explicar que chamamos de grandeza tudo o que pode ser contado e medido, como massa, distância, tempo, entre outras. Para exemplificar melhor a questão, pedir aos alunos que trabalhem em conjunto para a resolução da proposta a seguir.

• Imagine que você esteja ajudando a sua família a fazer um bolo utilizando a receita a seguir

Ingredientes

• 300 gramas de açúcar

• 450 gramas de farinha de trigo

• 60 gramas de manteiga

• 3 ovos

• 250 mL de leite

• 10 gramas de fermento

Essa receita rende 10 porções de bolo de 100 gramas por pedaço. Porém, há 20 pessoas para comer o bolo. Quais soluções existem para que todos comam um pedaço de bolo do mesmo tamanho?

Deixar que os alunos respondam o que fazer diante da situação e anotar as respostas na lousa. Provavelmente, existirão duas respostas mais recorrentes: uma indicando que seja feito mais bolo; outra, que se diminuam as porções de cada pedaço de bolo. Mostrar que as duas podem ser feitas, levando a resultados diferentes.

Se uma receita serve 10 pessoas, para servir 20 pessoas, mantendo o tamanho de cada porção, precisaríamos do dobro da quantidade de bolo, ou seja, de duas receitas. Explicar que para dobrar a receita precisamos dobrar, também, a quantidade de cada ingrediente. Pedir que montem uma nova receita, alterando a quantidade dos ingredientes, para servir as 20 pessoas, conforme representado a seguir.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Ingredientes

• 600 gramas de açúcar

• 900 gramas de farinha de trigo

• 120 gramas de manteiga

• 6 ovos

• 500 mL de leite

• 20 gramas de fermento

Mostrar que existe, nesse caso, grandezas proporcionais: ao dobrarmos a quantidade dos ingredientes da receita, também dobramos o número de pessoas que podem ser servidas, com a mesma proporção. Representar na lousa o quadro a seguir, sem o preenchimento dos dados do número de pessoas servidas, e solicitar aos alunos que o completem com essas informações.

Depois, pedir aos alunos que imaginem que acabaram os ingredientes e que não é possível fazer uma nova receita. Então, para que todas as pessoas sejam servidas, é necessário diminuir o tamanho da porção servida a cada pessoa.

Se cada porção tinha 100 gramas e servia 10 pessoas, qual é o tamanho necessário da porção para que sejam servidas 20 pessoas? Representar na lousa um novo quadro, sem os dados do número de pessoas servidas, para que os alunos o completem com as informações solicitadas.

Explicar aos alunos que essas grandezas são inversamente proporcionais, uma vez que, ao aumentarmos o valor de uma, diminuímos o da outra na mesma proporção.

Ao final da aula, verificar se os alunos compreenderam as ideias sobre as relações de proporcionalidade apresentadas. Para isso, realizar uma roda de conversa e propor questões

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas

sob os mesmos parâmetros.

como: ao aumentar a quantidade dos ingredientes, a quantidade de porções obtidas aumentou ou diminuiu? Espera-se que eles respondam que aumentou. Ao reduzir o tamanho da porção, a quantidade de pessoas servidas aumentou ou diminuiu? Espera-se que eles respondam que aumentou

Para a próxima aula, pedir aos alunos que pesquisem com pessoas adultas que moram com eles alguma receita culinária que seja preparada com certa frequência. Destacar que eles devem anotar a quantidade de cada ingrediente, o modo de preparo e o rendimento (quantidade de porções obtidas). Esses registros devem ser providenciados para a próxima aula.

Aula 6

Nesta aula, a ideia é retomar o trabalho com proporcionalidade desenvolvido na aula anterior. Em uma roda de conversa, retomar o que foi estudado anteriormente, esclarecendo possíveis dúvidas.

Organizar os alunos em grupos de 3 ou 4 integrantes. Propor, a cada grupo, que escolha uma receita culinária entre as que eles trouxeram. Em seguida, cada grupo deve calcular a quantidade dessa receita que será preparada para que, no mínimo, todos os alunos da turma recebam uma porção. Por exemplo, considerar a lista de ingredientes, a seguir, da receita de bolo apresentada na aula anterior, cujo rendimento é de 10 porções (pedaços de 100 gramas):

Ingredientes

• 300 gramas de açúcar

• 450 gramas de farinha de trigo

• 60 gramas de manteiga

• 3 ovos

• 250 mL de leite

• 10 gramas de fermento

Supondo que a turma tenha 38 alunos, será necessário preparar 4 receitas dessas, pois 38 ÷ 10 = 3 e resto 8. Nesse caso, é importante que os alunos deem significado ao resto da divisão. Por exemplo, verificar se eles notaram que 3 receitas dessas rendem 30 porções, ou seja, uma quantidade insuficiente para servir uma porção por aluno.

Assim, de acordo com essas informações, a lista da quantidade dos ingredientes é dada por:

Ingredientes

• 1 200 gramas de açúcar (4 × 300 = 1 200)

• 1 800 gramas de farinha de trigo (4 × 450 = 1 800)

• 240 gramas de manteiga (4 × 60 = 240)

• 12 ovos (4 × 3 = 12)

• 1 000 mL de leite (4 × 250 = 1 000)

• 40 gramas de fermento (4 × 10 = 40)

Em seguida, pedir aos grupos que façam o registro da receita de acordo com as quantidades de ingredientes calculadas. Cada grupo deve realizar uma apresentação oral aos demais grupos, explicando a receita trabalhada, ou seja, indicando a quantidade de cada ingrediente, o rendimento de porções e o modo de preparo.

Ao final das apresentações, se for possível e conveniente, uma das receitas apresentadas pode ser preparada na escola. Para isso, verificar a possibilidade de realizar esse preparo na cozinha da escola e com o apoio de outros profissionais (cozinheiras e outros professores), sempre zelando pela segurança dos alunos.

Para a próxima aula, pedir aos alunos que tragam uma fotografia impressa, de qualquer tamanho.

Aula 7

Iniciar a aula, propondo aos alunos as questões a seguir.

• Todas as fotografias impressas ou reveladas têm o mesmo tamanho?

• Existe relação entre as dimensões de alguns formatos de fotografias?

Após deixar os alunos conversarem entre si sobre essas questões, por cerca de 5 minutos, explicar a eles que as fotografias costumam ser impressas em formato retangular e podem ter tamanhos diferentes. Listar na lousa algumas dimensões mais comuns de impressão de fotografias, conforme representado a seguir.

Dimensão das fotografias (formato retangular)

• 10 cm × 15 cm

• 10 cm × 20 cm

• 13 cm × 18 cm

• 15 cm × 21 cm

• 20 cm × 25 cm

• 20 cm × 30 cm

• 30 cm × 45 cm

• 30 cm × 60 cm

• 40 cm × 50 cm

• 40 cm × 60 cm

Em seguida, pedir aos alunos que meçam com a régua as dimensões da fotografia que trouxeram e que verifiquem se possuem alguma das dimensões apresentadas.

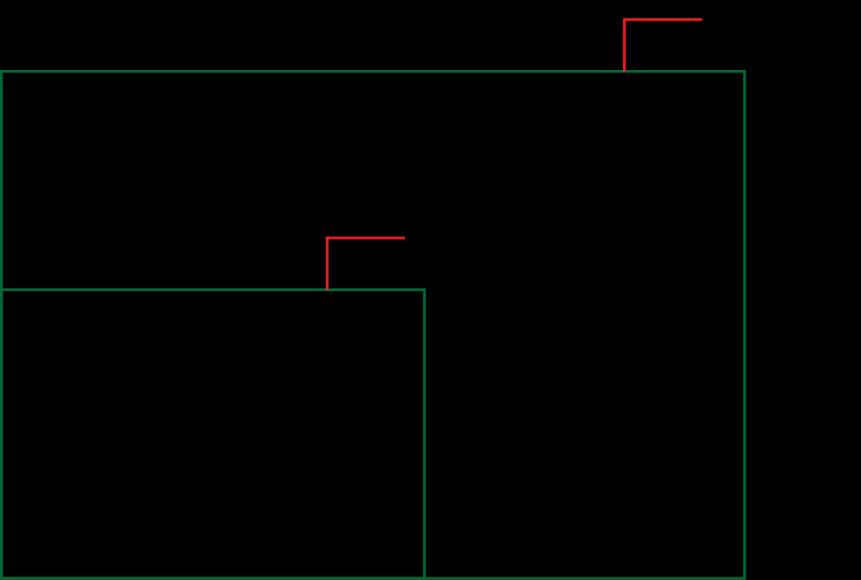
Explicar aos alunos que alguns dos formatos apresentados correspondem a ampliações ou reduções uma das outras. Por exemplo, nesse caso, uma fotografia pode ser ampliada ou reduzida, sem distorção ou corte da imagem, de maneira a obter outro formato com dimensões maiores ou menores. Para exemplificar, pedir que considerem uma fotografia com dimensões 20 cm × 30 cm, conforme representação a seguir (imagem fora de escala).

EDITORIA DE ARTE

Em seguida, pedir aos alunos que multipliquem por 2 cada dimensão da fotografia original. Nesse caso, obtêm-se as dimensões 40 cm × 60 cm (2 × 20 = 40; 2 × 30 = 60). Explicar a eles que a fotografia com essas dimensões calculadas corresponde a uma ampliação da fotografia original. Na lousa, desenhar a representação a seguir.

EDITORIA DE ARTE

Depois, pedir aos alunos que dividam por 2 cada dimensão da fotografia original, ou seja, de dimensões 20 cm × 30 cm. Nesse caso, obtêm-se as dimensões 10 cm × 15 cm (20 ÷ 2 = 10; 30 ÷ 2 = 15). Explicar a eles que a fotografia com essas dimensões calculadas corresponde a uma redução da fotografia original. Na lousa, desenhar a representação a seguir.

EDITORIA DE ARTE

Para consolidar o trabalho com proporcionalidade, que envolve ampliação e redução de figuras, propor aos alunos as seguintes atividades.

1. Considere uma fotografia com dimensões 20 cm × 25 cm. Ao dobrar as dimensões dessa fotografia, obtém-se uma ampliação ou redução dela? Quais são as dimensões da fotografia obtida?

Obtém-se uma ampliação com dimensões 40 cm × 50 cm (2 × 20 = 40; 2 × 25 = 50).

2. Carlos tem uma fotografia emoldurada com dimensões 30 cm × 60 cm. Ele deseja realizar uma redução dessa fotografia, de maneira que esta tenha dimensões 10 cm × 20 cm. Explique como pode ser calculada cada dimensão da fotografia reduzida em relação à fotografia original.

Espera-se que os alunos indiquem que cada dimensão da fotografia original seja dividida por 3, ou seja, 30 ÷ 3 = 10 (10 cm) e 60 ÷ 3 = 20 (20 cm).

3. Com as medidas das dimensões da fotografia que você trouxe, calcule a medida de cada dimensão de uma ampliação ou redução dela. Descreva como podem ser relacionadas as dimensões da fotografia original e dessa ampliação ou redução. A resposta depende das dimensões da fotografia que o aluno trouxe

Aula 8

Outra aplicação de proporcionalidade é o trabalho com a representação de informações em linha do tempo, assunto a ser trabalhado nesta aula. Inicialmente, perguntar aos alunos o que eles sabem sobre linha do tempo. Nesse momento, deixar que eles exponham seus conhecimentos prévios sobre esse assunto, registrando na lousa as respostas.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Explicar aos alunos que a linha do tempo corresponde a uma representação gráfica e cronológica de acontecimentos, ferramenta utilizada na indicação de fatos históricos.

Pedir aos alunos que escrevam no caderno alguns fatos históricos que aconteceram na vida deles, começando pelo próprio nascimento. Para cada fato desses, eles devem indicar o ano do acontecimento. Compartilhar com os alunos o exemplo a seguir.

Fatos históricos da vida de Rafaela

Nascimento: 2013

Comecei a andar: 2014

Adotei um cachorro: 2016

Primeiro dia na escola: 2017

Nascimento da irmã: 2020

Pedir aos alunos que indiquem ao menos 5 fatos acontecidos em anos diferentes. Na lousa, desenhar uma linha reta, marcar o ponto na extremidade esquerda e indicar o primeiro fato histórico do exemplo, conforme representado a seguir

Depois, dizer aos alunos que, nessa representação de linha do tempo, a distância entre dois anos consecutivos será representada por 10 cm de comprimento. Então, a partir do ponto correspondente a 2013, medir 10 cm com régua, e indicar o próximo fato histórico do exemplo.

EDITORIA DE ARTE

Em seguida, perguntar aos alunos como eles fariam para indicar o próximo fato histórico do exemplo nessa linha do tempo. Conduzir a conversa de maneira que eles percebam que, como o próximo fato histórico ocorreu 2 anos após o anterior, é necessário indicá-lo com o dobro da distância entre os fatos de 2013 e 2014. Após essa compreensão, medir na lousa 20 cm (2 × 10 = 20) na linha do tempo, a partir do ponto anterior, e indicar o fato histórico seguinte.

EDITORIA DE ARTE

disponibilizado em licença aberta do tipo

Atribuição

comercial

Material

Creative Commons –

não

(CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Com procedimentos análogos aos apresentados anteriormente, com os alunos, terminar de indicar os fatos históricos usados como exemplo, calculando as multiplicações correspondentes.

Em seguida, retomar com os alunos a atividade inicial proposta a eles, de relacionar fatos históricos de suas próprias vidas. Em uma folha avulsa, na posição paisagem, pedir a eles que tracem com a régua uma linha reta horizontal. Explicar a eles que procedam da mesma maneira que no exemplo apresentado, porém devem usar 3 cm como distância entre um ano e o seguinte. Para verificar se compreenderam, questionar quantos centímetros na linha do tempo devem corresponder a um período de 2 anos (6 cm, 2 × 3 = 6), de 3 anos (9 cm, 3 × 3 = 9) e de 4 anos (12 cm, 3 × 4 = 12). Disponibilizar para a produção da linha do tempo cerca de 25 min. Nesse período, circular entre as carteiras para esclarecer possíveis dúvidas dos alunos.

Ao final, promover uma exposição das linhas do tempo produzidas pela turma.

Sequência didática 4: Figuras geométricas espaciais

O objetivo desta sequência didática é auxiliar os alunos a reconhecerem as figuras geométricas espaciais e suas respectivas planificações, relacionando-as com objetos do dia a dia e classificando-as em poliedros e não poliedros

É proposta, ainda, a realização de dois jogos: "Bingo das planificações" e "Cartas com figuras geométricas espaciais" O objetivo é possibilitar que os alunos analisem as características de figuras geométricas espaciais, para identificarem a figura correta.

Objetivos de aprendizagem

• Identificar objetos que lembrem figuras geométricas espaciais.

• Associar a figura geométrica espacial à sua planificação.

• Identificar o número de arestas, vértices e faces em figuras geométricas espaciais.

• Classificar poliedros em prismas e pirâmides e identificar suas faces, suas arestas e seus vértices

• Caracterizar figuras geométricas espaciais.

• Desenvolver o olhar espacial geométrico.

Plano de aulas

Aula 1: Reconhecer e nomear figuras geométricas espaciais, associando-as a objetos do dia a dia e classificá-las em poliedros e não poliedros.

Aula 2: Associar figuras geométricas espaciais a suas respectivas planificações.

Aula 3: Associar figuras geométricas espaciais a suas respectivas planificações e explorar os conceitos de vértice, face e aresta.

Aula 4: Resolver problemas associados à planificação de figuras geométricas espaciais e aos conceitos de vértice, face e aresta.

Aula 5: Aplicar os conceitos associados a figuras geométricas espaciais em um jogo educativo.

Aula 6: Comparar figuras geométricas espaciais com base em vértices, arestas e faces.

Aula 7: Construir um jogo educativo sobre características de figuras geométricas espaciais.

Aula 8: Revisar os conhecimentos desenvolvidos por meio de um jogo educativo, confeccionado pelos próprios alunos

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita.

Competências gerais da Educação Básica: 2, 9 e 10.

Competências específicas de Matemática: 2 e 8.

Habilidade: EF05MA16.

Materiais necessários: Representações de figuras geométricas espaciais, papel-cartão, folhas com a planificação de algumas figuras geométricas espaciais, cartolina ou papel sulfite, tesoura com pontas arredondadas, cola, folha com imagem de um boneco de papel, lápis de cor, imagens de objetos que lembram as figuras geométricas espaciais, blocos de madeira ou de acrílico que lembram figuras geométricas espaciais e objetos do dia a dia que lembram figuras geométricas espaciais

Aula 1

Esta primeira aula tem como proposta a familiarização dos alunos com o tema "figuras geométricas espaciais" Para isso, são propostas atividades que possibilitam aos alunos observar, comparar e classificar as figuras geométricas espaciais de acordo com as suas características.

Para iniciar a aula, mostrar aos alunos algumas figuras geométricas espaciais específicas, que podem ser montadas com papel-cartão colorido ou apresentadas com a utilização de um projetor de imagens. Garantir que haja pelo menos dois poliedros e dois não poliedros nas figuras mostradas Observe a seguir exemplos de figuras geométricas espaciais que podem ser apresentadas aos alunos.

EDITORIA DE ARTE

Para explorar o conhecimento prévio dos alunos, perguntar a eles qual é o nome de cada uma das figuras geométricas espaciais apresentadas. Em seguida, registrar na lousa

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

os nomes apontados por eles e, se necessário, corrigi-los. Caso os alunos não demonstrem saber os respectivos nomes, introduzir os que faltam, registrando-os, também, na lousa.

Em seguida, pedir que os alunos se reúnam em grupos de 4 integrantes e respondam às questões a seguir

1. Escreva o nome de um objeto que vocês utilizam, ou têm contato, no dia a dia, que lembre uma dessas figuras geométricas espaciais.

Sugestões de resposta: dado (cubo); caixa (prisma); telhado (pirâmide); bola (esfera); lata (cilindro); chapéu de aniversário (cone)

2. Classifique, em dois grupos, as figuras geométricas espaciais mostradas, de acordo com suas características.

Sugestões de resposta: grupo 1 – poliedros (cubo, prisma de base hexagonal, pirâmide de base quadrada); grupo 2 – não poliedros (esfera, cilindro, cone).

Após os alunos responderem a essas duas questões, organizar uma roda de conversa e pedir que compartilhem, coletivamente, quais objetos cotidianos podem ser associados a essas figuras geométricas espaciais.

Solicitar que um representante de cada grupo explique como fizeram para classificar as figuras geométricas espaciais em dois grupos. Em seguida, realizar uma sistematização comentando que uma possibilidade de resposta para a classificação das figuras geométricas espaciais é agrupá-las em poliedros, quando todas as partes da superfície da figura geométrica espacial são planas, e não poliedros, quando há alguma parte arredondada na superfície da figura.

Aula 2

Ao iniciar a aula, propor algumas perguntas para retomar os conceitos sobre figuras geométricas espaciais, discutidos na aula anterior. Incentivar os alunos a participarem desse momento de levantamento dos conhecimentos construídos. Se julgar necessário, complementar as respostas deles e estimular a comparação entre objetos (que estejam presentes na sala de aula ou que façam parte do ambiente escolar) e figuras geométricas espaciais. Para isso, dizer o nome de alguns objetos (sem mostrá-los) para que eles digam o nome da figura geométrica espacial que cada objeto lembra.

Após essa conversa inicial, pedir a eles que formem grupos com no máximo quatro alunos e entregar, para cada grupo, uma planificação de alguma das figuras geométricas espaciais estudadas na aula anterior, como cubo, bloco retangular, pirâmide, cone, cilindro e prisma. É importante que não haja indicação de quais figuras geométricas espaciais correspondem a essas planificações, pois espera-se que os próprios alunos consigam observar essa relação.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Após entregar as diferentes planificações, solicitar que os alunos reproduzam a planificação que receberam em uma folha avulsa, recortem-na e, depois, tentem montá-la utilizando cola.

Quando todos tiverem terminado, solicitar que os grupos apresentem a planificação inicial que cada um recebeu e a relacionem com a figura geométrica espacial que eles montaram. Nesse momento, solicitar a participação coletiva da turma, de maneira que os próprios alunos indiquem o nome de cada figura geométrica espacial montada

A seguir, são apresentadas algumas planificações que podem ser entregues aos alunos. Se julgar necessário, acrescentar outras figuras para que sejam trabalhadas diversas planificações.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial

(CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

EDITORIA DE ARTE

EDITORIA DE ARTE

EDITORIA DE ARTE

EDITORIA DE ARTE

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

EDITORIA DE ARTE

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

O objetivo desta aula é retomar alguns conteúdos explorados anteriormente, especificamente as ideias de vértice, face e aresta. Para isso, em um primeiro momento, questionar os alunos a respeito do que se lembram desse assunto. Em seguida, mostrar aos alunos algumas imagens e realizar uma discussão coletiva com eles, explicitando as diferenças entre aresta, face e vértice. Observar a seguir exemplos de imagens que podem ser exploradas com os alunos.

EDITORIA DE ARTE

Após explicitar o significado dos elementos dessas figuras geométricas espaciais, solicitar que os alunos determinem a quantidade de arestas, faces e vértices que possui cada uma das figuras anteriores Espera-se que eles respondam que o prisma de base triangular tem 6 vértices, 5 faces e 9 arestas e a pirâmide de base quadrada tem 5 vértices, 5 faces, 8 arestas.

Aproveitar essa discussão para perguntar aos alunos qual é o nome dessas figuras geométricas espaciais. Espera-se que eles respondam que a primeira é um prisma; a segunda, uma pirâmide.

Para ampliar, conversar com os alunos a respeito da planificação dessas figuras geométricas espaciais. Para isso, perguntar se eles lembram como seriam essas planificações e se conseguem desenhá-las com régua e papel. Depois, apresentar as imagens a seguir, relacionando-as com as produções dos alunos e corrigindo se for necessário.

EDITORIA DE ARTE

Iniciar a aula com a retomada de alguns conceitos discutidos na aula anterior. Depois, entregar uma folha de papel com a imagem a seguir ou apresentá-la com o auxílio de um projetor.

EDITORIA DE ARTE

Representação de boneco construído com caixa de papelão.

Em seguida, perguntar aos alunos: existe ao menos uma parte desse boneco que lembre alguma figura geométrica espacial que você conheça? Qual figura? Espera-se que os alunos respondam que a cabeça do boneco lembra um bloco retangular.

Depois de os alunos reconhecerem qual figura espacial a cabeça do boneco lembra, escrever as questões a seguir na lousa e pedir que eles as copiem em uma folha avulsa.

1. Quantos vértices tem essa figura?

8 vértices.

2. Qual é a quantidade de arestas?

12 arestas.

3. Qual é a quantidade de faces?

6 faces.

4. Qual das imagens a seguir melhor representa a planificação dessa figura espacial? EDITORIA

Espera-se que os alunos percebam que a imagem que melhor representa a planificação de um bloco retangular é a segunda imagem (figura da direita).

Ao término da atividade, pedir aos alunos que entreguem as questões resolvidas. Em seguida, entregar a eles a representação de uma planificação de bloco retangular, como a apresentada a seguir, e solicitar que montem e confiram as respostas das questões. EDITORIA

Aula 5

Para iniciar a aula, perguntar aos alunos quais figuras geométricas espaciais eles conhecem. Anotar na lousa as figuras mencionadas por eles. Depois, continuar a conversa e perguntar: quais características são parecidas e quais são diferentes entre essas figuras?

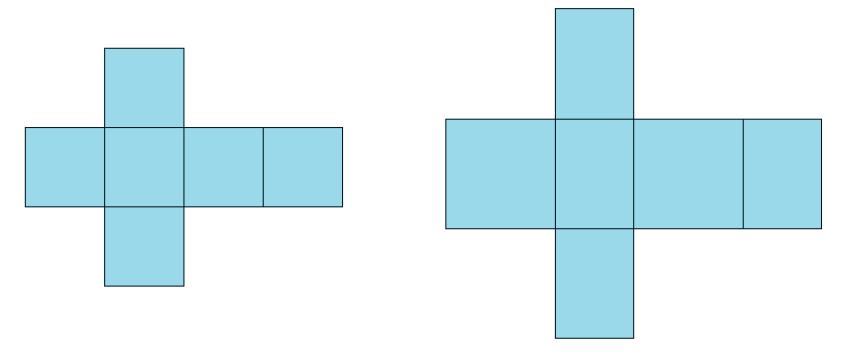
Nesta aula, será necessário trazer blocos de madeira ou acrílico que lembram figuras geométricas espaciais. Sugere-se trabalhar com figuras como o cubo, o bloco retangular, a pirâmide (de base quadrada), o tetraedro (pirâmide de base triangular), o cone e o cilindro Após essa conversa, organizar os alunos em grupos, cada um com no máximo cinco integrantes, e entregar uma folha com cinco ou seis planificações de figuras espaciais a cada um. A seguir, há algumas planificações.

Para obter um resultado melhor com a atividade, entregar aos alunos planificações diferentes.

Em seguida, pedir que os alunos anotem em uma folha avulsa as informações que considerarem importantes para que eles identifiquem as figuras posteriormente. Por exemplo: a figura é formada por quatro triângulos e um quadrado (descrição referente à pirâmide de base quadrada).

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Explicar que o nome do jogo é Bingo das planificações. Colocar, de antemão, os blocos de madeira ou acrílico dentro de uma caixa e, durante o jogo, retirá-los e mostrá-los aos alunos Eles deverão verificar se têm consigo a planificação que lembra esse objeto e marcá-la. Vencerá o grupo que assinalar corretamente primeiro todas as planificações da folha.

Ao final, pedir aos alunos que tragam, na próxima aula, um objeto que lembre uma das figuras geométricas espaciais estudadas nas aulas anteriores.

Aula 6

Iniciar a aula perguntando se resta alguma dúvida quanto ao que foi abordado nas aulas anteriores. Depois de sanar as dúvidas, dar continuidade à aula dispondo sobre a mesa os objetos levados pelos alunos.

Pedir que anotem em uma folha de caderno os seguintes dados sobre cada uma das figuras representadas pelos objetos dispostos na mesa.

• Número de vértices.

• Número de arestas.

• Número de faces.

Em seguida, perguntar aos alunos: o objeto faz lembrar qual figura geométrica espacial? As respostas devem ser compartilhadas com toda a turma.

Promover mais uma rodada de conversa e perguntar se há dúvidas, retomando o que for preciso. Depois, desenhar na lousa um quadro com as características das figuras geométricas com as quais os alunos tiveram contato, conforme o exemplo a seguir.

Em seguida, pedir que entreguem as anotações feitas no caderno e questioná-los se ainda possuem alguma dúvida em relação à identificação do número de faces, arestas e vértices.

Provavelmente, alguns alunos ainda se confundem ao contar as faces, as arestas e os vértices das figuras geométricas espaciais. Por isso, se julgar oportuno, retomar as planificações, os objetos apresentados e aqueles que os alunos trouxeram para esclarecer essas questões e promover uma contagem conjunta com a turma. Se possível, por meio de um projetor, mostrar imagens dessas figuras à turma.

Aula 7

Nesta aula, os alunos vão compor os materiais necessários para a realização do jogo Cartas com figuras geométricas espaciais, que será explorado na aula seguinte. Para isso, selecionar 7 figuras geométricas espaciais e organizar os alunos em 7 grupos. Alguns exemplos de figuras estão listados a seguir.

• Cubo.

• Bloco retangular

• Pirâmide de base quadrada

• Pirâmide de base triangular

• Prisma triangular

• Prisma hexagonal

• Cone.

Cada grupo receberá três cartas iguais, que devem ter a representação de uma figura geométrica espacial e seu respectivo nome.

Os grupos devem ficar responsáveis pela confecção dos materiais correspondentes a essas três cartas. Em cada uma delas, no verso do desenho, serão descritas dicas, pelos próprios alunos, que se associam à figura geométrica espacial representada. Essas dicas definem o tipo de carta do jogo e devem ser escritas conforme indicado a seguir.

• Carta do tipo 1: apresenta alguma característica da figura geométrica espacial. Por exemplo, ter uma das faces representada por um triângulo, ter todas as partes compostas de figuras planas, ser um não poliedro, entre outras.

• Carta do tipo 2: apresenta o número de vértices, faces e arestas da figura geométrica espacial.

• Carta do tipo 3: apresenta a planificação da figura geométrica espacial. É importante que o tipo de carta também seja indicado em cada uma

Após a confecção das cartas do jogo, os alunos já estarão preparados para jogá-lo na aula seguinte. Pedir que os grupos tragam materiais de referência, na próxima aula, como os registros realizados nas aulas anteriores, que podem ajudar no desempenho do jogo.

Aula 8

Nesta aula, os alunos vão jogar o jogo com cartas de figuras geométricas espaciais. Para isso, organizar os alunos nos mesmos grupos que confeccionaram os materiais do jogo na aula anterior. Em seguida, ler as regras a seguir para a turma.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Regras do jogo

• Este é um jogo de adivinhação.

• Em cada rodada, um grupo terá sua vez de jogar. A ordem das rodadas será determinada por sorteio.

• Para cada grupo, o professor fará o sorteio de uma carta, e a mostrará para todos os alunos. Essa carta descreve, de algum modo, uma figura geométrica espacial.

• O grupo da rodada terá 30 segundos para tentar adivinhar a resposta. Ou seja, nesse período, o grupo deverá adivinhar qual figura geométrica espacial é descrita por aquela carta.

• Caso o grupo não saiba, ele pode escolher outro grupo para tentar adivinhar a resposta, que também terá 30 segundos para tentar descobri-la. Esse momento será estratégico. Portanto, uma possibilidade de escolha é a do grupo que possuir menor pontuação.

• Se o grupo não acertar a resposta ou não a encontrar no tempo disponível, o professor apresentará a resposta da carta, que se encontra em seu verso.

• Ao acertar a figura geométrica espacial, o grupo ganha pontos de acordo com o tipo de carta. Se for uma carta do tipo 1, o grupo ganha 10 pontos. Se for do tipo 2, o grupo ganha 9 pontos e se for do tipo 3, o grupo ganha 8 pontos. O professor registrará a pontuação de cada grupo na lousa.

• Caso o grupo erre a figura geométrica espacial ou não a determine no tempo destinado, ele não ganhará pontos.

• Ao final da aula, o grupo com maior pontuação vencerá o jogo. Quando todos os alunos compreenderem as regras, iniciar o jogo.

Sugestões

• O MUNDO e as formas geométricas Conexão Escola Disponível em: https://sme.goiania.go.gov.br/conexaoescola/ensino_fundamental/o-mundo-e-asformas-geometricas/ Acesso em: 13 abr. 2021

• FUNDAÇÃO CULTURAL PALMARES. Reinos e impérios africanos: civilização egípcia. Disponível em: www.palmares.gov.br/?p=53916 Acesso em: 13 abr. 2021.

• POLYPAD. Mathigon. Disponível em: https://pt.mathigon.org/polypad. Acesso em: 8 jan. 2022.

• COLEÇÃO Matemática Multimídia: o que é poliedro? São Paulo: Matemática Multimídia, 19 set. 2020.Podcast Disponível em: https://anchor.fm/matematicamultimidia/episodes/Srie-O-que O-que poliedro-ejsp2i Acesso em: 21 jan. 2022.

Sequência didática 5: Os números na forma de fração

O objetivo desta sequência didática é ampliar o trabalho com números racionais na forma fracionária por meio da manipulação de material concreto, da realização de jogos e da resolução de situações-problema, de maneira que os alunos sejam capazes de identificar e compreender o significado de frações, como a ideia da relação parte-todo, de relacionar diferentes representações de frações e de comparar frações.

Objetivos de aprendizagem

• Reconhecer as diferentes representações de um número racional.

• Compreender o significado de frações equivalentes.

• Utilizar a ideia de frações equivalentes para fazer a comparação de frações.

• Ideia de fração como relação parte-todo.

• Compor um inteiro por meio de adição de frações.

• Representação de frações unitárias.

Plano de aulas

Aula 1: Representar frações unitárias por meio de confecção de fichas.

Aula 2: Comparar frações unitárias e relacionar essas frações ao inteiro, utilizando fichas.

Aula 3: Compor o inteiro com adições de frações unitárias por meio de um jogo.

Aula 4: Reconhecer e representar, utilizando figuras e números, frações não unitárias, por meio da resolução de situações-problema.

Aula 5: Representar numericamente e por extenso uma mesma fração na confecção de fichas de jogo.

Aula 6: Associar diferentes representações, numérica e por extenso, de uma mesma fração, por meio da realização de um jogo.

Aula 7: Comparar e ordenar frações utilizando fichas.

Aula 8: Comparar frações por meio de um jogo.

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita.

Competências gerais da Educação Básica: 9 e 10.

Competências específicas de Matemática: 3 e 8

Habilidades: EF05MA03, EF05MA04 e EF05MA05.

Materiais necessários: Caderno, fichas quadradas de cartolina (5 cm × 5 cm), folhas avulsas, lápis de cor, cartolina nas cores branca, amarela, rosa, vermelha, azul, roxa e laranja, no tamanho de uma folha de papel sulfite A4 e tesouras com pontas arredondadas

Inicialmente, promover uma atividade para identificar os conhecimentos prévios dos alunos sobre frações. Para isso, providenciar antecipadamente as folhas de cartolina nas cores branca, amarela, rosa, vermelha, azul, roxa e laranja (devem ser 7 cores diferentes de cartolina; se não houver cartolina nas 7 cores, usar somente a branca e pedir aos alunos que façam marcações de diferentes cores). Recortar as folhas de cartolina no tamanho de uma folha de papel A4 e disponibilizar sete "partes" de cartolina de mesmo tamanho (A4) para cada aluno. Em seguida, pedir aos alunos que façam dobras (considerando a posição paisagem da cartolina), conforme instruções a seguir. Escrever as instruções na lousa.

• Dobrar a cartolina amarela ao meio, da direita para a esquerda, formando duas partes iguais.

• Dobrar a cartolina rosa ao meio, de baixo para cima, formando duas partes iguais.

• Dobrar a cartolina vermelha em três partes iguais.

• Dobrar a cartolina azul em quatro partes iguais.

• Dobrar a cartolina roxa em seis partes iguais.

• Dobrar a cartolina laranja em oito partes iguais.

• A cartolina branca é a única que ficará sem dobras.

Se julgar necessário, fazer as dobras com os alunos, mostrando onde cada folha deverá ser dobrada.

Após terem dobrado todas as folhas de cartolina, conforme as instruções anteriores, pedir aos alunos que recortem cada uma nos vincos formados pelas dobras e escrevam a fração que cada uma das peças representa da cartolina original (A4).

Eles devem obter as seguintes peças. EDITORIA

Ao final, pedir aos alunos que analisem as peças e verifiquem a relação de cada uma com a cartolina branca. Verificar se eles compreenderam que as partes da mesma cor, juntas, formam um inteiro (cartolina branca). Por exemplo, as 8 partes da cartolina laranja formam um inteiro; assim, cada uma dessas partes representa 1 8

Pedir aos alunos que guardem o material confeccionado, pois será utilizado na próxima aula.

Aula 2

No início da aula, organizar os alunos em duplas e pedir que peguem as cartolinas coloridas confeccionadas na aula anterior. Permitir a eles que, por cerca de 5 minutos, observem, manipulem e conversem sobre as cartolinas e as frações representadas por elas. Reforçar com eles que essas frações são consideradas a partir do inteiro representado pela cartolina branca.

Em seguida, pedir às duplas que construam no caderno um quadro, conforme representado a seguir.

Propor aos alunos que preencham o quadro fazendo comparações das cartolinas de cada cor com a cartolina branca. Por exemplo, são necessárias 3 cartolinas vermelhas para sobrepor exatamente a cartolina branca. Observe a seguir o quadro preenchido.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Cor da cartolina Fração representada Quantidade de cartolinas para formar um inteiro

Cor da cartolina Fração representada Quantidade de cartolinas para formar um inteiro

Com o quadro preenchido, promover uma roda de conversa com os alunos, a partir da seguinte questão: como podemos comparar essas frações indicadas no quadro e ordená-las de maneira decrescente, ou seja, da maior para a menor?

Conduzir a discussão de maneira que os alunos percebam que a fração 1 2 é a maior delas, pois são necessárias apenas duas partes das cartolinas amarelas ou rosa para formar um inteiro. Já a fração 1 8 é a menor delas, pois são necessárias 8 partes das cartolinas de cor laranja para formar um inteiro

Após esse momento, pedir às duplas que escrevam no caderno as frações que já estão indicadas no quadro em ordem decrescente:

 11111 23468

Então, propor às duplas a seguinte questão: acrescentem as frações 1 7 , 1 5 , 1 10 e 1 9 à ordenação escrita anteriormente. Deixar que eles utilizem as estratégias que preferirem. É possível que, coletivamente, algumas duplas percebam que, por exemplo, para representar a fração 1 7 , seria necessário recortar um pedaço de cartolina colorida de tamanho A4 em 7

partes iguais, sendo cada parte desta correspondente a 1 7 . Assim, seriam necessárias 7 cartolinas para formar um inteiro. Com esse raciocínio, as duplas podem escrever esta nova ordenação de frações:

 111111111

2345678910

Para finalizar a aula, providenciar um conjunto de cartolinas idênticas às produzidas por eles e compor, na sala de aula, um varal no qual as cartolinas devem ser penduradas em ordem decrescente das frações representadas por elas, conforme representado a seguir.

EDITORIA DE ARTE

Pedir aos alunos que guardem suas peças de cartolina, pois elas serão reutilizadas na próxima aula.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Representação do varal de frações.

Aula 3

Retomar com os alunos as atividades trabalhadas nas aulas anteriores e solicitar que peguem as peças de cartolina que confeccionaram.

Construir, antecipadamente, dados que, em cada face, tenham cada uma das seguintes frações: 1 2 , 1 3 , 1 4 , 1 4 , 1 4 , 1 6 e 1 8

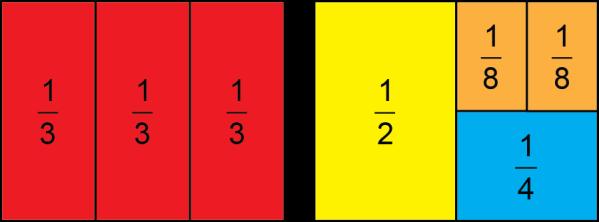
Organizar os alunos em grupos de três ou quatro integrantes e explicar as instruções a seguir

• Cada aluno deve ter, na sua frente, o conjunto com as 26 peças de cartolina confeccionadas anteriormente.

• A cartolina branca ficará separada do conjunto e vai ser utilizada como base de comparação pelo aluno.

• Um aluno por vez joga o dado e retira do conjunto a peça que representa a fração da face que ficar para cima.

• Ganha o jogo o aluno que conseguir formar exatamente um inteiro primeiro, sobrepondo, sem sobras, a cartolina branca com peças sorteadas.

• O inteiro pode ser formado por peças de cores diferentes ou iguais.

Se julgar conveniente, apresentar a eles algumas composições diferentes para vencer uma partida desse jogo, conforme os exemplos a seguir.

Ao final de cada partida, pedir aos alunos que expliquem como conseguiram formar o inteiro, se utilizaram peças da mesma cor ou de cores diferentes. Neste momento, é importante verificar se eles perceberam que podem utilizar, por exemplo, duas peças que representam 1 4 , no lugar de uma que representa 1 2 . Novas partidas desse jogo podem ser propostas, alterando a composição das duplas.

Para esclarecer as dúvidas dos alunos e consolidar as ideias de frações trabalhadas, propor questões com o objetivo de fazê-los perceber quantas peças de cada cor são necessárias para formar um inteiro ou quantas peças de determinada cor são necessárias para formar uma peça de outra cor, entre outras.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

Aproveitar a oportunidade para analisar de que forma os alunos estão agindo para chegar às respostas: se manipulando as peças e sobrepondo umas às outras ou se realizando os cálculos mentais a partir da fração que cada peça representa.

Aula 4

Iniciar a aula conversando com os alunos sobre o estudo de frações realizado nas aulas anteriores. Deixar que eles expressem o que aprenderam sobre o assunto e sanar possíveis dúvidas. Explicar a eles que, nesta aula, também serão estudadas frações não unitárias, ou seja, aquelas em que o numerador é diferente de 1.

Na lousa, escrever e propor aos alunos que resolvam o problema a seguir.

• O planeta Terra tem a maior parte de sua superfície coberta por água. Se dividíssemos igualmente toda essa superfície em quatro partes, veríamos que três delas corresponderiam à água. Represente a superfície da Terra por uma figura e destaque a parte correspondente à água. Depois, escreva uma fração para representar essa parte em relação a toda a superfície do planeta.

Logo após propor o problema, conversar com a turma sobre possíveis estratégias para realizar a representação por meio de uma figura. Nessa conversa, propor as questões a seguir.

• No problema, sugere-se que a superfície da Terra seja dividida em quantas partes iguais?

• E quantas dessas partes corresponderiam à água?

Assim, espera-se que os alunos compreendam que a figura deve ser dividida em 4 partes iguais, sendo destacadas 3 delas para representar a água da superfície terrestre. Propor aos alunos que construam a figura recortando inicialmente um círculo com uma folha avulsa. Para isso, eles podem contornar na folha um objeto circular. Depois, orientá-los a dobrar esse pedaço circular de papel ao meio duas vezes consecutivas. Ao desdobrá-lo, pedir que tracem linhas retas sobre os vincos marcados, conforme representado a seguir. EDITORIA DE ARTE

Então, pedir a eles que pintem de azul as partes da figura obtida que correspondem à superfície da Terra coberta por água. Observar a representação a seguir.

Explicar aos alunos que, ao considerarmos essa figura como um inteiro, a quantidade de partes iguais em que ela foi dividida corresponde ao denominador da fração. Já as partes consideradas, ou seja, aquelas destacadas na figura, correspondem ao numerador da fração. Dessa maneira, junto com eles, escrever na lousa a fração correspondente à parte da superfície da Terra coberta por água.

Para finalizar a aula, propor aos alunos que, em duplas, resolvam as questões a seguir.

1. Qual fração da superfície da Terra não é coberta por água?

2. Gabriel preparou um bolo e dividiu-o igualmente em 8 fatias. A que fração do bolo correspondem 3 dessas fatias?

3. Joana vende balões na praça da cidade. Certa tarde, ela vendeu 9 balões, sendo 7 na cor amarela. Qual fração dos balões vendidos são da cor amarela?

4. Carlos comprou 2 pacotes de figurinhas de animais para sua coleção. Cada pacote desses tem 5 figurinhas. Após abrir os pacotes, ele identificou que 4 figurinhas eram repetidas. Qual fração das figurinhas compradas por Carlos eram inéditas?

Observar as estratégias que os alunos utilizam para resolver as questões, bem como os registros deles. Observar, também, se as duplas reconhecem, em cada problema, o inteiro a ser considerado. Na questão 1, por exemplo, o inteiro corresponde a toda a superfície terrestre. Já na questão 2, o inteiro corresponde ao bolo preparado.

Aula 5

Propor uma atividade para mobilizar os conhecimentos prévios dos alunos sobre a representação de frações e sua escrita por extenso. Para isso, providenciar antecipadamente fichas de cartolina ou um papel mais grosso, no formato de quadrado com 5 cm de lado. Cada aluno deverá receber 30 fichas.

Pedir aos alunos que separem dois conjuntos com 15 fichas cada um. No primeiro conjunto, eles deverão escrever uma fração em cada ficha, sem repeti-las. Pode-se estabelecer com eles o critério de que tanto o numerador quanto o denominador das frações sejam números naturais de 1 até 10. Por exemplo: EDITORIA DE ARTE

No segundo conjunto, os alunos deverão escrever por extenso a fração de cada uma das fichas do primeiro conjunto. Por exemplo: EDITORIA DE ARTE

Orientar os alunos a fazerem essa atividade individualmente, para que as fichas tenham valores diferentes. Acompanhar a produção dos alunos e, se algum deles apresentar dúvidas na escrita por extenso, auxiliá-lo fazendo questionamentos que o possibilitem chegar à forma escrita correta sem dizer prontamente a resposta.

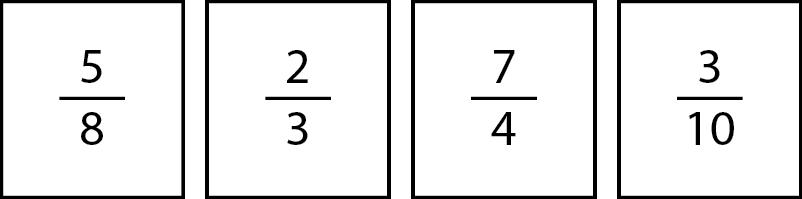
Ao final, pedir a alguns alunos que apresentem as fichas confeccionadas e, depois, solicitar que as guardem, pois serão utilizadas nas aulas seguintes.

Aula 6

Ao iniciar a aula, pedir aos alunos que peguem as fichas confeccionadas na aula anterior. Dizer a eles que formem duplas com os colegas para brincarem com o Jogo da memória.

Para cada partida desse jogo, serão utilizadas as fichas confeccionadas por um dos integrantes da dupla. Na partida seguinte, deverão ser utilizadas as fichas confeccionadas pelo outro integrante.

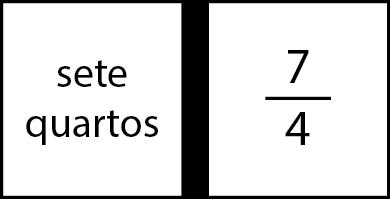
Explicar que eles devem embaralhar as 30 fichas e, viradas com as frações para baixo, organizá-las em 5 linhas e 6 colunas. Um aluno de cada vez vira duas cartas e verifica se elas correspondem à mesma fração, ou seja, a representação numérica é a correspondente da escrita por extenso. Se forem correspondentes, o aluno fica com as duas fichas; caso contrário, elas são viradas para baixo, devolvidas às mesmas posições, e a vez passa para o outro integrante da dupla. Observar um par de fichas correspondentes, representada a seguir como exemplo.

A partida termina quando não houver mais fichas na mesa e ganha quem tiver arrecadado mais fichas.

Para tornar a aula mais dinâmica e possibilitar aos alunos que analisem mais frações, promover algumas vezes a troca das duplas. Durante a realização das partidas, circular entre as duplas para verificar a dinâmica do jogo e esclarecer possíveis dúvidas. Ao final, pedir aos alunos que guardem as fichas, pois serão utilizadas nas aulas seguintes.

Aula 7

Ao iniciar a aula, pedir aos alunos que peguem as fichas que confeccionaram. Porém, devem ser separadas apenas aquelas em que as frações estão representadas com algarismos.

Com as 15 fichas em mãos, dizer aos alunos que organizem as fichas em grupos com aquelas de denominadores iguais. Então, propor a eles que organizem, em cada grupo desses, as fichas de forma que as frações fiquem dispostas em ordem crescente. Nesse momento, é possível avaliar se os alunos conseguem comparar frações com denominadores iguais. Se necessário, relembrá-los de que, ao comparar duas frações com denominadores iguais, a maior delas é a de maior numerador. Observar, a seguir, um exemplo de organização.

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

EDITORIA DE ARTE

Após conferir a realização da atividade, propor um trabalho semelhante, porém, agora, as 15 fichas devem ser organizadas em grupos de fichas com numeradores iguais. Se necessário, relembrá-los de que, ao comparar duas frações com numeradores iguais, a maior delas é a de menor denominador. Observar, a seguir, um exemplo de organização.

EDITORIA DE ARTE

Depois de conferir a segunda atividade realizada pelos alunos, ampliar a proposta pedindo a eles que organizem as 15 fichas em ordem crescente. Nesse momento, se for necessário, relembrar aos alunos como comparar frações com denominadores e com numeradores diferentes. Nesse caso, se julgar conveniente, realizar a comparação das frações 3 4 e 5 6 , obtendo algumas frações equivalentes a elas. Destacar que, para isso, o numerador e o denominador da fração podem ser multiplicados ou divididos por um mesmo número natural diferente de zero.

• 36912 481216 ====

• 5101520 6121824 ====

Nesse caso, como 39 412 = e 510 612 = e sabendo que 109 1212 > , temos que 53 64 > .

Após todos os alunos organizarem as 15 fichas em ordem crescente das frações, permitir a eles que caminhem pela sala de aula observando as organizações realizadas pelos colegas. Quando necessário, esclarecer possíveis dúvidas que possam surgir.

Ao final da aula, pedir aos alunos que guardem as fichas para que possam ser utilizadas na aula seguinte.

Aula 8

Retomar o que foi trabalhado na aula anterior e pedir aos alunos que peguem as 15 fichas que confeccionaram em que as frações são indicadas com algarismos. Orientá-los a se organizar em duplas para a realização de um jogo, em que será trabalhada a comparação de frações.

Explicar a eles que, nesse jogo, cada um deve embaralhar suas fichas e dispô-las em um monte com as frações voltadas para baixo. Em cada rodada, os alunos de cada dupla devem virar uma ficha do seu monte ao mesmo tempo que o colega. Eles devem observar as frações e compará-las: quem estiver com a fração que representa o maior número fica com as duas fichas, que deverão ser colocadas de lado. É importante que os alunos das duplas façam a comparação das frações, realizando cálculos quando necessário.

A partida termina quando acabarem as fichas dos montes. Vence o aluno da dupla que tiver arrecadado mais fichas.

Por exemplo, se em uma rodada as fichas viradas foram as representadas a seguir, o aluno que virou a ficha com a fração 7 4 vence a rodada e guarda para si ambas as fichas, pois 75714145 e 484888 

Estipular um tempo para que os alunos joguem pelo menos duas partidas, que pode ser de 25 a 30 minutos. Durante o jogo, observar quais são as estratégias que eles utilizam para a comparação das frações. As duplas, também, podem ser alteradas a cada partida.

Caso os alunos apresentem dificuldade no desenvolvimento das atividades, identificar as principais dúvidas para poder elaborar outras estratégias em sala de aula. A partir do momento que a dúvida for diagnosticada, escolher a melhor forma para que os alunos possam esclarecê-las. É interessante ajudá-los a sanar suas dúvidas, mas sem resolvê-las de imediato, e lembrá-los de que a solução sempre deve ser da dupla.

Sugerir aos alunos que façam desenhos para representar as frações, sempre partindo do mesmo inteiro. Se necessário, retomar o estudo de frações equivalentes, o que contribui para a comparação de frações com denominadores diferentes.

Sequência didática 6: Os números na forma decimal

Esta sequência didática aborda situações que envolvem a comparação e a ordenação de números racionais, na forma fracionária e na forma decimal, e propõe situações de adições e de subtrações com números racionais escritos na forma decimal. Além disso, aborda divisão de números naturais com quociente decimal.

Os alunos participarão de atividades em grupo e individuais e serão envolvidos tanto em situações de criação de lojas quanto na confecção de peças de jogos que abordam os conteúdos. Para a resolução das atividades, os alunos poderão utilizar estratégias pessoais e técnicas operatórias convencionais.

Com essas aulas, o professor poderá utilizar materiais simples, como folhas avulsas, que serão importantes no desenvolvimento dos conceitos.

Objetivos de aprendizagem

• Ler e escrever números na representação decimal.

• Comparar e ordenar números decimais.

• Representar numericamente partes de um todo-referência.

• Efetuar adições e subtrações com números decimais.

• Explorar situações-problema que envolvam números decimais.

• Decompor números decimais.

• Localizar números na reta numérica.

• Analisar as diferentes representações de um mesmo número racional.

Plano de aulas

Aula 1: Representar o valor de objetos em números decimais, por meio de atividade lúdica, elaborar um quadro de preços e efetuar adições e subtrações com os valores dos objetos.

Aula 2: Representar o valor de objetos em números decimais, elaborar um quadro de preços, por meio de atividade lúdica, e efetuar adições e subtrações com os valores dos objetos.

Aula 3: Compreender as relações no Sistema de Numeração Decimal e comparar números decimais por meio de atividade que envolve as medidas das alturas dos alunos.

Aula 4: Resolver cálculos e problemas envolvendo números decimais.

Aula 5: Relacionar frações decimais, números decimais e posição na reta numérica por meio de jogo.

Aula 6: Efetuar divisão de números naturais com quociente decimal e elaborar um Jogo da memória com os resultados obtidos.

Aula 7: Ler, escrever e representar números decimais com auxílio de figura.

Aula 8: Reconhecer frações equivalentes por meio de figuras.

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita

Competências gerais da Educação Básica: 4 e 9

Competências específicas de Matemática: 2, 3 e 8.

Habilidades: EF05MA02, EF05MA04, EF05MA05, EF05MA07 e EF05MA08

Materiais necessários: Representações de moedas e cédulas de papel, caderno, régua, lápis grafite, lápis de cor, borracha, calculadora, trena ou fita métrica, malha quadriculada, folhas avulsas e saquinhos de papel.

Aula 1

Inicialmente, propor uma atividade lúdica que envolva situações de compra e venda com troco. Para isso, organizar os alunos em cinco grupos; quatro grupos representarão as lojas de materiais escolares e um representará os clientes.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Explicar aos alunos que deverão "montar" a loja e colocar os preços em cada um dos itens do quadro a seguir. Cada grupo vai confeccionar placas com preços para os produtos da loja, utilizando folhas avulsas. Os preços não podem ser inteiros de real (por exemplo, R$ 2,00), ou seja, eles devem ter os centavos diferentes de zero (por exemplo, R$ 2,45). A definição do preço de cada item deve ser feita pelo grupo, que pode usar estimativa ou pesquisar em sitesde papelarias.

Os alunos que serão os clientes das lojas deverão fazer uma pesquisa de preços e montar um quadro na lousa, conforme o modelo a seguir

Itens Loja 1 Loja 2 Loja 3 Loja 4

Lápis R$ R$ R$ R$

Borracha R$ R$ R$ R$

Caderno R$ R$ R$ R$

Régua R$ R$ R$ R$

Calculadora R$ R$ R$ R$

Estojo R$ R$ R$ R$

Com o quadro completo, solicitar aos alunos que, em grupos, respondam às questões a seguir no caderno

1. Qual é o valor da compra de todos os itens em cada loja de materiais escolares?

2. Quanto o cliente economizará se comprar na loja que oferece o menor preço total, comparando com a que oferece o maior preço total?

3. Quanto o cliente economizará se comprar todos os produtos pagando o menor preço em cada produto?

Ao final, socializar as respostas e promover uma roda de conversa para que os alunos expliquem as impressões sobre a atividade, quais dificuldades tiveram e como fizeram para resolvê-las. Aproveitar para explicar sobre o consumo consciente e responsável. A atividade pode ser realizada outras vezes, alternando as funções dos grupos.

Aula 2

Retomar com os alunos os conceitos trabalhados na aula anterior. Para isso, promover uma conversa e relembrar a situação de compra e venda que desenvolveram, utilizando a adição e a subtração de números decimais.

Em seguida, organizar novamente os alunos em cinco grupos, porém de forma que todos os grupos "montem" suas lojas. Os preços devem ter os centavos diferentes de zero (por exemplo, R$ 3,75). A definição do preço de cada item deve ser feita pelo grupo, que pode

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

usar estimativa ou pesquisar em sitesde papelarias. Cada grupo vai confeccionar um quadro de produtos em uma folha avulsa, conforme o modelo a seguir

Itens Loja

Lápis R$

Borracha R$

Caderno R$

Régua R$

Calculadora R$

Estojo R$

Total R$

Após todos os grupos preencherem seus quadros, um aluno de cada grupo deve ser escolhido para escrever o valor total dos produtos na lousa. Nesse momento, conversar com os alunos sobre qual loja é mais atrativa para um cliente que deseja gastar menos. Propor agora que cada grupo (loja) altere o valor de seus produtos de forma que os totais sejam menores em todas as lojas (por exemplo, se o menor valor dos totais for R$ 23,75, solicitar que readequem para R$ 22,75 seus totais e os valores dos produtos).

Discutir com os alunos a estratégia utilizada por cada grupo para fazer a readequação dos valores. Feito isso, solicitar que formem um quadro na lousa e, em grupos, discutam as questões a seguir, respondendo-as na folha avulsa.

1. Após adequar os valores, há uma loja que é melhor para um cliente que deseja economizar? Justifique.

2. Para comprar um kitcomposto de 1 lápis, 1 borracha, 1 caderno e 1 calculadora, em qual loja o valor seria menor? Justifique.

Socializar as respostas escolhendo um novo representante de grupo para ir ao quadro. Conversar com os alunos sobre as adequações feitas nos valores totais e como elas influenciam no valor individual de cada produto

Outros kitspodem ser propostos a fim de que, empiricamente, os alunos percebam a diferença entre comprar nas diferentes lojas.

Aula 3

Nesta aula, relembrar brevemente a adição e a subtração de números decimais. Em seguida, escolher cinco alunos com diferentes alturas e, utilizando uma fita métrica ou uma trena, medir a altura de cada um, em metro, registrando-as na lousa.

Por exemplo: 1,32 m; 1,27 m; 1,40 m; 1,25 m e 1,22 m.

Solicitar aos alunos que, em duplas, resolvam as atividades a seguir e as registrem no caderno.

1. Coloque em ordem crescente as medidas da altura dos colegas.

2. Qual é a maior altura registrada?

3. Qual é a menor altura?

4. Qual é a diferença, em metros, entre a maior e a menor altura registradas?

Estipular um tempo para a resolução desta atividade, que pode ser de 25 minutos. Em seguida, socializar as respostas e as estratégias utilizadas pelos alunos. Fazer a correção na lousa, resolvendo as possíveis dúvidas e dificuldades apresentadas pelos alunos.

Agora é a vez de os alunos fazerem as medições. Disponibilizar, para cada dupla, uma trena ou fita métrica e solicitar que meçam e registrem a altura de cada um. Depois, pedir que comparem as medidas e respondam às questões a seguir.

5. Qual é a altura do mais alto e a do mais baixo?

6. Quanto o mais alto mede a mais que o mais baixo?

Estipular um tempo para a resolução desta atividade, que pode ser de 15 minutos. Ao término, verificar se os alunos chegaram às respostas corretas e quais estratégias utilizaram.

Aula 4

Ao iniciar a aula, conversar com os alunos com o objetivo de identificar dúvidas que possam ter em relação às aulas anteriores. Nesta aula, serão abordados tanto o cálculo quanto a resolução de problemas envolvendo números decimais. No caso de dúvidas em relação à comparação ou à adição e subtração de números decimais, uma alternativa é incentivar a utilização do quadro de classes e ordens. Porém, aproveitar as situações para que os alunos que ainda utilizam o quadro de classes e ordens nos cálculos passem a compreender e utilizar o algoritmo. Pedir a eles que resolvam no caderno as seguintes adições e subtrações:

a) 2,85 + 0,37 = 3,22

b) 4,5 + 3,42 = 7,92

c) 15,7 – 8,9 = 6,8

d) 32,5 – 12,15 =

20,35

e) 0,018 + 0,37 = 0,388

f) 16 – 0,018 = 15,982

Auxiliar os alunos individualmente na tarefa, de forma a reconhecer as dificuldades de cada um. Utilizar essas dúvidas ao corrigir coletivamente a atividade. Uma dúvida comum é o fato de os números com os quais se realizaram a adição e a subtração terem quantidades diferentes de casas decimais. O uso do quadro de classes e ordens pode ser uma alternativa eficiente nesses casos.

Em seguida, solicitar aos alunos que resolvam no caderno, individualmente, a atividade a seguir.

• Rafael colocou em uma balança os produtos que deseja comprar e verificou a massa de cada um deles. A sacola retornável que ele vai usar para carregar os produtos suporta, no máximo, 3,5 kg. Observe as massas dos produtos e responda às questões.

Saco com maçãs: 1,286 kg

Saco com uvas: 0,933 kg

Saco com laranjas: 1,685 kg

a. Rafael conseguirá carregar todos esses produtos na sacola que levou? Justifique.

Não, pois 1,286 + 0,933 + 1,685 = 3,904; 3,904 kg > 3,5 kg.

b. Rafael decidiu colocar somente dois tipos de frutas na sacola, para que ela fique com a maior massa possível. Qual das frutas deve ficar de fora da sacola? Justifique.

O saco com uvas, pois a massa é a menor entre as três.

Novamente, corrigir a atividade coletivamente. Aproveitar o momento e questionar os benefícios da utilização de sacolas retornáveis Discutir sobre o impacto das sacolas plásticas no meio ambiente.

Aula 5

Inicialmente, propor uma atividade para mobilizar os conhecimentos prévios dos alunos sobre a relação das representações de um número racional: forma decimal e forma de fração. Para isso, organizar os alunos em quatro grupos e explicar-lhes que participarão de um jogo.

Escrever na lousa os dois quadros representados a seguir.

Transpor, também, para a lousa a reta numerada a seguir, de 0 a 3

Pedir a cada grupo que escolha um integrante para representá-los na primeira rodada. Entregar a cada representante um giz colorido, de modo que cada equipe tenha uma cor própria.

Explicar à turma que vai dizer um número na forma decimal (ou de fração). Supondo que diga um número decimal, os grupos devem identificar a fração correspondente. Em seguida, o representante do grupo que identificar primeiro a fração deve ir à lousa, marcá-la e representar o decimal na reta numérica.

Se acertar a fração e localizar o decimal corretamente na reta, a equipe do representante ganhará dois pontos. Se acertar somente a fração e não a representar corretamente, a equipe ganhará um ponto. Se errar a fração, a equipe não ganhará nenhum ponto, mesmo que a representação na reta numérica do decimal correspondente esteja correta.

Por exemplo, dizer " zero vírgula quatro". O aluno que levantar a mão primeiro deve ir à lousa, marcar 4 10 e 0,4 e representar o número na reta.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Pedir aos grupos que escolham outro representante. Dizer outro número e prosseguir o jogo como na rodada anterior. Fazer nove rodadas; a equipe que fizer mais pontos ganhará o jogo.

Ao final, pedir aos alunos que registrem no caderno os números da atividade realizada e, depois, promover uma roda de conversa para verificar o que acharam da atividade e quais dificuldades tiveram.

Aula 6

Nesta aula, será abordado o conteúdo de divisão dos números naturais com quociente decimal, por meio de atividade lúdica do Jogo da memória.

Para começar a aula, dividir os alunos em duplas e solicitar que, utilizando o algoritmo de divisão, resolvam os itens a seguir:

Auxiliar os alunos individualmente na tarefa, de forma a reconhecer as principais dificuldades deles Sanar as dúvidas ao corrigir coletivamente a atividade.

Agora, cada dupla deverá confeccionar suas fichas do Jogo da memória. Para isso, entregar duas folhas avulsas (A4) para cada dupla. Pedir que dobrem cada folha ao meio três vezes, de forma que, ao desdobrá-la, obtenham 8 retângulos representados. Esses retângulos serão os campos em que os alunos deverão escrever a fração decimal ou número decimal correspondente, de acordo com os resultados das divisões realizadas anteriormente, como no exemplo a seguir.

Desta forma, eles deverão recortar as peças usando os vincos na folha e começar a organização do jogo. Solicitar que virem as peças com a escrita para baixo, embaralhem e as espalhem pela mesa. Cada aluno deverá levantar duas peças de uma vez, tentando encontrar o par formado pela fração e o número decimal correspondentes. Se as peças viradas não corresponderem, o aluno deverá devolver as duas peças, com a escrita para baixo, e passar a vez. Caso as peças correspondam, ele poderá ficar com elas. Ganhará quem tiver a maior quantidade de fichas ao final do jogo.

O Jogo da memória é praticado tradicionalmente em duplas, porém a atividade poderá ser realizada em trios dependendo da quantidade de alunos da turma

Aula 7

Retomar com os alunos o que foi trabalhado nas aulas anteriores e pedir a eles que formem duplas. Entregar a cada dupla uma folha com malha quadriculada de 10 cm × 10 cm, dois lápis de cores diferentes e um saquinho com papéis dobrados, contendo números decimais de 0 a 1. Explicar que eles sortearão um papel de cada vez e pintarão a quantidade de quadradinhos referentes ao número sorteado, considerando a malha inteira como a unidade. Ver a seguir uma sugestão de números e a malha quadriculada.

EDITORIA DE ARTE

Se julgar conveniente, representar uma malha quadriculada na lousa e mostrar um exemplo aos alunos. Explicar que, se sortearem um papel que tenha o número 0,13, por exemplo, devem saber quantas partes pintar na malha quadriculada. Tomando esse exemplo, pois, se = 13 0,13 100 a malha corresponde à unidade e tem 100 quadradinhos, devem ser pintados 13 deles.

O jogo terminará quando todos os quadradinhos estiverem pintados, e ganhará quem tiver pintado mais quadradinhos.

Caso algum aluno tenha dificuldade para fazer as atividades propostas, é importante retomar o conteúdo e incentivar os alunos, que conseguiram resolvê-las, a auxiliarem os colegas.

Aula 8

Iniciar a aula retomando o que foi estudado anteriormente, em particular as representações fracionária e decimal de um mesmo número.

Então, propor aos alunos a seguinte atividade.

• Em malhas de mesmas dimensões, mas formadas por figuras de quadradinhos de tamanhos diferentes, Ricardo e Beatriz pintaram partes de verde. Observe e responda às questões a seguir.

a) Qual fração da malha que pertence a Ricardo corresponde à parte pintada de verde? 24 40

b) Qual fração da malha que pertence à Beatriz corresponde à parte pintada de verde? 6 10

c) Essas frações são equivalentes? Por quê?

Sim; porque as partes em verde correspondem à mesma parte das malhas de dimensões iguais: 246 4010 =

d) Escreva o número decimal correspondente a essas frações. Com base em qual das frações você escreveu o número na forma decimal?

0,6 Espera-se que os alunos respondam que escreveram com base na fração 6 10

Esta atividade pode ser corrigida coletivamente, mas questionar os alunos que fizeram de forma diferente.

Para complementar, propor aos alunos que dividam todas as partes que compõem a unidade pertencente à Beatriz em partes iguais, como no exemplo a seguir, e descubram novas frações equivalentes. Em relação ao exemplo a seguir, temos: 54246 904010 ==

Para finalizar a aula, pegar uma folha avulsa (A4) e dizer aos alunos que a considerem como sendo a unidade. Dobrar a folha ao meio, desdobrar e pintar uma das partes determinadas pelo vinco. Então, mostrar a folha aos alunos e perguntar: qual fração representa a parte pintada? Espera-se que os alunos digam 1 2 . Em seguida, dobrar a folha como feito anteriormente, e, depois, dobrar ao meio novamente. Então, desdobrá-la, mostrar aos alunos e perguntar: qual fração representa a parte pintada? Espera-se que os alunos digam 2 4 . Procedendo de modo análogo, é possível mostrar, na prática, a equivalência de algumas frações, por exemplo: === 1248 24816 .

Uma alternativa é possibilitar aos alunos que, em pequenos grupos, desenvolvam esta atividade prática. Ao separar os grupos, propor que, inicialmente, dobrem a folha em 3 partes iguais e, ao desdobrá-la, escolham colorir 1 ou 2 partes. A partir daí, pedir que façam novas dobras ao meio e relatem as frações equivalentes encontradas e suas conclusões. Ao finalizar a atividade, recolher a folha de um dos grupos que escolheu colorir 1 parte, uma folha de um grupo que tenha colorido 2 partes e usá-las para explicar a importância de as partes obtidas na dobra serem iguais. Questionar os alunos sobre outras situações do cotidiano, que podem relacionar com a atividade desenvolvida, em que partes de um todo podem ser novamente divididas de forma que as partes sejam iguais, como, por exemplo, alguns alimentos como bolo, pizza , tortas ou até brinquedos de montar.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial

(CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Sequência didática 7: Estatística e probabilidade

O objetivo desta sequência didática é ampliar o trabalho com a leitura e a interpretação de gráficos e tabelas, de modo que os alunos possam reconhecer as informações apresentadas neles, compreendê-las e sintetizar conclusões. Ainda nesta sequência didática, os alunos terão a oportunidade de se familiarizar com os termos utilizados em probabilidade e participar de dinâmicas que possibilitam compreender e determinar a probabilidade de ocorrência de um resultado em eventos aleatórios.

Objetivos de aprendizagem

• Ler e interpretar gráficos.

• Organizar informações em tabelas.

• Ler informações e dados apresentados em tabelas.

• Elaborar gráficos com base em tabelas.

• Coletar, organizar e descrever dados.

• Interpretar dados apresentados por meio de tabelas e gráficos, para identificar características previsíveis ou aleatórias de acontecimentos.

• Ler e interpretar dados apresentados de maneira organizada e construir representações.

• Escrever textos com base na interpretação de gráficos e tabelas.

• Identificar espaço amostral e evento aleatório com base em situações-problema.

• Determinar a probabilidade de um evento ocorrer.

Plano de aulas

Aula 1: Organizar dados em tabela e gráfico.

Aula 2: Interpretar dados de tabela, realizar uma pesquisa e construir um gráfico lúdico.

Aula 3: Ler e interpretar dados apresentados em gráficos de barras, de setor e de segmentos.

Aula 4: Comparar características de gráficos e realizar uma pesquisa.

Aula 5: Analisar e escolher o gráfico mais adequado para organizar os dados de uma pesquisa.

Aula 6: Elaborar texto que sintetize os resultados de um ou de mais gráficos

Aula 7: Determinar a probabilidade de um evento ocorrer e identificar o espaço amostral.

Aula 8: Apresentar todos os possíveis resultados de um experimento aleatório e, a partir disso, elaborar estratégias para brincar com um jogo.

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita.

Competências gerais da Educação Básica: 2 e 9

Competências específicas de Matemática: 2, 6 e 8

Habilidades: EF05MA22, EF05MA23, EF05MA24 e EF05MA25.

Materiais necessários: Folha com atividades (uma para cada dupla), lápis, caneta, folhas avulsas, folhas de cartolina, tesoura com pontas arredondadas, cola, jornais e revistas, rolo de papel higiênico (um por aluno), papel Kraft(1 metro de altura por 1 metro de largura), fita dupla face, canetas hidrocor, tinta guache (preta, verde e azul), pincel (um por trio), bolinhas de isopor (9 por trio de alunos), saco não transparente (um por trio) e folha com quadro para preencher (uma para cada aluno)

Aula 1

Nesta aula, os alunos vão retirar informações de um jogo, anotá-las em uma tabela e esboçar um gráfico. Para começar, organizar os alunos em duplas para que confeccionem as cartas do jogo "Esquentando a cuca". Distribuir uma cartolina a cada dupla e pedir que recortem 40 cartas de mesmo tamanho e numerem de 1 a 10 todas elas, ou seja, quatro cartas com o número 1, quatro cartas com o número 2, quatro cartas com o número 3, e assim sucessivamente.

Para anotarem as pontuações de cada rodada, esboçar uma tabela na lousa para que os alunos reproduzam no caderno, como no exemplo a seguir.

Depois de confeccionadas as 40 cartas e já com a tabela reproduzida no caderno, explicar as regras do jogo. O jogo consiste em 10 rodadas, sendo que, em cada uma, apenas ointegrante que vencer vai pontuar.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Pontuação do jogo Esquentando a cuca

Fonte: Turma do 5º ano.

A dupla deve embaralhar as cartas e distribuí-las em dois montes, um para cada integrante. Sem ver as cartas, cada integrante deve tirar duas cartas do seu monte e levar até a testa de modo que só o adversário possa ver os números. Em seguida, o integrante 1 deve iniciar a brincadeira tentando adivinhar a soma dos números que estão em sua testa. Cada integrante tem direito a três tentativas de acertar a soma. O integrante 2, por sua vez, que está vendo os números das cartas e, consequentemente, sabe qual é a soma, deve dizer se ela está certa ou não. Se estiver incorreta, é a vez do integrante 2 tentar adivinhar, em três tentativas, a soma dos números que estão em sua testa, e o integrante 1 dizer se está correta ou não. Quem acertar a soma primeiro pontua, sendo que a pontuação será o valor dessa soma. Assim que um dos integrantes acertar, ambos devem deixar as cartas que estavam segurando na testa em outro monte e, em seguida, cada um deve pegar mais duas cartas e levar até a testa novamente para começar a segunda rodada.

Vencerá aquele que conseguir a maior pontuação no final das 10 rodadas. Para verificar quem venceu, os alunos podem utilizar as anotações da tabela e somar.

Pontuação do jogo Esquentando a cuca

Ao final da aula, pedir que esbocem um gráfico de barras ou colunas a fim de apresentarem a pontuação final de cada integrante da dupla, como no exemplo a seguir.

Fonte: Turma do 5º ano.

Fonte: Turma do 5º ano.

Após o esboço do gráfico, pedir que os integrantes das duplas troquem entre si seus resultados apresentados em tabelas e gráficos.

Pedir aos alunos que guardem as cartas que confeccionaram nesta aula, pois serão utilizadas posteriormente.

Aula 2

Inicialmente, promover uma roda de conversa com os alunos sobre o conteúdo que será abordado. Depois, apresentar a situação a seguir

Cecília está no 5º ano e o professor de Matemática está trabalhando com gráficos e tabelas. Para ampliar esse estudo, ele pediu aos alunos que fizessem uma pesquisa e apresentassem os dados em uma tabela. Após decidirem qual seria o tema da pesquisa, os alunos elaboraram a seguinte pergunta para fazer a cada entrevistado: você tem um celular com acesso à internet? Depois decidiram quem seriam os entrevistados: pais ou responsáveis dos alunos de uma turma de 3º ano, de uma de 4º ano e de uma de 5º ano.

Observe a seguir a tabela com as respostas dos entrevistados.

Você tem um celular com acesso à internet?

Turma Sim Não

3º ano 20 15

4º ano 25 20

5º ano 30 10

Fonte: Turma do 5º ano.

a)Se você não tivesse lido todo o texto que antecede a tabela, saberia do que se trata essa pesquisa? Como?

Espera-se que os alunos respondam que sim. É possível saber do que se trata a pesquisa, por meio do título e da fonte da tabela, que fornecem essas informações. Ou seja, de acordo com a fonte indicada, a pesquisa foi realizada pelos alunos do 5º ano e o objetivo era pesquisar qu al entrevistado tem um celular com acesso à internet.

b)Quantos entrevistados responderam "sim"? E quantos responderam "não"?

Para saber quantos alunos responderam "sim", espera- se que os alunos realizem a seguinte adição: 20 + 25 + 30 = 75; 75 entrevistados têm celular com acesso à internet. O mesmo deve ser feito para saber quantos entrevistados responderam "não": 15 + 20 + 10 = 45; 45 entrevistados não têm celular com acesso à internet.

c)Ao todo, quantos foram os entrevistados?

Espera-se que os alunos adicionem 75 + 45 = 120; foram entrevistadas 120 pessoas. Mas, também, é possível que alguns alunos resolvam adicionar todos os dados da tabela, fazendo: 20 + 25 + 30 + 15 + 20 + 10 = 120.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Agora, realizar uma pesquisa com os alunos da turma e anotar as respostas na lousa. A intenção é que, ao final da pesquisa, os alunos confeccionem, juntos, um gráfico de colunas, utilizando papel Krafte colagem de rolos de papel higiênico.

Para realizar a pesquisa, perguntar a eles: quantos irmãos você tem?

Anotar a resposta de cada um fazendo um risquinho na quantidade indicada de irmãos. Por exemplo:

Em seguida, fixar na lousa o papel Kraft de mais ou menos 1 metro de largura e 1 metro de altura. Esboçar a estrutura de um gráfico, contendo os dois eixos "Quantidade de irmãos" e "Quantidade de alunos"; o título "Quantidade de irmãos dos alunos do 5º ano " e a indicação "Fonte: Turma do 5º ano.", como no exemplo a seguir.

EDITORIA DE ARTE

Quantidade de irmãos dos alunos do 5º ano

Fonte: Turma do 5º ano.

Ao montar a estrutura do gráfico, pedir ajuda aos alunos para que identifiquem quais elementos são necessários e quais sugestões vão dar para os nomes dos eixos e do título.

EDITORIA DE ARTE

Assim que a estrutura estiver pronta, cada aluno colará com fita dupla face um rolinho feito com papel higiênico na coluna que corresponder à quantidade de irmãos que ele tem. Chamar um aluno por vez para colar o rolo.

EDITORIA DE ARTE

Quantidade de irmãos dos alunos do 5º ano

Se preferir, a dinâmica da colagem dos rolinhos de papel higiênico no gráfico pode acontecer paralelamente às anotações na lousa.

Assim que o gráfico estiver finalizado, perguntar:

• Observando o gráfico, é possível perceber que a altura das colunas varia? Qual é a relação entre a altura da coluna e a quantidade de alunos que responderam à pesquisa?

Espera-se que os alunos percebam que a altura da coluna varia de acordo com a quantidade de alunos que responderam quantos irmãos têm, ou seja, quanto maior o número de alunos que têm 0 irmão, ou 1 irmão, ou 2 irmãos, ou 3 irmãos ou 4 irmãos ou mais, mais alta será a coluna.

Expor o gráfico do lado de fora da sala de aula para que os outros alunos e colaboradores da escola possam ver o trabalho realizado.

Aula 3

Inicialmente, promover uma roda de conversa com os alunos sobre o conteúdo que será abordado. Depois entregar uma folha com as seguintes situações-problema e pedir que as resolvam

1. Roberto, Júlio, Daniel e Marcos participaram de um campeonato de natação. Observe, no gráfico de barras a seguir, o tempo que cada um levou para concluir a prova na modalidade nado livre.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Fonte: Turma do 5º ano.

Agora, responda às questões a seguir.

a) Quanto tempo Roberto levou para concluir a prova?

Espera-se que os alunos concluam que Roberto concluiu a prova em 70 segundos.

b) Júlio terminou a prova em quanto tempo?

Espera-se que os alunos concluam que Júlio terminou a prova entre 50 e 60 segundos.

c) Quem venceu a prova? Qual foi o seu tempo?

Espera-se que os alunos concluam que Marcos venceu, pois ele concluiu a prova no menor tempo: entre 40 e 50 segundos.

d) Podemos afirmar que, entre o primeiro e o último colocados, a diferença de tempo foi superior a 20 segundos? Justifique.

Espera-se que os alunos concluam que sim, pois o vencedor (Marcos) obteve o tempo inferior a 50 segundos, enquanto o último colocado (Daniel) demorou mais de 70 segundos.

2. Márcia tem uma lanchonete e, preocupada em atender melhor os clientes, resolveu fazer uma pesquisa para saber como eles avaliam a qualidade dos lanches servidos. Para isso, Márcia entrevistou 100 clientes. Observe o gráfico a seguir com os resultados.

Fonte: Dados fictícios.

Fonte: Lanchonete da Márcia

Agora, responda às questões a seguir.

a) Qual setor do gráfico é maior, o dos clientes que consideram o lanche ótimo ou o dos clientes que consideram o lanche bom?

O maior setor é o vermelho, que representa os clientes que consideram o lanche bom.

b) Qual é a porcentagem de pessoas que consideram o lanche ótimo? 28%.

c) Qual é a porcentagem de pessoas que consideram os lanches ruim ou péssimo?

A porcentagem de pessoas que consideram os lanches ruim é 10% e a porcentagem de pessoas que consideram o lanche péssimo é 2%. Assim, a porcentagem de pessoas que consideram os lanches ruins ou péssimos é 12% (10% + 2% = 12%).

d) Sabe-se que 100 pessoas foram entrevistadas. Quantas pessoas consideram o lanche regular?

251

25% 1004 ==

100 ÷ 4 = 25; 25 pessoas consideram o lanche regular.

3. André comprou uma loja e resolveu fazer um estudo para saber como foram as vendas nos últimos meses. Observe a seguir o resultado do estudo transposto para um gráfico, que mostra o faturamento da loja nos últimos seis meses.

Agora, responda às questões a seguir.

a) Em que mês a loja teve o maior faturamento?

Em maio.

b) O faturamento da loja foi maior em junho ou em janeiro?

Em junho, pois neste mês o faturamento esteve entre R$ 10000,00 e R$ 20000,00, enquanto em janeiro esteve abaixo de R$ 10000,00.

Fonte: Dados fictícios.

Assim que os alunos terminarem de resolver a atividade, organizá-los em duplas e pedir que troquem suas resoluções com o colega a fim de verificarem divergências e discutirem os resultados. Enquanto isso, circular pela sala de aula para sanar possíveis dúvidas. Ao final, corrigir as atividades na lousa.

Aula 4

Levar jornais e revistas para a sala de aula. Dividir a turma em grupos de três ou quatro alunos e pedir que procurem os tipos de gráfico que já estudaram. Pedir que recortem os gráficos escolhidos e os colem em folha de cartolina. Lembrar aos alunos que informações como título, legenda e fonte dos gráficos devem ser recortadas com o respectivo gráfico. Assim que todos tiverem recortado e colado seus gráficos, pedir a um grupo por vez que fale sobre alguns deles, informando aos colegas de que tipo são eles, seu título e sua fonte e o que mais lhe chamou atenção. Depois que os grupos expuserem os gráficos, conduzir um debate perguntando se é conveniente usar um gráfico de setores para representar o crescimento de algo (vendas, por exemplo) ao longo do tempo. Questioná-los de modo que concluam que o gráfico de setores é mais adequado para representar partes de um todo, e o gráfico de segmentos é usado mais para comparar o crescimento ou a queda no valor de uma variável durante um intervalo de tempo.

Em seguida, pedir aos alunos que continuem no mesmo grupo e orientá-los a realizar uma pesquisa na escola. Sugerir que selecionem um tema que lhes interesse e realizem a pesquisa com os próprios colegas de turma.

Pedir a eles que organizem, em uma folha avulsa, as perguntas que serão feitas na pesquisa. Elaborar perguntas cujas respostas sejam SIM ou NÃO, com exceção das perguntas como nome, gênero e idade. Observar a seguir um modelo com possíveis perguntas sobre o tema consumo consciente.

Consumo consciente

Resposta: SIM ou NÃO

( ) Você evita deixar lâmpadas acesas em ambientes desocupados?

( ) Você fecha a torneira enquanto escova os dentes?

( ) Você fecha a torneira enquanto se ensaboa no banho?

( ) Você desliga os aparelhos eletrônicos quando não estão em uso?

( ) Você costuma usar o verso de folhas de papel já utilizadas?

( ) Você costuma comer todo o alimento que põe no prato?

Para esta dinâmica, pedir que cada integrante do grupo entreviste um dos integrantes de outro grupo e vice-versa, até que todos os grupos sejam entrevistados. Orientar os alunos a guardarem os dados coletados, pois serão utilizados na aula seguinte.

Aula 5

Iniciar a aula retomando o que foi trabalhado na aula anterior e a formação dos mesmos grupos.

Com as respostas das pesquisas em mãos, pedir a eles que organizem uma tabela com os dados obtidos e, depois, escolham um tipo de gráfico que usarão para dispor os dados da pesquisa. Lembrar os alunos de inserir o título e a fonte do gráfico e, se necessário, escrever também as legendas. Caso os alunos optem por gráfico de setor, a construção pode ser realizada utilizando planilhas eletrônicas. Para isso, verificar a possibilidade de levá-los a um laboratório de informática.

Se algum aluno apresentar dificuldade na compreensão dos dados dos gráficos de colunas, de setores e de segmentos, propor uma conversa sobre as especificidades de cada um. Incentivar os alunos a compartilharem suas dúvidas, anotá-las na lousa para retomar o que for necessário e ajudar a saná-las.

Se julgar necessário, retomar as situações propostas. Além disso, é importante trabalhar não só a leitura dos dados nos gráficos, como também a compreensão de como eles são elaborados. É interessante pedir aos alunos que registrem suas dúvidas e as atividades realizadas, pois, ao analisar essas anotações, o professor pode pensar em outras atividades que ajudem os alunos a ampliar a aprendizagem.

Aula 6

Retomar o que foi estudado na aula anterior e perguntar aos alunos se ficou alguma dúvida.

Em seguida, propor algumas questões para os grupos formados na aula anterior, a fim de eles refletirem sobre os resultados que obtiveram e sintetizarem suas conclusões.

• Quantas pessoas foram entrevistadas?

• Qual é a porcentagem de meninas entrevistadas?

• Qual das perguntas mais apresentou resposta afirmativa?

• Qual das perguntas mais apresentou resposta negativa?

• Qual é a probabilidade de um entrevistado ser menino?

Então, pedir aos alunos que descrevam em uma folha avulsa os gráficos que estudaram, seus elementos e os tipos que devem ser usados em diferentes situações. Além disso, pedir para cada grupo elaborar uma conclusão com os resultados obtidos a partir da análise dos gráficos ou da tabela e a partir das respostas das questões.

Para ampliar os estudos sobre os gráficos de colunas, setores e de segmentos, propor aos alunos que, no mesmo grupo em que realizaram a pesquisa, analisem os principais erros que cometeram ao organizar os dados e relatem as estratégias usadas para solucionar esses

problemas. Em seguida, organizar um debate para que os grupos compartilhem as experiências e para cada grupo apresentar sua pesquisa e seus resultados.

Uma sugestão é pedir que os integrantes do grupo se apresentem à frente da sala de aula para explicarem sua entrevista e mostrarem seus resultados.

Aula 7

Para esta aula, separar os alunos em trios e pedir a eles que pintem 3 bolinhas de isopor na cor verde, 3 na cor preta e 3 na cor azul. Depois, fazer algumas dinâmicas e questionamentos.

Propor que os alunos coloquem somente as bolinhas de cor azul em um saco não transparente e perguntar que cor eles acham que seria sorteada caso fosse retirada uma bolinha ao acaso.

Espera-se que eles respondam que a cor seria azul, pois só há bolas azuis no saco não transparente. A fim de testarem essa estratégia, pedir que façam alguns sorteios entre eles.

Em seguida, pedir aos alunos para acrescentarem uma bolinha preta junto com as azuis e perguntar se é possível ter certeza qual é a cor da bolinha que será retirada no sorteio Nesse caso, espera-se que os alunos digam que não é possível ter certeza, pois há duas opções de cor, porém é mais provável retirar uma bolinha azul, já que no saco há 3 bolinhas azuis e apenas uma preta.

Pedir que realizem vários sorteios e que anotem em seus cadernos quais cores saíram em cada um. Assim, eles podem comprovar que é mais provável retirar uma bolinha azul do que retirar uma bolinha preta. Lembrar os alunos que eles devem devolver para o saco a bolinha retirada em cada sorteio.

Agora, pedir que tirem as bolinhas do saco não transparente e coloquem 3 bolinhas pretas e 2 verdes. Perguntar: qual cor vocês acham que será sorteada? Por quê?

A ideia é que os alunos percebam que é mais provável retirar uma bolinha na cor preta, pois há mais bolinhas pretas do que verdes. Sugerir que façam diversos sorteios e que anotem em seus cadernos a cor de cada bolinha sorteada. No final, espera-se que comprovem que é mais provável sortear uma bolinha preta do que uma bolinha verde.

Pedir, então, aos trios que montem uma situação na qual a chance de sortear uma cor seja a mesma de sortear a(s) outra(s) cor(es). Depois, pedir que apresentem para a turma qual combinação pensaram. Existem várias possibilidades de combinações para a situação proposta. Os alunos podem escolher:

• 1 bolinha azul, 1 preta e 1 verde;

• 2 bolinhas azuis, 2 pretas e 2 verdes;

• 3 bolinhas azuis, 3 pretas e 3 verdes;

• 1 bolinha azul e 1 preta;

• 1 bolinha azul e 1 verde;

• 1 bolinha preta e 1 verde;

• 2 bolinhas azuis e 2 pretas;

• 2 bolinhas azuis e 2 verdes;

• 2 bolinhas pretas e 2 verdes.

Por último, para que os alunos se familiarizem com os termos utilizados em probabilidade, os trios devem colocar, no saco não transparente, 3 bolas azuis, 2 verdes e 1 preta e pensar nas seguintes questões: qual é a probabilidade de ser sorteada uma bola azul? E uma verde? E uma preta?

Pode-se estabelecer uma ficha para ser preenchida de acordo com a explicação de como proceder para responder a essas questões, conforme exemplo a seguir

Evento aleatório: ____________________

Espaço amostral: ______________

Probabilidade: _______

Evento aleatório: ___________________

Espaço amostral: __________________

Probabilidade: _______

Evento aleatório:

Espaço amostral: _____

Probabilidade: ________

Para as três questões, o espaço amostral é o mesmo, ou seja, é formado por seis elementos, que corresponde ao total de bolinhas que podem ser sorteadas (A1, A2, A3, V1, V2, P1), sendo A (azul), V (verde) e P (preta). O evento aleatório "Sortear uma bola azul" é formado por 3 elementos, o evento "Sortear uma bola verde" é formado por 2 elementos e o evento "Sortear uma bola preta" é formado por 1 elemento. Portanto, a probabilidade de sortear uma bola azul é 31 612 = , de sortear uma bola verde é 21 63 = e de sortear a bola preta

Relembrar os alunos de que a probabilidade de ocorrência de um evento aleatório é a razão entre a quantidade de elementos de um evento e a quantidade de elementos do espaço amostral.

Aula 8

Orientar os alunos a recuperarem 20 cartas da aula 1, sendo duas cartas de cada número, para acompanharem esta aula.

Antes de iniciar a atividade, relembrar os alunos sobre as regras do jogo Esquentando a cuca e questionar se eles utilizaram alguma estratégia para tentar adivinhar a adição dos valores das cartas. Nesse momento, deixar que troquem experiências e informações.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

A partir daí, distribuir uma folha avulsa com um quadro para o aluno preencher com todos os possíveis resultados de adição das cartas do jogo. A intenção é que os alunos avaliem quais adições têm maior frequência.

Após o quadro preenchido com a soma dos números da linha e dos números da coluna, pedir aos alunos que analisem os resultados por um tempo e, depois, dizer para eles colorirem ou contornarem com a mesma cor os resultados que têm a mesma soma. Por exemplo, colorir de verde todas as adições iguais a 5, colorir de vermelho todas as adições iguais a 6, e assim por diante.

Perguntar aos alunos quais somas têm mais chance de ocorrer.

Espera-se que seja notório que 11 é a soma que mais ocorre, em seguida, a soma 10 e a soma 12, depois a soma 9 e a soma 13, a soma 8 e a soma 14, e assim por diante.

Depois dessa análise, sugerir aos alunos que se organizem em duplas e brinquem novamente com o jogo, a fim de verificar se eles utilizam outras estratégias, como dar os palpites dos números que possuem as maiores chances de serem os resultados das adições.

Sequência didática 8: Algumas grandezas e unidades de medida

A proposta desta sequência didática é promover uma reflexão sobre unidades de medida cotidianas, o que possibilita o desenvolvimento do conceito de medida como o metro e o centímetro. Além disso, trabalha com a utilização de múltiplos e submúltiplos de unidades de medida, para que os alunos concluam que é preciso escolher a unidade de medida mais adequada e, quando necessário, saibam fazer a conversão. Para isso, serão abordadas medidas de massa, medidas de comprimento e medidas de superfície.

Objetivos de aprendizagem

• Efetuar a medição do comprimento usando unidades de medida não convencionais.

• Reconhecer, selecionar e utilizar instrumentos de medida adequados para a grandeza, com compreensão do processo de medição e das características do instrumento escolhido.

• Fazer registros para comunicar o resultado de uma medição, explicando, quando necessário, o modo como ela foi obtida.

• Comparar comprimento de dois ou mais objetos para identificar o maior, o menor, os iguais, o mais alto, o mais baixo etc.

• Desenvolver conceitos relacionados às medidas de comprimento, medidas de massa e medidas de superfície.

• Desenvolver a habilidade de conversão entre as unidades de medidas mais usuais de comprimento e de massa.

Plano de aulas

Aula 1: Introduzir a discussão a respeito das medidas de massa, particularmente o quilograma e o grama.

Aula 2: Confeccionar um jogo para comparação de medidas de massa.

Aula 3: Rever conceitos de medidas de massa por meio de um jogo confeccionado pelos próprios alunos.

Aula 4: Introduzir o conceito de medidas de comprimento.

Aula 5: Relacionar unidades padronizadas de medida de comprimento.

Aula 6: Explorar relações entre múltiplos e submúltiplos das unidades de medida de comprimento.

Aula 7: Explorar individualmente com os alunos a escolha da melhor unidade de medida para mensurar um determinado comprimento.

Aula 8: Introduzir o conceito de área como medida de superfície.

Componentes essenciais para a alfabetização: Compreensão de texto

Competências gerais da Educação Básica: 2 e 9

Competências específicas de Matemática: 2 e 8

Habilidade: EF05MA19

Materiais necessários: Régua, fita métrica, folhas avulsas, folhetos de mercado, tesoura com pontas arredondadas, cola, cartolina, folha de atividades e canetas hidrocor.

Aula 1

O objetivo desta aula é discutir algumas unidades de medida de massa, particularmente o quilograma e o grama. Para isso, inicialmente, promover uma roda de conversa sobre o conteúdo a ser explorado na aula. Perguntar aos alunos quais unidades de medida de massa eles conhecem e onde é possível encontrá-las. Fazer uma discussão geral, de maneira a envolver os alunos no tema. Se julgar necessário, registrar alguns pontos chaves da discussão na lousa. Destinar um tempo para que os alunos relatem suas próprias experiências.

Comentar que o quilograma e o grama são unidades de medida de massa utilizadas em diversos contextos. Perguntar aos alunos se conhecem locais que utilizam unidades de medida de massa em suas transações de venda. É possível que eles citem mercados, farmácias, feiras livres, entre outros.

Solicitar que os alunos indiquem alguns produtos que são comercializados por grama e quilograma. É possível que eles citem: grama – pastas de dente, sabonetes, conservas, temperos; quilograma – arroz, feijão, sal, açúcar, entre outros.

Nesse momento, comentar com os alunos que há uma relação direta entre grama e quilograma. Perguntar se eles conhecem essa relação. É esperado que os próprios alunos apontem que 1 quilograma corresponde a 1 000 gramas Em seguida, registrar na lousa essa relação.

Explorar, ainda, o significado matemático dessa relação a partir da seguinte ideia: " ao dividir 1 kg em 1 000 partes iguais, cada uma dessas partes corresponde a 1 g" Assim:

1 g = 1 1000 = 0,001 kg

Após esse momento, discutir com os alunos algumas conversões para unidades de medida de massa, de quilograma para grama, e de grama para quilograma. A seguir, há uma sugestão de conversão.

• 8 kg = 8 × 1 000 g = 8 000 g

• 5 g = 5 1000 kg = 0,005 kg

• 700 g = 700 1000 kg = 0,7 kg

• 90 kg = 90 × 1 000 g = 90 000 g

Perguntar, então, aos alunos se eles sabem como essas medidas de massa podem ser indicadas, por algum instrumento, instantaneamente. Espera-se que os alunos respondam que isso é possível por meio de balanças. Orientar a discussão de maneira que eles apresentem essa resposta.

Em seguida, questioná-los a respeito de quais os modelos de balança que eles conhecem. Espera-se que, pelas próprias experiências deles, as balanças digitais sejam apontadas.

Comentar com os alunos que existem outros tipos de balança, como a de dois pratos. Dizer a eles que a balança de dois pratos tem como princípio a comparação entre massas. Os objetos são colocados nos pratos para que suas massas sejam comparadas. Quando os objetos colocados em um prato possuem, juntos, a mesma massa que os objetos colocados no outro prato, os pratos ficam alinhados. Quando possuem massas diferentes, os pratos não ficam alinhados. O lado que pende para cima é o de menor massa. Comentar que a balança de dois pratos é antiga e que, aos poucos, foi substituída pela balança digital.

Aula 2

O objetivo desta aula é produzir um jogo para comparação de medidas de massa. Sendo assim, os próprios alunos confeccionarão as cartas que irão compor um jogo, que deverá ser jogado por eles na próxima aula. Para isso, propor que a turma seja organizada em 9 grupos. Após os alunos se organizarem, explicar que esse jogo será utilizado posteriormente e que, nessa aula, eles irão confeccionar os materiais necessários para esse fim.

Inicialmente, distribuir para cada grupo 6 cartas em branco, já cortadas pelo professor no tamanho escolhido. Sugere-se que o tamanho seja parecido com as cartas de um baralho. Elas podem ser confeccionadas de diversos materiais, como cartolina, papel sulfite com maior gramatura, papelão, papel-cartão, entre outros.

Explicar aos alunos que eles podem escolher de 1 a 3 tipos de elementos distintos, presentes no quadro a seguir, para registrar em cada carta. Indicar que para cada elemento escolhido, a quantidade pode ser variada. É importante que cada aluno tenha uma cópia desse quadro.

Elemento

Massa aproximada

1 pacote de arroz 5 kg

1 pacote de açúcar 2 kg

1 ventilador 2,4 kg

1 tomate 100 g

1 maçã 130 g

1 castanha-do-pará 5 g

1 ferro de passar 0,5 kg

1 cadeira 8 kg

1 pera 133 g

1 faca 40 g

1 pacote de farinha 1 kg

1 pacote de feijão 1 000 g

1 caneta 0, 015 kg

1 estojo 200 g

1 tablet 0,78 kg

1 celular 140 g

1 computador 7 kg

1 saco de cimento 25 kg

1 notebook 3 kg

1 par de alianças de ouro 5 g

1 automóvel 2 000 kg

1 formiga 0,15 g

A ideia é que os próprios alunos componham cada carta. Se necessário, mostrar o exemplo de uma carta já pronta, como a representada a seguir.

5 pacotes de açúcar 10 maçãs

Comentar que os alunos devem escrever as quantidades com canetas coloridas e decorar como acharem necessário. Dizer a eles que esse jogo também será utilizado em outras turmas. Portanto, eles devem caprichar na confecção das cartas

Conforme os grupos forem produzindo as cartas, acompanhar as discussões fazendo intervenções, quando achar necessário. Garantir que eles reflitam a respeito das quantidades que escolherem para compor a carta. Fazer questionamentos de maneira que eles próprios

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

percebam que utilizar uma quantidade exagerada para determinado elemento pode fazer com que eles tenham dificuldade no decorrer do jogo.

Para a próxima aula, o professor pode escrever no verso de cada carta a quantidade total de massa de todos os elementos juntos. A ideia é que seja um gabarito para organizar as ações na hora do jogo. Além disso, deixar junto às cartas, quatro cartas em branco.

Aula 3

O objetivo desta aula é revisitar os conceitos de medidas de massa por meio de um jogo confeccionado pelos próprios alunos. Para isso, organizar a turma em 9 grupos e mostrar, coletivamente, as regras do jogo Adivinhe qual elemento tem maior massa

Regras do jogo

O nome do jogo é: Adivinhe qual elemento tem maior massa.

• Cada grupo terá sua vez de jogar. Essa ordem será estabelecida por sorteio.

• O professor irá embaralhar, na frente dos alunos, todas as cartas.

• Para cada rodada, o professor sorteará 2 cartas. Após o sorteio, ele realizará a leitura de cada uma delas em voz alta.

• O grupo da vez terá que adivinhar qual das 2 cartas possui maior massa total de elementos.

• O tempo para adivinhação é de 30 segundos. Cada grupo poderá utilizar como referência o quadro apresentado na aula anterior.

• Caso acerte na primeira tentativa, o grupo ganhará 2 pontos.

• Caso erre, o grupo não ganhará pontos e não participará da próxima rodada.

• Se o grupo selecionar uma carta em branco, sua pontuação será dobrada.

• O grupo que tiver maior quantidade de pontos, após todos os grupos terem participado, vencerá a partida.

Após os alunos jogarem, solicitar que permaneçam em grupos. Em seguida, pedir que analisem o quadro que foi a base para o jogo. Perguntar a eles quais dos elementos do quadro são, comumente, representados por outras unidades de medidas de massa. É possível que eles digam que o feijão é vendido, geralmente, por quilograma e que a massa do tablet , geralmente, é representada por grama.

Após os alunos responderem, focar a discussão em um elemento do quadro: o automóvel. Comentar com os alunos que para objetos que possuem "grande massa", é interessante utilizar outra unidade de medida de massa: a tonelada. Perguntar a eles se já ouviram falar desse termo. Em seguida, comentar que a unidade de medida de massa tonelada é representada pela letra t e apresentar a seguinte relação:

1 t = 1 000 kg ou = 1 1kgt 1000

Comentar que essa ideia também é válida para elementos que possuem uma " massa muito pequena", como as formigas. Argumentar que, nesse caso, podemos utilizar outra unidade de medida de massa: o miligrama. Apresentar aos alunos o miligrama, que é representado pelas letras mg e que as seguintes relações podem ser estabelecidas:

1 g = 1 000 mg ou = 1 1mgg 1000

Por fim, solicitar aos alunos que representem a massa do automóvel em tonelada e a massa da formiga em miligrama. Espera-se que eles respondam 2 t e 150 mg.

Aula 4

O objetivo desta aula é introduzir o conceito de medidas de comprimento. Para isso, inicialmente, promover uma roda de conversa com os alunos sobre esse conteúdo. Perguntar quais unidades de medida eles ouvem falar no dia a dia e se conhecem alguma medição.

Propor uma atividade para que estimem o comprimento de alguns objetos. Pedir a eles que escolham objetos presentes no ambiente da sala de aula, da escola em geral ou no dia a dia deles. Eles devem listar os objetos em uma folha avulsa ou no caderno e escolher a unidade de medida que será usada para fazer as estimativas.

É importante que a unidade de medida a ser utilizada pelos alunos esteja de acordo com o objeto escolhido por eles. Ou seja, existem unidades de medida de comprimento que são mais adequadas para objetos específicos. Mostrar o seguinte exemplo para eles: se escolherem uma caneta esferográfica, devem escrever a unidade de medida de comprimento mais adequada para ela: o centímetro. Não é representado, usualmente, o comprimento de uma caneta em metro, por exemplo. Caso os alunos não tenham entendido o que é estimativa, esclarecer o significado do termo.

Depois desta atividade, entregar a eles réguas e fitas métricas e pedir que formem grupos. Deixar que os alunos façam algumas medições, como o comprimento de um livro, dos estojos de lápis ou mesmo a altura de um colega, e anotem os resultados. Se possível, pedir, também, que meçam alguns objetos cujo tamanho foi estimado anteriormente para realizarem comparações. Esse tipo de procedimento ajuda os alunos a se acostumarem com alguns instrumentos de medida e a terem clareza sobre a unidade de medida mais apropriada para medir cada objeto.

Aula 5

O objetivo desta aula é relacionar as unidades de medida padronizadas de comprimento. Na aula anterior foi desenvolvida uma atividade em que os alunos precisavam fazer estimativas e medições de alguns objetos. Conversar com eles para se certificar de que

não restaram dúvidas. Caso seja necessário, explicar como medir com régua e fita métrica. Após essa conversa, para verificar se eles sabem relacionar as unidades de medida padronizadas, entregar a eles uma folha com as seguintes atividades.

1. Complete as igualdades fazendo as conversões necessárias.

a) 25 cm = ______ dm

b) 50 cm = ______ mm

c) 135 mm = ______ cm

d) 80 mm = ______ cm

e) 1 m = ______ cm

f) 85 cm = ______ m

g) 1 km = _____ m

a) 2,5 dm; b) 500 mm; c) 13,5 cm; d) 8 cm; e) 100 cm; f) 0,85 m; g) 1 000 m.

2. Letícia, Paulo, Pedro e Beatriz mediram suas alturas em centímetros. Observe o quadro com os resultados.

a) Escreva a altura de cada um em metros.

Letícia: 1,24 m; Paulo: 1,41 m; Pedro: 1,47 m; Beatriz: 1,32 m.

b) Pedro tem quantos centímetros a mais que Letícia?

147 – 124 = 23. Pedro é 23 cm mais alto que Letícia.

c) Qual é a diferença entre a altura de Paulo e a de Beatriz?

141

132 = 9. A diferença entre as alturas de Paulo e de Beatriz é de 9 cm.

d) Quem é mais alto? Converta essa medida de altura para decímetros.

O mais alto é Pedro (147 cm). 147 cm = 14,7 dm.

3. Qual é a unidade de medida de comprimento mais adequada para medir:

a) o comprimento de um celular?

Centímetro ou milímetro.

Letícia Paulo Pedro Beatriz

b) a altura de uma pessoa?

Metro ou centímetro.

c) a espessura da capinha de um celular? Milímetro ou centímetro.

d) a espessura de uma borracha com formato que lembra um bloco retangular? Milímetro ou centímetro.

e) a distância entre duas cidades?

Quilômetro ou metro.

Corrigir, coletivamente, as respostas destas atividades. Para ampliar esse estudo, segurar em cada mão um lápis e uma caneta que tenham um tamanho com diferença quase imperceptível quando não estão lado a lado. Perguntar: qual desses objetos tem um comprimento maior? É provável que fiquem confusos a princípio. Nesse momento, organizar a discussão para que os alunos percebam que, em alguns casos, realizar comparações apenas por estimativas pode ser uma tarefa bastante complexa. Por isso, para algumas situações, indica-se utilizar uma régua ou algum outro instrumento de medição.

Perguntar aos alunos se eles têm alguma dúvida sobre as conversões estudadas e, caso necessário, retomar o conteúdo utilizando exemplos que facilitem a compreensão deles.

Aula 6

O objetivo desta aula é explorar relações entre múltiplos e submúltiplos de unidades de medida de comprimento.

Para isso, a aula será dividida em dois momentos:

• No primeiro momento, os alunos devem reconhecer a importância da existência de múltiplos e submúltiplos das unidades de medida. Para isso, utilizaremos o metro como unidade de trabalho.

• No segundo momento, o foco será a conversão do metro para seus múltiplos e submúltiplos.

Dessa maneira, iniciar a aula pedindo aos alunos que deem exemplos de elementos que podem ser medidos com unidades de medida de comprimento. Por exemplo, o comprimento de um lápis, a altura de uma pessoa, a largura de uma rua, a distância entre duas cidades etc. É importante que haja exemplos das mais diversas grandezas, desde objetos com comprimento bem pequeno (um grão de arroz, por exemplo) até elementos com comprimento bem grande (como a distância entre duas cidades).

Anotar na lousa alguns desses exemplos e solicitar aos alunos que deem uma medida aproximada de cada um, em metro. Nesse momento, alguns números serão "muito grandes"

e outros "muito pequenos" É possível que os alunos tenham alguma dificuldade para determinar medidas diminutas, visto que o trabalho com números decimais continua em desenvolvimento.

Depois de os alunos darem estimativas das medidas, anotar na lousa alguns números "muito grandes", outros "muito pequenos" e outros ainda que sejam um "meio-termo". Esses números são importantes, pois servirão de base para as seguintes perguntas a serem feitas aos alunos: é prático trabalhar com valores tão grandes e com valores tão pequenos? O que pode ser feito para mudar esses números?

Não se espera que a resposta seja "trabalhar com outra unidade de medida", mas sim que os alunos, que provavelmente já realizaram atividades com outras unidades de medida, utilizem esse conhecimento para sugerir o uso de algumas delas, como o centímetro, o milímetro e o quilômetro.

Após essa argumentação, é hora de fechar a primeira etapa da aula apresentando essas unidades como múltiplos e submúltiplos do metro, destacando a importância delas nas medições cotidianas. Apresentar estas igualdades:

1 000 milímetros = 100 centímetros = 10 decímetros = 1 metro = 0,001 quilômetro

Destacar que multiplicações e divisões por 10, 100 e 1 000 convertem uma unidade de medida em outra. Destacar essas divisões e multiplicações explorando o cálculo mental realizado pelos alunos. Apresentar alguns outros exemplos, se for necessário. Se julgar conveniente, as características desses cálculos (regularidades) podem ser retomadas com o auxílio de uma calculadora.

Para sanar eficientemente as dúvidas dos alunos, é importante detectar precisamente onde se encontram as dificuldades.

Por se tratar de um conteúdo que exige diversos pré-requisitos (multiplicação, divisão, conhecimento de outras unidades de medida), verificar se as dúvidas estão relacionadas com o conteúdo atual ou com algum desses pré-requisitos. Para isso, pedir aos alunos que têm dúvidas que expliquem passo a passo o conteúdo apresentado. Em algum ponto, o aluno demonstrará onde está a dificuldade e o que precisa ser sanado.

Caso julgar pertinente, esse trabalho pode ser feito em grupos ou em duplas, sempre mesclando os alunos que têm dúvidas com aqueles que já manifestam o desenvolvimento das habilidades desejadas.

Aula 7

Esta aula terá como objetivo principal explorar individualmente com os alunos a escolha da melhor unidade de medida para mensurar um determinado comprimento e a conversão entre a unidade apresentada e a unidade escolhida pelo aluno. Para isso, entregar para os alunos uma folha com atividades que tenham essa abordagem, como por exemplo:

1. Observe os casos a seguir e determine em cada um deles qual é a unidade de medida mais apropriada para a medição e faça a conversão para essa unidade.

a) Uma viagem de 13 400 000 centímetros.

b) Um lápis de 0,15 metro de comprimento.

c) Um prédio com 50 000 milímetros de altura.

d) Um parafuso de 0,00001 quilômetro.

Respostas esperadas: a) quilômetro; 134 quilômetros. b) centímetro; 15 centímetros; c) metro; 50 metros; d) milímetro; 10 milímetros.

2. Alberto vai de carro a outro estado e decidiu escrever um diário de viagem com sua lapiseira preferida. Sem dúvida, ele levará bastante grafite para abastecer a lapiseira. Escreva a seguir o que pode ser mencionado em um texto de viagem que tenha um comprimento mensurável e qual é a unidade de medida mais adequada para fazê-lo em cada caso.

Sugestão de resposta: viagem (quilômetro); carro (metro); diário (centímetro); lapiseira (centímetro); grafite (milímetro).

3. Michelle decidiu fixar quatro prateleiras em uma parede de seu quarto, uma acima da outra. Sabendo que essas prateleiras ocuparão toda a extensão da parede, que é bem comprida, que a madeira para as prateleiras precisará ter uma larga espessura para suportar peso e que precisa haver uma distância entre as prateleiras, responda quais unidades de medida são mais adequadas para expressar:

a) O comprimento da parede.

b) A espessura da madeira.

c) A distância entre as prateleiras.

Espera-se que os alunos respondam: a) metro; b) centímetro ou milímetro; c) centímetro.

Após a conclusão da atividade, fazer uma correção coletiva, permitindo aos alunos explicar como chegaram às conclusões e quais estratégias adotaram para responder a essas atividades. Nesse momento, é importante que os alunos expliquem como resolveram as questões.

Por fim, solicitar aos alunos que elaborem uma situação-problema relacionada a medidas de comprimento. Em seguida, pedir que eles troquem o problema com um colega para que resolvam os problemas elaborados. Ao final, solicitar que, juntos, confiram as resoluções.

O objetivo desta aula é introduzir a ideia de área como uma medida de superfície. Para isso, organizar os alunos em grupos de três alunos, e solicitar que um deles leia em voz alta a seguinte atividade.

• Para uma aula coletiva de yoga , o piso do salão de uma academia foi revestido com placas de EVA em formato quadrado. Observe a imagem a seguir e responda às questões

EDITORIA DE ARTE

a) Quantas placas de EVA foram utilizadas para revestir o piso desse salão? 40 placas.

b) Se cada placa de EVA custou R$ 12,20, quanto foi gasto pela academia para revestir o piso de todo o salão?

R$ 488,00 (40 x 12,20 = 488,00)

Após um aluno ler a atividade em voz alta, perguntar se algum outro aluno tem alguma dúvida sobre o enunciado. Em seguida, solicitar que tentem resolver nos grupos essa atividade.

No momento em que eles tentam resolver, acompanhar os grupos e realizar intervenções, se julgar conveniente. Alguns questionamentos são importantes nesse momento, por exemplo:

• Como vocês resolveram a questão?

• Por que vocês desenvolveram essa estratégia?

• Justifique como você resolveu.

• Tente convencer seu colega de que está certo.

• Como vocês realizaram para determinar a quantidade total de placas de EVA?

Esses questionamentos permitem a percepção sobre as estratégias utilizadas pelos alunos. Além disso, permitem que os próprios alunos reconheçam estratégias que, porventura, são inadequadas.

Após os alunos resolverem as questões, solicitar que um representante de cada grupo apresente suas resoluções dos itens a e b Em seguida, relacionar as resoluções dos grupos,

discutindo semelhanças e diferenças entre elas. Por fim, sistematizar a ideia de área, formalizando com os alunos que a quantidade de placas de EVA corresponde à medida da superfície ou da área do piso do salão, tomando como unidade de medida cada placa de EVA. Nesse sentido, pode-se dizer que a medida da área do salão corresponde a 40 placas de EVA.

Após chegar nessa sistematização, problematizar o modo com que os alunos podem ter determinado a quantidade total de placas de EVA. Nessa discussão, problematizar os seguintes modos de obter essa quantidade:

• Podemos contar todas as placas, uma a uma;

• Uma fileira tem 10 placas de EVA. Como há 4 fileiras, basta realizar a seguinte adição: 10 + 10 + 10 + 10 = 40;

• Uma fileira tem 10 placas de EVA. Como há 4 fileiras, basta multiplicar 10 (quantidade de placas em uma fileira) por 4 (quantidade de fileiras), ou seja, 10 × 4 = 40.

Comentar que, nesse caso, pode-se realizar essa multiplicação, pois a região é retangular.

Após realizada essa formalização, comentar que nesta atividade a unidade de medida utilizada foi a superfície de uma placa de EVA. Porém, existem algumas unidades de medida de superfície que são padronizadas. Uma delas é chamada metro quadrado (m²). Nesse momento, perguntar aos alunos se eles já ouviram falar nesse tipo de medida. Em seguida, registrar na lousa que 1 metro quadrado equivale à área de um quadrado com 1 m de lado. Se necessário, realizar o desenho na lousa.

Por fim, propor a pergunta a seguir aos alunos.

• Se a placa de EVA da atividade anterior tiver 1 m², qual será a medida da área do piso do salão, sendo o metro quadrado a unidade utilizada?

40 m²

Sugestões

• MUSEU IBRAN GOIÁS. Balança Disponível em:

https://museusibramgoias.acervos.museus.gov.br/museu-das-bandeiras/balanca-2/ Acesso em: 15 dez 2021.

• MENDES, Daniela. Faça uma balança de pratos e ensine Álgebra usando garrafas PET! Laboratório Sustentável de Matemática, c2022. Disponível em:

https://www.laboratoriosustentaveldematematica.com/2014/05/faca-uma-balanca-depratos-ensine-algebra-garrafas-pet.html Acesso em: 21 jan. 2022.

Relatórios e indicadores do acompanhamento da aprendizagem

O processo avaliativo exige do professor um olhar reflexivo permanente sobre o desenvolvimento da aprendizagem dos alunos e, consequentemente, sobre a sua própria prática pedagógica. Dessa forma, instrumentos de avaliação, como provas, testes, questionários, redações, trabalhos, seminários, entre outros, não devem ser encarados como instrumentos pontuais de avaliação, mas, sim, como ferramentas de coleta de indicadores que descrevem o desempenho dos alunos e possibilitam uma análise coletiva e individual dos avanços e dos pontos de melhoria da aprendizagem.

Os indicadores de aprendizagem devem auxiliar o professor no acompanhamento do desenvolvimento das aprendizagens dos alunos, apontando se os objetivos, as competências, as habilidades e os conteúdos previstos em seu plano de trabalho estão sendo alcançados ou se há necessidade de intervenção no processo de aprendizagem para que possam ser atingidos.

Esses indicadores de aprendizagem, isoladamente, nada apontam, uma vez que os resultados são fruto da análise do professor com base em objetivos, competências e habilidades desenvolvidos em determinado contexto educacional. Assim, com o apoio da avaliação dos indicadores de aprendizagem, é necessário que sejam produzidos relatórios descritivos das análises, considerações e observações a respeito do processo de aprendizado e desenvolvimento dos alunos e de sua prática pedagógica em sala de aula.

Produção de relatórios

Os relatórios escolares são registros que devem ser realizados periodicamente (a cada bimestre, trimestre ou semestre) a respeito do desenvolvimento de diferentes aprendizagens dos alunos ao longo do processo de ensino-aprendizagem.

Dentro do processo de aprendizagem escolar, os relatórios, entre outras finalidades, deverão:

• Possibilitar ao educador compreender de forma significativa o processo de aprendizagem dos alunos, respeitando suas individualidades, particularidades e diferenças.

• Produzir informações e dados significativos sobre o processo de aprendizagem de modo a planejar intervenções pedagógicas com base em objetivos, conteúdos, competências e habilidades a serem desenvolvidos.

• Fornecer subsídios teóricos para as reuniões de conselho de classe para que professores, coordenadores pedagógicos e diretores da escola possam analisar o desempenho individual e coletivo dos alunos e, consequentemente, discutir formas,

ações, intervenções, estratégias e métodos de melhoria do processo de ensino-aprendizagem com base no Projeto Político Pedagógico da escola.

• Realizar uma comunicação orientada, assertiva e planejada com pais ou responsáveis de modo a engajá-los no processo de aprendizagem, contribuindo desse modo para o desenvolvimento dos alunos e a efetividade do ensino.

• Proporcionar ao aluno o direito de acompanhar o próprio processo de aprendizagem, de modo a oportunizar a superação de suas dificuldades.

Apesar de não existir um modelo fixo de relatório a ser seguido, alguns pontos importantes podem ser considerados na elaboração desse material. O texto do relatório deverá ser escrito de forma clara, concisa e objetiva, de modo que o leitor o compreenda. Devem ser registrados os conteúdos trabalhados e como foram avaliados, assim como todas as considerações julgadas pertinentes ao processo de ensino-aprendizagem. É importante, também, descrever quais foram os encaminhamentos adotados em caso de dificuldade dos alunos.

Se possível, os relatórios devem ainda captar as diferentes dimensões envolvidas nas experiências dos alunos no grupo, ou seja, devem trazer aspectos relacionados a sentimentos, afetos, emoções, movimentos e cognição.

Os relatórios podem conter apresentações visuais e gráficas dos dados coletados, de modo a facilitar a compreensão das informações que estão sendo transmitidas. Pode-se elaborar um gráfico de barras comparando a distribuição percentual dos resultados quantitativos da aprendizagem dos alunos a respeito de competências gerais, de competências específicas e de habilidades em um período, como no exemplo a seguir.

Fonte: Dados fictícios.

Gráficos e tabelas podem ser elaborados por meio de um editor de planilhas eletrônicas, como o LibreOffice, que é um software livre e gratuito, disponível em: https://pt-br.libreoffice.org/ (acesso em: 10 dez. 2021).

Indicadores do acompanhamento da aprendizagem

De modo geral, o termo "indicadores" é usado para apontar parâmetros que avaliam certa realidade em determinado intervalo de tempo. Um médico, por exemplo, examina vários indicadores antes de oferecer um diagnóstico a um paciente. Um economista também se utiliza de indicadores para analisar se a inflação de um país aumentou ou diminuiu. Já no contexto escolar, os indicadores do acompanhamento da aprendizagem têm como objetivo mapear os diferentes níveis de desenvolvimento das aprendizagens dos alunos.

Uma vez que o processo de aprendizagem ocorre simultânea e interativamente nas dimensões cognitiva, afetiva e psicomotora, os indicadores de aprendizagem a serem observados e avaliados deverão abarcar aspectos tanto quantitativos quanto qualitativos do processo de aprendizagem dos alunos, garantindo, assim, uma visão ampla e significativa desse processo.

Os aspectos qualitativos dos indicadores de aprendizagem, geralmente, são aqueles ligados às competências gerais e socioemocionais que expressam a voz, as percepções, as crenças, os sentimentos, os pensamentos, as emoções, as atitudes e os modos de agir dos educandos. São eles que possibilitam ao educador avaliar se os alunos alcançaram a construção e a formação de atitudes e valores, como autonomia, responsabilidade, empatia, resiliência, determinação, criticidade e capacidade de ouvir, ser ouvido e dialogar.

Já os aspectos quantitativos dos indicadores de aprendizagem são aqueles que descrevem quantidades ou percentuais da consecução do processo de ensino-aprendizagem. São esses aspectos quantitativos que permitem ao professor fazer uma avaliação do quanto os alunos estão avançando em relação aos objetivos, competências, habilidades e conteúdos, gerais ou específicos, de determinada área do conhecimento, previstos em seu plano de trabalho.

São apresentados, a seguir, quatro modelos de fichas com sugestões de indicadores que podem ser obtidos por meio do processo avaliativo que julgar mais conveniente. Esses modelos podem ser impressos e preenchidos com os dados dos alunos ou da turma.

O primeiro modelo é o de Ficha de avaliação diagnóstica. Nela, estão presentes alguns indicadores que poderão servir de subsídio para que seja reconhecido o domínio dos alunos a respeito de alguns conteúdos, no início do ano letivo.

O segundo modelo é o de Ficha de acompanhamento das aprendizagens, na qual são apresentadas as habilidades da BNCC indicadas para o ano de escolaridade, as Competências específicas de Matemática para o Ensino Fundamental, as Competências gerais da Educação Básica e os componentes essenciais para a alfabetização. Nela, há uma coluna para preenchimento de observações mais detalhadas.

O terceiro modelo é o de Ficha deverificaçãode resultados, em que estão indicados, a cada ano de escolaridade, alguns objetivos de aprendizagem categorizados como focais, por influenciarem de modo mais evidente o desenvolvimento vinculado às Competências gerais e às Competências específicas da área de Matemática para o Ensino Fundamental.

Por fim, considerando a ideia de educação integral, também é preciso avaliar o desenvolvimento das dimensões sociais e emocionais dos alunos. Para tanto, o quarto modelo é o de Ficha de acompanhamento do desenvolvimento de competências socioemocionais, que apresenta indicadores para que seja apontada a frequência com que essas competências são reconhecidas nas atitudes dos alunos.

Os modelos de fichas aqui apresentados são apenas proposições para apoiar o processo de ensino-aprendizagem. É fundamental que o trabalho pedagógico seja planejado com intencionalidade para explorar todos os potenciais de aprendizagem e garantir as condições de desenvolvimento pleno e integral de cada aluno. Essa tarefa requer a participação de toda a comunidade escolar, envolvendo professores, gestores e os responsáveis pelos alunos.

RECURSO EDUCACIONAL DIGITAL

Ficha de avaliação diagnóstica

Professor:

Turma:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de avaliação diagnóstica

Números Álgebra Geometria Grandezas e medidas Estatística Probabilidade

Aluno Identificar características do Sistema de Numeração Decimal com base na composição e decomposição de números naturais até 99 999.

Compreender propriedades das operações para o desenvolvimento de diferentes estratégias de cálculo com números naturais.

Reconhecer propriedades de uma igualdade.

Figuras geométricas planas: reconhecer, nomear e comparar atributos, considerando características como lados e vértices.

Figuras geométricas espaciais: analisar, nomear e comparar atributos.

Estabelecer relações entre as unidades de medida mais usuais.

Leitura, interpretação e representação de dados em tabelas (simples ou de dupla entrada) e gráficos.

Analisar chances de eventos aleatórios.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de acompanhamento das aprendizagens

Professor:

Turma:

Aluno:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de acompanhamento das aprendizagens (Matemática)

Habilidades C PC NC Observações

(EF05MA01) Ler, escrever e ordenar números naturais até a ordem das centenas de milhar com compreensão das principais características do sistema de numeração decimal.

(EF05MA02) Ler, escrever e ordenar números racionais na forma decimal com compreensão das principais características do sistema de numeração decimal, utilizando, como recursos, a composição e decomposição e a reta numérica.

(EF05MA03) Identificar e representar frações (menores e maiores que a unidade), associando-as ao resultado de uma divisão ou à ideia de parte de um todo, utilizando a reta numérica como recurso.

(EF05MA04) Identificar frações equivalentes.

(EF05MA05) Comparar e ordenar números racionais positivos (representações fracionária e decimal), relacionando-os a pontos na reta numérica.

(EF05MA06) Associar as representações 10%, 25%, 50%, 75% e 100% respectivamente à décima parte, quarta parte, metade, três quartos e um inteiro, para calcular porcentagens, utilizando estratégias pessoais, cálculo mental e calculadora, em contextos de educação financeira, entre outros.

(EF05MA07) Resolver e elaborar problemas de adição e subtração com números naturais e com números racionais, cuja representação decimal seja finita, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.

(EF05MA08) Resolver e elaborar problemas de multiplicação e divisão com números naturais e com números racionais cuja representação decimal é finita (com multiplicador natural e divisor natural e diferente de zero), utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.

(EF05MA09) Resolver e elaborar problemas simples de contagem envolvendo o princípio multiplicativo, como a determinação do número de agrupamentos possíveis ao se combinar cada elemento de uma coleção com todos os elementos de outra coleção, por meio de diagramas de árvore ou por tabelas.

(EF05MA10) Concluir, por meio de investigações, que a relação de igualdade existente entre dois membros permanece ao adicionar,

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

subtrair, multiplicar ou dividir cada um desses membros por um mesmo número, para construir a noção de equivalência.

(EF05MA11) Resolver e elaborar problemas cuja conversão em sentença matemática seja uma igualdade com uma operação em que um dos termos é desconhecido.

(EF05MA12) Resolver problemas que envolvam variação de proporcionalidade direta entre duas grandezas, para associar a quantidade de um produto ao valor a pagar, alterar as quantidades de ingredientes de receitas, ampliar ou reduzir escala em mapas, entre outros.

(EF05MA13) Resolver problemas envolvendo a partilha de uma quantidade em duas partes desiguais, tais como dividir uma quantidade em duas partes, de modo que uma seja o dobro da outra, com compreensão da ideia de razão entre as partes e delas com o todo.

(EF05MA14) Utilizar e compreender diferentes representações para a localização de objetos no plano, como mapas, células em planilhas eletrônicas e coordenadas geográficas, a fim de desenvolver as primeiras noções de coordenadas cartesianas.

(EF05MA15) Interpretar, descrever e representar a localização ou movimentação de objetos no plano cartesiano (1º quadrante), utilizando coordenadas cartesianas, indicando mudanças de direção e de sentido e giros.

(EF05MA16) Associar figuras espaciais a suas planificações (prismas, pirâmides, cilindros e cones) e analisar, nomear e comparar seus atributos.

(EF05MA17) Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e desenhá-los, utilizando material de desenho ou tecnologias digitais.

(EF05MA18) Reconhecer a congruência dos ângulos e a proporcionalidade entre os lados correspondentes de figuras poligonais em situações de ampliação e de redução em malhas quadriculadas e usando tecnologias digitais.

(EF05MA19) Resolver e elaborar problemas envolvendo medidas das grandezas comprimento, área, massa, tempo, temperatura e capacidade, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais.

(EF05MA20) Concluir, por meio de investigações, que figuras de perímetros iguais podem ter áreas diferentes e que, também, figuras que têm a mesma área podem ter perímetros diferentes.

(EF05MA21) Reconhecer volume como grandeza associada a sólidos geométricos e medir volumes por meio de empilhamento de cubos, utilizando, preferencialmente, objetos concretos.

(EF05MA22) Apresentar todos os possíveis resultados de um experimento aleatório, estimando se esses resultados são igualmente prováveis ou não.

(EF05MA23) Determinar a probabilidade de ocorrência de um resultado em eventos aleatórios, quando todos os resultados possíveis têm a mesma chance de ocorrer (equiprováveis).

(EF05MA24) Interpretar dados estatísticos apresentados em textos, tabelas e gráficos (colunas ou linhas), referentes a outras áreas do conhecimento ou a outros contextos, como saúde e trânsito, e produzir textos com o objetivo de sintetizar conclusões.

(EF05MA25) Realizar pesquisa envolvendo variáveis categóricas e numéricas, organizar dados coletados por meio de tabelas, gráficos de colunas, pictóricos e de linhas, com e sem uso de tecnologias digitais, e apresentar texto escrito sobre a finalidade da pesquisa e a síntese dos resultados.

Competências específicas de Matemática para o Ensino Fundamental C PC NC Observações

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial

(CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações se jam licenciadas sob os mesmos parâmetros.

Competências gerais da Educação Básica C PC NC Observações

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Componentes essenciais para a alfabetização

Conhecimento alfabético

Fluência em leitura oral

Desenvolvimento de vocabulário

Compreensão de textos

Produção de escrita

Ficha de verificação de resultados

Professor:

Turma:

Sugestão de critérios de avaliação

C = consolidado (aluno faz sozinho); PC = em processo de consolidação (aluno precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (aluno não consegue realizar a atividade proposta)

Ficha de verificação de resultados

Principais objetivos de aprendizagem

Aluno Ler, escrever, comparar, compor e decompor números naturais até 999 999.

Plano cartesiano: coordenadas cartesianas (1º quadrante) e representação de deslocamentos no plano cartesiano.

Representação fracionária dos números racionais: reconhecimento, representações e significados.

Compreender o significado de frações equivalentes e utilizar na comparação de frações.

Ler, escrever, comparar e ordenar números racionais na representação decimal.

Problemas: adição e subtração de números racionais cuja representação decimal é finita.

Determinar a probabilidade de um evento ocorrer.

Identificar espaço amostral e evento aleatório com base em situações-problema.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Professor:

Turma:

Aluno:

Competências socioemocionais Sempre Frequentemente Raramente Nunca

Determinação

Foco

Organização

Persistência

Responsabilidade

Empatia

Respeito

Confiança

Tolerância ao estresse

Autoconfiança

Tolerância à frustração

Iniciativa social

Assertividade

Entusiasmo

Curiosidade para aprender

Imaginação criativa

Interesse artístico

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Catálogo dos audiovisuais

Nesta seção, são disponibilizados detalhamentos, como objetivos de aprendizagem e conteúdos abordados, entre outros aspectos, acerca de cada um dos audiovisuais que compõem a coletânea desta coleção. Também, para cada audiovisual, são descritas sugestões de utilização e são sugeridas propostas de atividades, a fim de apoiar pedagogicamente o uso desses recursos digitais audiovisuais. Tais informações visam trazer insumos para favorecer o planejamento de aplicação deles de acordo com a realidade da comunidade escolar e da turma em que forem trabalhados.

Audiovisuais da coletânea

Relação de audiovisuais da coletânea

Cara ou coroa? Neste audiovisual, é explorado o estudo da probabilidade a partir de uma situação envolvendo o lançamento de moedas. Dessa forma, os alunos vão aprender como obter todos os resultados possíveis de um experimento aleatório e como calcular a probabilidade de ocorrência de um resultado e representálo utilizando fração

Coleta seletiva de materiais recicláveis

Neste audiovisual, é abordada a importância da separação correta do lixo e da reciclagem para a preservação do meio ambiente. Além disso, é explorada a construção de uma tabela em uma planilha eletrônica, por meio de uma situação fictícia na qual os alunos organizam os dados referentes à quantidade de materiais reciclados coletados por eles em uma ação de coleta seletiva.

• Determinar os possíveis resultados de um experimento aleatório equiprovável.

• Determinar a probabilidade de ocorrência de um resultado de um experimento aleatório equiprovável.

• Escrever a probabilidade de ocorrência de um evento aleatório utilizando fração.

• Refletir sobre a importância de realizar o descarte adequado do lixo

• Refletir sobre a importância da reciclagem para o meio ambiente.

• Reconhecer a importância da organização de dados em situações cotidianas.

• Organizar dados em tabelas utilizando uma planilha eletrônica.

• Construir gráfico em uma planilha eletrônica a partir dos dados organizados em uma tabela.

• Espaço amostral: análise dos resultados de um experimento aleatório equiprovável

• Cálculo de probabilidade de resultados e experimento aleatório equiprovável.

• Reciclagem

• Tecnologias digitais

• Tabelas

• Gráficos

Consumo consciente de energia elétrica

Neste audiovisual, é abordada a importância do consumo consciente de energia. Nele, também é mencionado que a maior fonte de energia no Brasil são as usinas hidrelétricas e são apresentadas atitudes que podem contribuir para a economia de energia. Além disso, explora o cálculo de operações com números racionais ao calcular quanto uma lâmpada LED consome de quilowatts-hora por mês ao ficar ligada 5 horas por dia.

Rios voadores Neste audiovisual, são apresentadas informações sobre os rios voadores e a importância da Floresta Amazônica para a formação de chuva em diferentes regiões do país. Além disso, para apresentar algumas informações referentes aos rios voadores são utilizadas as medidas de comprimento, capacidade e volume.

Coordenadas e Batalha naval Neste audiovisual, é abordado o plano cartesiano a partir da apresentação do jogo Batalha naval. Ao explorar esse jogo, é apresentado o 1º quadrante do plano cartesiano e como localizar pontos no plano utilizando coordenadas cartesianas.

• Identificar os elementos de uma tabela: título e fonte.

• Refletir sobre a importância do consumo consciente de energia.

• Reconhecer qual é a principal fonte de energia do Brasil.

• Identificar atitudes que podem contribuir para reduzir o consumo de energia.

• Resolver operações de multiplicação envolvendo números racionais cuja representação decimal é finita.

• Energia

• Multiplicação com números racionais cuja representação decimal é finita.

• Compreender o que são os rios voadores.

• Reconhecer a importância da Floresta Amazônica para as diferentes regiões do Brasil.

• Reconhecer a utilização de unidades de medida para interpretar informações de outras áreas do conhecimento.

• Compreender o sistema de coordenadas cartesianas.

• Identificar pontos no plano cartesiano (1º quadrante)

• Localizar pontos no plano cartesiano (1º quadrante).

• Rios voadores

• Floresta Amazônica

• Grandezas e medidas

• Plano cartesiano: coordenadas cartesianas (1º quadrante)

Orientações para o uso dos audiovisuais

Cara ou coroa?

Este audiovisual pode ser apresentado de maneira introdutória ao estudo de Probabilidade. A partir de uma situação envolvendo moedas, são apresentados como obter todos os resultados possíveis de um experimento aleatório e como calcular a probabilidade de ocorrência de um resultado e a representação da probabilidade na forma de fração. Se

possível, disponibilizar alguns dados e fazer alguns experimentos com os alunos após a exibição do vídeo.

Durante o vídeo, logo após ser apresentada a representação da probabilidade na forma de fração, fazer uma pausa e perguntar aos alunos se eles compreenderam esse conteúdo. Caso não tenham compreendido, retomar a explicação na lousa.

Ao terminar a exibição do vídeo, propor aos alunos que investiguem se, ao lançar um dado, é mais fácil obter a face 1 ou obter a face 6 Para isso, orientar os alunos a seguirem o passo a passo apresentado no vídeo, ou seja, eles devem observar todos os resultados possíveis e a quantidade de cada resultado possível (1, 2, 3, 4, 5, 6). Em seguida, pedir que indiquem a probabilidade de cada resultado na forma de fração e respondam se é mais fácil obter a face 1 ou a face 6. É importante que os alunos observem que as duas situações têm a mesma chance de ocorrer.

A partir desta atividade envolvendo dados, explorar outras perguntas para que os alunos calculem probabilidades. Por exemplo, perguntar: qual é a probabilidade de o resultado ser par ou de o resultado ser ímpar? Qual é a probabilidade de o resultado ser maior ou igual a 5 ou menor que 5? Quanto mais situações forem exploradas, mais os alunos irão se familiarizar com esses cálculos.

Após a exibição do vídeo, sugere-se a resolução das atividades propostas a seguir ou de atividades semelhantes.

Sugestões de atividades

1. Lia e Josué estão brincando com uma roleta de cores.

EDITORIA DE ARTE

a) Qual cor tem mais chance de ser sorteada?

Espera-se que os alunos respondam que a vermelha tem mais chance de ser sorteada porque, das seis partes da roleta, há três partes vermelhas, duas partes verdes e uma parte azul.

b) Pinte a roleta com as cores vermelha, azul e verde de modo que elas tenham a mesma chance de serem sorteadas.

Espera-se que os alunos pintem duas partes de cor vermelha, duas partes de cor verde e duas partes de cor azul (a posição das cores não importa).

2. Escreva o significado da frase "A probabilidade de sair o resultado 1 no lançamento de um dado é de 1 em 6".

Espera-se que os alunos respondam que há um resultado 1 para um total de 6 resultados possíveis.

a) Represente as probabilidades indicadas a seguir na forma de fração.

• "A probabilidade de selecionar um número par é de 3 em 5": 3/5

• "A probabilidade de selecionar um menino de um determinado grupo é de 6 em 8":

6/8

• "A probabilidade de selecionar a cor amarela de um determinado grupo de cores é de 3 em 6":

3/6

b) Qual das probabilidades do item a é equivalente a 1/2?

Espera-se que os alunos respondam 3/6, pois 1/2 e 3/6 são equivalentes.

3. Pinte as fichas a seguir de azul, verde, amarelo e laranja de modo que, ao colocá-las em uma sacola para retirar uma ficha aleatoriamente, a probabilidade de sair uma ficha em uma dessas cores seja:

• azul: 1/8 • verde: 4/8 • amarelo: 1/8 • laranja: 2/8

• Agora, pinte as fichas de modo que a probabilidade de sair a ficha azul, verde, amarela ou laranja seja a mesma.

Coleta seletiva de materiais recicláveis

Este audiovisual pode ser apresentado de maneira introdutória ao estudo de tabelas e de gráficos ou como retomada do conteúdo. Nele, o narrador explora a construção de tabela e de gráfico em uma planilha eletrônica a partir de dados sobre coleta de materiais recicláveis.

Caso este vídeo seja utilizado como introdução ao conteúdo, sugere-se iniciar a aula com a exibição dele Para isso, fazer uma pausa logo após a apresentação das quatro cores das lixeiras da coleta seletiva e conversar com os alunos sobre a importância do tema apresentado. Perguntar a eles por que a reciclagem é importante e como nós podemos ajudar a reduzir a produção de lixo. Perguntar, também, se eles já viram as lixeiras de coleta seletiva em algum lugar, se eles fazem o descarte correto dos materiais ou se conhecem alguém que faz o descarte corretamente. A partir das respostas dos alunos, outras perguntas podem ser exploradas.

Após esse momento de conversa sobre reciclagem, retomar a exibição do vídeo. Depois, fazer outra pausa logo após a apresentação da tabela com os dados sobre os materiais coletados pelos alunos de Manaus. Reproduzir essa tabela na lousa para a turma visualizar a construção dela, fora da planilha eletrônica e, em seguida, dar continuidade à exibição do vídeo.

Quando a exibição do vídeo terminar, construir um gráfico com os dados da tabela na lousa para os alunos visualizarem as etapas dessa construção. Em seguida, pedir a eles que observem o gráfico e tirem conclusões sobre os dados apresentados. Se achar pertinente, organizar a turma em grupos com quatro integrantes e propor que cada um faça uma pesquisa, sobre algum tema, com os próprios alunos da turma. Em seguida, pedir que eles apresentem os dados em tabela e em gráfico.

Caso o vídeo seja utilizado como retomada de conteúdo, sugere-se as propostas anteriores e, se for possível, a exploração de planilhas eletrônicas. Propor aos alunos que construam tabelas e gráficos em uma planilha eletrônica, com os dados coletados nas pesquisas feitas com os próprios colegas de turma. Os alunos, também, podem reproduzir os dados da atividade 2 na planilha eletrônica para gerar a construção do gráfico. Depois, pedir que interpretem os dados apresentados.

Em seguida, propor as atividades seguintes ou atividades semelhantes envolvendo gráficos e tabelas.

Sugestões de atividades

1. Escreva exemplos de materiais utilizados no cotidiano que podem ser descartados nas lixeiras indicadas a seguir.

a) Lixeira de metal

Sugestões de resposta: lata de tinta; tampa de metal de garrafa de vidro.

b) Lixeira de papel:

Sugestões de resposta: folha de papel; folheto de mercado, sacola de papel.

c) Lixeira de plástico:

Sugestões de resposta: embalagem de macarrão; garrafa PET

d) Lixeira de vidro

Sugestões de resposta: pote de alimento em conserva; garrafa de suco.

2. Os alunos de duas turmas do 5º ano fizeram uma campanha para arrecadar brinquedos para doar. Observe na tabela a quantidade de brinquedos que eles arrecadaram.

Campanha de arrecadação de brinquedos das turmas do 5º ano

Fonte: Turmas do 5º ano

a) Escreva qual brinquedo as turmas A e B arrecadaram em maior quantidade cada uma.

Turma A: arrecadou mais carrinhos; turma B: arrecadou mais bolas.

b) Qual brinquedo cada turma arrecadou em menor quantidade?

As duas turmas arrecadaram quebra-cabeças em menor quantidade.

c) Quantos brinquedos cada turma arrecadou no total?

A turma A arrecadou 128 brinquedos e a turma B arrecadou 173 brinquedos.

3. Observe o gráfico dos materiais coletados pelos estudantes de Manaus, em 2022. Em seguida, escreva um texto com as conclusões que você pode tirar por meio desse gráfico.

Resposta pessoal. Espera-se que os alunos escrevam um texto baseado nas informações apresentadas no gráfico.

Consumo consciente de energia elétrica

Este audiovisual pode ser utilizado como retomada do conteúdo operações com números racionais. Nele, é apresentada a importância do consumo consciente de energia elétrica. Se for possível, selecionar previamente algumas imagens de equipamentos eletrônicos com o Selo Procel de Eficiência Energética.

Para iniciar a aula, sugere-se apresentar o vídeo à turma. Após a exibição, pedir aos alunos que compartilhem com os colegas o que mais lhes chamou a atenção na apresentação e fazer perguntas a eles como: o que é consumo consciente? Por que é importante consumir energia elétrica de modo consciente? O que podemos fazer para diminuir o consumo de energia elétrica? Vocês utilizam energia elétrica de forma consciente em casa, na escola e em outros ambientes? Depois, propor aos alunos que deem exemplos do que eles fazem para reduzir esse consumo.

Apresentar as imagens de equipamentos eletrônicos com o Selo Procel de Eficiência Energética e pedir que os alunos respondam quais deles são mais eficientes dentro de sua categoria.

Em seguida, propor as atividades descritas a seguir ou atividades semelhantes. Na atividade 3, que envolve operações com números racionais, outras propostas de perguntas podem ser realizadas. Uma atividade que pode ser criada a partir dela é propor aos alunos

Fonte: Dados coletados pelos alunos.

que estimem quanto tempo cada equipamento da tabela é utilizado em sua residência, qual seria o custo mensal (em reais) de cada um, considerando os dados da tabela e qual é o custo mensal desses equipamentos juntos.

Sugestões de atividades

1.Responda às questões a seguir de acordo com o vídeo a que você assistiu.

a)Qual é a principal fonte de energia no Brasil?

As usinas hidrelétricas.

b)Que soluções podemos adotar para economizar energia elétrica?

Espera-se que os alunos citem uma ou mais soluções apresentadas no vídeo: comprar, sempre que possível, aparelhos que tenham Selo Procel de Eficiência Energética e que precisam de uma menor quantidade de energia para funcionar; deixar cortinas e janelas abertas durante o dia; tomar banho rapidamente; pegar tudo que precisa da geladeira de uma só vez; substituir lâmpadas incandescentes comuns por lâmpadas LED.

2.Faça uma pesquisa sobre como a energia elétrica chega até a nossa casa. Anote as informações que você encontrou e, depois, compartilhe com os colegas. Resposta pessoal.

3.Observe a tabela a seguir.

Equipamentos eletrônicos: custo mensal em reais por tempo de uso diário em 1 hora Equipamento eletrônico (por unidade) Custo mensal (em reais)*

Fonte: SIMULADOR DE CONSUMO. Disponível em https:// enel-rj.simuladordeconsumo.com.br/ Acesso em: 22 jan. 2022.

*Custo mensal em uma determinada região e com base em alguns modelos de aparelhos específicos. O custo mensal pode ser maior ou menor dependendo da região e dos modelos dos aparelhos.

a) Qual é o assunto da tabela?

O custo mensal, em reais, de alguns equipamentos eletrônicos por tempo de uso diário de 1 hora.

b) Quais aparelhos têm o maior custo mensal considerando-se que eles ficam ligados na tomada por 1 hora todos os dias? E qual tem o menor custo mensal?

Maior custo: chuveiro elétrico; menor custo: aparelho celular.

c) Se uma pessoa utilizar o ar-condicionado por 6 horas, todos os dias, quantos reais ela irá pagar por esse uso?

R$ 102, 54 (6 × 17,09 = 102,54).

d) Qual é o custo mensal, em reais, de uma geladeira considerando-se que ela fica ligada o dia todo?

R$ 100,32 (24 × 4,18 = 100,32).

e) Qual é o custo mensal, em reais, de 3 lâmpadas considerando-se que elas ficam ligadas por 5 horas, todos os dias?

R$ 23,10 (1 lâmpada: 5 × 1,54 = 7,70; 3 lâmpadas: 3 × 7,70 = 23,10).

f) Considerando os dados da tabela anterior, qual desses equipamentos você acha que tem um custo maior na conta de energia da sua casa? Quantos reais, aproximadamente?

Resposta pessoal.

Rios voadores

Este audiovisual pode ser utilizado como retomada do estudo sobre grandezas e medidas. Nele, são apresentadas informações sobre os rios voadores e a importância da Floresta Amazônica para a sua formação e para as chuvas em diferentes regiões do país. Os alunos irão precisar de dicionário para compreender algumas palavras presentes no audiovisual que são desconhecidas por eles

Sugere-se que a aula seja iniciada com a exibição do vídeo. Após a exibição, fazer algumas perguntas à turma. Por exemplo: o que são rios voadores e a sua importância? Qual é a importância da Floresta Amazônica para a formação dos rios voadores? Qual é a importância da Floresta Amazônica para as chuvas nas regiões Centro-Oeste, Sudeste e Sul do Brasil? Por que as chuvas são importantes? Deixar que os alunos respondam de acordo com que aprenderam com o vídeo e, se julgar necessário, fazer intervenções.

Depois, retomar as informações matemáticas presentes no vídeo. Para efeito de comparação, pedir aos alunos que deem exemplos de algo que tenha 20 metros de comprimento para eles terem uma noção do diâmetro da árvore dada como exemplo no vídeo. O mesmo pode ser feito com a quantidade de água que uma árvore pode transferir

para a atmosfera. Para isso, perguntar aos alunos quantos galões de 10 ou 20 litros poderiam ser preenchidos com 1 000 litros de água, quantidade que equivale ao que evapora de uma árvore (com as características apresentadas no vídeo) em um único dia de sol.

É importante ressaltar aos alunos que a árvore com 20 metros de diâmetro é apenas um exemplo, pois árvores com diferentes tamanhos contribuem para esse fenômeno.

Em seguida, propor as atividades a seguir ou atividades semelhantes relacionadas ao conteúdo estudado. Na atividade 4, sugere-se propor aos alunos outras perguntas relacionadas aos dados apresentados no gráfico.

Sugestões de atividades

1. Responda de acordo com o vídeo a que você assistiu.

a) O que são rios voadores?

Espera-se que os alunos respondam que os rios voadores são fluxos de vapor de água que ganham força na Floresta Amazônica e, depois de fazer o seu trajeto, chegam às regiões Centro-Oeste, Sudeste e Sul do Brasil transformando-se em chuva nesses estados

b) Por que os rios voadores são importantes para o nosso país?

Espera-se que os alunos respondam que os rios voadores são importantes porque eles formam nuvens de chuva em algumas regiões do Brasil.

c) Por que a preservação da Floresta Amazônica é importante para as chuvas no nosso país?

Espera-se que os alunos respondam que a preservação da Floresta Amazônica é importante porque os vapores de água que se formam nela se transformam em nuvens de chuva em outras regiões do Brasil.

2. Faça uma pesquisa sobre a Floresta Amazônica. Depois, registre as informações que você encontrou e compartilhe com os colegas. Resposta pessoal.

3. De acordo com o vídeo, segundo o Projeto Rios Voadores, em um dia de sol, uma árvore frondosa com uma copa de 20 metros de diâmetro consegue transferir para a atmosfera o equivalente a 1 000 litros de água.

a) Essa quantidade de água transferida por uma árvore dessa daria para encher o equivalente a quantos baldes de 20 litros?

50 baldes (1 000 ÷ 20 = 50).

b) Em 30 dias de sol, essa única árvore consegue transferir para a atmosfera o equivalente a quantos litros de água?

30 000 litros (1 000 x 30 = 30 000).

c)Quantos litros de água 10 árvores com essas características conseguem transferir, juntas, para a atmosfera?

10 000 litros (1 000 × 10 = 10 000).

d) Cada árvore, com essas características, que é cortada pela raiz corresponde a quantos litros de água a menos na atmosfera, aproximadamente?

1 000 litros.

4.Observe o gráfico a seguir.

a)Qual é o assunto desse gráfico?

O desmatamento da Amazônia Legal Brasileira, em km², de 2014 a 2021.

b)O que é a Amazônia Legal Brasileira? Faça uma pesquisa e compartilhe com os colegas as informações que você encontrou.

Espera-se que os alunos respondam que a Amazônia Legal Brasileira é a área de Floresta Amazônica pertencente ao Brasil, como o próprio nome sugere, que abrange os estados do Acre, do Amapá, do Amazonas, do Mato Grosso, do Pará, de Rondônia, de Roraima, do Tocantins e de parte do Maranhão.

c)A partir do gráfico, o que é possível observar sobre o desmatamento da Amazônia Legal?

Resposta pessoal. Sugestão de resposta: o desmatamento aumentou, principalmente a partir de 2019, em relação aos anos anteriores apresentados no gráfico.

Mate rial disponibilizado em licença aberta do tipo

Commons

Atribuiçã o n ã o comercial (CC BY NC – 4.0 International). Permitida a cria çã o de obra derivada

fins n ã o comerciais, desde que seja atribu í do cr é dito autoral e as cria çõ es sejam licenciada s

com

Fonte: INPE. Monitoramento do desmatamento da floresta amazônica brasileira por satélite Disponível em: http://www.obt.inpe.br/OBT/assuntos/programas/amazonia/prodes. Acesso em: 13 jan. 2022.

Coordenadas e Batalha naval

Este audiovisual pode ser utilizado como introdução ao estudo do plano cartesiano. A partir da apresentação do jogo Batalha naval, serão apresentados o 1º quadrante do plano cartesiano e como localizar pontos no plano utilizando coordenadas cartesianas. Selecionar previamente folhas de papel quadriculado para que os alunos, em dupla, joguem Batalha naval.

Para iniciar a aula, sugere-se apresentar o vídeo à turma. Fazer uma pausa logo após a explicação de como localizar o ponto de coordenada (3,4) no plano cartesiano. Perguntar aos alunos se eles entenderam a explicação e, caso não tenham entendido, explicar novamente.

Depois, perguntar a eles por que acham que, em uma coordenada, sempre devemos considerar o primeiro número como sendo referente ao eixo x, e, o segundo número, ao eixo y. É importante que os alunos percebam que, caso não houvesse essa regra, haveria duas possibilidades de representação do ponto no plano cartesiano: considerando o 3 no eixo x e o 4 no eixo y e vice-versa. Por isso, é importante essa ordem: o primeiro número da coordenada corresponde ao eixo x, e, o segundo, ao eixo y.

Em seguida, dar continuidade à exibição do vídeo e fazer uma pausa logo após a localização no plano cartesiano do ponto de coordenada (5,2). Pedir aos alunos que mostrem na tela a localização do ponto (2,5), e, depois, sugerir que localizem outros pontos também. Finalizar a exibição do vídeo. Após o término da exibição, sugere-se fazer perguntas sobre o que foi apresentado e verificar se os alunos compreenderam o sistema de coordenadas cartesianas, se identificam os eixos x e y corretamente e se compreenderam como localizar pontos do plano cartesiano sendo dadas as suas coordenadas. Se possível, construir um plano cartesiano na lousa para retomar essas explicações.

Verificar, também, se os alunos compreenderam o jogo Batalha naval e, caso não tenham entendido, retomar a explicação do jogo.

Em seguida, propor as atividades a seguir ou atividades semelhantes. Para a atividade 1, serão necessárias as folhas de papel quadriculado selecionadas previamente.

Sugestões de atividades

1. Na folha de papel quadriculado, desenhe o sistema de coordenadas do jogo Batalha naval conforme o modelo. Em seguida, distribua as embarcações na folha pintando o total de quadrinhos com a respectiva cor de cada embarcação.

Escolha um colega para ser o seu oponente no jogo.

• Quem venceu o jogo?

O vencedor será o aluno que conseguir "afundar" todas as embarcações.

2. No plano cartesiano, marque os pontos B, C e D cujas coordenadas são dadas a seguir.

disponibilizado

licença

Ligue os pontos em ordem alfabética, formando o contorno de um polígono e, depois, pinte a figura. Qual polígono será formado?

Um retângulo

3. Escreva a coordenada de cada ponto do plano cartesiano.

BNCC

A Base Nacional Comum Curricular (BNCC), homologada em 2018, é um documento oficial e normativo sobre as aprendizagens (e suas progressões) da Educação Básica (Ensino Infantil, Ensino Fundamental e Ensino Médio). A BNCC estrutura as etapas de aprendizagens em competências, mais abrangentes, e habilidades, mais específicas; e, dessa forma, objetiva garantir a progressão das aprendizagens entre os diferentes anos/ciclos da Educação Básica.

A BNCC tem como objetivo assegurar o direito de uma aprendizagem de qualidade a todos os alunos, buscando colaborar com a formação de uma sociedade mais justa, democrática e inclusiva. Seu caráter normativo colabora com esse objetivo ao ser um documento que orienta a elaboração e a revisão de currículos, a formação inicial e continuada de professores e as avaliações e exames nacionais.

A seguir, são apresentadas na íntegra as Competências gerais da Educação Básica, as Competências específicas da área de Matemática e suas Tecnologias para o Ensino Fundamental e as cinco unidades temáticas com os respectivos objetos de conhecimento e habilidades para o 5º ano do Ensino Fundamental, que podem ser encontrados nas páginas 9, 10, 267, 294, 295, 296 e 297da BNCC (BRASIL, 2018).

Competências gerais da Educação Básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o

consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Competências específicas de Matemática para o Ensino Fundamental

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Matemática – 5º ano

Unidades temáticas Objetos de conhecimento Habilidades

Números Sistema de numeração decimal: leitura, escrita e ordenação de números naturais (de até seis ordens)

Números racionais expressos na forma decimal e sua representação na reta numérica

Representação fracionária dos números racionais: reconhecimento, significados, leitura e representação na reta numérica

Comparação e ordenação de números racionais na representação decimal e na fracionária utilizando a noção de equivalência

Cálculo de porcentagens e representação fracionária

(EF05MA01) Ler, escrever e ordenar números naturais até a ordem das centenas de milhar com compreensão das principais características do sistema de numeração decimal.

(EF05MA02) Ler, escrever e ordenar números racionais na forma decimal com compreensão das principais características do sistema de numeração decimal, utilizando, como recursos, a composição e decomposição e a reta numérica.

(EF05MA03) Identificar e representar frações (menores e maiores que a unidade), associando-as ao resultado de uma divisão ou à ideia de parte de um todo, utilizando a reta numérica como recurso.

(EF05MA04) Identificar frações equivalentes.

(EF05MA05) Comparar e ordenar números racionais positivos (representações fracionária e decimal), relacionando-os a pontos na reta numérica.

(EF05MA06) Associar as representações 10%, 25%, 50%, 75% e 100% respectivamente à décima parte, quarta parte, metade, três quartos e um inteiro, para calcular porcentagens, utilizando estratégias pessoais, cálculo mental e calculadora, em contextos de educação financeira, entre outros.

Problemas: adição e subtração de números naturais e números racionais cuja representação decimal é finita

Problemas: multiplicação e divisão de números racionais cuja representação decimal é finita por números naturais

(EF05MA07) Resolver e elaborar problemas de adição e subtração com números naturais e com números racionais, cuja representação decimal seja finita, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.

(EF05MA08) Resolver e elaborar problemas de multiplicação e divisão com números naturais e com números racionais cuja representação decimal é finita (com multiplicador natural e divisor natural e diferente de zero), utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.

Álgebra

Problemas de contagem do tipo: “Se cada objeto de uma coleção A for combinado com todos os elementos de uma coleção B, quantos agrupamentos desse tipo podem ser formados?”

Propriedades da igualdade e noção de equivalência

(EF05MA09) Resolver e elaborar problemas simples de contagem envolvendo o princípio multiplicativo, como a determinação do número de agrupamentos possíveis ao se combinar cada elemento de uma coleção com todos os elementos de outra coleção, por meio de diagramas de árvore ou por tabelas.

(EF05MA10) Concluir, por meio de investigações, que a relação de igualdade existente entre dois membros permanece ao adicionar, subtrair, multiplicar ou dividir cada um desses membros por um mesmo número, para construir a noção de equivalência.

Grandezas diretamente proporcionais Problemas envolvendo a partição de um todo em duas partes proporcionais

(EF05MA11) Resolver e elaborar problemas cuja conversão em sentença matemática seja uma igualdade com uma operação em que um dos termos é desconhecido.

(EF05MA12) Resolver problemas que envolvam variação de proporcionalidade direta entre duas grandezas, para associar a quantidade de um produto ao valor a pagar, alterar as quantidades de ingredientes de receitas, ampliar ou reduzir escala em mapas, entre outros.

(EF05MA13) Resolver problemas envolvendo a partilha de uma quantidade em duas partes desiguais, tais como dividir uma quantidade em duas partes, de modo que uma seja o dobro da outra, com compreensão da ideia de razão entre as partes e delas com o todo.

Geometria Plano cartesiano: coordenadas cartesianas (1º quadrante) e representação de deslocamentos no plano cartesiano

(EF05MA14) Utilizar e compreender diferentes representações para a localização de objetos no plano, como mapas, células em planilhas eletrônicas e coordenadas geográficas, a fim de desenvolver as primeiras noções de coordenadas cartesianas.

(EF05MA15) Interpretar, descrever e representar a localização ou movimentação de objetos no plano cartesiano (1º quadrante), utilizando coordenadas cartesianas, indicando mudanças de direção e de sentido e giros.

Figuras geométricas espaciais: reconhecimento, representações, planificações e características

Figuras geométricas planas: características, representações e ângulos

Ampliação e redução de figuras poligonais em malhas quadriculadas: reconhecimento da congruência dos ângulos e da proporcionalidade dos lados correspondentes

Grandezas e medidas Medidas de comprimento, área, massa, tempo, temperatura e capacidade: utilização de unidades convencionais e relações entre as unidades de medida mais usuais

Áreas e perímetros de figuras poligonais: algumas relações

(EF05MA16) Associar figuras espaciais a suas planificações (prismas, pirâmides, cilindros e cones) e analisar, nomear e comparar seus atributos.

(EF05MA17) Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e desenhá-los, utilizando material de desenho ou tecnologias digitais.

(EF05MA18) Reconhecer a congruência dos ângulos e a proporcionalidade entre os lados correspondentes de figuras poligonais em situações de ampliação e de redução em malhas quadriculadas e usando tecnologias digitais.

(EF05MA19) Resolver e elaborar problemas envolvendo medidas das grandezas comprimento, área, massa, tempo, temperatura e capacidade, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais.

(EF05MA20) Concluir, por meio de investigações, que figuras de perímetros iguais podem ter áreas diferentes e que, também, figuras que têm a mesma área podem ter perímetros diferentes.

Noção de volume

(EF05MA21) Reconhecer volume como grandeza associada a sólidos geométricos e medir volumes por

meio de empilhamento de cubos, utilizando, preferencialmente, objetos concretos.

Probabilidade e estatística Espaço amostral: análise de chances de eventos aleatórios

Cálculo de probabilidade de eventos equiprováveis

Leitura, coleta, classificação interpretação e representação de dados em tabelas de dupla entrada, gráfico de colunas agrupadas, gráficos pictóricos e gráfico de linhas

(EF05MA22) Apresentar todos os possíveis resultados de um experimento aleatório, estimando se esses resultados são igualmente prováveis ou não.

(EF05MA23) Determinar a probabilidade de ocorrência de um resultado em eventos aleatórios, quando todos os resultados possíveis têm a mesma chance de ocorrer (equiprováveis).

(EF05MA24) Interpretar dados estatísticos apresentados em textos, tabelas e gráficos (colunas ou linhas), referentes a outras áreas do conhecimento ou a outros contextos, como saúde e trânsito, e produzir textos com o objetivo de sintetizar conclusões.

(EF05MA25) Realizar pesquisa envolvendo variáveis categóricas e numéricas, organizar dados coletados por meio de tabelas, gráficos de colunas, pictóricos e de linhas, com e sem uso de tecnologias digitais, e apresentar texto escrito sobre a finalidade da pesquisa e a síntese dos resultados.

Referências bibliográficas comentadas

• AMANCIO, Daniel de Traglia; SANZOVO, Daniel Trevisan. Ensino de Matemática por meio das tecnologias digitais. Revista Educação Pública, v. 20, n 47, 8 dez. 2020. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/20/47/ensino-de-matematica-pormeio-das-tecnologias-digitais Acesso em: 5 jan. 2022.

No artigo, é apresentada uma discussão sobre as contribuições da utilização das tecnologias digitais no ensino-aprendizagem de Matemática.

• BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática. 6. ed. Belo Horizonte: Autêntica, 2019. (Coleção Tendências em educação matemática).

No livro, os autores apresentam resultados de um trabalho sobre informática educativa, como questões pedagógicas sobre o uso do computador e da calculadora.

• CARAÇA, Bento de Jesus. Conceitos fundamentais da Matemática. Lisboa: Gradiva, 1991.

O livro oportuniza ao leitor entrar em contato com ideias e práticas para o desenvolvimento de aulas de Matemática.

• COLL, César; TEBEROSKY, Ana. Aprendendo Matemática. São Paulo: Ática, 2000.

No livro, são apresentados conceitos matemáticos de diversos campos, compreendendo estruturas e ideias fundamentais.

• EVES, Howard. Introdução à história da Matemática. Tradução de Hygino H. Domingues. Campinas: Editora da Unicamp, 2004.

Na obra, são apresentados tópicos importantes da história da Matemática.

• GAUTHIER, Clermont; BISSONNETTE, Steve; RICHARD, Mario. Ensino explícito e desempenho dos alunos. Tradução de Stephania Matousek. Petrópolis: Vozes, 2014.

Os autores do livro se propõem a oferecer aos leitores detalhamento da prática docente por meio das ideias do ensino explícito.

• IFRAH, Georges. História universal dos algarismos: a inteligência dos homens contada pelos números e pelo cálculo. Tradução de Alberto Muñoz e Ana Beatriz Katinsky. Rio de Janeiro: Nova Fronteira, 1997. v. 1

O livro tem enfoque no desenvolvimento de sistemas de numeração ao longo do tempo, em particular o Sistema de Numeração Decimal.

• LOPES, Maria Laura M. Leite. Tratamento da informação: explorando dados estatísticos e noções de probabilidade a partir de séries iniciais. Rio de Janeiro: Instituto de Matemática/UFRJ-Projeto Fundão, 2005.

No livro, a autora propõe apoiar o professor no ensino de conceitos relacionados à estatística e à probabilidade nos Anos Iniciais do Ensino Fundamental.

• LUCKESI, Cipriano C. Avaliação da aprendizagem escolar: estudos e proposições. 22. ed. São Paulo: Cortez, 2011.

No livro, são apresentados estudos críticos sobre avaliação escolar, possibilitando ao educador refletir sobre sua prática avaliativa.

• MACHADO, Nílson José. Matemática e língua materna: análise de uma impregnação mútua. 5. ed. São Paulo: Cortez, 2001.

O autor apresenta uma reflexão sobre a relação entre o alfabeto e o Sistema de Numeração Decimal, com o objetivo de contribuir com o ensino da Matemática.

• MORAN, José Manuel; MASETTO, Marcos Tarciso; BEHRENS, Marilda Aparecida. Novas tecnologias e mediação pedagógica. 21. ed. Campinas: Papirus, 2013. (Coleção Papirus Educação).

No livro, é abordada uma reflexão sobre a inserção da informática e da telemática na educação.

• NEVES, Iara Conceição Bitencourt etal Ler e escrever: compromisso de todas as áreas. 9.ed. Porto Alegre: Editora da UFRGS, 2011.

No livro, são discutidas questões relacionadas à leitura e à escrita nos textos dos diferentes componentes curriculares, inclusive na Matemática.

• POLYA, George. A arte de resolver problemas: um novo aspecto do método matemático. Tradução de Heitor Lisboa de Araújo. Rio de Janeiro: Interciência, 1995.

O autor apresenta reflexões sobre a resolução de problemas e propostas didáticas práticas para o trabalho com problemas em sala de aula.

• SANT'ANA, Claudinei de Camargo; AMARAL, Rúbia Barcelos; BORBA, Marcelo de Carvalho O uso desoftwaresna prática profissional do professor de Matemática

Revista Ciência & Educação, Bauru, v 18, n 3, p. 527-542, 2012. Disponível em: https://doi.org/10.1590/S1516-73132012000300003 Acesso em: 10 dez. 2021.

Os autores apresentam uma discussão sobre a incorporação de softwaresna prática docente.

• TOLEDO, Marília; TOLEDO, Mauro. Teoria e prática de Matemática: como dois e dois. São Paulo: FTD, 2010.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Os autores apresentam informações relevantes sobre o processo de ensino-aprendizagem da Matemática, como reflexões com base em práticas de sala de aula.

Documentos oficiais

• BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília: SEB, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pd f. Acesso em: 5 jan. 2022.

Documento de caráter normativo que define o conjunto de aprendizagens essenciais que os alunos devem desenvolver ao longo das etapas e modalidades da educação básica, de modo que tenham assegurados seus direitos de aprendizagem e desenvolvimento.

• BRASIL. Ministério da Educação. PNA: Política Nacional de Alfabetização. Brasília: Sealf, 2019. Disponível em: http://alfabetizacao.mec.gov.br/images/pdf/caderdo_final_pna.pdf Acesso em: 5 jan. 2022

O documento instituído pelo Ministério da Educação, por meio da Secretaria de Alfabetização (Sealf), apresenta políticas que visam melhorar os processos de alfabetização e combater o analfabetismo no Brasil.

• BRASIL. Ministério da Educação. Relatório Nacional de Alfabetização Baseada em Evidências (Renabe) Brasília: Sealf, 2020. Disponível em: http://alfabetizacao.mec.gov.br/images/pdf/renabe_web.pdf Acesso em: 5 jan. 2022.

Relatório que apresenta pesquisas recentes sobre alfabetização, literacia e numeracia e cujo objetivo é contribuir para a melhoria nas políticas públicas e nas práticas de ensino no Brasil.

Leituras complementares para o professor

• FERREIRA, Mariana K. Leal. Ideias matemáticas de povos culturalmente distintos. São Paulo: Global, 2002. (Série antropologia e educação).

No livro, são reunidos relatos de atividades matemáticas aplicadas em diversos países, possibilitando ao leitor refletir sobre sua prática docente.

• LINDQUIST, Mary Montgomery; SHULTE, Albert P. (org.). Aprendendo e ensinando Geometria. Tradução de Hygino H. Domingues. São Paulo: Atual, 1994.

A obra contém artigos relevantes sobre o ensino-aprendizagem da Geometria em diferentes faixas etárias.

• MONTEIRO, Alexandrina; POMPEU JUNIOR, Geraldo. A Matemática e os temas transversais. São Paulo: Moderna, 2001.

Os autores propõem reflexões sobre os temas transversais, com especial atenção às aulas de Matemática.

• SOUZA, Eliane R. de etal . A Matemática das sete peças do tangram. 2. ed. São Paulo: Caem/IME-USP, 1997.

No livro, há textos e atividades para serem desenvolvidas com o tangram nas aulas de Matemática.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos