saperi

Didattica laboratoriale Logica
Problematicamente
Ra-giocando Storie matematiche
ELi Oltre l’insegnamento Educ Ability
Alfia Lucia Fazzino • Paola Hippoliti
5 Matematica con QUADERNO OPERATIVO Il piacere di apprendere
Gruppo Editoriale
2
3
4 I NUMERI ROMANI
5 Le regole per scrivere i numeri romani
6 NUMERI GRANDI: MILIONI E MILIARDI
7 Esercizi
8 I NUMERI DECIMALI
9 Approssimare i numeri decimali
10 I NUMERI RELATIVI
11 Confrontare i numeri relativi
12 DEBITI E CREDITI
LE QUATTRO OPERAZIONI
14 OPERAZIONI E PROPRIETÀ
18 RELAZIONE TRA LE OPERAZIONI
18 Addizione e sottrazione
19 Moltiplicazione e divisione
20 I NUMERI 0 E 1 NELLE QUATTRO OPERAZIONI
21 MOLTIPLICARE E DIVIDERE I DECIMALI PER 10, 100, 1 000
22 Esercizi
24 LE POTENZE
25 Le potenze del 10
26 LE ESPRESSIONI
27 Le espressioni con le parentesi
28 MULTIPLI E DIVISORI
29 I numeri primi
Il crivello di Eratostene
30 Scomposizione in fattori primi
31 I criteri di divisibilità
32 Esercizi
34 LA CALCOLATRICE: USO RAGIONATO
35 Le proprietà della calcolatrice
36 PROBLEMATICAMENTE
37 Esercizi
38 ARITMETICA DELL’OROLOGIO
Storie matematiche
40 Un triangolo speciale
LE FRAZIONI
44 LA FRAZIONE
45 Esercizi
46 Frazioni minori, uguali e maggiori di 1
48 Frazioni a confronto
49 Frazioni equivalenti
50 Dall’intero alla frazione
54
56
96 Area del rettangolo e del quadrato
97 Area del triangolo e del parallelogramma
98 Area del rombo
99 Area del trapezio
100 Esercizi
Storie matematiche
102 Pitagora: mito e leggenda
106 I POLIGONI REGOLARI
108 L’area dei poligoni regolari
109 L’apotema dei poligoni regolari
Storie matematiche
110 La leggenda di Didone
114 LA CIRCONFERENZA E IL CERCHIO
115 Esercizi
116 La circonferenza
117 Area del cerchio
118 FESTA DELLA MATEMATICA
120 PROBLEMATICAMENTE
122 Esercizi
I SOLIDI
124 RICONOSCERE I SOLIDI
125 Classificare i poliedri
127 La superficie di un solido
128 Esercizi
130 IL VOLUME DEI SOLIDI Volume del parallelepipedo Volume del cubo
131 Esercizi
132 LE MISURE DI VOLUME
RELAZIONI, DATI E PREVISIONI
134 L’INDAGINE STATISTICA
136 LA MODA
137 LA MEDIA
138 IL PIANO CARTESIANO
139 Esercizi
140 LA PROBABILITÀ
143 PROBABILITÀ E PERCENTUALI
144 COMPITO DI REALTÀ Un piccolo spazio verde
147 TAPPA COMPETENZE Verso l’Invalsi
154 PROVE INVALSI
157 QUADERNO OPERATIVO
Dalla frazione all’intero
La frazione: un legame fra due o più cose
51
52
Esercizi
Frazioni decimali e numeri decimali
La frazione come percentuale 60 Percentuali e grafici
La percentuale nel commercio 62 PROBLEMATICAMENTE 63 Esercizi 64 PROBLEMI DEL “MUCCHIO” LA MISURA 66 MISURARE: CHE COSA SIGNIFICA? 67 Unità di misura, multipli e sottomultipli 68 Esercizi 70 Esprimere in maniera diversa la misura 71 Trasformare nel nostro Sistema di Misura 72 LE MISURE DI TEMPO 74 L’EURO 75 Sistemi monetari europei 76 Esercizi 78 PROBLEMATICAMENTE 79 Esercizi 80 GIORNATA MONDIALE DELLE API LE ISOMETRIE 82 LA SIMMETRIA 83 LA TRASLAZIONE 84 LA ROTAZIONE 85 Esercizi 86 INGRANDIMENTI E RIDUZIONI SPAZIO E FIGURE 88 I POLIGONI 89 Poligoni speciali 90 I TRIANGOLI: RIPASSIAMO INSIEME 91 Classifichiamo i triangoli rispetto ai lati Classifichiamo i triangoli rispetto agli angoli 92 I QUADRILATERI: RIPASSIAMO INSIEME 93 Classifichiamo i quadrilateri 94 LA SUPERFICIE 95 Esercizi
NUMERI
58
61
I
NUMERI
I
NATURALI
DI
IL NOSTRO SISTEMA
NUMERAZIONE
I NUMERI
I NUMERI NATURALI
• Osserva e rispondi.
• Quanti pesci ci sono nella boccia? I pesci sono
• Che cosa hai fatto per sapere quanti sono i pesci?
I numeri che usi per contare sono i numeri naturali Si chiamano così perché sono dei segni che gli esseri umani hanno inventato per contare e ordinare gli oggetti intorno a loro.
• Aiuta Sofia a rispondere, sfidando un compagno o una compagna a questo gioco.
Copri le Fig. 2 e 3; mostragli/le la Fig. 1, conta fino a due e poi coprila.
• È stato/a in grado di dirti che numero è? Sì No
Se ha risposto correttamente, mostragli/le la Fig. 2, conta di nuovo fino a 2 e poi coprila.
• È stato/a in grado di dirti che numero è? Sì No
Prova nello stesso modo con la Fig. 3.
• È stato/a in grado di dirti che numero è? Sì No
• Se hai risposto no, secondo te perché non ci è riuscito/a?

È sempre necessario contare?
HO CAPITO CHE...
Le persone riconoscono a colpo d’occhio solo piccole quantità di oggetti. Per riconoscere quantità maggiori devono contare. A ciascuna quantità è associato un simbolo e per scrivere i numeri ci sono delle regole. L’insieme dei simboli e delle regole usati per scrivere i numeri forma il sistema di numerazione.
Fig. 1
Fig. 2
Fig. 3
2
IL NOSTRO SISTEMA DI NUMERAZIONE
Cecilia e Giorgio giocano a “Combina il numero” usando due dadi e una matita colorata per ciascuno.
Chi tira i dadi colora le caselle che contengono i numeri formati dalle due cifre visibili sulle facce superiore.
Vince chi colora per primo/a l’ultima casella.
• Osserva la tabella di gioco e rispondi.
• Perché il primo numero è e l’ultimo è ?
• Completa il tabellone di gioco scrivendo i numeri che mancano. Spiega la regola usata.
Giorgio ha tirato i dadi, ha formato un numero e ha colorato la casella 13.
• Quali cifre saranno comparse sui dadi di Giorgio?
• Quale altro numero può formare con quelle cifre?
• Quindi colora anche la casella
• Che cosa hanno in comune questi due numeri?
• I due numeri hanno lo stesso valore? Sì No
• Confronta i due numeri poi completa la tabella.
13
Precedente Numero Successivo 13
Il nostro sistema di numerazione è decimale e posizionale È decimale, perché contiamo in base 10, cioè usiamo dieci cifre: 0, 1, 2, , , , , , , e raggruppiamo le quantità per 10 (10 u = 1 da; 10 da = 1 h ecc.)
È posizionale, perché il valore di ogni cifra dipende dalla posizione che occupa all’interno del numero.
È anche ordinato, perché ogni numero è maggiore del suo precedente e minore del suo successivo.
51 61 66 31 26 25 24 23 22 21 16 15 14 13 12 11 VIA STOP
41
I numeri 3
I NUMERI ROMANI
Passeggiando per la tua città o per il tuo paese avrai avuto modo di osservare orologi, iscrizioni o nomi di vie che contengono i segni che vedi nelle immagini: sono i numeri che usavano gli antichi Romani.


• Osserva i simboli che gli antichi Romani usavano per scrivere i numeri.

• Quanti simboli sono?
• Esiste un simbolo per indicare il numero 0? Sì No
I Romani non avevano inventato lo zero. Infatti, siccome lo zero equivaleva al niente, ritenevano che non fosse necessario usare un simbolo per indicarlo.
Il trattino sopra a una lettera indica che il valore di quel segno va moltiplicato per
Il numero si forma sommando il valore di ciascun simbolo
PROVO IO


1. Scrivi il valore di ciascun simbolo, poi scrivi in cifre il numero ottenuto.
I V X L C D M 1 5 10 50 100 500 1000
V X L C D 5000 10000 50000 100000 500000
+ + +
+ + + + =
= + + + +
MDXX = + + + =
VIII = 5
= XVIII = 10
CLXII
=
I numeri 4
LE REGOLE PER SCRIVERE I NUMERI ROMANI
• Osserva e completa.
I II III
1 1 + 1 1 + 1 + 1
1 2 3
III XXX CCC 3 30 300
V L D
5 50 500
VI XI LX CX
Se lo stesso simbolo viene ripetuto due o tre volte in successione il suo valore si ...........................................................................
I simboli I, X, C, M possono essere scritti di seguito, al massimo 3 volte.
I simboli V, L, D possono essere scritti una sola volta.
5 + 1 10 + 1 50 + 10 100 + 10
6 11 60 110
IV IX XL XC
5 – 1 10 – 1 50 – 10 100 – 10
4 9 40 90
XIX 10 + (10 – 1) 19
PROVO IO

Se un simbolo è seguito da un altro di valore minore, allora si il valore dei due simboli.
Se un simbolo è preceduto da uno di valore minore, allora si il valore del simbolo minore.
Quando un simbolo è fra due simboli di valore maggiore, si sottrae il suo valore al simbolo che si trova alla sua destra.
VIII = IX = XIV = XXXII = LXVI = DCCIX =
MMCCCXX =
MDCCCXXXV =
XMDC =
10 = 55 = 36 = 124 = 218 =
532 = 450 = 249 = 1571 =
1. Scrivi i numeri romani nel nostro sistema di numerazione.
2. Scrivi in numeri romani.
I numeri 5 Quaderno pp. 158-159
NUMERI GRANDI: MILIONI E MILIARDI
Il Sole è la stella più vicina alla Terra ed è quella che fornisce la luce e il calore necessari alla vita.
La Terra dista dal Sole 149597870 km… ma come si legge un numero così grande?
Sai già che per scrivere i numeri grandi si separano le cifre in gruppi di tre, cominciando da destra.
Ogni gruppo di tre cifre forma una classe e ogni classe è suddivisa in 3 ordini: unità (u), decine (da), centinaia (h).
Ogni classe viene separata dalle altre da uno spazio vuoto o da un punto.

• Completa la tabella scrivendo il numero che indica la distanza della Terra dal Sole.
Classe dei miliardi
Classe dei milioni
Classe delle migliaia
Classe delle unità semplici
Leggi il numero scritto in ogni classe seguito dal nome della classe. Ricorda che la lettura di un numero si esegue andando sempre da sinistra verso destra!
54305213
cinquantaquattroMILIONI trecentocinqueMILA duecentotredici
Se le cifre di una classe sono tutti 0, allora non la leggi.
135000214
centotrentacinqueMILIONI duecentoquattordici
hG daG uG hM daM uM hk dak uk h da u 100 miliardi 10 miliardi 1 miliardo 100 milioni 10 milioni 1 milione 100 mila 10 mila 1 mille 100 unità 10 unità 1 unità 8 7 0 ottocentosettanta
I numeri 6 Quaderno pp. 160-161
1 Disegna sul quaderno la tabella e inserisci i numeri, come nell’esempio.
Ricorda di andare da destra a sinistra, che ciascuna classe è formata da tre ordini (u, da, h) e che ogni tre cifre devi lasciare uno spazio vuoto.
52678913 • 2583614 • 98504170 • 21084301225 • 6320091454 • 301584000963
2 Scomponi ciascun numero dividendolo in classi, come nell’esempio.
684126545116 = 684 G, 126 M, 545 k, 116 u
74214607 = 140526980741 =
302694012 = 56317985 = 630458120006 = 129003654 =
3 Separa ciascuna classe con un trattino, poi scrivi in cifre i numeri, come nell’esempio.
Duemilionisettecentotrentaquattromiladuecentoventi 2734220
Trentacinquemilionitrecentoquarantatremilacinquecentosedici
Tremiliardiquattrocentomilioniseicentosettantacinquemilacentoottantasei
Ventiquattromiliardicentotremilioniottocentosettemilacinquecentotrentanove
4 Riscrivi i numeri lasciando uno spazio vuoto per individuare ciascun ordine. Poi scrivili in lettere.
132658140 =
4389147600 =
500652315 =
5 Scrivi in cifre i seguenti numeri.
Scrittura corretta
Numero hG daG uG hM daM uM hk dak uk h da u
5 2 6 7 8 9 1 3 52678913
52678913
1 da + 9 uk + 4 h = 2000 + 30000 + 50 + 700000 = 5 h + 3 dak + 2 uM + 9 u = 800 + 5 + 70 + 60000 + 4000 = 3 uk + 3 hk = .................................... 9000000 + 700000 + 80000 = .............................................................................. 7 ESERCIZI
I NUMERI DECIMALI
: 1 2 3
1 2 3
• Completa la tabella eseguendo solo le divisioni che hanno resto 0. Lascia vuote le caselle che non completi.
• Scrivi le divisioni che avresti dovuto fare nelle caselle vuote.
1 : 2 • • •
Osserva l’operazione 3 : 2 sulla linea dei numeri:
Puoi eseguire queste divisioni usando i numeri decimali. In linguaggio matematico 3 : 2 = 1,5 infatti 1,5 x 2 = 3
0 1 2 3
Conosci già i numeri decimali perché li hai incontrati quando hai usato le unità di misura e li trovi scritti sulle etichette di molti prodotti al supermercato.

2,50 m

€ 0,95

1,3 kg
I numeri 2,50 • 0,95 • 1,3 sono numeri decimali.
• Inserisci nella tabella i numeri dei prodotti che vedi sopra.
Parte intera Parte decimale h da u d c m Si legge
2 , 5 0
2 unità e 50 centesimi

In ogni numero decimale la virgola separa la parte delle unità intere dalla parte decimale.
HO I numeri 8 Quaderno pp. 162-163
La divisione può generare i numeri decimali 24 : 5 = 4,8 CAPITO CHE...
APPROSSIMARE I NUMERI DECIMALI
I nonni hanno regalato a Pietro € 60 per comprare lo zaino e l’astuccio per il nuovo anno scolastico.
Al supermercato Pietro vede queste offerte:

€ € 25,50 €31,87 2
Di quale offerta potrà approfittare Pietro con i soldi che possiede?
Pietro calcola a mente quanto spenderà nei due casi.
Per semplificare il calcolo approssima i numeri, cioè li sostituisce con numeri vicini meno precisi, ma più facili da calcolare.
Per fare questo segue le stesse regole usate per approssimare un numero intero:
• sceglie a quale cifra approssimare;
• osserva la cifra a destra: se è 0, 1, 2, 3, 4 approssima per difetto; se è 5, 6, 7, 8, 9 approssima per eccesso
• Aiuta Pietro a eseguire questa approssimazione. Completa.
Numero approssimato € 38
• Calcola in modo approssimato quanto spende se:
• compra la prima offerta: 38 + =
• compra la seconda offerta: + =
I numeri 9 Quaderno pp. 164-165

Costo oggetto Approssimazione Zaino € 38,35 Astuccio € 23,74 Zaino € 31,87 Astuccio € 25,50 Approssima alle unità di euro € 38, 35 38 approssimato per difetto € 23,74 approssimato per eccesso ....................................................... .......................................................
• Che cosa potrà comprare Pietro con i soldi che ha a disposizione? 38,35 € 23,74 1
• Completa la tabella della sottrazione. Poi rispondi.
• Hai completato tutta la tabella? Sì No
• Quali sottrazioni avresti dovuto fare nelle caselle vuote?
1 – 2 • •
Per eseguire queste sottrazioni servono altri numeri.
• Leggi, osserva e completa.
Disegna una linea dei numeri su un foglio, poi piegalo in modo che la piega passi sullo 0 e ricalca con il verde la linea sull’altra parte del foglio; quindi riaprilo.
Hai ottenuto due linee uguali e simmetriche che hanno verso opposto, così come questa:
Scrivi i numeri che mancano sulla linea simmetrica a quella disegnata.
Ora colora il numero 3: sai quale casella colorare? Sì No
Perché?
La risposta non è unica, perché ci sono due caselle che indicano lo stesso numero e che si trovano alla stessa distanza da 0.
Per risolvere questa ambiguità i matematici e le matematiche hanno indicato con il segno + i numeri a destra dello 0 e li hanno chiamati numeri positivi. Questi numeri, in realtà, già li conosci perché sono i numeri naturali.
Hanno invece indicato con il segno – i numeri che si trovano a sinistra dello 0 e li hanno chiamati numeri negativi
Adesso completa la linea dei numeri aggiungendo i segni. Quale numero è rimasto senza segno?
I numeri relativi sono i numeri preceduti dal segno + o dal segno – e si chiamano “relativi” perché il loro valore dipende dal segno che hanno davanti.
Lo zero è senza segno perché è l’origine della linea dei numeri, sia di quelli positivi sia di quelli negativi.

I NUMERI RELATIVI
2 1 0 1 2 3 4 5 6 – 1 2 3 1 0 2 1 3 2
I numeri 10
HO CAPITO CHE...
CONFRONTARE I NUMERI RELATIVI
I seguenti termometri riportano le temperature minime e massime registrate in alcune città italiane.
• Colora di rosso le temperature massime e di blu quelle minime.
Bolzano L’Aquila Bologna Pisa
max +4 min –4 max +3 min –5 max +5 min –3 max +6 min –1
• Scrivi i nomi delle città in ciascun riquadro.
ll numero negativo più vicino allo 0
è maggiore di un numero negativo più lontano dallo 0
Puoi dire che i numeri negativi sono in ordine:
crescente decrescente
ll numero positivo più vicino allo 0
è minore di un numero positivo più lontano dallo 0
Puoi dire che i numeri positivi sono in ordine:
crescente decrescente
HO CAPITO
I numeri positivi sono a destra dello zero e sono in ordine crescente. + 8 > + 5
I numeri negativi sono a sinistra dello zero e sono in ordine decrescente. – 3 > – 7
CHE...
–6 –5 –4 –3 –2 –1 +1 +2 +3 +4 +5 +6 0
°C -20 -10 0 10 20 30 40 °C -20 -10 0 10 20 30 40 °C -20 -10 0 10 20 30 40 °C -20 -10 0 10 20 30 40 °C -20 -10 0 10 20 30 40 °C -20 -10 0 10 20 30 40 °C -20 -10 0 10 20 30 40 °C -20 -10 0 10 20 30 40
I numeri 11 Quaderno pp. 166-167
DEBITI E CREDITI
Martina è in gita scolastica e per ricordo vuole comprare per sé un cappellino che costa € 7 e per suo fratello una tazza che costa € 8. Guarda nel portafoglio e vede che ci sono € 10.
Le basteranno?
Aiutati con linea dei numeri per capire quanto spende. Martina compra prima la tazza:

• Scrivi l’operazione eseguita.
10 – 8 =
A Martina restano Le bastano per comprare anche la tazza?
Che cosa suggeriresti di fare a Martina per risolvere il suo problema?

Una sua compagna gentile decide di aiutarla.
Martina, non ti preoccupare.
Te li presto io e quindi ti faccio credito
Aiuta Martina a calcolare quanto le manca usando la linea dei numeri.
Martina ha € 2, quindi sulla linea posizionati a +2. Sottrai i 7 euro del cappellino spostandoti di 7 passi verso sinistra.
• Scrivi l’operazione eseguita.
+2 =
Quindi a Martina mancano €
Questa è una sottrazione particolare perché il minuendo è minore del sottraendo.
Hai potuto comunque eseguirla? Sì No
–10 –9 –8 –7 –6 –5 –4 –3 –2 –1 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 0
–10 –9 –8 –7 –6 –5 –4 –3 –2 –1 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 0
I numeri 12
L’amica presta a Martina i 5 euro che le mancano.


Grazie, sono in debito con te di 5 euro.
1. Completa le piramidi usando anche i numeri negativi, poi scrivi l’operazione che hai eseguito.
Operazione: ............................................................
2. Completa i quadrati magici.
Operazione: ............................................................
Operazione: ............................................................
Inserisci i numeri che mancano sapendo che la somma dei numeri posti in ciascuna riga, colonna o diagonale è sempre lo stesso numero. Non puoi scrivere due volte lo stesso numero.
+4 –3 +5 –2 –10 +3
0 –5 –3 –1 +1 0 –1 +1 –2 –2 +3 0 +2 +6
I numeri 13
PROVO IO
LE QUATTRO OPERAZIONI
OPERAZIONI E PROPRIETÀ
RIPASSIAMO INSIEME
ADDIZIONE
I termini
h da u,
5 0 6 +
1 8 2 =
Addendi
Totale o somma
Con i numeri decimali: esegui l’addizione con la stessa procedura che usi per i numeri interi, facendo attenzione a incolonnare i numeri rispettando il valore posizionale delle cifre
MOLTIPLICAZIONE
I termini
2
1 3 2 x
2 5 = 6
0
0 =
3 3 0 0
Fattori Prodotto

Aiutati con le proprietà delle operazioni!
506 + 182
è difficile da eseguire!
Con i numeri decimali: esegui la moltiplicazione con la stessa procedura che segui con i numeri interi. Poi individua quante sono le cifre decimali dei fattori che hai moltiplicato, conta lo stesso numero di cifre decimali nel prodotto finale partendo da destra e metti la virgola.
Per l’addizione e la moltiplicazione valgono le seguenti proprietà:
Associativa: i numeri si possono associare come ci sembra meglio
Addizione: 3 + 6 + 7 = (3 + 7) + 6 = 10 + 6
Moltiplicazione: 2 x 4 x 6 = (2 x 4) x 6 = 8 x 6
Commutativa: si può cambiare l’ordine dei numeri
Addizione: 5 + 7 = 7 + 5
Moltiplicazione: 6 x 8 = 8 x 6
rifare disegni
1 3, 2 x 4, 6 = 7 9 2 + 5 2 8 0 = 6 0, 7 2
6
4
6
14
Solo per la moltiplicazione vale anche la proprietà distributiva
Esegui 8 x 27 applicando la proprietà distributiva:
8 x 27 = 8 x (20 + 7) = scomponi uno dei fattori in una somma (8 x 20) + (8 x 7) = moltiplica l’altro fattore per i singoli addendi 160 + 56 = 216 somma i prodotti parziali
La proprietà vale anche se uno dei fattori lo scomponi in una differenza:
8 x 27 = 8 x (30 – 3) = scomponi uno dei fattori in una differenza (8 x 30) – (8 x 3) = moltiplica l’altro fattore per il minuendo e il sottraendo 240 – 24 = 216 sottrai i prodotti parziali
PROVO IO

1. Scomponi utilizzando le proprietà commutativa e associativa, come nell’esempio.
53 + 18 = 50 + 3 + 10 + 8 = (50 + 10) + (3 + 8) = 60 + 11 = 71
125 + 44 = 100 + + + 40 + = (100 + ) + 20 + (5 + ) =
356 + 70 = + 50 + + 70 = + 120 + =
234 + 158 = + 30 + 4 + 100 + + = + 100 + + 30 + + 4 = = + + =
2. Scomponi e arrotonda al multiplo di 10 più vicino, come nell’esempio.
64 + 73 = 64 + 70 + 3 = (64 + 70) + 3 = 134 + 3 = 137
32 + 19 = 32 + 20 – 1 = 52 – 1 = 51
125 + 190 = 125 + 200 – = – 10 =
142 + 180 =
3. Scomponi uno dei fattori e utilizza la proprietà distributiva, come nell’esempio.
43 x 4 = (40 + 3) x 4 = 40 x 4 + 3 x 4 = 160 + 12 = 172
96 x 3 = (90 + ) x 3 = 90 x + x 3 = + =
5 x 158 = 5 x (100 + 50 + ) = 207 x 11 = ( + ) x =
4. Scomponi uno dei fattori, poi associali per eseguire moltiplicazioni più semplici, come nell’esempio.
20 x 18 = 20 x 3 x 3 x 2 = 60 x 3 x 2 = 180 x 2 = 360
25 x 6 = 25 x 2 x 3 =
35 x 21 =
Le quattro operazioni 15
SOTTRAZIONE
I termini
Con i numeri decimali: esegui la sottrazione con la stessa procedura che usi per i numeri interi, facendo attenzione a incolonnare i numeri rispettando il valore posizionale delle cifre
DIVISIONE
I termini
Con i numeri decimali: esegui la divisione con la stessa procedura che usi con i numeri interi. Dividi la parte intera del numero e quando inizi a dividere la parte decimale metti la virgola anche al quoziente.
Per la sottrazione e la divisione vale la proprietà invariantiva
h da u, d c m 6 9 3, 5 8 2 –3 2, 5 6 = ,
8,64 : 4 = 8, 6 4 4 8 2, 1 6 0 6 4 2 4 2 4 0
sottraendo. 18 – 13 = 5 18 – 13 = 5 (18 + 2) – (13 + 2) (18 – 3) – (13 – 3) 20 – 15 = 5 15 – 10 = 5 Nella divisione: moltiplica o dividi per lo stesso numero il dividendo e il divisore 150 : 50 = 3 150 : 50 = 3 (150 : 10) : (50 : 10) (150 x 2) : (50 x 2)
: 5 = 3 300 : 100 = 3 uk h da u 2 8 7 9 –1 5 7 2 = Sottraendo 1 3 0 7 Resto o ............................................. 8 6 4 : 4 = dividendo divisore quoziente Le quattro operazioni 16
Nella sottrazione: aggiungi o togli lo stesso numero al minuendo e al
15
Solo per la divisione vale anche la proprietà distributiva
Esegui 200 : 5 applicando la proprietà distributiva:
200 : 5 = (150 + 50) : 5 = scomponi il dividendo in una somma (150 : 5) + (50 : 5) = dividi poi i singoli addendi per il divisore 30 + 10 = 40 somma i quozienti parziali
La proprietà vale anche se scomponi il dividendo in una differenza:
200 : 5 = (250 – 50) : 5 = scomponi il dividendo in una sottrazione (250 : 5) – (50 : 5) = dividi minuendo e sottraendo per il divisore 50 – 10 = 40 sottrai i quozienti parziali
Ricorda
I numeri in cui scomponi il dividendo devono essere multipli del divisore.
PROVO IO

1. Scomponi i numeri per ottenere sottrazioni più semplici, come nell’esempio.
38 – 16 = (38 – 10) – 6 = 28 – 6 = 22
45 – 18 = (45 – 15) – = – 3 =
124 – 38 = [(124 – 20) – 10) – 4] – 4 =
232 – 121 =
422 – 208 =
2. Scomponi il divisore per ottenere divisioni più semplici, come nell’esempio.
84 : 12 = (84 : 4) : 3 = 21 : 3 = 7
96 : 6 = (96 : 3) : = : 2 =
105 : 15 =
273 : 21 =
432 : 12 =
3. Scomponi il dividendo e applica la proprietà distributiva.
96 : 8 = (80 + 16) : 8 =
102 : 3 =
116 : 4 = 115 : 5 =
432 : 8 =
324 : 12 =

.........................................................................................................................................................................................................
Le quattro operazioni 17 Quaderno pp. 168-171
Le quattro operazioni
RELAZIONE TRA LE OPERAZIONI
ADDIZIONE E SOTTRAZIONE
Maddalena e Filippo giocano con due dadi. Vince chi ottiene il numero più alto sommando i numeri che escono. Maddalena lancia i dadi e ottiene questo:


Descrivi la situazione in linguaggio matematico.
5 5 =
Filippo per vincere deve fare 11. Lancia il primo dado e compare 5. Quale numero deve uscire nel secondo dado?

Descrivi la situazione in linguaggio matematico.
+ = 11 oppure + = 11
Per scoprire il valore del secondo dado puoi usare l’operazione inversa dell’addizione, cioè la sottrazione.
11 – 5 = , infatti + 5 = 11
Puoi usare questa proprietà per il calcolo veloce.
• Completa le piramidi.
Puoi rappresentare così:
Ricorda la regola: il numero che sta nel mattone in alto è la somma dei numeri che stanno nei mattoni in basso.
HO CAPITO CHE...
La sottrazione è l’operazione inversa dell’addizione
– 5 + 5
11
19 26 12 32 15 24 41 37 66 42 18 25 50 35
18 Quaderno pp. 172-173
MOLTIPLICAZIONE E DIVISIONE
Maddalena e Filippo cambiano il gioco. Questa volta vince chi ottiene il numero 20 moltiplicando i numeri che escono.
Inizia Filippo: lancia i dadi e ottiene questo:

Descrivi la situazione in linguaggio matematico.
3 6 = oppure 6 3 =
Maddalena lancia il primo dado ed esce ..................... . Per vincere, quale dovrà essere il numero sull’altro dado?

Descrivi la situazione in linguaggio matematico.
................. x = 20 oppure x ................. = 20
Per scoprire il valore del secondo dado puoi usare l’operazione inversa della moltiplicazione, cioè la divisione: 20 : 4 = , infatti x 4 = 20
Puoi rappresentare così: 20 : 4 ..........
Puoi usare questa proprietà per il calcolo veloce.
• Completa le piramidi.
Ricorda la regola: il numero che sta nel mattone in alto è il prodotto dei numeri che stanno nei mattoni in basso.
HO
La divisione è l’operazione inversa della moltiplicazione
CAPITO CHE...
20 3 5 120 6 2 8 12 84 4 24 3 63 7
Le quattro operazioni 19 Quaderno pp. 172-173
Le quattro operazioni
I NUMERI 0 E 1 NELLE QUATTRO OPERAZIONI
IL NUMERO 0
• Completa.
ADDIZIONE E SOTTRAZIONE
8 + 0 = 8 – 0 =
MOLTIPLICAZIONE E DIVISIONE
4 x 0 vuol dire 0 + 0 + 0 + 0 quindi 4 x 0 =
Nella divisione puoi dire che 6 : 2 = 3 perché vedi che 3 x 2 = 6
Prova a verificare con lo 0.
5 : 0 = 0 verifica: 0 x 0 può formare 5? Sì No
5 : 0 = 5 verifica: 5 x 0 può formare 5? Sì No
IL NUMERO 1
• Completa.
ADDIZIONE
Se aggiungo o tolgo 0 a un numero, il risultato è il numero iniziale.
Nella moltiplicazione, lo 0 annulla tutto il prodotto.
Non puoi dividere un numero per 0
0 + 1 + 1 + 1 + 1 + 1
Se a un numero aggiungi 1, ottieni il numero successivo. Non esiste un ultimo numero perché puoi sempre aggiungere 1, per questo motivo i numeri sono
SOTTRAZIONE
Se a un numero togli 1, ottieni il numero ; se continui a togliere 1, si arriva al numero
MOLTIPLICAZIONE E DIVISIONE
9 x 1 = 9 : 1 =
L’1 non modifica il numero che moltiplica o che divide.
– 1 – 1 – 1 – 1 – 1 5
20 Quaderno p. 174
MOLTIPLICARE E DIVIDERE I DECIMALI PER
10, 100, 1 000
Per moltiplicare o dividere un numero decimale per 10, 100 o 1000 devi seguire lo stesso ragionamento usato con i numeri interi.
• Osserva le tabelle e completa le uguaglianze. MOLTIPLICARE
1,235 x 10 = 1467 : 10 =
1,235 x 100 = 1467 : 100 =
1,235 x 1000 = 1467 : 1000 =
, ,
Un numero moltiplicato per 10, 100, 1000 aumenta il suo valore di 10, 100, 1000 volte. La virgola separa le unità intere dalla parte delle unità decimali.
PROVO IO

1. Esegui le operazioni.
h da u d c m 2 3, 1 8 x 10 h da u d c m 6, 8 9 x 100 h da u d c m 4 7, 1 2 : 10 h da u d c m 1 9 2, 5 : 100 , , , ,
DIVIDERE
uk h da u d c m 1, 2 3 5 x 10 1 2, 3 5 x 100 1 2 3, 5 x 1000 1 2 3 5 uk h da u d c m 1 4 6 7 : 10 1 4 6, 7 : 100 1 4, 6 7 : 1000 1, 4 6 7
Se invece dividi un numero, il suo valore diminuisce di 10, 100, 1000 volte. La virgola separa sempre la parte delle unità intere dalla parte delle unità decimali. Le quattro operazioni 21 Quaderno p. 175
1 Sul quaderno, applica le proprietà commutativa e associativa per trovare tutti i modi possibili per scrivere queste operazioni.
52 + 15 + 8 3,5 + 1,24 + 0,5 + 8 8 x 3 x 6 4,2 x 7 x 1,8
2 Sul quaderno, associa gli addendi in modo opportuno e calcola, come nell’esempio.
9 + 3 + 1 + 4 = (9 + 1) + 3 + 4 = 10 + 3 + 4 = 17
13 + 15 + 7 + 2 65 + 12 + 35 + 8
3,4 + 6,2 + 7,1 + 4,5 5,2 + 2,5 + 8,1 + 5
29 + 3 +14 + 11
7,1 + 2,3 + 8,4 + 3,7
3 Per semplificare le moltiplicazioni scomponi i numeri, poi sul quaderno associali, come nell’esempio.
70 x 5 20 x 8 = 7 x 50 =
10 x 7 x 5 80 x 4 = 9 x 30 =
10 x 35 = 350 70 x 9 = 5 x 90 =
4 Indica con una X le operazioni nelle quali è stata applicata la proprietà distributiva in modo corretto. Dove ci sono errori, riscrivi correttamente.
6 x (2 + 13) = (6 x 2) + 13
4 x (18 + 5) = (4 x 18) + (4 x 5)
(20 + 3) x 7 = 20 + (3 x 7)
(30 + 8) x 5 = (30 x 5) + (8 x 5)
12 x (9 +3) = 12 + (9 x 3)
5 Sottrarre 10 è più semplice: applica la proprietà invariantiva formando multipli di 10, come nell’esempio.
23 – 9 37 – 28 = 92 – 53 = 156 – 31 = +1 +1
45 – 37 =
86 – 34 = 179 – 139 =
24 – 10 = 14 245 – 126 = 184 – 62 = 509 – 321 =
6 Sul quaderno, semplifica il calcolo applicando la proprietà invariantiva, come nell’esempio.
800 : 200 =
(800 : 100) : (200 : 100) =
8 : 2 = 4
900 : 300 = 2000 : 500 = 1200 : 40 =
210 : 30 = 330 : 55 = 420 : 70 =
45 : 15 = 64 : 32 = 84 : 14 =
22 ESERCIZI
7 Risolvi sul quaderno.
a. In un negozio di articoli sportivi le combinazioni di oggetti hanno i prezzi che vedi.
Puoi acquistare anche un oggetto singolarmente. Quanto costa uno dei palloni da calcio?
49 euro
117,60 euro
b. Osserva il disegno accanto. Anna ha 3 scatole di caramelle e Lella ha 2 scatole. Ogni scatola contiene lo stesso numero di caramelle. Quante caramelle ha Anna e quante ne ha Lella, se in tutto hanno 120 caramelle?
Spiega come hai trovato la risposta.

408 6 79




51 3 2

d. Osserva il trenino “matematico”.
c. Osserva la figura: sei numeri sono scritti su altrettanti foglietti.
Accostando tutti i sei foglietti puoi formare dei numeri di dieci cifre.
Qual è il numero più piccolo che puoi formare?
Spiega come hai trovato la risposta.
4 6 10 18
Quale sarà il numero scritto sul sesto vagone?
E sull’ultimo vagone?
e. Giulia va in gita a Torino con i suoi amici e le sue amiche. Prepara la valigia e come vestiti mette un paio di jeans, un paio di pantaloni neri e 3 magliette: una bianca a fiori, una a righe e una blu.
In quanti modi diversi potrà vestirsi Giulia?

34 ? ? ? ? ?
23
Le quattro operazioni
LE POTENZE
Sugli oggetti sporchi ci sono animaletti talmente piccoli che non li vedi: si chiamano batteri. Quando tocchi gli oggetti, i batteri si attaccano alle tue mani e si trovano così bene che si riproducono velocemente. In poche ore diventano un esercito! Devi sapere che ogni 30 minuti ogni batterio si divide e ne forma due, come vedi nello schema sotto.
Perché prima di mangiare devo lavarmi le mani?
È questione di numeri!

Dopo 2 h
Dopo 1,30 h
Dopo 1 h
Dopo 30 min















• Completa disegnando i batteri che si riproducono in due ore, poi completa. Questo schema si chiama grafico ad albero perché somiglia appunto a un albero.
Nella prima mezz’ora i batteri raddoppiano, nella seconda raddoppiano ancora e continuano a raddoppiare ogni mezz’ora.
Dopo due ore quante volte si sono riprodotti?
E quanti batteri sono nati? Calcola.
2 x 2 x 2 x 2 =
Questa espressione è formata solo da moltiplicazioni con fattori uguali, pertanto la puoi scrivere in una forma abbreviata che si chiama potenza:
2 x 2 x 2 x 2 = 24 si legge “2 alla quarta” oppure “2 elevato alla quarta”.
HO CAPITO CHE...
La potenza indica un’espressione composta solo da moltiplicazioni con tutti i fattori uguali.
24
Le quattro operazioni

Come si chiamano i termini di una potenza?
La potenza indica un’operazione i cui termini sono:
potenza
indica quante volte la base si deve moltiplicare per se stessa indica il fattore che si ripete 2 4
esponente base
Nelle potenze ci sono dei casi particolari:
• se l’esponente è 1, si considera la base una volta sola, quindi 21 = 2
• se l’esponente è 0, il risultato è uguale a 1, quindi 20 = 1
• se la base è 0, quale sarà il risultato? Verifica: 03 = 0 x x = È
• se la base è 1, quale sarà il risultato? Verifica: 13 = 1 x x = È
LE POTENZE DEL 10
Senza saperlo, hai già usato le potenze del 10 scrivendo i numeri, perché la nostra numerazione è scritta in base dieci. Vuol dire che per passare da un ordine a quello successivo si moltiplica ogni volta x 10
Per scrivere il valore di una potenza di 10, si scrive 1 seguito da tanti zeri quanti ne sono indicati dall’esponente: 103 ha esponente 3 quindi 1000
Le potenze del 10 sono utili per scomporre i grandi numeri:
423000 = 4 x 100000 + 2 x 10000 + 3 x 1000 = = 4 x 105 + 2 x 10 4 + 3 x 103
PROVO IO

Ma se la base è 10?

HO CAPITO CHE...
L’esponente delle potenze di 10 indica quanti zeri vanno scritti dopo la cifra 1.
hk 100000 dak 10000 uk 1000 h 100 da 10 u 1 105 10 x x x x 104 10 x x x 103 10 x x 102 10 x 10 101 10 100 1
1. Scrivi in forma di potenza.
4 elevato alla terza
5 elevato alla quarta
7 elevato alla nona
6 x 6 x 6 = 8 x 8 x 8 x 8 x 8 x 8 = 10 x 10 x 10 x 10 = 3 x 3 x 3 x 3 =
2. Trasforma in potenze.
25 Quaderno pp. 178-179
LE ESPRESSIONI
La maestra conta quanti gessi sono rimasti nell’armadio in classe.
Ci sono 8 scatole con dentro 6 gessi di vari colori e 5 scatole con 6 gessi rossi.
• Scrivi in linguaggio matematico che cosa sta facendo la maestra.
1. Conta il numero dei gessi di vari colori: 6 x =
2. Conta il numero dei gessi rossi: 6 x =
3. Infine somma i prodotti ottenuti: + = gessi.
Puoi scrivere le tre operazioni fatte dalla maestra con un’unica frase, cioè con una sola espressione, scrivendo così:
6 x 8 + 6 x 5 = + =
oppure 6 x (8 + 5) = 6 x =
Le due scritture vengono chiamate espressioni aritmetiche.
La parola “espressione” significa “frase che serve per comunicare”.

È molto importante l’ordine in cui vanno eseguite le operazioni, perché ci sono
delle operazioni che hanno la precedenza.
Per eseguire 15 x 4 + 36 : 12 – 10 procedi così: al prodotto di 15 e 4 somma il quoziente di 36 e 12, poi sottrai 10
In linguaggio matematico: 60 + 3 – 10
• Quali operazioni hai eseguito per prima? e
• Quali operazioni dovrai eseguire dopo? e
HO CAPITO CHE...
Un’espressione aritmetica è una sequenza di operazioni. Prima si eseguono la moltiplicazione e la divisione, poi l’addizione e la sottrazione nell’ordine in cui compaiono.

1. Risolvi le espressioni sul quaderno.
a. 4 x 10 – 10 : 2 + 9 = b. 12 + 5 x 7 + 42 : 7 – 38 =
Se ci sono tante operazioni, in quale ordine dovrò eseguirle?

5
PROVO IO
c. 18 + 2 x
– 24 : 8 – 25 =
26
Le quattro operazioni
Le quattro operazioni
LE ESPRESSIONI CON LE PARENTESI
Nelle espressioni le parentesi ti indicano l’ordine con il quale le operazioni devono essere effettuate.
• Osserva e completa.
6 x 2 + 3 = 6 x (2 + 3) =
Al prodotto di 6 e 2 x = Moltiplica la somma di 2 e 3 2 + 3 = aggiungi 3 + 3 per 6 x 6 ottieni ottieni
Le due espressioni hanno lo stesso risultato? Sì No È successo perché nella prima espressione hai eseguito prima la ....................................................... poi l’ , mentre nella seconda espressione hai eseguito prima l’operazione dentro alla parentesi, cioè l’ , e solo dopo hai eseguito la
Nelle espressioni con le parentesi segui quest’ordine:
1. esegui prima le operazioni nelle parentesi tonde ( );
2. poi quelle nelle quadre [ ];
3. infine quelle nelle graffe { }
All’interno delle parentesi si eseguono le operazioni seguendo l’ordine che già conosci.
Quindi:
8 + {3 x [20 : (3 + 2) – 3]} =
8 + {3 x [20 : – 3]} =
8 + {3 x [ – 3]} =
8 + {3 x } =
8 + =
HO CAPITO CHE...
Se ci sono le parentesi in un’espressione, per prime si eseguono le operazioni nelle parentesi tonde, poi si eseguono quelle nelle quadre e infine quelle nelle graffe, con le stesse regole di prima.
1. Esegui i calcoli nella parentesi tonda.
2. Esegui la divisione nella parentesi quadra.
3. Esegui la sottrazione nella parentesi quadra.
4. Esegui l’operazione nella parentesi graffa.
5. Esegui l’operazione fuori dalle parentesi.
PROVO IO

1. Risolvi le espressioni sul quaderno.
8 + (15 – 6 x 2) + 3 – 2 x 5 = 4 x [6 + (7 – 3)] =
9 + (3 + 1) – {4 x [5 – (2 + 1)]} = 5 + {6 x [10 : (8 – 3)]} =
2. Traduci queste frasi in espressioni e risolvi sul quaderno.
Al numero 48 aggiungi il quoziente tra i numeri 72 e 8
Al numero 84 sottrai la somma dei numeri 52 e 32
27 Quaderno pp. 180-181
Le quattro operazioni
MULTIPLI E DIVISORI
Marta ha 12 biglie colorate e le dispone in modo lineare














Marta trova queste soluzioni:







Ha disposto le biglie in una riga da ................. biglie e si scrive: Si chiede in quanti altri modi le può disporre formando dei rettangoli.






















2 righe da biglie ciascuna 6 righe da biglie ma anche ................. righe da ................. biglie ................. righe da ................. biglie




























• Completa le moltiplicazioni che corrispondo agli schieramenti.
12 x 1 = 12 2 x 6 = 6 x = 3 x = x =
Hai ottenuto 12 moltiplicando 1 e 12, oppure 2 e 6, o 3 e 4, quindi si dice che
12 è multiplo di 1, di 2, di 3, di 4, di 6 e di 12
I multipli si ottengono moltiplicando un numero per un qualsiasi altro numero naturale. Poiché i numeri sono infiniti, anche i multipli sono infiniti
Poiché la divisione è l’operazione inversa alla moltiplicazione, possiamo associare alle moltiplicazioni le rispettive dvisioni: 12 : 2 = 12 : 6 = 12 : = : 3 = 12 : =
Queste divisioni hanno tutte resto , quindi puoi dire che i numeri 1, 2, 3, 4, 6 sono i divisori di 12.
È la stessa cosa di dire che “12 è divisibile per 1, 2, 3, 4, 6”.
Tra i divisori di 12 c’è anche 12? Prova 12 : 12 = con resto
Quindi
HO CAPITO CHE... 12
3 multiplo divisore
Le relazioni “essere divisore” ed “essere multiplo” sono l’una l’inversa dell’altra.
PROVO IO

I divisori dividono un numero in modo esatto, cioè con resto zero.
1. Circonda i numeri che non sono multipli di 4.
2. Circonda i numeri che sono multipli di 3.
54
4 • 14 • 8 • 22 • 26 • 30
14 • 17 • 21 • 30 • 25 • 33 •
•
38
28




Marta perde una biglia e gliene restano 11. Inizia a disporle in forma lineare.




è 1 riga da biglie.
Le moltiplicazioni corrispondenti sono 1 x oppure 11 x
• Scrivi le divisioni che corrispondo a queste moltiplicazioni.

11 : = 11 : = 1
Marta si domanda: “Posso ancora disporle a forma di rettangolo?” Sì No
Quindi i divisori di 11 sono solo e
Per questo motivo si dice che 11 è un numero primo.
IL CRIVELLO DI ERATOSTENE
I numeri primi hanno solo due divisori: il numero 1 e se stessi.
I numeri che hanno più di due divisori invece si chiamano numeri composti.
Il matematico greco Eratostene (III secolo a.C.) scoprì un sistema per trovare i numeri primi minori di 100.
Regalò al re Tolomeo III una lastra di metallo con i numeri fino a 100, segnando i numeri non-primi con dei fori. Per questo, la lastra sembrava un setaccio, che allora si chiamava “crivello”.
Ripercorriamo il lavoro di Eratostene cercando i numeri primi fino a 100. Osserva e completa:
Il numero 1 ha solo un divisore e non è un numero primo.
Continua tu e cancella con i colori indicati:
• verde tutti i multipli di 2 tranne il due;
• giallo tutti i multipli di 3 tranne il tre;
• celeste tutti i multipli di 5 tranne il cinque;
• arancione tutti i multipli di 7 tranne il sette.
Elenca i numeri rimasti:
Questi sono i numeri primi minori di 100.
Scrivi i numeri primi che hai trovato:
Osservali: a eccezione del 2, sono tutti numeri
PROVO IO

I NUMERI
PRIMI
14 = 11 + 3 22 • 30 • 26 • 8 • 38 • 10 • 20 • 50 • 44 • 36 • 100 • 72 • 112
1. Scrivi questi numeri pari come somma di due numeri primi, come nell’esempio.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
Le quattro operazioni 29
Le quattro operazioni
SCOMPOSIZIONE IN FATTORI PRIMI
Ricorda che puoi scrivere un numero in tanti modi:
12 = 6 + 5 + 1 12 = 20 – 8 12 = 24 : 2
• Puoi scriverlo anche in forma di prodotto.
12 = 3 x oppure 12 = 2 x
In questi prodotti i numeri 3 e 2 sono numeri , ma 4 e 6 non lo sono.
• Puoi scrivere anche il 4 e il 6 come prodotto di numeri primi? Prova. 4 = 2 x ................ 6 = 3 x ................
Ora riscrivi 12, sostituendo a 4 e 6 il loro prodotto in fattori primi.
12 = 3 x 4 3 x 2 x 2
12 = 2 x 6 2 x x
A che cosa servono i numeri primi?

Quindi puoi scrivere il numero 12 come 12 = 3 x x oppure 12 = x x
Puoi dire che 3 x 2 x 2 = 2 x 3 x 2 perché vale la proprietà commutativa.
Siccome 2 e 3 sono numeri , l’espressione 3 x 2 x 2 si chiama scomposizione in fattori primi, perché esprime 12 come prodotto di soli numeri
HO CAPITO CHE...
I numeri primi sono i “mattoni” con i quali si formano tutti i numeri.
Ogni numero naturale può essere espresso come prodotto di numeri primi. Questa espressione è unica e si dice scomposizione in fattori primi.
PROVO IO

1. Completa le scomposizioni in fattori primi. 2. Scomponi in fattori primi.
28 x 4 x 28 =
18 x 9 x 18 =
50 = 5 x .......................... = .....................................................................................
70 = 7 x =
24 = 4 x =
20 = 2 x =
18 = 3 x =
27 = 3 x =
30 Quaderno pp. 182-183
Le
I CRITERI DI DIVISIBILITÀ
È facile trovare i numeri che dividono i numeri primi, perché sai che hanno come divisori solo
il numero e se stessi.
Per trovare i divisori di un numero che non sia primo ti viene in aiuto la scomposizione in fattori.
• Completa.
Scomponi in fattori primi il numero 18
18
2 x ............
3 x
Scrivi in riga: 18 = 2 x x quindi puoi dire che i numeri 2 e 3 sono divisori primi di 18
Per trovare gli altri divisori di 18 moltiplica fra loro i divisori primi che hai trovato:
3 x 3 = 2 x 3 = 2 x 3 x 3 =
Adesso conosci i divisori di 18. Scrivili: 1, 2, , , ,
Siccome questi numeri , sono i divisori di 18, puoi anche dire che 18 è divisibile per 1, 2, 3, 4, 6, 9 e 18.
2
3
Come si trovano i divisori di un numero? PROVO IO

Un altro modo per stabilire quali sono i divisori di un numero è quello di conoscere i criteri di divisibilità.

Un numero è divisibile per... Esempio
se è
0, 2, 4, 6, 8 2 24 36 48 70
pari, cioè termina con
se la
multiplo di 3 681 6 + 8 + 1 = 15 5 se il numero termina con 0 oppure con 5 5 10 205 340 10 se termina con 0 320 580 1990 100 se termina
00 300 700 1000
somma delle sue cifre è un
con
Circonda
3 7 12 65 84 89 123 5 52 150 356 1025 154 2 123 264 89 941 246 2. Completa la tabella indicando con una X. Divisibile per... 2 3 5 10 100 832 700 1221
1.
i numeri divisibili per il numero nel quadratino.
31 Quaderno pp. 182-183
quattro operazioni
ESERCIZI
1 Completa i calcoli seguendo la strategia indicata.
Operazione Strategia Calcolo
Siccome 4 = 2 x 2
55 x 4
Allora puoi calcolare così:
55 x 2 x 2
Siccome 5 = 10 : 2
63 x 5
Allora puoi calcolare così:
63 x 10 : 2
28 x 9
64 x 11
2 Completa le tabelle.
Siccome 9 = 10 – 1 allora
28 x 10 – 28 x 1
Siccome 11 = 10 + 1 allora
64 x 10 + 64 x 1
55 x 2 x 2 (55 x 2) x 2
110 x =
63 x 10 : 2 (63 x ) :
: =
28 x 10 – 28 x 1 (28 x ) – (28 x )
– =
64 x 10 + 64 x 1 (64 x ) + (64 x )
+ =
3 Quali operazioni si possono riscrivere sotto forma di potenza? Indicale con una X e, quando puoi, scrivile.
4 Quale espressione rappresenta il numero indicato nel riquadro? Indica con una X.
x 10 x 100 x 1000 1,2 23,5 69,15 5,31 : 10 : 100 : 1000 247 32 4416 3584
Sì No Potenza 3 x 3 x 3 x 3 5 + 5 + 5 + 5 + 5 2 x 4 x 3 x 5 x 8 6 x 6 x 6 Sì No Potenza 7 + 7 + 7 + 7 5 x 3 x 6 x 1 2 x 2 x 2 x 2 x 2 4 x 4
34 29 70 36 (4 + 6) x 5 (5 + 8) x 3 5 + 2 x 2 x 5 50 – 4 x 9 + 6 : 3 4 x 6 + 5 (5 + 3) x 8 (5 + 2) x (2 x 5) 50 – 4 x (9 + 6) : 3 4 + 6 x 5 5 + 3 x 8 2 x 5 + 2 x 5 50 – (4 x 9 + 6) : 3
32
5 Collega ciascuna espressione scritta alla sua espressione in linguaggio matematico. Scrivi l’espressione che manca.
È la differenza fra 8 e la somma di 4 e 2
È la somma di 5 col prodotto di 4 e 2 (4 + 2) x (5 – 3)
È la somma del prodotto di 5 e 3 con il prodotto di 4 e 2 5 x 3 + 4 x 2
È la differenza fra il prodotto di 4 e 2 e la somma di 5 e 3 8 – (4 + 2)
È il prodotto fra la somma di 4 e 2 e la differenza fra 5 e 3 5 + 4 x 2
6 Risolvi le espressioni sul quaderno.
a. 7 + 5 + 12 – 3 – 5
40 – 15 – 5 + 6 + 2
6 x 2 : 4
3 x 5 : 5 x 2
b. 15 + 6 x 4 – 13
10 x 4 – 6 x 5 + 7
30 : 6 + 14 : 2 – 10
16 + 18 : 9 – 3 x 3 + 4
7 Scopri la regola e completa la successione. 52 56
I numeri trovati sono tutti multipli di e di
I numeri trovati sono tutti divisibili per e per
c. 4 x (7 + 8 – 5) : 5
229 – (15 + 4) x (6 + 4)
42 + (2 x 7 x 2) : 2
(15 x 4 – 3 x 10) : 3 + 2 x 8 : 4
8 Della successione che hai completato nell’esercizio precedente, riscrivi i numeri che sono divisibili: per 3:
per 5: per 10:
Osserva i numeri che hai scritto: quale numero è multiplo di 3, di 5 e di 10?
9 Scomponi in numeri primi completando gli schemi, poi riscrivi il numero con un’espressione unica. 24 6
18 9
Espressione: Espressione:
...........................................................................................................
33
Le quattro operazioni
LA CALCOLATRICE: USO RAGIONATO
La calcolatrice è uno strumento che ti aiuta a eseguire calcoli particolarmente complessi o ti può servire per verificarli, se li hai fatti a mente o in colonna.
• Disegna sul quaderno la tua calcolatrice e descrivi com’è fatta.
Alcuni tasti sono intuitivi, riesci a capire da solo il loro significato: scrivi nei riquadri il significato di quelli che già conosci, mentre lascia vuoti quelli che non conosci.

Qui a lato puoi leggere quali funzioni svolgono alcuni tasti:
C oppure CE oppure ON/C = cancella tutto.
AC = cancella solo l’ultimo dato inserito.
• Completa lo schema sopra scrivendo il significato dei tasti che hai lasciato vuoti.
• Usa la calcolatrice per comporre i numeri 360 e 2794 e scrivi che cosa vedi apparire sul display ogni volta che digiti un tasto.
Digito on 3 6
Vedo 0 3
Digito on 2 7
Vedo 0 2
• Esegui 35 + 24 prima a mente, poi con la calcolatrice. Scrivi come hai proceduto. Calcolo a mente:
Con la calcolatrice:
Digito on 3 5 +
Vedo
• Hai proceduto nello stesso modo? Sì No
........................................................................ ........................................................................
........................................................................................................
34
LE PROPRIETÀ DELLA CALCOLATRICE
• Esegui le operazioni prima con carta e penna, poi con la calcolatrice. Spiega le strategie usate.
Con carta e penna: 8 + 34 + 12 =
8 + 12 = 20
20 + =
Con la calcolatrice: 8 + 34 + 12 =
Digito
Vedo
Con carta e penna hai applicato: la proprietà e la proprietà
Hai dovuto scrivere i risultati intermedi? Sì No
Con la calcolatrice hai proceduto come nel calcolo a mente? Sì No
Hai registrato i risultati intermedi? Sì No
Con carta e penna: 24 + 12 x 5 =
Esegui prima la moltiplicazione e poi
l’addizione:
12 x 5 = ................ ................ + 24 = ................
Con la calcolatrice: 24 + 12 x 5 = (esegui i calcoli così come sono scritti in riga)
Digito .............. .............. .............. .............. .............. .............. ..............
Vedo
Hai ottenuto lo stesso risultato dell’operazione eseguita con carta e penna? Sì No
Ora esegui ordinando le operazioni come hai fatto con carta e penna.
Digito .............. .............. .............. .............. .............. ..............
Vedo
Hai ottenuto lo stesso risultato? Sì No
• Conosci il tasto = ? Esegui come indicato in tabella per scoprire un’altra funzione di questo tasto.
Digito 5 + 3 = = = =
Vedo .............. .............. .............. .............. .............. .............. ..............
Che cos’è successo digitando ripetutamente il segno = ?
Hai ottenuto lo stesso risultato? Sì No
HO CAPITO CHE...
Con la calcolatrice eseguo operazioni digitando meno tasti possibili.
Non importa registrare i risultati intermedi.
Con alcune calcolatrici è necessario ordinare le operazioni prima di eseguirle.
quattro operazioni 35
Le
PROBLEMATICAMENTE
Osserva con attenzione la tabella e il disegno. Poi rispondi.
TIRO ALLE CESTE
1 Quali informazioni ricavi senza effettuare calcoli?
• Quanti tiri ha effettuato ciascun giocatore: Sì No
• I punti di ciascuna cesta: Sì No
• Il punteggio totale di ciascun giocatore: Sì No
• Quanto tempo hanno giocato: Sì No
• Quante persone hanno partecipato al gioco: Sì No
• Il punteggio effettuato da ciascun giocatore per ogni tiro: Sì No
• Dove hanno giocato: Sì No
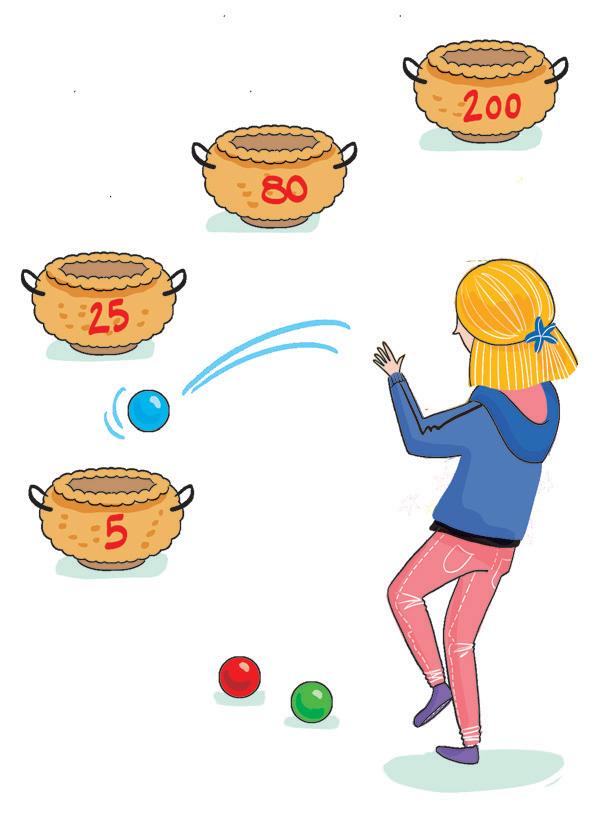
2 Indica con una X le domande alle quali puoi rispondere effettuando i calcoli necessari.
Quanti punti ha realizzato in ogni tiro ciascun giocatore?
Chi ha vinto?
Quanti anni ha ciascun giocatore?
Quanto hanno speso per partecipare alla gara?
3 Ora completa il testo del problema scegliendo una o più domande dall’esercizio precedente.
Per la festa del Paese di Villagioiosa hanno organizzato dei giochi in piazza…
4 Risolvi il problema.
Totale punteggio
Anna
Filippo
Nome 1° tiro 2° tiro 3° tiro
Tommy 25 25 130 Caterina 5 5 25
.................. .................. 0 30
25 110
................................................................................................................................................................................................................................................................................................................................
36
1 Risolvi sul quaderno.
a. Gino, il maestro di ginnastica, sta preparando un percorso in palestra per i suoi alunni. Ogni due passi Gino mette in terra un cerchio rosso, ogni quattro passi mette un cerchio blu e ogni sette passi mette un cono verde. Qui vedi l’inizio del percorso.









Si fermerà quando metterà tutti e tre gli oggetti insieme. Quanti passi avrà fatto Gino a questo punto? Quanti attrezzi di ciascun tipo avrà usato? Spiega come hai trovato la risposta.
b. I fratelli Michele e Martin hanno contato gli scalini che vanno dalla porta di casa al portone di ingresso del palazzo dove abitano e hanno scoperto che in tutto sono 36 scalini. Un giorno decidono di scendere le scale saltando. Michele è più grande e salta tre scalini alla volta, mentre Martin, che è più piccolo, li salta due alla volta. Quanti salti fa ciascun bambino per scendere le scale? Ci sono scalini sui quali saltano entrambi i bambini. Quali sono?
Spiega come hai trovato la risposta.
c. Leonard ha preparato dei biscotti e li sistema dentro a delle scatoline per regalarli.
Se Leonard mette 3 biscotti in ogni scatolina, gliene avanza uno; se ne mette 4, gliene avanza sempre uno, mentre se ne mette 5 in ogni scatolina, non gliene avanza nessuno.
Quanti biscotti ha preparato Leonard?

d. La cartolaia Maria ha speso € 970 per comprare uno scatolone di quaderni per la scuola. Nello scatolone ci sono 10 scatole, in ogni scatola ci sono 10 pacchi e in ogni pacco ci sono 10 quaderni.
Quanto ha pagato Maria ogni quaderno?
e. Sara ha speso € 48 per comprare 6 magliette. Poi compra ancora 3 paia di pantaloncini che costano ciascuno come una maglietta. Quanto ha speso in tutto?

37 ESERCIZI
ARITMETICA DELL’OROLOGIO
ARITMETICA DELL’OROLOGIO

Che bello!
Questa scatola era proprio quello che mi serviva per finire il mio robot.
Non sempre nella vita quello che resta è inutile; infatti, è proprio grazie alla scatola buttata via che Filippo riesce a finire il suo robot. Anche in Matematica ci sono operazioni nelle quali ciò che conta non è tanto il risultato quanto piuttosto quello che rimane: il resto.
Vengo a trovarti fra 12 giorni
Se oggi è martedì, che giorno della settimana sarà quando viene a trovarmi?
In questo caso la Matematica ti può venire in aiuto. Poiché la settimana è formata da 7 giorni, immagina di avere un orologio a forma di ettagono, cioè con 7 vertici. Su questo orologio invece delle ore scrivi i giorni della settimana e li numeri.
38
• Completa l’orologio.
Nel tuo orologio martedì è il giorno 2, quindi inizia a contare da 2 ed aggiungi 12. L’amica arriverà di che corrisponde al numero ..........................
• Scriviamo in linguaggio matematico l’operazione che hai eseguito.
Hai iniziato da martedì 2 e hai aggiunto 12 passi: 2 + 12 =
Poiché la settimana è formata da 7 giorni, ogni 7 giorni la lancetta dell’orologio fa un giro completo e torna al punto di partenza, cioè a domenica 7
Quanti giri completi fa la lancetta in 14 giorni?
Calcola: 14 : 7 resto
Considera solo il resto: quale giorno corrisponde a 0 nell’orologio?
• Prova ancora.
Oggi è mercoledì: fra 23 giorni che giorno sarà?
Nell’orologio mercoledì è il numero
Quindi + 23 =
26 : 7 resto
Che giorno della settimana corrisponde al resto, cioè a 5?
Questa cosa del resto funziona solo con i giorni della settimana o anche con le ore? Prova. Sono le 10 del mattino e Lisa ha il corso di ginnastica fra 7 ore. A che ore inizia il corso? Aiutati con l’orologio: sono le e devi aggiungere le 7 ore che mancano per arrivare all’ora in cui inizia il corso. In linguaggio matematico: + 7 =
Che ore indicherà l’orologio?
Questa volta stai lavorando con l’insieme dei numeri dell’orologio che sono 12, quindi devi dividere per 12, così: 17 : 12
....................... resto .......................
Il resto ti dice dove si ferma la lancetta delle ore, disegnala sull’orologio. Ora sai che il corso di ginnastica inizia alle ore del pomeriggio.
0 Domenica 1 Lunedì 2 M 3 M 4 5 6 0 Domenica 1 Lunedì 2 M 3 M......................... 4 ............................. 5 6 ............................. 2 3 9 4 8 57 6 12 11 10 1
39


La vita di Niccolò non fu semplice: suo padre morì quando era ancora piccolo, la sua
Il 19 febbraio del 1512, infatti, la città di Brescia venne presa d’assalto dalle truppe francesi e nella battaglia vennero ferite moltissime persone; fra queste anche Niccolò, che aveva solo 12 anni e che riportò dei tagli al viso che gli danneggiarono il palato e la mascella: da allora non riuscì più a parlare con facilità e cominciò a “tartagliare” (cioè a balbettare).
Proprio perché tartagliava, cioè parlava in modo confuso e stentato, i suoi amici lo soprannominarono “Tartaglia”. Niccolò fece suo questo soprannome e con esso firmò i libri che scrisse in seguito.
Tartaglia, nonostante le difficoltà famigliari, non abbandonò mai lo studio. Divenne bravissimo in Matematica e, una volta adulto, iniziò a insegnare questa materia, prima a Verona e poi a Venezia.
Tartaglia è diventato famoso per gli studi che ha fatto su di un triangolo speciale, a cui, in seguito, è stato dato proprio il suo nome: “il triangolo di Tartaglia”.
In realtà questo triangolo era già conosciuto in Cina, ma Niccolò scoprì nuove proprietà e le spiegò scrivendole in un libro.

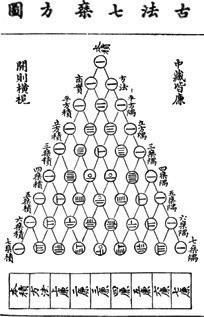
40
Che cosa avrà mai di speciale questo triangolo?
Osservalo con attenzione e, come Tartaglia, scopri alcune delle sue caratteristiche.


Questo che vedi è un pezzo del triangolo. Da che cosa è formato?
Lungo il contorno del triangolo c’è scritto
sempre lo stesso numero: quale? .......................
.........................
Quale regola è stata usata per scrivere i numeri nei cerchi?
....................
Il numero che sta nel cerchio sotto è ......................................................
Inserisci i numeri che mancano seguendo la regola che hai scoperto.
• Nello scrivere i numeri avrai scoperto già un’altra caratteristica di questo triangolo. Quale?
Se non l’hai notata, colora i cerchi che contengono i numeri 1, 2, 6, 20, 70, 252 e uniscili tracciando un segmento.
In quante parti hai diviso il triangolo?
• Osserva i numeri che compongono la parte che sta a destra con quella che sta a sinistra: come sono fra loro?
Puoi dire allora che il segmento che hai tracciato è del triangolo.
Storie matematiche 41
...............................................................................................................................
...............................................................................................................................
1 1 1 1 1 1 1 1 1 20 1 1 5 10 10 5 1 1 4 16 4 1 1 3 3 1 1 2 1 1 1 1
Storie matematiche
Ci sono ancora altre scoperte matematiche da fare.
Osserva la fila indicata dalla freccia rossa. Scrivi i primi cinque numeri della fila: Li riconosci? Che cos’hanno di speciale?
Sono i numeri triangolari che hai studiato lo scorso anno!
Sono numeri che possono essere disposti a forma di triangolo e che furono studiati da Pitagora.
• Adesso parti dal numero 3 e colora tutti i suoi multipli. Ottieni un’altra !
Ti lanciamo una sfida. Somma i numeri in diagonale da sinistra verso destra: troverai la successione 1 • 1 • 2 • Che successione sarà?
Questo triangolo ha un sacco di proprietà: è proprio speciale!
42
1 8 1 1 7 1 1 6 15 20 15 1 1 5 10 10 5 1 1 4 16 4 1 1 3 3 1 1 2 1 1 1 1
Il triangolo nasconde delle configurazioni interessanti.
Colora con un solo colore tutti i numeri pari e con un altro colore tutti i numeri dispari.
Che cosa succede? Adesso ricalca questo triangolo e colora tutti i numeri divisibili per 3.
Poi ricalca di nuovo e colora tutti i numeri divisibili per 4.
E se colori i numeri divisibili per 5?
Wow! I frattali! Che belli!
Più grande farai il triangolo, più belli risulteranno.
Storie matematiche 43 1 15 1 1 14 1 1 13 1 1 12 1 1 11 1 1 10 1 1 9 1 1 8 1 1 7 1 1 6 1 1 5 10 10 5 1 1 4 6 4 1 1 3 3 1 1 2 1 1 1 1
LE FRAZIONI
LA FRAZIONE
Anna ha 12 caramelle.
Mette 1 4 delle caramelle in una scatolina triangolare per regalarle alla sua amica Jenny.
Poi prende ancora 1 4 e le mette in una scatolina rettangolare.
Disegna le caramelle nella scatola.
Le caramelle messe nei due contenitori sono la stessa quantità? Sì No
Le caramelle sono sempre 1 4 , però sono state disposte in modo diverso.
Ginevra ha preparato due torte.
• Che parte è una fetta rispetto a tutta la torta?
• In ciascuna fetta, scrivi la frazione di torta che rappresenta.
• Puoi dire che ciascuna fetta indica la stessa quantità di torta? Sì No
• Hanno anche uguale forma? Sì No
La seconda torta è stata divisa in modo diverso.
• In quante parti è stata divisa? Ciascuna fetta è 1 4 della torta.
• In ciascuna fetta, scrivi la frazione di torta che rappresenta.
• Ciascuna fetta è la stessa quantità di torta? Sì No
• Le fette hanno tutte uguale forma? Sì No
HO CAPITO CHE...
Frazionare significa dividere in parti uguali
Se si fraziona una superficie, ogni parte ha uguale estensione, ma non per forza anche la stessa forma.
Le fette non hanno uguale forma, ma indicano tutte 1 4 della torta.
Se si fraziona una quantità di oggetti, ogni parte ha la stessa quantità. In linguaggio matematico:
1 numeratore
4 denominatore linea di frazione
Quaderno p. 186
44
1 Indica con una X i casi che non sono stati “frazionati bene”.
2 Per ciascun caso, indica con una X se è stato “frazionato bene” oppure no.
Sì No
Sì No
Sì No
Sì No
Sì No
Sì No
Sì No Sì No
3 Fraziona ciascuna immagine come indicato. in sesti in ottavi
quarti terzi settimi dodicesimi
4 Se necessario, completa la suddivisione e poi scrivi le frazioni rappresentate in ciascuna figura.
45
ESERCIZI
FRAZIONI MINORI, UGUALI E MAGGIORI DI 1
David piega un foglio di forma rettangolare prima lungo le due mediane, poi lungo le due diagonali e infine riapre il foglio.
• Prova anche tu e disegna qui accanto che cosa hai ottenuto.
Osserva: hai diviso un rettangolo in parti fra di loro
• Colora una parte.
Hai colorato una parte su , si scrive:
Ti ricordi come si chiama? È l’unità ............................................................ Il rettangolo intero è
Con un foglio di carta trasparente David ricalca l’unità frazionaria e, usandola più volte, ottiene questa figura.
• Prova anche tu, poi scrivi quello che hai fatto.
1
8 + + = 8
Osservala: è minore, maggiore o uguale al rettangolo di partenza?
perché hai ripetuto l’unità frazionaria solo ............................................................ volte.
La frazione 3 8 ha il numeratore maggiore minore del denominatore, indica una parte minore dell’intero e quindi è minore di 1
In linguaggio matematico si scrive 3 8 < 1
David costruisce una nuova figura.
• Scrivi quante volte ha ripetuto l’unità frazionaria.
1 8 + =
HO
CAPITO CHE...
Quando una frazione ha il numeratore minore del denominatore è minore di 1.
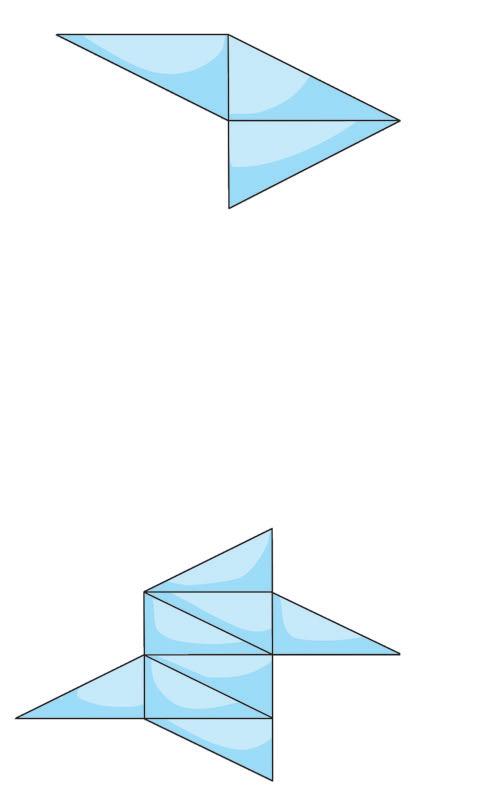
La frazione ha il numeratore al denominatore e indica tutto l’intero. Infatti è formata dallo stesso numero di unità frazionarie del rettangolo, ma David le ha disposte in modo differente. Puoi scrivere che 8 8 = 1
HO CAPITO CHE...
Quando una frazione ha il numeratore uguale al denominatore è uguale a 1.
Le frazioni 46
David si diverte a costruire ancora altre figure.
• Osserva la figura accanto, rispondi e completa.
• Quante volte ha ripetuto l’unità frazionaria?
1
8 + = 8
• Ha ottenuto una figura maggiore o minore del rettangolo di partenza?
• Di quanto è maggiore? Infatti 10 8 = 8 8 +
Siccome 8 8 = 1, puoi scrivere anche così: 10 8 = 1 + 2 8
HO CAPITO CHE...
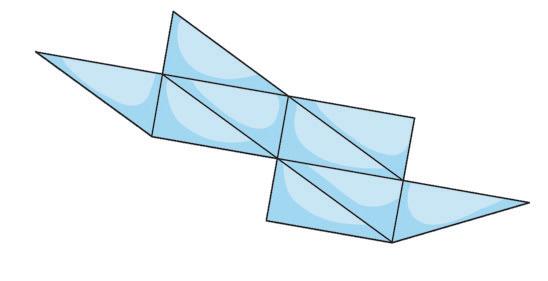
Quando una frazione ha il numeratore maggiore del denominatore indica una quantità maggiore dell’intero.

1. Per ciascuna figura, scrivi la frazione corrispondente rispetto a quella di partenza.
a.
PROVO IO 4 4 = 1 1 3 3 =
b.
2. Se è 1 3 dell’intero, colora la figura che corrisponde al suo intero.
Delle altre figure, scrivi le frazioni corrispondenti.
3. Circonda di verde le frazioni maggiori di 1 e di rosso le frazioni minori di 1.
.......... ..........
..........
..........
6 6 2 6 5 4 12 12 15 9 23 16 18 27 7 12 30 30 34 45 Quaderno p. 187 Le frazioni 47
FRAZIONI A CONFRONTO
Luca e Matteo giocano con le costruzioni.
• Colora le torri seguendo le indicazioni date dai due bambini e scrivi la frazione che indica il numero dei mattoncini gialli in ciascuna torre.
Nella mia torre i mattoncini gialli sono 3 4 .

Nella mia invece i mattoncini gialli sono 2 4 .

Osserva le torri: hanno un numero di mattoncini diverso uguale, ma il numero dei mattoncini gialli è diverso uguale.
Puoi osservare la stessa cosa confrontando le due frazioni: hanno denominatori diversi uguali, ma i numeratori sono diversi uguali. In quale torre ci sono più mattoncini gialli?
Puoi dire allora che 3 4 è di 2 4 e si scrive 3 4 > 2 4
I due bambini costruiscono due nuove torri.
• Colorale seguendo le indicazioni e scrivi per ciascuna torre la rispettiva frazione.
• 2 6 dei mattoncini della torre di Luca sono rossi
• 2 3 dei mattoncini della torre di Matteo sono rossi
Osserva le torri: hanno un numero di mattoncini diverso uguale, ma il numero dei mattoncini rossi è diverso uguale.
Puoi osservare la stessa cosa confrontando le due frazioni: hanno denominatori diversi uguali, ma i numeratori sono diversi uguali.
In quale torre ci sono più mattoncini rossi?
Puoi dire allora che 2 6 è di 2 3 e si scrive 2 6 < 2 3
Quaderno p. 188
Matteo
Le frazioni 48
Luca
FRAZIONI EQUIVALENTI
Lucy costruisce un muretto con i suoi mattoncini.
• Scrivi dentro ai mattoncini che valore hanno rispetto al mattoncino giallo e quanti, di ciascun tipo, ne ha usati.
• Alcune frazioni indicano la stessa parte di muretto: osserva e scrivile.
1
• Scrivi la frazione che indica la parte rosa. Poi completa. Come sono state ottenute queste frazioni equivalenti?
I numeratori sono stati I numeratori sono stati moltiplicati per divisi per I denominatori sono stati I denominatori sono stati moltiplicati per divisi per
Come si trovano le frazioni equivalenti?

1 = 1 2 + 1 2 = 2 2
1 = 1 3 + + =
1 = 1 =
1 = ..................................................................................................
HO CAPITO CHE...
Le frazioni che indicano la stessa parte dell’intero si dicono equivalenti e si possono scrivere in modi diversi.
HO CAPITO CHE...
Per trovare una frazione equivalente a un’altra si applica la proprietà invariantiva: moltiplica o dividi il numeratore e il denominatore per lo stesso numero.
2
2 4
= 1 3 = 1 4 = 2
= 2 2 = = = = 1
=
=
3 = =
1 2 4 1 2
x x : : 2 3 4 6 8 12 8 12 4 6 2 3 x x : :
Quaderno p. 189 Le frazioni 49
Le frazioni
DALL’INTERO ALLA FRAZIONE
Sofia ha sistemato le medaglie vinte nelle gare di pattinaggio.
3 5 delle medaglie sono d’oro, di quelle che restano 3 4 sono d’argento e le altre sono di bronzo.
• Colora le medaglie.
Ricorda
Ricorda che cosa significa 3 5 :
3 indica quante sono le unità frazionarie considerate
5 parti nelle quali è stato diviso l’intero
• Procedi così per scoprire quante sono le medaglie d’oro.
1. Conta quante sono tutte le medaglie vinte da Sofia: sono
2. Dividile per trovare il valore dell’unità frazionaria:
= è 1 5

3. Ripeti il valore dell’unità frazionaria per quante sono le medaglie d’oro:
3 5 = 1 5 + + quindi 4 + + =
Colora le medaglie d’oro.
• Adesso considera le medaglie d’argento.
Sai già quante sono, ma in forma di frazione sono ..........
Procedi così per scoprire quante devi colorarne.
1. Conta quante medaglie non colorate sono rimaste: sono
2. Dividile per trovare il valore dell’unità frazionaria: : = è 1 4
3. Ripeti il valore dell’unità frazionaria per quante sono le medaglie d’argento:
3 4 = 1 4 + + quindi 2 + + =
Colora le medaglie d’argento.
• Ora rispondi: quante sono quelle di bronzo?

:
Quaderno pp. 190-191
50
DALLA FRAZIONE ALL’INTERO
I cioccolatini che vedi sono 2 5 di tutti quelli che c’erano.
Quanti cioccolatini c’erano nella scatola?
• Per scoprirlo, rifletti su che cosa significa 2 5 .
2 5 , il denominatore indica in quante parti
sono stati divisi i cioccolatini quando la scatola era piena. Quindi in frazione, tutti i cioccolatini erano 5 5
2 5 , il numeratore indica che le parti rimaste sono ....................., quindi i cioccolatini che vedi sono 2 parti su 5
Per scoprire quanti cioccolatini c’erano all’inizio devi sapere quanti ce ne sono in 1 5 .
Sai che 2 5 sono .........., quindi 20 : 2 = .......... sono 1 5 dei cioccolatini. Circondali.
Sai che tutti i cioccolatini erano 5 5 , cioè 1 5 + 1 5 + + + , quindi tutti i cioccolatini
erano + + + + , cioè x 5 =
PROVO IO

1. Le uova che vedi sono e sono 3 7 di tutte le uova che c’erano nel cestino. Quante uova c’erano nel cestino?

a. Il numero 7 indica in quante parti sono state divise, quindi in frazione tutte le uova erano 7
b. Scopri quante sono 1 7 6 : = Circondale nel disegno.
c. Ora che sai quant’è 1 7 , trova quante sono 7 7 x =
2. I fiori sono 8 15 di tutti i fiori del terrazzo di Anna.
a. Conta i fiori: sono
b. L’intero in frazione è
c. Trova 1 15 cioè 8 : =
d. Trova l’intero: x =
Quaderno pp. 192-193
Le frazioni 51
LA FRAZIONE: UN LEGAME FRA DUE O PIÙ COSE
• Osserva il disegno e completa.
Anna Gloria
Quanti sono i sacchetti di caramelle di Anna? E quelli di Gloria?
Quanti sacchetti possiede Anna rispetto a Gloria? . Si scrive 1 3
Gloria invece ha sacchetti uguali a quello di Anna, cioè ha 3 volte i sacchetti di Anna. Si scrive 3 1
Nello schema è rappresentata la situazione. Scrivi i nomi delle bambine.
1 3 dei sacchetti di 3 volte i sacchetti di
Se nei 3 sacchetti di Gloria ci sono 36 caramelle, quante caramelle ci saranno in ciascun sacchetto?
36 : = caramelle in ciascun sacchetto.
E Anna quante caramelle avrà?

1. Osserva e completa.
• Il triangolo A rispetto al tutto il rettangolo è
• Tutto il rettangolo rispetto al triangolo è
• Il triangolo A rispetto al trapezio B è ..........
• Il trapezio B rispetto al triangolo A è
• Il rettangolo C rispetto a tutto il rettangolo è
• Tutto il rettangolo rispetto al rettangolo C è
• Il rettangolo C rispetto al trapezio B è
A C
B
PROVO IO Le frazioni 52
Antonio ha 50 g di cioccolata e sono 2 3 della cioccolata di Giorgio.
Quanti grammi di cioccolata ha Giorgio?
• Rappresentiamo la situazione con un disegno. Scrivi il nome dei bambini.
50 g ?
Quante tavolette ha Antonio? ....................
E Giorgio? ....................
Puoi dire allora che Antonio rispetto a Giorgio ha tavolette su , in frazione si scrive
• Inserisci i nomi dei bambini nello schema che rappresenta la situazione.
2 3 della cioccolata di
3 2 della cioccolata di
HO CAPITO CHE...
Se la relazione cambia verso, devo invertire la frazione, cioè scambio il numeratore con il denominatore.
Per scoprire quanti grammi di cioccolata ha Giorgio, devi sapere quanto pesa una tavoletta.
Antonio ha grammi di cioccolata divisi in tavolette.
In linguaggio matematico si scrive: : = g di cioccolata di una tavoletta.
Sai che Giorgio ha 3 tavolette, quindi 3 x = g di cioccolata.
PROVO IO

1. Osserva e rispondi.
• Quante sono le palline rosse rispetto alle palline gialle?
• E le gialle rispetto alle rosse?
• Quante sono le palline rosse rispetto alle palline verdi?
• E le palline verdi rispetto alle rosse?
• E le palline verdi rispetto a tutte le palline?
• E tutte le palline rispetto alle palline verdi?
Le frazioni 53
1 Se necessario, completa il frazionamento, poi colora le parti indicate.
2 Metti il simbolo giusto, come nell’esempio.
3 Completa in maniera adatta.
4 Per scrivere la durata di un suono si usano le note musicali. Osserva il valore di ciascuna nota.
Nota intera: i Le altre note:
Scrivi i valori delle seguenti note e calcola.
In quanti modi diversi puoi formare 4 5 ? Disegnali sul quaderno.
5 Che numero segna l’orologio se sono:
• le 9 e tre quarti:
• le 18 e un quarto:
• le 11 e mezza:
• un quarto alle 15:
a. 4 7 > 2 7 5 6 3 6 4 9 8 9 2 5 1 5 6 8 8 8 4 3 2 3 4 4 5 4 10 8 12 8 5 5 3 5 1 2 2 2 b. 2 6 2 4 6 7 6 9 3 7 3 5 4 7 4 9 8 10 8 9 4 3 4 6 1 6 1 2 5 8 5 3 3 2 3 4 9 6 9 10 1 2 2 9 2 8
5 8 > 2 6 < 1 3 < 4 4 = 3 9 < 9 10 > .......... < 3 4 .......... > 2 6 .......... = 1 2 .......... < 6 8 .......... < 1 3 .......... > 5 7
4 4 2 4 1 4 1 8
= + = = + = = + + = = + + =
54
ESERCIZI
6 Per ciascuna frazione, scrivi una frazione minore avente lo stesso denominatore. 3
7 Se ho 13 mezze arance, quante arance intere ho tagliato?
8 In un giardino ci sono 50 alberi da frutto, di cui 20 sono alberi di arance. Scrivi quattro frazioni che indicano la parte di arance rispetto a tutti gli alberi da frutto.
9 Rappresenta le frazioni sull’intero e poi fai la somma.
10 Piegando un foglio di carta, Gregorio ha costruito il viso di una volpe.
Quale parte rappresenta l’orecchio della volpe rispetto a tutto il viso?
Quale parte rappresenta il musetto?
Apre il foglio e ripassa con la matita le pieghe.
Quali poligoni riesci a vedere? Sul quaderno scrivi che parte è ciascun poligono rispetto al foglio quadrato. C’è un poligono che non è una parte frazionata del quadrato. Qual è?
11 Osserva e rispondi.
Il quadrato A rispetto a tutto il quadrato grande è
Il rettangolo B rispetto al quadrato grande è
Il quadrato grande rispetto al rettangolo B è
Il rettangolo C rispetto al quadrato A è
Il rettangolo C rispetto al quadrato grande è
Il quadrato grande è ................. rispetto al rettangolo C. C B
A
5 9 7 2 4 6 4 8
3
2 9 + 4 9 = 3 8 + 2 8 = 5 16 + 9 16 = 1 4 + 2 4 =
55
Le frazioni

I bambini e le bambine della 5a C si sono divertiti a scrivere alla lavagna queste frazioni.
• Scrivi i denominatori delle frazioni.
Le frazioni che hanno al denominatore 10, 100, 1000 si chiamano frazioni decimali
Considera la frazione 7 10 . Puoi scriverla anche in altri modi:
• a parole sette decimi
• come numero decimale 7 : 10 = 0,7 quindi 7 10 = 0,7
Puoi trasformare una frazione decimale in numero decimale dividendo il numeratore per il denominatore, infatti la linea di frazione indica l’operazione aritmetica della divisione.
Ma posso fare anche il contrario, cioè scrivere un numero decimale finito in frazione decimale?
Considera il numero 4,32 u.
È formato da u e centesimi
Siccome 32 sono centesimi, trasforma tutto il numero in centesimi:
4,32 x = c
Si legge: quattrocentotrentaduecentesimi e puoi scriverlo in frazione:
432 100
Osserva: 432 100 È il numero decimale a cui hai tolto la virgola. È il numero 1 con tanti zeri quante sono le cifre decimali.
Le frazioni decimali indicano un numero decimale e si leggono nello stesso modo: 2 10 = 0,2 = due decimi
Ciascun numero decimale si può trasformare in frazione decimale:
0,9 = 9 10
6,78 = 678 100
0,563 = 563 1000
7 10 4 10 2 100 19 100 54 1000 6 1000
FRAZIONI DECIMALI E NUMERI DECIMALI
HO CAPITO CHE...
56

E le frazioni che non sono decimali possono diventare numeri decimali?
Considera la frazione 1 5 . È una frazione decimale? Sì No
• Osserva e rispondi.
Confronta le due frazioni: come sono fra loro?
In linguaggio matematico 1 5 = 2 10
La frazione 1 5 non è una frazione decimale, ma puoi trasformarla in 2 10 , che è una frazione decimale a essa equivalente.
Sai che la frazione 2 10 2 : 10 = e la frazione 1 5 1 : 5 =

Dipende dai denominatori!
I numeri decimali che hai ottenuto sono ...................................., quindi 1 5 = 2 10 = ......................
Hai scoperto che la frazione 1 5 indica il numero decimale 0,2

Posso trasformare anche 3 20 in numero decimale?
Trasformala nella frazione decimale equivalente 3 20
x 5 x 5
• 3 20 è una frazione decimale? Sì No
Sai che la frazione 15 100 15 : 100 = e la frazione 3 20 3 : 20 = 0,15
I numeri decimali che hai ottenuto sono , quindi 3 20 = 15 100 =
Hai scoperto che la frazione 3 20
indica il numero decimale 0,15.
HO CAPITO CHE...
• Osserva: i denominatori delle frazioni 1 5 e 3 20 .
• 5 è un divisore di 10, 100, 1000? Sì No
• 20 è un divisore di 100, 1000? Sì No
Ogni frazione che ha al denominatore un divisore di 10, di 100, di 1 000 è equivalente a una frazione decimale, quindi è un numero decimale finito. 3 25 = 3 : 25 = 0,12
pp. 194-195
Quaderno
1 5
Le frazioni 57
LA FRAZIONI COME PERCENTUALE
Alla corsa campestre della scuola partecipano 100 concorrenti; di questi, 42 sono femmine.
• Scrivi il numero delle femmine in frazione.
Le frazioni con denominatore 100 si chiamano percentuali e si possono scrivere usando il simbolo %. 42 100 = 42%
• Scopri quanti sono i maschi che hanno partecipato alla gara.
Sai che tutti i partecipanti sono e che le femmine sono .
Calcola: – = sono i maschi scritti in frazione.
Ora scrivi il numero dei maschi in percentuale: ................ %
Le percentuali si usano per indicare preferenze, costi, scelte…


La mamma di Eleonora è stata eletta come rappresentante di classe con il 65% delle preferenze.
Significa che delle persone hanno votato la mamma di Eleonora.
Qual è la percentuale dei voti contrari?
Per la partita di calcio sono stati venduti 85% dei biglietti.
Significa che i biglietti
Qual è la percentuale di biglietti che non sono stati venduti?

........................................................................................................................................................................ Le frazioni 58

Come calcolare la percentuale?
Al centro commerciale, un negozio di abbigliamento ha ribassato il costo dei vestiti del 50%.
Significa che

• Osserva il disegno in basso e completa.
Il papà di Valeria ha un acquario con 25 pesci colorati. Il 40% sono pesci pagliaccio. Quanti sono i pesci pagliaccio?
La percentuale 40% indica che 40 pesci su 100 sono i pesci pagliaccio; in frazione si scrive .......... .
Per rispondere alla domanda devi calcolare i 40 100 di Sai già come fare!
25 : 100 x 40 =
Quanti sono i bambini con gli occhiali? su , in frazione .......... .
Posso trasformare una frazione decimale in percentuale?

Quaderno pp. 196-198
Le frazioni 59
Le
frazioni
PERCENTUALI E GRAFICI
Spesso è necessario trasformare i dati numerici in percentuale, per renderli più chiari, e rappresentarli con un grafico.
• Leggi e completa.
Gli iscritti al corso di ginnastica artistica sono 60. Alla fine del mese l’insegnante osserva che ci sono stati 15 assenti.
• Scrivi la frazione che indica il numero degli assenti: ..........
• Trasforma la frazione in percentuale:
15 : 60 = 0,25 0,25 = = % degli assenti

PROVO IO

Quale grafico si usa per rappresentare le %?
1. All’interno del negozio Tuttobici c’è una esposizione di 80 biciclette. Alla fine del mese sono state vendute 16 biciclette. Calcola la percentuale delle biciclette non vendute.
• Scrivi in frazione le biciclette vendute:
• Trasformala in numero decimale: 16 : =
• Scrivi il numero decimale ottenuto in centesimi: 100
• Corrisponde alla percentuale del
• Adesso puoi rispondere: qual è la percentuale delle biciclette non vendute? %

• Quanti sono stati i presenti in tutto il mese? 60
LA PERCENTUALE NEL COMMERCIO
Spesso sui volantini pubblicitari trovi scritte le percentuali che indicano lo sconto.
Lo sconto è una quantità di denaro che viene sottratta al prezzo iniziale.

€ 220
Costo iniziale del tablet: €
Calcola il 20% di 220
220 : 100 x 20 = € sconto
220 – 44 = € prezzo scontato
Sicuramente qualche volta avrai sentito dire che i prezzi sono aumentati.
L’aumento è una quantità di denaro che viene aggiunta al prezzo iniziale e viene espressa spesso in percentuale.
Il corso di nuoto che costava € 160 quest’anno è aumentato del 5%
Costo iniziale del corso €
Calcola il 5% di 160.
160 : 100 x 5 = € aumento
160 + 8 = € prezzo attuale

PROVO IO

1. Completa la tabella.
2. Il corso di tennis l’anno scorso costava € 200. Quest’anno è aumentato di € 16.
A quale percentuale corrisponde l’aumento? In frazione si scrive 40 100 .
• Scrivi come numero decimale: 16 : =
• Scrivi in frazione: .......... =
Prezzo iniziale % di sconto Sconto Prezzo scontato Scarpe € 80 25% € € Jeans € 65 15% € .................................. € ..................................
Quaderno p. 199 Le frazioni 61
PROBLEMATICAMENTE
Nella piscina di Bellavista si disputa la finale del campionato di pallanuoto. Per assistere alla partita sono disponibili 1600 posti sugli spalti e altri 140 nel piano vasca. Non sono stati occupati tutti i posti disponibili, infatti i responsabili della biglietteria hanno calcolato che 2 10 dei biglietti non sono stati venduti, mentre 1 20 dei biglietti sono stati regalati ai parenti dei giocatori delle due squadre.
Rifletti sul testo per risolvere il problema

1 Indica con una X le domande che sono coerenti con il testo, cioè sono domande alle quali puoi trovare una risposta.
Quanti spettatori sono andati a vedere la partita?
Qual è stato il miglior giocatore?
Quanti biglietti sono stati regalati?
Quanti posti a sedere ci sono nella piscina?
Quanto tempo è durata la partita?
2 Scomponi il testo in tre parti, una per ciascuna domanda coerente. Alla fine di ciascuna parte, scrivi la sua domanda.
a.
b.
c. Domanda:
d.
e.
f. Domanda:
g.
h.
i. Domanda:
3 Risolvi il problema sul quaderno.
62
1 Risolvi sul quaderno.
a. La zia di Gisella e Lina ha regalato a ciascuna delle sue nipoti una confezione con 20 cioccolatini. Gisella ha mangiato 2 5 della sua confezione, mentre sua sorella Lina ne ha mangiati 1 4 Quale delle due sorelle ha mangiato più cioccolatini?
b. Sulla Luna ogni oggetto pesa 1 6 di quanto pesa sulla Terra. Calcola quanto peserebbero sulla Luna: un uomo di 78 kg; un bambino di 36 kg; una macchina di 960 kg.
c. Liam ha un grande acquario con dentro 64 pesci. 2 4 dei pesci sono tropicali, 1 4 sono rossi e, di quelli che restano, la metà sono pesci pappagallo. Quanti sono i pesci pappagallo?
d. Asia desidera comprare una collana, ma ha 10 euro e sono solo 5 8 del prezzo intero della collana. Quanto costa la collana che vuole comprare Asia?
e. Vittoria va a comparare alcuni dolci per fare una festa. Al supermercato trova alcuni prodotti a prezzi “speciali”. Calcola sul quaderno e completa la tabella.
Prodotto
Torrone Biscotti Succo di frutta Brioches Gelato al limone
f. Il corso di yoga di Luisa costa € 160 all’anno. Quest’anno ha subito un aumento del 12%. Quando costa il corso? Siccome Luisa è una vecchia iscritta ha diritto a uno sconto del 5%. Quanto spenderà?
g. Beatrice vuole andare a trovare una sua amica e cerca su Internet i prezzi per dormire una notte in albergo. Per prenotare una camera dovrà lasciare un anticipo che corrisponde a 2 5 del prezzo intero della camera.
Hotel Bellosguardo Anticipo € 40
Hotel Dormibene Anticipo € 30
Hotel Stella Anticipo € 32
Se Beatrice vuole spendere al massimo 85 euro, in quale albergo potrà soggiornare?
h. La nonna di Roberto ha 81 anni. La mamma di Roberto ha 5 9 dell’età della nonna e Roberto ha 2 5 dell’età della mamma. Calcola l’età di Roberto e della sua mamma.

Prezzo iniziale in euro € 8 € 9 € 1,80 € 4,20 € 3,30 Sconto in % 40% 33% 20% 30% 20% Sconto in euro € € € € €
63 ESERCIZI
PROBLEMI DEL “MUCCHIO“

Puoi sapere con precisione quante sono le caramelle di Stefano o quanti sono i sassi di Emma? Sì No
La parola mucchio non dà informazioni precise su quante sono le caramelle o i sassi, ma indica solo un numero sconosciuto di oggetti.
Per indicare questo numero sconosciuto gli antichi Egizi usavano la parola “aha”, cioè mucchio.
Nel linguaggio matematico oggi, invece, si usa la parola incognita.
Ma se un numero è sconosciuto, si può scoprire che numero è? Prova.
Lisa e suo fratello Luca hanno terminato la lezione di tennis e hanno raccolto le palline rimaste nel campo mettendole in carrelli uguali.
Quante palline ha raccolto Luca? Quante palline ha raccolto Lisa?
• Osserva l’immagine, poi rispondi.
• Puoi sapere quante palline ha raccolto ciascun bambino? Sì No
• Perché?
• Puoi capire chi ne ha raccolte di più? Sì No
• Perché?
64
Luca e Lisa confrontano i loro carrelli: che cosa si diranno?
• Scegli la frase giusta e scrivila nel fumetto.
• Ho la metà delle tue palline.
• Ho tante palline quante ne hai tu.
• Ho il doppio delle tue palline.
• Adesso puoi conoscere quante palline ha raccolto Luca? Sì No
Però sai quante palline ha Luca rispetto a Lisa, cioè hai un dato relazionale
Scriviamo in linguaggio matematico la situazione: palline di Luca = 2 volte le palline di Luca = 2 x
• Rifletti.
Lisa ha un cestino di palline (un mucchio) mentre Luca ne ha il Insieme hanno carrelli di palline.
Se hanno raccolto in tutto 48 palline, puoi scrivere: mucchio + mucchio + mucchio = 48 e quindi puoi determinare il numero delle palline di ogni mucchio.
: = palline di ogni mucchio
Sai che le palline di Luca = il doppio delle palline di Lisa quindi Luca = 2 x .................... = ....................................................................
E se avessero raccolto 54 palline?
65
LA MISURA
MISURARE: CHE COSA SIGNIFICA?
Misurare e contare sono la stessa cosa?
• Completa la tabella.
Oggetto Che cosa conti? Che cosa misuri?



Il delle caramelle.
Il peso delle caramelle; le dimensioni del pacchetto.
Il delle pagine. Il del quaderno; le dimensioni del Il delle bottiglie.
Il ........................................................ della confezione; la di liquido in ogni bottiglia.
Come vedi, contare e misurare non sono la stessa cosa: quando conti valuti una quantità, quando misuri, invece, valuti la proprietà di un oggetto.
Qualsiasi proprietà di un oggetto può essere misurata?
• Puoi misurare:
• la bellezza di un paesaggio? Sì No
• la durata di una canzone? Sì No
• l’altezza di un bambino? Sì No
• la simpatia di una persona? Sì No
• Ordina le azioni che compi quando misuri.
Ricorda
Non tutte le proprietà di un oggetto si possono misurare. La proprietà che misuri si chiama “grandezza”.
Confronti l’unità di misura con la grandezza che vuoi misurare.
Conti quante volte l’unità di misura entra nella grandezza che stai misurando.
Scegli come unità di misura una grandezza omogenea a quella che vuoi misurare, cioè una grandezza dello stesso tipo.
Quali strumenti usi per misurare?
• Scrivi il nome dello strumento e la grandezza che misura.





66
UNITÀ DI MISURA, MULTIPLI E SOTTOMULTIPLI
Poiché ogni Paese per misurare aveva una propria unità di misura, gli studiosi e le studiose, per evitare confusione, hanno trovato una unità di misura comune e hanno fissato delle regole che hanno scritto nel documento “Sistema Internazionale di Misure”.
• Completa le tabelle.
Misure
Misure di MASSA MULTIPLI UNITÀ SOTTOMULTIPLI
Quaderno pp. 200-203
Misure di LUNGHEZZA MULTIPLI UNITÀ SOTTOMULTIPLI km chilometro 1 x = m hm ettometro 1 x = m dam decametro 1 x = m m metro 1 dm decimetro 1 : = m cm centimetro 1 : = m mm millimetro 1 : = m
1
1
di CAPACITÀ MULTIPLI UNITÀ SOTTOMULTIPLI h<l ettolitro
x .................. = <l da<l decalitro
x .................. = <l <l litro 1 d<l decilitro 1 : .................. = <l c<l centilitro 1 : .................. = <l m<l millilitro 1 : .................. = <l
1
Megagrammo Mg 1 x = kg h di kg 1 x = kg da di kg 1 x = kg chilogrammo kg 1 ettogrammo hg 1 : = kg decagrammo dag 1 : = kg grammo g 1 : = kg grammo g 1 decigrammo dg
: = g centigrammo cg 1 : = g milligrammo mg 1 : = g
1
1
1
10 u
0,1 c 1
0,01
Sistema di NUMERAZIONE MULTIPLI UNITÀ SOTTOMULTIPLI uk
x = h
x = da
x =
1 d 1 : =
: =
m 1 : =
La misura 67
1 Completa scrivendo l’unità di misura adatta.
La capacità di una lattina è di 0,33
La mamma pesa 67
La distanza fra Milano e Venezia è di 250
2 Indica la misura espressa da ciascuno strumento.
<l
Il passo di Chiara è lungo 55
Il peso della medaglietta d’oro è di 5
Una bottiglietta contiene 0,5 ............. di tè.
3 Colora solo le misure che possono essere corrette.
Oggetto
Misure possibili
Lunghezza di un temperamatite. 2,5 m 2,5 mm 2,5 cm
Peso di una mela. 180 g 180 kg 180 mg
Capacità di una tazzina da caffè. 50 <l 50 m<l 50 d<l
Capacità di un bicchiere di tè. 20 da<l
Peso di un’automobile.
Lunghezza di un furgoncino.
4 Scrivi la lunghezza di ciascun segmento.
<l 20 c<l
Mg 1460 g 1460 kg
m 5821 cm 5,821 km
11121314151617181920 012345678910
20
1460
A
Segmento B
Segmento C
A B C AB = 45 mm CD = 3,2 cm EF = 39 mm
5,821
Segmento
=
=
=
11121314151617181920 012345678910
10 1 2 3 4 5 6 7 8 9 1 0 100 200 300 400 600 700 800 900 1 2 150 149 147148 130131132133134135136137138139140141142143144145146 129 128 127 126 125 124 123 122 121 .................
5 Disegna sul righello tre segmenti che abbiano le lunghezze indicate. ESERCIZI 68
6 Indica il valore di ciascuna cifra nella sua unità di misura. Osserva gli esempi e completa sul quaderno. 17 m 7,3 <l 13 g
dam m <l d<l dag g
18 dam 33,1 da<l 37 dag
3,8 dam 5,17 <l 2351 mg
2315 m 418 <l 13,5 g
47,18 hm 138 c<l 8,17 kg
5,12 m 7,18 da<l 32,8 hg
3,8 km 2300 m<l 2,13 dag
7 Scomponi le misure inserendole prima in tabella. Ricorda di inserire la cifra indicata dall’unità di misura e poi le altre. Segui l’esempio.
8 Scomponi sul quaderno come hai fatto nel precedente esercizio. Puoi anche non disegnare la tabella.
dag 171 dg
9 Aggiungi la quantità che manca per ottenere la misura indicata.
hm 8,973 m
5 cm 2,5 cm 30 mm 0,8 cm ................................ 15 mm 6 d<l 1,4 d<l 25 c<l 48 c<l 0,2 d<l ................................ 2 <l 1,5 <l 0,75 <l 8 d<l ................................ 30 c<l 1 dag 3 g 40 dg 650 cg 4,5 g ................................
136 cm 2634 cm 571 mm m dm cm 3 6 dam m dm cm 136 cm = 1 m + 3 dm + 6 cm 2634 cm = 571 mm = 100 cm + 30 cm + 6 cm ........................................................................................................ .............................................................................. a. 175 cg 1150 cg 3370 cg 148 g 3102 g 12300 mg c. 41,6 c<l 4,5 h<l 4,35 <l 1,17 da<l 3,76 h<l 120,5 <l b. 714
d. 32,6
1,48
0,251 kg 1581 dg 1847 dg 4,36 dag
dm 1,235 dam 33,51 dam
12,06 dam
69
ESPRIMERE IN MANIERA DIVERSA LA MISURA
L’insegnante ha distribuito dei fili colorati ai bambini e alle bambine della 5a C per misurare l’altezza dei banchi della classe, che sono tutti uguali. Questi sono i fili ricevuti da Asia, Fanny e Carla.
Asia
Fanny Carla
• Sovrapponi uno spago a ciascun filo e taglialo in modo da ottenere tre fili uguali a quelli delle tre bambine.
• Adesso confrontali a due a due sovrapponendoli e completa.
• Il filo di Fanny rispetto a quello di Asia è la metà, invece rispetto a quello di Carla è
• Il filo di Carla rispetto a quello di Asia è , mentre rispetto a quello di Fanny è
Asia misura l’altezza del suo banco e scopre che è alto 6 fili gialli.

PROVO IO
Aiuta Fanny a eseguire questa trasformazione.
Sai che 1 filo giallo è uguale a rosa, quindi quanti fili rosa saranno uguali a 6 fili gialli?
6 x = fili
Ora trasforma in fili blu la misura dell’altezza del banco fatta con i fili gialli.
Sai che 1 filo giallo è uguale a fili blu, quindi quanti fili blu saranno uguali a 6 fili gialli?
6 x = fili
HO CAPITO CHE...
Una stessa grandezza si può misurare anche con unità di misura diverse

1. Calcola l’altezza del banco di Fanny in fili arancioni, verdi e viola sapendo che:
• 1 filo arancione = 4 fili rosa
• 1 filo verde = 2 fili gialli
• 1 filo viola = 16 fili blu
La misura 70
TRASFORMARE NEL NOSTRO SISTEMA DI MISURA
La nonna ha chiesto a Elia di comprare 1 kg di pane.
Elia arriva tardi al forno e trova solo filoni di pane di questo tipo.
Quanto pesa un filone?
Elia si chiede: “Sarà 1 kg?”
• Aiutalo: per scoprirlo devi fare una trasformazione.
Rifletti
Il peso del filone resta sempre lo stesso, quello che cambia è l’unità di misura che usi per esprimerlo. L’unità di misura scelta corrisponde all’unità del numero.
250 g

La virgola è il segno che serve per dividere la parte intera del numero (a sinistra della virgola) dalla parte decimale (a destra).
• Colora di rosso l’unità di misura scelta e completa.
a. Nel cartellino il peso del pane è espresso in , quindi scrivi così: .................. g
b. Trasforma : 250 g = ? dag
In questo caso l’unità di misura scelta sono i .................. , quindi la parte intera del numero inizia dai dag. Ripassali di rosso. Ora sai che 250 g = dag
c. Trasforma: 250 g = hg
L’unità di misura scelta sono gli .................., quindi la parte intera del numero inizia dagli
d. Trasforma: 250 g = kg
L’unità di misura scelta sono i , che però non hai, quindi ci scrivi 0.
HO CAPITO CHE...
Per trasformare una misura in un’altra devo:
• scegliere l’unità di misura;
Parte intera del numero u Parte intera del numero
kg hg dag g dg cg mg
2 5 0 , kg hg dag g dg cg
2 5 0 , kg hg dag g dg
2 5 0 , kg hg dag g .............. 2 5 0 ,
• leggere le cifre che indicano la quantità riferita all’unità di misura scelta e separare con la virgola le cifre che indicano quantità minori dell’unità di misura scelta.
La misura 71
LE MISURE DI TEMPO
• Osserva e rispondi.
Ho impiegato 20 minuti per tornare da scuola.
Fai una merenda leggera, tra 25 minuti inizi l’allenamento!

• A che ora è uscito Andrea da scuola?
• Quando inizia l’allenamento?
• A che ora lo finisce, di solito?
• Quanto tempo si è allenato oggi? ..................................
L’unità di misura del tempo è il secondo (s).
• Osserva e completa.
Oggi ho fatto un quarto d’ora in più di allenamento.
Per rispondere alle domande hai misurato l’intervallo di tempo trascorso fra un evento e un altro e hai usato l’orologio come strumento di misura.
Per misurare intervalli di tempo lunghi, però, si usano i giorni, i mesi o gli anni.
1
Giorno d Ora h Minuti min Unità secondo s 1 x 24 h = h h = 1 d 1 min x 60 = min min = 1 h 1 s x 60 = s 60 s = 1 min 1 Anno A Mese M Settimana S Giorno d 1 d x 365 = d A = ............... d 1 d x 30 = d M = ............... d 1 d x 7 = d S = ............... d 1 h x 24 = h d = ............... h
S x 52 = S
= S
M x 12 = M A = M
A
1
La misura 72
Gli intervalli di tempo molto lunghi si misurano in secoli (100 anni) e in millenni (1000 anni). Noi misuriamo il tempo in relazione alla nascita di Cristo: gli anni successivi sono indicati con d.C. (“dopo Cristo”), gli anni precedenti vengono indicati con a.C. (“avanti Cristo”).
avanti Cristo (a.C.)
NASCITA DI CRISTO
dopo Cristo (d.C.)
primo millennio a.C.
primo millennio d.C.
Aiutati con la linea del tempo per scrivere in quale secolo e in quale millennio si trovano i seguenti anni.
Anno Secolo Millennio
250 d.C.
480 a.C.
820 a.C.
• In quale secolo stai vivendo?
PROVO IO

1. Scrivi nelle sveglie le ore indicate.
Anno Secolo Millennio
1240 d.C.
610 d.C.
2021 d.C.
• E in quale millennio?
2. Trasforma.
1000 900 800 700 600 500 400 300 200 100 100 200 300 400 500 600 700 800 900 1000 X secolo IX secolo VIII secolo VII secolo VI secolo V secolo IV secolo III secolo II secolo I secolo I secolo II secolo III secolo IV secolo V secolo VI secolo VII secolo VIII secolo IX secolo X secolo
Quaderno pp. 204-205
22 ore 15 minuti 9 ore 20 minuti 7 ore 5 minuti ore minuti
a. 1 d h 1 h min 1 h s 1 min s 1 d ........... min 1 d ........... s 3 h ........... min 2 d ........... h b. 10 min s 20 min s 2 h min mezz’ora min 2 h e mezza min 1 h e 25 min min 2 d h 1 d e 60 min h 1 S h 73 La misura
Nei Paesi che appartengono all’Unione Europea si usa come moneta di scambio l’euro. È stato scelto come simbolo €, perché rappresenta la lettera iniziale della parola “Europa”.
• Scopri come è stato costruito questo sistema monetario: osserva e completa.




















Le monete e le banconote che formano il nostro sistema monetario sono tutte multipli di 1.
Possono essere anche multipli di oppure di
• Scrivi le monete che sono:
• multiple di 2:
• multiple di 5:
• Scrivi le banconote che sono:
• multiple di 2:
• multiple di 5:
• Siccome 2 x 5 = 10, allora ci sono anche monete multiple di 10: e banconote multiple di 10:
• Siccome 5 x 10 = 50, allora ci sono monete multiple di 50: e banconote multiple di 50:
x .......... x .......... x5 x2 x 2 x 5 x 2 x 5 x 2 x 5
............................................................................................................................................................................................................................................................................................
La misura 74
L’EURO
SISTEMI MONETARI EUROPEI
Non tutte le Nazioni in Europa usano l’euro come moneta di scambio. La Svizzera, la Danimarca, l’Inghilterra e altre Nazioni hanno una moneta nazionale; quando viaggi in questi Paesi devi cambiare gli euro con i soldi locali.
• Osserva quale moneta usano alcune di queste Nazioni.
Nazione
Svizzera
Nome della moneta in uso Moneta Valore in euro ottobre 2023
franco svizzero CHF
Danimarca corona danese (krone) kr
Gran Bretagna sterlina £



€ 1 = chf 0,97
€ 1 = kr 7,46
€ 1 = £ 0,87
• Cerca quali altri Paesi europei non usano l’euro come moneta di scambio.
Disegna una tabella come questa e completala.
PROVO IO

1. Quanto costa in…? Completa.
Nazione Zaino Diario Astuccio
Italia
€ 45 € 13,50 € 12
Svizzera CHF CHF CHF
Danimarca Kr Kr Kr
Gran Bretagna £ £ £
2. Durante il suo viaggio a Londra, Marco decide di comprarsi una maglietta di un supereroe.
Lui ha € 20 e la maglietta che gli piace costa £ 16,53.
Marco ha abbastanza soldi per comprare la maglietta? Spiega perché.
Quaderno pp. 206-207
75 La misura
1 Inserisci le misure di lunghezza nelle tabelle ed esegui le equivalenze, come nell’esempio.
14 dam e 5 m
km hm dam m dm cm mm
1 4 5
145 m 1,45 hm
1450 dm 14,5 dam
48 m e 5 dm
km hm dam m dm cm mm m hm dm dam
31 hm e 9 m
km hm dam m dm cm mm
km dam hm m
2 Esegui le equivalenze.
3 Collega le misure equivalenti.
4 Colora nello stesso modo le misure equivalenti.
37 hm e 14 m
km hm dam m dm cm mm
dam km m hm
276 dam e 28 dm
km hm dam m dm cm mm m hm dm dam
4 m e 6 dm
km hm dam m dm cm mm cm m mm dm
4 m = dm 7 dm = m 2,6 hm = m 37,14 m = cm 31,17 dm = mm 1,8 hm = m 700 m = hm 900 cm = m 5 hm = dam 18 m = dam 170 cm = dm 3,5 dam = mm 30 da<l 3 da<l 33 <l 3,3 <l 700 cg 0,7 g 0,07 dag 70 cg 30,3 <l 3,3 h<l 330 <l 303 d<l 7 g 700 cg 7 dg 7 g 3,33 h<l 333 <l 0,3 h<l 3 h<l 77 cg 7 dag 70 g 7,7 dg
4 cm 440 cm 2 dm 20 dm 7000 m 77 hm 4,4 m 6 cm 2000 cm 200 dm 77 dam 1,7 km 0,6 dm 40 dm 2 m 20 cm 170 dam 7,7 hm 4 m 0,4 dm 20 dm 2 m 7,7 km 7 km
76
ESERCIZI
5 Esegui le equivalenze.
3600 m dam hm km dm
7 kg hg dag g dg
80000 m<l
d<l
c<l <l da<l
6 Trascrivi sul quaderno in ordine crescente le seguenti misure.
8 m 0,8 m 1800 m 750 cm 5 dm
500 <l 18,8 h<l 4,8 da<l 8,1 h<l 45 <l
7 hg 62 dag 3000 dg 4,45 g 7000 mg
7 Risolvi sul quaderno.
a. Giovanni sta organizzando la partenza per le vacanze. L’aereo che deve prendere parte alle ore 9:15, ma lui dovrà essere all’aeroporto un’ora prima della partenza. Questi sono gli orari di partenza dell’autobus che può prendere per andare all’aeroporto.
Sapendo che l’autobus impiega 1 h e 20 min per arrivare all’aeroporto, quale dovrà prendere Giovanni?
40 hg kg dg g dag
0,6 h<l <l
d<l da<l
c<l
Orari autobus
6:45 8:15 7:15
b. Nadia deve preparare dei dolcetti e dei salatini da portare a scuola e ha scelto queste ricette:
Biscotti al cioccolato
Farina 400 g
Zucchero 200 g
Burro 150 g
Uova 5
Latte 220 m<l
Gocce cioccolato 300 g
Salatini al formaggio
Farina 180 g
Burro 50 g
Uova 1
Latte 50 m<l
Formaggio 100 g
Rotolo alla crema
Farina 250 g
+ 50 g per la crema
Uova 3
+ 5 per la crema
Latte 500 m<l
Zucchero 150 g
Scrivi la lista della spesa di Nadia: quanti kg di farina e di zucchero dovrà comprare in tutto?
Quanti litri di latte?
Osserva i prezzi dei prodotti e calcola quanto dovrà spendere.
1 kg farina € 0,95 1 kg di zucchero € 1,80 confezione da 10 uova € 1,65 confezione da 6 uova € 1,10 1 <l di latte € 1,40 formaggio € 9,70 all’etto burro da 125 g € 1,70 burro da 0,5 kg € 2,45 gocce di cioccolato da 0,5 kg € 3,10
77
PROBLEMATICAMENTE
Cerca nel volantino le informazioni necessarie per rispondere alle domande e scrivi il numero della domanda a cui si riferiscono.
Informazioni
Apertura parco dal 1° giugno al 1° novembre
Apertura dal giovedì alla domenica compresa, dalle ore 10:00 alle ore 19:00
Costo per l’utilizzo delle attrezzature:
€ 10 fino a 10 anni; € 15 ragazzi e adulti; gratis bambini accompagnati da un genitore
All’interno del parco potrete trovare percorsi attrezzati, parete d’arrampicata, circuito MTB, itinerari fantastici, area bimbi, noleggio bici, servizio ristoro
Noleggio bici fino agli 11 anni € 4,50 l’ora oppure € 15 giornata intera; dai 12 anni in su € 6,50 l’ora oppure € 20 giornata intera

1 Che cosa pubblicizza il volantino?
2 Dove si trova?
Come arrivare
Località Campotto:
da Bologna 50 min
da Modena 1 h e 30 min da Milano 2 h 50 min da Firenze 1 h e 50 min
Autostrade
A1 Milano-Bologna-Firenze A22 Modena-Brennero
Sconto del 10% Sulla SpeSa totale per gruppi famiglia
Superiori a 4 perSone
3 È necessario portarsi da mangiare? Perché?
4 Qual è il periodo di apertura durante l’anno?
Rifletti sul testo per risolvere il problema
9 Quanto spende un bambino di 10 anni per entrare? E se vuole affittare anche la bicicletta per due ore?
10 Quanto spenderà un adulto per entrare e per affittare la bicicletta tutto il giorno?
5 Qual è l’orario di apertura settimanale?
6 Qual è il costo per le attrezzature?
7 A quale città è più vicino?
8 È necessario portarsi la bicicletta? Perché?
11 Quanto spende per entrare una famiglia formata da due adulti e un bambino di 5 anni, uno di 9 e uno di 12?
12 Quanto spendono se vogliono affittare anche le biciclette per un’ora?
Scegli una domanda, le informazioni necessarie e inventa un problema sul quaderno.
78
1 Risolvi sul quaderno.
a. Marco e Lisa sono arrivati al parcheggio e stanno guardando la cartina per fare l’escursione fino alla vetta. Per fare una salita meno ripida, all’andata vogliono percorrere il sentiero più lungo, mentre al ritorno vogliono fare quello più corto. Quali sentieri dovranno scegliere?

b. Ugo vuole sistemare la recinzione del suo campo. Se mette nel terreno un palo ogni 0,50 m, quanti pali gli serviranno per una lunghezza di 6 m?
c. Giorgio si allena in una piscina lunga 25 m. Il suo allenatore stima che oggi dovrà fare 0,6 km. Quante vasche dovrà fare Giorgio?
Il suo amico Nico invece si allena in una vasca lunga 50 m e oggi ha fatto 15 vasche. Si è allenato di più o di meno di Giorgio?
d. Nel negozio dietro l’angolo vendono le costruzioni a peso. Stefano ha comprato un sacchetto da 1,6 kg, che contiene 400 mattoncini tutti uguali. Quanti grammi pesa ogni mattoncino?
e. Una confezione in promozione al supermercato contiene tre succhi di frutta da 125 m<l ciascuno. Jona si chiede quanti litri di succo di frutta contiene la confezione intera. Aiutalo a rispondere.
h. La tabella accanto rappresenta gli orari dei voli Milano-Parigi. Mario si reca a Parigi per un appuntamento alle ore 14. Quale volo dovrà prendere? Quanto durerà il viaggio? Quanto tempo avrà a disposizione per raggiungere il luogo dell’appuntamento?
f. Per la sua festa Alessio ha portato dei bicchieri da 200 m<l ciascuno. Se vuole offrire un bicchiere di succo a ciascuno dei suoi 24 compagni, quante bottiglie da 1 <l dovrà comprare?
g. Andrea deve andare da Roma Termini a Bologna Centrale, quindi consulta gli orari. Quale treno impiegherà meno tempo per fare quella tratta? Di quanto sarà la differenza?
IC 1584 Dolomiti
P. Roma Termini 7.42
A. Bologna Centrale 11.01
EC 84 Michelangelo
P. Roma Termini 7.54
A. Bologna Centrale 11.18
E per andare da Firenze S. M. Novella a Milano Centrale? Quale treno impiegherà meno tempo e di quanto sarà la differenza?
IC 988 Vesuvio
P. Firenze SMN 11.25
A. Milano Centrale 14.40
IC 582 Il Verrocchio
P. Firenze SMN 14.19
A. Milano Centrale 17.20
Volo Partenza Arrivo giornaliero giornaliero giornaliero venerdì AF461 AF463 AF465 AF121 9.30 14.30 19.30 22.00 10.50 15.30 20.50 23.20
0,6
79 ESERCIZI
800m 1,2km 1,6 km 700 m 850m
km
GIORNATA
Le api sono insetti preziosi per l’essere umano perché producono il miele, la cera e la propoli, che usiamo per produrre candele, medicine naturali, dolci e prodotti di bellezza. Sono preziose soprattutto perché consentono l’impollinazione di moltissime specie di piante. Infatti, quando si spostano tra i fiori alla ricerca del nettare, trasportano il polline che resta attaccato al loro corpo.
Negli ultimi decenni è diminuito moltissimo il numero delle api soprattutto a causa dei pesticidi. Per questo motivo è stata dedicata una giornata all’anno a questi animali, per diffondere la conoscenza dei pericoli che corrono e per progettare attività che garantiscano la loro sopravvivenza.
Gioco


Le api che hanno il compito di procurare il nettare si chiamano “api bottinatrici” e devono fare molti viaggi per trasportare il nettare dai fiori al proprio alveare. Per fare meno fatica possibile, volano di fiore in fiore senza percorrere mai due volte la stessa strada. Quali fra questi tragitti possono essere percorsi da un’ape?
A B C D 80
Giornata mondiale delle api 20magg i o
MONDIALE DELLE API

Gioco
Gli apicoltori e le apicoltrici allevano le api costruendo per loro delle casette chiamate “arnie” e le dispongono in fila, una accanto all’altra.
Poi colorano le arnie usando colori differenti per aiutare ciascuna ape a ritrovare con facilità la propria arnia.
Le api vedono i colori in modo differente da noi. Come noi vedono solo il giallo, l’arancione, il blu e il verde.
Laura fa l’apicoltrice e ora ha ben 47 arnie. Le ha disposte in fila una accanto all’altra in modo che due arnie dello stesso colore non si tocchino. Quelle che vedi sono alcune delle sue arnie.
123456789101112131415161718
In quale successione le ha disposte?
Continua a colorarle seguendo la successione.
Di quale colore sarà la 30esima arnia?
Spiega come hai trovato la risposta.
Gioco
Hai a disposizione un barattolo di colore azzurro, uno di colore giallo e uno arancione.
Usando sempre tutti e tre i colori, in quanti modi differenti puoi colorare queste arnie?
E la 42esima?
81
LE ISOMETRIE
LA SIMMETRIA
Hai mai visto decorazioni simili a quelle che puoi osservare in queste immagini?



Sono decorazioni formate da un disegno detto “modulo”, che si ripete.
Queste decorazioni si chiamano fregi.
• Osserva il fregio a lato: la parte colorata è il modulo usato per formarlo. Con un foglio di carta trasparente ricalcalo e scopri quale movimento è stato fatto per disegnare il fregio. Il modulo è stato
Lin ha iniziato a disegnare un fregio e ha colorato il modulo di partenza.
• Qual è il movimento che ha scelto per ripetere il modulo? ................................................................................................................
• Continua tu completando e colorando il disegno.
• Verifica se hai disegnato correttamente.
Ricorda che per essere simmetrica la figura deve avere:
• la stessa forma e le stesse dimensioni del modulo: il disegno ha la stessa forma e le stesse dimensioni del modulo? Sì No
• il verso opposto alla figura di partenza: il disegno ha il verso opposto? Sì No
• i segmenti che uniscono i vertici corrispondenti delle due figure devono essere perpendicolari all’asse di simmetria: unisci i vertici corrispondenti e verifica.
• i punti corrispondenti con la stessa distanza dall’asse: verifica la distanza utilizzando il lato di quadretto come unità di misura.
Quaderno pp. 210-211
82
LA TRASLAZIONE
• Completa il fregio disegnando le figure simmetriche rispetto all’asse di simmetria tratteggiato.
A
• Ora confronta le figure, completa e rispondi.
Le figure 1 e 2 sono fra di loro
Le figure 2 e 3 sono fra di loro
• Com’è ciascuna figura rispetto alla precedente e alla successiva?
• Ripassa di blu gli assi di simmetria: come sono fra di loro?
• Le figure 1 e 3 sono uguali? Verifica ricalcando la figura 1 con la carta trasparente e poi falla scivolare fino a sovrapporla alla figura 3
• Si sovrappongono perfettamente? Sì No
Quindi puoi dire che
La figura 3 è congruente alla figura 1, ma ha diversa posizione sul piano perché è stata traslata.
• Segui le indicazioni per rispondere a Said.
• Scegli un vertice della figura di partenza, ad esempio il vertice A. Cerca il suo corrispondente nella figura 3 e nominalo A1.
• Disegna il segmento che unisce i due vertici.
Questo segmento indica la direzione dello spostamento.
In quale direzione, in quale verso e di quanto si è spostata?

• Per conoscere il verso dello spostamento in corrispondenza del punto A1 metti la freccia al segmento.
• Per capire di quanto si è spostata la figura, conta quanti lati di quadretto è lungo il segmento.
Questo segmento orientato si chiama vettore e indica la direzione, il verso e la misura dello spostamento
PROVO IO

Quaderno pp. 212-213
Fig. 1 Fig. 2 Fig. 3
1. Disegna il vettore e misura lo spostamento.
Le isometrie 83
LA ROTAZIONE
• Osserva il disegno. Poi con la carta trasparente ricalca il disegno della bandierina, trova il punto di incontro delle due semirette e con la matita blocca in quel punto la carta trasparente.
a
B
F
b Ruota la carta fino a sovrapporre la semiretta a con la semiretta b e fora i vertici della bandierina: hai lasciato le impronte dei vertici. Aiutati con il modellino e unisci le impronte trovate.
In questo modo hai ottenuto il disegno della bandierina dopo aver eseguito una rotazione. Adesso hai due disegni della stessa figura: hanno la stessa forma e le stesse dimensioni? Sì No
Puoi dire allora che le due figure sono congruenti, è cambiata solo
la loro posizione sul piano perché è la figura stata ruotata

• Osserva il disegno.
Di quanto è ruotata la seconda figura rispetto alla prima?
Le due semirette a e b si incontrano in un punto detto centro di rotazione e formano un angolo. Colora l’angolo e misuralo. La misura di questo angolo indica di quanto hai ruotato la figura e si chiama ampiezza della rotazione. La rotazione può avvenire in senso orario o in senso antiorario. Puoi dire che questa figura è stata ruotata di in senso
A C D E F B a
A
b
C D E
Quaderno pp. 214-215 Le isometrie 84
1 Traccia gli assi di simmetria, poi rispondi.
2 Disegna la figura simmetrica rispetto all’asse di simmetria.
• Ci sono carte con 3 assi di simmetria?
3 Colora la figura traslata. Disegna il vettore e misura lo spostamento.
4 Copia le figure sul quaderno. Poi traslale secondo le indicazioni dei vettori.
5 Osserva la lancetta dei minuti nel primo orologio: nei tre orologi accanto, misura l’ampiezza della rotazione avvenuta in senso orario rispetto al primo.
................................................... ................................................... ................................................... 12 6 57 8 4 3 9 10 2 1 11 12 6 57 8 4 3 9 10 2 1 11 12 6 57 8 4 3 9 10 2 1 11 12 6 57 8 4 3 9 10 2 1 11
A 15 8
A 5 A A 4 85 ESERCIZI
3
INGRANDIMENTI E RIDUZIONI
Martina ha fatto una foto al suo cane e l’ha ingrandita per fare un poster.
• Osserva le due foto.
Le immagini del cane sono uguali nella forma e nella posizione; cambiano solo le

In questo caso si dice che le due figure sono simili.
• Anche i poligoni possono essere simili?

Questi due parallelogrammi sono simili?

• Scopri insieme a Martina come distinguere figure simili.
• Osserva la figura A e la figura B: hanno la stessa forma? Sì No
• Le misure dei lati delle due figure sono uguali? Sì No
I lati della figura B sono più dei lati della figura A.
Di quanto? Verifica la tua risposta misurando i lati.
Figura A lato lungo = cm lato corto = cm
Figura B lato lungo = ............................ cm lato corto = ............................ cm
I lati della figura A sono il rispetto a quelli della figura B, quindi i lati della figura B sono la rispetto a quelli della figura A.
Allora puoi dire che la figura A è stata ingrandita rispetto alla figura B, mentre la figura B è stata ridotta rispetto alla figura A.
• Ora osserva gli angoli. Confrontali con la carta trasparente o misurandoli con il goniometro: sono uguali o diversi? Sono
Quindi la figura A e la figura B sono simili perché hanno una relazione di ingrandimento o di riduzione fra i lati e gli angoli uguali.
Fig. B
Le isometrie 86
Fig. A
• Anche questi due parallelogrammi sono simili?
Verifica la relazione fra i lati.
Misura i lati.
Fig. C lato lungo = cm lato corto = cm
Fig. D lato lungo = ................. cm lato corto = cm
Fra i due poligoni esiste una relazione di riduzione tra la figura ................. e la figura .................
• Misura adesso gli angoli: sono uguali? Sì No
Gli angoli uguali.
• Le due figure sono simili? Sì No
Le due figure non sono simili perché tra i lati c’è una relazione di riduzione ma gli angoli non sono uguali.
HO CAPITO CHE...
Due poligoni sono simili se fra i lati c’è una relazione di ingrandimento o di riduzione e hanno gli angoli uguali.
PROVO IO

1. Secondo te, tra questi poligoni quali sono quelli simili?
Colora nello stesso modo le figure che sono fra loro simili.
pp. 216-217
Quaderno
Fig. C
Fig. D
B C D Le isometrie 87
2.
A
SPAZIO E FIGURE I POLIGONI
Il poligono è una parte di piano limitata da una linea spezzata chiusa semplice
• Colora di rosso i poligoni e di verde le figure che non sono poligoni.
Gli elementi di un poligono sono: i lati, i vertici, gli angoli e le diagonali La diagonale è un segmento che unisce due vertici non consecutivi.
• Completa i cartellini della figura. .................................
Un poligono è:
• convesso se ha tutti gli angoli minori di 180° e i prolungamenti dei lati sono esterni al poligono;
• concavo se ha almeno un angolo maggiore di 180° e i prolungamenti dei lati dell’angolo concavo attraversano il poligono.
Il nome di un poligono dipende dal numero dei lati e degli angoli:
Triangolo = 3 lati e 3 angoli Ettagono = 7 lati e 7 angoli
Quadrilatero = 4 lati e 4 angoli
Pentagono = 5 lati e 5 angoli
Esagono = 6 lati e 6 angoli
Ottagono = 8 lati e 8 angoli
Ennagono = 9 lati e 9 angoli
• Scrivi se le seguenti figure sono concave o convesse.
88
POLIGONI SPECIALI
• Osserva e completa.
Poligono equilatero se ha tutti i uguali
Poligono equiangolo se ha tutti gli uguali.
Poligono regolare se ha tutti i lati e gli angoli
Il perimetro di un poligono è la somma della misura della lunghezza dei lati
I poligoni che hanno il perimetro uguale sono isoperimetrici L’area è la misura della superficie di un poligono.
I poligoni che hanno l’area uguale sono equivalenti o equiestesi
PROVO IO

un
I poligoni isoperimetrici sono e ; i poligoni equivalenti sono e
1. Colora solo i poligoni concavi.
A = P = A = P = A = P =
Fig. 1
Fig. 2
Fig. 3
2. Calcola perimetro e area dei poligoni usando come unità di misura il lato di
quadretto per il perimetro e un quadretto per l’area. Poi completa.
Spazio e figure 89 Quaderno pp. 218-219
I TRIANGOLI: RIPASSIAMO INSIEME
• Prendi 9 strisce di cartoncino con le misure uguali a quelle disegnate qui sotto e prova a costruire 3 triangoli.
a.
• Puoi sempre costruire un triangolo? Sì No È possibile nel caso ............................................
• Che cosa succede con le striscioline del caso b?
Riesci a costruire il triangolo solo nel caso con i lati che misurano
Quindi:
il triangolo esiste solo se il lato più è minore della degli altri due.
• Puoi costruire un poligono con meno di tre lati? Sì No
Infatti, il triangolo è il poligono più piccolo che si può costruire.
• Disegna un triangolo e colora in modo diverso i suoi angoli. Ritaglia gli angoli, disponili uno accanto all’altro facendo combaciare un lato e incollali nel riquadro.
• Che cosa ottieni?
La somma degli angoli interni di un triangolo è , cioè un angolo

Quanto misura la somma degli angoli interni di un triangolo?
2 cm 5 cm 10 cm b. 4 cm 6 cm 10 cm
10 cm 8 cm 12 cm
c.
Spazio e figure 90
CLASSIFICHIAMO I TRIANGOLI RISPETTO AI LATI
• Osserva e ripassa in ciascun triangolo i lati uguali, se ci sono. Poi completa.
È isoscele se ha 2 lati
ISOSCELE
EQUILATERO
È equilatero se ha i lati ...........................................
Un triangolo equilatero è anche un triangolo isoscele?
Rifletti: il triangolo equilatero ha due lati della stessa lunghezza? Sì No
Allora è anche
SCALENO
È scaleno se ha i lati ...........................................
CLASSIFICHIAMO I TRIANGOLI RISPETTO AGLI ANGOLI
• Osserva e completa.
Il triangolo è rettangolo se ha un
Individua l’angolo retto sul disegno e coloralo.
Il triangolo con un angolo ottuso è Individua l’angolo ottuso sul disegno e coloralo.
Il triangolo acutangolo ha
L’altezza è il segmento perpendicolare che congiunge un vertice con il lato opposto.
In ciascun triangolo ci sono 3 vertici e 3 lati, quindi puoi disegnare altezze.
• Disegna l’altezza relativa al lato AB di ciascun triangolo.
A B C A B C A B C
Spazio e figure 91 Quaderno pp. 220-223
I QUADRILATERI: RIPASSIAMO INSIEME
• Prendi 12 strisce di cartoncino con le misure uguali a quelle disegnate qui sotto e prova a costruire 3 quadrilateri.
a.
• Puoi sempre costruire un quadrilatero? Sì No
• È possibile nel caso
• Che cosa succede con le striscioline del caso b? Riesci a costruire il quadrilatero solo nel caso con i lati che misurano
Puoi costruire un quadrilatero solo se il lato più è minore della degli altri tre.
• Costruisci un quadrilatero con le misure dei lati a piacere.
Premendo leggermente su un vertice il quadrilatero cambia perché è articolabile.
• Costruisci un triangolo a piacere e premi su un vertice.
• Il triangolo cambia forma? Sì No
Perché il triangolo è una figura rigida, cioè indeformabile
• Nel quadrilatero accanto, disegna le diagonali.
• Quante ne puoi disegnare?
Perché i quadrilateri hanno coppie di vertici non consecutivi.
In un poligono la diagonale
è il segmento che unisce due vertici non consecutivi
2 cm 5 cm 4 cm 13 cm
3 cm 6 cm 5 cm 14 cm c. 6 cm 4 cm 7 cm 12 cm
b.
Spazio e figure 92
• Disegna un quadrilatero su un foglio e colora in modo diverso i suoi angoli.
Ritaglia gli angoli, disponili uno accanto all’altro facendo combaciare un lato e incollali su un foglio del tuo quaderno.
• Che cosa ottieni?
In un quadrilatero la somma degli angoli interni è , cioè un angolo giro.
CLASSIFICHIAMO I QUADRILATERI
• Osserva e completa la classificazione dei quadrilateri.
Trapezi: quadrilateri con due lati paralleli. Un trapezio può essere:
isoscele, se i lati non paralleli sono uguali.
scaleno, se i lati non paralleli sono

Quanto misura la somma degli angoli interni di un quadrilatero?
rettangolo, se uno dei lati è perpendicolare e ha due angoli
Parallelogrammi: quadrilateri con i lati uguali e paralleli a due a due.
Il parallelogramma ha gli angoli opposti uguali.
Il rombo ha tutti i lati e le diagonali perpendicolari.
Il rettangolo ha tutti gli angoli uguali e le diagonali
Il quadrato ha tutti i lati e gli angoli e diagonali uguali e
Spazio e figure 93 Quaderno pp. 224-227
LA SUPERFICIE
L’unità di misura per le superfici è il metro quadrato (m2), cioè la superficie di un quadrato con il lato di 1 metro.
chilometro quadrato ettometro quadrato decametro quadrato metro quadrato decimetro quadrato centimetro quadrato millimetro quadrato
• Osserva e completa.
1 km2
1 hm2
1 dam2
= hm2 = dam2 = m2
Se leggi la tabella da sinistra verso destra, ti accorgi che ogni misura è 100 volte più grande della successiva.
Se leggi la tabella da destra verso sinistra, ti accorgi che ogni misura è 100 volte più piccola di quella precedente.
• Esegui le trasformazioni.
• Scrivi le cifre del numero partendo dai m2.
• Osserva le cifre che indicano i dam2. Metti la virgola per separare le cifre che indicano le quantità minori del dam2
1324 m2 = dam2
km2 hm2 dam2 m2 da u da u da u da u
• Scrivi le cifre del numero partendo dai dam2 Continua fino ad arrivare ai dm2; se le cifre non bastano aggiungi zeri.
14,65 dam2 = dm2
m2 dm2 cm2 da u da u da u da u
MULTIPLI UNITÀ SOTTOMULTIPLI
km2 hm2 dam2 m2 dm2 cm2 mm2
m2
da u da u 1 1 ........... ........... 1 ........... ...........
km2 hm2 dam2
da u da u
m2 dm2 cm2 mm2 da u da u da u da u 0, 0 1 1 1 1 mm2 = cm2 1 cm2 = dm2 1 dm2 = m2
1 4 6 5 0 0 MULTIPLI UNITÀ SOTTOMULTIPLI km2 hm2 dam2 m2 dm2 cm2 mm2
dam2
1 3 2 4 ,
Spazio e figure 94 Quaderno pp. 228-229
ESERCIZI
1 Completa.
• Un triangolo acutangolo ha angolo/i
• Un triangolo rettangolo ha angolo/i
• Un triangolo ottusangolo ha angolo/i
2 Puoi costruire un triangolo con strisce di questa lunghezza?
5 cm • 4 cm • 8 cm Sì No 7 cm • 21 cm • 10 cm Sì No
3 In ciascun triangolo, disegna l’altezza rispetto al lato colorato di verde.
4 Per ciascuna affermazione, indica con una X se è vera (V) o falsa (F).
• I quadrilateri possono essere concavi. V F
• I rettangoli sono poligoni regolari. V F
• I rettangoli e i quadrati hanno sempre gli angoli retti. V F
• Un trapezio rettangolo può avere 3 angoli retti. V F
5 Per ciascuna caratteristica, scrivi i nomi dei quadrilateri.
• Hanno le diagonali di uguale lunghezza:
6 Aiutati con la tabella e fai le trasformazioni.
• Hanno le diagonali perpendicolari: dam2 m2 dm2 cm2 mm2 da u da u da u da u da u
3 dam2 =
4 m2 =
30 m2 = 500 dm2 =
3 0 0
7 Esegui le trasformazioni. Aiutati con una tabella.
1 km2 = dam2
2,25 m2 = dm2
375 dm2 = m2
0,22 cm2 = mm2
= 300 m2
= dm2
= dam2 = m2
4550 km2 = hm2
458 m2 = hm2
95
Spazio e figure
AREA DEL RETTANGOLO E DEL QUADRATO
• Osserva e completa.
Il rettangolo disegnato è formato da quadratini con lato lungo 1 cm.
La superficie di ogni quadratino è cm2.
• Quanti cm2 ci sono in ogni riga? ............. E quante sono le righe? .............
Se moltiplichi il numero dei cm2 di ogni riga per il numero delle righe, trovi l’
In linguaggio matematico cm2 x 4 = = area
Puoi trovare l’area moltiplicando la misura di un lato per la misura dell’altro lato.
HO CAPITO CHE...
Un lato del rettangolo può essere considerato come base (b) e l’altro come altezza (h), quindi l’area del rettangolo è: A = b x h
• Osserva e completa.
x h : h
b A
Se procedi da sinistra verso destra, trovi l’area.
Se procedi da destra verso sinistra, trovi la base.
Il quadrato è un quadrilatero con i lati tutti ed è anche un rettangolo, perché ha tutti gli angoli
• Per trovare l’area puoi usare la formula del rettangolo? Sì No
Quindi, l’area del quadrato si trova: misura del lato per del lato.
HO CAPITO CHE...
x b : b
h A
Se procedi da sinistra verso destra, trovi l’area.
Se procedi da destra verso sinistra, trovi l’altezza.

L’area del quadrato si trova moltiplicando la misura del lato per se stesso. A = l x l oppure A = l2
E l’area del quadrato?
96 Quaderno pp. 232-234
AREA DEL TRIANGOLO E DEL PARALLELOGRAMMA
• Osserva e completa.
Con due triangoli uguali puoi formare un , quindi la superficie del triangolo è: la metà il doppio di quella del rettangolo.
h h
Il lato lungo del rettangolo è uguale alla del triangolo. L’altezza del rettangolo è all’altezza del triangolo.
Puoi quindi trovare l’area del triangolo partendo da quella del rettangolo: (b x h), ma siccome il triangolo è metà rettangolo, l’area andrà divisa a metà.
HO CAPITO CHE...
Per calcolare l’area del triangolo si moltiplica la misura della base per la misura dell’altezza e si divide il prodotto per 2. A = b x h : 2
• Osserva lo schema e rifletti. Poi aiuta Marco a rispondere.
Come si misura l’area degli altri quadrilateri?

HO CAPITO CHE...
La figura ABCD è un Marco traccia l’altezza dal vertice A.
Ha ottenuto un : coloralo di giallo. Marco prende il triangolo giallo e lo trasla a destra del parallelogramma, ottiene un rettangolo. quadrato.
Il rettangolo ha l’area a quella del parallelogramma.
La base del rettangolo è alla base del L’altezza del rettangolo è uguale all’altezza del
Per calcolare l’area del parallelogramma si moltiplica la misura della base per la misura dell’altezza. A = b x h
b b
b A x h : 2 : h x 2 h A x b : 2 : b x 2 oppure
A
D C
D C
B
A B
Spazio e figure 97 Quaderno pp. 234-235
Spazio e figure
AREA DEL ROMBO
E l’area del rombo?
… Secondo me si può trasformare anche il rombo!

Marco
Omar
• Aiuta i due amici.
Sul quaderno disegna un rombo e traccia una sua diagonale.
Colora uno dei triangoli che hai ottenuto.
Taglia lungo la diagonale e poi dividi a metà il triangolo che hai colorato.
Fai ruotare i triangoli colorati e portali sotto al triangolo bianco come nella
figura accanto.
Hai ottenuto un che ha l’area uguale all’area del rombo.
La base del rettangolo è alla diagonale del rombo.
L’altezza del rettangolo è uguale a metà dell’altra diagonale.
• Quindi, per calcolare l’area puoi usare la formula del rettangolo? Sì No
Se l’area del rettangolo è h x b
l’area nel rombo diventa (d : 2) x d
quindi A = (d x d) : 2
In schema:
Sai che il quadrato è un rombo; puoi quindi trovare la sua area anche così (d x d) : 2
HO CAPITO CHE...
d A

x d : 2 : d x 2
Per calcolare l’area del rombo devo moltiplicare la misura delle lunghezza delle diagonali e dividere per 2. A = (d x d) : 2
d
12,5 cm d
6 cm A
1. Completa. PROVO IO
=
=
= d = 14 cm A = 42 cm2 d =
98 Quaderno pp. 236-237
AREA DEL TRAPEZIO
• Aiuta Gianni.
Sul quaderno, disegna due trapezi uguali. Ritaglia uno dei trapezi, ribaltalo e fai combaciare uno dei lati non paralleli.
E il trapezio, allora, in quale quadrilatero può essere trasformato per misurare la sua area?
b b b b b
h b
h h
Hai ottenuto un parallelogramma formato da 2
L’area del trapezio, quindi, è la dell’area del
La base del parallelogramma è la somma delle basi del trapezio, ma l’altezza è
Se l’area del parallelogramma è b x h
l’area del trapezio, allora, sarà (b + b) x h : 2
• Aiuta Sofia a rispondere.
Ricalca il trapezio rettangolo, ritaglialo e ribaltalo come hai fatto prima.

E se fosse un trapezio rettangolo?
Hai ottenuto un la cui area è il dell’area del trapezio. Anche in questo caso l’area del trapezio è (b + b) x h : 2

HO CAPITO CHE...
L’area del trapezio si calcola moltiplicando la somma delle misure delle basi per la misura dell’altezza e dividendo il prodotto per 2. A = (b + b) x h : 2
PROVO IO

1. Dividi ciascuna figura in modo da ottenere sempre due trapezi congruenti. Poi rispondi.
• Ciascun trapezio quale parte rappresenta dell’intera figura?
Misura la lunghezza dei lati e calcola l’area di ciascun trapezio.
Spazio e figure 99 Quaderno pp. 238-239
1 Calcola l’area e il perimetro delle seguenti figure. Usa come unità di misura il lato del quadretto per il perimetro e il quadretto per l’area. Poi completa.
Fig. Fig. Fig.
• Ci sono figure equivalenti: quali sono?
• Ci sono figure isoperimetriche: quali sono?
2 Calcola.
3 Calcola il perimetro e l’area.
A = A = A = A = A = A = P = P = P = P = P = P = P = A = P = A = P = A = P = A = P = A = P = A = h = 12 cm 7 cm 16 cm h = 6 cm 12 cm 5 cm 10 cm 13 cm 8 cm 1 4 5 6 2 3
Fig. 1 Fig. 2 Fig. 3 Fig. 4 Fig. 5 Fig. 6
5 cm 4 cm 12 cm 7 cm 7 cm 5 cm 6 cm 14 cm 4 cm 8 cm 6 cm 5 cm
Fig. Fig. Fig.
P
P
A
A
=
=
=
=
d = 4 cm d = 8 cm 13 cm ESERCIZI 100
4 Il perimetro di un quadrato è 64 cm. Calcola la misura di un lato e l’area.
5 Questi due triangoli hanno lo stesso perimetro. Quanto misura l’area del triangolo equilatero se l’altezza è 10,4 cm?
14 cm 8 cm
6 Un rombo ha l’area di 48 cm2. Se una diagonale misura 8 cm, quanto misura l’altra diagonale?
7 Trova il perimetro e l’area del seguente triangolo rettangolo isoscele.
30 cm
42 cm
30 cm
8 Un rombo ha una diagonale di 10 cm e l’altra la diagonale di 4 cm. Calcola l’area.
9 In un rettangolo una dimensione misura 9 cm e l’altra 4. Rispondi.
• Quanto misura l’area del rettangolo? .....................................................
• Quanto misura il perimetro del rettangolo?
• Quanto misura il perimetro di un quadrato isoperimetrico?
• Quanto misura il lato del quadrato?
• Quanto misura l’area del quadrato? .....................................................
10 Osserva il disegno, poi rispondi.
• Quanti rettangoli ci sono? ................ Quanti triangoli? ................
• Quant’è l’area di un triangolo rispetto al rettangolo?
• Quant’è l’area del rettangolo di partenza rispetto a un triangolo?
• Come sono i due triangoli? .....................................................
Copia e ritaglia i vari pezzi.
Usali tutti e costruisci un trapezio isoscele e un parallelogramma.
Il trapezio e il parallelogramma sono sicuramente
101
Storie matematiche

PITAGORA: MITO E LEGGENDA
Ti ricordi di Pitagora? Quel ragazzo nato nell’isola di Samo che vinse le Olimpiadi nella disciplina sportiva del pugilato e che pensava che i pianeti, muovendosi nel cielo, producessero un suono celestiale?
Siamo nell’antica Grecia e Pitagora è ormai cresciuto, è diventato adulto. Curioso e desideroso di conoscere il mondo, ha viaggiato per moltissimi anni recandosi dagli studiosi più importanti della sua epoca.
Con loro ha condiviso le sue conoscenze e al tempo stesso ha imparato moltissime cose nuove. Pitagora è diventato un filosofo, cioè un “amante della sapienza”, come lui stesso amava definire le persone che cercavano di dare una spiegazione agli eventi naturali senza fare ricorso alla mitologia o a spiegazioni che richiamano l’intervento divino.
Pitagora, però, sente il bisogno di ritornare nell’isola dov’è nato e cresciuto. Lì viene accolto con affetto dai suoi concittadini e fonda una scuola nella quale insegna tutto quello che aveva imparato nei suoi lunghi viaggi: geometria, alchimia, cosmologia, fisica, medicina e musica.
102

Il suo amico d’infanzia Policrate con il passare degli anni prende il comando dell’isola e ne diventa il tiranno. È lui, infatti, che decide tutto, senza ascoltare o chiedere consiglio agli altri cittadini.
Se da bambini erano stati amici, da adulti non vanno più d’accordo. A Policrate non piacciono le idee di fratellanza, di giustizia e libertà che Pitagora diffonde nella sua scuola. Si racconta che, un giorno, Pitagora andò a parlargli e Policrate, per dispetto, lo fece aspettare per molto tempo in una sala.
Mentre se ne stava seduto ad aspettare, Pitagora si mise a osservare le piastrelle quadrate del pavimento e fu colto da un’illuminazione.
Che cosa avrà visto Pitagora in quelle mattonelle?
Proviamo a scoprirlo insieme.
• Osserva il disegno accanto.
Rappresenta le piastrelle quadrate.
Che tipo di triangolo è quello colorato di azzurro?
• Ricalca i quadrati gialli su di un foglio, dividili a metà lungo la diagonale e ritagliali.
Quanti triangoli hai ottenuto?
Che proprietà hanno? Sono
• Usa questi triangoli per ricoprire la superficie del quadrato con il contorno arancione. Riesci a ricoprirla completamente? SÌ NO
Allora puoi dire che la superficie del quadrato grande è uguale diversa alla somma delle superfici dei due quadrati piccoli, cioè le superfici sono equivalenti.
Storie matematiche 103
Ma questa proprietà varrà solo per i triangoli rettangoli isosceli o vale per qualsiasi triangolo rettangolo? Proviamo a scoprirlo!
• Osserva il disegno accanto.
Questa volta il triangolo azzurro è
Il quadrato piccolo ha il lato uguale al del triangolo
Il lato del quadrato medio ha il lato
uguale al del triangolo.
il quadrato rosso ha il lato uguale al
• Ricalca i due quadrati gialli.
Dividi un quadrato in 4 parti uguali come nel disegno.
Hai ottenuto 4 uguali
Ciascun rettangolo è / del quadrato.
Quindi il quadrato è volte il rettangolo.
Usa tutti i 5 pezzi per ricoprire il quadrato con il contorno rosso.
Riesci a ricoprirlo completamente? SÌ NO
Quindi la proprietà vale anche per un triangolo rettangolo scaleno.
Questa proprietà è conosciuta da tutti come il teorema di Pitagora, ma, in realtà, già i Babilonesi, vissuti 1 000 anni prima di Pitagora la conoscevano.
Gli anni passano e Policrate diventa sempre più potente e presuntuoso, per cui Pitagora è costretto a fuggire dalla sua tirannia. Emigra a Crotone, nella Magna Grecia dove fonda una nuova scuola: la Scuola Pitagorica.
Il motto di Pitagora è “Tutto è Numero”: ogni aspetto della vita è fondato sui numeri naturali. Secondo Pitagora il numero è l’elemento che forma tutto.
I Pitagorici immaginavano i numeri come un insieme di palline disposte in modo da formare figure geometriche: sono i numeri triangolari, quadrati e rettangolari che hai incontrato nel Sussidiario di quarta. Per ricordarli, facciamo un gioco.
104 Storie matematiche
Gioca con I numeri di Pitagora!
• Considera il numero quadrato 3² e il suo precedente 2².
3² = 3 x 3 = 2² =
Quello che vedi è il disegno dei due numeri quadrati.
3² 2²
• Ora calcola la loro differenza sovrapponendo i numeri.
Quante palline verdi restano? ...........
Scrivi in linguaggio matematico l’operazione eseguita: 3² – 2² = 9 – ........... = ...........
È un numero pari o dispari? .......................................
Prova ancora; calcola la differenza dei due numeri quadrati 4² e 3².
Disegnali nel rettangolo accanto e confrontali come hai fatto prima.
Quante palline restano? ...........
Scrivi in linguaggio matematico ciò che hai fatto: 4² – ........... = ........... – ........... = ...........
È un numero pari o dispari? ...........
Anche questa volta hai trovato un numero .....................
Puoi dire allora che ogni numero dispari si può ottenere come differenza tra due numeri ..................... consecutivi.
Con il passare dei secoli Pitagora è diventato un mito in tutto il mondo e su di lui si raccontano storie incredibili. Si dice che un fiume lo abbia salutato, che abbia accarezzato un’aquila bianca e che, grazie a questo gesto, questa sia diventata docile.
Si dice che, mentre fuggiva da un suo nemico, si sia trovato di fronte ad un campo di fave. Poiché le odiava, piuttosto che mettersi in salvo attraversando il campo, ha preferito farsi catturare ed uccidere.
Non sappiamo se questi episodi siano davvero avvenuti, ma una cosa è certa: Pitagora fu il primo a considerare la Matematica come la regina delle Scienze
Storie matematiche 105
I POLIGONI REGOLARI
Un poligono è regolare se ha tutti i e gli angoli
• Colora i poligoni regolari e traccia le diagonali che escono da un vertice.
• Completa il poligono sotto: è un esagono e il segmento blu è una delle sue diagonali, ma è anche un asse di simmetria. Disegna le altre diagonali dell’esagono, che sono anche assi di simmetria, osserva e rispondi.
Quante sono?
Quanti assi di simmetria ha un poligono regolare?

• Osserva l’esagono sotto e completa. I segmenti verdi che vedi tratteggiati uniscono i punti medi di due lati opposti del poligono.
• Quanti sono? ..................
• Ciascuno di questi segmenti è anche un asse di simmetria? Sì No
Osserva: degli assi di simmetria dell’esagono coincidono con le diagonali e coincidono con i segmenti che uniscono i punti medi dei lati. In tutto sono Confronta gli assi di simmetria con i lati dell’esagono. I lati sono e gli assi di simmetria sono , quindi sono
Il punto d’incontro degli assi di simmetria è il centro del poligono (o centro di simmetria).
Spazio e figure 106
• Aiuta Samuela a rispondere osservando questo pentagono.

Individua nel pentagono il punto medio di ciascun lato.
Spazio e
figure
E se il poligono ha un numero dispari di lati?
Traccia nel pentagono i segmenti che uniscono un vertice con il punto medio del lato opposto, che si chiamano mediane. Quante ne hai disegnate?
• Sono anche assi di simmetria? Sì No
• Conta i lati: sono
• Conta gli assi di simmetria: sono Puoi dire allora che gli assi di simmetria sono tanti il numero dei lati. Anche in questo caso il punto d’incontro degli assi di simmetria è il centro del poligono.
HO CAPITO CHE...
Tutti i poligoni regolari hanno tanti assi di simmetria quanti sono i lati.
Ciascun poligono regolare ha un centro di simmetria
PROVO IO

1. Disegna tutte le diagonali in questi poligoni regolari. Poi rispondi.
• C’è qualche poligono regolare che non ha diagonali? Sì No Qual è?
2. Disegna tutti gli assi di simmetria nei seguenti poligoni regolari, poi completa.
È un e ha assi di simmetria. Tutti gli assi partono da un e arrivano al opposto.
È un ................................................... e ha ....................... assi di simmetria. Due assi sono le .............................................; gli altri due assi partono dalla metà di un e arrivano alla metà del opposto e sono le 107 Quaderno pp. 240-241
L’AREA DEI POLIGONI REGOLARI
Il perimetro di un poligono è la somma della lunghezza dei lati.
• Come si trova l’area di un poligono regolare? Completa.
Trova il centro del poligono tracciando leggermente gli assi di simmetria.
Con la matita rossa, unisci il centro con i vertici.
Hai diviso il poligono in triangoli, cioè tanti quanti sono i suoi lati.
Sono tutti triangoli uguali e un loro lato coincide con un lato del poligono.
Traccia l’altezza di un triangolo.
L’altezza di uno dei triangoli è l’apotema del poligono.
Ricalca su un foglio e ritaglia i triangoli ottenuti e mettili uno accanto all’altro. Ora raddoppia i triangoli e disponili come in figura.
Osserva la figura ottenuta: è un
Il lato lungo che fa da base, che parte del poligono è? È il
Disegna la sua altezza: con quale parte del poligono coincide? Con l’
Quindi, per trovare l’area del poligono puoi utilizzare la formula dell’area del parallelogramma, ma poi devi dividerla in due, poiché l’area del poligono è la metà dell’area del parallelogramma.
Area parallelogramma b x h
Area poligono p x a : 2
HO CAPITO CHE... 1.
PROVO IO

L’area di un poligono regolare si trova moltiplicando la misura del perimetro per la misura dell’apotema e dividendo il prodotto per 2.
A = P x a : 2
Calcola.
l = 8 cm a = 6,9 cm P = A = ............................ l = 5 cm a = 3,4 cm P = A = ............................
Spazio e figure 108
L’APOTEMA DEI POLIGONI REGOLARI
I matematici e le matematiche hanno dimostrato che c’è una relazione tra il lato di un poligono regolare e il suo apotema. Scopriamola insieme.
• Osserva questi quadrati.
Hanno i lati , ma sono tutti divisi in triangoli
• Misura il lato e l’apotema in ciascun quadrato e completa.
Quadrato blu Quadrato verde Quadrato rosso lato = ................. lato = ................. lato = ................. apotema = apotema = apotema = a : l = a : l = a : l =
• Osserva il quoziente che hai ottenuto in ciascuna divisione: è sempre
Il numero 0,5 è il numero fisso del quadrato; vuol dire che in qualsiasi quadrato il rapporto fra l’apotema e il suo lato è sempre 0,5
PROVO IO

1. Disegna il centro in ciascun poligono, poi esegui.
• In ciascun poligono, unisci il centro con i vertici.
....................
• Scrivi in quanti triangoli hai diviso ciascun poligono.
• Traccia l’apotema.
In ciascun poligono regolare, il rapporto tra l’apotema e il lato del poligono è il numero fisso a : l = n° fisso
a n° fisso : l x l
1 cm 2 cm 3 cm
HO CAPITO CHE...
Spazio e figure 109 Quaderno p. 240-241


Storie matematiche
LA LEGGENDA DI DIDONE
Didone viveva a Tiro, città fenicia posta nei territori che oggi corrispondono alla Libia. Era una principessa: era la sorella di Pigmalione, re della città, e moglie di Sicheo, un sacerdote molto ricco. Un giorno il marito fu ucciso e Didone scoprì che il responsabile della morte era suo fratello, che lo aveva fatto uccidere per impossessarsi delle ricchezze. Didone capì allora di essere anche lei in pericolo e decise di fuggire da Tiro di nascosto, con l’aiuto di un piccolo gruppo di amici fedeli. La principessa viaggiò a lungo per il Mar Mediterraneo, finché approdò sulle coste dell’Africa Settentrionale, nei pressi dell’attuale Libia.

 I VIAGGI DI DIDONE
I VIAGGI DI DIDONE
110
Si innamorò del luogo e così contattò Iarba, il re del posto, per chiedergli di vendergli una porzione di terreno per costruire la sua città. Il re non voleva e così, in modo sprezzante, diede a Didone la pelle di un bue dicendole che avrebbe potuto prendere tanto terreno quanto poteva contenerne quella pelle.


Riesci a immaginare quanto grande può essere la pelle di un bue? Ci avrebbe potuto costruire una città, secondo te?
Didone, però, era una donna intelligente e non si perse d’animo. Escogitò un astuto stratagemma riuscendo ad accaparrarsi una bella porzione di terreno, compresa la collina sulla quale voleva costruire la rocca. Sai che cosa fece? Ordinò di tagliare la pelle in tante strisce sottilissime e poi le fece legare insieme ottenendo una lunghissima corda.
Storie matematiche 111
Che cosa aveva in mente Didone?
Scopriamolo insieme.
• Ricalca e ritaglia 4 strisce uguali a quelle che vedi disegnate. Ogni striscia sarà per noi una delle strisce preparate da Didone con la pelle di bue, ma per comodità le abbiamo fatte un po’ più alte.
• Piega le strisce lungo le linee tratteggiate che vedi disegnate, poi unisci le estremità senza sovrapporle e chiudile con lo scotch, come vedi in figura.
• Osserva l’impronta: che figure hai ottenuto?
Un triangolo, un ........................................................................
Siccome per costruirle hai usato strisce della stessa lunghezza, queste figure hanno tutte lo stesso ......................
• Ora ricopri con uno strato di ceci, biglie di plastica o di perline la superficie del triangolo, poi svuotala e usa gli stessi ceci per ricoprire la superficie del quadrato.
Ricopri interamente la sua superficie o restano spazi vuoti?


• Procedi nello stesso modo riempiendo gli altri poligoni e infine prova con il cerchio. Se restano spazi vuoti, aggiungi ceci, perline o biglie.
Quale figura contiene più ceci, biglie o perline? .....................................................................................................
L’avresti mai immaginato? A parità di perimetro, il ...................................................... ha l’area massima!
112 Storie
matematiche
...............................................................................................................................
.....

Ecco perché le città medievali hanno le mura di forma circolare!
Pensa alla cittadina di Monteriggioni in Toscana, le cui mura, ancora intatte, ci permettono di conoscere le strategie usate in quell’epoca! Meno confine da difendere, più superficie per le città.
Anche gli animali lo sanno!
Le pecore chiuse nell’ovile si dispongono in cerchio per proteggere più pecore dai predatori.


E tu quando senti freddo ti rannicchi! Perché?
Allora Didone avrà costruito la sua città di forma circolare!
Certamente no! Perché? Fu talmente astuta, ma talmente astuta, che costruì la sua città a forma di semicerchio, per avere ancora più superficie. Con la pelle fece congiungere le rive dei lati opposti dell’altura, acquisendo così la collina e un comodo sbocco sul mare. Che furba!
Il problema di Didone è diventato molto famoso in Matematica come “il problema dei poligoni isoperimetrici”.
Storie matematiche 113
LA CIRCONFERENZA E IL CERCHIO
Nella realtà e in natura ci sono diversi elementi che ci ricordano la forma di cerchio.

• Leggi e completa.

Il cerchio è una figura piana racchiusa da una linea la circonferenza.


Tutti i punti della circonferenza hanno la stessa distanza dal
Lo strumento che utilizziamo per disegnare questa figura è il
cerchio
circonferenza
La corda è il segmento che unisce due punti sulla circonferenza.
Il diametro è la corda che passa per il centro. Tra tutte le corde il diametro è quella più lunga.
Il raggio è il segmento che unisce il centro con un punto qualsiasi della circonferenza e corrisponde alla metà del diametro.
centro
• Osserva e completa.
Il diametro divide il cerchio in parti uguali; ogni parte si chiama semicerchio.
Il diametro divide anche la circonferenza in due parti uguali: semicirconferenza.
Il settore circolare è la parte di cerchio compreso tra due raggi.
HO CAPITO CHE...
Il cerchio è la parte di piano racchiusa da una linea curva detta circonferenza.
...............................................
Spazio e figure 114 Quaderno p. 244
1 Completa con i nomi corretti.
2 Usa il righello per misurare e completa.
3 Disegna un quadrato nel cerchio unendo solo
4 punti di quelli disegnati sulla circonferenza.
Il raggio è cm
Il diametro è cm
Il raggio è la del diametro.
Il diametro è il del raggio.
4 Questi segmenti rappresentano, in ordine sparso, i raggi e i diametri di tre circonferenze.
Usando il righello, collega ciascun raggio al corrispondente diametro. RAGGI
5 Osserva, rifletti e rispondi.
• Quanti punti puoi disegnare sulla circonferenza?
• Quanti raggi può avere un cerchio?
• Quanti diametri?
• Se metti uno specchio sul centro del diametro, noti che è un
DIAMETRI
115 ESERCIZI
Spazio e figure
LA CIRCONFERENZA
• Aiuta Liam a rispondere.
Per misurare la circonferenza del portapenne quale oggetto puoi usare? Circondalo.



Liam prova a misurare la circonferenza del suo nastro adesivo:
Come si trova la misura della circonferenza?

prende uno spago e lo mette intorno al nastro adesivo e segna dove arriva.
Lo taglia nel segno che ha preso e lo distende così:
Ha ottenuto un che è la circonferenza rettificata.
La lunghezza del segmento è la misura della ........................................................

Usando lo spago, misura anche il diametro del nastro adesivo e lo distende.

• Esegui e rispondi.
Quante volte il diametro è contenuto nella circonferenza?
Prendi uno spago lungo quanto la lunghezza del diametro e riportalo sulla circonferenza rettificata.
Quante volte il diametro entra nella circonferenza? volte e avanza un pezzettino.
Quindi la circonferenza è lunga volte e un pezzettino il suo diametro.
I matematici e le matematiche hanno indicato questo valore con il simbolo p che si legge “pi greco”.
Il matematico Archimede approssimò il valore di p a 3,14.
Siccome circonferenza : diametro = p allora d x p = circonferenza se approssimi p, scrivi d x 3,14 = circonferenza
HO CAPITO CHE...
Per calcolare la misura della circonferenza devo moltiplicare la misura del diametro per p. C = d x p
116
AREA DEL CERCHIO
Per trovare l’area del cerchio, non è possibile scomporlo in poligoni che conosci, perché il cerchio è limitato da una linea curva.
Possiamo, però, paragonare il cerchio a un poligono che gli assomiglia.
• Sul quaderno, disegna un cerchio e dividilo in sei settori circolari uguali.
Ritaglia i settori e sistemane tre uno accanto all’altro e gli altri tre sopra a incastro. Ottieni una figura che assomiglia a un parallelogramma.
Ripeti lo stesso procedimento dividendo il cerchio in 8 settori: ricalca il cerchio rosa, ritaglia i settori e incollali nel rettangolo accanto.
E se lo dividi in più parti?

Il quadrilatero che ottieni assomiglia sempre più a un , quindi, più settori hai, più l’area del cerchio diventa quasi uguale all’area del
Il parallelogramma che ottieni ha la base uguale alla lunghezza di metà circonferenza e l’altezza al raggio.
Puoi calcolare l’area usando la formula del parallelogramma?
Sì No A = h x b
Nel cerchio diventa A = r x C : 2 oppure A = r2 x p che, approssimando p, diventa A = r2 x 3,14
HO CAPITO CHE...
Per calcolare l’area del cerchio devo moltiplicare il quadrato del raggio per p. A = r² x p
Spazio e figure 117 Quaderno pp. 244-245

3,1415
FESTA DELLA MATEMATICA
Il 14 marzo è il giorno dedicato alla festa della Matematica. Come simbolo di questo giorno è stato scelto un numero importantissimo chiamato PI GRECO. È grazie a esso che gli architetti e le architette possono costruire archi, gallerie e tunnel.
La “prima volta” che incontri questo numero è nello studio del cerchio. Infatti esso indica il rapporto che c’è tra il diametro del cerchio e la sua circonferenza, cioè quante volte il diametro sta nella lunghezza della circonferenza. Che numero è?
Per scoprirlo, calcola il rapporto fra il diametro e la lunghezza della circonferenza in ciascuno di questi cerchi.
circonferenza:
diametro:
circonferenza:
diametro:
circonferenza:
diametro:
Che numero hai ottenuto ciascuna volta?
Adesso scrivi la data del 14 marzo in forma abbreviata, scrivendo prima il mese e poi il giorno:
Confronta la data che hai scritto con il numero abbreviata: che cosa osservi?
In realtà il numero è molto più grande e ancora oggi non è stato scoperto del tutto.
Nell’agosto del 2021 in Svizzera è stato battuto il record calcolando ben 62800 miliardi di cifre decimali:
3,1415926535 8979323846 2643383279 5028841971 6939937510 58209…
E ora gioca con puzzle di quadrati
Osserva questo rettangolo.
• È formato da quadratini.
• È stato diviso in quadrati più grandi: quanti sono?
• Riesci a dividerlo in un numero minore di quadrati? Prova.
/
118
Happy day 3,1415
• Prova ora con questo rettangolo.
Secondo te, è possibile dividerlo in sei quadrati? Sì No

E questo rettangolo, in quanti quadrati riesci a dividerlo?
Confrontati con i compagni e le compagne: avete diviso il rettangolo nello stesso modo?
Qualcuno/a è riuscito a dividerlo in un numero minore di quadrati rispetto a te?
• Secondo te, sarà più facile dividere un quadrato rispetto al rettangolo? Verifica ciò che hai pensato dividendo questi quadrati.
In quanti quadrati è stato diviso? .................
Puoi dividerlo in meno quadrati?
È possibile dividere questo in 10 quadrati?
Prova, poi confrontati con i compagni e le compagne.
119
PROBLEMATICAMENTE
Leggi e completa
1 Con 5 ritagli di cartoncino di forma poligonale Silvia ha composto l’iniziale del suo nome. Quali forme possono avere i cartoncini usati da Silvia?
2 Per trovare la risposta dividi la S in 5 poligoni. Scrivi il nome di ciascun poligono e le misure dei suoi lati. Misura i lati con il righello.
• Poligono 1:
Misure lati:
• Poligono 2:
Misure lati:
• Poligono 3:
Misure lati:
• Poligono 4:
Misure lati:
• Poligono 5:
Misure lati:
3 C’è un altro modo di dividere la figura? Prova e disegna la nuova suddivisione.
• Poligono 1:
Misura lati: ........................................................................................................................
• Poligono 2:
Misura lati:
• Poligono 3:
Misura lati: ........................................................................................................................
• Poligono 4:
Misura lati:
• Poligono 5:
Misura lati:
4 Confronta le tue soluzioni con quelle dei compagni e delle compagne e rispondi. Avete suddiviso la S tutti nello stesso modo? Sì No
Perché?
.......................................................................................................................................................................................................................................................................................................................... 120
Adesso risolvi il problema
5 Le soluzioni possibili quindi sono molte. Ma quali saranno i poligoni trovati da Silvia?
I suoi appunti ti potranno aiutare. Infatti lei aveva scritto su un foglietto come ha calcolato l’area di ciascun poligono trovato.
Osserva le misure che ha scritto e scopri a quale poligono appartengono, seguendo il procedimento scritto sotto. Usa il lato di quadretto come unità di misura.

3 x 3
[(6 + 3) x 3] : 2
(6 x 3) : 2
9 x 3
[(9 + 6) x 3] : 2
Poligono 1: area = 9 x 3
Osserva: c’è solo una possibilità per disegnare un poligono di 9 x 3 lati di quadretti.
Qual è questo poligono?
quadrato rettangolo triangolo
rombo trapezio
Disegnalo nella figura a lato.
6 Procedi nello stesso modo per trovare gli altri poligoni e disegnali nella figura.
Poligono 2: area = 3 x 3
Poligono 4: area = [(6 + 3) x 3] : 2
Poligono 3: area = (6 x 3) : 2
Poligono 5: area = [(9 + 6) x 3] : 2
7 Calcola la misura dell’area della figura S.
121
1 Risolvi sul quaderno.
a. Per la festa della scuola, Luisa deve bordare con del nastro 12 bandierine a forma di triangolo equilatero. Il lato di ciascuna bandierina è 12 cm. Quanti cm di nastro servono a Luisa?
b. Marco ha un telo da mare formato da 10 quadrati rossi e gialli. Il lato di un quadrato è 15 cm. Di quanti cm2 è la superficie del telo?
f. Nella scuola di Nina c’è un giardino di forma quadrata con il perimetro di 80 m. Quanto misura un lato del giardino? Quanto misura la superficie?
g. Calcola l’area della parte con l’erba di questo giardino.
1,2 m
2 m
6 m
h. Dentro un piazzale a forma di cerchio è stata ricavata un’aiuola quadrata. Calcola:
c. Omar si allena tutti i giorni in questo campo sportivo. Ogni giorno fa 10 volte il giro del campo.
Quanti km percorre in un giorno? E in 5 giorni?
50 m
d. Il perimetro di un quadrato è 64 cm. Trova la misura di un lato e l’area.
e. A casa della nonna c’è un vecchio tappeto di forma esagonale formato da triangoli equilateri con il lato di 0,8 m e l’altezza di 0,69 m. Quanto misura l’area del tappeto?
30 m
• la lunghezza del raggio del piazzale, sapendo che la diagonale dell’aiuola è lunga 5 m;
• l’area e la misura della circonferenza del piazzale.
i. Calcola il perimetro e l’area del campo da gioco della squadra di Paesebello.
P = A = ....................................................................
8 m
15 m
122
ESERCIZI
l. Il nonno di Elisa ha un terreno a forma di rettangolo, con i lati di 18 m e 7 m.
I 2 3 della superficie del terreno sono coltivati, mentre il resto è giardino. Quanto misura l’area del giardino?
7 m
m. Greta, con gli avanzi di stoffa, vuole fare una coperta a patchwork. Ritaglia dagli avanzi
68 rombi tutti uguali con le diagonali di 64 cm e di 24 cm e li cuce insieme. Quanto misura la superficie della coperta?

18 m
n. Il nonno di Luca vuole recintare un pezzo del suo terreno per fare un piccolo orto. Vuole farlo bello ampio, ma è indeciso se farlo rettangolare o quadrato. Aiutalo tu: disegna figure di perimetro uguale a quello disegnato dal nonno, usando come unità il lato del quadretto. Quale forma sceglierà il nonno? Perché?
o. In cucina c’è un tavolo rotondo che ha il diametro di 70 cm. Leonardo vuole realizzare una tovaglia che sporga 15 cm dal bordo del tavolo. Quale sarà il diametro della tovaglia?
Decide poi di bordare la tovaglia con del nastro: quanti centimetri di nastro gli serviranno?
p. Osserva i triangoli della figura sotto e rispondi aiutandoti con il righello.
• Quanti e quali triangoli colorati vedi?
• Sono tutti equivalenti? Perché?
• Sono isoperimetrici? Perché?
Spiega il tuo ragionamento.
123
SOLIDI
RICONOSCERE I SOLIDI
Guardando nella cesta dei giochi, Amelia trova queste costruzioni in legno.
l I
Decide di metterle in ordine suddividendole in due scatole.
• Osserva il criterio scelto da Amelia e sistema ciascuna costruzione nella scatola giusta. Poi rispondi.
Scatola 1
Scatola 2
Costruzioni con facce formate solo da poligoni. .................................................................................
Costruzioni con facce formate solo da poligoni:
Le costruzioni di Amelia si chiamano solidi.
I solidi delimitati solo da poligoni si chiamano poliedri.
• Quale delle due scatole contiene i poliedri?
Costruzioni con facce formate solo da poligoni. .................................................................................
Costruzioni con facce formate anche da non poligoni:
I poligoni che delimitano un poliedro si chiamano facce del poliedro, i lati del poligono sono gli spigoli del poliedro, mentre i vertici del poligono sono anche i vertici del poliedro.
e
c
a b d
h f g i
• Scrivi in questi solidi il nome delle parti indicate. 124
• Giochiamo: la formichina F vuole raggiungere la briciola di pane B . Per arrivarci può camminare solo lungo gli spigoli del cubo.
Trova il percorso minimo che può fare per raggiungere la briciola.
C’è un solo percorso minimo? Se ce ne sono altri, mostrali.
E in questi casi, invece, quali cammini minimi può fare? Mostrali.
CLASSIFICARE I POLIEDRI
• Osserva questa scatola e descrivila dal punto di vista geometrico.

• Osserva i solidi di Amelia e rispondi.
È un solido che ha ................ facce, ................ vertici e ................ spigoli. Le facce sono dei , quindi puoi dire che la scatola
è un poliedro? perché è delimitata da Le facce opposte di questo poliedro sono fra di loro parallele e uguali.
• Quali poliedri hanno le caratteristiche sopra descritte? I poliedri
• Tutti i poliedri hanno le facce opposte uguali e parallele? Sì No
• Tutti i solidi hanno due basi uguali e parallele? Sì No
• Quali poliedri hanno due basi? I poliedri
• Quale poliedro ha una sola base, mentre le altre facce sono tutti triangoli?
F B F B F B
I solidi 125
In base alle caratteristiche che hai osservato, possiamo dividere i poliedri in 2 gruppi.
a) PRISMI
Sono i poliedri che hanno 2 facce opposte uguali e parallele, le altre sono rettangoli.
b) PIRAMIDI
Sono i poliedri che hanno una faccia che può essere un poligono qualsiasi e le altre sono tutti triangoli.
cubo
prisma a base pentagonale
parallelepipedo prisma a base esagonale piramide a base pentagonale
• Fra i solidi trovati da Amelia, quali sono i prismi?
• E quali le piramidi?
• Quali sono i solidi che non sono né prismi né piramidi?
piramide a base triangolare
piramide a base quadrata
• Questi che vedi sono dei poliedri speciali: come mai? Scopriamolo!
Osserva le facce di ciascun poliedro: sono tutte uguali diverse
A B C D E
• Scrivi da quali poligoni è formato ciascun poliedro: nel poliedro A sono tutti triangoli ; nel B sono tutti ; nel C sono tutti triangoli ; nel D sono tutti ; nel E e sono tutti Ricorda che, oltre al pentagono regolare, anche il triangolo equilatero e il quadrato sono poligoni regolari. I poliedri formati da poligoni regolari sono poliedri regolari.
• Conta quanti sono:
Quaderno pp. 246-247 I solidi 126
LA SUPERFICIE DI UN SOLIDO
Giulia ha questa scatolina che vuole rivestire con della carta da regalo. Per essere sicura di avere abbastanza carta, decide di aprire la scatola lungo gli spigoli e di distenderla sul piano.
• Indica con una X quale delle due figure ottiene.

• Da quali poligoni è formata? Da 4 .......................................................... e ..........................................................
Questi poligoni formano lo sviluppo in piano del parallelepipedo.
• Secondo te, avrebbe potuto aprire la scatola in questi altri modi?
Scoprilo usando carta e scotch: disegna 4 rettangoli uguali e 2 quadrati uguali, disponili secondo gli sviluppi che vedi sotto e poi prova a ricostruire la scatola.
• Colora di giallo le due facce considerate come basi di appoggio e di verde le facce restanti che formano la superficie laterale della scatola.
Sì No I solidi 127
Sì No
• Usa lo stesso colore per mettere in evidenza i lati dei poligoni che si toccano fra di loro quando costruisci il parallelepipedo. Quaderno pp. 248-249
1 Completa lo sviluppo dei solidi disegnando le facce mancanti. Usa lo stesso colore per colorare le facce opposte.
parallelepipedo cubo
2 Usa come unità di misura un cubetto per misurare i volumi e la faccia di un cubetto per misurare la superficie, poi rispondi.
• Tutti i solidi hanno lo stesso volume? Sì No Perché?
• Tutti i solidi hanno la stessa superficie? Sì No Perché?
Devi dipingere con la tempera la superficie di ciascuno dei tre solidi non considerando le facce su cui appoggiano. Rispondi.
• Quale solido richiederà più tempera?
• Perché? ....................................................................................................................................................................................................................................................................................................
• Quale invece ne richiederà di meno?
• Perché?
A B C
............................................................................................................................................................................................................................................................................................................................
ESERCIZI 128
3 Osserva questi due sviluppi, poi rispondi.
1 2
• Osserva la figura 1: secondo te, di quale solido è lo sviluppo?
La figura 2 potrebbe essere lo sviluppo dello stesso solido?
Verifica le tue risposte ricalcando i due sviluppi e provando a ricostruire i solidi.
• Aiutandoti con il modellino dei due solidi che hai costruito, rispondi.
Osserva lo sviluppo del solido 1.
Da quante facce è formato?
Quanti sono gli spigoli?
E i vertici?
• Ora osserva lo sviluppo del solido 2.
Da quante facce è formato?
Quanti sono gli spigoli?
E i vertici?
• Quali poligoni compongono lo sviluppo del solido 1?
E del solido 2?
• In tutte e due gli sviluppi, usa lo stesso colore per colorare i poligoni uguali.
Puoi dire che entrambi sono formati dagli stessi poligoni? Sì No
Quale solido è un poligono regolare? 129
IL VOLUME DEI SOLIDI
Il volume è la misura dello spazio occupato dal solido.
VOLUME DEL PARALLELEPIPEDO
Scopriamo quant’è grande questo parallelepipedo utilizzando un cubetto da 1 cm³ come unità di misura.
• Lo strato colorato di blu è la base del parallelepipedo.
Da quanti cubetti è formata?
Sono 5 cubetti ripetuti per volte: 5 x = cubetti
Hai trovato la misura della base in unità cubetti.
• Quanti strati uguali alla base sono stati fatti per riempire tutto il parallelepipedo?
Allora calcola: 15 x = cubetti
Il volume di questo solido è di cubetti.
VOLUME DEL CUBO
Procedi come prima:
La base del cubo è formata da cubetti ripetuti per 4 volte, quindi 4 x = cubetti
Hai trovato la misura della del cubo.
Da quanti starti come la base è formato il cubo?
Quindi per trovare il volume del cubo fai: ............. x ............. = ............. cubetti totali
PROVO IO
 1. Calcola il volume dei solidi.
1. Calcola il volume dei solidi.
Quaderno pp. 250-251 I solidi 130
ESERCIZI
1 Calcola il volume dei solidi usando come unità campione il cubetto disegnato sotto a ciascuno. V =
Ricorda
Il volume è il numero delle volte che l’unità campione è contenuta nel solido.
2 Calcola il volume dei solidi usando l’unità campione disegnata. unità
V =
Volume A =
Volume B =
I solidi hanno lo stesso volume? Sì No
Ricorda
Solidi con lo stesso volume sono equivalenti
3 Scrivi il volume di ciascun solido e rispondi. unità
Volume A = Volume B = Volume C = Volume D =
Quale solido ha il volume maggiore?
Quali solidi sono equivalenti?
Quale solido ha il volume minore?
V =
A B
A B C D 131
I solidi 132
LE MISURE DI VOLUME
Tutto ciò che ti circonda occupa uno spazio. Per sapere “quanto” spazio occupano gli oggetti bisogna misurare il volume usando un’unità di misura che abbia 3 dimensioni, perché lo spazio ha 3 dimensioni.
Paolo misura il volume della sua scatola usando campioni differenti: biglie, palline e sassolini.
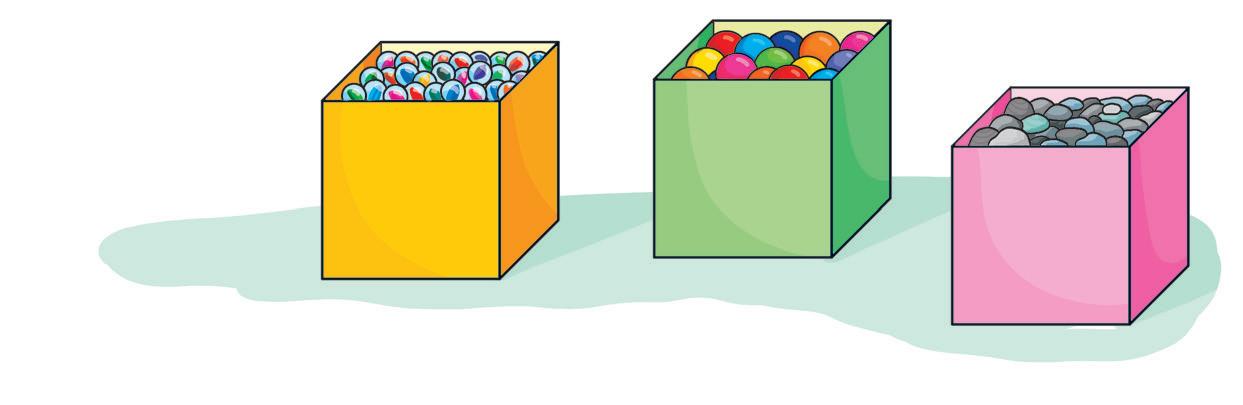
Nel Sistema Internazionale, quindi, l’unità di misura per il volume è il metro cubo, cioè un cubo con lo spigolo di 1 m.
Si scrive m3; il 3 ti ricorda le tre dimensioni.
1
m 1 m 1
Ogni misura è 1000 volte più piccola di quella che precede e 1000 volte più grande della successiva.
m3
• Anche il metro cubo ha multipli e sottomultipli. Osserva e completa. MULTIPLI UNITÀ SOTTOMULTIPLI chilometro cubo ettometro cubo decametro cubo metro cubo decimetro cubo centimetro cubo millimetro cubo km3 hm3 dam3 m3 dm3 cm3 mm3 m3 m3 1000 m3 1 m3 0,001 m3 m3 m3
1m
• Osserva, poi rifletti.
Sono tutte unità di misura con 3 dimensioni, ma nessuna di queste è adatta, perché lascia dei piccoli spazi vuoti e, quindi, non riempie completamente le scatole. Per evitare questo problema i matematici e le matematiche hanno scelto come unità campione un cubo, perché ha 3 dimensioni uguali e questo consente di non lasciare spazi vuoti.
• Completa le trasformazioni inserendo i numeri in tabella.
m3 dm3 cm3 mm3
h da u h da u h da u h da u
1 m3
3 dm3
4 cm3
2000 dm3
5000 cm3
7000 mm3
1 0 0 0 3 4
= 1000 dm3 = cm3 = mm3
m3 dm3 cm3 mm3 h da u h da u h da u h da u
2 0 0 0
• Segui le indicazioni per eseguire queste trasformazioni.
3246 m3 = dam3
hm3 dam3 m3
h da u h da u h da u
3 2 4 6 ,
12,35 hm3 = ......................... dam3
hm3 dam3 m3
h da u h da u h da u
1 2 3 5
PROVO IO

= 2 m3 = dm3 = cm3
Scrivi le cifre che compongono il numero partendo da m3
Osserva le cifre che indicano i dam3, metti la virgola per separare le quantità minori del dam3
Scrivi le cifre che formano il numero partendo da hm3 e arriva ai dam3
Se le cifre non bastano aggiungi gli zeri.
1. Aiutati con la tabella ed esegui le trasformazioni.
8000 m3 = dam3 234 dam3 = hm3
0,057 dam3 = m3
0,41 hm3 = dam3
hm3 dam3 m3 h da u h da u h da u
Quaderno pp. 252-253 I solidi 133
RELAZIONI, DATI E PREVISIONI
L’INDAGINE STATISTICA
Anna e Matteo vivono nella città di Siena e stanno studiando la loro regione. Sono curiosi di vedere quali città della Toscana sono più popolate di Siena.
• Colora il riquadro con l’informazione che i due bambini devono cercare per scoprirlo.
Numero di città presenti in Toscana
Numero di abitanti di ogni regione dell’Italia
Numero di abitanti di ogni città della Toscana
• Per trovare questa informazione possono fare un’indagine diretta, cioè porre direttamente alle persone interessate una domanda? Sì No
• Quindi, in questo caso, dovranno svolgere un’indagine indiretta, cioè dovranno usare tabelle o grafici compilati da altre persone che si sono occupate di raccogliere queste informazioni.
• Secondo te, dove dovranno cercare per trovare il numero di abitanti di ogni città della Toscana?
Dopo alcune ricerche insieme a una persona adulta, i due bambini trovano su Internet la tabella qui sotto.
Città
Siena 247197 250000
Lucca 397876 400000
Massa-Carrara 198878
Livorno 347832
Grosseto 200629
Firenze 1000349
Prato 248716
Arezzo 352654
Pisa 402037
Pistoia 299473
Per semplificare il confronto fra le città decidono di approssimare i numeri alle dak.
• Completa per loro la tabella.
 Grosseto
Siena
Arezzo
Firenze
Pisa
Pistoia Lucca Livorno
Prato Massa Carrara
Grosseto
Siena
Arezzo
Firenze
Pisa
Pistoia Lucca Livorno
Prato Massa Carrara
Popolazione (residenti) Approssimazione alle dak
....................................................
134
Per vedere a colpo d’occhio e con facilità il numero degli abitanti delle province toscane, Anna e Matteo decidono di rappresentarli con un ideogramma
• Completa l’ideogramma.
Siena (SI)
Lucca (LU)
Massa-Carrara (MC)
Livorno (LI)
Grosseto (GR)
Firenze (FI)
Prato (PO)
Arezzo (AR)
Pisa (PI)
Pistoia (PT)
Legenda: = 100000 abitanti = 50000 abitanti
Gli stessi dati si possono rappresentare anche con un altro grafico che si chiama diagramma
a
• Completa il grafico, poi rispondi sul quaderno.
a. I due grafici rappresentano le stesse informazioni?
b. Quali informazioni rappresentano?
c. Quale dei due grafici ti sembra più facile da leggere? Perché?
d. Sul quaderno scrivi le città in ordine crescente di popolazione.
e. Anna e Matteo hanno capito quali sono le città più popolate di Siena? Quali sono?
1 00 000 2 00 000 3 00 000 4 00 000 5 00 000 6 00 000 7 00 000 8 00 000 9 00 000 1 000 000
SI LU MC LI GR FI PO AR PI PT
Quaderno pp. 254-257 Relazioni, dati e previsioni 135
LA MODA
Gli istruttori di nuoto della piscina di Bellacqua stanno organizzando una giornata di festa per i 60 bambini e bambine che frequentano i corsi di nuoto. Hanno deciso di regalare un costume da bagno a ciascun partecipante come ricordo della festa. Per comprare i costumi è stato incaricato l’istruttore Mario.
L’istruttore chiede a ciascun partecipante quale taglia di costume porta: l’indagine gli permetterà di capire quanti costumi prendere di ogni taglia.
• Completa.
Quali taglie di costume portano?
Quanti costumi dovrò comprare per ogni taglia?


• Quanti sono i maschi intervistati da Mario? E le femmine?
Per i maschi, Mario comprerà:
Per le femmine comprerà:
• Quale taglia compare con maggiore frequenza fra i maschi? Quindi la moda è il numero ................. E tra le femmine? ................. Quindi la moda è il numero .................
taglia 22
taglia 24
taglia 26
taglia 28 ; taglia 30
;
;
;
taglia 22 ; taglia 24 ; taglia 26 ; taglia 28 ; taglia 30
Numero taglia Risposte maschi Totale risposte maschi Risposte femmine Totale risposte femmine 22 X X 2 X X X 24 7 5 26 X X X X X X X X X X X X X X X X 28 X X X X X X X X X 7 30 6 5
.
CAPITO CHE...
dati e previsioni 136
La moda è il dato che compare con la frequenza più
alta
HO
Relazioni,
LA MEDIA
Nella squadra di basket sono entrati due nuovi giocatori, Joseph e Andrea. L’allenatore li ha osservati per tutto il campionato e ha registrato i punti che hanno fatto durante le partite.
Joseph Andrea
Alla fine del campionato l’allenatore confronta i loro punteggi.
• Calcola i punteggi e rispondi.
Joseph: Andrea: Chi ha fatto meno punti?
I due atleti hanno giocato lo stesso numero di partite? Sì No
Non puoi dire che Andrea ha giocato peggio, perché ha fatto partite in meno di Joseph.
1. Ha rappresentato i di ciascuna partita con un diagramma a barre;
2. ha tolto i punti dalle colonne più alte e li ha spostati sulle colonne più basse;
13344889911
13344889911
Joseph
66556767
66556767
Andrea
Calcola la media di Joseph.
1
13344889911
13344889911
66556767
66556767
3. ha proceduto in questo modo fino a quando le colonne hanno raggiunto tutte la stessa altezza; colorale.
L’altezza delle colonne indica la media.
La media dei punti di Joseph è ..................
La media dei punti di Andrea è In linguaggio matematico: somma tutti i dati e dividi per il numero totale dei dati.
60 : 10 = 6 media dei punti
punti fatti nelle partite totale punti : numero delle partite
Calcola la media di Andrea
6 + + + + + + + = : = media dei punti
Quaderno pp. 258-259 Relazioni, dati e previsioni 137
9
9
+ 3 + 3 + 4 + 4 + 8 + 8 +
+
+ 11 = 60 punti
punti fatti nelle partite totale punti : numero delle partite 1a 2a 3a 4a 5a 6a 7a 8a 9a 10a 1 3 3 4 4 8 8 9 9 11 1a 2a 3a 4a 5a 6a 7a 8a 6 6 5 5 6 7 6 7
Se vuole confrontare i punteggi, l’allenatore deve calcolare la media. Osserva come ha proceduto.
IL PIANO CARTESIANO
L’allenatore ha capito che Joseph e Andrea hanno fatto in media lo stesso numero di punti.
Questo significa che avranno giocato nello stesso modo durante il campionato?
Per capirlo, disegna il loro punteggio usando un altro grafico.
• Osserva e completa.
Grafico di ..................................................... Grafico di .....................................................
Il piano cartesiano è formato da due semirette, chiamate x e y, che sono fra loro perpendicolari. I numeri scritti sulla semiretta x sono le partite, i numeri scritti sulla semiretta y indicano i Incrociando le informazioni delle semirette l’allenatore ha individuato i punti sul piano cartesiano e poi li ha uniti con dei segmenti ottenendo un grafico. Il primo grafico già disegnato rappresenta il punteggio di Completa il secondo grafico inserendo ciò che manca.
• Confronta i due grafici e completa.
Osserva il grafico di Joseph: procedendo da sinistra verso destra noti che è andato crescendo. Significa che Joseph durante il campionato è
Osserva il grafico di Andrea: noti che all’inizio parte più in alto rispetto a Joseph ma poi si mantiene, più o meno, sempre alla stessa altezza. Significa che durante il campionato Andrea ha giocato in modo più regolare di Joseph.
HO CAPITO CHE...
Nel piano cartesiano il grafico indica come varia un dato nel tempo.
0 1a 2a 3a 4a 5a 6a 7a 8a 9a 10a x x 5 10 15 y y 0 1a 2a 3a 4a .................... 5
Quaderno pp. 260-261 Relazioni, dati e previsioni 138
1 Individua l’argomento di ciascuna indagine, poi completa le tabelle di frequenza e calcola la moda.
Verdura Scelte Frequenza
insalata X X X X X X X 7
spinaci X X X
carote X X X X X
zucchine X X X
cavolo X
Argomento indagine: ...........................................................................
Quanti sono stati intervistati:
Il dato che compare con maggiore frequenza, cioè la moda, è
Questo significa che la verdura preferita è
Argomento indagine:
Quanti sono stati intervistati: ...............
Il valore che compare con maggiore frequenza, cioè la moda, è
Questo significa che il numero di scarpe più diffuso è il
2 Nella società sportiva Vivalosport, gli allievi e le allieve sono divisi in gruppi.
Calcola l’età media di ciascun gruppo.
Corso Età allievi/e Calcolo dell’età media
N. scarpe Scelte Frequenza 33 X X 2 34 4 35 2 36 10 37 7
corsa di velocità 8, 10, 9, 9, 10, 7, 10 + + + + + + = .................... : .................... = .................... corsa a ostacoli 17, 15, 16 .......... + .......... + .......... = .............. : = salto in lungo 9, 13, 11, 12, 10 + + + + = : = salto in alto 12, 10, 10, 11, 12, 11 + + + + + = .................... : .................... = .................... 139 ESERCIZI
LA PROBABILITÀ
Nella vita di ciascuno di noi capitano tanti avvenimenti che in linguaggio statistico vengono chiamati “eventi”. Alcuni eventi è impossibile che accadano: è impossibile che andando a scuola si incontri un dinosauro!
Altri eventi, invece, possono accadere oppure no, sono cioè eventi possibili: se tiri un calcio di rigore è possibile che tu faccia gol.
Fra gli eventi possibili ce ne sono alcuni che è certo che accadano: se oggi è domenica, è certo che domani sarà lunedì.
Proviamo a misurare la probabilità che un evento accada.
Lucia vuole giocare a “Pesca il pesce” con Sofia. Vince chi, per prima, a occhi bendati, riesce a pescare un pesce blu. Sofia è indecisa.
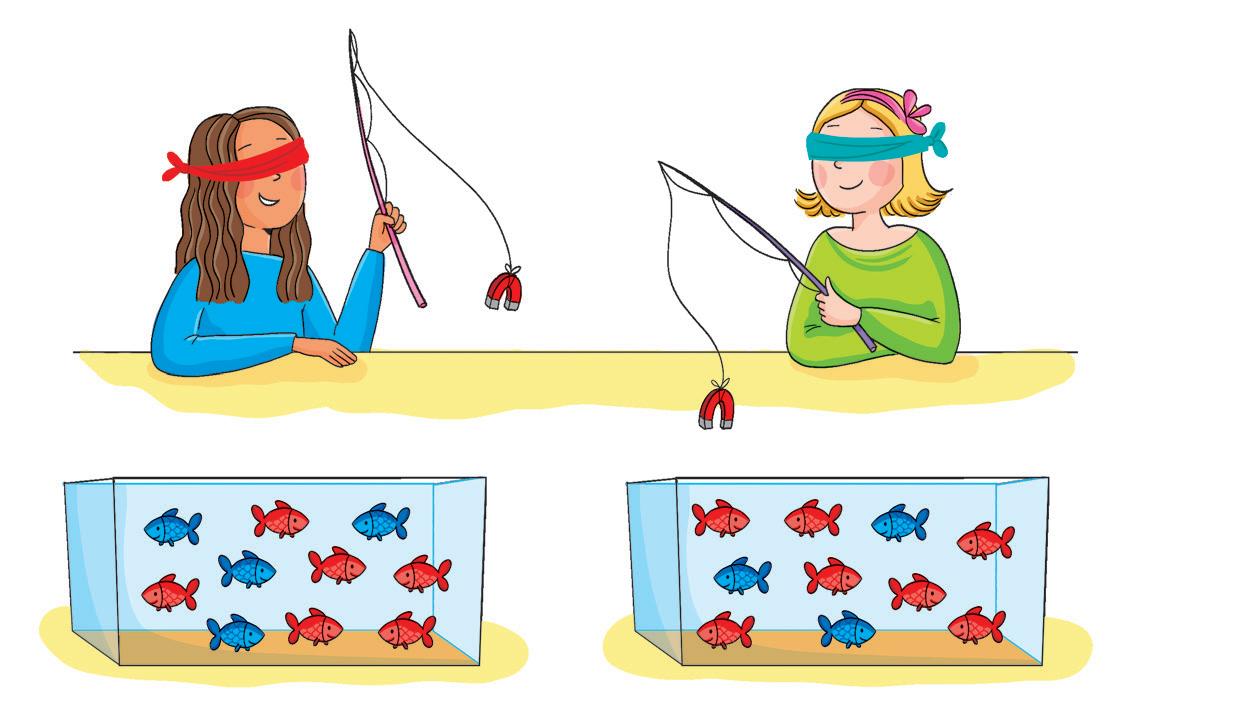
In quale vaschetta mi converrà pescare per avere maggiori probabilità di vincere? A B
• Aiuta Sofia a trovare la probabilità di pescare un pesce blu. La probabilità si può misurare quando riusciamo ad attribuire a un evento un valore numerico. Questo valore si esprime con una frazione.
Il numeratore della frazione indica il numero dei casi favorevoli, mentre il denominatore indica il numero dei casi possibili.
Relazioni, dati e previsioni 140
• Misura la probabilità che accada l’evento “pescare un pesce blu”.
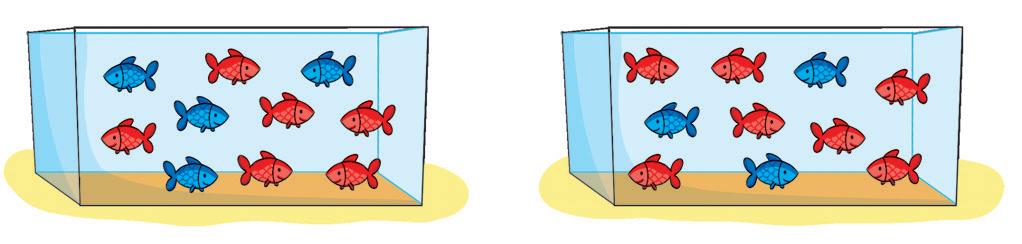
A B
• Osserva la vaschetta A e completa.
I casi possibili, cioè tutti i pesci, sono
I casi favorevoli, cioè “pescare un pesce blu” sono ............... su 10.
In linguaggio matematico: la probabilità di “pescare un pesce blu” è ..........
L’evento “pescare un pesce blu” è possibile e la probabilità che questo avvenga è .
Procedi nello stesso modo per la vaschetta B.
Casi possibili: Casi favorevoli: La probabilità è
Confronta le due frazioni: <
Sofia avrà maggiore probabilità di pescare un pesce blu se prende la vaschetta
• Misura adesso l’evento “pescare un pesce” da una vaschetta.
I casi possibili, cioè tutti i pesci, sono
I casi favorevoli, “pescare un pesce qualsiasi”, sono su 10
In linguaggio matematico si dice che la probabilità di “pescare un pesce” è 10
In questo caso puoi dire che l’evento è certo, cioè è sicuro che Sofia pescherà un pesce.
• Misura ora la probabilità di “pescare un pesce viola”.
I casi possibili, cioè tutti i pesci, sono ...............
I casi favorevoli, “pescare un pesce viola”, sono 0 perché non
In linguaggio matematico: la probabilità di “pescare un pesce viola” è
In questo caso puoi dire che l’evento è impossibile, perché non ci sono pesci viola.
Relazioni, dati e previsioni 141
E se le due vaschette hanno lo stesso numero di pesci blu?
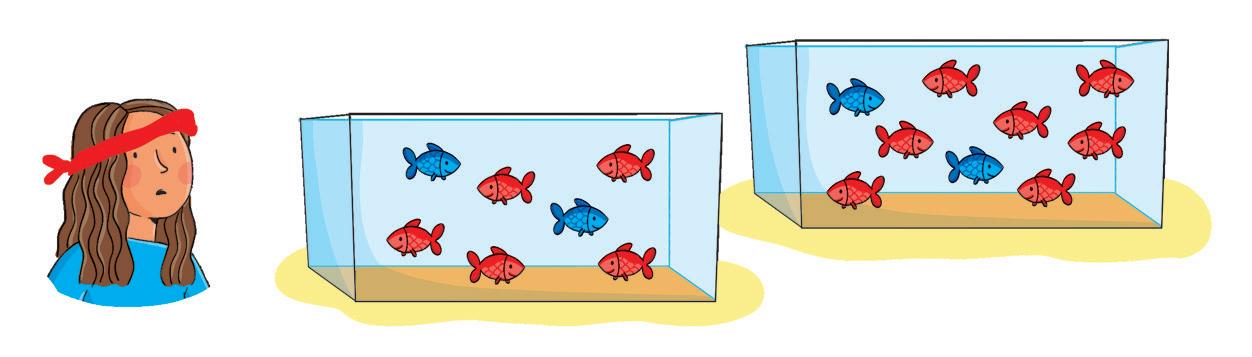
A
• Osserva le vaschette e completa.
Vaschetta A
I casi possibili sono .................
I casi favorevoli sono
La probabilità di “pescare un pesce blu”
è di su
In linguaggio matematico:
Confronta le due frazioni ottenute: ..........
< ..........
A Sofia conviene pescare dalla vaschetta perché A B
Vaschetta B
B
I casi possibili sono .................
I casi favorevoli sono
La probabilità di “pescare un pesce blu”
è di su
In linguaggio matematico:
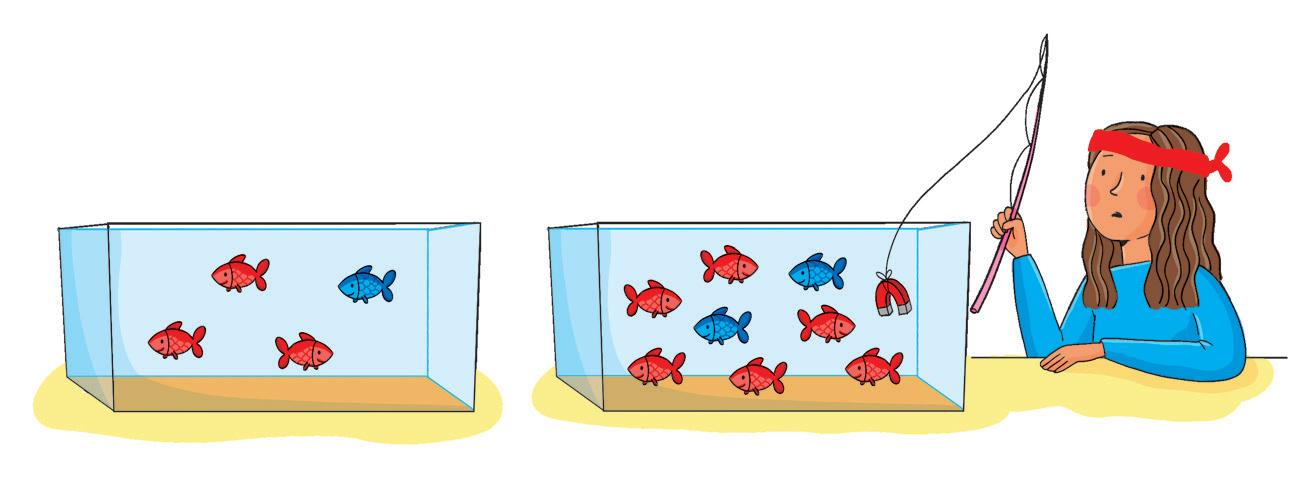
• Osserva le vaschette e completa.
E in questo caso, in quale vaschetta
c’è maggiore probabilità di pescare un pesce blu?
La probabilità di pescare un pesce blu nella vaschetta A è: ; la probabilità di pescare un pesce blu nella vaschetta B è:
Osserva: 1 4 x 2
Le due frazioni sono x 2
Puoi dire, quindi, che la probabilità di pescare un pesce blu è
...........................................
Quaderno pp. 262-263 Relazioni, dati e previsioni 142
PROBABILITÀ E PERCENTUALI
• Leggi, osserva e completa.
Michela ha comprato un sacchetto di cioccolatini.
Quanti sono:
• tutti i cioccolatini?
• quelli alle nocciole?
• quelli bianchi?
• quelli fondenti? ..................
A Michela piacciono di più i cioccolatini alle nocciole. Se pesca dal sacchetto senza guardare, quale probabilità avrà di prendere uno dei suoi cioccolatini preferiti?
• Osserva e completa.
I casi possibili sono ; i casi favorevoli sono ; quindi la probabilità è di
Trasforma la frazione 6 12 in una frazione equivalente con il denominatore 100
Come fare?
Esegui la divisione 6 : 12 =
Ora moltiplica il numero decimale trovato per 100 cioè 0,50 x 100 = ; quindi in percentuale è %
Puoi dire quindi che Michela ha il di probabilità di pescare un cioccolatino alle nocciole.
• Ora calcola la percentuale degli altri cioccolatini. Completa la tabella.
fondenti su : =
Per calcolare la percentuale di un evento trasformo la frazione che indica la probabilità in un numero decimale e moltiplico per 100.
Quaderno p. 264
Cioccolatini Probabilità di uscita In frazione Numero decimale Moltiplico x 100 Percentuale bianchi 3 su 12 .......... 3 : 12 = 0,25 0,25 x 100 = 25%
HO CAPITO CHE... Relazioni, dati e previsioni 143
Un piccolo spazio verde
Nella scuola di Michela ogni classe si affaccia su un piccolo cortile. Ai bambini e alle bambine è stata data la possibilità di abbellire lo spazio progettando una piccola area verde.
Progetta con loro un piccolo spazio verde per abbellire il cortile davanti all’aula della classe 5a
Fase 1 • Il luogo
Lavoro individuale e in piccoli gruppi
• Osserva il disegno del cortile che si vuole abbellire e confrontalo con la sua pianta; riporta sulla pianta gli elementi che compongono il cortile: porta di accesso, muretto con rete, muro, muretto con accesso per andare nel cortile della classe accanto.
• Calcola le misure reali del cortile e scrivile sulla pianta dove ci sono le .
• Divisi in piccoli gruppi, individuate sulla pianta le zone del cortile che avete pensato di abbellire e coloratele con la matita verde; calcolate le misure reali degli spazi individuati.
Scala di riduzione 1:100 aula 5a aula 4a aula 3a
144 COMPITO di REALTÀ
Fase 2 • I vasi
Lavoro in piccoli gruppi
• Osservate alcune idee per capire che cosa può servire per creare uno spazio verde.


Fig. 1
100 x 50 cm
terriccio 350 <l € 35 a cassetta

Fig. 3
100 x 50 x 60 cm
terriccio 450 <l
€ 150 la struttura
• Osservate le misure nelle immagini e riducetele usando il rapporto di riduzione di 1:100 cm, lo stesso usato per la pianta del cortile. Copiate questa tabella sul quaderno e fate i calcoli per ciascun contenitore.

Fig. 2
50 x 20 cm
terriccio per vaso 20 <l € 15 a vaso
Fig. 4
50 x 50 cm
terriccio 80 <l
€ 29 a vaso
Fig. Misure reali Misura in scala 1:100 cm
1 100 x 50 1 x 0,5
2 50 x 20 3 4
• Scegliete i contenitori e disegnateli nella pianta rispettando le riduzioni in scala. Calcolate il costo totale con una tabella simile a questa.
Tipologia contenitori Quantità Costo unitario Costo totale
Fase 3 • Le piante e il terriccio
Lavoro in piccoli gruppi
• Documentatevi sulle piante che vivono in vaso all’aperto e che sono resistenti sia al caldo sia al freddo. Scegliete le piante e fate una stima di quante piante di ciascun tipo serviranno.
• Calcolate il costo totale usando una tabella simile a questa.
Piante Quantità Costo unitario Costo totale
145
• Calcolate in tabella la quantità di terriccio necessaria a riempire i contenitori e il numero dei sacchi.



Fase 4 • La spesa
Lavoro in piccoli gruppi
• Calcolate il preventivo della spesa necessaria a realizzare il progetto in una tabella conclusiva come questa:
Costo contenitori Costo piante Costo terriccio Spesa totale
il mio PERCORSO
Fase 5 • Il progetto e la cura
Lavoro in piccoli gruppi
• Ciascun gruppo disegna su un foglio A3 il progetto del cortile con un rapporto di ingrandimento di 2 : 1 cm.
• Ciascun gruppo presenta il proprio progetto, con il preventivo della spesa, alla classe. Scegliete il criterio di valutazione per l’approvazione del progetto e votate.
• Pianificate gli interventi di manutenzione.
• Che cosa pensi del lavoro che hai fatto? Mi è piaciuto. Non mi è piaciuto. Non so.
• Pensi sia stato importante lavorare in gruppo? Sì No
• Scrivi tre cose che hai imparato dall’attività che hai appena svolto e che potranno esserti utili per un lavoro successivo.
1.
2.
3.
• In che modo?
• Quali vantaggi o svantaggi hai incontrato?
• Scegli tre aggettivi che secondo te descrivono meglio l’attività che hai svolto e sottolineali: divertente, impegnativa, noiosa, semplice, complessa, istruttiva, coinvolgente, inutile, utile, improduttiva.
Terriccio Quantità Costo unitario Costo totale € 14,50 50 <l € 25,00 80 <l € 12,50 20 <l
146 COMPITO di REALTÀ
1 Osserva le divisioni e indica con una X se ciascuna affermazione è vera (V) o falsa (F).
a. 5 è un divisore di 40 V F
b. 7 è un divisore di 25 V F
c. 40 è divisibile per 5 V F
d. 25 è un multiplo di 7 V F
2 Scrivi quattro numeri a due cifre che siano:
a. divisibili per 2:
b. divisibili per 3:
c. divisibili per 5:
d. divisibili per 10:
e. 4 è un divisore di 36 V F
f. 6 è un divisore di 21 V F
g. 36 è divisibile per 4 V F
h. 21 è un multiplo di 6 V F
3 Dei numeri che hai scritto nell’esercizio precedente, riscrivi solo quelli che:
a. sono multipli di 2 e di 10
b. sono multipli di 3 e di 5
c. sono multipli di 2 e di 5
d. sono multipli di 5 e di 10
4 Esegui le seguenti espressioni.
(6 + 7) x 3 – 2 x 4 =
5 + 4 x 8 – 18 : 3 =
5 Riscrivi l’espressione inserendo le parentesi che mancano perché l’uguaglianza sia vera.
14 + 12 : 2 – 5 = 8
15 + 17 : 2 x 4 = 4
25 + 5 : 2 – 3 + 4 = 8
6 Metti il segno = (uguale) oppure ≠ (non uguale).
7 Metti in ordine crescente i numeri.
43
5 7 4 3 4 0 5 0 8 3 6 4 0 9 2 1 6 3 2
2
72 14 33 6 24 8 62 36 53 15 103 1000
• 45 • 42 • 46 52 • 23 • 43 • 15 V erso l’Invalsi 147 TAPPA
Competenze L’alunno/L’alunna padroneggia le diverse rappresentazioni di un numero naturale e si muove con sicurezza nel calcolo mentale; riconosce e utilizza rappresentazioni diverse di oggetti matematici.
COMPETENZE
1 Confronta le frazioni scrivendo il segno adatto. a.
3 Osserva la sequenza numerica e rispondi.
2 Circonda di verde le frazioni maggiori di 7 10 e di rosso quelle minori.
Quali tra questi numeri puoi inserire nella sequenza?
a.
4 Nell’aiuola della scuola sono fiorite 20 calle: 1 5 sono gialle, 1 4 sono rosa e tutte le altre bianche.
Le calle bianche sono , in frazione le bianche sono
5 Trasforma le frazioni decimali in numeri decimali. a.
6 Trasforma le percentuali in frazioni e viceversa.
7 Calcola il valore della percentuale.
6% di 500 =
di 700 =
8 Calcola il valore dell’intero. 10% 50
di 1000 =
di 2000 =
68
9 Nel paese di Solaria lo scorso anno gli abitanti erano 400. Quest’anno sono aumentati di 12 unità.
A quale percentuale corrisponde l’aumento degli abitanti?
a. 5% b. 8% c. 3% d. 7%
Competenze L’alunno/L’alunna riconosce e utilizza rappresentazioni diverse di oggetti matematici.
4 4
c. 1 2 6 2 b. 9 2
2 d. 11 4 9 4
8 8
3
0,135 0,134 0,078
0,25 0,225 0,215
0,16 b. 0,148 c. 0,153
7 5 7 15 7 13 7 4 7 20 7 7 7 9 7 19
Le calle gialle sono 4 5 8 Le calle rosa sono 4 5 6
10
b. 8 100
c. 58 10
d.
1000
6
=
=
=
614
=
35% = .......... • 72% = .......... • 18 100 = • 15 100 = • 4% = .......... • 90% = .......... • 75 100 = • 38 100 =
15%
7%
14%
17%
TAPPA
V erso l’Invalsi 148
COMPETENZE
1 Le alunne e gli alunni sono andati a mangiare 40 minuti fa.
A che ora sono andati a mangiare?
a. 13:48 b. 13:38 c. 12:58 d. 12:48
2 Samuele ha disegnato l’ora in cui ha iniziato a fare i compiti e l’ora in cui ha finito.
Quanto tempo ha impiegato per fare i compiti?
a. 1 ora e 56 minuti
b. 1 ora e 36 minuti
c. 1 ora e 46 minuti
d. 1 ora e 26 minuti
3 Da una bottiglia di tè da 1,5 <l vengono riempiti 10 bicchieri da 1,2 d<l .
Quanto tè è rimasto nella bottiglia?
a. 4 d<l o 0,4 <l b. 3 d<l o 0,4 <l c. 3 d<l o 0,3 <l d. 4 d<l o 0,3 <l
4 Gabriella prepara dei ghiaccioli. In ciascuno stampino ci stanno 8 c<l di succo. Quanti ghiaccioli riesce a fare con 1 <l ?
a. 12 e mezzo b. 12 c. 11 d. 13
5 Se a 4 m aggiungi 5 cm, ottieni:
a. 4,5 m b. 45 cm c. 4,05 m d. 45 m
8 Scrivi l’unità di misura corretta.
a. 1,37 hg = 137
6 Se a 8 kg togli 2 hg ottieni:
a. 78 hg c. 82 hg
b. 8,2 kg d. 82 kg
7 Se a 3 <l aggiungi 2 h<l ottieni:
a. 23 <l c. 2,3 h<l
b. 203 <l d. 20,3 <l
0,3 m = 300
9 Una bottiglietta contiene 100 m<l di profumo e costa € 12. Quanto costa quel profumo al litro?
a. 140 euro b. 200 euro c. 120 euro d. 130 euro
10 Completa.
Articolo Costo Paghi Resto
lattina € 2,50 € 10
maglietta € 18 € 50
Articolo Costo Paghi Resto gelato € € 2 € 0,20
penna € € 5 € 2,70
Competenze L’alunno/L’alunna misura grandezze utilizzando unità di misura convenzionali.
b.
c.
46,5
3,17 h<l
31,7 150 cm
2,9 kg
29000 12,4 c<l
0,124 30 mm
0,3 inizio compiti fine compiti 12 6 57 8 4 3 9 10 2 1 11 12 6 57 8 4 3 9 10 2 1 11 12 6 57 8 4 3 9 10 2 1 11 12 6 57 8 4 3 9 10 2 1 11
32 <l = 3200
dg = 0,465
=
= 0,15
=
=
=
V erso l’Invalsi 149
TAPPA COMPETENZE
1 Osserva e indica con una X se ciascuna affermazione è vera (V) o falsa (F).
A B C D
a. La figura A è equivalente alla figura B. V F
b. L’area della figura B è maggiore dell’area della figura C. V F
c. L’area della figura D è minore dell’area della figura A. V F
d. La figura A è equivalente alla figura C. V F
2 Colora di rosso i poligoni regolari e, in ciascuno, traccia le diagonali quando è possibile.
3 L’area dell’esagono è 30 cm². Quale sarà l’area del rombo verde?
a. 5 cm² b. 15 cm² c. 20 cm² d. 10 cm²
4 Questa figura è formata da due triangoli equilateri e da un quadrato. Indica con una X se ciascuna affermazione è vera (V) o falsa (F).
a. La figura è un poligono regolare. V F
b. La figura ha tutti i lati uguali. V F
c. La figura ha un solo asse di simmetria. V F
d. La figura è un esagono. V F
5 I due cerchi che vedi sono uguali e hanno raggio 5 cm. Quale sarà l’area del rettangolo?
a. 50 cm2 c. 200 cm2
b. 100 cm2 d. 110 cm2
Competenze L’alunno/L’alunna riconosce le forme del piano e ne coglie le relazioni tra gli elementi; ne determina le misure.
TAPPA COMPETENZE V erso l’Invalsi 150
TAPPA COMPETENZE
1 Colora di rosso uno spigolo, di blu una faccia e di verde un vertice delle seguenti figure.
2 Quale sviluppo corrisponde alla scatola bicolore disegnata accanto?
3 Indica con una X le figure che rappresentano lo stesso solido ma in due posizioni diverse.
4 Questo cubo è stato verniciato di verde all’esterno. Rispondi.
a. Quanti cubetti hanno solo 3 facce verdi?
b. Quanti cubetti hanno solo 2 facce verdi?
c. Quanti cubetti hanno solo 1 faccia verde?
d. Quanti cubetti non hanno facce verniciate?
Trova
Volume = Volume = Volume = Volume =
5
il volume dei seguenti prismi.
a. c.
d. A B C D
b.
b. c.
151
a.
d. V erso l’Invalsi
Competenze L’alunno/L’alunna riconosce e rappresenta forme del piano e dello spazio; descrive, denomina e classifica figure in base a caratteristiche geometriche.
1 Indica con una X se ciascuna affermazione è vera (V) o falsa (F).
a. La Statistica è una parte della Matematica. V F
b. La Statistica si occupa di svolgere indagini, raccogliere dati, ordinarli,
c. rappresentarli e interpretarli. V F
d. Non vengono usate tabelle per raccogliere i dati di un’indagine. V F
e. I dati vengono rappresentati con dei grafici. V F
f. Il grafico sul piano cartesiano mostra come varia un fenomeno nel tempo. V F
g. La moda è il valore che compare con minore frequenza. V F
2 Osserva e indica con una X.
Sport Preferenze
nuoto
pallavolo
danza
calcio
pattinaggio
Quali informazioni puoi ricavare dal grafico?
a. Quante sono le persone intervistate. Sì No
b. Quanti sono i maschi e quante le femmine. Sì No
c. Quanti anni hanno le persone intervistate. Sì No
d. Da quanto tempo praticano lo sport scelto. Sì No
e. Qual è lo sport meno praticato. Sì No
f. Quali sport sono praticati dallo stesso numero di persone. Sì No
Legenda: = 5 ragazzi/e
V erso l’Invalsi 152
TAPPA COMPETENZE
3 Leggi, osserva e indica con una X.
Il grafico rappresenta le iscrizioni degli alunni e delle alunne al 1° anno di scuola superiore.
350
300
250
200
150
100
50
0
a. Si tratta di un’indagine: diretta. indiretta.
Liceo classico
Liceo scienti co
Liceo linguistico
Liceo artistico
Istituto professionale
Istituto tecnico
b. Le persone iscritte al Liceo linguistico sono: 3 30 300
c. Le persone iscritte all’Istituto professionale sono:
30 in più rispetto al Liceo artistico.
il doppio di quelle iscritte all’Istituto tecnico.
lo stesso numero di quelle iscritte al Liceo scientifico.
d. Quale coppia di scuole indicate ha lo stesso numero di iscritti:
Istituto professionale • Istituto Tecnico
Liceo artistico • Liceo classico
e. Quale scuola ha il doppio delle iscrizioni rispetto al Liceo classico:
f. La moda è: Liceo scientifico Istituto professionale Liceo linguistico
4 Scrivi i punti che puoi ottenere lanciando un dado.
Poi indica con una X se ciascuna affermazione è vera (V) o falsa (F).
a. La probabilità che esca il numero 2 è di 4 6 V F
b. La probabilità che esca un numero pari è del 50%. V F
c. La probabilità che esca il numero 6 è maggiore della probabilità che esca il numero 4 V F
5 Sottolinea i nomi nei quali la probabilità di estrarre una vocale corrisponde al 50%.
CANE LATTE CARTA ANNA GIANLUCA
Competenze L’alunno/L’alunna ricava informazioni da dati rappresentati in tabelle e grafici; riconosce e quantifica situazioni, in casi semplici, di incertezza.
153
NUMERI
A1. Quale numero si avvicina di più al numero ottenuto con questa operazione?
14053 + 36 =
a. 14100 b. 14050 c. 14500 d. 14000
A2. Giovanni deve risolvere questo esercizio scritto alla lavagna.

Approssima i numeri
335 e 775
alle centinaia più vicine e poi
calcola la somma dei numeri ottenuti.
Quale operazione deve eseguire Giovanni per risolvere l’esercizio?
a. 400 + 800 = 1200
b. 300 + 700 = 1000
c. 340 + 780 = 1120
d. 300 + 800 = 1100
A3. Indica con una freccia dove si trovano il numero: 245 millesimi e il numero 75 centesimi.
0123456789101112131415161718192021222324252627282930
A4. Quanto manca per arrivare a 2?
0,43 + = 2
a. 2,57 b. 1,57 c. 1,6
PROVE INVALSI 154
SPAZIO E FIGURE
B1. Cancella con una X il poligono tra quelli celesti che non puoi usare per ricoprire il fiore. Dei tre poligoni che restano, scrivi quanti te ne servono di ciascun tipo per ricoprirlo.
1. Del ..................................................................................................... ne servono .....................................................................................................
2. Del ne servono
3. Del ne servono
B2. Se disegni la figura simmetrica rispetto ai vari assi di simmetria, quale figura otterrai?
A B C D
PROVE INVALSI 155
a. b. c.
RELAZIONI, DATI E PREVISIONI
C1. Osserva il grafico e rispondi.
temperatura a Verona il 21 luglio
a. Qual è stata la temperatura minima? A che ora?
b. Qual è stata l’ora più calda della giornata? Con quanti gradi?
c. In quali ore del giorno a Verona c’è stata la stessa temperatura?
d. Che differenza di temperatura c’è stata fra le 6:00 del mattino e le 6:00 del pomeriggio?
C2. Quale dei due grafici rappresenta i dati riportati?
Videogiochi 27%
Lettura 10%
Sport 35%
Giochi da tavolo 5%
Giochi all’aperto 23%
00:00 0 5 10 15 20 25 30 35 (°C) 02:0001:0006:00 22:00 20:00 18:00 16:00 14:00 12:00 10:00 08:00
A B
PROVE INVALSI 156
I NUMERI
158 I numeri romani /
160 Grandi numeri: milioni e miliardi /
162 I numeri decimali /
164 Approssimare i numeri decimali /
166 I numeri relativi /
LE QUATTRO OPERAZIONI
168 Proprietà dell’addizione /
169 Proprietà della sottrazione /
170 Proprietà della moltiplicazione /
171 Proprietà della divisione /
172 Operazioni inverse /
174 I numeri 0 e 1 /
175 Moltiplicare e dividere i decimali per 10, 100, 1 000 /
176 Calcolo a mente /
178 Le potenze /
180 Le espressioni /
182 Multipli, divisori, criteri di divisibilità e fattori primi /
184 Problemi /
LE FRAZIONI
186 Frazioni /
187 Frazioni maggiori, minori, uguali a 1 /
188 Confrontare frazioni /
189 Frazioni equivalenti /
190 Dall’intero alla frazione /
192 Dalla frazione all’intero /
194 Frazioni e numeri decimali /
196 Frazioni e percentuali /
199 La percentuale nel commercio /
LA MISURA
200 Le misure /
204 Le misure di tempo /
206 L’euro /
208 Ra-Giocando
Le indicano gli esercizi graduati su livelli
LE ISOMETRIE
210 La simmetria /
212 La traslazione / 214 La rotazione /
216 Figure simili /
SPAZIO E FIGURE
218 I poligoni /
220 I triangoli /
224 I quadrilateri /
228 Le misure di superficie /
230 L’area /
232 Area del rettangolo e del quadrato /
234 Area del triangolo e del parallelogramma /
236 Area del rombo /
238 Area del trapezio /
240 I poligoni regolari /
242 Aree di poligoni /
244 Circonferenza e cerchio /
I SOLIDI
246 I solidi /
248 La superficie dei solidi /
250 Il volume /
252 Le misure di volume /
RELAZIONI, DATI E PREVISIONI
254 L’indagine statistica /
258 La moda e la media /
260 Il piano cartesiano / 262 La probabilità /
264 Probabilità e percentuali /
1
I numeri romani
Completa la tabella con l’operazione e il corrispondente numero arabo.
Numero romano Operazione Numero arabo
XI 10 + 1 11
IX 10 – 1 9
LXIII CCLXII ................................ ................................
XC CD MDXXV CM
3
Completa le scritture dei numeri.
2
Scrivi il numero contenuto in ciascun riquadro. Poi, per ciascuna coppia, colora il numero maggiore.
XXXV XXIV CLXII CCX
MCLI MCXXV XLVII LII ..................... ..................... ..................... .....................
CCCXXI DCXXV MCCXXXV MCDLVIII
MCXL MCXX CCCII CCIX
28 = XX 83 = LX 92 = X
275 = CC
309 = C 853 = DC 955 = CM 1 631 = MD
4
Sul quaderno, scrivi in numeri romani.
a. I numeri da 5 a 30
b. Numera per 100, da 300 a 1000
c. I numeri: 4, 9, 40, 90, 104, 109, 140, 190.
d. I numeri: 400, 900, 1040, 1090, 1400, 1900.
e. I numeri: 6, 11, 60, 110, 160, 210.
f. I numeri: 600, 1100, 2100.
5
Scrivi in numeri romani.
La tua età: Giorno/mese/anno di nascita: / /
Quante lettere ha il tuo nome: Quante lettere ha il tuo cognome:
Il numero della tua classe: Il numero dei tuoi compagni di classe:
La data del giorno in cui stai eseguendo questo compito: / /
158 I numeri
6
7
Inserisci in cifre romane i numeri indicati dalle definizioni: leggendo in successione dall’alto verso il basso le lettere scritte nelle caselle evidenziate leggerai l’anno in cui hanno iniziato a costruire il Colosseo.
Il doppio di 32
1 3 di 96
Il triplo della metà di 12
Il prodotto di 7 e 6
La differenza fra 33 e 26
Hanno iniziato a costruire il Colosseo nel d.C.
8
Inserisci i numeri che mancano in ciascuna serie. V

Colora le caselle che contengono i simboli necessari per formare il numero indicato, poi scrivi il numero.
In ciascun quadrato, usa i simboli rimasti per scrivere almeno altri 2 numeri.
159 I numeri Obiettivo di apprendimento Conoscere sistemi di notazione dei numeri che sono stati in uso in tempi diversi dai nostri.
XXV
CCCL
X
CC CCL
DC DCL DCC
C IV X I L VI X II IX C C XX X L II VI IV I I V II M C C L D VI M I VI V M X L X C 152 = 146 = 1256 = 2020 =
..................................................................................................................................................................................................................................................................................................................................
Grandi numeri: milioni e miliardi
Completa scrivendo il nome di ciascuna classe, come nell’esempio. Poi leggi il numero.
Nella scrittura di alcuni numeri è sbagliata la divisione in classi: correggi riscrivendo solo i numeri sbagliati. 12369125
Completa la tabella scrivendo il valore della cifra 5, come nell’esempio.
Scrivi tre numeri che contengano rispettivamente: 6 daM
160 I numeri
12369456 12 milioni 369 migliaia 456 unità semplici 3697581420 3 ............................................. 697 ......................................... 581 ......................................... 420 ......................................... 2569107 2 569 107 43296764 43 296 764 65200413745 65 200 413 745 1
in cifre ciascun
25 mila = 3 uG = 7 milioni = 6 daM = 142 milioni
5 hk =
9
4
Scrivi
numero.
=
263 mila =
daG = 2 miliardi =
hM = 2
• 256421360 • 78346012523 • 2364565 • 645982300
3
Numero Valore cifra 5 espresso in parole Valore cifra 5 espresso in numero 256 5 decine 50 89562100 ................................................... ................................................... 526321964807 642257834123 215364900470
4
5
4 hk
6
Dato il numero 45236538901, scrivi il numero che ottieni se:
• inverti la cifra delle uk con quella delle daM
• inverti la cifra delle uG con quella delle dak
• inverti la cifra delle hM con quella delle uk
Riscrivi in ordine crescente i numeri che hai ottenuto.
7
Osserva la tabella e rispondi sul quaderno.
8
2005
2006
2007 58223000
2008 58652000
2009 59000000
2010 59190000
2011 59364000
2012 59394000
2013 60782000
• Qual è l’oggetto di questa indagine?
• In quali anni la popolazione italiana è stata minore di 59 milioni di persone?
• Quando è stata invece superiore a 59 milioni e 500 mila?
• La popolazione in Italia è sempre cresciuta ogni anno?
• Scrivi i numeri nei quali la cifra delle uM è uguale a quella delle dak.
Scrivi il numero in cifre, poi indica quale dei due numeri accanto è maggiore di quello che hai scritto.
161 I numeri Obiettivo di apprendimento Leggere, scrivere e ordinare numeri naturali.
Numero Numero in cifre Qual è maggiore? 6 milioni 8200 9200000 8 miliardi 13000000000 9500000 5 mila ...................................................... 7500 650 15 miliardi 15100000000 16000000 23 milioni 24000 24000000
Popolazione italiana
Anno
57874000
58064000
1
I numeri decimali
Collega ciascun numero alla scatola a cui appartiene.
2
Numeri interi Numeri decimali
In ciascun numero, circonda le cifre che formano la parte decimale.
3 Con le cifre 2 • 0 • 5 forma tutti i numeri decimali possibili.
In ciascun numero, circonda la parte del numero che indica le unità intere.
4
Scrivi il numero maggiore: e il numero minore:
Riscrivi in ordine crescente i numeri formati:
5 Completa le successioni.
Scomponi i numeri sul quaderno, come nell’esempio.
9,36 = 9 unità, 3 decimi e 6 centesimi = 9 + 0,3 + 0,06
162 I numeri
0,35 210 5,63 12,06 849 3 2604 74,1 10,347
33,06 1,894 456,7 12,906 1256 6,1 97,82 19
2,006 65,2 47 9,23 467,2 1,324 256,9 54,32 0,04
36,8 2,45 4,365 12,04 73,8 3,009 5,43 8,01
+0,1 1 1,1 1,2 2 +0,1 4,3 5,3 +0,1 7,7 8,7 +0,01 2,32 2,42 +0,01 8,15 8,25
6
7 Circonda i numeri che hanno 23 unità.
Scrivi il valore della cifra 4 in ciascun numero, come nell’esempio.
42,1 4 decine, cioè 40
8
9
i numeri che hanno 18 centesimi.
10
i numeri che hanno 7 decimi.
11
Indica con una X la scrittura corrispondente al numero 27,065.
12
Riscrivi in cifre i numeri scritti in forma scomposta, come nell’esempio. 0,6
13
Fra i numeri scritti, circonda quello che corrisponde alle indicazioni.
Ha tre cifre nelle unità frazionarie decimali.
Ha una cifra nelle unità intere.
Ha 7 centesimi.
Ha 2 millesimi.
Scrivi numeri decimali di cinque cifre che abbiano:
163 I numeri Obiettivo di apprendimento Leggere, scrivere e ordinare numeri decimali.
24,6 7,04 1,274 12,43 6,54 15,649 1245,8 1,004
23,4 2,38 0,231 23,9 3,24 0,23 23,7 23,5
Circonda
4,28 3,18 1,8 7,218 6,18 31,8 45,18 182,3
Circonda
2,67 7,36 1,347 4,76 74,3 671 5,79 1,74
20 + 7 + 0,6 + 0,05 20 + 7 + 0,06 + 0,05 20 + 7 + 0,06 + 0,005
35,64 4 + 0,7 + 0,09 = 0,03 + 5 + 0,6 + 0,002 = 0,4 + 50 + 0,07 + 3 = 100 + 0,6 + 8 + 30 + 0,01 = 0,009 + 8 + 10 + 0,07 = 60 + 0,9 + 0,003 + 4 =
+ 35 + 0,04 =
7 decimi 4 unità 9 millesimi 2 centesimi 14 3,715 24,06 15,427 8,971 1,672 543,6 6,17
1
Approssimare i numeri decimali
Completa le rette con i numeri mancanti, poi indica il numero intero a cui è più vicino ciascun numero dato.
2
Esegui le divisioni, se vuoi, aiutandoti con la calcolatrice. Trascrivi in tabella il numero ottenuto scrivendo le cifre solo fino ai millesimi, poi esegui le approssimazioni richieste.
Divisione da eseguire Numero ottenuto Approssima ai centesimi Approssima ai decimi
• Riscrivi in ordine decrescente i numeri approssimati ai decimi.
• Riscrivi in ordine crescente i numeri approssimati ai centesimi.
164 I numeri
0 1 2 1,4 0,3 0,7 1,6 1,2 0,5
7 4 : 7 7 : 12 6 : 7 9 : 11 12 : 45 23 : 52
1 :
2,8 2,81 3 2,9 2,96 2,87 2,82 2,99 2,81
4
L’allenatore ha svolto un’indagine per sapere all’incirca quanto sono alti i giocatori della sua squadra. Completa la tabella e rispondi.
ai decimi di metro
L’allenatore fa un calcolo e stabilisce che la media delle altezze dei ragazzi è di 1,64 m.
Chi si avvicina maggiormente alla media?
Nei riquadri sono scritti dei numeri approssimati ai decimi. Di quale numero sono l’approssimazione? Colora quello corretto.
5
Circonda l’operazione il cui risultato si avvicina maggiormente al numero indicato. Aiutati approssimando alle unità i fattori di ciascuna operazione.
165 I numeri Obiettivo di apprendimento Approssimare numeri decimali.
in metri
Erik 1,66 Giancarlo 1,54 Ferdinando 1,72 Michele 1,77 Lorenzo 1,50 Tommaso 1,63 Leopoldo 1,69 ....................................... 3 1,8 1 1,83 1,87 6,1 6,14 4,9 6,23 5 5,8 4,8 5,7 2,7 2,53 2,78 2,68 7,1 6,05 7 7,9 3,5 2,55 3,54 3,58
Nome allievo Altezza espressa
Approssima
50 2,6 x 10,3 10,1 x 4,8 x = x = 63 7,5 x 8,2 9,7 x 5,4 .......... x .......... = .......... .......... x .......... = .......... 34 5,6 x 4,9 7,1 x 5,4 x = x = 42 6,2 x 7,1 8,2 x 9,1 x = x =
I numeri relativi
Con una freccia, inserisci sulla retta ciascun numero.
–5 +3 –12 +5 –3 +12
1 0 +15 –15
2 0
Colloca sulla retta i numeri, poi colora nello stesso modo le coppie di numeri simmetrici.
+7 –2 +8 –3 –7 +2 +5 +3 –8
3
• Quale numero fra quelli inseriti non ha il suo simmetrico?
Scrivi al posto dei puntini il numero simmetrico a quello dato.
+10 –7 +9 –1 +5 –3
In ciascun riquadro sono indicate le temperature minime e massime di alcune città.
Circonda la temperatura massima.
6
In ciascun riquadro sono indicate le temperature minime e massime di alcune città. Circonda la temperatura minima.
Esprimi la misura con un numero intero relativo, come nell’esempio.
Profondità di un pozzo di 60 m –60 m
Altezza di un ponte di 15 m
Altezza del trampolino di una piscina di 10 m
Profondità di una piscina di 5 m
Profondità di un lago di 12 m
166 I numeri
+2 °C +5 °C –1 °C 0 °C +9 °C +4 °C –2 °C +1 °C –5 °C –1 °C +10 °C +3 °C –3 °C –6 °C
4
–8 °C –2 °C +6 °C +3 °C 0 °C +3 °C –2 °C –1 °C +6 °C 0 °C –2 °C +2 °C –5 °C –6 °C
5
7
Segna sulla linea del tempo le date indicate. Fondazione di Roma 750 a.C. circa Nascita di Giulio Cesare 100 a.C. Incendio di Roma 64 d.C. Costruzione terme di Caligola 40 d.C.
8
Aiutati con la linea dei numeri per eseguire queste operazioni.
– 5 – 3 = – 7 + 4 = + 10 – 8 = + 5 – 9 =
9
10
Alle squadre che partecipano alla corsa vengono attribuiti dei punti e assegnate delle penalità per ciascun percorso. Calcola il punteggio ottenuto da ciascuna squadra.
Squadra Punti assegnati Penalità Totale punteggio
Scoiattoli +9 –2
Falchi +3 –4
Cervi +5 –1
Lupi +4 –4
Scrivi l’ordine di arrivo delle squadre.
1°
2°
3° 4°
Scrivi la temperatura indicata da ciascun termometro. Poi osserva la variazione di temperatura segnata sotto e disegna dove arriva la colonnina. Infine, scrivi la temperatura raggiunta.
Variazione: +5 °C
Temperatura
raggiunta:
Obiettivo
Variazione: –3 °C
Temperatura
raggiunta:
Variazione: +8 °C
Temperatura
raggiunta:
Variazione: –6 °C
Temperatura
raggiunta:
167 I numeri
di apprendimento Leggere, scrivere e ordinare numeri relativi.
Anno 0 1000 1000 900 900 800 700 600 500 300 400 200 100 800 700 600 500 400 300 200 100
0 –15 –14 –13 –12 –11 –10 +10 +11 +12 +13 +14
–9 –8 –7 –6 –5 –4 –3 –2 –1 +1 +2 +3 +4 +5 +6 +7 +8 +9
+15
°C -10 0 10 20 30 40 °C -10 0 10 20 30 40 °C -10 0 10 20 30 40 °C -10 0 10 20 30 40
1
Proprietà dell’addizione
Esegui le addizioni, poi applica la proprietà commutativa per verificare l’esattezza del calcolo e rispondi, come nell’esempio.
35 + 27 = 62 Verifico: 27 + 35 = 62 Hai calcolato in modo corretto? Sì
16 + 34 = Verifico: = Hai calcolato in modo corretto? Sì No
51 + 42 = Verifico: = Hai calcolato in modo corretto? Sì No
37 + 45 = Verifico: = Hai calcolato in modo corretto? Sì No
2
Sul quaderno, associa gli addendi per semplificare i calcoli, come nell’esempio.
30 + 50 + 70 = (30 + 70) + 50 = 100 + 50 = 150
a. 80 + 10 + 20 • 60 + 50 + 50 • 10 + 80 + 90 • 70 + 40 + 30 + 60 • 20 + 80 + 70 + 30
b. 350 + 120 + 380 + 150 • 140 + 230 + 260 + 170 • 220 + 180 + 310 + 190
3
Applica la proprietà opportuna e calcola.
21 + 14 + 39 = ..................................................................................................................................................................................................................................................................................
76 + 15 + 24 =
85 + 47 + 13 + 15 =
Quali proprietà hai applicato?
4
Sul quaderno, associa gli addendi per semplificare i calcoli, come nell’esempio.
120 + 310 + 490 + 180 = (120 + 180) + (310 + 490) = 300 + 800 = 1100
a. 30,5 + 10,2 + 70,3 + 10,6 • 20,3 + 60,1 + 40,5 + 80,4 • 10,5 + 50,3 + 20,4 + 50,6
b. 140,3 + 250,4 + 60,2 + 150,5 • 110 + 30,6 + 270,2 + 190,3
5
Sul quaderno, scomponi ciascun numero in unità intere e in unità frazionarie decimali, poi applica la proprietà associativa, come nell’esempio.
2,34 + 12,5 =
scomponi 2 + 0,34 + 12 + 0,5 =
p. associativa (2 + 12) + (0,34 + 0,5) =
14 + 0,84 = 14,84
a. 48,35 + 6,23 + 14,04 =
b. 352,13 + 5,36 + 71,005 =
c. 46,02 + 2,152 + 23,18 =
d. 126,4 + 2,008 + 42,3 =
e. 30,05 + 4,3 + 18,72 =
f. 9,3 + 25,6 + 3,204 =
168 Le quattro operazioni
Obiettivo di apprendimento Eseguire addizioni con i numeri naturali e decimali usando le proprietà per semplificare i calcoli.
1
Proprietà della sottrazione
Sottrarre 10 è più facile! Sul quaderno, applica la proprietà invariantiva con le coppie del 10 al sottraendo, come nell’esempio.
28 – 9 + 1 + 1
29 – 10 = 19
2
a. 37 – 8 =
– 7 =
– 5 =
b. 86 – 24 =
– 29 =
– 32 =
c. 84 – 67 = 68 – 35 = 99 – 73 =
Applica la proprietà invariantiva scegliendo il numero che ti conviene togliere al sottraendo per semplificare il calcolo.
3
In ciascuna sottrazione è stata applicata la proprietà invariantiva. Scrivi l’operazione effettuata per trasformare i numeri, poi esegui il calcolo. 45 –
=
–
Scrivi l’operazione effettuata per trasformare i numeri, poi trasformali una seconda volta. 83 –
169 Le quattro operazioni Obiettivo di apprendimento Eseguire sottrazioni con i numeri naturali e decimali usando le proprietà per semplificare i calcoli.
45
91
45
73
a. 38 – 24 – = 95 – 62 – = 179 – 46 – = 128
88 – = b. 82 – 57 – = 78 – 29 – = 163
58 – = 184
26 – = c. 84
33 – = 67 – 35 – = 72
39 – = 173
46 – =
–
–
–
–
–
–
21
20
87
57 80
50
92
37 95
40 = 81
18 83
20
76
34 72
30
44 –
–
=
–
–
–
–
=
–
–
=
54
51 – = 97 – 46 96 – 45 – = 59 – 27 60 – 28 – = 64
35 67
38 – =
80 –
–
–
4
2
Proprietà della moltiplicazione
Esegui le moltiplicazioni, poi applica la proprietà commutativa per verificare l’esattezza del calcolo e rispondi.
9 x 12 = ..................... Verifico: ...................................... = ..................... Hai calcolato in modo corretto? Sì No
13 x 7 = Verifico: = Hai calcolato in modo corretto? Sì No
24 x 6 = Verifico: = Hai calcolato in modo corretto? Sì No
Sul quaderno, associa in due modi diversi i fattori per semplificare i calcoli.
a. 5 x 7 x 2 • 10 x 6 x 2 • 4 x 20 x 3 • 2 x 2 x 4 x 5 • 15 x 2 x 2 x 5
b. 3 x 8 x 2 • 5 x 3 x 20 • 50 x 3 x 4 • 3 x 5 x 5 x 2 • 32 x 10 x 3
3
4
Sul quaderno, riscrivi il primo fattore in forma additiva, poi applica la proprietà distributiva, come nell’esempio.
25 x 6 = (20 + 5) x 6 = (20 x 6) + (5 x 6) = 120 + 30 = 150
a. 37 x 4 = 43 x 8 = 234 x 4 =
b. 29 x 7 = 52 x 9 = 406 x 5 =
c. 80 x 3 = 75 x 2 = 516 x 3 =
5
Scrivi quali proprietà sono state applicate.
4 x (7 + 3) = (4 x 7) + (4 x 3) = 28 + 12
6 x 2 x 3 x 10 = 6 x (2 x 3) x 10 = 6 x 6 x 10
8 x 6 x 2 x 5 = (8 x 2) x (6 x 5) = 16 x 30
Sul quaderno, scomponi ciascun numero in unità intere e in unità frazionarie decimali, poi applica la proprietà distributiva, come nell’esempio.
3,7 x 4 =
scomponi (3 + 0,7) x 4 = p. distributiva (3 x 4) + (0,7 x 4) = 12 + 2,8 = 14,8
a. 2,4 x 3 = 5,8 x 2 = 3,5 x 4 = 6,1 x 7 = 7,4 x 4 =
b. 4,25 x 2 = 3,06 x 4 = 12,3 x 6 = 7,20 x 5 = 9,32 x 3 =
Nell’applicare la proprietà distributiva sono stati commessi degli errori: correggi e completa il calcolo sul quaderno.
(18 + 25) x 4 = 18 + (25 x 4) = 6 x (14 + 26) = (6 x 14) + (6 + 26) =
2 x (22 + 13) = (2 x 22) + 13 = (24 + 12) x 5 = 24 + (12 x 5) =
170 Le quattro operazioni
Obiettivo di apprendimento Eseguire moltiplicazioni con i numeri naturali e decimali usando le proprietà per semplificare i calcoli.
1
6
..........................................................................................................................................................................................................
Proprietà della divisione
Completa le tabelle, come nell’esempio.
a.
In ciascuna divisione è stata applicata la proprietà invariantiva. Scrivi l’operazione effettuata per trasformare i numeri, poi esegui il calcolo.
171 Le quattro operazioni
Obiettivo di apprendimento Eseguire divisioni con i numeri naturali e decimali usando le proprietà per semplificare i calcoli.
Operazione Applica la proprietà invariantiva Divisione trasformata Numero ottenuto 280 : 70 (280 : 10) : (70 : 10) 28 : 7 4
: 900
: 40
:
Operazione Applica
Divisione trasformata Numero ottenuto 3,6 : 1,2 4,8 : 0,24 ............................................................................................................................................ .................................... ....................................
: 0,9
0,06
4500
8400
9300
300 b.
la proprietà invariantiva
7,2
3,24 :
1
60 : 20 6 : 2 = 96 : 24 48 : 12 = 70 : 35 14 : 7 = 15 : 3 45 : 9 = 4 : 2 16 : 8 = 2
l’operazione effettuata
trasformare
3500 : 250 350 : 25 : = 2800 : 400 28 : 4 : = 16,8 : 8,4 8,4 : 4,2 : = 50 : 2,5 500 : 25 : = 3
Scrivi
per
i numeri, poi trasformali una seconda volta.
1
2
3
Operazioni inverse
Trasforma ciascuna moltiplicazione in due divisioni.
6 x 8 = 48 perché .............................................................................. oppure ..............................................................................
9 x 3 = perché oppure
6 x 9 = perché oppure
10 x 8 = perché oppure
24 x 5 = ................ perché .............................................................................. oppure ..............................................................................
Trasforma ciascuna divisione in due moltiplicazioni.
56 : 8 = 7 perché .............................................................................. oppure ..............................................................................
20 : 5 = perché oppure
250 : 50 = perché oppure
168 : 7 = perché oppure
Scrivi il numero che manca, poi scrivi l’operazione eseguita per trovarlo.
4
Completa scrivendo nel riquadro il numero che manca e nell’ovale l’operazione inversa.
172 Le quattro operazioni
5 + 8 = + 5 8 + 13 6 x 12 10 : 140 7 + 6 21 – 20 x 8 : 3 8 40 25
42 + 10 21 – 6 18 + 12 70 : 10 32 x 8 9 : 4
5
Scopri il numero di partenza o di arrivo in queste successioni.
6
7
Scrivi i numeri che mancano, poi scrivi le operazioni eseguite per trovarli.
Infine, inventa tu due schemi.
173 Le quattro operazioni Obiettivo di apprendimento Usare le operazioni inverse per verificare calcoli e per trovare numeri naturali.
x 3 + 5 x 2 16 – 6 : 10 x 6 – 4 80 x 4 31 + 9 x 2 x 4 – 9
+ 15 50 53 46 28 – 30 18 15 30 24 x 5 10 11 88 15 : 24 6 8 12 6
Completa le tabelle.
–– –26 8 15 + + + + + + 41 23 5 : : : 180 3 6 x x x 24 20 4 x x x
I numeri 0 e 1
Completa le tabelle. Se non puoi eseguire un’operazione, lascia vuota la casella.
2
Sottolinea le operazioni che danno come risultato 0.
4 + 0 5 x 0 27 – 0 18 : 0 15 + 0 13 x 0 60 – 0 35 : 0
Sottolinea le operazioni che non si possono eseguire.
9 – 0 17 + 0 24 x 0 36 : 0 7 + 0 8 : 0 21 + 0 14 : 0
4
In alcune operazioni c’è un errore: trovalo e correggilo. 13 = 13 x 1 27 = 27 x 0 15 = 15 : 0 20 = 19 + 1 36 = 37 – 1
Quale operazione corrisponde alle seguenti affermazioni? Scrivila al posto dei puntini. aggiungi uno • togli uno • moltiplichi per uno • dividi per uno
Se si ottiene il numero precedente.
Se il numero rimane uguale a se stesso.
Se si ottiene il numero successivo.
Se il numero rimane uguale a se stesso.
174 Le quattro operazioni
a. 27 18 64 17,5 x 0 7 36 8,9 47,2 : 0 87 43 4,91 78,6 + 0 37 91 7,79 32,4 – 0 b. 64 71 2,6 64,1 x 1 78 59 7,3 19,2 : 1 79 47 8,7 5,8 + 1 90 53 4,2 17,9 – 1
1
3
di apprendimento
le
con i numeri 1 e 0.
5 Obiettivo
Eseguire
quattro operazioni
1
Moltiplicare e dividere i decimali per 10, 100, 1000
Trasforma in centesimi.
a. € 5 = cent
€ 23 = cent
€ 48 = cent
2
Esegui le divisioni.
a. 698 : 10 =
b. € 2,50 = cent
€ 1,88 = cent
€ 7,65 = cent
c. € 32,40 = cent
€ 71,15 = cent
€ 143,99 = cent
b. 3218 : 100 = c. 12850 : 1000 =
2,4 : 10 = 2806 : 100 = 3624,8 : 1 000 =
9,01 : 10 =
3
1320,7 : 100 = 2155 : 1 000 =
400 : 10 = 19,58 : 100 = 542,9 : 1000 =
È stato moltiplicato o diviso per 10, 100 o 1000? Completa le uguaglianze inserendo il numero che manca.
a. 230 = x 23
b. 68000 = 68 x c. 6100 = 61 x 1500 = x 1,5
= x 790
= x 340 0,8 = 80 :
= 72,3 :
= 9210 :
= 4506 :
= 844 :
= 1763 :
175 Le quattro operazioni Obiettivo di apprendimento Eseguire calcoli a mente con i numeri naturali e decimali.
79000
3400
9,21
8,44
7,23
45,06
1,763
Completa le tabelle. 24 353 18,7 94,6 :10 4 61,2 0,7 763 :100 12 0,25 45,217 12 040 :1000 4 14,36 1436 143,6 1,436 1436 940 9,4 0,94 94 9400 6,35 635 63,5 6350 6,35 Scrivi se è stato moltiplicato o diviso per 10, per 100 o per 1000. 5
Calcolo a mente
Collega ciascuna operazione all’opportuna strategia di calcolo. 29 x
2
Completa la tabella inserendo i numeri che mancano.
Operazione Strategia Numero ottenuto
20 x 4 20 x 2 x
50 x 9 (50 x 10) – ( x )
14 x 5 (14 x 10) :
38 x 11 (38 x ..............) + (38 x ..............)
3
Completa le tabelle inserendo i numeri che mancano.
Operazione Strategia Numero ottenuto
60 x 4 60 x 2 x .....................................
35 x 4
32 x 4
120 x 4 250 x 4
Operazione Strategia Numero ottenuto 15 x 5 (15 x 10) :
Operazione Strategia Numero ottenuto 20 x 9 (20 x 10)
176
Le quattro operazioni
5 29
11 29
29
9
10) : 2
10)
10)
1)
x
x 4
x
29 x 2 x 2 (29 x
(29 x
– (29 x 1) (29 x
+ (29 x
1
22
160
640
...............................
x 5 46 x 5
x 5
x 5
( x )
........................................................................................................................ ...............................
–
12 x 9 60 x 9 45 x 9
39 x 9
Per ciascuna operazione, scrivi la strategia per effettuare il calcolo rapidamente. Poi calcola, come nell’esempio.
18 x 5 (18 x 10) : 2 = 180 : 2 = 90
36 x 4
26 x 9
37 x 11
18 x 5
120 x 5
150 x 4
210 x 4
40 x 11
38 x 9
5
Collega ciascuna strategia di calcolo con la moltiplicazione a cui si riferisce.
a. (4 x 10) : 2 4 x 4
(4 x 10) + (4 x 1) 4 x 11
4 x 2 x 2
x 9
(4 x 10) – (4 x 1) 4 x 5
b. (47 x 10) + (47 x 1)
(47 x 10) : 2
(47 x 10) – (47 x 1)
x 4
x 11
c. (56 x 10) + (56 x 1)
x 2 x 2
(56 x 10) – (56 x 1)
(56 x 10) : 2
d. 291 x 2 x 2
(291 x 10) – (291 x 1)
x 9
x 5
x 11
x 4
x 9
x 5
x 9 47 x 2 x 2
(291 x 10) + (291 x 1)
x 5
(291 x 10) : 2
Quale strategia è stata applicata? Scrivi la moltiplicazione a cui si riferisce ciascun calcolo.
(18 x 10) + (18 x 1) =
18 x 2 x 2 =
(18 x 10) : 2 =
(18 x 10) – (18 x 1) =
Calcola a mente usando le strategie imparate. Sul quaderno, scrivi le operazioni fatte a mente indicando i passaggi.
13 x 4 = 32 x 5 = 16 x 9 = 14 x 11 =
36 x 4 = 43 x 5 =
130 x 4 = 184 x 5 =
x 9 =
x 9 =
x 11 =
x 11 =
x 11
x 4
177 Le quattro operazioni Obiettivo di apprendimento Usare strategie di calcolo mentale.
4
6
4
56
56
56
56
56
47
47
47
47
291
291
291
291
34
28
140
7
136
quattro operazioni
Le potenze
Quanti quadretti formano la superficie di questi quadrati? Scrivi in forma di moltiplicazione e di potenza.
Moltiplicazione: x
Potenza:
Completa.
• Quali forme sono queste?
• Da quanti cubetti sono formate?
• Calcola.
Cubo 1
Moltiplicazione: x x
Potenza:
Cubo 2
Moltiplicazione: x x
Potenza:
Scrivi in forma di moltiplicazione, poi calcola il valore.
Moltiplicazione: x
Potenza:
Indica con una X.
1 2
178 Le
1
2
32 = = 202 = = 23 = = 81 = = 53 = ........................................... = ................. 1002 = ........................................... = .................
3
44? 4 + 4 + 4 5 x 4 4 x 4 x 4 5 + 4 4 x 3 4 x 4 x 4 x 4 3 x 3 x 3 x 3 5 x 5 x 5 x 5 4
Quale scrittura di 43 è corretta? E di
Scrivi in cifre il numero espresso con una potenza, come nell’esempio.
12 x 102 = 12 x (10 x 10) = 12 x 100 = 1200
a. 9 x 103 = ............................................................................................................................................................................................................................................................................................
3 x 102 =
5 x 104 =
103 x 8 =
b. 102 x 23 =
57 x 103 =
38 x 101 = 104 x 84 =
c. 104 x 519 = 167 x 103 = 236 x 102 = 103 x 862 =
Completa il grafico ad albero, come nell’esempio.
179 Le quattro operazioni
Obiettivo di apprendimento Calcolare le potenze di un numero.
5
Potenza Base Esponente Operazione Valore della potenza 82 26 53 104 15 63 8 Calcola le potenze. 70 = 19 = 52 = 30 = 103 = 06 = 32
..................... 62 = ..................... 42 = 22 = 10
91 = 6 ..................... 1 = 20
Completa la tabella.
=
=
7
Le espressioni
Indica con una X l’espressione corretta per risolvere ciascuna situazione.
a. Filippo gioca a carte con Piero. Nella prima partita Filippo ha guadagnato 6 punti e ne ha persi 2; nella seconda partita ha invece guadagnato 7 punti.
6 – (2 + 7)
6 – 2 + 7
b. Piero ha guadagnato 10 punti con la prima partita, nella seconda ne ha persi prima 5 e poi ancora 2.
10 – (5 + 2)
10 – (5 – 2)
c. Nel carrello di Michele ci sono 2 confezioni da 125 g di mandorle e 2 confezioni da 250 g. 2 x 125 + 250 x 2 2 x (125 + 250) x 2
Indica con una X se le affermazioni sono vere (V) o false (F).
Se l’espressione ha solo addizioni e sottrazioni, si eseguono i calcoli nell’ordine in cui si trovano.
Se l’espressione ha solo moltiplicazioni e divisioni, si eseguono prima le divisioni e poi le moltiplicazioni.
Se nell’espressione ci sono le parentesi, si eseguono prima le operazioni nelle parentesi quadre [ ], poi quelle nelle parentesi tonde ( ) e infine quelle nelle graffe { }
Se nell’espressione ci sono solo divisioni e moltiplicazioni, si eseguono i calcoli nell’ordine in cui si trovano.
Se nell’espressione ci sono parentesi, si eseguono prima le operazioni nelle parentesi tonde ( ).
Confronta il valore delle seguenti espressioni, come nell’esempio.
18 – (3 + 4) < 18 – 3 + 4
a. 21 – (5 + 6) 21 – 5 + 6
35 – (20 – 5)
29 + (10 – 8)
50 – 12 + 13
35 – 20 – 5
29 + 10 – 8
50 – (12 + 13)
V F
b. 80 : (10 : 2) 80 : 10 : 2
48 x 2 x 8
9 x 3 x 2
20 x 20 : 4
48 x (8 : 2)
9 x (3 x 2)
20 x (20 : 4)
180 Le quattro operazioni
1
2
3
4
Scrivi in linguaggio matematico l’espressione scritta con le parole.
È la somma di 8, 5 e 3: ......................................................................
Sottrai 9 alla somma di 12 e 8:
È la somma di 10 con la differenza fra 18 e 5:
Al prodotto di 7 e 6 somma la differenza fra 18 e 7:
È la differenza fra la somma di 16 e 4 e la differenza fra 23 e 17: ......................................................................
È la differenza fra il prodotto di 3 e 8 e la somma di 5 e 3:
5
Scrivi l’espressione con le parole.
7 + 5 + 3 è ...............................................................................................................................................................................................................................................................................................
9 – (4 + 3) è
5 x (2 + 6) è
(10 + 5) – (13 – 4) è
(6 + 8) x (9 – 3) è .............................................................................................................................................................................................................................................................................
6
Sul quaderno, esegui le seguenti espressioni.
a. 70 – [2 x (3 + 5) + (12 – 8)] =
81 : (2 + 4 + 3) + 56 : (2 x 8 – 12) =
7
b. 14 + [50 : (2 x 8 – 2 x 7) – (3 x 9 – 4)] – 8 =
450 – [(79 + 21) x 3 – (6 x 8 + 2 x 11)] =
Usa i numeri 4 • 3 • 5 • 10 per comporre delle espressioni. Scrivi una sola volta ciascun numero all’interno della stessa espressione. Poi risolvile sotto.
a. + – + – – +
b. x – x x + :
181 Le quattro operazioni
di apprendimento Rispettare l’ordine di
Obiettivo
esecuzione di una serie di operazioni.
1
Multipli, divisori, criteri di divisibilità e fattori primi
Completa.
Un numero è divisibile per 2 se è
Un numero è divisibile per se termina con 5 o 0.
Un numero è divisibile per se la somma delle sue cifre è un multiplo di 3
Un numero è divisibile per se termina per 0
2
Scrivi quattro numeri:
• divisibili per 2:
• divisibili sia per 5 sia per 10:
3
Inserisci i numeri nella tabella. Alcuni vanno scritti due volte.
Maggiori di 40
Minori di 40
4 Espressione:
Multipli di 5 Multipli di 3
Circonda i numeri primi.
• Ci sono numeri che non hai saputo dove mettere?
• Se sì, quali?
• Perché?
Scomponi i numeri come prodotto di numeri primi e riscrivili in un’unica espressione. I cerchi celesti ti aiutano a individuare i numeri primi ottenuti.
Espressione:
Sul quaderno, completa le scomposizioni.
54
182 Le quattro operazioni
5 • 8 • 9 • 10 • 11 • 23 • 26 • 21 • 30 • 1 • 33 • 19 • 27
x x 12
x x x 24 x x x 40
Espressione:
= 9 x 48 = x 8 81 = 9 x
6
50 • 18 • 63 • 15 • 11 • 25 • 9 • 45 • 36 • 65 • 23
5
Completa inserendo una cifra in modo da ottenere
8
Rispondi.
• Qual è il numero più piccolo divisibile per 4?
• Qual è il numero più piccolo di 3 cifre divisibile per 2?
• Qual è il più grande divisore di 200? E di 3457?
• Qual è il numero più piccolo divisibile sia per 6 sia per 8?
• Qual è il numero più piccolo divisibile per 5, 10 e 20?
Completa la tabella con numeri compresi fra 0 e 40.
9 Multipli di 5 Multipli di 3
Se un numero occupa più caselle, puoi scriverlo più volte.
Multipli di 2
Multipli di 10
Scrivi i seguenti numeri come prodotto di numeri primi.
50 • 42 • 28 • 60
11
Completa le scomposizioni in fattori primi, poi riscrivi il numero usando le potenze.
28 = 14 x =
48 = 12 x =
81 = 9 x =
40 = 4 x =
54 = 9 x =
Scrivi con le potenze:
Scrivi con le potenze:
Scrivi con le potenze:
Scrivi con le potenze:
Scrivi con le potenze:
183 Le quattro operazioni Obiettivo di apprendimento Individuare multipli e divisori di un numero. Usare criteri di divisibilità per trovare i divisori di un numero. Scomporre in fattori un numero primo.
un
2 1.............. 5.............. 3..............2 14.............. 37.............. 7..............8 ..............34 … per 3 2 3 7 1 6 9 2 29 1 0 … per 5 4 6 18 43 2 5 10 64 … per 10 3 9 12 24 56 32 43
numero divisibile… … per
7
..................................................................................................................................................................................................................................................................................................................................
10
Problemi
Risolvi.
a. Ai piedi di una quercia uno scoiattolo trova molte ghiande. Portando 4 ghiande alla volta e facendo 20 viaggi, riesce a trasportarne un bel po’ nella sua tana. Lo scoiattolo gira ancora per il bosco e trova delle noci, così decide di trasportare anche queste alla tana, prendendone 3 alla volta. Alla fine della giornata conta le ghiande e le noci che ha trasportato ed è molto soddisfatto perché ha in tutto 125 pezzi. Quanti viaggi ha fatto per portare le noci?
CONTO
Antipasto € 6 x 5€ 30
Pizza € 6 x 8........
Birra ..... x 8€ 32
Dolce € 2,5 x 4
Totale
Spesa a testa
........
€ 15 ........
b. Alcuni amici sono andati a mangiare la pizza tutti insieme nella pizzeria “Burlamacco”. Chiedono di dividere la spesa in par ti uguali ma ricevono il conto con alcuni dati che non si leggono bene perché nella stampante della cassa sta finendo l’inchiostro. Aiuta gli amici a capire il conto inserendo le informazioni che mancano.
c. I 44 gatti della famosa canzone sono in fila per 6 “col resto di 2”; perché con il resto di 2?
Quanti gatti devi mettere in ogni fila per non far “avanzare gatti”?
Spiega come hai trovato la risposta.
d. La maestra Elena deve comprare 18 quaderni. In cartoleria trova confezioni da 2 quaderni con la copertina blu, confezioni da 3 con la copertina gialla e confezioni da 5 con la copertina rossa. Vuole avere quaderni con le copertine di vario colore. Quante e quali confezioni potrà comprare? C’è una sola soluzione? Spiega come hai trovato la risposta.
e. Pusy e Popy sono due foche del circo “Italia”; la prima ha 4 anni e l’altra ne ha 13. Quando accadrà che Popy avrà il doppio degli anni di Pusy?
Spiega come hai trovato la risposta.
184 Le quattro operazioni
1
f. Matteo ha una scatola con 64 cioccolatini e li ha messi in modo che in ogni lato della scatola ci siano 18 cioccolatini, disposti come vedi nel disegno. Li offre alle sue amiche che ne mangiano 8. Matteo vuole divertirsi e lancia una sfida alle amiche: – Riuscite a disporre ancora 18 cioccolatini su ogni lato della scatola? E se ne mangiate altri 8 potete di nuovo disporne 18 per ogni lato?
Riusciranno le amiche a vincere la sfida? Spiega come hai trovato la risposta.
g. Andrea e Daniela vanno al campo sportivo il lunedì, il mercoledì, il venerdì dalle 18 alle 19. Valentina ci va il lunedì e il venerdì sempre dalle 18 alle 19. Carlo va anche lui dalle 18 alle 19 ma solo il martedì e il venerdì.
Quando si ritrovano tutti insieme al campo sportivo? C’è un giorno in cui Andrea e Daniela non incontrano nessuno degli amici? C’è un giorno in cui nessuno di loro va al campo sportivo? Spiega come hai trovato la risposta.
h. I 22 alunni e alunne della classe 5a B, per festeggiare la fine dell’anno scolastico, decidono di preparare una macedonia per tutta la classe usando la ricetta che leggi accanto. Quante fragole, banane, kiwi e zucchero saranno necessari per fare la macedonia per tutta la classe?
Macedonia: ogni 4 alunni/e = 6 = 2 = 2 = 3 = 2
i. Per il suo compleanno Anna ha invitato 11 amiche; come torta prepara la crostata di marmellata perché è il suo dolce preferito. La ricetta che possiede è per 8 persone e prevede 200 g di farina e 120 g di burro, oltre agli altri ingredienti.
Anna però dovrà farla per più persone, così controlla le sue scorte e trova: 320 g di farina e 180 g di burro.
Le basteranno gli ingredienti che ha?
l. Marco e Davide giocano con un mazzo da 52 carte. Alla fine della partita Marco ha quattro carte in più del triplo delle carte di Davide. Quante carte ha ciascuno dei due ragazzi?
m. Miriam ha comprato un sacchetto con dentro 14 dolcini. Le caramelle sono la metà dei lecca lecca e il doppio dei cioccolatini. Quanti sono i cioccolatini? E i lecca lecca? Spiega come hai trovato la risposta.
185 Le quattro operazioni
2 2 14 2
14 14 14
2
4 4 2 2 5 5 3 3 A A
Frazioni
1
Alcune figure non sono state frazionate. Modifica in modo da frazionare ciascuna figura.
2
3
Rebecca aveva 15 fiori da mettere nei vasi. Voleva mettere 1 5 dei fiori in vaso. Ha sistemato correttamente i fiori? Se ha sbagliato, correggi.
4
Finisci di frazionare le figure, poi scrivi la frazione che rappresenta la parte bianca rispetto alla figura intera.
5
Osserva il sacchetto di dolci e completa.
Quale parte di tutti i dolci sono: Le caramelle rispetto ai cioccolatini:
le caramelle: .......... I cioccolatini rispetto alle caramelle: ..........
i cioccolatini: I lecca lecca rispetto ai cioccolatini:
i lecca lecca: .......... I cioccolatini rispetto ai lecca lecca: ..........
Scrivi le frazioni che rappresentano le figure.
Se = 1 4 , allora = = =
Se = 1 2 , allora = =
186 Le frazioni
Obiettivo di apprendimento Rappresentare e leggere frazioni.
Frazioni maggiori, minori, uguali a 1
Per ciascuna figura, scrivi la frazione corrispondente rispetto al quadrato. Poi circonda le frazioni maggiori di 1.
Il triangolo colorato è 1 2 del quadrato. Indica se le figure disegnate rappresentano la frazione 3 2 . 2
Circonda le frazioni minori di 1.
Circonda le frazioni maggiori di 1.
Aggiungi la frazione complementare per formare 1.
Scrivi un numero adatto per rendere le frazioni:
187 Le frazioni Obiettivo di apprendimento Rappresentare e leggere frazioni.
1
1 7 • 4 8 • 3 2 • 6 4 • 8 8 • 5 9 • 9 6 • 5 5
3
Sì No Sì No Sì No
3 5 • 6 4 • 7 9 • 2 2 • 5 3 • 8 5 • 9 3 • 6 8
4
1 = 3 5 + 1 = 4 7 + 1 = 8 9 + 1 = 3 8 +
5
• minori
1: .......... 9 • 4 • 3 • .......... 6 • 18 • .......... 12 • 35 • 1 • uguali a 1: 5 • 1 • 7 • 16 • 4 • 29 • 34 • 71 • maggiori di 1: 6 • 4 • 3 • 14 • 22 • 31 • 47 • 52
di
6
Confrontare frazioni
Scrivi le frazioni corrispondenti alla parte colorata di ciascuna figura, poi confrontale, come nell’esempio.
Luca e Gilberto stanno attaccando dei cartellini sulla linea dei numeri.
Completa la linea e poi collega i cartellini che non hanno ancora appeso.
Confronta le frazioni inserendo il segno opportuno.
Completa mettendo il numero che manca per rendere vere le relazioni.
Scrivi una frazione compresa fra le coppie delle frazioni.
Obiettivo
188 Le frazioni
di apprendimento Rappresentare, leggere e confrontare frazioni.
1
3 2 1 2 • 4 6 5 6 • 3 3 2 3 • 4 9 3 9 • 2 5 2 6 • 7 4 7 7 • 5 7 5 3 • 6 8 6 3
3
1 1 3 4 4 1 2 1 4 3 4 2 4 2 3 0 12 12 12 12 12 12 12 12 12 12 12 12 < 1 3 1 3 1 2 1 2
2
5 > 4 5 • 3 7 < 7 • 5 8 < 3 .......... 6 > 3 6 • 6 9 > 9 • 2 5 > 1 .......... 3 < 1 • 4 5 > 6 • 2 6 < 2 3 < 3 3 • 5 7 > 5 • 2 9 > 2
4
a. 2 8 6 8 • 5 9 ....... 2 9 • 7 12 ....... 5 12 • 15 40 ....... 18 40 • 3 20 ....... 5 20 b. 3 6 3 9 • 6 10 6 6 • 3 7 3 5 • 7 8 7 12 • 4 15 4 13 5
Frazioni equivalenti
Per ciascuna parte colorata, scrivi il suo valore e una frazione a essa equivalente.
Valore: 1
Valore:
Valore:
Valore: Fraz. equivalente: Fraz. equivalente: Fraz. equivalente: Fraz. equivalente:
In ciascuna figura, colora e scrivi la frazione corrispondente a:
L’allenatrice ha segnato i tiri e i canestri fatti dalle giocatrici. Completa la tabella e rispondi.
Giocatrice Tiri Canestri N. canestri rispetto ai tiri
Alessandra 15 3
Nicole 12 4
Proprietà invariantiva Frazione equivalente
Farida 24 8 .......... ..........
Viola 10 5 ..........
• Chi ha fatto più canestri rispetto ai tiri fatti?
189 Le frazioni
Obiettivo di apprendimento Rappresentare, leggere e calcolare frazioni equivalenti.
1
2 8 2 : 2 8 : 2
Giorgia 8 2
3
......... 15
:
:
..........
3
1 5 2 3 1 4 3 5
/ = / / = / / / = / / = / / = =
2
1
Dall’intero alla frazione
Scrivi che frazione rappresentano rispetto a tutte le figure:
• i quadrilateri:
• i triangoli:
• i triangoli rettangoli:
• i poligoni con almeno 1 angolo retto:
• i poligoni regolari:
• i poligoni con i lati paralleli:
Colora secondo le indicazioni, poi rispondi.
2 8 blu • 3 8 a righe Quanti cerchi sono rimasti bianchi? In frazione:
Prima disegna l’intero, poi calcola la parte frazionaria indicata, come nell’esempio.
2 3 di 21 21 è la parte intera
Calcola:
21 : 3 = 7 che è 1 3 2
190 Le frazioni
1 3 7
2
=
3 + 1 3 , quindi, 7 + 7
x 2 = 14 3 4 di 24 • 5 7 di 28 • 8 9 di 36 • 4 5 di 45 • 4 7 di 35 • 2 3 di 144
3
1
oppure 7
3
4
Risolvi.
Clelia e Caterina stanno preparando due collane e hanno a disposizione 100 perline. Per fare la sua collana Clelia ha scelto le perline di colore rosso e quelle color perla, mentre Caterina ha scelto le perline rosse e quelle oro. 2 4 di tutte le perline sono rosse, 2 5 sono color perla e quelle color oro sono 2
20 .
Riuscirà ogni bambina a fare una collana da 30 perline usando metà perline di un colore e metà dell’altro? Spiega come hai trovato la risposta.
5
Trova almeno 6 modi diversi per frazionare questa figura. Colora e scrivi l’unità frazionaria.
6
Risolvi.
a. Un gruppo di amici sta correndo la maratona di Firenze. Il percorso è lungo 42 km.
Marco è a 5 7 del percorso, Lisa è a 1 3 , Gianni è a 4 6 e Francesca è a 1 2
Sul quaderno scrivi gli amici in ordine, da chi ha percorso meno strada a chi ne ha percorsa di più.
b. In un negozio di sport sono esposte 12 biciclette: 1 6 delle bici sono da strada; di quelle che restano, 2 5 sono da corsa; di quelle che restano, togliendo anche quelle da corsa, 1 3 sono mountain bike.
Quelle che restano sono per i bambini piccoli: quante sono?
191 Le frazioni
Obiettivo di apprendimento Calcolare la frazione di un numero.
Dalla frazione all’intero
Ciascun triangolo è la metà di un rettangolo. Quanti rettangoli interi puoi formare?
2
Calcola l’intero dopo aver rappresentato le quantità graficamente, come nell’esempio.
Se 1 4 è 15 1 4 15 15 x 4 = 60, quindi, l’intero corrisponde a 60.
Se 1 3 è 20
Se 1 5 è 20
Se 1 6 è 15
Se 1 7 è 9
Calcola l’intero, come nell’esempio.
Se 1 4 è 12
Se 1 2 è 36
Se 1 15 è 10
Se 1 8 è 8
8 è 2 5 di , significa che 8 sono 2 delle 5 parti che formano l’intero.
Se 2 parti sono 8, trova da quanto è formata 1 parte: 8 : 2 = 4
Se 4 è 1 5 , allora 5 5 sono 4 x 5 = 20
Calcola: 9 è 3 4 di 12 è 3 5 di 24 sono 4 7 di
192 Le frazioni
1
42 sono 6 7 di 150 sono 3 4
45 sono 5 8 di
di 3
Alcuni alunni e alunne hanno registrato le pagine lette in una settimana. Completa la tabella, esegui i calcoli e rispondi.
193 Le frazioni Obiettivo di apprendimento Ricostruire l’intero conoscendo il valore di una parte.
4
Osserva la frazione e disegna la figura intera.
Bambino/a Pagine lette In frazione, rispetto al totale Totale pagine libro Franca 15 1 3 Marta 21 3 8 Alessandro 18 2 5 Lucia 14 7 12 Duccio 20 2 3 5
Chi ha il libro con più pagine?
1 4 1 2 1 3 2 4 2 3 3 5
• Chi ha il libro con uguale numero di pagine?
1
Frazioni e numeri decimali
Scrivi prima in frazione, poi come numero decimale, come nell’esempio.
Numero Frazione Numero decimale Numero Frazione Numero decimale
9 decimi
4 centesimi
3 millesimi
34 decimi ..........
2
3
Usa una sola volta i seguenti simboli per comporre:
3 1 6 ,
• il numero minore:
• il numero maggiore:
Usa una sola volta i seguenti simboli per comporre:
5 8 7 ,
• due numeri compresi fra 7 e 8:
• un numero compreso fra 5,7 e 5,8:
• un numero minore di 8: .......................
centesimi
millesimi ..........
Circonda la cifra dei decimi, poi riscrivi solo i decimi, come nell’esempio.
Circonda la cifra dei centesimi, poi riscrivi solo i centesimi.
6 Cancella gli zeri inutili, se ce ne sono.
Sul quaderno, riscrivi il numero scomposto prima a parole e poi in cifre, come nell’esempio.
7 Sul quaderno, riscrivi in ordine crescente.
194 Le frazioni
9 10 0,9 18
millesimi
................................... 67
centesimi ...................................
217
369
7, 5 6 5 decimi 0,5 0,27 78,369 724,3 3,607 4
25,34 51,073 714,526 0,237 ..................................... ............... 5
3,19 = tre unità + un decimo + nove centesimi = 3 + 0,1 + 0,09 6,34 • 12,8 • 1,385 • 0,37 • 25,73 • 312,8 • 6,357 • 78,009 • 0,607
00,308 • 1,280 • 35,070 • 4,200 • 27,05 • 012,60 • 0,370 • 0,06
23,56 • 2,356 • 23,65 • 2,536 • 23,62 14,79 • 14,97 • 147,9 • 14,69 • 1,497 8
9
10
Usa i simboli 1 4 6 , per comporre tutti i numeri possibili sul quaderno: in ogni numero puoi usare una sola volta ciascun simbolo. Poi riscrivi i numeri trovati in ordine crescente.
Sul quaderno, scrivi i numeri naturali fra i quali
compreso il numero decimale, come nell’esempio.
11
12
Scrivi un numero decimale compreso tra i due numeri dati.
13
Sul quaderno, scomponi i numeri, poi applica la proprietà associativa per eseguire i calcoli, come nell’esempio.
32,93 + 3,18 =
scomponi i numeri (30 + 2 + 0,9 + 0,03) + (3 + 0,1 + 0,08) =
associa (30 + 2 + 3) + (0,9 + 0,1) + (0,03 + 0,08) = calcola 35 + 1 + 0,11 = 36,11
a. 73,59 + 47,8 =
417,96 + 135,2 =
90,26 + 3,75 =
b. 826,7 + 35,2 =
178,36 + 3,57 =
85,023 + 47,38 =
c. 30,60 + 18,23 =
2,77 + 15,87 =
364,17 + 64,36 =
14
195 Le frazioni Obiettivo di apprendimento Identificare il rapporto tra frazione e numeri decimali.
Completa, come nell’esempio. 1 u = 10 d = 100 c = 1000 m 7 u = d = c = m 2,04 u = c = d = m 3,2 u = d = c = m 34,27 u = m = d = c 8,65 u = d = c = m 30,065 u = m = c = d
2 2,36 3 9,52 • 3,54 • 8,6 • 1,09 • 7,276 • 11,36 • 13,127
è
Completa con
compreso
0,8 1 1,4 27,6 1 28,2 13,5 1 14,4 5,2 1 6,5
un numero naturale adatto,
tra i due numeri dati.
11 12 18 19 7,7 8 6 6,2 1,18 1,19 25 26
Frazioni e percentuali
Sul quaderno, riscrivi il numero in frazione e poi in percentuale, come nell’esempio.
0,20 = 20 100 = 20%
2
Sul quaderno, riscrivi in frazione e poi in numero, come nell’esempio.
30% = 30 100 = 0,30
Disegna sul quaderno un rettangolo con l’area di 100 quadretti. Colora il 32% di rosso, il 20% di blu, il 12% di verde. Qual è la percentuale non colorata?
Completa inserendo il simbolo adatto, come nell’esempio.
4 Indica con una X se le uguaglianze sono vere (V) o false (F).
=
=
=
6
3 Scrivi la percentuale o quella complementare.
=
196 Le frazioni
0,83 • 0,40 • 0,07 • 0,5 • 0,74 • 2,1 • 0,68 • 12,3 • 6,2 • 3,9 • 2,46 • 8,4 • 1,35 1
Percentuale Percentuale complementare 15% ..................................... 75% 29% Percentuale Percentuale complementare 35% ..................................... 60% 89% Percentuale Percentuale complementare ..................................... 48% 94% 13%
60% • 25% • 47% • 90% • 36% • 413% • 234% • 18% • 124% • 230%
2 100 < 10% • 30% 6 100 • 65% 68 100 • 45 100 40% • 60 100 6% • 100% 1 • 18% 23 100 • 4 100 4% • 7 100 60% • 85% 87 100 • 70% 70 100
V
2 100
20% 72%
72 100 124%
24 100 90 100
90% 180%
180 100 5
F
=
7
Calcola sul quaderno.
a. 50% di 200
10% di 200
75% di 200
25% di 200
b. 25% di 7500
15% di 8300
24% di 7200
8% di 32000
c. 11% di 2800
7% di 4900
41% di 200
52% di 300
8
Scrivi la frazione rappresentata in ciascun quadrato: aiutati contando i quadretti più piccoli.
Trasforma poi la frazione in una frazione decimale equivalente con denominatore 100.
Infine, riscrivi il numero in percentuale.
197 Le frazioni
1 = = ........% x 50 x 50 1 = .......... = % x 20 x 3 = .......... = % x x 10 3 .......... = = % x x 20 20 = .......... = % x x 3 4 = 75 = % x 25 x 25
Sul quaderno, applica la proprietà invariantiva per trasformare le frazioni in frazioni decimali equivalenti con denominatore 100. Poi riscrivi la frazione decimale come percentuale, come negli esempi.
Trasforma le frazioni in percentuali dopo aver eseguito le divisioni, come negli esempi.
Aiutati con una calcolatrice per eseguire le divisioni. Scrivi il numero ottenuto fino alla cifra dei millesimi, poi approssimalo ai centesimi e trasforma in percentuale, come nell’esempio.
198 Le frazioni
1 4 = 25 100 = 25% 7 50 • 9 25 • 13 20 • 5 10 • 3 5 • 16 25 • 8 25 • 12 20 • 49 50 180 200 = 90 100 = 90% 80 200 • 92 200 • 360 400 • 384 400 • 90 300 • 126 300 • 200 500 • 320 500 9 x 25 x 25 : 2 : 2
1 4 = 1 : 4 = 0,25 25 100 = 25% 5 10 = 5 : 10 = 0,5 0,50 50 100 = 50% 10 50 20 0 0 10
Frazione Numero Numero approssimato Percentuale 8 14 0,571 0,57 57% 5 27 7 18 12 37 11 6 5 = : = = % 4 25 = : = = % 9 15 = : = = % 7 14 = : = = % 3 4 = : = = % 1 2 = : = = % Obiettivo di apprendimento Riconoscere e calcolare le percentuali. Calcolare e rappresentare percentuali con areogrammi.
La percentuale nel commercio
Completa la tabella.
2
Risolvi.
a. Barbara ha comprato una libreria con lo sconto del 30%, pagandola € 210. Quanto costava prima dello sconto la libreria di Barbara?
b. Un paio di rollerblade costavano € 50, ma il prezzo
è aumentato del 10%.
Quanto costano adesso? € 50
c. Lo zio di Matilde, che ha uno stipendio mensile di € 1 350, ha ricevuto un aumento del 7%.
Qual è il suo nuovo stipendio?
d. Clotilde compra un’automobile che costa € 24550. Paga subito il 70% del costo totale. Quanto gli resta ancora da pagare?
e. Che cosa costa di meno: una maglia da € 55 scontata del 12% oppure una maglia da € 50 scontata del 15%? E quanto di meno?
f. Quale percentuale rimane da pagare se sul prezzo di un libro c’è lo sconto del 20%?
g. Nel piccolo paese di Poggiobello gli abitanti erano 500. Quest’anno sono arrivati 25 nuovi residenti. A quale percentuale corrisponde l’aumento di abitanti?
h. Una bicicletta costava € 400. Il suo prezzo è stato prima aumentato del 15%, ma poi il prezzo aumentato è stato scontato del 15%. Qual è il prezzo finale?
199 Le frazioni Obiettivo di apprendimento Calcolare percentuali in contesti concreti.
Merce Prezzo iniziale Percentuale di sconto Sconto in
finale in
Pantaloni € 25 15% T-shirt € 14 10% Felpa € 45 12%
€ Prezzo
€
1
2
Le misure
Stima quanto sono lunghe le parti del tuo corpo, poi verifica misurandole in centimetri.
• Lunghezza del dito indice: stima .............. misura ..............
• Lunghezza spanna: stima misura
• Lunghezza dell’avambraccio (dal gomito al polso): stima misura
• Lunghezza del piede: stima misura
• Lunghezza degli arti superiori (dalla spalla alla punta delle dita): stima .............. misura ..............
• Lunghezza degli arti inferiori (dall’anca al tallone): stima misura
Osserva i prodotti, poi completa. Se necessario, svolgi le equivalenze sul quaderno.
3
succhi marmellata
Scrivi i prodotti che pesano:
• meno di 1 kg:
• 1 kg:
• più di 1 kg:
Scrivi l’unità di misura necessaria per misurare la massa (peso) di:
• 1 barattolo di marmellata:
• 1 cane: ....................
• 1 pennarello:
• 1 vagone del treno:
• 1 piuma d’oca:
• 1 bicicletta: ....................
• 1 auto:
• 1 astuccio:
• 1 bustina di tè:
4
Scrivi i prodotti che hanno una capacità:
• minore di 1 <l :
• di 1 <l :
• maggiore di 1 <l :
Scrivi l’unità di misura necessaria per misurare la capacità d’acqua contenuta in:
• 1 bicchiere:
• 1 cucchiaino: ....................
• 1 vasca da bagno:
• 1 pentola:
• 1 siringa:
• 1 bottiglietta: ....................
• 1 innaffiatoio:
• 1 contagocce:
• 1 bottiglia di aranciata:
200 La
misura
1
5
Completa gli schemi.
c<l + 150 c<l
.............
18 d<l + d<l
210 c<l + c<l
20 dag + dag
............. g + 1100 g hg + 9 hg
m + 350 m dm + 4300 dm
16 dam + dam
3 <l
2 kg
20 d<l + ............. d<l m<l + 1200 m<l
2600 m<l + m<l
14 hg + hg
800 g + g dag + 130 dag
25 dam + dam
5 hm
20 m + m
3000 dm + dm
Esegui le equivalenze.
a. 369 c<l = ................. <l
91657 m<l = d<l
2546 m<l = d<l
4,5 d<l = da<l
52 d<l = ................. h<l
508 c<l = da<l
b. 364 dag = kg
24 mg = g
32649 dg = ................. hg
651,3 cg = g
19 dag = kg
17,4 dag = hg
In ciascuna bottiglia, aggiungi la quantità di acqua necessaria a raggiungere la capacità indicata.
30 c<l + 30 c<l + 30 c<l + 30 c<l + 30 c<l + 30 c<l + 7
• Riscrivi in ordine crescente le misure inserite:
Trasforma nelle unità di misura indicate, come nell’esempio.
254 <l = 25,4 da<l
319 m<l = d<l 462 <l = h<l
Obiettivo
c<l = d<l 304 m<l = <l
201 La misura
di apprendimento Operare trasformazioni fra
grandezze omogenee.
6 60 c<l 10 20 30 40 50 60 70 80 90 100 110 120 450 m<l 10 20 30 40 50 60 70 80 90 100 110 120 1 <l 10 20 30 40 50 60 70 80 90 100 110 120 8 d<l 10 20 30 40 50 60 70 80 90 100 110 120 5,5 d<l 10 20 30 40 50 60 70 80 90 100 110 120 0,4 <l 10 20 30 40 50 60 70 80 90 100 110 120
8
37,4
Le misure
1
Scrivi la marca che manca, come nell’esempio.
16 m = 1600 cm = 16000 mm
a. 8 dag = 0,08 = 80
260 g = 2,6 = 0,26
610 g = 61 = 0,61
4,6 hg = 460 ............ = 46 ............
2
b. 248 dg = 2,48 = 2480
327 cg = 3,27 = 0,327
2,9 kg = 2900 = 29
7,5 cg = 75 ............ = 0,075 ............
Indica con una X se le uguaglianze sono vere (V) o false (F).
V F
7,8 km = 7800 m
234 cm = 2,34 m
15 cm = 150 dm
6 m = 0,06 hm
41 cg = 410 mg
8 hg = 80 kg
42,6 dag = 0,426 kg
0,94 kg = 940 g
Scrivi in litri a quanto corrispondono le frazioni indicate.
V F
V F
34,8 c<l = 3,480 <l
63 d<l = 0,63 da<l
12 h<l = 120 da<l
3 <l = 0,03 h<l
202 La
misura
1 litro
1 2
3 4 di litro
1 4 di litro = 2 litri e 3 4 = 4 litri e 1 2 = 1 litro e 2 4 =
1 2 kg = 250 g = 2 kg e 1 2 = 750 g = 4 Collega le misure equivalenti. 200 <l 202 d<l 0,2 h<l 2000 c<l 2 da<l 2 da<l 20 <l 2 h<l 200 d<l 20,2 <l
e
=
=
3 Scrivi in chilogrammi a quanto corrispondono i pesi indicati.
5
6
Esegui le operazioni con le misure di lunghezza, come nell’esempio.
8 m + 20 dm + 300 cm =
8 m + 20 dm + 300 cm =
8 m + 2 m + 3 m = 13 m
a. 12 m + 200 dm + 1200 cm = m
26 hm + 11 km + 1300 m = hm
127 m + 3,4 km + 44 dam = hm
13,4 dm + 480 cm + 1770 mm = ................................................................................................................ m
b. 3700 g – 140 dag = kg
7800 mg – 44 dg = g
9,86 kg – 75 hg = dag
2,46 g – 126 cg = dg
Aiutati con le tabelle e trasforma nelle unità di misura indicate, come negli esempi.
14 <l = m<l
3,6 da<l = c<l
L’unità di misura in cui trasformare i 14 <l L’unità di misura in cui trasformare i 3,6 da<l sono i m<l. sono i c<l.
h<l dah<l h<l dh<l ch<l mh<l 1 4 0 0 0
h<l da<l <l d<l c<l m<l 3 6 0 0
5,7 <l = c<l 3,4 h<l = d<l 6,82 da<l = c<l
<l d<l c<l m<l h<l da<l <l d<l da<l <l d<l c<l
45 d<l = m<l 28 da<l = <l 7 da<l = d<l
<l d<l c<l m<l h<l da<l <l d<l h<l da<l <l d<l
203 La misura
Obiettivo di apprendimento Operare trasformazioni fra grandezze omogenee.
7
1
Le misure di tempo
Inserisci i numeri adatti per completare le frasi.
a. In un millennio ci sono anni.
b. In un millennio ci sono secoli.
c. In un secolo ci sono ........................ anni.
d. In un anno ci sono mesi.
e. Una settimana è formata da giorni.
2
Scrivi le date indicate dalle frecce.
primo millennio avanti Cristo (a.C.)
f. In un giorno ci sono ore.
g. In un’ora ci sono minuti.
h. In un minuto ci sono ........................ secondi.
i. I mesi che hanno 31 giorni sono
NASCITA DI CRISTO
primo millennio dopo Cristo (d.C.)
• Quale data è più vicina alla nascita di Cristo? Qual è più lontana?
3
Trasforma in secondi.
1 min e mezzo = s
3 min = s
5 min e mezzo = s
10 min = s
20 min = s
15 min = s
5
Trasforma in ore.
Trasforma in minuti.
6
1 d = h mezza giornata = h 2 d e mezzo = h
180 min = h 90 min = h 480 min = h
Calcola il tempo trascorso.
Dalle 8:30 alle 12:00
Dalle 15:10 alle 15:55
Dalle 21:35 alle 00:10
Dalle 23:50 alle 2:25
Dalle 9:00 alle 11:15
Dalle 19:20 alle 20:10
Dalle 20:18 alle 22:00
Dalle 4:32 alle 6:13
204 La misura
1000 900 800 700 600 500 400 300 200 100 100 200 300 400 500 600 700 800 900 1000 X secolo IX secolo VIII secolo VII secolo VI secolo V secolo IV secolo III secolo II secolo I secolo I secolo II secolo III secolo IV secolo V secolo VI secolo VII secolo VIII secolo IX secolo X secolo
1 h e 1 2 = min 2 h e 15 min = min Mezz’ora = min 3 4
min 1 h e 3 4 = min 3 h e 20 min = min 4 h = min 2
4 =
4
d’ora =
h e 1
min
8
Ciascun orologio segna l’ora sbagliata. Segui le indicazioni e scrivi l’ora giusta.
9
10
È 12 min indietro. È 8 min avanti. È 16 min indietro. È 19 min avanti.
Ora esatta: Ora esatta: Ora esatta: Ora esatta:
Leggi l’ora indicata dall’orologio e poi completa.
Che ore erano: 3 ore fa?
2 10 11 12 1
9 3 6 57 8 4
1 ora e mezzo fa?
2 ore e 1 4 fa?
Che ore saranno: fra 2 ore? .......................
fra 4 ore e mezzo?
fra 24 ore?
Fabio guarda la televisione dalle 17:30 alle 18:15, mentre Alberto la guarda per 1 ora e mezzo e Leonardo la guarda dalle 17:20 alle 18:10. Quale bambino guarda meno televisione?
Ludovica e Gabriel vanno al cinema a vedere lo spettacolo delle 17:15. Il film durerà 90 minuti, fra il primo e il secondo tempo ci sarà un intervallo di 10 minuti e altri 10 minuti serviranno per uscire.
A che ora devono dire ai loro genitori di venirli a prendere fuori dal cinema?
11
Alessandro e Andrea sono due compagni di classe e festeggiano il compleanno lo stesso giorno. Oggi Andrea compie 11 anni.
a. In quale anno è nato Alessandro?
b. Alessandro ha una sorella maggiore di 4 anni. In quale anno è nata?
c. La mamma di Alessandro ha il quadriplo degli anni del figlio e cinque anni in meno del marito.
Quanti anni hanno i genitori di Alessandro?
d. Per festeggiare è stata invitata a cena una persona nata nel 1945.
Chi pensi che sia?
Quanti anni ha?
Obiettivo
205 La misura
di apprendimento Calcolare intervalli di tempo. Operare trasformazioni fra grandezze omogenee.
7
9 3 6 57 8 4 2 10 11 12 1
Indica il numero di monete o banconote necessario per formare i seguenti numeri. Usa meno monete e banconote possibili, come nell’esempio.













Forma 10 euro usando:
• solo banconote:
• banconote e monete:
• 6 monete:
• 9 monete:
• 14 monete:
• banconote e 8 monete:
Osserva le sterline britanniche, poi scrivi quanti soldi Amy ha nei suoi salvadanai.































206 La misura
L’euro
16,45 1 1 1 2 1 48,55 94,70 69,03 130,05 319,50 1 1 penny 2 pence 5 pence 10 pence 20 pence 50 pence 1 pound 2 pounds sterline
sterline e
2
3
5
Sul quaderno, scrivi le combinazioni di oggetti che può comprare Emily con € 20.
€ 13,50
€ 8,90
€ 119
€ 5,90
€ 11,90
Anita vuole mangiare un panino, un dolce e bere qualcosa. Osserva, scrivi tre menù possibili per Anita e calcola la spesa. Poi completa.
6
acqua € 1,50 lattina € 2,50 bicchiere tè € 1
Il meno caro:
Il più caro:
Un menù a tua scelta:
crostata € 3,50 gelato € 2,80 tiramisù € 3,80
piadina € 4,50 hot dog € 3,60 hamburger € 5,50
Scrivi in euro il valore del seguente denaro, sapendo che 1 sterlina è uguale a 0,84 euro.

= euro = x = euro

1 sterlina 2 sterline


50 pence = : = euro = =

Quanti euro sono? Se serve, aiutati con la calcolatrice.
15 sterline = € 23 sterline = €
36 sterline = € ............... 13 sterline = € ...............

Scopri quanto costa ciascun fiore. 8
7 £3,80 £3,50 £4,20
71 sterline = € 47 sterline = €
57 sterline = € 51 sterline = €
100 sterline = € 200 sterline = €
Margherita
207 La misura
di apprendimento Operare trasformazioni tra sistemi monetari differenti. Risolvere problemi relativi al sistema monetario.
Obiettivo
4
=
Rosa Tulipano
= = =
Quanto vale ciascun simbolo?
Ra-Giocando
2
Nei rettangoli c’è la somma dei numeri collegati. Trova i numeri mancanti.
Quanto pesa ciascuna pallina? 3


208 GIOCA CON LA LOGICA
+
22 x = 44 + + = 24 = = = 3 x x = 12 x = 18 + – = 8 = = = 6 x x = 128 x x = 80 + – x = 16 = = = + + + + = 21 + + + + + + + = 30 = = 1
=
11 kg 19 kg 14 kg 53 27 49 48 65 7 13 16 38 12 16
4
Disegna queste forme nelle caselle vuote e completa in modo che ciascuna riga, ciascuna colonna e ciascun settore contengano tutte le 4 forme senza ripetizione.
5
Trova il valore del cubetto in ciascun esercizio.
a. + + 4 = 20 =
6
b. 5 x – 8 = 17 =
c. 3 x + 8 = 20 =
7
d. 7 x – 15 = 34 = ..................
Completa la colonna azzurra in modo da ottenere un numero che sia il doppio di 232. Segui le istruzioni.
1. Ha tre cifre uguali e la loro somma è 6
2. Il doppio di trenta più quattro.
3. Il primo numero dispari.
4. Sei elevato alla seconda.
5. 74 decine e 4 unità.
Lisa ha 5 mele. Scambia tutte le sue mele perché vuole solo ciliegie. Quante ciliegie può ottenere?
Ciliegie =
209 GIOCA CON LA LOGICA
1 2 3 4 5
= = =
1
Colora le figure simmetriche a quelle colorate.
La simmetria
2
Disegna gli assi di simmetria di ciascuna figura.


3
5
La lettera M si guarda allo specchio: come si vedrà? Disegna l’immagine riflessa.
M• Che cosa noti?
• Quali altre lettere si comportano come la M?

4

La lettera B si specchia in una pozza d’acqua: come si vedrà? Disegna l’immagine riflessa.
B• Che cosa noti?
• Quali altre lettere si comportano come la B?
Disegna poligoni di forme differenti che abbiano almeno un asse di simmetria.
210 Le isometrie
.......................................................................................................................................
6
Disegna tutti gli assi di simmetria presenti nelle figure e poi scrivi quanti sono.
7
Indica con una X qual è la figura simmetrica a quella data.
8
Disegna la figura simmetrica rispetto all’asse dato.
9
Circonda con lo stesso colore le coppie di rettangoli che, unite, formano un quadrato celeste al loro interno.
211 Le isometrie
Obiettivo di apprendimento Riconoscere ed effettuare movimenti nel piano di punti e figure. Identificare assi di simmetria.
1
La traslazione
Riproduci il disegno effettuando gli spostamenti indicati dal vettore. Poi misura la lunghezza dello spostamento e rispondi.
Spostamento
A • A1:
A1 • A2:
A2 • A3:
2
A
A1 A2 A3
• Sono uguali le figure A e A1? Sì No
• E le figure A e A2? Sì No
• E le figure A e A3? Sì No
• Che cosa hanno tutte di diverso fra loro?
Con il righello, disegna il vettore che unisce i punti indicati nelle figure, misura lo spostamento e scrivi quanto misura.
3
Disegna i vettori che indicano i possibili spostamenti:
• degli uccelli azzurri e degli uccelli bianchi
• dei cigni bianchi e dei cigni celesti
212 Le isometrie
.............................................................................................................................
.................................
4
Verifica se il vettore disegnato è corretto e, dove serve, correggi. Poi misura la traslazione.
5
La chiocciola si sta muovendo lentamente: disegna il vettore che indica lo spostamento.
Di quanto si è spostata ciascuna volta? In vettore ha direzione e verso uguale, ma possono essere presi punti di riferimento diversi.
6
1° spostamento: verso di 2° spostamento: verso di
Disegna il vettore che indica, ciascuna volta, lo spostamento fatto dalla coppa. Poi rispondi.
1o spostamento: cm
2o spostamento: cm
3o spostamento: cm
• In quale caso si è spostata di più?
7
Stabilisci quale movimento ha effettuato la figura A per andare da:
•
•
•
213 Le isometrie
di apprendimento Riconoscere ed effettuare movimenti
Obiettivo
nel piano di figure: la traslazione.
A 1:
1 2:
2 3: A 1 3 2 ................................. A
B C
coppa
1
Colora di blu le coppie di figure che sono state traslate e di giallo le coppie di figure ruotate.
3
Osserva il cerchio a sinistra. Sapendo che il cerchio ruota ciascuna volta intorno al suo centro, quale lettera si trova al posto dello ?
Aiutati con il goniometro disegnato per misurare l’ampiezza della rotazione effettuata dalla bandiera in senso orario.
214 Le isometrie
90 80 100 110 120 130140 150 160 170 180 70 60 50 40 30 20 10 0 0 180 170 10 20 30 40 50 60 70 80 160 150140130120110 100 90 80 100 110 120 130140 150 160 170 180 70 60 50 40 30 20 10 0 0 180 170 10 20 30 40 50 60 70 80 160 150140130120110 100 90 80 100 110 120 130140 150 160 170 180 70 60 50 40 30 20 10 0 0 180 170 10 20 30 40 50 60 70 80 160 150140130120110 100
La rotazione
.......................... .......................... ..........................
E
2 A C
A D F A E B C A D E B C
4
Di quanto è ruotato il vigile ciascuna volta rispetto alla posizione di partenza?
posizione di partenza
5
6
In senso antiorario di 90°. In senso antiorario di 180°. In senso orario di 180°. In senso orario di 90°. In senso antiorario di 90°. In senso orario di 90°.
Indica il senso e l’ampiezza del movimento di rotazione che deve effettuare il triangolo numero 3 per sovrapporsi:
• al triangolo 4: senso orario di ....................................
2
1 4
3
• al triangolo 1: senso orario di
• al triangolo 2: senso orario di
E per riportarlo su se stesso? Senso
In quale altro senso può ruotare il triangolo 3?
Di quanto ruota, allora, nell’altro senso per sovrapporsi:
• al triangolo 1: senso di
• al triangolo 2: senso di
• al triangolo 4: senso di
Traccia i segmenti che uniscono i punti A e A1 al centro di rotazione (O). Poi indica il verso di rotazione e di quanto è ruotato il punto A.
215 Le isometrie Obiettivo di apprendimento Riconoscere ed effettuare movimenti nel piano di figure: la rotazione.
O O O O A A1 A1 A1 A1 A A A .......... .......... .......... ..........
1
Osserva e rispondi.
Figure simili

2
Osserva e rispondi.
Nicolas ha costruito il rettangolo A. Lo schiaccia e ottiene la figura B.
• I lati hanno la stessa misura? Sì No
Stefano gioca con l’ombra della sua mano.
• La mano e la sua ombra hanno la stessa forma? Sì No
• Se Stefano allontana la mano dal muro, come diventa la sua ombra? E se la avvicina?
• Puoi dire allora che, se Stefano avvicina o allontana la mano dal muro, l’ombra cambia dimensioni? Sì No
• Cambia anche la forma? Sì No
• E gli angoli corrispondenti hanno la stessa ampiezza? Sì No
• Le due figure hanno la stessa forma? Sì No
• Puoi dire allora che le due figure sono simili? Sì No
A B
3
Leggi e rispondi.
Ricalca il triangolo celeste con la carta trasparente e sovrapponilo agli altri triangoli.
Colora solo i triangoli che hanno la stessa forma e gli angoli di uguale ampiezza rispetto a quello celeste.
• I triangoli hanno tutti la stessa grandezza? Sì No
• Hanno tutti la stessa forma? Sì No
• Gli angoli corrispondenti hanno la stessa ampiezza? Sì No
Conosci questi strumenti? Sul quaderno scrivi il loro nome e a che cosa servono. Poi completa la frase colorando il termine corretto.
Tutti e tre gli strumenti si usano per ingrandire rimpicciolire un oggetto.



216 Le isometrie
4
5
Copia le figure sul quaderno e ingrandiscile secondo il rapporto di ingrandimento indicato.
6
Copia le figure sul quaderno e riducile secondo il rapporto di riduzione indicato.
7
In ciascun riquadro, misura i lati della figura colorata. Poi individua e colora la figura che è stata ridotta di 1:2 rispetto a quella colorata.
8
In ciascun riquadro, colora la figura che è stata ingrandita di 3:1 rispetto a quella colorata.
217 Le isometrie
1:3 1:2 1:2 1:4
3:1 2:1 4:1 4:1
Obiettivo di apprendimento Riconoscere figure simili e usare le regole della similitudine per ingrandire e ridurre le figure.
Spazio e figure
1
I poligoni
Colora di giallo le figure che non sono parti di piano racchiuse da una linea spezzata chiusa semplice. Poi completa.
2
• Le figure rimaste bianche sono
Scrivi in tabella il numero delle figure che hanno le caratteristiche indicate.
Non sono poligoni Poligoni concavi Poligoni convessi
Disegna le diagonali dove è possibile. Poi rispondi. 3
• Hai disegnato le diagonali in tutti i poligoni? Sì No
• Ci sono poligoni senza diagonali? Sì No Quali sono?
• Quali poligoni hanno due diagonali?
• Quante diagonali ha il pentagono?
218
A B C D E F G H I L
1 8 7 4 3 2 5 6
A B C D E F
4
Metti una X nei poligoni equilateri e un 3 nei poligoni equiangoli. Poi rispondi.
5
• Ci sono poligoni equilateri ed equiangoli? Sì No • Quali sono?
Prendi come unità di misura il lato del quadretto e calcola il perimetro dei poligoni.
6
Prendi come unità di misura il lato del quadretto e calcola il perimetro dei poligoni.
Poi disegnane uno isoperimetrico accanto.
219 Spazio e figure Obiettivo di apprendimento Riconoscere, denominare e descrivere le proprietà.
P = P = P = P = A B C D E P = P = ...................... P = P =
I triangoli
Classifica i triangoli in base agli angoli. 1
triangolo triangolo triangolo
Classifica i triangoli in base ai lati. 2
Triangoli isosceli Triangoli scaleni Triangoli equilateri
In questi triangoli, traccia l’altezza rispetto al lato celeste.
220 Spazio e figure
3
1 2 3 4 6 7 5
4
Indica con una X in quali triangoli l’altezza è stata disegnata correttamente.
5
Calcola il perimetro del triangolo scaleno.
A
6
8,4
9,2 cm
221 Spazio e figure Obiettivo di apprendimento Riconoscere, denominare e descrivere le proprietà dei triangoli.
13cm 11 cm 7 cm 12 cm 12 cm 10 cm 5cm 5 cm 5 cm P = P = P =
C
12cm 18
P = 10cm
B
cm
Calcola il perimetro dei seguenti triangoli.
cm 14,4cm 13 cm A
Sapendo che i triangoli A e B hanno lo stesso perimetro, calcola i lati del triangolo isoscele B. 7
B
I triangoli
Indica con una X quale terna di angoli può indicare gli angoli interni di un triangolo.
2
Completa la tabella, come nell’esempio.
3
Calcola l’ampiezza dell’angolo con il punto interrogativo.
Stabilisci in quali casi si può costruire il triangolo e indica con una
222 Spazio e figure
60° 35° 28° 42° 65° 83° 36° 64° 80° 1
X. Misure dei lati Il triangolo si può costruire? 8 cm 7 cm 17 cm Sì No 9 cm 18 cm 9 cm Sì No 21 cm 10 cm 14 cm Sì No
4
Misure degli angoli Tipo
50° 30° 100° ottusangolo
70° 50°
25° 65°
55° 75°
Triangolo 1
Triangolo 2
Triangolo 3
Triangolo 4
40° ? 45° 62° ?
5
6
Sapendo che tutti i lati del triangolo B sono la metà dei lati del triangolo A, calcola il perimetro dei due triangoli.
6,2 cm 10,2cm
P = P = A B
12 cm
Tutti i triangoli hanno la base della stessa lunghezza. Indica con una X se le affermazioni sono vere (V) o false (F).
Triangolo 1 Triangolo 2 Triangolo 3
Tutti i triangoli hanno lo stesso perimetro.
Il triangolo 2 ha il perimetro maggiore.
Il triangolo 1 ha il perimetro maggiore.
Il triangolo 3 ha il perimetro maggiore.
7
Quanti triangoli vedi in questa figura?
8
Osserva la figura e calcola l’ampiezza dell’angolo con il punto interrogativo.
42°
Nomina i vertici di tutti i triangoli.
I triangoli sono:
• Quali triangoli sono rettangoli?
40° ?
223 Spazio e figure Obiettivo di apprendimento Classificare i triangoli secondo proprietà geometriche e determinare il perimetro.
V
F
1
I quadrilateri
Osserva i quadrilateri, poi rispondi.
2
• Quali quadrilateri hanno tutti i lati uguali?
• Quali quadrilateri hanno due coppie di lati uguali e paralleli? ................................................................
• Quali quadrilateri hanno solo una coppia di lati paralleli?
• Quale quadrilatero non ha nessuna delle proprietà scritte sopra?
Disegna le diagonali nei seguenti quadrilateri, poi rispondi.
• In quali quadrilateri le diagonali sono uguali?
• In quali quadrilateri le diagonali sono perpendicolari?
Quando è possibile, traccia tutti gli assi di simmetria, poi rispondi. 3
• In quale quadrilatero gli assi di simmetria coincidono con le diagonali?
224 Spazio e figure
1 2 3 4 7 8 6 5
A D B E C F
A B C D
4
Osserva la figura, poi rispondi.
5
Osserva la figura, poi rispondi.
6
• Quanti quadrati ci sono? .................
• Quanti trapezi vedi? Indica quanti sono i:
• trapezi rettangoli
• trapezi isosceli
• trapezi scaleni
Giacomo, giocando con le matite, fa un disegno astratto. Subito dopo si accorge di aver ottenuto dei quadrilateri. Osserva il disegno: colora e scrivi i nomi di tutti i quadrilateri che riconosci.
7
Per ciascuna caratteristica, scrivi i nomi dei quadrilateri che la possiedono.
• Hanno i lati tutti uguali:
• Hanno due coppie di lati paralleli:
• Hanno gli angoli tutti uguali:
• Hanno le diagonali perpendicolari: .....................................................................................................................................................................................
8
Completa.
• Un quadrilatero si può costruire se il lato più è minore della somma degli altri
• La somma degli angoli interni di un quadrilatero è
225 Spazio e figure
Obiettivo di apprendimento Riconoscere, denominare e descrivere i quadrilateri.
1
Indica con una X le quaterne che contengono gli angoli interni di un quadrilatero.
60° 70° 140°
30°
A D
90°
C ^ = 40° B ^ = ..................
A ^ = 90° D ^ = 90°
B ^ = 110° C ^ = ..................
A ^ = 33° B ^ = 82°
C ^ = D ^ = 225°
A ^ = 150° B ^ = 95°
226
e figure
Spazio
I quadrilateri
Con il righello, misura i lati dei quadrilateri e calcola il perimetro. 3 50°
70° 150° 10° 45° 135° 135° 45°
A ^ = 90° D ^ = 90°
90° 40° B C
D A D C
B B C
C ^ = D ^ = 50
A D 90° 110° 90° B C
A
P = P = P =
Trova l’ampiezza dell’angolo mancante. 2
Sapendo che i lati del rettangolo B sono la metà dei lati del rettangolo A, calcola il perimetro dei due rettangoli. 5
6
Sapendo che il rettangolo A e il quadrato B hanno lo stesso perimetro, calcola:
• il perimetro del rettangolo: ................................................
• il perimetro del quadrato:
• la misura del lato del quadrato:
Usa i dati che hai a disposizione per trovare la lunghezza dei segmenti indicati. 7
AB = 38 cm
DC = 16 cm
BH =
HA =
AB = 32 cm
CD = 8 cm
AK =
227 Spazio e figure Obiettivo di apprendimento Riconoscere le caratteristiche dei quadrilateri e calcolare il perimetro.
P
P = P = 9 cm 4,5 cm 3,5 cm D C A B Calcola il perimetro.
4 cm 5,5 cm A D C B 3 cm A C B D
=
4
9 cm
B
14 cm 9 cm P (A) = P (B) = A B 16 cm
A
C
KB = A D C B K H
D B A H
1
Le misure di superficie
Sottolinea la misura adatta per la superficie di:
• un cartoncino.
4250 cm2
425 m2
4,25 dm2
2
Scrivi il valore delle cifre evidenziate.
• una stanza.
3
Inserisci le misure in tabella ed esegui le trasformazioni, come nell’esempio.
534,85 hm2 = 53 485 dam2
a. 0,07 cm2 = mm2
123 hm2 = m2
123 dm2 = m2
9,632 hm2 = cm2
b. 9 dam2 = m2
0,8 m2 = mm2
1,86 m2 = dam2
23,8 m2 = dm2
200000 mm2
200 dm2
20 m2 km 2 hm 2 dam 2 m 2 dm 2 cm 2 mm 2 da u da u da u da u da u da u da u
5 3 4 8 5
dm2
228 Spazio e figure
le tabelle. km 2 hm 2 34 0,9 123 4,2 m 2 dm 2 0,6 0,13 47,9 42 dam 2 hm 2 0,7 0,56 134 52
Completa
4
42
68 32,45
32
5689
56
2412 m2 24
4028
28
20,41
41
42,33 m2
36,68 dm2
km2
100 hm2 1
cm2
..............
..............
cm2
..............
..............
5
Nelle seguenti misure, sottolinea le cifre che indicano:
• i metri quadrati.
• i centimetri quadrati.
•
6
Evidenzia le cifre che si riferiscono alla marca. Poi scomponi, come nell’esempio.
2345,65 m2 = 23 dam2
9842 hm2 = 98 .................. 42 ..................
67,80 km2 = 67 80
7
Esegui le trasformazioni.
48 m2 = dam2
hm2 = m2
8
dm2 = 75 81
dam2 = 0 .................. 45 ..................
km2 = dam2 2 m2 = hm2
Inserisci l’unità di misura corretta, come nell’esempio.
9 Completa.
Colora nello stesso modo le misure di superficie equivalenti.
Esegui le seguenti trasformazioni.
Obiettivo
229 Spazio e figure
di apprendimento Riconoscere e denominare le unità di misura della superficie. Operare trasformazioni tra grandezze omogenee.
5041 m2 72,42
5689
34,68
m2
dm2
dam2
68,32 cm2 7,96 dm2 4567 mm2 3121 cm2
i decimetri quadrati. 34,86 dm2 9588 cm2 9,25 m2 3420 cm2
45
65
7581
m2
dm2
0,45
1235,78
cm2 = 12 35 78
324
0,2
1,9
7
dm2 = m2
dm2 = cm2
= 7 cm2 0,8 km2 = 8000 500 dm2
5 0,2 m2
2000 1 hm2 = 10000 75,9 dam2
759000
700 dm2
=
=
=
4000 m2 40000 dm2 0,04 hm2 4 dam2 400 m2 0,04 hm2 40 dam2 400 m2
1 m2 = 30 dm2 + 1 cm2 = 98 mm2 + 1 km2 = 70 hm2 + 1 dm2 = 75 cm2 + 1 dam2 = 50 m2 + 1 mm2 = 0,4 mm2 +
10
1,20 dm2 = m2 3245 mm2 = dm2 80,5 m2 = hm2 42500 dam2 = km2 456 cm2 = ....................................... dm2 54 m2 = ....................................... hm2 11
L’area
1
Scegli un’unità di misura a piacere e calcola l’area dei poligoni disegnati.
2
Usando il quadretto come unità di misura, calcola l’area dei poligoni e disegna accanto un poligono equivalente a ciascuno di esso.
3
Stabilisci quali poligoni sono isoperimetrici e quali sono equivalenti.
A B C D
Poligoni isoperimetrici e Poligoni equivalenti e
230 Spazio e figure
A
= A = A = A =
4
Osserva la figura e completa.
• Nella figura l’unità di misura u1 entra volte.
• L’unità di misura u2 entra volte.
• Il valore dell’area cambia se si cambia l’ di misura.
5
Leggi e completa.
Conta i lati del poligono qui a lato e scrivi il suo perimetro.
Ora misura la sua superficie.
L’area è
Quale unità di misura hai usato?
Scegli una nuova unità di misura e misura nuovamente.
L’area è
6
Osserva le figure e indica con una X le affermazioni vere.
A B
L’area della figura A è la metà dell’area della figura B.
L’area della figura A è il triplo dell’area della figura B.
L’area della figura A è il doppio dell’area della figura B.
L’area della figura A è 1 4 dell’area della figura B.
7
Osserva il disegno e rispondi.
• Se l’area della figura è 24 u2 quale unità di misura è stata usata?
• E se l’area è 12 u2?
• E se l’area è di 6 u2 ?
231 Spazio e figure Obiettivo di apprendimento Determinare il perimetro e l’area di figure piane.
Spazio e figure
Area del rettangolo e del quadrato
Sapendo che il quadretto azzurro è 1 cm2, esegui quanto richiesto.
Colora un rettangolo formato da 4 cm2.
Avevi 1 cm2 e l’hai per volte.
Scrivi in linguaggio matematico:
cm2 x volte = cm2
1 cm
2
Osserva e completa.
Da quanti cm2 è formato il rettangolo azzurro?
Scrivi in linguaggio matematico:
1 cm2 x = cm2
Da quanti cm2 è formato il quadrato?
Scrivi in linguaggio matematico: cm2 x = cm2
Osserva e completa.
Quale poligono è la figura a lato?
Per misurare la sua superficie procedi così:
quanti cm2 ci sono in una riga?
Quante righe sono in tutto? ...................................
cm2 x = cm2
Sul quaderno, calcola quanto richiesto per ciascuna figura. 4
232
perimetro e area 4,2 cm 2,4 cm perimetro e area 6 cm lunghezza lato e area perimetro = 12,8 cm
1
3
5 Completa.
Completa.
Se in un quadrato conosci la misura della diagonale, puoi calcolare l’area? Sì No
Scrivi come fai ............................................................................................
In questo quadrato la diagonale misura 2,8 cm, calcola l’area.
6 Completa.
Nel rettangolo a lato il perimetro è 24 cm. La base è 4 cm e l’altezza è il doppio della base. Calcola l’area.
7 A B C D
Il rettangolo e il quadrato qui sotto sono isoperimetrici. Calcola perimetro e area del rettangolo e del quadrato.
AB = 12 cm
BD = 9 cm
Perimetro rettangolo =
Area rettangolo =
8
Esegui sul quaderno.
Perimetro quadrato =
Area quadrato =
a. Disegna un quadrato di lato 2 cm e un altro con il lato doppio rispetto al precedente. Poi calcola l’area dei quadrati. Quanti quadrati uguali a quello piccolo entrano nel quadrato grande?
b. Un lato di un rettangolo è 20 cm e l’altezza è 5 4 del lato. Calcola il perimetro e l’area del rettangolo.
c. Un lato di un rettangolo è 16 cm e l’altro lato è 3 8 del primo. Trova la misura del lato e calcola l’area e il perimetro del rettangolo.
d. Un quadrato ha il lato di 4 cm. Calcola l’area. Se il lato aumenta di 0,4 cm, di quanto aumenta la sua area?
e. Calcola l’area e il perimetro di un rettangolo sapendo che un lato è lungo 12,3 cm e che è il triplo dell’altro lato.
f. Calcola il perimetro e l’area di un quadrato di lato 6 cm. Se si triplica il lato, di quanto cambia il perimetro? E l’area?
233 Spazio e figure Obiettivo di apprendimento Determinare il perimetro e l’area di figure piane.
1
Area del triangolo e del parallelogramma
Completa la tabella sapendo che le misure si riferiscono a dei parallelogrammi.
Base 9 cm 8,5 cm
Altezza 5 cm 12 cm
Area 60 cm2 34 cm2
2
Completa.
a.
Sapendo che:
la base = 3,5 cm • l’altezza relativa al lato = 5,2 cm
Calcola l’area:
h
b. A B
C
Sapendo che:
BC = 7,5 cm • h = 4 cm
Calcola l’area:
c.
14cm 8cm
d.
Calcola l’area:
Usa il righello per prendere le misure necessarie a calcolare l’area del triangolo e del parallelogramma.
Area triangolo:
Area parallelogramma: ..................................................................................................................................................
234 Spazio e figure
3
Completa.
Il parallelogramma ha la base doppia dell’altezza.
Disegna l’altezza e calcola l’area.
lato = 12 cm
altezza =
Area =
4
Completa.
Questo triangolo ha un lato lungo 24 cm.
Sapendo che l’altezza relativa è 1 3 del lato.
Calcola quanto richiesto.
5
Calcola quanto richiesto.
a. Un triangolo ha l’altezza di 24 cm e la base è 3 2 dell’altezza.
Calcola la misura della base e l’area.
b. L’area di un parallelogramma misura 375 cm2 e la base è 25 cm. Calcola la misura dell’altezza.
c. La base di un parallelogramma misura 16 cm e l’altezza è la metà della base. Calcola la sua area.
d. L’area di un triangolo è di 108 cm2 e l'altezza è 18 cm. Calcola la base del triangolo.
e. Calcola l’area del quadrato e del triangolo isoscele sapendo che il perimetro del quadrato è 52 cm.
altezza =
Area =
235 Spazio e figure Obiettivo di apprendimento Riconoscere le proprietà e determinare il perimetro e l’area del triangolo e del parallelogramma utilizzando le formule.
Area del rombo
1
Osserva le figure, rispondi e completa.
• Quale poligono è la figura A? ....................................................
• E la figura B?
Misura la superficie dei due poligoni usando come unità di misura uno dei triangoli da cui sono composti: area rombo: ....................................... area rettangolo: .......................................
Confronta le misure delle aree: sono Ricalca su di un foglio di carta trasparente il rettangolo e sovrapponilo al rombo in modo che il lato lungo del rettangolo e la diagonale più lunga del rombo coincidano: come sono i due segmenti fra loro?
Sovrapponi adesso la diagonale più corta del rombo e il lato corto del rettangolo.
Puoi dire che il lato corto del rettangolo è la della diagonale corta del rombo oppure che la diagonale corta del rombo è il del lato corto del rettangolo.
Figura B
Figura A
2
Colora i termini corretti.
L’area del rombo è uguale all’area di un rettangolo che ha la lunghezza del lato più lungo uguale alla lunghezza della diagonale più corta diagonale più lunga del rombo e la lunghezza del lato più corto è la metà il doppio della lunghezza della diagonale più corta diagonale più lunga del rombo.
3
Completa aiutandoti con lo schema.
236
e figure
Spazio
d A x d : 2 : d x 2
Area del rombo = d x ................................................................................ Diagonale del rombo = A x .................................................................
4
Completa le tabelle.
5
In un rombo, una diagonale misura 2 cm e l’altra diagonale misura il doppio della prima. Colora il rombo che rappresenta correttamente queste informazioni.
6
Con il righello, misura i segmenti che ti servono per calcolare la misura del contorno e della superficie di ciascun rombo, poi completa.
Rombo A: perimetro: area:
Rombo B: perimetro: area:
Rombo C: perimetro: area:
Sul quaderno, calcola il perimetro e l’area del rettangolo
ABCD e l’area del rombo EFGH. Poi rispondi.
AE = 8 cm AH = 3 cm
• Com’è l’area del rombo rispetto a quella del rettangolo?
237 Spazio e figure Obiettivo di apprendimento Riconoscere le proprietà del rombo e determinare il perimetro e l’area usando le formule.
Diagonale 1 Diagonale 2 Area del rombo 12 6 6 15 20 12 Diagonale 1 Diagonale 2 Area del rombo Calcolo 10 65 25 100
32 7 140
4
A B E G F C H D
A B C
1
Osserva e completa.
A B
Area del trapezio
La figura che vedi è un
Unisci i punti A e B.
Hai diviso il in due poligoni che si chiamano e sono fra loro
Sai che l’area del parallelogramma è di 84 cm2.
Calcola l’area di un trapezio.
2
Leggi, rispondi e completa.
Unisci i punti B ed E, poi colora di rosso il lato AB del trapezio e il lato corrispondente nell’altro trapezio.
Colora di verde il lato FE e il lato corrispondente.
Infine colora di celeste l’altezza di un trapezio.
Osserva: il lato lungo del rettangolo da che cosa è formato?
E il lato corto del rettangolo è uguale dei trapezi.
Sai che i lati del rettangolo sono lunghi 24 cm e 8 cm.
Calcola l’area del rettangolo:
area di ogni trapezio:
Puoi trovare il perimetro di uno dei trapezi?
Perché?
Osserva e completa.
3 È un
A B C D
Lato parallelo = 4,2 cm è il lato AB
Lato parallelo = 7,2 cm è il lato
Altezza = 5 cm è il lato
Calcola l’area: ................................................................................................................
238
e figure
Spazio
A F E C D B
4
Osserva e completa.
A B H D C
È un
5 A F
6
Lato parallelo = 8,3 cm è il lato
Lato parallelo = 11,5 cm è il lato
Altezza = 4,5 cm è il segmento
Calcola l’area:
Sul quaderno, calcola il perimetro e l’area del quadrato e l’area dei trapezi.
AF = 9 cm
BC = 6 cm
B
C D E
In un trapezio isoscele uno dei lati paralleli è lungo 6,4 cm e l’altro è lungo il doppio, mentre l’altezza è di 3,2 cm. Rispondi e completa.
Com’è l’altezza rispetto al lato lungo di 6,4 cm?
Cerca fra i trapezi disegnati qui sotto quello che ha un lato parallelo lungo il dell’altro e l’altezza
lunga la del lato parallelo più corto. Coloralo.
Calcola l’area del trapezio sul quaderno.
7 14 cm 12 cm
Usa le misure che hai a disposizione per calcolare il perimetro e l’area del trapezio.
P = A =
12 cm 3 cm
239 Spazio e figure Obiettivo di apprendimento Riconoscere le proprietà del trapezio e determinare il perimetro e l’area usando le formule.
Spazio
I poligoni regolari
1
Completa.
Un poligono si dice regolare se ha tutti i ......................... uguali e tutti gli angoli .........................
2
Colora i poligoni regolari.
3
Scrivi il nome dei poligoni e in ciascuno disegna un apotema.
4
Traccia le diagonali uscenti da un vertice qualsiasi del poligono e rispondi.
• Quante diagonali hai tracciato?
• In quanti triangoli hanno diviso il poligono? ..................
• Quanto misura la somma degli angoli interni di ogni triangolo?
La somma degli angoli del poligono è 180° x =
5
Leggi e completa.
Traccia tutti gli assi di simmetria del poligono.
Il poligono è un e ha assi di simmetria.
Tre assi sono le e tre sono i
6
Traccia tutti i segmenti che uniscono il centro del poligono con i vertici, poi rispondi e completa.
• In quanti triangoli hai diviso il poligono?
• Che tipo di triangoli sono?
Traccia l’altezza di un triangolo relativa al lato che coincide con il lato del poligono. L’altezza del triangolo è .......................................................................... del poligono.
240
e figure
7
Rispondi.
Quanti lati ha un poligono regolare che ha il perimetro di 150 cm e un lato di 30 cm?
Numero di lati = ....................................; quindi è un ....................................
8
Un esagono ha il perimetro di 72 cm. Calcola il lato di un quadrato e di un triangolo equilatero isoperimetrici all’esagono.
Lato quadrato =
Lato triangolo = ....................................................................
9
Completa e rispondi.
Ogni poligono regolare si può dividere in tanti triangoli quanti sono i lati. Se un poligono è stato diviso in 10 triangoli isosceli, quanti lati ha?
10
In questo pentagono regolare l’area del triangolino celeste è 6,8 cm2. Rispondi e completa.
• Quanti triangoli uguali a quello celeste puoi disegnare?
Puoi calcolare l’area del pentagono anche come somma delle di tutti i triangoli.
In linguaggio matematico:
cm2 + cm2 + cm2 + cm2 + cm2 = cm2
11
L’ottagono regolare qui a lato ha l’apotema di 9,6 cm e il lato di 8 cm.
Disegna l’apotema e calcola.
Perimetro
Area
12
In questo triangolo equilatero l’area è 209 cm2 e l’altezza è 19 cm.
Calcola il perimetro del triangolo, rispondi e completa.
• Se raddoppi la misura del lato, il perimetro raddoppia? Sì No
• Anche l’area raddoppia? Sì No
Spiega la tua risposta con un esempio.
241 Spazio e figure
Obiettivo di apprendimento Riconoscere e operare con poligoni regolari.
.................................................................................................................................................................................................................
2
Sapendo che il lato di un quadrato misura 2 cm, calcola:
• quanto misura l’area di tutta la figura.
• quanto misura l’area della parte colorata.
• che frazione rappresenta l’area della parte colorata
• rispetto a tutta la figura.
• l’area della parte colorata rispetto a quella bianca.
La somma delle aree del quadrato e del rettangolo che compongono la figura accanto è 300 cm2 e l’area del quadrato è 1 3 dell’area dell’intera figura.
Calcola sul quaderno l’area del quadrato. Sapendo che la base del rettangolo ABCD è 30 cm, trova il perimetro.
3
Osserva, rispondi e calcola.
• Da quali poligoni è formato questo trapezio?
• Quanto misura l’altezza del trapezio?
• Quanto misurano i lati paralleli?
• Calcola l’area del trapezio:
4
Osserva la figura e trova le misure delle parti mancanti. Poi rispondi e completa.
• Da quali poligoni è formata?
Calcola il perimetro e l’area della figura.
P =
5
La tovaglia di Andrea misura 24 e 28 cm.
Vuole decorarla ai bordi con un nastro di 2 cm.
Qual è la superficie del bordo?
242
e figure
Spazio
Aree di poligoni
28 cm 24 cm A D C B
1
10 cm
.........................................................................................................................................................................
3 cm 6 cm 10 cm
..........................................................................
A =
6
7
Carlo ha ritagliato un quadrato e due triangoli rettangoli isosceli. Facendo combaciare ciascuna volta due lati uguali, ha costruito questi poligoni. Osserva e rispondi.
8
• Quali poligoni ha costruito Carlo?
• Ricorda che lati dello stesso colore hanno la stessa lunghezza. Sono più lunghi i lati grigi o i lati celesti?
• Come sono le aree dei poligoni? ..................................................................... Perché? ........................................................................
Usando come unità di misura i lati grigi e i lati celesti, scrivi i perimetri dei poligoni dell’esercizio precedente, poi rispondi.
Fig. 1 Perimetro = lati grigi e lati celesti
Fig. 2 Perimetro =
Fig. 3 Perimetro =
• Quali figure sono isoperimetriche?
• Se il lato celeste misura 5 cm e il lato grigio misura 7 cm, quanto misurano l’area e il perimetro di ogni poligono?
Osserva la figura ed esegui.
Usa i dati scritti in figura per ricavare i dati necessari per calcolare:
• l’altezza di tutta la figura;
• l’area della figura.
3 cm 2,5 cm 1,5 cm
2 cm 2 cm
243 Spazio e figure Obiettivo di apprendimento Determinare il perimetro e l’area di figure per scomposizione o utilizzando le formule.
Fig. 1
Fig. 2
Fig. 3
1
Circonferenza e cerchio
Ripassa di verde la circonferenza e colora di giallo il cerchio.
2
Inserisci i nomi delle parti indicate, poi rispondi.
Misura con il righello le lunghezze e completa. 3
AB =
OB =
O A B O
H
Circonferenza = ...................
Area =
OH =
Circonferenza =
Area =
• Quanti assi di simmetria ha un cerchio?
4
Risolvi.
a. Lucrezia è molto sportiva. Per tenersi allenata, tutte le mattine corre facendo 14 giri intorno alla pista circolare del suo paese. Il diametro della pista è di 25 m. Quanti metri percorre in una mattina?
b. Omar cammina lungo il bordo di un’aiuola come quella della figura. Quanto è lungo il percorso che fa?
30 m
244 Spazio e figure
c. La ruota della bicicletta di Diego ha il raggio di 25 cm. Quanto misura la circonferenza della ruota?
Se la ruota compie 200 giri completi, quanti metri percorre Diego?
d. L’apertura di questo barattolo è a forma circolare. La sua circonferenza misura 34,54 cm.
Quale coperchio è più adatto per chiudere il barattolo? Indicalo.
= d = 11 cm
= d = 13 cm A B
e. Un orologio segna le 9:00. Quali angoli formano le lancette?
Le lancette formano un settore circolare all’interno del quadrante dell’orologio: coloralo.
Quant’è l’area del settore rispetto all’area dell’orologio intero?
Per trovare l’area del settore puoi fare : 4
Se il raggio è 7 cm, calcola l’area di tutto l’orologio. Calcola l’area del settore circolare.
f. Il cerchio disegnato in basso ha il diametro di 40 cm. Quanto misura il lato del quadrato all’esterno?
Calcola l’area della parte colorata.
g. Il lato del quadrato disegnato in basso misura 8,5 cm.
Quale delle due figure ha il perimetro più piccolo?
E di quanto più piccolo?
245 Spazio e figure Obiettivo di apprendimento Riconoscere e denominare gli elementi caratteristici del cerchio e della circonferenza.
I solidi
1
Colora di giallo i prismi e di verde le piramidi.
2
Inserisci i termini dati al posto giusto.
spigolo • faccia • vertice
3
In ciascun poliedro, colora uno spigolo di rosso, un vertice di blu e una faccia di verde.
4
Completa la tabella.
246 I solidi
Nome N. spigoli ...................................................... ...................................................... ...................................................... ...................................................... N. vertici N. facce
5
Scrivi il nome di ciascun poliedro e colora di rosso la faccia d’appoggio (base) e, se presente, la faccia parallela a essa.
6
Osserva i poliedri dell’esercizio precedente e completa.
• Ha due basi uguali e parallele:
• È racchiuso da sei quadrati uguali:
• È racchiuso da sei facce, che sono tutti rettangoli uguali e paralleli a due a due:
• Ha solo una base:
Indica con una X.
• Un prisma ha sempre: due basi uguali e parallele. due basi.
• Una piramide ha: una base e tutte le facce triangolari. una base e le facce rettangolari.
• Il cubo è delimitato da: rettangoli tutti uguali. quadrati tutti uguali.
• Una piramide ha: due basi. una base.
247 I solidi Obiettivo di apprendimento Classificare i solidi in base alle proprietà.
....................................................
7
1
La superficie dei solidi
Collega ciascun solido al suo sviluppo in piano.
2
Per ciascuno sviluppo in piano, scrivi il nome del solido.
Per ciascuno sviluppo in piano, colora le basi di verde e le facce laterali di giallo.
248 I solidi
3
4
6
Collega ciascun solido alla faccia su cui appoggia (base) e scrivi il nome della figura piana corrispondente.
Per ciascun solido, sono disegnati due sviluppi: colora solo quello corretto.
5 Quali numeri bisogna scrivere sulle facce vuote di questi sviluppi affinché la somma dei numeri delle facce opposte sia sempre 7? Completa.
249 I solidi Obiettivo di apprendimento Riconoscere gli sviluppi piani di solidi noti. Identificare uno stesso solido da diversi punti di vista.
1 3 ............... 5 5 6 4
1
Il volume
Calcola il volume di ciascuna delle seguenti costruzioni, usando come unità di misura un cubetto .
2
Volume = cubetti
Volume = cubetti
3
Volume = cubetti
Volume = cubetti
Calcola il volume del solido usando come unità di misura un cubetto .
Poi, usando come unità di misura una faccia del cubetto, calcola anche l’area totale.
Volume = cubetti
Area totale = facce di cubetto
Calcola i volumi sapendo che = 1 cm3. Poi completa.
250 I solidi
Volume A
cm3 Volume B = Volume C = Mettili in ordine decrescente, dal più grande al più piccolo: Obiettivo di apprendimento Determinare il volume dei solidi noti usando le più comuni formule.
=
4
5
I tre amici Luca, Gianni e Giacomo, stanno giocando con i cubi e hanno fatto queste costruzioni. Osserva e rispondi.
Costruzione di Luca
Costruzione di Gianni
Costruzione di Giacomo
6
• Quanti cubetti ha utilizzato ciascuno di loro per fare la propria costruzione? Scrivi a lato.
• Chi ha usato più cubetti? Spiega come hai contato il numero dei cubetti usati da ciascun bambino.
Carla ha fatto questa costruzione con dei cubi tutti uguali.
Disegna nel quadrettato accanto il solido visto di fronte, di lato e dall’alto.
vista di fronte vista di lato vista dall’alto
lato 9,5 mm
Questa scala è fatta di cubi. Questi che vedi sono i cubi necessari per formare i primi tre scalini.
Quanti cubi saranno necessari per arrivare al dodicesimo scalino?
Spiega il tuo ragionamento.
251 I solidi Obiettivo di apprendimento Usare unità di misura omogenee per calcolare il volume di un solido. Determinare i volumi di solidi per scomposizione.
Le misure di volume
Quanti decimetri cubi ci sono in 1 m3? Leggi e completa.
Il decimetro cubo è un cubo con lo spigolo di 1 dm.
• Lungo lo spigolo del metro cubo quanti dm3 puoi sistemare? dm3
• Quante file da dm3 servono per ricoprire la base?
10 x = dm3
Quindi su tutta la base ci sono dm3
• Per riempire tutto il cubo quanti “piani” da 100 dm3 servono? ............. piani da ............. dm3, cioè 100 dm3 x ............. = ........................ dm3 1 m3 = dm3
2
Evidenzia le cifre a cui si riferisce la marca, poi inserisci i numeri nella tabella, come nell’esempio.
Multipli
Unità di misura Sottomultipli
km3 hm3 dam3 m3 dm3 cm3 mm3 h da u h da u h da u h da u h da u h da u h da u
15,767 m3 1 5, 7 6 7
0,5432 km3
535,88 dam3
7643 mm3
1,6754 m3
Evidenzia le cifre che si riferiscono alla marca, poi scomponi, come negli esempi.
dm3
252 I solidi
1
m3 = 235
45
3 456 cm3 = 3 dm3 456 cm3
dm3 = 571 327 700800 mm3 = 700 800 76598 cm3 = 76 598 58,420 dm3 = 58 420 896,432 dam3 = 896 432 78453 cm3 = 78 453 3
235,45
m3
571,327
4
Esegui le trasformazioni aiutandoti con la tabella. Se necessario, aggiungi gli zeri.
6
Esegui le trasformazioni.
Quanti cubetti sono stati usati per realizzare la costruzione che vedi?
253 I solidi Obiettivo di apprendimento Conoscere il concetto di volume. Operare trasformazioni tra grandezze omogenee.
hm 3 dam 3 m 3 dm 3 cm 3 mm 3 h da u h da u h da u h da u h da u h da u
hm3 = dam3
cm3 = mm3
=
dm3 = m3
=
=
=
12,54
5,765
6500 m3
dam3 2100
9780 dam3
hm3 50 m3
dm3 62,3 dam3
hm3
m 3 dm 3 4,6 ......................... 45700 65000 9,3 dm 3 cm 3 0,6 ......................... 5200 8,52 1,20 cm 3 mm 3 9400 5,73 ......................... 10000 3,42
5
1
L’indagine statistica
Indica con una X in quali casi, per raccogliere le informazioni, si può fare un’indagine diretta e in quali casi è necessario, invece, svolgere un’indagine indiretta.
Indagine
Numero abitanti dei capoluoghi di regione.
Quanto tempo impiegano per andare a scuola i bambini e le bambine della 5a C.
I film preferiti nelle classi quinte.
Il numero di automobili vendute in Italia nel 2019.
Diretta
Indiretta
2
Le frasi contengono tutte un’informazione statistica. In ciascuna frase, individua l’oggetto di indagine, a chi è stata rivolta (popolazione statistica) e l’informazione individuata (frequenza).
1. La scorsa estate hanno frequentato il centro estivo 43 maschi e 47 femmine.
2. Nella famiglia di Carlotta 2 persone hanno gli occhi azzurri.
3. Nella prima settimana di gennaio la temperatura è scesa sotto zero per 4 giorni.
4. Nella classe 5a B 6 bambini festeggiano il compleanno a novembre.
5. La merenda preferita dai cugini di Lorenzo è la focaccia.
6. Il fiore preferito dalle maestre della scuola di Anna è il papavero.
Oggetto di indagine
1. Quanti maschi e quante femmine hanno frequentato il centro estivo.
A chi è stata rivolta (popolazione statistica)
Agli educatori e alle educatrici del centro estivo.
Informazione individuata (frequenza)
43 maschi
47 femmine
254 Relazioni, dati e previsioni
.............................................................................................. .............................................................................
2.
3. 4. 5. 6.
Gli alunni e le alunne della 5a C hanno disegnato questo grafico. Completa la tabella di frequenza con i dati corretti.
3 Taglia di scarpe Scarpe Frequenza
Taglia di scarpe Tabella di frequenza
35 36
37
38
39
35 X X X
4
Sul quaderno, rappresenta i dati scritti nelle tabelle di frequenza, prima con un ideogramma e poi con un diagramma a barre.
Osserva la tabella e rispondi sul quaderno.
Dolce preferito in 5 a A
1. Qual è l’oggetto di indagine?
2. Quale domanda è stata posta?
3. A chi è rivolta l’indagine?
4. Quanti sono?
5. È un’indagine diretta o indiretta?
6. Come si chiama il valore che aiuta a capire il dolce preferito?
7. Se un bambino volesse regalare un dolcetto ai compagni, quale converrebbe comprare per soddisfare i gusti del maggior numero di bambini?
255 Relazioni, dati e previsioni Obiettivo di apprendimento Leggere e interpretare dati statistici.
Zone d’Italia dove vive l’orso bruno Frequenza Trentino-Alto Adige 50 Friuli-Venezia Giulia 35 Appennino centrale 60 Biciclette vendute in Italia Frequenza biciclette tradizionali 150000 biciclette da corsa 90000 mountain bike 130000 e-bike 170000
Preferenze Frequenza
X X X X X X
X X X X X
X X X marshmallow X X X X X X X
cioccolatino
lecca-lecca
biscotto
5
L’indagine statistica
Sul quaderno, disegna la tabella di frequenza di ciascun grafico.
a. Chicchi di grano di una spiga.
c. Altezza alunni/e (cm)
b. Precipitazioni annue a La Spezia.
d. Materie preferite alla Scuola Secondaria di 1° grado.
Educazione sica
Geogra a Storia Inglese Italiano
Matematica
Per ciascuna tabella, disegna sul quaderno un grafico adatto.
256 Relazioni, dati e previsioni
135 140 142 145 146 1
Distribuzione acqua e terre emerse acqua 71% terre emerse 29%
dell’acqua sulla Terra oceani 97% calotte polari 2% fiumi e laghi 1% 2 45102030 antichità1 5001 8001 900oggi 200 160 120 80 40 0 8 8 296 44566 1210 G N FMG LASDO AM giorni 1020304050607080
Distribuzione
3
Osserva e rispondi. Ciascuna coppia di grafici rappresenta le stesse informazioni?
a.
Genere musicale preferito da bambini e bambine di 10 anni
Genere musicale preferito da bambini e bambine di 10 anni
musica
pop
musica leggera musica rock musica pop musica leggera musica rock
Sì No
b.
Lettrici
4 Animali domestici in Europa cani 7000000 gatti 7500000 piccoli mammiferi 1800000 rettili 1300000
Lettrici e lettori italiani oltre i 6 anni
maschi
femmine
Sì No
Fra i due grafici indicati nei riquadri sotto, colora quale sceglieresti per rappresentare le informazioni scritte in ciascuna tabella.
a.
a
Diagramma a barre Grafico sul piano cartesiano
257 Relazioni, dati e previsioni
di apprendimento Leggere e rappresentare dati statistici.
Obiettivo
0 50 100
24% 14% 62%
58% Maschi 42% 0 60 100 40 20
e lettori italiani oltre i 6 anni Femmine
Diagramma a barre Grafico sul piano cartesiano Sport praticati alunni classe 5
b. danza 9 calcio 1 pallavolo 2 basket 3 judo 2 niente 4
La moda e la media
Gli alunni e le alunne della 5a B fanno un’indagine per stabilire quale fiore mettere nell’aiuola del giardino della scuola. Completa la tabella dove hanno registrato le preferenze e rispondi.
Fiori Preferenze Frequenza
tulipano X X X X X X X X
margherita 4
rosa X X X X X X X X X X X X
ortensia
2
• Quale fiore è stato il più scelto?
Quindi la moda è
• Conoscere la media in questa situazione è un dato utile?
Sì No
3
La moda a dicembre è .............................................
La moda a febbraio è .............................................
Significa che il dolce più venduto a dicembre sono ................................................................................................................,
mentre il dolce più venduto a febbraio sono
Calcolare la media in questo caso è utile? Sì No
Questi sono il numero di messaggi giornalieri mandati da Sofia nei primi 5 giorni di scuola. Osserva e completa.
64 • 58 • 32 • 45 • 36
Calcola la media dei messaggi giornalieri:
C’è la moda?
4
castagnole
frittelle canestrelli
mantovane
Queste sono il numero di pagine del libro delle vacanze che Martina ha fatto ogni giorno per una settimana. Osserva e completa.
4 • 4 • 0 • 2 • 4 • 5 • 2
Calcola quante pagine ha fatto in media ogni giorno:
Qual è la moda?
Vuol dire che sono di più i giorni nei quali lei ha completato pagine.
258 Relazioni, dati e previsioni
i grafici e completa.
1 Osserva
Dolci venduti a dicembre panettone 100 60 40 20 80 0 pandoro panpepato torrone alle mandorle 100 60 40 20 80 0
Dolci venduti a febbraio
5
6
Per lo spettacolo di fine anno gli alunni e le alunne delle tre quinte devono indossare una maglietta gialla. Per risparmiare verrà fatto un acquisto complessivo. Osserva la tabella e rispondi sul quaderno.
Taglie small medium large
N. bambini/e 12 32 7
a. Quali informazioni sono riportate in tabella?
b. Per quale motivo è stata svolta questa indagine?
c. La moda è il numero 32. Che cosa significa?
d. Quanti sono gli alunni e le alunne delle classi quinte?
e. Puoi sapere con certezza da quanti alunni e alunne è formata ciascuna classe? Perché?
f. Puoi sapere quanti alunni e alunne ci sono, in media, in ciascuna classe? Se sì, calcola la media.
Osserva il grafico e completa.
Faccende sbrigate in casa da bambini e bambine della 5 a A
apparecchiare
sparecchiare
fare il letto
spazzare
La frequenza maggiore è
Bambini/e Frequenza
Significa che il lavoretto compiuto dalla maggior parte dei bambini e bambine della 5a A è
Conoscere la media in questo caso fornisce informazioni utili? Sì No
Leggi e completa.
La zia ha regalato a Duccio una scatola di cioccolatini. Ne ha mangiati in media 3 al giorno e, dopo 6 giorni, la scatola è finita. Puoi sapere con certezza quanti cioccolatini ha mangiato ogni giorno? Sì No
Potrebbe averli mangiati in questo modo?
259 Relazioni, dati e previsioni Obiettivo di apprendimento Interpretare grafici utilizzando indici statistici.
1° giorno 2° giorno 3° giorno 4° giorno 5° giorno 6° giorno 3 1 2 4 4 4 Sì No
7
Trova almeno altri quattro modi diversi.
Il piano cartesiano
L’insegnante ha chiesto alla classe di registrare in un grafico cartesiano i libri che hanno letto in un anno scolastico. Questo è il grafico di Luca: osserva e rispondi sul quaderno.
a. Qual è il mese nel quale ha letto più libri?
b. C’è un mese nel quale ne ha letti di meno?
c. Qual è la moda?
d. Qual è la media dei libri letti?
Completa il grafico inserendo le informazioni che mancano.
260 Relazioni, dati e previsioni
1
0 1 3 2 4 5 settott nov dicgen feb maraprmag giu
Giorno N. ingressi in piscina LUN 25 MAR 15 MER 40 GIO 15 VEN 35 SAB 60 DOM 55 2 0 5 10 15 20 25 30 35 40 45 50 55 60
MERGIOVENSABDOM
Rappresenta le informazioni nel grafico.
LUN MAR
Mesi Quantità di pioggia caduta in mm Gen 25 Feb 20 Mar 10 Apr 5 Mag 8 Giu 40 Lug 10 Ago 32 Sett 15 Ott 30 Nov 12 Dic 33 3 GFMAMGLASOND 0 50 45 40 35 30 25 20 15 10 5
5
Alla pizzeria “Sotto Casa”, in una settimana, sono state registrate le seguenti presenze.
Disegna il grafico nel piano cartesiano e poi calcola la moda e la media.
Lun 15 persone
Mar 30 persone
Mer —
Gio 60 persone
Ven 75 persone
Sab 90 persone
Dom 75 persone
• Qual è il giorno nel quale ci sono stati più clienti?
• C’è un giorno di chiusura?
Il grafico rappresenta le temperature rilevate a Torino alle ore 10 nei primi 15 giorni del mese di ottobre.
Calcola la temperatura media.
Osserva il grafico e rispondi sul quaderno. 6
Temperatura media a Roma
123456789101112131415
a. Quali informazioni sono rappresentate?
b. Quali informazioni sono scritte sull’asse delle ordinate y?
c. E sull’asse delle ascisse x?
d. Che temperatura media c’è stata ad aprile? E a febbraio?
e. Ci sono mesi nei quali la temperatura media è rimasta la stessa? E mesi nei quali la temperatura è andata sotto lo zero?
f. Qual è la temperatura media minima a Roma? E la massima?
g. Qual è la differenza tra la temperatura media di luglio e di maggio? gen
y feb maraprmag giu lugago
261 Relazioni, dati e previsioni Obiettivo di apprendimento Leggere e rappresentare dati mediante il piano cartesiano.
4 15 30 45 60 75 90 0 DOM SAB VEN GIO MER MAR LUN
x
24° 21° 18° 30° 27° 15° 12° 9° 6° 3° 0° -3°
22 24 26 28 30 (°C) 20 18 16 14 12 10
La probabilità
Indica con una X se ciascuno dei seguenti eventi è certo, possibile o impossibile.
Evento
Pescare una caramella da un sacchetto di cioccolatini.
Ottenere un numero da 1 a 6 lanciando un dado.
Sapere che domani sarà un giorno di sole.
Estrarre il numero 50 giocando a tombola.
Ottenere il numero 1 lanciando 2 dadi.
Certo Possibile Impossibile
2
Prima Marco e poi Giulia usano tutti i cartellini che vedi a sinistra per formare un grande numero. Scrivi se l’evento è certo, possibile oppure impossibile.
• Marco forma un numero pari. .........................................................................................................................
• Marco forma un numero dispari.
• Marco forma un numero che termina con la cifra 8
• Marco forma un numero di quattro cifre.
• Marco forma un numero che termina con la cifra 3
• Giulia forma un numero pari. ..........................................................................................................................
• Giulia forma un numero dispari. ....................................................................................................................
• Giulia forma un numero di otto cifre. ..........................................................................................................
• Giulia forma un numero di due cifre.
• Giulia forma un numero superiore a 9000
In un sacchetto ci sono 7 caramelle al limone e 3 alla fragola. Estraendo una sola volta e senza guardare nel sacchetto, che probabilità c’è che:
si estragga una caramella all’arancia?
si estragga una caramella al limone?
si estragga una caramella alla fragola?
262 Relazioni, dati e previsioni
1
6 1 9 5 0
4 2 8
3
4
Indica la probabilità di estrarre ciascuna pallina.
5
Colora le palline secondo le probabilità indicate.
6
Scrivi la probabilità.
a. Evento: estrazione da un sacchetto con 10 palline.
10 palline
8 bianche 2 nere
Estrai una pallina:
• è bianca
• è nera ..........
7
b. Evento: lancio del dado.
• Esce il 6
• Esce il 3
• Esce un numero pari
• Esce un numero dispari
• Esce 4 o 5
c. Evento: estrazione da un mazzo di 40 carte.
Estrai una carta:
• è un asso
• è una figura
• è una figura di picche
• è una carta di cuori ..........
• è una carta di fiori o di quadri
Al centro sportivo ci sono 4 distributori con 10 gomme da masticare in ciascuno. Sul quaderno, disegna i 4 distributori con dentro le gomme necessarie a rendere vere tutte le affermazioni date.
È impossibile estrarre una gomma gialla.
È più probabile estrarre una gomma rossa di una gialla.
È certo di estrarre una gomma blu.
C'è la stessa probabilità di estrarre una gomma rossa e una blu.
263 Relazioni, dati e previsioni Obiettivo di apprendimento Valutare la possibilità che accada un evento.
5 20 8 20 3 20 4 20
Collega ciascuna frazione di probabilità alla sua scrittura in percentuale.
2
Colora nello stesso modo le scritture equivalenti.
3
Scrivi prima con una frazione, poi con una percentuale, quale parte di tutte le figure sono:
• i solidi. In frazione: In percentuale:
• i prismi In frazione: In percentuale:
• le piramidi. In frazione: In percentuale:
Colora ciascuna figura rappresentando la percentuale indicata. 4
264 Relazioni, dati e previsioni
Obiettivo di apprendimento Esprimere il grado di probabilità che accada un evento. 50% 25% 75% 100%
Probabilità e percentuali
45 100 3 100 1 4 18 100 1 2 75 100 25% 3% 50% 45% 75% 18% 1
15% 5% 51% 51 100 5 100 15 100 0,5 0,51 0,15
Responsabile editoriale: Mafalda Brancaccio
Coordinamento redazionale: Valentina Dell’Aprovitola
Consulenza didattica: Chiara Tannoia
Redazione: Cecilia Barletta, Giulia De Giorgi
Responsabile di produzione: Francesco Capitano
Progetto grafico: Ilaria Raboni
Impaginazione: Bluedit - Torino
Illustrazioni: Francesca Galmozzi, Mauro Sacco ed Elisa Vallarino
Copertina: A come Ape di Alessia Zucchi
Illustrazione di copertina: Silvia Colombo
Ricerca iconografica: Paola Rainaldi
Referenze iconografiche: Shutterstock
Stampa: Tecnostampa – Pigini Group Printing Division Loreto – Trevi 24.84.067.0
Per esigenze didattiche i testi sono stati quasi tutti ridotti e/o adattati. L’editore è a disposizione degli aventi diritto tutelati dalla legge per eventuali e non volute omissioni o errori di attribuzione.
È assolutamente vietata la riproduzione totale o parziale di questa pubblicazione, così come la trasmissione sotto qualsiasi forma o con qualunque mezzo, senza l’autorizzazione della Casa Editrice.
Produrre un testo scolastico comporta diversi e ripetuti controlli a ogni livello, soprattutto relativamente alla correttezza dei contenuti. Ciononostante, a pubblicazione avvenuta, è possibile che errori, refusi, imprecisioni permangano. Ce ne scusiamo fin da ora e vi saremo grati se vorrete segnalarceli al seguente indirizzo: redazione@elionline.com
Tutti i diritti riservati
© 2024 Cetem, Gruppo Editoriale ELi info@gruppoeli.it
EquiLibri • Progetto Parità è un percorso intrapreso dal Gruppo Editoriale ELi, in collaborazione con l’Università di Macerata, per promuovere una cultura delle pari opportunità rispettosa delle differenze di genere, della multiculturalità e dell’inclusione.
Si tratta di un progetto complesso e in continuo divenire, per questo ringraziamo anticipatamente il corpo docente e coloro che vorranno contribuire con i loro suggerimenti al fine di rendere i nostri testi liberi da pregiudizi e sempre più adeguati alla realtà.
Matematica saperi
classe 5
AMBITO ANTROPOLOGICO
• Sussidiario Storia con Quaderno operativo 5
• Sussidiario Geografia con Quaderno operativo 5
ISBN per l’adozione: 9788847307438



Atlante multidisciplinare 4-5
Allegato biennale


AMBITO SCIENTIFICO
• Sussidiario Matematica con Quaderno operativo 5
• Sussidiario Scienze e Tecnologia con Quaderno operativo 5
ISBN per l’adozione: 9788847307445
• KIT DOCENTE comprensivo di guida alla programmazione, risorse didattiche, percorsi semplificati e tutto il necessario per il corso
• LIBRO DIGITALE (scaricalo subito seguendo le istruzioni all’interno della copertina) con LIBRO LIQUIDO ACCESSIBILE: volumi sfogliabili, esercizi interattivi, VIDEO, carte storiche e geografiche digitali, audiolibri, percorsi semplificati stampabili

Ambiente di apprendimento interattivo per la verifica delle competenze disciplinari.
ISBN per l’adozione: 9788847307469


#PROGETTOPARITÀ equilibri Sistema Digitale Accessibile AGENDA 2030 PACK UNICO AMBITO
EAMBITO
ANTROPOLOGICO
SCIENTIFICO
IL GIOCO DELLO SVILUPPO SOSTENIBILE Gamification
MISSION 2030
#altuofianco
Allegato a NEL CUORE DEI SAPERI 5 Non vendibile separatamente www.gruppoeli.it


































































































































 I VIAGGI DI DIDONE
I VIAGGI DI DIDONE




























 Grosseto
Siena
Arezzo
Firenze
Pisa
Pistoia Lucca Livorno
Prato Massa Carrara
Grosseto
Siena
Arezzo
Firenze
Pisa
Pistoia Lucca Livorno
Prato Massa Carrara































































