
Programmazioni
Didattica per competenze e compiti di realtà
Valutazione e autovalutazione
Didattica inclusiva e soft skills
Percorsi stem e laboratori di tinkering
Didattica laboratoriale
Sezioni metodologiche
Schede su due livelli


Programmazioni
Didattica per competenze e compiti di realtà
Valutazione e autovalutazione
Didattica inclusiva e soft skills
Percorsi stem e laboratori di tinkering
Didattica laboratoriale
Sezioni metodologiche
Schede su due livelli
Nel cuore dei saperi è un progetto moderno e innovativo , con una didattica versatile e inclusiva , pensato per formare i cittadini e le cittadine del mondo di domani. Un progetto didattico in linea con i Nuovi Scenari delle Indicazioni Nazionali e le Raccomandazioni del Consiglio Europeo
È caratterizzato da scelte didattiche innovative: approccio laboratoriale nelle discipline scientifiche, percorsi STEM , laboratori di Tinkering , pensiero computazionale e Storytelling
Filo conduttore del progetto è l’ Educazione Civica e Ambientale , con approfondimenti sulla Costituzione , sulla Cittadinanza digitale e sugli Obiettivi per lo Sviluppo Sostenibile dell’Agenda 2030
Nel cuore dei saperi è proposto in quattro volumi con quaderno integrato , per caratterizzare ogni disciplina con le sue specificità, pur inserita in un progetto strutturato.
Il corso è pensato per costruire, in modo graduale, un metodo di studio efficace e competenze durature , con una didattica versatile e inclusiva che si adatta ai diversi livelli dei singoli e del gruppo classe.
Tutte le discipline sono organizzate in unità con una struttura chiara e lineare , che permette ai bambini e alle bambine di lavorare in autonomia. Il linguaggio è semplice e accessibile a tutti; le fotografie e le tavole illustrate integrano il testo e forniscono esemplificazioni necessarie alla comprensione dei contenuti.
L’organizzazione chiara e ordinata delle pagine permette agli alunni e alle alunne di orientarsi facilmente in ciascuna disciplina.




I volumi sono completati da un Atlante , di Storia , Geografia e Scienze . L'Atlante è sono uno strumento prezioso che consente di approfondire le conoscenze, di fornire risposte ad alcune curiosità e di fissare i concetti chiave.

Nei volumi di Storia, Geografia, Scienze e Tecnologia
• Ripasso facile e Mappa
• Facciamo il punto e autovalutazione
• Compiti di realtà e situazioni non note
Nel volume di Matematica
• Verifiche delle conoscenze, verifiche delle competenze e autovalutazione
• Compito di realtà
• In apertura di unità, le civiltà sono introdotte da carte geostoriche con attività di CARTE GEOSTORICHE e dalla LINEA DEL TEMPO per sviluppare da subito le competenze specifiche della disciplina.
• Pagine dedicate alle FONTI per imparare a ricavare informazioni da fonti di vario tipo.
• Pagine dedicate alla TECNOLOGIA
• Pagine dedicate all’EDUCAZIONE CIVICA e all’EDUCAZIONE AL PATRIMONIO
• Proposte per attività di CLIL
• Pagine di STORYTELLING.
• ATLANTE STORICO per l’approfondimento.


• Fin dalle prime pagine, ampio spazio dedicato agli STRUMENTI della Geografia (carte, grafici, dati e tabelle, fotografie, immagini satellitari).
• Rubriche dedicate alla scoperta di AMBIENTE e PATRIMONIO STORICO e ARTISTICO e alla loro tutela.
• Approfondimenti sugli OBIETTIVI e TRAGUARDI dell’AGENDA 2030
• Rubriche pagine di EDUCAZIONE CIVICA
• Pagine di STORYTELLING
• ATLANTE GEOGRAFICO per l’approfondimento.


• Approccio laboratoriale ed esperienziale. Pagine di ESPERIMENTI e attività da svolgere in classe per far sì che i bambini e le bambine imparino a procedere secondo il metodo di indagine della ricerca scientifica.
• Pagine di STEM con laboratori di Tinkering
• Pagine di STORYTELLING
• Pagine di EDUCAZIONE CIVICA
• ATLANTE SCIENTIFICO per l’approfondimento.


• Il percorso è strutturato per presentare la Matematica come disciplina universale che aiuta gli alunni e le alunne a compiere scelte logiche e diventare responsabili del proprio apprendimento.
• Pagine con un approccio operativo (OPERO E ANALIZZO), fase di sintesi (HO CAPITO CHE) e infine il consolidamento (PROVO IO) per mettere subito in pratica le conoscenze.
• Ampio apparato di ESERCIZI che consente ai bambini e alle bambine di mettersi alla prova.
• Pagine di strategie per la comprensione dei problemi, PROBLEMATICAMENTE
• Pagine di STORYTELLING (STORIE MATEMATICHE).


Il percorso di Matematica , in linea con le Indicazioni Nazionali, adotta come principio metodologico fondante quello di valorizzare l’esperienza degli alunni e delle alunne
Il volume inoltre ripropone l’importanza della connessione tra Matematica e realtà e la pone al centro del lavoro in classe. La didattica del volume mette gli alunni e le alunne in condizione di “fare Matematica” appropriandosi loro stessi delle conoscenze a partire dalle situazioni proposte nelle pagine.

Il percorso inoltre è ampio per numero di pagine e argomenti trattati: numeri naturali , frazioni e numeri decimali , problemi , misura , spazio e figure , simmetria , relazioni , dati e previsioni .
Il percorso, strutturato e innovativo, propone una didattica laboratoriale finalizzata a un insegnamento inclusivo

Fin dall’inizio del percorso, i vari argomenti sono introdotti in modo da stimolare un atteggiamento di curiosità verso la realtà circostante e spingere gli alunni e le alunne a riflettere sui fenomeni che accadono, ponendosi le domande scientifiche.




La spiegazioni e le rubriche di sintesi sono organiche , con un linguaggio chiaro e accessibile a tutti, rivelandosi uno strumento utile per favorire l’apprendimento.
Gli argomenti sono presentati secondo una scansione equilibrata degli argomenti.
Le pagine del volume base sono strutturate attraverso 3 passaggi per la costruzione di competenze durature:
• OPERO E ANALIZZO , per un approccio operativo.
• SINTETIZZO (HO CAPITO CHE) , per una immediata sintesi dei concetti.
• CONSOLIDO (PROVO IO) , per mettere subito in pratica le conoscenze.


Le pagine PROBLEMATICAMENTE offrono strategie per la comprensione dei problemi e attività di logica. Vengono introdotti problemi legati a situazioni che interessano i bambini e le bambine per poi cercare strategie e strumenti utili alla risoluzione, dopo aver compreso la richiesta dell’attività.
Tutte le sezioni propongono pagine di attività laboratoriale
Il modo migliore perché l’alunno e l’alunna apprenda, infatti, è che costruisca da sé la propria conoscenza , diventando responsabile del proprio apprendimento e in questo, il lavoro di gruppo è più efficace del lavoro individuale.



Il Sussidiario presenta inoltre una ricca e ampia sezione esercitativa Sono presenti pagine intere di esercizi di riepilogo nel volume e un corposo Quaderno ricco di attività innovative; l’insegnante avrà la possibilità di scegliere tra una vasta gamma di esercitazioni da proporre agli alunni e alle alunne.
Le pagine scaricabili di VERIFICA DELLE CONOSCENZE al termine di ogni unità valutano gli apprendimenti e ne verificano l’acquisizione; al termine permettono anche un’autovalutazione da parte dell’alunno e dell’alunna.
Le pagine di VERIFICA DELLE
COMPETENZE • VERSO L’INVALSI sono utili per allenare gli alunni e le alunne ad affrontare preparati la prova Invalsi.

Le pagine di STORYTELLING, STORIE MATEMATICHE , gli alunni e le alunne possono approfondire, sempre attraverso un approccio operativo, episodi e personaggi della storia della Matematica.

Al termine del volume di Matematica sono dedicate tre pagine al COMPITO DI REALTÀ in cui gli alunni e le alunne devono affrontare un compito autentico e devono dimostrare di aver raggiunto i traguardi di competenza programmati.
Nella Guida didattica sono presenti le indicazioni utili per affrontare il compito, le competenze coinvolte e la valutazione.




Il QUADERNO è integrato nel volume e strettamente connesso con esso. Rimandi puntuali e costanti dal volume al quaderno permettono un uso immediato di questo strumento.
Nel quaderno, gli esercizi sono declinati su due livelli , indicati da una o due stelline ★ : in questo modo l’insegnante ha la facoltà di graduare la difficoltà degli esercizi proposti alla classe, oppure di diversificarli in base alle diverse esigenze degli alunni e delle alunne.
Un nuovo scenario per l’inclusione, la pluralità e la parità di genere
Con EquiLibri • Progetto Parità , il Gruppo Editoriale Eli si impegna a proporre, all’interno delle proprie pubblicazioni editoriali, argomenti costantemente aggiornati e strettamente legati al sempre più complesso mondo di oggi. L’obiettivo è quello di ampliare gli scenari delle studentesse e degli studenti, del corpo docente e delle famiglie fornendo esempi aderenti ai valori di giustezza sociale , parità di genere e valorizzazione delle differenze , favorendo, quindi, una cultura dell’inclusione
#equilibri #progettoparità
In quest’ottica, il Gruppo Editoriale Eli ha stretto una collaborazione e aperto un tavolo di lavoro con il Dipartimento di studi umanistici dell’Università di Macerata , al fine di individuare e arginare gli stereotipi di genere nei libri scolastici
“Nei testi scolastici occorre introdurre una rappresentazione equilibrata di donne e uomini; si richiede un equilibrio nella frequenza con la quale i generi vengono rappresentati, nel grado e nell’importanza dei ruoli e delle attività svolte, nonché nelle loro rappresentazioni sia come individui sia in testi collettivi. […] È auspicabile infine che i libri di testo offrano una lettura sempre più aderente allo sviluppo della nostra società in direzione della multiculturalità e della multietnicità.“
(Dal Codice di autoregolamentazione Polite, www.aie.it)
Il Gruppo Editoriale Eli si impegna “a operare per una sempre più puntuale qualificazione dei libri” attraverso:
• attenzione ai contenuti al fine di agevolare conoscenza e consapevolezza in uno scenario equilibrato da un punto di vista sociale e culturale;
• valutazione iconografica ragionata per sensibilizzare a una cultura di parità attraverso il linguaggio visivo;
• utilizzo di un linguaggio testuale inclusivo, puntuale e idoneo a qualificare entrambi i generi, oltre ogni stereotipo.
a cura di Maria Grazia Bertarini
STEAM è un acronimo composto dalle iniziali di alcune discipline:
• S cience – Scienze, lo studio del mondo e dei fenomeni della natura.
• T echnology – Tecnologia, non solo digitale, che comprende qualsiasi artefatto oppure opera che derivi da un processo trasformativo intenzionale da parte dell’essere umano. Per questo motivo, ogni prodotto creato dai ragazzi e dalle ragazze per la risoluzione di un problema è tecnologia. Tecnologia comprende il Coding.
• E ngineering – Ingegneria, il processo di progettazione che i ragazzi e le ragazze mettono in atto per risolvere un problema.
• A rt – Arte, intesa sia come espressione della creatività presente in qualsiasi processo di invenzione e innovazione, tecnica, scientifica o letteraria, sia come estetica della produzione.
• M ath – Matematica, il linguaggio dei numeri, delle forme, dei grafici, delle quantità e delle formule.
Le discipline STEAM comprendono dunque Scienze, Tecnologia, Ingegneria, Arte e Matematica. Tuttavia, queste non sono considerate materie di studio indipendenti: l’approccio STEAM non è la somma delle loro parti, bensì una metadisciplina che consente la risoluzione di problemi contestualizzati.
La didattica STEAM si basa sull’integrazione e sull’applicazione di conoscenze matematiche e scientifiche con lo scopo di creare, attraverso le fasi del metodo scientifico, del processo ingegneristico di invenzione e costruzione o della programmazione informatica, soluzioni a problemi reali. Per raggiungere questo obiettivo vengono chiamate in gioco competenze globali – o life skills – tra cui pensiero critico, problem solving , creatività e innovazione, collaborazione e imprenditorialità.
1 La base di una didattica STEAM è il pensiero computazionale , ovvero un’attitudine mentale che permette di risolvere problemi di varia natura seguendo metodi specifici. Il pensiero computazionale è un processo logico-creativo che consente di scomporre un problema complesso in problemi più semplici, quindi più gestibili se affrontati uno dopo l’altro. Trovando una soluzione a ciascuno di essi è possibile risolvere il problema originario.
2 Il contesto è motivante , coinvolgente e apre le porte della scuola al mondo reale esplicitando il senso e lo scopo di ciò che si fa in classe.
3 Il lavoro di gruppo , la comunicazione efficace e le abilità interpersonali hanno un’importanza fondamentale e preludono a quella che sarà la vita sociale e lavorativa dei ragazzi e delle ragazze del ventunesimo secolo, nel quale la quantità e diversità di informazioni rende poco plausibile, se non impossibile, lo svolgimento di qualsiasi lavoro in totale autonomia.
4 Il programma è fortemente inclusivo , per l’importanza che ogni membro riveste all’interno del gruppo, a seconda delle proprie peculiari abilità.
5 Il pensiero critico , il problem solving , la capacità di prendere decisioni, di essere creativi e innovativi, sono una palestra significante che allena i ragazzi e le ragazze all’approccio con qualsiasi branca del sapere, sia essa umanistica o scientifica, e alla vita sociale.
6 L’errore assume il significato positivo di crescita personale. Sbagliare è considerata come possibilità sia di nuove scoperte, sia di rimettersi in gioco in un ambiente sicuro e protetto, per allenarsi alla resilienza.
7 In un percorso STEAM non esiste la soluzione giusta o corretta, perché innovazione e creatività sono sempre al primo posto.
8 La classe lavora in gruppi e l’insegnante assume il ruolo di guida applicando la metodologia dell’ Inquired Based Learning, ovvero una metodologia didattica basata sull’investigazione, volta a stimolare nello studente e nelle studentesse la formulazione di domande e azioni per risolvere problemi e capire fenomeni.
9 Il nucleo della didattica STEAM consiste nell’applicazione del metodo scientifico, del Tinkering , della progettazione ingegneristica e del Coding
Gli scienziati e le scienziate sono uomini e donne che svolgono ricerche per scoprire sempre più informazioni sul mondo che ci circonda. Nel loro lavoro applicano un metodo sempre uguale caratterizzato da fasi ben precise:
• osservare;
• formulare una domanda;
• raccogliere informazioni;
• fare ipotesi;
• svolgere esperimenti;
• registrare i dati;
• trarre conclusioni;
• condividere i risultati.
L’esperimento è naturalmente il centro del metodo scientifico, tuttavia la didattica STEAM presuppone che l’esperimento autoconclusivo, che fino a ora si proponeva in classe per dimostrare un fatto noto, sia appunto una dimostrazione che non coinvolge creatività, pianificazione, logica e soprattutto che non porta a nuove scoperte. Nelle STEAM quindi, la dimostrazione è l’ input , il primo passo da cui partire per stimolare nuove domande, ricerche, sperimentazioni e scoperte autonome.
Il Tinkering , che in lingua originale vuol dire “armeggiare”, “trafficare con”, “darsi da fare”, nasce più di dieci anni fa negli Stati Uniti e precisamente nel Museo delle Scienze di San Francisco, con lo scopo di appassionare i bambini e le bambine alla scienza, alla tecnologia e alla matematica. Lo scopo del Tinkering è costruire oggetti di vario genere e meccanismi funzionanti, utilizzando materiali di recupero, facilmente reperibili anche in casa, e lavorando in gruppo. Possiamo quindi considerarlo una fase che anticipa il processo di progettazione ingegneristica
Gli ingegneri e le ingegnere utilizzano le conoscenze e le scoperte fatte dagli scienziati e dalle scienziate per inventare ciò che può migliorare la vita e il mondo intorno a noi. Nel loro lavoro applicano un metodo sempre uguale caratterizzato da step ben precisi:
• identificare il problema;
• raccogliere informazioni;
• immaginare;
• pianificare;
• creare;
• verificare sul campo;
• migliorare;
• condividere.
Una distinzione importante nella didattica STEAM è quella tra attività e sfida . I prodotti realizzati dai bambini e dalle bambine seguendo precise indicazioni rientrano nelle attività, mentre parliamo di sfide quando i bambini e le bambine sono coinvolti nel mettere in gioco creatività, pensiero critico e logica creando un prodotto con uno scopo preciso, secondo la loro immaginazione.
Coding significa programmazione . La programmazione informatica è una vera e propria lingua, una scrittura in codice che permette di interagire con macchine, per assegnare l’esecuzione di comandi e compiti. Il coding ha lo scopo di incentivare l’attitudine al problem solving con la ricerca di nuove soluzioni attraverso tentativi ed errori; favorisce lo sviluppo dei processi logici e creativi attraverso la scomposizione dei problemi in più parti per una risoluzione a step; favorisce l’acquisizione di competenze trasversali , quali memoria, attenzione, concentrazione e logica.
Per dare la possibilità di conoscere e sperimentare il coding anche ai bambini e alle bambine delle scuole non ancora attrezzate a livello informatico, proporremo attività di coding unplugged , ovvero su carta.
Tutte le attività e le sfide STEAM sono contestualizzate in un racconto , affinché ogni lavoro che i bambini e le bambine affrontano abbia uno scopo, un senso e soprattutto favorisca un coinvolgimento emotivo
Le Scienze sono lo sfondo integratore all’interno del quale si muovono i personaggi. Le note a piè di pagina vi danno la possibilità di inquadrare subito l’argomento principale affrontato nella pagina stessa, anche se ricordiamo che la didattica STEAM non è la somma di diverse discipline, ma bensì una metadisciplina che le comprende tutte.
Le attività di tecnologia e coding unplugged si basano su realizzazioni di Pixel Art, percorsi, decodificazione di codici, scrivere e interpretare un algoritmo.
Le attività di ingegneria permettono ai bambini e alle bambine un approccio alla routine del processo di progettazione ingegneristica in modo semplice e naturale proponendo realizzazioni che procedono attraverso tutti gli step del processo:
• identificare il problema;
• raccogliere informazioni;
• immaginare;
• pianificare;
• creare;
• verificare sul campo;
• migliorare;
• condividere.
Le attività di Scienze stimolano la curiosità e offrono lo spunto per ricerche e nuove scoperte attraverso tutte le fasi del metodo scientifico:
• osservare;
• formulare una domanda;
• raccogliere informazioni;
• fare ipotesi;
• svolgere esperimenti;
• registrare i dati;
• trarre conclusioni;
• condividere i risultati.
La Matematica è alla base di tutte le attività che implicano misurazioni e registrazione di dati, mentre l’ Arte è coinvolta nella risultanza di gradevolezza in ogni realizzazione e in sfide specifiche.
All’inizio della scuola allestite l’ angolo STEAM dell’aula . Procuratevi alcune scatole, anche di diverse dimensioni, e coinvolgete i bambini e le bambine nella raccolta di alcuni dei materiali di riciclo utili per lo svolgimento delle attività durante l’anno. Prima di dare il via a una sfida o un’attività, controllate sempre di avere a disposizione i materiali necessari.
I materiali che il vostro angolo STEAM potrà includere, oltre al consueto corredo scolastico, e ai materiali che sceglieranno i bambini e le bambine nelle sfide in cui viene loro richiesto, sono:
• cannucce riciclabili di diversi diametri;
• bicchieri di carta di diverse dimensioni;
• rotoli vuoti di carta igienica o di carta da cucina;
• graffette;
• spago di diverse dimensioni;
• lana;
• tovagliolini di carta;
• succo di limone, mela, carota;
• plastilina;
• vasetti di vetro;
• coloranti alimentari;
• ghiaccio;
• vaselina;
• guanti protettivi di plastica;
• piccoli contenitori di plastica o vetro;
• etichette;
• palette;
• semi;
• un frullatore;
• bacinelle;
• diversi tipi di terreno (ghiaioso, sabbioso, umifero, argilloso).
Soluzioni dei messaggi
• Pagina 159
SONO ALLO STAGNO VI ASPETTO
• Pagina 166
NON CATTURARE LE FARFALLE
• Pagina 169
BOMBE DI SEMI
• Pagina 172
Terreno GHIAIOSO
Terreno SABBIOSO
Terreno UMIFERO
Terreno ARGILLOSO
• Pagina 174
1: B-4
2: C-7
3: D-2
4: F-1
5: G-4
6: G-6
In via di prima acquisizione Base Intermedio Avanzato
Identificare il problema
Raccogliere informazioni
Immaginare
Non coglie il senso del problema. Non mostra interesse o curiosità.
Coglie il senso del problema solo in parte, ma mostra interesse o curiosità.
Raccoglie informazioni generiche da una sola fonte, digitale / non digitale. Non cita la fonte. Non verifica l’informazione. Raccoglie informazioni da fonti, digitali e non. Non cita le fonti. Non verifica le informazioni.
Non considera nessuna possibile soluzione.
Pianificare
Non c’è un elenco dei materiali e degli strumenti. La pianificazione è confusa.
Creare Non cerca di creare un prototipo o un modello che risolva il problema.
Verificare sul campo Non raccoglie i dati necessari. Non ripete il test.
Migliorare
Condividere
Non cerca di migliorare l’invenzione, nonostante non funzioni.
L’esposizione è disordinata e mancante delle informazioni richieste. Presenta le informazioni in modo difficile da seguire.
Lavoro di gruppo Non collabora. Comunica in modo negativo. Non si impegna.
Considera solo un’idea e una soluzione.
L’elenco dei materiali e degli strumenti non è completo. La pianificazione è chiara solo a tratti.
Crea un prototipo che non segue la propria pianificazione.
Raccoglie solo i dati che provano l’efficacia dell’invenzione. Ripete il test ma non registra il risultato.
Non cerca di migliorare l’invenzione, perché funziona.
L’esposizione è disordinata e alcune frasi sono incomplete o confuse. Presenta alcuni fatti in ordine.
Collabora in modo limitato. Comunica in modo a volte negativo. Il suo impegno è limitato.
Riesce a cogliere il senso del problema e mostra interesse o curiosità.
Raccoglie informazioni da più fonti, digitali e non. Non cita le fonti.
Verifica occasionalmente le informazioni.
Considera i punti deboli e i punti di forza di più di un’idea.
L’elenco dei materiali e degli strumenti è completo. La pianificazione
Crea un prototipo che segue la propria pianificazione.
Raccoglie la maggior parte dei dati necessari e li registra in un grafico. Ripete il test e registra il risultato.
Migliora l’invenzione nei punti che ritiene critici.
L’esposizione è organizzata e include immagini. Le frasi sono complete. Presenta tutti i fatti in ordine rendendo possibile la comprensione.
Collabora in molte occasioni. Comunica in modo perlopiù positivo. Si impegna.
Riconosce le varie componenti del problema. Mostra interesse o curiosità.
Raccoglie informazioni da più fonti, digitali e non. Cita le fonti.
Verifica le informazioni.
Considera i punti deboli e i punti di forza di più di un’idea. Arricchisce le idee con dettagli e spiegazioni.
L’elenco dei materiali e degli strumenti è chiaro e completo. La pianificazione è chiara e dettagliata.
Crea un prototipo che segue la propria pianificazione e lo corregge quando necessario.
Raccoglie i dati necessari e li registra correttamente in un grafico. Ripete il test e registra il risultato.
Rivaluta tutti i particolari e i dettagli dell’invenzione.
L’esposizione è ben organizzata e include immagini e materiali appropriati. Presenta tutti i fatti in ordine e rende la presentazione interessante.
Collabora in modo attivo e produttivo. Comunica in modo efficace. Si impegna con entusiasmo.
In via di prima acquisizione
Osservare Non coglie il senso della dimostrazione. Non mostra interesse o curiosità.
Formulare una domanda
Raccogliere informazioni
Formula domande non inerenti.
Raccoglie informazioni da una sola fonte, digitale / non digitale. Non cita la fonte. Non verifica l’informazione.
Fare ipotesi Le ipotesi non sono plausibili e appropriate al contesto.
Fare esperimenti Non c’è un elenco dei materiali e degli strumenti. La pianificazione è confusa. L’esperimento non è ripetuto.
Registrare dati Non raccoglie i dati necessari.
Trarre conclusioni Non collega la domanda iniziale al risultato dell’esperimento.
Condividere i risultati
L’esposizione è disordinata e mancante delle informazioni richieste. Presenta le informazioni in modo disordinato.
Lavoro di gruppo Non collabora. Comunica in modo negativo. Non si impegna.
Base Intermedio
Osserva con attenzione. Mostra interesse o curiosità.
Formula solo qualche domanda appropriata la cui risposta non è misurabile.
Raccoglie informazioni da fonti, digitali e non. Non cita le fonti. Non verifica le informazioni.
Le ipotesi sono plausibili e appropriate al contesto, ma un po’ confuse.
L’elenco dei materiali e degli strumenti non è completo. La pianificazione è chiara solo a tratti. L’esperimento è ripetuto due volte.
Raccoglie solo i dati che provano l’ipotesi.
Le conclusioni non sono sempre supportate dai dati.
L’esposizione è disordinata e alcune frasi sono incomplete o confuse. Presenta alcuni fatti in ordine.
Collabora in modo limitato. Comunica in modo a volte negativo. Il suo impegno è limitato.
Osserva con attenzione e fa qualche associazione di idee. Mostra interesse e curiosità.
Formula domande appropriate ma solo una misurabile.
Raccoglie informazioni da più fonti, digitali e non. Non cita le fonti. Verifica occasionalmente le informazioni.
Le ipotesi sono formulate in modo chiaro. Sono plausibili e appropriate al contesto.
L’elenco dei materiali e degli strumenti è completo. La pianificazione è chiara. L’esperimento è ripetuto due volte.
Raccoglie la maggior parte dei dati necessari e li registra in un grafico.
Le conclusioni non sono chiaramente supportate dai dati.
L’esposizione è organizzata e include immagini. Le frasi sono complete. Presenta i fatti in ordine rendendo possibile la comprensione.
Collabora in molte occasioni. Comunica in modo perlopiù positivo. Si impegna.
Avanzato
Osserva con attenzione e fa associazioni di idee e analogie. Mostra interesse o curiosità.
Formula domande appropriate, e misurabili.
Raccoglie informazioni da più fonti, digitali e non. Cita le fonti. Verifica le informazioni.
Le ipotesi sono formulate in modo chiaro e dettagliato. Sono plausibili e appropriate al contesto.
L’elenco dei materiali e degli strumenti è chiaro e completo. La pianificazione è chiara e dettagliata. L’esperimento è ripetuto più volte.
Raccoglie i dati necessari e li registra correttamente in un grafico.
Le conclusioni sono chiaramente supportate dai dati.
L’esposizione è ben organizzata e include immagini e materiali appropriati. Presenta tutti i fatti in ordine e rende la presentazione interessante.
Collabora in modo attivo e produttivo. Comunica in modo efficace. Si impegna con entusiasmo.
In via di prima acquisizione Base Intermedio Avanzato
Pixel art Svolge l’attività in modo lento e con frequenti imprecisioni.
Riordino di sequenze –diagrammi di flusso
Percorsi
Codici e decodificatori
Interpretare algoritmi
Scrivere algoritmi
Fatica ad individuare la successione dei fatti.
Fatica a orientarsi nella griglia e a seguire la sequenza di indicazioni. Perde spesso la concentrazione.
Svolge l’attività lentamente con qualche imprecisione.
Individua con qualche esitazione la successione dei fatti.
Riesce a orientarsi nella griglia e a seguire la sequenza di indicazioni con solo qualche incertezza. Perde spesso la concentrazione.
Utilizza codici e decodificatori in modo confuso. Perde spesso la concentrazione. Non mostra interesse.
Legge con molta difficoltà semplici algoritmi per risolvere problemi.
Fatica a orientarsi nella griglia.
Scrive con molta difficoltà semplici algoritmi per risolvere problemi.
Fatica a orientarsi nella griglia.
Lavoro di gruppo Non collabora. Comunica in modo negativo. Non si impegna.
Utilizza codici e decodificatori in modo talvolta incerto. Occasionalmente perde la concentrazione. Mostra curiosità e interesse.
Legge in modo discreto semplici algoritmi per risolvere problemi, con l’aiuto dell’insegnante. A volte perde l’orientamento nella griglia.
Scrive in modo discreto semplici algoritmi per risolvere problemi, con l’aiuto dell’insegnante. A volte perde l’orientamento nella griglia.
Collabora in modo limitato. Comunica in modo a volte negativo. Il suo impegno è limitato.
Svolge l’attività con precisione e accuratezza.
Individua la successione dei fatti.
Si orienta nella griglia e segue la sequenza di indicazioni con poche incertezze. Mantiene un buon livello di concentrazione.
Svolge l’attività velocemente con precisione e accuratezza.
Individua facilmente la successione dei fatti.
Si orienta nella griglia e segue la sequenza di indicazioni in modo sicuro e autonomo Mantiene un buon livello di concentrazione e svolge velocemente l’attività.
Utilizza codici e decodificatori in modo autonomo con un buon livello di concentrazione. Mostra curiosità e interesse.
Legge in modo discreto semplici algoritmi per risolvere problemi. Occasionalmente perde l’orientamento nella griglia.
Scrive in modo discreto semplici algoritmi per risolvere problemi. Occasionalmente perde l’orientamento nella griglia.
Collabora in molte occasioni. Comunica in modo perlopiù positivo. Si impegna.
Utilizza codici e decodificatori in modo autonomo e con entusiasmo anche al di fuori dall’attività richiesta. Mostra curiosità e interesse.
Legge in modo autonomo semplici algoritmi per risolvere problemi.
Scrive in modo autonomo semplici algoritmi per risolvere problemi.
Collabora in modo attivo e produttivo. Comunica in modo efficace. Si impegna con entusiasmo.
Nella nostra quotidianità, ci capita con frequenza di ammirare una persona per le sue competenze nell’affrontare una certa situazione. In tal caso, quando ci riferiamo a una competenza, ci troviamo concordi sul significato di questa parola, tanto da ritenere competente una persona che possiede la piena capacità di orientarsi in un determinato campo; in parole più semplici, viene riconosciuta competente la persona che mostra adeguate performance nell’affrontare e risolvere compiti e problemi insiti nel proprio lavoro, che cioè lo sa svolgere in modo efficace ed efficiente anche in situazioni inusuali, superando con successo ostacoli nuovi e imprevisti.
Proprio perché l’ essere competenti è fortemente legato a un ambito piuttosto che a un altro, è pressoché inverosimile che una persona possa essere competente in tutto e che persone diverse tra loro per formazione, per modo di essere e di porsi nei confronti degli altri, dimostrino lo stesso livello di competenza nell’affrontare e risolvere la medesima situazione.
Infatti, la competenza è strettamente ancorata alla dimensione del “ saper essere ” (dimensione sociale e metodologica, capacità personali…), oltre all’irrinunciabile bagaglio delle conoscenze, cioè “ il sapere ” (risultato dell’assimilazione di informazioni), e all’acquisizione di determinate abilità, il “ saper fare ” in termini cognitivi e pratico-procedurali, cioè il saper utilizzare e applicare know-how alle conoscenze acquisite.
Tale concetto risulterà più accessibile se facciamo riferimento a una diffusa competenza molto calata nella realtà: la competenza alla guida di un’auto. Per essere abilitati alla guida, il percorso è obbligatorio per tutti: lezioni di teoria con relativo esame da superare e lezioni di guida con “prova” finale (compito di realtà o, meglio, compito situato). Se questo è il percorso obbligatorio, allora tutti noi potremmo definirci ugualmente competenti nella guida, ma… ben sappiamo che non è così, tant’è che non tutti i patentati sono allo stesso livello di un pilota di F1 o di rally. Ma anche un pilota di F1 non ha le medesime competenze di uno di rally, eppure sono molto più esperti di qualunque altro soggetto abilitato alla guida.
Da che cosa viene determinata una competenza?
In quale misura servono le conoscenze informali, non formali e formali che abbiamo acquisto e le abilità che siamo in grado di esercitare?
Per rispondere a tali domande, ci può essere d’aiuto l’efficace immagine metaforica del Professor Mario Castoldi1 (Figura 1), nella quale rappresenta la “forma” della competenza associandola a quella di un iceberg.
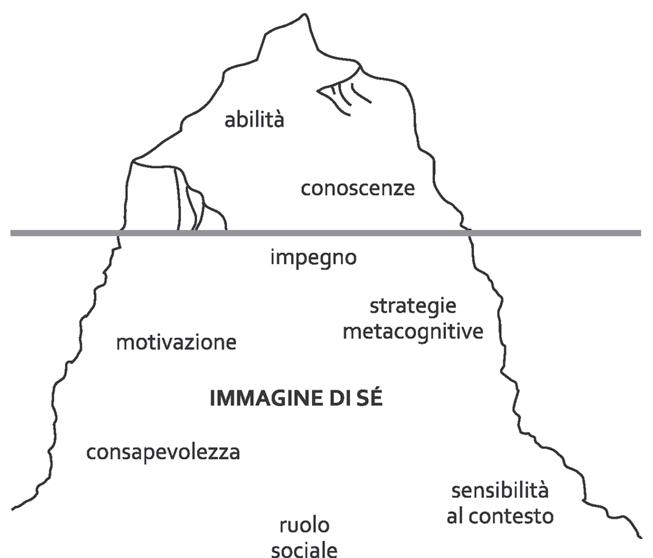
Componente visibile, esplicita , che si manifesta con l’osservazione delle prestazioni del soggetto.
Componente latente, implicita , che richiede l’esplorazione di dimensioni interiori connesse ai processi motivazionali, volitivi, socioemotivi.
Nella parte emersa, visibile ma quantitativamente inferiore a quella immersa non visibile, si colloca tutto ciò che una persona è in grado di acquisire e apprendere attraverso esperienze informali, non formali e formali come possono essere quelle del percorso di studi. Si tratta delle conoscenze e delle abilità, componenti facilmente osservabili, misurabili e valutabili, in quanto si possono rilevare durante una pluralità di “prestazioni standard” (quanto un soggetto, in un determinato ambito, sa e sa fare, in quale misura lo sa e lo sa fare).
Tornando all’esempio delle persone patentate, le conoscenze acquisite (codice stradale e sanzioni in caso di trasgressione, cartellonistica stradale verticale e orizzontale, parti costitutive del motore, parti elettriche e parti meccaniche con le specifiche funzioni, procedure per una corretta guida e per la sostituzione di una ruota…) non sono sufficienti per potersi mettere alla guida di un’auto. Occorre infatti “trasformare” parti di queste conoscenze in abilità e dimostrare di saperle applicare in modo corretto (portare il sedile
1 M. Castoldi, Valutare le competenze, Carocci, 2009, p. 52. Mario Castoldi è docente associato di Didattica generale presso l’Università degli Studi di Torino.
Figura 1di guida nella posizione adatta alla propria statura, allacciare la cintura di sicurezza, controllare ed eventualmente regolare lo specchietto retrovisore e gli specchietti laterali…).
Con il tempo – si direbbe con la famigerata esperienza – tali abilità diventano automatismi, al punto che non ci facciamo più caso.
Nella parte immersa dell’iceberg si colloca tutto ciò che afferisce alla sfera del “saper essere” di una persona, cioè le attitudini e le “ qualità ” proprie di un individuo (impegno, motivazione, strategie metacognitive, consapevolezza, ruolo sociale, immagine di sé, sensibilità al contesto) che, come tali, non sono acquisibili se non implementandole attraverso adeguati e costanti processi metacognitivi.
Si tratta dei processi che “entrano in gioco” ogni qualvolta un individuo si trova ad affrontare e risolvere una situazione inedita e, quindi, di per sé sfidante (non replicabile):
• il “saper fare relazionale” (capacità collaborative efficaci);
• il “saper fare cognitivo” (processi relativi alle operazioni intellettuali);
• le risorse socio-affettive (gestione delle relazioni);
• le risorse psicologiche (gestione delle energie);
• le attitudini e le qualità personali (modalità proprie nell’affrontare un compito/lavoro).
Tali componenti contribuiscono a “fare la differenza” quando si affronta una situazione inedita e imprevista (compito in situazione/compito di realtà/compito autentico) per cui, oltre a ricorrere alle conoscenze acquisite e alle abilità esercitate, entra in gioco la componente riferita ai processi motivazionali, volitivi, socio-emotivi. Questo è il motivo per cui le competenze non sono statiche nel tempo; al contrario, sono in continua evoluzione, in una sorta di spirale virtuosa: più aumentano le nostre conoscenze e le nostre abilità e più vengono parallelamente implementate le dimensioni interiori, maggiore sarà il livello dimostrato nell’affrontare e risolvere in modo efficace una situazione inedita.
Ritornando all’esempio delle performance di guida, risulta maggiormente comprensibile cogliere la differente competenza fra un qualunque soggetto patentato, un pilota di F1 e uno di rally. Le conoscenze e le abilità di una persona che guida in situazioni di quotidianità non possono essere le stesse di quelle dei piloti e nemmeno le dimensioni interiori sono le medesime, proprio perché, nelle “prove” sfidanti che di volta in volta vengono affrontate, le componenti della dimensione visibile (conoscenze e abilità) vengono esercitate in modo differente, “intrecciandosi” in modo altrettanto differente con quelle della dimensione latente (dimensioni interiori).
Ma anche fra “comuni” soggetti patentati, la competenza di guida non è la stessa. Pur avendo acquisito le medesime conoscenze teoriche a livello dichiarativo e procedurale e pur esercitando le stesse abilità necessarie a mettersi al volante, c’è chi si sente sicuro solo se percorre itinerari noti e chi non se ne fa un problema, chi è in difficoltà se si mette alla guida di un’auto che non è quella abituale e chi affronta con sicurezza la guida di un qualsiasi modello, chi si destreggia nel traffico cittadino e chi lo teme, chi è in grado di capire se c’è qualche problema di tipo meccanico o elettrico e chi nemmeno se ne accorge...
Come a dire che la medesima competenza si “attesta” su differenti livelli di prestazione
Le competenze chiave europee per l’apprendimento permanente
La popolare affermazione “Non si finisce mai di imparare”, pur nella sua semplicità, è il concetto che sta alla base di quanto sancito anche nel testo della Raccomandazione sulle competenze chiave per l’apprendimento permanente (22 maggio 2018), elaborata dal Consiglio europeo. L’apprendimento è dunque permanente ( lifelong learning ) e, come
tale, non è esclusiva prerogativa del percorso di studi. Tale documento è comune a tutti gli Stati dell’Unione Europea, proprio perché
“ogni persona ha diritto a un’istruzione, a una formazione e a un apprendimento di qualità inclusivi, al fine di mantenere e acquisire competenze che consentano di partecipare attivamente alla società […]. Promuovere lo sviluppo delle competenze è uno degli obiettivi della prospettiva di uno spazio europeo dell’istruzione […]. È necessario che le persone posseggano il giusto corredo di abilità e competenze […] necessarie per la realizzazione personale, la salute, l’occupabilità e l’inclusione sociale […]”.2
A tal fine, il documento, prima ancora di delineare gli otto tipi di competenze chiave necessarie per l’apprendimento permanente (Tabella A, pag. 23 della presente Guida), ne sottolinea gli scopi e la definizione.
“Le competenze chiave sono quelle di cui tutti abbiamo bisogno per la realizzazione e lo sviluppo personali, la salute, l’occupabilità, l’inclusione sociale, uno stile di vita sostenibile, una vita fruttuosa in società pacifiche, una gestione della vita attenta alla salute e la cittadinanza attiva. Esse si sviluppano in una prospettiva di apprendimento permanente , dalla prima infanzia a tutta la vita adulta, mediante l’apprendimento formale e non formale in tutti i contesti, compresi la famiglia, la scuola, il luogo di lavoro, il vicinato e altre comunità.
Le competenze chiave sono considerate tutte di pari importanza; ognuna di esse contribuisce a una vita fruttuosa nella società. Le competenze possono essere applicate in molti contesti differenti e in combinazioni diverse. Esse si sovrappongono e sono interconnesse; gli aspetti essenziali per un determinato ambito favoriscono le competenze in un altro. Elementi quali il pensiero critico, la risoluzione di problemi, il lavoro di squadra, le abilità comunicative e negoziali, le abilità analitiche, la creatività e le abilità interculturali sottendono a tutte le competenze chiave.”
DEFINIZIONE
“[…] Le competenze sono definite come una combinazione di conoscenze, abilità e atteggiamenti, in cui:
• la conoscenza si compone di fatti e cifre, concetti, idee e teorie che sono già stabiliti e che forniscono le basi per comprendere un certo settore o argomento;
• per abilità si intende sapere ed essere capaci di eseguire processi e applicare le conoscenze esistenti al fine di ottenere risultati;
• gli atteggiamenti descrivono la disposizione e la mentalità per agire o reagire a idee, persone o situazioni.”3
2 Raccomandazione sulle competenze chiave per l’apprendimento permanente (22 maggio 2018), Consiglio europeo.
3 Ibidem
Competenze chiave
Competenza alfabetica funzionale
Competenza multilinguistica
Competenza matematica e competenza in scienze, tecnologie e ingegneria
Competenza digitale
Competenza personale, sociale e capacità di imparare a imparare
Competenza in materia di cittadinanza
Competenza imprenditoriale
Competenza in materia di consapevolezza ed espressione culturali
Cenni di descrizione
Le persone dovrebbero possedere l’abilità di comunicare in forma orale e scritta nelle varie situazioni e di adattare la propria comunicazione in funzione della situazione. Questa competenza comprende anche la capacità di distinguere e utilizzare fonti di diverso tipo, di cercare, raccogliere ed elaborare informazioni, di usare ausili, di formulare ed esprimere argomentazioni in modo convincente e appropriato al contesto, sia oralmente sia per iscritto. Essa comprende il pensiero critico e la capacità di valutare informazioni e di utilizzarle in base ai propri obiettivi.
Questa competenza richiede la conoscenza del vocabolario e della grammatica funzionale di lingue diverse e la consapevolezza pragmalinguistica.
La competenza matematica è la capacità di sviluppare e applicare il pensiero e la comprensione matematici per risolvere problemi in situazioni quotidiane. Partendo da una solida padronanza della competenza aritmetico-matematica, l’accento è posto sugli aspetti del processo e dell’attività oltre che sulla conoscenza. La competenza matematica comporta, a differenti livelli, la capacità di usare modelli matematici di pensiero e di presentazione (formule, modelli, costrutti, grafici, diagrammi) e l’essere disposti a farlo.
La competenza digitale presuppone l’interesse per le tecnologie digitali e il loro utilizzo con padronanza nonché spirito critico e responsabile per apprendere, lavorare e partecipare alla società. Essa comprende l’alfabetizzazione informatica e digitale, la comunicazione e la collaborazione, l’alfabetizzazione mediatica, la creazione di contenuti digitali (inclusa la programmazione), la sicurezza (compreso l’essere a proprio agio nel mondo digitale).
La competenza personale, sociale e la capacità di imparare a imparare consiste nella capacità di riflettere su se stessi, di gestire efficacemente il tempo e le informazioni, di lavorare con gli altri in maniera costruttiva, di mantenersi resilienti e di gestire il proprio apprendimento e la propria carriera. Comprende la capacità di far fronte all’incertezza e alla complessità, di imparare a imparare, di favorire il proprio benessere fisico ed emotivo, di mantenere la salute fisica e mentale, nonché di essere in grado di condurre una vita attenta alla salute.
La competenza in materia di cittadinanza si riferisce alla capacità di agire da cittadini/e responsabili e di partecipare pienamente alla vita civica e sociale.
La competenza imprenditoriale presuppone la consapevolezza che esistono opportunità e contesti diversi nei quali è possibile trasformare le idee in azioni nell’ambito di attività personali, sociali e professionali, e la comprensione di come tali opportunità si presentano. Le capacità imprenditoriali si fondano sulla creatività, che comprende anche l’immaginazione.
Questa competenza richiede la conoscenza delle culture e delle espressioni locali, nazionali, regionali, europee e mondiali, comprese le loro lingue.
“Le competenze indicano la comprovata capacità di usare conoscenze, abilità e capacità personali, sociali e/o metodologiche, in situazioni di lavoro o di studio e nello sviluppo professionale e/o personale; le competenze sono descritte in termini di responsabilità e autonomia.”4
Di tale definizione di Pellerey, che richiama fedelmente l’immagine dell’iceberg delle competenze di Castoldi, la parola chiave è “comprovata”; infatti una competenza – in quanto processo dinamico di mobilizzazione di una pluralità di risorse che si mettono in moto in modo pertinente in un preciso contesto situato – si dimostra sul campo. Pertanto, le competenze non si memorizzano come le conoscenze e non si esercitano come le abilità. Alla luce di tale definizione, proviamo allora a mettere in relazione il testo della Raccomandazione con quanto previsto in quello delle Indicazioni Nazionali per il curricolo della scuola dell’infanzia e del primo ciclo di istruzione
Partendo dal presupposto che la costruzione di competenze è un processo lungo, costante e dinamico, fondato su un percorso formativo il più possibile organico e ad andamento spiralico, per ogni “segmento” scolastico – pur caratterizzato da una sua specificità organizzativa, strettamente correlata al modificarsi delle strutture cognitive dei bambini e delle bambine, della costruzione dell’immagine di sé e dell’autonomia – viene delineato uno specifico auspicabile profilo.
A conclusione del capitolo La Scuola dell’Infanzia, nel paragrafo Dalla Scuola dell’Infanzia alla Scuola Primaria , vengono esplicitate le competenze di base che “è ragionevole attendersi che ogni bambino/a abbia sviluppato […]” (si veda pag. 25 della presente Guida).5 Praticamente, viene tratteggiato l’auspicabile profilo di bambino/a competente che, al termine del percorso triennale della Scuola dell’Infanzia, costituisce il profilo in entrata alla scuola dell’obbligo (principio di continuità del sistema formativo).
Altresì, nel capitolo Finalità generali , a partire dalle otto competenze chiave del documento europeo ( Raccomandazione …), viene descritto, in forma essenziale, il Profilo delle competenze al termine del primo ciclo di istruzione (pag. 25 della presente Guida), nel quale si indicano “le competenze riferite alle discipline di insegnamento e di pieno esercizio della cittadinanza”6, specificando che tale “profilo costituisce l’obiettivo generale del sistema educativo e formativo italiano”.7
4 M. Pellerey, Competenze. Sintesi di didattica generale e speciale, Università degli Studi di Parma.
5 Indicazioni Nazionali per il curricolo della Scuola dell’Infanzia e del primo ciclo di istruzione
6 Ibidem
7 Ibidem
• Riconosce ed esprime le proprie emozioni, è consapevole di desideri e paure, avverte gli stati d’animo propri e altrui.
• Ha un positivo rapporto con la propria corporeità, ha maturato una sufficiente fiducia in sé, è progressivamente consapevole delle proprie risorse e dei propri limiti, quando occorre sa chiedere aiuto.
• Manifesta curiosità e voglia di sperimentare, interagisce con le cose, l’ambiente e le persone, percependone le reazioni e i cambiamenti.
• Condivide esperienze e giochi, utilizza materiali e risorse comuni, affronta gradualmente i conflitti e ha iniziato a riconoscere le regole del comportamento nei contesti privati e pubblici.
• Ha sviluppato l’attitudine a porre e a porsi domande di senso su questioni etiche e morali.
• Coglie diversi punti di vista, riflette e negozia significati, utilizza gli errori come fonte di conoscenza.
• Sa raccontare, narrare, descrivere situazioni ed esperienze vissute, comunica e si esprime con una pluralità di linguaggi, ut ilizza con sempre maggiore proprietà la lingua italiana.
• Dimostra prime abilità di tipo logico, inizia a interiorizzare le coordinate spazio-temporali e a orientarsi nel mondo dei simboli, delle rappresentazioni, dei media, delle tecnologie.
• Rileva le caratteristiche principali di eventi, oggetti, situazioni, formula ipotesi, ricerca soluzioni a situazioni problema tiche di vita quotidiana.
• È attento alle consegne, si appassiona, porta a termine il lavoro, diventa consapevole dei processi realizzati e li documenta
• Si esprime in modo personale, con creatività e partecipazione, è sensibile alla pluralità di culture, lingue, esperienze.
Profilo delle competenze al termine del primo ciclo di istruzione
Lo studente al termine del primo ciclo, attraverso gli apprendimenti sviluppati a scuola, lo studio personale, le esperienze ed ucative vissute in famiglia e nella comunità, è in grado di iniziare ad affrontare in autonomia e con responsabilità le situazioni di vita tipiche della propria età, riflettendo ed esprimendo la propria personalità in tutte le sue dimensioni.
Ha consapevolezza delle proprie potenzialità e dei propri limiti, utilizza gli strumenti di conoscenza per comprendere se stess o e gli altri, per riconoscere e apprezzare le diverse identità, le tradizioni culturali e religiose, in un’ottica di dialogo e d i rispetto reciproco. Interpreta i sistemi simbolici e culturali della società, orienta le proprie scelte in modo consapevole, rispetta le regole condivise, collabora con gli altri per la costruzione del bene comune esprimendo le proprie personali opinioni e sensibilità. Si impegna per portare a compimento il lavoro iniziato da solo o insieme ad altri.
Dimostra una padronanza della lingua italiana tale da consentirgli di comprendere enunciati e testi di una certa complessità, di esprimere le proprie idee, di adottare un registro linguistico appropriato alle diverse situazioni. Nell’incontro con persone di diverse nazionalità è in grado di esprimersi a livello elementare in lingua inglese e di affrontare una comunicazione essenziale, in semplici situazioni di vita quotidiana, in una seconda lingua europea.
Utilizza la lingua inglese nell’uso delle tecnologie dell’informazione e della comunicazione.
Le sue conoscenze matematiche e scientifico-tecnologiche gli consentono di analizzare dati e fatti della realtà e di verificare l’attendibilità delle analisi quantitative e statistiche proposte da altri. Il possesso di un pensiero razionale gli consente d i affrontare problemi e situazioni sulla base di elementi certi e di avere consapevolezza dei limiti delle affermazioni che riguardano questioni complesse che non si prestano a spiegazioni univoche.
Si orienta nello spazio e nel tempo dando espressione a curiosità e ricerca di senso; osserva e interpreta ambienti, fatti, fen omeni e produzioni artistiche.
Ha buone competenze digitali, usa con consapevolezza le tecnologie della comunicazione per ricercare e analizzare dati e informazioni, per distinguere informazioni attendibili da quelle che necessitano di approfondimento, di controllo e di verifica e pe r interagire con soggetti diversi nel mondo.
Possiede un patrimonio di conoscenze e nozioni di base ed è allo stesso tempo capace di ricercare e di procurarsi velocemente nuove informazioni e impegnarsi in nuovi apprendimenti anche in modo autonomo.
Ha cura e rispetto di sé, come presupposto di un sano e corretto stile di vita. Assimila il senso e la necessità del rispetto della convivenza civile. Ha attenzione per le funzioni pubbliche alle quali partecipa nelle diverse forme in cui questo può avvenire: momenti educativi informali e non formali, esposizione pubblica del proprio lavoro, occasioni rituali nelle comunità che frequenta, azioni di solidarietà, manifestazioni sportive non agonistiche, volontariato ecc.
Dimostra originalità e spirito di iniziativa. Si assume le proprie responsabilità e chiede aiuto quando si trova in difficoltà e sa fornire aiuto a chi lo chiede.
In relazione alle proprie potenzialità e al proprio talento si impegna in campi espressivi, motori e artistici che gli sono congeniali. È disposto ad analizzare se stesso e a misurarsi con le novità e gli imprevisti.
La complessità e l’ampiezza delle competenze di tale profilo viene resa maggiormente esplicita e accessibile attraverso quanto descritto nei Traguardi per lo sviluppo delle competenze che, per la Scuola Primaria e la Secondaria di 1° grado, costituiscono le linee guida riferite a ogni disciplina/materia. In quanto traguardi, indicano la meta che ogni scuola è chiamata a rispettare, costituiscono i riferimenti prioritari e ineludibili a partire dai quali organizzare le scelte e le pratiche didattiche e, al contempo, costituiscono gli indicatori (i criteri) per la valutazione delle competenze.
Per tali motivi, i traguardi sono da considerarsi elementi vincolanti di cui ogni singola istituzione scolastica deve tener conto.
Per orientare maggiormente i/le docenti nella scelta e nell’organizzazione delle azioni didattiche da mettere in campo, per ogni disciplina/materia vengono indicati gli obiettivi di apprendimento, cioè “[…] conoscenze e abilità ritenute indispensabili al fine di raggiungere i traguardi per lo sviluppo delle competenze”.8
Per quanto riguarda la Scuola Primaria, escludendo Musica, Arte e Immagine, Educazione fisica e Tecnologia, gli obiettivi di apprendimento, che comunque non sono vincolanti ma orientativi, vengono indicati sia al termine della classe 3ª sia al termine della classe 5ª, con l’intento di fornire ai/alle docenti un supporto orientativo a livello di progettazione, nel rispetto degli apprendimenti irrinunciabili. In altre parole, gli obiettivi costituiscono le linee guida per i/le docenti in quanto descrivono che cosa l’alunno/a deve sapere (conoscenze) e saper fare (abilità) in ogni specifica disciplina.
Ed è proprio negli obiettivi di apprendimento che risiede il margine di discrezionalità delle singole scuole: a partire da quelli delle Indicazioni Nazionali , si declinano gli obiettivi in linea con la propria offerta formativa, anche prevedendo una scansione maggiormente dettagliata progressiva classe per classe (Curricolo di istituto).
Se per verificare e valutare gli obiettivi di apprendimento (conoscenze e abilità) i/le docenti hanno a disposizione un collaudato ventaglio di strumenti (verifiche diagnostiche, formative e sommative orali o scritte con quesiti di diversa tipologia), per la certificazione delle competenze il documento di riferimento è quello delle Linee guida per la certificazione delle competenze nel primo ciclo di istruzione (9 gennaio 2018).
Il riferimento a tale documento è fondamentale per inquadrare la funzione e la progettazione dei compiti di realtà (pagg. 39-42 della presente Guida), quali dispositivi per mettere alla prova gli alunni e le alunne in un compito complesso, in forma di situazione inedita reale (compito autentico) o realistica/verosimile (compito di realtà), finalizzato a osservare e a valutare le prestazioni delle dimensioni di una competenza attraverso specifiche rubriche valutative.
Al termine della Scuola Primaria, unitamente al documento di valutazione, gli alunni e le alunne ricevono un ulteriore documento: la certificazione delle competenze. In attesa della ridefinizione del Profilo dello studente come individuato dalle Indicazioni Nazionali per il
Per lo sviluppo delle competenze: presupposti normativi
curricolo della scuola dell’infanzia e del primo ciclo di istruzione in coerenza con le nuove competenze chiave europee del 2018, si utilizzerà il modello indicato dal MIUR nella nota del 4 aprile 2019, che fa riferimento alle competenze chiave della Raccomandazione del parlamento europeo e del consiglio del 18 dicembre 2006.
Tale modello:
• si riferisce al Profilo dello studente/della studentessa nelle Indicazioni Nazionali per il curricolo della scuola dell’infanzia e del primo ciclo di istruzione ;
• è ancorato alle competenze chiave individuate dall’Unione europea, così come recepite nell’ordinamento italiano;
• definisce, mediante enunciati descrittivi, i diversi livelli di acquisizione delle competenze;
• valorizza eventuali competenze significative, sviluppate anche in situazioni di apprendimento non formale e informale;
• è coerente con il piano educativo individualizzato per le alunne e gli alunni con disabilità;
• indica, in forma descrittiva, il livello raggiunto nelle prove a carattere nazionale distintamente per ciascuna disciplina oggetto della rilevazione e certificazione sulle abilità di comprensione e uso della lingua inglese.9
9 https://www.orizzontescuola.it/
In più parti del documento Raccomandazione sulle competenze chiave per l’apprendimento permanente si fa esplicito riferimento al ruolo e alla funzione della scuola nel promuovere la costruzione delle competenze. In particolare, il documento si sofferma su tre ambiti di intervento:
a) favorire percorsi di studio a carattere interdisciplinare in contesto laboratoriale, utilizzando metodologie didattiche collaborative, interpellando continuamente gli alunni e le alunne, affinché acquisiscano consapevolezza critica del proprio percorso formativo, e costruendo prove in situazione che li stimolino nella messa in atto delle competenze;
b) formare e sostenere i/le docenti nella messa in atto di metodologie didattiche innovative, comprese quelle che fanno uso di strumenti e tecnologie digitali;
c) valutare competenze acquisite in contesti formali e non formali con opportuni quadri di riferimento dei risultati appresi, da affiancare alle più tradizionali valutazioni diagnostiche, formative e sommative.
Il primo ambito di intervento è proprio quello che pone l’accento sulla didattica orientata alle competenze e, quindi, merita particolare attenzione da parte dei/delle docenti, anche perché è interdipendente con il terzo ambito: non si può parlare di processo di insegnamento/apprendimento senza parlare di valutazione.
Come sostiene Morain, occorre “allenare il pensiero dei bambini e degli adolescenti a dare un senso alla frammentarietà delle informazioni, a ritrovare il filo rosso che connette le parti, anche imparando a selezionare ciò che è importante e scartando ciò che è superfluo”.1 L’approccio interdisciplinare nel processo di insegnamento/apprendimento consente di affrontare contemporaneamente aspetti differenti, così da ottenere una più adeguata visione di insieme della complessità, proprio perché qualsiasi ambito/aspetto del reale quotidiano non è mai “mono-disciplinare”. Spesso, infatti, la distanza tra l’apprendimento in contesti reali (dove concorrono simultaneamente conoscenze e abilità afferenti a più discipline) e quello nel contesto scolastico rende quest’ultimo artificioso e scollato dalla realtà. Pertanto non va dimenticato che “le discipline, così come le conosciamo, sono state storicamente separate le une dalle altre da confini convenzionali che non hanno alcun riscontro con l’unitarietà tipica dei processi di apprendimento. Ogni persona, a scuola come nella vita, impara infatti attingendo liberamente dalla sua esperienza, dalle conoscenze o dalle discipline, elaborandole con un’attività continua e autonoma”. 2
Ne consegue che l’eccessiva frammentazione disciplinare dell’apprendimento, così come spesso accade nella scuola, sia una forzatura innaturale e pertanto necessita di una sostanziale revisione della funzione e valenza didattica delle discipline.
1 E. Morain, La testa ben fatta, Riforma dell’insegnamento e riforma del pensiero, Raffaello Cortina Editore, 2000.
2 Indicazioni Nazionali per il curricolo della scuola dell’infanzia e del primo ciclo di istruzione.
Esempi significativi dell’interdipendenza delle discipline sono quelli che, nella nostra tradizione scolastica, proponiamo alla classe quando si parla del lavoro dello storico e della storica e di quello del geografo e della geografa, accennando alla indispensabile collaborazione che tali figure devono mettere in atto con altri specialisti che, attraverso le loro ricerche e i loro studi, concorrono alla completa analisi, comprensione, interpretazione, definizione di fatti, fenomeni, eventi, processi ecc. 3
Conferire significatività all’apprendimento, orientato alla costruzione di competenze, significa allora immergere gli alunni e le alunne in esperienze didattiche interdisciplinari attraverso le quali sperimentare e comprendere il ruolo specifico di ogni singola disciplina e, contestualmente, la loro “corresponsabilità” didattica rispetto a un medesimo ambito di conoscenza.
Progettare nell’ottica interdisciplinare consente allora di ricondurre la frammentarietà del sapere disciplinare all’unitarietà e alla complessità tipiche del sapere non scolastico. Se, per esempio, pensiamo a un contenuto di Storia, è naturale contestualizzarlo dal punto di vista geografico (interdipendenza fra risorse e limiti del territorio con lo sviluppo di una civiltà…), tecnologico e scientifico (quali scoperte e in che modo esse hanno contribuito allo sviluppo di una civiltà…) e via dicendo. Lo stesso vale per qualsiasi argomento di Geografia in quanto ogni territorio, così come lo possiamo conoscere oggi, è il risultato di fenomeni naturali spiegabili scientificamente, ma anche nelle trasformazioni apportate nel tempo dall’uomo per soddisfare bisogni di natura sociale, economica, politica… E la Matematica, in ogni caso, entra giocoforza con la Statistica, la Geometria, l’Aritmetica quali strumenti disciplinari per interpretare aspetti di fenomeni di natura storica, geografica e scientifica.
Una didattica orientata allo sviluppo delle competenze può allora essere supportata da una progettazione che fa dell’interdisciplinarità un punto di forza.
Le metodologie didattiche attive (cooperative learning, peer education, flipped classroom, didattica laboratoriale…) si realizzano solo se nell’ambiente di apprendimento è presente uno stile relazionale flessibile, che concede spazio agli interessi degli alunni e delle alunne e alle loro esperienze, privilegiando l’esperienza diretta. Tali pratiche sono da considerarsi le più efficaci per favorire non solo l’acquisizione di conoscenze, ma soprattutto di abilità finalizzate alla costruzione di competenze, fra cui quella di “imparare a imparare” e, parallelamente, per valorizzare il potenziale di apprendimento di ciascun alunno/a e favorire la sua autonomia.
Il laboratorio per eccellenza, nella tradizione del nostro sistema scolastico, viene collocato quasi esclusivamente in Scienze, disciplina di cui l’approccio sperimentale di tipo laboratoriale rappresenta la dimensione costitutiva.
Partendo però dal presupposto che per laboratorio non si intende esclusivamente un luogo fisico in cui maneggiare e manipolare materiali, strumenti e sostanze per scoprire, interpretare e comprendere un fenomeno o un processo, è possibile estendere l’idea di laboratorio scientifico a tutti gli altri ambiti disciplinari.
3 “Se in ogni scienza noi vediamo un ramo dell’albero della sapienza, allora ogni scienza ci appare in tutto il suo significato. Capiamo allora anche il giusto significato della specializzazione scientifica, il giusto senso della professionalità che non isola dal resto del sapere, non esclude il dialogo con le altre discipline, non esclude l’impegno, sia didattico che divulgativo, di comunicare i contenuti della propria scienza a qualsiasi pubblico.” (E. De Giorgi, Valore sapienziale della Matematica, in DISF - Documentazione Interdisciplinare di Scienza & Fede, vol. I, pp. 846-847).
Il laboratorio , didatticamente parlando, è infatti un approccio metodologico più che un luogo fisico deputato, per le sue caratteristiche, a svolgere una determinata attività pratico-concreta, attraverso il quale far sperimentare e favorire lo sviluppo di conoscenze contestualizzate e non artificiosamente frammentate. D’altra parte, nella vita quotidiana si apprende in azione, mentre “si fa” qualcosa, giusta o sbagliata che sia: l’apprendimento avviene in modo spontaneo e naturale proprio perché è fondato su attività e non su contenuti da apprendere. “Se faccio imparo” dovrebbe essere la condizione imprescindibile per garantire un apprendimento significativo, quello che passa cioè attraverso un fare operativo, non solo in termini di manipolazione di materiali, ma anche di sperimentazione di ipotesi, conoscenze informali, non formali e formali, in cui l’errore assume valenza didattica. Di conseguenza, la didattica laboratoriale si configura anche come occasione metacognitiva per destrutturare una procedura o una soluzione al fine di rintracciarvi la possibilità di rivedere le proprie scelte, qualora si siano rivelate inefficaci o errate.
Qualsiasi tipo di laboratorio deve allora poter effettivamente garantire il learning by doing, cioè l’apprendimento attraverso il fare e l’agire (materiale e mentale), dove la strategia indiscussa è il problem solving . Gli alunni e le alunne, immersi/e in un’esperienza diretta, attraverso l’osservazione, l’analisi, il confronto dialettico di procedure e soluzioni, i tentativi, la pratica dell’errore (sbagliando si impara!), la condivisione, la riflessione sul fare proprio e su quello altrui, mettono in atto gli stessi processi cognitivi e metacognitivi dell’apprendimento in contesti reali. E l’insegnante, in un ambiente di apprendimento predisposto per favorire l’approccio laboratoriale, assume il ruolo di regia, offrendo stimoli e rilanciandone di nuovi, valorizzando e rinforzando positivamente l’operatività degli alunni e delle alunne, senza anticipare concetti, esiti, risposte e, soprattutto, sospendendo qualsiasi forma di giudizio/valutazione sulle procedure e sui processi mentre sono in atto. In altre parole, l’insegnante deve far propria l’arte della maieutica socratica come modello didattico per far emergere le potenzialità cognitive degli alunni e delle alunne. Per sua natura, poi, il laboratorio si avvale anche del confronto e della condivisione di una pluralità di punti di vista (quelli dei compagni e delle compagne, che non sempre affrontano uno stesso problema mettendo in atto le medesime strategie). In tale ottica, l’apprendimento diventa, quindi, anche una “questione sociale”: il prodotto (sia di tipo materiale sia culturale) dell’attività laboratoriale sarà allora il frutto di una riflessione continua e di una naturale revisione del proprio procedere in relazione a quello altrui.
La massima espressione di una didattica collaborativa risiede nel lavoro di gruppo, non certamente inteso come semplice aggregazione di alunni e alunne che lavorano attorno a uno stesso argomento, aiutandosi più o meno vicendevolmente.
Se è pur vero che l’apprendimento è un’attività mentale individuale, lo si raggiunge più facilmente e con risultati più duraturi, nonché con maggior soddisfazione, quando ciascun appartenente al gruppo viene messo nelle condizioni di apportare il proprio personale contributo, nella misura in cui ha un ruolo attivo che lo rende responsabile nei confronti dell’esito o della soluzione del problema/compito affrontato. In tal senso, il lavoro di gruppo si configura come un’ottima metodologia inclusiva che consente la costruzione comune di nuovi saperi.
Il lavoro di gruppo non si improvvisa, ma richiede un processo – non sempre facile e certamente non breve – nel quale gli alunni e le alunne, fin dalle prime classi, vengono guidati a sperimentare l’importanza della collaborazione (iniziando dapprima solo con la condivisione di materiali, di giochi, di spazi…), per poi arrivare alla progressiva sperimentazione della
cooperazione ( cooperative learning ), passando attraverso il lavoro a coppie. L’ambiente di apprendimento basato su un autentico lavoro di gruppo impone la progressiva applicazione dei suoi principi fondanti:
• interdipendenza positiva nel gruppo (i membri del gruppo fanno affidamento gli uni sugli altri per raggiungere lo scopo; se qualcuno nel gruppo non fa la propria parte, anche gli altri ne subiscono le conseguenze);
• responsabilità personale (sebbene l’obiettivo sia unico per il gruppo e tutti concorrano per il suo conseguimento, ogni membro ha una responsabilità individuale per ciò che ha fatto);
• interazione promozionale faccia a faccia (verifica del proprio ragionamento, delle conclusioni, delle difficoltà, senza timore di esporre la propria opinione);
• importanza delle competenze sociali (la comunicazione efficace, l’ascolto, la funzione di guida, il rispetto del proprio ruolo e di quello altrui…);
• controllo o revisione ( riflessione ) del lavoro svolto insieme (critiche sulle procedure messe in atto e non sui membri del gruppo);
• valutazione individuale e di gruppo (l’autovalutazione fornisce valore alle proprie responsabilità e al lavoro sia individuale sia di gruppo).
Effettuare un’uscita sul territorio, realizzare un origami, preparare un cartellone, riprodurre un esperimento scientifico, intraprendere la corrispondenza epistolare con gli alunni e le alunne di un’altra classe, costruire un lapbook … non possono essere considerate attività che mettono l’alunno/a in una situazione in cui dimostrare quanto sa essere competente. Di conseguenza, pur essendo attività pratiche, anche se stimolanti e distanti dalla didattica frontale, non hanno in sé il carattere di quella sfida inedita che contraddistingue i compiti di realtà/autentici. Non si tratta, quindi, di una semplice questione di tipo lessicale, per cui basta sostituire l’espressione “esperienza concreta” con il termine compito di realtà/autentico, come spesso erroneamente viene inteso.
Assodato che i compiti di realtà/autentici, in quanto tali, dovrebbero avvicinarsi il più possibile a situazioni rintracciabili nelle pratiche quotidiane, vanno progettati tenendo conto di alcuni “tratti” distintivi imprescindibili:
• devono riguardare un compito-problema inedito , quindi che non si è mai affrontato prima e che, per sua natura, non può essere replicabile nel modo di affrontarlo e risolverlo;
• vanno intesi come un compito-problema aperto , cioè che si presta a una pluralità di possibili soluzioni, consentendo agli alunni e alle alunne di percorrere quella che ritengono maggiormente congeniale/vantaggiosa per l’esito richiesto;
• sono complessi , in quanto richiedono la selezione e la messa in gioco concomitante di conoscenze e abilità afferenti a più contenuti disciplinari oltre che alle risorse personali, cognitive, metacognitive, sociali;
• implicano intenzionalità e progettualità nell’individuare le attività necessarie per procedere nella soluzione, in quanto non sono strutturati in modo completamente definito;
• prevedono necessariamente un prodotto finale , che può essere differente in base alle scelte operate dal singolo o dal gruppo;
• offrono la possibilità di collaborare tra pari ( peer education );
• oltre alla valutazione coerente con la natura del compito da parte dell’insegnante, si prestano all’ autovalutazione (individuale e di gruppo) sia in itinere sia sull’esito del prodotto finale.
I tratti distintivi qui sopra enunciati impongono ai/alle docenti un’attenta progettazione dei compiti di realtà/autentici, che non possono avere carattere di estemporaneità né di occasionalità. Infatti, se gli alunni e le alunne hanno a disposizione i cinque anni della Scuola
Primaria per dimostrare in quale misura hanno raggiunto i traguardi di competenza attesi, i/le docenti hanno a disposizione lo stesso arco temporale per progettare compiti di realtà/ autentici di complessità crescente, modulandoli e graduandoli in base alle conoscenze e alle abilità da mettere in campo, in una sorta di spirale virtuosa, mettendo più volte gli alunni e le alunne nella medesima situazione sfidante.
I compiti di realtà/autentici si configurano allora anche come eccellente occasione per la pratica di una didattica attiva, attraverso l’interdisciplinarità, l’approccio laboratoriale e il lavoro di gruppo.
Nel terzo ambito di intervento rintracciabile nel documento Raccomandazione sulle competenze chiave per l’apprendimento permanente , viene indicato un primo distinguo in materia di valutazione delle competenze, laddove si parla di:
• contesti formali e non formali;
• opportuni quadri di riferimento;
• affiancamento alle più tradizionali forme di valutazione.
È quindi lecito pensare che la valutazione delle competenze sia altra rispetto alla valutazione di conoscenze e abilità, che pur deve essere mantenuta, sia negli strumenti, sia nelle modalità, sia nella forma valutativa.
Se la verifica e la relativa valutazione di conoscenze acquisite e abilità esercitate rispetto a un determinato contenuto/argomento disciplinare costituiscono una pratica ormai collaudata nel processo di insegnamento/apprendimento, la valutazione delle competenze implica un “cambio” di rotta e di prospettiva non indifferenti, come sollecitato nel documento Linee guida per la certificazione delle competenze (D.M. 742/2017), laddove si precisa che “Progettare l’attività didattica in funzione delle competenze e della loro certificazione richiede una professionalità docente rinnovata e attenta alle domande, anche e soprattutto implicite, che possono venire dagli alunni”.
Considerata la natura complessa, dinamica e processuale delle competenze 1, è impensabile poterle valutare una volta e per sempre, come avviene per le conoscenze e le abilità disciplinari che si cristallizzano nel tempo, ma “occorre assumere la consapevolezza che le prove utilizzate per la valutazione degli apprendimenti [verifiche in forma orale o scritta per accertare l’acquisizione di conoscenze e l’esercizio di abilità] non sono affatto adatte per la valutazione delle competenze” 2, anche se “spostare l’attenzione sulle competenze non significa in alcun modo trascurare il ruolo determinante che i più tradizionali risultati di apprendimento, identificati principalmente nelle conoscenze e nelle abilità, svolgono in funzione di esse. Non è infatti pensabile che si possano formare delle competenze in assenza di una sicura padronanza delle strumentalità di base. La competenza costituisce il livello di un uso appropriato e consapevole di tutti gli oggetti di apprendimento, ai quali si applica con effetti elaborativi, metacognitivi e motivazionali”. 3
Se il compito di realtà/autentico è il dispositivo che consente di osservare le evidenze/prove della messa in campo di una o più competenze, lo strumento per la valutazione delle competenze ne rispecchia la complessità. Infatti, a differenza delle verifiche di tipo contenutistico finalizzate a valutare l’esito degli apprendimenti disciplinari, la competenza si apprezza a
1 Linee guida per la certificazione delle competenze (D.M. 742/2017): “[…] complessità in quanto prende in considerazione i diversi aspetti della valutazione: conoscenze, abilità, traguardi per lo sviluppo delle competenze, atteggiamenti da utilizzare in un contesto problematico e più articolato rispetto alla semplice ripetizione e riesposizione dei contenuti appresi. […] Processualità in quanto tale operazione non può essere confinata nell’ultimo anno della Scuola Primaria e della Scuola Secondaria di Primo grado, ma deve sostanziarsi delle rilevazioni effettuate in tutti gli anni precedenti”.
2 Linee guida per la certificazione delle competenze (D.M. 742/2017).
3 Ibidem
differenti livelli di prestazione di una evidenza/prova sia con la valutazione del prodotto finale atteso sia con la valutazione del processo messo in atto per conseguire quel risultato. Poiché la natura del processo non è statica né materiale/visibile, la modalità per esprimerne la valutazione non potrà essere numerica, ma di tipo narrativo/descrittivo.4
Ritornando all’immagine metaforica di Castoldi (pag. 20), risulta più chiaro comprendere che anche le dimensioni non visibili incidono – e non da poco! – in una qualsiasi prestazione competente, tanto da essere oggetto della valutazione in quanto determinano il livello stesso della prestazione. Nel documento Linee guida per la certificazione delle competenze , gli indicatori di competenza vengono esplicitati nei seguenti termini:
• autonomia : è capace di reperire da solo strumenti o materiali necessari e di usarli in modo efficace;
• relazione : interagisce con i compagni, sa esprimere e infondere fiducia, sa creare un clima propositivo;
• partecipazione : collabora, formula richieste di aiuto, offre il proprio contributo;
• responsabilità : rispetta i temi assegnati e le fasi previste del lavoro, porta a termine la consegna ricevuta;
• flessibilità , resilienza e creatività : reagisce a situazioni o esigenze non previste con proposte divergenti, con soluzioni funzionali, con utilizzo originale di materiali ecc.;
• consapevolezza : è consapevole degli effetti delle sue scelte e delle sue azioni.
Poiché, come più volte sottolineato, qualsiasi competenza, per sua natura, è caratterizzata dalla complessità, anche lo strumento per la sua valutazione è altrettanto articolato. Gli strumenti per eccellenza finalizzati alla valutazione di una competenza sono le rubriche valutative, da considerarsi parte integrante del compito di realtà/autentico e che, quindi, vanno predisposte in fase di progettazione. Infatti la rubrica valutativa può essere considerata come la matrice generatrice per articolare in modo analitico e chiaro le evidenze delle prestazioni da tenere sotto controllo e, di conseguenza, per progettare le caratteristiche delle attività di apprendimento che maggiormente si prestano a rilevare gli aspetti delle stesse prestazioni (didattica per competenze). Ne consegue che, per ogni compito autentico progettato, è necessario predisporre uno strumento di tipo descrittivo, per una valutazione qualitativa e articolata della prestazione. In tale ottica, si assume la valutazione come risorsa formativa utile a orientare e promuovere il processo di apprendimento.
4 Linee guida per la certificazione delle competenze (D.M. 742/2017) “le prove utilizzate per la valutazione degli apprendimenti non sono affatto adatte per la valutazione delle competenze. È ormai condiviso a livello teorico che la competenza si possa accertare facendo ricorso a compiti di realtà (prove autentiche, prove esperte ecc.), osservazioni sistematiche e autobiografiche cognitive […] che permettono agli insegnanti di rilevare il processo, ossia le operazioni che compie l’alunno per interpretare correttamente il compito, per coordinare conoscenze e abilità già possedute, per ricercarne altre, qualora necessarie, e per valorizzare risorse esterne […] e interne”.
Nel documento Certificazione delle competenze al termine della scuola primaria , viene indicata la gradualità della valutazione , che si attesta su quattro livelli5, come a dire che, anche per ogni compito autentico progettato, la rubrica/griglia per la valutazione di una competenza va predisposta sulla base di prestazioni effettivamente osservabili e dei relativi indicatori di tipo descrittivo per il livello raggiunto: rispetto alla competenza individuata, se ne valuta la prestazione attraverso le dimensioni che la caratterizzano e i quattro livelli descrittivi che non contemplano il livello negativo (assenza della competenza).
Gli elementi irrinunciabili che compongono una rubrica solitamente sono:
• una prestazione individuata (oggetto della valutazione), complessa e osservabile all’interno del compito di realtà/autentico;
• l’elenco delle dimensioni ;
• una scala di valore (quattro livelli);
• i descrittori dei livelli per ciascuna dimensione espressi in termini di comportamenti attesi effettivamente osservabili.
La rubrica valutativa, quindi, si attesta come strumento attraverso il quale descrivere:
• le competenze dell’alunno/a al termine di un percorso formativo, attraverso le evidenze delle prestazioni;
• i livelli di padronanza della competenza stessa, dimostrati dall’alunno/a.
Ne consegue che le rubriche valutative, qualunque sia il livello di attestazione della competenza, restituiscono all’alunno/a l’apprezzamento di ciò che è stato in grado di fare in quella specifica situazione, fornendogli quindi il feedback delle proprie prestazioni e l’occasione per riflettere sulle proprie modalità di miglioramento. In tali aspetti risiede il motivo per cui le rubriche valutative possono essere considerate lo strumento per eccellenza di un’autentica valutazione formativa. Infatti, il principio di fondo sotteso alla valutazione formativa richiama il valore dei processi metacognitivi come strumenti di consapevolezza e controllo del proprio apprendimento; in tale prospettiva, la valutazione diviene una formidabile opportunità per sollecitare e potenziare l’attività metacognitiva, per “imparare a imparare”.
La valutazione delle competenze, attraverso le dimensioni più importanti relative a una prestazione complessa, per salvaguardare la sua dimensione formativa non si può ridurre al nostro feedback , ma necessita di essere supportata dall’autovalutazione dell’alunno/a attraverso una specifica rubrica.
5 A AVANZATO. L’alunno/a svolge compiti e risolve problemi complessi, mostrando padronanza nell’uso delle conoscenze e delle abilità; propone e sostiene le proprie opinioni e assume in modo responsabile decisioni consapevoli.
B INTERMEDIO. L’alunno/a svolge compiti e risolve problemi in situazioni nuove, compie scelte consapevoli, mostrando di saper utilizzare le conoscenze e le abilità acquisite.
C BASE. L’alunno/a svolge dei compito semplici anche in situazioni nuove, mostrando di possedere conoscenze e abilità fondamentali e di saper applicare basilari regole e procedure apprese.
D INIZIALE. L’alunno/a, se opportunamente guidato/a, svolge compiti semplici in situazioni note.
La scelta più efficace sarebbe quella di guidare progressivamente gli alunni e le alunne nella costruzione di rubriche autovalutative , sul modello di quelle utilizzate dall’insegnante per la sua valutazione. Il processo di costruzione di tale griglia assumerebbe allora il valore aggiunto della consapevolezza del proprio processo di apprendimento. In alternativa, l’insegnante può predisporre rubriche autovalutative strutturate in modo che ogni alunno/a, nella descrizione dei livelli di prestazione di ciascuna dimensione, possa ritrovare il comportamento che ritiene di aver messo in atto. Si tratta di una autovalutazione che richiede meno impegno a livello cognitivo, in quanto gli alunni e le alunne non sono chiamati in prima persona a ripercorrere a posteriori, passo dopo passo, l’approccio di apprendimento che hanno messo in atto, ma a individuare i descrittori che, a posteriori, meglio lo rappresentano.
Nel Sussidiario Nel cuore dei saperi è stata fatta la scelta di fornire rubriche autovalutative già predisposte “a misura di alunno/a”, ma su modello di quelle che utilizzerà l’insegnante.
Una competenza è fortemente radicata nelle conoscenze e nelle abilità acquisite in ambito disciplinare, quindi il sapere e il saper fare ne sono parte integrante. Ciò che cambia rispetto a una didattica tradizionale è l’approccio con cui vengono proposti i contenuti di apprendimento, che è quello di situarli in modo da conferire a essi valore di significatività. Nel concetto di significatività dell’apprendimento, oltre a entrare in gioco le scelte metodologiche relative alla didattica attiva, assume valore di irrinunciabilità la scelta di situare le occasioni di apprendimento in un percorso formativo del quale l’autenticità del proprio agire costituisca il carattere distintivo. In tale scelta, ci vengono in aiuto una pluralità di occasioni reali che spaziano dal contesto scolastico (organizzazione dell’ Open Day , dell’accoglienza dei futuri primini, di una mostra, di una visita di istruzione, dell’utilizzo di spazi interni ed esterni per i momenti ricreativi…), alla vita quotidiana (organizzazione di una festa in famiglia, di una gita/una breve vacanza, predisposizione di un menu settimanale nel rispetto delle esigenze e dei gusti dei propri familiari e in linea con i principi di una sana alimentazione…), alla comunità di appartenenza (ottimizzazione di uno spazio pubblico del territorio, valorizzazione di un luogo rilevante per il territorio, riqualificazione di un’area del territorio, organizzazione di una iniziativa culturale o di utilità sociale per il territorio…). La progettazione per eccellenza di un compito di realtà/autentico dovrebbe prendere avvio dalla scelta di una competenza da promuovere, in base alla quale procedere alla predisposizione della rubrica valutativa in linea con i traguardi e gli obiettivi di apprendimento. In base alle dimensioni individuate rispetto alla prestazione indicata, l’insegnante attinge dal mondo del reale una situazione-problema sfidante e inedita, prevedendo quali attività proporre e con quali scelte didattiche. Certamente, questa è la progettazione più impegnativa, in quanto richiede una collaudata pratica nella predisposizione delle rubriche per la valutazione e l’autovalutazione e nella pratica progettuale.
Una scelta più semplice è quella di individuare il prodotto finale da realizzare in base al quale, procedendo a ritroso, prevedere le attività necessarie alla sua realizzazione, con i relativi obiettivi di apprendimento e i traguardi per lo sviluppo delle competenze, per poi predisporre le rubriche valutativa e autovalutativa sulla prestazione attesa, articolata in dimensioni descritte in quattro livelli di attestazione.
A prescindere dalla scelta progettuale, tre possono essere gli approcci metodologici per la progettazione dei compiti di realtà/autentici:
• 1° approccio • partire da conoscenze e abilità disciplinari già acquisite e fatte oggetto di valutazione; in tal caso, la sfida per gli alunni e le alunne risiede nella richiesta di ricorrere a quanto sanno e sanno fare, selezionando le conoscenze e le abilità da mettere in campo per procedere in modo funzionale nell’affrontare il compito inedito richiesto;
• 2° approccio • si progetta un compito in cui l’alunno/a viene messo/a nelle condizioni di acquisire nuove conoscenze ed esercitare nuove abilità direttamente in situazione, conferendo a essi valore di significatività assoluta rispetto al compito stesso, in quanto strettamente funzionali al procedere; ciò implica che il docente, in fase di progettazio -
ne, debba prevedere anche interventi e modalità di lavoro funzionali ai nuovi apprendimenti;
• 3° approccio • è un approccio “integrato”, in quanto la progettazione prevede fasi di riutilizzo integrato di conoscenze e abilità già acquisite (1° approccio), alternate a fasi di lavoro di apprendimento situato (2° approccio).
Se nel 2° approccio risiede la vera essenza dell’apprendimento significativo, in quanto l’alunno/a viene messo/a nelle condizioni di comprendere l’effettiva necessità di impossessarsi dei necessari strumenti disciplinari per procedere nel compito, va riconosciuto che risulta quello maggiormente impegnativo sia per la classe sia per il/la docente che lo deve progettare. Qualunque sia la tipologia di approccio metodologico-didattico che si ritiene opportuno adottare per la propria classe, la fase della progettazione del compito di realtà/autentico è comunque indispensabile.
I compiti di realtà proposti nel Sussidiario Nel cuore dei saperi e le relative schede di progetto inserite di seguito non sono da intendersi vincolanti, ma possono costituire un’ottima “palestra” sia per i/le docenti che desiderano accostare e sperimentare tale modello didattico sia per gli alunni e le alunne che, in alcuni casi, si trovano a dover passare da un modello di apprendimento più tradizionale a quello per competenze.
In quanto hanno valore e funzione di proposte, nel pieno rispetto della libertà di insegnamento, va da sé che ogni docente può assumere in toto tali compiti di realtà, così come pure può valutare di utilizzarli quali modello di riferimento, ma anche di riprogettarli in base all’approccio che ritiene, al momento, più adatto per la realtà della propria classe.
Poiché una competenza, come definita dal Pellerey, è “la manifestazione della mobilitazione di risorse interne (‘conoscenze, abilità e disposizioni stabili’) e di risorse esterne ( ‘persone, strumenti e materiali’ ) ” 1, non può essere considerata come la sommatoria di elementi del sapere (conoscenze), del saper fare (abilità) e del saper essere (atteggiamenti e attitudini), per cui la sua valutazione richiede un “dispositivo” ad hoc , quale il compito di realtà/autentico, proprio perché essa non è misurabile in termini quantitativi ma si avvale di descrittori qualitativi.
Nel compito di realtà proposto in Matematica, per la valutazione e l’autovalutazione della prestazione di competenze, si è scelto di utilizzare rubriche analitiche (“suddividono” la competenza per dimensioni), nelle quali una prestazione viene scomposta nei suoi elementi costituenti, al fine di valutare ogni suo elemento.
Ritratti fruttuosi
a cura di Alfia Lucia Fazzino e Paola Hippoliti
Griglia di progettazione
Competenze chiave europee da attivare
• Competenza matematica e competenza in scienze, tecnologia e ingegneria
• Competenza digitale
• Competenza personale, sociale e capacità di imparare a imparare
• Competenza in materia di cittadinanza
• Competenza imprenditoriale
• Competenza in materia di consapevolezza ed espressione culturali
Traguardi per lo sviluppo delle competenze al termine della Scuola Primaria
• Si muove con sicurezza nel calcolo mentale e scritto.
• Ricerca dati per ricavare informazioni e costruisce rappresentazioni (tabelle e grafici).
• Legge rappresentazioni e tabelle al fine di ricavare informazioni utili alla soluzione del problema.
• Risolve facili problemi in ogni ambito di contenuto, mantenendo il controllo sia sul processo risolutivo, sia sui risultati.
Obiettivi di apprendimento
• Eseguire le quattro operazioni con i numeri naturali e decimali mediante calcolo mentale o scritto.
• Applicare procedimenti di misura in contesti differenti.
• Effettuare indagini.
• Rappresentare dati.
• Risolvere semplici problemi in ogni ambito di contenuto.
• Formulare e giustificare il processo risolutivo.
• Cooperare alla riuscita di un progetto.
• Effettuare ricerche.
Consegna operativa
Per l’Expo avvenuta a Milano nel 2015 il tema scelto fu “Nutrire il pianeta, energia per la vita” e fu realizzata una mascotte fatta di frutta chiamata “Foody”. Il suo autore si è ispirato a un pittore milanese del 1500 chiamato Giuseppe Arcimboldo autore di numerosi ritratti fatti tutti con frutta, verdura e altri oggetti. Prendendo ispirazione da G. Arcimboldo, realizza un ritratto utilizzando la frutta fresca di stagione.
Prodotto atteso
Ritratto realizzato con frutta fresca.
TEMPI STIMATI
MATERIALI E STRUMENTI
VALUTAZIONE
AUTOVALUTAZIONE
1a fase: presentazione da parte dell’insegnante dell’Expo 2015, della sua mascotte e del pittore Arcimboldo. Richiesta agli alunni e alle alunne di realizzare un ritratto con l’uso di frutta fresca di stagione.
2a fase : lavoro individuale o a coppie di ricerca su libri e/o al PC di notizie sul pittore G. Arcimboldo e sulle sue opere.
3a fase : lavoro collettivo per il confronto delle ricerche individuali e per l’analisi di un ritratto di Arcimboldo scelto fra quelli presentati dagli alunni e dalle alunne.
4a fase: lavoro in piccoli gruppi per la ricerca della frutta di stagione e dei luoghi di produzione. Creazione di una tabella riassuntiva.
5a fase : lavoro collettivo di indagine in classe per individuare la frutta preferita. Rappresentazione dei dati con grafico e loro interpretazione mediante indici statistici (moda).
6a fase: lavoro in piccoli gruppi per realizzare il disegno del progetto del ritratto scegliendo la frutta di stagione dalla tabella prodotta nella fase 4. Elenco della frutta necessaria e stima delle quantità necessarie.
7a fase: a ogni gruppo viene dato il volantino di un supermercato; ogni gruppo ha il volantino di un supermercato differente.
Usando i prezzi indicati sul proprio volantino, ogni gruppo calcola la spesa per l’acquisto della frutta necessaria alla realizzazione del ritratto e stabilisce il costo per ciascun componente del gruppo.
8a fase : lavoro collettivo per confrontare le spese calcolate da ogni gruppo, motivare le differenze e scegliere in quale supermercato effettuare la spesa.
9a fase : lavoro in piccoli gruppi per realizzare il ritratto con la frutta acquistata.
Esposizione dei ritratti, fotografarli e… mangiarli!!!
1a fase : 30 minuti
2a fase : 1 ora
3a fase : 1:30 ore
4a fase : 30 min
5a fase : 2 ore
6a fase : 2 ore
7a fase : 1 ora
8a fase : 30 min
9a fase : 2 ore
Sussidiario, testi di consultazione, computer, foto, fogli da disegno, volantini supermercati, frutta di stagione, piatti di carta, scodelle.
Rubrica sulle prestazioni insite nella/e competenze da valutare su quattro descrittori dei livelli di competenza.
Rubrica sulle prestazioni insite nella/e competenze da valutare su quattro descrittori dei livelli di competenza.
Alunno/a
Classe
a.s.
Periodo
Competenze chiave europee da attivare
• Competenza matematica e competenza in scienze, tecnologia e ingegneria
• Competenza digitale
• Competenza personale, sociale e capacità di imparare a imparare
• Competenza in materia di cittadinanza
• Spirito di iniziativa
• Competenza in materia di consapevolezza ed espressione culturali
COMPETENZA DA VALUTARE
• Competenza matematica e competenza in scienze, tecnologia e ingegneria
Dimensioni Iniziale
Uso delle procedure
Uso di sussidi e strumenti
Fatica ad utilizzare in modo autonomo procedure e algoritmi standard.
Fatica a ricavare informazioni dal materiale messo a disposizione.
PRESTAZIONI
Usare procedure e algoritmi • Usare sussidi e strumenti Progettare • Lavoro di gruppo
Base Intermedio Avanzato
Mostra incertezze nell’usare procedure e algoritmi standard.
Ricava semplici informazioni dal materiale messo a disposizione; utilizza le informazioni per effettuare ragionamenti riferiti a singole situazioni.
Usa procedure e algoritmi standard. Usa procedure e algoritmi con sicurezza, mostrando il controllo delle procedure utilizzate.
Utilizza il materiale a disposizione per ricavare informazioni, ricerca il materiale che manca; usa le informazioni ricavate per effettuare ragionamenti.
Utilizza il materiale a disposizione per ricavare informazioni, ricerca in modo autonomo le informazioni che mancano; organizza le informazioni in forma coerente e le usa per effettuare ragionamenti.
Modellizzazione
Realizza parzialmente il modello elaborato dai compagni/dalle compagne.
Efficacia del proprio ruolo Fatica a trovare un proprio ruolo e ad accettare idee e proposte altrui.
Usando parzialmente le informazioni ricavate, elabora singoli elementi del modello.
Svolge il ruolo assegnatogli in modo corretto, senza fornire particolari contributi.
Usando le informazioni ricavate, organizza le principali fasi di elaborazione del modello e le realizza.
Si attiva per trovare un ruolo; accoglie le proposte altrui e collabora nell’organizzazione del lavoro.
Usando le informazioni ricavate, organizza le fasi di elaborazione del modello e mantiene il controllo del processo di elaborazione.
Si attiva per trovare un ruolo; avanza proposte, mostrando capacità critiche; accoglie le proposte altrui, promuove la collaborazione.
Alunno/a
Classe a.s.
Periodo
Nel ricercare le informazioni necessarie alla realizzazione del progetto...
Ho avuto difficoltà a capire quali informazioni dovevo cercare e dove trovarle.
Mi hanno aiutato a cercare le informazioni, ma poi le ho sapute organizzare.
Nello svolgere l’indagine sulla frutta preferita...
Ho avuto difficoltà a capire come svolgere l’indagine e non ricordavo come si disegna un istogramma.
Ho saputo svolgere l’indagine, ma ho avuto bisogno di aiuto per rappresentare i dati con l’istogramma.
Nel calcolare il costo della frutta necessaria...
Mi sono fatto/a aiutare. Ho saputo calcolare solo il costo di alcuni frutti.
Nel realizzare il quadro...
Ho avuto difficoltà nel capire come realizzarlo e nel mettermi d’accordo con i compagni/con le compagne.
Ho ricercato le informazioni e le ho organizzate.
Ho svolto l’indagine e ho rappresentato i dati con l’istogramma.
Ho ricercato senza difficoltà le informazioni e le ho organizzate. Sono stato/a d’aiuto ai compagni/alle compagne del mio gruppo.
Ho svolto l’indagine, ho rappresentato i dati con l’istogramma e ho saputo ricavare informazioni dal grafico.
Ho saputo calcolare il costo di tutta la frutta necessaria.
Ho capito come si doveva realizzare, ma ho avuto difficoltà a mettermi d’accordo con i miei compagni/con le mie compagne di gruppo. Ho collaborato con i compagni/le compagne per la realizzazione del quadro facendo quanto mi hanno detto.
Ho calcolato la spesa totale. Sono stato/a di aiuto ai compagni/alle compagne del mio gruppo.
Ho collaborato con i compagni/le compagne alla realizzazione proponendo idee ed organizzando il lavoro.
a cura di Piercarla Colombo e Luisella Meda
L’iter legislativo relativo alla pratica valutativa, che ha accompagnato il testo delle Indicazioni Nazionali del 2012, va nella direzione di una valutazione PER l’apprendimento (e non DELL’apprendimento).
• Decreto n. 122 del 2009 : provvede al coordinamento delle disposizioni concernenti la valutazione degli alunni e delle alunne, tenendo conto anche dei disturbi specifici di apprendimento e delle disabilità ed enuclea le modalità applicative.
• Decreto legislativo n. 62/2017 : fornisce norme in materia di valutazione e di certificazione delle competenze, confermando il principio che la valutazione formativa va nella direzione della documentazione dello sviluppo dell’identità personale di ogni studente e studentessa, e promuove l’autovalutazione di ciascuno in relazione alle acquisizioni di conoscenze, abilità e competenze, anche al fine di favorire l’orientamento per la prosecuzione degli studi. “La valutazione ha per oggetto il processo formativo e i risultati di apprendimento di alunni e alunne […] ha finalità formativa ed educativa e concorre al miglioramento degli apprendimenti e al successo formativo degli stessi, documenta lo sviluppo dell’identità personale e promuove l’autovalutazione di ciascuno in relazione all’acquisizione di conoscenze, abilità e competenze”.
• DM n. 742/2017 : introduce i modelli nazionali di certificazione nazionale delle competenze al termine della scuola primaria e del primo ciclo di istruzione.
• Nota n. 1865 del 10 ottobre 2017 : fornisce indicazioni in merito a valutazione, certificazione delle competenze ed Esame di Stato nelle scuole del primo ciclo di istruzione.
• Ordinanza n. 172 del 4 dicembre 2020 : decreta che la valutazione periodica e finale degli apprendimenti delle alunne e degli alunni delle classi della scuola primaria sia espressa attraverso un giudizio descrittivo in coerenza con la certificazione delle competenze. “A decorrere dall’anno scolastico 2020/2021 la valutazione periodica e finale degli apprendimenti è espressa, per ciascuna delle discipline di studio previste dalle Indicazione nazionali, ivi compreso l’insegnamento trasversale di Educazione Civica […], attraverso un giudizio descrittivo riportato nel documento di valutazione , nella prospettiva formativa della valutazione e della valorizzazione del miglioramento degli apprendimenti. […] I giudizi descrittivi sono riferiti agli obiettivi oggetto di valutazione definiti nel curricolo di Istituto . […] Nel curricolo di Istituto sono individuati per ciascun anno di corso e per ogni disciplina […], riferiti alle Indicazioni Nazionali, con particolare attenzione agli obiettivi disciplinari e ai traguardi di sviluppo delle competenze”.
• Linee guida. La formulazione dei giudizi descrittivi nella valutazione periodica e finale della scuola primaria : documento in cui si precisa che “L’ottica è quella della valutazione per l’apprendimento , modificando le attività in funzione di ciò che è stato osservato e a partire da ciò che può essere valorizzato”.
Risulta evidente che i suddetti documenti, in modo particolare le Linee guida, “rivoluzionano” l’idea di valutazione praticata da anni, quella con i voti in decimi, tendente a misurare numericamente un apprendimento, senza fornire ad alunni/e, docenti e genitori elementi indispensabili per rappresentare e descrivere la complessità del processo di apprendimento, che va oltre la mera quantificazione dell’esito di una o più prestazioni.
Tali documenti attribuiscono alla valutazione un nuovo ruolo, ponendo l’accento sulla centralità della valutazione formativa per l’apprendimento (e non solo dell’apprendimento), quindi un “dispositivo” che ben si presta a evidenziare gli aspetti processuali messi in atto nell’apprendimento ed è finalizzato a:
• conferire trasparenza ai processi di apprendimento messi in atto dagli alunni e dalle alunne per raccogliere evidenze utili al proprio miglioramento e al proprio successo formativo;
• promuovere negli alunni e nelle alunne azioni di miglioramento, sostenendo i processi di apprendimento di ciascuno/a, spostando l’attenzione ai processi di apprendimento piuttosto che ai prodotti;
• porre al centro il soggetto che apprende in tutte le sue specificità (originalità, autonomia, punti di forza e di debolezza, continuità, canali apprenditivi preferenziali, consapevolezza dei processi mesi in atto…);
• fornire elementi indispensabili agli/alle insegnanti per la riorganizzazione della propria azione didattica per garantire il successo formativo di ciascun alunno/a in termini di apprendimenti autentici e significativi (personalizzazione).
Se ne evince che l’attenzione va prioritariamente spostata sul piano della didattica che viene messa in atto, in quanto si caratterizza come strumento principale attraverso la quale:
• i/le docenti hanno l’effettiva possibilità di “monitorare” in itinere i processi di apprendimento messi in atto da ciascun alunno/a (vedi Per una didattica inclusiva pag. 51 e Il laboratorio e la didattica laboratoriale pag. 58), come specificato nelle Linee guida di accompagnamento all’ordinanza n. 172 del 4 dicembre 2020: “[…] le informazioni rilevate sono utilizzate anche per adattare l’insegnamento ai bisogni educativi concreti degli alunni e ai loro stili di apprendimento […]”;
• gli alunni e le alunne, attraverso specifici e personali feedback forniti via via dagli insegnanti, hanno la possibilità di mettere in atto una sorta di controllo meta-cognitivo (riflessione e analisi critica in itinere e a posteriori del processo messo in atto), in un’ottica autovalutativa, per migliorare il proprio percorso di apprendimento.
Ne consegue che una valutazione autentica, come quella formativa, avendo una finalità educativa e anche certificativa, non si può limitare a controllare, misurare, verificare, classificare gli apprendimenti in base a standard predefiniti di tipo prettamente contenutistico e scolastico, ma deve aiutare a far sì che gli alunni e le alunne maturino un apprendimento, un’educazione, una consapevolezza e una maturazione globale delle proprie competenze per tutta la vita ( lifelong learning ).
Le innovazioni didattiche richiedono di norma di intervenire su tre aspetti che caratterizzano il processo di insegnamento: progettazione , azione didattica e valutazione
Nell’ottica della pratica valutativa in funzione formativa, i tre aspetti sopra elencati costituiscono l’indispensabile triangolazione a processo spiralico, sinergico e dialogante in cui la valutazione si configura come anello di congiunzione e strumento insostituibile per monitorare l’efficacia della propria azione didattica in relazione all’obiettivo o agli obiettivi prioritario/i selezionato/i per la sua/loro significatività, come esplicitato nel testo delle Indicazioni Nazionali per il curricolo, 2012: “Gli obiettivi di apprendimento individuano i campi del sapere, conoscenze e abilità ritenuti indispensabili al fine di raggiungere i traguardi per lo sviluppo delle competenze. Essi sono utilizzati dalle scuole e dai docenti nelle loro attività di progettazione didattica, con attenzione alle condizioni di contesto, didattiche e organizzative, mirando a un insegnamento ricco ed efficace”.
La fase della progettazione didattica prende quindi necessariamente avvio da “che cosa” si intende valutare, individuando pertanto:
• gli obiettivi da verificare (disciplinari e trasversali);
• “come” valutarli (Quali strumenti? Con quale modalità? Quali osservazioni e con quali strumenti? Quando?...);
• con quali modalità/strumenti promuovere il processo autovalutativo di ciascun alunno/a.
Le scelte operate in questa fase determinano le azioni didattiche funzionali a garantire agli alunni e alle alunne un efficace processo di apprendimento, prevedendo la possibile e auspicata alternanza di metodologie attive. L’azione didattica dell’insegnante si configura quindi come lo strumento indispensabile per monitorare in itinere il processo di apprendimento e, di conseguenza, autoregolare le proprie azioni metodologico-didattiche e le proprie scelte di mediazione didattica, privilegiando sempre le metodologie attive. Ne consegue che la fase della mediazione didattica si configura come un processo in continuo divenire e non come successione predefinita a monte di attività da proporre in una successione temporale prestabilita.
Una perplessità che ricorre spesso tra i/le docenti è quella riferita alla somministrazione di prove/schede di verifica in itinere e a come valutarle.
Precisato che verifica e valutazione non sono tra loro sinonimi, ma costituiscono due facce del processo di insegnamento/apprendimento, le prove di verifica di tipo esclusivamente contenutistico hanno senso se utilizzate come strumenti per raccogliere evidenze/informazioni utili ad accertare le conoscenze acquisite e le abilità messe in atto rispetto a uno a più obiettivi opportunamente selezionati in fase di progettazione.
Come precisato nella nota n. 2158 di accompagnamento all’O.M. n. 172, sono da considerarsi come “appunti di viaggio” che, oltre a “ dar conto innanzitutto del progresso negli apprendimenti […] consentono altresì agli insegnanti di rimodulare la propria attività e di progettare momenti di individualizzazione e personalizzazione, che sono strumenti preposti al successo formativo delle classi a loro affidate”.
Per assolvere a tale funzione, è auspicabile che gli strumenti per la verifica siano predisposti differenziandone la tipologia ( prove note e non note ), in base alle informazioni che riteniamo necessario rilevare, e variando la formulazione dei quesiti. In ogni caso, l’esito di tali prove va integrato e messo a confronto con gli elementi raccolti attraverso altre forme e strumenti di rilevazione degli apprendimenti (osservazioni sistematiche in
forma narrativo-descrittiva, trascrizione delle parole degli alunni, checklist, griglie, tabelle, diario di bordo…).
Fermo restando che tali prove, somministrate in itinere per monitorare il “procedere” degli alunni e delle alunne su quanto si sta proponendo, hanno ragione di essere predisposte solo se considerate come uno degli strumenti per conferire alla valutazione il carattere formativo, l’esito non necessita di essere quantificato né con il voto né con punteggi o in percentuali.
In ogni caso, le prove di verifica note non possono essere valutate per livelli (avanzato, intermedio, base, in via di prima acquisizione), che vanno assegnati solo sul documento di valutazione in quanto vene a mancare la possibilità di rilevare la continuità, che con le altre tre dimensioni ( autonomia , tipologia della situazione , risorse mobilitate ) costituisce il quadro delle dimensioni per l’apprendimento
Per una restituzione formativa dell’esito delle prove di verifica (sia note sia non note), è importante fornire all’alunno/a, in forma individuale, il feedback , che altro è dagli appezzamenti positivi o negativi ( Molto bene!, Nemmeno questa volta hai fatto attenzione! ) o da incoraggiamenti generici ( Fai attenzione ai calcoli!, Se la prossima volta farai attenzione, certamente farai meno errori! ) oppure limitandosi a segnalare gli errori e/o mostrare le correzioni apportate.
La funzione formativa del feedback , espresso in forma orale oppure scritta, fa leva sulla motivazione intrinseca , poiché fornisce all’alunno/a informazioni utili per migliorare, in futuro, la propria prestazione. Perché sia efficace, il feedback va utilizzato in modo costante nel tempo , con un linguaggio chiaro e adeguato all’età dell’alunno/a e sempre in riferimento all’obiettivo o agli obiettivi da raggiungere, che vanno esplicitati. Il feedback risulta efficace se:
• fornisce all’alunno/a i punti di forza e quelli di debolezza rispetto all’obiettivo o agli obiettivi riferiti all’attività richiesta, facendogli capire “dove si trova” in quello specifico percorso di apprendimento;
• fornisce suggerimenti puntuali per progredire nel raggiungimento dell’obiettivo o degli obiettivi esplicitato/i.
Nel paragrafo precedente, per quanto riguarda le prove di verifica da assegnare, si è sottolineata l’importanza e la necessità di diversificarle per:
a) tipologia (note e non note) ;
b) differenziazione dei quesiti e delle relative modalità di soluzione.
Per la prima volta, ai fini della valutazione formativa si pone l’accento sulla differente tipologia delle prove per la verifica degli apprendimenti. Non si tratta di una banalità o di un sofismo, in quanto la situazione stessa proposta come attività di verifica costituisce la possibilità di mettere in atto processi molto diversi tra loro anche ai fini della valutazione e dell’autovalutazione.
a) Tipologia delle prove
• Per prove note si intendono tutte quelle situazioni “standard”, riferite alla routine applicativa di conoscenze, concetti, abilità già percorsi in situazioni simili. Si tratta di attività nelle quali gli alunni e le alunne si sono già precedentemente confrontati in forma di esercitazione o “allenamento” e che, pertanto, non consentono loro di esercitare le risorse interne. Si tratta di “compiti routinari”, in cui viene richiesto di replicare conoscenze e/o abilità che implicano una sola risposta esatta con la riproduzione di
procedure e/o la memorizzazione di contenuti e che, pertanto, richiedono un “basso” coinvolgimento cognitivo, metacognitivo, emotivo, motivazionale oltre a ricorrere esclusivamente alle risorse messe a disposizione dall’insegnante (risorse esterne). Il vantaggio nell’utilizzo di tali prove di verifica è quello di rilevare contemporaneamente per tutto il gruppo classe un elevato numero di conoscenze e abilità riferite all’obiettivo o agli obiettivi selezionato/i.
Ciò non significa che le prove note debbano essere bandite, anche perché consentono di verificare un primo livello (livello base) di acquisizione, ma in fase di progettazione è necessario:
– stabilire quando e perché proporle all’interno di un certo percorso di apprendimento, avendo anche l’accortezza di variare le tipologie dei quesiti;
– prevedere l’azione di feedback , preferibilmente in forma scritta, predisponendo quindi un modello da utilizzare ad hoc
Poiché le prove note riguardano compiti/attività routinari, in cui gli alunni e le alunne sono chiamati a mettere in atto processi passivi ( memorizzazione , applicazione , ripetizione ), per poter acquisire informazioni utili alla formulazione del giudizio descrittivo quadrimestrale per scheda di valutazione non è possibile avvalersi unicamente di tali tipologia di verifica.
• Se la valutazione per essere formativa nella descrizione dei livelli deve prevedere anche le dimensioni relative alle risorse e alla continuità , occorre ricorrere giocoforza alle prove non note (vedi esempio di modello per la tabulazione delle informazioni di tipo processuale a pag. 51), in quanto, per la loro complessità e articolazione, consentono agli alunni di mettere in atto processi concettuali
Si tratta di situazioni inedite, quindi mai sperimentate durante il percorso proposto, che, in quanto tali:
– sono aperte a più soluzioni, anche con percorsi risolutivi differenti;
– richiedono la messa in campo di una varietà di abilità e di comportamenti;
– sono caratterizzate da un impegno “alto” a tutti i livelli (cognitivo, metacognitivo, emotivo, motivazionale);
– implicano l’impegno di processi complessi come il problem-solving;
– coinvolgono sia il corpo che la mente e più sensi;
– implicano l’utilizzo di una pluralità di codici (verbali, iconici, musicali…), di strumenti e di materiali diversi;
– sono caratterizzate da un coinvolgimento attivo degli alunni e delle alunne (che possono anche lavorare in piccolo gruppo).
In ogni caso, è consigliabile ricorrere a entrambe le tipologie di prova di verifica (note e non note), bilanciandole a seconda dell’obiettivo o degli obiettivi selezionato/i e del percorso proposto. In tal modo, si avrà la possibilità di raccogliere un maggior numero di informazioni ed evidenze nel momento della descrizione dei livelli da inserire nel documento di valutazione. È altresì auspicabile un graduale sbilanciamento verso le prove non note in quanto offrono la possibilità di una valutazione più autentica.
b) Differenziazione dei quesiti
Nelle prove note è auspicabile la diversificazione della tipologia dei quesiti, inserendo in una stessa prova domande a risposta chiusa e a risposta aperta.
Se le azioni di feedback costellano in modo continuativo la restituzione dell’esito delle varie prove di verifica, con domande orientate a far riflettere l’alunno/a sulla natura dei propri errori, sulle difficoltà incontrate e sulle modalità/strategie da mettere in atto per superarle, già creiamo le condizioni necessarie a favorire la capacità di autovalutarsi per autoregolarsi . Pertanto l’autoregolazione, cioè la capacità di riconoscere e capire le proprie difficoltà ma anche le proprie potenzialità, costituisce il dispositivo che orienta e supporta i bambini e le bambine nel processo per “imparare a imparare”.
Sono però le situazioni di apprendimento complesso (compiti non noti, compiti di realtà/ autentici…) a creare le condizioni maggiormente favorevoli a sviluppare la capacità di autoregolazione. Infatti essendo situazioni aperte a più soluzioni, il bambino e la bambina si trovano nelle condizioni di mettere in atto strategie diverse, provando e riprovando (didattica dell’errore) fino a pervenire a quella maggiormente efficace.
Per rafforzare nei bambini e nelle bambine l’idea che l’autovalutazione e la conseguente autoregolazione sono dispositivi di cui possono (e devono) disporre per migliorare il proprio successo formativo, è necessario, in fase di progettazione didattica, individuare i momenti e gli strumenti maggiormente idonei per favorire tali processi. Molteplici sono gli strumenti aperti o chiusi che si possono costruire e utilizzare per promuovere il processo metacognitivo in fase autovalutativa per accompagnare ciascun alunno/a a “fare il punto della situazione” rispetto al proprio processo di apprendimento. Qui si è fatta la scelta di prendere in considerazione tre tipi di strumenti, ciascuno con una sua propria specificità:
a) la rubrica per l’autovalutazione ;
b) l’autobiografia cognitiva ;
c) la checklist
a) La rubrica per l’autovalutazione – Uno degli strumenti che può favorire il processo di autovalutazione di atteggiamenti e strategie messi in atto durante un determinato percorso di apprendimento è la rubrica per l’autovalutazione , calibrata nella declinazione degli aspetti processuali e cognitivi su quattro livelli di prestazione (vedi pag. 36).
b) L’autobiografia cognitiva – Un ulteriore strumento che facilita e orienta il processo finalizzato all’autovalutazione è costituito dall’autobiografia cognitiva (vedi esempi di domande a pag. 50), particolarmente adatta a prove non note, con la quale, attraverso una serie di domande-stimolo aperte, opportunamente calibrate rispetto alla prova stessa e debitamente argomentate, si accompagna ciascun alunno/a a soffermarsi maggiormente sugli aspetti:
• cognitivi (strategie messe in atto, soluzione/i più efficaci, difficoltà incontrate e come sono state superate, ipotesi/propositi di miglioramento…);
• emotivi (livello di soddisfazione, impressioni su come è stata portata a termine la prova…);
• relazionali (ruolo e collaborazione nel gruppo di lavoro).
c) La checklist è un ulteriore strumento che, a differenza della rubrica per l’autovalutazione e dell’autobiografia cognitiva, consente all’alunno/a un’ autovalutazione in momenti diversi di una stessa prova, per poi comparare le risposte date:
• in fase preventiva, prima di somministrare la prova: l’alunno/a è chiamato/a a fare ipotesi circa le sue abilità nell’affrontare i singoli contenuti previsti;
• a prova conclusa: l’alunno/a è chiamato/a a indicare come pensa di aver risolto ogni tipo di item;
• dopo la restituzione della prova corretta (valutazione dell’insegnante tramite feedback ): l’alunno/a registra l’esito relativo a ciascun contenuto di apprendimento. A seguito della comparazione delle tre registrazioni, è consigliabile richiedere, all’alunno/a di esprimere una propria valutazione qualitativa rispetto alle proprie previsioni e all’esito della prova corretta.
A partire dal mese di marzo 2020, con i lockdown e la conseguente chiusura totale delle scuole a causa della pandemia dovuta al Coronavirus, la scuola ha dovuto rivedere, per non dire rivoluzionare, il modo di “fare scuola”.
Alunni/e, insegnanti e famiglie si sono ritrovati a interagire dietro a schermi, lontani, con una socialità quasi annullata, a utilizzare strumenti “nuovi” e a sviluppare in tempi brevissimi abilità, conoscenze e competenze rispetto a un modo di fare scuola che fino ad allora non era mai stato contemplato, reinventandosi completamente, dalla gestione delle lezioni, ai rapporti sociali a distanza fino ai metodi di valutazione.
Rivedere e ristrutturare da zero il “modo di fare scuola”, non è stato semplice, specie per quel che ha riguardato i cambiamenti da mettere in atto nella divulgazione delle informazioni e nella valutazione del lavoro svolto dagli alunni e dalle alunne.
Fin dall’inizio della pandemia, i/le docenti hanno assicurato le prestazioni didattiche nelle modalità a distanza, rimodulando però gli obiettivi di apprendimento, i mezzi, gli strumenti, le metodologie e riprogettando le attività da proporre attraverso l’utilizzo di piattaforme digitali. Si era pertanto reso necessario integrare le modalità di valutazione anche in base a quanto suggerito dalla nota 388 del 17 marzo 2020, dove si recita che la valutazione degli apprendimenti deve essere elemento indispensabile di verifica dell’attività svolta, di restituzione, di chiarimento e tesa alla promozione e alla valorizzazione delle capacità e delle caratteristiche individuali dello studente. Doveva inoltre essere caratterizzata dai principi di tempestività e trasparenza.
Le forme, le metodologie e gli strumenti per procedere alla valutazione in itinere degli apprendimenti, propedeutica alla valutazione finale, rientrano nella competenza di ogni docente e hanno come riferimento i criteri approvati dai Collegi Docenti. Con l’art.3 dell’Ordinanza Ministeriale n. 11 del 16.05.2020, nella quale si afferma che i docenti contitolari della classe procedono alla valutazione sulla base dell’attività didattica effettivamente svolta in presenza e a distanza, gli alunni e le alunne venivano ammessi alla classe successiva anche in presenza di voti inferiori ai sei decimi in una o più discipline. Per chi era stato ammesso alla classe successiva in presenza di votazioni inferiori ai sei decimi o comunque di livelli di apprendimento non adeguatamente consolidati, gli/le insegnanti dovevano predisporre un Piano di Apprendimento Individualizzato (P.A.I.), in cui erano indicati, per ciascuna disciplina gli obiettivi di apprendimento da conseguire o da consolidare nonché le specifiche strategie per il raggiungimento degli stessi.
Titolo del compito:
Data del compito:
Data della mia valutazione del compito:
• Ti è piaciuto svolgere questo compito? Perché?
• Quale fase/attività di questo compito hai preferito? Perché?
• Quale fase/attività di questo compito hai trovato più noiosa? Perché?
• Quale fase/attività di questo compito è stata più semplice per te? Perché?
• Quale fase/attività di questo compito è stata più difficile per te? Perché?
• In quale momento del lavoro o in quale attività di questo compito ti sei sentito/a più tranquillo/a? Perché?
• In quale momento del lavoro o in quale attività di questo compito ti sei sentito/a meno tranquillo/a? Perché?
• Sei soddisfatto/a di come hai lavorato? Perché?
• Sei soddisfatto/a del risultato ottenuto? Perché?
• Che cosa sapevi già fare?
• Che cosa hai imparato a fare?
• Ti è piaciuto lavorare con i compagni del tuo gruppo? Perché?
• Hai saputo collaborare con i compagni del tuo gruppo? Se sì, in che cosa e in che modo?
• Come valuti il lavoro svolto? Perché?
• Quali modifiche proporresti nel modo in cui avete lavorato in gruppo? Perché?
Possibile modello per la tabulazione delle informazioni di tipo processuale nelle prove
Alunno/a
Disciplina Data
Obiettivo/i d’apprendimento ......................................................................................…………
Breve descrizione della prova ( tipologia dei quesiti/compito di realtà/… , orale/scritta, tempo a disposizione per l’esecuzione, individuale/in piccolo gruppo… )
DIMENSIONI
SITUAZIONE RISORSE AUTONOMIA 1 CONTINUITÀ 4
nota interne completa presente
non nota esterne non consolidata 2 da sollecitare 3 da supportare in modo continuativo
saltuaria 5 assente
EVIDENZE OSSERVATE
1 In riferimento a strategie e/o comportamenti/atteggiamenti specifici osservabili messi in atto nell’esecuzione della prova, cioè in relazione al conseguimento dell’obiettivo o degli obiettivi, ma anche riferiti al ruolo all’interno del piccolo gruppo, ai punti di forza e a quelli di debolezza.
2 È da considerarsi non consolidata se, durante la prova, di tanto in tanto richiede l’approvazione o conferme dell’insegnante o, se sta lavorando in gruppo, dei compagni o delle compagne.
3 Riferita alla necessità dell’alunno/a di essere incoraggiato/a.
4 Da intendersi in relazione a una abilità e/o un comportamento positivi già manifestati in precedenti prove, alla presenza/assenza di compiere transfer tra un dominio del sapere e l’altro, di tener conto di propri precedenti errori per non ripeterli…
5 È da ritenersi “saltuaria” se una stessa abilità richiesta nel tempo con prove differenti risulta circoscritta a una sola prova.
Uno degli elementi di valore della scuola italiana consiste sicuramente nell’impegno profuso per favorire la rimozione e il superamento di ogni ostacolo alla promozione della persona e per consentire a tutti e a ognuno di trovare gli strumenti per esprimere al meglio le proprie potenzialità.
Fin dal 1977, la scuola italiana si è dotata di strumenti normativi, organizzativi e professionali realizzando un modello di inclusione che continuamente si arricchisce grazie all’eterogeneità delle classi.
Per la valorizzazione degli alunni e delle alunne Diversamente abili e per il riconoscimento degli alunni e delle alunne con DSA (Disturbi Specifici di Apprendimento) e con BES (Bisogni Educativi Speciali), nel corso degli anni si è cercato di delineare un piano complesso che di fatto vede la valorizzazione dei diversi modi di affrontare i processi di apprendimento.
Sicuramente per la scuola questa complessità comporta un importante impegno in termini di tempo e di risorse; ma consente anche un arricchimento, personale e professionale, altrettanto significativo.
Oltre a ciò che la normativa espressamente richiede, come i Piani Educativi Personalizzati (PEI) o i Piani Didattici Personalizzati (PDP), va sottolineato come sia necessario che il team docente si adoperi congiuntamente per adottare strategie di insegnamento che contemplino l’arco degli stili cognitivi.
Accanto agli strumenti compensativi o dispensativi, previsti dall’apposita normativa, sarebbe opportuno fare ricorso a metodologie attive che affianchino le più consuete, predisporre o adottare materiali facilitati e/o semplificati , fornire mappe di sintesi, usare strumenti digitali ...
Va considerato, inoltre, che la presenza di disturbi specifici ha spesso delle ricadute importanti sul piano emotivo. Le aspettative della famiglia, i risultati delle prestazioni e la loro corrispondenza con il livello di impegno profuso, l’idea di sé e del proprio processo di apprendimento sono fattori che incidono pesantemente e che possono creare demotivazione.
Ecco perché l’attenzione dell’insegnante dovrebbe andare oltre il mero livello degli apprendimenti.
Tutto questo si traduce in una costante autoformazione dell’insegnante che, grazie alle sollecitazioni di gruppi classi complessi e variegati, ha la necessità di dotarsi di strumenti e di mediatori didattici sempre più efficaci.
Leggendo con attenzione il Sussidario Nel cuore dei saperi possiamo cogliere come siano suggerite e/o dichiarate alcune metodologie attive che ben si prestano a supportare una didattica inclusiva
Le domande stimolo, il riconoscimento e la valorizzazione delle preconoscenze degli alunni e delle alunne, il richiamo al presente e all’esperienza personale, sono solo alcune delle proposte che, mettendo al centro il bambino e la bambina, accrescono la loro autostima,
li fanno sentire promotori del proprio processo di apprendimento, sottolineano il rispetto e la considerazione per le loro opinioni e il loro vissuto.
LE METODOLOGIE ATTIVE • Lavorare in cerchio
Nel Sussidiario gli alunni e le alunne sono invitati a mettere in comune le proprie esperienze e idee ingenue. Nelle fasi iniziali e introduttive di una Unità, può essere utile fare ricorso al Circle time in modo da esplorare la situazione-problema in tutte le sue sfaccettature e delinearla. Obiettivo del Circle Time è quello di facilitare la comunicazione tra pari, approfondendo la conoscenza reciproca, creando integrazione, e di valorizzare le competenze dei singoli e del gruppo. È così chiamato perché discenti e docente si siedono in cerchio, in situazione di parità e guardandosi in faccia. Affinché sia davvero efficace, richiede una progettazione attenta da parte del/della docente.
In altre pagine, il Sussidiario Nel cuore dei saperi invita al lavoro cooperativo e di gruppo. Lavorare alla pari con i compagni e le compagne e in un contesto ridotto consente a tutti i componenti del gruppo di esprimersi liberamente, di proporsi con le proprie risorse e di fare affidamento sugli altri, liberandosi da tensioni individualistiche, sperimentando il valore della fiducia verso l’altro.
Il gruppo, inoltre, sollecita nuove idee e soluzioni impreviste, grazie allo scambio e all’interazione fra i diversi componenti, e permette di riconoscere l’altro come competente.
LE METODOLOGIE ATTIVE • Lavorare in modo cooperativo
L’ apprendimento cooperativo è un metodo che coinvolge gli studenti e le studentesse nel lavoro di gruppo per raggiungere un fine comune. A differenziarlo da un lavoro di gruppo sono le caratteristiche seguenti:
1. interdipendenza positiva • ogni componente è consapevole e responsabile del proprio personale apprendimento ma anche dell’apprendimento degli altri membri del gruppo, su cui fare affidamento per raggiungere il fine condiviso;
2. responsabilità individuale • ogni componente deve rendere conto sia della propria parte di lavoro sia di quanto ha appreso;
3. interazione faccia a faccia • il lavoro dei componenti deve essere interattivo;
4. uso delle abilità • i/le componenti vanno incoraggiati/e a esprimere le proprie capacità e a misurarsi in ruoli e compiti diversi;
5. valutazione del lavoro : il feedback deve essere continuo, in modo da individuare i possibili cambiamenti utili per procedere in modo efficace ed efficiente.
La possibilità di usare strumenti digitali offre un ulteriore canale di facilitazione e mediazione nel processo di apprendimento, prima di tutto perché l’immagine cattura immediatamente l’attenzione degli alunni e delle alunne, che vivono immersi in un mondo prevalentemente iconico. Inoltre, consente all’insegnante di focalizzare l’attenzione su alcuni aspetti del Sussidiario ingrandendo le immagini, zoomando sui particolari, evidenziando parole-chiave, condividendo operazioni cognitive ecc.
Il libro di testo Nel cuore dei saperi è scaricabile e questo, oltre a consentire il lavoro con tutta la classe tramite l’uso della LIM o del videoproiettore, permette l’adozione di un’altra metodologia attiva che sta diventando sempre più diffusa nelle nostre classi.
LE METODOLOGIE ATTIVE
• Lavorare capovolti
Per la Flipped Classroom , o classe capovolta, la lezione diventa compito a casa mentre il tempo-classe viene usato per attività collaborative e laboratoriali, scambio di esperienze, spazio di dibattito. Richiede una libreria di contenuti, corredata da video online, opportunatamente scelti dal docente, a cui l’alunno e l’alunna possono accedere a casa con tempi propri.
Altro punto fondamentale per una scuola inclusiva è il ricorso ad attività di tipo trasversale . Favorire la capacità di cogliere le interrelazioni fra le discipline permette il superamento di una visione settoriale dell’insegnamento; inoltre, consente agli alunni e alle alunne di mettere in gioco anche altre abilità e competenze, così da vivere con minor disagio eventuali difficoltà nell’una o nell’altra disciplina.
La trasversalità è anche un modo tangibile per far cogliere come la cultura sia debitrice di tanti e vari apporti, non solo disciplinari, e come non ne esista una soltanto. Il Sussidiario Nel cuore dei saperi presenta, infatti, spunti volti a superare una visione eurocentrica della cultura presentando, per esempio, le civiltà di Paesi Altri, offrendo un input per invitare gli alunni e le alunne a cercare informazioni al fine di costruire e approfondire i quadri di civiltà.
LE METODOLOGIE ATTIVE • Lavorare in rete
Una metodologia strategica è l’interdisciplinarità . Grazie a essa si possono mettere in evidenza tutte le interrelazioni fra gli elementi che compongono una situazione-problema, favorendone la comprensione ampia e articolata.
Il Sussidiario Nel cuore dei saperi , aprendo inoltre a percorsi e riflessioni ampie (STEM, Agenda 2030, Educazione Civica), sollecita riflessioni su temi oggi assolutamente attuali come il contrasto verso ogni forma di disuguaglianza e di prevaricazione, la necessaria adozione di comportamenti improntati al rispetto, con l’intento di far riflettere sul valore della persona e dell’ambiente.
Infine il Sussidiario Nel cuore dei saperi invita all’adozione di una didattica laboratoriale di cui si parlerà diffusamente nei prossimi capitoli. In un processo di apprendimento è però necessario prevedere anche fasi di lavoro individuale , consentendo così all’alunno e all’alunna di misurarsi con una sfida cognitiva in cui mettere in campo le proprie risorse.
Queste fasi vanno però ben progettate dall’insegnante per non mettere in difficoltà l’alunno o l’alunna, proponendo un lavoro troppo al di sopra o al di sotto delle sue reali possibilità e provocando demotivazione.
Attraverso il metodo euristico si può condurre gradualmente l’alunno o l’alunna a scoprire da solo/a ciò che si desidera conosca, mediante un costante e attivo coinvolgimento nei percorsi di ricerca e di interpretazione. Questo permette all’alunno/a di padroneggiare le conoscenze e le abilità acquisite, mettendole a disposizione del gruppo di lavoro nelle fasi di apprendimento successivo.
Nel Sussidiario Nel cuore dei saperi è posta molta attenzione nella predisposizione di queste fasi.
L’utilizzo di parole-chiave, di immagini, di schemi e tabelle funge da gancio per richiamare alla memoria le informazioni, i processi, i termini fondamentali e specifici degli argomenti via via proposti.
Le esercitazioni sono numerose e graduali, nel Quaderno presentano livelli diversi di difficoltà , richiedendo agli alunni e alle alunne di interagire tra i testi in un continuo rimando concettuale e operativo.
Le schede operative propongono attività talvolta finalizzate a sollecitare abilità, altre volte a puntualizzare o ad approfondire conoscenze, così da arrivare alla graduale mobilizzazione di competenze.
A queste si aggiungono anche le schede proposte all’interno della Guida che, oltre a presentare esercitazioni semplificate , prevedono anche quelle per il consolidamento , al fine di contemplare la gamma di risorse e di potenzialità degli alunni e delle alunne.
Considerando che la verifica resta sempre una fase delicata, appare utile sostenere l’alunno/a nella decodifica delle consegne, nell’abituarlo/a a rintracciare nel testo di studio la pagine dove reperire le risposte, nella pratica della revisione condivisa così da riprendere e chiarire laddove si sono evidenziate delle criticità.

Sul sito del Gruppo, la sezione “ altuofianco sostegno ” offre una vasta gamma di strumenti, materiali e risorse utili per supportare l’insegnamento e l’apprendimento degli studenti con bisogni educativi speciali
Per la Scuola Primaria, il materiale è creato dall’Associazione IL MONDO DI DIEGOSAURO , che si occupa di creare materiale didattico adatto a disabilità complesse

Il progetto è nato con l’idea di adeguare le unità di apprendimento già presenti nei libri di testo per renderle adatte veramente a tutti, anche attraverso l’uso della C.A.A.

• È la prima volta che un gruppo di specialisti del settore collabora attivamente con un editore di scolastica. Tutto il materiale è creato e visionato da figure professionali quali: logopedisti, neuropsicomotricisti, psicologi.
• L’associazione offre supporto e assistenza durante tutto l’anno scolastico anche con percorsi formativi (online e in presenza).
• Il materiale è pensato per essere utilizzato anche dal gruppo classe : tutte le schede o attività didattiche usano infatti strategie di comunicazione alternativa aumentativa, in modo da semplificare l’apprendimento degli alunni e il lavoro agli insegnanti.

• Il materiale è di semplice utilizzo ed è di valido supporto anche per gli alunni stranieri.
• Il sito è in costante aggiornamento e settimanalmente viene caricato materiale nuovo in aggiunta.
• Letture semplificate con supporto immagini e, su richiesta dell’insegnante, possibile traduzione in pittogrammi Arasaac ( autorizzazione speciale ricevuta dall’Associazione ).
• Alfabetieri individuali riadattati; passaporto comunicativo.
• Discipline fornite in diversi formati già strutturati: powerpoint, slide in pdf da inserire nel portalistino, video animato per LIM, flashcard di ripasso per argomento.
• Verifiche facilitate.
• Volumi extra, scaricabili in pdf: veri e propri libri per la formazione degli insegnati: tombole sillabiche, volume di preparazione al grafismo.
• Agende visive, token economy, task analysis.
• Attività extra gioco, narrative in pittogrammi, storie sociali e… molto altro ancora!



a cura di Alfia Lucia Fazzino e Paola Hippoliti
In una società così complessa come quella di oggi, con la velocità del cambiamento, la molteplicità degli stimoli che i bambini e le bambine ricevono e le numerose opportunità alle quali hanno più facilmente accesso, la scuola sta vivendo un profondo cambiamento nella definizione delle proprie finalità e dei modi di operare.
Diversamente dal passato, compito della scuola di oggi non è più quello di permettere l’accesso all’informazione che, al contrario, è ormai facilmente raggiungibile da tutti, quanto piuttosto sviluppare quelle competenze e quelle capacità cognitive e sociali trasversali che operano nella vita di tutti i giorni e che consentano al bambino e alla bambina di misurarsi con la realtà in modo concreto e attivo, dandole senso e significato.
Questi profondi cambiamenti sono stati ben interpretati e rielaborati nelle Indicazioni Nazionali che sottolineano il nuovo ruolo formativo della scuola e fanno esplicito riferimento ad:
“ attività didattiche in forma di laboratorio per favorire l’operatività e allo stesso tempo per favorire il dialogo e la riflessione su quello che si fa. Il laboratorio, se ben organizzato, è la modalità di lavoro che meglio incoraggia la ricerca e la progettualità, coinvolge gli alunni nel pensare, realizzare, valutare attività vissute in modo condiviso e partecipato con gli altri”.
Nelle Indicazioni Nazionali , il laboratorio viene presentato come “elemento fondamentale per lo sviluppo delle competenze necessarie alla formazione culturale delle persone e della comunità”. Le competenze si costruiscono sulla base di conoscenze e di abilità e si esplicano sulla base di comportamenti; si tratta di disposizioni a saper scegliere, utilizzare e padroneggiare conoscenze e abilità idonee a risolvere un problema dato.
La didattica laboratoriale da alcuni anni è al centro di profonde riflessioni teoriche, volte alla ricerca di metodologie capaci di produrre modifiche significative ai risultati dei processi di insegnamento/apprendimento.
Nonostante se ne discuta soprattutto da quando sono entrate in vigore le Indicazioni Nazionali , è una metodologia che ha origini lontane e affonda le sue radici nelle riflessioni teoriche di importanti pedagogisti del passato, come J. Dewey che sottolinea la stretta relazione tra apprendere e fare, J.B. Bruner che evidenzia lo stretto legame esistente tra riflessione, linguaggio e azione, e come F. Fabbroni che vede nel laboratorio il luogo privilegiato per promuovere l’osservazione, la scoperta, la rielaborazione e la ri-costruzione delle conoscenze da parte dell’allievo e dell’allieva.
Questa metodologia è considerata una pratica di insegnamento che può consentire il superamento di quelle pratiche didattiche tradizionali dominate ancora dall’idea della separazione fra i momenti di costruzione della conoscenza da quelli di utilizzo, che si possa proporre un percorso metodologico unico adeguato indifferentemente a tutti gli studenti e le studentesse, nonostante le diversità di stili cognitivi, personalità e contesti culturali di
provenienza, dominate ancora dall’idea che la teoria abbia più valore della pratica e che conta quanto è stato fatto piuttosto che come è stato appreso.
Nella società di oggi, queste pratiche si sono dimostrate inadeguate a rispondere ai bisogni formativi di alunni/e, poiché non favoriscono lo sviluppo di quelle competenze necessarie a capire come e quando utilizzare il bagaglio di conoscenze appreso.
È stato rilevato, infatti, che gli alunni e le alunne del nostro tempo non sanno effettuare transfert e avvalersi delle conoscenze apprese al di fuori dell’aula scolastica: in contesti meno strutturati e appositamente predisposti, dimostrano di non saper riconoscere quali siano le conoscenze pertinenti e come utilizzarle in modo efficace.
“ Bisogna interessare l’allievo, stimolarlo alla ricerca e dargli di continuo il sentimento e l’illusione che sia lui che scopre ciò che gli si insegna. Fortifica il suo spirito di iniziativa e si abitua alla ricerca […] E se l’allievo è stato condotto all’acquisto della verità in modo da sembrargli che essa sia stata scoperta da lui, saprà più facilmente ritrovarla da sé nei casi ove l’abbia dimenticata […] In tal modo i giovinetti, mentre elaborano la loro cultura, elaborano la loro mente; l’insegnamento così diviene a un tempo informativo e formativo ”.
(Giovanni Antonio Colozza)

Nella didattica laboratoriale per laboratorio non si intende uno spazio fisico, quanto piuttosto un contesto di apprendimento intenzionalmente pensato dai/dalle docenti nel quale l’allievo e l’allieva diventano protagonisti del proprio processo di apprendimento grazie all’interazione con situazioni predisposte, spazi organizzati, materiali e strumenti appositamente strutturati e all’interno di un contesto cooperativo dove adulti e pari interagiscono al fine di costruire un sapere condiviso.
■ Il laboratorio è inteso come pratica del fare, quindi, dove l’allievo/a procede secondo la metodologia della ricerca in contesti problematici per lui/lei significativi, in quanto vicini al proprio vissuto. Non più passivi ricettori di un sapere elaborato dall’insegnante, gli allievi e le allieve nell’agire operativamente si confrontano concettualmente con la complessità dei saperi, si attivano nella progettazione, nella sperimentazione, nella ricerca di stili e modi di apprendimento, nella costruzione e rielaborazione del proprio sapere.
■ Il laboratorio è un contesto sociale poiché il processo di apprendimento si realizza all’interno di un confronto fra pari, mediante il lavoro a coppie o in gruppi, tramite la condivisione e la costruzione collettiva di un sapere condiviso che implicano l’ascolto reciproco e la partecipazione di tutti, ognuno secondo le proprie competenze e caratteristiche.
■ Il laboratorio è un contesto inclusivo , in quanto l’insegnante attiva forme molteplici di intelligenza e promuove processi cognitivi che coinvolgono ogni allievo/a contemporaneamente su più livelli. Questo permette di attivare in ciascuno/a le proprie intelligenze, di adeguare l’esperienza cognitiva al livello di maturazione e di conoscenza di ciascuno/a, consentendo a tutti/e di esprimere le proprie potenzialità e di sviluppare nuove competenze.
■ Il laboratorio non è un luogo specifico . La parola “laboratorio” fa pensare a uno spazio appositamente attrezzato con strumentazioni particolari dove realizzare esperimenti o produrre qualcosa. In realtà, essendo una metodologia, si può realizzare nei più svariati contesti fisici: all’interno della scuola, nella propria aula, in cortile, in palestra, nella biblioteca, ma anche all’esterno della scuola in un luogo specifico della città (un parco, un museo, un sito).
Nella didattica laboratoriale, l’azione educativa stravolge la propria prospettiva, concentrando la sua azione sui “processi del far apprendere e del riflettere sul fare” piuttosto che sui contenuti da insegnare. Cambia così il ruolo dell’insegnante che, da attore principale dell’azione educativa, diventa prima sceneggiatore e poi regista. Da semplice esecutore di “un programma da svolgere”, l’insegnante diventa ricercatore e costruttore di contesti di apprendimento che, partendo dai bisogni e dagli interessi degli allievi e delle allieve e manipolando gli oggetti della conoscenza, li/le stimoli a procedere in modo autonomo nella costruzione del proprio sapere.
Sulla base delle Indicazioni Nazionali , delle proprie competenze e della conoscenza epistemologica della disciplina, il/la docente sceglie gli aspetti fondanti del sapere intorno ai quali gli allievi e le allieve possano costruire le proprie rappresentazioni della realtà e progetta percorsi didattici adatti alle loro caratteristiche cognitive, diversificando materiali, strumenti e metodologie a seconda delle necessità.
La pratica del laboratorio rende indispensabile la particolare cura nella progettazione dell’intero percorso didattico e richiede attenzione a una serie di azioni che lo realizzano nella sua complessità.
Nella stesura del percorso laboratoriale, il/la docente:
• rivisita i saperi disciplinari per individuare il nodo concettuale da sviluppare;
• individua le conoscenze disciplinari insite nel concetto scelto, dei concetti che sottostanno a esso, di quelli per i quali esso è prerequisito, dei suoi possibili e ulteriori sviluppi;
• individua la successione con la quale procedere nello sviluppo dei sottoconcetti e dei relativi obiettivi di apprendimento ( Prima lavoro su…, poi su…, infine… );
• partendo dai bisogni e dagli interessi degli allievi e delle allieve, predispone situazioni motivanti individuando attività operative “aperte”, rimodellabili o riproponibili a seconda del contesto e dei feedback ricevuti dagli allievi/dalle allieve;
• sceglie i mediatori didattici con i quali e/o tramite i quali operare;
• organizza gli spazi per favorire attività di confronto e di scambio fra pari.
Una volta definito il percorso di apprendimento, l’insegnante predispone l’attività da realizzare in classe, che si può sviluppare secondo le seguenti fasi.
1. Attivazione mediante situazione-stimolo, cioè domande, situazione-problema, manipolazione di oggetti o materiali, esplorazione di parole-chiave, gioco, immagini.
2. Esperienze di tipo manipolativo con l’“oggetto” della riflessione, per promuovere l’esplorazione dell’oggetto stesso mediante un approccio globale e cominciare a osservarlo e conoscerlo. È importante sottolineare che per “oggetto” di riflessione non intendiamo necessariamente un oggetto materiale, ma anche entità astratte che comunque garantiscano esperienze cognitive significative e vicine agli allievi e alle allieve.
3. Ritornare su quanto fatto mediante una riflessione individuale, in coppia o in piccoli gruppi, mediante domande guida per promuovere un’ osservazione più attenta e analitica dell’“oggetto” di riflessione.
4. Condivisione collettiva delle riflessioni e produzioni per giungere a sintesi ed esplicitare con linguaggio condiviso i concetti scoperti.
Durante l’attività laboratoriale, il ruolo del/della docente non è più quello di dispensatore di saperi e di risposte, quanto quello di attivatore di quei processi che consentono di sviluppare competenze.
Durante l’attività di tipo laboratoriale, il/la docente:
• pone problemi;
• fa domande per stimolare a osservare, analizzare, fare collegamenti, costruire schemi interpretativi;
• chiede di motivare le proprie proposte, le riflessioni e le scelte;
• invita a esporre e a sintetizzare riflessioni e conclusioni;
• sollecita a riflettere sul proprio modo di progettare e di procedere;
• guida a riflettere sui processi attivati;
• invita ad assumersi la responsabilità dei propri apprendimenti;
• predispone contesti collaborativi di lavoro.
All’interno del laboratorio, cambia anche il ruolo dell’alunno/a che da spettatore passivo e ricettivo di conoscenze diventa attivo costruttore del proprio processo di apprendimento. All’interno di un contesto motivante, perché sollecitato dalla ricerca di risposte a problemi significativi, l’alunno/a si attiva in percorsi di rielaborazione e ri-costruzione del proprio sapere tramite esperienze dirette e in situazioni di scambio comunicativo e costruttivo fra pari e con il/la docente.
Durante l’attività di tipo laboratoriale, l’alunno/a:
• osserva;
• analizza;
• si pone domande;
• fa collegamenti;
• sviluppa ipotesi;
• si confronta con i compagni, le compagne e gli adulti;
• organizza il proprio percorso di ricerca;
• produce idee e oggetti;
• sostiene e motiva le proprie idee;
• ascolta i punti di vista degli altri e con essi si confronta;
• valuta risultati e processi;
• elabora sintesi;
• collabora con gli altri;
• si assume la responsabilità del proprio operare di fronte a sé e agli altri.
In una modalità di lavoro che promuove la ricerca, gli errori che si compiono durante il cammino sono elementi integranti il percorso. Fermarsi a riflettere su di essi insieme agli alunni e alle alunne per comprenderli e chiarirli costituisce un momento arricchente del processo stesso. L’errore non è più visto, quindi, come qualcosa da condannare, ma è fattore integrante del processo di apprendimento.
Lo sviluppo di competenze e la costruzione di un metodo di apprendimento sono un processo molto lungo, lento e laborioso che richiede tempi distesi per promuovere prolungate attività che, a partire dai vari campi di esperienza della Scuola dell’Infanzia, prosegue nella Scuola Primaria e, pertanto, richiede un forte elemento di continuità fra tutti i “segmenti scolastici” per giungere al suo pieno sviluppo.
L’ arte del narrare è certamente antica quanto l’umanità. Da sempre, molto prima della nascita della scrittura, gli uomini e le donne hanno utilizzato il racconto come strumento per trasmettere sapere e conoscenza, per avviare e coltivare relazioni, per raccontare un territorio e indicare itinerari, per educare le nuove generazioni e guidarle verso il futuro.
I miti che ogni antica cultura ha elaborato per trovare una spiegazione ai fatti della realtà sono un primo esempio di storytelling : come sappiamo, infatti, il significato del termine greco mythos è proprio parola, narrazione, racconto.
Ancora oggi, dopo migliaia di anni, continuiamo a raccontare storie . Amano le storie i più piccoli, fin dalla primissima infanzia: le fiabe, ma non solo, anche le storie di famiglia e di amici, che riguardano persone reali. Continuano ad amare le storie ragazzi e ragazze: le ascoltano a scuola, se le raccontano tra loro, le leggono nei libri, le scoprono attraverso i media. Anche noi adulti apprezziamo le storie, anzi non possiamo farne a meno: dalla cronaca quotidiana o da luoghi lontani nello spazio e nel tempo, sono un nutrimento essenziale della nostra vita cerebrale e della nostra psiche.


Ecco, allora, che lo storytelling si rivela uno strumento appropriato e perfetto, efficace e inclusivo, a cui ricorrere anche per lavorare a scuola , in qualsiasi ciclo di istruzione e tipologia di istituto.
Lo storytelling sollecita la curiosità . Nel trattare un argomento, presentare un tratto di vita di un personaggio, raccontare un progetto, seguire un’esperienza in contesti particolari, magari in luoghi lontani e poco conosciuti, stimola il desiderio di saperne di più, di approfondire.
Lo storytelling permette di mantenere l’attenzione . Se il racconto è in grado di continuare la tensione narrativa, infatti, è possibile conquistare il lettore (o l’ascoltatore) per un buon lasso di tempo, naturalmente variabile a seconda dell’età e di altri fattori interni ed esterni.
Lo storytelling attiva nel nostro cervello una comunicazione multisensoriale . Le parole e le frasi di un racconto permettono di esprimere sensazioni che arrivano a tutti e cinque i sensi, consentendo così una percezione completa, “a tutto tondo”. In pratica, quando ci viene raccontata una storia la nostra mente si attiva come se vivessimo gli eventi della storia stessa, in ogni suo aspetto. Lo storytelling porta perciò a interiorizzare il racconto , a trasformare la storia come un’esperienza personale, non di rado sollecitando il desiderio di raccontarla ad altri, in famiglia o ai coetanei.
Lo storytelling aiuta a prolungare il ricordo . Più la soglia di attenzione è stata alta ed elevato l’impatto emotivo, maggiore sarà la memorizzazione nel lungo periodo.
Lo storytelling favorisce l’inclusione . Le storie ben narrate, infatti, arrivano a tutti e tutte, trasmettendo contenuti anche a chi presenta difficoltà più o meno gravi in alcune fasi dell’apprendimento.
Nel percorso di Matematica i concetti affrontati si sviluppano nei due volumi secondo una prospettiva verticale , venendo di volta in volta ripresi e approfonditi.
Ogni concetto è stato introdotto da una piccola situazione reale vicina al vissuto dei bambini/delle bambine ed è seguito da una serie di domande o frasi da completare che aiutano gli alunni/le alunne a effettuare osservazioni mirate, riflessioni e collegamenti per giungere all’elaborazione finale del concetto.
Le proposte didattiche sono pensate in modo da costituire uno strumento utile all’insegnante al fine di realizzare in classe esperienze di tipo laboratoriale come Indicato dalle I.N. Seguendo alcune indicazioni presenti nella Guida o elaborando in modo personale gli spunti offerti dai contesti suggeriti nel Sussidiario, l’insegnante in un primo momento realizza l’attività in classe, avvicinando i bambini al concetto tramite la manipolazione di oggetti o modelli che stimolino l’osservazione, l’analisi, la scoperta di proprietà e di regolarità, promuovendo la formazione di nuove idee e la rielaborazione di quelle che già possiede.
In un secondo momento procede a effettuare la sintesi collettiva e condivisa su quanto osservato e scoperto seguendo le domande e gli spunti di riflessione presenti nelle pagine del Sussidiario.


Alla fine di ogni capitolo, o di una fase didattica particolarmente significativa, vengono presentati esercizi di consolidamento per aiutare l’alunno/l’alunna ad appropriarsi del concetto appena acquisito, mentre nel quaderno operativo gli esercizi predisposti su due livelli di difficoltà, i compiti di realtà e le proposte di riflessione, offrono suggerimenti e attività per consolidare i concetti affrontati. Non è stato dedicato un capitolo ai problemi non essendo né un concetto né un contenuto da sviluppare separatamente. I problemi costituiscono situazioni e opportunità che promuovono non solo lo sviluppo di conoscenze e abilità matematiche, ma anche abilità cognitive e metacognitive. Per questo motivo le situazioni problematiche sono state poste , secondo modalità e forme differenti, all’interno dei vari capitoli. Sono presenti come contesto introduttivo e motivante a un’attività, oppure come domande poste in forma di fumetto o al termine di alcuni capitoli in una modalità che guidi l’alunno/l’alunna all’analisi del problema secondo approcci di volta in volta differenti che attivino le componenti coinvolte nel processo di analisi e di soluzione.
L’attività viene introdotta e poi sviluppata con una piccola situazione problematica vicina al contesto quotidiano del bambino/della bambina.
Un esempio .
Gli alunni e le alunne della 4a C vogliono decorare i vetri rettangolari delle finestre della loro aula, ricoprendoli con forme geometriche fatte di pellicola trasparente colorata.
Divisi in gruppi, disegnano dei rettangoli per rappresentare i vetri e progettano come decorarli.
L’insegnante può promuovere un’attività di tipo laboratoriale secondo le modalità indicate nella Guida oppure si può appropriare della situazione introduttiva proposta realizzando l’attività in classe con i propri alunni/le proprie alunne.
Successivamente guida i propri alunni/le proprie alunne nell’operazione di sintesi riflettendo sugli elementi più significativi che concorrono alla formazione del concetto tramite le domande o i testi cloze presenti nel testo.
Al termine del paragrafo, in un box, viene definito il concetto.
Frazionare significa dividere un intero in parti di uguale superficie. Le parti possono avere
anche forme diverse
Successivamente vengono proposti esercizi che aiutino il bambino/la bambina a focalizzare gli aspetti più importanti del concetto appena acquisito.

1. Osserva e rispondi. Rappresenta una frazione?
In fondo al capitolo vengono indicate le pagine del Quaderno operativo dove l’alunno/l’alunna avrà modo di trovare gli esercizi di consolidamento.
Il progetto costituisce un sistema integrato dove ogni elemento (il Sussidiario, il quaderno operativo, il fascicolo delle verifiche e la Guida) acquista una propria valenza educativa e di conoscenza.
C lasse 4 a
Competenze chiave europee di riferimento
• Competenza matematica e competenze di base in scienze e tecnologie.
• Capacità di imparare ad imparare.
• Competenza sociale e civica in materia di cittadinanza.
• Competenza imprenditoriale.
Competenze dal profilo dello studente al termine della Scuola Primaria
• Utilizza le sue conoscenze matematiche e scientifico-tecnologiche per trovare e giustificare soluzioni a problemi reali.
• Possiede un patrimonio di conoscenze e nozioni di base ed è in grado di ricercare ed organizzare nuove informazioni.
• Rispetta le regole condivise, collabora con gli altri per la costruzione del bene comune.
• Dimostra originalità e spirito di iniziativa. È in grado di realizzare semplici progetti.
Traguardi per lo sviluppo delle competenze al termine della Scuola Primaria
• Utilizzare con sicurezza le tecniche e le procedure del calcolo aritmetico e algebrico, scritto e mentale, anche con riferimento a contesti reali e saper valutare l’opportunità di ricorrere a una calcolatrice.
• Riconoscere e utilizzare rappresentazioni diverse di oggetti matematici. Obiettivi
• Leggere, scrivere ed ordinare numeri naturali.
• Eseguire le quattro operazioni con i numeri naturali mediante il calcolo mentale o scritto.
• Il sistema posizionale decimale.
• Riconosce il valore posizionale delle cifre.
• Compone e scompone numeri naturali.
• Rappresenta i numeri naturali sulla retta e li confronta.
• Effettua approssimazioni di numeri naturali.
• Il concetto di addizione, sottrazione, moltiplicazione e divisione.
• Gli algoritmi per il calcolo scritto.
• Le proprietà delle operazioni.
• Strategie di calcolo a mente.
• Esegue le quattro operazioni con i numeri naturali mediante il calcolo menatale e scritto.
• Usa le proprietà delle operazioni per semplificare il calcolo.
• La classe delle migliaia.
• L’addizione e le sue proprietà.
• La sottrazione e la proprietà invariantiva.
• Calcolo mentale: addizioni e sottrazioni.
• Addizioni e sottrazioni in colonna.
• Le proprietà della moltiplicazione.
• Moltiplicazioni: calcolo mentale.
• Usare le proprietà delle operazioni per semplificare i calcoli.
• Usare rappresentazioni diverse per scrivere numeri naturali.
• Riconoscere classi di numeri (multipli e divisori).
• Usare le frazioni in situazioni reali come operatore sull’intero e su un insieme di oggetti.
• La forma dei numeri.
• Identificare il rapporto tra frazione e numero decimali.
• Leggere, scrivere e ordinare i numeri decimali.
• Calcolare con i numeri decimali.
Spazio e figure
• Riconoscere e disegnare gli enti geometrici fondamentali.
• Scrittura trasparente e scrittura non trasparente di un numero.
• Multipli e i divisori di un numero
• Usa strategie di calcolo mentale.
• Verifica i calcoli effettuati.
• Riconosce e descrive regolarità in una sequenza di numeri o di figure.
• Scrive numeri naturali utilizzando strutture operative differenti.
• Utilizza e riconosce il concetto di uguaglianza.
• Individua i multipli e i divisori di un numero.
• Le moltiplicazioni in colonna.
• La divisione: tabella e proprietà.
• Divisioni in colonna.
• Multipli, divisori e numeri primi.
• Il concetto di frazione e la sua rappresentazione simbolica.
• Frazioni maggiori, minori o uguali a 1.
• Frazione complementare.
• Frazione equivalente.
• Rappresenta, legge, confronta e ordina frazioni.
• Individua e calcola la frazione complementare.
• Riconosce e calcola frazioni equivalenti.
• Calcola la frazione di un numero.
• Ricostruisce l’intero conoscendo il valore di una parte.
• Le frazioni decimali e i numeri decimali.
• Il piano, il punto, rette, semirette e segmenti.
• Il concetto di parallelismo e incidenza.
• L’angolo.
• Legge, scrive e ordina frazioni decimali e numeri decimali.
• Riconosce, rappresenta e confronta numeri decimali.
• Colloca numeri decimali sulla linea dei numeri.
• Esegue trasformazioni.
• Esegue le quattro operazioni con i numeri decimali.
• Costruisce ed utilizza modelli materiali come supporto per visualizzare figure nel piano e nello spazio.
• Riconosce e disegna gli enti geometrici fondamentali.
• Utilizza e distingue i concetti di parallelismo e perpendicolarità.
• Frazioni e frazioni decimali.
• Frazioni maggiori, minori, uguali a 1.
• Frazioni e linea dei numeri, confronto di frazioni.
• Frazioni complementari ed equivalenti.
• Frazionare quantità e numeri.
• Moltiplicazioni e divisioni per 10, 100, 1000.
• Dalle frazioni decimali ai numeri decimali.
• I numeri decimali sulla linea dei numeri.
• Le quattro operazioni con i numeri decimali.
• Riconoscere, confrontare e misurare angoli mediante proprietà e strumenti.
La simmetria
• Riconoscere ed effettuare movimenti di figure nel piano: simmetrie, traslazioni e rotazioni.
• Riconosce le parti costitutive dell’angolo.
• Classifica gli angoli in base alle caratteristiche.
• Confronta e misura angoli utilizzando le proprietà e gli strumenti.
• Le isometrie: il concetto di simmetria, traslazione e rotazione.
Le figure piane
• Riconoscere, denominare e descrivere le proprietà delle figure piane.
• I poligoni.
• Poligoni equilateri, equiangoli, regolari.
• Il concetto di perimetro.
• Il concetto di area.
• L’unità di misura dell’area.
• Il concetto di isoperimetria, equiestensione ed equiscomponibilità.
• Riconosce le regole della simmetria.
• Riconosce movimenti sul piano di punti, linee e figure.
• Disegna movimenti sul piano di punti linee e figure: simmetria, traslazioni e rotazioni.
• Punti, linee, angoli.
• Le figure piane: i triangoli.
• Figure deformabili e non.
• Il criterio di componibilità di un triangolo.
• Caratteristiche e proprietà dei triangoli.
• L’altezza nei triangoli.
• I quadrilateri: caratteristiche e proprietà.
• Classificazione dei quadrilateri.
• Area del rettangolo, del quadrato e del triangolo.
• Riconosce le proprietà dei poligoni e li classifica.
• Determina il perimetro e l’area di una figura con unità di misura non convenzionali e convenzionali.
• Confronta grandezze lineari e di superficie.
• Riconosce e disegna figure equivalenti ed isoperimetriche.
• Riconosce e disegna figure equicomposte ed equiscomponibili.
• Descrive, denomina e classifica triangoli.
• Individua e traccia altezze, assi di simmetria.
• Descrive, denomina e classifica quadrilateri: trapezio, parallelogramma, rettangolo, rombo e quadrato.
• Determina l’area del rettangolo, quadrato e triangolo per scomposizione o utilizzando le più comuni formule.
• La simmetria.
• Rotazioni e traslazioni.
• I poligoni e la loro classificazione.
• I triangoli e le loro caratteristiche.
• I quadrilateri e le loro caratteristiche.
• Il perimetro.
• Il concetto di area: congruenza ed equivalenza di superfici.
• Area delle principali figure piane.
Esprimere misure
• Il concetto di misura.
• Misure di lunghezza, massa, capacità, tempo.
• Il sistema monetario.
• Stabilisce relazioni fra grandezze e misure.
• Associa alla grandezza da misurare lo strumento appropriato.
• Riesce a fare una stima delle misure.
• Effettua misurazioni con unità di misura non convenzionali e convenzionali.
• Opera trasformazioni tra grandezze omogenee.
• Calcola intervalli di tempo.
Relazioni, dati e previsioni
• Applicare sistemi e procedimenti di misura in contesti differenti.
• I dati dell’indagine statistica.
• Utilizza gli elementi di rilevazione statistica per effettuare indagini.
• Legge ed interpreta grafici.
• Il S.M.D.: le misure di lunghezza.
• Il S.M.D.: le misure di capacità.
• Il S.M.D.: le misure di massa.
• Peso lordo, tara, peso netto.
• I problemi del S.M.D.
• Le misure di tempo.
• Le misure di valore.
• La compravendita.
• Effettuare indagini.
• Leggere e rappresentare dati.
• Interpretare grafici utilizzando gli indici statistici.
• Formulare previsioni attendibili e giustificate.
• Analizzare e comprendere testi di varia tipologia che coinvolgano aspetti logici e matematici.
• Risolvere semplici problemi in ogni ambito di contenuto.
• Formulare e giustificare il processo risolutivo.
• Rappresentarli con schemi di vario tipo.
• Rappresentazione dei dati: tabella di frequenza, ideogramma, istogramma.
• Indici statistici: moda e media.
• II concetto di evento.
• Evento certo, possibile, impossibile.
• La misura di un evento.
• Rappresenta dati mediante tabelle di frequenza e grafici.
• Interpreta dati statistici mediante indici: la moda e la media.
• Valuta la probabilità che accada un evento.
• Esprime mediante un numero il grado di probabilità di un evento.
• Individua nel testo la richiesta.
• Manipola il testo del problema ai fini di ricavare informazioni utili alla ricerca di strategie risolutive.
• Ricerca e utilizza strategie risolutive.
• Descrive il processo risolutivo e lo giustifica.
• Utilizza schemi di vario tipo per rappresentare la struttura del problema.
• Individuare e interpretare le informazioni essenziali fornite da istogrammi, ideogrammi e areogrammi.
• Dati statistici: media, moda, mediana.
• Compiere semplici indagini statistiche.
• Le tabelle di frequenza per tabulare i dati raccolti.
• Eventi certi, possibili, impossibili, probabili.
• La probabilità di un evento.
• Problemi con due domande e due operazioni.
• Problemi con la domanda nascosta.
• Problemi con le frazioni.
• Problemi con il S.M.D.
• Problemi sulla compravendita, sul valore totale/unitario e sul rapporto costi/misure.
• Problemi sul calcolo del perimetro.
Aiutiamo i bambini e le bambine a comprendere che i simboli e le regole che utilizzano quando fanno Matematica costituiscono il linguaggio che questa disciplina usa per descrivere situazioni e per comunicare idee e concetti.
Scegliamo alcune immagini e osserviamo come comunicano le altre discipline:




1. La lingua italiana si esprime usando parole e regole grammaticali;
2. la Geografia usa simboli e disegni per costruire le carte geografiche;
3. l’Arte si esprime attraverso punti, linee e colori;
4. i movimenti del corpo sono il linguaggio della danza. Che cosa usa la Matematica per esprimersi?
Dall’analisi di queste immagini i bambini e le bambine potranno cogliere facilmente le ca-


1. al posto delle parole usa dei simboli (le cifre, + , x , < , = , % ….);
2. i bambini e le bambine di altre nazioni utilizzano gli stessi nostri simboli; questo significa che i simboli della Matematica sono uguali in tutto il mondo. Il linguaggio matematico infatti è l’unica lingua universale ;
3. è semplice ed essenziale perché attraverso pochi simboli si esprimono situazioni anche complesse.
Affinché i bambini e le bambine trovino senso nell’apprendere la Matematica, è importante che riescano a vederla nel mondo che li circonda e si rendono conto di come spesso la utilizzano senza esserne consapevoli.
Riflettiamo insieme a loro su questa affermazione di Galileo Galilei: La natura è un libro scritto a caratteri matematici.
Chiediamo alla classe: “Che cosa avrà voluto dire?” e, dopo aver ascoltato le loro riflessioni, chiediamo di analizzare alcuni contesti a loro vicini.
– Cerca la Matematica che:
c’è… in te



In quale data sei nato/a?
Quanti anni hai?
Quanto pesi ?
Quanto sei alto/a ?
Qual è il tuo numero di scarpe?
Mentre salti appoggi i piedi seguendo questo ordine che è quello dello schema della “campana”.










Quanto costa il maglione? Come lo piegheresti per far combaciare due metà ? Perché?
Riproduci sul quaderno il motivo della decorazione nella parte superiore.


Questa torta è per 4 persone e per farla sono stati usati 200 g di farina e 4 uova . Se si vuole fare una torta per 12 persone , quanta farina e quante uova serviranno?

Scopri le figure che si formano in ciascuno dei due fiori unendo i vertici di ogni petalo evidenziati con un pallino celeste.
Quali figure hai ottenuto?
Prova a disegnare una linea per dividere a metà questi due fiori. La puoi disegnare in entrambi? Perché?

Quali figure compongono il quadro?
Da che cosa sono formate?
Quale tipo di linee vedi?
Come sono tra loro?
Proponiamo il gioco del piccolo/della piccola detective e chiediamo di continuare a cercare “la Matematica intorno a loro”. Proponiamo la seguente attività: – Prendi carta e matita e, per un giorno, tutte le volte che “incontri la Matematica” scrivi di cosa si tratta.
In classe si confronta ciò che hanno annotato per mettere in evidenza che la Matematica non è fatta solo da numeri e operazioni; poi si effettua una prima classificazione dei nuclei tematici nei quali sono state suddivise le conoscenze matematiche: Aritmetica, Geometria, Statistica, Probabilità.

In classe quarta ormai il concetto di numero è acquisito e il nostro sistema di numerazione è conosciuto. Si possono predisporre delle attività in forma di gioco per riprendere le conoscenze pregresse e per consolidarle.
Che cosa sai sul sistema di numerazione?
Proponiamo ai bambini e alle bambine un brainstorming durante il quale lavorano in modalità cooperativa.
• Ciascun alunno/alunna scrive sul proprio quaderno, nel modo che ritiene più opportuno, con uno schema, sotto forma di elenco o con una mappa, che cosa sa sui numeri. (15 min. circa)
• Dopo aver recuperato le sue conoscenze, confronta il proprio elaborato con quello del compagno/della compagna di banco ed entrambi integrano quanto scritto individualmente con le informazioni dimenticate che trovano scritte nel quaderno del compagno/della compagna. (10 min. circa)
• A questo punto, l’insegnante distribuisce dei biglietti e chiede che ogni coppia si divida le informazioni ricordate e le scriva sui biglietti, una in ogni biglietto. (15 min. circa)
• L’insegnante chiede a un alunno/un’alunna di portare uno dei biglietti che ha scritto e di attaccarlo alla lavagna. Si legge ad alta voce, tutte le coppie verificano se possiedono fra i loro biglietti quell’informazione e la eliminano. Si procede nello stesso modo con gli altri biglietti. (20 min.)
• Una volta che le informazioni sono tutte attaccate alla lavagna, in modo collettivo si organizzano costruendo una mappa concettuale. (20 min.)
Attività 2
Scopri il numero
Per consolidare il concetto relativo alla differenza fra cifra/numero, il sistema di numerazione e la composizione e scomposizione di numeri possiamo proporre il gioco
“
Scopri il numero ”.
L’insegnante scrive su un foglietto un numero segreto di due cifre diverse.
Gli alunni/Le alunne, lavorando a piccoli gruppi, devono indovinare il numero.
Regole del gioco
Gli alunni/Le alunne propongono un numero che viene scritto alla lavagna.
Accanto a ogni numero proposto viene scritta una legenda con dei pallini di colore rosso e verde.
Se nel numero proposto è stata indovinata una o più cifre, ma nella posizione sbagliata, allora si mette il pallino rosso, uno per ogni cifra indovinata; se viene indovinata la cifra e si trova in una posizione corretta, si mette un pallino verde, uno per ogni cifra corretta.
Il gruppo che indovina si sostituisce all’insegnante e il gioco continua.
Es.: numero segreto 39
Alunni: 53 Legenda: (rosso)
Alunni: 38 Legenda: (verde)
Alunni: 34 Legenda: (verde)
Si capisce che è stato indovinato il 3, quindi va cambiata la cifra 4.
Per tentativi arriveranno alla conclusione giusta: 39 (verde) (verde)
Il gioco può essere proposto anche con un numero a tre cifre.
Attività 3
Dove sei stato/a in vacanza?
Ai bambini/Alle bambine piace molto raccontare dove sono stati in vacanza, pertanto si può partire dal loro racconto per proporre questa attività a carattere interdisciplinare fra Matematica e Geografia.
Materiali
– Una carta geografica e una carta geografico-politica dell’Italia da appendere in classe;
– carta muta dell’Italia politica in fotocopia per ciascun alunno/ciascuna alunna. Ciascun alunno/Ciascuna alunna scrive su di un foglietto semi-adesivo il nome del luogo di villeggiatura dove è stato in vacanza. Uno alla volta ciascun bambino/ciascuna bambina individua sulla carta geografica appesa al muro il luogo e attacca il suo foglietto, esplicitando l’ambiente (mare, montagna, città…) e la regione nella quale si trova. I compagni/Le compagne collocano nella propria fotocopia muta dell’Italia politica il luogo indicato dal compagno/dalla compagna e scrivono il nome della regione. Una volta individuate le regioni dei luoghi di villeggiatura, si procede cercando sull’Atlante geografico o in Internet la loro estensione superficiale, aggiungendo anche quella delle regioni che non sono state visitate.
Si fanno raccogliere i dati in una tabella come la seguente.
Nome regione Superficie
Numero approssimato alle decine di migliaia
Si può lavorare con i numeri trovati chiedendo di:
• riscriverli con le parole;
• riscriverli scomponendoli;
• trovare altre scritture del numero;
• scrivere il numero precedente e quello successivo;
• confrontare l’estensione territoriale fra coppie di regioni;
• riscriverli in ordine crescente o decrescente, facendo una classifica delle regioni sulla base della loro estensione territoriale.
L’introduzione delle frazioni nel percorso didattico dell’insegnamento della Matematica è giustificato dal fatto che i bambini/le bambine, nella vita quotidiana, incontrano situazioni che non si possono esprimere facendo riferimento ai soli numeri naturali. Il concetto di frazione è però molto complesso perché implica molti significati fra loro interconnessi. Alcuni di questi significati sono:
1. è parte di un intero , che può essere continuo (per esempio la superficie di una figura) o discreto (cioè una quantità numerica come 7 penne, 7 caramelle…);
2. è un operatore : 2 3 di 15 caramelle;
3. esprime una percentuale : 25% = 25 100 ; anche se le due scritture formalmente sono fra loro equivalenti possiedono significati differenti tant’è che nella vita quotidiana la percentuale non si indica con la scrittura frazionaria;
4. esprime una misura ;
5. in probabilità esprime il rapporto fra i casi possibili che accada un evento e quelli favorevoli ;
6. è un numero razionale ;
7. esprime un rapporto, una relazione fra due grandezze o quantità.
Nella Scuola Primaria si privilegia lo sviluppo dei primi 5 significati di frazione.
Nel Sussidiario sono state operate scelte che riteniamo importante esplicitare dal punto di vista teorico.
Nel significato di frazione come parte di un intero è essenziale una riflessione insieme agli alunni su cosa si intenda per “dividere un intero in parti uguali”.
Mentre se dividiamo una quantità , l’aggettivo uguali significa “ ugualmente numerosi ” e questa suddivisione può essere effettuata in un solo modo, se dividiamo una superficie , significa di “ uguale area ”. Avere uguale area non vuol dire avere necessariamente anche uguale forma , essere cioè congruenti. Per evitare che i bambini/le bambine pensino alla frazione unicamente come a una divisione in parti congruenti, è importante avviare con loro una riflessione in tale senso e usare modelli nei quali la figura sia stata frazionata in parti equiestese, ma non congruenti. Le pagine di avvio al concetto di frazione presenti nel Sussidiario, sia nel volume di quarta che in quello di quinta, offrono spunto di riflessione in tale senso.
Riteniamo inoltre che sia importante sviluppare il significato di frazione come parte di un tutto contemporaneamente, sia nell’ambito di grandezze continue che di quantità numeriche. Sebbene per i bambini/per le bambine sia più facile cogliere l’intero di riferimento se è una grandezza continua (una figura, un foglio, tavolette di cioccolata sono fra gli oggetti più usati e più vicini all’esperienza di tutti i bambini e le bambine), sviluppare inizialmente il concetto usando solo grandezze continue rischia di rendere più difficile trasferirlo al frazionamento di una quantità.
In quest’ottica sono state proposte le pagine 46, 47 e 48 del volume di classe quarta.



Per aiutare i bambini/le bambine a cogliere più facilmente l’intero anche nel caso in cui si frazionino quantità discrete , può essere di aiuto fare riferimento all’unità intera: “un pacchetto” con dentro 15 caramelle, “un sacchetto” con dentro 20 biscotti, “una scatola” con 12 cioccolatini.
Nello sviluppare il significato di frazione come rapporto fra uno/tutto, le definizioni di frazione propria, impropria, apparente non sono significative.
Riflettiamo su un esempio: 167 500 è una frazione propria. Se con il termine propria intendiamo che l’intero si può frazionare in 500 parti e ne possiamo considerare 167, ha senso dire che questa frazione è “propria” se fraziono una pizza o un foglio? Quando mai nell’esperienza quotidiana avviene una tale divisione?
La frazione 6 5 si dice che è “impropria” perché se dividi una tavoletta di cioccolata in 5 parti non ne puoi considerare 6. Ciò avviene però se l’intero è una tavoletta, ma se l’intero sono due tavolette allora diventa una frazione possibile.
Evitiamo pertanto di indirizzare i bambini in meccanismi che sembrano semplificare (“guarda il numero che c’è al denominatore, se è ... allora la frazione è …), ma che invece svuotano di significato un apprendimento e che, per questo, diventano oppositivi alla vera acquisizione di senso, mentre piuttosto concentriamoci sulla relazione e sul significato che di volta in volta vengono espressi dalla frazione.
Secondo noi è opportuno stimolare i bambini a fare riferimento all’unità, parlando di frazioni minori, maggiori



o uguali a 1, come proposto nel volume di quarta alle pagine 50, 51 e 52 e in quello di quinta alle pagine 46 e 47. Inoltre è consigliabile introdurre e consolidare bene il concetto di frazione mediante esperienze concrete e quindi lavorare inizialmente con frazioni minori o uguali a 1 e solo successivamente introdurre le frazioni maggiori di 1.
Tali frazioni non possiedono un significato immediatamente intuibile e per questo sono più difficili da capire: a volte l’intero è 1, ma a volte è formato da più interi, come nel caso della tavoletta di cioccolato di cui si parlava sopra.

Attività 1
In quanti modi possiamo fare a metà?
Per iniziare a riflettere sulla differenza che c’è tra frazionare una unità continua (la superficie di un foglio) o una unità discreta (16 caramelle) possiamo proporre la situazione presente nel volume di quarta alle pagine 46, 47 e 48 ma chiedendo inizialmente solo di frazionare a metà.
Distribuiamo ai bambini/alle bambine un foglio di forma rettangolare e chiediamogli di dividerlo a metà, lasciandoli/e liberi/e di procedere senza dare nessuna indicazione sul come. Sicuramente si verificherà che qualcuno divide il foglio in orizzontale e qualcuno in verticale, così:
Perfetto: confrontiamo le metà che hanno ottenuto e chiediamo: possiamo dire che ciascuna parte è metà del foglio? Sì.
Rappresentiamo la situazione in linguaggio matematico: 1 foglio : 2 = 1 2 foglio e scriviamo l’unità frazionaria su ciascuna metà.
Prendiamo due metà differenti e confrontiamole: posso dire che sono uguali? Qualcuno dirà di sì, qualcuno di no. Approfondiamo allora chiedendo: che cosa hanno di uguale? I bambini/Le bambine noteranno che entrambi sono rettangoli, ma hanno una forma un po’ diversa. Passiamo a confrontare le superfici sovrapponendole e tagliamo la parte di metà che avanza e mettiamola sotto all’altra.
Notiamo facilmente che le due metà hanno uguale superficie.
Soffermiamo l’attenzione dei bambini/delle bambine sul fatto che hanno già trovato due modi diversi per dividere a metà il foglio.
Chiediamo allora: Ci sono altri modi per dividere a metà questo foglio? Distribuiamo un altro foglio, uguale al primo, e chiediamo di provare a dividerlo in altri modi.
Ecco alcuni esempi:
Prendiamo nuovamente due metà e confrontiamole per sovrapposizione, come fatto in precedenza.
Noteremo facilmente che tutte le metà anche se non hanno uguale forma hanno uguale superficie, per cui si può dire che abbiamo frazionato il foglio in parti uguali e che tutte sono una metà.
Si può poi procedere a frazionare, seguendo lo stesso ragionamento, anche in quarti, in ottavi e poi in terzi e in sesti.
Lavoriamo adesso sul frazionare a metà una unità discreta, cioè un sacchetto di 16 caramelle presentando questa semplice situazione: il nonno ha regalato ai suoi due nipoti un sacchetto con 16 caramelle tutte uguali e gli dice di fare a metà. Portato in classe il sacchetto, simuliamo la situazione e facciamo dividere le caramelle a metà fra due bambini. Chiediamo: Da quante caramelle è formata una metà? 8. E l’altra?
8. Si potevano dividere in un altro modo? No.
Rappresentiamo la situazione in linguaggio matematico:
1 sacchetto : 2 bambini = 1 2 sacchetto per ogni bambino
Sostituiamo l’intero sacchetto con le caramelle: 16 caramelle : 2 bambini = 8 caramelle per ogni bambino, cioè 1 2 del sacchetto.
Riprendiamo le 16 caramelle, mettiamole in un altro contenitore, per esempio una scatolina, facciamo notare che la disposizione delle caramelle non è uguale a prima e chiediamo nuovamente di dividerle a metà. Quant’è la metà adesso? Sarà sempre
8. Riflettiamo insieme sul fatto che la metà di 16 è sempre 8, in qualsiasi modo vengano disposte le caramelle.
Chiediamo: E se i nipotini fossero stati 4, come si possono frazionare le caramelle?
Ripetiamo l’operazione e rappresentiamola in linguaggio matematico:
1 sacchetto : 4 bambini = 1 4 di sacchetto per ogni bambino
Sostituiamo l’intero sacchetto con le caramelle:
16 caramelle : 4 bambini = 4 caramelle per ogni bambino, cioè 1 4 del sacchetto
Soffermiamo nuovamente l’attenzione sul fatto che in qualunque modo vengano disposte le caramelle, un quarto di 16 è sempre 4.
Possiamo proporre la situazione presentata nel volume di quarta a pagina 48, per concludere nuovamente che in qualsiasi modo si dividano le caramelle, nel caso di una unità discreta il modo di frazionare può essere uno solo.
È importante che i bambini/le bambine abbiano compreso che nel caso in cui si divida una unità discreta, la parola “uguali” significa di uguale quantità e che questa quantità non può essere che unica; nel caso di una unità continua l’aggettivo “uguali” si riferisce all’uguaglianza di superfici e non necessariamente anche di forma. Le parti frazionate possono avere uguale superficie, ma non uguale forma oppure avere entrambe le due caratteristiche e quindi essere congruenti.
Nel volume di quinta il capitolo sulle frazioni inizia consolidando questo concetto alle pagine 46 e 47.

Le bandiere delle classi quarte
La situazione motivante all’attività proposta nel volume di quarta alle pagine 46 e 47 può essere realizzata in classe chiedendo ai bambini/alle bambine di progettare la decorazione di un vetro della loro classe. Dividiamo i bambini e le bambine in coppie e chiediamo loro di creare il progetto tenendo in considerazione queste indicazioni: il vetro deve avere forma rettangolare e deve essere frazionato in quarti.
Una volta realizzati i progetti, ogni coppia presenta il suo e si verifica se la condizione “essere divisi in quarti” è stata rispettata da tutti.
Si attaccano tutti i progetti in un cartellone e poi verrà scelto quello che piace di più. Per le riflessioni di sintesi si completano le pagine 46 e 47 del volume di quarta.
I bambini/Le bambine che frequentano la Scuola Primaria si trovano, secondo Piaget, nella fase dello sviluppo cognitivo caratterizzato dal pensiero operatorio concreto : sono cioè capaci di effettuare operazioni mentali ragionando in modo più sistematico e iniziando a svincolarsi dal modo in cui accadono le cose, ma hanno bisogno di supportare le proprie operazioni mentali con la manipolazioni di oggetti


Ciò significa che i bambini/le bambine di questa età hanno bisogno di oggetti concreti sui quali agire per sviluppare quelle operazioni di pensiero necessarie alla formazione delle rappresentazioni mentali necessarie alla costruzione di un concetto. Tuttavia le caratteristiche di astrazione che possiedono i concetti matematici rendono spesso difficile fare utilizzare o fare riferimento a oggetti concreti e, per questo motivo, spesso si utilizzano dei mediatori didattici fra i quali ci sono anche rappresentazioni di vario genere: disegni, schemi, grafici, modellini.
Il problema nasce dal fatto che nessuna rappresentazione può descrivere in modo corretto tutte le caratteristiche del concetto che veicola, poiché non possiede quelle caratteristiche di astrattezza, generalità e perfezione che invece possiede il concetto stesso. Per questo motivo, nessuno dei modelli o delle rappresentazioni scelte riuscirà a rappresentare il concetto nella sua completezza, ma ne evidenzierà solo alcune caratteristiche. Il bambino/La bambina che opera mediante il modello e sviluppa tramite esso il concetto, rischia di costruirlo in modo errato a causa dei limiti del modello stesso.
Per evitare questo rischio è necessario che l’insegnante conosca bene le potenzialità e i limiti dei modelli che propone come mediatori e che li alterni il più possibile per evitare che il bambino/la bambina identifichi il concetto col modello, sviluppando in modo errato il concetto stesso.
Per esempio, proporre come modello di quadrato una figura orientata nel piano sempre nello stesso modo, porta a identificare il concetto con la sua posizione nel piano e a non riconoscerlo se orientato in altro modo:
È un quadrato
Se lo ruoto… non è più un quadrato, diventa un rombo!
Un altro esempio:
angolo A
angolo A maggiore dell’angolo B
angolo B
Il modello di angolo se proposto sempre con l’archetto porta a identificare l’angolo con la superficie racchiusa dall’archetto, ostacolando l’idea d’infinito dell’angolo e identificando l’ampiezza dell’angolo con la grandezza dell’archetto.
La staticità dei modelli e delle rappresentazioni oltre a non supportare l’alunno/l’alunna con la manipolazione di oggetti concreti, facilita la formazione di misconcetti, cioè la costruzione non corretta del concetto che rischia di ostacolare in futuro lo sviluppo di ulteriori aspetti del concetto stesso o la costruzione di altri a esso correlati.
Un modello statico, quale può essere il disegno, non aiuta l’alunno/alunna ad analizzare la situazione da diversi punti di vista e a “vedere oltre”, ma consente l’osservazione solo di alcuni aspetti, è poco stimolante e di conseguenza suscita meno domande e riflessioni.
La dinamicità di un modello concreto invece mette l’alunno/alunna al centro del proprio apprendimento attraverso l’esplorazione diretta: toccare, percepire la tensione di un filo elastico, vedere la trasformazione della figura accende la curiosità, stimola l’osservazione e la nascita spontanea di domande, di osservazioni, di collegamenti.
Ciò che conta non è più il prodotto finale, ma il processo attivato per costruirlo.
Per questo motivo riteniamo importante proporre attività nelle quali i bambini/le bambine possano manipolare modelli semplici ma dinamici che consentano loro di scoprire proprietà e relazioni difficili da cogliere con la sola osservazione di una figura o semplicemente leggendone la descrizione o definizione su di un libro.
Punto
Nell’introduzione della Geometria è consuetudine partire dai concetti di punto e linea . Gli enti geometrici possono essere compresi facendo riferimento ad altri concetti precedenti, ma il punto e la linea sono enti geometrici primitivi , cioè sono enti che non possono derivare da altre entità geometriche e, per questo motivo, non possono essere espressi mediante una definizione. Questo significa che per l’insegnante nasce il problema di come sviluppare nei bambini/nelle bambine tali concetti senza poterli definire . Inoltre, non esistono nel mondo tangibile e quindi non sono manipolabili direttamente e quando li disegniamo costruiamo solo delle loro rappresentazioni. I bambini/ Le bambine però, nelle loro esperienze di vita, muovendosi ed esplorando lo spazio intorno, sviluppano tali concetti in modo intuitivo

Per questi motivi proponiamo una semplice attività che dia una spiegazione intuitiva di questi concetti.
Attività 1
La linea e il punto
Diamo ai bambini/alle bambine fogli di dimensioni differenti, chiediamo di fare una piega qualunque, schiacciandola bene, poi facciamo riaprire il foglio e chiediamo di descrivere che cosa vedono. I bambini/Le bambine osserveranno che si è formata una linea. Chiediamo: Quali proprietà possiede? Osserveranno che è lunga, quindi ha una lunghezza. Chiediamo: è anche larga? Qualcuno cercherà di misurarne la larghezza ed è proprio questo che stimolerà l’idea che è larga quasi zero, un quasi che non è quantificabile, per cui si può concludere che si possa dire che è larga zero
Successivamente facciamo fare un’altra piega che incontri la prima, apriamo il foglio e osserviamo quanto accaduto: le due linee si incontrano in un punto. Chiediamo: Quali proprietà possiede il punto? È lungo? È largo? Poiché la linea non ha larghezza, i bambini/le bambine si renderanno conto che il punto è senza dimensioni , però individua una posizione nel foglio. Ogni bambino/bambina incollerà il foglietto sul proprio quaderno e scriverà le osservazioni fatte.
Alla fine dell’attività si può continuare il lavoro usando il volume di quarta a pagina 91. Quando l’insegnante lavorerà con le figure piane e quelle solide ritroverà vertici, linee, spigoli e lati e in questo caso potrà ulteriormente sviluppare i concetti di linee parallele, linee incidenti e perpendicolari.
Il concetto di angolo è difficile per i bambini/le bambine ed è opportuno ritornare su di esso più volte. La staticità di un’immagine come quella di un disegno porta a identificare l’angolo con le due linee che lo limitano, o con il punto d’incontro delle linee (vertice) o addirittura con l’archetto che spesso viene usato per indicarlo. Tutto ciò crea dei misconcetti nei bambini/nelle bambine, che identificano l’ampiezza dell’angolo con l’archetto e non lo vedono come parte di piano che, partendo dal vertice, si apre (come un ventaglio) nel piano infinito.
Riflettiamo insieme ai bambini/alle bambine sui diversi significati che ha l’angolo nel linguaggio comune iniziando proprio dalla pagina 93 del volume di quarta. Chiediamo poi di scrivere altre frasi del linguaggio comune nelle quali si usa la parola angolo e arricchirle con immagini che incolleranno sul quaderno.

Per osservare le caratteristiche dell’angolo utilizziamo le istruzioni di pagina 288 del Quaderno di quarta per far costruire ai bambini/alle bambine un ventaglio.
Attività 1
Il ventaglio
Iniziamo con una prima fase di gioco e di esplorazione del modello usando il libro di quarta a pagina 94. Aprendo e chiudendo il ventaglio facciamo formare vari tipi di angolo: l’angolo “zero”, l’angolo giro e l’angolo retto. I bambini/Le bambine possono vedere e toccare con le loro mani che l’angolo si forma perché uno dei lati del ventaglio si muove ruotando rispetto all’altro.
Attività 2
Discutiamo sull’ampiezza dell’angolo
A ogni coppia chiediamo di formare con i propri ventagli un angolo più grande e uno più piccolo e chiediamo: Come puoi stabilire qual è il più grande? Registriamo alla lavagna la risposta data da ciascuna coppia. Individuiamo fra le risposte date quella condivisa da tutti per giungere alla conclusione che la “grandezza” di un angolo dipende dall’ampiezza e questa viene determinata dall’apertura di uno dei suoi lati.
Attività 3
Riflettiamo sulla lunghezza dei lati dell’angolo
Facciamo aprire ai bambini/alle bambine il ventaglio ad angolo retto. Anche l’insegnante fa la stessa cosa con un ventaglio più grande rispetto a quello dei bambini/ delle bambine e con i lati abbastanza lunghi. Facciamo confrontare l’angolo dell’insegnante con quello dei bambini/delle bambine e chiediamo: Gli angoli sono uguali? Giuste o sbagliate che siano, è necessario fare una verifica delle loro risposte mettendo a confronto i vari angoli con una semplice sovrapposizione. Lasciamo liberi i bambini/le bambine di fare ipotesi per arrivare alla condivisione che l’angolo è uguale nei vari ventagli e concludere che l’ampiezza di un angolo non dipende dalla lunghezza dei lati.
Attività 4
Ancora sul concetto di ampiezza di un angolo
Facciamo disegnare, colorare e ritagliare un angolo; poi, chiediamo di tagliarlo per “rimpicciolirlo”. Esaminiamo i vari tipi di tagli. Chi non ha compreso il concetto di ampiezza lo taglia scorciando i lati (errore ricorrente), mentre chi ha compreso dovrebbe fare un taglio passante per il vertice, quindi diminuire l’ampiezza. Quando siamo arrivati alla condivisione si rifà il disegno, si rimpicciolisce e si incolla l’angolo sul quaderno mettendo accanto il pezzo tagliato, come in figura.
Attività 5
Conclusioni sull’ampiezza dell’angolo
Disegniamo un angolo con delle corde (o lo scotch di carta) sul pavimento in classe (o in palestra, nel corridoio). Chiediamo: Come posso fare a portare l’angolo sul quaderno senza misurare?
Le risposte saranno le più svariate, ma sicuramente qualcuno proporrà di ricalcarlo con un foglio molto grande. È proprio questa proposta che si deve sfruttare per far riflettere ancora sulla lunghezza dei lati e sull’ampiezza di un angolo, affinché i bambini/le bambine arrivino alla conclusione che è sufficiente ricalcare solo una piccola parte dell’angolo partendo dal vertice.
Arriviamo alla condivisione, poi facciamo ricalcare l’angolo, ritagliare e incollare sul quaderno. A questo punto l’insegnante può continuare il lavoro sul libro.
Nel volume le isometrie sono presentate partendo dalla simmetria assiale per sviluppare successivamente la traslazione e la rotazione, perché si ottengono dalla composizione di più simmetrie: la traslazione con una doppia simmetria con assi paralleli, la rotazione una doppia simmetria con assi incidenti.
Ricordiamo le proprietà che caratterizzano la simmetria assiale :
• è uno spostamento rigido di una figura a 2D ;

• lo spostamento avviene nello spazio perché è un ribaltamento della figura rispetto a un asse ;
• l’ asse è unico , pertanto la sua direzione non ha significato ai fini della costruzione del concetto;
• i vertici corrispondenti della figura di partenza e della sua riflessa sono equidistanti dall’asse di simmetria ;
• i segmenti che uniscono i vertici corrispondenti sono perpendicolari rispetto all’asse e paralleli fra loro ;
• la figura riflessa è uguale a quella di partenza ma è orientata diversamente perché ha verso opposto
Considerando le proprietà della simmetria, riflettiamo su quali siano gli insegnamenti più diffusi nelle pratiche didattiche che sono inutili, o addirittura controproducenti, alla costruzione del concetto stesso.
Spesso nei libri si trovano indicazioni di questo genere:
In realtà l’ asse è unico e la sua posizione nel piano (verticale, orizzontale, obliquo, interno ed esterno) non modifica nessun aspetto del concetto di simmetria; pertanto è inutile, o addirittura fuorviante, obbligare gli alunni/le alunne a cogliere questa distinzione.
L’ asse può essere in qualsiasi posizione
È consuetudine inoltre introdurre la simmetria come completamento di una figura poiché facilmente intuibile dagli alunni/dalle alunne. In realtà tale proposta non aiuta a cogliere le proprietà della simmetria soprattutto l’equidistanza dei punti corrispondenti dall’asse di simmetria, poiché alcuni di questi punti sono sull’asse stesso, e può far pensare che per simmetria si intenda solo il completamento di una figura come si legge nel box in basso.
La retta che divide una figura in due metà sovrapponibili si chiama asse di simmetria della figura. Le due parti che formano la figura sono tra loro simmetriche .
Le proposte didattiche presenti nel Sussidiario pertanto propongono attività che pongano gli alunni/le alunne in situazioni nelle quali l’intuizione abbia un ruolo meno rilevante e che, proprio per questo, li stimolino a osservare e li guidino a cogliere le proprietà della simmetria. Come attività preliminari a quella presente nel volume di quarta alle pagine 102, 103 si possono realizzare le seguenti proposte.
Attivita 1
Il gioco dello specchio
L’insegnante chiama una bambina, pone davanti a lei per terra una corda che indichi la posizione dello specchio e poi chiama un’altra bambina, che si metta in modo da giocare a fare la figura riflessa. Istintivamente sarà molto probabile che la seconda bambina si ponga di fronte alla prima: stimoliamo i compagni/le compagne a riflettere sulla posizione chiedendo perché ha scelto proprio quel posto e se cambia qualcosa se si colloca in un altro punto.

Il gioco inizia e la prima bambina fa dei movimenti mentre la seconda li esegue come se fosse l’immagine riflessa. Mediante domande mirate, guidiamo i bambini/le bambine nell’osservazione per cogliere il verso: se la bambina alza la mano destra, il suo riflesso alza la sinistra; se si sposta a sinistra, il riflesso si sposta a destra; se ruota a destra lei ruota a sinistra.
Continuiamo osservando la distanza dalla corda/specchio: che cosa fa l’immagine riflessa se la bambina si allontana dallo specchio?
E se si avvicina? Mettiamo la bambina/riflessa a una distanza dalla corda differente rispetto alla prima bambina e chiediamo se va bene, ed eventualmente perché non va bene. Aiutiamo i bambini/le bambine a concludere che il riflesso si muove con verso opposto rispetto alla bambina che si specchia, mentre invece la sua distanza dalla corda/specchio rimane sempre la stessa.
Attività 2
Il verso dello specchio
Osserviamo alcune immagini allo specchio. Si distribuiscono degli specchi fatti con cartoncini rigidi di carta lucida e delle immagini che non siano simmetriche ma che abbiano un verso ben definito.


Il bambino/La bambina:
• osserva la sua immagine e quella riflessa e argomenta e scrive le sue osservazioni;
• muove la sua immagine e osserva che cosa succede all’immagine riflessa;
• muove lo specchio allontanandolo e avvicinandolo e osserva che cosa succede all’immagine riflessa;
• cambia posizione allo specchio disponendolo in qualsiasi direzione e verbalizza nuovamente le sue osservazioni.
Ciascun bambino/Ciascuna bambina scrive individualmente le proprie osservazioni che poi verranno lette con quelle dei compagni/delle compagne, per giungere a una sintesi collettiva condivisa.
Successivamente si può realizzare in classe l’attività presente nel volume di quarta alle pagine 102 e 103 ed eseguire gli esercizi di consolidamento proposti nel quaderno operativo. In quinta invece si ritrovano le conoscenze su tale concetto ripercorrendo la sintesi proposta a pagina 82 ed eseguendo gli esercizi di consolidamento presenti nel quaderno operativo.
Spesso i bambini/le bambine confondono l’area con la lunghezza del perimetro e faticano a rappresentarsi il concetto di equiestensione. In generale sanno calcolare il perimetro e l’area di una figura con l’uso di formule, invece stentano a mettere in relazione il perimetro e l’area di una stessa figura. Le difficoltà nascono dal fatto che nel linguaggio comune i termini superficie e area vengono usati come sinonimi (spesso dagli stessi insegnanti, anche se involontariamente). In realtà la superficie è una estensione , mentre l’ area è la misura di questa estensione . La stessa cosa vale per contorno e perimetro, infatti sappiamo che il contorno è una linea chiusa , mentre il perimetro è la misura del contorno
È importante iniziare con delle attività molto semplici che permettano osservazioni e confronti tra figure.
Attività 1
Facciamo osservare il disegno dato in fotocopia e chiediamo:
Le figure hanno la stessa area?
Ogni gruppo dà la propria risposta spiegando agli altri quale procedura hanno usato per calcolare l’area. Concludiamo che le figure hanno la stessa area anche se la forma è diversa.
Diamo una nuova immagine e chiediamo: Quanto misura l’area colorata se prendi come unità di misura un rettangolo ? Un mezzo rettangolo ? Un doppio rettangolo ?
Oppure, possiamo proporre l’attività al contrario dando il disegno su fotocopia e chiedere:
Se l’area della figura è 12 u, quale unità di misura è stata usata?
Se l’area è 6 u? E se è 24 u?
Successivamente lavoriamo su fogli quadrettati e stimoliamo a confrontare le aree e i perimetri. Proponiamo figure come queste.
Chiediamo: Se usiamo come unità di misura un quadretto, quanto misura l’area di ciascuna figura?
Se usiamo il lato del quadretto come unità di misura, quanto misura il perimetro? Ci sono figure equivalenti? Ci sono figure isoperimetriche?
I bambini/Le bambine coglieranno che non esiste una relazione diretta tra forma e area e nemmeno tra aree e perimetro ; infatti figure diverse possono avere la stessa area, ma perimetri diversi e, viceversa, le figure possono avere lo stesso perimetro, ma aree diverse. Possiamo anche chiedere ai bambini/alle bambine di disegnare una figura a piacere di area 20 quadretti del loro quaderno (non importa se i quaderni non hanno gli stessi quadretti) e chiediamo di calcolare il perimetro. Facciamo notare che i perimetri delle figure disegnate non sono tutti uguali. Ripetiamo facendo disegnare un’altra figura di area 20 quadretti e di perimetro diverso rispetto al primo. Successivamente aggiungiamo una ulteriore difficoltà chiedendo di disegnare una figura di area 20 quadretti, ma che abbia il perimetro di 24 lati di quadretto. A questo punto l’insegnante può continuare il lavoro sul volume di quarta alle pagine 110 e 112.




Avendo lavorato a lungo sulle unità di misura lineari dove il rapporto tra una misura e la sua successiva o precedente è 10, i bambini/le bambine fanno fatica a rappresentarsi mentalmente la misura quadrata. La difficoltà sta nel comprendere che ogni misura quadrata contiene 100 volte la misura immediatamente precedente e viceversa, cioè servono 100 misure quadrate per comporre la misura immediatamente successiva. Per aiutarli nella comprensione e superare le difficoltà possiamo guidare i bambini/le bambine nella costruzione del metro quadrato a misura reale.
Costruzione del metro quadrato a misura reale
L’insegnate disegna un quadrato di lato 1 dm, fa diverse fotocopie su fogli colorati e li distribuisce ai bambini/alle bambine divisi in piccoli gruppi in modo che ciascun gruppo abbia fotocopie di un solo colore. Chiediamo a ciascun gruppo di ritagliare più di 10 quadrati per arrivare ad averne a disposizione della classe 100.
Su un foglio sufficientemente grande, preparato dall’insegnante, il primo gruppo incolla i propri quadrati disponendone 10 lungo una riga, un altro gruppo ne incolla sopra altri 10 e così via fino a comporre un grande quadrato.
Chiediamo: Quanti quadrati avete messo in ogni riga? 10.
Quante righe avete incollato? 10
Quanti quadrati ci sono in tutto? 100 quadrati piccoli.
Formalizziamo in linguaggio matematico come i bambini/le bambine hanno proce-
duto al conteggio:
10 dm x 10 dm = 100 dm2
I bambini/Le bambine vedono facilmente che 1 m2 è formato da 100 dm2.
Attività 2
Lavoriamo su carta millimetrata
Per visualizzare concretamente le unità di superficie facciamo ritagliare su carta millimetrata il dm2, come in figura, lo facciamo incollare sul quaderno e chiediamo di colorare un quadratino che corrisponde a 1 cm2 e poi di colorare il mm2. Chiediamo di contare da quanti cm2 è formato un dm2, da quanti mm2 è formato un cm2 e chiediamo di calcolare da quanti mm2 è formato un dm2: 100 mm2 x 100 volte.
Usiamo ancora la carta millimetrata per far disegnare ai bambini/alle bambine delle figure di diversa forma che abbiano stessa area o con area diversa, come in figura.
Facciamo calcolare l’area, contando di volta in volta con unità di misura differenti, per completare poi una tabella come questa.
Se l’insegnante lo ritiene opportuno, è possibile chiedere di misurare anche il perimetro, come si vede in tabella.
Come esercizio per casa, chiediamo di disegnare su carta millimetrata figure di area 6 cm2; 25 mm2; 100 mm2 ecc…, di ritagliarle e poi incollarle nel quaderno, scrivendo sotto a ciascuna il relativo perimetro esprimendolo sia in cm che in mm.
Per i bambini/le bambine è facilmente intuibile che due figure congruenti hanno uguale area , ma faticano a riconoscere la stessa uguaglianza nel caso di due poligoni che hanno forma diversa , cioè che non sono congruenti.
Per superare tale difficoltà è utile lavorare sull’equiscomponibilità e sull’equicomponibilità di poligoni, proponendo attività che stimolino il bambino/la bambina a confrontare le superfici di figure equivalenti ma non congruenti, chiedendo di dividerle in poligoni noti più piccoli e fra loro congruenti. Facciamo poi confrontare le superfici e verificare che, siccome sono composte dagli stessi poligoni , sono equiestese
Possiamo procedere anche al contrario facendo scomporre una figura in poligoni noti più piccoli e chiedendo di utilizzare gli stessi pezzi per comporre altri poligoni che, quindi, risulteranno fra loro equicomposti e, pertanto, equiestesi.
Nel volume di quarta dalla pagina 114 alla pagina 117 sono proposte attività e riflessioni che permettono di sviluppare tali concetti e consentono di comprendere che le figure equicomposte sono equivalenti e che figure equivalenti non sempre sono anche isoperimetriche.
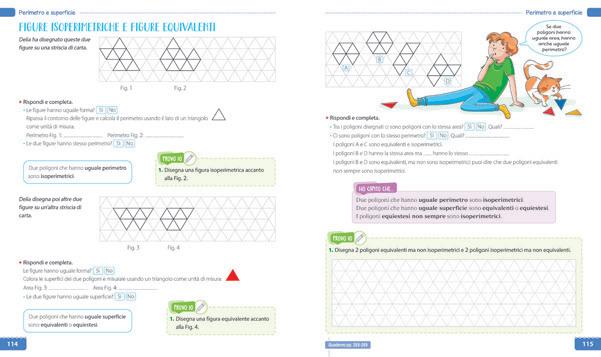

Per consolidare il lavoro svolto sul Sussidiario, successivamente, si può proporre la seguente attività.
Attività 1
Chiediamo di disegnare un rettangolo a piacere e una sua diagonale. Facciamo ritagliare lungo la diagonale per ottenere due triangoli rettangoli scaleni uguali. Scegliamo con gli alunni/le alunne un colore per evidenziare nei due triangoli lo stesso lato, poi concordiamo un altro colore per un altro lato e così per il terzo. Tutti gli alunni/ le alunne avranno usato gli stessi colori per indicare gli stessi lati nei due triangoli, come in figura.
Chiediamo di comporre tutte le figure che si possono ottenere ruotando o ribaltando i triangoli in modo da far combaciare i lati uguali. Ogni figura composta verrà disegnata sul quaderno e nominata. Le figure che otterranno sono le seguenti:
Guidiamo i bambini/le bambine nell’osservazione chiedendo: Quante figure diverse avete ottenuto? Da quali poligoni è formata ogni figura?
Concludiamo che le figure sono equicomposte perché formate sempre dagli stessi due triangoli e che quindi sono sicuramente equiestese.
Osserviamo il perimetro e chiediamo: Saranno anche isoperimetriche?
Per verificare le risposte, giuste o sbagliate che siano, chiediamo di calcolare il perimetro senza misurare i lati, ma facendo una stima (utilizziamo dei colori per far vedere le uguaglianze dei lati, il colore è utile per la discussione).
Ricordiamo che i lati di uguale lunghezza hanno lo stesso colore e facciamo scrivere da quali lati è formato il contorno del rettangolo: due lati rossi (||) e due lati blu (|||).
Stimoliamo i bambini a trovare una scrittura più sintetica, come la seguente: 2 rossi (||) + 2 blu (|||).
Continuando a riflettere sulla scrittura è possibile che qualche bambino abbrevi ulteriormente la scrittura e proponga l’espressione 2r + 2b.
Facciamo calcolare nello stesso modo i perimetri di tutte le figure e poi confrontiamoli:
Ci sono figure isoperimetriche?
L’insegnante potrà continuare con attività simili per capire che è possibile fare Matematica senza effettuare misurazioni , ma cogliendo solo le relazioni tra i lati
Stimoliamo i bambini/le bambine a scoprire alcune proprietà dei triangoli proponendo le seguenti attività.
Attività 1
Deformabile oppure no?
Facciamo costruire ai bambini/alle bambine con delle striscioline di cartoncino rigido di diverse lunghezze, preparate dall’insegnante, un quadrilatero generico e un triangolo. Chiediamo di premere su un vertice del quadrilatero e osserviamo che cambia forma; ripetiamo la stessa cosa con il triangolo e osserviamo che rimane com’era.
Chiediamo: che cosa è cambiato nel quadrilatero? Sicuramene noteranno che ha cambiato forma, ma il perimetro non è cambiato perché i lati sono gli stessi. Il triangolo invece non si deforma , quindi una volta costruito rimane sempre lo stesso.
Successivamente prepariamo 4 strisce di cartoncino. Pieghiamo due strisce in modo da costruire due quadrati distinti fissando le estremità con dello scotch senza sovrapporle. Pieghiamo le altre due strisce in tre parti in modo da formare 2 triangoli che chiuderemo come prima. Sulla cattedra appoggiamo i quadrati su un lato in posizione verticale e, un po’ più distante, i due triangoli uno accanto all’altro come nel disegno.
Appoggiamo una penna sui quadrati e osserviamo che si schiacciano rapidamente, mentre la costruzione triangolare resiste anche con più penne sopra.
Chiediamo ai bambini/alle bambine: Perché la prima costruzione si piega subito mentre la seconda no? Lasciamo ai bambini/alle bambine il tempo di fare le loro riflessioni. Soffermiamoci sul triangolo che resiste al peso delle penne ed è proprio questa sua caratteristica che fa sì che il triangolo sia molto usato nelle costruzioni , come per esempio le capriate dei tetti, nelle costruzioni di edifici, ponti e torri.
Stimoliamo i bambini/le bambine a cercare nella realtà che li circonda e a fotografare costruzioni che contengono triangoli oppure a ricercare su giornali, cartoline, riviste e/o sul web (insieme a una persona adulta) immagini di costruzioni che hanno il triangolo, per poi incollarle sul quaderno. Sotto a ogni immagine scriveranno il nome della costruzione e coloreranno su di essa i triangoli o il triangolo che la compongono.
Ripercorriamo l’esperienza leggendo la pagina 118 del volume di quarta.
Con 3 striscioline è sempre possibile costruire un triangolo?
I bambini/Le bambine vengono divisi in coppie e ogni coppia sceglie tre strisce per costruire un triangolo fermando le strisce con i fermacampioni. Intanto l’insegnante prepara un cartellone diviso a metà in verticale, sulla destra lascia uno spazio bianco e sulla sinistra scrive una tabella, come questa.
Lunghezza lato più lungo
Somma della lunghezza dei lati rimanenti (lato 2 + lato 3)
Ottengo un triangolo Non ottengo un triangolo
Ogni coppia attaccherà il proprio triangolo e completerà la sua riga sulla tabella.
Una volta incollati tutti i triangoli e completata la tabella chiediamo:
Siete riusciti tutti a costruire un triangolo con le vostre strisce?
In quali casi è possibile costruire un triangolo?
Invitiamo i bambini/le bambine a osservare le informazioni inserite nella tabella e lasciamo il tempo di esprimere le riflessioni fino ad arrivare a una condivisione del concetto di costruibilità . Insieme poi si giunge, per aggiustamenti linguistici, alla relazione che scriveranno nel quaderno.
Osserviamo nuovamente la tabella per evidenziare i casi in cui non è stato possibile costruire il triangolo. Se fra le scelte degli alunni/delle alunne mancasse una terna di strisce che non dà luogo alla costruzione di un triangolo, sarà l’insegnante stesso a proporre il caso. Lasciamo agli alunni/alle alunne il tempo e i tentativi per esprimere la condizione di impossibilità. Consolidiamo quanto scoperto con l’attività a pagina 119.
Stimoliamo i bambini/le bambine a scoprire alcune proprietà dei quadrilateri proponendo le seguenti attività.


Si ripete l’attività 2 fatta con i triangoli, dando ai bambini/alle bambine 4 strisce di cartoncino di diverse lunghezze. Dopo aver costruito i quadrilateri, averli attaccati nel cartellone e completato la tabella, si procede all’analisi dei risultati chiedendo: Siete riusciti tutti a costruire un quadrilatero con le vostre strisce?
In quali casi è possibile costruire un quadrilatero?
Invitiamo i bambini/le bambine a osservare le informazioni inserite nelle tabelle e lasciamo loro il tempo di fare tentativi e di intuire la condizione di costruibilità e di esprimerla correttamente. Non sarà difficile capire che il lato maggiore deve essere minore della somma degli altri tre. Insieme poi si giunge alla condivisione del concetto e, per aggiustamenti linguistici, a esplicitare in linguaggio matematico la relazione che scriveranno nel quaderno.
Una novità rilevante rispetto al triangolo è la deformabilità dei quadrilateri ottenuti
Osserviamo nuovamente la tabella per evidenziare i casi in cui non è stato possibile costruire il quadrilatero. Se fra le scelte degli alunni/delle alunne mancasse una quaterna di strisce che non dà luogo alla costruzione del quadrilatero, sarà l’insegnante a proporre il caso. Lasciamo agli alunni/alle alunne il tempo e i tentativi per esprimere la condizione di impossibilità. Consolidiamo quanto scoperto con l’attività a pagina 122 del volume di quarta.
Attività 2
Procediamo all’analisi delle caratteristiche dei quadrilateri sviluppando ulteriormente le attività proposte nel volume di quarta alle pagine 124 e 125. L’insegnante disegna alla lavagna una linea come quella in figura 1 che i bambini/le bambine copieranno sul quaderno. Facciamo descrivere la linea disegnata per arrivare a riconoscere che:
• è una linea spezzata aperta;
• è formata da 3 segmenti di diversa lunghezza;
• non ci sono segmenti paralleli né perpendicolari tra loro.
Con un fermacampione facciamo attaccare all’estremità del segmento superiore la striscia di cartoncino, come in figura 2.
Facciamo muovere il lato mobile e osservare che cosa si ottiene chiedendo: Quali figure ottenete muovendo il lato? Tanti quadrilateri.
Hanno tutti la stessa forma? No.
Soffermiamoci su un quadrilatero qualsiasi e guidiamoli a osservare come sono fra loro i lati per scoprire eventuali relazioni: Ci sono lati paralleli? Ci sono lati perpendicolari?
Procedendo per tentativi e correzioni, muovendo l’asticella lentamente, guidiamo i bambini/le bambine alla ricerca del trapezio fino ad arrivare alla figura 2. Nella posizione indicata otteniamo un trapezio, cioè un quadrilatero che ha due lati opposti paralleli
Riproponiamo la stessa attività partendo però da una linea spezzata che ha già due segmenti paralleli, come in figura, e ripetiamo la costruzione di prima.
Fig. 2
Facciamo muovere il lato e chiediamo: Quali quadrilateri si ottengono?
Si tratta di tanti trapezi. Facciamo osservare e scrivere via via che scoprono le figure, le relazioni dei lati di ogni trapezio per giungere alla loro classificazione: scaleni, isosceli e rettangoli.
Dopo la scoperta del trapezio rettangolo, muovendo lentamente l’asticella, si va alla ricerca del parallelogramma, cioè un trapezio con i lati opposti uguali e paralleli a due a due.
Questi due semplici modellini aiutano a capire che i trapezi sono quadrilateri e che tra tutti i trapezi c’è il parallelogramma, quindi possiamo affermare che il parallelogramma è un trapezio.
Si può consolidare quanto scoperto leggendo e completando le pagine del Sussidiario partendo dalla pagina 124 del volume di quarta.
Per promuovere la scoperta delle caratteristiche dei quadrilateri nel Sussidiario è stato proposto un percorso che parte dall’analisi della figura che possiede meno proprietà, il trapezio, per giungere all’analisi di quella che ne ha di più, cioè il quadrato. Nel considerare le aree invece è stato svolto, più o meno, il percorso inverso, infatti parte dallo scoprire come si calcola l’ area del rettangolo per arrivare a quella del trapezio

Trovare l’area di una figura significa calcolare quante misure quadrate sono necessarie per ricoprire la superficie del poligono che stiamo esaminando. Le attività presenti nel Sussidiario guidano il bambino/la bambina alla scoperta della regola utile a calcolare l’area di un poligono, lavorando in modo opportuno sull’equiscomponibilità, coinvolgendolo in un percorso di osservazione e di manipolazione. Le formule per il calcolo delle aree, pertanto, costituiscono la tappa finale di un ragionamento che con queste viene sintetizzato e formalizzato in linguaggio matematico. L’obiettivo da perseguire non è quello di giungere alla formalizzazione delle formule per poi memorizzarle e applicarle in modo meccanico, quanto piuttosto di promuovere nell’alunno/a la capacità di procedere il più autonomamente possibile nella manipolazione di figure e in percorsi di analisi e di sintesi che gli/le consentano di calcolare l’area di un poligono in qualsiasi contesto. L’insegnante può appropriarsi delle proposte presenti nel Sussidiario nei volumi di quarta e di quinta relative al calcolo dell’area di ciascun poligono, costruendo insieme agli alunni/ alle alunne i modelli proposti e manipolandoli secondo il ragionamento presentato. Sul quaderno ogni alunno/alunna attaccherà il proprio modellino e spiegherà con le sue parole il ragionamento seguito per scoprire come calcolare l’area. Per effettuare la sintesi collettiva, ripercorrendo in modo guidato le riflessioni spontanee emerse in classe durante la manipolazione, si possono usare le pagine del Sussidiario.
Ulteriori riflessioni
Consideriamo la formula A = b x h
La formula dell’area è un’uguaglianza tra una grandezza scritta a sinistra (l’area) e una espressione che contiene altre grandezze (base e altezza) scritte a destra del simbolo che la esplicita ( = ). Questa uguaglianza consente di trovare la misura di un’incognita, in questo caso l’area, conoscendo le altre grandezze.
Trattandosi di un’uguaglianza, può essere letta in entrambi i versi:
A = b x h
pertanto possiamo scrivere A = b x h, ma anche b x h = A
Inserendo i fattori in uno schema aiutiamo i bambini/le bambine a cogliere le relazioni esistenti fra essi:
b A x h
e a capire che, essendo un’uguaglianza, la relazione è leggibile in entrambi i versi, per cui si può conoscere l’area conoscendo la lunghezza dei lati (base ed altezza), ma si può anche conoscere la lunghezza di un lato se si conosce l’area e la lunghezza dell’altro lato.
b A x h : h h A x b : b
Essendo un’uguaglianza e non essendoci un verso obbligato di lettura (da sinistra a destra o da destra a sinistra), non esistono “formule inverse” e per questo motivo nel Sussidiario non se ne parla. Chiarito bene con i bambini/le bambine tale concetto, non è necessario obbligarli all’inutile fatica di memorizzare tutte le formule perché le sapranno ricavare da soli procedendo, in modo autonomo, nel ragionamento sopra indicato.
Nel testo, infine, non sono state presentate “formule” relative al calcolo del perimetro. Essendo la formula la “rappresentazione, mediante opportuni simboli, di una relazione che colleghi due o più enti matematici” (Enciclopedia Treccani), diventa una regola che generalizza la relazione espressa.
Nel caso del calcolo del perimetro non esiste una regola, è la definizione stessa di perimetro che indica come si calcola: è la misura del contorno, quindi si ottiene sommando le lunghezze di tutti i lati di un poligono.
Nel caso di poligoni equilateri il calcolo del perimetro si può esprimere con la scrittura P = l x numero dei lati , ma si tratta comunque della somma della lunghezza dei lati che però è stata espressa con una struttura moltiplicativa. È una generalizzazione a cui giungono spontaneamente i bambini/le bambine quando hanno capito che cos’è il perimetro, pertanto non è necessario esplicitarla e farla memorizzare.
La nostra conoscenza della Matematica in Mesopotamia deriva dal ritrovamento di più di 400 tavolette in scrittura cuneiforme.
I popoli della Mesopotamia usavano un sistema basato sul 6 e sul 10. Scrivevano i numeri sommando questi segni: usavano quindi un sistema addizionale . Per scrivere un numero grande usavano molti segni. Per scrivere i numeri fino a 59 usavano incidere 5 cunei larghi (ciascuno rappresentava 10 unità) disposti di lato e 9 cunei verticali che rappresentavano l’unità.
Anche gli Egizi usavano un sistema addizionale . Questi erano i loro simboli.
I simboli potevano essere ripetuti quanto era necessario, fino a 9 volte. Ad esempio, il numero 4622 (presente su una iscrizione nel tempio di Karnak) era scritto così:
• Schede operative
• Mappe
• Percorso STEAM
1 Inserisci i numeri nella tabella, poi scrivi la scomposizione come nell’esempio.
3 Completa scrivendo il valore di ciascun simbolo o disegnando il numero.
1 Usa sempre tutte le cifre 8, 7, 1, 3 per scrivere il numero pari più piccolo e il numero pari più grande.
Numero pari più piccolo ➔
Numero pari più grande ➔
2 Usa le cifre per scrivere due numeri formati da due cifre la cui differenza sia la maggiore possibile.
Numeri: Differenza 3 Completa le relazioni inserendo numeri opportuni.
1 Esegui l’operazione e scrivi al posto giusto i suoi termini.
3° addendo 1° addendo somma 2° addendo somma o totale
2 Completa la tabella e colora il completamento giusto. +
• Se a un numero sommi 0 ottieni:
lo stesso numero. il numero successivo.
• Se a un numero sommi 1 ottieni:
lo stesso numero. il numero successivo.
3 Segui le indicazioni per eseguire le addizioni.
48 + 52
scomponi i due addendi
40 + 8 + +
cambia l’ordine degli addendi
associa gli addendi
il secondo addendo
il primo addendo
1 Calcola a mente e collega ogni addizione al nome della o delle proprietà applicate.
14 + 36 = 36 + 14 =
18 + 12 + 35 = (18 + 12) + 35 =
17 + 34 + 26 = 17 + (34 + 26) =
36 + 13 + 17 + 24 = (36 + 24) + (13 + 17) =
commutativa e associativa
commutativa
2 Trova due modi per calcolare il numero da inserire nel cerchio in alto.
Quale proprietà hai applicato nel secondo modo?
3 Scomponi i numeri 11, 22, 33. Poi applica la proprietà associativa.
Ricorda che: 11 = 10 + 1 22 = 20 + 2 33 = 30 + 3
11 + 37 = 10 + 1 + 37 = 10 + ( + )
= 56 + 22 = 56 + 20 + = (56 + 20) + = + = 33 + 18 = + + 18 = + ( + 18) =
4 Completa le successioni.
Ricorda che 9 = 10 – 1, quindi aggiungi prima 10 e poi togli 1. + 9 + 9 + 9
Ricorda che 99 = 100 – 1, quindi puoi aggiungere 100 e poi togliere 1. + 99 + 99 + 99 + 99 41 Proprietà associativa
Nome Classe Data
1 Esegui l’operazione e scrivi al posto giusto i suoi termini. minuendo differenza sottraendo resto o differenza
2 Completa la tabella, lasciando vuote le caselle se non è possibile eseguire l’operazione richiesta. Poi colora il completamento giusto.
• Se a un numero sottrai 0 ottieni: lo stesso numero. il numero successivo.
• Se a un numero sottrai 1 ottieni: lo stesso numero. il numero precedente. il numero successivo.
• La sottrazione fra numeri naturali è possibile solo se: il minuendo è minore del sottraendo. il minuendo è maggiore o uguale al sottraendo.
3 Calcola a mente, poi collega ogni operazione al nome della proprietà che è stata applicata.
54 – 27 = (54 – 4) – (27 – 4) =
328 – 113 = (328 + 2 ) – (113 + 2) =
71 – 33 = (71 – 3) – (33 – 3) =
Proprietà commutativa
Proprietà invariantiva
Proprietà associativa
1 In ciascun insieme scegli i numeri e inventa tutte le sottrazioni possibili. Puoi usare più volte uno stesso numero.
Quali operazioni non puoi eseguire?
2 In ogni sottrazione è stata applicata la proprietà invariantiva. Scrivi l’operazione effettuata per trasformare i numeri e poi esegui il calcolo.
3 Usa tutti i numeri indicati e l’addizione e la sottrazione come operatori per ottenere il numero scritto nella stella.
Nome Classe Data
1 Esegui la moltiplicazione e scrivi al posto giusto i suoi termini. moltiplicando prodotto prodotto parziale moltiplicatore prodotto parziale
2 Completa la tabella e colora il completamento giusto.
• Se moltiplichi un numero per 0 ottieni: lo stesso numero. il numero 0.
• Se moltiplichi un numero per 1 ottieni: lo stesso numero. il numero successivo.
3 Segui le indicazioni per eseguire le moltiplicazioni applicando le proprietà indicate. x
Proprietà associativa
8 x 5
Proprietà associativa
6 x 5 x 7
( x ) x scegli due fattori e moltiplicali calcola
Proprietà commutativa x cambia l’ordine dei due fattori calcola +
34 x 8
scomponi il moltiplicando moltiplica i due addendi calcola
(30 + ) x 8
(30 x 8) + ( x 8)
Nome Classe Data
1 Segui le indicazioni per eseguire le moltiplicazioni applicando le proprietà.
24 × 4
riscrivi il moltiplicatore come prodotto
24 × 2 × 2
applica la proprietà associativa calcola
(24 × 2) ×
32 × 4
riscrivi il moltiplicatore come prodotto
15 × 4
riscrivi il moltiplicatore come prodotto
applica la proprietà associativa calcola
applica la proprietà associativa calcola
2 Sul quaderno segui gli stessi passaggi che hai usato nell’esercizio precedente per eseguire le seguenti moltiplicazioni.
3 Esegui le moltiplicazioni applicando la proprietà associativa. 6
4 Esegui le moltiplicazioni associando i fattori in maniera opportuna.
1 Inserisci al posto giusto i termini: divisore • dividendo • quoziente • quoto • resto
2 Completa la tabella, lasciando vuote le caselle se non è possibile eseguire l’operazione richiesta. Poi colora il completamento giusto.
•
dividi un numero per 1 ottieni: lo stesso numero. il numero successivo.
• Dividere un numero per 0 è: impossibile. possibile.
• Se dividi 0 per un numero ottieni: 1 0
3 Dario ha eseguito queste divisioni in maniera distratta, controlla se ha fatto bene. Fai i calcoli sul quaderno, se ci sono errori, correggi. a. 325 : 25 = 13
152 : 3 = 384
: 8 = 255
450 : 30 = 15
: 5 = 953
944 : 6 = 324
4 Esegui i calcoli in colonna sul quaderno, poi trascrivi i risultati.
1 Calcola la metà della metà, come nell’esempio.
20 : 4 = Calcolo prima la metà (20 : 2) : (4 : 2) e poi ancora la metà 10 : 2 = 5 80 : 4 = 28 : 4 =
1 Dividi per 3 i seguenti numeri.
45 : 3 = con resto
19 : 3 = con resto
27 : 3 = con resto 24 : 3 = con resto
53 : 3 = con resto
123 : 3 = con resto
Classificali in base alla proprietà indicata.
Numeri divisi per 3 con resto 0. Numeri divisi per 3 con resto diverso da 0.
Riscrivi solo i numeri con resto 0, cioè che sono divisibili per 3:
2 Completa gli schemi.
18 : 6 = con resto perché x 6 = quindi 18 è divisibile per 6; 6 è divisore di 18; 18 è multiplo di 6
35 : 7 = con resto perché x 7 = quindi 35 è per 7; 7 è divisore di ; 35 è multiplo di
84 : 4 = con resto perché x =
quindi è per ; è divisore di ; è multiplo di
3 Colora solo le nuvolette che contengono i multipli di 2, 4 e 5.
Nome Classe Data
1 Completa la tabella eseguendo solo le divisioni che hanno resto 0. Poi completa. :
di
– Quale divisore è comune a tutti i numeri?
– Quale divisore è comune a tutti
i numeri pari?
Scrivi i multipli di 1 e i multipli di 2
– Quale numero è multiplo di 3 e di 5?
– Quali numeri sono multipli di 2 e di 5?
2 Inserisci nella tabella i numeri al posto giusto. Fai attenzione: ci sono numeri che possono essere collocati anche in due caselle.
21
Numeri
Numeri
3 Inserisci i numeri in tabella e completa.
Scrivi i numeri che sono sia multipli di 7 sia multipli di 3:
30 • 15 • 80 • 21 • 45 • 28 • 40 • 20 • 42 Multipli
– Riscrivi i numeri multipli sia di 3 sia di 5:
– Riscrivi i numeri multipli sia di 4 sia di 5:
– Riscrivi i numeri multipli sia di 4 sia di 7:
– Riscrivi i numeri multipli sia di 3 sia di 7:
Nome Classe Data
Ingresso singolo € 6,50
Abbonamento 10 ingressi € 60
Abbonamento 20 ingressi € 108
Quanto costano 10 ingressi singoli?
• E se prendi l’abbonamento da 10 ingressi, quanto risparmi?
• Quanto costa 1 ingresso se compri l’abbonamento da 20 ingressi?

1 Scrivi la frazione che indica la parte colorata.
2 Colora la parte corrispondente alla frazione.
3 Scrivi le frazioni complementari a quelle date.

5 Risolvi i problemi sul quaderno.
• In una scatola Emma aveva 992 perline di tutti i colori. Se ne ha già usate i 3 8 , quante perline sono rimaste nella scatola?
• Il mio album contiene 258 figurine; ne ho già attaccate i 4 6 . Quante me ne mancano?
• Lara ha avuto in regalo dai nonni 150 euro. Se ha speso i 3 10 dei suoi soldi, quanto le resta?
il valore della cifra 3 nei seguenti numeri decimali, come nell’esempio.
1 Incolonna inserendo la virgola nelle tabelle e poi esegui le operazioni.
1 Esegui le addizioni in colonna.
42,78 + 35,18 = • 76,29 + 19,175 = • 345,6 + 134,74 = • 44,5 + 17,309 =
2 Esegui le sottrazioni in colonna. 135 – 4,29
3 Esegui le moltiplicazioni in colonna. 719 × 4,5 =
7,8 × 4,2 =
46,7 × 83 =
4 Esegui le divisioni in colonna. 74,64 : 12 =
: 18
1 Quale unità di misura è più adatta a misurare:
– l’altezza del tuo banco?
– il peso di una penna?
– la quantità di succo in un bicchiere?
– il peso della tua gomma per cancellare?
– il tempo che trascorri a scuola?
2 Completa la tabella ed esegui le trasformazioni.
MISURE DI LUNGHEZZA
Nome Classe Data ©
MISURE DI CAPACITÀ
MISURE DI
3 Trasforma le durate di tempo in giorni e ore e viceversa, come negli esempi.
26 h = 1 d e 2 h 1 d e 4 h = 28 h
38 h = 1 d e 10 h =
48 h = 2 d e 1 h =
32 h = 3 d =
4 Trasforma le durate di tempo in ore e minuti e viceversa, come nell’esempio.
80 min = 1 h e 1 h e 5 min = 72 min = 1 h e 40 min =
100 min = 2 h e 10 min = 120 min = 3 h e 12 min =
1 Quale unità di misura è più adatta a misurare:
– l’altezza del tuo banco?
– il peso di una penna?
– la quantità di succo in un bicchiere?
– il peso della tua gomma per cancellare?
– il tempo che trascorri a scuola?
– il tempo che impieghi a fare colazione?
2 Esegui le equivalenze nelle tabelle, come negli esempi.
g = Nome Classe Data
3 Scomponi indicando il valore di ogni cifra.
Mg =
g =
dg =
hg =
dag =
cg =
4 Indica il valore delle unità intere e delle unità decimali, come nell’esempio.
l = 18 l e 34 cl
dam =
dag =
Nome Classe Data
1 Quali monete puoi utilizzare per comporre le seguenti cifre?
Osserva l’esempio e completa.
euro
euro
euro
euro
euro
2 Osserva i disegni e completa gli schemi corrispondenti. peso lordo 30 kg tara 2 kg peso netto
euro
peso netto 500 kg peso lordo tara 5 000 kg
Caffè Caffè Caffè Caffè Caffè Caffè
Caffè Caffè Caffè Caffè Caffè Caffè Caffè Caffè Caffè CaffèCaffè Caffè
tara peso netto 500 g tara –peso netto tara + peso netto
peso lordo 600 g
3 Completa le tabelle.
Nome Classe Data
1 Quali monete puoi utilizzare per comporre le seguenti cifre? Osserva l’esempio e completa.
2 Completa la tabella.
Peso lordo Peso netto Tara
3 cassette di uva kg 15 kg 27 hg
1 scatola di spaghetti 500 g g 35 g
5 vasetti di olive verdi g 18 hg 750 g
4 sacchetti di biscotti 31,20 hg 3020 g g
2 casse di pesce 26 kg kg 180 dag
6 panettoni in scatola 6 kg 530 dag dag
3 Completa le tabelle.
Costo di 1 dm:
Costo di 1 m di stoffa: 20,00 €
Costo di 1 kg di prosciutto: 30,00 €
Costo di 3 m:
Costo di 1 2 m:
Costo di 1 kg e mezzo:
Costo di 3 kg:
Costo di 4 hg:
4 Risolvi il problema sul quaderno.
Un negoziante vende una partita di 180 bottiglie di acqua minerale a 0,45 euro l’una.
Per ogni bottiglia il negoziante guadagna
0,15 euro.
Qual è stata la spesa totale del negoziante?
Nome Classe Data
1 Nomina i punti corrispondenti, poi unisci e disegna la figura simmetrica.
2 Disegna la figura simmetrica.
3 Disegna ogni volta la figura simmetrica rispetto agli assi disegnati. Poi colora le figure traslate.
4 Esegui le seguenti traslazioni della figura: 10 ➔ , 5 ➔ , 8 ➔ .
Nome Classe Data
1 Disegna la figura simmetrica rispetto agli assi tratteggiati.
2 Disegna ogni volta la figura simmetrica rispetto agli assi disegnati.
Poi colora le figure traslate.
3 Esegui le seguenti traslazioni della figura: 13 ➔ , 6 ➔ , 11 ➔ .
Nome Classe Data
1 Osserva e completa.
• La linea curva chiusa semplice è:
• La linea curva chiusa intrecciata è:
• La linea curva aperta semplice è:
• La linea curva aperta intrecciata è:
2 Scrivi al posto giusto: retta • semiretta • segmento.
3 Completa con: parallele • incidenti • perpendicolari.
• a e b sono rette
• c e d sono rette
• e e f sono rette
4 Scrivi i nomi dei seguenti angoli.
Nome Classe Data
1 Osserva e completa. a b c d e f g h
• Le linee curve chiuse sono:
• Le linee spezzate chiuse sono:
• Le linee curve aperte sono:
• Le linee spezzate aperte sono:
2 Scrivi al posto giusto: retta • semiretta • segmento. a A B c
3 Negli spazi disegna due segmenti: paralleli incidenti perpendicolari
4 Completa come nell’esempio.
• È un angolo di 90°. ➔ angolo retto
• È un angolo che misura meno di 90°. ➔
• È un angolo che misura più di 90° e meno di 180°. ➔
• È un angolo di 180°. ➔
• È un angolo di 360°. ➔
1 Scrivi P solo all’interno dei poligoni.
2 Collega con una freccia ogni termine alla parte di figura corrispondente. lato angolo vertice diagonale
3 Osserva i poligoni e completa la tabella.

Nome Classe Data
1 Fai una 8 sui poligoni e completa la tabella per i soli poligoni.
poligono concavo o convesso? n° lati nome
2 Scrivi il nome delle parti indicate dalle frecce.
3 Completa le frasi.
• Un poligono è regolare quando ha tutti i e gli congruenti.
• Un poligono che ha solo i lati uguali si dice
• Un poligono che ha solo gli angoli uguali si dice
4 Colora solo i poligoni regolari.
1 Classifica i triangoli rispetto ai lati e agli angoli segnando con una 8. equilatero isoscele scaleno ottusangolo acutangolo rettangolo
2 Completa la classificazione: scrivi i nomi dei quadrilateri nei cartellini.
quadrilateri
1 Misura i lati dei triangoli e completa la tabella. triangoli isosceli triangoli equilateri triangoli scaleni
2 Completa le tabelle.
1 Disegna un quadrato con il lato di 6 quadretti e un rettangolo che abbia lo stesso perimetro.
2 Completa calcolando il perimetro delle figure disegnate.
quadrato perimetro triangolo scaleno perimetro
rettangolo perimetro triangolo equilatero perimetro
3 Calcola il perimetro dei seguenti poligoni.
• Triangolo equilatero con lato di 6 cm ➔
• Quadrato con lato di 8 dm ➔
• Rombo con lato di 11 cm ➔
• Rettangolo con base di 4,5 m e altezza di 2 m ➔
4 Calcola sul quaderno e trascrivi qui i risultati.
• Un triangolo isoscele ha la base di 26 dm e il lato obliquo di 22 dm.
Perimetro:
• Uno specchio quadrato ha il lato di 60 cm.
Perimetro:
Nome
1 Disegna almeno 3 poligoni isoperimetrici.
2 Completa calcolando il perimetro delle figure disegnate.
triangolo isoscele perimetro rombo perimetro
parallelogramma perimetro trapezio isoscele perimetro
3 Calcola la misura dei lati dei seguenti poligoni.
• Quadrato con il perimetro di 48 cm ➔
• Triangolo equilatero con il perimetro di 126 cm ➔
• Rombo con il perimetro di 60 cm ➔
• Rettangolo con il perimetro di 60 cm e l’altezza di 25 cm ➔
4 Calcola sul quaderno e trascrivi qui i risultati.
• Un rettangolo ha la base che misura 16 dam e l’altezza di 8 dam.
Perimetro :
• Un campo quadrato ha il perimetro di 240 cm.
Lato :
Nome Classe Data
1 Quale unità di misura useresti per misurare i seguenti elementi? Indicala.
km2 hm2 dam2 m2 dm2 cm2 mm2 aula quaderno piazza Italia
2 Inserisci nella tabella le seguenti misure, come nell’esempio.
65,24 m2 • 6,57 dm2 • 87,12 km2 • 9 148 cm2
km2 hm2 dam2 m2 dm2 cm2 mm2 da u da u da u da u da u da u da u 6 5 2 4
3 Collega con una freccia la descrizione e la marca corrispondente.
È un quadrato con il lato di 1 cm. dm2
È un quadrato con il lato di 1 dm. km2
È un quadrato con il lato di 1 km. cm2
4 Scrivi da quanti cm2 è formata ogni figura.
1 Quale unità di misura useresti per misurare gli elementi indicati? Indicala con una 8.
2 Scomponi, come nell’esempio.
3 Completa le tabelle.
4 Metti in ordine crescente, dopo aver calcolato l’area in unità di quadretto .
Nome Classe Data
1 La superficie di una figura piana è la misura: della sua larghezza. del suo confine. della sua estensione.
2 Disegna un rettangolo con la base di 9 quadretti e l’altezza di 4 quadretti. Poi disegna altri due poligoni che abbiano la stessa area del rettangolo disegnato.
3 Completa calcolando l’area delle figure disegnate. quadrato triangolo scaleno rettangolo triangolo equilatero
1 Due figure equiestese hanno uguale: perimetro. area. base.
2 Disegna 2 poligoni equiestesi, ma con perimetri diversi.
3 Completa calcolando l’area delle figure disegnate.
1 Nella vasca di un acquario ci sono 10 pesci rossi, 2 neri, 5 grigi e 6 gialli. Rappresenta i dati e realizza il grafico. Poi rispondi.
= 1 pesce
pesci rossi
pesci neri
pesci grigi
pesci gialli
• Quanti sono in tutto i pesci nella vasca?
• Immergendo una retina nella vasca, avresti maggiori probabilità di pescare un pesce nero o un pesce rosso?
• Potresti pescare un pesce blu?
2 Osserva la tabella e completa il grafico.
1 Nella vasca di un acquario ci sono 25 pesci rossi, 15 neri, 10 grigi e 20 gialli. Rappresenta i dati, disegnando l’ideogramma. Poi rispondi.
= 5 pesci
pesci rossi
pesci neri
pesci grigi
pesci gialli
• Quanti sono in tutto i pesci nella vasca?
• Immergendo una retina nella vasca, qual è la probabilità di pescare:
– un pesce rosso? La probabilità è su , cioè
– un pesce nero? La probabilità è su , cioè
– un pesce grigio? La probabilità è su , cioè
– un pesce giallo? La probabilità è su , cioè
2 Osserva la tabella e completa il grafico.
La proprietà commutativa
Se cambi l’ordine dei fattori, il prodotto non cambia.
14 x 5 = 70
5 x 14 = 70
La proprietà associativa
Se a due o più fattori sostituisci il loro prodotto, il risultato non cambia.
8 x 5 x 2 = 80
8 x (5 x 2)
8 x 10 = 80
MOLTIPLICAZIONE
È l’operazione che permette di ripetere una quantità per il numero di volte richiesto.
La proprietà distributiva rispetto all’addizione
Il prodotto non cambia se:
• scomponi un fattore in una somma di due addendi;
• moltiplichi l’altro fattore per ciascun addendo e sommi i due prodotti.
4 x 16 = 64
4 x (10 + 6) =
(4 x 10) + (4 x 6) =
40 + 24 = 64
DIVISIONE
È l’operazione che permette di ripartire delle quantità.
La proprietà invariantiva
Se moltiplichi o dividi per uno stesso numero il dividendo e il divisore, il risultato non cambia.
64 : 16 = 4
: 8 : 8
8 : 2 = 4
70 : 5 = 14
x 2 x 2
140 : 10 = 14
Frazionare significa dividere in parti uguali. 2
8
Numeratore
Linea di frazione
Denominatore
frazioni minori di 1
Le frazioni in cui il numeratore è minore del denominatore rappresentano una quantità minore
Le frazioni in cui il numeratore è maggiore del denominatore rappresentano una quantità maggiore di 1. frazioni maggiori di 1
Due o più frazioni sono complementari se, sommate, formano l’intero.
Due o più frazioni sono tra loro equivalenti se hanno lo stesso valore.
Tra due frazioni con lo stesso numeratore è maggiore la frazione con il denominatore minore:
Le frazioni che hanno come denominatore 10, 100, 1 000 si chiamano frazioni decimali.
Le frazioni decimali possono essere scritte sotto forma di numero decimale.
La virgola divide la parte intera dalla parte decimale.
per 10, 100, 1000
Quando dividi un numero per 10, 100, 1 000 il numero diminuisce del suo valore di 10, 100, 1 000 volte.
L’unità di misura fondamentale delle lunghezze è il metro; il simbolo è m.
L’unità di misura fondamentale dei pesi è il chilogrammo; il simbolo è kg.
peso lordo, peso netto, tara
• Il peso lordo è il peso del contenuto e del contenitore.
• Il peso netto è il peso del contenuto.
• La tara è il peso del contenitore.
La linea retta non cambia mai direzione; si indica con una lettera minuscola (a, b, c...).
Se fissi un punto su una retta, ottieni due semirette.
I punti sulla retta si indicano con una lettera maiuscola (A, B, C...).
Se fissi due punti su una retta ottieni un segmento, cioè una parte di retta delimitata dai due punti.
Le linee rette possono essere:
parallele: quando non hanno nessun punto in comune e sono sempre alla stessa distanza.
incidenti: quando hanno un punto in comune e formano 4 angoli uguali a due a due.
perpendicolari: sono due rette incidenti che incontrandosi formano 4 angoli retti.
I poligoni sono figure che hanno per contorno una linea spezzata chiusa.
• Ciascuno dei segmenti che delimitano un poligono si chiama lato.
• Il punto che unisce due lati consecutivi si chiama vertice.
• Il segmento che unisce due vertici opposti si chiama diagonale.


• Due lati consecutivi formano un angolo.
I TRIANGOLI sono poligoni convessi con 3 lati, 3 angoli, 3 vertici. La somma degli angoli interni di un triangolo è 180°.
In base ai lati si distinguono:


triangolo equilatero
In base agli angoli si distinguono:
triangolo rettangolo
triangolo isoscele
triangolo ottusangolo
triangolo scaleno



triangolo acutangolo
I QUADRILATERI sono poligoni con 4 lati, 4 angoli, 2 diagonali. La somma degli angoli interni di un quadrilatero è 360°.
I trapezi sono quadrilateri con una coppia di lati paralleli.
I parallelogrammi sono quadrilateri con due coppie di lati paralleli e congruenti. I parallelogrammi sono anche trapezi. angolo diagonale lato
trapezio scaleno trapezio isoscele trapezio rettangolo
delle migliaia
centinaia di migliaia decine di migliaia unità di migliaia
hk dak uk
addizione e sottrazione
È l’operazione che permette di raggruppare più quantità.
La proprietà commutativa Se cambi l’ordine degli addendi, il risultato non cambia.
24 + 16 = 40
16 + 24 = 40
La proprietà associativa Se a due o più addendi sostituisci la loro somma, il risultato non cambia.
7 + 25 + 15 = 47
7 + (25 + 15)
7 + 40 = 47
SOTTRAZIONE
È l’operazione che permette di calcolare un resto o una differenza fra due quantità.
La proprietà invariantiva Se aggiungi o sottrai la stessa quantità ai due termini dell’operazione, il risultato non cambia.
24 – 5 = 19
+ 5 + 5
29 – 10 = 19
33 – 13 = 20
– 3 – 3
30 – 10 = 20
Emy e Chris sono felici: oggi faranno una visita alla nuovissima fattoria didattica. I due gemelli amano la natura e adorano Renata, che è la responsabile della fattoria e ha fatto avere loro uno speciale pass pieno di simbolini strani. Quando il maestro li accompagna all’ingresso, ancora non sanno che cosa li aspetta, ma tu hai la certezza che... saranno un sacco di guai!

Per uscirne dovranno: risolvere problemi , costruire oggetti salva guai , decifrare codici , fare esperimenti scientifici , e naturalmente... usare il cervello !
Eh sì, è proprio un bel lavoro, ma se li aiuterai, tutto diventerà più semplice. E allora, buona giornata alla fattoria didattica e buon divertimento!

Il maestro lascia i bambini all’ingresso della fattoria. Emy e Chris mostrano il pass alla biglietteria, in un attimo sono dentro e subito corrono all’ufficio di Renata.
– Renata, siamo qui! Siamo arrivati! – gridano entusiasti.
Ma niente, nessuna risposta. La porta è chiusa e alla maniglia è appesa una busta con la scritta: “Per Emy e Chris”.
– Che strano, chissà perché non è qui ad aspettarci? – sussurra Emy prendendo la busta. – Beh, aprila! – dice impaziente il fratello. Emy apre la busta. – C’è un foglio, ma non c’è scritto niente. Guarda, Chris. Solo disegnini!
– Non sono disegnini, è un messaggio in codice! – si entusiasma Chris. – E il pass che ci ha fatto avere Renata è il decodificatore!
Scrivi in ordine le 26 lettere dell’alfabeto per completare il decodificatore.

Aiuta Emy e Chris a decodificare il messaggio di Renata.
Il messaggio è:
– Ok andiamo! – esclama Chris, ma dove sarà lo stagno?
– Aspetta un attimo. Nella busta c’è un altro foglio – replica la sorella.
Chris è perplesso: – Un altro enigma!
– Sì, ma questa volta so io come risolverlo! – esclama Emy.
l’algoritmo per portare Emy e Chris a destinazione.
Ripassa il percorso.

Grazie a te e alla tua classe, i gemelli arrivano allo stagno, ma ad accoglierli c’è Renata che è mooolto preoccupata. – Ragazzi, per fortuna siete arrivati! Guardate che disastro!
– Io non vedo niente – replica Chris.
– Appunto! Tutte le anatre dello stagno sono scomparse. E proprio il giorno prima dell’inaugurazione!
Aiuta Emy, Chris e Renata. Costruisci un richiamo per anatre.
MATERIALI:
Una cannuccia di carta



Tagliala in modo che diventi a punta.
Appiattisci bene un’estremità della cannuccia.
Soffia nell’estremità a punta della cannuccia. Ascolta il richiamo.
Ora sperimenta, completa la tabella e rispondi.

La lunghezza della cannuccia influenza il suono? In che modo? Il diametro della cannuccia influenza il suono? In che modo? cm / mm cm / mm cm / mm
Lunghezza
Diametro
Suono

I tre iniziano a soffiare e... soffiano, soffiano, soffiano, fino a quando ecco che le anatre in formazione compaiono all’orizzonte e una dopo l’altra planano nello stagno.
Renata è felice: – Grazie! Sapevo che mi avreste aiutato, ma... ma allora potete risolvere anche il mistero dei polli e delle galline scomparsi! Presto, andiamo al pollaio: magari riuscirete a costruire anche un “richiamapolli”.
Aiuta Emy, Chris e Renata. Costruisci un richiamo per polli e galline.

MATERIALI: Ripassa il percorso. Forbici Ripassa il percorso. Un bicchiere di carta Ripassa
percorso. Una graffetta
Un tovagliolino di carta

Fissa un pezzo di spago a una graffetta.
il
Buca il fondo del bicchiere e infila lo spago.
Ora sperimenta e scopri. Poi registra i dati nella tabella.
La dimensione del bicchiere influenza il suono?
Il tipo di spago o filato influenza il suono?
Se invece di un tovagliolino di carta usi altri materiali, il suono cambia?
Dimensione
Tipo di spago
Materiali
Bagna il tovagliolino, afferra lo spago e tira verso il basso con brevi strappi.



Tutti i volatili della fattoria sono tornati al loro posto: i polli e le galline nel pollaio e le anatre nello stagno.
– Ehi, ehi! – esclama all’improvviso Renata. – Da dove arrivano tutte queste formiche?
Dovrebbero essere in letargo rinchiuse nei loro nidi, ma con questo caldo... Stanno anche rubando tutti i semi dei pulcini. Presto bisogna fare qualcosa!
Aiuta Emy, Chris, Renata e soprattutto i pulcini. Scopri un liquido naturale per allontanare le formiche. Osserva le immagini: scrivi che cosa ti serve e le fasi dell’esperimento, poi rispondi.


Secondo te, quale liquido non riusciranno ad attraver sare le formiche?
Che bello! Pio pio pio... i pulcini adesso beccano felici i loro semi.
– Certo che fa proprio un bel caldo! – esclama a un tratto Renata.
– Chissà se ho caldo io o se è proprio la temperatura che sta aumentando?
– Per saperlo ci vorrebbe un termometro – suggerisce Chris.
Costruisci un termometro per scoprire se la temperatura sta aumentando.
MATERIALI:
Una cannuccia larga di silicone
Un vasetto di vetro stretto e alto
Una bacinella con cubetti di ghiaccio

Riempi il vasetto per metà di acqua.
Una bacinella con acqua calda

Aggiungi qualche goccia di colorante, un cubetto di ghiaccio e mischia.


Infila la cannuccia nel vasetto e sigilla con la plastilina. La cannuccia non deve toccare il fondo del vasetto.
Testa il tuo termometro.
Se lo metti nell’acqua calda il livello di acqua nella cannuccia si alza?
Se lo metti nel ghiaccio il livello di acqua nella cannuccia si abbassa?
sì NO NO sì
Controlla di aver seguito bene le fasi!
Il termometro è pronto per essere usato!
– Dovrebbero esserci le farfalle, invece... nemmeno una! –osserva Chris.
– Ragazzi miei, per le creature più belle dell’intero pianeta, la situazione è grave. In Italia, come in tutto il mondo, si stanno estinguendo!
– Non ci credo! – esclama Emy incredula.
– È proprio così! L’IUCN dice che il loro stato di conservazione è grave.
– E chi sarebbe questo signor IUCN? – si stizzisce Chris.
– L’IUCN non è una persona, è un’organizzazione –sorride Renata.
Cerca, insieme a una persona adulta, su Internet informazioni sull’IUCN e raccontale a Emy e Chris.


Quali dati raccoglie?
Che cos’è la lista rossa IUCN?

il percorso. Le piante e gli animali sono classificati secondo lo schema che vedi sotto.
Estinta in ambiente selvatico
Estinta EW
Minacciata
In pericolo critico
In pericolo
Vulnerabile
NT Quasi minacciata
LC Minor preoccupazione
Continua le ricerche e scopri quali sono le specie di farfalle nella Lista Rossa dell’IUCN in Italia. Disegnane tre e specifica il loro stato di conservazione. Poi decifra il messaggio.
Ripassa il percorso. Ripassa il percorso.
Ripassa il percorso.
Ripassa il percorso.
Ripassa il percorso.
Ripassa il percorso.
Nome:
Ripassa
Stato di conservazione:
EX CR VU EW EN NT LC
Nome: Ripassa
Stato di conservazione:
EX CR VU EW EN NT LC
Ripassa il percorso. Ripassa il percorso.
Ripassa
Nome:
Ripassa il percorso. Ripassa
percorso. Stato di conservazione:
Ripassa
EX CR VU EW EN NT LC

– Ma perché le farfalle si stanno estinguendo? – chiede Emy.
– Una delle cause è l’inquinamento dell’aria – risponde Renata.
– Allora è colpa dell’aria inquinata. Io sento una puzza... –afferma Emy.
– Io non sento niente, come fai a sapere che l’aria è inquinata?
Mica si vede... – ironizza Chris.

Fai un esperimento e poi racconta come si può vedere lo stato di inquinamento dell’aria.

Numera i quadrati dall’1 al 7.

Il giorno in cui inizi ricopri il quadrato 7 con un leggero strato di vaselina.
Incolla il quadrato 7 alla striscia di cartoncino e posizionala all’aperto.

Il giorno seguente ricopri di vaselina il quadrato 6 e incollalo sulla striscia.
Continua per altri 5 giorni.
Ripassa il percorso.
La differenza di colore tra il quadrato numero 7 e il quadrato numero 1 è data dall’inquinamento nell’area in cui hai svolto l’esperimento. Purtroppo tutto quello sporco entra nei nostri polmoni.
Ripassa il percorso.
Ripassa il percorso.

Anche utilizzando solo un quadrato di cartoncino puoi verificar e lo stato di inquinamento in diverse zone della città o in differenti stanze della casa.
Lavora con un compagno o una compagna e decidete che cosa potete fare anche voi per ridurre l’inquinamento dell’aria.
– Far tornare anatre, polli e galline è stato facile – afferma
Chris – ma con le farfalle come si fa? Non possiamo certo ripulire tutta l’aria del mondo!
– Non da un momento all’altro. Ma se ci impegniamo tutti insieme, si può fare molto! – interviene Renata.
– Già, ma l’inaugurazione è domani... quindi spremiamoci le meningi e pensiamo a che cosa può essere un richiamo per farfalle – suggerisce Emy.
– Ma certo: i fiori! – si entusiasma Chris. – Sono i fiori che attirano le farfalle e allora facciamo delle...




Strappa la carta in piccoli pezzi e mettili in una bacinella con dell’acqua per qualche ora.
Scola la carta e frulla in un frullatore.

Dividi la poltiglia in tre ciotoline diverse. Aggiungi un po’ di colore alimentare in ogni ciotola e mischia.
Fai delle palline di poltiglia di carta e semi.
Emy è perplessa: – Quali semi mettiamo nelle bombe?
– Possiamo mettere dei semi di avocado. Gli avocado hanno fiori a grappolo bianchi e gialli. Secondo me, alle farfalle piacciono! – suggerisce Chris.
– Ma quanto diventa grossa una bomba di semi di avocado? – sorride Renata.
– Forse è meglio pensare a qualcos’altro.
Suggerisci a Emy e Chris i nomi dei fiori preferiti dalle farfalle. Se non li riconosci, chiedi a una persona esperta.






La persona esperta a cui ho chiesto informazioni è perché
– Io vorrei fare arrivare le farfalle anche a casa mia – dice Chris, ma noi non abbiamo un giardino.
– Puoi sempre mettere le bombe di semi nei vasi – suggerisce Renata. – Sì, ma dove trovo la terra?
– Quella la troviamo dappertutto – interviene Emy.
Chris non è convinto: – Ma se poi è quella sbagliata e non cresce niente?
Aiuta Emy e Chris a scoprire come si riconoscono i diversi tipi di terreno.
Guanti di plastica Ripassa
Una paletta Ripassa
3 contenitori Ripassa
Etichette
Una penna biro

Pensa ai luoghi dove puoi raccogliere del terreno con caratteristiche diverse l’uno dall’altro.

il percorso. Fatti accompagnare da un adulto e raccogli i tuoi campioni indossando sempre i guanti

Etichetta i contenitori e scrivi dove hai raccolto i campioni.
raccogliere informazioni.
Ora che hai i tuoi campioni puoi procedere con l’osservazione del terreno.
È formato da tanti sassolini? sì


Metti i diversi tipi di terreno in vasi differenti. Poi pianta le tue bombe di semi. Osserva in quale vaso i semi germogliano prima e in quale i fiori crescono meglio.
Coding: decodificare un messaggio.

Tutti sono molto contenti, grazie a te e alla tua classe ora sanno quali fiori attirano le farfalle e in quale tipo di terreno crescono meglio. Renata già pensa di realizzare tantissime aiuole fiorite in tutta la fattoria didattica. – Emy, Chris, siete stati davvero eccezionali, ma si è fatto tardi, il maestro vi sta aspettando all’ingresso. Su correte! E fate attenzione a non calpestare le talpe. Ecco dove sono le loro tane.

Avanti (x3)
Girati a destra
Avanti
2
Avanti
Girati a sinistra
Avanti (x3)
3
Girati a destra
Avanti
Girati a destra
Avanti (x5)
4
Avanti
Girati a sinistra
Avanti (x2)
5
Avanti
Girati a sinistra
Avanti (x3)
6
Avanti (x2)
Girati a sinistra
Avanti (x2)
Girati a sinistra
Avanti
Ora che hai scoperto dove sono le tane delle talpe, indicale con una ✘ e scrivi l’algoritmo per accompagnare Emy e Chris dal maestro.


Fuori dalla fattoria didattica Emy e Chris non stanno zitti nemmeno un secondo. Che giornata entusiasmante!
– Complimenti ai due gemelli! – dice Renata. Emy e Chris si guardano l’un l’altra stupiti. – Che cosa abbiamo fatto?
– Avete superato una grande prova! Avete dimostrato non solo di amare la natura, ma anche di saper essere davvero in gamba e saper risolvere problemi, così ho deciso che sarete per tutta l’estate consulenti ufficiali della fattoria didattica!
I due gemelli sono entusiasti, ma anche leali e sanno che se un loro sogno si è avverato è solo merito tuo e della tua classe!