Model behaviour in social networks



New network models have been developed over recent years that could help researchers gain deeper insights into the spread of disease. We spoke to Professor Johannes Lengler about his work in refining geometric inhomogenous random graphs (GIRGs), and how they could improve epidemic modelling and inform more effective quarantine strategies.
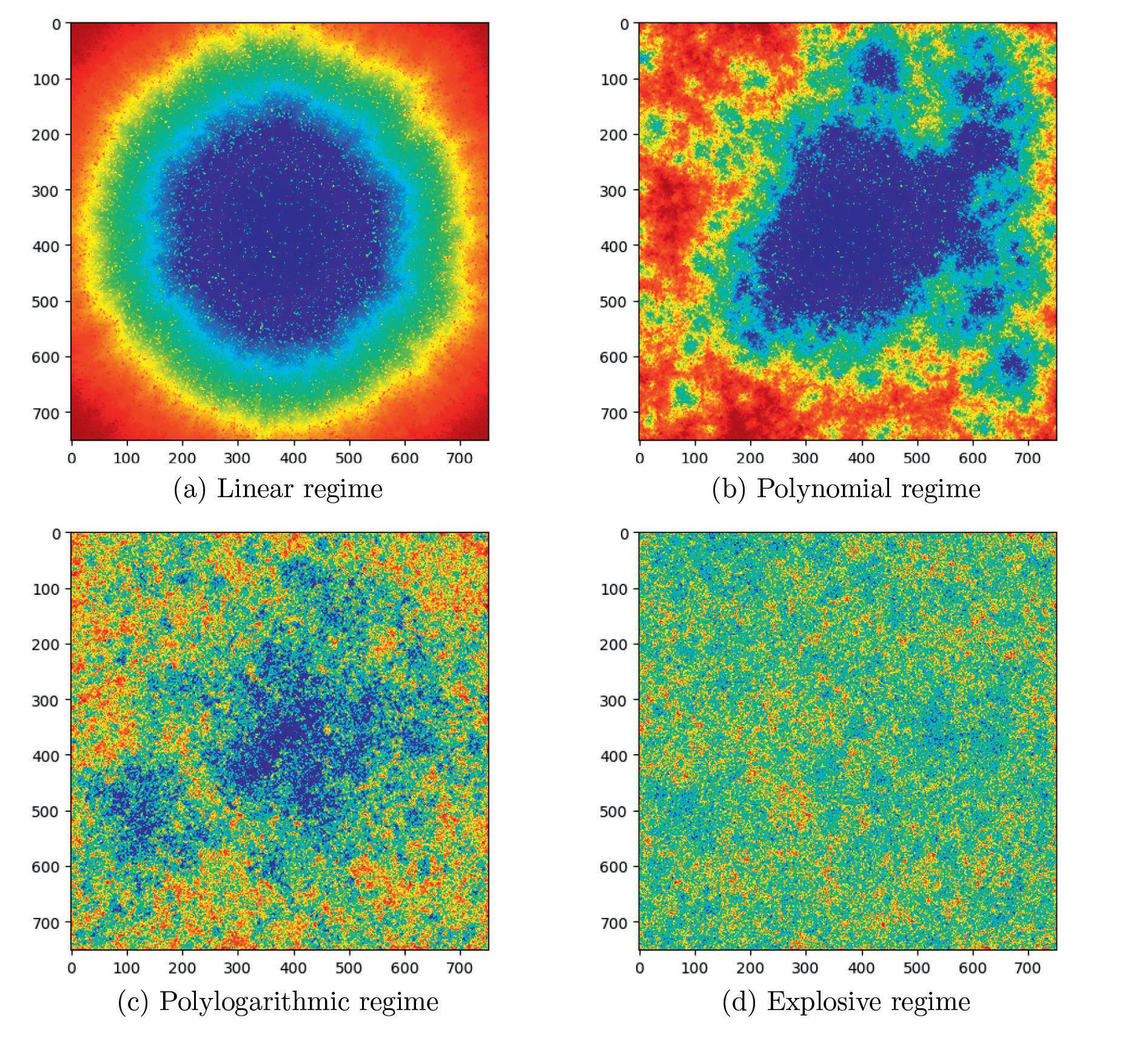
A variety of highly sophisticated network models have been developed over the years to look at the dynamics of social interaction, for example the way that rumours filter through a social network and how diseases spread across populations. One prominent type are inhomogenous network models, which can generate clear results. “For example, we see with inhomogenous network models that information can spread very fast,” outlines Johannes Lengler, Professor of Computer Science at ETH Zurich. Another type are geometric models, which while capturing certain aspects of social networks in the real world, may generate results contradictory to those from inhomogenous network models. “For example, if you look at the spread of epidemics, then it’s extremely fast if you look at the inhomogenous models, then it’s very slow if you look at the other type, the geometric models. So this raises the question, which is the right one?” asks Professor Lengler.
DynaGIRG project
This is a topic Professor Lengler is exploring further in the DynaGIRG project, an initiative backed by the Swiss National Science Foundation (SNSF), in which he and his colleagues are looking at the dynamics of social interaction in network models that combine these characteristics. This research centres around geometric inhomogenous random graphs (GIRGs), a new type of network model which Professor Lengler says is highly flexible. “There is a lot of freedom in the model definition, and it’s quite a robust model,” he explains. In the project Professor Lengler is working to refine these GIRGs and build a deeper understanding of their component structure. “I am taking the GIRG model, trying to improve it, and to make it even more flexible,” he continues. “Another part involves looking at certain processes on the model, including bootstrap percolation, routing and the progression of epidemics.
The project’s agenda also includes research into how information is transmitted through social networks, a topic addressed in Stanley Milgram’s famous ‘small-world’ experiment in 1967. In this experiment two people were randomly selected in two entirely different locations, and one was asked to send a letter to another, with only limited information. “They knew their address and a little personal information, but person A was not allowed to send the letter to person B directly. They were only allowed to send the letter to one of their friends, who was then asked to send a letter on to one of their friends, and so on. Was it possible with such a chain to reach B?” says Professor Lengler. This was indeed found to be possible, and letters needed just six hops on average before they reached their intended recipient. “Even if you have only a little information, you will be able to find a friend who is better at finding the intended recipient,” continues Professor Lengler.
This routing process has been modelled on GIRGs, and researchers have been able to essentially reconstruct the chain of intermediaries which passed on the letters, as well as to analyse what happens in each of the different phases. As part of his work in the project, Professor Lengler is now looking to check whether these insights also hold in terms of how information filters through social networks. “The most obvious question is, how many steps does it take to get to the intended recipient? We can also look at the route of messages and what happens when a lot of messages are sent. Do all these paths go through the same few vertices in the model, or are all these paths very different from each other?” says Professor Lengler. “We have found that these messages do indeed all go through a very small set of well-connected vertices, which is what we would expect to see in social networks.”
A parallel can be drawn here with the epidemiology case, where a single individual may play a particularly significant role in the spread of a disease, a so-called superspreader. The first step towards becoming a super-spreader is to meet a lot of people, yet Professor Lengler says other factors are also involved. “A person can be a super-spreader if they have a high viral load. However, it’s
not the case that if you have 100 times more contacts then you will also spread a disease to 100 times more people, and we study the effects of this,” he says. The project has largely focused on the role of people in spreading disease, but Professor Lengler also intends to look at the importance of events and meetings in future. “One type of meeting would be between close-by vertices, where one vertex invites others, and usually they know each other,” he continues. “Another type of event is where vertices which are very different from each other come together.”
Epidemiology
The project’s research holds wider relevance in terms of understanding how diseases spread and in developing quarantine strategies to control or limit their transmission. Epidemiological models were used extensively during the Covid-19 pandemic for example to assess the likely impact of restrictions on the spread of the disease. “If you impose restrictions on flights, if you try to force vertices not to move very far but otherwise don’t restrict them very much, does this change the dynamics of disease spread?” outlines Professor Lengler. The GIRG models can provide a more detailed picture than standard epidemic models in this respect. “Standard epidemic models
DynAGIRG
Dynamic Processes on Geometric Inhomogeneous Random Graphs
Project Objectives
The project aims to understand how epidemics and other dynamic processes spread in networks that combine inhomogeneity with clusterlike characteristics. In particular, researchers aim to understand under which circumstances processes spread exponentially, and in which circumstances they spread even faster or slower.
Project Funding
This project is funded by the SNSF.
Contact Details
Project Coordinator,
Prof. Dr. Johannes Lengler
ETH Zürich
Department of Computer Science
OAT Z 14.1
Andreasstrasse 5 8050 Zürich
E: johannes.lengler@inf.ethz.ch
W: https://as.inf.ethz.ch/people/members/ lenglerj/index.html
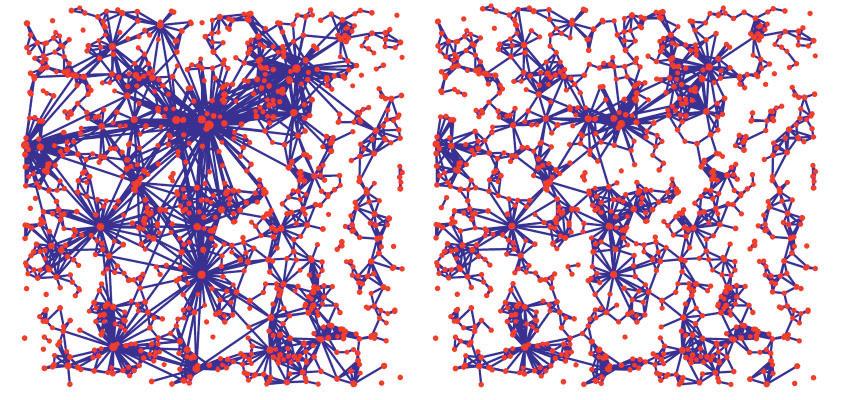
Depending on the parameters, the macroscopic structure of the networks differs. Left: strong heterogeneity. Shortest paths mostly use nodes with many neighbors. Right: weak heterogenity. Shortest paths mostly use nodes with few neighbors. Image created by Joost Jorritsma.
build on the hidden assumption that when one vertex infects another, then this new vertex is found at random from the whole population. So if someone in the UK infects someone else there, then this second person is just uniformly at random, you will not see geometric information,”
This geometric information was not typically available in the models used during the Covid-19 pandemic, a major motivation behind Professor Lengler’s work. The hope is that these new models will add a further dimension in epidemiology and allow researchers to gain a fuller picture of how diseases spread. “We have looked at how geometry affects the spread of a disease. It

Johannes Lengler is a Professor in the Department of Computer Science at ETH Zurich. He gained his PhD at the University of Saarland before moving to Zurich, and has conducted research in both pure and applied mathematics.


similar properties. “This is about the extent to which vertices are sorted by similarities of degrees. How does this distribution compare to a baseline? For a popular vertex, do we see a lot more vertices in a neighbourhood which are also popular?” outlines Professor Lengler. The overall picture seems to be that there is a high degree of positive assortativity in social networks, where for example stars associate with other stars, while negative assortativity has been observed in certain technological networks. “The central nodes and servers here tend not to connect so much to other central nodes and servers, but rather to low degree and low weight nodes,” continues Professor Lengler.
“The spread of epidemics is extremely fast if you look at the inhomogenous models, then it’s very slow if you look at the geometric models. So this raises the question, which is right?”
may or may not have a very strong impact, and this depends on the characteristics of the disease and the contact network,” says Professor Lengler. Some infections are known to spread exponentially, but there are also others which grow polynomially, and Professor Lengler says GIRGs can be used in both of these different scenarios. “These models can show both types of behaviours. Earlier models had a lot of trouble modelling infections like ebola or aids, because they did not have the geometry in them, while the GIRG model takes this into account,” he explains.
The evidence suggests that GIRGs are highly effective in terms of replicating the features of real-world social networks, and Professor Lengler is now actively working to improve them further. One major topic of interest is assortativity, the tendency for vertices to associate with others with
The GIRG model as currently defined is entirely neutral with respect to assortativity, a topic that Professor Lengler and his colleagues hope to address in future. The idea will be to develop a method to control assortativity. “We can then have strong positive assortativity, or strong negative assortativity in a model,” says Professor Lengler. This would add a further dimension to GIRGs, and open up deeper insights into not just how diseases spread, but also other scenarios. “We can look at how two competing opinions spread in the network for example, opinions A and B. Let’s say that a vertex changes, perhaps with a bit of randomness, to the majority opinion in a neighbourhood. Can there be bubbles where both of these opinions are stable?” continues Professor Lengler. “This can happen in some types of network, while in others this would be unstable, and one opinion would take over in the end.”
