












Åse Marie Bugten
Audun Rojahn Olafsen

∙
Elevboka og lærerveiledningen er nært knyttet sammen og danner en komplett enhet i læreverket Volum
Lærerveiledningen har som hovedmål å gi faglig og didaktisk støtte til læreren i arbeidet med å nå elevenes kompetansemål. Lærerveiledningen kan brukes i forarbeidet til hver time og er ei nyttig håndbok å ha med seg i timen.
Lærerveiledningen gir hjelp til strukturering og gjennomføring av timen.
For hver økt i elevboka har lærerveiledningen ∙ faksimile som viser til elevboka ∙ forslag til plan og gjennomføring av timen ∙ kommentarer til oppgaver og aktiviteter, samt forslag til veiledning av elevene

Læringsmål sammenfatter lærestoffet som elevene skal øve på. ∙ Oppstart introduserer dagens emne med definisjon av begreper og utredning av aktuell teori. Her kan læreren finne forslag til spørsmål og drøfting knyttet til forståelse av og framgangsmåten i oppgavene.
∙ Arbeid med oppgavene inneholder forslag til organisering av arbeidet, utdyping av matematisk innhold og didaktiske vinklinger.
∙ Avslutning gir forslag til gjennomgang av sentrale oppgaver som oppsummerer øktens læringsmål. Her er det rom for spørsmål fra elevene og drøfting av spesielle utfordringer og misoppfatninger.
Kommentarer til oppgavene og hvordan veilede elevene God veiledning forutsetter matematisk kunnskap og kjennskap til egnede didaktiske metoder. Et overordnet prinsipp er at læreren skal veilede og ikke forelese. Det er derfor svært viktig at de faglige og didaktiske kommentarene til oppgavene brukes til å stille ledende spørsmål til elevene. Den matematiske samtalen skal bidra til undring og analytisk tenkning hos elevene. Dette krever tid, tålmodighet og arbeidsro.
Kommentarene til aktivitetssidene i elevboka gir utfyllende forklaring til hvordan spill og aktiviteter kan gjennomføres. Det gis praktiske tips, forslag til variasjon og alternativ gjennomføring der det er aktuelt.
Noe av hemmeligheten til læring ligger kanskje i glede og mestring? Grunntanken i verket bygger på å skape et trygt læringsfellesskap der elevene motiveres til å ha tro på utvikling av egne evner. Lærerens innsats er avgjørende for å støtte og inspirere den enkelte elev i sitt arbeid med å utforske, prøve og feile, og drøfte tanker og ideer med medelever. God veiledning!
LEKSJON 1 TALLENE 0–20 4
LEKSJON 2 TALLENE 0–20 12
LEKSJON 3 ADDISJON OG SUBTRAKSJON 0–20 20
LEKSJON 4 LENGDER 0–20 28
LEKSJON 5 ULIKHETER OG KJØP MED PENGER 36
LEKSJON 6 TALLENE 0–100 44
LEKSJON 7 ADDISJON UTEN TIEROVERGANG 52
LEKSJON 8 SUBTRAKSJON UTEN TIEROVERGANG 60
LEKSJON 9 ADDISJON OG SUBTRAKSJON PÅ TALLINJA 68
LEKSJON 10 SPEILSYMMETRI 76
LEKSJON 11 FORSKYVING 84
LEKSJON 12 MØNSTER MED SPEILING OG FORSKYVING 92
LEKSJON 13 DOBLING OG HALVERING 100
LEKSJON 14 PARTALL OG ODDETALL 108
• Elevene repeterer tallene 0–10 og øver på å forstå tallverdiene.

• kopioriginal med ti-rutenett
• brikker












Del ut ti-rutenett til hver elev. Elevene kan arbeide parvis og lage oppgaver til hverandre. Begge elevene legger opp brikker i sitt rutenett. Deretter skal de fortelle hvor mange brikker den andre har.
Tegn ti-rutenettet på tavla med eksempler der brikkene fyller én full rad (5) og to fulle rader (10).
• La elevene svare på hvor mange brikker det er i hver rad.
• Spør om de nå vil kunne klare å svare uten å telle.
Fyll rutenettene med 4, 6 og 9 brikker.
• Klarer elevene å svare uten å telle?

• Spør elevene hva som kjennetegner disse tallene. Disse tallene er én mindre og én mer enn 5, og én mindre enn 10.



Generelt er det viktig å være klar over at oppgavene i alle økter er differensiert med hensyn til kompleksitet og vanskelighetsgrad. Det er derfor ikke en målsetting at alle elevene skal gjøre alle oppgavene. Men alle skal øve på noen oppgaver med sentralt lærestoff i hver økt. Når de mestrer disse, kan de velge hvilke oppgaver de ønsker å jobbe med videre. Veiled elever som trenger hjelp til å finne oppgaver med passe utfordring. Oppgavene kan også kortes ned, for derved å rekke å regne flere oppgavetyper.
Legg merke til at faksimilene inneholder en del løsninger på utregninger og tegneoppgaver.


Gjennomgå oppgave 6. Hvilke svar har elevene fått? Tegn ei tallinje på tavla som kan brukes til å illustrere tallmengdene.




















Elevene vil oppdage at det mangler én prikk i hver figur. Be elevene forsøke å plassere prikken slik at det blir et fint mønster. Slike figurer kalles figurtall og kan hjelpe oss med å gjenkjenne visse antall.


Hvilke tall er ikke større enn fire? 4, 3, 2, 1 og 0. Det vil si at alle andre tall kan fargelegges. Se faksimilen for å se bildet.
Strekene danner avgrensede felt som skal fargelegges. Se faksimilen.
Oppgave 4



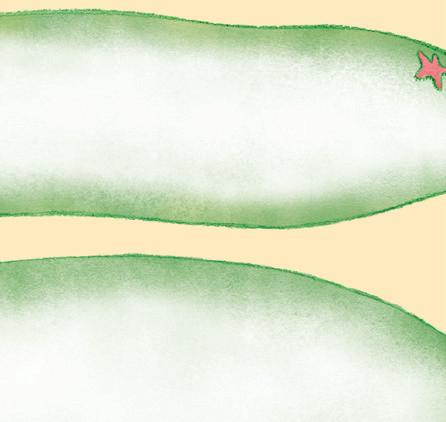
Høydene finnes ved å lese av verdiene på den loddrette aksen. Aksen viser høyden i cm.
Oppgave 5
Her kan elevene gjerne tegne den loddrette aksen og skrive på tall. Referansen er venstre fisk som er 5 cm.












Elevene kan bruke brikker og ti-rutenett eller tallinje som hjelpemiddel.
Oppgave 7






Elevene skal finne hvilken veibeskrivelse som passer til hvilken ball. Klarer de å finne en strategi som hjelper dem? Tips: Tegn svakt med blyant, og visk ut under utprøving av alternative veier.


• Elevene skal arbeide med tall og mengder i tallområdet 0–20.
• kopioriginal med ti-rutenett
• brikker







Del ut ti-rutenett til hver elev.
Tegn ti-rutenett på tavla med følgende antall brikker: én full rad (5), to fulle rader (10), tre rader (15) og fire rader (20).
• La elevene svare på hvor mange brikker det er i hver rad.

• Gjenta spørsmålene og be elevene forsøke å svare uten å telle. Fyll rutenettene med 4, 6, 9, 11, 14, 16 og 19 brikker.
• Klarer elevene å svare uten å telle?





• Spør elevene hva som kjennetegner disse tallene. Disse tallene er én mindre eller én mer enn 5, 10 og 15 og én mindre enn 20.

Kjerneoppgaven som alle skal løse, er nummer 8. Veiled elever som trenger hjelp til å finne oppgaver med passe utfordring, og kort ned oppgavene ved behov.
Gjennomgå oppgave 8. Ser elevene en enkel teknikk for å finne svaret når et tall legges til 10? Velg én eller flere tallfølger fra oppgave 11. Hva er differansen mellom tallene?

Tegn de mest kjente figurtallene i oppgave 10 på tavla. Klarer elevene å anslå antallet i noen figurer, uten å telle? Figurtallene kommer igjen senere, så det kan være lurt å øve.























Bruk gjerne ti-rutenett og brikker som hjelp. 10 + 6 og 10 + 7 er oppgavene som mangler.
Hva er summen på venstre og høyre side? 16 og 19 er i nærheten av hverandre, men må justeres litt. Hva må legges til 10 for å få 19? Kan 6-tallet gjøres om til et 9-tall?



Klarer elevene å plassere steinen som mangler, slik at figuren blir et figurtall? Figurtall er gjenkjennelige figurer med et bestemt antall.







Studer tallene i de gule rutene og finn differansen mellom dem. 1, 6 og 11 viser økning på 5. Neste tall i tallfølgen blir derfor 11 + 5 = 16.


Naboruter kan velges vannrett, loddrett og diagonalt.
I midterste tegning kan elevene forsøke å bruke samme rekkefølge som i øverste oppgave, men de vil se at dette ikke fører fram. Den nederste oppgaven, med prikk til prikk, gir heller ikke løsningen fordi det mangler ett linjestykke. Dette er allikevel det nærmeste vi kan komme.

• Elevene skal bruke tallene 0–20 i praktisk sammenheng.


Oppgave 14 Forklar veien krever mest konsentrasjon, og det anbefales at elevene starter med denne aktiviteten.

I aktivitetene på de røde sidene samarbeider elevene i utgangspunktet to og to.
Dersom det er én elev til overs, blir det en gruppe på tre elever. I oppgave 14 kan da to elever følge instruksene til elev 1 og forsøke å finne hullet som forklares. Elevene rullerer og bytter roller.

Tunnelspillet i 15 fungerer bra med tre elever. Hver spiller trenger en spillebrikke.
Det er lurt å lære elevene faste rutiner på opprydding av konkretene for å unngå tap.

En del av læringsprosessen er å gjøre elevene bevisste og kritiske. I denne aktivitetsøkta kan elevene gis øvelse i dette ved at du ber om tilbakemeldinger på aktivitetene. Har noen forslag til endringer?



























14 Forklar veien.
Elev 1 legger ei brikke på et kryss i rutenettet i boka si. Se eksempel med blå brikke i figuren under.
Elev 2 legger ei brikke på samme sted i sin bok. Elev 1 skal forklare hvordan den andre eleven skal flytte brikka slik at den tre er et bestemt hull. De skal ikke se på hverandre. Dersom elev 2 bommer, prøver de på nytt. Deretter bytter de roller.
14 Forklar veien.
Formålet med oppgaven er å øve elevene i å orientere seg. De trenger å bruke begrepene vannrett til venstre, vannrett til høyre, loddrett ned og eventuelt loddrett opp. Gå gjerne gjennom begrepene ved å knytte dem til illustrasjoner på tavla, før elevene starter.

Forbered elevene. For å treffe rett hull må elevene være

• nøyaktige når de teller antall ruter
• presise når de forklarer veien
• konsentrerte når de lytter på instruksen
Følg med og rettled elever som trenger hjelp.

15 Tunnelspill.
To spillere slår en terning annenhver gang. Følg den grønne tunnelen.
2 spillere Dere trenger
• 2 brikker
Spillet egner seg for 2–3 elever.
Brikkene fungerer som spillebrikker som flyttes fra start til mål.
• 1 terning eller snarveier.
Ved landing på rosa og lysegrønne felt, må spillerne følge pilene som gir omveier

Gå gjennom spilleregelene.
Den mørkegrønne traseen er korteste vei fra start til mål.
Men underveis kan spillerne havne på rosa ruter som innebærer en omvei.




Motsatt vil landing på en lysegrønn rute bringe spilleren raskere fram gjennom en snarvei.
For å gjøre spillet litt mer utfordrende, kan elevene lage noen regnestykker som må løses, dersom en spiller lander på lysegrønn rute.
Hver elev lager to regnestykker. De kan se på oppgavene på de foregående sidene dersom de trenger ideer.
Den nye spilleregelen kan for eksempel lyde slik: «For å bruke denne snarveien, må du finne svaret på følgende regnestykke.»
Deretter vises spilleren ett regnestykke som må løses med rett svar, for å komme videre. Ved feil svar kan snarveien ikke brukes. Elev 1 velger startpunkt et sted øverst i spillebrettet. Se den blå brikka.

Brikkene skal plasseres og bevege seg på kryssene i rutenettet – ikke legges inni rutene.
Hullet som brikka skal ende i, befinner seg også i et kryss.
• Elevene skal øve på rekkefølgen av tallene 0–20 og regne med mengder i samme tallområde.












I denne økta repeteres læringsinnholdet i leksjonen: tallene 0–20. Elevene skal derfor arbeide selvstendig og regne oppgaver som viser at de mestrer kjernestoffet.
De mest sentrale oppgavene er 16, 19, 20 og 21. Det er gunstig om elevene får prøvd seg på forskjellige typer oppgaver. Hjelp elevene med å finne et ønsket utvalg, og velg ett eller flere delstykker som passer, fra hver av disse oppgavene.
Elevene kan bla tilbake for å se på forklaringer i gule bokser og regnestykker dersom de er usikre.
Etter at elevene har arbeidet så langt de klarer, kan de sammenholde og drøfte løsninger med en naboelev.
Det er viktig å observere hver elev for å oppdage og rette opp misoppfatninger. Gi flere øvingsoppgaver ved behov.



Hvilke utfordringer hadde elevene? Diskuter og få innspill fra elevene på ulike måter å tenke og regne på.









brikker. Det mangler brikker.
brikker.



a) Tenk på et tall mellom 1 og 9.
Legg til 9.
Summer sifrene i svaret.
Hva får du?
Gjør det samme flere ganger med ulike tall.
b) Tenk på et tall mellom 1 og 9. Legg til 10.
Trekk fra 1.
Summer sifrene i svaret.
Hva får du?
Gjør det samme med flere ulike tall. Kan du forklare hva du fant ut?
Ved å studere tallene vil elevene finne at de stiger jevnt i hver rad.
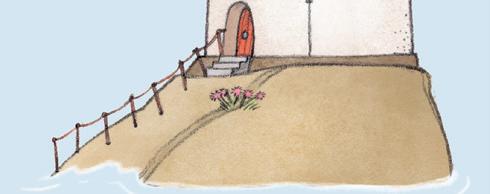
Finn lengden på tauene ved å sammenlikne med lengden på det grønne tauet, eller måle med linjal.
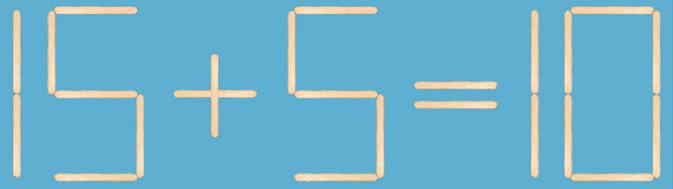
Sammenlikn verdiene på hver side av likhetstegnet. Hva kan endres for å få riktig regnestykke? Et ledd, svaret eller tegnene +, – eller =. Linje 1: 13 + 5 = 18 Linje 2: 15 – 5 = 10 Linje 3: 15 = 5 + 10 Linje 4: 15 – 5 = 10
To ti-rutenett rommer 20 brikker. Følg med på elevenes strategi. Det vil ofte være mer effektivt å regne i stedet for å telle tomme ruter. Linje 3: Det mangler 3 + 10 = 13. Linje 4: Det mangler 10 – 3 = 7.


I addisjonsstykker med oppgitt sum kan vi regne: 10 + _ = 13 ↔ 13 – 10 = 3










Subtraksjonsstykker: 20 – _ = 13 ↔ 20 – 13 = _.

Elevene må se an stykket og prøve seg fram med ulike tegn. 20 – 17 = 3, og 20 = 17 + 3.
Vi velger for eksempel tallet 2 i a): 2 + 9 = 11. Summen av sifrene i svaret er 1 + 1 = 2. Svaret er altså lik tallet vi valgte å starte med. Gjenta utregningen med flere tall. Hvorfor blir svaret det samme som tallet? La elevene sammenlikne regnestykkene og forsøke å forklare hva som skjer. b) Vi velger tallet 3: 3 + 10 = 13. 13 – 1 = 12. 1 + 2 = 3. Flere utregninger gir samme resultat som i a). Ved å studere regnestykket ser vi at 10 legges til og 1 trekkes fra, altså det samme som å legge til 9, som i a).

c) 16 er det eneste tallet der sifrene har sum lik 7. 16 kan skrives som summen av to like tall: 8 + 8.
Elevene lærer om tallene fra 0 til 20 og øver på rekkefølge, tallposisjoner og sifre, plassering av tall og mengder på tallinja, samt addisjon.




Først en kort repetisjon. Tegn ei tallinje med 21 markeringer (0–20), og la elevene fortelle hvilket tall som skal stå ved hver markering. Pek på tallene fra 0 til 20 og la klassen telle høyt fram og tilbake.
Hvordan er tallene fra 0 til 20 bygd opp?
• Se først på tallene 0–9: Hvilke tallsymboler brukes? Snakk om tallposisjonene – står sifrene på enerplassen eller tierplassen?
• Tallene 10–20: Hvilke tallsymboler brukes? Disse tallene har ingen nye symboler, vi kombinerer bare symbolene 0–9. Finnes det flere?












På hvilken plass står sifrene i tallene? Fra 10 til 20 inneholder tallet både enere og tiere

• Drøft sammenhengen mellom tallordene og tallene. Hvilke tallord ender på ten?
Veiled elevene med å velge oppgaver med passe vanskelighetsgrad. Noen deloppgaver kan strykes for å frigjøre tid til å øve på flere oppgavetyper.
Sørg for at elever som trenger hjelp, har tilgjengelig rutenett med brikker og tallinje. Elevene kan tegne ei tallinje i kladdeboka si, eller bruke tallinja som står på permen i elevboka.

Oppgave 4: Kan vi summere uten å regne?
La elevene lese tallordene de kom fram til i oppgave 5


For å finne hvilke tall som mangler, må elevene studere tallene i tallfølgen. Tallfølgene kan være stigende eller synkende.
Dersom elevene trenger hjelp, kan tallinje eller rutenett være nyttig. Hvordan kan svarene kontrolleres? Addenden øker med én for hvert stykke, og dermed øker også summen med én.

Se fargelegging av figuren i faksimilen. Elevene kan finne at tallet 18 mangler.
Se figuren i faksimilen. Hvor mange sidekanter er det i trekanter, firkanter og åttekanter?




Husker elevene at de må legge sammen tallet i vannrett rad med tallet i loddrett kolonne for å regne ut tallet i skjæringspunktet, det vil si ruta inne i tabellen?
Hva er kjent? Verdien av et brunt skjell er 10 + 2 = 12. To hvite skjell er lik 12, dermed er ett skjell lik 6. Vi setter inn verdiene for skjellene i øverste linje og regner ut at blått skjell er lik 12 + 6 = 18.






Oppgave 10
Elevene skal lære å løse denne typen oppgaver ved å oppfylle ett og ett krav. Tallet befinner seg på tallinja, og tallordet er skrevet med fire bokstaver. Null, fire, åtte og tolv er derfor aktuelle tall.
4 er summen av 2 + 2, og 8 er summen av 4 + 4. Både 4 og 8 oppfyller kravene.
Oppgave 11
Se fargelagt oppgave i faksimilen.

• Bli kjent med mengder og myntverdier knyttet til tallene 0–20.
• ti-rutenett og brikker
• mynter fra konkretene

















Be elevene forklare sammenhengen mellom mynter, rutenett og tallinje i de fem eksemplene i gul boks.
Følg med på at alle elevene forstår sammenhengen mellom tall, mengder og mynter. Dette er grunnleggende stoff som det vil bygges videre på.
Dersom elevene har tid, kan de arbeide med oppgavene nedenfor og/eller lage liknende oppgaver til hverandre.
1) Hvilke andre myntkombinasjoner kan du bruke i eksemplene i gul boks? Eksempelvis kan 16 kr betales med: 16 kronestykker
1 tier og 6 kronestykker



2 femmere og 6 kronestykker



1 femmer og 11 kronestykker

3 femmere og 1 krone







2) Marker tallet 9 på tallinja. Legg samme antall brikker i rutenettet. Hvilke mynter tilsvarer 9 kr?

3) Start med 18 brikker i rutenettene. Marker tallet på tallinja. Vis beløpet 18 kr med mynter. Finnes det flere løsninger med myntene som gir riktig beløp?
4) Vis minst to ulike myntsamlinger som blir 12 kr. Marker tallet på tallinja. Legg rett antall brikker i rutenettene.




Oppgave 16: Tegn et prikkart med 3 x 3 prikker, der start er øverste prikk til venstre og mål er nederste prikk til høyre. Hvilke veier gir korteste vei fra start til mål? Vi kan ikke gå diagonalt. Kan vi bruke dette for å svare på a)?


















Elevene bør først skrive summen ved siden av rutenettene og myntene.































Hver linje har en tallfølge med ulike sprang mellom tallene. Elevene kan finne differansen ved å telle fra ett tall til det neste. Nederst: Fra 16 til 20 teller vi fire. Det er altså fire tall fra 16 til 20 og to tall fra 16 til det ukjente. 16 + 2 = 18, 16 – 2 = 14, 14 – 2 = 12, 10 – 2 = 8.























Det kan være lurt å tegne svakt med blyant under utprøving av veivalg. Finnes det mer enn én vei som gir korteste vei fra start til mål? Se drøfting av løsning under Avslutning.

Det kan opplyses om at figurene er symmetrisk bygd opp. Tegningene er gjort for hånd, så det finnes små uregelmessigheter.



















De røde klossene kan deles opp i enheter som består av de 7 fremre klossene. Det er tre lag av disse, og regnestykket blir 7 + 7 + 7 = 21, altså 21 klosser.






De grønne klossene kan deles i enheter med 4 klosser: 3 klosser i høyden, pluss 1 kloss. I tillegg kan vi se 1 kloss i sentrum. Spørsmålet er om det finnes 1 kloss under denne? Be elevene bruke sin erfaring fra bygging med klosser for å finne svaret.

Hva kan regnes ut? 2 vannløpere (i midten) er lik 6, 1 vannløper = 3.








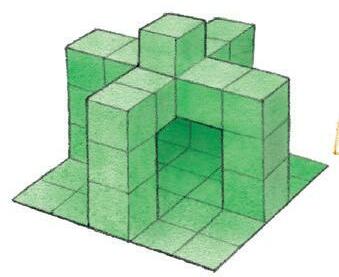



Sett inn denne verdien i øverste linje: Salamander + 3 = 10, gir at salamander = 7. Sett inn denne verdien i nederste linje: Grønn bille + 7 = 20, gir at grønn bille = 13.
















• Elevene skal undersøke tallordene null til tjue og deres sammenheng med tallsymbolene.
• Praktisk forståelse av plassering i en rekke.

19 Tallordene 0–20.
a) Hvor mange tallord
• slutter på ten • begynner på bokstaven «t» • begynner på bokstaven «f»
b) Er det slik at dersom du tar et tall mellom 1 og 10 og legger til «ten», så får du et tall mellom 11 og 20?






trenger • 1 terning per par






Fortell kort hva oppgavene går ut på, slik at elevene kan velge hvilken de ønsker å starte med.
Oppgave 19 Tallordene 0–20 fokuserer på tallordenes navn og deres kopling til tallene. Oppgave 20 Skrytepave dreier seg om plasseringer i konkurransesammenheng.
Oppgave 21 er et terningspill med avkryssing av ruter i spillebrettet.
Elevene kan samarbeide parvis i alle aktivitetene.
Hvilke konklusjoner kom elevene til i oppgave 19 og 20? Ta imot alle forslag og diskuter. Jamfør kommentarene til oppgavene. Illustrer gjerne løsningen i oppgave 20, som beskrevet.
c) En mattelærer synes at tallene etter 9 til og med 19 burde vært skrevet slik: enti, entien, entito, ... Hva synes dere om forslaget?
20 Skrytepave.
a) Bo skryter hele tiden. Hvilken plass fikk han egentlig?
Bo sier høyt:
«Det var 12 deltakere, og jeg ble nr. 2.» Bo legger til lavt: «Bakfra.»

b)
Hvor mange deltakere var det? Bo sier: «Jeg ble nr. 10.» Dere: «Bakfra eller forfra?» Bo : «Det er det samme.»
19 Tallordene 0–20.
a) Svarene på spørsmålene finnes ved å ramse opp tallordene, eller se på oversikten over tallordene i gul boks i økt 1.
b) Elevene vil finne at dette ikke stemmer for to, men er riktig for tre, fem, seks og ni. Om vi legger til -ten etter fire, sju og åtte, får vi tallord som likner litt på fjorten, sytten og atten.
c) Ved å dele opp ordet entien vil enti bety én tier og den siste delen av ordet en bety én ener. På samme måte vil entito bety én tier og to enere.




Dette er en oppgave det er lett å gjøre feil på. La elevene gruble og tegne for å nærme seg riktig løsning. Hvis de trenger hjelp, så still spørsmål som kan lede dem videre i tankegangen.

Løsningsforslag:
a) Tegn 12 streker, én for hver deltaker. Nr. 1 bakfra er deltaker nr. 12. Nr. 2 bakfra er deltaker nr. 11.
b) Ved å tegne én strek per deltaker vil den tiende streken være deltaker nr. 10. Hvor mange flere streker/deltakere må du tegne for at deltaker nr. 10 skal ha plass nr. 10 bakfra? Svaret er 19.



Spillet er tilsynelatende enkelt. Spillerne kaster én terning annenhver gang og krysser ut like mange ruter som øynene på terningen viser.
Dersom en spiller får 5 i sitt terningkast, skal spilleren, om mulig, krysse ut 5 ruter ved siden av hverandre, vannrett eller loddrett.

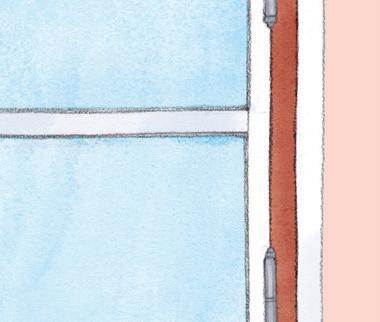





Målet er å få krysset ut alle rutene i sitt spillebrett først.
Elevene vil oppdage at det er lurt å tenke seg om og tenke strategisk på grunn av kravet om at kryssene må settes etter hverandre.


En variant av spillet vil være å tillate å krysse ut ruter som ligger diagonalt i forhold til hverandre.


• Elevene repeterer tallene 0–20, rekkefølge og regning med forskjellige enheter.














































Denne økta inneholder for det meste kjente oppgavetyper. Elevene skal arbeide selvstendig med repetisjonsoppgavene og vise hva de mestrer av kjernestoffet.









Oppfordre elevene til å bla tilbake til forklaringer i gule bokser og regnestykker de har regnet tidligere, dersom de er usikre.

Gi et mindre utvalg av oppgaver til elever som trenger mer tid. Blant de utplukkede oppgavene kan antall deloppgaver reduseres. Eksempelvis holder det å bestemme én mengde med klosser i oppgave 23 og fylle ut ett rutenett i oppgave 28. På denne måten får de testet kunnskapene sine på flest mulige områder.











Etter at elevene har gjort så mange oppgaver som de klarer, kan de sammenholde og drøfte løsninger med en naboelev.
I denne økta er det mange konkrete oppgaver. Reflekter litt over hvilke typer oppgaver ulike elever liker og mestrer. Dette kan det være nyttig å vite ved tilpasning av arbeid til den enkelte elev.

De blå øktene avsluttes ofte med en eller flere grubleoppgaver av problemløsende art. Elever som har god kontroll på lærestoffet, kan redusere eller hoppe over enklere oppgaver, slik at de får tid til å arbeide med de mer komplekse.








Ta imot spørsmål fra elevene. Hvordan fant elevene tallfølgene i den nederste tabellen i oppgave 28?
Elever som ikke har rukket å gjøre oppgave 24, kan gjerne tegne på denne hjemme. Røp derfor ikke løsningen.















Myntene kan summeres ved hoderegning. En sikrere måte å summere myntene på er å skrive addisjonsstykket: 1 kr + 1 kr + 10 kr = 12 kr.





Elevene ser ikke alle klossene og kan derfor ikke telle alle. Spør om hvordan vi kan regne ut antallet.
Ferdig tegning kan ses i faksimilen.
Om elevene er usikre – spør hvor mange sidekanter det er i en femkant og i en sekskant.






For å finne hvilke tall som mangler, må elevene undersøke tallfølgene. Hva er differansen mellom nabotallene?

I nederste tabell, linje 1, kan vi regne 4 – 1 = 3. Det skal altså telles 3 videre: 4, 7, 10, 13, 16, 19.
Linje 2: 8 – 2 = 6. Skal 6 legges til? Tallet 2 øker med 6 over to plasser, det gir en økning på 3 for hver plass: 2, 5, 8, 11, 14, 17, 20.


























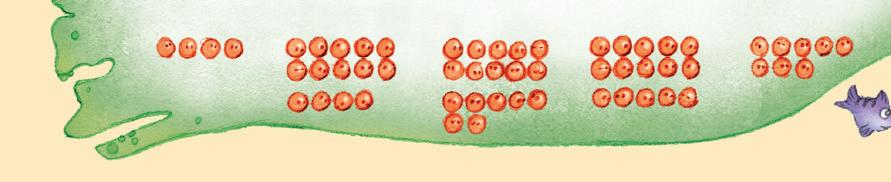
Dere kan først diskutere hva som skal regnes som armer og bein hos selene og beverne. Svaret på dette er ikke så viktig, elevene trenger kun å vite hva som skal telles med.
Heller ikke her kan vi se alle klossene. Én måte å løse dette på er å tegne klossene lag for lag, slik at antallet vises.

Det kan være en idé å tegne de forskjellige maurveiene med hver sin farge. Regn ut tiden for hver vei, og finn den korteste og den lengste turen.


– et nytt læreverk i matematikk for barneskolen etter fagfornyelsen 2020.
Lærerveiledningen er lærerens verktøykasse for å oppfylle VOLUMs grunnideer om å gi elevene læringsglede og mestring i matematikkfaget. Undring og tid til å diskutere matematikk i fellesskap står sentralt.
Boka gir faglig og didaktisk støtte til undervisningen gjennom forslag til struktur, gjennomføring av timen og veiledning til oppgaver og aktiviteter.
Lærerens rolle som veileder er uvurderlig for elever på alle nivåer, og lærerveiledningen utfyller elevboka underveis i dette viktige arbeidet.
I et trygt og raust læringsfellesskap kan elevene argumentere og dele ideer – og på den måten bidra til å utvikle et felles, presist og hensiktsmessig matematisk språk.
Les mer om verket på www.fagbokforlaget.no
Matematikk finner du alle steder!
