A New Type of Neutrosophic Set in Pythagorean Fuzzy Environment and Applications by Florentin Smarandache

ANewTypeofNeutrosophicSetinPythagoreanFuzzyEnvironment andApplicationstoMulti-criteriaDecisionMaking

MahmutCanBozy˙ ı ˘ g ˙ ıt 1,MuratOlgun2,FlorentinSmarandache3 ,Mehmet ¨ Unver2

1AnkaraYıldırımBeyazıtUniversity,FacultyofEngineeringandNaturalSciences,Departmentof Mathematics,06010AnkaraTurkey

2AnkaraUniversity,FacultyofScience,DepartmentofMathematics,06100AnkaraTurkey

3 MathematicsDepartment,UniversityofNewMexico,705GurleyAve.,Gallup,NM87301,USA

Emails:mcbozyigit@aybu.edu.tr,olgun@ankara.edu.tr,smarand@unm.edu,munver@ankara.edu.tr

Abstract

Inthispaper,weintroducetheconceptsofPythagoreanfuzzyvaluedneutrosophicset(PFVNS)andPythagorean fuzzyvaluedneutrosophic(PFVNV)constructedbyconsideringPythagoreanfuzzyvalues(PFVs)insteadof numbersforthedegreesofthetruth,theindeterminacyandthefalsity,whichisanewextensionofintuitionisticfuzzyvaluedneutrosophicset(IFVNS).BymeansofPFVNSs,thedegreesofthetruth,theindeterminacy andthefalsitycanbegiveninPythagoreanfuzzyenvironmentandmoresensitiveevaluationsaremadebya decisionmakerindecisionmakingproblemscomparedtoIFVNSs.Inotherwords,suchsetsenableadecision makertoevaluatethedegreesofthetruth,theindeterminacyandthefalsityasPFVstomodeltheuncertainty intheevaluations.Firstofall,weproposetheconceptsofPythagoreanfuzzy t-normand t-conormandshow thatsomePythagoreanfuzzy t-normsand t-conormsareexpressedviaordinarycontinuousArchimedean tnormsand t-conorms.ThenwedefinetheconceptsofPFVNSandPFVNVandprovideatooltoconstruct aPFVNVfromanordinaryneutrosophicfuzzyvalue.Wealsodefinesomesettheoreticoperationsbetween PFVNSsandsomealgebraicoperationsbetweenPFVNVsvia t-normsand t-conorms.Withthehelpofthese algebraicoperationsweproposesomeweightedaggregationoperators.TomeasurediscriminationinformationofPFVNVs,wedefineasimplifiedneutrosophicvaluedmodifiedfuzzycross-entropymeasure.Moreover, weintroduceamulti-criteriadecisionmakingmethodinPythagoreanfuzzyvaluedneutrosophicenvironment andpracticetheproposedtheorytoareallifemulti-criteriadecisionmakingproblem.Finally,westudythe comparisonanalysisandthetimecomplexityoftheproposedmethod.

Keywords: Pythagoreanfuzzyvaluedneutrosophicset;aggregationoperators;multi-criteriadecisionmaking

1Introduction

Zadeh42 introducedtheconceptoffuzzyset(FS)definedbyamembershipfunction µA fromauniversal set X toclosedunitinterval [0, 1] inordertohandletheuncertaintyinvariousreal-worldproblems.Then usingamembershipfunction µA : X → [0, 1] andanon-membershipfunction νA : X → [0, 1] under thecondition µA(x)+ νA(x) ≤ 1 for x ∈ X,Atanassov2 proposedtheconceptofintuitionisticfuzzyset (IFS)whichisanextensionoftheconceptofFS.Thepair ⟨µA(x),νA(x)⟩ iscalledanintuitionisticfuzzy value(IFV)forafixed x ∈ X.ThetheoryofIFShasbeenusedtosolveproblemsinmanyapplications asmulti-criteriadecisionmaking(MCDM),classification,patternrecognitionandclusteringandithasbeen studiedinmanyareasbyresearchers.Theconceptsofentropyandcross-entropyareimportantmeasurement methodsusedintheinformationtheoryandtheseconceptswereproposedbyShannon.23,24 Thentheconcept ofcross-entropywasimprovedbyKullbackandLeibler13,14 anditwasmodifiedbyLin.15 Inordertomeasure https://doi.org/10.54216/IJNS.200208 Received:July08,2022Accepted:January11,2023

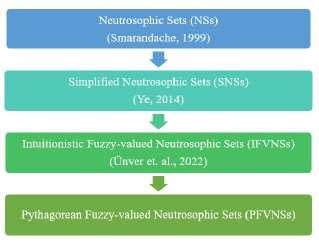
InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

107

Figure1:Thedevelopmentoftheoryofneutrosophicset discriminationinformationbetweenIFSs,WeiandYe31 introducedanimprovedintuitionisticfuzzycrossentropytoovercomethedrawbackofintuitionisticfuzzycross-entropygivenbyVlachosandSergiadis.30 The conceptofaggregationoperatorthattransformsseveralinputvaluesintoasingleoutputvalueisanimportant toolinthedecisionmakingtheory.Aseriesofaggregationoperatorshavebeenproposedbymanyresearchers. Particularly,variousgeneralizationsofaggregationoperatorsforIFSs(seee.g.3,7)weredefinedviaseveral typesof t-normsand t-conormson [0, 1].FurtherstudiesonMCDMwithFSsandaggregationoperatorscan befoundin.1,9,17,27,29,39–41

AsageneralizationofIFS,theconceptofPythagoreanfuzzyset(PFS)wasdevelopedbyYager,33,34 whichis definedbyamembershipfunction µA : X → [0, 1] andanon-membershipfunction νA : X → [0, 1] underthe condition µ2 A(x)+ ν2 A(x) ≤ 1 for x ∈ X.APFSismorecapablethananIFStoexpressuncertainty.Inother words,PFSsenhanceflexibilityandpracticabilityofIFSsandhavewiderareathanIFSswhiledescribing theuncertainty.ThereforetheoryofPFShasbeenstudiedbymanyresearcherstomodeltheuncertainty.

LaterYager34,35 proposedarangeofaggregationoperatorsforPFSs.Afterthat,Penget.al.20 presentedthe axiomaticdefinitionsofdistancemeasure,similaritymeasure,entropyandinclusionmeasureforPFSs.

Smarandache26 introducedtheconceptofneutrosophicset(NS)whereeachelementhasthedegreesoftruth, indeterminacyandfalsifyinthenon-standardunitinterval.Thereisnorestrictiononthemembershipfunctions forNSs.Duetothedifficultyofapplyingneutrosophicsetstopracticalproblems,theconceptofsimplified neutrosophicsets(SNSs)wasproposedbyYe.37 ASNSisconstructedbyatruth,anindeterminacyanda falsifymembershipfunctiondefinedfrom X to [0, 1].Ithasbeenusedinvariousnumericalapplications. Moreover,theconceptofsinglevaluedneutrosophicmulti-set(SVNMS)thatischaracterizedbysequencesof truth,indeterminacyandfalsifymembershipfunctionshasbeenproposedbyYeandYe.36

SchweizerandSklar21 introducedtheconceptoftriangularnorm(t-norm)andtriangularconorm(t-conorm), followingtheconceptofprobabilisticmetricspacesproposedbyMenger,16 whichisageneralizationofmetricspaces.ThesenotionsareusefultoolstodefinealgebraicoperationsandaggregationoperatorsforFSs. Deschrijveret.al.6 proposedtheconceptsofintuitionisticfuzzy t-normandintuitionisticfuzzy t-conorm, whichareextensionsoftheconceptsof t-normand t-conorm,respectively,byturningintointerval [0, 1] to {(x1,x2): x1,x2 ∈ [0, 1] and x1 + x2 ≤ 1}.Inthispaper,weintroducetheconceptsofPythagoreanfuzzy t-normandPythagoreanfuzzy t-conormwhichareextensionsofnotionsofbothordinaryandintuitionistic fuzzy t-normand t-conorm,respectively. Unveret.al.28 proposedtheconceptofintuitionisticfuzzyvaluedneutrosophicmulti-set(IFVNMS)bycombiningNStheoryandIFStheorywiththehelpofintuitionistic fuzzyvaluesinsteadofnumbersinmembershipsequences.Motivatingfromthisidea,weproposetheconceptsofPythagoreanfuzzyvaluedneutrosophicset(PFVNS)andPythagoreanfuzzyvaluedneutrosophic value(PFVNV)bycombiningNStheoryandPFStheory.APFVNVconsistsofatripleofPythagoreanfuzzy values(PFVs)andaPFVNSconsistsofPFVNVs.Thenwedevelopamethodtotransformfuzzyvaluesand givesomesettheoreticandalgebraicoperationswiththehelpofPythagoreanfuzzy t-normsand t-conorms. Byusingthesealgebraicoperationswedefinesomeweightedarithmeticandgeometricaggregationoperators. Entropyisausefultoolformeasuringuncertaininformation.Theconceptoffuzzyentropywasintroducedby Zadeh.43 Later,afuzzycross-entropymeasureandasymmetricdiscriminationinformationmeasurebetween FSswereproposedbyShangandJiang.22 WeiandYe31 definedamodifiedintuitionisticfuzzycross-entropy measurebetweenIFSs.Withsimilarmotivation,weintroduceasimplifiedneutrosophicvaluedmodifiedfuzzy

https://doi.org/10.54216/IJNS.200208

Received:July08,2022Accepted:January11,2023

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

108

cross-entropyforPFVNVs.Finally,usingtheseconceptsweprovideaMCDMmethodinthePythagorean fuzzyvaluedneutrosophicenvironment.

Somemaincontributionsofthepresentstudycanbelistedasfollows:

• WiththehelpofPythagoreanfuzzy t-normsand t-conormswestudyinthefuzzyenvironmentwhile conductingtheaggregationprocessindecisionmakingproblemsratherthandefuzzifiedenvironment thatprovidesuswithmoresensitivesolutions.

• BymeansofPFVNSs,thedegreesofthetruth,theindeterminacyandthefalsitycanbegiveninthe Pythagoreanfuzzyenvironmentandmoresensitiveevaluationsaremadebydecisionmakersinreal lifeproblems.Inotherwords,suchsetsenableadecisionmakerevaluatethedegreesofthetruth,the indeterminacyandthefalsityasPFVsindecisionmakingprocess.Thus,theuncertaintyinthedecision maker’sevaluationsisrepresentedwiththehelpofmorecapableFSnotion.

• Theproposedcross-entropymeasuremeasuresthediscriminationoftheinformationbetweenPFVNVs inafuzzyenvironment.Thusmoresensitiveevaluationscanbemadeindecisionmakingproblems beforedefuzzifyingtheenvironment.

Therestofthepaperisorganizedasfollows.InSection2,weintroducetheconceptsofPythagoreanfuzzy tnormand t-conormandshowthatsomePythagoreanfuzzy t-normsand t-conormsareexpressedviaordinary continuousArchimedean t-normsand t-conorms.InSection3,weintroducetheconceptofPFVNS,which isanextensionofthenotionofintuitionisticfuzzyvaluedneutrosophicset(IFVNS)whereanIFVNSis anIFVNMSwithsequencelength 1.Thenwedevelopamethodtotransformsimplifiedneutrosophicvalues (SNVs)toPFVNVs.WealsogivesomesettheoreticalandalgebraicoperationsviaPythagoreanfuzzy t-norms and t-conormsforPFVNVs.InSection4wedefinesomeweightedaggregationoperatorsusingthesealgebraic operations.InSection5,motivatingbythemodifiedintuitionisticfuzzycross-entropymeasuredefinedbyWei andYe,31 wegiveasimplifiedneutrosophicvaluedmodifiedfuzzycross-entropy.InSection6,wepropose aMCDMmethodandapplytheproposedtheorytoaMCDMproblemfromtheliterature.Wealsocompare theresultsoftheproposedmethodwiththeexistingresults.Finally,wecalculatethetimecomplexityofthe MCDMmethod.InSection7,weconcludethepaper.

2PythagoreanFuzzy t-normsand t-conorms

Inthissection,werecallsomefundamentaldefinitionsabout t-normsand t-conormsanddefinetheconcepts ofPythagoreanfuzzy t-normand t-conorm.

Definition2.1. 10,21 A t-normisafunction T :[0, 1] × [0, 1] → [0, 1] thatsatisfiesthefollowingconditions:

(T1) T (x, 1)= x forall x ∈ [0, 1],

(T2) T (x,y)= T (y,x) forall x,y ∈ [0, 1],

(T3) T (x,T (y,z))= T (T (x,y),z) forall x,y,z ∈ [0, 1],

(T4) T (x,y) ≤ T (x′,y′) whenever x ≤ x′ and y ≤ y′ .

Definition2.2. 10,21 A t-conormisafunction S :[0, 1] × [0, 1] → [0, 1] thatsatisfiesthefollowingconditions:

(S1) S(x, 0)= x forall x ∈ [0, 1],

(S2) S(x,y)= S(y,x) forall x,y ∈ [0, 1],

(S3) S(x,S(y,z))= S(S(x,y),z) forall x,y,z ∈ [0, 1],

(S4) S(x,y) ≤ S(x′,y′) whenever x ≤ x′ and y ≤ y′

https://doi.org/10.54216/IJNS.200208

Received:July08,2022Accepted:January11,2023

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

109

Definition2.3. 33,34 Afuzzycomplementisafunction N :[0, 1] → [0, 1] satisfyingthefollowingconditions:

(N1) N (0)=1 and N (1)=0,

(N2) N (a) ≥ N (b) whenever a ≤ b forall a,b ∈ [0, 1],

(N3)Continuity,

(N4) N (N (a))= a forall a ∈ [0, 1].

Thefunction N :[0, 1] → [0, 1] definedby N (a)=(1 ap)1/p where p ∈ (0, ∞) isafuzzycomplement introducedbyYager.33,34 When p =2, N (a)= √1 a2 iscalledthePythagoreanfuzzycomplement.

Definition2.4. 12 Let T bea t-normandlet S bea t-conormon [0, 1].If T (x,y)= N (S(N (x),N (y))) and S(x,y)= N (T (N (x),N (y))) forafuzzynegator N ,then T and S aresaidtobedualwithrespectto N

Remark2.5. Let T bea t-normon [0, 1] andlet N (a)= √1 a2.Thenthedual t-conormSwithrespectto N is S(x,y)= 1 T 2 1 x2 , 1 y2

Astrictlydecreasingfunction g :[0, 1] → [0, ∞] with g(1)=0 iscalledtheadditivegeneratorofa t-norm T ifwehave T (x,y)= g 1(g(x)+ g(y)) forall (x,y) ∈ [0, 1] × [0, 1]

Proposition2.6. 12 Let g :[0, 1] → [0, ∞] betheadditivegeneratorofa t-norm T ,let S bethedual tconormof T andlet N beafuzzycomplement.Thestrictlyincreasingfunction h :[0, 1] → [0, ∞] definedby h(t)= g(N (t)) istheadditivegeneratorof S andso S (x,y)= h 1 (h (x)+ h (y))

Notethat T isanArchimedean t-normifandonlyif T (x,x) <x forall x ∈ (0, 1) and S isanArchimedean t-conormifandonlyif S(x,x) >x forall x ∈ (0, 1) 10 KlementandMesiar11 provedthatcontinuous Archimedean t-normshaveusefulrepresentationsviatheiradditivegeneratorsasfollows.

Theorem2.7. 11 Let T bea t-normon [0, 1].Thefollowingareequivalent:

(i) T isacontinuousArchimedean t-norm.

(ii) T hasacontinuousadditivegenerator.

BeforeintroducingtheconceptsofPythagoreanfuzzy t-normand t-conormwerecalltheconceptofPFS. Throughoutthispaperweassume X = {x1,...,xn} isafiniteset.

Definition2.8. 33,34 APFS A on X isdefinedby

A = {⟨xj ,µA(xj ),νA(xj )⟩ : j =1,...,n} where

: X → [0, 1] arethemembershipandnon-membershipfunctionsrespectivelywithcondition that

Motivatingby6 wenowintroducethenotionsofPythagoreanfuzzy t-normandPythagoreanfuzzy t-conorm. Considertheset P ∗ definedby

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

µA

µ2 A(xj )+ ν2 A

≤

α = ⟨µα,να⟩ = ⟨µA(xj ),νA(xj )⟩.

,ν

(

)

1 forany j =1,...,n.Forafixed j =1,...,n aPFVisdenotedby

P ∗ = {x =(x1,x2): x1,x2 ∈ [0, 1] and x 2 1 + x 2 2 ≤ 1} Weusethepartialorder ⪯ on P ∗ thatisdefinedby x ⪯ y ⇔ x1 ≤ y1 and x2 ≥ y2 for x =(x1,x2),y =(y1,y2) ∈ P ∗

Received:July08,2022Accepted:January11,2023 110

https://doi.org/10.54216/IJNS.200208

Definition2.9. APythagoreanfuzzy t-normisafunction T : P ∗ × P ∗ → P ∗ thatsatisfiesthefollowing conditionsforany x =(x1,x2),y =(y1,y2),z =(z1,z2) ∈ P ∗

(PT1) T (x, (1, 0))= x forall x ∈ P ∗ ,

(PT2) T (x,y)= T (y,x) forall x,y ∈ P ∗ ,

(PT3) T (x, T (y,z))= T (y, T (x,z)) forall x,y,z ∈ P ∗ ,

(PT4) T (x,y) ⪯T (x′,y′) whenever x ⪯ x′ and y ⪯ y′ .

Definition2.10. APythagoreanfuzzy t-conormisafunction S : P ∗ × P ∗ → P ∗ thatsatisfiesthefollowing conditionsforany x =(x1,x2),y =(y1,y2),z =(z1,z2) ∈ P ∗ .

(PS1) S(x, (0, 1))= x forall x ∈ P ∗ ,

(PS2) S(x,y)= S(y,x) forall x,y ∈ P ∗ ,

(PS3) S(x, S(y,z))= S(y, S(x,z)) forall x,y,z ∈ P ∗ ,

(PS4) S(x,y) ⪯S(x′,y′) whenever x ⪯ x′ and y ⪯ y′ WedefinetheconceptofPythagoreanfuzzynegatorasanextensionofthenotionoffuzzynegator.

Definition2.11. APythagoreanfuzzynegatorisafunction N : P ∗ → P ∗ satisfyingthefollowingconditions:

(PN1) N ((1, 0))=(0, 1) and N ((0, 1))=(1, 0),

(PN2) N (x) ⪰N (y) whenever x ⪯ y.

If N (N (x))= x forall x ∈ P ∗,thenwecall N involutive.Themapping Ns : P ∗ → P ∗ givenby Ns((x1,x2))=(x2,x1) isaninvolutivePythagoreanfuzzynegatorwhichiscalledthestandardnegator.

FollowingtheoremshowsthataPythagoreanfuzzy t-conormcanbeobtainedfromaPythagoreanfuzzy t-norm viaPythagoreanfuzzynegators.

Theorem2.12. Let T beaPythagoreanfuzzy t-normandlet N beaninvolutivePythagoreanfuzzynegator. Thefunction S definedby S(x,y)= N (T (N (x), N (y))) forany x,y ∈ P ∗ isa t-conorm.

Proof. (PS1)Forall x =(x1,x2) ∈ P ∗ weget

S x, (0, 1)

= N (T (N (x1,x2), N (0, 1)))

= N (T (N (x1,x2), (1, 0)))

= N (N (x1,x2))

= x.

(PS2)Forall x,y ∈ P ∗ weobtain

S(x,y)= N T (N (x), N (y))

= N T (N (y), N (x))

= S(y,x)

https://doi.org/10.54216/IJNS.200208

Received:July08,2022Accepted:January11,2023

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

111

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

(PS3)Forall x,y,z ∈ P ∗ wehave S(x, S(y,z))= S x, N (T (N (y), N (z))

= N T (N (x), N N (T (N (y), N (z)

= N T (N (x), (T (N (y), N (z))

= N T (N (y), (T (N (x), N (z))

= N T (N (y), N N (T (N (x), N (z)

= S y, N (T (N (x), N (z))

= S(y, S(x,z))

(PS4)Forall x,x′,y,y′ ∈ P ∗ wehave x ⪯ x ′ and y ⪯ y ′ ⇒N (x) ⪰N (x ′) and N (y) ⪰N (y ′)

⇒T N (x), N (y) ⪰T N (x ′), N (y ′)

⇒N T N (x), N (y) ⪯N T N (x ′), N (y ′)

⇒S(x,y) ⪯S(x ′ ,y ′).

Therefore, S isaPythagoreanfuzzy t-conorm.

The t-conorm S inTheorem2.12iscalledthedualPythagoreanfuzzy t-conormof T withrespecttonegator N .FollowingtheoremstatesthatPythagoreanfuzzy t-normsand t-conormscanbeproducedbyordinary t-normsand t-conorms.

Theorem2.13. Let T bea t-normandlet

S bea t-conormon [0, 1].If T (a,b) ≤ 1 S2 1 a2 , 1 b2 forall a,b ∈ [0, 1], (1) thenthefunction T : P ∗ × P ∗ → P ∗ definedby T (x,y)= T (x1,y1),S(x2,y2) isaPythagoreanfuzzy t-normandthefunction S : P ∗ × P ∗ → P ∗ definedby S(x,y)= S(x1,y1),T (x2,y2) isthedualPythagoreanfuzzy t-conormof T withrespectto Ns Proof. As S isincreasing,from(1)wehaveforany x,y ∈ P ∗ that T 2(x1,x2)+ S2(x2,y2) ≤ 1 S2 1 x2 1, 1 x2 2 + S2(x2,y2) ≤ 1 S2 1 x2 1, 1 x2 2 + S2 1 x2 1, 1 x2 2 =1 whichyieldsthat T (x,y) isin P ∗ . (PT1)Forany x =(x1,x2) ∈ P ∗ wehave T (x, (1, 0))=(T (x1, 1) ,S (x2, 0)) =(x1,x2) = x (PT2)Forany x,y ∈ P ∗ weget T (x,y)=(T (x1,y1) ,S (x2,y2)) =(T (y1,x1) ,S (y2,x2)) = T (y,x).

Received:July08,2022Accepted:January11,2023 112

https://doi.org/10.54216/IJNS.200208

Therefore T isaPythagoreanfuzzy t-norm.Similarly,itcanbeshownthat S isaPythagoreanfuzzy tconorm.

ContinuousArchimedean t-normsand t-conormson [0, 1] canbegeneratedbytheiradditivegenerators.Sowe canconstructaPythagoreanfuzzy t-normandaPythagoreanfuzzy t-conormusingtheseadditivegenerators. Notethatifa t-norm T anda t-conorm S aredualwithrespecttothePythagoreanfuzzycomplement,then(1) issatisfied.

Corollary2.14. Let g :[0, 1] → [0, ∞] betheadditivegeneratorofacontinuousArchimedean t-norm T andlet h :[0, 1] → [0, ∞] betheadditivegeneratorofthedualcontinuousArchimedean t-conorm S where h(t)= g(√1 t2).Thenthefunction

isthedualPythagoreanfuzzy t-conormof S withrespectto NS .Inthiscase T and S arecalledPythagorean fuzzy t-normandPythagoreanfuzzy t-conormgeneratedby g and h,respectively.

Proof. ItistrivialfromTheorem2.13andRemark2.5.

Example2.15. Considerthefunctions g :[0, 1] → [0, ∞] definedby g(t)= log t2 and h :[0, 1] → [0, ∞] definedby h(t)= log(1 t2).ThentheAlgebraicPythagoreanfuzzy t-normis T (x,y)= x1y

andtheAlgebraicdualPythagoreanfuzzy t-conormwithrespectto Ns is

3PythagoreanFuzzyValuedNeutrosophicSets

WestartthissectionrecallingtheconceptofIFVNSobtainedbytakingthesequencelengthequalto 1 in IFVNMSs.ThenwedefinetheconceptsofPFVNSandPFVNV.

https://doi.org/10.54216/IJNS.200208 Received:July08,2022Accepted:January11,2023

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

T (x, T (y,z))= T (x1,x2), T y1,z1),S(y2,z2) = T x1,T (y1,z1) ,S x2,S(y2,z2) = T y1,T (x1,z1) ,S y2,S(x2,z2) = T (y1,y2), T x1,z1),S(x2,z2) = T (y, T (x,z)).

∈

∗ wehave x ⪯ x ′ and y ⪯ y ′ ⇒ x1 ≤ x ′ 1 , x2 ≥ x ′ 2 and y1 ≤ y ′ 1 , y2 ≥ y ′ 2 ⇒ T (x1,y1) ≤ T (x ′ 1,y ′ 1) and S(x2,y2) ≥ S(x ′ 2,y ′ 2) ⇒T (x,y) ⪯T (x ′ ,y ′)

(PT3)Forall x,y,z ∈ P ∗ weobtain

(PT4)Forall x,x′,y,y′

T : P ∗ × P ∗ → P ∗ definedby T (x,y)= g 1(g(x1)+ g(y1)),h 1(h(x2)+

S : P ∗ × P ∗ → P ∗ definedby S

)= h 1(h(x1)+ h(y1)),g 1(g(x2)+ g

h(y

)) isaPythagoreanfuzzy t-normandthefunction

(x,y

))

2 2

2 2y2 2

, x2 2 + y

x,y)= x2 1 + y2 1 x2 1y2 1 ,x2y2

(

113

Definition3.1. 28 AnIFVNS A on X isdefinedby

However,anIFVNScannotberepresentedasastandardSNS(see,e.g.,Example3.2).

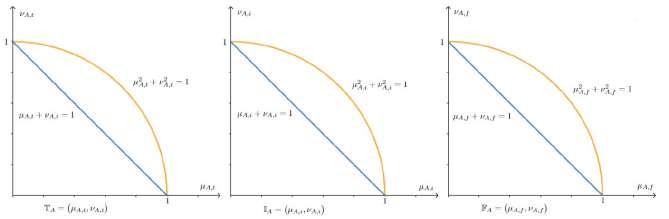
Insomedecisionmakingproblems,thesumofthemembershipandnon-membershipdegreesthataredeterminedbythedecisionmakerscanbelargerthan1.Therefore,PFVsaremorecapablethanIFVsformodelling vaguenessinthedegreesofthetruth,theindeterminacyandthefalsityinthepracticalproblemsasshownin Figure2.UsingPFVsforthedegreeofthetruth,theindeterminacyandthefalsity,wedefinetheconceptof PFVNSandproposesomesettheoreticalandalgebraicoperationsbetweenPFVNSs.ByutilizingPFVNSs, theuncertaintyinthedecisionmaker’sevaluationscanbemodeledinamorecapableenvironment.

Definition3.4. APFVNS A on X isdefinedby

arethetruth,theindeterminacyandthefalsitymembershippairsofPFVs,respectively,

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

A = ⟨xj , Tj A, Ij A, Fj A⟩ : j =1,...,n where Tj A, Ij A and Fj A arethetruth,theindeterminacyandthefalsitymembershippairsofIFVs,respectively, i.e.,for j =1,...,n Tj A = µA,t(xj ),νA,t(xj ) with µA,t(xj ),νA,t(xj ) ∈ [0, 1] suchthat µA,t(xj )+ νA,t(xj ) ≤ 1 Ij A = µA,i(xi),νA,i(xj ) with µA,i(xj ),νA,i(xj ) ∈ [0, 1] suchthat µA,i(xj )+ νA,i(xj ) ≤ 1 Fj A = µA,f (xj ),νA,f (xj ) with µA,f (xj ),νA,f (xj ) ∈ [0, 1] suchthat µA,f (xj )+ νA,f (xj ) ≤ 1 AnIFVNVisdenotedby α = ⟨Tα, Iα, Fα⟩ := ⟨Tj A, Ij A, Fj A⟩ forafixed j =1,...,n Example3.2. Let X = {x1,x2}. A = {⟨x1, (0.7, 0.3), (0.3, 0.5), (0.1, 0.8)⟩, ⟨x2, (0.4, 0.3), (0.1, 0.6), (0.2, 0.75)⟩} isanIFVNS.

ThenotionofIFVNSisanewextensionofthenotionofSNS,sinceeachSNShastheform A = xj ,TA(xj ),IA(xj ),FA(xj ) : j =1,...,n = xj , µA,t(xj ), 0 , µA,i(xj ), 0 , µA,f (xj ), 0 : j =1,...,n .

Remark3.3.

A = ⟨xj , Tj A, Ij A, Fj A⟩ : j =1,...,n

Tj A, Ij A and Fj

i.e.,for j =1,...,n Tj A = µA,t(xj ),νA,t(xj ) with µA,t(xj ),νA,t(xj ) ∈ [0, 1] suchthat µ 2 A,t(xj )+ ν 2 A,t(xj ) ≤ 1 Ij A = µA,i(xi),νA,i(xj ) with µA,i(xj ),νA,i(xj ) ∈ [0, 1] suchthat µ 2 A,i(xj )+ ν 2 A,i(xj ) ≤ 1 Fj A = µA,f (xj ),νA,f (xj ) with µA,f (xj ),νA,f (xj ) ∈ [0, 1] suchthat µ 2 A,f (xj )+ ν 2 A,f (xj ) ≤ 1 APFVNVisdenotedby α = ⟨Tα, Iα, Fα⟩ := ⟨Tj A, Ij A, Fj A⟩ forafixed j =1,...,n Example3.5. Let X = {x1,x2} A = {⟨x1, (0 4, 0 3), (0 5, 0 5), (0 1, 0 9)⟩, ⟨x2, (0 3, 0 7), (0 7, 0 6), (0 2, 0 2)⟩} isaPFVNS. https://doi.org/10.54216/IJNS.200208 Received:July08,2022Accepted:January11,2023 114

where

Figure2:ComparisonofconceptsofPFVandIFVforthetruth,theindeterminacyandthefalsitymembership degrees

Remark3.6. EachIFVNSisaPFVNSbuttheconverseofthisstatementisnottrueingeneral.Forexample, A isaPFVNS,but A isnota IFVNS inExample3.5since 0 7+0 6=1 3 > 1 for I2 A =(0 7, 0 6)

SNVscanbeconvertedtoPFVNVswiththefollowingmethod.AsimilarmethodwasproposedforIFSsin.25 Proposition3.7. Let ρ :[0, 1] → [0, 1] beafunctionsuchthat ρ(t) ≤ √t forany t ∈ [0, 1].Considera number µα ∈ [0, 1].Then

)⟩ isaPFV.

Proof. Let µα ∈ [0, 1]

So α isa PFV

Wecantransforma SNV intoa PFVNV byusingProposition3.7asinthefollowingexample.

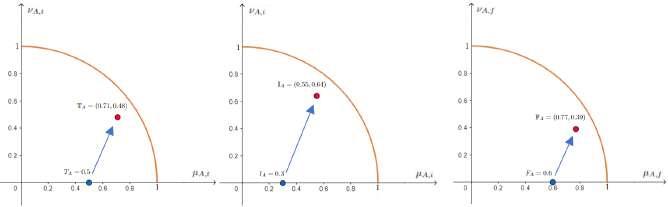
Example3.8. ConsidertheSNV A = ⟨0 5, 0 3, 0 6⟩ andthefunction ρ :[0, 1] → [0, 1] definedby ρ(t)= sint.FromProposition3.7,weobtainaPFVNVfrom A asfollows:

WevisualizethistransformationinFigure3.

NowwedefinethesetoperationsbetweenPFVNSs.ThroughoutthispaperthesetoperationsforPFSsare denotedby ⊂(pyt), ∪(pyt), ∩(pyt), ( )c(pyt) ”(see,34).

https://doi.org/10.54216/IJNS.200208

Received:July08,2022Accepted:January11,2023

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

Figure3:TheSNVandPFVNVinExample3.8

α = ⟨√

µα,ρ(1 µ

√µα + ρ 2(1 µα) ≤ µα + 1 µα 2 = µα +1 µα =1

A = ⟨(0 71, 0 48), (0 55, 0 64), (0 77, 0 39)⟩

115

Definition3.9. Let

c) Ac = xj , Fj A, Ij A c(pyt) , Tj A : j =1,...,n whereforall j =1,...,n

Ij A c(pyt) = νA,i(xj ),µA,i(xj )

d) A ∪ B = xj , Tj A ∪(pyt) Tj B , Ij A ∩(pyt) Ij B , Fj A ∩(pyt) Fj B : j =1,...,n where

Tj A ∪(pyt) Tj B = max µA,t(xj ),µB,t(xj ) , min νA,t(xj ),νB,t(xj )

Ij A ∩(pyt) Ij B = min µA,i(xj ),µB,i(xj ) , max νA,i(xj ),νB,i(xj )

Fj A ∩(pyt) Fj B = min µA,f (xj ),µB,f (xj ) , max νA,f (xj ),νB,f (xj ) .

e) A ∩ B = xj , Tj A ∩(pyt) Tj B , Ij A ∪(pyt) Ij B , Fj A ∪(pyt) Fj B : j =1,...,n where

Tj A ∩(pyt) Tj B = min µA,t(xj ),µB,t(xj ) , max νA,t(xj ),νB,t(xj )

Ij A ∪(pyt) Ij B = max µA,i(xj ),µB,i(xj ) , min νA,i(xj ),νB,i(xj )

Fj A ∪(pyt) Fj B = max µA,f (xj ),µB,f (xj ) , min νA,f (xj ),νB,f (xj )

Example3.10. Let X = {

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

A = ⟨xj , Tj A, Ij A, Fj A⟩ : j =1,...,n and B = ⟨xj , Tj B , Ij B , Fj B ⟩ : j =1,...,n betwoPFVNSs.Setoperationsamong A and B aredefinedasfollows.

Tj A ⊂(pyt) Tj B i.e. µA,t(xj ) ≤ µB,t(xj ) and νA,t(xj ) ≥ νB,t(xj ) Ij A ⊃(pyt) Ij B i.e. µA,i(xj ) ≥ µB,i(xj ) and νA,i(xj ) ≤ νB,i(xj ) Fj A ⊃(pyt) Fj B i.e. µA,f (xj ) ≥ µB,f (xj ) and νA,f (xj ) ≤ νB,f (xj ).

⊂ B ifandonlyifforallj=1,...,n

A = B ifandonlyif A ⊂ B and B ⊂ A.

andconsiderthePFVNSs A = x1, (0 2, 0 3), (0 7, 0 4), (0 4, 0 7) , x2, (0 4, 0 8), (0 7, 0 3), (0 7, 0 1) and B = x1, (0.4, 0.3), (0.4, 0.5), (0.1, 0.9) , x2, (0.6, 0.5), (0.2, 0.6), (0.2, 0.2) . Then A ⊂ B.Ontheotherhand,itiseasytoobtainthat Ac = x1, (0 4, 0 7), (0 4, 0 7), (0 2, 0 3) , x2, (0 7, 0 1), (0 3, 0 7), (0 4, 0 8) A ∪ B = x1, (0 4, 0 3), (0 4, 0 5), (0 1, 0 9) , x2, (0 6, 0 5), (0 2, 0 6), (0 2, 0 2) and A ∩ B = x1, (0 2, 0 3), (0 7, 0 4), (0 4, 0 7) , x2, (0 4, 0 8), (0 7, 0 3), (0 7, 0 1) NextweshowthatsetoperationsdefinedinDefinition3.9satisyDeMorgan’srules. Theorem3.11. Let A = ⟨xj , Tj A, Ij A, Fj A⟩ : j =1,...,n and B = ⟨xj , Tj B , Ij B , Fj B ⟩ : j =1,...,n betwoPFVNSs.Thefollowingarevalid. a) (A ∪ B)c = Ac ∩ Bc b) (A ∩ B)c = Ac ∪ Bc https://doi.org/10.54216/IJNS.200208 Received:July08,2022Accepted:January11,2023 116

}

NowweintroducesomealgebraicoperationsforPFVNVsviaPythagoreanfuzzy

α, Iβ , S Fα, Fβ

Remark3.13. If g istheadditivegeneratorofacontinuousArchimedean t-normand h(t)= g(√1 t2), thenfromCorollary2.14weget

FollowingpropositionisthevalidationofthatthesumandtheproductoftwoPFVNVsarealsoPFVNVs.

Proposition3.14. Let α and β betwoPFVNVs,let T beAPythagoreanfuzzy t-normandlet S bethedual Pythagoreanfuzzy t-conormwithrespecttoaPythagoreanfuzzynegator N .Then, α ⊕ β and α ⊗ β arealso PFVNVs.

Proof. Since T and S haverange P ∗ , α ⊕ β and α ⊗ β arePFVNVs.

Nextwedefinemultiplicationbynon-negativeconstantandnon-negativepowerofPFVNVsusingadditive generatorsofcontinuousArchimedean t-normand t-conormon [0, 1]

https://doi.org/10.54216/IJNS.200208 Received:July08,2022Accepted:January11,2023

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023 Proof. a)Weget (A ∪ B)c = xj , Tj A ∪(pyt) Tj B , Ij A ∩(pyt) Ij B , Fj A ∩(pyt) Fj B : j =1,...,n c = xj , Fj A ∩(pyt) Fj B , Ij A ∩(pyt) Ij B c(pyt) , Tj A ∪(pyt) Tj B : j =1,...,n = xj , Fj A ∩(pyt) Fj B , Ij A c(pyt) ∪(pyt) Ij B c(pyt) , Tj A ∪(pyt) Tj B : j =1,...,n = Ac ∩ Bc b)Weget (A ∩ B)c = xj , Tj A ∩(pyt) Tj B , Ij A ∪(pyt) Ij B , Fj A ∪(pyt) Fj B : j =1,...,n c = xj , Fj A ∪(pyt) Fj B , Ij A ∪(pyt) Ij B c(pyt) , Tj A ∩(pyt) Tj B : j =1,...,n = xj , Fj A ∪(pyt) Fj B , Ij A c(pyt) ∩(pyt) Ij B c(pyt) , Tj A ∩(pyt) Tj B : j =1,...,n = Ac ∪ Bc .

-conorms. Definition3.12. Let α = ⟨Tα, Iα, Fα⟩ and β = ⟨Tβ , Iβ , Fβ ⟩ betwoPFVNVs,let T beaPythagoreanfuzzy t-normandlet S bethedualPythagoreanfuzzy t-conormof T withrespecttoaPythagoreanfuzzynegator N .Then α ⊕ β := S Tα, Tβ , T Iα, Iβ , T Fα, Fβ and α ⊗ β := T Tα, Tβ , S I

t-normsand t

µα,t

β,t

να,t

g 1 g(µα,i)+ g

µβ,i) ,h 1 h(να,i)+ h(νβ,i) , g 1 g(µα,f )+ g(µβ,f ) ,h 1 h(να,f )+ h(νβ,f ) and α ⊗ β = g 1 g(µα,t)+ g(µβ,t) ,h 1 h(να,t)+ h(νβ,t) , h 1 h(µα,i)+ h(µβ,i) ,g 1 g(να,i)+ g(νβ,i) , h 1 h(µα,f )+ h(µβ,f ) ,g 1 g(να,f )+ g(νβ,f )

⊕ β = h 1 h(

)+ h(µ

) ,g

)+ g(νβ,t) ,

(

117

Definition3.15. Let α = ⟨Tα, Iα, Fα⟩

ThefollowingpropositionverifiesthatmultiplicationbyconstantandpowerofPFVNVsarealsoPFVNVs.

whichyieldsthat Tλα isaPFV.Similarly,itcanbeeasilyshownthat

, Iαλ and Fαλ arePFVs. Therefore λα isaPFVNV.

Followingtheoremgivessomebasicpropertiesofalgebraicoperations.

Theorem3.17.

λ,γ ≥ 0,let g betheadditivegeneratorofacontinuousArchimedean t-normandlet h(t)= g(√1 t2).Then,

i) α ⊕ β = β ⊕ α

ii) α ⊗ β = β ⊗ α

iii) (α ⊕ β) ⊕ θ = α ⊕ (β ⊕ θ)

iv) (α ⊗ β) ⊗ θ = α ⊗ (β ⊗ θ)

v) λ(α ⊕ β)= λα ⊕ λβ

vi) (λ + γ)α = αλ ⊕ γα

vii) (α ⊗ β)λ = αλ ⊗ βλ

viii) αλ ⊗ αγ = αλ+γ

Proof. (i)and(ii)aretrivial.

iii) ItisclearfromDefinition3.12that

Tα⊕β = h 1 h(µα,t)+ h(µβ,t) ,g 1 g(να,t)+ g(νβ,t) . https://doi.org/10.54216/IJNS.200208 Received:July08,2022Accepted:January11,2023

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

≥ 0

1 t2

λα = h 1 λh µα,t ,g 1 λg να,t , g 1 λg µα,i ,h 1 λh να,i , g 1 λg µα,f ,h 1 λh να,f and α λ = g 1 λg µα,t ,h 1 λh να,t , h 1 λh µα,i ,g 1 λg να,i , h 1 λh µα,f ,g 1 λg να,f .

beaPFVNV,let λ

,let

:[0, 1] → [0, ∞] betheadditivegenerator ofacontinuousArchimedean t-normandlet h(t)=

(√

).Then

beaPFVNV,let λ ≥ 0,let g :[0, 1] → [0, ∞] betheadditivegeneratorofa

t-normandlet h(t)= g(√1 t2).Then λα and αλ arePFVNVs.

Weknowthat h 1(t)= 1 [g 1(t)]2 and g(t)= h(√1 t2).Since µα,t ≤ 1 ν2 α,t and h,h 1 areincreasing,weobtain 0 ≤ h 1(λh(µα,t)) 2 + g 1(λg(να,t)) 2 ≤ h 1 λh 1 ν2 α,t 2 + g 1(λg(να,t)) 2 =1 g 1 λh 1 ν2 α,t 2 + g 1(λg(να,t)) 2 =1 g 1(λg(να,t)) 2 + g 1(λg(να,t)) 2 =1

Proposition3.16. Let α

continuousArchimedean

Proof.

Iλα, Fλα Tαλ

Fα⟩

β = ⟨Tβ , Iβ , Fβ ⟩ and θ = ⟨Tθ, Iθ, Fθ⟩

Let α = ⟨Tα, Iα,

bePFVNVs,let

118

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

Therefore,weobtain

T(α⊕β)⊕θ = S(Tα⊕β , Tθ)

= h 1 h h 1 h(µα,t)+ h(µβ,t) + h µθ,t ,

g 1 g g 1 g(να,t)+ g(νβ,t) + g νθ,t

= h 1 h(µα,t)+ h(µβ,t)+ h(µθ,t) ,

g 1 g(να,t)+ g(νβ,t)+ g νθ,t

= h 1 h(µα,t)+ h h 1 h(µβ,t)+ h(µθ,t) ,

g 1 g(να,t)+ g g 1 g(νβ,t)+ g νθ,t

= S(Tα, Tβ⊕θ) = Tα⊕(β⊕θ)

Similarlyitcanbeeasilyobtainedthat I(α⊕β)⊕θ = Iα⊕(β⊕θ) and F(α⊕β)⊕θ = Fα⊕(β⊕θ) iv) ItisclearfromDefinition3.12that

Therefore,wehave

Tα⊗β = g 1 g(µα,t)+ g(µβ,t) ,h 1 h(να,t)+ h(νβ,t)

T(α⊗β)⊗θ = T (Tα⊗β , Tθ)

= g 1 g g 1 g(µα,t)+ g(µβ,t) + g µθ,t , h 1 h h 1 h(να,t)+ h(νβ,t) + h νθ,t

= g 1 g(µα,t)+ g(µβ,t)+ g(µθ,t) , h 1 h(να,t)+ h(νβ,t)+ h νθ,t

= g 1 g(µα,t)+ g g 1 g(µβ,t)+ g(µθ,t) , h 1 h(να,t)+ h h 1 h(νβ,t)+ h νθ,t = T (Tα, Tβ⊗θ)

= Tα⊗(β⊗θ)

Similarlyitcanbeseenthat I(α⊗β)⊗θ = Iα⊗(β⊗θ) and F(α⊗β)⊗θ = Fα⊗(β⊗θ)

v) ItisclearfromDefinition3.12andDefinition3.15that

Tα⊕β =(µα⊕β,t,να⊕β,t)= h 1 h(µα,t)+ h(µβ,t) ,g 1 g(να,t)+ g(νβ,t) and Tλα =(µλα,t,νλα,t)= h 1 λh µα,t ,g 1 λg να,t

Therefore,weget

Tλ(α⊕β) = h 1 λh(µ

α⊕β,t) ,g 1 λg(να⊕β,t) = h 1 λh(h 1 h(µα,t)+ h(µβ,t)) ,g 1 λg(g 1 g(να,t)+ g(νβ,t) = h 1 λh(µα,t)+ λh(µβ,t)) ,g 1 λg(να,t)+ λg(νβ,t) = h 1 h h 1 λh(µα,t) + h h 1 λh(µβ,t) , g 1 g g 1 λg(να,t) + g g 1 λg(νβ,t) = h 1 h µλα,t + h µλβ,t ,g 1 g νλα,t + g νλβ,t = Tλα⊕λβ https://doi.org/10.54216/IJNS.200208 Received:July08,2022Accepted:January11,2023 119

Similarlyitcanbeshownthat

vi)

vii)

4WeightedAggregationOperatorsforPFVNVs

Aggregationoperatorshaveavitalrolewhiletransforminginputvaluesrepresentedbyfuzzyvaluestoa singleoutputvalue.Inthissection,weintroduceaweightedarithmeticaggregationoperatorandaweighted geometricaggregationoperatorforcollectionsofPFVNVsbyusingalgebraicoperationsgiveninSection3.

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

Iλ(α⊕β) = Iλα⊕λβ and Fλ(α⊕β) = Fλα⊕λβ

Itisclearthat T(λ+γ)α = h 1 (λ + γ)h µα,t ,g 1 (λ + γ)g να,t = h 1 λh µα,t + γh µα,t ,g 1 λg να,t + γg να,t = h 1 h h 1 λh µα,t + h h 1 γh µα,t , g 1 g(g 1 λg να,t + g(g 1 γg να,t = h 1 h µλα,t + h(µγα,t ,g 1 g νλα,t + g νγα,t = Tλα⊕γα Similarlyitcanbeobtainedthat I(λ+γ)α = Iλα⊕γα and F(λ+γ)α = Fλα⊕γα.

Weknowthat

α⊗β =(µα⊗β,t,να⊗β,t)= g 1 g(µα,t)+ g(µβ,t) ,h 1 h(να,t)+ h(νβ,t) and Tαλ =(µαλ,t,ναλ,t)= g 1 λg µα,t ,h 1 λh να,t Therefore,weobtain T(α⊗β)λ = g 1 λg(µα⊗β,t) ,h 1 λh(να⊗β,t) = g 1 λg(g 1 g(µα,t)+ g(µβ,t)) ,h 1 λh(h 1 h(να,t)+ h(νβ,t) = g 1 λg(µα,t)+ λg(µβ,t)) ,h 1 λh(να,t)+ λh(νβ,t) = g 1 g g 1 λg(µα,t) + g g 1 λg(µβ,t) , h 1 h h 1 λh(να,t) + h h 1 λh(νβ,t) = g 1 g µαλ,t + g µβλ,t ,h 1 h ναλ,t + h νβλ,t = Tαλ⊕βλ Similarlyitcanbeseenthat I(α⊗β)λ = Iαλ⊕βλ and F(α⊗β)λ = Fαλ⊕βλ

Tαλ+γ = g 1 (λ + γ)g µα,t ,h 1 (λ + γ)h να,t = g 1 λg µα,t + γg µα,t ,h 1 λh να,t + γh να,t = g 1 g g 1 λg µα,t + g h 1 γg µα,t , h 1 h(h 1 λh να,t + h(h 1 γh να,t = g 1 g µαλ,t + g(µαγ ,t ,h 1 h ναλ,t + h ναγ ,t = Tαλ⊗αγ Similarlyitcanbeobtainedthat Iαλ+γ = Iαλ⊗αγ and Fαλ+γ = Fαλ⊗αγ

viii) Wehave

Received:July08,2022Accepted:January11,2023 120

https://doi.org/10.54216/IJNS.200208

4.1AWeightedArithmeticAggregationOperator

Asseeninthenexttheorem,weightedarithmeticaggregationoperatorscanbeexpressedviaadditivegeneratorswhenever t-normand t-conormarecontinuousArchimedean.

Proof. ItisclearfromPropositions3.14and3.16that WA PFVVNV (

1,...,αn) isaPFVNV.Using mathematicalinductionweshowthatthesecondpartisvalid.If n =2,weobtain

https://doi.org/10.54216/IJNS.200208

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

Let {αj = ⟨Tαj , Iαj , Fαj ⟩ : j =1,...,n} beacollectionofPFVNVs.Aweightedarithmetic aggregationoperator WA PFVNV isdefinedby WA PFVNV (α1,...,αn):= n j=1 wj αj where w =(w1,...,wn)T isaweightvectorsuchthat 0 ≤ wj ≤ 1 forany j =1,...,n and n j=1 wj =1

Definition4.1.

Theorem4.2. Let {αj = ⟨Tαj , Iαj , Fαj ⟩ : j =1,...,n} beacollectionofPFVNVs,let w =(w1,...,wn)T beaweightvectorsuchthat 0 ≤ wj ≤ 1 forany j =1,...,n and n j=1 wj =1 andlet g betheadditivegeneratorofacontinuousArchimedean t-normandlet h(t)= g(√1 t2).Then WA PFVVNV (α1,...,αn) isa PFVNV andwehave WA PFVNV (α1,...,αn)= h 1 n j=1 wj h(µαj ,t) ,g 1 n j=1 wj g(ναj ,t) , g 1 n j=1 wj g(µαj ,i) ,h 1 n j=1 wj h(ναj ,i) , g 1 n j=1 wj g(µαj ,f ) ,h 1 n j=1 wj h(ναj ,f )

Tw1α1⊕w2α2 = S(Tw1α1 , Tw2α2 ) = h 1 h(µw1α1 )+ h(µw2α2 ) ,g 1 g(νw1α1 )+ g(νw2α2 ) = h 1 h(h 1(w1h(µα1 )))+ h(h 1(w2h(µα2 ))) , g 1 g(g 1(w1g(να1 ))+ g(g 1(w2g(να2 ))) = h 1 w1h(µα1 )+ w2h(µα2 ) ,g 1 w1g(να1 )+ w2g(να2 ) = h 1 2 j=1 wj h(µαj ) ,g 1 2 j=1 wj g(ναj ) Nowassumethat TAn 1 =  h 1   n 1 j=1 wj h(µαj )  ,g 1   n 1 j=1 wj g(ναj )    ,

Received:July08,2022Accepted:January11,2023 121

Remark4.3. Usingparticularadditivegeneratorsweobtainsomeparticularcasesof WA PFVNV as follows:

a) Letgbetheadditivegeneratordefinedby g(t)= log t2.ThenwegetAlgebraicweightedarithmetic aggregationoperatorgivenby

b) Letgbetheadditivegeneratordefinedby g(t)=log( 2 t2 t2 ).ThenwegetEinsteinweightedarithmetic aggregationoperatorgivenby

n j=1

TAn = TAn 1 ⊕ wnαn = S TAn 1 , Twnαn = S h 1 n 1 j=1 wj h(µαj ) ,g 1 n 1 j=1 wj g(ναj ) , h 1(wnh(µαn,t)),g 1(wng(µαn,t)) = h 1 h h 1 n 1 j=1 wj h(µαj ) + h h 1(wnh(µαn,t)) , g 1 g g 1 n 1 j=1 wj g(ναj ) + g g 1(wng(µαn,t)) = h 1 n 1 j=1 wj h(µαj )+ wnh(µαn,t) ,g 1 n 1 j=1 wj g(ναj )+ wng(µαn,t) = h 1 n j=1 wj h(µαj ) ,g 1 n j=1 wj g(ναj )

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023 where An :=

αj .Thenweobtain

Similarproofisalsovalidforindeterminacyandfalsity.

WAA PFVNV (α1,...,αn)= 1 n j=1 (1 µ2 αj ,t)wj , n j=1 ν wj αj ,t , n j=1 µ wj αj ,i, 1 n j=1 (1 ν2 αj ,i)wj , n j=1 µ wj αj ,f , 1 n j=1 (1 ν2 αj ,f )wj

WAE PFVNV (α1,...,αn)= n j=1(1+ µ2 αj ,t)wj n j=1(1 µ2 αj ,t)wj n j=1(1+ µ2 αj ,t)wj + n j=1(1 µ2 αj ,t)wj , √2 n j=1 νwi αj ,t n j=1(2 ν2 αj ,t)wj + n j=1(ν2 αi,t)wj , √2 n j=1 µwj αj ,i n j=1(2 µ2 αj ,i)wj + n j=1(µ2 αj ,i)wj , n j=1(1+ ν2 αj ,i)wj n j=1(1 ν2 αj ,i)wj n j=1(1+ ν2 αj ,i)wj + n j=1(1 ν2 αj ,i)wj , √2 n j=1 µwj αj ,f n j=1(2 µ2 αj ,f )wj + n j=1(µ2 αj ,f )wj n j=1(1+ ν2 αj ,f )wj n j=1(1 ν2 αj ,f )wj n j=1(1+ ν2 αj ,f )wj + n j=1(1 ν2 αj ,f )wj

Definition4.4. Let {αj = ⟨Tαj , Iαj , Fαj ⟩ : j =1,...,n} beacollectionofPFVNVs.Aweightedgeometric aggregationoperator WG PFVVNV isdefinedby WG PFVVNV (α1,...,αn):= n j=1 α wj j https://doi.org/10.54216/IJNS.200208 Received:July08,2022Accepted:January11,2023 122

4.2WeightedGeometricAggregationOperator

where w =(w1,...,wn)T isaweightvectorsuchthat 0 ≤ wj ≤

Asseeninthenexttheorem,weightedgeometricaggregationoperatorscanbeexpressedviaadditivegeneratorswhenever t-normand t-conormarecontinuousArchimedean.

Theorem4.5.

Proof. ItcanbeprovedsimilartoTheorem4.2. Remark4.6. Byusingparticularadditivegeneratorswealsoobtainsomeparticularcasesof

5ASimplifiedNeutrosophicValuedModifiedFuzzyCross-EntropyMeasureforPFVNVs

ThenotionofSNSwasproposedbyYe37 torelievethedifficultyofapplyingNSstopracticalproblems.

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

1 forany j =1,...,n and

j=1 wj =1

⟨Tαj , Iαj , Fαj ⟩ : j =1,...,n} beacollectionofPFVNVs,let w =(w1,...,wn)T beaweightvectorsuchthat 0 ≤ wj ≤ 1 forany j =1,...,n and n j=1 wj =1,let g betheadditivegeneratorofacontinuousArchimedean t-normandlet h(t)= g(√1 t2).Then WG PFVVNV (α1,...,αn) isaPFVNVand WG PFVVNV (α1,...,αn)= g 1 n j=1 wj g(µαj ,t) ,h 1 n j=1 wj h(ναj ,t) , h 1 n j=1 wj h(µαj ,i) ,g 1 n j=1 wj g(ναj ,i) , h 1 n j=1 wj h(µαj ,f ) ,g 1 n j=1 wj g(ναj ,f )

Let {αj =

WG PFVNV

g(t)= log t2.ThenwegetAlgebraicweightedgeometric aggregationoperatorgivenby WGA PFVVNV (α1,...,αn)= n j=1 µ wj αj ,t, 1 n j=1 (1 ν2 αj ,t)wj , 1 n j=1 (1 µ2 αj ,i)wj , n j=1 ν wj αj ,i , 1 n j=1 (1 µ2 αj ,f )wj , n j=1 ν wj αj ,f .

g(t)=log( 2 t2 t2 ).ThenwegetEinsteinweightedgeometric aggregationoperatorgivenby WGE PFVVNV (α1,...,αn)= √2 n j=1 µwj αj ,t n j=1(2 µ2 αj ,t)wj + n j=1(µ2 αj ,t)wj , n j=1(1+ ν2 αj ,t)wj n j=1(1 ν2 αj ,t)wj n j=1(1+ ν2 αj ,t)wj + n j=1(1 ν2 αj ,t)wj , n j=1(1+ µ2 αj ,i)wj n j=1(1 µ2 αj ,i)wj n j=1(1+ µ2 αj ,i)wj + n j=1(1 µ2 αj ,i)wj , √2 n j=1 νwi αj ,i n j=1(2 ν2 αj ,i)wj + n j=1(ν2 αi,i)wj , n j=1(1+ µ2 αj ,f )wj n j=1(1 µ2 αj ,f )wj n j=1(1+ µ2 αj ,f )wj + n j=1(1 µ2 αj ,f )wj , √2 n j=1 νwi αj ,f n j=1(2 ν2 αj ,f )wj + n j=1(ν2 αi,f )wj

asfollows. a)Letgbetheadditivegeneratordefinedby

b)Letgbetheadditivegeneratordefinedby

123

https://doi.org/10.54216/IJNS.200208 Received:July08,2022Accepted:January11,2023

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

Definition5.1. 37 ASNS A on X isgivenby

A = {⟨xj ,TA(xj ),IA(xj ),FA(xj )⟩ : j =1,...,n}

where TA,IA,FA : X → [0, 1] arethetruth,indeterminacyandfalsifymembershipfunctions.Forconvenience,aSNVisdenotedby

α = ⟨Tα,Iα,Fα⟩ = ⟨TA(xj ),IA(xj ),FA(xj )⟩

forafixed xj ∈ X

SomealgebraicoperationsofSNVisrecalledinthenextdefinition.

Definition5.2. 18 Let A = ⟨TA,IA,FA⟩ and B = ⟨TB ,IB ,FB ⟩ beSNVs.Assumethat g :[0, 1] → [0, ∞] istheadditivegeneratorofacontinuousArchimedean t-normand h :[0, 1] → [0, ∞] istheadditivegenerator ofacontinuousArchimedean t-conorm.SomealgebraicoperationsbetweenSNVsaredefinedasfollow:

Thefollowingpropositionverifiesthatasimplifiedneutrosophicvaluedmodifiedfuzzycross-entropymeasure between α and β isaSNV.

Proposition5.4. E(α,β) isaSNV.

Proof. AccordingtoShannon’sinequality,15 weknowthateachcomponentof E(α,β) isequalorgreaterthan 0.Ontheotherhand,sincetherelation

istrue,eachcomponentof E(α,β) isequalorlessthan1.Therefore E(α,β) isaSNV.

Itisclearthat E(α,β) = E(β,α) ingeneral.Tomaketheconceptsymmetricwecandefinethefollowing.

Definition5.5. Let α and β betwoPFVNVs.Asimplifiedneutrosophicvaluedsymmetricdiscrimination informationmeasurebasedon E isgivenby

wheremultiplicationbyscalar 1 2 isinthesenseof(iii)ofDefinition5.2.

https://doi.org/10.54216/IJNS.200208

i) A ⊕SNV B = h 1(h(TA)+ h(TB )),g 1(g(IA)+ g(IB )),g 1(g(FA)+ g(FB ))

λA = h 1

λh

TA)),g 1(λg(IA)),g 1(λg(FA)) .

Let α = ⟨Tα, Iα, Fα⟩ and β = ⟨Tβ , Iβ , Fβ ⟩ betwoPFVNVs.Asimplifiedneutrosophic

α and β isdefinedby E(α,β):= 1 ln2 µ 2 α,t ln 2µ2 α,t µ2 α,t + µ2 β,t + ν 2 α,t ln 2ν2 α,t ν2 α,t + ν2 β,t + π 2 α,t ln 2π2 α,t π2 α,t + π2 β,t , 1 1 ln2 µ 2 α,i ln 2µ2 α,i µ2 α,i + µ2 β,i + ν 2 α,i ln 2ν2 α,i ν2 α,i + ν2 β,i + π 2 α,i ln 2π2 α,i π2 α,i + π2 β,i , 1 1 ln2 µ 2 α,f ln 2µ2 α,f µ2 α,f + µ2 β,f + ν 2 α,f ln 2ν2 α,f ν2 α,f + ν2 β,f + π 2 α,f ln 2π2 α,f π2 α,f + π2 β,f where π2 α,. =1 µ2 α,. ν2 α,. ,and π2 β,. =1 µ2 β,. ν2 β,..Asin,5 weusetheconvention(basedoncontinuity arguments)that 0ln 0 p =0 for p ≥ 0.

ii)

(

Definition5.3.

valuedmodifiedfuzzycross-entropymeasurebetween

1 ln2 µ 2 α,. ln 2µ2 α,. µ2 α,. + µ2 β,. + ν 2 α,. ln 2ν2 α,. ν2 α,. + ν2 β,. + π 2 α,. ln 2π2 α,. π2 α,. + π2 β,. ≤ 1 ln2 µ 2 α,. ln2+ ν 2 α,. ln2+ π 2 α,. ln2 =1

E∗(α,β)= 1 2 E(α,β) ⊕SNV 1 2 E(β,α)

124

Received:July08,2022Accepted:January11,2023

E∗ canbeexpressedviaadditivegeneratorsofcontinuousArchimedean t-normsand t-conorms.

Theorem5.6. Let α and β betwoPFVNVs,let g betheadditivegeneratorofacontinuousArchimedean t-normand h(t)= g(1 t).Then

Byusingparticularadditivegeneratorswecanobtainsomeparticularcasesof E∗ .

Remark5.7. Let g betheadditivegeneratordefinedby g(t)= log t.ThenwegetAlgebraicsimplified neutrosophicvaluedsymmetricdiscriminationinformationmeasurebasedon E givenby

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

E∗(α,β)= h 1 1 2 h TE(α,β) + h TE(β,α) ,g 1 1 2 g IE(α,β) + g IE(β,α) , g 1 1 2 g(FE(α,β) + g FE(β,α) .

Wehave E∗(α,β)= 1 2 E(α,β) ⊕SNV 1 2 E(β,α) = h 1 h T 1 2 E(α,β) + h T 1 2 E(β,α) ,g 1 g I 1 2 E(α,β) + g I 1 2 E(β,α) , g 1 g(F 1 2 E(α,β) + g F 1 2 E(β,α) = h 1 h h 1 1 2 h(TE(α,β)) + h h 1 1 2 h TE(β,α)) , g 1 g g 1 1 2 g(IE(α,β)) + g g 1 1 2 g IE(β,α)) , g 1 g g 1 1 2 g(IE(α,β)) + g g 1 1 2 g IE(β,α)) whichyieldsthat E∗(α,β)= h 1 1 2 h TE(α,β) + h TE(β,α) ,g 1 1 2 g IE(α,β) + g IE(β,α) , g 1 1 2 g(FE(α,β) + g FE(β,α)

Proof.

E∗ A(α,β)= 1 (1 TE(α,β))(1 TE(β,α)), IE(α,β)IE(β,α), FE(α,β)FE(β,α) . Let g betheadditivegeneratordefinedby g(t)=log( 2 t t ).ThenwegetEinsteinsimplifiedneutrosophic

E givenby E∗ E (α,β)= (1+ TE(α,β))(1+ TE(β,α)) (1 TE(α,β))(1 TE(β,α)) (1+ TE(α,β))(1+ TE(β,α))+ (1 TE(α,β))(1 TE(β,α)) , 2 IE(α,β)IE(β,α) IE(α,β)IE(β,α) + (2 IE(α,β))(2 IE(β,α)) , 2 FE(α,β)FE(β,α) FE(α,β)FE(β,α) + (2 FE(α,β))(2 FE(β,α))

Received:July08,2022Accepted:January11,2023 125

valuedsymmetricdiscriminationinformationmeasurebasedon

https://doi.org/10.54216/IJNS.200208

Since E∗ isaSNV,ascorefunctionisneededtorankthevaluesof E∗.Inthispaper,weusethefollowing scorefunction.

Definition5.8. 32 Let A =(TA,IA,FA) beaSNV.Ascorefunctionisdefinedby

Theorem5.9. Let α and β betwoPFVNVs.Themodifiedcross-entropymeasure E∗ satisfiesthefollowing properties.

i) E∗(α,α)= ⟨0, 1, 1⟩,

ii) 0 ≤ N (E∗(α,β)) ≤ 1,

iii) E∗(α,β)= E∗(β,α),

iv) N (E∗(α,α))=0

Proof.

Weknowthat

6AnApplicationof PFVNVs ToAMCDMProblem

Inthissection,weprovideaMCDMmethodinPythagoreanfuzzyvaluedneutrosophicenvironment.Then wesolveaMCDMproblemfromtheliteraturebyusingtheproposedmethod.

https://doi.org/10.54216/IJNS.200208

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

IA +1 FA 3

N (

E(α,α)= 1 ln2 µ 2 α,t ln 2µ2 α,t µ2 α,t + µ2 α,t + ν 2 α,t ln 2ν2 α,t ν2 α,t + ν2 α,t + π 2 α,t ln 2π2 α,t π2 α,t + π2 α,t , 1 1 ln2 µ 2 α,i ln 2µ2 α,i µ2 α,i + µ2 α,i + ν 2 α,i ln 2ν2 α,i ν2 α,i + ν2 α,i + π 2 α,i ln 2π2 α,i π2 α,i + π2 α,i , 1 1 ln2 µ 2 α,f ln 2µ2 α,f µ2 α,f + µ2 α,f + ν 2 α,f ln 2ν2 α,f ν2 α,f + ν2 α,f + π 2 α,f ln 2π2 α,f π2 α,f + π2 α,f = ⟨0, 1, 1⟩ Thereforeweobtain E∗(α,α)= h 1 1 2 h TE(α,α) + h TE(α,α) ,g 1 1 2 g IE(α,α) + g IE(α,α) , g 1 1 2 g(FE(α,α) + g FE(α,α) = TE(α,α),IE(α,α),FE(α,α) = ⟨0, 1, 1⟩ ii) Since E∗(α,β) isaSNVweobtainthat 0 ≤ N (E∗(α,β)) ≤ 1.

Itistrivialfromdefinitionof E∗

Itistrivialfrom(i)anddefinitionof N .

iii)

iv)

Received:July08,2022Accepted:January11,2023 126

Table1:SNVsofalternativesaccordingtocriteria

6.1AMCDMmethod

Inthissub-section,wegiveaMCDMmethodinthePythagoreanfuzzyvaluedneutrosophicenvironment.The proposedmethodisappliedtoaMCDMproblemadaptedfromtheliterature37,38 toseetheeffectivenessof theproposedmethod.Thestepscanbesummarizedasfollows.

Step1: FormaMCDMproblemwithalternatives

Step2: Theweightsofcriteriaaredetermined.

Step3: Theevaluationresultsofthealternativesareexpressedbytheexpertas SNVs foreachcriterion.

Step4: UsingProposition3.7,evaluationresultsofalternativesinStep3areconvertedfromSNVsto PFVNVs.

Step5: EvaluationvaluesexpressedasPFVNVsforeachalternativeaccordingtocriteriaaretransformedtoa valueexpressedasaPFVNVbyutilizingproposedweightedaggregationoperators.

Step6: Positiveidealalternativeforeachsampleisdefinedby

Here,allofthecriteriaareassumedtobebenefitcriteria.Ifthereexistsacostcriterion,thenwecantake compliment.

Step7: Byusing E∗ definedinDefinition5.5thesymmetricdiscriminationinformationmeasurebetween aggregatedvalueofeachalternativeandpositiveidealalternativearecalculated.

Step8: Thescoresofthese SNVs areobtainedbyusingascorefunction.

Step9: Alternativesarerankedsothattheminimumscorevalueisthebestalternative.

6.2Anapplication

Asanapplication,weconsideraninvestmentcompanywhichwantstoinvestasumofmoneyinthebest opinion.Thisproblemisadaptedfrom.37,38 Therearefouralternativesforinvestingthemoney:(1) A1 (a carcompany);(2) A2 (afoodcompany);(3) A3 (acomputercompany);and(4) A4 (anarmscompany).The investmentcompanywantstomakeadecisionusingthefollowingthreecriteria:(1) C1 (therisk);(2) C2 (thegrowth);and(3) C3 (thetheenvironmentalimpact).Theweightvectorofthecriteriaisconsideredby w =(0 35, 0 25, 0 4) andthedecisionmatrixgiveninTable1isusedasin.37,38

Let fδ(t)= sinδt with δ ∈ [0, 1].Itisclearthat fδ(t)= sinδt ≤ √t for t ∈ [0, 1] (seealsoFigure4).

Nowweconvert SNVs ofalternativesinTable1to PFVNVs byusingProposition3.7.For δ =1,we

https://doi.org/10.54216/IJNS.200208

Received:July08,2022Accepted:January11,2023

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023 C1 C2 C3 A1 ⟨0 4, 0 2, 0 3⟩⟨0 4, 0 2, 0 3⟩⟨0 2, 0 2, 0 5⟩ A2 ⟨0 6, 0 1, 0 2⟩⟨0 6, 0 1, 0 2⟩⟨0 5, 0 2, 0 2⟩ A3 ⟨0 3, 0 2, 0 3⟩⟨0 5, 0 2, 0 3⟩⟨0 5, 0 3, 0 2⟩ A4 ⟨0.7, 0.0, 0.1⟩⟨0.6, 0.1, 0.2⟩⟨0.4, 0.3, 0.2⟩

A = {A1,...,An} andcriteria C = {C1,...,Ck}

A+ = ⟨(µ+ t ,ν+ t ), (µ+ i ,ν+ i ), (µ+ f ,ν+ f )⟩ withalternatives A = {A1,...,An} = {⟨(µ1 t ,ν1 t ), (µ1 i ,ν1 i ), (µ1 f ,ν1 f )⟩,..., ⟨(mn t ,νn t ), (µn i ,νn i ), (µn f ,νn f )⟩} and µ+ t =max j∈{1,...,n} µj t , ν+ t =min j∈{1,...,n} νj t , µ+ i =min j∈{1,...,n} µj i , ν+ i =max j∈{1,...,n} νj i , µ+ f =min i∈{1,...,n} µj f , ν+ f =max i∈{1,...,n} νj f

127

alternatives

Figure4:Thegraphsof y = √t and fδ with δ ∈ [0, 1]

Table2:PFVNVsofalternativesobtainedfor

https://doi.org/10.54216/IJNS.200208

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

C1 C2 A1 ⟨(0.63, 0.56), (0.45, 0.72), (0.55, 0.64)⟩⟨(0.63, 0.56), (0.45, 0.72), (0.55, 0.64)⟩ A2 ⟨(0 77, 0 39), (0 32, 0 78), (0 45, 0 72)⟩⟨(0 77, 0 39), (0 32, 0 78), (0 45, 0 72)⟩ A3 ⟨(0 55, 0 64), (0 45, 0 72), (0 55, 0 64)⟩⟨(0 71, 0 48), (0 45, 0 72), (0 55, 0 64)⟩ A4 ⟨(0 84, 0 3), (0 0, 0 84), (0 32, 0 78)⟩⟨(0 77, 0 39), (0 32, 0 78), (0 45, 0 72)⟩ C3 A1 ⟨(0.45, 0.72), (0.45, 0.72), (0.71, 0.48)⟩ A2 ⟨(0.71, 0.48), (0.45, 0.72), (0.45, 0.72)⟩ A3 ⟨(0 71, 0 48), (0 55, 0 64), (0 45, 0 72)⟩ A4 ⟨(0 63, 0, 56), (0 55, 0 64), (0 45, 0 72)⟩

δ =1 PFVNV A1 ⟨(0 57, 0 62), (0 43, 0 76), (0 6, 0 62)⟩ A2 ⟨(0 76, 0 41), (0 37, 0 76), (0 43, 0 74)⟩ A3 ⟨(0.6, 0.59), (0.55, 0.74), (0.45, 0.68)⟩ A4 ⟨(0 74, 0 44), (0 0, 0 68), (0 48, 0 69)⟩ A+ ⟨(0 76, 0 41), (0 0, 0 76), (0 43, 0 74)⟩ Table3:AggregatedPFVNVaccordingto WAA PFVNV andpositiveidealalternative A+ AlgebraicsymmetricdiscriminationinformationmeasuresSNV E∗ A(A+,A1) ⟨0.06, 0.97, 0.97⟩ E∗ A(A+,A2) ⟨0 0, 0 99, 1⟩ E∗ A(A+,A3) ⟨0 04, 0 93, 0 99⟩ E∗ A(A+,A4) ⟨0 003, 0 99, 0 99⟩ Table4:Algebraicsymmetricdiscriminationinformationmeasuresbetweenpositiveidealalternativeand

Received:July08,2022Accepted:January11,2023 128

Table5:ScoresofAlgebraicsymmetricdiscriminationinformationmeasuresbetween A+ and Aj (j = 1, 2, 3, 4)

Table6:Thecomparisonofsomepreviousmethodswithproposedmethod obtainTable2.When PFVNVs ofeachalternativewithrespecttocriteriaareaggregatedbyutilizing WAA PFVNV ,Table3containingthepositiveidealalternativeisobtained.

Algebraicsymmetricdiscriminationinformationmeasure E∗ A betweenpositiveidealalternative A+ andalternativesarecalculated.TheresultsareshowninTable4.

Scorefunction N recalledinDefinition5.8isusedtorankthevalueof E∗ A.Thesmallerthevalueof N (E∗ A(Aj ,A+)) is,thebetterthealternative Aj is.Intheotherwords,thealternative Aj isclosertopositiveidealalternative A+ as N (E∗ A(Aj ,A+)) getssmaller.TheresultsofscorefunctionareshowninTable5. Asaresult, A2 isthebestalternative.

6.3Comparativeanalysis

6.3.1Comparisonwiththeliterature

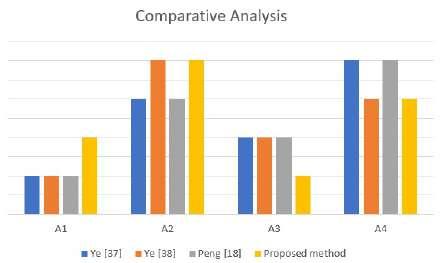
WecomparetheresultsofsomeexistingmethodswiththeresultsoftheproposedmethodinSub-section6.1. SoastosolvetheMCDMproblemgiveninSub-section6.2,somemethodswereproposedunderdifferent fuzzyenvironments.Ye38 gaveaweightedcorrelationcoefficientforSVNSs,utilizedittosolvethesame investmentproblemandobtainedtheranking A1 ≺ A3 ≺ A4 ≺ A2.Usingdifferentaggregationoperatorsand asimilaritymeasureforSNSs,Ye37 solvedthesameproblemandobtainedtheranking A1 ≺ A3 ≺ A2 ≺ A4. Similarly,Peng18 proposedsomeaggregationoperatorsvia t-normsand t-conorms,appliedthemtoinvestigate sameproblemandgottheranking A1 ≺ A3 ≺ A2 ≺ A4.Thebestalternativeobtainedwiththepresent methodremainssamewiththeoneof37 and38 forsome δ.Thecomparisonresultsofproposedmethodwith theexistingonesareshowninTable6andillustratedinFigure5.

Score N (E∗ A(A+,A1)) 0.039 N (E∗ A(A+,A2)) 0.0048 N (E∗ A(A+,A3)) 0.041 N (E∗ A(A+,A4))0.0051

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

MethodRankingorderBestAlternative Ye37 A1 ≺ A3 ≺ A2 ≺ A4 A4 Ye38 A1 ≺ A3 ≺ A4 ≺ A2 A2 Pengetal.18 A1 ≺ A3 ≺ A2 ≺ A4 A4 Proposedmethod A3 ≺ A1 ≺ A4 ≺ A2 A2

129

Figure5:Thecolumnchartcomparisonoftheothermethodsandproposedmethod

https://doi.org/10.54216/IJNS.200208 Received:July08,2022Accepted:January11,2023

Table8:Theresultswithrespectto WGA PFVNV whentheparameter δ variesfrom 0 1 and 1

6.3.2Comparisonwithrespecttoparameter δ

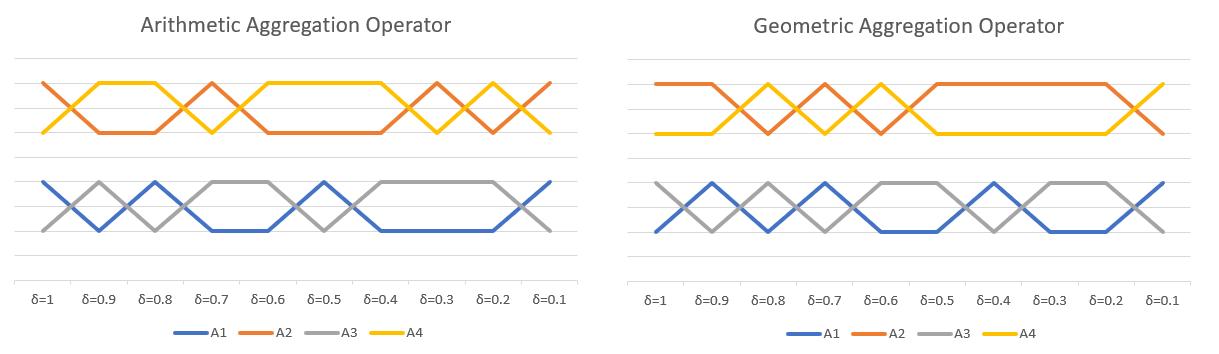
Weinvestigatetheeffectoftheparameter δ ontherankingofalternativeswithrespectto WAA PFVNV and WGA PFVNV .TheresultsaresummarizedinTable7andTable8.Fromtheseresults,itisconcluded thattherankingofthealternativeis

when

equalsto 0.1 and 1 withrespectto

.8 for

A PFVNV .When δ equalsto 0 1 and 1 withrespectto WAA PFVNV ,weconcludethat A2 isthebestalternative,whileby using WGA PFVNV ,thebestalternativeis A4 when δ equalsto 0 6 and 0 8.Thegraphicalrepresentation ofthebehaviourofthealternativeswiththe δ variationisshowninFigure6.

6.4TimecomplexityoftheproposedMCDMmethod

Inthissub-sectionweanalysisthecomplexityoftheMCDMmethodproposedinSub-section6.1.Actuallywe evaluatethetimecomplexitythatdependsonthenumberoftimesofmultiplication,exponential,summation

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023 δ RankingorderBestalternative δ =1 A3 ≺ A1 ≺ A4 ≺ A2 A2 δ =0 9 A1 ≺ A3 ≺ A2 ≺ A4 A4 δ =0 8 A3 ≺ A1 ≺ A2 ≺ A4 A4 δ =0.7 A1 ≺ A3 ≺ A4 ≺ A2 A2 δ =0 6 A1 ≺ A3 ≺ A2 ≺ A4 A4 δ =0 5 A3 ≺ A1 ≺ A2 ≺ A4 A4 δ =0 4 A1 ≺ A3 ≺ A2 ≺ A4 A4 δ =0 3 A1 ≺ A3 ≺ A4 ≺ A2 A2 δ =0.2 A1 ≺ A3 ≺ A2 ≺ A4 A4 δ =0 1 A3 ≺ A1 ≺ A4 ≺ A2 A2 Table7:Theresultswithrespectto WAA PFVNV whentheparameter δ variesfrom 0 1 and 1 δ RankingorderBestalternative δ =1 A1 ≺ A3 ≺ A4 ≺ A2 A2 δ =0 9 A3 ≺ A1 ≺ A4 ≺ A2 A2 δ =0 8 A1 ≺ A3 ≺ A2 ≺ A4 A4 δ =0 7 A3 ≺ A1 ≺ A4 ≺ A2 A2 δ =0.6 A1 ≺ A3 ≺ A2 ≺ A4 A4 δ =0 5 A1 ≺ A3 ≺ A4 ≺ A2 A2 δ =0 4 A3 ≺ A1 ≺ A4 ≺ A2 A2 δ =0 3 A1 ≺ A3 ≺ A4 ≺ A2 A2 δ =0 2 A1 ≺ A3 ≺ A4 ≺ A2 A2 δ =0.1 A3 ≺ A1 ≺ A2 ≺ A4 A4

A3 ≺ A1 ≺ A4 ≺ A2

WAA PFVNV while A1 ≺ A3 ≺ A2 ≺ A4 when δ equalsto 0.6

and

https://doi.org/10.54216/IJNS.200208 Received:July08,2022Accepted:January11,2023 130

Figure6:Effectoftheparameter δ tothesolution

asin4 and.8 ConsideraMCDMproblemwith n alternativesand k criteria.InStep2weneed k operations,in Step3weneed 3kn operations,inStep4weneed 6kn operations,inStep5weneed 3n (6k +2) operations ifweusetheaggregationoperator WGA PFVNV andweneed n(75k +21) operationsifweusethe aggregationoperator WGE PFVNV .InStep6weneed 3n operations,inStep7weneed 98n operations andinStep8weneed 5n operations.Sothetimecomplexity Tnk oftheMCDMmethodis

T A nk = k +27kn +112n

fortheaggregationoperator WGA PFVNV and

T E nk = k +84kn +127n

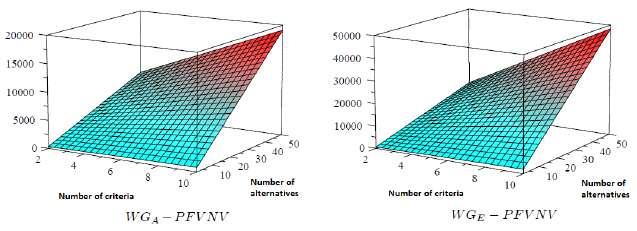
fortheaggregationoperator WGE PFVNV .Clearlythebi-variatefunctions gA,gE :[2, ∞)2 → R definedby gA(x,y)= x +27xy +112y and gE (x,y)= x +84xy +127y bothtakeabsoluteminimumat point (2, 2).Figure7illustratesthechangeofthetimecomplexitywithrespecttothechangeinthenumbers ofthealternativesandthecriteriafor WGA PFVNV and WGE PFVNV .

7Conclusion

ThemainaimofthisstudyistointroducetheconceptofPFVNSconstructedbyconsideringPFVsrather thannumbers,inspiredbyIFVNSs.Thus,aPFVNSisanextensionofIFVNSs.PFVNSsareusedtoexpress uncertaintyinamoreextendedfuzzyenvironment.Therefore,largerinformationcanbekeptwhilethedata isconvertedtoaFS.Inthisway,informationlossisprevented.Inthisstudy,somesetoperationsbetween PFVNSsareproposed.WealsointroducePythagoreanfuzzy t-normsand t-conormswithmotivationfrom intuitionisticfuzzy t-normsand t-conorms.WeshowthatsomePythagoreanfuzzy t-normsand t-conorms areexpressedviacontinuousArchimedean t-normsandcontinuousArchimedean t-conormson [0, 1].Then wedefinesomealgebraicoperationsbetweenPFVNVsbyutilizingcontinuousArchimedean t-normandcontinuousArchimedean t-conormson [0, 1].Bywayofthesealgebraicoperations,someweightedaggregation operatorsareproposed.InputvaluesrepresentedbyPFVNVsaretransformedtoasingleoutputvaluebyusingweightedaggregationoperators.Also,weintroduceamethodthatconvertsneutrosophicfuzzyvaluesto PFVNVs.Bydefiningasimplifiedneutrosophicvaluedmodifiedfuzzycross-entropymeasurewemanageto rankoutputvaluesrepresentedbyPFVNVswiththehelpofascorefunctioninsimplifiedneutrosophicenvironment.NextaMCDMmethodisgiventoseepracticabilityoftheproposedtheory.Theproposedmethodis madeuseoftosolveaMCDMproblemadaptedfromtheliteratureinPythagoreanfuzzyvaluedneutrosophic environment.Acomparisonanalysisandacomplexityanalysisarealsoprovided.Inthefuture,differentkind ofaggregationoperatorsandcross-entropymeasurescanbeconsidered.Theapplicationsoftheproposed theorycanbeextendedtosomedecisionmakingproblemssuchasfacerecognitionsystems,classificationand medicaldiagnosis.

Funding “TheresearchofMahmutCanBozyi˘githasbeensupportedbyTurkishScientificandTechnological ResearchCouncil(TUBITAK)Program2211.”

ConflictsofInterest: “Theauthorsdeclarenoconflictofinterest.”

https://doi.org/10.54216/IJNS.200208

Received:July08,2022Accepted:January11,2023

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

Figure7:TimecomplexityoftheproposedMCDMmethod

131

References

[1] Abdullah,L.,Fuzzymulticriteriadecisionmakinganditsapplications:abriefreviewofcategory. Procedia-SocialandBehavioralSciences,97,131-136,2013.

[2] Atanassov,K.T.,Intuitionisticfuzzysets.InIntuitionisticfuzzysets(pp.1-137).Physica,Heidelberg, 1999.

[3] Beliakov,G.,Bustince,H.,Goswami,D.P.,Mukherjee,U.K.,Pal,N.R.,Onaveragingoperatorsfor Atanassov’sintuitionisticfuzzysets.InformationSciences.181,1116-1124,2011.

[4] Chang,D.Y.,ApplicationsoftheextentanalysismethodonfuzzyAHP.Europeanjournalofoperational research,95(3),649-655,1996.

[5] Cover,T.M.,andThomas,J.A.,Elementsofinformationtheory2ndedition(wileyseriesintelecommunicationsandsignalprocessing),2006.

[6] Deschrijver,G.,Cornelis,C.,Kerre,E.E.,Ontherepresentationofintuitionisticfuzzy t-normsand t-conorms.IEEEtransactionsonfuzzysystems,12(1),45-61,2004.

[7] Garg,H.,Arora,R.,GeneralizedMaclaurinsymmetricmeanaggregationoperatorsbasedon Archimedean t-normoftheintuitionisticfuzzysoftsetinformation.ArtifIntellRev54:3173-3213,2021.

[8] Junior,F.R.L.,Osiro,L.,andCarpinetti,L.C.R.,AcomparisonbetweenFuzzyAHPandFuzzyTOPSIS methodstosupplierselection.Appliedsoftcomputing,21,194-209,2014.

[9] Kahraman,C.,(Ed.)Fuzzymulti-criteriadecisionmaking:theoryandapplicationswithrecentdevelopments(Vol.16).SpringerScienceandBusinessMedia,2008.

[10] Klement,E.P.,Mesiar,R.,Pap,E.,Triangularnorms,KluwerAcademicPublishers,Dordrecht,2002.

[11] Klement,E.P.,Mesiar,R.,Pap,E.,Triangularnorms.PositionpaperIII:continuous t-norms,FuzzySets andSystems,145(3)439-454,2004.

[12] Klir,G.Yuan,B.,FuzzySetsandFuzzyLogic:TheoryandApplications,PrenticeHall,UpperSaddle River,NJ,1995.

[13] Kullback,S.,Leibler,R.A.,Oninformationandsufficiency.AnnalsoftheInstituteofStatisticalMathematics.4:99–111,1951.

[14] Kullback,S.,Informationtheoryandstatistics.Wiley,NewYork,1959.

[15] Lin,J.,DivergencemeasuresbasedonShannonentropy,IEEETrans.InformationTheory37(1)145-151, 1991.

[16] Menger,K.,Statisticalmetrics.ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesof America,28(12),535,1942.

[17] Naz,S.,andAkram,M.,Noveldecision-makingapproachbasedonhesitantfuzzysetsandgraphtheory. ComputationalandAppliedMathematics,38(1),1-26,2019.

[18] Peng,J.J.,Wang,J.Q.,Wang,J.,Zhang,H.Y.,Chen,X.H.,Simplifiedneutrosophicsetsandtheir applicationsinmulti-criteriagroupdecision-makingproblems.Internationaljournalofsystemsscience, 47(10),2342-2358,2016.

[19] Peng,X.,Yang,Y.,SomeresultsforPythagoreanfuzzysets.InternationalJournalofIntelligentSystems, 30(11),1133-1160,2015.

[20] Peng,X.,Yuan,H.,Yang,Y.Pythagoreanfuzzyinformationmeasuresandtheirapplications.InternationalJournalofIntelligentSystems,32(10),991-1029,2017.

[21] Schweizer,B.andSklar,A.,Probabilisticmetricspaces,North-Holland,NewYork,1983.

[22] Shang,X.G.,Jiang,W.S.,Anoteonfuzzyinformationmeasures.PatternRecognitionLetters,18(5), 425-432,1997.

https://doi.org/10.54216/IJNS.200208

Received:July08,2022Accepted:January11,2023

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

132

[23] Shannon,C.,Amathematicaltheoryofcommunication.BellSyst.,Tech.J.27:379-423,1948.

[24] Shannon,C.,Weaver,W.,Themathematicaltheoryofcommunication.Urbana:UniversityofIllinois Press,1949.

[25] Singh,A.,Joshi,D.K.,Kumar,S.,Anovelconstructionmethodofintuitionisticfuzzysetfromfuzzyset anditsapplicationinmulti-criteriadecision-makingproblem.InAdvancedComputingandCommunicationTechnologies(pp.67-75).Springer,Singapore,2019.

[26] Smarandache,F.,Aunifyingfieldoflogics.Neutrosophy:Neutrosophicprobability,setandlogic.AmericanResearchPress,Rehoboth,1998.

[27] Sun,B.,Tong,S.,Ma,W.,Wang,T.,andJiang,C.,AnapproachtoMCGDMbasedonmulti-granulation Pythagoreanfuzzyroughsetovertwouniversesanditsapplicationtomedicaldecisionproblem.Artificial IntelligenceReview,55,1887–1913,2022.

[28] Unver,M.,Turkarslan,E.,Olgun,M.,Ye,J.,Intuitionisticfuzzy-valuedneutrosophicmulti-setsand numericalapplicationstoclassification.ComplexandIntelligentSystems,1-19,2022.

[29] Unver,M.,Olgun,M.,andT¨urkarslan,E.,CosineandcotangentsimilaritymeasuresbasedonChoquet integralforSphericalfuzzysetsandapplicationstopatternrecognition.JournalofComputationaland CognitiveEngineering,1(1)21-31,2022.

[30] Vlachos,I.K.,Sergiadis,G.D.,Intuitionisticfuzzyinformation-Applicationstopatternrecognition, PatternRecognitionLetters28(2007)197-206,2007.

[31] Wei,P.,Ye,J.,Improvedintuitionisticfuzzycross-entropyanditsapplicationtopatternrecognitions.In 2010IEEEInternationalConferenceonIntelligentSystemsandKnowledgeEngineering(pp.114-116). IEEE,2010.

[32] Wu,X.H.,Wang,J.Q.,Peng,J.J.,Chen,X.,H.Cross-entropyandprioritizedaggregationoperatorwith simplifiedneutrosophicsetsandtheirapplicationinmulti-criteriadecision-makingproblems.InternationalJournalofFuzzySystems,18(6),1104-1116,2016.

[33] Yager,R.R.,Pythagoreanmembershipgradesinmulticriteriadecisionmaking.IEEETransactionson FuzzySystems,22(4),958-965,2013a.

[34] Yager,R.R.,Pythagoreanfuzzysubsets.In2013jointIFSAworldcongressandNAFIPSannualmeeting (IFSA/NAFIPS)(pp.57-61).IEEE,2013b.

[35] Yager,R.R.,andAbbasov,A.M.,Pythagoreanmembershipgrades,complexnumbers,anddecision making.InternationalJournalofIntelligentSystems,28(5),436-452,2013.

[36] Ye,S.,Ye,J.,Dicesimilaritymeasurebetweensinglevaluedneutrosophicmultisetsanditsapplication inmedicaldiagnosis.NeutrosophicSetsSyst.6:48-53,2014.

[37] Ye,J.,Amulticriteriadecision-makingmethodusingaggregationoperatorsforsimplifiedneutrosophic sets.JournalofIntelligentandFuzzySystems,26(5),2459-2466,2014.

[38] Ye,J.,Multicriteriadecision-makingmethodusingthecorrelationcoefficientundersingle-valuedneutrosophicenvironment.InternationalJournalofGeneralSystems,42(4),386-394,2013.

[39] Ye,J.,Single-ValuedNeutrosophicClusteringAlgorithmsBasedonSimilarityMeasures.Journalof Classification,34(1),2017.

[40] Ye,J.,T¨urkarslan,E., Unver,M.,Olgun,M.,AlgebraicandEinsteinweightedoperatorsofneutrosophic enthalpyvaluesformulti-criteriadecisionmakinginneutrosophicmulti-valuedsetsettings.Granular Computing,1-9,2021.

[41] Yeni,F.B.,and Ozc¸elik,G.,Interval-valuedAtanassovintuitionisticFuzzyCODASmethodformulti criteriagroupdecisionmakingproblems.GroupDecisionandNegotiation,28(2),433-452,2019.

[42] Zadeh,L.A.,Fuzzysets.Informationandcontrol.8(3):338-353,1965.

[43] Zadeh,L.A.,Probabilitymeasuresoffuzzyevents.Journalofmathematicalanalysisandapplications, 23(2),421-427,1968.

https://doi.org/10.54216/IJNS.200208

InternationalJournalofNeutrosophicScience(IJNS)Vol.20,No.02,PP.107-134,2023

133

Received:July08,2022Accepted:January11,2023