Some Results on the Graph Theory for Complex Neutrosophic Sets by Florentin Smarandache

SomeResultsontheGraphTheoryforComplex NeutrosophicSets

ShioGaiQuek 1,*,SaidBroumi 2,GaneshsreeSelvachandran 3 ID ,AssiaBakali 4 , MohamedTalea 2 andFlorentinSmarandache 5 ID

A-LevelAcademy,UCSICollegeKLCampus,Lot12734,JalanChooLipKung,TamanTayntonView, Cheras56000,KualaLumpur,Malaysia

2 LaboratoryofInformationProcessing,FacultyofScienceBenM’Sik,UniversityHassanII,B.P7955 SidiOthman,Casablanca,Morocco;broumisaid78@gmail.com(S.B.);taleamohamed@yahoo.fr(M.T.)

3 DepartmentofActuarialScienceandAppliedStatistics,FacultyofBusiness&InformationScience, UCSIUniversity,JalanMenaraGading,Cheras56000,KualaLumpur,Malaysia;ganeshsree86@yahoo.com

4 EcoleRoyaleNavale,BoulevardSourJdid,B.P16303Casablanca,Morocco;assiabakali@yahoo.fr

5 DepartmentofMathematics,UniversityofNewMexico,705GurleyAvenue,Gallup,NM87301,USA; fsmarandache@gmail.comorsmarand@unm.edu

* Correspondence:quekshg@yahoo.comorquekshg@ucsicollege.edu.my;Tel.:+60-17-5008359

Received:25February2018;Accepted:21May2018;Published:31May2018

Abstract: Fuzzygraphtheoryplaysanimportantroleinthestudyofthesymmetryandasymmetry propertiesoffuzzygraphs.Withthisinmind,inthispaper,weintroducenewneutrosophicgraphs calledcomplexneutrosophicgraphsoftype1(abbr.CNG1).Wethenpresentamatrixrepresentation foritandstudysomepropertiesofthisnewconcept.TheconceptofCNG1isanextensionofthe generalizedfuzzygraphsoftype1(GFG1)andgeneralizedsingle-valuedneutrosophicgraphsof type1(GSVNG1).TheutilityoftheCNG1introducedhereareappliedtoamulti-attributedecision makingproblemrelatedtoInternetserverselection.

Keywords: complexneutrosophicset;complexneutrosophicgraph;fuzzygraph;matrixrepresentation

1.Introduction

Smarandache[1]introducedanewtheorycalledneutrosophictheory,whichisbasicallyabranch ofphilosophythatfocusesontheorigin,nature,andscopeofneutralitiesandtheirinteractions withdifferentideationalspectra.Onthebasisofneutrosophy,Smarandachedeﬁnedtheconcept ofaneutrosophicset(NS)whichischaracterizedbyadegreeoftruthmembership T,adegreeof indeterminacymembership I,andadegreeoffalsitymembership F.Theconceptofneutrosophicset theorygeneralizestheconceptofclassicalsets,fuzzysetsbyZadeh[2],intuitionisticfuzzysetsby Atanassov[3],andinterval-valuedfuzzysetsbyTurksen[4].Infact,thismathematicaltoolisaptfor handlingproblemsrelatedtoimprecision,indeterminacy,andinconsistencyofdata.Theindeterminacy componentpresentinNSsisindependentofthetruthandfalsitymembershipvalues.Tomakeitmore convenienttoapplyNSstoreal-lifescientiﬁcandengineeringproblems,Smarandache[1]proposed thesingle-valuedneutrosophicset(SVNS)asasubclassofneutrosophicsets.Lateron,Wangetal.[5] presentedtheset-theoreticoperatorsandstudiedsomeofthepropertiesofSVNSs.TheNSmodeland itsgeneralizationshavebeensuccessfullyappliedinmanydiverseareas,andthesecanbefoundin[6]. Graphsareamongthemostpowerfulandconvenienttoolstorepresentinformationinvolving therelationshipbetweenobjectsandconcepts.Incrispgraphs,twoverticesareeitherrelatedornot relatedtooneanotherso,mathematically,thedegreeofrelationshipiseither0or1.Infuzzygraphs ontheotherhand,thedegreeofrelationshiptakesonvaluesfromtheinterval[0,1].Subsequently,

Symmetry 2018, 10,190;doi:10.3390/sym10060190 www.mdpi.com/journal/symmetry

symmetry SS Article

ShannonandAtanassov[7]deﬁnedtheconceptofintuitionisticfuzzygraphs(IFGs)usingﬁvetypes ofCartesianproducts.Theconceptfuzzygraphsandtheirextensionshaveacommonpropertythat eachedgemusthaveamembershipvalueoflessthan,orequalto,theminimummembershipofthe nodesitconnects.

Intheeventthatthedescriptionoftheobjectortheirrelationsorbothisindeterminateand inconsistent,itcannotbehandledbyfuzzy,intuitionisticfuzzy,bipolarfuzzy,vague,orinterval-valued fuzzygraphs.Forthisreason,Smarandache[8]proposedtheconceptofneutrosophicgraphsbased ontheindeterminacy(I)membershipvaluestodealwithsuchsituations.Smarandache[9,10]then gaveanotherdeﬁnitionforneutrosophicgraphtheoryusingtheneutrosophictruth-values(T, I, F) andconstructedthreestructuresofneutrosophicgraphs:neutrosophicedgegraphs,neutrosophic vertexgraphsandneutrosophicvertex-edgegraphs.Subsequently,Smarandache[11]proposednew versionsoftheseneutrosophicgraphs,suchastheneutrosophicoffgraph,neutrosophicbipolargraph, neutrosophictripolargraph,andneutrosophicmultipolargraph.Presently,worksonneutrosophic vertex-edgegraphsandneutrosophicedgegraphsareprogressingrapidly.Broumietal.[12]combined theSVNSmodelandgraphtheorytointroducecertaintypesofSVNSgraphs(SVNG),suchasstrong SVNG,constantSVNG,andcompleteSVNG,andproceededtoinvestigatesomeofthepropertiesof thesegraphswithproofsandexamples.Broumietal.[13]thenintroducedtheconceptofneighborhood degreeofavertexandclosedneighborhooddegreeofavertexinSVNGasageneralizationofthe neighborhooddegreeofavertexandclosedneighborhooddegreeofavertexfoundinfuzzygraphs andintuitionisticfuzzygraphs.Inaddition,Broumietal.[14]provedanecessaryandsufﬁcient conditionforaSVNGtobeanisolatedSVNG.

Recently,Smarandache[15]initiatedtheideaoftheremovaloftheedgedegreerestrictionfor fuzzygraphs,intuitionisticfuzzygraphsandSVNGs.Samantaetal.[16]proposedanewconceptcalled generalizedfuzzygraphs(GFG)anddefinedtwotypesofGFG.Heretheauthorsalsostudiedsomeof themajorpropertiesofGFGs,suchasthecompletenessandregularityofGFGs,andverifiedtheresults. In[16],theauthorsclaimthatfuzzygraphsandtheirextensionsarelimitedtotherepresentationsof onlycertainsystems,suchassocialnetworks.Broumietal.[17]thendiscussedtheremovaloftheedge degreerestrictionofSVNGsandpresentedanewclassofSVNG,calledgeneralizedSVNGoftype1, whichisanextensionofgeneralizedfuzzygraphsoftype1proposedin[16].Sincetheintroduction ofcomplexfuzzysets(CFSs)byRamotetal.in[18],severalnewextensionsofCFSshavebeen proposedinliterature[19–25].ThelatestmodelrelatedtoCFSisthecomplexneutrosophicset(CNS) modelwhichisacombinationofCFSs[18]andcomplexintuitionisticfuzzysets[21]proposedbyAli andSmarandache[26].TheCNSmodelisdefinedbythreecomplex-valuedmembershipfunctions whichrepresentthetruth,indeterminate,andfalsitycomponents.Therefore,acomplex-valued truthmembershipfunctionisacombinationofthetraditionaltruthmembershipfunctionwiththe additionofthephaseterm.Similartofuzzygraphs,complexfuzzygraphs(CFG)introducedby Thirunavukarasuetal.[27]haveacommonpropertythateachedgemusthaveamembershipvalueof lessthanorequaltotheminimummembershipofthenodesitconnects.

Inthispaper,weextendtheresearchworksmentionedabove,andintroducethenovelconcept oftype1complexneutrosophicgraphs(CNG1)andamatrixrepresentationofCNG1.Tothebest ofourknowledge,thereisnoresearchonCNGsintheliteratureatpresent.Wealsopresentan investigationpertainingtothesymmetricpropertiesofCNG1inthispaper.Inthestudyoffuzzy graphs,asymmetricfuzzygraphreferstoagraphstructurewithoneedge(i.e.,twoarrowsonopposite directions)ornoedges,whereasanasymmetricfuzzygraphreferstoagraphstructurewithnoarcsor onlyonearcpresentbetweenanytwovertices.Motivatedbythis,wehavededicatedanentiresection inthispaper(Section 7)tostudythesymmetricpropertiesofourproposedCNG1.

Theremainderofthispaperisorganizedasfollows:inSection 2,wereviewsomebasicconcepts aboutNSs,SVNSs,CNSs,andgeneralizedSVNGsoftype1;inSection 3,theformaldeﬁnitionofCNG1 isintroducedandsupportedwithillustrativeexamples;inSection 4 arepresentationmatrixofCNG1 isintroduced;someadvancedtheoreticalresultspertainingtoourCNG1ispresentedinSection 5,

Symmetry 2018, 10,190 2of32

followedbyaninvestigationontheshortestCNG1inSection 6;thesymmetricpropertiesofordinary simpleCNG1ispresentedinSection 7;andSection 8 outlinestheconclusionofthispaperandsuggests directionsforfutureresearch.Thisisfollowedbytheacknowledgmentsandthelistofreferences.

2.Preliminaries

Inthissection,wepresentbriefoverviewsofNSs,SVNSs,SVNGs,andgeneralizefuzzygraphs thatarerelevanttothepresentwork.Wereferthereadersto[1,5,17,18,27]forfurtherinformation relatedtotheseconcepts.

ThekeyfeaturethatdistinguishestheNSfromthefuzzyandintuitionisticfuzzyset(IFS)models isthepresenceoftheindeterminacymembershipfunction.IntheNSmodeltheindeterminacy membershipfunctionisindependentfromthetruthandfalsitymembershipfunctions,andweareable totelltheexactvalueoftheindeterminacyfunction.Inthefuzzysetmodelthisindeterminacyfunction isnon-existent,whereasintheIFSmodel,thevalueoftheindeterminacymembershipfunctionis dependentonthevaluesofthetruthandfalsitymembershipfunctions.Thisisevidentfromthe structureoftheNSmodelinwhich T + I + F ≤ 3,whereasitis T + F ≤ 1 and I = 1 T F intheIFS model.Thisstructureisreflectiveofmanyreal-lifesituations,suchasinsports(wining,losing,draw), voting(for,against,abstainfromvoting),anddecision-making(affirmative,negative,undecided), inwhichtheproportionsofoneoutcomeisindependentoftheothers.TheNSmodelisabletomodel thesesituationsmoreaccuratelycomparedtofuzzysetsandIFSsasitisabletodeterminethedegreeof indeterminacyfromthetruthandfalsitymembershipfunctionmoreaccurately,whereasthisdistinction cannotbedonewhenmodellinginformationusingthefuzzysetsandIFSs.Moreover,theNSmodel hasspecialstructurescalledneutrosophicoversetsandneutrosophicundersetsthatwereintroduced bySmarandachein[11],inwhichthevaluesofthemembershipfunctionscanexceed1orbebelow0, inordertocatertospecialsituations.ThismakestheNSmoreflexiblecomparedtofuzzysetsand IFSs,andgivesittheabilitytocatertoawiderrangeofapplications.Theflexibilityofthismodeland itsabilitytoclearlydistinguishbetweenthetruth,falsity,andindeterminacymembershipfunctions servedasthemainmotivationtostudyabranchofgraphtheoryofNSsinthispaper.Wereferthe readersto[28,29]formoreinformationonthedegreeofdependenceandindependenceofneutrosophic sets,and[11]forfurtherinformationontheconceptsofneutrosophicoversetsandundersets.

Deﬁnition1[1]. LetXbeaspaceofpointsandlet x ∈ X. Aneutrosophicset A ∈ X ischaracterizedbya truthmembershipfunction T, anindeterminacymembershipfunction I, andafalsitymembershipfunction F Thevaluesof T, I, F arerealstandardornonstandardsubsetsof ] 0,1+ [,and T, I, F : X →] 0,1+ [ A neutrosophicsetcanthereforeberepresentedas: A = {(x, TA (x), IA (x), FA (x)) : x ∈ X} (1) SinceT, I, F ∈ [0,1], theonlyrestrictiononthesumofT, I, Fisasgivenbelow: 0 ≤ TA (x) + IA (x) + FA (x) ≤ 3+ (2)

AlthoughtheoreticallytheNSmodelisabletohandlevaluesfromtherealstandardor non-standardsubsetsof ] 0,1+ [,itisoftenunnecessaryorcomputationallyimpracticaltousevalues fromthisnon-standardrangewhendealingwithreal-lifeapplications.Mostproblemsinengineering, andcomputersciencedealwithvaluesfromtheinterval[0,1]insteadoftheinterval ] 0,1+ [,andthis ledtotheintroductionofthesingle-valuedneutrosophicset(SVNS)modelin[5].TheSVNSmodelis aspecialcaseofthegeneralNSmodelinwhichtherangeofadmissiblevaluesarefromthestandard intervalof[0,1],therebymakingitmorepracticaltobeusedtodealwithmostreal-lifeproblems. TheformaldeﬁnitionoftheSVNSmodelisgiveninDeﬁnition2.

Symmetry 2018, 10,190 3of32

Deﬁnition2[5]. Let X beaspaceofpoints(objects)withgenericelementsin X denotedby x. Asingle-valuedneutrosophicset A (SVNSA)ischaracterizedbyatruth-membershipfunction TA (x), anindeterminacy-membershipfunction IA (x), andafalsity-membershipfunction FA (x). Foreachpoint x ∈ X, TA (x), IA (x), FA (x) ∈ [0,1].TheSVNS A canthereforebewrittenas: A = {(x, TA (x), IA (x), FA (x)) : x ∈ X} (3)

Definition3[26]. Denote i = √ 1.Acomplexneutrosophicset A definedonauniverseofdiscourse X, which ischaracterizedbyatruthmembershipfunction TA (x), anindeterminacy-membershipfunction IA (x), anda falsity-membershipfunction FA (x) thatassignsacomplex-valuedmembershipgradeto TA (x), IA (x), FA (x) forany x ∈ X Thevaluesof TA (x), IA (x), FA (x) andtheirsummaybeanyvalueswithinaunitcircle inthecomplexplaneandisthereforeoftheform TA (x) = pA (x)eiµA (x) , IA (x) = qA (x)eiνA (x) , and FA (x) = rA (x)eiωA (x) Alltheamplitudeandphasetermsarereal-valuedand pA (x), qA (x), rA (x) ∈ [0,1], whereas µA (x), νA (x), ωA (x) ∈ (0,2π], suchthatthecondition: 0 ≤ pA (x) + qA (x) + rA (x) ≤ 3(4) issatisfied.AcomplexneutrosophicsetAcanthusberepresentedinsetformas: A = { x, TA (x) = aT , IA (x) = aI , FA (x) = aF : x ∈ X},(5) where TA : X → {aT : aT ∈ C, |aT| ≤ 1}, IA : X → {aI : aI ∈ C, |aI| ≤ 1}, FA : X → {aF : aF ∈ C, |aF| ≤ 1}, andalso:

|TA (x) + IA (x) + FA (x)| ≤ 3.(6)

Definition4[26]. Let A = {(x, TA(x), IA(x), FA(x)) : x ∈ X} and B = {(x, TB(x), IB(x), FB(x)) : x ∈ X} be twoCNSsinX TheunionandintersectionofAandBareasdefinedbelow.

(i) TheunionofAandB,denotedasA∪ N B,isdeﬁnedas:

A∪ N B = {(x, TA∪ B (x), IA∪ B (x), FA∪ B (x)) : x ∈ X},(7) whereTA∪ B (x), IA∪ B (x), FA∪ B (x) aregivenby:

TA∪ B (x) = max(pA (x), pB (x)) eiµA∪ B (x) , IA∪ B (x) = min(qA (x), qB (x)) eiνA∪ B (x) , FA∪ B (x) = min(rA (x), rB (x)) eiωA∪ B (x)

(ii) TheintersectionofAandB,denotedasA∩ N B, isdeﬁnedas:

A∩ N B = {(x, TA∩ B (x), IA∩ B (x), FA∩ B (x)) : x ∈ X},(8)

whereTA∩ B (x), IA∩ B (x), FA∩ B (x) aregivenby:

TA∩ B (x) = min(pA (x), pB (x)) eiµA∩ B (x) , IA∩ B (x) = max(qA (x), qB (x)) eiνA∩ B (x) , FA∩ B (x) = max(rA (x), rB (x)) eiωA∩ B (x)

Theunionandtheintersectionofthephasetermsofthecomplextruth,falsityandindeterminacy membershipfunctionscanbecalculatedfrom,butnotlimitedto,anyoneofthefollowingoperations:

Symmetry 2018, 10,190 4of32

(a) Sum:

(b) Max:

µA∪ B (x) = µA (x) + µB (x), νA∪ B (x) = νA (x) + νB (x), ωA∪ B (x) = ωA (x) + ωB (x)

µA∪ B (x) = max(µA (x), µB (x)), νA∪ B (x) = max(νA (x), νB (x)), ωA∪ B (x) = max(ωA (x), ωB (x)).

µA∪ B (x) = min(µA (x), µB (x)), νA∪ B (x) = min(νA (x), νB (x)), ωA∪ B (x) = min(ωA (x), ωB (x)).

(d) “Thegameofwinner,neutral,andloser”:

µA∪B (x) = µA (x) ifpA > pB µB (x) ifpB > pA ,

νA∪B (x) = νA (x) ifqA < qB νB (x) ifqB < qA ,

ωA∪B (x) = ωA (x) ifrA < rB ωB (x) ifrB < rA

Deﬁnition5[17]. Letthefollowingstatementshold:

(a) Visanon-voidset.

(b) ˘ ρT , ˘ ρI , ˘ ρF arethreefunctions,eachfromVto [0,1].

(c) ωT , ωI , ωF arethreefunctions,eachfromV × Vto [0,1]. (d) ˘ ρ = ( ˘ ρT , ˘ ρI , ˘ ρF ) and ˘ ω = ( ˘ ωT , ˘ ωI , ˘ ωF ). Thenthestructure ˘ ξ = V, ˘ ρ, ˘ ω issaidtobeageneralizedsinglevaluedneutrosophicgraphoftype1 (GSVNG1). Remark1.

(i) ˘ ρ dependson ˘ ρT , ˘ ρI , ˘ ρF and ˘ ω dependson ˘ ωT , ˘ ωI , ˘ ωF Hencetherearesevenmutuallyindependent parametersintotalthatmakeupaCNG1:V, ˘ ρT , ˘ ρI , ˘ ρF, ˘ ωT , ˘ ωI , ˘ ωF

(ii) Foreachx ∈ V, xissaidtobeavertexof ξ TheentiresetVisthuscalledthevertexsetof ξ (iii) Foreachu, v ∈ V, (u, v) issaidtobeadirectededgeof ˘ ξ. Inparticular, (v, v) issaidtobealoopof ˘ ξ (iv) Foreachvertex: ˘ ρT (v), ˘ ρI (v), ˘ ρF (v) arecalledthetruth-membershipvalue,indeterminatemembership value,andfalse-membershipvalue,respectively,ofthatvertex v. Moreover,if ˘ ρT (v) = ˘ ρI (v) = ˘ ρF (v) = 0, thenvissaidtobeavoidvertex.

(v) Likewise,foreachedge (u, v) : ˘ ωT (u, v), ˘ ωI (u, v), ˘ ωF (u, v) arecalledthetruth-membershipvalue, indeterminate-membershipvalue,andfalse-membershipvalue,respectivelyofthatdirectededge (u, v) Moreover,if ˘ ωT (u, v) = ˘ ωI (u, v) = ˘ ωF (u, v) = 0, then (u, v) issaidtobeavoiddirectededge.

Hereweshallrestatetheconceptofcomplexfuzzygraphoftype1.Moreover,foralltheremaining partsofthispaper,weshalldenotetheset{z ∈ C: |z| ≤ 1}as O1

Deﬁnition6[27]. Letthefollowingstatementshold:

Symmetry 2018, 10,190 5of32

(a) Visanon-voidset.

(b) ρ isafunctionfromVtoO1

Then:

(i) thestructure ξ = V, ρ, ω issaidtobeacomplexfuzzygraphoftype1(abbr.CFG1).

(ii) Foreachx ∈ V,xissaidtobeavertexof ξ.TheentiresetVisthuscalledthevertexsetof ξ (iii) Foreachu, v ∈ V, (u, v) issaidtobeadirectededgeof ξ.Inparticular, (v, v) issaidtobealoopof ξ.

3.ComplexNeutrosophicGraphsofType1

Byusingtheconceptofcomplexneutrosophicsets[26],theconceptofcomplexfuzzygraphof type1[27],andtheconceptofgeneralizedsinglevaluedneutrosophicgraphoftype1[17],wedeﬁne theconceptof complexneutrosophicgraphoftype 1asfollows:

Deﬁnition7. Letthefollowingstatementshold:

(a) Visanon-voidset.

(b) ρT , ρI , ρF arethreefunctions,eachfromVtoO1 (c) ωT , ωI , ωF arethreefunctions,eachfromV × VtoO1. (d) ρ = (ρT , ρI , ρF ) and ω = (ωT , ωI , ωF ).

Thenthestructure ξ = V, ρ, ω issaidtobeacomplexneutrosophicgraphoftype1(abbr.CNG1). Remark2. ρ dependson ρT , ρI , ρF,and ω dependson ωT , ωI , ωF.Hencetherearesevenmutuallyindependent parametersintotalthatmakeupaCNG1:V, ρT , ρI , ρF, ωT , ωI , ωF.Furthermore,inanalogytoaGSVNG1:

(i) Foreachx ∈ V,xissaidtobeavertexof ξ.TheentiresetVisthuscalledthevertexsetof ξ (ii) Foreachu, v ∈ V, (u, v) issaidtobeadirectededgeof ξ.Inparticular, (v, v) issaidtobealoopof ξ (iii) Foreachvertex: ρT (v), ρI (v), ρF (v) arecalledthecomplextruth,indeterminate,andfalsitymembership values,respectively,ofthevertex v.Moreover,if ρT (v) = ρI (v) = ρF (v) =0,then v issaidtobea voidvertex.

(iv) Likewise,foreachdirectededge (u, v) : ωT (u, v), ωI (u, v), ωF (u, v) arecalledthecomplextruth, indeterminateandfalsitymembershipvalue,ofthedirectededge (u, v).Moreover,if ωT (u, v) = ωI (u, v) = ωF (u, v) = 0, then (u, v) issaidtobeavoiddirectededge.

Forthesakeofbrevity,weshalldenote ω(u, v) = (ωT (u, v), ωI (u, v), ωF (u, v)) and ρ(v) = (ρT (v), ρI (v), ρF (v)) foralltheremainingpartsofthispaper.

Asmentioned,CNG1isgeneralizedfrombothGSVNG1andCFG1.Asaresult,wehave ωT , ωI and ωT beingfunctionsthemselves.Thisfurtherimpliesthat ωT (u, v), ωI (u, v) and ωT (u, v) canonly besinglevaluesfromO1.Inparticular, ωT (v, v), ωI (v, v),and ωT (v, v) canonlybesinglevalues.

Asaresult,eachvertex v inaCNG1possessasingle,undirectedloop,whethervoidornot. Andeachofthetwodistinctvertices u, v inaCNG1possess two directededges,resultingfrom (u, v) and (v, u),whethervoidornot.

Recallthatinclassicalgraphtheory,weoftendealwithordinary(orundirected)graphs,andalso simplegraphs.TofurtherrelateourCNG1withit,wenowproceedwiththefollowingdeﬁnition.

Deﬁnition8. Let ξ = V, ρ, ω beaCNG1.

(a) If ω(a, b) = ω(b, a),then {a, b} = {(a, b), (b, a)} issaidtobean(ordinary)edgeof ξ.Moreover, {a, b} issaidtobeavoid(ordinary)edgeifboth (a, b) and (b, a) arevoid.

Symmetry 2018, 10,190 6of32

(b) If ω(u, v) = ω(v, u) holdsforall u, v ∈ V, then ξ issaidtobeordinary(orundirected),otherwiseitis saidtobedirected.

Deﬁnition9. Let ξ = V, ρ, ω beanordinaryCNG1.Ifforall u, v ∈ V with u = v,thereexistnon-void edges {u = w1, w2}, {w2, w3}, , {wn 1, wn = v} forsomen ≥ 2,then ξ issaidtobeconnected.

Deﬁnition10. Let ξ = V, ρ, ω beanordinaryCNG1.Letu, v ∈ V.Then:

(a) {u, v} issaidtobeadjacenttou(andtov).

(b) u(andvaswell)issaidtobeanend-pointof {u, v}

WenowdiscussareallifescenariothatcanonlyberepresentedbyaCNG1. 3.1.TheScenario

Note:Allthelocationsmentionedareﬁctional

SupposethereisaresidentialareainMalaysiawithfourfamilies: a, b, c, d.Allofthemhave Internetaccess.Inotherwords,theyareInternetclients,whichwillaccesstheInternetserversfrom aroundtheworld(includingthoseserverslocatedwithinMalaysia)dependingonwhichwebsitethey arevisiting.

Iftheyaccesstheinternetontheirown,theoutcomescanbesummarizedasgivenintheTable 1 andFigure 1.

Table1. Theoutcomesofindividuals,forScenario3.1.

Activities abcd

Somememberswill seekexcitement (e.g.,playing onlinegames)

Somememberswill wanttosurfaround (e.g., onlineshopping)

Somememberswill needtorelax (e.g.,listening tomusic)

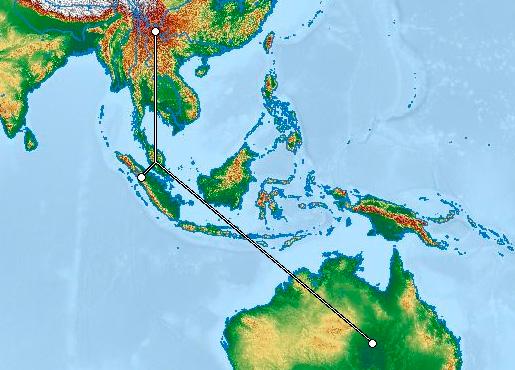
Happenson80%oftheday,and thosewillbeconnecting towards0◦ (becausethatserver islocatedinChina )

Happenson50%oftheday,and thosewillbeconnecting towards130◦ (becausethat serverislocatedinAustralia )

Happenson20%oftheday,and thosewillbeconnecting towards220◦ (becausethat serverislocatedinSumatra ,Indonesia)

Happenson70%of theday,andthose willbeconnecting towards30◦

Happenson60%of theday,andthose willbeconnecting towards180◦

Happenson30%of theday,andthose willbeconnecting towards200◦

( )asillustratedinFigure 1

Happenson90%of theday,andthose willbeconnecting towards120◦

Happenson20%of theday,andthose willbeconnecting towards340◦

Happenson50%of theday,andthose willbeconnecting towards40◦

Happenson80%of theday,andthose willbeconnecting towards250◦

Happenson40%of theday,andthose willbeconnecting towards200◦

Happenson10%of theday,andthose willbeconnecting towards110◦

Moreover,thefollowing(unordered)pairsofthefourfamiliesareclosefriendsorrelatives: {a, b},{a, c}, {a, d}, {b, d}.

Thus,eachpairoffamilymentioned(e.g., {a, b})mayinviteoneanotherforavisit,accessingthe Internetasoneteam.Inparticular:

(i) When {a, b} or {a, d} accesstheinternettogether,theywillsimplysearchfor“aplaceofcommon interest”.Thisisregardlessofwhoinitiatestheinvitation.

(ii) a and c rarelymeet.Thus,eachtimetheydo,everyone(especiallythechildren)willbesoexcited thattheywouldliketotrysomethingfresh,soallwillseekexcitementandconnecttowardsto alocalbroadcastingserverat240◦ towatchsoccermatches(thatserverwilltakecareofwhich countrytoconnectto)fortheentireday.Thisisalsoregardlessofwhoinitiatesthevisitation.

2018

10,190 7of32

Symmetry

excitement (e.g., playing online games)

Some members will want to surf around (e.g., online shopping)

connecting towards 0° (because that server is located in China ⋇)

those will be connecting towards 30°

those will be connecting towards 120°

those will be connecting towards 250°

Happens on 50% of the day, and those will be connecting towards 130° (because that server is located in Australia ⋇)

Happens on 60% of the day, and those will be connecting towards 180°

Happens on 20% of the day, and those will be connecting towards 340°

Happens on 40% of the day, and those will be connecting towards 200°

Symmetry 2018, 10,190 8of32

(iii) Thesizeandthewealthof d farsurpasses b. Thus,itwouldalwaysbe d whoinvites b totheir house,nevertheotherway,andduringtheentirevisit,membersof b willcompletelybehavelike membersof d and,therefore,willvisitthesamewebsitesas d.

Some members will need to relax (e.g., listening to music)

Happens on 20% of the day, and those will be connecting towards 220° (because that server is located in Sumatra ⋇, Indonesia)

Happens on 30% of the day, and those will be connecting towards 200°

Happens on 50% of the day, and those will be connecting towards 40°

Denotetheﬁrsttermoftheorderedpair (u, v) asthefamilywhoinitiatestheinvitation,andthe secondtermasfamilywhoreceivestheinvitationandvisittheotherfamily.Theoutcomesoftheseven possibleteams (a, b), (a, c), (a, d), (b, a), (c, a), (d, a), (d, b) are,thus,summarizedbyTable 2

Happens on 10% of the day, and those will be connecting towards 110° (⋇) as illustrated in Figure 1.

Figure 1. The illustration of the servers’ relative positions using a public domain map, for Scenario 3.1.

Figure1. Theillustrationoftheservers’relativepositionsusingapublicdomainmap,forScenario3.1.

Moreover, the following (unordered) pairs of the four families are close friends or relatives: { , }, { , }, { , }, { , }

Table2. Theoutcomesofteamsinpairs,forthescenario.

Activities (a, b),(b, a)(a, c),(c, a)(a, d),(d, a)(d, b)

Thus, each pair of family mentioned (e.g., { , }) may invite one another for a visit, accessing the Internet as one team. In particular:

Somememberswill seekexcitement

Happenson80%of theday,andthose willbeconnecting towards15◦

Happensonthe entireday,allwill beconnecting towards240◦

Happenson80%of theday,andthose willbeconnecting towards305◦

(i) When { , } or { , } access the internet together, they will simply search for “a place of common interest”. This is regardless of who initiates the invitation.

Happenson80%of theday,andthose willbeconnecting towards250◦

Somemembers willwanttosurf around

Somemembers willneedtorelax

Happenson60%of theday,andthose willbeconnecting towards155◦

Happenson30%of theday,andthose willbeconnecting towards210◦

Doesnothappen

Happenson50%of theday,andthose willbeconnecting towards165◦

(ii) and rarely meet. Thus, each time they do, everyone (especially the children) will be so excited that they would like to try something fresh, so all will seek excitement and connect towards to a local broadcasting server at 240° to watch soccer matches (that server will take care

Happenson40%of theday,andthose willbeconnecting towards200◦

Doesnothappen

Happenson50%of theday,andthose willbeconnecting towards40◦

Happenson10%of theday,andthose willbeconnecting towards110◦

Ontheotherhand, {c, b} and {d, c} aremutualstrangers.So c and b willvisiteachother.Thesame goesto d and c

3.2.RepresentationoftheScenariowithCNG1

Wenowfollowallthestepsfrom(a)to(e)inDeﬁnition7,torepresentthescenariowitha particularCNG1.

(a) Take V0 = {a, b, c, d}.

(b) Inaccordancewiththescenario,deﬁnethethreefunctionson V0: ρT , ρI , ρF,asillustratedin Table 3

Table3. k(v) ,where k representsanyofthe3functionson V0 ρT , ρI , ρF,forthescenario. AlsomentionedinSection 4.2.

k v abcd

ρT 0.8ei2π 0.7ei π 6 0.9ei 2π 3 0.8ei 25π 18 ρI 0.5ei 13π 18 0.6eiπ 0.2ei 17π 9 0.4ei 10π 9 ρF 0.2ei 11π 9 0.3ei 10π 9 0.5ei 2π 9 0.1ei 11π 18

Table4. Theoutcomesof ωT (u, v) ,forthescenario.AlsomentionedinSection 4.2. u v abcd a 0 0.8ei π 12 1ei 4π 3 0.8ei 61π 36 b 0.8ei π 12 000 c 1ei 4π 3 000 d 0.8ei 61π 36 0.8ei 25π 18 00

Table5. Theoutcomesof ωI (u, v) ,forthescenario.AlsomentionedinSection 4.2 u v abcd a 0 0.6ei 31π 36 0 0.5ei 33π 36 b 0.6ei 31π 36 000 c 0000 d 0.5ei 33π 36 0.4ei 10π 9 00

Table6. Theoutcomesof ωF (u, v) ,forthescenario.AlsomentionedinSection 4.2 u v abcd a 0 0.3ei 7π 6 0 0.5ei 2π 9 b 0.3ei 7π 6 000 c 0000 d 0.5ei 2π 9 0.1ei 11π 18 00

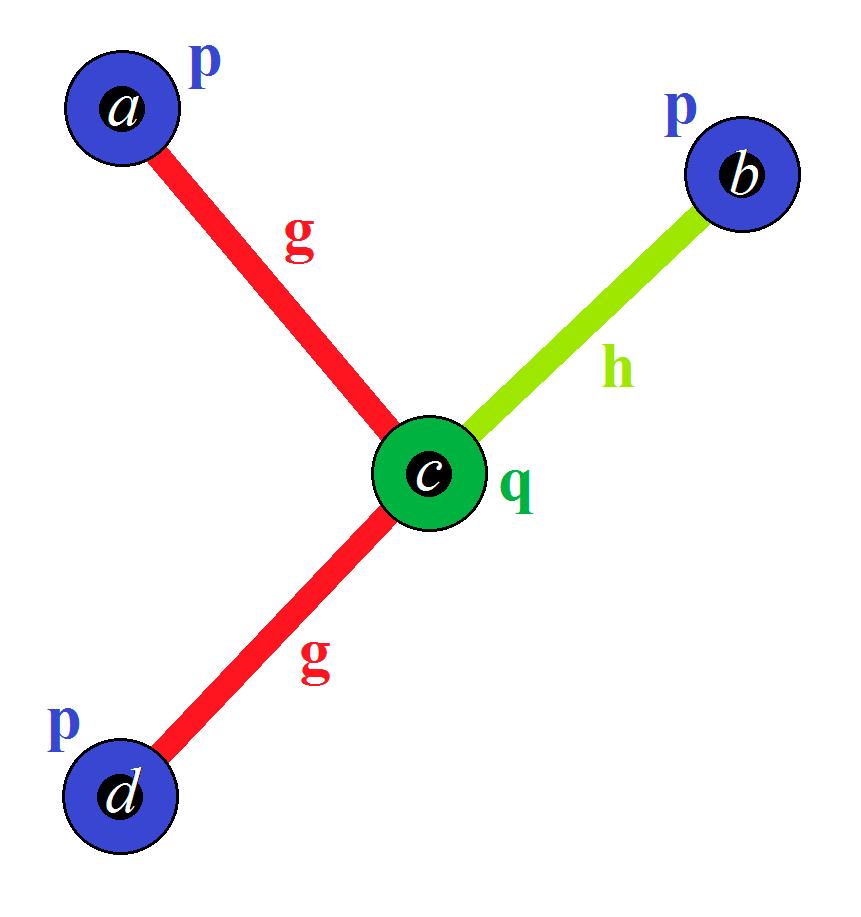
(d) Bystatement(d)fromDeﬁnition7,let ρ0 =(ρT , ρI , ρF),and ω0 =(ωT , ωI , ωF).Wehavenow formedaCNG1 V0, ρ0, ω0

Oneofthewayofrepresentingtheentire V0, ρ0, ω0 isbyusingadiagramthatisanalogous withgraphsasinclassicalgraphtheory,asshownintheFigure 2

Symmetry 2018, 10,190 9of32

(d) By statement (d) from Definition 7, let = ( , , ), and = ( , , ). We have now formed a CNG1 〈 , , 〉

One of the way of representing the entire 〈 , , 〉 is by using a diagram that is analogous with graphs as in classical graph theory, as shown in the Figure 2.

Symmetry 2018, 10,190 10of32

Figure 2. A diagram representing 〈 , , 〉, for the scenario.

Figure2. Adiagramrepresenting V0, ρ0, ω0 ,forthescenario.

In other words, only the non-void edges (whether directed or ordinary) and vertices are to be drawn in such a diagram.

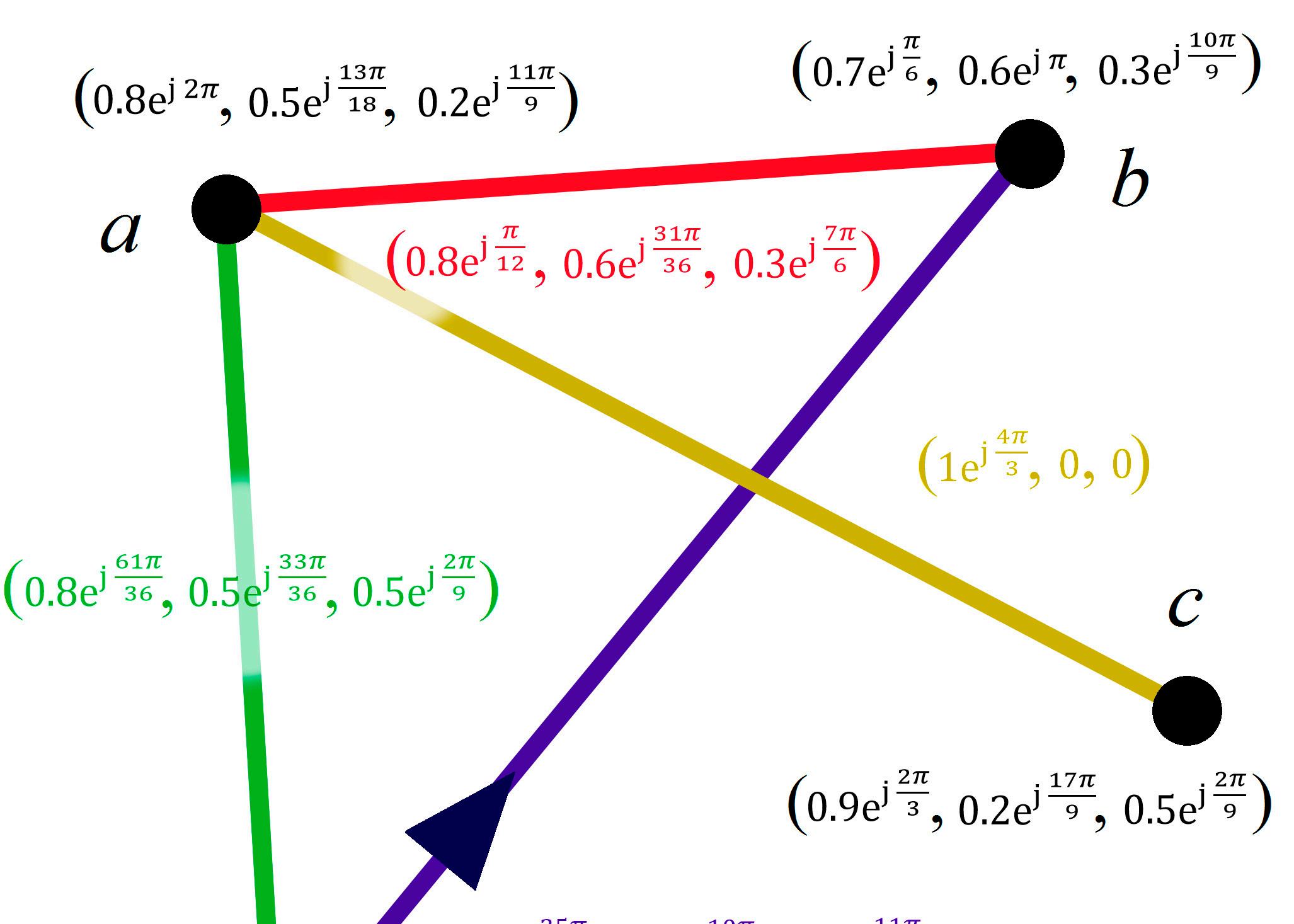
Inotherwords,onlythenon-voidedges(whetherdirectedorordinary)andverticesaretobe drawninsuchadiagram.

Hence,wehaveshownhowaCGN1canbeconstructedfromadatasetwithfourhomes.Thesame conceptmentionedcancertainlybeusedonalargerdataset,suchasonewiththousandsoflocations andthousandsofhomes,whichwillresultinamorecomplicateddiagrambeinggenerated.However, onewilldeﬁnitelyrequirecomputeralgebraicsystems,suchasSAGE,toprocessthedataandto displaythedataindiagramform.

Additionally,recallthat,inclassicalgraphtheory,agraphcanberepresentedbyanadjacency matrix,forwhichtheentriesareeitherapositiveinteger(connected)or0(notconnected).

ThismotivatesustorepresentCNG1usingamatrixaswell,inasimilarmanner.Nonetheless, insteadofasinglevaluethatiseither0or1,wehave three valuestodealwith: ωT , ωI , ωF,witheach ofthemcapableofbeinganywherein O1.Moreover,eachoftheverticesthemselvesalsocontain ρT , ρI , ρF,whichmustbetakenintoaccountaswell.

Inthissection,wediscusstherepresentationofCNG1intwoways,whicharebothanalogousto theoneencounteredinclassicalliterature.

Inotherwords,eachelementofthematrix M isitselfanorderedsetofthreeelements,insteadof justanumberofeither0or1intheclassicalliterature.

Remark3. Since ξ canonlypossessundirectedloops,wedecidednottomultiplythemaindiagonalelementsof M by 2,asseeninadjacencymatricesforgraphsclassicalliterature(2forundirected,1fordirected, 0 forvoid)

4.RepresentationofaCNG1byanAdjacencyMatrix 4.1.TwoMethodsofRepresentation

ρ, ω

M = ai,j n =       a

. . . a

     

Let ξ = V,

beaCNG1wherevertexset V ={v1,v2, ... ,vn}(i.e.,CNG1hasﬁnitevertices). Weﬁrstforman n × n matrixasshown:

1,1 a1,2

2,1 a2,2 a1,n a2,n

n,1 an,2 an,n

, where ai,j = ω vi, vj forall i, j

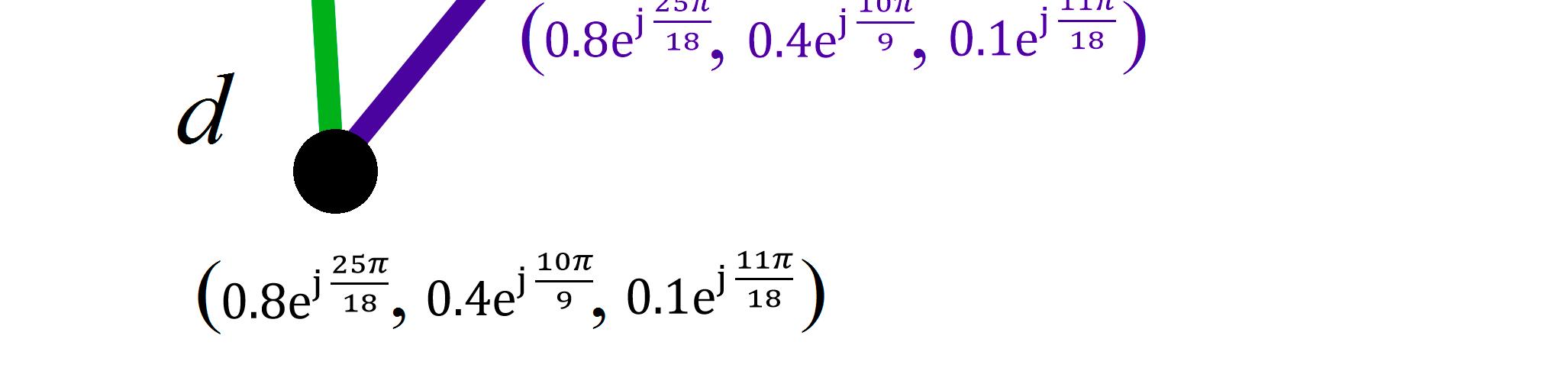
Meanwhile,alsorecallthateachoftheverticesin ξ contains ρT , ρI , ρF,whichmustbetakeninto accountaswell. Thus,weformanothermatrix K asshown: K = [ki ]n,1 =   

k1 k2 . kn



,where ki = ρ(vi )foralli.



  

a1,n a2,n . . . kn an,1 an,2 an,n



   

Although[K|M]isan n × (n+ 1)matrixandthereforenotasquare,thisrepresentationwillsave usanother separate orderedsettorepresentthe ρT , ρI , ρF valuesoftheverticesthemselves.

Sometimesitismoreconvenienttoseparatelydealwitheachofthethreekindsofmembership valuesforbothedgesandvertices.Asaresult,hereweprovideanothermethodofrepresentingthe entire ξ:usingthree n × (n+ 1)matrices, [K|M] T , [K|M] I ,and [K|M] F,eachderivedfrom [K|M] by takingonlyonekindofthemembershipvaluesfromitselements: [K|M] T =[KT |MT ]

     







      , [K|M] I =[KI |MI ]      

  

  

Remark4. If [K|M] I = [K|M] F = [0]n,n+1, KT = [1]n,1,alltheentriesof MT areeither1or0,then ξ is reducedtoagraphinclassicalliterature.Furthermore,ifthat MT issymmetricalandwithmaindiagonal elementsbeingzero,then ξ isfurtherreducedtoasimpleordinarygraphintheclassicalliterature.

Remark5. If [K|M] I = [K|M] F = [0]n,n+1,andalltheentriesof [K|M] T arerealvaluesfromtheinterval [0,1],then ξ isreducedtoageneralizedfuzzygraphtype1(GFG1).

Remark6. Ifalltheentriesof [K|M] T , [K|M] I ,and [K|M] F arerealvaluesfromtheinterval [0,1],then ξ is reducedtoageneralizedsinglevaluedneutrosophicgraphsoftype1(GSVNG1).

Symmetry 2018, 10,190 11of32

  

    

Toaccomplishoneofourmethodsofrepresentingtheentire ξ we,therefore,augmentthematrix K with M,formingthe adjacencymatrixof CNG1,[K|M],asshown: [K|M]= 



k1 a1,1 a1,2 k2 a2,1 a2,2



, where ai,j = ω vi, vj ,and ki = ρ(vi ),forall i, j

ρT (v1) ωT (v1, v1) ωT (v1, v2) ρT (v2) ωT (v2, v1) ωT (v2, v2) ··· ωT (v1, vn ) ωT (v2, vn ) . . . . . ρT (vn ) ωT (vn, v1) ωT (vn, v2) ωT (vn, vn )

ρI (v1) ωI (v1, v1) ωI (v1, v2) ρI (v2) ωI (v2, v1) ωI (v2, v2) ωI (v1, vn ) ωI (v2, vn ) . . .

ρI (vn ) ωI (vn, v1) ωI (vn, v2) ωI (vn, vn )

     , [K|M] F =[KF |MF ]

   

ρF (v1) ωF (v1, v1) ωF (v1, v2) ρF (v2) ωF (v2, v1) ωF (v2, v2) ωF (v1, vn ) ωF (v2, vn ) . . ρF (vn ) ωF (vn, v1) ωF (vn, v2) ωF (vn, vn )

[K|M] T , [K|M] I , and [K|M] F shall,thus,becalled,respectively,the truth-adjacencymatrix, the indeterminate-adjacencymatrix,andthe false-adjacencymatrix of ξ.

Remark7. If MT , MI ,and MF aresymmetricmatrices,then ξ isordinary.

4.2.IllustrativeExample

Forthesakeofbrevity,wenowgiverepresentationforourexampleforthescenarioin3.1bythe lattermethodusingthreematrices: [K|M] T , [K|M] I , and [K|M] F: [K|M] T

0.8ei2π 00.8ei π 12 1ei 4π 3 0.8ei 61π 36 0.7ei π 6 0.8ei π 12 000 0.9ei 2π 3 1ei 4π 3 000 0.8ei 25π 18 0.8ei 61π 36 0.8ei 25π 18 00

0.5ei 13π 18 00.6ei 31π 36 00.5ei 33π 36 0.6eiπ 0.6ei 31π 36 000 0.2ei 17π 9 0000 0.4ei 10π 9 0.5ei 33π 36 0.4ei 10π 9 00

0.2ei 11π 9 00.3ei 7π 6 00.5ei 2π 9 0.3ei 10π 9 0.3ei 7π 6 000 0.5ei 2π 9 0000 0.1ei 11π 18 0.5ei 2π 9 0.1ei 11π 18 00

AsinSection 3,wehaveshownhowamatrixrepresentationofaCNG1with |V| = 4 canbe constructed.Likewise,thesameconceptmentionedcancertainlybeusedonalargerCNG1but,again, onewilldeﬁnitelyrequirecomputeralgebraicsystems,suchasSAGEtoprocessthedataandtodisplay suchamatrixrepresentation.

5.SomeTheoreticalResultsonOrdinaryCNG1

WenowdiscusssometheoreticalresultsthatfollowsfromthedeﬁnitionofordinaryCNG1, aswellasitsrepresentationwithadjacencymatrix.SinceweareconcernedaboutordinaryCNG1,all theedgesthatwewillbereferringtoareordinaryedges.

Deﬁnition11. Let ξ = V, ρ, ω beanordinaryCNG1.Let V = {v1, v2,..., vn } bethevertex setof ξ.Then,foreach i,theresultantdegreeof vi,denotedas D(vi ),isdeﬁnedtobetheorderedset (DT (vi ), DI (vi ), DF (vi )), forwhich:

(a) DT (vi ) = n ∑ r=1 ωT (vi, vr ) + ωT (vi, vi ),

(b) DI (vi ) = n ∑ r=1 ωI (vi, vr ) + ωI (vi, vi ), (c) DF (vi ) = n ∑ r=1 ωF (vi, vr ) + ωF (vi, vi )

Remark8. Inanalogytoclassicalgraphtheory,eachundirectedloophasbothitsendsconnectedtothesame vertex,soiscountedtwice.

Remark9. EachofthevaluesofDT (vi ),DI (vi ),andDF (vi ) neednotbeanintegerasinaclassicalgraph.

Deﬁnition12. Let ξ = V, ρ, ω beanordinaryCNG1.Let V = {v1, v2,..., vn } bethevertexsetof ξ Then,theresultantamountofedgesof ξ,denotedasEξ ,isdeﬁnedtobetheorderedset(ET , EI , EF)forwhich:

(a) ET = ∑ {r,s}⊆{1,2,...,n} ωT (vr, vs ),

Symmetry 2018, 10,190 12of32

    

    

     

      [

] F =      

   

[K|M] I =

K|M





(b) EI = ∑ {r,s}⊆{1,2,...,n} ωI (vr, vs ), (c) EF = ∑ {r,s}⊆{1,2,...,n} ωF (vr, vs )

Remark10. Asinclassicalgraphtheory,eachedgeiscountedonlyonce,asshownby {r, s} ⊆ {1,2,..., n} in theexpression.Forexample,if ωT (va, vb ) isadded,wewillnotadd ωT (vb, va ) againsince {a, b} = {b, a}. Remark11. Eachofthevaluesof ET , EI and EF neednotbeanintegerasinaclassicalgraph.Asaresult, wecallitthe“amount”ofedges,insteadofthe“number”ofedgesasintheclassicalliterature.

Foreachvertex vi,justbecause D(vi ) equals0,thatdoesnotmeanthatalltheedgesconnect to vi arevoid.Itcouldbetwodistinctedges {vi, v1} and {vi, v2} with ωT (vi, v1) = ωT (vi, v2), ωI (vi, v1) = ωI (vi, v2) and ωF (vi, v1) = ωF (vi, v2) (i.e.,equalinmagnitude,butoppositeinphase). Thesamegoestothevalueof Eξ Thisdiffersfromtheclassicaltheoryofgraphsand,therefore, itmotivatesustolookataCNG1inyetanotherapproach.We,thus,furtherdefinethefollowing: Definition13. Let ξ = V, ρ, ω beanordinaryCNG1.Let V = {v1, v2,..., vn } bethevertex setof ξ.Then,foreachi,theabsolutedegreeof vi,denotedas |D|(vi ),isdefinedtobetheorderedset (|D|T (vi ), |D|I (vi ), |D|F (vi )),forwhich:

(a) |D|T (vi ) = n ∑ r=1 |ωT (vi, vr )| + |ωT (vi, vi )|,

(b) |D|I (vi ) = n ∑ r=1 |ωI (vi, vr )| + |ωI (vi, vi )|,

Deﬁnition14. Let ξ = V, ρ, ω beanordinaryCNG1.Let V = {v1, v2,..., vn } bethevertexsetof ξ. Then,theabsoluteamountofedgesof ξ,denotedas |E|ξ ,isdeﬁnedtobetheorderedset(|E|T , |E|I , |E|F)for which:

(a) |E|T = ∑ {r,s}⊆{1,2,...,n} |ωT (vr, vs )|, (b) |E|I = ∑ {r,s}⊆{1,2,...,n} |ωI (vr, vs )|, (c) |E|F = ∑ {r,s}⊆{1,2,...,n} |ωF (vr, vs )|

Ontheotherhand,sometimesweareparticularlyconcernedaboutthenumberofnon-voidedges inanordinaryCNG1.Inotherwords,wejustwanttoknowhowmanyedges vi, vj with: ω vi, vj = (0,0,0)

Insteadofamerevisualinterpretation,wemusthoweverformaprecisedeﬁnitionasfollows:

Deﬁnition15. Let ξ = V, ρ, ω beanordinaryCNG1.Let V ={v1, v2, , vn}tobethevertexsetof ξ Then,thenumberofnon-voidedgesof ξ,denotedasMξ ,isdeﬁnedtobethecardinalityoftheset: vi, vj ⊆ V ω vi, vj = (0,0,0) .

Deﬁnition16. Let ξ = V, ρ, ω beanordinaryCNG1.Let V ={v1, v2, , vn}tobethevertexsetof ξ Then,thenumberofverticesof ξ,denotedasNξ ,isdeﬁnedtobethecardinalityofthesetVitself.

Symmetry 2018, 10,190 13of32

Remark12. Inthispaper,weoftendealwithboth Mξ and Nξ atthesametime.Thus,wewillnotdenote Nξ as |V|.

Remark13. ByDeﬁnition7,Visnon-void,soNξ ≥ 1 follows.

Lemma1. Let ξ = V, ρ, ω beanordinaryCNG1.Let V = {v1, v2,..., vn } bethevertexsetof ξ.Then, foreachi:

(a) DT (vi ) = n ∑ r=1 ωT (vr, vi ) + ωT (vi, vi ), (b) DI (vi ) = n ∑ r=1 ωI (vr, vi ) + ωI (vi, vi ), (c) DF (vi ) = n ∑ r=1 ωF (vr, vi ) + ωF (vi, vi )

Proof. Since ξ isordinary, ω(vr, vi ) = ω(vi, vr ) forall i and r.Thelemmathusfollows.

Lemma2. Let ξ = V, ρ, ω tobeanordinaryCNG1.If ξ issimple.then,foreachi:

(a) DT (vi ) = ∑ r∈{1,2,...,n}−{i} ωT (vi, vr ), (b) DI (vi ) = ∑ r∈{1,2,...,n}−{i} ωI (vi, vr ), (c) DF (vi ) = ∑ r∈{1,2,...,n}−{i} ωF (vi, vr ).

Proof. Since ξ issimple, ω(vi, vi ) = (0,0,0) forall i.Thelemmathusfollows.

Lemma3. Let ξ = V, ρ, ω beanordinaryCNG1.Let V = {v1, v2,..., vn } bethevertexsetof ξ.Then, foreachi:

(a) |D|T (vi ) = n ∑ r=1 |ωT (vr, vi )| + |ωT (vi, vi )|, (b) |D|I (vi ) = n ∑ r=1 |ωI (vr, vi )| + |ωI (vi, vi )|, (c) |D|F (vi ) = n ∑ r=1 |ωF (vr, vi )| + |ωF (vi, vi )|.

Proof. TheargumentsaresimilartoLemma1.

Lemma4. Let ξ = V, ρ, ω beanordinaryCNG1.If ξ issimple.then,foreachi:

(a) |D|T (vi ) = ∑ r∈{1,2,...,n}−{i} |ωT (vi, vr )|, (b) |D|I (vi ) = ∑ r∈{1,2,...,n}−{i} |ωI (vi, vr )|, (c) |D|F (vi ) = ∑ r∈{1,2,...,n}−{i} |ωF (vi, vr )|.

Proof. TheargumentsaresimilartoLemma2.

Lemma5. Let ξ = V, ρ, ω beanordinaryCNG1.Then n ∑ r=1 |D|(vr ) = (0,0,0) ifandonlyif |D|(vi ) = (0,0,0) foralli.

Symmetry 2018, 10,190 14of32

Wenowproceedwithtwoofourtheoremswhichbothserveasgeneralizationsofthewell-known theoreminclassicalliterature: “Foranordinarygraph,thesumofthedegreeofallitsverticesisalwaystwicethenumberof itsedges”. Theorem1. Let ξ = V, ρ, ω beanordinaryCNG1.Then n ∑ r=1 D(vr ) = 2Eξ

Proof. As D(vi ) = (DT (vi ), DI (vi ), DF (vi ))forall i,and Eξ =(ET , EI , EF).Withoutlossofgenerality, itsufﬁcestoprovethat2ET = n ∑ r=1 DT (vr ):

ET =∑{r,s}⊆{1,2,...,n} ωT (vr, vs ) = ∑ {r, s}⊆{1,2,..., n} r = s

Since {r, s} = {s, r} forall s and r,itfollowsthat: 2ET = 2∑ {r, s}⊆{1,2,..., n} r = s

= ∑ r ∈{1,2,..., n} s ∈{1,2,..., n} r = s

ωT (vr, vs ) + ∑n r=1 ωT (vr, vr )

ωT (vr, vs ) + 2∑n r=1 ωT (vr, vr )

= ∑ r ∈{1,2,..., n} s ∈{1,2,..., n} ωT (vr, vs ) + ∑n r=1 ωT (vr, vr ) = ∑n r=1

n ∑ s=1 ωT (vr, vs ) + ∑n r=1 ωT (vr, vr ) = ∑n r=1( ∑n s=1 ωT (vr, vs ) + ωT (vr, vr )) = ∑n r=1 DT (vr )

Thiscompletestheproof. Theorem2. Let ξ = V, ρ, ω beanordinaryCNG1.Then n ∑ r=1 |D|(vr ) = 2|E|ξ Proof. TheargumentsaresimilartoTheorem1andcanbeeasilyprovenbyreplacingalltheterms ωT vi, vj with ωT vi, vj .

Lemma6. Let ξ = V, ρ, ω beanordinaryCNG1,with n ∑ r=1 D(vr ) = (0,0,0).IfMξ > 0,thenMξ ≥ 2 Proof. ByTheorem1, n ∑ r=1 D(vr ) = 2Eξ ,so Eξ = (0,0,0) aswell.

Symmetry 2018, 10,190 15of32

Theorem 2. Let = 〈 , , 〉 be an ordinary CNG1. Then ∑| |( ) =2| | .

Proof. The arguments are similar to Theorem 1 and can be easily proven by replacing all the terms ( , ) with ( , ) . □

Lemma 6. Let = 〈 , , 〉 be an ordinary CNG1, with ∑ ( ) = (0,0,0). If >0, then ≥2

Ifonlyoneedgeisnon-void,then ω(vr0 , vs0 ) = (0,0,0) onlyforoneparticularset {r0, s0}. Thisimpliesthat:

Proof. By Theorem 1, ∑ ( ) = 2 , so = (0,0,0) as well.

If only one edge is non-void, then ( , ) ≠ (0,0,0) only for one particular set { , }. This implies that:

= ∑ ( , ) { , }⊆{ , ,…, } = ( , ),

= ∑ ( , ) { , }⊆{ , ,…, } = ( , ), which contradicts the statement that = (0,0,0). □

ET = ∑{r,s}⊆{1,2,...,n} ωT (vr, vs ) = ωT (vr0 , vs0 ), EI = ∑{r,s}⊆{1,2,...,n} ωI (vr, vs ) = ωI (vr0 , vs0 ), EF = ∑{r,s}⊆{1,2,...,n} ωF (vr, vs ) = ωF (vr0 , vs0 ), whichcontradictsthestatementthat Eξ = (0,0,0)

Since Mξ ≥ 2,onemayhavethoughteither Mξ or Nξ mustbeeven.However,thisisproventobe false,evenbyletting ξ tobesimpleandbyletting D(v) = (0,0,0) forall i,asshownbythefollowing counter-example(Figure 3):

Since ≥2, one may have thought either or must be even. However, this is proven to be false, even by letting to be simple and by letting ( ) = (0,0,0) for all i, as shown by the following counter-example (Figure 3):

Figure 3. A counterexample, showing that or need not be even. = e , e , e , = e , e , e , = e , e , e . Figure3. Acounterexample,showingthat Mξ or Nξ neednotbeeven. a = 1 5 e𝒻2π , 1 5 e𝒻 4 3 π , 1 5 e𝒻 2 3 π , b = 1 5 e𝒻 4 3 π , 1 5 e𝒻 2 3 π , 1 5 e𝒻2π , c = 1 5 e𝒻 2 3 π , 1 5 e𝒻2π , 1 5 e𝒻 4 3 π

forwhich Mξ = 7, Nξ = 5,andwithallverticesbeingend-pointsofsomeedges.Moreover,such aresultisnotrelatedtothevalueof ρ(v) foranyofthevertex v Thismotivatestoconsiderwhatistheleastpossiblevaluesof Mξ and Nξ ,forthespecialcaseof anordinary ξ beingsimple,with D(v) = (0,0,0) and ρ(v) = (1,0,0) forallofitsvertices v.

6.TheShortestCNG1ofCertainConditions

Wenowproceedwiththefollowingdeﬁnitions.

Deﬁnition17. Let ξ = V, ρ, ω beanordinaryCNG1. ξ issaidtobenetifallofthefollowingaresatisﬁed: (a) ξ issimple. (b) ξ isconnected. (c) forallv ∈ V,D(v) = (0,0,0) and ρ(v) = (1,0,0).

Furthermore, ξ issaidtobe trivial iftheentire ξ consistofonesinglevertex v with ρ(v) = (1,0,0) Ontheotherhand, ξ issaidtobe gross ifitisnotnet.

Lemma7. Let ξ = V, ρ, ω beanon-trivialnetCNG1.Theneachvertexmusthaveleasttwonon-voidedges adjacenttoit.

Proof. Let v ∈ V.Since Nξ ≥ 2 and ξ isconnected,theremustexistanon-voidedge {v, u} forsome u ∈ V {v}.

If {v, u} istheonlynon-voidedgeadjacentto v,then D(v) = ω(v, u) = (0,0,0).Thisa contradiction.

Symmetry

16of32

2018, 10,190

Symmetry 2018, 10,190

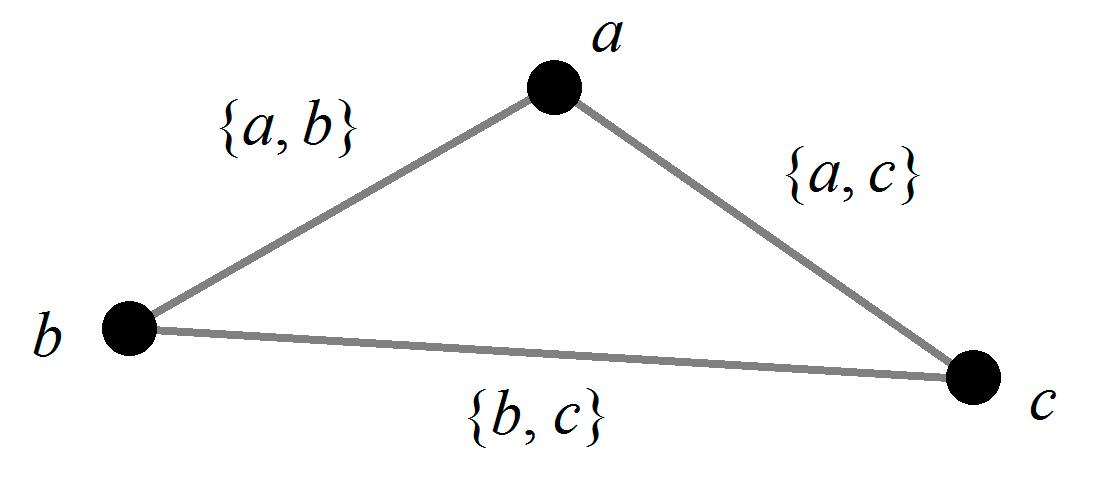
Theorem3. Let ξ = V, ρ, ω beanon-trivialnetCNG1.Then Mξ ≥ 4.Moreover,twoofthosenon-void edgesmustbe {a, b} and {a, c},forsomemutuallydistinctverticesa,b,c.

Proof. Since Nξ ≥ 2 and ξ isconnected,non-voidedge(s)mustexist,so Mξ > 0.Furthermore, D(v) = (0,0,0) forall v ∈ V wouldimply ∑ v∈V D(v) = (0,0,0) Mξ ≥ 2nowfollowsbyLemma6.

Let a beanend-pointofsomeofthosenon-voidedges.FromLemma7,weconcludethatatleast twonon-voidedgesmustbeadjacentto a

Since ξ issimple,itnowfollowsthatthose2non-voidedgesmustbe {a, b} and {a, c},with a, b, c being3mutuallydistinctverticesof ξ

If Mξ = 2: {a, b} and {a, c} arethereforetheonlytwonon-voidedges.ByLemma7,both {a, b} and {a, c} mustbeadjacentto b.Thisisacontradiction.

Symmetry 2018, 10, x FOR PEER REVIEW 16 of 28

If Mξ = 3: Therecanonlybeonemorenon-voidedgesbesides {a, b} and {a, c}

ByLemma7: b mustbeanend-pointofanothernon-voidedgebesides {a, b};and c mustalsobe anend-pointofanothernon-voidedgebesides {a, c}

Proof. By Theorem 3, ≥4, and two of those non-void edges must be { , } and { , }, for some mutually distinct vertices , , .

Wenowdeducethatthethirdnon-voidedgemustthereforebeadjacenttoboth b and c.Thisyields Figure 4:

Suppose 4. Since ξ is simple, the maximum possible number of edges (whether it is void or not) is 3+ (3−3)=3 4, which is a contradiction. ≥4 now follows. □

Figure 4. The triangle formed when { , }, { , } and { , } are all non-void. Mentioned in Theorem 3, 6.

Figure4. Thetriangleformedwhen {a, b}, {a, c} and {b, c} areallnon-void.MentionedinTheorem 3,6.

Theorem 5. The smallest non-trivial net CNG1 must be of the structure in Figure 5:

Since {a, b} and {c, a} arenonvoid, ω(a, b) = k = ω(c, a) forsome k = (0,0,0). Since {b, c} isadjacenttoboth b and c, ω(b, c) = k = k.Thisisagainacontradiction. Mξ ≥ 4nowfollows.

Theorem4. Let ξ = V, ρ, ω beanon-trivialnetCNG1.ThenMξ ≥ 4 andNξ ≥ 4

Proof. ByTheorem3, Mξ ≥ 4,andtwoofthosenon-voidedgesmustbe {a, b} and {a, c},forsome mutuallydistinctvertices a, b, c

Suppose Nξ < 4.Since ξ issimple,themaximumpossiblenumberofedges(whetheritisvoid ornot)is3 + 3 2 (3 3) = 3 < 4,whichisacontradiction. Nξ ≥ 4nowfollows.

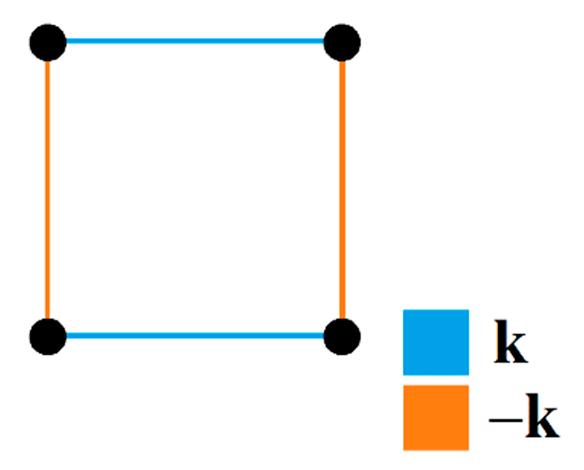
Theorem5. Thesmallestnon-trivialnetCNG1mustbeofthestructureinFigure 5:

Figure 5. The smallest non-trivial net CNG1. Mentioned in Theorem 5 and Example 4. ≠ (0,0,0)

Proof. Let = 〈 , , 〉 be a non-trivial net CNG1. By Theorem 4, ≥4 and ≥4. By Theorem 3, two of those non-void edges must be { , } and { , }, with , , being three mutually distinct vertices of

Proof. Let ξ = V, ρ, ω beanon-trivialnetCNG1.ByTheorem4, Mξ ≥ 4 and Nξ ≥ 4.ByTheorem3, twoofthosenon-voidedgesmustbe {a, b} and {a, c},with a, b, c beingthreemutuallydistinctvertices of ξ

Considerthescenariowhere Mξ = 4and Nξ = 4(i.e.,theleastpossiblenumber).

Consider the scenario where =4 and =4 (i.e., the least possible number).

Iftheedge {b, c} isnon-void,thenwewouldhaveformedFigure 4,asmentionedintheproofof Theorem3

If the edge { , } is non-void, then we would have formed Figure 4, as mentioned in the proof of Theorem 3

That leaves us with only one vertex and only one extra non-void edge being adjacent to This is a contradiction.

There is now only one choice left: both the edges { , } and { , } must be non-void. This gives rise to the following structure in Figure 6:

Without loss of generality, let ( , ) = . Then both ( , ) = − and ( , ) = − must

17of32

leaving

the only valid option.

follow,

us with ( , ) as

Figure 4. The triangle formed when { , }, { , } and { , } are all non-void. Mentioned in Theorem 3, 6.

Thatleavesuswithonlyonevertex d andonlyoneextranon-voidedgebeingadjacentto d.Thisis acontradiction.

Theorem 5. The smallest non-trivial net CNG1 must be of the structure in Figure 5:

Symmetry 2018, 10, x FOR PEER REVIEW 17 of 28

Theorem 6. Let = 〈 , , 〉 be a non-trivial net CNG1 with both and being odd numbers. Then ≥7 and ≥5.

Figure5. Thesmallestnon-trivialnetCNG1.MentionedinTheorem5andExample4. k = (0,0,0)

Figure 5. The smallest non-trivial net CNG1. Mentioned in Theorem 5 and Example 4. ≠ (0,0,0).

Proof. Let = 〈 , , 〉 be a non-trivial net CNG1. By Theorem 4, ≥4 and ≥4. By Theorem 3, two of those non-void edges must be { , } and { , }, with , , being three mutually distinct vertices of

Thereisnowonlyonechoiceleft:boththeedges {d, b} and {d, c} mustbenon-void.Thisgives risetothefollowingstructureinFigure 6:

Proof. Let ξ= 〈 , , 〉 be a non-trivial net CNG1. By Theorem 4, ≥4 and ≥4. By Theorem 3, two of those non-void edges must be { , } and { , }, for some , and being three mutually distinct vertices of Since both and are odd, it follows that ≥5 and ≥5. So in addition to , , , there exist another 2 vertices , Consider the scenario where =5 and =5 (i.e., the least possible number).

Consider the scenario where (i.e., the least possible number). If the edge { , } is non-void, then we would have formed Figure 4, as mentioned in the proof of Theorem 3

That leaves us with only one vertex and only one extra non-void edge being adjacent to This is a contradiction.

There is now only one choice left: both the edges { , } must be non-void. This gives rise to the following structure in Figure 6:

Without loss of generality, let ( , ) = − and ( , ) = − must follow, leaving us with ( , ) = We are therefore left with the only way of assigning as shown by the theorem. □

Lemma 8. Let = 〈 , , 〉 be a non-trivial net CNG1. Then ≥

Figure 6. The only choices left because eace vertex must have at least 2 adjacent non void edges. Mentioned in Theorem 5, 6.

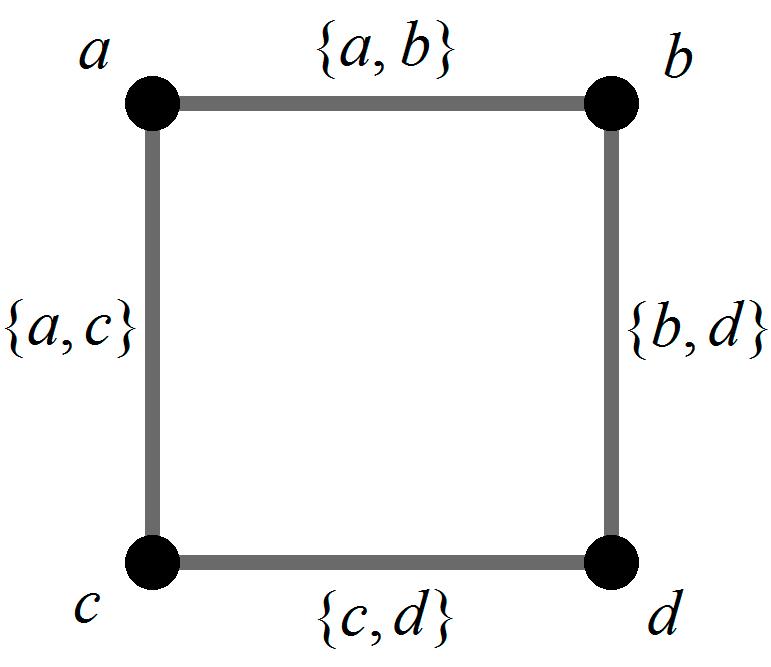
Figure6. Theonlychoicesleftbecauseeacevertexmusthaveatleast2adjacentnonvoidedges. MentionedinTheorem5,6.

Case 1. Suppose the edge { , } is non-void. Then we would have formed Figure 4, as mentioned in the proof of Theorem 3.

Withoutlossofgenerality,let ω(a, b) = k.Thenboth ω(b, d) = k and ω(a, c) = k mustfollow, leavinguswith ω(c, d) = k astheonlyvalidoption.

Proof. Every single non-void edge is connected to two vertices. Thus, if we count the total number of adjacent non-void edges for each vertex, and then summing the results for all the vertices together, the result will be 2 (note: this paragraph is analogous to classical graph theory).

Wearethereforeleftwiththeonlywayofassigning ω asshownbythetheorem.

By Lemma 7, each vertex must have at least two non-void edges connect to it. We now have 2 ≥2 , so ≥ follows. □

That leaves us with two vertices and , and two extra non-void edge, which both of them must be adjacent to . Even if { , } is non-void, the other non-void edge adjacent to cannot possibly be { , } itself. Therefore, we have, at most, one non-void edge being adjacent to . This is a contradiction.

Lemma8. Let ξ = V, ρ, ω beanon-trivialnetCNG1.ThenMξ ≥ Nξ

Case 2. Without loss of generality, suppose the edges { , } and { , } are non-void. Then we would have formed Figure 6, as mentioned in the proof of Theorem 5.

Proof. Everysinglenon-voidedgeisconnectedtotwovertices.Thus,ifwecountthetotalnumberof adjacentnon-voidedgesforeachvertex,andthensummingtheresultsforalltheverticestogether,the resultwillbe2Mξ (note:thisparagraphisanalogoustoclassicalgraphtheory).

That leaves us with only one vertex and only one extra edge being adjacent to , which is, again, a contradiction.

ByLemma7,eachvertexmusthaveatleasttwonon-voidedgesconnecttoit.Wenowhave 2Mξ ≥ 2Nξ ,so Mξ ≥ Nξ follows.

Case 3. Without loss of generality, suppose the edges { , } and { , } are non-void. Then, besides { , }, another edge must be adjacent to Likewise, besides { , }, another edge must be adjacent to Since we are left with one edge, it must, therefore, be { , } . This gives rise to the following structure in Figure 7:

Theorem6. Let ξ = V, ρ, ω beanon-trivialnetCNG1withboth Mξ and Nξ beingoddnumbers. ThenMξ ≥ 7 andNξ ≥ 5.

Proof. Let ξ = V, ρ, ω beanon-trivialnetCNG1.ByTheorem4, Mξ ≥ 4 and Nξ ≥ 4.ByTheorem3, twoofthosenon-voidedgesmustbe {a, b} and {a, c},forsome a, b and c beingthreemutuallydistinct verticesof ξ

Sinceboth Mξ and Nξ areodd,itfollowsthat Mξ ≥ 5 and Nξ ≥ 5.Soinadditionto a, b, c,there existanother2vertices d, e

Symmetry 2018

18of32

, 10,190

Figure 6. The only choices left because eace vertex must have at least 2 adjacent non void edges. Mentioned in Theorem 5, 6.

Considerthescenariowhere Mξ = 5and Nξ = 5(i.e.,theleastpossiblenumber).

Case 1. Suppose the edge { , } is non-void. Then we would have formed Figure 4, as mentioned in the proof of Theorem 3.

Case1. Supposetheedge {b, c} isnon-void.ThenwewouldhaveformedFigure 4,asmentioned intheproofofTheorem3.

Thatleavesuswithtwovertices d and e,andtwoextranon-voidedge,whichbothofthemmust beadjacentto d.Evenif {d, e} isnon-void,theothernon-voidedgeadjacentto d cannotpossiblybe {d, e} itself.Therefore,wehave,atmost,onenon-voidedgebeingadjacentto e.Thisisacontradiction.

Case2. Withoutlossofgenerality,supposetheedges {b, d} and {c, d} arenon-void.Thenwe wouldhaveformedFigure 6,asmentionedintheproofofTheorem5.

Case 2. Without loss of generality, suppose the edges { , } and { , } are non-void. Then we would have formed Figure 6, as mentioned in the proof of Theorem 5.

Thatleavesuswithonlyonevertex e andonlyoneextraedgebeingadjacentto e,whichis,again, acontradiction.

Case3. Withoutlossofgenerality,supposetheedges {b, d} and {c, e} arenon-void.Then,besides {b, d},anotheredgemustbeadjacentto d Likewise,besides {c, e},anotheredgemustbeadjacentto e Sinceweareleftwithoneedge,itmust,therefore,be {d, e}.Thisgivesrisetothefollowingstructure inFigure 7:

That leaves us with only one vertex and only one extra edge being adjacent to , which is, again, a contradiction.

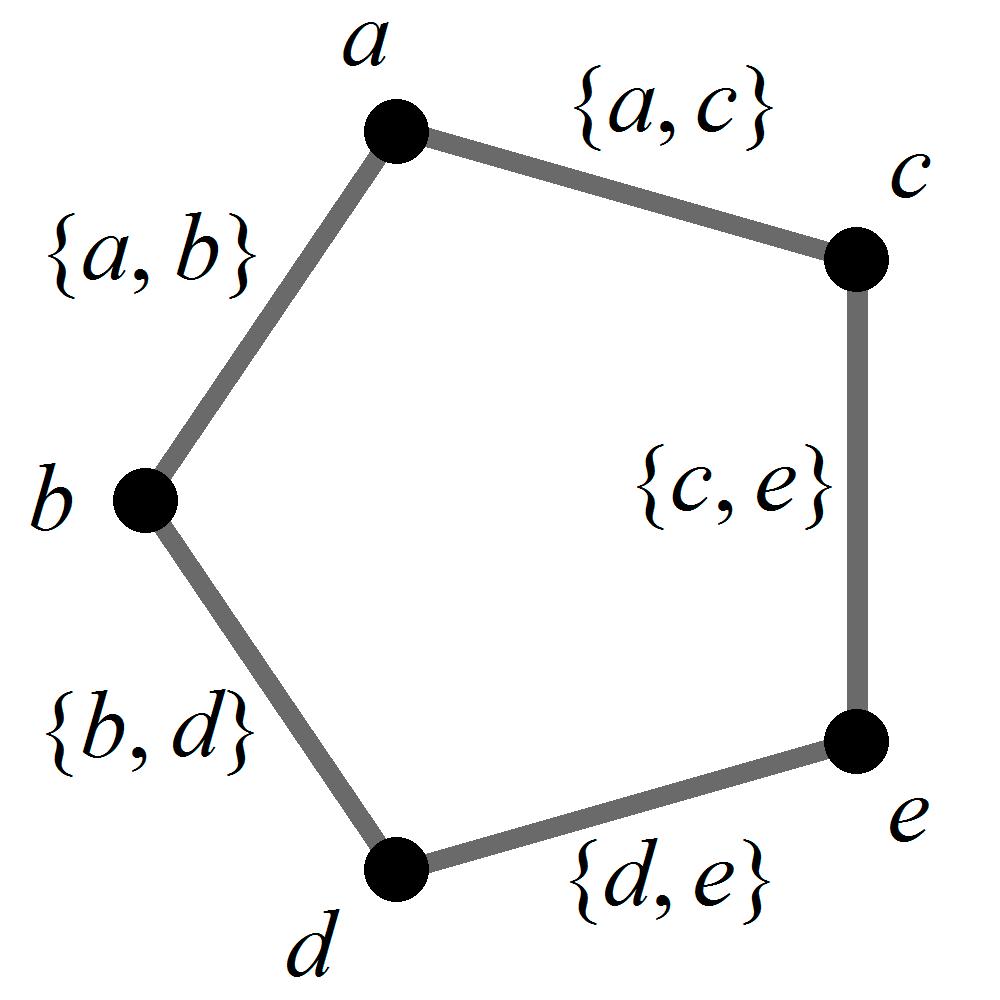
Figure7. Theonlychoiceleftforthecaseof5non-voidedgesconnectingto5vertices.Mentionedin Theorem6.

Figure 7. The only choice left for the case of 5 non-void edges connecting to 5 vertices. Mentioned in Theorem 6.

Withoutlossofgenerality,let ω(a, b) = k.Thenboth ω(b, d) = k and ω(a, c) = k mustfollow, leavinguswithboth ω(c, e) = k and ω(d, e) = k. Wehave,thus,arrivedat D(e) =2k = (0,0,0),againacontradiction. Hence,itiseither Mξ > 5or Nξ > 5. Sinceboth Mξ and Nξ areodd,eitheroneofthefollowingmusthold:

(a) Mξ ≥ 7and Nξ ≥ 7.

(b) Mξ = 7and Nξ = 5.

Furthermore,byLemma8, Mξ ≥ Nξ Hence(c)willnotoccur,whichimpliesthat Mξ ≥ 7 and Nξ ≥ 5.Thiscompletestheproof.

Theorem7. Thesmallestnon-trivialnetCNG1 ξ,withboth Mξ and Nξ beingoddnumbers,mustbeofthe structureasshowninFigure 8:

Proof. Let ξ = V, ρ, ω beanon-trivialnetCNG1withboth Mξ and Nξ beingoddnumbers. Then Mξ ≥ 7and Nξ ≥ 5. Considerthescenariowhere Mξ = 7and Nξ = 5(i.e.,theleastpossiblenumber).

Symmetry 2018, 10,190 19of32

Hence, it is either >5 or >5.

Since both and are odd, either one of the following must hold: (a) ≥7 and ≥7 (b) =7 and =5. (c) =5 and =7

Symmetry 2018, 10,190

Furthermore, by Lemma 8, ≥ Hence (c) will not occur, which implies that ≥7 and ≥5. This completes the proof. □

Since ξ isanordinaryCNG1,eachvertexmusthave5edgesadjacenttoit(whethervoidornot). Since ξ issimple,oneoftheﬁveedgesforeachvertex,whichisaloop,mustbevoid.Asaresult, wenowconcludethateachvertexmusthaveatmost4non-voidedgesadjacenttoit.

Ontheotherhand,byLemma7,eachvertexmusthaveatleasttwonon-voidedgesadjacenttoit.

Theorem 7. The smallest non-trivial net CNG1 , with both and being odd numbers, must be of the structure as shown in Figure 8:

Figure 8. The smallest non-trivial net CNG1, with both M and N being odd numbers. . Mentioned in Theorem 7 and Example 5. + + =(0,0,0); | + |, | + | ≤1.

Figure8. Thesmallestnon-trivialnetCNG1, withboth Mξ and Nξ beingoddnumbers..Mentioned inTheorem7andExample5. p + q + r = (0,0,0); |p + r| , |q + r| ≤ 1.

Proof. Let = 〈 , , 〉 be a non-trivial net CNG1 with both and being odd numbers. Then ≥7 and ≥5

Sinceeverysinglenon-voidedgeisadjacenttotwovertices.Thus,ifwecountthetotalnumberof adjacentnon-voidedgesforeachvertex,andthensummingtheresultsforalltheverticestogether,the resultwillbe7 × 2 = 14(note:thisparagraphisanalogoustoclassicalgraphtheory).

Consider the scenario where =7 and =5 (i.e., the least possible number).

Since ξ is an ordinary CNG1, each vertex must have 5 edges adjacent to it (whether void or not). Since ξ is simple, one of the five edges for each vertex, which is a loop, must be void. As a result, we now conclude that each vertex must have at most 4 non-void edges adjacent to it.

Hence,thesetrepresentingthenumberofnon-voidedgesadjacenttoeachoftheﬁvevertices, mustbeoneofthefollowing:

(a) {2,3,3,3,3} (most“widelyspread”possibility)

(b) {2,2,3,3,4} (c) {2,2,2,4,4} (most“concentrated”possibility)

On the other hand, by Lemma 7, each vertex must have at least two non-void edges adjacent to it. Since every single non-void edge is adjacent to two vertices. Thus, if we count the total number of adjacent non-void edges for each vertex, and then summing the results for all the vertices together, the result will be 7×2=14 (note: this paragraph is analogous to classical graph theory).

Hence, the set representing the number of non-void edges adjacent to each of the five vertices, must be one of the following:

Wenowconsidereachthethreecases: Case1. {2,3,3,3,3} Withoutlossofgenerality:

(a) {2,3,3,3,3} (most “widely spread” possibility) (b) {2,2,3,3,4} (c) {2,2,2,4,4} (most “concentrated” possibility)

Let a bethatonevertexwhichisanend-pointtoonly2 non-voidedges {a, b} and {a, c} (i.e., {a, d}, {a, e} arevoid)(Figure 9) (9) Symmetry 2018, 10, x FOR PEER REVIEW 19 of 28

We now consider each the three cases:

Case 1. {2,3,3,3,3}

Without loss of generality:

Let be that one vertex which is an end-point to only 2 non-void edges { , } and { , } are void) (Figure 9) (9)

Then, each one among , , must be an end-point of three non-void edges. Besides { , } and { , }, which are both void, there are three more edges adjacent to : { , }, { , }, { , }

Figure 9. The 2 non-void edges { , } and { , }, for all the 3 cases of Theorem 7.

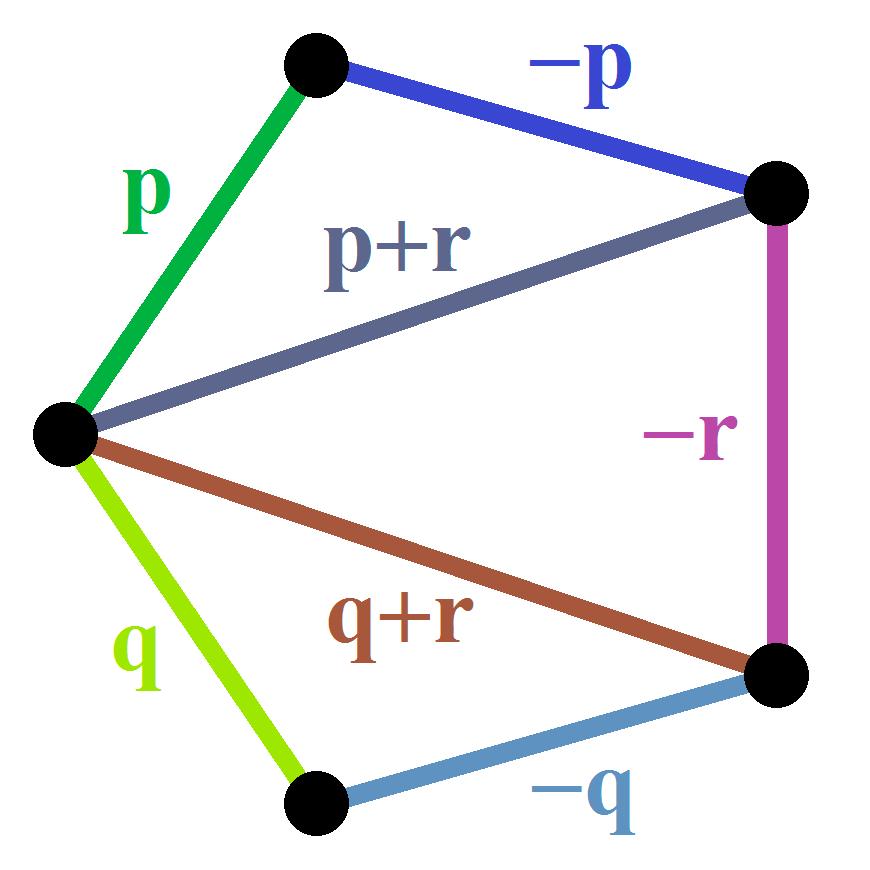
Figure9. The2non-voidedges {a, b} and {a, c},forallthe3casesofTheorem7.

Since d is an end-point of exactly three non-void edges, we conclude that: { , }, { , }, { , } are all non-void (10)

Then,eachoneamong b, c, d, e mustbeanend-pointofthreenon-voidedges. Besides {d, a} and {d, d},whicharebothvoid,therearethreemoreedgesadjacentto d: {d, b}, {d, c}, {d, e}

Similarly, besides { , } and { , }, which are both void, there are three more edges adjacent to : { , }, { , }, { , }

Since e is also an end-point of exactly three non-void edges, we conclude that: { , }, { , }, { , } are all non-void. (11)

From (10) and (11), we conclude that: { , } { , } { , } { , } { , }={ , } are all non void.

20of32

(12)

Since d isanend-pointofexactlythreenon-voidedges,weconcludethat:

Figure 9. The 2 non-void edges { , } and { , }, for all the 3 cases of Theorem 7.

{d, b},{d, c}, {d, e} areallnon void(10)

Since d is an end-point of exactly three non-void edges, we conclude that:

{ , }, { , }, { , } are all non-void (10)

Similarly,besides {e, a} and {e, e},whicharebothvoid,therearethreemoreedgesadjacentto e: {e, b}, {e, c}, {e, d}.

Since e isalsoanend-pointofexactlythreenon-voidedges,weconcludethat:

{ , }, { , }, { , } are all non-void (10)

Similarly, besides { , } and { , }, which are both void, there are three more edges adjacent to : { , }, { , }, { , }

{e, b},{e, c}, {e, d} areallnon void(11)

Since e is also an end-point of exactly three non-void edges, we conclude that:

From(10)and(11),weconcludethat:

{ , }, { , }, { , } are all non-void. (11)

Since e is also an end-point of exactly three non-void edges, we conclude that: { , }, { , }, { , } are all non-void. (11)

{d, b},{d, c}, {e, b}, {e, c}, {d, e} = {e, d} areallnon void(12)

From (10) and (11), we conclude that: { , }, { , }, { , }, { , }, { , }={ , } are all non void. (12)

From(9)and(12),wehaveobtainedallthesevennon-voidedges:

From (9) and (12), we have obtained all the seven non-void edges: { , }, { , }, { , }, { , }, { , }, { , }, { , }.

{d, b},{d, c}, {e, b}, {e, c}, {d, e}, {a, b}, {a, c}.

Hence, {b, c}, {a, d}, {a, e} mustbeallvoid.We,thus,obtainthefollowingstructure(Figure 10):

Hence, { , }, { , }, { , } must be all void. We, thus, obtain the following structure (Figure 10):

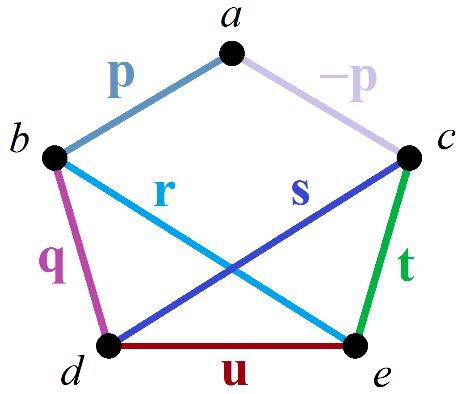
Figure 10. The only possible way of connection for {2,3,3,3,3}.

Figure 10. The only possible way of connection for {2,3,3,3,3}

Let ( , ) = p, ( , ) = q, ( , ) = r, ( , ) = s, ( , ) = t, ( , ) = u.

Since { , } and { , } are the only two non-void edges adjacent to , we now have ( , ) = − (Figure 11).

Figure10. Theonlypossiblewayofconnectionfor {2,3,3,3,3} ω(a, b) = p, ω(b, d) = q, ω(b, e) = r, ω(c, d) = s, ω(c, e) = t, ω(d, e) = u. {a, b} and {a, c} aretheonlytwonon-voidedgesadjacentto a,wenowhave ω(a, c) = p (Figure 11).

Since { , } and { , } are the only two non-void edges adjacent to , we now have ( , ) = − (Figure 11).

Figure 11. The labeling of the non-void edges for {2,3,3,3,3}

Figure 11. The labeling of the non-void edges for {2,3,3,3,3}. Figure11. Thelabelingofthenon-voidedgesfor {2,3,3,3,3}

Wehowhave: r + q + p = s + t p = s + q + u = r + t + u = (0,0,0) Thisfurtherimpliesthat: r + q + p + s + t p = s + q + u + r + t + u = (0,0,0)

Therefore, q + r + s + t = q + r + s + t + 2u,whichimpliesthat u = (0,0,0).Thisis acontradiction.

Case2. {2,2,3,3,4}

Symmetry 2018, 10,190 21of32

Symmetry 2018, 10, x

We how have: + + = + − = + + = + + =(0,0,0)

This further implies that: + + + + − = + + + + + =(0,0,0)

We how have: + + = + − = + + = + + =(0,0,0) This further implies that: + + + + − = + + + + + =(0,0,0) Therefore, + + + = + + + +2 , which implies that =(0,0,0) . This is a contradiction.

We how have: + + = + − = + + = + + =(0,0,0).

Therefore, + + + = + + + +2 , which implies that =(0,0,0) . This is a contradiction.

Case 2. {2,2,3,3,4}

This further implies that: + + + + − = + + + + + =(0,0,0). Therefore, + + + = + + + +2 , which implies that =(0,0,0) . This is a contradiction.

Withoutlossofgenerality:

Case 2. {2,2,3,3,4}

Without loss of generality:

Let a bethatonevertexwhichisanend-pointtoonlytwonon-void edges {a, b} and {a, c} (i.e., {a, d } , {a, e} arevoid) (13)

asshowninFigure 9.

Let be a vertex which is an end-point to only two non-void edges { , } and { , }. (i.e., { , }, { , } are void) (13)

Let be a vertex which is an end-point to only two non-void edges { , } and { , }. (i.e., { , }, { , } are void) (13) as shown in Figure 9.

Let be a vertex which is an end-point to only two non-void edges { , } and { , } (i.e., { , }, { , } are void) (13)

Since {a, d}, {a, e} arevoid,both d and e cannotbethatvertexwhichisanend-pointtofour non-voidedges.

as shown in Figure 9.

Since { , }, { , } are void, both and cannot be that vertex which is an end-point to four non-void edges.

as shown in Figure 9.

Since { , }, { , } are void, both and cannot be that vertex which is an end-point to four non-void edges.

Bysymmetry,ﬁx b tobethatvertexwhichisanend-pointtofournon-voidedges.Then:

By symmetry, fix to be that vertex which is an end-point to four non-void edges. Then: { , }, { , }, { , }, { , } are all non-void. (14)

{b, a},{b, c}, {b, d}, {b, e} areallnon void.(14)

From(13)and(14),wehavenowarrivedatthefollowingstructure(Figure 12):

From (13) and (14), we have now arrived at the following structure (Figure 12):

By symmetry, fix to be that vertex which is an end-point to four non-void edges. Then: { , }, { , }, { , }, { , } are all non-void. (14)

From (13) and (14), we have now arrived at the following structure (Figure 12):

Figure 12.

Figure12. Theﬁrst5non-voidedgesfor {2,2,3,3,4}.

Figure 12. The first 5 non-void edges for {2,2,3,3,4}

Figure 12. The first 5 non-void edges for {2,2,3,3,4}.

Suppose { , } is void. Then exactly one out of { , } and { , } must be non-void. Similarly, exactly one out of { , } and { , } must be non-void. By symmetry and the rules of graph isomorphism, fix { , } to be non-void, then would have been an end-point of three non-void edges: { , }, { , }, { , }. So { , } must be void and, therefore, { , } is non-void. We, thus, obtain the following structure (Figure 13):

Suppose {d, e} isvoid.Thenexactlyoneoutof {d, c} and {d, a} mustbenon-void.Similarly, exactlyoneoutof {e, c} and {e, a} mustbenon-void.Bysymmetryandtherulesofgraphisomorphism, ﬁx {d, a} tobenon-void,then a wouldhavebeenanend-pointofthreenon-voidedges: {d, a}, {b, a}, {c, a}.So {e, a} mustbevoidand,therefore, {e, c} isnon-void.We,thus,obtainthefollowingstructure (Figure 13):

Figure 13. The only possible way of connection for {2,2,3,3,4}, if { , } is void.

Figure13. Theonlypossiblewayofconnectionfor {2,2,3,3,4},if {d, e} isvoid.

Figure 13. The only possible way of connection for {2,2,3,3,4}, if { , } is void.

Suppose { , } is non-void. Then we now arrived at the following structure (Figure 14):

Suppose {d, e} isnon-void.Thenwenowarrivedatthefollowingstructure(Figure 14):

Suppose { , } is non-void. Then we now arrived at the following structure (Figure 14):

Figure 14. The first 6 non-void edges for , for the case of non-void { , }.

Figure 14. The first 6 non-void edges for {2,2,3,3,4}, for the case of non-void { , }

Figure 14. The first 6 non-void edges for {2,2,3,3,4}, for the case of non-void { , } Figure14. Theﬁrst6non-voidedgesfor {2,2,3,3,4},forthecaseofnon-void {d, e}

2018

22of32

Symmetry

, 10,190

FOR PEER REVIEW 20 of 28

Symmetry 2018, 10, x FOR PEER REVIEW 20 of 28

Symmetry 2018, 10,190 23of32

2018, 10, x FOR PEER REVIEW

Symmetry 2018, 10, x FOR PEER REVIEW 21 of 28

By symmetry, fix to be a vertex which is an end-point of three non-void edges. Then exactly one edge out of { , } and { , } must be non-void. By the rules of graph isomorphism, we can fix { , } to be non-void. Again we obtain the following structure (Figure 15):

Bysymmetry,ﬁx a tobeavertexwhichisanend-pointofthreenon-voidedges.Thenexactlyone edgeoutof {a, d} and {a, e} mustbenon-void.Bytherulesofgraphisomorphism,wecanﬁx {a, d} to benon-void.Againweobtainthefollowingstructure(Figure 15):

Figure 15. The only possible way of connection for {2,2,3,3,4}, if { , } is non-void.

Figure15. Theonlypossiblewayofconnectionfor {2,2,3,3,4},if {d, e} isnon-void.

Let ( , ) = g, ( , ) = h, ( , ) = k, ( , ) = p, ( , ) = q

Let ( , ) = g, ( , ) = h, ( , ) = k, ( , ) = p, ( , ) = q.

Let ω(a, b) = g, ω(c, b) = h, ω(a, c) = k, ω(b, d) = p, ω(b, e) = q.

Since { , } and { , } are the only two non-void edges adjacent to , we now have ( , ) = − .

Since {a, d} and {b, d} aretheonlytwonon-voidedgesadjacentto d,wenowhave ω(a, d) = p. Likewise,since {c, e} and {b, e} aretheonlytwonon-voidedgesadjacentto e,wenowhave ω(c, e) = q (Figure 16).

Since { , } and { , } are the only two non-void edges adjacent to , we now have ( , ) = − Likewise, since { , } and { , } are the only two non-void edges adjacent to , we now have ( , ) = − (Figure 16).

Likewise, since { , } and { , } are the only two non-void edges adjacent to , we now have ( , ) = − (Figure 16).

Figure 16. The labeling of the non-void edges for {2,2,3,3,4}.

Figure 16. The labeling of the non-void edges for {2,2,3,3,4}

Figure16. Thelabelingofthenon-voidedgesfor {2,2,3,3,4}

We how have: + + + = + − = + − =(0,0,0)

Wehowhave: p + q + g + h = g + k p = h + k q = (0,0,0). Therefore, g = p k, h = q k .Asaresult: p + q + p k + q k = 2p + 2q 2k = (0,0,0), whichimplies p + q k = (0,0,0).

Therefore, = − , = − . As a result: + + − + − =2 +2 −2 =(0,0,0), which implies + − =(0,0,0)

Therefore, = − , = − . As a result: + + − + − =2 +2 −2 =(0,0,0), which implies + − =(0,0,0). Denote − = . Then = + , = + , and + + =(0,0,0) follows. We have, thus, formed the structure as mentioned in this theorem. Case 3. {2,2,2,4,4}

Denote k = r.Then g = p + r, h = q + r,and p + q + r = (0,0,0) follows.Wehave,thus, formedthestructureasmentionedinthistheorem.

Case3. {2,2,2,4,4}

Denote − = . Then = + , = + , and + + =(0,0,0) follows. We have, thus, formed the structure as mentioned in this theorem. Case 3. {2,2,2,4,4}

Withoutlossofgenerality:

Without loss of generality:

Let a beoneofthattwoverticeswhichisanend-pointtofournon-voidedges.Then:

Without loss of generality:

Let be one of that two vertices which is an end-point to four non-void edges. Then: { , }, { , }, { , }, { , } are non-void. (15)

{a, b},{a, c}, {a, d}, {a, e} arenon void.(15)

Let be one of that two vertices which is an end-point to four non-void edges. Then: { , }, { , }, { , }, { , } are non-void. (15) Let be the other one vertices which is also an end-point to four non-void edges. Then: { , }, { , }, { , }, { , } are non-void. (16)

Let b betheotheroneverticeswhichisalsoanend-pointtofournon-voidedges.Then: {b, a},{b, c}, {b, d}, {b, e} arenon void.(16)

Let be the other one vertices which is also an end-point to four non-void edges. Then: { , }, { , }, { , }, { , } are non-void. (16)

From (15) and (16), we have obtained the seven non-void edges: { , }, { , }, { , }, { , }, { , }, { , }, { , }.

From (15) and (16), we have obtained the seven non-void edges: { , }, { , }, { , }, { , }, { , }, { , }, { , }

From(15)and(16),wehaveobtainedthesevennon-voidedges:

Hence, { , }, { , }, { , } are all void. We, thus, obtain the following structure (Figure 17):

{a, c},{a, d}, {a, e}, {b, c}, {b, d}, {b, e}, {a, b}

Hence, { , }, { , }, { , } are all void. We, thus, obtain the following structure (Figure 17):

Hence, {c, d}, {c, e}, {d, e} areallvoid.We,thus,obtainthefollowingstructure(Figure 17):

21 of 28

Symmetry

Symmetry 2018, 10, x FOR PEER REVIEW

(i) Such 𝒻 issaidtobeanisomorphismfrom ξ to ζ,andweshalldenotesuchcaseby 𝒻[ξ ] ≡ ζ. (ii) ξ and ζ aresaidtobeisomorphic,andshallbedenotedby ξ ∼ = ζ

Remark 15. As both and are ordinary, ( , ) = ( , ) and ( ( ), ( )) = ( ( ), ( )) follow for all , ∈

Remark15. Asboth ξ and ζ areordinary, ω(u, v) = ω(v, u) and ψ(𝒻(u), 𝒻(v)) = ψ(𝒻(v), 𝒻(u)) follow forallu, v ∈ V.

Example 1. Consider = 〈 , , 〉 and = 〈 , , 〉 as follows: = { , , , , , } = { , , , , , } ( ) = , ( ) = , ( ) = , ( ) = , ( ) = , ( ) = , ( ) = ( ) = , ( ) = ( ) = ( ) = , ( ) = ( , ) = ( , ) = ( , ) = , ( , ) = ( , ) = , ( , ) = ( , ) = , ( , ) = ( , ) = , ( , ) = ( , ) = , ( , ) = ( , ) = , ( , ) = ( , ) = , ( , ) = ( , ) = , ( , ) = ( , ) = , ( , ) = ( , ) = , ( , ) = ( , ) = , ( , ) = ( , ) = ( , ) = , otherwise, ( , ) = (0,0,0). otherwise, ( , ) = (0,0,0).

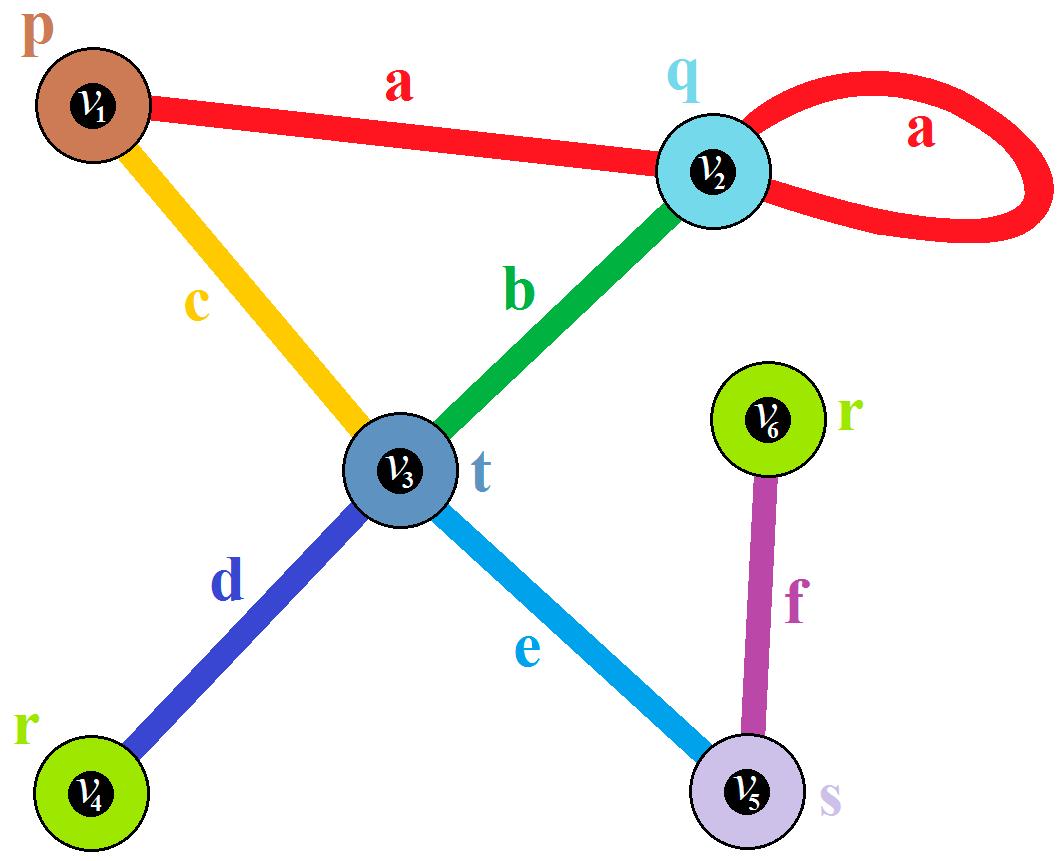
Example1. Consider ξ0 = V0, ρ0, ω0 and ζ0 = W0, ς0, ψ0 asfollows: V0 = {v1, v2, v3, v4, v5, v6}.W0 = {w1, w2, w3, w4, w5, w6} ρ0(v1) = p, ρ0(v2) = q, ρ0(v3) = t, ς0(w1) = t, ς0(w3) = p, ς0(w4) = s, ρ0(v4) = ρ0(v6) = r, ρ0(v5) = s ς0(w2) = ς0(w4) = r, ς0(w6) = q ω0(v1, v2) = ω0(v2, v1) = ω0(v2, v2) = a, ψ0(w1, w2) = ψ0(w2, w1) = d, ω0(v1, v3) = ω0(v3, v1) = c, ψ0(w1, w3) = ψ0(w3, w1) = c, ω0(v2, v3) = ω0(v3, v2) = b, ψ0(w1, w4) = ψ0(w4, w1) = e, ω0(v3, v4) = ω0(v4, v3) = d, ψ0(w4, w5) = ψ0(w5, w4) = f, ω0(v3, v5) = ω0(v5, v3) = e, ψ0(w1, w6) = ψ0(w6, w1) = b, ω0(v5, v6) = ω0(v6, v5) = f, ψ0(w3, w6) = ψ0(w6, w3) = ψ0(w6, w6) = a, otherwise, ω0(u, v) = (0,0,0) otherwise, ψ0(w, ν) = (0,0,0)

Moreover, |{p, q, r, s, t}| = 5 and |{a, b, c, d, e, f}| = 6(Figure 19).

Moreover, |{ , , , , }| =5 and |{ , , , , , }| =6 (Figure 19).

Figure 19. Two isomorphic CNG1’s, as mentioned in Example 1.

Figure19. TwoisomorphicCNG1’s,asmentionedinExample1.

Thus, we define the bijection : → as: ( ) = , ( ) = , ( ) = , ( ) = , ( ) = , ( ) = .

Thus,wedeﬁnethebijection 𝒻0 : V → Was:

It now follows that is an isomorphism from to , so ≅ . Still, ≢ in accordance with Definition 18.

𝒻0 isanisomorphismfrom ξ0 to ζ0,so ξ0 ∼ = ζ0. Still, ξ0ζ0 inaccordancewith

In all the following passages of this paper, let ℐ: → be the identity mapping from to itself. Like classical graph theory, whenever ≡ , ℐ is an isomorphism from to itself in accordance with Definition 19. It is, therefore, motivational to investigate if there are other nonidentity bijections from to itself, which is also an isomorphism from to itself. Additionally, recall that, in classical graph theory, an isomorphism from a graph to itself will be called an automorphism on that graph. Thus, we proceed with the following definition:

Inallthefollowingpassagesofthispaper,let ℐ : V → V betheidentitymappingfrom V toitself. Likeclassicalgraphtheory,whenever ζ ≡ ξ, ℐ isanisomorphismfrom ξ to ξ itselfinaccordance withDeﬁnition19.Itis,therefore,motivationaltoinvestigateifthereareothernon-identitybijections from V toitself,whichisalsoanisomorphismfrom ξ to ξ itself.Additionally,recallthat,inclassical graphtheory,anisomorphismfromagraphtoitselfwillbecalledanautomorphismonthatgraph. Thus,weproceedwiththefollowingdeﬁnition:

Definition 20. Let be a non-void set. Let = 〈 , , 〉 be an ordinary CNG1’s. Let : → be a bijection such that: (a) ( ) = ( ( )) for all ∈ (b) ( , ) = ( ( ), ( )) for all , ∈ Then is said to be an automorphism of

Symmetry 2018

25of32

, 10,190

𝒻0

Remark 16. As is ordinary, ( , ) = ( , ) follows for all , ∈ . 0

(v1) = v3,

(v2) = v6, 𝒻0(v3) =

1, 𝒻

(v4) = v2, 𝒻0(v5) = v

, 𝒻

(v6) = v5

Itnowfollowsthat

Deﬁnition18.

Symmetry 2018, 10,190

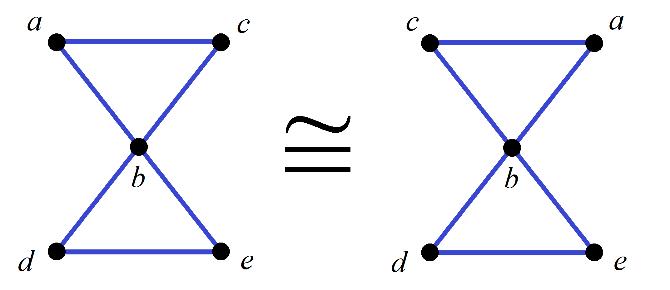
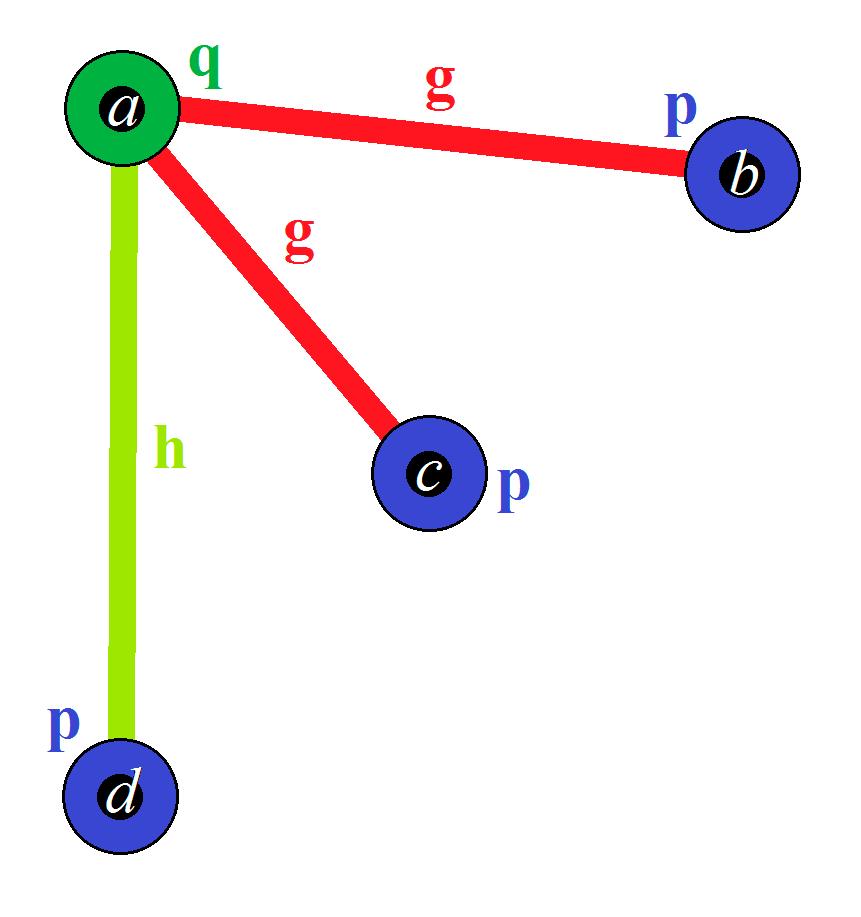
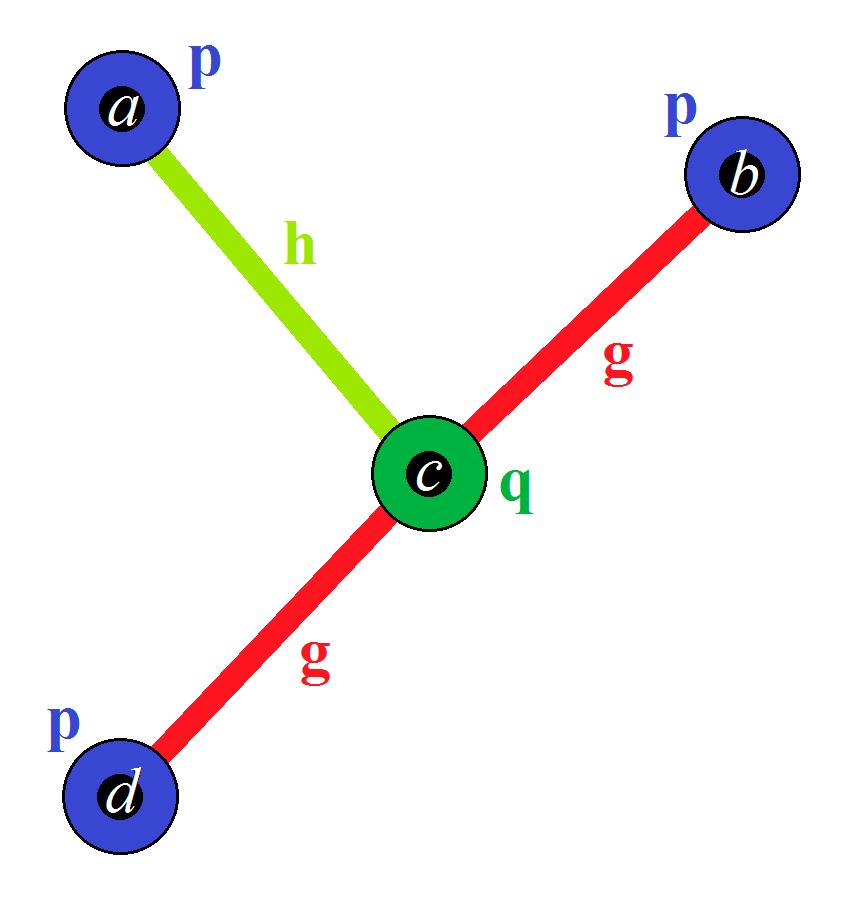
Deﬁnition20. Let V beanon-voidset.Let ξ = V, ρ, ω beanordinaryCNG1’s.Let 𝒻 : V → V bea bijectionsuchthat: (a) ρ(u) = ρ(𝒻(u)) forallu ∈ V (b) ω(u, v) = ω(𝒻(u), 𝒻(v)) forallu, v ∈ V. Then 𝒻 issaidtobeanautomorphismof ξ Remark16. As ξ isordinary, ω(u, v) = ω(v, u) followsforallu, v ∈ V. Remark17. Justbecause ρ(u) = ρ(𝒻(u)) and ω(u, v) = ω(𝒻(u), 𝒻(v)),doesnotmeanthat u = 𝒻(u) or v = 𝒻(v). Remark18. ℐ isthuscalledthetrivialautomorphismof ξ. Example2. Consider ξ1 = V1, ρ1, ω1 asshowninFigure 20: V1 = {a, b, c, d} ρ1(a) = ρ1(b) = ρ1(d) = p, ρ1(c) = q ω1(a, c) = ω1(c, a) = h, ω1(b, c) = ω1(c, b) = ω1(d, c) = ω1(c, d) = g, otherwise, ω1(u, v) = (0,0,0) |{p, q}| = |{g, h}| = 2.

Symmetry 2018, 10, x FOR PEER REVIEW 24 of 28 Remark 17. Just because ( ) = ( ( )) and ( , ) = ( ( ), ( )), does not mean that = ( ) or = ( ). Remark 18. ℐ is thus called the trivial automorphism of Example 2. Consider = 〈 , , 〉 as shown in Figure 20: = { , , , } ( ) = ( ) = ( ) = , ( ) = ( , ) = ( , ) = , ( , ) = ( , ) = ( , ) = ( , ) = , otherwise, ( , ) = (0,0,0) |{ , }| = |{ , }| =2.

Figure 20. as mentioned in Example 2. Let , , : → be three bijections defined as follows: (a) ( ) = , ( ) = , ( ) = , ( ) = (b) ( ) = , ( ) = , ( ) = , ( ) = (c) ( ) = , ( ) = , ( ) = , ( ) =

Figure20. ξ1 asmentionedinExample2. Let 𝒻1, 𝒷1, 𝒽1 : V1 → V1 bethreebijectionsdeﬁnedasfollows: (a) 𝒻1(c) = a, 𝒻1(a) = d, 𝒻1(d) = c, 𝒻1(b) = b (b) 𝒷1(b) = a, 𝒷1(d) = d, 𝒷1(c) = c, 𝒷1(a) = b. (c) 𝒽1(b) = d, 𝒽1(a) = a, 𝒽1(c) = c, 𝒽1(d) = b.

Then: (i) is an isomorphism from to the following ordinary CNG1 (Figure 21).

Then: (i) 𝒻1 isanisomorphismfromV1 tothefollowingordinaryCNG1(Figure 21). whichisnotequalto ξ1 inaccordancewithDeﬁnition 18. 𝒻1 isthereforenotanautomorphismof ξ1 (ii) 𝒷1 isanisomorphismfromV1 tothefollowingordinaryCNG1(Figure 22). whichisalsonotequalto ξ1 inaccordancewithDeﬁnition 18. Likewise 𝒷1 is,therefore,notan automorphismof ξ1 (iii) 𝒽1 isanisomorphismfrom V1 toitselfand,therefore,itisanautomorphismof ξ1.Notethat,evenif 𝒽1(b) = d and 𝒽1(d) = b,as ρ1(b) = ρ1(d) = p and ω1(b, c) = ω1(d, c) = g,so 𝒽1[ξ1] ≡ ξ1 stillholds.

26of32

(b) ( ) = , ( ) = , ( ) = , ( ) = (c) ( ) = , ( ) = , ( ) = , ( ) =

Then:

Symmetry 2018, 10,190

(i) is an isomorphism from to the following ordinary CNG1 (Figure 21).

Symmetry 2018, 10, x FOR PEER REVIEW 25 of 28

which is not equal to in accordance with Definition 18. is therefore not an automorphism of . (ii) is an isomorphism from to the following ordinary CNG1 (Figure 22).

Figure21. Thisisnotanautomorphismof ξ1 asmentionedinExample2.

Figure 21. This is not an automorphism of as mentioned in Example 2.

Figure22. Thisisnotanautomorphismof ξ1 asmentionedinExample2.

Figure 22. This is not an automorphism of as mentioned in Example 2. which is also not equal to in accordance with Definition 18. Likewise is, therefore, not an automorphism of . (iii) is an isomorphism from to itself and, therefore, it is an automorphism of . Note that, even if ( ) = and ( ) = , as ( ) = ( ) = and ( , ) = ( , ) = , so [ ] ≡ still holds.

Deﬁnition21. Let ξ = V, ρ, ω beanordinarysimpleCNG1. ξ issaidtobetotalsymmetricif,for all {u1, v1}, {u2, v2} ⊆ V,with |{u1, v1}| = |{u2, v2}|,thereexistanautomorphismof ξ, 𝒻,suchthat u2 = 𝒻(u1),v2 = 𝒻(v1).

Remark19. Inotherwords, {u1, v1}, {u2, v2} caneitherbetwoedges,ortwoverticesaswhen u1 = v1 and u2 = v2

Definition 21. Let = 〈 , , 〉 be an ordinary simple CNG1. is said to be total symmetric if, for all { , }, { , } ⊆ , with |{ , }| = |{ , }| , there exist an automorphism of , , such that = ( ), = ( )

Example3. Withthisdeﬁnition,thefollowingCNG1(Figure 23)is,thus,totally-symmetric.

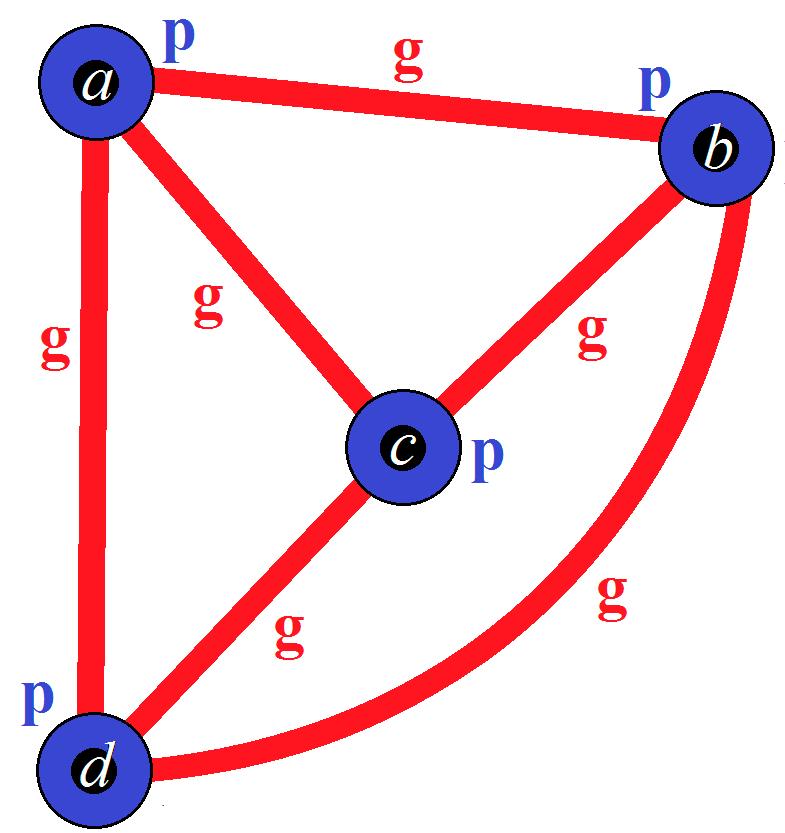
Remark 19. In other words, { , }, { , } can either be two edges, or two vertices as when = and = Example 3. With this definition, the following CNG1 (Figure 23) is, thus, totally-symmetric.

However,unlikesymmetryofclassicalgraphs,theconceptoftotalsymmetrytakesalltheedgesintoaccount, whethervoidornot.Asaresult,thefollowinggraph(Figure 24),thoughlooksfamiliartotheclassicalliterature, isnottotally-symmetric.

27of32

(a) ( ) = , ( ) = , ( ) = , ( )

Symmetry 2018, 10,190 28of32

Remark 19. In other words, { , }, { , } can either be two edges, or two vertices as when = and =

(connected).TogivemorecharacterizationofsymmetryamongordinarysimpleCNG1,wenowproceed withthefollowingdeﬁnitions.

Example 3. With this definition, the following CNG1 (Figure 23) is, thus, totally-symmetric.

Symmetry 2018, 10, x FOR PEER REVIEW 26 of 28

However, unlike symmetry of classical graphs, the concept of total symmetry takes all the edges into account, whether void or not. As a result, the following graph (Figure 24), though looks familiar to the classical literature, is not totally-symmetric.

Figure 23. A totally-symmetric CNG1, as mentioned in Example 3. Figure23. Atotally-symmetricCNG1,asmentionedinExample3.

Figure24.

Figure 24. This graph is not totally-symmetric. Mentioned in Example 3.

Deﬁnition22. Let ξ = V, ρ, ω beanordinarysimpleCNG1. ξ issaidtobestrongedge-wisesymmetric (abbr.SES)if:Forall {u1, v1}, {u2, v2} ⊆ V withboth ω(u1, v1) and ω(u2, v2) non-void,thereexistan automorphism 𝒻 of ξ,suchthatu2 = 𝒻(u1),v2 = 𝒻(v1)

As a result, the concept of total-symmetry in ordinary simple CNG1 proves even more stringent than the concept of symmetry in classical ordinary simple graphs. Additionally, recall that edges and vertices in CNG1 have three membership values instead of only 0 (disconnected, void) and 1 (connected). To give more characterization of symmetry among ordinary simple CNG1, we now proceed with the following definitions.

Remark20. As ξ issimple,itfollowsthat |{u1, v1}| = |{u2, v2}| = 2.

Definition 22. Let = 〈 , , 〉 be an ordinary simple CNG1. is said to be strong edge-wise symmetric (abbr. SES) if: For all { , }, { , } ⊆ with both ( , ) and ( , ) non-void, there exist an automorphism of , such that = ( ), = ( ).

Remark21. AnordinarysimpleCNG1withalledgesbeingvoidisclassiﬁedasstrongedge-wisesymmetric aswell.

Deﬁnition23. Let ξ = V, ρ, ω beanordinarysimpleCNG1. ξ issaidtobestrongpoint-wise(orvertex-wise) symmetric(abbr.SPS)if:Forall u1, u2 ∈ V withboth ρ(u1) and ρ(u2) non-void,thereexistsanautomorphism 𝒻 of ξ,suchthatu2 = 𝒻(u1)

Remark 20. As is simple, it follows that |{ , }| = |{ , }| =2.

Remark 21. An ordinary simple CNG1 with all edges being void is classified as strong edge-wise symmetric as well

Remark22. AnordinarysimpleCNG1withallverticesbeingvoidisclassiﬁedasstrongpoint-wisesymmetric aswell.

Definition 23. Let = 〈 , , 〉 be an ordinary simple CNG1. is said to be strong point-wise(or vertexwise) symmetric (abbr. SPS) if: For all , ∈ with both ( ) and ( ) non-void, there exists an automorphism of , such that = ( )

Remark 22. An ordinary simple CNG1 with all vertices being void is classified as strong point-wise symmetric as well.

Thisgraphisnottotally-symmetric.MentionedinExample3.

Deﬁnition24. Let ξ = V, ρ, ω beanordinarysimpleCNG1. ξ issaidtobestrongsymmetric(abbr.SS)if itisbothstrongedge-wisesymmetricandstrongpoint-wisesymmetric.

Deﬁnition25. Let ξ = V, ρ, ω beanordinarysimpleCNG1. ξ issaidtobeweakedge-wisesymmetric(abbr. wES)if:Forall {u1, v1}, {u2, v2} ⊆ V with ω(u1, v1) = ω(u2, v2) = (0,0,0),thereexistsanautomorphism 𝒻 of ξ,suchthatu2 = 𝒻(u1),v2 = 𝒻(v1).Otherwise, ξ issaidtobeedge-wiseasymmetric(abbr.EA).

Remark23. Again,as ξ issimple,itfollowsthat |{u1, v1}| = |{u2, v2}| = 2.

Symmetry 2018, 10, x FOR PEER REVIEW 27 of 28

Remark24. AnordinarysimpleCNG1withallnon-voidedgeshavingdifferentmembershipvalueisclassiﬁed asweakedge-wisesymmetricaswell.

Definition 26. Let = 〈 , , 〉 be an ordinary simple CNG1. is said to be weak point-wise (or vertexwise) symmetric (abbr. wPS) if: For all , ∈ with ( ) = ( ) ≠ (0,0,0) , there exists an automorphism of , such that = ( ). Otherwise, is said to be point-wise asymmetric (abbr. PA).

Deﬁnition26. Let ξ = V, ρ, ω beanordinarysimpleCNG1. ξ issaidtobeweakpoint-wise(orvertex-wise) symmetric(abbr.wPS)if:Forall u1, u2 ∈ V with ρ(u1) = ρ(u2) = (0,0,0),thereexistsanautomorphism 𝒻 of ξ,suchthatu2 = 𝒻(u1).Otherwise, ξ issaidtobepoint-wiseasymmetric(abbr.PA).

Remark 25. An ordinary simple CNG1 with all non-void vertices having different membership value is classified as weak point-wise symmetric as well.

Remark25. AnordinarysimpleCNG1withallnon-voidverticeshavingdifferentmembershipvalueisclassiﬁed asweakpoint-wisesymmetricaswell.

Definition 27. Let = 〈 , , 〉 be an ordinary simple CNG1. is said to be asymmetric if it is both edgewise asymmetric and point-wise asymmetric

Deﬁnition27. Let ξ = V, ρ, ω beanordinarysimpleCNG1. ξ issaidtobeasymmetricifitisboth edge-wiseasymmetricandpoint-wiseasymmetric.

Based on the definition, we now state such symmetric properties on the smallest non-trivial net CNG1, as mentioned in Theorem 5, as well as the smallest non-trivial net CNG1 with both and being odd numbers, as mentioned in Theorem 7.

Basedonthedeﬁnition,wenowstatesuchsymmetricpropertiesonthesmallestnon-trivialnet CNG1,asmentionedinTheorem5,aswellasthesmallestnon-trivialnetCNG1withboth Mξ and Nξ beingoddnumbers,asmentionedinTheorem7.

Example 4. With regards to the structure of Figure 5, as mentioned in Theorem 5, with ( ) = ( ) = ( ) = ( ) = (1,0,0). Consider the following three automorphisms , , of , : (a) ( ) = , ( ) = , ( ) = , ( ) = , (b) ( ) = , ( ) = , ( ) = , ( ) = , (c) ( ) = , ( ) = , ( ) = , ( ) = , together with ℐ , the trivial automorphism of As a result, , is thus strong point-wise symmetric (SPS) and weak edge-wise symmetric (wES).

Example4. Withregardstothestructureof Figure 5,asmentionedinTheorem5, with ρ(a) = ρ(b) = ρ(c) = ρ(d) = (1,0,0)

Considerthefollowingthreeautomorphisms 𝒻, 𝒷, 𝒽 of ξ4,4:

(a) 𝒻(a) = b, 𝒻(b) = a, 𝒻(c) = d, 𝒻(d) = c, (b) 𝒷(a) = c, 𝒷(b) = d, 𝒷(c) = a, 𝒷(d) = b, (c) 𝒽(a) = d, 𝒽(b) = c, 𝒽(c) = b, 𝒽(d) = a, togetherwith ℐ ,thetrivialautomorphismof ξ. Asaresult, ξ4,4 isthusstrongpoint-wisesymmetric(SPS)andweakedge-wisesymmetric(wES).

Example 5. With regards to the structure of Figure 8, as mentioned in Theorem in Theorem 7, with + + =(0,0,0); | + |, | + | ≤1; and ( ) = ( ) = ( ) = ( ) = ( ) = (1,0,0).

Example5. WithregardstothestructureofFigure 8,asmentionedinTheoreminTheorem7,with p + q + r = (0,0,0); |p + r|, |q + r| ≤ 1; and ρ(a) = ρ(b) = ρ(c) = ρ(d) = ρ(e) = (1,0,0)

In this case, as non-void vertices having different membership values, only one automorphism of , , which is the identity mapping ℐ: → where ℐ( ) = for all ∈ . As ℐ( ) ≠ , , is, thus, point-wise asymmetric (PA). It is, nonetheless, weak edge-wise symmetric (wES).

Inthiscase,asnon-voidverticeshavingdifferentmembershipvalues,onlyoneautomorphismof ξ5,7,which istheidentitymapping ℐ : V → V where ℐ (v) = v forall v ∈ V.As ℐ (a) = b, ξ5,7 is,thus,point-wise asymmetric(PA).Itis,nonetheless,weakedge-wisesymmetric(wES).

We now give an example of CNG1 which is asymmetric (i.e., both edge-wise and point-wise). Example 6. = 〈 , , 〉 has the structure as shown in Figure 25:

WenowgiveanexampleofCNG1whichisasymmetric(i.e.,bothedge-wiseandpoint-wise).

Example6. ξ = V, ρ, ω hasthestructureasshowninFigure 25:

Figure 25. A which is both point-wise asymmetric and edge asymmetric, as mentioned in Example 6. with |{ , , }| =3, |{ , }| =2.

Figure25.A ξ whichisbothpoint-wiseasymmetricandedgeasymmetric,asmentionedinExample6.

Only the trivial automorphism ℐ can be formed. As ℐ( ) ≠ , is point-wise asymmetric. Moreover, as ℐ( ) ≠ , is edge asymmetric. We end this section by giving a conjecture, which shall be dealt with in our future work:

Symmetry 2018, 10,190 29of32

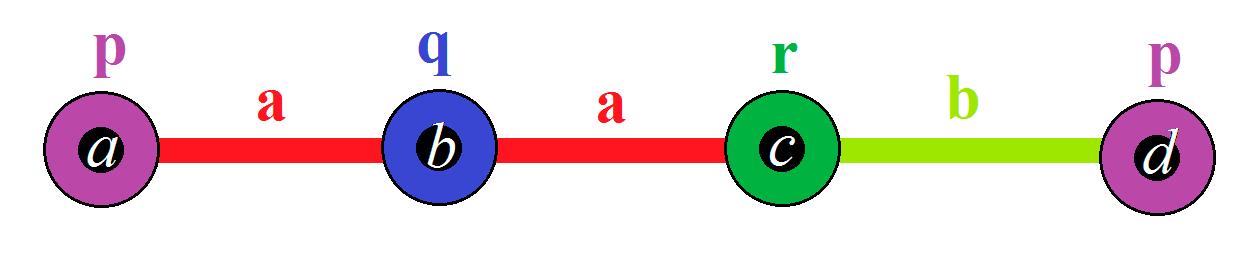
Symmetry 2018, 10,190

with |{p, q, r}| = 3, |{a, b}| = 2. Onlythetrivialautomorphism ℐ canbeformed.As ℐ (a) = d, ξ ispoint-wiseasymmetric.Moreover, as ℐ (a) = b, ξ isedgeasymmetric.

Weendthissectionbygivingaconjecture,whichshallbedealtwithinourfuturework: Conjecture1. Thesmallestnon-trivialnetCNG1 ξ,withboth Mξ and Nξ beingoddnumbers,andisbothSPS andwES,mustbeofthestructureasshowninFigure 26: Symmetry 2018, 10, x FOR PEER REVIEW 28 of 28

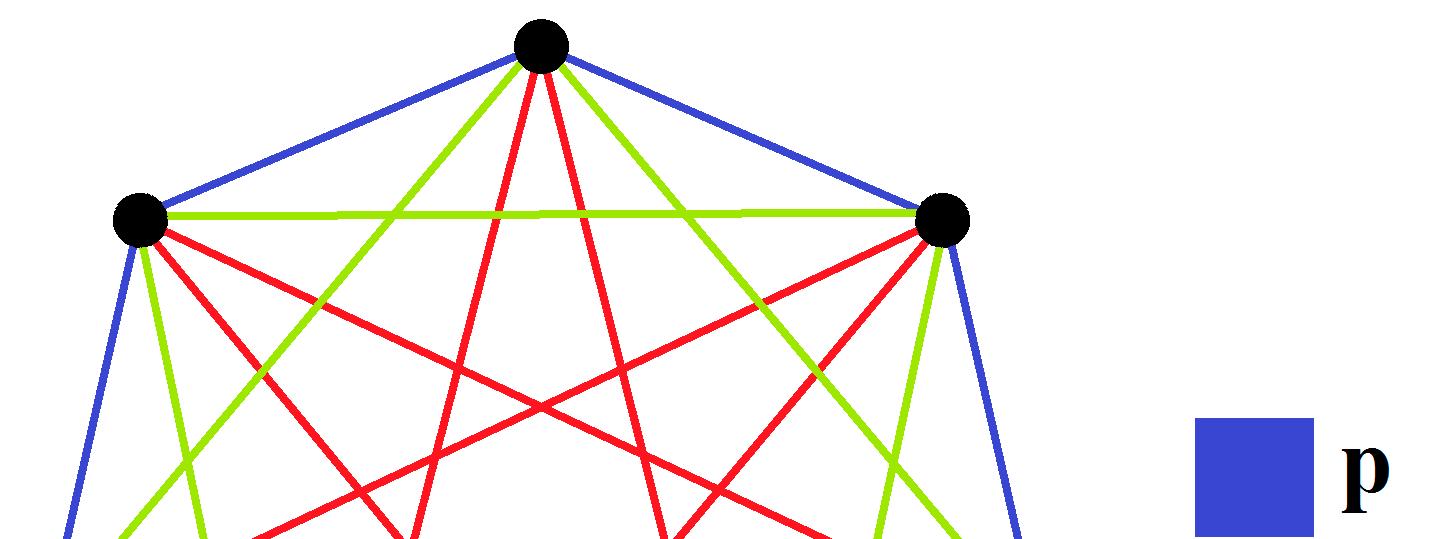
Figure 26. for conjecture 1. + + =(0,0,0).

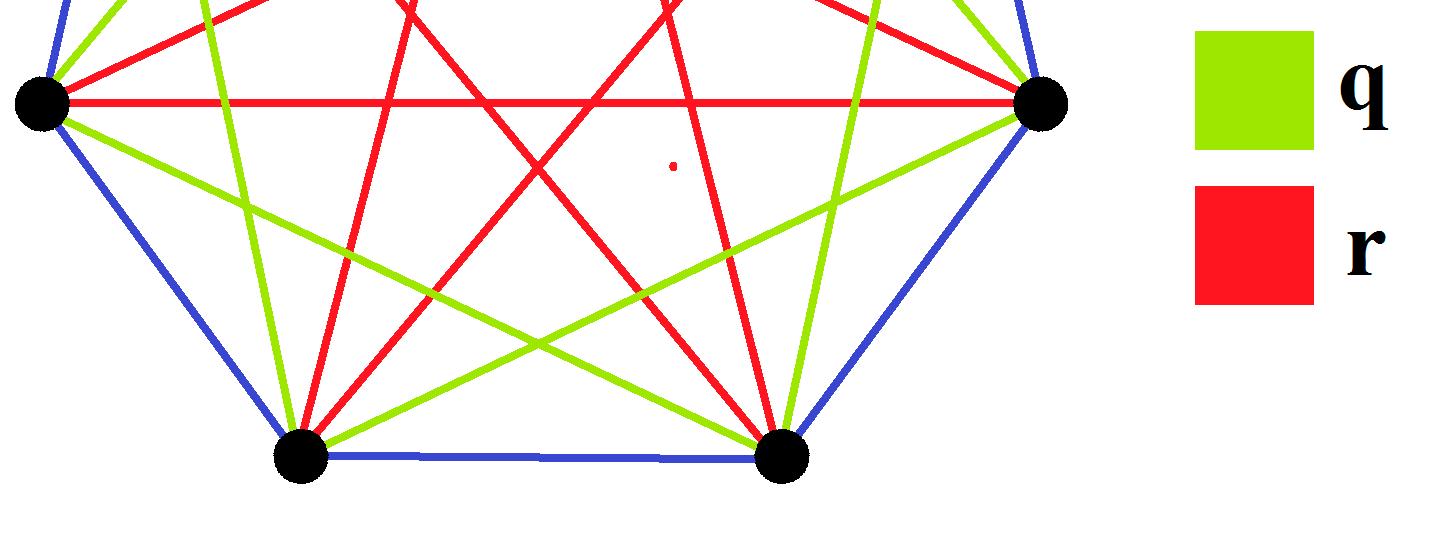
Figure26. ξ forconjecture1. p + q + r = (0,0,0)

8. Conclusions

8.Conclusions

In this article, we presented a new concept of the neutrosophic graph called complex neutrosophic graphs of type 1 (CNG1), and also proceeded to present a matrix representation of it.

Inthisarticle,wepresentedanewconceptoftheneutrosophicgraphcalledcomplexneutrosophic graphsoftype1(CNG1),andalsoproceededtopresentamatrixrepresentationofit.

The strength of CNG1 lies in the presence of both magnitude and direction for the parameters involved, as has been illustrated in Section 3. As the parameters have directions, even when the resultant degree of a vertex is zero, the edges to that vertex need not necessarily be void. Thus the concept of CNG1 may also be used in engineering, such as in metal frameworks, for example in the construction of power lines, so that even when the beams are under tension, the resultant force at a point (possibly being a cornerstone) joining all those beams are zero.

ThestrengthofCNG1liesinthepresenceofbothmagnitudeanddirectionfortheparameters involved,ashasbeenillustratedinSection 3.Astheparametershavedirections,evenwhenthe resultantdegreeofavertexiszero,theedgestothatvertexneednotnecessarilybevoid.Thusthe conceptofCNG1mayalsobeusedinengineering,suchasinmetalframeworks,forexampleinthe constructionofpowerlines,sothatevenwhenthebeamsareundertension,theresultantforceata point(possiblybeingacornerstone)joiningallthosebeamsarezero.

The concept of CNG1 can also be applied to the case of bipolar complex neutrosophic graphs (BCNG1). We have plans to expand on this interesting concept in the near future, and plan to study the concept of completeness, regularity, and CNGs of type 2.

TheconceptofCNG1canalsobeappliedtothecaseofbipolarcomplexneutrosophicgraphs (BCNG1).Wehaveplanstoexpandonthisinterestingconceptinthenearfuture,andplantostudy theconceptofcompleteness,regularity,andCNGsoftype2.

As we can see in Section 6, when the choices of and becomes more restrictive, the smallest non-trivial net CNG1 increases in complexity. This makes us wonder what will be the smallest non-trivial net CNG1 in the case when both and are not divisible by all primes up to 5 (7, 11, etc.), as well as whether their symmetric properties, as outlined in Section 7. However, the proof of such cases will become much more tedious and, therefore, we would have to utilize computer programs, such as MATLAB and SAGE, in order to find those non-trivial net CNG1 Therefore our future research in this area involves plans to deal with those non-trivial net CNG1 We are motivated by the interest to know if there exist some general patterns or general theorems governing such smallest non-trivial net CNG1 as and become more restrictive.

AswecanseeinSection 6,whenthechoicesof Mξ and Nξ becomesmorerestrictive,thesmallest non-trivialnetCNG1 ξ increasesincomplexity.Thismakesuswonderwhatwillbethesmallest non-trivialnetCNG1 ξ inthecasewhenboth Mξ and Nξ arenotdivisiblebyallprimesupto5(7,11, etc.),aswellaswhethertheirsymmetricproperties,asoutlinedinSection 7.However,theproof ofsuchcaseswillbecomemuchmoretediousand,therefore,wewouldhavetoutilizecomputer programs,suchasMATLABandSAGE,inordertoﬁndthosenon-trivialnetCNG1 ξ.Therefore ourfutureresearchinthisareainvolvesplanstodealwiththosenon-trivialnetCNG1 ξ.Weare motivatedbytheinteresttoknowifthereexistsomegeneralpatternsorgeneraltheoremsgoverning suchsmallestnon-trivialnetCNG1as Mξ and Nξ becomemorerestrictive.

We are currently working on developing a more in-depth theoretical framework concerning the symmetric properties of CNG1, and have plans to extend this to other types of fuzzy graphs in the future. We are also motivated by the works presented in [30–32], and look forward to extending our work to other generalizations of neutrosophic sets, such as interval complex neutrosophic sets, and apply the work in medical imaging problems and recommender systems.

Wearecurrentlyworkingondevelopingamorein-depththeoreticalframeworkconcerningthe symmetricpropertiesofCNG1,andhaveplanstoextendthistoothertypesoffuzzygraphsinthe future.Wearealsomotivatedbytheworkspresentedin[30–32],andlookforwardtoextending ourworktoothergeneralizationsofneutrosophicsets,suchasintervalcomplexneutrosophicsets, andapplytheworkinmedicalimagingproblemsandrecommendersystems.

AuthorContributions: Conceptualization,S.G.Q.,S.B.,A.B.,andM.T.;Methodology,S.B.;Software,S.G.Q.; Validation,G.S.,S.B.andS.G.Q.;FormalAnalysis,G.S.andF.S.;Writing-OriginalDraftPreparation,S.B.; Writing-Review&Editing,G.S.andF.S.;Visualization,S.G.Q.;Supervision,G.S.andF.S.

Author Contributions: Conceptualization, S.G.Q., S.B., A.B., and M.T.; Methodology, S.B.; Software, S.G.Q.; Validation, G.S., S.B. and S.G.Q.; Formal Analysis, G.S. and F.S.; Writing-Original Draft Preparation, S.B.; Writing-Review & Editing, G.S. and F.S.; Visualization, S.G.Q.; Supervision, G.S. and F.S.

Funding: This research was funded by the Ministry of Education, Malaysia under grant no. FRGS/1/2017/ STG06/UCSI/03/1 and UCSI University, Malaysia under grant no. Proj-In-FOBIS-014.

Acknowledgments: The authors would like to thank the Editor-in-Chief and the anonymous reviewers for their valuable comments and suggestions.

30of32

Funding: ThisresearchwasfundedbytheMinistryofEducation,Malaysiaundergrantno.FRGS/1/2017/STG06/ UCSI/03/1andUCSIUniversity,Malaysiaundergrantno.Proj-In-FOBIS-014.

Acknowledgments: TheauthorswouldliketothanktheEditor-in-Chiefandtheanonymousreviewersfortheir valuablecommentsandsuggestions.

ConﬂictsofInterest: Theauthorsdeclarenoconﬂictofinterest.

References

1. Smarandache,F. NeutrosophicProbability,Set,andLogic;ProQuestInformation&Learning:AnnArbor,MI, USA,1998;105p.

2. Zadeh,L.A.Fuzzysets. Inform.Control 1965, 8,338–353.[CrossRef]

3. Atanassov,K.T.Intuitionisticfuzzysets. FuzzySetsSyst. 1986, 20,87–96.[CrossRef]

4. Turksen,I.Intervalvaluedfuzzysetsbasedonnormalforms. FuzzySetsSyst. 1986, 20,191–210.[CrossRef]

5. Wang,H.;Smarandache,F.;Zhang,Y.;Sunderraman,R.Singlevaluedneutrosophicsets. Multispace Multistruct. 2010, 4,410–413.

6. NeutrosophicSetTheory.Availableonline: http://fs.gallup.unm.edu/NSS/ (accessedon1December2017).

7. Shannon,A.;Atanassov,K.Aﬁrststeptoatheoryoftheintuitionisticfuzzygraphs.InProceedingsofthe FirstWorkshoponFuzzyBasedExpertSystems,Soﬁa,Bulgaria,28–30September1994;Akov,D.,Ed.;1994; pp.59–61.

8. Smarandache,F. SymbolicNeutrosophicTheory;EuropanovaAsbl:Brussels,Belgium,2015.

9. Smarandache,F.Reﬁnedliteralindeterminacyandthemultiplicationlawofsub-indeterminacies. NeutrosophicSetsSyst. 2015, 9,58–63.

10. Smarandache,F.TypesofNeutrosophicGraphsandneutrosophicAlgebraicStructurestogetherwiththeir ApplicationsinTechnology.InProceedingsoftheSeminarUniversitateaTransilvaniadinBrasov,Facultatea deDesigndeProdussiMediu,Brasov,Romania,6June2015.

11. Smarandache,F.(Ed.)Neutrosophicoverset,neutrosophicunderset,neutrosophicoffset.In Similarly forNeutrosophicOver-/Under-/Off-Logic,Probability,andStatistics;PonsEditions:Brussels,Belgium,2016; pp.158–168.

12. Broumi,S.;Talea,M.;Bakali,A.;Smarandache,F.Singlevaluedneutrosophicgraphs. J.NewTheory 2016, 10, 86–101.

13. Broumi,S.;Talea,M.;Smarandache,F.;Bakali,A.Singlevaluedneutrosophicgraphs:Degree,orderandsize. InProceedingsoftheIEEEInternationalConferenceonFuzzySystems,Vancouver,BC,Canada,24–29July 2016;IEEE:Piscataway,NJ,USA,2016;pp.2444–2451.

14. Broumi,S.;Bakali,A.;Talea,M.;Hassan,A.;Smarandache,F.Isolatedsinglevaluedneutrosophicgraphs. NeutrosophicSetsSyst. 2016, 11,74–78.

15. Smarandache,F.(Ed.)Nidusidearum.In Scilogs,III:VivalaNeutrosophia;Ponsasbl:Brussels,Belgium,2017; ISBN978-1-59973-508-5.

16.

17.

Samanta,S.;Sarkar,B.;Shin,D.;Pal,M.Completenessandregularityofgeneralizedfuzzygraphs. SpringerPlus 2016, 5,1–14.[CrossRef][PubMed]

Broumi,S.;Bakali,A.;Talea,M.;Hassan,A.;Smarandache,F.Generalizedsinglevaluedneutrosophicgraphs ofﬁrsttype.InProceedingsofthe2017IEEEInternationalConferenceonInnovationsinIntelligentSystems andApplications(INISTA),GdyniaMaritimeUniversity,Gdynia,Poland,3–5July2017;pp.413–420.

18. Ramot,D.;Menahem,F.;Gideon,L.;Abraham,K.ComplexFuzzySet. IEEETrans.FuzzySyst. 2002, 10, 171–186.[CrossRef]

19. Selvachandran,G.;Maji,P.K.;Abed,I.E.;Salleh,A.R.Complexvaguesoftsetsanditsdistancemeasures. J.Intell.FuzzySyst. 2016, 31,55–68.[CrossRef]

20.

Selvachandran,G.;Maji,P.K.;Abed,I.E.;Salleh,A.R.Relationsbetweencomplexvaguesoftsets. Appl.SoftComp. 2016, 47,438–448.[CrossRef]

21. Kumar,T.;Bajaj,R.K.Oncomplexintuitionisticfuzzysoftsetswithdistancemeasuresandentropies. J.Math. 2014, 2014,1–12.[CrossRef]

22. Alkouri,A.;Salleh,A.Complexintuitionisticfuzzysets. AIPConf.Proc. 2012, 1482,464–470.

23. Selvachandran,G.;Hafeed,N.A.;Salleh,A.R.Complexfuzzysoftexpertsets. AIPConf.Proc. 2017, 1830,1–8. [CrossRef]

31of32

Symmetry 2018, 10,190

24. Selvachandran,G.;Salleh,A.R.Interval-valuedcomplexfuzzysoftsets. AIPConf.Proc. 2017, 1830,1–8. [CrossRef]

25. Greenﬁeld,S.;Chiclana,F.;Dick,S.Interval-valuedComplexFuzzyLogic.InProceedingsoftheIEEE InternationalConferenceonFuzzySystems,Vancouver,BC,Canada,24–29July2016;IEEE:Piscataway,NJ, USA,2016;pp.1–6.

26. Ali,M.;Smarandache,F.Complexneutrosophicset. NeuralComp.Appl. 2017, 28,1817–1834.[CrossRef]

27. Thirunavukarasu,P.;Suresh,R.;Viswanathan,K.K.Energyofacomplexfuzzygraph. Int.J.Math.Sci. Eng.Appl. 2016, 10,243–248.

28. Smarandache,F.Ageometricinterpretationoftheneutrosophicset—Ageneralizationoftheintuitionistic fuzzyset.InProceedingsoftheIEEEInternationalConferenceonGranularComputing,NationalUniversity ofKaohsiung,Kaohsiung,Taiwan,8–10November2011;Hong,T.P.,Kudo,Y.,Kudo,M.,Lin,T.Y.,Chien,B.C., Wang,S.L.,Inuiguchi,M.,Liu,G.L.,Eds.;IEEEComputerSociety;IEEE:Kaohsiung,Taiwan,2011; pp.602–606.

29. Smarandache,F.Degreeofdependenceandindependenceofthe(sub)componentsoffuzzysetand neutrosophicset. NeutrosophicSetsSyst. 2016, 11,95–97.

30. Ali,M.;Son,L.H.;Khan,M.;Tung,N.T.SegmentationofdentalX-rayimagesinmedicalimagingusing neutrosophicorthogonalmatrices. ExpertSyst.Appl. 2018, 91,434–441.[CrossRef]

31. Ali,M.;Dat,L.Q.;Son,L.H.;Smarandache,F.Intervalcomplexneutrosophicset:Formulationand applicationsindecision-making. Int.J.FuzzySyst. 2018, 20,986–999.[CrossRef]

32. Ali,M.;Son,L.H.;Thanh,N.D.;Minh,N.V.Aneutrosophicrecommendersystemformedicaldiagnosis basedonalgebraicneutrosophicmeasures. Appl.SoftComp. 2017.[CrossRef]

© 2018bytheauthors.LicenseeMDPI,Basel,Switzerland.Thisarticleisanopenaccess articledistributedunderthetermsandconditionsoftheCreativeCommonsAttribution (CCBY)license(http://creativecommons.org/licenses/by/4.0/).

32of32

Symmetry 2018, 10,190