Strong Interval-valued Neutrosophic Intuitionistic Fuzzy Graph

InternationalJournalofPureandAppliedMathematics

Volume120No.52018,1251-1272

ISSN:1314-3395(on-lineversion) url: http://www.acadpubl.eu/hub/ SpecialIssue http://www.acadpubl.eu/hub/

Strong Interval-valued Neutrosophic Intuitionistic Fuzzy Graph

Abstract

2 1

Dr. K. Kalaiarasi

1 and R.Divya

Assistant Professor, PG and research Department of Mathematics, Cauvery College for Women, Trichy-18, Tamil Nadu, India. 2

Assistant Professor, PG and research Department of Mathematics, Cauvery College for Women, Trichy-18, Tamil Nadu, India.

In this paper, the strong interval-valued neutrosophic intuitionistic fuzzy graphs are suggest. Cartesian product, composition and clamp of two strong interval-valued neutrosophic intuitionstic fuzzy graphs defined. Some propositions involving strong interval-valued neutrosophic intuitionistic fuzzy graphs are stated and proved. We introduce the opinion of product of two interval-valued intuitionistic fuzzy graphs and investigate some of their properties. We discuss some propositions on Cartesian product and define some properties on it. Strong interval-valued neutrosophic intuitionistic fuzzy graphs allows attaching the truthmembership(t), indeterminacy-membership(i) and falsity –membership degrees (f) both to vertices and edges. Combining the strong interval valued neutrosophic set with graph theory, a new graph model emerges, called strong interval neutrosophic intuitionistic fuzzy graph.

Keywords: Intuitionstic fuzzy graph, Interval valued intuitionstic fuzzy graph.

1. Introduction

In 1965, Zadeh [21] inaugurated the conception of fuzzy set as a method of finding uncertainty. In 1986, Atanassov proposed Intuitionistic Fuzzy set (IFS) [3] which looks more accurately to uncertainty quantification and provides the opportunity to precisely model the problem based on the existing knowledge and observations. After three years Atanassov and Gargov [4] introduced Interval-Valued Intuitionistic Fuzzy Set (IVIFS) which is helpful to model the problem precisely.

In 1975, Rosenfeld [14] introduced the concept of fuzzy graphs. Yeh and Bang [8] also introduced fuzzy graphs independently. Fuzzy graphs are useful to represent relationships which deal with uncertainty and it differs greatly from classical graphs. It has numerous applications to problems in computer science, electrical engineering, system analysis, operations research, economics, networking routing, transportation, ect. Interval-Valued Fuzzy Graphs (IVFG) are defined by Akram and Dudec [1] in 2011. Atanassov [4] introduced the concept of intuitionistic fuzzy relations and Intutionistic Fuzzy Graph (IFG).In fact, interval-valued fuzzy graphs and

interval valued intuitionistic fuzzy graphs are two different models that extend theory of fuzzy graph. S.N.Mishra and A.Pal [9] introduced the product of interval valued intuitionistic fuzzy graph. Akram and Bijan Davvaz [1] introduced Strong Intuitionistic Fuzzy Graphs(SIFG). In this paper, The opinion of Strong Interval-Valued Intuitionistic Fuzzy Graphs (SIVIFG) are introduced.

Many works on fuzzy graphs, intuitionistic fuzzy graphs and interval valued intuitionistic fuzzy graphs (Antonios K et al. 2014; Bhattacharya 1987; Mishra and pal 2013; Nagoor Gani and shajitha Begum 2010; Nagoor Gani and Latha 2012; Shannon and atanassov 1994) have been carried out and all of them have considered the vertex sets and edge sets as fuzzy and/or intuitionistic fuzzy sets.Further on, Broumi et al. (2016b) introduced a new neutrosophic graph model, This model allows attaching the membership (t), indeterminacy(i) and non-membership degrees (f) both to vertices and edges.

2. Preliminaries

In this section, the authors mainly recall some notions related to neutrosophic graphs, strong interval valued neutrosophic sets, intuitionistic fuzzy graphs, Strong interval valued neutrosophic intuitionistic fuzzy graphs, proper to the present work. The readers are consulted for further details to (Broumi et al.2016b; Mishra and Pal 2013; Nagoor Gani and Basheer Ahamed 2003;Parvathi and Karunambigai 2006;Smarandache 2006;wang et al.2010; Wang et al. 2005a).

3.Interval-Valued Intuitionistic Fuzzy Graph

In this section, we introduce the Interval valued intuitionstic fuzzy graph and the conception of Strong interval valued intuitionstic fuzzy graph.

Definition 3.1



V

v u 





and UM

are the lower and upper limits of M.



, ( *

Definition 3.2

An intuitionistic fuzzy graph with underlying set V is defined to be a pair G =

) , ( B A where (i) the functions [0,1] :  V A and [0,1] :  V A denote the degree of membership and non membership of the element V x  respectively, such that 0 1 ) ( ) (    x x A A   for all V x  (ii) the function [0,1] :    V V E B and [0,1] :    V V E B are defined by )) ( ), ( min( )) , (( y x y x A A B     and )) ( ), ( max( )) , (( y x y x A A B     such that 0 1 )) , (( )) , ((    y x y x B B   , ) , ( E y x  

Definition 3.3

An intuitionistic fuzzy graph ) , ( B A G  is called strong intuitionistic fuzzy graph if )) ( ), ( min( ) ( y x xy A A B     and )) ( ), ( max( ) ( y x xy A A B     , for all E xy

Definition 3.4

An interval valued intuitionistic fuzzy graph with underlying set V is defined to be pair G = ) , ( B A where 1) The functions [0,1] : D V M A  and [0,1] : D V N A  denote the degree of membership and non membership of the element V x  , respectively such that 1 ) ( ) ( 0    x N x M A A

for all V x  2) The functions [0,1] : D V V E MB    and [0,1] : D V V E NB    are defined by )) ( ), ( min( )) , (( y M x M y x M AL AL BL 

such that 1 )) , (( )) , (( 0    y x N y x M BU BU . ) , ( E y x   Strong Interval-Valued Intuitionistic Fuzzy Graph

and )) ( ), ( max( )) , (( y N x N y x N AL AL BL  , and )) ( ), ( min( )) , (( y M x M y x M AU AU BU 

and )) ( ), ( max( )) , (( y N x N y x N AU AU BU 

and )) ( ), ( max( ) ( y N x N xy N AL AL BL 

, if )) ( ), ( min( ) ( y M x M xy M AU AU BU 

, E xy  

and )) ( ), ( max( ) ( y N x N xy N AU AU BU  InternationalJournalofPureandAppliedMathematicsSpecialIssue 1253

Example 3.1

Figure 1 is an SIVIFG G=(A,B) where A=        ,[07,05],[03,01] , ,[05,06],[01,03] , ,[04,06],[02,03] z y x B=        ,[0.4,0.6],[0.3,0.1] , ,[0.5,0.6] , ,[0.4,0.6],[0.2,0.3] xz yz xy

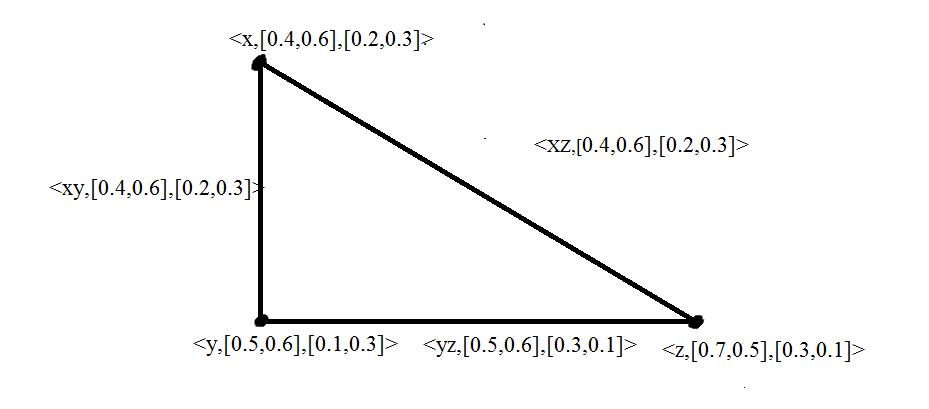
Figure-1 Strong Interval Valued Intuitionistic Fuzzy Graph

Definition 3.6

Let 1A

and 2B

and 2A

be interval-valued intuitionistic fuzzy subsets of 1V

and 2V respectively. Let 1B

interval-valued intuitionistic fuzzy subsets of 1E

respectively. The Cartesian product of two SIVIF SG 1G

and 2G

and 2E

and is defined as follows: 1) )) ( ), ( min( ) , )( ( 2 1 2 1 2 1 2 1 x M x M x x M M L A L A L A L A   )) ( ), ( min( ) , )( ( 2 1 2 1 2 1 2 1 x M x M x x M M U A AU U A AU   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x N x N x x N N L A L A L A L A   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x N x N x x N N U A AU U A AU  

is denoted by ) , ( 2 1 2 1 2 1 B B A A G G    

, 2 2 1 1 , V x V x   

2) )) ( ), ( min( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x M x M y x x x M M L B L A L B L B   )) ( ), ( min( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x M x M y x x x M M U B AU U B U B   )) ( ), ( max( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x N x N y x x x N N L B L A L B L B   )) ( ), ( max( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x N x N y x x x N N U B AU U B U B   2 2 2 1 1 , E y x V x   

3)

)) ( ), ( min( )) , )( , )(( ( 2 1 2 1 1 1 1 1 z M y x M z y z x M M L A L B L B L B   )) ( ), ( min( )) , )( , )(( ( 2 1 2 1 1 1 1 1 z M y x M z y z x M M U A U B U B U B   )) ( ), ( max( )) , )( , )(( ( 2 1 2 1 1 1 1 1 z N y x N z y z x N N L A L B L B L B   )) ( ), ( max( )) , )( , )(( ( 2 1 2 1 1 1 1 1 z N y x N z y z x N N U A U B U B U B   1 1 1 2, E y x V z   

Theorem 3.1

= )), ( ), ( min(min( 2 2 1 x M x M U A AU ))) ( ), ( min( 2 2 1 y M x M U A AU

= )) ( ), ( ), ( min( 2 2 2 2 1 y M x M x M U A U A AU

Hence, ( ) 2 1 L B L B M M  )) , )( , (( 2 2 y x x x

= )) , )( ),( , )( min(( 2 2 2 1 2 1 y x M M x x M M L A L A L A L A  

= )) , )( ),( , )( min(( 2 2 2 1 2 1 y x M M x x M M U A AU U A AU  

( ) 2 1 U B U B M M  )) , )( , (( 2 2 y x x x InternationalJournalofPureandAppliedMathematicsSpecialIssue 1255

Similarly, we can show that (

) 2 1 L B L B N N  )) , )( , (( 2 2 y x x x =

)) , )( ),( , )( max(( 2 2 2 1 2 1 y x N N x x N N L A L A L A L A  

Example:3.2 Consider the fuzzy graph with five vertices given in figure Figure-2 Strong Interval Valued Intuitionistic Fuzzy Graph

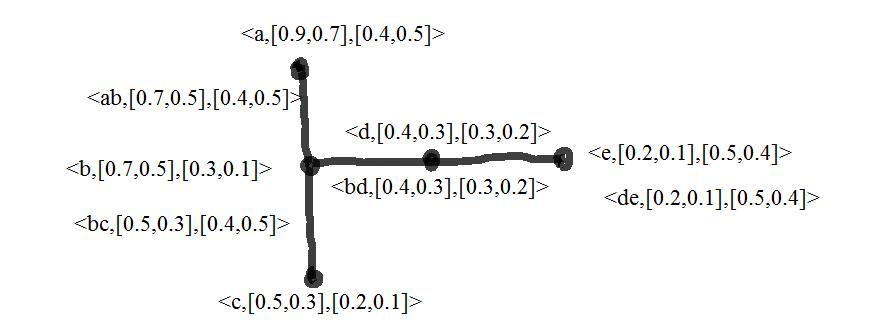
A={   5] 4,0 7],[0 9,0 ,[0a ,   1] 3,0 5],[0 7,0 ,[0b ,   1] 2,0 3],[0 5,0 ,[0c , , 2] 3,0 3],[0 4,0 ,[0  d   ,[0.2,0.1],[0.5,0.4]e

} B={   ,[0.7,0.5],[0.4,0.5]ab

}.

,   ,[0.5,0.3],[0.3,0.1]bc

,   4] 5,0 1],[0 2,0 ,[0de

,   ,[0.4,0.3],[0.3,0.2]bd

4. Operation on Strong Interval-Valued Neutrosophic Intuitionistic Fuzzy Graph

Definition 4.1 By an Strong Interval-Valued Neutrosophic Intuitionistic Fuzzy Graph G* =(V,E) one means a pair G=(A,B), Where A=< [TAL,TAL], [TAU,TAU], [IAL,IAL], [IAU,IAU],[FAL,FAL], [FAU,FAU] > is an Strong Interval-Valued Neutrosophic Intuitionistic set on V and B=< [TBL,TBL], [TBU,TBU], [IBL,IBL], [IBU,IBU],[FBL,FBL],[FBU,FBU] > is an Strong Interval-Valued Neutrosophic Intuitionistic relation on E satisfying the following condition:

1. V={v1,v2,…..vn} such that TAL:V

[0,1]  , TAU:V

[0,1]  , IAL:V

[0,1]  , and FAL:V

[0,1]  , FAU :V

[0,1]  , IAU:V

[0,1]  denote the degree of truth-membership, the degree of inderminancy membership and falsity-membership of the element y V , respectively, and 1, ) ( ) ( ) ( 0     i A i A i A v F v I v T for every vi

V

2.The functions TBL:V V [0,1]  , TBU:V V [0,1]  , IBL:V V [0,1]  , IBU:V V [0,1]  and FBL:V V [0,1]  , FBU:V V [0,1]  , such that )] ( ), ( min[ ) , ( j AL i AL j i BL v T v T v v T  )] ( ), ( min[ ) , ( j AU i AU j i BU v T v T v v T  )] ( ), ( max[ ) , ( j BL i BL j i BL v I v I v v I  )] ( ), ( max[ ) , ( j BU i BU j i BU v I v I v v I  And )] ( ), ( max[ ) , ( j BL i BL j i BL v F v F v v F  )] ( ), ( max[ ) , ( j BU i BU j i BU v F v F v v F 

Denote the degree of truth-membership, the degree of inderminancy membership and falsity-membership of the degree ( E v v j i  ) , respectively, where 1 ) , ( ) , ( ) , ( 0     j i B j i B j i B v v F v v I v v T for all ( E v v j i  ) ,

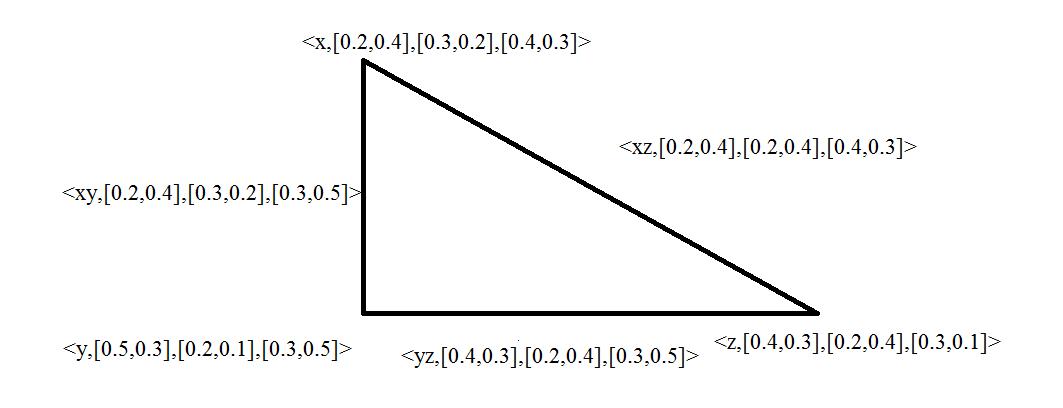
y,[0.5,0.3],[0.2,0.1],[0.3,0.5] ,   1] 3,0 4],[0 2,0 3],[0 4,0 ,[0z

} and B an Strong Interval Valued Neutrosophic Intuitionistic Fuzzyset of V V E   B=    , 3] 4,0 2],[0 3,0 4],[0 2,0 ,[0 { xy

yz,[0.4,0.3],[0.2,0.4],[0.3,0.5] ,   3] 4,0 2],[0 3,0 4],[0 2,0 ,[0zx InternationalJournalofPureandAppliedMathematicsSpecialIssue 1257

}.

Figure-3

Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graph

By routine computations, it is easy to see that G=(A,B) is an Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graph of G*

Definition 4.2 Let ) , ( * 2 * 1 * E V G G G    be the Cartesian product of two graphs where 2 1 V V V   and     } , )/ , )( , {( 2 2 2 1 1 2 2 E y x v x y x x x E } , )/ , )( , {( 1 1 1 2 1 1 E y x v z z y z x   ; then, the Cartesian product ) , ( 2 1 2 1 2 1 B B A A G G G      is an Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graph defined by 1) )) ( ), ( min( ) , )( ( 2 1 2 1 2 1 2 1 x T x T x x T T L A L A L A L A   )) ( ), ( min( ) , )( ( 2 1 2 1 2 1 2 1 x T x T x x T T U A AU U A AU   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x I x I x x I I L A L A L A L A   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x I x I x x I I U A AU U A AU   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x F x F x x F F L A L A L A L A   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x F x F x x F F U A AU U A AU  

2)

.

for all V x x  ) , ( 2 1

)) ( ), ( min( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x T x T y x x x T T L B L A L B L B  

)) ( ), ( min( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x T x T y x x x T T U B AU U B U B  

)) ( ), ( max( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x I x I y x x x I I L B L A L B L B  

)) ( ), ( max( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x I x I y x x x I I U B AU U B U B  

3)

)) ( ), ( max( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x F x F y x x x F F L B L A L B L B   )) ( ), ( max( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x F x F y x x x F F U B AU U B U B   ,

2 2 2 1, E y x V x    

)) ( ), ( min( ) , )( , )( ( 2 1 2 1 1 1 1 1 z T y x T z y z x T T L A L B L B L B   )) ( ), ( min( ) , )( , )( ( 2 1 2 1 1 1 1 1 z T y x T z y z x T T U A U B U B U B   )) ( ), ( max( ) , )( , )( ( 2 1 2 1 1 1 1 1 z I y x I z y z x I I L A L B L B L B   )) ( ), ( max( ) , )( , )( ( 2 1 2 1 1 1 1 1 z I y x I z y z x I I U A U B U B U B   )) ( ), ( max( ) , )( , )( ( 2 1 2 1 1 1 1 1 z F y x F z y z x F F L A L B L B L B   )) ( ), ( max( ) , )( , )( ( 2 1 2 1 1 1 1 1 z F y x F z y z x F F U A U B U B U B   , 1 1 1 2, E y x V z    

Example 4.2 Let ) , ( 1 1 * 1 B A G  and ) , ( 2 2 * 2 B A G  be two graphs where V1={a,b}, V2={c,d}, E1={a,b} and E2={c,d}. Consider two Strong Interval Valued Neutrosophic Intuitionistic Graphs:    ,[03,04],[05,01],[02,04] { 1 a A ,   3] 1,0 4],[0 2,0 1],[0 5,0 ,[0b }, B1={<ab,[0.3,0.4],[0.5,0.1],[0.2,0.4]>};    ,[02,05],[03,02],[05,02] { 2 c A ,   ,[0.3,0.2],[0.4,0.1],[0.2,0.4]d }, B2={<cd,[0.2,0.5],[0.4,0.1],[0.5,0.2]>};

Figure-4 Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graph G1

Figure-5 Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graph G2

Figure-6 Cartesian product of Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graph

E we have )) ( ), ( min( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x T x T y x x x T T L B L A L B L B   

min ))) ( ), ( ),min( ( ( 2 2 2 2 1 y T x T x T L A L A L A = min(min( ))) ( ), ( 2 2 1 x T x T L A L A

,min(min( ))) ( ), ( 2 2 1 y T x T L A L A = min ) , )( ),( , )( (( 2 2 2 1 2 1 y x T T x x T T L A L A L A L A  

), )) ( ), ( min( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x T x T y x x x T T U B AU U B BU   

= min(min( ))) ( ), ( 2 2 1 x T x T U A AU

min ))) ( ), ( ),min( ( ( 2 2 2 2 1 y T x T x T U A U A AU

,min(min( ))) ( ), ( 2 2 1 y T x T U A AU

), )) ( ), ( max( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x I x I y x x x I I L B L A L B L B   

= min ) , )( ),( , )( (( 2 2 2 1 2 1 y x T T x x T T U A AU U A AU  

max ))) ( ), ( ),max( ( ( 2 2 2 2 1 y I x I x I L A L A L A

,max(max( ))) ( ), ( 2 2 1 y I x I L A L A

= max(max( ))) ( ), ( 2 2 1 x I x I L A L A InternationalJournalofPureandAppliedMathematicsSpecialIssue 1260

= max

) , )( ),( , )( (( 2 2 2 1 2 1 y x I I x x I I L A L A L A L A   ), )) ( ), ( max( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x I x I y x x x I I U B AU U B BU    max

))) ( ), ( ),max( ( ( 2 2 2 2 1 y I x I x I U A U A AU = max(max( ))) ( ), ( 2 2 1 x I x I U A AU ,max(max( ))) ( ), ( 2 2 1 y I x I U A AU = max ) , )( ),( , )( (( 2 2 2 1 2 1 y x I I x x I I U A AU U A AU   ),)) ( ), ( max( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x F x F y x x x F F L B L A L B L B    max ))) ( ), ( ),max( ( ( 2 2 2 2 1 y F x F x F L A L A L A = max(max( ))) ( ), ( 2 2 1 x F x F L A L A ,max(max( ))) ( ), ( 2 2 1 y F x F L A L A = max ) , )( ),( , )( (( 2 2 2 1 2 1 y x F F x x F F L A L A L A L A   ), )) ( ), ( max( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x F x F y x x x F F U B AU U B U B   max ))) ( ), ( ),max( ( ( 2 2 2 2 1 y F x F x F U A U A AU = max(max( ))) ( ), ( 2 2 1 x F x F U A AU ,max(max( ))) ( ), ( 2 2 1 y F x F U A AU = max ) , )( ),( , )( (( 2 2 2 1 2 1 y x F F x x F F U A AU U A AU   )

Similarly, we prove ((x1,z)(y1,z))  E Hence )) , )( , )(( ( 1 1 2 1 z y z x T T L B L B  = min )), , )( ),( , )( (( 1 1 2 1 2 1 z y T T z x T T L A L A L A L A   )) , )( , )(( ( 1 1 2 1 z y z x T T U B BU  = min ) , )( ),( , )( (( 1 1 2 1 2 1 z y T T z x T T U A AU U A AU   ), )) , )( , )(( ( 1 1 2 1 z y z x I I L B L B  = max ) , )( ),( , )( (( 1 1 2 1 2 1 z y I I z x I I L A L A L A L A   ), )) , )( , )(( ( 1 1 2 1 z y z x I I U B BU  = max ) , )( ),( , )( (( 1 1 2 1 2 1 z y I I z x I I U A AU U A AU   ), )) , )( , )(( ( 1 1 2 1 z y z x F F L B L B 

), )) , )( , )(( ( 1 1 2 1 z y z x F F U B BU 

) Hence proved

= max ) , )( ),( , )( (( 1 1 2 1 2 1 z y F F z x F F L A L A L A L A  

= max ) , )( ),( , )( (( 1 1 2 1 2 1 z y F F z x F F U A AU U A AU  

be the composition of two graphs where

1)

)) ( ), ( min( ) , )( ( 2 1 2 1 2 1 2 1 x T x T x x T T L A L A L A L A   )) ( ), ( min( ) , )( ( 2 1 2 1 2 1 2 1 x T x T x x T T U A AU U A AU   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x I x I x x I I L A L A L A L A   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x I x I x x I I U A AU U A AU   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x F x F x x F F L A L A L A L A   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x F x F x x F F U A AU U A AU   2 2 1 1 , V x V x    ; 2)

)) ( ), ( min( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x T x T y x x x T T L B L A L B L B   )) ( ), ( min( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x T x T y x x x T T U B AU U B U B   )) ( ), ( max( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x I x I y x x x I I L B L A L B L B   )) ( ), ( max( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x I x I y x x x I I U B AU U B U B   )) ( ), ( max( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x F x F y x x x F F L B L A L B L B   )) ( ), ( max( ) , )( , )( ( 2 2 1 2 2 2 1 2 1 y x F x F y x x x F F U B AU U B U B   , 2 2 2 1, E y x V x     ;

3)

)) ( ), ( min( ) , )( , )( ( 2 1 2 1 1 1 1 1 z T y x T z y z x T T L A L B L B L B   )) ( ), ( min( ) , )( , )( ( 2 1 2 1 1 1 1 1 z T y x T z y z x T T U A U B U B U B   )) ( ), ( max( ) , )( , )( ( 2 1 2 1 1 1 1 1 z I y x I z y z x I I L A L B L B L B   )) ( ), ( max( ) , )( , )( ( 2 1 2 1 1 1 1 1 z I y x I z y z x I I U A U B U B U B   )) ( ), ( max( ) , )( , )( ( 2 1 2 1 1 1 1 1 z F y x F z y z x F F L A L B L B L B   )) ( ), ( max( ) , )( , )( ( 2 1 2 1 1 1 1 1 z F y x F z y z x F F U A U B U B U B  

, 1 1 1 2, E y x V z    

where }. , )/ , )( , {( 2 2 1 1 1 2 1 2 1 0 y x E y x y y x x E E    

Example 4.3 Let

) , ( 1 1 * 1 E V G  and

) , ( 2 2 * 2 E V G 

be two graphs where V1={a,b}, V2={c,d}, E1={a,b} and E2={c,d}. Consider two Strong Interval Valued Neutrosophic Intuitionistic Graphs:    ,[05,03],[03,02],[01,03] { 1 a A ,

  ,[0.3,0.4],[0.5,0.2],[0.1,0.2]b }, B1={<ab,[0.3,0.4],[0.5,0.2],[0.1,0.3]>};    ,[03,02],[05,02],[01,04] { 2 c A ,   ,[0.1,0.3],[0.3,0.2],[0.4,0.3]d }, B1={<cd,[0.1,0.3],[0.5,0.2],[0.4,0.3]>};

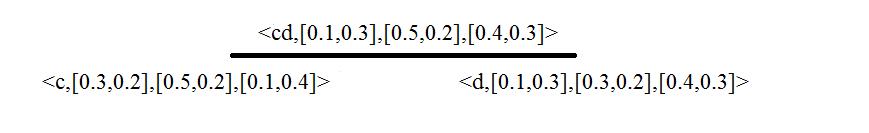
Figure-7 Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graph G1

Figure-8 Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graph G2

Figure-9 Composition of Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graph

Proposition 4.2 If G1 and G2 are the Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graphs then the Composition 2 1 G G  is a Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graphs. Proof: Let ) , ( 2 1 2 1 2 1 B B A A G G    

max ))) ( ), ( ),max( ( ( 2 2 2 2 1 y I x I x I L A L A L A = max(max( ))) ( ), ( 2 2 1 x I x I L A L A

,max(max( ))) ( ), ( 2 2 1 y I x I L A L A = max ) , )( ),( , )( (( 2 2 2 1 2 1 y x I I x x I I L A L A L A L A  

), )) ( ), ( max( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x I x I y x x x I I U B AU U B U B   

max ))) ( ), ( ),max( ( ( 2 2 2 2 1 y I x I x I U A U A AU = max(max( ))) ( ), ( 2 2 1 x I x I U A AU

,max(max( ))) ( ), ( 2 2 1 y I x I U A AU

), )) ( ), ( max( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x F x F y x x x F F L B L A L B L B   

= max ) , )( ),( , )( (( 2 2 2 1 2 1 y x I I x x I I U A AU U A AU  

max ))) ( ), ( ),max( ( ( 2 2 2 2 1 y F x F x F L A L A L A

= max(max( ))) ( ), ( 2 2 1 x F x F L A L A

,max(max( ))) ( ), ( 2 2 1 y F x F L A L A

= max ) , )( ),( , )( (( 2 2 2 1 2 1 y x F F x x F F L A L A L A L A   InternationalJournalofPureandAppliedMathematicsSpecialIssue 1264

),

))) ( ), ( ),max( ( ( 2 2 2 2 1 y F x F x F U A U A AU = max(max(

))) ( ), ( 2 2 1 x F x F U A AU ,max(max(

) , )( ),( , )( (( 2 2 2 1 2 1 y x F F x x F F U A AU U A AU   ). Consider E z y z x  ) , )( , ( 1 1 )) ( ), ( min( )) , )( , )(( ( 2 1 2 1 1 1 1 1 z T y x T z y z x T T L A L B L B L B    min ))) ( ),min( ( ),( ( ( 2 1 1 1 1 z T y T x T L A L B L B = min(min( ))) ( ), ( 2 1 1 z T x T L A L B ,min(min( ))) ( ), ( 2 1 1 z T y T L A L B = min ) , )( ),( , )( (( 1 1 2 1 2 1 z y T T z x T T L A L B L A L B   ), )) ( ), ( min( )) , )( , )(( ( 2 1 2 1 1 1 1 1 z T y x T z y z x T T U A U B U B U B    min ))) ( ),min( ( ),( ( ( 2 1 1 1 1 z T y T x T U A BU BU = min(min( ))) ( ), ( 2 1 1 z T x T U A U B ,min(min( ))) ( ), ( 2 1 1 z T y T U A U B = min ) , )( ),( , )( (( 1 1 2 1 2 1 z y T T z x T T U A U B U A U B   ), )) ( ), ( max( )) , )( , )(( ( 2 1 2 1 1 1 1 1 z I y x I z y z x I I L A L B L B L B    max ))) ( ),max( ( ),( ( ( 2 1 1 1 1 z I y I x I L A L B L B = max(max( ))) ( ), ( 2 1 1 z I x I L A L B

))) ( ), ( 2 2 1 y F x F U A AU = max

,max(max( ))) ( ), ( 2 1 1 z I y I L A L B = max ) , )( ),( , )( (( 1 1 2 1 2 1 z y I I z x I I L A L B L A L B   ), )) ( ), ( max( )) , )( , )(( ( 2 1 2 1 1 1 1 1 z I y x I z y z x I I U A U B U B BU   

max ))) ( ),max( ( ),( ( ( 2 1 1 1 1 z I y I x I U A U B BU = max(max( ))) ( ), ( 2 1 1 z I x I U A U B

,max(max( ))) ( ), ( 2 1 1 z I y I U A BU = max ) , )( ),( , )( (( 1 1 2 1 2 1 z y I I z x I I U A U B U A U B  

), )) ( ), ( max( )) , )( , )(( ( 2 1 2 1 1 1 1 1 z F y x F z y z x F F L A L B L B L B   

= max(max( ))) ( ), ( 2 1 1 z F x F L A L B

max ))) ( ),max( ( ),( ( ( 2 1 1 1 1 z F y F x F L A L B L B

,max(max( ))) ( ), ( 2 1 1 z F y F L A L B

), )) ( ), ( max( )) , )( , )(( ( 2 1 2 1 1 1 1 1 z F y x F z y z x F F U A BU U B BU   

= max ) , )( ),( , )( (( 1 1 2 1 2 1 z y F F z x F F L A L B L A L B  

max ))) ( ),max( ( ),( ( ( 2 1 1 1 1 z F y F x F U A U B U B

,max(max( ))) ( ), ( 2 1 1 z F y F U A U B

= max(max( ))) ( ), ( 2 1 1 z F x F U A U B InternationalJournalofPureandAppliedMathematicsSpecialIssue 1265

) , )( ),( , )( (( 1 1 2 1 2 1 z y F F z x F F U A U B U A U B   ), Consider

E E y y x x  0 2 1 2 1 ) , )( , ( )) ( ), ( ), ( min( )) , )( , )(( ( 1 1 2 2 2 1 2 1 1 2 2 2 1 y x T y T x T y y x x T T L B L A L A L B L B    min ))) ( ), ( ),min( ( ), ( ( 1 1 2 2 2 1 2 2 y T x T y T x T L A L A L A L A = min(min( )) ( ), ( 2 1 2 1 x T x T L A L A ),min(min( ))) ( ), ( 2 1 2 1 y T y T L A L A = min ) , )( ),( , )( (( 2 1 2 1 2 1 2 1 y y T T x x T T L A L A L A L A   ), )) ( ), ( ), ( min( )) , )( , )(( ( 1 1 2 2 2 1 2 1 1 2 2 2 1 y x T y T x T y y x x T T U B U A U A U B U B   min ))) ( ), ( ),min( ( ), ( ( 1 1 2 2 2 1 2 2 y T x T y T x T U A AU U A U A = min(min( )) ( ), ( 2 1 2 1 x T x T U A AU ),min(min( ))) ( ), ( 2 1 2 1 y T y T U A AU = min ) , )( ),( , )( (( 2 1 2 1 2 1 2 1 y y T T x x T T U A AU U A AU   ), )) ( ), ( ), ( max( )) , )( , )(( ( 1 1 2 2 2 1 2 1 1 2 2 2 1 y x I y I x I y y x x I I L B L A L A L B L B    max ))) ( ), ( ),max( ( ), ( ( 1 1 2 2 2 1 2 2 y I x I y I x I L A L A L A L A = max(max( )) ( ), ( 2 1 2 1 x I x I L A L A ),max(max( ))) ( ), ( 2 1 2 1 y I y I L A L A = max ) , )( ),( , )( (( 2 1 2 1 2 1 2 1 y y I I x x I I L A L A L A L A   ), )) ( ), ( ), ( max( )) , )( , )(( ( 1 1 2 2 2 1 2 1 1 2 2 2 1 y x I y I x I y y x x I I U B U A U A U B U B    max ))) ( ), ( ),max( ( ), ( ( 1 1 2 2 2 1 2 2 y I x I y I x I U A AU U A U A = max(max( )) ( ), ( 2 1 2 1 x I x I U A AU

This completes the proof.

= max

),max(max( ))) ( ), ( 2 1 2 1 y I y I U A AU = max ) , )( ),( , )( (( 2 1 2 1 2 1 2 1 y y I I x x I I U A AU U A AU   ), )) ( ), ( ), ( max( )) , )( , )(( ( 1 1 2 2 2 1 2 1 1 2 2 2 1 y x F y F x F y y x x F F L B L A L A L B L B   

max ))) ( ), ( ),max( ( ), ( ( 1 1 2 2 2 1 2 2 y F x F y F x F L A L A L A L A = max(max( )) ( ), ( 2 1 2 1 x F x F L A L A

),max(max( ))) ( ), ( 2 1 2 1 y F y F L A L A = max ) , )( ),( , )( (( 2 1 2 1 2 1 2 1 y y F F x x F F L A L A L A L A  

), )) ( ), ( ), ( max( )) , )( , )(( ( 1 1 2 2 2 1 2 1 1 2 2 2 1 y x F y F x F y y x x F F U B U A U A U B U B   

= max(max( )) ( ), ( 2 1 2 1 x F x F U A AU

max ))) ( ), ( ),max( ( ), ( ( 1 1 2 2 2 1 2 2 y F x F y F x F U A AU U A U A

= max ) , )( ),( , )( (( 2 1 2 1 2 1 2 1 y y F F x x F F U A AU U A AU  

),max(max( ))) ( ), ( 2 1 2 1 y F y F U A AU

).

2 1 G G  is Strong Interval Valued Netrosophic Intuitionistic Fuzzy Graph then at least G1 or G2 must be strong Proof: Suppose that G1 and G2 are not SIVNIFG, there exist , i i i E y x  i=1,2 such that 1) )) ( ), ( min( ) , )( ( 2 1 2 1 2 1 2 1 x T x T x x T T L A L A L A L A   )) ( ), ( min( ) , )( ( 2 1 2 1 2 1 2 1 x T x T x x T T U A AU U A AU   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x I x I x x I I L A L A L A L A   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x I x I x x I I U A AU U A AU   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x F x F x x F F L A L A L A L A   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x F x F x x F F U A AU U A AU       } , )/ , )( , {( 2 2 2 1 1 2 2 E y x v x y x x x E } , )/ , )( , {( 1 1 1 2 1 1 E y x v z z y z x   Consider, , ) , )( , ( 2 2 E y x x x  we have )) ( ), ( min( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x T x T y x x x T T L B L A L B L B    min ))) ( ), ( ),min( ( ( 2 2 2 2 1 y T x T x T L A L A L A = min(min( ))) ( ), ( 2 2 1 x T x T L A L A

,min(min( ))) ( ), ( 2 2 1 y T x T L A L A = min ) , )( ),( , )( (( 2 2 2 1 2 1 y x T T x x T T L A L A L A L A   ), )) ( ), ( min( )) , )( , )(( ( 2 2 2 2 2 1 2 1 y x T x T y x x x T T U B AU U B BU   

min ))) ( ), ( ),min( ( ( 2 2 2 2 1 y T x T x T U A U A AU = min(min( ))) ( ), ( 2 2 1 x T x T U A AU

) )) ( ), ( min( ) , )( ( 2 1 2 1 2 1 2 1 x T x T x x T T L A L A L A L A   )) ( ), ( min( ) , )( ( 2 1 2 1 2 1 2 1 x T x T x x T T U A AU U A AU   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x I x I x x I I L A L A L A L A   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x I x I x x I I U A AU U A AU   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x F x F x x F F L A L A L A L A   )) ( ), ( max( ) , )( ( 2 1 2 1 2 1 2 1 x F x F x x F F U A AU U A AU  

,min(min( ))) ( ), ( 2 2 1 y T x T U A AU = min ) , )( ),( , )( (( 2 2 2 1 2 1 y x T T x x T T U A AU U A AU   InternationalJournalofPureandAppliedMathematicsSpecialIssue 1267

)) , )( ),( , )( min(( 2 2 2 1 2 1 y x T T x x T T U A AU U A AU   = ))) ( ), ( )),min( ( ), ( min(min( 2 2 2 1 2 1 y T x T x T x T U A AU U A AU =

)) ( ), ( ), ( min( 2 2 2 2 1 y T x T x T U A U A AU )) , )( ),( , )( max(( 2 2 2 1 2 1 y x I I x x I I U A AU U A AU   = ))) ( ), ( )),max( ( ), ( max(max( 2 2 2 1 2 1 y I x I x I x I U A AU U A AU = )) ( ), ( ), ( max( 2 2 2 2 1 y I x I x I U A U A AU

Hence,  )) , )( , )(( ( 2 2 2 1 y x x x T T L B L B  min )) , )( ),( , )( (( 2 2 2 1 2 1 y x T T x x T T L A L A L A L A   ),  )) , )( , )(( ( 2 2 2 1 y x x x T T U B BU  min ) , )( ),( , )( (( 2 2 2 1 2 1 y x T T x x T T U A AU U A AU   ),  )) , )( , )(( ( 2 2 2 1 y x x x I I L B L B  max ) , )( ),( , )( (( 2 2 2 1 2 1 y x I I x x I I L A L A L A L A   ),  )) , )( , )(( ( 2 2 2 1 y x x x I I U B U B  max ) , )( ),( , )( (( 2 2 2 1 2 1 y x I I x x I I U A AU U A AU   ), Similarly, we can show that )) , )( , )(( ( 2 2 2 1 y x x x F F L B L B   max ) , )( ),( , )( (( 2 2 2 1 2 1 y x F F x x F F L A L A L A L A   ), )) , )( , )(( ( 2 2 2 1 y x x x F F U B U B   max ) , )( ),( , )( (( 2 2 2 1 2 1 y x F F x x F F U A AU U A AU   ). Hence, 2 1 G G  is not Strong Interval Valued Netrosophic Intuitionistic Fuzzy Graph, Which is a contradiction. This completes the proof.

Conclusion

In this Paper, Cartesian product, Composition and join of two SIVIFG and SIVNIFGs are discussed. Our future plan to extend our research to some other operations on Strong Interval Valued Neutrosophic Intuitionistic Fuzzy Graph.

References

1. M.Akram and W.A. Dudec, Interval-valued fuzzy graphs, Computers and Mathematics with Applications, 61 (2011) 289-299.

2. Antonios, K., Stefanos, S., Lazaros, I., & Elias, P. (2014). Fuzzy graphs: algebraic structure and syntactic recognition, Artificial Intelligence Review, vol 42, Issu 3:479-490.

3. K.T. Atanassov, Intuitionistic fuzzysets: Theory and Applications, Studies in fuzziness and soft computing, New York, Physica-Verl., 1999.

4. K.T. Atanassov, Intuitionistic fuzzysets, Fuzzy sets and Systems, 20(1986) 87-96.

5. Bhattacharya, P. (1987). Some remarks on fuzzy graphs, Pattern Recognition Letters, 6: 297-302.

6. K R Bhutani, On automorphisms of fuzzy graphs, Pattern Recognition Letters, 9 (1989) 159-162

7. J.N Mardeson and C.S. Peng, Operation on fuzzy graphs, Information Sciences, 19 (1994) 159-170.

8. J.N Mardeson, P.S. Nair, Fuzzy Graphs and Fuzzy Hypergraphs, Physica-Veriag, Newyork, 2000.

9. Mishra S. N. & Pal, A. (2013). Product of Interval Valued Intuitionistic fuzzy graph, Annals of Pure and Applied Mathematics, Vol. 5, No.1:37-46.

10. Nagoor, G.A., & Shajitha Begum, S. (2010). Degree, Order and Size in Intuitionistic Fuzzy Graphs, International Journal of Algorithms, Computing and Mathematics, (3)3:11-16.

11. Nagoor, G.A., & Latha, S.R. (2012). On Irregular Fuzzy Graphs. Applied Mathematics Sciences, Vol.6, No.11:517-523.

12. Nagoor, G.A., & Basheer Ahamed, M. (2003). Order and Size in Fuzzy Graphs, Bulletin of Pure and Applied Sciences, Vol 22E (No.1):145-148.

13. Parvathi, R., Karunambigai, M.G. (2006). Intuitionistic Fuzzy Graphs. Computational Intelligence, Theory and applications, International Conference in Germany, 18-20.

14. A. Rosenfeld, Fuzzy graphs, in: L.A. Zadeh, K.S. Fu, M. Shimura (Eds), Fuzzy sets and their Applications to Cognitive and Decision Processes, Academic Press, New York, 1975,pp. 77-95.

15. Shannon, A., & Atanassov, K.(1994). A first step of the intuitionistic fuzzy graph, Proceeding of the first Workshop on fuzzybased Expert Systems, Sofia, Sept. 28-30; 59-61.

16. M.S. Sunitha, A. Vijayakumar, A characterization of fuzzytrees, Information Sciences,

113 (1999) 293-300.

17. M.S. Sunitha, A. Vijayakumar, Some metric aspects of fuzzy graphs, in: R. Balakrishna, H.M. Mulder, A. Vijayakumar(Eds.), Proceedings of the Conference on Graph Connections CUSAT, Allied Publishers, Cochin, 1999, pp. 111-114.

18. M.S. Sunitha, A. Vijayakumar, Complement of a fuzzy graph, Indian Journal of Pure and Applied Mathematics, 33 (2002) 1451-1464.

19. M.S. Sunitha, A. Vijayakumar, Blocks in fuzzy graphs, The Journal of Fuzzy Mathematics, 13 (2005) 13-23.

20. R.T. Yeh, S.Y. Beng, Fuzzy relations fuzzy graphs and their applications to clustering analysis, in; L.A. Zadeh, K. S. Fu, M. Shimura(Eds.), Fuzzy Sets and Their Applications, academic Press, 1975, pp. 125-149.

21. L A Zadeh, Fuzzy sets, Information and Control, 8(1965) 338-353.

22. K. Kalaiarasi, R. Divya, Fuzzy Colouring of Interval-Valued Fuzzy Graph, International Journal of Fuzzy Mathematical Archive, Vol. 14, No.1,2017, pp 47-57.

23. K.Kalaiarasi, Optimization of Fuzzy Integrated Vendor-Buyer Inventory models, Annals of Fuzzy Mathematics and Informatics, Volume 2, No. 2, (Oct 2011), pp. 239-257