Study of Decision Framework of Shopping Mall Photovoltaic Plan Selection

StudyofDecisionFrameworkofShoppingMall PhotovoltaicPlanSelectionBasedonDEMATELand ELECTREIIIwithSymmetryunderNeutrosophic SetEnvironment

JiangboFeng 1,* ID ,MinLi 2 andYansongLi 1

1 SchoolofElectricalandElectronicEngineering,NorthChinaElectricPowerUniversity,Beijing102206, China;fyh@ncepu.edu.cn

2 SinopecNanjingEegineeringandConstructionInc.,Nanjing210000,China;yxglc@sina.com

* Correspondence:fengjiangbo1995@163.com;Tel.:+86-18810727102

Received:23April2018;Accepted:3May2018;Published:9May2018

Abstract: RooftopdistributedphotovoltaicprojectshavebeenquicklyproposedinChinabecause ofpolicypromotion.Before,therooftopsoftheshoppingmallhadnotbeenoccupied,anditwas urgedtohaveadecision-makingframeworktoselectsuitableshoppingmallphotovoltaicplans. However,atraditionalmulti-criteriadecision-making(MCDM)methodfailedtosolvethisissueat thesametime,duetothefollowingthreedefects:theinteractionsproblemsbetweenthecriteria, thelossofevaluationinformationintheconversionprocess,andthecompensationproblemsbetween diversecriteria.Inthispaper,anintegratedMCDMframeworkwasproposedtoaddressthese problems.Firstofall,thecompositiveevaluationindexwasconstructed,andtheapplicationof decision-makingtrialandevaluationlaboratory(DEMATEL)methodhelpedanalyzetheinternal influenceandconnectionbehindeachcriterion.Then,theinterval-valuedneutrosophicsetwas utilizedtoexpresstheimperfectknowledgeofexpertsgroupandavoidtheinformationloss.Next, anextendedeliminationetchoicetranslationreality(ELECTRE)IIImethodwasapplied,andit succeedinavoidingthecompensationproblemandobtainingthescientificresult.Theintegrated methodusedmaintainedsymmetryinthesolarphotovoltaic(PV)investment.Lastbutnotleast, acomparativeanalysisusingTechniqueforOrderPreferencebySimilaritytoanIdealSolution (TOPSIS)methodandVIKORmethodwascarriedout,andalternativeplanX1ranksfirstatthesame. Theoutcomecertifiedthecorrectnessandrationalityoftheresultsobtainedinthisstudy.

Keywords: shoppingmall;photovoltaicplan;decision-makingtrialandevaluationlaboratory (DEMATEL);interval-valuedneutrosophicset;extendedELECTREIII;symmetry

1.Introduction

Thefrequentoccurrenceoffogorhazeandothernegativetypesofclimatechangeinrecent decadesisthegraverealitythatthewholeworldisexperiencing.Thepivotalreasonbehindthese environmentalproblemsisatmosphericpollutantsandgreenhousegasemissions,mainlyproducedby fossilfuelconsumption.Fossilfuelsuppliesapproximately80%oftheworld’senergy,anditisdrying upwiththerapidincreaseoftheworldenergydemand[1].

Tofacethissituation,manycountrieshaveendorsedpoliciestosubmitfossilfuelutilization withrenewableenergygeneration.Amongdiversetypesofalternativeenergy,solarphotovoltaic (PVhereinafter)energyisrecognizedaspromising,sincesunlightisunlimitedandwidespreadand theconvertingefficienciesofphotovoltaicaregettinghigherandhigherwhilethemanufacturingcosts arebecominglowerandlower[2].

Symmetry 2018, 10,150;doi:10.3390/sym10050150 www.mdpi.com/journal/symmetry

Symmetry 2018, 10,150 2of20

ThepastfiveyearshaswitnessedtheastonishingincreaseininstalledcumulativeglobesolarPV capacity,whichnearlyquintupledfrom70GWin2011,to275GWin2016.Chinaisfollowingthe worldwidetrendwithsolarPVrapiddevelopmentandgainedthenumberonecumulativePVcapacity of65.57GWin2016.Itisworthnotingthatthelarge-scalegroundPVpowerstation,newlyinstalled, had28.45GWcapacitythisyear,andgrewby75%comparedtothelastyear,accountingfor89%of allnewPVpowerplantsin2016,whilethedistributedPV,newlyinstalled,with3.66GWcapacity thisyear,increasedby45%incomparisontolastyear,andaccountedfor11%ofcapacityofnew installationsin2016.ThescaleofdistributedPVdevelopmentissignificantlylowerthanthatofthe large-scalegroundPV.

The past five years has witnessed the astonishing increase in installed cumulative globe solar PV capacity, which nearly quintupled from 70 GW in 2011, to 275 GW in 2016. China is following the worldwide trend with solar PV rapid development and gained the number one cumulative PV capacity of 65.57 GW in 2016. It is worth noting that the large-scale ground PV power station, newly installed, had 28.45 GW capacity this year, and grew by 75% compared to the last year, accounting for 89% of all new PV power plants in 2016, while the distributed PV, newly installed, with 3.66 GW capacity this year, increased by 45% in comparison to last year, and accounted for 11% of capacity of new installations in 2016. The scale of distributed PV development is significantly lower than that of the large-scale ground PV.

Underthesecircumstances,theChinaauthoritieshavelaunchedthefeedintariffadjustment. ThefeedintariffofgroundsolarPVgenerationwilldecreasetosomeextent,butincontrasttothat ofdistributedPV,willnotdecreaseatall.AsshowninFigure 1,accordingtothe13thfive-year (2016–2020)solarenergyplanningobjectivesofChina,thegoalistobuildatotalinstalledcapacity of150GWsolarPV,inwhichmorethan40%ofthenewinstalledcapacitywillbefromdistributed PV,andtobuild100distributedPVdemonstrationareas.Infact,Chinaisacountrywithhigh potentialofsolarradiation,andofgenerouspolicysubsidiestopromoteachievingtheambitious plan.Obviously,inChina,distributedsolarPVgenerationisgovernmentencouraged,well-resourced, environmentallyfriendly,andcloselyfollowingtheworldtrend.Itisworthconsideringinvestmentin suchapromisingproject.

Under these circumstances, the China authorities have launched the feed in tariff adjustment. The feed in tariff of ground solar PV generation will decrease to some extent, but in contrast to that of distributed PV, will not decrease at all. As shown in Figure 1, according to the 13th five-year (2016–2020) solar energy planning objectives of China, the goal is to build a total installed capacity of 150 GW solar PV, in which more than 40% of the new installed capacity will be from distributed PV, and to build 100 distributed PV demonstration areas. In fact, China is a country with high potential of solar radiation, and of generous policy subsidies to promote achieving the ambitious plan. Obviously, in China, distributed solar PV generation is government encouraged, well-resourced, environmentally friendly, and closely following the world trend. It is worth considering investment in such a promising project.

Figure1. Chinesephotovoltaicpowerstructure,2012–2016.

Figure 1. Chinese photovoltaic power structure, 2012–2016

Numerousvacantroofsofbuildingorstructuresinthecitiesprovidethebest-fittinglocation fordistributedsolarPV,andfarsightedinvestorshavebeenpreemptingoutstandingroofresources. Therearevarioustypesofbuildings,suchasgovernmentbuilding,hospitals,schools,coliseums, orresidentialandindustrialbuildings.Amongallthesetypes,theshoppingcenterspossessesplenty ofadvantages,superiortotheothertypesofbuildings,andareoneofthemostpromisingplacesworth preemptingforPVinstallation.

Numerous vacant roofs of building or structures in the cities provide the best-fitting location for distributed solar PV, and farsighted investors have been preempting outstanding roof resources. There are various types of buildings, such as government building, hospitals, schools, coliseums, or residential and industrial buildings. Among all these types, the shopping centers possesses plenty of advantages, superior to the other types of buildings, and are one of the most promising places worth preempting for PV installation.

Firstofall,previousconstructioncharactersofshoppingcentersfacilitatetherooftopPV installation.Accordingtoliterature[3],theavailabilityrateofroofspaceisbetween60%and65% inshoppingmalls,butjust22%and50%inresidentialbuildings.Thatistosay,doubleortriplePV capacitycanbeinstalledintheformerroofs,comparedtothelatterone.Secondly,theshopping mallsneedalargeamountofelectricityconsumptiondaily,themostgenerationcanfeedthe themselves-consumption.Besides,itisusuallycitedindowntownareasandpopulatedareas.Onthe

First of all, previous construction characters of shopping centers facilitate the rooftop PV installation. According to literature [3], the availability rate of roof space is between 60% and 65% in shopping malls, but just 22% and 50% in residential buildings. That is to say, double or triple PV capacity can be installed in the former roofs, compared to the latter one. Secondly, the shopping malls need a large amount of electricity consumption daily, the most generation can feed the themselvesconsumption. Besides, it is usually cited in downtown areas and populated areas. On the one hand, there have a so complete transmission and distribution network that the surplus generation can efficiently feed local electricity consumption. On the other hand, brand advertisement and promotion

Symmetry

onehand,therehaveasocompletetransmissionanddistributionnetworkthatthesurplusgeneration canefficientlyfeedlocalelectricityconsumption.Ontheotherhand,brandadvertisementand promotionofthePVmanufacturerandtherisinglevelofawarenessofthecitizentowardssustainable effortscanbegreatlyobtainedforthelargevisitorsthere.Lastbutnotleast,facingthenon-manageable featurethroughelectricitygenerationinPVfacilities,technicalmanagementmeasuresneedtobetaken forprotectingdistributionsystem[4].Fortunately,theshoppingmallsequippedprofessionalstaffand equipmentforenergysupply,security,airconditioning,andsoon.So,thepreviousstaffinshopping mallscancondemnthewholenewchallengetoreducetheextraexpenditureinPVmanagement.

ItisdesirabletoadoptapropermethodologyforevaluatingtheshoppingmallPVplaninorder todemonstratetheoptimalpossibleselectionsforaninvestment.Sincethefollowingthreeproblems existedinthisissue,whicharetheinteractionproblemsbetweenthecriteria,thelossofevaluation informationintheconversionprocess,andthecompensationproblemsbetweendiversecriteria. Thereisnodoubtthattraditionalmulti-criteriadecision-making(MCDM)methodfailedtosolvethe threeproblemsatthesametime.Nevertheless,thedecision-makingtrialandevaluationlaboratory (DEMATEL)methodcanhelpanalyzetheinternalinfluenceandconnectionbehindeachcriterion, andtheinterval-valuedneutrosophicsetisaccomplishedinexpressingtheimperfectknowledgeof expertsgroup.Besides,anextendedELECTREIIImethodasanoutstandingoutrankingmethodcan succeedinavoidingthecompensationproblem,andtheintegratedmethodusedmaintainedsymmetry inthesolarPVinvestment.Therefore,inthiscontext,theintegratedDEMATELmethodandextended ELECTREIIImethodunderinterval-valuedneutrosophicsetenvironmentforsearchingtheoptimal shoppingmallsolarPVplanhasbeendevised.

2.LiteratureReview

MCDM(multi-criteriadecision-making)hasbeensuccessfullyappliedinenergyplanning problems.Forexample,areviewofMCDMmethodstowardsrenewableenergydevelopmentidentified MCDMmethodsasoneofthemostsuitabletoolstofindingoptimalresultsconcernedwithenergy planningprogressincomplexscenarios,includingvariousindicators,andconflictingobjectivesand criteria[5].Forexample,FaustoCavallaroetal.useanintuitionisticfuzzymulti-criteriaapproach combinedwithfuzzyentropytorankdifferentsolar-hybridpowerplantssuccessfully[6].

Inarealcase,itisdifferentfordecisionmakerstoexpresspreferenceswhenfacinginaccurate, uncertain,orincompleteinformation.Althoughthefuzzset,intuitionisticfuzzysets,interval-valued intuitionisticfuzzysets,andhesitantfuzzysetscanaddressthesituation.However,whenbeing askedtheevaluationonacertainstatement,theexpertscanusetheinterval-valuedneutrosophicset (IVNNS)expressingtheprobabilitythatthestatementistrue,false,andthedegreeofuncertaintycan beaccuratelydescribed,respectively[7].TheIVNNS,combinedwithoutrankmethods,hasaddressed manyMCDMproblemssuccessfully[8].Forexample,theIVNNScombinedwithVIKORwasapplied tosolveselectionoflocationforalogisticterminalproblem[9].Hong-yuZhangetal.developed twointervalneutrosophicnumberaggregationoperatorsandappliedthemtoexploremulti-criteria decision-makingproblems[10].

TheindependenceofcriteriaremainsinmostoftheMCDMmethodologies.Inrecentyears,lotsof methodsappearedtosolvetheproblem,andtheDEMATELmethodispopularlyused.Accordingto thestatisticcensusedinarticle[11],oftheuseofMCDMmethodsinhybridMCDMmethods,thetop fivemethodsareAnalyticalNetworkProcess(ANP),DEMANTEL,AnalyticHierarchyProcess(AHP), TOPSIS,andVIKOR.

TheDEMATELmethodologyhasbeenacknowledgedasapropertoolfordrawingthe relationshipsconcerninginterdependenciesandtheintensityofinterdependencebetweencomplex criteriainanevaluationindexsystem[12,13].Asapowerfultooltodescribetheeffectrelationship, ithelpevaluatetheenablersinsolarpowerdevelopments[11]andevaluatefactorswhichinfluencing industries’electricconsumption[14].TheapplicationofDEMATELcontributedtodeterminingthe weightcoefficientoftheevaluationcriteria,andsuccessfullyhelpedidentifythesuitablelocations

forinstallationofwindfarms.ItistheDEMATELmethodthathelpedtheinvestorsimprovetheir decisionswhentherearemanyinterrelatedcriteria.Thus,theconnectionrelationshipoftheclimate andeconomycriteriathatexistsinthisstudyisofgreatneedoftheapplicationofDEMATELmethod. ThecommonlyusedoutrankmodelsareTOPSIS,AHP,ANP,preferencerankingorganization methodforenrichmentevaluations(PROMETHE),andELECTRE,ofwhichELECTREmethods arepreferredbydecisionmakersinenergyplanningprogress.AmongtheELECTREmethods, ELECTREIIImethodconveysmuchmoreinformationthantheELECTREIandELECTREII methods[15].Intheliterature[16],economicsofinvestmentinthefieldofPV,aninclusive decision-makingstructureusingELECTREIIIthatwouldhelpphotovoltaic(PV)systemowners, bureaucrats,andthebusinesscommunitiestodecideonPVtechnologies,financialsupportsystems andbusinessstrategieswerefeatured.ELECTREIIIwasusedtostructureamulti-criteriaframework toevaluatetheimpactofdifferentfinancialsupportpoliciesontheirattractivenessfordomesticPV systemdeploymentonamultinationallevel[17].Duetothecompensationproblemininformation processing,incompleteutilizationofdecisioninformation,andinformationloss,ELECTREIIIwas chosentobuildaframeworkforoffshorewindfarmsiteselectiondecisionintheintuitionisticfuzzy environment.TheseliteraturestudiesimprovetheapplicationofELECTREIIImethodintheenergy planningprocess,andterrifytheeffectivenessofevaluationindecisionmakingprogress[18].

Inconclusion,basedonthementionedevolvement,theshoppingmallPVplanevaluationresult willbemorescientificandreasonablethanbefore.

3.DecisionFrameworkofSMPVPlanSelection

Theevaluationcriteriaarebasictotheentireevaluation,sothattheyareofgreatimportancetothe shoppingmallphotovoltaicplanselection.Inviewofthespecialcharacteristicsofphotovoltaic planandtheshoppingmalls,sixfactorsweretakenintoconsideration,namelyarchitectural elements,climate,photovoltaicarray,economy,risk,contribution.Table 1 showssixcriteriaand twenty-onesubcriteria.

Table1. Analysisofevaluationattributesofshoppingcentersphotovoltaicplanselection.

3.1.ArchitecturalElements

Notalltheshoppingmallsaresuitabletoallocatethephotovoltaics,andarchitecturalelements aretheprimaryintrinsiclimitations.Steeproofpitchandwrongorientationwillincreasethedifficulty ofallocationandmaintenance.Inaddition,buildingobstructions,andvegetationshadingpartof thespacearenotabletoallowfortheallocationofPVequipment,whichcanbemeasuredbythe coveringratioestimatedbyEquation(2).Lastbutnotleast,thephotovoltaicroofspaceneededto becalculatedbytheEquation(1).Colmenar-Santos,Antonioetal.[15]assessedthephotovoltaic potentialinshoppingmallsbycalculatingthephotovoltaicroofspace.Wedecidedtorefertothis researchmethod.

RSPV = RS × α (1)

RSPV isPVroofspace, RS standforroofspace, α isavailabilityratio

CR = L/(a + b)= tan ϕ tan (αs )α sin ϕ tan (αs )α + sin ϕ tan ϕ sin (γs )a (2)

CR iscoveringratio. (αs )α solaraltitudeangle (γs )a ϕ solarazimuthangle.Thevalueisatnine o’clockonthewintersolsticeineachlocation.

3.2.Climate

Notallthelocationsoftheshoppingmallshavetheoptimalclimateforsolarpowergeneration. Itisundoubtedthatthesolarresourcedependsonlocalclimate.Thus,theannualaveragesolar radiation,landsurfacetemperature,andannualsunshineutilizationhours,arethefourtypicalcriteria tojudgewhetherthelocalsolarenergyresourceisinabundance.

3.3.PhotovoltaicArray

Itiswellknownthattheperformanceofphotovoltaicarrayswillimpacttheelectricitygeneration reliabilityandstability.Thedustinthephotovoltaiccellpanelwillreducethesolarenergyconversion efficiency,meanwhile,sincethephotovoltaiccellpaneldamageandfaultsaredirectlyrelatedtothe electricitysupplyreliability,therepairandcleanrateshouldbepondered.Inaddition,itisworth concerningwhetherthespecifiedtypeofthephotovoltaicpanelisabsolutelysuitabletothelocal solarregime.ThetotalPVareaaffectstheelectricitygeneratedwhichiscalculatedbyEquation(3). PVgeneration(yearlyelectricitygeneration)isestimatedbyEquation(4). Apanel = RSPV × CR (3) E = H × Apanel × ε × κ (4) H isthetotalyearlysolarirradiation. Apanel isthetotalareaofPVpanel. ε istheefficiencyofthe panel. κ isthecomprehensivefacilityperformanceefficiency,whichis0.8[19],and0.28istheempirical conversioncoefficientofthePVmoduleareatothehorizontalarea.

3.4.Economy

Itisbeyonddoubtthattheeconomyoftheshoppingmallphotovoltaicplansoughttobetaken intoaccountbythedecisionmakers.Thereareplentyofstudiestoassessthefinancialaspectsof thephotovoltaicprojects.IndrajitDasetal.[23]presentedaninvestor-orientedplanningmodelfor optimumselectionofsolarPVinvestmentdecisions.RodriguesSandyetal.[24]conductedeconomic analysisofphotovoltaicsystemsunderChina’snewregulation.Theeconomicassessmentmethods therearesosuitableandscientificthattheyareworthreferringtointhispaper.Thesignificant

economicattributesweconsideredarepaypackperiod,totalinvestment,totalprofit,andannualrate ofreturn,whicharecalculatedbyEquations(5)–(7).

I = C × Apanel × ppanel apanel (5)

I isthetotalinvestment, C istheaveragecostofbuildingperWroofPVprojects. ppanel isthe maxpowerpin(W)underSTCsituationofthesolarpanel, apanel istheareaofperphotovoltaicpanels.

B = PE × tLC + PS × tS I × tLC O × tLC (6)

B isthetotalprofit, PE istheelectricitypricebuyingfromthepowersupplycompany, PS isthe electricitypricesubsidy, tLC isthetimeofPVprojectslifecycle, tS isthetimesubsidylasting, O isthe costforoperationandmaintenance.

ROI = B I × tLC (7)

ROI istheannualrateofreturn.

TPB isthepaypackyear.

3.5.Contribution

TPB = I PE + PS I O (8)

AlthoughtheenvironmentalandsocialcontributionstheSMPVprojectsmademaynotbe calculatedexplicitlyaseconomicprofit,thereisnodenyingthatthesebenefitsresultinincreaseinlocal economyandemployment,andenvironmentprotectionandpublicityeffectsareworththefocusof attention.Particularly,theshoppingmallholdsagreatnumberofvisitors.Ontheonehand,itobtains, easily,thebrandadvertisementandpromotionwhenPVequipmentofaparticularcompanyoccupies therooftopofalargecommercialbuilding.Ontheotherhand,itiseffectivetoraisethelevelof awarenessofthecitizentowardsrenewableenergyandsustainableefforts.

3.6.Risk

Expectthatfortheaboveattributes,theriskfacedcannotbeneglected.Firstofall,thegovernment subsidespolicyislikelytochange,andtheimpartiality,sufficiency,stability,andconstancyofthe subsidyisunabletobeensured.Secondly,thegeneratingcapacityisinfluencedbytheclimateheavily, sotheprofitswillreducewhenfacingconsecutiverainydays.Thirdly,therooftopusageneedsthe allowancefromalltheowners,however,therooftopownershipandoccupancydisputesareavery commonrisk.Lastbutnotleast,theconnectedphotovoltaicgridisunabletobringanybenefitstothe gridenterprisebecauseoftheintermittentpoweroutput.Thus,howlongthesupporttophotovoltaic gridconnectedfromthegridenterprisecanexistisuncertain.

Allinall,theSCPVplanalternativesoughttobeappraisedfromarchitecturalelements,climate, photovoltaicarrayperformance,economy,risk,contributionattributes.Theuniquecustom-made frameworkofcriteriaandsubcriteriaissetupinviewoftheactualSMPVplansandnationalconditions.

4.ResearchMethodology

AdecisionframeworkofSMPVselectionhasbeenproposedinthissection,andthereare fourphasesinthisframework,asshowninFigure 2.Theresearchframeworkisdescribedinthe followingsubsections.

Figure 2. The flowchart of the research methodology. DEMATEL: decision-making trial and evaluation laboratory

Figure2. Theflowchartoftheresearchmethodology.DEMATEL:decision-makingtrialand evaluationlaboratory.

4.1 Preliminary Knowledge in the Neutrosophic Set Environment

4.1.PreliminaryKnowledgeintheNeutrosophicSetEnvironment

Due to the existence of many uncertainties in real decision-making problems, such as indeterminate and inconsistent, the neutrosophic set (NS) is used in the MCDM method, and definition of NS is introduced in this section.

Definition 1 [25]. Let X be a space of objects with a generic element in X denoted by x . A NS A in X is defined using three functions: truth-membership function ()A Tx , indeterminacy-membership function ()A Ix and falsity-membership function ()A Fx . These functions are real standard or nonstandard subsets of ]0,1[  , that is, ():]0,1[ A TxX

, ():]0,1[A IxX

 and ():]0,1[A FxX

Duetotheexistenceofmanyuncertaintiesinrealdecision-makingproblems,suchas indeterminateandinconsistent,theneutrosophicset(NS)isusedintheMCDMmethod,anddefinition ofNSisintroducedinthissection. Definition1 [25]. Let X beaspaceofobjectswithagenericelementin X denotedby x.ANS A in X is definedusingthreefunctions:truth-membershipfunction TA (x),indeterminacy-membershipfunction IA (x) andfalsity-membershipfunction FA (x).Thesefunctionsarerealstandardornonstandardsubsetsof ]0 ,1+ [, thatis, TA (x) : X →]0 ,1+ [ , IA (x) : X →]0 ,1+ [ and FA (x) : X →]0 ,1+ [ .Andthatthesumof TA (x), IA (x) andFA (x) satisfiesthecondition 0 ≤ supTA (x)+ supIA (x)+ supFA (x) ≤ 3+

. And that the sum of ()A Tx , ()A Ix and ()A Fx satisfies the condition 0sup()sup()sup()3 AAA TxIxFx

. Since the non-standard unit interval ]0,1[  is hard to apply in practice, and the degree of truth, falsity, and indeterminacy about a certain statement could not be described precisely in the practical evaluation, the interval-valued neutrosophic set (IVNNS) of standard intervals has been proposed by

Sincethenon-standardunitinterval ]0 ,1+ [ ishardtoapplyinpractice,andthedegreeoftruth, falsity,andindeterminacyaboutacertainstatementcouldnotbedescribedpreciselyinthepractical evaluation,theinterval-valuedneutrosophicset(IVNNS)ofstandardintervalshasbeenproposed byWang[26],andafewdefinitionsandoperationsofIVNNSareintroducedintheGPPtechnology selectionMCDMproblem.

Definition2 [26]. Let X beaspaceofobjectswithagenericelementin X denotedby x.AnIVNNS A canbe definedas A = { x, TA (x), IA (x), FA (x) : x ∈ X} (9) where TA (x) : X → [0,1] , IA (x) : X → [0,1] , FA (x) : X → [0,1] .Foreachelement x in X,thesefunctions canbeexpressedas TA (x)= [infTA (x), supTA (x)] ⊆ [0,1], IA (x)= [infIA (x), supIA (x)] ⊆ [0,1], FA (x)= [infFA (x), supFA (x)] ⊆ [0,1] and 0 ≤ supTA (x)+ supIA (x)+ supFA (x) ≤ 3, x ∈ X.Forconvenience, theinterval-valuedneutrosophicnumber(IVNN)canbeexpressedas a = TL a , TU a , I L a , IU a , FL a , FU a , andL, UrepresenttheinferiorsandsuperiorsofIVNNrespectively.

Definition3 [10] Let

, I

,

and b

,

,

TL b , TU b , I L b , IU b , FL b , FU b betwo IVNNs,and λ isarealnumberfornotlessthan0.Whichoperationalrulescanbeexpressedasfollows

TheoriginaldataofselectionofSPPVarecollectedandprocessedinthisphase.Thealternative plansoftheGPPprojectareevaluatedbytheexperts,firstlyaccordingtothelocaltechnicalcondition dataandpracticalexperience.Then,thedecisionmatricesareexpressedintheformofIVNNs, whichcanhandleincompleteandindeterminateinformation.Finally,acomprehensivedecision matrixisformedbasedoninterval-valuedneutrosophicnumberweightedgeometricoperator (IVNNWG)operator.Let Ai denotethetechnologyalternatives(i = 1,2, ··· m),and Cj denotethe criteria(j = 1,2, ··· n).Itisassumedthat ak ij canbeusedtorepresenttheevaluationvalueofattribute ofalternativefromeveryexpert Ek (k = 1,2, ··· h)

Definition4 [27]. Let Ak ij = ak ij m×n betheIVNN-decisionmatrixofthe k-thDM, k = 1,2, h, and ak ij = TL ak ij , TU ak ij , I L ak ij , IU ak ij , FL ak ij , FU ak ij .AnIVNNWGoperatorisamapping: IVNNn → IVNN , suchthat IVNNWGω a1 ij, a2 ij, , ah ij = k=h ∏ k=1 ak ij ωk = k h ∏ k=1 TL ak ij

ωk , k h ∏ k=1 TU ak ij

ωk , 1 k h ∏ k=1 1 IL ak ij

ωk ,1 k h ∏ k=1 1 IU ak ij

4.2.PhaseIIdentificationofAlternativeSMPVPlans

ωk , 1 k h ∏ k=1 1 FL ak ij

ωk ,1 k h ∏ k=1 1 FU ak ij

ωk (14) where ω = (ω1, ω2, , ωh )T representstheweightvectorofDMs,satisfying Σh k=1ωk = 1, ωk ∈ [0,1]

Atthisstage,agroupofexpertsconsistingofseveraldoctorateengineerswillbeconstitutedby theinvestor.Alltheexpertspossessabundantworkingexperienceinsolarenergyinvestmentfield, andarespecializedinsolarphotovoltaicandpowergridtechnologies.

Morethantwentyfamousinfluentiallarge-scaleshoppingmallslocatedinthosecitieswithboth abundantsunshineandgeneralpolicysubsidiesneedtobecollected,andbasedonthatinformation, lessthantenalternativeplansroughlyscreenedout,basedontheplentitudeofdocumentsand investigation.Afterthat,theinvestigationwillbecarriedoutbytheexpertsgroup,andinvolve meetingtheDevelopmentandReformCommission,theMeteorologicalBureau,andthelocalpower

supplycompanies,inordertogatherinformationaboutsolarresources,cityplanningandconstruction, localsolarsubsidypolicies,distributedsolarpowerplanning,economicassessment,andapproved shoppingmallrooftopsforconstruction.Lastly,therewillbelessthanfiveofthemostpotential alternativeplacespresentedforthenextevaluation.

4.3.PhaseIIDeterminationoftheWeightsofCriteriaBasedonDEMATELMethod

TheimportanceofthecriteriaonGPPtechnologyselectionisdifferent,sotheDEMATELmethod isusedtodecidetheweightofcriteriainthisphase.Thedirectandindirectcausalrelationsamong criteriaareconsideredintheDEMATELmethod,andthesubjectivejudgmentofDMsisalsoconsidered. ThestepsofdeterminingtheweightsbasedontheDEMATELmethodareshownasfollows[28]:

Step1.Determinetheinfluencefactorsinthesystem

TheinfluencefactorsofGPPtechnologyselectionsystemaredeterminedbasedonexpertopinions andliteraturereviews,whichiscalledthecriteria,asshowninTable 1

Step2.Constructthedirect-relationmatrixamongthecriteria

Thedirect-relationmatrix X = xpq n×n isconstructedinstages,where xpq isusedtorepresent thedegreeofdirectinfluenceof pthcriterionon qthcriterionwhichisevaluatedbytheexperts,and n isthenumberofcriteria.

Step3.Normalizethedirect-relationmatrix

Thedirect-relationmatrix X = xpq n×n isnormalizedinto Y = ypq n×n .Anormalization factor[29] s isappliedinthenormalizedcalculation,andthenormalizeddirect-relationmatrix Y is calculatedbyusingEquations(1)and(2). Y = s X (15) s = Min 1 Max1≤p≤n ∑n q=1 xpq , 1 Max1≤q≤n ∑n p=1 xpq (16)

Step4.Calculatethecomprehensive-relationmatrix. Thecomprehensive-relationmatrix T isobtainedbyusingEquation(3). T = ∞ ∑ λ=1 Yλ = Y(I Y) 1 (17) where T = tpq n×n, p, q = 1,2, n,and tpq isusedtorepresentthedegreeoftotalinfluenceof pth criterionon qthcriterion. I representsfortheidentitymatrix.

Step5.Determinetheinfluencerelationamongcriteria

Theinfluencedegreeandinfluenceddegreeofthecriteriaisdeterminedafterobtainingthe comprehensive-relationmatrix T.Thesumoftherowandcolumnvaluesofmatrix T canbeobtained bytheEquations(4)and(5).Thesumofrowvaluesof T,denotedby D,whichrepresentstheoverall influenceofagivencriteriononothercriteria.Thesumofcolumnvaluesof T,denotedby R,which impliestheoverallinfluenceofothercriteriaonagivencriterion. D = dp n×1 = ∑n q=1 tpq (18) R = rq 1×n = ∑n p=1 tpq (19)

Thecausaldiagramisobtainedbasedonthe D + R and D R values.The D + R valueindicates theimportanceofindicatorintheSMPVplanselectionsystem,thegreaterthe D + R value,themore importantthecorrespondingindicatoris.Ontheotherhand,the D R valueindicatestheinfluence

betweenacertainindicatorandtheotherindicators,whichcanbeseparatedintocauseandeffect groups.Theindicator,whichhaspositivevaluesof D R,belongstothecausegroup,anddispatches effectstotheotherindicators.Otherwise,theindicator,whichhasnegativevaluesof D R,belongsto theeffectgroup,andreceiveseffectstotheotherindicators.

Step6.Determinetheweightofcriteria

Thecriteriaarerepresentedby j,andsatisfying j = 1, ··· p, ··· q, ··· n,thentheweightsofcriteria aredeterminedbasedonthefollowingEquations(6)and(7)[30]. wj = dj + rj 2 + dj rj 2 1/2 (20) wj = wj ∑n j=1 wj (21) where wj denotestherelativeimportanceoftheindicators,and wj denotestheweightsoftheindicators inSMPVtechnologyselection.

4.4.PhaseIIICalculationIVNNsPerformanceScore

ELECTREisafamilyofmethodsusedforchoosing,sortingandranking,multi-criteriaproblems. ELECTREIIIwasdevelopedbyRoyin1978m,whichisvaluedoutrankingrelation.

A = {a1, a2,..., an } isthefinitesetofalternatives, Y = {y1, y2,..., ym } isthefinitesetofcriteria, yj (a) representstheperformanceofalternativeaoncriterion yj ∈ Y.Assumethatallthecriteria areofthegaintype,whichmeansthegreaterthevalue,thebetter. qj istheindifferencethreshold, whichrepresentstwoalternativesintermsoftheirevaluationsoncriterion yj.Ingeneral, qj isa functionofattributevalue qj (ai ),whichcanbedenotedas qj (yj (ai )); pj (yj (ai )) ispreferencethreshold, whichindicatesthatthereisaclearstrictpreferenceofonealternativeovertheotherintermsoftheir evaluationsoncriterion yj.Inaddition, vj (yj (ai )) isavetothresholdthatindicatesthattheattribute value yj (ai ) ofscheme ai islowerthantheattributevalue yj (ak ) ofscheme ak,andwhenitreachesor exceeds vj (yj (ai )),itisnotrecognizedthatthe ai ispreferredtothe ak yj (ai ) yj (ak ) whichindicates thesituationofpreferenceof ai over ak forcriterion Cj.Aweight wj expressestherelativeimportance ofcriterion yj,asitcanbeinterpretedasthevotingpowerofeachcriteriontotheoutrankingrelation. Where yj (ai ) and yj (ak ) areexpressedintheformofIVNNsinthepaper,thatis, yj (ai ) = TL i , TU i , I L i , IU i , FL i , FU i , yj (ak ) = TL k , TU k , I L k , IU k , FL k , FU k .Inthecalculationof Equation(8),let

(23) andso yj(ai) yj(ak) = TL i + TU i TL k TU k + I L i + IU i I L k IU k + FL i + FU i FL k FU k (24) Tij =

i amin i aij (i ∈ θC, amin i = 0)

i (1 aij amax i )(i ∈ θC, amin i = 0)

i aij amax i (i ∈ θB )

i amin i aij (i ∈ θC, amin i = 0)and µi (1 aij amax i )(i ∈ θC, amin i = 0) Fij Fij U = 1 TL ij I L ij Fij L = 1 TU ij IU ij

(25)

The δ, λ refertothecertaintyparametersofthebenefitcriteriaandcostcriteria,respectively[23], whilethe ε, µ standfortheuncertaintyparametersofthebenefitcriteriaandcostcriteriarespectively, andtheyobeyrule0 < δi + εi ≤ 1,0 < λi + µi ≤ 1.

4.5.PhaseIVCalculationofOutrankingRelationofIVNNsBasedonExtendedELECTRE-III

Step1.Definetheconcordanceindex

Theconcordanceindex c(ai, ak ) thatmeasuresthestrengthofthecoalitionofcriteriathesupport thehypothesis“isatleastasgoodas”, c(ai, ak ) iscomputedforeachorderedpair ai, ak ∈ A asfollows: c(ai, ak )= n ∑ j=1 wj cj (ai, ak )/ n ∑ i=1 wj (26) andthepartialconcordanceindex c(ai, ak ) isdefinedas cj (ai, ak )= 



 0 (yj (ai ) yj (ak ) ≤ qj [yj (ai )]) 1 (yj (ai ) yj (ak ) ≤ qj [yj (ai )]) yj (ai ) yj (ak ) qj [yj (ai )] pj [yj (ai )] qj [yj (ai )] (others) (27)

Step2.Definethediscordanceindex

Thediscordanceindex dj (ai, ak ) isdefinedasfollows: dj (ai, ak )=        0 (yj (ak ) yj (ai ) ≤−qj [yj (ai )]) 1 (yj (ak ) yj (ai ) ≥ vj [yj (ai )]) yj (ak ) yj (ai )+qj [yj (ai )] vj [yj (ai )]+qj [yj (ai )] (others) (28)

Step3.Definethedegreeofcredibilityoftheoutrankingrelation

Theoverallconcordanceandpartialdiscordanceindicesarecombinedtoobtainavalued outrankingrelationwithcredibility s(ai, ak ) ∈ [0,1] definedby: s(ai, ak )=    c(ai, ak )(∀j, dj (ai, ak ) ≤ c(ai, ak )) c(ai, ak ) ∏ j∈J(ai ,aj )

1 dj (ai ,ak ) 1 c(ai ,ak ) (others) (29) where j(ai, ak ) isthesetofcriteriaforwhich dj (ai, ak ) > c(ai, ak )

Step4.Definetherankingofthealternatives

∑ s(ai ak ) meansthesumdegreeofcredibilitythatalternative ai outranksalltheother alternatives,and ∑ s(ak ai ) meansthesumdegreeofcredibilitythatalltheotheralternatives outrankalternative ai.Thus, ∆S(ai ) representstherankingofthealternative ai,andthehigherthe ∆S(ai ) valueis,themoresuperiortheoutrankingorderis.

∆S(ai )= ∑ s(ai ak ) ∑ s(ak ai )(k = 1,2... n) (30)

5.ARealCaseStudy

AChineserenewableenergyinvestmentcompanywantstobuildashoppingcenterrooftop photovoltaicpowerproject.Inordertoseektheoptimalshoppingmallforrooftopphotovoltaicpower plants,furthermore,onemustjudgetheweightandtheinfluencenetworkofthecriteria.Agroup ofexpertsconsistingofthreedoctorateengineers(referredtoasE1,E2,E3)wasconstitutedbythe

Symmetry 2018, 10,150

Symmetry 2018, 10, x FOR PEER REVIEW 13 of 21

company.Allthreeexpertspossessmorethan15years’workingexperienceinsolarenergyinvestment field,andarespecializedinsolarphotovoltaicandpowergridtechnologies.Thecollaborationof thealltheexpertswasneeded,thus,apseudo-delphimethodwasappliedinwhicheachexperthas nointeraction.

Considering the development target and the investment capacity of the company, the famous influential large-scale shopping malls located in those cities, with both abundant sunshine and general policy subsidies, have been roughly screened out based on the plentitude of documents and investigation. The investigation involved several potential shopping malls located in Beijing, Shanghai, Guangzhou, Chengdu, Hangzhou, and Nanjing. The experts group met the Development and Reform Commission, the Meteorological Bureau, and the local power supply companies, in order to gather information about solar resources, city planning and construction, local solar subsidy policies, distributed solar power planning, economic assessment, and approved shopping mall rooftops for construction. There are four potential shopping malls picked out after the first filter, and they are the Golden Resources shopping mall in Beijing, Super Brand Mall in Shanghai, Deji Plaza in Nanjing, Jiangsu province, The Mixc shopping mall in Shenzhen, Guangdong province (hereafter referred to as X1, X2, X3, X4), as shown in Figure 3.

Consideringthedevelopmenttargetandtheinvestmentcapacityofthecompany,thefamous influentiallarge-scaleshoppingmallslocatedinthosecities,withbothabundantsunshineand generalpolicysubsidies,havebeenroughlyscreenedoutbasedontheplentitudeofdocuments andinvestigation.TheinvestigationinvolvedseveralpotentialshoppingmallslocatedinBeijing, Shanghai,Guangzhou,Chengdu,Hangzhou,andNanjing.TheexpertsgroupmettheDevelopment andReformCommission,theMeteorologicalBureau,andthelocalpowersupplycompanies,inorder togatherinformationaboutsolarresources,cityplanningandconstruction,localsolarsubsidypolicies, distributedsolarpowerplanning,economicassessment,andapprovedshoppingmallrooftopsfor construction.Therearefourpotentialshoppingmallspickedoutafterthefirstfilter,andtheyarethe GoldenResourcesshoppingmallinBeijing,SuperBrandMallinShanghai,DejiPlazainNanjing, Jiangsuprovince,TheMixcshoppingmallinShenzhen,Guangdongprovince(hereafterreferredtoas X1,X2,X3,X4),asshowninFigure 3

Figure 3. The alternative shopping malls geography distribution

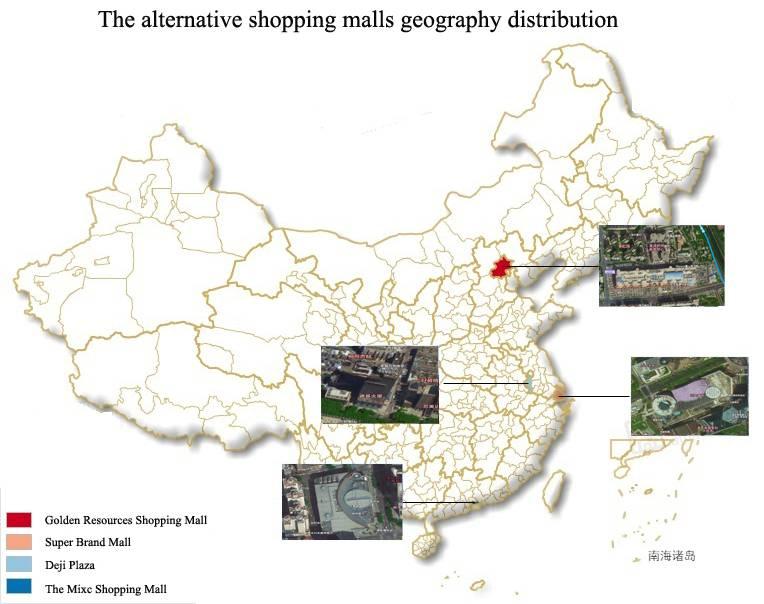
Figure3. Thealternativeshoppingmallsgeographydistribution.

Firstly, based on the evaluation criteria, the influence of each criteria to the other one criteria was accessed by the experts. Then, the three experts discussed with each other and obtained a consensus about the influence of each criteria, as shown in Table 2. According to the DEMANTEL method, the weight of criteria and subcriteria was calculated based on Equations (15)–(21), and shown in Table 2. For the intuitive and simple understanding and analysis of the criteria and subcriteria, Figures 4 and 5 were drawn. As shown in Figure 4, the horizontal axis represents the importance of a criteria, while the vertical axis indicates the influence between the criteria, and the arrow is from the sender of this influence to the receiver. As we can see, the (b) economy (0.286) obtained the most importance, but was vulnerable to other criteria. The (a) architectural element and (c) climate (0.88) seemed not particularly important, however, they had significant direct impacts to the other four criteria. The (f) risk (0.188), (d) photovoltaic array (0.162), and (e) contribution (0.151) were considered of medium importance, and among them, (f) and (d) had more of an impact, while (e) received more impact. Horizontal histogram clearly and intuitively shows the weight of each subcriteria in Figure 5. It is obvious that the (b1) Total investment, (b2) Total profit, and (b3). Annual rate of return acquired the highest weight, in addition to the (f4) Government subsidies reduction, (e2) Publicity effects and (d2). PV area was considered to be less but also very important. Therefore, it can be imagined that the SMPV plan alternatives which obtained high scores in these criteria are more likely to win the competition

Firstly,basedontheevaluationcriteria,theinfluenceofeachcriteriatotheotheronecriteria wasaccessedbytheexperts.Then,thethreeexpertsdiscussedwitheachotherandobtaineda consensusabouttheinfluenceofeachcriteria,asshowninTable 2.AccordingtotheDEMANTEL method,theweightofcriteriaandsubcriteriawascalculatedbasedonEquations(15)–(21),andshown inTable 2.Fortheintuitiveandsimpleunderstandingandanalysisofthecriteriaandsubcriteria, Figures 4 and 5 weredrawn.AsshowninFigure 4,thehorizontalaxisrepresentstheimportanceof acriteria,whiletheverticalaxisindicatestheinfluencebetweenthecriteria,andthearrowisfrom thesenderofthisinfluencetothereceiver.Aswecansee,the(b)economy(0.286)obtainedthemost importance,butwasvulnerabletoothercriteria.The(a)architecturalelementand(c)climate(0.88) seemednotparticularlyimportant,however,theyhadsignificantdirectimpactstotheotherfour criteria.The(f)risk(0.188),(d)photovoltaicarray(0.162),and(e)contribution(0.151)wereconsidered ofmediumimportance,andamongthem,(f)and(d)hadmoreofanimpact,while(e)receivedmore

Symmetry 2018, 10,150 13of20

impact.HorizontalhistogramclearlyandintuitivelyshowstheweightofeachsubcriteriainFigure 5. Itisobviousthatthe(b1)Totalinvestment,(b2)Totalprofit,and(b3).Annualrateofreturnacquiredthe highestweight,inadditiontothe(f4)Governmentsubsidiesreduction,(e2)Publicityeffectsand(d2). PVareawasconsideredtobelessbutalsoveryimportant.Therefore,itcanbeimaginedthattheSMPV planalternativeswhichobtainedhighscoresinthesecriteriaaremorelikelytowinthecompetition.

Symmetry 2018, 10, x FOR PEER REVIEW 15 of 21

Roof pitch and orientation PV roof space Total profit Pay back year Land surface temperature

0.023 0.028 0.037 0.064 0.075 0.074 0.074 0.054 0.030 0.042 0.039 0.056 0.032 0.034 0.050 0.057 0.043 0.046 0.039 0.048 0.054

0.023 0.028 0.037 0.064 0.075 0.074 0.074 0.054 0.030 0.042 0.039 0.056 0.032 0.034 0.050 0.057 0.043 0.046 0.039 0.048 0.054

Figure 4. The weights of subcriteria

Figure 4. The weights of subcriteria.

D-R D+R

(c) Climate (0.125) (f) Risk (0.188) (d) Photovoltaic array (0.162) (e) Contribution （0.151）

-3.5 -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 0 1 2 3 4 5 6 7 8 9

D-R D+R

(a)Architectural elements (0.088) (b) Economy (0.286)

(c) Climate (0.125) (f) Risk (0.188) (d) Photovoltaic array (0.162) (e) Contribution （0.151）

Figure 5. Influential network relationship map within systems

Figure5. Influentialnetworkrelationshipmapwithinsystems.

Secondly, there are two types of criteria, one is quantitative, and the other is qualitative. On one hand, for the quantitative subcriteria, searching from the NASA atmospheric science data center, the data for c1, c2, c3 were obtained. Through using the Google earth map, the roof space data were obtained. Then, according to Equations (1)–(8), the data for a3, b1–b4, d2, d3 were estimated. Because the Equations (1)–(8) are just for rough estimate, these data were not highly accurate. Considering the uncertainty and fuzziness of the data, Equation (25) was used to turn the numerical value into an IVNN value. The performance scores of the quantitative subcriteria are shown in Table 3. On the other hand, for the qualitative subcriteria, the experts group devoted their efforts to investigate the alternative plans and evaluate the performance score for the subcriteria a1, a2, d1, d4, e1–e3, f1–f4. The performance scores of the qualitative subcriteria were shown in Table 4. In addition, the subcriteria were divided into positive and negative. The score of positive criteria higher and negative criteria lower means the alternative better. In this paper, subcriteria b1, d4, f1, f3, f4 are negative and the others are positive.

Figure 5. Influential network relationship map within systems.

Secondly,therearetwotypesofcriteria,oneisquantitative,andtheotherisqualitative.Onone hand,forthequantitativesubcriteria,searchingfromtheNASAatmosphericsciencedatacenter, thedataforc1,c2,c3wereobtained.ThroughusingtheGoogleearthmap,theroofspacedata wereobtained.Then,accordingtoEquations(1)–(8),thedatafora3,b1–b4,d2,d3wereestimated. BecausetheEquations(1)–(8)arejustforroughestimate,thesedatawerenothighlyaccurate. Consideringtheuncertaintyandfuzzinessofthedata,Equation(25)wasusedtoturnthenumerical valueintoanIVNNvalue.TheperformancescoresofthequantitativesubcriteriaareshowninTable 3 Ontheotherhand,forthequalitativesubcriteria,theexpertsgroupdevotedtheireffortstoinvestigate thealternativeplansandevaluatetheperformancescoreforthesubcriteriaa1,a2,d1,d4,e1–e3,f1–f4. TheperformancescoresofthequalitativesubcriteriawereshowninTable 4.Inaddition,thesubcriteria weredividedintopositiveandnegative.Thescoreofpositivecriteriahigherandnegativecriteria lowermeansthealternativebetter.Inthispaper,subcriteriab1,d4,f1,f3,f4arenegativeandtheothers arepositive.

Secondly, there are two types of criteria, one is quantitative, and the other is qualitative. On one hand, for the quantitative subcriteria, searching from the NASA atmospheric science data center, the data for c1, c2, c3 were obtained. Through using the Google earth map, the roof space data were obtained. Then, according to Equations (1)–(8), the data for a3, b1–b4, d2, d3 were estimated. Because the Equations (1)–(8) are just for rough estimate, these data were not highly accurate. Considering the uncertainty and fuzziness of the data, Equation (25) was used to turn the numerical value into an IVNN value. The performance scores of the quantitative subcriteria are shown in Table 3. On the other hand, for the qualitative subcriteria, the experts group devoted their efforts to investigate the alternative plans and evaluate the performance score for the subcriteria a1, a2, d1, d4, e1–e3, f1–f4. The performance scores of the qualitative subcriteria were shown in Table 4. In addition, the subcriteria were divided into positive and negative. The score of positive criteria higher and negative criteria lower means the alternative better. In this paper, subcriteria b1, d4, f1, f3, f4 are negative and the others are positive.

Table2. Thescoreofinfluenceamongeachsubcriteria.

a1a2a3b1b2b3b4c1c2c3d1d2d3d4e1e2e3f1f2f3f4DRW a1034111100400000410000 0.500.03 0.023 a2205322202401000000000 0.600.05 0.028 a3000554400003112320000 0.750.25 0.037 b1000035500033224441100 0.891.05 0.064 b2000005500001115420203 0.681.47 0.075 b3000000200001115420203 0.491.51 0.074 b4000002000001224331102 0.501.51 0.074 c1000555505533021021012 1.160.08 0.054 c2000444400022010000010 0.580.27 0.030 c3000444403003030020010 0.720.54 0.042 d1000333300403110013002 0.710.47 0.039 d2000253300030012245003 0.820.90 0.056 d3000153300432031000000 0.640.26 0.032 d4000153300333001000000 0.570.48 0.034 e1000110000000000412003 0.301.05 0.050 e2000210000000002013304 0.421.17 0.057 e3000000000000000503204 0.360.86 0.043 f1000354400005001220003 0.740.66 0.046 f2005554400002002200000 0.740.39 0.039 f3000154455544001001000 1.040.06 0.048 f4000555500001002223000 0.750.91 0.054

Table3. IVNNperformancescoresofalternativeSMPVplansonthequantitativesubcriteria.

SubcriteriaS1S2S3S4

(a3) ([0.90,0.90],[0.10,0.10],[0.00,0.00])([0.32,0.32],[0.04,0.04],[0.65,0.65])([0.26,0.26],[0.03,0.03],[0.71,0.71])([0.42,0.42],[0.05,0.05],[0.54,0.54]) (b1) ([0.41,0.41],[0.10,0.10],[0.49,0.49])([0.70,0.70],[0.08,0.06],[0.23,0.25])([0.26,0.26],[0.03,0.03],[0.71,0.71])([0.50,0.50],[0.06,0.06],[0.44,0.44]) (b2) ([0.90,0.90],[0.03,0.03],[0.07,0.07])([0.40,0.40],[0.04,0.06],[0.56,0.54])([0.90,0.90],[0.10,0.10],[0.00,0.00])([0.53,0.53],[0.05,0.05],[0.42,0.42]) (b3) ([0.90,0.90],[0.03,0.03],[0.07,0.07])([0.65,0.65],[0.07,0.07],[0.28,0.28])([0.53,0.53],[0.06,0.06],[0.41,0.41])([0.63,0.63],[0.07,0.07],[0.30,0.30]) (b4) ([0.90,0.90],[0.03,0.03],[0.07,0.07])([0.72,0.72],[0.08,0.08],[0.20,0.20])([0.60,0.60],[0.07,0.07],[0.33,0.33])([0.60,0.60],[0.07,0.07],[0.33,0.33]) (c1) ([0.90,0.90],[0.03,0.03],[0.07,0.07])([0.79,0.79],[0.10,0.10],[0.11,0.11])([0.81,0.81],[0.09,0.09],[0.10,0.10])([0.81,0.81],[0.09,0.09],[0.09,0.09]) (c2) ([0.53,0.53],[0.06,0.06],[0.41,0.41])([0.70,0.70],[0.08,0.08],[0.22,0.22])([0.62,0.62],[0.07,0.07],[0.31,0.31])([0.90,0.90],[0.10,0.10],[0.00,0.00]) (c3) ([0.90,0.90],[0.03,0.03],[0.07,0.07])([0.71,0.71],[0.08,0.08],[0.21,0.21])([0.69,0.69],[0.08,0.08],[0.23,0.23])([0.73,0.73],[0.08,0.08],[0.19,0.19]) (d2) ([0.90,0.90],[0.03,0.03],[0.07,0.07])([0.53,0.53],[0.06,0.06],[0.41,0.41])([0.41,0.41],[0.05,0.05],[0.54,0.54])([0.74,0.74],[0.08,0.08],[0.17,0.17]) (d3) ([0.90,0.90],[0.03,0.03],[0.07,0.07])([0.47,0.47],[0.05,0.05],[0.48,0.48])([0.37,0.37],[0.04,0.04],[0.59,0.59])([0.67,0.67],[0.07,0.07],[0.25,0.25])

Table4. IVNNperformancescoresofalternativeSMPVplansonthequalitativesubcriteria.

SubcriteriaX1X2X3X4

(a1) ([0.45,0.56],[0.18,0.30],[0.13,0.50])([0.68,0.79],[0.18,0.30],[0.13,0.50])([0.56,0.68],[0.18,0.24],[0.38,0.67])([0.79,0.90],[0.12,0.18],[0.25,0.50]) (a2) ([0.50,0.50],[0.06,0.06],[0.44,0.44])([0.85,0.85],[0.09,0.09],[0.06,0.06])([0.80,0.80],[0.09,0.09],[0.12,0.12])([0.90,0.90],[0.10,0.10],[0.00,0.00]) (d1) ([0.80,0.90],[0.15,0.23],[0.13,0.33])([0.50,0.60],[0.23,0.30],[0.38,0.67])([0.40,0.60],[0.15,0.23],[0.25,0.50])([0.60,0.80],[0.23,0.30],[0.25,0.50]) (d4) ([0.20,0.23],[0.12,0.20],[0.25,0.33])([0.45,0.60],[0.20,0.30],[0.13,0.17])([0.60,0.90],[0.15,0.20],[0.13,0.14])([0.30,0.45],[0.10,0.12],[0.20,0.50]) (e1) ([0.70,0.90],[0.08,0.15],[0.21,0.33])([0.50,0.60],[0.23,0.30],[0.36,0.58])([0.30,0.50],[0.08,0.15],[0.43,0.58])([0.60,0.80],[0.15,0.30],[0.14,0.25]) (e2) ([0.50,0.60],[0.23,0.30],[0.33,0.75])([0.70,0.80],[0.15,0.23],[0.33,0.75])([0.70,0.90],[0.15,0.23],[0.17,0.50])([0.80,0.90],[0.15,0.23],[0.17,0.50]) (e3) ([0.79,0.90],[0.12,0.18],[0.17,0.50])([0.68,0.90],[0.06,0.12],[0.17,0.75])([0.68,0.79],[0.18,0.24],[0.33,0.75])([0.68,0.79],[0.24,0.30],[0.33,0.75]) (f1) ([0.30,0.45],[0.20,0.26],[0.33,0.43])([0.45,0.90],[0.26,0.30],[0.38,0.43])([0.23,0.45],[0.20,0.23],[0.38,0.43])([0.30,0.90],[0.23,0.26],[0.38,0.50]) (f2) ([0.45,0.68],[0.08,0.15],[0.44,0.56])([0.45,0.68],[0.15,0.23],[0.39,0.56])([0.23,0.45],[0.15,0.23],[0.44,0.56])([0.68,0.90],[0.23,0.30],[0.33,0.44]) (f3) ([0.23,0.26],[0.12,0.20],[0.25,0.33])([0.60,0.90],[0.20,0.30],[0.13,0.17])([0.60,0.90],[0.15,0.20],[0.13,0.14])([0.30,0.45],[0.10,0.12],[0.20,0.50]) (f4) ([0.30,0.34],[0.15,0.30],[0.25,0.50])([0.30,0.39],[0.15,0.30],[0.17,0.25])([0.68,0.90],[0.03,0.04],[0.13,0.25])([0.68,0.90],[0.04,0.05],[0.17,0.25])

Thirdly,basedontheweightofthesub-criteriaandtheIVNNscoresofeachalternativeoneach subcriteria,thefinalcompositescoreswerecalculatedbyimprovedELECTRICIIImethod.Afterbeing toldthat qj istheindifferencethreshold, pj isthepreferencethresholdand vj isthevetothreshold, theexpertsgroupsuggestedthat ∑ s(ai, ak ) ∑ s(ak, ai )(k = 1,2 ... n),respectively.Theconcordance index c(Xi, Xk ) andthepartialconcordanceindex cj(Xi, Xk ) werecalculatedbyEquations(26)and(27), asshowninTable 5.Thediscordanceindex dj (Xi, Xk ) wasachievedbyEquation(28),asshownin Table 6.Then,overallconcordanceandpartialdiscordanceindiceswasobtainedbyEquation(29) asshowninTable 7.Finally,thedegreeofcredibilityoftheoutrankingrelationwascalculatedby Equation(30),andtherankingsofalternativeX1,X2,X3,X4wasshowninTable 8

FromTable 8,theSMPVplanX1oftheGoldenResourcesshoppingmallinBeijingistheoptimal selection.ThealternativeX1isparticularlysuperiortootheralternativeplansintermsoftheeconomy, photovoltaicarray,andcontributioncriteria,whilethesethreecriteriaweighedmorethanahalfofthe entirecriteriaweights,sothereisnodoubtthatplanX1obtainedthebestposition.However,planX1 performsbadlyintheriskandarchitecturalelementscriteria.Respectively,PlanX2havestrengthon theeconomy,butareweakonphotovoltaiccriteria.Yet,planX2ismuchbetterthanplanX3andX4, sothatitcanbethestand-bychoice.

Table5. TheconcordanceindexandthepartialconcordanceindexforeachpairofSMPVplans.

a1a2a3b1b2b3b4c1c2c3d1

c(X1 ≥ X2)0.000.001.000.001.000.620.430.240.000.460.83 c(X1 ≥ X3)0.050.001.000.360.000.920.740.200.000.500.61 c(X1 ≥ X4)0.000.001.000.000.930.680.740.190.000.410.45 c(X2 ≥ X1)0.260.850.000.700.000.000.000.000.410.000.00 c(X2 ≥ X2)0.340.100.111.000.000.260.280.000.190.010.00 c(X2 ≥ X3)0.000.000.000.470.000.020.280.000.000.000.00 c(X3 ≥ X1)0.000.720.000.000.000.000.000.000.200.000.00 c(X3 ≥ X2)0.000.000.000.001.000.000.000.010.000.000.19 c(X3 ≥ X4)0.000.000.000.000.930.000.000.000.000.000.00 c(X4 ≥ X1)0.440.990.000.190.000.000.000.000.920.000.00 c(X4 ≥ X2)0.150.110.220.000.300.000.000.020.480.020.35 c(X4 ≥ X3)0.520.240.370.590.000.210.000.000.690.050.13 d2d3d4e1e2e3f1f2f3f4C c(X1 ≥ X2)0.911.000.000.740.000.120.000.030.000.000.38 c(X1 ≥ X3)1.001.000.000.780.000.460.020.350.000.000.40 c(X1 ≥ X4)0.370.550.000.140.000.540.000.000.000.000.32 c(X2 ≥ X1)0.000.000.440.000.320.000.260.000.700.210.18 c(X2 ≥ X2)0.280.230.000.010.000.300.320.290.000.000.19 c(X2 ≥ X3)0.000.000.240.000.000.380.060.000.530.000.11 c(X3 ≥ X1)0.000.000.850.000.660.000.000.000.811.000.19 c(X3 ≥ X2)0.000.000.370.000.300.000.000.000.080.810.16 c(X3 ≥ X4)0.000.000.650.000.000.050.000.000.650.000.13 c(X4 ≥ X1)0.000.000.170.000.720.000.170.220.131.000.20 c(X4 ≥ X2)0.510.490.000.560.370.000.000.280.000.780.21 c(X4 ≥ X3)0.820.750.000.610.030.000.220.600.000.000.25

Table6. ThediscordanceindexforeachpairofSMPVplans.

d(Xi ≥ Xj)a1a2a3b1b2b3b4c1c2c3d1 d(X1 ≥ X2)0.000.001.000.000.910.470.340.210.000.360.61 d(X1 ≥ X3)0.080.001.000.300.020.680.560.190.000.390.46 d(X1 ≥ X4)0.000.000.880.000.680.510.560.170.000.330.35 d(X2 ≥ X1)0.220.630.000.520.000.000.000.000.330.000.00 d(X2 ≥ X2)0.280.110.120.800.000.230.240.000.170.050.00 d(X2 ≥ X3)0.000.000.000.370.000.060.240.000.000.000.00 d(X3 ≥ X1)0.000.540.000.000.020.000.000.000.180.000.00 d(X3 ≥ X2)0.000.000.000.000.910.000.000.050.000.000.17 d(X3 ≥ X4)0.000.000.000.000.680.000.020.010.000.000.00 d(X4 ≥ X1)0.350.720.000.180.000.000.000.000.680.000.00 d(X4 ≥ X2)0.150.120.200.000.250.000.000.060.370.060.29 d(X4 ≥ X3)0.410.210.300.450.000.190.020.030.520.080.13 d(Xi ≥ Xj)d2d3d4e1e2e3f1f2f3f4 d(X1 ≥ X2)0.670.780.000.550.000.130.000.060.000.00 d(X1 ≥ X3)0.890.960.000.580.000.360.060.290.000.00 d(X1 ≥ X4)0.300.430.000.140.000.410.000.000.000.00 d(X2 ≥ X1)0.000.000.350.000.270.000.230.000.520.19 d(X2 ≥ X2)0.240.200.000.050.000.250.260.250.000.00 d(X2 ≥ X3)0.000.000.210.000.000.310.090.000.410.00 d(X3 ≥ X1)0.000.000.630.000.500.000.000.000.600.77 d(X3 ≥ X2)0.000.000.300.000.250.000.000.000.100.60 d(X3 ≥ X4)0.000.000.490.000.000.080.000.000.490.05 d(X4 ≥ X1)0.000.000.160.000.540.000.160.190.130.75 d(X4 ≥ X2)0.390.380.000.430.300.000.000.240.000.58 d(X4 ≥ X3)0.610.560.000.460.070.000.200.460.000.00

Table7. TheoverallconcordanceandpartialdiscordanceindicesforeachpairofSMPVplans.

s(Xi ≥ Xj)a1a2a3b1b2b3b4c1c2c3d1 s(X1 ≥ X2)1.621.670.001.670.150.881.101.321.671.070.64 s(X1 ≥ X3)1.541.670.001.181.630.540.741.361.671.020.90 s(X1 ≥ X4)1.481.480.181.480.470.730.661.221.481.000.96 s(X2 ≥ X1)0.950.451.220.581.221.221.221.220.821.221.22 s(X2 ≥ X2)0.881.091.080.251.230.950.941.231.021.171.23 s(X2 ≥ X3)1.121.121.120.701.121.050.851.121.121.121.12 s(X3 ≥ X1)1.230.571.231.231.201.231.231.231.011.231.23 s(X3 ≥ X2)1.191.191.191.190.101.191.191.131.191.190.98 s(X3 ≥ X4)1.141.141.141.140.361.141.121.131.141.141.14 s(X4 ≥ X1)0.820.341.251.031.251.251.251.250.401.251.25 s(X4 ≥ X2)1.091.121.021.270.951.271.271.200.801.200.91 s(X4 ≥ X3)0.791.060.940.731.331.081.301.290.641.221.16 s(Xi ≥ Xj)d2d3d4e1e2e3f1f2f3f4s s(X1 ≥ X2)0.550.361.670.751.671.451.671.561.671.670.38 s(X1 ≥ X3)0.190.061.670.691.671.071.571.191.671.670.40 s(X1 ≥ X4)1.040.851.481.271.480.871.481.481.481.480.32 s(X2 ≥ X1)1.221.220.791.220.891.220.941.220.580.980.18 s(X2 ≥ X2)0.940.981.231.161.230.920.910.931.231.230.19 s(X2 ≥ X3)1.121.120.881.121.120.781.021.120.661.120.11 s(X3 ≥ X1)1.231.230.461.230.621.231.231.230.490.280.19 s(X3 ≥ X2)1.191.190.831.190.891.191.191.191.070.470.16 s(X3 ≥ X4)1.141.140.581.141.141.061.141.140.581.090.13 s(X4 ≥ X1)1.251.251.051.250.581.251.051.011.080.320.20 s(X4 ≥ X2)0.770.791.270.720.891.271.270.971.270.540.21 s(X4 ≥ X3)0.520.591.330.711.241.331.070.721.331.330.25

Table8. FinalcompositescoresandrankingsofalternativeSMPVplans.

Xi ∑ s(ai ak ) ∑ s(ak ai ) ∆S(ai )

X10.730.290.44 X20.470.370.1 X30320.39 0.07 X40.561.02 0.47

TherankingorderusingELECTRIIIIisX1>X2>X3>X4.Inordertocheckthevalidityofthe results,TOPSISandVIKORmethodswereusedtoreorderthealternativeSMPVplansasshownin Table 9.TheresultobtainedbyTOPSISmethodisX1>X4>X3>X2,whiletheresultachievedby VIKORmethodisX1>X4>X3>X2.fromthesethreerankings,alternativeplanX1istheoptimal selection,nomatterwhatmethodwasused.Thatistosay,thealternativeX1ismuchbetterthan theremainingalternatives,andthereisnodoubtinchoosingX1first.However,therankingsforX2, X3,andX4aredifferentbetweenthesethreemethods.Thereisthevetothreshold,whichindicates whenthevalueofalternativeXiislowerthanthevalueofalternativeXj,andthelowervalueexceeds thevetothreshold,anditisnotrecognizedthatXiispreferredtotheXjingeneral.However,itis theotherterminTOPSISmethodandVIKORmethod,andsomereallybadperformanceinacertain criterioncanbetoleratedandremediedbyothergoodperformancesinothercriteria.Inthatcase, analternativewithsomefataldefectinacertaincriterionofanalternativemaybeneglected,which leadstoanunsatisfactoryselection.Whenanalternativeisvetoedbetterthantheotheralternativein ELECTREIII,itcanstillcomeoutinfrontintheTOPSISandVIKORmethods.ThatwhytheX2,X3, X4rankeddifferentlyinTOPSISandVIKORmethods.

Table9. TherankingsofSMPVplansusingTOPSISandVIKOR.

MethodTOPSISVIKOR

y+y CRankingssrQRankings

X10.621.430.701 2.57 0.120.001 X21.170.470.2941.881.180.9224 X31.350.710.353 1.74 1.060.5262 X40.760.740.4922.741.010.9193

6.Conclusions

TheselectionofSMPVplaniscrucialtotheentirelifeofSMPVproject.Althoughtherehasbeen someresearchonthisissue,severalquestionsstillneedaddressing.Firstly,theinteractionofthecriteria layintheevaluationcriteria.Secondly,thelossofevaluationinformationexitedintheinformation conversionprocess.Thirdly,thecompensationproblembetweenbestandworstperformancein diversecriteriawasnoteasilytoavoided.

Inthispaper,anintegratedMCDMframeworkwasproposedtoaddresstheSMPVplanselection problem.Firstofall,thecompositiveevaluationindexwasconstructed,andtheapplicationof DEMATELmethodhelpedanalyzetheinternalinfluenceandconnectionbehindeachcriterion. Fromtheinfluentialnetwork-relationshipmap,wediscoveredthatthecriteria(b)economyobtained themostimportancebutwasvulnerabletoothercriteriaaswellasthe(a)architecturalelementand(c) climatehadsignificantdirectimpactstotheotherfourcriteria.Thesethreecriteriashouldbethefirstfor thedecisionmakertoconsiderwhenselectingtheSMPVplan.Then,theinterval-valuedneutrosophic setisutilizedtoexpresstheimperfectknowledgeofexpertsgroup.SincetheapplicationofIVNNS, theexpertscanclearlyexpresstheirevaluationinformation,includingtheircertainty,uncertainty, aswellashesitationattitude.Followingthis,anextendedELECTREIIImethodasanoutstanding outrankingmethodwasapplied,anditsucceedinavoidingthecompensationproblemandobtaining thescientificresult.InthecaseofChina,theintegratedmethodhasbeensuccessfullyappliedtoselect

theSMPVplanX1astheoptimalselectionwhichisparticularlysuperiortootheralternativeplansin termsoftheeconomy,photovoltaicarray,andcontributioncriteria.Also,theintegratedmethodused maintainedsymmetryinthesolarPVinvestment.Lastbutnotleast,acomparativeanalysisusing TOPSISmethodandVIKORmethodwascarriedout,andalternativeplanX1ranksfirstatthesame. Theoutcomecertifiedthecorrectnessandrationalityoftheresultsobtainedfromthispaper.

Therefore,thisstudyhasnotonlyservedtoevaluatetheSMPVplans,ithasalsodemonstrated howitispossibletocombineIVNNS,DEMATELmethod,andELECTREIIImethodforapplicationin handlingMCDMproblemsinthefieldofsolarenergy.

AuthorContributions: M.L.designedthedecisionframeworkofshoppingmallphotovoltaicplanselection, andstudiedtheproposedmethod.Then,J.F.collectedtherelativedata,calculatedtheresult,anddraftedthe paper.Next,Y.L.adjustedtheformatofthepaperandformattedthemanuscriptforsubmission.

ConflictsofInterest: Theauthorsdeclarenoconflictofinterest.

References

1. Zhang,L.;Wang,J.;Wen,H.;Fu,Z.;Li,X.OperatingPerformance,IndustryAgglomerationandItsSpatial CharacteristicsofChinesePhotovoltaicIndustry. Renew.Sustain.EnergyRev. 2016, 65,373–386.[CrossRef]

2. Sánchez-Lozano,J.M.;Teruel-Solano,J.;Soto-Elvira,P.L.;García-Cascales,M.S.GeographicalInformation Systems(GIS)andMulti-CriteriaDecisionMaking(MCDM)MethodsfortheEvaluationofSolarFarms Locations:CaseStudyinSouth-EasternSpain. Renew.Sustain.EnergyRev. 2013, 24,544–556.[CrossRef]

3. Zhang,L.;Zhou,P.;Newton,S.;Fang,J.;Zhou,D.;Zhang,L.EvaluatingCleanEnergyAlternativesfor Jiangsu,China:AnImprovedMulti-CriteriaDecisionMakingMethod. Energy 2015, 90,953–964.[CrossRef]

4. Liu,P.;Yu,X.2-DimensionUncertainLinguisticPowerGeneralizedWeightedAggregationOperatorandIts ApplicationinMultipleAttributeGroupDecisionMaking. Knowl.BasedSyst. 2014, 57,69–80.[CrossRef]

5. Kumar,A.;Sah,B.;Singh,A.R.;Deng,Y.;He,X.;Kumar,P.;Bansal,R.C.AReviewofMultiCriteriaDecision Making(MCDM)towardsSustainableRenewableEnergyDevelopment. Renew.Sustain.EnergyRev. 2017, 69,596–609.[CrossRef]

6. Cavallaro,F.;Zavadskas,E.K.;Streimikiene,D.ConcentratedSolarPower(CSP)HybridizedSystems. RankingBasedonAnIntuitionisticFuzzyMulti-CriteriaAlgorithm. J.Clean.Prod. 2018, 179,40416. [CrossRef]

7. Peng,J.J.;Wang,J.Q.;Zhang,H.Y.;Chen,X.H.AnOutrankingApproachforMulti-CriteriaDecision-Making ProblemswithSimplifiedNeutrosophicSets. Appl.SoftComput. 2014, 25,336–346.[CrossRef]

8. Zhang,H.;Wang,J.;Chen,X.AnOutrankingApproachforMulti-CriteriaDecision-MakingProblemswith Interval-ValuedNeutrosophicSets. NeuralComput.Appl. 2016, 27,615–627.[CrossRef]

9. Bausys,R.;Zavadskas,E.K.MulticriteriaDecisionMakingApproachbyVikorunderIntervalNeutrosophic SetEnvironment. Econ.Comput.Econ.Cybern.Stud.Res. 2017, 49,33–48.

10. Zhang,H.Y.;Wang,J.Q.;Chen,X.H.Intervalneutrosophicsetsandtheirapplicationinmulticriteriadecision makingproblems. Sci.WorldJ. 2014, 2014,645953.[CrossRef][PubMed]

11. Zavadskas,E.K.;Govindan,K.;Antucheviciene,J.;Turskis,Z.HybridMultipleCriteriaDecision-Making Methods:AReviewofApplicationsforSustainabilityIssues. Econ.Res.-Ekon.Istraž. 2016, 29,857–887. [CrossRef]

12. Tsai,W.H.;Chou,W.C.SelectingManagementSystemsforSustainableDevelopmentinSmes:ANovel HybridModelBasedonDEMATEL,ANP,andZOGP. ExpertSyst.Appl. 2009, 36,1444–1458.[CrossRef]

13. Xia,X.;Govindan,K.;Zhu,Q.AnalyzingInternalBarriersforAutomotivePartsRemanufacturersinChina UsingGrey-DEMATELApproach. J.Clean.Prod. 2015, 87,811–825.[CrossRef]

14. George-Ufot,G.;Qu,Y.;Orji,I.J.SustainableLifestyleFactorsInfluencingIndustries’ElectricConsumption PatternsUsingFuzzyLogicandDEMATEL:TheNigerianPerspective. J.Clean.Prod. 2017, 162,624–634. [CrossRef]

15. Azzopardi,B.;Martinez-Cesena,E.A.;Mutale,J.DecisionSupportSystemforRankingPhotovoltaic Technologies. IETRenew.PowerGener. 2013, 7,669–679.[CrossRef]

16. Matulaitis,V.;Straukaite,G.;Azzopardi,B.;Martinez-Cesena,E.A.Multi-CriteriaDecisionMakingforPV DeploymentonaMultinationalLevel. Sol.EnergyMater.Sol.Cells 2016, 156,122–127.[CrossRef]

17. Wu,Y.;Zhang,J.;Yuan,J.;Shuai,G.;Haobo,Z.StudyofDecisionFrameworkofOffshoreWindPower StationSiteSelectionBasedonELECTRE-IIIunderIntuitionisticFuzzyEnvironment:ACaseofChina. EnergyConvers.Manag. 2016, 113,66–81.[CrossRef]

18. Colmenar-Santos,A.;Campinez-Romero,S.;Perez-Molina,C.;Mur-Pérez,F.AnAssessmentofPhotovoltaic PotentialinShoppingCentres. Sol.Energy 2016, 135,662–673.[CrossRef]

19. Wu,Y.;Geng,S.Multi-CriteriaDecisionMakingonSelectionofSolar–WindHybridPowerStationLocation: ACaseofChina. EnergyConvers.Manag. 2014, 81,527–533.

20.

Tahri,M.;Hakdaoui,M.;Maanan,M.TheEvaluationofSolarFarmLocationsApplyingGeographic InformationSystemandMulti-CriteriaDecision-MakingMethods:CaseStudyinSouthernMorocco. Renew.Sustain.EnergyRev. 2015, 51,1354–1362.[CrossRef]

21. Long,S.;Geng,S.DecisionFrameworkofPhotovoltaicModuleSelectionunderInterval-ValuedIntuitionistic FuzzyEnvironment. EnergyConvers.Manag. 2015, 106,1242–1250.[CrossRef]

22. Patlitzianas,K.D.;Skylogiannis,G.K.;Papastefanakis,D.AssessingThePVBusinessOpportunitiesinGreece. EnergyConvers.Manag. 2013, 75,651–657.[CrossRef]

23. Das,I.;Bhattacharya,K.;Canizares,C.;Muneer,W.Sensitivity-Indices-BasedRiskAssessmentofLarge-Scale SolarPVInvestmentProjects. IEEETrans.Sustain.Energy 2013, 4,370–378.[CrossRef]

24. Rodrigues,S.;Chen,X.J.;Morgado-Dias,F.EconomicAnalysisofPhotovoltaicSystemsfortheResidential MarketunderChina’sNewRegulation. EnergyPolicy 2017, 101,467–472.[CrossRef]

25. Smarandache,F. AUnifyingFieldinLogics.Neutrosophy:NeutrosophicProbability,SetandLogic;American ResearchPress:Rehoboth,NM,USA,1999.

26. Wang,H.;Smarandache,F.;Zhang,Y.-Q.;Sunderraman,R. IntervalNeutrosophicSetsandLogic:Theoryand ApplicationsinComputing;Hexis:Phoenix,AZ,USA,2005.

27. Lee,Y.C.;Li,M.L.;Yen,T.M.;Huang,T.H.Analysisofadoptinganintegrateddecisionmakingtrialand evaluationlaboratoryonatechnologyacceptancemodel. ExpertSyst.Appl. 2010, 37,1745–1754.[CrossRef]

28. Tzeng,G.H.;Chiang,C.H.;Li,C.W.Evaluatingintertwinedeffectsine-learningprograms:Anovelhybrid MCDMmodelbasedonfactoranalysisandDEMATEL. ExpertSyst.Appl. 2007, 32,1028–1044.[CrossRef]

29. Quader,M.A.;Ahmed,S.;Ghazilla,R.A.R.;Ahmed,S.;Dahari,M.EvaluationofcriteriaforCO2 capture andstorageintheironandsteelindustryusingthe2-tupleDEMATELtechnique. J.Clean.Prod. 2015, 120,207–220.[CrossRef]

30. Bouyssou,D.;Marchant,T.AnaxiomaticapproachtononcompensatorysortingmethodsinMCDM,I: Thecaseoftwocategories. Eur.J.Oper.Res. 2007, 178,217–245.[CrossRef]

© 2018bytheauthors.LicenseeMDPI,Basel,Switzerland.Thisarticleisanopenaccess articledistributedunderthetermsandconditionsoftheCreativeCommonsAttribution (CCBY)license(http://creativecommons.org/licenses/by/4.0/).