Study On Neutrosophic Graph with Application in Wireless Network

CAAITransactionsonIntelligenceTechnology

ResearchArticle

Studyonneutrosophicgraphwithapplication inwirelessnetwork

YaoFei

ISSN2468-2322

Receivedon16thMay2020 Revisedon24thJune2020 Acceptedon29thJune2020 doi:10.1049/trit.2020.0093 www.ietdl.org

CollegeofInformationScienceandTechnology,GansuAgriculturalUniversity,Lanzhou730070,People’sRepublicofChina ✉ E-mail:yaofei111111@sina.com

Abstract: Aneutrosophicnetworkisanextensionofanintuitio nisticfuzzynetworkthat providesmoreprecision compatibilityandflexibilitythananintuitionisticfuzzygraphinstructuringandmodellingmanyreal-lifeproblems.The authorshaveexploredtheuseofaneutrosophicnetwo rkformodellingthepassiveopticalnetwork,mobile adhoc network(MANET),andwirelesssensorgraph.Theyhavepresentedtheideaofstrongarc,weakarcstrongdomination numbers,andstrongperfectdominationofneutrosophicnetwork.Theyhavedescribedthemethodtofindthevalues ofstrongandstrongperfectdominationofneutrosophicn etwork.Finally,theyuseth eideaofastrongarcstrong dominationnumberinMANETandwirelesssensorgraphs.

1Introduction

Graphtheories[1–3]haveseveralreal-lifeapplicationsintheareaof computerscience,transportation,physics,systemsanalysis,biology, economics,astronomy,andoperationsresearch.Inthoseproblems, thegraphemergesasamathematicalgraphicalmodelofthe observedreal-lifeproblems.Let G= (V , E )beagraph,where V representsthenon-emptysetofallnodes/verticesand E represents thesetofallarcs/edgesofthegraph G.Twonodes k and l ina graph G aredefinedasanadjacentnodein G ifandonlyif(k , l )is anarcof G.Thegraph G isasimplegraphif G hasnomultiple arcsandloops.Asimplegraph G issaidtobeacompletegraphif andonlyifeverypairofdistinctnodesof G isjoinedbyanarc. Ifthecompletegraph G has n numberofnodesthenithasalways n(n 1)/2arcs.Inthisstudy,wehaveworkedondifferenttypes ofneutrosophicnetworks.Manydecision-makingproblems, e.g.trafficplanning,texturemapping,shortestpathproblem, spanningtreeproblemetc.canbemodelledasagraph,which consistsofobjects/items/elementsandrelationships.Expertsuse thenodesofthegraphtorepresenttheobjects/items/elementsand edgestorepresenttherelationshipbetweenobjectsoftheproblem. Inalmosteverydecision-makingproblem,theusableinformation isgenerallyapproximateorimpreciseduetomanydistinctreasons suchaslackofevidence,imperfectstatisticalinformation,lossof information,inaccuratedata,andinsufficientinformation.

Thebasicideaofthecrispsettheoryhasbeenintroducedby Cantor,whichisusedinclassicalgraphtheory.Inagraph,forany nodeorarc,thereexisttwodistinctpossibilities:the firstone eitherpresentinthegraphorisnotpresentinthegraph.Owingto thisreason,thesimplegraphtheoryisunabletomodeluncertain real-lifeproblemsproperly.Fuzzyset[4]isanupperversionofa crispset,whereeachandeveryitem/elementshavevarying membershipgrade.Itcanshowthatitselementshavedistinct membershipgradesbetweenintervals1and0.Theideaof membershipdegreesisdifferentfromprobability.

TheideaofafuzzygraphhasbeenpresentedbyKaufmann[5] usingthefuzzyrelation.In[6],Rosenfeldhasdescribedthe variousideasoffuzzybridges,fuzzycycles,fuzzypaths,fuzzy trees,andfuzzyconnectednesstoafuzzygraphandpresented someofthepropertiesofthem.Severalmathematicians,suchas RashmanlouandPal[7],SamantaandPal[8],GhoraiandPal[9], Paramik etal.[10],Rashmanlou etal. [11, 12],Nandhiniand Nandhini[13],andBorzooei etal.[14]haveresearchedalotin theareaofthefuzzygraphanditsapplicationsinreal-life

problems.Atanassov[15–17]haspresentedthenewtypeoffuzzy set,i.e.intuitionisticfuzzyset,asamodificationoftype1fuzzy set.Thetype1fuzzysetshaveonlyasinglemembershipgrade; however,theintuitionisticfuzzysetalwaysconsiderstwo independentmembershipgrades:membershipgradeand non-membershipgradeforeachandeveryelement.Shannonand Atanassov[18]haveforthe firsttimedescribedtheconceptof intuitionisticfuzzysetrelationshipandintuitionisticfuzzygraphs. Theyhavepresentedseveralproprieties,theorems,andprovedin [18].Forfurtherstudyonintuitionisticfuzzygraphs,pleaserefer to[19–25].However,thefuzzygraphandintuitionisticfuzzy graphbothareemployedtorepresentmanyreal-lifeproblems,but uncertaintyduetotheinconsistentinformationandindeterminate informationofanyreal-lifedecision-makingproblemcannotbe handledpreciselybyafuzzygraphorintuitionisticfuzzygraph. Therefore,anexpertrequiresothernewconceptstohandlethese scenarios.

In[26],Smarandachehasdescribedtheneutrosophicset,by extendingtheideaofafuzzyset.Itcanmanagewith indeterminate,vague,uncertain,andinconsistentdataofany real-worldproblem.Theneutrosophicsetismainlyanextension oftheclassicalset,fuzzyset,andintuitionisticfuzzyset.A neutrosophicset[27–34]hasthreemembershipgrades:truth, indeterminate,andfalseofeachandeveryelement.Thosethree membershipgradesarealwaysindependentandliebetweenthe interval]0,1[.In[27],theauthorsintroducedamodifiedscore functionto findtherankofthesingle-valuedneutrosophicsetas wellastheinterval-valuedneutrosophicset.Theyhavealso describedadecision-makingmethodbasedontheproposed function.GargandNancy[28]introducedanon-linear programmingmodelto findthesolutionstoadecision-making probleminwhichparametersarerepresentedbyinterval neutrosophicnumbers.GargandNancy[29]describesomenew aggregatingoperatorsforneutrosophicinformation.Theyhave usedthoseoperatorsto findthesolutiontothemulti-criteria decision-makingproblems.GargandNancy[28]introducedsome hybridaggregationoperatorsusingarithmeticaggregation operatorsandgeometricaggregationoperators.Theyhavealso presentedadecision-makingapproachtosolvethemulti-criteria decision-makingproblem.

Thesingle-valuedneutrosophicsetsareappliedtographtheory andpresentanewtypeofgraphicalstructurewhichisdefinedasa single-valuedneutrosophicgraph.Theideaofneutrosophicgraph theory(NGT)isbasedonneutrosophicrelationships.TheNGT

CAAITrans.Intell.Technol.,2020,Vol.5,Iss.4,pp.301–307 301 ThisisanopenaccessarticlepublishedbytheIET,ChineseAssociationforArtificialIntelligenceand ChongqingUniversityofTechnologyundertheCreativeCommonsAttribution-NoDerivsLicense(http://creativecommons.org/licenses/bynd/3.0/)

canbeappliedtomodeltherelationshipsbetweenseveral objects/individualsinreal-lifeproblems.Adecision-makermay usetheNGTinnumerousreal-lifeapplicationsindiverseareas suchasmodernengineeringandsciences,databasetheory, imageprocessing,datamining,artificialneuralnetworks,cluster analysis,expertsystems,andcontrolsystems.Itisanextension ofcrispgraphtheory,fuzzygraphtheory,andintuitionistic fuzzygraphtheory.TheideaofNGTisamoreefficient graphicalrepresentingmethodfordealingwithinconsistency, indeterminacy,anduncertaintiesinthereal-lifeinformation comparedtofuzzygraphandintuitionisticfuzzygraph. Neutrosophicgraph[9, 35]canefficientlyrepresentthereal-life problem.Severalresearchershaverecentlyresearchedneutrosophic networktheory,forinstance,Yang etal. [36],Borzooei etal.[37], Naz etal. [38],Ye[39],Wang[40],Arkam etal.[41],Arkam [42],PrasertpongandSiripitukdet[43],AkramandSiddique[44], andAkrama[45].

Thedominationnumberisusefulinformationtoanalyseany graph.Borzooei etal.[46]describedthenewideasofdominating setsforvaguegraphsanddescribedtheideaofstrongvague dominationnumbersforvaguegraphs.Theneutrosophicgraphis morepreciseand flexibletomodelthedecision-makingproblem whenitcompareswiththevaguegraphmodel.Thus,the importanceofconsideringneutrosophicnetworksareinevitable tomodelthemanydecision-makingproblems[39, 44, 47–52]in real-worldscenariosanditisrequiredtointroducetheideaof strongarc,weakarcstrongdominationnumbers,andstrong perfectdominationoftheneutrosophicnetwork.Inthisstudy, wehavedescribedseveralideasoftheneutrosophicnetwork. Then,wehaveintroducedtheideaofstrongarc,weakarcstrong dominationnumbers,andstrongperfectdominationofthe neutrosophicnetwork.Wehaveexploredtheuseofaneutrosophic networkformodellingthepassivemobile adhoc graph[mobile adhoc network(MANET)]andwirelesssensorgraph.Wehave describedthemethodto findthevaluesofstrongandstrong perfectdominationoftheneutrosophicnetwork.

2Preliminaries

Definition2: Aneutrosophicnetwork G=K, L () isdefinedasa strongneutrosophicnetworkif

(), IL k , l () = IK k () ^ IK l (), FL k , l ()= FK k () _ FK l ()∀k , l [ E (3)

Definition3: Let GK, L () beaneutrosophicnetwork.Anedge kl in G iscalledaneffectiveedgeif

T L kl ()=F K k () ^ F K l () T L kl ()=F K k () ^ F K l () F L kl ()=F K k () _ F K l () (4)

Definition4: Aneutrosophicnetwork G iscalledastrong neutrosophicnetworkif

T L kl ()=F K k () ^ F K l ()

T L kl ()=F K k () ^ F K l ()

F L kl ()=F K k () _ F K l ()∀kl [ E

Aneutrosophicnetworkisastrongneutrosophicnetworkifeachand everyedgehaseffectiveedges.

Definition5: Aneutrosophicnumber G iscalledacomplete neutrosophicnetworkifforevery k , l [ V ,

T L kl ()=F K k () ^ F K l () T L kl ()=F K k () ^ F K l () F L kl ()=F K k () _ F K l () (6)

Acompleteneutrosophicnetworkwith n verticesisrepresented by Kn

3Strongandweakneutrosophicedges

Definition6: Let GK, L () beaneutrosophicnetwork.

(i)Aneutrosophicpath p in G isacollectionofdifferentvertices y0 , y1 , y2 , , yl 1 , yl suchthat T L yi 1 yi , I L yi 1 yi , F L yi 1 yi . 0, i = 1, , l (7)

Here l describesthelengthofthepath p.Thetwonodes k and l areconnectedbyapathwithlength l suchas ˜ p:x = x0 , x1 , x2 , ..., xl 1 , xk = y then T k L kl (), I k L kl (),and F k L kl () are determinedby

T l L kl (), I l L kl (), F l L kl () = sup T L x, x1 ^ T L x1 , x2 ^ ^ T L xl 1 , y , inf I L x, x1 _ I L x1 , x2 _ _ I L xl 1 , y , inf F L x, x1 _ F L x1 , x2 _ ... _ F L xl 1 , y

(8)

Thestrengthofneutrosophicconnectednessbetweenanytwo neutrosophicnodes(k and l )withinaneutrosophicnetwork G is definedasfollows: T 1 L kl (), I 1 L kl (), F 1 L kl () = sup l [N T l L kl () ,inf l [N F l L kl () ,inf l [N F l L kl () (9)

Definition7: Anedge kl in G iscalledastrongedgeifandonly if T L kl ()≥T 1 L kl (), I L kl ()≤I 1 L kl (),and F L kl ()≤F 1 L kl (). Forany k, l [ V ,ifandonlyifthereexistsanystrongedge betweenthenodes k and l thenthenode k isdominatedbythe node l in G

Definition8: LetNDSbeaneutrosophicsubsetofthevertices V in G NDSissaidtobeaneutrosophicdominatingsetif,forall y [ V \NDS ,thereexistsomeneutrosophicnodes x [ NDS suchthatnode k dominatesnode y.Aneutrosophicdominating setNDSin G iscalledaminimalneutrosophicdominatingset ifthereexistsnopropersubsetofNDSinaneutrosophic dominatingset.

CAAITrans.Intell.Technol.,2020,Vol.5,Iss.4,pp.301–307 302ThisisanopenaccessarticlepublishedbytheIET,ChineseAssociationforArtificialIntelligenceand ChongqingUniversityofTechnologyundertheCreativeCommonsAttribution-NoDerivsLicense(http://creativecommons.org/licenses/ by-nd/3.0/)

Inthissection,theneutrosophicstrongandneutrosophic strongneighbourhooddominationnumbersaredefinedforthe neutrosophicnetwork.Wepresenttheideasofneutrosophicstrong sizeandneutrosophicstrongorderofaneutrosophicnetwork.

Definition9: Let GK, L () beaneutrosophicnetworkandnode k [ V .Thentheneutrosophicnode y [ V issaidtobea neutrosophicstrongneighbournodeofneutrosophicnode x,ifand onlyifneutrosophicedge kl isastrongedge.Thesetofall neutrosophicstrongneighbournodeof k isrepresentedby Ns k () Theneutrosophicclosedstrongneighbourhoodvertexof k is describedas Ns x [] = Ns k () < x {}

Definition10: Let GK, L () beaneutrosophicnetworkandthenode k [ V .Theneutrosophicstrongdegreeofanode l isdefinedas follows: ds l ()= k [Ns l () T L kl (), k [Ns l () I L kl (), k [Ns l () F L kl () (10)

Definition11: Let GK, L () beaneutrosophicnetworkandthenode k [ V .Theneutrosophicstrongneighbourhooddegreeofa neutrosophicnode l isdefinedasfollows: dsN l ()= k [Ns l () T K x (), k [Ns l () T K x (), k [Ns l () F K x () (11)

Here kl isastrongarc.Theneutrosophicstrongorderofthe neutrosophicnetwork G isdefinedasfollows:

Os G ()= kl [E

T K l ()+I K kl ()+ 1 −F K k () 3 (17)

Here, l isanendvertexofastrongedge.

Definition16: Let D beaneutrosophicdominatingsetina neutrosophicnetwork G.Thenodeweightandarcweightof D are definedasfollows:

Wx D ()= k [D,y[Ns k () ^ T K k () + _ I K k () + 3 _ F K k () 3

We D ()= k [D,y[Ns k () ^ T L kl () + _ I L kl () + 3 _ F L kl () 3

(18)

(19)

Theneutrosophicstrongdominationnumberofaneutrosophic network G isdefinedastheminimumneutrosophicarccostin G= (K, L)anditisdenotedby gs G ()

Theneutrosophicstrongneighbourhooddominationnumberof G isdefinedasminimumneutrosophicnodecostin G= (K, L)andit isdenotedby gsN G ()

T L kl ()+I L kl ()+ 3 −F L kl () 3 (12)

Definition12: Let GK, L () beaneutrosophicnetworkandthenode k [ V .Theneutrosophicstrongdegreecardinalityofnode l is definedasfollows: ds l () = k [Ns l ()

Definition13: Let GK, L () beaneutrosophicnetworkandthenode k [ V .Theneutrosophicstrongneighbourhooddegreecardinality ofnode l isdefinedasfollows: dsN l () = k [Ns l ()

T K k ()+I K k ()+ 3 −F K k () 3 (13)

Definition14: Themaximumandminimumneutrosophicstrong degreeof G= (K, L)aredeterminedasfollows: Ds G ()= _ ds l () ∀y [ V ds G ()= ^ ds l () ∀y [ V (14)

Theminimumandmaximumstrongneighbourhooddegreeof G= (K, L)aredeterminedasfollows: DNs G ()= _ dNs l () ∀y [ V dNs G ()= ^ dNs l () ∀y [ V (15)

Definition17: Let GK, L () beaneutrosophicnetwork.Thegraph G isacompletebipartiteneutrosophicnetworkifthevertexset V can bepartitionedintotwonon-emptysets p1 and p2 suchthat T L p1 p2 , I L p1 p2 , F L p1 p2 = 0,1 () for p1 , p2 [ p1 or p1 , p2 [ p2 Moreover T L kl (), I L kl (), F L kl () =T K k () ^ T K l (), I K k () ^ I K l (), F K k () _ F K l () (20) for k [ y1 and y [ V 2.

5Strongperfectdominationnumber

Inthissection,theideaofneutrosophicperfectdominatingsetand neutrosophicstrongperfectdominationnumberofaneutrosophic networkareintroduced.Thenweshowthatundersomespecific criteria,theneutrosophicstrongdominationnumberandthe neutrosophicstrongperfectdominationnumberinaneutrosophic network G= (K, L)arealwaysequalled.Finally,we finda maximumboundforstrongperfectdominationnumbersin neutrosophicnetworks.

Definition18: Let GK, L () beaneutrosophicnetwork.A neutrosophicsubset D ofvertexset V issaidtobeperfect neutrosophicdominatingsetor Dp in G= (K, L),ifallthe nodesof y [ V \D,thereisoneandonlynode k [ D suchthat node k dominatesnode y.The Dp iscalledtheminimalperfect neutrosophicdominatingsetifforeach y [ Dp , Dp \ v {} isnota perfectdominatingsetin G

T L kl () +I L kl () + 1 −F L kl () 3 (16)

Remark1: Let G= (K, L)beavaguegraph.If tA and fA areconstant functions,then ds G ()= dsN G () and Ds G ()= DsN G () Definition15: Theneutrosophicstrongsizeoftheneutrosophic network G isdefinedasfollows: Ss G ()= kl [E

Definition19: Thestrongperfectdominationnumberofavague graph G isdefinedastheminimumarcweightofperfect dominatingsetsof G= (K, L),whichisdenotedby gsp G ()

CAAITrans.Intell.Technol.,2020,Vol.5,Iss.4,pp.301–307 303 ThisisanopenaccessarticlepublishedbytheIET,ChineseAssociationforArtificialIntelligenceand ChongqingUniversityofTechnologyundertheCreativeCommonsAttribution-NoDerivsLicense(http://creativecommons.org/licenses/bynd/3.0/)

Theideaofasemi-complementaryneutrosophicnetworkand semi-neutrosophicdominatingsetinaneutrosophicnetwork G are presentedinthissection.

Definition20: Let GK, L () beaneutrosophicnetwork,then semi-complementaryneutrosophicnetworkof G= (K, L), i.e. GSC =KSC , LSC ,isdescribedby

(i) T SC K l ()=T K l (), I SC K l ()=I K l (),and F SC K l ()=F K l () (ii) E SC = uv E , ∃w, uw, wv [ E {} whereforany kl [ E SC , T SC L kl () =T K k () ^ T K l (), I SC kl () =I K k () _ I K l (), and F SC kl ()=F K k () _ F K l ().

Definition21: Let GK, L () beaneutrosophicnetwork.

(i)Theneutrosophicsubset D isdefinedasasemi-neutrosophic dominatingsetinaneutrosophicnetwork G= (K, L)ifandonly iftheneutrosophicsubset D isaneutrosophicdominatingsetfor bothneutrosophicnetwork(G= (K, L))andsemi-complementary neutrosophicnetwork GSC (ii)Asemi-neutrosophicdominatingsetisdefinedasminimal semi-neutrosophicdominatingsetifandonlyif ∀y [ DS , DS \ v {} isnotaglobaldominatingsetin G

Definition22: Thestrongsemi-neutrosophicdominationnumberofa neutrosophicnetwork G isdescribedastheminimumedgecostof semi-neutrosophicdominatingsetin G.

whichisplacedinthemainbranchoftheserviceprovider’s(hub) andsomeopticalnetworkterminalsandopticalnetworkunits (ONUs),neartoend-userpoints.APONsystemcanreducethe costofthemainbranchequipmentand fibreneededcompared withapointtopointtechnology.Itisaspecialtypeof fibreoptic accesstelecommunicationgraph.PONisgenerallyusedasatree structure.Atreeisnothingbutaconnectedcircuitlessgraph.A serviceprovidercompanywantstoprovideaPONtoacity.We canrepresentthecitymapusinganeutrosophicnetwork.The roadsareusedasthecommunicationlinks(arc)andtheroad junctionstogetherwiththeONUandOLTsareconsideredasthe nodesoftheneutrosophicnetwork.Thedecisionmakerconsiders theweightsofthecommunicationlinksbasedonthelengthofthe correspondingroads.InthePONsystem,theOLTislocatedinthe mainbranchanditisusedasarootofthetree.TheONUis consideredastheleavesofthetreeandtheyareplacednearthe end-users.TheOLTandONUsbothareconsideredaspassive elementsofthe fibresandtheopticalsplittersarespread.Inthe PON,useraccesspointsarelinkedtotheONUsviaclassical engineeringsuchascoaxlinesorcopper.AnexampleofaPONis showninFig. 1.Mostoftheprojectcosthastobeusedfor diggingthelineductstoinstallanewPONinacity.Thedecision makerhasto findtheshortestpaths,whichconnectalltheONUs withthesingleOLTinthePON.Ithelpsto findminimisethe projectcost.Fromtheneutrosophicnetworkrepresentation,this neutrosophicoptimisationproblemcanbeconvertedintothe neutrosophicminimumSteinertreeproblem.Thedecision-maker wantstodetermineaneutrosophictreeoftheneutrosophic network,whichconsistsofasubsetofneutrosophicvertices whosesumoftheweightsoftheselectedarcsbecomesminimal.

8Someapplicationsofstrongdomination numbers

AneutrosophicsetisgeneralisedofAtanassov’sintuitionisticfuzzy setwhichconsistsofthreemembershipgrades:truthmembership, indeterminatemembership,andfalsemembership.The neutrosophicnetworkisanextensionofavaguegraphand intuitionisticfuzzygraphwhichprovidesmore flexibility, precision,andcompatibilitytodesignthereal-lifeproblemwhen Fig.1

ThePONisa fibreoptictelecommunicationgraphthatusesthe singlepointtomultipointtechnologyandopticalsplittertosend databetweenasinglesourcepointtomultipleend-users.APON systemmainlyconsistsofasingleopticallineterminal(OLT),

CAAITrans.Intell.Technol.,2020,Vol.5,Iss.4,pp.301–307 304ThisisanopenaccessarticlepublishedbytheIET,ChineseAssociationforArtificialIntelligenceand ChongqingUniversityofTechnologyundertheCreativeCommonsAttribution-NoDerivsLicense(http://creativecommons.org/licenses/ by-nd/3.0/)

comparedwiththeintuitionisticfuzzygraphs.Neutrosophicgraph modelsarerecentlyusingtomodelmanyreal-lifeproblemsin severaldifferentareasofengineeringandscience.Inthisstudy, weintroducetheideaofadominatingsetinneutrosophicnetwork theory.Thedominationintheneutrosophicnetworkcanbeused tosolvemuchreal-lifeproblem.Here,insociety,aswellasin administration,theinfluenceoftheindividualdependsonthe strengththathederivesfromhissupporters,andtheseeffectsmay benoteffective.Besides,theindividualhastodependmoreonhis supportersthanonhimself.

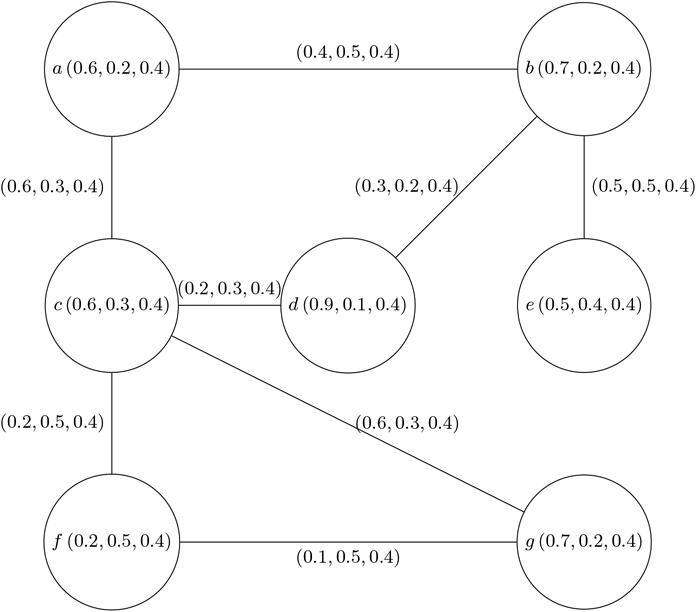
Now,weexpressanapplicationofdominatingset.Anoffice consistsofsevenemployeesandelectionsarebeingheldto determinethenewhead.Weshowthatafewemployeescanselect aperson G= (K, L)(whodoesnothaveconsiderableinfluenceon allemployees)astheheadbyusingadominationsetofavague graph.First,werepresenttheofficewithavaguegraph G asinFig. 2

Inthisvaguegraph,thenodesandarcsrepresentemployeesand friendshipsbetweenthem,respectively.Truemembershipfunction foreachnodeisconsideredasthesignificanceofthenodeinthe office,includinglevelofeducation,workexperienceetc.,andfalse membershipfunctionforeachnodeisevaluatedaslackof compatibilitybetweeneducationalmajorandoccupation,lackof ability,andothercases.Inthisexample,weseethat ac, cd, bd, de, cf,and cg arestrongarcs,andthereisastrongrelationship betweenthem.Hence, D1 = c, d {}, D2 = c, b, d {},and D3 = c, d , e {} aredominatingsetsinthisvaguegraphandweightsare

We D1 = 0 2 + 0 5 + 0 5 + 0 6 = 1 8

We D2 = 0 2 + 0 5 + 0 5 + 0 6 + 0 5 + 0 8 = 3 1 We D3 = 0 2 + 0 5 + 0 5 + 0 6 + 0 5 + 0 6 = 2 9

Also,so D1 isaminimaldominationsetinthisexample.Sincethe nodesindominatingsethavethemostinfluenceontheother

memberswhoarenotin D1 ,therefore,bythisinfluence,theycan selectoneoftheirownas G= (K, L)oranyoneelseasheadof office.(However,weseethatthecrispgraph,whichismadeup ofemployeesandrelationshipsbetweenthem, D = c, e {} isa minimaldominationsetthathaslessinfluenceontheother membersascomparedto D1 )

Inthefollowing,wehavesomemoreapplicationsofstrong dominationnumbersineverydaylife.

8.1Mobile

adhoc graph(MANET)

Amobile adhoc graph(MANET)isadecentralisemobilegraph, whichiscontinuouslyself-organising,self-configuring,and infrastructurelessgraphusedtocommunicateoverwireless channel.InthisMANET,eachmobiledevicecanfreelymovein anydirectionandthelinksbetweenothermobiledeviceswill changefrequently.EachdeviceinaMANETmustsendthetraffic totheirownuse.ThemainchallengeinmodellingaMANETisto equipeachmobiledevicetoprovidetheexactinformationneeded tohandletheroutetrafficproperly.WecanrepresenttheMANET asaneutrosophicnetworkwheretheverticesrepresentthemobile deviceandedgesdescribepatternofmessagingamongthemobile devices.Theideaofneutrosophicnetworkcanhandlethe uncertaintyofMANET.Wecanusethedominatingsetto find theroutingtableinMANET.Thesmalldominatingsetis consideredasabackboneforMANET.Ifadeviceisnotpresent inthedominatingsetthenthedevicetransmitsthemessagesusing theneighbourdevicesintheset.Thestrongedgesareonly consideredinthedominatingsetofaneutrosophicnetworkandif anydeviceisnotpresentindominatingsetofgraph(neutrosophic network)thenithasalwaysastrongneighbourinthedominating set.Wecantransmitmessagefastertoitsneighbourintheset. Thestrongdominationnumberdescribesthesmallestnumberof mobiledeviceindominatingsetoftheneutrosophicnetwork.The transmissionspeedandroutingofmessagecanbeimprovedusing dominatingset,anditcanhelptominimisetheconstructioncost oftheMANET.

CAAITrans.Intell.Technol.,2020,Vol.5,Iss.4,pp.301–307

ThisisanopenaccessarticlepublishedbytheIET,ChineseAssociationforArtificialIntelligenceand ChongqingUniversityofTechnologyundertheCreativeCommonsAttribution-NoDerivsLicense(http://creativecommons.org/licenses/bynd/3.0/)

8.2Computercommunicationgraphs

Theideaofneutrosophicdominatingsetplaysanimportantrolein computerandcommunicationgraphstoroutetheinformation betweenthenodes.Neutrosophicgraphcanbeusedtomodelthe computergraphwheretheeachnoderepresentsthecomputerand twonodesareconnectedbyadirectedarcifthereexistsanydirect communicationlinebetweenthetwocomputers.Informationis collectedfromthecomputerandeachcomputercantransmitthe informationtoothercomputers,whichhavedirectcommunication linewithit.Inthisproblem,weneedto findasmallsetof computersinthegraph,whichdirectlycommunicatewithallother computers.Wecansolvethisproblemusingtheideaofminimum neutrosophicdominatingsetofthecorrespondingneutrosophic network.Theinformationmaybecollectedbymakingeach processortorouteitsinformationtooneofthesmallsetsof collectingprocessor,whichisconstructedbyadominatingsetof thecorrespondinggraph.

8.3Wirelesssensorgraph

Awirelesssensorgraph[wirelesssensornetwork(WSN)]isan infrastructurelessandself-configurewirelessgraph.Itiscollection oftransducers,whichcanmonitorandrecordtheconditionsof differentlocations.Itgenerallymonitorstheparameterssuchas pressure,temperature,humidity,pollutantlevels,windspeed, powerlinevoltage,winddirection,chemicalconcentrations,sound intensity,andilluminationintensity.TheWSNismainly constructedofsensornodes,whicharegenerallyspreadinthe graph.Thesensornodesgathertheinformationfromothersensor nodesandgraphs.Thetopologycontrolisthemostbasicproblem inWSN.WecanmodeltheWSNasaneutrosophicnetworksince theplaceofeachnodeisindefiniteandcanconveyeverypieceof information,evendestructive,toothernodesand,thereforeinduce interventioninthegraph.Asaresult,wecandefinetrue (regardinglevelofimportance,necessity,effect,paceof conveyanceetc.)andfalse(regardingthedegreeofintervention, vaguenessetc.)membershipfunctionsandalsovaluateseacharc consideringimportanceandnecessityofconveyanceof informationetc.Accordingly,sinceeachdominatingsetinavague graphisgainedusingstrongarcs,wecan,insodoing,makethe smallestandthemosteffectiveminimalbackbonesetbygaining minimaldominatingset(byusingminimumarcweight).Virtual backboneisnecessaryforfaulttoleranceandrouting flexibility.

9Conclusion

Inthispaper,wehaveexploredtheuseofneutrosophicnetworkfor modellingthePON,mobile adhoc graph(MANET),andwireless sensorgraph.Wehavepresentedtheideaofstrongarc,weakarc strongdominationnumbers,andstrongperfectdominationof neutrosophicnetwork.Wehavedescribedthemethodto findthe valuesofstrongandstrongperfectdominationofneutrosophic network.Finally,weusetheideaofstrongarcstrongdomination numberinMANETandwirelesssensorgraph.

10References

[1]Zheng,W.,Qiao,J.,Feng,L., etal.: ‘Optimalcooperativevirtualmulti-inputand multi-outputnetworkcommunicationbydoubleimprovedantcolonysystemand geneticalgorithm’ , IAENGInt.J.Comput.Sci.,2018, 45,(1),pp.89–96

[2]Intan,R.,Chan,S.H.G.: ‘Extendedgeneralizationoffuzzyroughsets’ , IAENG Int.J.Comput.Sci.,2019, 46,(2),pp.257–263

[3]Yang,L.,Li,B.,Xu,H.: ‘NovelpoweraggregationoperatorsbasedonEinstein operationsforintervalneutrosophiclinguisticsets’ , IAENGInt.J.Appl.Math., 2018, 48,(4),pp.475–484

[4]Zadeh,L.A.: ‘Fuzzysets’ , Inf.Control,1965, 8,(3),pp.338–353

[5]Kaufmann,A.: ‘Introductiontothetheoryoffuzzysubsets’,vol.2(Academic Press,Germany,1975)

[6]Rosenfeld,A.: ‘Fuzzygraphs’ in ‘Fuzzysetsandtheirapplicationstocognitive anddecisionprocesses’ (Elsevier,Spain,1975),pp.77–95

[7]Rashmanlou,H.,Pal,M.: ‘Somepropertiesofhighlyirregularinterval-valued fuzzygraphs’ , WorldAppl.Sci.J.,2013, 27,(12),pp.1756–1773

[8]Samanta,S.,Pal,M.: ‘Irregularbipolarfuzzygraphs’,arXivpreprint arXiv:12091682,2012

[9]Ghorai,G.,Pal,M.: ‘Certaintypesofproductbipolarfuzzygraphs’ , Int.J.Appl. Comput.Math.,2017, 3,(2),pp.605–619

[10]Pramanik,T.,Samanta,S.,Pal,M., etal.: ‘Interval-valuedfuzzy j-tolerance competitiongraphs’ , SpringerPlus,2016, 5,(1),p.1981

[11]Rashmanlou,H.,Samanta,S.,Pal,M., etal.: ‘Astudyonvaguegraphs’ , SpringerPlus,2016, 5,(1),p.1234

[12]Rashmanlou,H.,Samanta,S.,Pal,M., etal.: ‘Astudyonbipolarfuzzygraphs’ , J.Intell.FuzzySyst.,2015, 28,(2),pp.571–580

[13]Nandhini,S.P.,Nandhini,E.: ‘Stronglyirregularfuzzygraphs’ , Int.J.Math. Arch.,2014, 5,(5),pp.110–114.

[14]Borzooei,R.A.,Rashmanlou,H.,Samanta,S., etal.: ‘Newconceptsofvague competitiongraphs’ , J.Intell.FuzzySyst.,2016, 31,(1),pp.69–75

[15]Atanassov,K.T.: ‘Intuitionisticfuzzysets’ , FuzzySetsSyst.,1986, 20,(1), pp.87–96

[16]Atanassov,K.: ‘Intuitionisticfuzzysets,1983’,VIIITKR’sSession,Sofia (deposedinCentralSci-TechnicalLibraryofBulgAcadofSci,1697/84)(in Bulgarian)

[17]Atanassov,K.T.: ‘Intuitionisticfuzzysets’,in ‘Intuitionisticfuzzysets’ (Springer, Verlag,Berlin,Heidelberg,1999),pp.1–137

[18]Shannon,A.,Atanassov,K.: ‘Onageneralizationofintuitionisticfuzzygraphs’ , NIFS,2006, 12,(1),pp.24–29

[19]Parvathi,R.,Karunambigai,M.: ‘Intuitionisticfuzzygraphs’,in ‘Computational intelligence,theoryandapplications’ (Springer,VerlagBerlinHeidelberg,2006), pp.139–150

[20]Parvathi,R.,Thamizhendhi,G.: ‘Dominationinintuitionisticfuzzygraphs’ , NotesIntuitionisticFuzzySets,2010, 16,(2),pp.39–49

[21]Parvathi,R.,Karunambigai,M.,Atanassov,K.T.: ‘Operationsonintuitionistic fuzzygraphs’.2009IEEEInt.Conf.onFuzzySystems,Spain,2009, pp.1396–1401

[22]Rashmanlou,H.,Samanta,S.,Pal,M., etal.: ‘Bipolarfuzzygraphswith categoricalproperties’ , Int.J.Comput.Intell.Syst.,2015, 8,(5),pp.808–818

[23]Akram,M.,Akmal,R.: ‘Operationsonintuitionisticfuzzygraphstructures’ , FuzzyInf.Eng.,2016, 8,(4),pp.389–410

[24]Rashmanlou,H.,Borzooei,R.,Samanta,S., etal.: ‘Propertiesofintervalvalued intuitionistic(s,t)–fuzzygraphs’ , PacificSci.Rev.A,Nat.Sci.Eng.,2016, 18,(1), pp.30–37

[25]Sahoo,S.,Pal,M.: ‘Differenttypesofproductsonintuitionisticfuzzygraphs’ , PacificSci.Rev.A,Nat.Sci.Eng.,2015, 17,(3),pp.87–96

[26]Smarandache,F.: ‘Aunifying fieldinlogics:neutrosophiclogic.Neutrosophy, neutrosophicset,neutrosophicprobability’ (InfiniteStudy,USA,2005)

[27]Garg,H.,Nancy: ‘Animprovedscorefunctionforrankingneutrosophicsetsand itsapplicationtodecision-makingprocess’ , Int.J.Uncertain.Quantif.,2016, 6, (5),pp.377–385

[28]Garg,H.,Nancy: ‘Non-linearprogrammingmethodformulti-criteriadecision makingproblemsunderintervalneutrosophicsetenvironment’ , Appl.Intell., 2018, 48,(8),pp.2199–2213

[29]Garg,H.,Nancy: ‘Multi-criteriadecision-makingmethodbasedonprioritized Muirheadmeanaggregationoperatorunderneutrosophicsetenvironment’ , Symmetry,2018, 10,(7),p.280

[30]Garg,H.,Nancy: ‘Somenewbiparametricdistancemeasuresonsingle-valued neutrosophicsetswithapplicationstopatternrecognitionandmedical diagnosis’ , Information,2017, 8,(4),p.162

[31]Garg,H.: ‘AnovelimprovedaccuracyfunctionforintervalvaluedPythagorean fuzzysetsanditsapplicationsinthedecision-makingprocess’ , Int.J.Intell. Syst.,2017, 32,(12),pp.1247–1260

[32]Garg,H.,Nancy: ‘Somehybridweightedaggregationoperatorsunder neutrosophicsetenvironmentandtheirapplicationstomulticriteria decision-making’ , Appl.Intell.,2018, 48,(12),pp.4871–4888

[33]Garg,H.: ‘Anovelaccuracyfunctionunderinterval-valuedPythagoreanfuzzy environmentforsolvingmulticriteriadecisionmakingproblem’ , J.Intell. FuzzySyst.,2016, 31,(1),pp.529–540

[34]Garg,H.,Nancy: ‘Newlogarithmicoperationallawsandtheirapplicationsto multiattributedecisionmakingforsingle-valuedneutrosophicnumbers’ , Cogn. Syst.Res.,2018, 52,pp.931–946

[35]Smarandache,F.: ‘Extensionofhypergraphton-superhypergraphandto plithogenicn-superhypergraph,andextensionofhyperalgebraton-ary (classical-/neutro-/anti-)hyperalgebra’ , NeutrosophicSetsSyst.,2020, 33,(1), pp.290–296

[36]Yang,H.L.,Guo,Z.L.,She,Y., etal.: ‘Onsinglevaluedneutrosophicrelations’ , J.Intell.FuzzySyst.,2016, 30,(2),pp.1045–1056

[37]Borzooei,R.A.,Rashmanlou,H.,Samanta,S., etal.: ‘Regularityofvague graphs’ , J.Intell.FuzzySyst.,2016, 30,(6),pp.3681–3689

[38]Naz,S.,Rashmanlou,H.,Malik,M.A.: ‘Operationsonsinglevalued neutrosophicgraphswithapplication’ , J.Intell.FuzzySyst.,2017, 32,(3), pp.2137–2151

[39]Ye,J.: ‘Single-valuedneutrosophicminimumspanningtreeanditsclustering method’ , J.Intell.Syst.,2014, 23,(3),pp.311–324

[40]Wang,J.: ‘Anovel fireflyalgorithmforportfoliooptimizationproblem’ , IAENG Int.J.Appl.Math.,2019, 49,(1),pp.45–50

[41]Akram,M.,Waseem,N.,Dudek,W.A.: ‘Certaintypesofedgem-polarfuzzy graphs’ , IranianJ.FuzzySyst.,2017, 14,(4),pp.27–50

[42]Akram,M.: ‘Certainbipolarneutrosophiccompetitiongraphs’ , J.Indonesian Math.Soc.,2017, 24,(1),pp.1–25

CAAITrans.Intell.Technol.,2020,Vol.5,Iss.4,pp.301–307 306ThisisanopenaccessarticlepublishedbytheIET,ChineseAssociationforArtificialIntelligenceand ChongqingUniversityofTechnologyundertheCreativeCommonsAttribution-NoDerivsLicense(http://creativecommons.org/licenses/

[43]Prasertpong,R.,Siripitukdet,M.: ‘Applyinggeneralizedroughsetconceptsto approximationspacesofsemigroups’ , IAENGInt.J.Appl.Math.,2019, 49, (1),pp.51–60

[44]Akram,M.,Siddique,S.: ‘Neutrosophiccompetitiongraphswithapplications’ , J.Intell.FuzzySyst.,2017, 33,(2),pp.921–935

[45]Akrama,M.: ‘Single-valuedneutrosophicplanargraphs’ (InfiniteStudy,USA, 2016)

[46]Borzooei,R.A.,Darabian,E.,Rashmanlou,H.: ‘Strongdominationnumbers ofvaguegraphswithapplications’ , Appl.Math.E-Notes,2016, 16, pp.251–267

[47]Broumi,S.,Bakali,A.,Talea,M., etal.: ‘Spanningtreeproblem withneutrosophicedgeweights’ , ProcediaComput.Sci.,2018, 127, pp.190–199

[48]Broumi,S.,Talea,M.,Smarandache,F., etal.: ‘Decision-makingmethodbased ontheintervalvaluedneutrosophicgraph’.2016FutureTechnologiesConf. (FTC),London,UK,2016,pp.44–50

[49]Dey,A.,Broumi,S.,Bakali,A., etal.: ‘Anewalgorithmfor findingminimum spanningtreeswithundirectedneutrosophicgraphs’ , GranularComput.,2019, 4,(1),pp.63–69

[50]Liu,Q.: ‘Onmaximalincidenceenergyofgraphswithgivenconnectivity’ , IAENGInt.J.Appl.Math.,2018, 48,(4),pp.429–433 [51]Yang,L.,Li,B.: ‘Anextendedsingle-valuedneutrosophicnormalizedweighted BonferronimeanEinsteinaggregationoperator’ , IAENGInt.J.Appl.Math., 2018, 48,(4),pp.373–380 [52]Chen,X.,Liu,S.: ‘Adjacentvertexdistinguishingproperedgecoloringsof bicyclicgraphs’ , IAENGInt.J.Appl.Math.,2018, 48,(4),pp.401–411

CAAITrans.Intell.Technol.,2020,Vol.5,Iss.4,pp.301–307 307 ThisisanopenaccessarticlepublishedbytheIET,ChineseAssociationforArtificialIntelligenceand ChongqingUniversityofTechnologyundertheCreativeCommonsAttribution-NoDerivsLicense(http://creativecommons.org/licenses/bynd/3.0/)