TestingofGroupedProductfortheWeibull DistributionUsingNeutrosophicStatistics
MuhammadAslam* andOsamaH.Arif
DepartmentofStatistics,FacultyofScience,KingAbdulazizUniversity,Jeddah21589,SaudiArabia; oharif@hotmail.com
* Correspondence:magmuhammad@kau.edu.saoraslam_ravian@hotmail.com;Tel.:+966-593-329-841
Received:21August2018;Accepted:11September2018;Published:15September2018
Abstract: Partsmanufacturersusesuddendeathtestingtoreducethetestingtimeofexperiments. Thesuddendeathtestingplanintheliteraturecanonlybeappliedwhenallobservationsoffailure time/parametersarecrisp.Inpracticehowever,itisnotedthatnotallmeasurementsofcontinuous variablesareprecise.Therefore,theexistingsuddendeathtestplancanbeappliediffailuredata/or parametersareimprecise,incomplete,andfuzzy.Theclassicalstatisticshavethespecialcaseof neutrosophicstatisticswhentherearenofuzzyobservations/parameters.Theneutrosophicfuzzy statisticscanbeappliedforthetestingofmanufacturingpartswhenobservationsareimprecise, incompleteandfuzzy.Inthispaper,wewilldesignanoriginalneutrosophicfuzzysudden deathtestingplanfortheinspection/testingoftheelectronicproductorpartsmanufacturing. WewillassumethatthelifetimeoftheproductfollowstheneutrosophicfuzzyWeibulldistribution. Theneutrosophicfuzzyoperatingfunctionwillbegivenandusedtodeterminetheneutrosophic fuzzyplanparametersthroughaneutrosophicfuzzyoptimizationproblem.Theresultsofthe proposedneutrosophicfuzzydeathtestingplanwillbeimplementedwiththeaidofanexample.

Keywords: neutrosophicfuzzystatistics;fuzzyapproach;neutrosophicfuzzyplanparameters;fuzzy optimizationproblem;risks
1.Introduction
Inlifetestingexperiments,arandomsampleofitemsisusuallyselected,andasingleitemis installedonasingletesterforthelotsentencing.Thistypeoftestingiscostlyasthenumberoftesters isequaltothenumberofitemsthatareselectedforthetestingpurpose.Alternatively,thegroup samplingschemeisappliedforthetestingofmorethanoneitemonthesingletester.Suddendeath testingisimplementedingroupstoreducethetesting/inspectioncostoftheproduct.Insudden deathtesting,arandomsampleofsize n isequallydistributedto g groupshaving r itemsineach ofthe g groups.Reference[1]proposedthesuddentestfortheWeibulldistribution.Accordingto Reference[1]“Thespecimensineachgrouparetestedidentically&simultaneouslyondifferenttesters. The1stgroupofspecimensisrununtilthe1stfailureoccurs.Atthispoint,thesurvivingspecimens aresuspended&removedfromtesting.Anequalsetofnewspecimensnumberingisnexttested untilthe1stfailure.Thisprocessisrepeateduntilonefailureisgeneratedfromeachofthegroups”. Thesamplingplanforsuddendeathtestinghasbeenconsideredbyseveralauthorsintheliterature, seeforexampleReferences[1–3].
Inthemodernera,productsaremanufacturedusingadvancedtechnology,whichresultinhigh qualityandreliability.Forthetesting/inspectionofahighlyreliableproduct,itmaynotbepossibleto waitforthefailuresoftheproductforthelotsentencing.Thetwotypesofcensoringwidelyapplied toreducethetestingcostforahighlyreliableproduct,areknownastype-Icensoringandtype-II censoring.Thetestingissaidtobetype-Icensoringifthetimeofexperimentisfixed,andtype-IIif
Symmetry 2018, 10,403;doi:10.3390/sym10090403 www.mdpi.com/journal/symmetry
thenumberoffailuresisspecifiedforthetesting/inspectionoftheproduct.Theacceptancesampling plansfortype-Iandtype-IIcensoringwhenthelifetimefollowstheWeibulldistributionisdesignedby anumberofresearchers,including,forexample,References[4–10].
Thefuzzyapproachiswidelyusedwhenthereissomeuncertaintyintheproportionofdefectives. Inpractice,theexperimentermaybeindeterminateaboutthepercentageofdefectives.Inthiscase, thetraditionalsamplingplanscanbeappliedfortheinspectionofthelot.Hence,anumberof peoplehavedesignedefficientsamplingplansusingthefuzzyapproach,including,forexample, References[11–26].
Partsmanufacturersusesuddendeathtestingtoreducethetestingtimeoftheexperiment. Thesuddendeathtestingplanintheliteraturecanonlybeappliedwhenallobservationsoffailure time/parametersarecrisp.AccordingtoReference[27],“allobservationsandmeasurementsof continuousvariablesarenotprecisenumbersbutmoreorlessnon-precise.Thisimprecisionis differentfromvariabilityanderrors.Therefore,lifetimedataarealsonotprecisenumbersbutmore orlessfuzzy.Thebestup-to-datemathematicalmodelforthisimprecisionisso-callednon-precise numbers”.Therefore,theexistingsuddendeathtestplancanbeappliediffailuredataorparameters areimprecise,incomplete,andfuzzy.Theclassicalstatisticshavethespecialcaseoftheneutrosophic statisticswhentherearenofuzzyobservations/parameters.Thus,theneutrosophicfuzzystatistics canbeappliedforthetestingofmanufacturingpartswhenobservationsareimprecise,incomplete, andfuzzy.Recently,theauthorsofReference[28]introducedtheneutrosophicstatisticsintheareaof acceptancesamplingplan.
Byexploringtheliterature,andtothebestoftheauthor’sknowledge,thereisnoworkonthe designofneutrosophicfuzzysuddendeathtestingplanusingtheWeibulldistribution.Inthispaper, wewilldesignanoriginalneutrosophicfuzzysuddendeathtestingplanfortheinspection/testing oftheelectronicproductorpartsmanufacturing.Wewillassumethatthelifetimeoftheproduct followstheneutrosophicfuzzyWeibulldistribution.Theneutrosophicfuzzyoperatingfunctionwill begivenandusedtodeterminetheneutrosophicfuzzyplanparametersthroughaneutrosophicfuzzy optimizationproblem.Theresultsoftheproposedneutrosophicfuzzydeathtestingplanwillbe implementedwiththeaidofanexample.
2.DesignofProposedPlan
Supposethat TNi {TL, TU } = i =1,2,3, ... , nN beingarandomsamplefromtheneutrosophic fuzzyWeibulldistributionwithneutrosophicfuzzyshapeparameter mN andneutrosophicfuzzyscale parameter λN .TheneutrosophicfuzzyWeibulldistributionisdefinedby: FN (tN ; mN , λN ) = 1 exp (tN /λN )mN , tN ≥ 0(1)
SomemoredetailsonfuzzybasedWeibulldistributioncanbeseeninReferences[29,30].
Itisassumedthatitemsaretestedidenticallyandsimultaneouslyineachgroup.Wepropose followinganeutrosophicfuzzysuddendeathtestingplan.Thequalitycharacteristicbeyondthelower specificationlimit L isdefinedasdefective.Thus,theprobabilityofdefectivenessisgivenby: pN = prN {TN < L} = FN (L) (2)
Forthegiven pN ,thecorresponding λN L fromEquation(2)isgivenby: wN = ln(1 pN ) = (λN L)mN (3)
Step1. Selectarandomsample nN {nL, nU } anddistribute r itemsinto gN {gL, gU } groups. Step2. Recordfirstfailurefrom ithgroup (i = 1,2,... gN ) andcalculateneutrosophicfuzzystatistic vN = ∑gN i=1 Ym iN ; gN {gL, gU }, vN {vL, vU }.
Symmetry 2018, 10,403
Step3. Acceptlotoftheproductif vN ≥ kN Lm , kN {kaL, kaU } isaneutrosophicfuzzy acceptancenumber.
Symmetry 2018, 10, x FOR PEER REVIEW 3 of 9
sampling plan reduces to the plan in Reference [1] when ���� =���� =�� and ������ =������ =�� The operational process of the proposed plan is also shown in Figure 1.
Theproposedplanhastwoneutrosophicfuzzyparameters gN {gL, gU } and kN {kaL, kaU } TheproposedsamplingplanistheextensionoftheplanproposedinReference[1].Theproposed samplingplanreducestotheplaninReference[1]when gL = gU = g and kaL = kaU = k TheoperationalprocessoftheproposedplanisalsoshowninFigure 1
Figure 1. Operational procedure of proposed plan
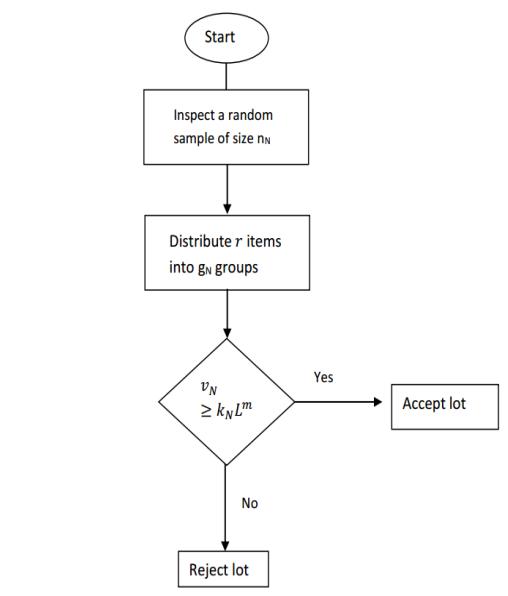
Figure1. Operationalprocedureofproposedplan.
By following Reference [1] that ������ �� in ���� =∑ ������ �� ���� ��=1 follows the i i d neutrosophic exponential distribution with neutrosophic parameter ���� ��������, so ���� follows the neutrosophic fuzzy gamma distribution with neutrosophic parameters (����,���� ��������) ; ������{����,����} The neutrosophic fuzzy operating function (NFOC) will be derived as follows: ��(����)=1 ��2����(2������������); ������{������,������} (4) where ������ is the neutrosophic fuzzy cumulative distribution function of the neutrosophic fuzzy gamma with a neutrosophic degree of freedom ����
2.1. Neutrosophic Fuzzy Non-Linear Optimization
ByfollowingReference[1]that Ym iN in vN = ∑gN i=1 Ym iN followsthei.i.d.neutrosophicexponential distributionwithneutrosophicparameter λmN N rN ,so vN followstheneutrosophicfuzzygamma distributionwithneutrosophicparameters gN , λmN N rN ; gN {gL, gU }.Theneutrosophicfuzzy operatingfunction(NFOC)willbederivedasfollows: L(pN ) = 1 G2gN (2rN kN wN ); kN {kaL, kaU } (4) where GδN istheneutrosophicfuzzycumulativedistributionfunctionoftheneutrosophicfuzzy gammawithaneutrosophicdegreeoffreedom δN NeutrosophicFuzzyNon-LinearOptimization
Let �� and �� respectively be the producer’s risk and consumer’s risk. The plan parameters ������{����,����} and ������{������,������} will be determined ��(��������)≥1 �� at acceptable quality level (AQL = ��1) and ��(��������)≤�� at limiting quality level (LQL = ��2) Therefore, the neutrosophic fuzzy plan parameters of the proposed plan will be determined by following the neutrosophic fuzzy non-linear optimization problem: minimize ������{����,����} (5) ��(��������)=(1 ��2����(2������������0))≥1 ��,������{����,����}; ������{����,����} (6) ��(��������)=(1 ��2����(2������������1))≤��, ������{����,����}; ������{����,����} (7)
The plan parameters ������{����,����} and ������{������,������} will be determined through Equations (5) –(7) using the grid search method. The following algorithm is used to determine the plan parameters
Step 1. Specify the value of r. Step 2. Determine the values of ���� and ���� using the search grid method through Equations (5)–(7)
Step1. Specifythevalueof r. Step2. Determinethevaluesof gN and kN usingthesearchgridmethodthroughEquations(5)–(7). Step3. Choosetheparametersfortheplanwhereindeterminacyintervalin gN isminimum. Thecombinationsthathavesmallervaluesof nN {nL, nU } areselectedandreportedinTables 1 and 2.Table 1 reportsfor gN {gL, gU } and kN {kaL, kaU } when r =5andTable 2 reportsfor gN {gL, gU } and kN {kaL, kaU } when r =10.FromTables 1 and 2,wenotedthefollowingtrend in gN {gL, gU } and kN {kaL, kaU }
1. Forthefixedvaluesofneutrosophicparameters, gN {gL, gU } and kN {kaL, kaU } decreaseas r increasesfrom5to10.
2. Forthefixedvaluesofneutrosophicparameters, gN {gL, gU } and kN {kaL, kaU } decreaseas LQLincreases.
Table1. Theneutrosophicplanoptimalparameterswhen r =5. p1 p2 gN kN L CAQL L CLQL 0.001
0.002 Min192473.20.9521630.099984 Max212717.50.9627120.095018 0.003 Min8783.60.9534900.099964 Max10953.30.9758000.095052 0.004 Min6462.90.9691750.099899 Max8592.60.9888450.095073 0.006 Min4222.10.9734340.099858 Max6311.30.9946800.095147 0.008 Min3132.60.9701670.099792 Max5201.20.9962390.095123 0.010 Min3106.00.9832130.099699 Max5160.80.9985550.095117 0.015 Min251.50.9719990.099838 Max489.40.9988310.095418 0.020 Min238.60.9835920.099255 Max466.90.9995990.095298
0.0025
0.005 Min19987.80.9524440.099978 Max211085.30.9629750.095069 0.010 Min6184.60.9694620.099904 Max8236.30.9889890.095133 0.015 Min488.50.9736910.099564 Max6123.90.9947850.095364 0.020 Min352.70.9834390.099924 Max580.00.9963210.095083
Min342.10.9834900.099512 Max563.80.9986000.095342 0.030 Min225.60.9584240.099282 Max444.40.9974420.095051 0.050 Min215.20.9840440.099320 Max426.30.9996240.096062
0.025
Table1. Cont.
p1 p2 gN kN L CAQL L CLQL
0.005
0.010
Min19492.70.9528850.099908 Max21541.30.9633710.095048 0.015 Min8155.80.9543350.099875 Max10189.50.9763770.095086 0.020 Min691.90.9698490.099547 Max8117.50.9892430.095381
0.030 Min443.90.9742400.099688 Max661.50.9949310.095194
0.040 Min326.10.9712000.099658 Max539.50.9964910.096118 0.050 Min320.80.9839450.099161 Max531.50.9986680.095215
0.100 Min27.40.9847870.099317 Max412.80.9996580.096182 0.01
0.020 Min19245.10.9538350.099928 Max21269.20.9642730.095309
0.030 Min877.30.9554500.099925 Max1094.00.9771230.095270 0.040 Min539.20.9500250.099569 Max752.00.9824090.095945 0.050 Min426.10.9557410.099193 Max636.50.9887050.095461 0.100 Min310.20.9846420.096525 Max515.30.9988130.096244 0.150 Min24.80.9751900.099150 Max48.30.9990950.096094 0.200 Min23.50.9862320.098790 Max46.00.9997290.099160 0.03
0.060 Min1980.10.9572440.099165 Max2187.90.9674180.095266 0.090 Min825.00.9595160.099143 Max1030.30.9800980.096447 0.120 Min512.60.9543650.096610 Max716.60.9850150.096118 0.150
Min48.30.9604070.096094 Max611.50.9908330.096298 0.300
Min22.20.9549640.097352 Max54.50.9992850.098199 0.05
0.100 Min1844.90.9537780.098375 Max2049.40.9656430.096049
0.150 Min814.50.9638780.099439 Max1017.60.9825850.095869 0.200 Min57.20.9601310.097749 Max79.50.9875050.096649 0.250 Min44.70.9657610.095135 Max66.50.9926910.096047 0.500 Min21.20.9613240.080608 Max62.70.9999150.095643
Table2. Theneutrosophicplanoptimalparameterswhen r =10.
p1 p2 gN kN L CAQL L CLQL
0.002 Min191236.60.9521630.099984 Max211358.70.9627240.095049 0.003 Min8391.80.9534900.099964 Max10476.60.9758150.095115
0.001
0.004
Min6231.50.9691470.099791 Max8296.30.9888450.095073 0.006 Min4111.10.9733960.099670 Max6155.60.9946880.095301 0.008 Min366.30.9701670.099792 Max5100.60.9962390.095123 0.010 Min353.00.9832130.099699 Max580.40.9985550.095117 0.015 Min225.80.9718990.099239 Max444.70.9988310.095418 0.020 Min219.30.9835920.099255 Max433.40.9996020.095903
0.005 Min19493.90.9524440.099978 Max21542.60.9630040.095147 0.010 Min692.30.9694620.099904 Max8118.10.9890140.095364 0.015 Min444.30.9735970.099096 Max661.90.9948050.095754 0.020 Min326.40.9704500.099229 Max540.00.9963210.095083 0.025 Min321.10.9833870.098644 Max531.90.9986000.095342 0.030 Min212.80.9584240.099282 Max422.20.9974420.095051 0.050 Min27.60.9840440.099320 Max413.10.9996290.097616 0.005
0.0025
0.010 Min19246.40.9528090.099739 Max21270.60.9634300.095205 0.015 Min877.90.9543350.099875 Max1094.70.9764510.095405 0.020 Min646.00.9697130.099008 Max858.70.9892940.095848 0.030 Min422.00.9740540.098745 Max630.70.9949700.095980 0.040 Min313.10.9709200.098260 Max519.70.9965290.097257 0.050 Min310.40.9839450.099161 Max515.70.9986860.096635 0.100 Min23.70.9847870.099317 Max46.40.9996580.096182
Table2. Cont.
p1 p2 gN kN L CAQL L CLQL
0.020 Min19122.60.9536860.099588 Max21134.60.9642730.095309 0.030 Min838.70.9551760.099196 Max1047.00.9771230.095270
0.040 Min519.60.9500250.099569 Max726.00.9824090.095945
0.01
0.050 Min413.10.9552310.097616 Max618.20.9888430.096790
0.100 Min35.10.9846420.096525 Max57.60.9988470.099210 0.150 Min22.40.9751900.099150 Max33.30.9952490.097215 0.200 Min21.80.9854820.090371 Max43.00.9997290.099160
0.060 Min1940.10.9568140.098132 Max2143.90.9677450.096233 0.090 Min812.50.9595160.099143 Max1015.10.9804900.098475 0.120 Min56.30.9543650.096610 Max78.30.9850150.096118 0.150 Min44.20.9589440.091311 Max76.50.9957040.098411 0.300 Min21.10.9549640.097352 Max31.50.9886710.098094 0.05
0.03
0.100 Min1822.50.9529810.096593 Max2024.70.9656430.096049 0.150 Min87.30.9626500.095621 Max108.80.9825850.095869 0.200 Min53.60.9601310.097749 Max85.30.9931160.097357 0.250 Min42.40.9634760.086889 Max84.10.9985010.098851 0.500 Min20.60.9613240.080608 Max81.70.9999960.099397
3.ApplicationofProposedPlan
Theapplicationoftheproposedplanwillbegivenontheballbearingqualityassurance,asthe qualitycharacteristicismeasurableandasthereisachancethatsomeobservationsmaybefuzzy. Supposethattheballbearingmanufacturerisinterestedinapplyingtheproposedsamplingplan, butisnotcertainhowtoselectsuitableplanparametersforthetestingofhisproduct.Supposehe decidestoinstallfiveitemsonthesingletester.LetAQL=AQL=0.001,LQL=0.010, α =0.05and β =0.10.FromTable 1,wehave gN {3,5} and kN {106.0,160.8}.Hence,hecanselect g between3 and5.Supposeexperimenterdecidestoselectarandomsamplesize n =25and g =5.
Step1. Selectarandomsample25anddistributefiveitemsintofivegroups. Step2. Performsuddendeathtestingandnotedownthefirstfailurefromeachofthefivegroups (i = 1,2,...,5).Thenumberoffirstfailuresfromthefivegroupsare Y1 =[220,230], Y2 =[300,320], Y3 =285,Y4 =[155,165]andY5 =[365,375].Thelifetimeofballbearingfollows
theneutrosophicWeibulldistributionwithparameter mN {2,2} andlowerspecificationlimit L =200.Thestatistic vN iscalculatedas: vN = gN ∑ i=1 Ym iN ; gN {3,5}, vN {106.0,160.8}
vN = [2202,2302]+[3002,3202]+[2852,2852]+[1552,1652]+[3652,3752]=[376875,404375].Now kN LmN {4240000,6432000}.As vN < kN LmN ,sorejectthelotofballbearingproduct.
4.ComparisonStudy
Inthissection,wewillcomparetheefficiencyoftheproposedplanusingtheneutrosophic statisticsandthesuddendeathsamplingplanproposedinReference[2]usingtheclassical(crisp) statisticsintermsofplanparameter g.Forfaircomparison,wewillconsiderthesameplanparameter values.BycomparingTable 1 oftheproposedplanwithTable 1 ofReference[2]when r =5,itcan beseenthattheproposedplanprovidessmallervaluesof g ascomparedtotheplaninReference[2]. Foreasyreference,wepresentthecomparisonin gN betweentheproposedplanandReference[2]in Table 3.Forexample,whenAQL=0.001andLQL=0.002inTable 3,theproposedplanhasaminimum valueof g =17andamaximumvalueof g =21,whiletheplanin[2]providesacrispvalueof g = 231. Therefore,theproposedplanneedsasamplesizeof n = r*g between85and105.Bycomparison,the existingplanneedsasamplesizeof1155forthetestingofthesamelotoftheproduct.FromTable 3, wenotethattheproposedplanhasasmaller gN forallcombinationsofAQLandLQL.Therefore, theproposedplanrequiredasmallersamplesizefortheinspectionofthesameproduct.Hence,less inspectioncostisneededwhentheproposedsamplingplanisimplemented.
Table3. ThecomparisonofproposedplanwiththeplaninReference[2]. p1 p2
ProposedPlanExistingPlan gN g 0.001
0.002[19,21]231 0.003[8,10]154 0.004[6,8]115 0.006[4,6]77 0.008[3,5]58 0.05 0.100[18,20]34 0.150[8,10]16 0.200[5,7]8
5.ConcludingRemarks
Inthispaper,wehavedesignedaneutrosophicfuzzysuddendeathtestingplanforthe inspection/testingoftheelectronicproductorpartsmanufacturing.TheNFOCandneutrosophicfuzzy non-linearoptimizationproblemareusedtoevaluatetheproposedsamplingplan.Theproposedplan canbeappliedforthetestingofpartswhensomeobservationsorparametersarefuzzy.Theproposed planistheextensionofasuddendeathplanbasedonclassicalstatistics.However,theproposed planismoreflexiblethantheplanbasedonclassicalstatistics.Sometablesaregivenanddiscussed withthehelpofaballbearingexample.Theproposedplancanbeappliedfortestingproductsinthe automobile,aerospaceandelectronicsindustries.Theproposedplanhasthelimitationthatitcanonly beappliedwhenthefailuretimefollowstheneutrosophicfuzzyWeibulldistribution.Theproposed planforsomeotherdistributioncanbeconsideredasfutureresearch.Theproposedsamplingplan usingbigdatacanalsobeconsideredasfutureresearch.
Symmetry 2018, 10,403
AuthorContributions: Conceivedanddesignedtheexperiments,M.A.;Performedtheexperiments,M.A. Analyzedthedata,M.A.andO.H.A.;Contributedreagents/materials/analysistools,M.A.;Wrotethepaper,M.A. andO.H.A.
Funding: ThisarticlewasfundedbytheDeanshipofScientificResearch(DSR)atKingAbdulazizUniversity, Jeddah.Theauthors,therefore,acknowledgewiththanksDSRtechnicalandfinancialsupport.
Acknowledgments: Theauthorsaredeeplythankfultoeditorandreviewersfortheirvaluablesuggestionsto improvethequalityofthismanuscript.
ConflictsofInterest: Theauthorsdeclarenoconflictofinterestregardingthispaper.
References
1. Jun,C.-H.;Balamurali,S.;Lee,S.-H.VariablessamplingplansforWeibulldistributedlifetimesundersudden deathtesting. IEEETrans.Reliab. 2006, 55,53–58.[CrossRef]
2. Aslam,M.;Azam,M.;Balamurali,S.;Jun,C.-H.Anewmixedacceptancesamplingplanbasedonsudden deathtestingundertheWeibulldistribution. J.Chin.Inst.Ind.Eng. 2012, 29,427–433.[CrossRef]
3. Balamurali,S.;Subramani,J.ConditionalvariablesdoublesamplingplanforWeibulldistributedlifetimes undersuddendeathtesting. BonfringInt.J.DataMin. 2012, 2,12.
4. Fertig,K.;Mann,N.R.Life-testsamplingplansfortwo-parameterWeibullpopulations. Technometrics 1980, 22,165–177.[CrossRef]
5. Kwon,Y.ABayesianlifetestsamplingplanforproductswithWeibulllifetimedistributionsoldunder warranty. Reliab.Eng.Syst.Saf. 1996, 53,61–66.[CrossRef]
6. Balasooriya,U.;Saw,S.L.;Gadag,V.ProgressivelycensoredreliabilitysamplingplansfortheWeibull distribution. Technometrics 2000, 42,160–167.[CrossRef]
7. Tse,S.-K.;Yang,C.ReliabilitysamplingplansfortheWeibulldistributionunderTypeIIprogressivecensoring withbinomialremovals. J.Appl.Stat. 2003, 30,709–718.[CrossRef]
8. Chen,J.;Choy,S.;Li,K.-H.OptimalBayesiansamplingacceptanceplanwithrandomcensoring. Eur.J. Oper.Res. 2004, 155,683–694.[CrossRef]
9. Chen,J.;Chou,W.;Wu,H.;Zhou,H.Designingacceptancesamplingschemesforlifetestingwithmixed censoring. Nav.Res.Logist. 2004, 51,597–612.[CrossRef]
10. Balasooriya,U.;Low,C.-K.CompetingcausesoffailureandreliabilitytestsforWeibulllifetimesundertype Iprogressivecensoring. IEEETrans.Reliab. 2004, 53,29–36.[CrossRef]
11. Kanagawa,A.;Ohta,H.Adesignforsinglesamplingattributeplanbasedonfuzzysetstheory. FuzzySetsSyst. 1990, 37,173–181.[CrossRef]
12. Tamaki,F.;Kanagawa,A.;Ohta,H.Afuzzydesignofsamplinginspectionplansbyattributes. Jpn.J.Fuzzy TheorySyst. 1991, 3,211–212.
13. Cheng,S.-R.;Hsu,B.-M.;Shu,M.-H.Fuzzytestingandselectingbetterprocessesperformance. Ind.Manag. DataSyst. 2007, 107,862–881.[CrossRef]
14. Zarandi,M.F.;Alaeddini,A.;Turksen,I.Ahybridfuzzyadaptivesampling—RunrulesforShewhartcontrol charts. Inf.Sci. 2008, 178,1152–1170.[CrossRef]
15. Alaeddini,A.;Ghazanfari,M.;Nayeri,M.A.Ahybridfuzzy-statisticalclusteringapproachforestimating thetimeofchangesinfixedandvariablesamplingcontrolcharts. Inf.Sci. 2009, 179,1769–1784.[CrossRef]
16. SadeghpourGildeh,B.;BalouiJamkhaneh,E.;Yari,G.Acceptancesinglesamplingplanwithfuzzyparameter. Iran.J.FuzzySyst. 2011, 8,47–55.
17. Jamkhaneh,E.B.;Sadeghpour-Gildeh,B.;Yari,G.Inspectionerroranditseffectsonsinglesamplingplans withfuzzyparameters. Struct.Multidiscip.Optim. 2011, 43,555–560.[CrossRef]
18. Turano˘glu,E.;Kaya, I.;Kahraman,C.Fuzzyacceptancesamplingandcharacteristiccurves. Int.J.Comput. Intell.Syst. 2012, 5,13–29.[CrossRef]
19. Divya,P.Qualityintervalacceptancesinglesamplingplanwithfuzzyparameterusingpoissondistribution. Int.J.Adv.Res.Technol. 2012, 1,115–125.
20. Jamkhaneh,E.B.;Gildeh,B.S.Acceptancedoublesamplingplanusingfuzzypoissondistribution. WorldAppl. Sci.J. 2012, 16,1578–1588.
21. Jamkhaneh,E.B.;Gildeh,B.S.SequentialsamplingplanusingfuzzySPRT. J.Intell.FuzzySyst. 2013, 25, 785–791.
Symmetry 2018, 10,403 10of10
22.
23.
24.
Venkateh,A.;Elango,S.AcceptancesamplingfortheinfluenceofTRHusingcrispandfuzzygamma distribution. AryabhattaJ.Math.Inform. 2014, 6,119–124.
Afshari,R.;Gildeh,B.S.Constructionoffuzzymultipledeferredstatesamplingplan.InProceedingsofthe 2017Joint17thWorldCongressofInternationalFuzzySystemsAssociationand9thInternationalConference onSoftComputingandIntelligentSystems(IFSA-SCIS),Otsu,Japan,27–30June2017;pp.1–7.
Afshari,R.;Gildeh,B.S.;Sarmad,M.Multipledeferredstatesamplingplanwithfuzzyparameter. Int.J. FuzzySyst. 2017, 20,549–557.[CrossRef]
25. Elango,S.;Venkatesh,A.;Sivakumar,G.Afuzzymathematicalanalysisfortheeffectoftrhusingacceptance samplingplans. Int.J.PureAppl.Math. 2017, 117,1–7.
26. Afshari,R.;SadeghpourGildeh,B.;Sarmad,M.Fuzzymultipledeferredstateattributesamplingplaninthe presenceofinspectionerrors. J.Intell.FuzzySyst. 2017, 33,503–514.[CrossRef]
27.
28.
29.
30.
Viertl,R.Onreliabilityestimationbasedonfuzzylifetimedata. J.Stat.Plan.Inference 2009, 139,1750–1755. [CrossRef]
Aslam,M.Anewsamplingplanusingneutrosophicprocesslossconsideration. Symmetry 2018, 10,132. [CrossRef]
Huang,H.-Z.;Zuo,M.J.;Sun,Z.-Q.Bayesianreliabilityanalysisforfuzzylifetimedata. FuzzySetsSyst. 2006, 157,1674–1686.[CrossRef]
Pak,A.;Parham,G.A.;Saraj,M.InferencefortheWeibulldistributionbasedonfuzzydata. Rev.Colomb.Estad. 2013, 36,337–356.
© 2018bytheauthors.LicenseeMDPI,Basel,Switzerland.Thisarticleisanopenaccess articledistributedunderthetermsandconditionsoftheCreativeCommonsAttribution (CCBY)license(http://creativecommons.org/licenses/by/4.0/).

