GreenSupplierEvaluationandSelectionUsing CloudModelTheoryandtheQUALIFLEXMethod
Ke-QinWang 1,Hu-ChenLiu 2,*,LipingLiu 3 andJiaHuang 2
1 SchoolofManagement,NorthwesternPolytechnicalUniversity,Xi’an710072,China; keqinwang@nwpu.edu.cn
2 SchoolofManagement,ShanghaiUniversity,Shanghai200444,China;jiahuangshu@foxmail.com
3 BusinessSchool,NanjingNormalUniversity,Nanjing210023,China;lpliu1016@163.com
* Correspondence:huchenliu@foxmail.com;Tel.:+86-21-6613-3703;Fax:+86-21-6613-7931
AcademicEditor:AndreaAppolloni
Received:24January2017;Accepted:24April2017;Published:27April2017
Abstract: Nowadays,companieshavetoimprovetheirpracticesinthemanagementofgreensupply chainwithincreasedawarenessofenvironmentalissuesworldwide.Selectingtheoptimumgreen supplieriscrucialforgreensupplychainmanagement,whichisachallengingmulti-criteriadecision making(MCDM)problem.Moreover,whileevaluatingtheperformanceofalternativesuppliers, decisionmakerstendtodeterminetheirassessmentsusinglinguisticdescriptorsduetoexperts’ vagueknowledgeandinformationdeficiency.Therefore,thispaperdevelopsanintegratedMCDM modelbasedonthecloudmodelandQUALIFLEX(qualitativeflexiblemultiplecriteriamethod) approachtoassessthegreenperformanceofcompaniesundereconomicandenvironmentalcriteria. Fortheintroducedmodel,thelinguisticterms,expressedinnormalclouds,areutilizedtoassess alternativesagainsteachselectioncriterion.Alinearprogrammingmodelisestablishedtocompute theweightsofcriteriawithunknownorincompletelyknownweightinformation.Anextended QUALIFLEXapproachisproposedandusedtoselectthemostsuitablegreensupplier.Finally,the proposedgreensupplierselectionmethodisdemonstratedbyanempiricalexampleofanauto manufacturertoconfirmitsrationalityandeffectiveness.

Keywords: greensupplychainmanagement;supplierselection;cloudmodel;QUALIFLEXapproach
1.Introduction
Currently,companies,particularlyinthedevelopingnations,havetoenhancetheeffectiveness oftheirgreensupplychainmanagementactivitiestosurviveintheglobalmarketplace.Ontheone hand,governmentsarepayingmoreattentiontoenvironmentalissuesandhaveissuedaseries ofenvironmentalregulationsduetodiminishingrawmaterials,increasinglevelsofpollution,and deteriorationoftheenvironment.Besides,avarietyofpressuresfromconsumersaremakingcompanies morecautiouswithregardstothedetrimentalinfluencesoftheirbusinessesoperationsonthe environment[1].Inthisregard,numerousgreensupplierdevelopmentprograms,suchasgreen purchasing,designforenvironment,andreverselogistics,havebeeninvestedbyorganizationsto enhancetheirgreenperformancewithrespecttothesupplychain[2,3].Accordingto[4],greensupply chainmanagementisanapproachtothephilosophyofmanagementtakingenvironmentalconcerninto accountinthesupplychainmanagement,whichconsistsofproductdesign,rawmaterialextraction, productionprocesses,producttransportationaswellasdisposingoftheend-of-lifeproduct.Giventhe increasingawarenessofenvironmentalprotection,itismoresignificantforcompaniestoconduct greensupplychainmanagementpracticestominimizeoreliminatethenegativeenvironmentaleffects oftheirbusinessoperations.Inrecentyears,greensupplychainmanagementhasreceivedincreasing interestamongbothacademicsandpractitioners[4–6].
Sustainability 2017, 9,688;doi:10.3390/su9050688 www.mdpi.com/journal/sustainability
Withingreensupplychainmanagement,organizationsarerequiredtoassessthegreenperformance oftheirsuppliersandselectthemostappropriateone(s)indifferentstagesofproductlifecycle[7]. Greensupplierselectionisachallengingmulti-dimensionalissueinthecompetitive environment[8,9], whichcanberesolvedbymulti-criteriadecisionmaking(MCDM)methods.TheQUALIFLEX(qualitative flexiblemultiplecriteriamethod)[10]isanefficientoutrankingMCDMmethodthatassessesall possiblerankingsofconsideredalternativesandfindstheoptimumonebyusingthemaximum concordance/discordanceindex.ThesalientfeaturesoftheQUALIFLEXmethod,comparedtoother MCDMmethods,arethat:(1)Itcansimultaneouslydealwithcardinalandordinalinformationinthe decisionprocess;(2)Itcanperfectlyaddressthecomplexdecisionmakingproblemswithnumerous criteriaandlimitedalternatives;(3)Itdoesnotrequirecomplicatedcomputationsinthemultiplecriteria decisionanalysis.Moreover,theuseoftheQUALIFLEXforgreensupplierselectionispracticalandhas demonstratedsatisfactoryresults[11–13].Therefore,itisnaturaltoutilizetheQUALIFLEXapproachto managethegreensupplierselectionproblemsinvolvingcomprehensivecriteria.
Ontheotherhand,intheprocessofgreensupplierevaluation,decisionmakersmayhavedifficulty inevaluatingcandidatecompanieswithspecificnumericalvaluesduetotheuncertaintyofinput data,andinparticular,thevaguenessofhumanthinking.Asisstressedbymanyresearchers[14,15], itisnaturalfordecisionmakerstodeterminetheirjudgmentsbasedonlinguisticexpressions,i.e., inexactandunquantifiableinformation,inreal-lifegreensupplierselectionproblems.Computingwith wordsisthekeytotransforminglinguisticvariablesintoquantitativevalues,andthecurrentmethods ofdealingwithlinguisticinformationcanbemainlyclassifiedintothreetypes,i.e.,thelinguistic computationalmodelbasedonmembershipfunctions[16],thelinguisticsymbolicmodelbasedon ordinalscales[17]andthe2-tuplelinguisticmodel[18].However,asindicatedbyWangetal.[19], thelinguisticsymbolicmodelandthe2-tuplelinguisticmodelcannotproduceaclearerdescription ofeitherfuzzinessorrandomnessofqualitativeinformation.Thelinguisticcomputationalmodel candescribefuzzinessbutnotrandomness.However,thecloudmodel[20]notonlydescribesthe fuzzinessandrandomnessoflinguistictermsbutalsomakesthetransformationbetweenquantitative valuesandqualitativeconceptsmucheasierandinterchangeable.Inthisway,thecloudmodelisof greatvalueinsolvingthelinguisticgreensupplierevaluationproblems.
Basedonthediscussionsabove,thisarticleisaimedatproposinganintegrateddecisionsupport frameworkbasedoncloudmodeltheoryandtheQUALIFLEXmethodfortheevaluationofqualified greensupplierswithinalinguisticenvironment.Themaincontributionsofthisstudyaresummarized asfollows:First,thecloudmodelisintroducedforthepurposeofhandlingthefuzzinessand randomnessoflinguisticexpressionsprovidedbydecisionmakers.Second,wecreateanoptimization modeltoobtainthecriteriaweightsthataresupposedtobetotallyunknownorincompletelyknown. Third,anextendedQUALIFLEXalgorithmisdevelopedtoprioritizetheperformanceofdifferent alternativesuppliersandrecommendtheoptimalone(s)forcooperation.Inaddition,thefeasibility andeffectivenessoftheproposedgreensupplierselectionapproachareindicatedbyacaseexample concerninganautomobilemanufacturingcompany.Theremainingpartofthisarticleisstructured asbelow:Section 2 reviewstherelatedliteratureofgreensupplierselection,thecloudmodeltheory andtheQUALIFLEXmethod.Section 3 introducessomebasicconceptsrelatedtocloudmodeltheory. InSection 4,weproposethegreensupplierselectionapproachusingthecloudmodelandQUALIFLEX method.InSection 5,anillustrativeexampleispresentedtodemonstratethedevelopedapproach,and thesolutionresultsarecomparedwiththosederivedbyotherexistingmethods.Finally,inSection 6, theconclusionsanddirectionsforfutureworkcompletethepaper.
2.RelatedLiterature
2.1.GreenSupplierSelectionMethods
Toseeksolutionsforcomplexgreensupplierselectionproblems,anabundanceofdecision-making tools,especiallythosebasedonMCDMmodels,hasbeendevelopedintheliterature.Forexample,
UygunandDede[15]proposedacomprehensiveMCDMmodelusingfuzzydecision-makingtrial andevaluationlaboratory(DEMATEL),fuzzyanalyticalnetworkprocess(ANP)andfuzzytechnique fororderpreferencebasedonsimilaritytoidealsolution(TOPSIS)methodsforassessingcompanies’ greensupplychainmanagementperformance.Wangetal.[21]proposedanintegratedMCDM methodbycombiningfuzzyAHPwithfuzzyTOPSISforselectinggreensuppliersinlinewiththe economicandenvironmentalcriteria.Banaeianetal.[8]appliedthreefuzzyMCDMapproaches, i.e.,fuzzyTOPSIS,fuzzyVIKOR(VlseKriterijuskaOptimizacijaIKomoromisnoResenje)andfuzzy greyrelationalanalysis(GRA),forgreensupplierevaluationandselectionintheagri-foodindustry. Tsuietal.[22]usedahybridMCDMmethodwithDEMATEL-basedANP(DANP)andPROMETHEE toappraiseandimprovetheperformanceofgreensuppliersinthethinfilmtransistorliquidcrystal displayindustry.Liouetal.[23]suggestedahybridMCDMapproachonthebasisofDANPand modifiedCOPRAS-G(COmplexPRoportionalASsessmentofalternativeswithGreyrelations)for rankingandimprovingsuppliersingreensupplychainmanagement.Kannanetal.[14]reporteda fuzzyaxiomaticdesign-basedmethodologyforgreensupplierselectionandutilizeditforaSingapore plasticmanufacturingcompany,andKannanetal.[24]appliedthefuzzyTOPSISapproachtoan electronicscompanyinBrazilforgreensupplierevaluationinaccordancewithgreensupplychain managementpractices.Hashemietal.[25]developedacombinedMCDMapproachusingANPand improvedGRAtodeterminetheoptimalgreensupplierfromeconomicandenvironmentalaspects. Yazdanietal.[26]proposedanintegratedgreensupplierselectionframeworkinwhichDEMATELwas usedtoaddressestheinter-relationshipsbetweencustomerrequirements;qualityfunctiondeployment wasadoptedtoidentifytherelationshipdegreebetweencriteriaandcustomerrequirements,and COPRASwasappliedtoprioritizeandrankthealternativesuppliers.Bakeshlouetal.[27]addressed thegreensupplierselectionproblemusingahybridmultiobjectivedecisionmakingalgorithmin whichfuzzyDEMATELwasusedtounderstandtheinterrelationshipsamongcriteria;fuzzyANP providedthecriteriaweightsconsideringtheirdependencies.Inaddition,asystematicliterature reviewontheMCDM-basedgreensupplierevaluationandselectionapproachescanbefoundin[5].
2.2.ApplicationsofQUALIFLEXMethod
Overthepastdecades,researchershaveextendedtheQUALIFLEXmethodtomodelandmanage MCDMproblemswithindifferentdecision-makingenvironments.Forinstance,Zhang[28]proposed aPythagoreanfuzzyQUALIFLEXmodelbasedontheclosenessindex-basedmethodforhierarchical multiplecriteriadecisionmakinginthePythagoreanfuzzyandinterval-valuedPythagoreanfuzzy contexts.Zhang[29]proposedtwointerval-valuedhesitantfuzzyQUALIFLEXapproachesusinga likelihood-basedcomparisonmethodtosolveMCDMproblemsundertheinterval-valuedhesitantfuzzy environment.Xueetal.[30]elaboratedonacombinedlinguisticMCDMmodelintegratinghesitant 2-tuplelinguistictermsetsandtheQUALIFLEXmethodinordertodealwithrobotselectionproblems withincompleteinformationofcriteriaweights.Tianetal.[31]proposedasimplifiedneutrosophic linguisticQUALIFLEXapproachforgreenproductdesignselectionconsideringriskattitudesofdecision makers,andTianetal.[32]proposedanextendedQUALIFLEXapproachwithalikelihood-based comparisonmethodtohandleMCDMproblemsinthecontextofhesitantfuzzylinguisticinformation. Pengetal.[33]presentedtwocrossentropymeasuresforprobabilitymulti-valuedneutrosophicnumbers andproposedaprobabilitymulti-valuedneutrosophicQUALIFLEXmethodtoaddressMCDMproblems. Wangetal.[34]developedalikelihood-basedQUALIFLEXmodeltodealwithdecision-makingproblems underthecontextofintervaltype-2trapezoidalfuzzysets.Chen[35]suggestedaninterval-valued intuitionisticfuzzyQUALIFLEXapproachusinglikelihood-basedcomparisonmethodtoresolveMCDM issues.Inaddition,othermeaningfulextensionsoftheQUALIFLEXtechniqueinpreviousstudiesinclude theinterval-valuedintuitionisticfuzzyQUALIFLEX[36],theintervaltype-2fuzzyQUALIFLEX[37], andthehesitanttrapezoidalfuzzyQUALIFLEX[38].
2.3.ApplicationsofCloudModelTheory
Inrecentyears,thecloudmodeltheoryhasattractedincreasingattentionandhasbeensuccessfully appliedinmanyfields.Forexample,Zhangetal.[39]developedahybridinformationfusionapproach thatintegratesthecloudmodel,Dempster-ShaferevidencetheoryandMonteCarlosimulationfor perceivingsafetyriskofbuildingsadjacenttotunnelingexcavations.Wuetal.[40]proposedacloud model-baseddecisionframeworkforlow-speedwindfarmsiteselectionwithinapure2-tuplelinguistic environment.WangandWang[41]reportedanevolvingTakagi-Sugenoapproachbasedonaggregated trapeziumcloudsthatcouldbeusedforanomalydetectioninlargedatasets.Shietal.[42]establishedan integrateddecision-makingmodelusingthecloudmodelandMABACmethodforassessinghealthcare wastetreatmenttechnologiesfromamultiplestakeholderperspective.Basedonthecloudmodel andcombinedweightingmethod,Caoetal.[43]developedanassessmentmodelfortheanalysisof debris-flowhazard.InZhangetal.[44],atrustevaluationmethodbasedonthecloudmodelisproposed todetectmaliciousnodesandensuresecurityinclusteredwirelesssensornetworks.Lietal.[45]applied fuzzyAHPandthecloudmodelforenergyutilizationevaluationofcarbonperformanceinpublic projects,andZhaoandLi[46]usedthecloudmodelandfuzzycomprehensiveevaluationmethodto evaluatetheriskofultra-highvoltageprojects.Furthermore,anuncertainlinguisticgroupMCDM methodandaninterval-valuedintuitionisticlinguisticdecisionmakingmethodwereproposedby Wangetal.[47]andWangetal.[48],respectively,basedoncloudmodeltheory.
3.Preliminaries
3.1.CloudModelTheory
ThecloudmodelisanewcognitionmodeldefinedbyLi[20]torepresenttheuncertainty (fuzzinessandrandomness)ofqualitativeconcepts.Inthispart,somebasicconceptsandoperations relatedtocloudmodeltheoryareintroduced.
Definition1. SupposingaqualitativeconceptTdefinedonauniverseofdiscourseU,let x, x ∈ U bearandom realizationoftheconceptTand µT (x) ∈ [0,1] bethemembershipdegreeofxbelongingtoT,whichcorresponds toarandomnumberwithastabletendency.ThenthedistributionofxintheuniverseUiscalledacloudand everyxiscalledaclouddrop [20].
Definition2. Thecharacteristicsofacloudyaredepictedbythreeparameters:expectationEx,entropy EnandhyperentropyHe.Here,Existhecentervalueofthequalitativeconceptdomain,Enmeasuresthe randomnessandfuzzinessofthequalitativeconcept,andHereflectsthedispersiondegreeoftheclouddropsand theuncertaintyofthemembershipfunction.Generally,acloudcanbedenotedbyy = (Ex, En, He) [20].
Definition3. Consideranytwonormalclouds y1 = (Ex1, En1, He1) and y2 = (Ex2, En2, He2) inthedomain U,thebasicoperationsofnormalcloudsaredefinedasfollows[19]:
(1)
Definition4. Let yi = (Exi, Eni, Hei )(i = 1,2,..., n) bennormalcloudsintheuniverseofdiscourseU,and w = (w1, w2,..., wn )T betheirassociatedweightswith wi ∈ [0,1] and ∑n i=1 wi = 1, thenthecloudweighted averaging(CWA)isdefinedas[19]: CWAw (y1, y2,..., yn ) = n ∑ i=1 wi yi = n ∑ i=1 wi (Exi, Eni, Hei ) = n ∑ i=1 wi Exi, n ∑ i=1 wi En2 i , n ∑ i=1 wi He2 i .
Definition5. Let y1 = (Ex1, En1, He1) and y2 = (Ex2, En2, He2) betwoarbitrarynormalcloudsinthe domainU,thenthedistancebetweenthemiscomputedby [47]: d(y1, y2) = 1 (En1 + He1) Ex1 Ex1 1 (En2 + He2) Ex2 Ex2 .(2)
Definition6. Let y = (Ex, En, He) beanormalcloudinthedomainU,thenthesigneddistanceof y fromthe origin 0 isdeterminedby d y, 0 = 1 (En + He) Ex Ex.(3)
Notethatthesigneddistancesfromnormalcloudsto 0 arerealnumbers,whichsatisfythelaw oftrichotomy.
Definition7. Let y1 = (Ex1, En1, He1) and y2 = (Ex2, En2, He2) betwonormalcloudsinthedomainU. Thenthesigneddistance-basedcomparisonofnormalcloudsisdefinedasfollows:
(1) Ifd y1, 0 > d y2, 0 , then y1 isbetterthan y2, i.e., y1 > y2;
(2) Ifd y1, 0 < d y2, 0 , then y1 isworsethan y2, i.e., y1 < y2; (3) Ifd y1, 0 = d y2, 0 , then y1 isindifferentto y2, i.e., y1 = y2
Definition8. Let yi = (Exi, Eni, Hei )(i = 1,2,..., n) beasetofnormalcloudsintheuniverseofdiscourseU, and ω = (ω1, ω2,..., ωn ) beanassociatedweightvectorsatisfying ωj ∈ [0,1] and ∑n j=1 ωj = 1, thenthecloud orderedweightedaveraging(COWA)iscomputedby [19]: COWAω (y1, y2,..., yn ) = n ∑ j=1 ωj yσ(j) = n ∑ j=1 ωj Exσ(j), n ∑ j=1 ωj En2 σ(j), n ∑ j=1 ωj He2 σ(j) , (4) where yσ(j) = Exσ(j), Enσ(j), Heσ(j) isthejthlargestelementof yi (i = 1,2,..., n).
3.2.LaplaceDistribution-BasedMethod
Definingtheaggregationweightvector ω isonekeyissueinthetheoryoftheorderedweighted averaging(OWA)operator[49].Recently,Mohammedetal.[50]developedanewmethodbasedon theLaplacedistributiontocalculatetheOWAweightvector.Thismethodhastheabilitytoreducethe effectof“false”or“biased”opinionsonthedecision-makingresultsbyassigninghigherweightsto themedianelementsoftheorderedargumentsandlowerweightstothetailelements.
Sustainability 2017, 9,688 6of17
Sustainability 2016, 8, 688
Definition9. Accordingtotheargument-dependentmethodbasedonLaplacedistribution,theassociated weightingvectoroftheOWAoperatorisobtainedby [50]: ωj = 1 2λn e |i µn | λn ∑n j=1 1 2λn e |i µn | λn
(5)
is the mean of the number of the argument, and n is the scale of the Laplace distribution. The parameter n is calculated by 1 11 , 22 n
n is the number of aggregated arguments,
nn n n
the Laplace distribution standard deviation
= e |i µn | λn ∑n j=1 e |i µn | λn , j = 1,2,..., n,(5) wherenisthenumberofaggregatedarguments, µn isthemeanofthenumberoftheargument,and λn isthe scaleoftheLaplacedistribution.Theparameter µn iscalculatedby µn = 1 n n(1 + n) 2 = 1 + n 2 ,(6) andtheLaplacedistributionstandarddeviation σn isdefinedas σn = √2λn = 1 n
n ∑ j=1 (j µn )2.(7)
4. The Proposed Green Supplier Selection Methodology
4.TheProposedGreenSupplierSelectionMethodology
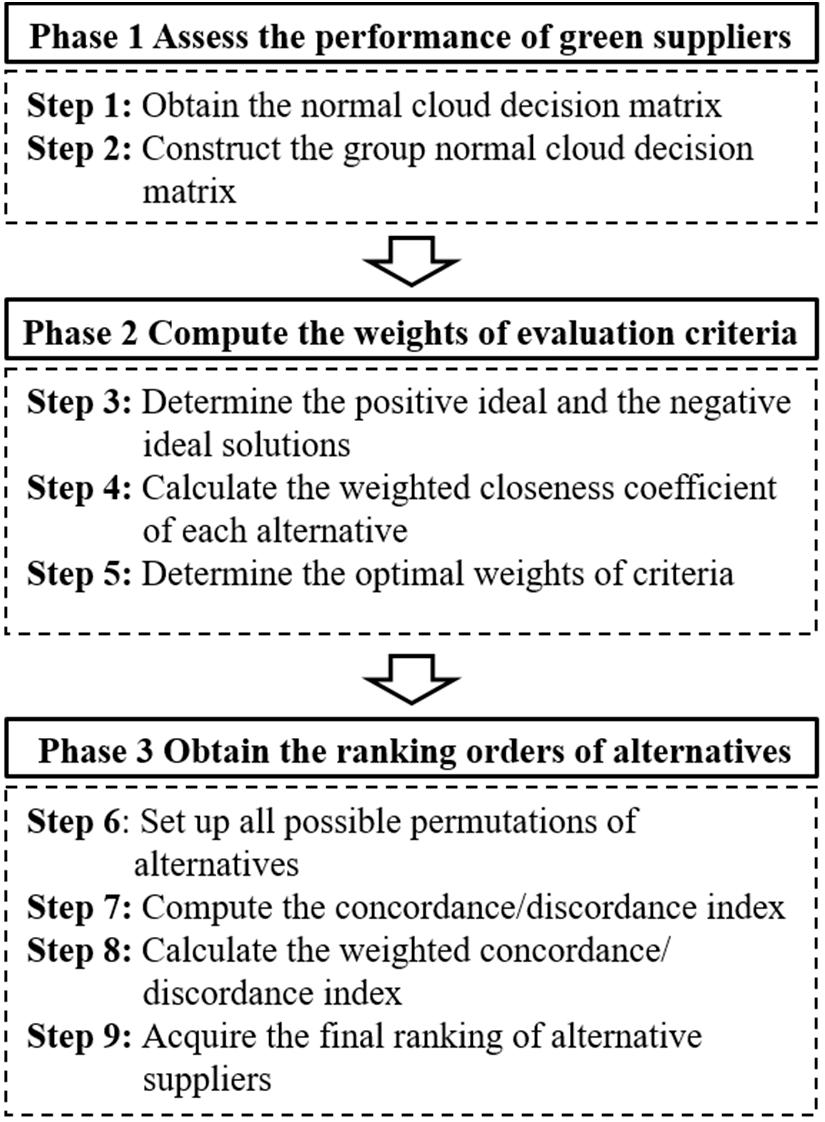
Green supply chain management has become a challenging issue for companies to maintain their competitive positions due to the increased public concern of environmental issues and stricter governmental regulations. In this section, we introduce a novel decision support framework by combining the cloud model and QUALIFLEX method for addressing the green supplier selection problem with unknown or incomplete weight information. In a nutshell, the proposed methodology to select the optimum green supplier is comprised of three phases: assessing the performance of green suppliers based on normal clouds, acquiring the weights of evaluation criteria by a linear programming model, and determining the ranking orders of alternatives with the QUALIFLEX method. The procedure of the proposed green supplier selection approach is depicted in Figure 1, and the detailed explanations are presented as below.
Greensupplychainmanagementhasbecomeachallengingissueforcompaniestomaintaintheir competitivepositionsduetotheincreasedpublicconcernofenvironmentalissuesandstrictergovernmental regulations.Inthissection,weintroduceanoveldecisionsupportframeworkbycombiningthecloud modelandQUALIFLEXmethodforaddressingthegreensupplierselectionproblemwithunknownor incompleteweightinformation.Inanutshell,theproposedmethodologytoselecttheoptimumgreen supplieriscomprisedofthreephases:assessingtheperformanceofgreensuppliersbasedonnormal clouds,acquiringtheweightsofevaluationcriteriabyalinearprogrammingmodel,anddetermining therankingordersofalternativeswiththeQUALIFLEXmethod.Theprocedureoftheproposedgreen supplierselectionapproachisdepictedinFigure 1,andthedetailedexplanationsarepresentedasbelow.
Figure 1. Flowchart of the proposed green supplier selection approach. Figure1. Flowchartoftheproposedgreensupplierselectionapproach.
4.1.AssessthePerformanceofGreenSuppliers
Assumeagreensupplierselectionproblemwith m feasiblealternatives (Ai, i = 1,2,..., m),which areassessedbyacommitteeof l decisionmakers (DMk, k = 1,2,..., l) onthebasisof n evaluationcriteria
Cj, j = 1,2,..., n .Let Dk = dk ij m×n bethelinguisticdecisionmatrix,where dk ij isthesuitability assessmentofalternativeAi versuscriterionCj providedbythedecisionmaker DMk.Next,thecloud modeltheoryisusedtomodelthelinguisticevaluationsonalternativesgivenbythedecisionmakers. Step1: Obtainthenormalclouddecisionmatrix Xk
Asdiscussedbefore,thecloudmodeltheoryisverypracticalfordepictingthefuzziness andrandomnessofdecision-makingproblems.Accordingly,theproposedgreensupplierselection approachutilizesthelinguistictermsrepresentedbynormalcloudstoassesstheperformanceof alternativesuppliersregardingvariousselectioncriteria.Forinstance,theselinguistictermscanbe representedbythenormalcloudsshowninTable 1
Table1. Linguisticratingsforalternativesuppliers.
LinguisticTermsNormalClouds
VeryPoor(VP)(1,0.45,0.05) Poor(P)(2,0.45,0.05) MediumPoor(MP)(3,0.45,0.05) Fair(F)(5,0.45,0.05)
MediumGood(MG)(6,0.45,0.05) Good(G)(8,0.45,0.05) VeryGood(VG)(9,0.45,0.05)
Basedonthelinguisticratingsofeachdecisionmaker,thefirststepistotransformtheminto normalcloudsasperthelinguisticscaleinformationtoobtainthenormalclouddecisionmatrix Xk = xk ij m×n ,where xij = Exij, Enij, Heij , i = 1,2,..., m; j = 1,2,..., n.
Step2: Establishthegroupnormalclouddecisionmatrix X Normally,theremayexist“false”or“biased”judgementsinthegreensupplierselectionpractice; thatistosay,somedecisionmakersmaygiveexcessivelyhighorexcessivelylowratingstotheir preferredorrepugnantsuppliers.Todealwithsuchcases,theCOWAoperatorisadoptedtocombine thedecisionmakers’performanceassessmentsintorepresentativegroupassessments. ByapplyingtheCOWAoperator,theaggregationofindividualcloudmatrices Xk = xk ij m × n (k = 1,2,..., l) isperformedtoconstructthegroupnormalclouddecision matrix X = xij m×n,i.e., xij
4.2.ComputetheWeightsofEvaluationCriteria
Itiscommonthatinthegreensupplierselectionproblems,theinformationconcerningcriteria weightsmaybecompletelyunknownorpartiallyknown.Thus,itisveryinterestingandimportantto focusonthisissue.TheTOPSISproposedbyHwangandYoon[51]isaclassicalMCDMtechnique, whichselectsthemostsuitablealternativewiththeshortestdistancefromthepositive-idealsolution
andthefarthestdistancefromthenegative-idealsolution.Theaimofthisstageistobuildan optimizationmodelfollowingtheideaoftheTOPSISmethodforobtainingthecriteriaweights objectively.Suppose w = (w1, w2,..., wn )T istheweightvectorofthecriteria Cj (j = 1,2,..., n),whichis unknownapriori.Inthefollowingsection,thedetailprocessesofdeterminingcriteriaweights arepresented.
Step3: Definethepositive-idealandthenegative-idealsolutions
Withinthecloudenvironment,thepositive-idealandthenegative-idealsolutions,denotedas A+ and A ,canberespectivelydenotedby
A+ = x+ j 1×n = max i xijforbenefitcriteria min i xijforcostcriteria ,(9) A = xj 1×n = min i xijforbenefitcriteria max i xijforcostcriteria .(10)
Step4: Determinetheweightedclosenesscoefficientsofalternatives
ByusingEquation(11),theclosenesscoefficientofeachalternativeagainstthecriteriaiscomputed asfollows: Dij = d xij, xj d xij, x+ j + d xij, xj , i = 1,2,..., m, j = 1,2,..., n,(11) where d xij, x+ j d xij, xj isthedistanceofAi from A+(A )concerningthecriterionCj.
ThentheweightedclosenesscoefficientofalternativesAi isdeterminedby Di = n ∑ j=1 wj Dij = n ∑ j=1 wj d xij, xj d xij, x+ j + d xij, xj , i = 1,2,..., m.(12)
Step5: Calculatetheoptimalweightsofcriteria
Theweightedclosenesscoefficient Dj representstherelativeclosenessofalternativeAi totheideal solution,thatis,thelargerthevalueof Dj,thebetterthealternative.Consideringallthe m alternatives asawhole,thefollowinglinearprogrammingmodelcanbecreatedforobtainingthecriteriaweights whentheweightinformationiscompletelyunknown: (M 1)
n ∑ j=1 wj Dij s.t. n ∑ j=1 wj = 1, wj ≥ 0, j = 1,2,..., n.
maxD(w) = m ∑ i=1 Di = m ∑ i=1
(13)
Byresolvingtheabovemodel,theoptimalsolutionsarenormalizedtoobtaintheweightsof criteriaas wj =
m ∑ i=1 Dij n ∑ j=1
m ∑ i=1 Dij .(14)
Furthermore,therearestillsomecaseswheretheinformationregardingcriteriaweights isidentifiedpartially.Theobtainedweightinformationnormallyconsistsofthefollowingfive structuralforms[52,53],for i = j:(1)Aweakranking: H1 = wi ≥ wj ;(2)Astrict ranking: H2 = wi wj ≥ βj βj > 0 ;(3)Arankingofdifferences: H3 = wi wj ≥ wk wl
(j = k = l);(4)Arankingwithmultiples: H4 = wi ≥ βj wj 0 ≤ βj ≤ 1 ;(5)Anintervalform: H5 = {βi ≤ wi ≤ βi + εi } (0 ≤ βi ≤ βi + εi ).Forthesakeofconvenience, H isassumedtobeaset ofrecognizedweightinformationand H = H1 ∪ H2 ∪ H3 ∪ H4 ∪ H5.Forthesesituations,thesingle objectiveoptimizationmodelinEquation(15)canbeestablished.
(M 2)
n ∑ j=1 wj Dij s.t. w ∈ H, n ∑ j=1 wj = 1, wj ≥ 0, j = 1,2,..., n.
maxD(w) = m ∑ i=1 Di = m ∑ i=1
(15)
Byexecutingmodel(M 2)withLingosoftware,theoptimalcriteriaweightscanbeobtainedas w = (w1, w2,..., wn )T
4.3.DeterminetheRankingOrdersofAlternatives
Greensupplierselectionrequiresmulti-dimensionaltechniques,andtheQUALIFLEXmethod[10] isapragmaticandreliableoutrankingMCDMtechniquetorankandselectalternatives.Thus,inthe thirdphraseofourproposedframework,weextendtheclassicalQUALIFLEXapproachtothecloud settinginordertodeterminethebestsuppliers.Tosumup,theproposedcloudQUALIFLEXforthe generationofrankingofgreensuppliersincludesthefollowingsteps: Step6: Setupallpossiblepermutationsofalternatives
Forthe m alternatives Ai (i = 1,2,..., m), m! permutationsoftherankingordersofalternatives exist.Assumethatthe ρthpermutationdenotedby Pρ isdefinedas: Pρ = ...,Aχ ,...,Aη ,... , ρ = 1,2,..., m!,(16) where Aξ and Aζ , ξ, ζ = 1,2,..., m,arethesuppliersunderconsideration,and Aξ isrankedlargerthan orequaltoAζ Step7: Acquiretheconcordance/discordanceindex
Weusethefollowingformulatocomputetheconcordance/discordanceindex φρ j Aξ ,Aζ inthe ρthpermutationagainstthecriterionCj foreachpairofalternatives Aξ ,Aζ φρ j Aξ ,Aζ = d rξ j, 0 d rζ j, 0 , j = 1,2,..., n.(17)
AccordingtothecomparisonmethodofnormalcloudsintroducedinDefinition7, φρ j Aξ ,Aζ > 0, φρ j Aξ ,Aζ < 0,and φρ j Aξ ,Aζ = 0representconcordance,discordanceandexaequo,respectively.
Step8: Determinetheweightedconcordance/discordanceindex
Usingtheweightvectorofcriteria w = (w1, w2,..., wn )T acquiredinthesecondstage,theweighted concordance/discordanceindex φρ Aξ ,Aζ isdeterminedbyEquation(18)forthealternatives Aξ ,Aζ regardingpermutation Pρ φρ Aξ ,Aζ = n ∑ j=1 φρ j Aξ ,Aζ wj.(18)
Step9: Acquirethebestrankingofalternativesuppliers
Foreachpermutation Pρ ,weobtainthecomprehensiveconcordance/discordanceindex φρ throughEquation(19). φρ = ∑ ξ,ζ =1,2,...,m
n ∑ j=1 φρ j Aξ ,Aζ wj.(19)
For each permutation P , we obtain the comprehensive concordance/discordance index through Equation (19).
A higher comprehensive concordance/discordance index value indicates that the ranking order of the alternatives is better. Hence, the optimum ranking of the considered suppliers can be identified via the comparison of the comprehensive concordance index values 1,2,...,! m
. That is, the permutation with the highest value, i.e.,
should be the final ranking of the alternatives.
Ahighercomprehensiveconcordance/discordanceindexvalueindicatesthattherankingorder ofthealternativesisbetter.Hence,theoptimumrankingoftheconsideredsupplierscanbeidentified viathecomparisonofthecomprehensiveconcordanceindexvalues φρ (ρ = 1,2,..., m!).Thatis, thepermutationwiththehighest φρ value,i.e., P∗ = max ρ=1,2,...,m!{φρ } shouldbethefinalranking ofthealternatives.
5.IllustrativeExample
5. Illustrative Example
Takingthegreensupplierselectionforanautomanufacturingcompanyasanexample,the applicabilityandefficacyoftheproposedgreensupplierevaluationmodelaredemonstratedin thissection.
Taking the green supplier selection for an auto manufacturing company as an example, the applicability and efficacy of the proposed green supplier evaluation model are demonstrated in this section.
5.1.BackgroundDescription
5.1. Background Description
Inthisstudy,weconsideranautomanufacturingcompanyinShanghai,Chinasincethegreen initiativesareexpectedtobeimplementedwithinitsoperations.Tocomplywithenvironmental regulationsandadapttosocialconcerns,topmanagementofthiscompanydecidedtoadjustits businessstrategyandbecomeacompanydevotedtothepublichealthandenvironmentbycommitting itselftosocialresponsibility.Currently,determinationofthequalifiedgreensupplierfortheautomotive component,instrumentpanel,forimprovingthecompany’ssupplychainenvironmentalperformance isneeded.Anexpertpanelincludingfivedirectmanagers(denotedasDM1,DM2, ,DM5)was establishedtoratethreealternativecompanies,A1,A2andA3.
Generally,variousquantitativeandqualitativeevaluationcriteriamustbeconsideredtodetermine thebestgreensupplier.Accordingtotheliteraturesurveys[5,6]anddecisionmakers’opinions,green design,greenpurchasing,greenproduction,greenlogisticsandgreenrecyclingaredetermined asevaluationdimensionsforthegreensupplierselection.Further,severalrelatedcriteriaofeach dimensionareidentifiedforevaluatingthealternativesuppliersinmoredetail(seeFigure 2).Then, thefivedecisionmakersareaskedtorateeachsupplierwithregardtotheabovecriteriausingthe linguisticassessmenttermsshowninTable 1.Thecompletedassessmentmatricesprovidedbythe expertgrouparepresentedinTable 2.
In this study, we consider an auto manufacturing company in Shanghai, China since the green initiatives are expected to be implemented within its operations. To comply with environmental regulations and adapt to social concerns, top management of this company decided to adjust its business strategy and become a company devoted to the public health and environment by committing itself to social responsibility. Currently, determination of the qualified green supplier for the automotive component, instrument panel, for improving the company’s supply chain environmental performance is needed. An expert panel including five direct managers (denoted as DM1, DM2, …, DM5) was established to rate three alternative companies, A1, A2, and A3. Generally, various quantitative and qualitative evaluation criteria must be considered to determine the best green supplier. According to the literature surveys [5,6] and decision makers’ opinions, green design, green purchasing, green production, green logistics and green recycling are determined as evaluation dimensions for the green supplier selection. Further, several related criteria of each dimension are identified for evaluating the alternative suppliers in more detail (see Figure 2). Then, the five decision makers are asked to rate each supplier with regard to the above criteria using the linguistic assessment terms shown in Table 1. The completed assessment matrices provided by the expert group are presented in Table 2.
Figure 2. Dimensions and related criteria for green supplier selection. Figure2. Dimensionsandrelatedcriteriaforgreensupplierselection.
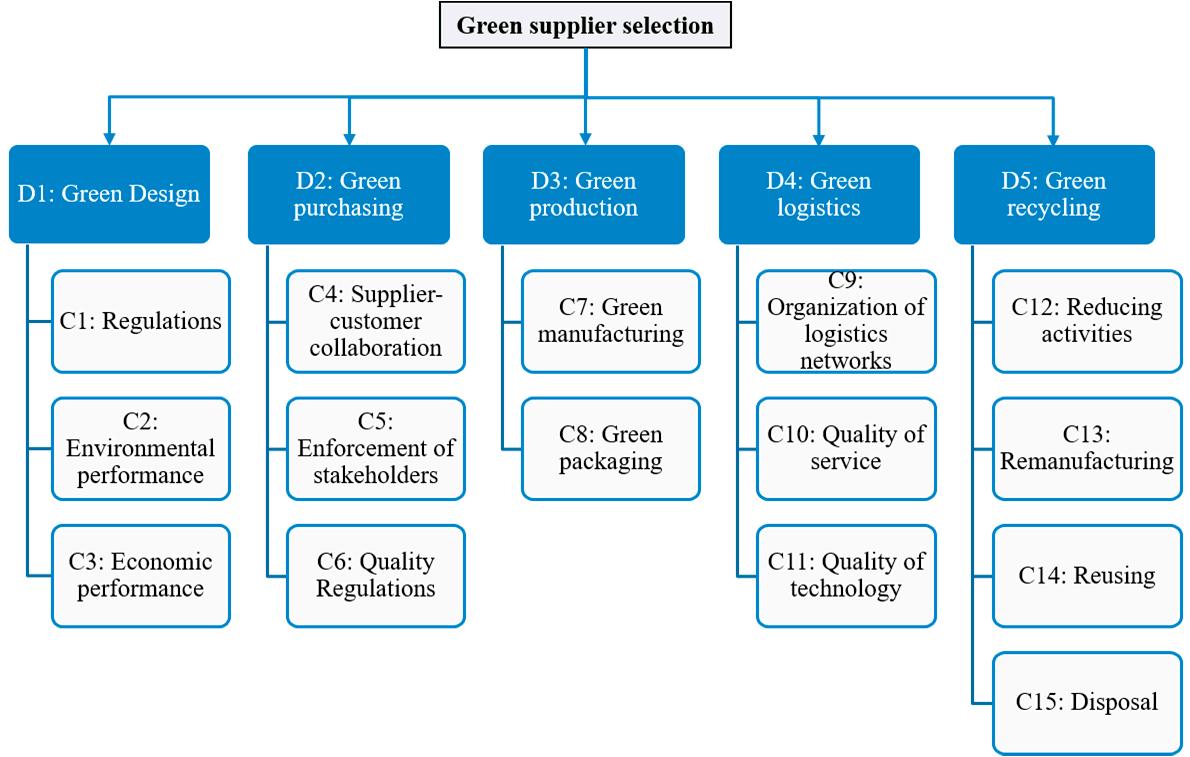
Table2. Linguisticassessmentsofalternativesprovidedbytheexpertgroup.
Decision Makers Alternatives
DM1
DM2
DM3
DM4
DM5
Criteria
C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12 C13 C14 C15
A1 GMPVGVPPGFP MG GGFVGPG
A2 FPVGPVPVGVGPPGFGFVPF
A3 P MG GFFGFPGFMP MGMG FG
A1 GMPGPPVG MG PFVGF MG VGMPVG
A2 MPMP MG VPMPGGPVPG MG GFPF
A3 FGGVP MG VGVGFFVGMPFFFP
A1 GFGVPVPVGFMPFGPFVGPVG
A2 MPP MG PFVGVGVPPVGF MG FMPMP
A3 MP MG VGMPGGVGMPGPFFMP MG F
A1 GMPVGVPVPGFMPGGF MG GMPVG
A2 FP MG PVPVGGVPVPVG MG GFVPF
A3 FG MG FFGVGMPGGP MG FPF
A1 VGMPGPPGMP MG VG MGMG FGVPVG
A2 FPFVPVPVGVGPPGGFFVPP
A3 P MG GP MG VGG MG GFFMPMPGF
5.2.ApplicationandResults
Thegreensupplierselectionproblemissolvedbyapplyingtheproposedmodelandthe implementationprocedureisdescribedasfollows.
Step1: Obtainthenormalclouddecisionmatrixofeachdecisionmaker
Thelinguisticratingsofthefivedecisionmakerscanbetransformedintonormalcloudseasily basedonTable 1 toconstructthenormalclouddecisionmatrixes Xk = xk ij 3×15(k = 1,2,...,5)
Step2: Establishthegroupnormalclouddecisionmatrix X
Theproducednormalclouddecisionmatrixes Xk (k = 1,2,...,5) areaggregatedbyusingthe COWAoperatortoestablishthegroupclouddecisionmatrix X = xij 3×15.Theresultsobtained arepresentedinTable 3.NotethattheweightingvectoroftheCOWAoperatorisdetermined asω = (0.068,0.183,0.498,0.183,0.068) withtheLaplacedistribution-basedmethod.
Table3. Thegroupclouddecisionmatrix X
C1 C2 C3 C4 C5
A1 (8.07,0.45,0.05)(3.14,0.45,0.05)(8.25,0.45,0.05)(1.25,0.45,0.05)(1.75,0.45,0.05)
A2 (4.50,0.45,0.05)(2.07,0.45,0.05)(6.14,0.45,0.05)(1.75,0.45,0.05)(1.64,0.45,0.05)
A3 (3.25,0.45,0.05)(6.50,0.45,0.05)(7.93,0.45,0.05)(3.18,0.45,0.05)(5.89,0.45,0.05)
A+ (8.07,0.45,0.05)(6.50,0.45,0.05)(8.25,0.45,0.05)(3.18,0.45,0.05)(5.89,0.45,0.05)
A (3.25,0.45,0.05)(2.07,0.45,0.05)(6.14,0.45,0.05)(1.25,0.45,0.05)(1.64,0.45,0.05) C6 C7 C8 C9 C10
A1 (8.25,0.45,0.05)(4.93,0.45,0.05)(2.95,0.45,0.05)(6.32,0.45,0.05)(7.93,0.45,0.05)
A2 (8.93,0.45,0.05)(8.75,0.45,0.05)(1.75,0.45,0.05)(1.75,0.45,0.05)(8.25,0.45,0.05)
A3 (8.25,0.45,0.05)(8.55,0.45,0.05)(3.50,0.45,0.05)(7.80,0.45,0.05)(5.62,0.45,0.05)
A+ (8.93,0.45,0.05)(8.75,0.45,0.05)(3.50,0.45,0.05)(7.80,0.45,0.05)(8.25,0.45,0.05)
A (8.25,0.45,0.05)(4.93,0.45,0.05)(1.75,0.45,0.05)(1.75,0.45,0.05)(5.62,0.45,0.05)
C11 C12 C13 C14 C15
A1 (5.18,0.45,0.05)(5.25,0.45,0.05)(8.75,0.45,0.05)(2.18,0.45,0.05)(8.93,0.45,0.05)
A2 (5.89,0.45,0.05)(7.43,0.45,0.05)(5.00,0.45,0.05)(1.32,0.45,0.05)(4.43,0.45,0.05)
A3 (3.43,0.45,0.05)(5.12,0.45,0.05)(4.57,0.45,0.05)(5.18,0.45,0.05)(5.00,0.45,0.05)
A+ (5.89,0.45,0.05)(7.43,0.45,0.05)(8.75,0.45,0.05)(5.18,0.45,0.05)(8.93,0.45,0.05)
A (3.43,0.45,0.05)(5.12,0.45,0.05)(4.57,0.45,0.05)(1.32,0.45,0.05)(4.43,0.45,0.05)
Step3: Definethepositive-idealandthenegative-idealsolutions
UsingEquations(9)and(10),thepositive-idealandthenegative-idealsolutions A+ and A can bederivedaslistedinthelasttworowsofTable 3.
Step4: Determinetheweightedclosenesscoefficientsofalternatives
TheweightedclosenesscoefficientiscalculatedviaEquations(11)and(12)foreachalternative, andtheresultsareasfollows:
D1 = w1 + 0.241w2 + w3 + 0.026w4 + 0.687w8 + 0.756w9 + 0.879w10 +0.714w11 + 0.059w12 + w13 + 0.224w14 + w15,
D2 = 0.259w1 + 0.258w4 + w6 + w7 + w10 + w11 + w12 + 0.104w13, D3 = w2 + 0.849w3 + w4 + w5 + 0.947w7 + w8 + w9 + w14 + 0.127w15
Step5: Calculatetheoptimalweightsofcriteria
TheweightsofthefifteencriteriaareacquiredbyEquation(14)as
w = (0.06,0.059,0.088,0.06,0.049,0.047,0.092,0.08,0.083,0.089,0.081,0.05,0.052,0.058,0.053)T .
Step6: Setupallpossiblepermutationsofalternatives
Thereare6(=3!)permutationsoftherankingsforthethreepotentialgreensuppliers,i.e.,
P1 =(A1,A2,A3),P2 =(A1,A3,A2),P3 =(A2,A1,A3), P4 =(A2,A3,A1),P5 =(A3,A1,A2),P6 =(A3,A2,A1).
Step7: Acquiretheconcordance/discordanceindex
ByusingEquation(17),wecancomputetheconcordance/discordanceindex φρ j Aξ ,Aζ foreach pairofsuppliers Aξ ,Aζ inthe ρthpermutationconcerningeverycriterionCj.Forinstance,the calculationresultsforthepermutation P1 arepresentedinTable 4
Table4. Theresultsoftheconcordance/discordanceindexfor P1 P1 φ1 j (A1,A2 ) φ1 j (A1,A3 ) φ1 j (A2,A3 ) C1 3.5704.8171.247 C2 1.068 3.366 4.434 C3 2.1150.319 1.796 C4 0.498 1.932 1.434 C5 0.111 4.136 4.247 C6 0.6810.0000.681 C7 3.817 3.6130.204 C8 1.204 0.549 1.753 C9 4.570 1.477 6.047 C10 0.3192.3152.634 C11 0.7021.7492.451 C12 2.1790.1362.315 C13 3.7494.1830.434 C14 0.864 3.000 3.864 C15 4.5023.932 0.570
Step8: Determinetheweightedconcordance/discordanceindex
Theweightedconcordance/discordanceindex φρ Aξ ,Aζ isacquiredbyemployingEquation(18) foreachpairofalternatives Aξ ,Aζ (ξ, ζ = 1,2,3) andTable 5 showsthecomputationalresults. Step9: Acquirethebestrankingofalternativesuppliers
Finally,thecomprehensiveconcordance/discordanceindexes φρ (ρ = 1,2,...,6) aredetermined byutilizingEquation(19)asfollows:
φ1 = 0.178, φ2 = 1.640, φ3 = 1.818, φ4 = 1.640, φ5 = 1.818, φ6 = 0.178.
Basedonthecomprehensiveconcordance/discordanceindexes φρ (ρ = 1,2,...,6),itisclear that P∗ = max ρ=1,2,...,6{φρ } = φ5.Thereby,theoptimalrankingofthethreealternativecompaniesis A3 >A1 >A2,andthemostappropriategreensupplierissupplierA3 forthevehiclemanufacturer.
Table5. Theresultsoftheweightedconcordance/discordanceindexes.
P1 P2 P3
φ1(A1,A2) 0.820 φ2(A1,A3) 0.089 φ3(A2,A1) 0.820 φ1(A1,A3) 0.089 φ2(A1,A2) 0.820 φ3(A2,A3) 0.909 φ1(A2,A3) 0.909 φ2(A3,A2) 0.909 φ3(A1,A3) 0.089 P4 P5 P6
φ4(A2,A3) -0.909 φ5(A3,A1) 0.089 φ6(A3,A2) 0.909 φ4(A2,A1) -0.820 φ5(A3,A2) 0.909 φ6(A3,A1) 0.089 φ4(A3,A1) 0.089 φ5(A1,A2) 0.820 φ6(A2,A1) 0.820
5.3.DiscussionunderIncompleteWeightInformation
Thefollowingisthesituationwheretheweightinformationfortheassessmentcriteriais incompletelyknownandthegivenweightinformationisasfollows:
w1 ≤ 0.04, w2 ≤ w1, w3 ≤ 0.03,0.1 ≤ w4 ≤ 0.13, w5 ≥ 0.7w4, w6 ≥ 0.05, 0.1 ≤ w7 ≤ 0.17,0.06 ≤ w8 ≤ 0.11, w4 w9 ≥ 0.02,0.06 ≤ w8 ≤ 0.10, w10 = w11,0.008 ≤ w12 ≤ 0.012, w13 ≤ 0.008, w13 = w14, w15 ≤ w13
Then,usingEquations(9)–(12),thefollowinglinearprogrammingmodelcanbeestablished: maxD(w) = 1.2589w1 + 1.2409w2 + 1.8492w3 + 1.2578w4 + 1.0261w5 + w6 + 1.9466w7 +1.6868w8 + 1.7557w9 + 1.8789w10 + 1.7136w11 + 1.0587w12 + 1.1038w13 +1.2236w14 + 1.1266w15 s.t.
Basedontheabovemodel,theweightvectorofthefifteencriteriaiscomputedas w = (0.04,0.04,0.03,0.013,0.091,0.05,0.17,0.11,0.11,0.1,0.1,0.008,0.008,0.008,0.005)T
Accordingly,thecomprehensiveconcordance/discordanceindexes φρ (ρ = 1,2,...,6) are computedas φ1 = 1.921, φ2 = 0.173, φ3 = 2.094, φ4 = 0.173, φ5 = 2.094, φ6 = 1.921. Hence,the optimalpriorityorderofthethreealternativesuppliersisA3 >A1 >A2,whichisexactlythesameas therankingresultearlier.Thisimpliesthattheproposeddecisionsupportframeworkisalsousefulfor thegreensupplierselectionproblemswhenthecriteriaweightinformationisincompletelyknown.
5.4.ComparativeStudy
Next,acomparativeanalysisisconducedtoshowtheeffectivenessofourproposeddecision supportapproachwithrespecttoothergreensupplierselectionmethods.Webasetheanalysisonthe samecaseexampleandchoosethefuzzyVIKOR[1],thefuzzyTOPSIS[15],theimprovedGRA[25]to
facilitatethecomparisonanalysis.Therankingresultsofthethreealternativesdeterminedbythese methodsaretabulatedinTable 6.
Table6. Rankingresultsofdifferentmethods.
AlternativesFuzzyVIKORFuzzyTOPSISImprovedGRATheProposedMethod
A1 2222 A2 2333 A3 1111
FromtheresultsofTable 6,itiseasilyseenthatthemostsuitablegreensupplierfortheconsidered applicationremainsthesame,i.e.,A3,accordingtotheproposedapproachandthelistedmethods. Further,therankingordersofthesupplierswiththeproposedapproacharetotallyinagreementwith theresultsacquiredviathefuzzyTOPSISandtheimprovedGRAmethods.Thisprovesthevalidity oftheproposedgreensupplierselectionmodel.However,incomparisonwiththelistedmethods, thedistinctadvantagesoftheapproachbeingproposedinthisstudyareasbelow:(1)Byusingthe cloudmodeltheory,theproposedmodeleffectivelypreventsthelossofinformationinthesemantic transformationandalsoeasilycompletesaninterchangeableconversionbetweenqualitativeconcepts andquantitativeinformation;(2)Theimpactof“false”or“biased”assessmentsofdecisionmakerson thedecisionresultcanbedecreasedbyusingtheCOWAoperatorinaggregatingpersonaljudgments intooverallassessments;(3)AgainstthebasicruleoftheTOPSIS,theproposedmodelcanbeusedto managethegreensupplierselectionproblemswheretheweightinformationofcriteriaiscompletely unknownorpartlyidentified;(4)WiththeaidoftheextendedQUALIFLEXalgorithm,anaccurateand crediblerankingofavailablesupplierscanbeobtained.Inparticular,theproposedmethodissuitable forgreensupplierselectionproblemshavingalargenumberofcriteriabutlimitedalternatives.
6.Conclusions
Inthisstudy,wepresentapracticalintegratedMCDMframeworkbasedonthecloudmodel andQUALIFLEXmethodtoassessandselectthemostappropriategreensupplierconsidering botheconomicandenvironmentalcriteria.Thecloudmodelisusedforrepresentingthelinguistic assessmentsofdecisionmakerswithrespecttoalternativecompaniesandanextensionoftheclassical QUALIFLEXisappliedtogenerategreensupplierrankings.Inaddition,forthesituationswherethe informationofcriteriaweightisunknownorpartlyknownpreviously,theproposedapproachcan derivethecriteriaweightsbyusingaTOPSIS-basedoptimizationmodel.Theproposedgreensupplier selectionmethodisvalidatedwithareal-lifecasecompanyoftheautomobilemanufacturingindustry setup.Theresultsshowthatourproposedframeworkismoreexpressiveincapturinguncertaintyand vaguenessofdecisionmakers’judgementsandisveryusefultoyieldthebestgreensupplieringreen suppliermanagement.
Evenwiththeadvantagesofourproposedapproach,therearesomelimitationsandroom forfurtherresearch.First,interactionsofcriteriaarenotconsideredintheproposedgreensupplier selectionapproachalthough,insomesituations,varioustypesofrelationshipsmayexistamongcriteria. Inthefuture,theChoquetintegraltechniqueshouldbeincorporatedintotheproposedmodelto analyzetheinter-dependenteffectsbetweenevaluationcriteria.Second,theproposedmethodassumes thatdecisionmakersprovidedeterministiclinguisticmeasurementsonthealternativesuppliers. Intherealworld,however,decisionmakersmayuserandomvariablestoexpresstheirassessments owingtotimelimitationsandtheincreasingcomplexityofgreensupplierselectionproblems.Thus,it isapromisingdirectiontoapplystochasticMCDMmethods[54,55]forgreensupplierselection. Inaddition,considerablecomputationsareinvolvedintheproposeddecision-makingalgorithm. Therefore,infutureresearch,softwarecanbedevelopedsothatmanufacturersandserviceproviders canapplytheproposedapproachconvenientlytodeterminethemostsuitableoneforcooperation.
Sustainability 2017, 9,688
Acknowledgments: Theauthorsareverygratefultotheeditorandreviewersfortheirinsightfulandconstructive commentsandsuggestions,whichareveryhelpfulinimprovingthequalityofthepaper.Thisworkwaspartially supportedbytheNationalNaturalScienceFoundationofChina(Nos.71671125and71402090),theProgram forProfessorofSpecialAppointment(YoungEasternScholar)atShanghaiInstitutionsofHigherLearning (No.QD2015019),andtheMinistryofEducationFoundationofHumanitiesandSocialScience(No.12YJC630201).
AuthorContributions: Theindividualcontributionandresponsibilitiesoftheauthorswereasfollows: Ke-QinWangandHu-ChenLiudesignedtheresearch,LipingLiuandJiaHuangprovidedextensiveadvice throughoutthestudyregardingtheabstract,introduction,researchdesign,researchmethodology,findings andrevisionofthemanuscript.Thediscussionwasateamtask.Allauthorshavereadandapprovedthe finalmanuscript.
ConflictsofInterest: Theauthorsdeclarenoconflictofinterest.
References
1. Rostamzadeh,R.;Govindan,K.;Esmaeili,A.;Sabaghi,M.ApplicationoffuzzyVIKORforevaluationof greensupplychainmanagementpractices. Ecol.Indic. 2015, 49,188–203.[CrossRef]
2. Awasthi,A.;Kannan,G.GreensupplierdevelopmentprogramselectionusingNGTandVIKORunderfuzzy environment. Comput.Ind.Eng. 2016, 91,100–108.[CrossRef]
3. Bai,C.;Sarkis,J.Greensupplierdevelopment:Analyticalevaluationusingroughsettheory. J.Clean.Prod. 2010, 18,1200–1210.[CrossRef]
4. Srivastava,S.K.Greensupply-chainmanagement:Astate-of-the-artliteraturereview. Int.J.Manag.Rev. 2007, 9,53–80.[CrossRef]
5. Govindan,K.;Rajendran,S.;Sarkis,J.;Murugesan,P.Multicriteriadecisionmakingapproachesforgreen supplierevaluationandselection:Aliteraturereview. J.Clean.Prod. 2015, 98,66–83.[CrossRef]
6. Igarashi,M.;deBoer,L.;Fet,A.M.Whatisrequiredforgreenersupplierselection?Aliteraturereviewand conceptualmodeldevelopment. J.Purch.SupplyManag. 2013, 19,247–263.[CrossRef]
7. Bai,C.;Sarkis,J.Integratingsustainabilityintosupplierselectionwithgreysystemandroughset methodologies. Int.J.Prod.Econ. 2010, 124,252–264.[CrossRef]
8. Banaeian,N.;Mobli,H.;Fahimnia,B.;Nielsen,I.E.;Omid,M.Greensupplierselectionusingfuzzygroup decisionmakingmethods:Acasestudyfromtheagri-foodindustry. Comput.Oper.Res. 2016.[CrossRef]
9. Sarkis,J.;Dhavale,D.G.Supplierselectionforsustainableoperations:Atriple-bottom-lineapproachusinga Bayesianframework. Int.J.Prod.Econ. 2015, 166,177–191.[CrossRef]
10. Paelinck,J.H.P.Qualiflex:Aflexiblemultiple-criteriamethod. Econ.Lett. 1978, 1,193–197.[CrossRef]
11. Li,J.;Wang,J.Q.AnextendedQUALIFLEXmethodunderprobabilityhesitantfuzzyenvironmentfor selectinggreensuppliers. Int.J.FuzzySyst. 2017.[CrossRef]
12. Zhang,X.;Xu,Z.S.HesitantfuzzyQUALIFLEXapproachwithasigneddistance-basedcomparisonmethod formultiplecriteriadecisionanalysis. ExpertSyst.Appl. 2015, 42,873–884.[CrossRef] 13. Peng,J.J.;Wang,J.Q.;Yang,W.E.Amulti-valuedneutrosophicqualitativeflexibleapproachbasedon likelihoodformulti-criteriadecision-makingproblems. Int.J.Syst.Sci. 2017, 48,425–435.[CrossRef]
14. Kannan,D.;Govindan,K.;Rajendran,S.Fuzzyaxiomaticdesignapproachbasedgreensupplierselection: AcasestudyfromSingapore. J.Clean.Prod. 2015, 96,194–208.[CrossRef]
15. Uygun,Ö.;Dede,A.Performanceevaluationofgreensupplychainmanagementusingintegratedfuzzy multi-criteriadecisionmakingtechniques. Comput.Ind.Eng. 2016, 102,502–511.[CrossRef]
16. Zadeh,L.A.Theconceptofalinguisticvariableanditsapplicationtoapproximatereasoning—I. Inf.Sci. 1975, 8,199–249.[CrossRef]
17. Xu,Z.S.Amethodbasedonlinguisticaggregationoperatorsforgroupdecisionmakingwithlinguistic preferencerelations. Inf.Sci. 2004, 166,19–30.[CrossRef]
18. Herrera,F.;Martínez,L.A2-tuplefuzzylinguisticrepresentationmodelforcomputingwithwords. IEEETrans.FuzzySyst. 2000, 8,746–752.
19. Wang,J.Q.;Peng,L.;Zhang,H.Y.;Chen,X.H.Methodofmulti-criteriagroupdecision-makingbasedon cloudaggregationoperatorswithlinguisticinformation. Inf.Sci. 2014, 274,177–191.[CrossRef]
20. Li,D.Y.;Liu,C.Y.;Gan,W.Y.Anewcognitivemodel:Cloudmodel. Int.J.Intell.Syst. 2009, 24,357–375. [CrossRef]
21. WangChen,H.M.;Chou,S.Y.;Luu,Q.D.;Yu,T.H.K.AfuzzyMCDMapproachforgreensupplierselection fromtheeconomicandenvironmentalaspects. Math.Probl.Eng. 2016, 2016.[CrossRef]
22. Tsui,C.W.;Tzeng,G.H.;Wen,U.P.AhybridMCDMapproachforimprovingtheperformanceofgreen suppliersintheTFT-LCDindustry. Int.J.Prod.Res. 2015, 53,6436–6454.[CrossRef]
23. Liou,J.J.H.;Tamošaitiene,J.;Zavadskas,E.K.;Tzeng,G.H.NewhybridCOPRAS-GMADMmodelfor improvingandselectingsuppliersingreensupplychainmanagement. Int.J.Prod.Res. 2015, 54,114–134. [CrossRef]
24. Kannan,D.;deSousaJabbour,A.B.L.;Jabbour,C.J.C.SelectinggreensuppliersbasedonGSCMpractices: UsingfuzzyTOPSISappliedtoaBrazilianelectronicscompany. Eur.J.Oper.Res. 2014, 233,432–447. [CrossRef]
25. Hashemi,S.H.;Karimi,A.;Tavana,M.Anintegratedgreensupplierselectionapproachwithanalyticnetwork processandimprovedgreyrelationalanalysis. Int.J.Prod.Econ. 2015, 159,178–191.[CrossRef]
26. Yazdani,M.;Chatterjee,P.;Zavadskas,E.K.;HashemkhaniZolfani,S.IntegratedQFD-MCDMframework forgreensupplierselection. J.Clean.Prod. 2017, 142,3728–3740.[CrossRef]
27. Bakeshlou,E.A.;Khamseh,A.A.;Asl,M.A.G.;Sadeghi,J.;Abbaszadeh,M.Evaluatingagreensupplier selectionproblemusingahybridMODMalgorithm. J.Intell.Manuf. 2017, 28,913–927.[CrossRef]
28.
Zhang,X.MulticriteriaPythagoreanfuzzydecisionanalysis:AhierarchicalQUALIFLEXapproachwiththe closenessindex-basedrankingmethods. Inf.Sci. 2016, 330,104–124.[CrossRef]
29. Zhang,Z.Multi-criteriadecision-makingusinginterval-valuedhesitantfuzzyQUALIFLEXmethodsbased onalikelihood-basedcomparisonapproach. NeuralComput.Appl. 2016.[CrossRef]
30. Xue,Y.X.;You,J.X.;Zhao,X.;Liu,H.C.AnintegratedlinguisticMCDMapproachforrobotevaluationand selectionwithincompleteweightinformation. Int.J.Prod.Res. 2016, 54,5452–5467.[CrossRef]
31. Tian,Z.P.;Wang,J.;Wang,J.Q.;Zhang,H.Y.Simplifiedneutrosophiclinguisticmulti-criteriagroup decision-makingapproachtogreenproductdevelopment. GroupDecis.Negot. 2017, 26,597–627.[CrossRef]
32. Tian,Z.P.;Wang,J.;Wang,J.Q.;Zhang,H.Y.Alikelihood-basedqualitativeflexibleapproachwithhesitant fuzzylinguisticinformation. Cogn.Comput. 2016, 8,670–683.[CrossRef]
33. Peng,H.G.;Zhang,H.Y.;Wang,J.Q.Probabilitymulti-valuedneutrosophicsetsanditsapplicationin multi-criteriagroupdecision-makingproblems. NeuralComput.Appl. 2016.[CrossRef]
34. Wang,J.C.;Tsao,C.Y.;Chen,T.Y.Alikelihood-basedQUALIFLEXmethodwithintervaltype-2fuzzysetsfor multiplecriteriadecisionanalysis. SoftComput. 2015, 19,2225–2243.[CrossRef]
35. Chen,T.Y.Interval-valuedintuitionisticfuzzyQUALIFLEXmethodwithalikelihood-basedcomparison approachformultiplecriteriadecisionanalysis. Inf.Sci. 2014, 261,149–169.[CrossRef]
36. Chen,T.Y.DataconstructionprocessandQUALIFLEX-basedmethodformultiple-criteriagroupdecision makingwithinterval-valuedintuitionisticfuzzysets. Int.J.Inf.Technol.Decis.Mak. 2013, 12,425–467. [CrossRef]
37. Chen,T.Y.;Chang,C.H.;RachelLu,J.F.TheextendedQUALIFLEXmethodformultiplecriteriadecision analysisbasedonintervaltype-2fuzzysetsandapplicationstomedicaldecisionmaking. Eur.J.Oper.Res. 2013, 226,615–625.[CrossRef]
38. Zhang,X.;Xu,Z.;Liu,M.HesitanttrapezoidalfuzzyQUALIFLEXmethodanditsapplicationinthe evaluationofgreensupplychaininitiatives. Sustainability 2016, 8.[CrossRef]
39. Zhang,L.;Wu,X.;Zhu,H.;AbouRizk,S.M.Perceivingsafetyriskofbuildingsadjacenttotunneling excavation:Aninformationfusionapproach. Automat.Constr. 2017, 73,88–101.[CrossRef]
40. Wu,Y.;Chen,K.;Zeng,B.;Yang,M.;Li,L.;Zhang,H.Aclouddecisionframeworkinpure2-tuplelinguistic settinganditsapplicationforlow-speedwindfarmsiteselection. J.Clean.Prod. 2017, 142,2154–2165. [CrossRef]
41. Wang,M.X.;Wang,J.Q.AnevolvingTakagi-Sugenomodelbasedonaggregatedtrapeziumcloudsfor anomalydetectioninlargedatasets. J.Intell.FuzzySyst. 2017, 32,2295–2308.[CrossRef]
42. Shi,H.;Liu,H.C.;Li,P.;Xu,X.G.Anintegrateddecisionmakingapproachforassessinghealthcarewaste treatmenttechnologiesfromamultiplestakeholder. WasteManag. 2017, 59,508–517.[CrossRef][PubMed]
43. Cao,C.;Xu,P.;Chen,J.;Zheng,L.;Niu,C.Hazardassessmentofdebris-flowalongthebaichariverin HeshigtenBanner,InnerMongolia,China. Int.J.Environ.Res.PublicHealth 2017, 14,30.[CrossRef][PubMed]
44. Zhang,T.;Yan,L.;Yang,Y.Trustevaluationmethodforclusteredwirelesssensornetworksbasedoncloud model. Wirel.Netw. 2016.[CrossRef]
Sustainability 2017, 9,688
45.
Li,L.;Fan,F.;Ma,L.;Tang,Z.Energyutilizationevaluationofcarbonperformanceinpublicprojectsby FAHPandcloudmodel. Sustainability 2016, 8,630.[CrossRef]
46. Zhao,H.;Li,N.RiskevaluationofaUHVpowertransmissionconstructionprojectbasedonacloudmodel andFCEmethodforsustainability. Sustainability 2015, 7,2885–2914.[CrossRef]
47.
Wang,J.Q.;Peng,J.J.;Zhang,H.Y.;Liu,T.;Chen,X.H.Anuncertainlinguisticmulti-criteriagroup decision-makingmethodbasedonacloudmodel. GroupDecis.Negot. 2015, 24,171–192.[CrossRef]
48. Wang,J.Q.;Wang,P.;Wang,J.;Zhang,H.Y.;Chen,X.H.Atanassov’sinterval-valuedintuitionisticlinguistic multicriteriagroupdecision-makingmethodbasedonthetrapeziumcloudmodel. IEEETrans.FuzzySyst. 2015, 23,542–554.[CrossRef]
49. Yager,R.R.Onorderedweightedaveragingaggregationoperatorsinmulticriteriadecisionmaking. IEEETrans.Syst.ManCybern. 1988, 18,183–190.[CrossRef]
50. Mohammed,E.A.;Naugler,C.T.;Far,B.H.BreasttumorclassificationusinganewOWAoperator. ExpertSyst.Appl. 2016, 61,302–313.[CrossRef]
51. Hwang,C.L.;Yoon,K. MultipleAttributesDecisionMakingMethodsandApplications;Springer: Berlin,Germany,1981.
52. Zhang,X.;Xu,Z.S.;Wang,H.Heterogeneousmultiplecriteriagroupdecisionmakingwithincomplete weightinformation:Adeviationmodelingapproach. Inf.Fusion 2015, 25,49–62.[CrossRef]
53. Liu,H.C.;You,J.X.;Li,P.;Su,Q.Failuremodeandeffectanalysisunderuncertainty:Anintegratedmultiple criteriadecisionmakingapproach. IEEETrans.Reliab. 2016, 65,1380–1392.[CrossRef]
54. Zhou,H.;Wang,J.Q.;Zhang,H.Y.Stochasticmulticriteriadecision-makingapproachbasedon SMAA-ELECTREwithextendedgraynumbers. Int.Trans.Oper.Res. 2017.[CrossRef]
55. Yu,S.M.;Wang,J.;Wang,J.Q.Anintervaltype-2fuzzylikelihood-basedMABACapproachanditsapplication inselectinghotelsonatourismwebsite. Int.J.FuzzySyst. 2017, 19,47–61.[CrossRef]
© 2017bytheauthors.LicenseeMDPI,Basel,Switzerland.Thisarticleisanopenaccess articledistributedunderthetermsandconditionsoftheCreativeCommonsAttribution (CCBY)license(http://creativecommons.org/licenses/by/4.0/).

