TriangularSingleValuedNeutrosophicData EnvelopmentAnalysis:ApplicationtoHospital PerformanceMeasurement
WeiYang 1,LuluCai 2,SeyedAhmadEdalatpanah 3,*andFlorentinSmarandache 4
1 STATEGRIDQuzhouPowerSupplyCompany,QuzhouUniversity,Quzhou324000,China; easteryang@163.com
3
2 DepartmentofElectricalAutomation,QuzhouUniversity,Quzhou324000,China;ysu-fbg@163.com
DepartmentofAppliedMathematics,QuzhouUniversity,Quzhou324000,China
4 DepartmentofMathematics,UniversityofNewMexico,Gallup,NM87301,USA;smarand@unm.edu

* Correspondence:saedalat@yahoo.com
Received:22February2020;Accepted:18March2020;Published:8April2020
Abstract: Theforemostbroadlyutilizedstrategyforthevaluationoftheoverallperformance ofasetofidenticaldecision-makingunits(DMUs)thatuseanalogoussourcestoyieldrelated outputsisdataenvelopmentanalysis(DEA).However,thewitnessedvaluesofthesymmetryor asymmetryofdifferenttypesofinformationinreal-worldapplicationsaresometimesinaccurate, ambiguous,inadequate,andinconsistent,sooverlookingtheseconditionsmayleadtoerroneous decision-making.Neutrosophicsettheorycanhandletheseoccasionsofdataandmakesanimitation ofthedecision-makingprocedurewiththeaidofthinkingaboutallperspectivesofthedecision. Inthispaper,weintroduceamodelofDEAinthecontextofneutrosophicsetsandsketchan innovativeprocesstosolveit.Furthermore,wedealwiththeproblemofhealthcaresystemevaluation withinconsistent,indeterminate,andincompleteinformationusingthenewmodel.Thetriangular single-valuedneutrosophicnumbersarealsoemployedtodealwiththementioneddata,andthe proposedmethodisutilizedintheassessmentof13hospitalsofTehranUniversityofMedicalSciences ofIran.Theresultsexhibittheusefulnessofthesuggestedapproachandpointoutthatthemodelhas practicaloutcomesfordecision-makers.
Keywords: single-valuedneutrosophicset;triangularneutrosophicnumber;dataenvelopment analysis;healthcaresystems;performanceevaluation
1.Introduction
Asastronganalyticaltoolforbenchmarkingandefficiencyevaluation,DEA(dataenvelopment analysis)isatechniqueforevaluatingtherelationefficiencyofdecision-makingunits(DMUs), developedinitiallybyCharensetal.[1]onaprintedpapernamedtheCharnes,Cooper,andRhodes (CCR)model.TheyextendedthenonparametricmethodintroducedbyFarrell[2]togaugeDMUs withmultipleinputsandoutputs.TheBanker,Charnes,andCooper(BCC)modelisanextensionof thepreviousmodelundertheassumptionofvariablereturns-to-scale(VRS)[3].Withthistechnique, managerscanobtaintherelativeefficiencyofasetofDMUs.Intime,manytheoreticalandempirical studieshaveappliedDEAtoseveralfieldsofscienceandengineering,suchashealthcare,agriculture, bankingsupplychains,andfinancialservices,amongothers.Formoredetails,thereaderisreferredto thestudiesof[4–14].
ConventionalDEAmodelsrequirecrispinformationthatmaynotbepermanentlyaccessiblein real-worldapplications.Nevertheless,innumerouscases,dataareunstable,uncertain,andcomplicated; therefore,theycannotbeaccuratelymeasured.Zadeh[15]firstproposedthetheoryoffuzzysets(FSs)
Symmetry 2020, 12,588;doi:10.3390/sym12040588
www.mdpi.com/journal/symmetry
againstcertainlogic.Afterthiswork,manyresearchersstudiedthistopic;detailsofsomeapproaches canbeobservedin[16–20].SeveralresearchersalsoproposedsomemodelsofDEAunderafuzzy environment[21–25].
However,Zadeh’sfuzzysetsconsideronlythemembershipfunctionandcannotdealwithother parametersofvagueness.Toovercomethislackofinformation,Atanassov[26]introducedanextension ofFSscalledintuitionisticfuzzysets(IFSs).TherearealsoseveralmodelsofDEAwithintuitionistic fuzzydata:see[27–30].
AlthoughthetheoryofIFSscanhandleincompleteinformationforvariousreal-worldissues, itcannotaddressalltypesofuncertaintysuchasinconsistentandindeterminateevidence.Therefore, Smarandache[31,32]establishedtheneutrosophicset(NS)asarobustoverallframeworkthat generalizesclassicalandallkindsoffuzzysets(FSsandIFSs).
NSscanaccommodateindeterminate,ambiguous,andconflictinginformationwherethe indeterminacyisclearlyquantified,anddefinethreekindsofmembershipfunctionindependently.
Inthepastyears,someversionsofNSssuchasintervalneutrosophicsets[33,34],bipolar neutrosophicsets[35,36],single-valuedneutrosophicsets[37–39],andneutrosophiclinguisticsets[40] havebeenpresented.Inaddition,inthefieldofneutrosophicsets,logic,measure,probability,statistics, pre-calculusandcalculus,andtheirapplicationsinmultipleareashavebeenextended:see[41–44].
Inrealcircumstances,somedatainDEAmaybeuncertain,indeterminate,andinconsistent, andconsideringtruth,falsity,andindeterminacymembershipfunctionsforeachinput/outputof DMUsintheneutrosophicsetshelpdecision-makerstoobtainabetterinterpretationofinformation. Inaddition,byusingtheNSinDEA,analystscanbettersettheiracceptance,indeterminacy,andrejection degreesregardingeachdatum.Moreover,withNSs,wecanobtainabetterdepictionofrealitythrough seeingallfeaturesofthedecision-makingprocedure.Therefore,theNScanembraceimprecise, vague,incomplete,andinconsistentevidencepowerfullyandefficiently.Althoughthereareseveral approachestosolvevariousproblemsunderneutrosophicenvironments,therearenotmanystudies thathavedealtwithDEAunderNSs.
TheutilizationofneutrosophiclogicinDEAcanbetracedtoEdalatpanah[45].Kahramanetal.[46] proposedahybridalgorithmbasedonaneutrosophicanalytichierarchyprocess(AHP)andDEAfor bringingasolutiontotheefficiencyofprivateuniversities.EdalatpanahandSmarandache[47],based onsomeoperatorsandnaturallogarithms,proposedaninput-orientedDEAmodelwithsimplified neutrosophicnumbers.Abdelfattah[48],byconvertinganeutrosophicDEAintoanintervalDEA, developedanewDEAmodelunderneutrosophicnumbers.Althoughtheseapproachesareinteresting, somerestrictionsexist.Oneofthemisthatthesemethodshavehighrunningtimes,mainlywhen wehavemanyinputsandoutputs.Furthermore,themainflawof[48]istheexistenceofseveral productionfrontiersinthestepsofefficiencymeasure,andthisleadstothelackofcomparability betweenefficiencies.
Therefore,inthispaper,wedesignaninnovativesimplemodelofDEAinwhichallinputsand outputsaretriangularsingle-valuedneutrosophicnumbers(TSVNNs),andestablishanewefficient strategytosolveit.Furthermore,weusethesuggestedtechniquefortheperformanceassessmentof 13hospitalsofTehranUniversityofMedicalSciences(TUMS)ofIran.
Thepaperunfoldsasfollows:somebasicknowledge,concepts,andarithmeticoperationsonNSs andTSVNNsarediscussedinSection 2.InSection 3,someconceptsofDEAandtheCCRmodelare reviewed.InSection 4,weestablishthementionedmodelofDEAundertheneutrosophicenvironment andproposeamethodtosolveit.InSection 5,thesuggestedmodelisutilizedforacasestudyof TUMS.Lastly,conclusionsandfuturedirectionsarepresentedinSection 6.
2.Preliminaries
Inthissection,wediscusssomebasicdefinitionsrelatedtoneutrosophicsetsandsingle-valued neutrosophicnumbers,respectively.
Smarandacheputforwardanindeterminacydegreeofmembershipasanindependentcomponent inhispapers[31,32],andsincetheprincipleofexcludedmiddlecannotbeappliedtonew logic,hecombinesnon-standardanalysiswiththree-valuedlogic,settheory,probabilitytheory, andphilosophy.Asaresult,neutrosophicmeans“neutralthinkingknowledge.”Giventhismeaning andtheuseofthetermneutral,alongwiththecomponentsoftruth(membership)andfalsity (non-membership),itsdistinctionismarkedbyfuzzysetsandintuitionisticfuzzysets.Here,itis appropriatetogiveabriefexplanationofthenon-standardanalysis.
Intheearly1960s,Robinsondevelopednon-standardanalysisasaformofanalysisandabranch oflogicinwhichinfinitesimalsarepreciselydefined[49].Formally, x iscalledaninfinitesimalnumber ifandonlyifforanynon-nullpositiveintegernwehave |x| ≤ 1 n Let ε> 0 beaninfinitesimalnumber; then,theextendedrealnumbersetisanextensionofthesetofrealnumbersthatcontainstheclassesof infinitenumbersandtheinfinitesimalnumbers.Ifweconsidernon-standardfinitenumbers 1+ = 1 + ε and 0 = 0 ε, where 0 and 1 arethestandardpartsand ε isthenon-standardpart,then ] 0,1+ [ is anon-standardunitinterval.Itisclearthat 0,1,aswellasthenon-standardinfinitesimalnumbers thatarelessthanzeroandinfinitesimalnumbersthataremorethanonebelongtothisnon-standard unitinterval.Now,letusdefineaneutrosophicset:
Definition1 ([31,32,41])(neutrosophicset). AneutrosophicsetinuniversalUisdefinedbythreemembership functionsforthetruth,indeterminacy,andfalsityofxintherealnon-standard ] 0,1+ [,wherethesummationof thembelongsto[0,3].
Definition2 ([34]). IfthethreemembershipfunctionsofaNSaresingletonintherealstandard[0,1],thena single-valuedneutrosophicset(SVNS) ψ isdenotedby: ψ = x, τψ(x), ιψ(x), νψ(x) x ∈ U , whichsatisfiesthefollowingcondition: 0 ≤ τψ(x) + ιψ(x) + νψ(x) ≤ 3.
Aℵ (x)=
Aℵ (x)=
,
Definition4 ([38]). Let Aℵ = al , am , au , bl , bm , bu , cl , cm , cu and Bℵ = dl , dm , du , el , em , eu , f l , f m , f u betwoTSVNNs,wheretheirelementsarein [L1, U1] Then,Equations(1)to(3) aretrue:
(i)Aℵ ⊕ Bℵ = min(al + dl , U1 , min(am + dm , U1), min(au + du , U1); min(bl + el , U1 , min(bm + em , U1), min(bu + eu , U1); min(cl + f l , U1 , min(cm + f m , U1), min(cu + f u , U1) , (1)
(ii) Aℵ = au , am , al , bu , bm , bl , cu , cm , cl ,(2) (iii)λAℵ = λal , λam , λau , λbl , λbm , λbu , λcl , λcm , λcu , λ> 0.(3)
Definition5 ([38]). Consider Aℵ = al , am , au , bl , bm , bu , cl , cm , cu asaTSVNN.Then,theranking functionofAℵ canbedefinedwithEquation(4): ξ Aℵ = al + bl + cl + 2(am + bm + cm) + (au + bu + cu) 12 (4)
Definition6 ([20]). SupposePℵ andQℵ aretwoTSVNNs,then:
(i) Pℵ ≤ Qℵ ifandonlyif ξ Pℵ ≤ ξ Qℵ , (ii) Pℵ < Qℵ ifandonlyif ξ Pℵ <ξ Qℵ
3.DataEnvelopmentAnalysis
Letasetof n DMUs,witheachDMUj ( j = 1,2, ... , n) using m inputs pij (i = 1,2, ... , m) produce s outputs qrj(r = 1,2, ... , s).IfDMUo isunderconsideration,thenthe input-orientedCCRmultiplier modelfortherelativeefficiencyiscomputedonthebasisofEquation(5)[1]: θo ∗ = max s r=1 vrqro m i=1 uipio (5) s.t: s r=1 vrqrj m i=1 uipij ≤ 1, j = 1,2, ... , n vr, ui ≥ 0r = 1, , s, i = 1, , m where vr and ui aretherelatedweights.Theabovenonlinearprogrammingmaybeconvertedas Equation(6)tosimplifythecomputation: θo ∗ = max s r=1 vrqro (6) s.t: m i=1 uipio = 1 s r=1 vrqrj m i=1 uipij ≤ 0, j = 1,2, ... , n vr, ui ≥ 0r = 1, , s, i = 1, , m
TheDMUo isefficientif θo ∗ = 1;otherwise,itisinefficient.
4.NeutrosophicDataEnvelopmentAnalysis
Likeeveryothermodel,DEAhasbeenthesubjectofevolution.Oneofthecriticalimprovements inthisfieldisrelatedtocircumstanceswheretheinformationofDMUsischaracterizedandmeasured beneathconditionsofuncertaintyandindeterminacy.Indeed,oneofthetraditionalDEAmodels’ assumptionsistheircrispnessofinputsandoutputs.
However,itseemsquestionabletoassumethedataandobservationsarecrispinsituations whereuncertaintyandindeterminacyareinevitablefeaturesofarealenvironment.Inaddition,most managementdecisionsarenotmadebasedonknowncalculations,andthereisalotofuncertainty, indeterminacy,andambiguityindecision-makingproblems.TheDEAunderaneutrosophic environmentismoreadvantageousthanacrispDEAbecauseadecision-maker,inthepreparationofthe problem,isnotobligedtomakeasubtleformulation.Furthermore,becauseofalackofcomprehensive knowledgeandevidence,precisemathematicsarenotsufficienttomodelacomplexsystem.Therefore, theapproachbasedonneutrosophiclogicseemsfitforsuchproblems[31,32].Inthissection,we establishDEAunderaneutrosophicenvironment.
Considertheinputandoutputforthe jthDMUasfollows: p ij = ai pij, bi pij, ci pij = [a1 p ij, a2 p ij, a3 p ij] , [ b1 p ij, b2 p ij, b3 p ij], [c1 p ij, c2 p ij, c3 p ij] , q rj = ai qrj , bi qrj, ci qrj = [a1 q rj, a2 q rj, a3 q rj] , [ b1 q rj, b2 q rj, b3 q rj], [c1 q rj, c2 q rj, c3 q rj] ,
whichareTSVNNs.Then,thetriangularsingle-valuedneutrosophicCCRmodelcalledTSVNN-CCR isdefinedasfollows:
θℵ∗ o = max s r=1 vr q ro (7) s.t: m i=1 ui ... p io = 1 s r=1 vr q rj m i=1 ui p ij ≤ 0, j = 1,2, ... , n vr, ui ≥ 0r = 1, , s, i = 1, , m
Next,tosolveModel(7),weproposethefollowingalgorithm:
Algorithm1. ThesolutionofTSVNN-CCRModel
Step1.ConstructtheproblembasedonModel(8). Step2.UsingDefinition3(ii,iii),transformtheTSVNN-CCRmodelofStep1into Model(8): θℵ∗ o = max s r 1 [vr a1 q ro, vr a2 q ro, vr a3 q ro], [vr b1 q ro, vr b2 q ro, vr b3 q ro], [vr c1 q ro, vr c2 q ro, vr c3 q ro] (8) s.t: m i 1 [ui a1 p io, ui a2 p io, ui a3 p io] , [ui b1 p io, ui b2 p io, ui b3 p io], [ui c1 pio, ui c2 pio, ui c3 pio] = 1 s r=1 [vr a1 q rj, vr a2 q rj, vr a3 q rj] , [vr b1 q rj, vr b2 q rj, vr b3 q rj], [vr c1 q rj, vr c2 q rj, vr c3 q rj] ⊕ m i=1 [ ui a3 p ij, ui a2 p ij, ui a1 p ij] , [ ui b3 p ij, ui b2 p ij, ui b1 p ij], [ui c3 pij, ui c2 pij, ui c1 pij] ≤ 0, vr, ui ≥ 0r = 1, , s, i = 1, , m
Step3.TransformModel(8)intothefollowingmodel:
θℵ∗ o = max s r=1 vr a1 q ro, s r=1 vr a2 q ro, s r=1 vr a3 q ro , s r=1 vr b1 q ro, s r=1 vr b2 q ro, s r=1 vr b3 q ro , s r=1 vr c1 q ro, s r=1 vr c2 q ro, s r=1 vr c3 q ro (9) s.t: m i=1 ui a1 p io, m i=1 ui a2 p io, m i=1 ui a3 p io , m i=1 ui b1 p io, m i=1 ui b2 p io, m i=1 ui b3 p io , m i=1 ui c1 pio, m i=1 ui c2 pio, m i=1 ui c3 pio = 1 s r=1 vr a1 q rj ⊕ m i=1 ui a3 p ij, s r=1 vr a2 q rj ⊕ m i=1 ui a2 p ij, s r=1 vr a3 q rj ⊕ m i=1 ui a1 p ij , s r=1 vr b1 q rj ⊕ m i=1 ui b3 p ij, s r=1 vr b2 q rj ⊕ m i=1 ui b2 p ij, s r=1 vr b3 q rj ⊕ m i=1 ui b1 p ij , s r=1 vr c1 q rj ⊕ m i 1 ui c3 pij, s r=1 vr c2 q rj ⊕ m i 1 ui c2 pij, s r=1 vr c3 q rj ⊕ m i 1 ui c1 pij ≤ 0, vr, ui ≥ 0r = 1, , s, i = 1, , m Step4.BasedonDefinitions4–5,convertTSVNN-CCRModel(9)intocrispModel(10): θo ∗ ≈ ξ θℵ∗ o = max s r=1 ξ [vr a1 q ro, vr a2 q ro, vr a3 q ro] , [vr b1 q ro, vr b2 q ro, vr b3 q ro], [vr c1 q ro, vr c2 q ro, vr c3 q ro]
(10) s.t: m i=1 ξ [ui a1 p io, ui a2 p io, ui a3 p io] , [ui b1 p io, ui b2 p io, ui b3 p io], [ui c1 pio, ui c2 pio, ui c3 pio] = 1 s r=1 ξ [vr a1 q rj, vr a2 q rj, vr a3 q rj], [vr b1 q rj, vr b2 q rj, vr b3 q rj] , [vr c1 q rj, vr c2 q rj, vr c3 q rj] ⊕ m i=1 ξ ui a3 p ii, ui a2 p ij, ui a1 p ij , ui b3 p ij, ui b2 p ij, ui b1 p ij , ui c3 pij, ui c2 pij, ui c1 pij ≤ 0, vr, ui ≥ 0r = 1, , s, i = 1, , m Step5.RunModel(10)andgettheoptimalefficiencyofeachDMU.
5.NumericalExperiment
Inthissection,acasestudyofaDEAproblemunderaneutrosophicenvironmentisusedtoreveal thevalidityandusefulnessoftheproposedmodel.
CaseStudy:TheEfficiencyoftheHospitalsofTUMS
Performanceassessmentsinhealthcareframeworksareanoteworthyworryofpolicymakers sothatreformstoimproveperformanceinthehealthsectorareonthepolicyagendaofnumerous nationalgovernmentsandworldwideagencies.Intherelatedliterature,variousmethodssuchas leastsquaresandsimpleratioanalysishavebeenappliedtoassesstheperformanceofhealthcare systems(seeforinstance:[50–52]).Nonetheless,duetotheapplicabilityofDEAinthesolutionof problemswithmultipleinputsandoutputs,itismostcommonlyusedinhealthcaresystems[53]. TheutilizationsofDEAinthehealthcaresectorcanbefoundinseveralworksofliterature,includingfor crispdata[54–56],fuzzydata[57,58],andintuitionisticfuzzydata[59].Tothebestofourknowledge, noneofthesecurrentworksassessedtheefficiencyofhealthcareorganizationswithneutrosophicsets. Therefore,toassesstheefficiencyofthementionedsystemsunderaneutrosophicenvironment,we usedtheproposedmodeltoevaluate13hospitalsofTUMS.Itisworthemphasizingthatduetoprivacy policies,thenamesofthesehospitalsarenotshared.Furthermore,fortheselectionofthemostsuitable andacceptableitemsofthehealthcaresystem,whicharecommonlyusedformeasuringefficiency
intheliterature,weconsideredtwoinputs,namelythenumberofdoctorsandnumberofbeds,and threeoutputs,namelythetotalyearlydaysofhospitalizationofallpatients,numberofoutpatient departmentvisits,andoverallpatientsatisfaction.
Foreachhospital,wegatheredtherelateddatafromthemedicalrecordsunitofthehospitals, CenterofStatisticsoftheUniversityofMedicalSciences,thereliablelibrary,onlineresources,andthe judgmentsofsomeexperts.Aftercollectingdata,wefoundthattheinformationwassometimes inconsistent,indeterminate,andincomplete.Theinvestigationrevealedthatseveralreformsbythe mentionedhospitalsandotherissueshaveledtoconsiderableuncertaintyandindeterminacyabout thedata.Asaresult,weidentifiedthemastriangularsingle-valuedneutrosophicnumbers(TSVNNs). Forexample,for“PatientSatisfaction,”wecollecteddataintermsof“satisfaction,”“dissatisfaction,” and“abstention,”andforeachterm,therelateddatawasexpressedbyatriangularfuzzynumber. Inaddition,eachtriangularfuzzynumberwasconstructedbasedonmin,average,andmax.Alldata wereexpressedbyusingTSVNNs,andcanbefoundinTables 1 and 2
Table1. Inputinformationofthenomineehospitals.
DMU
Inputs1 NumberofDoctors
Inputs2 NumberofBeds
1 [404,540,674] , [350,440,560], [420,645,700] [520,530,535] , [520,525,530], [532,534,540]
2 [119,136,182] , [122,125,137], [125,178,200] [177,180,188] , [173,175,179], [185,189,195]
3 [139,145,158] , [139,140,147], [146,155,167] [208,214,218] , [195,209,215], [210,217,230]
4 [86,93,151] , [83,85,87], [89,138,160] [114,116,118] , [114,115,117], [116,118,125]
5 [84,93,143] , [84,89,120], [90,140,155] [110,117,121] , [105,112,120], [113,119,128]
6 [101,113,170] , [110,112,115], [112,120,177] [101,107,111] , [95,100,104], [108,112,115]
7 [561,694,864] , [510,640,750], [582,857,930] [492,495,508] , [492,494,500 ], [493,506,520]
8 [123,179,199] , [122,125,130], [195,200,205] [66,68,73] , [63,67,69], [68,70,78]
9 [101,153,155] , [140,145,150], [145,149,167] [192,195,198] , [185,193,197], [194,196,205]
10 [147,164,170] , [147,160,167], [165,169,180] [333,340,357] , [335,338,350], [338,347,364]
11 [130,158,192] , [110,144,173], [146,177,205] [96,100,114] , [97,99,103], [99,110,129]
12 [128,137,187] , [128,133,164], [134,184,199] [213,220,224] , [208,215,223], [216,222,231]
13 [151,160,210] , [151,156,187], [157,207,222] [320,327,331] , [315,322,330], [323,329,338]
Next,weusedAlgorithm1tosolvetheperformancevaluationproblem.Forexample,Algorithm1 forDMU1 canbeusedasfollows:
First,weconstructaDEAmodelwiththementionedTSVNNs:
max θ1 ≈ [121.13,139.24,140.04] , [138.64,139.14,139.81], [139.14,140.02,141.17] v1⊕ [38,41,45] , [38,40,43], [41,44,49] v2⊕ [104.23,114.04,278.51] , [102.37,109.15,235.72], [104.81,275.25,279.88] v3 s.t: [404,540,674] , [350,440,560], [420,645,700] u1 ⊕ [520,530,535] , [520,525,530], [532,534,540] u2 = 1, ( [121.13,139.24,140.04] , [138.64,139.14,139.81], [139.14,140.02,141.17] v1 ⊕ [38,41,45] , [38,40,43], [41,44,49] v2 ⊕ [104.23,114.04,278.51] , [102.37,109.15,235.72], [104.81,275.25,279.88] v3) ( [404,540,674] , [350,440,560], [420,645,700] u1 ⊕ [520,530,535] , [520,525,530], [532,534,540] u2) ≤ 0, ( [31.54,34.93,38.89] , [31.54,34.15,38.27], [34.86,38.15,39.83] v1 ⊕ [40,44,47] , [35,52,45], [41,46,50] v2 ⊕ [34.54,36.98,54.82 ] , [36.45,36.80,41.57], [47.61,54.25,55.35] > v3 ) ( < [109,126,172] , [112,115,127], [115,168,190] u1 ⊕ [ 177,180,188 ], [173,175,179], [185,189,195] u2) ≤ 0,
( [81.62,82.07,85.51] , [81.41,81.94,83.35], [81.78,85.49,88.16] v1 ⊕ [18,20,29] , [19,21,23], [28,30,35] v2 ⊕ [ 157.75,177.57,264.52 ], [157.75,176.68,250.75], [180.29,263.98,272.16] v3)
( [139,145,158] , [139,140,147], [146,155,167] u1 ⊕ [208,214,218] , [195,209,215], [210,217,230] u2) ≤ 0, ( [19.54,20.41,20.59] , [20.15,20.25,20.32], [20.54,20.58,20.70] v1 ⊕ [18,21,25] , [15,19,23], [20,24,30] v2 ⊕ [32.89,35.56,87.74 ] , [35.25,35.50,35.61], [87.50,87.94,88.30] v3)
( [86,93,151] , [83,85,87], [89,138,160] u1 ⊕ [114,116,118] , [114,115,117], [116,118,125] u2) ≤ 0,
( [23.89,24.60,26.09] , [23.56,23.60,23.68], [25.97,26.35,26.72] v1 ⊕ [30,36,41] , [34,35,37], [35,40,57] v2 ⊕ [63.23,69.58,120.73 ] , [63,65.17,94.93], [64.47,118.75,124.75 ] v3)
( [84,93,143] , [84,89,120], [90,140,155] u1 ⊕ [110,117,121] , [105,112,120], [113,119,128] u2) ≤ 0,
( [21.33,21.49,23.31] , [20.94,24.25,22.68 ], [21.38,23.14,23.94 ] v1 ⊕ [50,55,60] , [50,53,57], [56,59,70] v2 ⊕ [72.84,82.84,94.18 ] , [82.15,82.68,84.89 ], [85.75,93.50,97.18 ] v3) ( [101,113,170] , [110,112,115], [112,120,177] u1 ⊕ [101,107,111] , [95,100,104], [108,112,115] u2) ≤ 0,
( [145.77,148.28,169.01], [145.77,147.16,168.31], [150.69,168.95,175.18] v1 ⊕ [40,44,46], [42,43,45], [43,44,55] v2 ⊕ [147.59,150.37,227.12 ], [147.30,147.45,148.25], [218.24,224.61,229.63] v3) ( [561,694,864], [510,640,750], [582,857,930] u1 ⊕ [492,495,508], [492,494,500 ], [493,506,520] u2) ≤ 0, ( [11.56,11.74,12.96] , [11.42,11.61,11.98], [11.58,12.64,13.16] v1 ⊕ [60,75,80] , [55,60,62], [78,83,85] v2 ⊕ [189.37,202.08,284.99 ] , [189.37,200.52,281.63], [270.16,284.55,289.12] v3) ( [123,179,199] , [122,125,130], [195,200,205] u1 ⊕ [66,68,73] , [63,67,69], [68,70,78] u2) ≤ 0,
( [57.55,62.67,63.03] , [62.15,62.50,62.93], [62.50,62.97,63.61] v1 ⊕ [32,35,38] , [32,33,35], [34,36,45] v2 ⊕ [14.63,14.85,29.40] , [14.70,14.75,15.25], [24.75,28.36,32.64] v3)
( [101,153,155] , [140,145,150], [145,149,167] u1 ⊕ [192,195,198] , [185,193,197], [194,196,205] u2) ≤ 0,
( [73.21,76.03,81.90 ] , [75.76,76.05,76.25], [81.67,82.27,82.64] v1 ⊕ [22,25,40] , [20,24,27], [23,25,29] v2 ⊕ [96.77,97.27,110.39] , [96.77,96.89,105.14], [99.76,108.62,115.27] v3)
( [147,164,170] , [147,160,167], [165,169,180] u1 ⊕ [333,340,357] , [335,338,350], [338,347,364] u2) ≤ 0,
( [22.90,27.71,35.56] , [22.90,26.45,31.28], [27.92,34.62,39.41] v1 ⊕ [20,23,26] , [21,22,24], [22,25,30] v2 ⊕ [171.53,182.46,384.99 ] , [171.12,178.65,210.34], [175.59,270.65,400.12] v3) ( [130,158,192] , [110,144,173], [146,177,205] u1 ⊕ [96,100,114] , [97,99,103], [99,110,129] u2) ≤ 0, ( [58.41,59.12,60.61], [58.08,58.12,58.20], [60.49,60.87,61.24 ] v1 ⊕ [25,31,37] , [29,30,32], [30,35,52] v2 ⊕ [59.87,66.22,117.37 ], [59.64,61.81,91.57], [61.11,115.39,121.39 ] v3) ( [128,137,187], [128,133,164], [134,184,199] u1 ⊕ [213,220,224] , [208,215,223], [216,222,231] u2) ≤ 0, ( [66.97,67.68,69.17] , [66.64,66.68,66.76], [69.05,69.43,69.80] v1 ⊕ [20,27,31] , [23,26,28], [24,30,46] v2 ⊕ [96.97,103.32,154.47 ] , [96.74,98.91,128.67], [98.21,152.49,158.50 ] v3) ( [151,160,210] , [151,156,187], [157,207,222] u1 ⊕ [320,327,331] , [315,322,330], [323,329,338] u2) ≤ 0, vr, ui ≥ 0, r = 1,2,3, i = 1,2.
Table2. Outputinformationofthenomineehospitals.
DMU Outputs1 DaysofHospitalization (inThousands)
1
2
3
4
[121.13,139.24,140.04] , [138.64,139.14,139.81], [139.14,140.02,141.17]
[31.54,34.93,38.89] , [31.54,34.15,38.27] , [34.86,38.15,39.83]
[81.62,82.07,85.51] , [81.41,81.94,83.35], [81.78,85.49,88.16]
[19.54,20.41,20.59] , [20.15,20.25,20.32], [20.54,20.58,20.70]
Outputs2 PatientSatisfaction(%)
[38,41,45] , [38,40,43], [41,44,49]
[40,44,47] , [35,42,45], [41,46,50]
[18,20,29] , [19,21,23], [28,30,35]
[18,21,25] , [15,19,23], [20,24,30]
Outputs3 NumberofOutpatients (inThousands)
[104.23,114.04,278.51] , [102.37,109.15,235.72], [104.81,275.25,279.88]
[34.54,36.98,54.82 ] , [36.45,36.80,41.57], [47.61,54.25,55.35]
[157.75,177.57,264.52 ] , [157.75,176.68,250.75], [180.29,263.98,272.16]
[32.89,35.56,87.74 ] , [35.25,35.50,35.61], [87.50,87.94,88.30]
5
6
[23.89,24.60,26.09] , [23.56,23.60,23.68], [25.97,26.35,26.72 ]
[21.33,21.49,23.31] , [20.94,24.25,22.68 ], [21.38,23.14,23.94 ]
7 [145.77,148.28,169.01] , [145.77,147.16,168.31], [150.69,168.95,175.18]
8 [11.56,11.74,12.96] , [11.42,11.61,11.98], [11.58,12.64,13.16]
[30,36,41] , [34,35,37], [35,40,57]
[50,55,60] , [50,53,57], [56,59,70]
[40,44,46] , [42,43,45], [43,44,55]
[60,75,80] , [55,60,62], [78,83,85]
[63.23,69.58,120.73 ] , [63,65.17,94.93], [64.47,118.75,124.75 ]
[72.84,82.84,94.18 ] , [82.15,82.68,84.89 ], [85.75,93.50,97.18 ]
[147.59,150.37,227.12 ] , [147.30,147.45,148.25], [218.24,224.61,229.63]
[189.37,202.08,284.99 ] , [189.37,200.52,281.63], [270.16,284.55,289.12]
9
[57.55,62.67,63.03 ] , [62.15,62.50,62.93 ], [62.50,62.97,63.61]
[32,35,38] , [32,33,35], [34,36,45]
[14.63,14.85,29.40 ] , [14.70,14.75,15.25 ], [24.75,28.36,32.64 ] 10 [73.21,76.03,81.90 ] , [75.76,76.05,76.25], [81.67,82.27,82.64]
[22,25,40] , [20,24,27], [23,25,29]
[96.77,97.27,110.39 ] , [96.77,96.89,105.14], [99.76,108.62,115.27] 11
[22.90,27.71,35.56 ] , [22.90,26.45,31.28], [27.92,34.62,39.41]
[20,23,26] , [21,22,24], [22,25,30]
[171.53,182.46,384.99 ] , [171.12,178.65,210.34], [175.59,270.65,400.12] 12
[58.41,59.12,60.61] , [58.08,58.12,58.20], [60.49,60.87,61.24 ]
[66.97,67.68,69.17] , [66.64,66.68,66.76], [69.05,69.43,69.80]
[25,31,37] , [29,30,32], [30,35,52]
[59.87,66.22,117.37 ] , [59.64,61.81,91.57], [61.11,115.39,121.39 ] 13
[20,27,31] , [23,26,28], [24,30,46]
[96.97,103.32,154.47 ], [96.74,98.91,128.67], [98.21,152.49,158.50 ]
Finally,basedonDefinition4,weconverttheabovemodeltothefollowingmodel:
max θ1 ≈ 138.0608v1+42v2 + 175.2v3
s.t:
529.8333u1 + 529.5833u2 = 1, 138.0608v1+42v2 + 175.2v3 529.8333u1 529.5833u2 ≤ 0, 35.7792v1 + 43.5v2 + 43.8667v3 146.9167u1 182.0833u2 ≤ 0, 83.4025v1 + 24.5v2 + 209.9733v3 148u1 213u2 ≤ 0, 20.36v1 + 21.5833v2 + 57.1075v3 104.3333u1 116.8333u2 ≤ 0, 24.9175v1+38v2 + 86.5092v3 110u1 116.0833u2 ≤ 0, 22.6117v1 + 56.4167v2 + 86.2525v3 122.9167u1 106u2 ≤ 0, 156.9592v1 + 44.4167v2 + 180.2492v3 714.9167u1 499.5833u2 ≤ 0, 12.0533v1 + 71.3333v2 + 239.9117v3 165.1667u1 68.9167u2 ≤ 0, 62.3375v1 + 35.3333v2 + 20.6075v3 146u1 194.9167u2 ≤ 0, 78.3442v1 + 25.75v2 + 102.4717v3 163.5u1 343.9167u2 ≤ 0, 29.7942v1 + 23.5833v2 + 231.4342v3 159.5u1 104.6667u2 ≤ 0, 59.4375v1 + 33.0833v2 + 83.1492v3 154u1 219.0833u2 ≤ 0, 67.9975v1 + 28.1667v2 + 120.25v3 177u1 326.0833u2 ≤ 0, vr, ui ≥ 0, r = 1,2,3, i = 1,2.
AftercomputationswithLingo,weobtained θ∗ 1 = 0.6673 for DMU1.Similarly,fortheother DMUs,wereportedtheresultsinTable 3.Fromtheseresults,wecanseethatDMUs3,6,8,and11are efficientandothersareinefficient.
Table3. Theefficienciesofthedecision-makingunits(DMUs)bythetriangularsingle-valued neutrosophicnumber-Charnes,Cooper,andRhodes(TSVNN-CCR)model.
DMUsEfficiency Ranking 10.66739 20.80576 31.001 40.595010 50.87544 61.001 70.70247 81.001 90.91162 100.87513 111.001 120.85365 130.75878
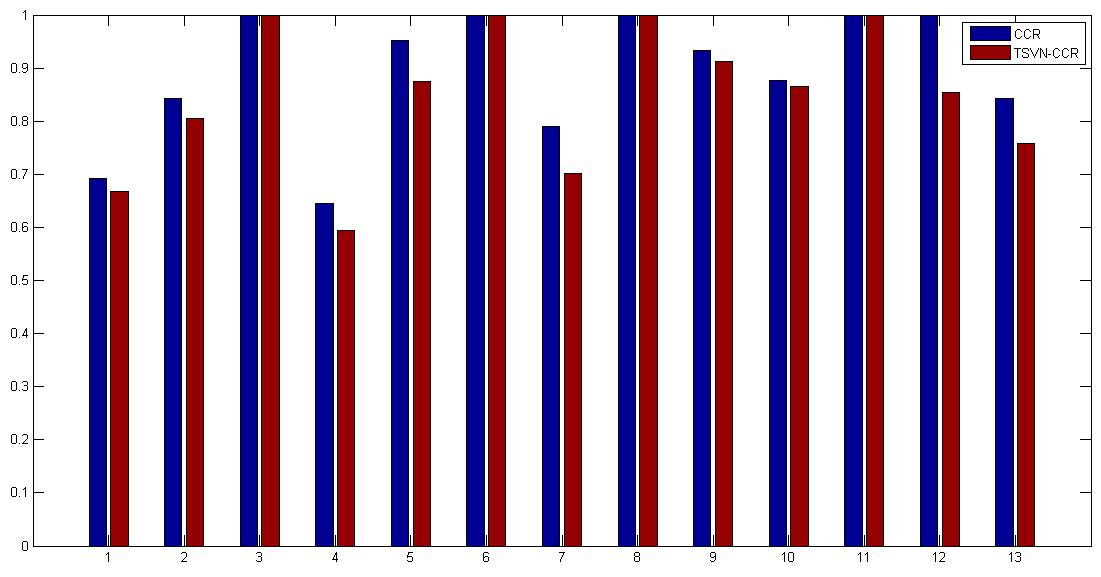
Toauthenticatethesuggestedefficiencies,theseefficiencieswerecomparedwiththeefficiencies obtainedbythecrispCCR(Model(6)),andaregiveninFigure 1.Inthisfigure,theefficienciesof DMUsarefoundtobesmallerforTSVNN-CCRcomparedtocrispCCR.
ItisinterestingthatDMU12isefficientincrispDEA,butitisinefficientwithanefficiencyscore of0.8536usingTSVNN-CCR.Therefore,TSVNN-CCRismorerealisticthancrispCCR.Inaddition, crispCCRandTSVNN-CCRmaygivethesameefficienciesforcertaindata.However,thecrispCCR modeldoesnotdealwiththeuncertain,indeterminate,andincongruousinformation.Therefore, TSVNN-CCRismorerealisticthancrispCCR.
Figure1. Comparisonofsuggestedandcrispmodels.
Figure 1. Comparison of suggested and crisp models.
6.ConclusionsandFutureWork
It is interesting that DMU 12 is efficient in crisp DEA, but it is inefficient with an efficiency score of 0.8536 using TSVNN-CCR Therefore, TSVNN-CCR is more realistic than crisp CCR. In addition, crisp CCR and TSVNN-CCR may give the same efficiencies for certain data. However, the crisp CCR model does not deal with the uncertain, indeterminate, and incongruous information. Therefore, TSVNN-CCR is more realistic than crisp CCR.
Inthispaper,anewapproachfordataenvelopmentanalysiswasproposedinthatindeterminacy, uncertainty,vagueness,inconsistent,andincompletenessofdatawereshownbyneutrosophicsets. Furthermore,thesortingofDMUsinDEAhasbeenpresented,andusingade-neutrosophication technique,arankingorderhasbeenextracted.Theefficiencyscoresoftheproposedmodelhavea similarmeaningandinterpretationwiththeconventionalCCRmodel.Finally,theapplicationof theproposedmodelwasexaminedinareal-worldcasestudyof13hospitalsofTUMS.Thenew modelisappropriateinsituationswheresomeinputsoroutputsdonothaveanexactquantitative value,andtheproposedapproachhasproducedpromisingresultsfromcomputingefficiencyand performanceaspects.
6. Conclusions and Future Work
In this paper, a new approach for data envelopment analysis was proposed in that indeterminacy, uncertainty, vagueness, inconsistent, and incompleteness of data were shown by neutrosophic sets. Furthermore, the sorting of DMUs in DEA has been presented, and using a deneutrosophication technique, a ranking order has been extracted. The efficiency scores of the proposed model have a similar meaning and interpretation with the conventional CCR model. Finally, the application of the proposed model was examined in a real-world case study of 13 hospitals of TUMS. The new model is appropriate in situations where some inputs or outputs do not have an exact quantitative value, and the proposed approach has produced promising results from computing efficiency and performance aspects.
Theproposedstudyhadsomebarriers:first,theindeterminacy,uncertainty,andambiguity inthepresentreportwaslimitedtotriangularsingle-valuedneutrosophicnumbers,buttheother formsofNSssuchasbipolarNSsandinterval-valuedneutrosophicnumberscanalsobeusedto indicatevariablescharacterizingtheneutrosophiccoreinglobalproblems.Second,thepresented modelwasinvestigatedunderaconstantreturns-to-scale(CRS),butthesuggestedmethodcanalsobe extendedunderaVRSassumption,soweplantoextendthismodeltotheVRS.Moreover,although thearithmeticoperations,model,andresultspresentedheredemonstratetheeffectivenessofour methodology,itcouldalsobeconsideredinothertypesofDEAmodelssuchasnetworkDEAandits applicationstobanks,supplierselection,taxoffices,policestations,schools,anduniversities.While developingdataenvelopmentanalysis,modelsbasedonbipolarandinterval-valuedneutrosophic dataisanotherareaforfurtherstudies.Asforfutureresearch,weintendtostudytheseproblems.
AuthorContributions: Theauthorscontributedequallytowritingthisarticle.Allauthorshavereadandagreed tothepublishedversionofthemanuscript.
Funding: ThisworkwassupportedbyQuzhouUniversity.
ConflictsofInterest: Theauthorsdeclarenoconflictsofinterest.
The proposed study had some barriers: first, the indeterminacy, uncertainty, and ambiguity in the present report was limited to triangular single-valued neutrosophic numbers, but the other forms of NSs such as bipolar NSs and interval-valued neutrosophic numbers can also be used to indicate variables characterizing the neutrosophic core in global problems. Second, the presented model was investigated under a constant returns-to-scale (CRS), but the suggested method can also be extended under a VRS assumption, so we plan to extend this model to the VRS. Moreover, although the arithmetic operations, model, and results presented here demonstrate the effectiveness of our methodology, it could also be considered in other types of DEA models such as network DEA and its applications to banks, supplier selection, tax offices, police stations, schools, and universities. While developing data envelopment analysis, models based on bipolar and interval-valued neutrosophic data is another area for further studies. As for future research, we intend to study these problems.
Author Contributions: The authors contributed equally to writing this article. All authors read and approved the final manuscript.
Funding: This work was supported by Quzhou University.
Conflicts of Interest: The authors declare no conflicts of interest.
Abbreviations: List of Acronyms
Abbreviations:ListofAcronyms
DEADataEnvelopmentAnalysis
DMUDecision-MakingUnits
CCRmodelCharnes,Cooper,Rhodesmodel
BCCmodelBanker,Charnes,Coopermodel
CRSConstantReturns-to-Scale
VRSVariableReturns-to-Scale
AHPAnalyticHierarchyProcess
TUMSTehranUniversityofMedicalSciences
FSFuzzySet
IFSIntuitionisticFuzzySet
NSNeutrosophicSet
SVNSSingle-ValuedNeutrosophicSet
TSVNNTriangularSingle-ValuedNeutrosophicnumber
References
1. Charnes,A.;Cooper,W.W.;Rhodes,E.Measuringtheefficiencyofdecisionmakingunits. Eur.J.Oper.Res. 1978, 2,429–444.[CrossRef]
2. Farrell,M.J.Themeasurementofproductiveefficiency. J.R.Stat.Soc. 1957, 120,253–290.[CrossRef]
3. Banker,R.D.;Charnes,A.;Cooper,W.W.Somemodelsforestimatingtechnicalandscaleinefficienciesin dataenvelopmentanalysis. Manag.Sci. 1984, 30,1078–1092.[CrossRef]
4. Sahoo,B.K.;Tone,K.Decomposingcapacityutilizationindataenvelopmentanalysis:Anapplicationto banksinIndia. Eur.J.Oper.Res. 2009, 195,575–594.[CrossRef]
5. Lee,Y.J.;Joo,S.J.;Park,H.G.AnapplicationofdataenvelopmentanalysisforKoreanbankswithnegative data. BenchmarkingInt.J. 2017, 24,1052–1067.[CrossRef]
6. Jiang,H.;He,Y.ApplyingDataEnvelopmentAnalysisinMeasuringtheEfficiencyofChineseListedBanks intheContextofMacroprudentialFramework. Mathematics 2018, 6,184.[CrossRef]
7. Karasakal,E.;Aker,P.AmulticriteriasortingapproachbasedondataenvelopmentanalysisforR&Dproject selectionproblem. Omega 2017, 73,79–92.
8. Lacko,R.;Hajduová,Z.;Gábor,V.DataEnvelopmentAnalysisofSelectedSpecializedHealthCentresand PossibilitiesofitsApplicationintheTermsofSlovakRepublicHealthCareSystem. J.HealthManag. 2017, 19, 144–158.[CrossRef]
9. Ertay,T.;Ruan,D.;Tuzkaya,U.R.Integratingdataenvelopmentanalysisandanalytichierarchyforthe facilitylayoutdesigninmanufacturingsystems. Inf.Sci. 2006, 176,237–262.[CrossRef]
10. Düzakın,E.;Düzakın,H.Measuringtheperformanceofmanufacturingfirmswithsuperslacksbasedmodel ofdataenvelopmentanalysis:Anapplicationof500majorindustrialenterprisesinTurkey. Eur.J.Oper.Res. 2007, 182,1412–1432.[CrossRef]
11. Jahanshahloo,G.R.;Lotfi,F.H.;Valami,H.B.Malmquistproductivityindexwithintervalandfuzzydata, anapplicationofDataenvelopmentanalysis. Int.Math.Forum 2006, 1,1607–1623.[CrossRef]
12. Shafiee,M.;Lotfi,F.H.;Saleh,H.Supplychainperformanceevaluationwithdataenvelopmentanalysisand balancedscorecardapproach. Appl.Math.Model. 2014, 38,5092–5112.[CrossRef]
13. Soheilirad,S.;Govindan,K.;Mardani,A.;Zavadskas,E.K.;Nilashi,M.;Zakuan,N.Applicationofdata envelopmentanalysismodelsinsupplychainmanagement:Asystematicreviewandmeta-analysis. Ann.Oper.Res. 2018, 271,915–969.[CrossRef]
14. Krmac,E.;Djordjevi´c,B.ANewDEAModelforEvaluationofSupplyChains:ACaseofSelectionand EvaluationofEnvironmentalEfficiencyofSuppliers. Symmetry 2019, 11,565.[CrossRef]
15. Zadeh,L.A.Fuzzysets. Inf.Control 1965, 8,338–353.[CrossRef]
16. Hsu,T.;Tsai,Y.;Wu,H.Thepreferenceanalysisfortouristchoiceofdestination:AcasestudyofTaiwan. Tour.Manag. 2009, 30,288–297.[CrossRef]
17. Finol,J.;Guo,Y.K.;Jing,X.D.Arulebasedfuzzymodelforthepredictionofpetrophysicalrockparameters. J.Pet.Sci.Eng. 2001, 29,97–113.[CrossRef]
18. Najafi,H.S.;Edalatpanah,S.A.Animprovedmodelforiterativealgorithmsinfuzzylinearsystems. Comput.Math.Modeling 2013, 24,443–451.[CrossRef]
19. Hosseinzadeh,A.;Edalatpanah,S.A.Anewapproachforsolvingfullyfuzzylinearprogrammingbyusing thelexicographymethod. Adv.FuzzySyst. 2016.[CrossRef]
20. Das,S.K.;Edalatpanah,S.A.;Mandal,T.Aproposedmodelforsolvingfuzzylinearfractionalprogramming problem:NumericalPointofView. J.Comput.Sci. 2018, 25,367–375.[CrossRef]
21. Hatami-Marbini,A.;Emrouznejad,A.;Tavana,M.Ataxonomyandreviewofthefuzzydataenvelopment analysisliterature:Twodecadesinthemaking. Eur.J.Oper.Res. 2011, 214,457–472.[CrossRef]
22. Emrouznejad,A.;Tavana,M.;Hatami-Marbini,A.Thestateoftheartinfuzzydataenvelopmentanalysis. In PerformanceMeasurementwithFuzzyDataEnvelopmentAnalysis;Springer:Berlin/Heidelberg,Germany, 2014;pp.1–45.
23. Emrouznejad,A.;Yang,G.L.Asurveyandanalysisofthefirst40yearsofscholarlyliteratureinDEA: 1978–2016. Socio-Econ.Plan.Sci. 2018, 61,4–8.[CrossRef]
24. Yen,B.T.;Chiou,Y.C.Dynamicfuzzydataenvelopmentanalysismodels:Caseofbustransportperformance assessment. RAIRO-Oper.Res. 2019, 53,991–1005.[CrossRef]
25. Lotfi,F.H.;Ebrahimnejad,A.;Vaez-Ghasemi,M.;Moghaddas,Z. DataEnvelopmentAnalysiswithR;Springer: Cham,Switzerland,2020.
26. Atanassov,K.T.Intuitionisticfuzzysets. FuzzySetsSyst. 1986, 20,87–96.[CrossRef]
27. Rouyendegh,B.D.TheDEAandintuitionisticfuzzyTOPSISapproachtodepartments’performances:Apilot study. J.Appl.Math. 2011,1–16.[CrossRef]
28. Puri,J.;Yadav,S.P.Intuitionisticfuzzydataenvelopmentanalysis:Anapplicationtothebankingsectorin India. ExpertSyst.Appl. 2015, 42,4982–4998.[CrossRef]
29. Edalatpanah,S.A.Adataenvelopmentanalysismodelwithtriangularintuitionisticfuzzynumbers. Int.J. DataEnvel.Anal. 2019, 7,47–58.
30. Arya,A.;Yadav,S.P.Developmentofintuitionisticfuzzydataenvelopmentanalysismodelsandintuitionistic fuzzyinput–outputtargets. SoftComput. 2019, 23,8975–8993.[CrossRef]
31. Smarandache,F. AUnifyingFieldinLogics.Neutrosophy:NeutrosophicProbability,SetandLogic;American ResearchPress:Rehoboth,MA,USA,1999.
32. Smarandache,F.Aunifyingfieldinlogics:Neutrosophiclogic.In Neutrosophy,NeutrosophicSet,Neutrosophic ProbabilityandStatistics,3rded.;AmericanResearchPress:Rehoboth,MA,USA,2003.
33. Broumi,S.;Smarandache,F.Correlationcoefficientofintervalneutrosophicset. Appl.Mech.Mater. 2013, 436, 511–517.[CrossRef] 34. Ye,J.Similaritymeasuresbetweenintervalneutrosophicsetsandtheirapplicationsinmulticriteria decision-making. J.Intell.FuzzySyst. 2014, 26,165–172.[CrossRef] 35. Broumi,S.;Smarandache,F.;Talea,M.;Bakali,A.Anintroductiontobipolarsinglevaluedneutrosophic graphtheory. Appl.Mech.Mater. 2016, 841,184–191.[CrossRef] 36. Wang,L.;Zhang,H.Y.;Wang,J.Q.FrankChoquetBonferronimeanoperatorsofbipolarneutrosophicsetsand theirapplicationtomulti-criteriadecision-makingproblems. Int.J.FuzzySyst. 2018, 20,13–28.[CrossRef] 37. Ye,J.Multicriteriadecision-makingmethodusingthecorrelationcoefficientundersingle-valuedneutrosophic environment. Int.J.Gen.Syst. 2013, 42,386–394.[CrossRef]
38. Chakraborty,A.;Mondal,S.P.;Ahmadian,A.;Senu,N.;Alam,S.;Salahshour,S.DifferentFormsofTriangular NeutrosophicNumbers,De-NeutrosophicationTechniques,andtheirApplications. Symmetry 2018, 10,327. [CrossRef]
39. Garg,H.NewLogarithmicoperationallawsandtheirapplicationstomultiattributedecisionmakingfor single-valuedneutrosophicnumbers. Cogn.Syst.Res. 2018, 52,931–946.[CrossRef]
40.
Garg,H.Linguisticsingle-valuedneutrosophicprioritizedaggregationoperatorsandtheirapplicationsto multiple-attributegroupdecision-making. J.AmbientIntell.Hum.Comput. 2018, 9,1975–1997.[CrossRef]
41. Smarandache,F. AboutNonstandardNeutrosophicLogic:AnswerstoImamura’s“NoteontheDefinitionof NeutrosophicLogic”;InfiniteStudy:Coimbatore,India,2019.
42. Garg,H.Algorithmsforpossibilitylinguisticsingle-valuedneutrosophicdecision-makingbasedonCOPRAS andaggregationoperatorswithnewinformationmeasures. Measurement 2019, 138,278–290.[CrossRef]
43. Kumar,R.;Edalatpanah,S.A.;Jha,S.;Broumi,S.;Dey,A.Neutrosophicshortestpathproblem. Neutrosophic SetsSyst. 2018, 23,5–15.
44.
Edalatpanah,S.A.Nonlinearapproachforneutrosophiclinearprogramming. J.Appl.Res.Ind.Eng. 2019, 6, 367–373.
45. Edalatpanah,S.A.NeutrosophicperspectiveonDEA. J.Appl.Res.Ind.Eng. 2018, 5,339–345.
46. Kahraman,C.;Otay,I.;Öztay¸si,B.;Onar,S.C.AnIntegratedAHP&DEAMethodologywithNeutrosophic Sets.In FuzzyMulti-CriteriaDecision-MakingUsingNeutrosophicSets;Springer:Cham,Switzerland,2019; pp.623–645.
47.
Edalatpanah,S.A.;Smarandache,F.DataEnvelopmentAnalysisforSimplifiedNeutrosophicSets. NeutrosophicSetsSyst. 2019, 29,215–226.
Abdelfattah,W.Dataenvelopmentanalysiswithneutrosophicinputsandoutputs. ExpertSyst. 2019, 36,e12453.[CrossRef] 49. Robinson,A. Non-StandardAnalysis;PrincetonUniversityPress:Princeton,NJ,USA,2016.
48.
50.
Aristovnik,A.Measuringrelativeefficiencyinhealthandeducationsector:ThecaseofEastEuropean countries. ActualProbl.Econ. 2012, 136,305–314.
51. Barros,C.P.;deMenezes,A.G.;Vieira,J.C.Measurementofhospitalefficiency,usingalatentclassstochastic frontiermodel. Appl.Econ. 2013, 45,47–54.[CrossRef]
52. Colombi,R.;Martini,G.;Vittadini,G.Determinantsoftransientandpersistenthospitalefficiency:Thecase ofItaly. HealthEcon. 2017, 26,5–22.[CrossRef][PubMed]
53. Bryce,C.L.;Engberg,J.B.;Wholey,D.R.Comparingtheagreementamongalternativemodelsinevaluating HMOefficiency. HealthServ.Res. 2000, 35,509.[PubMed]

54. Kalhor,R.;Amini,S.;Sokhanvar,M.;Lotfi,F.;Sharifi,M.;Kakemam,E.Factorsaffectingthetechnical efficiencyofgeneralhospitalsinIran:Dataenvelopmentanalysis. J.Egypt.PublicHealthAssoc. 2016, 91, 20–25.[CrossRef]
55. Chen,H.;Liu,J.;Li,Y.;Chiu,Y.-H.;Lin,T.Y.ATwo-stageDynamicUndesirableDataEnvelopmentAnalysis ModelFocusedonMediaReportsandtheImpactonEnergyandHealthEfficiency. Int.J.Environ.Res. PublicHealth 2019, 16,1535.[CrossRef]
56. Kohl,S.;Schoenfelder,J.;Fügener,A.;Brunner,J.O.TheuseofDataEnvelopmentAnalysis(DEA)in healthcarewithafocusonhospitals. HealthCareManag.Sci. 2019, 22,245–286.[CrossRef]
57. Ji,A.B.;Qiao,Y.;Liu,C.FuzzyDEA-basedclassifieranditsapplicationsinhealthcaremanagement. Health CareManag.Sci. 2019, 22,560–568.[CrossRef]
58. Dotoli,M.;Epicoco,N.;Falagario,M.;Sciancalepore,F.Across-efficiencyfuzzydataenvelopmentanalysis techniqueforperformanceevaluationofdecisionmakingunitsunderuncertainty. Comput.Ind.Eng. 2015, 79, 103–114.[CrossRef]
59. Otay, I.;Oztaysi,B.;Onar,S.C.;Kahraman,C.Multi-expertperformanceevaluationofhealthcareinstitutions usinganintegratedintuitionisticfuzzyAHP&DEAmethodology. Knowl.BasedSyst. 2017, 133,90–106. © 2020bytheauthors.LicenseeMDPI,Basel,Switzerland.Thisarticleisanopenaccess articledistributedunderthetermsandconditionsoftheCreativeCommonsAttribution (CCBY)license(http://creativecommons.org/licenses/by/4.0/).
