Blackbody Radiation and Planck's Constant Edward Wei

Blackbody Radiation and Planck’s Constant

Edward Wei (Year 10, Peel)

By the late 19th century, it was the general consensus that nothing more could be discovered in physics. Physicists could calculate the motion of material objects using Newton’s laws of classical mechanics, and describe the properties of radiant energy using Maxwell’s mathematical relationships. The universe appeared to be a simple and orderly place, containing matter (which consisted of particles that had mass and whose location and motion could be accurately described) and light (which was viewed as having no mass and whose exact position in space cannot be fixed). Matter and energy were considered distinct and unrelated phenomena. However, there were several contradictions that continued to puzzle classical physicists. The one we will be looking at is known as the “ultraviolet catastrophe”.

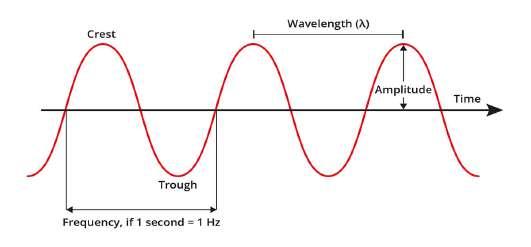
Figure 1: A diagram of an electromagnetic wave

(Source: Clinuvel) Light or electromagnetic radiation is a form of energy which travels in a wave, as shown in Figure 1 (Note: this is a simple depiction, but for our purposes it is enough). The crest is the tip of a wave; the trough is the bottom. The wavelength is the distance between the crests of 2 waves (measured in meters), and the amplitude is the distance between the crest and the trough divided by 2 (measured in meters). The wave period or frequency is the time taken to complete one cycle - as shown in Figure 1. It is measured in 1/time in seconds or Hertz. The frequency and wavelength of a wave are inversely proportional to each other.

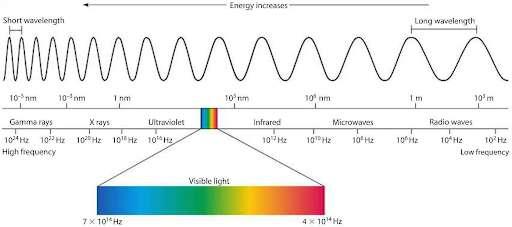
Figure 2: Diagram of the electromagnetic spectrum.

(Source: Mini Physics)

The electromagnetic spectrum categorizes light into several categories as its frequency/wavelength varies. Higher frequencies or shorter wavelengths equate to higher energy and vice versa. The relevant part is the visible section, which is the only part of the entire spectrum that we can see. Our eyes are not sensitive enough to detect infrared whilst the lenses of our eyes block out ultraviolet (it is harmful to cells). We are able to see objects because they either emit light themselves, or they absorb light and reflect it in all directions, and some of the light reflected just so happens to enter our eyes.

The contradiction that continued to puzzle classical physicists came in the form of 'black bodies'. Black bodies are idealized physical objects that do not simply reflect the light that they absorb: they absorb all frequencies of electromagnetic radiation that falls upon them and they can also emit radiation of any wavelength, but it is not usually in the visible light range, so we do not see it. However, the highest intensity wavelength emitted depends on temperature (Figure 3).

The radiation emitted from it is the kind released by any object with temperatures above absolute 0 (-273˚C). We do not usually see this radiated energy: at ambient temperature, the wavelength of the emitted radiation falls beyond the visible light spectrum, such as infra-red wavelengths. This is why we can feel hot things, even when we don’t come into direct contact with them or see any glow. Let’s take a real life example: molten iron glows red because while most of the energy radiated from it is within the infra-red spectrum, a portion of the energy has a high enough frequency to be visible red light. As objects get hotter, they emit radiation with shorter and shorter wavelengths, so it is within the visible spectrum or even shorter.

Classical physicists use the equation I = 2f 2 k B T/c 2 or the Rayleigh–Jeans Law to approximate the total energy in terms of electromagnetic radiation as a function of wavelength from a black body at a given temperature, where f is frequency, k B is Boltzmann’s constant, T is the temperature (in Kelvin) and c is the speed of light (in metres per second).

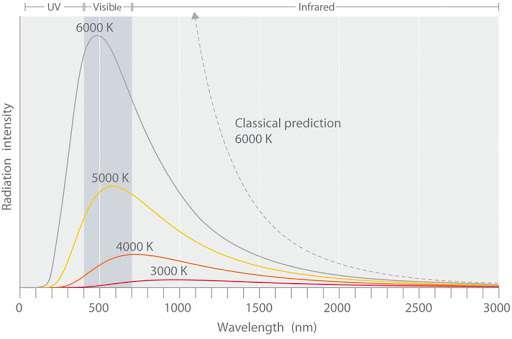
Figure 3: A graph comparing radiation intensity predicted by the Rayleigh-Jeans Law and the actual data. (Source: chem.libretexts.org)

The equation predicts that as the wavelength decreases, radiation intensity should increase without a limit at any temperature, as shown by the dotted line. It does not explain the sharp decrease in the radiation intensity emitted at shorter wavelengths. In fact, it does such a poor job of describing what really happens that it was dubbed the “ultraviolet catastrophe”. This contradiction was solved when German physicist Max Planck proposed that the energy of electromagnetic waves was quantized.

We say something is quantized when the number of possible values is limited to certain discrete magnitudes, which are multiples of a constant value (quanta). Although quantization may be an unfamiliar concept, it’s all around us. For example, US money is an integral multiple of pennies. Musical instruments such as the piano can only produce certain musical notes like C or F sharp. Even electrical charges are quantized - ions can have a charge of 1 or -2, but not 1.46.

En = nhv

E = the energy in joules and represents the total amount of energy radiated from a black body (although generally E now represents the amount of energy in a light beam) n = the number of protons in the light beam, a very large integer. h = 'Planck’s constant', 6.626 x 10 -34 joule-seconds v = the frequency of the light wave in hertz

Planck explained that at low temperatures, radiation with relatively large wavelengths (low frequencies) is emitted. As temperature increases, the emission of radiation with shorter wavelengths (higher frequencies) becomes more probable. This is why hotter black bodies are able to emit electromagnetic radiation at higher maximum intensities. However, at any given temperature, objects would rather emit many low-energy photons over a single high energy photon of equivalent total energy.

The 'discovery' of the quantized nature of electromagnetic radiation was an incredible breakthrough. In the early 20th century, physicists were so sure that they had discovered everything that one respected member even said,

“There is nothing new to be discovered in physics now. All that remains is more and more precise measurement.” Lord Kelvin 1

Planck’s discovery led to a new branch of Physics: Quantum Physics, opening a vast world that we have barely scratched the surface of. This discovery fundamentally changed the way physicists perceived the world. In the past, physicists viewed mass as a “thing” with a definite location and velocity, like a car travelling west at 10m/s. However, we now know that the concepts of location, velocity and even existence itself blur at the atomic and subatomic level. For reasons we do not understand, electrons exist everywhere at once, with the probability of them “existing” in certain areas being higher than other areas. This fundamental difference in the way mass exists at the macro and the micro still befuddles physicists today.

AFTERNOTE

Max Planck didn’t actually know why the energy of electromagnetic waves was quantized. He derived this equation according to the graph of real data and through the assumption that energy carried by electromagnetic radiation was quantized. Similarly, he was able to guess that n is a very large integer, but was unable to identify its exact value. It was only explained later on when Albert Einstein discovered that light could have both wavelike and particle-like properties. This is because the energy that can be carried by a single photon (light particle) is fixed. The equation above actually calculates the energy within a light beam, which is why n is a large integer, as there are many photons in a light beam. The equation that calculates the energy of a single photon is E photon packets, because you cannot have half a photon of energy. = hv. The radiation comes in discrete

Now you may be asking, why does Planck’s equation conclude that energy is quantized? Sure, h is a constant, but isn’t v (frequency) an infinitely variable quantity? If so, how can the energy of a photon have only certain values? Yes, the spectrum of “allowed” energies of a photon is continuous i.e. a photon can have any energy, but for a given frequency, the energy exchange can only take place in jumps of hv. For example, if object A’s initial energy is equal to hv and we increase its energy by giving it another photon of energy with equal frequencies, object A has E Initial + hv worth of energy. It is impossible for object A to have a final energy in between E Initial and E Initial + hv.

Khan Academy

https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_-_The_Central_ Science_(Brown_et_al.)/06._Electronic_Structure_of_Atoms/6.2%3A_Quantized_Energy_and_ Photons

https://www.youtube.com/watch?v=GgD3Um_f0DQ

https://www.physicsforums.com/threads/how-can-energy-be-quantized-with-e-hv.338298/

https://www.youtube.com/watch?reload=9&v=pmM28gQZTXc

https://en.wikipedia.org/wiki/Rayleigh–Jeans_law