Study on Non-Negative Integer Solutions of Exponential Diophantine Equation 512x + 1728y = z3 and 27 by IRJET Journal

Study on Non-Negative Integer Solutions of Exponential Diophantine Equation

512x + 1728y = z3 and 271x + 9y = z3

Parakram Singh

Department of Mathematics, Planetskool Research centre, Sonipat, (HR) India

Abstract – The aim of the present paper is to demonstrate the problem of existence of the solution of exponential nonlinear Diophantine equation as there are no general methods to find solution with natural number. This is an attempt to find numerical solutions (if any) of the equations 512x + 1728 y = z3 , and the 271x + 9y = z3 , where (x, y, z) are non-negative integers.

Keywords: Exponential Diophantine equation, Number Theory, Non-Negative Integers Solution

Mathematics Subject Classification (ASM): 11D61, 11D79

1. INTRODUCTION

ThetheoryofNumberisanelegantbranchofmathematics that primarily concerned with the study of non-negative integers,orcountingnumbers,andtheirpropertiesaswell as the solvability of equations in whole numbers It has a veritablylonganddifferenthistory,andsomeofthetopmost mathematicians of all time, similar as Euclid, Euler, and Gauss,havemadesignificantbenefactionstoit. Hardyand Wright,[9]discussedagreatdiversityofdifferenttopicsof theoreticalnumbertheoryandfoundaremarkableselection ofarithmeticproblemstreatedwithconsummateclarityand distinction.Burton[7]suggestedthestudyofElementary& classicalnumbertheoryandtoimpartsomeofthehistorical backgroundinwhichthesubjectevolved. Nivenetal.[11] havediscussedthe introductiontothetheoryofnumbers andexpandthebinomialtheorem,calculationmethods for numericalandapublickeycryptographysection.Contains anoutstandingsetofproblems.Baker,[1]and[2]provided comprehensive initiation to all the major branches of number theory including elements of cryptography and primality testing, an account of number fields in the arithmetic of elliptic curves. The particular type of Exponential Diophantine equation is analyzed and generalized by the method of Catalan's conjecture, its primaryCyclotomicunits,andproofwasgivenbyMihailescu [15].

Algebraic equations with non-negative integer amounts having integer solutions are Diophantine equations. For findingthesolutiontotheseequations,there'snouniversal manner available yet, so the investigators are keenly interested in developing new techniques for unravelling theseequations.Whilehandlinganycognateequation,three issuesarise,that'swhethertheproblemisresolvableornot;

ifresolvable,possiblenumberofsolutionsandfinallytofind thecompleteresults.Diophantineequationsarefrequently usedinthefieldofAbstractalgebra,Coordinategeometry, Grouptheory,Linearalgebra,Trigonometry,Cryptography andasunderaswellaswecandefinethenumberofrational pointsonacircle.IninvestigationsonDiophantineequations ofsteps,twosignificantsuccesseswerescoredonlyinthe 20thcentury.ItwasprovedbyA.Thue[4].Diophantusfrom Alexandria such equations are vociferated Diophantine equations.Mordell[12]studiedtheDiophantineequations. Acu [6] has studied the elementary solutions for the Diophantineequationofax +by =cz Suvarnamanietal [3] analyzedtwoDiophantineequations4x+7y=z2and4x+11y = z2. Sroysang [5] obtained the solutions for Diophantine Equations 2x + 3y = z2. Cohen [10] studied the Number Theory and also gave its tools he also dealt with many aspectsofnumbertheory, mainlythecentral theme being thesolutionofDiophantineequations Cipuetal [13]have revealedthenumberofextensionsforafixedDiophantine triple. Burshtein [14], considered the general equation of threeconsecutiveprimeintegersoftheformpx +(p+1)y + (p+2)z =M3 ,whereMrepresentsapositiveintegerandp represents prime with p ≥ 2, x, y ≥ 1, & z ≤ 2, also he determined all solutions of the above exponential Diophantine equations. Janaki and Shankari [8] have discussed various implementable ways to tackle multivariableandmulti-degreeDiophantineproblemsand obtain the solution of these exponential Diophantine equations.

The paper is organized as follows. Section 2 presents the Preliminary work of the paper by using Lemma and theorems.Section3and4,presentstheworkingstrategyto solve the main exponential Diophantine equations of this paper. The conclusions about the obtained solutions are containinsection5.Therestofthepaperlistedtherelated workasreferences.

2. Preliminary

2.1 Lemma: (Miheailescu’sTheorem)[15]TheDio-phantine equationax by =1hastheuniquesolution(a,b,x,y)= (3,2,2,3),wherea,b,xandyareintegerswithmin{a, b,x,y}>1.

2.2 Lemma: Therearenosolutionsinintegerx,y,zwithx, y, z > 0, of xn + yn = zn when n ≥ 3, also known as Fermat'sLastTheorem,wasprovedbyWiles[16]

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 11 Issue: 10 | Oct 2024 www.irjet.net p-ISSN: 2395-0072

3. Main work for Equation 1: 512x +1728y =z3

Theorem 3: The Diophantine 512x + 1728y = z3, has no solutioninnon-negativeintegers,wherex,y,z>0

Proof: letwefindthetrivialsolutionfor 512x +1728y =z3 (3)

Letx=0

1+1728y =z3,thenz3 >1orz>1

or z3 – 1728y = 1, byLemma 2.1,ycanonlytakethe value 0 and1, for y = 0 and 1, the equation 1 + 1728y = z3 giveszhasnointegervalue

Nowlety=0

512x+1=z3,alsoherez3>1orz>1,thenequationz3–512x =1,byLemma2.1,says,xcantakethevaluelessthan2in integersthatarex=0,1 forx=0and1equation512x +1= z3 implyingz3 =2and513respectively,itgiveszhasnota positiveintegervalue.Hence,theequation512x+1728y=z3 hasnotrivialsolution.

Nowfindthenontrivialsolutionforequation,(3) or 512x +1728y =z3

canberewriteoftheform

83x +123y =z3 (3.1)

⟹ 2|z

zisevenbecauseLHSiseven,ifzisoddthenz3 isalsoodd

Dividingequation(3.1)by8weget

83x-1 +123y-3 ∙63 =(z/2)3

Ingeneral,ifwedivide(3.1)by8, i timesthen

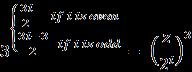
fori>1 (3.2)

We cannot divide by 8 infinitely many times. In equation (3.2) when i = min {3x, 2y, L} where L is the logarithm of highestpowerof2dividingzonbase2,itcannotbedivided by8.Weassumein(3.1)thatthetermisreducedifitstops theequationtodivideby8andcanbeaninteger,first.

Case 3.1: if123yreducesbeforeorwithz3 or83x

Afterkeepondividingby8,2ytimes,then

83x-2y +33y =(z/22y)3

3x-2y≥0

83x-2y+33y=t3 [t=z/22y]

(23x-2y)3+(3y)3=t3

Leta=23x-2y,b=33y

a3 +b3 =t3 whichtakesformofx3 +y3 =z3 andhasnosolutionduetoLemma2.2.

if123y willnotreducefirstgotothenextcase

Case 3.2: let83x reducesfirstbeforez3

1+123y-9x ∙69x =(z/8x)3

Put,m=3x 1+(12y-m ∙6m)3 =(z/2m)3` (3.2.1)

z/2m >1

as z/2m iseven

As123y hasnotreduced,soy-m>0ory>m

12y-m ∙6m>1andbyCatalanconjectureLemma2.1,wehave nosolutionforthiscase.

Case 3.3: ifz3 reducesfirsttoletsayk3 andbefore83x

Let z=2mk,

Dividingby8uptomtimesofequation(3.1)

83x-m +123y-3m ∙ 63m =k3

And it can be clearly seen that parity of LHS and RHS are different

Case 3.4: ifz3 and83x reduceboth

Afterreducing,weget 1+(63x ∙12y-3x)3 =k3 , wherez=23xk

(8isdivided3xtimes)

If n=63x ∙123y-3x , 1+n3 =k3

Now, n>1,k>0

Ifkis1thennis0whichisnotpossiblesok>1whichhas nosolutionbyLemma2.1.

Hence, the equation 512x + 1728y =z3 has no solution in non-negativeintegers.

4.

Main work for Equation 2: 271x +9y=z3

Theorem 4: Let x, y, z be non-negative integers then the equation271x +9y=z3 hasasolution(1,3,10).

Proof: Now initially check the trivial solution for the equation

271x +9y=z3 (4)

Letx=0,

1+9y =z3 Sincez3 >1,soz>1

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 11 Issue: 10 | Oct 2024 www.irjet.net p-ISSN: 2395-0072

or z3 –9y =1,

BytheLemma2.1,ycantakethevalueonlylessthan2,that is,y=0,1.ify=0,theequation1+9y =z3 givesz3 =2,which showszisnotanintegervalue.Similarly,fory=1,then1+ 91 =z3 orz3 =10whichgivesagain,zisnotanintegervalue Nowlety=0

271x +1=z3 Sincez3 >1,z>1 or z3 –271x =1

ByLemma2.1,ifanequationoftheformax –by =1then(a, b,x,y)canonlytakethepossiblesolutionis(3,2,2,3)for min {a, b, x, y} > 1. So, x can take the value less than 2 in integers,thatare x=0,1.

forx=0and1,theequation271x +1=z3 ,implyz3 =2and 272 respectively for both cases shows z is not a positive integer. Hence the equation 271x + 9y = z3 has no trivial solution.

Nowcheckthenontrivialsolutionforequation(4) x,yandz are the non-negative integers and the equation as given below-

Let, 271x +9y=z3 zisevenso, z3 ≡0(mod8), 9y ≡1(mod8), 271≡-1(mod8),hencexisodd

Nowforfindingy,consideritundermodulo3thenthereare followingcasesarise:

Case 4.1: Lety=3k,thenequation(4)becomes

271x +93k =z3

271x =z3 –(9k)3

271x =(z–9k)(z2 +9kz+92k)

Letx=u+v.forfactoring271x togetvaluesofz–9k andz2 +9kz+92k .

271u =z–9k (4.1.1)

271v =z2 +9kz+92k (4.1.2)

From(4.1.1),z=271u +9k

substitutingthisinequation(4.1.2)

271v =(271u +9k)2 +9k(271u +9k)+92k =2712u +3∙9k(271u +9k)=2712u +3∙9kz

32k+1 ∙z=271v –2712u =2712u(271v-2u –1)

Obviously,v>2uand271 LHShenceu=0andv=x

∵ x=u+v;

Then, 32k+1 ∙z+1=271x

or z3 –32k+1 ∙z–(36k +1)=0

whichgives, z=(32k +1),(-32k –1±√(-4∙32k+1))

Now,consideronlyrealvalueofz=32k +1,then

32k+1(32k +1)+1=271x

34k+1 +32k+1 =271x -1x

34k-2 +32k-2 =10(271x–1 +271x–2 +…+2712 +271+1)

Ifk=1,then34–2 +32–2 =10=10*1

Hence,x=1andz=10so,(1,3,10)isasolution

Ifk>1,then3|271x–1 +271x–2 +…+2712 +271+1

Sincealltermsare1(mod3)so3|x, let x=3m

(271m)3+(9k)3 =z3 ,whichisnotpossiblebyLemma2.2or Fermat’s last theorem represents no solution would be appearforthiscase.

Case 4.2: Lety=3k+1forequation(4),then

271x +93k+1 =z3 (4 2.1)

here,weconsidertwocasesfork,eitherithasthevaluek>0 orat,k=0

Subcase 4.2 (A): k>0

93k+1 ≡0(mod81)

Letx=2m+1andz=2t,

∵xisoddandziseven

Thenequation(4.2.1)becomes

2712m+1 +81∙93k-1 =8t3

2712m+1 +271∙93k-1 -190∙93k-1 =8t3

271(2712m +93k-1)=2(4t3 +95∙93k-1)

((2712m +93k-1)/2)=((4t3 +95∙93k-1)/271)=a (say) (4.2.A.1)

from1&3ratioofequation(4.2.A.1)

2712m +93k-1 =2a

⇒ 93k-1 =2a–2712m (4.2.A.2)

Alsoconsiderfrom2&3ratioofequation(4.2.A.1)

271a=4t3 +95∙93k-1 =4t3 +190a-95∙2712m by(4.2.A.2)

81a =4t3 -95∙2712m

0≡4t3 -14∙282m(mod81)

or 0≡4t3 -14∙55m(mod81) (4.2.A.3)

Weconstructthetablestofindthevaluefordifferentm andt,of14∙55mand4t3 modulo81

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 11 Issue: 10 | Oct 2024 www.irjet.net p-ISSN: 2395-0072

Table -1: ToFindallthepossiblevaluesof1455m (mod 81)

Find all the possible values of 14∙55m (mod 81)

m 55m (mod81) 14∙55m (mod81)

form>3,repeatthevaluesunder(mod81)

Table -2: ToFindallthepossiblevaluesof4t3 (mod81)

Find all the possible values of 4t3 (mod 81)

t t3(mod81) 4t3(mod81)

Subcase 4.2 (B): k=0

Lettheequation(4.2.1)at,k=0

271x +9=z3 (4.2.B.1)

We consider different modulo for the equation (4.2. B.1), Firstconsidermodulo5,then

271x +9≡z3 (mod5)

271x +9≡0(mod5), [∵271≡1(mod5)]

⇒ z≡0(mod5)

⇒ z3 ≡0(mod25)

From,(4.2.B.1),considermodulo25,then

⇒ 21x ≡16(mod25),

∵ 271≡21(mod25)

271x can be 21, 16, 11, 6, 1 (mod 25), if x takes the value from1,2,3,4and5resp.so,hereweseex>5,itwillrepeat thevalues.

Hence x≡2(mod5)

Nowfromequation(4.2.B.1),

271x +9≡z3 (mod31)

23x +9≡z3 (mod31)

(23x +9)canbe1,11,24,13,8,17,7,25,5,10(mod31),ifx takesthevaluefrom1to10respectivelyandmore So,we takex>10,itwillrepeatthevalues.

∵ x≡2,7(mod10)

Hence, z3≡7,11(mod31) Whichcontradicts,becausez3can nevertakesthevalue7or11under(mod31),sosubcase42 (B)unabletoshowthesolutionatk=0.

fort>8,repeatthevaluesunder(mod81)

wecan compare these values of t and m, according to the congruence (4.2.A.3) then here, z = 2t and t ≡ 5(mod 9) becauset>8,repeatthevaluesunder(mod81)

z≡1(mod9)andm≡0(mod3)

⇒ z3 ≡1(mod81)andx≡1(mod3).

Letx=3n+1

Sincez3 ≡1(mod81)and93k+1 ≡0(mod81),fromequation (4.2.1)

⇒ 271x ≡1(mod81)

⇒ 271∙(2713)n ≡1(mod81)

While,

271≡28(mod81)

which is a contradiction as 1 and 28 are not congruent to eachotherundermodulo81.So,the equation(42.1)hasno solutionforthiscase.

Case 4.3: y=3k+2,thenequation(4)becomes

Let 271x +93k+2 =z3 (4.3.1)

93k+2 ≡0(mod81)

Letx=2m+1andz=2t [∵xisoddandziseven]

Thenequation(4.3.1)becomes

2712m+1 +81∙93k =z3

271(2712m +93k)=2(4t3 +95∙93k)

Tofactorout542because271isafactorof542,Sinceboth sideoftheaboveequationisdivisibleby542,letitbe542a then,

2712m +93k =2a

⇒ 93k =2a–2712m

Also,271a=4t3 +95∙93k =4t3 +95(2a–2712m)

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

=4t3 +190a-95∙2712m

81a=4t3 -95∙2712m

Usingsubcase4.2(A);ithasnosolution.

Hencetheequation271x +9y=z3 hasasolution(1,3,10).

5. CONCLUSIONS

We have examined the equation 512x + 1728y = z3 has no solution in Z+ and also obtained the solution of the nonlinear exponential Diophantine equation 271x + 9y = z3 , where(x,y,z)=(1,3,10)arenon-negativeintegers.

REFERENCES

[1] A. Baker, “A Concise Introduction to the Theory of Numbers”, Cambridge University Press, Cambridge, 1994.

[2] A.Baker,“AComprehensiveCourseinNumberTheory” , CambridgeUniversityPress,Cambridge,2012

[3] A.Suvarnamani,A.Singta,andS.Chotchaisthit,“Ontwo diophantineequations4x+7y=z2and4x+11y =z2”,Sci. andTech.RMUTTJour,Vol.1,No.1,2011,pp.25–28.

[4] A. Thue,“Über Annäherungswerte algebraischer” , Zahlen.J.reineangew.Math.,Vol.135,1909,pp.284–305.

[5] B.Sroysang,“MoreontheDiophantineEquations2x+3y = z2” , Int. Jour. of Pure and Appl. Math., Vol. 84, No. 2, 2013,pp.133-137

[6] D.Acu,“Onthediophantineequationoftypeax+by=cz,” GeneralMath.,Vol.13,No.1,2005,pp.67-72.

[7] D.M. Burton, “Elementary Number Theory”, Allyn and Bacon,Inc.,1980.

[8] G.Janaki,andA.G.Shankari,“Exponentialdiophantine equation(n2 -1)u +n2v =w2,n=2,3,4,5”,Ind.J.ofSci. andTech.,Vol.17,No.2,2024,pp.166-170.

[9] G.H. Hardy and E. M. Wright, “An Introduction to the TheoryofNumbers”,OxfordSci.Pub.,1979.

[10] H. Cohen, “Number Theory. Volume I: Tools and DiophantineEquations”,SpringerVerlag,Berlin,2007

[11] I. Niven, H.S. Zuckerman and H.L. Montgomery, “An introduction to the theory of numbers”, fifth edition. JohnWileyandSons,Inc,1991.

[12] L.J.Mordell,“Diophantineequations”,AcademicPress, NewYork,1969.

[13] M. Cipu, Y. Fujita, T. Miyazaki, “On the number of extensions of a Diophantine triple”, Int. J. Number Theory,Vol.14,2018, pp.899–917.

[14] N Burshtein, “All the solutions of the diophantine equationspx +(p+1)y +(p+2)z=M3whenpisprime and1≤x,y,z≤2”,Anls.ofPureandAppl.Math.,Vol.22, No.1,2021,pp.7-15.

[15] P.Mihailescu,“OnprimaryCyclotomicunitsandaproof ofCatalan'sconjecture”,J.ReineAngew.Math.,Vol.27, 2004,pp.167-195.

[16] A. Wiles,“ Modular elliptic curves and Fermat's Last Theorem”,Ann.ofMath.,Vol.141,No.3,1995,pp.443551.