"Evolution of Coding Techniques: From Morse code to Matrix-Based Cryptography for Secure Communicati by IRJET Journal

"Evolution of Coding Techniques: From Morse code to Matrix-Based Cryptography for Secure Communication"

- Saba

Abstract:Thispaperinvestigatesdifferentcodinganddecodingtechniques,fromclassicmethodssuchasMorsecodeto moresophisticatedmethodsusingmatrixmultiplicationandinversion.ThesimplicityandeffectivenessofMorsecodeare being evaluated asa reliable form of basiccommunication, especiallyin low-tech environments. Yet, its basic nature also constrainsitssafetyincontemporaryuses.Ontheotherhand,thearticleexplorestheapplicationofmatrixmultiplication for encrypting messages, converting information into a safe form through mathematical procedures. The decryption procedure,whichinvolvesaccuratelycalculatingtheinversematrix,introducesastronglevelofprotection,renderingitan effectivetoolincryptography.Byextensivelycomparingthesemethods,thepapershowcaseshowcodingtechniqueshave evolved from basic to advanced, mirroring the increasing need for secure communication in the digital age. The results highlightthesignificanceofchoosingsuitableencodinganddecodingtechniquesaccordingtothespecificrequirementsof thecommunication,beitforsimplicity,speed,orsecurity.

KEYWORDS:Coding,Decoding,Morsecode,Matrices

WhyIchosethistopic:

1. Introduction:

The common concept of coding and decoding to the forms of changing over data from one organize into another (coding) and after that changing over it back to its unique frame (translating). This concept is essential in different areas,suchascommunication,computing,informationhandling,andphonetics.

 Coding Definition: Coding is the method of transforming information or data into a distinctive arrange employing a particular strategy or calculation. This prepare is regularly done to plan the information for transmission,capacity,orhandling.

Examples:

1. ContentEncoding:ChangingovercharactersintoparallelinformationutilizingdesignslikeASCIIorUTF8.

2. Encryption: Changing over plain content into a ciphertext to ensure the data (e.g., utilizing calculations likeAESorRSA).

3. InformationCompression:Decreasingthemeasureofinformationforcapacityortransmission(e.g.,using ZIPorMP3groups).

 Decoding:Decodingisthemethodofchangingovercodedorencodedinformationbackintoitsuniqueorganize. Thispermitsthedatatobecaughtonorhandledasplanning.

Examples:

1. ContentInterpreting:Changingovertwofoldinformationbackintodiscernablecontent.

2. Unscrambling:Changingoverciphertextbackintotheinitialplaincontent.

3. InformationDecompression:Growingcompressedinformationbacktoitsoriginalmeasureandorganize.

 Applications

1. Communication: In advanced communication, information is regularly encoded to guarantee that it can be transmitted proficiently and safely. At the receiver's conclusion, the information is decoded to its unique frame.

2. Computing: In computers, various forms of encoding (e.g., machine code) are utilized to permit the processortoexecuteenlightening.Interpretingisvitalfordecipheringthoseenlightening.

3. Multi media: Sound and video records are encoded to diminish record measure for capacity or gushing. Playbackgadgetstranslatetherecordstorenderthemediaappropriately.

Significance:CodingandDecodingarebasicforguaranteeingthatinformationremainsintaglio,secure,and usable all through its travel from creation to end-user. Whether in computing, communication, or informationcapacity,theseformsplayavitalpartinpresentdayinnovation.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 11 Issue: 09 | Sep 2024 www.irjet.net

2. Computer Programming:

p-ISSN:2395-0072

Computer programming is the art of writing instructions for a computer. These instructions are called “programs.” As “smart”astheyseemtothelayperson,computerscan’tdoanythingontheirown.Everythingacomputerdoesistheresult ofprogramspeopledeveloptosolveproblems,meetneeds,orachievegoals.

Codingisacombinationofsequencesthatyougivetoyourcomputerforittoperformvarioustasks.Whatexcitesmeabout codingishowarandomsequenceofcharacterscancreatemultimillionworthofwebsitesandapplications.Itisawayto communicatewithyourmachines.Codingplaysahuge impactonourdaytodaylives.Trafficlights,Calculators,smartTV and even some cars use internal coding. All the top running businesses around the globe require an application that can run in as many platforms as possible, which is again only possible because of coding. Programming is more fun and astonishinglyusefulasitbuildyourcreativityandcreatesnewcareerdoorsforthosepassionateaboutit.Learningtocode hasbeenanempoweringexperienceforme.Asithelpedmecreatethingsthatoncelivedinmyimagination.

It wouldn’t be easy to imagine things we use today that do not rely either fully or partially on software in one form or another. Code powers the world we live in today. Coding has a widespread use in multiple areas such as automation of repetitivetasks,softwaredevelopment,complexproblemsolving,datamanagement,webdevelopment,andinnovationof new technologies such as artificial intelligence and machine learning. A SaaS application, smartphone apps, desktop productivity tools, an apple watch, and even microwave and washing machines rely on code written by software programmersinordertooperate.Evenwhenjobsofrepetitivenaturewouldbereplacedbymorestrategicjobsasaresult ofwidespreadautomation,coderswouldultimatelycontrolwhatistobeautomatedandcodethemachinesaccordingly. In thenextphaseofAIevolution,whenmachineslearnandbeginto“code”themselves,humanswillcreateandprogramme thenextgenerationofartificialintelligence.Hencecodingisgoingtostayforeverandremainasimportantasitistoday, if notmore.

Sincecomputersdonotcommunicatelikehumans,codingactsasatranslator.Codeconvertshumaninputintonumerical sequences that computers understand. Once computers receive these messages, they complete assigned tasks such as changingfontcolorsorcenteringanimage.

3. Coding Decoding in Different Sectors:

A. CODINGINMILITARYSECTOR

ComputersystemsareacriticalcomponentintheMilitary.Computerprogrammingprinciplesimplementedtoday influencehowtechnologies,suchas3Dprintingandartificialintelligence,willsupportfutureMilitaryoperations. Computer programmers and developers write, analyze, design, and develop programs that are critical to warfighting capabilities. From maintenance tracking programs to programs that organize and display intelligence data, they ensure that the Military has the software and programs needed to complete missions efficiently and effectively.

B. CODINGINAVIATION

Withoutsoftwareprogramming, modernaviation wouldnot exist.It wouldn’tbe possible tomanageflightplans, air traffic control, autopilot systems and complex maintenance routines. There are a lot of automated software systemsthataviationcurrentlyrelieson. Computers software are crucial to an airport's air traffic control services. While the communication between air traffic controllers and pilots occurs through radio, the system by which this communication is synthesized with radarandweatherdataisbasedoncomputers.

C. HEALTHCAREADVANCEMENTS

TheBiotechindustryisleaningmoreandmoreoncodeastimepasses.AI,bioinformatics,anddataanalysismade possible the fastest-in-history development of the COVID-19 vaccine. In addition, patient management systems make it easier for patients to find healthcare providers and maintain clinic operations. Healthcare information management also used to require shocking amounts of paperwork. Still, those days are no more, now that informationaboutmedicalvisitscanbeeasilyencodedandstoredinpatientdatabases.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 11 Issue: 09 | Sep 2024 www.irjet.net p-ISSN:2395-0072

D. GOVERNMENTSERVICES

Code-basedinterfaceshave made student loanapplications,vaccine registrations,filingtaxes, income assistance, and many other services easier. Facial recognition is being increasingly used when scanning passports in internationalairports,whichhashelpedmaketheverificationprocess90%faster.

E. CLIMATECHANGE

Coding continues to play a vital role in developing new technologies to address global challenges like climate change. Carbon emissions data is often stored and sorted manually, which can be taxing due to its magnitude. Automatingthiscanincreasedataaccuracy,improvingtheresolutionsthatcanbeobtained.

F. MEDIAANDCOMMUNICATION

Codingisthekeytothedevelopmentofsocialmediaplatforms.Codingisneededtobuildtheentireinfrastructure ofsocialmediaplatforms,creatingauserfriendlyinterface,contentmanagement,networking,dataanalyticsand personalisation,andfixingbugstoensuresmoothoperationandusersatisfaction.

G. CODINGINSPACECRAFT

Programmingallowsustodesignanddevelopcutting-edgesystemsthatpowerrockets,satellites,andspacecraft. We may imagine complex mathematical equations and cutting-edge technologies when we think of space exploration.However,attheheartofeveryspacemissionliesthecodethatcontrolsthespacecraft,itssensors,and its instruments. Various coding programs are used in spacecraft innovation to improve performance, efficiency, reliability and safety of the spacecraft. Coding also plays a crucial role in mission control, allowing operators to interactwithspacesystems,analyzedata,andmakeinformeddecisions.

4. Types of Coding and Decoding:

A. BINARYCODE

 Coding: Represents data using two symbols, typically 0 and 1. Binary code is the foundation of all modern computinganddigitalcommunication.

 Decoding:Convertsbinarydatabackintoitsoriginalform,suchastext,images,orexecutableinstructions.

 Example:Theletter"A"inbinaryis01000001.

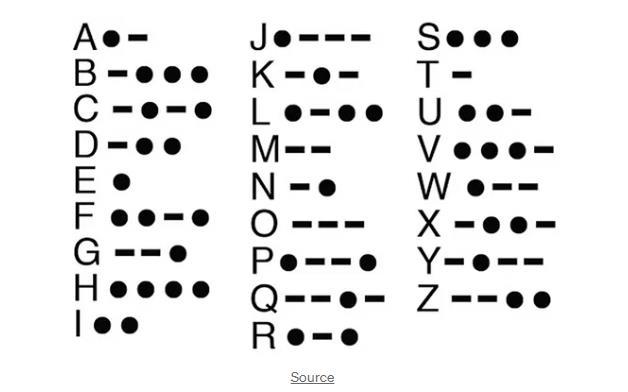
B. MORSECODE

 Coding: Uses a series of dots (short signals) and dashes (long signals) to represent letters, numbers, and punctuation.Originallydesignedfortelegraphcommunication

 Decoding:Convertsthesequenceofdotsanddashesbackintoreadabletext.

 Example:Theletter"A"inMorsecodeis.-

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 11 Issue: 09 | Sep 2024 www.irjet.net p-ISSN:2395-0072

C. ASCII(AmericanStandardCodeforInformationInterchange)

 Coding: Encodes text characters into a 7-bit or 8-bit binary number, allowing computers to store and communicatetextdata.

 Decoding:Convertsthebinarynumbersbackintotextcharacters.

 Example:Thecharacter"A"inASCIIis65indecimal,whichcorrespondsto01000001inbinary.

D. UNICODE

 Coding: Extends ASCII to supporta vastarray of charactersfrom various languages and symbol sets,using a varietyofencodingforms(UTF-8,UTF-16,etc.).

 Decoding:ConvertstheencodedUnicodedatabackintocharactersthatcanbedisplayedonthescreen.

 Example:Thecharacter"A"inUnicodecanbeU+0041.

E. HEXADECIMALCODE

 Coding:Representsbinarydatainamorehuman-readableformatusingbase-16numbering(0-9andA-F).

 Decoding:Convertshexadecimalnumbersbackintobinaryorotherdataforms.

 Example:Thebinary01000001is41inhexadecimal.

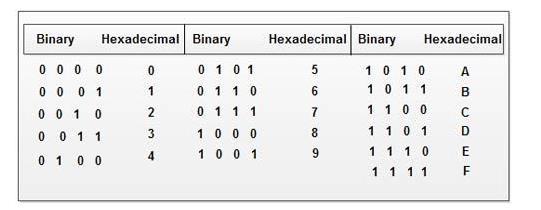
Fiq2:Binary,Hexadecimalcodes

F. BASE64ENCODING

 Coding: Converts binary data into a text string using 64 different ASCII characters (A-Z, a-z, 0-9, +, /). Often usedtoencodebinaryfileslikeimagesfortransmissionovertext-basedprotocols(e.g.,email).

 Decoding:ConvertstheBase64-encodedtextbackintobinarydata.

 Example:Thetext"Hello"inBase64isSGVsbG8=.

G. QRCODES

 Coding:Encodestext,URLs,orotherdataintoatwo-dimensionalmatrixofsquares,whichcanbescannedbya QRcodereader.

 Decoding:TheQRcodereaderinterpretsthepatternofsquarestoretrievetheoriginaldata.

 Example:AQRcodemightencodeaURLlikehttps://example.com

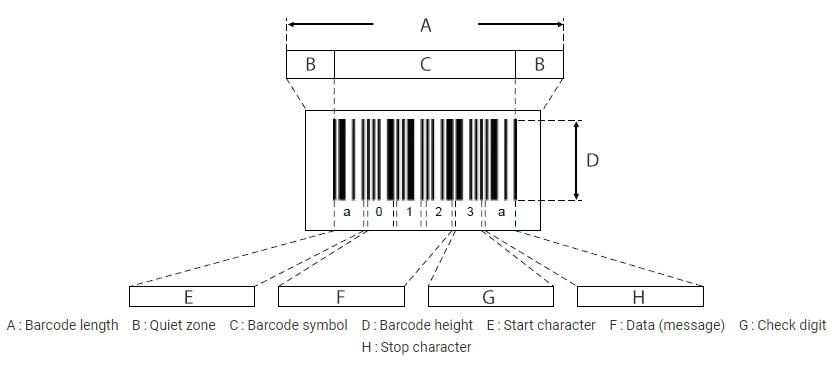
H. BARCODES

 Coding: Uses a series of vertical bars of varying widths and spaces to represent numbers or other data, typicallyforproductidentification.

 Decoding:Barcodescannersinterpretthepatternofbarstoretrievetheencodeddata.

 Example:AUPCbarcodeencodesaproductnumberlike012345678905.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 11 Issue: 09 | Sep 2024 www.irjet.net p-ISSN:2395-0072

I. HUFFMANCODING

 Coding:Acompressiontechniquethatusesvariable-lengthcodesfordifferentcharacters,withmorecommon charactersreceivingshortercodes.

 Decoding:TheencodeddataisexpandedbackintotheoriginalformusingtheHuffmantree.

 Example: In a text file, common letters like "e" might be encoded with a shorter bit sequence than less commonletterslike"z".

J. GRAYCODE

 Coding: A binary numeral system where two successive values differ in only one bit, often used in error correctionindigitalcommunication.

 Decoding:ConvertsGraycodebackintostandardbinaryordecimalform.

 Example:Thebinarynumber0011(3indecimal)is0010inGraycode.

K. REED-SOLOMONCODE

 Coding: Used in error correction to detect and correct errors in data transmission or storage, particularly in CDs,DVDs,andQRcodes.

 Decoding:TheReed-Solomonalgorithmcorrectserrorsandretrievestheoriginaldata.

 Example:Usedtocorrectuptotwoerroneoussymbolsinasequenceof255symbols.

L. CAESARCIPHER

 Coding: Asimple encryption technique where eachletterin thetextisshifted bya fixed number of placesin thealphabet.

 Decoding:Shiftsthelettersbackbythesamenumbertoretrievetheoriginaltext.

 Example:Thetext"HELLO"shiftedby3becomes"KHOOR".

M. RUN-LENGTHENCODING(RLE)

 Coding:Asimpleformofdatacompressionwheresequencesofthesamedatavaluearestoredasasingledata valueandcount.

 Decoding:Expandsthecompresseddatabackintoitsoriginalform.

 Example:ThestringAAAAAABBBBcouldbeencodedas6A4B.

Thesearejustsomeofthemanycodinganddecodingsystemsusedinvariousapplications,eachwithitsownpurposeand advantages.

Fiq3:Barcode

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 11 Issue: 09 | Sep 2024 www.irjet.net p-ISSN:2395-0072

5. Matrix in Coding Decoding:

Matrix coding and decoding typically refers to the process of encoding data into a matrix format and then decoding it backtoitsoriginalform.Thistechniqueiscommonlyusedinvariousfields,includingerrorcorrection,cryptography,and digitalcommunications.Herearesomeofthekeyconceptsrelatedtomatrixcodinganddecoding:

A.Error-CorrectingCodes(ECC)

Matrixcodingisoftenusedinerror-correctingcodes,whicharedesignedtodetectandcorrecterrorsindatatransmission orstorage.Somecommontypesofmatrix-basederror-correctingcodesinclude:

o Hamming Code:

 Coding:Dataisarrangedin amatrix,andparitybitsareaddedinspecificpositionstodetectandcorrect single-biterrors.

 Decoding:Thereceiveddataischeckedagainsttheparitybitstoidentifyandcorrectanyerrors.

 Example:A7-bitHammingcodecancorrectasingle-biterroranddetecttwo-biterrors.

o Reed-Solomon Code:

 Coding:Dataisencodedintoamatrix,andextrarowsorcolumnsareaddedwithredundantinformation tocorrectmultipleerrors.

 Decoding:Thematrixisanalyzedtoidentifyandcorrecterrorsusingtheredundantinformation.

 Example:UsedinQRcodes,CDs,andDVDstocorrectbursterrors.

o LDPC (Low-Density Parity-Check) Code:

 Coding: Data is represented in a sparse matrix with a low density of 1s, which helps in efficiently detectingandcorrectingerrors.

 Decoding:Iterativealgorithmsareusedtodecodethedatabycheckingparityconstraints.

 Example:UsedinmoderncommunicationsystemslikeWi-Fiandsatellitecommunications.

B.BlockCodes

In block coding, data is divided into fixed-size blocks, and each block is encoded separately. The encoding and decoding processesofteninvolvematrixoperations.

o Generator Matrix (G):

 Coding:Theoriginaldatavectorismultipliedbyageneratormatrix(G)toproduceacodeword.

 Decoding: The received codeword is multiplied by the inverse or transpose of the generator matrix (if applicable)toretrievetheoriginaldata.

 Example:Inasimple(7,4)blockcode,4bitsofdataareencodedintoa7-bitcodeword.

o Parity-Check Matrix (H):

 Decoding: The received codeword is multiplied by a parity-check matrix (H) to detect and possibly correcterrors.

 Example:Iftheresultofthemultiplicationiszero,thecodewordisvalid;otherwise,errorsarepresent.

C.Matrix-BasedCryptography

Matrix coding and decoding are also used in cryptographic algorithms, where matrices are employed to transform plaintextintociphertextandviceversa.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 11 Issue: 09 | Sep 2024 www.irjet.net p-ISSN:2395-0072

o HillCipher:

 Coding: The plaintext is divided into blocks, each block is treated as a vector, and then multiplied by an encryptionmatrixtoproducetheciphertext.

 Decoding:Theciphertextismultipliedbytheinverseoftheencryptionmatrixtoretrievetheplaintext.

 Example: If the encryption matrix is AAA and the plaintext vector is XXX, the ciphertext YYY is Y=AXY = AXY=AX

D.MatrixCodinginDigitalCommunications

Matrixcodingisusedindigitalcommunicationsystemstoimprovedatatransmissionreliability.

o MIMO (Multiple Input Multiple Output):

 Coding: Data is transmitted over multiple antennas using matrix-based algorithms to increase throughputandreliability.

 Decoding:Thereceiverusesmatrixdecodingtechniquestoseparatethesignalsandretrievethe original data.

 Example:MIMOtechnologyisusedin4Gand5Gwirelesscommunicationsystems.

E.Reed-MullerCodes

 Coding: Data is encoded using a matrix-based approach where the generator matrix is derived from Boolean functions.Thisallowsthecreationoflong,complexcodesthatcancorrectmultipleerrors.

 Decoding:Specificalgorithmsareusedtodecodethereceiveddataandcorrectanyerrorsbasedonthestructure ofthecode.

 Example: Reed-Muller codes are used in deep-space communication and other applications requiring high reliability.

Summary

Matrix coding and decoding involve representing data as matrices and using matrix operations to encode and decode information. These techniques are widely used in error correction, cryptography, and digital communication to ensure dataintegrity,security,andreliability.

6. Coding Decoding basic sentences using Matrices:

Let’scodeandDecodebasicsentencesusingmatricesinmathematics.

GivingnumberstoalltheAlphabets.

Takingabasicsentencetocode:

1. “MYNAMEISSANA”

Givingnumberstoeachalphabetofsentence:

IfIwriteinnumbers,anyonecandecodeitbyusingnumbersgiventothealphabets.

Soforcodelanguage,Ihavetousematrixmultiplicationmethod.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 11 Issue: 09 | Sep 2024 www.irjet.net p-ISSN:2395-0072

Let’sconsideranymultiplicationmatrixas,A= [1 2 3 4]

Thismatrixwillbeknowntoreceiveronlysothathecandecodeit.

So,let’scodeMYoutofthewholesentence: [1 2 3 4]*[1325]=[13+50 39+100]=[63139](forMY,whereM=13andY=25)

Let’scodeforotheralphabetsto, �� [141], �� [135], �� [919],, �� [191],, �� [141]

ForNAME,

[��]= [1 2 3 4]*[141]=[14+242+4]=[1646]

[��]= [1 2 3 4]*[135]=[13+10 39+20]=[2359]

ForIS, [��]= [1 2 3 4]*[919]=[9+3827+76]=[47103]

ForSANA,

[��]= [1 2 3 4]*[191]=[14+257+4]=[2161]

[��]= [1 2 3 4]*[141]=[14+242+4]=[1646]

CodedMessage,

Fordecodingthecurrentmessage,wewilluseinverseofmatrix, ForfindinginverseofA,weneedadjA, For2x2matrixwecaninterchangediagonalelementsandchangingsignsofdiagonalelementstogetadjA, SoadjA= [ 4 2 3 1 ]

DeterminantofA=1*4–2*3=-2

So.InverseofA,A-1 =[ 4 2 3 1 ]/-2=[ 2 1 3/2 1/2]

Togetoriginalmessage,wehavetomultiplyA-1andcodedmessage,

ForMY, [��]= [ 2 1 3/2 1/2]*[63139]=[ 126+139 (189 139)/2]= [1325]

ForNAME,

[��]= [ 2 1 3/2 1/2]*[1646]=[ 32+46 (48 46)/2]=*[141]

[��]= [ 2 1 3/2 1/2]*[2359]=[ 46+59 (69 59)/2]=[135]

ForIS,

[��]= [ 2 1 3/2 1/2]*[47103]=[ 94+103 (141 103)/2]=[919]

ForSANA,

[��]= [ 2 1 3/2 1/2]*[2161]=[ 42+61 (63 61)/2]=[191]

[��]= [ 2 1 3/2 1/2]*[1646]=[ 32+46 (48 46)/2]=[141]

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 11 Issue: 09 | Sep 2024 www.irjet.net

Decodemessage,

2. “BELIEVEINYOURSELF”

Let’sconsideraquote“Believeinyourself”

Wewillbreakthewordsinto3alphabetsgroups, LikeBEL=[2,5,12] Forspacewewillconsideritas0.

Let’sconsidermultiplicationmatrixas,A

5 7 6 8]∗ [9 5 22]= [85121209]

2 3

6 8]∗ [5 0 0]= [5 5 35] ForIN,

4 5

2 3 1 4 5 7 6 8]∗ [914 0 ]= [ 37 4721] ForYOURSELF,

2 3

4 5 7 6 8]∗ [25 15 21]= [55 35 85]

�� ]=[ 1 2 3 1 4 5 7 6 8]∗ [18 195]= [71 83 52] [��]=[ 1 2 3 1 4 5 7 6 8]∗ [12 6 202]= [24 12 48]

Codedmessage,

Decoding, FordecodingweneedtofindA-1 , ForcalculatingA-1byadjointmethod,weneedtofindcofactors,

A11=32+30=62

A12 =-(8-35)=43

A13 =6-28=-22

A21 =-(16+18)=-34

A22 =8-21=-13

A23 =-(6-26)=20

A31 =10-12=-2

A32 =-(5+3)=-8

2395-0072

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 11 Issue: 09 | Sep 2024 www.irjet.net p-ISSN:2395-0072

A33 =4+2=6 Co-factormatrix=[ 62 43 22 34 13 22 2 8 6 ] |A|=1*62+2*43+38*(-22)=82 AdjA=(cofactor)transpose =[

2 43 13 8 22 22 6 ] A-1=adjA/|A|=1/82*[ 62 24 2 43 13 8 22 22 6 ] A-1 =[31/41 17/41 1/41 43/82 12/82 4/41 11/41 10/41 3/41 ] ForBELIEVE,

=[31/41 17/41 1/41 43/82 12/82 4/41 11/41 10/41 3/41 ]∗ [48 78 80]= [82/41 410/82 492/41]=[2 5 12]

��]=[31/41 17/41 1/41 43/82 12/82 4/41 11/41 10/41 3/41 ]∗ [85121209]= [9 5 22] [��]=[31/41 17/41 1/41 43/82 12/82 4/41 11/41 10/41 3/41 ]∗ [ 5 5 35]= [5 0 0]

ForIN, [��]=[31/41 17/41 1/41 43/82 12/82 4/41 11/41 10/41 3/41 ]∗ [ 37 4721]= [9140] ForYOURSELF,

��]=[31/41 17/41 1/41

43/82 12/82 4/41 11/41 10/41 3/41 ]∗ [71 83 52]= [18 195]

43/82 12/82 4/41 11/41 10/41 3/41 ]∗ [55 47 85]= [25 15 21] [�� ]=[31/41 17/41 1/41

=[31/41 17/41 1/41 43/82 12/82 4/41 11/41 10/41 3/41 ]∗ [24 12 48]= [12 6 0]

7. Conclusion:

Ultimately, studying different coding and decoding methods, such as Morse code and matrix operations, offers a holistic perspectiveonsecureinformationtransmissionandretrieval.Dependingonthesituationandthedesiredlevelofsecurity, eachapproachhasitsownsetofbenefitsanddifficulties.

Morse code, a prime example, depends on a basic but efficient method of using dots and dashes for encoding data. Its longevityisattributedtoitssimplicityanduser-friendliness,especiallyinscenarioswithlimitedtechnologyorwhenquick communicationisessential.Nevertheless,itsstraightforwardnessalsorendersitvulnerabletocurrentdecodingmethods, emphasizingthenecessityformoresophisticatedapproachesinspecificsituations.

On the flip side, employing matrix multiplication and matrix inverses brings a more advanced strategy to coding and decoding.Thisapproachencodesmessagesinamannerthatishardtodecodewithoutunderstandingthespecificmatrix by representing messages as vectors and utilizing matrices for transformation. Decoding includes calculating the matrix inverse, providing an extra layer of security by only revealing the original message with the correct inverse matrix.

| Page

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 11 Issue: 09 | Sep 2024 www.irjet.net p-ISSN:2395-0072

Matrix-basedmethodsareespeciallyimportantincryptography,whereensuringthesecurityoftransmittedinformationis crucial.ComparingthesemethodstoMorsecodeshowshowcodinganddecodingstrategieshaveevolved,highlightingthe demandforincreasinglysecureandintricatesystemsinthedigitalera.

Overall, this discussion underscores the importance of choosing the appropriate method based on the specific requirementsofthecommunicationprocess,whetheritbethesimplicityandreliabilityofMorsecodeorthemathematical rigor of matrix operations. The continued study and development of these methods are crucial for advancing secure communicationinanincreasinglyinterconnectedworld.

8. Biographies :

Saba:

- Highschoolgraduate2024,‘BlueStarSeniorSecondaryPublicSchool,Hamirpur’

- Disciplinecaptainintheschoolcabinet.

- PresidentofCulturalActivitiesClub(2023-24)

- Founderofcodingclubatmyschool,asaninitiativetohelpyoungstudentsbuildprogrammingskills.

- OrganisedSymposium-2024forpharmacyandpharmaceutics.

- Organisedaspringcleaningdriveinmycommunity.(2024)

- IBMFullStackDeveloperProfessionalCertification(2023-24)

- Volunteeratregionalhospitalforcovidvaccination(2021)

- Firstinenvironmentdaypostermakingcompetition(2022)

- Secondininterschoollandscapepaintingcompetition(2023)

- 1stinclassicalmusiccompetition(synthesizer)(2022)

- ParticipatedinregionalandstatelevelTableTennistournaments(2021-24)

- ParticipatedinnationalandstatelevelKarate-KumitebyKIO(KarateIndiaOrganisation)(2021-24)

- FirstinregionalMTBtournament(2023)

- IntermediateCourseinsnowskiing(2020)

- Advancecourseinsnowskiing(2021)

- Wintericeskatingcourse(2021-24)

- Advancemountaineeringcourse(2022)

- Firstinschoollevelmarch-pastcompetition(2021)

- Organisedandparticipatedinblooddonationcamp(2024)anddonatedbloodtwiceinthesameyear.

Undertheguidanceof:

Dr. Mamta Jain

- M.Sc(Mathematics)(Doublegoldmedalist)

- M.Phil(ComputerApplications)withhonorsFromUniversityofRoorkee(nowIITRoorkee)

- PhD(Mathematics)-Variouspaperspublishedininternationaljournals

- FormerLeadAuditorISO9001,ISO-22000SchoolAccreditationExaminerbyQCI

- 26yearsofteachingexperience

- VariousResearchPaperPublished

Er. Raunaq Jain

- B.EMechanicalEngineeringFromThaparInstituteofEngineeringandTechnology

- DistrictPhysicsTopper

- ContentWriterandgraphicdesigner

- MechanicalMentorfromsession2019-2020

- TechnicalDataAnalystatDeloitte