The Minimum Height of a Strike Point of a Follow Shot with a Billiard Ball Yong Kyung Jo

The Minimum Height of a Strike Point for a Follow Shot with a Billiard Ball

By: Yong Kyung Jo | Art By: Lilian Kong

Introduction

Billiards is an easily accessible sport that is favored by many people. I myself enjoy billiards, and regularly go to the billiard room at least twice a week. In billiards, one hits a ball with a long stick known as a cue. Skills for playing billiards revolve around hitting the exact location on the ball (called the strike point), hitting with precise thickness, and hitting with an appropriate amount of force. All of these factors act together to lead to a successful billiard shot, and among them, this paper will focus on how to aim and hit at the exact strike point. This focus can be justified by the fact that all techniques in billiards require preciseness in aiming and striking. There are a variety of techniques in billiards (examples would be follow shots, draw shots, and masse etc.), and while all of these techniques seem almost physically impossible, the fundamental principle is that they all require one to hit at the exact strike point. In other words, the rotation that a strike gives to the ball changes its direction and course, which makes it the most important factor when performing various skills in billiards.

Among all of these, let’s first take a look at follow shots. In order to perform a follow shot in a desired direction, hence, in order to have a ball proceed in a specific direction even after colliding with another ball, what kind of conditions should be met? The answer to this question would be that the billiard ball requires an advancement of rotations, meaning that the ball needs to roll across the billiard table without sliding. This is what allows for the ball to proceed in direction the player intends to send it. By intuition, it’s possible to see that a ball will roll by hitting at a point higher than its midpoint. However, the occurrence of a slide may be the cause of the ball being unable to head in the desired direction, and thus results in a missed shot. Consequently, this research aims to find the minimum height of a strike point that will allow the ball to roll without sliding.

Body

To find the minimum height of a strike point that will allow the ball to roll without sliding, it is necessary to have some physical knowledge on an object in rotational motion. Just like an object with translational motion has velocity, acceleration, and mass, an object with rotational motion has angular velocity, angular acceleration, and moment of inertia.

Angular velocity is a physical quantity that measures how fast an object rotates relative to a certain axis, and is denoted by the symbol ω. While acceleration is defined as the rate of change of velocity with respect to time, angular acceleration is the rate of change of angular velocity with respect to time, and is referred to as α. Hence,

α = dω/dt

The last physical quantity, the moment of inertia, is defined as the torque needed for change in angular acceleration, and is represented by the symbol I. The moment of inertia is determined by the body’s mass distribution and the axis of rotation, it is given by the following equation

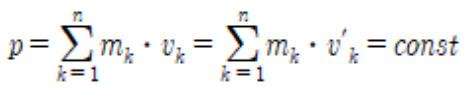
(Here, r denotes the distance between the material point and the axis of rotation.)

So far, basic terminology has been defined. Now, rotating objects will be examined, and physical laws will be derived to explain their movements.

First of all, the following physical laws explain the translational motion of an object. 1. Newton’s Laws of Motion: An object with a constant speed (or at rest) will maintain its state unless acted upon by a force (Law of Inertia). The net force that acts upon an object is equivalent to the product of mass and acceleration of the object. Mathematically, this is expressed as ΣF=Ma (Law of Acceleration). Also, all forces that are exerted between two objects exist in equal magnitude and opposite direction (Law of Action and Reaction). 2. Momentum Conservation Principle: The momentum of an object — the product of mass and velocity — remains unchanged unless an external force is applied to it. Hence, even if n different objects collide against each other, the equation

3. holds. ( is the velocity before collision, while is the velocity after collision) Impulse-Momentum Theorem: The change in momentum of an object is equal to the impulse that is

applied to it. Mathematically, this can be expressed as ∆p = m∆v = f∆t. (f is the force of impulse, and is the external force that acts upon an object.) 4. Law of Conservation of Energy: A system always has the same amount of total energy. Hence, its overall energy remains unchanged during conversion or transfer. Note that energy created by translational motion involves potential energy — energy by virtue of an object’s position (Ep = mgh), and kinetic energy — energy by velocity (Ek = 1/2mv2).

Now, let’s examine the physical laws involved in rotational motion by examining how they correspond to the laws of translational motion. 1. An object in rotational motion has the tendency to maintain its initial direction of rotation, and the overall torque that acts upon the object is equivalent to the product of moment of inertia and angular acceleration. Mathematically, this can be expressed as ∆τ = Iα. 2. Law of Conservation of Angular Momentum: The angular momentum of a rotating object — the product of moment of inertia and angular velocity — remains unchanged unless an external torque is applied to it. Hence, even if different objects rotate while colliding against each other, the equation

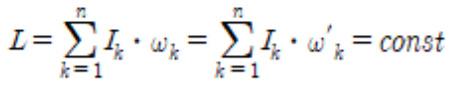
3.

4. (ωk is the angular velocity before collision, while ω’k is the angular velocity after collision.) Angular Momentum and Impulse: Let’s take a look at the relationship between change in angular momentum and the impulse that an object receives. First of all, angular momentum is the product of moment of inertia and acceleration, but can also be expressed as the vector product (cross product) between the momentum of translational movement and angular velocity. Hence, L = rp. If we assume, for convenience, that rotational motion is circular motion, then the cross product of the momentum and the distance vector between the axis of rotation and the material point, always has a constant direction. The change in angular momentum can hence be expressed as ∆L = r∆p = rm∆v = rf∆t, or ∆L = I∆ω. Therefore, ∆L = I∆ω = rf∆t (f is the external force that acts upon an object in motion). Law of Conservation of Energy: The fundamental concept that a system always has the same amount of total energy holds for rotational motion as it does for translational motion. Hence, its overall amount of energy remains unchanged during conversion or transfer. The difference between the two is that while translational motion involved potential energy and kinetic energy, rotational motion involves an additional type of energy — rotational kinetic energy ( Er = 1/2ω^2).

Of course, there are situations in which an object can be in both rotational motion and translational motion. In such cases, the velocity of the translational motion of a rotating object satisfies the equation v = rω, as well as the physical laws (which have been stated above) for both rotational and translational motion. In simultaneous rotation and translation, it is necessary to first separately consider the forces an object receives in each type of motion. This will allow identification of the force that causes rotation, and when rotation and translation are considered together, will then ultimately lead to finding the final velocity and acceleration.

The movement of a billiard ball, which is the subject of this research, can also be thought of as a combination of rotational and translational movement. Torque, moment of inertia, the relationship between translational and rotational motion, and the concept of a ‘strike’ are all involved in the movement of a billiard ball. Consequently, the main goal of this research would be to use the relationship between the change in momentum and impulse to identify the minimum height of the strike point that is necessary for the billiard ball to roll without sliding. Note that this experiment is based on the assumption that there is no air resistance.

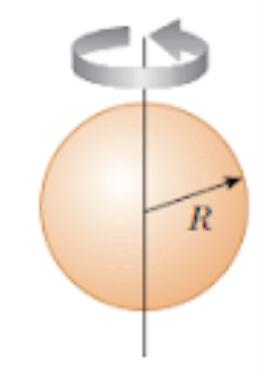
Now, let’s start the process of finding the minimum height of a strike point that is required for the billiard ball to roll without sliding. In order to do so, it is necessary to find the moment of inertia of a billiard ball. A billiard ball can be considered a solid sphere with fixed density, and hence the next step would be to find the moment of inertia of a full sphere with radius R and mass M.

It’s important to be aware of the fact that within the equation for moment of inertia the variable r does not represent the radius, but the distance to the axis of rotation. Hence, the axis of rotation can become the z-axis, and the equation for a sphere can be expressed as Consequently, a solid sphere can be considered a infinitesimal set of thin solid cylinders that are perpendicular to the z-axis, as depicted in the figure below. Image 3: A sphere as an infinitesimal set of thin solid spheres.

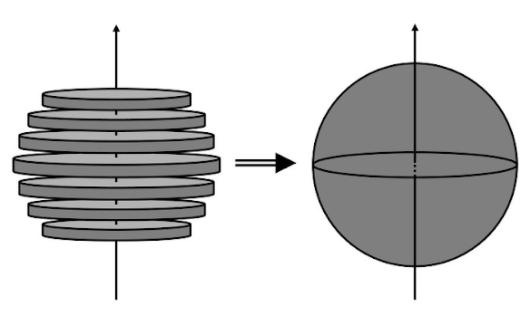
Now, since the moment of inertia of this sphere can be considered the sum of the same physical quantity for sufficiently thin cylinders, let’s first find the moment of inertia of a cylinder.

Suppose a cylinder has a radius of R’ and a mass of M’. Its surface area would then be π(R’)2, so A= πR2, and differentiating both sides of this equation with respect to r results in dA/dr = 2 πr. Thus,

dA = 2πrdr

Also, since this process of derivation was based on the supposition that the heights of the all of the cylinders are infinitesimally thin and uniform,

Image 2: A full sphere with radius R

x2 + y2 + z2 = R2 . Hence, T he moment of inertia of a cylinder would thus be

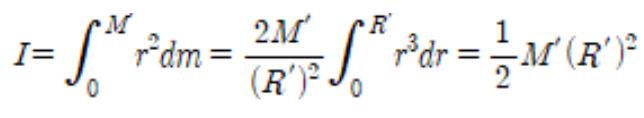
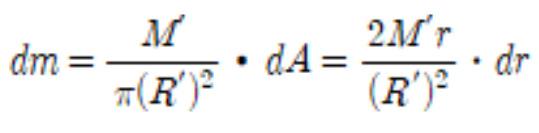
Now, to obtain the moment of inertia of the sphere, the same quantities for the cylinders should be stacked with respect to the z-axis.

Hence,

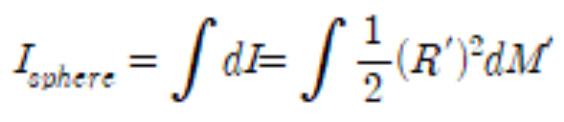
and the changes in the mass of the thin cylinders can be considered as follows.

Also, since the Pythagorean theorem gives (R’)2 = R2 - z2 , the equation on the moment of inertia of the sphere can be organized in terms of . Calculations lead to

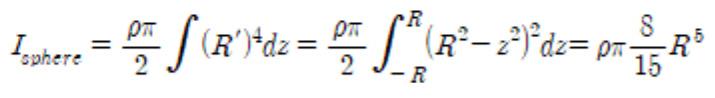
Substituting ρ = M/V = (3m)/(4πR3) into this equation yields

Isphere = 2/5 (MR2)

Now, if a billiard ball has a mass of m, radius of r, and a strike is made at a height of h, then it is clear that h>r, since the strike must be above the center of the ball. Also, the moment of inertia of this billiard ball would be I = 2/5 (mr2). Now, suppose a force of f is exerted on the strike point for a short period of time (∆t seconds), and the ball thus started to roll across the table without sliding. The force f is assumed to be horizontal, i.e. parallel to the billiard table. The motions of the ball can then be considered based on its states in the three following moments. 1. State 1: The moment in which a force of f is exerted on a billiard ball initially at rest for ∆t seconds. 2. State 2: The moment in which a still ball starts moving at a velocity of vo due to the force f, and hence starts to receive a kinetic friction force. The ball starts moving precisely at this movement, so it is possible to assume that it only has translational movement and no rotational movement. 3. State 3: The moment in which translational movement and rotational movement occur together. Hence, the ball starts moving forward with a velocity of v1, and advances while rotating with an angular velocity of ω1 . The ball does not slide, so the relationship v1 = r ω 1 holds.

The movement of a billiard ball was divided into three stages for convenience, and it is important to note that these stages do not occur in order, but occur simultaneously. Thus, the physical quantities within these stages should ultimately be equal. Now, let’s compare the physical quantities within each of the stages, based on the physical laws that were organized above. This will lead to h, the height of a strike point.

I. Comparison between State 1 and 3

These states each refer to the initial state created due to a strike, and the final state that results from the movement. Thus, we are able to construct an equation in terms of h — the desired variable. Since a force of f was exerted on a stationary ball from a height of h, it can be stated that an external force exists from the perspective of an object going through translational movement. This allows us to think of the relationship between momentum and impulse. According to the physical laws that we’ve organized above, the equation m∆v = f∆t holds, and hence the following equation can be obtained.

If motion is observed from the perspective of rotational motion, it can be said that an external force exists. Hence, it would be necessary to examine the relationship between angular momentum and impulse. As stated within the physical laws above, ∆L = I∆ω = rf∆t, in which r is not the radius, but the distance between the strike point (the point on which a force was exerted) and the center of rotation. Since the center of rotation in such movement is the center of the billiard ball, h-r would be the distance between the strike point and the rotation center. It is thus possible to derive the following equation.

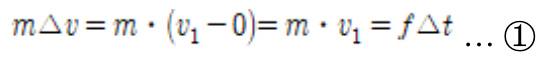
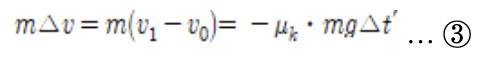
II. Comparison between State 2 and 3

The moment in which state 2 occurs can be considered as follows. A billiard ball that starts moving at a velocity of due to an external force will be affected by frictional force, and thus have its velocity decreased in state 3, to , a velocity of translational motion. Also, the momentum acts upon the center of mass of the ball, i.e. the geometric center of the ball, but frictional force acts upon the point at which the ball and the billiard table make contact. It can thus be said that the rotational motion of the ball is created due to friction.

As done in the previous comparison, let’s first think from the perspective of translational motion. In between state 2 and 3 acts an external force called kinetic friction force, so the law of conservation of momentum does not hold. We can thus examine the relationship between momentum and impulse, as done above.

First of all, the magnitude of the kinetic friction — the external force that acts upon the billiard ball — can be expressed as the product of coefficient of kinetic friction μk and the normal force N. Since the billiard ball does not move in a perpendicular direction, it is possible to discover that the normal force is equal to the gravitational force that acts upon the ball. Hence, N = mg, and the friction thus is F = μkmg. Now, since f = F within the equation m∆v = f∆t, ∆t would be different from the quantity ∆t above, and hence is ∆t’. Both stages are single moments, but are different in that ∆t refers to the time during which the force was applied, while ∆t’ refers to the time that elapsed while moving on from transitional motion to rotational motion. Therefore, the following equation holds.

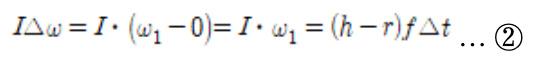
The negative sign in this equation signifies that the frictional force acts upon the ball in a direction opposite from the movement of the ball.

Next, we should consider that in the perspective of rotational

motion, an external force called friction exists. Hence, it is necessary to check the relationship between angular momentum and impulse. In state 2, the ball has no rotational motion, and thus ω o = 0. Also, since the distance between the ball’s center of mass and the point which friction acts upon is r, substitution into ∆L = I∆ω = rf∆t yields the following.

The rotation created by friction is a rotational advancement in which the ball moves forward, so the signs in the equation above are all equal.

Now, let’s form a system of equations with 1~2, and find h, the height of the strike point.

First, let’s substitute I = (2/5)mr2, the moment of inertia of the sphere, into the equation

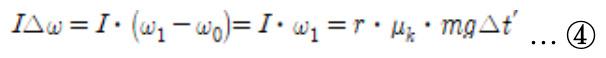
With this equation, ω 1 can be expressed in an organized form as shown below.

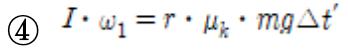
With v 1 = rω 1, one obtains

Substituting the value of v1 into 3 yields

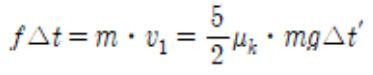
Also, substituting the final velocity (v1) (which we’ve found through the equation above) into equation 1 results in mv 1 = f∆t. Thus,

Lastly, let’s look at the equation

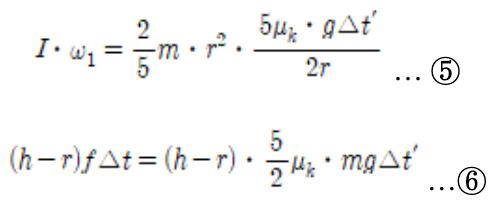
Substituting the three equations f∆t = (5/2)μkmg∆t’, ω 1 = [5μkg∆t’]/2r, and I = (2/5)mr2 into 2 results in the two equations at right.

5=6, so dividing both sides of this equation by μkmg∆t’ leads to (5/2)(h-r) = r. Consequently, the minimum height of the strike point — that will allow the ball to roll without sliding — is obtained by solving for h.

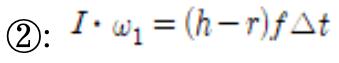
h = (7/5)r

Conclusion

Previously, we’ve used a system of equations with the physical laws of translational motion and rotational motion in order to find the minimum height required for a billiard ball to roll without sliding. Consequently, it was possible to obtain the conclusion that a player should aim and hit at a point with a height of at least h = (7/5)r.

Now, let’s take a look at what would happen at a strike point of h > (7/5)r. Even if the billiard ball is hit with the same force of f for the same period of time, ∆t seconds, the distance between the ball’s center of rotation and the strike point would have grown, and hence the magnitude of the torque would have increased. Consequently, ω1, the angular velocity of the billiard ball, would also increase, and v1, the velocity at which the ball advances forward, would increase in accordance.

However, if the billiard table and billiard ball are made up of the same material as in the previous situation, then the magnitude of frictional force would be equal. If so, even in the current situation where the ball’s angular velocity and rate of advancement have both increased, could we still state that the ball is moving forward without sliding?

To state the conclusion first, the billiard ball would still roll without sliding. To see why, let’s refer to state 2 among the 3 states that the ball can be divided into after a strike is made.

A ball in state 2 is at an instant where rotational motion is about to occur with translational motion for the first time ever since force was initially exerted on it. However, since v1, the final velocity, has increased, the initial velocity of translational motion (vo) has also increased, and ∆t’, which is the time for which state 2 lasts, has increased in accordance. Hence, we can identify that the duration of the moment has slightly increased, and after it ends, the ball will roll. Therefore, if one strikes a point with a height greater than or equal to (7/5)r, then the billiard ball will roll without sliding.

References [1] Beer F P. Mechanics for Engineers: Dynamics. New York, NY: McGraw-Hill; 2017. [2] Johnston R Jr. Mechanics of Materials. London: Pearson; 2015. [3] Walker J, Principles of Physics. Hoboken, NJ: Wiley; 2014. [4] Serway Raymond A. Physics. Austine, TX: Holt McDougal; 201. [5] Stamps Robert. Solid State Physics. London: Elsevier; 2017 [6] Serway Raymond A. Physics for Scientist and Engineers. Belmont, CA: Thomson-Brooks/Cole; 2004 [7] Sibley Thomas Q. The Foundations of Mathematics. Hoboken, NJ: Wiley; 2008