29 minute read
A Comparison and Analysis of Different Tuning Systems and Temperaments and Their Use in the Baroque Period
Evan Martschenko
Over the centuries, the world of western music has used many different tuning systems, mathematical organizations of notes within an octave. Each system has the capability to drastically change the music that they are being used in through expressive differences in color and feeling that varied scales can bring about. Thus, tuning systems have become topics of debate for musicologists and performers for centuries and were under constant reassessment and modification until the early 20th century (Duffin, 2007, p. 112). An edited tuning system is known as a temperament — it is important to note that the terms “tuning system”10 and “temperament”11 are not interchangeable, though often they are incorrectly used as synonyms (Barbour, 2004, p. 5). These everinteresting topics dominate the modern performance of older music today, certainly not excluding Baroque music.
Advertisement
This paper will serve as an analysis and introduction to the commonly used tuning systems and temperaments, and their pertinence to Baroque music. This paper will be written with the expectation that the reader understands basic musical terminology but is entirely new to tuning. Early on, a few crucial topics and terms will be explained that the
10 Tuning System — A mathematical organization of notes within an octave. reader must understand before reading the remainder of the paper. Every term will be defined when it is first used in the paper, as well as in a glossary on page 18 for ease of reference. For the sake of relevance to the reader, the tuning systems will all be compared to equal temperament, as it is most familiar to the modern ear. Therefore, equal temperament will quickly be explained first before the other tunings and revisited later on in more depth. A brief timeline of tunings and their use will be provided for each tuning alongside the scientific and sonic aspect of each system. A chart with important intervals will accompany the tuning systems and temperaments examined in the paper, and an appendix on page 18 will have a large amalgamation of each smaller chart. Additionally, each system and temperament will be explained in its relevance to period instruments, particularly keyboard instruments, and its effect on Baroque history and the modern practice of Baroque music.
On the Issue of Tuning
While the true origin of the musical scale and musical intervals is unknown, it is clearly linked to what is known as the harmonic series. This is a natural phenomenon in which a wavelength halves itself over and over
11 Temperament — An edit to a pre-existing tuning system, slightly adjusting an established system.
to form higher frequencies, often called overtones or partials based on the initial fundamental pitch. Each partial diminishes by half of the previous partial; for example, if the original wavelength were 100 units, the first partial would be 50 units, the second partial 25, 12.5, 6.25, and so on, decreasing in size forever. These sizes are usually expressed in ratios instead of specific lengths or complex fractions. The pitches produced by the first five partials follow the ratios and values shown below in Figure 1.
Fig. 1: Partial ratios and cent values. 12
Interval (above Fundamental) Ratio Cent Value13
Perfect Octave 2:1 1200
Perfect Fifth 3:2 702
Perfect Fourth 4:3 498
Major Third 5:4 386
Minor Third 6:5 316
These naturally occurring intervals came to be known as “just intervals,” sometimes called “pure.” Just intervals are generally considered to be the most desirable and pleasing to the ear due to their occurrence in nature and started out being the standard for what an “in-tune” interval would sound as. The issue arrives when one attempts to use all of these intervals across multiple octaves. David Dolata uses an effective analogy in comparing pitches within an octave to inches in a foot (2016, p. 71). Imagine having to fit 13 standard inches into one foot. Without changing the definition of an inch, it is
12 Thomas Donahue, A Guide to Musical Temperament (Lanham, Maryland. Scarecrow Press, Inc., 2005) p. 5. impossible to fit all 13. The inches could all be shortened equally, or some shortened more than others, or most of the inches can be left as true inches while some are reduced greatly. This is very applicable to the concept of fitting twelve pitches into a scale. As will be explained below, the octave cannot consist of only justly tuned pitches and, like the inches, some pitches must be compromised. A superparticular ratio is any tempered, or compromised, ratio that lies between any two adjacent partials in the harmonic series, and therefore is a term used often in temperaments (Donahue, 2005, p. 6). For simplicity, the modern term of a cent can be used, which was coined by Alexander Ellis in the early 20th century. His system divides an octave into 1200 cents, and therefore leaves 100 in a semitone (Rasch, 2002, p. 210). Starting on one pitch and moving through the entire circle of fifths using pure fifths should theoretically bring back the same beginning pitch seven octaves higher after twelve perfect fifths. In essence, twelve perfect fifths should equal seven octaves, or 8400 cents. However, when multiplying 12 perfect fifths by the pure value of 702 cents each, we end up with 8424 cents. This difference of 24 cents is referred to as a “ditonic comma,” sometimes a “Pythagorean comma,” a correlation that will be explored when talking about Pythagoras (Donahue, 2005, p. 7).
Additionally, a major third can be found by taking four perfect fifths and then moving down two octaves: for example, C-G-D-A-E. When using
13 Explained just below, and also defined in the glossary.
just perfect fifths, we can multiply 4 by 702 cents to get 2808 cents, subtracted by two octaves (2400 cents) to end up with a major third of 408 cents. This is 22 cents higher than a just major third (386 cents), a difference called a “syntonic comma” (Donahue, 2005, p. 8). The 22 cents difference has the superparticular ratio of 80:81 and is roughly equal to one-fifth of a semitone, enough of a difference to make even someone completely untrained in music say a note is “out of tune.”
These discrepancies make it clear that the vastly common intervals of fifths and major thirds cause issues immediately when attempting to tune with their just tunings. Just like it is impossible to fit thirteen inches into a foot, it is mathematically impossible to tune all seven diatonic pitches to their just value without compromising the octave, something that cannot be done for obvious reasons (Blackwood, 1985, p. 67). Across the world, every culture ubiquitously recognizes that two pitches an octave apart are the same pitch class, regardless of the tuning system used within the octave. This could be due to not only the octave being the first partial in the harmonic series, but also men, women, and children singing folk tunes in unison separated by octaves. So, while the octave is inflexible, the smaller intervals can be altered, and thus starts the history of tuning systems. Before continuing to talk about varied tuning systems, it is important to have a frame of reference with which to understand the differences in each of these systems and temperaments. The entire western world has been using equal
14 Donahue, A Guide to Musical Temperament, p. 5. temperament for over a hundred years and is what most people now refer to as “in tune,” no longer the just intervals from the harmonic series. Modern ears are accustomed to equally tempered intervals, and thus much of this paper will be a comparison to equal temperament. The temperament as we know it today did not truly come into place until the early 20th century, when William Braid used new mathematical principles such as logarithms to perfect the equal temperament that had been attempted by many tuners before him (Rasch, 2002, p.210). In 1917, John Ellis took Braid’s work and gave it the unit of a cent, which was explained above.
Fig. 2: Naturally just intervals.
Intervals Just
Cent Value14 Equally Tempered
Cent Value
Minor Third 316 300
Major Third 386 400
Perfect Fifth 702 700
In short, equal temperament features 12 semitones of exact same value. This results in narrow minor thirds, wide major thirds, and slightly flat perfect fifths. The advantage of equal temperament is that everything is evenly out of tune as compared to just intervals; nothing is great, but nothing is worse than anything else. This is beneficial to highly chromatic music such as jazz or post-tonal music and is a necessity for both, though it does hinder many stylistic and expressive possibilities that other
tuning systems excel in (Helmholtz, 1877, p. 327).
Pythagorean Tuning
It is no mystery that the Pythagorean tuning system comes from the famous Greek mathematician. True to the rest of his work, Pythagoras developed this tuning system by means of mathematics. Two hundred years later, Aristoxenus critiqued Pythagoras for his blending of mathematics and music, claiming that musicians should use their ears and leave math to itself (Barbour, 2004, p. 2). As the next couple of millennia would be filled with mathematical debate over musical tuning, it is obvious that Aristoxenus’ opinion did not last. Pythagoras paved the way for such conversations, and his own tuning system stayed in practice for many hundreds of years following.
Fig. 3: Pythagorean intervals.
Interva l Pythagorea n Cent Value15 Equal Temperame nt Cent Value Just Cent Valu e
Minor Second Minor Third Major Third Perfect Fifth 90 100 112
294 300 316
408 400 386
702 700 702
This tuning system is based off of rather simple mathematics, as Pythagoras only attempted to keep the
15 Helmholtz, 1877, p. 313. 16 It is important to clarify that tuning a perfect fifth justly will result in a just perfect fourth — likewise, octaves and perfect fifths just. He used a method of ascending by a just perfect fifth and then removing octaves, the exact same method used for the ditonic comma, hence its nickname being the Pythagorean comma. In short, Pythagorean tuning is based solely on the just perfect fifth, and every other interval is tuned consequently from the perfect fifths. Therefore, the major thirds suffer, being a syntonic comma too wide. This leaves the Pythagorean major third 8 cents higher than an equally tempered major third. Additionally, the minor thirds are approximately a syntonic comma too narrow, leaving them around 7 cents smaller than an equal minor third (Rasch, 2002, p. 196). However, for Pythagoras and musicians for centuries after him, these horribly out of tune thirds do not pose a huge issue. Music of the antiquity and medieval periods is heavily based on fifths. Church music for many centuries was based on monophony and eventually organum at the fifth. Pythagorean tuning served plainchant well with its small melodic semitones and its pure perfect fifths.16 But as music progressed, a need for acceptable thirds and sixths arose, which brought about new and differing tuning systems.
Just Intonation
Toward the end of the fifteenth century, the next important tuning system started to gather the interest of theorists. Composers wanted the sweet sound of just perfect fifths to be retained in the increasingly popular thirds. Therefore, many different theorists attempted to keep the octave,
a wide major third will yield a narrow minor sixth. Intervallic inversions remain true when dealing with tuning.
fifth, and major third pure. While often attributed to the Spanish theorist Ramos de Pareja, the theoretical discovery of the third is more accurately credited to the Oxford mathematician, Walter Odington, around 1480 (Riemann, 1962, p. 280). In a time largely ruled by Pythagorean tuning, Odington’s proposal was certainly a brave one. However, the idea of just intonation may have been a bit too optimistic, and technically impossible for fixed pitch instruments, like keyboards. On a keyboard, the black key between D and E can be tuned to a just major third above B, or a major third below G, but not both. This brings about the technical impossibility for keyboards to play in just intonation. There would need to be two black keys in this instance, with one tuned to D# and one to Eb. While some intervals may be tuned very well in just intonation, others are far from pure. Many fifths end up being off by a syntonic comma and some major thirds end up being sharp by as much as 35 cents (Rasch, 2002, p. 200). These huge differences are obviously an issue, particularly to keyboard players. Therefore, it was always known that just intonation, while great in theory, could never actually be used in practice, as no one could tolerate such a gross mistreatment of so many intervals in the scale. However, many theorists believe that the idea of just intonation should not be thrown away completely. In the 16th century, theorist Gioseffo Zarlino said that vocalists, fretless violins, and
17 Contemporary musicians, often jazz musicians, claim to use just intonation in an attempt to change the color of certain chords, namely and recently Jacob Collier, though John Adams has fallen victim to the same fallacy. While they may tune the third trombones/sackbuts should do their best to play in just intonation when possible (Barbour, 2004, p. 197). This opinion is shared by some modern musicologists as well, such as Ross W. Duffin.17 Nevertheless, there are counterarguments to this. J. Murray Barbour argues that this is an unrealistic request because of other things relating to performance, such as vibrato, sliding/portamento, and in the case of singers, an exceptionally good ear is required, as well as the ability to sing a difference as small as 7-10 cents (2004, p. 198). Regardless of this debate, just intonation was incapable of fixing the errors of Pythagorean tuning.
Meantone Temperament
Music up until the late 14th century heavily favored the perfect fifth over the third, but as modal and eventually triadic harmony found its way to the western world, this preference had to shift. Meantone temperament is the first instance of a system where certain keys are strongly favored over others. A tuner could tune a harpsichord to be wonderfully in tune in C, and the closely surrounding keys would be similarly pleasant. However, the farther away one travels from that key, the worse the distant keys will sound. This fact was known, and composers would use more distant keys and chords for expressive effect. The first recorded instance of a meantone temperament comes from Giovanni Maria Lanfranco in 1533, who said that the fifths should be so flat that “the ear is not well
of the chord justly, it is not accurate to claim that it is “just intonation,” as every pitch would have to be altered, especially in such chromatic music. Rather, they are using equal temperament, unafraid of occasionally altering specific tunings.
pleased,” and the thirds “as sharp as can be endured,” in a treatise on the newly arising meantone temperaments (Barbour, 2004, p. 45). This was written in a time dominated by Pythagorean tuning, which leads musicologists to believe that meantone temperament was intended to be a temperament of the Pythagorean system. This theory is backed by mathematics, as meantone temperament is obtained by a similar method to Pythagorean tuning.
Fig. 4: 1/4-c meantone intervals.
Interv al 1/4-c Meantone Temperam ent Cent Value18 Equal Temperam ent Cent Value Just Cent Value
Minor Secon d
Minor Third Major Third Perfec t Fifth Diatonic117 Chromatic77 100 See append ix
310 300 316
386 400 386
696 700 702
Just as Pythagoras did, the meantone temperaments stack perfect fifths around the circle of fifths to find other intervals. However, the fifths are no longer just. To keep the thirds pure, the fifth had to be sacrificed. This is achieved by flattening the fifth by anywhere between 1/5 (4.4 cents) to 1/3 (7.3 cents) of a syntonic comma. The most common amount is 1/4 (5.5 cents), which is referred to as “quartercomma meantone,” and is exemplified in the chart above. This results in great major thirds (identical to just major thirds), rather good minor thirds, but unfortunately flat perfect fifths. 1/4-c
18 Rasch, 2002, p. 204. meantone also has semitones which are not truly half a tone, which requires some further tempering. Therefore, the concept of diatonic and chromatic semitones had to be introduced. A diatonic semitone (E-F) was larger and more pleasant, usually 117 cents. The chromatic semitone (CC#) was horribly small, about 77 cents, and was typically avoided (Rasch, 2002, p. 204). Additionally, meantone tuning actually worsened a problem that both Pythagorean tuning and just intonation also suffered from. Successions of perfect fifths, just or tempered, cause the issue of the ditonic comma mentioned above; the final fifth is far too wide. This fifth came to be known as the “wolf fifth,” its name coming from the howling sound it makes. Pythagorean and just tuning both had wolf fifths, but neither was used in a time period where such modulations were viable, whereas meantone temperament was. The wolf fifth (technically a diminished sixth) could be placed anywhere that the tuner deemed it least likely to be used, which was most commonly between G# and Eb. The two issues of chromatic semitones and wolf fifths meant that the “black keys” of a keyboard could not be made to serve as enharmonics, as a modern musician is used to on a piano. Usually, the pitches chosen for the black keys were C#, Eb (occasionally D#), F#, G#, and Bb (Rasch, 2002, p. 204). This only affects keyboard players, as they could not freely adjust the tuning of their black keys. This effectively rules out a chord like F minor, as the G# is not the same as an Ab, and therefore is not in tune with the F or C.
These may seem like unmanageable or unnegotiable compromises to the modern musician, but meantone temperament was actually the first widely successful system for its repertoire since Pythagorean tuning. Meantone temperament was popular in the late renaissance through the early Baroque period, a time marked by modal and hexachordal harmony, not traditional triadic harmony used by composers like Bach and beyond. Hexachordal harmony is instead based on fifths, and triads then built off of those fifths. For instance, the natural hexachord consists of the chords FM, CM, GM, Dm/DM, Am/AM, Em/EM, which only calls for an F#, G#, and C#, all of which are accounted for and in tune with a meantone temperament based around C (Huener, 2015, p. 1). As successful as these temperaments were for their music, it could not last for very long, as tertian harmony eventually exposed the limitations of these “single-use black keys,” and yet another temperament had to be produced.
Well and Equal Temperaments
In 1722, J.S. Bach finished writing his “Well Tempered Clavier,” a collection of pieces for keyboard in which all 24 keys are used. If the name does not give it away, such a work would be impossible in meantone temperament due to the use of the entire circle of fifths, not to mention the intense chromatic harmony that Bach uses. By the time the prelude in Ab Major starts, the wolf fifth of meantone temperament would have been far too noticeable. Bach did not invent well temperament, but his music is a great example of the necessary push to such a system. An organist named Andreas Werckmeister is considered the father of well temperament (Rasch, 2002, p. 215), though technically the earliest welltempered tuning can be traced all the way back to Aristoxenus in his critique of Pythagoras (Barbour, 2004, p. 2). Werckmeister drew up his own well temperament in the late 17th century in which he tempered certain “central” fifths (C-G, G-D, D-A, B-F#) by 1/4 of a syntonic comma—the same temperament as the most common meantone temperament, the difference being that these were the only fifths tempered as such (Rasch, 2002, p. 215). The result is a temperament in which every key, chord, and interval is acceptable to the ear, but even more importantly each is different from each other. The key of D major had a distinctly different color than A major, the chord C minor rang out unlike F minor, and the minor second between G and A♭ pulled up dissimilar to E and F. Werckmeister tuned his organ to this temperament as a means of being able to explore farther reaches of the circle of fifths. This specific temperament was decently successful, though most theorists borrowed Werckmeister’s principle of tempering central fifths, rather than the precise measurements of his temperament. Well temperaments used a wide variety of syntonic comma fractions to take off of specific fifths, namely 1/2, 1/4, 1/5, 1/6, 1/7, 1/8, and 1/12 (Rasch, 2002, p. 215). The biggest difference between well and meantone temperaments is that while meantone temperaments coincidentally produce very good keys and chords due to an even tempering of each fifth, the placement of good and bad keys is intentional in well temperament, because tuners would decide where
and how much to temper fifths. Tuners were no longer sacrificing F# major so they could have a great C major, but instead purposefully thinking about which keys they wanted to be good and which they did not, as well as thinking about how good or bad either extreme could be.
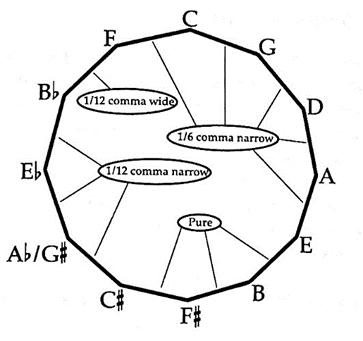
Fig. 5: Bach-Lehman Well Temperament.
19
In his 2005 article, Bradley Lehman claims to have uncovered a hidden secret on the title page of Bach’s “Well Tempered Clavier” manuscript, a wildly famous work in which there is a prelude and fugue for all twenty-four keys, moving chromatically upward (C major, C minor, C# Major, etc.) (p. 3). Lehman believes that what appears to be a simple drawing is actually a key for the specific temperament that Johann Sebastian was asking for. Whether or not this is actually what Bach intended is irrelevant, as the temperament proposed by Lehman is sound and typical of the time period, nonetheless. It features five fifths from F to E all lowered by 1/6 comma (3.6 cents), three pure fifths from E to C#, three fifths from C# to A# lowered by 1/12 comma (1.8 cents), and one fifth, A# to F, raised by 1/12 comma. This
19 Duffin, How Equal Temperament Ruined Harmony, p. 37. temperament removes any wolf intervals, and while there are four different kinds of fifths, each is acceptable to the ear. Well temperaments also rid the system of chromatic semitones, which allows a performer to play the C# major prelude and fugue immediately after the one in C minor (Rasch, 2002, p. 206).
Until the late 16th century, theories of tuning were always found by means of simple arithmetic and produced on an ancient single string instrument called a monochord. The next two hundred years were aided by the new mathematical practice of root extraction, a method with which to simplify irrational equations by squaring both sides of an equation, left with two linear equations. This allowed mathematicians and tuners to produce even more accurate figures for tuning. The process was refined yet again in the mid-18th century with the invention of logarithms (Rasch, 2002, p. 193, 206). In 1753, C.P.E. Bach published “On the true art of playing the clavier,” in which he called particularly for “equal” temperament. This equal temperament is a precursor to the modern standard tuning, though it would remain “incorrect” to a modern ear for more than a century. To C.P.E. Bach and musicians after him, equal tuning simply meant a well temperament in which every interval is equal to intervals of the same type. This started as a well tempering of the fifths by 1/12 of a syntonic comma, though this was crude and difficult to reproduce. Nonetheless, the idea of equal temperament fascinated theorists, and before the year 1800 meantone temperament had become
obsolete (except within the community of organists) (Rasch, 2002, p. 208). That is not to say that equal temperament had been agreed upon as the superior tuning. In 1806, important theorists were seemingly divided on the acceptance of equal temperament (Jorgensen, 1991, p. 293). This argument may be due to the fact that true equal temperament had not been produced by anyone yet. Simon Stevin was a relatively successful scientist of the early 17th century who also studied the humanities extensively. Stevin published a paper where he rejected the inequality of semitones. In his writings is found an equal temperament using the ratio of the twelfth root of two to find an equal division of the octave into 12 equal semitones, the same method that is used today (Rasch, 2002, p. 206). However, Stevin was reckless with the rounding of decimals, so it was not until the late 19th century, when Hermann Helmholtz and John Ellis revisited the math proposed by Stevin nearly three centuries earlier, that equal temperament truly became effective. Even still, the math is rather complicated, and tuners had little guidance on how to tune to this temperament, especially because one cannot count the beats20 of an equally tempered interval, as they all use complicated superparticular ratios; for example, a perfect fifth is 31:12. In 1917, William Braid published a book on tuning to equal temperament that finally perfected the system. At the same time, Alexander Ellis coined the term “cent,” further helping tuners
20 “Counting beats” is a practice of tuning in which a tuner will listen to the oscillations between two pitches to hear how well the higher pitch is tuned. The number of beats is derived from the ratio of the with the difficult equal temperament and finally providing a means of measurement for tuning that did not include lengths of monochord strings (Duffin, 2007, p. 113-115). Unfortunately, with universally accepted mathematical principles came the end of an era. Tuning was once an art form with endless possibilities for variation, differing greatly from one tuner to the next, and giving composers much more to think about in terms of expressivity.
Timeline of Tuning and Temperament
Before explaining the relevance of each of these tuning systems during the Baroque period, a quick summary of the timeline given above is helpful. The earliest form of tuning that musicologists can identify and recreate is Pythagorean tuning, which survived virtually untouched for nearly a millennium and a half. Its success is due largely to the fact that the music it served used primarily perfect fifths, which is the interval that Pythagorean tuning is based on. However, as music progressed and the interval of a third came to be desired, new tuning systems had to be made. Just intonation maintained a similar principal as its predecessor in that it wanted to keep both the fifths and the thirds pure, but such an ideal is not mathematically possible. In the early 16th century, tuners started to compromise the long-preserved fifth
two pitches; for example, a just perfect fifth with the ration 2:1 would beat twice on the higher pitch for every once on the lower.
in order to obtain the highly soughtafter third, thus introducing meantone temperament. This was the first truly successful system since Pythagorean tuning, and served the repertoire of its time exceptionally well with its sweetly tuned thirds and expressive reaches of the circle of fifths. However, meantone temperament had a limit that late 17th century composers and theorists wanted to push. If meantone temperament was brought about in an attempt to introduce the use of the third, well temperaments were brought about in an attempt to use more thirds; that is, in an effort to make more thirds usable around the circle of fifths. In essence, well temperament allowed composers to access farther keys than before thought acceptable, while still maintaining the expressive differences in keys. As time moved on and music became even more chromatic, particularly for the keyboard, early mid-19th century composers and theorists became increasingly interested in the idea of equal temperament, so much so that meantone temperament became obsolete. Through the mathematical efforts of many theorists and scholars, equal temperament was perfected by 1917 and now dominates the world of western music.
Tuning Systems Used in the Baroque Era
The history of tuning and temperament, then, is chiefly the history of its adoption upon keyboard instruments (Barbour, 2004, p. 6). Pythagorean tuning was not used at all in the Baroque era. Just intonation was certainly an ideal on the minds of Baroque theorists, but such a system has never been successful in practice. Vincenzo Galilei pointed out that fretted string instruments were incapable of anything other than equal temperament, as the octaves would have been out of tune across different strings (Barbour, 2004, p. 8). For a mild example, the twelfth fret on a lute G string and the seventh fret on a C string would both produce a G, though the former would be tuned as a just octave above G, and the latter a just fifth above C; a difference of four cents. Yet at the same time, keyboard instruments would not be pushed toward equal temperament for another two hundred years. This clash of differing temperament types would likely have brought about equal tuning much sooner were it not for the everrising popularity of fretless string instruments in the early Baroque era. Such an instrument had freedom to play in even the unusable just intonation and may have distracted baroque musicians from the viability of equal temperament. This is not to say equal temperament was unknown to Baroque theorists and performers. It was just simply another option, particularly to fretted string players. In the early Baroque world of hexachords, meantone temperament was exceedingly useful and clearly superior to well temperaments, just as highly chromatic and triadic music of the late Baroque required more inventive well temperaments. Meantone temperaments could no longer account for tonal music, which allows historians to clearly mark the difference is uses of meantone and well temperaments right in the middle of the Baroque period. And still, even with the popularity of well
temperament in the early tonal world, equal temperament was on the mind of theorists and composers, though it was not widely accepted until well into the classical period, and not perfected until the 20th century.
Conclusions
The only real test is the sound . . . I think it worthwhile, however, to use our ears as best we can, and hope for a well-informed consensus to confirm our perceptions or improve upon them (Lehman, 2005, p. 211). For over 2000 years, tuning has been an integral part of the performance and enjoyment of western music. It has fascinated musicians, mathematicians, and scientists alike. Much like the invention and innovation of instruments, harmony, form, and style have evolved to match the musical desires of different periods, so has tuning. The baroque period is a crucial point in the story of western tuning, as it coincided with the shift toward functional tertian harmony, which closed a few doors in relation to tuning, but opened up countless more regarding new and individualized temperaments. That same individuality may have been halted with the standardization of equal temperament in the 20th century, but it was undoubtedly a necessary misfortune to accommodate the styles of jazz and post-tonal practices. Nonetheless, tuning and temperament is by no means a lost art. There remains much research to be done on not only the past of tuning, but also the present and future.
References
Barbour, J. Murray. Tuning and Temperament; A Historical Survey. Mineola, New York. Dover Publications, Inc., 2004. Blackwood, Easley. The Structure of Recognizable Diatonic Tunings. Princeton, New Jersey. Princeton University Press, 1985. Dolata, David. Meantone Temperaments on Lutes and Viols. Indiana. Indiana University Press, 2016. Donahue, Thomas. A Guide to Musical Temperament. Lanham, Maryland. Scarecrow Press, Inc., 2005. Duffin, Ross W. How Equal Temperament Ruined Harmony (and Why You Should Care). New York, New York. W.W. Norton & Company, 2007. Helmholtz, Hermann L. F. On the Sensations of Tone as a Physiological Basis for the Theory of Music. New York. Dover Publications, Inc., 1877. Huener, Thomas J. A Mid-17th-Century Post-Modal Pitchscape. Greenville, 2015. Jorgensen, Owen H. Tuning. East Lansing, Michigan. Michigan State University Press, 1991. Lehman, Bradley. “Bach’s Extraordinary temperament: our Rosetta Stone — 1,” Early Music vol. 33/1 (2005). pp. 3-23. Lehman, Bradley. “Bach’s Extraordinary temperament: our Rosetta Stone — 2,” Early Music vol. 33/2 (2005). pp. 211-231. Rasch, Rudolf. “Tuning and Temperament,” The Cambridge History of Western Music. Thomas Christensen. Cambridge: Cambridge University Press, 2002, pp. 193-222. Riemann, Hugo. History of Music Theory Books I and II. Raymond H. Haggh. Lincoln: University of Nebraska Press, 1962.
Appendix and Glossary
Interval Pythagorean Tuning
Just Intonation 1/4 -Comma Meantone Bach-Lehman Well Temperament Modern Equal Temperament Naturally Pure Interval
Minor Second 90 112 D*-117
C*-76 94-110 100 N/A
Minor Third 294 316 310 294-306 300 316
Major Third
Perfect Fifth 408 386 386 392-406 400 386
702 702 696 698-704 700 702
Intervals chosen are based on their relevance to this paper. Given in modern cent values. Lehman-Bach Well Temperament uses ranges as each interval is unique. The harmonic series has widely varied semitones, hence the unavailable semitone here. *D-Diatonic Semitone, C-Chromatic Semitone.
Cent- A measurement of pitch variance; 1200 cents in one octave. Chromatic Semitone- A semitone stepping outside of a diatonic scale; i.e. C-C#, 77 cents. Ditonic Comma- The difference between 12 just fifths and 7 just octaves; 24 cents. Diatonic Semitone- A semitone within a diatonic scale; i.e. E-F, 117 cents. Equal Temperament- A well temperament based on equal semitones in which everything is equally out of tune; the modern standard. Harmonic Series- The naturally occurring order of pitches based on a fundamental/sounding pitch. Just Intervals- The tuning of a pitch as it occurs in the harmonic series; sometimes called pure. Just Intonation- A tuning system that attempted to maintain just fifths and thirds; impractical. Meantone Temperament- A temperament of Pythagorean tuning that is based on narrow fifths; perfect for hexachordal and modal music of the renaissance and early baroque. Pythagorean Tuning- A tuning system based on pure fifths; very fitting for music of the antiquity to organum. Superparticular Ratio- Any ratio that lies between two adjacent partials in the harmonic series. Syntonic Comma- The difference between 4 just fifths (subtracted by two octaves) and a just major third; 22 cents. Temperament- An edit to a pre-existing tuning system; slightly adjusting an established system. Tuning System- A mathematical organization of notes within an octave. Well Temperament- A temperament based on fifths of varying sizes; well suited for chromatic music of the late baroque period. Wolf Fifth- The result of the ditonic comma; horribly out of tune twelfth fifth.




