Grundsystemets opbygning

Elevbog/Web

Reflex 2A, Elevbog/Web indeholder 9 kapitler, der tager udgangspunkt i udvalgte faglige begreber og arbejdsmetoder. Hvert kapitel indledes med en stilladseret undersøgelse efterfulgt af opgave og aktiviteter, der er organiseret i varierende samarbejdsformer.

Lærervejledning/Web reflex.alinea.dk

Reflex 2A Lærervejledning/Web indeholder introduktion til tankerne bag grundsystemet og en beskrivelse af tilrettelæggelsen af undervisningen med Reflex herunder de gennemgående elementer. Derudover indeholder denne lærervejledning beskrivelse af de enkelte opgaver og aktiviteter i elevbogen herunder anvendelsen af digitale ressourcer, der er tilgængelige på det tilhørende website, arbejdsark og faglige film. Det er også her, man kan læse om målet med opgaverne, supplerende aktiviteter og særlige opmærksomhedspunkter.

Reflex er et Har du bog, har du web system. Når du har købt Reflex 2A Elevbog/Web eller Reflex Lærervejledning 2A/Web, får du samtidig adgang til websitet på reflex.alinea.dk, der indeholder følgende:

• Samtalebilleder fra elevbogen til visning på en skærm i klassen

• Faglige film, som beskriver de matematiske begreber, der indgår i hvert kapitel

• Film, der viser spilvejledninger og anvendelsen af diverse hjælpemidler

• Digitale ressourcer til udvalgte opgaver

• GeoGebra-opgaver

• Selvrettende fordybelsesopgaver og færdighedsevalueringer

• Mulighed for elevbesvarelser ved hjælp af lydoptagelser

• Differentierede evalueringsopgaver på tre niveauer

• Fælles Mål og læringsmål for hvert kapitel

• Arbejdsark og Hjælpeark

• Facitliste til elevbogen

• Tavlebog

Tankerne bag Reflex

Reflex er organiseret med baggrund i tre didaktiske hjørnesten: Videnskonstruktion, Den nysgerrige samtale og Det anerkendende læringsrum. Hjørnestenene repræsenterer de særlige læringsmæssige betoninger i Reflex og udgør de vigtigste didaktiske kendetegn for systemet. De er tænkt som gennemgående læringsprincipper, hvor der fokuseres på tilegnelse af viden, varierende arbejdsformer og kulturen i læringsrummet.

Elevernes Videnskonstruktion er stilladseret i en genkendelig struktur af matematiske undersøgelser, konsoliderende opgaver, samt formative og summative evalueringer.

I Den nysgerrige samtale er der fokus på den læringsmæssige værdi i at dele ideer, løsningsmuligheder og viden med hinanden.

I Den nysgerrige samtale kommer kommunikation og sproglig begrebsdannelse derfor særligt til udtryk.

Det anerkendende læringsrum danner rammen om Den nysgerrige samtale og elevernes tilegnelse af matematisk viden. Centralt for Det anerkendende læringsrum er elevens aktive deltagelse i undersøgelser, samtaler om løsninger, vidensdeling og feedback i evalueringerne. Det anerkendende læringsrum indebærer en læringskultur, hvor det at prøve sig frem og lære, både af fejlslagne forsøg og af andre, ses som en værdifuld måde at konstruere viden på.

Videnskonstruktion

Konstruktionen af viden skal forstås som elevernes evne til at tilegne sig matematisk viden ud fra refleksioner over matematiske pointer og sammenhænge.

I Reflex foregår elevernes refleksioner både selvstændigt og i samarbejde med andre. Når eleverne diskuterer med hinanden og udveksler løsningsforslag, udfordres den enkeltes viden, hvilket vil styrke elevens matematiske forståelse. Den enkeltes aktive deltagelse gennem spørgsmål, undren og svar vil andre også kunne drage fordel og blive motiveret af samt opleve at kunne bygge videre på. Den enkelte elevs bidrag bliver således en værdifuld kilde både til egen og andres tilegnelse af viden.

Det er særlig vigtigt, at eleverne undervejs i processen får mulighed for at deltage aktivt og udtrykke sig undrende og spørgende. Et ufuldstændigt svar er et vigtigt skridt på vejen mod en mere fuldstændig besvarelse. Processen med at opbygge viden og den opnåede forståelse bliver dermed hinandens styringsredskaber, fordi den nye forståelse bliver grundlaget for den videre konstruktion af viden.

I Reflex er der i indledningen til hvert kapitel lagt særlig vægt på at understøtte den undersøgende proces og aktivitet. I undersøgelserne arbejder eleverne med at prøve sig frem, dele ideer med hinanden og samle op på de faglige pointer i fællesskab. I de efterfølgende opgaver lægges der op til, at de anvender og afprøver deres viden i forskellige sammenhænge for derigennem at konsolidere de nye faglige pointer som matematisk viden.

Den nysgerrige samtale

For at styrke elevernes Videnskonstruktion er der særligt fokus på samtalen i Reflex. Det kommer til udtryk i Den nysgerrige samtale hvor elevernes udveksling af ideer og begrundelser for løsninger har afgørende betydning for deres tilegnelse af viden. I samtalerne er der både fokus på nysgerrighed og en undersøgende tilgang. Det, der kan opfattes som forkerte besvarelser, vil i denne sammenhæng blive en værdifuld ressource, idet forkerte eller skæve svar skaber en oplagt mulighed for nytænkning. Nysgerrighed og åbenhed over for, hvad eleverne har tænkt giver desuden indsigt i elevernes faglige ståsted.

I elevernes interaktion med andre er det hensigten, at de skal opleve, at den enkeltes bidrag er værdifuldt, og at alle elevers forslag derfor skal inddrages så meget som muligt. I samtalerne lægges der op til at lade eleverne beskrive deres faglige pointer, sådan at potentialerne i deres forslag bliver italesat, og forskellige betragtninger bliver diskuteret. Der gives i lærervejledningen forslag til spørgsmål og samtaleemner, der kan støtte eleverne i at italesætte deres bidrag. Hensigten er, at de mundtlige opsamlinger dermed vil styrke italesættelsen af elevernes viden, så de på den måde hjælpes til at forholde sig både til egne og andres refleksioner.

Det anerkendende læringsrum

Det anerkendende læringsrum udgør både rammen for Den nysgerrige samtale og elevernes konstruktion af viden. Det anerkendende læringsrum understøtter elevernes undersøgende tilgang og styrker vekselvirkningen mellem den enkeltes refleksioner og konstruktion af viden. Den nysgerrige samtale får således optimale betingelser, når Det anerkendende læringsrum er etableret. Et væsentligt element i Det anerkendende læringsrum er elevernes bevidsthed om, at matematik ikke alene handler om at finde løsninger og svar, men i høj grad også om den proces, der er forbundet med at afklare og behandle et matematisk problem.

I Reflex er det centralt, at eleverne oplever matematik som et fag, hvor man undrer sig, tør tage chancer og dele sine foreløbige tanker med hinanden. Når klassen dyrker det anerkendende fællesskab, dannes der grundlag for udvikling af læring, tillid og respekt for andre. I dette anerkendende fællesskab skabes der tryghed og mulighed for at være nysgerrig, udveksle og afprøve ideer samt lære af egne og andres foreløbige og fejlslagne forsøg. Ved at vise foreløbige løsninger, forklare valg og gøre sig nye erfaringer kan eleverne udvide deres forståelse og opleve værdien af at skabe viden sammen med andre.

Det anerkendende læringsrum understøtter samtidig muligheden for differentiering i undervisningen, fordi elevernes bidrag i form af halve og hele løsninger er værdifulde for konstruktionen af viden. Alle behøver således ikke at kunne det samme eller være på samme niveau. Det er hensigten, at eleverne engageres, fordi selve det at deltage skaber muligheder og ressourcer både for den enkelte og for fællesskabet. Anerkendelse af eleverne for at deltage og turde give foreløbige bud bliver dermed et vigtigt værktøj til at motivere elevernes deltagelse i samtalerne om matematik.

Lærerens rolle

De tre hjørnesten afspejler den gennemgående didaktiske organisering i Reflex og dermed også lærerens rolle i undervisningen. Særligt Den nysgerrige samtale og Det anerkendende læringsrum er idealer for den didaktik, der ligger til grund for tilrettelæggelse og gennemførelse af undervisningen med Reflex. I Reflex er der konkrete anvisninger til, hvordan man som lærer aktivt kan realisere denne didaktik.

I Reflex lægges der stor vægt på at skabe et anerkendende læringsmiljø. Ved at skabe trygge rammer øges mulighederne for, at eleverne tør kaste sig ud i aktiviteter, som de ikke umiddelbart kender metoder til eller løsninger på. Og i stedet for blot at konstatere, at et opgavesvar er rigtigt eller forkert, lægges der op til at spørge nysgerrigt ind til, hvordan eleven er nået frem til sit bud på en metode eller løsning. Formålet med dette er dels at forstå elevernes tankegang, dels at give eleverne mulighed for at erkende gennem andres iagttagelser, bud og forsøg, og dels bedre at kunne guide eleverne videre i læringsprocessen.

Hvis eleven fx fejlagtigt svarer, at 16 + 5 = 31, kan man som lærer spørge ind til, hvordan eleven er nået frem til 31. På det spørgsmål vil eleven evt. svare: ”16 plus 4 er 20. Så mangler jeg at lægge 1 til, fordi det var 5, der skulle lægges til. Nu har jeg 21, og så lægger jeg tieren til.”

Ved at spørge ind til, hvordan eleven har tænkt, bliver det tydeligt, hvad der kan bygges videre på, og hvordan eleverne kan guides i at nå frem til en holdbar og korrekt metode. I første omgang bruger eleven en regnestrategi ved at dele 5 op i 4 plus 1, så udtrykket gør tierovergangen lettere. Herefter lægges der så fejlagtigt en tier til. Dette kan hænge sammen med, at eleven fra andre additionsopgaver er blevet opmærksom på, at man skal huske tierne, men ud fra den regnestrategi, som eleven har valgt, går det galt. I eksemplet giver det derfor mening at spørge ind til, hvor tieren kommer fra og at gøre eleven opmærksom på, at hvis man bruger denne metode, er det netop vigtigt at huske at få den nye tier lagt til den tier, der indgår i 16. Det kan også være en god idé at spørge de andre elever, hvad de tror, eleven har tænkt, og lade dem forklare.

Eleven kan præsenteres for den samme opgave på flere måder med det formål netop at opdage og arbejde med flere mulige strategier. Det kan fx ske ved at bruge centicuber eller ved at tegne og skrive en matematikhistorie. Man kan også opfordre eleven til at regne opgaven ved at bruge en tallinje, talslange eller taltavle, så det bliver klart, at man når frem til 21 og ikke 31, når man begynder ved 16 og hopper fem gange. Som opfølgning kan man eventuelt stille en tilsvarende opgave, som fx 14 + 9.

Der vil naturligvis opstå situationer, hvor eleverne kan få brug for en anden form for vejledning. Hvis en elev fx svarer, at 5 + 7 er 100, så giver det sandsynligvis ikke mening at spørge ind til de bagvedliggende tanker, men vil give mere mening at starte et helt andet sted. Det er vigtigt at vurdere, om et svar er rent gætteri, eller om der er brug for at støtte eleven i at vurdere, om et svar er rimeligt eller ej.

Ved at spørge nysgerrigt ind til elevernes arbejdsmetode og tankegang kan man danne sig et billede af deres udfordringer og umiddelbare formåen, hvilket både kan bruges i dialogen og i det fremadrettede arbejde. Samtidig udnyttes diversiteten i klasserummet, fordi der er fokus på understøttende dialog, fremadrettet feedback og det, at eleverne oplever deres bidrag som en værdifuld del af undervisningen.

Det er i sig selv både lærerigt og inspirerende at bevæge sig ind i disse processer, da de ofte afspejler en mangfoldighed af svar, som man også kan dele med eleverne. Synliggørelsen af mangfoldigheden af svar kan berige faget, medvirke til at mindske matematikangst og understøtte udviklingen og opbygningen af en anerkendende læringskultur. Eleverne skulle gerne føle, at det både er trygt og spændende at kaste sig ud i forskellige undersøgelser, og at de kan lære en masse både af de gode ideer og tankerne undervejs i processen.

De matematiske kompetencer

Kompetencer kan også beskrives som evner og færdigheder til at handle hensigtsmæssigt ud fra givne udfordringer og situationer. De matematiske kompetencer drejer sig om at kunne forstå, beskrive, bearbejde og løse matematiske problemstillinger indenfor alle fagets områder. De matematiske kompetencer fokuserer på det at kunne handle aktivt og hensigtsmæssigt ud fra andet end selve den faglige viden og den færdighedsmæssige kunnen. Nedenfor er de enkelte kompetencer beskrevet ud fra deres betydning for indholdet i Reflex. Til indholdet i elevbogen er der på web opstillet læringsmål og tilhørende tegn på læring formuleret ud fra Fælles Mål for matematik.

Kilde til nedenstående afsnit om de matematiske kompetencer: Faghæftet for matematik på emu.dk.

Problembehandling

Denne kompetence vedrører opstilling og løsning af matematiske problemer, der ikke udelukkende kan besvares ved hjælp af rutineprægede metoder. Et matematisk problem kan lægge op til en undersøgelse i form af fx gæt-og-prøv-efter-strategier, afprøvning af hypoteser eller udførelse af eksperimenter. For at opøve kompetence i problembehandling skal eleverne i indskolingen arbejde med at behandle enkle matematiske problemer og være i stand til at gennemføre en matematisk undersøgelse. En undersøgelse indeholder eksperimenter, herunder systematiske afprøvninger og ræsonnementer. Konkrete materialer samt egne skitser og noter er vigtige elementer i elevernes undersøgelser. Det er gennem undersøgelser og eksperimenter, at eleverne på hele trinforløbet udvikler deres selvstændige tilgang til problembehandling, samtidig med at de tilegner sig arbejdsmetoder til systematisering og strategier til problembehandling.

Problembehandling kommer i Reflex til udtryk i de opgaver, hvor eleverne skal undersøge deres omgivelser. I flere af opgaverne skal eleverne vurdere noget, før de besvarer en opgave - fx gætte vægten af eller længden på genstande, før de måler efter. Det kan være opgaver, hvor eleverne skal undersøge, hvilke varer man kan købe for et bestemt beløb, eller hvilke ting man kan have i kufferten, når vægten ikke må overstige et kilo. Alt sammen opgaver, hvor eleverne kan gætte, eksperimentere og prøve efter. Problembehandling kommer desuden til anvendelse i de undersøgelser, der indleder hvert kapitel. Undersøgelserne er tilrettelagt, så de lægger op til, at eleverne eksperimenterer med svarmuligheder og får erfaring med forskellige metoder til at tilgå matematiske problemstillinger.

Modellering

Denne kompetence vedrører evnen til at vurdere og opstille matematiske modeller. Det kan være processer, hvor matematik enten anvendes til at behandle konkrete situationer eller til at analysere og vurdere matematiske modeller, som beskriver forhold i virkeligheden. For at opøve kompetence i modellering, skal eleverne arbejde med at anvende matematik til at tolke, undersøge og beregne enkle hverdagssituationer. Eleverne skal i stigende grad gennem indskolingsforløbet kunne tolke resultaterne af deres matematiske arbejde i forhold til hverdagssituationer, og de skal kunne vurdere, om deres resultater er realistiske i forhold til det problem fra virkeligheden, som de har arbejdet med. Hvis resultaterne ikke er realistiske, skal eleverne være i stand til at genstarte modelleringsprocessen, fx ved at gætte på ny og prøve efter.

Modellering kommer i Reflex fx til udtryk i arbejdet med matematikhistorier, hvor eleverne deler deres arbejde med at omsætte et hverdagsproblem til matematik og derefter igen omsætter det til hverdagssprog. Modellering kommer også til udtryk i elevernes undersøgelser. Dette gælder særligt i indledningen til hvert kapitel, hvor eleverne skal gøre sig antagelser om virkeligheden og efterprøve forskellige hypoteser. Elevernes erfaringer fra virkeligheden og hverdagen inddrages desuden i samtalerne om de introtegninger, der indleder hvert kapitel.

Ræsonnement og tankegang

Denne kompetence vedrører matematisk argumentation og karakteristika ved matematisk tankegang. Eleverne skal kunne genkende, stille og besvare spørgsmål, som er karakteristiske for faget matematik og blive i stand til at argumentere for deres tankegang. Elevernes udvikling af kompetence i ræsonnement og tankegang skal bl.a. bygge på nysgerrige spørgsmål, der leder eleven videre i den proces, som eleven er i. Gode spørgsmål kan derfor være: ”Hvad nu, hvis…?” ”Hvordan kan du vide, at…?” og ”Kan du forklare, hvorfor…?” I indskolingen arbejder eleverne med kendetegnene ved det matematiske sprog gennem enkle matematiske spørgsmål, svar og forklaringer.

Ræsonnement og tankegang kommer i Reflex til udtryk, når eleverne skal undersøge egenskaber ved geometriske figurer eller sammenhænge mellem regningsarter. Det samme gælder, når eleverne skal beskrive, hvordan talmønstre fortsætter, eller når de argumenterer for, hvordan en opgave er løst. Ræsonnement og tankegang kommer desuden til udtryk, når eleverne efter de indledende undersøgelser deler deres erfaringer, undrer sig, stiller spørgsmål, giver forklaringer og argumenterer for deres tankegang, samt i den opsamlende samtale efter undersøgelsen, hvor eleverne reflekterer over den viden, som de har opnået.

Repræsentation og symbolbehandling

Denne kompetence vedrører anvendelsen og forståelsen af repræsentationer i matematik, herunder matematisk symbolsprog. Repræsentation og symbolbehandling er særlig central for elevernes muligheder for at arbejde abstrakt med matematiske emner, som når de fx opstiller regneudtryk eller tolker pindediagrammer. Anvendelse af konkrete materialer er vigtig i arbejdet frem mod de symbolske repræsentationer. Undervejs suppleres de konkrete materialer med visuelle repræsentationer, der inddrages sammen med elevernes egne, måske mere uformelle repræsentationer i form af tegninger og notater. Det alsidige valg af repræsentationer har til formål at støtte elevernes mulighed for at skabe forbindelser mellem de matematiske symboler og de konkrete visuelle repræsentationer. Samtidig understøttes elevernes arbejde med at løse matematiske problemer og udvikle begreber og metoder.

I forbindelse med de matematiske symboler bør undervisningen i indskolingen lægge vægt på tal og regnetegn. Matematiske symboler er helt særlige og vigtige repræsentationer, som eleverne har brug for at se gentaget og anvendt, for at kunne tilegne sig dem. Det er centralt, at eleverne gennem undervisningen får mulighed for at skabe forbindelse mellem de nye matematiske symboler og de konkrete og visuelle repræsentationer, der kan fungere som støtte for den enkelte elev. Digitale læremidler, herunder forskellige typer af apps, kan på samme måde både understøtte kompeten- cen og elevernes erfaring med, at der kan være flere forskellige metoder til at repræsentere matematiske begreber.

Repræsentation og symbolbehandling kommer i Reflex til udtryk, når regneudtryk enten er repræsenteret ved en illustration eller en matematikhistorie. På den måde får eleverne vist regneudtrykket på flere forskellige måder, som fx ved hjælp af symbolsk opskrivning, sproglige formuleringer og tegninger, der passer til. Eleverne ser tal repræsenteret på mange forskellige måder, blandt andet som talbilleder fx i form af øjne på terningesider eller prikker på dominobrikker. De ser også tal vist som et antal genstande, digitale tal og med talsymboler i forskellige regneudtryk. Geometriske figurer bliver vist på mangfoldige måder, både som geometriske flade figurer, former på hverdagsgenstande, rumlige og sammensatte figurer. Dette sker for at afhjælpe den fejlopfattelse, at de geometriske figurer, cirkel, kvadrat og ligesidet trekant, kun repræsenterer cirkler, firkanter og trekanter generelt. I Reflex kommer repræsentation og symbolbehandling desuden til udtryk i elevernes undersøgelser, hvor uformelle repræsentationer af egne og andres tanker gennem tegninger og brug af konkrete materialer er nødvendigt for at kommunikere det, som eleverne har erfaret.

Kommunikation

Denne kompetence vedrører det at udtrykke sig med og om matematik samt at fortolke andres udtryk med og om matematik. For at opøve kompetencen, skal eleverne i undervisningen bruge et matematikholdigt sprog. Det betyder, at de skal arbejde med at formulere forklaringer på, hvordan bestemte opgaver skal forstås og løses, og at de også øver sig i at forstå og sætte sig ind i andres forklaringer. Eleverne skal også arbejde med visuel kommunikation både ved brug af digitale værktøjer til lydoptagelser samt stillbilleder.

Eleverne skal have mulighed for at forklare, vise, lytte og diskutere matematik i matematikundervisningen. Der skal være fokus på, at eleverne lærer at udtrykke sig matematisk præcist både mundtligt, skriftligt og visuelt, samt at de kan sætte sig ind i andres matematiske fortællinger, beskrivelser, udsagn og forklaringer. I indskolingen består en begyndende skriftlig kommunikation af uformelle noter og illustrative tegninger. Denne form for kommunikation skal støtte eleverne i deres matematiske tænkning, fastholde tanker, idéer og metoder samt hjælpe eleverne til efterfølgende at kunne forklare tanker og løsninger. Eleverne skal også arbejde med at kunne anvende enkle fagord og begreber både mundtligt og skriftligt og med en begyndende præcision i deres egne forklaringer af disse fagord og begreber. Desuden indgår begyndende læsning af matematikhistorier, tekster med fagord, opgaver og matematiske problemer.

Kommunikation kommer i Reflex til udtryk, når eleverne gennem leg og aktivitet skal sige og forklare matematiske begreber. Det kan fx være, når eleverne stiller hinanden spørgsmål om og med matematik, hvor begreber sættes ind i en kontekst, som fx talnavne, lige, ulige, figurnavne, flest og færrest. Eleverne sætter også ord på matematikken, når de forklarer deres regnestrategier for hinanden. Eleverne skal fortælle matematikhistorier, som enten bygger på et bestemt regneudtryk, eller hvor der indgår bestemte begreber, som fx en historie om et datasæt eller en historie om figurer. Kommunikationen kan både foregå samlet i klassen, flere elever imellem og alene, når eleverne indtaler lyd på web.

Kommunikation kommer desuden til udtryk, når elevernes forforståelse aktiveres i samtalen om introtegningens matematiske indhold og om elevernes hverdagserfaringer med matematik. I Reflex er der lagt vægt på den visuelle kommunikation, hvor eleverne afkoder billedet for information og selv fremstiller billeder. Derudover kommer kommunikation til udtryk, når eleverne forklarer resultater af undersøgelser, og når de præsenteres for levende visuel kommunikation, som fx i film, der handler om disse begreber. Det kommer også til udtryk i den opsamlende samtale efter undersøgelserne, hvor eleverne gør sig overvejelser omkring viden, tanker og ideer, og hvor spørgsmål kan stilles og besvares.

Hjælpemidler

Denne kompetence vedrører kendskab til anvendelse og valg af relevante hjælpemidler i matematik. Eleverne skal udvikle færdigheder i brug af hjælpemidler og viden om, hvilke hjælpemidler det er hensigtsmæssigt at anvende i bestemte situationer. For at opøve kompetencen, skal eleverne arbejde med konkrete materialer og redskaber samt digitale hjælpemidler ved undersøgelser, beregninger og tegninger. Det centrale er, at eleverne har adgang til en bred vifte af konkrete og digitale hjælpemidler. Papir og blyant til tegning og noter er fx vigtige hjælpemidler for at kunne fastholde systematiske planer for undersøgelser samt kreative ideer. I indskolingen skal eleverne bruge konkrete materialer som støtte for begrebsdannelse, undersøgelse af sammenhænge, efterprøvelse af hypoteser og grundlæggelse af færdigheder. Eleverne skal introduceres for et dynamisk geometriprogram, lommeregnere og senere også for regneark og CAS-værktøjer.

Hjælpemiddelkompetencen kommer i Reflex til udtryk, når eleverne bruger forskellige konkrete materialer og redskaber, som fx linealer, vægte eller spejle, og når de løser regneudtryk ved hjælp af centicuber, taltavler, tallinjer eller lommeregnere. Med digitale hjælpemidler kan eleverne udføre undersøgelser, som er besværlige at håndtere ved brug af papir og blyant. I GeoGebra kan eleverne fx nemt rykke rundt på hjørner og kanter og dermed se sammenhænge, som det ville tage lang tid at tegne med papir og blyant. Med lommeregnere kan eleverne desuden undersøge, hvilke varer der kan købes hos købmanden og afprøve mange muligheder, når de fx skal finde regneudtryk, der giver resultatet 4. Hjælpemidler kan desuden bestå af konkrete materialer, som fx brikker, centicuber, papir, farveblyanter, sakse og lim. Blyanten er et vigtigt redskab til tegning, noter og skriblerier. Digitale tegninger i dynamiske geometriprogrammer er også vigtige, idet eleverne her nemt kan få succes med at tegne mere præcist, og hvor de får erfaring med, at det, de skaber, både er flot og af høj kvalitet.

Matematik med Reflex

Med afsæt i de tre didaktiske hjørnesten og de matematiske kompetencer er undervisningen med Reflex tilrettelagt ud fra en genkendelig struktur i hvert kapitel. Strukturen afspejler en progression gennem stilladsering af elevernes undersøgelser, konsolidering af deres viden og færdigheder samt en løbende evaluering, dialog og feedback. Denne struktur er illustreret i nedenstående lærebogsmodel.

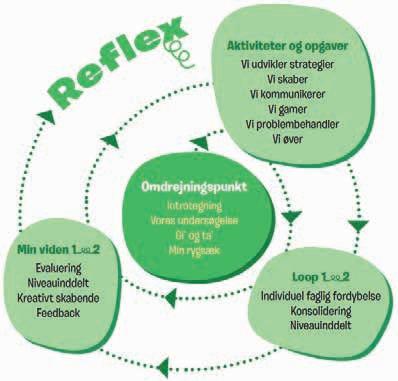
undersøgelse gennemfører eleverne en undersøgelse. Herefter deler eleverne i fase 3 Gi’ og ta’ deres løsningsforslag med hinanden, før der samles op på den opnåede viden i fase 4, Min rygsæk.

Omdrejningspunktet danner baggrund for det faglige indhold, som eleverne efterfølgende skal arbejde med i kapitlet. De fire faser er uddybet nedenfor.

Fase 1 Introtegning

I første fase introduceres eleverne til kapitlets faglige indhold gennem en Introtegning, der danner udgangspunkt for en klassesamtale. Formålet med Introtegningen og samtalen er at aktivere elevernes forforståelse og umiddelbare opfattelse af emnet. Samtalen tager udgangspunkt i elevernes hverdagserfaringer med det faglige emne. På Introtegningen vises hver gang den samme lærer, som stiller et spørgsmål til eleverne, der er ment som en inspiration til at opdage tegningens faglige indhold. I side til side-vejledningen er der til hver Introtegning givet forslag til supplerende spørgsmål for at støtte eleverne i deres udforskning af tegningens indhold. Introtegningerne er tilgængelige på web, så de kan vises på en skærm i klassen, mens eleverne går på opdagelse i indholdet. Efter at have aktiveret elevernes forforståelse og umiddelbare opfattelse, skal de efterfølgende udføre deres egen undersøgelse.

Hvert kapitel er tilrettelagt til en varighed på 2 til 3 uger svarende til 10 til 15 lektioner. Opgaverne på opslagene kan vælges til og fra således at tidsrammen for arbejdet med kapitlet kan tilpasses det der er til rådighed. På modellen kan det ses, at et kapitel tager udgangspunkt i et Omdrejningspunkt, hvor elevernes undersøgelse er en central del. Nedenfor beskrives både omdrejningspunktet, og hvordan de tre didaktiske hjørnesten indrages.

Efter at have gennemførtomdrejningspunktet arbejder eleverne med aktiviteter og opgaver, hvor deres viden og færdigheder udvikles og konsolideres. Midtvejs i hvert kapitel fordyber eleverne sig i selvrettende Loop 1 opgaver på web, hvorefter evalueringerne gennemføres i Min viden 1 på et af de tre niveauer. Loop 1 og Min viden 1 er ligeledes uddybet i det efterfølgende.

Anden halvdel af kapitlet følger den samme struktur som første halvdel. Eleverne arbejder med aktiviteter og opgaver, hvorefter kapitlet afsluttes med et nyt sæt opgaver i Loop 2 og en afsluttende evaluering i Min Viden 2. Opgaverne i Loop 2 i anden del af kapitlet er differentieret på de samme tre niveauer, sådan at eleverne kan afslutte fordybelsen i kapitlet ud fra deres individuelle forståelse af det faglige indhold. I Min viden 2 arbejder eleverne videre med det produkt, de skabte i Min viden 1 og giver og modtager feedback. Pilen, der peger ud af modellen, viser overgangen til et nyt kapitel, der følger den samme struktur.

Omdrejningspunktet

Hvert kapitel indledes med et Omdrejningspunkt, der er inddelt i fire genkendelige faser. I den første fase, Introtegning, aktiveres elevernes forforståelse af kapitlets faglige indhold. I fase 2 Vores

Fase 1 afspejler især Den nysgerrige samtale, som er en af de tre didaktiske hjørnesten. Elevernes nysgerrighed vækkes i forhold til indholdet på Introtegningen, hvor elevernes opdagelser og begrundelser deles i den fælles samtale i klassen. Samtidig afspejles også Det anerkendende læringsrum og Videnskonstruktion, idet der tages udgangspunkt i elevernes umiddelbare fund på tegningen og i deres umiddelbare opfattelse af indholdet.

Fase 2 Vores undersøgelse

I fase 2 skal eleverne udføre en undersøgelse. Undersøgelsen indledes med et nøglespørgsmål, der præsenterer eleverne for den problemstilling, de skal undersøge. Nøglespørgsmålet findes på web, så det kan vises på en skærm i klassen, når elevernes undersøgelse sættes i gang. Undersøgelserne kan være formuleret som mere eller mindre åbne eller lukkede problemstillinger. Hensigten er at fokusere på den matematiske viden, der både er nødvendig for at kunne besvare dette spørgsmål, og som eleverne skal bruge i de efterfølgende opgaver i kapitlet. Det væsentlige i undersøgelsen er, at eleverne får mulighed for at arbejde eksperimenterende med ideer og løsningsforslag.

For at støtte den undersøgende proces findes der i hvert kapitel forslag til vejledende spørgsmål, som skal støtte elevernes besvarelse af nøglespørgsmålet. Spørgsmålene findes både i lærervejledningen og på det tilhørende arbejdsark. Spørgsmålene lægger op til, at eleverne kan give differentierede svar, ligesom de både kan fungere som ideer til de elever, der kan have vanskeligt ved at komme i gang, og til andre, der har brug for yderligere udfordringer. På arbejdsarket er der plads til at notere nogle af elevernes eksempler og pointer fra undersøgelsen, som efterfølgende kan indgå i den opsamlende samtale under Min rygsæk. Der kan både noteres forskellige ideer og løsningsforslag samt elevernes undren eller foreløbige forslag. Noter også elevernes navne, så de selv kan fortælle pointerne i den opsamlende samtale.

Fase 2 afspejler især Det anerkendende læringsrum, som er en af de tre didaktiske hjørnesten. Eleverne arbejder undersøgende, og der sker en vekselvirkning mellem deres egne og andres refleksioner. Undersøgelserne giver mulighed for differentiering, da de er tilrettelagt, så eleverne kan svare på baggrund af deres aktuelle viden og dermed motiveres til en nysgerrig tilgang. Samtidig vil de erfare, at de kan bidrage til at skabe viden i fællesskab med

Fase 3 afspejler særligt Den nysgerrige samtale, som er en af de tre didaktiske hjørnesten. Eleverne udveksler deres eksempler fra undersøgelsen og begrunder deres forslag. Alle elever kan deltage, fordi udgangspunktet er deres egne eksempler og forslag fra undersøgelsen. Øvelsen lægger desuden op til, at eleverne er nysgerrige efter at høre om hinandens eksempler, og at elevernes egen viden styrkes ved, at de ser og hører, hvordan andre har grebet undersøgelsen an.

Fase 3 Gi’ og ta’

I Gi’ og ta’ deler eleverne deres ideer og løsninger fra undersøgelsen med hinanden. Gennem samtale kan eleverne enten få nye ideer til løsninger, eller opdage at forskellige tilgange kan løse den samme problemstilling. For at skærpe elevernes opmærksomhed på andres ideer og løsninger skal de efterfølgende i luppen tegne og notere et eksempel, som de har fået beskrevet af en anden. Eksemplerne inddrages i den efterfølgende fælles opsamling. Under Gi’ og ta’ noteres udvalgte elevers ideer og løsningsforslag fortsat på arbejdsarket.

Gi' og ta'-aktiviteten

Fase 4 Min rygsæk

I Min rygsæk samles der op på den nye viden, som eleverne har opnået i Vores undersøgelse. I den afsluttende fase vil eleverne blive støttet i overgangen fra konkrete erfaringer til matematisk viden. For at styrke denne overgang, vises først filmene om de faglige begreber. I filmene præsenteres eleverne for de centrale begreber fra første del af kapitlet, som dannede udgangspunkt for deres undersøgelse. Efterfølgende tales der om, hvad eleverne ved om de faglige begreber. Begreberne er også vist i elevbogen.

Herefter drøftes det i klassen, hvilke faglige pointer der kan bringes med videre i rygsækken. Ideer og pointer noteres først på tavlen ved en fælles brainstorm om, hvad der kom ud af undersøgelsen. Der henvises i den forbindelse til den foregående undersøgelse og elevernes tegninger i luppen. Elevernes eksempler, som blev noteret på arbejdsarket, mens de arbejdede med Vores undersøgelse samt Gi’ og ta’-øvelsen, bringes ind i samtalen. Vær opmærksom på, at den opsamlende samtale dækker de faglige begreber, der er præsenteret i de faglige film, og at den samtidig repræsenterer en bred vifte af elevernes eksempler. Det anbefales at bruge den viden, som notaterne rummer, til at præsentere elevernes pointer i en hensigtsmæssig rækkefølge. Begynd med de mest almindelige eksempler og vent med de dybere ræsonnementer og generaliseringer. Som afslutning tegner og noterer eleverne hver især de faglige pointer, som de vil have med i rygsækken.

Fase 4 afspejler særligt Videnskonstruktion, som er en af de tre didaktiske hjørnesten. Eleverne forbinder deres erfaringer fra undersøgelsen med kapitlets faglige begreber på baggrund af en fælles klassesamtale om egne og andres eksempler og forslag. I Min rygsæk lægges der samtidig fortsat op til nysgerrighed overfor andres bidrag, når eleverne reflekterer over de matematiske pointer og sammenhænge, som er indgået i undersøgelsen.

M in rygsæk

vanskeligheder benytte de samme primitive strategier. Effektiv brug af strategier kan læres gennem undervisning. Eleverne vil ikke nødvendigvis selv forlade de primitive strategier, tællestrategierne, da de kan opleves som hurtigere, når tallene er små. Derfor lægger Reflex op til at, der undervises i strategier, så elevernes metoder kan blive mere effektive. Det har vist sig, at netop systematisk strategioplæring har en positiv indflydelse på udviklingen af matematisk kompetence. Det er med andre ord vigtigere at forstå hvad og hvordan man regner end at resultatet er korrekt.

En strategi er i matematisk forstand en teknik til at løse en opgave, og i opgaveløsning er det væsentlig at have mange forskellige strategier at trække på. Regnestrategier kan opdeles i to typer:

• Primitive tællestrategier, også kaldet backup-strategier.

• Effektive regnestrategier, også kaldet retrieval-strategier.

Primitive tællestrategier

Rygsækken i elevbogen.

Faglige begreber

De faglige begreber, der indgår i hvert kapitel, danner udgangspunkt for tilrettelæggelsen af elevernes arbejde, kapitlets organisering og evalueringen af elevernes viden. Begreberne er illustreret i elevbogen og er beskrevet i film, der findes på det tilhørende website. Filmene vises i forbindelse med opsamlingen af elevernes undersøgelser. Filmene vises desuden forud for evalueringerne i Min viden 1 og 2 for at give eleverne mulighed for at genopfriske kapitlets faglige indhold. De faglige film kan også indgå individuelt undervejs i elevernes arbejde, hvis de har brug for at repetere begrebernes indhold.

Udover faglige film findes der på reflex.alinea.dk film med spilinstruktioner, forklaringer af strategier og beskrivelser af, hvordan matematikredskaber og digitale værktøjer anvendes. Dette er angivet med et webikon i elevbogen og i side til side-vejledningen.

Regnestrategier

I arbejdet med udviklingen af strategier er elevernes forskellige bidrag vigtige. Når eleverne oplever andres løsningsmetoder, forholder de sig samtidig til deres egne. Fra forskningen ved vi at elever, der har svært ved matematik, bruger primitive tællestrategier gennem hele skoleforløbet. Mens deres jævnaldrende klassekammerater udvikler flere og smartere strategier, vil elever med

At tælle på fingre, bruge streger på et stykke papir eller andet til at tælle med er backupstrategier. Svaret kan altså ikke bare hentes fra hukommelsen, hvilket betyder, at eleven ofte finder frem til svaret på en langsom, synlig og oftest hørbar metode. Tællestrategier er basale og vigtige, men mest effektive ved små tal. Når tallene bliver større, og regnestykkerne mere komplekse er det godt at kombinere tællestrategier med hukommelsesstrategier, hvor eleverne arbejder videre fra lært viden. Mange elever udvikler ikke af sig selv regnestrategier, bl.a. fordi de føler sig trygge ved tællestrategier. Det er derfor meget vigtigt, at eleverne opfordres til at forlade tællestrategierne også selv om de oplever, at det tager længere tid, at løse opgaverne.

Eleverne skal undervises i strategier, så de ikke holder fast i primitive tællestrategier gennem hele skoleforløbet. Disse strategier belaster nemlig arbejdshukommelsen i sådan en grad, at eleverne vil miste overblikket. Når de senere i skoleforløbet møder komplicerede matematikopgaver, vil de bruge alt, deres energi på at finde svaret på en enkel opgave, hvilket vil resultere i, at de går glip af vigtig læring og dermed kommer i større og større vanskeligheder.

Effektive regnestrategier

Disse strategier er kendetegnet ved at være hurtige og effektive. Svaret hentes nærmest automatisk fra hukommelsen. Enten kender eleven svaret eller også bruges et delsvar, som hjælp til hurtigt at finde frem til svaret. I takt med at eleverne automatiserer flere talbilleder og resultater af additions- og subtraktionsstykker, som fx 10’er- og 100-venner (8 + 2 = 10 og 10 – 8 = 2 samt 80 + 20 = 100 og 100 – 80 = 20) samt de små og store pluspar (3 + 3 = 6 og 6 – 3 = 3 samt 30 + 30 = 60 og 60 – 30 = 30), vil elevernes regnestrategier blive mere og mere effektive, så der ikke skal tælles forfra hver gang, og så allerede kendt viden kan anvendes i nye sammenhænge. I Reflex arbejder eleverne med at udvikle strategier med fokus på at tilegne sig smarte regnemetoder og på at automatisere 10’er- og 100-venner, samt små og store pluspar i forbindelse med både addition og subtraktion. Eleverne skal hver især lære at se efter muligheder, for at finde venner eller pluspar, for at gøre der lettere at finde frem til en løsning. Eleverne skal afprøve forskellige strategier, og tage stilling til hvilke, der er smarte at bruge i nye sammenhænge. Når eleverne har kendskab til mange forskellige strategier, vil de kunne bruge dem fleksibelt, udvikle nye strategier og have blik for hvornår en strategi er smartere end en anden.