Love Symposium DRAFT

Lower Sixth/Year 12

SYMPOSIUM

O Tell Me The Truth About Love

Spring / Summer 2023

The Royal Society, Carlton House Terrace, London

26

Meeting on a Random Walk

Aryan, Chloe, Genevieve, Oscar

30

Love as a Drug

Rithi, Nur, Tamir, JB, Misha

34

Love & Eukaryotic Genomes

Flora, Adriana, June, Lovin

38

Fluid Dynamics & Champagne

Bea, Joey, Leela, Luke, Lydia

42

Loving Local Politics?

Chris, Elizabeth, Krish, Vivien

46

Lab-grown Diamonds

Alicia, Michel, Henry

50

The Economics of Loving Teaching

Ava, Dome, Harinee, James

hundred years ago, whilst reading Lauréamont’s 1869 Chants de Maldoror, the great Surrealist leader André Breton came across the phrase “as beautiful as a sewing machine and an umbrella on a dissection table”.

O Tell me The Truth About Love A

The Surrealists believed that chance encounters are a source both of beauty and of deeper knowledge. In their artistic, psychological, and political pursuits, they enthusiastically forced such encounters. They were, of course, especially interested in love.

Academic projects run by schools must serve the needs of students: exposure to advanced material challenges us to use knowledge in new contexts, and understand where school-level learning might be point to. The ability to collaborate with new people on difficult challenges is, of all the skills in life, perhaps the most helpful of all.

But equally, as Alastair Land once put it, education can’t all be “an endless rehash of self-consciously worthy pursuits”. Where space emerges for creativity, for the love of ideas, projects are suffused with a new energy. Colleagues from both schools spend holidays debating what overarching theme might lend itself to multidisciplinary explorations. Prestigious mentors from leading universities come on board, providing extraordinary inspiration. Preparing the questions and allocating groups is a huge labour of love. Students then throw themselves into dissecting extraordinarily complex concepts.

Indeed, it all becomes very serious, and also enormous fun.

This collection of essays is therefore quite the surreal collage. No sewing machines and no umbrellas (I think…), but instead Leukocyte Antigens, Ealing Council, sp3 hybrid orbitals, and Paradise Lost, passionately assembled on a dissecting table, and possibly even producing, in the unlikeliness of the juxtapositions, something really rather beautiful.

Ms Madeleine Copin Deputy Head (Academic)

Notting Hill & Ealing High School

An endorsement

The theme of love in all its aspects provided the focus for a remarkable symposium. The authority and sparkle with which students from Notting Hill & Ealing High School and Harrow School presented work from the length and breadth of the academic spectrum made for an exhilarating day. The talks, grouped around eleven subject areas, displayed not only a breathtaking command of the disciplines concerned but also a determination to share knowledge and enthusiasms across and beyond disciplinary boundaries. The day had been planned as “an interdisciplinary adventure”, and it fulfilled precisely that vision. Pure and applied science and medicine jostled with mathematics, law and philosophy, literary and linguistic studies, and the contemporary practicalities of politics and economics. The tone was outward-looking, and the quality of the excellent questions and strikingly composed replies that ended the day was the measure of a highly successful event.

Underlying the conception of the symposium was a belief in the importance of openness in an age in which academic disciplines, especially though not only in the sciences, can too easily become areas of expertise accessible only to specialists. The counterweight lies in communication, in the manner of the lively, informative talks we heard on 25 May. The skills required in bridging the divide between specialists and non-specialists do not come easily. They call for thoughtfulness on both sides and a keen eye for the impediments to understanding. They call, too, for the kind of cooperation and collaboration within and between groups that went into the weeks of preparation for the day. And we should never forget the contribution, during those weeks, of teachers and external advisors. Without them, none of this could have happened.

For an occasion devoted to the exchange of ideas, the gracious rooms of the Royal Society provided a setting as appropriate as it was comfortable. The society’s membership includes many of the world’s greatest scientists, as it has done since its foundation in 1660. As an elite body of some 1800 fellows and foreign members (more than eighty of them Nobel Laureates), it is unyielding in its priority of promoting scientific excellence. But it is equally mindful of a parallel mission aimed at encouraging public engagement with science. One of its most widely read journals, Notes and Records, of which I was editor some years ago, is typical of the mission in offering scholarly articles not on the achievements and debates of today but on science in human history in all periods and cultures. As part of a programme of lectures, exhibitions, and other activities open to scientists and non-scientists alike, the journal plays its part in a society proud to be a place of interaction with the world beyond its doors as well as a force for the advancement of specialized research at the highest level.

On a memorable day, many values were reaffirmed. Belief in the primacy of academic achievement went hand in hand with the importance of critical thinking and presentational skills, exemplified in two school communities, students and teachers, working together and at their very best. It was an occasion of which Notting Hill & Ealing High School and Harrow School have every reason to be proud.

Robert Fox

Emeritus Professor of the History of Science University of Oxford

The Law

To what extent is love a defence?

Jurisdictional

differences in ‘crimes of passion’ and their public policy interactions.

Acrime of passion entails a sudden loss of control with an imminent reaction to a provocation; to an extent, there must be an impairment of judgement which enables the provoked to react imminently. Concerning crimes of passion, in order to use love as a defence, the qualifying trigger must provoke a loss of control related to love; anything short of a complete loss of control due to love would be nullified. Here, the separation between love and sexual possessiveness is crucial in determining whether a crime is manslaughter or murder. This begs the question; how far can a situation be extended before it becomes a qualifying trigger, and can love carry as defence in court?

Evangeline (NHEHS)

James (HARROW)

James (HARROW)

Shobhitha (NHEHS)

Crimes of passion serve to eliminate the incriminating element of ‘premeditation’

Crimes of passion are typically considered as concepts within law with difficult parameters to enforce - the boundaries of crime committed as a result of compromised judgement due

to intense emotion are complex and laboriously defined by legal criterion. However, though the reasoning of crimes of passion tends to rely on the fickle nature of emotion, thus rendering the defendant’s capacity diminished, the lawful boundaries are evident. Crimes of passion serve to eliminate the incriminating element of ‘premeditation’, in which the defendant argues that they acted immediately upon the ‘rise of passion’ without the time for ‘a cooling of the blood’ (Legal Dictionary | Law. com). Thus the parameters of intense emotion, beyond rationale and reason, are established, alongside the immediacy of incriminating action, following the rise in emotion. For a legitimate case of crime of passion, the defendant must have also responded directly to a provocation, then leading to the sharp rise in emotion and subsequently the crime. Provocation is therefore essential in serving as partial defence for a genuine crime of passion, as the defendant must have a

qualifying trigger for the crime committed – under UK law, this rejects revenge as reasonable cause and similarly “loss of control triggered by sexual infidelity, cannot, on its own, qualify as a trigger” (‘R v. Clinton,’ 2012). Vitally, the nature of method in committing the act does not change the legal consequences, as intention supporting the crime is consistently through crimes of passion a “loss of control” rather than a specific extremity of action, and focuses on the provocation “[inflaming] the passions of a reasonable person” (Wex, US Law). It was similarly decided that any crime committed after the perpetrator could have had a reasonable amount of time to reflect on their action was not subject to the defence: “the loss of control need not be sudden, but it must have been lost” (‘R v. Clinton,’ 2012), implying that the driving force is emotion rather than general immediacy.

Through our own discussions, we concluded that love was a “deeply rooted attachment for a person or object so strong that it causes you to overcome rational self-interest.” Of course, many crimes of passion are likely to take place when someone feels a sense of betrayal due to infidelity. So it may seem illogical that English law does not allow for it as a crime of passion and that we agreed with this. Our first problem was that allowing crimes of passion in relation to infidelity has a disproportionate impact on women and can lead to huge problems in relation to domestic violence. Alongside this, if provisions for defending murder due to infidelity are allowed, it could pose a serious threat to personal freedoms. The ethics of infidelity are not questionable, but it should not be within the reach of a government’s policy making, and it certainly should not be permissible to murder someone on the basis of infidelity if it was decriminalised in 1857. Allowing people to punish others unimpeded by the law for something the law does not itself criminalise would be absurd.

Another problem with the idea is the misconception that infidelity and adultery are identical. Infidelity is not limited to marriage and includes both emotional and sexual betrayal. If there is no legal recognition of a relationship, how can we bind people to non-existent terms of relationships to which they have not legally acknowledged their commitment? What would be even more ludicrous would be permitting the punishment of partners who violate these non-existent terms and not holding the perpetrators accountable for their crimes. In the judgement of R v. Clinton, the judge cited R v. Stingel, 1990, where a jealous stalker killed his quarry for having relations with someone else. They were not in a relationship together and whether they were in a relationship should not change the outcome of any criminal proceedings. In the words of Mr Birnbaum, “Why should the law exclude one kind of betrayal by a lover but not another?”

against murder. Prior to 1975, the French Penal Code of 1810 stated in article 324 that “in the case of adultery, murder committed upon the wife as well as upon her accomplice, at the moment when the husband shall have caught them in the fact, in the house where the husband and wife dwell, is excusable.” This is significant as it suggests that it is not love that is the defence, but the purely disrespectful nature of the location. In theory, this legislation was to provide the convicted with a one-to-five-year prison sentence, however many domestic violence cases ended in acquittal for the accused. France’s modern stance on crimes of passion is harsh in the sense that love is not used as a valid defence and other factors of the case, like mens rea and provocation are generally more important.

The nature of method in committing the act does not change the legal consequences, as intention supporting the crime is consistently through crimes of passion a ‘loss of control’

This is also the general consensus in modern Western cultures such as Australia. In Brisbane’s case of R v. Koani, Christopher Koani was sentenced to life for the murder of Natalie Leaney, his girlfriend. Koani had initially pleaded guilty to manslaughter, however, this plea was rejected. Koani’s defence of love was

There is also international provision of legislation for cases that involve crimes of passion; however, the countries that even consider entertaining the philosophy that love is an acceptable defence are all Western cultured. The most notable of examples in which crimes of passion have affected foreign jurisdiction is in France, following this theme. In the past, France was notorious for supporting crimes of passion as a defence

invalid as it demonstrated that the crime was committed out of sexual possessiveness/jealousy; he was then unable to be convicted of a crime of passion and manslaughter and instead was charged with murder. This exemplifies Australia’s rejection of love as a defence and their prioritisation of other factors that may contribute to a crime, and adds to the general feel that love is not a defence.

When debating if love is truly a defence, a crucial consideration is the choice between including the psychological factors of the appellant and disregarding them. If someone is non compos mentis, they are unable to have a clear sense of control over their mind and clear intent. In English law, if a person of the same “sex, age, with a normal degree of tolerance and self restraint, and in the same circumstances” of the appellant were to react in a similar way, the qualifying

When debating if love is truly a defence, a crucial consideration is the choice between including the psychological factors of the appellant and disregarding them.

trigger is justified and the appellant is of sound mind. If the appellant is under 18 or suffering from mental illness, love may not qualify as a defence. As an adolescent, an underdeveloped prefrontal cortex, which does not fully develop until the age of 25, implies that an appellant’s sense of impulse-control may be ineffective. While they can use a lack of the ability to process and control their reaction to certain provocations as a defence, this also nullifies their ability to use love as a defence, as adolescents cannot adequately comprehend the concept of love or justify love to be the catalyst of their actions.

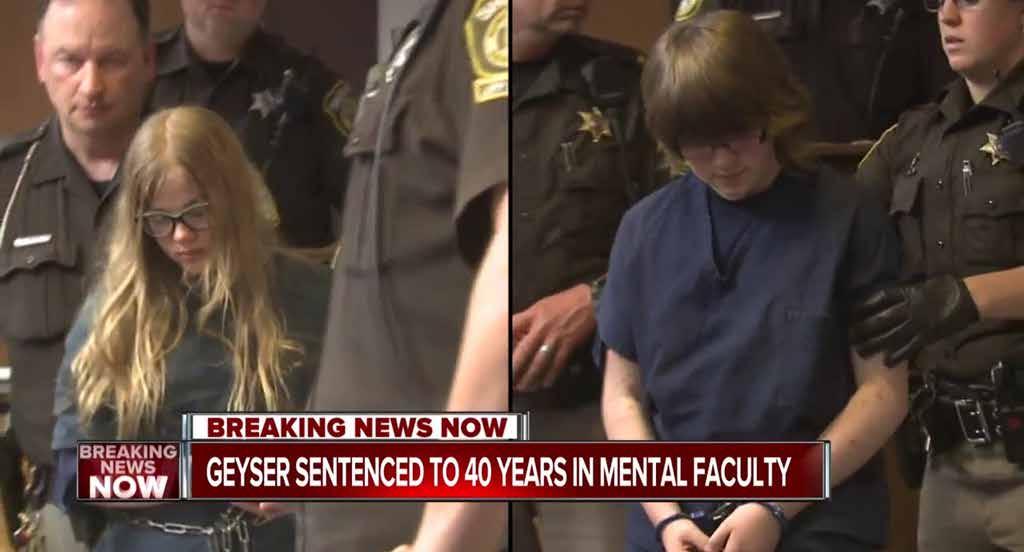
In 2014, Anissa Weier and Morgan Geyser lured Payton Leutner into a forest and proceeded to stab her 19 times to ‘appease’ the fictional character Slender Man. Later, Geyser was diagnosed with early-onset

childhood schizophrenia and, three years later, found not guilty by mental disease or defect. She could not be charged with a crime of passion as her rational thinking was already compromised meaning mental illness was the trigger for her actions. Consequently, crimes of passion can only be limited to those of sound mind as mental illness and other psychological factors, such as love, prevent the perpetrator from having sufficient control over their impulses. This makes it virtually impossible for them to lose said control, or comprehend whether love is the trigger for their criminal impulses.

Therefore we find that the defendant must prove that they possessed a reasonable qualifying trigger, not including revenge or infidelity, and the defence relies on the defendant being compos mentis, thus limiting its usages and applications. Subsequently, love may only serve as a defence to a limited extent, as the abuse of crimes of passion as a partial defence may be the deciding factor of justice or fundamental grievance.

Milton & Marriage

What did John Milton truly believe about marriage?

When evaluating the question of what John Milton truly believed about marriage, it is important to explore the historical context in which Milton lived, as well as his own experience with this form of legal partnership.

As a writer of poetry and prose, John Milton’s work extended over three key periods in England’s history: the English Civil War (1642-1648), the Commonwealth and Protectorate period (1649-1660) and finally the Restoration, from 1660 onwards. Having been raised in an upper-middleclass, Puritan household, it is highly probable that Milton’s view on marriage would have had Puritan beliefs at its core. To an extent, this can be said to be true. A key term in Puritan vocabulary at the time was that of “helpmate” which is also seen in Milton’s most famous works, such as Paradise Lost (1667) and The Doctrine and Discipline of Divorce (1643). The word “helpmate” suggests that Milton strongly believed in the

Andrew (Harrow)

Ash (NHEHS)

Natasha (NHEHS)

Sebastian (Harrow)

importance of companionship, equality and mutual respect in marriage. Though at first glance, Milton appears to agree with the Puritan view that the main objective of marriage should be to achieve mutual comfort and support, the viewpoints diverge on the subject of divorce. John Milton married three times, and during his first marriage to Mary Powell in 1642, it is documented that the couple entered a period of separation for three years. Though formal separation never took place, Milton during this period wrote the aforementioned The Doctrine and Discipline of Divorce (1643), in which he espoused the view that if marriage’s purpose of providing mutual comfort could not be achieved, a divorce was permissible.

Milton’s focus on the distinctiveness of marriages is unsurprising given that his writing came after the Protestant Reformation. In the aftermath of the Reformation, the move away from a predominantly Catholic outlook on life led to Milton’s increased focus on the individual and unique

identities. In order to analyse further the context in which Milton’s views of marriage were formed, it is important also to establish the extent to which Milton’s views contrasted with the increasing Puritan viewpoint of the time. During the mid-17th century, the large majority of Puritans and Catholics oversimplified marriage, assigning roles in the companionship to man and woman on the basis of their sex. Milton saw this viewpoint to be irreconcilable, neglecting the view that marriage was necessary for man and woman to avoid sin. Instead Milton, rather radically for his time, argued that promiscuity, infidelity, disease and prostitution could be curbed if the laws on divorce were reformed.

John Milton’s poetry gives us an insight into his beliefs on what he believed constituted a marriage and what made a marriage strong. As one of the first people to argue that divorce should be allowed on the grounds of spousal incompatibility, it is important to look at Milton’s poetry to question the verisimilitude of his work in relation to his beliefs and the template he lays out, especially in Paradise Lost, for what a perfect marriage should be.

in congruence with each other: “Each with thir kinde, lion with lioness.” He claims that “bird and beast, or fish and fowle” (VIII, 393-395) cannot coexist together in a relationship and thus he needs a partner of the same species. God grants Adam his request by creating another being (Eve) from Adam’s rib. In Book VIII Milton agrees with the traditional Christian view of the time of marriage being ordained by God, as he grants Adam a spouse in Eve. The implication from this creation story is that spouses should remain with each other through their whole life, contrasting with his views in the Divorce Tracts, which also include The Judgment of Martin Bucer, Tetrachordon and Colasterion.

Throughout Paradise Lost, Milton makes it clear that marriage, with both religious and emotional unity is a holy and beneficial thing for mankind.

Milton’s most famous poetic work is Paradise Lost: an epic that tells the story of Adam and Eve’s journey from creation to expulsion from the Garden of Eden, and their temptation by Satan. Published in 1667, Paradise Lost consists of ten books written in blank verse.

Throughout Paradise Lost, Milton makes it clear that marriage, with both religious and emotional unity, is a holy and beneficial thing for mankind. In Book VIII Adam begs God for a partner in an almost comedic scene as he lists animals that live

Sonnet 23 was first published in 1673 and was written by Milton after the death of his second wife Katherine Woodcock in 1657. In this sonnet, Milton talks about seeing his “late espoused Saint brought to me […] from the grave.” The poet tries to embrace his dead wife, but he wakes before he can wrap his arms around her. Judging by the fact Milton deliberately chose to write a Sonnet about his dead second wife returning from the grave, we can safely assume this sonnet supports the views he expresses in the Divorce Tracts, as he writes about Woodcock with emotion and passion even though she wasn’t his first wife. If Milton didn’t really believe in what he claims in the Divorce Tracts, he would not have written this deeply emotional sonnet.

John Milton, outside of the poetry he is best known for, also published several tracts on religion, the church and other contemporary matters. Of these tracts, a number of them focus on marriage and divorce, namely The Doctrine of Discipline

and Divorce (1st ed. 1643, 2nd ed. 1644), The Judgement of Martin Bucer Concerning Divorce (1644), Tetrachordon (1645) and Colasterion (1645), all of which were written during the breakdown of his first marriage. To attempt to distil Milton’s views on marriage, he argued that for a marriage to be true, it must be a marriage of minds, not one borne out of physical desire and that, in the event of a union between two incompatible minds, a no-fault divorce is permissible in the eyes of God.

In The Doctrine of Discipline and Divorce, Milton wrote that “in God’s intention, a meet and happy conversation is the chiefest and noblest end of marriage.” Milton reasoned that as God created Eve to remedy the “solitarines” of Adam, and thus woman to remedy that of man, God intended marriage to provide mental companionship, and not to have a purely physical basis. Milton wrote that “a marriage can be no marriage whereto the most honest end is wanting”; a marriage without “happy conversation” is not a marriage at all, at least not a marriage as designed by God. That is not to say that marriage has no physical element, but that without a mental union “all corporall delight will soon become unsavoury and contemptible”;

this requirement of mental compatibility in the marriage is in fact a “provision against the impediment of carnall performance”.

A true marriage, to Milton, is beyond law and exists within God.

Moreover, in Tetrachordon, Milton makes the point that marriage as it is in law, is a “civill and ordain’d relation”, not a natural one. Adam and Eve were joined in a “unity of mind and heart”; a marriage of compatible souls that only death could separate. A true marriage, to Milton, is beyond law and exists within God. Considering that “a marriage can be no marriage whereto the most honest end is wanting”, a legal marriage between two incompatible people is just that: legal, not holy. If the marriage is not a true marriage in God, but purely one in law, then divorce should be permissible.

Indeed, in Considerations Touching the Likeliest Means to Remove Hirelings Out of the Church (1659), Milton elaborated on this sentiment, having written that he

found “no ground in scripture” that marriage was not holy without a priest’s benediction, and that marriage is a “household contract, a thing indifferent and free to the whole race of mankind”, and “not therefore invalid or unholy without a minister”.

But then, can divorce from incompatibility not be avoided by simply getting to know one’s fiancé? The Doctrine of Disciple and Divorce accounts for this argument: the “bashful mutenes of a virgin” may hide a

“naturall sloth which is really unfit for conversation”. That is to say that, until marriage, the true nature of one’s partner can remain hidden. Therefore, Milton argued that “one forbidd’n to divorce, is in effect, forbidd’n to marry”, as an unbreakable marriage vow may end up becoming a trap.

In both Milton’s poetic and prosaic works, the message that, for a marriage to succeed, it must be between two alike souls, is repeated over and over again. At first glance, Milton’s traditional upbringing may contradict the idea that divorce can be sanctioned under terms of mutual incompatibility. This influence can be seen through his lexical choices, for instance the Puritan concept of the aforementioned “helpmate”, allowing the reader to denote a foundational belief in traditional partnership forged in equality. Through deeper

exploration however, Milton’s own tumultuous romantic life no doubt influenced his work to an equal extent, shown in his more personal poetry and contemporary tracts. Passionate odes to his second marriage become key in understanding his belief in partnerships grounded in “happy conversation” and mental attraction aside from the physical. This is expressed in key texts such as The Doctrine of Discipline and Divorce and Tetrachordon. Thus, whether it be a result of a timely reformation of religious tradition, or simply his personal experiences of love and loss, Milton shows a resounding belief in the legitimacy of divorce. Yet, most crucially, this divorce must specifically involve a break from his definition of marriage within the confines of legality, and removed from genuine godly union, which remains sanctified.

Hall’s Marriage Theorem

A proof, and some applications.

1 Introduction

Hall’s Marriage Theorem is a result in combinatorics. It can be stated in several equivalent forms, the most common of which is about finding a matching in bipartite graphs. The name comes from an application to matchmaking: given a list of potential matches among an equal number of brides and grooms, the theorem gives a necessary and sufficient condition on the list for everyone to be married to an agreeable match. The theorem is equivalent to several celebrated results in combinatorics, including Dilworth’s theorem. All the equivalent theorems tend to have a similar flavour in saying that an obvious necessary condition is in fact sufficient: they say that in order to guarantee that some structure exists, it’s enough to check that there’s no obvious reason it shouldn’t.

We’ll first explain the theorem and some applications before giving the proof.

2 Bipartite graphs and the statement of the theorem

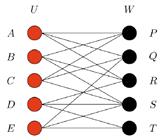
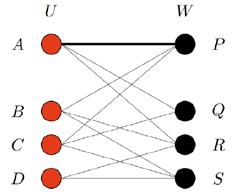
A bipartite graph G is a structure made of two sets of vertices joined by edges which link one vertex from each set. We will formally call the vertex sets U and W and informally call them the ‘left set’ and ‘right set’. One bipartite graph is shown in Figure 1 below. The left set has 3 vertices, the right set has 4 vertices, and there are 6 edges linking them.

In the traditional ‘marriage’ interpretation, the left set is a set of men and the right set is a set of women; each edge pairs a man and a woman who could happily marry (for short, we’ll say that the man and woman like each other). Thus in Figure 1, every woman likes man A, whereas only woman X likes man B, and man D doesn’t like anyone.

A matching is a way of pairing up all the men and women in a bipartite graph in happy marriages.[3] This is impossible in Figure 1 for several reasons: first, there are more men than women; second, man D cannot be paired with anyone; and third, both man B and man C only like woman X, and they cannot both marry her.

Hall’s Marrage Theorem will say that if there aren’t obvious problems like this, then a matching is possible.

2.1 Hall’s condition

First, the theorem. We write it formally and explain it intuitively afterwards:

Mark (Harrow)

Derja (NHEHS)

Hall’s Marriage Theorem: Let G be a bipartite graph with left set U and right set W, with |U| = |W| = n, say. A necessary and sufficient condition for G to have a matching is given by Hall’s condition: for every subset X ⊂ U, we must have |NG(X)| ≥ |X|.

In this statement, |X| denotes the size of the set X, so by |U| = |W| we mean that the left set and right set have the same size (ie there are an equal number n of men and women). By NG(X) we mean the set of neighbours of X in the graph G - that is, all the vertices that are joined by an edge to some element of X. In particular, if X is part of the left set (a set of men), then NG(X) is part of the right set (a set of women). So we can restate the theorem:

Hall’s Marriage Theorem, intuitive version: Suppose we have a set of n men and a set of n women whom we want to pair into n couples. A necessary and sufficient condition is Hall’s condition: for every k men, there must be at least k women they like between them.

2.2 Examples

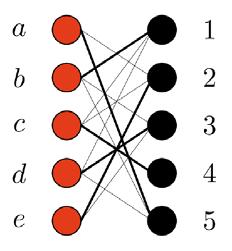
We give an example of a graph where Hall’s condition fails, so there is no matching, and a graph where Hall’s condition holds, so there is a matching. Example 1: Consider the bipartite graph of Figure 2.

Figure 2: A bipartite graph without a matching

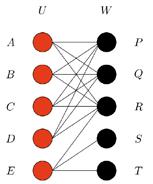
In this graph, consider the subset {A,B,C,D} of the left set. This is a set of 4 men who only like 3 women (P,Q and R) between them. This means that a matching is impossible, and {A,B,C,D} is the set X in Hall’s condition (whereas NG(X) = {P,Q,R}).

You might have noticed another reason that this graph doesn’t have a matching: namely, the women S and T both only like man E. This isn’t covered by Hall’s condition, since the condition is asymmetric: it says that every k men must like at least k women between them, and doesn’t require anything from the women. It’s a nice and surprising fact that if the condition holds for the men, then an equivalent condition must hold for the women automatically. You might want to think about how the sets {A,B,C,D} of men and {S,T} of women are related, and so deduce Hall’s condition for women as a consequence of Hall’s condition for men.

Figure 1: A bipartite graph

Example 2: Instead, consider the bipartite graph of Figure 3.

We check that Hall’s condition holds for this graph; that is, we check that every k men (elements of the left set) like at least k women (elements of the right set) between them. In principle, there are 25 subsets to check but we can avoid checking every case by noticing that each man likes 3 women. This means that the condition definitely holds for k = 1,2,3, and it’s also true for k = 5 (the five men like five women between them) so we just need to check for k = 4. The only way that 4 men could like fewer than 4 women is if all 4 like the same three women, which doesn’t happen (eg as each woman only likes 3 men). This means that we’ve checked all cases and Hall’s condition holds, so a matching must exist even though we haven’t found one yet. One possible matching is shown in Figure 4.

Some people state Hall’s Marriage Theorem to allow cases where there are fewer men than women, where a matching marries all the men (and leaves some women left over). They may also allow infinite sets of men and women. For simplicity, we will work with the same (finite) number of men and women. The variants tend to be easy to prove given our standard version.

3 Applications of matchings

of S. Note that if instead, we try to pick 2 from the first set and 3 from the second set, then there is no choice of element from the third set that leads to a transversal - we have already picked both of its elements. Consider instead another

S′ = {s1,s2,s3,s4} with

• s′ 1 = {1,2,3,4}

• s′ 2 = {3,4}

• s′ 3 = {3}

• s′ 4 = {4}

There does not exist a valid transversal in the family S′. To see this, consider the subfamily

R = {s′2, s′3, s′4}. There are 3 elements of R, but between them they only contain two elements of {1,2,3,4}, so we cannot choose a different member of each set.

It’s easy to represent the problem of finding a transversal using bipartite graphs.

Hall’s Marriage Theorem has various applications in different areas of mathematics, computer science, combinatorics and graph theory, with links to society more generally. Here we give an overview of some of the significant applications and related problems.

3.1 Combinatorics

Here is an equivalent statement of Hall’s Marriage Theorem which doesn’t use the language of graph theory. Let S be a family of n finite sets and let X = {x1,x2,...,xn} be its union. Here elements in S can be repeated. A transversal T is defined as a subset of X that can be obtained by choosing a distinct element from each set in S. This can be formally represented by an injective function f : S → X such that f(T) ∈ T for each T ∈ S.[5]

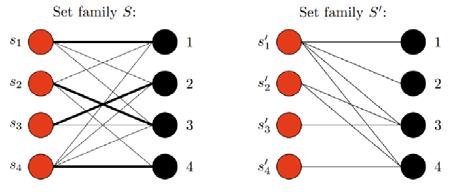
As an example: suppose that

X = {1,2,3,4}, and S = {s1,s2,s3,s4} where:

• s1 = {1,2,3}

• s2 = {1,3,4}

• s3 = {2,3}

• s4 = {1,2,3,4}

A transversal (1,3,2,4) can be generated by picking 1 from s1 (the first set), 3 from s2 (the second set), 2 from s3 (the third set), and 4 from s4 (the fourth set). Other transversals (1,4,2,3) and (1,4,3,2) could also be generated by picking the elements from their corresponding subsets

We use S to label the left set, and we use X to label the right set, with an edge showing which elements of S contain which elements of X. Figure 5 draws these bipartite graphs for the two set families of Figure 5.

In Figure 5, the transversal (1,3,2,4) for S is drawn as a matching with thick lines. There is no matching for S′ because the three elements of the left set have between them only 2 neighbours in the right set. This violates Hall’s condition. Notice that this argument is just a rephrasing of our earlier argument for S′ not having a transversal. Similar rephrasing lets us rephrase the theorem:

Hall’s Marriage Theorem, transversal version If S is a family of n sets whose elements are drawn from X = {x1,x2,...,xn}, then a necessary and sufficient condition for S to have a transversal is Hall’s condition: every subfamily R of S must contain at least as many different members as its number of sets. Formally,

3.2 The Stable Marriage Problem

The Stable Marriage Problem is a strengthening of Hall’s Marrige Theorem that allows the participants to have ranked preferences. The problem is stated as follows:

Given n men and n women, suppose that each person ranks all members of the other gender in order of preference. We seek to find a set of n marriages that is stable, meaning that there’s no pair of a man and woman who would both prefer to be with each other rather than being with their existing partner. For example, if all participants agree on preference, a stable matching would pair the two most attractive people together, then the next two most attractive, and so on.

Figure 3: A bipartite graph with a matching

Figure 4: One example of a matching from Figure 3

Figure 5: Bipartite graphs corresponding to set families

Techniques similar to Hall’s Marriage Theorem can be used to show that a stable matching always exist; the many algorithms for finding a solution to the stable marriage problem have applications to the other matching problems described in this article.

3.3 Network Flow

A large-scale application practical application of matchings in bipartite graphs comes from the Internet and network flows. In this context, the left set of the graph is a set of Internet users, and the right set is a set of distributed servers. Edges link users to servers that are closer to them, and so can give a faster response time. (In practice, a server can handle multiple users so we could make several different vertices for the different connections to one server). Hall’s Marriage Theorem can be used to check if users can be matched to servers. If it’s not possible to find a matching, we could modify the network by tolerating slower response times, which would add edges to the bipartite graph and so would make a matching more likely to exist. Content delivery networks that distribute much of the world’s content and services use load balancers to solve this large and complex stable marriage problem. By finding optimal matches between users and servers many times a minute, they enable billions of users to be matched up with their respective servers that can provide the requested web pages, videos, or other services.

3.4 Large-scale Assignments

Matching in bipartite graphs also applies in many more situations, whre different people must be assigned different objects. A common example is the assignment of graduating medical students to their first hospital appointments for their residency. Similary, admitting students to various colleges, assigning students to their preferred classes, and assigning workers to jobs in a country can all be represented with bipartite graphs. There are also economic applications like stable resource allocations and market designs. Many of these circumstances have nuances not captured by the simple mathematical model which means that research in this area is ongoing.

3.5 Latin squares

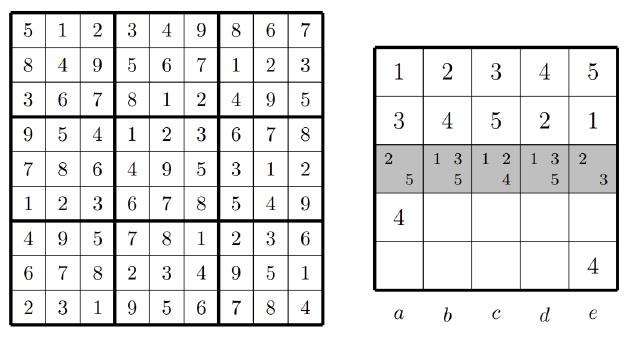
We finish with an elegant example of Hall’s Marriage Theorem in its purest form. A Latin square is an n×n array filled with n different symbols such that each symbol occurs exactly once in every row and exactly once in every column. Puzzles like Sudoku are based on Latin squares.

The left of Figure 6 shows a 9 × 9 Latin square which is the solution to a sudoku puzzle [4] (so as well as being a Latin square, it satisfies an extra rule about 3 × 3 boxes). The right of Figure 6 shows a partially filled 5 × 5 Latin square, where the top two rows have been filled, as well as two extra digits (both 4). In the middle row (shaded), the possible digits in each cell have been written in using small numbers. For example, the cell in column a could potentially contain either 2 or 5 - it could not contain 1,3,or 4, because those are already in the column. (We don’t know without trying it whether the options 2 and 5 can lead to a complete Latin square; they’re just the options that aren’t obviously impossible).

Let’s say we want to continue the 5×5 Latin square by putting numbers in the shaded row. We can represent this task as a bipartite graph: the left set will be the cells of the row, and the right set will be the numbers {1,2,3,4,5}. Edges will link cells to numbers that could go in them. This is shown in Figure 7, along with one matching for this bipartite graph.

In this case, a matching did exist, and we could fill in at the least the next row of

the grid consistently (you can check that the matching suggested extends to a full Latin square). It is not too hard to use Hall’s theorem to prove the following result: Theorem: Suppose we are given a partially filled n × n Latin square, where the first k rows are completely filled and the remaining n − k rows are empty, such that no symbol repeats in a row or a column. Then it’s always possible to complete the grid to an n × n Latin square.

This is a surprising result: if you’ve ever made a mistake in a Sudoku puzzle, you’ll know that it’s possible for a grid to look like it could give a Latin square, but then fail after many deductions. This theorem says that if the given digits in a Latin square are in a nice pattern (they fill up entire rows), then there can’t be any subtle reasons a Latin square is impossible - if it isn’t obviously impossible to make a Latin square, then a Latin square can be found. We notice how similar this is to Hall’s theorem, which says that if a matching isn’t obviously impossible, then a matching can be found.

Sudoku is also a good motivator for the proof of Hall’s theorem, which we’ll conclude with in the next section. When solving a Sudoku, you normally start with the most constrained options (eg a number that can only go in one place in a row). In proving Hall’s theorem, we’ll also find the most constrained cases let us make the most deductions, and that’s where we start in building a possible matching.

4 Proving Hall’s Marriage Theorem

Our proof of Hall’s Marriage Theorem will be structured as a proof by induction. Induction is a technique for structuring mathematical arguments, which is used when we want to prove a statement for large numbers by using the result for smaller numbers. This is sensible for Hall’s theorem: if we want to find a matching for 10 men and 10 women, we could start by marrying some couple, and then looking at the remaining 9 men and

Figure 7: The bipartite graph for a row of a Latin square

Figure 6: Examples of Latin squares

women. If we can choose the first couple cleverly so that Hall’s condition holds for the remaining 9 couples, and if we’ve already proved the result for 9 men and 9 women, we’ll be done.

This example motivates the structure of an induction. First, we’ll prove the base case: that is, we prove the theorem for 1 man and 1 woman. Next, we’ll use this to get the result for bigger numbers: pick some number k where we know that the theorem is true for up to k men and women. We’ll prove the theorem for k + 1 men and women, using the cases we already know are true. This will complete the proof for all numbers of men and women: since we know it’s true for k = 1, it’s true for k = 2; then, since it’s true for k = 2, it’s true for k = 3; and so on forever.

4.1 Setting up the proof

Let G be a bipartite graph. Let its left set be U and let its right set be V ; we’ll also refer to U as the set of men, and V as the set of women. Hall’s Marriage Theorem is an if-and-only-if statement so we need to prove an implication in both directions. One of these implications is that if there is a matching, then Hall’s condition holds: as we’ve remarked, this is almost obvious (if a complete matching is possible, then certainly any number of men must like at least as many women between them). The difficult direction is showing that if Hall’s condition holds, then a matching is possible.

The base case of our induction will be when |U| = |V | = 1. That is, there is one man and one woman; by Hall’s condition, they must like each other, so can be married.

We now turn to the inductive step. So take |U| = |V | = k + 1. That is, we have

k +1 men and k +1 women whose preferences satisfy Hall’s condition. We assume the inductive hypothesis that any smaller group of men and women who satisfy Hall’s condition can be married. The clever idea of the proof is to split into two cases depending on how restricted the graph is. If there are lots of edges (so there are lots of possible marriages) then we will have freedom to marry any two people and there will still be enough possibilities left for Hall’s condition to hold on the remainder. If on the other hand there are fewer edges - say 3 men who only like 3 women between them - then we can use this extra structure to deduce what a matching must look like. We do these cases in detail now.

The easy case: suppose that for every subset X ⊂ U with X ≠ U, we have that |X| < |NG(X)|. That is, every proper subset of l men likes more than l women between them: every man

likes at least 2 women, every 2 men like at least 3 women between them, and so on. One such example with k+1 = 4 men is depicted in Figure 8.

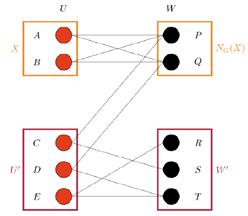
In this case, we start by marrying any man and woman who like each other

U′ with the remaining women W′. This is illustrated in Figure 9.

Let’s show how to find a matching on this graph using the inductive hypothesis. First consider the bipartite graph with vertex sets X and NG(X); Hall’s condition definitely holds for this graph (if it failed, it would fail for the whole graph with sets U and W). So we can definitely match the l men in subset X with l women.

It remains to show that Hall’s condition holds for the graph with vertex sets U′ and W′. This is harder, because some of the women that are liked by men in U′ have already been married to men in X, and so there are fewer options. For example, in Figure 9, C liked both P and S, but P was married to A in the first step, so C now only has one option - which is only just enough.

(we’ll call them A and P, like in the picture). Looking at the unmarried people, we have a bipartite graph with k people, which means that our inductive hypothesis applies: we can find a matching so long as Hall’s condition holds for this new bipartite graph. But this is easy to check: consider any set X of l men. Before P was married, they liked more than l women between them - that is, they liked at least l + 1 women. Now P is married, she is removed from the set NG(X) of women they like, but that still leaves l women. This means that any l men like at least l women between them, Hall’s condition applies for the smaller graph, and we can get a total matching.

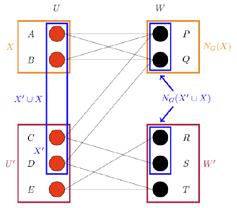
The hard case: if we’re not in the easy case, there is some subset X ⊂ U (with X ≠ U) such that |X| = |NG(X)|. That is, there is a set of l particular men who like precisely l women between them. In order to find a matching, the only thing we can hope to do is to match X with NG(X), and match the remaining men

So let X′ be a subset of U′ of size m, say. We want to show that the m men of X′ like at least m women between them. The trick here is to apply Hall’s condition not to X′ alone, but to X′∪X as pictured in Figure 10. This is a set of l +m men who like at least l +m women between them, by Hall’s condition. Of these l + m women, only l of them are liked by the fussy men in subset X (that’s how we chose X). So the remaining women in NG(X′∪ X) must be liked by men in X′. There are at least m of these women, and they’re in W′ not NG(X), so Hall’s condition holds - the m men of X′ like at least m women. This means (by induction) that the bipartite graph with parts U′ and W′ also has a matching - we can match the remaining men to the remaining women and we’re done.

5 Algorithms and final thoughts

This completes the proof of Hall’s Marriage Theorem. Although the result is mathematically satisfying, it can be hard to check in practice. In fact, Hall’s condition requires checking every subset of a vertex set, which is an exponentially growing number of subsets. Also, the theorem alone

Figure 8: An illustration of the easy case

Figure 9: An illustration of the hard case

Figure 10: The strategy for the hard case

doesn’t tell you how to find a matching; it just guarantees that one exists. There are algorithms for finding explicit matchings which work in O(n √n) time, much faster than exponential, but these seem to require knowledge of Hall’s theorem to prove that the algorithm will terminate.

In conclusion, Hall’s Marriage Theorem is a powerful tool that has numerous applications in various fields, including combinatorics, graph theory, and computer

science. The theorem provides a sufficient condition for the existence of a perfect matching in a bipartite graph, which has important implications for solving many realworld problems, such as matching medical residents to hospitals, assigning servers to tasks, and optimizing network flows. Moreover, Hall’s Marriage Theorem can be used in conjunction with other mathematical concepts, such as Latin squares, to develop efficient algorithms for large-

scale assignments. Overall, Hall’s Marriage Theorem remains an important area of active research and has the potential to drive further innovation in many fields.

We are deeply grateful to Dr Richard Freeland for his support in preparing this article for publication.

Thank you!

Audience feedback

“Confident presentation style highlighting cultural differences”

“Excellent research evident with strong use of examples”

“Successfully navigated the challenge of being the first presenter”

“Skillful balance in presentation, walking a fine line effectively”

“Engaging flow with a relaxed delivery, minimal reliance on notes “

“Enthusiastic and passionate approach to the subject”

“Effective use of humor to enhance understanding and engagement”

“Diverse collection of thoughts and perspectives explored”

Presenters’ advice for future teams

“Practise in front of a large group to alleviate nervousness”

“Ensure each speaker receives equal time at the podium”

“Foster audience engagement by posing questions during the presentation”

“Refrain from reading directly from notes; engage with the audience”

“Enhance clarity by breaking down complex ideas into understandable phrasing.”

“Ensure a moderate speaking pace to enhance understanding.”

“Include more illustrations on slides for better comprehension.”

“Move away from the lectern but avoid standing in front of the screen.”

Linguistics

To what extent is the English verb love just a stronger form of the verb like?

The earliest ancestor of the English word ‘love’ is the Indo-European root ‘Leubh’, which is most accurately translated as ‘to care’ or ‘to desire’. Since then, the definition of the word has gone through various transformations. Initially, according to the Bloomsbury Dictionary of Word Origins, the word ‘love’ meant ‘find pleasing’. This resembles the current definition of the word ‘like’: to find somebody or something pleasant, attractive or of a good enough standard. Over time, the definition of ‘love’ became associated with the concepts of ‘praise’ and ‘trust’. In a way, this etymology reflects the way we feel love. It is initially a feeling of pleasure, admiring another person; similar to just ‘liking’ someone. However, as the bond becomes stronger, being in love entails much more than that. It is a fusion of

Bronwen (NHEHS)

Florence (NHEHS)

Melvin (Harrow)

Ollie (Harrow)

passion, devotion, trust, and a myriad of emotions which make up a feeling that is not conveyed through ‘like’ in the way that it is with ‘love’.

Over time, the definition of ‘love’ became associated with the concepts of ‘praise’ and ‘trust’. In a way, this etymology reflects the way we feel love.

The strength of the words ‘like’ and ‘love’ is entirely dependent on the context in which they are used. Whilst it may at first seem bizarre to suggest that ‘like’ could convey the same emotion as ‘love’, pragmatics allows us to understand how context plays a large role in conversations. Pragmatics is the contribution of context to conversations and understanding how the unspoken parts and relations in a conversation contribute to the overall meaning. The inferences of ‘like’ and ‘love’ are dependent on the situation and the same word can convey different meanings when used in different contexts.

For example:

“Does Eve love Adam?”

“Eve likes Adam.”

In this example a scale is formed between ‘like’ and ‘love’ and the implicature is that Eve likes but does not love Adam. Evidently here ‘love’ is a stronger form of the verb ‘like’.

On the other hand, this example demonstrates that this is not always the case:

“Do you like Adam?”

“Yes.”

From this response the person asking the question may infer that the speaker does not love Adam. However, the speaker may love them but not think saying ‘love’ was appropriate in the context of the conversation.

Language philosopher Grice created four maxims which people implicitly rely on when communicating. In this example, replying that you ‘love’ them, after only having been asked if you ‘like’ them, is not relevant to the conversation, breaking Grice’s maxim of relevance. In the context of this conversation the verb ‘to like’ conveys the most amount of affection possible suggesting that ‘love’ is not always a stronger form of the verb ‘to like’. The same can be shown in the context of other situations. ‘Warm/hot’ and ‘believe/know’ are similar, as scales can be formed between

‘So desperately in love,’ emphasises the immense effect that loving someone can have. The word, ‘Desperately,’ contains connotations of trauma and insanity, and when this is placed in close alignment with, ‘Love,’

the meaning of the words. However there are often situations where one term is more appropriate than another. Due to pragmatics’ contribution to the meaning of a statement, only to a certain extent can ‘love’ be considered a stronger form of the verb ‘like’. Literary usage can also tell us a great deal about the relationship between ‘like’ and ‘love’. In Jane Austen’s Sense and Sensibility, this relationship is encapsulated in the dichotomy between the ever-composed Elinor and the fiercely passionate Marianne. Although both women are in the early stages of their romances, Marianne’s fiery passions and her willingness to use the word ‘love’ suggest a lot about how the word could be utilised. There are mentions of Marianne’s devotion to Willoughby throughout the novel; however, the description of her as, “So desperately in love”, emphasises the immense effect that loving someone can have. The word ‘desperately’ contains connotations of trauma and insanity, and when this is placed in close alignment with ‘love’, a rather overwhelming image is conveyed, as if Marianne has fallen into a state of yearning where her only medicine is the man she is addicted to. This is important because the image appreciates the potential power of love, demonstrating that one could be reduced to crisis if it were experienced in the wrong way. It is highlighted as an enabler of compulsion; an extremely influential attribute that cannot really be replicated by the word ‘like’.

Marianne’s sister Elinor is portrayed in a significantly more composed manner throughout the novel, depicting her character almost as the perfect ambassador for the meaning behind the word ‘like’. After her mother’s “I love him already”, Elinor responds with the quick but reserved “I think you will like him”, when talking about her love interest, Edward. The direct contrast and almost subtle correction accentuated through Elinor’s quote highlights her understanding of the different magnitudes linked to ‘love’ and ‘like’. This is significant because it highlights a very personal and real-world portrayal of the words ‘love’, and ‘like’, by demonstrating the difference between the two in separate characters. Marianne’s incredibly emotive description takes the form of ‘love’, a feeling that can evoke all sorts of actions within someone. On the other hand, Elinor’s reserved and slightly cautious nature is similar to the undertones of ‘like’, a word that represents the first stage of attraction, where people still maintain caution. The clear differences between the sisters and their uses of ‘love’ and ‘like’ accentuate the idea that the words are actually quite different and should also be appreciated in different ways.

For hundreds of years psychologists and linguists alike have discussed whether men and women are different in the way that they use language. John Gray’s popular self-help book Men Are from Mars, Women Are from Venus claimed that the inability of the two sexes to communicate effectively was one reason that explained relationship conflict. It is therefore

The rapid emergence of the middle class created a kind of ‘new women’, exposing domestic femininity as a choice rather than a destiny.

important to explore how gender plays a role in the use of the verbs ‘to love’ and ‘to like’, in order to understand whether men and women use them differently when

referring to personal relationships or opinions. Initially, one might assume that men use these terms in a less intimate and meaningful way than women do, due to societal views that they should repress their feelings and inhibit the expression of their emotions. However, an article titled ‘Women and Men in Love: Who Really Feels It and Says It First’ by Marissa A. Harrison and Jennifer C. Shorthall argued that this is not actually the case and that in fact, men tend to say “I love you” more quickly than women do. From an evolutionary point of view, this is because women have to be more guarded about falling for someone in order to select the best partner for reproduction as they tend to be the main caregivers, whereas men supposedly have less to lose. On the other hand, women are thought to say “I love you” more frequently than men. Abdul-Ghani et al (2022) conducted an investigation into whether there are gender differences in the use of emotive language. Its hypothesis was that

I love you I love you

I love you

female online reviewers of restaurants use words such as ‘love’ more frequently than male reviewers and the results supported this, whereas there was no gender difference in the use of ‘like’. Interestingly, an emotive review by a man containing the verb ‘love’ resulted in a higher evaluation of the restaurant than ‘like’. This study demonstrates that not only do women express emotions more frequently than men, but it highlights that because men do not use emotive language as often, when they do use it, it is viewed as more meaningful than when women do.

The most common way to say ‘I love you’ in French is ‘je t’aime’.

Interestingly, saying ‘je t’aime

bien’ (I love you a lot) does not strengthen your declaration of affection for someone.

The relationship between ‘love’ and ‘like’ varies across languages. French has various means of expressing the feeling. The most common way to say “I love you” in French is “je t’aime”. Interestingly, saying “je t’aime bien” (“I love you a lot”) does not strengthen your declaration of affection for

someone. In fact, it is used only for friends, as the word ‘bien’ removes the romantic sense. ‘Adorer’ also means ‘to love’; you could say “je t’adore” to a close friend and it would still mean “I love you”, but not in a romantic sense. However, when we are talking about inanimate things, ‘adorer’ is stronger than ‘aimer’, and in a way, the meanings of the two words switch. ‘Aimer’ becomes more similar to ‘like’, whilst adorer is more like ‘love’. This complex interrelationship between ‘aimer’ and ‘adorer’ highlights, in a better way than the English language does, the distinction between ‘love’ and ‘like’.

To conclude, the English words ‘love’ and ‘like’ have gone through transformations throughout history, and their meanings have always been heavily dependent on the context in which they are used. Although it is the general perception that ‘love’ is a stronger form of the word ‘like’, it is not that simple. By examining the contribution of context to conversations, we can more accurately interpret the different meanings of the two words. The true meanings of ‘love’ and ‘like’ depend not only on linguistic context, but also on psychological circumstances, which is shown in the way that men and women differ in their use and interpretation of the words. The portrayal of love in literature suggests that love is a powerful sentiment of its own, separate to the feeling of liking someone. Ultimately, while ‘love’ can be used simply as a stronger version of ‘like’, the two words have very different meanings and should be appreciated as separate entities.

Maths

Serendipity: Random Walks - finding the probability that two people on a random walk will meet.

Our task is to find the probability that two people on a random walk will meet. In order to solve this numerically, we will have to restrict this to a model where we have two walkers on a 1-dimensional plane (also known simply as a number line), who each simultaneously take 1 step either forward or backward, each with a probability of ½. This can be further extended to 2 dimensions and higher. The problem is therefore to prove whether or not the random walkers will be in the same position after n steps for any n, and if we are to prove that this will always eventually happen, then the probability, p, of this occurring must be 1. To solve the problem, we must first find the probability of a single walker on a random walk returning to any given point in a 1-D then 2-D plane. This can then be transferred to solving the larger problem.

There are two states of a random walk; a transient state and a recurrent state. A transient state refers to one where the probability of returning to the origin at least once is less than 1 and thus the expected number of returns is finite. This will occur for dimensions other than 1-D and 2-D. In order to show that any particle on an infinitely long random walk in a 1-D state will always return to the origin, it must be shown that the state is recurrent. This means that the probability of returning to the origin at least once is equal to 1 and therefore the expected number of returns must be infinite.

The expected number of returns is the summed probability of the particle being at the origin after exactly 1 step or 2 steps or 3 ad infinitum. Therefore, the expected number of returns can be modelled as the sequence:

Aryan (Harrow)

Chloe (NHEHS)

Genevieve (NHEHS)

Oscar (Harrow)

where E(V) is the expected number of returns, and P (n)/00 is the probability that the particle has returned to the origin in n steps

This can also be written as:

This summation must diverge to show a recurrent state. In order to return to the origin, the particle must have travelled the same number of steps forwards as backwards so that it has a total displacement of 0. Therefore, P(n)/00 for any odd n will be equal to 0. To find P(n)/00, the probability of taking n/2 forwards steps must be multiplied by the probability of taking n/2 backwards steps. As the probability of taking a forwards step and the probability of taking a backwards step are equal to ½, this will be equal to

This must be multiplied by the number of potential routes that can be taken to reach the return point in n steps. This is done by finding the number of unique combinations of forward and backwards steps that can be formed from n steps: or Thus:

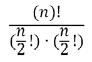
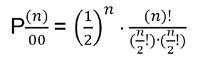
Stirling’s Formula can be used to approximate factorials: ( thus, )

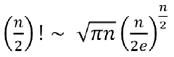
Which allows us to simplify P(n) as follows:

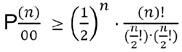
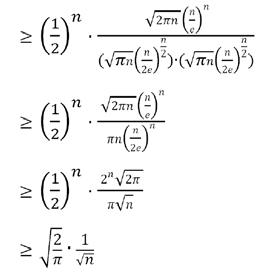
Hence

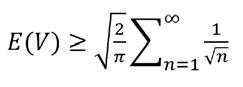
As demonstrated by the following graph

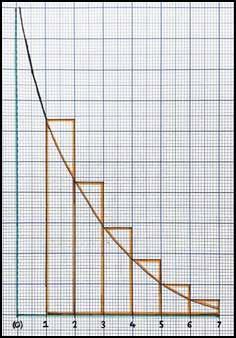
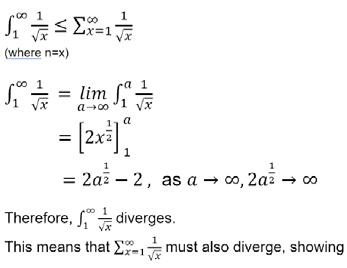
that the state is recurrent (P(return)=1).

Therefore, in 1-D, any particle on a random walk must return to the origin, infinitely many times. It is also important to note that recurrence at the origin implies recurrence at any other point (every point will be visited infinitely many times).

This proof can be replicated for a 2-D state. Here (as shown in the figure below),

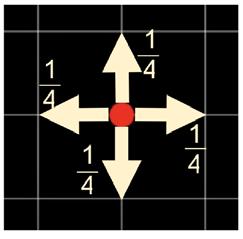
the particle can move upwards, downwards, forwards or backwards, each with an equal probability of occurrence of ¼. The expected number of returns E(V) can still be modelled as:

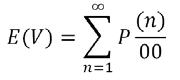
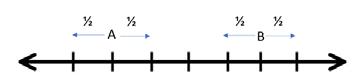
For the particle to return to the origin, the number of forwards and backwards steps must be equal, same with the number of upwards and downwards steps (as displacement must be 0). This is shown in figure here.

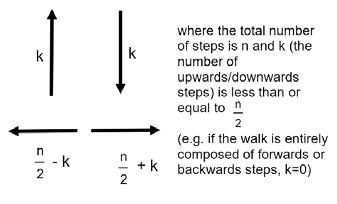
To find P((n))/00 when n is even, the probability of taking k upwards and downwards steps and (n/2-k) forwards and backwards steps must be found. This is then multiplied by the number of unique arrangements of this set of vertical and horizontal steps. However, as 0≤k≤n/2 , this calculation of the arrangements must be repeated for each value of k to find the final probability. Therefore,

walker, and Bn is the position of the second walker, then the distance between the 2 walkers can be expressed by An – Bn . Therefore, if we state that Zn= An – Bn (where Zn evolves as two-steps of a random walk), then the problem is equivalent to finding the probability that Zn returns to 0 (the origin).

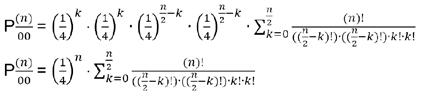
This simplifies (using Stirling’s Formula as mentioned above) such that:

Thus

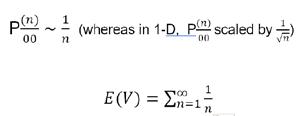
This is the harmonic series, which means that E(V) diverges, proving that the probability of the particle returning to the origin is equal to 1. Therefore, any random walk on a 2-D lattice is also certain to return to the origin. However, it is important to note that in dimensions higher than 2, the state is transient, meaning that the probability of the particle returning to the origin is less than one, leading to the saying “a drunk man will find his way home, but a drunk bird may be lost forever”.

In order to apply this to 2 particles on a random walk on a 1-D lattice, if An is the position of the first

The steps that can be taken by the walkers are outlined in the table below.

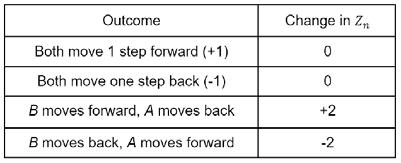
As this is modelled in a 1-D lattice, and we have proven that the probability of a random walk returning to the origin is 1, this is certain to occur as long as the step number is even. Therefore, assuming they start an even number of steps away from each other, two people on a random walk in a 1-D plane will always meet again.

Finally, let’s look at the expected value of n when Zn first returns to 0 (how long it takes for Zn to return to 0).

This is outlined in Bertrand’s ballot problem, where

the probability that the number of forward steps remains greater than or equal to the number of backward steps at all times is 1 / ((n/2) + 1).

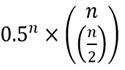
This must be multiplied by since each step carries a probability of 0.5 of going either way, and there are ( n choose n/2) different paths. We therefore get an expected value of n,

E(n) =

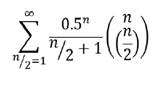
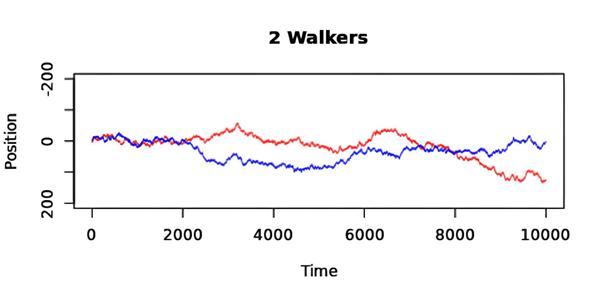
where n only takes even positive integer values (n = 2,4,6,8…). This infinite sum diverges, and thus we can see that the expected time for the random walk to return to 0 is infinite. The figure below shows Simulations of 2 random walks done on random walks.

This is a surprising result, since we have proved that the random walk will always return to 0 at some point, and yet it is expected to take infinitely long to do so.

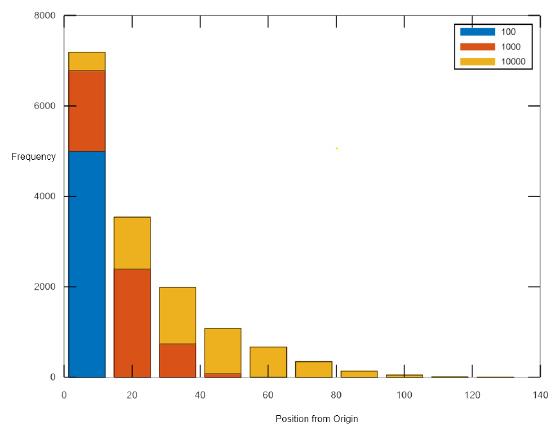
The figure above is a Matlab plot of the position of a particle after 100, 1,000 and 10,000 steps. The data was collected from 15,000 simulations.

Biochemistry

Love is a drug… or is it?

Romantic love is “a state of intense longing for union with another” according to Hatfield and Rapson (1987), and can be divided into two stages: infatuation and attachment. While infatuation is the initial stage of love, synonymous with an intense attraction between individuals, attachment is associated with comfort and a deeper emotional connection that requires time to develop (Langeslag and van Strien, 2017). When looking at the effects of alcohol, a highly addictive drug classified as a central nervous system depressant, alcohol addiction can be divided into either a state of regulated relapse or a state of compulsive alcohol addiction. The initial stage is a regulated relapse where an individual’s alcohol intake is controlled, whereas the later stage involves compulsive alcohol intake, in which the neuroplasticity of the brain is altered. While romantic love is glamorised by society, alcohol addiction is considered shameful and stigmatised by society. It could be argued that romantic love (although it shares similar cognitive operations with alcohol addiction) is not a physical addiction, but a behavioural one.

Rithi (NHEHS)

Nur (NHEHS)

Tamir (Harrow)

JB (Harrow)

Misha (Harrow)

During the initial infatuation stage of romantic love, individuals experience exhilaration synonymous with how one feels when intoxicated.

During the initial infatuation stage of romantic love, individuals experience exhilaration synonymous with how one feels when intoxicated. This is due to dopamine, a neurotransmitter that activates the brain’s reward circuit, leading to a euphoric experience similar to alcohol addiction. This not only raises levels of serotonin, but also triggers an increase in production of oxytocin, a hormone associated with prosocial behaviours such as trust and empathy. These neurotransmitters play a role in the reward system, which is when the brain associates different stimuli with a positive or desirable outcome. However, there are also adverse effects from the high levels of hormones. While high levels of dopamine trigger giddiness and euphoria, they also lead to insomnia or a bad appetite.

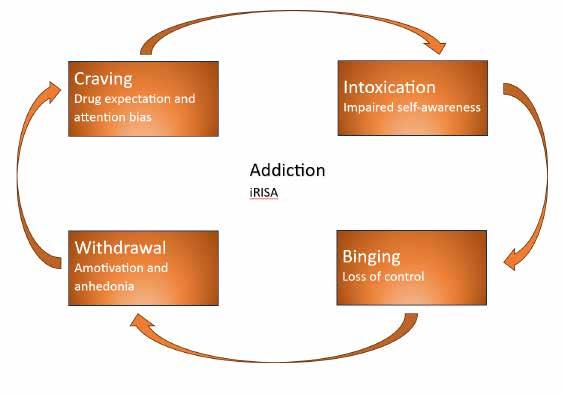
Additionally, levels of the stress hormone cortisol increase, which causes a decrease in levels of the neurotransmitter serotonin, hence leading to the obsessive behaviours and thoughts associated with infatuation (Edwards, 2015).

There are three main stages that lead to alcohol addiction (National Institute on Alcohol Abuse and Alcoholism, 2021). Firstly, there’s the intoxication stage, in which the rewards of alcohol are the main focus, and any negatives are expressed temporarily. These rewards include euphoria, similar to infatuation, and stress reduction, with cortisol levels decreasing. This differs from infatuation in romantic love, where cortisol levels increase. The neural mechanism of this stage involves the activation of the basal ganglia and its relay of dopamine neurons. This surge of dopamine due to alcohol, makes one feel ‘good’, increasing the likelihood of further consumption. Repeated activation of the basal ganglia triggers changes in the way an individual responds to specific stimuli associated with alcohol, such as certain scents or glassware, which can become stimuli that urge them to drink again. Secondly, the withdrawal stage is when the individual stops drinking and consequently experiences

Romantic love can be referred to as the satisfaction of a yearning or desire, which is synonymous with what addictive behaviour entails..

uncomfortable or dangerous withdrawal symptoms. Diminished activation of the reward system, and increased activation of the brain’s stress system in the extended amygdala, cause anxiety and agitation. Consequently, the person drinks to escape the lows, rather than experience the highs. Finally, there is the craving stage which involves becoming preoccupied with seeking alcohol. The prefrontal cortex, which is responsible for organising thoughts and prioritising tasks, has temporarily reduced bilateral activation, which plays a significant role during alcohol addiction.

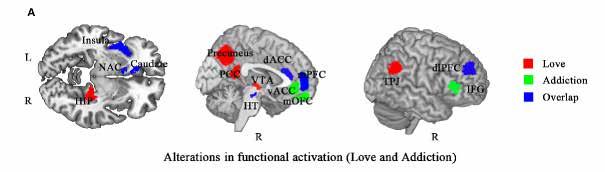
Romantic love can be referred to as the satisfaction of a yearning or desire, which is synonymous with what addictive behaviour entails. In recent studies concerning the neurocognition of drug addiction and romantic love, additional associations have been detected consisting of overlapping brain regions and their activity. When exposed to partner-related cues, like an image of an individual’s partner, ‘lovers’ tend to show significant activation in the ventral tegmental area (VTA), dorsal anterior cingulate cortex (dACC), posterior cingulate cortex (PCC), and the hippocampus (Zou et al., 2016). When addicts are exposed to drug-related cues,

significant activity is also seen in the VTA, dACC, and PCC, as well as other areas such as the inferior frontal gyrus and amygdala. Through these studies, it is evident that although some activated brain regions are unique to romantic love (like the hippocampus) and some to drug addiction (like the amygdala), there are significantly more brain regions that overlap between the two.

As a relationship develops, the addictive nature of infatuation wears off, and obsessive desires are soon replaced by feelings of comfort and safety. The neural pathways activated in response to an attractive face differ to those activated in response to attachment to a longterm partner. For instance, liking someone during the stage of infatuation activates the left VTA, whilst wanting someone during the attachment phase activates the right VTA (Fisher et al., 2016). The VTA is used to regulate the reward system and is responsible for addictionrelated behaviours due to the dopaminergic neurons it releases. In a longitudinal study, it was found that the number of years a couple was married had a positive correlation with the neural activity in the right nucleus accumbens and caudate nucleus (Acevedo et al., 2011).

This is because most of the neurons in the caudate nucleus use GABA, a γ-Aminobutyric acid, as their main neurotransmitter (Driscoll, Bollu and Tadi, 2021). Its main function is to reduce the ability of nerve cells to receive and send chemical messages to one another resulting in less neuronal excitability throughout the nervous system. Consequently, GABA is known for its calming effect, explaining why the later stage of romantic love is associated with less anxiety than the earlier stage. Additionally, increased activation in the PCC leads to social cognition and trustworthiness increasing with the duration of a relationship.

Compulsive alcohol addiction involves constant changes in the brain known as neuroadaptations. The key change in the brain is regarding the mesolimbic dopamine system which plays a crucial role in the reward pathway, and is activated at the initial stages of alcohol addiction.

Chronic use results in an alteration of this reward circuit, causing a decrease in dopamine receptors and an increase in stress hormones, which can in turn lead to increased tolerance, dependence, and more severe withdrawal symptoms. Prolonged alcohol use does not just affect the brain’s neurochemicals but also changes the brain on a cellular level. Whilst it is false that alcohol kills neurons, there is evidence suggesting it reduces the number of new hippocampal neurons made (Geil et al., 2014). Increasingly, chronic alcohol use can also lead to changes in brain structures, namely a reduction in the size of the prefrontal cortex responsible for executive function (Abernathy et al., 2010). Furthermore, neuroadaptations caused by compulsive alcohol addiction are

long-lasting, increasing the risk of relapse even after years of stopping usage. Long-term alcohol addiction is much like opioid addiction, characterised by patterns of bingeing, and followed by withdrawal driven by intense craving in response to various stimuli, whether negative or positive, or more importantly, stimuli that are associated with drinking.

While very similar in earlier stages, romantic love and compulsive alcohol addiction differ in later stages. In terms of similarities, long-term romantic love and chronic alcohol use both induce the plastic changes of both the DA (dopamine) and the OT (oxytocin) system, as the constant dopamine reward reinforces the dependency on either romantic love or alcohol. Another more social similarity is the inability of most people to stop an alcohol addiction in a similar way to struggling to remove themselves from abusive relationships, since neurologically they cannot bear to be without the constant reward from what they perceive as ‘love’. In a study by Dr Sandra Langeslag (BBC Science Focus Magazine, n.d.), it was found that romantic love leads to decreased cognitive control. Participants were asked to carry out a shortterm memory task whilst presented with pictures of a loved one, friend, or stranger; those presented with a picture of a loved one completed the tasks slower and more poorly. Regarding differences, in the later stages, romantic love is considered more of a behavioural addiction, and there are significant differences in the OT system between the two. There is also increasing research suggesting that romantic love is better defined

as a natural addiction experienced by most humans, that has resulted through the process of evolution, so that human beings can conserve their mating energy and time to find one specific partner (Fisher et al., 2016).

... natural addiction experienced by most humans, that has resulted through the process of evolution ...

To conclude, although romantic love and drug addiction share many attributes when assessed holistically, it is evident that time is a crucial factor to consider. In early-stage romantic relationships, lovers exhibit several characteristics synonymous with addiction, however, this tends to abate as the relationship progresses. By comparing the early stages of romantic love and alcohol addiction, as well as detecting neural correlates between the two, new treatments for alcohol addiction may be developed in the foreseeable future.

Medicine

To what extent does the process of ‘falling in love’ affect (dis)regulation of eukaryotic genomes?

Flora (NHEHS)

Adriana (NHEHS)

June (Harrow)

Lovin (Harrow)

Initiating romatic love, or ‘falling in love’, affects eukaryotic genome regulation; however, preprogrammed genetic mutations also impact an individual’s ability to develop romantic relationships. Chemicals produced in response to extreme states of emotion modify the eukaryotic genome which often results in the dysregulation of biological processes. Nevertheless, oxytocin receptor gene (OXTR) alleles associated with disorders of social functioning such as OXTR rs13316193 T>A,C, rs2254298 G>A,T, rs1042778 G>A,C,T, rs2268494 G>A,C,T, and rs2268490 C>G,T reduce empathetic responses to partner distress (Schneiderman et al., 2013). Since empathy correlates to long-term romantic relationships, OXTR alleles impact the ability to initiate and sustain love. Furthermore, the heritability of partner preferences suggests that attraction is, to an extent, preprogrammed. Therefore, the initiation of love weakly affects the regulation of the eukaryotic genome.

Oxytocin (Oxt) is a pleiotropic (influences the expression of two or more phenotypes) peptide hormone

“... the heritability of partner preferences suggests that attraction is, to an extent, preprogrammed...”

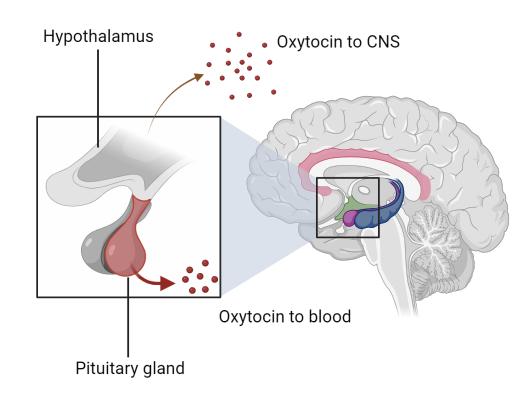
commonly associated with romantic love (Dantzer and Swanson, 2017). Produced in the hypothalamus and secreted by the posterior pituitary gland, Oxt stimulates the oxytocin receptor commonly found in the gonads, uterus, corpus luteum, kidneys, and heart (Figure 1) (Carter et al., 2020; Acevedo et al., 2011; Gimpi and Fahrenholz, 2001). The activation influences various physiological changes. Indeed, Oxt decreases the transcription of the corticotropin releasing factor gene (Crf) by acting as a transcription factor, reducing adrenocorticotropic hormone and cortisol production to support healing and stress-coping immune mechanisms, preventing exaggerated stress responses (Jurek et al., 2015). However, the imbalance between Oxt and Crf activity due to Oxt gene dysregulation may cause cyclic alterations in depressive and manic symptoms in Bipolar Disease (Guo et al., 2022). Oxt is the neurobiological substrate for pair bonding and empathy, peaking in the initial stages of romantic relationships (Schneiderman et al., 2013). Indeed, some researchers recognise Oxt as one of the “ancient” hormones, facilitating inherent “selfish” altruism in genetically similar individuals (Carter et al., 2020, Williams, 2008). The hormone’s significant immunological impact provides insight into the association between emotions and genetics.

Love’s impact on the endocrine and immune systems emphasises that environmental factors such as romantic love can regulate the genome. New lovers exhibit high, prolonged cortisol and noradrenaline levels compared to controls (Seshadri, 2016). Neural signals drive hypothalamo-pituitaryadrenocortical (HPA axis) secretion of cortisol and noradrenaline precursors

Image Caption

Image Caption

Figure 1. The production and secretion of oxytocin in the limbic system. Oxytocin for the brain and CNS remains in the hypothalamus, whereas oxytocin for the body enters the blood via the pituitary gland.

(Krugers et al., 2012). Test subjects show increased activity in the ventral tegmental area (VTA) and the midbrain neurones that link the VTA to the HPA when shown images of their partners (Aron et al., 2005; Di et al., 2020). Thus, visual stimuli seem to trigger “love” in the VTA; signals activate the HPA axis, creating a fight-or-flight stress level in preparation for initial love. The moderate stress level encourages individuals to try out new mates; positive social interactions elevate Oxt secretion to subsequently reduce stress, facilitating long-term relationships (Seshadri, 2016). Cortisol induced from the HPA axis acts as a transcription factor through the activation of the glucocorticoid receptor (GR). Thus, love-related stimuli cause impulses that promote Crf transcription in the neurosecretory cells within the paraventricular nucleus of the hypothalamus (Raadsheer et al., 1993). Therefore, the link between physical stimuli, VTA, and the HPA axis suggests that love can alter the transcription of the eukaryotic genome.

Humans selectively upregulate genes involved in immune responses to fight viral infections, increasing Type 1 interferon (IFN) transcription and dendritic cell (DC) activity (Amit et al., 2009). Most human cells express the receptor for IFNs; IFN-induced antiviral effector proteins such as ISG15 and Mx (myxovirus resistance) proteins block viral transcription and degrade viral RNA (McNab et al., 2015; Sadler and Williams, 2008). DCs initiate all antigen-specific immune responses, acting as an antigen-presenting cell (APC) to generate the correct T cells for adaptive immune response (Mellman, 2013). Sexually active women exhibit increased IFN transcription and DC activity; indeed, the responses protect the female reproductive tract from pathogens and viruses and prepare for sexual reproduction (Fung et al., 2013; Mor et al., 2011). Comparison between single, partnered, and recently separated females discovered a similar increased IFN transcription and DC activity in partnered women above and beyond the effects of sexual reproduction (Murray et al., 2018). The results suggest that falling in love may affect immune system transcription and activation in preparation for reproduction, supporting the claim that love regulates the eukaryotic genome.

Figure 2. (A) Regional brain response interactions with OXTR rs53576 (G versus A-alleles) and change in romantic love scores from T1 (time of wedding) to T2 (one year after wedding); (B) Scatterplot showing correlation between OXTR rs53576 (G versus A-alleles) and Left VTA at T1; (C) Scatterplot showing correlation between OXTR rs53576 (G versus A-alleles) and Left VTA at T2.

Lovesickness, or the intense emotional longing and romantic infatuation accompanied by physical symptoms such as heart palpitations, butterflies in the stomach and difficulty sleeping or eating, supports the above conclusion. Lovesickness increases the activity of genes such as Crf and the glucocorticoid receptor gene (GR) related to stress responses. The upregulation may be due to the heightened emotion and physiological arousal that comes with being lovesick and suggests that the body’s stress response system may be dysregulated in lovesick individuals (Acevedo et al., 2012).

Cortisol regulates stress responses by binding to GR in the cell, triggering a complex signalling cascade that activates the euchromatin to expose the nucleosomes and enable gene transcription for stress-terminating factors. Thus, cortisol can select to transcript or not transcript genes, altering the expression of genes involved in stress and inflammation. Cortisol can also bind to specific DNA sequences called glucocorticoid response elements (GREs) located near the target genes and influence the rate of RNA synthesis by recruiting or blocking transcription factors.

Furthermore, rejection can also make you ill. Another study found that people who had recently gone through a romantic breakup had changes in the expression of genes related to inflammation and immune function. Specifically, the researchers found increased expression of genes related to pro-inflammatory cytokines in those who had experienced a breakup compared to those who were still in a relationship. Thus, breakup stress and emotional turmoil can impact the body’s immune system, potentially leading to increased susceptibility to illness (Eisenberger et al., 2011). The increased expression of pro-inflammatory cytokines is thought to be related to the activation of the stress response and the release of stress hormones, including cortisol. Cortisol can activate pro-inflammatory pathways in the immune system and lead to the production of inflammatory cytokines. Overall, this study suggests that the stress of a romantic breakup can have a physiological impact on the body’s immune system, potentially increasing the risk of developing health problems associated with chronic inflammation.

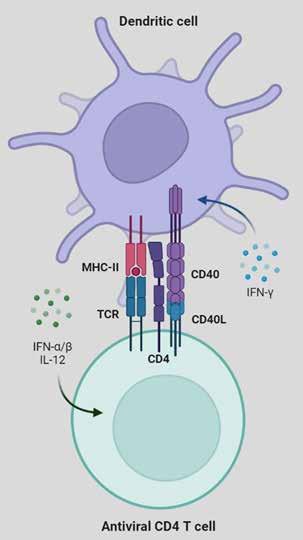
However, being lovesick may even give you increased tolerance for pain. For example, one study found that oxytocin increased the expression of the mu-opioid receptor gene (OPRM1) in the spinal cord, which is involved in the endogenous opioid system and plays a role in pain modulation (Gutierrez and Loh, 2014). Another study found that oxytocin increased the expression of the gene encoding for the potassium channel KCNQ5, which modulates the excitability of pain-sensitive neurons (Loken et al., 2009). Overall, lovesickness’ impact on the endocrine, immune, and nervous system highlights that love affects genome regulation to a significant extent.

On the other hand, the strong association between Human Leukocyte Antigen (HLA) and partner selection suggests that romantic attraction is preprogrammed and does not significantly impact genome regulation (Kromer et al., 2016). HLA is a protein complex on APCs that allows antigen presentation to T/B cells (Markov and Pybus, 2015). Each

HLA complex presents processed antigens of target pathogens (epitopes), activating T killer cells (caused by Class I complex) or Helper T cells (Class II complex). Thus, increased HLA diversity facilitates immune response to a wider set of pathogens (Markov and Pybus, 2015). Humans can differentiate HLA types in people’s odours; although humans lack vomeronasal organs, test subjects could identify self HLA from a mixture of odours when instructed to select the smell of “themselves” (Milinski et al., 2013). Corroborating research shows that humans and mice prefer partners with nonself and nonparental HLA (Kromer et al., 2016; Yamazaki and Beauchamp, 2007). The results show that HLA types influence humans’ romantic attraction and partner choice. Since genes of the HLA super locus on chromosomal position 6p21 code, or “program” an individual’s HLA set, one can argue that romantic

Genes indirectly influence preferred physical and emotional traits, highlighting the preprogrammed nature of love.

attraction is preprogrammed via one’s HLA set (Shiina et al., 2009). Research involving OXTR gene variability (OXTR rs13316193 T>A,C, rs2254298 G>A,T, rs1042778 G>A,C,T, rs2268494 G>A,C,T, rs2268490 C>G,T) sheds light on the strong association between love and the preprogrammed genome. Empathy, or the capacity to understand emotions (r = .19, p < .05) positively correlates with longerterm and happier romantic relationships (r = .04, p < 0.5) (Table 1) (Ulloa et al., 2017). Oxt is responsible for such pair-bonding behaviour; central Oxt facilitates mate selection in females and shows a substantial increase in the blood plasma during the first year of human romantic love (Insel and Hulihan, 1995; Williams et al., 1994;

Schneiderman et al., 2012). Twin experiments suggest a moderate inheritability of social traits (Ebstein et al., 2010). Indeed, OXTR alleles carry different risk factors for susceptibility to decreased social functioning. Single nucleotide polymorphism (SNP) rs13316193 C/C is associated with empathy (Wu et al., 2012); T/T of the same SNP has fewer Oxt receptors in the brain and increased Autism Spectrum Disorder risk; SNP rs2254298 A/G implicates higher ASD, depression, and anxiety risk (Lerer et al., 2007; Kawamura et al., 2010; Jacob et al., 2007, Costa et al., 2009). Researchers used the above SNPs to assign cumulative risk values to five OXTRs by summing the number of SNPs on which the individual was homozygous for the risk allele, discovering that individuals with higher cumulative risk engaged in less empathetic behaviour during simulated interactions with their partners. Furthermore, men were more empathetic than women; although the underlying reason is unclear, elevated stress-related cortisol levels in women and increased male brain response to attachment-related cues, potentially due to increased attentiveness, may explain the difference

(Schneiderman et al., 2013). The results highlight that the Oxt genotype influences pair-bonding capabilities in humans and thus impacts the ability of individuals to form healthy romantic relationships.

Genes indirectly influence preferred physical and emotional traits, highlighting the preprogrammed nature of love. Attraction and relationships aim to seek the best mate for reproduction on the evolutionary scope. The definition of a “best” mate relies on physical traits, intelligence, attractiveness, and ability to provide resources. Indeed, those with polymorphisms associated with Oxt and antidiuretic hormone such as AVPR1a rs3, OXTR rs53576, DRD47R, and COMT rs4680 were in relationships that reported higher sexual satisfaction and altruism, demonstrating elevated levels of attraction (Acevedo et al., 2020). In newlyweds, fMRI scans at T1 (time of

wedding) and T2 (one year after wedding) show a strong association between the polymorphisms and the substantia nigra and ventral tegmental area (SN/VTA) (Acevedo et al., 2020). Indeed, OXTR rs53576 (G versus A-alleles) shows a significant correlation with Left VTA activation (Figure 2). SN/VTA is a dopamine-rich region, responsible for motivation, reward, and addiction (Kalivas, 1993). The association suggests that certain genetic variations motivate individuals to maintain long-term romantic relationships, highlighting the preprogrammed nature of attraction. On the other hand, social and economic factors also impact partner preferences, demonstrating that the environment influences love to an extent. Indeed, men living in countries with greater gender equality did not significantly value attractiveness when seeking a mate, highlighting the influence the environment has on the traits that one is attracted to, despite significant genetic correlations (Buss, 1989).

Certain genetic variations motivate individuals to maintain long-term romantic relationships, highlighting the preprogrammed nature of attraction.

exposure to toxins can cause epigenetic changes that alter gene expression and modify the effect of SNPs. On the other hand, polymorphism is characterized by random, permanent, and easy-to-understand changes to genetic information; epigenetic gene regulation is volatile, induced, and reversible (Maggert, 2012). SNP’s permanent effect on the eukaryotic genome and allelic variations suggest that SNPs are preprogrammed. Thus, inherited social capabilities and attractions from SNP variation demonstrate that love is preprogrammed.

SNP influence of preference for physical traits in potential partners demonstrates that romantic love is preprogrammed. Indeed, DRD4 is associated with high levels of novelty-seeking behaviour, preferring frequently changing, short-term relationships. AVPR1a rs3 is associated with strong social bonds and romantic relationships (Walum et al, 2008). However, to substantiate the conclusion, scientists must consider whether SNPs are “preprogrammed”. Stress and

Falling in love influences the genetic up- and down-regulation of immunological factors such as IFN and DCs that prepare women for sexual reproduction; lovesickness significantly alters the transcription of stress-factor genes. Thus, love dysregulates the eukaryotic genome to a significant extent (Murray et al., 2018). Socioeconomic and environmental factors affect social skills and partner preferences (Venney et al., 2020; Buss, 1989). However, the significant association of OXTR cumulative risk with failed relationships and partner preference genetic predetermination logged with fMRI studies highlights love’s pre-programmed nature (Schneiderman et al., 2013). Therefore, ‘falling in love’ significantly affects the dysregulation of the eukaryotic genome; genetic pre-programming determines romantic attraction in collaboration with cultural and environmental factors.

Physics

Scientifically-speaking, what is the best shape for a champagne glass?

In order to determine the ‘best’ shape of a champagne glass, it is important to consider the following factors: aroma, how long bubbles last and how quickly they rise. These factors are caused by vortices, the diffusion velocity of the bubbles and the radius and depth of the cup.

The flûte à champagne (champagne flute) became popular in France in the 1750s. This glass shape was specifically designed with a deeper, thinner cone which allowed the foam and bubbles to be better shown off. The champagne coupe (‘saucer’ in English) then began to emerge in the late 1830s. This was the preferred champagne glass as it allowed people to pour and drink the bubbly drink easily and quickly. There were also many disadvantages of the champagne coupe shape, therefore people quickly fell out of favour with it during the 1920s. In this time, the tulip shape, the shape of a typical modern wine glass, became more popular among champagne drinkers. This is because the smaller width of the top of the glass allowed people to capture the aromas of the champagne more easily.

Lydia (NHEHS)

Leela (NHEHS)

Bea (NHEHS)

Luke (Harrow)

Joey (Harrow)

Champagne is notoriously used in romantic situations in the hope of creating a spark between the two drinkers. The drinking of champagne in order to create love dates back to the 18th century where champagne was seen by the public to represent love, purity and tenderness. This sort of advertising meant that champagne had a reputation for being a symbol of lust, admiration and ardour.

Concerning the process of making champagne, it is split into two stages. Following the pressing and picking of grapes (stage one), still white wine is combined with reserve wines to produce champagne wine and the second fermentation commences: the champagne wine is mixed with yeast and sugar, resulting in the production of an alcohol and carbon dioxide, hence why champagne typically has high concentrations of carbon dioxide (10 grams per litre.) As for the storage of the finished product, it can be kept under a maximum of six atmospheres of pressure, whilst equilibrium after removing the cork can be maintained by the release of carbon dioxide.

Champagne is notoriously used in romantic situations in the hope to create a spark between the two drinkers. pheromones.

Fick’s Law is one of the two principal factors that influence the rate at which carbon dioxide is released from champagne, and is the only relevant phenomenon when the liquid is in a stagnant state. Indeed, this law of diffusion states that the rate of diffusion from a liquid is directly proportional to both the surface area and concentration difference of the liquid, but is inversely proportional to thickness. In this investigation, surface area is the only factor that affects the rate at which carbonation is reversed when a liquid is stationary. Given that the retention of carbonation is 80% dependent on this phenomenon, it is safe to assume that the shape of a champagne glass can produce varying rates at which carbon dioxide escapes. Likewise, the loss of carbon dioxide can also occur through convective transfer, where a mass loss occurs due to the desorption of carbon dioxide and other volatile compounds. The champagne would undergo evaporation and diffusion stages, caused by

ascending bubble-driven convective flow patterns. Therefore, the greater the velocity of the convective patterns, the quicker the rate at which carbon dioxide is lost.

To deduce the best glass for champagne, we used the study in the paper ‘Unsteady evolution of the two-phase flow in sparkling wine tasting and the subsequent role of glass shape’ by Fabien Beumont, Gerard Liger-Belair and Guillame Polidori¹.

In this experiment, they used 100ml of sparkling wine in each glass, because it has a similar refractive index to champagne, meaning that the two liquids

behave in similar ways. When they were evaluating the glasses, they ensured that the nucleation was controlled. The two main things which were assessed were the vorticity or vortices created in the glasses and the velocity of the gas bubbles in each glass; they compared four different glasses which we also used to compare.

Effervescence and bubble magnitude are key attributes and ways of gauging the quality of champagne. The shape of the glass that the liquid is poured into also affects the perceived quality, and impacts the sensory attributes of the drinking experience. For the purposes of this study we have assumed that the metric of maximum volume flux of CO2 just after pouring correlates to optimal sensory experience. When the champagne is poured into the glass,

The shape of the glass that the liquid is poured into also affects the perceived quality, and impacts the sensory attributes of the drinking experience.

tiny air pockets trapped inside the structure are absorbed on the glass wall and offer interfaces for CO2 dissolved molecules.

We will now review aroma, and how it is mainly affected by the

depth of the glass. As a coupe is shallow the bubbles do not rise very far, and this means that the ‘bubble engine’ is very slow, so aroma is delivered to the surface slowly, but escapes the glass quickly. It is useful for the flavour to be delivered gradually, as it allows it to develop complexity.

The flute acts the opposite, as it is much taller and narrower than the coupe. However, due to the small amount of air space at the top of the flute, most flavour is lost to the surrounding air. Moreover, in a champagne flute the aroma is more concentrated so the carbon dioxide is more concentrated, which could burn your nose.

The rim of the ISO tasting glass contains all of the aromas and the large, rounded cup allows the aromas to spread when swirled. Meanwhile for the long-stemmed glass, the angular gob means that the aromas will not be lost to the surroundings quickly.

The diffusion velocity of the gas is how quickly a bubble leaves the liquid and diffuses into the air. This velocity is dependent on how the liquid acts inside of each glass.

The coupe has a relatively low diffusion velocity of gas compared to the flute and long-stemmed glass and this decreases at a slow rate.

Flute glasses have a narrow neck which means a smaller radius. Along with its extended height, the narrow aperture of the flute allows the bubbles to reach a higher velocity, meaning there is higher force on

the surrounding liquid. In an experiment carried out by Fabien Beaumont, Gerard Liger-Belair and Guillaume Polidori in 2019, it was discovered that the average velocity of the bubbles in a flute has the highest extended rate. This demonstrates how there is a better flow of gas in a flute glass, maximising CO2 gas dispersal at the surface. This effervescence produced by the pour is a key attribute of the physical look and feel of the champagne. The aromatics are transported with the CO2 to amplify the sensory experience whilst drinking.

Vortices are formed in the champagne by the bubbles rising in the liquid, and these are useful as they mix the champagne, causing the aromas to diffuse above the surface.

We also know that CO2 volume fluxes are higher in a coupe than a flute. This movement is acute in the initial

minutes after the pour but after a while this reverses and the rate of volume flow of CO2 becomes higher in a flute. This ability to maintain the effervescence is a key reason why flutes are the most suitable carriers for champagne.

The ISO tasting glass has a relatively similar gas velocity to that of the coupe and the decrease in speed of the bubbles over time is much slower than that of the flute and long-stemmed glass. So the bubbles leave the ISO tasting glass slowly from the start whereas the bubbles leave the flute and long stemmed glass very quickly initially, but this speed decreases over the time, providing an aroma whilst also ensuring that the sparkling wine or champagne is not too fizzy or too flat.

The maximum flow velocities were measured in the long-stemmed glass so this means the gas will escape this glass much faster than the others.

Vortices are formed in the champagne by the bubbles rising in the liquid, and these are useful as they mix the champagne, causing the aromas to diffuse above the surface of the champagne. In addition, a vortex flow makes it an appealing visual experience as well as improving the taste. As the bubbles rise they get continuously larger as they absorb molecules of carbon dioxide that are dissolved in the champagne. The bubbles ‘act like objects in motion’ and so their displacement in the fluid causes motion in the nearby fluid layers. Bubbles and surrounding liquid move upwards and this induces a rotational flow in the liquid.

For the champagne flute, two alike and constant vortices are created on either side with an upwards stream in the middle. The same happens for the coupe, however due to its wide and shallow nature, only about half the liquid contains this vortex pattern, in the other half there is no movement. The whole liquid bulk was homogeneously mixed up to several minutes after the pouring process. This is due to the larger height (causing the bubbles to reach a higher velocity, meaning there is higher force on surrounding liquid) and the narrow open aperture.

For the long-stemmed glass, due to its shape, there was more opportunity for a vortex to be developed in comparison to the flute. A second vortex ring also

formed with a ‘lower intensity’ and rotating in a different direction to the main vortex. From this it was concluded that “in a glass with a narrow shape and high filling height (for example the flute), the vorticity of CO2 molecules released from the liquid medium will be significant.” So a taller, narrower shape increases the amount of CO2, and therefore bubbles, released from the glass. The long-stemmed glass will release bubbles at a high (but not the highest) speed so it will stay fizzier for longer than the flute but will release less aroma.

Another thing to consider is that the turbulence of the pouring process can cause a significant loss of dissolved CO2 during champagne serving. In a narrow aperture this can mean that excess foam is formed on the pour, meaning more CO2 loss which affects the sensory experience. This increase in the volume of gas of a bubble can often irritate the drinker’s nose and leave an unpleasant sensation as the liquid is over-bubbly and too effervescent. This also means that there may have to be two or three stages of pouring due to the foam forming at the top of the glass, to prevent the glass from overflowing and having a large, unnecessary foam-toliquid ratio.

For the coupe, only about half of the liquid medium was found to be mixed by the flow of ascending bubbles arising from the bottom of the coupe. The external periphery of the coupe is characterised by a ‘dead-zone’, where the champagne is at rest.

For the ISO tasting glass, the speed of the bubbles was lower and the speed at which the vortexes ‘swirl’ is also much less. These mean that there are fewer bubbles released from the sparkling wine, so it will stay fizzy for longer; however there will be less of an aroma.

This experiment demonstrated that there was a close link between the ascending bubbles and glass shape as well as the fact that “bubbles enhance the release of dissolved gas species and aromas under tasting conditions.”

Another factor to consider when deciding upon the most suitable champagne glass for the user is their personal taste. It is clear that many people will enjoy the sharp aromatic bubbles that the champagne offers, whilst others may prefer a more calm glass of fizz.

As mentioned in the history of the champagne glass, coupes were used to gulp down champagne without appreciation for its true attributes. As champagne production got more sophisticated and the quality increased with the number of bubbles, there was a higher demand to maintain the turbulence of the bubbles for longer. If this type of champagne is favoured by the drinker, a flute or tulip-shaped glass would be recommended. Studies have shown that these glasses are able to release a highly concentrated number of bubbles over a long period of time, due to their long stems and small apertures.

On the other hand, if the person drinking is in favour of the subtle, delicate taste of champagne and therefore would not appreciate the flute or tulip-shaped glass, they may find the large number of bubbles being emitted from the surface of the glass overwhelming, as the bubbles may give them an unpleasant sensation whilst drinking the champagne. In this situation, they may find that the coupe and ISO tasting glass are more appropriate for their experience. This will prevent the volume fluxes of the champagne from being too intense for the drinker and therefore the aromatic bubbles may overpower the original taste of the champagne.

Politics

To what extent do Consultations help people love their local area?

Consultations form a part of the political framework associated with the topic of local government. Léon Dion pellucidly refers to how consultation can be an “indispensable bridge” in working out how consulting can bring the public’s love and effusive, unimpeachable knowledge about their local area to dreary, paperstacked, Leviathan-like desk corridors that create our bureaucracy. But how has this impacted how people love their area and how effective local politics is? This article will aim to digest a particular case study about a leisure centre in Ealing, and how this pertains to the interface between the government and citizens emotionally, philosophically, and politically.

Ultimately, consultations are programmes which seek counsel or advice for political matters in a prospective policy. An ideal survey should try to be open and balanced in the political arena, which should not be symbiotic (done on predetermined outcomes) based on

Chris (Harrow)

Elizabeth (NHEHS)

Krish (Harrow)

Vivien (NHEHS)

what industry wants, and not in a ‘dark room’ which does not reflect ‘real life.’ Democracy was quite consultative and survey-based, back in Athens thousands of years ago, in which, 40 times a year, local, people-led groupings created foreign policies and revised laws –direct democracy, in which people rather than politicians do politics.

Through time, this form of politics has been shown to be largely unworkable in large states, compared to the small hippodrome-sized Athens in Ancient Greece. Modern direct democracy can often be found in referenda, but the ‘tyranny of the majority’ can affect this significantly. The Burkean form of democracy, which is around using the modern-day politicians’ so-called superior knowledge to create ideas, (not dissimilar to Plato’s paradise of technocrats running the world) goes against the ideas that are more prevalent today, such as resemblance (diversity), but too often political influence can corrupt this system of government.

A study in Rotterdam[1] proved that local amenities and exercise infrastructure, driven by political policies to do this, can help improve people’s happiness of the area.

Another study in China underlined how political participation in local areas can not only try to repair the damaged amount of trust there is between the public and politicians, but also two in five Britons do not feel part of their local community, and political participation in areas for economic improvement of your ordinary Tom, Dick or Harry can actually aid in long-term happiness and personal fulfilment. The condition is that this is done by local people, and not politicians.

Ealing’s government structure as a London metropolitan borough gives them power over planning permission. They usually have a cabinet which

leads the council overseeing departments, which usually hold meetings, consult with the public and talk to interest groups to help drive changes in the webs of local bureaucracy. Consultation meetings are usually quite technocratic and highbrow. Oftentimes, an average citizen will have a knowledge deficit when being involved in the policy-making process. The key thing to note is a ‘competence disparity’ giving way to a ‘confidence disparity’ as people may not have the competence to interact effectively with the process, but also, they lose faith in the governmental system itself, as it tells them to ‘talk to the hand.’

Dion, in his seminal article, ‘The Politics of Consultation’, believes that consulting councils can be a “bridge between the social and political system” and it can benefit councils by giving them “popular esteem.” Over time these systems have become a “major cog” and, according to the referenced Rokkan[3], “decisions are not made through the counting of heads but complex consideration.” Despite democracy appearing to be representative by politicians and voting for them, it is bureaucrats and people giving advice that form the bedrock of our laws.

People felt let down both by their representatives and by the lack of input they themselves were given within a decision that would shape the spaces which they inhabited, the spaces which they loved.

Club, the largest swimming club in the country with over 1650 members. The council wanted to rebuild the centre with large apartment blocks to fund it, and so it sought consulting help to make decisions on how it should look, designs and whether it should go ahead. This last point is where the sounding board came in: they disagreed over the use of a mixed-use (multi-purpose) project by the council and wanted alternatives (possibly council tax, borrowing or leisure income) to be used to fund this project (due to the impacts of former such projects by the council causing unease). On the sounding board were community associations, residents’ groups and sports groups, who concerned four times to conclude that the centre ought to go ahead but without the tower-block housing development.

Dion expands on this by outlining how it would be a “fallacy” that ministers are all “equally competent, involved and influential” and so encourages more consultation to act as a ‘counterpoise’ to this. The weakness of this governmentally comes when political interest infects consultation. Dion describes how the “cloak” of impartiality of many organisations can have a damaging impact, especially given that Cllr Martin on a Trader’s Association in the sounding board was a Labour politician.

Ealing Council recognised the need for a new generating leisure provision to replace the Gurnell Leisure Centre, which closed during the Covid-19 pandemic, and had been home to Ealing Swimming

The sounding board were, in their damning evaluation of council meetings, incandescent about the public survey the Council put out, in which they had “no input”, and disagreed about the premise of using Gurnell as a mixed-use development rather than a purely ‘like-for-like’ leisure centre replacement, pointing to even better places to put housing, such as that a “two-minute walk away” from Pitshanger Lane.

The reaction to the Council’s original plans for the redevelopment of the Gurnell site was overwhelmingly negative. A government body had proposed a plan that was felt by the community to be unreflective of the desires of the population of that community itself. People felt let down both by their representatives and by the lack of input they themselves were given within a decision that would shape the spaces which they inhabited, the spaces which they loved. This widespread outrage led to the creation of the Gurnell Sounding Board in 2022: a sounding board that would theoretically “provide a way for community and leisure stakeholders to assist in steering the Gurnell project.”[4]

The sounding board was created as a direct response to the public outcry that arose from the original redevelopment plans of Gurnell. Its effectiveness in achieving its aims of collaboratively forging a future for Gurnell have largely been inconclusive. Members of the group Save Gurnell, who participated within this sounding board declared that, despite their membership, they had been unable to have “seen the Council officer’s report and recommendations to Cabinet or had the opportunity to comment on them before the meeting.”[4]

give voice to stakeholders within the community, a voice that these same people felt had been given too late, and the progress of the sounding board has only furthered their distrust in the system of which they are a part.

The sounding board was created as a direct response to the public outcry that arose from the original redevelopment plans of Gurnell.

The creation of the sounding board has been undermined by the utilisation of the group by Ealing Council. As a result of this, both members of the Ealing community and the Council itself find themselves unable to reach conclusive decisions over a project that has proven to elicit passionate responses within the community. The sounding board was created to

Sounding boards have not been effectively utilised within the Gurnell project and have served little purpose beyond offering an official avenue to ‘leisure and community stakeholders’ as members of the sounding board feel unheard and underappreciated within that role. As has been established, sounding boards can be an effective means of including local, unelected citizens within local Government decisions, but in the case of Gurnell, they were not used to their fullest potential.

Given the drawbacks of the sounding board, we look towards other solutions; other frameworks through which we can effectively garner public opinion.

One example, which Léon Dion himself discusses, is the use of town hall meetings – relatively large gatherings of local citizens to discuss and debate a certain topic. He acknowledges how successful such a scheme can be, directly commenting: “the town hall meeting has a long and venerable tradition as the forum par excellence for the expression of popular opinion in democratic societies” (Dion, 1991, p. 105). Indeed he is not wrong, as town hall meetings do serve as an effective tool to foster engagement and understand public opinion.

Compared to soundboards, they can also be more efficient as they force policymakers not to simply understand and acknowledge public opinion, but to immediately take action on it. Despite the long and winding process of modern promulgation and planning, this allows new laws and new projects – like the Gurnell Sports Centre – to be passed. One may argue though, that this quick decision-making can negatively impact the quality of legislation, thereby forcing the council to make the wrong decision. However, it is important to

remember the principal purpose of the sounding board, to garner public opinion and act on this – in this way then, town hall meetings serve perfectly, as they allow for efficient execution of such events, preventing public dismay and mistrust. Co-incidentally, Gurnell Council is already planning to introduce such a system in the form of town forums, where diverse bodies of the towns meet regularly to discuss the implementation of new council projects and schemes.

It is not to say, however, that such a system does not come with its own problems. Similar to the sounding board, and indeed as Dion recognises, town hall meetings can suffer from accessibility issues which impacts diversity in the board, thus skewing results. As an example, someone from a poorer household may not be able to afford the travel to Ealing town hall to express their opinion on a certain topic, this would lead to their opinion being ignored, thus skewing the process entirely as the council’s decision no longer represents the will of people. Furthermore, those who have strong social views but are generally less politically engaged may simply not attend, considering the process ‘too much of a hassle.’

Local governments have various powers that can be utilised in order to try to maintain communities that residents are not only content with living in but towards which they also feel a sense of pride and attachment.

For instance, local governments are able to foster a sense of community by promoting engagement and interaction among residents. This is done by providing public spaces, such as parks, supporting local businesses, and organising community events. A recent example was displayed in celebrations for the Queen’s Jubilee, where the Ealing Council allowed planning parties to be able to “request a grant of up to £150” (Ealing Council News, 2023). Such events can unite a community with the promotion of social interaction reducing feelings of isolation; a prevalent problem amongst older individuals. From making residents feel as if they love the area where they live, there is a correlation to increased civil engagement as residents are more enthusiastic about sharing political views and helping shape policy decisions that affect them.

Similar to the sounding board, and indeed as Dion recognises, town hall meetings can suffer from accessibility issues which impacts diversity in the board, thus skewing results.

These issues could be solved to some extent. In the modern era, to improve accessibility, one could hold such meetings online but even this has its own issues, as online meetings may lead people to dismiss the importance, and thus their engagement in such topics: the effectiveness which the town hall system champions will be diminished. Furthermore, older and less wealthy individuals may not have access to the internet, and so to provide this the council will need to pay a cost – with a large sample, this may end up costing greatly.

Conservation of the physical environment through the upkeep of parks, well-lit streets, and waste management can create a greater sense of general safety whilst more appealing surroundings can reduce stress and encourage residents to take part in more physical activity. As a result, residents are more likely to spend their leisure time in their immediate local area instead of travelling to more central areas.

As seen in the Gurnell Sounding Board, local governments often utilise methods which are a direct outreach to citizens, who are given a forum to voice their opinions. Alongside a sounding board, local governments are able to call public meetings, which de-restrict who can provide input, and surveys in order to obtain a diverse range of opinions.

Chemistry

To what extent will lab-grown diamonds dismiss natural diamonds and what will be the social consequences?

The value of diamonds comes from their chemical and physical properties, which make them sought out both as gems and for making tools. However, diamonds are scarce and expensive to mine. The quality of the production of lab-grown diamonds has become such that many can only be distinguished using photoluminescence spectroscopy or other similar techniques, not by the human eye. While the market for synthetic diamonds has already grown significantly, we suggest that when synthetic diamonds advance to the point that they are completely indistinguishable from natural diamonds, they will become a dominant force in the gem market.

Diamond is a giant covalent molecule composed of carbon atoms covalently bonded in a tetrahedral shape. Carbon atoms in diamond form 4 bonds so they are sp3 hybridised. Strong covalent bonds in diamond and its regular arrangement make diamond strong.

The unit cell of diamond is a face-centred cubic unit cell with a lattice constant of 0.3567nm. Layers of carbon atoms stack in an ABCABC arrangement. Diamond can often have impurities in this lattice arrangement, which will be further explored later.

Interestingly, there also exists a form of diamond with a hexagonal unit cell and crystal structure known as lonsdaleite. Lonsdaleite has the same density as face centred cubic diamond (3.52 g/cm2). However, lonsdaleite is only found in small samples, likely due to its irregularity, which hinders formation. Lonsdaleite has lattice constants of a=0.252nm and c=0.412nm in addition to stacking in an ABAB form.

Like many inorganic materials, a crystal orbital model can be applied to diamond in order to explain its microscopic structure.

As explained earlier, valence electrons in diamond occupy hybrid orbitals (as predicted by the quantum mechanical model) and these hybrid orbitals overlap to form strong covalent bonds between atoms. This can be seen in Figure 1.2.1 where two sp3 hybrid orbitals combine linearly to produce a bonding molecular orbital (which is lower in energy as a result of an in-phase combination) and an anti-bonding molecular orbital (which higher in energy due to an out of phase combination).

Alicia (NHEHS)

Michel (Harrow)

Henry (Harrow)

The diagram above showing the linear combination of two sp3 hybrid orbitals to form a bonding molecular orbital (σ) and an anti-bonding molecular orbital (σ*).

In diamond, the MOs (molecular orbitals) that are formed from two carbon atoms overlap with other MOs formed from different pairs of carbon atoms. Due to its giant, repeating structure (see Figure 1.1.1), many combinations of these MOs occur to form bands containing infinitely many energy levels. These bands can form from both bonding and anti-bonding interactions, hence forming two distinct bands (sp3 σ) and (sp3 σ*). In addition to this, a band can be formed from similar interactions between 1s orbitals of carbon atoms. Hence, three distinct bands are formed and the energy between the bands is known as the ‘band gap’. This model can be used to calculate the bond index of diamond, which is a measure (from 0 to 1) of how covalent or ionic a crystal structure is. The integrated (average) crystal orbital index for diamond is 0.95 , suggesting that it is almost purely a covalent structure. Diamond has a high thermal conductivity at room

temperature. Many common diamond testers use thermal conductivity to distinguish diamond from similar looking gems such as moissanite. The thermal conductivity of diamond can also be used to distinguish between some forms of synthetic and lab-grown diamonds. 2a diamonds (a classification which shall be explained later) vary greatly in thermal conductivity depending on their origin. Synthetic 2a diamonds have a thermal conductivity of 3400 W/mK whilst natural 2a diamonds have a thermal conductivity of 200 W/mK.

Diamond also has a low thermal expansion coefficient. The averaged value of the coefficient of linear thermal expansion of diamond from 20-100°C is 1.34 x 10-6 cm/ cm/°C whilst from 20-800°C it is 3.12 x 10-6 cm/cm/°C. This is significant because in order to test the fluorescence of diamonds and use spectroscopy techniques, it must be cooled to low temperatures. Because of its low thermal expansion coefficient, diamond does not break when cooled to extreme temperatures.

The most notable property of diamond is its hardness. This means that in addition to being a durable and long-lasting gem, diamond can also be used for making tools. Diamond has a Knoop Hardness which ranges from 68.7-98.1 kN/m2. The hardness of diamond varies as a function of crystallographic orientation. Diamond is more likely to shear depending on which face has force applied to it. Diamond is brittle and cleaves readily on the 111 plane. Due to this fracturing, diamond is self-sharpening. The majority of diamonds used to make tools such as drill bits are synthetic diamonds because they are cheaper.

Diamond is fairly unreactive and inert to inorganic acids. A key exception to this is the fact that diamond is soluble in metals such as Fe and Ni. Thus, at high temperatures, such as a drill bit, diamonds can react with these metals. This limits the use of diamond in making tools.

Diamonds are classified into four types: 1a, 1b, 2a, 2b. This classification is based on the presence and positioning of impurities in the diamond lattice, particularly nitrogen and boron impurities.

Most natural diamonds are type 1a and contain 2500 ppm nitrogen. 1a diamonds contain platelets which are visible by transmission electron microscopy on the 100 planes which are indicative of N-N or C-N clusters.

These impurities interfere with the dislocation motion and give type 1a diamonds a higher high temperature bending strength than other forms such as 2b diamonds

2a diamonds have the highest thermal conductivity of all diamonds. They are transparent out to 10.6 micrometres and include some of the rarest and most well-known diamonds such as the hope diamond.

Type 1b diamonds can be formed from the treatment of brown 2a diamonds. By annealing at high temperatures 2a diamonds can be lightened, increasing their market value.

2b diamonds contain significant amounts of boron (0.225 ppm), causing blue colouration.

There are two main methods used to create synthetic diamonds: High Pressure High Temperature (HPHT) and Chemical Vapour Deposition (CVD). HPHT diamonds are made by mimicking the environment of the Earth’s crust. The temperature and pressure required for diamond formation are typically around 1,000 to 1,300 degrees Celsius and 5 to 8 gigapascals. This means to synthetically create diamonds, temperatures have to be at least 100 °c hotter for faster growth. The HPHT process begins with a small diamond seed, this seed is a small piece of a pre-existing diamond (2-4 millimetres in size, natural or synthetic) which is used to begin the manufacture of larger HPHT diamonds by acting as a nucleus and allowing a larger more valuable diamond to develop. This seed is then placed into a capsule which contains carbon and a metallic flux (often iron, nickel or cobalt) to dissolve the carbon, remove impurities and to aid the growth. Depending on the desired carat, (size of diamond) a HPHT diamond can be grown between an hour and a few weeks. The metallic flux is crucial to the development of a high pressure high temperature diamond as the metal catalysts react with the carbon to form carbides to then migrate onto the diamond seed and crystallise.

On the contrary, CVD (chemical vapour deposition) diamonds are made in a vacuum chamber through powders and microcrystalline structures. Once the diamond seed is inside the chamber, a gas mixture or plasma is introduced. These reactants consist of hydrocarbon fragments from hydrogen and methane feed gases. A feed gas is a gas introduced for a specific purpose. Furthermore, the gases will be ionised through microwave plasma (consisting of free radicals and ions) so the new individual atoms can be deposited onto the substrate forming a layered microcrystalline structure, eventually forming a diamond. To form diamonds via CVD, the optimum growth conditions are: temperatures ranging between 600-1200°c whilst pressure ranges from 30-13,000 Pascals. This low pressure reduces the risk of impurities such as nitrogen and boron, as they are less likely to bond to the substrate. In addition, other limiting factors involve the composition of the gas mixture, the strength of the energy source and the diamond substrate.

Several spectroscopic techniques are available to scientists who are investigating crystal structures, however, many choose to adopt Photoluminescence (PL) spectroscopy when exploring synthetic and natural diamonds. PL spectroscopy works through

analysing the emissions recorded by a spectrometer after a sample (cooled with liquid N2 and coated with graphite to minimise reflection from non-target areas) is illuminated with a laser. This non-destructive technique, which allows scientists to identify spatial distributions of defects within diamonds, can be used to detect whether a diamond is synthetic or not.

When the light illuminates the sample, electrons move into higher energy levels and then return to their original energy levels, emitting light in the process. The light re-emitted from this process is called scattered light. Although the scattered light normally has the same wavelength as that of which it is absorbed (known as Rayleigh scattering), occasionally the scattered wavelength is different from the source.

If the emitted wavelength is greater than that which it absorbed, Raman scattering occurs. This does not occur very often and so these peaks have low intensity, hence a specialised Raman spectrometer is used to enhance the precision of the PL spectrum. A Raman spectrometer is also used to obtain the rest of the peaks due to Rayleigh scattering.

A sample PL spectrum is shown in Figure 3.1.1, with the intensity of the scattered light emission plotted on the y-axis and the wavelength (or its wave number equivalent) plotted on the x-axis.

Pure diamond has 8 distinct monochromatic frequency emissions, 7 of which are so small that they are not picked up by even a Raman spectrometer while the emission at 1333 cm-1 has a very high intensity. This makes distinguishing natural and synthetic diamonds relatively easy: a pure diamond will have one very strong peak (as shown in (b) below) while a synthetic diamond will have many strong peaks (shown in (a)).

However, it is more challenging to distinguish a CVD and HPHT diamonds due to their variety in production and colour. An example of a distinguishable difference is the presence of a SiV- peak at doublet at 736.6 and 736.9 nm, which are common in CVD diamonds but are much rarer in HPHT diamonds.

Diagram above showing both Rayleigh scattering (when the wavelength of the laser and the scattered light are the same) and Raman scattering (when the wavelength of the laser is less than that of the scattered light).

Moreover, the NV- peak (at approximately 640 nm) intensity (proportional to the impurity’s concentration) of a CVD diamond is much higher than that of a HPHT diamond.

The trade of conflict diamonds is widely regarded as immoral due to its association with human rights violations and the financing of armed conflicts against governments. Diamonds are often referred to as blood diamonds in less economically developed countries, due to the fact

diamonds are often mined in war zones, then sold to finance additional armed conflicts against governments. Whilst many diamonds are sold overseas to precisely cut these gems, countries such as Sierra Leone, Angola and the Democratic republic of Congo sell many of these ‘rough diamonds’ on the black market. This is so they can purchase AK-47s, land mines and political favours, it is estimated that this illegal activity makes up to 10% of the US $7billion dollar annual rough

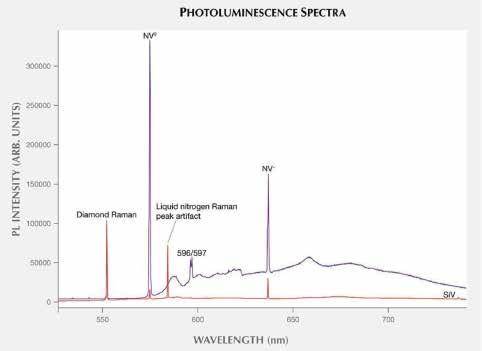
The figure above shows a sample PL spectrum of two synthetic diamond types: CVD (shown in purple) and HPHT (shown in red). The two graphs have been scaled such that the diamond peak at 552 nm (1333 cm-1) have equal intensity. (b) A PL spectrum of a pure diamond sample.

diamond market. Rough diamonds are small and easy to smuggle out of a country so are ideal for the groups that run the trade. Statistics show that one mind in Angola produces $8 million worth of diamonds in a month, enough to buy 160,000 AK-47s. The future for this rough diamond market is growth, due to the demand for these

diamonds and how simple it is to ship out of Africa into developed countries, this will not halt anytime soon. Many other African countries have corrupt governments who buy and sell these diamonds to eastern European countries and countries with weapons from the Cold War.

The Kimberley Process is an international regulation which was established to prevent the trade of war diamonds and ensure that instead, diamonds are sourced from ethical and legitimate sources. This scheme was set up in May 2000 to prevent the trade of these conflict diamonds entering international markets but has a fatal flaw in which any country just has to state they are ‘willing and able to meet the requirements’. This flaw enables countries to keep selling blood diamonds because there are ineffective monitoring mechanisms.

Diamond mining is not considered sustainable as there is a finite amount of material on Earth. In order for there to be continued growth in the diamond industry, firms will need to introduce more synthetic diamonds in

order to make revenue as the current diamond mining rate will deplete the resource. Diamond mining is damaging to ecosystems and wildlife through: water pollution, air pollution, loss of habitat and increased risk of animal extinction. It has been estimated that for one carat of mined diamond, 250 tons of earth has to be moved, moving this much material requires large amounts of energy. It is likely that this energy in LEDC (less economically developed countries) comes from burning fossil fuels and so 160 kilograms of greenhouse gases is released into the atmosphere per polished carat.

In Zimbabwe, hundreds of cattle died from drinking contaminated water from the Odzi River. This river is located downstream from a diamond processing plant who released all the contaminated water into the stream, this incident can also happen with local residents. Marine diamond mining creates light,noise and machinery pollution for ecosystems and sediment removed from mining can take from two to ten years to return. However many companies are making an effort to improve their techniques due to an increased number of strict regulations. However, due to natural diamonds growing hundreds of metres underground, and the increased demand for diamonds, the environmental impact will not stop.

It is predicted that the future of the diamond market will not be dominated by natural or synthetic diamonds alone but that they will coexist in the market. Many people will still choose the traditional diamond (natural), as they hold significant value and appeal especially for those who appreciate scarcity and chronicle. However, the advantage that lab grown diamonds have over natural diamonds is that they are a lower cost making them more accessible to those who aren’t willing or able to pay at the high price level. Synthetic diamonds are judged to be morally correct and more environmentally friendly as there are no blood diamonds involved or mass mineral mining. In conclusion, the choice of the two diamonds will adapt the market in order to: promote responsible mining, sustainable growth and increase transparency between governments, producers and consumers.

Economics

To what extent does a teacher who loves teaching inspire a student to love learning?

In today’s rapidly developing world, effective education is a vital tool to sculpt the population into cultivated and valuable members of society. A competent teacher is essential in ensuring that the youth receive high-quality education that prepares them for success in life. But what makes a good teacher? Is it their relatability, mastery, and love for the subject? Or could it be their ethnicity, race, and social status? This question has long been debated by researchers, as the implications of education possess great influence on the long-run health of society and the economy. We will be exploring the various determinants of effective teaching and why it’s crucial for society’s progression.

What makes a good teacher?

In today’s society, teachers have a responsibility not only to impart academic knowledge to their students but also to cultivate their soft skills. The Behavioural Insights Team, based in the UK, advises that teachers give great importance to developing potentially overlooked attributes in their students, such as emotional intelligence and stress management. Teachers are therefore crucial as they shape both the intellectual and emotional competence of future generations. But what makes a good teacher?

Ava (NHEHS)

Dome (Harrow)

Harinee (NHEHS)

James (Harrow)

Multiple research studies have been conducted to explore whether students’ ability to perform academically is affected by them being able to relate with their teachers demographically.

The Indian Constitution abolished the caste system in 1950; however, it is still visible in society today. As part of an initiative to improve access to schooling, the government made schools within walking distance of rural households. The residents of these rural areas live in habitations that are organised along historical caste lines, which means that the caste system inadvertently came into effect in the education system. Lower-caste children attended schools that were in poor physical condition due to a lack of funding, which was reflected in their low attainment. In 2004, Hoff and Pandey conducted a study to investigate the educational outcomes of the caste system. They found that discrimination against lower-caste students was driven by teachers of a lower caste, and teachers from higher castes appeared to not discriminate at all. Furthermore, when the caste of the students was not publicly revealed, there appeared to be no significant gap in the performance of children from different castes. This signifies that the attainment of students is largely limited by the teachers’ perception of their caste rather than their academic capability.

Multiple research studies have been conducted to explore whether students’ ability to perform academically is affected by them being able to relate with their teachers demographically. A paper published in 2010 entitled ‘Akin to My Teacher’[3] investigated the impact of students and teachers sharing the same gender, religion, and caste. The paper referenced a 2007 study by Aslam and Kingdom, which concluded that “girls benefit from having female teachers.” This is largely due to the different classroom management practices adopted by male and female teachers, with girls being more responsive to the females’ approach. While this study does not conclude that all students will benefit from having a teacher who shares their gender, it suggests that girls, in particular, can succeed academically under those conditions.

Students and teachers sharing demographic characteristics can have positive and negative impacts on schooling outcomes. The concept of ‘role model effects’ suggests that students are more engaged, better behaved and perform better when their teacher shares their gender, caste, and/or religion. For example, in the mid-1980s in Sri Lanka there was a surge in young teachers of plantation community origin. These teachers, who shared the ethnic identity of many of their students, acted as motivational role models and inspired women to gain government jobs. The negative aspect of this can be shown by the ‘Pygmalion effect’. This refers to students self-fulfilling negative expectations that their teachers have of them due to their demographic characteristics. Teachers that operate on these preconceived judgements inhibit equity within the schooling system and encourage students to perpetuate existing stereotypes.

Does a love of teaching change the learning environment?

There is evidence to suggest that a teacher who loves teaching can inspire their students to start learning. When teachers are passionate and enthusiastic about their subject matter, it can create a positive and engaging classroom environment that can motivate students to become interested in the topic at hand. Research has shown that teacher enthusiasm and passion can positively impact student engagement, academic achievement, and motivation to learn. For example, a study conducted by the University of Michigan found that teacher enthusiasm was one of the strongest predictors of student engagement in the classroom. Similarly, a study by the University of California, Berkeley found that teacher enthusiasm was positively correlated with student motivation, particularly with students who were initially less interested in the subject matter. Overall, it appears that when teachers are passionate about teaching, and demonstrate a love for their subject matter, it can have a formidable effect on their students’ motivation to learn and engagement in the classroom.

When teachers are passionate and enthusiastic about their subject matter, it can create a positive and engaging classroom environment that can motivate students to become interested in the topic at hand.

and society as a whole. Education plays a crucial role in promoting democracy, civic engagement, and social mobility, among other benefits. A well-educated population is more likely to vote and volunteer, which translates to better representation of the population and more effective governance. Increased engagement from society will lead to increased accountability from the government, which results in more effective policies from greater cooperation between citizens and government. Moreover, education nurtures cultural awareness and appreciation, which promotes greater tolerance and respect for diversity. When people from diverse backgrounds participate in elections, it can help foster a sense of social cohesion and shared identity. This can help reduce polarisation and promote greater understanding and collaboration between different groups. Both these factors of increased civic engagement and intercultural cooperation will pave the path to the smooth operation of the economy and society.

There are several economic benefits derived from teachers enjoying their profession. Being taught by enthusiastic and passionate teachers piques student engagement which leads to higher levels of academic success and in turn good job opportunities, high salaries and increased economic activity. This style of teaching also means that the quality of education increases, creating a more productive workforce in the future. This means there is potential for actual economic growth in the long run. When students are taught by effective teachers who enjoy teaching, they may be better prepared to compete in a global economy. This can improve the competitiveness of the workforce and contribute to increased economic growth and development. Therefore an influx in teachers who are passionate about what they do can lead to higher levels of academic achievement, increased productivity, and improved competitiveness, all of which can contribute to increased economic growth and prosperity.

Qualitative and quantitative implications of education on society

Even with competent teachers, will there be any tangible benefits for society to reap? The answer is yes, the impact of good education cannot be overstated. Not only does it lead to personal growth and contentment, but it also has extensive implications for the economy

Education comes with many benefits not originally seen within the syllabus; this is known as the hidden curriculum, an idea commonly presented by Karl Marx. The hidden curriculum is lessons that students learn outside of the classroom, such as in assemblies, sports, extracurricular and other experiences that students have on a daily basis within the school environment. It helps prepare students for adult life and influences their beliefs, attitudes and morals towards certain situations. The hidden curriculum highlights the importance of hard work, responsibility and self-discipline which causes students to develop a strong work ethic, ergo leading to an increase in productivity and a decrease in cost of

production for firms. However, the hidden curriculum emphasises conformity and obedience, students may be less likely to question authority or challenge the status quo, which can limit innovation and creativity in the workforce.

In addition to the qualitative aspects, education also has undeniable quantitative benefits. Excellent education enriches economic outcomes, including higher earning capacity, reduced poverty, and increased tax revenue. Studies have found a direct correlation between high levels of education and high GDP per capita, as well as lower levels of poverty. For example, an analysis by the University of Oxford found that every additional year of education can increase one’s earnings by 10%. A more educated workforce means one that is skilled and knowledgeable, which is essential for innovation and competitiveness in a global economy. In fact, businesses often prioritise hiring employees with the highest levels of education because it is a good indication of expertise and proficiency needed to succeed in a workplace. Additionally, a welleducated population is also less likely to engage in criminal activities, leading to a reduction in crime rates and associated opportunity cost for handling it. Ultimately, these features

of improved economic growth, reduced crime, and higher earnings, all lead to a better standard of living and quality of life within a society.

Humanitarian significance of education

Education is not only important for economic growth and development, but it also has a crucial humanitarian dimension. For individuals, education can provide essential skills and knowledge that can improve their health and wellbeing, increase their opportunities for

Education comes with many benefits not originally seen within the syllabus, thus known as the hidden curriculum, an idea commonly presented by Karl Marx.

employment and economic security, and enable them to participate more fully in their communities and in civic life. For societies, education can help to build more resilient and equitable communities, promote peace and stability, and provide the foundation for sustainable development.

A benefit of education is that it encourages gender and racial equality, and teaches girls about

contraception: a study at the World Bank report found that “an extra year of schooling for girls reduces teen pregnancy rates by six per cent”. A fall in teen birth rates allows more women to go to work and therefore decreases unemployment across the country. As more women join the workforce, their income rises, leading to an increase in consumption hence an increase in aggregate demand. Simultaneously education also helps to reduce child mortality as “a child born to a mother who can read is 50 per cent more likely to survive past the age of five” according to UNESCO. A decrease in child mortality subsequently frees up more space in hospitals which allows the government expenditure to increase in other sectors within the economy such as defence. Education can also promote social and cultural awareness as it allows students to gain a further understanding and appreciation of the diverse world around them.

Challenges and potential solutions

If teaching is such a vital aspect of a functioning society, why do we see little emphasis placed on good education around the world? There are a number of reasons as to why teaching doesn’t have the desired effects on society, ranging from the quality of teachers to the motivation driving the teachers to perform well

in their job.

One of the most prominent reasons as to why the education system is flawed is due to society’s view on the system. Being a teacher is seen as a lesser profession in society’s eyes, especially in the developed world. This stigma about the job means that the brightest and most fitting people won’t want to work in the education sector and so the sector attracts candidates that aren’t as good as they could be. This then creates a stronger stigma against the teaching profession and so it is a self-fulfilling cycle. Due to this stigma of teaching being an easy profession, many of the world’s teachers are under-trained. This lack of training means that the teachers aren’t equipped to properly educate and help the children under their care, not just academically, but to a much higher degree in areas outside of the classroom, such as mental health or character development from an early stage. This lack of proficiency from teachers leads to their children not gaining the basic skills needed to succeed in life and so they don’t reap many of the benefits of education. To prevent this cycle from occurring, we need to change the way that society views teachers. This could be done by increasing teachers’ pay to increase the profile of the job so that it is seen as a more important job and attracts

more highly qualified candidates or it could be done by fostering a society that places a large importance on education and learning for the youth. On top of changing society’s views, we need to place a greater importance on education outside of academic life, so that the children coming out of school have better social skills and can foster a better society in the future.

Another reason as to why education isn’t having the desired effect is due to the fact that education is a merit good. This means that people don’t see the real benefits of education in the long run, as they operate in the short term and so when deciding whether to undergo education, they don’t think about how it may improve their lifestyle or their job in the future, they only see the early mornings and negatives that it brings along in the short term. Due to this myopic outlook from society, education isn’t seen as being as important as it really is for the advancement of society. This means that fewer people than optimum take part in the education system. This misunderstanding of the benefits of education could be fixed by trying to offer reward schemes to people who pursue further education, to try and incentivise members of society to take up further education and allow them to truly understand the

benefits of education and to consume education to the optimum level. This extra consumption of education will increase the positive effects as educated people increase the standard of living for people around them and improve the economy in the process.

Conclusion

Teachers are absolutely vital to a well-functioning society. They need to not only be efficient in educating the children under their care academically, but also giving them a wider education outside the classroom so that they can truly develop into active, high-quality members of society. What makes a good teacher is, to a great degree, dependent on the type of education they are in as well as what their pupils are like and their background. However, it is commonly accepted that an outstanding teacher won’t only love their subject and want to share their knowledge, but they will care for the children and seek to improve their quality of life as they head into the future.

A teacher’s importance in society cannot be overstated and should not be underestimated as they are the people who are shaping the future of our world every day; whether it be in the classroom or on the sports field, teachers are creating a better tomorrow for everyone.

Symposium Team 2023

Dr Adam Bowditch, Dr Thomasin Bailey, Miss Emily Chappell, Mr Luke Cryer, Ms Madeleine Copin, Dr Joe Cooper, Dr Chris Cummins, Mr Scott Elgersma, Mr Thomas Rodgers Endersby, Dr Richard Freeland, Mr Julian Gallant, Miss Hannah Fox, Dr Callum Hayes-Smith, Dr Emon Keshavarz, Dr Roberta Klimt, Dr Lukas Kowalik, Mr Alastair Land, Miss Catherine McHenry, Mr Phil Nelkin, Dr Richard Pearce, Dr Shenila Rawal, Mr Harry Sellen, Mr Chiin-Zhe Tan, Mrs Gaelle Valcke, Mr John Wright

The Notting Hill & Ealing High School and Harrow School

Year 12/Lower Sixth Symposium

SPRING 2023