AWhile…forWiles
AndrewWilesdiscoveredFermat’slasttheoremasatenyearold,whenhefoundabookabout itinhislocallibrary.Hewassurprisedthatanideathatwassoeasytounderstand,stilllacked a proof. He decidedto make this hislife goal, dedicating twenty years of his life to furthering his understanding of maths. During this period, Wiles made several advances in the field of ellipticcurves.ThesecontributionswouldlaterleadhimtohisproofofFermat’slasttheorem.
Many of his contemporaries aimed to dissuade him, claiming that the theorem had no proof. Wilesrefusedtolisten.Hespentsevenyearsinisolation,workingsecretlyandindependently. This isnot commonfor mathematicians,whotendtodiscusstheir ideaswith othercolleagues to ensure they are moving in the right direction, and to gain different perspectives. However, Wileswasdeterminedtoprovethetheory,cuttinghimselfofffromtheworld.Andafterseven long years, it would seem it had paid off: in 1993, he presented a proof to fellow mathematiciansataconferenceinCambridge.Manypushedhimtopublishhisfindings,eager topulltheveiloffthiselusiveproof.
Wileshesitated.
Hefelt that something was not right. Hedecided to hold offfrom publishing his proof then; a veryprudentmovesinceaflawwassoondiscoveredinhisproof.Ratherthandisregardingthe whole proof, or giving up, Wiles spent more than a year trying to mend the hole. Along with thehelpofRichardTaylor,aformerstudent,Wileswasabletoofficiallycompletehisfindings. In 1995, he published both papers, finalising the proof, and distributing it to the rest of the world.
WecanalllearnavaluablelessonfromAndrewWiles;wedon’tevenneedtosolveanage-old problem.
Wilesfoundadream,andhewasn’tafraidtocontinuepursuingit,evenashegrewolder.
This dream involved doing something some people thought was impossible. Fermat’s last theorem is a very simple idea. It is also known as Fermat’s great theorem, and it states that there are no natural numbers (1, 2, 3, …) ��,��,�� such that�� +�� =�� where�� is a natural number greater than 2. For example, Fermat’s last theorem states that there are no numbers ��,��,�� where��3 +��3 =��3.ThisistheexamplethatPierredeFermatmentionedin1637,inhis copyof Arithmetica byDiophantusofAlexandria.Heclaimedthat“Itisimpossibleforacube to be a sum of two cubes, a fourth power to be a sum of two fourth powers, or in general for anynumberthatisapowergreaterthanthesecondtobethesumoftwolikepowers.”
However, he was writing this in the margin of the book, and so did not enlighten us with his proof,andhisnextwordswere,“Ihavediscoveredatrulyremarkableproof[ofthistheorem], butthismarginistoosmalltocontainit.”Thiscommentstumpedmathematiciansforcenturies, because although individual cases were proved, it seemed impossible to find a general proof. Duetothelargeamountoftimethatpassedbeforeananswerwasfound,manymathematicians believethatFermathadn’tactuallyfoundaproof,butsimplygotabitaheadofhimself.
-Rali
Tangents–People September23 5
PaulErdős
Mathematicians are often thought tobe highly eccentric, and Paul Erdős is certainly one who fits that stereotype. His eccentricity accompanied a highly intelligent mind, and he is rememberedforhavingthoughtaboutmoreproblemsthananyothermathematicianinhistory, withatotalofaround1500publishedpapers.Manyofthesepaperswereco-authored,andthe 485 mathematicians with whom he published a paper are said to have an Erdős number of 1. Those mathematicians who had worked with someone with an Erdős number of 1 have an Erdős number of 2, and so on; in other words, Erdős numbers are the degree of separation of any person from Erdös, based on mathematical collaboration. Erdős numbers are a mathematical topic in their own right, with papers on Erdős numbers scattered around mathematicalliterature,andagraph(inthemathematicalsenseofagroupofverticesconnected by edges) called the Collaboration Graph has also been produced. The highest known Erdős numberofanyworkingmathematicianiscurrently7.
Erdőswasundoubtedlyagenius,and,asherecalls,“fellinlovewithnumbersatayoungage”. He was born in Hungary in 1913, to Jewish parents, who were also both high school mathematics teachers. By age 3, Erdős could perform complex mental calculations and went ontodiscovernegativenumbersatage4.HeenteredthePéterPázmányUniversityinBudapest at17 and completed his undergraduate and PhD in 4 years. During this time,he made quite a


Tangents–People September23 6
name for himself with his simple proof of Bertrand’s postulate (also known as Chebyshev’s Theorem),whichstatesthatforeveryinteger ��,aprimenumbermustexistbetween �� and 2��.
In 1934, Erdős moved to the UK for a fellowship at the University of Manchester, due to the riseofantisemitisminHungary.In1938,hemovedyetagain,thistimetoAmerica–originally forafellowshipatPrinceton,however,Princetonconsideredhim“uncouthandunconventional” andrefusedtorenewhisfellowship,leadingErdőstomovetoMadison,whereStanislawUlam wasbased.
For the rest of his life, Erdős continued to devote his time solely to mathematics – he had no wife,children,orhome,butrathermovedbetweenfellowmathematicians’homes,workingon theorems together before finding another place to stay. His life was free of all but the most basic of material objects (and his prized notebooks), and much of the money he earned in his lifetime he donated to others. During the last 25 years of his life, Erdős regularly clocked in 19-hour days, with the help of caffeine and amphetamine, for, as he would often say, “A mathematicianisamachineforturningcoffeeintotheorems”.
Erdös’ main focus was on number theory, graph theory, and combinatorics. One of his most notable results is the Prime Number Theorem, which gives an approximation for the number ofprimeslessthanorequaltoanyintegern.Interestingly,Erdősworkedonthisproblemwith Atle Selberg, and initially they agreed to publish their papers together, each outlining their work. However, at the last minute, Selberg decided to publish his proof first, and was consequentlygivenmuchofthecredit,andwasalsoawardedtheFieldsMedalinthefollowing year.Nevertheless,Erdősdidreceivehisfairshareofprizes,includingtheWolfPrizein1983. Erdős did not only solveproblems but was also“theabsolute monarch of problem posers”, to quoteErnstStrauss.Erdőswouldofferpaymentstounresolvedproblems,theamountofmoney depending on the difficulty and significance of each problem. Some of these problems have sincebeensolved–includingtheCollatzconjecture,andErdös’conjectureonprimegaps,but othersremainyetunsolved,suchashisconjectureonarithmeticprogressions(whichstatesthat: if the sum of the reciprocals of a sequence of integers diverges, then the sequence contains arithmeticprogressionsofarbitrarylength).
Aside from his mathematical genius, Erdős was full of quirks, one of these being his use of a special vocabulary. He often spoke of the SF (Supreme Fascist) which translated to God, and ‘The Book’, which he believed contained the most elegant proof to every problem. He called childrenepsilons(astheGreekletterepsilonisusedtorepresentsmallquantities),womenwere “bosses”andmenwere“slaves”.Ifsomeonehad“died”,theyhadstoppeddoingmathematics, andiftheyhadreallydied,Erdőswouldsaytheyhad“left”.
His signaturewas also notable,and he accumulatedquitea fewletters during his life, signing off as Paul Erdős P.G.O.M.L.D.A.D.L.D.C.D. These stood for Poor Great Old Man, Living Dead(addedat60),ArchaeologicalDiscovery(at65),LegallyDead(at70),andCountsDead (at75).
Erdőscontinuedworkinguntilhisdeathattheageof83inHungary,thusdefyingthecommon notion that mathematicians are productive only in their youth and contributing immensely to mathematicsintheprocess.
-Sara
Tangents–People September23 7
M.C.Escher
“The laws of the phenomena around us - order, regularity, cyclical repetition, and renewalshaveassumedgreaterandgreaterimportanceforme.Theawarenessoftheirpresencegivesme peace and provides me with support.” wrote M.C. Escher about the laws of maths and specifically, of symmetry. “I try in my prints to testify that we live in a beautiful and orderly world,andnotinaformlesschaos,asitsometimesseems.".
Bornin1898,theDutchartistMauritsCornelisEscherwasfarfrompromisingasastudent.A sickly child, his grades were often dire, and his academic future unpromising. He began to study woodwork at age 13, which he continued at Haarlem School of Architecture and DecorativeArts.ThispromptedhimtoembarkongreattravelsthroughItalyandSpainin1922, where his interest was piqued by Roman landscapes, Moorish architecture and the repetitive geometricpatternsthatadorntheAlhambra.
A later 1936 revisit to the Alhambra would throw him into deep obsession with such tessellations – interlocking patterns with no gaps in between (think tetris) – and with regular divisions of the plane. Using geometric grids, he created highly complex interlocking tessellating designs, often with faunal themes inspired by his time in the Italian countryside. Describing his tessellations as a “real mania to which I have become addicted”,Escherlongedforasubstantialtheoreticalunderstandingtothemathematicalarthe was already intuitively creating. In the same year he returned to study maths, focusing on symmetry groups, an area of group theory which explores the groupof transformations under which a shape is invariant. Having created artistic representations of 43 different types of symmetries,heengagedinfurtherintense‘empirical’research,bycreatingwoodcutsofothers andrecordinghisfindings.Hisworkandresearchinthisperiodisrecognisedandusedbymany mathematicians to illustrate such complexities, and some of his work was even investigated mathematically–alldespitehislackofformaleducation.Inthefollowingyears,Escherwould explore other mathematical and physical concepts in his art, including hyperbolic geometry (attracting the attention and admiration of the famous mathematician and physicist Roger Penrose), relativity and physical-law-bending depictions of ‘reality’. He is known for his unique,fascinatingandinnovativeartworks,acoupleofwhichcanbeseenbelow.
His work primarily took the form of sketches, lithograph prints and woodcuts, the latter of which are especially time-consuming and challenging to produce, which highlights his talent andcraftmanshipfurther.Despitethisandhisimmensecreativity,Escherfacedmuchcriticism and dismissal from art critics who declared that his artlacked emotional depth and other such things.Afterhisdeath,hisworksbecamemoreacceptedintheartworld.However,thecritical reception to his work exposes the interesting gap of the incomplete tessellation that links the worlds of art and science. Now renowned, Escher built a bridge over this gap, bringing the worldsofartandscienceeversoslightlyclosertogether–asheprovedinhiswork,theyought to be. In his own, ever tessellating language, Escher said on this, “Science and art sometimes can touch one another, like two pieces of the jigsaw puzzle which is our human life, and that contactmaybemadeacrosstheborderlinebetweenthetworespectivedomains”,apromisehe defiedalloddsandnormalitiestoachieve.
-Amelia
Tangents–People September23 8
SophieGermain
SophieGermainwasaFrenchmathematicianwho livedfromApril1,1776,toJune27,1831, in Paris, France. She contributed greatly to the subject of science and technology, especially thestudy ofacoustics (atypeof physics that describes the properties of sound), elasticity(the abilityofamaterialbodytoreturntoitsoriginalshapeandsizewhentheforcesactinguponit aretakenaway),andthe theoryof numbers (abranch ofmathematicsregardingtheproperties ofallpositiveintegers).
As a girl, Sophie was already highly interested in maths and was known to have read many books using her father’s library. She later went to École Polytechnique, an engineeringschoolinPariswhereshemetthemathematician Joseph-Louis Lagrange; he helped Germain in many ways and was a strong support and encouragement to her career. Herearlyworkwasmainlybasedonnumbertheory,shewas inspiredbyAdrien-MarieLegendreandCarlFriedrichGauss, who both researched and wrote works on this. The subject was a very important part of her career, and it occupied her throughoutherlife,bringingherthemostsignificantresults.

In 1809, the French Academy of Sciences opened a competition conducted by a German physicist for a mathematical account of the phenomena witnessed in experiments on vibrating plates.In1811, Germain submitted an anonymous response,but the prizewasnotawarded.Thecompetitionreopenedtwicemore,oncein1813andoncein1816, and Germain submitted a memoir on both chances. She finally won the prize on the third memoir she wrote, which explained vibrations of curved as well as flat surfaces and was publishedprivatelyin1821.Duringthe1820ssheworkedonresearchinelasticity,butbecause she was isolated from the community based on her gender, she was very unaware of the developmentstakingplaceinthetheoryofelasticityandmadeverylittleprogress.
Meanwhile, Germain had decided to start working on number theory again, and in 1819 she wrote to Gauss explaining her strategy for a solution to Fermat’s last theorem, whichstates that there is no solution to the equation xn + yn = zn if n is an integer greater than 2 and x, y and z are non-zero integers. Her work first appeared in 1825 in the second edition of Legendre’s Théories des nombres. She worked for a long time with Legendre, and Germain’s method formed the basis for his proof of the theorem for the case where n = 5. In 1995, the theorem wasthenproved forallcasesbyEnglishmathematicianAndrewWiles.
In1829,Germainwasdiagnosedwithbreastcanceranddiedtwoyearslater.Thatyearin1831, Gauss had arranged for her to receive an honorary doctorate from a German university, but it couldnotbeawardedtoher.Sophiewas amassivehelpbothintheresearchofmathsandina step towards allowing women to have more freedom and right of speech. Despite initial

Tangents–People September23 9
opposition from her parents and difficulties presented by society and her place, she became knownasoneofthegreatestmathematiciansinthe19th century.
-Vittoria
Tangents–People September23 10
Mathsandpeople:howismathematicalpsychologyusefultopeople?
-Amber
Mathematicalpsychologyfocusesontheuseofmathematicalandcomputationalmodelstoaccuratelyexplainandpredict humanbehaviour,includingcognitiveprocesses,socialbehaviour,personality,personaldevelopment,andmentalhealth. Thisbranchofpsychologycanbeusefultopeopleinmanyareassuchaseducation,marketing,andmentalhealth.


Howismathematicalpsychology usedineducation?
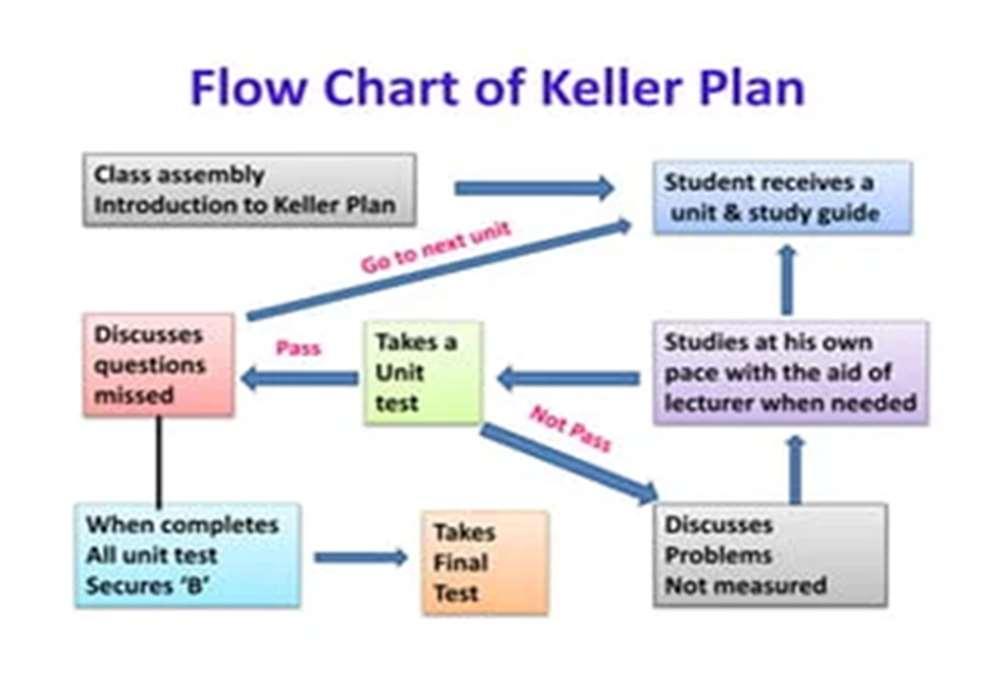
Mathematical psychology has contributed to education through the development of effective educational programsenablinglearning through the use ofinteractive digital tools. Mathematicalmodels of learningare able to formulate computational learning programs specifically tailoredto each student’s individual needs and ability.An example is the Personalised System of Instruction (PSI), alsoknownastheKellerPlan,developedinthemid-1960s byFredS.KellerwithJ.GilmourSherman,CarolinaBori, and Rodolpho Azzian. The PSI is an individualised learning system using mathematical models of student aptitudetotrackstatisticalprogressandprovideadditional support where necessary, mainly in higher education but also in primary and upper school. Its key elements are based on mathematical psychology, such as unit mastery, which requires students to learn a small quantity of information and pass a test with a certain percentage. If theydonotpassthetest,theymustrestudytheinformation andcontinuetakingthetestuntiltheyaredeemedtohave masteredthematerial.ThePSI,andothersimilarsystems, use mathematical psychology to design tests that are effective in measuring student mastery of units, and analysedatafromtheteststoidentifyareaswherestudents need more support, and factors essential to student success, which can help improve the software and the progressmadebystudents.



Tangents–People September23 11
Howismathematicalpsychologyusedinmarketing?



Mathematical psychology uses mathematical models in marketing to help professionals predict how consumers will react to the release of products. Data analysis and mathematical-based research suggests that people are slower to make choices when they are faced with a greater number of options, and researchers can quantify this difference in reaction time to develop more effective ad campaigns. In addition, mathematical psychology aids marketing professionals in evaluating these ad campaigns withmathematical models of consumerbehaviour. For example, Florida Atlantic University and collaborators developed and introduced a new mathematical innovation model generating qualitative and quantitative predictions of adoption trends of new products to improve their success rate upon release. Researchers labelled consumers as 1 of 4 different psychological profiles: the innovator (thought to make independent purchase decisions), early adopter, majority, or laggard, and assigned particular preferences for adoption trends based on these profiles to predict the sales data of 200 supermarket chain products across 4 years. The study suggests that differenttypesofconsumersseekdifferentpropertiesofadoptiontrends to inform their purchasing decisions, which can be formulated mathematically with provable predictions. Findings indicate evidence of these 4 different types of consumer behaviour, and, crucially, illustratetheusefulnessinquantifyingpsychologicalbehaviourinsocial contexts,combiningmathswithpsychology.
Howismathematicalpsychologyusedinmentalhealth?


Mathematical psychologists study the way that mental health problems affect people'sbehaviourandusemathstomodelmethodsusedfor prevention,diagnosis, and treatment. Mathematical models have been used to devise treatment interventions, evaluate treatments, predict patient outcomes, improve the design of clinicaltrials,personalisementalhealthcare,anddevelopdiagnostictoolsformental health disorders. For example, mathematical psychology was used to develop the Beck Depression Inventory (BDI), a multiple choice 21-item self-report questionnaire measuring characteristic attitudes and symptoms of depression. He employed mathematical methods when formulating the inventory, such as factor analysisforitemselection,whichidentifiedtheunderlyingdimensionsofdepression as affective,cognitive,motivational, and somatic symptoms,validation of the BDI, and scaling. As a quantitative assessment of depression, the BDI has a numerical scoring scale from 1 to 63 as a total score for people to compare their own against and assign a level to. Still widely used today, it has helped people recognise their depression,providedmanywithasenseofperspectiveabouttheircondition,andhas also enhanced healthcare professionals’understanding of depression as a disorder significantly impacted by patients’ own thoughts and cognitions. This, and other diagnostictoolsusingmathematicalmodelsandmethods,allowforbetterdiagnosis ofmentalhealthdisordersandprovidetheopportunityfordifferentiatedtreatment.

To conclude,mathematicalpsychology isa vitaldiscipline beneficialto peopleina wide range of fields. Its studyofthe humanmind,patternsofbehaviour,statisticalanalysis,andmathematicalmodelsmakesitausefulbranchofpsychology applicable to education, marketing, and mental health, whether it be through the development of interactive educational onlinetools,forecasts ofretailsales, or thediagnosisof mental healthdisorders.Hopefully,asitcontinuesto evolve and develop, in the future, many more people will be able to benefit from the inventions of this invaluable marriage of psychology,andmaths.

Tangents–People September23 12
References
TheDuelintheCrown(MrThorogood)
Wikipedia.(n.d.). Evariste Galois. Wikipedia.https://en.wikipedia.org/wiki/%C3%89variste_Galois
AWhile…ForWiles(Rali)
Castelvecchi,D.(2016).Fermat'slasttheoremearnsAndrewWilestheAbelPrize. Nature 531,287. https://doi.org/10.1038/nature.2016.19552
EncyclopaediaBritannica.(2023,April7). Andrew Wiles
https://www.britannica.com/biography/Andrew-Wiles
PaulErdos(Sara)
Hoffman,P.(1998). The man who loved only numbers (1st ed.).Hyperion.
Wikipedia.(n.d.). Paul Erdős. Wikipedia.https://en.wikipedia.org/wiki/Paul_Erd%C5%91s#
O’Connor,J.J.&Robertson,E.F.(2000,January). Paul Erdős.MacTutor.https://mathshistory.standrews.ac.uk/Biographies/Erdos/
Hoffman,P.(2023,August2). Paul Erdős.EncyclopediaBritannica. https://www.britannica.com/biography/Paul-Erdos
M.C.Escher(Amelia)
Anon,(n.d.).ThePlaneSymmetryGroups: theirRecognitionandNotation. https://www.york.ac.uk/depts/maths/histstat/symmetry/schattschneider.pdf
Christie’s.(n.d.).The‘mindscapes’ofM.C.Escher.https://www.christies.com/en/stories/collectingguide-the-mindscapes-of-m-c-escher-0801512f6553478fa0404f6ae511d5bf
Ranucci,E.R.(n.d.).MasterofTessellations:M.C.Escher,1898-1972. https://www.jstor.org/stable/41182465
SophieGermain(Vittoria)
O’Connor,J.J.,&Robertson,E.F.(2020,November). Sophie Germain https://mathshistory.standrews.ac.uk/Biographies/Germain/
Barrow-Green,J.(2023,June23). Sophie Germain.EncyclopediaBritannica. https://www.britannica.com/biography/Sophie-Germain
MathematicalPsychology(Amber)
Smith,P.,Liu,Y.,Townsend,J.T.,&vanZandt,T.(2020).MathematicalPsychology. https://doi.org/10.1093/OBO/9780199828340-0266
Tangents–People September23 13
BestPsychologyDegrees.com.(n.d.) What is Mathematical Psychology?
https://www.bestpsychologydegrees.com/faq/what-is-mathematical-psychology/
Wikipedia.(n.d.). Keller Plan
https://en.m.wikipedia.org/wiki/Keller_Plan
Wikipedia.(n.d.). Beck Depression Inventory
https://en.m.wikipedia.org/wiki/Beck_Depression_Inventory
Wikipedia.(n.d.). Mathematical Psychology.
https://en.m.wikipedia.org/wiki/Mathematical_psychology
Hillmayr,D.,Ziernwald,L.,Reinhald,F.,Hofer,S.I.,&Reiss,K.M.(2020). Computers and Education, 153 https://doi.org/10.1016/j.compedu.2020.103897
IGI Global.(n.d.). What is Keller Plan.https://www.igi-global.com/dictionary/keller-plan/16126
MarketBusinessNews.(n.d.). Keller Plan https://marketbusinessnews.com/financial-glossary/kellerplan/
PsychologySchoolGuide.(n.d.). Mathematical Psychology Career Guide.
https://www.psychologyschoolguide.net/psychology-careers/mathematical-psychologist/
FloridaAtlanticUniversity.(2023,May8). Mathematical model based on psychology predicts who will buy trendy products. https://phys.org/news/2023-05-mathematical-based-psychology-buytrendy.html
FloridaAtlanticUniversity.(2023,May8). Math Meets Psychology to Target Trendy Buyers.
https://scienceblog.com/537742/math-meets-psychology-to-target-trendy-buyers/
RoskildeUniversity.(2016,May4). Mathematical model can improve depression diagnosis
https://ruc.dk/en/news/mathematical-model-can-improve-depression-diagnosis
AmericanPsychologyAssociation.(n.d.). Beck Depression Inventory
https://www.apa.org/pi/about/publications/caregivers/practice-settings/assessment/tools/beckdepression
IndianaStateMedicalAssociation.(n.d.). Beck’s Depression Inventory
https://www.ismanet.org/doctoryourspirit/pdfs/Beck-Depression-Inventory-BDI.pdf
Cohen,A.(2008).TheunderlyingstructureoftheBeckDepressionInventoryII:Amultidimensional scalingapproach. Journal of Research in Personality, 42 (3),779-786.
https://doi.org/10.1016/j.jrp.2007.09.007
Tangents–People September23 14