ARMADURAS Y VIGAS

Alcos Ventura, Kevin Alfaro Paico, Darwin Castilla Espinoza, Ariana Moreno Ballena, Marcelo Rojas Morán, Alex

Ingeniería Civil Ambiental, USAT

I. INTRODUCCIÓN

Desde tiempos remotos, en el mundo de la ingeniería civil, la viga ha sido considerado uno de los principales elementos constructivos gracias a que es de quien depende el soporte de todas las estructuras que vemos hoy en día. Por mucho tiempo esta estructura fue elaborada únicamente con madera, pero gracias al desarrollo de la tecnología y los diversos avances que ha proporcionado, se ha logrado fabricar vigas de distintos materiales tales como el hierro o el acero brindando a la estructura diferentes propiedades químicas, físicas y mecánicas

Por ejemplo, en el caso del acero, este es un material isotrópico, lo que brinda una mayor resistencia tanto a tracciones como compresiones y representa un menor peso con respecto al hormigón.

De mismo modo existe una tipología estructural que no puede pasar desapercibida por sus innumerables aplicaciones en las obras civiles. Estamos hablando de las armaduras. Podemos definirlas como un sistema estructural reticular de barras rectas interconectadas en nudos articulados formando triángulos. Los elementos conforman, comúnmente, uno o varios triángulos en un solo plano y se disponen de forma tal que las cargas externas se aplican a los nudos, por lo que, en teoría, solo causan efectos de tensión o de compresión, dos condiciones que deben estar presentes para que dicho sistema estructural funcione satisfactoriamente. En la realidad, algunos esfuerzos de flexión pueden ocurrir como resultado de la fricción en las uniones y de cargas distribuidas aplicadas a los miembros entre las juntas, por lo general estos esfuerzos son menores comparados con las fuerzas axiales y, comúnmente se ignoran para propósitos analíticos.

a. REALIDAD PROBLEMÁTICA

Las vigas, tanto de concreto como metálicas u otro material, tienen serias limitaciones para cubrir grandes luces, no solo para hacer cumplir el estado límite de resistencia, sino fundamentalmente el estadodedeflexión.Alaumentarlaluzaumentaladeflexióndelaviga, y para disminuirla es necesario aumentar su sección transversal, logrando de esta manera una inercia satisfactoria que pueda controlar dicha deflexión. Sin embargo, esto genera un aumento en el peso propio de la viga que automáticamente aumenta la carga y esta a su vez, incrementa la deflexión, de tal manera que para grandes luces la deflexión es incontrolable. Es por esto que, a modo de solución a la deflexión, es necesario buscar otras alternativas estructurales tales como las armaduras

Las armaduras seusan,esencialmente,de la mismaformaquelasvigas de alma llena, pero preferentemente para cubiertas de luces considerables. Una cubierta o entrepiso de relativamente gran luz, formada por vigas, se convierte en antieconómica como consecuencia de la utilización incompleta del material y la posibilidad de pandeo lateral. En estos casos, la viga de alma llena se debe sustituir por un sistema reticular, una armadura, cuyos elementos o barras, sometidos a cargas concentradas aplicadas en los nudos, trabajan a compresión o tensión; lo que permiten un aprovechamiento casi total del material, evitando la marcada deflexión y los negativos efectos que esta genera. Sin embargo, el problema radica en que actualmente no existen guías estandarizadas en cuanto a los tipos de armadura a utilizar de acuerdo al área y cargas actuantes. Dicha problemática se ve reflejada al momento de preguntarse qué tipo de armadura se debe usar para tener un diseño óptimo que se adecúe a las solicitaciones sísmicas, viento, entre otros y cumpla con los requisitos mínimos.

b. CONTENIDO A DESARROLLAR

El presente informe académico, titulado “Armaduras y Vigas” ha sido desarrollado por los estudiantes de la escuela de Ingeniería Civil y Ambiental de la Universidad Católica Santo Toribio de Mogrovejo. Este tema trata de ahondar fundamentos de dimensionamiento, esfuerzos,momento,cargas y deformaciones tanto de armaduras como de vigas dándole un mayor enfoque e importancia a estas. Por ello se han definido conceptos técnicos de nuestro campo profesional a través de teorías, describiendo en algunos casos sus ventajas y desventajas en la ingeniería civil.

c. ANTECEDENTES

El informe de investigación y aplicación práctica presentado ha considerado como antecedentes las tesis de licenciatura e investigaciones de diversos autores, los cuales llegaron a las conclusiones citadas a continuación.

Según Juan Vidal Gutiérrez Lozano (2018) una armadura está compuesta por un conjunto de miembros rectos articulados conectados en los puntos denominados nudos. Estos a su vez se conectan en sus extremos por lo tanto no se prolongan más allá del nudo. Las barras de las armaduras pueden soportar muy pequeñas cargas laterales, por eso es necesario que todas las cargas recaigan en los nudos y no en las barras.En otras palabras, al ser delgados los miembros de la armadura, éstos son incapaces de soportar grandes cargas laterales, es por esto

que es necesario que todas las cargas sean aplicadas en las uniones o nodos.

De igual forma Gutiérrez Lozano (2018) llegó a la conclusión de que se pueden obtener estructuras rígidas añadiendo dos barras a una armadura triangular básica, si estas se unen a 2 nudos diferentes y se conectan en un nuevo nudo se conoce como “Armadura Simple”. A partir de lo cual podemos afirmar que una estructura rígida está diseñada de modo que presente grandes deformaciones bajo la acción de cargas pequeñas.

Con respecto al material con el que es elaborada la viga, Gutiérrez Lozano (2018) afirma que las armaduras construidas con madera presentan ventajas para solución de puentes y cubiertas en general, cubriendo luces mayores usando sistemas a base de viguetas, logrando una mayor flexibilidad en el diseño. Por lo tanto, por su bajo peso se hacen más manejables que en otros sistemas como podría ser el metálico.

En lo que a vigas respecta, realizar ensayos de flexión nos beneficia de modo que ayudan a determinar el comportamiento de las vigas, a la vez que arrojan resultados sobre sus cargas máximas, fisuras y los esfuerzos cortantes a los que pueden estar sometidas. (Ramos Alfaro, García Reyes, Castañeda Monterroso, López Guerrero, & Morales Cruz, 2014). Dicho de otro modo, el objetivo del ensayo de flexión en vigas es determinar las propiedades mecánicas de las mismas, relacionadas con los esfuerzos y deformaciones

Otro antecedente tomado en cuenta hace referencia a que cuando la parte inferior de la viga está en tensión y la superior en compresión o viceversa, en alguna región de la viga existe una superficie neutra y su intersección con cualquier plano transversal es llamado eje neutro. (Guzmán Rosales, 2008). Es decir, la superficie que separa la zona comprimida de la zona traccionada en una viga deformada por flexión es llamada “eje neutro”.

d. OBJETIVOS

El objetivo general de este informe es hacer un enfoque sencillo y simpledel diseño de vigas y armaduras,empleando un lenguaje simple y cotidiano, tratando que el lector entienda los conceptos de manera clara, ya que en el código del ACI y NTP el lenguaje empleado es técnico y no se logra un entendimiento claro si no se tiene una base sólida en los conceptos relacionados

De mismo modo, los objetivos específicos se centran en desarrollar en los estudiantes la capacidad de analizar, entender y dar solución a los distintosproblemas detorsión odeflexiónpresentes en vigas y conocer los distintos tipos de armaduras existentes a la par que se calculan las fuerzas presentes en estas.

e. DESARROLLO DE LA INVESTIGACIÓN

Por último, cabe mencionar que el método empleado en el presente estudio hasido la consulta dediversas fuentes bibliográficas y técnicas para analizar la información del fichaje. El equipo de investigación estuvo formado por cinco integrantes, los cuales, todos en igual mediad, aportaron información relevante y vital para el correcto desarrollo de la investigación y la satisfactoria culminación de la misma.

II. MARCO TEÓRICO a. ARMADURAS

Las armaduras son estructuras que actualmente se usan con mucha frecuencia en la ingeniería. Esta proporciona una solución práctica y económica para muchas situaciones de ingeniería, en especial para el diseño depuentes y edificios.Son estructuras estacionarias concebidas para soportar cargas, compuesta únicamente de barras conectadas por articulaciones, las fuerzas siguen la dirección de las barras. Por tanto, son elementos sujetos a dos fuerzas,esto es,elementos sobre los cuales actúan dos fuerzas iguales y opuestas que están dirigidas a lo largo del elemento.Estas fuerzas pueden ser detensión o compresión.Si tienden a estirar el elemento, está en tensión; por el contrario, si tienden a comprimirlo, está en compresión.

1. ARMADURAS SIMPLES

Una armadura es una estructura compuesta de elementos esbeltos unidos entre sí en sus puntos extremos. Los elementos usados comúnmente en construcción consisten en puntales de madera o barras metálicas. En particular, las armaduras planas se sitúan en un solo plano y con frecuencia se usan para soportar techos y puentes. En toda armadura las cargas están transmitidas en sus puntos de conexión o nodos. El elemento constitutivo básico de toda armadura es el triangula, esta figura geométrica es la que mejor se comporta frente a las cargas que se aplican. Las armaduras degran tamaño se construyen uniendo varios triángulos.

Los elementos que conforman la armadura se unen en sus puntos extremos por medio de pasadores lisos sin fricción localizados en una placa llama "Placa de Unión”, o por medio de soldadura, remaches, tornillos,clavos opernos en el caso dearmadurasde madera,para formar un armazón rígido. Si a una armadura triangular rígida le agregamos dos nuevos elementos y los conectamos en un nuevo nodo se obtiene una estructura rígida., por lo tanto, se pueden expandir repitiendo este procedimiento. Se puede comprobar que en una armadura simple exista el número total de elementos m y de los nodos n mediante la siguiente relación:

2. CONEXIONES

Se usan dos tipos de conexiones para unir elementos deuna estructura:

- Conexiones rígidas

- Conexiones flexibles o articuladas

Una junta o conexión rígida previene translaciones relativas y rotacionesenlosextremosdeloselementosconectadosaunnodorígido tienen las mismas translaciones y rotaciones. En otras palabras, los ángulos iniciales entre los elementos que se interceptan en el nodo rígido se mantienen después de que la estructura se ha deformado bajo la acción de las cargas. Tales nodos son capaces de transmitir fuerzas al igual que momentos entre los elementos.

3. TIPOS DE ARMADURAS SIMPLES

➢ Warren

Estructura de celosía y se identifica fácilmente por su construcción a partir de triángulos equiláteros y distribución de manera uniforme.

➢ Fink

Estructura que tiene forma básica que se caracteriza por tener un patrón V en su diseño son eficientes para transmitir cargas al soporte.

➢ Pratt

Esta armadura se diferencia de Howe porque las barras son inclinadas en el sentido contrario. Usada en pendientes muy grandes, generalmente soportadas por perfiles de sección en caja.

➢ Howe

Los montantes de esta armadura son verticales entre el borde superior y el borde inferior. Las diagonales se unen en cada extremo, exactamente en donde coincide un montante con el tirante en la parte inferior, y con la diagonal en la parte superior.

b. ANÁLISIS DE ARMADURAS

1. MÉTODO DE NODOS

Una armadura puede ser considerada como un grupo de pernos y elementos sometidos a la acción de dos fuerzas. Por tanto, la armadura sepuede analizar apartirdesudiagrama decuerpolibrepara cadaperno y para cada elemento. Cada elemento está sometido a la acción de dos fuerzas, una en cada uno de sus extremos; ambas tienen la misma magnitud, misma dirección y sentidos opuestos. Como las líneas de acción de todas las fuerzas internas en una armadura son conocidas, el estudio de una armadura se reduce a calcular las fuerzas en los elementos que las constituyen y a determinar si cada uno de dichos elementos está en tensión o compresión

Como la armadura en su totalidad está en equilibrio, cada perno debe estar en equilibrio. El que un perno este en equilibrio se expresa dibujando un diagrama de cuerpo libre y escribiendo dos ecuaciones de equilibrio.

Por tanto, si una armadura tiene �� pernos, habrá

En el caso de una armadura simple, se tiene que �� = 2�� 3, esto es, Esto significa que las fuerzas en todos los elementos, las dos componentes de la reacción ���� y la reacción ���� se determinan considerando los diagramas de cuerpo libre de los pernos.

El arreglo de los pernos y elementos en una armadura simple es tal que siempre será posible encontrar un nodo que involucre únicamente a dos fuerzas desconocidas. Estas fuerzas se determinan por medio de las dos ecuaciones de equilibrio y sus valores se transfieren a los nodos adyacentes tratándolos como cantidades conocidas en dichos nodos, este procedimiento se repite hasta determinar todas las fuerzas desconocidas.

2. METODO DE SECCIONES

Si se desea determinar la fuerza en un elemento, se realizará un corte a través de tres elementos de la armadura, de los cuales uno debe ser el elemento deseado, esto es,dicha porción se obtienedibujando una línea que divide a la armadura en dos partes complementarias separadas pero que no interseque a más de dos elementos. Cualquiera de las dos porciones de la armadura que se obtenga después de que los elementos

intersecados han sido removidos puede utilizarse como el cuerpo libre. Para el estudio por método de secciones utilizaremos la armadura que se muestra a continuación.

equilibrio. Las cargas transversales están constituidas por cargas concentradas (N, lb) o cargas distribuidas, uniformemente o no, expresadas en kN/m y kips/ft respectivamente.

A diferencia de otros elementos estructurales, en una viga se presentan 2 efectos claramente definidos, a saber:

• Fuerza cortante (V)

• Momento flector (M)

Para entender mejor la naturaleza tanto de la fuerza cortante como del momento flector considérese una viga prismática bajo la acción de una carga P como se muestra en la figura, donde se corta dicha viga mediante un plano transversal A-A’ localizado a una distancia X con respecto a la reacción de la izquierda y por último se traza el diagrama de cuerpo libre de dicha sección.

En la figura se ha realizado un corte ���� a través de los elementos ����, ���� y ���� y se ha seleccionado la porción ������ de la armadura como el cuerpo libre. Las fuerzas que actúan sobre el diagrama de cuerpo libre son las cargas P1 y P2 que están aplicadas en los puntos �� y �� y las tres fuerzas desconocidas ������ , ������ y ������.

Como no se sabe si los elementos removidos estaban a tensión o compresión, de manera arbitraria se dibujan las tres fuerzas alejándose del cuerpo libre como si los elementos estuvieran en tensión.

El hecho de que el cuerpo rígido ������ esta en equilibrio se puede expresar con tres ecuaciones,las cuales pueden resolverse para encontrar tres fuerzasdesconocidas.Si solo sedeseadeterminar la fuerza ������,solo se necesita escribir una ecuación, siempre y cuando dicha ecuación no contenga a otras incógnitas.

Por tanto, la ecuación

�� =0

Como sepuedeobservar enla figura,la fuerza cortanteVtiendeacortar o deslizar una sección con respecto a otra y el momento flector “M” tiende a “doblar” o flexionar a la viga.

Las principales características de la fuerza cortante y del momento flector se describen a continuación:

• Fuerza cortante (V)

✓ Para que exista equilibrio en segmento de viga, debe haber una fuerza vertical interna V que satisface sumatoria de fuerzas en “y” igual a 0.

proporciona el valor de la magnitud

F

BD ��������������������������

Un signo positivo en el resultado indicara que la suposición original en relación con el sentido de ������ fue correcta y que el elemento ���� está en tensión; por el contrario, un signo negativo indicara que la suposición adoptada fue incorrecta y que ���� está en compresión.

c. VIGAS

Las vigas son elementos estructurales que soportan cargas aplicadas perpendicularmente a su eje longitudinal y son elementos relativamente esbeltos (una dimensión es mucho mayor que las otras dos). Otro tipo de definición acerca de viga es todo elemento que se flexiona bajo la acción de una carga no importando su tamaño ya que puede ser tan grande que forme parte de un puente o edificio o tan pequeño como el diente de engrane.

Se clasifican por ser estáticamente determinadas o indeterminadas. Las segundas no pueden resolverse mediante las ecuaciones básicas del

✓ Esta fuerza cortante V es igual a la suma de todas las componentes verticales de las fuerzas externas, pero tiene sentido contrario.

• Momento flector (M)

✓ La tercera condición de equilibrio sumatoria de momentos igual a 0 se satisface con un momento interno que se opone al originado por las fuerzas externas.

✓ Es de la misma magnitud, pero de sentido contrario.

✓ Como tiende a causar flexión en la viga, se le llama momento flector.

✓ Para hallar las fuerzas internas en viga expuesta a una carga concentrada P1 y una carga distribuida ωa donde hay que calcularse las reacciones en los apoyos. Averiguar el valor del momento flector máximo se logra auxiliándose en el diagrama de momento flector. Lo mismo para la fuerza cortante.

✓ Estos efectos producen a su vez esfuerzosdecorte(τ)ynormales o de flexión (σ) que varían de una sección a otra de la viga dependiendo de las condiciones de carga de esta.

1. ESFUERZOS DE FLEXIÓN EN VIGAS

Si en una viga prismática como la que se muestra en la figura se dibujan dos planos A y B paralelos entre sí, y, si a continuación se aplica una fuerza puntual P, se puede notar que después de hacerlo, en la parte superior de los planos se acercan, y, en la de abajo se alejan, en consecuencia, se puede deducir, que en la parte por arriba con respecto al eje neutro, se presentan fuerzas de compresión y en la de abajo, de tensión,siendocero,las fuerzasque actúansobrelasfibras quecoinciden con el eje neutro.

Para el diseño de vigas se utiliza la expresión siguiente:

Donde

S = I / c conociéndose como módulo de sección elástico.

2. ESFUERZOS CORTANTES EN VIGAS

La consideración del esfuerzo cortante vertical como tal,se hace en muy pocas ocasiones en el análisis y diseño de vigas, sin embargo, estos esfuerzos se relacionan con los esfuerzos cortantes horizontales y por esto, es de importancia en algunos aspectos en el diseñode vigas, así, los esfuerzos cortantes horizontales deben considerarse en las dos aplicaciones que se describen a continuación:

a) El material usado para lavigatiene una baja resistencia al esfuerzo cortanteen unadirección (generalmente la horizontal).Esto ocurre en materiales como la madera.

b) Las partes fabricadas de la viga deben estar unidas en forma segura.

La acción de los esfuerzos cortantes horizontales supone que una viga está compuesta de varias placasdelgadas,apiladas una sobre la otra,pero sin estar unidas de forma alguna. Cuando se aplica una carga a la viga y ocurre la deformación, las superficies de contacto entre las placas se deslizarán y sus posiciones finales se ilustran en la figura.

Las fuerzas producidas crean asu vez esfuerzos normales o de flexión, que se pueden calcular con ayuda de la ec. siguiente:

Donde:

σ: esfuerzo normal y: distancia que existe entre el centroide y la fibra de interés I: Momento de inercia del área

En el caso de secciones geométricas no simétricas el esfuerzo es diferente en las fibras superiores y en las fibras inferiores, en consecuencia, los esfuerzos de flexión se pueden calcular así:

Si las placas estuvieran unidas por algún medio antes de que se aplique la carga (por ejemplo, pernos), la viga actuará como una unidad, ya que dichos medios de unión impedirán el deslizamiento de las superficies individuales, por lo que los pernos estarían ejerciendo fuerzas horizontales.

Si la viga está compuesta de un solo bloque, y se aplica una fuerza P, cada superficie horizontal tiende a deslizarse con respecto a la superficie adyacente. Realmente el deslizamiento no ocurre, pues la resistencia de la viga al esfuerzo cortante (fuerzas internas aportadas por el material) lo impide. Así, el esfuerzo cortante longitudinal se puede evaluar con ayuda de la expresión siguiente:

Donde:

τ = esfuerzo cortante horizontal

V = fuerza cortante vertical en la sección

Q = momento estático del área que queda arriba (o abajo) del corte

I = momento de inercia de toda el área de la sección transversal con respecto al eje neutro

b = ancho de la sección del corte

III. EJERCICIOS:

a. CASO 1: ARMADURAS

Determinar las fuerzas en los elementos FH, GH y GI, de la siguiente armadura

∑���� =0

����∗15 4����∗10 4����∗5 + ��������������∗8= 0

������ = 34����

1. ANALÍTICO

→ ���� + ���� 50����= 0

���� + ���� = 50����

(14����)∗(5) (14����)∗(10) (14����)∗

(15) (4����)∗(20) (4����)∗(25)+����∗

(30)=0

����= 20���� ����= 30����

Fuerza en el elemento FH. Se mueve FFH a lo largo de su línea de acción hasta que actué en el punto F y se calcula el momento para la sección de la armadura con respecto a G.

Fuerza en el elemento GI. Se pasa la sección n-n a través de la armadura como se muestra en la figura. Utilizando la porción HLI de la armadura como cuerpo libre, se puede obtener el valor de FGI.

������ = 34000��(����������������ó��) ∑���� =0

����∗10 4����∗5 ������ ∗ 2 3 8= 0

������ = 3375����

������ = 33750��(������������ó��) ∑����=0

FuerzaenelelementoGH.SemueveFGBalolargodesulíneadeacción hasta que actué en el punto G y se calcula el momento para la sección de la armadura con respecto a L.

4����∗5 + 4����∗10 ������ ∗��������∗15= 0

������ =5.4827����

������ =5482.7��(������������ó��)

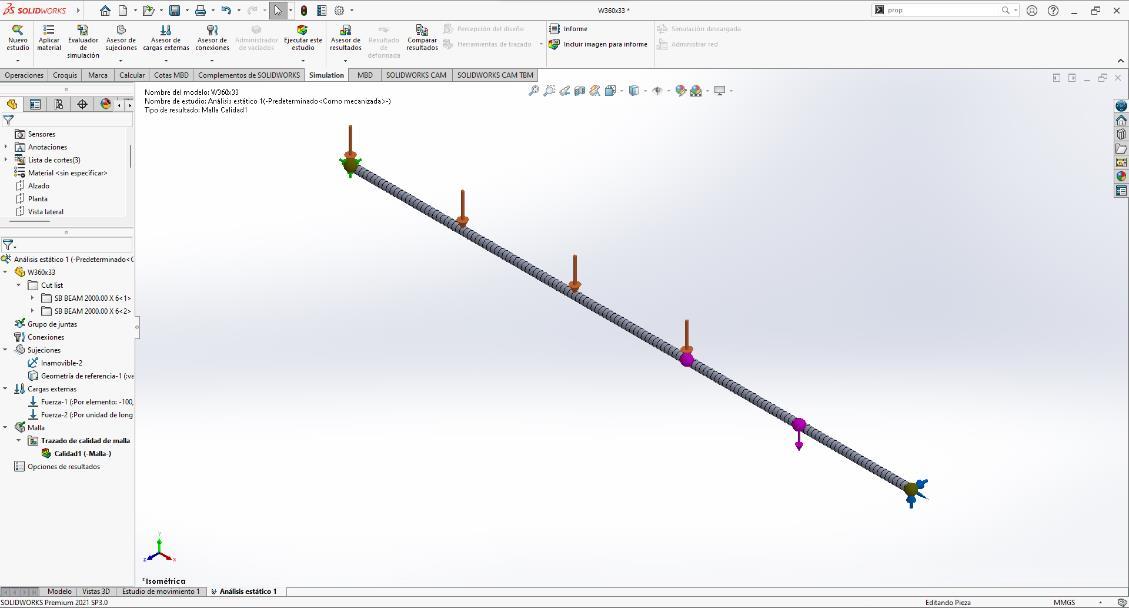
2. SOLIDWORKS

b. CASO 2: VIGAS

Una viga de acero simplemente apoyada de 10 m de largo, AD, debe soportar las cargas distribuida y concentrada que se muestran en la figura. Si el esfuerzo normal permisible para el grado de acero utilizado es de 320 MPa, seleccione el perfil de patín ancho que deberá utilizarse.

Segmento FH

1. ANALÍTICO

Reacciones. Considerando todala viga como un cuerpo libre, se escribe

+↺ ���� =0

D(10m) (240kN)(3m) (100kN)(8m)=0

�� =1520kN D=1520kN↑

Segmento GI

Segmento GH

+→ ���� =0: ���� =0

+↑ ���� =0:���� +1520kN 240kN 100kN=0

���� =188.0kN ��=188.0kN ↑

Diagrama de cortante. El cortante justo a la derecha de �� es ���� =

���� =+188.0����. Como el cambio en el cortante entre A y B es igual a menos el área bajo la curva de carga entre estos dos puntos se tiene

���� = 1880kN 240kN= 52Kn

El esfuerzo cortante permanece constante entre B y C, donde cae a -152 kN, y conserva este valor entre C y D. Se localiza la sección E de la viga donde �� = 0 escribiendo:

���� ���� = ����

0 1880kN= (40kN/M)��

Despejando x se encuentra que x = 4.70 m.

Determinación de |M|máx. El momento flector es máximo en E, donde �� = 0.Ya que M es cero en el apoyo A,su máximovalor en E es igual al área bajo la curva de corte entre A y E. Se tiene, por tanto, que |M|máx = ME = 439.537 kN  m.

Módulo de sección mínimo permisible. Sustituyendo en la ecuación el valor dado de perm y el valor de |M|máx que se encontró, se escribe:

= |��|máx perm = 439537kN m 320MPa

=1373.5531×10 6 m3

=13735531×103 mm3

2. SOLIDWORKS

IV. CONCLUSIONES

• Cuando se desea conocer las fuerzas en todos los elementos de la armadura el método de nodos es más eficiente. Sin embargo, si se desea calcular la fuerza de un elemento o en un número muy reducido de elementos, el método de secciones es el más recomendado.

• Seconcluyequelasvigassoportancargaslocual siseusaunaviga, esta deberá tener resistencia al esfuerzo cortante el cual dependerá del material usado, por lo tanto es importante considerar el análisis y diseños de vigas en la ingeniería civil.

V. BIBLIOGRAFÍA

• C. Arias Palomino and K. N. Betancourt Irusta, “Análisis no lineal elástico en Vigas de Concreto a través del modelo fijo de grietas Dispersas,” repositorioacademico.upc.edu.pe, 24-Jan2020. [Online]. Available: https://repositorioacademico.upc.edu.pe/handle/10757/648868.

• “Conclusiones - UPC universitat politècnica de catalunya.” [Online]. Available: https://upcommons.upc.edu/bitstream/handle/2099.1/3341/3446 3-9.pdf?sequence=9.

• “Marlon - César Vallejo University.” [Online]. Available: https://repositorio.ucv.edu.pe/bitstream/handle/20.500.12692/2 5672/Guevara_FMJ.pdf?sequence=4.

• “Pirhua - Universidad de Piura.” [Online]. Available: https://pirhua.udep.edu.pe/bitstream/handle/11042/5356/ICI_21 22.pdf?sequence=1.

• “Universidad San Ignacio de Loyola.” [Online]. Available: https://repositorio.usil.edu.pe/server/api/core/bitstreams/98f939e54675-419a-b82d-4e46a466f388/content.

VI. ANEXOS

• Capturas de la resolución del ejercicio de armaduras en el programa de SolidWorks:

• Capturas de la resolución del ejercicio de vigas en el programa de SolidWorks: