Unit
mathematics and statistics for Aotearoa New Zealand2
Unit
1
Independent practice
1 Group in 10s, then count.
2 Match the pictures with the numbers.
3 Draw counters to show 47.
Extended practice
1 Who am I?
a I have 5 tens.
I have 9 ones.
I am .
c I have 2 tens.
I am less than 21.
I am .
2 What is …
a 2 more than 48?
b 2 less than 61?
b I have 1 ten. I have 6 ones. I am .
d I have 8 tens.
I am more than 88.
I am .
FINAL
c 1 more than 4 tens?
d 1 less than 3 tens?
Unit 1: Topic 2
Reading and writing numbers
Numbers can be shown with: words twenty-four
rua tekau ma¯ wha¯
Guided practice
1 Write the numerals.
numerals 24 pictures
a twelve b twenty-eight
c fifteen d fifty-three
e fourteen f forty-five
FINAL
2 Circle the correct way to write the numbers.
a 18 eighty eighteen eighty-one
b 46 fourty six sixty-four forty-six All compound numbers are written with a hyphen in them –twenty-four, thirtythree, ninety-nine.
Independent practice
1 Match the player with the shirt.
I wear number ninety-four.
I’m number ninety.
My number is ninety-five.
2 Write in words. a 71 b 62 c 38 d 100
I wear number nineteen.
Match the words, pictures and numerals.
I wonder why “nine” doesn’t change to make the word “ninety”, but “five” changes to make “fifty”?
Extended practice
1 Write words and numerals for:
a Words
Numeral
b Words
Numeral
c Words
Numeral
d Words
Numeral
e Words
Numeral
Unit
Guided
1 Colour the correct word.
2 Colour the correct word.
1 Colour the number between:
2
Extended practice
1 Write:
a the biggest number
b the smallest number
c the number with a 4 in the tens place
d the numbers smaller than 50
2 Write the numbers in the correct place.
3 Write the
Unit 2: Topic 1
Finding the nearest 10
Estimating
Estimating is making a guess based on information you have.
We know this is 5 without counting.
Guided practice
a Lizzy wants to estimate the number of strawberries. She says that there are closer to 20 than 30.
Does this seem right? Yes No
b Check how many strawberries there are by putting them into the ten frames.
a Lizzy wants to estimate the number of lollies. She says that there are closer to 30 than 20.
Does this seem right? Yes No
b Check how many lollies there are by putting them into the ten frames.
c How many lollies are there?
Finding the nearest 10 Ten frames and number lines help you find the nearest 10.
13 is 3 away from 10, and 7 away from 20. So, the nearest 10 to 13 is 10.
1 a Circle 12 on the number line. 01234567891011 121314151617181920
b Is 12 closer to 10 or 20?
c Circle 28 on the number line.
d Is 28 closer to 20 or 30?
2 Circle the numbers below on the number line. 8, 19, 38, 22, 35, 14
Extended practice
When a number ends with 5, it rounds up. So the closest 10 to 15 is 20!
1 Circle the closer number. a 20 or 30 b 30 or 40 c 10 or 20 d 20 or 30
a 16 The nearest 10 is .
3 Circle the closer number. a 8 b 19 c 38 d 22 e 35 f 14 10 20 or 10 20 or 30 40 or 30 40 or 10 20 or 20 30 or b 24 The nearest 10 is
2 Use the ten frames to draw these numbers. Write the nearest 10 for each number.
Unit 2: Topic 2 Number facts
A number bond is a pair of numbers added together to make a bigger number.
What are other number pairs that could go in the squares?
Each pair makes 20.
Guided practice
1 Recall number bonds to 10.
2 Fill in the gaps.
Independent practice
Can you find any pattern here?
2
Find different number bonds that make the number on Robostar’s nose.
3 Fill in the gaps.
Extended practice
Guess my mystery number!
We can use number bonds that we already know to find a missing number.
The mystery number + 8 = 10 + 5 … We know that 10 + 5 = 15.
The mystery number + 8 = 15 … What + 8 = 15?
7 + 8 = 15 … The mystery number is 7. ?
1 Find the mystery ( ? ) numbers.
a 6 + ? = 2 + 8 b 7 + ? = 10 + 4 c 5 + ? = 6 + 7 ? = ? = ? = d 3 + ? = 12 + 8 e 15 + 2 = ? + 9 f 9 + 6 = 5 + ?
= ? = ? = g ? + 16 = 7 + 9 h 14 + ? = 12 + 7
2 True or false?
a 7 + 6 = 8 + 5
b 12 + 7 = 13 + 5
c 18 – 7 = 5 + 6
d 19 – 7 = 3 + 8
False
False
False
False
13 and 4 is 17
01234567891011 121314151617181920
Guided practice
Start from the bigger number to count on –13, 14, 15, 16, 17. So, 13 + 4 = 17.
1 Count on to find the answers.
a 9 and 3 is .
Why is it easier to count on from the number?
01234567891011 121314151617181920
b 11 and 6 is
01234567891011 121314151617181920
c 2 and 15 is .
01234567891011 121314151617181920
Independent practice
1 Circle the bigger number. Then count on.
a 14 and 5 is .
01234567891011 121314151617181920
b 3 + 16 =
01234567891011 121314151617181920
2 Show on the number line and solve. 0123568910121315 47 1114161718192021 222324252627282930
a 20 + 4 =
c 2 and 21 is 20
b 24 + 5 =
c 41 + 6 =
3 Show 12 + 17.
a Draw the bigger number in red
b Draw the smaller number in blue.
c How many now?
4 Show 23 + 14.
a Draw the bigger number in red
b Draw the smaller number in blue.
c How many now?
5 Show 35 + 11.
FINAL
a Draw the bigger number in red.
b Draw the smaller number in blue.
c How many now?
Extended practice
1 Use the number line to count on by tens. a
b
2
Partitioning means separating.
23 can be partitioned as:
Guided practice
1 Record how the numbers have been partitioned. How else could you partition 23? 23 is a is 19
is is and ten and and and 10 and 13 and 3 ones. 15 and 8
FINAL
tens ones tens and ones tens and ones
Independent practice
1 Draw counters to show the partitions. Then fill in the gaps.
a is the same as 18 and 6
b is the same as 20 and
FINAL
c is the same as 16 and
d is the same as and
2 Partition each number into 2 parts.
When do you think it would be useful to partition numbers?
Extended practice
1 Partition each number 2 ways.
a 14 is the same as and OR and is the same as and OR and b 25 is the same as and OR is the same as and OR and and
2 Find 4 ways to partition:
a 28 and is 28. and is 28. and is 28. and is 28.
b 57 and is 57. and is 57. and is 57. and is 57.
Independent practice
1 Circle the starting number. Then count back.
a 14 take away 2 is .
01234567891011 121314151617181920
b 18 take away 8 is .
01234567891011 121314151617181920
c 16 − 12 =
01234567891011 121314151617181920
2 Show on the number line and solve.
a 20 − 6 =
b 20 − 9 =
c 19 – 9 =
a How many?
b Cross out 4 and count back.
c How many now? How could you use counting on to check your answers? 4 a How many?
b Cross out 7 and count back.
c How many now?
5 a Draw 29.
b Cross out 17 and count back.
c Complete the number sentence. − =
6 a Draw 28.
b Cross out 11 and count back.
c Complete the number sentence.
Extended practice
1 Count back to find the answers.
a 27 − 5 = b 49 − 8 =
c 57 − 33 = d 68 – 24 =
2 Draw each story and use counting back to solve the problem.
a Koa had 9 apples. He ate 3. How many are left?
=
b 12 eggs were in a box. 4 broke. How many are left?
FINAL
c Aroha blew 18 bubbles. 5 of them popped. How many are left?
Unit 2: Topic 6
Skip counting
Guided practice
1 Finish by skip counting.
a Count by 2s.
Counting by 2s
Counting by 5s
Counting by 10s
Why do you think it’s called “skip counting”?
b Count by 5s.
c Count by 10s.
Independent practice
1 Skip count on the number line: 02
by 2s.
2 Fill in the gaps.
3
Skip count to find how many balloons, chips and rabbits.
Extended practice
1 Skip count by 2s to help the kiwi get to the tree.
2 Colour the squares to skip count by 5s from 5 and find the secret number.
Secret number: Can you see a number pattern when you skip count by 2s?
A group of 6 cakes is shared between a group of 3 children.
6 shared between 3 is 2.
Guided practice
1 Complete the sentences. a
What does it mean if the shares are “equal”?
8 shared between 2 is .
9 shared between 3 is .
Independent practice
a Share the sandwiches onto the plates.
b How many on each?
a Share the flowers into the vases. 2
b How many in each?
a Share the mushrooms onto the pizzas. 3
b How many on each?
4 Complete the number sentences.
shared between is
shared between is .
shared between is
FINAL
shared between is .
In maths, “division” is another word for “sharing”.
Extended practice
1 a Draw 12 shared between 3.
b Fill the gap.
12 shared between 3 is .
2 a Draw 15 shared between 5.
FINAL
b Fill the gaps.
shared between is .
Write the equation. 1
2 × 4 =
6 Use the array to help you fill in the multiplication facts for two. a 2 × 2 = c 2 × 5 = e 2 × 8 =
2 × 7 =
2 × 10 =
Draw the array.
×
10 × 3 = I wonder if 10 × 3 is the same as 3 × 10.
If the arrows continue, will they land on:
14? Yes No 18? Yes No 20? Yes No
How many donuts?
25? Yes No 21? Yes No 30? Yes No Show how you got your answer.
3 Use a method of your choice to find the total number of players if there are three teams with 10 players on each. Describe or draw how you worked out the answer.
Unit 3: Topic 1
Guided practice
1 Draw a square around the whole objects. This is a whole. This is a half. This is a quarter. This is an eighth.
2 Circle the fractions.
3 Shade 1 2 of each shape.
How many halves make a whole?
Independent practice
1 What fraction has been shaded?
2 What is the size of the piece inside the red rectangle? Write your answer as a fraction.
3 Look at question 2. Which fraction is the biggest?
4 Look at question 2. Which fraction is the smallest?
5 Label the fractions.
6 Draw a line from the fraction to the matching picture.
7 If half is 4 pieces of orange, how many pieces are needed to make a whole orange?
Extended practice
1 Circle the pictures that show quarters.
2
a Shade 1 2 purple.
b Shade 1 8 red.
c Shade 1 4 green.
3
This circle has been halved.
a Draw how it would look if you halved it again. What is each piece called?
b Draw how it would look if you halved it again. What is each piece called?
Guided practice
1 Colour 1 2 of each group.
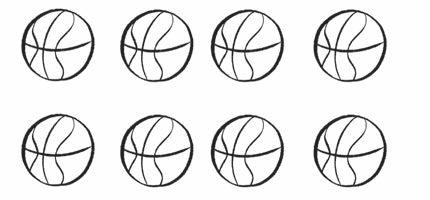
2 Colour 1 4 of each group.
3 Colour 1 8 of each group.
Independent practice
1 What fraction is this?
2 What fraction of the group are:
a the yellow blocks?
FINAL
b the red blocks?
c the blue blocks?
a Circle 1 2 .
b Circle 1 4 .
1 2 of 4 is . 1 4 of 8 is .
c Circle 1 8 . d Circle 1 4 .
1 8 of is . 1 4 of is .
a Colour 1 2 red.
b Colour 1 4 blue.
c Colour 1 8 green.
What does the number on the bottom of the fraction mean?
Extended practice
1 Circle which is bigger.
Unit 4: Topic 1
New Zealand notes and coins
There are five New Zealand coins.
There are five New Zealand notes.
Guided practice
1
a Circle the silver coins.
b Circle the gold coins.
FINAL
c Which coin is bronze?
d Which coin is the biggest in size?
e Which coin is the smallest in size? Who is on the “heads” side of all our coins?
Independent practice
1 Match the coins and pictures.
2
a Circle the $20 notes.
b How many $20 notes are there?
FINAL
c How many $50 notes?
d How many $10 notes?
3
Match the values, pictures and descriptions.
10c
20c
50c
$1
$2
The bird on me cannot fly.
I have a koruru, or carved head.
I have a ship.
The bird on me can fly.
I have a carving of Pu¯ kaki.
Extended practice
a How many silver coins?
b How many gold coins?
c How many of the smallest-sized silver coin?
d How many of the biggest-sized gold coin?
2
a Circle the two notes that equal $25.
b Circle the two notes that equal $60.
Unit 4: Topic 2
Ordering notes and coins
To make $1, you can use:
To make $5, you can use:
Guided practice
1 Draw a line to match each coin with its value.
FINAL
2
a List the coins in order of value from most to least.
b Which coins are worth more than 50c?
c Which coin is worth the least?
a Number the notes in order of value from most to least. 1
b Which notes are worth more than a $20 note?
FINAL
c Which note is worth the least?
2 Circle the coin that is worth the most in each group.
3 Circle the note that is worth the least in each group.
4 Draw the coins in order of value from least to most.
5 Draw the notes and coins in order of value from smallest to biggest.
Which notes and coins are missing from question 5? Where would they go in order of value?
Extended practice
1 Circle coins that equal:
$1
20c
2 Circle notes that equal:
$20
$2
70c
$50
Unit 5: Topic 1 Patterns
ABBB AA
The rule for this colour pattern is red, green.
Guided
practice
1 Finish the colour patterns.
a
The rule for this letter pattern is A, B. b
What other sorts of patterns are there?
2 Finish the letter patterns. a b
1 Are these 2 or 3 patterns?
2 a Continue the pattern.
b What is the rule?
3 a Complete the pattern.
This type of pattern is called a repeating pattern.
b What is the rule?
4 a Circle the error.
b What should the colour be?
5 a Circle the error.
b What should the letter be?
Extended practice
1 Finish the growing patterns. 2 a Create a colour pattern.
b What is the rule? 3 a Create a shape pattern.
b What is the rule?
Unit 6: Topic 1
Length and perimeter
Length
Guided practice
1 How long?
a
The carrot is 5 paperclips long.
How much of the paperclip is left over? Half, less than half or more than half?
c
2 Which is the longest?
The cucumber is 8 paperclips long. paperclips long corn
b paperclips long
less than halfhalfmore than half Circle how much of the last paperclip is left over.
zucchini chilli
Independent practice
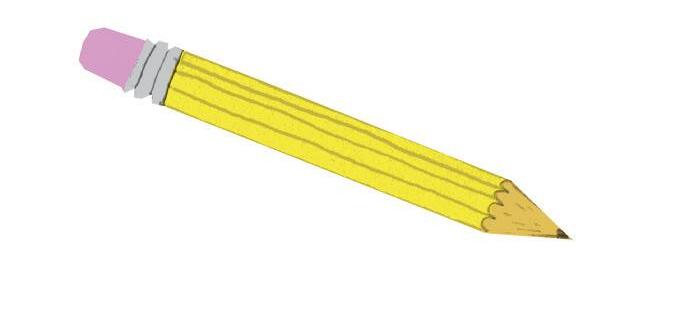
1 Estimate and measure with paperclips:
a the length of your pencil.
b the length of your student book.
c the length of your shoe.
d the length of this line.
Estimate: paperclips
Length: paperclips
FINAL
Estimate: paperclips
Length: paperclips
Estimate: paperclips
Length: paperclips
Estimate: paperclips
Length: paperclips
2 Draw the shortest item from question 1.
Perimeter
Perimeter is the total length of all the sides of a shape.
2 groups of 2 paperclips = 4 paperclips
5 groups of 2 paperclips = 10 paperclips
The perimeter of this rectangle is 14 paperclips.
3 Find the perimeter of each shape.
Extended practice
1 Find the perimeter of your desk:
a using paperclips.
b using pencils.
paperclips pencils
c Which did you need more of?
2 Find the length of the whiteboard in your class. paperclips pencils
a Circle which one is better to use to measure the whiteboard.
paperclips pencil this textbook
b Es timate the length of the whiteboard. paperclips pencils textbooks
c Measure the whiteboard with the item you chose. Record the length and identify the item you chose to measure with.
What else can you measure your whiteboard (or desk) with?
Unit 6: Topic 2
Area measures the surface of something.
The placemat has an area of 12 tiles.
Guided
practice
1 Find the area.
The photo has an area of 6 tiles.
FINAL
Do you notice how there are no gaps? What would happen if the tiles did not fit perfectly? tiles
c tiles
d Which has the smallest area? book rug calendar Dictionary Dictionary tiles
Independent practice
1 Estimate and measure with tiles or blocks:
a the area of your student book.
b the area of a poster.
c the area of your lunch box lid.
d the area of this rectangle.
2 Which has the biggest area?
Estimate: tiles or blocks
Area: tiles or blocks
Estimate: tiles or blocks
Area: tiles or blocks
Estimate: tiles or blocks
Area: tiles or blocks
Estimate: tiles or blocks
Area: tiles or blocks
Extended practice
1 Find the area of this book:
a using blocks to measure. blocks
b using sticky notes to measure. sticky notes
2 Which did you need more of? blocks sticky notes
a Measure the area of your object using blocks. blocks
4 Which did you need more of?
5 Billy measured the area of his dictionary using big tiles. blocks sticky notes
How many tiles did he use and how much of the tiles is left over?
3 Find an object with a smaller area than this book. sticky notes left over
b Measure the area of your object using sticky notes. tiles
Dictionary
Unit 6: Topic 3
Volume and capacity
Volume is how much space an object takes up.
This box has a volume of 4 cubes.
This box has a volume of 6 cubes.
Guided practice
1 Write the volume of these objects. a
FINAL
Which of the two boxes has the bigger volume?
cubes
cubes
c d cubes
cubes
Independent practice
1 Use cubes to make each object. Record the volume. a b cubes cubes c d cubes cubes
2 a Circle in blue the object that needed the most cubes. b Circle in red the object that needed the fewest cubes.
3
FINAL
A B C D
a Which item has the biggest volume?
b Which item has the smallest volume?
Capacity is how much a container can hold.
This bowl has a capacity of 4 cups.
This bowl has a capacity of 10 cups.
Guided
practice
1 Write the capacity of each jug in cups.
Which of the two bowls has the bigger capacity?
Independent practice
1 Circle the unit you would use to measure the capacity of the items.
c d
2
FINAL
a Draw an item with a bigger capacity. b Draw an item with a smaller capacity.
c Circle the unit you would use to measure the capacity of the items you drew.
Extended practice
a Make and draw an object with a volume of 8 cubes. 1
b Make and draw a different object with a volume of 8 cubes.
2 Find a cup and two larger containers.
a Draw your containers.
b Estimate the capacity of each container.
c Measure and record the capacities.
Guided practice
1 Draw something lighter on the scales. a b I am heavy. I am light.
How can you tell which animal is heavier on the balance scale?
2 Draw something heavier on the scales. a b
Independent practice
1 Choose pairs of items from below and draw them on the correct sides of the scales.
FINAL
2 Estimate and then check if each item is lighter or heavier than your pencil case.
a a ruler
My estimate: lighter heavier
Result: lighter heavier
b a s tapler
My estimate: lighter heavier
Result: lighter heavier
c this book
My estimate: lighter heavier
Result: lighter heavier
d a pencil
My estimate: lighter heavier
Result: lighter heavier
e a drink bottle f scissors
My estimate: lighter heavier
Result: lighter heavier
My estimate: lighter heavier
Result: lighter heavier
How will you know which items are lighter than your pencil case?
Extended practice
a 1 cube 1 Collect some counters and cubes. Use a scale to find how many counters balance:
c 5 cubes counters
b 2 cubes counters
2 Redraw the items from lightest to heaviest . counters
d 10 cubes counters
Lightest
Heaviest
Unit 6: Topic 5
Telling time
Guided practice
1 O’clock or half past? a b
Where is the hour hand for o’clock time? Where is it for half past time? 1 o’clock half past 1 2 o’clock half past 2 o’clock half past c o’clock half past o’clock half past
2 What is the time?
Independent practice
1 Match the o’clock times.
2 Show:
3 Match the half past times.
half past 3 half past 11 half past 7 half past 2
4 Write the numbers on the timeline to show which order the events happened in. 1:00 1:05 1:10 1:15 1 2
Extended practice
1 Match the clocks and their times.
2 Write the times. 6:30 12:00 5:30 12:30 5:00
3 Draw or write events on the timeline from your school day in the right order. Arrive
Unit
Months and seasons
December
January
1 summer a Write the months of the year in order.
February March April May June July August September October November
Guided practice
b Write the season each month is in. autumn winter spring
Month
January
FINAL
Season
How many months are in a year? How many seasons are in a year?
Independent practice
1 In what season is …
a Mother’s Day?
2nd Sunday in May
d Father’s Day?
1st Sunday in September
b Valentine’s Day? 14th February
c Anzac Day? 25th April
e King’s Birthday holiday?
2nd Monday in June f Waitangi Day? 6th February
2 Put the events above in the order they occur in the year.
Waitangi Day
FINAL
3 What month and season is the regional anniversary day where you live in 2025?
4
a Write down the birthdays of 10 people in your class.
Name Birthday
What month is your birthday in? What season is it in?
b Write the 10 birthdays in the order they occur in the year.
c Write the season each birthday is in.
Name Birthday Season
FINAL
Extended practice
1 Traditionally, Ma¯ ori ancestors (tupuna) used the Maramataka (Ma¯ ori seasonal calendar). The Maramataka is based on the moon cycles.
Seasons Takurua Winter Koanga Spring
Months Pipiri (May–Jun)
Hongongoi (Jun–Jul)
Hereturikoka (Jul–Aug)
Mahuru (Aug–Sep)
Whiringa-a-Nuku (Sep–Oct)
Whiringa-a-Rangi (Oct–Nov)
Raumati Summer Ngahuru Autumn
Hakihea (Nov–Dec)
Poututerangi (Feb–Mar)
Kohitatea (Dec–Jan) Paengawhawha (Mar–Apr)
Hui Tanguru (Jan–Feb)
Haratua (Apr–May)
a Why does a Maramataka month span over two months?
b What are the other differences with the Maramataka?
c Which months are in Kohita¯ tea?
d Is each Maramataka month listed below in summer, winter, autumn or spring?
Maramataka month Summer, winter, autumn or spring?
Pipiri
Whiringa-a¯-Nuku
Whiringa-a¯-Rangi
Hui Tanguru
Poutu¯ terangi
Haratua
1
2
The first day of January was a Monday.
The first Sunday in January was the 7th.
The last day of January was a Wednesday.
a What is the first day of February?
b What date is the first Sunday in February?
c What is the last day in February?
a How many Sundays are in November?
b How many Saturdays?
c What day is the 13th of November?
d What date is the last day in November?
Independent practice
1
a How many days are in each month?
b On this calendar, which months have 5 Sundays?
c On this calendar, which months start on a Thursday?
a If today is the 4th, what will be the day and date in 2 weeks?
b What day is 9 days after the 13th of May?
c Which days are there 5 of in the month?
d If you went on holidays on the 3rd of May for 11 days, on which day would you get back?
e How many days is it from the 17th to the 23rd of May?
f Which month comes after May?
g Which month comes before May?
Does May always start on a Wednesday?
Extended practice
a Fill in the name of the current month.
b Fill in the dates on the correct days.
c What day does the month start on?
d How many days are in the month?
2 This calendar shows one month of the year.
a Could it be February?
b Which months could it be?
c How many full weeks are there?
d What date is the third Thursday of the month?
Guided practice
“Duration” means how long something lasts.
1 Hours, days, weeks or months?
a 12 in a year.
b 24 in a day.
c 30 in April.
FINAL
d 4 in February.
e 6 1 2 in a school day.
f 3 in spring.
Independent practice
going to a friend’s house eating a cupcake lunchtime at school building a house
1 Think about the activities in the pictures above. Write the activities (A, B, C, D) in order from the shortest to the longest time they take.
Shortest time
Longest time
2 Think about four activities that you do in a normal school day.
a Write and draw a picture of you doing each activity in the boxes.
b Does each activity take longer or shorter than eating breakfast? Write “longer” or “shorter” under each activity.
FINAL
Extended practice
1 Circle the activity that takes less than a minute to do.
writing a two-page story eating dinner counting to 10
2 Write these units of time from shortest to longest. minute, second, day, hour
3 Think about these activities.
eating one pizzacounting to 10 growing long hair
long hair
growing long hair
eating one pizzacounting to 10
eating one pizzacounting to 10
a Which would take a few seconds to do?
b Which would take a few minutes to do?
c Which would take a few months to do?
4 Draw or write something you do that matches each time.
It takes about one hour. It takes about one minute.It takes 10 minutes.
5 Timing an activity
a How long do you think it would take to write the alphabet neatly?
b Time yourself when writing the alphabet. How long did it take?
c How many times can you write your full name in 30 seconds?
This rectangle has:
2 horizontal lines 4 corners
2 vertical lines 4 sides
Guided practice
1 How many:
a
Which way do horizontal lines go?
Which way do vertical lines go?
horizontal lines? corners?
vertical lines? sides?
b horizontal lines? corners?
vertical lines? sides?
c horizontal lines? corners?
vertical lines? sides?
d horizontal lines? corners?
vertical lines? sides?
Unit 7: Topic 1 2D shapes
Independent practice
1 Colour the shapes with:
a 1 horizontal line in green.
b 2 vertical lines in red.
All four-sided shapes are quadrilaterals quadrilaterals. How many quadrilaterals can you see? What other names do they have?
2 Match the shapes and descriptions.
1 vertical side
2 horizontal sides
sides in
corners
vertical
vertical sides
0 vertical sides
0 horizontal sides 4 sides in total 4 corners
a triangles blue.
b quadrilaterals red.
c pentagons yellow.
d hexagons green.
e octagons purple.
FINAL
a How many triangles?
b How many rectangles?
1 Colour the:
a ovals red.
b circles blue.
c semi-circles green.
2 a Circle two shapes.
FINAL
b Write two things that are the same about the shapes you chose.
c Write two things that are different about the shapes you chose.
Unit 7: Topic 2
Symmetry
An object is symmetrical if one side is a mirror image of the other. This square is symmetrical. This butterfly is symmetrical. This hand is not symmetrical.
Guided practice
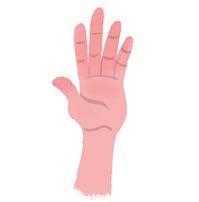
Line symmetry can be horizontal, vertical or even diagonal.
1 Tick if each item is symmetrical or not.
Independent practice
1
Draw 1 line of symmetry on each shape.
2 Draw 1 line of symmetry on each shape.
FINAL
Does any shape have more than 1 line of symmetry?
3
Read the instructions and draw lines of symmetry on each shape.
a Draw a vertical line of symmetry.
b Draw a horizontal line of symmetry.
4 Circle the shapes with line symmetry.
FINAL
c Draw a diagonal line of symmetry. Are you symmetrical?
d Draw vertical, horizontal and diagonal lines of symmetry.
Extended practice
1 Draw a symmetrical shape picture.
2 Create a symmetrical picture on the grid. Make sure that one side of the picture is a reflection of the other side.
FINAL
Unit 7: Topic 3 3D shapes
The faces of a rectangular prism are rectangles.
Guided practice
2 Tick the shapes with a circle-shaped face. face corner
A face is a flat surface of a 3D shape.
1 Match the labels to the picture.
face corner edge hemisphere rectangular prism cube cone
Independent practice
1 Circle the shape with:
a 6 faces.
b 3 faces.
c 0 corners.
d 8 corners.
e 0 edges.
f 12 edges.
FINAL
2 Circle the shapes with curved faces.
How many:
a cubes?
b cones?
c rectangular prisms?
d spheres?
e hemispheres?
A prism is a shape that has two end faces that are the same shape. All the other faces are rectangles.
4 Match the shapes and faces.
Extended practice
1 Who am I?
a I have:
• 6 faces
• 8 corners
• 12 edges
• all edges are the same length.
b I have:
• 1 face that is a circle
• 1 curved face
2 Draw the shape you would see:
• 1 corner. cube cylinder rectangular prism cone sphere hemisphere a from the top. b from the front. c from the side.
FINAL
Unit 8: Topic 1
Guided practice
1 Where is:
The cat is on the chair.
The mouse is under the chair.
The dog is in the box.
What other words can you use to describe the position of something?
FINAL
a the bird? on the bench in the tree under the car
b the car? in the shed in the tree on the bench
c the cat? on the car in the shed next to the tree
d the snake? on the bench in the tree under the car
Independent practice
1 In the box below, draw:
a a cat under the table.
b a ball on the rug.
c a chair next to the ball.
d a book in the bookshelf.
How would you describe where I am sitting on the page?
e a person between the table and the bookshelf.
FINAL
2 What is:
a next to the brown bear?
b under the robot?
How many different ways can you describe where the train is?
c between the boat and the drum?
d above the ball?
3 Where is:
a the panda?
b the drum?
1 Describe the position of:
a the pirate.
b the treasure.
FINAL
2 a Draw a dog on the map.
b Describe where you drew it.
Unit 8: Topic 2
Measures of turn
Guided practice clockwise
Clockwise is the direction the hands on a clock move. Anticlockwise is the opposite direction. anticlockwise
1 Which way should the cat move to:
a find the mouse first?
clockwise anticlockwise
b find the fish first?
clockwise anticlockwise
FINAL
2 Which way should the hippo move to:
a find the lion first?
clockwise anticlockwise
b find the zebra first?
clockwise anticlockwise
half turn quater turn to the right
1 Half turn or quarter turn?
half turn quarter turn
FINAL
half turn quarter turn
half turn quarter turn c d half turn quarter turn
Turns can be made in a clockwise or anticlockwise direction.
2 Draw what happens if you do a: a half turn. d half turn. b quarter turn. c quarter turn.
3
Decide whether the pattern is showing half turns or quarter turns, then continue the pattern.
a
b half turn quarter turn half turn quarter turn
Extended practice
1 Draw the shapes after a:
half turn. quarter turn.
FINAL
half turn. quarter turn.
Animals
Guided practice
1
Independent practice
1 How many: a triangles?
c circles?
2 Show on the picture graph.
10 b rectangles? d hexagons?
3 Use the data to finish the picture graph.
a Which fruit was the most popular?
b Which two fruits were equally popular?
BananaAppleCherry Orange
a Ask 10 people their favourite chip flavour. Record with ticks.
b Use the data to make a picture graph.
Unit 9: Topic 2
Recording and interpreting data
Guided practice
1 Answer the questions.
Blue is the most popular colour.
Green is the least popular colour.
Two people like pink best. Four people like red best.
How many people are represented on the graph? How do you know?
c How many people have green eyes?
d How many people have brown eyes?
e The number of people with green eyes is the same as people with blue eyes.
f You would meet more people with brown eyes than people with blue eyes in 2T. agree disagree agree disagree
Independent practice
1
a Use the data in the table to make a tally chart.
b Use the data in the table to complete the graph.
Favourite fruit
Apple Jack, Beth, Kaia, Simon, Keanu
Banana Taika, Hu
Orange Blaise, Mai, Kora
Cherry Hemi, Tayla
Favourite fruit tally chart
Apple
Banana Orange Cherry
Favourite fruit graph
c Which fruit is most popular?
d Which is least popular?
e How many people like cherries best?
f How many people like bananas best?
g Which fruit does Taika like?
Favourite
Year
Reading Sport
Art
Maths
Music
2 Answer the questions.
a Which subject is most popular?
b Which is least popular?
c Which subject is the favourite of nine people?
d Which two subjects do the same number of people like?
e How many people like sport best?
f Is reading or art more popular?
g Circle the statement that best describes the graph.
The second most popular subject is reading.
The number of students that like sport is double the number that like music.
Many people like art.
Extended practice
1
a Ask 10 students in your class what kind of pet they have. Record their answers using tally marks.
b Make a picture graph showing the data.
Pets in our class
Cat Dog Fish
Other No pet
c Which has the most? cat dog fish other no pet
d Which has the least? cat dog fish
e How many dogs?
no pet
Unit 10: Topic 1
An elephant will fly a helicopter over the school.
ImpossibleUnlikely Likely Certain A pop star will visit today. You will eat lunch today. You will do maths today.
Guided practice
What does “certain” mean?
1 Choose a word that matches each situation. Impossible Unlikely Likely Certain a It will rain today. b It will be cold today.
FINAL
c It will get dark tonight. d You will go shopping today.
2
Circle the event that is possible to happen today.
Rolling a 5 on this die
Independent
practice
1 Match the descriptions to the boxes.
There is a live dinosaur in the playground.
cer tain to pick a red ball
impossible to pick a red ball
unlikely to pick a green ball
likely to pick a blue ball
2 Describe the chances of pulling out a: a red teddy. b blue teddy. c yellow teddy.
3 John has 6 teddies.
a List the possible outcomes if he picks one teddy.
b Circle true or false. If John picks one teddy, it is: certain that he’ll pick a green teddy. true false impossible that he’ll pick a black teddy. true false likely that he’ll pick a blue teddy. true false unlikely that he’ll pick a green teddy. true false
Extended practice
1 The teacher of 2F made a game for the class. You win the game if you pick the yellow marble.
a Circle the chance of picking a yellow marble.
impossible less likely likely certain
b Compete the sentences below. Match the sentences with the correct fraction.
c Which colour are you more likely pick? red yellow
2 The teacher of class 2B made the same game. They put four marbles in a box.
a Which class’s game do you have more chance of winning?
2F 2B
b Complete the sentence below. The yellow marbles are out of . Write the missing words as a fraction.
Glossary
addition The joining or adding of two numbers together to find the total. Also known as adding, plus and sum.
Example:
3 and 2 is 5
anticlockwise Moving in the opposite direction to the hands on a clock.
base The bottom edge of a 2D shape or the bottom face of a 3D shape.
base
calendar A chart or table showing the days, dates, weeks and months in a year.
Date
area The size of an object’s surface.
Example: It takes 12 tiles to cover this placemat.
array An arrangement of items into even columns and rows that make them easier to count.
balance scale Equipment that balances items of equal mass – used to compare the mass of different items. Also called pan balance or equal arm balance.
capacity The amount that a container can hold.
Example: The jug has a capacity of 4 cups.
cups 2 cups 1 cup
category A group of people or things sharing the same characteristics.
centimetre A unit for measuring the length of smaller items.
Example: Length is 15 cm. 80cm 4 cups
Green Pink
circle A 2D shape with a continuous curved line that is always the same distance from the centre point.
data Information gathered through methods such as questioning, surveys or observation.
day A period of time that lasts 24 hours.
clockwise Moving in the same direction as the hands on a clock.
cone A 3D shape with a circular base that tapers to a point.
corner The point where two edges of a shape meet. Also called a vertex
cube A rectangular prism where all six faces are squares of equal size. corner
difference (between) A form of subtraction or take away.
Example: The difference between 11 and 8 is 3.
digit The single numerals from 0 to 9. They can be combined to make larger numbers.
Example: 24 is a 2-digit number. 378 is a 3-digit number.
division/dividing Sharing into equal groups.
Example: 9 divided by 3 is 3.
cylinder A 3D shape with 2 parallel circular bases and one curved surface.
double/doubles Adding two identical numbers or multiplying a number by 2.
Example: 4 + 4 = 8 2 × 4 = 8
duration How long something lasts.
Example: The school week lasts for 5 days.
edge The side of a shape or the line where two faces of a 3D shape meet.
eighth One part of a whole or group divided into eight equal parts. edge edge
1 8
Eighth of a whole
Eighth of a group
equal Having the same number or value.
Example:
Equal size
Equal numbers
equation A written mathematical problem where both sides are equal.
Example: 4 + 5 = 6 + 3
estimate A thinking guess.
face The flat surface of a 3D shape.
f lip
To turn a shape over horizontally or vertically. Also known as reflect
face vertical flip horizontal flip
fraction An equal part of a whole or group.
Example: One out of two parts or 1 2 is shaded.
friendly numbers Numbers that are easier to add to or subtract from.
Example: 10, 20 or 100
half One part of a whole or group divided into two equal parts. Also used in time for 30 minutes.
Example:
Half of a whole
Half of a group
Half past 4
hexagon A 2D shape with 6 sides.
horizontal Parallel with the horizon or going straight across.
line
method A way to solve a problem. In maths you can often use more than one method to get the right answer.
Example: 32 + 27 = 59
Jump method
Split method
+ 2 + 20 + 7 = 30 + 20 + 2 + 7 = 59
metre A unit for measuring the length or height of larger objects.
jump method A way to solve number problems that uses place value to “jump” along a number line by hundreds, tens and ones.
Example: 16 + 22 = 38
length How long an object is from end to end.
Example: This poster is 3 pens long.
3 m
month The time it takes the moon to orbit the Earth. There are 12 months in a year.
near doubles A way to add two nearly identical numbers by using known doubles facts.
Example: 4 + 5 = 4 + 4 + 1 = 9
number line A line on which numbers can be placed to show their order in our number system or to help with calculations.
number sentence A way to record calculations using numbers and mathematical symbols.
Example: 23 + 7 = 30
numeral A figure or symbol used to represent a number.
Example:
octagon A 2D shape with 8 sides.
ordinal numbers Numbers that show the order or position of something in relation to others.
pair Two items that go together.
Example: Pairs that make 4
Pair of socks 2 and 2 3 and 1
parallel lines Straight lines that are the same distance apart and so will never cross.
parallelparallelnot parallel
partitioning Dividing or separating an amount into parts.
Example: Some of the ways 10 can be partitioned are: 5 and 5 4 and 6 9 and 1
pattern A repeating design or sequence of numbers.
Example: Shape pattern
Number pattern 2, 4, 6, 8, 10, 12
pentagon A 2D shape with 5 sides.
picture graph A way of representing data using pictures to make it easy to understand.
Example: Favourite juices in our class
place value The value of a digit depending on its place in a number.
position Where something is in relation to other items.
Example: The boy is under the tree that is next to the house.
prism A 3D shape with parallel bases of the same shape and rectangular side faces.
rectangle A 2D shape with four sides and four right angles. The opposite sides are parallel and equal in length.
pyramid A 3D shape with a 2D shape as a base and triangular faces meeting at a point.
triangular prism rectangular prism hexagonal prism square pyramid hexagonal pyramid right angle
quadrilateral Any 2D shape with four sides.
rhombus A 2D shape with four sides, all of the same length and opposite sides parallel.
skip counting Counting forwards or backwards by the same number each time.
Example: Skip counting by 5s: 5, 10, 15, 20, 25, 30
Skip counting by 2s: 1, 3, 5, 7, 9, 11, 13
slide To move a shape to a new position without f lipping or turning it. Also known as translate
quarter One part of a whole or group divided into four equal parts. Also used in time for 15 minutes.
Example:
Quarter of a whole Quarter of a group Quarter past 4 1 4
sphere A 3D shape that is perfectly round.
split method A way to solve number problems that involves splitting numbers up using place value to make them easier to work with.
Example: 21 + 14 = 35
square A 2D shape with four sides of equal length and four right angles. A square is a type of rectangle.
right angle
subtraction The taking away of one number from another number. Also known as subtracting, take away, difference between and minus
Example: 5 take away 2 is 3
survey A way of collecting data or information by asking questions.
Strongly agree Agree Disagree Strongly disagree
table A way to organise information that uses columns and rows.
tally marks A way of keeping count that uses single lines with every fifth line crossed to make a group.
three-dimensional or 3D A shape that has three dimensions – length, width and depth. 3D shapes are not f lat.
trapezium A 2D shape with four sides and only one set of parallel lines.
triangle A 2D shape with three sides.
turn Rotate around a point.
two-dimensional or 2D A f lat shape that has two dimensions – length and width.
unequal Not having the same size or value.
Example:
Unequal sizeUnequal numbers
value How much something is worth.
Example:
This coin is worth 10c. This coin is worth $1.
vertical At a right angle to the horizon or straight up and down.
week A period of time that lasts 7 days.
FINAL
volume How much space an object takes up.
Example: This object has a volume of 4 cubes.
whole All of an item or group.
Example: A whole shapeA whole group width How wide an object is from one side to the other.
Example: This poster is 2 pens wide.
year The time it takes the Earth to orbit the Sun, which is approximately 365 days.
1: Topic 1
Guided practice
1 a 22 23 24 b 36 37 38
c 54 55 56 d 67 68 69 e 71 72 73 f 29 30 31
Independent practice
1 a 26, 27, 28, 29, 30, 31, 32 , 33, 34
b 43, 44, 45, 46, 47, 48 , 49, 50, 51
c 66, 67, 68 , 69, 70, 71, 72 , 73, 74
2 a b c d
Guided practice
1 a tens? 2; ones? 1; altogether? 21 b tens? 5; ones? 3; altogether? 53
c tens? 3; ones? 8; altogether? 38 d tens? 6; ones? 2; altogether? 62
Unit 1: Topic 2
practice
1 a 59 b 16 c 20 d 89
2 a 50 b 59 c 41 d 29 3536373840414344 39 42 45
2 Teacher to check. Look for answers that show ability to make reasonable estimations about where the numbers should go, and that space the numbers accurately and order the numbers correctly.
1 a Words: forty-five; Numeral: 45
b Words: thirty-one; Numeral: 31
c Words: thirteen; Numeral: 13
d Words: seventy-seven; Numeral: 77
e Words: one hundred and two; Numeral: 102
Unit 1: Topic 3
Guided practice
Unit 2: Topic 1
Guided practice
1 a Yes
b Teacher to check. In the ten frames, students should fill 22 squares with strawberries.
2 a No
b Teacher to check. In the ten frames, students should fill 29 squares with lollies. c 29 Independent practice 1 a b 10 c d 30 01234567891011 121314151617181920
3 a
Extended practice
1
Unit 2: Topic 2
Guided practice
1 a 10 b 9 c 8
d 7 e 6 f 5
g 4 h 3 i 2
j 1 k 0
2 a 9 b 8 c 7 d 6 e 5 f 4
g 3 h 2 i 1 j 0
Independent practice
1 a 5 b 8 c 17
2 a Teacher to check that the number bonds total 17.
b Teacher to check that the number bonds total 19
3 a 7 + 6 = 13
6 + 7 = 13
13 − 6 = 7
13 − 7 = 6
b 12 + 8 = 20
8 + 12 = 20
20 − 8 = 12
20 − 12 = 8
Extended practice
1 a 4 b 7 c 8
d 17 e 8 f 10
g 0 h 5 i 12
2 a True b False
c True d False
Unit 2: Topic 3
2 a 24. Teacher to check number line. Look for answers that accurately show the equation on the number line, using steps of 1, 2 or 4 to reach the total.
b 29. Teacher to check number line. Look for answers that start at the bigger number (24) to find the answer, and use steps of 1 or 5 to accurately show the solution.
c 47. Teacher to check number line.
Independent practice 1 a b c
Extended practice
1 a & b Teacher to check. Look for answers that successfully identify combinations that add to the required total and that use both drawings and numbers.
2 a & b Teacher to check. Look for answers that successfully identify combinations that add to the required total and that demonstrate an understanding of place value as a basis for partitioning.
Unit 2: Topic 5
Guided practice 1 a 9 b 3 c 12 d 13
Independent practice
Unit 2: Topic 4
Guided practice
1 a 1 ten and 9 ones b 26, 2 tens and 6 ones c 35, 3 tens and 5 ones
1 a 12 b 10 c 4
01234567891011 121314151617181920
01234567891011 121314151617181920
01234567891011 121314151617181920
2 a 14. Teacher to check the number line. Look for answers that accurately show the equation on the number line, using steps of 1 or 2 to reach the correct answer.
b 11. Teacher to check. Look for answers that start at the bigger number (20) to find the answer and show steps of an appropriate size (e.g. 1 or 3) to accurately reach the solution.
c 10. Teacher to check. Look for students who start at the bigger number and count back by 1s, 2s, 5s or 10s to find the correct answer.
NOTE: for questions 3–6 the specific counters crossed out are not important, as long as the correct number has been crossed out.
practice
Unit 2: Topic 6
Guided practice
1 a 0, 2, 4, 6, 8 , 10, 12 , 14, 16, 18 , 20
b 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
c 0, 10, 20, 30, 40
Independent practice
1 a b
c
2 a 38, 40, 42, 44, 46, 48 , 50, 52 , 54, 56
b 35, 40, 45, 50, 55, 60, 65, 70, 75, 80
c 10, 20, 30, 40, 50, 60, 70, 80, 90, 100
d 24, 22, 20, 18, 16, 14, 12, 10, 8, 6
e 45, 43, 41, 39, 37, 35, 33, 31, 29, 27
3 a 5, 10, 15, 20, 25
b 10, 20, 30, 40, 50
c 2, 4, 6, 8, 10, 12, 14
Unit 2: Topic 7
Guided practice 1 a 4 b 3 Independent practice 1 a
Extended practice
demonstrate an understanding of equality by dividing the total into five equal groups. b 15 shared between 5 is 3.
Unit 2: Topic 8
Guided practice
practice
1 a Teacher to check. Look for answers that show ability to successfully represent 12 items and that demonstrate an understanding of equality by dividing the total into three equal groups.
b 4
2 a Teacher to check. Look for answers that show ability to successfully represent 15 items and that
Teacher to check. Look for answers that show ability to use repeated addition or multiplication knowledge to work out the correct answer.
3 Teacher to check. Look for answers that show ability to understand that multiplication can be used to solve the equation.
Unit 3: Topic 1
Guided practice
1 The whole apple and the whole pizza should have a square drawn around them.
2 The half apple and the pizza slice should have a circle drawn around them.
Unit 3: Topic 2
Guided practice
1 a 4 items should be coloured in. b 5 items should be coloured in. 2 a
item should be coloured in. b 3 items should be coloured in.
Independent practice 1
5 a 1 2 There are 2 pieces.
1 4 There are 4 pieces.
1 8 There are 8 pieces.
Extended practice
1 The following figures should be circled: c and e
2 a–c Teacher to check: some combination of the following:
3 a–b Teacher to check diagrams. Look for students who can draw fractions with reasonable accuracy.
OR 1 4
eighth or 1 8
8 of 16 is 2. d 3 items should be circled. 1 4 of 12 is 3.
4 a 12 items should be coloured red.
b 6 items should be coloured blue.
c 3 items should be coloured green.
Extended practice
Unit 4: Topic 2
Unit 4: Topic 1
Unit 6: Topic 2
2 a & b Teacher to check. Look for answers that demonstrate an understanding of repeating colour patterns and that accurately describe the pattern created.
3 a & b Teacher to check. Look for answers that demonstrate an understanding of either a repeating or a growing pattern using shapes and that accurately describe the pattern created.
Unit 6: Topic 1
Guided practice
1 a 6 paperclips long
b 9 paperclips long
Unit 5: Topic 1
Guided practice
1
1 a 3 b 2 c 2 d 3
2 a
b two green triangles, two orange rectangles
3 a b blue circle, red circle, purple triangle
c half
2 zucchini
Independent practice
1 a–c Teacher to check. Look for reasonable estimates of the length of the items in paperclips and answers that have been measured accurately by placing the paperclips end to end with no gaps.
d Approximately 5 small or 4 large paperclips long.
2 The pencil is likely to be the shortest item. Look for answers that include reasoning using language of measurement such as shorter and longer.
3 a 8 paperclips
b 15 paperclips
c 14 paperclips
Extended practice
1 a–b Teacher to check. Look for answers that demonstrate accurate measurement techniques, placing the items end-to-end with no gaps or overlaps.
c paperclips
2 a this textbook
b–c Teacher to check.
Guided practice
1 a 8 tiles b 24 tiles
c 4 tiles d calendar
Independent practice
1 a–d Teacher to check. Look for reasonable estimates of the area of the items, taking into account the size of the block or tile being used, and for answers that demonstrate an ability to accurately measure by placing the tiles or blocks with no gaps.
2 Teacher to check; most likely to be the poster. Look for answers that include reasoning and that demonstrate an understanding of the concept of area.
Extended practice
1 a–b Teacher to check. Look for answers that demonstrate accurate measurement techniques, placing units in rows with no gaps or overlaps.
2 Teacher to check – answers will vary depending on the size of the blocks and sticky notes used. Look for answers that include reasoning using the language of measurement.
3 a–b Teacher to check. Look for answers that demonstrate that students can competently compare the area of two different objects and can accurately measure using informal units.
4 Teacher to check. Answers will vary depending on the size of the blocks and the sticky notes used. Look for answers that include reasoning using the language of measurement.
5 3 tiles used; 1 2 a tile left over
Unit 6: Topic 3
Guided practice
1 a 3 cubes b 6 cubes
c 9 cubes d 7 cubes
Independent practice
1 a 6 cubes b 4 cubes
c 12 cubes d 9 cubes
Teacher to check students’ models. Look for responses that accurately make the model using cubes and that can use the physical model to identify the volume.
2 a Model c should be circled in blue. b Model b should be circled in red.
3 a B b D
Guided
practice
1 a 4 cups b 6 cups c 10 cups d 8 cups
Independent practice
1 a spoon b mug c mug d bucket
There may be an opportunity to discuss the concept of the most appropriate units to use as students respond to this question. For example, it is possible to measure the capacity of the fish tank using the coffee mug but it is not the quickest or most efficient way of doing it.
2 a–b Teacher to check. Look for reasonable estimates of items that have a greater and smaller capacity than the saucepan and justification of answers using the language of capacity.
c Answers will vary depending on the items drawn in a & b. Most likely the mug or bucket will be appropriate for the first item and the spoon or mug for the second. Look for answers that provide justification and that demonstrate an understanding of how to choose the most appropriate unit.
Extended practice
1 a–b Teacher to check. Look for students who are able to construct two different models with a volume of 8 cubes, and who can describe their models using the language of volume.
2 a–c Teacher to check. Look for students who are able to make reasonable estimates of the capacity of their chosen containers in cups, and who are then able to accurately measure and record the results.
Unit 6: Topic 4
Guided practice
1 a–b Teacher to check. Look for answers that show an understanding of the concepts of lighter and heavier and that demonstrate reasonable choices in comparison with the items shown – e.g. a glue stick would be lighter than the paint can and a pencil would be lighter than the calculator.
2 a–b Teacher to check. Look for answers that show an understanding of the concepts of lighter and heavier and that demonstrate reasonable choices in comparison with the items shown – e.g. a bottle of water would be heavier than the cupcake and a car would be heavier than the pumpkin.
Independent practice
1 a–d Teacher to check. Look for answers that show ability to choose pairs with an obvious difference in mass, and to put the heavier and lighter item in each pair on the correct side of the pan balance.
2 Answers will vary depending on the mass of each student’s pencil case and the versions of the items chosen. Look for answers that show ability to use methods such as hefting to accurately predict the results and ability to correctly use a pan balance to check. Likely results are:
a lighter b heavier c heavier d lighter e heavier f lighter
Extended
practice
1 a–d Answers will vary depending on the size of the cubes and counters used. Look for answers that demonstrate ability to achieve a reasonable balance between the given number of cubes and the required number of counters and that demonstrate an understanding of equality of mass.
2 teabag, teaspoon, coffee mug, milk, kettle
Accept slight variances if students can justify their responses – e.g. the kettle may be lighter than the milk container if it is empty.
Unit 6: Topic 5
Guided practice
1 a o’clock b o’clock c half past d half past e o’clock f half past
2 a 5 o’clock b half past 8 c half past 3 Independent practice
a 8:00 b 7:30 c 6:00 d 3:30 e 11:30 f 11:00
3 Teacher to check. Look for answers that demonstrate an understanding of sequencing.
Unit 6: Topic 6
Guided practice
Waitangi Day February
Valentine’s Day February
Anzac Day April
Mother’s Day May
King’s Birthday holiday June
Father’s Day September
4 a–c Teacher to check. Look for answers that show students’ ability to accurately sequence months and to match the months to the correct seasons.
Extended practice
1 a It does not use the same dates for months.
b Teacher to check. Answers could be about the calendar starting in Winter, months having different dates, etc.
c December and January
d Maramataka month Summer, winter, autumn or spring?
Pipiri Winter
Whiringa-aNuku Spring
Whiringa-aRangi Spring
Hui Tanguru Summer
Poututerangi Autumn
Haratua Autumn
Unit 6: Topic 7
Guided practice
1 a Tuesday b 6th February
c Monday
2 a 4 b 5
c Wednesday d Saturday 30th
Independent practice
1 a
Month Days
January 31
February 28
March 31
April 30
May 31
June 30
July 31
August 31
September 30
October 31
November 30
December 31
b April, July, September and December
c February, March, November
2 a Saturday 18th May
b Wednesday 22nd May
c Wednesday, Thursday and Friday
d Tuesday 14th May
e 6 f June
g April
Extended practice
1 a–d Teacher to check. Look for answers that show students’ ability to correctly identify and write the current month and to accurately label the dates. Also check that students can use the information they have provided to correctly identify the first day of the month and the number of days in the month.
2 a No
b April, June, September or November
c 3
d 17th
Unit 6: Topic 8
Guided practice
1 a months b hours c days d weeks e hours f months
Independent practice
1 B, C, A, D
2 Teacher to check.
Extended practice
1 counting to 10
2 second, minute, hour, day
3 a counting to 10
b eating one pizza
c growing long hair
4 Teacher to check.
5 Teacher to check.
Unit 7: Topic 1
Guided practice
1 a 2 horizontal lines, 2 vertical lines, 4 corners, 4 sides
b 2 horizontal lines, 0 vertical lines, 6 corners, 6 sides
c 1 horizontal line, 1 vertical line, 3 corners, 3 sides
d 1 horizontal line, 2 vertical lines, 5 corners, 5 sides
Independent practice
1 a & b
Extended practice
2 a–c Teacher to check. Answers will depend on shapes chosen by students and the features they choose to compare.
Unit 7: Topic 2
Guided practice
1 a symmetrical
b symmetrical
c not symmetrical
d not symmetrical
e not symmetrical
f symmetrical
Independent practice
1 In some cases, more than one answer is possible. The most likely responses are shown here.
2 Teacher: Some of the shapes have more than one line of symmetry. The most likely responses are shown, but accept any correct responses.
Unit 7: Topic 3
Guided practice
1 2 hemisphere, cone
Independent practice
1 The following shapes should be circled:
a cube b cylinder
c sphere, hemisphere
d cube
e sphere, hemisphere
f rectangular prism
2 The cone, sphere and hemisphere should be circled.
3 a 3 b 2 c 3
4
d 2 e 3
Extended practice
1 a–b Answers will vary. Look for answers that show ability to accurately use positional language such as above, below, near, between, etc. to describe the position of each item.
2 a–b Teacher to check. Look for answers that show an understanding of positional language in describing where the dog is.
Unit 8: Topic 2
Guided practice
FINAL
3 Teacher to check. For questions a and b, only one correct answer is possible. In questions c and d, there is more than one possible correct answer. Teachers could use this as a point of discussion.
4 a, c and d should be circled
Extended practice
1 Teacher to check. Look for students who can apply their knowledge of symmetry to make a simple picture that has either horizontal or vertical line symmetry.
2 Teacher to check. Look for students who can demonstrate an understanding of line symmetry as two halves that are a reflection of each other.
Extended practice
1 a cube b cone
2 a drawing of a rectangle
b drawing of a rectangle
c drawing of a square or a smaller rectangle that shows the proportion of the side view
Unit 8: Topic 1
Guided practice
1 a in the tree b in the shed
c next to the tree d under the car
Independent practice
1 a–e Teacher to check. Look for answers that show ability to accurately interpret positional language to correctly place the items.
2 NOTE: accept either written or drawn answers from students.
a the train b the boat
c the blocks d the duck
3 a & b Answers will vary. Look for answers that show ability to accurately use positional language such as above, next to, left of, etc. to describe the position of each item.
1 a clockwise b anticlockwise
2 a anticlockwise b clockwise
Independent practice
1 a clockwise b anticlockwise
c anticlockwise d clockwise
2 a b c d
3 a b
Extended practice
1 a b
Unit 9: Topic 1
Unit 9: Topic 2
Guided
1
c apple d cherry and banana
e 2 f 2 g banana
2 a sport b art c maths
1 a Answers will vary. Look for answers that show ability to accurately record the responses of 10 people in the table using ticks or tally marks.
b Answers will vary. Look for answers that show ability to use the data from the previous question to make an accurate picture graph using one-to-one correspondence.
d reading and music e 12 f reading
g The number of students that like sport is double the number that like music.
Extended practice
1 a Answers will vary. Look for answers that show ability to accurately record classmates’ responses in the table. Note that in some instances the total responses might be more than 10 if some students surveyed have more than one pet.
b Responses will vary depending on data collected. Look for answers that demonstrate ability to accurately represent the data in a picture graph.
c–e Responses will vary depending on the data collected. Check that the answers accurately interpret the data.
Unit 10: Topic 1
Guided practice
1 a, b and d Teacher to check. Look for answers that show students’ ability to justify their selections using the language of chance.
c certain
2 rolling a 5 on the die Independent practice
1
certain to pick a red ball
impossible to pick a red ball
unlikely to pick a green ball
likely to pick a blue ball
2 a likely b unlikely
c impossible
3 a red, blue, green b false, true, true, true
Extended practice
1 a less likely
b The red marbles are three out of four. 3 4 The yellow marble is one out of four. 1 4
c red
2 a 2B
b The yellow marbles are two out of four.
2 4 or 1 2
Working space
Working space
Oxford University Press is a department of the University of Oxford. It furthers the University’s objective of excellence in research, scholarship and education by publishing worldwide. Oxford is a registered trademark of Oxford University Press in the UK and in certain other countries.
Published in Australia by
Oxford University Press
Level 8, 737 Bourke Street, Docklands, Victoria 3008, Australia © Oxford University Press 2025
The moral rights of the author have been asserted.
First published 2025
First edition
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, transmitted, used for text and data mining, or used for training artificial intelligence, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, by licence, or under terms agreed with the reprographics rights organisation. Enquiries concerning reproduction outside the scope of the above should be sent to the Rights Department, Oxford University Press, at the address above.
You must not circulate this work in any other form and you must impose this same condition on any acquirer.
ISBN 9780190351007
Reproduction and communication for educational purposes
The New Zealand Copyright Act 1994 (the Act) allows educational institutions that are covered by remuneration arrangements with Copyright Licensing New Zealand to reproduce and communicate certain material for educational purposes. For more information, see copyright.co.nz.
Illustrated by Daniel Rieley
Typeset by Newgen KnowledgeWorks Pvt. Ltd., Chennai, India
Proofread by Carly Tenille Slater
Printed in New Zealand by Webstar
Oxford University Press Australia & New Zealand is committed to sourcing paper responsibly.
Disclaimer
Links to third party websites are provided by Oxford in good faith and for information only. Oxford disclaims any responsibility for the materials contained in any third party website referenced in this work.
Acknowledgements
Cover: Paul Cumberland/Alamy Stock Photo; Shysheep/Shutterstock, p.37, p.56 (kiwi); Zhuna/ Shutterstock, p.55, p.56, p.58, p.60, p.61, p.62, (bank notes); GoodStudio/Shutterstock, p.56 (egret); Shysheep/Shutterstock, p.79 (sheep).
Internal illustrations of the cover animal copyright © Katherine Quinn 2025