A leading whole-school primary maths program updated for the NESA Syllabus
Tried and trusted for more than 20 years, Maths Plus is a leading mathematics program for K–6, that follows a spiral approach to learning. Students explore and re-visit mathematical concepts throughout the year, building their skills, developing their understanding, and making connections over time.
Maths Plus offers explicit instruction, practice and consolidation, problem-solving tasks, mentals and homework activities.
Maths Plus allows teachers and students to build on and re-visit mathematical content over time. The spiral approach helps students develop robust recall of information, consolidating learning and increasing their mathematical fluency.
Student Books
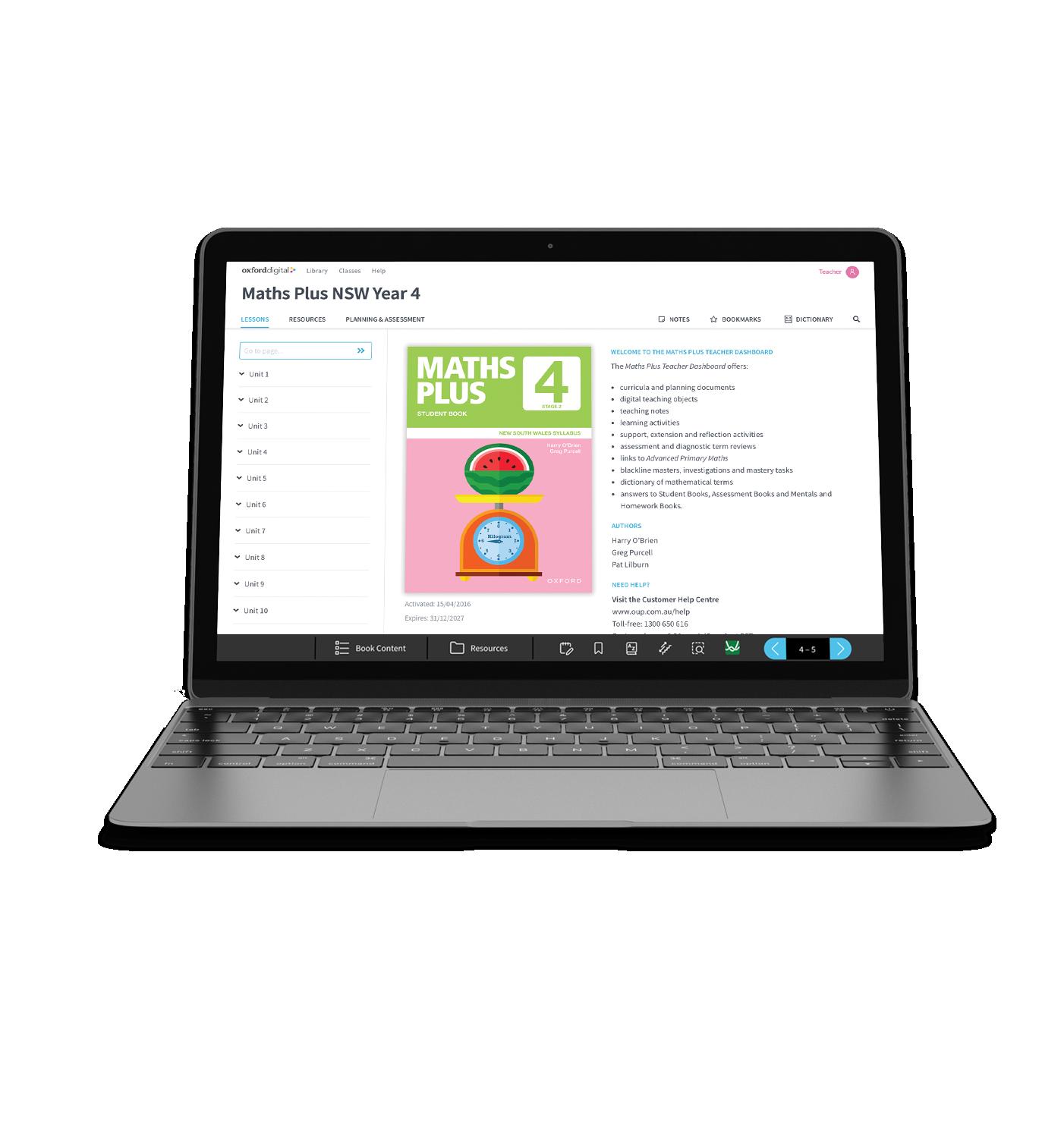
Activities are colour-coded and supported by diagnostic term reviews to assess students’ understanding of concepts and skills. Content descriptions, proficiency strands, and cross-curriculum area references are included on every page.
Assessment Books
Easy-to-use assessments support end-of-year reporting and provide samples of students’ skills and understanding of key mathematical concepts.
Mentals and Homework Books
Activities feature revision, practice, and consolidation activities and directly correspond to the concepts and units of work presented in the Student Books.
Student and Teacher Dashboards
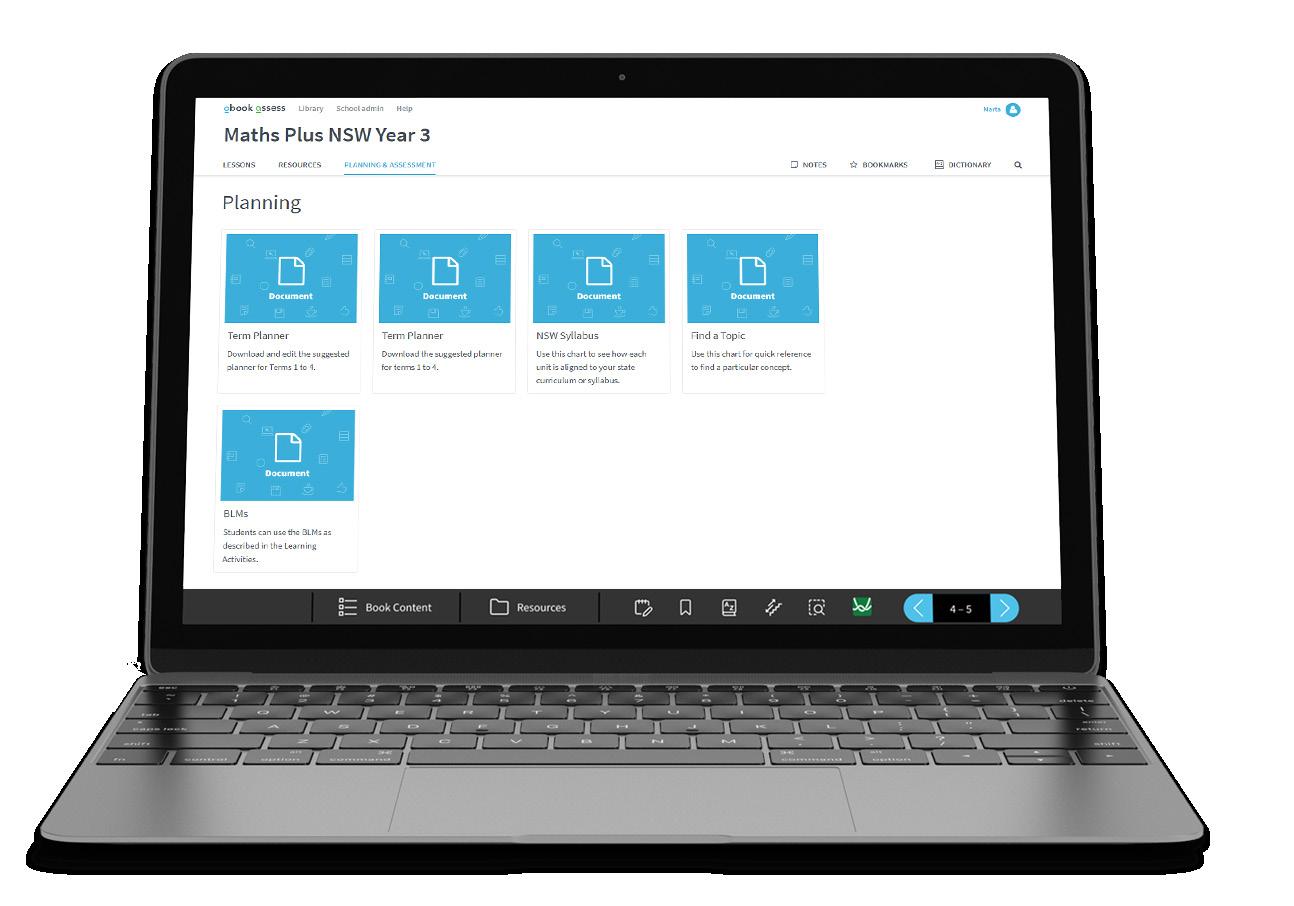
Student and Teacher Dashboards make learning and teaching easier. They include teacher notes*, term planners, blackline masters, investigations pages and more.
* Teacher notes are also available in a Teacher Book format
Practise, master, assess Nsw Curriculum Change for years F-6
• Maths Plus is fully aligned with the outcomes of the NESA Syllabus for Years K to 6, to be implemented in 2023/2024. The series covers content organised within the strands of number and algebra, measurement and space, and statistics and probability. Learning activities incorporate the ‘working mathematically’ processes of communicating, understanding and fluency, reasoning and problem solving.
NESA Syllabus Years K–6
With Maths Plus, teachers can be confident that students will
• develop understanding and fluency by exploring and connecting mathematical concepts
• use logical, critical and creative thinking
• identify, explain and use patterns and relationships in mathematical thinking
• develop reasoning and problem-solving abilities, choosing and applying appropriate strategies and techniques
• apply mathematical knowledge and understanding to real-world situations
Sample pages from
Practise, master, assess
NSW Syllabus Outcomes
Units 1234 56789
NUMBER AND ALGEBRA
MA3-RN-01
Applies an understanding of place value and the role of zero to represent the properties of numbers
MA3-RN-02
Compares and orders decimals up to 3 decimal places
MA3-RN-03
Determines percentages of quantities, and finds equivalent fractions and decimals for benchmark percentage values
MA3-AR-01
Selects and applies appropriate strategies to solve addition and subtraction problems
MA3-MR-01
Selects and applies appropriate strategies to solve multiplication and division problems
MA3-MR-02
Constructs and completes number sentences involving multiplicative relations, applying the order of operations to calculations
MA3-RQF-01
Compares and orders fractions with denominators of 2, 3, 4, 5, 6, 8 and 10
MA3-RQF-02
Determines 1 2 , 1 4 , 1 5 and 1 10 of measures and quantities
MA3-GM-01
Locates and describes points on a coordinate plane
MA3-GM-02
Selects and uses the appropriate unit and device to measure lengths and distances including perimeters
MA3-GM-03
Measures and constructs angles, and identifies the relationships between angles on a straight line and angles at a point
MA3-2DS-01
Investigates and classifies two-dimensional shapes, including triangles and quadrilaterals, based on their properties
MA3-2DS-02
Selects and uses the appropriate unit to calculate areas, including areas of rectangles
MA3-2DS-03
Combines, splits and rearranges shapes to determine the area of parallelograms and triangles
MA3-3DS-01
Visualises, sketches and constructs three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations
MA3-3DS-02
Selects and uses the appropriate unit to estimate, measure and calculate volumes and capacities
MA3-NSM-01
Selects and uses the appropriate unit and device to measure the masses of objects
MA3-NSM-02
Measures and compares duration, using 12- and 24-hour time and am and pm notation
MA3-DATA-01
Constructs graphs using many-to-one scales
MA3-DATA-02
Interprets data displays, including timelines and line graphs
AND SPACE
MA3-RQF-02
MA3-GM-01
MA3-GM-02
MA3-GM-03
MA3-2DS-01
MA3-2DS-02
MA3-2DS-03
MA3-3DS-01
STATISTICS AND PROBABILITY
MA3-NSM-01
MA3-NSM-02
MA3-DATA-01
MA3-DATA-02
MA3-CHAN-01 MA3-CHAN-01
Conducts chance experiments and quantifies the probability
MAO-WM-01 Working mathematically
Develops understanding and fluency in mathematics through exploring and connecting mathematical concepts, choosing and applying mathematical techniques to solve problems, and communicating their thinking and reasoning coherently and clearly
MAO-WM-01 Working
MA3-RN-01
MA3-RN-02
MA3-RN-03
MA3-AR-01
MA3-MR-01
MA3-MR-02
MA3-RQF-01
MA3-3DS-02
SPACE
MA3-RN-01
MA3-RN-02
MA3-RN-03
MA3-AR-01
MA3-MR-01
MA3-MR-02
MA3-RQF-01
MA3-RQF-02
MA3-GM-01
MA3-GM-02
MA3-GM-03
MA3-2DS-01
MA3-2DS-02
MA3-2DS-03
MA3-3DS-01
MA3-3DS-02
MA3-NSM-01
MA3-NSM-02 PROBABILITY
MA3-DATA-01
MA3-DATA-02
MA3-CHAN-01
MAO-WM-01 Working mathematically
MEASUREMENT AND SPACE
STATISTICS AND PROBABILITY
Sample pages from ____
Practise, master, assess
Partitioning/Know 1, know 4
The 4 facts associated with this array are: 4 × 3 = 12 3 × 4 = 12
Write 4 facts you can derive from each array. 1
Associative and commutative laws
The commutative law of multiplication tells us that two factors of a multiplication number sentence can be multiplied in reverse and it will not change the answer. 3 × 4 has the same result as 4 × 3.
The associative law states that it does not matter which order factors are multiplied. 3 × 2 × 4 has the same result as 4 × 2 × 3.
Complete these pairs of number sentences. 2
Write some division number sentences to find out if division is commutative. 3
Sample pages from ____
Recognising angles
An angle is the amount of opening between two arms. They can be measured and named according to the size of their opening. This common angle is called a right angle. It is equal to a 1 4 turn of the hands on a clock face.
Angles are classified according to the amount of turn between two arms.
8 Right angle Square corner; 90° Obtuse angle Larger than a right angle; greater than 90°
Acute angle Smaller than a right angle; less than 90°
Straight angle
Reflex angle
Can be made from two right angles; 180°
Label the angles either right angle, obtuse, acute, reflex or straight.
Larger than a straight angle; greater than 180°
Identify which shape is being described.
a I have four right angles.
b I have one obtuse angle, one acute angle and two right angles.
c I have three acute angles.
d I have three right angles and two obtuse angles.
e I have six obtuse angles. 9
Find two acute angles and two obtuse angles in your classroom.
Sample pages from ____
Practise, master, assess
Column graph
A column graph is a graph that uses columns to record the frequency of events.
For example, in this survey six people selected C.
Ashton threw a set of three dice forty times and recorded the totals on a column graph. Use his graph to answer the questions.
a Which score occurred most frequently?
b What was the frequency of the second most frequent score?
c Which scores occurred 2 times?
d Which scores did not appear at all in this sample?
e Explain why the scores 10, 11 and 12 account for 50% of the results.
Class 5G were given a Quick Quiz about Australia. Madeleine and Grace recorded the scores on this column graph.
Answer true or false to these statements.
a 13 correct answers was the most common score.
b Most scores were between 11 and 16.
c 5 and 20 were scores apart from the main cluster.
d 30 people participated in the quiz.
Sample pages from
Multiplication
Mentally calculate the answers to these questions.
1 5 × 5 =
2 5 × 50 = 6 9 × 80 = 7 4 × 62 =
3 6 × 6 =
4 6 × 60 =
5 9 × 8 = 8 5 × 73 = 9 7 × 84 = 10 5 × 123 =
Calculate the answers to these multiplications.
11 3 4 8 × 6 3 × 4 = 12 So: 3 × 4 tens = 12 tens (120) 3 × 40 = 120
× 4 =
30 × 4 = 120 2 × 4 = 8 120 + 8 = 128
Use the area model to find these products. The first one has been done for you.
16 3 × 38 = 17 4 × 54 = 18 5 × 65 = 19 4 × 365 =
Use the distributive property of multiplication to find these products. The first one has been done for you.
20 6 × 462 6 × (400 ÷ 60 ÷ 2) = 2400 + 360 + 12 2772
21 5 × 643
22 8 × 395
23 4 × 527
24 7 × 328
1 In which shape above are all the angles acute angles?
2 In which shape above are all the angles obtuse angles?
3 In which shape above are all the angles right angles? Measure these angles using a protractor.
Sample pages from ____
Madison has made a column graph to show how she spends her weekly wages. Answer true (T) or false (F).
1 Madison saves $60 per week.
2 The total amount she spends on rent, food and her car is $150.
$10
$0 Categories
How many members are under 10 years old?
3 She spends about $15 per week on clothes.
4 She spends twice as much on sport as she does on clothes.
5 Her total wage is $255.
6 At what time was the highest temperature?
7 What was the rise in temperature between 8 am and 10 am?
8 What was the fall in temperature between 4 pm and 7 pm?
9 At what times of the day was the temperature 20°C?
10 Estimate the temperature at these times:
• 9:30 am
• 12:30 pm • 10:30 am
4:30 pm • = 2 people
11 How many members are in the 14–17 year age group?
12 How many members are over 21 years?
13 How many members are under 10 years old?
14 How many members belong to the club?__________
15 Which group represents 1 4 of the total membership? ___________
Practise, master, assess
1 7 + 5
2 11 − 5 3 8 + 7 4 12 − 6
5 4 × 4
6 5 × 5
7 6 × 6
8 1368c = $
9 12 ÷ 4
10 20 ÷ 5
11 What is the sum of 16 and 7?
12 What is the product of 5 and 8?
13 Divide 24 by 4.
14 What is the value of 7 in 7326?
Peter had $87 but spent $36. How much did he have left?
Sample pages from ____
7 + 5
8 − 3
9 − 7 5 6 × 4
6 8 × 5
7 9 × 3
8 $6.80 = c
9 49 ÷ 7
10 48 ÷ 6
11 What is the product of 9 and 4?
12 What is the sum of 9 and 11?
13 Divide 42 by 6.
14 What is the value of 4 in 964?
15 A bag of lollies cost 25c. How much would 10 bags cost?
13 Share 85 lollies among 6 children.
14 Share 37 balls among 4 groups.
15 Share 55 books among 7 children.
16 Share $95 among 5 boys.
17 Share 89 pencils among 8 girls.
18 Sascha bought 4 movie tickets and paid for them with a $50 note and received $14 change. How much was each movie ticket?
Statistics and Probability Column graphs
Mr Evans created this column graph to record how many of each type of birthday card his shop sells.
1 Which price card is most popular?
2 Do many people pay $10 for a birthday card?
3 Which cards were not sold at all?
4 What was the total amount of money received from the sale of the $4, $5 and $6 cards?
