Jeen-Shang Lin, PhD, P.E

725 Benedum Hall | 3700 O’Hara Street | Pittsburgh, PA 15261 P: 412-624-8158

jslin@pitt.edu http://www.engineering.pitt.edu/JeenShangLin/ Associate Professor

Mechanics of Rock Cutting and Modeling

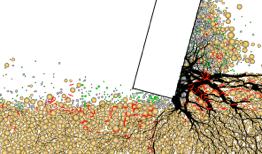
Rock cutting is a fundamental problem facing engineers, as any structure that is placed on or in rocks would involve some degree of rock cutting. Yet it is a challenging problem from a modeling perspective. This challenge appears as a sequence of difficult problems: A contact problem first arises as a cutter advances and interacts with the target rock material. This is followed by the problem of determining when and whether or not the rock would fail. Subsequently, the problem of how to initiate the fragmentation process after the material failure has to be resolved. This cycle of problems then repeats starting with a new contact problem after new surfaces are generated because of fracture. We have successfully applied both the discrete element and the finite element methods in capturing the various fracture phases of the fragmentation during rock cutting. We have also demonstrated the feasibility of modeling a drilling operation using computation mechanics. Other focus of our study included the modeling of failure mode transition from ductile to brittle as the depth of cut increases. In fact, we have shown that rock cutting also follows a size law if the depth of cut is used as the measure of size.

Continuum-Discrete Analysis

Many problems of importance involve interaction of continuum with discontinuum. For instance, bones may be viewed as discrete objects and tissues and muscles the continuum; dams the continuum and the fracture rocks foundation the discrete objects. A continuum may also rupture into several discrete objects. This class of problems requires a dedicated, efficient computational approach. We have worked on continuum damage mechanics together with element erosion in FEM to model fracture. We have also developed algorithms in a mesh based partition of unity method, also known as the numerical manifold method, to address interaction across discontinuities.

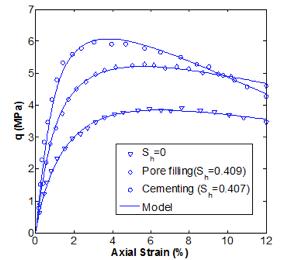
Constitutive Modeling of Hydrate-Bearing Soils

Methane hydrates have been touted as an important potential future source of energy. Production of gas hydrates faces significant challenges, such as the geomechanical changes brought about by hydrate dissociation. Specifically, the dissociation of gas hydrates could affect the structural integrity of unconsolidated hydrate-bearing sediments. In this connection, a good grasp of the geomechanics of hydrate-bearing sediments is also crucial in addressing potential geohazards resulting from global warming. We have been funded by NETL and successfully developed a new constitutive law for methane hydrate-bearing soils. We are currently focusing on implementation of this new law, and on coupling geomechanics code with multiphase flow code.