Vado bene in... Matematica 5 by Gruppo Editoriale Raffaello

V. Cantillo S. Mischianti

F. Perez

iN...

VADO BENEmatematica 5

verifiche delle competenze prove modello INVALSI pagine semplificate compiti di realtà percorso CODING

Il libro continua online!

Accedi al sito www.raffaellodigitale.it , clicca su VADO BENE IN... MATEMATICA 5 e digita il codice sotto riportato.

CODICE

Coordinamento: Corrado Cartuccia

Redazione: Corrado Cartuccia, PaginaQuarantanove, Sara Ortenzi (sezione di Coding)

Grafica e impaginazione: Claudio Campanelli, PaginaQuarantanove

Illustrazioni e colore: Monica Fucini

Copertina: Claudio Campanelli, Mauro Aquilanti

Stampa: Gruppo Editoriale Raffaello

Scratch è sviluppato dal Lifelong Kindergarten Group dei Media Lab del MIT. Vedi http://scratch.mit.edu

Questo testo tiene conto del codice di autoregolamentazione Polite (Pari Opportunità Libri di Testo), per la formazione di una cultura delle pari opportunità e del rispetto delle differenze.

Raffaello Libri S.p.A. Via dell’Industria, 21 60037 - Monte San Vito (AN) www.grupporaffaello.it - info@grupporaffaello.it

Ristampa:

Per esigenze didattiche alcuni testi sono stati ridotti e/o adattati. L’Editore è a disposizione per eventuali omissioni o inesattezze nella citazione delle fonti. Tutti i diritti sono riservati. È vietata la riproduzione dell’opera o di parti di essa con qualsiasi mezzo, compresa stampa, fotocopia, microfilm e memorizzazione elettronica, se non espressamente autorizzata dall’Editore.

matematica 5

I numeri

2 I numeri grandi

3 Componi e scomponi in polinomi

4 Le potenze

5 I numeri relativi

6-8 CI PROVO IO!

9 Le espressioni

10 Criteri di divisibilità

11 I numeri primi

12-14 CI PROVO IO!

15 L’addizione e le sue proprietà

16 La sottrazione e la sua proprietà

17 La moltiplicazione e le sue proprietà

18 La divisione e le sue proprietà

19 Problemi: addizione o sottrazione?

20 Problemi: moltiplicazione o divisione?

21-23 CI PROVO IO!

24 Le frazioni

25 Frazioni proprie, improprie, apparenti

26 Le frazioni complementari

27 Confronto di frazioni

28 La frazione come operatore

29 Operazioni con le frazioni

30 Le frazioni decimali

31-33 CI PROVO IO!

34 I numeri decimali

35 Più e meno con i decimali

36 Moltiplicazione e divisione con i decimali

37-39 CI PROVO IO!

40 La percentuale

41 Lo sconto

42-43 CI PROVO IO!

La misura

44 Le misure di lunghezza

45 Le misure di capacità

46 Le misure di peso

47 Peso lordo, peso netto e tara

48 Le misure di valore

49 La compravendita

50 Le misure di tempo

51 Le misure di superficie e di volume

52 Problemi di misure

53 Ancora problemi di misure

54-57 CI PROVO IO!

Spazio e figure

58 Le linee

59 Gli angoli

60 Le figure piane

61 Ripasso veloce

Perimetro e area del quadrato e del rettangolo

Perimetro e area del triangolo

Perimetro e area del trapezio

Perimetro e area del rombo

Perimetro e area del parallelogramma

67 I poligoni regolari: perimetro, area e apotema

68 Ancora apotema e area

69 Circonferenza e cerchio

70 Circonferenza e area del cerchio

71 I poligoni regolari

72-75 CI PROVO IO!

76 I solidi geometrici

77 Il cubo e il parallelepipedo

78 Il prisma e la piramide

79 Il cilindro e il cono

80 Il volume

81 Problemi di solidi

82-85 CI PROVO IO!

86 Ingrandire e rimpicciolire

Relazioni, dati e previsioni

La probabilità

La frequenza e la percentuale

La moda e la media

Gli operatori logici

91 Logica e problemi

Un’indagine nell’areogramma

93-95 CI PROVO IO!

Verso la secondaria

96 Operare con i decimali

98 Operare con le frazioni

100 Operare con le misure

103

106

108

Operare con area e volume

Risolvere problemi di vario tipo

Disegno geometrico

I NUMERI GRANDI

RICORDA...

I numeri sono organizzati in classi (unità semplici, migliaia, milioni, miliardi) e in ordini che si ripetono nelle varie classi: ordine delle unità (u), delle decine (da), delle centinaia (h). Conoscere il valore posizionale è importante per capire come leggere e scrivere i numeri.

Scrivi in tabella il numero, seguendo l’esempio. 1

1 789 350 • 3 420 598 070 • 6 300 842 005 • 9 740 055 800 7 439 • 2 873 500 • 2 950 000 • 7 896 005 800

Classe dei miliardi G Classe dei milioni M Classe delle migliaia k Classe delle unità semplici

Collega ogni simbolo al suo valore. 2 uk

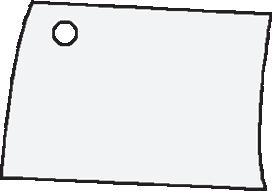
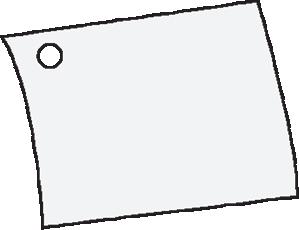
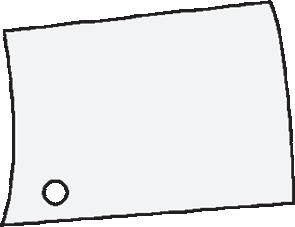
decine di migliaia decine di milioni centinaia di miliardi unità di migliaia dak hG daM

Obiettivo Leggere e scrivere i numeri oltre il milione.

COMPONI E SCOMPONI IN POLINOMI

RICORDA...

Un polinomio è la somma di più moltiplicazioni. È utile per scrivere numeri molto grandi.

Osserva la tabella, poi scomponi i numeri seguendo l’esempio. 1

Il numero ha 8 zeri Il numero ha 7 zeri Il numero ha 6 zeri Il numero ha 5 zeri Il numero ha 4 zeri Il numero ha 3 zeri Il numero ha 2 zeri Il numero ha 1 zero Il numero non ha zeri

4 329 862 = (4 × 10 6) + (3 × 105) + (2 × 10 4) + (9 × 103) + (8 × 102) + (6 × 101) + (2 × 1) = 4 000 000 + 300 000 + 20 000 + 9 000 + 800 + 60 + 2 =

8 438 665 = = 12 875 498 = =

795 788 230 = =

Scomponi i numeri in polinomi seguendo l’esempio. 2

476 329 = (4 × 100 000) + (7 × 10 000) + (6 × 1 000) + (3 × 100) + (2 × 10) + (9 × 1) = = 400 000 + 70 000 + 6 000 + 300 + 20 + 9 =

7 437 =

90 654 337 =

139 000 =

Obiettivo Comporre e scomporre i numeri in polinomi.

LE POTENZE

La potenza si esprime attraverso due numeri:

esponente

52 = 5 × 5 = 25

Scrivi come si leggono le potenze.

Trasforma le potenze in moltiplicazioni.

54 = 5 × 5 × 5 × 5

RICORDA...

Si legge “5 alla seconda”.

La base è il numero che deve essere moltiplicato per se stesso.

L’esponente, il numero scritto in alto a destra, indica quante volte la base deve essere moltiplicata per se stessa.

Trasforma in potenze.

Completa la tabella.

Obiettivo Calcolare le potenze.

I NUMERI RELATIVI

RICORDA...

I numeri relativi sono i numeri preceduti dal segno + o − .

Sono detti numeri relativi positivi quando sono maggiore di 0; numeri relativi negativi quando sono minori di 0.

+4 −4 numero relativo positivo numero relativo negativo

Lo zero non ha segno. Separa i numeri positivi da quelli negativi.

Cerchia in rosso i numeri negativi e in blu quelli positivi.

1 +5 • −1 • +4 • +9 • +15 • −27 • −3 • 0 • +6

Completa la linea dei numeri. 2

Indica con una X se le affermazioni sono vere (V) o false (F). 3

• +19 è un numero relativo negativo. V F

• −5 è un numero relativo negativo. V F

• +14 è un numero relativo positivo. V F

• –7 è un numero relativo positivo. V F

Osserva e scrivi le temperature registrate in quattro città alle 8:00 del mattino.

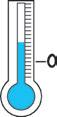
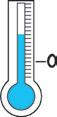
• Qual è la città più calda alle 8:00 del mattino?

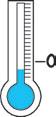
Milano: Torino: Palermo: Firenze: − 3 0 + 1

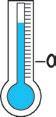
• Se la temperatura aumenta di 3 gradi alle 12:00, quale sarà la temperatura in ogni città?

Obiettivo Conoscere e confrontare i numeri relativi. Operare con i numeri relativi.

MILANO

TORINO PALERMO FIRENZE

CI PROVO IO!

Leggi i numeri e scrivili in lettere. 1

55 660 =

1 438 978 =

3 894 =

436 520 000 =

12 000 000 =

Componi. 2

3 uM 7 uk 9 u =

2 daM 6 hk 0 h 8 da =

3 hk 1 dak 6 uk 5 u = 8 dak 3 h 6 u = 9 uM 5 dak = 7 uM 5 uk 1 u =

Ordina dal maggiore al minore.

Scomponi i numeri in polinomi

46 583 =

129 654 =

217 365 =

128 664 298 =

Scrivi sotto forma di potenza. 5

4 × 4 × 4 =

2 × 2 =

5 × 5 × 5 × 5 × 5 =

8 × 8 × 8 =

3 × 3 × 3 × 3 × 3 =

7 × 7 × 7 × 7 × 7 × 7 × 7 × 7 =

Confronta le coppie di numeri relativi inserendo il segno > o <. 6

Verificare le competenze Conoscere, confrontare e ordinare i numeri grandi e i numeri relativi.

CI PROVO IO!

Calcola il valore delle seguenti potenze.

Colora gli spazi secondo le indicazioni. 2

• rosa = potenze di 3

• blu = potenze di 2

• arancione = potenze di 10

• verde = potenze di 5

Calcola. 3

+5 −3 =

−3 +7 =

−9 +6 = +12 −10 = +4 +2 = −3 +5 =

Completa la tabella con le differenze tra temperatura massima e temperatura minima. 4

Verificare le competenze Conoscere, confrontare e ordinare i numeri grandi e i numeri relativi.

CI PROVO IO!

Indica con una X se le affermazioni sono vere (V) o false (F). 1

28 dak = 28 000 u V F

18 hk = 1 800 u V F

5 uM = 5 000 000 u V F

21 hk = 21 000 u V F

105 hk = 105 000 u V F

13 daM = 13 000 000 u V F

Confronta i numeri e inserisci >, < o = .

Scrivi sotto forma di potenza.

9 × 9 × 9 × 9 =

3 × 3 × 3 × 3 × 3 =

10 × 10 × 10 × 10 × 10 × 10 =

× 5 =

× 6 =

In ogni fiore, colora di viola il petalo con il valore minore.

Verificare le competenze Conoscere e calcolare potenze. Operare con i numeri relativi.

LE ESPRESSIONI

RICORDA...

L’espressione aritmetica è un insieme di numeri uniti tra loro da segni di operazione. Nelle espressioni si eseguono prima le moltiplicazioni e le divisioni, poi le addizioni e le sottrazioni. Alcune delle operazioni sono racchiuse da parentesi e, quando ci sono, si eseguono prima le operazioni nelle parentesi tonde (…), poi le operazioni nelle parentesi quadre […] e infine quelle nelle parentesi graffe {…}

Sottolinea di verde le operazioni da svolgere per prime, poi risolvi. 1

5 × 10 − 20 : 2 =

3 × 4 + 18 : 2 =

6 × 2 + 27 : 9 − 5 =

48 − 5 × 4 + 48 : 6 =

Risolvi le espressioni senza parentesi. 2

10 : 2 + 4 × 4 + 15 : 5 − 10 : 2 =

50 : 10 + 45 : 9 − 6 =

800 : 100 + 54 : 9 − 2 + 3 × 6 =

9 : 9 + 10 × 3 − 15 : 5 =

180 − 50 : 10 + 2 × 9 − 6 =

Risolvi rispettando le parentesi. 3

210 − (8 × 3) =

(40 + 30) : 10 =

18 − [2 + (25 : 5) − 1] + [12 − (18 : 2)] =

2 + [15 : (9 − 4) + 6 × 3] =

{2 + [5 + (9 × 6) − 3] + 4} : 2 =

(7 × 3) + 15 − (72 : 9) =

Obiettivo Eseguire le espressioni aritmetiche senza e con le parentesi.

CRITERI DI DIVISIBILITÀ

RICORDA...

Un numero è divisibile per 2 quando termina con 0 o una cifra pari.

Un numero è divisibile per 3 quando la somma delle sue cifre è un numero divisibile per 3. Un numero è divisibile per 4 se termina con due zeri o se le ultime due cifre formano un numero divisibile per 4. Un numero è divisibile per 5 se termina per 5 o per 0.

Cerchia di rosso i numeri divisibili per 2 e di verde quelli divisibili per 3. Attenzione: alcuni numeri sono divisibili per entrambi i numeri.

Nello spazio vuoto scrivi una o due cifre in modo da ottenere un numero:

• divisibile per 2

• divisibile per 3

• divisibile per 4

• divisibile per 5

RICORDA...

Un numero è divisibile per 10, 100 o 1 000 quando termina con 1, 2, 3 o più zeri.

Colora di giallo le bandierine con i numeri divisibili per 5 e di viola le bandierine con i numeri divisibili per 3. Attenzione: alcuni numeri sono divisibili per entrambi i numeri.