Los números y otros retos matemáticos


Manual Parte 6


Dra.MaríaTeresa
AliciaSilvayOrtiz 6
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6

Dedicatoria
Paratiorientadorquequieresformarteparapoderguiaraotrosenel caminodelavidaparaaprovecharsuspotencialidadesydarlomejorde símismos.

MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
1. El concepto de número
El conocimiento lógico-matemático no existe por sí mismo en la realidad de los objetos. La fuente de este razonamiento está en el sujeto y se construye por abstracción reflexiva. De hecho, se deriva de la coordinación de las acciones que el sujeto realiza con los objetos. En otras palabras, la fuente del conocimiento físico son los objetos del mundo externo; pelota, carro, tren, leche, etc. En contraste, si hay tres objetos frente a uno, en ningún lado se ve el “tres”, esta noción es más bien producto de una abstracción de la interacción del sujeto en donde se encuentran tres objetos. Esto significa que este tipo de conocimiento se construye al relacionar las experiencias obtenidas con la manipulación de objetos y no sólo de la observación, como al tocar y comparar se diferencia una textura áspera de otra lisa. Antes de llegar a las operaciones lógico-matemáticas, el niño necesita construir estructuras internas y manejar ciertas nociones adquiridas a través de su interacción con el medio y la relación con los objetos y personas para que pueda aprender a clasificar, seriar y adquirir la noción de número.
1.1
Conservación
a) Percepción y manipulación de los objetos:
azul rojo rojo rojo azul azul
b) Alineamiento: de los objetos, continuos o discontinuos. Los elementos que escoge son heterogéneos.
amarillo amarillo rojo azul
c) Objetos colectivos: colecciones de dos o tres dimensiones, formadas por elementos semejantes y que constituyen una unidad geométrica.
Azul Rojo
Azul rojo
Azul rojo
d) Objetos complejos: iguales caracteres de la colectiva, pero con elementos heterogéneos. De variedades: formas geométricas y figuras representativas de la realidad.
• Forma colecciones de parejas y tríos: al comienzo de esta sub-etapa el niño todavía mantiene la alternancia de criterios, más adelante mantiene un criterio fijo.
Triángulos cuadrados
• Colecciones con subcriterios: forma agrupaciones que abarcan más y que pueden a su vez dividirse en subcolecciones.
Triángulos
triángulos rojos triángulos amarillos triángulos azules
1.2 Clasificación
Constituye una serie de relaciones mentales en función de las cuales los objetos se reúnen por semejanzas, se separan por diferencias, se define la presencia del objeto a una clase y se incluyen en ella subclases. En conclusión, las relaciones que se establecen son las semejanzas, diferencias, pertenencias (relación entre un elemento y la clase a la que pertenece) e inclusiones (relación entre una subclase y la clase de la que forma parte). La clasificación en el niño pasa por varias etapas:
• Transitividad: Consiste en poder establecer deductivamente la relación existente entre dos elementos que no han sido comparados efectivamente a partir de otras relaciones que si han sido establecidas perceptivamente.
• Reversibilidad: Es la posibilidad de concebir simultáneamente dos relaciones inversas, es decir, considerar a cada elemento como mayor que los siguientes y menor que los anteriores.
1.3 Seriación
La seriación es una operación lógica que, a partir de un sistema de referencias, permite establecer relaciones comparativas entre los elementos de un conjunto, y ordenarlos según sus diferencias, ya sea en forma decreciente o creciente. Pasa por las siguientes etapas:
• Primera etapa: Parejas y Tríos (formar parejas de elementos, colocando uno pequeño y el otro grande) y Escaleras y Techo (el niño construye una escalera, centrándose en el extremo superior y descuidando la línea de base). A los 5 años: sin conservación de la cantidad, ausencia de correspondencia término a término.
• Segunda etapa: Serie por ensayo y error (el niño logra la serie, con dificultad para ordenarlas completamente). Entre los 5 y 6 años: Establecimiento de la correspondencia término a término, pero sin equivalencia durable.
• Tercera etapa: el niño realiza la seriación sistemática y se da la conservación del número.
Según Piaget, saber contar no significa entender el concepto de número, pues requiere entender dos ideas: la correspondencia uno a uno y la conservación.
La correspondencia uno a uno permite establecer que dos conjuntos cualesquiera son equivalentes en número si a cada objeto de un conjunto le corresponde otro objeto en el segundo conjunto.
La conservación se refiere al hecho de que, si dos conjuntos son iguales en el número, sin importar cómo acomode los objetos en cada uno, por ejemplo, apilándolos en el primero y esparciéndolos en el segundo, habrá siempre el mismo número de objetos en ambos. Esto es, el número se conserva y no se altera porque sea diferente la configuración perceptiva.
2. Cómo se logra el conocimiento cognoscitivo
Ningún conocimiento es una copia de lo real, porque incluye, forzosamente, un proceso de asimilación de estructuras anteriores; es decir, una integración de estructuras previas. De esta forma, la asimilación maneja dos elementos: lo que se acaba de conocer y lo que significa dentro del contexto del ser humano que lo aprendió. Por esta razón, conocer no es copiar lo real, sino actuar en la realidad y transformarla.
La lógica, por ejemplo, no es simplemente un sistema de notaciones inherentes al lenguaje, sino que consiste en un sistema de operaciones como clasificar, seriar, poner en correspondencia, etc. Es decir, se pone en acción la teoría asimilada. Conocer un objeto, para Piaget, implica incorporarlo a los sistemas de acción y esto es válido tanto para las conductas sensoriomotoras como las combinaciones lógicas-matemáticas.
Los esquemas más elementales que se asimilan son reflejos o instintos, en otras palabras, información hereditaria. A partir de la conformación genética se responde al medio al que se pertenece; pero a medida que se incrementan los estímulos y conocimientos, se amplía la capacidad de respuesta; ya que se asimilan nuevas experiencias que influyen en la percepción y en la forma de responder al entorno.
Las conductas adquiridas llevan consigo procesos autorreguladores, que indican cómo se deben percibir y aplicar. El conjunto de las operaciones del pensamiento, en especial las operaciones lógico-matemáticas, son un vasto sistema autorregulador, que garantiza al pensamiento su autonomía y coherencia.
Dentro de la regulación está el número que es un concepto lógico por naturaleza, distinto al conocimiento físico o social, ya que no se extraer directamente de las propiedades físicas de los objetos ni de las convenciones sociales, sino que se construye a través de un proceso de abstracción reflexiva de las relaciones entre los conjuntos que expresan número. Según Piaget, la formación del concepto de número es el resultado de las operaciones lógicas como la clasificación y la seriación; por ejemplo, al contar, se tiende a agrupar determinado número de objetos o se ordena en serie. Las operaciones mentales sólo pueden tener lugar cuando se logra la noción de la conservación de la cantidad y la equivalencia término a término. Consta de las siguientes etapas:
• Regulaciones orgánicas, que tienen que ver con las hormonas, ciclos, metabolismo, información genética y sistema nervioso.
• Regulaciones cognoscitivas, tienen su origen en los conocimientos adquiridos previamente por los individuos.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
Actividad # 1 Clasificando los bloques lógicos


Instrucciones. Vamos a ordenar los bloques lógicos respetando los criterios de color, forma, tamaño y espesor.
Actividad # 2 Las serpientes
Instrucciones. Utiliza los bloques lógicos para hacer serpientes de colores La primera es libre, la segunda pide ir cambiando de color, la tercera es adivinar el criterio y la cuarta seguir los colores de las etiquetas





3. Consideraciones generales de la teoría cognoscitiva
De manera general se puede decir que el desarrollo cognoscitivo ocurre con la reorganización de las estructuras cognoscitivas como consecuencia de procesos adaptativos al medio, a partir de la asimilación de experiencias y acomodación de estas de acuerdo con el equipaje previo de las estructuras cognoscitivas de los aprendices. Si la experiencia física o social entra en conflicto con los conocimientos previos, las estructuras cognoscitivas se reacomodan para incorporar la nueva experiencia y es lo que se considera como aprendizaje. El contenido del aprendizaje se organiza en esquemas de conocimiento que presentan diferentes niveles de complejidad. La experiencia escolar, por tanto, debe promover el conflicto cognoscitivo en el aprendiz mediante diferentes actividades, tales como las preguntas desafiantes de su saber previo, las situaciones desestabilizadoras, las propuestas o proyectos retadores, etc.
La teoría de Piaget ha sido denominada epistemología genética porque estudia el origen y el desarrollo de las capacidades cognoscitivas desde su base orgánica, biológica, genética, encontrando que cada individuo se desarrolla a su propio ritmo. Describe el curso del desarrollo cognoscitivo desde la fase del recién nacido, donde predominan los mecanismos reflejos, hasta la etapa adulta caracterizada por procesos conscientes de comportamiento regulado.
En el desarrollo genético del individuo se identifican y diferencian periodos del desarrollo intelectual, tales como el sensorio-motriz, el de operaciones concretas y el de las operaciones formales. Piaget considera al pensamiento y a la inteligencia como procesos cognoscitivos que tienen su base en un substrato orgánicobiológico determinado que va desarrollándose en forma paralela con la maduración y el crecimiento biológico.
En la base de este proceso se encuentran dos funciones denominadas asimilación y acomodación, que son fundamentales para la adaptación del organismo a su ambiente. Esta adaptación se entiende como un esfuerzo cognoscitivo del individuo para encontrar un equilibrio entre él mismo y su ambiente. Mediante la asimilación el organismo incorpora información al interior de las estructuras cognoscitivas a fin de ajustar mejor el conocimiento previo que posee. Es decir, el individuo adapta el ambiente a sí mismo y lo utiliza según lo concibe.
La segunda parte de la adaptación denominada acomodación como ajuste del organismo a las circunstancias exigentes, es un comportamiento inteligente que necesita incorporar la experiencia de las acciones para lograr su cabal desarrollo. Estos mecanismos de asimilación y acomodación conforman unidades de estructuras cognoscitivas que Piaget denomina esquemas. Estos esquemas son representaciones interiorizadas de cierta clase de acciones o ejecuciones, como cuando se realiza algo mentalmente sin realizar la acción. Puede decirse que el esquema constituye un plan cognoscitivo que establece la secuencia de pasos que conducen a la solución de un problema.
Para Piaget el desarrollo cognoscitivo se lleva a cabo de dos maneras: la primera, la más amplia, corresponde al propio desarrollo cognoscitivo, como un proceso adaptativo de asimilación y acomodación, el cual incluye la maduración biológica, la experiencia, la transmisión social y el equilibrio cognoscitivo. La segunda forma de desarrollo cognoscitivo se limita a la adquisición de nuevas respuestas para situaciones específicas o a la adquisición de nuevas estructuras para determinadas operaciones mentales específicas.
En el caso del salón de clases, Piaget considera que los factores motivacionales de la situación del desarrollo cognoscitivo son inherentes al estudiante y no son, por lo tanto, manipulables directamente por el profesor.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
La motivación del estudiante se deriva de la existencia de un desequilibrio conceptual y de la necesidad del estudiante de restablecer su equilibrio.




La enseñanza debe ser planeada para permitir que el estudiante manipule los objetos de su ambiente, transformándolos, encontrándoles sentido, disociándolos, introduciéndoles variaciones en sus diversos aspectos, hasta estar en condiciones de hacer inferencias lógicas y desarrollar nuevos esquemas y nuevas estructuras mentales.
El desarrollo cognoscitivo, en resumen, ocurre a partir de la reestructuración de las estructuras cognoscitivas internas del aprendiz, de sus esquemas y de sus estructuras mentales, de tal forma que al final de un proceso de aprendizaje deben aparecer nuevos esquemas y estructuras como una nueva forma de equilibrio.
Actividad # 3


Atributos de los bloques lógicos









Instrucciones. Pon en cada espacio la figura que indica la tarjeta con base en los atributos que se señalan






MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
Actividad # 4 Atributos de los bloques lógicos
Instrucciones. Con un juego de diez barras o varillas, se ordenan de menor a mayor y después de mayor a menor.
Actividad # 5 Figuras con Tangram



Instrucciones. Construye las figuras con el tangram con base en las tarjetas que se te van entregando. Cuenta una historia.

4. Ejercicios preparatorios para el cálculo mental

Los ejercicios preparatorios se enmarcan en el eje programático. Los números, sus relaciones y sus operaciones.
Estos ejercicios responden a dos propósitos muy claros: preparar a los estudiantes para el conocimiento del método mediante la presentación de situaciones matemáticas que puedan ser ilustradas en su totalidad en un gráfico, y ofrecer a los educandos estrategias alternativas para promover el cálculo mental.
4.1 Conversión de cantidades continuas y discontinuas


Una función es continua si su gráfica puede dibujarse de un solo trazo, es decir, si no presenta puntos de discontinuidad, saltaos o interrupciones.
A. Función Discontinua
Las gráficas que presentan algún punto aislado, saltos o interrupciones, es decir, que no están hechas de un sólo trazo en un intervalo determinado, son llamadas funciones discontinuas.
Una función es discontinua si tiene puntos en los cuales una pequeña variación de la variable independiente produce un salto o interrupciones en los valores de la variable dependiente.
Los puntos de discontinuidad pueden ser de dos tipos:
• Puntos en los que la función no está definida, los puntos que no pertenecen al dominio de la función.
• Puntos en los que la gráfica presenta un salto, gráfica.
4.2 Números finitos ordinales y cardinales.
Los números ordinales finitos (así como los cardinales finitos) son los números naturales 0, 1, 2,..., puesto que dos órdenes totales de un conjunto finito son isomorfos en cuanto al orden
Los números cardinales son aquellos números ordinales que no tienen la misma cardinalidad que cualquier ordinal menor. Por ejemplo, todos los números ordinales finitos (vistos como conjuntos) son a su vez números cardinales.
Esta noción es por lo tanto distinta del ordinal, que caracteriza el lugar de un elemento en una sucesión. Cinco difiere de quinto, aunque obviamente existe una relación entre ambos. Se dice que dos conjuntos tienen el mismo cardinal si existe una biyección entre ellos. Contrariamente a los ordinales, esta biyección no tiene que respetar el orden (además los conjuntos no tienen que ser ordenados).
Actividad # 6
Instrucciones. Ordena a los búhos y ponles su etiqueta para identificar cuál es su lugar. Coloréalos.
¿Cuál es su lugar?
4.3 Cuantificadores
Los cuantificadores sirven para comprender los cálculos matemáticos que vinculan una serie de variables. Los cuantificadores determinar un valor como verdadero y falso, valido o invalido. Hay dos tipos de cuantificadores:
a) El cuantificador universal donde puede declararse como: para todo “X”, es verdad que “P” existe por lo menos un y tal que “Q” es verdad, a partir de la simbología correspondiente.

b) El cuantificador existencial, es empleado para identificar que por lo menos un elemento de un conjunto, “X”, está acorde con una propiedad.
Los cuantificadores sirven para enseñar a los niños los conceptos numéricos de muchos y pocos, arriba y abajo, todoso ninguno. El buen uso de los cuantificadores, en cuanto a expresión del juicio lógico, favorecerá en el niño la noción de conservación, la construcción de la noción de clase y la coordinación de su extensión.

Actividad # 7
¿Dónde hay más, dónde hay menos?
Instrucciones. Utiliza tarjetas con distintas órdenes para que el orientado vaya comprendiendo la diferencia entre mucho, poco, nada; más, menos, etc.


MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
4.4 Función y expresión verbal y simbólica
Las funciones de la expresión verbal en los orientados emiten a los juicios de valor de sus expresiones verbales cotidianas, cuando ellos afirman que un objeto tiene o no ciertas características que lo distinguen de los demás. Los aprendices son muy evidentes en su aptitud lógica, ya que hacen público sí reconocen lo falso y verdadero de los objetos ante sus propiedades.
Otra manera de detectar su razonamiento lógico es cuando centran su atención en algún objeto en específico y se preocupan por buscar elementos en común y diferencias entre otros objetos.
Los niveles de madurez cognoscitiva los van adquiriendo en su expresión verbal, la cual puede ser reforzada mediante más experiencias que le permitan seguir ampliando su aprendizaje.
Actividad # 8
Encuentra las diferencias
Instrucciones. Encuentra las diferencias de los dibujos y enciérralas en un círculo. En los pájaros 3 y en los peces 4 diferencias.


4.5 Noción de consecución y de clase
El intervalo es un subconjunto de la recta real y contiene a todos los números reales que están comprendidos entre dos.

Geométricamente los intervalos corresponden a segmentos de recta, semirrectas o la misma recta real.
Los intervalos de números correspondientes a segmentos de recta son intervalos finitos, los intervalos correspondientes a semirrectas y a la recta real son intervalos infinitos.
a) Los intervalos finitos pueden ser cerrados, abiertos o semiabiertos.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
b) Intervalo cerrado Es el conjunto de números reales formado por a, b y todos los comprendidos entre ambos.
[a, b] = { x / a £ x £ b}
c) Intervalo abierto. Es el conjunto de los números reales comprendidos entre a y b.
(a, b) = {x / a < x < b}
d) Intervalo semiabierto a izquierda (o semicerrado a derecha) Es el conjunto de números reales formado por b y los números comprendidos entre a y b.
(a, b] = {x / a < x £ b}
e) Intervalo semiabierto a derecha (o semicerrado a izquierda) Es el conjunto de números reales formado por a y los números comprendidos entre a y b.

[a, b) = { x / a £ x < b}
4.6 Conceptos numéricos
Para que le niño pueda comprender el número es necesario que lo conceptualice, es decir, necesita de dos condiciones psicológicas para la elaboración de este concepto:


La conservación del todo: el todo es un conjunto de partes que se puede distribuir como se quiera. Tiene que haber reversibilidad del pensamiento para que haya conservación.
La seriación de los elementos: el número se construye en la medida que los elementos de la serie son concebidos a la vez como equivalentes y no equivalentes.
Actividad # 8 Series y relaciones
Instrucciones. Completa la serie. Une las dos columnas.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
4.6.1. Conceptos formales y naturales
El niño debe adquirir una serie de conceptos básicos como son: poco, mucho, demasiado, suficiente; una vez que esto se ha adquirido el niño está listo para contar y con esto entender el sistema métrico decimal, captar el concepto de número, su uso y su sentido, los diferentes órdenes de unidades y el valor posicional en números de varias cifras.
Los niños adquieren parte de estos aprendizajes a través de las experiencias informales y otros en sus experiencias escolares; los niños con Dificultades de Aprendizaje de las Matemáticas (DAM) suelen tardar más tiempo y necesitar más situaciones estimulantes que el resto de los niños para realizar estos aprendizajes.
Contar implica una serie de subhabilidades, los niños pueden contar objetos cuando han dominado cinco principios:
• Correspondencia uno a uno o correspondencia biunívoca entre los números y los objetos: a cada objeto de una colección le corresponde un solo número; los niños dominan este principio desde los 2 años.
• Orden estable: los nombres de los números siguen un orden estable y fijo, la asignación del número a los objetos que se cuentan debe realizarse en ese orden. Esto no se consigue hasta los 3-4 años.
• Cardinalidad: el último número de una secuencia numérica es el cardenal de ese conjunto, el que indica el número de objetos que hay en el conjunto; este principio se consigue en torno a los 5 años.
• Abstracción: permite saber cuáles son los objetos que son enumerables y que los principios se aplican a diferentes grupos de objetos, independientemente de sus características o cualidades físicas; hacia los 3 años ya han adquirido la abstracción.
• Irrelevancia del orden: la posición del objeto en una secuencia no es importante, los niños se dan cuenta de esto alrededor de los 4 años.
4.6.2. Fundamentos y propuestas metodológicas
Dentro de las propuestas se deben realizar actividades para el desarrollo del esquema corporal y la lateralidad, presentando especial atención a las coordenadas espaciales arriba-abajo, delante-detrás, derecha-izquierda en relación con el propio cuerpo
Ejercicios de coordinación motriz. Desarrollo de las etapas homolateral, contralateral y lateral.
Actividades que aumenten la coordinación viso-motriz, y proporcionen un sentido del ritmo y del equilibrio.
Al mismo tiempo que se fortalece en el niño la capacidad de secuenciar lo establecido, es decir, saber ubicar el pasado, el presente y el futuro en un cierto esquema establecido, así también puede identificar el valor numérico en determinadas situaciones, ejemplo: 4 < 9 y 8 > 2, con este conocimiento previo podrá sortear retos como son la resolución de secuencias entre otras.
4 6.3. Formas geométricas elementales
Son conocidas como figuras elementales: el cuadrado, el rectángulo, el círculo y el triángulo.
Una vez que el niño se encuentra en una edad apta para trabajar con este tipo de figuras, ya sea en forma de juego o pequeñas labores estaremos trabajando las destrezas básicas del pensamiento matemático: observación, comparación, clasificación, y seriación; con el uso constante estaremos reforzando el pensamiento lógico.

Como material de apoyo podemos encontrar entre otros el uso del tangram y de los bloques lógicos de Dienes.


4.6.4. Concepto de número y comparación numérica





Número: Propiedad de un todo que indica una cantidad total. Para la comparación numérica es necesario que el concepto de número este bien entendido, de este modo y haciendo uso de un lenguaje especifico el niño será capaz de diferenciar las características que encierra el número, es decir mediante la experiencia previa el niño es capaz de determinar que 8 es mayor a 3, pues ya lo ha integrado en un esquema alfanumérico, en un principio se tuvo que apoyar por objetos contados uno a uno.
Actividad # 9 Mayor, menor o igual que
Instrucciones. Decir la relación que hay entre los números: si es mayor que, menor que o igual que. En la siguiente parte, poner el signo.


De este modo llega a la conclusión de que un número está conformado por unidades que en un momento representan un todo además le es posible comprender que la adicción de objetos a un todo representa un nuevo concepto numérico.
4.6.5. Conversión de números decimales a fracciones.
Para convertir un número decimal a facción se debe de tomar en cuenta las siguientes indicaciones:
• Se escribe el número decimal y se divide por 1.
• Multiplica los números de arriba y abajo por 10 una vez por cada número. (ejemplo, si hay dos números luego del decimal, multiplícalos por 100 y si hay tres se utiliza 1000 y así sucesivamente.)

• Se simplifica la fracción.
Ejemplo: 0.75 como fracción se escribe: 0.75 1
Multiplica el número de abajo y el de arriba por 100 (porque hay 2 dígitos luego de la coma): × 100
0.75 = 75 1 100 × 100
El número de arriba se convierte en entero.
Simplifica la fracción:
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
÷ 25
75 = 3
100 4
÷ 25
El resultado es ¾ esto es una fracción común y 75/100 es una fracción decimal.
Actividad # 10 Fracciones

Instrucciones. Elige la opción que represente cada uno de los dibujos.


Siguen las instrucciones. Escribe cuál es la fracción de cada círculo.



5. Didáctica de las relaciones lógicomatemáticas y cuantificación
El contenido de este trabajo hace referencia a un programa que se ha elaborado para atender las dificultades de aprendizaje en matemáticas bajo el paradigma de la discalculia.
El objetivo es que el lector analice este programa y haga las adaptaciones que considere pertinentes para que sea adecuado a la población que atiende.
5.1 Discalculia
Se hace un breve repaso sobre el tema, el cual ha sido tratado ampliamente en el manual de esta serie y en otros números.
¿A qué hace referencia el término discalculia?
El término discalculia hace referencia a un amplio rango de problemas relacionados con el aprendizaje de las habilidades matemáticas. No existe una forma única de estas alteraciones. Las dificultades que se presentan varían de una persona a otra, les afecta de manera diferente y también depende del momento en el ciclo vital que se encuentren.
¿Cómo se define la discalculia?
Aunque hay muchas definiciones, quizá la más práctica y adecuada sea, la inhabilidad o dificultad para aprender a realizar operaciones aritméticas, a pesar de recibir toda instrucción convencional, en contraste con una capacidad intelectual normal del alumno.

¿Qué impacto tiene la discalculia en quien lo padece?
Si no se trata precozmente, puede arrastrar un importante retraso educativo. En los niños esta dificultad causa mucho sufrimiento, especialmente en los primeros años escolares en los que el dominio de las "bases conceptuales" es de gran importancia, pues el aprendizaje de la matemática es de tipo "acumulativo", por ejemplo, no es posible entender la multiplicación sino se entiende la suma. Los efectos que tienen estas dificultades de aprendizaje en las matemáticas son diferentes en cada persona.
Algunas de ellas, por ejemplo, pueden estar asociados con el procesamiento verbal, por lo tanto, los desafíos serán diferentes a quienes presentan dificultades en las relaciones visoespaciales. Otras personas pueden tener problemas para recordar y mantener una secuencia adecuada, en fin, hay muchas variantes.
¿Cómo se enseña generalmente las matemáticas?
En el sistema tradicional de enseñanza se ha perdido la conexión con la raíz de las matemáticas, enseñando al alumno a memorizar y manejar símbolos, olvidando que estos son sólo representaciones de algo concreto, y a memorizar procedimientos y formulas sin saber lo que está haciendo: generalmente cuando se le pregunta al orientado qué está haciendo cuando está sumando con llevadas y ¿cuál es la razón por la que se lleva una?, suele responder. “porque así me dijo mi maestra”. La clave está en "como hacer la transición desde el material concreto, hasta el papel y lápiz". Mediante la integración de patrones numéricos para llegar a la abstracción del dígito.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
¿Cómo proceder?
En vista de que cada caso es único, sólo se pueden sugerir algunos lineamientos comunes a considerar en las distintas etapas del desarrollo. Aquí se comentará brevemente: primera infancia, edad escolar, adolescentes y adultos.
a) Primera infancia. Construir una base sólida sobre distintas habilidades que les permita comprender el significado de los números; la agrupación de objetos con base en su forma, tamaño, color o textura; reconocer grupos y patrones; comparar opuestos utilizando conceptos contrastantes, como grande-chico, altobajo, por ejemplo. Aprender a contar, reconocer números y emparejar números con determinadas cantidades.
b) Edad escolar. Atender el procesamiento verbal, pues generalmente les cuesta trabajo comprender el lenguaje matemático; ayudarlos a dominar las cuatro operaciones básicas: adiciones, sustracciones, multiplicaciones y divisiones. Los temas que generalmente se les dificultan son:
• Recordar hechos matemáticos básicos: tablas, unidades de medida, valor posicional de los números, sistema decimal.
• Resolver problemas matemáticos: comprender cómo se plantean, qué se está preguntando, valorar sus respuestas.
• Fallas en las habilidades visoespaciales: como cuando si entiende los hechos matemáticos, pero se le dificulta ponerlos y organizarlos en el papel, les cuesta trabajo entender lo que está escrito en el pizarrón o en un libro.
c) Adolescentes y adultos: Si no han dominado las habilidades matemáticas básicas, entonces habrá complicaciones en aplicaciones más avanzadas: en el procesamiento verbal por no comprender la terminología matemática, les falta vocabulario suficiente para construir el conocimiento matemático y para realizar tareas multipaso: no visualizan patrones diferentes en los problemas ni identifican la información necesaria para resolver una ecuación o problemas más complejos.
¿Cuáles son las características del orientado con discalculia?
El orientado que empieza a tener problemas en aritmética suele manifestar:
a) Dificultades en la organización del espacio. Problemas para organizar los números en columnas o para seguir la direccionalidad apropiada del procedimiento.
b) Dificultades de procedimiento. Omisión o adición de un paso del procedimiento aritmético; aplicación de una regla aprendida para un procedimiento a otro diferente, como sumar cuando hay que restar.
c) Dificultades de juicio y razonamiento Errores tales como que el resultado de una resta es mayor a los números sustraídos y no hacer la conexión de que esto no puede ser.
d) Dificultades con la memoria mecánica Tropiezos para recordar las tablas de multiplicar y para recordar algún paso de la división... este problema se incrementa conforme el material es más complejo.
e) Especial dificultad con los problemas razonados. Particularmente los que involucran multipasos (como cuando hay que sumar y luego restar para encontrar la respuesta).
f) Poco dominio de conceptos como clasificación, medición y secuenciación especial interés por ver y entender lo que se le pide en un problema. Se les dificulta seguir procedimientos sin saber el cómo y porqué
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
¿Cuáles son las señales de alerta?
Son muy diversos, por eso se requiere una evaluación neuropsicológica para obtener un diagnóstico diferencial que permita identificar la naturaleza exacta de su problemática con el fin de poder programar los pasos más adecuados en cada caso. Es recomendable considerar lo siguiente:
• Nivel de desarrollo del lenguaje, lectura y escritura en contraste con su dificultad para aprender a contar y a resolver problemas matemáticos.
• Memoria para las palabras escritas en contraste con su habilidad para leer números y/o recordar secuencias numéricas.
• Comprensión de conceptos matemáticos generales y nivel de frustración al realizar cálculos específicos.
• Dificultad para ordenar cronológicamente conceptos, para recordar hechos agendados, estimación de tamaños, longitud, volumen, peso, entre otros.
• Noción derecha-izquierda, direccionalidad y lateralidad.
• Sentido de orientación, efecto en los cambios de su rutina.
• Memoria a corto, mediano y largo plazo. Si presenta alteraciones al realizar funciones matemáticas: un día lo hace bien, pero después es incapaz de recordarla.
• Pobre capacidad para estimar a grandes rasgos costos, tamaños, distancias temporales, por ejemplo.
• Dificultad con juegos estratégicos, como el ajedrez, damas, barajas, o juegos electrónicos.
• Dificultad para seguir las puntuaciones en los juegos.
¿Cómo prevenir y/o corregir la discalculia?
La discalculia suele presentarse en una etapa muy temprana, siendo el primer síntoma la dificultad en el aprendizaje de los dígitos. Ello se debe a que el orientado no entiende la correspondencia entre el dígito y la cantidad, y comienza a ver que las matemáticas son complicadas. La correspondencia entre lo concreto (la cantidad) y lo abstracto (el símbolo), es un paso que quien padece discalculia, no llega a comprenderla.
Se utilizan patrones (que sirven para hacer la transición) y plastilina (que sirven para que aprendan el concepto), que están basados en la forma en que los antiguos comprendían las matemáticas, ya que trabajaban con materiales concretos (semillas, barras de arcilla, cuerdas con nudos…). El ábaco es un intento bastante bueno para acercar a los niños a lo concreto; sin embargo, en los colegios enseguida se pasa al papel y lápiz.
La metodología ha de basarse en una correcta transición de lo concreto a lo abstracto a través de una serie de actividades donde el orientado aprenda de forma más rápida y eficiente, entendiendo el cómo y por qué de las cosas.
Este método se aplica tanto a niños visuales (niños con un estilo diferente de aprender y percibir debido a que piensan con imágenes y no con palabras), como a los no visuales, a partir de 7 años
El método consiste en realizar actividades y representaciones en material concreto (principalmente, aunque no limitado, en plastilina) junto con el estudiante, quién va descubriendo paso a paso cómo pasar del material concreto al cuaderno, gracias a un diseño especial en el que se aprenden las cantidades mediante unos "patrones". Héctor Linares explica que la idea de "patrones" la tomó del sistema numérico de los mayas. Aunque en un principio el método fue creado pensando en ayudar específicamente a niños con discalculia, el método beneficia a todos en general.
5.2 Didáctica de las relaciones lógico-matemáticas
¿Cuál sería el punto de partida para la didáctica de las relaciones lógicomatemáticas y cuantificación?
Según la UNICEF, si se toma como punto de partida que las matemáticas no es el arte de calcular sino el arte de comprender, que hay aprendizaje cuando la experiencia presenta desafíos interesantes para los orientados, cuando tienen la oportunidad de jugar con las respuestas antes de escoger una de ellas, cuando expresan diferentes alternativas antes de llegar a una conclusión definitiva y donde puedan compartir, dialogar, observar y también experimentar. En síntesis, se busca que los orientados desarrollen habilidades matemáticas que posibiliten, en forma autónoma, la búsqueda de posibles soluciones a problemáticas que surgen de la vida cotidiana, que confronten las soluciones encontradas, que busquen diferentes caminos de solución, que formulen nuevos problemas, que comprendan que equivocarse es parte del aprendizaje, es decir, asumir un rol de un investigador que busca permanentemente caminos para resolver situaciones.
¿Cómo está organizado este contenido?
El contenido de esta sección está ordenado de la siguiente manera: lenguaje matemático, concepto de número, conocimiento del espacio, orientación temporal, medidas y sus magnitudes, resolución de problemas y diferentes formas de registro. Se pone especial atención al carácter lúdico de cada una de las experiencias, pues son un medio privilegiado para favorecer los aprendizajes, las habilidades y los valores esenciales.
Los juegos colaborativos surgen como una valiosa oportunidad para desafiar, contar con una mayor organización, definición de reglas del juego, compromiso a respetar y cumplir dichas reglas, ayudarse mutuamente, aceptar las diferentes opiniones, construir en grupo, además refuerza los valores solidarios como compartir y respetar a los demás, etc.
¿Cómo se adquieren las nociones matemáticas?
Las nociones matemáticas se adquieren a través de un largo proceso de construcción continuo y permanente que abarca toda la vida de las personas. En este sentido, los educadores cumplen un papel primordial en la transmisión y producción de los saberes, entre ellos el saber matemático.
La integración de este núcleo a partir de la más temprana edad obedece a la necesidad de contar con instrumentos, habilidades y conceptos matemáticos que le permitan: interactuar, comprender y modificar el medio, dado que favorece la integración activa al entorno social y tecnológico. El aprendizaje de los conceptos matemáticos contribuye al desarrollo de la capacidad de interpretación y creación simbólica.
¿Cuál es el objetivo del aprendizaje de las habilidades matemáticas?
El aprendizaje de las habilidades matemáticas ha de llevar al alumno a ser capaz de organizar mentalmente sus impresiones referidas a las cosas en sí mismas (números), sus atributos (cantidad, forma, características) y las relaciones que existen o podrían existir entre ellas (comparación, correspondencia, posición espacial, etc.). Cada uno de estos aspectos va a sentar las bases o estructuras cognoscitivas requeridas para enfrentar las operaciones formales en la Educación Básica.
¿Cómo enseñar las matemáticas?
El modelo clásico de la enseñanza de las matemáticas estuvo centrado mayoritariamente en la transmisión de los contenidos, es decir, el educador
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
introduce algunas nociones, presenta los ejercicios y los alumnos tienen que ejercitarlos una y otra vez.
Hoy, luego de haber superado este modelo, cambia el enfoque y propone una enseñanza centrada en la actividad de los orientados, utilizando métodos activos en los cuales cobran importancia sus aprendizajes, sus intereses, las motivaciones, y sus necesidades. Tanto el educador como el niño tienen un papel activo, el primero en relación con la generación de estrategias que garanticen la apropiación de los conceptos matemáticos y los niños como constructores de sus saberes.
¿Cómo debe proceder el educador?
En síntesis, el educador:
• Escucha, responde a sus intereses, le ayuda a buscar diferentes fuentes de información.
• Selecciona los aprendizajes esperados que desea proporcionar.
• Crea experiencias de aprendizaje que estén relacionadas con los intereses y situaciones de la vida cotidiana.
• Acompaña y facilita el proceso de aprendizaje para que los alumnos construyan sus saberes.
• Propone problemas o situaciones de aprendizaje que sean significativos para los orientados
• Crea espacios para que puedan interaccionar y participar en trabajos cooperativos, lo que permite que éstos busquen soluciones, intercambien puntos de vista, favoreciendo de esta manera, la reflexión sobre su propio pensamiento y la construcción en conjunto de diversas posibilidades de solución.
• Favorece la autonomía, pues el desarrollo del pensamiento lógico matemático requiere de parte de los alumnos una construcción que surge desde adentro, es decir, algo que únicamente el niño puede hacer con la ayuda de otros.
• Reconoce que los alumnos traen un bagaje de experiencias previas y concepciones diversas respecto al pensamiento lógico matemáticas como: concepto de número, unidades de medida, nociones espaciales, geométricas, etc.
• Explora las potencialidades informales de los alumnos para que en la enseñanza formal (escuela) sea significativa e interesante; por ejemplo, las primeras concepciones informales de la adición (en tanto que añadir más) y la de sustracción (en cuanto a quitar algo), guiando sus intentos para construir procedimientos aritméticos informales.
¿Cómo deben ser las experiencias de aprendizaje?
Cada experiencia de aprendizaje debe tener una fuerte intencionalidad o finalidad, es decir, experiencias que desafíen a los alumnos buscar y encontrar posibles soluciones a los problemas planteados. A través de estas acciones se va adquiriendo sentido en el conocimiento matemático.
¿Cómo debe ser el aprendizaje conceptual?
Cualquier aprendizaje conceptual que se desee alcanzar, ha de surgir a partir de la acción concreta sobre los objetos, por ejemplo, seriación es un concepto y una operación. La estrategia didáctica para que efectivamente se produzca la conexión entre concepto y operación es el lenguaje, es decir, permitir que los alumnos verbalicen constantemente la propia acción, estimularlos para que hablen sobre lo que han hecho, cómo lo han hecho o lo que piensan hacer. Al respecto, la siguiente expresión refuerza lo anteriormente expuesto "... si el objeto de conocimiento está demasiado alejado de las posibilidades de comprensión del alumno, no se produciría desequilibrio alguno en los esquemas de asimilación o
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
bien el desequilibrio provocado sería de una magnitud tal que el cambio quedaría bloqueado. Si, por el contrario, el objeto de conocimiento se deja asimilar totalmente por los esquemas ya disponibles, no habría razón alguna para modificarlos y el aprendizaje sería igualmente imposible. En consecuencia, la intervención pedagógica debe concebirse en términos de diseño de situaciones que permitan un grado óptimo de desequilibrio, es decir, que superen el nivel de comprensión del alumno pero que no lo superen tanto que no puedan ser asimilados o que resulte imposible restablecer el equilibrio...".
¿Cuáles serían las estrategias para el trabajo pedagógico?
Las estrategias para el trabajo pedagógico serían:
• Las situaciones de aprendizaje que propone el educador para ir construyendo los conceptos lógico-matemáticos, han de considerar permanentemente una intencionalidad pedagógica, que le permita al educador, partiendo de los saberes y de los intereses de los niños, plantear situaciones problemáticas que involucren los aprendizajes esperados seleccionados, sin perder el aspecto lúdico.
• El juego al ser una actividad espontánea favorece la creatividad, el cumplimiento de normas, la búsqueda de estrategias, la autonomía, conocimientos, etc. Este acto involucra al niño en los diferentes ámbitos de su ser, afectivo, cognitivo, social, cultural.
• Se pueden proponer diferentes tipos de juegos, algunos que resultan interesantes son aquellos que pueden ser reglados, tanto por el educador como por los orientados. Generalmente estos juegos pueden fomentar aspectos como la autonomía, respeto por los acuerdos tanto a nivel individual como grupal.
¿Qué tipo de juegos se pueden proponer?
En este sentido Constance Kamii y Rheta Devries (1985) plantean algunos juegos colectivos que presentan las siguientes características:
• Deben proponer algo interesante y estimulante para que los niños piensen en cómo hacerlo.
• Deben posibilitar que los propios niños evalúen el éxito.
• Deben permitir que todos los jugadores participen activamente durante todo el juego.
¿Cómo poner situaciones de aprendizaje interesantes y estimulantes?
Cuando se habla de proponer situaciones de aprendizaje interesantes y estimulantes, se refiere fundamentalmente a cómo el juego va asociado o unido a un obstáculo a resolver, para ello existen una serie de materiales (dados, tableros) donde el educador analiza junto con los niños quiénes avanzaron más, quiénes menos, por qué, si les gustó o no, cómo podrían mejorar el juego, qué cambiarían, etc.
¿Cuáles serían algunas actividades para realizar todos los días?
Algunas actividades que se realizan diariamente como son:
• El registro de asistencia (cuántos niños asistieron, cuántos faltaron) y meteorológico (cuantos días a la semana llovió, hubo sol, estuvo nublado), préstamo de cuentos, revistas u otros de la biblioteca de aula podrían utilizarse como un interesante y significativo momento para que los niños comparen cantidades, establezcan relaciones de causa y efecto, investiguen, planteen hipótesis, etc., además con la guía del educador podrían graficar los resultados.
• El reparto de los materiales de trabajo puede convertirse en una situación problema factible de solucionar por los propios niños: ¿qué hacer si los materiales para pintar y/o dibujar no alcanzan para todos los grupos?, ¿qué
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
hacer para que todos los materiales estén permanentemente ordenados?, ¿cómo los podemos organizar?, ¿dónde ubicar un nuevo material didáctico?, ¿por qué ha de ubicarse en un área y no en otra?, etc.
• Una experiencia puede ser más desafiante o interesante para los niños en la medida que el educador plantee un problema a resolver (plantea el qué), y el niño busca los diferentes caminos para resolverlo (el cómo).
• Decidir o seleccionar el tipo de organización de las actividades o situaciones pedagógicas. El conocimiento matemático, en tanto saber cultural y social, se construye en interacción con otros. Por tanto, es importante promover las relaciones entre los niños, educador-niño, para así contribuir a los saberes. Esta organización puede darse en pequeños grupos, lo que favorece la comunicación entre ellos, intercambio de ideas, procedimientos, confrontación de los saberes, búsqueda de posibles soluciones. Además del trabajo grupal, el trabajo individual ha de permitir al educador, considerar otros aspectos puntuales que requiere observar y fortalecer en forma particular.
5.3 Desarrollo del lenguaje matemático
¿Por qué se requiere el aprendizaje del lenguaje matemático?
Las matemáticas son una expresión simbólica de ideas que posibilita la comunicación y, por ende, el desarrollo del pensamiento. A través de su lenguaje es posible establecer un puente con la realidad, conceptualizarla, establecer relaciones, explicarse situaciones y construir nuevos conocimientos. Por ello, es importante, que al iniciar el proceso de enseñanza de las matemáticas se incorpore la terminología correspondiente que implica, no sólo el manejo del nombre de los números, sino además la capacidad para explicarse la realidad, comunicar las diferentes relaciones que se establecen entre diferentes situaciones, comunicar nuevos descubrimientos, etc.
¿Cuáles son los propósitos del lenguaje matemático?
El lenguaje matemático cumple tres propósitos fundamentales: lúdicos, comunicativos y representativos.
a) Función lúdica: se expresa principalmente a través de los juegos reglados donde se ponen en práctica conocimientos matemáticos que requieren del cálculo, estrategias espaciales, anticipación, etc.
Al respecto el educador ha de crear experiencias que desafíen a los niños a resolver pequeñas dificultades, que impliquen efectivamente un reto atractivo y, considerando los espacios suficientes para que exprese verbalmente cómo lo hizo, qué más le costó resolver y qué aprendió con la experiencia.
b) Función representativa: implica la utilización de signos para representar cantidades o relaciones, figuras geométricas y otras formas conocidas, etc. Durante los primeros años los niños se irán acercando a los signos convencionales del lenguaje escrito de las matemáticas, a través de experiencias que surgen de la vida cotidiana; por ejemplo: en lugar de dibujar cinco objetos podrá escribir el signo que represente esa cantidad. Para llegar a conocer y utilizar un lenguaje matemático objetivo y universal (los signos en numeración obedecen a convenciones rigurosas que permiten una sola interpretación) es necesario previamente ofrecer experiencias significativas donde puedan una y otra vez contar, seleccionar, agrupar, etc.
c) Función comunicativa: permite informar, dar a conocer la realidad, explicar y cuantificar la realidad; por ejemplo: frente a la pregunta: ¿Dónde ven los números y para qué sirven?, podríamos tener las siguientes respuestas " en los autos para saber de quién es, en los buses para saber dónde ir, en los canales
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
de TV para saber qué canal es, etc.”. En cada uno de estos ejemplos los números no representan cantidad ni orden, se han utilizado combinaciones de números para informar. Es a través de estas situaciones simples que los niños construirán sus ideas previas sobre la numeración.
5.4 Concepto de número
¿Qué es el número?
El número es el símbolo matemático por excelencia y éste no se construye en su totalidad durante los primeros años en la educación infantil. El primer uso que hacen los niños del número es para cuantificar una serie de objetos o de hechos relacionados con sus acciones, por ejemplo, la cantidad de dulces o bolitas que tienen en un bolsillo. Por lo general, lo que hacen es recitar la serie numérica atribuyendo una palabra número a cada objeto o acción, pero sin tener sentido de la cantidad.
¿Qué implica la numeración?
La numeración implica fundamentalmente:
• Saber los números (no conceptualmente, sino verbalmente), se repiten una y otra vez con distintas presentaciones (aspecto cardinal).
• Reconocer la cantidad de las cosas en términos globales; por ejemplo: nada, muchos, pocos (uso de cuantificadores).
• Diferenciar el lugar que ocupa un objeto dentro de una serie; por ejemplo, en un estante de libros el niño puede pedir el que está en el primer lugar o al final (aspecto ordinal).
• Para identificar, por ejemplo, el número de la casa, número de hermanos, el dinero para comprar dulces, el teléfono.
• Para medir (peso, capacidad, tiempo y longitud);
• Para repartir, por ejemplo, ¿una torta mediana nos alcanza para que todos los niños del grupo puedan comer?
¿Por qué se necesitan distintos materiales?
Los alumnos utilizan los números permanentemente a través de experiencias de la vida cotidiana, integradas en su contexto y que dan sentido a su aprendizaje. Es importante, por tanto, disponer de variedad de materiales como, por ejemplo, dados, dominós, cartas, con el propósito de clasificar, ordenar, etc. Éstos podrán servir de base para contar, además facilitar la comprensión del concepto de número en su aspecto cardinal (percibir el número como cantidad) y en su aspecto ordinal, al compararlos y ordenarlos físicamente.
¿Cómo trabajar la numeración?
Para trabajar la numeración se sugiere comenzar con experiencias de tipo oral, las que pueden realizarse en forma individual o en pequeños grupos. El conteo es vital en el proceso de construcción del concepto de número y los alumnos la pueden utilizar para investigar aspectos cuantitativos de elementos que se encuentran en su entorno. Para aprender la secuencia numérica, se puede realizar la siguiente experiencia: contar ellos el número de mesas que tiene el salón, la cantidad de sillas en cada mesa, la cantidad de sillas y mesas que habría que integrar si llegaran cinco compañeros, el tiempo que tardan, por ejemplo, ordenar sus materiales, colgar la mochila, guardar sus libros, colocarse el delantal, jugar al escondite contando hasta 10, cantar canciones donde van apareciendo los números sucesivamente ("un elefante se balanceaba ..."), canciones; juegos como "Corre, corre la patita...", para ver quién empieza una actividad, o bien otras como:
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
"En un café, se rifa un pez, al que le toca el número 10, 1,2,3,4,5,6,7,8,9 y 10, En un café, se rifa un gato, al que le toque el número cuatro, 1,2,3,4.
¿En dónde están los números?
Los números están en todas partes, pues dan información y se recibe, transmiten diversos mensajes de acuerdo con el contexto al cual hacen referencia; por ejemplo, el significado del número 13 es diferente de acuerdo con la situación a que se haga referencia. Puede significar: el número del colectivo para regresar a casa, el número del anexo del teléfono, los $ 13 pesos que faltan para el pasaje, las 13 fotos del último paseo, etc. Se puede señalar que en el número trece hay 1 decena y 3 unidades, que el 12 es anterior al 13 y el 14 es posterior, que es número non, etc.
5.5 El concepto de número a través de materiales concretos
¿Por qué son importantes los materiales concretos?
Los materiales concretos son muy importantes para la asimilación del concepto de número. De ahí, que sea necesario disponer en el salón de actividades que utilicen materiales continuos y discontinuos.
• Materiales continuos: aquellos materiales no divisibles en elementos, por ejemplo: el agua, la arena, arroz, plastilina, barro, peso, etc., pero que pueden trasvasijarse de un recipiente a otro: el trabajo con estos materiales favorece la consolidación de la idea de cantidad y la asimilación de su conservación.
• Materiales discontinuos: están formados por unidades singulares, por ejemplo: palillos, lápices, pelotas, conchitas, piedras, camiones, etc., y se relacionan más con el trabajo de los números y las correspondencias.
¿Por qué es necesario trabajar el concepto de número a través de la actividad lúdica?
Para comprender las matemáticas con base en la realidad, es decir, enmarcarla en el entorno en que se vive y actuar sobre él. Los nuevos enfoques de la enseñanza de las matemáticas pretenden potenciar este carácter funcional.
¿Por qué razón los juegos cobran un importante rol?
Los juegos son clave debido a que:
• El juego está vinculado a la vida de los niños, su vida es jugar, por lo tanto, le da un sentido fundamental.
• Generalmente los juegos poseen elementos matemáticos, no sólo porque se cuantifica la realidad, sino también por la posición que ocupan los elementos en el espacio.
• El juego es una excelente estrategia para aprender, pues ayuda y motiva a al niño a pensar
• Presta atención a la diversidad, todos los niños se integran al juego de acuerdo con sus intereses, necesidades y ritmos particulares.
• El juego abre permanentemente posibilidades para la imaginación, el gozo, la creatividad y la libertad.
• Todos los niños, sin excepción, saben jugar.
¿Cuáles serían algunos juegos que favorecen el concepto de número?
Algunos juegos que favorecen el concepto de número en sus aspectos cardinales y ordinales:
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
Juegos de competencia:
a) Cartas (naipes) de números del 1 al 10. Dos jugadores. Se reparten las cartas entre dos jugadores, las cartas se dejan boca abajo. Dan la vuelta una a una del montón, la comparan y el que tiene la mayor se lleva las dos. Así con todas. Gana el que ha conseguido más cartas.



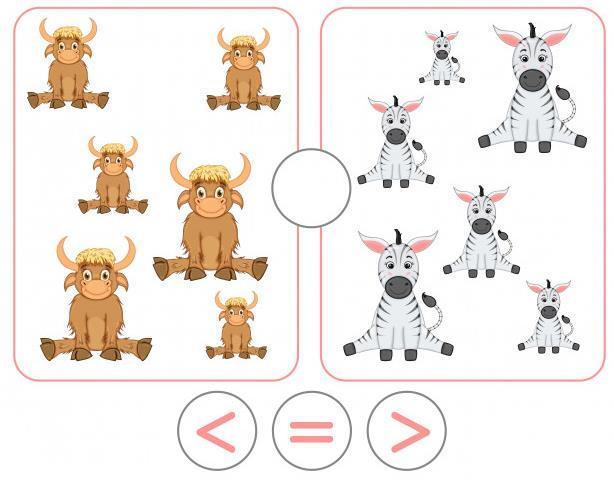
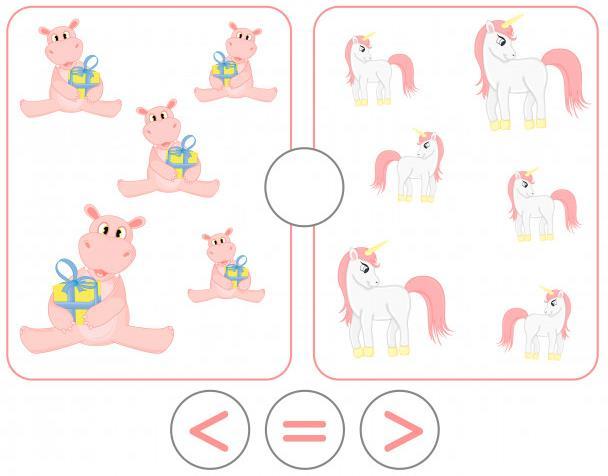
Actividad # 11 Comparación de números
Instrucciones. Elige el signo correcto en cada tarjeta y ponlo en el círculo. Gana quien vaya llenando las tarjetas lo más rápido posible.




b) Adivinar un número: se trata de descubrir el número que ha pensado o escrito un niño. Los demás dirán uno, sí aciertan, se les dirá sí; si no aciertan, se les darán las pistas sobre si es mayor o menor.

c) Elaborar una caja de lógica matemática: puede ser confeccionada con la familia. Consiste en una caja con diferentes divisiones y variedad de materiales que permitan a los niños trabajar el número y la serie numérica, el espacio (geometría), medidas, magnitudes, etc.





d) Los materiales que la integran pueden ser los siguientes: cartas pequeñas del 1 al 10, palos de diferentes tamaño y grosor, plastilina, cintas de diferentes colores y largos, botones diferentes formas, tamaño y colores, una cinta para medir, semillas variadas, monedas de diferentes valores y tamaños, recipientes de diferentes tamaños, etc. El material debe permitir trabajar al interior y al exterior del salón, en conexión con situaciones concretas, reales que surgen de su vida cotidiana. El educador puede salir a un parque para investigar el entorno y decidir con los niños qué elementos se pueden ocupar, por ejemplo, para saber cuál de los tallos de las plantas es más largo, qué elementos se pueden utilizar para clasificar las hojas recogidas, la cantidad que agua que necesitan algunas plantas de acuerdo con el macetero donde estén, etc.

MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
¿Con qué se continúa una vez que se ha trabajado la numeración en forma oral?
Una vez que se han trabajado experiencias de numeración de forma oral, se pueden iniciar experiencias en cifras de acuerdo a un ordenamiento lógico. Los niños conocen los números y los diferencian perfectamente de las letras; por tanto, es necesario crear situaciones que les permita usarlos, tanto para representar como para interpretar la realidad.
¿Cómo comenzar el contacto con los números escritos?
Los números sirven para cuantificar, medir el tiempo, la estatura, el peso, para ordenar, etc., y permiten el acercamiento paulatino al mundo de los números escritos, por tanto, es importante integrar en el salón diferentes elementos, como: el calendario, la recta numérica, los números de la lista, fecha, mes y año, escritos en el pizarrón, el friso, etc. Estos materiales han de estar ubicados en un lugar visible y accesible para que sirvan de consulta y manipulación.
¿Cómo qué tipo de materiales se sugieren?
Los materiales que se sugieren son los siguientes:
• Una recta numérica colocada o pintada en la pared a la altura de los niños, con tantas divisiones y números como niños haya en el salón. La separación entre cada número puede ser de 10 cm y el tamaño de los números de 2 x 6 cm.
• Una recta numérica pintada en el suelo, para trabajar actividades que requieran desplazamientos.
• Huellas de pisadas pegadas en el piso, con el número escrito en el centro de la huella en forma correlativa.
• Un formato de calendario en blanco para ir construyéndolo cada día.
• Lista por orden alfabético con el número de orden delante.
• Números escritos en cartulina con una cinta para realizar juegos.
¿Cómo se podría jugar con estos materiales?
Los orientados se ubican en el centro del y se les va dando instrucciones simples como: quienes tengan el número cuatro, párense en el círculo rojo, los que tengan el número tres en el círculo amarillo... o bien, mostrarles cifras simples (12) para que ellos formen el número, o bien que se ordenen en forma correlativa, etc.
5.6 Orientación en el espacio y geometría
¿Por qué preocuparse del conocimiento espacial en los primeros años?
El conocimiento del espacio requiere ser trabajado en forma intencional en los primeros años, pues permite su familiarización con su espacio más próximo y vital, para así adaptarse al mundo tridimensional, y comprender las distintas formas y expresiones espaciales que presenta su entorno más cercano.
¿Cómo se adquiere la noción del espacio?
Desde los primeros meses de vida se van elaborando poco a poco la noción de espacio, producto de la actividad constructiva que el propio niño ejerce en su espacio más próximo como, por ejemplo: su cuna, sus juguetes, el biberón, etc., y con las relaciones espaciales entre los objetos y las personas; todo esto le permite estructurar el espacio en forma espontánea desde que nace.
¿Entonces por qué es necesario enseñarlo?
Estas nociones van sufriendo cambios a medida que se van adquiriendo otras habilidades como las motoras: el desplazamiento permite establecer otro tipo de
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
relación entre él y los espacios; más adelante será capaz transformar los espacios (cambiar elementos de un lugar a otro, esconder objetos, ordenar materiales) y, posteriormente, representar los espacios, como dibujar un garabato y decir que es su perro jugando en el patio. Por tanto, se le debe promover y proporcionar las herramientas necesarias para dominar sus relaciones con el espacio, representarlo, describirlo, comunicar las posiciones de los objetos y de las personas, así como su desplazamiento.
¿Qué se necesita para lograr esto?
Para que esto suceda es necesario manejar un lenguaje que permita comunicar posiciones, describir e identificar objetos, indicar oralmente movimientos, etc. Las relaciones espaciales consideran las relaciones en el objeto, entre los objetos y los desplazamientos. Las relaciones espaciales en los desplazamientos permiten comprender que los movimientos y los objetos provocan modificaciones en las relaciones espaciales.
¿Cuáles serían los desafíos para el educador?
Esto trae como consecuencia los siguientes desafíos para el educador:
• Crear situaciones de aprendizaje que permitan una acción directa sobre los objetos y situaciones, así como la reflexión de estas
• La búsqueda permanente de situaciones problemáticas de la vida cotidiana para encontrar soluciones que permitan el dominio del espacio circundante, pasar del espacio concreto al de las representaciones.
¿Cómo utilizar el espacio con los cuerpos geométricos?
Respecto a los cuerpos geométricos, se han de incluir tanto las relaciones espaciales como el reconocimiento de las nociones, las propiedades y los atributos geométricos en los cuerpos y las figuras geométricas en dos dimensiones, en objetos, dibujos y construcciones. Para el trabajo con los cuerpos geométricos y figuras, se sugiere manipular diferentes cuerpos de distintos tamaños (grande, pequeño), grosor, observarlas, experimentar con ellas; hasta llegar a la descripción.
¿Por qué distinguir los cuerpos de las figuras geométricas al trabajar?
Al trabajar con las figuras geométricas es importante tener presente la diferencia que existe entre cuerpos y figuras. Los cuerpos ocupan un lugar en el espacio, en cambio las figuras son representaciones que se plasman en un plano, por ejemplo, un dibujo en un papel.
¿Qué comprende las relaciones espaciales en el objeto?
Las relaciones espaciales en el objeto, comprende el reconocimiento de algunos atributos geométricos como: caras, vértices, lados, rectas, curvas, en los cuerpos y en las figuras. Esto permite percibir la posición que adquieren los objetos en el espacio y su relación con otros objetos y con el sujeto. Es importante ofrecer experiencias para darse cuenta que un mismo objeto no se ve de igual forma cuando está en distintas posiciones.
¿Cuáles serían algunas experiencias de aprendizaje?
Algunas experiencias de aprendizaje serían:
• Conociendo y recorriendo diferentes caminos: dibujar en el patio líneas rectas, curvas, en zigzag para recorrerlas tomando el tiempo (reloj de arena) y determinar en cuánto tiempo se demora uno al recorrer cada una. Comparar. Mencionar que un trozo de una recta se llama segmento.
• Curvas: buscar en el medio circundante o naturaleza líneas curvas (arco iris), los arcos en las construcciones (conocer y reconocer diferentes construcciones,
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
dibujarlas y compararlas entre sí y con diferentes construcciones a lo largo de la historia; por ejemplo, los castillos, iglesias, casas, edificios, etc.). Al trabajar sobre las líneas curvas plantear que aquellas que están cerradas (como las ruedas de la bicicleta) distan lo mismo desde todos sus puntos al centro y esto se llama circunferencia.
• Paralelas: buscar en el espacio circundante cómo se relacionan las rectas, aquellas que nunca se tocan, por ejemplo, las líneas del tren (rectas paralelas), investigar dónde se pueden encontrar (vías del tren, mapa de las calles principales donde se encuentran su casa y el colegio), recorrido que hacen los autos en una carretera, etc.
• Figuras simétricas: aquellas que tienen una mitad igual que la otra y cuyas líneas, por donde se doblan para que coincidan, se llaman eje de simetría. Se recomienda buscar alrededor figuras y cosas simétricas; por ejemplo: el cuerpo (la parte derecha del cuerpo es simétrica con relación a la parte izquierda).
Plantear preguntas como: ¿Una hoja de árbol es simétrica? ¿En qué se parece un libro a una pelota? Permitir el descubrimiento de los cuerpos geométricos en tres dimensiones (largo, ancho y alto), en cay compararlo con las figuras geométricas en dos dimensiones.
• Investigar cómo se construyeron los monumentos: de la antigüedad (templos, pirámides, castillos) y modernos (pirámide de vidrio, llamada Pirámide del Louvre). Introducir el concepto de esferas observando, por ejemplo, catedrales, la tierra, etc.
• Construir a partir de conos (de hilo) diferentes objetos como: sombreros, personajes para después elaborar sus propias historias.
• ¿Sirve la geometría para pintar?: visitar museos, iglesias que posean en sus ventanas mosaicos decorativos que estén llenos de rectas y curvas; murales (arabescos); alfombras, etc.
• La geometría en la naturaleza: buscar y seleccionar piedras de diferentes tamaños, formas y colores (piedras preciosas); tirar piedras en un lago (al caer se forman circunferencias); observarlas como material de construcción, en la casa, la escuela, la calle.
• Tierra y los planetas: utilizar un microscopio y observar pequeñas partículas, describir, dibujar y buscar su relación con las figuras geométricas, etc.
5.7 Orientación temporal
¿Cómo formar las nociones de tiempo?
Las nociones de tiempo son básicas para las relaciones lógico-matemáticas y de cuantificación en diversas situaciones cotidianas, por lo tanto, es necesario trabajar las secuencias: antes-después; mañana y tarde; día y noche; ayer hoy y mañana; semanas, meses; estaciones del año; la duración: más, menos; y velocidad: rápido, lento.
¿Cuáles serían algunas de las actividades a realizar en relación con la orientación temporal?
Entre las actividades para la orientación temporal se sugieren:
• Elaborar su historia personal: con la cooperación de la familia, hacer un álbum con recortes, dibujos, recuerdos, etc., de los diferentes momentos de su vida, peguen fotos y los padres escriban sus impresiones y las de sus hijos.
• Investigar algunas noticias: de impacto y hacer una secuencia a través de fotos. Se sugiere que los propios niños anoten la fecha de los acontecimientos.
• Anotar las fechas más importantes: cumpleaños, santos, día de la amistad, de los abuelos, etc.
• Ordenar hechos y situaciones en el tiempo: mañana, tarde-noche.
5.8 Las medidas y sus magnitudes
¿Por qué son importantes las medidas?
A diario las personas se ven obligadas a realizar diversos tipos de mediciones para resolver situaciones de la vida cotidiana; por ejemplo, calcular cuántos pliegos de cartulina se necesitan para hacer una decoración en la sala, pesarse para saber cuántos kilos han subido después de las vacaciones, calcular la cantidad de cintas que se necesitan para envolver 10 regalos, etc.
¿Qué tipo de medidas se usaban en la antigüedad?
En épocas pasadas las personas utilizaban medidas antropométricas (uso partes de su cuerpo), el brazo, la mano, el codo, los pies. Otros objetos como las ramas y piedras. Para medir la capacidad utilizaban vasijas de formas y tamaños diferentes. Para el peso confeccionaron balanzas y pesas de distintos materiales. A partir del año 1791, en Francia, se acuerda el uso de un sistema de medición métrico decimal. (Sistema Métrico: su base es el metro y decimal, pues sigue el principio de la numeración de base 10). Pero ¿qué significa en términos cotidianos medir? Esto implica calcular cuántas veces entra la unidad elegida en el objeto que se desea medir.
¿Cómo cuantificar en el aula?
Para cuantificar una situación de la realidad se tiene dos posibilidades: contar y medir. Si desea contar por ejemplo la cantidad de puzles, cuentos, juegos que hay en la sala, se contarán (cantidad discontinua); la unidad que se utiliza es el número. Si se desea saber cuántos litros de jugo se necesitan para 30 niños o el recorrido que deberá hacerse para salir al museo en un determinado tiempo, hace referencia a las cantidades continuas, pues estas situaciones requieren ser medidas.
¿Cómo trabajar la medida con los niños?
Los aprendizajes esperados de la medida se trabajan en forma intencionada, pues se sabe que desde muy pequeños los alumnos tienen experiencias con situaciones de medida de manera cotidiana. Por ejemplo: cuando lo llevaban al pediatra lo pesan y miden, sabe cuándo es la hora de comer y dormir. Es a través, de la interacción con el medio como se van construyendo estas nociones, pero a pesar de ello no es suficiente, se requiere de un trabajo intencionado de parte del educador. Se pueden plantear diversas situaciones problemas que surgen de la vida cotidiana para que los niños experimenten y apliquen. Por ejemplo: plantear preguntas dentro de un contexto temático (proyectos): ¿cuántas cartulinas se necesitarán para pegar los trabajos realizados?
¿Cuántas cajas se necesitarán para guardar los libros de cuentos?, etc. Se debe dar oportunidad para resolver sus problemas, plantar su hipótesis y verificarla, explorarla, observar, experimentar, etc.
¿Con qué se mide?
No todos los objetos y elementos se cuantifican de la misma manera. En la vida cotidiana hay situaciones que, al no poder ser contadas, necesitan para su cuantificación del uso de unidades específicas que permitan medirlas. Estas unidades pueden ser: el kilo, minutos, litro, metro. A continuación, se presentan algunas experiencias que lo ejemplifican:
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
• Longitud: la unidad de medida es el metro. Se sugiere utilizar diferentesmetros: metro de madera, plegadizo que utilizan los carpinteros, el que utilizan las modistas, cinta métrica de metal (automática), regla de plástico. Las situaciones de aprendizaje han de motivar la observación y la experimentación con diferentes tipos de metros; estimen la longitud y su verificación, ordenen objetos según su longitud, se midan (utilizando medidas con el cuerpo, pies, manos, dedos, etc.) y lo comparen con otros niños y, posteriormente, lo registre (yo mido 8 pies y tres dedos).
• Peso: la unidad es el kilo. El instrumento que se utiliza para medir la masa de un cuerpo es la balanza. Contar con diferentes tipos de balanzas y sus respectivos usos (electrónicas, farmacia, frutería, joyería, etc.). Se sugiere iniciar estas experiencias pesando su propio cuerpo: manos, pies, espalda, observen y experimenten con diferentes balanzas, exploren las balanzas de platillos (equilibrio y desequilibrio), comparen objetos que tengan: igual forma y diferente peso, diferente forma e igual peso.
• Capacidad: la unidad de medida es el litro. Matemáticamente hablando la capacidad consiste en la facultad de los envases huecos para alojar algo, sea líquido o sólido continuo, por ejemplo, arena. Por lo tanto, la capacidad de un recipiente es el volumen de líquido o del sólido que puede contenerlo. El instrumento que se utiliza para medir la capacidad de un recipiente es el vaso graduado; para ello se pueden comprar diferentes vasos que traen sus medidas indicadas, así como vasos de probetas de laboratorio. Sugerir actividades con un problema que surja en el salón para experimentar con diferentes recipientes (tamaño, forma), estimar las capacidades (hipótesis) y verificar, etc.
• Tiempo: el instrumento que se utiliza para medir el tiempo es el reloj. Se mide a través de las horas, minutos y segundos. Poner actividades donde se pueda comparar la duración de varias situaciones, tiempos para jugar, ordenar, comer, leer cuentos, etc., estimar la duración de las canciones, bailes, los calendarios, almanaques, el ordenar la jornada diaria, la duración de algunos juegos, ubicar las manecillas del reloj durante el tiempo que están en casa (ver TV, comer, jugar, lavarse y dormir, horas de descanso), etc.
5.9 Resolución de problemas
¿Cómo entender un problema?
El problema se ha de entender como una situación que se plantea al alumno sin que conozcan las estrategias para resolverlo, o bien como un conjunto de datos o informaciones de su entorno para que determinen el tipo de preguntas que pueden responder, o los datos que necesitan para responder a tales preguntas, o los diferentes caminos que se pueden seguir para llegar a la meta, o las posibles interpretaciones que se les pueden dar a los resultados obtenidos, a través, de la aplicación de las operaciones matemáticas, como la adición y la sustracción. Lo importante es encontrar diferentes alternativas para resolver una situación dada, y comprender que ante un mismo problema se pueden entregar varias soluciones
¿Para qué se trabajan los problemas?
Uno de los propósitos de trabajar los problemas es ejercitar habilidades de pensamiento y no sólo el resultado final. Para lograrlo hay que dar oportunidades a los alumnos de analizar la situación, se imaginen las cantidades, aprendan a explicar lo que han pensado y, sí hace falta, realicen el cálculo. En suma, es necesario plantear problemas abiertos donde se puedan ofrecer más de una solución, fomente una diversidad de respuestas, aquellas que verdaderamente hacen pensar.
¿Dónde enfatizar en las operaciones de adición y sustracción?
En las operaciones de adición y sustracción es importante enfatizar su significado, en vez de la operatoria. Para ello, se pueden utilizar situaciones de la vida cotidiana significativas, como las siguientes:
• Describir situaciones en las que se agrega o quitan elementos de un conjunto dado y relacionarlas con las operaciones matemáticas de adición y sustracción.
• Dada cierta información determinar qué preguntas pueden responder; qué datos se necesitan para responder una pregunta; qué información se puede obtener a partir de una operación de adición o sustracción.
• Resolver problemas matemáticos simples involucrando las operaciones de adición y sustracción.

¿Cómo registrar?
Hay dos distinciones para hacer el registro, esto es, en las cantidades discontinuas: se cuenta y se utilizan los números y en las cantidades continuas se mide, por tanto, se requiere seleccionar una unidad y contar las veces en que estaría incluida en el objeto a medir. Esto implica que el registro debe indicar un número y una unidad. Por ejemplo: una botella de dos litros tiene que ser llenada con jugo utilizando para ello un vaso chico (100cc) y otro grande (250 cc). Frente a esta situación los alumnos pueden:
• Registrar la cantidad de vasos que se necesitan para llenar la botella utilizando el número (6 vasos) pero sin especificar la unidad de medida (vaso de 100 cc o 250 cc).
• Representar (dibujar) la cantidad de vasos (vaso de 100 cc o 250 cc) y su tamaño para indicar las veces en que se usó cada uno de ellos.
• Representar la cantidad de vasos y el tamaño.
• Utilizar el número para representar la cantidad y del dibujo del vaso para indicar la unidad seleccionada.
¿Estas sugerencias son válidas para la atención de las DAM?
Justifica tu respuesta
Actividad # 59 Los cohetes
Instrucciones. Realiza las operaciones de cada cohete con la mayor velocidad posible.


Apéndice # 1. Vocabulario matemático básico (Frances Schoning, 1990:176)
abajo demasiado longitud raro adelante dentro lleno rebaño algo derecho más recto alguno (a) desde más abajo reducir al lado después más pequeño respuesta alrededor detrás más que resta alto diferencia medio restar a medio camino disminuir mejor resto ancho dividir menor segundo anchura dos menos semejante añadir dos veces mitad siempre a partir de dualidad muchedumbre simple arriba elevado mucho sin atrás encima multiplicar sobre bajo enfrente de muy solamente banda enorme nada suma bastante entero ninguno suprimir bien entre no sus cada espalda nuevo tal vez cada uno esquina nulo tamaño cada vez menos estrecho número tanto cambio exacto par (es) tarde camino fin parada tiempo casi final pareja todavía central fondo parte todo centro fracaso pequeño toma (lo) cerca gemela pesado tropa cerca de gemelo peso único cerrado grande poco unidad cerrar grosor por debajo último cima grueso por detrás uno cociente grupo por encima uno y otro columna hora por último vacío comparar hueco precio varios correcto igual primero venta corto izquierda probablemente verdad cuando joven producto verificar cumbre junto profundo vez curvo justo programar viejo de lado progresivo zurdo debajo largo próximo delante lejos (de) quinto delgadez lento quitar
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
Apéndice # 2. Nombres de las figuras geométricas

3 lados = Triángulo
4 lados = Cuadrilátero
5 lados= Pentágono
6 lados = Hexágono
7 lados= Heptágono
8 lados= Octágono
9 lados= Nonágono o Eneágono
10 lados= Decágono
11 lados= Endecágono o Undecágono
12 lados= Dodecágono
13 lados= Tridecágono
14 lados = Cuatorsiavilono
15 lados= Pentadecágono
20 lados= Icoságono
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte
Glosario
Acalculia
Término acuñado por Henschen, para designar un trastorno adquirido de la habilidad de cálculo. En neuropsicología, la acalculia engloba una serie de trastornos que van desde la inhabilidad para reconocer un número hasta la dificultad para efectuar operaciones aritméticas. Implica hablar de una serie de habilidades cognoscitivas. Su habilidad está influida por factores socioculturales, con lo cual la habilidad propiamente dicha se encuentra en líneas generales en toda la población con unos niveles de eficiencia muy variables, lo que provoca, sin duda, dificultades a la hora de poder baremar y validar tareas dirigidas a su evaluación neuropsicológica.
Acalculia (tipos)
Aunque la clasificación puede variar según el autor, se reconocen los siguientes tipos de acalculia:
a) Alexia y agrafía numérica. Algunos autores la denominan Acalculia afásica, pero la afasia no es la condición necesaria ni suficiente para la aparición de este déficit. Básicamente habría tres tipos de alexia agrafía numérica que se pueden combinar entre sí.
1. Incapacidad de leer- escribir dígitos individuales.
2. Incapacidad de leer-escribir correctamente cifras de varios dígitos, asignando a cada uno su valor de acuerdo con el lugar que ocupan en la cifra, según las normas del sistema arabigodecimal (errores gramaticales 50 por 500, secuenciales como 3.004 por 4.003)
3. 3. Incapacidad de leer-escribir comprender signos aritméticos (x,+,-, <, >, etc.)
b) Acalculia espacial. Consiste en la incorrecta alineación de los números en la cifra, en las fases iniciales del proceso computacional, bien en la inadecuada colocación en el espacio de los resultados parciales de las multiplicaciones por más de un dígito, de los restos de las divisiones, etc.
Los déficits asociados a este tipo son alteraciones visoconstructivas, confusión direccional, trastornos óculomotores, agnosia espacial unilateral y global, apraxia del vestido y deterioro cognitivo global.
c) Anaritmética. De acuerdo con Hecaen, se excluye la alexia-agrafia numérica y la Acalculia espacial, pero se asocian otros déficits de tipo neurológico y neuropsicológico como afasia, alteración visoconstructiva, alexia verbal, déficit cognitivo global, confusión direccional, déficit visual, trastornos óculomotores y déficit somatosensitivos. Se describen casos con incapacidad selectiva para recordar valores tabulados de operaciones aritméticas simples, pero conservando el concepto de la operación matemática concreta, casos con déficit selectivos de determinadas operaciones matemáticas, con conservación de otras y casos con desproporcionada alteración en funciones que se les llama “ejecutivas” en el cálculo (como llevar un número y sumar el número llevado), por un problema atencional al ser estas tareas duales, problema en secuenciación de operaciones matemáticas simples en el contexto de una operación compleja en el que intervendría la memoria de trabajo con la capacidad de planificación.
Algoritmo
En matemáticas lógica, un algoritmoes un conjunto prescrito de instrucciones o reglas bien definidas, ordenadas y finitas que permite realizar una actividad mediante pasos sucesivos que no generen dudas a quien deba realizar dicha actividad. Dados un estado inicial y una entrada, siguiendo los pasos sucesivos se
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
llega a un estado final y se obtiene una solución. Es un conjunto ordenado y finito de operaciones que permite hallar la solución de un problema. Método y notación en las distintas fórmulas del cálculo. Esto significa que el algoritmo constituye un método para resolver un problema mediante una secuencia de pasos a seguir. Dicha secuencia puede ser expresada en forma de diagrama de flujo con el fin de seguirlo de una forma más sencilla.
Discalculia
• Trastorno que proviene de dificultades específicas en el aprendizaje del cálculo, con independencia del nivel mental, de los procederes pedagógicos, de la asiduidad escolar y de trastornos afectivos.
• Según madame Borell, la discalculia aparece frecuentemente unida a trastornos de lenguaje. Otros autores encuentran tres tipos distintos de discalculia:
a) Dificultad para el aprendizaje de los signos numéricos, que suele presentarse asociado a problemas de lenguajes oral y escrito.
b) Dificultad para adquirir los automatismos necesarios para realizar las operaciones aritméticas, que también acompaña a alteraciones de lenguaje;
c) Dificultad para ordenar los números, de acuerdo con una estructura espacial. Se asocia con desorientación espaciotemporal
• Se pueden establecer dos grupos con características diferenciales: a) Verbal, que determina la dificultad de simbolización (aprendizaje de los símbolos matemáticos) y su relación con la noción de cantidad; b) Espacial, que determina la dificultad de ordenación de cifras y colocación de cantidades.
Discalculia (tipos)
• Discalculia primaria. Trastorno específico y exclusivo del cálculo, unido a lesión cerebral.
• Discalculia secundaria. Mala utilización de símbolos numéricos y mala realización de operaciones, especialmente las inversas. Va asociada a otros trastornos como dificultades del lenguaje, desorientación espaciotemporal y baja capacidad de razonamiento.
• Disaritmética. Gran dificultad para comprender el mecanismo de la numeración, retener el vocabulario, concebir la idea de las cuatro operaciones básicas, contar mentalmente y utilizar sus adquisiciones en la resolución de problemas.
• Discalculia espacial. Dificultad para ordenar los números según una estructura espacial. Suele ir acompañada de apraxia constructiva y desorientación espacio temporal.
Áreas
de las matemáticas
• Aritmética. Se encarga de estudiar las estructuras numéricas elementales, así como las propiedades de las operaciones y los números en sí mismos en su concepto más profundo, construyendo lo que se conoce como teoría de números.
• Álgebra. Estudia las estructuras, las relaciones y las cantidades (en el caso del álgebra elemental). El álgebra elemental es la forma más básica del álgebra- A diferencia de la aritmética, en donde sólo se usan los números y sus operaciones aritméticas (como +, −, ×, ÷), en álgebra los números son representados por símbolos (usualmente a, b, c, x, y, z).
• Trigonometría. Es la subdivisión de las matemáticas que se encarga de calcular los elementos de los triángulos. Para esto se dedica a estudiar las relaciones entre los ángulos y los lados de los triángulos. El objetivo de la trigonometría es establecer las relaciones matemáticas entre las medidas de las longitudes de los segmentos que forman los lados de un triángulo con las medidas de las
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
amplitudes de sus ángulos, de manera que resulte posible calcular las unas mediante las otras.
• Geometría. Trata de estudiar unas idealizaciones del espacio en que vivimos, que son los puntos, las rectas y los planos, y otros elementos conceptuales derivados de ellos, como polígonos o poliedros, estudia las propiedades del espacio, que se emplean para representar con exactitud las figuras y los cuerpos geométricos.
• Estadística. Se ocupa de los métodos y procedimientos para recoger, clasificar, resumir, hallar regularidades y analizar los datos, siempre y cuando la variabilidad e incertidumbre sea una causa intrínseca de los mismos; así como de realizar inferencias a partir de ellos, con la finalidad de ayudar a la toma de decisiones y en su caso formular predicciones.
• Puede ser Descriptiva, es decir, sólo importa el conjunto de datos e Inferencial cuando se busca derivar conclusiones de un conjunto de datos más amplio.
• Cálculo diferencial e integral. Es una herramienta que surge en el siglo XVII para resolver algunos problemas de geometría y física. El problema de hallar una recta tangente a la gráfica de una función en un punto dado y la necesidad de explicar racionalmente los fenómenos de la astronomía o la relación entre distancia, tiempo, velocidad y aceleración, estimularon la invención y el desarrollo de los métodos del Cálculo. Mientras el Cálculo Diferencial busca descomponer los elementos, el Cálculo Integral va integrar los elementos que se encuentran aislados.
Cálculo aritmético
El cálculo aritmético es el que se realiza con números enteros o racionales; puede realizarse de cabeza (exacto, aproximado o estimado), por escrito o con la ayuda de materiales manipulativos como el ábaco o electrónicos como la calculadora. El cálculo estimado se realiza con datos que proceden de un juicio o valoración, suelen ser números redondos acabados en cero. El cálculo aproximado se realiza con datos que proceden de la medición, están condicionados por la inexactitud de los instrumentos de medida, lo que hace que a menudo números con cifras decimales, siendo un tipo de cálculo del que se puede conocer el margen de error.
Capacidad
Conjunto de recursos y aptitudes que tiene un individuo para desempeñar una determinada tarea. En este sentido, esta noción se vincula con la de educación, siendo esta última un proceso de incorporación de nuevas herramientas para desenvolverse en el mundo. El término capacidad también puede hacer referencia a posibilidades positivas de cualquier elemento. En general, cada individuo tiene variadas capacidades de la que no es plenamente consciente. Así, se enfrenta a distintas tareas que le propone su existencia sin reparar especialmente en los recursos que emplea. Esta circunstancia se debe al proceso mediante el cual se adquieren y utilizan estas aptitudes. En un comienzo, una persona puede ser incompetente para una determinada actividad y desconocer esta circunstancia; luego, puede comprender su falta de capacidad; el paso siguiente es adquiriry hacer uso de recursos de modo consciente; finalmente, la aptitud se torna inconsciente, esto es, la persona puede desempeñarse en una tarea sin poner atención a lo que hace. Un ejemplo claro puede ofrecerlo el deporte: un atleta utiliza técnicas sin pensar en ellas. Esto se debe a que ha alcanzado un nivel en el cual su capacidad se ha interiorizado profundamente. No obstante, no todas las capacidades del hombre son adquiridas. Muchas de ellas son innatas.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
Capacidades superiores
Son aquellas que se caracterizan por su alto grado de complejidad y sintetizan intencionalidades educativas. Son las que permiten desarrollar el pensamiento crítico, pensamiento creativo, resolución de problemas y toma de decisiones. Las capacidades superiores son interpretación, análisis, evaluación, inferencia, explicación, autorregulación, producción, construcción, síntesis, asociación, relajación, creación, diseño, investigación.
Coeficiente intelectual
El coeficiente intelectual, también conocido como cociente intelectual, es un número que resulta de la realización de una evaluación estandarizada para medir las habilidades cognitivas de una persona en relación con su grupo de edad. Este resultado se abrevia como CI o IQ, por el concepto inglés de intelligence quotient Como estándar, se considera que el CI medio en un grupo de edad es 100. Esto quiere decir que una persona con un CI de 110 está por sobre la media entre las personas de su edad. Lo más normal es que la desviación típica de los resultados sea de 15 o 16 puntos, ya que las pruebas se diseñan de tal forma que la distribución de los resultados sea aproximadamente una distribución normal. Se considera como sobresalientes a aquellos que se sitúan por encima del 98% de la gente.
Habilidad Matemática
Es aquella en que eres capaz de comprender conceptos, proponer y efectuar algoritmos y desarrollar aplicaciones a través de la resolución de problemas. En estas se consideran tres aspectos:
• En Aritmética, operaciones fundamentales (suma, resta, multiplicación, división, potenciación y radicación) con números enteros y racionales, cálculos de porcentajes, proporciones y promedios, series numéricas y comparación de cantidades.
• En Álgebra, operaciones fundamentales con literales, simplificaciones de expresiones algebraicas, simbolización de expresiones, operaciones con potencias y raíces, factorización, ecuaciones y funciones lineales y cuadráticas.
• En Geometría, perímetros y áreas de figuras geométricas, propiedades de los triángulos (principales teoremas), propiedades de rectas paralelas y perpendiculares y Teorema de Pitágoras.
Incapacidad
De acuerdo con la OMS es toda restricción o pérdida (causada por un defecto) de la capacidad para llevar a cabo una actividad del modo o en la medida que se consideran normales en un ser humano. Es la consecuencia de una anomalía en el funcionamiento del organismo que obstaculiza el normal desempeño de las actividades habituales de los individuos.
Inteligencia.
Existen muchas definiciones de inteligencia.
• La American Psychological Association la define como: “Los individuos difieren unos de otros en su habilidad de comprender ideas complejas, de adaptarse eficazmente al entorno, así como aprender de la experiencia, en encontrar varias formas de razonar y de superar obstáculos mediante la reflexión. A pesar de que estas diferencias individuales puedan ser sustanciales, éstas nunca son completamente consistentes: las características intelectuales de una persona variarán en diferentes ocasiones, en diferentes dominios, y con diferentes criterios. El concepto de "inteligencia" es una tentativa de aclarar y organizar este conjunto complejo de fenómenos”.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
• Una segunda definición de inteligencia viene del Mainstream Science on Intelligence", que fue firmada por 52 investigadores de la inteligencia en 1994: Una muy general capacidad mental que, entre otras cosas, implica la habilidad de razonar, planear, resolver problemas, pensar de manera abstracta, comprender ideas complejas, aprender rápidamente y aprender de la experiencia. No es un mero aprendizaje de los libros, una habilidad estrictamente académica, ni un talento para superar pruebas.
• La inteligencia para Howard Gardner es la capacidad para resolver problemas cotidianos, generar nuevos problemas para resolver y crear productos u ofrecer servicios valiosos dentro del propio ámbito cultural.
Lógica matemática
La Lógica estudia la forma del razonamiento. La Lógica Matemática es la disciplina que trata de métodos de razonamiento. En un nivel elemental, la Lógica proporciona reglas y técnicas para determinar si es o no valido un argumento dado. El razonamiento lógico se emplea en Matemáticas para demostrar teoremas, sin embargo, se usa en forma constante para realizar cualquier actividad en la vida.
Matemáticas
Ciencia que trata de la cantidad, sea en abstracto (matemáticas puras), sea con relación a objetos o fenómenos determinados (matemáticas mixtas o aplicadas).
La historia de la matemática se inicia con el descubrimiento que el hombre realiza en su propio cuerpo del primer módulo para medir y contar (codo, pie, brazo, etc.).
La noción de notación por posición, del valor relativo de las unidades según su posición se alcanzó en la India en el s. IX, junto con la de fijación de los signos actuales para las nueve primeras cifras y la invención del 0. Los momentos de actividad matemática se corresponden con las fases de invención o de renovación. Los pueblos orientales (caldeos y egipcios) descubrieron el número y sus notaciones.
En la Edad Media, los árabes, que se ponen en contacto con la vieja ciencia caldea, asiria, griega e hindú, son los representantes de la actividad matemática de los siglos medios y en el s. IX dan el paso decisivo hacia la generalización, es decir hacia la verdadera ciencia matemática al introducir el álgebra. Las matemáticas modernas no se limitan a la magnitud, el número y el espacio intuitivos; los elementos con los cuales razonan son estructuras lógicas.
El desarrollo de las matemáticas modernas proviene de la formalización y sistematización de la lógica. Cada teoría matemática parte de un sistema de axiomas o de definiciones primeras a los que se aplica el instrumental lógico para obtener nuevas verdades lógico-matemáticas.
Son la ciencia de las estructuras, es decir, un conjunto de relaciones abstractas que comprenden y permiten el estudio de los números, de las formas, del movimiento, del razonamiento lógico, del azar, de la posición, de la simetría o de la proximidad.
Estas estructuras pueden ser reales o imaginarias, visuales o mentales, estáticas o dinámicas, cualitativas o cuantitativas, útiles o sólo con un interés recreativo. Pueden tener su origen en el mundo que nos rodea, en las profundidades del espacio y del tiempo o provenir exclusivamente de la actividad de la mente humana.
Las matemáticas son la única ciencia no empírica, es decir, no dependen de demostraciones experimentales. Y se deben tomar en cuenta que sus áreas son interdependientes y su estructura es jerárquica.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte
Niveles lógicos del pensamiento
El concepto de niveles lógicos de aprendizaje y cambio fue formulado inicialmente por el antropólogo Gregory Bateson, identifica cuatro niveles básicos de aprendizaje y cambio que abarcan y organizan cada uno de los elementos del nivel situado por debajo de él, y ejercen un grado de impacto progresivamente creciente sobre el individuo, el organismo o el sistema. El término de “niveles lógicos” se refiere a la jerarquía de niveles de procesos (mentales) en el individuo o del grupo. La función de cada nivel consiste en sintetizar, organizar, dirigir, las interacciones en el nivel inmediatamente inferior. Cambiar algo en un nivel superior “irradiará” necesariamente hacia abajo, precipitando el cambio en los niveles inferiores. Sin embargo, cambiar algo en un nivel inferior no tiene por qué afectar necesariamente a los niveles superiores.
Niveles lógicos del pensamiento (clasificación)
Los diferentes niveles de pensamiento o estratos de la mente son, de forma ascendente:
• Espiritual que es el nivel de trascendencia, donde yo soy parte de algo más, de un sistema más vasto y donde estoy consciente que lo que haga o deje de hacer, afecta a todos los que me rodean, aun cuando ya no esté en este mundo.
• Identidad donde según el concepto que tengo de mí mismo voy a desarrollar una "misión" en mi vida y va a desarrollar mis creencias para poder lograrlo. Tiene que ver con el verbo ser.
• Creencias o valores, yo creo que soy o no soy capaz de lograr algo en mi vida y según esto voy a desarrollar, o no, mis capacidades. Tiene que ver con el verbo creer
• Capacidades, son mis aptitudes o la falta de ellas, y según esto yo me conduzco en mi contexto. Tiene que ver con el verbo poder.
• Conductas, es lo que hago o dejo de hacer y es cómo me conduzco en mi contexto. Tiene que ver con el verbo hacer.
• Medio ambiente, es mi contexto, y la manera en que éste me afecta.
Operadores aritméticos.
Los operadores aritméticos nos permiten, básicamente, hacer cualquier operación aritmética, que necesitemos (ejemplo: suma, resta, multiplicación, etc ). En la siguiente tabla se muestran los operadores de los que disponemos en C y su función asociada.
Operador Acción Ejemplo
Resta
Decremento
Razonamiento matemático
Sirve para medir habilidades para aplicar las matemáticas en situaciones nuevas y diferentes, esto es de gran importancia para el éxito en cualquier trabajo práctico. Las preguntas miden tu habilidad para procesar, analizar y utilizar información en la Aritmética, el Álgebra y la Geometría, es evidente que estas habilidades se relacionan también con el éxito en las materias que se estudian en el nivel universitario.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
Receptor matemático
Un receptor también es el conductor en el que la energía eléctrica produce un efecto energético diferente del efecto Joule, y que, en consecuencia, está dotado de fuerza contra electromotriz. Aparato utilizado para recibir señales eléctricas, telegráficas, telefónicas u ondas electromagnéticas. Todo elemento o dispositivo que realiza la recepción como, por ejemplo, el aparato que recoge las ondas del radiotransmisor. En las transmisiones hidráulicas, dispositivo sobre el que actúa el fluido, y que transforma la energía comunicada en un par que aplica a un árbol o eje de transmisión.
Símbolos básicos de comparación
Símbolo Palabras Ejemplos de uso
= Igual a 1 + 1 = 2
≠ No igual a 1 + 1 ≠ 1
> Mayor que 5 > 2
< Menor que 97 < Cuadro # 36 Símbolos básicos de comparación.
Bibliografía
• Aller, C. y Pérez, P. (1998). Cuentos de los primeros números. Sevilla: Quercus.
• Alonso Tapia, J. y otros. (1992). Leer, comprender y pensar. Nuevas estrategias y técnicas de evaluación. Madrid: MEC/CIDE.
• Alsina, C. y otros. (1996). Enseñar matemáticas. Barcelona: Grao.
• Andonegui, M. (2004). El desarrollo del pensamiento lógico. Caracas: procesos educativos.
• Ansari, D. y Karmiloff-Smith, A. (2002). “Atypical trajectories of number development: a neuroconstructivist perspective”. Trends in Cognitive Sciences 6 (12): 511–516
• APA (1995) DSM-IV. Manual diagnóstico y estadístico de los trastornos mentales. Barcelona: Masson.
• Ashman, A. F. y Conway, R. N. (1990). Estrategias cognoscitivas en educación especial. Madrid: Santillana.
• Ashman, A. y Conway, R. N. F. (1990). Estrategias cognitivas en E.E. Madrid: Santillana.
• Bandura, A. (1988). Pensamiento y acción. Fundamentos sociales. Barcelona: Martínez Roca.
• Barrody, A.J. (1988). El pensamiento matemático de los niños. Un marco evolutivo para maestros de Preescolar, Ciclo Inicial y Educación Especial. Madrid: Visor-MEC.
• Bell, A. (1987). “Diseño de la enseñanza diagnóstica en matemáticas”. En A. Álvarez (comp.), Psicología y educación. Realizaciones y tendencias actuales en la investigación y en la práctica. Madrid: Visor/MEC.
• Beltrán, J.; Santiuste, V. y otros. (1987). Psicología de la educación. Madrid: Eudema.
• Bermejo, V. (1990). El niño y la aritmética. Instrucción y construcción de las primeras nociones aritméticas. Barcelona: Paidós.
• Bermejo, V. (1993). “Perspectivas innovadoras en la enseñanza-aprendizaje de las matemáticas: investigación cognoscitiva y practica educativa”. En J. Beltrán, V. Bermejo, M. D. Genovard (eds.) Psicología de la instrucción I. Variables y procesos básicos. Madrid: Síntesis.
• Bermejo, V. (1996). “Cardinality development and counting”. Developmental Psychology, 32 (2), 263-268.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
• Bermejo, V. (1998). “Enseñar a comprender las matemáticas”. En J. Beltrán, V. Bermejo y C. Vence (eds.) Intervención psicopedagógica. Madrid: Pirámide.
• Bermejo, V. (2004). Cómo enseñar matemáticas para aprender mejor. Madrid: CCS.
• Bermejo, V. y Bermejo, M. P. (2004). Aprendiendo a contar. En Bermejo (coord.), Como enseñar matemáticas para aprender mejor (pp. 15-32). Madrid: CCS.
• Bermejo, V. y Lago, O. (1991). Aprendiendo a contar. Su relevancia en la comprensión y fundamentación de los primeros conceptos matemáticos Madrid: C.I.D.E.
• Bermejo, V. y Rodríguez, M.R. (1990). La operación de sumar. En V. Bermejo (dir.), El niño y la aritmética. Instrucción y construcción de las primeras nociones aritméticas (pp. 107-150). Barcelona: Paidós.
• Bermejo, V.; Lago, M. O., y Rodríguez, P. (1998). “Aprendizaje de la adición y sustracción. Secuenciación de los problemas verbales según su dificultad”. Revista de Psicología General y Aplicada, 51 (3-4), 533-552.
• Bermejo, V.; Lago, M.O., y Rodríguez, P. (1998). “Aprendizaje de la adición y sustracción. Secuenciación de los problemas verbales según su dificultad”. Revista de Psicología General y Aplicada, 51 (3-4), 533-552.
• Bermejo, V.; Morales, S. y García de Osuna, Y. (2004). “Supporting children's development of cardinality understanding”. Learning and Instruction, 14, 381398.
• Blanco, M. y Bermejo, V (2004). Dificultades de aprendizaje en matemáticas. En Bermejo (coord.), Cómo enseñar matemáticas para aprender mejor (pp. 215-238). Madrid: CCS.
• Blanco, M. y Bermejo, V (2004). Dificultades de aprendizaje en matemáticas. En Bermejo (coord.), Como enseñar matemáticas para aprender mejor (pp. 215-238). Madrid: CCS.
• Brissiau, D. (1993). El aprendizaje del cálculo. Madrid: Visor.
• Brown, J. S. y Burton, R. (1978). “Diagnostic models for procedural bugs in basic mathematic skis”. Cognitive Science, 2, 155-168.
• Bryant, B. R. y Rivera, D.P. (1997). “Educational assessment of mathematics skills and abilities”. Journal of learning disabilities, 30, 57-68.
• Bull, R. y Johnston, R.S. (1997). “Children´s arithmetical difficulties: contributions from processing speed, item identification y short-term memory”. Journal of Experimental Child Psychology, 65, 1-24.
• Carpenter, T.P. y Moser, J.M. (1983). The acquisition of addition and subtraction concepts. En R. Lesh y M. Landau (comps.), Acquisition of mathematics: Concepts and processes (pp. 7-14). Nueva York: Academic Press.
• Cascallana, M. T. (1988): Iniciación a la matemática. Materiales y recursos didácticos. Madrid: Santillana.
• Castro E. y otros (1987). Números y operaciones. Madrid: Síntesis
• Collins, A.; Brown, J. S. y Newman, S. (1989). “Cognitive apprenticeship: Teaching the craft of reading, writing and mathematics”. En L. B. Resnick (ed.), Knowing, learning and instruction. Hillsdale, Nueva Jersey: Lawrence Erlbaum Associates.
• Company Rico, J. y otros (1988). El aprendizaje del cálculo y la resolución de problemas. Currículo educativo. Alicante: Benissa.
• Corbalán, F. (1995). La matemática aplicada a la vida cotidiana. Barcelona: Grao
• De Corte, E. (1993). “La mejora de las habilidades de resolución de problemas matemáticos: hacia un modelo de intervención basado en la investigación”. En J. Beltrán, V. Bermejo, M. D. Prieto y D. Vence (eds.) Intervención psicopedagógica. Madrid: Pirámide.
• Deaño, M. (1994). “Dificultades selectivas de aprendizaje: Matemáticas”. En S. Molina (ed.). Bases psicopedagógicas de la Educación Especial. Alcoy: Marfil.
• Derry, S. J. (1989). “Strategy and expertice in solving Word problems”. En Ch. B. McCormic, G. M. Miller y M. Presslely (eds.), Cognitive strategy research: From basic research to educational applications. Nueva York; Springer-Verlag.
• Dickson, L. y Gibson, O. (1991). El aprendizaje de las matemáticas. Barcelona: Labor/MEC.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
• Dubrovsky, S. (2002). El valor de la teoría socio-histórica de Vigotski, para la comprensión de los problemas de aprendizaje escolar, En Dubrovsky, S. (comp.), Vigotski su proyección en el pensamiento actual. (pp 61-73). Buenos Aires: Novedades educativas.
• Enciclopedia de pedagogía práctica. (2004). Escuela para Maestros. Grupo Dasa: Colombia.
• Engelmann, S.; Carnine, D. y Steely, D. G. (1991). “Making Connetions in Mathematics”. Journal of Learning Disabilities, 24(5), 292-301.
• Fayol, M., Barrouillet, P. y Marinthe, C. (1998). “Predicting arithmetical achievement from neuro-psychological performance: A longitudinal study”. Cognition, 68, B63-B70.
• Fuson, K. C. (1992). Research on whole number addition and subtraction. En D. A Grouwns (Ed.,) Handbook of Research on Mathematics Teaching and Learning. A project of the National Council of Teachers of Mathematics (pp. 243276). Nueva York: McMillan Publishing Company.
• Fuson, K. C. y Briars, D. J. (1990). “Using a base-ten blocks learning/teaching approach for first and second-grade place-value and multidigit addition and subtraction”. Journal for Research in Mathematics Education, 21, 180-206.
• Fuson, K. C. (2000). Pre-K to Grade 2 Goals and Standards: Achieving 21st Century Mastery for All. Ponencia presentada en la Conference on Standards for Preschool and Kindergarten Mathematics Education, State University of New York at Buffalo. Extraído del sitio Web:
• Gallistel, C. R. y Gelman, R. (1992). “Preverbal and verbal counting and computation”. Cognition, 44, 43-74.
• Geary, D. C.; Hamson, C. O. y Hoard, M. K. (2000). “Numerical and arithmetical cognition: a longitudinal study of process and concept deficits in children with learning disability”. Journal of Experimental Child Psychology, 77, 236-263.
• Gelman, R. y Gallistel, C. R. (1978). The child´s understanding of number. Cambridge, Massachusetts: Harvard University Press.
• Giménez, J., y Girondo, L. (1993): Cálculo en la escuela. Barcelona: Grao.
• Ginsburg, H. P., Klein, A. y Starkey, P. (1998). The Development of Children's Mathematical Thinking: Connecting Research with Practice. En Handbook of Child Psychology, vol. 4, Child Psychology in Practice (404-476). Ed. John Wiley and Sons, Nueva York.
• Godino, J. D. y Batanero, C. (1996). Relaciones Dialécticas entre teoría, desarrollo y práctica en educación Matemáticas: Un meta-análisis de tres investigaciones. España: Departamento de Didáctica de las Matemáticas. Universidad de Granada.
• Gross, J. y Manzano, P. (2004). Necesidades educativas especiales en educación primaria. Una guía práctica. España: Morata.
• Guzmán, P. (1994). Metodología de la matemática. En J.L. Castillejo, J.L. y otros, El curriculum en la escuela infantil. Diseño, realización y control (pp. 241258). Madrid: Aula XXI-Santillana.
• Hernán, F. y Carrillo, E. (1988). Recursos en el aula matemática. Madrid: Síntesis.
• Hernández, F., y Soriano, E. (1999): Enseñanza y aprendizaje de las matemáticas en la Educación Primaria. Madrid: La Muralla.
• Jiménez, J. E. (1999). Psicología de las dificultades del aprendizaje. Madrid: Síntesis.
• Jordan, N.C.; Kaplan, D. y Hanich, L.B. (2002). “Achievement growth in children with learning difficulties in mathematics: Findings of a two-year longitudinal study”. Journal of Educational Psychology, 94 (3), 586–597.
• Kamii, C. K. (1995): Reinventando la aritmética. Madrid: Visor.
• Luceño, J. L. (1986): El número y las operaciones. Alcoy: Marfil.
• Macnab, D. S., y Cunmine, J. A. (1982): La enseñanza de las matemáticas de 11 a 16. Un enfoque centrado en la dificultad. Madrid: Aprendizaje Visor.
• Manso Luengo, A. J. (1996). Dificultades de aprendizaje: escritura, orto-grafía y cálculo. Madrid: Centro de Estudios Ramón Areces.
• Martínez Montero, J. (1991): Numeración y operaciones básicas en la Educación Primaria. Madrid. Escuela Española.
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
• Martínez Montero, J. (2000): Una nueva didáctica del cálculo para el siglo XXI. Barcelona: CISS-PRAXIS.
• Maza, C. (1989). Sumar y restar. Madrid: Visor.
• Maza, C. (1991). Enseñanza de la multiplicación y división. Madrid: Síntesis.
• Maza, C. (1991). Enseñanza de la suma y de la resta. Madrid: Síntesis.
• Mercer, C. D. (1998). Dificultades de aprendizaje. España: CEAC-
• Ministerio de Educación Y Ciencia (1991). Real Decreto 1333/91 de 6 de septiembre por el que se establece el currículo de la Educación Infantil. Boletín Oficial del Estado de 9 de septiembre.
• Ministerio de Educación y Ciencia (1992a). Resolución del 5 de marzo de 1992 por la que se regulan los proyectos curriculares para la Educación Infantil y se establecen orientaciones para la distribución de objetivos y contenidos para cada uno de los ciclos. Boletín Oficial del Estado del 23 de marzo.
• Ministerio de Educación Y Ciencia (1992b). Orden de 12 de noviembre de 1992 sobre evaluación en Educación Infantil. Boletín Oficial del Estado 280/92 de 21 de noviembre.
• Ministerio de Educación Y Ciencia (1992c). Cajas Rojas. Madrid, Servicio de Publicaciones del M.E.C.
• Miranda, A. Fortes, C. y Dolores Gil, M.: (1999): Dificultades de aprendizaje en matemáticas. Un enfoque evolutivo.
• Miranda, A., y otros (1998). Dificultades del aprendizaje de las matemáticas. Archidona: Aljibe.
• Ostad, S.A. (1999). “Developmental progression of subtraction strategies: A comparison of mathematically normal and mathematically disabled children”. European Journal of Special Needs Education, 14 (1), 21-36.
• Piaget, J. (1995). Seis estudios de psicología. Colombia: Labor.
• Porras, R., y García, I. (1995). Fichero autocorrectivo de cálculo y problemas. Madrid: EOS.
• Puig, L., y Cerda, F. (1988). Problemas aritméticos escolares. Madrid: Síntesis.
• Resnick, L. B. (1989). “Developing mathematical knowledge”. American Psychologist, 44, 162-169.
• Resnick, L. B. y Ford, W. W. (1990). La enseñanza de las matemáticas y sus fundamentos psicológicos. Paidos: Madrid.
• Resnick, L. B., y Ford, W. W. (1990): La enseñanza de las matemáticas y sus fundamentos psicológicos. Madrid: MEC-Paidós.
• Resnick, L.B. y Ford, W.W. (1991). La enseñanza de las matemáticas y sus fundamentos psicológicos. Barcelona: Paidós-MEC.
• Rivera, D. P. (1997). “Mathematics education and students with learning disabilities: introduction to special series”. Journal of learning disabilities. 30, 2, 2-19.
• Rogoff, B. (1993). Aprendices del pensamiento. El desarrollo cognitivo en el contexto social. Barcelona: Paidós.
• Schoning, F. (1990). Problemas de aprendizaje. México: Trillas.
• Siegler, R.S. (1988a). “Strategy choice procedures and the development of multiplication skill”. Journal of Experimental Psychology General, 117, 258-275.
• Stacey, K., y Groves, S. (1999): Resolver problemas: estrategias. Unidades para desarrollar el razonamiento matemático. Madrid: Narcea.
• Waterman, B. (1994). Assessing children for the presence of a disability. Nichcy news digest, 4 (1).
• Whimbey, A., Y Lochhead, J. (1993): Comprender y resolver problemas. Madrid: Visor
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
Sitios Web
• Cibeles L. Jean Piaget y su influencia en la pedagogía
https://www.academia.edu/27899851/JEAN_PIAGET_Y_SU_INFLUENCIA_EN _LA_PEDAGOG%C3%8DA
• Acertijos de matemáticas:
https://acertijos.elhuevodechocolate.com/de1a12/matematicas.html
• Disfruta las matemáticas: https://www.disfrutalasmatematicas.com/
• Eduteka: https://www.eduteka.org/CapacidadesMentales.php
• Frases célebres: http://www.frasescelebresde.com/HABILIDAD-YDESTREZA/1/
• Las nuevas capacidades mentales en adolescentes.
https://feandalucia.ccoo.es/docu/p5sd5092.pdf
• Matemáticas en educación infantil y primaria
https://www.infantilyprimaria.com/mate.html
• Caalmoco. https://caalmoco.wordpress.com/2014/06/23/desarrollo-delpensamiento-logico-matematico-segun-piaget/
• Sabidurías.com
https://www.sabidurias.com/tags/destreza/es/1474
• Scribd.com. actividades matemáticas.
https://es.scribd.com/s/Matematicas%20para%20ninos
• Scribd.com. Discalculia. https://es.scribd.com/doc/250848262/DISCALCULIA
• Santamaría S. Teorías de Piaget.
https://www.monografias.com/trabajos16/teorias-piaget/teorias-piaget.shtml
• Wikipedia https://es.wikipedia.org/wiki/Destreza
• Wikipedia: https://es.wikipedia.org/wiki/Matem%C3%A1ticas
• Revista suma. https://revistasuma.fespm.es/
• Dibujos para pintar y colorear: https://www.dibujos.net/
Enlaces interesantes que se te recomienda visitar
• 250 ideas material didáctico 2021.
https://www.pinterest.com.mx/caroh95/material-did%C3%A1ctico/
• 67 ideas material didáctico preescolar.
https://www.pinterest.com.mx/andrucel33/material-did%C3%A1ctico/
• 900 ideas estimulación cognoscitiva.
https://www.pinterest.es/SraMetamorfosis/estimulaci%C3%B3n-cognitiva/
• 95 ideas material didáctico: estimulación temprana.
https://www.pinterest.com.mx/malenabermoll2/material-did%C3%A1ctico/
• Buena forma para multiplicar
https://www.youtube.com/watch?v=dXKN3Y4agCw
• Capotemath.
https://www.youtube.com/channel/UCwjoPg9bkpCmLhHbNhWBFPw
• Discalculia. https://es.slideshare.net/caluva23/discalculia-8210104
• Libros de tela. https://www.pinterest.com.mx/bere_tmz/materialdid%C3%A1ctico/
• Matemáticas inclusivas. https://www.matematicasinclusivas.com/
• Material educativo. https://materialeducativo.org/
• Math2me.Tiene una serie de videos tutoriales
https://www.youtube.com/results?search_query=math2me
• Método ABN. https://www.actiludis.com/2012/01/09/decoracion-de-numeros/
• Pedagogía y psicología.
https://psicopedagogias.blogspot.com/2008/01/discalculia.html
• Pina y homeschooler. https://www.pinayhomeschooler.com/2016/11/highlyrecommended-montessori-materials.html
• Problemas en las matemáticas.
https://www.slideshare.net/ROSHAUN/problemas-matemticas-7455410
• Psicodiagnosis.https://www.psicodiagnosis.es/areaclinica/trastornosenelambito escolar/trastornodelcalculodiscalculia/index.php
MaríaTeresaAliciaSilvayOrtiz. Los números y otros retos matemáticos. Parte 6
• Retomanía. http://retomania.blogspot.com/
• Tete a modeler. https://www.teteamodeler.com/montessori
• Unidades y decenas. https://es.slideshare.net/idoialariz/la-decena-41178832
• Unidades y decenas https://www.pinterest.com.mx/pin/586945763912687723/
Juegos
• 75 juegos matemáticos conteo números y operaciones básicas.
https://www.imageneseducativas.com/75-nuevos-juegos-matematicos-conteonumeros-operaciones-basicas-etc/
• Actitudes. Material educativo accesible y gratuito. https://www.actiludis.com/
• Childtopia. Materiales educativos.
https://didactalia.net/comunidad/materialeducativo/recurso/childtopia-juegoseducativos/91631928-e927-4195-acc0-844193956586
• Dos príncipes aprenden Montessori.
http://dosprinceses.blogspot.com/2014/04/barras-numericas-ii-aritmetica.html
• Figuras geométricas divertidas.
https://www.slideshare.net/epapadi/httpsblogsschgrsfairastideuterahttpblogsschgrgoma-httpblogsschgrepapadi-191997667
• Mash up Math. https://www.mashupmath.com/freemathpuzzles/
• Material Montessori. https://montessoriprintshopusa.com/products/sensorialextensions-bundle
Consulta estos libros
• “Cómo obtener lo mejor de tus hijos” Tim Seldin.
• “Enséname a hacerlo sin tu ayuda” Maja Pitamic.
• “La mente absorbente del niño” María Montessori
• “Educar para un nuevo mundo” María Montessori
• “La educación de las potencialidades humanas” María Montessori
• “Formación del hombre” María Montessori
• “Ideas generales del método” Ángel Gómez Moreno
• “Jugar y aprender. El método Montessori” Lesley Britton.
• El método de la pedagogía Científica, María Montessori
• Montessori explicado a los padres, de Charlotte Poussin
• Montessori en casa, de Cristina Tébar
• Cómo educar niños maravillosos con el método Montessori
• La mente absorbente del niño, de María Montessori
• El niño, el secreto de la infancia, de María Montessori
