Batería básica para las DAM Yo y las matemáticas

Parte 1


Dra. María Teresa
Alicia Silva y Ortiz 7

María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Batería básica para el diagnóstico presuntivo de las DAM
Yo y las Matemáticas Parte 1
Introducción
Las matemáticas es una de las materias con mayor índice de reprobación en todos los niveles educativos. En gran medida se debe a la deficiencia en los procedimientos didácticos que se emplean, por diversos motivos. Sin embargo, está el otro lado de la moneda, ¿cómo se encuentra el aprendiz para poder recibir este tipo de conocimientos y aprenderlas de manera natural y como un proceso natural de enseñanza-aprendizaje.
La UNESCO (1994) menciona que el orientado con una necesidad educativa especial, como es el caso de las matemáticas, tiene una condición significativa que le impide u obstaculiza aprender a través del uso de los medios educativos de la escuela común, por lo tanto, requiere ser enseñado con base en sus requerimientos especiales.
El origen de las dificultades de aprendizaje puede ser inherentes a diferencias significativas en la adquisición y uso de e las capacidades de comprensión oral, lectura, escritura, razonamiento y para la matemática. Estos desordenes pueden ser intrínsecos del aprendiz, debido a una disfunción del Sistema Nervioso Central y afectarlo a lo largo de toda la vida, o son de funcionalidad y, al atenderse apropiadamente, se logra compensar y lograr un desempeño como es esperado.
Los problemas en comportamientos que requieren autocontrol, percepción e interacciones sociales pueden coexistir con las dificultades de aprendizaje, pero no constituyen en sí mismos una dificultad en el aprendizaje. En este escrito no se contemplan los casos asociados con impedimentos físicos severos, como alteraciones visuales, auditivas, del aparato locomotor o intelectuales de carácter permanente. En contraste, es competencia de este contenido el aprendiz que en apariencia es semejante a sus coetáneos, pero por alguna dificultad en su desarrollo su rendimiento es inapropiado o se le considera como fracaso escolar en cualquier momento de su escolarización. Estos casos se consideran transitorios, es decir, factibles de superar con una intervención a la medida.
Las preguntas frecuentes que se plantean en torno a esta condición suelen ser:
¿Qué son las dificultades en el aprendizaje?
¿Qué conductas presenta un niño con dificultades en el aprendizaje?
¿A qué edad se pueden detectar o presentar las dificultades en el aprendizaje?
¿Cuál es el origen de las dificultades en el aprendizaje?
¿Cómo se debe evaluar e intervenir a los niños que presentan dificultades en el aprendizaje en el aula?
¿Qué tipo de especialista o maestro puede atender a un niño con dificultades en el aprendizaje? ¿Un niño con dificultades en el aprendizaje debe ser atendido en un aula de clase regular o en Escuela de Educación Especial?
¿Quiénes son los responsables de atender a un niño con dificultades en el aprendizaje?
¿Si actualmente se habla de necesidades educativas especiales (NEE), dónde queda el concepto de dificultades en el aprendizaje?
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
En la “escuela para todos” se requiere contar con adecuaciones escolares que permitan atender a todos los aprendices. Las dificultades más comunes están asociadas a la atención, comprensión, dominio de conceptos básicos, codificación, descodificación grafémica, asociación y resolución de problemas, etc., que pueden compensarse mediante estrategias didácticas ajustadas a su nivel y condición, que suponen el empleo de acciones como:
Ajuste de los ritmos de enseñanza a los ritmos de aprendizaje del alumno.
Entrenamiento perceptivo
Dominio de conceptos espaciales y temporales.
Adecuación del vocabulario básico.
Comprensión lectora
Mecanismos de resolución de problemas y cálculo operatorios
Desarrollo del esquema corporal: orientación espacial y temporal, lateralidad y direccionalidad.
Motivación a la lectura
Articulación en el lenguaje oral y dominio de la comunicación verbal
Dominio del trazo para el aprendizaje de la escritura
Desarrollo de los procesos cognitivos básicos: razonamiento, atención y memoria a partir de las funciones mentales como: deducir, inducir, sintetizar, analizar, evocar, discriminar y retener
Técnicas de estudio
Estrategias de trabajo intelectual
Habilidades sociales
Autoestima
Motivación para aprender
Myers y Hammill (1982) agrupan en seis rasgos característicos que pueden estar presentes en el niño con dificultades en el aprendizaje:
Trastornos en la percepción: de las formas y el espacio.
Trastornos en la atención: insuficiente o excesiva.
Trastornos en la memoria: auditiva o visual.
Trastornos en la actividad motora: hiperactividad, hipoactividad, carencias en la coordinación, perseverancia.
Trastornos en el lenguaje: afásicos y trastornos del habla.
Trastornos en la personalidad: ansiedad, inestabilidad emocional, bajo autoconcepto y autoestima, inquietud y desobediencia, poco control en sí mismo, dificultades para mantener la atención, tensión nerviosa, etc.
Desafortunadamente, en el país, hay una fuerte tendencia en detectar las dificultades en el aprendizaje en la escuela primaria en la mayoría de los casos, cuando ya se han manifestado de alguna manera. Eso se debe a que no se cuenta con suficiente personal para ocuparse de ello ni se tiene un mecanismo de detección estructurado con los más pequeños ni en el jardín de niños.
Una detección oportuna en los primeros años permite la intervención temprana de las necesidades educativas especiales y, por consiguiente, prevenir las dificultades en el aprendizaje del siguiente nivel.
En la Educación Primaria es recomendable, prestar atención en el primer año, especialmente desde el momento en que el niño domina los aprendizajes instrumentales básicos, ya que es a partir de aquí cuando suelen presentarse las primeras manifestaciones en los ritmos de aprendizaje.
1. El diagnóstico psicopedagógico.
En esta especial es de vital importancia prepararse en los procedimientos e instrumentos que generalmente se utilizan para detectar dificultades de aprendizaje en los orientados, con el fin de que se le atienda de acuerdo con sus necesidades educativas especiales y cuente con un programa que le permita ir avanzando en sus estudios.
Cuando los aprendices no son atendidos como es debido oportunamente, generalmente se van quedando rezagados, teniendo graves problemas que lo van a ir afectando durante su vida académica
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
y, muy probablemente, en la personal y laboral. Desafortunadamente esto se recrudece con sentimientos de inseguridad, frustración y pérdida por aprender y asistir a una escuela que lo prepare para un futuro productivo.
¿Qué es el diagnóstico psicopedagógico?
Es un proceso que permite describir, clasificar, predecir y, en caso necesario, explicar el comportamiento del aprendiz en el contexto escolar, relacionándolo con otros sistemas implicados en su educación, como la familia y la comunidad.
¿Cuál es el propósito de hacer este tipo de estudio?
En términos generales se trata de un proceso donde se involucran una serie de actividades que sirven para medir y evaluar el desempeño del aprendiz con el fin de ofrecer una orientación específica para que siga adelante con su educación formal. Esto implica hacer una valoración del nivel de desarrollo y de aprendizaje de la persona en estudio, así como sus habilidades, capacidades y hábitos, además de sus procesos afectivos.
¿Cuál es el objetivo del diagnóstico psicopedagógico?
El objetivo del diagnóstico psicopedagógico es detectar dificultades específicas en cada uno de estos casos, de tal manera que se pueda diseñar una intervención que le ayude a salir adelante con éxito. Esto implica involucrar tanto a profesores como a los familiares.
Específicamente se puede resumir de la siguiente manera:
1. Comprobar el progreso del alumno en relación con las metas del currículo escolar, especialmente en las áreas cognoscitiva, afectiva y psicomotriz.
2. Identificar factores que puedan interferir en su educación: esto es, sus puntos fuertes y sus áreas de oportunidad en el proceso de aprendizaje, tanto personales como las que son determinantes en su ambiente, como una familia disfuncional, falta de recursos económicos, círculo social inexistente o muy pobre, por ejemplo.
3. Adecuar la enseñanza-aprendizaje de manera que se empleen estrategias educativas que lo ayuden en este proceso, respetando su ritmo de trabajo, de manera que pueda ir superando las dificultades que no le permiten seguir avanzando en la escuela.
¿Cuáles son las funciones del diagnóstico psicopedagógico? Como principales funciones se señalan:
1. Prevención y predicción: para conocer las partes fuertes y las que requieren ser atendidas con el fin de que su desarrollo sea satisfactorio al igual que su aprendizaje.
2. Identificación del problema y gravedad: averiguar las causas, tanto personales como ambientales que le están impidiendo su desarrollo y aprendizaje, por ejemplo.
3. Orientación: una vez detectadas sus necesidades, se diseña un plan de intervención tomando como punto de partida lo obtenido en el diagnóstico psicopedagógico con el fin de atender aquello que requiere para mejorar su desarrollo y aprendizaje.
4. Corrección: con el fin de hacer un ajuste que permita reorganizar las condiciones y situaciones en las que se encuentra el aprendiz para llevar a cabo una intervención adecuada junto con las recomendaciones que se requieren poner en práctica tanto en la familia como en la escuela y grupos sociales en que participe o se necesite que acuda.
¿Cuáles son los principios esenciales del diagnóstico psicopedagógico?
Al elaborar un diagnóstico psicopedagógico es necesario tomar en cuenta estos principios de manera que su educación se administre de acuerdo con lo que el orientado requiere evitando caer en supuestos o por condiciones socioculturales, por ejemplo. Aquí se comentan cuatro principios fundamentales.
1. Su medio: es decir, tomar en cuenta el contexto donde se desenvuelve, sus costumbres, tradiciones, lenguaje, modismos, oportunidades socioeconómicas, por citar unos ejemplos.
2. Su personalidad: estar consciente de cuáles son sus rasgos de carácter, su perfil, lo que lo hace único e irrepetible de manera integral.
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
3. Seguimiento: la orientación no termina con el diagnóstico y la intervención. Implica el acompañamiento que permite dar la retroalimentación oportuna y los ajustes que deben irse haciendo a medida que va avanzando en los distintos grados escolares.
4. Sistémico: esta orientación debe tener una visión integrada del aprendiz que correlacione su desarrollo psicosomático y su relación con su medio.
¿Cuáles son los principales medios implicados?
Durante este proceso debe trabajar en armonía la escuela, el profesor, el alumno, la familia y el psicopedagogo.
a) La escuela: es la que integra el entorno social del aprendiz al compartir funciones con otros sistemas, como el familiar, por ejemplo. Son complementarios en este proceso de aprendizaje, por lo tanto, no puede ser fuentes de conflictos.
b) El profesor: es una figura fundamental en el proceso educativo, y es un profesional que pertenece y actúa en diferentes subsistemas simultáneamente. Es quien se comunica con los padres y otros profesores implicados en la educación del educando, lo ayuda en la formación de hábitos y valores, patrones de conducta, conocimientos adecuados para que sea una persona autónoma y responsable.
c) El alumno: también juega varios roles en el proceso educativo, siendo el eje de su proceso enseñanza-aprendizaje, y está inmerso en otros sistemas, como el familiar, el religioso, el comunitario, entre otros.
d) La familia: tiene una función psicosocial y está comprometida a proteger a sus miembros, de tal manera que puedan desenvolverse e integrarse a su cultura de manera favorable. Tanto el contexto sociocultural de la familia como su ideología, hábitos y valores son de gran influencia en la educación del aprendiz. Cuando la escuela y la casa entran en conflicto, el orientado queda en medio y se afecta su educación, provocando tensiones, frustración y descontrol en todos los involucrados.
e) El psicopedagogo: es quien une a los sistemas del orientado. Puede formar parte del equipo de la escuela o ser un profesional externo dedicado a la detección y diagnóstico de los problemas de aprendizaje y/o la orientación familiar. Su principal contribución es establecer un contexto de colaboración entre los implicados, en especial los profesores y padres de familia para acordar cómo proceder en beneficio de la educación del aprendiz.
¿Cuáles son las dimensiones y áreas de actuación?
Toma en cuenta varias dimensiones personales y ambientales del orientado, empezando por el contexto educativo y familiar del aprendiz, así como su familia, escuela y comunidad que influyen en su desarrollo físico, emocional y psicológico.
A nivel personal están las dimensiones biológica, psicomotora, cognoscitiva, de motivación, afectiva y social. En las dimensiones socioambientales están: el centro educativo, el grupo de padres, la familia y la comunidad.
a) Biológico: desarrollo físico y madurez, salud física y bienestar, estado psicofisiológico, sensaciones y percepciones.
b) Psicomotricidad: motricidad gruesa y fina, coordinación, lateralidad, conciencia corporal (concepto, imagen y esquema corporal), noción derecha-izquierda, direccionalidad.
c) Cognoscitivo: desarrollo intelectual, inteligencia general, capacidades y habilidades específicas, potencial y estilos de aprendizaje, conocimientos, creatividad, lenguaje. A esto se suman las creencias, memoria, imaginación, resolución de problemas.
d) Motivación: expectativas, atribuciones, intereses y actitudes.
e) Afectividad: historia personal, estabilidad emocional, personalidad, adaptación personal, autoconcepto.
f) Social: desarrollo y adaptación social, habilidades sociales, interacción con los demás.
g) Centro educativo: aspectos físicos y arquitectónicos, recursos, organización y funcionamiento, proyecto educativo, servicios de apoyo, socio demografía, aspectos psicosociales.
h) Grupo de padres: aspectos socio estructurales, procesuales y socio académicos.
i) Familia: relaciones con la familia y la comunidad, aspectos socioeconómicos y socio académicos.
j) Comunidad: aspectos socio estructurales y demográficos, procesuales (valores, actitudes, intereses) y aspectos socio académicos.
2. Necesidad de efectuar una evaluación inicial
¿Por qué evaluar durante el proceso de enseñanza aprendizaje?
El proceso de enseñanza y del aprendizaje del alumnado se dirige hacia el logro de una serie de objetivos valiosos, lo que implica partir de un "estado inicial" (que debe conocerse) sobre el que se irán operando los cambios producidos por la enseñanza y el aprendizaje.
El conocimiento de los niveles, características y necesidades de los alumnos nos permitirán tomar una serie de decisiones relativas a:
• Planificar y programar las actividades docentes.
• Adoptar medidas de atención a la diversidad en el aula.
• Metodologías para emplear.
¿Qué se debe contemplar en la toma de decisiones?
Al tratarse de decisiones que afectan a un equipo docente es necesario que exista un intercambio de opiniones e información entre los miembros del equipo educativo. La evaluación inicial de los alumnos es un primer paso en el proceso de evaluación continua que lleva a cabo el equipo educativo, se sospeche que tenga DAM o no.
¿Qué aspectos interesa evaluar?
El proceso de evaluación inicial exige que se atienda más a los posibles recursos y capacidades del alumnado que a las posibles deficiencias que presenten, aunque sin olvidar éstas. Parece ser más productivo analizar las expectativas e intereses y las potencialidades que poseen los estudiantes con el fin de proporcionarles una educación adaptada a ellos que simplemente "constatar el bajo nivel que poseen".
¿Por dónde empezar?
Se sugiere tomar en cuenta lo siguiente:
a) Si se toma como punto de partida este supuesto, lo primero que conviene explorar y conocer son sus actitudes frente al área o grupo de áreas, y en general a los grandes temas que pueden tratarse desde un punto de vista disciplinar. El conocimiento de estas actitudes proporcionará datos valiosos para organizarles actividades que promuevan su "motivación por aprender". El orientador puede completar esta "radiografía" del alumno con sus actitudes frente a temas más generales (los estudios, ambiente familiar y social, etc.).
b) En segundo lugar, interesa conocer las capacidades de los alumnos en relación con los procedimientos. Interesará conocer el nivel de desarrollo de sus capacidades generales (lectura, escritura, identificación, análisis...) ya que tienen una influencia en todas las áreas. También, han de conocerse el grado de dominio de los procedimientos básicos de las matemáticas que caben ser considerados como prerrequisitos en el área; esto permitirá iniciar algunas medidas de refuerzo en caso necesario.
c) En tercer lugar, conviene explorar en cada caso los procedimientos centrales del área, aunque sólo sea a modo de anticipación respecto a lo que será el trabajo en el área o grupo de áreas a lo largo del curso y los grados de dominio en relación con los conceptos. En este caso interesa observar no sólo la adquisición o no de determinados conceptos relacionados con las matemáticas, sino los procesos seguidos que los han llevado a concepciones erróneas. Las capacidades que podrían explorarse en este caso pueden ser: identificación, selección, interrelación, definición y aplicación a la resolución de problemas.
En estas tareas es importante disponer de la información acumulada sobre el alumno a lo largo de su escolarización en el Instituto, aunque suelen en cada curso cambiar los profesores, los alumnos suelen permanecer en el colegio unos seis años en primaria en promedio. Debido a que esta información histórica puede, en algunos casos, incitar a la sobrevaloración y en otros a una subvaloración del alumno, es importante conocer estos riesgos de sesgo.
¿Cómo evaluar los diferentes aspectos?
En primer lugar, debe considerarse que la evaluación es un proceso encomendado al equipo docente de modo colectivo. Esto permitirá un intercambio de informaciones y opiniones que podrán facilitar una enseñanza basada en las necesidades y características del alumnado.
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
En los casos especiales, es importante contemplar una evaluación inicial que sirve de base para la intervención, el seguimiento del caso para ver su evolución e ir haciendo los ajustes pertinentes y la evaluación final.
Los instrumentos para recoger la información relevante para la evaluación inicial no tienen que basarse necesariamente en pruebas escritas.
Este tipo de pruebas puede ser adecuado para determinados procedimientos y algunos contenidos conceptuales, pero no con carácter general; entre sus ventajas destaca que se dispone de un material escrito, individualizado y siempre revisable, pero tiene la desventaja de que supone un gran esfuerzo para su corrección y que no es adecuada en algunos casos.
Como complemento a la prueba escrita se puede trabajar en grupos de debate, en técnicas en pequeño grupo, etc., lo que nos indicará las tendencias generales del grupo. La observación de los alumnos y su anotación en un registro (escrito, de audio, de video...) nos dará información individualizada.
En todo caso, las actividades grupales conviene planificarlas rigurosamente: qué se pretende evaluar, cómo se organizará el trabajo del grupo, cómo se va a evaluar, cómo se registrará la información...
Otro instrumento que puede utilizarse es la entrevista, que puede realizarse de modo formal o informal, o simplemente mediante preguntas en clase. En cualquier caso, debe planificarse y seleccionarse las preguntas en función de los objetivos que se pretendan.
Puede emplearse una amplia gama de instrumentos en esta evaluación inicial, sobre todo de tipo cualitativo, pero el objetivo que debe guiar su selección y utilización ha de permitir conocer algo de las posibilidades y recursos del orientado. No debe tratarse con una actitud clasificatoria, aunque si debe y puede servir para detectar pronto problemas y dificultades de aprendizaje en algunos de ellos. Una parte importante de la información puede obtenerse de la autoevaluación del orientado o mediante actividades o ejercicios que impliquen un alto grado de su propia valoración.
3. La evaluación inicial
Debido a que este trabajo se centra en la evaluación inicial del razonamiento lógico-matemático, se comenta brevemente en que consiste la evaluación inicial en general. Ésta comienza cuando se detecta que el rendimiento escolar de un alumno no es satisfactorio, es decir, hay una discrepancia entre lo que está rindiendo y lo que se cree que puede rendir, por lo que se hace conveniente que se realice una observación continua en el aula, a fin de valorar si estas necesidades educativas que presenta el alumno pueden ser atendidas sólo por la maestra regular o con el apoyo de algún especialista o requiere de ser derivado, a algún servicio especial para su atención.
Si la escuela común puede resolver estos casos, entonces estos aprendices no pertenecen al área de dificultades de aprendizaje propiamente dicho, pues sus deficiencias pueden deberse a una enseñanza poco eficaz o que no se les enseñó y les faltan esos conocimientos. Entonces, al ajustarse como es requerida, se superan y pueden continuar con sus estudios como es esperado.
Sería deseable que antes de derivar el caso a algún servicio externo, se haya intentado resolver las dificultades del alumno dentro del aula regular con la colaboración de otros profesores y/o profesionales del centro educativo, a fin de proponer las adecuaciones curriculares pertinentes y coherentes a las necesidades educativas presentadas por el alumno en la adquisición de los aprendizajes.
El procedimiento sugerido es la recogida de datos que interesan, como son los del entorno, la familia, médica, evolutiva y escolar, y la aplicación de una evaluación psicopedagógica que permita obtener una visión completa e integradora del alumno, es decir; una evaluación:
Centrada en el orientado y sus contextos.
Contempla habilidades y necesidades generales y específicas.
Analiza características, aptitudes, habilidades y tareas
Asociada con la enseñanza y el desarrollo global
Con la aplicación pruebas formales e informales referidas a criterios definidos.
Que mide registros tanto cuantitativos como cualitativos
Se considera que no es posible plantear un programa de intervención si previamente no se ha logrado describir exhaustivamente las potencialidades y las carencias del sujeto con detalle, así
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
como las características de los sistemas familiar, social y escolar en los que se manifiesta y se desarrolla su existencia.
¿Cuándo realizar la evaluación inicial?
El momento más adecuado para realizarla es a comienzo de curso ya que puede facilitar pautas para la adaptación del proyecto curricular a las características y necesidades del alumnado. Normalmente será necesario dedicar varias sesiones para alcanzar un conocimiento mínimo.
Al comienzo de las diversas unidades didácticas pueden realizarse "minievaluaciones" como recurso y como activador de organizadores previos. En este caso se puede atender de modo más concreto a las necesidades del área.
A modo de resumen se presenta un breve esquema:
Cuadro # 1 Esquema de evaluación inicial
¿Qué tipo de técnicas y procedimientos son recomendables?
Esta tarea puede realizarse mediante técnicas y procedimientos tales como:
• Intercambio de información del equipo educativo.
• Autoevaluación de los propios estudiantes.
• Entrevistas.
• Simulación de situaciones, debates, ...
• Pruebas escritas y orales.
• Si se sospecha DAM, pruebas formales para su detección y diagnóstico.
4. Evaluación de las dificultades en el aprendizaje de las matemáticas

Cualquier intervención educativa debe ser precedida de un diagnóstico diferencial en que se identifiquen las DAM.
Velasco y Jabonero (1984) señalan que la evaluación tradicional examinaba variables como:
• Nivel de desarrollo del razonamiento: conservación, clasificación, seriación, etc.
• La realización de cálculos aritméticos: numeración y operaciones.
• Conceptos matemáticos que posee, su comprensión y expresión verbal.
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
• Planteamiento de problemas y modo de resolverlos.
• Los elementos gnosopráxicos: estructuración espaciotemporal y dominio del espacio gráfico.
El enfoque cognoscitivo se centra especialmente en los procesos de aprendizaje:
• Conceptos correctos o erróneos.
• Estrategias adecuadas o no para afrontar las tareas.
• Examina tanto conocimiento formal como informal, pues puede ser insuficiente y dificultar el acceso a las matemáticas.
• Detallar los puntos fuertes y débiles del niño.
• La precisión y eficacia de las técnicas matemáticas básicas.
• Su grado de automatización.
• Estrategias seguidas para llegar a una solución.
• Los errores sistemáticos que comete.
• Conocer las insuficiencias de los conocimientos subyacentes. Los instrumentos que se pueden emplear para el diagnóstico diferencial pueden apoyarse en pruebas estandarizadas, muy útiles por su solidez en su construcción (fiabilidad y validez), estandarización y baremación, pues permite comparaciones con grupos de pares. En general no se usan pruebas aisladas sino una batería de pruebas específicas para identificar los factores que intervienen.
A. Pruebas Psicológicas
Finalidad: identificar déficits de aptitudes específicas asociadas con el rendimiento matemático, la inteligencia general, memoria, hábitos de estudio, autoconcepto académico, comprensión lectora y resolución de problemas. Entre las pruebas que hay en el mercado se toman las subpruebas que se relacionan directamente con este tema. Algunos ejemplos son:
Pruebas Edad/aplicación Objetivo
Escalas de inteligencia Wechsler
Escalas McCarthy de aptitudes y psicomotricidad
Pruebas de factor g: Factor g de Cattell
Matrices progresivas de Raven
DAT: test de aptitudes diferenciales
WPPSI: 4 a 6 ½ años
WISC-R: 6 a 16 años
WAIS: 16 en adelante Aplicación individual
MSCA: 2 ½ a 8 ½ años Aplicación individual
A partir de los 4 años Aplicación colectiva
A partir de los 14 años Aplicación colectiva
Muy utilizadas en la evaluación psicopedagógica
• Subtests: aritmética, memoria auditiva inmediata (dígitos)
• Perfil: puede ayudar en la interpretación neurológica.
Escala numérica con tres subpruebas:
• Recuento y distribución
• Cálculo
• Memoria numérica
• Miden inteligencia general
Prueba de desarrollo de la percepción visual de Frostig
3 a 7 años
Algunos aspectos de inteligencia general:
• Razonamiento abstracto
• Razonamiento verbal
• Aptitud numérica
• Rapidez y precisión perceptiva
• Razonamiento mecánico
• Relaciones espaciales.
Relevante para el diagnóstico de geometría
• Coordinación visomotora
• Discriminación figura – fondo
• Constancia de forma
• Posición en el espacio
• Relaciones espaciales
Prueba gestáltica visomotora de Bender
4 años hasta adultos
• Valora la integración visomotora
• Alteraciones neurológicas
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Batería Luria – DNI A partir de los 7 años Evalúa trastornos neuropsicológicos
• Escritura numérica: pide escribir y leer números de izquierda a derecha y de arriba hacia abajo, decidir qué número de entre arios que lee o escucha es mayor.
• Operaciones aritméticas: resolver sumas, restas, multiplicaciones, completar operaciones en las que falta un número o el signo y contar hacia atrás de tres en tres.
Cuestionario de personalidad Cattell
(ESPQ, CPQ y HSPQ)
De 6 años hasta adultos Aplicación individual
Es importante conocer la personalidad del niño y su forma de reaccionar, pues puede influir en su rendimiento académico.
Cuadro # 2. Pruebas psicológicas.
B. Pruebas pedagógicas
Finalidad: ayudan a determinar el grado de dominio de la diversidad de conceptos y procedimientos propios de las matemáticas.
a) Habilidad para comprender y usar los conceptos de cantidad, combinaciones, número, forma, tamaño, posición y medida.
b) Habilidad para sumar, restar, multiplicar y dividir números naturales, enteros y fracciones.
c) Habilidad para aplicar los conceptos matemáticos a la solución de problemas en situaciones personales y sociales: comprar y vender, calcular diferencias de tiempo, pesar y medir.
d) Habilidad para clasificar y categorizar datos y hechos matemáticos.
e) Adquisición de nociones e información específicamente matemática.
No difieren en mucho de las pruebas que elabora el profesor, pero están más estandarizadas, lo que permite comparar resultados obtenidos con los baremos disponibles del mismo nivel educativo. Algunos ejemplos son:
Pruebas Nivel/edad Objetivo
EAP de Terrasa, 1989. Pruebas pedagógicas graduadas para preescolar y ciclo inicial
Montesinos y otros (1991). Pruebas psicopedagógicas de evaluación individual
Palomino y Crespo
Pruebas de cálculo y nivel matemático
Preescolar Primero de primaria
Preescolar Primaria
• Reactivos graduados para distintos niveles de educación infantil y primer ciclo de primaria.
• Reactivos de lógica, cálculo y grafía de números, medida y geometría.
• Conocimiento de las cantidades
• Operaciones
• Problemas y otros contenidos
7 a 12 años Serie A: nociones previas:
• Conservación
• Seriación
• Previsión
• Clasificación
• Inclusión
Serie B: conocimiento de simbolización matemática:
• Dictado y lectura de números
• Concepto de valor
• Concepto de signos
• Conocimiento de figuras geométricas
• Conocimiento de cuerpos geométricos
Serie C: disposición para el cálculo y resolución de problemas:
• Repartición y resta
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
• Resolución de problemas con elementos concretos, con dificultad en el enunciado
• Problemas abstractos
Cuadro # 3 Pruebas pedagógicas.
5. La evaluación informal
La evaluación informal de las necesidades matemáticas, según Jean Gross y Pablo Manzano (2004), se puede realizar también a través de:
a) La observación: mientras el niño trabaja se puede uno dar cuenta de sus patrones de atención y concentración o la falta de ellos, la frecuencia con que pide ayuda, su forma de realizar la selección de los enfoques y los materiales que usa en las tareas prácticas, el lenguaje matemático que emplea y su capacidad para hacer generalizaciones y predicciones.
b) El análisis de errores: revisar con cuidado el tipo de faltas que comete el niño en los cálculos escritos con el fin de entender su forma de pensar.
c) Utilizar materiales de evaluación informal: diseñados para comprobar la comprensión de determinados objetivos básicos que logra conseguir el niño, su progreso mensual o trimestral, para involucrarlo en la supervisión y el establecimiento de sus objetivos.
d) Apoyarse de la entrevista informal: para sondear la comprensión del niño preguntándole cómo llega a determinadas conclusiones o como verificación rápida de los conceptos que ha dominado. Por ejemplo, elaborar un formato que permita evaluar en 15 minutos lo que el niño comprende acerca del tiempo, dinero, la medida, el valor posicional, el cálculo y el uso de la calculadora.
e) Combinar con las pruebas estandarizadas: con el fin de hacer una evaluación más detallada y poderla comparar con sus iguales.
Las ventajas de contar con una evaluación precisa sobre el desempeño del niño en esta área y sus dificultades:
• Se pueden plantear con precisión los objetivos de aprendizaje que requiere el niño.
• Desarrollar planes de acción.
• Obtener información sobre dónde se pierde el niño en matemáticas con el fin de ajustar los estilos y el proceso de enseñanza-aprendizaje.
• Encontrar alternativas específicas de cómo enseñarle, en lugar de limitarse a la guía de los contenidos correspondientes a su grado escolar.
Prueba # 1. Yo y las matemáticas
Empecemos por explorar cuál es la actitud que tiene el orientado hacia las matemáticas. Esta sencilla prueba es un primer paso. Instrucciones. Elige la opción que mejor te represente con base en la escala y, al final, haz un breve comentario sobre tu apreciación sobre las matemáticas.
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Comentario:
VIDEO: Contrasta tu resultado con el que obtengas del video Yo y las matemáticas: https://www.youtube.com/watch?v=qd0p2tEUFHs
Yo y las matemáticas
Es importante estar consciente de cuál es tu actitud ante las matemáticas. Es una materia poco popular debido a la forma como se enseña. Aprenderlas implica dominar su lenguaje y razonar con lógica. Es lo primero que has de indagar en el orientado, si es pertinente, ya que su actitud será determinante en el proceso de intervención.
Objetivo:
Explorar la relación que tiene el orientado con las matemáticas desde una perspectiva afectiva.
Evaluar la percepción que tiene el sujeto de cómo su familia, los profesores, sus compañeros y amigos confían en sus posibilidades de éxito en matemáticas.
Descripción:
Este ejercicio consta de un listado de situaciones que el orientado debe leer y responder. Estas situaciones se relacionan con la metacognición de su forma de trabajo escolar, la percepción que tienen los otros de él y la autopercepción frente a la asignatura.
Puntuación máxima: 68 puntos
Criterios de corrección:
Se le asigna el siguiente puntaje según la respuesta:
Se suma el puntaje obtenido, se saca el porcentaje y se ubica en el rasgo correspondiente:
➢ Muy buena percepción y actitud hacia las matemáticas
➢ Buena percepción y actitud hacia las matemáticas
➢ Regular percepción y actitud hacia las matemáticas

➢ Deficiente percepción y actitud hacia las matemáticas si ha obtenido menos de 40 puntos.
Interpretación:
Tener en cuenta la frecuencia con que se presenta cada rango para la programación.
Hoja de reflexión # 1 Yo y las matemáticas
Instrucciones. Después de haber resuelto y calificado la prueba, escribe en los recuadros tus estrategias de acción para la intervención.
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Estrategias de acción
¿Qué aspectos le ayudan a estar bien? ¿Qué quiero que conserve?
¿Qué aspectos le obstaculizan? ¿Qué necesita modificar?
¿Cómo pienso ponerle la práctica? ¿Cuál es el objetivo y en cuánto tiempo lo ha de lograr?
¿De qué me di cuenta?
¿Qué necesita modificar?
¿Cómo pienso ayudarlo?
Mi firmaPrueba # 2. Guía para la prueba de Capacidad de Comprensión. Forma “A”
Ficha técnica
• Nombre: Prueba de capacidad de comprensión.
• Mide: capacidad de comprensión del espacio, vocabulario y aritmética.
• Edad: 10 a 18 años.
• Administración: colectiva.
• Tiempo: 12 minutos.
• Material: guía de aplicación, protocolos, lápiz del # 2 o 2 ½, goma de borrar, hojas blancas, cronómetro, bicolor.
• Estructura: Tres tipos de ejercicios: contar bloques, vocabulario y problemas aritméticos.
• Evaluación: un punto por cada respuesta correcta según la clave. Sumar todo para obtener la PN y buscar en la tabla la PE (puntuación de escala) para obtener el nivel de comprensión.
• Área: inteligencia general: verbal y lógico-matemática.
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Instrucciones. Esta prueba comprende tres tipos de ejercicios: contar bloques, vocabulario y problemas aritméticos.
A. Contar bloques: ejemplos
1) ¿Cuántos bloques hay en este montón?
(A) 3 (B) 2 (C) 5 (D) 4………….... (D)
En el montón hay cuatro bloques; por lo tanto, la respuesta es (D), que es la letra que se ha escrito en el paréntesis situado al final de la línea de puntos. Aunque en el dibujo solamente se ven tres bloques, al levantar el bloque colocado en la parte superior se observa que debajo de éste se encuentra el cuarto bloque.
2) ¿Cuántos bloques hay en este montón?
(A) 3 (B) 2 (C) 5 (D) 2…………… (A)

Todos los bloques de un montón dado tienen el mismo tamaño y la misma forma, pero el tamaño y la forma de éstos puede cambiar de un ejercicio a otro.
B. Vocabulario: ejemplos
3) Grande aproximadamente significa:
(A) blanco (B) pequeño (C) voluminoso (D) negro ………… (C)
Puesto que el significado de grande es parecido al de voluminoso, se ha escrito la respuesta (C) en el paréntesis situado al final de la línea de puntos.
C. Problemas aritméticos: ejemplos
1) ¿Cuántos paquetes de cigarrillos de $ 50.00 cada uno se pueden comprar con $ 200.00?
(A) 5 (B) 4 (C) 40 (D) 10……………… (B)
La respuesta es 4, por consiguiente se ha escrito ( B ) dentro del paréntesis situado al final de la línea de puntos.
Los ejercicios de las páginas siguientes son similares a estos ejemplos. Resuelva todos los que pueda en el tiempo que se le concede para ello. Si no está seguro de cuál es la respuesta correcta de un ejercicio, elija la que considere más acertada, pero no adivine. No pierda el tiempo tratando de resolver un ejercicio que no entienda o cuya solución no conozca; déjelo y pase al siguiente
¡NO VUELVA LA PÁGINA HASTA QUE SE LO INDIQUEN! DISPONE DE 12 MINUTOS
NO ESCRIBA NADA EN ESTE CUESTIONARIO UTILICE SÓLO LA HOJA DE RESPUESTAS
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Prueba de Capacidad de Comprensión – Forma “A”
1) ¿Cuántos bloques hay en ese montón?
(A) 2 (B) 3 (C) 5 (D) 4 ( )
2) Responder aproximadamente significa:
(A) Fabricar (B) Hacer (C) Contestar (D) Venir ( )
3) ¿Cuántos son 6 paquetes de cigarrillos y 7 paquetes de cigarrillos?
(A) 15 (B)17 (C) 13 (D) 11 ( )
4) ¿Cuántos bloques hay en ese montón?
(A) 2 (B) 3 (C) 5 (D) 4 ( )
5) Asaltar aproximadamente significa:
(A) Abandonar (B) Regresar (C) Atacar (D) Retroceder ( )
6) Se repartieron varias hectáreas de tierra entre 7 personas, a partes iguales. Cada persona recibió 6 hectáreas. ¿Cuántas hectáreas se repartieron?
(A) 19 (B) 37 (C) 42 (D) 49 ( )
7) ¿Cuántos bloques hay en ese montón?
(A) 7 (B) 6 (C) 5 (D) 4 ( )
8) Decoración aproximadamente significa:
(A) Deuda (B) Deseo (C) Condición (D) Ornamento ( )
9) Juan tiene 93 vacas y su vecino tiene 59. ¿Cuántas vacas menos tiene su vecino?
(A) 41 (B) 34 (C) 19 (D) 21 ( )
10) ¿Cuántos bloques hay en ese montón?
(A) 4 (B) 8 (C) 6 (D) 12 ( )





11) Llamamos a una persona farsante cuando es:
(A) Detective (B) Explorador (C) Caballero (D) Mentiroso ( )
12) Si un camión recorre 9 kilómetros en 15 minutos, ¿qué distancia recorrerá en una hora?
(A) 6 Km. (B) 24 Km. (C) 36 Km. (D) 135 Km. ( )
13) ¿Cuántos bloques hay en ese montón?
(A) 14 (B) 11 (C) 15 (D) 16 ( )

14) Brotar aproximadamente significa:
(A) Hablar (B) Reducir (C) Vivir (D) Manar ( )
15) Tres hombres pescaron 81 peces. Si cada hombre se lleva un tercio de la pesca, ¿cuántos peces tendrán cada uno?
(A) 17 (B) 21 (C) 23 (D) 27 ( )
16) ¿Cuántos bloques hay en ese montón?
(A) 22 (B) 16 (C) 27 (D) 24 ( )
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
17) Privar a una persona de su libertad aproximadamente significa:
(A) Dársela (B) Quitársela (C) Restringírsela (D) Deseársela ( )
18) El sueldo básico de un jefe de ventas es de $ 9,000.00 por mes, más que el vendedor cuyo sueldo básico es de $ 12,000.00 mensuales. ¿Cuál es el sueldo básico mensual del jefe de ventas?
(A) $18,500 (B) $ 21,000 (C) $ 23,000 (D) $23,500 ( )
19) ¿Cuántos bloques hay en ese montón?
(A) 20 (B) 19 (C) 21 (D) 15 ( )
20) Una pregunta aproximadamente significa:
(A) Escuela (B) Narración (C) Una interrogación (D) Un bolso ( )
21) La escala de un mapa de carretera es de 1 cm = 22 Km. ¿A cuántos kilómetros de distancia se encuentran dos ciudades separadas en el mapa por 3,5 cm?
(A) 55 (B) 13 (C) 77 (D) 88 ( )
22) ¿Cuántos bloques hay en ese montón?
(A) 10 (B) 13 (C) 12 (D) 14 ( )
23) Una apertura aproximadamente significa:
(A) Una terminación (B) Una entrada o una salida (C) Un oráculo (D) Un ejercicio ( )
24) Un hombre participó en prácticas de tiro al blanco 8 veces, haciendo en total 192 puntos, ¿cuál fue su puntuación media?
(A) 19 (B) 24 (C) 29 (D) 37 ( )

25) ¿Cuántos bloques hay en ese montón?
(A) 17 (B) 22 (C) 18 (D) 21 ( )
26) Concurrente aproximadamente significa:
(A) Rebelde (B) Simultáneo (C) Capaz (D) Consciente ( )
27) El señor Pérez tiene la quinta parte de su dinero en una libreta de ahorros. La cantidad ahorrada asciende a $ 20,000.00, ¿Cuál es la suma total de dinero que posee el Sr. Pérez?
(A) $ 20.000 (B) $ 50,000 (C) $ 80,000 (D) $ 100.000 ( )
28) ¿Cuántos bloques hay en ese montón?
(A) 10 (B) 13 (C) 9 (D) 14 ( )
29) Ostentar aproximadamente significa:

(A) Ocultar (B) Exhibir (C) Expirar (D) Montar ( )
30) El ángulo A del triángulo ABC es de 40° y el ángulo B es de 60°, ¿cuántos grados tiene el ángulo C?


(A) 70° (B) 78° (C) 80° (D) 82° ( )

31) ¿Cuántos bloques hay en ese montón?
(A) 14 (B) 16 (C) 17 (D) 15 ( )
32) Dilema aproximadamente significa:
(A) Apuro (B) Evasiva (C) Consolidación (D) Granero ( )
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
33) Una propiedad fue tasada en $ 900,000.00. El tipo de impuesto fue de 4 5.50 por cada $ 100. ¿Cuál fue el impuesto sobre la propiedad?
(A) $ 45,500 (B) $ 49,500 (C) $ 51,500 (D) $ 54,500 ( )
34) ¿Cuántos bloques hay en ese montón?
(A) 9 (B) 12 (C) 10 (D) 13 ( )

35) Cuando una información es insuficiente significa:
(A) Incorrecta (B) Bastante (C) Escasa (D) Equivocada ( )
36) La superficie de un solar cuadrado es de 81 metros cuadrados. ¿Qué longitud tiene cada lado?
(A) 6 (B) 3 (C) 9 (D) 18 ( )

37) ¿Cuántos bloques hay en este montón?
(A) 7 (B) 9 (C) 8 (D) 10 ( )
38) Incurrir aproximadamente significa:
(A) Ganar (B) Introducir (C) Cometer (D) Aumentar ( )
39) A la misma hora que un arbusto de 40 cm de longitud, un árbol proyecta una sombra de 3.60 m de longitud. ¿Qué altura tiene el árbol?

(A) 4 m (B) 4.80 m (C) 5.40 m (D) 6 m ( )
40) ¿Cuántos bloques hay en ese montón?
(A) 9 (B) 8 (C) 7 (D) 6 ( )


41) La paga que devenga un obrero es el salario que:
(A) Va acumulando (B) Ya cobró (C) Disminuye (D) Desaparece ( )
42) Una persona ha invertido $ 35,000 al 8 % de interés anual. ¿Qué intereses le producirá su inversión en un año?
(A) $ 1,800 (B) $ 2,600 (C) $ 2,800 (D) 2,900 ( )
43) ¿Cuántos bloques hay en ese montón?
(A) 9 (B) 10 (C) 8 (D) 13 ( )
44) Una reprimenda es una cáustica cuando es:
(A) Displicente (B) Efectiva (C) Costosa (D) Mordaz ( )
45) Un terreno mide 100 m X 50 m. Una casa construida en el terreno mide 50 m X 25 m. ¿cuál es la superficie de terreno no edificada en metros cuadrados?
(A) 1.250 (B) 2.500 (C) 3.750 (D) 5,000 ( )
46) ¿Cuántos bloques hay en ese montón?
(A) 16 (B) 17 (C) 18 (D) 19 ( )
47) Indispensable aproximadamente significa:
(A) Inútil (B) Útil (C) Importante (D) Necesario ( )
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
48) ¿Cuántos grados de un gráfico circular deberían sombrearse para indicar que el 10 % de todas las personas fuman tabaco en una u otra forma?
(A) 10° (B) 15° (C) 18° (D) 36° ( )


49) ¿Cuántos bloques hay en ese montón?
(A) 17 (B) 18 (C) 19 (D) 20 ( )
50) Un vestigio aproximadamente significa:
(A) Una capa (B) Una pérdida (C) Una plaga (D) Un rastro ( )
51) Pedro y Juan tienen entre los dos $ 4,000.00. Si los ¾ del dinero de Pedro equivalen a la ½ del dinero de Juan, ¿cuánto dinero pertenece a Pedro?
(A) $ 1,200 (B) $ 1,500 (C) $ 1,600 (D) $ 2,400 ( )
52) ¿Cuántos bloques hay en ese montón?
(A) 11 (B) 12 (C) 13 (D) 14 ( )
53) Egregio aproximadamente significa:
(A) Apropiado (B) Congregante (C) Designado (D) Insigne ( )
54) Una casa valorada en $ 1,000,000.00 fue asegurada durante un año por el 90 % de su valor original a razón de $ 1.00 por cada $ 1,000. ¿A cuánto ascendió la prima anual del seguro de la casa?
(A) $ 900 (B) $ 1,000 (C) $ 9,000
(D) $ 10,000 ( )
¡DETÉNGASE AQUÍ! NO REPASE LOS EJERCICIOS
Protocolo para la Prueba de Capacidad de Comprensión - Forma “A” Instrucciones. Escriba dentro del paréntesis la letra que elija respuesta en cada uno de los reactivos.
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Clave para Calificar la Prueba de Capacidad de Comprensión Forma “A”

Instrucciones. Se dará un punto por cada respuesta que coincida con la siguiente clave:
Tabla para convertir la puntuación natural en niveles de comprensión Instrucciones. Se suman los aciertos y se ubican en la siguiente tabla para considerar los siguientes criterios:
Hoja de reflexión # 2
Capacidad de comprensión Instrucciones. Después de haber resuelto y calificado la prueba, escribe en los recuadros tus estrategias de acción para la intervención
Estrategias de acción
¿Qué aspectos le ayudan a estar bien? ¿Qué quiero que conserve?
¿Qué aspectos le obstaculizan? ¿Qué necesita modificar?
¿Cómo pienso ponerle la práctica? ¿Cuál es el objetivo y en cuánto tiempo lo ha de lograr?
¿De qué me di cuenta?
¿Qué necesita modificar?
¿Cómo pienso ayudarlo?
Prueba # 3. Cubos y Dibujos de Kohs
Ficha técnica
• Nombre: Cubos de Kohs o prueba de cubos y dibujos.
• Autor: S. C. Kohs
• Editorial: Cronopios. http://cronopios.cl/?prueba-cubos-de-kohs,29,,,3
• Fuente: http://es.scribd.com/doc/86149858/Protocolo-Test-Cubos-de-Kohs

• Tipo de prueba: estandarizada.
• Mide: inteligencia abstracta: percibir figuras para hacer su análisis y síntesis a través de la reproducción de las láminas estímulo.
• Edad: 5 a 20 años.
• Administración: individual.
• Material: 16 cubos con diseños iguales, tarjeta de ensayo, 16 tarjetas o láminas con los diseños, cronómetro, protocolo, pluma.

a) 16 cubos iguales, 2.5 cm., de arista, pintados de los siguientes colores:
o Una cara roja, una azul, una amarilla y una blanca.
o Una cara roja/azul; otra roja/blanca; roja/amarilla.
b) 16 láminas coloreadas en complejidad creciente que se han organizado con caras de un solo color y con caras de dos colores.
o Láminas 1 – 9: se construyen con cuatro cubos.
o Láminas 10 – 11: se construyen con nueve cubos.
o Láminas 12 – 16: se construyen con 16 cubos.
c) Tarjetas: tienen dos números: Los romanos indican el orden en que se han de presentar al sujeto; arábigos: el tiempo máximo asignado para su reproducción.
• Estructura: 16 reactivos.
• Áreas: matemáticas y perceptiva: posición en el espacio.
Objetivo:
Informar sobre la capacidad de integrar desde el punto de vista viso-perceptivo-motriz estímulos gráficos, analizar dichos estímulos y sintetizarlos en volumen.
Procedimiento:
1. Se le presenta al sujeto la primera lámina que sirve de entrenamiento
2. Se pide al sujeto que nombre los colores representados en cada una de las caras de un cubo. Si no fuera capaz de discriminar los colores, la prueba debe ser suspendida.
3. Se le pide que componga con los cubos el diseño mostrado.
4. La figura debe estar a la vista del sujeto en el momento de la ejecución. Siempre se le deben entregar los 16 cubos.
5. Si el examinado no es capaz de realizar la tarea, el orientador la armará lentamente hasta que se dé cuenta de lo que se le está pidiendo.
6. Si el sujeto falla o no entiende la orden, se suspende la prueba.
7. Instrucciones: “Usando estos cubos, arma la figura que está en el diseño”.
8. Vigilar que para la formación de la figura ocupe un plano horizontal. No se acepta en sentido vertical.
Valoración y normas
Para la valoración y normas, se sigue la sugerencia del Dr. Feldman y no la original pues, en esta última, el objetivo es medir la capacidad general del sujeto.
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Valoración: Se asignan los puntos que señala la tabla; si el tiempo de ejecución no excede el que corresponde, si lo excediera, no se otorgan puntos.
NOTA: La prueba se considera terminada cuando el examinado comete cinco (5) errores consecutivos.
Tabla de puntajes y Tiempos correspondientes
Cuadro # 5. Tabla de puntajes y tiempos correspondientes para los cubos.
Comparar edad cronológica con edad mental.
PN = Puntuación natural EM = Edad Mental
Tabla
Instrucciones. Buscar la edad mental del sujeto con base en la puntuación natural que obtuvo en la prueba.
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Cuadro # 6. Tabla de equivalencias EM para los cubos.
Protocolo de la Prueba de Cubos de
Kohs
Instrucciones. Registrar con cuidado el desempeño del sujeto con base en los datos sugeridos en la siguiente tabla.
Tabla de registro
Cuadro # 7. Tabla de registro.
Tabla de comparación
Edad cronológica Puntaje obtenido
Observaciones:
Análisis cualitativo:
Edad mental
Nombre y firma del orientador
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Material de la Prueba Cubos de Kohs
Instrucciones. Imprime las tarjetas, plastifícalas y sepáralas, de manera que estén las 16 tarjetas en forma independiente.

Recomendaciones
1. Es conveniente ponerle un mantel individual al examinado con el fin de que tenga delimitado su espacio de trabajo.
2. Los cubos deben estar colocados en la parte superior derecha del examinado, si éste es diestro; o del lado izquierdo si es zurdo. Las tarjetas se colocan arriba, al centro, de manera que el sujeto las pueda ver con facilidad.
Protocolo Ilustrado de Cubos de Kohs



















No. Lámina Tiempo Puntos por prueba Puntos acumulados
Figuras Puntaje Edad
12 13 14 15 16


Total: PN: EM: Cuadro # 8. Protocolo de registro de cubos de Kohs.







Hoja de reflexión # 3 Cubos y dibujos
Instrucciones. Después de haber resuelto y calificado la prueba, escribe en los recuadros tus estrategias de acción para la intervención


Estrategias de acción

¿Qué aspectos le ayudan a estar bien? ¿Qué quiero que conserve?
¿Qué aspectos le obstaculizan? ¿Qué necesita modificar?
¿Cómo pienso ponerle la práctica? ¿Cuál es el objetivo y en cuánto tiempo lo ha de lograr?
¿De qué me di cuenta?
¿Qué necesita modificar?
¿Cómo pienso ayudarlo?
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Prueba # 4. Precálculo
Ficha técnica
• Nombre: MPP – Prueba de precálculo. Editorial Universitaria
• Autores: Neva Milici, Sandra Schmidt (2002).
• Adaptación: Tere Silva.
• Fuente: http://es.scribd.com/doc/4727001/PRUEBA-PRECALCULO
• Aplicación: individual y colectiva
• Edad: 4 a 7 años
• Duración: 60 minutos aproximadamente
• Objetivo: evaluar el desarrollo del razonamiento matemático
• Baremos: normas en percentiles
• Material: manual, cuaderno de estímulos y protocolo.

¿Qué evalúa?
• Evalúa el desarrollo del razonamiento matemático.
• Pretende detectar a niños con alto riesgo de presentar problemas de aprendizaje de las matemáticas antes de que sean sometidos a la enseñanza formal de ellas, con el fin de poder proveer a estos niños de programas compensatorios y remediales en el momento oportuno.
• Además, orientar la rehabilitación de las áreas que aparecen deficitarias a través de técnicas de estimulación y apresto.
Áreas que considera y sus objetivos
• Se basa en 19 funciones psicológicas básicas expresadas en 118 ítems.
• Cada subprueba tiene un número variable de reactivos que oscila entre 4 y 25 preguntas, ordenadas en dificultad creciente.
Descripción de la prueba
La prueba está compuesta de 10 subpruebas que tratan de evaluar el desarrollo del razonamiento matemático en niños de 4 a 7 años. Específicamente, pretende detectar a niños con alto riesgo de presentar problemas de aprendizaje en matemáticas.
I. Conceptos básicos
• Cantidad * Orden *Tamaño *Espacio
• Dimensión * Relaciones * Forma * Distancia
II. Percepción visual
• Ubicar una figura diferente a una serie dada.
• Ubicar una figura igual al modelo
III. Correspondencia término a término
• Aparear cada uno de los objetos de un grupo con los de otro grupo.
IV. Números ordinales
• Establecer un orden.
V. Reproducción de figuras y secuencias
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
• Coordinación visomotriz.
VI. Reconocimiento de figuras geométricas
• Cuadrado
• Rectángulo.

VII. Reconocimiento y reproducción de números
• Identificar un número.
VIII. Cardinalidad
• Cantidad de elementos.
IX. Solución de problemas aritméticos
• Datos
• Operación
• Resultado
X. Conservación
• Los elementos de dos colecciones son iguales o diferentes.
¿Qué aspectos se deben tener en cuenta?
• La prueba no contempla tiempo fijo de aplicación.
• Las instrucciones se darán con voz clara, pareja y alta.
Subpruebas
1. Conceptos básicos
2. Percepción visual
3. Correspondencia término a término
4. Números ordinales
5. Reproducción de figuras y secuencias
6. Reconocimiento de figuras geométricas
7. Reconocimiento y reproducción de números
8. Cardinalidad
9. Solución de problemas aritméticos
10. Conservación
Materiales
• Examinador: manual con instrucciones, protocolo, pluma, reloj. Sacapuntas.



• Examinado: cuadernillo de respuestas, lápiz del # 2 o 2 ½
y protocolo
• Primera Parte: Describe algunas características del Razonamiento Matemático (Capítulo I), la descripción de la Prueba de Precálculo (Capítulo II) y la elaboración y Estudios experimentales de la prueba (Capítulo III).


• Segunda Parte: Presenta dos Aplicaciones Experimentales: Análisis Ítem a Ítem y Obtención de Normas (Capítulo IV y V), y las Características Psicométricas del Instrumento (Capítulo VI).
• Anexos: Instrucciones y baremos. Pauta de Corrección. Ejemplos de Puntuación de ítems. Protocolo para la puntuación de la Prueba; además de casuística y análisis de protocolos.
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
¿Cómo se administra?
Administración
• Puede aplicarse de manera individual o colectiva (en esta última modalidad es deseable contar con ayudantes).
▪ Si son menores de 5 años los grupos pueden tener hasta 3 niños.
▪ Si son mayores de 5 años los grupos pueden incluir como máximo 10 niños.
• Puede ser administrado por profesores de enseñanza básica, educadoras de jardín de niños, psicólogos, pedagogos y otros especialistas en el área de educación.
• Es indispensable estar familiarizado con el instrumento antes de utilizarlo, dominar las instrucciones y la pauta de corrección.
• Se debe tener cuidado con los distractores en el ambiente de aplicación.
• Se debe tener un registro del tiempo utilizado: desde que se inicia el test hasta que se termina descontando el tiempo utilizado en los recreos dados al niño.
• En el área de deficiencia mental se administra siempre en forma individual, y no hay límites de tiempo.
• Su evaluación es cuantitativa y cualitativa.
Instrucciones


I. Conceptos básicos
Evalúa: si están adquiridos los conceptos de cantidad, dimensión, orden, relaciones, tamaño, espacio, forma, distancia y tiempo ligados al lenguaje aritmético.
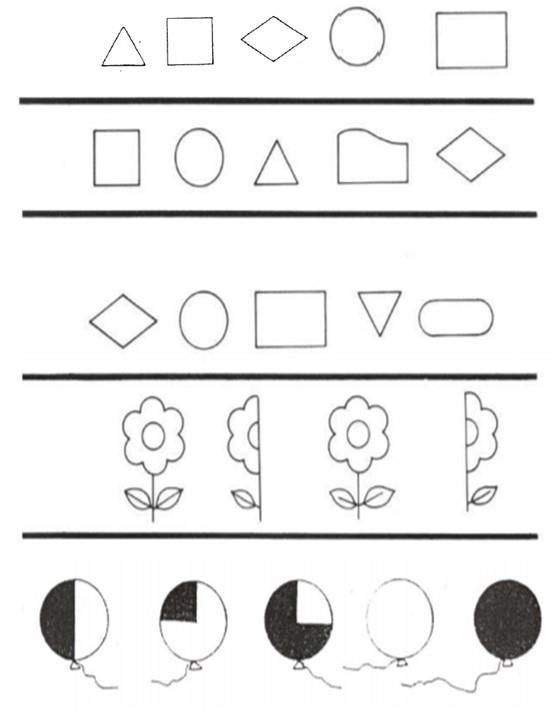
Ejemplo: En estos ítems, el niño debe marcar la figura según su tamaño (siguiendo las instrucciones del examinador). “En esta hoja:
15. Marca el instrumento que tiene más cuerdas.
16. Marca la palmera que tiene menos cocos
17. Marca la copa más ancha
18. Marca la botella más angosta.
19. Marca la chalina más angosta”.
II. Percepción visual
Evalúa: si el niño logra discriminar figuras igual al modelo, ubicar la figura diferente de una serie y reconocer un número dentro de una serie, igual al modelo con claves visuales próximas.
Ejemplo: En estos ítems, el niño debe reconocer la figura igual al modelo.
25. “En esta fila marca el que es igual al camión”.
26. “En esta fila marca el que es igual al círculo”.
III. Correspondencia término a
término
Evalúa: la capacidad para aparear objetos que se relacionan por su uso, es decir, evalúa el concepto de equivalencia de los grupos
Ejemplo: “Aquí hay dos filas de dibujos, une con una línea cada dibujo de esta fila (mostrar) con la figura que le corresponde de ésta otra fila” (mostrar)
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
IV. Números ordinales
Evalúa: el reconocimiento de los conceptos 1º, 2º, 3º y último.

Ejemplo: El niño debe reconocer el tercer oso y el primer gallo respectivamente.
52. Marca el tercer osito
53. Marca el primer gallo

V. Reproducción de figuras, números y secuencias
Evalúa: la coordinación visomotora, en el sentido de la reproducción de formas.

Ejemplo: El niño debe reproducir patrones perceptivos, según el modelo (ejemplo: ítem 65). Y dibujar la figura que continua de una serie
65. Pinta los círculos que están vacíos (mostrar) para que queden igual a éstos (mostrar).
VI. Reconocimiento de figuras geométricas

Evalúa: la habilidad perceptiva visual del niño en el reconocimiento de las formas geométricas básicas, lo cual supone un vocabulario geométrico y asociación de conceptos geométricos con los símbolos gráficos que los representan, y además el reconocimiento del concepto de mitad.

Ejemplo: El niño debe identificar el triángulo y la flor que está a la mitad.
83. Marca el rectángulo.

84. Marca las mitades de la flor.

VII. Reconocimiento y reproducción de números
Evalúa: la capacidad de identificar el número que lees nombrado dentro de una serie, reproducir un símbolo numérico cuando se le es nombrado; realizar operaciones simples: primero, agregando o quitándolos elementos pedidos.



Ejemplo: en el ítem 94 el niño debe dibujar 1 elemento más que el modelo, y en el ítem 96 dos elementos menos que el modelo dado.
94. Dibuja en este cuadro (mostrar) el mismo número de círculos que hay aquí (mostrar).
96. Dibuja aquí (mostrar) dos casitas menos de las que hay en el modelo (mostrar).
VIII. Cardinalidad
Evalúa: la capacidad para identificar y dibujar la cantidad de elementos pedidos.
Ejemplo: El niño debe dibujar el número que corresponde a una determinada cantidad de elementos dados
105. Escribe aquí (mostrar) el número que corresponde a la cantidad de círculos del conjunto
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
IX. Problemas aritméticos
Evalúa: la habilidad para realizar operaciones simples de adición y sustracción.
Ejemplo: En el primer caso el niño debe marcar la cantidad de bolitas que quedan después de quitar 2 a los que tenía originalmente. Y en el segundo caso el niño debe marcar la cantidad de helados que quedan después de haber agregado 3 a los 3 helados que tenía previamente.
109. Escucha bien lo que te voy a decir: “yo tenía cinco bolitas y perdí dos. En la fila de las bolitas, marca las que me quedaron”.
110. “Tú tenías tres paletas y tu mamá te regala tres más. En la fila de las paletas, marca los que tienes ahora”.
X. Conservación
Evalúa: la habilidad para juzgar si dos colecciones de objetos son iguales o diferentes respecto de su cantidad de elementos.
Ejemplo: El niño debe marcar los pares de conjuntos que tienen igual cantidad de elementos
113. “Fíjate en la primera fila, aquí (mostrar). Cuenta la cantidad de círculos que hay en cada conjunto… ¿son iguales?, si son iguales, márcalos. Si son distintos, no hagas ninguna marca.

Protocolo

Prueba de Precálculo No. Exp.:
Nombre:
Edad:
Fecha: Tiempo:
Instrucciones. Escribe en la primera columna (PN = puntuación natural) el número de ítems correctos que obtuvo en cada apartado. Busca en los baremos el percentil (Pc) correspondiente a cada puntuación.
Subpruebas
I. Conceptos básicos
II. Percepción visual
III. Correspondencia

IV. Números ordinales
V. Reproducción de figuras y secuencias
VI. Reconocimiento de figuras geométricas

VII. Reconocimiento y reproducción de números
VIII. Cardinalidad
IX. Problemas aritméticos
X. Conservación
Diagnóstico:
Pronóstico:
Observaciones:
Recomendaciones:
Total
Puntuación natural Percentiles
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Calificación e interpretación

• Respuesta correcta, se otorga 1 punto y si es incorrecta se señala 0 punto.
• Cómputo de resultados: se cuenta los ítems respondidos en forma correcta, para cada prueba se anotan estos puntajes y luego se suman para obtener el puntaje total de la prueba, pudiendo obtenerse un máximo de 118.
• Los puntajes brutos totales: (puntuación natural) y de las cinco subpruebas, se transforman en percentiles
PRUEBA DE PRECÁLCULO

Para evaluar el desarrollo del razonamiento matemático en niños de 4 a 7 años
Neva Milicic M. Sandra Schmidt M


















María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
Anexo
Cuadernillo de instrucciones de la prueba Precálculo
A. Instrucciones generales para el examinador
Esta prueba está destinada a evaluar el desarrollo del razonamientomatemático en niños cuyas edades fluctúan entre 4 y 7 años.
La prueba puede ser aplicada en forma individual o colectiva, entendiéndose por colectiva grupos de no más de tres niños entre 4 años 1 mes y 5 años. Para niños mayores de 5 años, el grupo puede incluir hasta 10 niños.
• En las aplicaciones colectivas es recomendable contar con un ayudante.
• Dadas las características la prueba, puede ser administrado por profesores de Enseñanza Básica, Educadores de Párvulos, Psicólogos y otros especialistas en educación.
• Es indispensable que el examinador, conozca previamente la prueba, tanto desde el punto de vista teórico como práctico.
• Se recomienda una primera aplicación individual, para familiarizarse con las instrucciones y la pauta de corrección.

Materiales
• Para el examinador: un cuadernillo de instrucciones, un cuadernillo de la prueba, lápices de reemplazo, sacapuntas y reloj para control de tiempo.
• Para el niño: Cuadernillo de la prueba y lápiz negro, de mina blanda. No se permitirá al niño el uso de lápices de colores, pasta, cera ni goma de borrar. Es importante dejar fuera del alcance de los niños cualquier elemento que distraiga o distorsiones el rendimiento en el test.
• Ambiente físico: por la influencia que tiene el ambiente sobre el rendimiento del niño es necesario considerar los siguientes aspectos: disponer de un espacio amplio que permita ubicar a los niños a una distancia de alrededor de un metro y medio entre uno y otro. Luz natural o artificial suficiente, ventilación adecuada.
Comentarios
• La prueba de Precálculo surge de la comprensión intuitiva de las experiencias.
María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
• Los niños que presentan dificultades en la Prueba deben ser considerados en términos de no haber logrado un determinado nivel de desarrollo, pero ello no autoriza a realizar inferencias clínicas.
• La Prueba de Precálculo es una útil herramienta que orienta las posteriores derivas de los niños evaluados: escolaridad normal, programas de estimulación, derivación clínica para diagnósticos diferenciales.
• En el área de deficiencia mental se administra siempre en forma individual, y no hay límites de tiempo.
• La Prueba de Precálculo es muy útil para orientar la rehabilitación de las áreas que aparecen deficitarias a través de técnicas de estimulación y apresto.
Indicaciones específicas
Poner en la portada:
• Nombre completo del examinado.
• Edad: años y meses.
• Fecha de aplicación.
• Hora de inicio y hora de termino.
• Descontar los descansos que se le den al examinado.
Nota: En la aplicación colectiva, el examinado puede sombrear la portada con el lápiz mientras espera que inicie la actividad.
El examinador debe decir lo siguiente:
• “En este cuadernillo vamos a jugar a hacer algunos ejercicios. Tienes que trabajar solo, no hablar con tus compañeros, y si tienes alguna pregunta que hacer, levanta el dedo; no hagas ninguna marca antes que te lo pidan, no abras el librito; mientras tanto, pinta el dibujo de la portada.
• Una vez que todos los niños tengan el cuadernillo, decir: “Abran el cuadernillo en la página de la manzana” (página 3).

• En este momento, anote la hora de comienzo.

I. Conceptos básicos



María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas


II. Percepción visual




María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas
III. Correspondencia término a término
IV. Números ordinales




María Teresa Alicia Silva y Ortiz. Batería básica para las DAM – Yo y las matemáticas