GENIE Fysica 5 Leerboek - Inkijkexemplaar by VAN IN

GENIE 5 Fysica

©VANIN

GENIE 5 Fysica ©VANIN

Via www.ididdit.be heb je toegang tot het onlineleerplatform bij GENIE Fysica leerboek 5. Activeer je account aan de hand van de onderstaande code en accepteer de gebruiksvoorwaarden. Kies je ervoor om je aan te melden met je Smartschool-account, zorg er dan zeker voor dat je e-mailadres aan dat account gekoppeld is. Zo kunnen we je optimaal ondersteunen.

!©VANIN

GENIE 5 Fysica

LET OP: DEZE LICENTIE IS UNIEK, EENMALIG TE ACTIVEREN EN GELDIG

VOOR EEN PERIODE VAN 12 MAANDEN NA ACTIVATIE.

Help, de activatiecode hierboven is al gebruikt!

Krijg je bij het activeren van de bovenstaande code de melding dat de activatiecode reeds in gebruik is? Dan ben je wellicht niet de eerste leerling die met dit leerboek aan de slag gaat. Op vanin.be/leerboeklicentie kun je terugvinden welke stappen je kunt ondernemen of hoe je een nieuwe licentie kunt aankopen.

Tip: Normaal gezien mag je niet schrijven in een leerboek. Per uitzondering mag jij na activatie de bovenstaande activatiecode doorstrepen.

Fotokopieerapparaten zijn algemeen verspreid en vele mensen maken er haast onnadenkend gebruik van voor allerlei doeleinden. Jammer genoeg ontstaan boeken niet met hetzelfde gemak als kopieën. Boeken samenstellen kost veel inzet, tijd en geld. De vergoeding van de auteurs en van iedereen die bij het maken en verhandelen van boeken betrokken is, komt voort uit de verkoop van die boeken.

In België beschermt de auteurswet de rechten van deze mensen. Wanneer u van boeken of van gedeelten eruit zonder toestemming kopieën maakt, buiten de uitdrukkelijk bij wet bepaalde uitzonderingen, ontneemt u hen dus een stuk van die vergoeding. Daarom vragen auteurs en uitgevers u beschermde teksten niet zonder schriftelijke toestemming te kopiëren buiten de uitdrukkelijk bij wet bepaalde uitzonderingen. Verdere informatie over kopieerrechten en de wetgeving met betrekking tot reproductie vindt u op www.reprobel.be.

Ook voor het digitale lesmateriaal gelden deze voorwaarden. De licentie die toegang verleent tot dat materiaal is persoonlijk. Bij vermoeden van misbruik kan die gedeactiveerd worden. Meer informatie over de gebruiksvoorwaarden leest u op www.ididdit.be.

De uitgever heeft ernaar gestreefd de relevante auteursrechten te regelen volgens de wettelijke bepalingen. Wie desondanks meent zekere rechten te kunnen doen gelden, wordt verzocht zich tot de uitgever te wenden.

Credits p. 10 foto IJzervijlsel staafmagneet: Dorling Kindersley / UIG © Science Photo Library, p. 60 Weerkaart temperatuur © Koninklijk Meteorologisch Instituut, p. 60 Weerkaart windsnelheid © Koninklijk Meteorologisch Instituut, p. 81 foto Metalen kooi: Peter Menzel © Science Photo Library, p. 81 foto Vliegtuig en bliksem: David Parker © Science Photo Library, p. 82 foto Diepte van de oceaan op de noordpool: NOAA © Science Photo Library, p. 82 foto Kinderen bij plasmabol: frantic00 © Shutterstock, p. 110 foto’s Elektromagneet 1 en 2: Turtle Rock Scientific / Science Source © Science Photo Library, p. 110 foto Paperclips aan hand © Science Photo Library, p. 111 foto Staafmagneet en hoefijzermagneet © Mathieu Marck, p. 113 Elektromagneet met paperclips: Giphotostock © Science Photo Library, p. 115 foto’s Kompasnaalden rechte geleider zonder en met stroom, Giphotostock © Science Photo Library, p.119 foto’s IJzervijlsel bij gelijksoortige en ongelijksoortige polen: Cordelia Molloy © Science Photo Library, p. 120 IJzervijlsel rechte stroomvoerende geleider: New York Public Library © Science Photo Library, p. 121 tekening Rechterhandregel rechte geleider: Mikkel Juul Jensen © Science Photo Library, p. 121 foto IJzervijlsel stroomvoerende lus: New York Public Library © Science Photo Library, p. 122 tekening Tweede rechterhandregel spoel: Mikkel Juul Jensen © Science Photo Library, p. 122 foto IJzervijlsel rond spoel: Andrew Lambert Photography © Science Photo Library, p. 137 foto Kompas en magneet: Giphotostock © Science Photo Library, p. 139 foto Teslameter: Public Health England © Science Photo Library, p. 139 foto Supergeleidende magneet: Belish © Shutterstock, p. 148 foto Kathodestraalbuis: Charles D. Winters / Science Source © Science Photo Library, p. 150 tekening Bouw van een beeldscherm © Science Photo Library, p. 161 foto Opstelling koperdraad balans: Trevor Clifford Photography © Science Photo Library, p. 177 foto Vrijevaltoren: FAG © Shutterstock, p. 193 foto Large Hadron Collider: Pascal Boegli © Getty Images, p. 206 foto Reconstructie Ötzi: Zigres © Shutterstock, p. 216 foto Albert Einstein: Library of Congress © Science Photo Library, p. 227 foto Portret Enrico Fermi: Bridgeman © Belga Image, p. 229 foto Controlestaven in een kernreactor: EOL Studios © Shutterstock, p. 230 foto Hiroshima: Everett Collection © Shutterstock, p. 234 foto Lawrence Livermore Laboratory: Zuma Press © Belga Image, p. 236 foto Fukushima: Fly_and_Dive © Shutterstock, p. 241 foto Pierre en Marie Curie: Bettmann / Contributor © Getty Images, p. 241 foto Henri Becquerel: Boyer / Contributor © Getty Images, p. 249 foto Alfastralers: Aquatarkus © Shutterstock, p. 275 kaart Radongas België © Federaal Agentschap voor Nucleaire Controle, p. 277 foto Handen Japanse vrouw: Rolls Press / Popperfoto / Contributor © Getty Images, p. 278 foto Afscherming kernreactor Tsjernobyl: German Meyer © Getty Images, p. 283 foto Kankerbehandeling radiotherapie: Nicolas Randall © Shutterstock

Eerste druk 2024

ISBN 978-94-647-0704-5

Vormgeving en ontwerp cover: Shtick

Tekeningen: Geert Verlinde, Tim Boers (Studio B) D/2023/0078/90

Art. 606871/01

NUR 120

Zetwerk: Zyncke Vanderplancke

INHOUD ©VANIN

THEMA 01: KRACHT EN VELD

` HOOFDSTUK 1

Kracht 11

1 Welke kenmerken hebben vectoriële grootheden? 11

1.1 Krachtvector 11

1.2 Scalaire en vectoriële grootheden 12

2 Hoe stel je vectoren samen? 13

2.1 De resulterende vector 13

2.2 Vectoren met dezelfde richting optellen 14

2.3 Vectoren met een verschillende richting optellen 15

3 Wat zijn de bewegingswetten van Newton? 18

3.1 Eerste wet van Newton 18

3.2 Tweede wet van Newton 19

3.3 Actie-reactie 21

` HOOFDSTUK 2

Elektrische kracht en gravitatiekracht 27

1 Wat is statische elektriciteit? 27

2 Hoe worden voorwerpen geladen? 29

2.1 Elektrisch gedrag van stoffen 29

2.2 Voorwerpen laden door wrijving 33

2.3 Geleiders laden door contact 35

3 Welke eigenschappen heeft de kracht tussen ladingen? 37

3.1 Elektrische kracht tussen twee puntladingen 37

3.2 Elektrische kracht tussen meerdere puntladingen 40

4 Hoe kan er een aantrekking zijn tussen een geladen voorwerp en een neutraal voorwerp? 43

4.1 Geleider 43

4.2 Isolator 45

5 Hoe is de krachtwerking tussen massa’s vergelijkbaar met de krachtwerking tussen ladingen? 47

5.1 Zwaartekracht bij hemellichamen 47

5.2 Massa van een voorwerp 48

5.3 Algemene gravitatiekracht 49

5.4 Analogie tussen de coulombkracht en de gravitatiekracht 52

` HOOFDSTUK 3

Elektrisch veld en gravitatieveld 59

1 Wat is een veld bij een veldkracht? 59 1.1 Veld 59 1.2 Soorten velden in de fysica 60 1.3 Veldkrachten en hun veld 62

2 Hoe kun je een elektrisch veld kwalitatief voorstellen? 63

2.1 Een elektrisch veld zichtbaar maken 63

2.2 Elektrische veldlijnen 64

2.3 Verschillende configuraties van elektrische velden 65

2.4 Kwalitatief verband tussen elektrische veldlijnen en elektrische veldkracht 67

3 Hoe kun je een gravitatieveld kwalitatief voorstellen? 68

3.1 Het gravitatieveld 68

3.2 Het gravitatieveld als radiaal veld 68

3.3 Het gravitatieveld benaderen als een homogeen veld 69

4 Welke grootheid beschrijft een gravitatieveld? 70

5 Welke grootheid beschrijft een elektrisch veld? 75

5.1 Elektrische veldsterkte 75

5.2 De elektrische veldsterkte in een radiaal veld 76

5.3 De elektrische veldsterkte in een homogeen veld 79 5.4 Elektrische schermwerking 80

` HOOFDSTUK 4

Energie in een gravitatieveld en in een elektrisch veld 88

1 Welke energieomzettingen zijn er in een stroomkring? 88

2 Wat is potentiële energie bij een veldkracht? 90

3 Hoe kun je de potentiële energie in een veld kwantificeren? 93

4 Wat is spanning? 96

4.1 Potentiaalverschil in het homogeen gravitatieveld 96

4.2 Potentiaalverschil in het homogeen elektrisch veld 99

` HOOFDSTUK 5

Eigenschappen van magneten 109

1 Welke soorten magneten bestaan er? 109

2 Welke kwalitatieve kenmerken heeft de magnetische kracht? 111

2.1 Krachtwerking tussen permanente magneten 111

2.2 Krachtwerking tussen een magneet en een magnetisch voorwerp 113

2.3 Krachtwerking tussen een magneet en een stroomvoerende geleider 115

3 Hoe ziet het veldlijnenpatroon rondom magneten eruit? 117

3.1 Magnetisch veld rond een permanente magneet 117

3.2 Magnetisch veld rond een elektromagneet 120

4 Hoe maak je van ferromagnetische materialen een magneet? 123

4.1 De microscopische structuur van ferromagnetische materialen 123

4.2 Magnetiseren 125

4.3 Permanente magneten demagnetiseren 127

5 Welke toepassingen hebben magneten? 127

5.1 Elektromagneten 127

5.2 Permanente magneten 128

5.3 De magnetische velden van hemellichamen 129

` HOOFDSTUK 6

Magnetische veldsterkte en magnetische kracht 137

1 Wat is magnetische veldsterkte? 137

2 Hoe groot is de magnetische veldsterkte bij een elektromagneet? 140

2.1 Algemeen 140

2.2 De magnetische veldsterkte bij een stroomvoerende spoel 140

2.3 De magnetische veldsterkte rondom een rechte stroomvoerende geleider 143

3 Hoe groot is de magnetische kracht op bewegende ladingen in een magnetisch veld? 145

` HOOFDSTUK 7

Elektromagnetische inductie 166

1 Hoe kun je spanning opwekken met een magnetisch veld? 166

1.1 Veranderend magneetveld 166

1.2 Fluxverandering 168

2 Welke eigenschappen heeft de inductiespanning? 171

2.1 Geïnduceerd magnetisch veld 171

2.2 Eigenschappen van de inductiespanning 172

3 Hoe wordt magnetische inductie gebruikt in technologische toepassingen? 173

3.1 Spanning opwekken in een elektrische kring 173

3.2 Wervelstromen in geleiders 176

©VANIN

3.1 Kracht op een stroomvoerende geleider 145

3.2 Kracht op bewegende ladingen 148

4 Hoe kun je de krachtwerking tussen magneten verklaren? 151

4.1 Kracht tussen elektromagneten 151

4.2 Kracht tussen permanente magneten 155

5 Hoe wordt de elektromagnetische krachtwerking gebruikt? 156

5.1 De laplacekracht op een elektromagneet 156

5.2 De lorentzkracht op een lading 158

THEMA 02: KERNFYSICA

` HOOFDSTUK 1

Stabiele en instabiele kernen 188

1 Hoe is een atoomkern opgebouwd? 188

1.1 Samenstelling van de kern 188

1.2 Isotope nucliden 191

1.3 De kleinste bouwstenen 192

2 Welke krachten bepalen de stabiliteit van de kern? 194

2.1 Stabiele kernen op de nuclidenkaart 194

2.2 De kernkrachten 196

2.3 De vier fundamentele interacties 198

3 Welke stabiele en instabiele kernen bestaan er? 200

4 Welke meetbare grootheid is een maat voor de stabiliteit van de kern? 203

4.1 De halveringstijd 203

4.2 Het verband tussen de halveringstijd en de stabiliteit van kernen 207

` HOOFDSTUK 2

Kernenergie

` HOOFDSTUK 3

Radioactief verval 240

1 Welke straling komt vrij bij radioactief verval? 240

1.1 Straling bij radioactief verval 240

1.2 Eigenschappen van straling 241

©VANIN

212

1 Wat is het verband tussen massa en energie? 212

1.1 De atomaire massa-eenheid 212

1.2 Massadefect 213

1.3 Equivalentie tussen massa en energie 215

1.4 De MeV als eenheid voor kernenergie 217

2 Wat is de energie van een nucleon in een kern? 218

2.1 De specifieke rustenergie 218

2.2 De energievallei 219

3 Hoe wordt kernenergie vrijgemaakt uit kernen? 220

3.1 De specifieke bindingsenergie 220

3.2 De relatie tussen de specifieke bindingsenergie en de specifieke rustenergie 222

3.3 Energie uit lichte en zware kernen 223

3.4 Energieopbrengst bij kernsplitsing 224

3.5 Energieopbrengst bij kernfusie 225

4 Hoe kunnen we kernsplitsingsenergie gebruiken? 226

4.1 Spontane en niet-spontane splitsing 226

4.2 De splitsing van 235U 226

4.3 Kettingreacties 227

4.4 Kernsplitsingsreactoren 229

5 Hoe kunnen we kernfusie-energie gebruiken? 231

5.1 Kernfusie in de zon 231

5.2 Kernfusie op aarde 233

1.3 De verschillende soorten straling bij radioactief verval 242

1.4 β–-straling en β+-straling 244

2 Wat is de oorzaak van de verschillende soorten radioactief verval? 246

3 Hoe veranderen de kernen van samenstelling bij de verschillende soorten radioactief verval? 248

3.1 Behoudswetten bij kernreacties 248

3.2 Kernreactie bij α-verval 249

3.3 Kernreacties bij β-verval 251 3.4 γ-verval 255

4 Wat gebeurt er als instabiele kernen naar andere instabiele kernen vervallen? 257

` HOOFDSTUK 4

Effecten van ioniserende straling op de mens 261

1 Welke impact heeft ioniserende straling op de mens? 261

2 Hoe kun je jezelf beschermen tegen ioniserende straling? 263

2.1 Besmetting en bestraling 263

2.2 Voorzorgsmaatregelen 264

3 In welke grootheden en eenheden worden stralingsdosissen uitgedrukt? 265

3.1 Grootheden om stralingshoeveelheden uit te drukken 265

3.2 De hoeveelheid straling uitgezonden door de bron (in becquerel) 265

3.3 De stralingsdosis geabsorbeerd door je lichaam (in gray) 268

3.4 De biologische schade in je lichaam (in sievert) 271

4 Aan hoeveel natuurlijke en kunstmatige radioactiviteit worden we blootgesteld? 274

4.1 Gemiddelde jaarlijkse effectieve dosis 274 4.2 Toegelaten waarden 277

5 Hoe kan ioniserende straling bijdragen tot een genezingsproces? 279

5.1 Diagnose en behandeling 279

5.2 Medische beeldvorming 279

5.3 Radiotherapie 283

©VANIN

KRACHT EN VELD 01 THEMA

Elektriciteit is niet weg te denken uit onze maatschappij. Je merkt dan ook her en der in het landschap hoogspanningsleidingen die de elektrische energie van de elektriciteitscentrales naar de verbruikers brengen. Als je onder hoogspanningskabels wandelt, hoor je soms een knisperend geluid als gevolg van ontladingen.

` Welke kracht zorgt ervoor dat de elektrische stroom zich door de hoogspanningskabels verplaatst?

` Hoe komt het dat er effecten van elektrische stroom merkbaar zijn in de buurt van een geleider?

` Hoe kunnen deze verschijnselen gebruikt worden in technologische toepassingen?

We zoeken het uit!

VERKEN

JE KUNT AL ...

• de statische en dynamische uitwerking van een kracht omschrijven;

• een kracht voorstellen als vector;

• de resulterende kracht berekenen.

• voorbeelden geven van elektriciteit in het dagelijkse leven;

• de bouw van een atoom, geleiders en isolatoren omschrijven;

• de zwaartekracht bij een hemellichaam omschrijven, voorstellen en berekenen.

• het begrip veldkracht omschrijven;

• de coulomb- en gravitatiekracht omschrijven, voorstellen en berekenen.

• de kenmerken van een (kracht)vector omschrijven;

• (kracht)vectoren samenstellen;

• de drie bewegingswetten van Newton formuleren en toepassen in eenvoudige situaties.

• statische elektriciteit en het begrip ‘elektrische lading’ omschrijven;

• beschrijven hoe voorwerpen op atomaire schaal elektrisch geladen worden;

• de vier kenmerken van de elektrische kracht bepalen en weergeven;

• de elektrische kracht vergelijken met de gravitatiekracht.

• velden in het algemeen en soorten velden in de fysica omschrijven;

• het elektrisch veld en het gravitatieveld voorstellen met veldlijnen;

• de eigenschappen van het elektrisch veld en het gravitatieveld interpreteren;

• de grootheden gravitatieveldsterkte en elektrische veldsterkte definiëren en gebruiken.

JE LEERT NU ...

• potentiële zwaarte-energie omschrijven en berekenen;

• de werking van een stroomkring omschrijven met behulp van energieomzettingen;

• stroomsterkte en spanning in een stroomkring omschrijven.

• voorbeelden geven van magneten in het dagelijkse leven;

• de werking van een kompas beschrijven;

• elektrische velden zichtbaar maken en voorstellen;

• de beweging van elektronen in een geleider en in een atoom beschrijven.

©VANIN

• potentiële energie in een homogeen gravitatieveld en homogeen elektrisch veld omschrijven en berekenen;

• een potentiaal(veld) in een homogeen gravitatieveld en homogeen elektrisch veld omschrijven, berekenen en voorstellen;

• spanning in een homogeen gravitatieveld en homogeen elektrisch veld omschrijven en berekenen;

• stroomkringen omschrijven in termen van energie, potentiaal en spanning.

• gelijkenissen en verschillen tussen permanente magneten en elektromagneten omschrijven;

• de krachtwerking van een magneet omschrijven;

• magnetische veldlijnenpatronen tekenen en interpreteren;

• de fenomenen ‘magnetiseren’ en ‘demagnetiseren’ verklaren op atomaire schaal;

• enkele technologische toepassingen van (elektro)magneten geven.

JE KUNT AL ...

JE LEERT NU ...

VERKEN

JE KUNT AL ...

• kwalitatieve eigenschappen van de kracht tussen magneten omschrijven;

• het ontstaan en de vorm van verschillende magnetische velden omschrijven;

• kracht en veld in de buurt van een lading en een massa omschrijven en berekenen.

• het ontstaan van een magnetisch veld door bewegende ladingen (= elektrische stroom) omschrijven;

• de krachtwerking op bewegende ladingen in een magnetisch veld omschrijven en berekenen;

• magnetische velden voorstellen en magnetische veldsterkte berekenen.

©VANIN

• het magnetisch veld beschrijven met de magnetische veldsterkte;

• de magnetische kracht op een stroomvoerende geleider en op bewegende ladingen beschrijven, tekenen en berekenen;

• de grootte van de magnetische veldsterkte bij elektromagneten berekenen;

• de waargenomen elektromagnetische krachtwerking verklaren voor verschillende situaties;

• enkele toepassingen van de elektromagnetische kracht geven, toelichten en beschrijven.

• de opwekking van spanning met behulp van een magneet beschrijven;

• de grootte en het teken van de opgewekte spanning bepalen;

• het ontstaan en de kenmerken van de inductiestroom omschrijven;

• enkele toepassingen van elektromagnetische inductie geven, toelichten en beschrijven.

JE LEERT NU ...

HOOFDSTUK 1

Kracht

©VANIN

Je leerde de afgelopen jaren al over de verschillende soorten krachten en hun uitwerkingen. In dit hoofdstuk herhaal je de belangrijkste kenmerken van krachten en de bewerkingen die je met (kracht)vectoren kunt uitvoeren. Je maakt kort kennis met de wetten van Newton, zodat je ze in de verdere hoofdstukken van dit thema kunt toepassen.

LEERDOELEN

M de kenmerken van een (kracht)vector omschrijven

M bewerkingen met (kracht)vectoren uitvoeren

M de drie bewegingswetten van Newton formuleren en toepassen in eenvoudige situaties

1 Welke kenmerken hebben vectoriële grootheden?

1.1 Krachtvector

Om een systeem van snelheid of vorm te laten veranderen, is er een kracht nodig. De kracht wordt uitgeoefend door een systeem op een ander systeem. De kracht die uitgeoefend wordt, kun je niet rechtstreeks zien.

Een persoon oefent een kracht uit op de band. Je ziet de inspanning, maar de duwkracht zie je niet.

Een kind beweegt op en neer door de zwaartekracht (uitgeoefend door de aarde) en de veerkracht (uitgeoefend door de elastiek).

De magneet oefent een kracht uit op de deur. Het blad ertussen wordt zo opgehangen.

Je kunt de uitgeoefende kracht voorstellen door de krachtvector F. Kracht is een vectoriële grootheid, die je kunt voorstellen met vier kenmerken:

• aangrijpingspunt: het punt van het voorwerp waar de kracht op inwerkt;

• richting: de oriëntatie van de rechte die je door de vector kunt tekenen;

• zin: de kant naar waar de pijlpunt wijst;

• grootte: de getalwaarde van de kracht, aangegeven door de lengte van de pijl.

De krachtgrootte stel je voor met de letter F

kracht F newton [F] = N

Een systeem is een voorwerp of een verzameling van voorwerpen.

We nemen de grootte van een vector altijd positief. Om dat te beklemtonen, wordt soms een normteken bij de vector (bijvoorbeeld ‖F‖) of een absolutewaardeteken bij de grootte (bijvoorbeeld |F|) toegevoegd. Onder andere bij het werken met vectorcomponenten zal in geval van twijfel expliciet duidelijk gemaakt worden waar het om de grootte gaat door absolutewaardetekens toe te voegen (zie leerjaar 6).

VOORBEELD KRACHTEN TIJDENS HET SPORTEN

In de fitnesszaal oefen je een kracht uit op toestellen om je spieren te trainen. Je kunt die krachten voorstellen met een vector.

Yena heft de halter op met een kracht van 800 N.

Margot trekt aan het touw met een kracht van 500 N.

AANGRIJPINGSPUNT halter touw

RICHTING verticaal horizontaal

ZIN naar boven naar rechts

GROOTTE

F = 800 N

1.2 Scalaire en vectoriële grootheden

F = 500 N

Sommige grootheden kun je volledig beschrijven met een getalwaarde en een eenheid. Ze hebben een grootte, maar geen aangrijpingspunt, richting of zin. Dat zijn scalaire grootheden. Voorbeelden zijn temperatuur, druk, volume, lengte en energie.

Naast kracht bestaan er nog andere vectoriële grootheden met een grootte, richting, zin en aangrijpingspunt. Je leerde al de snelheidsvector v, positievector x en verplaatsingsvector ∆x kennen.

VOORBEELD BEWEGING VOORSTELLEN MET VECTOREN

Een bus vertrekt, rijdt een tijdje met een constante snelheid en vertraagt nadien. Je kunt die beweging voorstellen met vectoren. x (m) 0 x4 x5 Δx4-5 1 cm 20 m

Afb. 4 Positie- en verplaatsingsvector van de bus na het vertrek

v1 = 0 v5 v8 v12 = 0

▲ Afb. 5 Snelheidsvectoren tijdens de verschillende deelbewegingen van de bus

Snelheid: 1 cm 20 km h (= 5,6 m s )

• Scalaire grootheden zijn grootheden die enkel een grootte hebben. Temperatuur, druk, volume, lengte en energie zijn voorbeelden van scalaire grootheden.

• Vectoriële grootheden zijn grootheden die een aangrijpingspunt, richting, zin en grootte hebben. Je stelt ze voor met een vector (= pijl) en benoemt ze met een letter met een pijltje erboven. De grootte van de vector noteer je zonder het pijltje op de letter en wordt altijd positief genomen. Kracht F en de bewegingsgrootheden (v, x en ∆x) zijn voorbeelden van vectoriële grootheden.

2 Hoe stel je vectoren samen?

2.1 De resulterende vector

Vectoriële grootheden kun je optellen en aftrekken. Je stelt de vectoren samen.

Op de slee werken verschillende krachten. De resulterende kracht is een samenstelling van alle krachten.

Tijdens een boottocht heb je een snelheid ten opzichte van het water. Het water heeft zelf een stroomsnelheid. De snelheid ten opzichte van de oever is een samenstelling van beide snelheden.

Een vallende bal verplaatst zich. De verplaatsingsvector is een samenstelling van de positievectoren op twee momenten.

instructiefilmpje: krachten met dezelfde richting optellen

In dit thema zul je vectoren enkel optellen. We beperken ons in de verdere uitleg tot de som van vectoren. De vectorsom noem je ook de resulterende vector of resultante. De kenmerken van de resultante worden bepaald door de onderlinge ligging van de vectoren.

De samenstelling van verschillende krachten die op een systeem inwerken, noem je de resulterende kracht Fres. Het is de som van alle krachten (F1, F2 Fn) die inwerken op een systeem.

In symbolen: F res = F 1 + F2 + ... + F n

VOORBEELD KRACHTEN DIE INWERKEN OP EEN SLEE

De beweging van de slee (zie afbeelding 6) wordt bepaald door alle krachten die erop inwerken:

F res = F

Daarbij is F 1 de zwaartekracht, F2 de normaalkracht, F3 een trekkracht, F4 een duwkracht en F5 de wrijvingskracht.

2.2 Vectoren met dezelfde richting optellen

Vectoren met dezelfde richting kunnen dezelfde of een tegengestelde zin hebben. Je construeert de resulterende vector met de kop-staartmethode. De vector ligt volgens dezelfde richting als de aparte vectoren.

OPLOSSINGSSTRATEGIE

F res = F 1 + F2

Krachten met eenzelfde richting en eenzelfde zin

F2 F 1

F res

Krachten met eenzelfde richting en een tegengestelde zin

F 1

©VANIN

F res

Je tekent de resulterende krachtvector met de kopstaartmethode:

• Je tekent de eerste krachtvector F 1

• Je tekent de tweede krachtvector F2 vanaf de pijlpunt van F1.

• Je tekent de resulterende krachtvector F res vanaf het begin van de eerste krachtvector tot aan de pijlpunt van de laatste krachtvector.

• Als er meer dan twee krachten ingrijpen, herhaal je dat:

—eerst voor krachtvectoren met een gelijke zin, —vervolgens voor krachtvectoren met een tegengestelde zin.

Om de grootte van de resulterende vector te berekenen, moet je rekening houden met de zin van de vectoren:

• vectoren met dezelfde zin: de som van de vectorgroottes berekenen;

• vectoren met een tegengestelde zin: het verschil tussen de grootste en kleinste vectorgrootte berekenen.

VOORBEELD BOBSLEE AFDUWEN

Vier atleten duwen een bobslee af. De slee ondervindt wrijving aan de twee glijders. Je kunt dat voorstellen met zes horizontale krachten: vier duwkrachten (uitgeoefend door de atleten op de slee en allemaal identiek, op het aangrijpingspunt na) en twee wrijvingskrachten (uitgeoefend door de ondergrond op de slee en identiek, op het aangrijpingspunt na).

©VANIN

Afb. 11 De krachten volgens de bewegingszin (

duw) en tegen de bewegingszin ( res, w) bepalen de resulterende kracht ( res).

Alle krachten hebben dezelfde richting. Je kunt de resultante construeren met de kopstaartmethode. De grootte kun je als volgt berekenen:

2.3 Vectoren met een verschillende richting optellen

Voor vectoren met een verschillende richting kun je de resulterende vector construeren met de kop-staartmethode of parallellogrammethode. De resulterende vector heeft een andere richting dan de aparte vectoren.

OPLOSSINGSSTRATEGIE

Je kunt de resulterende vector ook construeren met de kop-staartmethode:

• Je tekent de eerste krachtvector F 1

• Je tekent de tweede krachtvector F2 vanaf de pijlpunt van F1.

• Je tekent de resulterende krachtvector F res vanaf het begin van de eerste krachtvector tot aan de pijlpunt van de laatste krachtvector.

Er verschijnt een parallellogram waarvan de resultante de diagonaal is. Je kunt de resultante ook construeren door het parallellogram van de twee vectoren te tekenen. Dat noem je de parallellogrammethode.

instructiefilmpje: krachten met een verschillende richting optellen

Om de grootte van de resulterende vector te berekenen, maak je een onderscheid tussen twee situaties.

DE VECTOREN STAAN LOODRECHT OP ELKAAR.DE VECTOREN MAKEN EEN WILLEKEURIGE HOEK MET ELKAAR.

©VANIN

Je kunt de grootte bepalen met de stelling van Pythagoras

De vectoren a en b staan loodrecht op elkaar.

De resultante c = a + b is de diagonaal van de rechthoek (= parallellogram met hoeken van 90°). Dat is de schuine zijde van een rechthoekige driehoek, dus c2 = a2 + b2. Je kunt

de grootte van de resulterende vector als volgt berekenen:

c = a2 + b2

Je kunt de grootte bepalen met een variant van de cosinusregel

De vectoren a en b maken een hoek met elkaar. De resultante c = a + b is de diagonaal van een parallellogram. Je kunt de lengte van de diagonaal bepalen door de cosinusregel toe te passen voor de hoek φ = 180° – α:

c2 = a2 + b2 – 2 · a · b · cos φ

= a2 + b2 – 2 · a · b · cos(180° – α)

= a2 + b2 + 2 · a · b · cos α

Je kunt de grootte van de resulterende vector als volgt berekenen:

c = a2 + b2 + 2 · a · b · cos α

VOORBEELD PARACHUTESPRONG BIJ ZIJDELINGSE WIND

Hassan is een parachutist. Hij maakt een sprong op een dag met een horizontale wind:

• Na het openen van zijn parachute werken er twee krachten in verticale richting: de zwaartekracht F z en de weerstandskracht F w

• In de horizontale richting werkt een windkracht Fwind.

Je kunt de resulterende kracht bepalen als F res = F z + F w + Fwind.

Om de resulterende vector te construeren, bepaal je eerst de resulterende kracht in de verticale richting F res, vert = F z + F w met de kop-staartmethode. Je kunt de grootte van deze kracht bepalen door de (tegengestelde) krachten van elkaar af te trekken:

F res, vert = F w – F z = 1 250 N – 1 000 N = 250 N

De windkracht staat loodrecht op F res, vert. Je kunt de resulterende krachtvector F res = F res, vert + Fwind construeren met de kop-staartmethode of de parallellogrammethode. De resulterende kracht ligt volgens de diagonaal van de rechthoek gevormd door beide krachtvectoren.

Met de stelling van Pythagoras kun je de grootte van de resulterende kracht berekenen:

F res = F 2 res, vert + F 2 wind = (250 N)2 + (200 N)2 = 320 N

Afb. 12 De resulterende vector van twee loodrechte vectoren▲

13 De resulterende vector van twee vectoren die een hoek maken met elkaar

Krachten nadat de parachute net geopend is

©VANIN

Resulterende verticale kracht (F res, vert = F z + Fw) nadat de parachute net geopend is

Resulterende kracht (F res = F res, vert + Fwind) nadat de parachute net geopend is

VOORBEELD BOBSLEE VOORTTREKKEN

Twee atleten trekken een bobslee vooruit. Ze oefenen een kracht met een verschillende richting uit.

• Atleet 1 trekt met een kracht Ftrek, 1 met een richting schuin naar rechts en een grootte Ftrek, 1 = 200 N.

• Atleet 2 trekt met een kracht Ftrek, 2 met een richting schuin naar links en een grootte Ftrek, 2 = 200 N.

Je kunt de resulterende krachtvector F res = Ftrek, 1 + Ftrek, 2 construeren met de kop-staartmethode of de parallellogrammethode. De resulterende kracht ligt volgens de diagonaal van het parallellogram gevormd door beide krachtvectoren.

▲ Afb. 15 Krachten met een verschillende richting worden uitgeoefend op een bobslee

De hoek tussen beide krachten is α = 48°. Met de cosinusregel kun je de grootte van de resulterende kracht berekenen:

F res = F 2 trek, 1 + F 2 trek, 2 + 2 · Ftrek, 1 · Ftrek, 1 · cos α

▲ Afb. 14

▲ Afb. 16 Constructie van de resulterende krachtvector

Een versnelde beweging is een beweging waarbij de snelheidsvector v verandert.

Een resulterende vector is de vectoriële som van alle vectoren. De vectorsom noem je ook de resulterende vector of resultante. De resulterende vector kun je construeren met de kop-staartmethode of parallellogrammethode. De grootte van de resulterende vector kun je berekenen met de gepaste wiskundige methode, die bepaald wordt door de onderlinge ligging:

• vectoren met dezelfde richting:

– dezelfde zin: groottes van de vectoren optellen;

– tegengestelde zin: groottes van de vectoren aftrekken;

• vectoren met een verschillende richting:

– loodrecht op elkaar: stelling van Pythagoras;

– willekeurige hoek: cosinusregel.

©VANIN

3 Wat zijn de bewegingswetten van Newton?

Bij de meeste bewegingen is de snelheid niet constant. De grootte, de richting of de zin van de snelheidsvector v verandert tijdens de beweging. Er is een verandering van bewegingstoestand. Zulke bewegingen zijn versnelde bewegingen.

De snelheid neemt toe na het startschot.

De snelheid verandert van richting in de bocht.

De snelheidsgrootte neemt af na de finish.

Om een verandering van bewegingstoestand te veroorzaken, is er een kracht nodig.

Wetenschappers (Copernicus, Da Vinci, Galilei, Newton …) hebben dat verband nauwkeurig onderzocht. In 1687 formuleerde Isaac Newton de drie natuurwetten die de grondslag vormen voor de klassieke mechanica. Je krijgt hier een korte toelichting, zodat je ze in dit thema kunt toepassen. Volgend schooljaar ga je er dieper op in.

3.1 Eerste wet van Newton

Als de resulterende kracht op een voorwerp nul is, dan verandert de snelheid van het voorwerp niet:

1 Een voorwerp in rust blijft in rust.

2 Een voorwerp dat met een snelheid v beweegt, blijft met de zelfde snelheid v (grootte, richting en zin) bewegen.

Het voorwerp voert een ERB uit.

Dat is de eerste wet van Newton. De wet geldt ook omgekeerd: als een voorwerp in rust is of met een constante snelheid beweegt, dan is de resulterende kracht op dat voorwerp gelijk aan nul.

Om de snelheid van een voorwerp te veranderen, is er een kracht nodig. De neiging om de bewegingstoestand te bewaren, noemen we de traagheid of inertie van een voorwerp. Daarom heet deze wet, die voor het eerst zo geformuleerd werd door Isaac Newton, ook de traagheidswet of inertiewet.

Hoe groter de massa van een voorwerp, hoe moeilijker de snelheid (grootte, richting of zin) te veranderen is. Voorwerpen met een grotere massa hebben een grotere traagheid of inertie.

VOORBEELD FIETSER

Een renner in beweging blijft in beweging (met dezelfde snelheid v).

Als de fiets tegen de hindernis komt, ondervindt de fiets een kracht en wordt vertraagd. De persoon zelf ondervindt quasi geen kracht en blijft met dezelfde snelheid verder bewegen. De renner komt los van zijn fiets. Tijdens de zweeffase zal de zwaartekracht hem ook naar beneden doen versnellen en komt hij dus wat verder op de grond terecht.

3.2 Tweede wet van Newton

©VANIN

Als er een resulterende kracht F res op een voorwerp werkt, is er een dynamisch effect van de kracht: de bewegingstoestand verandert. De snelheid v verandert: er is een versnelling a. Hoe kleiner de massa m, hoe gemakkelijker het voorwerp versnelt. Omgekeerd, hoe groter de massa m, hoe moeilijker het voorwerp versnelt. Uit experimenten blijkt:

De versnelling neemt recht evenredig toe met een toenemende resulterende kracht.

a ~ F res

De versnelling ten gevolge van een resulterende kracht is omgekeerd evenredig met de massa.

a ~ 1 m

a = constante · F res m

a = F res m definiëring

Het verband tussen de resulterende kracht en de versnelling kun je als volgt noteren: F res = m · a

Zowel de versnelling als de kracht is een vectoriële grootheid. Het verband F res = m · a geldt ook vectorieel: F res = m · a. Dat is de tweede wet van Newton.

De eenheid newton is een afgeleide eenheid. Via de tweede wet van Newton vind je de basiseenheden terug:

[Fres] = [m] · [a], dus 1 N = 1 kg · 1 m s2 = 1 kg · m s2

De grootheid versnelling geeft het tempo van de snelheidsverandering aan. In symbolen: a = ∆v ∆t met als eenheid 1 m s2 . In jaar 6 bestudeer je dat in detail.

Dat de constante 1 is, volgt uit de definitie van de eenheid van kracht: een kracht die een voorwerp van 1 kg versnelt met een versnelling van 1 m s2 , heeft een grootte van 1 newton.

De definitie stamt pas uit 1946 en werd dus niet door Newton bepaald.

VOORBEELD WINKELKAR DUWEN

Je moet harder duwen tegen een volle winkelkar om de kar in beweging te krijgen dan tegen een lege winkelkar. Als de kar in beweging is, moet je meer kracht uitoefenen op een volle kar om ze tot stilstand te brengen.

Marwan oefent een kracht van 140 N uit om de volle winkelkar van 70 kg in beweging te brengen.

De versnelling is a = FMarwan m = 140 N 70 kg = 2,0 m s2

VOORBEELD PARACHUTESPRONG

Noa moet slechts een kracht van 20 N uitoefenen om een kar van 10 kg dezelfde versnelling te geven:

a = FNoa m = 20 N 10 kg = 2,0 m s2

Wanneer een parachutist uit een vliegtuig springt, neemt zijn snelheid niet gelijkmatig toe. Dat zie je in de video. Door zijn hoge snelheid en het grote contactoppervlak van de parachute is er een grote weerstandskracht. De beweging is geen vrije val. De valbeweging bestaat uit verschillende deelbewegingen. Die deelbewegingen worden elk bepaald door de grootte van de luchtweerstand op de verschillende momenten en de bijbehorende resulterende kracht.

BEGIN VAN DE SPRONG

©VANIN

NA EEN PAAR SECONDEN VALLEN

NA EEN TIJDJE VALLEN PARACHUTE NET GEOPEND NA EEN PAAR SECONDEN MET GEOPENDE PARACHUTE

EVRB minder snel versnellen ERB vertragen ERB

vrije val val met weerstand

De richting en de zin van a zijn hetzelfde als de richting en de zin van Fres. Je kunt de grootte van de versnelling voor elke situatie berekenen als a = F res m

3.3 Actie-reactie

Als een systeem A een kracht FAB uitoefent op een systeem B, dan oefent systeem B een even grote, maar tegengestelde kracht FBA uit op systeem A. In symbolen: FAB = – FBA

Dat is de derde wet van Newton. De kracht FAB is de actiekracht, de kracht FBA de reactiekracht. Die wet wordt ook de wet van actie en reactie genoemd.

De twee krachten (die elk op een ander systeem inwerken) noem je een actie-reactiepaar. De kracht FAB grijpt aan op systeem B, de kracht FBA grijpt aan op systeem A.

Je leerde vorige jaren al actie-reactieparen kennen:

1 Normaalkracht en gewicht

De kracht die het systeem uitoefent op zijn ondersteuning noem je het gewicht. De reactiekracht van het gewicht is de normaalkracht: dat is de kracht die de ondersteuning op het systeem uitoefent. De normaalkracht en het gewicht zijn even groot en hebben dezelfde richting, namelijk loodrecht op het oppervlak (ook bij een schuin oppervlak). Ze hebben echter een tegengestelde zin.

Het gewicht en de normaalkracht vormen een actie-reactiepaar.

VOORBEELD NORMAALKRACHT TIJDENS HET SPORTEN

Atleten staan op hun handen op de grond. Ze oefenen een gewicht uit op de grond.

De gewichtskracht grijpt aan op de grond.

De grond oefent een normaalkracht uit op de atleten. De normaalkracht grijpt aan op de atleten. De gewichtskrachten vormen een actie-reactiepaar met de normaalkrachten.

F n = –F g

©VANIN

CONCEPTVRAAG

Je duwt schuin tegen een verticale muur. Welke uitspraak is correct?

a Er is geen reactiekracht.

b De normaalkracht is de reactiekracht van de duwkracht en schuin gericht.

c De normaalkracht is de reactiekracht van de loodrechte component van de duwkracht en horizontaal gericht.

d Er is geen normaalkracht.

2 Veerkracht

Als een systeem een kracht uitoefent op een veer, dan oefent de veer een even grote maar tegengestelde kracht uit op dat systeem. De kracht die de veer uitoefent op het systeem, is altijd gericht volgens de veer en tegengesteld aan de vervorming. Die kracht noem je de veerkracht. Het aangrijpingspunt van de veerkracht ligt op het systeem. De uitgeoefende kracht en de veerkracht vormen een actie-reactiepaar.

VOORBEELD VEERKRACHT

Tijdens het fitnessen trekt Julia aan een veer. Ze oefent een kracht uit op de veer. De veer oefent een veerkracht uit op Julia. De spierkracht vormt een actie-reactiepaar met de veerkracht:

spier = –F v

©VANIN

KENMERK VECTOR Kracht op veer Fspier Veerkracht F v

AANGRIJPINGSPUNT op de veer op de hand RICHTING horizontaal

ZIN naar rechts, volgens de uitrekking naar links, tegen de uitrekking in GROOTTE Fspier = F v = 60 N

In de mechanica zijn drie basiswetten van Newton altijd geldig:

• Eerste wet (traagheidswet): als de (resulterende) kracht op een voorwerp nul is, dan verandert de snelheid van het voorwerp niet. Omgekeerd geldt: als een voorwerp in rust is of met een constante snelheid beweegt, dan is de resulterende kracht op dat voorwerp nul.

• Tweede wet: het verband tussen de resulterende kracht en de versnelling wordt gegeven door: F res = m · a.

• Derde wet (actie-reactiewet): als een systeem A een kracht FAB uitoefent op een systeem B, dan oefent systeem B een even grote maar tegengestelde kracht FBA uit op systeem A. In symbolen: FAB = – FBA

Sarah werkt op de achtste verdieping. Als ze in de lift stapt op de vierde verdieping, heeft Ismael de knop van de tweede verdieping al ingedrukt. De lift werkt de verdiepingen (elk 3,2 m hoog) af volgens de indrukvolgorde.

a Teken de x-as vanop de gelijkvloerse verdieping.

b Teken de positievector naar elke tussenstop (vierde, tweede en achtste verdieping).

c Teken de verplaatsingsvector voor elke deelbeweging.

Jeff vertrekt vanuit stilstand, zoals weergegeven op de afbeelding.

a Teken de afbeelding over.

b Vervolledig de afbeelding met de verplaatsingsen de snelheidsvector.

Een raket met een massa van 2 050 ton wordt gelanceerd met een motorkracht van 30 MN.

a Teken de zwaartekracht, de motorkracht en de resulterende kracht in een krachtenschema. Schat de onderlinge groottes.

b Bereken de grootte van de zwaartekracht en de grootte van de resulterende kracht.

c Klopt je voorspelling over de onderlinge groottes? Pas aan.

Twee krachten F 1 en F2 werken in dezelfde richting, met F 1 > F2. Neem de tabel over en vul aan.

Resulterende krachtvector

1 Krachten werken in dezelfde zin

2 Krachten werken in tegengestelde zin

Resulterende krachtgrootte

F res = F res =

Een trein rijdt met een snelheid van 80 km h . Je wilt naar een andere wagon gaan en stapt met een snelheid van 4,0 km h . Teken en bereken de resulterende snelheidsvector ten opzichte van de omgeving als je …

a in dezelfde zin als de treinbeweging stapt;

b in tegengestelde zin van de treinbeweging stapt.

Je zwemt de rivier over (loodrecht op de oever) met een snelheid van 2,0 m s . Het water stroomt met een snelheid van 5,0 m s .

a Teken de snelheidsvectoren en de resulterende snelheidsvector.

b Bereken de grootte van de resulterende snelheid.

Twee vrienden willen een boom neerhalen. Marlies trekt met een kracht van 450 N, Josse met een kracht van 400 N. Bereken de resulterende kracht als …

a de krachten loodrecht op elkaar staan;

b de krachten een hoek van 60° maken.

Op een rubberbootje worden twee krachten uitgeoefend: een kracht F horizontaal naar rechts en een kleinere kracht F’. De oriëntatie van F’ verandert. Rangschik de groottes van de resulterende krachten F 1 F6 van klein naar groot.

AAN DE SLAG

Bestudeer de verschillende situaties van de basketbal en de vectorvoorstellingen van de snelheid en de resulterende kracht.

a Verbind elke foto met de overeenkomstige vectorvoorstelling.

Verbind het voorbeeld met de juiste wet van Newton.

A Een veiligheidsgordel beschermt tegen verwondingen.

©VANIN

1 De bal krijgt een duw van de hand.

B De snelheid van een parachutespringer neemt toe tijdens de vrije val.

C Als je uit een bootje stapt, drijft het bootje weg.

D Een vrachtwagen heeft een grotere remafstand dan een auto.

2 De bal valt.

E In een bocht op de autosnelweg beweeg je naar de deur van de auto toe.

F Een hamer komt spontaan omhoog tijdens het inkloppen van een spijker.

G Als je een lade snel opentrekt, verschuiven de spullen die erin liggen.

3 De bal raakt net de hand.

1 eerste wet van Newton: traagheidswet

2 tweede wet van Newton (F res = m ∙ a)

3 derde wet van Newton: actie-reactiewet

4 De bal is weggegooid.

b Omschrijf een beweging van de basketbal die past bij de overblijvende vectorvoorstellingen.

Geef een voorbeeld van de drie wetten van Newton.

1 traagheidswet

2 tweede wet van Newton (F res = m ∙ a)

3 actie-reactiewet

Jo trekt met een horizontale kracht van 123 N naar rechts aan een kist met een massa van 18,7 kg. De wrijvingskracht is 86 N.

a Teken en benoem op een krachtenschema de trekkracht, de wrijvingskracht en de resulterende kracht.

b Bereken de grootte van de resulterende kracht en de grootte van de versnelling.

Rani en Louise houden een wedstrijdje touwtrekken.

Ze trekken beiden met een kracht van 200 N.

Louise kan een wrijvingskracht van 100 N uitoefenen met haar schoen op de grond, Rani een wrijvingskracht van 150 N.

a Teken een krachtenschema met de krachten (trekkracht en wrijvingskracht) die inwerken op elke persoon.

b Wie wint? Meerdere antwoorden zijn mogelijk.

1 degene die het hardste trekt

2 degene die de grootste wrijvingskracht uitoefent

3 degene die de grootste resulterende kracht levert

c Waarom zijn de trekkrachten altijd gelijk?

` Meer oefenen? Ga naar .

HOOFDSTUKSYNTHESE

KERNBEGRIPPEN

scalaire grootheid

vectoriële grootheid

NOTITIES

Scalaire grootheid heeft enkel een grootte (bijvoorbeeld temperatuur, druk, volume, lengte en energie).

Vectoriële grootheid stel je voor met een vector (= pijl).

Een vector heeft vier kenmerken: richting

F aangrijpingspunt zin grootte

• aangrijpingspunt: punt waar de vector inwerkt;

• richting: rechte waar de vector op ligt (bijvoorbeeld horizontaal, verticaal, schuin);

• zin: kant waar de pijlpunt van de vector naar wijst (bijvoorbeeld links, rechts, boven, onder);

• grootte: lengte van de vector die de grootte van de grootheid aangeeft. De grootte van de vector noteer je zonder het pijltje op de letter en is altijd positief.

(bijvoorbeeld kracht, snelheid)

vectoren samenstellen Vectoren samenstellen, is de vectoriële som nemen.

Bijvoorbeeld: F res = F 1 + F2 + … + F n

• constructie van F res met de kopstaartmethode

• berekening grootte F res met de geschikte wiskundige techniek

KRACHTEN MET DEZELFDE RICHTING:

F res = F 1 + F2

dezelfde zin

©VANIN

tegengestelde zin

loodrechte richting Pythagoras toepassen F res = F2 1 + F2 2

KRACHTEN MET VERSCHILLENDE RICHTING:

F res = F 1 + F2

willekeurige richting (hoek α tussen krachten)

wetten van Newton In de mechanica zijn drie basiswetten van Newton altijd geldig:

• Tweede wet: het verband tussen de resulterende kracht en de versnelling wordt gegeven door: F res = m · a

• Derde wet (actie-reactiewet): als een systeem A een kracht FAB uitoefent op een systeem B, dan oefent systeem B een even grote maar tegengestelde kracht FBA uit op systeem A.

In symbolen: FAB = –FBA

HOOFDSTUK 2

Elektrische kracht en gravitatiekracht

©VANIN

De oude Grieken stelden vast dat versteend boomhars (amber of barnsteen) kleine stukjes bladeren aantrok wanneer ze het opwreven met wol. Ze noemden dat ‘elektriciteit’ (het Griekse woord elektron betekent ‘amber’). Het duurde tot de achttiende eeuw voordat wetenschappers een correcte verklaring konden vinden voor dat verschijnsel.

In dit hoofdstuk bestudeer je hoe statische elektriciteit ontstaat en hoe groot de kracht tussen geladen voorwerpen is. Je vergelijkt de elektrische kracht met de zwaartekracht.

LEERDOELEN

M statische elektriciteit en het begrip ‘elektrische lading’ omschrijven

M beschrijven hoe voorwerpen op atomaire schaal elektrisch geladen worden

M de vier kenmerken van de elektrische kracht bepalen en weergeven

M de elektrische kracht vergelijken met de gravitatiekracht

1 Wat is statische elektriciteit?

In het dagelijks leven ondervind je regelmatig verschijnselen van statische elektriciteit

Een kous en een wollen trui die net uit de droogkast komen, trekken elkaar aan

Als je je haren borstelt met een plastic borstel, kunnen ze rechtop staan doordat ze elkaar afstoten.

Soms voel je een schokje wanneer je een auto aanraakt.

De term ‘statisch’ betekent dat iets onbeweeglijk, blijvend, onveranderlijk … is.

Wat gebeurt er als je opgewreven voorwerpen in de buurt van andere voorwerpen brengt?

1 Je leerkracht brengt ballonnen in de buurt van verschillende voorwerpen (papiersnippers, andere ballonnen, haar, plastic zakjes …).

2 Wat zal er volgens jou gebeuren?

Bespreek met je buur en test samen met je leerkracht uit.

3 Je leerkracht wrijft de ballonnen op en herhaalt dan het experiment.

4 Formuleer een antwoord op de onderzoeksvraag.

▲ Afb. 18

▲ Afb. 20

DEMO

CONCEPTVRAAG

Verklaar de waarnemingen op afbeelding 18 en 19.

Uit experimenten blijkt dat sommige voorwerpen door wrijving met andere materialen fenomenen als aantrekking, afstoting en zelfs schokjes veroorzaken. Je zegt dat die voorwerpen een elektrische lading krijgen. Er zijn twee soorten ladingen, die je ‘positief’ en ‘negatief’ noemt.

Je kunt aan een voorwerp niet zien of het geladen is. Door de invloed van het voorwerp op zijn omgeving kun je dat wel afleiden.

VOORBEELD KRACHTWERKING GELADEN VOORWERPEN

1 Aantrekking van papiersnippers

Als je een wollen doek over en weer wrijft op een ballon, wordt die ballon elektrisch geladen. Je ziet het effect van de lading doordat de ballon papiersnippers aantrekt.

©VANIN

papiersnippers

▲ Afb. 21 Een opgewreven ballon trekt papiersnippers aan.

2 Aantrekking en afstoting tussen geladen voorwerpen

Als je met een ballon over je haar wrijft, is er aantrekking tussen het haar en de ballon. Als je twee ballonnen door je haar wrijft, stoten de ballonnen elkaar af.

Het verschil in effect ontstaat door de twee soorten ladingen.

ballon haar

▲ Afb. 22 De opgewreven ballon en het haar hebben ongelijksoortige ladingen: de ballon is negatief en het haar positief geladen. Ze trekken elkaar aan.

▲ Afb. 23 De opgewreven ballonnen hebben gelijksoortige (negatieve) ladingen. Ze stoten elkaar af.

Statische elektriciteit ontstaat als een voorwerp (elektrisch) geladen wordt.

Er bestaan twee soorten (elektrische) ladingen, die je ‘positief’ en ‘negatief’ noemt:

• Gelijksoortige ladingen stoten elkaar af.

• Ongelijksoortige ladingen trekken elkaar aan.

ballon

Wanneer de elektrische lading op een voorwerp groot genoeg is, kan het voorwerp spontaan ontladen. Tijdens die elektrostatische ontlading is er kortstondig een elektrische stroom tussen het geladen voorwerp en de omgeving.

Wanneer je je trui uittrekt, hoor je soms geknetter. In het donker zie je vonkjes.

Bij een onweersbui ontstaat er een lading in de wolken. De ontlading zie je als bliksem.

2 Hoe worden voorwerpen geladen?

2.1 Elektrisch gedrag van stoffen

A Elektrische lading

Alle materie is opgebouwd uit atomen. Een atoom bestaat uit een kern, die omgeven is door een elektronenwolk. Die elektronenwolk bestaat uit een of meerdere schillen. De kern van het atoom bevat protonen en neutronen.

• De protonen (p+) van de kern hebben een positieve lading.

• De neutronen (n0) van de kern hebben geen lading.

• De elektronen (e–) hebben een negatieve lading.

• De elektronen op de buitenste schil noem je de valentie-elektronen.

©VANIN

Bekijk in de applet hoe de ontlading gebeurt.

▲ Afb. 24 Bouw van een atoom

‘Discreet’ betekent dat er uitsluitend gehele veelvouden van een bepaalde eenheid kunnen voorkomen.

• De natuurlijke getallen zijn discreet. Tussenliggende waarden zijn onmogelijk.

• Een geldbedrag is een discrete grootheid: elk bedrag is een geheel veelvoud van het kleinste muntstuk (de eurocent).

Lading is een grootheid met als symbool q. De eenheid is coulomb, met het symbool C.

Een lading van 1 C is vrij groot. In de praktijk zijn ladingen veel kleiner. Daarom gebruik je meestal voorvoegsels, zoals in millicoulomb (1 mC = 10–3 C), microcoulomb (1 µC = 10–6 C) en nanocoulomb (1 nC = 10–9 C).

GROOTHEID MET SYMBOOL

SI-EENHEID MET SYMBOOL lading q coulomb C

De lading van een proton is in absolute waarde gelijk aan de lading van een elektron. Het is de kleinste lading die afzonderlijk voorkomt. Dat noem je de eenheidslading e.

• lading van een proton: qp+ = e = 1,60 ∙ 10–19 C

• lading van een elektron: qe–= –e = –1,60 ∙ 10–19 C

Een atoom heeft evenveel elektronen als protonen en is neutraal.

Op figuren stelt men soms de ladingen van voorwerpen en soms elementaire ladingen voor. Om verwarring te vermijden, gebruiken we daarvoor verschillende symbolen.

POSITIEVE LADING q

NEGATIEVE LADING q

(VEELVOUD VAN) LADINGEN VAN PROTONEN(VEELVOUD VAN) LADINGEN VAN ELEKTRONEN + –

Een voorwerp lading geven of kortweg laden betekent dat er elektronen toegevoegd of afgevoerd worden naar een ander voorwerp. De totale lading bij de ladingsuitwisseling verandert niet. Je kunt geen elektronen scheppen of vernietigen. Je kunt ze enkel overdragen. Dat noem je de wet van behoud van lading

De nettolading van een voorwerp is altijd een geheel veelvoud van de eenheidslading. Lading is een discrete grootheid

NEGATIEF GELADEN VOORWERP

Er zijn meer elektronen dan protonen op het voorwerp. Er is een overschot aan elektronen

POSITIEF GELADEN VOORWERP

Er zijn minder elektronen dan protonen op het voorwerp. Er is een tekort aan elektronen

Je gebruikt # als symbool voor ‘aantal’.

De ladingsgrootte kun je als volgt berekenen: q = (#p+ – #e–) ∙ e #e– > #p+, dus q < 0 #p+ > #e–, dus q > 0

TIP

VOORBEELD OVERSCHOT EN TEKORT AAN ELEKTRONEN BEREKENEN

Je kunt de nettolading opmeten met een coulombmeter.

©VANIN

Een pvc-buis heeft een negatieve lading q = –30 nC.

(#p+ – #e–) = q e = –30 ∙ 10–9 C 1,60 ∙ 10–19 C = –1,9 ∙ 1011

Er zijn 1,9 ∙ 1011 elektronen te veel (= meer dan protonen) ten opzichte van de neutrale toestand.

Een glazen staaf heeft een positieve lading q = 16 nC.

(#p+ – #e–) = q e = 16 ∙ 10–9 C 1,60 ∙ 10–19 C = 1,0 ∙ 1011

Er zijn 1,0 ∙ 1011 elektronen te kort (= minder dan protonen) ten opzichte van de neutrale toestand.

B Geleiders en isolatoren

In een geleider kan de lading zich verplaatsen. In een isolator blijft de lading op de plaats waar ze werd aangebracht.

In een elektrische kring gebruikt men koper in de snoeren. Koper is een geleider

Om elektrocutie te vermijden, gebruikt men kunststoffen in elektrische toestellen. Kunststof is een isolator

Een haardroger in de badkamer kan gevaarlijk zijn. Door onzuiverheden is kraantjeswater een geleider

Macroscopisch beschrijft men geleiding met de grootheden weerstand en geleidbaarheid:

• Geleiders hebben een lage weerstand en een hoge geleidbaarheid.

• Isolatoren hebben een hoge weerstand en een lage geleidbaarheid.

▲ Afb. 25 ▲ Afb. 26 ▲ Afb. 27

kleine geleidbaarheid

lucht glas

kraantjeswater grafiet koper geleiders kleine weerstand

grote geleidbaarheid grote weerstand isolatoren

▲ Afb. 28 Enkele gerangschikte voorbeelden voor draden met identieke afmetingen die zouden bestaan uit de verschillende getoonde stoffen

Op atomair niveau wordt de geleidbaarheid bepaald door de aanwezigheid van vrije geladen deeltjes

In geleiders zijn er vrije elektronen en/of ionen:

• Bij metaalbindingen zijn de valentie-elektronen los. Daardoor ontstaan er positieve roosterionen en elektronen die vrij bewegen tussen de positieve roosterionen.

• Bij sommige stoffen in een oplossing en bij vloeistoffen kunnen de ionen vrij bewegen.

positief metaalionvrije elektronen

▲ Afb. 29 In een metaal kunnen de valentie-elektronen vrij bewegen.

In isolatoren zijn er geen vrije geladen deeltjes.

Voorwerpen zijn opgebouwd uit atomen.

Atomen bezitten elementaire ladingen: protonen in de kern en elektronen op de schillen.

ATOMAIR DEELTJE PLAATS SYMBOOL ELEKTRISCHE LADING proton kern p+ e = 1,60 · 10–19 C neutron kern n0 0 elektron wolk e– –e = –1,60 · 10–19 C

De lading q van een voorwerp wordt bepaald door het overschot (negatief geladen voorwerp) of het tekort aan elektronen (positief geladen voorwerp) ten opzichte van de neutrale toestand.

q = (#p+ – #e–) · e met e = 1,60 · 10–19 C

Materialen worden ingedeeld op basis van hun elektrische eigenschappen.

• Bij geleiders zijn er vrije geladen deeltjes (valentie-elektronen bij metalen of ionen in andere geleiders).

• Bij isolatoren zijn er geen vrije geladen deeltjes.

2.2 Voorwerpen laden door wrijving

DEMO

Welke invloed heeft de combinatie van materialen op de lading bij wrijvingsexperimenten?

1 Je leerkracht wrijft staven uit metaal, glas en pvc op met een wollen doek.

Daarna brengt je leerkracht de staven in de buurt van enkele papiersnippers.

2 Wat zal er volgens jou gebeuren?

Bespreek met je buur en test samen met je leerkracht uit.

3 Je leerkracht wrijft de staven op met papier en herhaalt dan het experiment.

4 Formuleer een antwoord op de onderzoeksvraag.

Wanneer je een staaf opwrijft met een doek, worden er valentie-elektronen losgemaakt en vervolgens overgedragen. Daardoor krijgen de staaf en de doek een lading. Het laden van voorwerpen door wrijving noem je het tribo-elektrisch effect

Bij een isolator kunnen de ladingen zich niet verplaatsen, waardoor de aangebrachte lading op de opgewreven plaats blijft zitten. Als dat stuk van de staaf in de buurt komt van neutrale voorwerpen, kun je de aantrekking waarnemen.

VOORBEELD PVC OPWRIJVEN MET WOL

Als je een pvc-buis opwrijft met een wollen doek, wordt de buis negatief geladen. Er worden elektronen overgedragen van de wollen doek naar de pvc-buis. De buis wordt op die manier negatief geladen en de doek wordt even sterk positief geladen. Wol en pvc zijn isolatoren: de ladingen blijven op de opgewreven plaats zitten.

demovideo: invloed van het materiaal

©VANIN

Afb. 30 Een pvc-staaf wordt (lokaal) negatief als je erover wrijft met een wollen doek.

τρɩβω (tribo) is het Griekse woord voor ‘wrijving’.

‘Aarden’ is met een geleider verbinding maken tussen een voorwerp en de aarde.

Het aantal overgedragen elektronen en de zin van de overdracht worden bepaald door de gebruikte materialen. De isolatoren (doek en staaf) zijn opgebouwd uit atomen met een bepaalde elektronegativiteit Atomen met een grotere elektronegativiteit zullen gemakkelijker elektronen opnemen. Op basis van die eigenschap kun je materialen ordenen in een tribo-elektrische reeks. Materialen die zich hoger bevinden in de reeks, staan gemakkelijker elektronen af dan materialen die onderaan staan.

Als je een materiaal hoger in de reeks opwrijft met een materiaal lager in de reeks, dan wordt het bovenste positief en het onderste negatief geladen. Hoe verder de materialen in de reeks uit elkaar staan, hoe duidelijker het effect is.

Ook als je een geleidende staaf opwrijft, worden er elektronen uitgewisseld. De geleidende staaf wordt echter weinig merkbaar geladen, omdat de elektronen in de geleider elkaar afstoten en de lading zich onmiddellijk verspreidt over (het grote oppervlak van) de geleider.

Als de opgewreven geleidende staaf geaard is, verspreidt de lading van de staaf zich verder naar de aarde totdat de staaf ontladen is.

CONCEPTVRAAG

In de video’s zie je hoe elektrostatische krachtwerking gebruikt wordt bij poedercoating van oppervlakken en sorteren van kunststoffen.

Tribo-elektrische reeks

gemakkelijkst positief te laden staat elektronen makkelijkst af

droge huid dierlijke pels glas menselijk haar nylon wol zijde aluminium papier katoen staal amber rubber nikkel, koper polyester polyethyleen pvc teflon

gemakkelijkst negatief te laden neemt elektronen makkelijkst op

©VANIN

Verklaar de waarnemingen (uit de demoproef) met de metalen staaf en de glazen staaf op basis van het deeltjesmodel.

Wanneer twee verschillende materialen met elkaar wrijven, kunnen er valentie-elektronen loskomen, die zich verplaatsen naar het materiaal dat onderaan staat in de tribo-elektrische reeks.

• Het voorwerp dat elektronen opneemt, wordt negatief geladen.

• Het voorwerp dat elektronen afstaat, wordt positief geladen.

Dat is het tribo-elektrisch effect.

Bij isolatoren blijft de lading ter plekke en is het effect van de lading merkbaar.

Bij geleiders verspreidt de lading zich en is het effect van de lading niet altijd merkbaar.

2.3 Geleiders laden door contact

Een elektroscoop is een eenvoudig toestel waarmee je ladingen kunt meten en andere elektrische verschijnselen kunt aantonen. Het bestaat uit een horizontale metalen kop (schijfje of bol), met daaronder een of twee beweeglijke metalen staafjes, die kunnen draaien rond een scharnierpunt (vergelijkbaar met de wijzer van een klok). De metalen staafjes noem je de beentjes van de elektroscoop. In sommige uitvoeringen wordt de elektroscoop ter bescherming omhuld door glas.

kop scharnierpunt

beentjes

Wat gebeurt er als je met een geladen staaf de kop van een elektroscoop aanraakt?

1 Je leerkracht laadt een glazen staaf.

Daarna brengt je leerkracht de staaf in contact met de kop van een elektroscoop.

2 Wat zal er volgens jou gebeuren?

Bespreek met je buur en test samen met je leerkracht uit.

3 Je leerkracht herhaalt het experiment met een geladen pvc-staaf.

4 Formuleer een antwoord op de onderzoeksvraag.

Wanneer je een geladen voorwerp in contact brengt met een geleider, verplaatsen de elektronen zich van of naar de geleider:

• Bij een negatief geladen voorwerp bewegen de elektronen zich naar de neutrale geleider.

• Bij een positief geladen voorwerp bewegen elektronen zich van de neutrale geleider naar het voorwerp.

De geleider krijgt hetzelfde ladingsteken als het geladen voorwerp. In de geleider verspreiden de extra elektronen zich maximaal door hun onderlinge afstoting.

▲ Afb. 31 Onderdelen van een elektroscoop

DEMO

demovideo: elektroscoop laden door contact

Zonder lading in de buurt is een elektroscoop neutraal.

Op de beentjes is er geen nettolading en dus ook geen afstoting. Er is geen uitwijking.

©VANIN

Als een geladen glazen staaf contact maakt met de elektroscoop, wijken de beentjes van de elektroscoop uit.

Als je de geladen glazen staaf verwijdert, blijft de uitwijking bestaan. De elektroscoop blijft geladen.

Je kunt die waarneming verklaren op atomair niveau. De glazen staaf is positief geladen.

Bij contact met de kop bewegen er elektronen van de elektroscoop naar de staaf.

De beentjes worden allebei positief geladen en stoten elkaar af. Als je de staaf verwijdert, blijft de elektroscoop geladen.

▲ Afb. 32 Symbolische weergave van de lading door contact met een positieve staaf

CONCEPTVRAGEN

1 Hoe kun je een elektroscoop negatief laden?

2 Hoe kun je het ladingsteken bepalen met een elektroscoop? Verduidelijk met het deeltjesmodel.

Door contact te maken met een geladen voorwerp, kunnen valentie-elektronen weg van of naar een neutrale geleider bewegen.

De elektronen verspreiden zich over de volledige geleider, die dezelfde lading krijgt als het geladen voorwerp

Je kunt het laden door contact bekijken via de animatie.

3.1 Elektrische kracht tussen twee puntladingen

DEMO

Welke factoren beïnvloeden de kracht tussen twee geladen voorwerpen?

1 Een geladen plastic staaf hangt op aan een touwtje.

2 Bespreek met je buur de mogelijke invloedsfactoren wanneer je met een tweede geladen staaf een kracht uitoefent op die plastic staaf.

3 Test samen met je leerkracht uit.

4 Formuleer een antwoord op de onderzoeksvraag.

Als geladen voorwerpen in elkaars buurt komen, oefenen ze een kracht uit op elkaar. Die kracht noem je de elektrische kracht of de coulombkracht. Je kunt het effect van die kracht zien doordat er aantrekking of afstoting is. De grootte van de kracht wordt beïnvloed door de grootte van de ladingen en de afstand tussen de ladingen.

VOORBEELD ELEKTRISCHE KRACHT TUSSEN GELADEN STAVEN

▲ Afb. 33 Als je een negatief geladen staaf in de buurt van een andere negatief geladen staaf brengt, is er afstoting.

De grootte van de coulombkracht neemt toe met:

▲ Afb. 34 Als je een positief geladen staaf in de buurt van een negatief geladen staaf brengt, is er aantrekking.

demovideo: elektrische kracht tussen twee puntladingen

©VANIN

• een toenemende lading van beide staven;

• een afnemende afstand tussen de staven.

Om de elektrische kracht of coulombkracht kwantitatief te bestuderen, gebruik je een vereenvoudigd model met puntladingen.

Tussen twee puntladingen q1 en q2 die zich op een afstand r van elkaar bevinden, werkt een elektrische kracht, oftewel de coulombkracht, met als symbool FC:

• Een puntlading q1 oefent op een puntlading q2 een coulombkracht F12 uit.

• Een puntlading q2 oefent op een puntlading q1 een coulombkracht F21 uit.

• F12 en F21 vormen een actie-reactiepaar. Uit de derde wet van Newton volgt dat F12 en F21 voor elke combinatie van puntladingen q1 en q2 even groot en tegengesteld zijn: F12 = –F21

Een puntlading is een model waarbij alle lading zich in één punt bevindt.

02 LABO

Om de benaming van de vector eenvoudig te houden, laten we het onderschrift C weg als het duidelijk is dat het om de coulombkracht gaat.

Men heeft de kenmerken van de coulombkracht FC experimenteel bepaald. Het aangrijpingspunt is de puntlading. De richting is de verbindingslijn tussen beide ladingen. De zin is afhankelijk van het ladingsteken. De grootte is afhankelijk van de ladingsgrootte en de onderlinge afstand.

INVLOED VAN HET LADINGSTEKEN

INVLOED VAN DE LADINGSGROOTTE

INVLOED VAN DE ONDERLINGE AFSTAND

• ongelijksoortige ladingen: aantrekking

• gelijksoortige ladingen: afstoting

De zin van de coulombkracht FC is aantrekkend voor ongelijksoortige ladingen en afstotend voor gelijksoortige ladingen

De grootte van de coulombkracht FC voor twee puntladingen q1 en q2 op een afstand r is gelijk aan:

FC = k ∙ |q1| ∙ |q2| r 2

Daarbij is k = k0 = 8,99 ∙ 109 N ∙ m2 C 2 een evenredigheidsconstante (voor lucht of een vacuüm), die men ook wel de constante van Coulomb noemt.

Je kunt het model van de puntladingen toepassen op bolvormig geladen voorwerpen en op willekeurige voorwerpen met afmetingen die klein zijn in vergelijking met de afstand tussen de ladingen. Het aangrijpingspunt is het middelpunt van het voorwerp en r de afstand tussen de middelpunten van de voorwerpen.

Een lading q1 oefent op een lading q2 een coulombkracht FC uit met deze kenmerken:

• aangrijpingspunt: een puntlading of het middelpunt van een (bolvormige) lading;

• richting: de verbindingslijn tussen de ladingen;

• zin: aantrekkend (ongelijksoortige ladingen) of afstotend (gelijksoortige ladingen);

• grootte: FC = k ∙ |q1| ∙ |q2| r 2 , waarbij r de afstand tussen de middelpunten van beide ladingen is en k = 8,99 ∙ 109 N ∙ m2 C 2 (in lucht of in een vacuüm).

Een proton en een elektron bevinden zich in een vacuüm op een afstand van 0,10 nm van elkaar.

1 Teken en bereken de coulombkracht op beide ladingen.

2 Bereken de afstand waarop de coulombkracht 0,5 nN bedraagt.

Gegeven:

• q1 = 1,60 ∙ 10–19 C

• q2 = –1,60 ∙ 10–19 C

• r = 0,10 nm

• FC’ = 0,50 nN

Gevraagd: 1 F12 = ?; F21 = ?

2 r’ = ?

▲ Afb. 35 Coulombkracht tussen een elektron en een proton

Oplossing: 1 F12 en F21 vormen een actie-reactiepaar, dus F12 = –F21 volgens de verbindingslijn. De krachten zijn aantrekkend, omdat een proton en een elektron een ongelijksoortig ladingsteken hebben. De grootte kun je berekenen met de wet van Coulomb:

2 FC’ = k ∙ |q1| ∙ |q2| r ’ 2 , dus r’ = k ∙ |q1| ∙ |q2|

= 6,8 ∙ 10–10 m = 0,68 nm

TIP

• Je kunt het rekenwerk beperken: groepeer de getalwaarden en de machten van 10. Geef in je rekentoestel enkel de getalwaarden in en vermenigvuldig de machten van 10 uit je hoofd.

• Noteer de tussenstap met de getalwaarden niet als je zeker bent van je (omgezette) formule en de nodige getalwaarden in de SI-eenheid.

• In formules hoef je het maalteken niet altijd te schrijven. Bij machten van 10 schrijf je wel altijd het maalteken.

Voorbeeld:

FC = k |q1||q2| r 2 = 8,99

1,6

10–19

(1,0 ∙ 10–10 m)2 = 2,3 ∙ 10–10 N = 23 nN

• Je kunt de constante k vóór de breuk of in de teller van de breuk schrijven: FC = k ∙ |q1| ∙ |q2| r 2 = k ∙ |q1| ∙ |q2| r 2

Reflectie: • Kloppen de richting en de zin?

Ja, volgens de verbindingslijn en aantrekkend.

• Kloppen de eenheid en de grootteorde?

Ja, de kracht is heel klein en wordt uitgedrukt in newton.

• Vergelijk de twee afstanden en de twee krachten. Klopt alles?

Ja, de kracht is ongeveer vijftig keer kleiner bij een afstand die bijna zeven keer groter is (72 = 49). r p + F21 F12 e–

©VANIN

Je kunt die constructiemethode ook bekijken in de animatie.

3.2 Elektrische kracht tussen meerdere puntladingen

Als er meerdere puntladingen zijn, ervaart elke puntlading de coulombkracht van de andere puntladingen. De resulterende coulombkrachtvector F 1 die een lading q1 ondervindt van de ladingen q2, q3, q4 …, is de vectoriële som van alle coulombkrachten:

F 1 = F res, 1 = F21 + F31 + F41 + …

Dat is de formule die je eerder al leerde voor de resulterende kracht (F res = F 1 + F2 + F3 + …), waarbij we nu de indices gebruiken om duidelijk te maken tussen welke ladingen de krachten werken.

VOORBEELD COULOMBKRACHT OP DRIE LADINGEN CONSTRUEREN

Drie even sterke ladingen bevinden zich op een kleine afstand van elkaar. De ladingstekens zie je op de figuur. Ze oefenen coulombkrachten op elkaar uit.

©VANIN

▲ Afb. 36 De totale coulombkracht op drie ladingen in elkaars buurt

Om de kracht F 1 = F21 + F31 op lading q1 te construeren, teken je de coulombkrachten F21 en F31 die q1 ondervindt van de andere ladingen:

• De krachten zijn gericht volgens de verbindingslijnen.

• Lading q1 wordt aangetrokken door de ladingen q2 en q3.

• r12 > r13 en omdat |q2| = |q3|, geldt dus: F21 < F31

Je kunt nu de resulterende krachtvector op elke lading construeren met de parallellogrammethode.

De krachten F2 = F12 + F32 op lading q2 en F3 = F23 + F13 op lading q3 construeer je op een analoge manier. De grootte van de actie-reactiekracht is telkens even groot.

VOORBEELDVRAAGSTUK

Een lading van 3,0 μC bevindt zich op 0,25 m afstand van een lading van 5,0 μC en op 0,30 m afstand van een lading van 6,0 μC. Teken en bereken de coulombkracht op de lading van 3,0 μC in de onderstaande situaties.

1 De lading staat op een rechte lijn met de twee andere ladingen (twee mogelijkheden).

2 De lading staat op een hoekpunt van een rechthoekige driehoek (twee mogelijkheden).

Gegeven:

• q1 = 3,0 ∙ 10–6 C

• q2 = 5,0 ∙ 10–6 C

• q3 = 6,0 ∙ 10–6 C

• r12 = 0,25 m

• r13 = 0,30 m

Gevraagd: F 1 in de verschillende situaties = ?

Oplossing: De kracht op lading q1 is in alle situaties gegeven door: F 1 = F21 + F31

Aangezien de ladingen en de afstanden niet van grootte veranderen, kun je de grootte van de coulombkrachten in elke situatie berekenen met de wet van Coulomb:

•

• F31 = k ∙ |q1|

De krachten F21 en F31 zijn allebei afstotend. Om de grootte, de richting en de zin van de resulterende kracht te bepalen, construeer je de resulterende krachtvector in de verschillende situaties.

1 De lading staat op een rechte lijn met de twee andere ladingen (twee mogelijkheden). LADING q1 TUSSEN

De krachten F21 en F31 hebben dezelfde richting, maar een tegengestelde zin.

De grootte van de resulterende kracht is het verschil van de grootte van beide krachten:

F 1 = F21 – F31 = 2,2 N – 1,8 N = 0,4 N

De krachten F21 en F31 hebben dezelfde richting en dezelfde zin. De grootte van de resulterende kracht is de som van de grootte van beide krachten:

F 1 = F21 + F31 = 2,2 N + 1,8 N = 4,0 N

2 De lading staat op een hoekpunt van een rechthoekige driehoek (twee mogelijkheden).

LADING q1 STAAT OP DE RECHTE HOEK IN EEN RECHTHOEKIGE DRIEHOEK MET LADINGEN q2 EN q3

LADING q1 STAAT OP EEN SCHERPE HOEK IN EEN RECHTHOEKIGE DRIEHOEK MET LADINGEN q2 EN q3

©VANIN

De krachten F21 en F31 staan loodrecht op elkaar.

De grootte van de resulterende kracht kun je berekenen met de stelling van Pythagoras:

(2,2 N)2 + (1,8 N)2 = 2,8 N

De krachten F21 en F31 vormen een hoek α met elkaar.

De grootte van de resulterende kracht kun je berekenen met de cosinusregel:

F 1 = F 21 2 + F 31 2 + 2 ∙ F21 ∙ F31 ∙ cos α = (2,2 N)2 + (1,8 N)2 + 2 ∙ 2,2

= 3,8 N

Daarbij geldt: cos α = r12 r 13 = 0,25 0,30 = 0,83

OPLOSSINGSSTRATEGIE

• Schets de situatie.

Benoem elke puntlading. Plaats bij elke lading het teken (+ of –). Teken de richting en de zin van de nodige coulombkrachten. Schat de grootte.

• Bereken de grootte van de nodige coulombkrachten op de lading.

• Corrigeer je schets van alle coulombkrachten op de lading. Werk op schaal.

• Bereken de grootte van de resulterende coulombkracht op de lading via de gepaste wiskundige methode.

De resulterende coulombkracht die een lading ondervindt door de verschillende ladingen in haar buurt, is de vectoriële som van alle onderlinge coulombkrachten die de lading ondervindt.

4 Hoe kan er een aantrekking zijn tussen een geladen voorwerp en een neutraal voorwerp?

DEMO

Welke invloed heeft het ladingsteken van een geladen staaf op het gedrag van voorwerpen in de buurt?

1 Je leerkracht brengt een opgewreven pvc-staaf in de buurt van een blikje, papiersnippers en een dunne waterstraal.

Daarna herhaalt je leerkracht dat met een glazen staaf.

2 Wat zal er volgens jou gebeuren?

Bespreek met je buur en test samen met je leerkracht uit.

3 Formuleer een antwoord op de onderzoeksvraag.

4 Probeer je waarnemingen te verklaren met het deeltjesmodel.

Door de lading in de buurt verschuiven de elektronen in het neutrale voorwerp. Dat noem je elektrische influentie of elektrostatische inductie. De manier waarop de ladingen verschuiven, verschilt voor geleiders en isolatoren.

4.1 Geleider

Als je een neutraal metalen voorwerp nadert met een geladen staaf, verschuiven de valentieelektronen. Het neutrale metaal krijgt daardoor een positieve en een negatieve kant. Dat noem je een ladingsverdeling. Er ontstaat een aantrekkende elektrische kracht tussen de staaf en de geleider (die zelf geen lading krijgt).

VOORBEELD AANTREKKING VAN EEN BLIKJE DOOR EEN NEGATIEVE STAAF

Je brengt een opgewreven pvc-staaf in de buurt van een blikje (= neutrale geleider). De vrije valentie-elektronen in het blikje worden afgestoten, waardoor ze verschuiven naar de tegenoverliggende rand van de geleider, die negatief wordt. De kant het dichtst bij de staaf heeft daardoor een tekort aan elektronen en wordt positief.

De resulterende coulombkracht wordt bepaald door de aantrekkingskracht van de voorkant en de afstotingskracht van de achterkant. Aangezien de achterkant verder verwijderd is van de geladen staaf, is volgens de wet van Coulomb de afstotingskracht kleiner dan de aantrekkingskracht. Daardoor wordt de geleider aangetrokken tot de staaf.

▲ Afb. 37 Verplaatsing van elektronen in een blikje door een negatieve staaf in de buurt F C

De begrippen ‘influentie’ en ‘inductie’ zijn afgeleid van Latijnse werkwoorden:

• influere: beïnvloeden;

• inducere: opwekken.

©VANIN

CONCEPTVRAAG

Verklaar de waarnemingen voor het blikje in de buurt van een glazen staaf. Doe dat door de ladingsverdeling te tekenen.

▲ Afb. 38 Het blikje wordt aangetrokken door de resulterende coulombkracht.

demovideo: ladingen verschuiven zonder contact

Hoe kun je een elektroscoop laden zonder contact te maken met een geladen voorwerp?

1 Brainstorm met je buur over de vraag hoe je een elektroscoop positief/negatief kunt laden zonder hem in contact te brengen met een positieve/negatieve staaf.

2 Test samen met je leerkracht uit.

3 Formuleer een antwoord op de onderzoeksvraag.

Je kunt een geleider een permanente lading geven door elektrische influentie. Als je een externe lading in de buurt van een geleider houdt (zonder dat de geleider contact maakt met het geladen voorwerp), verplaatsen de elektronen in de geleider zich en ontstaat er een ladingsverdeling. Als je een geleidende verbinding tussen de geleider en de aarde maakt (= aarding), kunnen de vrije valentie-elektronen in de geleider weg van of naar de aarde verschuiven. Door die aarding krijgt de geleider een permanente lading, die tegengesteld is aan de externe lading.

VOORBEELD ELEKTROSCOOP POSITIEF LADEN

©VANIN

Een neutrale elektroscoop zonder nabije lading.

Een negatieve staaf nadert, met een uitwijking als gevolg. De elektroscoop is onderaan negatief en bovenaan positief geladen (maar in zijn geheel neutraal!).

Door de geleiding met de grond (aarding) kunnen er elektronen (die nog altijd worden afgestoten door de staaf) weg. Onderaan wordt de elektroscoop neutraal en bovenaan positief geladen.

Je neemt de aarding weg, maar de geladen staaf blijft. Zo blijft de elektroscoop in de evenwichtsstand die de zwaartekracht had veroorzaakt.

Je neemt de staaf weg. De lading van de elektroscoop verplaatst zich naar de uiteinden boven- en onderaan, met een uitwijking als gevolg.

4.2 Isolator

Elektrische influentie leidt bij isolatoren tot twee mogelijke fenomenen.

1 Polariseerbare isolatoren

Polariseerbare isolatoren bestaan uit apolaire moleculen, die dipolen kunnen worden. Als er geen externe lading in de buurt is, zijn de ladingen binnen elke molecule gelijkmatig verdeeld. Als een externe lading de isolator nadert, verschuiven binnen elke molecule de elektronen door elektrische influentie. Elke molecule krijgt zo een positieve en een negatieve kant en is dus tijdelijk een dipool geworden. Er ontstaat een aantrekkende elektrische kracht tussen de staaf en de isolator ten gevolge van het afstandsverschil. Net zoals bij het blikje (zie p.43) wordt de ongelijksoortige pool meer aangetrokken dan dat de gelijksoortige pool wordt afgestoten. De isolator blijft gepolariseerd totdat je de uitwendige oorzaak (de lading in de buurt) weghaalt.

VOORBEELD AANTREKKING VAN PAPIER DOOR EEN POSITIEVE STAAF

©VANIN

‘Polariseren’ betekent: een tegenstelling doen ontstaan, bijvoorbeeld twee tegengestelde (= ongelijksoortige) ladingen.

Een dipool heeft een positieve en een negatieve kant.

▲ Afb. 40

A Een neutrale papiersnipper met apolaire moleculen

B Polarisatie en tijdelijke dipoolmoleculen

C Schematische voorstelling van een papiersnipper met gepolariseerde moleculen

D Schematische voorstelling van een gepolariseerde papiersnipper

In een papiersnipper zijn de ladingen binnen elke molecule gelijkmatig verdeeld. Als je papiersnippers nadert met een positief geladen glazen staaf, verplaatsen de elektronen binnen een molecule zich door elektrische influentie naar de positieve staaf. Aangezien alle dipolen die zo ontstaan in de moleculen van de papiersnipper, op dezelfde manier georiënteerd zijn, lijkt er in de papiersnipper een negatieve kant dicht bij de staaf en een positieve kant aan de andere zijde te ontstaan. Op afbeeldingen stelt men een gepolariseerde papiersnipper vaak voor als een dipool.

Aangezien de achterkant van elke molecule verder verwijderd is van de geladen staaf, is de afstotingskracht kleiner dan de aantrekkingskracht. Daardoor wordt de papiersnipper aangetrokken tot de staaf.

2 Polaire isolatoren

Polaire isolatoren bestaan uit polaire moleculen, die permanent een positieve en een negatievekant hebben (= dipolen). Als je polaire isolatoren nadert met een geladen staaf, ontstaat er een aantrekkende elektrische kracht tussen de ladingen op de staaf en die op de isolator als gevolg van een heroriëntatie van de polaire moleculen

CONCEPTVRAGEN

1 Maak de uitspraken correct door het juiste antwoord te kiezen.

©VANIN

a Binnen in de gepolariseerde snipper zijn de elektronen gelijkmatig / ongelijkmatig verdeeld.

b De gepolariseerde snipper als geheel is elektrisch neutraal / geladen.

c De moleculen veranderen wel / niet van plaats als je een geladen staaf in de buurt houdt.

2 Water bestaat uit polaire moleculen.

a Gebruik je voorkennis uit de lessen chemie om te verklaren hoe de dipool ontstaat.

b Verklaar je waarnemingen wanneer je een glazen staaf en een pvc-staaf in de buurt van een waterstraal houdt. Doe dat door de ladingsverdeling te tekenen.

Bij elektrische influentie of elektrostatische inductie verschuiven de ladingen in een neutraal voorwerp door een externe lading in de buurt, zonder dat er contact gemaakt wordt:

• Geleiders: de valentie-elektronen verschuiven.

• Isolatoren: er worden dipolen gevormd (bij apolaire stoffen die kunnen polariseren) of de dipolen heroriënteren zich (bij polaire stoffen).

Gevolgen: neutrale voorwerpen kunnen worden aangetrokken door externe ladingen en geleiders kunnen worden geladen zonder contact te maken met het geladen voorwerp door aarding.

5 Hoe is de krachtwerking tussen massa’s vergelijkbaar met de krachtwerking tussen ladingen?

5.1 Zwaartekracht bij hemellichamen

Een voorwerp met een massa ondervindt zwaartekracht op of in de buurt van een hemellichaam. De zwaartekracht is een vectoriële grootheid met als symbool Fz. De zwaartekracht grijpt aan in het zwaartepunt van een voorwerp. Ze heeft een verticale richting en een zin naar het middelpunt van het hemellichaam.

De grootte van de zwaartekracht is afhankelijk van de massa van het voorwerp, de massa van het hemellichaam en de afstand van het voorwerp tot het middelpunt van het hemellichaam.

Voor elke massa kun je de grootte van de zwaartekracht berekenen als het product van de massa en de zwaarteveldsterkte op die plaats:

F z = m ∙ g

VOORBEELD ZWAARTEKRACHT VANWEGE DE AARDE OF DE MAAN OP EEN PERSOON

Het zwaartepunt van een object is het centrale massa(evenwichts)punt.

‘Verticaal’ betekent ‘loodrecht op een wateroppervlak’. 1 2 3

De zwaartekracht op een volwassene is groter dan op een kind.

Eigenschap van het voorwerp: massa m

De zwaartekracht op aarde is groter dan op de maan.

De zwaartekracht op de evenaar is kleiner dan op de polen.

Eigenschap van het hemellichaam en afstand tot het middelpunt van dat hemellichaam: zwaarteveldsterkte g

De zwaartekracht F z grijpt aan ter hoogte van het bekken van de personen. De richting is voor alle voorwerpen verticaal en de zin naar het midden van de aarde of de maan. De grootte kun je berekenen met F z = m ∙ g, waarbij gBelgië = 9,81 N kg , gmaan = 1,62 N kg en gevenaar = 9,78 N kg

In de buurt van een hemellichaam ondervinden voorwerpen de zwaartekracht F z , met deze kenmerken:

• aangrijpingspunt: het zwaartepunt;

• richting: verticaal;

• zin: naar het middelpunt van het hemellichaam;

• grootte: F z = m ∙ g

Fz, volwassene Fz, kind

Fz, aarde

F z, maan

F z

In het dagelijks leven worden massa en gewicht door elkaar gebruikt. In de fysica is er een duidelijk onderscheid. De massa is een scalaire grootheid. Het gewicht is een kracht (vectoriële grootheid) die uitgeoefend wordt door een massa op een ondersteuning. In de meeste gevallen is het gewicht even groot als de zwaartekracht.

5.2 Massa van een voorwerp

De massa van een voorwerp is de hoeveelheid materie waaruit dat voorwerp is opgebouwd. De massa van een voorwerp wordt bepaald door het materiaal en het volume van het voorwerp.

VOORBEELD MASSA VAN AARDSE VOORWERPEN EN PLANETEN

De afmetingen van aardse voorwerpen en organismen zijn beperkt, waardoor ze een beperkte massa hebben.

Bijvoorbeeld: een vliegje heeft een massa van 80 mg, een mens een massa van 50 tot 100 kg en een olifant een massa van 6 ton (= 6 ∙ 103 kg).

©VANIN

De afmetingen en dus ook de massa’s van de planeten zijn veel groter dan die van aardse voorwerpen. De massa van de aarde is bijvoorbeeld 5,972 ∙ 1024 kg. Op afbeelding 42 zie je de relatieve massa van alle planeten van ons zonnestelsel in vergelijking met de aarde. De massa van elke planeet wordt bepaald door haar samenstelling en afmetingen.

Macroscopisch wordt de massa m van een voorwerp bepaald door de grootheden volume V en massadichtheid ρ:

m = ρ ∙ V

Daarbij is de massadichtheid een materiaalconstante.

Op atomair niveau kun je de massadichtheid verklaren met het deeltjesmodel:

• Hoe groter de afstand tussen de deeltjes van een stof, hoe kleiner de massadichtheid van die stof.

• Hoe groter de massa van de deeltjes, hoe groter de massadichtheid. De soorten deeltjes verschillen voor elke stof. Ze hebben bepaalde afmetingen en een bepaalde massa, afhankelijk van de atomen of moleculen waaruit ze zijn samengesteld.

▲ Afb. 42 De verschillende planeten in ons zonnestelsel, met hun relatieve massa ten opzichte van de aardmassa

NAAM

De massa kun je ook berekenen aan de hand van de stofhoeveelheid n en de molaire massa M: m = n ∙ M

Daarbij wordt de stofhoeveelheid bepaald door het aantal deeltjes via het getal van Avogadro (NA = 6,022 ∙ 1023 mol–1):

n = N N A

De molaire massa wordt bepaald door de samenstelling van de moleculen.

De massa van een voorwerp wordt bepaald door de hoeveelheid materie Materie bestaat uit deeltjes met een specifieke massa.

WEETJE

Hoe deeltjes massa krijgen, is lang een vraagstuk geweest in de theoretische en experimentele fysica. De oplossing blijkt het elementaire deeltje met de naam ‘higgsboson’, dat voor het eerst werd voorspeld in 1964 en experimenteel werd bevestigd in 2012. De ontdekkers, Peter Higgs en François Englert (een Belg), ontvingen er in 2013 de Nobelprijs voor.

5.3 Algemene gravitatiekracht

De aantrekking van de planeten op voorwerpen wordt veroorzaakt door de massa van de planeet en de massa van het voorwerp. Meer algemeen oefenen massa’s in elkaars buurt een aantrekkende kracht uit op elkaar. Die kracht noem je de gravitatiekracht. De grootte van de gravitatiekracht wordt beïnvloed door de grootte van de massa’s en de afstand tussen de massa’s.

Om de gravitatiekracht kwantitatief te bestuderen, gebruik je een vereenvoudigd model met puntmassa’s. Je kunt het model van de puntmassa’s toepassen op bolvormige voorwerpen met een homogene samenstelling en op willekeurige voorwerpen met afmetingen die klein zijn in vergelijking met de afstand tussen de massa’s.

Tussen twee puntmassa’s m1 en m2 die zich op een afstand r van elkaar bevinden, werkt een gravitatiekracht, met als symbool FG:

• Een puntmassa m1 oefent op een puntmassa m2 een gravitatiekracht F12 uit.

• Een puntmassa m2 oefent op een puntmassa m1 een gravitatiekracht F21 uit.

• F12 en F21 vormen een actie-reactiepaar. Uit de derde wet van Newton volgt dat F12 en F21 voor elke combinatie van puntmassa’s m1 en m2 even groot en tegengesteld zijn: F12 = –F21

Om de benaming van de vector eenvoudig te houden, laten we het onderschrift G weg als het duidelijk is dat het om de gravitatiekracht gaat.

CONCEPTVRAAG

Hoe kun je massa vergelijken met lading?

Een puntmassa is een model waarbij alle massa zich in één punt bevindt.

03 LABO

Een universele constante is in elk medium geldig. Voorbeelden zijn de universele gasconstante en de elementaire lading.

Verschillende wetenschappers hebben de kenmerken van de gravitatiekracht FG experimenteel bepaald. De gravitatiekracht FG heeft volgende kenmerken:

• aangrijpingspunt: in de puntmassa of het middelpunt van de bolvormige massa (F12 in m2 en F21 in m1);

• richting: volgens de verbindingslijn tussen de puntmassa’s of de middelpunten van de bolvormige massa’s;

• zin: altijd aantrekkend;

• grootte: hangt af van de twee massa’s en hun onderlinge afstand: FG = G

met m1 en m2 de twee massa’s en r de afstand tussen die twee massa’s. G = 6,67

is een evenredigheidsconstante, die men ook wel de universele gravitatieconstante noemt.

©VANIN

Aangezien de gravitatieconstante G erg klein is, is het effect van de gravitatiekracht tussen voorwerpen enkel merkbaar als minstens een van beide voorwerpen een grote massa heeft.

De kracht van een hemellichaam op een voorwerp in de onmiddellijke buurt is ook een gravitatiekracht, maar in dat geval gebruiken we de term zwaartekracht en het vereenvoudigd model F z = m · g. In het Engels blijft het gravity heten.

Op een vergelijkbare manier kun je spreken van de zwaartekracht op andere hemellichamen (bijvoorbeeld de zwaartekracht op de maan: F z = m · gmaan, waarbij gmaan = 1,6 N kg ).

Om de zwaartekracht te berekenen, kun je in alle situaties de algemene gravitatiewet gebruiken.

In het dagelijkse taalgebruik wordt ook wel de vertaling zwaartekracht gebruikt in de plaats van gravitatiekracht, bijvoorbeeld de zwaartekracht van de maan op de aarde of de zwaartekracht op de astronauten in het ISS.

WEETJE

VOORBEELDVRAAGSTUK

Kiran (mk = 78,3 kg) staat op 1,25 m van Saar (m s = 65,2 kg).

Bepaal hun onderlinge gravitatiekracht en de gravitatiekracht die de aarde op hen allebei uitoefent.

Gegeven:

Gevraagd:

• mk = 78,3 kg

• m s = 65,2 kg

• rks = 1,25 m

• Fks = ?

• Fsk = ?

• Fak = ?

• F as = ?

Oplossing: a De onderlinge gravitatiekracht is aantrekkend en werkt volgens de verbindingslijn tussen Kiran en Saar.

De grootte van de gravitatiekracht die ze op elkaar uitoefenen, is voor hen allebei gelijk:

©VANIN

= 1,25 m

b De gravitatiekracht door de aarde is aantrekkend en werkt volgens de verbindingslijn tussen het middelpunt van de aarde en het zwaartepunt van Kiran en Saar.

De grootte wordt bepaald door massa van de aarde (een grote massa: ma = 5,972 ∙ 1024 kg) en de afstand tussen de vrienden en het middelpunt van de aarde. Die afstand is de aardstraal (ra = 6 371 km). Fak = Fka = G

Reflectie: Vergelijk de gravitatiekrachten die je berekend hebt.

Wat stel je vast?

Tussen Kiran en Saar onderling werkt een verwaarloosbare gravitatiekracht, omdat ze allebei een kleine massa hebben.

Vergelijk het resultaat bij punt b van het voorbeeldvraagstuk met de kenmerken van de zwaartekracht op aarde zoals je ze tot nu toe bepaalde. Wat stel je vast? Verklaar.

Fak Fka

De (omgekeerde) kwadratenwet is een wet in de fysica die aangeeft dat een grootheid zich omgekeerd evenredig verhoudt tot het kwadraat van de afstand tot de bron van die grootheid. Die wet is geldig bij veel fenomenen, omdat de oppervlakte van een bol toeneemt met de straal in het kwadraat.

Tussen twee massa’s werkt gravitatiekracht FG met deze kenmerken:

• aangrijpingspunt: een puntmassa of het middelpunt van een homogene bolvormige massa;

• richting: de verbindingslijn tussen de massa’s;

• zin: aantrekkend;

• grootte: FG = G ∙ m1 ∙ m2 r 2 , waarbij r de afstand tussen beide massa’s is en G = 6,67 ∙ 10–11 N ∙ m2 kg 2 .

Dat noem je de algemene gravitatiewet.

In de context van hemellichamen wordt de gravitatiekracht ook ‘zwaartekracht’ genoemd.

©VANIN

5.4 Analogie tussen de coulombkracht en de gravitatiekracht

De coulombkracht is de kracht als gevolg van de lading van voorwerpen. De gravitatiekracht is de kracht als gevolg van de massa van voorwerpen. De kenmerken van beide krachten zijn sterk vergelijkbaar.

• aangrijpingspunt: het ladings- of massacentrum

• richting: volgens de verbindingslijn

• zin: aantrekkend of afstotend voor de coulombkracht, enkel aantrekkend voor de gravitatiekracht

• grootte bepaald door:

– het product van de groottes van beide ladingen of massa’s

– de onderlinge afstand volgens de omgekeerde kwadratenwet: twee keer verder weg zorgt voor een vier keer zwakkere kracht; drie keer verder weg zorgt voor een negen keer zwakkere kracht

– een evenredigheidsconstante:

• coulombconstante, afhankelijk van het medium: k = 8,99 ∙ 109 N ∙ m2 C 2 in lucht of in een vacuüm; lager in andere mediums

• gravitatieconstante, in elk medium: G = 6,67 ∙ 10–11 N ∙ m2 kg 2

Afb. 43 De omgekeerde kwadratenwet: grootheden nemen af volgens de toename van het boloppervlak

REEKS

Je brengt een geladen ballon en een geladen rietje in elkaars buurt. Welke stelling is correct? Verklaar.

a Er is aantrekking, want de voorwerpen bestaan uit verschillende materialen.

b Er is afstoting, want de voorwerpen bestaan uit verschillende materialen.

c De aantrekking of afstoting wordt ook bepaald door de stof waarmee je de voorwerpen hebt opgewreven.

d De aantrekking of afstoting wordt bepaald door de materialen waaruit de voorwerpen gemaakt zijn.

Je beweegt met een wollen broek over een polyester kussen.

a Welke lading krijgen de broek en het kussen? Verklaar.

b Hoe kun je die lading opmerken?

Bereken voor een goudklompje met een massa van 23 g (ZAu = 79; AAu = 197; me– = 9,11 · 10–31 kg; 1 u = 1,66 · 10–27 kg):

a de lading;

b de totale lading van de elektronen;

c de totale massa van de elektronen.

De beentjes van een geladen elektroscoop blijven staan in een bepaalde hoek. Hoe komt dat?

Twee metalen bollen met ladingen van 0,080 µC en –0,060 µC bevinden zich op 12 cm van elkaar. Teken en bereken de kracht op elke bol.

Twee puntvormige ladingen (q1 = 0,294 C en q2 = 0,147 C) oefenen een kracht van 4,80 N op elkaar uit.

Op welke afstand bevinden de ladingen zich van elkaar?

Wie heeft gelijk? Verklaar.

De appel oefent een heel kleine gravitatiekracht uit op de aarde.

©VANIN

Op een droge winterdag stapt Lisa uit haar auto. Door de wrijving met de autostoel krijgt haar jas een lading van –83 µC. Bereken:

a het aantal extra elektronen op haar jas; b haar massatoename.

De appel oefent op de aarde een gravitatiekracht uit die gelijk is aan mappel ∙ g

Alleen een vallende appel oefent een gravitatiekracht uit op de aarde.

Bereken de grootte van de gravitatiekracht tussen de twee voorwerpen.

Zoek de ontbrekende gegevens op.

a een massa van 3,2 kg en een massa van 1,0 kg op een afstand van 2,0 m

b twee neutronen op een afstand van 3,0 nm

c de aarde en de maan

Op het einde van de achttiende eeuw heeft Henry Cavendish G voor het eerst experimenteel bepaald.

Hij mat een gravitatiekracht van 1,45 ∙ 10–7 N tussen een lichte loden bol van 0,73 kg en een zware bol van 158 kg, waarbij de afstand tussen de middelpunten 23 cm bedroeg.

a Bereken het aantal looddeeltjes in beide bollen.

b Bepaal de waarde van G die Cavendish berekende.

A B

AAN

DE SLAG

Pluto is een dwergplaneet met een straal van 1 185 km, die net als de aarde (ma = 5,98 ∙ 1024 kg en ra = 6 371 km) rond de zon beweegt (op een ellipsbaan).

De aarde bevindt zich op een afstand van 7,5 miljard km van Pluto en oefent een kracht van 9,2 ∙ 1010 N uit op die dwergplaneet.

Bereken:

a de gravitatiekracht die Pluto uitoefent op de aarde; b de massa van Pluto;

c de grootte van de gravitatiekracht die een massa van 5,0 kg op Pluto ondervindt.

REEKS

Vul de uitspraken aan met ‘altijd’, ‘soms’ of ‘nooit’.

a Bij wrijvingsexperimenten worden er protonen uitgewisseld.

b Bij wrijvingsexperimenten ontstaat er een overschot aan protonen.

c Als je een glazen staaf opwrijft met een dierlijke pels, ontstaat er een overschot aan elektronen op de staaf en een overschot aan elektronen op de dierlijke pels.

d Als je een glazen staaf opwrijft met een wollen doek, ontstaat er een overschot aan protonen op de staaf en een overschot aan protonen op de wollen doek.

Verklaar onderstaande fenomenen.

a Je kunt stofdoekjes gebruiken om vuil, stof en haar in je huis op te vangen en vast te houden.

b Als je fijn materiaal zoals bloem, veevoeder of houtzaagsel overpompt, is er explosiegevaar.

Je laadt een metalen bol positief en zet die samen met een tweede geladen bol op een glazen plaat.

De afbeelding toont het bovenaanzicht van die situatie.

a Hoe zal de lading zich verdelen? Verklaar.

b Teken de ladingsverdeling op beide metalen bollen in de volgende situaties.

c Je legt de bol nu rechtstreeks op de grond. Wordt de aarde daardoor geladen? Verklaar.

Je hangt een metalen bolletje op met een isolerend touwtje. Het bolletje wordt aangetrokken door een positief geladen staaf.

Wat kun je besluiten over de lading op de bol?

a De bol is negatief geladen.

b De bol is positief geladen.

c De bol is niet geladen.

d De bol is negatief of niet geladen.

e De bol is positief of niet geladen.

Een grote geïsoleerde bol met straal r heeft een lading. Op een afstand s van zijn oppervlak plaats je een kleine lading. De grafiek toont het verband tussen de afstand en de coulombkracht op de grote bol.

Welke grootheid is weergegeven op de horizontale as?

a s

b (r + s)2

c 1 s 2

d 1 ( r + s ) 2

e Je kunt daar geen uitspraak over doen, omdat je de aard van de ladingen niet kent.

f Geen van bovenstaande want binnen in de bol is er geen elektrische kracht.

F C

Je brengt enkele puntladingen met verschillende ladingen op een afstand d en 2 ∙ d (tussen de middelpunten) van elkaar, zoals voorgesteld op de afbeelding. d

a Rangschik de kracht die de ladingen ondervinden, van klein naar groot.

b Neem de afbeelding over en teken de kracht op de linkse ladingen.

Twee ladingen (q1 = q2 = –7,8 nC) bevinden zich op 3,0 cm van elkaar. Op de verbindingslijn tussen de twee ladingen plaats je op 1,0 cm van een van beide ladingen een lading q3 = 3,0 nC.

Bereken de kracht op de twee oorspronkelijke ladingen.

De grafiek toont de kracht tussen twee puntladingen.

a Welke grafieklijn geeft het verband tussen de coulombkracht en de afstand tussen de puntladingen correct weer?

b Bepaal de mogelijke ladingen van q2 waarvoor de grafiek geldig is …

1 als q1 = 2,0 µC;

2 als beide ladingen even groot zijn.

Drie ladingen, waarvan er twee identiek zijn, bevinden zich op de hoekpunten van een gelijkzijdige driehoek. De afbeelding toont de resulterende kracht op een van de ladingen.

Wat kun je daaruit besluiten over de derde lading? q q q 3 F

a q3 = q

b q3 = –q

c |q3| > |q|

d |q3| < |q|

e Er bestaat geen lading q3 waarvoor dat de resulterende kracht is.

Drie identieke metalen staven zijn geïsoleerd van de grond. Ze worden verticaal en evenwijdig met elkaar in elkaars nabijheid gebracht. De linkse geleider wordt (door een generator) positief geladen.

a Welke uitspraak is correct?

1 De middelste staaf wordt positief geladen.

2 De middelste staaf wordt negatief geladen.

3 De middelste staaf blijft neutraal, met een positieve linkerkant.

4 De middelste staaf blijft neutraal, met een negatieve linkerkant.

b Wat gebeurt er als je de middelste en de rechtse staaf met elkaar verbindt?

c Wat gebeurt er als je de verbinding verbreekt en de rechtse staaf aardt?

Verklaar je antwoorden met het deeltjesmodel.

Een elektron bevindt zich op 1,5 ∙ 10–12 m van de kern van een ijzeratoom dat 26 protonen bevat.

a Welke uitspraak is correct?

1 De coulombkracht die de kern uitoefent op het elektron, is verwaarloosbaar.

2 De gravitatiekracht die de kern uitoefent op het elektron, is verwaarloosbaar.

3 De coulombkracht en de gravitatiekracht die de kern uitoefent op het elektron, zijn verwaarloosbaar.

4 De coulombkracht en de gravitatiekracht die de kern uitoefent op het elektron, zijn vergelijkbaar.

b Teken en bereken de coulombkracht en de gravitatiekracht vanwege de kern op het elektron.

c Hoe komt het dat het elektron niet wordt opgenomen in de kern?

De grafiek toont het verband tussen de zwaartekracht en de massa van een voorwerp.

Vul de legende bij de grafiek aan met de aarde en de hypothetische planeten.

In het ISS zweven de astronauten (gewichtloos) rond. Zijn de volgende uitspraken juist of fout?

a De astronauten hebben dezelfde massa als op aarde.

b Er is geen gravitatiekracht van de aarde in het ISS.

c Er is nooit zwaartekracht in de ruimte.

d De hoge snelheid van het ISS heft het effect van de zwaartekracht op.

e De astronauten en het ISS bevinden zich continu in vrije val naar het centrum van de aarde toe.

Een appel met een massa van 200 g en een doorsnede van 10 cm ligt op de grond.

a Hoe groot is de afstand tussen het middelpunt van de appel en het middelpunt van de aarde?

b Hoe groot is de zwaartekracht die de aarde uitoefent op de appel?

c Hoe groot zou de gravitatiekracht op de appel zijn als hij zich in het ISS bevond op 330 km boven het aardoppervlak?

d Op welke afstand van de aarde zou de appel zich moeten bevinden om helemaal geen gravitatiekracht van de aarde te ondervinden?

Je wilt een propje aluminiumfolie van 2,0 g met een lading van –9,0 nC boven de grond laten zweven door er een metalen bol met een lading van +2,0 μC en een straal van 4,0 cm boven of onder te houden.

a Moet je de bol boven of onder het propje monteren? Verklaar met een krachtenschema.

b Hoe ver moet het propje zich van de bol bevinden opdat je poging lukt?

a Planeet A heeft een massa die dubbel zo groot en een straal die drie keer zo groot is als die van de aarde.

b Planeet B heeft dezelfde massadichtheid en een straal die dubbel zo groot is als die van de aarde.

c Planeet C heeft dezelfde massadichtheid en een massa die dubbel zo groot is als die van de aarde.

d Planeet D heeft een massadichtheid die de helft is van die van de aarde en dezelfde afmetingen als de aarde.

REEKS

Verklaar hoe elektrostatica een rol speelt bij onderstaande technologische toepassingen. Ga op zoek naar een geschikte video op het internet.

a een printer

b een fotokopieertoestel

c systemen voor luchtzuivering

Twee geïsoleerde puntladingen bevinden zich op een afstand r van elkaar en oefenen een kracht met grootte FC op elkaar uit. Vervolgens vervang je een van de ladingen door een dubbel zo grote lading. Op welke afstand moet je die lading plaatsen opdat de kracht even groot zou blijven?

Vier puntladingen bevinden zich op de hoekpunten van een vierkant. De afbeelding toont het onderlinge verband tussen de ladingen.

2 q q q – q

Welke lading ondervindt …

a de grootste resulterende kracht?

b een resulterende kracht die naar de buitenkant van het vierkant gericht is?

c een resulterende kracht volgens de diagonaal van het vierkant?

d een resulterende kracht die even groot is als de resulterende kracht op een andere lading?

Twee puntladingen die zich op 5,00 m van elkaar bevinden, stoten elkaar in de lucht af met een kracht van 0,72 N. Je brengt ze met elkaar in contact en plaatst ze dan weer op dezelfde afstand van elkaar. Ze stoten elkaar nu af met een kracht van 0,81 N.

Hoe groot waren de oorspronkelijke ladingen?

Twee puntladingen (q1 en q2) bevinden zich op een afstand d van elkaar. Je plaatst een derde lading q3 tussen beide ladingen.

a Bepaal (indien mogelijk) de positie waar q3 in rust is als q1 = q2

b Bepaal (indien mogelijk) de positie waar q3 in rust is als q1 = –q2.

c Noteer in symbolen de algemene evenwichtsvoorwaarde opdat q3 in rust is.

Twee identieke bolletjes (met een massa m en een lading q) zijn opgehangen zoals op de afbeelding.

β l = 15,0 cm

m = 60 mg d = 8,0 cm

a Bereken de hoek β en de lading van elk bolletje voor de gegeven waarden.

b Noteer in symbolen de hoek waarbij er een evenwicht bereikt wordt voor bolletjes met een massa m en een lading q die opgehangen zijn aan een touwtje met lengte l

Bepaal de grootteorde van de verhouding tussen de coulombkracht en de gravitatiekracht die tussen een elektron en een proton werken.

 Meer oefenen? Ga naar .

HOOFDSTUKSYNTHESE

Kracht tussen puntladingen

Wet van Coulomb:

VAN HET LADINGSTEKENINVLOED

©VANIN

▲ Afb. 44 De coulombkracht wordt beïnvloed door het ladingsteken, de ladingsgrootte en de afstand tussen de ladingen.

Een lading q1 oefent op een lading q2 een coulombkracht FC uit met deze kenmerken:

• aangrijpingspunt: een puntlading of het middelpunt van een (bolvormige) lading;

• richting: de verbindingslijn tussen de ladingen;

• zin: aantrekkend (ongelijksoortige ladingen) of afstotend (gelijksoortige ladingen);

• grootte: FC = k ∙ |q1| ∙ |q2| r 2 , waarbij r de afstand tussen de middelpunten van beide ladingen is en k = 8,99

(in lucht of in een vacuüm).

Lading

• Materie bestaat uit atomen, die protonen en elektronen bevatten.

• De lading wordt bepaald door het overschot (negatief geladen) of het tekort (positief geladen) aan elektronen

• Voorwerpen laden door elektronen over te dragen bij:

1 wrijving met een andere stof (tribo-elektrisch effect);

2 contact met een geladen voorwerp;

3 aarding in de buurt van een geladen voorwerp (elektrostatische inductie met aarding).

Kracht tussen puntmassa’s

Gravitatiewet:

▲ Afb. 45 De gravitatiekracht wordt beïnvloed door de massa en de afstand tussen de massa’s.

Tussen twee massa’s werkt zwaartekracht of gravitatiekracht met deze kenmerken:

• aangrijpingspunt: een puntmassa of het middelpunt van een homogene bolvormige massa;

• richting: de verbindingslijn tussen de massa’s;

• zin: aantrekkend;

• grootte: FG = G ∙ m1 ∙ m2 r 2 , waarbij r de afstand tussen beide massa’s is en G = 6,67 ∙ 10–11 N ∙ m2 kg 2

Massa: materie bestaat uit atomen, die een massa hebben.

Vaak gebruikt men het begrip ‘zwaartekracht’ om de gravitatiekracht in de buurt van planeten te benoemen.

HOOFDSTUK 3

Elektrisch veld en gravitatieveld

Je kunt een schokje voelen zonder dat je contact maakt met een geladen voorwerp. Een appel valt zonder dat er contact is met de aarde. In het vorige hoofdstuk leerde je hoe je dat kunt verklaren aan de hand van de coulombkracht en gravitatiekracht als veldkrachten. Maar in welk gebied is de uitwerking van die krachten merkbaar? Welke invloed hebben de bron en de afstand tot de bron op de uitwerking? En hoe kun je dat (wiskundig) beschrijven?

In dit hoofdstuk leer je hoe je het effect van ladingen en massa’s kunt beschrijven en voorstellen met velden. Eerst geef je betekenis aan een veld in het algemeen en vervolgens definieer je het elektrisch veld en het gravitatieveld. Je leert om beide velden voor te stellen en hun grootte te berekenen.

LEERDOELEN

M velden in het algemeen en soorten velden in de fysica omschrijven

M het elektrisch veld en het gravitatieveld voorstellen met veldlijnen

M de eigenschappen van het elektrisch veld en het gravitatieveld interpreteren

M de grootheden gravitatieveldsterkte en elektrische veldsterkte definiëren en gebruiken

1 Wat is een veld bij een veldkracht?

1.1 Veld

In het woordenboek vind je een tiental definities van het begrip ‘veld’. Vaak bedoelt men: een gebied of ruimte waar zich een specifieke activiteit voordoet of kan voordoen. Je kunt het veld beschrijven zonder dat de specifieke activiteit er zich echt voordoet. De eigenschappen van het veld zijn bepalend voor het verloop van de activiteit.

VOORBEELD VOETBALVELD

Op een voetbalveld kun je voetballen, maar dan heb je wel een aantal zaken nodig op het veld: om te beginnen een bal, maar ook spelers zijn onmisbaar. Misschien heb je ook een scheidsrechter nodig om alles in goede banen te leiden.

Het voetbalveld kan er nat, droog of hard bij liggen. Er kunnen stenen aanwezig zijn op het veld. De eigenschappen van het veld bepalen hoe het voetbalspel zou verlopen als de spelers en de bal het veld betraden. Een modderig voetbalplein zorgt voor een heel andere wedstrijd dan een droge, groene grasmat.

Een veld is een gebied of ruimte waar een specifieke activiteit kan plaatsvinden. De beschrijving van het veld (zonder activiteit) is zinvol om te voorspellen wat er zou gebeuren in het veld met activiteit.

CONCEPTVRAAG

Pas de definitie van het begrip ‘veld’ toe op een landbouwveld.

▲ Afb. 46 Op een modderig voetbalveld krijg je een andere wedstrijd dan op een droge, groene grasmat.

1.2 Soorten velden in de fysica

Binnen de wetenschappen is een veld een ruimtelijke verdeling van een fysische grootheid, bijvoorbeeld vochtigheidsgraad, temperatuur, snelheid ... Dat noem je een veldgrootheid

Wetenschappers zijn geïnteresseerd in de eigenschappen van een veld, omdat die eigenschappen de activiteiten op of in dat veld beïnvloeden.

VOORBEELD WEERKAART

Een weerkaart is een voorstelling van fysische velden. Op de kaart worden veldgrootheden zoals temperatuur en windsnelheid voorgesteld. Hun getalwaarde wordt op verschillende plaatsen in het veld weergegeven. De combinatie van de verschillende grootheden laat wetenschappers toe om het weer te beschrijven.

Wanneer je op vakantie gaat, kijk je naar het weerbericht van je bestemming, zodat je weet welke kleding je het best meeneemt. Zo’n weerkaart is de beschrijving van het veld waar je naartoe gaat (via een grafische weergave van enkele veldgrootheden).

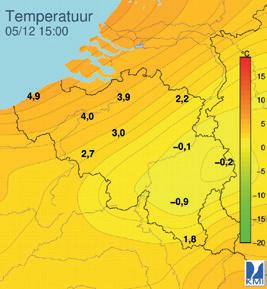
Er zijn twee soorten velden in de fysica:

1 Scalarveld

Een veld dat door een scalaire grootheid wordt beschreven, is een scalarveld. Aan elk punt van het veld wordt een getalwaarde verbonden. De weergave van het veld gebeurt met getallen in het veld, soms ondersteund door kleuren.

VOORBEELD TEMPERATUURVELD

Temperatuur is een scalaire grootheid. Op een weerkaart duidt men de temperaturen in verschillende regio’s soms aan met een getal (in graden Celsius) en een kleur voor een bepaald temperatuurbereik.

▲ Afb. 47 Weerkaart met de veldgrootheid temperatuur

▲ Afb. 48 Weerkaart met de veldgrootheid windsnelheid

2 Vectorveld

Een veld dat door een vectoriële grootheid wordt beschreven, is een vectorveld. Met elk punt van het veld wordt een vector met een getalwaarde (grootte), een richting en een zin verbonden. Je kunt het veld weergeven door op elke positie in het veld de corresponderende vector te tekenen. In paragraaf 2 leer je hoe je vectorvelden kunt voorstellen met lijnen.

VOORBEELD SNELHEIDSVELD

Snelheid is een vectoriële grootheid. Je kunt de stroming van bijvoorbeeld een rivier of de wind weergeven door een snelheidsvector te tekenen op verschillende plaatsen in het veld.

©VANIN

▲ Afb. 50 Het windveld boven Europa

CONCEPTVRAAG

Je kunt een vectorveld ook enkel scalair weergeven (bijvoorbeeld met kleuren).

Welke info mis je dan?

Kun je een scalarveld vectorieel weergeven? Verklaar kort.

Een veld beschrijf je in de fysica met een veldgrootheid.

Er zijn twee soorten velden:

• Scalarveld: de veldgrootheid is een scalar.

Bij elk punt van het veld hoort een getalwaarde.

• Vectorveld: de veldgrootheid is een vector.

Bij elk punt van het veld hoort een vector.

1.3 Veldkrachten en hun veld

Een veldkracht is een kracht die werkzaam kan zijn zonder dat er contact is (in tegenstelling tot een contactkracht). Het gebied waarin de (mogelijke) krachtwerking van de veldkracht beschreven wordt, noem je een veld.

In dit thema komen drie velden van veldkrachten aan bod. Je vindt hier al een korte omschrijving.

1 Elektrisch veld

Een elektrisch veld is een gebied waarin er een elektrische kracht werkt op elke lading die je in het gebied plaatst.

2 Zwaarteveld of gravitatieveld

Een zwaarteveld of gravitatieveld is een gebied waarin er een gravitatiekracht werkt op elke massa die je in het gebied plaatst.

©VANIN

3 Magnetisch veld

Een magnetisch veld is een gebied waarin er een magnetische kracht werkt op elke magneet of magnetische stof (zoals ijzer) die je in het gebied plaatst.

een parachutist aangetrokken door de aarde.

▲ Afb. 53 Rondom de U-vormige magneet heerst een magnetisch veld. Als je een kompasnaald (= kleine, langwerpige magneet) in de buurt brengt, neemt ze een bepaalde richting aan. Ook ijzervijlsel ondervindt een kracht in het magneetveld.

Een veld van een veldkracht is het gebied waar de veldkracht merkbaar is:

• elektrisch veld: daar waar een lading elektrische kracht ondervindt;

• gravitatieveld: daar waar een massa gravitatiekracht ondervindt;

• magnetisch veld: daar waar een magneet magnetische kracht ondervindt.

▲ Afb. 51 Rondom een geladen ballon heerst een elektrisch veld. Als er een metalen blikje in de buurt is, wordt het (na influentie) aangetrokken.

▲ Afb. 52 Rondom de aarde heerst een gravitatieveld. Daarin wordt bijvoorbeeld

2.1 Een elektrisch veld zichtbaar maken

DEMO

Hoe kun je een elektrisch veld zichtbaar maken?

1 Je leerkracht verbindt twee ronde elektroden met de uiteinden van een (band)generator of hoogspanningsbron en plaatst ze in een schaaltje op enkele centimeters van elkaar. De elektroden worden geladen met een even grote, maar tegengestelde lading. Dat zijn de bronladingen.

2 Wat zal er volgens jou gebeuren?

Bespreek met je buur en test samen met je leerkracht uit.

3 Je leerkracht giet nu ricinusolie in het schaaltje en strooit er griesmeelkorrels over. Daarna herhaalt je leerkracht stap 1.

4 Wat zal er volgens jou gebeuren?

Bespreek met je buur en test samen met je leerkracht uit.

5 Formuleer een antwoord op de onderzoeksvraag.

Rondom een of meerdere bronladingen is er een elektrisch veld, waarvan je meestal geen uitwerking ziet. Door kleine polaire of polariseerbare voorwerpen in de buurt te brengen, maak je een patroon van het elektrisch veld zichtbaar.

VOORBEELD DIPOOLVELD ZICHTBAAR MAKEN

Een elektrisch veld dat ontstaat door twee even grote, maar tegengestelde puntladingen, noem je een dipoolveld. Q1 Q2

Als je een andere lading in het dipoolveld plaatst, kan die een kracht ondervinden. Zonder proefladingen zie je geen uitwerking van het veld.

Als er griesmeelkorreltjes aanwezig zijn in het veld, zie je dat de korrels zich oplijnen. Er verschijnt een specifiek patroon in het dipoolveld.

demovideo: elektrisch veld

Een elektrode is een metalen voorwerp waaraan je een lading kunt geven.

Bronladingen zijn de ladingen die het elektrisch veld veroorzaken. Je stelt ze voor met de hoofdletter Q.

Proefladingen zijn externe ladingen die je in het elektrisch veld plaatst. Je stelt ze voor met de kleine letter q.

Je kunt het patroon dat verschijnt, verklaren met de polarisatie van de griesmeelkorreltjes. Een griesmeelkorreltje is een isolator en elektrisch neutraal. Het krijgt onder invloed van de geladen elektroden een positieve en een negatieve kant.

• De negatieve kant van de korrel wordt aangetrokken door de positieve elektrode en afgestoten door de negatieve.

• De positieve kant van de korrel wordt aangetrokken door de negatieve elektrode en afgestoten door de positieve.

Dat is hetzelfde fenomeen als bij de polarisatie van een papiersnipper (zie p.45).

▲ Afb. 54 Het patroon van gepolariseerde griesmeelkorrels in een dipoolveld

De gepolariseerde korrels ondervinden ook aantrekkingskrachten van de andere nabije korrels. Nadat de korrels zich in een patroon hebben herschikt, bewegen ze niet meer. Dat statische eindresultaat zie je op afbeelding 54.

Uit de demoproef blijkt dat de griesmeelkorreltjes een elektrische kracht ondervinden. Dat kan enkel als ze zich in een elektrisch veld bevinden. Dat elektrisch veld blijft aanwezig als je de griesmeelkorreltjes wegneemt. Alleen is er dan geen uitwerking van het veld merkbaar.

Je kunt het patroon van een elektrisch veld zichtbaar maken door polaire of polariseerbare voorwerpen in de buurt te brengen. Die voorwerpen lijnen zich op.

2.2 Elektrische veldlijnen

Je kunt het elektrisch veld voorstellen met elektrische veldlijnen. Dat lijnenpatroon is een visuele voorstelling van de richting, zin en grootte van het veld. Omwille van het verband tussen veld en veldkracht geeft het lijnenpatroon ook informatie over de richting, zin en grootte van de kracht die een proeflading op een bepaalde plaats in het veld zou ondervinden.

VOORBEELD VELDLIJNEN IN HET DIPOOLVELD

Op afbeelding 54 zie je hoe de gepolariseerde griesmeelkorreltjes een lijnvormig patroon vormen doordat ze zich richten. Je kunt dat patroon voorstellen door vloeiende lijnen te tekenen die het patroon volgen. Dat zijn de veldlijnen van het dipoolveld. Het veld is driedimensionaal. Ook zonder de griesmeelkorrels kun je het veld tekenen met die veldlijnen.

▲ Afb. 55 Vloeiende lijnen door de patronen van de korrels

Je kunt de veldlijnen een zin geven. Volgens afspraak is dat de zin waarin een positieve proeflading een kracht zou ondervinden. De zin van elektrische veldlijnen is dus altijd weg van de positieve bronlading(en) en naar de negatieve bronlading(en) toe. Aan de hand van de zin van de veldlijnen kun je de krachtzin op proefladingen bepalen. Bij onbekende bronladingen kun je door de veldlijnen hun ladingstekens achterhalen.

De dichtheid van de veldlijnen is een maat voor de relatieve sterkte van het veld. Hoe dichter de veldlijnen bij elkaar liggen, hoe sterker het veld is.

VOORBEELD STERKTE EN ZIN VAN HET DIPOOLVELD

Op afbeelding 56 zie je de zin van elke veldlijn van het dipoolveld. Dicht bij en op de verbindingslijn tussen de bronladingen liggen de veldlijnen dicht tegen elkaar. Daar is het veld sterker (gele zone A) dan op andere plaatsen, waar de veldlijnen verder uit elkaar liggen (groene zone B).

CONCEPTVRAAG

Wat verandert er aan het veldlijnenpatroon als een van de polen sterker geladen is dan de andere pool?

Je kunt het elektrisch veld voorstellen met veldlijnen

• Veldlijnen geven de richting van het elektrisch veld aan.

• De zin van de veldlijnen is per definitie weg van de positieve bronlading(en) en naar de negatieve bronlading(en) toe

• De dichtheid van de lijnen geeft aan waar het veld sterker of zwakker is.

2.3 Verschillende configuraties van elektrische velden

DEMO

Hoe ziet het veldlijnenpatroon van verschillende elektrodeopstellingen eruit?

1 Je leerkracht maakt verschillende configuraties van bronladingen met ricinusolie en griesmeelkorrels.

2 Welk patroon verwacht je?

Bespreek met je buur en test samen met je leerkracht uit.

3 Formuleer een antwoord op de onderzoeksvraag.

demovideo: veldlijnenpatronen

TIP applet: elektrisch veld

Bouw de situatie na in de applet om te zien welk elektrisch veld er ontstaat in specifieke situaties.

De verschillende configuraties geven elk een eigen veldlijnenpatroon.

In de tabel worden enkele veelvoorkomende types velden voorgesteld en besproken.

▲ Afb. 56 Dipoolveldlijnen met zin

TYPE VELD EIGENSCHAPPEN VAN DE VELDLIJNEN radiaal veld

▲ Afb. 57 Griesmeelkorreltjes rond een puntlading

▲ Afb. 58 Elektrische veldlijnen rond een positieve en een negatieve bronlading

Een radiaal veld ontstaat rondom een puntlading of rondom een geladen bol. Daarrond is er bolsymmetrie

dipoolveld

▲ Afb. 59 Griesmeelkorreltjes in een dipoolveld

• richting: rechte lijnen die door de bronlading of het middelpunt van de bolvormige lading lopen

• veldlijnendichtheid: het grootst dicht bij de lading; daar is het elektrisch veld het sterkst

• zin: afhankelijk van het teken van de lading die het veld opwekt: weg van een positieve bronlading of naar een negatieve bronlading toe

©VANIN

▲ Afb. 60 Elektrische veldlijnen

Een dipoolveld ontstaat in de buurt van twee puntladingen die even sterke, tegengestelde ladingen hebben. De aantrekking tussen de twee puntladingen (die allebei bronladingen zijn) is zichtbaar door veldlijnen die naar elkaar toe buigen.

homogeen veld

▲ Afb. 62 Elektrische veldlijnen in een

Een homogeen veld ontstaat tussen twee lange, evenwijdige elektroden met een tegengestelde lading. Je kunt dat begrijpen als heel veel dipolen naast elkaar, die elkaar beïnvloeden en zorgen voor een evenwijdig veldlijnenpatroon.

veld tussen gelijke polen

Afb. 63 Griesmeelkorreltjes in een veld bij twee gelijke ladingen

▲ Afb. 64 Elektrische veldlijnen in een veld bij twee gelijke ladingen

Als de twee ladingen even sterk en gelijksoortig zijn (twee gelijke positieve ladingen of twee gelijke negatieve ladingen), dan ontstaat er een patroon waarbij de afstoting tussen de twee polen (die allebei bronladingen zijn) duidelijk wordt door veldlijnen die afbuigen van elkaar.

• richting: tussen twee ladingen gebogen naar elkaar toe, buiten de ladingen (bijna) zoals bij een radiaal veld

• veldlijnendichtheid: het grootst dicht bij de bronladingen; daar is het elektrisch veld het sterkst

• zin: weg van de positieve bronlading en naar de negatieve bronlading toe

• richting: recht en evenwijdig met elkaar, loodrecht op de staven

• veldlijnendichtheid: constant; het elektrisch veld is overal even sterk

• zin: van de positieve naar de negatieve elektrode (net zoals bij dipolen)

• richting: tussen twee ladingen gebogen van elkaar weg, buiten de ladingen (bijna) zoals bij een radiaal veld

• veldlijnendichtheid: het grootst dicht bij de bronladingen; daar is het elektrisch veld het sterkst

• zin: afhankelijk van de tekens van de ladingen: weg van de positieve lading en naar de negatieve lading toe

in een dipoolveld

▲ Afb. 61 Griesmeelkorreltjes in een homogeen veld

homogeen veld

▲

2.4 Kwalitatief verband tussen elektrische veldlijnen en elektrische veldkracht

Elektrische veldlijnen geven op elke plaats de richting en de zin aan van de resulterende coulombkracht F res op een proeflading:

• De richting van de resulterende coulombkracht is altijd rakend aan de veldlijnen.

• De zin van de resulterende coulombkracht hangt af van het teken van de proeflading. Een positieve proeflading ondervindt een kracht in de zin van de veldlijnen, een negatieve lading een kracht tegen de zin van de veldlijnen in.

• De grootte van de resulterende coulombkracht wordt bepaald door de grootte van de proeflading en de sterkte van het elektrisch veld op de plaats waar de lading zich bevindt.

©VANIN

VOORBEELD KRACHT OP PROEFLADINGEN IN EEN DIPOOLVELD

Je brengt drie proefladingen (A, B en C) met een even grote absolute waarde op verschillende plaatsen in het dipoolveld. De proefladingen ondervinden een resulterende coulombkracht door de aantrekking en afstoting van de twee bronladingen van het dipoolveld.

• Proeflading A is positief en bevindt zich op de verbindingslijn tussen de bronladingen. De lading wordt aangetrokken door de negatieve bronlading en afgestoten door de positieve. Zonder de aparte coulombkrachten te tekenen, weet je dat de resulterende krachtvector (F res, A) aan de veldlijn raakt en dezelfde zin heeft als de veldlijnen.

65 Kracht op proefladingen in een dipoolveld

• Proeflading B is negatief en bevindt zich op een willekeurige plaats in het veld, een beetje dichter bij de positieve bronlading dan bij de negatieve. De proeflading ondervindt meer aantrekkingskracht door de positieve bronlading dan afstotingskracht door de negatieve. De resulterende krachtvector (F res, B) raakt aan de veldlijn. Ze heeft een zin die tegengesteld is aan die van de veldlijnen.

• Proeflading C is negatief en bevindt zich heel dicht bij de negatieve bronlading. De proeflading ondervindt veel meer afstotingskracht door de negatieve bronlading dan aantrekkingskracht door de positieve. De resulterende krachtvector (Fres, C) raakt aan de veldlijn. Haar zin is tegengesteld aan die van de veldlijnen.

De drie (resulterende) krachtvectoren raken aan de plaatselijke veldlijn. De drie proefladingen zijn even sterk, maar in C is de kracht het grootst. Je kunt dat zien doordat daar de veldlijnen het dichtst bij elkaar liggen. In B is de kracht het zwakst. De veldlijnen liggen er ver uit elkaar.

Voor een positieve proeflading werkt de kracht in de zin van de veldlijn, voor een negatieve proeflading tegen de zin van de veldlijn in.

CONCEPTVRAAG

Kunnen veldlijnen elkaar snijden?

Verklaar waarom (niet).

In alle punten van het elektrisch veld raakt de krachtvector aan de veldlijn. De zin van de coulombkracht hangt af van het teken van de proeflading en de zin van de veldlijnen. De relatieve grootte wordt zichtbaar gemaakt door de dichtheid van de veldlijnen.

CONCEPTVRAAG

Teken in een homogeen veld op drie verschillende plaatsen de krachten op een proton en een elektron.

• De bronmassa is de massa die het gravitatieveld opwekt.

• De proefmassa is de massa die in het veld wordt geplaatst.

3.1 Het gravitatieveld

Massa’s ondervinden in de buurt van een hemellichaam (of een andere massa) de gravitatiekracht. De gravitatiekracht is een veldkracht. Massa’s ondervinden de gravitatiekracht dus ook als er geen contact is met het hemellichaam. Het gebied rond het hemellichaam waarin massa’s de gravitatiekracht ondervinden, noem je het gravitatieveld. Het hemellichaam is de bronmassa en de massa in het gravitatieveld de proefmassa. De vorm van het veld stel je voor met veldlijnen. De gravitatiekrachtvector op een proefmassa heeft in elk punt van het veld dezelfde richting en zin als de veldlijn door dat punt. Door de krachtvectoren te tekenen, kun je het veldlijnenpatroon afleiden.

3.2 Het gravitatieveld als radiaal veld

Het gravitatieveld is radiaal. De veldlijnen lopen door het middelpunt van het hemellichaam.

VOORBEELD GRAVITATIEVELD ROND DE AARDE

Voorwerpen op of in de buurt van de aarde ondervinden de gravitatiekracht. Alle krachtvectoren op de proefmassa’s wijzen naar het middelpunt van de aarde (de bronmassa). Zo kun je de richting en de zin van het gravitatieveld bepalen.

• Richting: de krachtvectoren raken aan de veldlijnen. De veldlijnen gaan dus door het middelpunt van de aarde.

• Zin: de zin wordt gekozen volgens dezelfde zin als de gravitatiekracht, dus naar het middelpunt van de aarde toe.

▲ Afb. 66 De gravitatieveldlijnen van de aarde hebben dezelfde richting en zin als de krachtvectoren op een proefmassa op of in de buurt van de aarde.

Ook zonder proefmassa’s in de buurt bestaat het gravitatieveld van de aarde. Je kunt het voorstellen met een patroon van gravitatieveldlijnen: vloeiende lijnen die de richting en de zin van de mogelijke gravitatiekracht weergeven. De veldlijnen liggen dichter bij elkaar in de buurt van de aarde. Daar is het gravitatieveld dus sterker.

Rond de aarde is er een radiaal gravitatieveld aanwezig. De richting en de zin zijn naar het middelpunt van de aarde toe.

▲ Afb. 67 De veldlijnen zijn ook aanwezig als er geen proefmassa is.

3.3 Het gravitatieveld benaderen als een homogeen veld

Voor gebieden ver van het middelpunt van een hemellichaam kun je het gravitatieveld benaderen als een homogeen veld. Dat betekent dat de veldlijnen in een klein gebied (aangeduid met de gele rechthoekjes op afbeelding 68) benaderend evenwijdig en op gelijke afstand van elkaar lopen.

Hemellichamen zijn groot. Dat betekent dat de afstand van het oppervlak tot het middelpunt groot is. In de buurt van het oppervlak kun je het gravitatieveld dus als een homogeen veld benaderen. Laat je de afstand tot het oppervlak (en dus tot het middelpunt) verder toenemen, dan wordt de homogene benadering steeds beter.

Het gravitatieveld wordt steeds homogener.

VOORBEELD GRAVITATIEVELD IN DE BUURT VAN DE AARDE

©VANIN

▲ Afb. 68 Het donkerste rechthoekje bevindt zich het verst van het middelpunt. Daar kun je het veld het best benaderen als een homogeen veld.

In onze leefwereld is het aardoppervlak schijnbaar horizontaal. We bevinden ons ver genoeg van het middelpunt van de aarde om het gravitatieveld als homogeen te kunnen benaderen.

De veldlijnen staan loodrecht op het aardoppervlak en zijn naar de aarde toe gericht. Je tekent de veldlijnen overal even ver van elkaar om aan te geven dat het gravitatieveld overal even sterk is.

Na een regenbui of in de douche verschijnen er verticale lijnen op het raam. Ze stellen het veldlijnenpatroon in de buurt van het aardoppervlak voor. Het veldlijnenpatroon is homogeen.

Afb. 69 Nabij en verder weg van het aardoppervlak kun je

gravitatieveld benaderen als een homogeen veld.

CONCEPTVRAGEN

Afb. 70 Waterdruppels op een raam maken het homogene veldlijnenpatroon in de buurt van de aarde zichtbaar.

1 Is er enkel een gravitatieveld rond hemellichamen? Verklaar.

2 Is er enkel een radiaal gravitatieveld rond een bolvormig voorwerp? Verklaar.

Het gravitatieveld rond een bronmassa is radiaal, met de zin gericht naar het middelpunt van de bronmassa.

Als je je ver genoeg van het middelpunt van de bronmassa bevindt, dan kun je het veld als homogeen benaderen. Dat is het geval nabij en verder weg van het oppervlak van een hemellichaam.

▲

het

▲

4 Welke grootheid beschrijft een gravitatieveld?

In de buurt van hemellichamen ondervinden voorwerpen een zwaartekracht. De grootte wordt bepaald door de grootte van de massa m en de zwaarteveldsterkte g. Voor elke massa kun je de grootte van de zwaartekracht berekenen als het product van de massa en de zwaarteveldsterkte op die plaats: F z = m · g

Omgekeerd kun je bij een gekende zwaartekracht de zwaarteveldsterkte bepalen als de verhouding van de grootte van de zwaartekracht op een voorwerp (planeet, maan, ster …) tot de massa van dat voorwerp: g = Fz m . De zwaarteveldsterkte is een grootheid waarmee je de sterkte van het zwaarteveld (= de invloed van de bronmassa) uitdrukt. De grootte van g is de grootte van de zwaartekracht op een massa van 1 kg.

De zwaarteveldsterkte heeft, naast een grootte, ook een aangrijpingspunt, een richting en een zin. Het is een vectoriële grootheid: g = Fz m . Op een analoge manier kun je de gravitatieveldsterkte g definiëren.

GROOTHEID MET

gravitatieveldsterkte g = FG m [g] = N kg

VOORBEELD GRAVITATIEVELDSTERKTE

©VANIN

MET

Rondom de aarde en de maan is er een zwaarteveld en dus een gravitatieveld. De eigenschappen (de massa en de straal van de aarde of de maan) bepalen de gravitatieveldsterkte g. Die is onafhankelijk van de proefmassa in de buurt van het hemellichaam.

De gravitatiekracht op een volwassene is groter dan op een kind.

Eigenschap van de proefmassa m

De gravitatiekracht op aarde is groter dan op de maan. De gravitatiekracht op de evenaar is kleiner dan op de polen.

Eigenschap van het gravitatieveld in dat punt rond de bronmassa: gravitatieveldsterkte g

Het gravitatieveld is een vectorveld. Je kunt de gravitatieveldsterkte in elk punt voorstellen met de veldsterktevector.

SYMBOOL

EENHEID

SYMBOOL

Je bestudeert nu de gravitatieveldsterkte in een radiaal en in een homogeen veld.

A Gravitatieveldsterkte in een radiaal veld

Rond elke bolvormige bronmassa is er een radiaal gravitatieveld. De bronmassa kan een hemellichaam of een willekeurige massa zijn. Om de kenmerken van de gravitatieveldsterkte rond de bronmassa te bestuderen, onderzoek je de gravitatiekracht op een proefmassa in dat veld.

VOORBEELD GRAVITATIEVELDSTERKTE ROND DE AARDE

©VANIN

De massa van de aarde Maarde is de bronmassa van het gravitatieveld op en rond de aarde. Als je een proefmassa m in dat veld plaatst, ondervindt ze een gravitatiekracht naar het middelpunt van de aarde toe, met als grootte:

FG = G ∙ Maarde ∙ m r 2

De gravitatieveldsterkte op de plek van de proefmassa kun je bepalen als g = FG m .

Aangezien m positief is, heeft g dezelfde richting en zin als FG. De grootte kun je als volgt berekenen:

g = FG m = G ∙ Maarde ∙ m r 2 m = G ∙ Maarde r 2

CONCEPTVRAAG

Geef een voorbeeld van een positie waarbij:

• dezelfde massa een even grote gravitatiekracht ondervindt als de weergegeven massa;

• een grotere massa een even grote gravitatiekracht ondervindt als de weergegeven massa;

• de gravitatieveldsterkte voor een kleinere massa even groot is als voor de weergegeven massa.

Met die eigenschappen kun je de gravitatieveldsterkte g in een aantal willekeurige punten berekenen en construeren. Elke vector is naar het middelpunt van de aarde gericht.

De grootte g = G ∙ Maarde r 2 neemt af als de afstand r tot het middelpunt toeneemt.

Je kunt de opeenvolgende veldsterktevectoren verbinden met een veldlijn. Dan bekom je het radiale veldlijnenpatroon.

Voldoet de gravitatieveldsterkte aan de omgekeerde kwadratenwet? Verklaar. CONCEPTVRAAG

In elk radiaal gravitatieveld rond een willekeurige massa (zoals een hemellichaam) is er een gravitatieveldsterkte g met deze kenmerken:

• aangrijpingspunt: een willekeurig punt in het gravitatieveld;

• richting: radiaal naar het middelpunt van de bronmassa toe;

• zin: naar de bronmassa toe;

• grootte: g = G ∙ M r 2 , waarbij G de universele gravitatieconstante is, M de grootte van de bronmassa en r de afstand tot het middelpunt van de bronmassa.

Je kunt de eigenschappen van de gravitatieveldsterkte afleiden uit het veldlijnenpatroon:

©VANIN

• In elk punt van het gravitatieveld raakt de gravitatieveldsterkte aan de veldlijnen.

• De zin van de gravitatieveldsterkte is hetzelfde als de zin van de veldlijnen: naar de bronmassa toe.

• De grootte van de veldsterkte is gelinkt aan de veldlijnendichtheid: de dichtheid van de veldlijnen neemt af naarmate de afstand r tot het middelpunt toeneemt.

B Gravitatieveldsterkte in een homogeen veld

Nabij en verder van het oppervlak van een hemellichaam is het gravitatieveld bij benadering homogeen. Hemellichamen hebben een straal r van enkele duizenden kilometers. Als een voorwerp zich op een hoogte h van enkele meters of kilometers van het oppervlak bevindt, dan blijft de afstand van dat voorwerp tot het middelpunt van het hemellichaam bij benadering gelijk aan de straal van het hemellichaam (enkele duizenden kilometers). De afstand tot het middelpunt van het hemellichaam verandert dus in verhouding nauwelijks voor een hoogte h van enkele kilometers boven het oppervlak. Daardoor is g (bijna) constant in de buurt van het hemellichaam.

g = G ∙ M r 2 = G ∙ M (rhemellichaam + h)2 ≈ G ∙ M r2 hemellichaam

Ook de richting en de zin van g zijn overal hetzelfde: de vectoren lopen evenwijdig met elkaar, naar het oppervlak van de planeet toe.

VOORBEELD GRAVITATIEVELDSTERKTE NABIJ DE AARDE

Je kunt de gravitatieveldsterkte op verschillende plaatsen in de nabijheid van de aarde berekenen:

• op zeeniveau (h = 0):

g = G ∙ M r 2 = G ∙ Maarde

• bovenop een berg (h = 1 km):

g = G ∙ M r 2 = G ∙ Maarde (raarde + h)2 = 6,674

• op vliegtuighoogte (h = 10 km):

g = G ∙ M r 2 = G ∙ Maarde (raarde + h)2 = 6,674

5,9742 ∙ 1024 kg (6 381 ∙ 10 3 m) 2 = 9,793 N kg

De berekende waarde is (afgerond op twee beduidende cijfers) gelijk: g = 9,8 N kg

Die waarde stemt overeen met de zwaarteveldsterkte zoals je die je vroeger al geleerd hebt.

Ook de richting en de zin zijn voor alle vectoren gelijk. Met die eigenschappen kun je de gravitatieveldsterkte g in een aantal willekeurige punten tekenen: dat zijn voor elk punt identieke vectoren. Het bijbehorende veldlijnenpatroon is homogeen.

▲ Afb. 73 De gravitatieveldsterkte voor verschillende punten in het homogene veld rond de aarde

CONCEPTVRAAG

▲ Afb. 74 De gravitatieveldlijnen in het homogene veld rond de aarde

Als er in een punt een gravitatieveldsterkte is, is er daar dan ook een gravitatiekracht G? Leg in woorden het kwantitatieve verband tussen die twee grootheden uit.

VOORBEELDVRAAGSTUK

Mars heeft een massa van 6,42 · 1023 kg en een diameter van 6 779 km.

In de buurt van Mars bevindt zich een brokstuk met een massa van 4,0 kg.

1 Bepaal de grootte van de gravitatieveldsterkte op het oppervlak van Mars.

2 Bepaal de hoogte h waarop de gravitatieveldsterkte 2,00 N kg bedraagt.

3 Teken en bereken de gravitatiekracht op het brokstuk op het oppervlak en op hoogte h

Gegeven:

Gevraagd:

• MMars = 6,42 ∙ 1023 kg

• d = 6 779 ∙ 103 m

• gh = 2,00 N kg

• m = 4,0 kg

• gopp = ?

• hh = ?

• FG, opp = ?

• FG, h = ?

Oplossing: 1 Op het oppervlak is de afstand tot het middelpunt de straal (= d 2 ) van Mars. Je vindt de gravitatieveldsterkte aan de hand van de definitie:

©VANIN

2 Om de hoogte h te vinden, moet je de basisformule omvormen en als afstand tot het middelpunt rMars + h gebruiken:

3 De gravitatiekracht is op beide hoogtes verticaal naar het midden van Mars gericht, met als aangrijpingspunt het zwaartepunt van het brokstuk. Je kunt de grootte van de gravitatiekracht berekenen aan de hand van de gravitatieveldsterkte op beide hoogtes:

De gravitatieveldsterkte g is een grootheid waarmee je de eigenschappen van het gravitatieveld (= de invloed van de bronmassa) uitdrukt.

GROOTHEID MET SYMBOOL EENHEID MET SYMBOOL

gravitatieveldsterkte g = FG m [g] = N kg

Het gravitatieveld is een vectorveld waarbij g in elk punt de grootte, de richting en de zin van het gravitatieveld aangeeft. De grootte kun je als volgt berekenen: g = G ∙ M r 2 (waarbij G de universele gravitatieconstante is, M de grootte van de bronmassa en r de afstand tot het middelpunt van de bronmassa). Als een voorwerp zich ver van het middelpunt van een hemellichaam (bronmassa) bevindt, kun je het gravitatieveld als homogeen benaderen en is de gravitatieveldsterkte (bij benadering) constant.

Als je de gravitatieveldsterkte g in een punt van het veld kent, kun je de gravitatiekracht op een proefmassa m in dat punt als volgt bepalen: FG = m · g.

5.1 Elektrische veldsterkte

In een elektrisch veld ondervindt een proeflading q een coulombkracht FC.

Op een analoge manier als bij de gravitatieveldsterkte definieer je voor een elektrisch veld de elektrische veldsterkte E. De elektrische veldsterkte is een grootheid waarmee je de sterkte van het elektrisch veld (= de invloed van de bronlading) uitdrukt. De grootte van de elektrische veldsterkte is gelijk aan de grootte van de coulombkracht op een proeflading van 1 C.

GROOTHEID MET SYMBOOL

elektrische veldsterkte E = FC q [E] = N C

VOORBEELD ELEKTRISCH VELD ROND EEN PUNTLADING

©VANIN

Het ladingsteken en de grootte van de proeflading beïnvloeden de coulombkracht.

Eigenschap van de proeflading q

Het ladingsteken van de bronlading beïnvloedt de zin van de coulombkracht.

EENHEID MET SYMBOOL

De afstand tot de bronlading beïnvloedt de grootte van de coulombkracht.

Eigenschap van het elektrisch veld rond de bronlading Q: elektrische veldsterkte E

Rondom een puntlading (= bronlading) is er een elektrisch veld. De eigenschappen (ladingsgrootte, ladingsteken en afstand tot de bronlading) bepalen de elektrische veldsterkte E

Die is onafhankelijk van de proeflading in de buurt van de bronlading.

Het elektrisch veld is een vectorveld. Je kunt de elektrische veldsterkte in elk punt voorstellen met de veldsterktevector.

De elektrische veldsterkte E is een grootheid waarmee je de eigenschappen van het elektrisch veld (= de invloed van de bronlading) uitdrukt. Het elektrisch veld is een vectorveld

GROOTHEID MET SYMBOOL EENHEID MET SYMBOOL

elektrische veldsterkte E = FC q [E] = N C

Als je de elektrische veldsterkte E in een punt van het veld kent, kun je de coulombkracht op een proeflading q in dat punt als volgt bepalen: F c = q · E.

5.2 De elektrische veldsterkte in een radiaal veld

De puntlading die het veld opwekt, is de bronlading Q. Als je een proeflading q in het veld plaatst, ondervindt ze een coulombkracht die gericht is volgens de verbindingslijn met de bronlading. De grootte van de veldsterkte in een radiaalveld is gelijk aan:

E = FC | q | = k ∙ |Q| · |q| r 2 | q | = k ∙ |Q| r 2

Daarbij is k de coulombconstante, Q de grootte van de bronlading en r de afstand tot (het middelpunt van) de bronlading.

Als de proeflading q positief is, heeft E dezelfde richting en zin als FC op de proeflading.

Je kunt de elektrische veldsterktevectoren ook tekenen zonder dat er een proeflading met bijbehorende coulombkracht is. Elke veldvector is radiaal gericht. De zin wordt bepaald door het teken van de bronlading:

• Voor een positieve bronlading is de zin van de elektrische veldvector weg van de bronlading.

• Voor een negatieve bronlading is de zin van de veldvector naar de bronlading toe

De grootte van de veldvector wordt bepaald door de grootte van en de afstand tot de bronlading.

▲ Afb. 75 De coulombkracht en de elektrische veldsterkte voor een positieve proeflading in de buurt van een positieve bronlading

▲ Afb. 76 De coulombkracht en de elektrische veldsterkte voor een positieve proeflading in de buurt van een negatieve bronlading

▲ Afb. 77 Elektrische veldsterktes in de buurt van een positieve bronlading

CONCEPTVRAAG

▲ Afb. 78 Elektrische veldsterktes in de buurt van een negatieve bronlading

Hoe liggen de coulombkracht en de elektrische veldsterkte ten opzichte van elkaar bij een negatieve proeflading? Toon aan met formules en figuren.

Je kunt de opeenvolgende veldsterktevectoren verbinden met een veldlijn. Je bekomt het radiale veldlijnenpatroon:

• Het teken van de bronlading bepaalt de zin

• De grootte van de bronlading bepaalt de veldlijnendichtheid.

▲ Afb. 79 Elektrische veldlijnen in de buurt van:

een positieve bronlading

een negatieve bronlading

Je kunt de eigenschappen van de elektrische veldsterkte ook afleiden uit het veldlijnenpatroon:

• In elk punt van het elektrisch veld raakt de elektrische veldsterkte aan de veldlijnen: het veld is radiaal.

• De zin van de elektrische veldsterkte is hetzelfde als de zin van de veldlijnen: van de bronlading weg voor een positieve bronlading, naar de bronlading toe voor een negatieve bronlading.

• De grootte van de veldsterkte is gelinkt aan de veldlijnendichtheid: de dichtheid van de veldlijnen neemt af naarmate de afstand r tot het middelpunt toeneemt.

Als er meerdere puntladingen een elektrisch veld veroorzaken, dan is de resulterende veldsterkte E res de vectoriële som van de afzonderlijke veldsterktes: E res = E 1 + E2 + E3 + …

Scan de pagina en open de applet. Klik op ‘E-veld dipool’ en sleep met de proeflading in het veld. Je kunt ook de groottes van de bronladingen wijzigen en zien wat er gebeurt.

VOORBEELDVRAAGSTUK

Een puntlading van 3,0 pC en een andere puntlading van –2,0 pC liggen 5,0 cm uit elkaar. Een punt A ligt op 3,0 cm van de positieve proeflading en vormt samen met de twee puntladingen een rechthoekige driehoek, waarbij A in de rechte hoek ligt.

1 Construeer en bereken de (resulterende) elektrische veldsterkte in A.

2 Construeer en bereken de (resulterende) kracht op een elektron in A.

Gegeven:

• Q1 = 3,0 ∙ 10–12 C

• Q2 = –2,0 ∙ 10–12 C

• r12 = 0,050 m

• r1 = 0,030 m

• q = –e

Gevraagd:

• E r = ?

• FC op q = ?

applet:

Eveld dipool

Oplossing: 1 De resulterende veldsterkte E res in het punt A is de vectoriële som van de afzonderlijke veldsterktes: E res = E 1 + E2.

De veldsterktes worden veroorzaakt door puntladingen. Je kunt beide vectoren tekenen:

• E 1 wijst weg van de positieve Q1

• E2 wijst naar de negatieve Q2

• E2 is beduidend kleiner, omdat Q2 verder verwijderd is van A en omdat Q2 zwakker is.

De grootte van de veldsterkte door de puntladingen kun je als volgt berekenen:

m2 C 2

2,0 ∙ 10–12 C (0,050 m) 2 – (0,030 m) 2 = 11 N C

• De afstand tot de tweede puntlading kun je berekenen met de stelling van Pythagoras:

Je kunt E res construeren met de parallellogrammethode.

De grootte kun je berekenen met de stelling van Pythagoras (omdat E 1 en E2 een rechte hoek maken): E r = E2 1 + E2 2 = 32 N C

2 Je kunt de coulombkracht berekenen aan de hand van de definitie van elektrische veldsterkte: FC = q · E. Een elektron is negatief en ondervindt in A een coulombkracht tegen de zin van de elektrische veldsterkte in, met als grootte: FC = |q| ∙ E = e ∙ E res = 1,60 · 10–19 C · 32 N C = 5,1 ∙ 10–18 N

Reflectie:

• Kloppen de eenheden?

Ja, N C is de eenheid van veldsterkte en N de eenheid van kracht.

• Kloppen de grootteordes?

Ja, de elektrische veldsterktes zijn groot en de krachten zijn klein, omdat de proefladingen heel klein zijn.

OPLOSSINGSSTRATEGIE

• Schets de situatie.

• Benoem elke puntlading. Plaats bij elke lading het teken (+ of –).

• Teken de richting en de zin van de elektrische veldsterktes in het gekozen punt. Schat de grootte.

• Bereken de grootte van de elektrische veldsterktes.

• Corrigeer je schets van alle elektrische veldsterktes.

• Bereken de grootte van de resulterende elektrische veldsterkte via de gepaste wiskundige methode.

• Bereken en construeer de coulombkracht met de uitdrukking FC = q · E.

In een punt in een radiaal elektrisch veld rond een willekeurige bronlading is er een elektrische veldsterkte E met deze kenmerken:

• aangrijpingspunt: een willekeurig punt in de buurt van de bronlading;

• richting: radiaal;

• zin: – van de bronlading weg voor een positieve bronlading; – naar de bronlading toe voor een negatieve bronlading;

• grootte: E = FC | q | = k ∙ |Q| r 2 waarbij k de coulombconstante is, Q de grootte van de bronlading en r de afstand tot (het middelpunt van) de bronlading.

©VANIN

Als er meerdere puntladingen zijn, kun je het resulterende veld als volgt berekenen:

5.3 De elektrische veldsterkte in een homogeen veld

Een homogeen elektrisch veld ontstaat tussen twee lange, evenwijdige staven of platen met een tegengestelde lading. Je kunt dat resulterende elektrisch veld bekijken als de samenstelling van heel veel dipoolvelden, waarbij je de bronladingen met hetzelfde teken allemaal naast elkaar zet.

Je kunt dat nagaan door in applet 1 op ‘Dipole Row’ of in applet 2 op het derde icoon te klikken.

VOORBEELD VELDSTERKTE EN COULOMBKRACHT IN EEN HOMOGEEN ELEKTRISCH VELD

Elke bronlading veroorzaakt een radiale veldsterkte Ei. Twee tegengestelde bronladingen veroorzaken samen een dipoolveld. Veel dipoolvelden samen veroorzaken het resulterende homogene elektrisch veld Eres, of kortweg E. De veldlijnen vertonen een homogeen veldlijnenpatroon: ze lopen evenwijdig met en op gelijke afstand van elkaar. Ze staan loodrecht op de staven. De zin is van de positieve naar de negatieve staaf toe. Dat is de zin van de coulombkracht die op een positieve proeflading in het elektrisch veld zou werken. De veldsterktevectoren hebben in elk punt dezelfde richting en zin als de veldlijnen. Ze zijn allemaal even groot.

demovideo: schermwerking

In het veld ondervindt een proeflading een constante coulombkracht: FC = q · E.

• Een positieve proeflading ondervindt een kracht in dezelfde zin als de veldsterkte.

Een negatieve proeflading ondervindt een kracht tegen de zin van de veldsterkte in.

• Even grote proefladingen ondervinden een even grote coulombkracht, onafhankelijk van hun positie in het veld.

©VANIN

▲ Afb. 82 De coulombkracht op een positieve en een negatieve proeflading met dezelfde ladingsgrootte in een homogeen elektrisch veld. De proefladingen hebben dezelfde grootte.

CONCEPTVRAGEN

1 Teken een homogeen veld met de bijbehorende elektrische veldsterkte op verschillende plaatsen in het veld.

2 Teken de coulombkracht voor proefladingen met een verschillende ladingsgrootte op verschillende posities.

3 Verklaar waarom je de formule E = k ∙ |Q| r 2 niet mag toepassen in een homogeen veld.

Tussen twee tegengesteld geladen platen is de elektrische veldsterkte E constant. Het elektrisch veld is homogeen.

5.4 Elektrische schermwerking

DEMO

Welke invloed heeft een gesloten geladen geleider op de elektrische kracht en het elektrisch veld?

1 Je leerkracht neemt een gesloten metalen kooi. Vervolgens zet je leerkracht er één elektroscoop in en een andere erbuiten.

De kooi krijgt via een generator of een hoogspanningsbron een elektrische lading.

2 Welk resultaat verwacht je? Bespreek met je buur en test uit.

3 Formuleer een antwoord op de onderzoeksvraag.

Uit experimenten blijkt dat er binnen in een gesloten of een holle geleider nooit een elektrisch veld is. Je kunt dat verklaren door de vrije valentie-elektronen in een geleider. Als er over een geleider een elektrisch veld aangelegd wordt, ondervinden de vrije valentie-elektronen een elektrische kracht waardoor ze zich verplaatsen. Het resulterende elektrische veld binnen in de geleider neemt hierdoor af. De elektronen verspreiden zich over de buitenkant van de geleider totdat het resulterende elektrisch veld binnen in de geleider nul is.

Dat betekent dat de geleider de elektrische velden van buitenaf afschermt. Dat fenomeen noem je elektrische schermwerking.

VOORBEELD KOOI VAN FARADAY

In een kooivormige constructie van elektrisch geleidend materiaal, zoals koper of ijzer, kunnen elektrische velden niet doordringen Dat noem je een kooi van Faraday (naar de ontdekker).

Binnen in een gesloten geleider zijn personen en toestellen afgeschermd van elektrische velden. Omgekeerd schermt de kooi opgewekte elektrische velden af van de omgeving.

In een metalen kooi ondervind je geen invloed van (grote) velden errond.

Een auto en een vliegtuig zijn kooien van Faraday. Bij bliksem ben je er veilig.

Een microgolfoven is gemaakt uit metaal. Op het deurtje zit een metalen rooster. Het is een kooi van Faraday.

©VANIN

CONCEPTVRAAG

In een tunnel valt de gsm-ontvangst weg. Verklaar hoe dat komt.

Binnen in elke geladen geleider is de elektrische veldsterkte gelijk aan nul. Dat is het principe van elektrische schermwerking

▲ Afb. 83 De griesmeelkorrels binnen een metalen ring lijnen niet op. Ze ondervinden geen invloed van het homogene elektrisch veld.

Afb. 84 Het veldlijnenpatroon van een gesloten geleider in een homogeen elektrisch veld

AAN DE SLAG

REEKS

Bestudeer de twee afbeeldingen van oceanen waarin een veld wordt voorgesteld.

▲Oceaanstromen

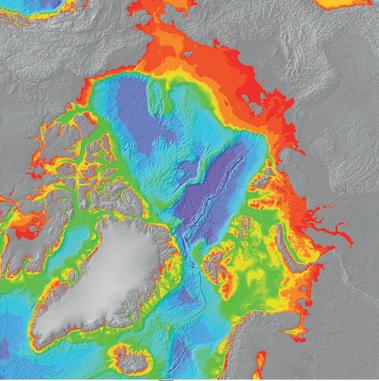
▲Diepte van de oceaan op de Noordpool

a Welke grootheden kun je koppelen aan de voorgestelde velden?

b Om welke soorten velden gaat het in beide gevallen?

c Geef voor elke afbeelding aan welke eigenschappen van de grootheid je kunt aflezen. 1 de grootte 2 de richting 3 de zin

Wie heeft gelijk? Verklaar.

Het elektrisch veld rond de plasmabol is er enkel als je een lading in de buurt brengt.

C

Er is nooit een elektrisch veld rond een plasmabol. Dat is er enkel bij opgewreven voorwerpen.

Het elektrisch veld rond de plasmabol is er altijd.

Bestudeer de elektrische veldlijnpatronen.

©VANIN

Zijn deze uitspraken juist of fout? Verklaar.

a Een ijzeren paperclip ondervindt nabij de aarde gravitatiekracht.

b Een ijzeren paperclip ondervindt nabij een magneet magnetische kracht.

c Een ijzeren paperclip ondervindt nabij een lading elektrische kracht.

a Welk patroon hoort bij een positieve lading van 2 µC en een negatieve lading van –1 µC?

b Verklaar je keuze.

c Geef een mogelijke combinatie van ladingen bij de twee andere patronen.

A B

A B C

Maak de uitspraken correct door ze aan te vullen met ‘altijd’, ‘soms’ of ‘nooit’.

a Elektrische veldlijnen lopen weg van een positieve bronlading.

b Elektrische veldlijnen lopen naar een negatieve bronlading toe.

c Elektrische veldlijnen lopen van een positieve naar een negatieve bronlading toe.

d Elektrische veldlijnen lopen van een negatieve naar een positieve lading toe.

e Elektrische veldlijnen in een homogeen veld zijn evenwijdig.

f Elektrische veldlijnen in een homogeen veld zijn verticaal.

g De zin van de coulombkracht op een proeflading is naar een positieve bronlading toe.

h De elektrische veldsterkte heeft dezelfde zin als de coulombkracht op een proeflading.

Venus heeft een diameter van 12,1 Mm.

Op het oppervlak is de gravitatieveldsterkte 8,87 N kg

Een brokstuk van 3,0 ton valt vanop 1 000 km hoogte naar het oppervlak van Venus.

Bereken:

a de massa van Venus;

b de gravitatieveldsterkte op 1 000 km boven het oppervlak van Venus;

c de toename van de grootte van de gravitatiekracht op het brokstuk aan de hand van de gravitatieveldsterkte.

Welke uitspraken zijn juist? Verklaar.

a De gravitatieveldsterkte op het aardoppervlak is op sommige plaatsen even groot als de gravitatieveldsterkte op het maanoppervlak.

b De gravitatieveldsterkte rond de aarde kan even groot zijn als de gravitatieveldsterkte rond de maan.

c De gravitatiekracht op het aardoppervlak kan even groot zijn als de gravitatiekracht op het maanoppervlak.

d De gravitatieveldsterkte is groter voor een ruimtetuig dan voor een astronaut op dezelfde hoogte.

Een punt A bevindt zich op 3,0 dm van een bronlading van 5,0 mC.

Teken en bereken:

a de elektrische veldsterkte in A;

b de coulombkracht op een lading van 0,20 nC in P.

In een punt P in de omgeving van een bronlading Q = 8,3 nC is de elektrische veldsterkte 7,2 ∙ 106 N C Hoe ver bevindt het punt P zich van de bronlading?

Op een afstand van 3,4 cm van een bronlading Qb is de grootte van de elektrische veldvector 1,8 ∙ 105 N C .

De vector is naar de lading toe georiënteerd.

a Bepaal het teken en de grootte van de bronlading.

b Welke proeflading q moet je in dat punt plaatsen, opdat de coulombkracht een grootte van 6,7 nN heeft en weg van Qb wijst?

Een bolvormige geleider met een straal van 9,0 cm heeft een lading van 16,0 µC.

a Bereken de grootte van de veldsterkte:

1 in een punt A op de bolwand;

2 in een punt B buiten de bol op 3,0 cm van de bolwand;

3 in een punt C op 6,0 cm van het middelpunt van de bol.

b Bereken de grootte van de coulombkracht op een lading van 5,0 nC in het punt B.

REEKS

Een atoomkern bestaat uit protonen en neutronen.

a Welke uitspraak is correct?

1 Rond een atoomkern werkt een elektrisch veld, maar geen gravitatieveld.

2 Rond een atoomkern werkt een gravitatieveld, maar geen elektrisch veld.

3 Rond een atoomkern werkt een sterk elektrisch veld en een zwak gravitatieveld.

4 Rond een atoomkern werkt een zwak elektrisch veld en een sterk gravitatieveld.

5 Welke van de bovenstaande uitspraken juist is, hangt af van de atoomkern.

b Controleer je antwoord door dat te berekenen voor een waterstofkern. Zoek de nodige gegevens op.

Bestudeer de afbeeldingen en beantwoord voor elke afbeelding de vragen.

a Bepaal het ladingsteken van de bronladingen.

b Geef de richting en de zin van de elektrische veldsterkte in elk van de punten.

c Rangschik de absolute waarde van de bronladingen volgens ladingsgrootte.

d Rangschik de elektrische veldsterktes in de punten A tot en met D van klein naar groot.

e Je plaatst een proeflading in elk van de punten. Welke uitspraken zijn correct? Verklaar.

1 Je kunt de richting van de coulombkracht bepalen.

2 Je kunt de zin van de coulombkracht bepalen.

3 Je kunt de coulombkrachten rangschikken van klein naar groot.

Bestudeer de grafiek van de elektrische veldsterkte in functie van de afstand rondom een bronlading.

E (kN) C

©VANIN

a Neem de tabel over.

1 Bepaal zonder rekentoestel de ontbrekende grootheden.

2 Vul de tabel aan.

3 Welke proeflading is niet realistisch? Verklaar.

r (m) 0,36

E ( kN C ) 10

KRACHT DIE WERKT OP PROEFLADING q F (N) F (N)

q = 1,0 nC

q = 4 ∙ 10–3

q = 3,0 C

b Bepaal de mogelijke bronladingen.

Een puntlading van 5,0 µC en een andere van –2,0 µC bevinden op 10,0 cm van elkaar. Het punt M bevindt zich in het midden op de verbindingslijn. Teken en bereken:

a de elektrische veldsterkte in M; b de resulterende coulombkracht op een lading van –4,0 pC in M.

Je brengt bolletjes met een verschillende lading op een afstand d of 2 ∙ d (tussen de middelpunten) van elkaar, zoals voorgesteld op de afbeelding. Rangschik de groottes van de veldsterkte in een punt M in het midden van de verbindingslijn van klein naar groot.

Een puntvormige bronlading Q wekt een elektrisch veld E op. Een proeflading q bevindt zich op een afstand r van de bronlading.

Welke vorm hebben de grafieken van de onderstaande verbanden?

Twee ladingen van 2,00 nC en 3,00 nC bevinden zich op 50,0 cm van elkaar.

Bepaal de ligging van het/de punt(en) op de verbindingslijn waar de grootte van de veldsterkte gelijk is aan 0 N C .

a E(Q)

b E(q)

c E(r)

d E(r²)

e E( 1 r 2 )

f F(q)

g F(r)

h F(r²)

i F( 1 r 2 )

j F(Q)

Een geladen zeepbel veroorzaakt een elektrisch veld in de punten A, B, C en D, zoals weergegeven op de afbeelding.

Wat gebeurt er met de veldsterkte in die vier punten als je de bel opblaast en de straal daardoor twee keer groter wordt?

r = 3,0 cm Q

r = 3,0 cm

r = 4,0 cm

r = 6,0 cm

r = 9,0 cm

Bestudeer de afbeelding van twee ladingen op de hoekpunten van een gelijkbenige rechthoekige driehoek.

Hoe groot is de veldsterkte in A?

a 0 N C

b 18 N C

c 9,0 N C

d 13 N C

e 4,5 N C

f 6,4 N C

Bestudeer de afbeelding.

Welke vector geeft de (resulterende) veldsterkte in A correct weer?

REEKS

Drie puntladingen

(Q1 = –3,0 µC, Q2 = 2,0 μC en Q3 = –1,0 µC) bevinden zich op de hoekpunten van een gelijkzijdige driehoek (zie afbeelding). Punt A ligt net in het midden van de basis van de gelijkzijdige driehoek.

a Teken de afbeelding over.

b Construeer de afzonderlijke en resulterende veldsterktes in het punt A.

c Bepaal de grootte van de resulterende veldsterkte in het punt A.

d Bereken de grootte van de kracht op een lading van +2 · e in het punt A.

Bestudeer de afbeelding van twee ladingen, waarbij |Q1| > |Q2|.

In welk(e) van de zeven punten op de verbindingslijn kan de veldsterkte nul zijn? Verklaar. A B x Q1 x C x D x E x Q2 x F x G x

Een metalen bolletje met een massa van 20 g en een lading van –10 pC hangt op aan een isolerend touwtje. Wanneer je het bolletje tussen twee tegengesteld geladen platen opstelt, wordt het naar links getrokken. Zo bereikt het een rustsituatie, waarbij de hoek tussen het touw en een verticale gelijk is aan 30° (zie afbeelding).

a Teken de afbeelding over.

Teken zes elektrische veldlijnen opgewekt door de platen, opdat die situatie zich voordoet.

b Bepaal de grootte van de elektrische veldsterkte tussen de platen.

Q1(1,0 nC)

Q2(–1,0 nC)

HOOFDSTUKSYNTHESE

KERNBEGRIPPEN

NOTITIES

veld Een veld is een gebied of ruimte waar een specifieke activiteit kan plaatsvinden. Een veld beschrijf je in de fysica met een veldgrootheid.

• Scalarveld: de veldgrootheid is een scalar (= getal).

• Vectorveld: de veldgrootheid is een vector (bijvoorbeeld: een veld van een veldkracht is het gebied waar de veldkracht merkbaar is).

veldlijnen Een veld is niet zichtbaar. Je kunt het (elektrisch of gravitatie-)veld voorstellen met veldlijnen.

• Veldlijnen geven de richting van het veld aan.

• De zin van de veldlijnen wordt bepaald door de bronlading en bronmassa

• De dichtheid van de lijnen geeft de sterkte van het veld aan.

ELEKTRISCH VELD

©VANIN

GRAVITATIEVELD

radiaal veld rond puntladingen

homogeen veld tussen geladen platen

• gravitatieveldsterkte: invloed van de bronmassa

GROOTHEID MET SYMBOOLEENHEID MET SYMBOOL

gravitatieveldsterkte g = FG m [g] = N kg

GROOTHEID MET SYMBOOLEENHEID MET SYMBOOL

elektrische veldsterkte E = FC q [E] = N C

radiaal, (bij benadering) homogeen veld dicht bij planeetoppervlak

veldsterkte De veldsterkte is een vectoriële grootheid waarmee je de eigenschappen van het veld van een veldkracht uitdrukt.

Hieruit volgt: FG = m · g

De grootte kun je berekenen als: g = G ∙ M r 2 (waarbij G de universele gravitatieconstante is, M de grootte van de bronmassa en r de afstand tot het middelpunt van de bronmassa).

• elektrische veldsterkte: invloed van de positieve of negatieve bronlading(en)

Hieruit volgt: FC = q · E

De grootte kun je berekenen voor een radiaalveld als: E = k ∙ |Q| r 2 (waarbij k de constante van coulomb is, Q de grootte van de bronlading en r de afstand tot het middelpunt van de bronmassa).

Als er meerdere puntladingen zijn, kun je de resulterende veldsterkte als volgt berekenen: E = E res = E 1 + E2 + E3 + …

Bijvoorbeeld: een elektrisch veld tussen geladen platen is een resulterend veld: je kunt daar de formule E = k ∙ |Q| r 2 niet gebruiken!

schermwerking In elke geladen geleider is de elektrische veldsterkte gelijk aan nul. Dat is het principe van elektrische schermwerking. Dat wordt de kooi van Faraday genoemd.

Energie in een gravitatieveld en in een elektrisch veld

Ladingen ondervinden de elektrische kracht in een elektrisch veld, massa’s de gravitatiekracht in een gravitatieveld.

Daardoor kunnen ze in beweging komen: ze bezitten energie. Hoe groot is die energie? Welke factoren van het veld beïnvloeden die energie? Hoe kunnen we de kennis over die energie en het bijbehorende energieveld gebruiken om stroomkringen optimaal te laten werken?

In dit hoofdstuk vertrekken we van je voorkennis over stroomkringen, energie en velden om potentiële energie in een homogeen gravitatieveld en een homogeen elektrisch veld te definiëren. Van daaruit ga je op zoek naar de betekenis van de grootheid spanning, die je al leerde kennen.

LEERDOELEN

M potentiële energie in een homogeen gravitatieveld en homogeen elektrisch veld omschrijven en berekenen

M potentiaal(veld) in een homogeen gravitatieveld en homogeen elektrisch veld omschrijven, berekenen en voorstellen

M spanning in een homogeen elektrisch veld omschrijven en berekenen

M stroomkringen omschrijven in termen van energie, potentiaal en spanning

1 Welke energieomzettingen zijn er in een stroomkring?

Een stroom is de netto beweging van bepaalde deeltjes in dezelfde richting en zin. Dat noem je een driftbeweging van die deeltjes. In een stroomkring is er een gesloten circuit waarin een energiebron energie levert aan deeltjes die hun energie kunnen overdragen aan een verbruiker.

De bouw van de energieomzetting in een elektrische stroomkring kun je vergelijken met een waterkringloop.

WATERKRINGLOOP

©VANIN

ELEKTRISCHE STROOMKRING

leiding kraantje waterrad

▲ Afb. 85 Een pomp zorgt ervoor dat het water potentiële zwaarteenergie krijgt, waardoor het water het rad kan doen draaien.

batterij conventionele stroomzin

elektronenstroom lamp

▲ Afb. 86 De batterij zorgt ervoor dat de elektronen potentiële elektrische energie krijgen, waardoor ze doorheen de stroomkring bewegen en een lamp kunnen doen branden.

1 Energieomzetting in een waterkringloop

In een waterkringloop kan het water stromen door het hoogteverschil. In vele watercircuits stroomt water door een drukverschil van een pomp, wat voor een verschil in potentiële zwaarte-energie zorgt. De potentiële energie van het water wordt omgezet in kinetische energie van het water. In de verbruiker wordt de kinetische energie van het water overgedragen naar energie van de verbruiker.

potentiële zwaarte-energie van het water → kinetische energie van het water → energie van de verbruiker

Om het water blijvend te laten stromen, moet de kring gesloten zijn en is er een energiebron nodig. De energiebron brengt het water omhoog. Die energiebron kan een pomp zijn (afbeelding 85) of de zon, die via verdamping de watercyclus op gang houdt.

2 Energieomzetting in een elektrische stroomkring

In een elektrische stroomkring zorgt de bron voor een verschil in potentiële elektrische energie van de ladingen tussen de pluspool en de minpool. Bij het doorlopen van de stroomkring wordt er potentiële energie van de ladingen omgezet in kinetische energie. In de verbruiker wordt de kinetische energie van de ladingen overgedragen naar energie van de verbruiker.

(potentiële) elektrische energie van de ladingen → kinetische energie van de ladingen → energie van de verbruiker

Om de ladingen blijvend te laten stromen, moet de kring gesloten zijn en is er een energiebron nodig. Die geeft de ladingen elektrische energie

In de energiebron (batterij, waterkrachtcentrale, kerncentrale …) wordt een andere vorm van energie omgezet in elektrische energie.

In een stroomkring zorgt de energiebron dat de deeltjes potentiële energie krijgen.

De potentiële energie wordt omgezet naar kinetische energie, die op haar beurt omgezet wordt naar energie van de verbruiker.

©VANIN

Je leerde vorig schooljaar de verschillende vormen van mechanische energie kennen:

• potentiële energie: energie doordat er een kracht inwerkt op een voorwerp en het voorwerp zich op een bepaalde plaats bevindt;

• kinetische energie: energie doordat een voorwerp een snelheid heeft.

Net zoals bij gravitatiekracht en zwaartekracht is gravitatie-energie een veralgemening van zwaarte-energie. In de buurt van een planeet (homogeen veld) zijn dat synoniemen.

2 Wat is potentiële energie bij een veldkracht?

Potentiële energie is energie die een voorwerp bezit op een bepaalde plaats (in een veld). Een voorwerp bezit energie als het in staat is om zichzelf of andere voorwerpen in beweging te brengen.

Door de hoogte en de zwaartekracht kom je van een duikplank in het water terecht.

Je bezit potentiële energie in het gravitatieveld.

De uitrekking en de veerconstante van de elastiek bepalen hoe ver het steentje afgeschoten wordt met een katapult. De katapult bezit potentiële energie.

Door de elektrische kracht kunnen de elektronen van de bron naar je hand bewegen die zich op de glaswand bevindt. De elektronen bezitten potentiële energie in het elektrisch veld.

Om potentiële energie te bezitten, moet er een kracht inwerken op het voorwerp en moet het voorwerp zich op een bepaalde plaats bevinden:

• Een massa bezit potentiële gravitatie-energie in het gravitatieveld door haar plaats ten opzichte van de bronmassa(‘s).

• Een veer bezit potentiële elastische energie door de vervorming.

• Een lading bezit potentiële elektrische energie in het elektrisch veld door haar plaats ten opzichte van de bronlading(en).

De potentiële energie is een scalaire grootheid. De grootte van de potentiële energie van een voorwerp, wordt altijd uitgedrukt ten opzichte van een (vrij te kiezen) referentiepunt waar E pot gelijk aan 0 J gekozen wordt.

Van voorwerpen waar een veldkracht op inwerkt, kun je potentiële energie beschrijven. Je bestudeert nu de grootte ervan in homogene velden.

©VANIN

1 Potentiële energie in een homogeen gravitatieveld

VOORBEELD POTENTIËLE

GRAVITATIE-ENERGIE VAN EEN BAL IN DE BUURT VAN DE AARDE

In het gravitatieveld van de aarde is de gravitatieveldsterkte g constant. Het gravitatieveld is homogeen. Op een bal (met massa m) in dat veld kun je de gravitatiekracht bepalen als F z = m · g.

Doordat je de bal optilt, bezit hij potentiële gravitatie-energie ten gevolge van zijn plaats in het gravitatieveld. Als referentiepunt kies je het laagste punt (h = 0) waar E pot, z = 0. Je kunt op iedere hoogte h de potentiële zwaarte-energie berekenen als: E pot, z = m · g · h

Als de bal vanuit rust losgelaten wordt, beweegt hij spontaan van een punt met hogere potentiële gravitatie-energie (P1) naar een punt met lagere potentiële gravitatie-energie (P2) door de gravitatiekracht.

CONCEPTVRAAG

Je kiest het referentiepunt op de hoogte van het trapje. Welke invloed heeft dat op de potentiële gravitatie-energie? Welke invloed heeft dat op de verandering van potentiële gravitatie-energie?

In de buurt van het oppervlak van een planeet is er een homogeen gravitatieveld met de planeet als bronmassa. Als je een (proef)massa in de buurt van het oppervlak brengt en loslaat, zal ze zich verplaatsen onder invloed van de gravitatiekracht. Doordat je de massa optilt, bezit ze potentiële gravitatie-energie ten gevolge van haar positie in het gravitatieveld. In een homogeen gravitatieveld kun je de potentiële gravitatie-energie berekenen als: E pot, z = m · g · h waarbij m de (proef)massa, g de grootte van de gravitatieveldsterkte en h de hoogte tot het oppervlak van de planeet is.

Als je een massa die potentiële gravitatie-energie bezit, loslaat, komt ze spontaan in beweging door de gravitatiekracht, die een veldkracht is. De potentiële gravitatie-energie wordt omgezet in kinetische energie.

2 Potentiële energie in een homogeen elektrisch veld

Tussen twee tegengesteld geladen platen is er een homogeen elektrisch veld. Als je een lading tussen de platen loslaat, zal ze zich verplaatsen onder invloed van de elektrische kracht. Doordat je de lading tussen de platen plaatst, krijgt ze potentiële elektrische energie ten gevolge van haar positie in het elektrisch veld. In een homogeen elektrisch veld kun je de potentiële elektrische energie (analoog aan de gravitatie-energie) berekenen als:

E pot, E = q · E · x waarbij q de (proef)lading, E de grootte van de elektrische veldsterkte en x de afstand tot het referentiepunt is. Als referentiepunt wordt meestal de negatieve plaat gekozen. Het teken van de potentiële elektrische energie hangt af van het teken van de proeflading. Dat verschilt van de potentiële gravitatie-energie, waar de proefmassa m altijd positief is.

▲ Afb. 90 Kracht F z en verplaatsing Δh van een massa m in het zwaarteveld

Als je een lading die potentiële elektrische energie bezit, loslaat, zal ze zich verplaatsen onder invloed van de elektrische kracht, die een veldkracht is. De potentiële elektrische energie wordt omgezet in kinetische energie.

VOORBEELD POTENTIËLE ELEKTRISCHE ENERGIE VAN EEN PUNTLADING TUSSEN TWEE GELADEN PLATEN

In het elektrisch veld tussen twee tegengesteld geladen platen is de elektrische veldsterkte E constant. Het elektrisch veld is homogeen. Op een puntlading (proeflading met lading q) in dat veld kun je de elektrische kracht bepalen als FC = q · E

Met als referentiepunt de negatieve plaat (x = 0) waar E pot, z = 0 geldt, kun je op iedere afstand x de potentiële elektrische energie berekenen als E pot, E = q · E · x

POSITIEVE PUNTLADING IN HOMOGEEN VELDNEGATIEVE PUNTLADING IN HOMOGEEN VELD

©VANIN

Voor een positieve puntlading is de potentiële elektrische energie tussen twee tegengesteld geladen platen positief.

Voor een negatieve puntlading is de potentiële elektrische energie tussen twee tegengesteld geladen platen negatief.

Als de lading losgelaten wordt, beweegt ze spontaan van P1 naar P2 door de elektrische kracht.

De potentiële energie is een scalaire grootheid die de hoeveelheid energie aangeeft ten gevolge van een positie in een veld. De potentiële energie kan berekend worden als:

• in een homogeen gravitatieveld: E pot, z = m · g · h waarbij m de (proef)massa, g de grootte van de gravitatieveldsterkte en h de hoogte tot het oppervlak van de planeet is;

• in een homogeen elektrisch veld: E pot, E = q · E · x waarbij q de (proef)lading, E de grootte van de elektrische veldsterkte en x de afstand tot de negatieve plaat is.

3 Hoe kun je de potentiële energie in een veld kwantificeren?

De grootte van potentiële energie wordt bepaald door de eigenschappen van het voorwerp (massa of lading) en door de eigenschappen van het veld dat ontstaat door de aanwezigheid van een of meerdere bronmassa’s/bronladingen. Het veld dat de energiegrootte bepaalt, noem je het potentiaalveld. De sterkte van het potentiaalveld wordt beschreven door de grootheid potentiaal.

We bespreken de potentiaal in een homogeen gravitatieveld en in een homogeen elektrisch veld.

1 Potentiaal in een homogeen gravitatieveld

In de buurt van hemellichamen bezit een massa potentiële gravitatie-energie. De grootte wordt bepaald door de grootte van de massa m, de zwaarteveldsterkte g en de hoogte h.

Voor elke massa kun je de grootte van de potentiële gravitatie-energie berekenen als E pot, z = m · g · h.

Net zoals je de krachteigenschappen van het gravitatieveld beschrijft met de gravitatieveldsterkte, gedefinieerd als F z m , kun je de energie-eigenschappen

in het potentiaalveld beschrijven met de (gravitatie)potentiaal, gedefinieerd als Epot, z m .

Aangezien potentiële gravitatie-energie en massa scalaire grootheden zijn, is de gravitatiepotentiaal een scalaire grootheid.

De gravitatiepotentiaal hangt enkel af van de eigenschappen van en de afstand tot de bronmassa, niet van de proefmassa. Hoe groter de gravitatiepotentiaal in een punt van het potentiaalveld, hoe meer energie een proefmassa in dat punt van het veld zal hebben.

De grootheid gravitatiepotentiaal heeft geen eigen symbool.

GROOTHEID MET DEFINITIE

©VANIN

EENHEID MET SYMBOOL

gravitatiepotentiaal E pot, z m joule per kilogram J kg

VOORBEELD POTENTIËLE GRAVITATIE-ENERGIE IN HET HOMOGEEN GRAVITATIEVELD

Een steen dicht in de buurt van de aarde of de maan bezit potentiële gravitatie-energie. Het gravitatieveld is homogeen. De grootte wordt bepaald door de massa van de steen, het hemellichaam en de hoogte ten opzichte van het hemellichaam.

mbruin = 3 · mzwart

De zware (bruine) steen bezit meer potentiële gravitatie-energie dan de lichte (zwarte) steen.

Eigenschap van het voorwerp: massa m

De potentiële gravitatieenergie is groter op de aarde dan op de maan.

De potentiële gravitatieenergie neemt toe met de afstand tot het aardoppervlak.

Eigenschap van de positie h en de veldsterkte g: potentiaal g · h

CONCEPTVRAAG

Bepaal de potentiaal voor drie equipotentiaallijnen die weergegeven zijn op afbeelding 94.

De eenheid volt is genoemd naar de natuurkundige Alessandro Volta, die de elektrische batterij ontdekte.

In het homogene gravitatieveld rondom een hemellichaam is de veldsterkte g constant

De gravitatiepotentiaal is gelijk aan g · h en dus niet constant, maar recht evenredig met de afstand tot het referentiepunt

In een homogeen gravitatieveld hebben alle punten op dezelfde hoogte dezelfde potentiaal (want g is een constante). Het hoogteveld is dus een potentiaalveld en de hoogtelijnen zijn equipotentiaallijnen

In een homogeen gravitatieveld zijn de equipotentiaallijnen evenwijdig met het oppervlak.

2 Potentiaal in een homogeen elektrisch veld

▲ Afb. 94 De hoogtelijnen rond een heuvel zijn equipotentiaallijnen.

Tussen twee tegengesteld geladen platen bezit een lading potentiële elektrische energie. De grootte wordt bepaald door de (proef)lading q, de elektrische veldsterkte E en de afstand x tot de negatieve plaat. Voor elke lading kun je de grootte van de potentiële elektrische energie berekenen als E pot, E = q · E

Net zoals je de krachteigenschappen van het elektrisch veld beschrijft met de elektrische veldsterkte, gedefinieerd als FC q , kun je de energie-eigenschappen in het potentiaalveld beschrijven met de elektrische potentiaal, gedefinieerd als Epot, E q . Aangezien potentiële elektrische energie en lading scalaire grootheden zijn, is de elektrische potentiaal een scalaire grootheid. De elektrische potentiaal hangt enkel af van de eigenschappen van en de afstand tot de bronlading, niet van de positieve proeflading. Hoe groter de elektrische potentiaal in een punt van het potentiaalveld, hoe meer energie een proeflading in dat punt van het veld zal hebben.

GROOTHEID MET DEFINITIE

EENHEID MET SYMBOOL

elektrische potentiaal V = Epot, E q joule per coulomb = volt

De eenheid joule per coulomb wordt de volt genoemd.

VOORBEELD ELEKTRISCHE POTENTIËLE ENERGIE IN EEN HOMOGEEN ELEKTRISCH VELD

Een positieve puntlading tussen twee tegengesteld geladen platen bezit potentiële elektrische energie. De grootte van de potentiële elektrische energie wordt bepaald door de ladingsgrootte van de puntlading, de elektrische veldsterkte (die afhangt van het ladingsverschil van de platen) en de afstand tot de negatieve plaat.

De positieve puntlading 2q bezit meer potentiële elektrische energie dan de positieve puntlading q.

Eigenschap van het voorwerp: lading q

De potentiële elektrische energie van een positieve puntlading neemt toe met de elektrische veldsterkte.

De potentiële elektrische energie van een positieve puntlading neemt toe met de afstand tot de negatieve plaat.

Eigenschap van de positie x en de veldsterkte E: potentiaal E · x

CONCEPTVRAAG

Werk het voorbeeld van p. 94 uit voor een negatieve puntlading.

In een homogeen elektrisch veld is de elektrische veldsterkte E constant. De potentiaal in een homogeen elektrisch veld is gegeven door

V = Epot, E q = q · E · x q = E · x

waarbij x de afstand tot de negatieve plaat is en als referentiepunt E pot, E = 0 J gekozen wordt op de negatieve plaat.

De potentiaal van de positieve plaat wordt genoteerd als V+, die van de negatieve plaat als V –. Als referentiepunt wordt (in de meeste gevallen)

V – = 0 V gekozen.

©VANIN

V 3 = 75 V V + = 100 V V 2 = 50 V V 1 = 25 V V –= 0 V

▲ Afb. 98 In een homogeen veld wordt de potentiaal bepaald door de afstand tot de negatieve plaat. Op een evenwijdig vlak (aangeduid met stippellijn) is de potentiaal constant.

Tussen de twee platen is de elektrische potentiaal niet constant: de grootte van de potentiaal in een homogeen elektrisch veld wordt bepaald door de afstand x tot de negatieve plaat. Er is een recht evenredig verband tussen de grootte van de potentiaal en de afstand tot de negatieve plaat (als V – = 0 V):

V ~ x

Op vlakken evenwijdig met de platen is zowel de afstand x tot de negatieve plaat als de elektrische veldsterkte E constant: de potentiaal is constant. Het evenwijdige vlak is een equipotentiaalvlak. Equipotentiaalvlakken met gelijke potentiaalverschillen liggen in een homogeen veld even ver van elkaar.

CONCEPTVRAAG

Geef het verband tussen V1, V2 en V3 op afbeelding 98. Leg uit.

Rond een bronmassa of een bronlading is er zowel een scalair als een vectorieel veld:

• Krachteigenschappen worden beschreven met de grootheid veldsterkte.

• Energie-eigenschappen worden beschreven met de grootheid potentiaal

VELD ROND BRONMASSA

VELD ROND BRONLADING gravitatieveldsterktegravitatiepotentiaalelektrische veldsterkte elektrische potentiaal

g = FG m E pot, z m E = FC q V = Epot, E q vectoriële grootheid scalaire grootheidvectoriële grootheidscalaire grootheid veld wordt voorgesteld met veldlijnen veld wordt voorgesteld met equipotentiaalvlakken

veld wordt voorgesteld met veldlijnen veld wordt voorgesteld met equipotentiaalvlakken

4.1 Potentiaalverschil in het homogeen gravitatieveld

A Energieverschil door hoogteverschil

De potentiële energie voor een bepaalde massa in het potentiaalveld wordt bepaald door de grootte van de massa, de zwaarteveldsterkte en de hoogte. Een verschil in potentiële gravitatie-energie ∆E pot, z wordt voor een bepaalde massa bepaald door het hoogteverschil. Een hoogteverschil bepaalt een potentiaalverschil.

VOORBEELD POTENTIAAL(VERSCHIL) EN POTENTIËLE ENERGIE(VERSCHIL) IN DE BUURT VAN DE AARDE

©VANIN

▲ Afb. 99 Potentiaal(verschil) op equipotentiaallijnen in het homogeen gravitatieveld van de aarde

h 4–3 De grootte van de zwaarteveldsterkte is in de buurt van de aarde g = 9,81 N kg . De potentiaal op het oppervlak is nul. De equipotentiaallijnen liggen even ver van elkaar op veelvouden van g · h. Het potentiaalverschil tussen twee equipotentiaallijnen wordt bepaald door het hoogteverschil.

Als je een voorwerp met massa m in de buurt van de aarde brengt, bezit het potentiële gravitatie-energie

E pot, z = m · g · h. De potentiële energie wordt bepaald door de massa en door de potentiaal. Het potentiaalverschil bepaalt het potentiële energieverschil ∆E pot, z voor een bepaalde massa.

▲ Afb. 100 Potentiële energie(verschil) van een massa op equipotentiaallijnen in het homogeen gravitatieveld van de aarde

CONCEPTVRAAG

Op afbeelding 99 liggen de equipotentiaalvlakken allemaal even ver van elkaar (je noemt dat equidistante equipotentiaalvlakken). Is dat noodzakelijk?

Als een massa losgelaten wordt, beweegt ze naar de aarde toe. Ze beweegt van hogere naar lagere potentiaal. De potentiële energie neemt af. Voor een proefmassa in het veld impliceert een potentiaalverschil een energieverschil

De potentiële gravitatie-energie wordt omgezet in kinetische energie. Voor een geïsoleerd systeem is er behoud van mechanische energie: ∆E pot, z = –∆Ekin. De toename van kinetische energie wordt volledig bepaald door het potentiaalverschil.

Je laat balletjes met verschillende massa’s vallen aan zee en op een berg. Je laat ze los op schouderhoogte. Ze bewegen van schouderhoogte (hogere potentiaal) naar het oppervlak (lagere potentiaal).

hogere potentiaal, hoge E pot, z

©VANIN

lagere potentiaal, lage E pot, z

v v hogere potentiaal, hoge E pot, z

lagere potentiaal, lage E pot, z

▲ Afb. 101 Snelheid van een vallend balletje op en naast een berg

Met het behoud van mechanische energie kun je de eindsnelheid van de balletjes bepalen. De eindsnelheid wordt volledig bepaald door het potentiaalverschil: veind = 2 · g · ∆h

Als de balletjes hetzelfde hoogteverschil (∆h) en dus hetzelfde potentiaalverschil (g · ∆h) doorlopen op de berg en in de vallei, komen ze met dezelfde snelheid aan. De massa’s (m groen ≠ mgeel) en de potentiaal (bepaald door hberg) hebben geen invloed.

CONCEPTVRAAG

Toon aan dat je de eindsnelheid kunt berekenen als: veind = 2 · g · ∆h

B Waterkringloop

In een waterkringloop wordt potentiële gravitatie-energie omgezet naar kinetische energie van het water. Het water beweegt spontaan van het hoogste punt (hogere potentiaal) naar het laagste punt (lagere potentiaal). De kinetische energie van het water wordt bepaald door het potentiaalverschil: hoe groter het potentiaalverschil (bepaald door het hoogteverschil), hoe meer potentiële energie van het water omgezet kan worden in kinetische energie en hoe groter de eindsnelheid van het water.

©VANIN

In de waterkringloop staat een verbruiker. Ter hoogte van de verbruiker is er een energieomzetting of energieoverdracht.

Om het potentiaalverschil te behouden, is er een pomp nodig. De pomp voegt energie toe, waardoor het water van lage naar hoge potentiaal beweegt.

hogere potentiaal, hoge E pot, z

∆h

lagere potentiaal, lage E pot, z

▲ Afb. 102 Een pomp zorgt ervoor dat het water potentiële zwaarte-energie krijgt, waardoor het water het rad kan doen draaien.

VOORBEELD TURBINE

In een stuwmeer wordt de potentiële gravitatie-energie van het water omgezet naar potentiële elektrische energie.

potentiële gravitatie-energie van het water → kinetische energie van het water → kinetische energie van de turbine → potentiële elektrische energie

Het water stroomt uit het stuwmeer door een potentiaalverschil. Het potentiaalverschil wordt in stand gehouden doordat de zon energie toevoegt: bij verdamping beweegt water van lagere potentiaal naar hogere potentiaal.

Het potentiaalverschil (g · ∆h) en de hoeveelheid water (m) bepalen de hoeveelheid elektrische energie die de turbine produceert.

▲ Afb. 103 Elektriciteitsproductie bij een stuwmeer

In een gravitatieveld zorgt een hoogteverschil voor een potentiaalverschil: een (proef)massa bezit op verschillende hoogtes een verschillende potentiële energie. Bij beweging naar het oppervlak toe neemt de potentiële energie af en de kinetische energie toe.

In een waterkringloop geeft een bron potentiële energie aan het water zodat het potentiaalverschil blijft bestaan.

A Energieverschil door spanning DEMO

Hoe kun je een elektrische stroom veroorzaken?

1 Ga op zoek om een lamp te laten branden:

a met een batterij;

b met een ballon; c met een plasmabol.

2 Probeer je waarnemingen te verklaren.

3 Formuleer een antwoord op de onderzoeksvraag.

De potentiële energie voor een bepaalde lading in het potentiaalveld wordt bepaald door die lading en de potentiaal. De verandering van potentiële elektrische energie ∆E pot, E wordt bepaald door die lading en de afstand tot de negatieve plaat. Tussen twee punten die op een verschillende afstand van de negatieve plaat liggen, is er een potentiaalverschil. Voor een elektrisch veld wordt het potentiaalverschil de spanning genoemd.

GROOTHEID MET SYMBOOL

©VANIN

EENHEID MET SYMBOOL

potentiaalverschil spanning U = V1 – V2 volt V

In de praktijk wordt vaak de positieve spanning (|U|=|∆V21|) gebruikt.

De potentiaal in een homogeen elektrisch veld is gegeven door V = E · x waarbij x de afstand tot de negatieve plaat is en als referentiepunt V – = 0 V gekozen wordt. Daaruit volgt:

De spanning tussen twee punten in een homogeen elektrisch veld neemt recht evenredig toe met de afstand tussen de twee punten.

Dat betekent dat als er een spanning verschillend van nul aanwezig is, er ook een elektrisch veld aanwezig is dat ervoor zorgt dat ladingen onder invloed van de elektrische kracht bewegen.

VOORBEELD POTENTIAAL, SPANNING EN POTENTIËLE ENERGIE TUSSEN TWEE TEGENGESTELD GELADEN PLATEN

CONCEPTVRAAG

Toon aan dat de eenheid van elektrisch veld ook als volt per meter kan uitgedrukt worden.

▲ Afb. 104 Potentiaal(verschil) tussen equipotentiaallijnen in een homogeen elektrisch veld tussen twee tegengestelde platen met een spanning van 20 V tussen de platen

De potentiaal in een punt is gedefinieerd als V = E · x.

De potentiaal hangt af van de afstand tot de negatieve plaat.

De spanning tussen twee punten is gegeven door:

U = V1 - V2 = E · x1 - E · x2

Dat betekent dat een lading eenzelfde potentiaalverschil ∆V doorloopt als ze eenzelfde afstand

∆x doorloopt. De spanning tussen twee punten hangt niet af van de afstand tot de platen. De spanning tussen de twee platen is gegeven door U = V + – V= E · d

©VANIN

▲ Afb. 105 Potentiële energie(verschil) van een lading op equipotentiaallijnen in een homogeen elektrisch veld tussen twee tegengesteld geladen platen met een spanning van 20 V tussen de platen

Als je een lading tussen de twee platen brengt, bezit ze potentiële elektrische energie. De potentiële energie wordt bepaald door de lading en door de potentiaal:

E pot, E = q · E · x = q · V

Daaruit volgt dat de verandering van potentiële elektrische energie bepaald wordt door de lading en het potentiaalverschil:

∆E pot, E = E pot, E, 2 – E pot, E, 1 = q · V2 – q · V1 = –q · U met E pot, E, 2 de potentiële energie in positie 2, het dichtst bij de negatieve plaat en E pot, E, 1 de potentiële energie in positie 1, het dichtst bij de positieve plaat.

• Voor een positieve lading is de potentiële elektrische energie maximaal bij de positieve plaat: E pot, E, max = q · U (waarbij U = V + – V–). Als de positieve lading van de positieve naar de negatieve plaat beweegt, neemt de potentiële energie af en is ∆E pot, E negatief.

• Voor een negatieve lading is de potentiële elektrische energie maximaal bij de negatieve plaat: E pot, E, max = q · U – = 0 J. Als de lading van de negatieve naar de positieve plaat beweegt, neemt de energie af en is ∆E pot, E negatief.

CONCEPTVRAGEN

1 Toon aan dat U12 = U23 = 5 V.

2 Bepaal E als de equipotentiaallijnen op 2,5 cm van elkaar liggen.

Als een lading losgelaten wordt, beweegt ze spontaan naar een van de platen toe:

• Een positieve lading beweegt naar de negatieve plaat. Ze beweegt van hogere naar lagere potentiaal

• Een negatieve lading beweegt naar de positieve plaat. Ze beweegt van lagere naar hogere potentiaal.

In beide situaties neemt de potentiële energie q · V af en is ∆E pot, E negatief. Het potentiaalverschil impliceert een energieverschil.

De potentiële elektrische energie wordt omgezet in kinetische energie. Dat wil zeggen dat de kinetische energie toeneemt (∆Ekin > 0) als de potentiële energie afneemt (∆E pot < 0). Voor een geïsoleerd systeem is er behoud van energie:

∆E pot, E = –∆Ekin q · V2 – q · V1 = –∆Ekin

De toename van kinetische energie wordt volledig bepaald door het potentiaalverschil.

VOORBEELDVRAAGSTUK

Een elektron en een proton worden losgelaten tussen twee tegengesteld geladen platen.

De spanning tussen de platen (op een afstand van 6,0 cm van elkaar) is 3,0 kV.

1 Maak een figuur met a de geladen platen; b elektrische veldlijnen; c de equipotentiaallijnen van 1,0 kV en 2,0 kV; d de positie waar het elektron en het proton moeten worden losgelaten om maximale snelheid te bekomen.

2 Bepaal de elektrische veldsterkte.

3 Bereken voor het elektron en het proton de potentiële energie op de positieve plaat, op de negatieve plaat, bij 1,0 kV en bij 2,0 kV.

4 Bereken de maximale snelheid voor het elektron en het proton.

Gegeven:

Gevraagd:

• U = 3,0 kV

• d = 6,0 cm

• E = ?

• E pot op verschillende plaatsen = ?

• v max = ?

Oplossing: 1

+ = 3,0 kV

2 = 2,0 kV

1 = 1,0 kV V –= 0 kV

▲ Afb. 106 Beweging van een elektron en een proton in een elektrisch veld

2 De elektrische veldsterkte E is van de positieve naar de negatieve plaat gericht. De spanning tussen twee punten in een homogeen veld kun je schrijven als U = ΔV21 = E · Δx. Voor twee platen op een afstand d van elkaar geldt:

E = U d = 3,0 · 103 V 6,0 · 10–2 m = 5,0 · 10 V m = 50 kV m = 50 kN C

Reflectie:

3 De potentiële energie in een homogeen elektrisch veld kun je berekenen als E pot, E = q · V

Met V – = 0 V gekozen wordt dat E pot, E = q · ΔV = q · U.

Positieve plaat

©VANIN

Negatieve plaat

4 Je kunt de snelheid bepalen met het behoud van energie. Na het loslaten wordt de potentiële elektrische energie omgezet in kinetische energie. Bij aankomst op de tegenovergestelde plaat is de kinetische energie maximaal.

Elektron: –e = –1,60

Beweging van negatieve plaat (lagere potentiaal) naar positieve plaat (hogere potentiaal)

Beweging van positieve plaat (hogere potentiaal) naar negatieve plaat (lagere potentiaal)

Behoud van energie: E

• Bestudeer de grootteorde van de potentiële elektrische energie. Wat stel je vast?

Dat is een heel kleine waarde omdat de lading van een proton en een elektron heel klein zijn.

• Wat gebeurt er met de potentiële energie tijdens de beweging?

Die neemt in beide gevallen af.

• Verklaar het verschil in maximale snelheid van het elektron en het proton. De massa van het elektron is 104 keer kleiner dan die van het proton.

De snelheid is daardoor een factor 102 keer groter.

LABO

B Elektrische stroomkring

In een elektrische stroomkring wordt potentiële elektrische energie van elektronen omgezet naar kinetische energie van elektronen. In de geleider ontstaat een homogeen elektrisch veld tussen de beide polen van de energiebron. De elektronen bewegen spontaan van de negatieve pool (lagere potentiaal) naar de positieve pool (hogere potentiaal). De stroomsterkte wordt bepaald door de spanning (= het potentiaalverschil): hoe groter het potentiaalverschil, hoe groter de stroomsterkte.

In de elektrische stoomkring staat een verbruiker. Ter hoogte van de verbruiker is er een energieomzetting.

conventionele stroomzin

elektronenstroom lamp

batterij

©VANIN

lagere potentiaal

hoge pot, E hogere potentiaal lage pot, E

▲ Afb. 107 Conventionele stroomzin (rode pijl) en elektronenstroom (blauwe pijlen) in een stroomkring. Elektronen bewegen van lagere naar hogere potentiaal.

Om het potentiaalverschil te behouden, is er een spanningsbron nodig. De spanningsbron zet een vorm van energie (chemische energie, windenergie, kernenergie ...) om in elektrische energie en brengt zo de elektronen terug op hogere potentiaal. Zo kunnen ze de stroomkring opnieuw doorlopen.

VOORBEELD BUREAULAMP

Door de stekker van een bureaulamp in het stopcontact te steken, zorg je ervoor dat ladingen een groot potentiaalverschil, namelijk 230 V, kunnen doorlopen en veel potentiële energie kunnen omzetten naar andere vormen van energie. De volgende energieomzettingen vinden plaats:

potentiële elektrische energie van de ladingen → kinetische energie van de ladingen → thermische energie (warmte) en stralingsenergie (licht) van de lamp

Uit metingen blijkt dat de spanning over de bron gelijk is aan de spanning over de lamp. Concreet betekent dat dat alle energie die in de kring wordt omgezet, omgezet wordt in de lamp zelf.

▲ Afb. 108 Schakeling van voltmeters in parallel om de spanning over de bron en een verbruiker op te meten

met

▲ Afb. 109 De spanning over de verbruiker is hetzelfde als de bronspanning.

Stroomsterkte is de hoeveelheid lading die per seconde door een oppervlak stroomt. Dat wordt uitgedrukt in ampère (1 A = 1 C s ).

C De elektronvolt als energie-eenheid

De joule is een grote eenheid en ladingen hebben een kleine waarde. Daardoor is de potentiële elektrische energie van ladingen uitgedrukt in joule altijd heel klein (zie voorbeeldvraagstuk in paragraaf A). Om de kleine machten van 10 te vermijden, heeft men een nieuwe eenheid ingevoerd: de elektronvolt.

1 elektronvolt is de energieverandering van een elektron dat een potentiaalverschil van 1 V doorloopt. 1 eV = e · U = 1,60 · 10–19 C · 1 V = 1,60 · 10–19 C · 1 J C = 1,60 · 10–19 J

©VANIN

VOORBEELD POTENTIËLE ENERGIE VAN EEN PROTON EN EEN ELEKTRON UITGEDRUKT IN eV

Je kunt de potentiële energie van het elektron en het proton bij de positieve plaat (V + = 3,0 kV) in het voorbeeldvraagstuk uitdrukken in eV.

• elektron: E pot, E = –e · V + = –e · 3,0 kV = –3,0 keV

• proton: E pot, E = e · V + = e · 3,0 kV = 3,0 keV

CONCEPTVRAAG

Kun je de energie in eV gebruiken om de snelheid te berekenen? Verklaar.

In een elektrisch veld zorgt een positieverschil voor een potentiaalverschil: (proef)ladingen op verschillende afstand tot de negatieve plaat bezitten een verschillende potentiële energie. Bij spontane beweging van een lading naar de tegengesteld geladen plaat (= pool) neemt de potentiële energie af en de kinetische energie toe. Een spanningsbron geeft in een stroomkring potentiële elektrische energie aan ladingen zodat het potentiaalverschil blijft bestaan.

GROOTHEID MET DEFINITIE EENHEID MET SYMBOOL

potentiaalverschil spanning U = V1 – V2 volt V

De energie van ladingen wordt vaak uitgedrukt in elektronvolt: 1 eV = 1,60 · 10–19 J

VERDIEPING

Je kunt de potentiële elektrische energie en de potentiaal ook definiëren in een radiaal veld. Je leert er meer over op

REEKS

Een bromvlieg (m = 80 mg) heeft een potentiële gravitatie-energie van 1,17 mJ. Bereken:

a de gravitatiekracht;

b de hoogte;

c de potentiaal.

Teken vijf equipotentiaallijnen in:

a een homogeen gravitatieveld in een appartementsgebouw van vier verdiepingen;

b een homogeen elektrisch veld met V + = 200 V.

Welke zin is correct? Verklaar.

a Equipotentiaaloppervlakken bestaan alleen in homogene velden.

b Het ISS beweegt op een equipotentiaaloppervlak.

c Er is geen potentiaal in de ruimte.

Ladingen van 6,0 µC en –6,0 µC worden op 3,0 cm van de negatieve plaat geplaatst in een homogeen elektrisch veld van 2,0 kN C

a Bereken voor beide ladingen:

1 de coulombkracht;

2 de potentiaal;

3 de potentiële elektrische energie.

b Bepaal de plaats waar de potentiaal verdubbeld is.

c Bereken voor beide ladingen op de plaats uit vraag b de coulombkracht en de potentiële elektrische energie.

Na een maanmissie brachten de astronauten verschillende maanstenen mee (mbruin = 3 · mzwart) die ze op korte afstand van het oppervlak houden. Rangschik de volgende situaties volgens toenemende ...

a E pot, z van de maanstenen; b potentiaal van de weergegeven posities;

c Ekin van de maanstenen bij landing op het oppervlak.

Verschillende ladingen (protonen p+ of e–) worden in een homogeen elektrisch veld geplaatst met V – = 0 V.

a In welke situaties is de potentiële elektrische energie negatief?

b Rangschik de volgende situaties volgens toenemende ...

1 E pot, E van de ladingen; 2 potentiaal van de weergegeven posities;

3 Ekin van de ladingen bij aankomst op de plaat.

Een lading q = 0,50 nC wordt vlak bij een positieve plaat in een punt P1 vrijgelaten in het veld tussen twee evenwijdige platen. De afstand tussen de platen is 20 mm. De spanning over de platen is 400 V. Punt P2 ligt precies in het midden tussen de twee platen en punt P3 bevindt zich op de negatieve plaat.

Neem de tabel over en vul aan.

GROOTHEID IN PUNT P1 IN PUNT P2 IN PUNT P3

elektrisch veld

elektrische kracht

elektrische potentiaal potentiële elektrische energie

Zijn deze beweringen juist of fout?

Verklaar je antwoord.

a Equipotentiaallijnen kunnen elkaar kruisen.

b Als de potentiaal nul is in een punt, is het elektrisch veld ook nul in dat punt.

c Als het elektrisch veld nul is in een punt, is de potentiaal ook nul in dat punt.

d Tussen twee platen met een even grote negatieve lading kan er een spanning bestaan.

e In een batterij bewegen elektronen van hoge naar lage potentiaal.

AAN DE SLAG

De spanning tussen vijf stellen van twee evenwijdige platen wordt opgemeten door de linkerplaat te verbinden met de pluspool van de voltmeter en de rechterplaat met de minpool.

Rangschik de afgelezen spanning van klein naar groot.

Vlinks Vrechts

10 V2,0 V

2–2,0 V0 V

32,0 V–2,0 V

42,0 V0 V

5–2,0 V–2,0 V

Een homogeen elektrisch veld wordt opgewekt door twee tegengesteld geladen platen die zich op 5,0 cm van elkaar bevinden.

a Waar moet een elektron vanuit rust losgelaten worden, om zo snel mogelijk te gaan? Waar bereikt het elektron zijn maximale snelheid?

b Hoe sterk moet het elektrisch veld zijn, opdat het elektron een snelheid van 100 m s zou kunnen halen?

Twee evenwijdige vlakke geleiders produceren met een spanning van 100 V een veldsterkte van 50 kN C

a Hoe ver bevinden de geleiders zich van elkaar?

b Bereken de energieverandering van een lading van 1,0 mC die zich verplaatst van:

1 de positieve plaat naar de negatieve plaat; 2 de negatieve plaat naar de positieve plaat.

Bereken de kinetische energie in joule en in elektronvolt van:

a een H+-ion dat vanuit rust versnelt over een spanning van 1,0 kV;

b Liesbeth (55,0 kg), die met een snelheid van 8,3 km h loopt.

Welke eenheid is in elke situatie het meest geschikt? Verklaar.

REEKS

Je plaatst verschillende ladingen tussen (en niet op) twee tegengesteld geladen platen en laat ze los. Je kiest als referentiepunt voor de potentiële energie de negatieve plaat. Maak de uitspraken correct door ze aan te vullen met ‘altijd’, ‘soms’ of ‘nooit’.

a Ladingen op een verschillende equipotentiaallijn bevinden zich op een andere afstand tot de negatieve plaat.

b Ladingen op een verschillende equipotentiaallijn hebben dezelfde potentiële elektrische energie.

c Tegengestelde ladingen hebben dezelfde potentiële elektrische energie.

d Tegengestelde ladingen hebben dezelfde kinetische energie.

e Een lading beweegt van de lage naar de hoge potentiaal.

f Een lading beweegt volgens de richting van het elektrisch veld.

g Een lading beweegt volgens de zin van het elektrisch veld.

5 000 Mg2+-ionen bezitten samen een potentiële elektrische energie van 33,7 nJ in een elektrisch veld van 7,8 MN C

a Noteer de potentiële elektrische energie in elektronvolt.

b Hoe ver van de negatieve plaat bevinden de ionen zich?

Het potentiaalverschil tussen twee evenwijdige geladen platen is –8,0 kV. In welk punt is de potentiaal –2,0 kV?

a In punt A.

b In punt B.

c In punt C.

d Niet te bepalen met deze gegevens.

Een elektron vertrekt vanuit rust en krijgt een snelheid v door een spanning U die aangelegd is tussen twee evenwijdige platen op een afstand d Welke snelheid zal het elektron (bij aankomst op de positieve plaat) hebben als de platen dubbel zo ver uit elkaar staan en ...

a de spanning verdubbelt?

b het elektrisch veld verdubbelt?

Het elektrische schokje dat je voelt als je in de buurt komt van geleidende voorwerpen op een droge winterdag, treedt op als het elektrisch veld zo sterk is (3 MV m ) dat ladingen doorheen de lucht kunnen bewegen na ionisatie van de luchtmoleculen. Er is doorslag tussen je hand en de klink, die zich 3,0 mm van elkaar bevinden. Bereken:

a de doorslagspanning;

b de potentiaal van je hand en de klink, net voordat de doorslag optreedt.

Jan koopt drie batterijen van 1,5 V voor een zaklamp met een lampje van 4,5 V en een buisvormige batterijhouder.

a Wat betekent 4,5 V hier?

b Teken de verschillende mogelijkheden om de batterijen te monteren. In welke situaties zal de lamp branden?

Bestudeer de afbeeldingen. Beantwoord voor beide schakelingen de vragen.

a Benoem de schakeling.

b Welk watermodel komt overeen met de schakeling?

c Noteer het verband tussen de totale spanning en de spanning over de weerstanden.

d Verklaar het spanningsverband met potentiaal en potentiële energie.

e Vergelijk met potentiaal en potentiële energie in het watermodel.

REEKS

Schakeling A Watermodel A

Schakeling B Watermodel B

Een proton bevindt zich op 13,6 cm van de positieve plaat in een verticaal homogeen elektrisch veld en ondervindt een elektrische kracht van 6,2 nN.

a Toon aan dat de verhouding van verandering van de potentiële energie in het zwaarteveld (ΔE pot, z) tot de potentiële energie in het elektrisch veld (ΔE pot, z) gelijk is aan F z F C (als je het nulniveau van de gravitationele potentiële energie samenlegt met de negatieve plaat). Bereken die verhouding.

b Bereken de totale kinetische energie op de positieve plaat, als het proton op die plaat aankomt.

Toon aan dat je in een elektrische kring het vermogen kunt berekenen als P = U · I.

Meer oefenen? Ga naar .

HOOFDSTUKSYNTHESE

WATERKRINGLOOP

potentiële zwaarte-energie van het water → kinetische energie van het water → energie van de verbruiker

ELEKTRISCHE STROOMKRING

(potentiële) elektrische energie van de ladingen → kinetische energie van de ladingen → energie van de verbruiker

Potentiële energie: energie ten gevolge van de kracht en de plaats in een veld. We bestuderen homogene velden.

E pot, z = m · g · h

waarbij m de (proef)massa, g de grootte van de gravitatieveldsterkte en h de hoogte tot het oppervlak van de planeet is.

E pot, E = q · E · x

waarbij q de (proef)lading, E de grootte van de elektrische veldsterkte en x de afstand tot het referentiepunt is.

Potentiaal: maat voor de energie-eigenschappen van een veld.

VELD ROND BRONMASSA VELD ROND BRONLADING

gravitatieveldsterkte potentiaalelektrische veldsterkte potentiaal g = FG m E pot, z m E = FC q V = Epot, E q

vectoriële grootheid scalaire grootheidvectoriële grootheidscalaire grootheid voorgesteld met veldlijnen

voorgesteld met equipotentiaalvlakken

voorgesteld met veldlijnen voorgesteld met equipotentiaalvlakken

Potentiaalverschil zorgt voor beweging van deeltjes: stroom

conventionele stroomzin

hogere potentiaal, hoge E pot, z

elektronenstroom lamp

lagere potentiaal, lage E pot, z batterij

potentiaalverschil spanning

HOOFDSTUK 5

Eigenschappen

van magneten

©VANIN

In de klassieke oudheid ontdekte men kristallen die elkaar aantrekken of afstoten afhankelijk van de richting waarin je ze in elkaars buurt brengt. Die kristallen noemde men ‘magnetiet’, naar de geografische locatie met de naam Magnesia (volgens sommige bronnen een landstreek in Thessalië, volgens andere dan weer steden in het oude Griekenland en Turkije) waar al meer dan 2 500 jaar lang magnetische brokken ijzererts worden gevonden. Het verschijnsel noemde men ‘magnetisme’ (λιθος Μαγνης (lithos Magnès), Grieks voor ‘magnetische stenen’). Onderzoek wees uit dat magnetiet een mineraal is dat samengesteld is uit ijzer(II, III)oxide (Fe2O3 of Fe3O4).

In dit hoofdstuk bestudeer je de eigenschappen van magneten en hun velden. Je leert hoe je stoffen magnetisch kunt maken, om zo tot technologische toepassingen te komen.

LEERDOELEN

M gelijkenissen en verschillen tussen permanente magneten en elektromagneten omschrijven

M de krachtwerking van een magneet omschrijven

M magnetische veldlijnenpatronen tekenen en interpreteren

M de fenomenen ‘magnetiseren’ en ‘demagnetiseren’ verklaren op atomaire schaal

M enkele technologische toepassingen van (elektro)magneten geven

1 Welke soorten magneten bestaan er?

In het dagelijks leven gebruik je regelmatig magneten.

Met magneten kun je voorwerpen ophangen op de koelkast.

Een smartphone of smartwatch wordt aangetrokken door de magneet in de oplader.

Je kunt deuren vanop een afstand openen door een elektromagneet uit te zetten.

Uit experimenten blijkt dat sommige voorwerpen ijzer aantrekken. Je zegt dat die voorwerpen magneten zijn. Je kunt aan een voorwerp niet zien of het een magneet is. Door de invloed van het voorwerp op zijn omgeving kun je dat wel afleiden.

05 LABO

In deze video zie je een elektromagneet in werking.

Permanente magneten hebben de magnetische eigenschap altijd. Het materiaal van de magneet is behandeld zodat het die eigenschap vertoont.

In deze video zie je een elektromagneet als deuropener.

©VANIN

Elektromagneten zijn magnetisch bij elektrische stroom. In de praktijk zijn dat doorstroomde geleiders.

In paragraaf 5 leer je hoe je permanente magneten en elektromagneten maakt.

VOORBEELD MAGNEET ALS DEUROPENER

Om een deur vanop een afstand te kunnen openen, bevestigt men op de deur een elektromagneet die de deur dichthoudt als de kring gesloten is. Nadat iemand heeft aangebeld, opent de elektrische kring en wordt de deur ontgrendeld. Vaak laat men tijdens de ontgrendeling een geluid weerklinken.

Een magneet is een voorwerp dat een invloed uitoefent op sommige voorwerpen (zoals ijzer) in de omgeving.

Er zijn twee soorten magneten:

• permanente magneten (kortweg ‘magneten’): het materiaal van de magneet vertoont de invloed continu;

• elektromagneten: je kunt de invloed aan- en uitschakelen.

▲ Afb. 113

▲ Afb. 114

▲ Afb. 115 Een elektromagneet die bevestigd is op een deur

2

2.1 Krachtwerking tussen permanente magneten

DEMO

Welke factoren beïnvloeden de kracht tussen twee permanente magneten?

1 Je leerkracht hangt een staafmagneet op aan een touwtje.

2 Bespreek met je buur de mogelijke invloedsfactoren wanneer je met een tweede staafmagneet een kracht uitoefent op die opgehangen staafmagneet.

3 Test samen met je leerkracht uit.

4 Formuleer een antwoord op de onderzoeksvraag.

Permanente magneten hebben twee polen: een noordpool N en een zuidpool Z. De naamgeving van de polen is gebaseerd op het gedrag van permanente magneten in de buurt van de aarde. Een draaibaar opgestelde staafmagneet (= kompas) oriënteert zich altijd op dezelfde manier volgens de geografische noord-zuidrichting. Bij permanente magneten geldt de volgende afspraak:

• De noordpool N wijst naar het geografische noorden.

• De zuidpool Z wijst naar het geografische zuiden.

B Een

Permanente magneten oefenen een kracht uit op sommige voorwerpen in hun omgeving zonder contact te maken. De magnetische kracht is een veldkracht Twee magneten in elkaars buurt oefenen een aantrekkende of afstotende kracht uit op elkaar. Die wordt bepaald door hun onderlinge oriëntatie.

demovideo: krachtwerking permanente magneten

Gelijksoortige magneetpolen stoten elkaar af. Ongelijksoortige magneetpolen trekken elkaar aan

Net zoals bij de elektrische dipool, zijn er twee ongelijksoortige polen. Om een duidelijk onderscheid te maken tussen de magneetpolen, kleurt men ze vaak. De zuidpool is blauw, groen of wit.

▲ Afb. 116 De noordpool van permanente magneten wordt meestal aangegeven in het rood.

Een hoefijzermagneet

staafmagneet

VOORBEELD KOMPAS

Een kompasnaald is een lichte, langwerpige, permanente magneet, vaak met scherpe punten aan de pooluiteindes, die vrij kan roteren om haar middelpunt.

ZN

In de nabijheid van een pool van een andere magneet wordt de gelijksoortige pool van het kompas afgestoten en de ongelijksoortige aangetrokken.

©VANIN

▲ Afb. 120 Een kompas in de buurt van een permanente magneet

De kompasnaald draait totdat de ongelijksoortige polen in elkaars verlengde liggen. De noordpool op het kompas wijst naar de zuidpool van de magneet.

▲ Afb. 121 De aarde is een permanente magneet.

Een kompasnaald oriënteert zich altijd naar hetzelfde punt van de aarde. Het is alsof er een staafmagneet in de aarde zit met een magnetische zuidpool in de buurt van de geografische Noordpool en een magnetische noordpool in de buurt van de geografische Zuidpool.

Een permanente magneet heeft een zuidpool en een noordpool Als je een andere permanente magneet in de buurt brengt, is er aantrekking tussen de ongelijksoortige polen en afstoting tussen de gelijksoortige polen

▲ Afb. 119 Een kompas draait in de buurt van een permanente magneet.

Europa

Afrika

Bekijk het aardmagnetisch veld in de applet.

2.2 Krachtwerking tussen een magneet en een magnetisch voorwerp

Als je een permanente magneet op een kleine afstand van voorwerpen uit ijzer en sommige andere stoffen (zoals nikkel, kobalt en hun legeringen) houdt, worden die voorwerpen aangetrokken. In de buurt van andere materialen is er geen krachtwerking. De stoffen die aangetrokken worden tot een magneet, noem je ferromagnetische stoffen of kortweg ‘magnetische stoffen’.

Bij aantrekking door een magneet worden voorwerpen uit ferromagnetisch materiaal zelf tijdelijk een magneet. Dat verschijnsel heet magnetische influentie. Magnetische influentie werkt op afstand en door sommige middenstoffen heen. In het voorwerp uit ferromagnetisch materiaal ontstaan ongelijksoortige magneetpolen. Het voorwerp wordt aangetrokken tot de polen. Als je de magneet verwijdert, verliest het voorwerp zijn magnetische eigenschap (bijna) helemaal. De sterkte van de influentie hangt af van de sterkte van de magneet, de afstand tot de magneet en het materiaal. Omdat het materiaal tijdens het proces polen krijgt, noem je dat fenomeen ook magnetische polarisatie

Ferrum is Latijn voor ‘ijzer’. Ferromagnetische stoffen gedragen zich zoals ijzer in de buurt van een magneet.

In de video zie je de krachtwerking tussen een magneet en voorwerpen.

©VANIN

Influere is Latijn voor ‘beïnvloeden’. De eigenschappen van het ferromagnetisch materiaal worden beïnvloed door de permanente magneet. Dat kun je vergelijken met elektrostatische inductie, waarbij materialen beïnvloed worden door ladingen in de buurt.

▲ Afb. 122 Een permanente magneet trekt ijzervijlsel aan door glas.▲ Afb. 123 Een elektromagneet trekt ijzeren paperclips aan door plastic.

Z N N Z

▲ Afb. 124 Paperclips krijgen een N- en een Z-pool als je ze aan een magneet hangt.

nikkel

©VANIN

magnetisch niet-magnetisch magnetisch

▲ Afb. 125 De samenstelling van de verschillende muntstukken

Muntstukken bestaan uit verschillende metalen, zodat ze elk hun specifieke kleur hebben. Bij een muntstuk is het belangrijk dat de geldwaarde van het metaal lager is dan de waarde die het muntstuk aangeeft. Zo bevatten de muntstukken van 1, 2 en 5 cent voornamelijk ijzer en maar een kleine fractie koper.

In de buurt van een magneet worden de muntstukken die een ferromagnetische stof (ijzer of nikkel) bevatten, aangetrokken. Tijdens die aantrekking worden de munten zelf een magneet met twee polen. Je noemt ze ‘magnetisch’.

CONCEPTVRAGEN

1 Maak de uitspraken correct door ze aan te vullen met ‘altijd’, ‘soms’ of ‘nooit’. a Een magneet wordt aangetrokken tot een opgewreven plastic staaf. b Een magneet wordt afgestoten door een opgewreven plastic staaf.

2 Test uit en verklaar.

Als je een permanente magneet in de buurt brengt van een voorwerp uit ferromagnetisch materiaal, is er (meestal) aantrekking, omdat het voorwerp zelf een magneet wordt.

Het magnetisch worden of magnetiseren van het ferromagnetisch materiaal noem je magnetische influentie of magnetische polarisatie

2.3 Krachtwerking tussen een magneet en een stroomvoerende geleider

DEMO

Welke invloed is er tussen een permanente magneet en een stroomvoerende geleider?

1 Je leerkracht brengt:

a een draaibare kompasnaald (= permanente magneet) in de buurt van een vaste geleider die aangesloten is aan een spanningsbron; b een beweegbare geleider (met bron) tussen de benen van een vaste hoefijzermagneet.

Je kunt de bron aan- en uitzetten en de stroomzin omwisselen.

2 Wat zal er volgens jou gebeuren?

Bespreek met je buur en test samen met je leerkracht uit.

3 Formuleer een antwoord op de onderzoeksvraag.

Uit experimenten blijkt dat er een verband bestaat tussen elektriciteit en magnetisme. De tak van de wetenschap die dat verband bestudeert, noem je elektromagnetisme.

Tussen een permanente magneet en een stroomvoerende geleider is er een krachtwerking. De bewegende ladingen maken van de geleider een magneet. Uit de derde wet van Newton volgt dat de kracht op de permanente magneet door een stroomvoerende geleider even groot als, maar tegengesteld is aan de kracht van de permanente magneet op de stroomvoerende geleider. Experimenteel kun je dat op twee manieren zien.

A Krachtwerking van een stroomvoerende geleider op een permanente magneet

Als je een permanente magneet (zoals een kompasnaald) in de buurt van een stroomvoerende geleider brengt, ontstaat er een krachtwerking op de permanente magneet. De stroomzin bepaalt de richting en de zin van de kompasnaaldjes (als die gemakkelijk kunnen draaien).

VOORBEELD KOMPASNAALDEN IN DE BUURT VAN EEN RECHTE GELEIDER

Als er geen stroom door een geleider loopt, richten kompasnaalden in de omgeving van de geleider zich volgens de noord-zuidrichting van de aarde.

Als er stroom door de geleider loopt, richten de kompasnaalden zich loodrecht op de geleider. De zin wordt bepaald door de stroomzin. Als de kompasnaalden in hetzelfde vlak loodrecht op de geleider liggen, vormen ze een cirkel.

demovideo: beweegbare geleider

B Krachtwerking van een permanente magneet op een stroomvoerende geleider

Als je een stroomvoerende geleider in de buurt van een permanente magneet brengt, kan de stroomvoerende geleider een kracht ondervinden doordat de stroomvoerende geleider een magneet wordt. (Dat bespreek je in detail in hoofdstuk 6.) De stroomzin en de oriëntatie van de magnetische polen bepalen de zin van de kracht.

VOORBEELD KOPERDRAAD TUSSEN DE POLEN VAN EEN HOEFIJZERMAGNEET

Koper is geen ferromagnetische stof.

Een koperen draad waar geen stroom door vloeit, ondervindt geen invloed van de magneet. Er is geen krachtwerking.

Een koperen draad waar een stroom door vloeit, ondervindt tussen de polen van een hoefijzermagneet een kracht. De kracht werkt loodrecht op de loodrechte verbindingslijn tussen de polen. De stroomzin bepaalt de zin van de kracht.

©VANIN

CONCEPTVRAAG

Leg uit waarom de uitwerking van de reactiekracht in beide gevallen niet zichtbaar is.

Een magneet en een stroomvoerende geleider oefenen een kracht uit op elkaar.

De bewegende ladingen maken van de geleider een magneet.

WEETJE

Oersted was een van de eersten die onderzoek deed naar elektromagnetische verschijnselen. Je kunt zijn onderzoek bekijken in de video.

3 Hoe ziet het veldlijnenpatroon

3.1 Magnetisch veld rondom een permanente magneet

Rondom een of meerdere magneten is er een magnetisch veld, waarvan je meestal geen uitwerking ziet. Als je kleine ijzerdeeltjes in de buurt brengt, wordt het patroon van het magnetisch veld zichtbaar.

Een staafmagneet heeft twee ongelijksoortige polen. Het veld noem je een magnetisch dipoolveld

VOORBEELD MAGNETISCH VELD RONDOM EEN STAAFMAGNEET

In de buurt van een staafmagneet ondervinden sommige voorwerpen (een andere magneet, ferromagnetisch materiaal of bewegende ladingen in een geleider) een magnetische kracht. Zonder die voorwerpen zie je geen uitwerking van het veld.

06 LABO

video: veldlijnenpatronen bij permanenten magneten

©VANIN

Met ijzervijlsel kun je de magnetische veldlijnen zichtbaar maken. De korrels lijnen zich op in de buurt van de staafmagneet. Er verschijnt een specifiek patroon van veldlijnen. Kompasnaalden richten zich volgens de veldlijnen.

Door ijzervijlsel met olie te mengen, zie je dat het magnetisch veld driedimensionaal is.

Je kunt het patroon dat verschijnt, verklaren met de magnetische polarisatie van de ijzervijlselkorreltjes. Elk korreltje krijgt onder invloed van de staafmagneet een zuidpool en een noordpool (= magnetische influentie).

• De noordpool van de korrel wordt aangetrokken tot de zuidpool van de magneet en de zuidpool tot de noordpool.

• De ongelijksoortige polen van naburige korreltjes trekken elkaar aan.

Op afbeelding 133 zie je het statisch eindresultaat.

Uit het veldlijnenpatroon blijkt dat de ijzerkorreltjes een magnetische kracht ondervinden. Dat kan enkel als ze zich in een magnetisch veld bevinden. Er is dus een magnetisch veld aanwezig. Dat magnetisch veld blijft aanwezig als je het ijzervijlsel wegneemt.

▲ Afb. 133 IJzerkorreltjes worden magneten in de buurt van een magneet.

▲ Afb. 130

▲ Afb. 131

▲ Afb. 132

Je kunt het magnetisch veld voorstellen met magnetische veldlijnen. Dat lijnenpatroon beschrijft het gedrag van kompasnaalden en ijzervijlsel (of andere ferromagnetische materialen) als je die in het veld plaatst. Ze visualiseren de eigenschappen van de ruimte rondom een magneet.

• Een kleine magneet, zoals een kompasje, neemt in het magneetveld een richting aan die raakt aan de veldlijn.

• Je kunt de veldlijnen een zin geven. Volgens afspraak is dat in de zin van de noordpool van een kompas: de zin van de magnetische veldlijnen is buiten de magneet altijd weg van de noordpool en naar de zuidpool toe. Magnetische veldlijnen zijn altijd gesloten lijnen, omdat een magneet altijd een dipool is. Dat is een verschil met elektrische veldlijnen: bij een puntlading (= monopool) zijn de veldlijnen niet gesloten.

• In de magneet lopen de veldlijnen van de zuid- naar de noordpool. Om figuren niet te zwaar te maken, tekent men die meestal niet.

• Net zoals bij elektrische velden en gravitatievelden, is de dichtheid van de veldlijnen een maat voor de relatieve sterkte van het veld. Hoe dichter de veldlijnen bij elkaar liggen, hoe sterker het veld is.

VOORBEELD VELDLIJNEN BIJ EEN STAAFMAGNEET

In elk punt in de omgeving van een staafmagneet raakt een kompasnaald aan de veldlijn die in dat punt wordt gezet. Rondom de staafmagneet is de zin van de veldlijn gelijk aan de zin waarnaar de noordpool van de kompasnaald wijst. Binnen in de magneet lopen de (gesloten) veldlijnen van de zuidpool naar de noordpool.

©VANIN

▲ Afb. 134

A Kompasnaalden in de buurt van een staafmagneet

B Veldlijnen in de buurt van een staafmagneet

C Veldlijnen in de buurt van en in een staafmagneet

In de paarse zone liggen de veldlijnen dichter bij elkaar dan in de gele zone. Het magnetisch veld van de staafmagneet is het sterkst aan de polen en het zwakst ter hoogte van het midden van de staafmagneet.

Verschillende magneten of configuraties veroorzaken elk een eigen veldlijnenpatroon. In de tabel op de volgende pagina zie je enkele voorbeeldconfiguraties met hun eigenschappen.

PATROON VAN IJZERVIJLSEL VELDLIJNEN

CONCEPTVRAGEN

EIGENSCHAPPEN

Twee gelijksoortige polen stoten elkaar af. Dat is zichtbaar door de veldlijnen, die tussen de twee afstotende polen van elkaar weg gericht zijn.

©VANIN

Twee ongelijksoortige polen trekken elkaar. Dat is zichtbaar door de veldlijnen, die tussen de twee aantrekkende polen naar elkaar toe gericht zijn, met een zin van de noordpool naar de zuidpool.

De benen van een hoefijzermagneet zijn twee lange, ongelijksoortige polen van een magneet.

Tussen de benen ontstaat er een homogeen magnetisch veld loodrecht op de benen, met een zin van de noordpool naar de zuidpool.

1 Hoe veranderen het patroon van het ijzervijlsel en de veldlijnen in de situaties met de twee staafmagneten in elkaars buurt (voorbeeldconfiguraties A en B) als je beide magneten omdraait?

2 Hoe komt het dat de veldlijnen buiten de hoefijzermagneet gekromd zijn?

Je kunt het patroon van een magnetisch veld zichtbaar maken door kompasnaalden of ijzervijlsel in de buurt te brengen, die zich volgens het magnetisch veld richten. Je kunt het magnetisch veld voorstellen met veldlijnen. Dat zijn lijnen die de richting en de zin van het magnetisch veld aangeven. Kleine, langwerpige, beweegbare magneetjes raken in elk punt van het veld aan de plaatselijke veldlijn en wijzen met hun noordpool in de zin van de veldlijn. De dichtheid geeft aan waar het veld sterker of zwakker is.

3.2 Magnetisch veld rondom een elektromagneet

DEMO

Hoe ziet het veldlijnenpatroon eruit bij verschillende vormen van stroomvoerende geleiders?

1 Je leerkracht monteert een stroomvoerende geleider zonder voorwerpen in de buurt.

2 Wat zal er volgens jou gebeuren?

Bespreek met je buur en test uit.

3 Je leerkracht strooit ijzervijlsel rond de geleider en zet er kompasnaaldjes rond.

4 Welk patroon verwacht je?

Bespreek met je buur en test uit.

5 Formuleer een antwoord op de onderzoeksvraag.

Rondom een stroomvoerende geleider (en dus bewegende ladingen) ontstaat er een magnetisch veld. Je noemt zo’n geleider een elektromagneet. Meestal zie je geen uitwerking van het opgewekte veld. Net zoals bij permanente magneten wordt het veldlijnenpatroon zichtbaar als je ijzervijlsel in de buurt brengt.

We bespreken drie situaties: een rechte stroomvoerende geleider, een stroomvoerende lus en een stroomvoerende spoel.

1 Rechte stroomvoerende geleider

De magnetische veldlijnen van een rechte stroomvoerende geleider zijn cirkels in een vlak loodrecht op de geleider, met de geleider als middelpunt.

In drie dimensies vormen de veldlijnen concentrische cilinders. Het magnetisch veld rond een rechte stroomvoerende geleider noem je een cilinderveld.

Een kompasnaald in een punt oriënteert zich volgens de raaklijn aan een cirkel. De zin van de veldlijn rondom de geleider is de zin waarin de noordpool van die kompasnaald wijst.

▲ Afb. 135 IJzervijlsel rond een rechte stroomvoerende geleider vormt een cirkelvormig patroon.

▲ Afb. 136 De stroomzin bepaalt de zin van de veldlijnen.

Zonder kompasnaalden kun je de zin van de veldlijnen vinden door met je rechterhand de geleider ‘vast te pakken’, zodat je duim in de zin van de stroom wijst. Je overige vingers geven dan de zin van de veldlijnen aan. Dat is de rechterhandregel voor de veldlijnen bij een geleider

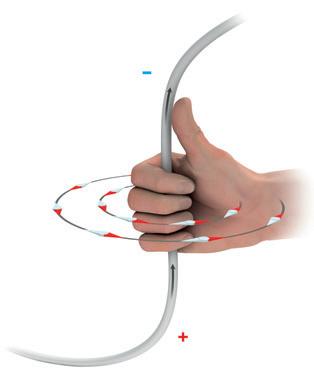
▲ Afb. 137 De rechterhandregel voor de bepaling van de zin van de veldlijnen bij een rechte geleider

©VANIN

▲ Afb. 138 Voorstelling van de magnetische veldlijnen bij een rechte stroomvoerende geleider

2 Stroomvoerende lus

Als een geleider gekromd wordt, ontstaat er een lus. Bij een lus kun je elk stukje van de geleider als een rechte geleider beschouwen. Dicht bij de twee overstaande delen van de geleider (aangeduid met A en B op afbeelding 139) verschijnen cirkels, zoals bij een rechte geleider. Meer naar het midden toe beïnvloeden de velden van beide geleiders elkaar en ontstaan er rechtere lijnen. In het midden is er één rechte lijn.

De richting van de veldlijnen kun je zien door een kompasnaald die zich oriënteert volgens de raaklijn aan de veldlijn. De zin van de veldlijnen bij een lus is de zin waarin de noordpool van een kompasnaald wijst. Je kunt de zin bepalen met de rechterhandregel voor een rechte geleider.

▲ Afb. 140 De rechterhandregel voor de bepaling van de zin van de veldlijnen bij een lus

Het magnetisch veld dat veroorzaakt wordt door een stroomvoerendelus (zie afbeelding 141 en 142 op p. 122), lijkt sterk op het veld van een staafmagneet: het magneetveld heeft een noorden een zuidpool. Er is een dipoolveld. Net zoals bij een staafmagneet gaan de magnetische veldlijnen in de lus van zuid naar noord en die buiten de lus van noord naar zuid.

▲ Afb. 139 IJzervijlsel rond een stroomvoerende lus vormt een cirkelvormig patroon rond de geleiders en rechte lijnen naar het midden toe.

De rechterhandregel is enkel een hulpmiddel om snel de polen te vinden.

De rechterhandregel voor de lus en de spoel zijn telkens een uitbreiding van de rechterhandregel voor de rechte geleider.

Bekijk de rechterhandregel voor de spoel in de video.

©VANIN

▲ Afb. 141 Het magnetisch veldlijnenpatroon bij een stroomvoerende lus

3 Stroomvoerende spoel

Meerdere lussen naast elkaar vormen een spoel of solenoïde. Het veldlijnenpatroon dat zichtbaar wordt met ijzervijlsel, kun je verklaren vanuit de magnetische velden rondom stroomvoerende lussen die dicht bij elkaar liggen. Naar het midden toe beïnvloeden de velden van beide geleiders elkaar en ontstaan er rechte lijnen

▲ Afb. 142 Het veld van een stroomvoerende lus (zijaanzicht) en dat van een staafmagneet vertonen veel gelijkenissen.

In een lange spoel lopen de veldlijnen evenwijdig met de lengterichting van de spoel. Het veld in de spoel is in elk punt gelijk. Binnen in de spoel is er een sterk homogeen magnetisch veld gevormd.

Het veld buiten de spoel is veel zwakker dan dat binnen de spoel en heeft dezelfde vorm als het veld rondom een staafmagneet: het is een dipoolveld. De kant waar de veldlijnen uit de spoel komen, is de noordpool. De kant waar de veldlijnen in de spoel binnenkomen, is de zuidpool.

Zonder kompasnaalden vind je de zin van de veldlijnen door met je rechterhand de spoel ‘te grijpen’, zodat je vingers gekromd zijn volgens de stroom. Je gestrekte duim geeft dan de zin van de veldlijnen in de spoel aan. Dat is de tweede rechterhandregel voor de veldlijnen bij een spoel.

▲ Afb. 144 Het magnetisch veldlijnenpatroon bij een stroomvoerende spoel

▲ Afb. 145 De tweede rechterhandregel voor de bepaling van de zin van de veldlijnen bij een spoel

▲ Afb. 146 Voorstelling van de magnetische veldlijnen bij een spoel

▲ Afb. 143 Men gebruikt spoelen met veel windingen (enkele honderden) om sterke magnetische velden op te wekken.

CONCEPTVRAGEN

1 Hoe veranderen het patroon in het ijzervijlsel, de oriëntatie van een kompasnaald en de zin van de veldlijnen als je de stroomzin omwisselt in de drie situaties (rechte geleider, lus en spoel)?

2 Je brengt twee stroomvoerende spoelen in elkaars buurt.

a Maak de uitspraken correct door ze aan te vullen met ‘altijd’, ‘soms’ of ‘nooit’.

• De spoelen worden aangetrokken tot elkaar.

• De spoelen worden afgestoten door elkaar.

b Verklaar.

Elektrische stroom (en dus bewegende ladingen) wekt een magneetveld op.

Er ontstaat een elektromagneet.

De vorm van de stroomvoerende geleider bepaalt de vorm van het magnetisch veld:

• Rechte geleider: cirkels rond de geleider vormen een cilinderveld

• Lus: er ontstaat een dipoolveld.

• Spoel: er ontstaan een dipoolveld buiten de spoel en een homogeen veld binnen de spoel

De stroomzin bepaalt de zin van de veldlijnen.

Je kunt die achterhalen met twee rechterhandregels

4 Hoe maak je van ferromagnetische materialen een magneet?

4.1 De microscopische structuur van ferromagnetische materialen

CONCEPTVRAGEN

Een staafmagneet breekt in tweeën.

1 Welke voorstelling geeft de polen correct weer?

2 Bedenk een experiment om je antwoord te controleren.

Als je een staafmagneet in kleinere stukken verdeelt, wordt elk stukje op zich een nieuwe magneet (met twee polen). Je kunt zo verdergaan tot je (in theorie) op moleculair vlak belandt bij een moleculair of elementair magneetje. Zo’n elementair magneetje kun je bekijken als een ondeelbaar magnetisch dipooltje en de staafmagneet als een grotere magnetische dipool die opgebouwd is uit een aaneenschakeling van dergelijke kleine dipooltjes.

Het atomaire dipooltje ontstaat door de beweging van elektronen (= negatieve ladingen) (zie afbeelding 148 op p. 124). Net zoals bewegende ladingen in een geleider een macroscopisch magneetveld opwekken, wekken de rotatie van een elektron rond een kern (= kringstroom) en de rotatie rond zijn eigen as (= elektronspin) een atomair magneetveld op.

rotatiebeweging

kringstroom (rotatie van een elektron rond de kern)

voorstelling van de stroom en het magneetveld

De weissgebieden zijn genoemd naar de Franse fysicus Pierre-Ernest Weiss, die ze ontdekte in 1907. De grootte van die gebieden is 10−8 tot 10−6 m. Binnen elk gebied bevinden zich ongeveer 106 tot 109 atomen.

▲ Afb. 148

elektronspin (rotatie van een elektron rond zijn eigen as)

N Z N Z

symbolische voorstelling als dipool of

I of

De polen van een magneet ontstaan door atomaire dipooltjes als gevolg van de kringstroom en de elektronspin.

In de meeste stoffen zijn de verschillende kringstromen en elektronspins niet geordend en heffen de effecten van de verschillende atomaire dipolen elkaar op. Er is meestal geen resulterende magnetische dipool.

Bij ferromagnetische stoffen is er een ordening van de atomaire dipolen in bepaalde gebieden. Een stuk ijzer (of een andere ferromagnetische stof die ijzer, kobalt of nikkel bevat) bestaat daardoor uit heel kleine magnetische gebiedjes, waarbij de dipolen dezelfde oriëntatie (richting en zin) hebben. Dat noem je weissgebieden

animatie: ijzer magnetiseren

geen extern magneetveld zwak extern magnetisch veld sterk extern magnetisch veld

▲ Afb. 149 weissgebieden in ongemagnetiseerd ijzer

Het stuk ijzer wordt een magneet als de weissgebieden georiënteerd worden door een magneetveld in de buurt. Bekijk dat in de animatie.

De magnetische eigenschappen van ferromagnetisch materiaal ontstaan als gevolg van de beweging van elektronen, die negatieve ladingen zijn. De elektronenbanen rond de kern en de elektronspin wekken kleine magnetische dipooltjes op. Bij ferromagnetische stoffen zijn die atomaire dipooltjes geordend in bepaalde gebieden, de weissgebieden. Net zoals (op macroscopisch niveau) bij elektromagneten wekken bewegende ladingen (op microscopisch niveau) een magnetisch veld op.

4.2 Magnetiseren

In een niet-magnetisch stuk ijzer zijn de weissgebieden willekeurig geordend, zodat ze elkaars magnetische werking opheffen. Het materiaal is dus niet-magnetisch. Als je een niet-magnetisch stuk ijzer in een magnetisch veld brengt (bijvoorbeeld in de buurt van een magneet of in een stroomvoerende spoel), oriënteren de weissgebieden zich. Het stuk ijzer wordt magnetisch. Dat is de atomaire verklaring voor magnetische influentie. Het proces waarbij een ferromagnetische stof magnetische eigenschappen krijgt, noem je magnetiseren.

Hoe een ferromagnetische stof magnetiseert, hangt af van de samenstelling van de stof.

1 Zuivere ferromagnetische stoffen (zuiver ijzer, kobalt en nikkel)

De weissgebieden oriënteren zich gemakkelijk, maar verdwijnen ook gemakkelijk door de thermische beweging van de deeltjes. Dat noem je week ijzer.

©VANIN

Bij een elektromagneet wordt een stuk week ijzer in een stroomvoerende spoel geschoven. Er is geen oriëntatie van de weissgebieden en dus geen magnetisme.

Als je de elektrische kring sluit, oriënteren de weissgebieden zich volgens het aangelegde veld (bepaald door de stroomzin). Het weke ijzer wordt een magneet met een noorden zuidpool.

Als je de kring opent of het ijzer uit de spoel verwijdert, verdwijnt de oriëntatie van de weissgebieden. Er is geen magnetisme meer.

2 Legeringen met ferromagnetische stoffen (legering van ijzer en koolstof)

De weissgebiedenoriënteren zich moeilijk, maar blijven bestaan nadat je het externe veld wegneemt. Dat noem je sterk ijzer

Om een permanente magneet te maken, schuif je een stuk sterk ijzer in een stroomvoerende spoel. Er is geen oriëntatie van de weissgebieden en dus geen magnetisme.

Als je de elektrische kring sluit, oriënteren de weissgebieden zich volgens het aangelegde veld (bepaald door de stroomzin).

Het sterke ijzer wordt een magneet met een noorden zuidpool.

Als je de kring opent of het ijzer uit de spoel verwijdert, blijft de oriëntatie van de weissgebieden bestaan. Het ijzer is een permanente magneet geworden. Om de polen duidelijk te maken, kleurt men die soms.

VOORBEELD MAGNETISCHE DATAOPSLAG

Op een bankkaart en een harde schijf wordt informatie magnetisch opgeslagen. De afwisseling van noorden zuidpolen zorgt voor een digitaal 0-1-signaal (bits).

Een harde schijf bestaat uit een aantal platen, gemaakt van memcor (een combinatie van glas en keramiek), met daarbovenop een dunne, ijzerhoudende laag (sterk ijzer) en een beschermlaag.

A Magnetisch beeld van de bits

©VANIN

B Topografisch beeld

Je kunt informatie op de schijf schrijven door op een gecontroleerde manier gebiedjes te magnetiseren met een extern magnetisch veld.

Met speciale microscopen die het oppervlak aftasten, kun je de vorm en de magnetische eigenschappen visualiseren. Als je de vorm van het oppervlak bestudeert, zie je geen structuur. Als je de magnetische eigenschappen bestudeert, zie je afwisselend de polen verschijnen.

Ferromagnetische stoffen worden gemagnetiseerd door de oriëntatie van weissgebieden onder invloed van een extern magnetisch veld. Die magnetisatie kan tijdelijk (week ijzer) of langdurig (sterk ijzer) zijn.

VERDIEPING

Zowel in fundamenteel onderzoek als in de toegepaste wetenschap doet men onderzoek naar (de eigenschappen van) magneten.

In 1931 toonde Paul Dirac aan dat er een magnetische monopool kon bestaan. In 2014 konden wetenschappers met een kleine wolk rubidiumatomen bij een temperatuur van (bijna) 0 kelvin een monopool creëren.

Bij lage temperaturen vertoont het magnetisme in sommige stoffen speciale eigenschappen. Dat maakt bij lage temperaturen magnetische levitatie (= optilling) mogelijk. De treinen van de toekomst zullen daardoor kunnen zweven over het spoor.

In de video’s en via de websites op leer je meer over de speciale eigenschappen van magnetisme.

▲ Afb. 157 Zo moet de losse noordpool er ongeveer uitzien.▲ Afb. 158 De maglevtrein in Shanghai

▲ Afb. 156 Stukje van 10 µm op 10 µm van een harde schijf

4.3 Permanente magneten demagnetiseren

Hoe kun je een spijker magnetiseren en demagnetiseren?

1 Ga samen met je leerkracht op zoek naar manieren om eerst van een spijker een magneet te maken en vervolgens de magnetische eigenschappen weer te verwijderen.

2 Formuleer een antwoord op de onderzoeksvraag.

Magnetisme gaat gepaard met een sterke ordening in een materiaal. Demagnetiseren betekent dat die ordening opgeheven wordt. Dat kan op verschillende manieren gebeuren:

• Als je een permanente magneet verhit, kan die minder magnetisch worden of zelfs helemaal gedemagnetiseerd worden. Doordat je de temperatuur verhoogt, wordt de thermische beweging van de atomen heviger en worden de weissgebieden minder gericht. Boven een bepaalde temperatuur, de curietemperatuur, is het niet meer mogelijk om het magnetisch materiaal magnetisch te maken. De atomen trillen dan zo hevig dat er geen oriëntering meer mogelijk is. De stof verliest haar magnetisme. De curietemperatuur is stofafhankelijk: voor ijzer bedraagt ze 767 °C, voor kobalt 1 137 °C en voor nikkel 357 °C.

• Door hevige mechanische schokken is er geen oriëntering meer mogelijk. Een permanente magneet verliest aan magnetische krachtwerking wanneer ze valt.

• Als je een tegengesteld magnetisch veld aanlegt, kun je de oriëntering tenietdoen. Je moet het tegengestelde magnetisch veld op tijd verwijderen om magnetisatie in de tegengestelde zin te voorkomen.

Permanente magneten worden gedemagnetiseerd als de ordening van de weissgebieden wordt opgeheven door hitte, mechanische schokken of een tegengesteld magnetisch veld.

5 Welke toepassingen hebben magneten?

5.1 Elektromagneten

Elektromagneten zijn magneten die hun magnetische eigenschappen enkel vertonen als er een elektrische stroom vloeit. We bespreken enkele voorbeelden.

VOORBEELD DEURBEL

Als je op een deurbel drukt, sluit de elektrische kring. De elektromagneet in de bel wordt aangezet, waardoor de ijzeren klepel na influentie wordt aangetrokken. Daardoor botst de klepel tegen de gong, maar wordt de kring ook geopend in punt P. De elektromagneet is uitgeschakeld en de klepel veert terug. De kring is opnieuw gesloten en het proces herhaalt zich.

Hier wordt de kring geopend. P

gong klepel

Hoe kun je gegevens van een harde schijf wissen? CONCEPTVRAAG

animatie: werking deurbel

schakelaar

elektromagneet

‘Permalloy’ = permanent + alloy.

Alloy is het Engelse woord voor ‘legering’.

VOORBEELD RELAIS

Elektromagneten worden op verschillende plaatsen in elektrische installaties gebruikt om de veiligheid van de kring te verhogen: bij zekeringen, de aardlekschakelaar en het relais.

Bij een magnetisch relais stuurt men met behulp van een ongevaarlijke schakeling (lage stroomsterkte) een grotere (gevaarlijkere) schakeling (grote stroomsterkte) met een verbruiker aan zonder rechtstreeks contact. Als men de kring met de elektromagneet sluit, wordt de ijzeren schakelaar in de kring met de verbruiker na influentie gesloten.

Men gebruikt een relais niet alleen voor de veiligheid, maar ook in domotica. Dat zijn systemen waarmee je vanop een afstand (bijvoorbeeld met je smartphone) toestellen kunt aan- en uitschakelen.

5.2 Permanente magneten

relais

©VANIN

kan gesloten worden op afstand

Permanente magneten zijn magneten die altijd magnetische eigenschappen vertonen, ook als er geen extern magnetisch veld in de buurt is.

VOORBEELD PERMALLOY

Sterk ijzer is altijd een legering. Legeringen die geschikt zijn om permanente magneten mee te maken, noem je permalloy. De eerste permalloy was een legering van 80 % nikkel en 20 % ijzer (uitgevonden in 1914). Materiaalwetenschappers zoeken altijd naar nieuwe legeringen, om zo steeds sterkere magneten te kunnen maken.

rolluik

▲ Afb. 159 Een vereenvoudigde voorstelling van een magnetisch relais om apparatuur vanop een afstand aan te schakelen (domotica)

▲ Afb. 160 Wanneer men rivieren proper maakt, haalt men voorwerpen (met een massa tot 500 kg) boven water met behulp van een sterke neodymiummagneet (een legering Nd2Fe14B van neodymium, ijzer en boor).

5.3 De magnetische velden van hemellichamen

Hemellichamen, zoals sterren en planeten, hebben een magnetisch veld dat ontstaat doordat ze bewegende ladingen bevatten. De noorden zuidpool hebben er meestal geen vaste positie. Ze verschuiven langzaam in de loop van de tijd. Op bepaalde tijden keert de zin van de elektrische stromen om en wisselen de magnetische noorden zuidpool dus ook. Het is niet te voorspellen wanneer de magnetische polen zullen omwisselen.

VOORBEELD AARDMAGNETISCH VELD

Het magnetisch veld van de aarde ontstaat door de bouw van de kern van de aarde: een ijzeren bol waarvan het hart vast en de buitenste laag vloeibaar is. Door de aardrotatie is er een geordende beweging van het vloeibare geïoniseerde ijzer en nikkel. Er ontstaan elektrische stromen in grote lussen, die een magnetisch veld creëren.

©VANIN

▲ Afb. 161 Het aardmagnetisch veld

(positief) ijzerion

(positief) nikkelion

▲ Afb. 162 Het ontstaan van het aardmagnetisch veld

Dat aardmagnetisch veld beschermt ons tegen gevaarlijke deeltjes uit de ruimte, vooral van de zon. Die stuurt constant schadelijke straling (de zonnewind) op ons af.

De magnetische polen van de aarde komen niet exact overeen met de geografische polen en verschuiven met een snelheid van ongeveer 15 km per jaar. De laatste keer dat er een omkering van de polen gebeurde, was zo’n 780 000 jaar geleden. Omdat de grootte van het magnetisch veld van de aarde in de laatste eeuwen sterk is afgenomen, nemen wetenschappers aan dat er over ongeveer tien eeuwen opnieuw een magnetische ompoling zal gebeuren.

De zonnewind is een stroom van geladen deeltjes die afkomstig zijn van de zon.

▲ Afb. 163 Het aardmagnetisch veld buigt de straling van de zon af en stuurt gevaarlijke deeltjes verder de ruimte in.

▲ Afb. 164 De beweging van de magnetische noordpool sinds 1831

Onderzoek is een voortdurende aanpassing van visies. Het onderzoek naar het magnetisch veld van de maan is daar een mooi voorbeeld van. De maan heeft geen magnetisch veld.

Onderzoekers besloten in 2020 dat de maan vroeger wel een magnetisch veld had, dat een miljard jaar geleden uitviel. In 2021 spraken nieuwe resultaten dat tegen: de maan heeft nooit een magnetisch veld gehad.

CONCEPTVRAAG

Welk verband is er tussen het ontstaan van magnetische eigenschappen op atomair, microscopisch, macroscopisch en planetair niveau? WEETJE

▲ Afb. 165 De aarde heeft een magnetisch veld, de maan niet.

REEKS

Zijn de volgende uitspraken juist of fout?

Verbeter indien nodig.

a Alle metalen worden aangetrokken door een magneet.

b Magneten zijn gemaakt uit ferromagnetisch materiaal.

c De noordpool van een kompas wijst naar de magnetische noordpool van de aarde.

d De magnetische kracht is een veldkracht.

e Door magnetische influentie worden alle voorwerpen zelf een magneet.

Bestudeer de afbeelding van een bloempot en een onderzetter.

a Welke uitspraak is correct?

1 De pot bevat een magneet, de onderzetter niet.

2 De onderzetter bevat een magneet, de pot niet.

3 Zowel de pot als de onderzetter bevat een magneet.

b Hoe komt het dat de pot kan zweven op een vaste plek?

Je hebt drie ijzeren staven, waarvan er twee gemagnetiseerd zijn.

Hoe kun je erachter komen welke staven gemagnetiseerd zijn?

Je zet een ijzeren latje horizontaal op een spil, zodat het kan roteren in een verticaal vlak. Naast het latje houd je een staafmagneet, zoals op de afbeelding. Welke uitspraak is correct?

a Het latje keert zich verticaal en krijgt onderaan een zuidpool.

b Het latje blijft horizontaal en krijgt rechts een zuidpool.

c Het latje keert zich verticaal en krijgt onderaan een noordpool.

d Het latje blijft horizontaal en krijgt rechts een noordpool.

Bestudeer het gedrag van ijzervijlsel en een kompasnaald bij verschillende oriëntaties van twee magneten.

3 a Bij welke kompasoriëntatie hoort het ijzervijlselpatroon uit situatie 1?

b Bepaal voor elke situatie alle mogelijke oriëntaties van de magneetpolen X en Y.

AAN DE SLAG

Welke kompasnaalden geven (ongeveer) de juiste richting aan?

C

Bestudeer de afbeeldingen.

a Teken de afbeeldingen over.

b Teken een klein kompasnaaldje in de aangeduide punten.

©VANIN

▲Het bovenaanzicht van een staafmagneet

▲Het vooraanzicht van een staafmagneet

Vier kompasnaalden bevinden zich rond een rechte stroomvoerende geleider die loodrecht op het vlak van het papier staat.

Gaat de stroom in het blad papier of komt ze eruit?

▲Het bovenaanzicht van een hoefijzermagneet

Teken de magnetische veldlijnen:

a rond een rechte geleider waarbij de stroom uit het blad naar je toe komt;

b in en rond een doorstroomde spoel met een zelfgekozen stroomzin;

c in en rond een doorstroomde lus waarvan de as evenwijdig is met die van de spoel, maar met een tegengestelde stroomzin.

Vul de uitspraken aan met ‘altijd’, ‘soms’ of ‘nooit’.

a Het magnetisch veldlijnenpatroon is gelijk aan dat van een staafmagneet.

b Magnetische veldlijnen lopen door in de magneet.

c Een kompasnaald oriënteert zich tegengesteld aan een veldlijn.

d In de buurt van een stroomvoerende geleider is er een magnetisch veld.

e Een stroomvoerende geleider die een magnetisch veld veroorzaakt, is gemaakt uit ferromagnetisch materiaal.

Bestudeer de magnetische veldlijnenpatronen in de verschillende situaties.

REEKS

Je schuift drie identieke ringvormige magneten over een staafje. Daarbij kunnen de magneten de drie posities aannemen die weergegeven zijn op de afbeelding.

©VANIN

Bepaal de polen van de magneten in de verschillende situaties. De noordpool van de onderste magneet zit onderaan.

a Rangschik voor elke situatie de sterkte van het magneetveld op de verschillende posities van klein naar groot.

b Geef de posities met een homogeen veld.

c Benoem de magnetische polen (aangeduid met X en Y) in situatie 1 en 2.

d Bepaal de stroomzin in situatie 3.

Een kompas bevindt zich vlak boven een horizontale rechte geleider. Als Tom de spanningsbron inschakelt, zodat er plots stroom door de geleider loopt, beweegt de kompasnaald niet. Zelfs als Tom even tegen het kompas tikt, verandert de naald niet van richting. Hoe kan dat?

a De geleider loopt evenwijdig met de kompasnaald en de stroom loopt naar het noorden.

b De geleider loopt evenwijdig met de kompasnaald en de stroom loopt naar het zuiden.

c De geleider staat loodrecht op de kompasnaald en de stroom loopt naar het westen.

d De geleider staat loodrecht op de kompasnaald en de stroom loopt naar het oosten.

Teken de afbeelding over.

Teken enkele veldlijnen in de spoel.

Duid hun zin aan.

AAN DE SLAG

Als je de schakelaar sluit, wijst de kompasnaald naar links.

Teken op een apart blad de bron met de negatieve en positieve pool.

Naast een spoel hang je twee staafmagneten op. Wat gebeurt er als je de schakelaar sluit?

Z N

a Beide magneten worden aangetrokken door de spoel.

b Beide magneten worden afgestoten door de spoel.

c De linkse magneet wordt aangetrokken, de rechtse afgestoten.

d De linkse magneet wordt afgestoten, de rechtse aangetrokken.

Na het productieproces liggen kompasnaalden dicht bij elkaar.

Hoe bewaar je de naalden het best? Verklaar.

Permanente magneten bestaan enkel in vaste vorm.

a Verklaar waarom.

b Hoe kan magneetverf dan toch bestaan?

Als alternatief voor grijpkranen gebruikt men soms elektromagneten. Bekijk de video.

elektromagneet verplaatst ijzeren platen.

a Kun je daarmee alle metalen optillen? Verklaar.

b Hoe werkt een hefmagneet?

c Teken de weekijzeren kern van de elektromagneet (die aan of uit staat) en het (opgetilde) voorwerp met … 1 de magnetische polen; 2 de oriëntatie van de weissgebieden.

©VANIN

elektromagneet

ijzeren plaat

▲Een

REEKS

Vier vrienden bestuderen tijdens de voorbereiding van een trektocht de werking van hun kompas. Wie heeft gelijk? Verklaar.

Met kompasnaald 3 hoeven we geen rekening te houden. Dat is een fout op de afbeelding.

Een kompasnaald wijst altijd naar het geografische noorden.

Een kompasnaald wijst nergens precies naar het geografische noorden.

Bestudeer de werking van een zekering en een aardlekschakelaar.

a Formuleer het doel van zekeringen en van een aardlekschakelaar. (Je leerde dat vorig schooljaar.)

b Beschrijf hoe men daarvoor elektromagneten kan gebruiken. (Raadpleeg eventueel het internet.)

 Meer oefenen? Ga naar .

Rond de evenaar

een kompas goed betrouwbaar om ons te oriënteren.

HOOFDSTUKSYNTHESE

• Magnetisme ontstaat ten gevolge van een geordende beweging van ladingen.

• Een magnetisch veld is een gebied waar de invloed van magnetische (veld)kracht werkzaam is.

Permanente magneten zijn materialen die hun magnetische eigenschappen continu vertonen door de geordende beweging van elektronen.

©VANIN

Ferromagnetische materialen (ijzer, kobalt, nikkel of hun legeringen) zijn materialen met geordende weissgebieden, die blijven bestaan.

Elektromagneten werken enkel als er een elektrische stroom loopt.

Stroomvoerende geleiders wekken een magnetisch veld op.

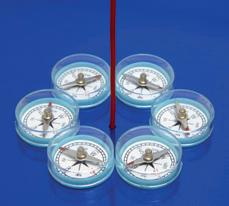
Toepassing: een stroomvoerende spoel rond ferromagnetisch materiaal waarvan geordende weissgebieden verdwijnen als je de stroom afzet. Polen bepaal je door de stroomzin via de rechterhandregel.

Aardmagnetisme: de magnetische noordpool (zuidpool) ligt in de buurt van de geografische zuidpool (noordpool).

• Magneten trekken elkaar aan of stoten elkaar af: dat wordt bepaald door de polen

• Magneten trekken ferromagnetische stoffen aan: dat heet magnetische influentie

HOOFDSTUK

Magnetische veldsterkte en magnetische kracht

©VANIN

Magneten kunnen elkaar aantrekken of afstoten. Dat lijkt eenvoudig, maar hoe ontstaat die bijzondere wisselwerking?

Hoe komt het dat permanente magneten en elektromagneten elkaar beïnvloeden? Hoe kun je, zoals bij andere veldkrachten (de coulombkracht en de gravitatiekracht), de veldsterkte definiëren? Welke toepassingen kunnen daar uit voortvloeien?

In dit hoofdstuk bestudeer je in detail de elektromagnetische krachtwerking, definieer je de magnetische veldsterkte en bestudeer je de eigenschappen ervan. Met die kennis leer je om de invloeden die je eerder bestudeerde, grondig te verklaren. Je maakt ook kennis met enkele praktische toepassingen.

LEERDOELEN

M het magnetisch veld beschrijven met de magnetische veldsterkte

M de magnetische kracht op een stroomvoerende geleider en op bewegende ladingen beschrijven, tekenen en berekenen

M de grootte van de magnetische veldsterkte bij elektromagneten berekenen

M de waargenomen elektromagnetische krachtwerking verklaren voor verschillende situaties

M enkele toepassingen van de elektromagnetische kracht geven, toelichten en beschrijven

1 Wat is magnetische veldsterkte?

In de buurt van een magneet ondervindt een kompasnaald een kracht, waardoor ze een bepaalde oriëntatie aanneemt.

Een kompasnaald geeft je informatie over de richting en de zin van het magnetisch veld van de aarde.

De zuidpool van een kompas wijst naar de noordpool van een nabije magneet.

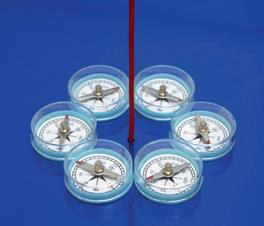
IRondom een stroomvoerende geleider oriënteren kompasnaalden zich in een cirkel.

De invloed van de magnetische kracht op een magneet of ferromagnetisch materiaal hangt af van de eigenschappen van het magnetisch veld in dat punt. Die eigenschappen kun je beschrijven met een vectoriële grootheid, de magnetische veldsterkte B

• Aangrijpingspunt: de veldvector B grijpt aan in een gekozen punt in het magnetisch veld.

• Richting: de veldvector B raakt in elk punt aan de veldlijnen.

• Zin: de veldvector B wijst in de zin van de veldlijnen (= dezelfde zin waarnaar de noordpool van een klein magneetje in dat veld wijst).

• Grootte: de grootte B beschrijft de sterkte van het veld, die je kwalitatief kunt afleiden uit de veldlijnendichtheid

©VANIN

▲ Afb. 169 Magnetische veldsterktevectoren in de

Afb. 170 Magnetische veldsterktevectoren in de buurt van een elektromagneet (3D- voorstelling en bovenaanzicht)

Het is moeilijk om een vectorpijl loodrecht op het vlak van het blad te tekenen. Daarom gebruik je een voorstelling die gebaseerd is op een dartspijltje.

Als een dartspijltje loodrecht in het blad prikt, zie je een kruisje. Daarom stel je een vector, veldlijn of stroomsterkte die loodrecht in het blad prikt, voor met een kruisje.

▲ Afb. 171 Een dartspijltje heeft vooraan een punt. De veren achteraan vormen een kruis.

Als een dartspijltje loodrecht uit het blad komt, zie je een puntje. Daarom stel je een vector, veldlijn of stroomsterkte die loodrecht uit het blad komt, voor met een puntje.

CONCEPTVRAAG

Teken de magnetische veldsterktevectoren tussen de benen van een hoefijzermagneet.

buurt van een staafmagneet

TIP

De grootte van de magnetische veldsterkte druk je uit in tesla

Je kunt ze opmeten met een teslameter.

Een teslameter

GROOTHEID MET SYMBOOL

EENHEID MET SYMBOOL magnetische veldsterkte B tesla [B] = T

De tesla is een grote eenheid. Meestal moet je voorvoegsels of hulpeenheden toevoegen.

VOORBEELD DE MAGNETISCHE VELDSTERKTE VAN VERSCHILLENDE MAGNETEN

Zodra er bewegende ladingen zijn, ontstaat er een magnetisch veld. Op afbeelding 173 zie je enkele voorbeelden.

hersenen

aarde

▲ Afb. 173 Magneten gerangschikt volgens toenemende magnetische veldsterkte

Op leer je meer over waar en hoe men magneten gebruikt in de wetenschap en de technologie, zoals in de geneeskunde (Magnetic Resonance Imaging) of in onderzoek naar kernfusie (supergeleidende magneet).

magneet

= 30 T

©VANIN

De magnetische veldsterkte B is een vectoriële grootheid die de eigenschappen van een magnetisch veld rondom een permanente magneet of een elektromagneet beschrijft.

• De richting en de zin vind je met een kompasnaald: rakend aan en in de zin van de veldlijn.

• De grootte is een maat voor de sterkte van het magnetisch veld.

GROOTHEID MET SYMBOOL

EENHEID MET SYMBOOL magnetische veldsterkte B tesla [B] = T

▲ Afb. 172

TIP

2 Hoe groot is de magnetische veldsterkte bij een elektromagneet?

2.1 Algemeen

DEMO

Welke factoren beïnvloeden de magnetische veldsterkte bij een elektromagneet?

©VANIN

Bekijk op de schematische voorstelling van de verschillende metingen.

1 Je leerkracht stelt verschillende elektromagneten (een stroomvoerende geleider, lus en spoel) op.

2 Welke factoren beïnvloeden de magnetische veldsterkte volgens jou?

Bespreek met je buur een onderzoeksaanpak en test samen met je leerkracht uit.

3 Formuleer een antwoord op de onderzoeksvraag.

2.2 De magnetische veldsterkte bij een stroomvoerende spoel

Spoelen vind je terug in veel toestellen. Elke toepassing vereist een specifieke magnetische veldsterkte.

In de motortjes van een ventilator worden spoelen gebruikt om kracht op te wekken.

Spoelen met verschillende windingen en middenstoffen worden gebruikt als elektronische component.

Deze industriële elektromagneet bestaat uit veel windingen (van koperdraad) rond een weekijzeren kern.

Uit het veldlijnenpatroon blijkt dat er binnen in de spoel een homogeen magnetisch veld ontstaat.

Voor dat homogene veld kun je de invloed van de stroomsterkte, de lengte van de spoel, het aantal windingen en de middenstof binnen de spoel onderzoeken.

Uit de experimenten volgt:

De magnetische veldsterkte neemt recht evenredig toe met een toenemende stroomsterkte.

B ~ I

De magnetische veldsterkte neemt recht evenredig toe met het aantal windingen:

B ~ N

De magnetische veldsterkte neemt omgekeerd evenredig af met de lengte:

B ~ 1 ℓ

De evenredigheidsconstante kun je berekenen uit kwantitatieve metingen. Experimenten tonen aan dat deze constante afhankelijk is van de middenstof. Je noemt deze constante de magnetische permeabiliteit, met als symbool μ

De grootte van de magnetische veldsterkte B voor een stroomsterkte I in een spoel met lengte ℓ en N windingen is gelijk aan:

B = μ ∙ N · I ℓ = μ · n · I

Daarbij is n = N ℓ de windingsdichtheid. Die geeft het aantal windingen per afstandseenheid weer, uitgedrukt in m–1

©VANIN

De magnetische permeabiliteit μ is een stofeigenschap. De magnetische permeabiliteit van het vacuüm is nauwkeurig bepaald en wordt als volgt genoteerd: μ0 = 4 · π · 10–7 T · m A

Alle andere middenstoffen hebben een magnetische permeabiliteit die kan uitgedrukt worden in verhouding tot µ0

In tabellen geeft men vaak de relatieve permeabiliteit

Het is een getal zonder eenheid.

In tabel 1 zie je enkele voorbeelden.

NIET-FERROMAGNETISCHE MATERIALEN

FERROMAGNETISCHE MATERIALEN

water 0,999 992ferriet (nikkel zink) 16-640 koper 0,999 994nikkel 100-600 waterstof 1,000 000 0 kobalt 400 lucht 1,000 000 37ferriet (mangaan zink) 640 (of meer) hout 1,000 000 43 staal 1 000-5 000

aluminium 1,000 022ijzer (99,8 % / 99,95 % zuiver)5 000/200 000 platina 1,000 265permalloy 100 000

neodymium magneet1,05

▲ Tabel 1 De relatieve permeabiliteit van enkele materialen

VOORBEELD PERMALLOYMAGNETEN

Voor ferromagnetische materialen is μr heel groot. Dat betekent dat ze heel grote magnetische velden kunnen opwekken.

Een hefmagneet kan tot 6 000 kg optillen. Daarvoor wikkelt men een spoel rond permalloy (een legering van neodymium, ijzer en boor: Nd2Fe14B). De magnetische veldsterkte is 1,5 T.

‘Permeabiliteit’ betekent ‘doorlaatbaarheid’ of ‘doordringbaarheid’. Het symbool μ is de Griekse letter mu. Ga de eenheid van magnetische permeabiliteit na.

CONCEPTVRAAG

VERDIEPING

Stoffen worden ingedeeld op basis van hun relatieve permeabiliteit (μr < 1, μr > 1 en μr >> 1).

Ferromagnetische materialen (legeringen die Fe, Ni of Co bevatten) hebben een heel grote relatieve permeabiliteit, waardoor je ze makkelijk kunt magnetiseren. Je leert er meer over op .

CONCEPTVRAGEN

1 Hoe groot zou de magnetische veldsterkte zijn als je de permalloy in de spoel van de hefmagneet …

• verwijdert?

• vervangt door staal?

2 Hoe kun je de sterkte van een elektromagneet (in toepassingen) het makkelijkst regelen (onder andere aan- en uitzetten)? Verklaar.

De grootte van de magnetische veldsterkte B voor een stroomsterkte I in een spoel met lengte ℓ en N windingen is gelijk aan:

B = μ ∙ N · I ℓ = μ · n · I

©VANIN

GROOTHEID MET SYMBOOL EENHEID

magnetische permeabiliteit µ T · m A

relatieve permeabiliteit μr = μ μ0 dimensieloos

windingsdichtheid n = N ℓ 1 m = m–1

2.3 De magnetische veldsterkte rondom een rechte stroomvoerende geleider

Spoelen zijn opgerolde geleiders. Je kunt de werking van een spoel beter begrijpen als je het magnetisch veld rond een rechte geleider bestudeert. Daarvoor onderzoek je de invloed van de stroomsterkte en de afstand tot de geleider.

Uit de experimenten volgt:

De magnetische veldsterkte neemt recht evenredig toe met een toenemende stroomsterkte.

B ~ I

De magnetische veldsterkte neemt omgekeerd evenredig af met een toenemende afstand.

B ~ 1 r B ~ I r of B = constante · I r

©VANIN

TIP

Bekijk op de schematische voorstelling van de verschillende metingen.

De evenredigheidsconstante kun je berekenen uit kwantitatieve metingen. Je schrijft ze meestal als μ 2 · π . De grootte van de magnetische veldsterkte B voor een stroomsterkte I op een afstand r van de rechte geleider is dan gelijk aan:

B = μ 2 · π ∙ I r

Daarbij is µ de magnetische permeabiliteit

Als er meerdere magneetvelden zijn, wordt de totale magnetische veldsterkte in een punt bepaald door de vectoriële som van de magnetische veldsterktes: B = B res = B 1 + B2 + B3 + …

CONCEPTVRAGEN

1 Bereken μ0 2 · π

2 Een rechte geleider bevindt zich in water, lucht en een vacuüm.

Bepaal µ en vergelijk met µ0.

3 Een punt P bevindt zich in het midden tussen twee stroomvoerende geleiders (met dezelfde stroomsterkte I en gelijke of tegengestelde stroomzin) in lucht op een afstand d van elkaar.

a Teken de aparte en totale magnetische veldsterktes.

b Geef de uitdrukking in symbolen voor de totale magnetische veldsterkte.

De factor 2 · π wijst erop dat de veldlijnen cirkelvormig zijn. In de noemer van de breuk herken je de omtrek van een cirkel: O = 2 · π · r.

VOORBEELD MAGNETISCHE VELDSTERKTE IN EEN LUS EN IN EEN SPOEL

Een lus is een gekromde geleider. Bij een lus kun je elk stukje van de geleider beschouwen als een rechte geleider. In het midden beïnvloeden de velden van de verschillende geleiders elkaar. De resulterende magnetische veldsterkte wordt bepaald door de vectoriële som van de magnetische veldsterktes van elk stukje. Uit metingen en berekeningen blijkt dat je voor het midden van een lus met straal R de veldsterkte als volgt kunt berekenen:

B = μ 2 I R

©VANIN

▲ Afb. 178 Het magnetisch veld in een lus

In een spoel zijn er heel veel lussen naast elkaar. Het magnetisch veld binnen in een spoel is daardoor erg sterk, omdat het de som is van de magnetische velden van alle stukjes geleider die deel uitmaken van de spoel. Hoe dichter de lussen bij elkaar liggen, hoe sterker het magnetisch veld. De windingsdichtheid n bepaalt de magnetische veldsterkte in een spoel: B = μ · n · I.

CONCEPTVRAAG

Op afbeelding 178 is het magneetveld binnen de lus als een homogeen veld voorgesteld. Leg uit waarom dat slechts een modelvoorstelling is.

De grootte van de magnetische veldsterkte B voor een stroomsterkte I op een afstand r van de geleider in een middenstof met magnetische permeabiliteit μ is gelijk aan:

B = μ 2 · π I r

3 Hoe groot is de magnetische kracht op bewegende ladingen in een magnetisch veld?

3.1 Kracht op een stroomvoerende geleider

A Richting en zin van de laplacekracht

DEMO

Herbekijk de demoproef uit hoofdstuk 5 op p. 115.

Een stroomvoerende geleider kan in een magnetisch veld een magnetische kracht ondervinden. Je noemt die kracht de laplacekracht, met als symbool FL. Met experimenten kun je de invloed van de stroomsterkte I en de magnetische veldsterkte B op de richting en de zin onderzoeken.

©VANIN

▲ Afb. 179 De richting en de zin van de laplacekracht op een stroomvoerende geleider in een magnetisch veld

Uit experimenten volgt:

• Als de stroom en de magnetische veldsterkte dezelfde richting hebben, is er geen laplacekracht.

• Als de stroom en de magnetische veldsterkte een verschillende richting hebben, is er een laplacekracht FL met deze kenmerken:

aangrijpingspunt: een punt op de stroomvoerende geleider (dat meestal in het midden van de geleider wordt getekend); – richting: loodrecht op de stroomsterkte I en op de magnetische veldsterkte B; – zin: bepaald door de zin van de stroomsterkte I en van de magnetische veldsterkte B

De magnetische kracht wordt vaak genoemd naar degene die de onderzoeken uitvoerde voor een specifieke opstelling. De laplacekracht is genoemd naar de Franse wiskundige en astronoom PierreSimon Laplace, die de magnetische kracht op een stroomvoerende geleider onderzocht.

▲ Afb. 180 Met de (derde) rechterhandregel bepaal je de zin van de laplacekracht: als de stroomsterkte volgens je wijsvinger gericht is en de magnetische veldsterkte volgens je middelvinger (tot je pink), dan is de laplacekracht gericht volgens je duim.

CONCEPTVRAGEN

▲ Afb. 181 Schematische voorstelling van de kracht op een geleider in een homogeen magnetisch veld dat loodrecht op de geleider staat en uit het blad komt

1 Bepaal de richting en de zin van de laplacekrachten op afbeelding 179. Stel ze schematisch voor zoals op afbeelding 181.

2 Wat gebeurt er met de geleider als de laplacekracht erop inwerkt? Verklaar de nieuwe evenwichtssituatie.

B Grootte van de laplacekracht

Uit experimenten blijkt dat de grootte van de laplacekracht op een stroomvoerende geleider wordt beïnvloed door vier factoren:

De grootte van de laplacekracht neemt recht evenredig toe met een toenemende magnetische veldsterkte.

FL ~ B

De grootte van de laplacekracht neemt recht evenredig toe met een toenemende stroomsterkte.

FL ~ I

De grootte van de laplacekracht neemt recht evenredig toe met de lengte van de geleider.

FL ~ ℓ

De grootte van de laplacekracht hangt af van de hoek α tussen het magnetisch veld en de stroom.

©VANIN

L ~ B · I · ℓ of FL = constante · B

FL = B · I · ℓ · sin α nauwkeurig onderzoek

sin α

Uit de uitdrukking FL = B · I · ℓ · sin α blijkt:

• Als de magnetische veldsterkte loodrecht op de geleider met lengte ℓ staat (α = 90°), dan: FL = B · I · ℓ · sin 90°= B · I · ℓ.

• Als de magnetische veldsterkte een willekeurige oriëntatie heeft ten opzichte van de geleider met lengte ℓ (B maakt een hoek α met de geleider), dan: FL = B · I · ℓ · sin α. Dat betekent dat enkel de loodrechte component B een invloed heeft op de laplacekracht, want B = B · sin α, dus FL = B · I · ℓ = B · sin α · I · ℓ = B · I · ℓ · sin α

▲ Afb. 182 De loodrechte component bepaalt de grootte van de laplacekracht.

CONCEPTVRAAG

Toon aan dat de uitdrukking FL = B · I · ℓ · sin α ook geldt voor een magnetische veldsterkte evenwijdig met de geleider.

VOORBEELDVRAAGSTUK

Door een hoogspanningslijn met een lengte van 50 m vloeit een stroom van 30 A. Bereken:

1 de laplacekracht als de hoogspanningslijn … a loodrecht op het aardmagnetisch veld staat; b evenwijdig loopt met het aardmagnetisch veld; 2 de hoek waarbij de laplacekracht 50 mN is.

Gegeven:

• ℓ = 50 m

• I = 30 A

• Baarde = 5,0 · 10–5 T

• α = 90°

• α’ = 0°

• FL = 50 mN

Gevraagd: 1 FL en FL’ = ?

2 α = ?

Oplossing: 1 De grootte van de laplacekracht kun je berekenen met deze formule:

Dus:

= 0 N

2 Als je de basisformule omvormt, krijg je: sin α = FL

De hoek α vind je als volgt: sin–1(0,67) = 42°.

Reflectie: Welke invloed heeft de hoek op de grootte van de laplacekracht? De laplacekracht is maximaal bij loodrechte stand, nul bij evenwijdige stand en een tussenliggende waarde bij de tussenliggende hoek.

CONCEPTVRAAG

Kun je de richting en de zin bepalen van de berekende laplacekrachten uit het voorbeeldvraagstuk? Verklaar.

▲ Afb. 183 Een hoogspanningslijn

demovideo: afbuiging kathodestraalbuis

C Definitie tesla

Als de geleider loodrecht op het magnetisch veld staat (α = 90°), dan is de laplacekracht als volgt gedefinieerd:

FL = B · I · ℓ

Daaruit volgt: B = FL I · ℓ

Aan de hand van die formule kun je de afgeleide eenheid voor de magnetische veldsterkte definiëren. Als er in een magneetveld op een geleider met een lengte van 1 meter waardoor een stroomsterkte van 1 ampère vloeit, een laplacekracht van 1 newton werkt, dan is de magnetische veldsterkte daar 1 tesla:

©VANIN

In een kathodestraalbuis produceert een elektronenkanon (negatieve pool, kathode) elektronen die naar de positieve pool (anode) bewegen. De elektronenbundels worden gefocust en botsen tegen een fluorescerend scherm, waardoor hun baan zichtbaar wordt.

De lorentzkracht werd genoemd naar de Nederlandse natuurkundige Hendrik Lorentz. Hij won de Nobelprijs in 1902.

1 T = 1 N 1 m · 1 A = 1 N m · A

Een stroomvoerende geleider ondervindt in een magnetisch veld een laplacekracht FL met deze kenmerken:

• aangrijpingspunt: op de geleider;

• richting: loodrecht op de stroomrichting (= de geleider) en op het magnetisch veld;

• zin: te bepalen met de derde rechterhandregel;

• grootte: FL = B · I · ℓ = B · I · ℓ · sin α, waarbij B de grootte van de magnetische veldsterkte is, I de stroomsterkte, α de hoek tussen B en de geleider (B = B · sin α), en ℓ de lengte van de geleider.

De uitdrukking voor de laplacekracht leidt tot een definitie van de eenheid tesla.

GROOTHEID MET SYMBOOL EENHEID MET SYMBOOL magnetische veldsterkte B tesla 1 T = 1 N m · A

3.2 Kracht op bewegende ladingen

DEMO

Welke invloed heeft een magnetisch veld op de bewegende elektronen?

1 Je leerkracht stelt een kathodestraalbuis op en brengt een permanente magneet in de buurt.

2 Wat zal er volgens jou gebeuren?

Bespreek met je buur en test samen met je leerkracht uit.

3 Formuleer een antwoord op de onderzoeksvraag.

Afb. 184 Een kathodestraalbuis

Elektrische stroom bestaat uit bewegende ladingen. Dat wil zeggen dat de laplacekracht op die bewegende ladingen inwerkt. Omdat de ladingen (vrije elektronen) in een stroomvoerende geleider netto dezelfde richting en zin hebben, ondervinden ze allemaal een magnetische kracht in dezelfde richting en zin. Daardoor wordt de draad in haar geheel naar dezelfde kant getrokken. De magnetische kracht die op één enkele bewegende lading inwerkt, noem je de lorentzkracht Het symbool voor die kracht is ook FL.

De elektrische stroom in een geleider ontstaat door elektronen die met een snelheid v bewegen. De richting van een bewegende lading is de richting van de snelheidsvector van de lading. De stroomzin bij een stroomvoerende geleider is de conventionele stroomzin, die van de pluspool naar de minpool loopt. Die zin is tegengesteld aan de beweging van de elektronen.

Dat betekent dat je met de rechterhandregel de richting en de zin vindt voor een positieve lading, waarbij je I vervangt door de richting en de zin van v, de snelheid van de lading. Voor een negatieve lading is de conventionele stroomzin I tegengesteld aan de zin van de snelheid v

©VANIN

De kenmerken van de lorentzkracht kun je afleiden uit de kenmerken van de laplacekracht:

• Het aangrijpingspunt van de lorentzkracht is de lading q.

• De richting van de lorentzkracht op een bewegende lading is loodrecht op het magnetisch veld en de snelheidsvector.

• De zin wordt bepaald door de zin van de snelheidsvector en het ladingsteken. Voor een positieve lading heeft de snelheidsvector dezelfde zin als de conventionele stroomzin. Voor een negatieve lading is de zin tegengesteld. Net als bij de laplacekracht kun je de zin van de lorentzkracht bepalen met de derde rechterhandregel.

• De grootte van de lorentzkracht kun je afleiden uit de laplacekracht Ze wordt gegeven door:

FL = B · I · ℓ (uitdrukking laplacekracht)

= B · |q| ∆t · ℓ (definitie stroomsterkte)

= B · |q| · ℓ ∆t

= B · |q| · v (definitie snelheid)

= B · |q| · v · sin α

De kracht die de bewegende lading ondervindt, staat loodrecht op de beweging.

Dat veroorzaakt een afbuiging, die bepaald wordt door de zin van de lorentzkracht. De snelheidsgrootte verandert niet.

CONCEPTVRAAG

B v v v v q q = 0 q > 0 q < 0

▲ Afb. 185 De invloed van het magnetisch veld op de baan van geladen deeltjes

Teken de baan en vier snelheidsvectoren van een proton dat beweegt in een homogeen magnetisch veld dat uit het blad gericht is (waarbij α = 90° (v B )).

VERDIEPING

De natuurkundige Lorentz formuleerde een vectoriële uitdrukking voor de totale kracht op een lading in een elektrisch veld en een magnetisch veld. Ben je geïnteresseerd in deze uitdrukking en in de diepere wiskunde achter de laplacekracht en de lorentzkracht? Ga dan naar . Daar leer je hoe je het vectoriële product kunt gebruiken als wiskundige tool om de richting en de zin van de laplacekracht en de lorentzkracht weer te geven.

VOORBEELDVRAAGSTUK

De eerste beeldschermen (ontworpen in 1897) waren beeldbuizen die kathodestralen produceerden. Het beeld op een beeldbuis ontstaat als je een kathodestraal (= elektronen) op de juiste plaats laat terechtkomen. Daarvoor kun je een verticaal magnetisch veld (met Y-platen) en een horizontaal magnetisch veld (met X-platen) aanleggen. Als je een magnetisch veld van 1,0 µT aanlegt (op een van de platen), buigen de elektronen (v = 1,0 · 108 m s ) verticaal af naar punt A, zoals voorgesteld op afbeelding 187.

elektronenkanon

anode Y-plaat X-plaat elektronenbundel vacuüm fluorescerend scherm A

1 Op welke plaat moet je een magnetisch veld aanleggen om de bundel af te buigen?

2 In welke zin moet je een magnetisch veld aanleggen om de bundel af te buigen?

3 Hoe groot is de lorentzkracht op een elektron?

Gegeven:

• B = 1,0 µT

• v = 1,0 · 108 m s

• q = –1,60 · 10–19 C

Gevraagd: 1 de plaat waarop het veld is aangelegd

2 de zin waarin het veld is aangelegd

3 FL = ?

Oplossing: 1 De snelheid v is horizontaal naar rechts gericht. De kracht moet (aanvankelijk) verticaal omlaag gericht zijn. Het veld is dus aangelegd op de X-plaat.

2 Met de derde rechterhandregel (voor een negatieve lading) vind je dat het magneetveld in het blad moet zijn gericht. Het moet dus loodrecht naar de achterste X-plaat gericht zijn.

©VANIN

F L

F L v ▲ Afb. 188 Met de (derde) rechterhandregel bepaal je de zin van de lorentzkracht.

▲ Afb. 189 Schematische voorstelling van de kracht op een elektron in een homogeen magneetveld dat loodrecht op de geleider staat en in het blad gaat

3 De snelheid staat loodrecht op het magneetveld. Je kunt de lorentzkracht dus als volgt berekenen: FL = B · |q| · v = B · |q| · v = 1,0 · 10–6 T · 1,60 · 10–19 C · 1,0 · 108 m s = 1,6 · 10–17 N

Reflectie: Bestudeer de grootte van de kracht. Wat stel je vast? Verklaar waarom het elektron toch zichtbaar afbuigt.

De lorentzkracht is heel klein, maar het effect op de beweging van het elektron is wel merkbaar, omdat de massa zo klein is.

▲ Afb. 186 Kathodestralen vormen het beeld op het scherm.

▲ Afb. 187 De bouw van een beeldscherm

Een lading q met snelheid v ondervindt in een magnetisch veld een lorentzkracht FL met deze kenmerken:

• aangrijpingspunt: op de lading;

• richting: loodrecht op de snelheidsvector en op het magnetisch veld;

• zin: te bepalen met de derde rechterhandregel;

• grootte: FL = B · |q| · v = B · |q| · v · sin α, waarbij B de grootte van de magnetische veldsterkte is, v de snelheidsgrootte en α de hoek tussen B en v

Door de inwerkende kracht verandert de lading van snelheidsrichting.

©VANIN

De kathodestraal leidde tot de ontdekking van het elektron door Thomson (1897). Je leert er meer over in de video.

4 Hoe kun je de krachtwerking tussen magneten verklaren?

4.1 Kracht tussen elektromagneten

DEMO

Wat gebeurt er als je twee stroomvoerende geleiders in elkaars buurt brengt?

1 Je leerkracht brengt twee stroomvoerende geleiders die vrij kunnen bewegen in elkaars buurt. De stroomsterkte en de stroomzin kunnen worden veranderd.

2 Wat denk je dat er zal gebeuren in verschillende situaties? Bespreek met je buur en test uit.

3 Probeer een verklaring te formuleren voor je waarneming bij verschillende situaties.

4 Formuleer een antwoord op de onderzoeksvraag.

Uit experimenten blijkt dat twee stroomvoerende geleiders (= elektromagneten) in elkaars buurt, die elkaar niet loodrecht kruisen, een kracht uitoefenen op elkaar. Je kunt die krachtwerking verklaren aan de hand van de magnetische velden die opgewekt worden door de elektrische stroom door de geleiders. Als een stroomvoerende geleider zich in de buurt van een andere geleider bevindt, dan ondervindt die de laplacekracht. De geleider bevindt zich dan immers in het magnetisch veld dat opgewekt wordt door de elektrische stroom in de andere geleider. Volgens het actie-reactieprincipe (derde wet van Newton) oefent de tweede geleider een even grote, maar tegengestelde kracht uit op de eerste geleider.

WEETJE

VOORBEELD

Als je twee beweegbare geleiders met dezelfde stroomzin in elkaars buurt plaatst, trekken ze elkaar aan. Je kunt dat verklaren met de eigenschappen van de laplacekracht.

De veldlijnen rond beide rechte geleiders zijn cirkels, loodrecht op de geleider en met de geleider als middelpunt. De magnetische veldsterktevector raakt in elk punt aan de veldlijn door dat punt.

©VANIN

▲ Afb. 190 Elke stroomvoerende geleider veroorzaakt een magnetisch veld in zijn omgeving.

De stroom I 1 in de eerste geleider veroorzaakt in het punt P op een afstand d van de geleider een magnetische veldsterkte B1. Als de tweede geleider zich in dat punt bevindt, werkt er een laplacekracht FL12 op de tweede geleider.

Met de derde rechterhandregel vind je de richting en de zin van die kracht. Als de stroom I 1 en I2 dezelfde zin hebben, is er aantrekking. Omgekeerd wekt de tweede geleider een magnetische veldsterkte B2 op op de plek van de eerste geleider waardoor die een laplacekracht FL21 ondervindt, de reactiekracht van FL12.

CONCEPTVRAGEN

▲ Afb. 191 De krachtwerking tussen twee stroomvoerende geleiders

1 Verklaar de kenmerken van FL21 op de eerste geleider.

2 Wat gebeurt er als de stroomzin in een van de geleiders of in beide geleiders verandert? Verklaar.

3 Wat gebeurt er als de stroomsterkte in een van de geleiders of in beide geleiders verandert?

Toon aan.

VOORBEELDVRAAGSTUK

In het elektriciteitssnoer van een laptop zijn twee geleiders tegen elkaar bevestigd. Ze bevinden zich op 0,50 cm van elkaar. Teken en bereken de kracht op de twee geleiders in een snoer van 1,00 m, als er een stroom van 4,75 A door het snoer van je laptop loopt. In de laptop is de stroom verschillend in functie van de weerstanden in de diverse kringen.

Gegeven: • d = 0,50 cm

• ℓ = 1,00 m

• I = 4,75 A

Gevraagd: • FL12 = ?

• FL21 = ?

Oplossing: De twee geleiders vormen een gesloten stroomkring. De stroomzin in beide geleiders is dus tegengesteld. Met de rechterhandregel vind je dat de laplacekracht afstotend is.

©VANIN

▲ Afb. 192 De laplacekracht tussen twee geleiders met een tegengestelde stroomzin

De grootte van de laplacekracht FL21 op een stuk van de eerste geleider met lengte ℓ1 is het gevolg van de stroomsterkte I 1 en het magnetisch veld B2 (veroorzaakt door de tweede geleider met stroomsterkte I2 op een afstand d).

Je kunt de grootte FL21 als volgt berekenen:

De geleiders zijn even lang en de stroomsterkte is gelijk, dus de onderlinge krachtgrootte is gegeven door:

Op analoge wijze geldt:

Reflectie: • Hoe kun je FL12 sneller bepalen?

Uit de derde wet van Newton volgt: FL12 = FL21.

• Hoe komt het dat je de geleiders toch bij elkaar kunt houden met een (isolerend) omhulsel?

De uitgeoefende kracht is verwaarloosbaar klein.

VOORBEELD KRACHT TUSSEN TWEE STROOMVOERENDE LUSSEN

Als je twee beweegbare lussen met een tegengestelde stroomzin in elkaars buurt plaatst, stoten ze elkaar af. Dat kun je verklaren met de eigenschappen van de laplacekracht. Je kunt de gemarkeerde stukken van de lussen beschouwen als twee geleiders in elkaars buurt: er is afstoting als de lussen een tegengestelde stroomzin hebben. Dat geldt voor elk stukje van de geleider, waardoor de lussen elkaar afstoten.

Je kunt dat ook verklaren aan de hand van de polen die ontstaan door de stroomsterkte. Met de rechterhandregel kun je de zin van de veldlijnen en de polen van beide lussen bepalen. Daaruit blijkt dat gelijksoortige (zuid)polen naar elkaar toe zijn gericht: er is afstoting.

Afb. 193 De krachtwerking tussen twee stroomvoerende lussen

©VANIN

Afb. 194 De magnetische veldlijnen en de polen bij stroomvoerende lussen

CONCEPTVRAGEN

1 Verklaar hoe twee spoelen elkaar kunnen aantrekken of afstoten. Werk uit zoals bij de lus.

2 Schets het verloop van de grafieken die de onderlinge krachtgrootte weergeven in functie van … a beide stromen; b de lengte van de geleider; c de afstand tussen de geleiders.

Twee elektromagneten oefenen een magnetische kracht uit op elkaar: FL21 = –FL12. De stroomzin bepaalt of er aantrekking of afstoting is. De grootte kun je bepalen met de geziene formules voor de laplacekracht.

4.2 Kracht tussen permanente magneten

Uit experimenten (zie hoofdstuk 5, paragraaf 2) blijkt dat twee permanente magneten in elkaars buurt een kracht uitoefenen op elkaar. Je kunt die krachtwerking verklaren aan de hand van de magnetische velden die opgewekt worden door de bewegende ladingen binnen in de magneet. Wat je macroscopisch waarneemt, is dus een gevolg van de microscopische eigenschappen van magneten. Op atomair niveau bewegen de elektronen rond de kern en hebben ze een spin. De ordening binnen de weissgebieden van het ferromagnetisch materiaal zorgt ervoor dat de permanente magneet een merkbaar magnetisch veld opwekt. Als een tweede permanente magneet, eveneens met geordende kringstromen en elektronspins, zich in het magnetisch veld van de eerste magneet bevindt, werkt er op die magneet een magnetische kracht. Door het actie-reactieprincipe (derde wet van Newton) oefent de tweede magneet een even grote, maar tegengestelde kracht uit op de eerste magneet.

VOORBEELD KRACHT TUSSEN TWEE ZUIDPOLEN VAN STAAFMAGNETEN

Twee staafmagneten met de zuidpolen naar elkaar toe gericht stoten elkaar af. Dat kun je verklaren aan de hand van de microscopische structuur binnen de staafmagneet. In beide magneten zijn de weissgebieden geordend. Dat betekent dat de baanbeweging van de elektronen en de elektronspin geordend zijn. Je kunt de atomaire stroomzin die nodig is om het waargenomen dipoolveld te veroorzaken, vinden met de (eerste) rechterhandregel.

©VANIN

▲ Afb. 195 Microscopische verklaring voor de afstoting tussen gelijksoortige polen van een staafmagneet

Voor magneten met gelijksoortige polen die naar elkaar toe gericht zijn, is de atomaire stroomzin tegengesteld. Daardoor is de onderlinge magnetische kracht (net zoals bij elektromagneten) afstotend.

CONCEPTVRAGEN

1 Verklaar de aantrekking tussen twee staafmagneten.

2 Verklaar de aantrekking tussen een staafmagneet en een ijzeren voorwerp.

3 Verklaar de aantrekking tussen een staafmagneet en een stroomvoerende spoel.

Twee permanente magneten oefenen een magnetische kracht uit op elkaar: F21 = –F12 De zin van de kringstromen en de elektronspins binnen de magneet bepalen of er aantrekking of afstoting is.

Je kunt de krachtwerking tussen permanente magneten onderling, tussen elektromagneten onderling en tussen permanente magneten en elektromagneten altijd verklaren aan de hand van de laplacekracht of lorentzkracht.

N Z N Z

F I

• Bij een translatie maken alle punten van het voorwerp dezelfde beweging, het voorwerp verplaatst.

• Bij een rotatie draaien alle punten over een vaste hoek rond een vast punt of een as. De verplaatsing van de punten is afhankelijk van het rotatiepunt (of de rotatieas).

5 Hoe wordt de elektromagnetische krachtwerking gebruikt?

5.1 De laplacekracht op een elektromagneet

Als een stroomvoerende geleider (= elektromagneet) zich in een magnetisch veld bevindt dat niet evenwijdig is met de geleider, ondervindt die geleider de laplacekracht. Die kracht kan voor een translatie of voor een rotatie van de geleider zorgen. Dat fenomeen heeft veel toepassingen.

DEMO

Hoe kun je een translatie of rotatie veroorzaken door de laplacekracht?

1 Bestudeer de onderstaande opstellingen. N Z permanente magneet Z N vaste staafmagneet beweegbare spoel

▲ Afb. 196 Gekromde stroomvoerende geleiders in een magneetveld

Afb. 197 Een beweegbare stroomvoerende spoel in de buurt van een staafmagneet

2 Welke opstelling is geschikt voor de rotatie en welke voor de translatie?

Bespreek met je buur en test uit.

3 Onderzoek de invloedsfactoren.

4 Beantwoord de onderzoeksvraag.

5 Formuleer een verklaring voor je waarneming.

1 Translatie van een elektromagneet

VOORBEELD LUIDSPREKER

In een luidspreker zit een permanente magneet met een vorm zoals op afbeelding 198. In de kleine luchtspleet tussen de magneetpolen is er een magneetveld waarin een spoel gewikkeld is.

Conus is het Latijnse woord voor ‘kegel’.

©VANIN

Je kunt de werking van een luidspreker bekijken in de video.

Wanneer er stroom door de spoel loopt, ondervinden de windingen de laplacekracht. Bij een wisselstroom zal de spoel heen en weer bewegen volgens de as van de spoel. De stroomzin bepaalt de zin van de laplacekracht en dus de bewegingszin van de spoel. De spoel zit vast aan de conus, die daardoor gaat meetrillen. Zo wordt de lucht in trilling gebracht en wordt er geluid geproduceerd.

zijaanzicht spoel conus

De bouw van een luidspreker

vooraanzicht

zijaanzicht

vooraanzicht

zijaanzicht

Of de permanente magneet de elektromagneet aantrekt of afstoot, hangt af van de stroomzin in de elektromagneet. Als er op de elektromagneet een voorwerp is bevestigd, komt dat voorwerp ook in beweging. Als je de elektrische stroom uitschakelt, is de laplacekracht niet meer actief en stopt de beweging van het voorwerp.

2 Rotatie van een elektromagneet

Als je een draaibare rechthoekige stroomvoerende geleider (= kader) in een homogeen magnetisch veld plaatst, dan werken er op het kader laplacekrachten. Er ontstaat een krachtenkoppel dat een rotatie veroorzaakt.

VOORBEELD GELIJKSTROOMMOTOR

Een gelijkstroommotor zet elektrische energie om in kinetische energie door een kader (dat bestaat uit meerdere windingen) te laten roteren in een magnetisch veld. Om ervoor te zorgen dat de beweging niet stilvalt en altijd in dezelfde draaizin verloopt, wordt, op het ogenblik dat het vlak van het kader loodrecht op het magnetisch veld staat, de stroomzin door het kader verwisseld door een commutator. De commutator bestaat uit geleidende koolborstels en twee halve, cirkelvormige ringen uit geleidend materiaal die bevestigd zijn op de as van het kader. Met de borstels wordt een elektrische verbinding gemaakt tussen een gelijkspanningsbron en de collectorringen.

▲ Afb. 199 De laplacekracht op een stroomvoerend kader

©VANIN

koolborstel

halve ringen commutator

▲ Afb. 200 De commutator zorgt ervoor dat de stroom telkens van zin verandert.

Welke kracht werkt op het stukje geleider tussen de hoekpunten R en S? Verklaar. CONCEPTVRAAG

koolborstel halve ring

1 Er vloeit stroom door de winding van A naar B. De kader roteert door de laplacekracht in tegenwijzerzin.

2 Er is even geen stroom. De winding draait verder met dezelfde zin als gevolg van traagheid.

3 De stroomzin is verwisseld (= gecommuteerd). De stroom vloeit nu van B naar A. De laplacekracht heeft dezelfde richting en zin als in stap 1. Het kader blijft in tegenwijzerzin draaien.

4 Er is opnieuw even geen stroom door de open stroomkring. Door traagheid blijft het kader verder draaien. De cyclus herhaalt zich.

Je kunt de werking van de gelijkstroommotor bekijken aan de hand van de applets.

Gelijkstroommotoren kennen veel toepassingen.

Door een gelijkstroommotor beweegt het papier in een printer tijdens het afdrukken. Als de stroomzin wordt omgekeerd, rolt het papier terug in de printer, zodat de achterkant kan worden bedrukt.

De snelheid van een blender wordt geregeld door de stroomsterkte die door de gelijkstroommotor vloeit.

De rijrichting en de snelheid van een elektrische auto worden bepaald door de stroom die door de gelijkstroommotor vloeit.

5.2 De lorentzkracht op een lading

Als een lading zich in een magnetisch veld bevindt, ondervindt die lading de lorentzkracht. Aangezien de lorentzkracht altijd loodrecht op de bewegingszin van de lading staat, verandert ze enkel de snelheidsrichting van de lading, niet de snelheidsgrootte. Je vindt er voorbeelden van in de natuur en toepassingen in de technologie.

VOORBEELD NOORDERLICHT

De zonnewind is een stroom van geladen deeltjes die ontsnapt van het oppervlak van de zon. Een deel van die deeltjes komt aan in het magnetisch veld van de aarde. Ze ondervinden de lorentzkracht en buigen grotendeels af. Het aardmagnetisch veld beschermt de aarde op die manier tegen de zonnewinden. Door de vorm van het magnetisch veld en de kracht die de deeltjes daardoor ondervinden, komen ze vooral bij de Noord- en de Zuidpool in de atmosfeer terecht. Aan de polen botsen de deeltjes met een hoge snelheid op zuurstof- en stikstofmoleculen, die daardoor in een hogere energietoestand komen.

©VANIN

▲ Afb. 205 A Het aardmagnetisch veld B Door de onderlinge ligging van het veld en de snelheidsvector bewegen de geladen deeltjes op spiraalbanen naar de polen toe.

geladen deeltje nadert de aarde geladen deeltje nadert de aarde

Als die moleculen terugvallen naar een lagere energietoestand, zenden ze het energieverschil uit in de vorm van licht: het pool- of noorderlicht. De kleuren (vooral groen, maar ook rood, violet, paars, wit en zelfs geel) worden bepaald door de samenstelling van de lucht en de energie van de deeltjes.

©VANIN

CONCEPTVRAGEN

1 Verklaar hoe de spiraalbaan ontstaat.

2 Bepaal het ladingsteken op afb 205 B.

VOORBEELD TESLAMETER

Een teslameter meet de grootte van een magnetisch veld. Dat gebeurt door een geleidend plaatje loodrecht op de veldlijnen van dat magnetisch veld te plaatsen. Als er door het plaatje een stroomsterkte I vloeit, bewegen de vrije elektronen met een snelheid v die tegengesteld is aan die (conventionele) stroomzin. Op elk elektron werkt een lorentzkracht FL die het elektron naar één kant afbuigt. Daardoor wordt die kant van de geleider negatief geladen. De andere kant heeft een tekort aan negatieve ladingen en is positief geladen. Over de geleider ontstaat een elektrisch veld en dus ook een spanning, die je hallspanning noemt. Ten gevolge van dat elektrisch veld ontstaat ook een coulombkracht op de vrije elektronen. De zin van de coulombkracht is tegengesteld aan die van de lorentzkracht. Als de coulombkracht even groot is als de lorentzkracht, werkt er geen resulterende kracht in op de elektronen en gaan ze rechtdoor.

De hallspanning neemt recht evenredig toe met de magnetische veldsterkte. Door de hallspanning te meten, bekom je een teslameter.

De hallspanning is genoemd naar de fysicus Edwin Hall (1879).

Je kunt het werkingsprincipe bekijken in de video.

Er bestaan nog andere toepassingen van de lorentzkracht.

Je leert er meer over op .

▲ Afb. 207 Het ontstaan van hallspanning in een geleider

▲ Afb. 208 Een teslameter meet de hallspanning.

▲ Afb. 206 Het noorderlicht

WEETJE

AAN DE SLAG

REEKS

Bestudeer de afbeeldingen.

Welke vectoren kunnen de magnetische veldsterkte correct weergeven?

Bestudeer de tabellen.

Verbind de opgemeten magnetische veldsterkte B met de kenmerken van de luchtledige spoel.

I (A) 2,00,50 1,5 3,02,01,0

N 100 1 000 50200150300

ℓ (m) 0,20 0,100,15 0,800,20 0,30

Een spoel heeft een lengte van 5,0 cm en 200 windingen.

De grootte van de magnetische veldsterkte in het midden van de spoel bedraagt 0,015 T. De spoel bevindt zich in lucht.

Hoe groot is de stroomsterkte door de spoel?

Een spoel met 1 200 windingen is 15,0 cm lang. In de spoel is een stalen staaf geschoven. Als de stroom door de spoel 0,30 A bedraagt, dan is de grootte van de magnetische veldsterkte in het midden van de spoel 0,40 T.

Hoe groot is de relatieve permeabiliteit van het staal waaruit de staaf is vervaardigd?

In het midden van een spoel is er een magnetische veldsterkte B

Hoe groot is de magnetische veldsterkte in de onderstaande situaties?

a De spoel wordt uitgerekt tot dubbele lengte en het aantal windingen blijft constant.

b Het aantal windingen verdubbelt en de lengte blijft constant.

c De lengte en het aantal windingen verdubbelen.

d De oppervlakte van elke winding verdubbelt.

Door een rechte geleider die zich in de lucht bevindt, loopt een stroom van 7,50 A.

a Hoe groot is de magnetische veldsterkte op een afstand van 3,00 cm van de geleider?

b Hoe groot is de magnetische veldsterkte op een afstand van 6,00 cm van de geleider?

De grootte van de magnetische veldsterkte in het veld van een rechte geleider bedraagt 0,250 mT in een punt op 2,00 cm afstand van de geleider. De geleider bevindt zich in lucht.

a Hoe groot is de stroom die door de geleider loopt?

b Op welke afstand van de geleider is de magnetische veldsterkte 16 keer kleiner?

Teken de afbeeldingen over.

Vul ze aan met de ontbrekende grootheden: FL, B of

Door een horizontale stroomdraad van 20,0 cm lengte vloeit een stroom van 6,0 A.

Hoe groot is de laplacekracht op die draad in een verticaal homogeen magneetveld van 300 mT?

Vier jongeren bestuderen een opstelling van koperdraad in een hoefijzermagneet op een balans.

Welke stelling is correct? Verklaar je antwoord.

a Met de massaverandering op de balans meet je de laplacekracht.

b Met de massaverandering op de balans meet je de reactiekracht van de laplacekracht.

c Je moet de koperdraad ergens aan vasthangen om de laplacekracht te kunnen meten.

d Met een balans kun je de laplacekracht niet bepalen.

Een stroomvoerende geleider bevindt zich in een homogeen magnetisch veld, waarbij α de hoek is tussen de geleider en het magnetisch veld.

Teken de FL(I)-, FL(B)- en FL(α)-grafiek.

Door een geleider met een lengte van 2,0 m loopt een stroom van 1,5 A. De laplacekracht bedraagt maximaal 180 mN.

a Hoe groot is het magnetisch veld?

b Welke voorstelling is correct, als de laplacekracht 100 mN bedraagt?

Welk van onderstaande uitdrukkingen zijn fout? Verklaar.

a E = FC q

b g = FZ m

c B = FL q · v · sin α

d B = FL q · v · sin α

e E = FC q

f G = FG m

g B = FL q · v · sin α

h B = FL q · v

AAN DE SLAG

Bestudeer de afbeeldingen van verschillende ladingen die bewegen met verschillende snelheden in hetzelfde homogene magnetisch veld. Teken de magnetische veldsterkte en de snelheid over. Vul de afbeeldingen aan met:

a (indien mogelijk) de lorentzkracht op schaal; b (indien mogelijk) de baan van de lading.

In een science game moet Jeroen drie deeltjes (p+, e– en n0) met een aangepaste snelheid afvuren door een homogeen magnetisch veld, zodat ze achtereenvolgens target 1, 2 en 3 raken.

a Welke afvuurvolgorde levert het goede resultaat op?

©VANIN

Door een koperen staafje met een lengte van 16,0 cm loopt een stroom van 20,0 A. Er werkt op het staafje een laplacekracht van 44,2 · 10–3 N als het zich in een homogeen magnetisch veld bevindt met een veldsterkte van 23,5 mT.

Bepaal de hoek tussen het staafje en het magnetisch veld.

Een proton beweegt met een snelheid van 3 000 km s door een homogeen magnetisch veld.

Op het proton werkt een kracht van 2,40 · 10–14 N.

Bepaal de grootte van de magnetische veldsterkte, als de hoek tussen de baan van het proton en de magnetische veldsterkte …

a 90° bedraagt; b 45° bedraagt.

1 p+, e–, n0

2 e–, n0, p+

3 n0, p+, e–

4 p+, n0, e–1

deeltjeswapen 2 3 B

b Is de snelheid van het elektron groter dan, gelijk aan of kleiner dan de snelheid van het proton (op de afbeelding)? Verklaar.

Twee rechte geleiders lopen parallel in een verticaal vlak. Ze hebben een tegengestelde stroomzin. De stroomsterkte IX is drie keer groter dan IY. In welk gebied kun je punten vinden waar de resulterende magnetische veldsterkte nul is? Verklaar.

a alleen boven geleider X

b alleen tussen geleider X en Y

c alleen onder geleider Y

d zowel boven geleider X als onder geleider Y

e zowel boven, tussen als onder de geleiders I x I y

Door twee evenwijdige rechte geleiders loopt een even grote stroom, maar met een tegengestelde zin. Als de stroom door elke geleider verdubbelt, dan zal de kracht die de geleiders op elkaar uitoefenen …

a constant blijven;

b verdubbelen;

c verviervoudigen;

d halveren.

REEKS

Bestudeer de opgemeten grafiek van de magnetische veldsterkte rondom een rechte geleider (Imax = 50 A).

Bestudeer de onderstaande afbeeldingen met stroomvoerende geleiders (gelijke stroomsterkte) op elk hoekpunt.

a Rangschik de situaties volgens toenemende magnetische veldsterkte in het punt P.

b In het punt P plaats je een geleider met een stroom die in het blad gaat. Teken de laplacekracht.

a Formuleer een geschikte onderzoeksvraag.

b Welke eenheid moet er op de verticale as staan?

c Welk verband bestaat er tussen beide metingen?

d Bepaal de constante grootheid voor beide metingen.

e Teken de B(I)-grafiek op 3 cm afstand.

Op twee overstaande hoekpunten van een rechthoek (2,0 cm op 4,0 cm) bevinden zich twee geleiders die loodrecht op het blad staan.

Door beide geleiders loopt een stroom van 3,0 A.

Beide geleiders lopen evenwijdig met elkaar over een afstand van 1,0 m. Bereken en teken:

a de kracht tussen beide geleiders;

b de magnetische veldsterkte in de twee andere hoekpunten.

Vul de uitspraken aan met ‘altijd’, ‘soms’ of ‘nooit’.

a Op een lading in rust werkt een lorentzkracht.

b De zin van de lorentzkracht op een bewegend proton is tegengesteld aan de zin van de lorentzkracht op een bewegend elektron in hetzelfde magnetisch veld.

c De snelheidsgrootte van een bewegend proton verandert door een magnetisch veld.

d De snelheidsrichting van een bewegend elektron verandert door een magnetisch veld.

e De kinetische energie van bewegende ladingen verandert door een magnetisch veld.

Bestudeer de onderstaande afbeeldingen.

Je plaatst vier geleiders op de hoekpunten van een vierkant.

Op welke geleider kan de resulterende kracht nul zijn? Toon aan met een figuur.

©VANIN

a Rangschik de situaties volgens toenemende kracht op de geleider.

b Hoe moet je de stroomsterkte in situatie B, C en D aanpassen om dezelfde krachtgrootte te bekomen als in situatie A?

c Hoe moet je het magnetisch veld aanpassen in situatie B, C en D om een tegengestelde, maar even grote kracht te bekomen als in situatie A?

Twee evenwijdige geleiders staan 16 cm uit elkaar. Er loopt door beide een stroom I. Je halveert de stroomsterkte door beide draden. Op welke afstand van elkaar moet je ze nu plaatsen, opdat de kracht die ze op elkaar uitoefenen, niet verandert?

REEKS

Aan de evenaar is het aardmagnetisch veld evenwijdig met het aardoppervlak en is de veldsterkte gelijk aan 25 µT. Je wilt een draad met een massa van 2,0 g en een lengte van 5,0 cm laten zweven.

a Hoe moet je de draad precies opstellen om dat te laten lukken?

b Hoe groot is de minimale stroomsterkte?

In een ampère- en voltmeter wijkt de wijzer uit door de magnetische kracht in een galvanometer. In een galvanometer zit er een vierkante winding tussen de polen van een U-vormige magneet.

a Teken de afbeelding over en duid de polen van de hoefijzermagneet aan, zodat de winding een draaiing maakt zoals aangegeven.

b In de U-vormige magneet is er een homogeen veld van 30 µT. Door de winding loopt 6,0 A. Bepaal de grootte van de kracht op geleider 1, 2 en 3 met lengte 3,0 cm, als die zich in de stand bevinden zoals op de afbeelding.

▲Elke analoge ampère- en voltmeter bevat een galvanometer, die uitwijkt door de laplacekracht.

HOOFDSTUKSYNTHESE

KERNBEGRIPPEN

NOTITIES magnetische veldsterkte

B B B B B B

magnetische veldsterkte bij elektromagneten

De magnetische veldsterkte B geeft de eigenschappen van het magnetisch veld weer:

• aangrijpingspunt: punt in de ruimte;

• richting: magnetische veldlijnen;

• zin: volgens noordpool kompasnaald;

• grootte: maat voor de sterkte van magnetisch veld.

GROOTHEID MET SYMBOOLEENHEID MET SYMBOOL magnetische veldsterkte B tesla[B] = T

Een elektrische stroom I (= bewegende ladingen) wekt een magnetische veldsterkte B op.

Voor een rechte geleider: B = µ 2 · π · I r (met r de afstand tot de geleider).

De magnetische permeabiliteit is een stofeigenschap: μ = µr · µ0

• Magnetische permeabiliteit van het vacuüm: µ0 = 4 · π · 10–7 T · m A

• Relatieve permeabiliteit van andere stoffen: µr

In alle andere configuraties geldt: B = B res = B 1 + B2 + B3 + …

Speciale configuraties:

• spoel: B = µ · n · I (met n = N l de windingsdichtheid);

• lus: B = µ 2 · I R (met R de straal van de lus).

magnetische krachtBewegende ladingen ondervinden een kracht in een magnetisch veld

STROOMVOERENDE GELEIDER MET LENGTE l EN STROOMSTERKTE I (LAPLACEKRACHT)

INDIVIDUELE LADING MET LADING q EN SNELHEID v (LORENTZKRACHT)

AANGRIJPINGSPUNT geleider lading

GROOTTE (IN MAGNETISCH VELD

DIE HOEK α MAAKT MET PAD VAN DE LADINGEN)

toepassingen • Wetenschap: de krachtwerking tussen permanente magneten en elektromagneten kan verklaard worden met de Lorentz- of Laplacekracht.

• Technologie: beeldscherm, gelijkstroommotor, teslameter

• Natuur: magnetische schermwerking door aardmagnetisch veld (merkbaar als noorderlicht)

Elektromagnetische inductie

In de vorige hoofdstukken maakte je al kennis met enkele elektromagnetische fenomenen waaruit blijkt dat elektriciteit en magnetisme nauw met elkaar verbonden zijn. Elektrische stroom wekt een magnetisch veld op (bijvoorbeeld: het aardmagnetisme ontstaat door bewegende ionen, elektromagneten ontstaan door stroomvoerende geleiders …).

Bewegende ladingen ondervinden een kracht in een magnetisch veld (bijvoorbeeld: de zonnewind buigt af door het aardmagnetisch veld, een stroomvoerende kader ondervindt kracht in een magnetisch veld en wordt zo een motor …).

Die belangrijkste ontdekkingen werden begin 19e eeuw gedaan. Wetenschappers vroegen zich al gauw af: als elektrische stromen een magnetisch veld opwekken, kan een magnetisch veld dan ook een elektrische stroom opwekken?

In dit hoofdstuk vind je een antwoord op die vraag.

LEERDOELEN

M beschrijven hoe spanning met behulp van een magneet opgewekt wordt

M de grootte en het teken van de opgewekte spanning bepalen

M het ontstaan en kenmerken van de inductiespanning en -stroom omschrijven

M enkele toepassingen van elektromagnetische inductie geven, toelichten en beschrijven

1 Hoe kun je spanning opwekken met een magnetisch veld?

1.1 Veranderend magneetveld

In het dagelijkse leven zijn er tal van voorbeelden (die je misschien niet bewust herkent) waarbij magneten gebruikt worden om elektriciteit op te wekken.

©VANIN

Je kunt met een dynamo je smartphone opladen. Door een magneet te draaien, wek je spanning op.

De magnetische informatie op een harde schijf wordt uitgelezen. De verandering van magnetische domeinen produceert een elektrisch signaal (= spanning).

Magneten worden gebruikt voor diefstalpreventie. Als je onbetaalde goederen door een scanner beweegt, zorgt de magneet voor een alarmsignaal.

Een verandering van magnetische veldsterkte kan in een nabij stuk metaal een spanning opwekken. In een gesloten kring zorgt dat voor een stroom.

07 LABO

VOORBEELD HISTORISCH EXPERIMENT VAN FARADAY

Michael Faraday was een van de wetenschappers die met een magneet een elektrische stroom probeerde op te wekken. Hij gebruikte twee spoelen rond een weekijzeren kern, een batterij en een kompas (zie afbeelding 212). Hij stelde vast dat de kompasnaald in de buurt van de tweede spoel beïnvloed werd door het openen of het sluiten van de kring met de eerste spoel. Dat betekent dat er op die momenten een magnetische kracht werkt op het kompas. Daaruit besloot hij dat er door de tweede spoel een stroom vloeit die een magneetveld opwekt.

Hij concludeerde dat een veranderend magneetveld door een spoel een spanning kan opwekken. In een gesloten kring veroorzaakt die spanning een elektrische stroom.

OPEN STROOMKRINGSLUITEN VAN DE

©VANIN

DE STROOMKRING

Het kompas wijst naar het geografische noorden.

Het kompas oriënteert zich volgens de veldlijnen van een rechte geleider.

Het kompas wijst naar het geografische noorden.

Het kompas oriënteert zich volgens de veldlijnen van een rechte geleider, maar in tegengestelde zin als bij het sluiten van de schakelaar.

Ook de Amerikaan Joseph Henry kwam tot dezelfde vaststellingen in dezelfde periode. Faraday publiceerde zijn resultaten echter eerder, waardoor het fenomeen bekend staat als de wet van Faraday.

VOORBEELD SPANNING OPWEKKEN MET EEN STAAFMAGNEET

Een gesloten winding is aangesloten op een voltmeter. Als je de winding nadert met een staafmagneet, zie je dat de meter uitwijkt. Er is een spanning opgewekt.

magneet beweegt naar de spoel toe (magnetische veldsterkte in spoel neemt toe)

magneet beweegt naar beneden (magnetische veldsterkte in spoel neemt af) N Z geen beweging (magnetische veldsterkte in spoel constant)

In de video leer je meer over de experimenten van Faraday.

Flux komt van het Latijnse fluere dat vloeien, stromen betekent. Flux betekent ‘doorstroom’. Magnetische flux wordt daarom ook soms magnetische stroom genoemd. Het symbool is de Griekse hoofdletter phi.

De oppervlaktevector A is gericht volgens de normaal. In fysica wordt als hoek vaak gekozen voor de hoek die een vector maakt met de normaal. Je leerde dat misschien al kennen bij optica.

CONCEPTVRAAG

Beschrijf hoe je met de opstelling uit de afbeelding onderaan p. 167 de voltmeter … a kunt laten uitwijken als je de staafmagneet stilhoudt; b op nul kunt laten staan als je de staafmagneet beweegt. Verklaar.

Een verandering van de magnetische veldsterkte kan spanning op wekken. Als er een gesloten kring is, ontstaat er een stroom.

1.2 Fluxverandering

Uitgebreidere experimenten tonen aan dat niet enkel de verandering van de magnetische veldsterkte, maar ook de oppervlakte van de lus of spoel een invloed heeft op de opgewekte spanning.

We definiëren hiervoor een nieuwe grootheid. De magnetische flux Φ is een maat voor het aantal magnetische veldlijnen dat een oppervlak doorkruist. De eenheid van magnetische flux is de weber.

GROOTHEID MET SYMBOOL

EENHEID MET SYMBOOL magnetische flux Φ weber Wb

De magnetische flux wordt beïnvloed door de grootte van de magnetische veldsterkte B, de grootte van het oppervlak A en de onderlinge ligging van de magnetische veldsterkte en het oppervlak. Om de oriëntatie van het oppervlak aan te geven, wordt de oppervlaktevector A gebruikt, die loodrecht op het oppervlak staat. De grootte van de vector komt overeen met de grootte van het oppervlak.

INVLOED VAN DE GROOTTE VAN DE MAGNETISCHE VELDSTERKTE

INVLOED VAN DE GROOTTE VAN HET OPPERVLAK

INVLOED VAN DE ONDERLINGE LIGGING

wordt beïnvloed door

Je kunt de magnetische flux voor een homogeen magnetisch veld berekenen als:

Φ = B · A · cos α

waarbij

• B · cos α de component van de magnetische veldsterkte B is, die loodrecht staat op het oppervlak. Je kunt ook zeggen dat B · cos α de component van de vector B is, die evenwijdig is met de oppervlaktevector A

• α de hoek is tussen de magnetische veldsterkte B en de oppervlaktevector A (0°≤ α ≤ 360°).

Uit de definitie van magnetische flux kun je de definitie van de eenheid van weber afleiden:

[Φ] = [B] · [A] dus 1 Wb = 1 T · m2

©VANIN

▲ Afb. 213 De magnetische flux door een oppervlak: Φ = B · A · cos α

CONCEPTVRAGEN

1 Het oppervlak voorgesteld op de figuren in de tabel op p. 168 is een vierkant.

a Teken de 2D-voorstelling van alle situaties, als je volgens de oppervlaktevector A kijkt.

b De flux voor de bovenste situatie kun je noteren als Φ = B · A · cos α = B · A. Bepaal de uitdrukking voor de flux voor alle andere situaties.

2 Wat betekent α = 0°; α = 90°, α = 180° voor de fluxgrootte en het teken van de flux?

Tijdens een fluxverandering, ontstaat er een elektrische spanning. Het opwekken van spanning door fluxverandering noem je elektromagnetische inductie. De elektrische spanning noem je de inductiespanning. De stroom die door de spanning opgewekt wordt, is de inductiestroom.

Bij een fluxverandering verandert het aantal magnetische veldlijnen door een oppervlak. Je kunt de inductiespanning opwekken door de verschillende factoren van de flux te veranderen. Je kunt:

• de grootte B van de magnetische veldsterkte veranderen;

• de grootte A van het oppervlak veranderen;

• de hoek α (tussen de magnetische veldsterkte B en de oppervlaktevector A) veranderen.

Induceren betekent opwekken. Bij elektromagnetische inductie wek je elektrische spanning op met een magneet.

VOORBEELD FLUXVERANDERING IN EEN LUS

FLUXVERANDERING DOOR BEWEGING NAAR DE LUS TOE

• Als de noordpool zich ver van de lus bevindt, gaan er weinig veldlijnen door het oppervlak. De magnetische flux is klein.

• Als de noordpool zich naar het oppervlak toe beweegt, gaan er meer veldlijnen door het oppervlak. De magnetische flux neemt toe.

FLUXVERANDERING DOOR DE GROOTTE VAN HET OPPERVLAK TE VERANDEREN

• Als de noordpool zich dichtbij in het verlengde van de lus bevindt, gaan er veel veldlijnen door het oppervlak. De magnetische flux is groot.

• Als het oppervlak van de lus verkleind wordt, gaan er minder veldlijnen door het oppervlak. De magnetische flux neemt af.

FLUXVERANDERING DOOR DE MAGNEET TE DRAAIEN

• Als de noordpool zich dichtbij en in het verlengde van de lus bevindt, gaan er veel veldlijnen door het oppervlak. De magnetische flux is groot.

• Als je de staafmagneet schuin draait, gaan er minder veldlijnen door het oppervlak. De magnetische flux neemt af.

Elektromagnetische inductie is het opwekken van spanning door een fluxverandering. De opgewekte elektrische spanning noem je de inductiespanning. De stroom die door de spanning opgewekt wordt, noem je de inductiestroom. Je kunt alle

CONCEPTVRAAG

Stel de fluxverandering van de drie situaties uit het voorbeeld voor op een 2D-figuur die het beeld geeft vanuit de lus naar de magneet toe.

Het aantal magnetische veldlijnen door een oppervlak beschrijf je met de grootheid magnetische flux. De flux is een maat voor het aantal veldlijnen.

GROOTHEID

2.1 Geïnduceerd magnetisch veld

DEMO

Welke kenmerken heeft de inductiestroom?

1 Een open en gesloten lus zijn op een draaibare staaf gemonteerd. Een permanente magneet wordt in de buurt gebracht.

2 Wat zal er volgens jou gebeuren bij de open en de gesloten lus als:

• de magneet ernaartoe beweegt?

• de magneet er van weg beweegt?

Bespreek met je buur en bekijk de video.

3 Formuleer een antwoord op de onderzoeksvraag.

Als in de buurt van een gesloten geleider een magnetische fluxverandering optreedt, dan ontstaat er een inductiestroom door de gesloten geleider. Door de inductiestroom wordt er een magnetisch veld met magnetische veldsterkte Bi opgewekt

De zin van de inductiestroom is zodanig dat het opgewekte magnetisch veld de oorspronkelijke fluxverandering tegenwerkt. Dat is de wet van Lenz

VOORBEELD ZIN VAN DE INDUCTIESTROOM IN EEN LUS

©VANIN

B i v I B

Als de magneet stilgehouden wordt voor de lus, is er geen magnetische fluxverandering. Er is geen inductiestroom (I = 0) en geen opgewekt magnetisch veld (Bi = 0). Z N

Als de noordpool van de magneet naar de lus toe beweegt, is er een fluxtoename in de lus (omdat de magnetische veldsterkte toeneemt). De lusvormige stroom vloeit in de zin zoals in de figuur aangegeven, zodat er een magnetische veldsterkte Bi opgewekt wordt, die de fluxverandering tegenwerkt.

Als de noordpool van de magneet van de lus weg beweegt, is er een fluxafname in de lus (omdat de magnetische veldsterkte afneemt).

Z I N

B i v B

CONCEPTVRAGEN

De lusvormige stroom vloeit in de zin zoals in de figuur aangegeven, zodat er een magnetische veldsterkte Bi opgewekt wordt, die de fluxverandering tegenwerkt.

a Controleer de zin van de inductiestroom.

b Wat gebeurt er als je de zuidpool van de staafmagneet naar en van de lus weg beweegt? Maak duidelijk met figuren.

Wet van Lenz: De magnetische fluxverandering wekt een inductiestroom op. De zin van de inductiestroom is zodanig dat het daardoor opgewekte magneetveld de fluxverandering tegenwerkt

▲ Afb. 214 Opstelling om de kenmerken van de geïnduceerde stroom te onderzoeken

2.2 Eigenschappen van de inductiespanning

DEMO

Welke factoren beïnvloeden de grootte en het teken van inductiespanning?

1 Je beschikt over verschillende spoelen en een staafmagneet.

2 Bespreek met je buur de mogelijke invloedfactoren op de inductiespanning.

3 Test samen met je leerkracht uit.

4 Formuleer een antwoord op de onderzoeksvraag.

©VANIN

Een fluxverandering bij een lus of spoel wekt een inductiespanning Ui op. De fluxverandering ∆Φ gebeurt in een bepaald tijdsinterval Δt door de grootte van de magnetische veldsterkte (B), de oppervlakte (A) of de hoek tussen de normaal op het oppervlak en de magnetische veldsterkte (α) te veranderen. Het tempo van de fluxverandering noteer je als ∆Φ Δ

CONCEPTVRAGEN

1 De flux door een oppervlak verandert van toestand 1 naar toestand 2. Noteer de fluxverandering voluit.

2 Geef de eenheid van de fluxverandering.

Uit de experimenten volgt:

inductiespanning neemt recht evenredig toe met het tempo van de fluxverandering Ui ~ ∆Φ Δt

inductiespanning neemt recht evenredig toe met toenemend aantal windingen Ui ~ N Ui ~ N

Ui = –N · ∆Φ Δt nauwkeurig onderzoek

In een lus of een spoel ontstaat door een fluxverandering een inductiespanning Ui die gegeven is door Ui = –N · ∆Φ Δt . Dat is de inductiewet van Faraday.

Het minteken in de inductiewet duidt erop dat er door de inductiespanning een inductiestroom opgewekt wordt, zodat de fluxverandering tegengewerkt wordt (wet van Lenz).

TIP

Je definieerde al de grootheid snelheid als het tempo van de positieverandering (v = ∆x Δt ).

De grootheid die het tempo van de fluxverandering beschrijft ( ∆Φ Δt ), heeft geen eigen naam.

Om het tempo van de fluxverandering op een bepaald moment te bestuderen, gebruik je een heel klein tijdsinterval (∆t → 0). Je bekomt de afgeleide lim Δt→0 ∆Φ Δt = dΦ dt .

Inductiewet van Faraday: in een lus of een spoel met N windingen veroorzaakt een fluxverandering ∆Φ een inductiespanning: Ui = –N · ∆Φ Δt

3.1 Spanning opwekken in een elektrische kring

A Generator

Een fluxverandering veroorzaakt een elektrische spanning. Door een magneet (periodisch) te bewegen ten opzichte van een spoel, wordt een spanningsbron gecreëerd.

©VANIN

In technologische toepassingen gebruikt men vaak een draaibeweging om de magneet en de spoel ten opzichte van elkaar te laten bewegen. De combinatie van een spoel en een magneet waarbij mechanische energie van een draaibeweging omgezet wordt in elektrische energie, wordt een generator genoemd.

Aangezien de relatieve beweging van de spoel ten opzichte van het magnetisch veld belangrijk is voor de fluxverandering, zijn er twee mogelijkheden:

1 De spoel heeft een vaste positie, de magneet draait. Om kleine spanningen op te wekken, monteer je een staafmagneet tussen spoelen. Als de magneet draait ten opzichte van de spoelen, verandert de flux door het oppervlak.

VOORBEELD DYNAMO

Je kunt met spierkracht een magneet laten draaien. Als die magneet tussen spoelen draait, ontstaat er een inductiespanning (tussen de punten 1 en 2 op de figuur). Als er een verbruiker (bijvoorbeeld een lamp, een smartphone) aangesloten is, wordt de draaiende magneet in combinatie met een spoel als spanningsbron gebruikt. Dat noem je een dynamo. Een ander bekend voorbeeld van een dynamo is een fietsdynamo.

▲ Afb. 215 Bouw van een kring met dynamo als spanningsbron▲ Afb. 216 Een smartphone kun je opladen door aan de hendel van de dynamo te draaien.

Je kunt de werking van de dynamo bekijken in de applet.

De snelheid bij een rechtlijnige beweging is gedefinieerd als v =

= x – x0

t0 = x t (als x0 = 0 bij t0 = 0 gekozen wordt). Op analoge manier kun je de hoeksnelheid bij een draaibeweging definiëren als ω = α t

2 De magneet heeft een vaste positie, de spoel draait. Bij generatoren die grote spanningen opwekken, wordt een draaibare spoel in een homogeen magneetveld gemonteerd. Aangezien het moeilijk is om zware magneten te laten ronddraaien, wordt de spoel rondgedraaid in een vaste magneet. De flux door een oppervlak is gegeven door Φ = B · A = B · A · cos α. Als de spoel draait, is er een fluxverandering.

magneet

sleepcontact I i winding

▲ Afb. 217 Ontstaan van een wisselspanning en een wisselstroom bij een volledige omwenteling (t omw = T)

Als je het oppervlak met een constante hoeksnelheid ω laat draaien, kan de hoek α geschreven worden als functie van de tijd: α = ω · t. De flux kun je dan schrijven als Φ = B · A · cos (ω · t).

/dt

De spanning die opgewekt is, kun je berekenen met de inductiewet van Faraday (voor (∆t→0)) als Ui = –N · dΦ dt = B · A · ω · sin (ω · t). Dat betekent dat de spanning een sinusfunctie is: er wordt wisselspanning opgewekt.

Bestudeer grafiek 1.

1 Hoe groot is de spanning als de fluxverandering maximaal is?

2 Hoe groot is de spanning als de flux maximaal is? Verklaar.

VOORBEELD GENERATOR BIJ ELEKTRICITEITSPRODUCTIE

De elektriciteit waarvan wij dagelijks gebruik maken, wordt grotendeels door generatoren opgewekt. Uit onze stopcontacten komt dus wisselspanning. Alleen fotovoltaïsche cellen (zonnepanelen) werken niet volgens dat principe. Die produceren gelijkspanning. Om zonnepanelen te kunnen aansluiten op het elektriciteitsnet, wordt de gelijkspanning daarom via een omvormer omgezet in wisselspanning.

©VANIN

zon wind water geothermisch biomassa kernenergie gas energiebron

omzetting naar elektrische energie

▲ Afb. 218 Verschillende manieren om elektrische energie te produceren

GENERATOR

CONCEPTVRAAG

Wekt een dynamo gelijkspanning of wisselspanning op?

1 Verklaar.

2 Hoe merk je dat in de praktijk?

omzetting naar warme

omzetting naar bewegingsenergie

Een sensor meet een natuurkundige grootheid. Met een sensor neemt een machine de omgeving waar (bijvoorbeeld: temperatuursensor, lichtsensor, bewegingssensor, stroomsensor ...). Het is een kunstmatige uitvoering van een zintuig bij organismen.

B Sensor

Als een magneet voor of in een spoel beweegt, verandert de flux en ontstaat er een spanning. Dat maakt het mogelijk om een beweging om te zetten in een elektrisch signaal. Op die manier heb je een sensor, meer bepaald een bewegingssensor. Uit de spanningsvariatie in de tijd kan informatie over de beweging geregistreerd worden en omgezet in de gewenste toepassing.

VOORBEELDEN INDUCTIESPANNING BIJ SENSOREN

Een fietscomputertje is verbonden met een bewegingssensor. Je bevestigt een magneet op de spaken en een detectielus op het fietsframe. Bij iedere doorgang verandert de flux door de detectielus en kan de afstand berekend worden uit de wielomtrek.

Een gitaarelement zet de trilling van de snaren (die gemaakt zijn uit een ferromagnetische stof) om in een elektrisch signaal. Het element bestaat uit een magneet die omwonden is met fijne koperdraad (enkele duizenden windingen). Wanneer de snaren trillen, verandert de magnetische flux waardoor een wisselspanning wordt opgewekt. De frequentie is gelijk aan de frequentie van het trillen van de snaren.

3.2 Wervelstromen in geleiders

DEMO

Wat gebeurt er als een metalen voorwerp door een magneetveld beweegt?

1 Een koper- of aluminium plaatje kan slingeren tussen de benen van een hoefijzermagneet (zoals op afbeelding 221).

2 Wat zal er volgens jou gebeuren? Bespreek met je buur.

3 Herhaal voor een plaatje met openingen.

4 Formuleer een antwoord op de onderzoeksvraag.

▲ Afb. 219 Bewegingssensor bij een fietscomputertje ▲ Afb. 220 Pick-upelement (= bewegingssensor) op een elektrische gitaar

Een inductiestroom loopt niet enkel via opgelegde paden zoals de draden in een elektrische kring. Zodra er een fluxverandering is door het oppervlak van een geleider, komen de vrije elektronen in beweging. De inductiestroom die op die manier ontstaat, noemt men een wervelstroom

De wervelstromen veroorzaken op hun beurt een magnetisch veld en warmte. Dat heeft zowel technologische toepassingen als nadelen.

1 Geïnduceerd magnetisch veld

Als een geleidend materiaal in een magneetveld beweegt, ontstaat er een fluxverandering door het oppervlak van de geleider. De bewegende elektronen wekken een magneetveld op die de beweging tegenwerkt. De geleider wordt afgeremd. Dat kan gebruikt worden als magnetische rem.

Zitjes in de vrijevaltoren worden magnetisch afgeremd. Je kunt de moeilijkheidsgraad op een hometrainer regelen door de wervelstromen groter of kleiner te maken.

2 Warmteontwikkeling

©VANIN

Treinen worden soms magnetisch geremd. Zo’n rem is slijtagevrij, maar ontwikkelt veel warmte in de spoorstaven.

De wervelstromen ondervinden weerstand. Daardoor is er warmteontwikkeling. (Dat leerde je vorig schooljaar kennen als het joule-effect). In motoren en generatoren is dat een nadelig neveneffect waarvoor oplossingen gezocht moeten worden. Het kan echter ook gebruikt worden om heel efficiënt een metaal op te warmen.

VOORBEELD INDUCTIEKOOKPLAAT

Bij een inductiekookplaat loopt er een wisselstroom in een spoel, die onder de glasplaat gemonteerd is. Door de spoel loopt een wisselstroom waardoor er een wisselend magnetisch veld opgewekt wordt. De fluxverandering veroorzaakt wervelstromen in de bodem van de metalen kookpot. Door de weerstand van het metaal warmt de bodem op. Die warmte wordt doorgegeven aan de inhoud van de pot.

De inductiekookplaat heeft een hoog rendement omdat de warmte in de kookpot ontwikkeld wordt. Een inductiekookplaat is tegelijk veilig (geen warmte zonder pot) en goed voor het milieu (geen verbrandingsgassen).

Inhoud van de pan wordt verwarmd door de panwanden

Pan wordt verwarmd door wervelstromen die opgewekt worden door magnetische velden

Magnetisch veld dat opgewekt wordt door elektrische stroom

Elektrische stroom in koperen spoel

Op vind je extra voorbeelden van toepassingen (detectielus voor auto’s, transformator, metaaldetector, nietferromagnetisch metaal scheiden uit PMD).

©VANIN

CONCEPTVRAGEN

1 Kun je een glazen pot gebruiken op een inductiekookplaat? Verklaar.

2 Verklaar de werking van de voorbeelden in het begin van dit hoofdstuk (Afb. 210 en 211)

VERDIEPING

De inductiewet van Faraday kent nog vele andere, soms meer complexe, toepassingen.

Theoretisch heeft de inductiewet van Faraday voor een grote doorbraak op het gebied van elektromagnetisme gezorgd. In combinatie met eerdere inzichten geeft het een cruciaal verband weer tussen elektrische en magnetische velden.

In een geleider ontstaat de elektrische stroom doordat er een elektrisch veld aangelegd wordt over de uiteinden van de geleider. Uit de inductiewet volgt dat een veranderende magnetische flux een stroom in een geleider opwekt. Gecombineerd is dat een belangrijke conclusie: een veranderende magnetische flux wekt een elektrisch veld op, die op zijn beurt een elektrische stroom opwekt als de geleider gesloten is.

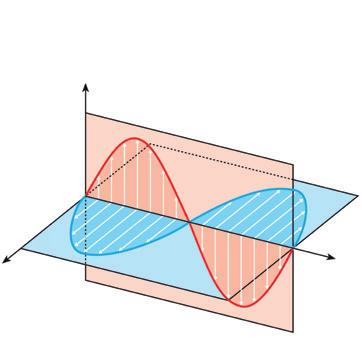
De nauwe band tussen elektrische en magnetische velden werd in 1884 door Maxwell in twintig vergelijkingen weergegeven. Later werden ze (door nieuwe wiskundige notaties) gereduceerd tot vier vergelijkingen. Ze staan bekend als de wetten van Maxwell. Het zijn de vier natuurkundige wetten van het elektromagnetisme, ze beschrijven de volledig theorie van elektrische en magnetische velden. Dat ligt ook aan de basis van het begrijpen en gebruiken van elektromagnetische golven. Veranderende magnetische velden wekken veranderende elektrische velden op, die op hun beurt opnieuw veranderende magnetische velden opwekken. Die velden kunnen zich bijvoorbeeld ook in een vacuüm voortplanten. Op die manier kan energie doorgegeven worden door velden zonder dat er materiedeeltjes aanwezig zijn. Zodra er een lading, bijvoorbeeld een elektron, in het elektromagnetische veld komt, zal het een elektromagnetische kracht ondervinden. Veranderende magnetische en elektrische velden kunnen dus niet alleen vele (kilo)meters ver, maar zelfs ook vele lichtjaren ver een elektromagnetische kracht veroorzaken.

▲ Afb. 226 Een ei op de plaat bakt niet. De warmte wordt ontwikkeld in de pan.

Je kunt het ontstaan van EMgolven als veranderende magnetische en elektrische velden bekijken in de applets.

REEKS

Bestudeer de onderstaande figuren.

a Rangschik de situaties volgens toenemende flux.

b Bereken de flux voor B = 0,500 T en een draadlus met een straal van 10 cm.

Welke uitspraak is correct?

a De magnetische flux is een vector.

b De magnetische flux is een veldeigenschap.

c De magnetische flux kan negatief zijn.

d De magnetische flux ontstaat door een bewegende magneet.

e De magnetische flux zorgt voor een spanning.

De magnetische flux door een metalen frame van 20 cm bij 20 cm bedraagt 5,5 · 10–7 Wb omdat het zich in het magnetisch veld van de aarde bevindt dat op die plaats een sterkte heeft van 4,0 · 10–5 T.

Welke hoek maakt de oppervlaktevector met de magnetische veldsterkte?

Kies het juiste antwoord en verklaar.

De flux door een ring met straal r waarvan de oppervlakte loodrecht staat op een homogeen magnetisch veld met veldsterkte B, is even groot als de flux door een ring …

a met dubbele straal in een veld dat twee keer zwakker is;

b met dubbele straal in een veld dat vier keer zwakker is;

c met dubbele straal in een veld dat twee keer sterker is;

d met dubbele straal in een veld dat vier keer sterker is.

Bestudeer de figuur. Hoe verandert de flux (met de figuur als beginsituatie)?

N Z

a De lus en de magneet bewegen niet

b De lus beweegt omhoog , de magneet staat stil.

c De lus beweegt niet, de magneet beweegt omhoog.

d De lus en de magneet bewegen samen omhoog.

e De lus verschuift naar rechts, de magneet staat stil.

f De lus wordt 90° gedraaid, de magneet staat stil.

g De lus wordt 180° gedraaid, de magneet staat stil.

Een lus bevindt zich tussen de benen van een hoefijzermagneet. Vul de uitspraken aan met ‘altijd’, ‘soms’, of ‘nooit’.

a De magnetische veldsterkte B staat loodrecht op het oppervlak van de lus.

b De magnetische veldsterkte B is evenwijdig met het oppervlak van de lus.

c De oppervlaktevector A staat loodrecht op het oppervlak van de lus.

d De oppervlaktevector A is evenwijdig met het oppervlak van de lus.

e De magnetische flux door het oppervlak is nul.

f De magnetische flux door het oppervlak verandert als je de lus verschuift.

g De magnetische flux door het oppervlak verandert als je de lus kantelt.

h De magnetische flux door het oppervlak verandert als je het oppervlak van de lus kleiner maakt.

AAN DE SLAG

De flux in een homogeen magnetisch veld in een spoel wordt opgemeten. Bestudeer de figuren.

a In welke situatie(s) ontstaat een inductiespanning?

b In welke situatie(s) ontstaat een inductiestroom?

Teken de zin van de inductiestroom in elke ring op de gevraagde momenten.

a De magnetische veldsterkte neemt toe.

b De staafmagneet beweegt van links naar rechts.

Een aluminium ring hangt in een homogeen magnetisch veld en draait met een constante hoeksnelheid.

Teken op één assenstelsel de Φ(t)-grafiek voor een volledige omwenteling (waarbij α de hoek is tussen A en B) in de gevraagde situaties.

©VANIN

c De lus passeert lijn 1, lijn 2 en lijn 3.

3 2 1

a De lus start zoals weergegeven op de figuur.

b De lus start een kwartslag naar rechts ten opzichte van de weergegeven situatie.

c De lus start zoals weergegeven op de figuur, de magnetische veldsterkte is verdubbeld.

d De lus start zoals weergegeven op de figuur, het oppervlak van de lus is verdubbeld.

REEKS

Door een spoel met 500 windingen met een doorsnede van 15,0 cm2 loopt een stroom van 8,25 A. De spoel is 10,0 cm lang. Bepaal de flux in deze spoel als …

a de spoel zich in lucht bevindt;

b in de spoel een kern wordt geplaatst met een relatieve permeabiliteit van 2 500.

Het oppervlak van een stroomvoerende spoel van 5,0 cm lang en 10 windingen (in lucht) kan vervormd worden. Met een fluxmeter die loodrecht op het homogene veld geplaatst wordt, registreer je onderstaande metingen.

meting 1meting 2

Je plaatst een staafmagneet op een draaibare schijf. De schijf begint te draaien vanuit de weergegeven positie en een omwenteling duurt 1,0 s.

a Welke verhouding bestaat er tussen de stroomsterkte door de spoel tijdens beide metingen?

b Hoe groot is de stroomsterkte in beide metingen?

c Hoe verandert de meting als de fluxmeter een hoek van 60° maakt met het magnetisch veld?

Een spoel is verbonden met een schakelaar en een bron. De spoel bevindt zich voor een metalen ring zoals op de figuur. Geef de zin van de (eventuele) inductiestroom in de onderstaande situaties.

Welke grafiek is correct?

A De schakelaar wordt gesloten.

B De schakelaar blijft gesloten.

C De schakelaar wordt geopend.

b Bepaal de frequentie waarmee het lampje knippert.

Een lus met een oppervlakte van 250 cm² staat loodrecht op de veldlijnen van een homogeen magnetisch veld met een magnetische veldsterkte van 0,300 T. De lus wordt in 0,20 s gedraaid tot een hoek van 30°.

a Bereken:

1 de flux door de lus in de beginpositie; 2 de flux door de lus in de eindpositie; 3 de inductiespanning.

b Kun je de inductiestroom berekenen? Verklaar.

Een vervormbare lus met een oppervlakte van 90 cm2 staat loodrecht op de veldlijnen van een sterk homogeen magnetisch veld met een magnetische veldsterkte van 1,00 T. De lus wordt vervormd tot ze nog een oppervlakte van 10 cm2 heeft. In welk tijdsinterval moet die vervorming gebeuren, opdat de gemiddelde inductiespanning over de lus 160 mV bedraagt?

(cm2)

AAN DE SLAG

Een spoel heeft 50 windingen met een oppervlakte van 30,0 cm2. Ze bevindt zich in een homogeen veld met een magnetische veldsterkte van 50,0 mT. De veldlijnen staan loodrecht op het oppervlak van de windingen. De magnetische veldsterkte wordt verviervoudigd in 20,0 ms. Hoe groot is de inductiespanning?

Je kunt een smartphone draadloos opladen. Als je de smartphone op de lader legt, wordt hij aangetrokken. Door welk fenomeen wordt de smartphone opgeladen? Verklaar.

a De magneet in de oplader sluit een elektrische kring met de smartphone en de netspanning.

b Door een spoel in de oplader vloeit een wisselstroom.

c Door een spoel in de oplader vloeit een gelijkstroom.

d Een magneet beweegt op en neer in een spoel in de oplader.

e In de oplader zit een batterij die opgeladen wordt door de netspanning.

REEKS

I toenemend

©VANIN

Je brengt een lus in de buurt van een stroomvoerende geleider. De kenmerken van de stroom in de stroomvoerende geleider zijn verschillend voor vijf situaties (zie figuur) en kunnen niet aangepast worden.

a In welke situatie(s) vloeit er een inductiestroom? Geef de stroomzin aan.

b Hoe kun je voor de andere situatie(s) een inductiestroom in tegenwijzerzin creëren?

I afnemend I constant I afnemend

I toenemend

Toon met SI-eenheden aan dat de eenheden volt en weber per seconde gelijk zijn aan elkaar.

Een spoel staat in een homogeen magnetisch veld, zodanig dat de as van de spoel een hoek maakt van 60° met de veldlijnen. Hoe moet je de spoel draaien opdat de flux zou verdubbelen? Toon aan.

Een winding beweegt met een constante snelheid zoals aangegeven in de figuur.

a Maak de Ф(x)-grafiek.

b Maak de I(x)-grafiek.

Wat zijn de gelijkenissen en de verschillen tussen een gelijkstroommotor en een generator?

Meer oefenen? Ga naar .

HOOFDSTUKSYNTHESE

Het aantal magnetische veldlijnen door een oppervlak beschrijf je met de grootheid magnetische flux

GROOTHEID

Wet van Lenz: de magnetische fluxverandering wekt een inductiestroom op zodat er een magnetische veldsterkte Bi opgewekt wordt die de fluxverandering tegenwerkt.

Als de magnetische flux door een oppervlak verandert, ontstaat een (inductie)spanning

Fluxverandering door verandering van:

• de grootte van de magnetische veldsterkte (B);

• de grootte van het oppervlak (A);

• de hoek tussen de magnetische veldsterkte B en de oppervlaktevector A (α en dus cos α).

In een lus of een spoel met N windingen veroorzaakt een fluxverandering ∆Φ een inductiespanning Ui = –N

(inductiewet van Faraday), die een inductiestroom I opwekt.

In een geleider zonder duidelijk pad: wervelstromen.

generator bewegingssensor

rem warmteontwikkeling wisselspanning

©VANIN

KERNFYSICA 02 THEMA

Kernreactoren spelen een belangrijke rol in onze elektriciteitsproductie. Ze halen meer en meer het nieuws als alternatief voor fossiele brandstoffen in de strijd tegen de klimaatopwarming. Ook in de medische wereld wordt vaak gebruik gemaakt van straling afkomstig van radioactieve kernen om diagnoses te stellen of kanker te behandelen. Nochtans hebben veel mensen schrik van alles wat met radioactiviteit te maken heeft.

` Wat bedoelt men precies met radioactiviteit?

` Worden radioactieve kernen door mensen gemaakt of komen ze ook in de natuur voor?

` Hoe kunnen we elektriciteit produceren door gebruik te maken van kernenergie?

` Hoe schadelijk is straling afkomstig van radioactieve kernen voor onze gezondheid?

We zoeken het uit!

VERKEN

• de bouw van een atoom omschrijven;

• de belangrijkste chemische elementen juist noteren;

• de kracht tussen (gelijksoortige) ladingen beschrijven.

• de bouw van een kern omschrijven;

• energieomzettingen beschrijven;

• voorbeelden geven van elektriciteitsopwekking met een dynamo in het dagelijkse leven.

©VANIN

• de bouw van een kern beschrijven en noteren;

• de stabiliteit van een kern beschrijven aan de hand van de krachten die in de kern werken;

• de vier fundamentele interacties en hun belangrijkste eigenschappen beschrijven;

• het verschil tussen natuurlijke en kunstmatige radionucliden beschrijven;

• de halveringstijd van radionucliden interpreteren.

• de uitdrukking E0 = m · c2 toelichten en toepassen;

• de stabiliteit van een kern beschrijven aan de hand van de specifieke rustenergie en de specifieke bindingsenergie;

• verklaren waarom er bij de fusie van lichte kernen en de splitsing van zware kernen enorme hoeveelheden energie vrijkomen;

• de werking van een kernsplitsingsreactor en de voor- en nadelen ervan beschrijven;

• de kracht en de problemen van kernfusie als energiebron beschrijven.

JE KUNT AL ...

JE LEERT NU ...

JE KUNT AL ...

• de bouw van een kern beschrijven;

• stabiele en instabiele kernen situeren op een nuclidenkaart;

• de rustenergie van een kern berekenen;

• het gedrag van geladen deeltjes in een elektrisch en magnetisch veld beschrijven.

• voorbeelden geven van radioactiviteit in het dagelijkse leven;

• het verschil tussen natuurlijke en kunstmatige radioactiviteit uitleggen;

• de kenmerken van de verschillende soorten ioniserende straling beschrijven;

• de halveringstijd van een kern interpreteren.

JE LEERT NU ...

• de begrippen ‘doordringend vermogen’ en ‘ioniserend vermogen’ toelichten en verbinden met de verschillende soorten verval;

• uitleggen waarom α-, β- en γ-straling voorbeelden van ioniserende straling zijn;

• de oorzaak van de verschillende soorten verval toelichten;

• de reactievergelijking voor de verschillende soorten radioactief verval weergeven;

• op de nuclidenkaart opzoeken hoe een nuclide vervalt.

• de impact van ioniserende straling op de mens beschrijven;

• beschermingsmaatregelen tegen ioniserende straling omschrijven;

• de verschillende grootheden en eenheden van ioniserende straling interpreteren en toepassen;

• de meest voorkomende bronnen van natuurlijke en kunstmatige ioniserende straling benoemen en beschrijven;

• een aantal medische toepassingen beschrijven.

HOOFDSTUK 1

Stabiele en instabiele kernen

De natuur dankt haar rijkdom aan de vele verschillende atomen die chemische bindingen aangaan en zo de wereld vormen. Atomaire elektronen en hun configuratie zijn bepalend voor hoe een atoom chemisch zal reageren. Het is echter de stabiliteit van de kern die bepaalt of een atoom kan bestaan of niet. De vraag ‘Welke atomen kunnen bestaan?’ is dus te herleiden tot de vraag ‘Welke kernen kunnen bestaan?’ of, nog concreter, ‘Uit hoeveel protonen en neutronen kan een kern bestaan en waarom?’. Dat is maar een van de vele vragen die kernfysici zich stellen en waarop je in dit eerste hoofdstuk een antwoord leert te geven. De kernfysica situeert zich namelijk op het (bijna) allerkleinste niveau (10–14 m), het niveau van de protonen en neutronen in kernen.

LEERDOELEN

M de bouw van een kern beschrijven en noteren

M de stabiliteit van een kern beschrijven aan de hand van de krachten die in de kern werken

M de vier fundamentele interacties en hun belangrijkste eigenschappen beschrijven

M het verschil tussen natuurlijke en kunstmatige radionucliden beschrijven

M de halveringstijd van radionucliden interpreteren

©VANIN

Nucleus is het Latijnse woord voor ‘kern’.

1 Hoe is een kern opgebouwd?

1.1 Samenstelling van de kern

In 1911 ontdekte Ernest Rutherford dat een atoom bestaat uit een kleine, positief geladen kern met daarrond atomaire elektronen, die in een bijna lege ruimte rond de kern draaien. Rond 1917 kon Rutherford voor het eerst een positief kerndeeltje isoleren en identificeren. Dat deeltje noemde hij een proton

Een proton is de kern van het eenvoudigste atoom, het waterstofatoom. Het heeft een positieve lading, die tegengesteld is aan de lading van het elektron. Zijn massa is ongeveer gelijk aan die van een waterstofatoom, maar is net iets kleiner omdat het waterstofatoom nog een atomair elektron bevat.

▲ Afb. 1 Voorstelling van een atoom. Een atoom bestaat uit een nuclide met protonen en neutronen en daarrond atomaire elektronen.

Het duurde tot 1932 voor James Chadwick een ander kerndeeltje, het neutron, kon isoleren en identificeren. Een neutron lijkt erg op een proton en heeft ongeveer dezelfde massa.

Zoals de naam aangeeft, is het echter elektrisch neutraal

Sindsdien stellen wetenschappers een kern voor als een samenvoeging van twee soorten deeltjes: positieve protonen en neutrale neutronen. Protonen en neutronen noem je ‘kerndeeltjes’ of nucleonen. Kernen noem je ook nucliden.

Kom in de video meer te weten over de ontdekking van het atoom, het proton en het neutron.

De atomaire elektronen bewegen in een wolk rond de kern. Ze verplaatsen zich niet willekeurig door die elektronenwolk, maar zijn verdeeld over een aantal schillen. In de chemie zijn die schillen van belang. In de kernfysica zijn enkel de protonen en neutronen in de kern belangrijk. Omdat de massa van de protonen en neutronen veel groter is dan de massa van de elektronen, bevat de nuclide bijna al de massa van het atoom.

ATOMAIR DEELTJE PLAATSSYMBOOL RUSTMASSA ELEKTRISCHE LADING

proton kern p+ 1,67262 · 10–27 kg +e = +1,60 · 10–19 C neutron kern n0

· 10–27 kg 0 elektron wolk e– 9,1095 · 10–31 kg –e = –1,60 · 10–19 C

Zowel het proton als het neutron werd ontdekt tijdens botsingsexperimenten.

• Rutherford bombardeerde stikstofgas met 4He-kernen. Hij detecteerde zuurstof en een nieuw deeltje: het proton.

• Chadwick bombardeerde beryllium met 4He-kernen. Hij detecteerde (naast andere deeltjes) het neutron.

4He-kern stikstof stikstof

4He-kern

▲ Afb. 2 De opstelling voor het botsingsexperiment van Rutherford

fluorescerend scherm protonen

microscoop

Chadwick ontving in 1935 de Nobelprijs voor zijn ontdekking van het neutron. Ook Rutherford kreeg de Nobelprijs, maar niet voor zijn ontdekking van het proton. Hij ontving de prijs al in 1908 voor ‘zijn onderzoek naar het uiteenvallen van elementen en de scheikunde van radioactieve substanties’.

Alle kernen bevatten zowel protonen als neutronen, behalve de waterstofkern. Die bestaat uit 1 proton.

• Het totale aantal nucleonen in de kern duid je aan met het massagetal . Dat getal noem je soms ook het nucleonental.

• Het protonental geeft het aantal protonen in de kern aan. In de chemie noem je Z het atoomnummer. In een neutraal atoom is het aantal atomaire elektronen gelijk aan het protonental Z. Daarom bepaalt het protonental om welk chemisch element het gaat. Zo heeft koolstof 6 protonen, stikstof 7 protonen, zuurstof 8 protonen, lood 82 protonen enzovoort.

• Het aantal neutronen van de nuclide wordt weergegeven door het neutronental . Er geldt: N = A – Z

proton

CONCEPTVRAAG

Wat zijn A, Z en N op afbeelding 1 op p. 188?

CONCEPTVRAAG

Wat ontbreekt er op afbeelding 4 om te kunnen spreken van een volledig 56Fe-atoom?

GROOTHEID SYMBOOL BETEKENIS FORMULE massagetal A aantal nucleonen N = A – Z

protonental Z aantal protonen neutronental N aantal neutronen

ATOOM

©VANIN

‘Femto’ is afgeleid van het Deense femten, dat ‘vijftien’ betekent. De term wordt pas sinds 1964 gebruikt.

KERN OF NUCLIDE positief geladen

NUCLEONEN

p+ = -

ELEKTRONENWOLK negatief geladen

n0 ELEKTRONEN e–

▲ Afb. 3 De opbouw van een atoom. In dit hoofdstuk focus je op de kern of nuclide.

De kern van element X met massagetal A en protonental Z noteer je vaak als A Z X:

massagetal element

protonental

Door de een-op-eenrelatie tussen het protonental en het chemisch element is het protonental Z overbodig in die notatie. Daarom kun je een kern ook noteren als AX.

VOORBEELD IJZERKERN

56 26Fe spreek je uit als ‘ijzer-56’. Dat staat voor een ijzerkern met 56 nucleonen (A = 56), waarvan 26 protonen (Z = 26) en 30 neutronen (N = 30). Je kunt ‘ijzer-56’ ook noteren als 56Fe.

▲ Afb. 4 Een 56Fe-kern

De afmetingen van nucleonen en de afstanden tussen nucleonen zijn van de grootteorde van 10–15 m. Je drukt ze meestal uit in de eenheid femtometer, die als symbool fm heeft: 1 fm = 10–15 m.

Elektronen zijn zeker duizend keer kleiner dan nucleonen. Dat is dezelfde verhouding als die tussen een speldenkop (1 mm) en een meter, of die tussen een meter en een kilometer.

: 10 000

©VANIN

• Een atoom bestaat uit een nuclide en atomaire elektronen. De nuclide bestaat uit Z protonen en N neutronen, waarbij Z het protonental en N het neutronental is. Protonen en neutronen noem je ook nucleonen. Een nuclide bevat A nucleonen, waarbij A het massagetal of nucleonental is. Er geldt: N

• De nuclide van element X met massagetal A en protonental Z noteer je vaak als A Z X of soms nog korter als AX

• De afmetingen van nucleonen en de afstanden tussen nucleonen zijn van de orde van 10–15 m. 10–15 m noem je ook een femtometer.

1.2 Isotope nucliden

Kernen die hetzelfde aantal protonen hebben, maar een verschillend aantal neutronen, noem je isotope nucliden of kortweg isotopen

Isotopen hebben dezelfde chemische eigenschappen, omdat ze hetzelfde aantal atomaire elektronen bezitten. Ze staan op dezelfde plaats in het periodiek systeem van de elementen. Natuurlijk helium kan bijvoorbeeld voorkomen als 4He en als 3He. Om de fysica van de kern te begrijpen, zijn isotopen echter wel van belang.

VOORBEELD NATUURLIJKE KOOLSTOFISOTOPEN

Koolstof bevat drie natuurlijke isotopen: 12C, 13C en 14C. Het percentage aan 14C is bijzonder klein, maar kan toch van belang zijn: die isotoop gebruiken wetenschappers om historische voorwerpen te situeren in de tijd. Zo werd de ouderdom van de mummie van Toetanchamon bepaald via de koolstof 14-dateringsmethode. De mummie dateert van (ongeveer) 1323 voor Christus.

NATUURLIJKE KOOLSTOFISOTOPEN

Het begrip ‘isotoop’ is een samentrekking van twee Griekse woorden: ἰσος (isos, ‘gelijk’) en τοπος (topos, ‘plaats’). Die samentrekking benadrukt dat de verschillende isotopen van een element dezelfde plaats innemen in het periodiek systeem.

Afb. 5 Het gouden grafmasker van Toetanchamon & Afb. 6 De kernen van drie koolstofisotopen

Isotope nucliden of isotopen zijn kernen met hetzelfde protonental Z, maar een verschillend neutronental N

1.3 De kleinste bouwstenen

In de jaren vijftig en zestig ontdekten fysici dat neutronen en protonen uit nog kleinere deeltjes zijn opgebouwd: de quarks. Voor zover wetenschappers tot nu toe weten, zijn quarks en deeltjes zoals het elektron niet samengesteld uit nog kleinere deeltjes. Daarom noem je ze fundamentele deeltjes of elementaire deeltjes

Er ontstond een nieuwe, fascinerende tak binnen de fysica: de elementaire deeltjesfysica.

©VANIN

Tak van de wetenschap

CHEMIE

KERNFYSICA

quark

▲ Afb. 7 De verschillende deeltjes in een atoom en hun afmetingen

VERDIEPING

Wil je meer weten over alle soorten deeltjes?

elektron

ELEMENTAIRE DEELTJESFYSICA

Ga dan naar .

Fundamentele of elementaire deeltjes zijn niet samengesteld uit nog kleinere deeltjes.

• Het elektron is een fundamenteel deeltje.

• Protonen en neutronen zijn samengesteld uit quarks. Protonen en neutronen zijn dus geen fundamentele deeltjes. Quarks zijn wel fundamentele deeltjes.

Wetenschappers onderzoeken de fundamentele deeltjes door in deeltjesversnellers protonen te versnellen tot ze bijna de lichtsnelheid bereiken, en ze dan met elkaar te laten botsen. De ‘brokstukken’ van die botsingen worden opgespoord door grote detectoren. Zowel de creatie van een protonenbotsing aan hoge snelheid, de detectie van de ‘brokstukken’, als de interpretatie van de experimentele gegevens in termen van fundamentele deeltjes is een waar huzarenstukje.

Een van de bekendste deeltjesversnellers is de Large Hadron Collider in CERN (Conseil Européen pour la Recherche Nucléaire), gelegen in Genève, Zwitserland.

©VANIN

▲ Afb. 8 Een deel van de Large Hadron Collider in CERN

video: Large Hadron Collider

2.1 Stabiele kernen op de nuclidenkaart

In de chemie gebruik je het periodiek systeem van de elementen (PSE). Atomen zijn er geordend volgens hun atoomnummer Z. De verschillende isotopen van één element zijn niet afzonderlijk opgenomen in het PSE.

Voor de kernfysica zijn de verschillende isotopen wel van belang. Wetenschappers ordenen ze op de zogenoemde nuclidenkaart. Dat is een grafiek met op de horizontale as het neutronental N en op de verticale as het protonental Z (soms ook omgekeerd). Alle kernen, gekarakteriseerd door N en Z, krijgen er hun unieke plaatsje. Isotopen van hetzelfde element hebben dezelfde waarde voor Z en staan daarom in dezelfde horizontale rij.

Sommige kernen zijn stabiel en zullen niet spontaan hun protonental Z of hun neutronental N veranderen. Andere kernen hebben te veel energie en zijn instabiel. Een instabiele kern kan spontaan naar een stabielere toestand overgaan door haar protonental Z en/of haar neutronental N aan te passen. De stabiele nucliden vormen de stabiliteitsband op de nuclidenkaart.

VOORBEELD SPONTAAN VERVAL VAN 146C NAAR 147N

146C is een instabiele kern. Ze vervalt spontaan tot 147N door een neutron om te zetten in een proton. 14N is wel een stabiele kern en zal haar protonen- en neutronental niet spontaan veranderen.

Wetenschappers kunnen bepaalde historische voorwerpen situeren in de tijd met behulp van 14C, juist doordat 14C instabiel is. Het aantal 14C-isotopen in die voorwerpen neemt af in functie van de tijd en is dus een maat voor de ouderdom van die voorwerpen.

andere deeltjes

©VANIN

C instabiel 14 6

nieuwe kern

N stabiel 14 7

▲ Afb. 9 Een instabiele 146C-kern vervalt spontaan tot een stabiele 147N-kern.

Grafiek 1 op de volgende pagina toont de stabiliteitsband op de nuclidenkaart: alleen de stabiele nucliden worden weergegeven. Later breiden we de nuclidenkaart uit met de instabiele nucliden.

Op de nuclidenkaart worden stabiele nucliden meestal voorgesteld met een zwarte stip of een zwart vakje.

• Nucliden met hetzelfde protonental Z, bijvoorbeeld 147Ni en 157Ni, staan in dezelfde rij.

• Nucliden met hetzelfde neutronental N, bijvoorbeeld 147Ni en 136C, staan in dezelfde kolom. Je kunt die voorbeelden zien op de groene uitvergroting van de grafiek.

▲ Grafiek 1 De stabiliteitsband op de nuclidenkaart geeft alle stabiele nucliden weer. Die worden voorgesteld door een zwarte stip. De oranje lijn stelt de rechte met vergelijking N = Z voor.

Uit de stabiliteitsband op de nuclidenkaart kun je een algemene tendens afleiden:

• Lichte stabiele kernen (Z < 20) bevatten (ongeveer) evenveel protonen als neutronen. De grafiek volgt bij benadering de rechte met vergelijking N = Z (zie uitvergroting in de blauwe cirkel op de grafiek). Voor die kernen geldt: N ≈ Z

126C, 136C, 147N en 157N zijn voorbeelden van lichte stabiele kernen. Voor die kernen geldt dat N en Z (ongeveer) gelijk zijn aan elkaar.

• Zwaardere stabiele kernen (Z > 20) bevatten meer neutronen dan protonen. De grafiek volgt de rechte met vergelijking N = Z niet meer. Voor die kernen geldt: N > Z. Er bestaan veel voorbeelden van dergelijke stabiele kernen: 10747Ag, 19779Au, 20882Pb …

CONCEPTVRAGEN

1 Bepaal voor de kernen 10747Ag, 19779Au en 20882Pb het neutronental , het protonental , het chemisch element en de plaats op de nuclidenkaart op .

2 Hoe kun je op de stabiliteitsband zien dat een element drie stabiele isotopen heeft?

3 Welk chemisch element hoort bij = 20?

4 Waarom staat 146C niet op de bovenstaande grafiek?

Stabiele kernen zijn kernen die niet spontaan hun protonental Z of hun neutronental N veranderen.

Instabiele kernen hebben te veel energie en gaan over naar een stabiele toestand door hun protonental Z en/of hun neutronental N aan te passen.

• Voor lichte stabiele kernen (Z < 20) geldt bij benadering: N ≈ Z.

• Voor zwaardere stabiele kernen (Z > 20) geldt: N > Z

CONCEPTVRAGEN

1 Voor afstanden tussen ≈ 0,5 fm en ≈ 2,5 fm is de sterke kernkracht negatief.

Wat betekent dat?

2 Voor afstanden groter dan ≈ 2,5 fm is de sterke kernkracht quasi 0.

Wat betekent dat?

2.2 De kernkrachten

Het is vreemd dat een verzameling protonen en neutronen een stabiele kern kan vormen. Alle protonen hebben immers dezelfde positieve elektrische lading en stoten elkaar dus af door de elektrische kracht FC = k ∙ |q1| ∙ |q2| r2 . Die kracht (~ 1 r2 ) wordt pas 0 op oneindig (zie groene curve op grafiek 2). Ze heeft een lang bereik. Bijgevolg werkt ze tussen alle protonen in een nuclide, ook als het om een grote nuclide met veel nucleonen gaat en de protonen ver uit elkaar zitten.

Een stabiele nuclide kan dan ook alleen maar bestaan als er nog een andere, aantrekkende kracht aanwezig is, die de nucleonen bij elkaar houdt. Omdat die kracht sterker is dan de elektrische kracht, wordt ze de sterke kernkracht genoemd.

Een belangrijke eigenschap van de sterke kernkracht is dat ze een kort bereik heeft. Grafiek 2 toont het verloop van de sterke kernkracht (rode curve). Ze is quasi 0 als de nucleonen zich op een afstand groter dan ≈ 2,5 fm van elkaar bevinden, en heeft dan geen invloed. Ze is sterk aantrekkend tussen nucleonen die op ongeveer 10–15 m (1 fm) van elkaar zitten, meer specifiek voor afstanden tussen ≈ 0,5 fm en ≈ 2,5 fm. Dat heeft als gevolg dat de sterke kernkracht in de kern enkel tussen naburige nucleonen aantrekkend is. Een nucleon (proton of neutron) ondervindt dus enkel de aantrekkingskracht van de naburige nucleonen, maar niet die van de nucleonen die verder zitten.

kracht (N)

AFSTOTING

©VANIN

In de video kom je meer te weten over de sterke kernkracht.

neutron proton

sterke kernkracht

elektrische kracht

AANTREKKING

elektrische kracht

1 2 3 4

sterke kernkracht

typische afstand tussen nucleonen

afstand tussen nucleonen (10–15 m)

▲ Grafiek 2 De elektrische kracht en sterke kernkracht in een kern

A De sterke kernkracht (rode vectorpijlen) en de elektrische kracht (groene vectorpijlen) zijn afstotend. De protonen (rode bolletjes) en neutronen (grijze bolletjes) stoten elkaar af.

B De aantrekkende sterke kernkracht (rode vectorpijlen) tussen de nucleonen is groter dan de afstotende elektrische kracht (groene vectorpijlen) tussen de protonen.

C De sterke kernkracht is verwaarloosbaar klein. De protonen stoten elkaar af door de elektrische kracht (groene vectorpijlen).

VERDIEPING

Op grafiek 2 kun je ook zien dat de sterke kernkracht afstotend is als de nucleonen zich op minder dan ≈ 0,5 fm van elkaar bevinden. Dat heeft als gevolg dat de nucleonen in een kern niet oneindig dicht bij elkaar kunnen komen. Ze plakken niet tegen elkaar.

Kernen met een laag protonental (Z < 20) hebben ongeveer evenveel neutronen als protonen nodig om stabiel te zijn: N ≈ Z. Alle protonen stoten elkaar af door de elektrische kracht. Die kernen zijn klein (orde van een paar fm) en de afstanden tussen de nucleonen beperkt. De nucleonen (protonen en neutronen) trekken elkaar aan als gevolg van de sterke kernkracht en houden de kern bij elkaar.

Voor zwaardere nucliden (Z > 20) zijn er meer neutronen dan protonen nodig. Omdat er meer nucleonen in zo’n kern aanwezig zijn, vergroot hun onderlinge afstand. Alle protonen stoten elkaar af door de elektrische kracht, die een lang bereik heeft. De sterke kernkracht is echter enkel aantrekkend tussen de naburige nucleonen. Opdat de kern toch bij elkaar blijft, zijn er extra neutronen nodig: N > Z

Wanneer Z > 83, wordt de elektrische afstotingskracht zo sterk dat de sterke kernkracht de afstotende elektrische kracht niet meer kan compenseren, ongeacht hoeveel neutronen er nog bij komen. De kernen vallen uit elkaar en zijn instabiel

VOORBEELD DE KERNKRACHTEN IN DRIE VERSCHILLENDE KERNEN

4He (helium-4) bevat 2 protonen en 2 neutronen.

De 2 protonen stoten elkaar af vanwege de elektrische kracht.

Alle nucleonen (protonen en neutronen) zijn buren van elkaar en trekken elkaar aan vanwege de sterke kernkracht.

De sterke kernkracht zorgt ervoor dat de 4 nucleonen samen een stabiele 4He-kern vormen.

127Ag (zilver-127) bevat 47 protonen en 80 neutronen.

Alle 47 protonen stoten elkaar af vanwege de elektrische kracht.

De sterke kernkracht werkt enkel tussen de nucleonen (protonen en neutronen) die buren zijn van elkaar.

Opdat de kern toch bij elkaar blijft, zijn er meer neutronen (N = 80) dan protonen (Z = 47).

238U (uranium-238) bevat 92 protonen en 146 neutronen.

Alle 92 protonen stoten elkaar af vanwege de elektrische kracht.

De sterke kernkracht werkt enkel tussen de nucleonen (protonen en neutronen) die buren zijn van elkaar.

De sterke kernkracht heeft een kort bereik en kan de kern niet bij elkaar houden. 238U is instabiel.

De stabiliteit van een atoomkern wordt bepaald door de aantrekkende sterke kernkracht tussen de nucleonen enerzijds en de afstotende elektrische kracht tussen de protonen anderzijds. Het evenwicht daartussen wordt bepaald door het aantal protonen en neutronen in de kern.

Neutronen zijn een bindmiddel voor de kern, net zoals maïzena een bindmiddel is voor saus. Maïzena werkt niet als je er te veel van gebruikt. Dan klontert de saus en valt ze uit elkaar. Ook op nucleair niveau is een kern instabiel als ze te veel neutronen bevat.

Loodkernen (chemisch symbool: Pb) zijn de op een na zwaarste stabiele kernen, met protonental Z = 82. Dat zorgt ervoor dat Pb een grote massadichtheid heeft. Lood wordt al sinds 5000-4500 voor Christus gebruikt omdat het wijdverspreid op aarde voorkomt en eenvoudig kan worden bewerkt. De Romeinen gebruikten erg veel lood. Ze maakten er van alles mee, van aquaducten tot kookgerei.

©VANIN

Dat leidde bij veel Romeinse burgers tot gezondheidsproblemen als gevolg van loodvergiftiging. Vandaag gebruikt men Pb vanwege zijn grote massadichtheid onder andere als bescherming tegen straling die het gevolg is van radioactief verval.

2.3 De vier fundamentele interacties

De sterke kernkracht is een veldkracht. In de natuur bestaan er vier soorten veldkrachten. Je noemt ze ook de fundamentele krachten. Ondertussen heb je al kennisgemaakt met de gravitatiekracht, de elektromagnetische krachten en de sterke kernkracht. Er bestaat nog een vierde soort veldkracht, namelijk de zwakke kernkracht.

Als deeltjes krachten uitoefenen op elkaar, wil dat zeggen dat ze met elkaar interageren. Zo is er bijvoorbeeld interactie tussen elektrische ladingen die een elektrische kracht uitoefenen op elkaar. Daarom spreek je in de fysica van de kleinste deeltjes ook over de vier fundamentele interacties.

Je krijgt hier een kort overzicht van de vier fundamentele interacties met hun belangrijkste eigenschappen en de rol die ze spelen binnen de kern.

1 De gravitationele interactie is verbonden met de gravitatiekracht. Het gaat om de aantrekking tussen massa’s. In de sterrenkunde is de gravitationele interactie belangrijk, omdat sterren en planeten grote massa’s hebben. Van alle interacties is de gravitationele interactie echter de zwakste. Ze heeft wel, net zoals de elektromagnetische interactie, een lang bereik. In een nuclide is de gravitationele interactie verwaarloosbaar, omdat de nucleonen erg kleine massa’s hebben.

2 Zowel elektrische als magnetische krachten werken enkel op geladen deeltjes. Ze zijn uitingen van de elektromagnetische interactie. De elektromagnetische interactie heeft net zoals de gravitationele interactie een lang bereik, maar ze is veel sterker. In een nuclide is de elektromagnetische interactie belangrijk, omdat ze voor de afstoting tussen protonen zorgt.

3 De sterke interactie houdt de protonen en neutronen bij elkaar in de kern. Het gaat in feite om een wisselwerking tussen de quarks, waaruit zowel protonen als neutronen zijn samengesteld. De interactie werkt niet in op bijvoorbeeld elektronen. De sterke interactie tussen de quarks is zo sterk dat ze ook buiten het nucleon voelbaar is. Het is de sterkste interactie tussen deeltjes, maar ze heeft wel een kort bereik

▲ Afb. 13

4 De zwakke interactie vindt plaats tussen alle materiedeeltjes (quarks, elektronen …). Net zoals de sterke interactie is de zwakke interactie enkel zichtbaar op het niveau van de kern en de elementaire deeltjes. Ze is sterker dan de gravitationele interactie, maar zwakker dan de elektromagnetische interactie. Net zoals de sterke interactie heeft ze een kort bereik De zwakke interactie is verantwoordelijk voor de omzetting van protonen in neutronen en omgekeerd. Daarover leer je meer in hoofdstuk 3.

Zoals je eerder al leerde, zijn het de elektromagnetische interactie en de sterke interactie die samen bepalen of de nucleonen in een nuclide bij elkaar blijven of niet.

©VANIN

Materiedeeltjes zijn de deeltjes waaruit materie is samengesteld, bijvoorbeeld quarks of elektronen. Niet alle deeltjes zijn materiedeeltjes. Zo is het foton geen materiedeeltje. Licht bestaat uit fotonen.

De vier fundamentele interacties zijn verbonden met de vier soorten veldkrachten in de natuur.

INTERACTIE

gravitationeledeeltjes met een massa langheel zwak elektromagnetischedeeltjes met een lading langsterk sterke quarks kortheel sterk zwakke alle materiedeeltjes (quarks, elektronen …) kortzwak

VERDIEPING

Vaak stellen wetenschappers de fundamentele interacties voor in zogenoemde feynmandiagrammen. Op afbeelding 14 zie je een feynmandiagram voor twee elektronen die elkaar afstoten vanwege de elektromagnetische interactie. In zo’n diagram worden de deeltjes voorgesteld door pijlen en de interacties door lijntjes die golvend zijn voor de elektromagnetische en de zwakke interactie, en door spiraalvormige lijntjes voor de gravitationele en de sterke interactie.

elektronen na de interactie

elektronen voor de interactie interactie

▲ Afb. 14 Feynmandiagram voor twee elektronen die elkaar afstoten vanwege de elektromagnetische interactie

3 Welke stabiele en instabiele kernen bestaan er?

De stabiliteit van een kern wordt in hoge mate bepaald door het protonental Z en het neutronental N. Zowel een teveel aan protonen als een teveel aan neutronen leidt tot instabiele kernen. Ze zullen hun protonental Z en/of hun neutronental N veranderen en zo tot een nieuwe kern met een andere samenstelling vervallen. Dat noem je radioactief verval. Een instabiele nuclide wordt daarom soms ook een radionuclide genoemd. Door radioactief te vervallen, verlaagt de radionuclide haar energie. Het energieverschil komt vrij doordat de nuclide straling uitzendt in de vorm van deeltjes of elektromagnetische golven (radiation in het Engels).

VOORBEELD HET RADIOACTIEVE VERVAL VAN 8BE

8Be (beryllium-8) is een uiterst instabiele radionuclide. Ze komt van nature niet op aarde voor, maar is wel in kleine hoeveelheden in sterren te vinden. 8Be vervalt tot 4He en doet dat door een andere 4He-kern uit te stoten. (Reken maar na!)

Kernen die vervallen door een 4He-kern uit te stoten, krijgen meestal een gele kleur op de nuclidenkaart (zie grafiek 3).

8Be 4

4He 2 instabiel

stabiel

▲ Afb. 15 8Be vervalt door een stabiele 4He-kern uit te stoten. Er blijft een stabiele 4He-kern achter.

Voor alle elementen tot en met 83Bi is er minstens één stabiele isotoop, met uitzondering van 43Tc (technetium) en 61Pm (promethium). Alle nucliden met Z > 83 zijn instabiel.

De elementen tussen 84Po (polonium) en 92U (uranium) bevatten natuurlijke radionucliden.

Dat zijn radionucliden die in de natuur voorkomen en niet het gevolg zijn van menselijke activiteit. Een ander bekend voorbeeld van een natuurlijke radionuclide is 14C.

Alle isotopen met Z ≥ 93 zijn door de mens gemaakt in laboratoria. Dat zijn allemaal kunstmatige radionucliden.

Er bestaan zo’n 280 stabiele nucliden, 70 natuurlijke radionucliden en meer dan 2 500 kunstmatig geproduceerde radionucliden.

Gebruik de applet om zelf stabiele en instabiele kernen (en atomen) te bouwen.

VOORBEELD NATUURLIJKE RADIONUCLIDEN

De aardkorst bevat verschillende natuurlijke radionucliden, bijvoorbeeld 238U (uranium-238), 232Th (thorium-232) en 40K (kalium-40).

In kerncentrales gebruikt men natuurlijk uraniumerts in

©VANIN

VOORBEELD KUNSTMATIGE RADIONUCLIDEN

Kunstmatige radionucliden worden soms aangemaakt voor wetenschappelijke doeleinden.

Ze hebben echter vaak ook een praktisch nut. Zo gebruikt men in de medische wereld veel kunstmatige radionucliden, onder andere voor medische beeldvorming en voor de behandeling van kanker. Voorbeelden zijn 18F (fluor-18) en 131I (jodium-131).

De volledige nuclidenkaart (grafiek 3) bevat alle stabiele en instabiele nucliden. De stabiele nucliden worden voorgesteld door zwarte vakjes, de instabiele nucliden door gekleurde.

Nucleonen boven de stabiliteitsband hebben te veel protonen in verhouding tot het aantal neutronen om stabiel te zijn. Ze zetten een proton om in een neutron en worden op de nuclidenkaart voorgesteld in het blauw (bijvoorbeeld 18F).

Nucleonen onder de stabiliteitsband hebben te veel neutronen in verhouding tot het aantal protonen om stabiel te zijn. Ze zetten een neutron om in een proton en worden op de nuclidenkaart voorgesteld in het roze (bijvoorbeeld 40K en 131I).

Elke kleur op de nuclidenkaart staat symbool voor de manier waarop de instabiele kern vervalt.

Tijdens experimenten ontdekken wetenschappers nog altijd nieuwe radioactieve isotopen. De nuclidenkaart wordt dan ook regelmatig aangepast aan de recentste status van het wetenschappelijk onderzoek.

▲ Afb. 16 Aeschyniet is een mineraal dat yttrium, cerium, calcium, thorium, niobium, titanium, zuurstof en waterstof bevat. Omdat natuurlijk thorium radioactief is, is ook aeschyniet radioactief. Je vindt het mineraal onder andere in de Alpen.

▲ Afb. 17

verrijkte vorm.

▲ Afb. 18 Voor medische doeleinden gebruikt men vaak kunstmatige radionucliden.

©VANIN

stabiele kern

instabiele kern

▲ Grafiek 3 De volledige nuclidenkaart. Stabiele nucliden worden in het zwart voorgesteld, radionucliden met een kleur. De verschillende kleurencodes geven de verschillende soorten radioactief verval weer. Daarover leer je meer in hoofdstuk 3. In professionele labo’s zul je de nuclidenkaart in deze vorm en met dezelfde kleurencodes terugvinden.

CONCEPTVRAAG

Wat is het verband tussen grafiek 1 (op p. 195) en grafiek 3?

In de natuur bestaan er stabiele isotopen en natuurlijke radionucliden

In laboratoria maakt men ook kunstmatige radionucliden. Radionucliden zijn instabiele kernen die bij radioactief verval straling uitzenden.

4.1 De halveringstijd

In de nucleaire geneeskunde worden radionucliden gebruikt die na enkele uren of dagen bijna allemaal vervallen zijn.

Radionucliden in radioactief afval worden als kortlevend beschouwd als de helft ervan in minder dan 30 jaar vervalt. Na 300 jaar zijn bijna alle kortlevende radionucliden vervallen.

Het radioactief verval van 14C wordt gebruikt om voorwerpen van duizend tot enkele duizenden jaren oud te dateren. Rotsen van 1 miljoen tot 4,5 miljard oud worden gedateerd door middel van het radioactief verval van 238U.

Elke instabiele nuclide vervalt naar een stabielere nuclide door radioactief verval. Voor vele toepassingen is het belangrijk om te weten hoe lang het duurt vooraleer de helft of bijna alle radionucliden vervallen zijn.

In een stof vervallen niet alle nucliden op hetzelfde ogenblik, ook niet als het om nucliden van dezelfde soort (zelfde Z en N) gaat die op hetzelfde moment gevormd werden. Het radioactief verval van instabiele nucliden is een statistisch proces: je kunt niet voorspellen wanneer een bepaalde nuclide zal vervallen, maar wel hoe een groot aantal nucliden zich zal gedragen. Het aantal instabiele nucliden als functie van de tijd van een groot aantal nucliden gedraagt zich altijd volgens hetzelfde patroon: hun aantal neemt exponentieel af als functie van de tijd.

Het enige verschil tussen die patronen van de verschillende soorten nucliden (verschillende Z en/of verschillende N) is de halveringstijd, ook wel halfwaardetijd genoemd, waarmee een nuclide vervalt. De halveringstijd T1/2 van een kern is de tijdsduur waarin de helft van het oorspronkelijk aantal nucliden vervalt. Is T1/2 de halveringstijd van een bepaalde nuclide, dan heeft deze nuclide 50 % kans om binnen die tijdsduur T1/2 te vervallen. Elke nuclide heeft een eigen specifieke halveringstijd.

instabiele kernen

vervallen kernen

Een statistisch proces is een proces waarbij je geen voorspellingen kunt doen over een individuele gebeurtenis, maar wel over een heel groot aantal gebeurtenissen. Dat komt omdat het geheel van een heel groot aantal gebeurtenissen zich altijd volgens eenzelfde patroon gedraagt.

08 LABO

Bergen is het veilig opslaan van radioactief afval voor huidige en toekomstige generaties.

Om het aantal overgebleven instabiele nucliden op een willekeurig tijdstip t te kennen, moet je het voorschrift van de van de dalende N(t)-functie kennen. Om het voorschrift te vinden, bestudeer je de regelmaat in het aantal overgebleven instabiele nucliden N op tijdstippen die veelvouden (n) zijn van de halveringstijd.

TIJDSTIP

t = 0 = 0 · T1/2

t = 1 · T1/2

t = 2 · T1/2

0 = N0 20

0 2 = N0 21

0 4 = N0 22

©VANIN

Uit de tabel blijkt dat het aantal overgebleven instabiele nucliden N(t) op een tijdstip

t = n · T1/2 gelijk is aan N(t) = N0 2n waarbij n = t T1/2

Daarmee wordt de uitdrukking voor het aantal overgebleven instabiele nucliden:

(t) = N0 2n = N0 2t/T1/2 = N

CONCEPTVRAGEN

• Welke fractie van de oorspronkelijke hoeveelheid radionucliden is er na drie halveringstijden nog over?

• Hoe lang duurt het vooraleer alle radionucliden van een radioactief materiaal zijn vervallen? Leg uit.

Vaak wil je weten wanneer alle radionucliden vervallen zijn. In theorie kan dat oneindig lang duren. Bij het bergen van radioactief afval wordt er vanuit gegaan dat het afval na 10 halveringstijden niet meer radioactief is. Dat wilt zeggen dat de resterende radioactiviteit na 10 halveringstijden minder is dan de natuurlijke radioactiviteit in de omgeving.

GROOTHEID MET SYMBOOL

EENHEID MET SYMBOOL halveringstijd T1/2 seconde (kan ook in: minuten, uren, dagen, jaren) s (kan ook in: m, h, d, y)

N(t) = N0 · 2–t/T1/2

met N(t) het aantal instabiele nucliden op het tijdstip t; N0 het aantal instabiele nucliden op t = 0; T1/2 de halveringstijd.

VOORBEELD KOOLSTOFDATERING

Koolstofdatering is een vorm van datering waarbij je de natuurlijke radioactiviteit van de nuclide 146C gebruikt om de ouderdom van (ooit) levend materiaal te bepalen.

Ontstaan van 14 6C in de atmosfeer

In de atmosfeer komt een kleine hoeveelheid 146C voor. Deze koolstofisotoop ontstaat als gevolg van kosmische straling. Dat zijn deeltjes die vanuit het universum invallen op de atmosfeer rond de aarde.

Sommige van die deeltjes komen van de zon. Die deeltjes zorgen mee voor lichteffecten zoals het noorderlicht. Ze hebben echter te weinig energie om bij te dragen aan de vorming van 146C. De hoogenergetische deeltjes van de kosmische straling ontstaan elders in ons universum. Ze zijn verantwoordelijk voor de vorming van 146C door te botsen met kernen van atomen in de atmosfeer. Daarbij komen neutronen vrij die op hun beurt kunnen botsen met de 147N-kernen in de atmosfeer. Bij botsingen van een neutron met een 147N-kern wordt 146C gevormd. n + 147N → 146C + p

Radioactief verval van 14 6C 146C vervalt terug naar 147N met een halveringstijd van 5 730 jaar.

Evenwicht tussen de vorming en het radioactief verval van 14 6C Omdat er ongeveer evenveel 146C-kernen in de atmosfeer gevormd worden dan er vervallen, is de hoeveelheid 146C in de atmosfeer al vele duizenden jaren min of meer constant.

andere deeltjes

©VANIN

14 6C in levende wezens

Levende wezens absorberen CO2 uit de lucht. De natuurlijke koolstof in deze molecule bestaat voor 98,9 % uit 126C (stabiele kern), voor 1,1 % uit 136C (stabiele kern) en voor 0,000 000 000 1 % uit 146C. Zolang planten of bomen in leven zijn, absorberen ze CO2. Mensen en dieren eten planten en nemen op die manier koolstof op. Omdat de verhouding van 146C en 126C in de lucht min of meer constant blijft, blijft de verhouding van die isotopen ook in levende organismen min of meer constant. Sterft het organisme, dan neemt de hoeveelheid 146C omwille van zijn radioactief verval af, terwijl de hoeveelheid 126C constant blijft.

Datering met 14 6C

Uit de verhouding 146C 126C van een organisme kun je bepalen hoe lang geleden het organisme gestorven is. Is de verhouding 146C 126C in een stuk hout of een bot bijvoorbeeld de helft van de verhouding in een levende boom of dier, dan is het stuk hout of het bot ongeveer 5 730 jaar oud.

▲ Afb. 23 Vorming van 14C

▲ Afb. 24

Radioactief verval van 14C

neutronen botsen met

kosmische straling botsingen in de atmosfeer VORMING 14C

3 000 jaar oud veel straling

▲ Afb. 25 Schematische voorstelling van koolstofdatering

©VANIN

000 jaar oud weinig straling

De datering van Ötzi

Op die manier werd bijvoorbeeld bepaald wanneer Ötzi leefde. Dat is een gemummificeerd lijk dat in 1991 door enkele bergwandelaars in de Alpen ontdekt werd. De verhouding 146C 126C in Ötzi was ongeveer 53 % van die in levende organismen. Dat laat toe om te schatten wanneer Ötzi ongeveer leefde:

N(t) = N0 · 2–t/T1/2

N(t) N0 = 2–t/T1/2

0,53 = 2–t/5 730 jaar

log2 0,53 = – t 5 730 jaar t = –5 730 jaar · log2 0,53 = –5 730 jaar · log 0,53 log 2 = 5 248 jaar

Ötzi leefde 5 248 jaar geleden, dus rond 3200 voor Christus.

Controle: in de literatuur vinden we dat Ötzi tussen 2900 en 3400 voor Christus leefde, afhankelijk van de bron.

Uranium-looddatering en kalium-argondatering

De halveringstijd van 14C is te kort om rotsen van miljoenen tot miljarden jaren oud te kunnen dateren. Geologen maken daarom gebruik van het radioactief verval van 238U en 40K (kalium-40) met een halveringstijd van respectievelijk 4,5 miljard jaar en 1,25 miljard jaar.

vrije

▲ Afb. 26 Reconstructie (links) en mummie (rechts) van Ötzi in het Zuid-Tiroler Archeologiemuseum in Bolsonaro, Italië.

Instabiele kernen vervallen volgens de radioactieve vervalwet: N(t) = N0 · 2–t/T1/2

met N(t) het aantal instabiele nucliden op het tijdstip t; N0 het aantal instabiele nucliden op t = 0; T1/2 de halveringstijd.

De halveringstijd is gedefinieerd als de tijdsduur waarin 50 % van het oorspronkelijk aantal instabiele kernen vervallen

Vaak wordt als vuistregel gehanteerd dat radioactief materiaal na tien halveringstijden niet meer radioactief is.

4.2 Het verband tussen de halveringstijd en de stabiliteit van kernen

©VANIN

▲ Afb. 27 Voorbeelden van kernen met verschillende halveringstijden

Halveringstijden variëren van vele miljarden jaren tot microseconden (10-6 s).

• Stabiele kernen zijn kernen die een halveringstijd hebben die zo lang is, dat tot nog toe geen radioactief verval van die kernen werd waargenomen.

• Sommige nucliden hebben halveringstijden die zo lang zijn, dat ze dikwijls als stabiel beschouwd worden. Voorbeelden hiervan zijn 209Bi met een halveringstijd van 1,9 · 1019 jaar, de wolfraamisotopen 180W, 182W, 183W, 184W en 186W met halveringstijden van meer dan 1018 jaar en 124Xe met een halveringstijd van 1,8 · 1022 jaar. Die halveringstijden zijn meer dan een miljard keer groter dan de leeftijd van ons heelal, namelijk 13,8 miljard jaar. De vraag is of elke kern ooit zal vervallen als je maar lang genoeg wacht.

• Instabiele kernen zijn kernen die als geheel zijn waargenomen en waarvan ook het radioactief verval is waargenomen. Hun halveringstijd is dus kort genoeg om radioactief verval tijdens de levensduur van het heelal te kunnen waarnemen, maar lang genoeg om de radionucliden als geheel, dus voor hun verval, te kunnen waarnemen. De bovengrens voor de halveringstijd van een instabiele kern wordt soms gelegd op een aantal keren de levensduur van ons universum, zijnde een aantal keren 13,8 miljard jaar. Is de halveringstijd langer, dan wordt de kern soms toch als stabiel beschouwd. De ondergrens is van de orde van (tienden van) milliseconden.

• Hoe korter de halveringstijd, hoe instabieler de kern. Extreem zware kernen of kernen met extreem veel protonen in verhouding tot het aantal neutronen of kernen met extreem veel neutronen in verhouding tot het aantal neutronen hebben heel korte halveringstijden. Je vindt ze aan de randen van de nuclidenkaart terug.

• Hoe langer de halveringstijd van een kern, hoe stabieler de kern.

• Hoe korter de halveringstijd van een kern, hoe instabieler de kern.

REEKS

Welke kenmerken onderscheiden de verschillende elementen in het PSE?

(Er kunnen meerdere antwoorden juist zijn.)

a het aantal elektronen in de kern

b het aantal atomaire elektronen in het neutrale atoom

c het aantal protonen in de kern

d het aantal neutronen in de kern

e het totale aantal kerndeeltjes

Bepaal voor de nuclide 226Ra:

a het nucleonental;

b het protonental;

c het neutronental.

Bepaal voor de nuclide 167X:

a het aantal nucleonen;

b het aantal protonen;

c het aantal neutronen.

Welk chemisch element is X?

Rangschik de nucliden 29P, 27Si, 28Si, 29Si en 27Al:

a volgens toenemend aantal nucleonen;

b volgens toenemend aantal protonen;

c volgens toenemend aantal neutronen.

Een nuclide van element X is opgebouwd uit 29 protonen en 25 neutronen.

a Uit hoeveel nucleonen bestaat die nuclide?

b Welk chemisch element is X?

c Is de nuclide stabiel of instabiel? Verklaar.

12C (koolstof-12) en 56Fe (ijzer-56) zijn twee stabiele nucliden.

12C heeft 6 protonen en 6 neutronen.

56Fe heeft 26 protonen en 30 neutronen.

Waarom heeft stabiel ijzer meer neutronen dan protonen en stabiele koolstof niet?

De enige stabiele kernen met meer protonen dan neutronen zijn 1 1H en 32He.

Waarom is Z > N zo zeldzaam?

Waarom valt een loodkern met 82 protonen niet uit elkaar?

a De positief geladen protonen en de negatief geladen neutronen houden elkaar in evenwicht.

b De positief geladen protonen en de negatief geladen atomaire elektronen houden elkaar in evenwicht.

c Protonen hebben geen lading binnen een kern.

d Ladingen voelen geen elektrische kracht binnen een kern.

e De gravitatiekracht houdt de protonen en neutronen bijeen.

f De sterke kernkracht houdt de protonen en neutronen bijeen.

Wie heeft gelijk? Verklaar je keuze.

De sterke kernkracht zorgt voor aantrekking tussen naburige protonen in een kern.

De sterke kernkracht zorgt voor afstoting tussen naburige protonen in een kern.

De sterke kernkracht zorgt voor afstoting tussen protonen als ze ver van elkaar zitten en niet elkaars buren zijn.

Vul de uitspraken aan met ‘altijd’, ‘soms’ of ‘nooit’.

a Kernen met een verschillend protonental Z hebben een verschillend nucleonental A.

b Het protonental Z is gelijk aan het aantal atomaire elektronen van een neutraal atoom.

c De sterke kernkracht tussen twee protonen is sterker dan de elektrische kracht tussen twee protonen.

d De gravitatiekracht is sterk genoeg om de nucleonen van de kern bij elkaar te houden.

e Radionucliden ontstaan als gevolg van menselijke activiteiten.

Bestudeer een stukje van de nuclidenkaart op de afbeelding.

a Noteer de stabiele isotopen van:

1 xenon; 2 jood.

b Geef een voorbeeld van:

1 een stabiele isotoop;

2 een nuclide die radioactief vervalt door een proton om te zetten in een neutron;

3 een nuclide die radioactief vervalt door een neutron om te zetten in een proton.

Op de grafiek staan het aantal instabiele kernen van drie soorten nucliden als functie van de tijd.

Rangschik de volgende grootheden voor de drie nucliden:

Rangschik het percentage overgebleven nucliden in volgende situaties van klein naar groot.

Zoek de ontbrekende gegevens in tabel 3 op p. 289-294.

a 22688Ra na 10 jaar

©VANIN

a de halveringstijd.

b het aantal overgebleven nucliden na twee minuten.

c het percentage verdwenen nucliden na twee minuten.

Je beschikt over 16 kg radioactief materiaal met een halveringstijd van 30 jaar. Hoeveel materiaal is nog radioactief na 90 jaar? Verklaar je antwoord.

b 21483Bi na 12 minuten

c 32 15P na 70 dagen

Vier klasgenoten bespreken een documentaire die ze zagen over Ötzi. Ötzi, de ijsmummie die door twee Duitse amateurbergbeklimmers op 19 september 1991 werd gevonden in de Italiaanse Ötzaler Alpen, is de oudste menselijke mummie die in Europa is gevonden. Met behulp van de koolstof-14 methode, heeft men kunnen bepalen wanneer deze man geleefd heeft. Wie heeft gelijk?

a Bart: “Koolstof-14 heeft een halfwaardetijd van 5 730 jaar. Dus met deze methode kun je geen uitspraak doen over de ouderdom als die groter is dan 11 460 jaar.”

b Karen: “Met deze methode kun je tot 50 000 jaar een relatief nauwkeurige datering doen.”

c Hector: “Volgens mij kun je enkel een zinnige datering doen als de ouderdom niet groter is dan 5 730 jaar.”

d Suzanne: “Ik had begrepen dat men niet Ötzi zelf heeft gebruikt voor de ouderdomsbepaling, maar wel de koperen bijl die hij bij zich had.”

REEKS

Twee protonen bevinden zich op een afstand van 1,2 fm van elkaar.

a Bereken de grootte van de coulombkracht en de gravitatiekracht die de protonen op elkaar uitoefenen.

b Is de gravitatiekracht sterk genoeg om de protonen bij elkaar te houden? Verklaar.

Toen de nazi’s tijdens de Tweede Wereldoorlog Noorwegen bezetten, kregen ze meteen ook toegang tot de enige Europese fabriek die zwaar water kon produceren: de centrale in Vemork, nabij het plaatsje Rjukan. In 1943 slaagden Noorse verzetsleden erin om de fabriek te saboteren, een erg gewaagde actie die later ook verfilmd werd.

Bestudeer de eigenschappen van zwaar water en superzwaar water.

Zoek de nodige informatie op.

a Geef de molecuulformule en het structuurmodel van:

1 gewoon water;

2 zwaar water;

3 superzwaar water.

b Welke uitspraken zijn correct? Verbeter de foute uitspraken.

1 Zwaar water is een vorm van water.

In levend materiaal is de verhouding van 146C ten opzichte van 126C gelijk aan 1 op 1,0 · 1012. Bij een Egyptische mummie waarvan men de leeftijd onderzoekt, blijkt de verhouding 0,60 op 1,0 · 1012. Maak een schatting van de leeftijd van die mummie. Controleer grafisch.

In 1950 werd bij Silkeborg (Denemarken) een veenlijk (de Man van Tollund) gevonden. Zoek op wanneer deze man leefde. Bepaal daarmee de verhouding 146C ten opzichte van 126C die men bij de datering constateerde.

REEKS

In het Excelbestand op iDiddit vind je twaalf reeksen nucliden.

De leerkracht verdeelt de klas in twaalf groepjes. Elk groepje neemt een reeks nucliden voor zijn rekening.

a Voer de Excelopdracht uit voor jouw reeks data.

b Breng de data van de twaalf reeksen samen in het tabblad ‘Alle data’ en voer de Excelopdracht uit.

c Vergelijk de bekomen grafieken met de stabiliteitsband van de nuclidenkaart op p. 195.

1 Welke gelijkenissen merk je op?

2 Welke verschillen merk je op?

©VANIN

2 Zwaar water heeft dezelfde kooktemperatuur en smelttemperatuur als gewoon water.

3 De molaire massa van water, zwaar water en superzwaar water verschilt.

4 Water, zwaar water en superzwaar water zijn isotopen.

5 Superzwaar water is radioactief.

c Zoek op waarom de geallieerden de fabriek in Noorwegen zo snel mogelijk wilden saboteren.

` Meer oefenen? Ga naar .

▲ De centrale in Vemork

HOOFDSTUKSYNTHESE

KERNBEGRIPPEN

nucleonen

massagetal of nucleonental A

protonental Z

neutronental N

nuclide of kern

isotope nucliden of isotopen

fundamentele of elementaire deeltjes

stabiele nucliden

instabiele nucliden of radionucliden

sterke kernkracht

NOTITIES

Protonen en neutronen worden nucleonen genoemd.

Het massagetal of nucleonental A is het aantal nucleonen in een nuclide.

©VANIN

fundamentele interacties

natuurlijke radionucliden

kunstmatige radionucliden

nuclidenkaart halveringstijd

radioactieve vervalwet

Het protonental Z geeft het aantal protonen in een nuclide weer.

Het neutronental N is het aantal neutronen in een nuclide: N = A – Z

Een nuclide of kern bevat A nucleonen, waarvan Z protonen en N neutronen. Een nuclide van het chemische element X noteer je als A ZX of AX

Nucliden met een hetzelfde protonental Z, maar een verschillend nucleonental A noem je isotope nucliden of isotopen.

Fundamentele of elementaire deeltjes zijn deeltjes je niet verder kan opsplitsen in nog kleinere deeltjes. Elektronen zijn elementaire deeltjes. Protonen en neutronen zijn geen elementaire deeltjes en bestaan uit quarks

Stabiele nucliden wijzigen Z of N niet spontaan.

Voor stabiele nucliden geldt: voor Z < 20: N ≈ Z en voor Z > 20: N > Z

Instabiele nucliden of radionucliden wijzigen Z en/of N om hun energie te verlagen

Nucleonen interageren met elkaar via de sterke kernkracht. Die is:

• quasi 0 voor afstanden groter dan ≈2,5 fm;

• sterk aantrekkend tussen naaste buren;

• sterk afstotend voor afstanden kleiner dan ≈0,5 fm.

De stabiliteit van een nuclide wordt bepaald door de elektrische kracht tussen de protonen en de sterke kernkracht tussen de nucleonen.

Tussen deeltjes werken vier soorten fundamentele interacties: de gravitationele, elektromagnetische, sterke en zwakke interactie

Natuurlijke radionucliden komen in de natuur voor.

Kunstmatige radionucliden worden door de mens gemaakt.

De nuclidenkaart is een grafiek met op de horizontale as N en op de verticale as Z. De nuclidenkaart bevat alle stabiele en instabiele nucliden.

De halveringstijd, T1/2, is de tijdsduur waarin 50% van het oorspronkelijk aantal instabiele kernen vervalt.

N(t) = N0 · 2–t/T1/2, met N(t) het aantal instabiele nucliden op tijdstip t, N0 het aantal instabiele nucliden op t = 0 en T1/2 de halveringstijd.

Kernenergie

‘Kernenergie’ is een woord dat tot de verbeelding spreekt. Je komt het vaak tegen in de actualiteit. Sommigen zien het gebruik van kernenergie als een oplossing voor de klimaatopwarming. Anderen hebben schrik voor een tweede Tsjernobyl of Fukushima. En iedereen weet wat er tijdens de Tweede Wereldoorlog in Hiroshima gebeurde …

In dit hoofdstuk geven we antwoord op een aantal vragen. Hoe halen we energie uit kernen, deeltjes met een diameter van amper 10–14 m? Is kernenergie gevaarlijk of kunnen we wel degelijk veilige kerncentrales bouwen? En wat met het radioactieve afval?

LEERDOELEN

M de uitdrukking E0 = m · c2 kunnen toelichten en toepassen

M de stabiliteit van een kern beschrijven aan de hand van de specifieke rustenergie en de specifieke bindingsenergie

M verklaren waarom er bij de fusie van lichte kernen en de splitsing van zware kernen enorme hoeveelheden energie vrijkomen

M de werking van een kernsplitsingsreactor en de voor- en nadelen ervan beschrijven

M de kracht en de problemen van kernfusie als energiebron beschrijven

1 Wat is het verband tussen massa en energie?

1.1 De atomaire massa-eenheid

De massa van kernen, atomen, elektronen … is erg klein. Het is niet praktisch om die massa uit te drukken in kilogram. Daarom kozen fysici een nieuwe massa-eenheid. Het idee achter die keuze was dat een kern met A nucleonen de massa zou hebben van A keer de nieuwe eenheid. Het bleek echter onmogelijk om een eenheid te vinden die strikt aan die voorwaarde voldeed, onder andere (maar niet alleen) doordat de massa van een neutron lichtjes verschilt van die van een proton.

©VANIN

▲ Afb. 28 De massa van de atomaire deeltjes

Sinds 1960 gebruiken we daarom de volgende definitie van de atomaire massa-eenheid u:

1 u = massa van een 126C–atoom 12

1 u = 1,660 54 · 10–27 kg

De onderstaande tabel toont de massa van een los proton, een los neutron, een los elektron en enkele kernen, met als eenheid de atomaire massa-eenheid u. Je kunt zien dat bij benadering, maar niet exact, geldt dat m(AX) ≈ A u.

DEELTJE

e–

ATOOM (ATOMAIRE ELEKTRONEN INBEGREPEN)

4He

12C

16O

56Fe

197Au

208Pb

CONCEPTVRAGEN

1 Voor welke kern geldt wel dat m(AX) = A u?

Waarom gaat de gelijkheid voor die kern wel op?

MASSA (u)

1,007 276

1,008 665

0,000 548 58

MASSA (u)

1,007 825

4,002 603

12,000 000

15,994 915

55,934 938

196,966 569

207,976 652

2 Welke massa uit de tabel wijkt sterk af van de andere massa’s? Verklaar.

De heel kleine massa van atomaire deeltjes, kernen en atomen wordt uitgedrukt in een aangepaste eenheid: de atomaire massa-eenheid u = massa van een 126C–atoom 12

1.2 Massadefect

Het is onmogelijk om een eenheid te definiëren waarvoor de kernmassa m(AX) precies gelijk is aan A keer die eenheid. Je kunt dat beter begrijpen als je de massa van een kern vergelijkt met de som van de massa’s van de protonen en de neutronen in die kern. We maken dat concreet voor een 4He-kern.

CONCEPTVRAAG

Een 4He-kern bestaat uit 2 protonen en 2 neutronen. Welke figuur stelt de situatie volgens jou correct voor? A B C

VOORBEELD MASSAVERSCHIL 42He

Een 4 2He-kern bestaat uit 2 protonen en 2 neutronen. Vergelijk de massa van een 4 2He-kern met de som van de massa’s van 2 protonen en 2 neutronen.

• Eerst bereken je som van de massa’s van 2 protonen en 2 neutronen:

2 ∙ m(n0) = 2 · 1,008 665 u = 2,017 330 u

2 ∙ m(p+) = 2 · 1,007 276 u = 2,014 552 u

som = 2 · m(n0) + 2 · m(p+) = 4,031 882 u

• Vervolgens bereken je de massa van een 4 2He-kern. In tabellen vind je de massa van een 4 2He-kern niet terug, maar wel de massa van een 4 2He-atoom, dus inclusief massa van de atomaire elektronen. Dat komt doordat men meestal de atomaire massa meet. Wil je de massa van een 4 2He-kern weten, dan moet je de massa van de 2 atomaire elektronen aftrekken van de atomaire massa.

m(42He-kern) = m(42He-atoom) - 2 · m(e–) = 4,002 603 u – 2 · 0,000 549 u = 4,001 505 u

• Het massaverschil ∆m wordt dan: ∆m = [2 · m(n0) + 2 · m(p+)] – [m(42He-kern)] = 4,031 882 u – 4,001 505 u = 0,030 377 u

Er is dus een massaverschil van 0,030 377 u.

2 · 1,008 665 u

2 · 1,007 276 u 4,031 882 u 4,001 505 u = + +? 0,030 377 u Δ

©VANIN

Kleine massaverschillen zijn belangrijk binnen de kernfysica. Om die massaverschillen te kunnen detecteren, moet je massa’s met voldoende nauwkeurigheid en dus met voldoende beduidende cijfers weergeven. Daarom gebruik je bij massaberekeningen veel (vijf tot zeven) beduidende cijfers.

Voor 4 2He is er een massaverschil van 0,030 377 u tussen de som van de massa’s van 2 protonen en 2 neutronen en de totale massa van de 4 2He-kern. Er is dus massa verdwenen. Dat geldt niet alleen voor 4 2He, maar voor alle kernen. De totale massa van een kern is altijd kleiner dan de som van de massa’s van de afzonderlijke protonen en neutronen.

Het verschil tussen de som van de massa’s van de protonen en neutronen van een kern en de totale massa van die kern noem je het massadefect ∆m:

∆m = [N · m(n0) + Z · m(p+)] – [m(AX)]

TIP

Het massadefect is de belangrijkste reden waarom je geen eenheid kunt vinden waarvoor exact geldt dat m(AX) = A eenheid, want de massa van een nucleon in een kern verschilt van de massa van een los nucleon.

GROOTHEID MET SYMBOOL

EENHEID MET SYMBOOL

totale kernmassa m(AX) atomaire massaeenheid u massadefect ∆m

©VANIN

Als losse protonen en neutronen samen een kern vormen, verdwijnt er massa. Het massadefect van een kern is het verschil tussen de som van de massa’s van de afzonderlijke nucleonen van een kern en de totale massa van die kern:

∆m = [N · m(n0) + Z · m(p+)] – [m(AX)]

1.3 Equivalentie tussen massa en energie

Waar komt het massadefect vandaan? Kan massa zomaar verdwijnen? Het antwoord komt van de speciale relativiteitstheorie, die Albert Einstein in 1905 publiceerde. Einstein leidde op basis van zijn berekeningen af dat een massa in rust overeenkomt met een hoeveelheid energie die hij de rustenergie E0 noemde:

E0 = m · c2

Daarbij is c de lichtsnelheid: c = 2,997 924 58 · 108 m s

GROOTHEID MET SYMBOOL

EENHEID MET SYMBOOL rustenergie E0 joule J

Een korte berekening in de speciale relativiteitstheorie leidde dus tot een spectaculaire ontdekking:

Massa kan worden omgezet in energie.

Energie kan worden omgezet in massa.

Als massa wordt omgezet in energie, dan komt die energie vrij in de vorm van straling en/of warmte. Dat neem je waar bij kernen. Wanneer losse protonen en neutronen samen een kern vormen, gaat er altijd een beetje massa verloren, namelijk het massadefect ∆m. Die massa wordt omgezet in energie. De hoeveelheid gevormde energie kun je berekenen met de wet ∆E0 = ∆m · c2

De rustenergie van een kern is de minimale energie die een kern kan hebben.

Massa kan worden omgezet in energie.

1 Hoeveel energie komt er vrij als er 1 g massa wordt omgezet in energie?

2 Hoeveel energie komt er vrij als er 1 u massa wordt omgezet in energie?

Gegeven: 1 m = 1 g

2 m = 1 u

Gevraagd: vrijgekomen energie E = ?

Oplossing: Als alle massa wordt omgezet in energie, dan is de vrijgekomen energie E volgens de wet van behoud van energie gelijk aan de rustenergie E0 van die massa:

1 E = E0 = m · c2 = 1 · 10–3 kg · (2,997 924 58 · 108 m s )2 = 8,987 551 79 · 1013 J

2 E = E0 = m · c2 = 1,660 54 · 10–27 kg · (2,997 924 58 · 108 m s )2 = 1,492 41 · 10–10 J

Reflectie: Vergelijk de bekomen resultaten voor een massa m = 1 g en m = 1 u.

Wat stel je vast?

De vrijgekomen energie bij de omzetting van 1 g massa is 1024 keer groter dan de vrijgekomen energie bij de omzetting van 1 u massa. Die energieverhouding is hetzelfde als de massaverhouding.

CONCEPTVRAAG

Waarom gebruiken we voor de uitwerking van het voorbeeldvraagstuk de SI-eenheden?

Het verband tussen de rustenergie en een massa in rust wordt gegeven door de formule

E0 = m · c2. Dat betekent dat massa kan worden omgezet in energie en energie in massa. Wanneer massa wordt omgezet in energie, dan komt die energie vrij in de vorm van straling en/of warmte.

De rustenergie van een kern is de minimale energie die een kern kan hebben.

WEETJE

Albert Einstein won in 1920 de Nobelprijs. Hij kreeg de prijs echter niet voor zijn pionierswerk in de relativiteitstheorie, maar wel voor zijn verklaring van het foto-elektrisch effect als een kwantummechanisch fenomeen.

©VANIN

1.4 De MeV als eenheid voor kernenergie

De joule is een erg grote eenheid als het gaat over de energie van kernen. Daarom gebruiken kernfysici meestal een andere eenheid: de elektronvolt eV en de veelvouden van de elektronvolt keV (= 103 eV) en MeV (= 106 eV).

1 elektronvolt (eV) is de energieverandering van een elektron dat een potentiaalverschil van 1 V doorloopt.

Uit |∆E| = |q · U| volgt de omzettingsfactor:

1 eV = 1,602 176 5 · 10–19 C · 1 V = 1,602 176 5 · 10–19 J

©VANIN

Als omgekeerde omzettingsfactor vind je:

1 J = 6,2415 · 1018 eV

GROOTHEID MET SYMBOOLEENHEID MET SYMBOOL

energie E elektronvolt eV1 eV = 1,602 176 5 · 10–19 J kilo-elektronvolt keV 1 keV = 103 eV = 1,602 176 5 · 10–16 J mega-elektronvoltMeV1 MeV = 106 eV = 1,602 176 5 · 10–13 J joule

J1 J = 6,2415 · 1018 eV

VOORBEELDVRAAGSTUK

Bereken de rustenergie van een massa van 1 u in MeV.

Gegeven: m = 1 u

Gevraagd: E0(1 u) = ?

Oplossing: E0(1 u) = m · c2 = 1,492 41 · 10–10 J = 1,492 41 · 10–10 J · 6,2415 · 1018 eV J = 1,492 41 · 6,2415 · 10–10 · 1018 eV = 9,3149 · 108 eV = 9,3149 · 102 MeV = 931,49 MeV

Gevolg: Je kunt schrijven: 931,49 MeV = 1 u · c2 c2 = 931,49 MeV 1 u = 931,49 MeV u

Dus: c2 = 931,49 MeV u

Voor een willekeurige massa uitgedrukt in u kun je de rustenergie uitgedrukt in MeV als volgt schrijven: E0 (in MeV) = m (in u) · 931,49 MeV u

CONCEPTVRAAG

Hoe kun je de rustenergie van een (kern)massa uitgedrukt in u snel en eenvoudig berekenen?

In de kernfysica gebruik je meestal de mega-elektronvolt MeV als eenheid voor energie.

1 eV = 1,602 176 5 · 10–19 J 1 MeV = 106 eV = 1,602 176 5 · 10–13 J

De rustenergie E0 van een massa m uitgedrukt in de atomaire massa-eenheid u kun je als volgt berekenen:

E0 (in MeV) = m (in u) · 931,49 MeV u

De rustenergie per atomaire massaeenheid u bedraagt 931,49 MeV u Dat getal zul je veel gebruiken in berekeningen. Het is dus handig als je het vanbuiten kent.

Elk (micro- en macroscopisch) systeem streeft naar minimale inwendige energie. Er vinden processen plaats totdat het systeem die evenwichtstoestand heeft bereikt.

2 Wat is de energie van een nucleon in een kern?

2.1 De specifieke rustenergie

De rustenergie van een kern kun je berekenen met de massa-energierelatie van Einstein: E0 = m · c2. Ze wordt groter naarmate de kern meer nucleonen bevat. Voor elk nucleon dat aan de kern wordt toegevoegd, zal de massa van de kern immers stijgen met ongeveer 1 u.

Om de energie van verschillende kernen te kunnen vergelijken, is het daarom interessanter om de gemiddelde rustenergie van een nucleon in de kern te berekenen. De gemiddelde rustenergie van een nucleon in een kern noem je de specifieke rustenergie van een kern of de rustenergie per nucleon

GROOTHEID MET SYMBOOL

specifieke rustenergie of rustenergie per nucleon

©VANIN

EENHEID MET SYMBOOL

E0 A mega-elektronvoltMeV

Zoals alle microscopische en macroscopische systemen, streven kernen naar minimale inwendige energie en dus naar minimale rustenergie en minimale specifieke rustenergie. Hoe lager de specifieke rustenergie van een kern, hoe stabieler ze is.

VOORBEELDVRAAGSTUK

Bereken de specifieke rustenergie van 197Au.

Gegeven: 197Au

Gevraagd: E0 A (197Au-kern) = ?

Oplossing: m(197Au-kern) = m(197Au-atoom) – 79 · m(e–) = 196,966 569 u – 79 · 0,000 549 u = 196,923 231 u

E0(197Au-kern) = 196,923 231 u · 931,49 MeV u = 183 432 MeV

E0 A (197Au-kern) = 183 432 MeV 197 = 931,13 MeV

De specifieke rustenergie van 197Au bedraagt 931,13 MeV.

Reflectie: Vergelijk je resultaat met de rustenergie van m = 1 u. Wat stel je vast?

De specifieke rustenergie is de gemiddelde energie van een nucleon in een kern en ligt dus in de buurt van (maar is niet gelijk aan) de rustenergie van een massa van 1 u, namelijk E0(1 u) = 931,49 MeV.

De specifieke rustenergie van een kern is gelijk aan E0 A , waarbij E0 de rustenergie van de kern is en A het nucleonental. Het is de gemiddelde rustenergie van een nucleon in de kern. Hoe lager de specifieke rustenergie van een kern, hoe stabieler ze is.

2.2 De energievallei

Je kunt voor elke nuclide van de nuclidenkaart de specifieke rustenergie berekenen. Door aan de nuclidenkaart een derde, verticale as met de specifieke rustenergie toe te voegen, krijg je een 3D-grafiek, zoals op afbeelding 33. Op de x-as het staat het neutronental N, op de y-as het protonental Z en op de z-as de specifieke rustenergie E0 A . Omdat die grafiek de vorm van een vallei heeft, wordt ze ook vaak de energievallei genoemd.

Energievallei

©VANIN

stabiele kern

instabiele kern

▲ Afb. 33 De energievallei is een driedimensionale uitbreiding van de nuclidenkaart, met als derde dimensie de specifieke rustenergie E0 A

De energievallei maakt een aantal trends zichtbaar:

• De stabiele kernen zijn zwart gekleurd. Ze bevinden zich in het dal van de vallei en hebben de laagste specifieke rustenergie.

• De lichtste kernen, zoals 1H, hebben een erg hoge specifieke rustenergie, ook al zijn ze stabiel Het is voor nucleonen dus energetisch voordeliger om samen zwaardere kernen te vormen. Bij erg zware kernen neemt de rustenergie opnieuw langzaam toe. De kernen met de laagste specifieke rustenergie zijn de middelzware kernen met een massagetal A tussen A ≈ 40 en A ≈ 80.

• Instabiele kernen zijn, net zoals op de nuclidenkaart, roze, blauw of geel gekleurd. Ze kunnen hun rustenergie verminderen door hun protonental Z en/of hun neutronental N te veranderen en zo een nieuwe kern te vormen die dichter bij het dal van de vallei ligt.

De energievallei is de nuclidenkaart waaraan een derde dimensie werd toegevoegd, namelijk de specifieke rustenergie van elke nuclide.

3 Hoe wordt energie vrijgemaakt uit kernen?

3.1 De specifieke bindingsenergie

In kerncentrales gebruikt men kernenergie om elektriciteit op te wekken.

Kernenergie wordt (jammer genoeg) ook gebruikt in atoombommen.

De zon geeft licht en warmte dankzij vrijgekomen kernenergie.

De energie die vrijkomt bij de vorming van nieuwe kernen, wordt als energiebron gebruikt in bijvoorbeeld kerncentrales, atoombommen of de zon.

De energie die vrijkomt als A losse nucleonen een kern AX vormen, noem je de bindingsenergie ∆E0 van de kern.

Omgekeerd is het ook de minimale energie die je aan een kern AX moet toevoegen om die te laten uiteenvallen in A losse nucleonen

De bindingsenergie ∆E0 is verbonden met het massadefect ∆m via de massa-energierelatie van Einstein: ∆E0 = ∆m · c2 .

©VANIN

Δ E 0 komt vrij bij vorming kern

Naar analogie met de specifieke rustenergie van een kern, definiëren we de specifieke bindingsenergie van een kern of de bindingsenergie per nucleon als de gemiddelde bindingsenergie van een nucleon in een kern: ∆E0 A .

Je kunt de specifieke bindingsenergie als volgt berekenen: ∆E0 A = ∆m · c2 A

Het is de gemiddelde energie per nucleon die vrijkomt als A losse nucleonen samen een kern AX vormen

Het is bij benadering de energie die vrijkomt als je een nucleon toevoegt aan een kern, of omgekeerd de energie die je aan een kern moet toevoegen om een nucleon vrij te maken. Δ E 0 nodig voor splitsing

▲ Afb. 34 Grafische voorstelling van de bindingsenergie ∆E0 ≈ komt vrij Δ E 0 A

nodig Δ E 0 A

▲ Afb. 35 Grafische voorstelling van de specifieke bindingsenergie

VOORBEELD DE BINDINGSENERGIE EN DE SPECIFIEKE BINDINGSENERGIE VAN EEN 42He-KERN

• Het massadefect van een 4 2He-kern bedraagt 0,030 376 u (zie paragraaf 1.2).

• De bindingsenergie van een 4 2He-kern bedraagt dan:

∆E0 = ∆m · c2 = Δm (in u) · 931,49 MeV u

= 0,030 376 u · 931,49 MeV u = 28,295 MeV

Wanneer 2 losse protonen en 2 losse neutronen samen een 4 2He-kern vormen, komt er 28,295 MeV energie vrij. Een 4 2He-kern heeft dus een bindingsenergie van 28,295 MeV.

2 · 1,008 665 u

2 · 1,007 276 u

4,001 505 u = + +

4,031 882 u

©VANIN

E 0 = 28,295 MeV

Δ E 0 = 28,295 MeV

bindingsenergie

▲ Afb. 36 Bij de vorming van een nuclide komt er energie vrij: de bindingsenergie.

• De specifieke bindingsenergie voor een 4 2He-kern bedraagt:

∆E0 A = 28,295 MeV 4 = 7,0737 MeV

Wanneer 2 losse protonen en 2 losse neutronen samen een 4 2He-kern vormen, verliest elk nucleon gemiddeld 7,037 MeV energie. Anders gezegd: het verschil tussen de gemiddelde rustenergie van een los nucleon en een nucleon in een 4 2He-kern bedraagt 7,037 MeV.

De specifieke bindingsenergie van een kern is van de orde van verschillende MeV. Dat is erg veel energie. Ter vergelijking: voor de ionisatie van een atoom is een energie van de grootteorde van 10 eV nodig. De energie die nodig is om een nucleon los te maken uit een kern, is met andere woorden honderdduizend keer groter dan de energie die nodig is om een atomair elektron los te maken van een atoom. Omgekeerd kunnen er enorme hoeveelheden energie vrijkomen als je nucleonen op de juiste manier bij elkaar brengt.

De specifieke bindingsenergie ∆E0 A is gelijk aan de gemiddelde energie per nucleon die vrijkomt als A nucleonen samen een kern vormen. Omgekeerd is het de minimale energie die je aan een kern moet toevoegen om een nucleon los te maken uit de kern.

Je kunt de specifieke bindingsenergie als volgt berekenen aan de hand van het massadefect ∆m:

∆E0 A = ∆m · c2 A

De specifieke bindingsenergie is van de orde van MeV. Dat is erg veel energie.

3.2 De relatie tussen de specifieke bindingsenergie en de specifieke rustenergie

Grafiek 4 toont de specifieke bindingsenergie van een aantal stabiele kernen en natuurlijke radionucliden als functie van het massagetal A. Je kunt voor diezelfde kernen ook een grafiek maken van de specifieke rustenergie als functie van het massagetal A

Specifieke bindingsenergie in functie van A

(MeV)

Specifieke rustenergie in functie van A

©VANIN

▲ Grafiek 4 De specifieke bindingsenergie en de specifieke rustenergie als functie van het massagetal A voor een aantal stabiele nucliden en natuurlijke radionucliden

Door de twee grafieken met elkaar te vergelijken, leer je het volgende:

• Hoe hoger de specifieke bindingsenergie, hoe meer energie de kern bij haar vorming afgegeven heeft en dus hoe lager de specifieke rustenergie

• De lichtste kernen hebben een lage specifieke bindingsenergie. Dat stemt overeen met het feit dat ze een hoge specifieke rustenergie hebben.

• De specifieke bindingsenergie stijgt naarmate A toeneemt, en bereikt een breed maximum bij ongeveer 8,7 MeV. Bij de middelzware kernen (met A tussen A ≈ 40 en A ≈ 80) zijn de nucleonen sterk aan de kern gebonden

• 56Fe heeft de hoogste specifieke bindingsenergie (en dus de laagste specifieke rustenergie) en is bijgevolg de stabielste kern. Het gevolg is dat 56Fe erg veel voorkomt in het heelal.

• Na het brede maximum, vanaf A ≈ 80, neemt de specifieke bindingsenergie langzaam af en de specifieke rustenergie langzaam toe. Dat betekent dat de nucleonen in zwaardere kernen iets minder sterk aan de kern gebonden zijn. Anders gezegd: het is iets gemakkelijker om nucleonen los te maken uit een zwaardere kern.

• De specifieke bindingsenergie toont bepaalde pieken. Een belangrijk voorbeeld van een dergelijke piek is de 4 2He-kern. Dat betekent dat 4 2He een erg stabiele nuclide is. Sommige radionucliden vervallen door een 4 2He-kern uit te sturen.

CONCEPTVRAAG

Situeer de nucliden 20 10Ne, 58 28Ni, 12753I, 18674W en 20882Pb op de grafiek van de specifieke bindingsenergie en op de grafiek van de specifieke rustenergie.

Hoe hoger de specifieke bindingsenergie, hoe lager de specifieke rustenergie. 56Fe is de stabielste kern.

De middelzware kernen hebben een hogere specifieke bindingsenergie en een lagere specifieke rustenergie dan de lichte en de zware kernen.

3.3 Energie uit lichte en zware kernen

Afhankelijk van hun massagetal A kunnen er op twee verschillende manieren grote hoeveelheden energie worden vrijgemaakt uit kernen (grafiek 5 en grafiek 6):

• Zware nucliden kunnen uiteenvallen in twee middelzware nucliden. Dat noem je kernsplitsing of kernfissie.

• Lichte nucliden kunnen samen een zwaardere nuclide vormen. Dat noem je kernfusie.

Specifieke bindingsenergie in functie van A

Specifieke rustenergie in functie van A

▲ Grafieken 5 en 6 Kernfusie en kernsplitsing in relatie tot de specifieke bindingsenergie en in relatie tot de specifieke rustenergie

Zowel bij kernsplitsing als bij kernfusie daalt de specifieke rustenergie van de kernen. De energie die gemiddeld per betrokken nucleon vrijkomt, met andere woorden de specifieke bindingsenergie, stijgt. Die vrijgekomen energie kan worden omgezet naar andere energiebronnen.

CONCEPTVRAAG

Komt er de meeste energie vrij bij kernsplitsing of bij kernfusie? Lees af op de grafieken van de specifieke bindingsenergie en de specifieke rustenergie in functie van

Er kunnen grote hoeveelheden kernenergie vrijkomen door:

• kernsplitsing: kernen die uiteenvallen;

• kernfusie: kernen die worden samengevoegd.

3.4 Energieopbrengst bij kernsplitsing

Bij een splitsingsreactie komt er enorm veel energie vrij. Je kunt de hoeveelheid berekenen aan de hand van de grafiek van de specifieke bindingsenergie op p. 222.

VOORBEELD ENERGIEOPBRENGST BIJ DE KERNSPLITSING VAN 1 KG 235U

Energieopbrengst bij de kernsplitsing van één 235U-kern:

• De specifieke bindingsenergie voor uranium is ongeveer 7,6 MeV. De specifieke bindingsenergie voor de splitsingselementen (A in het bereik van 80 tot 150) is ongeveer 8,5 MeV. Per betrokken nucleon komt er dus 8,5 MeV – 7,6 MeV = 0,9 MeV energie vrij. Er zijn 236 nucleonen betrokken bij de splitsingsreactie. De totale energie die vrijkomt per splitsing is dus 0,9 MeV nucleon ∙ 236 nucleonen ≈ 200 MeV.

Energieopbrengst bij de splitsing van 1 kg 235U:

• Per betrokken nucleon in één splitsingsreactie komt er ongeveer 0,9 MeV energie vrij. Een nucleon heeft een massa van ongeveer 1 u. Een massa van 1 u komt volgens de relatie E0 = m ∙ c2 overeen met een rustenergie van 931,49 MeV.

De energie die in een splitsingsreactie per nucleon vrijkomt (0,9 MeV), is dus ongeveer 1 1 000 van de rustenergie van een nucleon.

Volgens de relatie E0 = m ∙ c2 geldt dan ook dat ongeveer 1 1 000 van de massa van elk nucleon dat betrokken is bij de splitsingsreactie, wordt omgezet in energie.

Algemener geldt dat bij een splitsingsreactie ongeveer 1 1 000 van de massa van de splijtstof wordt omgezet in energie. Bij de splitsing van 1 kg splijtstof wordt er dus 1 g splijtstof omgezet in energie. Volgens de relatie E0 = m ∙ c2 geldt dan: E = 1 · 10–3 kg · (3 · 108 m s )2 = 9 · 1013 J.

1 kg splijtstof

3 ton

▲ Afb. 37 De splitsing van 1 kg splijtstof levert evenveel energie op als de

Bij de splitsing van 1 kg splijtstof wordt er 1 g splijtstof omgezet in energie. Er komt daardoor 9 · 1013 J energie vrij. Dat is evenveel energie als bij de verbranding van 3 ton steenkool.

CONCEPTVRAAG

9 · 1013 J komt overeen met 25 · 106 kWh. Een gemiddeld Vlaams gezin verbruikt zo’n 2 940 kWh elektriciteit per jaar. Met 1 kg 235U kun je dus 8 500 gezinnen een jaar lang van elektriciteit voorzien. Reken dat na.

Kernsplitsing levert enorm veel energie op: 1 kg splijtstof levert evenveel energie op als de verbranding van 3 ton steenkool.

steenkool

verbranding van 3 ton steenkool.

3.5 Energieopbrengst bij kernfusie

Kernfusie kan pas plaatsvinden als de twee kernen die samensmelten, elkaars afstotende elektrische kracht kunnen overwinnen. De elektrische kracht is het kleinst bij kernen met weinig protonen, dat wil zeggen bij lichte kernen. Als er een kernfusiereactie plaatsvindt, gaat het daarom dikwijls om waterstofkernen die samensmelten tot een heliumkern.

Afhankelijk van de waterstofisotopen (1H, 2H of 3H) en heliumisotopen (3He of 4He) die betrokken zijn, kan er tot 7 MeV per nucleon vrijkomen. Bij kernsplitsingsreacties gaat het om 0,9 MeV per nucleon. Kernfusie kan dus nog meer energie opleveren dan kernsplitsing.

deuterium helium

tritium

kernfusie neutron energie

▲ Afb. 38 Voorbeeld van een fusiereactie waarbij een 2H-kern (deuterium) en een 3H-kern (tritium) samen een 4He-kern en een neutron vormen

CONCEPTVRAAG

Lees op de grafiek van de specifieke bindingsenergie op p. 222 af wat de maximale energie per nucleon is die kan vrijkomen bij de fusie van waterstofkernen tot een heliumkern.

• Kernfusie kan enkel plaatsvinden als de twee kernen die samensmelten, elkaars afstotende elektrische kracht kunnen overwinnen

• Kernfusie kan nog meer energie opleveren dan kernsplitsing.

Zowel voor kernfusie- als voor kernsplitsingsreacties geldt dat het aantal protonen en het aantal neutronen voor en na de kernreactie gelijk blijft.

4

4.1 Spontane en niet-spontane splitsing

Spontane splitsing komt bijna uitsluitend voor bij extreem instabiele kunstmatige radionucliden met een erg hoog massagetal, zoals 264 106 Sg (seaborgium-264) en 278 111 Rg (röntgenium-278).

Op de nuclidenkaart op p. 202 staan de spontane splitsingskernen afgebeeld in het groen.

Kernen kunnen echter ook splitsen doordat er een neutron invalt op een zware kern. In principe kan elke zware kern splitsen, maar in de praktijk is de splitsingswaarschijnlijkheid enkel bij 235U (uranium- 235), 239Pu (plutonium-239) en 233U (uranium-233) groot genoeg om praktisch nut te kunnen hebben.

• Van die drie nucliden is enkel 235U een natuurlijke radionuclide.

• 239Pu en 233U moeten in laboratoria worden gemaakt.

©VANIN

splitsingsfragment

▲ Afb. 39 Kernsplitsing als gevolg van een invallend neutron

Daarom gebruikt men bij toepassingen van kernsplitsing meestal 235U.

In natuurlijk uranium komt maar 0,7 % 235U voor. Daarom verhoogt men voor praktische doeleinden het percentage 235U in natuurlijk uranium in een laboratorium tot 2 à 4 %. Dat proces noem je het verrijken van uranium.

• Meestal komt het kernsplitsingsproces op gang doordat er een neutron op een zware kern invalt. Spontane splitsing komt zelden voor.

• Voor toepassingen van kernsplitsing gebruikt men gewoonlijk 235U, omdat dat de enige natuurlijke radionuclide met een voldoende grote splitsingswaarschijnlijkheid is.

• Natuurlijk uranium bevat maar heel weinig 235U, namelijk 0,7 %. Daarom verhoogt men in laboratoria het percentage 235U in uranium (tot 2 à 4 %). Dat noem je het verrijken van uranium.

4.2 De splitsing van 235U

Het splitsingsproces wordt op gang gebracht door 235U te beschieten met neutronen. Dan zijn er verschillende splitsingsreacties mogelijk. Daarbij verschillen de gevormde kernen en het aantal vrijgekomen neutronen:

Bijvoorbeeld: 23592U + n0 → 14456Ba + 89 36Kr + 3 ∙ n0

Of: 23592U + n0 → 13953I + 95 39Y + 2 ∙ n0 enzovoort.

Voor alle kernsplitsingsreacties geldt dat het aantal protonen protonen en het aantal neutronen voor en na de splitsing gelijk blijft.

CONCEPTVRAAG

Wat is het element AX in deze splitsingsreactie?

23592U + n0 → A Z X + 90 37Rb + 2 ∙ n0? splitsingskern

Omdat zware kernen in verhouding meer neutronen bevatten dan middelzware kernen, hebben de splitsingsfragmenten, zoals 14456Ba, 89 36Kr, 13953I en 95 39Y, een overschot aan neutronen. Ze zijn met andere woorden instabiel en zullen radioactief vervallen door een neutron om te zetten in een proton.

Die splitsingsfragmenten zijn dan ook een belangrijke bron van radioactief afval. In tegenstelling tot andere vormen van vervuiling, is dat afval wel gemakkelijk op te vangen. Het komt dus niet zomaar in de natuur of in de nabijheid van mensen terecht. Een veilige berging van het nucleaire afval is belangrijk. Kortlevend radioactief afval heeft een halveringstijd van dertig jaar. Het moet tot driehonderd jaar (tien halveringstijden) worden opgeslagen vooraleer het niet meer radioactief is. Een kleine fractie van het afval is hoogradioactief en heeft een lange halveringstijd (langer dan dertig jaar). Dat afval moet gedurende duizenden jaren veilig worden opgeslagen.

• Wanneer een neutron botst met een 235U-kern, valt de 235U-kern uit elkaar in twee middelzware kernen en een paar neutronen. Er zijn verschillende combinaties van middelzware kernen en een aantal neutronen mogelijk.

• De splitsingsfragmenten hebben een teveel aan neutronen. Ze zijn daarom radioactief en vormen een belangrijke bron van radioactief afval. Een veilige berging van het radioactieve afval is belangrijk.

4.3 Kettingreacties

©VANIN

In België is NIRAS, de Nationale Instelling voor Radioactief Afval en verrijkte Splijtstoffen, verantwoordelijk voor het beheer van het radioactieve afval. In afwachting van definitieve berging wordt het nucleaire afval momenteel opgeslagen op een select aantal zeer streng bewaakte locaties: het terrein van Belgoprocess in Dessel en de kerncentrales in Doel en Tihange.

Om de enorme bron van splitsingsenergie aan te boren, is het belangrijk dat de kernsplitsing niet stopt na de splitsing van één 235U-kern. Bij de splitsing van een 235U-kern komen er gewoonlijk 2 of 3 neutronen vrij. De wetenschapper Fermi was een van de eersten die besefte dat je die vrijgekomen neutronen kunt gebruiken om nieuwe 235U-kernen te splitsen

Enrico Fermi won in 1938 de Nobelprijs voor ‘het aantonen van nieuwe radioactieve elementen door bestraling met neutronen, en daarmee samenhangend de ontdekking van kernreacties veroorzaakt door langzame neutronen’. Hij introduceerde als eerste de zwakke kernkracht en speelde een pioniersrol in de ontwikkeling van kernreactoren. Hij was ook betrokken bij de uitvinding van de atoombom.

WEETJE

▲ Afb. 40 Vaten met radioactief afval wachtend op verwerking in de opslagruimte van Belgoprocess in Dessel

WEETJE

▲ Afb. 41 Enrico Fermi

Een kettingreactie is een serie gebeurtenissen waarbij elke gebeurtenis wordt veroorzaakt door een vorige.

De 2 of 3 neutronen die bij de splitsing van een 235U-kern vrijkomen, kunnen op hun beurt invallen op nieuwe 235U-kernen en nieuwe kernsplitsingen veroorzaken. Daarbij komen er opnieuw neutronen vrij, die opnieuw kernsplitsingen veroorzaken. Zo ontstaat er een kettingreactie, die schematisch wordt weergegeven op afbeeldingen 42, 43 en 44.

Voor een zichzelf onderhoudende kettingreactie moet minstens een van de geproduceerde neutronen een nieuwe 235U-kern doen splitsen. Het verloop van de kettingreactie wordt dan ook bepaald door de vermenigvuldigingsfactor f: het gemiddelde aantal neutronen per splitsing dat een nieuwe splitsing veroorzaakt.

TYPE KETTINGREACTIE

gevaarlijk explosieve kettingreactie

Als f > 1, dan neemt het aantal splitsingen exponentieel toe. Het resultaat is een ongecontroleerde, gevaarlijke, explosieve kettingreactie. Op dat principe zijn atoombommen gebaseerd.

Afb. 42 Een kettingreactie met vermenigvuldigingsfactor f = 2. Die reactie is gevaarlijk explosief. ▶

veilige, gecontroleerde kettingreactie

Als f = 1, dan zorgt 1 neutron geproduceerd in de splitsing van één 235U-kern voor de splitsing van één nieuwe 235U-kern. De kettingreactie onderhoudt zichzelf zonder explosief te worden.

SCHEMATISCHE VOORSTELLING

Gebruik de applet ‘Kernsplitsing’ om de kettingreacties te simuleren. Kies voor ‘Chain Reaction’.

©VANIN

Afb. 43 Een kettingreactie met vermenigvuldigingsfactor f = 1 onderhoudt zichzelf zonder explosief te worden. ▶

stilvallende kettingreactie

Als f < 1, dan neemt het aantal splitsingen voortdurend af en dooft de kernreactie uit.

Afb. 44 Een kettingreactie met vermenigvuldigingsfactor f < 1 valt stil.

De neutronen die vrijkomen bij de splitsing van een 235U-kern, kunnen een nieuwe 235U-kern doen splitsen. Het gemiddelde aantal neutronen per splitsing dat een nieuwe splitsing veroorzaakt, noem je de vermenigvuldigingsfactor f.

• Als f > 1, dan ontstaat er een explosieve kettingreactie. Op dat principe zijn atoombommen gebaseerd.

• Als f = 1, dan onderhoudt de kernreactie zichzelf zonder explosief te worden.

• Als f < 1, dan dooft de kernreactie uit.

Een kerncentrale haalt haar energie uit een gecontroleerde kettingreactie van kernsplitsingen en zet die om in elektrische energie. De splitsingsreacties gebeuren in de kernreactor van de centrale. Voor een goede, gecontroleerde werking van een kernreactor is het essentieel dat men de vermenigvuldigingsfactor gelijk aan (of net iets kleiner dan) 1 houdt: f = 1. De kernreactor bevat daarom een moderator en controlestaven

1 De moderator verhoogt de vermenigvuldigingsfactor f door ervoor te zorgen dat de neutronen voldoende vertraagd worden. Vertraagde neutronen worden gemakkelijker opgenomen door een 235U-kern. Je kunt het vergelijken met een keeper die een voetbal moet pakken: dat is gemakkelijker bij een traag rollende bal dan bij een bal met een hoge snelheid. Een stof met lichte atomen is het meest geschikt als moderator.

▲ Afb. 45 Water in een kernreactor. De blauwe gloed noem je cherenkovstraling. Die straling ontstaat doordat geladen deeltjes, bijvoorbeeld hoogenergetische elektronen, sneller dan het licht door water bewegen. Dat is mogelijk doordat water het licht vertraagt. De geladen deeltjes komen vrij na radioactief verval van de splitsingsfragmenten.

In de huidige commerciële reactoren, zoals in Doel of Tihange, gebruikt men vaak water als moderator. De kernreactor van Tsjernobyl bevatte grafiet als moderator. Water is veel veiliger als moderator dan grafiet. Bij explosieve reacties wordt er veel warmte ontwikkeld, die ervoor zorgt dat het water verdampt en de kettingreactie stilvalt. Warm grafiet daarentegen zal de neutronen nog meer vertragen en de vermenigvuldigingsfactor doen toenemen.

2 De controlestaven verlagen de vermenigvuldigingsfactor f door neutronen te absorberen. Ze bestaan uit cadmium of boor, atoomsoorten waarvan de kernen gemakkelijk neutronen vangen. Door de controlestaven in en uit de reactor te schuiven, kunnen de operatoren de vermenigvuldigingsfactor f indien gewenst laten afnemen of toenemen.

©VANIN

Afbeelding 47 toont schematisch de werking van een volledige kerncentrale voor de productie van elektriciteit. In de kernreactor vinden de splitsingsreacties plaats. De brandstofstaven bevatten 235U. Het water in de container is de moderator en wordt opgewarmd door de vrijgekomen splitsingsenergie. Het warme water geeft zijn warmte via een warmtewisselaar af aan een stoomgenerator. De stoom laat de turbine draaien en de turbine laat op haar beurt de elektrische generator (een soort grote fietsdynamo) draaien. De stoom wordt door een derde watercircuit afgekoeld, condenseert in een condensor opnieuw tot water en wordt via een pomp weer naar de stoomgenerator gebracht. De restwarmte wordt via het derde watercircuit afgeleid naar de koeltorens, waar het haar warmte afgeeft aan de atmosfeer en in een rivier geloosd wordt. De elektrische generator is verbonden met het stroomnet.

Het grote voordeel van kerncentrales is dat ze, in tegenstelling tot gas- of steenkoolcentrales, geen CO2 uitstoten. Ze zijn ook erg energie-efficiënt: de energieopbrengst per kg splijtstof is groot. Als gevolg van de strijd tegen de klimaatopwarming is er daarom opnieuw meer interesse om bestaande kerncentrales te behouden of nieuwe te bouwen. Een nadeel is de productie van radioactief afval

▲ Afb. 46 De controlestaven van een kernreactor

Bekijk de video over de werking van een kerncentrale.

beveiligd gebouw

©VANIN

Kernreactoren functioneren bij f = 1. Daarom bevatten ze een moderator en controlestaven.

• De moderator verhoogt de vermenigvuldigingsfactor door de neutronen te vertragen. Tragere neutronen worden gemakkelijker opgenomen door de 235U-kernen.

• Controlestaven verlagen de vermenigvuldigingsfactor. Ze bestaan uit atomen waarvan de kernen gemakkelijk neutronen absorberen. Door de controlestaven in en uit de reactor te schuiven, kunnen operatoren de vermenigvuldigingsfactor aanpassen.

Er zijn voor- en nadelen aan kernreactoren:

• Voordeel: ze stoten geen CO2 uit en zijn energie-efficiënt

• Nadeel: ze produceren radioactief afval.

Het onderzoek naar kernsplitsing kende vooral tijdens de Tweede Wereldoorlog een snelle evolutie vanwege het militaire belang ervan. Op 6 augustus 1945 viel er een atoombom met uranium op de Japanse stad Hiroshima en op 9 augustus een tweede bom met plutonium op Nagasaki. Bij de ontploffing van de bommen ontstond er een explosieve kettingreactie van kernsplitsingen (f > 1). De gevolgen waren verwoestend:

Hiroshima enkele

nadat de stad werd getroffen door een atoombom. Alleen het geraamte van het Museum voor Wetenschappen en Industrie bleef overeind. Alle andere gebouwen in de omgeving werden van de kaart geveegd.

• Veel energie kwam vrij in de vorm van warmte. Dat veroorzaakte branden tot op 1 km van het trefpunt en brandwonden tot op 3,5 km van het trefpunt.

• De ontploffing ging gepaard met een enorme drukgolf. In Hiroshima werden woningen in een straal van 2 km met de grond gelijkgemaakt en in een straal van 6 km zwaar beschadigd.

• Veel hoogradioactieve splitsingsfragmenten kwamen in de atmosfeer terecht en werden verder door winden over het aardoppervlak verspreid. Door de regen kwamen de splitsingsresten in planten en dus in het plantaardige voedsel terecht. Op die manier belandden ze in het menselijk lichaam, waar ze schade konden berokkenen.

WEETJE

▲ Afb. 48 Foto van

dagen

video: atoombom Hiroshima

5 Hoe kunnen we kernfusie-energie gebruiken?

5.1 Kernfusie in de zon

Sterren, en dus ook de zon, zijn natuurlijke fusiereactoren. De temperaturen binnen in de zon lopen op tot 15 miljoen kelvin. Bij dergelijke temperaturen zijn alle atomen volledig geïoniseerd. De resulterende verzameling van kernen en elektronen is een plasma

De hoge temperaturen zorgen ervoor dat de kernen in de zon snel genoeg bewegen om de elektrische afstotingskracht te overwinnen en samen te smelten tot grotere kernen. Wetenschappers gaan ervan uit dat de energie die de zon uitstraalt, voornamelijk opgewekt wordt in een reeks fusiereacties. Bij alle fusiereacties van kernen lichter dan 56Fe komt er energie vrij.

Jonge sterren, zoals de zon, bevatten hoofdzakelijk waterstofkernen. Er vinden dus fusiereacties van waterstof plaats.

Bijvoorbeeld: 21H + 21H → 31H + 1 1H + 4,0 MeV

Of: 21H + 31H → 41He + n0 + 17,7 MeV enzovoort

Afbeelding 49 illustreert een mogelijke reeks van fusiereacties in de zon en andere sterren die uiteindelijk tot de vorming van 4He leidt. Bij elke fusiereactie komt er energie vrij.

©VANIN

▲ Afb. 49 De vorming van 4He door fusiereacties in de zon. Bij elke fusiereactie komt er energie vrij.

ander deeltje (positron) ander deeltje (neutrino) gammastraal

Per seconde wordt er in de zon 600 miljoen ton waterstof omgezet in 596 miljoen ton helium. De overige 4 miljoen ton wordt omgezet in energie.

Een plasma is een geïoniseerd gas: de deeltjes zijn geladen ionen die vrij kunnen bewegen.

21H + 32H → 42He + n0 + 17,7 MeV

De energie die vrijkomt, kun je berekenen aan de hand van het massaverlies bij de fusiereactie.

Totale massa vóór de fusie

m(21H-kern) = m(21H-atoom) – m(e–) = 2,014 102 u – m(e–)

m(31H-kern) = m(31H-atoom) – m(e–) = 3,016 049 u – m(e–)

som = 5,030 151 u – 2 · m(e–)

©VANIN

Totale massa na de fusie

m(42He-kern) = m(42He-atoom) – 2 · m(e–) = 4,002 603 u – 2 · m(e–)

m(n0) = 1,008 665 u

som = 5,011 268 u – 2 · m(e–)

Massaverlies = 5,030 251 u – 5,011 268 u = 0,018 983 u

Vrijgekomen energie ∆E = 0,018 983 u · 931,49 MeV u = 17,7 MeV

Bij de fusie van deuterium en tritium komt er 17,7 MeV energie vrij.

VERDIEPING + 4 2He+ 4 2He+ 4 2He+ 4 2He

Als er zich voldoende helium ophoopt in een ster, kunnen er verdere fusiereacties plaatsvinden: 3 · 4 2He → 126C en soms verder 126C 168O 20 10Ne 56 26Fe

Wil je meer weten over de evolutie van sterren? Ga dan naar .

In sterren en in de zon heersen erg hoge temperaturen. De snelheid van de kernen in sterren is dan ook hoog genoeg om de afstotende elektrische kernkracht te overwinnen en kernfusie mogelijk te maken. De energie die sterren uitstralen, wordt opgewekt door kernfusie.

5.2 Kernfusie op aarde

Kernfusie realiseren op aarde zou veel voordelen hebben:

• Het is een vrijwel onuitputtelijke bron van energie. We kunnen deuterium uit water halen. 1 op de 6 400 H-atomen is deuterium. Er zit dus heel veel deuterium in het water van de oceanen. Tritium wordt geproduceerd uit lithium. Zowel water als lithium is overvloedig aanwezig op aarde. De fusie van deuterium en tritium leidt onder andere tot de volgende fusiereactie:

21H + 31H → 42He + n0 + 17,7 MeV

• Het systeem maakt geen gebruik van kettingreacties, wat het erg veilig maakt. Een probleem leidt er automatisch toe dat de fusie stopt.

• Er is geen uitstoot van CO2 of andere vervuilende stoffen.

• Er is geen opslag van radioactief afval nodig.

Een van de uitdagingen voor de kernfysica is om kernfusie op aarde te realiseren. Het is echter erg moeilijk om de extreem hoge temperaturen die nodig zijn voor fusie, op aarde te creëren. De temperatuur van het plasma is zo hoog dat het in geen geval in aanraking mag komen met de wanden van een vat. De wanden zouden onmiddellijk sublimeren en de temperatuur van het plasma zou dalen. Daarom wordt het plasma opgesloten in een magnetisch veld. De ladingen maken dan door de magnetische kracht spiraalvormige bewegingen rond de magnetische veldlijnen (zie afbeelding 50).

geen magnetisch veld met magnetisch veld

magnetische veldlijnwaterstofkern

▲ Afb. 50 Ladingen kunnen bijeen worden gehouden door een magnetisch veld. Door de magnetische kracht zullen ze spiraalvormige bewegingen maken rond de magnetische veldlijnen.

▲ Afb. 51 Door de spiraalvormige bewegingen rond de magnetische veldlijnen raakt het plasma de wanden niet.

Op aarde zijn extreem hoge temperaturen en dus ook kernfusie moeilijk te realiseren. Kernfusie op aarde zou nochtans veel voordelen hebben:

• Het is een vrijwel onuitputtelijke bron van energie

• Het is erg veilig, want het systeem maakt geen gebruik van kettingreacties. Een probleem leidt er automatisch toe dat de fusie stopt.

• Er is geen uitstoot van CO2 of andere vervuilende stoffen.

• Er is geen opslag van radioactief afval nodig.

Twee belangrijke onderzoekscentra voor kernfusie zijn ITER in Frankrijk en JET in het Verenigd Koninkrijk. In die centrales wordt het plasma bijeengehouden in een torus (donutvorm). De neutronen die tijdens de fusiereactie ontstaan, zijn elektrisch neutraal en kunnen de torus verlaten. Ze produceren warmte door tegen de wand te botsen. Net zoals in een splitsingscentrale, is het de bedoeling om de gecreëerde warmte te gebruiken om water om te zetten in stoom. De stoom zet op zijn beurt een turbine en een elektrische generator in beweging.

JET is de eerste reactor waarin wetenschappers fusie op aarde hebben uitgevoerd. Daarbij werd er meer energie verbruikt dan er geproduceerd werd. ITER is momenteel in opbouw. Volgens de huidige planning wordt ITER in 2025 operationeel. Het is de bedoeling dat ITER tien keer meer energie zal produceren dan verbruiken, maar het zal nog vele jaren duren voordat het zover is.

©VANIN

In 2022 slaagden Amerikaanse wetenschappers er voor het eerst in om netto-energie uit kernfusie te halen. Ze hanteerden een ander principe dan de onderzoekers in JET of ITER. Ze stuurden intens laserlicht van 192 lasers op een piepkleine capsule met deuterium en tritium. Ze slaagden er op die manier in om een plasma te creëren dat implodeerde. Daarbij ontstonden er zulke hoge temperaturen dat de deuterium- en tritiumkernen samensmolten tot helium. Omdat de fusie enkel plaatsvond in een piepkleine capsule, kunnen we het principe jammer genoeg niet gebruiken voor commerciële fusiereactoren.

▲ Afb. 52 De fusiereactor van ITER in Frankrijk

▲ Afb. 53 In Lawrence Livermore National Laboratory konden wetenschappers netto-energie halen uit kernfusie.

REEKS

Waarom is de kernmassa uitgedrukt in de atomaire massa-eenheid u geen geheel getal, behalve voor 12C? (Er zijn meerdere antwoorden mogelijk.)

a De kernmassa is een gewogen gemiddelde van de verschillende isotopenmassa’s.

b De massa van een nucleon in de kern verschilt van de massa van een los nucleon.

c De kernmassa is altijd kleiner dan de massa van de samenstellende protonen en neutronen.

d Tabellen bevatten de atomaire massa. Daarom voegt men gemakkelijkheidshalve de massa van de atomaire elektronen toe aan de massa van de kern.

Op een uiterst nauwkeurige balans liggen aan de ene kant een proton en een neutron, en bevindt zich aan de andere kant een deuteriumkern 2H.

A B C

Wie heeft gelijk? Verklaar.

Een kern met een lagere specifieke bindingsenergie is stabieler dan een kern met een hogere specifieke bindingsenergie.

Ik denk dat een kern met een hogere specifieke bindingsenergie stabieler is dan een kern met een lagere specifieke bindingsenergie.

Volgens mij is een kern met een lagere rustenergie stabieler dan een kern met een hogere rustenergie.

©VANIN

a Welke afbeelding toont de juiste balans?

b Welke massa moet je toevoegen opdat de balans in evenwicht is?

Duid het juiste antwoord aan zonder te rekenen.

1 0 u

2 0,0024 u

3 1,0068 u

4 2,0136 u

Rangschik de nucliden 1H, 4He, 56Fe en 238U volgens:

a stijgende specifieke rustenergie;

b stijgende rustenergie;

c stijgende specifieke bindingsenergie.

Maak een inschatting van de gevraagde grootheden.

a de specifieke bindingsenergie van 59Co (kobalt-59) aan de hand van de grafiek op p. 222

b de totale bindingsenergie van 59Co aan de hand van de grafiek op p. 222

Een kern met een hogere specifieke rustenergie is stabieler dan een kern met een lagere specifieke rustenergie.

Welke uitspraken zijn correct?

Verbeter de foute uitspraken.

a Elk microscopisch en macroscopisch systeem streeft naar minimale kinetische energie.

b Een 1 1H-kern heeft een hogere rustenergie dan een 56 26Fe-kern.

c De projectie van de energievallei op het grondvlak is de nuclidenkaart.

d In een kerncentrale is het belangrijk dat er meer dan 1 neutron dat vrijkomt bij een splitsingsreactie van 235U, een nieuwe splitsingsreactie veroorzaakt. Zo valt de kettingreactie niet stil.

e De massa van de zon neemt geleidelijk aan toe.

Maak de uitspraken correct door ‘altijd’, ‘soms’ of ‘nooit’ toe te voegen.

a Middelzware kernen hebben een hoger specifieke bindingsenergie dan zware kernen.

b Als er bij een kernreactie massaverlies is, dan komt er energie vrij.

c Spontane kernsplitsing komt voor.

d Neutronen die vrijkomen bij een kernsplitsing, veroorzaken een nieuwe kernsplitsing.

e De heliumkernen in sterren zijn afkomstig van fusiereacties.

Op 11 maart 2011 vond er in de kerncentrale van Fukushima een kernramp plaats als gevolg van een zeebeving en een daaropvolgende tsunami. Hoewel de kernreactoren werden stilgelegd, bleef de temperatuur in de centrale oplopen omdat de koelsystemen beschadigd waren. Daardoor vond er in de drie kernreactoren een gedeeltelijke smelting plaats, waarbij ook grote hoeveelheden radioactieve stoffen vrijkwamen. Er werden zo’n 150 000 mensen geëvacueerd.

a Onmiddellijk na de beving werden de drie kernreactoren stilgelegd door middel van een noodstop. Wat heeft men heel concreet gedaan om de splitsingsreacties te stoppen?

b Was de vermenigvuldigingsfactor f groter dan, gelijk aan of kleiner dan 1 nadat de noodstop werd ingeschakeld? Verklaar je antwoord.

c Stopten alle splitsingsreacties onmiddellijk nadat de noodstop werd ingeschakeld? Verklaar je antwoord.

REEKS

Bereken voor de nuclide 16O:

a de rustenergie in MeV; b de specifieke rustenergie in MeV; c het massadefect in u; d de bindingsenergie in MeV; e de specifieke bindingsenergie in MeV.

Zoek de nodige gegevens op in de tabellen op p. 289-294.

Een neutron valt in op een 235U-kern.

De 235U-kern ondergaat daardoor de volgende splitsingsreactie:

23592U + n0 → 14156Ba + 92 36Kr + 3 · n0

a Leg uit hoe die splitsingsreactie een kettingreactie kan veroorzaken.

b Bereken de hoeveelheid kernsplitsingsenergie die vrijkomt.

Zoek de nodige gegevens op in de tabellen op p. 289-294.

2 tritiumkernen 31H smelten samen in een fusiereactie, waarbij er ook nog 2 neutronen vrijkomen.

a Welke fusiekern wordt er gevormd?

b Wat is de reactievergelijking?

c Hoeveel fusie-energie komt er vrij bij die reactie?

Zoek de nodige gegevens op in de tabellen op p. 289-294.

REEKS

Hoeveel energie is er minstens nodig om een proton uit een 20 10Ne-kern te verwijderen?

Zoek de nodige gegevens op in de tabellen op p. 289-294.

In het Excelbestand op iDiddit vind je twaalf reeksen nucliden.

De leerkracht verdeelt de klas in twaalf groepjes.

Elk groepje neemt een reeks nucliden voor zijn rekening.

a Voer de Excelopdracht uit voor jouw reeks data.

b Breng de data van de twaalf reeksen samen in het tabblad ‘Alle data’ en voer de Excelopdracht uit.

c Welke grafiek uit het handboek heb je min of meer nagemaakt? Bespreek de eventuele verschillen.

▲Fukushima na de tsunami

©VANIN

HOOFDSTUKSYNTHESE

Massadefect Δm:

∆m = [N · m(n0) + Z · m(p+)] – [m(AX)]

massadefect = som van de massa’s – massa kern van de afzonderlijke nucleonen

Massa van de kern verschilt van de som van de massa’s van de afzonderlijke nucleonen.

Massa-energierelatie van Einstein:

E0 = m · c2

©VANIN

rustenergie = massa · lichtsnelheid2

Massa kan worden omgezet in energie.

Energie kan worden omgezet in massa.

Atomaire massa-eenheid u:

1 u = massa van een 126C–atoom 12

1 u = 1,660 54 · 10–27 kg

E0 (in MeV) = m (in u) · 931,490 MeV u

Elektronvolt:

1 eV = 1,602 176 5 · 10–19 J

1 J = 6,2415 · 1018 eV

Kernsplitsingsreacties:

• Kernsplitsingsreacties beginnen gewoonlijk omdat er een neutron invalt op een 235U kern.

• Bij elke kernsplitsing komen neutronen vrij die een nieuwe kernsplitsing kunnen veroorzaken. → kettingreactie

• Het aantal neutronen per splitsing dat een nieuwe splitsing veroorzaakt, is de vermenigvuldigingsfactor f

- f < 1: kettingreactie valt stil.

- f = 1: situatie in kerncentrales.

-Moderator (vaak water of grafiet) verhoogt f door neutronen te vertragen.

-Controlestaven (vaak cadmium of boor) verlagen f door neutronen te absorberen.

- f > 1: atoombom

• Kernsplitsingsfragmenten hebben een teveel aan neutronen en zijn instabiel. → radioactief afval

Specifieke rustenergie van een kern =

E0 A rustenergie van de kern massagetal

= de gemiddelde energie van een nucleon in een kern

Specifieke bindingsenergie van een kern =

∆E0 A = ∆m · c2 A Δm = massadefect massagetal

= energie per nucleon die vrijkomt als nucleonen samen een kern vormen

Er kunnen grote hoeveelheden energie vrijkomen door:

• kernsplitsing: zware kernen die uiteenvallen;

• kernfusie : lichte kernen die worden samengevoegd.

Kernfusiereacties: Afstotende elektrische kracht moet overwonnen worden.

• Dat gebeurt in sterren omdat daar hoge temperaturen heersen.

• Onderzoek naar kernfusie op aarde: hoge temperaturen moeilijk te realiseren.

HOOFDSTUK 3

Radioactief verval

De straling die afkomstig is van radioactieve kernen, heeft vele toepassingen: in de geneeskunde voor diagnose en behandeling, in de archeologie om te dateren, in de voedingsmiddelenindustrie om te voorkomen dat voedsel bederft … Maar wat is radioactief verval precies? Welke soorten straling komen er vrij bij het verval en wat zijn hun eigenschappen? Hoe komt het dat er verschillende soorten radioactief verval bestaan?

Je gaat er in dit hoofdstuk dieper op in.

LEERDOELEN

M de begrippen ‘doordringend vermogen’ en ‘ioniserend vermogen’ toelichten en verbinden met de verschillende soorten verval

M uitleggen waarom α-, β- en γ-straling voorbeelden van ioniserende straling zijn

M de oorzaak van de verschillende soorten verval toelichten

M de nucleaire reactievergelijking voor de verschillende soorten radioactief verval weergeven

M op de nuclidenkaart opzoeken hoe een nuclide vervalt

1 Welke straling komt vrij bij radioactief verval?

1.1 Straling bij radioactief verval

‘Radioactiviteit’ komt van het Latijnse woord radius, dat ‘straal’ betekent, en het woord ‘actief’. Het begrip werd bedacht door Marie Curie.

©VANIN

In 1896 deed Henri Becquerel een belangrijke ontdekking: uraniumertsen zenden spontaan, zonder beïnvloeding van buitenaf, straling uit die een fotografische plaat zwart kleurt. Al snel ontdekten Marie en Pierre Curie nog twee andere, tot dan toe onbekende, elementen die spontaan straling uitzenden. De elementen kregen de namen polonium en radium. Het verschijnsel kreeg de naam radioactiviteit

Radioactiviteit is het proces waarbij instabiele nucliden vervallen naar andere (stabiele of instabiele) nucliden, om zo hun energie te verlagen. Instabiele kernen zenden tijdens hun verval straling uit en worden daarom radioactieve kernen genoemd. Materiaal dat radioactieve kernen bevat, noem je een stralingsbron

Straling is een vorm van energieoverdracht zonder rechtstreeks contact tussen stralingsbron en ontvanger. Er worden elektromagnetische golven of deeltjes uitgestuurd:

• Elektromagnetische golven zijn golven die geen middenstof nodig hebben om zich voort te planten. Een voorbeeld daarvan is zichtbaar licht.

• Bij deeltjesstraling gaat het om hoogenergetische deeltjes die maximaal de grootte van een nuclide hebben, bijvoorbeeld elektronen, neutronen, protonen of 4He-kernen. Ook elektromagnetische golven worden soms voorgesteld als deeltjes. Die deeltjes noem je fotonen. Je kunt dus zeggen dat zichtbaar licht uit fotonen bestaat.

• Radioactiviteit is het proces waarbij instabiele nucliden vervallen naar andere (stabiele of instabiele) nucliden. Ze zenden daarbij straling uit.

• Straling is een vorm van energieoverdracht zonder rechtstreeks contact tussen stralingsbron en ontvanger. Er worden elektromagnetische golven of deeltjes uitgestuurd.

©VANIN

In 1903 kregen Henri Becquerel en Pierre en Marie Curie samen de Nobelprijs. Becquerel kreeg de prijs ‘ter erkenning van de buitengewone diensten die hij heeft verricht door zijn ontdekking van spontane radioactiviteit’ en Pierre en Marie Curie ‘voor hun onderzoek naar de stralingsverschijnselen ontdekt door Henri Becquerel’.

Acht jaar later ontving Marie Curie opnieuw de Nobelprijs, deze keer voor scheikunde ‘als erkenning voor haar diensten ter bevordering van de scheikunde door de ontdekking van de elementen radium en polonium, door de isolatie van radium en de studie van de aard en samenstelling van dat opmerkelijke element’.

Marie Curie was de eerste vrouw die de Nobelprijs in ontvangst mocht nemen, en een van de vijf wetenschappers die de prijs twee keer mochten ontvangen.

1.2 De eigenschappen van straling

Straling die over voldoende energie beschikt om atomen en moleculen te kunnen ioniseren, noem je ioniserende straling. Voorbeelden van ioniserende straling zijn uv-straling en snelle neutronen die vrijkomen bij fusie- of splitsingsreacties. Alle straling die vrijkomt bij radioactief verval, is ioniserende straling.

Het ioniserend vermogen van straling is het vermogen om atomen en moleculen te ioniseren. Straling met een hoog ioniserend vermogen botst gemakkelijk met atomen en kan op die manier atomaire elektronen vrijmaken.

Afb. 56 Ioniserende straling

ioniserende straling

vrij elektron

Omdat de straling bij elke ionisatie energie afgeeft, verliest straling met een groot ioniserend vermogen heel snel haar energie. Dergelijke straling kan daarom niet ver doordringen in een materiaal.

▲ Afb. 54 Pierre en Marie Curie in hun laboratorium

Afb. 55 Henri Becquerel in zijn laboratorium

WEETJE

Het doordringend vermogen geeft aan hoe ver straling gemiddeld kan doordringen in een materiaal. Het is een statistisch proces: hoe ver stralingsdeeltjes in materie kunnen doordringen, hangt af van de botsingen die ze maken met de atomen en de moleculen in het materiaal, en hoeveel energie ze daarbij verliezen. Voor dezelfde soort straling zullen sommige stralingsdeeltjes verder in het materiaal doordringen dan andere.

Het ioniserend vermogen en het doordringend vermogen van straling zijn omgekeerd evenredig met elkaar. Als het ioniserend vermogen van straling hoog is, dan is het doordringend vermogen van die straling laag, en omgekeerd.

©VANIN

Ioniserende straling is straling die over voldoende energie beschikt om atomen en moleculen te ioniseren.

• Het ioniserend vermogen van straling is het vermogen om atomen en moleculen te ioniseren.

• Het doordringend vermogen geeft aan hoe ver straling kan doordringen in een materiaal.

Het ioniserend vermogen en het doordringend vermogen zijn omgekeerd evenredig met elkaar.

1.3 De verschillende soorten straling bij radioactief verval

In het begin van de twintigste eeuw ontdekte Rutherford op basis van experimentele waarnemingen dat bij radioactief verval drie soorten straling kunnen vrijkomen: α-, β- en γ-straling. Op basis van het gedrag van de verschillende soorten straling in een magnetisch en elektrisch veld kon Rutherford afleiden of de straling uit positief geladen, negatief geladen of elektrisch neutrale deeltjes bestond. Hij kon de verschillende soorten straling ook onderscheiden op basis van hun ioniserend en doordringend vermogen.

1 α-straling bestaat uit 4 2He-kernen, die soms ook α-deeltjes worden genoemd. Ze hebben een positieve lading, in overeenstemming met de waarnemingen van Rutherford. Ze zijn zwaar in vergelijking met andere stralingsdeeltjes, waardoor ze gemakkelijk botsen met atomen. Daarom hebben ze een groot ioniserend vermogen en een klein doordringend vermogen. Een blad papier of enkele centimeters lucht zijn voldoende om ze te stoppen.

2 β-straling bestaat uit β-deeltjes. β-deeltjes hebben een matig ioniserend vermogen en een matig doordringend vermogen. De β-deeltjes in het experiment van Rutherford waren elektronen. Deze β-deeltjes worden β–-deeltjes genoemd omwille van hun negatieve lading. Om β–-straling te stoppen, heb je een paar millimeter aluminium of enkele meters lucht nodig.

3 γ-straling bevat geen geladen deeltjes. Het gaat om hoogenergetische elektromagnetische golven, die je ook kunt voorstellen door fotonen. γ-straling heeft een klein ioniserend vermogen en een groot doordringend vermogen. Je hebt een paar centimeter lood nodig om γ-straling voor het grootste deel te kunnen stoppen.

VOORBEELD KWALITEITSCONTROLES MET BEHULP VAN STRALINGSBRONNEN

Bij de productie van metaalplaten of papier meet men de dikte met behulp van een stralingsbron. Hoe dikker de plaat of het papier, hoe meer straling er geabsorbeerd wordt. Door met een detector te meten welke fractie van de straling door het papier of de plaat gaat en welke fractie gestopt wordt, kan men de dikte bepalen.

Voor metaalplaten gebruikt men γ-straling, omdat die straling een groot doordringend vermogen heeft. Voor de diktebepaling van papier gebruikt men β–-straling, omdat die straling een matig doordringend vermogen heeft. Die techniek wordt ook gebruikt om vliegtuigvleugels, pijpleidingen, kabels van skiliften … te controleren op kleine barstjes.

©VANIN

stralingsbron

detector

staalplaat

stralingsbron metaalkabel holte detector

De verschillende soorten straling die afkomstig zijn van radioactieve kernen, kun je van elkaar onderscheiden op basis van een aantal experimentele waarnemingen.

STRALING SOORT DEELTJES IONISEREND VERMOGEN

DOORDRINGEND VERMOGEN

α-straling 4 2He-kernen groot klein

β–-straling elektronen matig matig

γ-straling fotonen klein groot

▲ Afb. 59 Diktecontrole bij een staalplaat

▲ Afb. 60 Kwaliteitscontrole van een metaalkabel

Het woord ‘annihilatie’ komt van het Latijnse annihilare. Daarin hoor je het woord nihil, dat ‘niets’ betekent, en het woord ad, dat ‘tot’ of ‘naar’ betekent.

1.4 β–-straling en β+-straling

De β-deeltjes in de experimenten van Rutherford waren elektronen en negatief geladen. Later werden er ook positief geladen β-deeltjes ontdekt. Sindsdien spreekt men van β–-straling voor negatief geladen β-deeltjes en van β+-straling voor positief geladen β-deeltjes:

• β–-straling bestaat uit hoogenergetische elektronen

• β+-straling bestaat uit hoogenergetische positronen.

Een positron, voorgesteld door het symbool e+, lijkt heel erg op een elektron, maar heeft een tegengestelde elektrische lading en is dus positief geladen. Het is het antideeltje van het elektron. Voor elk materiedeeltje, zoals een elektron of een quark, bestaat er ook een antideeltje. Deeltjes en antideeltjes hebben veel dezelfde eigenschappen, bijvoorbeeld de massa, maar ze hebben een tegengestelde elektrische lading.

Als een positron en een elektron interageren, wordt hun volledige massa omgezet in energie. Die energie komt vrij onder de vorm van twee γ-stralen: e– + e+ → γ + γ

Dat verschijnsel noem je positron-elektronannihilatie

VOOR NA

= 511 keV

▲ Afb. 61 Positron-elektronannihilatie

©VANIN

2 = 511 keV

VOORBEELD DE ENERGIE VAN DE γ-STRALEN BIJ POSITRON-ELEKTRONANNIHILATIE

Om de energie van de γ-stralen bij positron-elektronannihilatie te berekenen, stel je de energiebalans op.

De massa van het elektron bedraagt 0,000 548 580 u.

De bijhorende rustenergie is dan:

E0(e–) = 0,000 548 580 u · 931,49 MeV u = 0,051 100 MeV = 511,00 keV

Het positron is het antideeltje van het elektron en heeft dezelfde massa en rustenergie.

Het positron en het elektron hebben dus samen een rustenergie die gelijk is aan 2 · 511,00 keV.

Die energie wordt volledig omgezet naar de energie van de twee γ-stralen.

Dat wil zeggen dat elke afzonderlijke γ-straal een energie van 511,00 keV heeft.

Een materiaal bevat veel elektronen. Als een β+-deeltje op een materiaal invalt, interageert het dan ook quasi onmiddellijk met een elektron, waarna het samen met het elektron wordt omgezet in twee γ-stralen. Het β+-deeltje zelf kan dus niet ver in het materiaal doordringen, de γ-stralen die ontstaan door de positron-elektronannihilatie wel.

Er bestaan twee soorten β-straling:

• β–-straling bestaat uit hoogenergetische elektronen.

• β+-straling bestaat uit hoogenergetische positronen.

Positronen worden voorgesteld door het symbool e+. Het zijn de antideeltjes van elektronen. Ze hebben veel dezelfde eigenschappen als elektronen, maar hun elektrische lading is positief en dus tegengesteld aan die van elektronen.

Als β+-deeltjes invallen op een materiaal, worden ze quasi onmiddellijk omgezet in γ-stralen door positron-elektronannihilatie.

©VANIN

Carl Anderson, geboren in New York als zoon van Zweedse immigranten, ontdekte in 1932 het positron. Hij kreeg daarvoor in 1936 de Nobelprijs, samen met de Oostenrijkse fysicus Victor Franz Hess.

▲ Afb. 62 Carl Anderson

WEETJE

2 Wat is de oorzaak van de verschillende soorten radioactief verval?

Instabiele kernen kunnen hun specifieke rustenergie verlagen door radioactief te vervallen richting de stabiliteitsband. De soort straling die vrijkomt bij het radioactief verval, hangt af van de oorzaak van de instabiliteit van de kern. Het is de samenstelling van de kern (het aantal protonen Z en het aantal neutronen N) die bepaalt waarom de kern instabiel is en hoe de kern zal vervallen. Je kunt het soort verval van een kern aflezen op de nuclidenkaart.

Energievallei

©VANIN

1 α-verval

2 β-verval

Z nuclidenkaart

▲ Afb. 63 Het α-, β+- en β–-verval op de energievallei en de nuclidenkaart

stabiele kern

α-straler

β+-straler

β–-straler protonenemitter spontane splitser neutronenemitter

Kernen met meer dan 82 protonen zijn instabiel, omdat ze te veel nucleonen bevatten. De sterke kernkracht is niet meer in staat om ze bij elkaar te houden, vanwege het korte bereik van die kracht. Zware kernen kunnen hun energie verminderen door hun aantal nucleonen (protonen én neutronen) te verminderen. Meestal gebeurt dat via α-verval, waarbij een 4 2He-kern wordt afgestoten. Op de nuclidenkaart zijn die kernen geel gekleurd. 222Rn (radon-222) is een voorbeeld van een α-straler.

De flanken van de vallei worden gevormd door kernen met een teveel aan neutronen (bijvoorbeeld 40K, kalium-40) of een teveel aan protonen (bijvoorbeeld 18F, fluor-18). Kernen met te veel neutronen kunnen hun specifieke rustenergie verminderen door een neutron om te zetten in een proton (de roze kernen op de nuclidenkaart). Ze vervallen via β–-verval Op een analoge manier kunnen kernen met te veel protonen hun specifieke rustenergie verminderen door een proton om te zetten in een neutron (de blauwe kernen op de nuclidenkaart). Ze vervallen via β+-verval

3 γ-verval

Er bestaat ook een type verval waarbij het protonental en het neutronental ongewijzigd blijven: het γ-verval. Omdat N en Z ongewijzigd blijven, zijn γ-stralers niet terug te vinden op de nuclidenkaart. Ze worden ook niet weergegeven op de energievallei. Vóór het γ-verval heeft de nuclide een (totale) energie die hoger is dan haar (totale) rustenergie. Bij γ-verval verlaagt een kern haar energie door hoogenergetische fotonen (dat wil zeggen: hoogenergetische elektromagnetische golven) uit te zenden. Op die manier verlaagt de kern haar energie tot haar rustenergie bereikt is, zonder N of Z te wijzigen. Alle kernen kunnen meer energie bezitten dan hun rustenergie en via γ-verval vervallen, maar dikwijls volgt γ-verval op α-verval of β-verval.

©VANIN

4 Andere vormen van verval

Soms verminderen zware kernen hun specifieke rustenergie ook door spontane splitsing. Die kernen zijn groen gekleurd op de nuclidenkaart.

Kernen aan de rand van de nuclidenkaart kunnen ook vervallen door een proton af te stoten (oranje kernen op de nuclidenkaart) of een neutron af te stoten (paarse kernen op de nuclidenkaart).

CONCEPTVRAGEN

1 Zoek de kernen 222Rn, 40K, 131I en 18F op de nuclidenkaart en lees af hoe ze vervallen.

2 Zoek nog andere voorbeelden van α-stralers op de nuclidenkaart op .

3 Zoek nog andere voorbeelden van β–-stralers op de nuclidenkaart.

4 Zoek nog andere voorbeelden van β+-stralers op de nuclidenkaart.

Er bestaan verschillende soorten radioactief verval, omdat kernen om verschillende redenen instabiel kunnen zijn.

• Zware kernen vervallen meestal via α-verval, omdat ze te veel nucleonen hebben.

Ze verlagen hun specifieke rustenergie door een 4 2He-kern af te stoten en op die manier hun aantal nucleonen te verminderen.

• Kernen met te veel neutronen vervallen door een neutron om te zetten in een proton

Dat noem je ook β–-verval.

• Kernen met te veel protonen vervallen door een proton om te zetten in een neutron.

Dat noem je ook β+-verval

• Kernen kunnen ook vervallen zonder hun protonental of neutronental te wijzigen.

Dat is het geval wanneer hun energie groter is dan hun rustenergie

Ze vervallen dan via γ-verval en zenden een hoogenergetisch foton uit.

Een behoudswet is een natuurwet die stelt dat een bepaalde eigenschap (bijvoorbeeld lading of energie) van een systeem constant blijft als externe factoren geen rol spelen. Je kunt behoudswetten gebruiken om allerlei problemen op te lossen zonder ze in detail te beschrijven.

3 Hoe veranderen kernen van samenstelling bij de verschillende soorten radioactief verval?

3.1 De behoudswetten bij kernreacties

Je spreekt van een kernreactie als de samenstelling (aantal protonen Z en/of aantal neutronen N) van een kern verandert. α-verval, β-verval, kernfusie en kernsplitsing zijn voorbeelden van kernreacties.

©VANIN

Bij α-verval verandert de samenstelling van de kern. Het is een kernreactie.

Bij β-verval verandert de samenstelling van de kern. Het is een kernreactie.

Bij kernfusie verandert de samenstelling van de kernen. Het is een kernreactie.

Experimenten tonen aan dat bij elke kernreactie een aantal behoudswetten geldig zijn:

1 Het totale aantal nucleonen (weergegeven door het massagetal A) is voor en na de kernreactie gelijk

2 De totale elektrische lading is voor en na de kernreactie gelijk.

3 Bij de vorming van een extra deeltje wordt ook altijd een extra antideeltje gevormd.

De behoudswetten helpen om het radioactief verval beter te begrijpen.

Een kernreactie is een proces waarbij de samenstelling van een of meerdere kernen verandert

Bij kernreacties gelden drie behoudswetten:

• Het aantal nucleonen blijft behouden.

• De lading blijft behouden.

• Er kan enkel een extra deeltje worden gevormd als er een extra antideeltje wordt gevormd.

3.2 De kernreactie bij α-verval

Er bestaan zowel kunstmatige als natuurlijke radionucliden die spontaan via α-verval vervallen. Ze worden soms ook α-stralers genoemd. Een voorbeeld van een kunstmatige α-straler is 24195Am (americium-241). Voorbeelden van natuurlijke α-stralers zijn 23892U, 23592U, 22688Ra en 21084Po.

22688Ra en 21084Po zijn twee α-stralers die in 1898 door Pierre en Marie Curie werden ontdekt. Zij kregen daarvoor de helft van de Nobelprijs in 1903.

24195Am is een α-straler die nog niet zo lang geleden gebruikt werd in rookmelders.

23892U is een α-straler die gebruikt wordt om rotsen en gesteenten geologisch te dateren.

▲ Afb. 70 α-verval op de nuclidenkaart

α-stralers verminderen hun specifieke rustenergie door α-deeltjes (42He-kernen) uit te zenden. Wanneer een nuclide A ZX een α-deeltje uitstraalt, zal de samenstelling van de achtergebleven nuclide veranderd zijn: de nieuwe kern heeft 2 protonen en 2 neutronen minder, in overeenstemming met de behoudsregels voor kernreacties. De nuclide X is na het α-verval de nuclide – 4 – 2 Y geworden.

Je kunt de nucleaire reactievergelijking als volgt schrijven: X → – 4 – 2 Y + 4 2He

©VANIN

Afb. 71 De nucleaire reactievergelijking voor α-verval

▲ Afb. 67

▲ Afb. 68

▲ Afb. 69

▲

24195Am (americium-241) is een kunstmatige radionuclide die vervalt via α-verval. Ze werd vroeger vaak gebruikt in rookmelders.

De nucleaire reactievergelijking is:

24195Am → 23793Np + 4 2He waarbij 237Np de nuclide neptunium-237 is.

α-verval gebeurt volgens deze nucleaire reactievergelijking:

©VANIN

Rookmelders met radioactieve bron verboden Tot voor kort maakten veel rookmelders gebruik van het radioactieve 24195Am (americium-241) in de vorm van AmO2 24195Am is een α-straler met een halveringstijd van 432,52 jaar.

De α-straling ioniseert de zuurstof- en stikstofmoleculen in de lucht tussen twee tegengesteld geladen platen. De ionen die op die manier ontstaan, vormen een kleine elektrische stroom, die gemeten wordt door de elektronica van de rookmelder. Komt er rook tussen de elektrisch geladen platen van de rookmelder, dan wordt een deel van de α-straling geabsorbeerd door de rook in plaats van door de luchtmoleculen. De stroomsterkte daalt en er gaat een alarm af.

De stralingsdosis die van een rookmelder vrijkomt, is erg klein en relatief onschadelijk. De rookmelders kunnen wel schadelijk zijn voor het milieu als ze in het verkeerde afvalcircuit terechtkomen. Daarom zijn ze sinds 1 januari 2020 verboden.

De nieuwe generatie rookmelders zijn optische rookmelders. Die zenden licht uit. Als er rook aanwezig is, wordt het licht verstrooid en gaat er een alarm af.

▲ Afb. 72 Het α-verval van 24195Am op (een stukje van) de nuclidenkaart

WEETJE

▲ Afb. 73 Een oude rookmelder met binnenin een radioactieve bron

3.3 De kernreacties bij β-verval

Kernen die β-straling uitzenden bij hun radioactief verval, worden ook β-stralers genoemd. Er bestaan twee soorten β-stralers:

• β–-stralers zenden elektronen uit.

• β+-stralers zenden positronen uit.

Er bestaan zowel kunstmatige (6328Ni, 13178I …) als natuurlijke (31H, 146C …) β–-stralers. In de natuur bestaan geen radionucliden die spontaan via β+-verval vervallen. Spontane β⁺-stralers worden allemaal in het laboratorium gemaakt. Voorbeelden van spontane (maar kunstmatige) β+-stralers zijn 137N, 189F en 68 31Ga.

©VANIN

146C is een natuurlijke β–-straler die gebruikt wordt voor koolstofdatering.

63 28Ni is een kunstmatige β–straler die soms in nucleaire batterijen wordt gebruikt.

189F is een kunstmatige β+straler die voor medische beeldvorming wordt gebruikt.

Toch lijken β–-verval en β+-verval in vele opzichten op elkaar. Je bestudeert de twee soorten verval hieronder in meer detail.

A De kernreactie bij β–-verval

β–-stralers verlagen hun specifieke rustenergie door een neutron om te zetten in een proton. Ze zenden daarbij een hoogenergetisch elektron uit. De energie van die uitgezonden elektronen is zo groot dat ze niet afkomstig kunnen zijn van de atomaire elektronenmantel. Ze ontstaan in de kern zelf op het ogenblik dat een neutron wordt omgezet in een proton.

Volgens de derde behoudswet moet de vorming van een elektron gepaard gaan met de vorming van een antideeltje. Al in 1930 suggereerde Wolfgang Pauli het bestaan van een tot dan toe onbekend deeltje, maar het werd pas in 1953 voor het eerst gedetecteerd: het neutrino ν. Het neutrino heeft geen lading en een massa die zo klein is dat ze moeilijk te bepalen is. Het antideeltje van het neutrino is het antineutrino ν

Als er in een kern een neutron wordt omgezet in een proton, dan ontstaan er tegelijkertijd een elektron en een antineutrino: n → p + e– + ν̅.

CONCEPTVRAAG

Toon aan dat de omzetting n → p + e– + ν voldoet aan alle behoudswetten voor kernreacties.

VERDIEPING

Wil je meer weten over de verschillende soorten neutrino’s en antineutrino’s?

Ga dan naar

Het woord ‘neutrino’ is Italiaans voor ‘neutraaltje’. Het neutrino wordt voorgesteld door de Griekse letter ν (nu). Het antineutrino wordt voorgesteld door de Griekse letter met een streepje erboven: ν̅.

Wil je graag meer weten over nucleaire batterijen? Bekijk dan deze video.

Wanneer een nuclide A ZX een β–-deeltje (elektron) uitstraalt, zal de samenstelling van de achtergebleven nuclide veranderd zijn: de kern heeft een neutron omgezet in een proton. Na het verval heeft de nuclide dus 1 neutron minder (N – 1) en 1 proton meer (Z + 1). Het aantal nucleonen A is gelijk gebleven. De nuclide X is na het β–-verval de nuclide + 1 geworden.

▲ Afb. 77 β–-verval op de nuclidenkaart

Je kunt de nucleaire reactievergelijking als volgt schrijven: X

©VANIN

▲ Afb. 78 De nucleaire reactievergelijking voor β–-verval

VOORBEELD HET RADIOACTIEF VERVAL VAN 6328Ni

63 28Ni is een kunstmatige radionuclide die via β–-verval vervalt. Het is een van de radionucliden die in nucleaire batterijen worden gebruikt. Een nucleaire batterij maakt gebruik van de elektronen die bij β–-verval ontstaan om elektrische stroom en spanning te creëren.

De nucleaire reactievergelijking voor het radioactief verval van 63 28Ni is: 63 28Ni → 63 29Cu + e– + ν

▲ Afb. 79 Het β–-verval van 63 28Ni

29Cu

28Ni

▲ Afb. 80 Het β–-verval van 63 28Ni op (een stukje van) de nuclidenkaart

B De kernreactie bij β+-verval

β+-stralers verlagen hun specifieke rustenergie door een proton om te zetten in een neutron. Ze zenden daarbij een β+-deeltje uit. β+-deeltjes zijn positronen e+, de antideeltjes van elektronen. Als er een antideeltje ontstaat in de kern, moet er volgens de derde behoudswet nog een deeltje ontstaan: het neutrino ν

Als er in een kern een proton wordt omgezet in een neutron, dan ontstaan er tegelijkertijd een positron en een neutrino: p → n + e+ + ν

CONCEPTVRAAG

Toon aan dat de omzetting p → n + e+ + ν voldoet aan alle behoudswetten voor kernreacties.

De rustmassa van een los proton is lager dan de rustmassa van een los neutron. De rustenergie van een los proton is dus ook lager dan die van een los neutron. Daarom zal een los proton nooit spontaan vervallen naar een los neutron.

Protonen en neutronen in een kern kunnen zich echter anders gedragen dan losse protonen en neutronen. In de natuur bestaan er geen kernen die spontaan via β+-verval vervallen, maar spontane β+-stralers kunnen wel in laboratoria worden gemaakt. Voorbeelden zijn 189F en 68 31Ga.

▲ Afb. 81 β+-verval op de nuclidenkaart

Wanneer een nuclide A ZX een β+-deeltje (positron) uitstraalt, zal de samenstelling van de achtergebleven nuclide veranderd zijn: de kern heeft een proton omgezet in een neutron. Na het verval heeft de nuclide dus 1 proton minder (Z – 1) en 1 neutron meer (N + 1). Het aantal nucleonen A is gelijk gebleven. De nuclide X is na het β+-verval de nuclide + 1 Y geworden.

Je kunt de nucleaire reactievergelijking als volgt schrijven: X → – 1 Y + e+ + ν

©VANIN

▲ Afb. 82 De nucleaire reactievergelijking voor β+-verval

VOORBEELD HET RADIOACTIEF VERVAL VAN 189F

189F is een kunstmatige radionuclide die via β+-verval vervalt. De nuclide wordt gebruikt voor medische beeldvorming (zie ook hoofdstuk 4).

De nucleaire reactievergelijking voor het radioactief verval van 189F is:

189F → 188O + e+ + ν

©VANIN

▲ Afb. 83 Het β+-verval van 189F

▲ Afb. 84 Het β+-verval van 189F op (een stukje van) de nuclidenkaart

• β–-verval gebeurt volgens deze nucleaire reactievergelijking:

X → + 1 Y + e– + ν

• β+-verval gebeurt volgens deze nucleaire reactievergelijking:

X → – 1 Y + e+ + ν

VERDIEPING

Het is de zwakke interactie die zorgt voor de omzetting van een proton naar een neutron of een neutron naar een proton. Zwakke interactie maakt β-verval dus mogelijk.

3.4 γ-verval

Kernen die gevormd worden tijdens een kernreactie (fusiereactie, splitsingsreactie, α-verval, β-verval …), hebben vaak meer energie dan hun rustenergie. Zo vervalt 60 27Co eerst via β–-verval naar een hoge energietoestand in 60 28Ni, om vervolgens naar de grondtoestand van 60 28Ni te vervallen door twee γ-stralen uit te zenden.

99m43Tc is een γ-straler met een halveringstijd van 6 uur. De nuclide wordt heel vaak gebruikt wordt voor medische diagnoses.

Radionucliden zoals 60 27Co of 13755Cs worden gebruikt voor kwaliteitscontroles in de industrie. De γ-stralen die vrijkomen, gebruikt men voor diktemetingen van metaalplaten of om te zoeken naar kleine barstjes in vliegtuigvleugels.

γ-straling

Ook in de landbouw- en voedingsindustrie worden radionucliden zoals 60 27Co of 13755Cs gebruikt. Als voedsel bestraald wordt, zal het minder snel bederven. Ook insectenplagen bestrijdt men met behulp van γ-stralen.

Als kernen meer (totale) energie hebben dan hun (totale) rustenergie, bevinden ze zich in een aangeslagen toestand. Dat geef je aan door een sterretje toe te voegen bij het symbool van de kern: A ZX*.

De kernen vervallen naar een lagere energietoestand en uiteindelijk naar de grondtoestand door γ-stralen uit te zenden. γ-straling is hoogenergetische elektromagnetische straling. Die straling wordt vaak voorgesteld als hoogenergetische deeltjes. Je noemt zo'n deeltje een foton.

De verschillende energieniveaus van kernen hebben energieverschillen van de grootteorde van keV tot MeV. De energieniveaus van de elektronen in een atoom liggen maar een paar eV van elkaar verwijderd. γ-stralen zijn dan ook tot een miljoen keer energetischer dan fotonen die in de atomaire elektronenmantel ontstaan zijn, zoals de fotonen van zichtbaar licht.

Als een kern een foton uitzendt, blijft het aantal protonen Z en het aantal neutronen N in de kern behouden. In de nuclidenkaart blijft de kern op dezelfde plek staan.

Je kunt het uitzenden van γ-stralen als volgt schrijven: A ZX* → A ZX + γ

Een kern bevindt zich in een aangeslagen toestand als ze meer energie heeft dan haar rustenergie.

Soms kan een kern een tijdje in een aangeslagen toestand blijven vooraleer ze een γ-straal uitzendt. De kern bevindt zich in een metastabiele toestand en wordt een isomeer genoemd. Dat geef je weer door de letter m toe te voegen aan het symbool van de kern: Am ZX.

VOORBEELD DE 99m43Tc-ISOMEER

De 99m43Tc-isomeer wordt veel gebruikt voor medische beeldvorming vanwege zijn halveringstijd van 6,01 uur. Dat is lang genoeg om de nodige medische handelingen te kunnen uitvoeren. Het is ook kort genoeg om ervoor te zorgen dat de patiënt niet langdurig blootgesteld wordt aan radioactieve straling. De 99m43Tc-isomeer ontstaat door het β–-verval van 99 42Mo en zendt op zijn beurt een γ-straal uit.

Het gebeurt veel vaker dat kernen in een aangeslagen toestand onmiddellijk naar de grondtoestand vervallen. Dat is bijvoorbeeld het geval bij het verval van 66 27Co naar de grondtoestand van 60 28Ni.

©VANIN

▲ Afb. 89 Het vereenvoudigde vervalschema van 99 42Mo. De 99m43-isomeer ontstaat als gevolg van het β–-verval van 99 42Mo. De isomeer heeft een halveringstijd van 6,01 uur.

▲ Afb. 90 Het vervalschema van 6027Co. De aangeslagen energietoestanden van 6028Ni vervallen onmiddellijk verder naar het grondniveau, dat stabiel is.

γ-verval is radioactief verval waarbij hoogenergetische fotonen worden uitgestraald. Dat is het geval als de nuclide meer energie dan haar rustenergie bezit. Het aantal protonen Z en het aantal neutronen N blijven ongewijzigd.

Je kunt het uitzenden van γ-stralen als volgt schrijven: X* → X + γ

Soms kan een kern een tijdje in de hogere energietoestand blijven vooraleer ze een foton uitzendt. De kern bevindt zich in een metastabiele toestand en wordt een isomeer genoemd.

Insectenplagen aanpakken met γ-stralers Fruitgewassen zijn erg gevoelig voor insectenplagen. Nucleaire technieken vormen een alternatief voor pesticiden om de plagen in te dijken.

Mannetjesinsecten worden massaal gefokt en bestraald met γ-straling die afkomstig is van bijvoorbeeld 66 27Co of 13755Cs. Zo worden ze onvruchtbaar. Daarna worden ze vrijgelaten, maar ze kunnen zich niet meer voortplanten. Doordat men dat proces verschillende generaties na elkaar herhaalt, sterven de insecten geleidelijk aan uit. Op die manier werd de mediterrane fruitvlieg in Mexico uitgeroeid.

WEETJE

▲ Afb. 91 De mediterrane fruitvlieg

Wat gebeurt er als instabiele kernen naar andere instabiele kernen vervallen?

Als een kern vervalt door een α- of β-deeltje uit te stralen, kan de nieuwe kern op haar beurt radioactief zijn. Op die manier bestaan er reeksen van kernen die via radioactief verval van de ene kern in de andere overgaan, tot er uiteindelijk een stabiele kern wordt gevormd. Er bestaan kunstmatige vervalreeksen, maar in de natuur zijn er ook drie natuurlijke vervalreeksen. Ze vertrekken van 23290Th, 23892U en 23592U, en eindigen bij stabiele loodkernen, respectievelijk 20882Pb, 20682Pb en

82Pb.

Hieronder vind je het voorbeeld van de natuurlijke vervalreeks van 23892U.

©VANIN

▲ Afb. 92 De natuurlijke vervalreeks van 23892U op de vereenvoudigde nuclidenkaart. Alleen de nucliden van de vervalreeks zijn weergegeven.

Instabiele kernen kunnen zowel naar stabiele als naar instabiele kernen vervallen. Vervallen ze naar een instabiele kern, dan zal die op haar buurt ook vervallen. Zo ontstaan vervalreeksen. Er bestaan zowel natuurlijke als kunstmatige vervalreeksen.

REEKS

Zijn de volgende uitspraken juist of fout?

Verbeter indien nodig.

a α-deeltjes hebben dezelfde structuur als een 4He-atoom.

b β+- en β–-straling hebben hetzelfde doordringend vermogen.

c Elektromagnetische straling kan atomen ioniseren.

d Het aantal deeltjes voor en na een kernreactie is gelijk.

Een medisch laborante is aan het werk op een meter afstand van een stralingsbron die α-straling uitzendt.

a Wat moet ze minstens doen om zichzelf te beschermen tegen de straling?

1 Ze hoeft zichzelf niet te beschermen.

2 Ze moet een mondmasker dragen.

3 Ze moet voor een papieren afscheiding tussen zichzelf en de stralingsbron zorgen.

4 Ze moet voor een aluminium afscheiding tussen zichzelf en de stralingsbron zorgen.

5 Ze moet achter loodglas gaan staan.

b Herhaal deze oefening voor een stralingsbron die β–-straling en een stralingsbron die γ-straling uitzendt.

Vul de nucleaire reactievergelijkingen aan.

a A ZX → Y + e– + ν

b A ZX → Y + e+ + ν

c A ZX → X + γ

Bestudeer het radioactief verval van een aantal nucliden.

a Zoek de nuclide 34 17Cl op de nuclidenkaart op

b Via welk soort verval vervalt die kern?

Wie heeft gelijk? Verklaar.

α-straling is eigenlijk geen straling, want α-straling bestaat uit 4 2He-kernen.

Straling kun je enkel als elektromagnetische golven voorstellen.

Elektromagnetische golven kun je ook als deeltjes voorstellen, namelijk als fotonen.

©VANIN

c Naar welke kern vervalt 34 17Cl?

d Schrijf de volledige nucleaire reactievergelijking van dat verval op.

e Herhaal vraag a-d voor de nucliden 24294Pu en 69 28Ni.

Alleen de zon zendt straling uit.

Vul de uitspraken aan met ‘altijd’, ‘soms’ of ‘nooit’.

a Straling bestaat uit elektromagnetische golven.

b γ-stralen buigen af in een magnetisch veld.

c γ- stralen worden gestopt door een paar centimeter lood.

d β–-verval komt voor bij zware kernen (A > 200).

e β+-verval komt spontaan voor.

f In een magnetische veld buigt een α-deeltje sterker af dan een β-deeltje.

Is dit radioactief verval mogelijk?

Verklaar telkens waarom wel of niet.

a van 23592U naar 23693Np

b van 99m43Tc naar 99 43Tc

c α-verval van 31H

d β–-verval van 31H

e van 21182Pb naar 21183Bi

f van 8 4Be naar 4 2He

Antwoord telkens met de juiste nuclide(n).

Gebruik daarvoor de nuclidenkaart op

a Welke nuclide vervalt naar 198Hg door β–-straling uit te zenden?

b Welke nucliden vervallen naar 209Bi?

c Welke nucliden vervallen naar 208Pb?

d Welke nuclide vervalt naar 1H?

e Welke nuclide vervalt naar 2H?

A B

C D

REEKS

Construeer de vervalreeks van 235U.

Gebruik daarvoor de nuclidenkaart op

REEKS

21084Po vervalt naar 20682Po en zendt daarbij α-straling uit.

Je vindt het vervalschema van 21084Po hieronder. Po

MeV

De firma PapierGenie gebruikt een radioactieve bron om de dikte van papier te controleren. Zal de firma een stralingsbron met 99 42Mo, 60 27Co of 90 38Sr gebruiken? Verklaar je antwoord.

Je vindt de (vereenvoudigde) vervalschema’s van de drie radionucliden hieronder.

Mo 99 42

Tc 99m 43 67 h

12,5 % 1,86 MeV β

87,5 % 1,73 MeV

▲Het vervalschema van 99 42Mo

metastabiele toestand

Tc 99 43

2,12 · 105 y 6,01 h 0,14 MeV γ

0,803 MeV γ

▲Het vervalschema van 21084Po

a Op het vervalschema kun je lezen dat de energie van het α-deeltje die vrijkomt bij het radioactief verval van de grondtoestand van 21084Po naar de grondtoestand van 20682Pb, gelijk is aan 5,305 MeV.

Om welke energie gaat het precies?

1 de rustenergie van het α-deeltje

2 de kinetische energie van het α-deeltje

3 de totale energie van het α-deeltje

Hint: je kunt dat verifiëren door de energiebalans van de kernreactie op te schrijven.

b Bereken de snelheid van het α-deeltje met een energie van 5,305 MeV.

c Een kleine fractie van 21084Po vervalt niet naar de grondtoestand van 20682Pb, maar naar de eerste aangeslagen toestand. De energie van het α-deeltje die daarbij vrijkomt, is gelijk aan 4,502 MeV. Wat is de snelheid van dat α-deeltje?

d Vergelijk de snelheid van beide α-deeltjes.

▲Het vervalschema van 6027Co

Sr 90 38 Y 90 39

Zr 90 40 28,68 y 64,10 h stabiel 100 % 0,546 MeV

▲Het vervalschema van 9038Sr

 Meer oefenen? Ga naar

HOOFDSTUKSYNTHESE

oorzaak verval van instabiele kern te veel nucleonen in de kern te veel neutronen in de kern te veel protonen in de kern totale energie van de kern hoger dan de totale rustenergie van de kern

stralingsdeeltjes 4 2He-kernen elektronen e– positronen e+ fotonen (elektromagnetische golven)

nucleaire reactievergelijking

voorstelling op de nuclidenkaart

©VANIN

ioniserend vermogen (het vermogen om atomen en moleculen te ioniseren)

doordringend vermogen (geeft aan hoe ver straling kan doordringen in een materiaal)

hoog

matig

laag

Wordt gestopt door een blad papier of enkele centimeters lucht.

matig

Wordt gestopt door enkele millimeters aluminium of enkele meters lucht.

Positronelektronannihilatie: wordt bij interactie met een elektron samen met het elektron omgezet in energie onder de vorm van γ-stralen.

γ-stralers zijn niet terug te vinden op de nuclidenkaart.

laag

hoog

Wordt grotendeels gestopt door enkele centimeters lood.

blad papier enkele mm aluminium enkele cm lood

HOOFDSTUK 4

De effecten van ioniserende straling op de mens

©VANIN

Veel mensen zijn bang voor ioniserende straling, omdat die de gezondheid kan schaden. Toch gebruikt men ioniserende straling en radionucliden vaak in de medische wereld om diagnoses te stellen en mensen te behandelen. Welke impact heeft ioniserende straling op de mens? Welke stralingsdosissen zijn gevaarlijk en hoe kun je je beschermen? Aan welke bronnen van ioniserende straling worden we blootgesteld?

Op al die vragen krijg je een antwoord in dit hoofdstuk.

LEERDOELEN

M de impact van ioniserende straling op de mens beschrijven

M beschermingsmaatregelen tegen ioniserende straling omschrijven

M de verschillende grootheden en eenheden van ioniserende straling interpreteren en toepassen

M de meest voorkomende bronnen van natuurlijke en kunstmatige ioniserende straling benoemen en beschrijven

M een aantal medische toepassingen van radioactiviteit beschrijven

1 Welke impact heeft ioniserende straling op de mens?

Ioniserende straling beschikt over voldoende energie om atomen en moleculen te kunnen ioniseren. De straling afkomstig van kernreacties (α-, β- en γ-staling, snelle neutronen …) is hoogenergetische ioniserende straling met een energie van de grootteorde van 1 MeV. Voor de ionisatie van atomen en moleculen is er slechts een energie van de grootteorde van 10 eV nodig. Eén enkel stralingsdeeltje kan dus duizenden ionisaties veroorzaken.

Alle materialen, en dus ook biologische organismen zoals de mens, kunnen beschadigd worden als ze in contact komen met grote hoeveelheden ioniserende straling. Als de straling bindende elektronen van een molecule verwijdert, valt de molecule uit elkaar. Het is ook mogelijk dat de structuur van de molecule wijzigt, waardoor het gedrag van de molecule verandert en soms schadelijk wordt.

De gevolgen voor het lichaam hangen af van het aantal moleculen en de aard van de moleculen die door de ioniserende straling schade hebben opgelopen.

Meestal is het geen probleem als er een molecule in het menselijk lichaam verloren gaat. Een volwassen mens bestaat immers naar schatting uit 40 000 miljard cellen die elk uit vele miljarden moleculen opgebouwd zijn (zie Afb. 93). Een groep cellen die dezelfde functie hebben, vormen samen een weefsel, bijvoorbeeld het spierweefsel. Verschillende weefsels die samen een bepaalde taak uitoefenen, vormen samen een orgaan, bijvoorbeeld het hart of de spieren.

Een cel ondervindt gewoonlijk geen schade als er één molecule in die cel beschadigd raakt. Van de meeste moleculen zijn er voldoende kopieën aanwezig en kunnen er nieuwe kopieën worden bijgemaakt. Het DNA in de cel bevat de code voor de aanmaak van nieuwe moleculen. Als bepaalde moleculen niet of verkeerd worden aangemaakt omdat het DNA in de cel beschadigd is, kan de cel afsterven. Stralingsschade aan het DNA kan daarom ernstiger zijn.

Ook als er een lichaamscel afsterft, is dat normaal gezien geen probleem. Op enkele uitzonderingen na kan het lichaam een afgestorven cel vervangen door een nieuwe. Als er echter te veel cellen afsterven, kan het lichaam zichzelf mogelijk niet meer herstellen.

Soms overleeft de cel wel, maar is ze beschadigd. Door celdeling kunnen er op die manier veel defecte cellen ontstaan. Ioniserende straling kan dus kanker veroorzaken: een ongecontroleerde, snelle deling van abnormale cellen.

NORMALE CELONTWIKKELING

©VANIN

cel celkern

chromosoom

DNA

▲ Afb. 93 De structuur van een menselijke cel

celdeling

ABNORMALE CELGROEI gezond weefsel

normale cel normale cel beschadigde cel ongecontroleerde celdeling kwaadaardige tumor

▲ Afb. 94 De ontwikkeling van een tumor

Blootstelling aan straling, bijvoorbeeld bij medische toepassingen, moet dus altijd worden afgewogen tegen de eventuele voordelen ervan. Voor werknemers die beroepshalve vaak met radioactiviteit in contact komen, zijn er strenge veiligheidsmaatregelen uitgewerkt om de opgelopen stralingsdosis zo laag mogelijk te houden.

Blootstelling aan ioniserende straling kan lichaamsschade veroorzaken.

• Het menselijk lichaam heeft beschermingsmechanismen die ervoor zorgen dat het kan herstellen van beperkte schade: moleculen en cellen die verloren gaan, kunnen meestal worden vervangen door andere.

• Blijvende lichaamsschade ontstaat als er: – te veel cellen afsterven; – cellen defect zijn omdat het DNA binnen in de cel beschadigd is. Een ongecontroleerde deling van defecte cellen leidt tot kanker door de vorming van tumoren.

2 Hoe kun je jezelf beschermen tegen ioniserende

2.1 Besmetting en bestraling

Je kunt op verschillende manieren in contact komen met ioniserende straling. Het soort contact bepaalt de graad van gevaar.

contact met stralingsbron stralingsbron op afstand

uitwendige besmetting

inwendige besmetting

minste gevaar meeste gevaar bestraling

▲ Afb. 95 Het verschil tussen besmetting en bestraling

Ioniserende straling is het gevaarlijkst als je in rechtstreeks contact komt met de radionucliden van de stralingsbron.

Rechtstreeks contact met radionucliden wordt besmetting genoemd. Er zijn twee mogelijkheden:

• Bij inwendige besmetting zitten de radionucliden binnen in je lichaam. De meeste besmettingen gebeuren via het eten van voedsel. Ook de lucht bevat radionucliden die je kunt inademen.

• Bij uitwendige besmetting zijn de radionucliden aanwezig op je huid, haar of kleding. Dat kan het gevolg zijn van radionucliden in de lucht of het komt doordat je rechtstreeks een radioactieve bron hebt aangeraakt.

Je hebt onrechtstreeks contact met radionucliden als je bestraald wordt door een stralingsbron op afstand. Dat noem je bestraling. Ook dan kun je lichaamsschade oplopen.

CONCEPTVRAGEN

1 Word je zelf een stralingsbron als je besmet bent met radionucliden?

2 Word je zelf een stralingsbron als je bestraald wordt door een stralingsbron op afstand?

2.2 Voorzorgsmaatregelen

Om de stralingsschade te beperken, kun je voorzorgsmaatregelen nemen. Bij besmetting moet je de stralingsbron verwijderen om verdere lichaamsschade te voorkomen.

• Inwendige besmettingsbronnen kun je niet zomaar verwijderen. Het is dus belangrijk om niet inwendig met radionucliden besmet te worden.

• Uitwendige besmettingsbronnen kun je verwijderen door uitgebreid te douchen en zo de radionucliden op je huid en haar te verwijderen en andere kleren aan te trekken.

Wie beroepsmatig in aanraking komt met radioactieve bronnen, vermijdt rechtstreeks contact met de bronnen door beschermende kleding te dragen: overalls, handschoenen, schoenbeschermers, gezichtsmaskers enzovoort. Het is ook belangrijk om na het contact met een radioactieve bron altijd goed je handen te wassen.

VOORBEELD BESMETTING DOOR BANANEN

Wie lust er niet af en toe eens een banaan? Bananen zijn gezond. Nochtans bevatten bananen en ook ander fruit kalium. Een van de isotopen van kalium is de natuurlijke radionuclide 40K (kalium-40), met een natuurlijk voorkomen van 0,0117 %. 40K is een natuurlijke β–-straler. Door bananen te eten, besmet je jezelf dus met radionucliden. Gelukkig is de stralingsdosis die je op die manier oploopt, erg laag en ongevaarlijk. Je lichaam heeft sowieso kalium nodig om je bloeddruk te regelen en zenuwprikkels over te dragen.

Bij bestraling kun je de lichaamsschade beperken door:

• de blootstellingsduur te beperken;

• voldoende afstand te nemen van de bron;

• jezelf af te schermen van de bron door bijvoorbeeld loodglas of beschermende kleding te gebruiken.

©VANIN

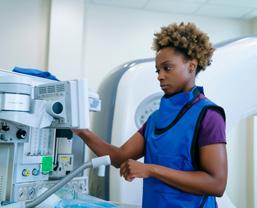
Bij besmetting is er rechtstreeks contact met radionucliden:

• bij inwendige besmetting in je lichaam;

• bij uitwendige besmetting op je haar, huid of kleren.

Uitwendige besmetting kun je verwijderen, inwendige besmetting niet.

Bij bestraling word je wel bestraald door ioniserende straling, maar is er geen rechtstreeks contact met de stralingsbron. Stralingsschade door bestraling kun je vermijden door de blootstellingsduur te beperken, afstand te houden van de bron en/of afscherming te voorzien.

▲ Afb. 96 Bananen: een stralingsbron

▲ Afb. 97 Een beschermende loodschort

In welke grootheden en eenheden worden stralingsdosissen uitgedrukt?

3.1 Grootheden om stralingshoeveelheden uit te drukken

Elke soort straling bevat een hoeveelheid energie. De energie uitgedrukt in MeV is echter onvoldoende om de impact van straling op de mens uit te drukken. De gevolgen van blootstelling aan ioniserende straling worden bepaald door drie factoren:

1 de sterkte van de radioactieve bron;

2 de hoeveelheid stralingsenergie die geabsorbeerd wordt door het organisme (de mens);

3 de biologische impact van de geabsorbeerde straling.

Elk van die factoren heeft een eigen grootheid, met indicatiewaarden die aangeven hoe groot de impact is en welke specifieke voorzorgsmaatregelen je moet nemen.

sterkte van de bron biologische impact geabsorbeerde energie

©VANIN

3.2 De hoeveelheid straling uitgezonden door de bron (in becquerel)

De stralingsschade hangt af van de sterkte van de radioactieve bron: hoe meer straling de radioactieve bron uitzendt, hoe groter de mogelijke stralingsschade. De hoeveelheid straling die een radioactieve bron uitzendt, is rechtstreeks verbonden met het aantal radioactieve kernen dat vervalt.

Bij elk verval is er een afname van het aantal instabiele kernen. Als N(t) het aantal instabiele kernen op een tijdstip t voorstelt, dan is het aantal vervallen kernen dus gelijk aan de verandering van het aantal instabiele kernen, namelijk ΔN.

De gemiddelde hoeveelheid straling die een radioactieve bron uitzendt, wordt gedefinieerd als het aantal vervallen kernen ΔN per tijdsinterval Δt: | ΔN Δt |. Die grootheid, die het tempo van het verval aangeeft, wordt de gemiddelde activiteit van de radioactieve bron genoemd en voorgesteld met het symbool A. De eenheid is becquerel (Bq): 1 Bq = 1 verval 1 s = 1 s–1

GROOTHEID MET SYMBOOL EENHEID MET SYMBOOL VERBAND MET SI-EENHEDEN activiteit A becquerelBq 1 Bq = 1 s–1

De eenheid Bq is vernoemd naar Henri Becquerel, die in 1896 radioactiviteit ontdekte.

▲ Afb. 98 Factoren die de impact van ioniserende straling op de mens beïnvloeden

Je kunt de activiteit op een bepaald tijdstip t, A(t), berekenen door Δt erg klein te maken: Δt → 0.

Je noteert dat als volgt: A(t) = lim Δ →0 | ΔN Δt | = | dN dt |. In de wiskunde noem je dat de afgeleide.

VOORBEELD HET MENSELIJK LICHAAM ALS STRALINGSBRON

Het menselijk lichaam heeft een natuurlijke radioactiviteit van ongeveer 120 Bq per kg. Die natuurlijke radioactiviteit komt hoofdzakelijk via voedsel in ons lichaam terecht. Een volwassene met een massa van 75 kg heeft dus een activiteit van 9 000 Bq.

Dat betekent dat er elke seconde 9 000 radioactieve kernen in een volwassene vervallen. Dat is een lage activiteit. Zo heeft 1 g 226Ra een activiteit van 37 miljard Bq.

©VANIN

120 Bq per kg

▲ Afb. 99 Het menselijk lichaam als radioactieve bron

Er bestaat een wiskundig verband tussen de activiteit van een radioactieve bron, het aantal instabiele kernen in die bron en hun halveringstijd:

Hoe meer instabiele kernen er zijn, hoe meer radioactieve vervallen er zullen plaatsvinden. Er is een recht evenredig verband tussen de activiteit en het aantal instabiele kernen:

A(t) ~ N(t)

Als de halveringstijd van de radioactieve kernen groot is, dan zullen de radioactieve vervallen over een langere tijd worden uitgesmeerd. Er is een omgekeerd evenredig verband tussen de activiteit en de halveringstijd:

A(t) ~ 1 T1/2

A(t) ~ N(t) T1/2

Je kunt dus schrijven dat:

A(t) = | dN dt |= constante · N(t) T1/2

Door de afgeleide dN dt wiskundig uit te rekenen, vind je dat de constante gelijk is aan 0,693 (= ln 2, zie oefening 15). De uitdrukking voor de activiteit A(t) van een radioactieve bron wordt dan:

A(t) = | dN dt |= 0,693 · N(t) T1/2

Soms schrijft men die uitdrukking ook als volgt:

A(t) = λ · N(t)

λ = 0,693 T1/2 en wordt de vervalconstante genoemd.

Grafisch is de activiteit A op een tijdstip t gelijk aan de grootte van de richtingscoëfficiënt van de raaklijn aan de N(t)-grafiek (grafiek 4). Je kunt zien dat de activiteit na verloop van tijd afneemt, omdat het aantal instabiele kernen N afneemt als functie van de tijd.

©VANIN

▲ Grafiek 4 Grafische voorstelling van de activiteit A

CONCEPTVRAGEN

1 Hoe kun je op de grafische voorstelling zien dat de activiteit afneemt als functie van de tijd?

2 Schat de verhouding tussen de aangeduide activiteiten.

De activiteit A van een radioactieve bron geeft aan hoeveel straling een radioactieve bron uitzendt, en is gelijk aan het aantal radioactieve vervallen per seconde:

A(t) = | dN dt |= 0,693 · N(t) T1/2

Daarbij is N(t) het aantal instabiele kernen op tijdstip t. De eenheid is becquerel (Bq).

De gray dankt zijn naam aan de Britse wetenschapper Louis Harold Gray (1905-1965). Hij was een van de eersten die de effecten van ioniserende straling op organismen bestudeerde.

3.3 De stralingsdosis geabsorbeerd door je lichaam (in gray)

De activiteit is een maat voor de radioactiviteit van een bepaalde bron. Als de activiteit hoog is, blijf je beter uit de buurt of moet je beschermende kleding dragen (die veel, maar niet alle straling tegenhoudt).

De activiteit zegt echter weinig over de hoeveelheid ioniserende straling die door je lichaam geabsorbeerd wordt. Niet alle straling die de bron uitzendt, valt immers in op iemand in de omgeving. De persoon in kwestie stond misschien redelijk ver van de bron of achter loodglas. Bovendien wordt niet alle straling die op een lichaam invalt, door dat lichaam geabsorbeerd.

©VANIN

activiteit (becquerel) geabsorbeerde dosis 1 (gray) geabsorbeerde dosis 2 (gray)

▲ Afb. 100 Niet alle uitgezonden ioniserende straling valt in op een persoon in de omgeving.

De grootheid geabsorbeerde dosis D is een maat voor de hoeveelheid stralingsenergie die je lichaam geabsorbeerd heeft. Ze wordt uitgedrukt in de eenheid gray. Een gray is gelijk aan de absorptie van een joule stralingsenergie door een kg materie.

GROOTHEID MET SYMBOOL

EENHEID MET SYMBOOL VERBAND MET SI-EENHEDEN geabsorbeerde dosis D gray Gy J kg

Hoe hoger de geabsorbeerde dosis, hoe meer stralingsenergie er in het lichaam opgenomen is en hoe meer ionisaties er mogelijk zijn. Voor elke ionisatie is er immers een bepaalde hoeveelheid energie nodig.

CONCEPTVRAAG

Zal de geabsorbeerde dosis het grootst zijn bij de persoon links of rechts op afbeelding 100? Verklaar.

VOORBEELDVRAAGSTUK

Benjamin is laborant. Hij heeft een massa van 82 kg en een lichaamsoppervlak van 1,9 m2.

Hij werkt deze voormiddag gedurende 4,0 uur op een afstand van 3,0 m van een 6027Co-bron met een activiteit van 1,0 · 109 Bq. Bij elk verval van 6027Co komen er onmiddellijk na elkaar twee γ-stralen vrij. De energieën van de γ-stralen zijn 1,33 MeV en 1,17 MeV (zie energieschema in hoofdstuk 3 op p. 256). Benjamins lichaam absorbeert 50 % van de invallende γ-stralen.

De andere γ-stralen passeren het lichaam ongehinderd.

▲ Afb. 101 Fractie van de straling die invalt op een persoon

1 Welke fractie van de straling die wordt uitgezonden door de bron, valt in op Benjamin?

2 Wat is de geabsorbeerde dosis van Benjamin?

Gegeven:

• m = 82 kg

• Alichaam = 1,9 m2

• t = 4,0 h

• d = 3,0 m

• A = 1,0 · 109 Bq

• E(γ1) = 1,33 MeV en E(γ2) = 1,17 MeV

• absorptie van 50 % van de γ-stralen

Gevraagd: 1 fractie van de radioactieve straling die invalt op Benjamin = ?

2 D = ?

Oplossing: 1 De bron zendt in alle richtingen evenveel straling uit.

De fractie van de straling die invalt op Benjamin, is gelijk aan zijn lichaamsoppervlak gedeeld door de oppervlakte van een bol met een straal van 3,0 m:

fractie = 1,9 m2

4 · π · d2 = 1,9 m2 4 · π · (3,0 m)2 = 1,7 · 10–2 = 1,7 %

Er valt 1,7 % van de bronstraling in op Benjamin.

2 Om de geabsorbeerde dosis D = E m te berekenen, moet je berekenen hoeveel energie het lichaam van Benjamin geabsorbeerd heeft.

De geabsorbeerde energie E kun je als volgt berekenen:

• Per verval van 60 27Co komen er twee γ-stralen vrij:

E(γ) = E(γ1) + E(γ2) = 1,33 MeV + 1,17 MeV = 2,50 MeV

• Er zijn 1,0 · 109 vervallen per seconde, wat overeenkomt met een uitgezonden energie van 2,50 · 1,0 · 109 MeV s

• 1,7 % van de uitgezonden straling valt in op Benjamin. 50 % van de straling die op Benjamin invalt, wordt geabsorbeerd. Benjamin absorbeert dus: 0,017 · 0,50 · 2,50 · 1,0 · 109 Mev s = 2,1 · 107 Mev s = 2,1 · 107 · 1,6 · 10–13 J s = 3,4 · 10–6 J s

Benjamin werkt 4,0 uur in het labo.

Hij absorbeert dus in totaal 3,4 · 10–6 J s · 4 h · 3 600 s h = 4,9 · 10–2 J.

De geabsorbeerde dosis is gedefinieerd als D = E m . Benjamin heeft een massa van 82 kg.

De geabsorbeerde dosis wordt:

D = 4,9 · 10–2 J 82 kg = 5,9 · 10–4 J kg = 5,9 · 10–4 Gy = 0,59 mGy

De geabsorbeerde dosis die Benjamin heeft opgelopen, bedraagt 0,59 mGy.

Reflectie: Is dat een schadelijke hoeveelheid straling of niet?

Met je huidige kennis is het moeilijk om het resultaat van 0,59 mGy te interpreteren. Daarvoor heb je meer informatie nodig. Je krijgt die in het vervolg van dit hoofdstuk.

©VANIN

3.4 De biologische schade in je lichaam (in sievert)

De geabsorbeerde dosis leert je hoeveel stralingsenergie een lichaam geabsorbeerd heeft. Hoewel dat een indicatie is voor de mogelijke stralingsschade die iemand heeft opgelopen, hangt de biologische schade ook af van de soort straling die het lichaam geabsorbeerd heeft, en van de organen die de straling absorberen. Daarom voerde men twee nieuwe grootheden in.

A De equivalente dosis

De grootheid equivalente dosis H eq, met als eenheid de sievert (Sv), brengt de soort straling in rekening door de geabsorbeerde dosis D te vermenigvuldigen met een stralingsweegfactor wR: H eq = D · wR

Daarbij wordt de stralingsweegfactor wR gedefinieerd als de dosis γ-straling die dezelfde biologische schade veroorzaakt als 1 gray van de betreffende straling. Het subscript R in het symbool wR komt van het Engelse woord radiation.

1 gray α-straling is tot twintig keer schadelijker dan 1 gray β- of γ-straling. Dat verschil wordt vooral veroorzaakt door het feit dat α-deeltjes zware stralingsdeeltjes zijn en door hun massa veel trager bewegen dan β- of γ-deeltjes met dezelfde energie. Daardoor veroorzaakt α-straling veel ionisaties dicht bij elkaar, wat het risico op onherstelbare schade in een cel verhoogt. De kans op blijvende biologische schade is kleiner als de geïoniseerde moleculen meer verspreid in het lichaam liggen, zoals bij β- of γ-straling. Ook neutronen hebben, afhankelijk van hun snelheid, een grote stralingsweegfactor: van 3 voor trage neutronen tot 20 voor snelle neutronen.

STRALING wR α 20 β– en β+ 1 γ 1 neutron3-20

©VANIN

De sievert is vernoemd naar Zweedse medische fysicus Rolf Maximilian Sievert (1896-1966). Hij bestudeerde de biologische effecten van ioniserende straling.

B De effectieve dosis

De effectieve dosis Heff, ook met de eenheid sievert (Sv), houdt niet alleen rekening met de soort straling, maar ook met het orgaan of het weefsel dat die straling geabsorbeerd heeft: Heff = H eq · w w = D · wR · w w

Daarbij is w w de weefselweegfactor, een weegfactor voor weefsels en organen. In sommige organen zijn de ionisaties immers veel schadelijker dan in andere. De onderstaande tabel en afbeeldingen lijsten de weefselweegfactoren voor verschillende weefsels en organen op. Als het volledige lichaam gelijkmatig aan de ioniserende straling wordt blootgesteld, is de weefselweegfactor gelijk aan 1. Dan zijn de equivalente dosis en de effectieve dosis gelijk aan elkaar.

WEEFSEL OF ORGAAN wW WEEFSEL OF ORGAAN wW voortplantingsorganen

0,20 lever

rood beenmerg 0,12 slokdarm

dikke darm 0,12 schildklier

longen 0,12 huid

maag 0,12 botoppervlak

blaas 0,05 rest van het lichaam 0,05 borsten 0,05 totaal 1

▲ Tabel 1 Weefselweegfactoren voor de verschillende lichaamsdelen

WEEFSELWEEGFACTOR

©VANIN

voortplantingsorganen: 0,20

skelet:

• rood beenmerg: 0,12

• botoppervlak: 0,01

blaas: 0,05 borsten: 0,05

spijsverteringsstelsel:

• dikke darm: 0,12

• maag: 0,12

• lever: 0,05

• slokdarm: 0,05 longen: 0,12

▲ Tabel 2 Weefselweegfactoren voor de verschillende lichaamsdelen

schildklier: 0,05huid: 0,01

GROOTHEID

equivalente dosis

effectieve dosis

De sievert is een grote eenheid. Vaak gebruikt men daarom de mSv (millisievert = 10–3 Sv) of μSv (microsievert = 10–6 Sv).

VOORBEELDVRAAGSTUK

BASISFORMULE

▲ Afb. 103 Schematische voorstelling van de verschillende eenheden

Benjamin is laborant. Zijn lichaam liep deze voormiddag een geabsorbeerde dosis van 0,59 mGy aan γ-straling op door de nabijheid van een 6027Co-bron die een γ-straler is.

Welke effectieve dosis heeft Benjamin opgelopen?

Gegeven:

• D = 0,59 mGy

• γ-straling

• absorptie van de γ-straling door heel zijn lichaam

Gevraagd: Heff = ?

Oplossing: Op afbeelding 102 en tabel 1 en 2 kun je aflezen dat:

• wR(γ) = 1

• ww(volledige lichaam) = 1

Daaruit volgt dat:

Heff = 0,59 · 10–3 · 1

1 Sv = 0,59 mSv

Benjamin heeft een effectieve dosis van 0,59 mSv opgelopen.

Reflectie: Waarom kun je de geabsorbeerde dosis en de effectieve dosis hier aan elkaar gelijk stellen? Als het volledige lichaam bestraald wordt met γ-straling, dan is de effectieve dosis (in sievert) gelijk aan de geabsorbeerde dosis (in gray).

De biologische stralingsschade hangt af van:

• de soort straling die het lichaam geabsorbeerd heeft;

• het orgaan of het weefsel dat de straling geabsorbeerd heeft.

De equivalente dosis H eq houdt rekening met de soort straling:

H eq = D · wR, waarbij D de geabsorbeerde dosis en wR de stralingsweegfactor is

De effectieve dosis Heff houdt rekening met de soort straling en het orgaan of het weefsel dat die straling absorbeert:

Heff = H eq · w w = D · wR · ww, waarbij w w de weefselweegfactor is

De eenheid is voor beide dosissen de sievert (Sv).

becquerel

sievert gray

CONCEPTVRAAG

Aan welke effectieve dosis word je blootgesteld gedurende een trans-Atlantische vlucht van tien uur op vijftien kilometer hoogte?

4 Aan hoeveel natuurlijke en kunstmatige radioactiviteit worden we blootgesteld?

4.1 Gemiddelde jaarlijkse effectieve dosis

Een gemiddelde Belg loopt per jaar een effectieve dosis van 4 mSv op:

• 2,5 mSv is het gevolg van natuurlijke radioactiviteit: – kosmische straling; – aardstraling; – inademing van natuurlijke radionucliden; – radionucliden in ons voedsel.

• 1,5 mSv is het gevolg van kunstmatige radioactiviteit: – Die ioniserende straling is bijna uitsluitend afkomstig van medische toepassingen – De opgelopen stralingsdosis door industriële toepassingen, bijvoorbeeld de aanwezigheid van kerncentrales, is verwaarloosbaar klein.

Natuurlijke radioactiviteit

kosmische straling (0,3 mSv/jaar)

natuurlijke radionucliden in de aardbodem (0,4 mSv/jaar)

inwendige besmetting door inademing van natuurlijke radionucliden (1,4 mSv/jaar)

inwendige besmetting door radionucliden in het voedsel (0,3 mSv/jaar)

Kunstmatige radioactiviteit

industriële toepassingen (0,01 mSv/jaar)

medische toepassingen (1,5 mSv/jaar)

▲ Afb. 104 De geschatte blootstelling aan ioniserende straling voor de gemiddelde Belg, gebaseerd op cijfers van het FANC

Er zijn zes bronnen van ioniserende straling waaraan de gemiddelde Belg wordt blootgesteld. Je bestudeert ze hierna meer in detail.

1 Kosmische straling

Kosmische straling is straling die in het universum ontstaat en voortdurend de aarde bombardeert. Een kleine fractie ervan ontstaat in de zon. Het grootste deel ontstaat in de andere sterren en de rest van het universum.

Als de kosmische straling de atmosfeer bereikt, botst ze met de luchtmoleculen. Dat leidt tot kernreacties waarbij (secundaire) straling vrijkomt, hoofdzakelijk β- en γ-straling. Omdat kosmische straling door de atmosfeer wordt geabsorbeerd, neemt de intensiteit sterk af naarmate je dichter bij het aardoppervlak komt. Ook het aardmagneetveld houdt veel van de geladen deeltjes van de kosmische straling tegen. Een kleine fractie bereikt uiteindelijk toch het aardoppervlak. Hoe hoger je je dus bevindt, aan hoe meer kosmische straling je wordt blootgesteld. Luchtvaartpersoneel dat regelmatig met lange vluchten meevliegt, kan daarom een aanzienlijke dosis straling oplopen.

2 Natuurlijke radionucliden in de aardbodem

De aarde bevat van nature radionucliden die in de bodem zitten. Het gaat daarbij vooral om 40K (kalium-40) en radionucliden uit de vervalreeksen van 238U en 232Th. 238U heeft een halveringstijd van 4,5 miljard jaar. Sinds het ontstaan van de aarde is dus ongeveer de helft van het 38U vervallen. 232Th heeft een halveringstijd van ruim 14 miljard jaar. Daarvan is dus pas een vijfde vervallen sinds het ontstaan van de aarde. 40K heeft een halveringstijd van ruim 1 miljard jaar.

Omdat bouwmaterialen zoals bakstenen gemaakt worden van bodemmateriaal, bevatten die ook kleine, meestal ongevaarlijke hoeveelheden radionucliden.

VOORBEELD BAKSTENEN

3 Inademing van natuurlijk radon

Bakstenen zijn gemaakt van klei uit de bodem en bevatten daardoor kleine hoeveelheden natuurlijke radionucliden (vooral 40K, 238U en 232Th). Wie in een bakstenen huis woont, loopt door de aanwezigheid van radionucliden in de muren een jaarlijkse effectieve dosis van 0,1-0,2 mSv op. De blootstelling aan ioniserende straling moet volgens Europese richtlijnen beperkt worden tot 1 mSv per jaar, bovenop de natuurlijke achtergrondstraling. De hoeveelheid straling die je oploopt door de aanwezigheid van radionucliden in de muren, ligt daar ver onder.

Halverwege de uraniumreeks ontstaat het radioactieve 222Rn (radon-222). Omdat dat een edelgas is, zal het vrijkomen uit de bodem en bepaalde bouwmaterialen. Het komt dan in de lucht terecht. 222Rn heeft een halveringstijd van vier dagen. Toch is het niet het radongas zelf dat schadelijk is. Bij het verval van 222Rn ontstaan er namelijk nieuwe radionucliden, ook wel radondochters genoemd. Die zijn niet gasvormig en hechten zich vast aan zwevende stofdeeltjes in de lucht. Als je die stofdeeltjes inademt, komen de radondochters in je longen terecht. Bij het verval van de radondochters komt zowel α-, β-, als γ-straling vrij. Door de stralingsschade in de longen kun je longkanker krijgen.

In Vlaanderen zijn de concentraties aan radongas erg laag. In Wallonië zijn er streken met hoge concentraties. In de buitenlucht is het radongas geen probleem, maar in slecht geventileerde huizen kan de concentratie aan radongas oplopen.

Zoek op de nuclidenkaart op welke radionucliden er gevormd worden bij het radioactief verval van 222Rn.

▲ Afb. 107 Radongas in België. Gegevens van het Federaal Agentschap voor Nucleaire Controle, situatie 2023.

▲ Afb. 106 Bakstenen gemaakt van klei

4 Natuurlijke radionucliden in voedsel

De natuurlijke radionucliden uit de aardbodem komen ook in ons voedsel terecht. Het gaat in de eerste plaats om 40K.

Zo zijn bananen gekend om hun relatief hoge activiteit, namelijk zo’n 18,4 Bq voor een grote banaan. Het is wel degelijk veilig om bananen te eten. Een volwassene heeft een activiteit van de orde van 9 000 Bq. Als die activiteit met 18,4 Bq toeneemt doordat je een banaan eet, maakt dat nauwelijks een verschil. Wanneer je een banaan eet, word je blootgesteld aan een effectieve dosis van ongeveer 0,1 μSv.

5 Medische toepassingen

©VANIN

In de medische wereld maakt men vaak gebruik van ioniserende straling en radionucliden. Je leert er meer over in paragraaf 5.

6 Industriële toepassingen

Straling die afkomstig is van industriële toepassingen, zoals de productie van elektriciteit, draagt nauwelijks bij tot de stralingsdosis waaraan de gemiddelde Belg wordt blootgesteld.

Meer dan de helft van de ioniserende straling waaraan we blootgesteld worden, is van natuurlijke oorsprong: kosmische straling, radionucliden in de aardbodem, 222Rn in de lucht en radionucliden in ons voedsel.

Ook bij medische toepassingen worden we aan relatief veel ioniserende straling blootgesteld.

We worden nauwelijks blootgesteld aan ioniserende straling die ontstaat bij industriële toepassingen, zoals kerncentrales.

▲ Afb. 108 Een banaan heeft een hoge activiteit.

4.2 Toegelaten waarden

De natuurlijke achtergrondstraling bedraagt in België ongeveer 2,5 mSv per jaar. De dosislimieten die je daarbovenop mag oplopen, zijn bij wet vastgelegd en terug te vinden op de website van het Federaal Agentschap voor Nucleaire Controle (FANC). De straling die je oploopt bij medische beeldvorming of andere medische behandelingen, is daarin niet inbegrepen.

DOSISLIMIETEN

effectieve dosis (Heff )

PUBLIEK

1 mSv per jaar

1 mSv tijdens de zwangerschap

BEROEPSHALVE BLOOTGESTELDE PERSONEN

20 mSv per twaalf opeenvolgende glijdende maanden

©VANIN

huid (gemiddelde dosis over een oppervlakte van 1 cm2) 50 mSv per jaar

equivalente dosis (Heq) ooglens 15 mSv per jaar

handen, voorarmen, voeten en enkels niet van toepassing

▲ Tabel 3 Toegelaten effectieve dosissen (gebaseerd op gegevens van het FANC).

20 mSv per twaalf opeenvolgende glijdende maanden

500 mSv per twaalf opeenvolgende glijdende maanden

Hogere dosissen kunnen leiden tot lichaamsschade. Bij erg hoge dosissen treden de zichtbare effecten van de schade al na enkele uren tot maanden op. Tabel 4 bevat een overzicht van de effecten bij bestraling van het hele lichaam.

Heff (Sv)

EFFECT

0,2-1 tijdelijke vermindering van het aantal witte bloedlichaampjes

1-2 lichte verschijnselen van stralingsziekte: vermoeidheid, braken, verminderde weerstand tegen ziekten

2-3 ernstige verschijnselen van stralingsziekte, eventueel overlijden binnen een maand als gevolg van inwendige bloedingen

3-4 ernstige verschijnselen van stralingsziekte, sterftekans meer dan 50 % binnen twee weken na de bestraling

4-10 sterftekans vrijwel 100 % binnen een maand

10-50darmsyndroom, overlijden binnen enkele dagen door vochtverlies > 50overlijden binnen enkele uren

▲ Tabel 4 Effecten bij bestraling van het hele lichaam afhankelijk van de opgelopen effectieve dosis

Effecten van bestraling op langere termijn zijn leukemie en andere vormen van kanker. Leukemie ontstaat typisch drie tot zes jaar na de bestraling. Tumoren verschijnen tien tot vijfentwintig jaar na de bestraling.

▲ Afb. 109 De handen van een Japanse vrouw in 1965. De vervormde vingers en de tumor zijn een gevolg van de atoombom op Hiroshima twintig jaar eerder.

Benjamin is laborant en wordt beroepshalve blootgesteld aan ioniserende straling. Hij werkt 250 dagen per jaar. In de voorbeeldvraagstukken rekende je uit dat Benjamin deze voormiddag 0,59 mSv opliep door de nabijheid van een 60 27Co-bron.

1 Liep Benjamin deze voormiddag een wettelijk toegelaten (en dus weinig schadelijke) stralingsdosis op?

2 Loopt Benjamin een wettelijk toegelaten stralingsdosis op als hij elke werkdag aan 0,59 mSv wordt blootgesteld?

3 Hoe kan Benjamin zijn stralingsdosis verlagen?

©VANIN

De dosislimiet voor personen die beroepshalve met ioniserende straling in contact komen, bedraagt 20 mSv per jaar en voor de rest van de bevolking 1 mSv per jaar (bovenop de achtergrondstraling).

Bij de kernramp in Tsjernobyl in 1986 werden sommige mensen blootgesteld aan een dosis van 10 Sv. Binnen een maand na de ramp stierven er 31 hulpverleners en technici. 3 mensen kwamen ter plaatse om en 28 mensen stierven in de weken daarna. De inwoners van de vlakbij gelegen stad (Pripjat, 55 000 inwoners tot 1986) en de omliggende dorpen werden pas na 36 uur geëvacueerd en liepen daardoor een gemiddelde dosis van 30 mSv op. De cijfers over hoeveel slachtoffers er de jaren daarna nog gevallen zijn door de gevolgen van de opgelopen straling, lopen sterk uiteen. Dat komt vooral doordat wetenschappers nog niet goed weten welk effect langdurige blootstelling aan lage stralingsdosissen heeft op het menselijk lichaam.

Na het ongeluk in de kerncentrale van Fukushima in 2011 werden de mensen in de omgeving veel sneller geëvacueerd. Daardoor werden ze aan veel minder straling blootgesteld. De gemiddelde dosis waaraan de bevolking in het eerste jaar na de ramp werd blootgesteld, door directe blootstelling aan ioniserende straling of door besmet voedsel te eten, was minder dan 10 mSv. Enkele medewerkers van de kerncentrale werden in het ziekenhuis opgenomen met stralingsziekte nadat ze tot 6 Sv straling hadden opgelopen.

▲ Afb. 110 Afscherming over de kernreactor van Tsjernobyl

WEETJE

5.1 Diagnose en behandeling

Radionucliden en ioniserende straling worden dagelijks in de medische wereld gebruikt om mensen met gezondheidsproblemen te helpen. Ze spelen een belangrijke rol bij het stellen van een juiste diagnose via medische beeldvorming. Ze worden ook ingezet voor allerlei behandelingen, zoals de behandeling van kankerpatiënten met radiotherapie.

Hoewel de meeste mensen zich bewust zijn van de mogelijke lichaamsschade door ioniserende straling, wegen de medische voordelen vaak zwaarder door dan het (kleine) risico op stralingsschade door de (kleine) opgelopen stralingsdosis.

5.2 Medische beeldvorming

Zowat iedereen heeft al eens een röntgenfoto laten nemen, maar er bestaan ook andere vormen van medische beeldvorming waarbij gebruik wordt gemaakt van ioniserende straling en radionucliden. Je bestudeert hieronder enkele beeldvormingstechnieken.

1 Röntgenfoto’s

Röntgenstralen bestaan, net zoals γ-stralen, uit hoogenergetische fotonen. De oorsprong van de fotonen is echter anders dan bij γ-stralen. Röntgenstralen ontstaan in een röntgenbuis doordat men snelle elektronen op een metalen plaatje laat botsen. De kinetische energie die de elektronen daarbij verliezen, komt vrij in de vorm van hoogenergetische fotonen.

Men neemt röntgenfoto’s om lichamelijke letsels in beeld te brengen. De patiënt wordt bestraald met röntgenstralen. De botten absorberen meer röntgenstralen dan de zachte weefsels van het lichaam en het bloed. Daardoor zijn ze goed zichtbaar op een röntgenfoto. Dat effect zorgt ervoor dat de foto’s letsels aan botten, zoals breuken of barstjes, goed in beeld kunnen brengen. Maar ook andere structuren in het lichaam, zoals nierstenen of letsels aan de longen, worden zichtbaar op een röntgenfoto.

Vroeger nam de patiënt plaats voor een fotografische plaat. Op plaatsen waar de röntgenstraling ongehinderd door het lichaam kon gaan, kleurde de fotografische plaat zwart. De rest van de plaat bleef wit. Nu is de fotografische plaat vervangen door een detector met stralingsgevoelige sensoren. De sensoren zetten de energie van de invallende fotonen om in een elektrisch signaal, dat naar een computer wordt gestuurd. De computer zet de elektrische signalen om in een digitaal beeld.

röntgenfoto

©VANIN

Röntgenstraling is genoemd naar de Nederlandse fysicus Wilhelm Conrad Röntgen, die straling ontdekte die ongehinderd door zachte materialen kan dringen. Hij noemde dat zelf x-stralen. In 1901 ontving hij daarvoor de eerste Nobelprijs voor Natuurkunde.

röntgenbuis

▲ Afb. 111 Het maken van een röntgenfoto

CT is de afkorting voor computertomografie. Het woord ‘computertomografie’ komt van het Griekse τομος (tomos, ‘plak’) en γραφειν (graphein, ‘schrijven’).

De onderstaande tabel geeft een overzicht van de stralingsdosissen die je oploopt bij een röntgenfoto. De dosissen bedragen dikwijls minder dan 0,1 mSv. Soms kan de dosis oplopen tot 2 mSv. Ter vergelijking: jaarlijks word je blootgesteld aan 2,5 mSv natuurlijke achtergrondstraling.

RADIOGRAFIE (RÖNTGENFOTO)

OPGELOPEN STRALINGSDOSIS Heff (mSv)

radiografie van de lage rug (volledig onderzoek) 1,9

radiografie van de buik 0,5 radiografie van het bekken 0,5 mammografie 0,3 radiografie van de longen (zijaanzicht) 0,06 radiografie van de longen (vooraanzicht) 0,04

gewone radiografie van de tanden 0,005

▲ Tabel 5 Opgelopen stralingsdosissen bij röntgenfoto’s van verschillende lichaamsdelen, gebaseerd op gegevens van het FANC

2 CT-scans

Een mogelijk probleem bij de interpretatie van röntgenfoto’s is dat lichaamsdelen en organen elkaar vaak overlappen. Als een röntgenfoto moeilijk te interpreteren is, nemen artsen soms een CT-scan van hun patiënt.

Bij een CT-scan maakt men verschillende röntgenfoto’s van de patiënt onder verschillende hoeken, door de röntgenbuis en de detector rond de patiënt te laten draaien. Ondertussen beweegt de patiënt langzaam in horizontale richting door de scanner. Op die manier worden er verschillende dwarsfoto’s van de patiënt gemaakt. De computer kan op basis van die dwarsdoorsneden een driedimensionaal beeld vormen.

ronddraaiende röntgenbuis röntgenstraling

©VANIN

röntgenbuis

detectoren

▲ Afb. 112 Bij een CT-scan schuift een patiënt horizontaal door een ring die kan ronddraaien. In de ring zitten een röntgenbuis en een CTscanner.

Omdat men bij een CT-scan een reeks van röntgenfoto’s maakt, wordt de patiënt aan een grotere dosis ioniserende straling blootgesteld dan bij één enkele röntgenfoto. De medische voordelen van een CT-scan moeten altijd worden afgewogen tegen de stralingsdosis die je oploopt.

CT-SCAN

OPGELOPEN STRALINGSDOSIS Heff (mSv) coronaire CT-angiografie (CT van het hart)

CT van de lage rug

CT van de buik

©VANIN

CT van de thorax

CT van het hoofd

CT van de sinussen

▲ Tabel 6 Opgelopen stralingsdosissen bij CT-scans van verschillende lichaamsdelen, gebaseerd op gegevens van het FANC

3 Scintigrafie

Scintigrafie is een beeldtechniek die gebruikmaakt van radioactieve tracers. Dat zijn radionucliden die men in het lichaam spuit om zo een medische diagnose te kunnen stellen. Meestal gaat het om γ-stralers, omdat γ-stralen een groot doordringend vermogen hebben en het lichaam dus gemakkelijk kunnen verlaten.

In 80 % van de gevallen kiest men voor 99mTc (de metastabiele toestand van technetium-99) als radioactieve tracer. 99mTc heeft immers een halveringstijd van zes uur, wat de radionuclide uiterst geschikt maakt. Een halveringstijd van zes uur is lang genoeg om de nodige technische en medische handelingen te kunnen uitvoeren, maar ook kort genoeg opdat de radioactieve besmetting van de patiënt snel spontaan verdwijnt.

Bij scintigrafie maakt men een chemische verbinding met een radioactieve tracer. De radioactieve molecule die op die manier ontstaat, wordt in het lichaam gespoten. De keuze van de chemische verbinding hangt af van het orgaan of het deel van het lichaam dat de artsen willen onderzoeken. De radioactief gemerkte stof concentreert zich in dat orgaan of deel van het lichaam en zendt γ-stralen uit.

Een bewegende detector meet op verschillende punten van het lichaam de hoeveelheid γ-stralen. De computer maakt daarvan een beeld. Als de gemeten stralingsintensiteit hoger of lager ligt dan de verwachte waarde, kan dat wijzen op een te snelle of te trage werking van dat orgaan, een bepaald letsel of een tumor.

Soms draait een γ-detector volledig rond het lichaam van de patiënt, om onder een groot aantal hoeken en op een groot aantal punten de intensiteit van de γ-straling te meten. De computer kan daarvan op een gelijkaardige manier als bij een CT-scan een driedimensionaal beeld maken. Een dergelijke scan wordt ook een SPECT-scan (Single Photon Emission Computer Tomography) genoemd.

Het woord ‘tracer’ is afgeleid van het Engelse trace, hetgeen ‘spoor’ betekent. Met een tracer spoor je letsels op.

Welke fractie van de oorspronkelijke hoeveelheid 99mTc blijft er over na 24 uur?

Scintigrafie wordt vaak gebruikt om het skelet, de schildklier of het hart te bekijken:

• Skeletscintigrafie wordt vooral gebruikt om botkanker te diagnosticeren.

• Schildklierscintigrafie wordt gebruikt om de werking van de schildklier te evalueren of om schildklierkanker op te sporen. Omdat de schildklier gemakkelijk jodium opneemt, gebruikt men voor een schildklierscintigrafie als tracer soms 131I (jodium-131) in plaats van 99mTc.

• Hartscintigrafie wordt gebruikt om het hart na te kijken. Na een hartinfarct kun je zien welk deel van het hart is aangetast. Ook de doorbloeding van het hart kan worden gecontroleerd.

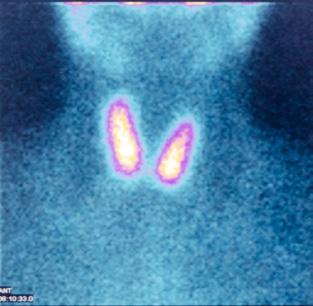
▲ Afb. 115 Scintigrafie van de schildklier

Bij een scintigrafie en een CT-scan loop je stralingsdosissen van dezelfde grootteorde op.

onderzoek doorbloeding van het hart (stress en rust) 4 onderzoek doorbloeding hersenen 6 onderzoek skelet 4 onderzoek doorbloeding longen 2 onderzoek schildklier 1 tot 2 onderzoek nieren 1 tot 1,5

▲ Tabel 7 Opgelopen stralingsdosissen bij scintigrafieën van verschillende lichaamsdelen, gebaseerd op gegevens van het FANC

4 Beeldvormingstechnieken zonder radioactiviteit

Er bestaan ook beeldvormingstechnieken die geen gebruik maken van ioniserende straling:

• Echografie gebruikt ultrasone geluidsgolven.

• Een MRI-scan (Magnetic Resonance Imaging) maakt gebruik van een combinatie van een extern magneetveld en laagenergetische fotonen.

Medische beeldvorming maakt vaak gebruik van ioniserende straling of radionucliden, bijvoorbeeld bij:

• röntgenfoto’s;

• CT-scans;

• scintigrafieën.

Er bestaan ook beeldtechnieken die geen gebruik maken van ioniserende straling Voorbeelden zijn:

• echografieën;

• MRI-scans.

©VANIN

Bij de keuze van medische beeldtechnieken moeten de medische voordelen altijd worden afgewogen tegen de nadelen van het gebruik van ioniserende straling.

Je vindt meer informatie over die technieken in deze video.

5.3 Medische behandeling: radiotherapie

Radiotherapie maakt gebruik van ioniserende straling om kanker te behandelen. Ioniserende straling kan immers cellen beschadigen. Dat kunnen gezonde cellen zijn, maar ook kankercellen.

Kankercellen zijn gevoeliger voor ioniserende straling dan normale, gezonde cellen, omdat ze zichzelf moeilijker kunnen herstellen. Ze worden dus gemakkelijker vernietigd, en daarvan maakt men gebruik bij radiotherapie.

1 Uitwendige bestraling

Bij uitwendige bestraling richt men een stralenbundel op de tumor of de plaats waar die zich bevond. Meestal bestaat de straling uit fotonen, maar ook elektronen, protonen of neutronen zijn mogelijk.

Om kankercellen te vernietigen, zijn er grote dosissen straling nodig. Die kunnen oplopen tot een equivalente dosis van een paar honderden mSv op de plaats van de tumor. Het is daarbij onvermijdelijk dat ook gezonde cellen beschadigd raken. Om dat zo veel mogelijk te vermijden …

• bestraalt men de tumor vanuit verschillende richtingen, zodat de gezonde cellen aan een kleinere stralingsdosis worden blootgesteld;

• splitst men de volledige bestralingsdosis op in meerdere kleine dosissen. Na elke deelbestraling hebben de gezonde cellen zo’n acht uur nodig om te herstellen.

stralingsbron

©VANIN

2 Inwendige bestraling

tumor

Soms gebruikt men ook inwendige bestraling, waarbij er een stralingsbron in het lichaam geïnjecteerd wordt op de plaats van de tumor of net ernaast. Het gaat om een stralingsbron die β–-straling uitzendt. β–-straling heeft een kleiner doordringend vermogen en een groter ioniserend vermogen dan γ-straling. Daardoor blijft de straling beperkt tot een klein gebied rond de tumor. Bij het gebruik van γ-stralers zou maar een kleine fractie van de straling door de tumor worden geabsorbeerd.

Voorbeelden van β–-stralers die voor inwendige bestraling worden gebruikt, zijn 166Ho (holmium-166), met een halveringstijd van 1,1 dagen, en 90Yt (yttrium-90), met een halveringstijd van 2,7 dagen. Ze worden onder andere gebruikt om leverkankers te behandelen.

Radiotherapie wordt gebruikt om kankercellen te doden

▲ Afb. 116 Bestraling van een tumor vanuit verschillende richtingen

▲ Afb. 117 Kankerbehandeling met radiotherapie

AAN DE SLAG

REEKS

Vul de uitspraken aan met ‘altijd’, ‘soms’ of ‘nooit’.

a Als een γ-straal op je lichaam invalt, ioniseert die een molecule.

b Als er ioniserende straling op je lichaam invalt, veroorzaakt dat kanker.

c Kanker is een ongecontroleerde deling van cellen.

d Kanker wordt veroorzaakt door ioniserende straling.

e Als een lichaamscel afsterft, is dat een probleem voor de menselijke gezondheid.

Aardappelen worden bestraald met γ-stralen om kiemvorming te voorkomen.

Welke uitspraak is correct?

a Na de bestraling bevatten de aardappelen zowel natuurlijke als kunstmatige radionucliden. De radionucliden blijven na de bestraling een tweetal dagen in een opslagplaats liggen, tot de activiteit van de kunstmatige radionucliden verwaarloosbaar klein geworden is ten opzichte van de activiteit van de natuurlijke radionucliden.

b Na de bestraling bevatten de aardappelen zowel natuurlijke als kunstmatige radionucliden. De activiteit van de kunstmatige radionucliden is echter verwaarloosbaar klein ten opzichte van de activiteit van de natuurlijke radionucliden. De aardappelen zijn veilig voor consumptie.

c Na de bestraling bevatten de aardappelen enkel natuurlijke radionucliden. Ze zijn veilig voor consumptie.

Zijn de volgende uitspraken juist of fout?

Verbeter indien nodig.

a De activiteit van een radioactieve bron is recht evenredig met het aantal instabiele kernen.

b De activiteit van een radioactieve bron is na een tijdsduur van één halveringstijd gelijk aan de helft van haar beginwaarde.

c Bij bestraling met γ-straling zijn de equivalente dosis en de effectieve dosis gelijk aan elkaar.

d De jaarlijkse stralingsdosis die we oplopen, is hoofdzakelijk het gevolg van industriële toepassingen.

e Ioniserende straling beschadigt gemakkelijker gezonde lichaamscellen dan kankercellen.

f Bij een CT-scan word je aan minder ioniserende straling blootgesteld dan bij een röntgenfoto.

Een radioactieve bron heeft een activiteit van 20 · 103 Bq en een halveringstijd van meerdere jaren.

Hoeveel kernen vervallen er in een kwartier?

In een radioactieve bron vervallen er in één uur gemiddeld 5 · 106 kernen. Bereken de gemiddelde activiteit van de bron tijdens dat uur.

Lees de onderstaande krantenkoppen.

Is er gevaar is voor besmetting, bestraling of beide?

Leg uit.

Radioactief afvalwater kerncentrale Fukushima wordt in zee geloosd

Bron: businessam.be

Emmers met uranium staan 20 jaar in museumgebouw Grand Canyon

Bron: www.standaard.be

Greenpeace vindt sporen van radioactiviteit bij Umicore Olen en in Molse Nete

Bereken de activiteit van beide stralingsbronnen op t = 150 s.

Welke uitspraak is correct? Verklaar.

©VANIN

In de buurt van de beschadigde kerncentrale van Fukushima werd een vis gevangen met een recordhoeveelheid radioactief 13755Cs van 7,4 MBq per kg. De halveringstijd van 13755Cs bedraagt dertig jaar.

a Wat is de activiteit van de vis, die 800 g woog?

b Onderzoekers besluiten om de vis in te vriezen voor verdere studies. Wat is de activiteit van diezelfde vis één maand nadat hij gevangen werd?

c Bereken het aantal actieve cesiumkernen op het ogenblik dat de vis gevangen werd.

De onderstaande mensen en dieren werden blootgesteld aan ioniserende straling.

Rangschik ze volgens toenemende opgelopen effectieve dosis. Zoek de nodige gegevens op in dit hoofdstuk.

a Didier is een bergbeklimmer. Hij verblijft zestig dagen in de Himalaya om de Mount Everest te beklimmen.

b Mieke laat een volledig radiografisch onderzoek van de lage rug uitvoeren.

c Amadu laat een radiografie van zijn tanden nemen.

d Bij James wordt een CT-scan van de lage rug genomen.

e Bij Sinem wordt een CT-scan van het hoofd genomen.

f Choco, het aapje van Jommeke, eet gedurende een jaar elke dag één banaan.

g Marie gaat op vakantie naar de Ardennen en verblijft daar gedurende twee weken in een huis met een hoge concentratie aan 222Rn (radon-222). Haar longen, met een massa van 0,500 kg, worden tijdens die vakantie blootgesteld aan 4,4 μJ stralingsenergie afkomstig van α-stralers.

a Gijs: Radioactief afval met een hoge halveringstijd moet langer veilig worden opgeslagen dan radioactief afval met een lage halveringstijd. Volgens mij is de activiteit van de bron dus hoger als de halveringstijd van de bron hoger is.

b Nia: Ik denk dat de activiteit van een radioactieve bron lager is als de halveringstijd van de radionucliden hoger is. Het aantal radioactieve vervallen wordt dan immers uitgesmeerd over een langere tijd.

c Lizzy: Elke radioactieve bron wordt gekenmerkt door haar activiteit. De activiteit is dus een constante, en de grootte van die constante is afhankelijk van de soort radionucliden in de bron.

d Charlie: α-straling is schadelijker voor de gezondheid dan β-straling en γ-straling. De activiteit van een radioactieve bron met α-stralers is dan ook groter dan de activiteit van een stralingsbron met β-stralers of γ-stralers.

AAN DE SLAG

REEKS

Een onderzoekster moet een detector voor α-straling afstellen. Ze heeft daarvoor een radioactieve bron met α-stralers nodig. De radioactieve bron heeft een activiteit van 1,0 · 106 Bq. Gedurende 3,0 minuten valt er 50 % van de uitgezonden straling van de bron op de hand van de onderzoekster. De massa van het bestraalde deel van de huid bedraagt 20 g. Dan verwijdert de onderzoekster zich van de bron en gaat ze haar handen wassen. De α-stralen hebben een energie van 4,5 MeV.

a Bereken de geabsorbeerde dosis waaraan de huid van de hand van de onderzoekster werd blootgesteld.

b Bereken de equivalente dosis waaraan de onderzoekster werd blootgesteld.

c Bereken de effectieve dosis waaraan de onderzoekster werd blootgesteld.

d Is dat een wettelijk toegelaten dosis?

e Hoe had de onderzoekster zichzelf beter kunnen beschermen?

Sarah woont in een huis waar de concentratie aan radongas (222Rn) erg hoog is. 222Rn is een natuurlijke radionuclide in de vervalreeks van 238U. Zowel bij het verval van 222Rn als bij het verval van haar dochterkernen komt α-straling vrij. Op die manier ontvangen de longen van Sarah jaarlijks 0,102 mJ aan stralingsenergie. Die energie komt terecht in 0,500 kg longweefsel. Bovendien krijgt Sarah dit jaar tijdens een behandeling voor borstkanker een equivalente dosis van 450 mSv.

Hoe groot is de effectieve dosis die Sarah dit jaar oploopt?

REEKS

Bereken de activiteit van 1,0 g 226Ra. 226Ra heeft een halveringstijd van 1 600 jaar.

Een man met prostaatkanker wordt behandeld door inwendige bestraling met een bron die radioactief 192Ir (iridium-192) bevat. Bij de behandeling moet een stukje weefsel van 3,0 g een stralingsdosis van 1,5 Gy absorberen. De behandeling duurt 3,0 uur.

De gemiddelde energie van de uitgezonden β–-deeltjes bedraagt 0,60 MeV. 192Ir heeft een halveringstijd van 74 dagen.

Bereken de gemiddelde activiteit van het geïnjecteerde preparaat met 192Ir.

Bewijs dat A(t) = 0,693 T1/2 N(t), met A(t) de activiteit van een radioactieve bron, N(t) het aantal instabiele kernen in die bron en T1/2 de halveringstijd van de instabiele kernen in de bron.

Doe dat via de onderstaande tussenstappen.

a Bewijs dat N(t) = N0 · e–t/τ door gebruik te maken van de radioactieve vervalwet.

Daarbij is N0 het aantal instabiele nucliden op tijdstip 0 en τ = T1/2 0,693 (τ is de Griekse letter tau).

b De grootheid τ wordt veel gebruikt binnen de kernfysica en wordt ook de levensduur van een kern genoemd. Is de levensduur τ korter of langer dan de halveringstijd T1/2?

c Bewijs dat na een tijd t = τ er nog 37 % van het oorspronkelijke aantal instabiele nucliden overblijft of, anders gezegd, dat 63 % van het oorspronkelijke aantal instabiele nucliden vervallen is.

d Bewijs dat A(t) = 0,693 T1/2 N(t).

 Meer oefenen? Ga naar

HOOFDSTUKSYNTHESE

KERNBEGRIPPEN

lichaamsschade door ioniserende straling besmetting bestraling becquerel

NOTITIES

Ioniserende straling kan atomen en moleculen in het lichaam ioniseren en daardoor lichaamscellen beschadigen.

Het lichaam kan moleculen en cellen die verloren gaan, meestal vervangen.

Blijvende lichaamsschade ontstaat als er te veel cellen afsterven of als beschadigde lichaamscellen zich ongecontroleerd delen. Dan ontstaat er kanker

Rechtstreeks contact met radionucliden is besmetting Je moet de stralingsbron verwijderen om verdere lichaamsschade te voorkomen.

Onrechtstreeks contact met radionucliden is bestraling Je wordt dan bestraald vanop een afstand. Je kunt lichaamsschade vermijden door de blootstellingsduur te beperken, afstand te houden van de bron en/of afscherming te voorzien.

Becquerel is de eenheid van activiteit

De activiteit A van de bron is het aantal radioactieve vervallen per seconde:

A(t) = | dN dt |, met N het aantal instabiele kernen in de bron.

GROOTHEID MET SYMBOOL EENHEID MET SYMBOOLVERBAND MET SI-EENHEDEN activiteit A becquerelBq 1 Bq = 1 s–1

gray Gray is de eenheid van geabsorbeerde dosis D. Een gray is gelijk aan de absorptie van een joule stralingsenergie door een kg materie.

GROOTHEID MET SYMBOOL EENHEID MET SYMBOOLVERBAND MET SI-EENHEDEN geabsorbeerde dosis D gray Gy J kg

sievert Sievert is de eenheid van equivalente dosis en effectieve dosis. Die dosissen zijn een maat voor de mogelijke biologische schade

GROOTHEID MET SYMBOOL EENHEID MET SYMBOOL VERBAND MET SI-EENHEDEN

©VANIN

BASISFORMULE

equivalente dosis H eq sievert Sv 1 Sv = 1 J kg H eq = D · wR met wR de stralingsweegfactor

effectieve dosis Heff sievert Sv 1 Sv = 1 J kg Heff = H eq · w w = D · w s · w w met w w de weefselweegfactor

gemiddelde jaarlijkse effectieve dosis

dosislimieten

medische beeldvorming

radiotherapie

De gemiddelde jaarlijkse effectieve dosis van een Belg bedraagt 4 mSv:

• 2,5 mSv als gevolg van natuurlijke radioactiviteit;

• 1,5 mSv als gevolg van kunstmatige radioactiviteit, bijna uitsluitend door medische toepassingen.

• personen die beroepshalve met ioniserende straling in contact komen: maximaal 20 mSv per jaar

• rest van de bevolking: maximaal 1 mSv per jaar (bovenop de achtergrondstraling)

Bij röntgenfoto’s, CT-scans, scintigrafieën … gebruikt men ioniserende straling, bij echografieën, MRI-scans ... niet.

Radiotherapie maakt gebruik van ioniserende straling om kanker te behandelen.

TABELLEN

TABEL 1: Massa en lading van enkele deeltjes

(u)

TABEL 2: Enkele constanten

176 5 · 10–19 C

eV 1,602 176 5 · 10–19 J 1 u 1,660 54 · 10–27 kg E0(u) = 931,490 MeV E0(m) = m (in u) · 931 MeV u

TABEL 3: De belangrijkste eigenschappen van een aantal kernen

1waterstofH1938,27271,008

2937,80702,014 0,015 3 936,3076 3,016 β– 12,3 j

2heliumHe3936,13113,016 0,0001 4931,84544,003 99,9

3lithiumLi6933,5869

5boorB10932,4443 0,013 19,8 11 932,050411,00980,2 12 932,3959 12,014 β– 0,0020 s

TABELLEN

6koolstofC10932,7580 10,017

13931,499213,003

7stikstofN12932,641212,019

14931,443514,003

15931,262515,000

8zuurstofO13932,958013,025

14931,774214,009

15931,412215,003

16 930,9429 15,99599,76 17931,206616,999 0,04 18931,224117,999

19931,454619,004

20931,479920,004

9fluorF18931,287318,001

19931,174218,998100

10neonNe20930,887119,99290,S

11 natriumNa 23 930,835622,990100 24 930,909623,991

13aluminiumAl 27 930,611526,982100

14siliciumSi28930,4714

15fosforP30930,5657

TABELLEN

17chloor Cl

18argonAr40930,3887 39,96299,6

19kaliumK

25mangaanMn 55 930,213154,938100

26ijzer Fe 54930,207053,9405,8 55 930,208054,938

56930,175355,93591,7

TABELLEN

931,2430 211,989

931,2925215,000

931,3358218,009

931,2866214,999