Paskín Matemático - Vol. 1 No. 1

https://editorial.konradlorenz.edu.co/paskin-matematico.html

e-mail: paskin@konradlorenz.edu.co

Editor

John A. Arredondo

Fundación Universitaria Konrad Lorenz alexander.arredondo@konradlorenz.edu.co

Comité Editorial

Ruth Alejandra Torres Julián Jiménez Cárdenas Fundación Universitaria Konrad Lorenz Universidad de los Andes rutha.torresr@konradlorenz.edu.co jo.jimenezc1@uniandes.edu.co

Camilo Ramírez Maluendas Andrés Mauricio Rivera Universidad Nacional de Colombia Pontificia Universidad Javeriana Sede Manizales Sede Cali camramirezma@unal.edu.co amrivera@javerianacali.edu.co

Leidy Catherinne Sánchez Jesús Muciño

Fundación Cardioinfantil Centro de Ciencias Matemáticas UNAM-Morelia lcascanio@lacardio.org muciray@matmor unam mx

Esta publicación puede ser difundida y reproducida con fines académicos y científicospor todos aquellos que tengan a bien hacer un correcto uso de su contenido.

ISSN 2665-2471

Fundación Universitaria Konrad Lorenz: Tel: (57 1) 347 23 11, Carrera 9 Bis No. 62- 43 Bogotá –Colombia, email: info@konradlorenz.edu. Carácter académico: Institución Universitaria. Personería Jurídica por Resolución 18537 del 4 de noviembre de 1981 del Ministerio de Educación Nacional. Institución de Educación Superior sujeta a inspección y vigilancia por el Ministerio de Educación Nacional (Art. 2.5.3.2.10.2, Decreto 1075 de 2015).

En este número

• Juan Pablo Hernández Rodas - El problema de las ocho reinaspag. 1

• Reynaldo Castaneira Ramírez - ¿Cicloide, braquistócrona o tautócrona - pag. 7

• César Augusto Lara Santana - Ventajas y desventajas de utilizar los modelos de función de transferencia - pag. 14

• Walter Garzón Gutiérrez - Representación gráfica y algebraica de las ecuaciones lineales y sus propiedades en el sistema seno - pag. 21

• Blanca Margarita Parra Mosqueda - Obstáculos en la concepción de los números negativos y de sus logaritmos - pag. 33

• Leidy Catherinne Sánchez Ascanio – MateKuento - pag. 39

• John A. Arredondo y Alejandro Cárdenas - Paskín Challengepag. 42

ELPROBLEMADELASOCHOREINAS

JuanPabloHern´andezRodas * jphernand@unal.edu.co

1.Resumen.

Elproblemadelas8reinasconsisteenencontrartodaslas posiblesformasenquesepuedenubicar8reinasenuntablerodeajedrezsinquesecomanentreellas.

Esteproblemafuepropuestoporunajedrecistaalem´anllamadoMaxBezzelen1848,yllam´olaatenci´ondemuchosmatem´aticosentreellosCarlFriedrichGauss,quienestrabajaron enlasoluci´ondeesteproblemacomoensugeneralizaci´ona untablerode n × n casillas.

Laideadelasoluci´onquevamosapresentar,utilizaherramientasdel ´ algebraconmutativaydel ´ algebracomputacional.

Vamosaasignarleunavariableacadacasilladeltableroparaluegoconsiderarelanillodepolinomiosenestasvariables. Enesteanilloconstruiremosunidealmonomialdetalmaneraqueelcocientedenuestroanilloporesteideal,tienela propiedaddequeladimensi´oncomoespaciovectorialdesu componentehomog´eneadegrado8,esprecisamenteeln´umerodeconfiguracionesdeochoreinaseneltablerodeajedrez quenosecomenentreellas.

2.Algunospreliminares.

Unaclaseespecialdeanillossonlosanillosgraduados. Losanillosgraduadossonunageneralizaci´ondelanillode polinomiosenelsiguientesentido.Enelanillodepolinomios R = K[x1,..., xn] elgradoasignadoacadamonomio,permiteescribir R = ⊕∞ i=0Ri,donde Ri esungrupoabelianoquees generadoportodoslosmonomiosdegrado i como K-espacio vectorialy RiR j ⊂ Ri+ j .Engeneralsetienelasiguientedefinici´ondeanillograduado.

Definici´on3. Unanillo R esunanillograduado,si

R = ∞ i=0 Ri

dondecada Ri esungrupoabelianoy RiR j ⊂ Ri+ j ,esdecir,si x ∈ Ri y z ∈ R j entonces xz ∈ Ri+ j .

img2.jpg

Paraelplanteamientoylasoluci´ondelproblemadelas ochoreinasquemostraremosm´asadelante,esnecesario mencionaralgunoshechosb´asicossobreelanillodepolinomiosyengeneralsobreanillosgraduados.

Sea K uncuerpoyconsideremoselanillo K[x1,..., xn] depolinomiosen n-variablesconcoeficientesen K.Este anillotienemuchaspropiedadesimportantes,porejemploes undominiodefactorizaci´on ´ unica,esNoetheriano,esdecir, todossusidealessonfinitamentegenerados,esunanillo graduado,entreotras.

Definici´on1. Dadoelanillodepolinomios R = K[x1,..., xn], definimosunmonomioen R comounelementodelaforma

x r1 1 x r2 2 xrn n donde ri ≥ 0paratodo i = 1, 2,..., n

Elanillodepolinomios R = K[x1,..., xn] esun K-espacio vectorialdedimensi´oninfinitaquetienecomobasea M ,donde M denotaelconjuntodetodoslosmonomiosenelanillo R.

Definici´on2. Dadounmonomio m ∈ M ,digamos m =

*DepartamentodeMatem´aticayEstad´ıstica,UniversidadNacionaldeColombia,sedeManizales

Ladefinici´ondeunanillograduadosepuedehacersobre cualquiermonoide,sinembargoparanuestrosintereses,la graduaci´onsiempresehar´asobreelconjuntodeenterosno negativos {0, 1, 2,... }

Notequedeladefinici´onanteriorsesigueque R0 esun subanillode R,yaquesi x, z ∈ R0 entonces xz ∈ R0.Adem´as, cada Ri esun R0-m ´ odulo.

Proposici´on1. Considereelanillodepolinomiosennvariables,R = K[x1,..., xn].SabemosqueR = ∞ i=0 Ri,donde Ri eselK-espaciovectorialgeneradoportodoslosmonomios degradoi.

CadaRi esunK-espaciovectorialdedimensi´onfinita,cuya baseeselconjuntodetodoslosmonomiosdegradoi.M´as a ´ un,

dimK (Ri)= n + i 1 n 1

enotraspalabras,eln´umerodemonomiosennvariablesde gradoiest´adadopor n+i 1 n 1 .

Demostraci´on. Unamaneradeprobarestoeslasiguiente. Considere n + i 1espaciosenblanco yubique n 1puntosentreesosespacios

•1 •2 •n 2 •n 1

Claramentedespu´esdeubicarestos n 1puntosnosquedan i espaciosvacios.Llenelosespaciosvaciosdelasiguiente forma:alaizquierdaddelpunto •1 llenelosespaciosconla

variable x1,luegoentreelpunto •1 yelpunto •2 llenelos espaciosconlavariable x2.Continuedeestaforma,esdecir, entrelospuntos • j 1 y • j llenelosespaciosconlavariable x j . Alfinal,losespaciosquesobrenaladerechadel ´ ultimopunto •n 1 ll´enelosconlavariable xn.Porejemploeneldibujo anterioralseguiresteprocedimientoobtenemos

Notequeconesteprocedimientosiempreseobtienealfinal unmonomiodegrado i.Veamosquedeestaformaseobtienen todoslosposiblesmonomiosdegrado i.Enefecto,consideremosunmonomio

.Tomemos n + i 1espacios enblanco 1 2 3 n+i 2 n+i 1 yubiquemos n 1puntosdela

siguientemanera:coloqueelprimerpuntoenlacasilla α1 + 1, deestaformavamosatenerlavariable x1 enlas α1 casillas queest´analaizquierdadeestepunto,esdecir,

Luegoubiqueelpunto •2 enlacasilla α1 + α2 + 2ydeesta formavamosatener α2 veceslavariable x2 enlascasillasque est´anentrelospuntos •1 y •2 x1 x1 x1 •1 x2 x2 x2 •2

Engeneral,ubiqueelpunto • j enlacasilla α1 + α2 + +

α j + j.Comoelpunto • j 1 est´aubicadoenlacasilla α1 +

α2 + ··· + α j 1 + j 1sesiguequeentrelospuntos • j 1 y • j hay α j casillasquecorrespondenalasqueser´anllenadascon lavariable x j .Alfinalobtenemosalgodelaforma

homog´eneos.

Recordemosqueengeneral,dadounanilloconmutativo R, decimosqueunsubconjunto I ⊂ R esunideal,si (I, +) esun subgrupoabelianode (R, +) ysiadem´asparatodo r ∈ R y paratodo x ∈ I setieneque rx ∈ I

Observaci´on1. Sea R = ∞ i=0 Ri unanillograduado.Alos elementosde Ri losllamaremoselementoshomog´eneosde grado i

Definici´on4. Dadounanillograduado R = ∞ i=0 Ri,decimos queunideal I de R eshomog´eneo,sidado f = f0 + f1 + ··· + fn ∈ R,con f j ∈ R j paratodo j = 0, 1,..., n,setiene que f ∈ I siysolosi f j ∈ I paratodo j = 0, 1,..., n,enotras palabras,cadaqueunelementode R est´aen I esporquetodas suscomponenteshomog´eneastambi´enloest´an.

Observaci´on2. Deladefinici´onanteriorsesiguequesiun ideal I ⊂ R eshomog´eneoentonces I esgraduado,ysugraduaci´onest´adadapor

Enelcasodelanillodepolinomios R = K[x1,..., xn],como esteanilloesNoetheriano,esdecir,todossusidealessonfinitamentegenerados,entoncessepuedeprobarqueunideal I eshomogen´eosiysolosiesgeneradoporelementoshomog ´ eneos.

Ejemplo1. Consideremoselanillo R = K[x, y, z].Delaobservaci´onanteriortenemosporejemploqueelideal I = ⟨x2 + yz, x y, z3 x2y⟩ esunidealhomog´eneo.

Notequealaderechadel ´ ultimopunto •n 1 hayprecisamente αn espaciosenblanco,yaquecomenzamoscon n + i 1espaciosenblancoyhemosllenado α1 + + αn 1 + n 1espacios,luegonosquedan n + i 1 (α1 + + αn 1 + n 1) espacios,esdecir, n + α1 + + αn 1 + αn 1 (α1 + + αn 1 + n 1)= αn espacios,quelosllenamosconlavariable xn.Porlotantotenemos

Engeneral,dadounanilloconmutativo R yunideal I ⊂ R,podemosconstruirelanillocociente R/I.Enelcasode anillosgraduados,altenerunanillograduado R yunideal I de R,elcociente R/I nonecesariamenteresultaserunanillo graduado.Sinembargo,cuandoelideal I eshomog´eneo,el anilloresultante R/I tieneunagraduaci´on.

quecorrespondealmonomio x α1 1 x αn 1 n 1 xαn n Claramentecadaubicaci´ondelos n 1puntosdetermina un ´ unicomonomio,porlotantopodemosconcluirquehay n+i 1 n 1 monomiosdegrado i en n variables.

Ejercicio1. Demuestrequeeln´umerodemonomiosenel anillodepolinomios R = K[x1,..., xn] degradomenoroigual a k est´adadopor n+k n .

Engeneralalestudiarlaestructuraalgebraicadeanillos, losidealespermitenconstruirpormediodecocientes,nuevos objetosconlamismaestructuraalgebraica.Enelcasode anillosgraduados,lossubconjuntosquealhacercocientepor ellosproducennuevamenteanillosgraduadossonlosideales

Teorema1. SeaR = ∞ i=0 Ri unanillograduadoyseaI ⊂ Runidealhomog´eneo.EntoncesR/Iesunanillograduado, m ´ asa ´ un, R/I = ∞ j=0 (I + R j )/I

Demostraci´on. Como I esunsubgrupodelgrupoabeliano I + R j ,entonceselcociente (I + R j )/I esungrupoabeliano. Porotrolado,como R/I esunanilloe I + Ri ⊂ R paratodo i ≥ 0,entonceslamultiplicaci´onde R/I induceunamultiplicaci´onentre (I + R j )/I e (I + Rk )/I.Siconsideramos x ∈ (I + R j )/I y z ∈ (I + Rk )/I,tomandorepresentantestenemos x = y + r j y z = w + rk donde y, w ∈ I, r j ∈ R j y rk ∈ Rk .Luego xz =(y + r j )(w + rk )= yw + r j w + rk y + r j rk ∈ I + R j+k .Esto muestraentoncesque x z ∈ (I + R j+k )/I

Solonosrestaverque R/I = ∞ j=0(I + R j )/I.Enefecto,tomemos x ∈ R/I.Altomarunrepresentante r ∈ R,esdecir,

x = r tenemosque x r ∈ I.Digamosque x = x0 + x1 + + xn

y r = r0 + r1 + + rn,luego x r =(x0 r0)+(x1 r1)+

+(xn rn) donde xi ri eslacomponentehomog´eneade grado i delelemento x r.Como x r ∈ I yadem´as I esun idealhomog´eneo,tenemosentoncesque x j r j ∈ I paratodo j ≥ 0,porlotanto x j r j = t j donde t j ∈ I.Estonospermiteescribir x =(t0 + r0)+(t1 + r1)+ ··· +(tn + rn) donde t j + r j ∈ I + R j .Altomarclasem´odulo I aamboslados,obtenemos

x = (t0 + r0)+(t1 + r1)+ +(tn + rn)+

= (t0 + r0)+ (t1 + r1)+ ··· + (tn + rn)+ ···

Finalmente,si (t0 + r0)+ (t1 + r1)+ + (tn + rn)= (l0 + f0)+ (l1 + f1)+ + (ln + fn) entonces

(r0 f0)+(r1 f1)+ +(rn fn) ∈ I, ycomo I esunidealhomog´eneoentonces r j f j ∈ I para todo j ≥ 0.Deaqu´ıpodemosconcluirque ti + ri = li + fi para todo i ≥ 0.

Observaci´on3. Consideremoselanillodepolinomios R = K[x1,..., xn].

Sea I unidealmonomialde R,esdecir,unidealgeneradopormonomios, I = ⟨m1,..., mk ⟩ donde m1,..., mk sonmonomios.Notequeenparticular I esunidealhomog ´ eneoyaqueesgeneradopormonomiosyenparticularunmonomioesunelementohomog´eneo. Porelteoremaanterior, R/I esunanillograduado.

R/I esun K-espaciovectorialgeneradoporlaclasede todoslosmonomiosde R quenopertenecena I,esdecir, B = {m : m monomio, m / ∈ I} esunabaseparael Kespaciovectorial R/I

Sea I unidealhomog´eneode R.Yasabemosque R/I es unanillograduado,peroenestecasopodemosdecira´un m ´ as,yesquelagraduaci´onde R/I sepuededarcomo

R/I = ∞ j=0 (R/I) j

donde (R/I) j esel K-espaciovectorialgeneradoportodaslasclasesdeequivalenciadem´onomiosen R degrado j quenopertenecena I

De ´ algebralinealpodemosconcluirentoncesqueuna baseparael K-espaciovectorial R/I sepuedeconstruir uniendolasbasesdecadaunadesuscomponenteshomog ´ eneas (R/I) j

3.Soluci´onalproblemadelasocho reinas.

Supongamosquetenemosuntablerodeajedrezubicado enelplanocartesianodetalmaneraquelosv´erticesinferioresderechosdecadacasillacorrespondenalospuntos

coordenados (i, j) con i, j = 1,..., 8,ylacasillaconv´ertice inferiorderecho (i, j) est´arotuladaconlavariable xij ,como sepuedeverenlasiguientefigura.

Figura1: Tablerodeajedrezrotuladoconlasvariables x11,..., x88,dondelacasillaconv´erticeinferiorderecho (i, j) est´amarcadaconlavariables xij .

Consideremoselanillodepolinomiosenestas64variables,esdecir, R = Q[x11,..., x81,..., x18,..., x88]. Notemosqueacadaconfiguraci´onde8reinasenestetablero, lepodemosasociarunmonomiodegrado8delanillode polinomios R,simplementemultiplicandotodaslasvariables correspondientesalasubicacionesdelasreinas.

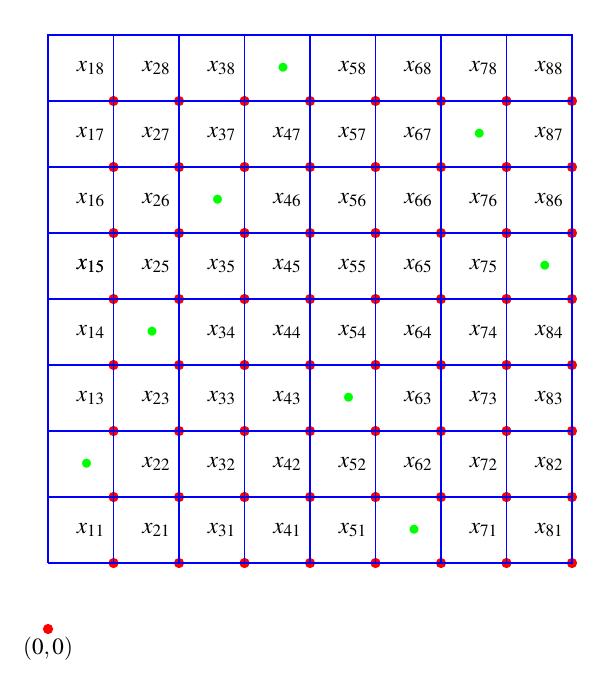
Enlafigura2sepuedeobservarunejemplodeunaconfiguraci´ondeochoreinasenuntablerodeajedrezquenose comenentreellas,juntoconsumonimioasociado.

Comoelanillo R esconmutativo,noimportaelorden enquesemultipliquenlasvariables.

Porcomodidad,vamosapermitirquevariasreinasest´enen unamismacasilla,yenestecasoconsideraremosquelas reinassecomenentreellas.Estonoafectalasoluci´ondel problema,yaqueloquepretendemosesencontrartodaslas configuracionesbuenas,enlascualesnopuedeocurrirque m ´ asdeunareinaest´eenunamismacasilla.

Loquevamosahaceracontinuaci´on,esconstruirun idealquecontengatodoslosmonomiosquecorrespondana configuracionesmalas,esdecir,quecorrespondana8reinas ubicadaseneltablero,dondeporlomenosdosdeellasse comen.

Dosreinassecomenentreellassiysolosiest´anenuna

mismacasilla,enunamismafila,enunamismacolumnao enunamismadiagonal.

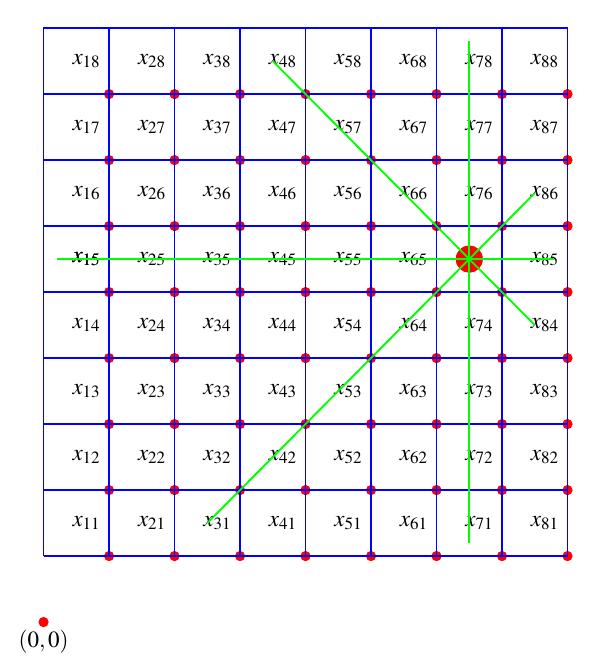
Enlafigura3sepuedeverunejemplodeuntablerode ajedrezconunareinaubicadaenunaposici´onespec´ıfica, juntocontodaslaslineasquerepresentantodoslosotros cuadrosdeltablerodondealubicarotrareina,estasecomen conlareinadada.

Comencemosidentificandotodoslosmonomiosdegrado dosquecorrespondenadosreinaseneltableroquesecomen entreellas.

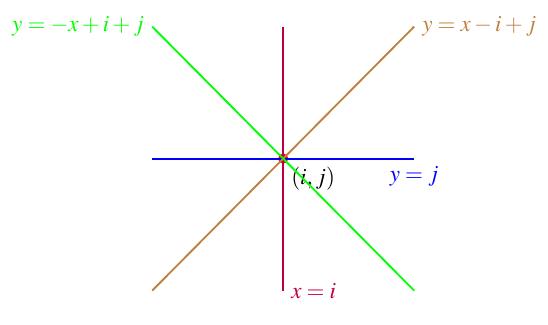
Paraesto,fijemosunareinaenlacasillacorrespondienteala variable xij ,1 ≤ i, j ≤ 8.Unamaneradeencontrartodaslas variables xkl talesquealubicarunareinaenlacasillamarcada conlavariable xkl ,estareinasecomaconlareinaubicadaen lacasillamarcadaconlavariable xij ,esparametrizandolassiguientesrectas:larectaverticalquepasaporelpunto (i, j),la rectahorizontalquepasaporelpunto (i, j) ylasrectasdiagonalesconpendientes1y 1quepasanpor (i, j).Enlafigura 4sepuedeobservarlagr´aficaylasecuacionesdeestascuatro rectas.

Todaslasconfiguracionesde2reinaseneltableroconuna deellasenlaposici´on (i, j) quesecomenentreellas,correspondenalossiguientesmonomiosdegrado2:

Figura3: Tablerodeajedrezconunareinaubicadaenlacasillamarcadaconlavariable x75,dondeloscuadrostocadospor lasl´ıneasverdescorrespodenatodaslasposicionesdondeno esposibleubicarotrareinasinquesecomaconlareinadada.

Paracada1 ≤ i, j ≤ 8,definamos Aij comolauni´ondelos siguientescuatroconjuntos:

{xij xik :1 ≤ k ≤ 8},

{xij xkj :1 ≤ k ≤ 8},

{xij xk(k i+ j) :max{1, 1 + i j}≤ k ≤ min{8, 8 + i j}},

{xij xk(i+ j k) :max{1, i + j 8}≤ k ≤ min{8, i + j 1}}.

Consideremoselideal I = 1≤i, j≤8 Aij

Notemosqueesteidealesmonomial,yaqueesgeneradopor monomios,porlotantoeshomog´eneo,yentonces R/I esun anillograduado.

Porotrolado,notequeunmonomiodegrado8corresponde aunasoluci´ondelproblema,esdecir,aunaconfiguraci´onde 8reinasquenosecomenentreellas,siysolosi,dichomonomionopertenecealideal I.Estoyaquesiunmonomio m degrado8pertenecea I,entoncesesdivisibleporunodelos generadoresde I,loqueimplicaqueelmonomiotienedos variablesquecorrespondenaposicionesdereinasquesecomen.Rec´ıprocamente,si m nopertencea I,entoncesning´un pardevariablesqueaparecenenelmonomio m puedenser elementosdelconjuntodegeneradoresde I,yestosignifica precisamentequelas8reinasubicadasenlasposicionescorrespondientesalasvariablesdelmonomio m,nosecomen entreellas.

Figura2: Configuraci´ondeochoreinasquenosecomenentre ellas,conmonomioasociado x12x24x36x48x53x61x77x85.Los puntosverdesrepresentanalasreinas.

Figura4: Gr´aficadelascuatrorectasquecodificanlasposicionesdeltableroquecorrespondenareinasquesecomen conlareinaubicadaenlacasillamarcadaconlavariable xij .

Ejercicio2. Sabemosque R/I esun Q-espaciovectorial.Demuestrequeenestecaso R/I tienedimensi´onfinitacomo Qespaciovectorialyqueadem´assugraduaci´onesfinita,m´as a ´ un, R/I =(R/I)0 ⊕ (R/I)1 ⊕···⊕ (R/I)8

Deloanteriortenemosentoncesquelosmonomiosde R degrado8quenoest´anen I,sonprecisamentelosdeunabasedel Q-espaciovectorial (R/I)8,porlotantoladimension como Q-espaciovectorialde (R/I)8 nosdaeln´umerodeconfiguracionesdistintasde8reinasenuntablerodeajedrezque nosecomenentreellas.M´asa´un,sicomputamosunabase para (R/I)8,obtenemosdichasconfiguraciones.

C´omputodedimQ(R/I)8 usandoMacaulay2.

1. L=() creaunasecuenciavac´ıa.

2. forifrom1to8doforjfrom1to8do L=append(L,x {i,j}) crealasecuenciaconlas64variables,unaporcadacasilladeltablerodeajedrez.

3. R=QQ[L] creaelanillodepolinomiosconcoeficientesen Q enlas 64variablesanteriores.

4. H=() creaunasecuenciavac´ıa.

5. forifrom1to8doforjfrom1to8doforkfrom1to8

doH=append(H,x {i,j}*x {i,k}).

6. forifrom1to8doforjfrom1to8doforkfrom1to8

doH=append(H,x {i,j}*x {k,j}).

7. forifrom1to8doforjfrom1to8do forkfrommax{1,1+i-j} tomin{8,8+i-j} do H=append(H,x {i,j}*x {k,k-i+j}).

8. forifrom1to8doforjfrom1to8do forkfrommax{1,i+j-8} tomin{8,i+j-1} do H=append(H,x {i,j}*x {k,i+j-k}). Los ´ ultimoscuatropasosproducenlasecuenciade generadoresdelideal I

9. I=idealH produceelideal I

10. s=hilbertSeriesI producelaseriedeHilbertdelanillocociente R/I como uncocientedepolinomios.

11. reduceHilberts producelaseriedeHilbertdelanillo R/I

AlrealizarlospasosanterioresenMacaulay2,finalmente elcomandoreduceHilbertsproduceelpolinomio

p(T )=1 + 64T + 1288T 2 + 10320T 3 + 34568T 4+ + 46736T 5 + 22708T 6 + 3192T 7 + 92T 8 , dondeelcoeficientequeacompanaalapotencia T 8 esladimensi´onde (R/I)8 como Q-espaciovectorial.

Deestamaneraconcluimosqueexisten92manerasdistintas deubicar8reinasenuntablerodeajedrezsinquesecoman entreellas.

Observaci´on4. Enelpolinomioobtenidoenelalgoritmoanterior,notemosqueloscoeficientesdecadapotencia T i con 1 ≤ i ≤ 8nosindicandecuantasmanerassepuedenubicar i reinasenuntablerodeajedrezsinquesecomanentreellas. Porejemplo,comoelcoeficientede T 7 es3192,estonosdicequeexisten3192formasdistintasdeubicar7reinasenun tablerodeajedrezsinquesecomanentreellas.

Generalizaci´ondelproblema.

Notemosqueenelprocedimientoanterior,noimport´o realmenteeltama˜nodeltableronieln´umerodereinas.Por lotanto,dadountablero n × n,podemosusarelmismo procedimientoparaentontrardecu´antasmanerassepueden ubicar m reinassinquesecomanentreellas.

Elprocedimentoser´ıaentoncesconstruirelanillodepolinomiosen n2 variables,definirelideal I generadopor todoslosproductosdedosvariablesquecorrespondana posicionesdondelasreinassecoman,luegoconsiderarel anillograduado R/I,yfinalmentecomputarladimensi´onde (R/I)m como Q-espaciovectorial,loquenosdar´ıacomo resultadoeln´umerodeformasdistintasenqueesposible ubicar m reinaseneltablero n × n sinquesecomanentreellas.

Finalmente,observequetampocoesimportantequeel tableroseacuadrado,porlotantosepuedeplantearelmismo problemaysolucionarlodelamismamanera,parauntablero detamano m × n

6Elproblemadelasochoreinas-JuanPabloHern´andezRodas

Referencias.

[Lan12] SergeLang, Algebra,SpringerScience&BusinessMedia,2012.

[Eis13] DavidEisenbud, Commutativealgebra:withaviewtowardalgebraicgeometry,SpringerScience&BusinessMedia,2013.

[Ati18] MichaelAtiyah, Introductiontocommutativealgebra,CRCPress, 2018.

Acercadelautor:ElprofesorJuanPablotrabajaenlas

´ areasde ´ algebraconmutativa, ´ algebrahomol´ogicaygeometr´ıaalgebraica,ytieneuninter´esengeneralporlamatem´aticaylasaplicacionesdeestacienciaaotras ´ areas. Amantedelaguitarracl´asica.

¿CICLOIDE,BRAQUIST ´ OCRONAO TAUT ´ OCRONA?

ReynaldoCastaneiraRam´ırez *

reynaldo.cr@itoaxaca.edu.mx

1.Resumen.

Enesteescritopresentamosbrevementeunamonograf´ıa delacicloide:suorigen,denominaci´oneinterpretaci´oncomosoluci´onadiferentesproblemasplanteadosporgrandes personajesatrav´esdelahistoriadelasmatem´aticas.

2.Introducci´on.

Elpresenteescritofuemotivadoporsimplecuriosidadsobreelorigendelacurva“conocida”comocicloide.Atrav´es demibrevepasoporlasmatem´aticasmeharesultadoperturbadorencontrarmeestacurvaenvarioscontextos,conpropiedadessorpresivamenteelegantesyunahistoriasingular. Lacicloidehasidodescubiertaalgunossiglosatras,estandoinclusoenlanaturalezamismacomolomencionaJohann Bernoulli.FueenelsigloXVIIcuandoestacurvasemanifest´oporprimeravezenlosdiversosestudiosdegrandespersonajesenlahistoriadelaciencia(B.Pascal,C.Huygens, G.Galilei,G.Leibniz,JohannBernoulli,G.L’Hˆopital,Jakob Bernoulli,I.Newton,L.Euler,J-LLagrange,entreotros).En aquellostiempos,sinexclusi´onactual,muchosdelosproblemasdeestudioeranb´asicamentesucesosofen´omenosque sepresentabanenel“mundoreal”einclusoquesepodian comprobarexperimentalmente.Porestaraz´on,noesquese estudiaralacicloidecomotal,sinoque ´ estasurgi´om´asbien comorespuestanaturaladistintosproblemasplanteados.Para entenderlaaparici´ondelacicloideendiversoscontextos,el escritoseestructuradelasiguientemanera:enlasecci´on2 presentolacicloideyalgunasdelaspropiedadesintr´ınsecas delacurvautilizandoherramientasactualmentebienconocidas,comoelc´alculodiferencialeintegral.1 Enlasecci´on 3abordamoselproblemadelataut´ocronaplanteadoporC. Huygensytratamosdejustificarsuresultado,elcualobtuvo experimentalmente.Finalmente,enlasecci´on4estudiamos elretodelabraquist´ocronaplateadoporJ.Bernoulli,lanzadoalacomunidadcient´ıficaeuropeadeaquellostiempos,y esbozamoslasoluci´onpresentadapor ´ elmismo.

*DepartamentodeCienciasB´asicas,Tecnol´ogicoNacionaldeM´exico/ I.T.deOaxaca

1RecordemosqueenelsigloXVII,elc´alculoa´unseencontrabaenuna etapaprematuraydesconocidaparamuchosdelospersonajesdela ´ epoca.

3.Cicloide.

Enmatem´aticas,entendemospor cicloide alacurvadescritaporunpuntodelacircunferencia,cuando ´ estaruedasin resbalarsobreunarecta.

Elorigendeestacurvaesincierto.Loshistoriadoresdela matem´aticaatribuyenadiferentespersonajesdelsigloXVI sudescubrimientoeinclusosecitandocumentosquesugierenquelacurvaprobablementeeraconocidaenlaantiguedad. Sinembargo,dadalaincertidumbresehangeneneradograndesdisputasporelt´ıtulo,porestaraz´onlacicloideesconocidacomo LaHelenadelosge´ometras,aunquealparecerfue hastafinalesdelsigloXVIenqueGalileoacunoelt´erminocicloideyfueelprimeroenhacerestudiosrigurososdelacurva [IHM94,WEA43].

Silacicloidesegeneramedianteunacircunferenciaderadio a queseapoyasobreeleje x enelorigen,surepresentaci´onenformaparam´etricaest´adadapor:

x(θ )= a(θ sin θ ), y(θ )= a(1 cos θ ), a > 0, donde θ eselpar´ametrocorrespondienteal ´ angulodegirodel c ´ ırculorodante.

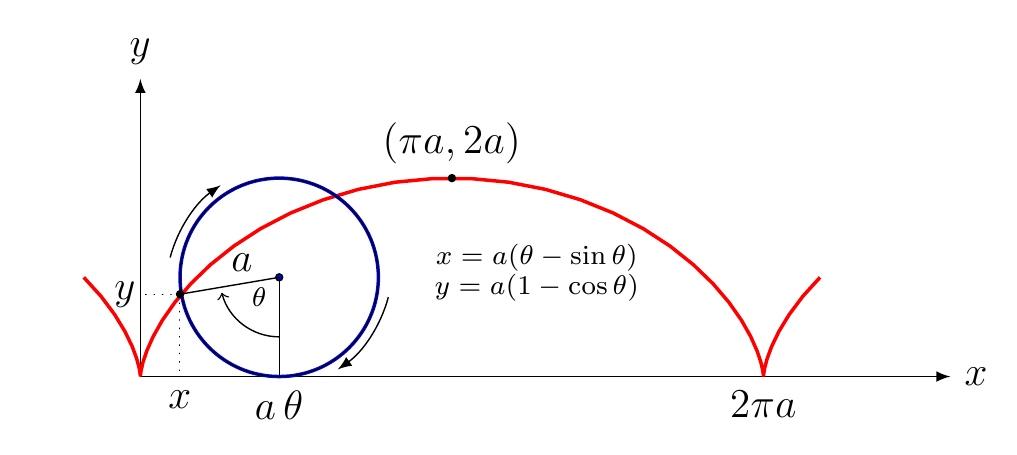
LaFigura2muestraelprimerarcodelacicloideparaun

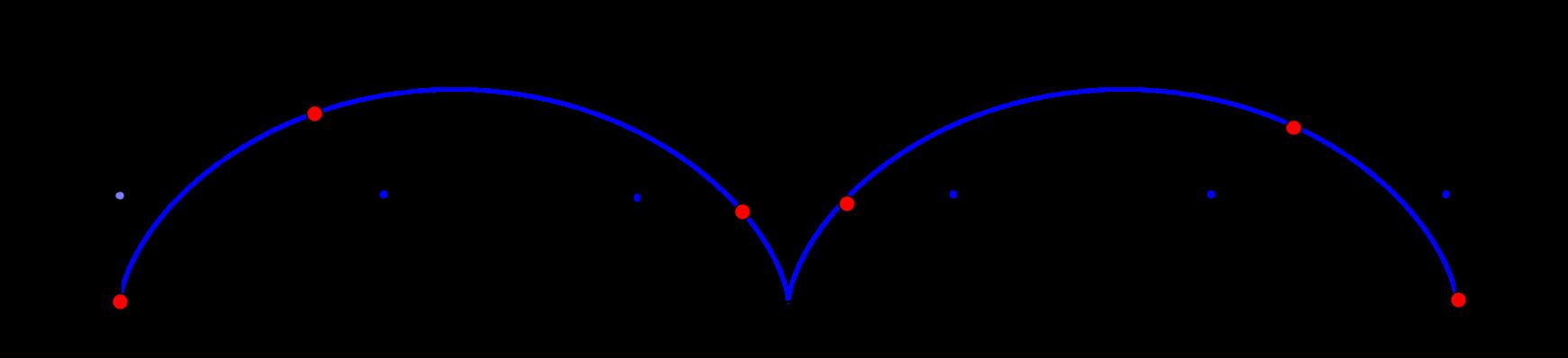Figura1: Cicloidegeneradaporunacircunferenciarodando sobreelejex.

Figura2: Parametrizaci´ondelacicloide.

8¿Cicloide,Braquist´ocronaoTaut´ocrona?-ReynaldoCastaneiraRam´ırez

c ´ ırculoderadio a.Paraun ´ angulo θ fijo,elcentrodelacircunferenciaest´aenenelpunto (x, y)=(aθ , a),lasintersecciones coneleje x ocurrenenlospuntosdonde

y(θ )= a(1 cos θ )= 0, esdecir,cuando θ esunm ´ ultiploenterode2π .Podemosobtenerlaformaparam´etricadelacicloideencoordenadascartesianasdespejandoelpar´ametro θ en y ysustituyendoen x:

x = a arccos 1 y a 2ay y2

Observequeestaf´ormulas´oloesv´alidapara y ∈ [0, 2a] ynos dalamitaddelprimerarcodelacicloide.Enestecaso,tenemos x = f (y).¿Puedeustedobtener y = g(x)?

El ´ arealimitadaporelprimerarcodelacicloideyeleje x es

As´ı,dela ´ ultimaintegralresulta

As´ıel ´ areabajoelprimerarcolacicloideestresvecesladel

2Hacia1632,Roberval(1602-1675)habıaobtenidounmetodosimilaral metododelosindivisiblesdeCavalieri.Robervalocupodesde1632hastasu muerteunacatedraenelCollegeRoyaldeParısyalparecerprefirionohacer publicossumetodosparaconservardichacatedra.Porestarazon,sevioenvueltoendiversaspolemicasrelacionadasconlaautorıadevariosresultados matem´aticos.Enparticular,en1634,logr´ocalcularel ´ areaencerradaporun arcodecicloideusandosum´etododeindivisibles,hallandoque,enefecto,el ´ areaencerradaporunarcodecicloideeraigualaltripledel ´ areadelc´ırculo quegeneralacicloide.Lanopublicaci´ondeestosresultadosleinvolucrar´ıa posteriormenteenunadesagradabledisputaconEvangelistaTorricelli(16081647),[HC86].

Entonces,lalongituddelprimerarcodelacicloide (α = 2π ), es8a. As´ıresultaquelalongituddelprimerarcodelacicloidees8veceselradio(o4veceseldi´ametro)delc´ırculo giratorio.3

El ´ areadelasuperficiequeseformaalhacergirarelprimer

3En1637,alatempranaedadde14anos,eljovenBlaisePascalcomienza aasistirconasiduidadalasreunionesorganizadasporMersenneenParıs. Trasobtenernuevosresultadosrelacionadosconlacurvacicloide,Pascaldecideplantearunreto,enelquesedebıanrespondercuestionesrelacionadas conelcentrodegravedaddelaregionplanaencerradaporlacicloide,ası comoconelvolumeny arealateraldelossolidosobtenidosporrevolucion dedichacurvarespectoauneje.Laresoluciondefinitivadelascuestiones planteadasporPascaltuvieronqueesperaralaapariciondelaobra Histoire delaroulette,publicadaporelpropioPascalafinalesdeeseano.

Unavezcerradoelplazodepresentaci´ondepropuestasalconcursoconvocadoporPascal,elarquitectoingl´esChristopherWren(1632-1723)comunicar´ıaaPascalunnovedosoresultadosobrelacicloide.Wrenhab´ıalogrado larectificaci´ondelacicloide,hallandoquelalongituddeunarcodecicloide eraigualacuatroveceseldi´ametrodelacircunferenciaquegeneralacurva.

arcodelacicloidealrededordeleje x est´adadopor

porloquelaevolutaparalaelipseesunastroide(asim´etrico). Retomandolacurvadenuestrointer´es,tenemosquelaevolutadelacicloideest´adescritaporloscentrosdecurvatura (ξ , η ) donde

ξ = a(θ + sen θ ),

η = a( 1 + cos θ )

Observequesitomamos φ = θ π ,entonces

ξ aπ = a(φ sen φ ),

η + 2a = a(1 cos φ )

Estasecuacionesmuestranquelaevolutadelacicloideesa suvezunacicloidesimilaralaoriginalsimplementetrasladadaalpunto (aφ , 2a)

Cuandoseestudiaunacurvaplanaexistendiversasmaneras dedefinirotrasasociadasaella,talcomola evoluta e involuta,lascualessurgenenaplicacionesdemaneranatural.Para nuestrosfines,aqu´ıs´oloestudiamoslaevoluta.

Sea σ : I → R2 , t → (x(t), y(t)) unacurvasinpuntosde inflexi´on(esdecir,puntosdondelosvaloresdeunafunci´on continuaen x pasandeuntipodeconcavidadaotra).Sedefine la evoluta σE de σ comolacurvaconrepresentaci´on

σE (t)= σ (t)+ 1 κ (t) n(t),

donde n(t) eselvectornormalalacurva σ (t) y t ∈ I.

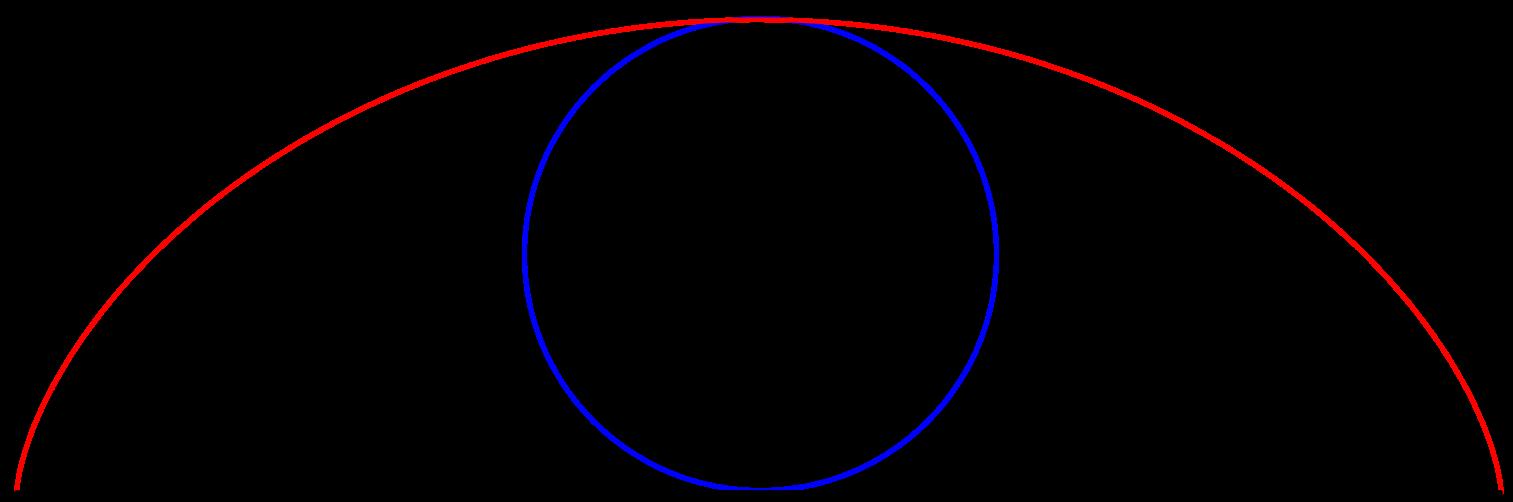
Paracada t0 ∈ I lacircunferenciaosculatriz(lamejoraproximaci´onalacurvaenunpuntoporcircunferencias)alacurva σ (t0) tienecentro σE (t0) yradio ρ = 1/κ (t0) llamadoradio decurvatura(elradiodelarcocircularquemejoraproximala curvaendichopunto),donde κ (t0) eslacurvatura(medida dequ´etantosedesv´ıalacurvadeunal´ınearecta)enelpunto

σ (t0).Lascurvastienenlamismatangenteenelpuntodecontacto.Porlotanto,laevolutacorrespondeallugargeom´etricodeloscentrosdecurvatura σE =(ξ , η ) de σ est´andados expl´ıcitamenteporlasexpresiones

ξ = x y x2 + y2 ˙ x ¨ y ˙ y ¨ x ,

η = y + ˙ x x2 + y2 xy yx

Sepuededemostrar,demanerasencilla,queparalaelipse

σ (t)=(a cos t, b sen t) con t ∈ [0, 2π ],0 < a < b secumple que

σ

t ∈ [0, 2π ].Unaexpresi´onimpl´ıcitadeestacurvaest´adadapor

4.Taut´ocrona.

Una taut´ocrona (isocr´ona)(delgriego, tauto-mismo y chrono-tiempo)eslacurvaparalacualeltiempotomadopor unobjeto,quedeslizasinrozamientoys´oloactuandolagravedad,hastallegarasupuntom´asbajoesindependientede supuntodepartida.

En1658,elastr´onomo,f´ısicoymatem´aticoholand´es ChristiaanHuygens(1629-1695)tratabademejorareldiseno delosrelojesdep´endulo,cuandoinspiradoporelretodePascal,estudiaelperiododeunp´enduloforzadoaseguiruna trayectoriacicloidal,descubriendoque ´ estossonis´ocronos. Huygensdescubreenbaseaconsideracionesgeom´etricasque lacurvacicloideinvertidaesunacurvataut´ocrona(isocrona). Elproblemadelatuat´ocrona,fueresueltogeom´etricamente porChristiaanHuygensen1659,aunquefuepublicadohasta 1673ensuobra Horologiumoscillatorium

Enunacicloidecuyoejeseelevasobrelaperpendiculary cuyov ´ erticeest´alocalizadoenelfondo,eltiempodedescenso enelcualuncuerpollegaalpuntom´asbajo,alv´ertice,despu ´ esdehaberpartidodesdecualquierpuntodelacicloide, esigualacualquierotro.

Lasecuacionesdelacicloideyevolutainvertidasson:

Figura4: Primerarcodelacicloideysuevoluta.

10¿Cicloide,Braquist´ocronaoTaut´ocrona?-ReynaldoCastaneiraRam´ırez

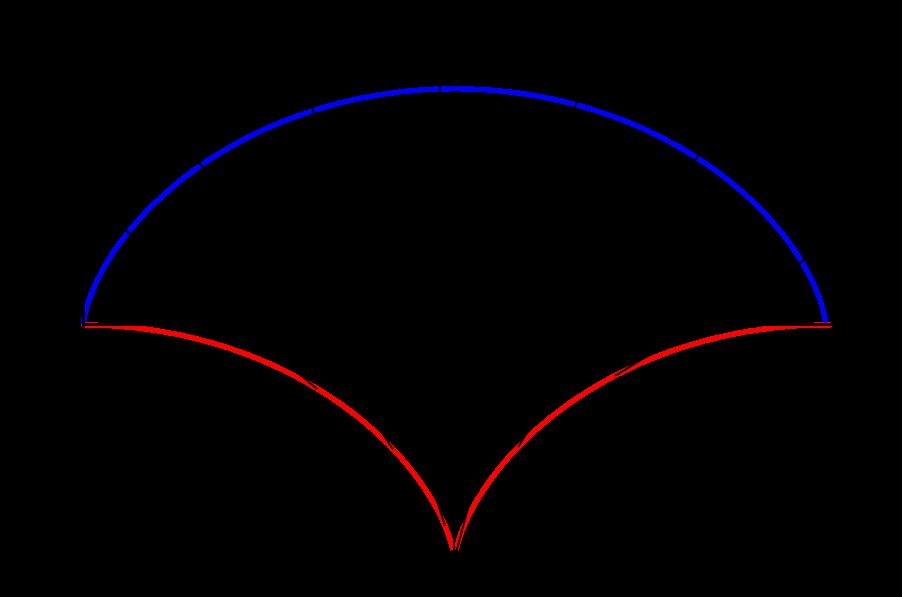
Respectivamente.Sidenotamosa P =(a(π + sen π ), a(1 cos π ))=(aπ , 2a) y M =(a(θ + sen θ ), a(1 cos θ )) puntos sobrelaevolutainvertiday N =(a(θ sin θ ), a( 1 + cos θ )) sobrelacicloideinvertida,comoenlaFigura5.

Observequeladistanciaentreelpunto M y N est´adada

cos β = cos2(β /2) sen2(β /2)= 2cos2(β /2) 1, cos α = 2cos2(α /2) 1, tenemosque

= 2gh = 2√ga cos2(β /2) cos2(α /2)

Usandoquelavelocidadeseldesplazamientoentreeltiempo, v = ds dt , donde ds = (dx)2 +(dy)2dα = 2a sin(α /2)dα

As´ı, dt = ds v = a g sen(α /2) cos2(β /2) cos2(α /2) dα

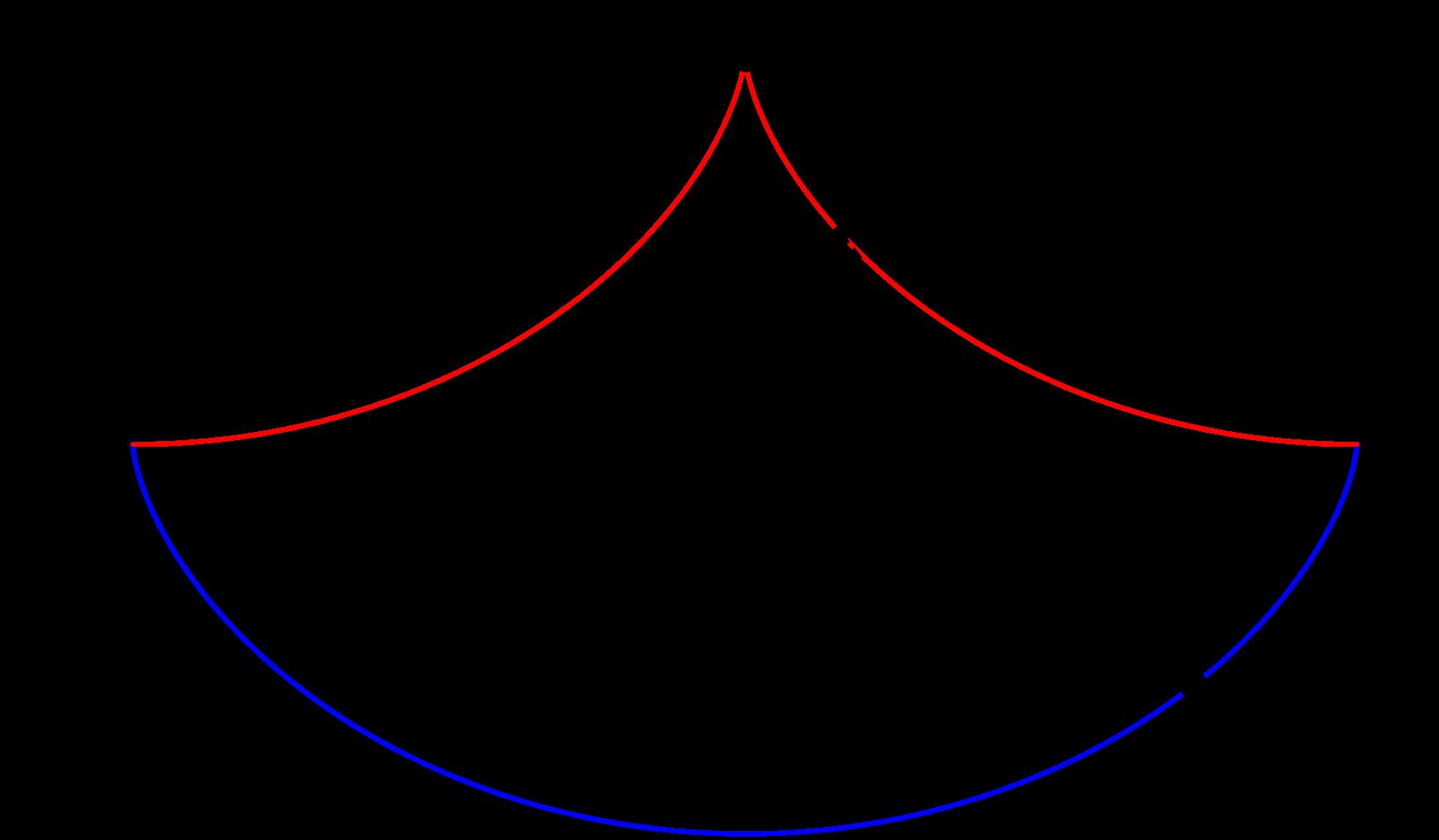
Porlotanto,tenemosqueeltiempoqueletomaalobjetoen laca´ıdaporlacicloidedesdeelpunto A alpuntom´asbajo B es

=

Porotrolado,sienlacicloidedejamoscaerunobjetodesde elpunto A hastaunpunto B,comoenlaFigura6,porlaley decaidalibre(leydeGalileo),llegar´aconunavelocidad

v = 2gh donde h = yB yA = a(cos β cos α )

Huygensfueelprimeroendescubrirestapropiedad(experimentalmente)en1673yendarleunaaplicaci´onpr´actica. Huygenshab´ıaestudiadoafondolosrelojesdep´enduloyobserv ´ oquecuandounrelojtieneunavariaci´onenlaamplitud delaoscilaci´ondelp´endulo,entoncesdejadecontareltiempo correctamente[HC86].Perosilalentejadelp´endulosemoviesenoenunacircunferencia,comoenelp´endulonormal, sinoalolargodeunacicloide,entoncesaunquelaamplitud

Figura5: Cicloideinvertidayevolutainvertida.

Figura6: ElobjetocaedesdeelpuntaAhastaelpuntoB. Como

deoscilaci´onfueramayoromenor,elperi´ododelp´endulo seguir´ıasiendoelmismo,comohemosvistoenlaecuaci´on (2).

Anosm´astarde,los m ´ etodosinfinitesimales deLeibniz (1646-1716)ejercer´ıanunaprofundainfluenciaenlosmatem´aticoseuropeos.Enparticular,sudisc´ıpulosuizoJakob Bernoulli(1654-1705)publicar´ıaenmayode1690untrabajo enlarevistaActaEruditorumdondeestablecelapropiedad taut´ocronadelacicloidehaciendousodelc´alculodiferencial eintegral.JakobBernoullimostr´oqueelproblemadelacurva taut´ocronasereduc´ıaalaresoluci´ondeunaecuaci´ondiferencialdeprimerorden.LostrabajosdeJakoben1690fueron relevantesparalahistoriadelc´alculoinfinitesimal,ladenominaci´on integral surgeporprimeravezconsusentidoactual comoprocesoinversoala diferenciaci´on

5.Braquist´ocrona.

Elproblemadelabraquist´ocrona(delgriego brachistos-m ´ ascorto, chronos-tiempo)fuepropuestoporJohann Bernoullien ActaEruditorum enJuniode1696.Laintroduci´ondelproblemafue:

Yo,JohannBernoulli,medirijoalosmatem´aticosm´as brillantesdelmundo.Nadaesm´asatractivoparalaspersonasinteligentesqueunproblemahonestoydesafiante, cuyaposiblesoluci´onotorgar´afamaypermanecer´acomo unmonumentoduradero.SiguiendoelejemplodePascal, Fermat,etc.,esperoganarmeelagradecimientodetodala comunidadcient´ıficaponiendoantelosmejoresmatem´aticos denuestrotiempounproblemaquepondr´aapruebasus m ´ etodosylafuerzadesuintelecto.Sialguienmecomunicala soluci´ondelproblemapropuesto,lodeclarar´ep´ublicamente dignodeelogio.

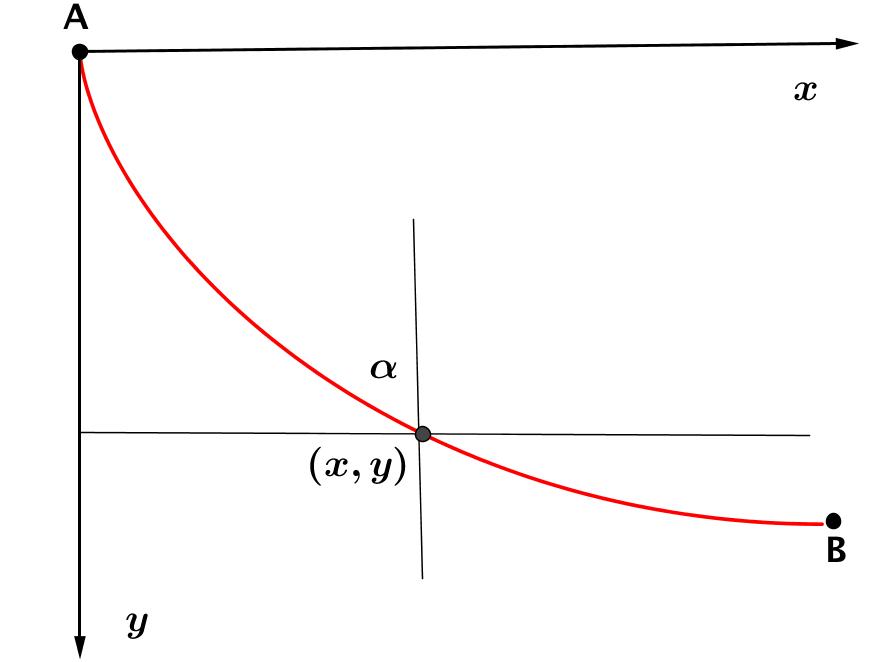
ElenunciadodelproblemaqueJohannpropusofue: Dados dospuntos4 AyBenunplanovertical,¿cu´aleslacurva trazadaporunpuntosobreelqueact´uasololagravedad, quecomienzaenAyllegaaBenelmenortiempo?

Alfinal,fueronJakobBernoulli(hermanodeJohann), Leibniz,NewtonyL’Hˆopitallas ´ unicaspersonasqueresolvieroncorrectamenteelproblema[IHM94].

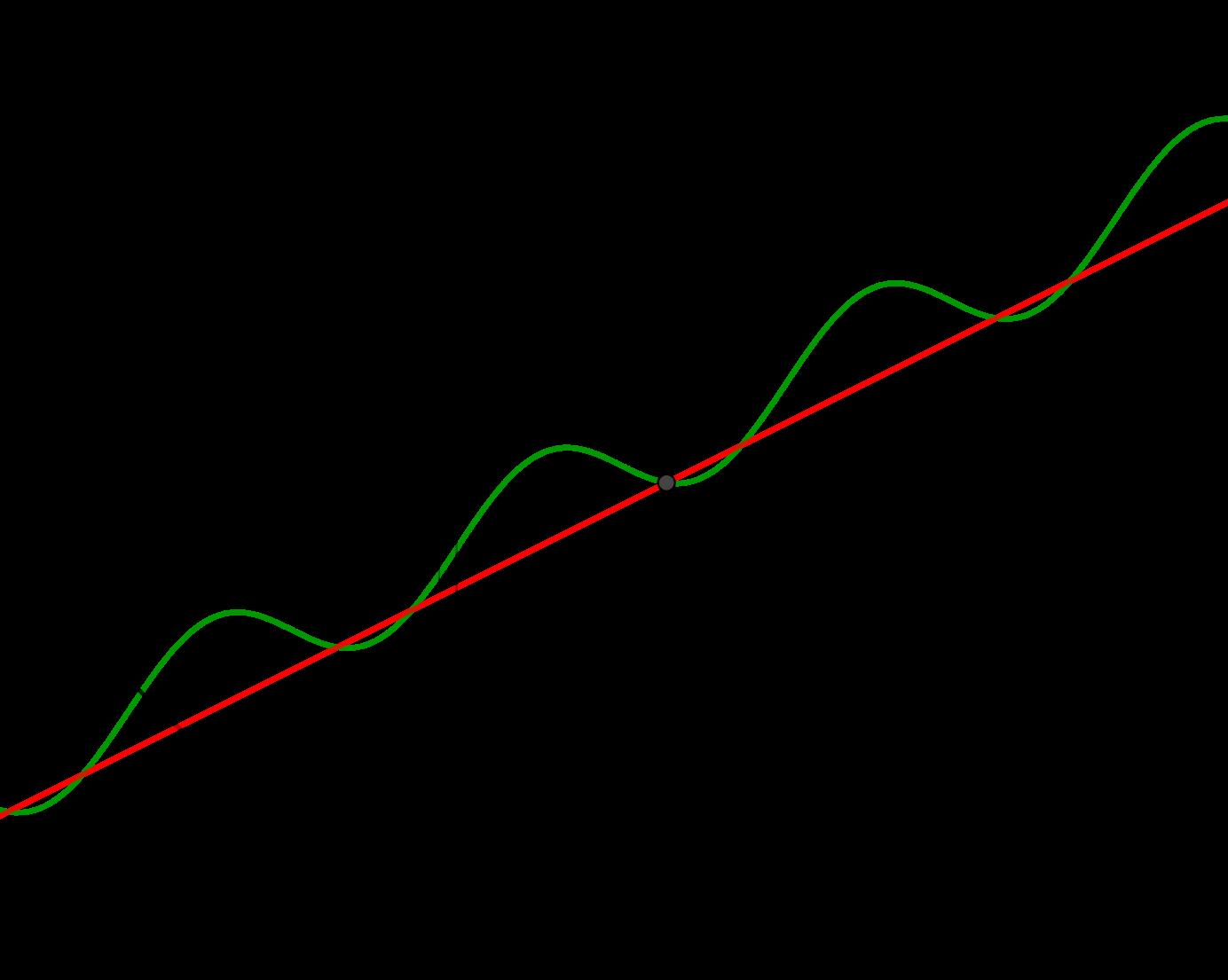
Presentamosaqu´ıs´ololasoluci´ondeJohann, ´ eldivide elplanoentirassuficientementedelgadasyasumequela part´ıculasigueunalinearectaencadatira.

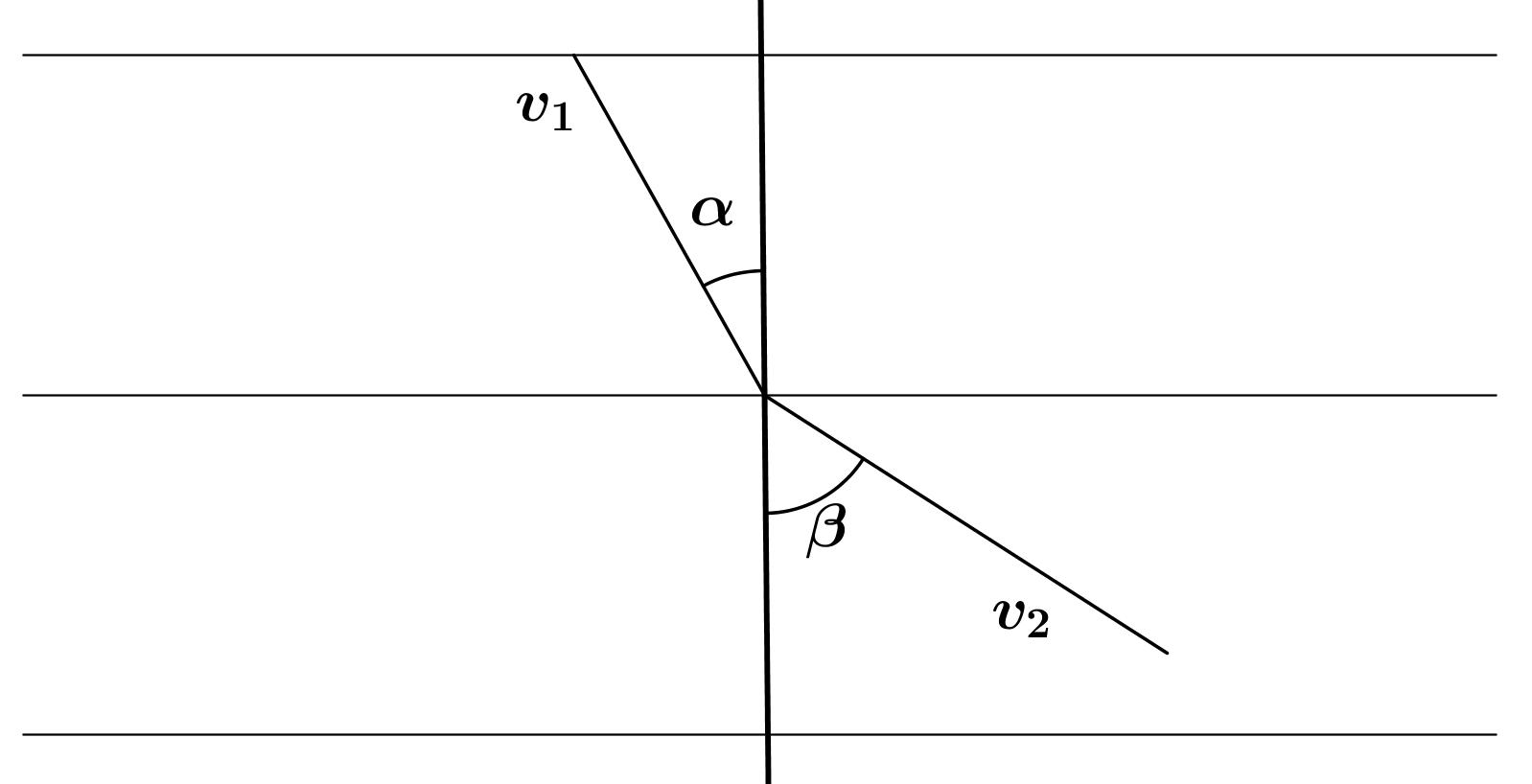
Figura7: Dospuntosendiferentestirasconsusrespectivos ´ angulosasociados.

Latrayectoriaentoncessonpedazosdelineas.Elproblemaesdeterminarel ´ angulodelalinea(segmento)encadatira. Parahaceresto ´ elrecurri´oal principiodeFermat,elcualestablecequelaluzviajadeunpuntoaotroenelm´ınimotiempo posible.Tambi´ensesabequelaluztienevelocidadesdistintas enmediosdistintos.

Entonces,si v eslavelocidadenunatiracon ´ angulo α respectoalaverticaly u lavelocidadenlasiguientetiracon ´ angulo β ,deacuerdoalaleyderefracci´onoleydeSnell:

sen α v = sen β u

Enell´ımite,cuandolastirassoncadavezm´asfinaslossegmentosdelasl´ıneastiendenaunacurvadondeencadapunto (x, y) el ´ anguloyelsegmentoconlaverticalesel ´ angulode latangenteconlavertical

4Sinp´erdidadegeneralidad,elpunto A debeest´arm´asarribaque B

Si v eslavelocidadenelpunto (x, y) y α esel ´ anguloque

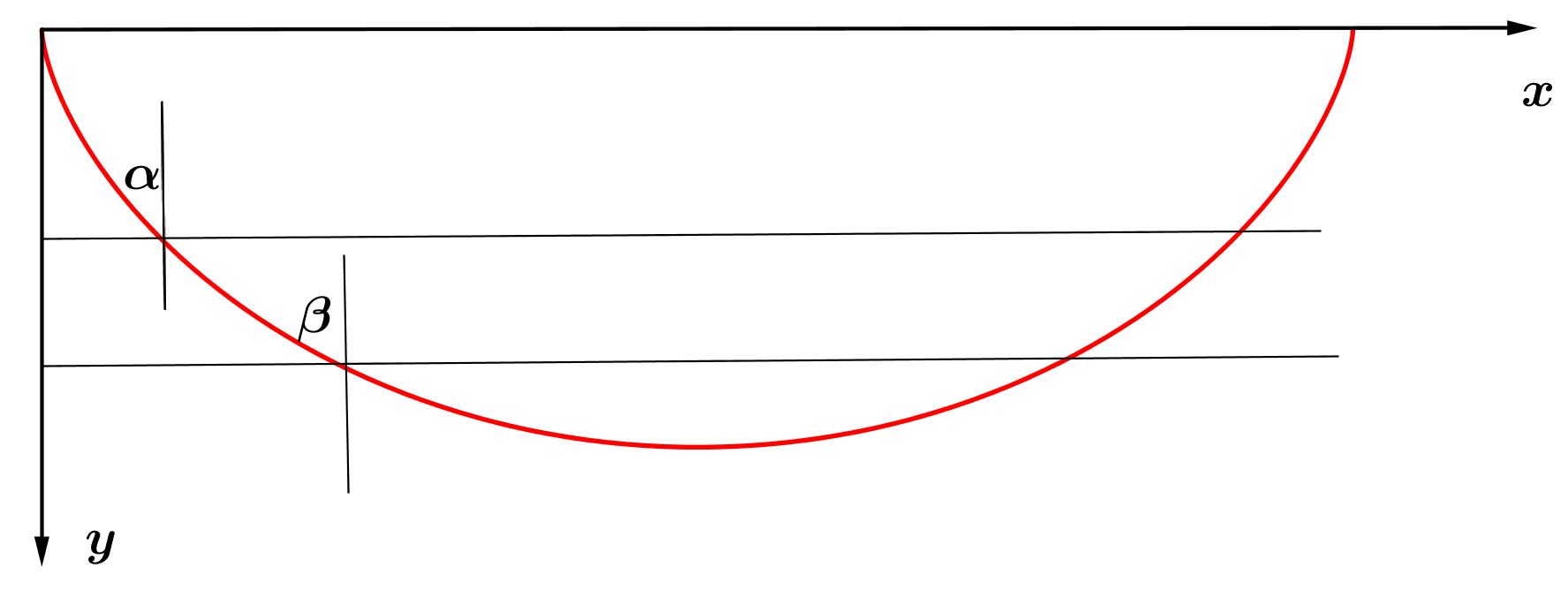
latangentehaceconlaverticalentonceslacurvasatisface

sen α

v = c, cconstante. (3)

LuegoporlaleydeGalileo:lavelocidad v dedescensodeun cuerpoesproporcionalalara´ızcuadradadeladistanciadesde dondecae,estoes, v satisface

v = 2gy,

donde g eslaaceleraci´ondebidoalagravedad.As´ı,alsustituir v en(3)tenemos

sen α √2gv = c, equivalentemente sin2 α 2gy = c 2 , porlotanto

y = k2 sen2 α , k2 = 1/(2gc 2) (4)

Porotrolado,delafiguraanterior,observeque y ′ = dy dx = cot α , y sen2 α = 1 1 + cos2 α sen2 α

= 1 1 + cot2 α = 1 1 +(y′)2 (5)

Delasecuaciones(3)y(5)seobtienequelacurva y (independientede α )debesatisfacerlaecuaci´ondiferencial:

y(1 +(y ′)2)= k2 (6)

Probemosahoraquelacicloidesatistaceestaecuaci´ondiferencial.Enefecto,si x = a(θ sen θ ) y y = a(1 cos θ ) entonces y ′ = dy dθ dθ dx = sen θ 1 cos θ

quebajocualquierotrahip´otesisdeber´ıamosnecesitardos curvas...

JohannBernoullinofueelprimeroenconsiderarelproblemadelabraquist´ocrona,aunquefue ´ elquienacunoelnombre.Galileoen1638hab´ıaestudiadoelproblemaensufamosa obra Discourseontwonewsciences [GG58].Suversi´ondel problemaconsist´ıaprimeroenencontrarlal´ınearectadesde unpuntoAhastaelpuntodeunal´ıneaverticalalquellegar´ıa m ´ asr ´ apido.Determin´ocorrectamentequetall´ıneadeAala l´ıneaverticalestar´ıaenun ´ angulode45◦,alcanzandolal´ınea verticalrequeridaenunpunto,B.

Calcul´oeltiemponecesarioparaqueelpuntosemoviera deAaBenl´ınearecta,luegomostr´oqueelpuntoalcanzar´ıa Bm´asr´apidamentesiviajabaalolargodelosdossegmentos del´ıneaACseguidodeCB,dondeCesunpuntoenunarco deunc´ırculo.

As´ı,lacicloidesatisfacelaecuaci´ondiferencial(6)con k = √2a

Johannterminasusoluci´ondelproblemadelaBraquist´ocronaconlassiguientespalabras:

Antesdeterminar,deboexpresarunavezm´aslaadmiraci´on quesientoporlainesperadaidentidaddelataut´ocrona deHuygensymibraquist´ocrona.Consideroespecialmente notablequeestacoincidencias´olopuedatenerlugarbajola hip´otesisdeGalileo,demodoqueinclusoobtenemosde ´ esto unapruebadesucorrecci´on.Lanaturalezasiempretiende aactuardelamaneram´assimple,porloqueaqu´ıpermite queunacurvasirvaparadosfuncionesdiferentes,mientras

AunqueGalileoestabaperfectamenteenlociertoenesto, luegocometi´ounerrorcuandoargument´oqueelcaminode descensom´asr´apidodeAaBser´ıaunarcodeunc´ırculo,lo cualfueunadeducci´onincorrectacomoacabamosdever.El m ´ etododeresoluci´onpropuestoporJakobBernoulli,elcual nomostramosaqu´ı,paraelproblemadelaBraquist´ocrona, esmuchom´asgeneralquelasoluci´onpropuestaporsuhermanoJohannyejerci´ounaprofundainfluenciaenLeonhard Euler(1707-1783),quien,juntoaJ.L.Lagrange(1736-1813), instaurar´ıalasbasesdeloqueactualmenteconocemoscomo C´alculodeVariaciones

Paraprofundizarenestatem´aticasepuedenconsultar [IHM94,WEA43,GG58,HC86]ylasreferenciasqueall´ıse encuentran.Tambi´ensepodr´aencontrarmaterialinteresante enlossiguientessitiosdelaweb:

1. https://mathshistory.st-andrews.ac.uk/ HistTopics/Brachistochrone/

2. http://www.mat.ucm.es/cosasmdg/cdsmdg/ 05edumat/geometriahoy/experimentosgeom/ ecua.htm

3. https://en.wikipedia.org/wiki/Cycloid

4. http://historiasdematematicas.blogspot. com/2017/04/historia-de-la-cicloide.html

Figura8: ProblemaconsideradoporGalileo.

Agradecimientos.

Elautoragradecealeditoryalr´eferian´onimoporsusvaliosasobservaciones.

Referencias.

[IHM94] IcazaHerreraM., Galileo,Bernoulli,LeibnizandNewtonaround thebrachistochroneproblem,Rev.MexicanaFis.,1994.

[WEA43] WhitmanE.A., SomeHistoricalNotesontheCycloid,TheAmericanMathematicalMonthly,1943.

[GG58] GalileoG., DialoguesConcerningTwoNewScience,DoverPublications,Inc.,NewYork,1958.TranslationbyHenryCrewand AlfonsodeSalvioofDISCORSIEDIMOSTRAZIONIMATEMATICHE,intorno’aduenuouescienze,Elsevier,Leiden,1638; firstpublishedbyMacmillan,1914.

[HC86] HuygensC., ThePendulumClockorGeometricalDemonstrations ConcerningtheMotionofPendula(sic)asAppliedtoClocks,IowaStateUniversityPress(Ames,Iowa,USA),1986.Translated byR.J.Blackwell.

[TGJ99] TeeG.J., Isochronesandbrachistochrones,NeuralParallelSci. Comput.,1999.

Acercadelautor:ReynaldoesdocentedelDepartamento deCienciasB´asicasenelInstitutoTecnol´ogicodeOaxaca,le apasionacontemplarlanaturalezaysembrar ´ arboles.Otrasde lascosasqueesperaesvercrecerasusninosyleeralgunos libros,quea´unesperanporabrirse.

VENTAJASYDESVENTAJASDEUTILIZARLOS MODELOSDE FUNCI ´ ONDE TRANSFERENCIA

C´esarAugustoLaraSantana * cesara.laras@konradlorenz.edu.co

Resumen

LosModelosdeFunci´ondeTransferencia(MFT)sonun tipodemodelosmatem´aticosdeenfoqueprobabil´ısticoque permitenresponderanecesidadesdecuantificaci´ondelamagnitud,sentidoyduraci´ondelosimpactosentrevariablesestad´ısticasqueseanalizanendiferentes ´ areasdelconocimiento.Estosmodelostienenlacapacidaddepoderidentificar siexistenseriesdetiempoquetienencorrelacioneslineales tantoenelmismomomentodeobservaci´oncomoenrezagostemporales.As´ı,elpresentedocumentobuscailustrarlas ventajasydesventajasdeutilizaresteobjetomatem´atico,el cualincluyelasprincipalesdefiniciones,procedimientometodol´ogicoyresultadosdeunaaplicaci´ondeunMFTsobre fen´omenosecon´omicos.Latransformaci´ondedatos,modelamientoydesplieguesehaceconelsoftwarelibreRjuntoalas librer´ıas,”TSA”,”tseries”,y”forecast”.

1.Introducci´on.

Endiferentessectoresdelasociedad,elan´alisisde fen´omenosinvolucracomprenderyproyectarelcomportamientodevariablesysusrespectivasinteracciones.Producto deestosan´alisismultivariados,surgenpreguntas,delascuales sepuedenmencionaralgunosejemplos,talescomo:¿Siaumentanlastasasdeinter´esdelosbancos,estopodr´ıaafectar lainflaci´on?¿Siaplicamosunmedicamentoveterinariosobre determinadogrupoanimal,cuandoseobservar´anlosefectos?

¿Porcu´antotiempodurar´anlosefectossignificativos?¿Los efectosser´anpositivosonegativos?

Dadoqueestaspreguntasconducenaproyectarelcomportamientodefen´omenosbajoincertidumbre,sehapropuestoelpresenteart´ıculoconelfindeintroducirlosconceptos deMFTcomounaalternativaprobabil´ısticapararespondera unapreguntacentral:¿Esposiblemodelarmatem´aticamente lamagnitud,sentidoyduraci´ondelasrelacionesentrediferentesvariablesendiferentesmomentos?

Elpresenteart´ıculoest´acompuestoporcuatrosecciones: inicialmente,sepresentaunaintroducci´onalosconceptosy definicionesnecesariasparaabordarlosModelosdeFunci´on deTransferencia(MFT).Enlasegundasecci´on,sedescribir´a elconjuntodedatosyseriesdetiempocontempladospara

*EstudiantedeMatem´aticas,Fundaci´onUniversitariaKonradLorenz,Bogot´aD.C.-Colombia

abordarelfen´omeno.Enlatercerasecci´onseilustranlosresultadosdelMFT,incluyendolaextrapolaci´ondelmodeloen unamuestraposterioralaventanadeentrenamientoutilizadaenlasegundasecci´on.Finalmente,seabordanlasconclusionestantoenlasventajasydesventajasdeimplementarun MFTcomoenlosresultadosobtenidosparaelconjuntode datosempleadoenelpresenteejercicio.

2.Conceptualizaci´on.

Comoconceptospreliminares,losMFTseenmarcanen last´ecnicasprobabil´ısticasparaelmodelamientomatem´atico.Estosmodelossonherramientasdelaestad´ısticaaplicada cuyautilidadradicaenquepuedeserempleadaparamodelar elcomportamientodeunavariablederespuestaatrav´esdelos impactosnocontempor´aneosdeunaovariasvariablesex´ogenastendiendopresenteelfactor tiempo.Algunosejemplosde estetipodemodelospuedenser:

Modelarelniveldelluviosidadenunaregi´onespec´ıfica enfunci´ondelahumedad,corrientesdevientoypresi´on atmosf´ericaobservadoenminutos,horasod´ıasprevios.

Establecerelimpactoenloscambiosdeniveldeglucosa delasangrehumanaapartirdelcambiodeingestade az ´ ucaresycarbohidratoshorasprevias.

Observarelporcentajedelavariaci´ondelProductoInternoBruto(PIB)teniendopresenteelcomportamiento ponderadodelospreciosinternacionalesdelosproductosexportablesensemanasomesesanteriores.

Acontinuaci´on,seenuncianalgunosdelosprincipales conceptosnecesariosparaabordarintegralmenteesteconcepto:

Definici´on2.1 (SeriedeTiempo). Esunavariablealeatoria xt definidadentrodelespaciodeestadosdeunprocesoestoc´astico x ∈ X ,lacualesmedidademanerarepetidaalo largodeltiempo[oS22].Adicionalmente,elconjuntode ´ ındices T = {t1, t2,..., tn} puedeserdefinidoentiempocontinuo otiempodiscreto.Paraefectosdelpresenteart´ıculo,seconsiderar´avaloresdelaseriedetiempomedidosenlosn´umeros realesyelconjuntode ´ ındicesmedidosentiempodiscretoy finito T = {t1, t2, · , tn},esdecir, x ⊂ R, t ⊂ Z+.Igualmente,

setrabajar´abajounmodelob´asicoconunasolavariablede respuesta yt yunasolavariabledeentrada xt .

Definici´on2.2 (ModelodeFunci´ondeTransferencia-MFT). Esunmodelomatem´aticoenelcualsedefineunaseriede tiempoespec´ıfica yt (entendidacomovariabledesalida)en funci´ondelacombinaci´onlinealdelastransformacionesde unaovariasseriesdetiempo xt (entendidascomovariables deentrada)medidasbajoelmismoconjuntode ´ ındices t [Wei06].Laecuaci´onfuncionaldeunMFTes:

yt = υ (B)xt + ηt (1) donde υ (B) esunpolinomioofiltroderezagosqueseaplicasobrelavariabledeentraday ηt esunaseriealeatoriaestacionaria,esdecir,tantolamediacomolavarianzadelaserie esconstanteparatodalaseriedetiempo.Enlaliteraturaestad´ıstica,estetipodemodelosesconocidotambi´encomolos modelosARMAX[LeB18].Esimportanteresaltarquelasseries xt , yt satisfacenlascondicionesdeestacionariedad(media yvarianzaconstante)conelfindepoderserobjetodemodelaci´onmedianteelm´etodoARMA.

Definici´on2.3 (Funci´ondeImpulsoRespuesta-FIR). Elpolinomio υ (B) esunoperadordetransformaci´onsobrelaserie detiempo xt (variabledeentrada),elcualgeneraunimpulsosobrelaseriedetiempo yt (variabledesalida),delacual segeneraunarespuesta.Larespuestasecalculamedianteestafunci´onpolin´omica υ (B),lacualest´acompuestaportres polinomios[Wei06]:

ω (B) eselpolinomioconloscoeficientesdeimpactorezagado(B)de xt sobrelavariable.Puedeserinterpretadocomoladuraci´ondelefectodelavariabledeentrada sobrelavariabledesalida.Estepolinomioesdeorden s ∈ N∗ .

δ (B) eselpolinomioquemideladuraci´ondelosimpactosautocorrelacionadosde yt sobres´ımisma.Esun polinomiodeorden r ∈ N∗

b eselordendelrezagoenelcualiniciaelimpactode latransferenciadelavariabilidadentreambasseriesde tiempo.

B eseloperadorderezagotemporalparaseriesdetiempo delaforma B(yt )= yt 1.

Porextensi´on,laecuaci´on(1)puededescomponersecon losdiferentespolinomiosqueconstituyenlaFunci´onde Impulso-Respuesta(FIR)delasiguientemanera[Sof99]:

laserie xt y yt [Abr85].Enelcasoque δ (B) notengasus ra ´ ıcesdentrodelc´ırculounitario,dichopolinomionopodr´ıa serinvertibleyenconsecuencia υ (B) nopodr´ıaserestimado. EsimportanteconsiderarqueunMFTseconsideracausalenlamedidaqueloscoeficientes,apartirdedeterminado rezago,tenganvalorcero,esdecir, υ j = 0para j < 0.

Definici´on2.4 (Funci´ondeCorrelaci´onCruzada-FCC). Es unafunci´onquetomavaloresenelrezago k ∈ Z yseobtiene elcoeficientedecorrelaci´onlinealluegodehaberrezagadola variableexplicativa k periodos[EC08].Losrezagosnegativos correspondenaimpactosoriginadosen yt yabsorbidospor xt k unidadesdetiempoposterior;losrezagospositivosson interpretadoscomoloschoquesgeneradosen xt loscualesson recibidosporlavariablerespuesta yt hastalos k unidadesde tiempoposteriores.

Comofunci´on,laFCCpuederepresentarsecomosedefine en[D´ı14]:

.Paraefectosqueelpolinomio υ (B) seadeordenfinito,esnecesarioquelasra´ıcesde δ (B) tenga susra ´ ıcesdentroc´ırculounitario,dadoqueestepolinomio correspondealconjuntodeimpactosdetransferenciaentre

donde µx :promediomuestraldelaserie xt , µy :promedio muestraldelaserie yt , Sx :desviaci´onest´andardelaserie xt , Sy :desviaci´onest´andardelaserie yt .

Estafunci´ontieneelprop´ositodeidentificarlamagnitud, signoyduraci´ondelascorrelacionesparcialesintertemporalesqueseanestad´ısticamentediferentesaceroentre xt y yt a diferentesrezagos.Dependiendodelpatr´ondedecaimientode lascorrelacionescruzadasobtenidasatrav´esdelFCC,sepudeidentificarlaformafuncionaldelpolinomio υ (B) definido enlaecuaci´on(1).

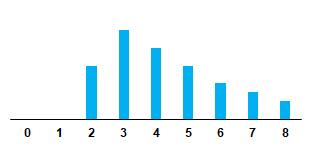
Conbasealodefinidoen[Wei06],enlasTablas1y2se ilustranelcomportamientote´oricodealgunascombinaciones delatupla (b, r, s) teniendorezagos k positivos,esdecir,considerandoquelavariable xt lfluct´uaprimeroquelavariable yt .Estosejemplosdeespecificaci´onfuncionalde υ (B) sirven comoelementoparaidentificarlaformafuncionaldelaFIR.

Cuadro1: FormasfuncionalesdelaFIRpara r = 0

Comohechocaracter´ıstico,enelCuadro1seobservaque cuando r = 0,laextensi´ondelaFIRsemantieneporcuantos rezagos s secontemplendespu´esdeocurridoelprimerimpactodelafunci´ondetransferenciaenelrezago k.Adicionalmente,cuando r = 1,sepresentaunprocesodedifuminaci´on odecaimientoexponencialdelimpactoobservado.Elproceso

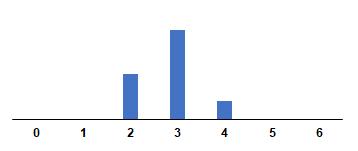
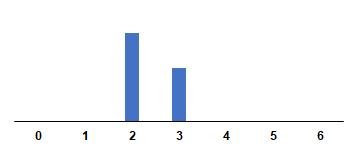
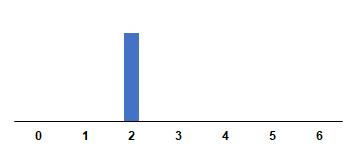
Cuadro2: FormasfuncionalesdelaFIRpara r = 1

deidentificaci´ondelospar´ametros (b, r, s) apartirdelafunci´ondecorrelaci´oncruzadafuncionadeformamuysimilar alaidentificaci´ondelospar´ametros p, q enunprocesoARIMA (p, q) haciendousodelcomportamientodelasfunciones deautocorrelaci´onsimpleyautocorrelaci´onparcial.

3.Losdatos.

ParaefectosdeilustrarlautilidaddelosMFTsobre fen´omenosecon´omicos,seproponetrabajarconlasseriesde tiempoasociadasalpreciodeactivosfinancierosagr´ıcolaso denominados commodities.LaguerraentreRusiayUcrania enfebrerode2022despert´oladiscusi´onentreacad´emicos, empresarios,consumidoresytomadoresdedecisi´onsobrelos efectosconcretosdelacontracci´onenlaproducci´ondecerealescomotrigo,sorgoysojasobrelaofertadeganadopara consumofinal.Bajoesteescenario,sebuscaconfirmarodesvirtuarmedianteevidenciaf´actica,lahip´otesisqueloscambiosenlospreciosdeinsumosenlaproducci´ondeinsumos agr ´ ıcolasparalaproducci´ondeganadopuedenafectarprecio deproductospecuarios.

Adicionalmente,comosecontemplanvariablesquereflejancontratosfuturos (t = h + k) (h eseltiempoactualy k eselperiodoadicionaleneltiempoenqueseproyectanlas expectativasdepreciodecontratosagropecuariosfuturos),las relacionesesperadasdecasualidadpodr´ıanreflejarunproceso contrarioaldelosprocesosdeOfertayDemandaen t = h.Por ejemplo:Losoperadoresburs´atilestomar´ıandecisionessobre laadquisici´ondecontratosfuturosdelasoya(comoinsumos deproducci´ondeganado)dependiendodec´omoevolucionen lospreciosdeloscontratosfuturosdeganado.

Lafuentedeinformaci´oncorrespondealvalorpactadoenlos contratosfuturossobreestosactivosfinancierospublicados enportalestransaccionales.Enparticular,elcuerpodedatos utilizadopararesponderalapreguntadeinvestigaci´onsedelimitasobrelossiguientesconceptos:

VariableNo.1: Gt :precioporcontratoderivadode 40.000lbsdecarnebovinaencanal,medidoenUSD. Fuente:[inv22].

VariableNo.2: St : ´ Indiceburs´atildelpromediodecontratodesoyade5.000Bushels(8galonesdegrano)me-

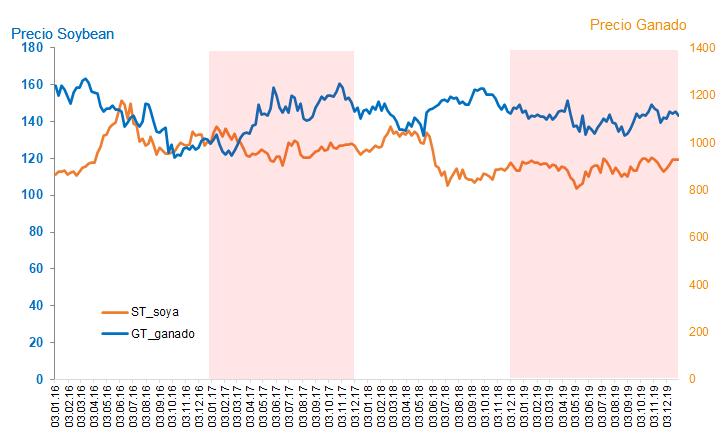
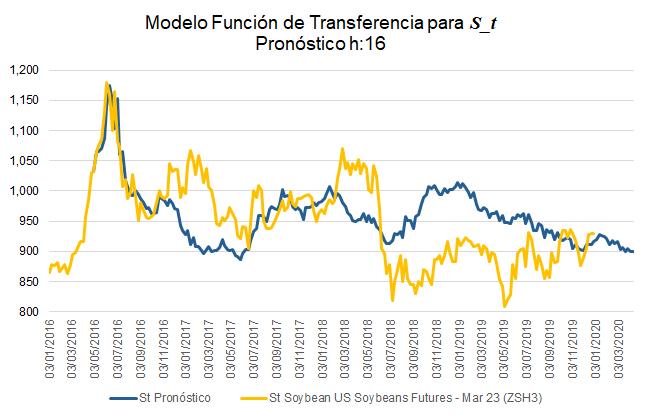
Figura1: Gr´aficodelasSeriesdeTiempo St (Preciodela Soya)y Gt (PreciodelGanado.)

didoenUSD.Fuente:[Edi22].

PeriododeEntrenamiento:01/01/2016-31/12/2019.

Frecuencia:Semanal(Agregaci´onporpromediosemanal dadoqueelreportedelaplataformaeselpreciodecierre diario).

PeriododeValidaci´on:01/01/2020-19/04/2020.

PeriododeComprobaci´on:01/01/2022-31/12/2022.

Tama˜nodeMuestra:Entrenamiento:209;Validaci´on: 52.

Mediantean´alisisgr´aficodelasseriesdisponiblesenlaFigura1seobservaqueexisteunpatr´onmuymarcadodecrecimientosostenidoentrelasseriesdetiempo St (Preciode laSoya)y Gt (PreciodelGanado).Sibienelcoeficientede correlaci´onlinealcontempor´anea(k = 0)entreambasseries ρ (Gt , St , 0) esbajo(0.00021),seobservaquelacorrelaci´on contempor´aneaporcadaanoevidenciaunaasociaci´onlineal moderadade(-0.4062;-0.4784;0.7878,0.4880)paralosanos 2016a2019,respectivamente.

Loanteriorinvitaaprofundizarsielrezagointertemporal permiteidentificarunaasociaci´onm´asfuerteentreambasserieseidentificar:1)siexistealgunarelaci´oncausalentrelos comportamientosdelpreciodesuinsumoprincipalrespecto alpreciofinaldelproductodecarnebovina;2)cualeslamagnituddeeseimpactoy3)cualeseltiempoquetomaobservar porprimeravezdichoimpactoysuduraci´on.

4.Metodolog´ıadeestimaci´ondel MFT.

LospasosparaconstruirlaMFTm´asadecuadapararesponderalobjetodeestainvestigaci´onson:

4.1.HacerelpreblanqueamientodelasSeries

Comoseobserv´oenlaFigura1,ambasseriesdetiempono satisfacenlascondicionesdeestacionariedaddeunaseriede

tiempo(mediayvarianzaconstante),conformeesrequerido parapoderconstruirelMFT.Siguiendolasrecomendaciones de[ECoS22],sehaceunareducci´ondelaescaladelasseries Gt St delasiguienteforma:

d1 log St = ∇(log(St )):correspondealaprimeradiferenciadellogaritmonaturaldelaserie St

d1 log Gt = ∇(log(Gt )):correspondealaprimeradiferenciadellogaritmonaturaldelaserie Gt

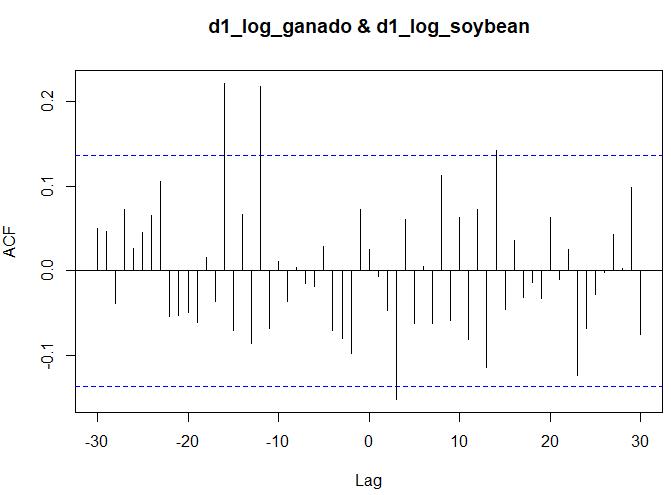
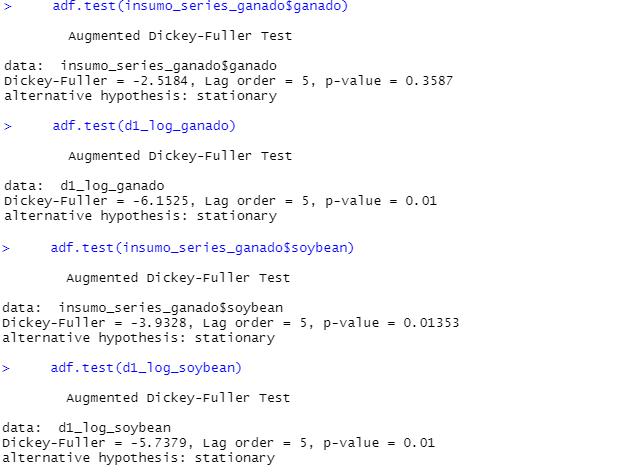
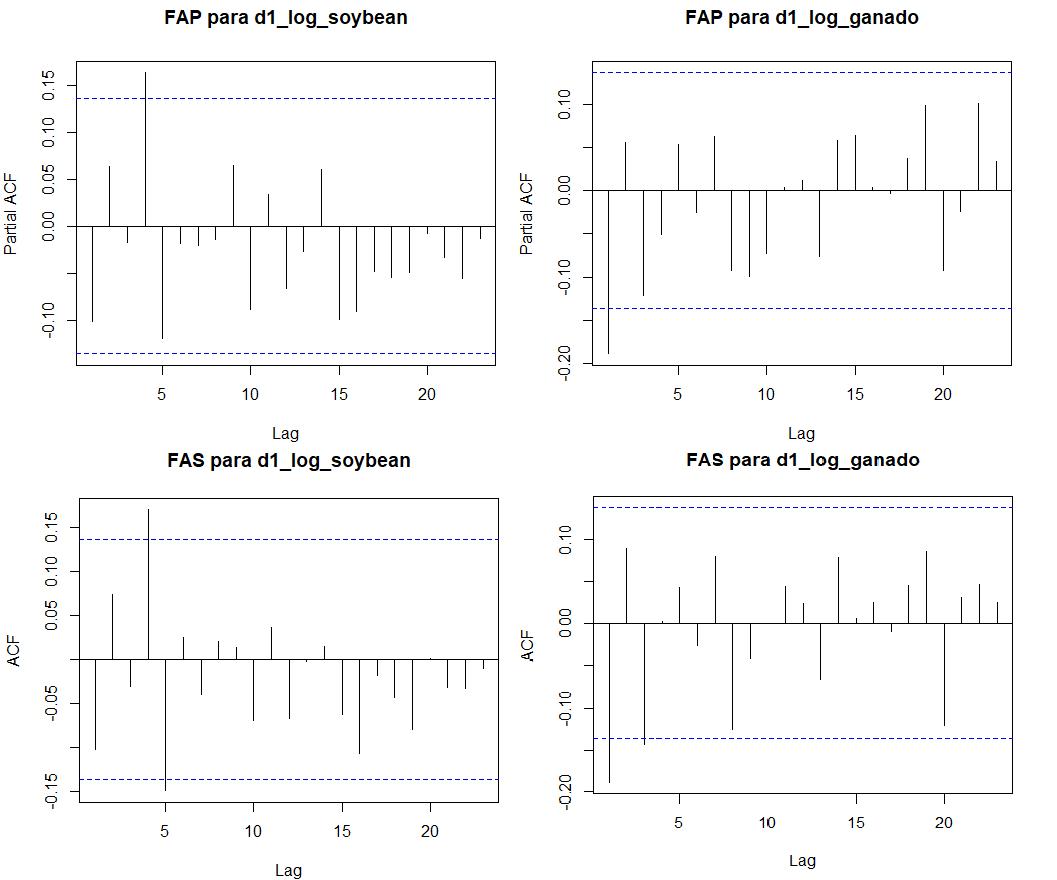
Losefectosdelaanteriortransformaci´onrindenfrutos,dadoquelapruebadeestacionariedaddeDickey-Fullerbrindaresultadossatisfactorios.Comosedemuestraenlafigura 2,lasseriessinaplicartransformaciones(’ganado,soybean’) demediayvarianzaobservanestad´ısticosdepruebadeestacionariedadDickey-F¨ullerquecaenenzonadeNo-Rezago (porejemplo:p-valorde0.35para Gt ).Luegodeaplicarlas transformaciones,(’d1 log ganado,d1 log soybean’)ambos p-valoresde Gt , St soninferioresa0.05,esdecir,seobtienenseriespreblanqueadaslistasparaserincorporadasenel procesodeestimaci´ondedelaFCC.

4.2.ConstruirlaFCCyFIRentre Gt y St .

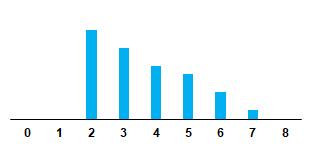
AlestimarlaFCC,seobservaenlaFigura3sobrelasseriestransformadas,seidentificantrescoeficientesdelaFCC cuyovalorestimadoessignificativamentesuperioralerror est´andardelaseriedecorrelacionescruzadas.Paralamuestradeentrenamiento,elerrorest´andar,seestimadelaforma

ladistribuci´onnormalest´andarconunniveldesignificancia de0.05.

Comohechoimportante,seevidenciaqueexistendoscoeficientesdecorrelaci´oncruzadasignificativamentesuperior alerrorest´andarenlosrezagos K = 12, 16cuyosrespectivosvaloresson (0,2170, 0,2212).Estoseinterpretacomolos cambiosocurridosen Gt reflejancambios12y16semanas despu´esen St .Esteresultadoesestad´ısticamentesignificativoypermiteevidenciarqueexisteunpatr´ondecorrelaci´on linealpositivaquenoseevidenciaalestimarlascorrelacionescontempor´aneas(k = 0),conlocualunMFTesunapropuestaadecuadaparaentenderestefen´omeno.Elprocesoa niveldescriptivonoevidenciaunprocesosecuencialestrictoentrelaserietransformada St sobre Gt enlamedidaque seobservauncoeficienteligeramentesignificativoenlosrezagos k = {4, 5}.Paraefectosdeestimarlarelaci´oncausal entreambasvariables,consideraremossolamentelosrezagos negativosenlaestimaci´onde υ (B).

Alanalizarlagr´aficadelaFCC,sepuedeproponerelsiguientemodelodefunci´ondetransferencia:

variabledeentrada: Gt

variabledesalida: St

ordenderezago b = 12

ordendeduraci´ondelimpacto s = 4.Dadoqueelimpactoalcanzaelrezago k = 16

ordendeduraci´onARIMA r = 1.Estimadoapartirdela Funci´ondeAutocorrelaci´onSimple(FAS)ylaFunci´on deAutocorrelaci´onParcial(FACP) St

Porloanterior,laformafuncionaldelmodelopropuestoes:

Figura2: ResultadosPruebadeEstacionariedadDickey-Fuller

Figura3: Funci´ondeCorrelaci´onCruzadaentre St sobrevariableexplicada Gt

Acontinuaci´onseenlistanlosprincipalespasosrequeridosparaabordarestetipodemodelamiento,conformelohan propuestopreviamente[Wei06]y[Ahm15],conbaseenla metodolog´ıaBox-Jenkins 1

Parapoderobtenerunmodelodefunci´ondetransferencia, serequieredescomponeresteprocesoenvariospasos:Enprimerainstancia,debeconstruirseunmodeloARIMAparala serieregresora Gt ,cuyopron ´ osticoservir´acomovariablede entradaenlamuestradeentrenamientodelaserie St .Posteriormente,seestimar´aunmodeloARIMAsobrelaserieobjetivo St ,incluyendoelcomportamientomodeladoparalaserie Gt .Esimportanteaclararquelaespecificaci´onfuncionalde lainteracci´onentreambasvariablesseestableceenelfiltro construidoconlaFIRylaFCCobtenidosenlasecci´on4.2.

4.3.1.Estimaci´onmodeloARIMAparalavariablede entrada Gt .

Mediantelaestimaci´ondelaFunci´ondeAutocorrelaci´on Simple(FAS)ylaFunci´ondeAutocorrelaci´onParcial(FAP), seidentificaque St sigueunprocesoARIMA(1,0,0),locual puedeserobservadoenlaFigura4.

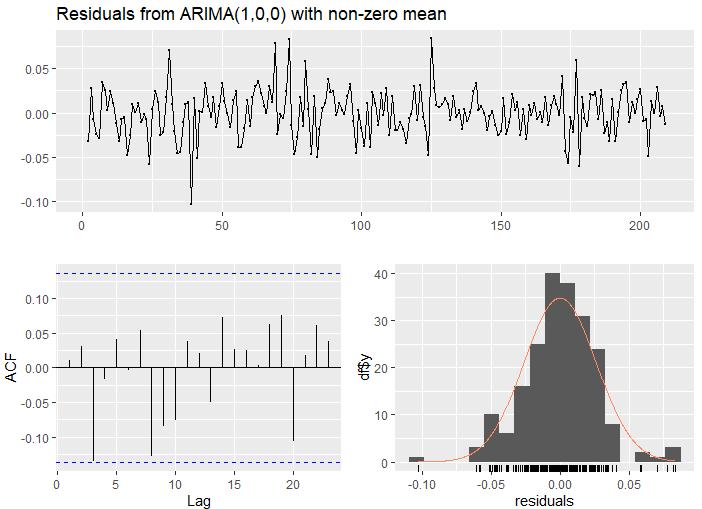
As´ı,laestimaci´ondelmodeloqueseajustaalasespecificacionespermiteobtenerunmodeloARIMA(1,0,0)para laseriepreblanqueada Gt ,cuyop-valoresmenora0.05.Es decir,serechazalahip´otesisnulaquesuestimadorseaestad´ısticamenteigualacero.Loanteriorsepuededetallaren laFigura5generadaporRalcorrerelmodeloenmenci´on. Adicionalmente,alverificarlascondicionesderuidoblanco paralosresiduosdelmodelo,seevidenciaquelosresiduosno sonautocorrelacionados,suvarianzaesconstantealolargo

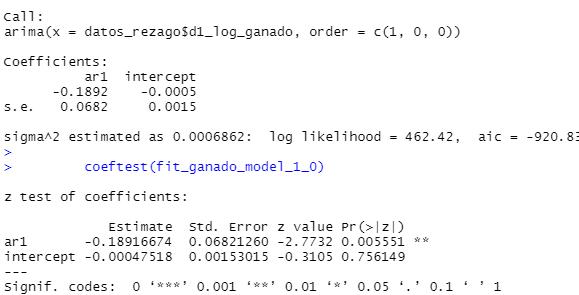
deltiempoytienemediaestad´ısticamenteigualacero(Ver Figura6).

Enesteproceso,soloseevidenciaunrezagoestad´ısticamentesignificativocuando k = 5,conlocualseproponeun modeloARIMA(5,0,0)paralaserieblanqueadadeacuerdo alaFASylaFAPestimadapara St .Noobstante,laestimaci´ondelmodelofinalilustradoenlafigura7evidenciaque losefectosautorregresivosde St nosonadecuadosparaconstruirelmodeloconlospar´ametros φ1, φ2, φ3 y φ4 yportanto sonexcluidosalnoobtenercoeficientesestad´ısticamentediferentesdecero.Esdecir,seestimar´ıaunprocesoARIMA concoeficientes {φ5,φ16} diferentesdecerocomo ´ unicoscoeficientes.

Conloselementosanalizadosenlasecci´onanterior,elmodelodefunci´ondetransferenciapropuestoes:

dondelafunci´ondetransferencia υ (B) tienelaespecificaci´on (b

Figura4: Funci´ondeCorrelaci´onCruzadaentre St y Gt

4.3.Estimarelmodelodefunci´ondeTransferencia.

1Lametodolog´ıaBox-Jenkinsesunodelosenfoquescl´asicosparaan´alisisdeSeriesdeTiempo.Paramayordetalle,puedeconsultarse[Wei06] Cap´ıtulo2-10.

Figura5: SalidaR-ModeloARIMA(1,0,0)para(∇ log Gt )

Figura6: An´alisisdeResiduosparamodeloARIMAsobre (∇ log Gt ).

4.3.2.Estimaci´onmodeloARIMAparalavariabledesalida St .

ElmejormodeloobtenidosepresentaaenlaFigura7de dondesepuedeconcluirqueent´erminosgenerales,elmodelo seajustaadecuadamentealaserieoriginalhastaantesdeocurrireldr´asticodescensodelvalordelpreciodelaSoyaentre junioyjuliode2018.Luegodeeseperiodo,seevidenciaun dr´asticocambiodenivelquenoesrecuperadoporelmodeloa pesardequelam´ımicadelaseriepronosticadasobrelaserie originalsemantienehastamayo2019.

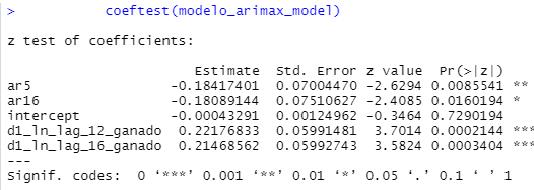
Ent´erminosdeconsistenciaestad´ıstica,losefectosautocorrelacionadosde St sobresimismasonestad´ısticamentesignificativos,cuyamagnitudysignosonconsistentesconlos evidenciadosenlasFASyFACP,tantoparaelrezagoautoregresivode St en k = 5comoparalosrezagosenlavariable regresora Gt 12 yGt 16.Estaafirmaci´onsebasaenlamedidaenquelaprobabilidaddesignificanciaestad´ısticadecada estimadoresmenoral0.016(verFigura8).

Encuantoelcomportamientodelaserieasociadaalos erroresdelmodelo ηt ,seevidenciaporan´alisisgr´aficoquedichovectordeerroressatisfacelacondici´ondeestacionariedad ent´erminosdemediayvarianza.Asuvez,lapruebaLjungBoxasociadaano-autocorrelaci´onenloserroresbrind´oresultadossatisfactorios.Estapruebavalidalahip´otesisnulaque loserroresnoevidencianprocesosautorregresivosdeorden k ([fSTN]).Laecuaci´onparaestimarelestad´ısticodeprueba es:

modeloARIMAestimadoenelmodelo5;enelcasodeles m = 19 3 0.

4.5.Verificarlaconsistenciadelmodeloenlas muestrasdevalidaci´onycomprobaci´on.

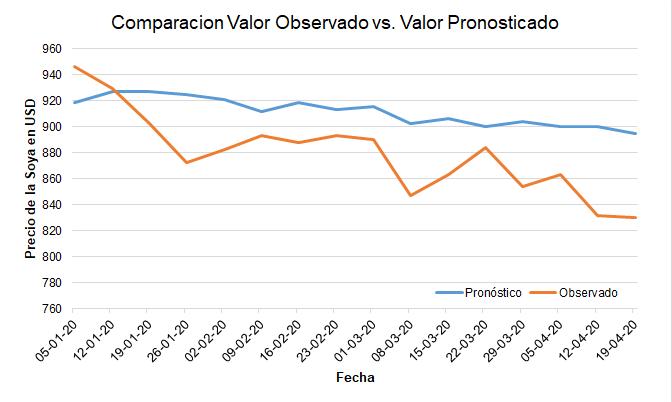
Alcompararlaserie St realcontrasupron´ostico( ˆ St )enla muestradevalidaci´on (T = 16),seevidenciaqueelpron´osticoesconsistentealidentificarlatendenciadecrecientedela serieoriginal(VerFigura9).Noobstante,seobservaqueel nivelovalorenelpron´osticoesm´asaltoencomparaci´oncon elvalorrealobservado,evidenciandoundesfaseent´erminos deniveldelaserie.

Paraelperiododecomprobaci´oncontemplado,seajustaun MFTbajolaespecificaci´onfuncionaldefinidaen5,dondelos resultadosnosonsatisfactorios,enlamedidaquelosestimadoresnoalcanzanasuperarelniveldesignificancianecesaria paraserestad´ısticamentedistintosdecero.

Unaposiblecausaqueexplicalap´erdidadeconsistenciade losestimadorespuedeserconstruirelmodeloincorporandoel efectodelcambioabruptodenivelentrejunioyjulio2018.

donde T eseltama˜nodemuestradelaseriedetiempo,

k eslacorrelaci´ondeloserroresy m eln´umeroderezagos aserprobados.Esteestad´ısticodepruebasecomparacontra unvalorcr´ıticoasociadoaunadistribuci´ondeprobabilidad Chi-cuadradocon h gradosdelibertad,elcualseobtienede operararitm´eticamentelospar´ametrosdelmodeloARIMAde laforma h = m p q,donde p y q sonlospar´ametrosdel

5.Conclusiones.

Conlaaplicaci´onhechadeunMFTsobreelfen´omeno econ ´ omicoabordadoenesteart´ıculo,podemoshacernosuna ideaqueestetipodemodelosesunaherramientamuyadecuadaparamodelarefectoscausales.Comolosprincipalesbene-

Figura7: ModelodeFunci´ondetransferenciapara St enfunci´onde St (∇ log St )= υ (B)∇ log Gt )+ ηt

4.4.Evaluarresultadosdelmodelo.

Figura8: Valor-pparacoeficientesMFT

Figura9: Predicci´ondelmodeloparah=16

ficiosobtenidosdeesteejercicio,seobtienequeloscoeficientesdelmodeloevidencianconsistenciaconlainterpretaci´on econ ´ omica,yasuvez,dichasestimacionesdelamagnitud, sentidosonestad´ısticamentesignificativas.Igualmente,laextrapolaci´ondelmodeloamuestrasdevalidaci´onycomprobaci´oncapturalatendenciademaneraaceptable,locualbrinda unvaloragregadoalmomentodegeneraran´alisisproyectivos sobreelcomportamientodelasvariablesylosfen´omenos.

Noobstante,seobservanciertasdesventajasenelempleo deestat´ecnica:porunlado,losestimadoressonsensiblesa perdersignificanciaestad´ısticaalreestimarelmodeloenla muestradecomprobaci´on.Adicionalmente,elmodelonocapturadeformaend´ogenacambiosabruptosdenivel,conlocual requiereajustestalescomolamodelaci´ondeintervenciones sobrelaseriedetiempo,aumentandoeln´umerodepar´ametrosdelmodelo.

Enconclusi´on,losMFTsonunesquemademodelamientoestad´ısticoquecuentaconm´aselementosafavorparaser utilizado,loscualestienenm´asrelevanciaquelosriesgoso sensibilidaddeinconsistenciadelaestimaci´onporcambios abruptosenlasseriesanalizadas.

Referencias.

[Abr85] BovasAbraham, Seasonaltimeseriesandtransferfunctionmodeling,JournalofBusinessandEconomicStatistics 3 (1985),no.4, 156.

[Ahm15] M.I.Ahmad, Ctransferfunctionmodelsforforecastingdomestic wateruse,JournalofSocialandDevelopmentSciences 6 (2015), no.2,52–56. https://pdfs.semanticscholar.org/996d/ 714395397dc0e9bd32c188b83c2ea7fbc01a.pdf

[Dı14] JoseManuelGuevaraDıaz, Usocorrectodelacorrelaci´oncruzadaenclimatologıa:elcasodelapresionatmosfericaentretaitı ydarwin,2014. ve.scielo.org/scielo.php?script=sci_ arttext&pid=S1012-70892014000100005

[EC08] JorgeMart´ınezElkinCastano, Usodelafunci´ondecorrelaci´on cruzadaenlaidentificaci´ondemodelosarma,RevistaColombianadeEstadıstica(2008),293a310. https://repositorio. unal.edu.co/handle/unal/40707

[ECoS22] PennStateUniversityEberlyCollegeofScience, 9.1prewhiteningasanaidtointerpretingthecc,2022.URL: https://online.stat.psu.edu/stat510/lesson/9/9.1.

[Edi22] BloombergUSEdition, Bcomsy:indbloombergsoybeanssubindex,2022. https://www.bloomberg.com/quote/BCOMSY: IND

[fSTN] NationalInstituteforStandardsandDepartamentodelComerciodelosEstadosUnidosdeAm´ericaTechnologyNIST, Box-ljungtest.URL: https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4481.htm.

[inv22] investing.com, Commoditieshistoricaldata,2022.us-soybeanmeal-historical-data,feed-cattle.

[LeB18] BlakeLeBaron, Armaxmodels-econ/fin250a:Forecastinginfinanceandeconomics,BrandeisUniversity,Massachusetts,2018. www.people.brandeis.edu/ blebaron/ classes/fin250a/regression/armax.html

[oS22] AustralianBureauofStatistics, Timeseriesanalysis:Thebasics, 2022. https://www.abs.gov.au/websitedbs/d3310114. nsf/home/time+series+analysis:+the+basics

[Sof99] StatisticalAnalysisSoftware, Notationforarimamodels,1999. https://www.sfu.ca/sasdoc/sashtml/ets/chap30/ sect13.htm

Acercadelautor:C´esarAugustoesestudiantedenoveno semestredeMatem´aticas.Igualmente,cuentaconunpregradoenEconom´ıayunaEspecializaci´onenEstad´ıstica.Enla actualidadsededicaalaconsultor´ıadem´etodoscuantitativos paraelsectordeinteligenciaestrat´egica.Ensutiempolibre, aprendealem´andeformaautodidactayesunpromotorincansabledelbuenusodelespanol.Acriteriodesushijos,esun carinosoydivertidoviejochochodecr´epito.

[Wei06] WilliamW.S.Wei, Timeseriesanalysis.univariateandmultivariatemethods,PearsonEducation,2006.

REPRESENTACI ´ ONGR ´ AFICAYALGEBRAICADELASECUACIONES

LINEALESYSUSPROPIEDADESENEL SistemaSeno

WalterGarz´onGuti´errez * walter.garzon01@usa.edu.co

1.Resumen.

Esteart´ıculomuestralosresultadosdeunestudio1 enfocadoenelcambioderepresentacionesdealgunosobjetos geom ´ etricos,vistoscomolasoluci´onaunaecuaci´onlineal comounconjuntodepuntosquecumplenunacondici´onmeramentegeom´etrica.Estoselograapartirdeunamaneradiferentedeubicarlospuntossobreunplanoenunosejescoordenadosdiferentesalcartesiano,enloscualesserepresentan gr ´ aficamentelasrectas(objetosgeom´etricos).Seestudianlas diferentesdefinicionesypropiedadesquecumplenestosobjetosenelsistemacoordenadocartesianoysemuestrasise cumplenonoenelnuevosistemadeubicaci´ondepuntos.

2.Introducci´on.

Endiferentescursosdec´alculoygeometr´ıasesuelerepresentarelconjuntodepuntossoluci´onaecuacionesdeprimer ysegundogradoenelplanocartesianodandounaideadesu representaci´on;porejemplo,siesunadeprimergrado,su gr ´ aficaesunal´ınearectaysiesunadesegundogrado,esuna c ´ onica.Enalgunosdeestoscursosseprofundizaunpocoen otrossistemascoordenadoscomoelpolar2,oblicuo3 oPAR4 EnlaFigura1semuestraquelarepresentaci´onvar´ıadependiendoelsistemaqueseest´eusandoparaconstruirlagr´afica. Estudiarlaspropiedadesdelosobjetosgeom´etricosendichos sistemasderepresentaci´onpuedellevaragrandeshallazgos muy ´ utilesparasolucionardiferentesproblemasqueenelsistemacartesianoavecessetornancomplicados,porejemplo, elcambiodecoordenadasalsistemapolarpuedeayudara determinarsolucionesaecuacionesdiferencialesointegrales

*Estudiantedelamaestr´ıaenmatem´aticasaplicadasdelaUniversidad Sergio ´ Arboleda.

1Tomadode[Gar19]

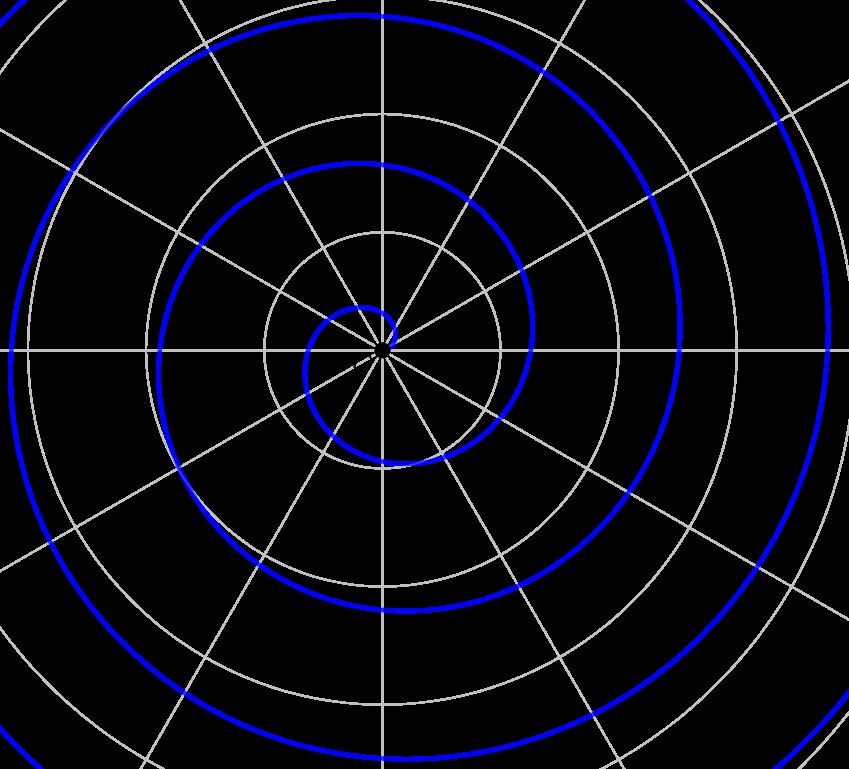
2Paraubicarunpuntoenelsistemapolarsetomaunalongitud r yun

´ angulo θ ,seubicaunvectordetalmaneraquetengalongitud r yformeel ´ angulo θ conlahorizontalylacabezadelvectorser´alaimagendelpunto [Leh89].

3Elsistemaoblicuoest´acompuestopordosrectasqueformanun ´ angulo α = 90.Paraubicarunpuntosetomandospuntos,cadaunosobreuneje,y setrazaunarectaperpendicularporcadapuntoalejeenelcualseencuentre elpunto,luegoelpuntodeintersecci´onentrelasdosrectasser´alaimagendel punto[MC11].

4ElsistemaPARest´acompuestopordosrectasparalelaslascualesrepresentanlosejes x y y.Paraubicarunpuntoseubicandospuntos,cadaunoen diferenteeje,ysetrazaunarectaquecontengaalosdospuntos.Estarecta ser ´ alaimagendelpunto[OP12].

demaneram´assencilla,comotambi´entienediferentes aplicacionesenbiolog´ıa,astronom´ıa,entreotras;elsistema PARpodr´ıatenerdiferentesaplicacionesenecuaciones diferenciales,puesunaecuaci´onlinealserepresentaconun puntoyestofacilitar´ıadiferentesc´alculosotransformaciones.

Conbaseenloanterior,elinter´esdeesteart´ıculoesestudiarlasrepresentacionesalgebraicasygeom´etricasenun sistemacoordenadodiferentealcartesiano(rectangular)que sedenomina SistemaSeno siguiendoundesarrolloparaleloal planteadoen[Leh89],elcualser´apresentadom´asadelantede maneraformal.Pensandoenlacomodidadycuriosidaddel lector,sehanpublicadoappletsdesarrolladosenGeoGebra, enloscualessepuedeexplorarycorroborardiferentesresultados.Loslinksestar´analfinaldecadasecci´onosubsecci´on.

3. SistemaSeno.

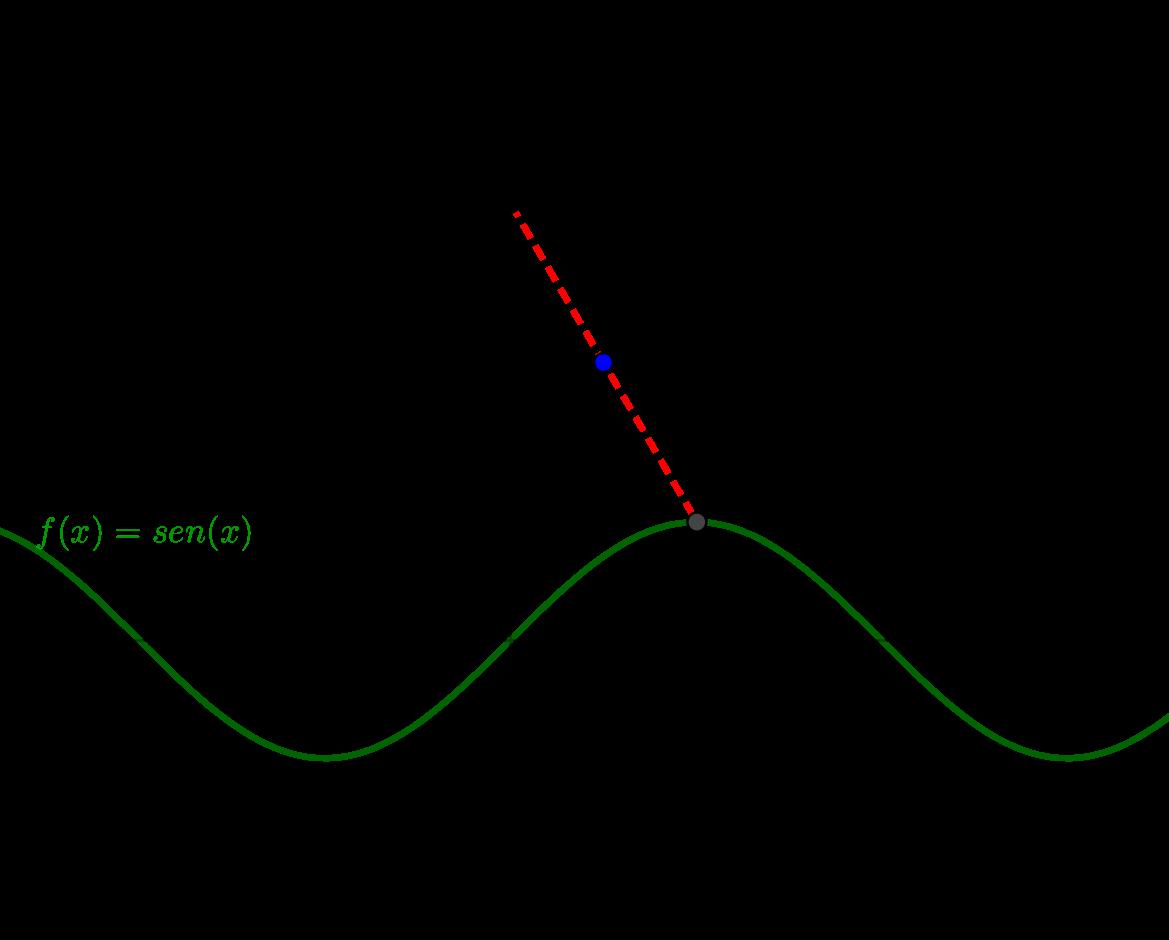
Estesistemaest´aconformadoporeleje y delsistemacartesianoylagr´aficadelafunci´on f (x)= sen(x) comoapoyopara

(a) SistemaPolar.

(b) SistemaOblicuo.

(c) SistemaPAR.

Figura1: Representaci´onde2x y = 0endiferentessistemas coordenados.

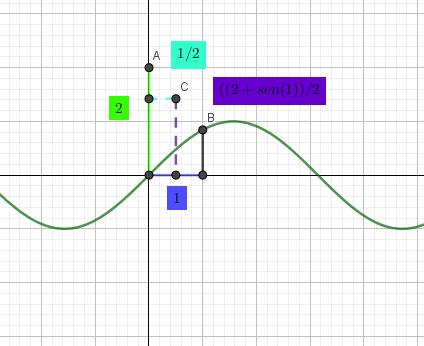
ubicarlospuntos.Paraubicarunpunto (x0, y0) sobreel SistemaSeno,setomaelpunto (x0, 0) enelsistemausual,setraza unaperpendicularporestepuntoaleje x ylaintersecci´onentrelaperpendicularylacurvadelafunci´on f (x)= sen(x) es elpunto A,luego,seubicaelpunto B concoordenadas (0, y0) enelsistemausual.Por ´ ultimo,seubicaelpuntomedio C entrelospuntos A y B yesteeslarepresentaci´onde (x0, y0) en el SistemaSeno.(v´easeFigura23).

Demostraci´onquefesinyectiva:Sean x, y, z, w en R, (x, y) y (z, w) en A y f (x, y)= f (z, w).Como f esunafunci´onbien definidasepuededecirque f (x, y)= P y f (z, w)= Q con P y Q puntosen α ,luego,existen A y B puntosdereferenciatal que A estasobrelacurvadelafunci´onsenoy B sobrelarecta verticaly P espuntomedioentre A y B,portransitividadse tieneque Q tambi´enespuntomediode A y B,portanto,las coordenadasde Q son (x, y).Porlaunicidadde A y B setiene que x = z y y = w,esdecirque (x, y)=(z, w) y Q = P,luego, es ´ unicoyenconclusi´on, f esinyectiva.

Demostraci´onquefessobreyectiva:Seaunpunto P en α . Comoel SistemaSeno estasobreelsistemacartesiano,el punto P tendr´acoordenadas (m, n) enelsistemacartesiano, luego,enel SistemaSeno elpunto P tienecoordenadas (2m, 2n sen(2m));comocadapuntosobreelplanotiene unacoordenadaenelplanocartesiano,entonces,tieneuna coordenadaenel SistemaSeno,porende,acadapunto P se lepuedeasignarunacoordenada (x, y) enel SistemaSeno oloqueesequivalente P = f (x, y),enconclusi´on, f es sobreyectiva.

Quedademostradoque f esunafunci´onbiyectivade A en α ypordefinici´onel SistemaSeno esunsistema coordenado.

Paradiferenciarlosejescoordenadosdelsistemacartesianoylosejesdel SistemaSeno sepondr´aunal´ıneasobre elnombredeleje,esdecir,losejes x y y ser ´ anlosejes coordenadosenel SistemaSeno yparalospuntosseusar´ala notaci´on (x0, y0)S.

Antesdeentraraestudiarlosdiferentesobjetosgeom´etricosenestesistema,sedemostrar´aqueel SistemaSeno efectivamenteesunsistemacoordenado.Paraelloseenunciala siguientedefinici´on:

Unconjuntodeparejasordenadas A esunsistemacoordenadoenunplano α siys´olosiexisteunafunci´on f biyectivade A en α .

Unafunci´onesbiyectivasiys´olosiesinyectivaysobreyectiva,esdecir,cumpleque:

Paratodo x, y, z, w en R,si f (x, y)= f (z, w) entonces (x, y)=(z, w)

Seaunpunto P en α entoncesexisten x, y en R talque P = f (x, y)

Porultimo,sedefinir´alafunci´on f como:

f : A −→ α , (x, y) −→ P

Seaelpunto S concoordenadas (x0, y0)S,sepuedeafirmar que S es ´ unico,yaqueporlamaneradeubicarlospuntosen el SistemaSeno,paratodo x y y en R existenpuntos ´ unicos Q y R dereferenciasobrelacurvadelafunci´onsenoysobre larectaverticalrespectivamente,ypordefinici´ondepunto medio, S es ´ unico.

3.1.EjesySemiejes.

Enestasecci´onsedefinenlosejesenel SistemaSeno,para ello,setienenencuentalassiguientesdefiniciones:

Eleje x eselconjuntodepuntostalesquesucoordenada esdelaforma (x, 0)

Eleje y eselconjuntodepuntostalesquesucoordenada esdelaforma (0, y).

Elsistemacartesianotienelaparticularidadquelarectaverticalqueseutilizaparaubicarlospuntoscoincideconeleje y ylarectahorizontalcoincideconeleje x,pero,enestesistemalarectaverticalcoincideconeleje y,aunas ´ ı,noocurrelo mismoconeleje x,m ´ asadelantesemostrar´aelporqu´edeesto.Porahora,sedefinelarectaverticalcomo Semieje y (que tambi´eneseleje y) ylacurvaSenocomo Semieje x.Enlas Figuras3y4semuestranlosejesylossemiejes.

Figura2: SistemaSeno.

Figura3: Semiejesdel SistemaSeno.

3.2.Cambiodecoordenadasentreel Sistema Seno yelsistemacartesiano.

Paracaracterizarelcambiodecoordenadasdel Sistema Seno alsistemacartesianosediceque:

∗ Dadounpunto (x, y)S enel SistemaSeno suscoordenadasenelsistemacartesianoser´an x 2 , y + sen(x) 2 C

∗ Dadounpunto (x, y)C enelsistemacartesianosuscoordenadasenel SistemaSeno ser ´ an (2x, 2y sen(2x))S.

Ejemplo3.1. Seubicar´aelpuntoCconcoordenadas (1, 2)S: UsandoelprimercambiodecoordenadassereemplazayC tendr´acoordenadas 1 2 , 2 + sen(1) 2 C .EnlaFigura5seobservaelpuntoCconlascoordenadasenelsistemacartesiano;paraelejexelcolorazulclaroyparaelejeycolor morado.YenelSistemaSeno;paraelsemieje xelcolorazul yparaelsemieje yelcolorverde.

4.Solucionesaecuacioneslinealesen el SistemaSeno.

Enestasecci´onsehaceundesarrolloparaleloalquehace Lehmannen[Leh89]enloscap´ıtulos1,2y3enloscuales estudiatodolorelacionadoalasrectasdesdesurepresentaci´ongr´aficayalgebraica,adem´as,demostrardefinicionesy propiedadescomocortesentrerectas,pendiente, ´ angulosy teoremasquecumplenall´ı.

4.1.Gr´aficadelaecuaci´on ax + by + c = 0 ycortesconlosejes.

Enloquesiguesepresentanlasrepresentacionesgr´aficas enel SistemaSeno delosconjuntossoluci´onalasecuaciones delaforma ax + by + c = 0cuandovar´ıanlasconstantes a, b y c.Serealizaapartirdecasosenloscualesseleasignan valoresalasconstantes a, b, c yseconstruyenalgunasgr´aficas delosconjuntossoluci´onloscualestienenelnombrede srectas.Paralelamenteseestudianloscortesconlosejes x y y yseconcluyeunaf´ormulaconlacualsepuedeencontrarel cortedecualquier s-rectaconlosejesusandoloscoeficientes a, b y c

Ejemplo4.1. Sia, b, c = 0:Enestecasosetienelaecuaci´on 0x + 0y + 0 = 0 ylospuntosquelasatisfacensontodoslos posiblespuntos (x, y)S conx, y ∈ R,esdecir,todoslospuntos delplano.

Ejemplo4.2. Sia, b = 0 yc = 0:D´andoleacvaloresdiferentesde 0 seconcluyequeparacualquieradeestos,enla ecuaci´onseencuentraunaincoherenciayaquequedadela formac = 0 ysecontradiceconlahip´otesis.

Ejemplo4.3. Sib = 0 ya, c = 0:Enestecasosetieneque las-rectaobtenidaporlaecuaci´onax + c = 0 notienecortes coneleje yocoincideentodossuspuntosconeleje y,el corteconeleje xsedaenelpunto ( c a , 0)S oenelsistema rectangular ( c 2a , 0)C .EnlaFigura6seilustralasoluci´on deestaecuaci´on.

Nota:Tengaencuentaquelamaneradeubicarlospuntos enelsemieje x noverificaqueladistanciade (0, 0)S a (a, 0)S sea a enel SistemaSeno

1◦ Caso:Si a = 0, b = 0 y c ∈ R. Elconjuntosoluci´ondelaecuaci´on y = 0(eje x),tomandoa

Figura4: Ejesdel SistemaSeno.

Figura6: Representaci´onalconjuntosoluci´onde ax + c = 0.

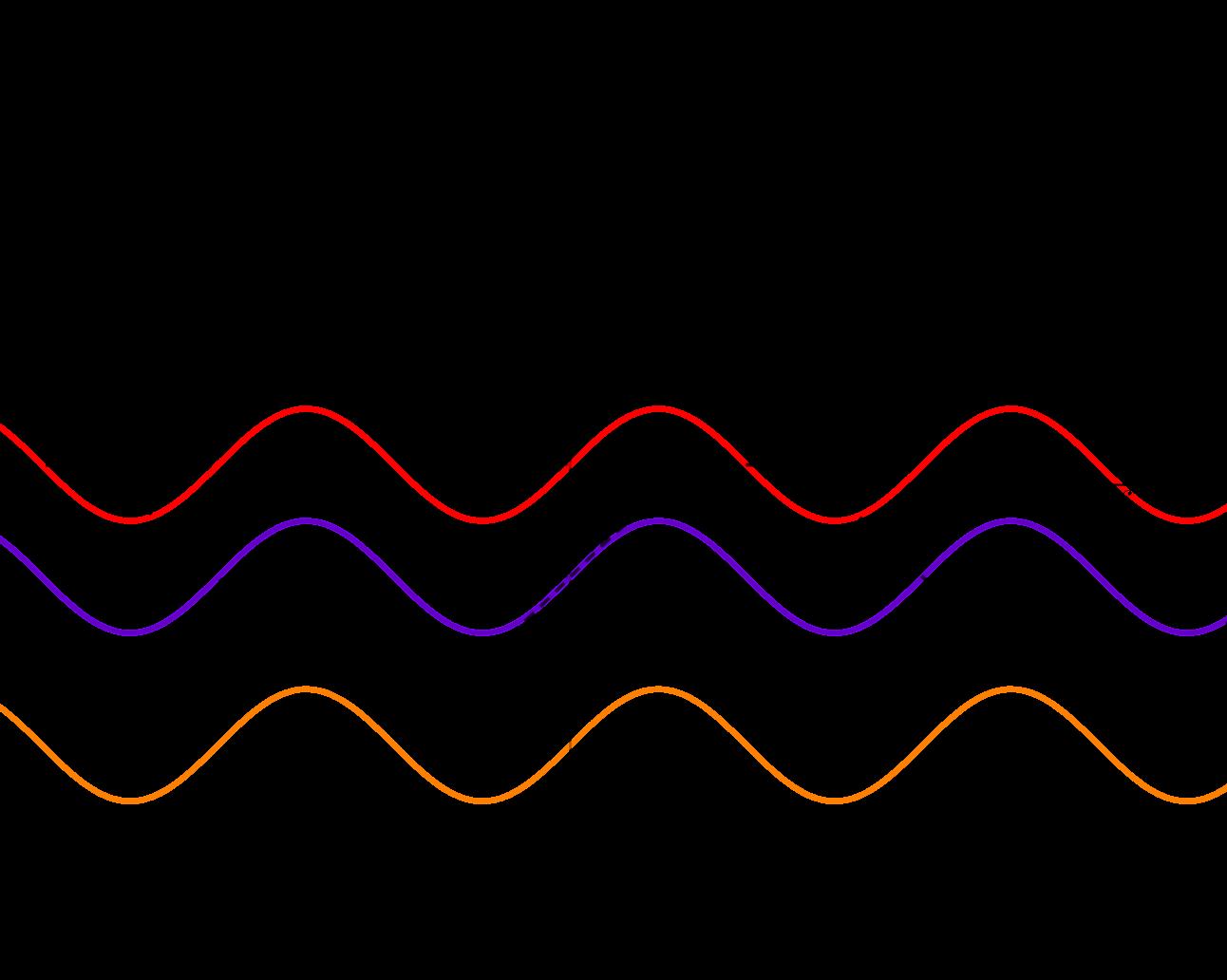
c = 0,sepuederepresentarenel SistemaSeno comoelconjuntodepuntosquecaenenlacurvamorada.Si c = 2el conjuntodepuntossoluci´onalaecuaci´on y 2 = 0serepresentanenlacurvaroja,ysi c = 3entonceslarepresentaci´on gr ´ aficade y + 3 = 0enel SistemaSeno seveenlacurvanaranja.Estasgr´aficassepresentanenFigura7.

ecuaci´ondelaforma ax + by = 0sucorteconeleje y ycon eleje x esenelpunto (0, 0)S.

3◦ Caso:Si a = 0, b = 0 y c = 0. Seiniciaconlosvalores a = 1, b = 2y c = 4,esdecir,la ecuaci´on x + 2y + 4 = 0.Sucorteconeleje y esenelpunto (0, 2)S yconeleje x esen ( 4, 0)S.Enelsistemacartesianosonlospuntos (0, 1)C y ( 2, 0,38)C .Larepresentaci´ongr´aficadelconjuntosoluci´onsemuestraenlaFigura9.

Figura7: Ejemplode s-rectas1◦ Caso.

Siseobservadetenidamenteloscortesconeleje y delas gr ´ aficasquesepresentanen7,setienequeelcortedela s-recta y = 0esenelpunto (0, 0)S,eldela s-recta y 2 = 0es en (0, 2)S yeldela s-recta y + 3 = 0esen (0, 3)S.Haciendo elrespectivocambiodecoordenadassediceque y = 0enel sistemacartesianotienecorteenelpunto 0 2 , 0 + sen(0) 2 C , resolviendo, (0, 0)C ;realizandoelmismoprocedimientocon losdem´aspuntos,las s-rectas y 2 = 0y y + 3 = 0tienen corteen (0, 1)C yen (0, 1,5)C respectivamente. Engeneral,sepuededecirquesisetieneunaecuaci´onde laforma by + c = 0sucorteconeleje y esen 0, c b S y ningunasecortaconeleje x,exceptuandolasquesondela forma by = 0quecoincideentodossuspuntos.Tambi´en,se puedeverquelas s-rectassemuevenhorizontalmente c b unidades.Si c b > 0entonceslagr´aficasetrasladahacia arribaseg´uneleje y,si c b < 0setrasladahaciaabajo.

2◦ Caso:Si a = 0, b = 0 y c = 0.

Sisetomaa a = 1y b = 1setienelaecuaci´on x + y = 0y elcortecon y yeleje x dela s-rectaesen (0, 0)S.(verFigura 8)

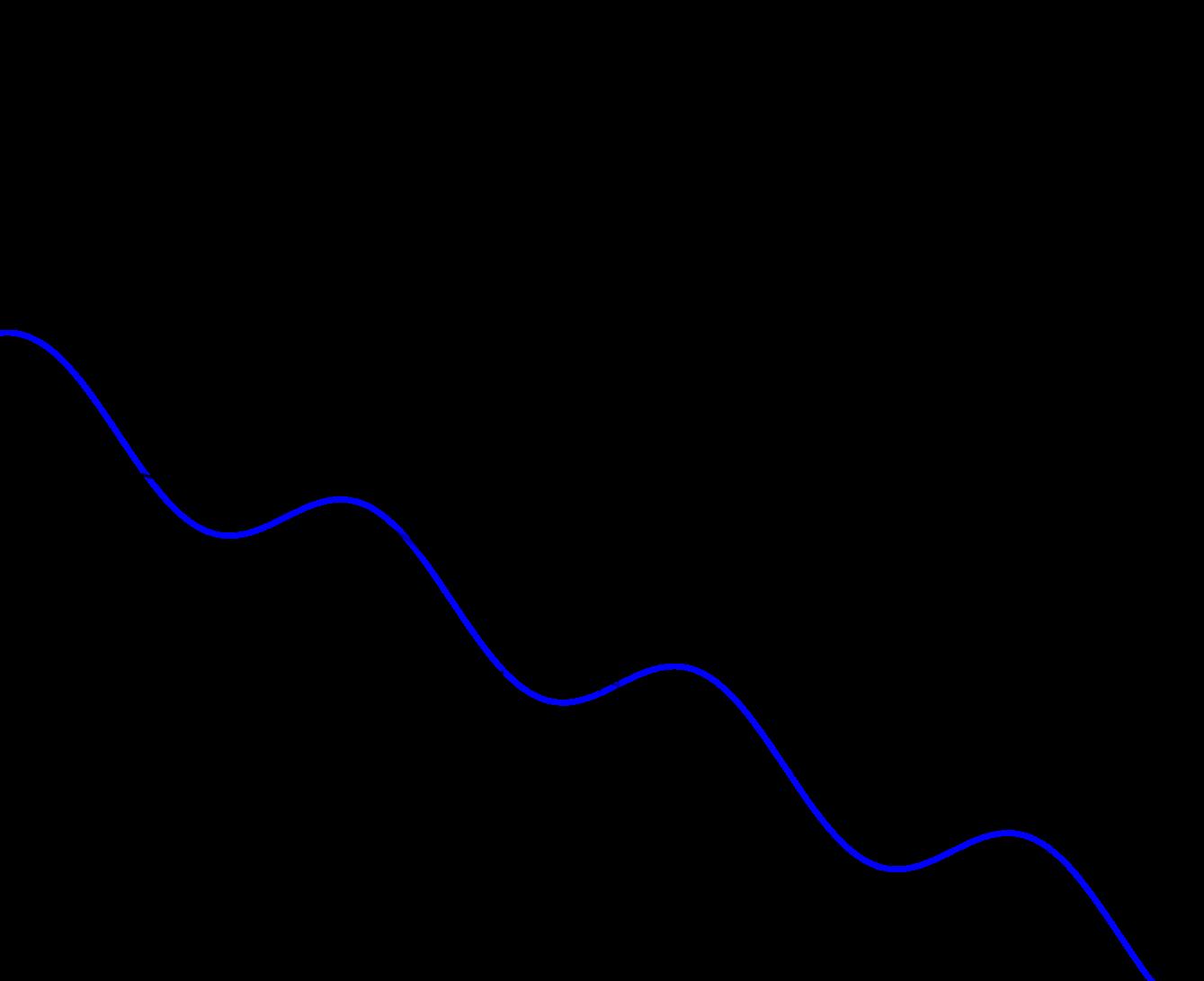
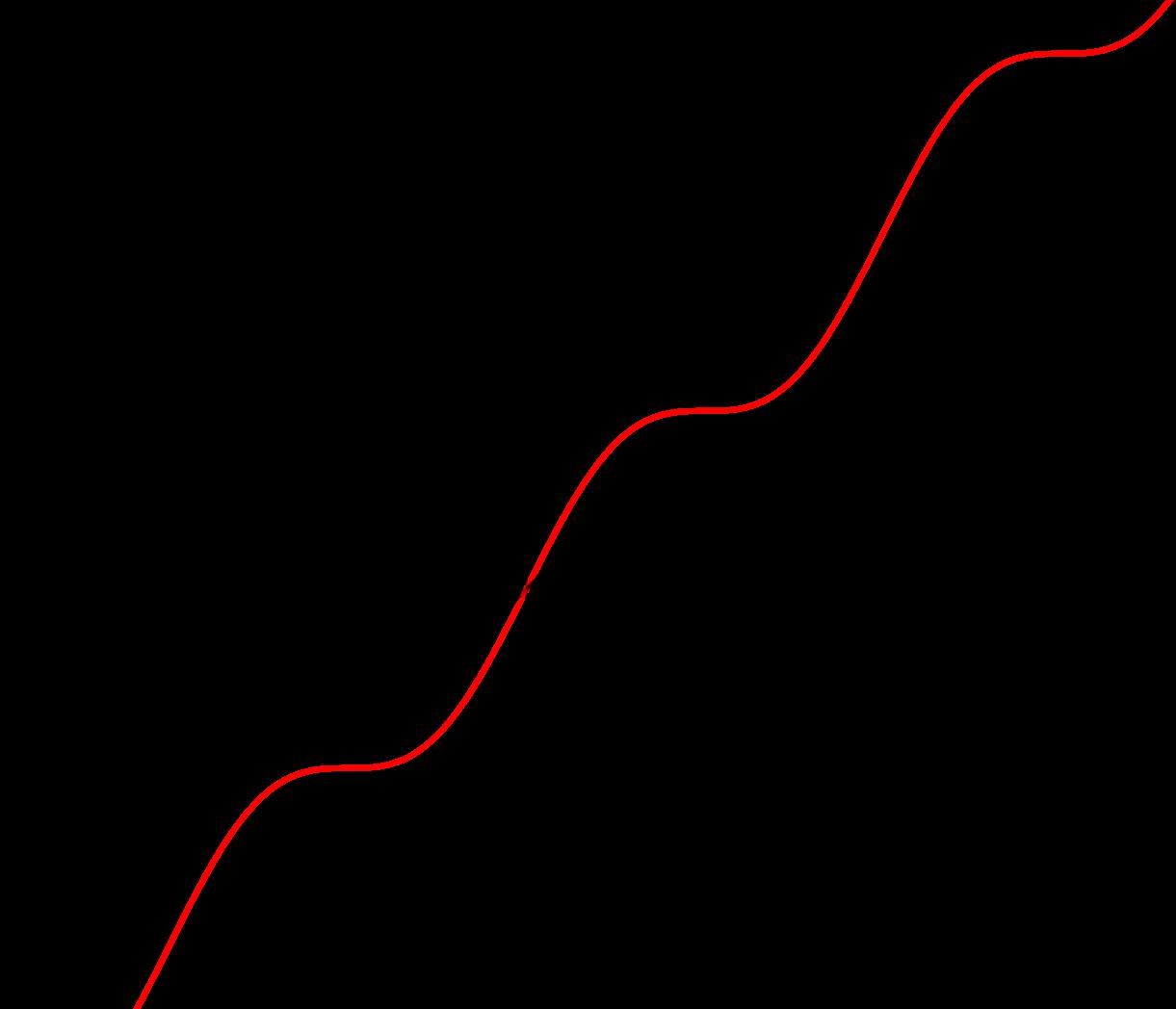
Sisetieneunaecuaci´on ax + by + c = 0enel SistemaSeno con a, b, c ∈ R elcorteconeleje y esenelpunto 0, c b S y coneleje x esen 0, c a S

Deestasecci´onseconcluyequealtenerlaecuaci´on ax + by + c = 0,laintersecci´ondelagr´aficaconeleje y se puedeencontrartomandoa x = 0ydespejandoa y,demanera an ´ alogaseencuentralaintersecci´onconeleje x.Sepudieron observarlastransformacionesquetienenlas s-rectasseg´un loscoeficientesdelaecuaci´onlinealenel SistemaSeno.En estasecci´onsoloseanalizaronloscortesconlosejes x y y pero,siobservanuevamente,puedenotarqueloscortescon elsemieje y coincidensiempreconlosdeleje y pero,en algunoscasoshaym´asdeuncorteconelsemieje x,estose analizar´aenlasiguientesubsecci´onyseexplicar´aporqu´ese cortaenvariospuntos.

Appletecuaci´onlineal: https://www.geogebra.org/m/jggssewy

4.2.Cortesconlossemiejes.

Sededicaestasecci´onalestudiodeloscortesconlos semiejes,enfoc´andoseparticularmenteenloscortesconel semieje x yaqueloscortesconelsemieje y sonlosmismos cortesconeleje y.Comoseobserv´oenlasecci´on4.1 loscortesconelsemieje x puedenservariosdependiendo dela s-rectaquesetome.Enestecasonoseencontraron solucionesgenerales,pero,seencontraronaproximacionesa lassolucionesutilizandom´etodosnum´ericos.

Demanerageneral,sepuededecirquesisetieneuna

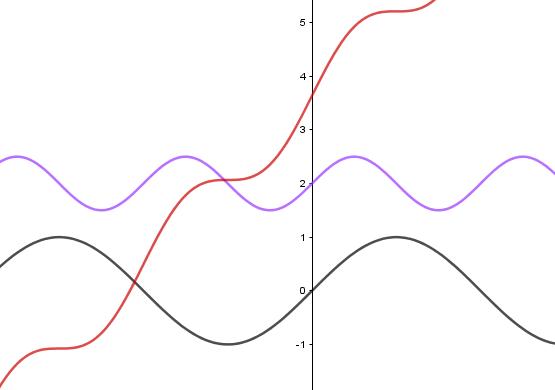
Parajustificaresteprocesote´oricamente,loprimeroque setieneencuentaesqueenel SistemaSeno elsemieje x

Figura8: Gr´aficade x + y = 0.

Figura9: Gr´aficade x + 2y + 4 = 0.

noesuna s-recta,esdecir,suformaalgebraicanosepuede escribircomo ax + by + c = 0,portanto,primeroseencuentra larepresentaci´onalgebraicadelsemieje x. Pordefinici´on,elsemieje x enelsistemarectangulares lafunci´onsenoquealgebraicamentesepresentacomo f (x)= sen(x),luego,lospuntosquepertenecenaesta funci´onser´andelaforma (x, sen(x))C .Usandoelcambiode coordenadasquesepresent´oenlasecci´on3.2,estospuntos enel SistemaSeno sondelaforma:

(x, sen(x))C =⇒ (2x, 2sen(x) sen(2x))S, luego,enel SistemaSeno eleje x tienecomoecuaci´on

y 2sen(x/2)+ sen(x)= 0

Ahora,comosequiereencontrarlasinterseccionesentreel semieje x yuna s-rectacualquierasedespeja y delaecuaci´on linealydelaecuaci´ondelsemieje x,seigualanyseobtiene lasiguienteecuaci´on:

ax + 2bsen(x/2) bsen(x)+ c = 0

Por ´ ultimo,secreaunconjuntoenelcualest´enlassoluciones alaecuaci´onyestasser´anlascoordenadasde x paralos cualeseleje x yla s-rectaseencuentren.

Secomprob´oquesi b = 0,suintersecci´ones ´ unicaen c a S.Amaneradeexploraci´onsepuedemostrarquesi

a = 0lospuntosdeintersecci´onsonfinitosy,adem´as,son unn ´ umeroimpardeintersecciones.Si a = 0,existeninfinitas interseccionessiaproximadamente 2,63 < c b < 2,63;ahora siaproximadamente c b < 2,63o c b > 2,63noexisteintersecci´onentrela s-rectayelsemieje x.

4.3.Pendientedeuna s-recta.

Sedefinelapendientedeuna s-recta t cuyaecuaci´ones

ax + by + c = 0comoelcocienteentre a y b ysedenotacon laletra m

m = a b . (1)

Lapendientetienelapropiedaddedescribirelmovimiento dedospuntosquepertenezcanalconjuntosoluci´ondela ecuaci´ondealguna s-recta,paraserm´asespec´ıficos,si lapendientees a b entonceslospuntosdela s-rectase mover ´ an b s-unidades hacialaderecha(enelsemieje x) y a s-unidades haciaarribaohaciaabajoenelsemieje y dependiendodelsignode a b ;siespositivo“sube”,sies negativo“baja”.

Nota: F´ıjesequeapareceelt´ermino s-unidad elcual eslaunidadenel SistemaSeno.Sediferenciadelasunidadesenelsistemarectangular,yaqueestanoserefiere aladistanciaentrelospuntos,sinoalcambiodecoordenadas.

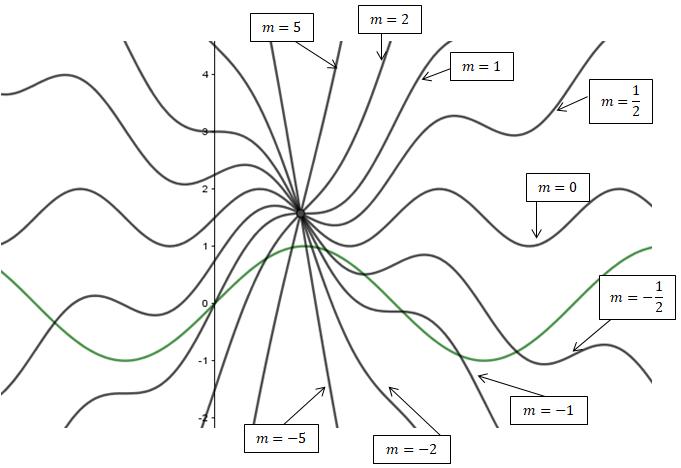
EnlaFigura10seobservanvarias s-rectascondiferentes pendientesyseevidenciaqueporunpuntocualquieraenel

SistemaSeno pasaninfinitas s-rectas,estosedebeaquepara cadan´umeroenelconjuntodelosn´umerosreales,sepuede construiruna s-rectaconestapendiente.

Conestet´erminodefinidoseestudianciertosteoremasque secumplenenel SistemaSeno comolosonel TeoremaPuntoPendiente y DosPuntos-Pendiente.

4.4.Cortesentre

Sedefineelcorteentredos s-rectas l y t conecuaciones

respectivamente,comolospuntos (x0, y0)S quepertenecena l y t simult´aneamente.Sedebetenerencuentaqueseest´a tomandola s-rectadesdesudefinici´onalgebraicayloque cambiaessurepresentaci´ongr´afica,portanto,apartirdesus ecuacionessepuedeconstruirunsistemalinealdospordos quesedesarrollausandoladeterminantedeestamatriz:siestatieneuna ´ unicasoluci´onentoncesseintersecanenun ´ unico punto,sinotienesoluci´onnoseintersecanysitieneinfinitas solucionesestasdos s-rectascoincidenentodossuspuntos, estoseilustragr´aficamenteenlasFiguras11,12y13.

Figura10: Hazde s-rectasenel SistemaSeno.

s-rectas.

Figura11: ´ Unicasoluci´on.

Figura12: Nohaysoluci´on.

Figura13: Infinitassoluciones.

4.5. ´ Anguloentre s-rectas.

Paraesteconceptoseestudiarondosformasdedeterminar el ´ anguloentredos s-rectas:elprimeroapartirde l´ıneastangentesauna s-recta yelsegundoapartirde l´ıneasasociadas auna s-recta.Acontinuaci´on,sepresentaladefinici´ondeestasl´ıneasylamanerageneraldeencontrarel ´ anguloentredos s-rectas.

4.5.1.Definici´ondel´ıneatangenteauna s-recta.

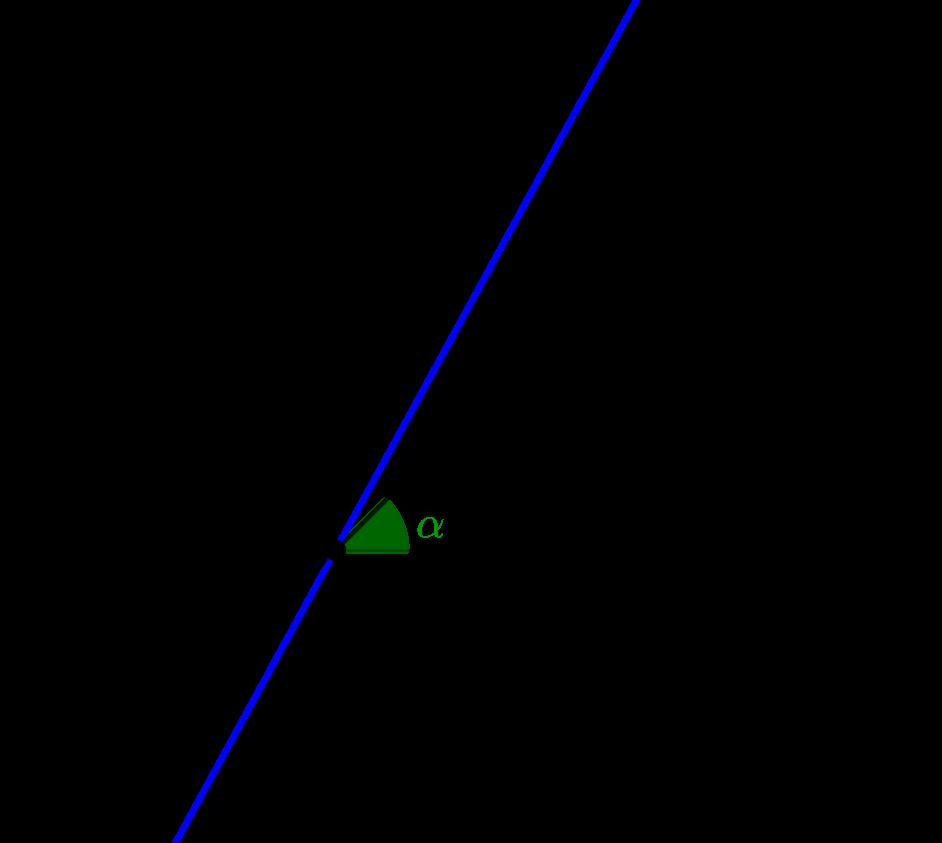
Sea l una s-rectaconecuaci´on ax + by + c = 0yunpunto A concoordenadas (x1, y1)S sobre l,sedenominal´ıneatangente a l por A alconjuntosoluci´ondelaecuaci´on:

a ′ x + b′ y + c ′ + b′ sen(x)= 0, (2)

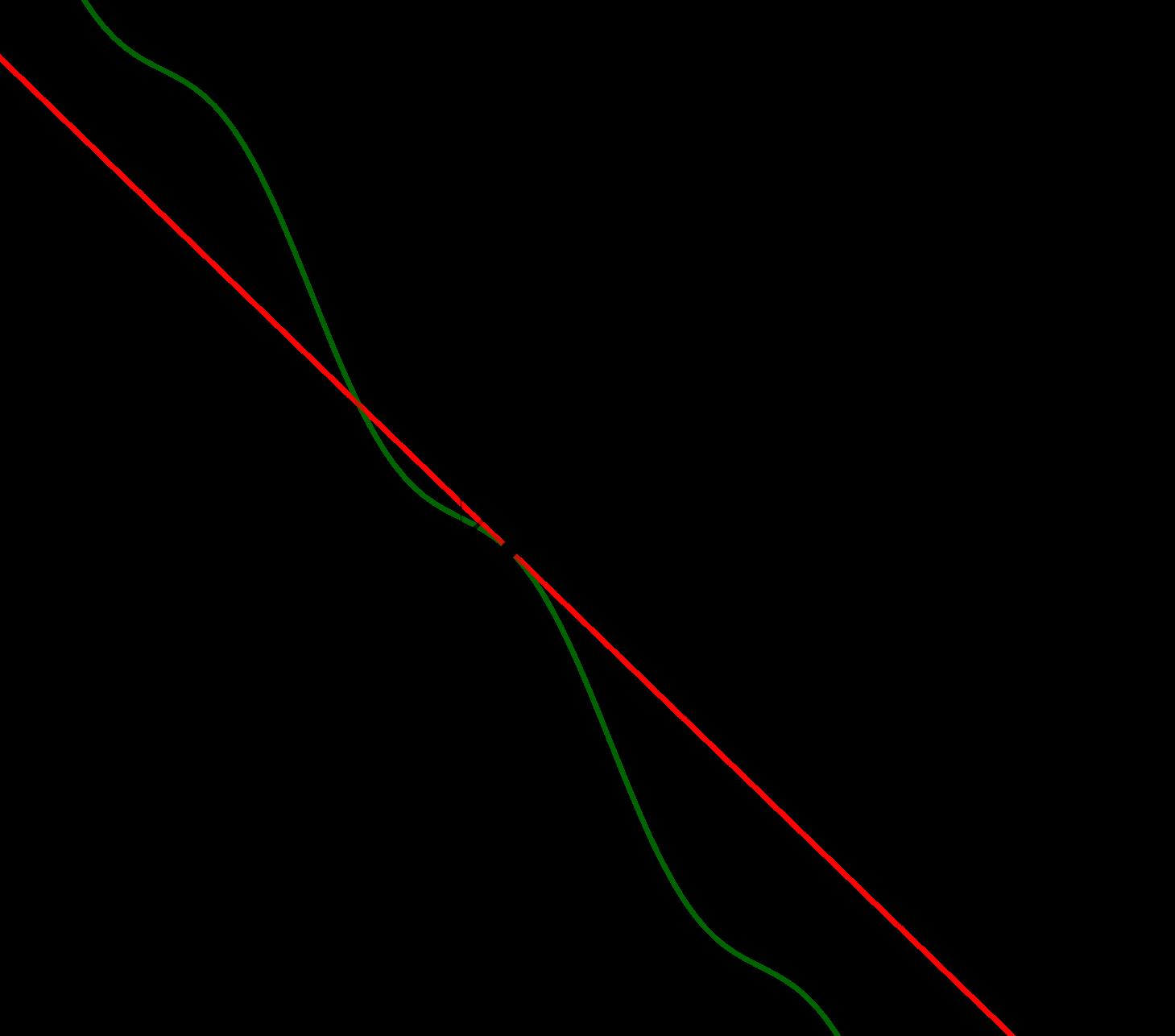
EnlaFigura14semuestralarepresentaci´ongr´aficadelal´ınea tangenteala s-recta l porelpunto (1, 1)S.

donde

a′ = a bcos(x1), b′ = b y

c′ = ax1 + bx1cos(x1) by1 bsen(x1)

Ejemplo4.4. Encuentrelal´ıneatangentealas-rectalcon ecuaci´on 3x + 2y 1 = 0 enelpunto (1, 1)S

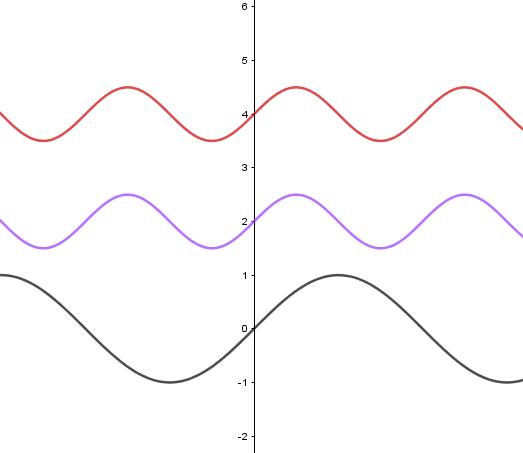
Soluci´on:Identificandoaloscoeficientes a = 3, b = 2, c = 1, x1 = 1y y1 = 1yreemplazandoen(2)setienequelos coeficientesdelaecuaci´ondel´ıneatangenteson:

a ′ = 3 2cos(1), b′ = 2, c ′ = 1 + 2cos(1) 2sen(1)

Luego,laecuaci´ondelal´ıneatangenteaesta s-rectaporel punto (1, 1)S ser ´ adelaforma:

y = 2cos(1) 3 2 x + 1 2cos(1)+ 2sen(1) 2 sen(x)

Appletl´ıneatangenteaunas-recta: https://www.geogebra.org/m/y8h8hmjr

4.5.2.Definici´ondel´ıneaasociadaauna s-recta.

Seala s-recta l conecuaci´on ax + by + c = 0yunpunto P concoordenadas (x0, y0)S sobre l,seledenominal´ınea asociadaa l por P alconjuntosoluci´ondelaecuaci´on:

ax + by + c ′ + bsen(x)= 0, (3)

con c′ = ax0 by0 bsen(x0).

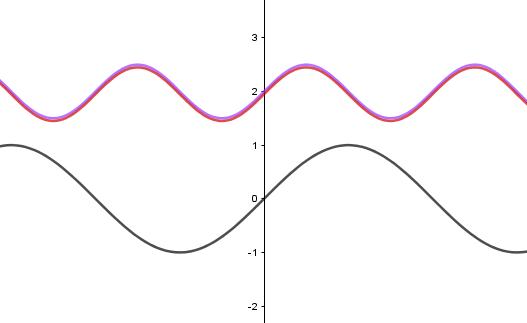
Ejemplo4.5. Encuentrelal´ıneaasociadaalas-rectapcon ecuaci´on x + 2y 5 = 0 enelpunto 4, 9 2 S .

Soluci´on:Primerosedetermina c′.Sustituyendoloscoeficientes a, b, c delaecuaci´ondela s-rectaylosvalores (x0, y0)S delpuntoen(3)setieneque:

c ′ = ( 1)(4) 2 9 2 2sen(4),

= 5 2sen(4)

Luego,laecuaci´ondelal´ıneaasociadaa p enelpunto 4, 9 2 S esdelaforma:

y = 1 2 x + 5 2 + sen(4) sen(x).

EnlaFigura15seobservalarepresentaci´ondelal´ıneaasociada(enrojo)ala s-recta(enverde)porelpuntodado.

Figura14: L´ıneatangentea l por (1, 1)

Paranombrarlasl´ıneas,seusar´anletrasgriegasyse especificar´aacu´altipodel´ıneaseest´ahaciendoalusi´on.Se puedeverquelasrectasdelsistemacartesiano(l´ıneas)no sonrectasenel SistemaSeno sinocurvas.F´ıjesequepara cadapuntosobreuna s-recta,setieneunal´ıneaasociadao tangentediferente.

Appletl´ıneaasociadaaunas-recta: https://www.geogebra.org/m/sgaysp4w

4.5.3.Definicionesde ´ angulo.

Acontinuaci´on,sepresentandosdefinicionesde ´ angulo entredos s-rectasapartirdel´ıneastangentesydel´ıneasasociadas.

´ Anguloentre s-rectasapartirdel´ıneastangentes:

Seanlas s-rectas l y t conun ´ unicopunto P encom ´ un ylasl´ıneas α y β tangentesa l y t respectivamente,por elpunto P.El ´ anguloentre l y t ser ´ ael ´ angulo θ determinadopor α y β

´ Anguloentre s-rectasapartirdel´ıneasasociadas: Seanlas s-rectas l y t conun ´ unicopunto P encom ´ un ylasl´ıneas α y β asociadasa l y t respectivamente,por elpunto P.El ´ anguloentre l y t ser ´ ael ´ angulo θ determinadopor α y β .

4.5.4. ´ Anguloapartirdel´ıneastangentes.

Seanlas s-rectas l y t conelpunto (x1, y1)S encom ´ uny ecuaciones

ax + by + c = 0,y lx + my + n = 0

respectivamente.Identificandoloscoeficientesparalasecuacionesdelasl´ıneas α y β tangentes l y t,setienequela ecuaci´onde α es: a′x + b′y + c′ + b′sen(x)= 0,

con a′ = a bcos(x1), b′ = b y c′ = ax1 +

bx1cos(x1) by1 bsen(x1) ylaecuaci´onde β ser ´ a:

l′x + m′y + n′ + m′sen(x)= 0,

con l′ = l mcos(x1), m′ = m y n′ = lx1 + mx1cos(x1) my1 msen(x1).Luego,el ´ anguloentre α y β est´adeterminadopor

θ = arctan a′m′ + b′l′ b′m′ + a′l′

Ypordefinici´onde ´ anguloentre s-rectasapartirdel´ıneas tangentes,el ´ anguloentre l y t es θ .

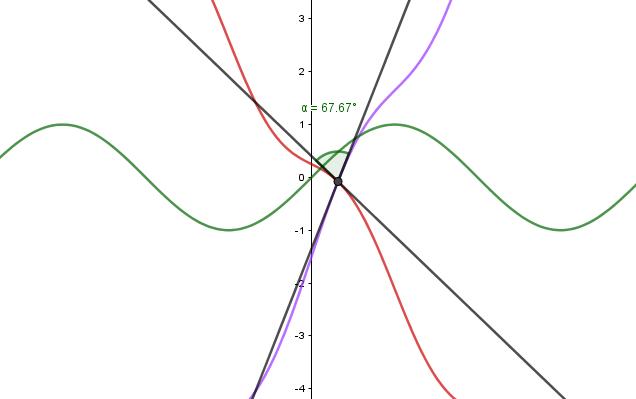
Paraejemplificaresteconceptosetomanlas s-rectas l y t quetienenencom´unelpunto (1, 1)S ytienenlasrespectivas ecuaciones

3x + 2y 1 = 0y4x 2y 6 = 0.

Identificandosuscoeficientessetieneque a = 3, b = 2, l = 4, m = 2, x1 = 1y y1 = 1,paraencontrarel ´ anguloentre ellassedeterminanlasecuacionesdelasl´ıneastangentesy loscoeficientes a′ , b′ , l′ , m′,portanto

a ′ = 3 + 2cos(1), b′ = 2, c ′ = 1 + 2cos(1) 2sen(1), l′ = 4 2cos(1), m ′ = 2, n ′ = 4 2cos(1)+ 2sen(1).

Reemplazandoestoscoeficientesen(4),resolviendoyrealizandolosprocedimientosalgebraicosnecesarios;setieneque el ´ anguloqueformanestasdos s-rectasenel SistemaSeno es:

θ = 67, 67◦ .

Sepuedevergr´aficamentecomosemuestraenlaFigura16.

Figura16: ´ Anguloentre l y t

Applet ´ anguloapartirdel´ıneastangentes: https://www.geogebra.org/m/uvd3ehah

4.5.5. ´ Anguloapartirdel´ıneasasociadas.

An´alogoalprocesodeladefinici´onde ´ anguloconl´ıneas tangentes,sisetienendos s-rectas l y t conecuaciones

ax + by + c = 0y lx + my + n = 0

respectivamente,ysusl´ıneasasociadas α y β conecuaciones

ax + by + c′ + bsen(x)= 0y lx + my + n′ + msen(x)= 0

Figura15: L´ıneaasociadaala s-recta x + 2y 5 = 0por 4, 9 2 S

respectivamente.El ´ angulo θ entre α y β determinadopor

θ = arctan am + bl bm + al , (5)

ser ´ ael ´ anguloentre l y t

Paraejemplificarestadefinici´onseencontrar´ael ´ angulo entrelassiguientes s-rectas:

l:3x + 2y 1 = 0y t:4x 2y 6 = 0

enelpuntodeintersecci´on (1, 1)S

Encontrandolaecuaci´ondelal´ınea α asociadaa l usando(3). Sedeterminaelcoeficiente c′

c ′ = (3)(1) 2( 1) 2sen(1),

= 1 2sen(1), luego,laecuaci´onde α es:

y = 3 2 x + 1 2 + sen(1) sen(x)

An´alogamente,seconcluyequelaecuaci´ondelal´ınea β asociadaala s-recta t es: y = 2x 3 + sen(1) sen(x)

Por ´ ultimo,sedeterminael ´ anguloentrelasl´ıneasasociadas usandolaecuaci´on(5).

θ = arctan (3)( 2)+(2)(4) (2)( 2)+(3)(4) , = arctan 7 4 , = 60,26◦

EnlaFigura17semuestragr´aficamenteel ´ anguloqueforman las s-rectas l y t corroborandolomencionadoenelprocedimientoanterior.

Dos s-rectas l y t conecuaciones

ax + by + c = 0y a′x + b′y + c′ = 0

sonparalelassi a b = a′ b′ .Si a′x + b′y + c′ = 0sepuedeescribircomo k(ax + by + c)= 0con k = 0entonces tambi´ensonparalelas.

Dos s-rectassonparalelassinuncaseintersecan ´ osise intersecanendosom´aspuntostambi´ensonparalelas.

4.7.Resultadosde s-rectasparalelasasociados adefinicionesde ´ angulos.

Enestasecci´onseanalizasisecumplenalgunosteoremas asociadosalasrectasysus ´ angulosdelsistemacartesianoen el SistemaSeno.

Teoremaparalelas- ´ anguloscorrespondientescongruentes:Seanlas s-rectas l y t paralelasconecuaciones

ax + by + c = 0y a′x + b′y + c′ = 0

respectivamente,ylas-recta s conecuaci´on dx + ey + f = 0secanteaellas.El ´ anguloqueforma l y s escongruenteal ´ anguloentre t y s.

Usandol´ıneastangentes: Como l y t sonparalelasentonces a b = a ′ b′ ;reemplazandoenlaecuaci´onde t setiene

ax + bx + c′b b′ = 0.

Seanlospuntos (x0, y0) y (x1, y1) lospuntosdeintersecci´on entre l y s y t y s respectivamente,ylasecuacionesdelas l´ıneastangentesacada s-rectaporlospuntosmostradasacontinuaci´on.

L´ınea δ1 tangentea s por (x0, y0)

a′′ 1 x + b′′ 1 y + c′′ 1 + b′′ 1 sen(x)= 0;

a′′ 1 = d ecos(x0), b′′ 1 = e,

c′′ 1 = dx0 + ex0cos(x0) ey0 esen(x0)

L´ınea α tangentea l por (x0, y0)

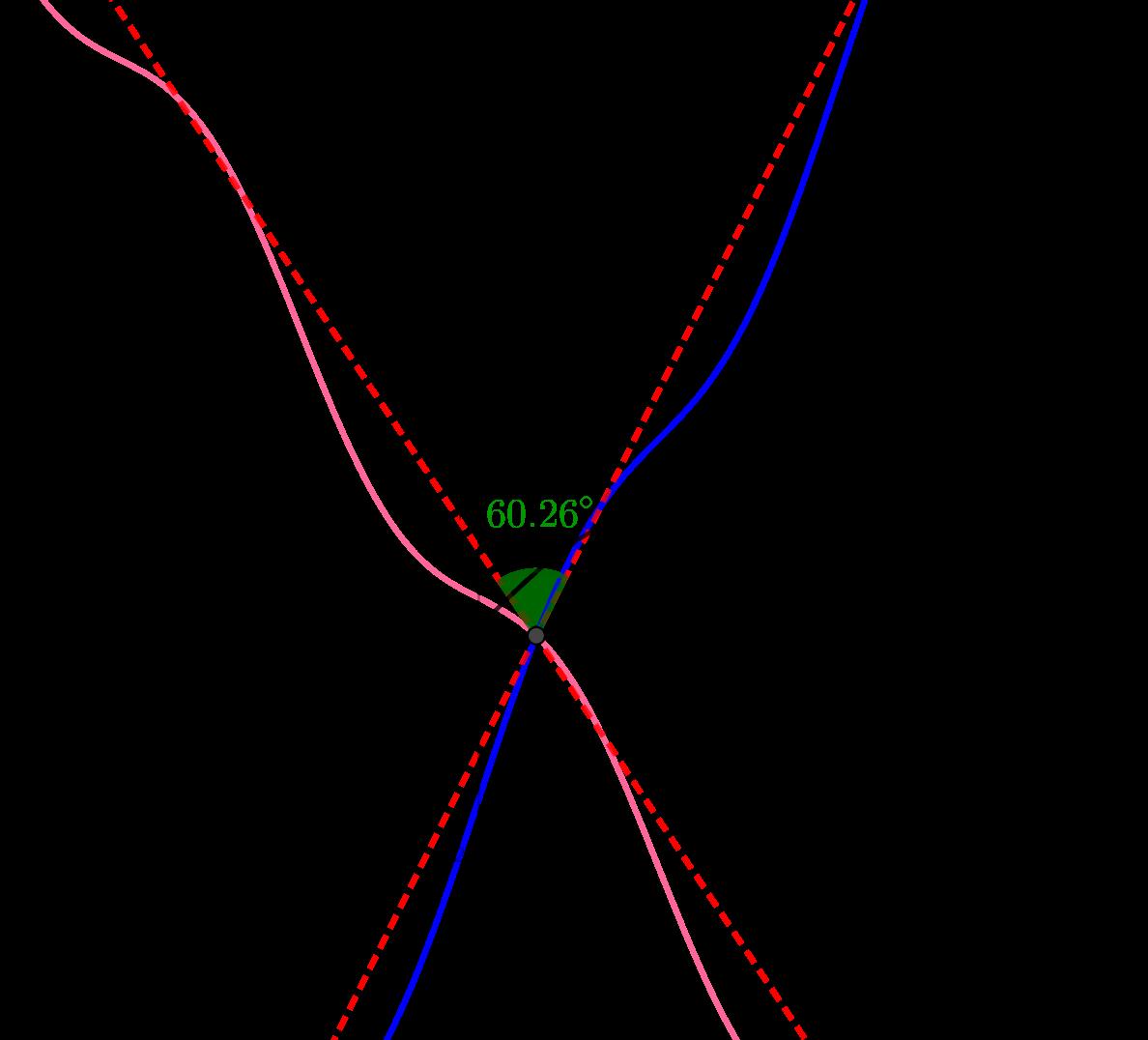
a′ 1x + b′ 1y + c′ 1 + b′ 1sen(x)= 0;

a′ 1 = a bcos(x0), b′ 1 = b,

c′ 1 = ax0 + bx0cos(x0) by0 bsen(x0)

L´ınea δ2 tangentea s por (x1, y1)

a′′ 2 x + b′′ 2 y + c′′ 2 + b′′ 2 sen(x)= 0;

Figura17: ´ Anguloentre l y t

Applet ´ anguloapartirdel´ıneasasociadas: https://www.geogebra.org/m/kujfzyyf

4.6. s-Rectasparalelas.

Sedefineelparalelismoentre s-rectasconlasdefiniciones anal´ıticaygeom´etricadelsistemacartesiano:

a′′ 2 = d ecos(x1), b′′ 1 = e,

c′′ 1 = dx1 + ex1cos(x1) ey1 esen(x1)

L´ınea β tangentea t por (x1, y1)

a′ 2x + b′ 2y + c′ 2 + b′ 2sen(x)= 0;

a′ 2 = a bcos(x1), b′ 2 = b,

c′ 2 = ax1 + bx1cos(x1) by1 bsen(x1)

Luego,porladefinici´onde ´ angulosapartirdel´ıneastangentes,los ´ angulosentre δ1 y α y δ2 y β son;

Paraquesecumplaque θδ1,α = θδ2,α lascoordenadasde lospuntosdeintersecci´ontienenquesatisfacerlassiguientes ecuaciones

eb(cos(x1) cos(x0))= 0, (db + ea + eb)(cos(x1) cos(x0))= 0

Enconclusi´on,los ´ angulosnosiempresoncongruentesluego, elteoremanosecumpleenel SistemaSeno conestadefinici´on(verFiguras18y19).

L´ınea δ1 asociadaa s por (x0, y0)

dx + ey + f ′ 1 + esen(x)= 0;

f ′ 1 = dx0 ey0 esen(x0)

L´ınea α asociadaa l por (x0, y0)

ax + by + c′ 1 + bsen(x)= 0;

c′ 1 = ax0 by0 bsen(x0)

L´ınea δ2 asociadaa s por (x1, y1)

dx + ey + f ′ 2 + esen(x)= 0;

f ′ 2 = dx1 ey1 e sen(x1)

L´ınea β asociadaa t por (x1, y1)

ax + by + c′ 2 + bsen(x)= 0;

c′ 2 = ax1 by1 bsen(x1)

Luego,porladefinici´onde ´ angulosapartirdel´ıneasasociadas,los ´ angulosentre δ1 y α y δ2 y β son;

θδ1,α = arctan ae + bd be + ad ,

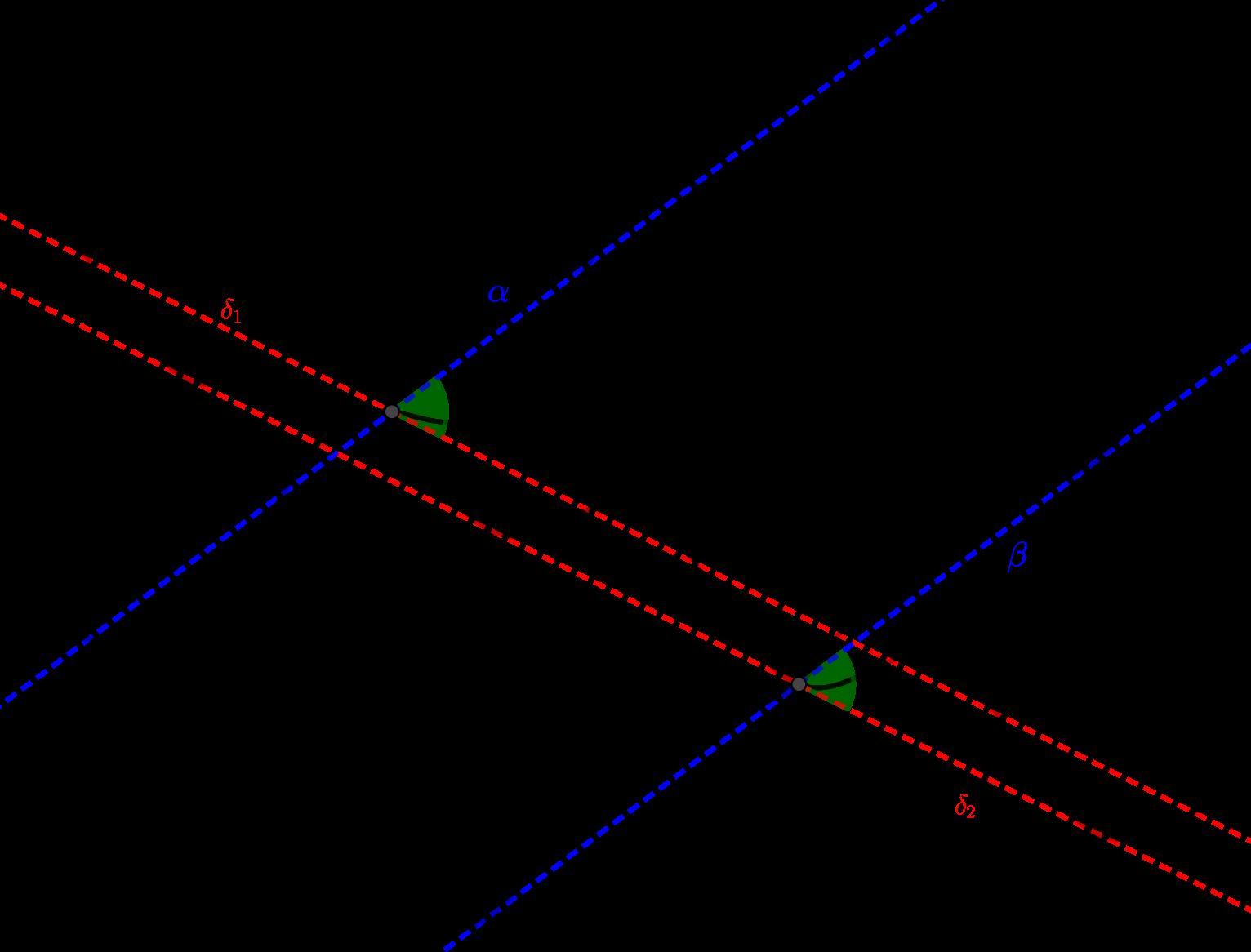
θδ2,β = arctan ae + bd be + ad .

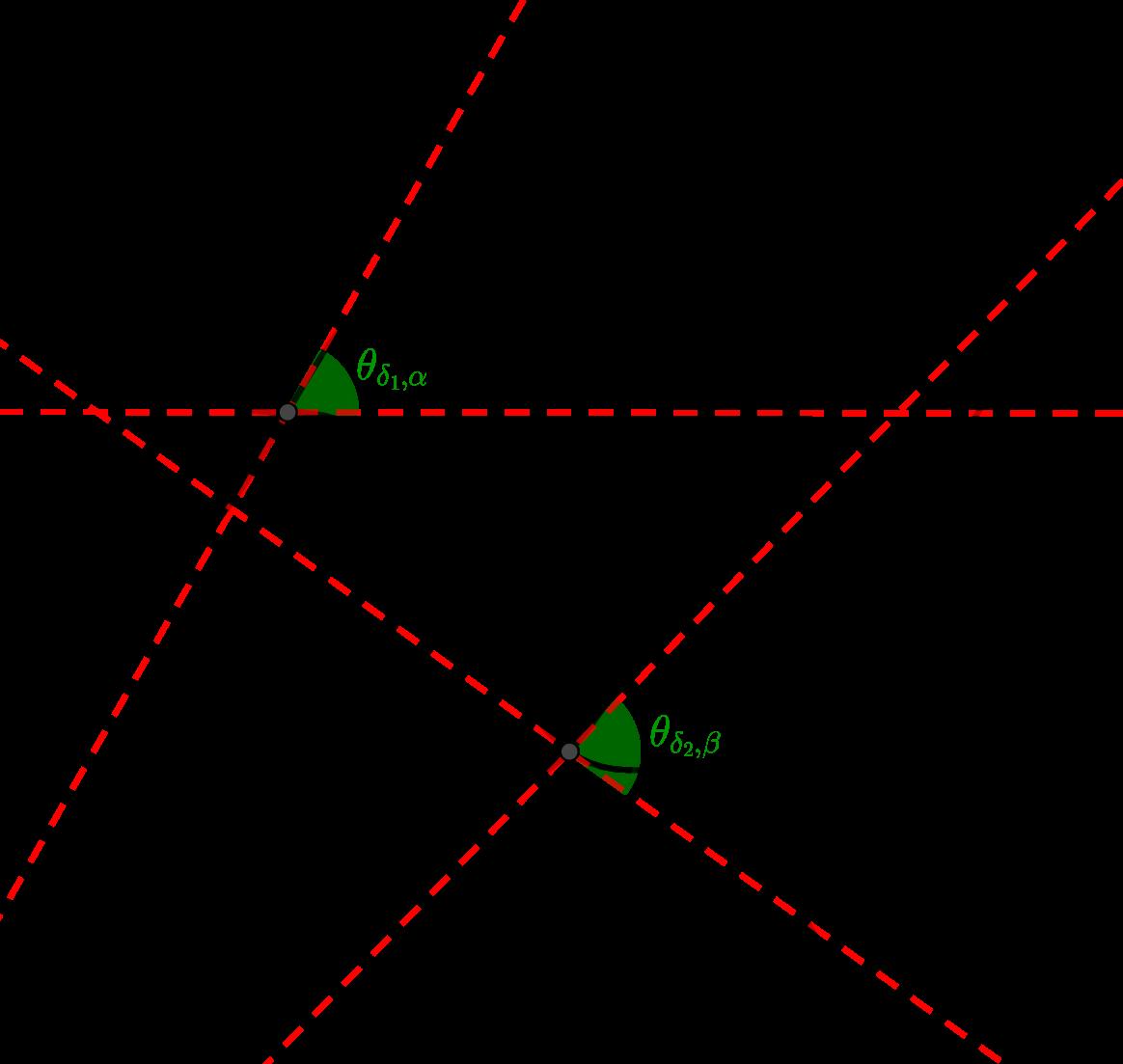
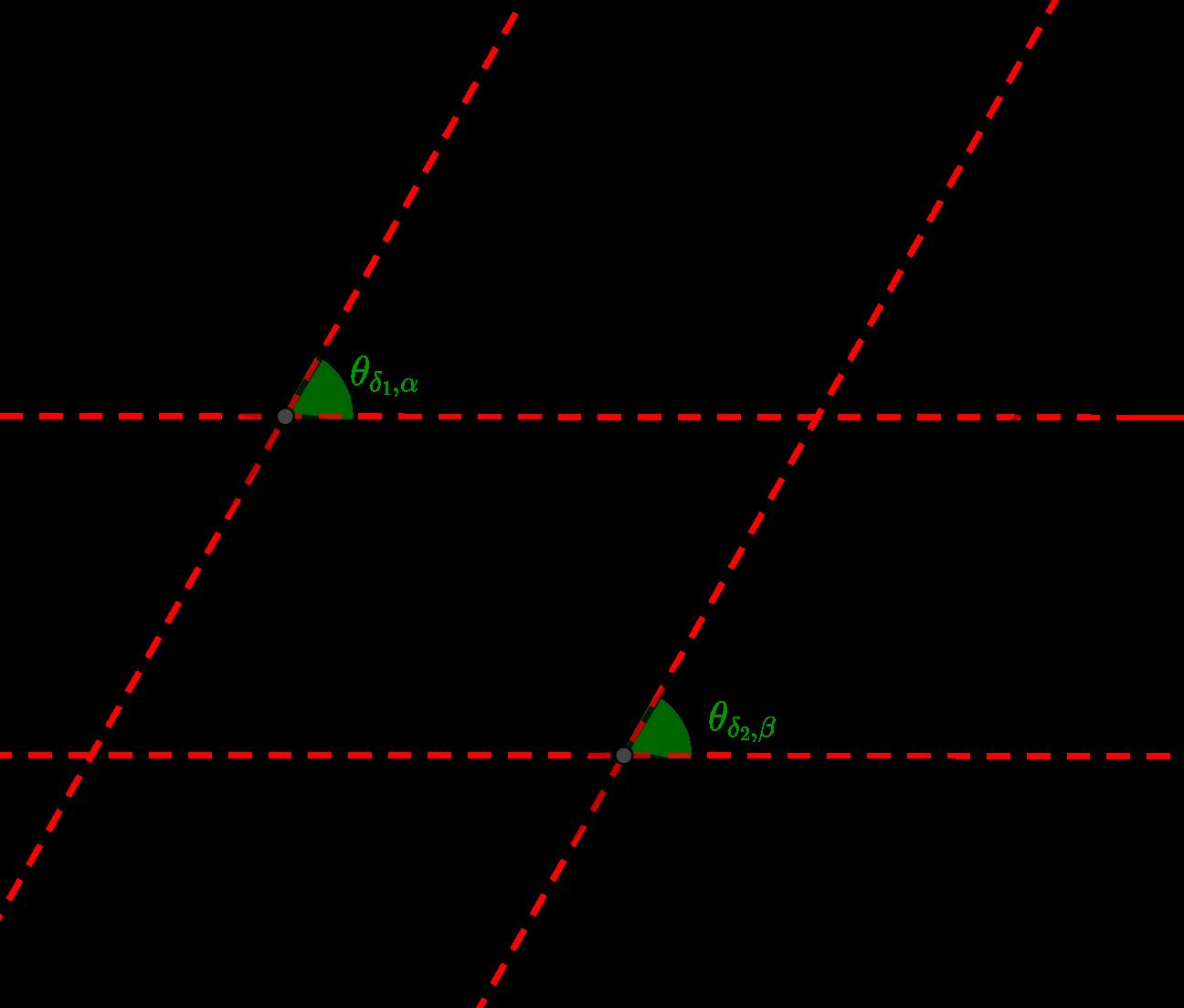
Enconclusi´on,los ´ angulossoncongruentes,luego,elteorema paralelas- ´ anguloscorrespondientescongruentes secumpleenel SistemaSeno conladefinici´onde ´ anguloapartirde l´ıneastangentes(v´easeFigura20).

Usandol´ıneasasociadas: Teniendolascondicionesdel teoremasetienequecomo l y t sonparalelasentonces a b =

a ′ b′ ,reemplazandoenlaecuaci´onde t setiene

ax + bx + c′b

b′ = 0

Seanlospuntos (x0, y0) y (x1, y1) lospuntosdeintersecci´on entre l y s y t y s respectivamente,lasecuacionesdel´ıneas asociadasacada s-rectaporlospuntosson:

Figura20: Conladefinici´onde ´ angulosapartirdel´ıneasasociadas.

Ejemplo4.6. Setienenlass-rectas

l −→−x + y = 0,t −→ 2x + y 4 = 0, k −→ 4x + 2y + 3 = 0

Porladefinici´onanal´ıticadeparalelismo,tesparalelaak.

Luego,lintersecaatenelpunto 4 3 , 4 3 S ylintersecaak

en 1 2 , 1 2 S .Ahora,sedeterminanlasecuacionesdelas l´ıneasasociadasacadas-rectaporlospuntosencontrados.

Figura18: Secumple.

Figura19: Nosecumple.

L´ınea δ1 asociadaalpor ( 1/2, 1/2)S y = x + sen( 1/2) sen(x)

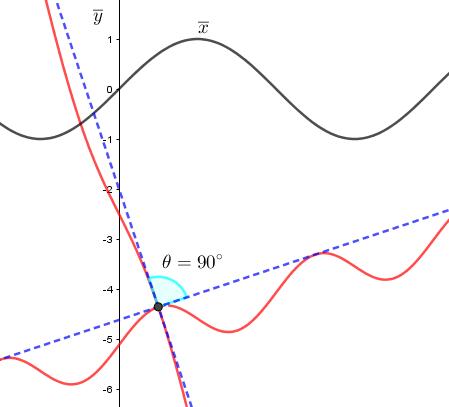
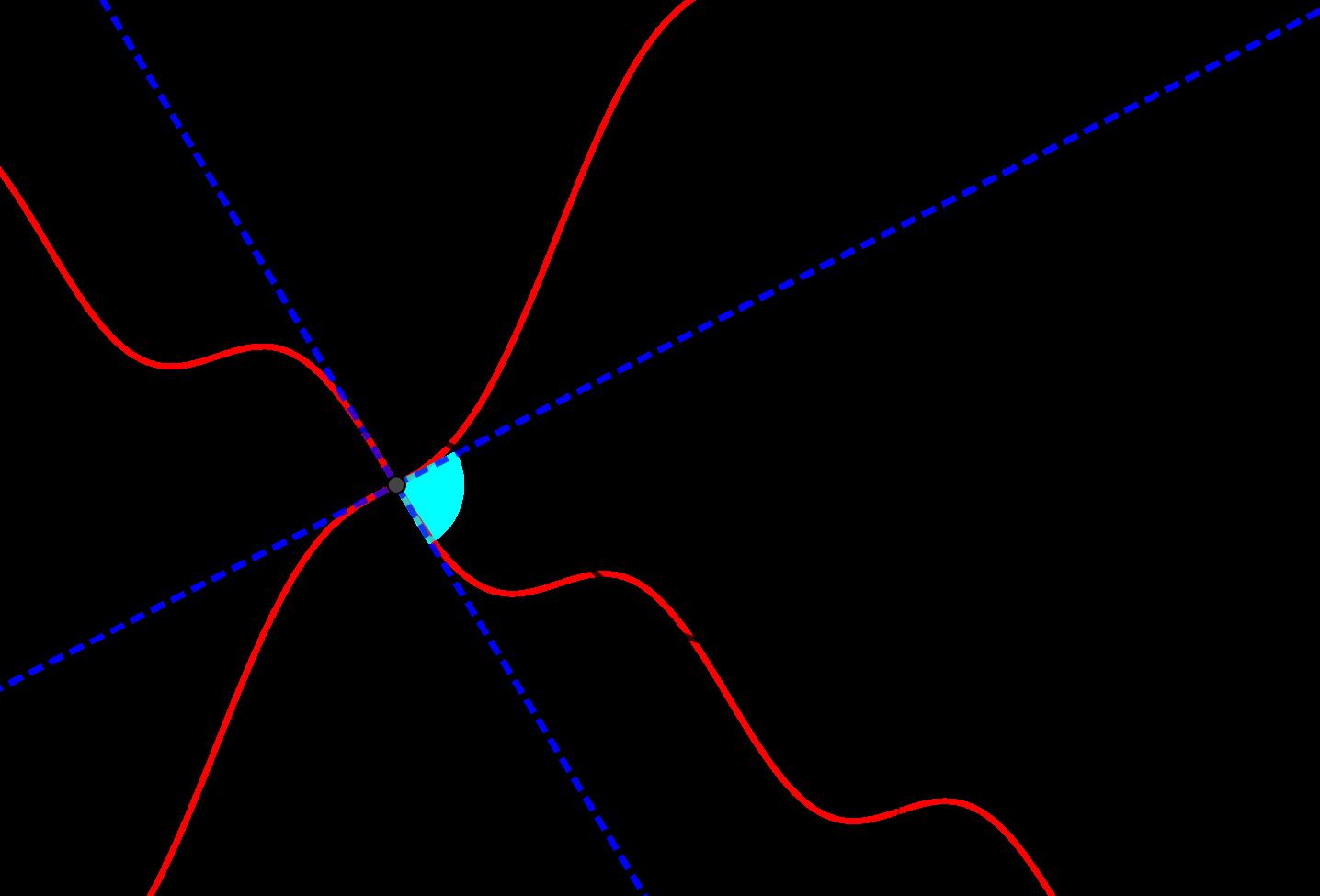
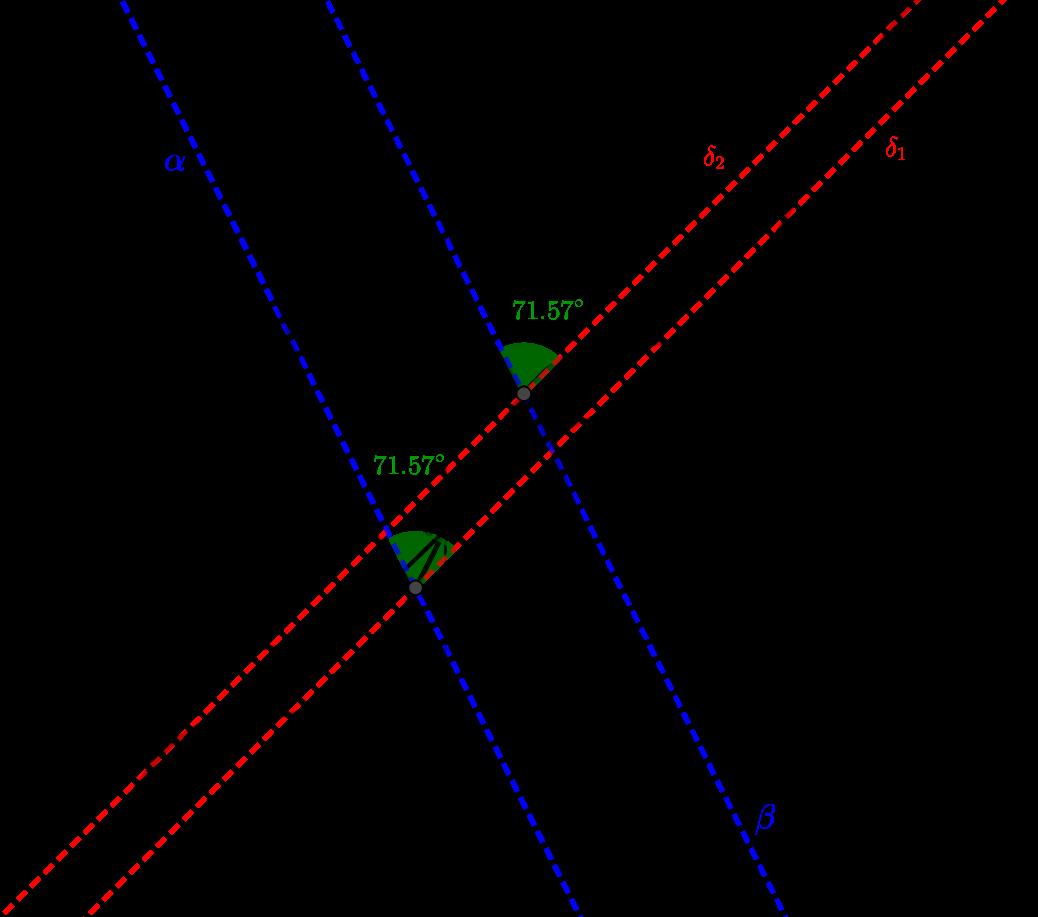
L´ınea α asociadaakpor ( 1/2, 1/2)S y = 2x 3/2 + sen( 1/2) sen(x)

L´ınea δ2 asociadaaspor (4/3, 4/3)S y = x + sen(4/3) sen(x)

L´ınea β asociadaatpor (4/3, 4/3)S y = 2x + 4 + sen(1/2) sen(x)

Los ´ angulosquedeterminan δ1 y α y δ2 y β son: θδ1,

Conladefinici´onde ´ anguloapartirdel´ıneastangentes: Seanlas s-rectas l y t conecuaciones2x + 3y + 15,2 = 0y 3x 2y + 30 = 0,respectivamente.Estascumplenque m1 · m2 = 1perolas s-rectasnoformanun ´ angulorecto.(ver Figura22).Ahora,tomandolas s-rectas t y l conecuaciones x + 3y + 30,71 = 0y3x + 1y + 5 = 0.Enestecasoel ´ angulo queformanporsupuntodeintersecci´onesde90◦ peroel productodelaspendientesnoes 1luego,nosecumplela equivalencia(verFigura23).

F´ıjesequeapesardequecadapuntosobre s tieneunal´ınea asociadadiferente,noinfiereenel ´ anguloquedetermina l y t, esdecir,sepuedetomarcualquierpuntosobrela s-rectapara determinarlal´ıneaasociadaaella.Tambi´en,sepuedemostrar otrosteoremasdelageometr´ıaEuclidianacomo paralelas´ angulosalternosinternoscongruentes oquelasumadelos ´ angulosinternosdeuntri´anguloes180◦,entreotros.

4.8.

An´alogoaldesarrollodelateor´ıaenelsistemacartesiano sedefinelaperpendicularidadentre s-rectascomo:

Seanlas s-rectas l y t,siel ´ angulo θ queforman l y t es de90◦ entonces l y t sonperpendiculares.

Las s-rectas l y t sonperpendicularessiysolosi m1 · m2 = 1

Enelestudiodeestaspropiedades,seencontr´oquelarelaci´on entreel ´ anguloyelproductodelaspendientessecumpleen el SistemaSeno usandoladefinici´onde ´ anguloapartirde l´ıneasasociadaspero,conladefinici´onde ´ anguloapartirde l´ıneastangentesnosecumple.

Estosedebeaque,comosemencion´ocuandoseestaba estudiandoel Teoremaparalelas- ´ anguloscorrespondientes congruentes desdeestadefinici´onde ´ angulo,siseconstruyen s-rectas ti perpendicularesporcadapuntodela s-recta l,las s-rectas ti forman ´ angulosdiferentescon l luego,puedeque algunascumplanconlapropiedadyotrasnocumplan.

Conladefinici´onde ´ anguloapartirdel´ıneasasociadas: Setomar´anlas s-rectas l y t conecuaciones

4x + 3y 10 = 0y3x + 4y 4 = 0,

luego,elproductodesuspendienteses 1yadem´assonperpendiculares.EnlaFigura24semuestralagr´aficadesus l´ıneasasociadasyel ´ angulorectoqueforman.

EnlaFigura21semuestralagr´aficadelass-rectasyl´ıneas asociadasyel ´ anguloqueseformaentreellas.

Figura21: ´ Anguloscongruentespara t y k conrespectoa k

s-Rectasperpendiculares.

Figura22: Delaspendientesal ´ angulo.

Figura23: Del ´ anguloalaspendientes.

Sesuponeuna s-recta l conecuaci´on ax + by + c = 0yun punto P(x0, y0)S fueradeella.Lospuntos Li quepertenecena l tienencoordenadas x

, luego,ladistanciaentre P ylospuntos Li,usando6,estar´a dadaporlasiguienteecuaci´on

4.9.Distanciaentredospuntos.

Seanlospuntos P1 y P2 concoordenadas (x1, y1)S y (x2, y2)S respectivamente,ladistanciaentreellossedenotar´a dP1P2 ysedeterminar´adelasiguientemanera:

dP1P2 = 1 2 (x1 x2)2 +(y1 y2 + sen(x1) sen(x2))2 . (6)

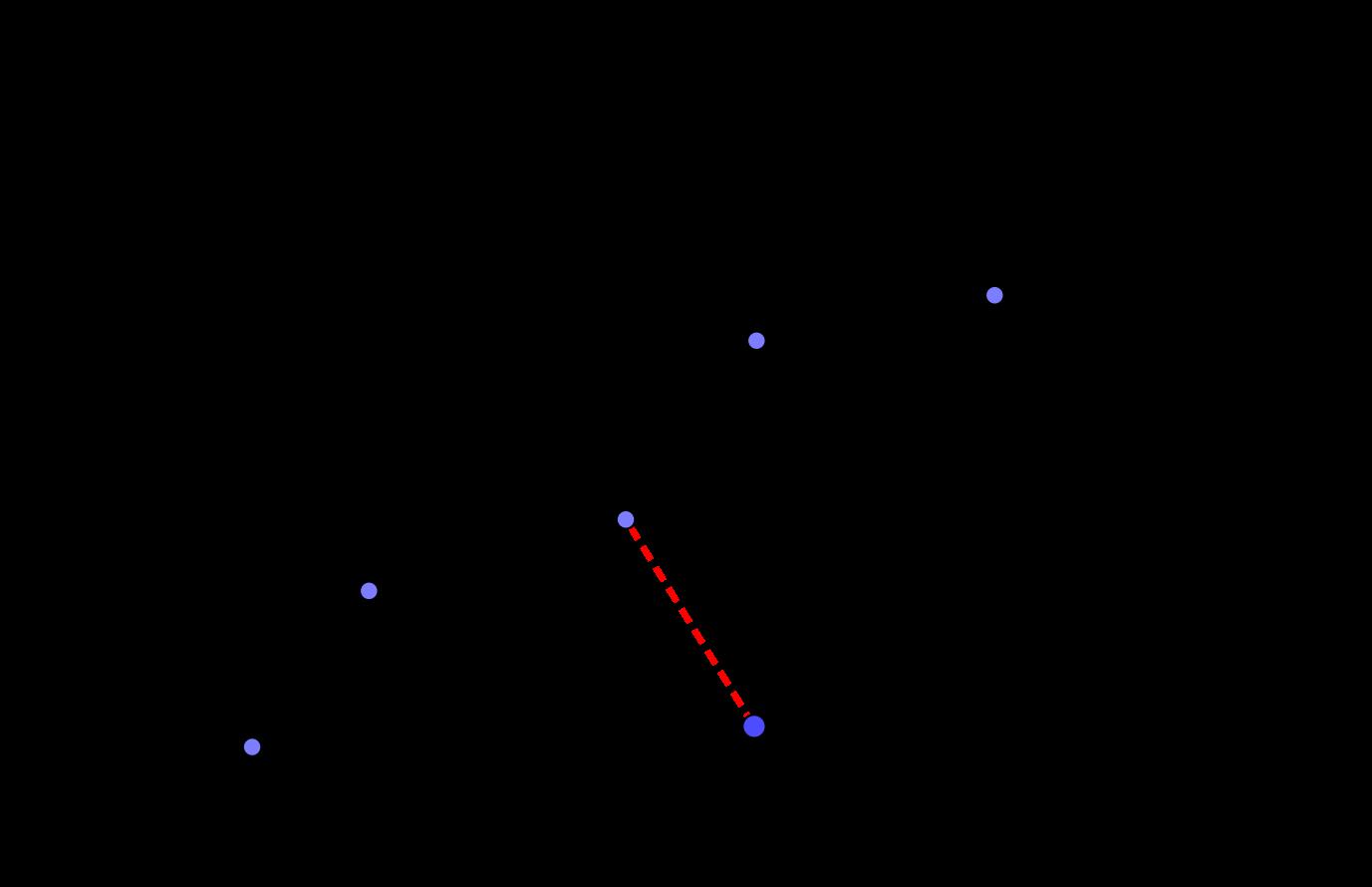
Estadistanciaseencuentraapartirdeladistanciaeuclidiana entredospuntos.

Appletdistanciaentredospuntos: https://www.geogebra.org/m/tdghkukg

4.10.Distanciadeunpuntoauna s-recta.

Paraestadefinici´onsetomaunpunto P fueradeuna s-recta l,sedeterminaladistanciaentrecadapunto Li sobre l.(ver Figura25)

Comosenecesitaencontrar min[dP,Li ] seusar ´ aelcriteriodela segundaderivadaviendoa dP,Li comounafunci´onent´erminosde x.Paracomodidaddelecturayescrituraseomitir´ael sub´ındice P, Li Laprimeraderivadade(7)es

porelcriteriodelaprimeraderivadalaecuaci´onanteriorse igualaa0ysedeterminaelconjunto

Loselementosdeesteconjuntosenombrancomo xA luego,la segundaderivadade(7)es:

(x)) ,

evaluandocada xA en d′′ sevanatomartodoslosvalorespositivos,esdecir,setomaelconjunto B como

B = xA | d′′(xA) > 0

Parafinalizar,setomanloselementosde B yseeval´uanen d, portanto,seconcluyequeelvalordeladistanciaentre P y l eselm´ınimodelosvaloresde d(xB).

dP,l = min[d(xB)].

Comosepuedeobservar,estademostraci´onest´acondicionada aque b = 0.Enelcasoque b = 0ladistanciaentrela s-recta l yelpunto P,seencontrar´aconlasiguienteecuaci´on:

dP,l = 1 2 x0 + c a

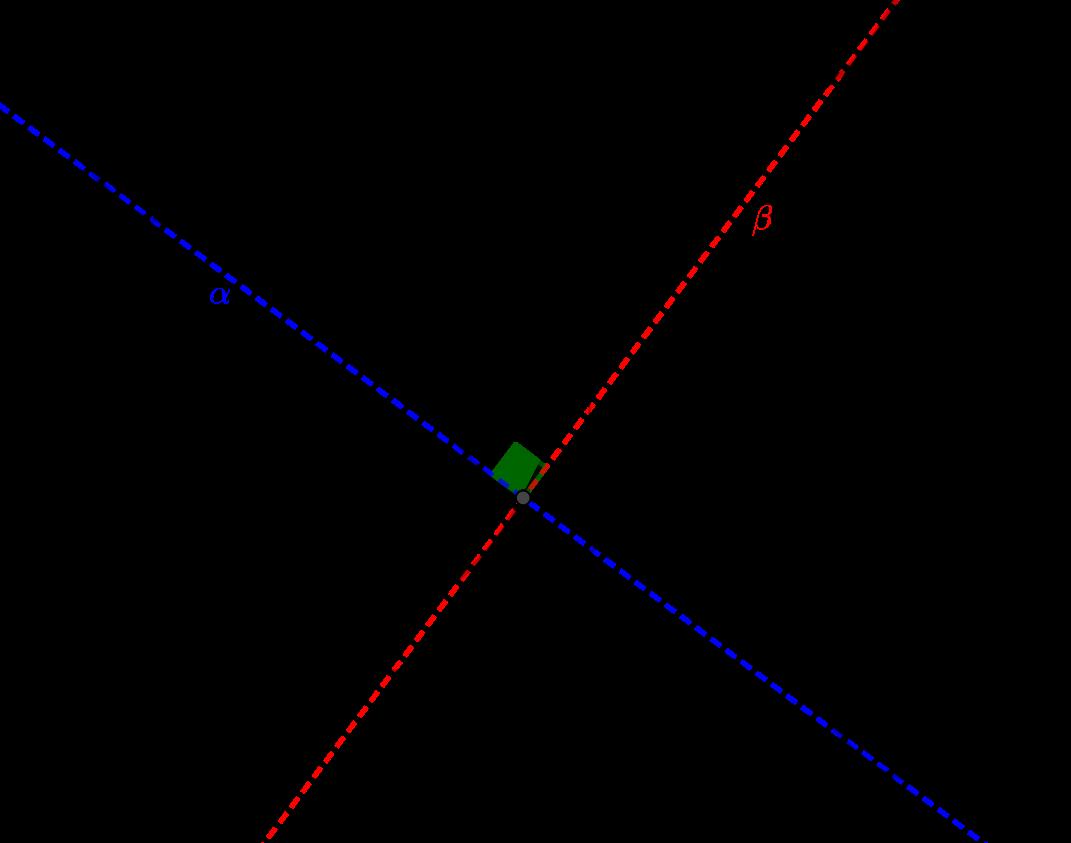
Ejemplo4.7. Sealas-rectalconecuaci´on x + y + 5 = 0 yel puntoPconcoordenadas (4, 3)S

Ladistanciaentre P y l ser ´ alam´ınimadistanciaencontrada entre P ylospuntossobre l (segmentorojo).

Seauna s-recta l ylospuntos L1, L2,..., L j , L j+1,... sobre l,unpunto P fueradeellay dP,Li ladistanciade P acada puntosobre l.Ladistanciade P a l ser ´ a dP,l = min[dP,Li ]

Siguiendoelprocedimientoanteriorsetienequelospuntos sobreltienencoordenadas

(x, x 5)S

yladistanciaentrePyestospuntosLi estadadapor

Figura24: ´ Anguloentre l y t.

Figura25: Distanciaentreunpuntoyuna s-recta.

luego,laderivadadeestafunci´ones

4dd′ = x 4 +(x + 8 sen(x)+ sen(4))(1 + cos(x))

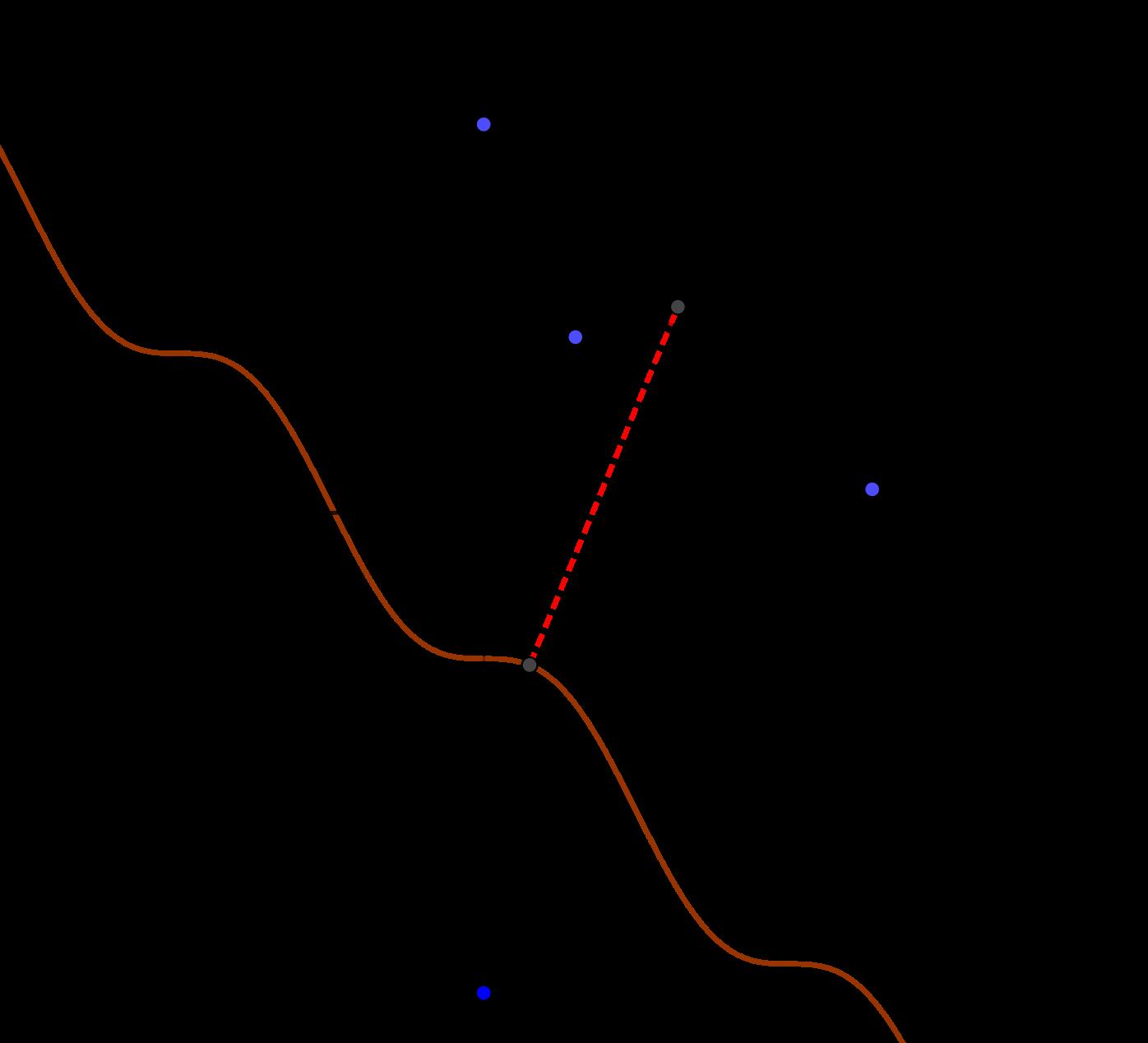
Ahora,porelcriteriodelaprimeraderivada,setieneelconjuntoA = { 3,34 , 1, 35 , 0, 94} talesqued′(xA)= 0 luego,lasegundaderivadaes:

4(d′2 + dd′′)= 1 +(1 cos(x))(cos(x) (x + 6 sen(x)+ sen(4))(sen(x))

yelconjuntoBtendr´aelelemento {0,94} talqued′′(xA) > 0, por ´ ultimo,seeval´uaendysetienequed(0,94)= 3,99 luego, ladistanciaentrePylser´ad(0,94)= 3,99.(verFigura26).

dP,Li = 3,99

Agradecimientos.

ADios,pordarmelaluzenmomentosdeoscuridad.Ami familia,porsersiempremimotivaci´on.AlprofesorJohn,por laoportunidaddepresentarestetrabajoenlarevista.

Referencias.

[Ap4] T.Ap´ostol, Calculus.VolI,Revert´e,Barcelona,1984.

[FS11] F.FernandezSanchez, Unestudiodelasrectasenplanosoblicuos perpendiculares,UniversidadPedagogicaNacional,Bogota,2011.

[Fil98] E.FilloyandF.Hitt, Visualizacionmatematica,representaciones, nuevastecnologıasycurriculum,GrupoEditorialIberoam´erica 10 (1998),23-45.

[Kle68] D.Kletenik, Problemasdegeometr´ıaanal´ıtica (1968).

[Kol06] B.KolmanandD.Hill, Algebralineal,Pearson,M´exicoD.F,2006.

[Leh89] C.Lehmann, Geometr´ıaanal´ıtica,Limusa,MexicoD.F,1989.

[Men16] A.Mendigano, Distanciausualentredospuntosendiferentessistemascoordenadosdelplanoyelespacio,UniversidadPedag´ogica Nacional,Bogot´a,2016.

[MC11] L.A.MorenoCeleitaandO.CarrenoG´omez, Untratamientoalas c ´ onicasapartirdediferentessistemascoordenados,Universidad Pedag´ogicaNacional,Bogot´a,2011.

[OP12] L.A.OrtizPuentes, Representaci´ongr´aficayalgebraicadela ecuaci´oncuadr´aticaenelsistemaPAR,UniversidadPedag´ogica Nacional,Bogot´a,2012.

[Ste89] J.StewartandR.HernandezandC.Sanmiguel, Introducci´onal C´alculo,1989.

[Gar19] W.Garz´onandS.Nino, Representaciongraficayalgebraicade lasecuacionescuadraticasyseccionesconicasenelSistemaSeno, UniversidadPedag´ogicaNacional,Bogot´a,2019.

Appletdistanciaentreunpuntoyunas-recta: https://www.geogebra.org/m/zwkfvy7w

5.Conclusiones.

Unareflexi´onacercadelarepresentaci´ondelosobjetos geom ´ etricosesque,usualmente,sepresentancomoobjetos conunasolarepresentaci´on,lacualesla ´ unicaquecumple laspropiedadesoladefinici´on.Coneldesarrollodeeste art´ıculoseevidenciaqueestonoescierto,sisetomanlas definicionesusualesono,sepuedecambiarlamanerade representarlosymostrarquelasmatem´aticassonflexiblesen muchosaspectos.

Acercadelasproyeccionesdeesteart´ıculosedejanalgunaspreguntassinresolverenel SistemaSeno como:

Teniendoencuentaladefinici´onde ´ anguloapartirde l´ıneastangentes,¿sepodr´ıaencontrarunarelaci´onentre laspendientesyel ´ anguloentredos s-rectaspararealizarunaequivalenciaentreladefinici´ongeom´etricayla definici´onalgebraicadelaperpendicularidad?

Enelsistemacartesiano,ladistanciaentredospuntos sepuededefinircomolalongituddelsegmentoderecta quelosune.Sisetomaestadefinici´onenel SistemaSeno ¿c ´ omocambiar´ıanlasrepresentacionesdelasdefinicionesqueseasociancondistancia?

Acercadelautor:Waltereslicenciadoenmatem´aticasde laUniversidadPedag´ogicaNacionalyactualmentecursael ´ ultimosemestredelamaestr´ıaenmatem´aticasaplicadasenla UniversidadSergioArboleda.Esapasionadoporlosdeportes comoelf´utbolylanataci´on,leencantasalirdeviaje,bailary compartirtiempoconsufamiliaycercanos.

Figura26: Distanciaentre (4, 3)S y x + y + 5 = 0.

OBST ´ ACULOSENLACONCEPCI ´ ONDELOSN ´ UMEROSNEGATIVOS YDESUSLOGARITMOS

BlancaMargaritaParraMosqueda * bparramosqueda@gmail.com

1.Resumen.

Eltextoquecompartoesunentretejidodeexperienciasy escritosalolargode46a˜nos.Almismotiempo,esunhomenaje/agradecimientoamismentores,losquemeincorporaron comocolegasinrepararencualquieradelascaracter´ısticas personalesque,enlostiemposactuales,sirvenparadiscriminarylimitarelcrecimientopersonalyprofesionaldeuna persona,especialmenteeldelasmujeres.

2.Introducci´on.

En1977,entallerescondocentesdematem´aticasdenivel secundaria,conJes´usAlarc´onBortolussicomomentor,detectamosparticularidadesensuconcepci´ondelconceptode n ´ umeronegativosinqueenesemomentopudi´eramosreferirlasacuestionessobreeldesarrollohist´oricodelconcepto,ni alosobst´aculosepistemol´ogicosqueseevidenciar´ıanposteriormente,alanalizarlaevoluci´ondelconcepto.Lasvisitas delprofesorGeorgesGlaeseraM´exiconospermitieronintroducirnosenesetipodean´alisis,conocerlaobradeBachelard[Bac67]respectoalosobst´aculosepistemol´ogicosenel desarrollodeunconceptoysurelevanciaeneldise˜nodesituacionesdid´acticasy,apartirdeah´ı,reconocerquelasexpresionesdelosdocentescorrespond´ıanaetapaseneldesarrollo delconceptoden´umeronegativoyque,dehecho,reproduc´ıan algunasdelasconcepcionessostenidaspormatem´aticoscomod’Alembertaltiempoquemanifestabanlossentimientos defrustraci´oneincomodidadque,comoalumnos,describen personajescomoSthendal,ensuautobiograf´ıa.Entre1981y 1984,encuestionariosyentrevistasquebuscabancomprender eldesarrollodelconceptodevariableenlosalumnos,apartirdequesonintroducidosalc´alculoalgebraico,enprimer gradodesecundaria,encontramoselmismotipodeconcepcionessobrelosn´umerosnegativosyalgunaspercepciones inusitadassobreeln´umerocero.

En1979Jean-LucVerley,entonceseditordelasecci´onde HistoriadelasMatem´aticasdela EnciclopediaUniversalis (Francia),pusoenmismanosunacopiadelasextamemoriaded’Alembert,lacualtratasobreloslogaritmosdecantidadesnegativas[Ale56]paraquehicieraunan´alisisepistemol´ogicodeltexto,conimplicacionesdid´acticas,loquepro-

*EscuelaNacionaldeEstudiosSuperiores(ENES)UNAMLe´onM´exico. Profesorainvitadapermanente.

dujounart´ıculoqueser´ıaincorporadoala EnciclopediaUniversalis.Denecesidad,llevaracabolatareaencomendadarequiri´olaconsultademuchasotrasfuentes,particularmentelos art´ıculos“N´egatifs”y“Logarithme”queelpropiod’Alembert escribi´oparalaEnciclopedia(Encyclop´edie,oudictionnaire raisonn´edessciences,desartsetdesm´etiers),editadaentre 1751y1772,decuyaedici´onfuecodirectorjuntoconDenis Diderot.

Porrazoneshist´oricas,enestetextoelrecorridocomienza coneldesarrollodelconceptodelogaritmo,contin´uaconlos conceptosdeceroyden´umeronegativoyconcluyeconuna partedelan´alisisrealizadoen1979,presentadoenuncoloquiollevadoacaboenmarzode1982enlaSecci´ondeMatem´aticaEducativadelCINVESTAV.

3.Or´ıgenesdelconceptodelogaritmo.

Unabuenapartedelconocimientomatem´aticom´asantiguoproviene,sinduda,delosmatem´aticossumerios(situadosenBabilonia,enloqueahoraesIrak).Enloquerespecta aloslogaritmos,O.Neugebauer[Neu69]senalaque“haymuchaevidenciadelashabilidadesdelosescribasdelantiguo per ´ ıodobabil´onico,eselper´ıodoquevade1800a1600antesdeCristo”–alrededordelreinadodeHammurabi–.Luego estableceque“nosolamenteesclarodelosproblemasquetienenqueverconinter´escompuestosinotambi´endelastablas num ´ ericasparalaspotenciasconsecutivasden´umerosdados. Porotrolado,setienentextosquetienenqueverconladeterminaci´ondelosexponentesden´umerosdados.Enotraspalabras,sehab´ıaexperimentadorealmenteconcasosespeciales delogaritmossinalcanzarunusogeneraldeestafunci´on.”. Posteriormente,enlasnotasdelcap´ıtulo2dellibrose˜nala que“Lastablasparaylascorrespondientesaloslogaritmos aparecenendocumentossumerios”,loscualesaparecen“ilustradosconfotograf´ıas,copias,transcripciones,traduccionesy comentarios”,endosdesuslibrosprevioscuyosacr´onimos sonMKTyMCT.

Loslogaritmos,comolosconocemosactualmente,sedebenaJohnNapier–matem´atico,f´ısicoyastr´onomo,quien vivi´oentre1550y1617–,perosuhistoriaseextiendedesde BabiloniahastaNewton,yunn´umeroconsiderabledeproblemasinteresantesysolucionesingeniosassepuedenencontrar enelcamino.

Laideaoriginaldelogaritmoseestablece,enpocaspala-

bras,comosigue:dadocualquiern´umerorealpositivoponemosencorrespondencialasdosprogresionessiguientes(una aritm´eticayunageom´etrica):

Progresi´onaritm´etica:-3,-2,-1,0,1,2,3,4.

Progresi´ongeom´etrica: a

Ydecimosqueloslogaritmosenlabasedelosn´umeros delaprogresi´ongeom´etricasonloscorrespondientesdela progresi´onaritm´etica.

Treselementosdistintos,peronoseparablescontribuyeron aldescubrimientodeNapier:suconocimientodelatrigonometr´ıaysutrabajocomocart´ografoyastr´onomo;cadaunode estosdominiosdeconocimiento,pors´ımismo,mereceatenci´onparacomprenderlamagnituddeldescubrimientodelos logaritmoscomoreglageneral,ysusaplicacionesac´alculos trigonom´etricosconn´umerosmuygrandes(omuypeque˜nos) comolosresultadosdelasobservacionesenastronom´ıa,la cualrequieredelregistrodedatosprecisosdemaneracontinuada.Napiersebenefici´o,adem´as,detodoelconocimiento griegodePit´agorasaEuclides,incluyendoaArqu´ımedes,por supuesto,ydelconocimientoalgebraicodesarrolladoporlos matem´aticosisl´amicosyloseuropeosdelossiglosqueleanteceden.Particularmente,diceItard[Ita84],“recordemosque NicolasOresmeyautilizabaexponentesfraccionarios,que Chuquetutilizabaexponentesnegativosynulos”.Adem´as,dice,fueronnumerososlosmatem´aticosqueestablecieronla estrecharelaci´onentrelasseriesaritm´eticaygeom´etrica,particularmenteChuquetyStifel.

Sinembargo,fueNapierquienproporcion´oalmismotiempounateor´ıas´olidayunm´etodopr´acticodelc´alculodelogaritmos.Suideadelaconstrucci´ondetablasdelogaritmosera ladecreartablasquepermitieranmultiplicarn´umerossinrealizarrealmenteesaoperaci´on,sinoutilizandolasuma(delos logaritmosdelosn´umeros).Napierconstruyesustablasdelogaritmosmediantelaextracci´onsucesivadera´ıcescuadradas abreviadasyconcomentariossensatos.Sinembargo,labase deloslogaritmosutilizadosporNapierdistabadesersimple. Poralgunaraz´on,diceIanStewart[Ste07],Napierescogi´ouna raz ´ onligeramentemenorque1,asaber0.9999999,Deesa manera,susucesi´ongeom´etricaibarecorriendohaciaatr´as unaserieden´umerosdelosmuygrandesalosm´aspequenos. Dehecho,contin´uaStewart,“comenz´ocon10,000,000yentoncesmultiplic´oporpotenciassucesivasde0.9999999.Si

escribimos Naplog(x) paraellogaritmodeNapierdeunvalor x,setieneque

Naplog(10,000,000)= 0

Naplog(9,999,999)= 1

ysesatisfacelaecuaci´on

Naplog(107xy)= Naplog(x)+ Naplog(y)”.

PosteriormenteHenryBriggs,unmatem´aticobrit´anico, trasvisitaraNapieryconsuaprobaci´on,desarroll´onuevas tablasdelogaritmos,haciendoqueellogaritmodelaunidad fueraceroyqueelde10fuera1–esdecir,loslogaritmos debase10–,ycalcul´oloslogaritmosvulgaresodecimales delosprimeros31,000enteros,conunaprecisi´ondehasta14 decimales,relataItard[Ita84].

4.Elcasodelosn ´ umerosnegativos.

Ensumuybiendocumentadoestudiosobrelaevoluci´on delconceptoden´umeronegativo,GeorgesGlaeser[Gla81] relataeldesarrolloepistemol´ogicodeeseconceptoque,en t´erminosescolaresactuales,parecieramuysimple.Ens´ıntesis,dice“senecesitaronm´asde1,500anosparaquela“regla delossignos”fueraconsideradaunlugarcom´unporlosmatem´aticos”.Ensutrabajohaceunestudiopormenorizadode textosquevandesdeDiofantohastafinalesdelsigloXX,en loscualessedetectanalgunosdelosobst´aculosepistemol´ogicosqueseinterpusieronenelcaminodelacomprensi´onde losn´umerosnegativos.Glaeserrefierelasdificultadesquecon esosn ´ umerosexperimentaronmatem´aticostannotablescomo Eulerod’Alembert,lascualestieneneco,todav´ıa,enlasrespuestasqueestudiantesydocentesdandevivavoz[Par81]y enalgunoscuestionarios[Par85].

ElmismoGlaeserdiceque“lapr´acticaclandestinadel c ´ alculodelosn´umerosrelativosprecedeen1600anosasu comprensi´on”.EnesesentidoStewart[Ste07]yNeugebauer [Neu69]datanelusoden´umerosnegativos,porconvenienciaparalosc´alculos,aliniciodelprimermilenio(unostreso cuatrosiglosantesdeDiofanto);losmatem´aticoschinosresolv´ıanecuacioneslinealesayud´andosedevarillasdecolores dispuestassobreunamesa;lasvarillasrojaseranutilizadas paralost´erminosquedeb´ıansumarsemientrasquelasvarillas negrasseutilizabanparalost´erminosquedeb´ıansustraerse. Stewartaclaraquelanotaci´onrojo/negronotratabaprecisamenteconn´umerosnegativos,sinosobrelaoperaci´onsustracci´on;sinembargo,ponelasbasesparaelconceptoden´umerosnegativos, chengfushu,yqueapartirdeah´ılosn´umeros negativosserepresentabanconunavarillapuestadiagonalmentesobrelasquesignificaban,dir´ıamos,elvalorabsoluto deln´umero.

EncuantoaDiofanto,PaulVerEecke[VE59]dicequeuna caracter´ısticaqueimpon´ıaasusproposicioneseraladesolamentereconocerlessolucionesracionales,dedonderesulta que,cuandounaecuaci´ondaparalainc´ognitaunvalorirracionaloimaginario,declaraquelasoluci´onalproblemaes “imposible”.Adem´as,comolanoci´ondelvalornegativoen s ´ ı,esdecirindependientedeunacantidadpositivadedonde unolaresta,eraextra˜naalosmatem´aticosgriegos,Diofantotampocoadmitelassolucionesnegativasy,entonces,cadavezquelasecuacionesconducenaunvalornegativode lainc´ognita,declaraqueesasecuacionesson“absurdas”.En todosloscasosenqueDiofantoencuentrasolucionesquerechaza,porimposiblesoabsurdas,utilizaunprocedimientode falsaposici´ony,enalgunoscasos,dedoblefalsaposici´onpara regresarsobresuspasosyconsiderarlag´enesisdelost´erminosdelaecuaci´onparalaquenoencuentrasoluci´onsatisfactoriaymodificarloscoeficientesnum´ericosdeesost´erminos, adoptandodeterminacionesarbitrariasdiferentesdelasenunciadasaliniciodelprocesoderesoluci´onqueloconduzcan asolucionespositivasracionales.Porsuparte,aldiscutirel tratamientoqueDiofantodaalasecuacionespuras,lascuales contienensolamenteunapotenciadelainc´ognita,independientementedelgrado,Heath[Hea07]senalaque“Diofanto

solamentereconoceunvalorde x quesatisfacelaecuaci´on; as ´ ı,silapotenciaespar, ´ elsolamenteda(comoresultado)el valorpositivo,puestoqueunvalornegativo perse erauna cosaque ´ elnoconceb´ıa”.

Probablementeparezcaunaobviedadqueparaconcebirun n ´ umeronegativonecesitamosconcebirelceronosolamente comos ´ ımbolopararepresentarelvalorposicionaldeund´ıgito enunaescrituranum´ericasinocomounn´umerosusceptible deoperarseconlosn´umerosdelsistemaqueyautiliz´abamos.

Alrededordelano500DC,elastr´onomoindioAryabhatasepropusodesarrollarunamaneraconcisadealmacenar n ´ umerosgrandes,diceRobertKaplanensumaravillosolibro TheNothingThatIs.ANaturalHistoryofZero [Kap99]. Susistemautilizabalasnuevevocalesdels´anscritoparalas posicionesdelosnueved´ıgitosposiblesenunn´umero.Pero, senalaKaplan,siendoastr´onomo,Aryabhatanecesitabaescribirn´umerosdem´asdenueveposicionesdecimales,loquelo llev´oaduplicarsusistemaa18posicionessinqueelceroestuvieraincluidoensusistema,aunqueelmismoAryabhata explicaraque“Lasnuevevocalesseempleanendosnueves delugares”yemplearalapalabra‘kha’parareferirsealespacioentredosposicionesdecimales;esapalabraser´ıaunade lasm´ascom´unmenteutilizadas,posteriormente,porlosmatem´aticosindiosparareferirsealcero.

ParaelsigloVIIDC,Brahmaguptaten´ıayaunaconcepci´ondelcero,alqueserefer´ıaconpalabrasequivalentesa ‘espacio’(kha)o‘vac´ıo’ypon´ıaunpuntosobrelosn´umeros quedeb´ıansersustra´ıdos.Hacia1150Bhaskarautilizabapequenosc ´ ırculos,adem´asdepuntos,sobrelossustraendos.El mismoBhaskara,retomandoalgunasideasdeBrahmagupta, estableci´oque“negativotomadodecifra(cero)seconvierte enpositivo;yafirmativo,seconvierteennegativo;negativo, menoscifra,esnegativo;positivoespositivo;cifra,nada”.Sin embargo,diceGlaeser,“lasobrasindiasdela ´ epocanoson m ´ asquecoleccionesdesentenciasacompa˜nadasdeunejemplodeaplicaci´onnum´erica.Peronosepreocupanporexplicar ah´ıporqu´e“lonegativomultiplicadoporlonegativodaafirmativo”.Esdecir,elconceptoden´umeronegativotodav´ıano exist´ıa.

Glaeser[Gla81b]refierelasdificultadesquemuchosdelos matem´aticosm´asnotablesexperimentabanantelaideadeincluirlascantidadesnegativasenelsistemaden´umeros.De Sim´onStevin(1540-1620)diceque,aunquemanifiestaque “nohayn´umerosabsurdos,irracionales,irregulares,inexplicablesosordos(losencontradosalolargodeldesarrollodel ´ algebraquehoyllamamossuperior,fundamentalmente),sino quehayenellostalexcelenciayconcordanciaquetenemos materiaparameditarnocheyd´ıaensuadmirableperfecci´on”, eln´umeronegativoaisladofaltaensulista.Nodicenadade suderechoalaexistenciaat´ıtulodes´ımbolodecantidad.

Lasra´ıces“falsas”deunaecuaci´onser´ıanevitadaspor matem´aticosdelatalladeFermatyDescartes,porejemplo,aunquecomienzanaaparecercomoresultadosdec´alculoscient´ıficosapartirdelsigloXVII.Perolasexplicaciones pedag´ogicassobrelosn´umerosnegativossedanent´erminos deresultadosdeunasustracci´on,aumentosydisminuciones,

deudasyganancias,etc.

Laobrapedag´ogicadeEuler(1707-1783),dequiennadie pondr´ıaendudasucapacidadytalentomatem´atico,esreveladora.EnelCap´ıtuloIIIdesus ElementosdeAlgebra [Eul] argumentaapartirdelainterpretaci´ondelosnegativoscomo deudas,considerandoquelamultiplicaci´ondecantidadescon signoesconmutativa,yrazonaporeliminaci´ondiciendoque, habiendoconsideradosolamenten´umerospositivoshastaese punto,nopuedehaberdudadequelosproductosquehemos vistosurgirsontambi´enpositivos: +a por +b debedarnecesariamente +ab.Perodebemosexaminarporseparadoqu´e producir´ıanlasmultiplicacionesde +a por b,yde a por b

32.Comencemospormultiplicar a por3o+3.Ahora puestoque a debeserconsideradocomounadeuda,esevidentequesitomamosesadeudatresveces,debevolversetres vecesm ´ asgrande,yconsecuentementeelproductorequerido es 3a.As´ı,simultiplicamos a por +b,obtenemos ba, o,loqueeslomismo, ab.Deaqu´ıconcluimos,quesiuna cantidadpositivasemultiplicaporunacantidadnegativa,el productodebesernegativo;ylareglaesque+por+hace+o m ´ as,yalcontrario+por-,o-por+da-,omenos.

33.Quedaporresolverelcasoenque-semultiplicapor -;o,porejemplo, a por b.Esevidente,aprimeravista, mirandolasletras,queelproductoser´a ab;peroesdudoso sidebeponersedelantedelproductoelsigno+oelsigno-; todoloquesabemosesquedebeserunouotrodeesossignos. Ahoradigoquenopuedeserelsigno-porque a por +b da ab,y a por b nopuedeproducirelmismoresultadoque a por +b;sinoquedebeproducirelcontrario,estoes, +ab; consecuentemente,tenemoslasiguienteregla:-multiplicado por-produce+,enlamismamaneraque+multiplicadopor +.

LoqueestosignificaesqueinclusoEulernoten´ıaunamejorjustificaci´ondelaregladelossignos.M´asa´un,aldeclararqueunn ´ umeronegativoserepresentaporunaletraprecedidadelsigno-(esdecir, a ser ´ ıasiemprenegativo),Euler muestradificultadesparacomprenderlaunificaci´ondelarectanum´erica.

Otromatem´aticoilustre,contempor´aneodeEuler,Jean LeRondd’Almbert(1717-1783)escribeparalaEnciclopedia(Encyclop´edie,oudictionnaireraisonn´edessciences, desartsetdesm´etiers,elnombrecompletodelaobra,de laquefuedirectorjuntoconDiderot,fuepublicadaentre 1751y1772)unart´ıculotituladoN´egatif,quetalvezes eltextom´asreveladordelpensamientoconfusosobrelos n ´ umerosnegativosenlasegundamitaddelsigloXVIII.LisaHefendehel-Hebeker[HH91]haceunabuenarecapitulaci´on sobrelosobst´aculosenlaconcepci´ondelosn´umerosnegativos,encontradosen ´ esteyotrosdocumentos,ysusefectos sobrequienespretend´ıanadentrarseenelconocimientode estosentesfant´asticos–comoenlanotableexperienciade Sthendal,descritaensuautobiograf´ıa–.Aqu´ıcitamosalgunos delosrazonamientosded’Alembert,extraidosdesuat´ıculo N´egatifs:

Lascantidadesnegativassonlocontariodelaspositivas:

dondeterminalopositivo,lonegativocomienza.

Decirquelacantidadnegativaest´am´asabajodelanada, esplantearunacosaquenosepuedeconcebir.

Sedeberecalcarquelascantidadesquesellamannegativasyquesevenfalsamentecomodebajodelcero, sonmuyamenudorepresentadasporcantidadesreales, comoenlaGeometr´ıaendondelasl´ıneasnegativasno difierendelaspositivasm´asqueporsusituaci´onconrespectodealgunal´ıneaconunpuntocom´un.

Elsigno queseencuentraantesdeunacantidadsirve paraenderezarycorregirunerrorquesehahechoenla hip´otesis.

Nohayentonces,realyabsolutamente,cantidadnegativa aislada:perosidigoqueunhombrehadadoaotros3 escudos,esoquieredecir,enlenguajeinteligible,quele haquitado3escudos.

Lainfluenciadelpensamientosobrelosn´umerosnegativos,externadosypublicadospormatem´aticosdelatallade Euleryd’Alembert,durar´ıatodav´ıaunsiglo.

En1815Augustin-LouisCauchy(1789-1857)fueadmitidocomoprofesordela ´ EcolePolytechniquedondepropuso cambiosenlaestructuradeloscursosdean´alisismatem´atico, paraelprimeranodeestudios,ydemec´anicaparaelsegundo ano.ElCursodean´alisis,comoeracostumbre,comenzar´ıa conunasecci´onsobrean´alisisalgebraico.Estasecci´oninicialintrodujotresnovedades,presentadascomounidadesdel curso:

“Expresionesimaginarias”,paraserense˜nadaantesde queseintrodujeranelteoremadeDeMoivreylaexponencialimaginaria;

Relativaaladiferenciaentrefuncionescontinuasyfuncionesdiscontinuas;untemaque,aparentemente,estaba totalmentedescuidadoenelprogramatradicional;

Referentealasnormasquerigenlaconvergenciadeseries.

En1821publicasucursosobrean´alisisestableciendo,en losPreliminares[Bra09],susconcepcionessobrelanaturalezadelosn´umeros:

Siempretomamoselsignificadodelosn´umerosenel sentidoqueseusaenaritm´etica,dondelosn´umerossurgendelamedidaabsolutadelasmagnitudes,ysoloaplicaremoselt´erminocantidadesacantidadesrealespositivasonegativas,esdeciran´umerosprecedidosporlos signos + o

Sinembargo,anadequeelsignodelascantidadesesasimiladoaunestadosimbolizadoporunadjetivo:magnitudes querepresentanagrandamientosvanrepresentadasporn´umerosprecedidosdelsigno +,ylasmagnitudesquedebenservirdedisminucionesporn´umerosprecedidosdelsigno

Alolargodedosp´aginasutilizaesamet´aforaparajustificar

laspropiedadesaditivasdelosn´umerosnegativos.Luego,sin m ´ as,dejadeladolamet´aforaparadarunaformadogm´atica delamultiplicaci´on,sinpreocuparseporlacomprensi´onde lasreglas:

En ´ algebra,usamosletraspararepresentarcantidadesy n ´ umeros.Puestoqueescostumbreclasificarlosn´umeros a comocantidadespositivas,podemosdenotarlacantidadpositivaquetienecomovalornum´ericoeln´umero A por +A o simplementepor A,mientrasquelacantidadnegativaopuestasedenotapor A.Asimismo,cuandolaletra a representa unacantidad,seacostumbraaconsiderarlasdosexpresiones a y +a comosin´onimos,ydenotarpor a lacantidadquees opuestaa +a.Estoscomentariosbastanparaestablecerloque llamamoslaregladelossignos

Enunciaas´ıunprimerteoremaenlaNotaI,queenrealidad eselprimerodelosap´endicesalfinaldesulibro:

Teorema4.1. Elproductodedossignossimilaresessiempre +,yelproductodedossignosopuestosessiempre-.

Lasreticenciasenlasconsideracionesdelosn´umeroscon signosever´anreflejadaseneltratamientodelosn´umeros complejosqueesunodelostemasintroducidosensucurso.CauchycomienzaeldesarrollodelCap´ıtulo7desulibro 1,“Sobrelasexpresionesimaginariasysusm´odulos”,declarandoque

Enan´alisis,llamamos expresi´onsimb´olica os ´ ımboloatodacombinaci´ondesignosalgebraicosquenosignificannada pors ´ ımismosoalosqueatribuimosunvalordiferentedelque naturalmentedeber´ıantener.Asimismo,llamamosecuaciones simb´olicasatodasaquellasque,tomandolasletrasylasinterpretacionesseg´unlasconvencionesgeneralmenteestablecidas,soninexactasonotienensentido,perodelascualespodemosdeducirresultadosexactosmodificandoyalterandolas ecuacionesmismasoloss´ımbolosquelascomponen,seg´un reglasfijas.Elusodeexpresionessimb´olicasoecuacioneses amenudounmedioparasimplificarlosc´alculosydeescribirenformaabreviadaresultadosqueparecenbastantecomplicados.Entreesasexpresionessimb´olicasoecuacionesque sondealgunaimportanciaenelan´alisis,convienedistinguir sobretodolasquellamamosimaginarias.Vamosamostrar c ´ omopodemosdarlesunbuenuso.

Inmediatamente,procedeaplantearlasidentidadestrigonom ´ etricasparaelsenoyelcosenodelasumadedos ´ angulos yaconsiderarelproductodelasexpresiones

cos(a)+ √ 1sin(a) y cos(b)+ √ 1sin(b)

“Comosi √ 1fueraunacantidadrealcuyocuadradoes iguala-1”.

Losn´umeroscomplejoshicieronsuaparici´onformalen el Artismagnae,sivederegulisalgebraicis (1545)deCardano(1501-1576),enelprocesoderesolverecuacionesc´ubicas[Car93].Sigloymediodespu´es,en1702,Bernoulliinvestigabaelprocesodeintegraci´onaplicadoalosrec´ıprocosde cuadr´aticas,locualnopresentabaproblemasi,alaplicarel

1Op.Cit.P´ags.138-139

m ´ etododeintegraci´onporfraccionesparciales,lacuadr´atica encuesti´onten´ıara´ıcesreales.Pero¿ysinofueraelcaso?

¿C´omopuedeintegrarseelrec´ıprocode x2 + 1,porejemplo?, planteaStewart[Ste07].

Bernoulliadmit´ıaunaanalog´ıaentrelosn´umerosreales yloscomplejos,as´ıcomolaexistenciadeloslogaritmosde losn´umeroscomplejos,graciasaunprincipiodepermanenciaestablecidoporAlbertGirard(1595-1632)seg´unelcual lasidentidadesobtenidasparalosn´umerosrealessontambi´en v ´ alidascuandosetrataden´umeroscomplejos.Estaconfianza ensuexistencialehab´ıapermitidollegararesultadostannotablescomoelestablecimientodeque Log(i)= 1 2 π i[Par82].

Sinembargo,estosc´alculosllevabanimpl´ıcitoslacreenciaenlaexistenciadeunafunci´onun´ıvocadefinidaparatodo n ´ umerocomplejo z nonulo,yconlasmismaspropiedadesde lafunci´onlogar´ıtmicadevalorreal.Peroeneldesarrollode laintegraci´ondefraccionesracionalessedebendeconsiderar loslogaritmosden´umerosrealesnegativos;mantenerlaunivocidaddelafunci´onconduceaunaseriedecontradicciones mayores.

5.Logaritmosden ´ umerosnegativos.

Lacontroversiaprovocadaporlascontradiccionesentorno deloslogaritmosden´umerosnegativoscomienzaentreelpropioBernoulliyLeibniz;elprimeroargumentabaqueelvalordeb´ıaserreal,mientrasqueelsegundoinsist´ıaenqueera complejo.Aladiscusi´onsesumaEuler,quienmuestraque,de hecho,lafunci´onesmultivaluada,ydavaloresexpl´ıcitosque resultandelosc´alculos;finalmenteseincorporad’Alembert ycomienzaunadisputaconEulersobreeltema.

Ensudiscusi´on,partiendodeldebateentreBernoulliy Leibniz,Eulerdiceque,loquepasaesque“sesuponeordinariamentequeacadan´umerosolocorrespondeun ´ unico logaritmoy,porpocoquesereflexione,seencontrar´aquetodaslasdificultadesycontradiccionessolamentesubsistenen tantoquesesupongaqueacadan´umerosolamentecorrespondeun ´ unicologaritmo”[Par82].

Stewarthaceunas´ıntesisdelosc´alculosdeEulerpara mostrarquelafunci´onlogaritmo,cuandoseaplicaacantidadesnegativas,esmultivaluada[Ste07].

Ensuart´ıculo“Logarithme”[Ale],enla Enciclopedia, despu´esdeexponerlateor´ıaconocidaenesemomentosobreloslogaritmosylasfuncionesdeunavariablereal, d’Alembertconcluyeconestep´arrafo:

Noustermineronscelui-ciparunequestionquia ´ et´efort agit´eeentreMM.L´eibnitz&Bernoulli.Leslogarithmesdes quantit´esn´egativessont-ilsr´eelsouimaginaires?M.L´eibnitz tenoitpourlesecond,M.Bernoullipourlepremier.Onpeut voirleslettresqu’ilss’´ecrivoient ` acesujet;ellessontimprim´eesdanslecommerciumepistolicumdecesdeuxgrands hommes,publi´een1745 ` aLausanne.J’eusautrefois(en1747 &1748)unecontroverseparlettresaveclec´elebreM.Eulersurlemˆemesujet;ilsoutenoitl’opiniondeM.L´eibnitz, &moicelledeM.Bernoulli.Cettecontroverseaoccasion´e unsavantm´emoiredeM.Euler,imprim´edanslevolumede

l’acad´emiedeBerlinpourl’ann´ee1709.Depuiscetems,M. deFoncenexatrait´elamˆemematieredanslepremiervolumedesm´emoiresdel’acad´emiedeTurin,&sed´eclarepour lesentimentdeM.Eulerqu’ilappuiedenouvellespreuves. J’aicompos´esurcesujetun ´ ecritdanslequeljemed´eclareaucontrairepourl’opiniondeM.Bernoulli.Commecet ´ ecritauraprobablementvulejouravantlapublicationdu pr ´ esentarticle,jenel’insereraipointici,&jemecontenteraid’yrenvoyermeslecteurs,ainsiqu’aux ´ ecritsdontj’ai parl´e;ilsytrouveronttouteslesraisonsqu’onpeutapporterpour&contreleslogarithmesimagi-nairesdesquantit´es n ´ egatives.Jemebornerai ` adireici,1°.Quesionprendentre deuxnombresr´eels&positifs,parexemple1&2,unemoyenneproportionnelle,cettemoyennepro-portionnellesera aussi-bien-2que+2,&qu’ainsilelogarithmede-2&celui de2serontlemˆeme,savoirlog.2/2.2°.Quesidansl’´equationy = cx &lelogarithmique(VoyezLOGARITHMIQUE& EXPONENTIEL)onfaitx = frac12,onaura,&qu’ainsile logarithmiqueauradesordonn´eesn´egatives&positives,en telnombrequ’onvoudra ` al’infini;d’o`uils’ensuitqueles logarithmesdecesordonn´eesserontlesmˆemes,c’est-`a-dire desquantit´esr´eelles.3°.Acesraisonsajoutezcellequisetire delaquadraturedel’hyperboleentresesasymptotes,queM. Bernoulliadonn´eelepremier,&quej’aifortifi´eepardenouvellespreuves;ajoutezenfinbeaucoupd’autresraisonsque l’onpeutliredansmonm´emoire,ainsiquemesr´eponses.

Enelfondo,d’Alembertrechazalaideadeunafunci´onde variablerealmultivaluada.Estanoci´on,apenaspresentadapor Euler,representaunarupturaconlaconstrucci´onmatem´atica deLeibnizyconlosdesarrollosdeBernoulli;alaceptarla, adem´as,hayqueecharportierraelfamoso“principiodepermanencia”deGirard.

Ensuargumentaci´on,d’Alembertdiceque“mepareceque M.Eulernorespondedeunamanerasatisfactoriaalaobjeci´onsacadadeque2log(+a)= 2log( a).Estaf´ormulasignifica(o,sino,hayquerenunciaratodaslasdenominaciones anal´ıticas)queeldobledellogaritmode +a esigualaldoble dellogaritmode a,ynoquelasumadedoslogaritmosdiferentesde +a esigualalasumadedoslogaritmosdiferentes de a”.ApesardelaclaridaddeEuler,d’Alembertnorenunciaasusentimientodelcar´acterrealy ´ unicodeloslogaritmos den´umerosnegativosybuscareafirmarsussentimientosapoyandolasideasdeBernoulli.

Lasdificultadesqued’Alembertmuestraalolargodesus desarrollosreposanenlanecesidaddemantenerprincipios hastaentoncesnocontradichos,losquehab´ıanpermitidoel desarrollodelc´alculodevariablesrealeshastaesemomento, sobreloscualessehab´ıaconstruidotambi´enunabuenaparte delateor´ıadelosn´umeroscomplejosycuyapuestaenduda significabaunaverdaderaruptura.

Agradecimientos.

MiagradecimientoalaFundaci´onUniversitariaKonrad LorenzyaJohnA.Arredondoporsumuyatentayespecial invitaci´onacolaborarenesten´umerodelPask´ınMatem´atico.

Ungranproyectoenapoyodeladivulgaci´ondelasmatem´aticas.

Referencias.

[Bac67] GastonBachelard, LaFormationdel’espritscientifique,Librairie philosophiqueJ.Vrin.,Par´ıs,1967.

[Ale56] JeanleRondd’Alembert, OpusculesMath´ematiques,TomePremier.,Par´ıs,1756.

[Neu69] ONeugebauer, TheExactSciencesinAntiquity,DoverPublications.,NewYork,1969.

[Ita84] JeanItard, Essaisd’histoiredesmath´ematiques,LibrairiescientifiqueettechniqueAlbertBlanchard.,Par´ıs,1984.

[Ste07] IanStewart, TheStoryofMathematics:FromBabyloneanNumeralstoChaosTheory,Quercus,2007.

[Gla81a] GGlaeser, Epist´emologiedesnombresrelatifs,RecherchesEnDidactiqueDesMath´ematiques,1981.

[Gla81b] , Epistemolog´ıadelosn´umerosrelativos,CINVESTAV., MexicoD.F.,1981.

[Par81] BlancaParra, An´alisisdeprocesodeuncursodeformaci´onparaprofesoresdelnivelmediob´asico,CINVESTAV.,MexicoD.F., 1981.

[Par85] , R´esultatsd’uneobservationsurlanotiondevariablechez les ´ el`evesmexicainsdudeuxi`emecycledusecondaireetdel’´ecole normalesup´erieuredeMexicoetd’une ´ etudecritiquedesmanuels, UniversidaddeParis.,Parıs,1985.

[VE59] PaulVerEecke, Diophanted”Alexandrie.Lessixlivresarithmetiquesetlelivredesnombrespolygones,Librairiescientifiqueet techniqueAlbertBlanchard,1959.

[Hea07] ThomasHeath, DiophantosofAlexandria;aStudyintheHistory ofGreekAlgebra,KessingerPublishing’sLegacyReprintSeries, 2007.

[Kap99] RobertKaplan, TheNothingThatIs.ANaturalHistoryofZero, TheNothingThatIs.ANaturalHistoryofZero,1999.

[Eul] LeonhardEuler, ElementsofAlgebra,KindleEdition.

[HH91] LisaHefendehl-Hebeker, NegativeNumbers:ObstaclesinTheir EvolutionfromIntuitivetoIntellectualConstructs,FortheLearningofMathematics,1991.

[Bra09] RobertBradley, Cauchy’sCoursd’analyse.AnannotatedTranslation,Springer,2009.

[Car93] GirolamoCardano, ArsMagna,or,TheRulesofAlgebra,Dover, 1993.

[Par82] BlancaParra, D’Alembertyloslogaritmosden´umerosnegativos, CINVESTAV.,M´exicoD.F.,1982.

[Ale] JeanleRondd’Alembert, Logarithme,UniversityofChicago.

Acercadelautor:BlancaMargaritaParraMosquedatieneunaLicenciaturaenF´ısicayMatem´aticasporelInstituto Polit´ecnicoNacionaldeM´exico,unamaestr´ıaenCienciasen Matem´aticaEducativaporelCINVESTAV,M´exico,yundoctoradoenDid´acticadelasMatem´aticasporlaentoncesFacultaddeCienciasdePar´ıs,ahoraUniversidadPar´ıs-Diderot.Su inter´essecentraeneldesarrollodepropuestasdid´acticassobrematem´aticas,orientadasaalumnosydocentesdetodoslos niveles,ejecutadasatrav´esdecursosytalleresyeldesarrollo demateriales.Pasatiempos:leer,conversar,cocinar.

Lapoci´oninfinita

Dominador,opresorypoderoso.As´ıeraZen´on,elreyde Eufros,unaantiguacivilizaci´onqueseven´ıadesarrollando entrelosr´ıosTigrisy ´ Eufrates.Apesardeello,Zen´onsab´ıa perfectamentec´omoocultarsuverdaderaidentidadparaconseguirhalagosporpartedetodoelmundo.

-EselejemploquehayquedaranuestrosdescendientesproclamabaelpresidentedelConsejodeAncianosenunode susdiscursos.

-Estaninteligenteyoptimista,seguramentehar´adeEufroslacivilizaci´onm´asimportantedetodas-comentabanlos comerciantesdelaciudad.

Peround´ıa,Uruk,elhermanodeZen´on,lleg´oalaciudad despu´esdehaberterminadosulargatraves´ıadedosa˜nospor elMediterr´aneo.Amedidaqueseibaacercandoalacomunidad,escuchabac´omotodoshablabandelreydeEufros-no ten´ıaniideadequi´ensetrataba-ycuandolleg´oalcentrode laciudad,qued´oalucinadoalobservarunaestatuade5metros dealtoquerepresentabaasuhermano.

-¡Conqueestefullerologr´oelreinadodeEufros!–Exclam´oUruk,sindisimularsuhielantesemejantenoticia.

YesqueUruktalvezerael ´ unicoservivientequeconoc´ıa aZen´onensutotalidad;fuetestigodetodaslasestafascon lasqueselucrabaensujuventud;erauntramposoquesiemprelograbaloquedeseabaapuntademanipulaci´on,ycomo siempre,sab´ıaexactamentec´omodeb´ıaactuarparalimpiarsu nombreantelasociedad.Endefinitiva,unimpostor.

Sinembargo,hab´ıaunsecretoquenadiem´asqueUruk sab´ıa.Suhermanohab´ıaasesinadoalantiguoreydeEufros paraquedarseconelreinadoenlaspr´oximasvotacionesyas´ı, formarladictaduram´asgrandedetodaslascivilizacionesvecinas.Zen´onamenaz´oaUrukconasesinarlosiestosal´ıaala luz,porloqueUrukdecidi´oolvidarsedesuhermano,olvidarsedeEufros-quequed´oamanosdelosescribasysacerdotes, mientrassedecid´ıaelfuturodelacivilizaci´on-yemprender unlargoviajequeterminar´ıatray´endolodenuevoalaciudad, puessusconstantesinsomniosacausadelaculpabilidadque sent´ıaporsucobard´ıadenohaberreveladolaverdadanteel pueblo,nolodejabantranquilonochetrasnoche.

-¡Tevasaarrepentirdehaberregresadoamipueblo!–pens ´ oZen´on,quienacababadeenterarsedelregresodesu hermanoalaciudad.

Atemorizadoeimpaciente,emprendi´ounaafanada b´usquedaporencontraralmejorhechicerodelpueblo,con elfindecomprarlelaf´ormuladeunapoci´ontalque,ald´arselaaUruk,estemurierainmediatamenteyconello,conseguir

quesusecretomuerieracon ´ el.As´ıqueconvoc´oatodoslos hechicerosdelpuebloalpalacioofreciendounagransuma dedineroparaaquelqueleconvencieradequeten´ıaelm´as potenteyefectivoveneno.

Despu´esdeunaagotantejornadaescuchandoacadauno deloshechicerosqueseibanacercandoalpalacio,entr´oLexi,unhechiceroreconocidoporcamuflarseencuerposajenos yconfundiralosciudadanossobresuverdaderaidentidad. Elhechiceronotuvoqueesforzarsemuchoparaconvencera Zen´ondeque ´ eleraelmejorhechicerodelpuebloydequesu poci´onnotendr´ıafalloalguno,as´ıqueprocedieronareunirseenlassalasarcanasdelpalacio,endondeLexirecibi´olas bolsasdedineroprometidasporZen´on.

-Prepararlapoci´onrequieredemuchaprecauci´on,una gotam´asounagotamenosqueviertasenelrecipiente,estropear ´ aelvenenoyyanofuncionar´a.Lom´asimportanteesel pesofinaldelapoci´on,1gramo-dijoelhechicero.

-¡Peroyosoyunrey,nouncient´ıfico,ninadasimilar! ¿C´omopretendequeyohagaeso?¿Acasonopodr´ıausted ayudarmeaprepararla?

-Nofuncionar´ıa.Yosoyhechicero,nuestrasenerg´ıasson muydiferentes,yaunqueparezcaincre´ıble,esteesunodelos ingredientesm´asimportantesenelproceso.Elvenenosolo servir´asiespreparadoporlapersonaquelovaautilizar.

Entonceselreycomenz´oaescucharconatenci´onlaspalabrasdelhechicero.

-Lamitaddelapoci´onestar´aconformadaporelsudorde lapalmeraSag´u.Luegotomar´asvariosliriosylosprensar´as, deall´ıtomar´as ´ unicamente0.25gramosdeesel´ıquido.Mientrassemezclanambassustancias,raspar´asunhabadecastor hastaobtenerunaoctavapartedetodoelveneno.

-¡Espere!–grit´oelrey-¿Yend´ondesesuponequehallar´e cadaunaesasplantastanex´oticasqueustedest´amencionando?

-Nosepreocupe,yohecultivadocadaunadeestasplantas porcientosdea˜nos,solotienequeiramijard´ınytomarlas quenecesite,lerespondi´oLexi.

-Est´abien,contin´ue.

-El6.25%delapoci´onlacompondr´ancristalesdeSchefflera.Aqu´ıdeber´apercatarsedequeloscristalesquetome seandecolorvioleta.Sitomacristalesdeotrocolor,har´aque lapoci´onnoseaefectiva.Recuerde,tododependedeusted. Finalmente,1/32gramoscorresponder´analn´ectardelasfloresdelAzafr´anCrocoylamitaddelpesodeestepertenecer´a aln´ectardelasfloresdelaKalanchoe.Todoslosingredien-

tesdebenmezclarsemuybienysabr´aqueest´alistocuandola mezclasetorneverdosa.

Unavezelhechicerotermin´odedarlasindicaciones,el reysedirigi´odirectoaljard´ınparacomenzarconsupreparaci´on.Sigui´otodaslasindicacionesdadasporelhechicero,iba pesandocadaunodelosingredientesparaasegurarsusproporcionesyunavezterminadalapoci´on,lacoloc´oencimade lab´asculagramera,pero,observ´oalgoextra˜no,elpesodela poci´onnoeradeungramo,talcomoselohab´ıaindicadoel hechicero,puesfaltabanaproximadamente0.015gramos.EntoncesZen´onvolvi´oaprepararlapoci´on,asegur´andoseuna vezm ´ asdeseguirtodaslasindicacionesdelhechicero,gramoporgramo,gotaporgota.Sinembargo,cuandovolvi´oa pesarlapoci´on,not´oquefaltabanlosmismos0.015gramos; aunas ´ ı,Zen´on,frustradoyalgoairado,pens´oquenoser´ıatan grave,pueseraunacantidaddemasiadoinsignificantecomo paraquearruinasesuplan.

Ycomplacidoelrey,combin´osupoci´onconunaarom´atica dehierbasfinas,provenientesdelasplantacionesm´asex´oticasqueseencontrabanplantadascercaalr´ıoTigris,ylaraz´on eraqueestaeralabebidaquetantoleencantabaasuhermano Uruk.Luego,contact´oaunodesusamigosterratenientesparaquefuese ´ elquienlebrindaseesabebidaaUruk,yas´ıponerfinasusecretom´aspreciado.Seescondi´odetr´asdeunas columnasdelaplazaparaobservardeunavezportodas,el momentoenelquesuhermanotomaralabebidaysucuerpo sefueraconsumiendolentamenteporelvenenodecadauna delasplantasqueconformaronlapoci´on.

Seacerc´oelterratenienteaUrukydespu´esdeunabuena charla,leofreci´olabebida,quien,alsentirelolordelasfinas hierbas,nodud´ounsegundoentomarunsorbo.Zen´onestaba afanosodeverasuhermanoyacermuertoenelsuelodela plaza,sinembargo,pasarondosminutosynohab´ıasucedido nada,suhermanoluc´ıacomosihubiesetomadounsorbode agua.

Furiosoycol´erico,sefueZen´onasupalacioeintentandobuscarunarespuestaalporqu´edelfracasodelapoci´on,se top´oconunodesusamigoshechicerosquehab´ıadecididorechazarylecont´oexactamentetodaslasindicacionesqueLexi lehab´ıadado,intentandoencontrarunarespuestaalfracaso delapoci´on.

-Paraempezar,yonoconozcomuybienaLexi,paramuchoshechiceros ´ elesnuevoaqu´ı,peroamigom´ıo,creoque ustedhasidotimado-ledijosuamigoelhechicero.

-¡Demonios!Esoesimposible,laestafaest´apenalizada enEufros.

-Pues,senor,estuverevisandolarecetadelvenenoque elhechiceroLexilepropusoyesasplantassolosepueden usarenunasproporcionesexactas,sivasautilizarotraplanta venenosa,suproporci´ondebeserlamitaddela ´ ultimaque utilizaste;creoquelefaltaunapartealapoci´on.

-¿Aqu´eserefiere?

-Hayalgoextra˜noconlasproporcionesdelosingredientes –ledijoelhechicero.

Ysac´osupapiroparaexplicarlealrey.

-S´ı,Lexiledijoquetodalapoci´onpesar´ıaungramo,¿no?

Entonceshagamosdecuentaqueesegramoest´arepresentado enestecuadradodeproporciones1cmx1cm–ydibuj´oel siguientecuadradoenelpapiro

-As´ı,todoslosingredientesquetienelapoci´onestar´an contenidosenelcuadrado.Veamos,dicequelamitaddela poci´onestar´aconformadaporelsudordelapalmeraSag´u, esolopodr´ıamosverdelasiguientemanera-ytraz´ounadiagonaldelcuadradopararepresentarestaproporci´on:

-Ahoradicequelosliriosrepresentan0.25,esdecir 1 4 de lapoci´on–ypint´oesacantidadas´ı:

-Sigamos;laoctavaparteesdelhabadecastor,esdecir–yvolvi´oatrazarotral´ıneaqueilustrar´ıalaproporci´ondeeste ingrediente:

Elhechicerosequed´opensandoporunosminutosycontinu ´ o.

-Nos´esiyasediocuenta–ledijoelhechicero.

-Creoques´ı,parecieraquelacantidaddelsiguienteingredienteeslamitaddelacantidaddelingredienteanterior.

-¡Nolopudodecirmejor!Noteustedquelacantidaddel siguienteingrediente,loscristalesdeSchefflera,corresponde aladieciseisavapartedelapoci´on,esdecirlamitaddela cantidaddelhabadecastor.Yas´ısucesivamente.

-Bueno,perosigosincomprendercu´aleslaideadeeste patr´on-respondi´oelrey

-Sisumamostodaslasproporcionesdelosingredientes–yescribi´oenelpapirolasumaquedeb´ıacalcularse:

-Esasumaesiguala 63 64 ,aproximadamente0.98gramos, poresaraz ´ onfall´oelveneno.Siseguimoscompletandonuestrocuadradoconlasproporciones,estosever´aas´ı–yelhechicerolemostr´osusnuevostrazos:

Contin´uohablandoelhechicero.

-Lexius´ounadelasseriesgeom´etricasm´asperversasdel mundodelahechicer´ıa,paradarlelapoci´on.

-¿Perversas?

-As´ıes,puesla ´ unicaformaparaobtenerungramodel venenoessumandounacantidadinfinitadeproporciones. Zenonseencontrabaanonadado.Estaeslaprimeravezque algolesal´ıamal.

-Porcierto,senor,nuncamecoment´oparaqu´enecesitaba eseveneno,¿aqui´endeseaasesinar?-lepregunt´oelhechicero.

-¿S´ılogravisualizarquehayunespacioquenosehalogradorellenar?Esorepresentaesaaproximaci´ondelos0.015 gramosquelehac´ıanfaltacuandopesabaelveneno.Noes queustedhubieseseguidomallasindicaciones,esquenose lasdieroncompletas–continuabaexplicandoelhechicero

Elreynopod´ıacreerloqueestabaviendo,peroseleocurri´ounaidea.

-Seguramentefaltaunoodosingredientesenlapoci´on paracompletarloquehacefalta,ycomoyadescubrimosel patr´on,talvezsiterminamoslapoci´onconotrasplantasvenenosasquedeprontoustedhayautilizado,podr´ıaservirel veneno-propusoelreyZen´on.

-Amigo,losiento,peroesaideaestotalmenteabsurda. Puedonotarqueustednohacomprendidoelpatr´onensutotalidad.Larealidadesquenuncavaatenerelvenenocompletoporquelefaltaninfinitosingredientesparalograrquepese exactamenteungramo.

-¡Absurdaessuideadequefaltaninfinitosingredientes! –lerespondi´oZen´onalhechicero.

-Volvamosalasumadelasproporciones–elhechicerole mostr´olasumaquehab´ıaescritoensupapiro–,siemprevaa haberunanuevafracci´onqueseincorporaalasumaynohay formadequeseacabe,notequeeldenominadordelafracci´on escadavezmayor,notienel´ımite–yvolvi´oaescribirsobre elpapiro

-Esonoesdesuincumbencia,nolotrajeaqu´ıparaqueme vengaacuestionar-ydespidi´oalhechiceroapresuradamente, temiendodequepudiesesospecharsusverdaderasintenciones.

¿Peroend´ondepodr´ıaestarLexi?,secuestionabaelfrustradoreymientrasibacaminandoasupalacio.Alparecernadieloconoc´ıa,¿ser´aquesefuedelpueblo?,¿porqu´eloengan ´ odeesamanera?Ymuchasotraspreguntasrondabanen lacabezadelrey.

LaverdadesqueLexia´unsegu´ıaenelpueblo,sinembargo,sol´ıacamuflarseenotroscuerposyconfundiralenemigo, unhechizoquenadiepudosiquieraigualar.YesqueLexi, noeraning´unhechicero,comohac´ıacreeralosdem´as;erael diosdelasabidur´ıa,Thot,ydesdequeayud´oalhijodeOsiris areconstruirlamayorpartedesuojo,piezaapieza-despu´es dehaberbatalladocontrasut´ıoSeth-Thotdedic´oelrestode suvidasalvarlasvidasdeaquellosqueeranamenazadospor suscodiciososycelososfamiliares.Enestaocasi´on,ibaen buscadeUruk,aquienobligar´ıaasalirdelpuebloparanunca m ´ asvolver.

FIN.

LeidyCatherinneS´anchezAscanio leidyc.sancheza@konradlorenz.edu.co Acercadelautor:Leidyesingenieraindustrialymatem´atica.Esunaamantedelasnovelaspoliciacasydelmundo profesionaldelcrimen;desdeesteanoseest´apreparandopara serboxeadoraprofesional,dondeesperahacersudebutantes dequefinaliceelano.

UnaturistavisitaBogot´aconelobjetivodeconocerelcentrodelaciudad.Despu´esdeleereninternetsobrelaciudad, cre ´ olasiguientelistadelugaresquequer´ıaconocer,eincluy´o eltiempoquedeseabapermanecerencadauno:

LaPlazadeBol´ıvar(45minutos).

ElMuseodelOro(6horas).

LaterrazadelaTorreColpatria(30minutos).

LaplazadelaPerseverancia(2horas).

Laexposici´ondelMuseoBotero(6horas).

LaBibliotecaLuis ´ AngelArango(7horas).

ElcerrodeMonserrate(5horas).

ElMuseoNacional(6horas).

ElMuseodeArteModerno(150minutos).

Laturistasehospedar´aenelHotelTequendama,ubicado enlaCarrera10#26-21.Estandoah´ı,planeainiciarsurecorridoaloslugaresdeinter´esalas8:00a.m.Despu´es,almorzar ´ atodoslosd´ıasentrelas12:00yla1:00p.m.,continuar´a surecorridoyregresar´aalhotelm´aximoalas5:00p.m.Dado quelaturistarealizar´atodoslosrecorridoscaminando,consideraremosquesedesplazar´aaunavelocidadconstantede4.5 km/hora.

Conelobjetivodeconocertodoslugaresenelmenortiempoposible,¿qu´elugaresdeber´aconocercadad´ıayenqu´e orden?

Pararesolverelproblematengaencuentalasiguienteinformaci´on:

•Elobjetivoconsisteendisenaruncronogramadetallado queminimicelom´asposibleeltiempoquelaturistaest´apor fueradelhotel.

•Paralosrecorridospodr´autilizarcualquiercaminoentrelacarrerad´ecima(sobrelaqueest´aubicadoelhotel)yla carrerasegundaeste(sobrelaqueest´aubicadalaentradaal cerrodeMonserrate),as´ıcomoentrelascalles31(sobrela queest´aubicadalaPlazadelaPerseverancia)ylacalle11 (sobrelaqueest´aubicadaeliniciodelaPlazadeBol´ıvar).

•Utilicelaaplicaci´onGoogleMapsparadise˜narelmapa quelaturistautilizar´a.

•Nosedebenconsiderartiemposdedesplazamientoparaalmorzarnibuscarrestaurantes,yaquelaturistaalmorzar´a siempreenalgunadelasatraccionestur´ısticas.Almorzarse puedehacerantes,duranteodespu´esdeunavisita.Encualquiercaso,esahoradealmuerzonosedebeincluircomoel tiempodevisitaaunsitio.

•Laturistapuederegresaralhotelencualquiermomento deld´ıa,peronuncadespu´esdelas5pm.Poreso,elcronogramadetalladodesuvisitadebetambi´enconsiderarlostiempos quetomanlosdesplazamientos.

•Lostiemposdecadadesplazamientosedebenredondear hac´ıaabajo.Porejemplo,siirdelpuntoAalpuntoBtoma3 minutosy45segundos,entoncesseconsideraqueeltiempo deldesplazamientoesde3minutos.

•Cadalugardebevisitarseenunsolod´ıaydemaneracontinua.Porejemplo,silavisitaalsitioAesde5horas,laturista nopuedepasar3horasund´ıayluego2horasotrod´ıa.Elalmuerzo,sinembargo,puedeinterrumpirlavisitayesel ´ unico casoenelcuallavisitaaunsitionoescontinua.

BasesdelConcurso:

Elegibilidad:

Estudiantesmenoresde18anos,decualquiernacionalidad ypertenecientesauncolegiocolombiano.

Duraci´on:

Elconcursofinalizaunanodespu´esdelapublicaci´ondel Pask´ınquepresentaelproblema,ohastaquehayaunapersonaganadora.

DocumentoSoluci´on:

Lasoluci´ondebepresentarsedemaneraindividualenun documentoformal,escritoenespanol,enelqueseexplique demaneradetalladalasoluci´onalproblemaplanteado.

Laprimerap´aginadeldocumentodebecontenerporlomenoslossiguientesseiselementos:

(1)Elnombrecompletodelapersonaparticipante.

(2)Elcursodelapersonaparticipante.

(3)Laedaddelapersonaparticipante.

(4)Elnombrecompletodelcolegiodelapersona.

(5)Municipioociudadderesidencia.

(6)Tel´efonoycorreoelectr´onicodecontacto.

Elcuerpodeldocumento,quesigueaestaprimerap´agina, puedetenercualquierextensi´onparainformarsobrelasoluci´on.

Losylasparticipantespuedenusarlibros,blogs,computadores,internet,programascomputacionales,peronopuedenconsultarointeractuarconningunaotrapersonadurante lasoluci´on.Ningunacontribuci´onpuedeserhechaporotra personaquenosealapersonaqueenv´ıalasoluci´on.

Aunquelosproblemasestar´andestinadosaunan´alisis te´orico,losparticipantespuedenrealizarexperimentosrelevantesypresentarlosdatosresultantesensutrabajosilodesean.

Encasodequeseutilicen,cadasoluci´ondebeincluiruna listadetodaslasreferencias.

Lassolucionespuedenusaralgoritmosyherramientas computacionalesexistentes(queincluyennosoloherramientasdisponiblesgratuitamente,sinotambi´enherramientasdentrodesistemascomoMatlaboMathematica),siempreque semencionenycitencorrectamenteylosm´etodosseexpliquenclaramenteenlasoluci´ondelproblema.Cualquierc´odigodeprogramaci´on,siseescribi´ouno,debeincluirsecomo unap ´ endicedelasoluci´on.Sinembargo,todoslosalgoritmos, m ´ etodosyresultadosdebenexplicarseeneltextoprincipaldel documentopararecibirconsideraci´ondurantelaevaluaci´on.

Lassolucionesenviadaspuedenincluirecuaciones,gr´aficos,figurasytablas.Cadasoluci´ondebeincluircomom´ınimo:

(1)Unacortaintroducci´ondelproblema,talcomolointerpret´olapersonaparticipante.

(2)Unaexplicaci´ondetodaslassuposicionesyaproximacionesrealizadas.

(3)Justificaci´ondetodoeltrabajorealizado.

(4)Unabrevediscusi´ondelasfortalezasydebilidadesdel enfoqueadoptado.

Env´ıodelasoluci´on:

Lassolucionespuedenenviarsecomoarchivos.pdf,.odf, .docodocx.Cadaparticipantedebeenviarsusoluci´onpor correoelectr´onicoapaskin@konradlorenz.edu.coylosdocumentosdebenrecibirseantesdequefinaliceelconcurso.Si lasoluci´onnoserecibeporcorreoelectr´onicoduranteladuraci´ondelconcurso,lasoluci´onnoser´aconsiderada.Eldocumentocompletodebeincluirsecomounarchivoadjuntoal correoelectr´onico.Noenv´ıeunenlacealdocumentoenun servicioenlanubecomoGoogleDocs,Dropbox,etc.Una vezrecibidalasoluci´onselenotificar´alarecepci´onenunplazomenoracincod´ıash´abiles.SiUd.norecibeconfirmaci´on, comun ´ ıqueseconeleditordelarevista.

Resultados:

Todasoluci´onrecibidaseir´aevaluandoenordendellegadahastalafinalizaci´ondelconcurso.Cuandounasoluci´onsea correcta,laoelparticipanteser´ainvitadaoinvitadoaexponer yjustificardemaneraverbalsusoluci´ondemaneraremota sincr´onicautilizandoalgunaplataformavirtualcomoTeams, ZoomoGoogleMeets.

Premiaci´on:

-Laprimerasoluci´oncorrectaser´apublicadaenunasiguienteedici´ondelPask´ın.Ser´aunaversi´onsimplificadade lasoluci´onrealizadaencolaboraci´onconelcomit´eeditorial, queincluir´aunacortaresenadelapersonaganadora.

-Certificado.Cadapersonaqueparticipeypresenteuna soluci´oncorrectarecibir´auncertificado.Elcertificadoseenviar´aporcorreoelectr´onicoaladirecci´onutilizadaparael env ´ ıodelasoluci´on.Esperevariassemanasdespu´esdeenviar susoluci´onpararecibirsucertificado.

-Lapersonaqueenvi´elaprimerasoluci´oncorrectarecibir´a unbonovirtualderegaloporunvalorde 500.000COP (quinientosmilpesoscolombianos.).Lapersonaganadorapuedeescogerelestablecimientocomercialquedesee,siemprey cuandoofrezcabonoselectr´onicosyelcomit´eeditorialpueda adquirirlos.

Política Editorial

El Paskín Matemático es una producción del Programa de Matemáticas de la Fundación Universitaria Konrad Lorenz. Está abierto a todos y todas. Si tienes interés en escribir un artículo con cualquier tipo de contenido matemático, reseñar a un personaje, comentar un problema o tienes comentarios sobre nuestra publicación, envía un mensaje a paskin@konradlorenz.edu.co

El Programa de Matemáticas de la Fundación Universitaria Konrad Lorenz fue creado en 1998. Conoce más acerca de nuestro programa en nuestra página institucional

https://www.konradlorenz.edu.co/programas/matematicas/

Bogotá, Colombia. 2023

PASK ´ INMATEM ´ ATICO Volumen5,No.2,2023

Contenido

• JuanPabloHern´andezRodas Elproblemadelasochoreinas.................................................................1

• ReynaldoCastaneiraRam´ırez ¿Cicloide,braquist´ocronaotaut´ocrona?.................................................7

• C´esarAugustoLaraSantana

Ventajasydesventajasdeutilizarlosmodelosdefunci´ondetransferencia.........................................................................................................14

• WalterGarz´onGuti´errez

Representaci´ongr´aficayalgebraicadelasecuacioneslinealesysus propiedadesenel sistemaseno................................................................21

• BlancaMargaritaParraMosqueda

Obst´aculosenlaconcepci´ondelosn´umerosnegativosydesuslogaritmos.......................................................................................................33

• LeidyCatherinneS´anchezAscanio MateKuento..........................................................................................39

• JohnA.ArredondoyAlejandroC´ardenas Pask´ınChallenge..................................................................................42

MATEMÁTICO

Enmuchasocasioneslal´ıneam´ascortaentredos verdadesdeldominiorealpasaatrav´esdeldominio complejo.

JacquesHadamard