PRÉ-CÁLCULO SEM MISTÉRIOS
Teoria e prática passo a passo
H´elio Vinicius Moreno Tozatti
Raimundo de Ara´ujo Bastos J´unior
PR ´ E-C ´ ALCULO SEM MIST ´ ERIOS
Teoria e pr´atica passo a passo
Volume 1
Acesse o gabarito aqui:

Pr´e-c´alculosemmist´erios:teoriaepr´aticapassoapasso,volume1 © 2024H´elioViniciusMorenoTozzatieRaimundodeAra´ujoBastosJ´unior EditoraEdgardBl¨ucherLtda.
Publisher EdgardBl¨ucher
Editor EduardoBl¨ucher
Coordenadoreditorial RafaelFulanetti
Coordena¸c˜aodeprodu¸c˜ao AndressaLira
Produ¸c˜aoeditorial KedmaMarques
Diagrama¸c˜ao Osautores
Revis˜aodetexto Maur´ıcioKatayama
Capa La´ercioFlenic Imagemdacapa iStockphoto
EditoraBlucher
RuaPedrosoAlvarenga,1245,4º andar
CEP04531-934–S˜aoPaulo–SP–Brasil Tel.:55113078-5366 contato@blucher.com.br www.blucher.com.br
SegundooNovoAcordoOrtogr´afico,conforme6.ed.do Vocabul´arioOrtogr´aficoda L´ınguaPortuguesa,AcademiaBrasileiradeLetras,mar¸code2012. ´ Eproibidaareprodu¸c˜aototalouparcialporquaisquermeiossemautoriza¸c˜aoescritadaeditora.Todos osdireitosreservadospelaEditoraEdgardBl¨ucherLtda.
DadosInternacionaisdeCataloga¸c˜aonaPublica¸c˜ao(CIP)
Ang´elicaIlacquaCRB-8/7057
Tozatti,H´elioViniciusMoreno.Pr´e-c´alculosemmist´erios,volume1:teoriaepr´atica passoapasso/H´elioViniciusMorenoTozatti,RaimundodeAra´ujoBastosJ´unior.S˜aoPaulo:Blucher,2024.226p.
ISBN978-85-212-2213-2(impresso)
ISBN978-85-212-2214-9(eletrˆonico)
1.Pr´e-c´alculoI.T´ıtuloII.BastosJ´unior,RaimundodeAra´ujo 24-4230CDD512
´ Indicesparacat´alogosistem´atico:1.Pr´e-c´alculo
Conte´udo
1Introdu¸c˜ao`ateoriadosconjuntos11
1.1Conceitoenota¸c˜ao.......................11
1.2Conjuntosuniverso,unit´arioevazio..............12
1.3Rela¸c˜aodepertinˆencia.....................13
1.4Rela¸c˜aodeinclus˜ao(subconjuntos)..............14
1.4.1Rela¸c˜aodeigualdadedeconjuntos...........15
1.4.2Subconjuntodefinidoporumapropriedade......15
1.4.3Subconjuntopr´oprio..................16 1.5Opera¸c˜oescomconjuntos....................17
1.5.1Uni˜aoeintersec¸c˜ao...................17
1.5.2Conjuntodiferen¸ca...................22
1.5.3Conjuntocomplementar................24 1.5.4LeisdeDeMorgan...................25
1.5.5DiagramasdeVenn-Euler...............27
1.5.6N´umerodeelementosdeumconjuntofinito.....29
1.6Conjuntodaspartesefam´ıliade conjuntos............................35
2Oconjuntodosn´umerosreais49
2.1Contextohist´orico.......................49
2.2Opera¸c˜oesaritm´eticas.....................52
2.3Propriedadesaritm´eticas....................55
2.4Desigualdades..........................61
2.5Potˆencias............................63
2.5.1Potˆenciadeexpoenteinteiron˜aonegativo......63
2.5.2Potˆenciadeexpoenteinteironegativo.........66
2.5.3Radicia¸c˜ao........................66
2.5.4Potˆenciadeexpoenteracional.............69
2.5.5Potˆenciadeexpoentereal...............70
2.6Inequa¸c˜oes,intervalosem´odulo................71
2.6.1Inequa¸c˜oes........................71
2.6.2Intervalos........................72
2.6.3M´odulo(valorabsoluto)................74
2.7Compara¸c˜oesentrepotˆencias..................77
2.8Problemasresolvidos......................79
2.9Exerc´ıciospropostos......................82
3Fun¸c˜oeselementares87 3.1Contextohist´orico.......................87 3.2Dom´ınioeimagemdeumafun¸c˜ao...............89
3.2.1Dom´ıniodeumafun¸c˜ao................89
3.2.2Opera¸c˜oesalg´ebricascomfun¸c˜oes...........91
3.3Gr´aficodeumafun¸c˜ao.....................93
3.4Fun¸c˜oesconstantes.......................95
3.5Fun¸c˜oeslineares.........................95 3.6Fun¸c˜oeslinearesafins......................96
3.6.1Exerc´ıciospropostos..................107
3.7Fun¸c˜oesquadr´aticas......................110
3.7.1Exerc´ıciospropostos..................126
3.8Fun¸c˜oespotˆencias........................130
3.8.1Problemasresolvidos..................134
3.8.2Exerc´ıciospropostos..................139
3.9Fun¸c˜oespolinomiais.......................143
3.9.1Fun¸c˜oesracionais....................144
3.9.2Divis˜aodefun¸c˜oespolinomiais.............145
3.9.3Sinaldasfun¸c˜oespolinomiais.............152
3.9.4Fun¸c˜oesalg´ebricaselementares............156
3.9.5Opera¸c˜oescomfun¸c˜oesracionaisealg´ebricaselementares...........................156
4
3.9.6Problemasresolvidos..................163
3.9.7Exerc´ıciospropostos..................167
´ Algebradasfun¸c˜oes173
4.1Opera¸c˜oesdasfun¸c˜oes.....................173
4.1.1Exerc´ıciospropostos..................177
4.2Paridadedasfun¸c˜oes......................178
4.2.1Fun¸c˜oespares......................178
4.2.2Fun¸c˜oes´ımpares....................180
4.2.3Exerc´ıciospropostos..................183
4.3Composi¸c˜aodasfun¸c˜oes....................185
4.3.1Exerc´ıciospropostos..................189
4.4Fun¸c˜oesmon´otonas.......................191
4.4.1Exerc´ıciospropostos..................195
4.5Fun¸c˜aoinversa.........................198
4.5.1Exerc´ıciospropostos..................205
5Apˆendice209
5.1F´ormuladeinterpola¸c˜aodeLagrange.............209
5.1.1Exerc´ıciospropostos..................213
5.2Fun¸c˜oesdefinidasporpartes..................214
5.2.1Exerc´ıciospropostos..................217
5.3BinˆomiodeNewton.......................219
5.4Tabeladef´ormulasdesomaediferen¸cadepotˆencia.....220
Bibliografia221
Cap´ıtulo1
Introdu¸c˜ao`ateoriadosconjuntos
1.1 Conceitoenota¸c˜ao
Oconceitoprimitivodeconjuntossurgiupelanecessidadedacontagem deobjetossobreumacorrespondˆenciaentrecadaanimal(carneiros/porcos/ bodes)dentrodeumcurralemumamarcaoupedra,usandoumregistrador (tally ),ouseja,abasedateoriadeconjuntosveiodaforma¸c˜aodecole¸c˜oes deanimais,pessoas,n´umerosouobjetosdequalquernatureza.Oprimeiro registrodeobjetomatem´aticomaisantigoconhecido´eumossodelobo querepresentaumtallyencontradonaRep´ublicaTchecaesculpidocom entalhesh´amaisde30milanos.Arepresenta¸c˜aodeumconjunto´efeita porletrasmai´usculasdo alfabetolatino (A,B,C,D,E,...).Osobjetos queconstituemumconjuntos˜aochamadosde elementosdoconjunto eusualmentes˜aorepresentadosporletrasmin´usculado alfabetolatino. Umconjuntoconsisteemescreverseuselementosentrechavesseparados porv´ırgula;chamamosissode formatabular doconjunto.
Considerandoasletrasvogais,podemosdeterminaroconjuntodasvogaisdaseguinteforma:
V = {a,e,i,o,u}.
Tamb´emdefinimosumconjuntodeterminandoaspropriedadesqueseus elementosprecisamsatisfazer,porexemplo:
P = {x | x ´eumn´umeropar} (P ´eoconjuntodoselementos x,taisque x ´eumn´umeropar.)
I = {x | x ´eumn´umero´ımpar}. (I ´eoconjuntodoselementos x,taisque x ´eumn´umero´ımpar.)
Chamamosesseformatode formadeconstru¸c˜aodeumconjunto Observequealinhavertical“|”´elida“talque”.
Cabeobservarqueaformaliza¸c˜aodessateoriafoiiniciadaapenasem 1874porGeorgFerdinandLudwigPhilippCantor1 (1845-1918).Juntocom otrabalhodeRichardDedekind2 (1831-1916)eGiuseppePeano3 (18581932),elesmostraramqueosistemadosn´umerosnaturaispodeserdefinido emtermosdeconceitosdateoriadosconjuntos.



GeorgCantor RichardDedekind GiuseppePeano
N˜aoiremosadotaraquiumaaxiomatiza¸c˜aodateoriadosconjuntospara n˜aoentrarmosemantinomiasouc´ırculosviciososexistentesnateoriageral dosconjuntos.AteoriadosconjuntosdeCantor,queestudaremos,´eregida peloseguinteconceito:“Porconjunto,entendemoscomosendoumacole¸c˜ao deobjetosdefinidosedistintosdenossaintui¸c˜aooudenossopensamento,e essesobjetoss˜aochamadosdeelementosdoconjunto”.Comessaimposi¸c˜ao nano¸c˜aodeconjuntoouprinc´ıpiodoc´ırculovicioso,evitamosantinomias conhecidasnateoriageraldosconjuntos.
1.2 Conjuntosuniverso,unit´arioevazio
Paraaconstru¸c˜aodealgumateoriamatem´atica,inicialmentetemosque determinaroconjuntoondeser˜aodesenvolvidostaisestudos.Chamamos esseconjuntode conjuntouniverso,queusualmentedenotamospelaletra
1 https://mathshistory.st-andrews.ac.uk/Biographies/Cantor
2 https://mathshistory.st-andrews.ac.uk/Biographies/Dedekind
3 https://mathshistory.st-andrews.ac.uk/Biographies/Peano
U .Fixadoumconjuntouniverso,ent˜aodefinimososconjuntoscompropriedadesexistentesrelacionadascomtalconjuntouniverso.Porexemplo,os n´umerosreaisformamoconjuntouniversonateoriadec´alculodiferencial eintegralemumavari´avel.
Al´emdoconjuntouniverso,existemoutrosconjuntosquelevamnomes espec´ıficos.Porexemplo,umconjuntoformadoapenasporumelemento ´echamadode conjuntounit´ario.Umconjuntoquen˜aopossuinenhum elemento´echamadode conjuntovazio (ou conjuntonulo).
Nota¸c˜ao: ∅ ou {}
.
Exemplo1.1. Dadooconjuntouniverso U = {1, 2, 3, 4, 5}, A = {3} ´e umconjuntounit´arioe B = {x | n´umerosmaioresque 5} = ∅ = {} ´eum conjuntovazio.
Observa¸c˜ao1.1. Oconjunto A = {∅} n˜aorepresentaoconjuntovazio, poisoconjunto A indicaquepossuisomentecomoelementooconjunto vazio,ouseja,oconjunto A ´eumconjuntounit´ario.
1.3 Rela¸c˜aodepertinˆencia
Indicamosarela¸c˜aodepertinˆenciapeloss´ımbolos ∈ (pertence)e ̸∈ (n˜ao pertence).Essarela¸c˜aoseestabeleceentreumelementoeumconjunto. Quandoumelemento a pertenceaoconjunto B,indicamospor a ∈ B Usualmente,nal´ogicamatem´atica(etamb´emnotrˆansito),utilizamosa barra“/”paradenotaranega¸c˜aodeums´ımbolo.Denotamosqueum elemento x n˜aopertenceaumconjunto B por x/ ∈ B.Paradeterminarmos seumelementopertenceoun˜aoaumdeterminadoconjunto,verificamos seeleest´aoun˜aorepresentadonoconjunto.Os´ımbolo ∈ foiestabelecido pelomatem´aticoGiuseppePeanoe´ealetragrega´epsilon.
Exemplo1.2. Dadooconjunto B = {1, 3,a,d},temosque 3 ∈ B; 2 / ∈ B; c/ ∈ B e d ∈ B.
Cap´ıtulo2
Oconjuntodosn´umerosreais
N˜aosabemosespecificamenteemque´epoca,civiliza¸c˜aooulocalsurgiu oconceitoden´umero. ´ Ecomumassociarmosahist´oriadosn´umeros`a necessidadedecontagem,conectadosaumacole¸c˜aodeobjetosconcretos. Osurgimentodoconceitoabstratoden´umero´ecomumenteassociadocom ainven¸c˜aodaescritaedatadoaproximadamentenoquartomilˆenioantesde Cristo.Oconjuntonum´ericoqueestudaremosaolongodolivro´eoconjunto dos n´umerosreais
2.1 Contextohist´orico
Inicialmente,representamosos n´umerosnaturais fixandoumaretaordenada,naqualmarcamosumpontonaretaeassociamosaessepontoo n´umero0(ouorigem).Fixandoumamedidaunit´aria,marcamos`adireita don´umerozeropontosequidistantes,conformeafiguraaseguir:
Cadan´umeronatural´eassociadoaumpontoemumaretaordenada.A nota¸c˜aousualparaoconjuntodosn´umerosnaturais´e:
Os n´umerosnegativos foramregistradospelaprimeiravezem628d.C. naobra BrhmasphudaSidd’hanta pelomatem´aticoindianoBrahmagupta1
1 https://mathshistory.st-andrews.ac.uk/Projects/Pearce/chapter-11/
Oconjuntodosn´umerosreais
(598-668),naturaldeUjjain,na ´ IndiaCentral.Omatem´aticoFran¸cois Vi`ete2 (1540-1603)introduziuoss´ımbolosatuaisde+, e=pararepresentarasopera¸c˜oesdeadi¸c˜ao,subtra¸c˜aoeigualdade,respectivamente. Noentanto,osmatem´aticoslevarammuitotempoparacompreenderprecisamenteosn´umerosnegativos.Nos´eculoXVIII,omatem´aticoColin Maclaurin3 (1698-1746)tratoudasdefini¸c˜oesdequantidadesnegativasem seulivro Tratadoda´algebra (1748),esuaconstru¸c˜aorigorosaapareceuno s´eculoXIXnostrabalhosdosmatem´aticosHermannHankel4 (1839-1873), OttoStolz5 (1842-1905),JulesTannery(1848-1910)6 eRichardDedekind7 (1831-1916).


ColinMaclaurin

Seguindoomesmoracioc´ınioutilizadopararepresentarosn´umerosnaturais,os n´umerosinteiros podemserrepresentadosemumaretaordenada,naqualon´umerozero´eopontodeorigem. ` Adireitadozeros˜ao representadososn´umerospositivose`aesquerdaosn´umerosnegativos. Anota¸c˜aoconvencionalparaoconjuntodosn´umerosinteiros´edada por:
= {··· , 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4
Aletra Z derivadapalavraalem˜a Zahlen,quesignifica“n´umeros”.Os n´umerospositivospodemserescritoscomousemosinalde+nafrente.
2 https://mathshistory.st-andrews.ac.uk/Biographies/Viete/
3 https://mathshistory.st-andrews.ac.uk/Biographies/Maclaurin/
4 https://mathshistory.st-andrews.ac.uk/Biographies/Hankel/
5 https://mathshistory.st-andrews.ac.uk/Biographies/Stolz/
6 https://mathshistory.st-andrews.ac.uk/Biographies/Tannery_Jules/
7 https://mathshistory.st-andrews.ac.uk/Biographies/Dedekind/
Pr´e-c´alculosemmist´erios:teoriaepr´aticapassoapasso,vol.1
Comessaconstru¸c˜ao,podemosafirmarqueoconjuntodosn´umerosnaturais N ´eumsubconjuntodosn´umerosinteiros,ouseja, N ⊂ Z.
Oconjuntodos n´umerosracionais ´erepresentadopor Q econsisteem todososn´umerosdaforma a b ,onde a e b s˜aon´umerosinteirose b ´ediferente dezero.Emoutraspalavras,temosque
Q = x | x = a b ,a,b ∈ Z eb =0
Essadefini¸c˜aonospermiteentenderqueosn´umerosracionaisincluem tantoosn´umerosinteirosquantoasfra¸c˜oes,bemcomosuasrepresenta¸c˜oes decimaisperi´odicasoufinitas.
Osprimeirosregistrosdos n´umerosracionais surgiram pormeiodoseg´ıpciosnoImp´erio Antigo(2700-2200a.C.).Naquela ´epoca,oseg´ıpciostinhamano¸c˜aode fra¸c˜aosomentepararegistrarpartes daunidade.Pararepresentaras fra¸c˜oes
1 2 , 1 4 , 1 8 , 1 16 , 1 32 e 1 64 ,utilizavam nota¸c˜oesespeciaisrepresentadaspor hier´oglifosconhecidoscomo“Olhode H´orus”ou“OlhodeWadjet”.
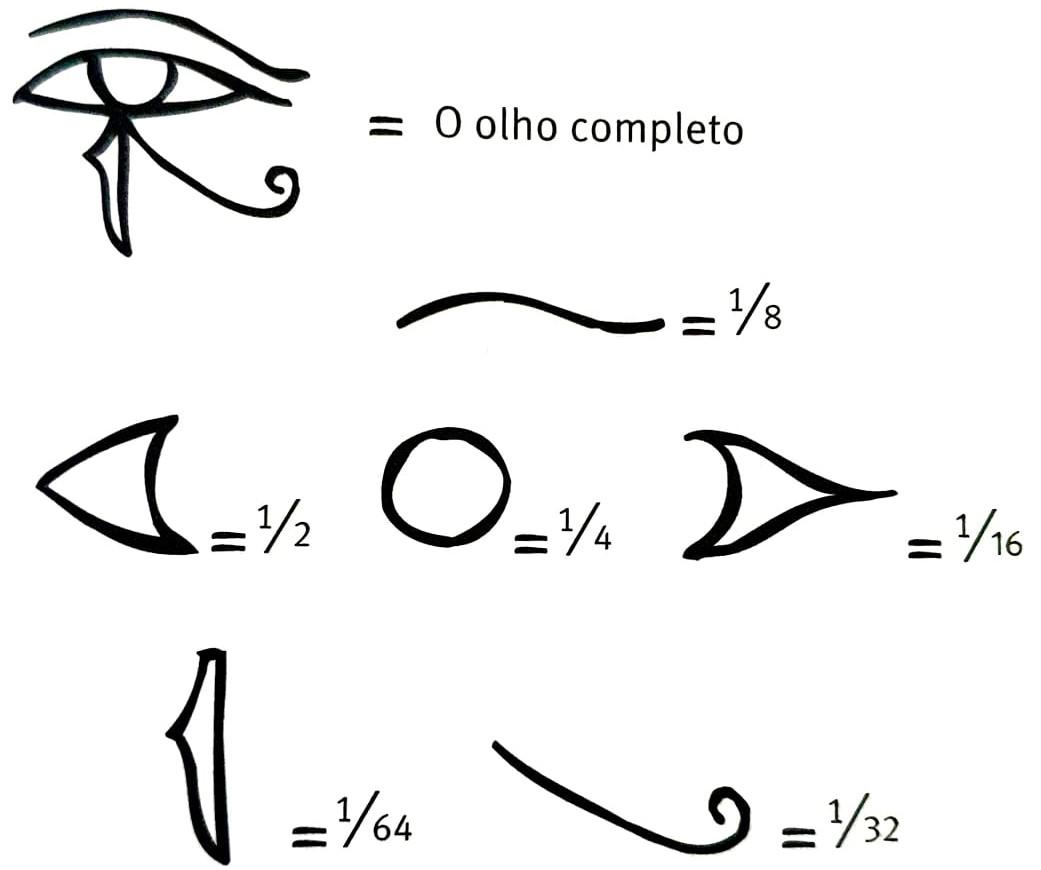
OlhodeH´orus
Aformacomodefinimosoconjuntodosn´umerosracionaisnospermite representarqualquern´umerointeiro a ∈ Z como a 1 .Portanto,consideramos queoconjuntodosn´umerosinteiros Z ´eumsubconjuntodosn´umerosracionais.Comooconjuntodosn´umerosnaturais´eumsubconjuntodosinteiros, podemosafirmarqueoconjuntodosn´umerosnaturais´eumsubconjunto dosn´umerosracionais,ouseja, N ⊂ Z ⊂ Q.
Ateoriados n´umerosirracionais foidesenvolvidaporEudoxode Cnido,ummatem´aticogregoqueviveuporvoltade370a.C.Asuaideiaera representarqualquergrandeza,sejaracionalouirracional,comoaraz˜aode doiscomprimentos.Entretanto,segundoumalenda,umdosseguidoresde Pit´agoras,HipasodeMetaponto,foioprimeiroaafirmarqueadiagonalde umquadradounit´ario´eumn´umeroirracional,ouseja,quearaizquadrada
Cap´ıtulo3 Fun¸c˜oeselementares
Naliteraturamatem´atica,asfun¸c˜oesconstantes,lineares,quadr´aticas, polinomiais,racionais,alg´ebricasedefinidasporpartess˜aocomumentechamadasde fun¸c˜oeselementares.Essenome´edevidoaoseuusofrequente emaplica¸c˜oese`asua“facilidade”nomanuseiodaspropriedadesdelimites, derivadaseintegrais.
3.1 Contextohist´orico


GottfriedW.Leibniz JohannBernoulli
Oestudodefun¸c˜oes´eamplamenteestabelecidona´areadamatem´atica. Oconceitodefun¸c˜ao´eumguiaefetivonodesenvolvimentodamatem´atica e´efundamentalnoscursosiniciaisdas´areasdeexatas.Aorigemdapalavrafun¸c˜aovemdolatim functus,eelafoiusadainicialmenteporGottfried
WilhelmLeibniz1 (1646-1716)emumacartaenviadaaJohannBernoulli2 (1667-1748)noanode1697.Essacartapodeserencontradano Conmercium PhilosophicumetMathematicumLeibnizetBernoulli,vol.I,1745.Emmeadosde1718,JohannBernoulliconsiderouqueumafun¸c˜ao´eumaexpress˜ao formadaporumavari´avelealgumasconstantes.Poucotempodepois,Euler conceituouqueumafun¸c˜aopodeserexpressaporumaequa¸c˜aoouf´ormula envolvendovari´aveiseconstantes.Essaideiacorrespondeaoconceitode fun¸c˜aousualmenteensinadonoscursoselementaresdematem´atica.


Esseconceitosemanteveinalteradoat´equeJosephFourier3 (1768-1830) considerouemsuaspesquisassobreapropaga¸c˜aodocalorasfun¸c˜oeschamadasdes´eriestrigonom´etricas.LejeuneDirichlet4 (1805-1859),emuma tentativadedarumadefini¸c˜aoamplaosuficiente,chegounaseguinteformula¸c˜ao:“Umavari´avel´eums´ımboloquerepresentaqualquerumdos elementosdeumconjuntoden´umeros.Seduasvari´aveis x e y est˜aorelacionadasdemaneiraque,sempreseatribuiumvalora x,corresponde automaticamente,poralgumaleiouregra,umvalora y,ent˜aosedizque y ´eumafun¸c˜ao(un´ıvoca)de x.Avari´avel`aqualseatribuemvalores´echamadade vari´avelindependente,eavari´avel y cujosvaloresdependemdos valoresde x ´echamadade vari´aveldependente.Osvaloresposs´ıveisonde x podemassumirconstituemocampodedefini¸c˜aodafun¸c˜ao.Osvalores assumidospor y constituemocampodevaloresdafun¸c˜ao”.
1 https://mathshistory.st-andrews.ac.uk/Biographies/Leibniz/
2 https://mathshistory.st-andrews.ac.uk/Biographies/Bernoulli_Johann/
3 https://mathshistory.st-andrews.ac.uk/Biographies/Fourier/
4 https://mathshistory.st-andrews.ac.uk/Biographies/Dirichlet/
Usualmenteusamosestadefini¸c˜aodeDirichletnocursodec´alculodiferencialeintegraldeumavari´avelreal.
3.2 Dom´ınioeimagemdeumafun¸c˜ao
Defini¸c˜ao3.1. Dados A e B subconjuntosde R.Uma fun¸c˜ao f : A → B ´eumaregraqueassociaacadaelementode A um´unicoelementode B.O conjunto A ´echamadode dom´ıniode f e´edenotadopor D(f ),enquanto B ´echamadode contradom´ınio(oucampodevalores)de f . ´ E comumsereferira y = f (x),onde x ´ea vari´avelindependente e y ´e a vari´aveldependente.Oelemento f (x) ∈ B ´eo valordafun¸c˜ao f noponto x,oua imagemde x por f .Oconjuntodetodosos valoresassumidospelafun¸c˜ao´edenominadode conjuntoimagemde f , denotadopor Im(f )
Nota¸c˜oes: f : A −→ B x −→ f
3.2.1 Dom´ıniodeumafun¸c˜ao
Naan´alisematem´atica,´ecomumtrabalharcomfun¸c˜oescujosdom´ınios s˜aosubconjuntosespec´ıficosdosn´umerosreais.Noentanto,emalgumas situa¸c˜oes,odom´ıniodeumadadafun¸c˜aopoden˜aoserexplicitado.Nesses casos,convencionamosqueodom´ıniodafun¸c˜ao´eoconjuntodetodosos n´umerosreais x,paraosquais´eposs´ıvelcalcular f (x).Essaconven¸c˜ao´e conhecidacomoo dom´ınionatural dafun¸c˜aoe´eamplamenteutilizada emv´ariosramosdamatem´atica,incluindoan´aliserealec´alculodiferencial eintegral. ´ Eimportanteobservarqueadefini¸c˜aododom´ınionaturalda fun¸c˜aodependedafun¸c˜aoemquest˜aoe,portanto,deveserdeterminada casoacaso.
Exemplo3.1. Afun¸c˜ao f (x)= 1 x ´edefinidacomoaregraqueassociaa cadan´umeroreal x on´umeroreal 1 x .Odom´ıniode f ´eoconjuntodetodos osn´umerosreais x paraosquais´eposs´ıvelcalcular f (x).Observamosque
Cap´ıtulo4
Algebradasfun¸c˜oes
4.1 Opera¸c˜oesdasfun¸c˜oes
Paraumestudomaisqualitativodasfun¸c˜oes,precisamosintroduziralgumasno¸c˜oesassociadasaosgr´aficoseopera¸c˜oesalg´ebricasemtermosdas fun¸c˜oesrelacionadas.Analogamenteaoconjuntodosn´umerosreais,podemosadicionar,subtrair,multiplicaredividirfun¸c˜oes.Porexemplo,dados f e g fun¸c˜oese x ∈ D(f ) ∩ D(g),ent˜ao f (x)e g(x)s˜aon´umerosreais.
Aomultiplic´a-los,obtemosumn´umeroreal f (x) · g(x).Comestaconstru¸c˜ao,definimosumanovafun¸c˜ao h queassociacadan´umero x comum aosdom´ıniosde f e g,aon´umero h(x)= f (x) · g(x).Seguindoomesmo racioc´ınioparatodasasopera¸c˜oesalg´ebricas,temosaseguintedefini¸c˜ao:
Defini¸c˜ao4.1. Sejam f e g fun¸c˜oesonde Dom(f ) ∩ Dom(g) = ∅
(a) A soma de f e g ´eafun¸c˜ao f + g definidapor
(f + g)(x)= f (x)+ g(x).
(b) A subtra¸c˜ao de f e g ´eafun¸c˜ao f g definidapor
(f g)(x)= f (x) g(x).
(c) O produto de f e g ´eafun¸c˜ao f · g definidapor
(f · g)(x)= f (x) · g(x).
´
(d) O quociente de f e g ´eafun¸c˜ao f g definidapor f g (x)= f (x) g(x)
Observa¸c˜ao4.1. Osdom´ıniosdasfun¸c˜oessoma,subtra¸c˜aoeproduto´eo conjunto Dom(f ) ∩ Dom(g) eodom´ıniodafun¸c˜aoquociente´e
D f g = {x ∈ Dom(f ) ∩ Dom(g) | g(x) =0}.
Quandon˜aoespecificado,ficasubentendidoqueocontradom´ıniodasfun¸c˜oes definidasanteriormente´eo“maior”subconjuntodosn´umerosreaisnos quaistaisfun¸c˜oespodemserdefinidas.
Observa¸c˜ao4.2. Se g = k ´eumafun¸c˜aoconstante,ent˜aotemosque (f · g)(x)=(g · f )(x)=(k · f )(x)= k · f (x).
Odom´ıniodafun¸c˜ao k·f coincidecomodom´ıniodafun¸c˜ao f . ´ Ecomum escrevermos (k · f )(x) aoinv´esde (f · k)(x),poisamultiplica¸c˜aodeum n´umeroreal k porumafun¸c˜ao f podeserinterpretadacomooescalonamento verticaldogr´aficodafun¸c˜ao f porumfator k.Ouseja,ovalordafun¸c˜ao f emumponto x ´emultiplicadopor k paraobtermosovalordafun¸c˜ao k · f nomesmoponto x.Essainterpreta¸c˜aofazcomqueaordemdasfun¸c˜oes namultiplica¸c˜aosejamenosrelevantedoqueaordemdosn´umerosreaisna multiplica¸c˜ao.
Exemplo4.1. Sejam f (x)=2x +5 e g(x)= x2 1 Ent˜ao:
(a) Asomade f e g ´edadapor
(f + g)(x)= f (x)+ g(x) =(2x +5)+(x2 1) = x2 +2x +4.
(b) Asubtra¸c˜aode f e g ´edadapor
(f g)(x)= f (x) g(x) =(2x +5) (x2 1) =2x +5 x2 +1 = x2 +2x +6
(c) Oprodutoentre f e g ´edadopor
(f · g)(x)= f (x) · g(x) =(2x +5) · (x2 1) =2x3 2x +5x2 5 =2x3 +5x2 2x 5.
(d) Oquocienteentre f e g ´edadopor f g (x)= f (x) g(x) = (2x +5) (x2 1) ,
sendoqueodom´ıniode f g ´eoconjuntodosn´umerosreaistaisque x2 1 =0,ouseja, Dom f g = R −{±1}.
Exemplo4.2. Dados f (x)= √7 x e g(x)= x 2 1 x ,podemosobservar
que D(f )=(−∞, 7].
Paradeterminarodom´ıniodafun¸c˜ao g,primeiramenteanalisamosos valores x,onde x =1 e x 2 1 x ≥ 0
• Quando x> 2,temosque x 2 > 0 e
Assim,podemosafirmarque x 2 1 x < 0. • Quando x< 1,temosque x 2
Assim,podemosafirmarque x 2 1 x < 0.
Cap´ıtulo5 Apˆendice
5.1 F´ormuladeinterpola¸c˜aodeLagrange
Quandoprecisamosacompanharocrescimentodeumaplantaoudeum animal,´e´utilobtermosumafun¸c˜aoqueforne¸ca,paracadamomento,a alturaoumassaaproximada.A f´ormuladeinterpola¸c˜aodeLagrange ajudaadeterminarumafun¸c˜aopolinomialquefornecetalaproxima¸c˜ao. Issoseguedofatodeque,dados n ≥ 2n´umerosdistintos x1,...,xn e n n´umerosquaisquer a1,...,an,podemosobterumafun¸c˜aopolinomial f ,de graumenorouiguala n 1,talque f (xi)= ai paracada i =1, 2,...,n.

JosephLouisLagrange1 (1736-1813)foiumdosmaioresmatem´aticos dos´eculoXVIII.NascidoemTurim,It´alia,veiodeumafam´ıliaoutrora abastadadeestirpefranco-italianaefoio´unicodeonzefilhosaatingira idadeadulta.EstudouemTurime,aindamuitojovem,tornou-seprofessor
1 https://mathshistory.st-andrews.ac.uk/Biographies/Lagrange/
dematem´aticanaacademiamilitarlocal.OinteressedeLagrangepela matem´aticacome¸couquandoeleleuumac´opiadolivrodeHalley,publicado em1693.Omundodamatem´aticadeveagradeceraopaideLagrangepelos seuspreju´ızosemespecula¸c˜oesfinanceiras,j´aqueLagrangeafirmou:“Seeu fosserico,provavelmenten˜aoteriamededicado`amatem´atica”.
Fun¸c˜oespolinomiaisauxiliares
Dados n pontosdistintos x1,...,xn,´eposs´ıvelconstruirimediatamente umafun¸c˜aopolinomialdegrau n,definidapor:
p(x)=(x x1)(x x2) ... (x xn); essafun¸c˜ao´enulaexatamentenosvalores x1,x2,...,xn.
Suprimindoomonˆomio(x x1)nessafun¸c˜aopolinomial,podemosconstruirafun¸c˜aopolinomial
p1(x)=(x x2)(x x3) ... (x xn),
naqual p1(x1) =0.Analogamente,podemosdefiniroutrasfun¸c˜oespolinomiais pi(x),dadaspor
pi(x)=(x x1) ... (x xi 1)(x xi+1) ... (x xn),
satisfazendo pi(xi) =0e pi(xj )=0paratodo j = i. Apartirdessasfun¸c˜oes polinomiais pi,obtemosfun¸c˜oespolinomiais fi degraumenorouiguala n 1,onde fi(xi)=1e fi(xj )=0paratodo j = i.Maisprecisamente, fi(x)= pi(x) pi(xi) .
Portanto, fi(xj )= pi(xj ) pi(xi) = 1, se i = j 0, se i = j
Explicitamente,asfun¸c˜oes fi s˜aodefinidaspor
fi(x)= (x x1) ··· (x xi 1)(x xi+1) ··· (x xn) (xi x1) ··· (xi xi 1)(xi xi+1) ··· (xi xn) = j=i x xj xi xj ,
sendoqueos´ımbolo j=i ´eumanota¸c˜aocompactaparadenotarumproduto dev´ariostermos.
Afun¸c˜aopolinomialinterpoladordeLagrange
Apartirdasfun¸c˜oespolinomiais fi definidasanteriormente,temoso seguinteresultado.
Teorema5.1. Dados n n´umerosdistintos x1,...,xn e n n´umerosquaisquer a1,...,an,existeumafun¸c˜aopolinomial f ,degraumenorouiguala n 1 talque
f (xi)= ai,i =1, 2,...,n.
Demonstra¸c˜ao:Como fi(xi)=1,para1 ≤ i ≤ n. ´ Eclaroque aifi(xi)= ai, para1 ≤ i ≤ n. Poroutrolado, fi(xj )= aifi(xj )=0para j = i.Assim, afun¸c˜ao
f (x)= a1f1(x)+ a2f2(x)+ ... + anfn(x)= n i=1 ai · j=i x xj xi xj
satisfazacondi¸c˜aodesejada,ouseja, f (xi)= ai para1 ≤ i ≤ n. □
Observa¸c˜ao5.1. Ademonstra¸c˜aobaseia-senaconstru¸c˜aode n fun¸c˜oes polinomiais fi,ondecadaumapossuiapropriedadedeque fi(xj )=0 para j = i e fi(xi)=1.Apartirdessasfun¸c˜oes,podemosobterafun¸c˜ao f comoumacombina¸c˜aolineardasfun¸c˜oes fi comcoeficientes ai.Afun¸c˜ao f ´e,portanto,degraumenorouiguala n 1 esatisfaz f (xi)= ai para i =1, 2,...,n.
Defini¸c˜ao5.1. (Fun¸c˜aopolinomialinterpoladordeLagrange)
Dados n pontosdistintosnoplanocartesiano (x1,a1), (x2,a2),..., (xn,an), a fun¸c˜aopolinomialinterpoladoradeLagrange ´edadapor: f (x)= n i=1 ai · j=i x xj xi xj
Essafun¸c˜ao´eumpolinˆomiodegraunom´aximo n 1 epassaportodos ospontosdados,ouseja, f (xi)= ai para i =1, 2,...,n
Parailustraradefini¸c˜aodeformamaisclara,vamosencontrarexplicitamenteafun¸c˜aopolinomialinterpoladoradeLagrangepara n =2e n =3.
O volume 1 do Pré-cálculo sem mistérios surge como uma solução para superar os obstáculos enfrentados por alunos ingressantes no ensino superior. Este livro foi elaborado para preencher as lacunas frequentemente encontradas nos cursos de cálculo diferencial e integral.
Embasando-se nas dúvidas recorrentes dos estudantes, a obra se aprofunda em temas fundamentais como conjuntos, números e funções. O texto estabelece uma ponte entre exemplos oriundos do ensino médio e tópicos mais avançados, garantindo uma transição harmoniosa e robusta ao ambiente acadêmico. Este é, sem dúvida, um investimento valioso para aqueles que buscam solidificar seus conhecimentos e adentrar com segurança o universo do cálculo.