

PRÉ-CÁLCULO SEM MISTÉRIOS
Teoria e prática passo a passo

H´elio Vinicius Moreno Tozatti
Raimundo de Ara´ujo Bastos J´unior
PR ´ E-C ´ ALCULO SEM MIST ´ ERIOS
Teoria e pr´atica passo a passo
Volume 2
Acesse o gabarito aqui:

Pr´e-c´alculosemmist´erios:teoriaepr´aticapassoapasso,volume2 © 2024H´elioViniciusMorenoTozattieRaimundodeAra´ujoBastosJ´unior EditoraEdgardBl¨ucherLtda.
Publisher EdgardBl¨ucher
Editor EduardoBl¨ucher
Coordenadoreditorial RafaelFulanetti
Coordena¸c˜aodeprodu¸c˜ao AndressaLira
Produ¸c˜aoeditorial KedmaMarques
Diagrama¸c˜ao Osautores
Revis˜aodetexto Maur´ıcioKatayama
Capa La´ercioFlenic Imagemdacapa iStockphoto
EditoraBlucher
RuaPedrosoAlvarenga,1245,4º andar
CEP04531-934–S˜aoPaulo–SP–Brasil Tel.:55113078-5366 contato@blucher.com.br www.blucher.com.br
SegundooNovoAcordoOrtogr´afico,conforme6.ed.do Vocabul´arioOrtogr´aficoda L´ınguaPortuguesa,AcademiaBrasileiradeLetras,mar¸code2012. ´ Eproibidaareprodu¸c˜aototalouparcialporquaisquermeiossemautoriza¸c˜aoescritadaeditora.Todos osdireitosreservadospelaEditoraEdgardBl¨ucherLtda.
DadosInternacionaisdeCataloga¸c˜aonaPublica¸c˜ao(CIP)
Ang´elicaIlacquaCRB-8/7057
Tozatti,H´elioViniciusMoreno.Pr´e-c´alculosemmist´erios,volume2:teoriaepr´atica passoapasso/H´elioViniciusMorenoTozatti,RaimundodeAra´ujoBastosJ´unior.S˜aoPaulo:Blucher,2024. 152p.
ISBN978-85-212-2215-6(impresso)
ISBN978-85-212-2209-5(eletrˆonico)
1.Pr´e-c´alculoI.T´ıtuloII.BastosJ´unior,RaimundodeAra´ujo 24-4231CDD512
´ Indicesparacat´alogosistem´atico:1.Pr´e-c´alculo
Conte´udo
1Fun¸c˜oesexponenciais11
2Fun¸c˜oeslogar´ıtmicas33
5Identidadestrigonom´etricas109 5.1Rela¸c˜oesfundamentaisdatrigonometria...........
5.3Somaesubtra¸c˜aodearcos...................
Cap´ıtulo1 Fun¸c˜oesexponenciais
NascidoemBasileia(Su´ı¸ca),LeonhardEuler1 (1707-1783),filhodeum pastorcalvinistaqueestudoucomJacobBernoulli2 (1655-1705),conseguiu umaindica¸c˜aodeJohannBernoulli3 (1667-1748)paraestudarcomele.Em 1727,Eulerfoiindicadopelosirm˜aosDanielBernoulli4 (1700-1782)eNicolausBernoulli5 (1657-1759)paraaAcademiadeS˜aoPetersburgo,criadapor Pedro,oGrande.Ap´osquatorzeanos,EuleraceitouoconvitedeFrederico, oGrande,parachefiarase¸c˜aodematem´aticadaAcademiadeBerlim,onde permaneceupor25anos.



DurantetodasuaestadianaPr´ussia,Eulerrecebiaumapens˜aoda R´ussiaporcausadoaltoprest´ıgioqueeleadquiriunessepa´ıs.Porisso,
1 https://mathshistory.st-andrews.ac.uk/Biographies/Euler/
2 https://mathshistory.st-andrews.ac.uk/Biographies/Bernoulli_Jacob/
3 https://mathshistory.st-andrews.ac.uk/Biographies/Bernoulli_Johann/
4 https://mathshistory.st-andrews.ac.uk/Biographies/Bernoulli_Daniel/
5 https://mathshistory.st-andrews.ac.uk/Biographies/Bernoulli_ Nicolaus(I)/
em1766, eleaceitouoconvitedeCatarina,aGrande,pararetornar`aAcademiadeS˜aoPetersburgo,ondeficouat´esuamortes´ubitaem1783, com76 anosdeidade.Curiosamente,Eulernuncaocupouumcargodeprofessor.
Euler´e,semd´uvida,umserinsuper´avelnahist´oriadamatem´atica.Sua produtividade´et˜aosurpreendenteque,mesmotendoficadocegopoucodepoisdeseuretornoaS˜aoPetersburgo(Eulerj´aeracegodoolhodireito desde1735),elecontinuouseutrabalhocomaajudadeumsecret´arioque anotavasuasideias.Aolongodesuavida,forampublicados530deseustrabalhos.Devidoaon´umerosubstancialdetrabalhosn˜aopublicados,mesmo ap´osasuamorte,outrosmanuscritosforampublicados,contribuindopor mais47anos`aspublica¸c˜oesdaAcademiadeS˜aoPetersburgo.
ASociedadeSu´ı¸cadeCiˆenciasNaturaisiniciouem1909umaedi¸c˜ao completadaobradeEuler,queresultouem886trabalhos,entrelivrose artigos.Anota¸c˜ao f (x)usadaparafun¸c˜aode x foiapresentadapelaprimeiravezporEulernoartigo Coment´ariosdePetersburgo (1734-1735).A partirda´ı,aideiadefun¸c˜aosurgiuemv´ariosartigosdean´alisematem´atica. Eulertamb´emfoioprimeiroausaraformaexponencial e parabasedos logaritmosnaturais,emuitasdasnota¸c˜oesmodernasdematem´aticas˜ao creditadasaele,porexemplo:sen, cos, tan, cot, sec, csc, e i = √ 1.
1.1 Defini¸c˜aoepropriedades
Paraentenderoconceitodeexponencial,considereasitua¸c˜aodeuma popula¸c˜aode b bact´eriasquedobraseun´umeroacada30minutos. ´ Eclaro que,emmeiahora,apopula¸c˜aoser´ade2 · b bact´erias,emumahora,apopula¸c˜aoser´ade2 (2 b)=22 b bact´eriase,ap´os5horas,ouseja,10per´ıodos de30minutos,apopula¸c˜aoser´ade210 · b bact´erias.Seguindooracioc´ınio,o n´umerode n bact´eriasdurante x per´ıodosde30minutos,´edadopelafun¸c˜ao n(x)=2x b. Essafun¸c˜aoquemodelatalsitua¸c˜ao´econhecidacomo fun¸c˜ao exponencial.Asfun¸c˜oesexponenciaisquedefiniremosaseguirdescrevem umagrandevariedadedeproblemas,porexemplo,proje¸c˜aopopulacional, desintegra¸c˜aoradioativa,velocidadesderea¸c˜oesqu´ımicas,avalia¸c˜aodeinvestimentos,an´alisedapropaga¸c˜aodeepidemias,circuitosel´etricos,estudo dosfenˆomenosdeaprendizagemeavalia¸c˜aodaconfiabilidadedeprodutos.
Cap´ıtulo2
Fun¸c˜oeslogar´ıtmicas
Noin´ıciodos´eculoXVII,os logaritmos surgiramcomointuitodefacilitarc´alculosdemultiplica¸c˜aoedivis˜aoemtermosdasopera¸c˜oesdesoma esubtra¸c˜ao.Consideradooinventordoslogaritmos,JohnNapier1 (15501617),oitavolordedeMarkinston,queagorafazpartedeEdimburgo,na Esc´ocia,eraumapessoam´ısticacominteressesteol´ogicos,tendofamade magoporacreditaremqueeleseenvolviacomalquimiaenecromancia.

Napierdedicouvinteanosdetrabalho`amatem´aticaparadesenvolver essateoriaat´esuapublica¸c˜aoem1614,notexto MirificiLogarithmorum canonisdescriptio (“Descri¸c˜aodamaravilhosaleidoslogaritmos”).
“J´aquen˜aoexistenadamaisenfadonho,colegasmatem´aticos, doqueograndeatrasosofridonot´ediodeextensasmultiplica¸c˜oes edivis˜oes,deencontrarraz˜oes,enaextra¸c˜aodera´ızesquadradasec´ubicas–e[...]osmuitoserrostrai¸coeirosquepodem
1 https://mathshistory.st-andrews.ac.uk/Biographies/Napier/
surgir–euestive,portanto,refletindosobreumaartesegurae r´apidaqueseriacapazdeaperfei¸coartaisdificuldadesmencionadas.Nofinal,ap´osmuitopensar,finalmentedescobriuma maneirasurpreendentedeabreviarosprocedimentos[...]e´e umatarefaprazerosaapresentartalm´etodoparausop´ublico dosmatem´aticos.”
EstetrabalhodespertouointeressedeHenryBriggs2 (1561-1631),o primeiroprofessordegeometrianoGreshamCollegedeLondrese,posteriormente,professoremOxford,quepossu´ıagrandeinteresseemnavega¸c˜aoe astronomia.Emmar¸code1615,BriggsescreveuumacartaaJamesUssher sobreessefatohist´oricodaciˆencia.
“Napier,lordedeMarkinston,colocouminhacabe¸caeminhas m˜aosparatrabalharcomseusnovoseadmir´aveislogaritmos. Esperovˆe-lonestever˜ao,seDeusquiser,poisnuncaviumlivro quemeagradassetantooumedeixassemaismaravilhado.”
Nomesmoano,Briggsviajouat´eEdimburgoparaencontrar-secom JohnNapieredarreconhecimentoaoinventordoslogaritmos.Duranteo encontro,NapiereBriggsconcordaramqueast´abuasdelogaritmosseriam mais´uteisselog1=0elog10=1,surgindoassimos logaritmosbriggsianos ou logaritmoscomuns.Inicialmentedenominadocomo n´umero artificial,apalavralogaritmocriadaporNapier´eacomposi¸c˜aodaspalavrasgregas logos (raz˜ao)e arithmos (n´umero).Briggsdedicoutodasassuas energiasnaconstru¸c˜aodeumat´abuacombasenestanovaideia,eem1624 publicousua Arithmeticalogarithmica,quecontinhaumat´abuadelogaritmoscomuns,comquatorzecasasdecimais,dosn´umerosde1a20.000ede 90.000a100.000.Quanto`aprioridadenainven¸c˜aodoslogaritmos,osu´ı¸co JobstB¨urgi(1552-1632)construiuumat´abuadelogaritmosindependente deNapierepublicouseusresultadosem1620. Originalmente,oslogaritmosforaminventadosantesdousodosn´umeros exponenciais(paramaisdetalhes,ver 3).Umadasutilidadesdoslogaritmos
2 https://mathshistory.st-andrews.ac.uk/Biographies/Briggs/ 3 http://www.17centurymaths.com/contents/napier/ademonstratiobookone. pdf
Cap´ıtulo3
Fun¸c˜oestrigonom´etricas
Noproblema51do papirodeRhind1 (tamb´emconhecidocomo papiro Ahmes),datadoaproximadamentede1650a.C.,encontra-seoprimeiro registroconhecidosobretrigonometria.Nessaquest˜ao,´eabordadooc´alculo da´areadeumtriˆangulois´osceles.
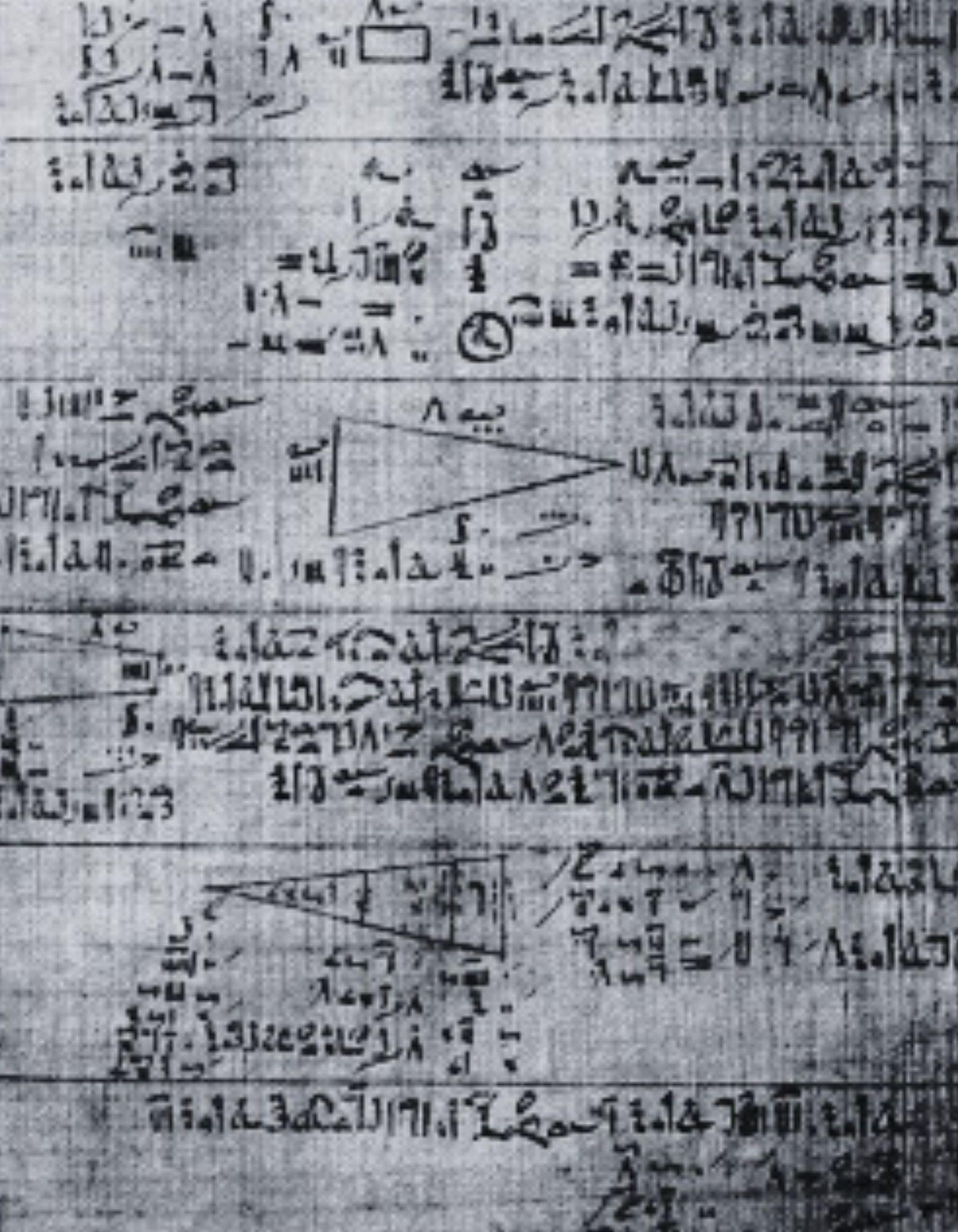
PapirodeRhind

AristarcodeSamos
Outroavan¸cosignificativosurgiuporvoltade260a.C.naobra Sobre ostamanhosedistˆanciasdoSoleaLua,deAristarcodeSamos2 (310-230 a.C.).Nessaobra,oautorapresentaadescobertadeque,quandoaLua est´anafasequartocrescente(momentoemqueoˆanguloTerra-Lua-Sol´e aproximadamentereto),oˆanguloentreaslinhasdevis˜aodoSoledaLua ´e 1 30 deumquadrantemenorqueumˆanguloreto.Esseresultadofoium avan¸cosignificativoparaa´epoca,permitindoumamelhorcompreens˜aoda geometriadoscorposcelesteseumimportantepassoparaodesenvolvimento
1 https://mathshistory.st-andrews.ac.uk/HistTopics/Egyptian_papyri/
2 https://mathshistory.st-andrews.ac.uk/Biographies/Aristarchus/
daastronomiacomociˆencia.
Emtermosmodernos,araz˜aodadistˆanciadaTerra`aLuaparaa distˆanciadaTerraaoSol´edadaporsen(3◦).Aoaplicaroseguinteteoremageom´etrico,expressopelasdesigualdades
sen(α) sen(β) < α β < tan(α) tan(β) ,
onde0 <β<α< 90◦,AristarcodeSamosconcluiuque 1 20 < sen(3◦) < 1 18 .IssosignificaqueadistˆanciadoSolat´eaTerra´emaisdedezoito vezesemenosdevintevezesmaiordoqueadistˆanciadaLuaat´eaTerra. Adistˆanciacorreta´edeaproximadamentequatrocentasvezes.Emborao m´etododeAristarcon˜aoestivesseincorreto,seuerrofoinaobserva¸c˜aodo ˆanguloentreaLua,aTerraeoSol,quenaverdade´edeaproximadamente 89◦50′ .
Oconceitode senodeumˆangulo surgiupelaprimeiraveznaobra Pancha-Siddhantika,doastrˆonomohinduVarahamihira3 (505-587d.C.). Apalavra“seno”temsuaorigememumatradu¸c˜aoincorretadapalavra jya (“corda”),queeraaabrevia¸c˜aodaspalavras ardha jya (“semicorda”)e jya ardha (“corda-metade”)utilizadaspelomatem´aticoindiano Aryabhata.Devido`apr´aticados´arabesdeomitirasvogais, jya sederivouemjˆıba,queeraumapalavraescritacomo jb equen˜aotinhasentido em´arabe.Posteriormente,escritoresquesedepararamcom jb comoabrevia¸c˜aodapalavrasemsentidojˆıbapassaramausar jaib,quefaziapartedo vocabul´ario´arabeesignificava“enseada”ou“ba´ıa”.QuandoGherardde Cremona4 (1114-1187)traduziu jaib paraolatim,eleempregouoequivalente`apalavralatina sinus,deondevemapalavraseno.
3.1 Senoecosseno
GeorgJoachimvonLauchenRhaeticus5 (1514-1576)criouadefini¸c˜aode senoecossenopormeioderaz˜oesentreosladosdeumtriˆanguloretˆangulo,
3 https://mathshistory.st-andrews.ac.uk/Biographies/Varahamihira/ 4 https://mathshistory.st-andrews.ac.uk/Biographies/Gherard/ 5 https://mathshistory.st-andrews.ac.uk/Biographies/Rheticus/
Cap´ıtulo4 Leistrigonom´etricas
Nestecap´ıtulo,realizaremosumas´ıntesedasrela¸c˜oesexistentesentreos elementosdeumtriˆangulo,conhecidascomoleisdossenosecossenos.
4.1 Leidossenos
Quando´enecess´ariodescreverumlugarouregi˜ao,´ecomumumtop´ografo recorreraoteodolito,uminstrumento´opticoquemedeˆangulosverticais, horizontaiseasrela¸c˜oesfornecidaspelatrigonometria.Porexemplo,na instala¸c˜aodeumcaboel´etricoentreumposte P eumacasa C que´eseparadaporumrio,´enecess´arioposicionarumteodolitonoponto C (casa) eoutroemumpontoacess´ıvel O paramedirosˆangulos P OC e OCP do triˆangulo △OPC.Medindoadistˆanciadoposteat´eoponto O eutilizando oteoremada leidossenos,obtemosamedidanecess´ariaparaainstala¸c˜ao docaboel´etrico(verFigura4.1).
Figura4.1:

Grossomodo,aleidossenos´eumaexpress˜aoquerelacionaoscompri-
Leistrigonom´etricas
mentosdosladoscomossenosdeseusˆangulosopostos.Ademonstra¸c˜ao queapresentaremosparaaleidossenosutilizaasseguintesexpress˜oesda ´areadeumtriˆangulogen´erico △ABC
Proposi¸c˜ao3. ( ´ Areadotriˆangulo)
Dado △ABC,ent˜aoa´areadasuperf´ıciedotriˆangulo´e
)= ab 2 ·
C)= ac 2 · sen(B),
onde:
• b e c s˜aooscomprimentosdosladosqueformamoˆangulo A;
• a e c s˜aooscomprimentosdosladosqueformamoˆangulo B;
• a e b s˜aooscomprimentosdosladosqueformamoˆangulo C
Demonstra¸c˜ao:Semperdadegeneralidade,demonstraremosesseresultadonoˆangulo A e b sendoabasedotriˆangulo △ABC.Nosoutroscasos, ademonstra¸c˜aoseguedemaneiraan´aloga.Assim,existemtrˆesposs´ıveis casosaconsiderarsobreoˆangulo A:
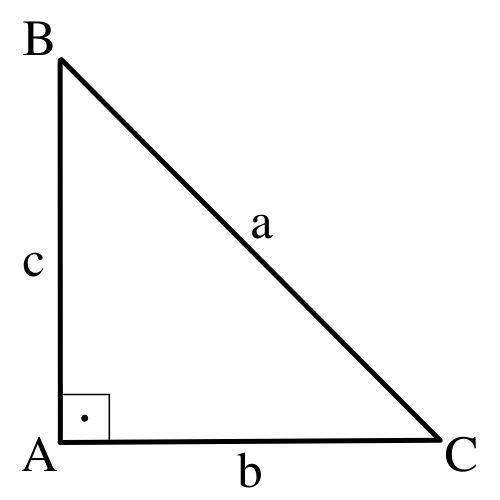
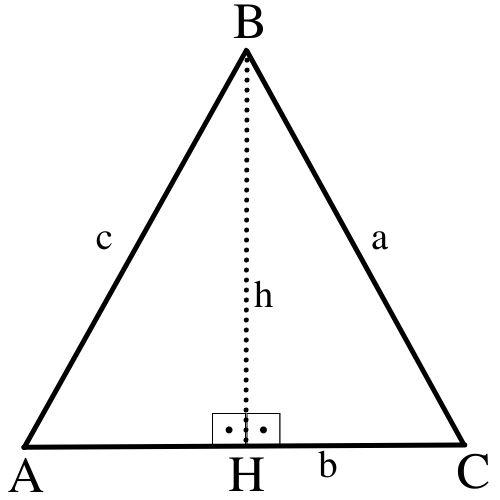
Figura4.4:
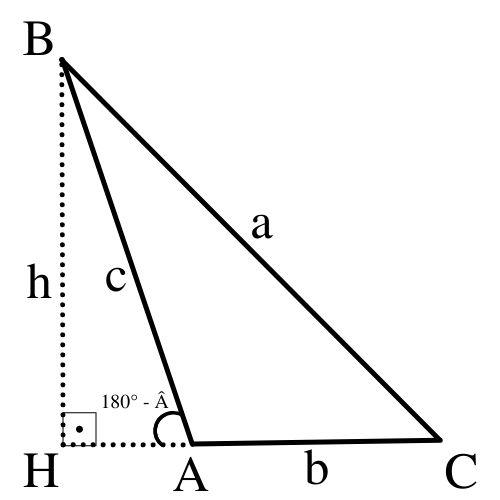
• Se A ´eumˆanguloreto(verFigura4.2),ent˜ao △ABC ´eumtriˆangulo retˆanguloe
2 · sen(A)
Cap´ıtulo5
Identidadestrigonom´etricas
Comoconhecimentoadquiridodasdefini¸c˜oesgeom´etricasdasfun¸c˜oes trigonom´etricas,podemosidentificaralgumasidentidadesques˜ao´uteispara simplificarexpress˜oesmatem´aticas.
5.1 Rela¸c˜oesfundamentaisdatrigonometria
Teorema7. Seja x ∈ R Ent˜ao
sen 2(x)+cos2(x)=1.
Demonstra¸c˜ao:Seja E(x)=(cos(x), sen(x)),onde x ∈ R.Quando E(x)´eiguala(1, 0),(0, 1),( 1, 0)ou(0, 1),temossen2(x)+cos2(x)=1. Quando E(x)pertenceaalgumquadrante,podemosidentificarotriˆangulo retˆanguloformadopelospontos P = E(x), A =(cos(x), 0)e O =(0, 0), onde O ˆ AP = π 2 (fa¸caoesbo¸coparacadaumdoscasos).Aplicandoo teoremadePit´agorasnotriˆanguloretˆangulo △OPA,temos PA2 + OA2 = OP 2.Independentedoquadranteemque E(x)esteja,temosque OP =1, OA = | cos(x)| e PA = |sen(x)|.Assim, (|sen(x)|)2 +(| cos(x)|)2 =12; (sen(x))2 2 + (cos(x))2 2 =1; sen2(x)+cos2(x)=1.
Identidadestrigonom´etricas
Teorema8. Dado x ∈ R,
(a) sec2(x) tan2(x)=1 para x = π 2 + nπ onde n ∈ Z;
(b) cot2(x) csc2(x)=1 para x = nπ onde n ∈ Z.
Demonstra¸c˜ao:Quando x = π 2 + nπ,onde n ∈ Z,temosquecos(x) =0. DividindoaidentidadedoTeorema7porcos2(x) =0,obtemos:
sen2(x)
cos2(x) + cos2(x) cos2(x) = 1 cos2(x) ;
tan2(x)+1=sec2(x);
sec2(x) tan2(x)=1.
Quando x = nπ,com n ∈ Z,temosquesen(x) =0.Dividindoa identidadedoTeorema7porsen2(x) =0,obtemos:
sen2(x)
sen2(x) + cos2(x)
sen2(x) = 1 sen2(x) ;
cot2(x)+1=csc2(x);
csc2(x) cot2(x)=1.
Nospr´oximosexemplos,aprenderemosquatrom´etodosutilizadosnas demonstra¸c˜oessobreidentidades.Paraisso,necessitamosrelembrardas seguintesigualdadesalg´ebricas:
Propriedades1. Dados a,b,c ∈ R.
(a) (a + b)2 = a2 +2ab + b2;
(b) (a b)2 = a2 2ab + b2;
(c) a2 b2 =(a + b)(a b);
O volume 2 do Pré-cálculo sem mistérios surge como uma solução para superar os obstáculos enfrentados por alunos ingressantes no ensino superior. Este livro foi elaborado para preencher as lacunas frequentemente encontradas nos cursos de cálculo diferencial e integral. Embasando-se nas dúvidas recorrentes dos estudantes, a obra se aprofunda em temas fundamentais como constante de Euler, funções exponenciais, funções logarítmicas e fundamentos da trigonometria. O texto estabelece uma ponte entre exemplos oriundos do ensino médio e tópicos mais avançados, garantindo uma transição harmoniosa e robusta ao ambiente acadêmico. Este é, sem dúvida, um investimento valioso para aqueles que buscam solidificar seus conhecimentos e entrar com segurança no universo do cálculo.



