Matematika za studente arhitekture i dizajna by Faculty of Architecture Zagreb

ManualiaUniversitatisstudiorumZagrabiensis UdˇzbeniciSveuˇciliˇstauZagrebu

Matematikazastudentearhitekturei

GoranaAras-Gazi´c Marija ˇ Simi´cHorvath DavidTarandek

Zagreb,2024.

IMPRESSUM

Matematikazastudentearhitektureidizajna

Autori

1.doc.dr.sc.GoranaAras-Gazi´c,SveuˇcilišteuZagrebuArhitektonskifakultet

2.doc.dr.sc.MarijaŠimi´cHorvath,SveuˇcilišteuZagrebuArhitektonskifakultet

3.DavidTarandek,mag.math.,SveuˇcilišteuZagrebuArhitektonskifakultet

Recenzenti

1.izv.prof.dr.sc.SlavicaIveli´cBradanovi´c,SveuˇcilišteuSplituFakultet gradevinarstva,arhitektureigeodezije

2.prof.dr.sc.EmaJurkin,SveuˇcilišteuZagrebuRudarsko-geološko-naftnifakultet

3.doc.dr.sc.IvaKodrnja,SveuˇcilišteuZagrebuGeodetskifakultet

Lektor

LedaFrani´cDragani´c,prof.hrvatskogjezika

Grafiˇckooblikovanje

LucijanaDuji´cRasti´c

Nakladnik

SveuˇcilišteuZagrebuArhitektonskifakultet

Zanakladnika

Prof.art.SinišaJusti´c

PublikacijujezaobjavuprihvatioSenatSveuˇcilištauZagrebu,naprijedlogPovjerenstvaza sveu ˇ cilišnunastavnuliteraturu,nasjedniciodržanoj15.listopada2024.(Klasa:032-01/2402/08,Urbroj:251-25-07-01/2-24-5).

ISBN978-953-8042-90-4

SADRŽAJ

0uvod 7

1vektori 9

1.1 Zbrajanjevektora 14

1 2 Množenjerealnogbrojaivektora 17

1 3 Linearnakombinacijavektora 19

1 4 Bazaikoordinatnisustav 26

1 5 Skalarniproduktvektora 32

1 6 Vektorskaprojekcija 38

1.7 Pravokutnikoordinatnisustav 41

1.8 Vektorskiproduktvektora 45

1.9 Mješovitiproduktvektora 54

2analiti ˇ ckageometrija 57

2.1 Jednadžbaravnine 57

2.2 Jednadžbapravca 59

DODATAK:Povežimoanalitiˇckuinacrtnugeometriju 77

2.AOsnovnielementi 77

2.A.1 Toˇcka 77

2.A.2 Pravac 78

2.A.3 Ravnina 78

2.A.4 Presjeˇcnicadvijuravnina 80

2.A.5 Probodištepravcairavnine 81

2.A.6 Pravacokomitnaravninu 82

2.BMetriˇckizadatci 82

2.B.1 Udaljenostdvijutoˇcaka 82

2.B.2 Udaljenosttoˇckeodravnine 83

2.B.3 Udaljenosttoˇckeodpravca 83

3elementarnefunkcije 85

4limesi 103

5derivacije 109

5 1 Deﬁnicijaderivacije 109

5 2 Derivacijeelementarnihfunkcijaipraviladeriviranja 113

5 3 L’Hospitalovopravilo 116

5.4 Rastipadfunkcije.Ekstremi 117

5.5 Zadatcizavježbu 132

6integrali 137

6.1 Neodredeniintegral 137

6.2 Metodasupstitucije 139

6.3 Odredeniintegral 141

6.4 Površineravninskihlikova 146

6.5 Volumenirotacijskihtijela 152

POPISSLIKA

Slika 1 0 1 Prikazvektora 9

Slika 1.0.2 Pravacnositeljvektora 10

Slika 1 0 3 Vektorisuprotnihorijentacija 10

Slika 1.0.4 ZadanielementiPrimjera 1 11

Slika 1 0 5 Kriterijzajednakostvektora 11

Slika 1.0.6 Nanošenjevektorautoˇcku 12

Slika 1 0 7 Nekolinearnivektori a i b 12

Slika 1.0.8 Paralelogramitrokutrazapetisdvanekolinearnavektora 13

Slika 1 0 9 Trostranapiramidarazapetastrinekomplanarnavektora 13

Slika 1.0.10 ˇ Cetverostranapiramidarazapetastrinekomplanarnavektora 13

Slika 1.0.11 Paralelopipedrazapetstrinekomplanarnavektora 14

Slika 1 1 1 Zbrajanjevektorapravilomtrokuta 14

Slika 1.1.2 Zbrajanjevektorapravilomparalelograma 15

Slika 1 1 3 Zbrajanjenadovezivanjem 15

Slika 1.1.4 Asocijativnostzbrajanjavektora 16

Slika 1 1 5 Komutativnostzbrajanjavektora 16

Slika 1 1 6 Suprotnivektori 16

Slika 1.1.7 Zbrajanjesila 17

Slika 1 1 8 Zbrajanjesilaistogsmjera 17

Slika 1.2.1 ZadanielementiZadatka 1 18

Slika 1 2 2 RješenjeZadatka 1 18

Slika 1.2.3 RješenjeZadatka 2 19

Slika 1 3 1 b = αa, α > 0, b = α a, α < 0 20

Slika 1.3.2 c = αa + βb 21

Slika 1 3 3 Nekomplanarnivektori (a, b, c) ivektor d 22

Slika 1.3.4 d = αa + βb + γc 22

Slika 1 3 5 RješenjeZadatka 3 23

Slika 1.3.6 RješenjeZadatka 4 24

Slika 1 3 7 RješenjeZadatka 5 24

Slika 1.3.8 ZadanielementiZadatka 6 25

Slika 1 3 9 RješenjeZadatka 6 26

Slika 1.4.1 Koordinatnisustav 28

Slika 1 4 2 RadijvektortoˇckeTukoordinatnomsustavu O, (a, b, c) 28

Slika 1 4 3 Vektorukoordinatnomsustavu O, (a, b, c) 29

Slika 1 4 4 Koordinatepolovištadužineukoordinatnom sustavu O, (a, b, c) 30

Slika 1.5.1 Kutizmeduvektora 32

Slika 1 5 2 ZadanielementiZadatka 14 34

Slika 1 5 3

Slika 1 5 4

RješenjeZadatka 14 34

RješenjeZadatka 15 36

Slika 1 5 5 ZadanielementiZadatka 16 37

Slika 1.5.6 RješenjeZadatka 16 37

Slika 1.6.1 Vektorskaprojekcija 39

Slika 1.6.2 RješenjeZadatka 17 40

Slika 1 7 1 Radijvektorupravokutnomkoordinatnomsustavu 41

Slika 1 7 2 Vektorupravokutnomkoordinatnomsustavu 42

Slika 1 7 3 Zlatnirez 44

Slika 1 8 1 Desnikoordinatnisustav 46

Slika 1 8 2 Lijevikoordinatnisustav 46

Slika 1.8.3 Vektorskiproduktvektora 47

Slika 1.8.4 Geometrijskainterpretacijamodulavektorskog produkta 47

Slika 1.8.5 ZadanielementiZadatka 22 48

Slika 1.8.6 RješenjeZadatka 23 52

Slika 1 8 7 RješenjeZadatka 24 53

Slika 1 9 1 Mješovitiproduktvektora a, b i c 54

Slika 2 1 1 Jednadžbaravnine 57

Slika 2 1 2 Ravninaparalelnasravninomxy 58

Slika 2.1.3 Ravninaparalelnasravninomyz 58

Slika 2.1.4 Ravninaparalelnasravninomxz 59

Slika 2.2.1 Jednadžbapravca 60

Slika 2.2.2

Slika 2 2 3

Slika 2 2 4

Slika 2 2 5

Slika 2 2 6

Slika 2.2.7

Slika 2.2.8

Slika 2.2.9

Slika 2.2.10

Slika 2 2 11

Slika 2 2 12

Slika 2 2 13

Slika 2.2.14

Slika 2.2.15

Rješenjezadatka 28 60

Rješenjezadatka 29 61

Rješenjezadatka 30 62

Rješenjezadatka 31 63

Rješenjezadatka 32 64

Rješenjezadatka 33 65

Rješenjezadatka 34 67

Rješenjezadatka 35 68

Rješenjezadatka 36 69

Rješenjezadatka 37 71

Rješenjezadatka 38 72

Rješenjezadatka 39 73

Rješenjezadatka 40 74

Rješenjezadatka 41 75

Slika 2.A.1 Toˇcka T 78

Slika 2.A.2 Pravac p 78

Slika 2.A.3 Prikazravnine 79

Slika 2.A.4

Projiciraju´ceravnine 79

Slika 2.A.5 Pravacuravnini 80

Slika 2.A.6

Slika 2.A.7

Slika 2.A.8

Horizontalniifrontalnipravciuravnini 80

Presjeˇcnicadvijuravnina 81

Probodištepravcairavnine 82

Slika 2.A.9 Pravacokomitnaravninu 82

Slika 2.B.1

Slika 2.B.2

Slika 2.B.3

Slika 3.0.1

Slika 3 0 2

Slika 3 0 3

Slika 3.0.4

Slika 3.0.5

Slika 3 0 6

Udaljenostdvijutoˇcaka 83

Udaljenosttoˇckeodravnine 83

Udaljenosttoˇckeodpravca 84

Grafkonstantnefunkcije 87

Graflinearnefunkcije 88

Grafkvadratnefunkcije 89

Grafeksponencijalnefunkcije 90

Graflogaritamskefunkcije 91

Trigonometrijskakružnica 92

Slika 3 0 7 Graffunkcijesinus 93

Slika 3.0.8 Graffunkcijekosinus 93

Slika 3.0.9 Graffunkcijetangens 94

Slika 3.0.10 Graffunkcijekotangens 95

Slika 3 0 11 Graffunkcijearkussinus 97

Slika 3 0 12 Graffunkcijearkuskosinus 98

Slika 3.0.13 Graffunkcijearkustangens 99

Slika 3.0.14 Graffunkcijearkuskotangens 99

Slika 3 0 15 Graffunkcije f (x)= 1 2 x

Slika 3 0 16 Graffunkcije f (

Slika 3.0.17 Grafkvadratnefunkcije 101

Slika 4.0.1 Okolinatoˇckea 103

Slika 4 0 2 Limesfunkcije f utoˇcki a 103

Slika 4 0 3 Vrijednostfunkcije f utoˇcki a nijejednakalimesufunkcije f utoˇcki a 104

Slika 4 0 4 Limesfunkcijeutoˇcki 105

Slika 5.1.1 Deﬁnicijaderivacije 109

Slika 5.1.2 Zadanielementizadatka 43 111

Slika 5 1 3 Rješenjezadatka 43 112

Slika 5 4 1 Eksponencijalnafunkcija 118

Slika 5.4.2 Rastipadfunkcije.Ekstremi. 119

Slika 5.4.3 Graffunkcije f (x)= x2 x 6 121

Slika 5 4 4 Graffunkcije f (x)= 1 3 x3 1 2 x2 6x 122

Slika 5 4 5 Graffunkcije f (x)= 2x2 6x 123

Slika 5.4.6 Graffunkcije f (x)= 2x+3 x2 123

Slika 5.4.7 Graffunkcije f (x)= 3 x 124

Slika 5 4 8 Graffunkcije f (x)= x3e x 124

Slika 5 4 9 Graffunkcije f (x)= x2 4 125

Slika 5 4 10 Graffunkcije f (x)= x + 4 x 126

Slika 5.4.11 Graffunkcije f (x)= lnx + 1 127

Slika 5.4.12 Graffunkcije f (x)= xlnx 127

Slika 5 4 13 Graffunkcije f (x)= x 128

Slika 5 4 14

Slika 5.4.15

Slika 5.4.16

Slika 5.4.17

Slika 5.4.18

Slika 6.3.1

Slika 6 3 2

Slika 6 3 3

Slika 6 4 1

Slika 6 4 2

Slika 6.4.3

Slika 6.4.4

Slika 6.4.5

Slika 6.4.6

Slika 6 4 7

Graffunkcije f (x)= 1 2 ln(1 + x2) 128

Graffunkcije f (x)= x2 + 3 129

Graffunkcije f (x)= x x2 2x+3 130

Rješenjezadatka 58 130

Rješenjezadatka 59 131

Površinaomedenagrafomfunkcije f ,pravcima

x = a, x = b iosi x 142

Donjaigornjaintegralnasuma 142

Donjaigornjaintegralnasuma 143

Površinaravninskoglika 146

Rješenjezadatka 67 147

Rješenjezadatka 68 148

Zadanielementizadatka 69 149

Rješenjezadatka 70 150

Zadanielementizadatka 71 151

Zadanielementizadatka 72 151

Slika 6 5 1 Volumenrotacijskogtijela 152

Slika 6 5 2

Slika 6 5 3

Zadanielementiprimjera 15 153

Rješenjeprimjera 15 153

Slika 6 5 4 Zadanielementiprimjera 16 154

Slika 6.5.5

Rješenjeprimjera 16 155

Slika 6.5.6 Zadanielementizadatka 74 155

Slika 6.5.7

Slika 6.5.8

Rješenjezadatka 74 156

Zadanielementizadatka 75 157

Slika 6.5.9 Rješenjezadatka 75 157

Slika 6 5 10 Zadanielementizadatka 76 158

Slika 6 5 11

Slika 6 5 12

Rješenjezadatka 76 158

Zadanielementizadatka 77 159

Slika 6 5 13 Rješenjezadatka 77 160

Udžbenik Matematikazastudentearhitektureidizajna namijenjenjestudentimaStudijaarhitektureiurbanizmatestudentimaStudijadizajna zauˇcenjeipolaganjekolegijaMatematikateMatematika 1 i 2 na ArhitektonskomfakultetuSveuˇcilištauZagrebu.Sadržajjepodijeljen u 6 poglavlja:Vektori,Analitiˇckageometrija,Elementarnefunkcije, Limesi,DerivacijeiIntegrali.DrugopoglavljeimaidodatakPovežimo analitiˇckuinacrtnugeometrijuukojemsupojedinezadaćeriješene metodamanacrtnegeometrije.Dakle,obradenisustandardnisadržaji kojisepredajunatehniˇckimfakultetima,aliprilagodenisatnicina ArhitektonskomfakultetuSveuˇcilištauZagrebutejevišestavljen naglasaknaprimjenuivizualizacijusadržaja,amanjenaformalni matematiˇckirjeˇcnikidokaze.Svakopoglavljezapoˇcinjemotivacijom, zatimslijedikratkiteorijskiuvodteriješeniprimjeriizadatci.Tekstje popraćenspreko 100 slikanapravljenihudigitalnomalatuGeogebri. Uprvompoglavljuuvedenjepojamvektoratesudefiniraneoperacije svektorimaitozbrajanjevektora,množenjerealnogbrojaivektorate skalarni,vektorskiimješovitiproduktvektora.

Udrugompoglavljukoristesealgebarskemetodezarješavanjegeometrijskihproblema.Pomo´cuvektorskograˇcunaizvodisejednažba pravcairavnineteseprouˇcavajumedusobniodnosiipoložajipravaca iravninauprostoru.Zasvakizadataknajprijejegraﬁˇckiprikazano prostornorješenje,azatimjedanoalgebarskorješenje.

Udodatkudrugompoglavlju,pojedinezada´cesuriješeneimetodama iznacrtnegeometrijetestudentimoguusporeditiiriješitiistezada´ce nadvanaˇcina.

Trećepoglavljeposvećenojeosnovnimelementarnimfunkcijama.Za svakufunkcijunacrtanjenjengraftesunavedenaosnovnasvojstva. Nakrajuovogpoglavljanalazesekratkizadatcizavježbu. Uˇcetvrtompoglavljudefiniranjepojamgraniˇcnevrijednostiililimesa funkcijetesunavodenasvojstvalimesaipravilazaraˇcunanjeosnovnih limesa.

Upetompoglavljudeﬁniranjepojamderivacijetejeprekoderivacije opisanoponašanjefunkcije.OvdjejetakodernavodenoL’Hospitalovo pravilozaraˇcunanjelimesafunkcija.

Uzadnjempoglavljudeﬁniranisuneodredeniiodredeniintegralte seuˇcetehnikeraˇcunanjaistih.Ovdjejenaglasakstavljennaraˇcunanje površinaravninskihlikovaomedenihgrafovimanekihfunkcijatena

raˇcunanjevolumenarotacijskihtijelakojanastajurotacijomgrafova funkcijaokoosi x ili y.

Nadamosedaćeovajudžbenikpribližitimatematiˇckisadržajiolakšatinjegovorazumijevanjestudentimanavedenihprofilateomogućiti primjenuugeometrijskimikonstrukcijskimkolegijima.

Nakraju,iskrenosezahvaljujemonašimrecezenticamaizv.prof.dr. sc.SlaviciIveli´cBradanovi´c,prof.dr.sc.EmiJurkinidoc.dr.sc.Ivi Kodrnjinakonstruktivnimsugestijamaikomentarimakojisudoprinijelipoboljšanjuudžbenika.

Autori

VEKTORI

Deﬁnicija 1: Orijentiranudužinuskrajnjimtoˇckamakodkojihrazlikujemopoˇcetnuizavršnutoˇckuzovemo vektor.Poˇcetnatoˇckaje poˇcetakvektora,akrajnjatoˇcka krajvektora.

Slika 1 0 1: Prikazvektora

Vektorˇcijijepoˇcetaktoˇcka A,akrajtoˇcka B, A = B,oznaˇcavat´cemo −→ AB.Vektorˇcijijepoˇcetaktoˇcka B,akrajtoˇcka A,nazivamo suprotni vektor vektora −→ AB ioznaˇcavamo −→ BA.Duljinavektorajeudaljenost izmedunjegovepoˇcetneikrajnjetoˇckeitojepozitivanrealanbroj kojegnazivamo modul ili normavektora ioznaˇcavamo |−→ AB|.Vidimo daje |−→ AB| = |−→ BA|. Smjer vektorajeodredenpravcemnakojemleživektor.Pravac p, odredenjetoˇckama A i B isadrživektor −→ AB,pakažemodajepravac p nositelj vektora −→ AB.Zavektorekojileženaparalelnimpravcima kažemodaimaju istismjer ilidasu kolinearni (oznaka ||).Usuprotnomsluˇcajugovorimoonekolinearnimvektorima.

Kakobismopotpunoodredilivektor,osimnjegoveduljineismjera moramopoznavatiinjegovu orijentaciju.Nacrtajmopravac p tena njemuistaknimo 3 toˇcke A, B i C takvedajetoˇcka B izmedu A i C

Vektori −→ AB, −→ AC i −→ BC sumedusobnojednakoorijentirani,avektori −→ BA i −→ BC sumedusobnosuprotnoorijentirani.

1 0 3: Vektorisuprotnihorijentacija

Deﬁnicija 2: Vektorjeodredensvojom duljinom, smjerom i orijentacijom,odnosno,kažemodasudvavektorajednakaakosepodudaraju poduljini,smjeruiorijentaciji.

Slika 1 0 2: Pravacnositeljvektora

Slika

Primjer 1. Vektori −→ AB i −→ CD saslike 1 0 4 imajuistismjer,alisusuprotno orijentiraniiimajurazliˇcitemodule.Vektori −→ AD i −→ BC imajurazliˇcitsmjeri orijentaciju,aistimodul.

Slika 1 0 4: ZadanielementiPrimjera 1

Kriterijzajednakostvektora

Vektori −→ AB i −→ DC jednakisuakoisamoakojeˇcetverokut ABCD paralelogram.

Dokaz: ⇒ Nekasuvektori −→ AB i −→ DC jednaki.Tadasuimpravcinositelji paralelniivrijedidaje |AB| = |DC|,atojedovoljnodaˇcetverokut ABCD budeparalelogram.

⇐ Nekajeˇcetverokut ABCD paralelogram.Tadasunasuprotne stranice AB i DC paralelogramaparalelneijednakeduljine,akakosu iorijentacijevektora −→ AB i −→ DC jednake,ondasutojednakivektori.

Slika 1.0.5: Kriterijzajednakostvektora

Temeljnistavakovektorima

Nekaje O bilokojatoˇckaprostorainekaje −→ AB vektor.Tadapostoji jedinstvenatoˇcka P prostorazakoju −→ OP = −→ AB.

Dokaz: Dokazovetvrdnjeslijediizˇcinjenicedapostojisamojedna toˇcka P prostoratakvadajeˇcetverokut OPBA paralelogram.Onda je −→ OP = −→ AB.Timesmopronašlivektorjednakpoˇcetnomkojiima poˇcetakuunaprijedzadanojtoˇcki O

Sobziromnagornjistavak,prirodnojevektoreoznaˇcavatibez isticanjapoˇcetneikrajnjetoˇcke,jednimsimbolomnpr. −→ a . Vektorkojemusupoˇcetakikrajuistojtoˇckizovemo nulvektor i oznaˇcavamo −→ 0 .Nulvektorimaduljinu 0 tenemasmjerniorijentaciju. Uravninipostojenajvišedvanekolinearnavektora.Pretpostavimo dasu −→ a i −→ b dvanekolinearnavektorateihnanesimospoˇcetkom utoˇckiO.Tadakažemodavektori −→ OA i −→ OB razapinju(odreduju) trokut OAB i paralelogram OACB

Slika 1 0 6: Nanošenjevektorautoˇcku

Slika 1.0.7: Nekolinearnivektori a i b

Slika 1 0 8: Paralelogramitrokutrazapetisdvanekolinearnavektora

Komplanarnivektori suvektorikojipripadajuistojiliparalelnim ravninama.Usuprotnomkažemodasuvektori nekomplanarni Oˇcitojedasukolinearnivektorinužnokomplanarni. Uprostorupostojenajvišetrivektorakojinisukomplanarni.Tri nekomplanarnavektora −→ a , −→ b i −→ c razapinju(odreduju)trostranu piramidu OABC, ˇcetverostranupiramidu OADBC i paralelopiped OADBCA D B

Slika 1 0 9: Trostranapiramidarazapetastrinekomplanarnavektora

Slika 1.0.10: ˇ Cetverostranapiramidarazapetastrinekomplanarnavektora

Slika 1.0.11: Paralelopipedrazapetstrinekomplanarnavektora

1.1 zbrajanjevektora

Deﬁnicija 3: Nekasuzadanivektori a i b tetoˇcke O, A i B takveda je −→ a = −→ OA i −→ b = −→ AB. Zbrojvektora a i b jevektor −→ c = −→ OB.Ovaj naˇcinzbrajanjavektoranazivase pravilotrokuta.

Slika 1.1.1: Zbrajanjevektorapravilomtrokuta

Vektoremožemozbrajatiipo praviluparalelograma.Zbrojvektora a = −→ OA i b = −→ OB jedijagonalaparalelograma c = −→ OC

Slika 1.1.2: Zbrajanjevektorapravilomparalelograma

Zazbrajanjevišeod 2 vektorakoristimopravilonadovezivanja, vidisliku 1.1.3.Svakisljede´civektorunizupostavljasetakoda mujepoˇcetakukrajnjojtoˇckiprethodnogvektora.Naslici 1.1.3 je −→ a6 = −→ a1 +

Slika 1.1.3: Zbrajanjenadovezivanjem

Zbrajanjevektoraimasljede´casvojstva:

1. (−→ a + −→ b )+ −→ c = −→ a +(−→ b + −→ c ) (asocijativnostzbrajanjavektora)

2 −→ a + −→ 0 = −→ a

3. zasvakivektor a postojivektor −→ a takavdaje −→ a + −→ a1 = −→ a1 + −→ a = −→ 0 −→ a1 - suprotnivektor vektora −→ a (oznaˇcavamoga −→ a )

4 −→ a + −→ b = −→ b + −→ a (komutativnostzbrajanjavektora)

Svojstvazbrajanjavektorasuprikazananasljede´cimslikama:

Slika 1 1 4: Asocijativnostzbrajanjavektora

Slika 1 1 5: Komutativnostzbrajanjavektora

Slika 1 1 6: Suprotnivektori

Oduzimanjevektorajezbrajanjesasuprotnimvektorom.Vektor −→ a +( −→ b ) kra´ceoznaˇcavamo −→ a −→ b inazivamo razlikavektora −→ a i −→ b

Primjer 2. Primjervektorskeveliˇcinejestsilajeruziznos,siluodreduju toˇckaukojojdjeluje(hvatište),pravacnakojemdjeluje(smjer),tenjezina orijentacija.Općenitoćemorezultantnusiludobitikaovektorskizbrojkomponenti.Pritomćemoupotrijebitipravilotrokutailipraviloparalelograma.

1 1 7: Zbrajanjesila

1 1 8: Zbrajanjesilaistogsmjera

1.2 množenjerealnogbrojaivektora

Množenjemrealnogbroja(skalara) λ ivektora a dobivamovektor λa zadannasljede´cinaˇcin:

• Akoje λ = 0ilije −→ a = −→ 0,ondaje λ−→ a = −→ 0

• Akoje λ > 0, ondajevektor λ−→ a jednakoorijentirankaoivektor −→ a ,aakoje λ < 0, vektori −→ a i λ−→ a susuprotnoorijentirani,za svaki −→ a = −→ 0

• Vektora λ−→ a imaduljinu |λ−→ a | = |λ||−→ a |

Nekasu λ i µ realnibrojevite −→ a i −→ b vektori.Operacijamnoženja skalaraivektoraimasljede´casvojstva:

• λ(−→ a + −→ b )= λ−→ a + λ −→ b

• (λ + µ)−→ a = λ−→ a + µ −→ a

• (λµ)−→ a = λ(µ −→ a ).

Jediniˇcnivektorvektora −→ a = −→ 0 vektorjeistogsmjeraiorijentacije kaovektor a ˇcijijemodul 1 ioznaˇcavamogas −→ a0 .Onjejednak −→ a0 = 1 |−→ a | −→ a = −→ a |−→ a | .Imaistismjeriorijentacijukaoivektor −→ a .

Zadatak 1. Naslici 1.2.1 prikazanjepravilanšesterokut ABCDEF sa središtemutoˇcki S.Nekaje G polovištestranice BC i H polovištestranice CD.Oznaˇcimovektore −→ AB i −→ BC s −→ m i −→ n .Izrazitevektore −→ AH, −→ GS, −→ AE, −→ GHi −→ GFprekovektora −→mi −→ n.

Slika

Slika 1 2 1: ZadanielementiZadatka 1

Rješenje:

Slika 1.2.2: RješenjeZadatka 1

1.3linearnakombinacijavektora 19

Zadatak 2. Uparalelogramu PQRS je −→ PQ = 2−→ a i −→ PS = −→ b .Toˇcka T je takvadavrijedi −→ PT = 2 −→ b .Akosepravci PR i QS sijekuutoˇcki X,apravci RSiQTutoˇckiY,prikažitevektore −→ TR, −→ PY, −→ QYi −→ XYpomo´cu −→ai −→ b.

Rješenje:

Slika 1.2.3: RješenjeZadatka 2

Primijetimonajprijedajeˇcetverokut SQRT paralelogram,pase dijagonale SR i QT raspolavljaju.

1 3 linearnakombinacijavektora

Deﬁnicija 4: Akosu −→ a1 ,..., −→ an vektorii λ1,..., λn skalari,ondavektor −→ a = λ1 −→ a1 + + λn −→ an nazivamo linearnakombinacijavektora

−→ a1 ,..., −→ an skoeﬁcijentima λ1,..., λn.Kažemojošdajevektor −→ a rastavljen(razvijen)povektorima −→ a1 ,..., −→ an .

Mi´cemoovdjepromatratidvodimenzionalanitrodimenzionalan vektorskiprostorte´cemoistražitivezuizmedualgebarskogpojma linearnekombinacijevektoraigeometrijskogpojmakolinearnostii komplanarnostivektora.

Nekaje −→ a = −→ 0 i −→ b vektorkolinearansvektorom −→ a .Tadapostoji jedinstvenirealnibroj α takavdaje −→ b = α −→ a Akojevektor −→ b jednakoorijentirankaoivektor −→ a ,ondaje α > 0.U suprotnomje α < 0. Slika 1.3.1: b = αa, α > 0, b = α a, α < 0

Nekaje (−→ a , −→ b ) uredeniparnekolinearnihvektora.Tadazasvaki vektor −→ c ,kojijekomplanarans −→ a i −→ b ,postojijedinstveniuredeni parrealnihbrojeva (α, β) takavdaje −→ c = α

Umjestodokazapogledajmosliku 1 3 2:

Slika 1.3.2: c = αa + βb

Nanesimovektor −→ c spoˇcetkomutoˇcki O tesadimamodaje

−→ c = −→ OC.Poˇcetkomvektora −→ c povucimopravac p paralelansvektorom −→ a ,akrajemvektora −→ c pravac q paralelansvektorom −→ b .Kako pravci p i q nisuparalelni,sijekuseutoˇcki P.Sadje −→ OC = −→ OP + −→ PC, gdjejevektor −→ OP kolinearansvektorom −→ a pasemožezapisatikao −→ OP = α −→ a ,a −→ PC jekolinearansvektorom −→ b pasemožezapisatikao −→ PC = β −→ b .Vektor αa + β −→ b zovemo linearnakombinacijavektora −→ a i −→ b skoeﬁcijentima α i β

Nekajesad (−→ a , −→ b , −→ c ) uredenatrojkanekomplanarnihvektora. Tadazasvakivektor −→ d postojijedinstvenauredenatrojkarealnih brojeva (α, β, γ) takvadaje

Umjestodokazapogledajmosljede´ceslike:

Slika 1 3 3: Nekomplanarnivektori (a, b, c) ivektor d

Nanesimovektorespoˇcetkomuistutoˇcku O.Nekaje −→ a = −→ OA, −→ b = −→ OB, −→ c = −→ OC i −→ d = −→ OD.Vidimodavektori −→ a i −→ b odreduju ravninu π tedavektor −→ c neležiutojravnini.Toˇckom D povucimo pravacparalelansvektorom −→ c .Onravninu π probadautoˇcki D .

Slika 1 3 4: d = αa + βb + γc

Sadje −→ OD = −−→ OD + −−→ D D.Poprethodnomjesluˇcaju −−→ OD = α −→ a + β −→ b ,akakojevektor −−→ D D kolinearansvektorom −→ c ,možemo ganapisatikao γ −→ c .Vektor α −→ a + β −→ b + γ −→ c zovemo linearnakombinacijavektora −→ a , −→ b i −→ c skoeﬁcijentima α, β i γ

Sad´cemobezdokazanavestidvateoremakojanamdajukarakterizacijukolinearnostiikomplanarnostivektora.

1.3linearnakombinacijavektora 23

Teorem 1. Dvavektora −→ a i −→ b kolinearnasuakoisamoakopostojibroj α ∈ R takavdaje −→ b = α −→ a.

Teorem 2. Trivektora −→ a , −→ b i −→ c komplanarnasuakoisamoakosesvaki odnjihmožeprikazatikaolinearnakombinacijaostalihdvaju.

Zadatak 3. Toˇcka C dijelidužinu AB uomjeru 2:1.Prikažitevektor −→ OC pomo´cuvektora −→ OAi −→ OB.

Rješenje:

Slika 1 3 5: RješenjeZadatka 3

Toˇckom C povucimopravacparalelansvektorom −→ OB kojivektor −→ OA sijeˇceutoˇcki D.Dobivamovektor −→ DC kolinearans −→ OB.Izsliˇcnosti trokuta ADC i AOB zakljuˇcujemodaje −→ DC = 2 3 −→ OB i −→ DA = 2 3 −→ OA,tj. −→ OD = 1 3 −→ OA.Slijedidaje −→ OC = 1 3 −→ OA + 2 3 −→ OB.

Zadatak 4. Nekasu A, B i C vrhovitrokuta, −→ a = −→ AB, −→ b = −→ AC inekaje −→ c = −→ AP orijentiranatežišnicatrokuta.Rastavitevektor −→ c usmjeruvektora −→ a i −→ b

Rješenje: Nadopunimotrokut ABC doparalelograma ABDC

1 3 6: RješenjeZadatka 4

Sadimamo:

Zadatak 5. Dokažitedaseuparalelogramudijagonaleraspolavljaju.

Rješenje: Oznaˇcimos E polovištedužine AC,as F polovištedužine BD.Moramodokazatidaje E = F,tj. −→ OE = −→ OF

1.3.7: RješenjeZadatka 5

Slika

Sadje

pajetimetvrdnjadokazana.

Zadatak 6. NekajezadanpravilantetraedarABCD.Rastavite

1 vektorvisine −−→ D D usmjeruvektora

2 vektorvisine

Rješenje:

Slika 1.3.8: ZadanielementiZadatka 6

1 3 9: RješenjeZadatka 6

1 4 bazaikoordinatnisustav

Uprethodnompoglavljuvidjelismodasvakivektormožemonapisati kaolinearnukombinacijutrinekomplanarnavektora.Zbogtoga kažemodajetrojkanekomplanarnihvektora baza uprostorusvih vektoraidajetajprostor trodimenzionalan

Istotako´ceuredeniparnekolinearnihvektorabitibazauprostoru svihvektorakojisukomplanarnistimvektorimaitajjeprostor dvodimenzionalan

Vektorrazliˇcitodnulvektorabit´cebazauprostorusvihvektora kolinearnihstimvektoromitajjeprostor jednodimenzionalan

Slika

Nekaje (−→ a , −→ b , −→ c ) bazainekaje −→ d vektor.Kaoštosmove´crekli, tadasevektor −→ d najedinstvennaˇcinmoženapisatikao

Uredenutrojku (α, β, γ) nazivamo trojkomskalarnihkomponenata vektora d ubazi (−→ a , −→ b , −→ c )

Zadatak 7. Nekaje (−→ a , −→ b , −→ c ) baza.Odreditex ∈ R takodavektori −→ m = −→ a + 2 −→ b + 3−→ci

cbudukolinearni.

Rješenje: Kakosu −→ m i −→ n kolinearni,vrijedi

izˇcegaslijedisustav

Zadatak 8. Nekaje (

bazainekasu

c komplanarnivektori.Prikažitevektor −→ m kao linearnukombinacijuvektora −→ni −→ p.

Rješenje: Uzmimodaje

Iztogadobivamosustav

Izprveidrugejednadžbedobivamodaje α =

2 , β = 1 2 .Kako dobiveni α i β zadovoljavajuitre´cujednadžbu,slijedidaje −→ m = 1 2

n + 1 2 −→ p . Nekaje O toˇcka,a (−→ a , −→ b , −→ c ) baza.Uredenipar O, (−→ a , −→ b , −→ c ) zovemo koordinatnisustav,atoˇcku O ishodištekoordinatnog sustava

Slika 1.4.1: Koordinatnisustav

Nekaje O, (−→ a , −→ b , −→ c ) koordinatnisustav.Svakivektorspoˇcetkomutoˇcki O nazivamo radijvektor. Nekaje T toˇcka.Njojpridružujemovektor −→ OT kojegnazivamo radijvektortoˇcke T ukoordinatnomsustavu O, (−→ a , −→ b , −→ c )

Slika 1 4 2: RadijvektortoˇckeTukoordinatnomsustavu O, (a, b, c)

Kakoje (−→ a , −→ b , −→ c ) baza,ondasevektor −→ OT najedinstvennaˇcin možezapisatikao −→ OT = x −→ a + y −→ b + z −→ c ,tj.vektoru −→ OT pridružena jetrojka (x, y, z) skalarnihkomponenataubazi (−→ a , −→ b , −→ c ).Trojku (x, y, z) zakojuje −→ OT = x −→ a + y −→ b + z −→ c nazivamo trojkom koordinatatoˇcke T ukoordinatnomsustavu O, (−→ a , −→ b , −→ c ) ioznaˇcavamo T(x, y, z)

Zadatak 9. Nekasu (x1, y1, z1) i (x2, y2, z2) trojkekoordinatatoˇcaka T1 i T2 ukoordinatnomsustavu O, (−→ a , −→ b , −→ c ) .Zapišiteudanomkoordinatnom

sustavuvektor −−→ T1 T2

Rješenje:

Slika 1.4.3: Vektorukoordinatnomsustavu O, (a, b, c)

Nekasu −−→ OT1 = x1 −→ a + y1 −→ b + z1 −→ c i −−→ OT2 = x2 −→ a + y2 −→ b + z2 −→ c radijvektoritoˇcaka T1 i T2 ukoordinatnomsustavu O, (−→ a , −→ b , −→ c )

Sadjevektor −−→ T1 T2 = −−→ OT1 + −−→ OT2 = x1 −→ a +

Zadatak 10. Nekasu (x1, y1, z1) i (x2, y2,

) trojkekoordinatatoˇcaka T1 i T2 ukoordinatnomsustavu O, (

) .Pokažitedapolovište P stranice T1, T2 imakoordinateP

Rješenje:Zaodreditikoordinatetoˇcke P moramoodreditiradijvektortoˇcke P.Sadimamodaje −→ OP = −−→ OT1 + −→ T1 P = −−→ OT1 + 1 2 −−→ T1 T2

Kakoskalarnekomponenteradijvektoratoˇckeubaziodgovarajukoordinatamatetoˇcke,dobivamoda P imakoordinate P

Slika 1 4 4: Koordinatepolovištadužineukoordinatnomsustavu O, (a, b, c)

Zadatak 11. Nekasu (x1, y1, z1), (x2, y2, z2) i (x3, y3, z3) trojkekoordinata toˇcaka T1, T2 i T3 ukoordinatnomsustavu O, (−→ a , −→ b , −→ c ) .Sliˇcnokao uprethodnomprimjerupokažitedatežištetrokuta T1 T2 T3 imakoordinate T x1 +x2 +x3 3 , y1 +y2 +y3 3 , z1 +z2 +z3 3

Rješenje: Zariješitizadatakkoristimokoordinatepolovištaizprethodnogzadatkateˇcinjenicudatežištedijelitežišnicuuomjeru 2:1 odvrha.

Zadatak 12. Leželitoˇcke T1, T2 i T3,zadanesvojimkoordinatamaunekomkoordinatnom sustavu O, −→ a , −→ b , −→ c ) ,najednompravcu?

1. T1(1, 3,5), T2(2,7,1)

Rješenje: 1.Toˇckeleženajednompravcuakosuvektori

kolinearni,apoTeoremu 1 tovrijediakoisamoakosevektor

možezapisatikao −−→ T1 T2 = α −−→ T1 T3.Sadimamo

Uvrštavanjemvektoraugornjujednakostdobivamo

Vidimodanemožemoprona´ci α takavdavrijedigornjajednakost,što znaˇcidavektorinisukolinearniidazadanetoˇckeneleženajednom pravcu.

2.Sliˇcnokaopod 1.raˇcunamo

Vidimodaje

T1 T2 = 2

T1 T3,tj.vektori

T1 T2 i

T1 T3 sukolinearni,pa toˇcke T1, T2 i T3 leženaistompravcu.

Zadatak 13.

Leželitoˇcke T1, T2, T3 i T4,zadanesvojimkoordinatamaunekomkoordinatnomsustavu O, (−→ a , −→ b , −→ c ) ,ujednojravnini?

1. T1(2,1, 2), T2(4,4, 1), T3(4, 1, 1), T4(4, 6, 1);

2. T1( 1,2,1), T2(0, 4,0), T3(1,0, 2), T4(2, 2,1).

Rješenje: 1.Toˇcke T1, T2, T3 i T4 ležeujednojravniniakosuvektori −−→ T1 T2, −−→ T1 T3 i −−→ T1 T4 komplanarni,apoTeoremu 2 tovrijediakoisamo akosejedanodnjihmožezapisatikaolinearnakombinacijaostala dva.Probajmosadzapisati

.Sadimamo

Uvrštavanjemovihvektoraugornjujednakostdobivamo

Izjednaˇcavanjemvektoraslijeveidesnestranedobivamo 3 jednadžbe s 2 nepoznanice:

Iz 2.i 3.jednadžbedobivamo β = 1 i α = 2.Vidimodadobiveni α i β zadovoljavajuiprvujednadžbu.Toondaznaˇcidasevektor −−→ T1 T2 možezapisatikao

pasusvatrivektora komplanarnaisveˇcetiritoˇckeležeujednojravnini. 2.Sliˇcnokaopod 1.sadimamo

tedobivamo

Izgornjejednakostislijedisustav

1 = 2α + 3β

Vra´canjemdobivenog α uprvujednadžbudobivamo β = 1 9 .Kako dobiveni α i β nezadovoljavajudrugujednadžbu,tj. 6 = 10 9 , zakljuˇcujemodasevektor −−→ T1 T2 nemožezapisatiprekovektora −−→ T1 T3 i −−→ T1 T4,štoznaˇcidavektorinisukomplanarni.

1 5 skalarniproduktvektora

Kakobismodeﬁniraliskalarniproduktvektoranajprijemoramodeﬁniratikutizmedudvavektora.Uzmimovektore −→ a = −→ 0 i −→ b =

ihnanesimospoˇcetkomuistutoˇcku O takodaje −→ OA

Kutizmeduvektora −→ a i −→ b jemanjikutoddvakutakojizatvaraju polupravci p i q nakojimaleževektori −→ a i −→ b pavrijedidaje 0 ≤ ∠(−→ a , −→ b ) ≤ π

Slika 1.5.1: Kutizmeduvektora

Deﬁnicija 5: Nekasudanivektori −→ a = −→ 0i −→ b = −→ 0inekaje ϕ = ∠(−→ a , −→ b ). Skalarniproduktvektora −→ a i −→ b jerealanbroj(skalar) −→ a −→ b = |−→ a ||−→ b |cos

Akoje −→ a = −→ 0 ili −→ b = −→ 0 ,onda ϕ = ∠(−→ a , −→ b ) nijedeﬁniranpa deﬁniramodaje

a −→ b = 0.

Uliteraturiˇcestosekoristiioznaka −→ a −→ b zaskalarniprodukt. Izdeﬁnicijeslijedidaje

tedaje

Zasvevektore −→ a , −→ b i −→ c tesvakirealanbroj λ,vrijedesljede´ca svojstvaskalarnogprodukta:

1 −→ a −→ b = −→ b −→ a (komutativnostskalarnogprodukta)

2. (λ−→ a )−→ b = λ(−→ a −→ b )

3. (−→ a + −→ b )−→ c = −→ a −→ c + −→ b −→ c (distributivnostskalarnogproduktapremazbrajanjuvektora)

4 −→ a −→ a ≥ 0.

Karakterizacijaokomitostidvajuvektora

Nekaje −→ a = −→ 0 i −→ b = −→ 0 .Vektori −→ a i −→ b okomitisuakoisamo akoje −→ a −→ b = 0.

Dokaz: ⇒ Nekasuvektori −→ a i −→ b okomiti.Tadajeskalarniprodukt jednak −→ a −→ b = |−→ a ||−→ b |cos π 2 = 0. ⇐ Nekajesad −→ a −→ b = 0. Kakoje −→ a = −→ 0 i −→ b = −→ 0 ,ondamora vrijeditidaje cos∠(−→ a , −→ b )= 0,izˇcegaslijedidaje ∠(−→ a , −→ b )= π 2 tj. −→ a ⊥ −→ b

Zadatak 14. Nekajedanpravilanšesterokut ABCDEF straniceduljine 2.Nekaje G polovištestranice BC i H polovištestranice AF.Izraˇcunajte duljinuvektora −→ ACtekutizmeduvektora −→ HGi −→ HE.

Rješenje: Nacrtajmopravilanšesterokut ABCDEF sasredištemu toˇcki S teoznaˇcimovektore −→ AB i −→ AF s −→ m i −→ n

1 5 2: ZadanielementiZadatka 14

Svetraženevektoreizrazit´cemoprekovektora −→ m i −→ n jerznamo daje |−→ m | = |−→ n | = 2 tedaje ∠(−→ m , −→ n )= 2π 3 pamožemoizraˇcunati skalarniprodukt −→ m −→ n = 2 2 cos 2π 3 = 2.

1.5.3: RješenjeZadatka 14

Slika

Najprijepronadimovektor

Sadje

Timesmoriješiliprvidiozadatka.

Sad´cemovektore −→ HG i −→ HE izrazitiprekovektora

,apotomim izraˇcunatimodule.Dobivamo:

Konaˇcnodobivamo

Zadatak 15. Nekajedanpravilantetraedar ABCD duljinestranice 3. Odrediteduljinuvektoravisine −−→ D D teduljinuvektoravisine −−→ D1 D stranice ABD.

Rješenje: Koristimosezadatkom 6 gdjesmovektore

ve´cizraziliprekovektora

Saddobivamo

Zadatak 16. Nekajedanpravilanoktaedar ABCDEF duljinestranice 2 Odrediteduljinuvektoradijagonale −→ FE tekutizmeduboˇcnihbridovairavnine ABCD.

Rješenje:

Slika 1 5 5: ZadanielementiZadatka 16

Uzmimodaje

Slika 1 5 6: RješenjeZadatka 16

Sadje

paje

Dobivamo

Ovajzadataksmoriješilipomo´cuskalarnogprodukta,alionsejednostavnomožeriješitiikorištenjemtrigonometrijepravokutnogtrokuta.

1.6 vektorskaprojekcija

Nekajedanuredeniparvektora (−→ a , −→ b ).Trebamona´ciuredenipar vektora (−→ x , −→ y ) takavdaje

= 0.(1)

Naslici 1 6 1 ilustriranjesluˇcajkadvektori −→ a i −→ b nisukolinearnii kadjeuvjet −→ y −→ a = 0 ekvivalentanuvjetuokomitosti −→ y ⊥ −→ a (jerako jevektor −→ b kolinearansvektorom −→ a ,ondaje −→ b = −→ x teje −→ y = −→ 0 ).

Uzmimosadnetrivijalnisluˇcajkadje −→ a = −→ 0 .Pretpostavimoda jeuredenipar (−→ x , −→ y ) rješenjedanogproblema.Izuvjeta −→ x ||−→ a i −→ a = −→ 0 slijedidapostojirealanbroj α takavdaje −→ x = α −→ a .Sad dobivamodaje −→ y = −→ b −→ x = −→ b α −→ a

Timesmodokazalidaakoproblem (1) imarješenje (

y ),ondaje nužno

Vektor

zovemo vektorskaprojekcijavektora

.Broj

zovemo skalarnaprojekcijavektora −→ b navektor −→ a .Apsolutna vrijednostskalarneprojekcijejednakajeduljinivektorskeprojekcije.

Slika 1.6.1: Vektorskaprojekcija

Zadatak 17. Nekajedantrokut ABC takavdaje

CC teduljinutogvektora.

Rješenje: Skicirajmotrokut ABC temuoznaˇcimovisinu CC

Slika 1 6 2: RješenjeZadatka 17

Sadvidimodajevektor −−→ AC vektorskaprojekcijavektora −→ AC na vektor −→ AB paidemogadobitipoprijeizvedenojformuli:

Sadje

1 7 pravokutnikoordinatnisustav

UPoglavlju 1.4 uvelismopojamkoordinatnogsustava.Definirali smogakaouredenipar O, (a, b, c) ,gdjeje O bilanekatoˇckakoju smozvaliishodištekoordinatnogsustava,auredenatrojka (a, b, c) tri nekomplanarnavektoraˇcinilajebazukoordinatnogsustava. SadćemokaonjegovspecijalnisluˇcajdefiniratipravokutniiliKartezijevkoordinatnisustav.NjegajeuveoRenéDescartesu 17.stoljeću, ˇcimejezapoˇceorazvojkoordinatnihsustavateomogućioprouˇcavanje geometrijskihtijelametodamaanalitiˇckegeometrijeialgebre.

Kažemodasu vektori a, b i c ortogonalni akoje a⊥b, a⊥c i b⊥c Akosuvektori a, b i c ortogonalni,ondanisukomplanarnipaˇcine bazu.Bazuortogonalnihvektorazovemo ortogonalnombazom.Ako suvektoriortogonalnebazejošijediniˇcni,takvubazuzovemo ortonormiranabaza.Izortogonalnebaze (a, b, c) jednostavnodobivamo ortonormiranubazu a |a| , b |b| , c |c| .

Kažemodaje koordinatnisustav O, (a, b, c) pravokutan akoje baza (a, b, c) ortonormirana.Koordinatetoˇckeupravokutnomkoordinatnomsustavunazivamo pravokutnimkoordinatamatoˇcke.Ortonormiranubazuoznaˇcavat´cemo (i, j, k),apravokutnikoordinatni sustav O, (i, j, k)

Pravactoˇckom O nakojemleživektor i nazivamo x-osili apscisa, pravactoˇckom O nakojemleživektor j nazivamo y-osili ordinata, apravactoˇckom O nakojemleživektor k nazivamo z-osili aplikata Koordinatneosiodreduju koordinatneravnine xy, xz i yz.

Naslikama 1.7.1 i 1.7.2.prikazanisuradijvektor −→ OT toˇcke T ivektor −→ AB upravokutnomkoordinatnomsustavu O, (i, j, k) .

Slika 1.7.1: Radijvektorupravokutnomkoordinatnomsustavu

Slika 1 7 2: Vektorupravokutnomkoordinatnomsustavu

Nekasusaddanivektori a = axi + ay j + azk i b = bxi + by j + bzk u pravokutnomkoordinatnomsustavu O, (i, j, k) .Izraˇcunajmosad skalarniprodukt ab pomo´cukomponenatatihvektoraubazi (i, j, k) Odredimonajprijeskalarneproduktevektorabaze:

Iztogaslijedidaje

Zadatak 18. Nekasudanetoˇcke A( 1,4,5), B(4, 3,1) i C( 1,0,4) u pravokutnimkoordinatama.Odrediteduljinuvektora −→ AB teskalarniprodukt −→ AB −→ AC.Kolikijekutizmeduvektora −→ ABi −→ AC?

Rješenje: Odredimonajprijevektore

Sadje

Zadatak 19. Odrediterealanparametar t takavdavektor −→ a = ti j 2k budeokomitnavektor −→ b = i + k.

Rješenje: Parametar t odredit´cemoizuvjetaokomitosti −→ a −→ b = 0. Sadimamo

Sad´cemoizvestijošjednuformulukojavrijedisamoupravokutnom koordinatnomsustavu.Nekajedanvektor a = axi + ay j + azk te oznaˇcimos α, β i γ kutevekojevektor a zatvarasvektorima i, j i k

Slijedidaje

Dobivamo

izˇcegaslijedidaje

Zadatak 20. Odreditoˇcku T(x, y, z) takvudaradijvektortoˇcke T imamoduljednak 6,s vektorima i i j zatvarakuteveod 45o i 60o tedajeaplikata(z-koordinata) toˇcke T negativna.Kolikijekutkojiradijvektortoˇcke T zatvarasvektorom −→ k?

Rješenje: Najprijezapišimoradijvektortoˇcke T(x, y, z),tj. −→ OT = xi + yj + zk.Sadpoprethodnimformulamaimamo

z =

OTk = 6cos120o = 6 · 1 2 = 3,

patoˇcka T imakoordinate T(3√2,3, 3).

Kažemodatoˇcka C ∈ AB dijelidužinu AB u omjeruzlatnogreza akoseduljidio |AC| dužine |AB| premakra´cemdijelu |CB| dužine |AB| odnosikaocijeladužina |AB| premaduljemdijelu |AC| dužine |AB|,tj. |AB| |AC| = |AC| |CB|

Oznaˇcimo a = |AB|, x = |AC|, a x = |BC| padobivamo a : x = x : (a x) x2 + ax a2 = 0.

Toˇcka C ležinadužini |AB| pajerješenje x = a 2 (√5 1)

duljinazlatnogreza |AC| dužine |AB| duljine a.

Slika 1.7.3: Zlatnirez

Zadatak 21. Zadanesutoˇcke A(3,5,1), B( 1,1,3).Naditetoˇcku C koja dužinu ABdijeliuomjeruzlatnogreza.

Rješenje:

Odredimoduljinudužine |AB|: |

Kakotoˇcka C dužinu AB dijeliuomjeruzlatnogreza,ondajeduljina dužine |AC| jednaka |AC| = 3(√5 1)

Sadje

paje

Toˇcka C imakoordinate

1 8 vektorskiproduktvektora

Nekaje (−→ a , −→ b , −→ c ) bazainekasu O, A, B i C toˇckezakojeje −→ OA = −→ a , −→ OB = −→ b i −→ OC = −→ c .Vektori −→ a i −→ b ležeuravnini π, dokvektor −→ c itoˇcka C nepripadajutojravnini. Akoseiztoˇcke C rotacijaizvektora −→ a uvektor −→ b vidikaopozitivnarotacija,ondakažemoda (−→ a , −→ b , −→ c ) desnabaza,odnosnodaje O, (−→ a , −→ b , −→ c ) desnikoordinatnisustav Napomenimo,pozitivnarotacijajerotacijausmjeruobratnomod kazaljkenasatu.

Slika 1.8.1: Desnikoordinatnisustav

Akoseiztoˇcke C rotacijaizvektora a uvektor b vidikaonegativnarotacija,ondakažemoda (−→ a , −→ b , −→ c ) lijevabaza,odnosnodaje

O, (−→ a , −→ b , −→ c ) lijevikoordinatnisustav

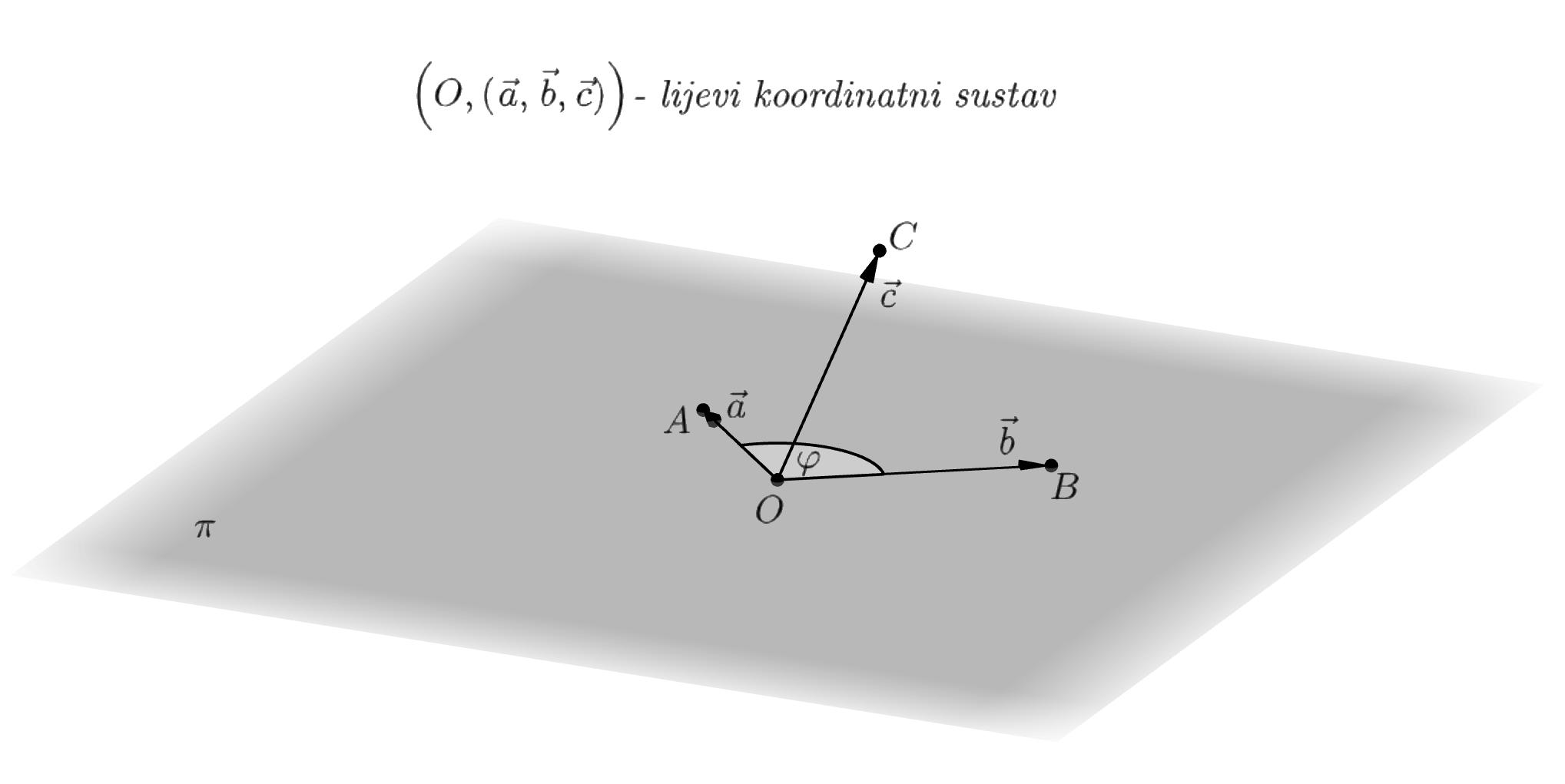
Slika 1 8 2: Lijevikoordinatnisustav

Nekaje (−→ a , −→ b ) uredeniparvektorai ϕ = ∠(−→ a , −→ b ). Vektorski produktvektora −→ a i −→ b jevektor −→ a × −→ b deﬁnirannasljede´cinaˇcin:

1 akoje −→ a ||−→ b ,ondauzimamodaje −→ a × −→ b = −→ 0

2 akovektori −→ a i −→ b nisukolinearni,ondauzimamodaje −→ a × −→ b vektorodredensljede´cimuvjetima:

• −→ a × −→ b jeokomitnavektor −→ a inavektor −→ b

• (−→ a , −→ b , −→ a × −→ b ) jedesnabaza

• |−→ a × −→ b | = |−→ a ||−→ b |sin∠(−→ a , −→ b ).

Slika 1 8 3: Vektorskiproduktvektora

Geometrijskainterpretacijamodulavektorskogprodukta |−→ a × −→ b | jestpovršinaparalelogramakojirazapinjuvektori −→ a i −→ b . Dokažimoovutvrdnju.Oznaˇcimos v visinuparalelogramais ϕ = ∠(−→ a , −→ b ) (vidisliku 1.8.4).Izpravokutnogtrokuta OB B dobivamo daje

paje

| Naravno,površinutrokuta OAB možemodobitikaopolovinupovršineparalelograma.

Slika 1 8 4: Geometrijskainterpretacijamodulavektorskogprodukta

Svojstvavektorskogprodukta

Zasvevektore −→ a , −→ b i −→ c izasvakirealanbroj λ vrijedi:

2 (−→

(distributivnostvektorskogproduktasobziromnazbrajanje)

) (antikomutativnostvektorskogprodukta)

Zadatak 22. Trokut ABC razapetjevektorima

,priˇcemuje |

.Odreditepovršinu trokutaABCivisinuizvrhaC.

Rješenje:

Slika 1 8 5: ZadanielementiZadatka 22

Vektorskiproduktupravokutnomkoordinatnomsustavu

Nekajesad

1.8vektorskiproduktvektora

vektorskiproduktvektora −→ a i −→ b pomo´cukomponentitihvektorau bazi (−→ i −→ j , −→ k ).Izraˇcunajmonajprijevektorskeproduktevektorabaze.

Kakoje −→ i ||−→ i , −→ j ||−→ j i −→ k ||−→ k ,ondauzimamodaje −→ i × −→ i = −→ 0 , −→ j × −→ j = −→ 0 i −→ k × −→ k = −→ 0 .Odredimosad −→ i × −→ j Nadimonajprije duljinutogvektora: |−→ i ×

Kakoje (−→ i × −→ j ) ⊥

(

i ×

j ) ⊥

j (aovosvojstvoimaivektor −→ k )tesu (−→ i , −→ j , −→ i × −→ j ) i (−→ i , −→ j , −→ k ) objedesnebaze,slijedida je −→ i × −→ j kolinearansvektorom −→ k .Kakosuobavektoraduljine 1,zakljuˇcujemodaje

bit´cesuprotno orijentiran,paje

izˇcegaslijedidaje

Determinantakvadratnematrice

Vektorskiproduktvektoraupravokutnomkoordinatnomsustavumožemoijednostavnijeraˇcunatikoriste´cideterminantematrica 2.i 3 reda.Kakobiobjasnilipojamdeterminante,najprijeuvodimopojam matrice.

Deﬁnicija 6: Pravokutnutablicuoblika

ˇcijisuelementirealnibrojevi,nazivamo realnamatricatipa m × n i oznaˇcavamo A ∈ Rmn Akoje m = n,tj.brojredakajejednakbroju stupaca,takvumatricunazivamo kvadratnamatrica

Determinanta A → detA funkcijajedeﬁnirananaskupusvihkvadratnihmatrica,apoprimavrijednostiizskupaskalara.Osimoznake detA zadeterminantukvadratnematrice A =

a11 a12 a1n a21 a22 a2n . . . . . . . an1 an2 ann

, ˇcestosekoristiioznaka

detA = a11 a12 ... a1n a21 a22 ... a2n . . . . . . . an1 an2 ... ann .

Determinantamatricedefiniraseinduktivno,tj.determinantamatrice n-togredadefinirasepomoćudeterminantematrice (n 1)-ogreda.

Akoje A = [a],ondajedetA = a Akoje

a11 a12 a21 a22

kvadratnamatrica 2.reda,tadajojmožemopridružitirealanbroj

a11 a12 a21 a22 = a11 a22 a21 a12

kojinazivamodeterminantakvadratnematrice 2.reda. Realnojmatrici 3.reda

a11 a12 a13 a21 a22 a23 a31 a32 a33

pridružujemodeterminantukojuraˇcunamonasljede´cinaˇcin:

a11 a12 a13 a21 a22 a23 a31 a32 a33 = a11 a22 a23 a32 a33 a12 a21 a23 a31 a33 + a13 a21 a22 a31 a32 = a11(a22 a33 a32 a23) a12(a21 a33 a31 a23)+ a13(a21 a32 a31 a22)

Determinantamatrice

reda n jebroj

det

Determinantumožemoraˇcunatitakodajurazvijemopobilokojem retkuilistupcu,naimevrijedisljede´citeorem:

Teorem 3. Laplaceovrazvojdeterminante NekajeA ∈ Rnn,n ≥ 2.Tadaje det A = n ∑ j=1 ( 1)i+j aij det Aij,

)

gdjeje Aij matrica (n 1)-ogredakojanastajeuklanjanjem i-togretkai j-togstupcaoriginalnematrice A.Jednakost (3) sezove Laplaceovrazvoj po i-tomretku,a (4) sezove Laplaceovrazvojpo j-tomstupcu

Mi´cemoovdjekoristitisamokvadratnematrice 2.i 3.reda.

Vektorskiproduktvektora

zadanihupravokutnomkoordinatnomsustavumožemojednostavnijedobitiinasljede´cinaˇcin:

Vidimodajeformula (6) jednakaformuli (3)

Zadatak 23. Odreditevolumenparalelopipeda ABCDA B C D akosu A(3, 5,2),B(1, 4,1) iD(6, 2, 1) trivrhaosnoviceiA (5, 2,1)

Rješenje:

Slika 1 8 6: RješenjeZadatka 23

Vektoridvajususjednihbridovaosnovicesu −→ AB = 2i + j k, −→ AD = 3 −→ i + 3 −→ j 3 −→ k .Raˇcunamovektorskiprodukt

i ( 3 + 3) −→ j (

+ 3)+ −→ k ( 6 3)= 9 −→ j 9 −→ k

Dakle, P = −→ AB × −→ AD = √81 + 81 = 9√2. Kakobismodobilivektorvisine −→ v moramonapravitivektorskuprojekcijuvektora −−→ AA navektor −→ AT.Najprijenadimovektor −−→ AA = 2 −→ i + 3 −→ j −→ k .Imamo −→ v = −→ AT −−→ AA |−→ AT|2 −→ AT = 27 + 9 √81 + 812 ( 9 −→ j 9 −→ k )= −→ j + −→ k , paje |−→ v | = √1 + 1 = √2. Konaˇcnoje V = P|−→ v | = 9√2√2 = 18.

Zadatak 24. Zadanesutoˇcke A(4,3, 2), B(3,5,1) i C(6,2,1) kojeˇcine bazuuspravnetrostraneprizme.Odreditepreostalatrivrhaprizmeakoje duljinanjenevisinev = √19

Rješenje:

Slika 1 8 7: RješenjeZadatka 24

Vektoristranicaosnovicesu

k .Sad´cemoizraˇcunativektorskiproduktvektoraosnovice kakobismodobilivektorokomitnaosnovicu:

Njegovaduljinaje

paje

A =(7,6, 3), B (6,8,0), C (9,5,0) Ovajzadatakimaidrugorješenje A , B , C kojedobijemoako uzmemosuprotnoorijentiranvektorvisine −→ v

1 9 mješovitiproduktvektora

Mješovitiproduktvektora −→

c realanjebroj

Geometrijskainterpretacijamješovitogprodukta Skicirajmoparalelopipedrazapetvektorima

1 9 1

Izpravokutnogtrokuta OCC dobivamodaje

kaonaslici

Sadraˇcunamomješovitiprodukt

gdje P oznaˇcavapovršinuparalelograma OADB,a V volumenparalelopipeda.Timesmopokazalidaprekomješovitogproduktavektora −→

c možemoizraˇcunativolumenparalelopipedarazapetogs vektorima

Slika 1 9 1: Mješovitiproduktvektora a, b i c

Kakokut ϕ izmeduvektora −→ c i −→ a ×

b možepoprimitisvevrijednostiizmedu 0 i π,kosinustogkutamožebitiinegativan,aondai volumenpoprimanegativnuvrijednost.Stogazavolumen V uzimamo |−→ c (−→ a × −→ b )|

1.9mješovitiproduktvektora 55

Akoimamoˇcetverostranupiramidurazapetusvektorima −→ a , −→ b i −→ c ,ondajenjenvolumenjednak 1 3 |−→ c (−→ a × −→ b )| jerjevolumenˇcetverostranepiramide 1 3 Pv.Volumentrostranepiramide,razapetes vektorima −→ a , −→ b i −→ c ,bit´ce 1 6 |−→ c (−→ a × −→ b )| jerjepovršinabazejednaka 1 2 P = 1 2 |−→ a × −→ b |.

Možemozakljuˇcitidajemješovitiproduktvektora −→ c (−→ a × −→ b )= 0 akoisamoakojebaremjedanodvektoranul-vektoriliakosuvektori komplanarni.

Nekasusaddanivektori

, −→ b = bx −→ i + by

koordinatnomsustavu O, (−→ i , −→ j , −→ k ) .Odredimomješovitiprodukt tihvektorapomo´cunjihovihkomponentiubazi (

Ovajproduktnajjednostavnijejeizraˇcunatikoriste´cideterminantu matrice 3.reda:

Zadatak 25. Vektori

razapinjutrostranupiramidu OABC. OdreditevolumenpiramideiduljinuvisineizvrhaCpiramide.

Rješenje: Koriste´cimješovitiproduktvektoraodredimovolumen piramide:

Sadnadimovektorskiproduktvektora a i b:

Površinaosnovice OAB iznosi

Konaˇcno,duljinavisineje

Zadatak 26. Odreditevolumenparalelopipeda ABCDA B C D akosu A(3, 5,2),B(1, 4,1) iD(6, 2, 1) trivrhaosnoviceiA (5, 2,1).

Rješenje: Ovajzadataksmove´criješilikoriste´cisamovektorski produkt(zadatak 23).Sadgamožetejednostavnijeriješitipreko mješovitogproduktavektora.Dakle,raˇcunamomješovitiprodukt vektora −→ AB, −→ AD i −−→ AA .Traženorješenjeje V = 18.

ANALITI ˇ CKAGEOMETRIJA

Uovompoglavljutoˇckeprostoraprikazanesuupravokutnimkoordinatamatepomo´cunjihdobivamoalgebarskejednadžbepravca iravnineuprostoru.Natajnaˇcingeometrijskezada´cerješavamo algebarskimmetodama.

Takoder,nekizadatciriješenisuikonstruktivnotejedanausporedba analitiˇckemetoderješavanjaimetodenacrtnegeometrije.

2.1 jednadžbaravnine

Nekaje T0 toˇckai −→ n = −→ 0 .Postojisamojednaravnina π koja sadržitoˇcku T0 iokomitajenavektor −→ n .Vektor −→ n nazivamo vektor normaleravnine π.Vektornormale −→ n ravnine π nijejedinstven. Svakivektorkolinearansvektorom −→ n takoderjevektornormale ravnine π

Slika 2.1.1: Jednadžbaravnine

Toˇcka T jeuravnini π akoisamoakoje T = T0 ili −→ T0 T ⊥ −→ n , atovrijediakoisamoakoje −→ T0 T−→ n = 0. Zbogtogrezultatauvjet −→ T0 T−→ n = 0zovemo karakterizacija(jednadžba)ravnine π ipišemo π −→ T0 T−→ n = 0.

Nekaje O, (−→ i , −→ j , −→ k ) desnipravokutnikoordinatnisustav, −→ n = A −→ i + B −→ j + C −→ k , T0(x0, y0, z0) i T(x, y, z).Sadje

T0 T =(x x0)

i +(y y0)

j +(z z0)−→ k ,paizkarakterizacije (jednadžbe)ravnine π, −→ T0 T−→ n = 0,dobivamo

A(x x0)+ B(y y0)+ C(z z0)= 0.(7)

Akosadoznaˇcimo D = Ax0 By0 Cz0,ondadobivamojednakost

Ax + By + Cz + D = 0(8)

kojuzovemo op´cioblikjednadžberavnine π

Primjer 3. Skicirajravninu π zadanujednadžbom π z + 3 = 0.

Rješenje:

Slika 2.1.2: Ravninaparalelnasravninomxy

Primjer 4. Skicirajravninu π zadanujednadžbom π x 3 = 0.

Rješenje:

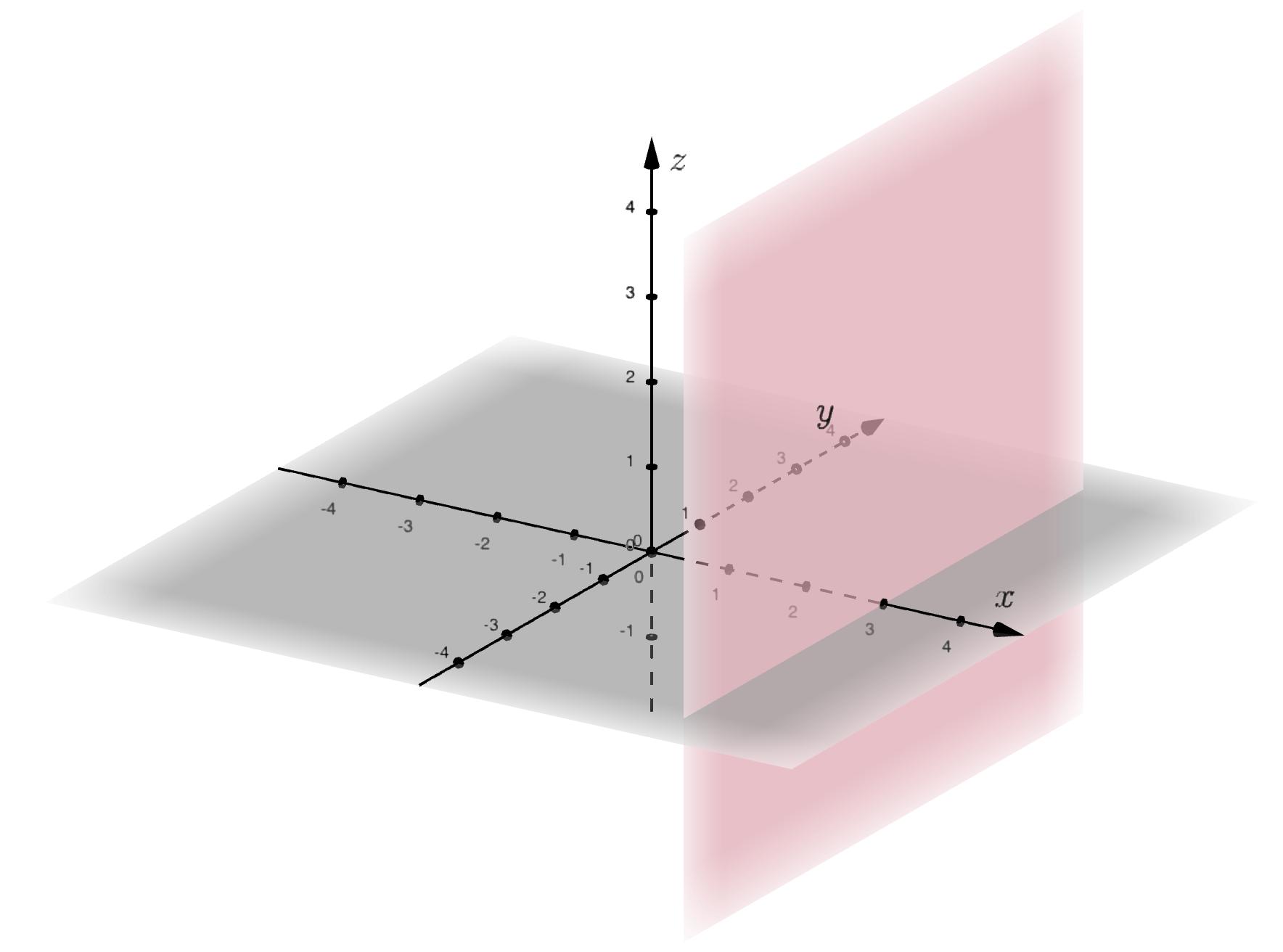
Slika 2.1.3: Ravninaparalelnasravninomyz

.2jednadžbapravca

Primjer 5. Skicirajravninu π zadanujednadžbom π y 2 = 0.

Rješenje: Slika 2.1.4: Ravninaparalelnasravninomxz

Zadatak 27. Napišiop´cioblikjednadžberavnine π kojaprolazitoˇckom

T0( 1,3,2) iokomitajenavektor −→ n = 2 −→ i 3 −→ j + −→ k.

Rješenje:

π ...2(x + 1) 3(y 3)+(z 2)= 0

π ...2x + 2 3y + 9 + z 2 = 0

π ...2x 3y + z + 9 = 0.

2 2 jednadžbapravca

Nekajedanatoˇcka T0 ivektor −→ q = −→ 0 .Postojitoˇcnojedanpravac p kojisadržitoˇcku T0 iimasmjervektora −→ q

Toˇcka T jenapravcu p akoisamoakojevektor −→ T0 T kolinearans vektorom −→ q ,atovrijediakoisamoakosevektor −→ T0 T možezapisati kao −→ T0 T = t−→ q , t ∈ R.Uvjet

−→ T0 T = t−→ q , t ∈ R nazivamo karakterizacija(jednadnadžba)pravca p ipišemo p −→ T0 T = tq, t ∈ R

Slika 2 2 1: Jednadžbapravca

Nekaje O, (−→ i , −→ j , −→ k ) desnipravokutnikoordinatnisustav,

R dobivamojednakosti

kojezovemo parametarskajednadžbapravca p.Eliminacijomparametra t dobivamo

kanonskioblikjednadžbepravca p

Zadatak 28. Toˇckom T( 2,2,3) ipravcem p ... x 1 2 = y 1 3 = z+1 1 postaviteravninu.

Rješenje:

Slika 2 2 2: Rješenjezadatka 28

Uzmimonekutoˇckupravca p,npr. P(1,1, 1).Sadje

PT = 3 −→ i + −→ j + 4 −→ k .Vektornormaleravnine π dobijemokao

vektorskiproduktvektorasmjera

j + −→ k pravca p i vektora −→ PT:

Dakle, −→ n

Zadatak 29. Postaviteravninukrozpravce

Rješenje:

Slika 2.2.3: Rješenjezadatka 29

Vidimodasupravci p1 i p2 paralelni(jersuimjednakivektori smjera −→ q1 = −→ q2 = 2 −→ i + 3 −→ j −→ k )paodredujuravninu.Kakobismo napisalijednadžburavninemoramoodreditivektornormale.Vektor normaledobivamokaovektorskiproduktdvavektoraravninestim danemožemouzetivektoresmjerapravaca p1 i p2 jersutokolinearni vektoripajenjihovvektorskiproduktjednaknulvektoru. Uzmimovektorsmjerapravca p1 (ilipravca p2) −→ q1 = 2 −→ i + 3 −→ j −→ k tetoˇcku A(1,1, 2) pravca p1 itoˇcku B(0,1,3) pravca p2.Sadje −→ AB = −→ i + 5 −→ k ,paje

1 ×

Jednadžbaravnine π sadglasi

π ...5(x 1) 3(y 1)+ z + 2 = 0

π ...5x 3y + z = 0.

Zadatak 30. Odreditejednadžburavnine π zadanetoˇckama A(5,4, 5), B(3,2, 3) iC(5,3, 4).

Rješenje:

Slika 2 2 4: Rješenjezadatka 30

Odredimovektore −→ AB = 2 −→ i 2 −→ j + 2

k i

AC = −→ j +

k . Vidimodadobivenivektorinisukolinearnipaodredujuravninu. Odredimovektornormaleravnine π

AB × −→ AC =

Sadjejednadžbaravnine π jednaka

...2(

Zadatak 31. Napravcu p x+3 1 = y+1 2 = z 2 2 naditetoˇckujednako udaljenuodprobodištapravcasravninama

1 x + y z + 2 = 0, π2 x y z 2 = 0.

Rješenje: Skicirajmotraženorješenje.Izjednadžbividimodaravninenisuparalelne.Trebamoprona´ciprobodištepravca p izadanih ravnina.Traženatoˇckajepolovištedobivenihprobodišta.

Slika 2.2.5: Rješenjezadatka 31

Zapišimopravac p uparametarskomobliku.Dobivamo

Sadpravacuvrštavamoujednadžberavninakakobismodobiliprobodišta:

10)

Sadjepolovište

Zadatak 32. Nekajedanpravac p x+1 1 = y 1 0 = z 2 2 iravnina π x + 2y z + 2 = 0.Odrediteortogonalnuprojekciju p pravca p uravninu π tepravacp simetriˇcanpravcupsobziromnaravninu π

Rješenje:

Slika 2.2.6: Rješenjezadatka 32

Odredimonajprijeprobodištepravca p iravnine π Zapišimopravac p uparametarskomobliku

= 2t + 2, t ∈ R, tegasaduvrstimoujednadžburavnine π:

+ 2 2t 2 + 2 =

⇒−t + 1 = 0 t = 1.

Dobivamodajeprobodištepravca p iravnine π toˇcka P(0,1,4).Kako bismoodredilivektorsmjerapravca p ,najprijepoformuli (2) izraˇcunajmovektorskuprojekciju −→ x vektorasmjerapravca p navektor normaleravnine π.Imamodaje

k paje

Sadje

Zadatak 33. Odreditejednadžburavnine π sobziromnakojusuravnine π1 ...2x y + 2z 2 = 0

+ 3 = 0 medusobno simetriˇcne.Takoder,odrediteudaljenostravnina π1 i π2.

Rješenje: Uoˇcimodasuravnine π1 i π2 medusobnoparalelnejerje

Slika 2 2 7: Rješenjezadatka 33

Uzmimotoˇcku T1 ∈ π1 tenjomepostavimopravacokomitna ravnine π1 i π2.Odaberimoproizvoljno 2 koordinate,npr. x = 0 i y = 0.Akoihuvrstimoujednadžburavnine π1 dobivamodaje z = 1 Dakle,toˇcka T1 imakoordinate T1(0,0,1) pajejednadžbapravca p

Odredimoprobodište T2 pravca p iravnine π2: 8t 2t 4(2t + 1)+ 3 = 0 ⇒ t = 1 18 ⇒ T2( 1 9 , 1 18 , 8 9 )

Polovište P dužine T1 T2 imakoordinate P 1 18 , 1 36 , 17 18 pajejednadžba ravnine π

...2x y + 2z 7 4 = 0.

Udaljenostravnina π1 i π2 dobijemotakodaizraˇcunamoudaljenost toˇcaka T1 i T2: d = 0 + 1 9 2 + 0 1 18 2 + 1 8 9 2 = 1

Skupsvihtoˇcakaprostorakojesujednakoudaljeneoddvijuravnina

π1 i π2 ležeujednojravninikojunazivamo simetralnomravninom ravnina π1 i π2

Vektorenormala −→ n i −→ n simetralnihravninadobivamokaovektore simetralakutevakojezatvarajuvektorinormalaravnina π1 i π2 tj.

Zadatak 34. Odreditejednadžberavninasobziromnakojesuravnine

π1 ... x y + 2z + 1 = 0 i π2 ...2x 3y + z + 1 = 0 medusobnosimetriˇcne(simetralneravnineravnina π1 i π2).Takoder,odreditekutizmedu ravnina π1 i π2.

Rješenje:

Slika 2 2 8: Rješenjezadatka 34

Najprijeodredimojednutoˇckupravcapresjeˇcniceravnina π1 i π2 Uzmimonpr.dajekoordinata x = 0teriješimosustav:

Dobivamo y =

Vektorenormalasimetralnihravninadobivamokaovektoresimetrala kutevakojezatvarajuvektorinormalaravnina π1 i π2 paje

Traženeravninesu

Kutizmeduravnina π1 i π2 jednakjekutuizmedunjihovihvektora normalapaimamo

Zadatak 35. OdrediteudaljenosttoˇckeT(2, 3,4) odravnine π ...2x y + z + 1 = 0.

Rješenje:

Slika 2 2 9: Rješenjezadatka 35

Toˇckom T postavimookomicunaravninu π.Dakle,vektorsmjera −→ q okomice p bit´cejednakvektorunormale −→ n ravnine π:

Sadjejednadžbapravca p

Odredimoprobodištepravca p iravnine π:

paje P( 2, 1,2).Sadjeudaljenost d toˇcke T odravnine π jednaka d(T, P)= (2 + 2)

Zadatak 36. Odreditetoˇckepravca p

Kolikoiznoseudaljenostitihtoˇcakaodravnina π1 i π2?

jednakoudaljene

Rješenje: Slika 2.2.10: Rješenjezadatka 36

Toˇckepravca p jednakoudaljeneodravnina π1 i π2 dobivamokao probodištapravca p sasimetralnimravninamaravnina π1 i π2 Zaodreditisimetralneravninenajprijeodredimojednutoˇckupravca

presjeˇcniceravnina π1 i π2.Uzmimonpr.dajekoordinata x = 0 te riješimosustav:

2z + 3 = 0 y + 2z 1 = 0.

Dobivamo y = 2 3 i z = 5 6 teje T(

1 ∩

2. Vektorenormalasimetralnihravninadobivamokaovektoresimetrala kutevakojezatvarajuvektorinormalaravnina π1 i π2 paje

Traženeravninesu

Odredimoprobodištapravca p sravninama π i π: (t 7 3 ) 2t + 2 3

paje P( 4 3 , 2,3),

paje Q( 38 3 , 62 3 ,3).

Udaljenostitoˇcke Q odravnina π1 i π2 dobijemotakodatoˇckom Q postavimookomicu o najednuodravnina,npr. π1 tetražimo probodišteokomiceiravnine.Dobivamodajejednadžbaokomice o jednaka o x+ 38 3

,aondajetraženoprobodištetoˇcka Q1( 7, 28 3 , 43 3 ).

Sadjeudaljenost d toˇcke Q odravnine π1 jednaka d(Q, Q1)= 7 + 38 3 2 + 28 3

Zadatak 37. Odrediteudaljenosttoˇcke T(2,2, 3) odpravca p x+2 1 = y 2 2 = z 1 3 .

Rješenje: Slika 2 2 11: Rješenjezadatka 37

Postavimoravninu π toˇckom T okomitonapravac p:

+ 2y + 3z + 3 = 0.

Sadodredimoprobodištepravca p iravnine π.Zapišimopravac p u parametarskomobliku

uvrstimogaujednadžburavnine π,padobivamo

pajeprobodište P 18 7 , 6 7 , 5 7 .Udaljenosttoˇcke T dopravca p jednakajeudaljenostitoˇcaka T i P,ataudaljenostiznosi:

Zadatak 38. Odreditekutizmedupravca p x 3 = y 1 2 = z 1 3 iravnine π x y + 2z 3 = 0

Rješenje:

Slika 2 2 12: Rješenjezadatka 38

Kutizmedupravca p iravnine π jednakjekutuizmedupravcai njegoveortogonalneprojekcijeuturavninu.

Vidimodajetajkut ϕ jednak ϕ = π 2 ϕ,gdjeje ϕ = ∠(−→ q , −→ n ) q = 3i 2j + 3k jevektorsmjerapravca p,a −→ n = −→ i −→ j + 2 −→ k vektornormaleravnine π.Sadje cosϕ =

⇒ ϕ = 16◦46 43 ⇒ ∠(p, p )= 73◦13 17

Zadatak 39. Odreditepravac q kojiprolazitoˇckom T(3,2,5),sijeˇcepravac p x 1 2 = y 1 1 = z 2 1 iparalelanjesravninom π x y + 2z 2 = 0.

Rješenje:

Slika 2.2.13: Rješenjezadatka 39

Toˇckom T postavimoravninu π paralelnusravninom π.Kakosu ravnineparalelne,imajuistivektornormalepaje −→ n = −→ n = −→ i −→ j + 2 −→ k .Sadje

π ... x 3 (y 2)+ 2(z 5)= 0

⇒ π x y + 2z 11 = 0.

Odredimoprobodištepravca p iravnine π .Napišimopravac p u parametarskomobliku p =

x = 2t + 1

= t + 1 z = t + 2, t ∈ R

tegauvrstimoujednadžburavnine π

2t + 1 (t + 1)+ 2(t + 2) 11 = 0 ⇒ t = 7 3 .

Probodište P imakoordinate P 17 3 , 10 3 , 13 3 Dakle,vektorsmjerapravca q je

pajednadžbapravca q glasi

Zadatak 40. Toˇckom T( 1,1,0) postavitepravac p kojisijeˇcepravac p1 x 1 1 = y 2 = z+1 1 iˇcijijevektorsmjeraokomitnavektorsmjerapravca p2 ... x 2 1 = y 1 1 = z 1 .

Rješenje:

Slika 2 2 14: Rješenjezadatka 40

Postavimoravninu π toˇckom T okomitonapravac p2.Dakle,vektor smjera −→ q2 pravca p2 normalajeravnine π ˇcijajednadžbaglasi

π ... x + y z = 0.Pronadimoprobodištepravca p1 iravnine π.Kako je p1 =

x = t + 1 y = 2t z = t 1, t ∈ R,

dobivamo t + 1 + 2t (t 1)= 0,izˇcegaje t = 1 pajeprobodište P(0, 2, 2).Vektorsmjerapravca p je −→ TP = −→ i 3 −→ j 2 −→ k paje p ... x+1 1 = y 1 3 = z 2 .

Zadatak 41. Visinauspravnogstošcajenapravcu p x 1 1 = y+1 2 = z 1 , toˇcka V(3,3,2) vrhjestošca,atoˇcka T(3, 2,0) naobodnojjekružnicibaze stošca.OdreditekoordinatesredištaSosnovicetevolumenstošca.

Rješenje:

Slika 2 2 15: Rješenjezadatka 41

Postavimoravninutoˇckom T okomitonapravac p.Dakle,vektor normaleravnineje −→ n = −→ i + 2 −→ j + −→ k panjenajednadžbaglasi

π ... x + 2y + z + 1 = 0.Sadodredimoprobodište S pravca p iravnine π.Pravac p zapišemouparametarskomobliku p =

x = t + 1 y = 2t 1 z = t, t ∈ R, uvrstimoujednadžburavninetedobivamo t = 0. Koordinatetoˇcke S glase S(1, 1,0). Volumenstošcaraˇcunamo r = d(S, T)=

d(S, V)=

DODATAK :POVEŽIMOANALITI ˇ CKUINACRTNU GEOMETRIJU

OvajudžbenikprvenstvenojenamijenjenstudentimaStudijaarhitektureiurbanizmateStudijudizajnakojinapoˇcetkusvogfakultetskog obrazovanjaslušajuikolegijenacrtnegeometrije.Nerijetkosedogadadastudentineuoˇcavajupoveznicuizmedusadržajaanalitiˇcke geometrijeobradeneuprethodnompoglavljuitogistogsadržajapromatranog”oˇcima”nacrtnegeometrije.Op´cenito,premanaˇcinunakoji rješavamogeometrijskeprobleme,geometrijudijelimona:

• analitiˇckugeometriju(alat:algebra)

• diferencijalnugeometriju(alat:diferencijalniraˇcun)

• sintetiˇckugeometriju(alat:logiˇcnozakljuˇcivanjeiprostornizor)

• nacrtnageometrija(alat:konstruktivnorješavanjemetodama projiciranja).

Podsjećamodajeprouˇcavanjegeometrijenužnozarazvijanjeprostornogzorairazumijevanjeraˇcunalnih 3Dprograma.Uovomdodatku riješitćemonekolikometriˇckihzadaćametodamaortogonalnogprojiciranja.Teistezadaćeobradenesuuprethodnompoglavljuna algebarskinaˇcin.Dakle,promatramoistemetriˇckeproblemeizdva razliˇcitakuta.Prirješavanjualatimanacrtnegeometrijepretpostavlja seosnovnoznanjeortogonalnogprojiciranja.Napominjemodaseu analitiˇckojgeometrijikoristidesnikoordinatnisustav,aunacrtnoj lijevikoordinatnisustav.

2.a osnovnielementi

Unacrtnojgeometrijiuvode´cibilokojumetoduprojiciranjapromatramotriosnovnageometrijskaelementa:toˇcku,pravac,ravninate njihoveodnose.

2.a.1 Toˇcka

Kodmetodeortogonalnogprojiciranjaprostornihﬁguraiodnosa medunjima,projiciramookomitimzrakamanatrimedusobnookomiteravnine Π1, Π2, Π3 (vidisliku 2.A.1a).Koordinatneosilijevog koordinatnogsustavasu

Toˇcka T zadanajekoordinatama (x, y, z),gdje x -koordinatapredstavljaudaljenosttoˇcke T odravnine Π3, y -koordinataudaljenostod ravnine Π2 i z -koordinataudaljenosttoˇcke T odravnine Π1.Okomite projekcijetoˇcke T naravnine Π1,Π2,Π3 soznakama T ,T ,T sutlocrt, nacrtibokocrttoˇcke.Ortogonalnaprojekcijatoˇcke T prikazanajena slici 2.A.1b.

(a) Koordinatnisustaviprostorniprikaz toˇcke T

(b) Ortogonalneprojekcijetoˇcke T

Slika 2.A.1: Toˇcka T

2.a.2 Pravac

Pravac p uortogonalnojprojekciji,kaoiuprostoru,odredenjedvjema toˇckama.Naravno,incidencijaseˇcuvauortogonalnimprojekcijama. Zapravac p uortogonalnimprojekcijamavezujusedvijebitnetoˇcke, P1 i P2.S P1 oznaˇcavamoprvoprobodištepravca,tj.probodištepravca p sravninom Π1,as P2 drugoprobodištepravca,tj.probodištepravca p sravninom Π2.Pravacuprostoruprikazanjenaslici 2.A.2a,a njegovaortogonalnaprojekcijana 2.A.2b

(a) Pravac p uprostoru (b) Pravac p uortogonalnimprojekcijama

Slika 2.A.2: Pravac p

2 a 3 Ravnina

Promotrimoop´curavninu P uprostoru,vidisliku 2.A.3a.Uortogonalnimprojekcijamaravninajeodredenasvojimtragovima,prvimi

drugimtragom.Prvitragravninejepresjeˇcnicaravnine P itlocrtne ravnine Π1,adrugitragravninejepresjeˇcnicaravnine P inacrtne ravnine Π2. Naslici 2.A.3b prikazjeravnineuortogonalnimprojekcijama.

(a) Ravninauprostoru (b) Tragoviravnine

Slika 2.A.3: Prikazravnine

Opisslike 2.A.3b:

1. r1 = P ∩ Π1, r1 jeprvitragravnine P

2. r2 = P ∩ Π2, r2 jedrugitragravnine P

3 r1 ∩ r2 ∈ x

Ravnineokomitena Π1,odnosno,na Π2 suprojiciraju´ceravninei prikazanesunaslikama 2.A.4a i 2.A.4b.

(a) Prvaprojiciraju´caravnina (b) Drugaprojiciraju´caravnina

Slika 2.A.4: Projiciraju´ceravnine

Toˇckaležinapravcuakoisamoakoprojekcijetoˇckeleženaodgovaraju´cim projekcijamapravca.

Pravacležiuravniniakoisamoakoprobodištapravcaleženaistoimenim tragovimateravnine,tj.P1 ∈ r1 iP2 ∈ r2

(a) Pravacuravnini

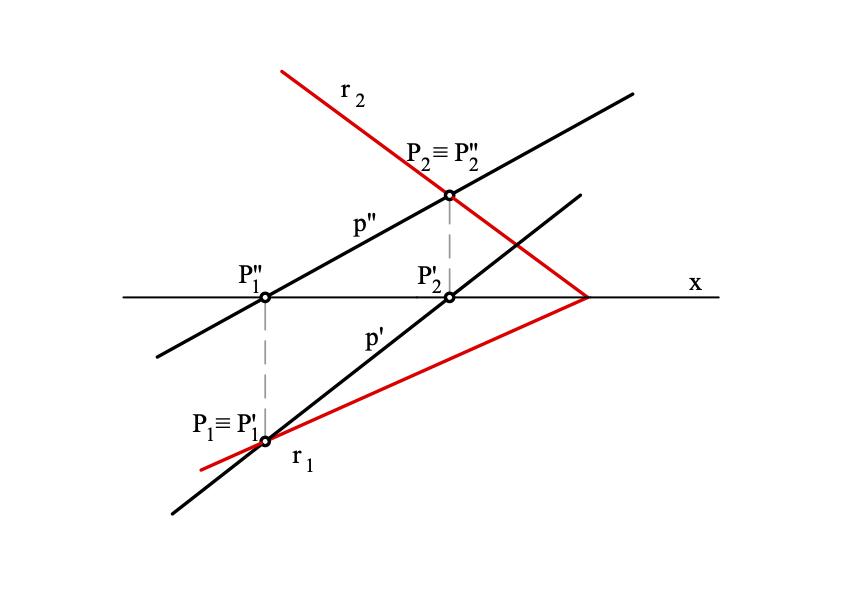
(b) Pravacuravnini-ortogonalne projekcije

Slika 2.A.5: Pravacuravnini

Horizontalniifrontalnipravciuravnini primjersupravacaravnineuposebnompoložaju:

(a) Horizontalnipravacuravniniortogonalnaprojekcija

(b) Frontalnipravacuravniniortogonalnaprojekcija

Slika 2.A.6: Horizontalniifrontalnipravciuravnini

2.a.4 Presjeˇcnicadvijuravnina

Zajedniˇckipravacdvijuravninazovese presjeˇcnica ravnina. Pravac´cebitipresjeˇcnicadvijuravninaakoisamoakoprobodišta pravcaleženatragovimatihravnina,vidisliku 2.A.7a

(a) Presjeˇcnicadvijuravnina

(b) Presjeˇcnicadvijuravnina-ortogonalne projekcije

Slika 2.A.7: Presjeˇcnicadvijuravnina

Zaprikazpresjeˇcniceuortogonalnojprojekciji(slika 2.A.7b)vrijedi:

3. p = P1 P2 ∧ p = P1 P2.

2 a 5 Probodištepravcairavnine

Zajedniˇckatoˇckaravnine P ipravca p zoveseprobodištepravcai ravnine.

Dabismonašli p ∩ P = N iuprostornomprikazu(slika 2.A.8a)iu ortogonalnimprojekcijama(slika 2.A.8b),radimoistipostupak:

1. Pravcem p postavljamopomo´cnuravninu ∆,usluˇcajuortogonalnogprojiciranjaravninu ∆ biramookomituna Π1 ili Π2.

2. Odredimopresjeˇcnicu q pomo´cneravnine ∆ ipolazneravnine P.

3 Sjecištepravca p ipresjeˇcnice q jetraženoprobodište N

Uortogonalnimprojekcijamatosesvodinasljede´ce:

1. p ⊂ ∆(d1, d2), npr. ∆(d1, d2)⊥Π2 ⇒ d2 ≡ p , d1⊥x

2. ∆(d1, d2) ∩ P(r1, r2)= q, q ≡ d2, q ≡ Q1Q2

3 p ∩ q = N ⇒ p ∩ q = N , N ∈ p

(a) Probodištepravcairavnine

(b) Probodištepravcairavnineortogonalneprojekcije

Slika 2.A.8: Probodištepravcairavnine

2.a.6 Pravacokomitnaravninu

Pravac n okomitjenaravninu P akojeokomitnabaremdva,aondai nasvepravceteravnine(slika 2.A.9a).

Pravac n nazivamo okomicom ili normalom.Uortogonalnimprojekcijama(slika 2.A.9b)vrijedi

n⊥P(r1, r2) ⇒ n ⊥r1 ∧ n ⊥r2

(a) Pravacokomitnaravninu

(b) Pravacokomitnaravninuortogonalneprojekcije

Slika 2.A.9: Pravacokomitnaravninu

2 b metri ˇ ckizadatci

2.b.1 Udaljenostdvijutoˇcaka

VidiPoglavlje 1 7,sliku 1 7 2

Akotražimoprostornuudaljenostdvijutoˇcaka A i B (slika 2.B.1a) tadauortogonalnimprojekcijamarotiramotrapez ABB A oko A B u Π1 ilitrapez ABB A oko A B uravninu Π2 (slika 2.B.1b).

(a) Udaljenostdvijutoˇcaka (b) Pravaveliˇcinaudaljenostidvijutoˇcaka

Slika 2.B.1: Udaljenostdvijutoˇcaka

2 b 2 Udaljenosttoˇckeodravnine

VidiZadatak 35,sliku 2 2 9

Odrediteudaljenosttoˇcke T odravnine P, T / ∈ P.

(a) Udaljenosttoˇckeodravnine

(b) Udaljenosttoˇckeodravnineortogonalneprojekcije

Slika 2.B.2: Udaljenosttoˇckeodravnine

Prostornorješenje:

1 T ∈ n, n ⊥ P (vidi 2.A.6 Pravacokomitnaravninu)

2 n ∩ P = N (vidi 2.A.5 Probodištepravcairavnine)

3 d(T, N) (vidi 2.B.1 Udaljenostdvijutoˇcaka).

Svakiodovihkorakariješenjeuprethodnimpromatranjima.Prikaz takvogrješenjauortogonalnimprojekcijamadanjenaslici 2.B.2b.

2.b.3 Udaljenosttoˇckeodpravca

Vidizadatak 37 isliku 2.2.11.

Odrediteudaljenosttoˇckeodpravca, T / ∈ p

Kodprostornogrješenjaspustimonormaluiztoˇcke T napravac p Takvorješenjenijemogu´ceuortogonalnimprojekcijamaosimuspecijalnimsluˇcajevima.Stogaradimosljede´ce:

1 T ∈ Σ, Σ ⊥ p

2. p ∩ Σ = P

3 d(T, p)= d(T, P)

KakopostavititoˇckomTravninu Σ okomitonapravac p?

1 a) T ∈ h, h Π1, h ∈ Σ(s1, s2) ⇒ T ∈ h , h ⊥p ∧ T ∈ h , h x (vidisliku 2.A.6a)

b) H2 = h ∩ x ∧ H2 ∈ h

c) H2 ∈ s2 ∧ s2⊥p , s1⊥p

2. p ∩ Σ(s1, s2)= P (vidi 2.A.5 Probodištepravcairavnine)

3 d(T, p)= d(T, P) (vidi 2.B.1 Udaljenostdvijutoˇcaka).

(a) Udaljenosttoˇckeodpravca

(b) Udaljenosttoˇckeodpravcaortogonalneprojekcije

Slika 2.B.3: Udaljenosttoˇckeodpravca

Studentimaprepuštamodapronadujošpoveznica.

ELEMENTARNEFUNKCIJE

Deﬁnicija 7: Funkcija ili preslikavanje uredenajetrojka (D, K, f ) koja sadržiskup D kojinazivamopodruˇcjedeﬁnicijeili domena funkcije, skup K kojinazivamopodruˇcjevrijednostiili kodomena funkcije inekopravilo f : D → K pokojemsesvakom x ∈ D pridružuje jedinstveni y ∈ K takavdaje y = f (x).

Deﬁnicija 8: Slikafunkcije jeskup

R( f )= { f (x) : x ∈ D} ⊆ K

Deﬁnicija 9: Skup Γ( f )= {(x, f (x)) : x ∈ D}

nazivamo graffunkcije f

Deﬁnicija 10: Zafunkciju f : D → K kažemodaje surjekcija akoza svaki y ∈ K postojibaremjedan x ∈ D takavdaje f (x)= y. Drugim rijeˇcima,funkcija f jesurjekcijaakojeslikafunkcijejednakakodomeni.

Zafunkciju f : D → K kažemodaje injekcija akovrijedisljede´ce:

zasve x1, x2 ∈ D, x1 = x2 ⇒ f (x1) = f (x2)

Zafunkciju f : D → K kažemodaje bijekcija akojefunkcijasurjekcija iinjekcija.

Deﬁnicija 11: Nekasu f : A → B i g : C → D dvijefunkcije.Akoje R( f ) ⊆ C,tadajejedinstvenoodredenafunkcija h : A → D takvada je h(x)= g( f (x))=(g ◦ f )(x) kojunazivamo kompozicijafunkcija f i g.

Deﬁnicija 12: Nekasu f : D → K i g : K → D funkcije.Kažemodaje g inverznafunkcija funkcije f akovrijedi

(g ◦ f )(x)= x,zasvaki x ∈ D,

( f ◦ g)(y)= y,zasvaki y ∈ K

Inverznufunkcijuoznaˇcavamos g = f 1

Inverznafunkcijapostojisamozabijektivnefunkcije.Grafinverzne funkcije f 1 simetriˇcanjegrafufunkcije f obziromnapravac y = x

Deﬁnicija 13: Nekaje Dg ⊆ D f i g(x)= f (x) zasvaki x ∈ Dg.Funkciju g nazivamo restrikcijailisuženjefunkcije f (oznaka g = f |Dg ),a funkciju f ekstenzijailiproširenjefunkcije g.

Miovdjeprouˇcavamofunkcijeukojimasu D ⊆ R i K ⊆ R,tj.kod kojihsudomenaikodomenapodskupoviskuparealnihbrojeva.

Deﬁnicija 14: Funkciju f nazivamo periodiˇcnom akopostojirealan pozitivanbroj P takavdavrijedi

f (x + P)= f (x), ∀x ∈ D.

Broj P nazivamo periodfunkcije f .

Deﬁnicija 15: Nekaje D ⊆ R takavdavrijedi

x ∈ D ⇒−x ∈ D,

tj. D je simetriˇcanskup sobziromnaishodište.

Kažemodaje f : D → R parnafunkcija akovrijedi

f ( x)= f (x), ∀x ∈ D.

Kažemodaje f : D → R neparnafunkcija akovrijedi

f ( x)= f (x), ∀x ∈ D

Deﬁnicija 16: Kažemodafunkcija f raste(strogoraste) napodruˇcju S ⊆ D akoje

f (x1) ≤ f (x2) ( f (x1) < f (x2))

zasve x1, x2 ∈ S, x1 < x2.

Kažemodafunkcija f pada(strogopada) napodruˇcju S ⊆ D akoje

f (x1) ≥ f (x2) ( f (x1) > f (x2))

zasve x1, x2 ∈ S, x1 < x2

Osnovneelementarnefunkcijesu:

• polinomi

• racionalnefunkcije

• eksponencijalnefunkcije

• logaritamskefunkcije

• op´capotencija

• trigonometrijskefunkcije

• ciklometrijskefunkcije.

Elementarnefunkcijesufunkcijekojesemogudobitiizosnovnih elemenarnihfunkcijapomo´cukonaˇcnogbrojaaritmetiˇckihoperacijai konaˇcnogbrojanjihovihkompozicija.

POLINOMI

Polinomn-togstupnja jefunkcija p : R → R oblika

p(x)= an xn + an 1 xn 1 + + a1

, an = 0.

Realnebrojeve a0, a1,..., an nazivamo koeﬁcijentima polinoma.Za n = 0 dobivamokonstantu p(x)= a0,za n = 1 linearnufunkciju p(x)= a1 x + a0,aza n = 2 kvadratnufunkciju p(x)= a2 x2 + a1 x + a0.

Konstantnafunkcija jefunkcija f : R → R oblika f (x)= c, c ∈ R

Primijetimodajekonstantnafunkcijapolinomstupnja0.

Primjer 6. Naslici 3.0.1 prikazanjegrafkonstante f (x)= 2.

Slika 3 0 1: Grafkonstantnefunkcije

Linearnafunkcija jefunkcija f : R → R oblika

f (x)= kx + l, k = 0, l ∈ R.

Primijetimodajelinearnafunkcijapolinomstupnja 1.Graflinearne funkcijejepravac y = f (x).Broj k nazivasekoeﬁcijentsmjera,a

predstavljatangenskuta α kojegpravaczatvaraspozitivnimdijelom osi x.Akoje k > 0 funkcijaraste,aakoje k < 0 funkcijapada.Broj l jeodsjeˇcakpravcanaosi y.Nultoˇckalinearnefunkcijejebroj x zakoji je f (x)= 0.

Primjer 7. Naslici 3 0 2 prikazanjegraflinearnefunkcije

f (x)= 1 2 x + 2.

Kvadratnafunkcija jefunkcija f : R → R oblika

f (x)= a2 + bx + c, a = 0, b, c ∈ R.

Primijetimodajekvadratnafunkcijapolinomstupnja 2.Grafkvadratnefunkcijejeparabola y = f (x).Kvadratnufunkcijumožemo zapisatiusljede´cemfaktoriziranomobliku:

f (x)= ax2 + bx + c = a(x x1)(x x2), gdjesu x1, x2 nultoˇckekvadratnefunkcije.Nultoˇckekvadratnefunkcijerješenjasujednadžbe f (x)= 0iraˇcunamoihpoformuli:

x1,2 = b ± √b2 4ac 2a

Koordinatetjemena T(xT , yT ) parabole y = f (x) raˇcunamopoformulama

xT = b 2a , yT = 4ac b2 4a .

Slika 3 0 2: Graflinearnefunkcije

Zarješenja x1 i x2 kvadratnejednadžbevrijedeiVièteoveformule

x1 + x2 = b a , x1 x2 = c a .

Primjer 8. Naslici 3.0.3 prikazanjegrafkvadratnefunkcije

f (x)= 2x2 3x 1.

Slika 3.0.3: Grafkvadratnefunkcije

RACIONALNEFUNKCIJE

Funkcija f oblika f (x)= p(x) q(x) , q(x) = 0,gdjesu p(x) i q(x) polinomi,nazivase racionalnafunkcija.Akojestupanjbrojnikamanji odstupnjanazivnika,ondakažemodajeto pravaracionalnafunkcija.

EKSPONENCIJALNEFUNKCIJE

Funkciju f : R → R+ oblika f (x)= ax , a > 0, a = 1 zovemo eksponencijalnafunkcijasbazoma Eksponencijalnafunkcijaimasljede´casvojstva: • ax1 ax2 = ax1 +x2 • ax1 ax2 = ax1 x2

• a0 = 1

• za a > 1funkcijajestrogorastu´ca

• za0 < a < 1funkcijajestrogopadaju´ca.

Primjer 9. Naslici 3.0.4 prikazanisugrafovieksponencijalnihfunkcija f (x)= 2x if (x)= 1 2 x .

Slika 3 0 4: Grafeksponencijalnefunkcije

LOGARITAMSKEFUNKCIJE

Logaritamskafunkcijasbazoma, f : R+ → R, f (x)= loga x, a > 0, a = 1,inverznajefunkcijaeksponencijalnefunkcije g(x)= ax

Logaritamskafunkcijaimasljede´casvojstva:

• loga(x1 x2)= loga x1 + loga x2

• loga x1 x2 = loga x1 loga x2

• loga 1 = 0

• loga xn = nloga x

• logan x = 1 n loga x

• loga x = logb x logb a

• za a > 1funkcijajestrogorastu´ca

• za0 < a < 1funkcijajestrogopadaju´ca.

Logaritamsbazom a = e,gdjeje e matematiˇckakonstantaaproksimativnogiznosa e = 2.71828,nazivamo prirodnilogaritam ioznaˇcavamogas f (x)= ln x. Logaritamsbazom a = 10 nazivamo dekadski logaritam ioznaˇcavamogas f (x)= logx.

Primjer 10. Naslici 3 0 5 prikazanisugrafovilogaritamskihfunkcija f (x)= log2 xif (x)= log 1 2 x.

Slika 3 0 5: Graflogaritamskefunkcije

OP ´ CAPOTENCIJA

Funkciju f : R+ → R+ oblika f (x)= xc =(elnx )c = eclnx , x > 0, c ∈ R nazivamo op´capotencija

TRIGONOMETRIJSKEFUNKCIJE

Slika 3 0 6: Trigonometrijskakružnica

Promotrimokružnicusasredištemuishodišturadijusa 1.Nekaje pravac p tangentanakružnicuutoˇcki A(1,0).Namatanjembrojevnog pravca p nakružnicu k(O,1) deﬁniranojepreslikavanjekojesvakom realnombroju t ∈ p pridružitoˇcku E(t) ∈ k(O,1),gdjejepoˇcetak utoˇcki A(1,0) ikre´ceseupozitivnomsmjeru.Ovopreslikavanje nazivamo eksponencijalnopreslikavanje.Usvakutoˇckukružnice preslikasebeskonaˇcnomnogotoˇcakabrojevnogpravcajervrijedi

E(t)= E(t + 2kπ), k ∈ Z

Funkcijakosinusdeﬁniranajekaoapscisa,afunkcijasinuskao ordinatatoˇcke E(t) nabrojevnojkružnici. Funkcijatangensdeﬁniranajekaoomjerfunkcijasinusikosinusnekog kuta,tj.

tgx = sinx cosx ,cosx = 0.

Dakle,tangensmožemopromatratikaonagibpravcakojizatvarataj kutspozitivnimdijelomosi x Funkcijakotangensdeﬁniranajekaoomjerfunkcijakosinusisinus nekogkuta,tj.

ctgx = cosx sinx ,sinx = 0.

Nasljede´cimslikamaprikazanisugrafovitrigonometrijskihfunkcija sinus,kosinus,tangensikotangens.

Funkcijasin: R → [ 1,1] :

Slika 3 0 7: Graffunkcijesinus

Funkcijasinusimasljede´casvojstva:

• sin( x)= sinx, ∀x (funkcijajeneparna)

• sin(x + 2π)= sinx, ∀x (funkcijajeperiodiˇcna).

Funkcijacos: R → [ 1,1] :

Slika 3.0.8: Graffunkcijekosinus

Funkcijakosinusimasljede´casvojstva:

• cos( x)= cosx, ∀x (funkcijajeparna)

• cos(x + 2π)= cosx, ∀x (funkcijajeperiodiˇcna).

Funkcijatg: R \{ π 2 + kπ, k ∈ Z}→ R :

Slika 3.0.9: Graffunkcijetangens

Funkcijatangensimasljede´casvojstva:

• tg( x)= tgx, ∀x (funkcijajeneparna)

• tg(x + π)= tgx, ∀x (funkcijajeperiodiˇcna).

Funkcijactg: R \{kπ : k ∈ Z}→ R :

Funkcijakotangensimasljede´casvojstva:

• ctg( x)= ctgx, ∀x (funkcijajeneparna)

• ctg(x + π)= ctgx, ∀x (funkcijajeperiodiˇcna).

Trigonometrijskiidentiteti

ˇ Cesto´cemouraˇcunskimoperacijamastrigonometrijskimfunkcijama koristititzv.trigonometrijskeidentitete.

Osnovnisutrigonometrijskiidentiteti

sin2 x + cos2 x = 1

tgx = sinx cosx ,cosx = 0

ctgx = cosx sinx ,sinx = 0

tj.tgx = 1

ctgx .

Formuleredukcijezasinusikosinusfunkcijusu

sin(π + x)= sinx

sin(π x)= sinx

cos(π + x)= cosx

cos(π x)= cosx

sin( π 2 + x)= cosx

Slika 3.0.10: Graffunkcijekotangens

sin( π 2 x)= cosx

cos( π 2 + x)= sinx

cos( π 2 x)= sinx

Trigonometrijskefunkcijezbrojairazlikesu

sin(x ± y)= sinxcosy ± cosxsiny

cos(x ± y)= cosxcosy ∓ sinxsiny tg(x ± y)= tgx ± tgy 1 ∓ tgxtgy

Trigonometrijskefunkcijedvostrukogkutasu

sin2x = 2sinxcosx

cos2x = cos2 x sin2 x tg2x = 2tgx 1 tg2 x

ctg2x = ctg2 x 1 2ctgx

Trigonometrijskefunkcijepoloviˇcnogkutasu

sin x 2 = ± 1 cosx 2

cos x 2 = ± 1 + cosx 2 .

Transformacijaumnoškauzbrojje

sinxcosy = 1 2 [sin(x + y)+ sin(x y)]

cosxsiny = 1 2 [sin(x + y) sin(x y)]

cosxcosy = 1 2 [cos(x + y)+ cos(x y)]

sinxsiny = 1 2 [cos(x y) cos(x + y)].

Transformacijazbrojauumnožakje

sinx + siny = 2sin x + y 2 cos x y 2

sinx siny = 2cos x + y 2 sin x y 2

cosx + cosy = 2cos x + y 2 cos x y 2

CIKLOMETRIJSKEFUNKCIJE

Ciklometrijskefunkcijesuinverznefunkcijerestrikcijatrigonometrijskihfunkcija.

Funkcijasinusjesurjekcija,alinijeinjekcija.Zatoradimorestrikciju funkcijesinusnanekiintervalkakobipostalainjekcija,alitakoderda ostanesurjekcija.Takodobivamofunkciju Sin = sin|[

kojajebijekcijapaimainverznufunkciju

kojunazivamo arkussinus.

Slika 3 0 11: Graffunkcijearkussinus

Sadnapravimorestrikcijufunkcijekosinusnainterval [0, π] kako bipostalainjekcija,alitakoderdaostanesurjekcija.Takodobivamo funkciju

Cos = cos|[0,π] : [0, π] → [ 1,1]

kojajebijekcijapaimainverznufunkciju

arccos = Cos 1 : [ 1,1] → [0, π]

kojunazivamo arkuskosinus

Slika 3 0 12: Graffunkcijearkuskosinus

Napravimorestrikcijufunkcijetangensnainterval

kojajebijekcijapaimainverznufunkciju

arctg = Tg 1 : R → π 2 , π 2

kojunazivamo arkustangens

Slika 3 0 13: Graffunkcijearkustangens

Napravimorestrikcijufunkcijekotangensnainterval < 0, π >.Takodobivamofunkciju

Ctg = ctg| 0,π : 0, π → R kojajebijekcijapaimainverznufunkciju

arcctg = Ctg 1 : R → 0, π kojunazivamo arkuskotangens

Slika 3.0.14: Graffunkcijearkuskotangens

ZADATCIZAVJEŽBU

1. Skicirajtegrafovefunkcija:

(a) f (x)= 1 2 x 3

Rješenje:

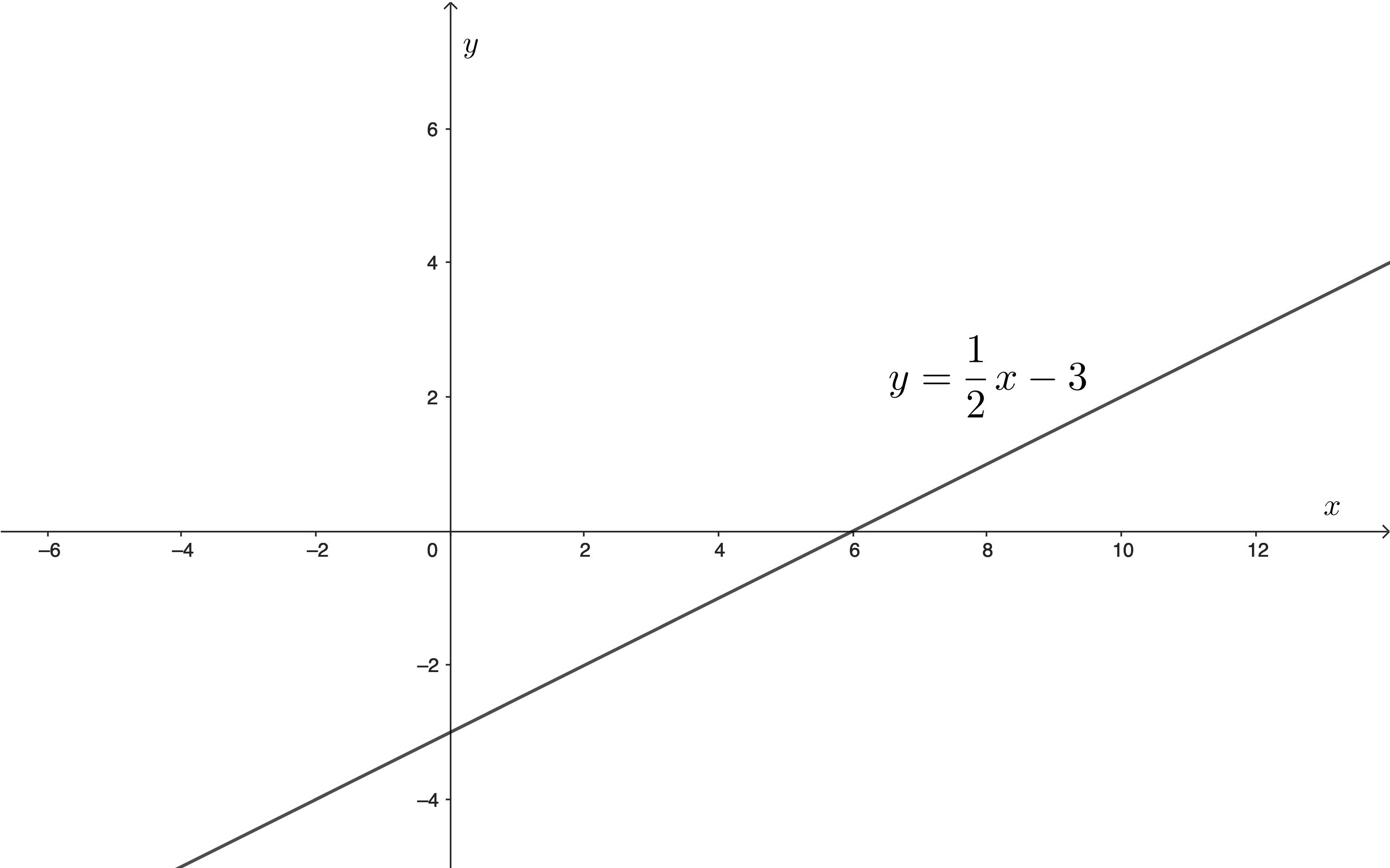
Slika 3 0 15: Graffunkcije f (x)= 1 2 x 3

(b) f (x)= x2 + x 12.

Rješenje:

Slika 3 0 16: Graffunkcije f (x)= x2 + x 12

2 Pronaditekvadratnufunkcijuzadanugrafom.

Rješenje: f (x)= 5 9 x2 + 5.

3 Riješijednadžbe:

(a) sin2x = √2 2

Rješenje: x = π 8 + kπ, k ∈ Z

(b) cosx = √3 2

Rješenje: x = π 6 + 2kπ, k ∈ Z.

4 Riješijednadžbe:

(a) lnx + 1 = 0

Rješenje: x = e 1

(b) e2x = 1

Rješenje: x = 0.

5 Dokažisljede´cetrigonometrijskeidentitete:

(a) cos4x cos2x sinxsin3x = 2

(b) cos( π 4 +x)+cos( π 4 x) cos( π 4 +x) cos( π 4 x) = ctgx

Slika 3.0.17: Grafkvadratnefunkcije

LIMESI

Graniˇcnavrijednostililimesfunkcije koristisekakobismoopisali ponašanjefunkcijekadsenjenargumentpribližavanekojtoˇckiilikad argumentpostajeproizvoljnovelik,tj.rasteubeskonaˇcnost.Graniˇcne vrijednostićemounastavkuovogpoglavljaiuidućempoglavlju koristitikakobismodefiniralineprekidnostiderivacijufunkcije.

Deﬁnicija 17: Nekaje > 0i a ∈ R.Otvoreniinterval < a , a + > zovemo okolina toˇcke a

Slika 4 0 1: Okolinatoˇckea

Deﬁnicija 18: Cauchyjevadeﬁnicijalimesa Nekajedanafunkcija f : D f → R, D f ⊆ R.Zarealanbroj l kažemo dajelimesfunkcije f utoˇcki a ∈ R akozasvaki > 0 postoji δ > 0 takavdaje a δ, a + δ \ {a} ⊆ D f idaiz x ∈ a δ, a + δ slijedi f (x) ∈ l , l +

Slika 4.0.2: Limesfunkcije f utoˇcki a.

Dakle,akopostojirealanbroj l takavdafunkcijskevrijednosti f (x) težeprematoˇcki l kadnezavisnavarijabla x težiprematoˇcki a,onda kažemodajetoˇcka l limesfunkcije f utoˇcki a ipišemo

lim x→a f (x)= l.

Izgornjedeﬁnicijevidimodajezapojamlimesafunkcije f utoˇcki a potrebnodafunkcijabudedeﬁniranananekojokolinitoˇcke a,aline nužnoiutoˇcki a.

Takodermožemozakljuˇcitidaakoipostojifunkcijskavrijednostu toˇcki a,onasenemorapoklapatislimesomfunkcijeutoˇcki a,štoje prikazanonaslici 4.0.3.

Slika 4 0 3: Vrijednostfunkcije f utoˇcki a nijejednakalimesufunkcije f u toˇcki a

Deﬁnicija 19: Nekaje a ∈ D f .Akopostoji limx→a f (x) iakoje limx→a f (x)= f (a), ondakažemodaje funkcija f neprekidnau toˇcki a.Kažemodaje funkcija f neprekidnanaskupu S ⊆ D f ako jeneprekidnausvakojtoˇcki x ∈ S.

Možemozakljuˇcitidafunkcijasaslike 4 0 3 nijeneprekidnautoˇcki a Nezavisnavarijabla x možetežititoˇcki a slijevaizdesnaitilimesi nemorajubitijednaki.

Vrijednost l je limesslijeva funkcije f utoˇcki a,odnosno

lim x→a f (x)= l

akozasvaki > 0 postoji δ > 0 takavdaiz x ∈ D f ∩ a δ, a slijedi | f (x) l| < .

Sliˇcno,vrijednost l je limessdesna funkcije f utoˇcki a,odnosno

lim x→a+ f (x)= l

akozasvaki > 0 postoji δ > 0 takavdaiz x ∈ D f ∩ a, a + δ slijedi | f (x) l| <

Primjer 11. Nacrtajmograffunkcijefzadanes

f (x)= x2 2, x < 1, x, x > 1.

Slika 4.0.4: Limesfunkcijeutoˇcki

Vidimodagornjafunkcijanemalimesutoˇcki 1 jerakosetoˇcki 1 približavamoslijevestrane,funkcijskevrijednostitežeprema 1,a akosepribližavamosdesnestrane,funkcijskevrijednostitežeprema 1.

Kodraˇcunanjalimesafunkcijakoristimoosnovnasvojstvalimesa koja´cemosadnavesti.Nekafunkcije f i g imajulimeseutoˇcki x0 Tadavrijedi:

Posebnovrijedilim

Unastavku´cemobezdokazanavestinekolikoosnovnihlimesa funkcijakoje´cemokoristitikodraˇcunanjalimesaostalihfunkcija:

1 limx→0 sinx x = 1

2 limx→0(1 + x) 1 x = e

3 limx→0 ln(1+x) x = 1

4 limx→0 ax 1 x = lna

5 limx→0 ex 1 x = 1.

Kodraˇcunanjalimesamogusepojaviti neodredenioblici 0 0 , ∞ ∞ , 0 · ∞, ∞ ∞, 00 , 1∞ , ∞0.Svitioblicitransformacijamasesvode najedanodoblika 0 0 i ∞ ∞ kodkojihmožemokoristiti L’Hospitalovo pravilo.Njega´cemouvestikaojednuodprimjenadiferencijalnog raˇcuna.Dotad´cemosekoristitidrugimtehnikamaraˇcunanjalimesa.

Zadatak 42. Izraˇcunajtelimese:

Rješenje:

DERIVACIJE

Derivacijafunkcijezajednosintegralnimraˇcunomˇciniosnovuinfinitezimalnograˇcunakojiimaširokuprimjenuuznanostiiinženjerstvu. Povijesnosudvapoprirodirazliˇcitaproblemabilaglavnamotivacija zarazvojdiferencijalnograˇcuna.Jedanodnjihjefiziˇckiproblem definiranjapojmabrzine.Drugiproblemjegeometrijskenaravi,a odnosisenapitanjepostojanjajedinstvenetangenteunekojtoˇckigrafa funkcije f . Derivacijaopisujebrzinupromjenefunkcijeuodnosunapromjenu argumentafunkcije.

5.1 definicijaderivacije

Slika 5 1 1: Deﬁnicijaderivacije

Oznaˇcimotoˇcke T0(x0, f (x0)) i T(x0 + ∆x, f (x0 + ∆x)) nagrafufunkcije f .Prisjetimosedajekoeﬁcijentsmjerapravcajednaktangensu kutakojipravaczatvaraspozitivnimdijelomosi x.Pravac s kroztoˇcke T0 i T nazivamo sekantomgrafafunkcije f .Vidimodajekoeﬁcijent smjerasekante

k = tgα = ∆ f ∆x = f (x0 + ∆x) f (x0) ∆x .

Kad ∆x → 0,toˇcka T sepografufunkcije"giba"dotoˇcke T0 isekanta s prelaziupravac t kojegnazivamo tangentomnagraffunkcije f u toˇcki x0.Dakle,akopostoji lim∆x→0,onćenamdatikoeficijentsmjera tangentefunkcije f utoˇcki x0.Tajlimesnazivamo derivacijafunkcije f utoˇcki x0 idefiniramogakao f (x0)= lim

x→0

x = lim

x→0 f (x0 + ∆x) f (x0) ∆x

Kažemodajefunkcija f derivabilnautoˇcki x0 akopostojilimes

lim∆x→0

(x0 +∆x) f (x0 )

x . Funkcija f je derivabilnanaintervalu a, b akojederivabilnausvakojtoˇckitogintervala.Zafunkciju f kažemo daje derivabilna akojederivabilnanacijelompodruˇcjudeﬁnicije. Kaoštosmove´crekli, k = tgα = f (x0)

Dakle,jednadžbatangentenagraffunkcije f utoˇcki x0 je t ... y f (x0)= f (x0)(x x0).

Oznaˇcimos D f skupsvihtoˇcakadomene D f funkcije f ukojima postojiderivacija f (x0).Funkciju

x → f (x), x ∈ D f

nazivamo derivacijafunkcije f Dakle, derivacijafunkcijeutoˇcki realanjebroj,a derivacijafunkcije jenovafunkcijakoja´cesvakojtoˇckidomenepridružitikoeﬁcijent smjeratangenteutojtoˇcki.

Derivabilnufunkciju f kojojjederivacija f neprekidnafunkcijanazivamo neprekidnoderivabilnailiglatkafunkcija.

Zadatak 43. Odreditejednadžbutangentenagraffunkcije f (x)= 1 2 x2 1 utoˇckix0 = 3 koriste´cisedeﬁnicijomderivacijefunkcije.

Rješenje: Dakle,moramoodredititangentukvadratnefunkcije f (x)= 1 2 x2 1udanojtoˇcki T0

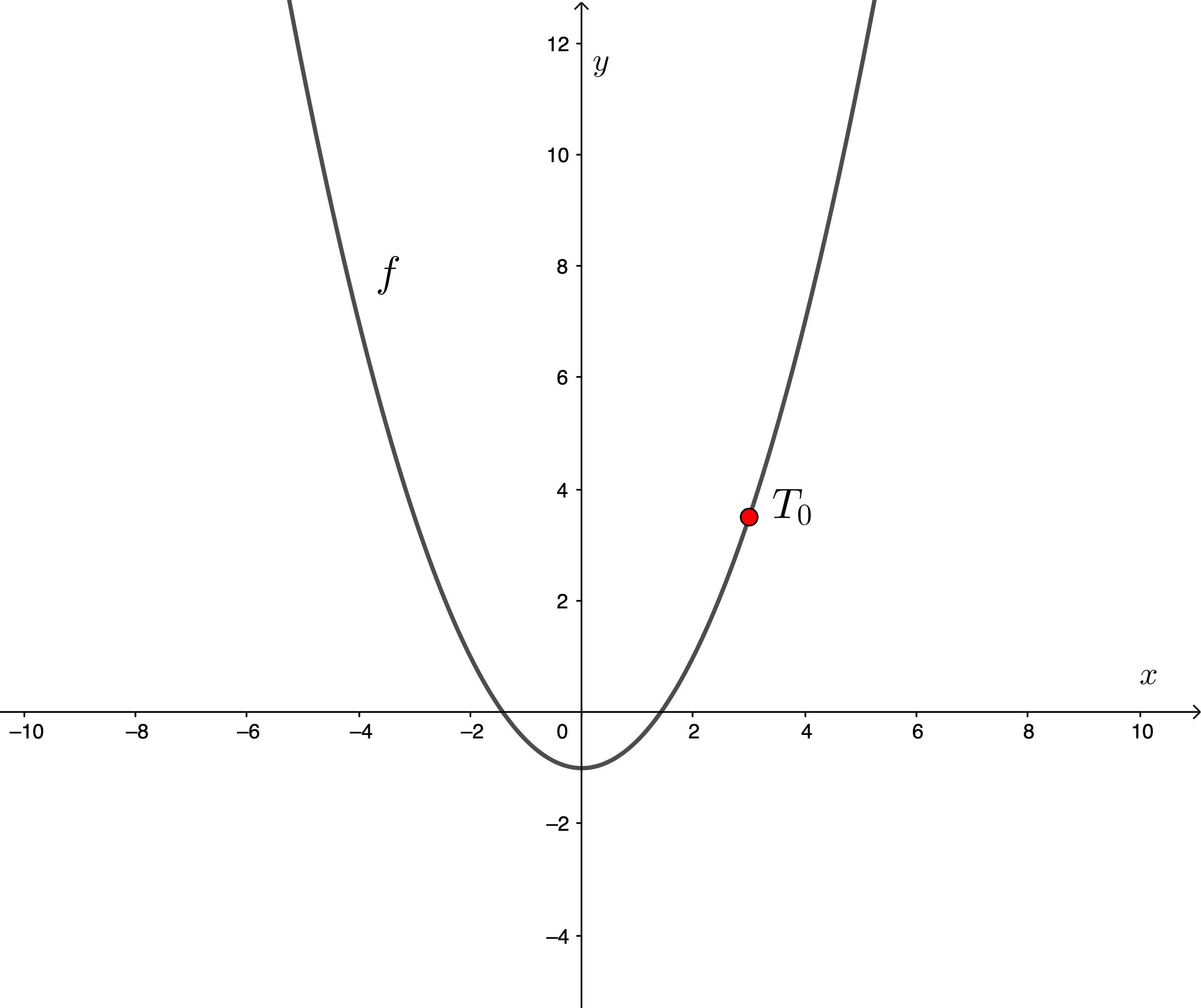
Slika 5 1 2: Zadanielementizadatka 43

Najprijeodredimokoordinatu y0 toˇcke T0:

Sadodredimokoeficijentsmjeratangenteutoˇcki T0 koristećisedefinicijomderivacije:

Jednadžbatangenteglasi

Akofunkciju f ipravac t prikažemograﬁˇcki,možemoseuvjeritidaje t tangentanagrafutoˇcki T0

Slika 5 1 3: Rješenjezadatka 43

Zadatak 44. Koriste´cisedeﬁnicijomderivacijefunkcijeodrediderivaciju funkcijef (x)= √x.

Rješenje:

Zadatak 45. Koriste´cisedeﬁnicijomderivacijefunkcijeodrediderivaciju funkcijef (x)= sin x.

.2derivacijeelementarnihfunkcijaipraviladeriviranja

Rješenje: f (x)=

)

Zadatak 46. Odreditejednadžbutangentenagraffunkcije f (x)= x2 u toˇckix0 = 2 koriste´cisedeﬁnicijomderivacijefunkcije.

Rješenje: y = 4x 4.

Zadatak 47. Koristećisedefinicijomderivacijeodreditederivacijesljedećih funkcija:

1. f (x)= x3

Rješenje: f (x)= 3x2

2 f (x)= cos x

Rješenje: f (x)= sin x

3. f (x)= tg x

Rješenje: f (x)= 1 cos2 x .

5 2 derivacijeelementarnihfunkcijaipraviladeriviranja

Koristećidefinicijuderivacijefunkcije,moguseizvestisvederivacije elementarnihfunkcija.Mićemonavestidobivenerezultatezaone funkcijekojećemokoristiti:

c = 0

(xn) = nx(n 1)

(cosx) = sinx

(sinx) = cosx

(ctgx) = 1 sin2 x

(tgx) = 1 cos2 x

(ax ) = axlna

(ex ) = ex

(loga x) = 1 xlna

(lnx) = 1 x .

Koristećidefinicijuderivacijetakoderizvodimopravilazaderivaciju zbroja,umnoškaikvocijentafunkcijatepravilozaderivacijusložene funkcije.Ovdjećemoihsvenavesti,anekeodnjihidokazati:

( f ± g) (x)= f (x) ± g (x)

( f g) (x)= f (x) g(x)+ f (x) g (x) f g = f (x)g(x) f (x)g (x) (g(x))2

( f (g(x)) = f (g(x))g (x)

Dokažimonpr.pravilozaderivacijuumnoška:

( f g) (x) = lim ∆x→0 ( f · g)(x + ∆x) ( f · g)(x)

(x + ∆x) ·

(x + ∆x)

(x) · g(x)

∆x→0 f (x + ∆x)g(x + ∆x) f (x)g(x)+ f (x)g(x + ∆x) f (x)g(x + ∆x) ∆x

lim ∆x→0

[ f (x + ∆x) f (x)] g(x + ∆x)+ f (x) [g(x + ∆x) g(x)] ∆x

lim ∆x→0

[ f (x + ∆x) f (x)] ∆x · g(x + ∆x)+ lim ∆x→0 f (x) · [g(x + ∆x) g(x)] ∆x = f (x)g(x)+ f (x)g (x)

Akostavimodaje f (x)= c, c ∈ R,dobivamo

(c g) (x)

= c · g(x)+ c · g (x) = 0 g(x)+ c g (x) = c · g (x)

Zadatak 48. Koriste´cisetabliˇcnimderivacijamaelementarnihfunkcijai pravilimaderiviranja,odreditederivacijesljede´cihfunkcija:

1. f (x)= sin x + x5

2. f (x)= x3 tg x

3. f (x)= 5ln x

4 f (x)= sin x x2

5 f (x)=(2 + x)2

6 f (x)=(2 + x)16

7 f (x)= sin(5x)

.2derivacijeelementarnihfunkcijaipraviladeriviranja

8 f (x)= ln(ln x + 5)

9. f (x)= ctg 1+x 1 x .

Rješenje:

1. Koristimopravilozaderivacijuzbrojadvijufunkcija:

f (x)= cosx + 5x4

2 Koristimopravilozaderivacijuumnoškadvijufunkcija:

)=(

3. Koristimopravilozaderivacijuumnoškakonstanteifunkcije:

f (x)= 5(lnx) = 5 x .

4. Koristimopravilozaderivacijukvocijentadvijufunkcija: f (x)= (sinx) x2 sinx(x2) (x2)2 = xcosx 2sinx x3

5 Zapišimofunkciju f uobliku:

f (x)= 4 + 4x + x2 .

Sadkoristimopravilozaderivacijuzbroja: f (x)= 0 + 4 + 2x = 4 + 2x.

6 Sadkoristimopravilozaderivacijusloženefunkcije: x g −→ 2 + x f −→ (2 + x)16 .

Dakle, g(x)= 2 + x,a f (x)= x16.Sadje

f (x)= 16(2 + x)15(2 + x) = 16(2 + x)15

7 Sadkoristimopravilozaderivacijusloženefunkcije: x g −→ 5x f −→ sin(5x).

Dakle, g(x)= 5x,a f (x)= sinx.Sadje

f (x)= cos(5x)(5x) = 5cos(5x)

8 Sadkoristimopravilozaderivacijusloženefunkcije: x g −→ lnx + 5 f −→ ln(lnx + 5)

Dakle, g(x)= lnx + 5,a f (x)= lnx.Sadje f (x)= 1 lnx + 5 (lnx + 5) =

9. Sadkoristimopravilozaderivacijusloženefunkcijeipraviloza derivacijukvocijenta: x g −→ 1 + x 1 x f −→ ctg 1 + x 1 x .

Dakle, g(x)= 1+x 1 x ,a f (x)= ctgx.Sadje

(x)=

Zadatak 49. Koriste´cisetablicomderivacijaelementarnihfunkcijaipravilimaderiviranja,odrediderivacijesljede´cihfunkcija:

1. f (x)= x ln x

Rješenje: f (x)= ln x 1 ln2 x

2 f (x)= x4 · ctg x

Rješenje: f (x)= x3 (2sin2x x) sin2 x

3 f (x)=(3x + 2)3

Rješenje: f (x)= 9(3x + 2)2

4. f (x)= cos(3x + 1)

Rješenje: f (x)= 3sin(3x + 1)

5 f (x)= ln 1 x 1+x

Rješenje: f (x)= 2 1 x2

5 3 l’ hospitalovopravilo

Kaoštosmove´cspomeniliuprethodnompoglavljukodraˇcunanja limesamožesepojavitijedanodsedamneodredenihoblika:

Limeseoblika 0 0 i ∞ ∞ jednostavnijemožemoriješitipomoćuL’Hospitalovog pravilakojećemonavestiunastavku.Ostalineodredenioblicisepomoćuodgovarajućihtransformacijasvodenajedanodovadvaoblika.

L’Hospitalovopravilo

Nekazafunkcije f , g : D → R vrijedi

lim x→c f (x)= 0,lim x→c g(x)= 0ili

lim x→c f (x)= ∞,lim x→c g(x)= ∞,

priˇcemuje c ∈ a, b ⊆ D.Nekasu f i g neprekidnenaskupu [a, b] ineprekidnoderivabilnenaskupu a, c ∪ c, b .Nekaje g(x) = 0 zasvaki x ∈ a, c ∪ c, b .Akopostoji limx→c f (x) g (x) = k,priˇcemuje k ∈ R ilije k = ∞ ilije k = ∞,tadaje

Zadatak 50. Izraˇcunajtelimese: 1

Rješenje:

5 4 rastipadfunkcije ekstremi

Unastavkućemokorištenjemprvederivacijedatikriterijezarastipad telokalneekstremefunkcije.Prisjetimosedefinicije(strogo)rastućei (strogo)padajućefunkcijeizpoglavlja 3,Elementarnefunkcije.

Deﬁnicija 20: Kažemodafunkcija f raste(strogoraste) napodruˇcju S ⊆ D akoje

f (x1) ≤ f (x2) ( f (x1) < f (x2))

zasve x1, x2 ∈ S, x1 < x2

Kažemodafunkcija f pada(strogopada) napodruˇcju S ⊆ D akoje

f (x1) ≥ f (x2) ( f (x1) > f (x2))

zasve x1, x2 ∈ S, x1 < x2.

Primjer 12. Jedanprimjersvugdjerastu´cefunkcijejeeksponencijalnafunkcijasbazomve´comod 1.

Slika 5 4 1: Eksponencijalnafunkcija

Deﬁnicija 21: Nekaje x0 ∈ D.Kažemodajetoˇcka f (x0) lokalni minimumfunkcije f akopostojiokolina x0 δ, x0 + δ toˇcke x0 na kojojje

zasvaki x ∈ x0 δ, x0 + δ

f (x0) ≤ f (x)

Kažemodajetoˇcka f (x0) lokalnimaksimumfunkcije f akopostoji okolina x0 δ, x0 + δ toˇcke x0 nakojojje

f (x0) ≥ f (x)

zasvaki x ∈ x0 δ, x0 + δ .

Naslici 5 4 2 nacrtanjegrafnekefunkcijetesunanjemupostavljene tangenteutoˇckama A, B i C

Slika 5.4.2: Rastipadfunkcije.Ekstremi.

Vidimodatoˇcka A ležinaintervalunakojemfunkcijastrogoraste, a B naintervalunakojemfunkcijastrogopada.Takodervidimodaje toˇcka C(x0, f (x0)) lokalnimaksimumfunkcijejerje f (x0) ≥ f (x),za svaki x iznekeokoline x0 δ, x0 + δ toˇcke x0

Pogledajmosadtangentuutoˇcki A.Prisjetimosedanamjederivacija funkcijeutoˇckidalakoeﬁcijentsmjeratangenteutojtoˇcki,tj. k1 = f (x1)= tgα1.Kakoje 00 < α1 < 900,ondaje f (x1) > 0. Sliˇcnoje tako k2 = f (x2)= tgα2.Kakoje900 < α2 < 1800,ondaje f (x2) < 0. Dakle,možemozakljuˇcitisljede´ce: pretpostavimodafunkcija f imaprvuderivacijuusvakojtoˇckinekog intervala a, b ; akoje

f (x) ≥ 0 f (x) > 0 ,zasvaki x ∈ a, b

ondafunkcija f raste(strogoraste)na a, b ; akoje

f (x) ≤ 0 f (x) < 0 ,zasvaki x ∈ a, b ondafunkcija f pada(strogopada)na a, b

Prouˇcimosadlokalneekstreme.Njihtražimoutoˇckama x0 ∈ D zakojepostojiokolinanakojojjefunkcija f deﬁniranaiukojimaje f (x0)= 0ilinepostoji f (x0)

Deﬁnicija 22: Nekaje f neprekidnafunkcijautoˇcki x0 Toˇcka x0 je stacionarnatoˇcka funkcije f akoje f (x0)= 0.Toˇcka x0 je kritiˇcna toˇcka funkcije f akoje x0 stacionarnatoˇckailiako f nijederivabilna utoˇcki x0

Dakle,kritiˇcnetoˇckesujedinetoˇckeukojimamogu(aliinemoraju) postojatilokalniekstremi.

Deﬁnicija 23: Nekaje f neprekidnautoˇcki x0.Akopostoji δ > 0 takavdaje f (x) ≤ 0, zasvaki x ∈ x0 δ, x0 i f (x) ≥ 0, zasvaki x ∈ x0, x0 + δ ,ondaje f (x0) lokalniminimum.Akopostoji δ > 0 takavdaje f (x) ≥ 0, zasvaki x ∈ x0 δ, x0 i f (x) ≤ 0, zasvaki x ∈ x0, x0 + δ ,ondaje f (x0) lokalnimaksimum.

Jednostavnijegovore´ci,akofunkcija f dotoˇcke f (x0) pada,aod toˇcke f (x0) raste,ondaje f (x0) lokalniminimum.Istotako,ako funkcija f dotoˇcke f (x0) raste,aodtoˇcke f (x0) pada,ondaje f (x0) lokalnimaksimum.

Upojedinimzadacimakojislijedeprokomentirat´cemoipostojanje asimptotanagraffunkcije.Stogaunastavkudajemoideﬁniciju asimptota.

Asimptotafunkcije jepravacsasvojstvomdaudaljenostizmedu toˇckegrafafunkcijeitogpravcatežiunulukadatoˇckanagrafutežiu beskonaˇcnost.Asimptotemogubitivertikalne,horizontalneikose.

Pravac x = x0 nazivamo vertikalnaasimptota funkcije f akovrijedi

limx→x0 f (x)= ±∞ ililim x→x0 + f (x)= ±∞.

Uprvomsluˇcajugovorimoovertikalnojasimptotislijevestrane,dok udrugomsluˇcajugovorimoovertikalnojasimptotisdesnestrane. Vertikalneasimptotemogusenalazitiutoˇckamaukojimafunkcija nijedeﬁniranailiuotvorenimrubovimadomene.

Horizontalneasimptote supravciparalelnis x-osi,dakleimaju koeﬁcijentsmjera k = 0.Pravac y = l nazivase desnahorizontalna asimptota funkcije f akopostoji

l = lim x→+∞ f (x)

Pravac y = l nazivase lijevahorizontalnaasimptota funkcije f ako postoji

l = lim x→−∞ f (x)

Preostajenamjošrazmotriti koseasimptote . Desnakosaasimptota jepravac y = kx + l zakojivrijedi

lim x→+∞ [ f (x) kx l] = 0.

Lijevakosaasimptota jepravac y = kx + l zakojivrijedi

lim x→−∞ [ f (x) kx l] = 0.

Koeﬁcijenti k i l zadesnukosuasimptotujednakisu

k = lim x→+∞ f (x) x ,

priˇcemuje k = 0, ∞, +∞ i

l = lim x→+∞ [ f (x) kx],

priˇcemuje l = ∞, +∞ Analognoodredujemokoeﬁcijente k i l za dobitilijevukosuasimptotutj. k = lim x→−

priˇcemuje k = 0, ∞, +∞ i l = lim x→−∞ [ f (x) kx],

priˇcemuje l = ∞, +∞.

Zadatak 51. Odrediteintervalerasta,intervalepadailokalneekstreme funkcijef (x)= 1 3 x3 1 2 x2 6x

Rješenje: Odredimoderivacijufunkcije f :

Kakobismodobiliintervalerastaipada,moramoodreditipredznakderivacije.Mi´cemotonapravititakodanacrtamoderivaciju,tj. kvadratnufunkciju f (x) x1,2 = ( 1) ± ( 1)2 + 24 2 = 1 ± 5 2 , x1 = 2, x2 = 3.

Slika 5 4 3: Graffunkcije f (x)= x2 x 6

Saslike 5 4 3 vidimodasuvrijednostikvadratnefunkcijepozitivne naintervalu ∞, 2 ∪ 3, ∞ ,anegativnenaintervalu 2,3 .To znaˇcida f rastenaintervalu ∞, 2 ∪ 3, ∞ ,apadanaintervalu

2,3

Stacionarnetoˇckesu x1 = 2, x2 = 3 jersmodobilidajeutim toˇckamaderivacijajednakanuli.Kakojelijevoodtoˇcke x1 = 2 f > 0,tj.funkcijaraste,adesnoje f < 0 pafunkcijapada,ondajeu toˇcki x1 = 2 lokalnimaksimumtj.lokalnimaksimumje f ( 2)= 22 3 . Istotako,lijevoodtoˇcke x2 = 3 funkcijapada,adesnorastepajeu tojtoˇckilokalniminimumtj.lokalniminimumje f (3)= 27 2 Dakle, M( 2, 22 3 ) jetoˇckalokalnogmaksimuma,a m(3, 27 2 ) toˇcka lokalnogminimumanagrafu.

Iakoseuzadatkutonetraži,ovdjejejošdodatnoskicirangraffunkcije f tesuoznaˇceninjenilokalniekstremi.Naskiciranomgrafumožemo provjeritidobiveneintervalerastaipada.

Slika 5.4.4: Graffunkcije f (x)= 1 3 x3 1 2 x2 6x

Zadatak 52. Odrediteintervalerasta,intervalepadailokalneekstreme funkcijef (x)= 2x+3 x2 .

Rješenje: Funkcijanijedeﬁniranau 0,dakle D = R\ {0}.Sad odredimoderivacijufunkcije f : f (x)= 2x2 2x( 2x + 3) x4 = 2x

Kakobismodobiliintervalerastaipada,moramoodreditipredznak derivacije.Vidimodajenazivnikpozitivanzasvaki x = 0 takoda nampredznakderivacijeovisiobrojniku,atojekvadratnafunkcija kojujednostavnomožemonacrtati.Odredimojojnultoˇcke:

2x(x 3)= 0 x1 = 0, x2 = 3.

Primijetimoda x1 = 0 ne´cebitiekstremjer x1 = 0/ ∈ D.Dakle, x1 = 0 jekritiˇcnatoˇckafunkcije f .

Slika 5 4 5: Graffunkcije f (x)= 2x2 6x

Saslike 5 4 5 vidimodasuvrijednostikvadratnefunkcijepozitivne naintervalu ∞,0 ∪ 3, ∞ ,anegativnenaintervalu 0,3 .Toznaˇci da f rastenaintervalu ∞,0 ∪ 3, ∞ ,apadanaintervalu 0,3 Stacionarnatoˇckaje x2 = 3 x1 = 0 nijestacionarnatoˇckajerne pripadadomeni D Kakolijevoodtoˇcke x2 = 3 funkcijapada,adesno raste,utojtoˇckijelokalniminimumionjejednak f (3)= 1 3 . Dakle, m(3, 1 3 ) jetoˇckalokalnogminimumanagrafu. Iakoseuzadatkutonetraži,ovdjejejošdodatnoskicirangraffunkcije f tejeoznaˇcennjenlokalniminimum.Naskiciranomgrafumožemo provjeritidobiveneintervalerastaipada.Primijetimodajepravac x = 0 lijevaidesnavertikalnaasimptota.Takoder,pravac y = 0 je lijevaidesnahorizontalnaasimptota.

Slika 5 4 6: Graffunkcije f (x)= 2x+3 x2

Zadatak 53. Odrediteintervalerasta,intervalepadailokalneekstreme funkcijef (x)= x3e x .

Rješenje: Odredimoderivacijufunkcije f : f (x)= 3x2e x + x3e x ( 1)= x2e x (3 x).

Kakobismodobiliintervalerastaipada,moramoodreditipredznak derivacije.Kakoje x2e x ≥ 0, predznakderivacijeovisiolinearnoj funkciji y = 3 x kojujednostavnomožemoskicirati.

Slika 5 4 7: Graffunkcije f (x)= 3 x

Vidimodajeprvaderivacijapozitivnanaintervalu ∞,3 ,anegativnanaintervalu 3, ∞ .Toznaˇcidafunkcijarastenaintervalu ∞,3 ,apadanaintervalu 3, ∞ .Stogaje M(3, f (3))= M(3,27e 3) toˇckalokalnogmaksimumanagrafu.

Iakoseuzadatkutonetraži,ovdjejejošdodatnoskicirangraffunkcije f tejeoznaˇcennjenlokalnimaksimum.Naskiciranomgrafumožemo provjeritidobiveneintervalerastaipada.Možemoprimijetitidaje pravac y = 0desnahorizontalnaasimptota.

Slika 5.4.8: Graffunkcije f (x)= x3e x

Zadatak 54. Odrediteintervalerasta,intervalepadailokalneekstreme funkcijef (x)= x + 4 x .

Rješenje: Napišimo f uobliku f (x)= x2 +4 x .Sadodredimoderivacijufunkcije f :

f (x)= 2x2 (x2 + 4) x2 = x2 4 x2 .

Kakobismodobiliintervalerastaipada,moramoodreditipredznak derivacije.Kakoje x2 > 0, za x = 0,predznakderivacijeovisio kvadratnojfunkciji y = x2 4 kojujednostavnomožemoskicirati.

Odredimonultoˇckekvadratnefunkcije:

x2 4 = 0

(x 2)(x + 2)= 0

x1 = 2, x2 = 2.

Slika 5.4.9: Graffunkcije f (x)= x2 4

Saslike 5 4 9 vidimodasuvrijednostikvadratnefunkcijepozitivne naintervalu ∞, 2 ∪ 2, ∞ ,anegativnenaintervalu 2,2 .To znaˇcida f rastenaintervalu ∞, 2 ∪ 2, ∞ ,apadanaintervalu 2,2 \{0}.

Stacionarnetoˇckesu x1 = 2 i x2 = 2.Kakolijevoodtoˇcke x1 = 2 funkcijaraste,adesnopada,ondajeutoˇcki x1 = 2 lokalni maksimumioniznosi f ( 2)= 4.Sliˇcnojeutoˇcki x2 = 2 lokalni minimumioniznosi f (2)= 4.Dakle, M( 2, 4) jetoˇckalokalnog maksimuma,a m(2,4) toˇckalokalnogminimumanagrafu. Iakoseuzadatkutonetraži,ovdjejejošdodatnoskicirangraffunkcije f tesuoznaˇceninjenlokalniminimumimaksimum.Naskiciranom

grafumožemoprovjeritidobiveneintervalerastaipada.Takoder vidimodajepravac x = 0lijevaidesnavertikalnaasimptota.

Slika 5 4 10: Graffunkcije f (x)= x + 4 x

Zadatak 55. Odrediteintervalerasta,intervalepadailokalneekstreme funkcijef (x)= x ln x.

Rješenje: Odredimoderivacijufunkcije f :

f (x)= 1 · lnx + x · 1 x = lnx + 1.

Kakobismodobiliintervalerastaipada,moramoodreditipredznak derivacije.Odredimonajprijestacionarnutoˇcku: lnx + 1 = 0 lnx = 1 x = e 1 .

Sadnacrtajmofunkcijulnx + 1:

Slika 5.4.11: Graffunkcije f (x)= lnx + 1

Vidimodajederivacijanegativnanaintervalu 0, e 1 ,apozitivna naintervalu e 1 , ∞ .Toznaˇcidafunkcijapadanaintervalu 0, e 1 , arastenaintervalu e 1 , ∞ teje m(e 1 , f (e 1))= m(e 1 , e 1) toˇcka lokalnogminimumumanagrafu. Jošjedodatnoskicirangraffunkcije f tejeoznaˇcenatoˇcka m(e 1 , e 1).

Slika 5 4 12: Graffunkcije f (x)= xlnx

Zadatak 56. Odrediteintervalerasta,intervalepadailokalneekstreme funkcijef (x)= 1 2 ln(1 + x2)

Rješenje: Odredimoderivacijufunkcije f : f (x)= 1 2 1 1 + x2 (1 + x2) = 1 2 1 1 + x2 2x = x 1 + x2 .

Kakobismodobiliintervalerastaipada,moramoodreditipredznak derivacije.Kakojenazivnikpozitivan,predznakovisiobrojniku,ato

jelinearnafunkcija.Stacionarnatoˇckaje x = 0.Skicirajmofunkciju y = x:

Slika 5.4.13: Graffunkcije f (x)= x

Izpredznakaderivacijevidimodafunkcija f rastenaintervalu ∞,0 ,apadanaintervalu 0, ∞ .Stogaje M(0, f (0))= M(0,0) toˇckalokalnogmaksimumanagrafu.

Ovdjejejošzaprovjeruskicirangraffunkcije f inanjemuoznaˇcena toˇcka M(0,0).

Slika 5 4 14: Graffunkcije f (x)= 1 2 ln(1 + x2)

Zadatak 57. Odrediteintervalerasta,intervalepadailokalneekstreme funkcijef (x)= x x2 2x+3

Rješenje: Odredimoderivacijufunkcije f : f (x)= 1 (x2 2x + 3) x(2x 2) (x2 2x + 3)2 = x2 2x + 3 2x2 + 2x (x2 2x + 3)2 = x2 + 3 (x2 2x + 3)2 .

Kakojenazivnikpozitivan,predznakderivacijeovisiokvadratnoj funkcijiubrojniku.Odredimojojnultoˇckeiskicirajmoje.Dobivamo x2 + 3 = 0 x1 = √3, x2 = √3.

Slika 5.4.15: Graffunkcije f (x)= x2 + 3

Izpredznakaderivacijevidimodafunkcijapadanaintervalu ∞, √3 ∪ √3, ∞ ,arastenaintervalu √3, √3 . Stogaje m( √3, f ( √3))= ( √3, 1 √3 4 ) toˇckalokalnogminimuma,a M(√3, f (√3))=(√3, 1+√3 4 ) toˇckalokalnogmaksimumanagrafu.

Ovdjejetakoderjošdodatnoskicirangraffunkcije f nakojemmožemovidjetiekstemefunkcijetelijevuidesnuhorizontalnuasimptotu y = 0.

Slika 5 4 16: Graffunkcije f (x)= x x2 2x+3

Zadatak 58. Odpravokutnogkartonaduljinastranica 12 i 20 napravite kutijubezpoklopcamaksimalnogvolumena.

Rješenje:

Nacrtajmopravokutniktes x oznaˇcimostranicekvadratakoje´cemo rezatipojednojunutarnjojstraniciisavijatizazalijepitikutiju.

Slika 5.4.17: Rješenjezadatka 58

Volumenkutijeiznosi

V(x)=(12 2x)(20 2x)x =(240 24x 40x + 4x2)x = 4x3 64x2 + 240x

Odredimo x takodavolumenbudemaksimalantj.nadimomaksimum funkcije V.Nadimoderivacijufunkcije V:

V (x)= 12x2 128x + 240.

Iz V (x)= 0 dobivamo x1,2 = 16±2√19 3 pasu x1 = 16 2√19 3 i x2 = 16+2√19 3 stacionarnetoˇcke.Domenafunkcije V je 0,6 .Kakoje V kvadratnafunkcija,slijedidaje 0, 16 2√19 3 intervalrasta,a 16 2√19 3 ,6

intervalpada.Stogajeutoˇcki x1 = 16 2√19 3 lokalnimaksimumion iznosi

V 16 2√19 3 ≈ 262.68.

Toˇcka x2 = 16+2√19 3 nepripadadomenifunkcije V

Zadatak 59. Bazauspravneprizmejejednakostraniˇcantrokut.Oplošje prizmeiznosi 600.Odreditedimenzijeprizmetakodavolumenbudemaksimalan.

Rješenje:

Oznaˇcimoosnovnibridprizmes a,avisinus v.

Slika 5 4 18: Rješenjezadatka 59

Volumenprizmeiznosi

Uvrstimo v uvolumenidobivamo

√

Zaprona´cimaksimumfunkcije V najprijejumoramoderiviratipa imamo

Stacionarnatoˇckesu a

i v > 0 dobivamodajedomenafunkcije V interval 0,20 4 √3 .Natojdomeni je 0, 20 4 √27 3 intervalrasta,a

intervalpada,paseutoˇcki

V jednakje

nepripadadomenifunkcije V. 5 5 zadatcizavježbu

Zadatak 60. Izraˇcunajtelimese:

4. lim t→0

Rješenje:

Zadatak 61. Podeﬁnicijiizraˇcunajtederivacijefunkcija:

1 f (x)= ctg x Rješenje:

2. f (x)= 2x

Rješenje:

3 f (x)= 3 √x Rješenje:

(x)= lim

Zadatak 62. Izraˇcunajtederivacijefunkcija: 1. f (x)= tg 2

Rješenje:

x ✟✟ 2x3 + 4x + ✟✟ 2x3 (2 x2)2 =

2. f (x)= xe x x2 +1

Rješenje: f (x)= (xe x ) (x2 + 1) (xe x )(x2 + 1) (x2 + 1)2 = (e x xe x )(x2 + 1) xe x2x (x2 + 1)2 = e x (1 x)(x2 + 1) 2x2 (x2 + 1)2 = e x (x2 + 1 x3 x 2x2) (x2 + 1)2 = e x ( x3 x2 x + 1) (x2 + 1)2 .

Zadatak 63. Odreditejednadžbutangentenagraffunkcije f (x)= x3

3x + 2 utoˇckiT(2, y0).

Rješenje: y0 = f (2)= 23 6 + 2 = 4 f (x)= 3x2 3 k = f (2)= 3 22 3 = 9 t ··· y y0 = k(x x0)

t y 4 = 9(x 2)

t ··· y = 9x 14.

INTEGRALI

6 1 neodreðeniintegral

Uovompoglavljuprouˇcavamosljede´ciproblem:akojezadanafunkcija f ,trebamona´cifunkcijuˇcijajederivacijajednaka f .Takvufunkciju F zakojuvrijedi

F (x)= f (x),zasvaki x ∈ a, b

zovemo primitivnafunkcijafunkcije f naintervalu a, b

Nekaje F primitivnafunkcijafunkcije f naintervalu a, b i c ∈ R.Tadaje

[F(x)+ c] = F (x)+ c = F (x)= f (x),zasvaki x ∈ a, b

paslijedidajei F + c primitivnafunkcijafunkcije f naintervalu a, b , tj.primitivnafunkcijajeskupkojisesastojiodbeskonaˇcnomnogo funkcijakojeserazlikujuzakonstantu.Skup

{F + c : c ∈ R}

zovemo neodredeniintegralfunkcije f ipišemo

f (x)dx = F(x)+ c.

Funkciju f nazivamo podintegralnafunkcija.

Primjer 13. Primitivnafunkcijafunkcije f (x)= x jefunkcija F(x)= 1 2 x2 + cjerje

F (x)= 1 2 x2 + c = 1 2 · 2x + c = x = f (x)

Svojstvaneodredenogintegrala:

f (x)dx = f (x)+ c

α f (x)dx = α f (x)dx, α ∈ R

Integralielementarnihfunkcija:

Zadatak 64. Izraˇcunajteneodredeneintegrale:

Rješenje:

4 ( 2 x4 + √x3 + 2 x )dx

Rješenje: ( 2 x4 + √x3 + 2 x )dx = 2 x 4dx + x 3 2 dx + 2 1 x dx = 2 x 3 3 +

6.2 metodasupstitucije

Nekajezadanintegral f (x)dx.

Pretpostavimoda f (x) možemozapisatiuobliku

f (x)= v (u(x)) u (x) tepretpostavimodamožemoprona´ciprimitivnufunkciju V od v,tj. V = v.Popraviluzaderivacijusloženefunkcijeimamo

[V (u(x))] = V (u(x)) u (x)= v (u(x)) u (x)= f (x),

tj.složenafunkcija V ◦ u jeprimitivnafunkcijafunkcije f .Slijedidaje f (x)dx = (V ◦ u) (x)+ c = V (u(x)) + c.

Naovojjednakostizasnivasemetodasupstitucije.

Primjer 14. Izraˇcunajteneodredeniintegral:

Rješenje:

Odaberimo

. Derivacijafunkcije u(x) je u (x)= 3x2.Primitivnafunkcijafunkcije v(x)= 4 3x je V(x)= 4 3 ln |x|. Tadaje

Sadje

Ovajpostupak´cemojednostavnijezapisivatinasljede´cinaˇcin

Zadatak 65. Izraˇcunajteneodredeneintegrale:

1. √4x 5dx

Rješenje:

x + 1)dx

Rješenje:

(x)= 4x 5

6 sin2 xdx

Rješenje: sin2 xdx = 1 cos2x 2 dx = 1 2 dx 1 2 cos2xdx = u(x)= 2x du = 2dx ⇒ dx = 1 2 du = 1 2 x + c 1 4 cos udu = 1 2 x 1 4 sin u + c = 1 2 x 1 4 sin2x + c

7. tgxdx

Rješenje: tg xdx = sin x cos x dx = u(x)= cos x du = sin xdx ⇒ sin xdx = du = 1 u du = ln |u| + c = ln | cos x| + c.

6.3 odreðeniintegral

Deﬁnicija 24: Zarealnufunkciju f kažemodaje omedena akopostoje realnibrojevi m i M zakojevrijedi m ≤ f (x) ≤ M zasvaki x na podruˇcjudeﬁnicije.

Deﬁnicija 25: Konaˇcanskuptoˇcaka D = {x0, x1,..., xn} sasvojstvom daje

nazivamo razdioba ili particija segmenta [a, b].Zaparticiju D kažemo daje proﬁnjenjeparticije D akoje D ⊆ D

Deﬁnicija 26: Nekaje A ⊆ R.Kažemodaje M ∈ R supremum skupa A,oznaka sup A akoje M gornjameda skupa A tj. a ≤ M zasvaki a ∈ A i M jenajmanjagornjameda.

Kažemodaje m ∈ R inﬁmum skupa A,oznaka inf A akoje m donja meda skupa A tj. a ≥ m zasvaki a ∈ A i m jenajve´cadonjameda.

Uzmimoomedenufunkciju f : [a, b] → R.Željelibismoizraˇcunati površinu P omedenugrafomfunkcije f ,pravcima x = a, x = b iosi x

Slika 6.3.1: Površinaomedenagrafomfunkcije f ,pravcima x = a, x = b iosi x

Kakojefunkcija f zakrivljena,miovupovršinunemožemoprekriti pravokutnicima,aliunjumožemoupisivatipravokutnikeilijuprekriti opisanimpravokutnicima.Zbrojpovršinaupisanihpravokutnikanazivamo donjaintegralnasuma,azbrojpovršinaopisanihpravokutnika gornjaintegralnasuma.Nasljedećimslikamavidimodajetražena površinaizmeduzbrojaupisanihizbrojaopisanihpravokutnika.Takoder,možemouoˇcitidaseuzimajućisvesitnijuparticijusegmenta [a, b],zbrojpovršinaupisanihpravokutnikapovećavailiostajeisti,a zbrojpovršinaopisanihpravokutnikasmanjujeiliostajeistiisvese višepribližavajutraženojpovršini.

Slika 6.3.2: Donjaigornjaintegralnasuma

Slika 6 3 3: Donjaigornjaintegralnasuma

Zadeﬁniratiodredeniintegraluzmimonajprijenekuparticiju D segmenta [a, b] tj.konaˇcanskuptoˇcaka D = {x0, x1,..., xn} sasvojstvomdaje a = x0 < x1 < ··· < xn = b Kakojefunkcija f omedena, nasvakompodsegmentu [xi 1, xi ], i = 1,..., n postojenenegativni brojevi mi, Mi takvidaje

mi = inf x∈[xi 1,xi ] f (x), Mi = sup x∈[xi 1,xi ] f (x), i = 1,..., n.

Akos P oznaˇcimopovršinuispodgrafafunkcije,vrijedi

.(11)

Štoje n ve´ci,donjaogradaaproksimacije (11) ´cerasti,agornjapadati.

Deﬁnirajmo s( f , P)= n ∑ i=1 mi (xi xi 1), S( f , P)= n ∑ i=1 Mi (xi xi 1).

Brojeve s( f , P) i S( f , P) nazivamo donja,odnosno gornjaDarbouxovasuma

Deﬁnicija 27: DonjiRiemanovintegral funkcije f na [a, b] deﬁnirase kao

f = sup {s( f , P) : Pparticijaod [a, b]} .

GornjiRiemanovintegral funkcije f na [a, b] deﬁnirasekao

f = inf {S( f , P) : Pparticijaod [a, b]} .

Deﬁnicija 28: Zaomedenufunkciju f : [a, b] → R kažemodaje Rintegrabilnaakoje f = f . Tajbrojtadanazivamo Riemanov integral ili odredeniintegral funkcije f nasegmentu [a, b] ioznaˇcavamo

(

)dx

Brojeve a i b zovemo donja,odnosno gornjagranicaintegracije. Svojstvaodredenogintegrala:

Zaraˇcunanjeodredenogintegralakoristit´cemosljede´citeorembez dokaza:

Teorem 4. (Newton-Leibnitzovaformula) Nekaje f neprekidnafunkcijana [a, b] i F primitivnafunkcijaod f .Tada vrijedi

Dakle,možemore´cidaodredeniintegralraˇcunamokaorazliku vrijednostiprimitivnefunkcijeugornjojidonjojgranicipromatranog integrala.

Zadatak 66. Izraˇcunajteodredeneintegrale:

Rješenje:

6 4 površineravninskihlikova

Promatramofunkcije f , g : [a, b] → R injihovegrafove.Željelibismo izraˇcunatipovršinuravninskoglikaomedenoggrafovimafunkcija f i g tepravcima x = a i x = b kaoštojeprikazanonaslici 6 4 1

Slika 6 4 1: Površinaravninskoglika

Kakoraˇcunanjem b a f (x)dx dobivamopovršinuispodgrafafunkcije f nasegmentu [a, b],araˇcunanjem b a g(x)dx površinuispodgrafa funkcije g nasegmentu [a, b],ondajetraženapovršinajednaka

Zadatak 67. Odreditepovršinulikauravninikojijeomedenparabolom y = x2 + x 12 ipravcemy = x 2

Rješenje: Nacrtajmopravaciparaboluioznaˇcimotraženupovršinu.

Slika 6 4 2: Rješenjezadatka 67

Kakobismoodrediligraniceintegracije,moramoprona´citoˇcke presjekapravcaiparabole:

x2 + x 12 = x 2

x2 10 = 0

(x √10)(x + √10)= 0

x1,2 = ±√10.

Sadraˇcunamotraženupovršinu:

Zadatak 68. Odreditepovršinulikaomedenogparabolom y = x2 2x + 3 ipravcemy = x.

Rješenje: Nacrtajmopravaciparaboluioznaˇcimotraženupovršinu.

Slika 6.4.3: Rješenjezadatka 68

Kakobismoodrediligraniceintegracije,moramoprona´citoˇcke presjekapravcaiparabole:

Sadraˇcunamotraženupovršinu:

Zadatak 69. Odreditepovršinulikasaslike 6 4 4

Slika 6.4.4: Zadanielementizadatka 69

Rješenje:

Zadatak 70. Odreditepovršinulikaomedenogparabolama y = x2 + 6xiy = x2 2x.

Rješenje: Nacrtajmozadaneparaboleioznaˇcimotraženupovršinu.

Slika 6 4 5: Rješenjezadatka 70

Kakobismoodrediligraniceintegracije,moramoprona´citoˇckepresjekaparabola:

Zadatak 71. Odreditepovršinulikasaslike 6 4 6

Slika 6 4 6: Zadanielementizadatka 71

Rješenje:

Kakobismoodrediligraniceintegracije,moramoriješitijednadžbu

Zadatak 72. Odreditepovršinulikasaslike 6.4.7.

Slika 6.4.7: Zadanielementizadatka 72

Rješenje:

Zadatak 73. Odreditepovršinulikaomedenogparabolama y = x2 5x i y = x2 + 9x 18

Rješenje: P = 15.62.

6.5 volumenirotacijskihtijela

Uzmimoneprekidnufunkciju f : [a, b] → R.Rotacijomlukakrivulje y = f (x) okoosi x nasegmentu [a, b] dobivamo rotacijskotijelo. Presjekrotacijskogtijelaravninomokomitomnaos x krugjeradijusa r(x) ˇcijajepovršina P(x)= πr2(x),gdjeje r(x)= | f (x)|

Slika 6 5 1: Volumenrotacijskogtijela

Zamislimodavolumenrotacijskogtijeladobivamozbrajanjempovršinabeskonaˇcnomnogokrugova.Analoganzbrajanjubeskonaˇcno površinabilobiintegriranjepovršinapovarijabli x,padobivamo formulu

V = π b a r2(x)dx

Nasliˇcannaˇcindobivasevolumenrotacijskogtijelakojenastajerotacijomkrivuljeokoosi y ilibilokojegpravcašto´cemopokazatiu zadatcimanakrajuovecjeline.

Višeovolumenurotacijskogtijelamožeseprona´ciuknjigama[1]i [11].

Primjer 15. Odreditevolumentijelakojinastajerotacijomlikasaslikeoko osix.

Slika 6 5 2: Zadanielementiprimjera 15

Rješenje: Skicirajmorotacijskotijelo:

Slika 6.5.3: Rješenjeprimjera 15

Primijenimoformuluzavolumenrotacijskogtijelakojenastajerotacijompravca y = 1 2 x nasegmentuod0do5.

Riješimosadgornjizadatakstandardnomformulomzavolumenstošca

Radijusosnovicestošcajednakje y koordinatisjecištapravaca y = 1 2 x i x = 5tj. r = 5 2 .Visinastošcaje v = 5.Saddobivamo

Primijetimodagornjerješenjeodgovararješenjukojesmodobiliupotrebomintegralneformulezavolumen.

Primjer 16. Odreditevolumentijelakojinastajerotacijomlikasaslikeoko osix.

Slika 6 5 4: Zadanielementiprimjera 16

Rješenje: Skicirajmorotacijskotijelo:

Slika 6 5 5: Rješenjeprimjera 16

Primijenimoformuluzavolumenrotacijskogtijelakojenastajerotacijompravca y = 2nasegmentuod0do5.

Riješimosadgornjizadatakstandardnomformulomzavolumenvaljka

V = r2πv

Radijusosnovicevaljkaiznosi r = 2,avisina v = 5.Saddobivamo

V = 22π · 5 = 20π.

Primijetimodagornjerješenjeodgovararješenjukojesmodobiliupotrebomintegralneformulezavolumen.

Zadatak 74. Odreditevolumentijelakojenastajerotacijomlikasaslike 6 5 6 okox-osi.

Slika 6.5.6: Zadanielementizadatka 74

Rješenje:

Slika 6 5 7: Rješenjezadatka 74

Najprijenapišimojednadžbupravca p kojiprolazikrozishodište itoˇcku T( 2π 3 , √3 2 ).Traženipravacje y = 3√3 4π x.Kakobismodobili volumentraženogrotacijskogtijela,moramoodvolumenatijelakoje nastajerotacijomgrafafunkcije f (x)= sinx oduzetivolumenstošca. Sadimamodajevolumentijela

avolumenstošcaradijusabaze

Zadatak 75. Odreditevolumentijelakojenastajerotacijomoko x-osilika omedenogparabolomy = x2 2 ipravcemy = 1

Rješenje: Skicirajmonajprijepovršinuomedenuzadanimfunkcijama.

Slika 6.5.8: Zadanielementizadatka 75

Dabismoodrediligraniceintegracije,moramona´cipresjekpravcai parabole:

Skicirajmotraženorotacijskotijelo.

Slika 6 5 9: Rješenjezadatka 75

Kakobismodobilivolumentraženogrotacijskogtijela,moramood volumenatijelakojenastajerotacijomgrafafunkcije y = x2 2 oduzeti volumenvaljka.Sadimamodaje

Zadatak 76. Odreditevolumentijelakojenastajerotacijomoko x-osilika omedenogparabolomy = x2 + 9 ipravcemy = x + 3.

Rješenje:

6.5.10: Zadanielementizadatka 76 x2 + 9 = x + 3 x1 = 3, x2 = 2

Slika 6.5.11: Rješenjezadatka 76

Slika

Zadatak 77. Odreditevolumentijelakojenastajerotacijomlikasaslike 6 5 12 okoy-osi.

Slika 6.5.12: Zadanielementizadatka 77

Rješenje: Najprijenapišimojednadžbuparabole:

Napišimojednadžbupravca(tangenteparaboleutoˇcki T( 2,0)):

Slika 6 5 13: Rješenjezadatka 77

Kakosmosadradilirotacijuokoosiy,radijusrotacijskogtijela´cemo izrazitikaofunkcijuuvarijabliy:

KAZALO

arkuskosinus, 98 arkuskotangens, 99 arkussinus, 97 arkustangens, 98 asimptotafunkcije, 120 baza, 26 bijekcija, 85

Cauchyjevadeﬁnicijalimesa, 103 ciklometrijskefunkcije, 97

dekadskilogaritam, 91 derivacijafunkcije, 110 derivacijafunkcijeutoˇcki, 110 desnikoordinatnisustav, 45 determinanta, 50 domena, 85 donjaDarbouxovasuma, 143 donjaintegralnasuma, 142 donjiRiemanovintegral, 143

eksponencijalnafunkcija, 89 eksponencijalnopreslikavanje, 92

ekstenzijailiproširenje funkcije, 86 funkcijailipreslikavanje, 85

gornjaDarbouxovasuma, 143 gornjaintegralnasuma, 142 gornjiRiemanovintegral, 143 graffunkcije, 85 horizontalnaasimptota, 120 inﬁmum, 141 injekcija, 85 inverznafunkcija, 85

jediniˇcnivektor, 17

jednadžbapravca, 59 jednadžbaravnine, 57 kanonskioblikjednažbe pravca, 60

karakterizacijaokomitosti, 33 kodomena, 85 kolinearnivektori, 9 komplanarnivektori, 13 kompozicijafunkcija, 85 konstanta, 87 koordinatnisustav, 27 kosaasimptota, 120 kosinus, 93 kotangens, 94 kritiˇcnatoˇcka, 119 kutizmeduvektora, 32 kvadratnafunkcija, 88

L’Hospitalovopravilo, 117 Laplaceovrazvojdeterminante, 51

lijevikoordinatnisustav, 46 limesfunkcije, 104 limessdesna, 105 limesslijeva, 104 linearnafunkcija, 87 linearnakombinacijavektora, 20 logaritamskafunkcija, 90 lokalnimaksimum, 118 lokalniminimum, 118 metodasupstitucije, 139 mješovitiproduktvektora, 54 množenjevektoraiskalara, 17 modulilinormavektora, 9 neodredeniintegral, 137 neodredenioblici, 106 neparnafunkcija, 86

neprekidnafunkcija, 104 NewtonLeibnitzovaformula, 144

normalaravnine, 57 nulvektor, 12

okolinatoˇcke, 103 omedenafunkcija, 141 op´capotencija, 91 op´cioblikjednadžberavnine, 58

ortogonalnabaza, 41 ortogonalnivektori, 41 ortonormiranabaza, 41

padaju´cafunkcija, 86, 118 parametarskioblikjednadžbe pravca, 60 parnafunkcija, 86 particijasegmenta, 141 periodfunkcije, 86 periodiˇcnafunkcija, 86 podintegralnafunkcija, 137 polinom, 87

površinaravninskoglika, 146 pravokutnekoordinate, 41 pravokutnikoordinatnisustav, 41

primitivnafunkcija, 137 prirodnilogaritam, 91

proﬁnjenjeparticije, 141 racionalnafunkcija, 89 radijvektor, 28 rastu´cafunkcija, 86, 118 realnamatrica, 49 restrikcijailisuženjefunkcije, 86

Riemanovintegral, 144 rotacijskotijelo, 152

sekanta, 109 sinus, 93 skalarnaprojekcija, 39 skalarniprodukt, 32 slikafunkcije, 85 stacionarnatoˇcka, 119 supremum, 141 surjekcija, 85

tangens, 94 tangenta, 110 vektor, 9 vektorskaprojekcija, 39 vektorskiprodukt, 46 vertikalnaasimptota, 120 volumenrotacijskogtijela, 152

zbrajanjevektora, 14 zlatnirez, 44

BIBLIOGRAFIJA

[1] AglićAljinović,Andrea;Brnetić,Ilko; ´ Cepulić,Vladimir;Elezović,Neven;Marangunić,Ljubo;Pašić,Mervan;Žubrinić,Darko; Županović,Vesna. 2014 Matematika 1,Element.

[2] Antoni´c,Nenad;Vrdoljak,Marko. 2001 Mjeraiintegral,PMFMatematiˇckiodjel.

[3] Babi´c,Ivanka;Horvati´c-Baldasar,Ksenija. 1997 Nacrtnageometrija, Sandd.o.o.,Zagreb.

[4] Beban-Brki´c,Jelena;Joviˇci´c,Damjan; 2007.DistanceFromPoint toLineandFromPointtoPlane, MIŠ 42, 61 - 68.

[5] Beban-Brki´c,Jelena;Šimi´cHorvath,Marija. 2014.Interaction amongCourses, Proceedingofthe 16thInternationalConferenceon GeometryandGraphics,InnsbruckUniversityPress, 690-696

[6] Elezovi´c,Neven. 2006. Linearnaalgebra,Element.

[7] Gorjanc,Sonja;Jurkin,Ema;Kodrnja,Iva;Koncul,Helena. Deskriptivnageometrija, http://www.grad.hr/geometrija/ udzbenik/

[8] Hrnˇcevi´c,Juraj. 2011. Matematika,Arhitektonskifakultet,SveuˇcilišteuZagrebu(neobjavljeninastavnimaterijal).

[9] https://arhitektzg.sharepoint.com/

[10] Slapniˇcar,Ivan. 2018. Matematika 1,Kartular,Split.

[11] Slapniˇcar,Ivan. 2019 Matematika 2,Kartular,Split.