6 minute read
3. Tabela de Frequências
A tabela de frequências é uma forma de organização dos valores das variáveis e, consoante o seu tipo (qualitativa ou quantitativa), esta pode conter apenas as frequências simples absolutas e relativas ou também conter as frequências acumuladas.
3.1 Tabela de Frequências Simples
Advertisement
Atividade 3
Considere a variável Assintomático. (a) Construa a tabela de frequências simples. (b) Indique a percentagem de doentes que são considerados assintomáticos.
Resolução: Selecione a folha do Excel Tab-Assint. (a) Para construir a tabela de frequências considere o seguinte procedimento. 1. Escrever em A3 e A4, Sim e Não, respetivamente, que são as categorias da variável Assintomático.
2. Cálculo das frequências absolutas simples. Colocar o cursor em B3 e selecionar a função CONTAR.SE, clicando em Mais Funções, seguido de Estatística. Escrever Assintomático no campo Intervalo e selecionar a célula A3 para o campo Critérios. Clicar em OK. Colocar o cursor no canto inferior direito da célula B3 e arrastar até B4.
3. Colocar o cursor na célula B5 e clicar no comando Soma Automática, conforme na figura seguinte. Clicar em Enter.

4. Cálculo das frequências relativas simples em percentagem. Introduzir em D3 o sinal de =, selecionar B3 e dividir pela soma (B5). Em D3 “Trancar” a célula B5, colocando um cifrão entre a letra B e 5 (=B3/B$5). Clicar em Enter. Arrastar D3 até D4.
5. Colocar o cursor na célula D5 e clicar no comando Soma Automática. Clicar em Enter.
O resultado será semelhante à tabela seguinte.

Para ver as fórmulas criadas basta clicar no separador Fórmulas, no comando Mostrar Fórmulas (no grupo Auditoria de Fórmulas), conforme na figura seguinte.

O resultado será semelhante à tabela seguinte.
(b) 13,3 % dos doentes são considerados assintomáticos.

3.2 Tabela de Frequências Simples e Acumuladas
Atividade 4
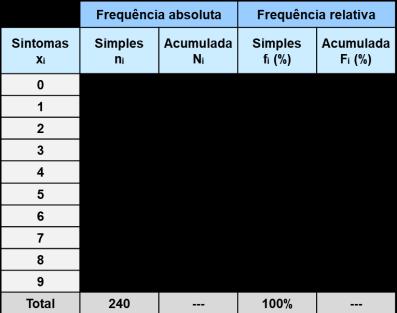
Considere a variável Sintomas. (a) Construa a tabela de frequências, simples e acumuladas. (b) Interprete os valores da linha da tabela associados a 5 sintomas.
Resolução: Selecione a folha do Excel Tab-Sinto.
(a) Para construir a tabela de frequências considere o seguinte procedimento. 1. Determinar o menor e o maior valor da variável Sintomas, introduzindo em quaisquer células da folha de Excel, as funções MÁXIMO e MÍNIMO para a variável Sintomas. 2. Na coluna A introduzir, de A3 a A12, os números inteiros entre o menor (0) e o maior valor (9). 3. Cálculo das frequências absolutas simples. Na célula B3, selecionar a função CONTAR.SE, escrevendo Sintomas no campo Intervalo e selecionando a célula A3 para o campo Critérios. Clicar em OK. Colocar o cursor no canto inferior direito da célula B3 e arrastar até B12.
4. Colocar o cursor na célula B13 e clicar no comando Soma Automática. Clicar em Enter.
5. Cálculo das frequências absolutas acumuladas. Colocar o cursor em C3 e introduzir o sinal de = . Clicar na célula B3, seguida de Enter. Na célula C4 introduzir o sinal de = , clicar na célula C3, introduzir o símbolo + da soma e clicar na célula B4, seguida de Enter. Arrastar C4 até C12. 6. Cálculo das frequências relativas simples em percentagem. Introduzir em D3 o sinal de = , selecionar B3 e dividir pela soma (B13). Em D3 “Trancar” a célula B13, colocando um cifrão entre a letra B e 13 (=B3/B$13). Clicar em Enter. Arrastar D3 até D12.
7. Colocar o cursor na célula D13 e clicar no comando Soma Automática.
8. Cálculo das frequências relativas acumuladas em percentagem. Proceder de forma análoga ao descrito no ponto 5 das frequências absolutas acumuladas.
O resultado será semelhante à tabela seguinte.

Para ver as fórmulas criadas basta clicar no item Mostrar Fórmulas.
O resultado será semelhante à tabela seguinte.
(b) Os valores a interpretar são: • 27 doentes apresentavam 5 sintomas, o que corresponde a 11,3% dos doentes; • 211 doentes apresentavam no máximo 5 sintomas, o que corresponde a 87,9% dos doentes.


Quando uma variável quantitativa assume muitos valores distintos é usual agrupá-la em classes.
Quantas classes deverão ser utilizadas?
• De acordo com a Regra de Sturges, o número de classes, ��, a utilizar é o menor natural tal que 2k ≥ n, onde n é a dimensão da amostra.
Nota: O número de classes deverá ser entre 5 e 20 inclusive.
• Amplitude total dos dados: AT = máximo – mínimo.
Para o caso em que as classes têm a mesma amplitude:
• Amplitude de cada classe: AC =
AT k .
Atividade 5
Pretende-se agrupar a variável Idade em classes. (a) Determine o número adequado de classes. (b) Apresente as classes e construa a tabela de frequências simples e acumuladas. (c) Interprete os valores da linha da tabela associados à classe [44,55[.
Resolução: Selecione a folha do Excel Tab-Idade.
(a) Como a dimensão da amostra é n = 240 então para determinar o número de classes adequado, ��, considera-se a regra 2k ≥ 240. Portanto, k = 8 (28 = 256) pois 8 é o menor número natural que verifica a condição.
(b) Considere o seguinte procedimento para determinar a amplitude de cada classe. 1. Começar por determinar o mínimo e o máximo da variável Idade. Nas células H3 e H4, escrever =MÍNIMO(Idade) e =MÁXIMO(Idade), respetivamente. Os valores obtidos são respetivamente 0,5 e 88. 2. Em H5, escrever =H4-H3, obtendo-se o valor da amplitude total que é 87,5. Para o cálculo da amplitude das classes considerar, em H6, =H5/8. O valor obtido é 10,9375. Assim, utilizar 8 classes de amplitude 11, considerando o arredondamento às unidades que têm que ser por excesso. 3. Existem várias opções que se podem considerar para definir as 8 classes, sendo que podem utilizar as opções:
• Opção 1: Considerar as classes [0;11[, [11;22[, [22;33[, [33;44[, [44;55[, [55;66[, [66;77[ e [77;88].
Nota: Optou-se por considerar a classe [77;88], fechada à direita em 88, para que esta inclua o valor máximo da variável presente na amostra, em vez do usual que seria [77;88[.
• Opção 2: Considerar as classes [0,5;11,5[, [11,5;22,5[, [22,5;33,5[, [33,5;44,5[, [44,5;55,5[, [55,5;66,5[, [66,5;77,5[ e [77,5;88,5[.
Considere a Opção 1, em que os cálculos das classes são mais simples. 4. Colocar o cursor na célula B3 e inserir a função =CONTAR.SE.S, a qual permite usar uma ou mais condições. Escrever Idade no campo Intervalo_critérios1 e escrever <11 no campo Critérios1, conforme se ilustra de seguida.

5. Clicar em OK.
6. Como a 2.ª classe é [11;22[, então é necessário contar todos os doentes que têm idade inferior a 22 anos, e que têm 11 anos ou mais. Como estão em causa duas condições então inserir, na célula B4, a função =CONTAR.SE.S. Preencher o quadro seguinte da forma como se ilustra.

7. Arrastar as células de B4 a B10. Nas células de B5 a B9, alterar os Critérios1 e Critérios2 com os limites das respetivas classes. Atenção, em B10, alterar o Critérios1 de <22 para <=88, pois a classe é fechada à direita em 88. 8. O preenchimento do resto da tabela (frequência absoluta acumulada, frequência relativa simples e frequência relativa acumulada) é efetuado de forma análoga à tabela de frequências da variável Sintomas da Atividade 4.
O resultado será semelhante à tabela seguinte.
Para ver as fórmulas criadas basta clicar no item Mostrar Fórmulas, obtendo-se uma tabela semelhante à seguinte.


Nota: A função CONTAR.SE.S permite especificar mais do que um critério enquanto CONTAR.SE permite especificar apenas um.
(c) Os valores a interpretar são: • 32 doentes tinham idade de pelo menos 44 anos, mas inferior a 55, o que corresponde a 13,3% dos doentes; • 161 doentes tinham idade inferior a 55 anos, o que corresponde a 67,1% dos doentes.





