Movimentosuniformeseuniformementevariados
Aceiteparapublica¸c˜aoem10deabrilde2023
Publica¸c˜aodebaixodeuma Licen¸caCreativeCommons daCasadasCiˆencias
Autor
PedroMiguelSousaCoelho
Agradecimentos
Osmeussincerosagradecimentos`aprofessoraM´onicaMeireles,professoradeF´ısico-Qu´ımicaAno AgrupamentodeEscolasdoCastˆelodaMaia,peladisponibilidadeededica¸c˜aonapropostadesolu¸c˜oes paramelhoraraaplica¸c˜aoPhysLabepelarevis˜aoecorre¸c˜aocient´ıficadetodoesteartigo.
1
Introdu¸c˜ao
Nestaatividadeexperimentalvamosdebru¸carmo-nossobreduas´areasmuitoimportantesdaF´ısica:a cinem´atica,queestudaomovimentodoscorposeadinˆamicaqueanalisaasintera¸c˜oesexistenteseas relacionacomostiposdemovimentosverificados.
Comvistaasuprimirafaltadematerialcomquealgumasescolassedeparamfoidesenvolvida umaaplica¸c˜ao”PhysLab”,parasmartphoneAndroid,comrecurso`aplataformaMITAppInventor. Estaaplica¸c˜aopermiteobterdadosexperimentaisutilizandocomosistemadeaquisi¸c˜aodessesdadoso telem´ovelpessoaldosalunos.Destaforma,asatividadesexperimentaispodemserrealizadasdeforma aut´onomapelosdiscentes,bemcomoorespetivotratamentodedados.
Estegui˜aotemcomoobjetivoexplicardequeformaaaplica¸c˜aopodeserpostaempr´atica.
2
AtividadeLaboratorialdeF´ısicaeQu´ımicaA
11º ano-AtividadeLaboratorial1.2.
For¸casnosmovimentosretil´ıneosaceleradoeuniforme
Nome: Grupo: Nº: Turma: Data: / /
Classifica¸c˜ao: AssinaturadoEncarregadodeEduca¸c˜ao:
1Objetivo
Oobjetivodestaatividadelaboratorial´edeterminarexperimentalmenteovalordam´odulodaacelera¸c˜aograv´ıtica.Paraissovamosestudaravaria¸c˜aotemporaldaacelera¸c˜ao,davelocidadeedo espa¸copercorridodeumcorpoA,ligadoaumcorpoBpormeiodeumfiotalqueocorpoAsemove aolongodeumaretahorizontaleocopoBsemoveaolongodeumaretavertical,easfor¸casque atuamnocorpoAenocorpoBantesedepoisdocorpoBatingirosolo.
2An´alisete´oricadoproblema
Comovemosnasimagensdamontagemexperimental,temosocarrinho(corpoA)ligadoaocilindro met´alico(corpoB)porumfio(demassadesprez´avel)quepassanumaroldana.Comoopesoea normaldocarrinhoseanulameastens˜oess˜aofor¸casinterioresaosistemacorpoA+corpoB,a resultantedasfor¸casqueatuanosistematemapenasacontribui¸c˜aodopesodeBedasfor¸casde atritoqueatuamsobreA.Aindapodemosverificarque,enquantoofioqueligaosdoiscorposestiver esticado,om´odulododeslocamentodocorpoAtemdeserigualaom´odulododeslocamentodocorpo B,om´odulodavelocidadedocorpoAtemdeserigualm´odulodavelocidadedocorpoBeom´odulo daacelera¸c˜aodocorpoAtemdeserigualm´odulodaacelera¸c˜aodocorpoB,at´eocorpoBcolidircom och˜ao.Esquematicamentetemosaseguintesitua¸c˜ao:
3
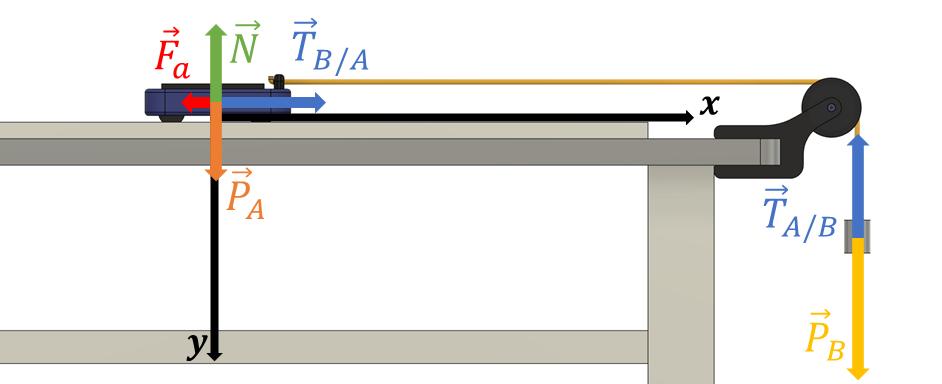
Figura1:For¸casqueatuamnosistema
Assimvamosconsiderarque x =0 m ∧ y =0 m,´eaposi¸c˜aoinicialdocarrinho,osentidopositivo doeixodasabcissas´eodomovimentodocarrinho(corpoA)eosentidopositivodoeixodasordenadas ´eodomovimentodocorpoB,talcomoserepresentaabaixo:
Figura2:For¸casqueatuamnosistemaereferencialescolhido
Consideremosaindaqueaordenadadaposi¸c˜aoinicialdocorpoB´e h1 eaordenadadaposi¸c˜ao finaldocorpoB,ouseja,quandoocorpoBatingeosolo,´e h2
Assimvamosestudarasequa¸c˜oesdomovimentodocarrinho,antesdocorpoBcolidircomoch˜ao, ouseja,enquantoodeslocamentodocorpoAformenorque h2 h1.Assimtemosque:
Ouseja: −→ P B + −→ F a = −→ F R Assim: g × mB Fa = aR × (mA + mB ) ⇔ ⇔ aR = gmB Fa mA + mB
a(t)= ax = gmB Fa mA+mB ay =0 [1] v(t)= vx = gmB Fa mA+mB × t vy =0 [2] r(t)= x = 1 2 gmB Fa mA+mB × t2 y =0 [3] 4
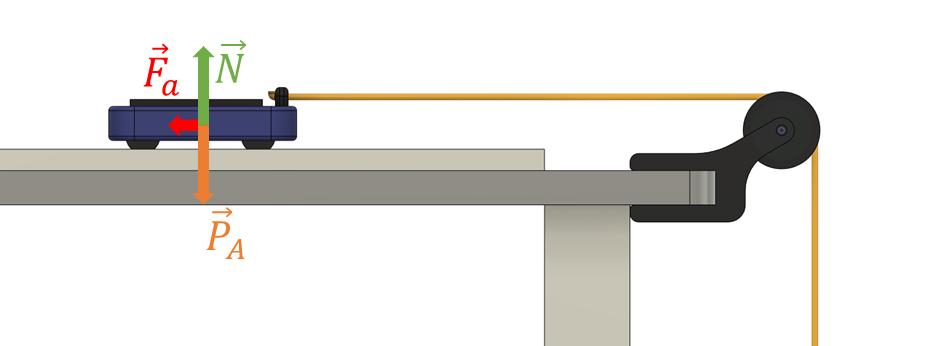
Eagoraanalisandoasitua¸c˜aodepoisdocorpoBcolidircomoch˜ao,ouseja,quandoodeslocamento docorpoAformaiorouiguala h2 h1,verificamosquearesultantedasfor¸casqueatuamnocarrinho (corpoA),emaisgeralmentenosistema,´eafor¸cadeatrito:
Figura3:For¸casqueatuamnosistemacorpoA,depoisdocorpoBentraremcontactocomosolo
h2 h1: 1 2 gmB Fa mA + mB × t2 <h2 h1 ⇔ ⇔ t2 < 2(mA + mB )(h2 h1) gmB Fa ∧ t ≥ 0 ⇒ ⇒ 0 ≤ t< 2(mA + mB )(h2 h1) gmB Fa Assumindoque: t1 = 2(mA + mB )(h2 h1) gmB Fa Temosque: 0 ≤ t<t1
Masodeslocamentotemdesermenorque
5
Assimpodemosescreverque:
Note-sequeaacelera¸c˜aodocarrinho(corpoA)depoisdocorpoBcolidircomosolo´e Fa/mA, umavezquearesultantedasfor¸casqueatuamnocarrinho(corpoA)´eafor¸cadeatrito(Fa). Juntandoagoraasduassitua¸c˜oesparaocorpoA,ouseja,asequa¸c˜oes[1],[2]e[3]e[4],[5]e[6]e, ainda,considerandoque:
a(t)= ax = Fa mA ay =0 v(t)= vx = gmB Fa mA+mB 2(mA+mB )(h2 h1) gmB Fa Fa mA (t t1) vy =0 r(t)= x = h2 h1 + gmB Fa mA+mB 2(mA+mB )(h2 h1) gmB Fa (t t1) Fa 2mA (t t1)2 y =0 Esimplificandoasexpress˜oes: a(t)= ax = Fa mA ay =0 [4] v(t)= vx = 2(gmB Fa)(h2 h1) mA+mB Fa mA (t t1) vy =0 [5] r(t)= x = h2 h1 + 2(gmB Fa)(h2 h1) mA+mB (t t1) Fa 2mA (t t1)2 y =0 [6]
t2 = t1 + mA Fa 2(gmB Fa)(h2 h1) mA + mB 6
Arestri¸c˜aotemporalde t2,deve-se`avelocidadedocorpoAnuncainverterosentidoquandoa resultantedasfor¸casqueatuamneste´eafor¸cadeatrito.
Agoraquededuzimosasequa¸c˜oesdomovimentoparaocorpoA(ocarrinho)aosubstituirmosas vari´aveisporvaloresrelativamentereal´ısticospodemosterumaideiadecomoser´aaformadogr´afico obtido.
Assimvamosconsiderarque:
• mA =0, 800kg
• mB =0, 060kg
• Fa =0, 050N
• g =9, 8ms 2
• h1 =0, 300m
• h2 =0, 800m
Temos: ax(t)= ax = gmB Fa mA+mB , 0 ≤ t<t1 ax = Fa mA ,t1 ≤ t ≤ t2 [7] vx(t)= vx = gmB Fa mA+mB t, 0 ≤ t<t1 vx = 2(gmB Fa)(h2 h1) mA+mB Fa mA (t t1) ,t1 ≤ t ≤ t2 [8] x(t)= x = gmB Fa 2(mA+mB ) t2 , 0 ≤ t<t1 x = h2 h1 + 2(gmB Fa)(h2 h1) mA+mB (t t1) Fa 2mA (t t1)2 , t1 ≤ t ≤ t2 [9]
7
Esubstituindoosvaloresnasexpress˜oes[7],[8]e[9]obtemososgr´aficos:
Legenda:
3Material
-Calhamet´alicadeatritoreduzido(opcional)-Polia
-Fioinextens´ıveldemassadesprez´avel-Corpomet´alico(corpoB)
-Carrinhocomrodasdeatritoreduzido(corpoA)-Telem´ovel
-El´asticosououtrotipodesuporteparaprenderotelem´ovel
-Barrasmet´alicas(opcional)
0 -0.2 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 t -0.2 0.2 0.4 0.6 0.8 1 1.2 1.4
a(t)(S.I.) v(t)(S.I.) x(t)(S.I.)
8
4Montagemexperimental
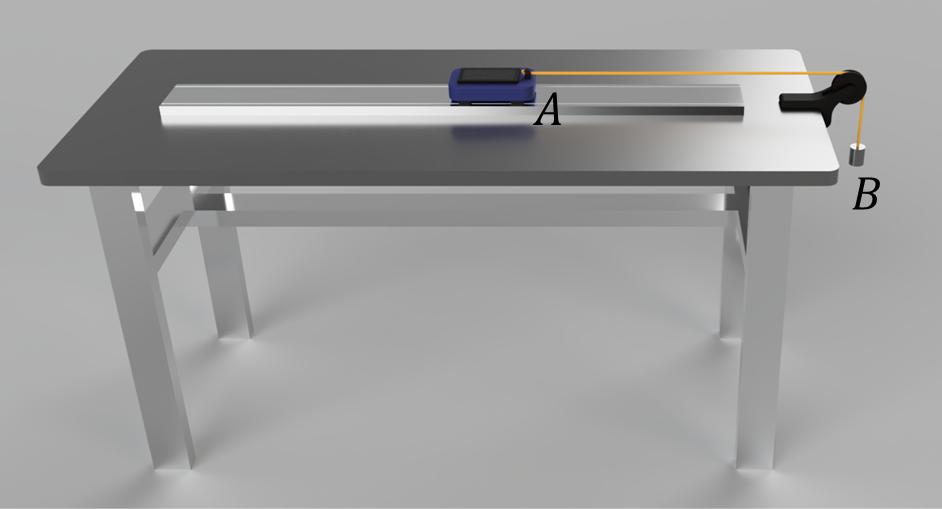
Abaixoencontram-sealgumasimagensqueilustramumaposs´ıvelmontagemexperimental.
Figura4:Vista1montagemexperimental
9
Figura5:Vista2montagemexperimental
Figura6:Vista3montagemexperimental
10
Figura7:Vista4montagemexperimental
Figura8:Vista5montagemexperimental
11
Figura9:Vista6montagemexperimental
5Procedimentoexperimental
Ap´osrealizarmosaan´alisete´oricaeefetuarmosamontagemexperimental,iremospassaraotrabalho experimentalpararecolherosdadosqueser˜aoposteriormenteanalisados.
Assim:
• Posicioneocarrinho,namontagemexperimental(montaracalha(opcional),eapolia),omais afastadodapoliaeprendaocorpoBcomumcomprimentodefio,talquecercademetade dodeslocamentodocarrinho´erealizadocomocorpoBsuspensopelofioeaoutrametade´e realizadacomocorpoBemrepousonosolo.Aten¸c˜ao:ofiotemdeestarnahorizontal,ouseja, paralelo`amesa.
• Abraaaplica¸c˜aoPhysLab,notelem´ovel.
• Seaindan˜aorealizouotutorial,fa¸ca-o,umavezqueesteexplicar´adetalhadamentecomoutilizar aaplica¸c˜ao.
• Cliqueem”MovementStudy”eposteriormenteem”RecolherDados”.
• Depoisdeposicionarefixardevidamenteotelem´ovelnocarrinhocliqueem”Start”parainiciar arecolhadedados.
• Largueocarrinhoetenteparararecolhadedadosomaispr´oximodocarrinhoatingirofim damesa.Aten¸c˜ao:Largueocarrinhocomcuidado,eviteabanaramesa,ouqueocarrinho realizemovimentosmuitobruscos,umavez,queestesmovimentosir˜aoafetarasmedi¸c˜oesdo aceler´ometrodotelem´ovel.
• Repitaolan¸camentodocarrinhopelomenos5vezes,eap´oscadalan¸camentoabraasec¸c˜ao ”AnalisarDados”everifiqueseduranteolan¸camenton˜aoocorreramerrosaleat´orioscomprometedoresdosresultadosobtidos.Seocorreramdescarteesseregisto.Oserrosaleat´oriosreferidos podemsermaioritariamentedetetadosquandoosgr´aficosdavelocidades˜aomuitoirregulares. Estasirregularidadespodemindicarqueamesatenhaabanadoouqueofion˜aoestavabem esticadoouqueficoupresonapolia.Oserrossistem´aticosquepodemafetarasmedi¸c˜oesde format˜aosubtilquen˜ao´epercet´ıvelpelaformadosgr´aficospodemseraindevidainclina¸c˜aoda mesaoudefeitosnacalhaounocarrinho.
Trabalhoexperimentalcoletivo!(opcional)
Paraagilizaraatividadeexperimental,5gruposdetrablhodeviamrealizaraexperiˆenciacommassas paraoscorposAeBdeacordocomaseguinteequa¸c˜ao:
mB grupoi mA grupoi + mB grupoi ≈ (0, 625+0, 375 × i) × mB grupo1 mA grupo1 + mB grupo1 , 1 ≤ i ≤ 5 Sendoque: 0, 015 ≤ mB grupo1 mA grupo1 + mB grupo1 ≤ 0, 020(S.I.) 12
5.1Exemplodeumaextra¸c˜aodedadosexperimentais
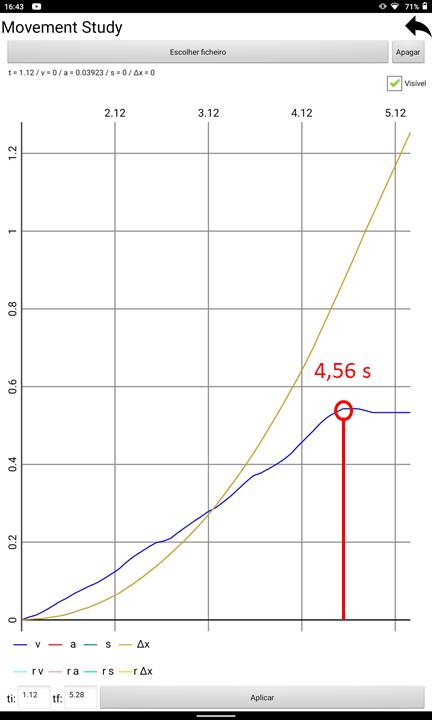
Ap´osselecionarmosointervalodetempoqueir´aseroalvodonossoestudo,deumdadolan¸camento, foiobtidooseguintegr´aficoparaavelocidadeedeslocamentoemfun¸c˜aodotempo.Temosagora deidentificaroinstantenoqualocorpoB(opeso)colidiucomosolo,ouseja,oinstantenoqual omovimentopassadeuniformementeaceleradoparauniforme.Esteponto´efacilmenteidentific´avel porseropontoangulosonoqualderepenteaacelera¸c˜aopassadeumvalorbastantemaiorquezero paraumvalormuitopr´oximodezero.Comovemosnogr´aficoabaixoesseinstanteocorreaos4,56 segundos.
Figura10:Gr´aficodavelocidadeedeslocamentodocarrinhoemfun¸c˜aodotempo(obtidonoPhysLab)
13
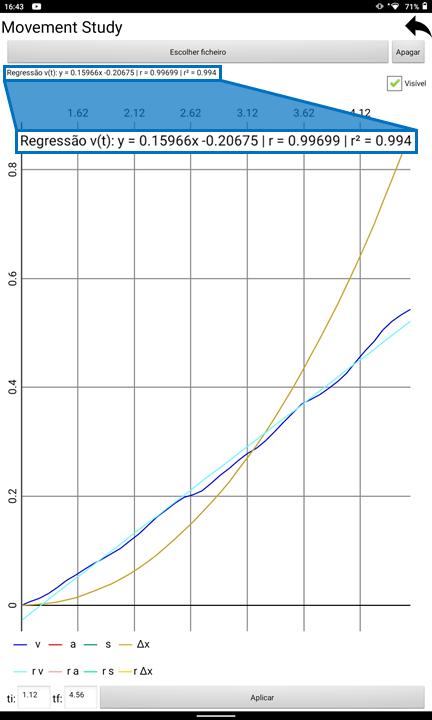
Depoisdaescolhadointervalodetempoadequado,nestecaso[1,12;4,56]segundos,fazemosaregress˜aodavelocidadeeodeclivedaretadeajustecorrespondenumericamenteaom´odulodaacelera¸c˜ao docorpo.Nestecasoobtivemosumaacelera¸c˜aode0, 15966ms 2,como´eposs´ıvelvernaimagem abaixo.
Figura11:Gr´aficodaregress˜aodavelocidadedocarrinhoemfun¸c˜aodotempo(obtidonoPhysLab)
14
5.2Tabelasean´alisededadosexperimentais
Massadocarrinho+barrasmet´alicas+telem´ovel(mA):
mA: kg
Massadopeso(mB ):
mB : kg
Deacordocomoprocedimentoexplicadoanteriormentepreenchaaseguintatabeladedadosexperimentais:
Agoracalculamosovalorm´ediodosresultadosobtidos:
Pelaequa¸c˜ao[1]sabemosqueteoricamente:
Lan¸camento(i) aRi m/s 2 1 2 3 4 5
aR = aR1 + aR2 + aR3 + aR4 + aR5 5 aR obtida: ms 2
aR = gmB Fa mA + mB 15
Mascomoassumimosqueoatrito´edesprez´avel(F
=0)temosque:
Assim:
Logooerropercentualobtidoser´a:
a
aR = gmB mA + mB
aR te´orica: ms 2
Erropercentual = |aR te´orica aR obtida| aR te´orica × 100% Erropercentual: %
δi = |aRi aR obtida| Lan¸camento(i) aRi m/s 2 δi 1 2 3 4 5 16
Quantoaodesviorelativo,temos:
Esendo δi max omaiorvalorque δi assume,temosqueodesviorelativoser´a:
Desviorelativopercentual = δi max aR obtida × 100%
Desviorelativopercentual: %
Trabalhoexperimentalcoletivo!
Ap´ostodososgruposteremchegadoaestapartepartedorelat´orio,seemcadagrupoodesviorelativo percentualfordepreferˆenciainferiora5%,podendosertoleradoserrosat´e10%,osgruposdevem partilharosseusdadosecompletaraseguintetabela:
6Quest˜oesP´os-Laboratoriais
1. Recorrendo`asfuncionalidadesdacalculadoragr´aficatracearetadeajusteaosvaloresdaColuna IIemfun¸c˜aodosvaloresdaColunaI,ouseja,considereosvaloresdaColunaIcomosendoavari´avel independenteeosvaloresdaColunaIIcomosendoavari´aveldependente,eapresentearespetiva equa¸c˜ao.
2. Qual´eosignificadof´ısicododeclivedaretaajusteobtidanaperguntaanterior,considerandoque afor¸cadeatrito´edesprez´avel?
3. Calculeoerropercentualdadetermina¸c˜aoexperimentaldom´odulodaacelera¸c˜aograv´ıticaconsiderandoqueovalortabeladodom´odulodaacelera¸c˜aograv´ıtica`asuperf´ıciedaterra´e g =9, 81ms 2
ColunaI ColunaII Grupo(i) mB grupoi mA grupoi+mB grupoi aR obtidagrupoi m/s 2 1 2 3 4 5
17
4. Parasimplificaraatividadeexperimental,ofiotemdeestarnahorizontal(paralelo`amesa),mas n˜aonecessariamenteistoteriadeacontecer.Expliqueporquˆequeofioestandonahorizontalsimplifica otratamentodedadosdestaatividadelaboratorial.
5. Tendoemcontaoqueaprendeuacercaderoldanas,escrevaumaexpress˜aoparaaacelera¸c˜ao resultantedocorpoA,noSistema1(verFigura12),emfun¸c˜aode g, mA, mB e α,considerandotodas asfor¸casdeatritodesprez´aveis.
Figura12:Sistema1
6. Umaformamuitoeficazdetestarrapidamenteaplausibilidadedeumaf´ormula´etest´a-laparaos casosextremos.Testeseaf´ormulaquededuziuanteriormentefuncionaparaocaso α =0,casono qual:
7. Calculeoˆangulo αmax,paraoqualomovimentodocorpoB´edescendente,emfun¸c˜aode mA, mB e g,considerandotodasasfor¸casdeatritodesprez´aveisequeinicialmenteAeBest˜aoemrepouso.
8. Qual´eatens˜aoexercidanofioemfun¸c˜aode g, mA, mB e α,considerandotodasasfor¸casdeatrito desprez´aveis.
9. Sup˜oeque mA =1, 500kg, mB =0, 800kge g =9, 81ms 2.Sabendoqueatens˜aom´aximaqueo fiosuportaantesderebentar´e8N,qual´eoˆangulom´aximodoplanoincinadoantesdofioromper? Apresentaoresultadocomumacasadecimal.
gm
mA + mB
aR =
B
18
7Exemploderesultadosexperimentais
Grupo1 mA:1, 214kg mB :0, 02459kg Lan¸camento(i) aRi m/s 2 1 0,20359 2 0,19390 3 0,19230 4 0,18708 5 0,18754 aR obtida:0, 19288ms 2 aR te´orica:0, 19476ms 2 Erropercentual:0, 96529% Lan¸camento(i) aRi m/s 2 δi 1 0,20359 0,01071 2 0,19390 0,00102 3 0,19230 0,00058 4 0,18708 0,00580 5 0,18754 0,00534 Desviorelativopercentual:5, 5527% Grupo2 mA:1, 290kg mB :0, 04025kg Lan¸camento(i) aRi m/s 2 1 0,29070 2 0,28684 3 0,29566 4 0,30483 5 0,29998 aR obtida:0, 29560ms 2 aR te´orica:0, 29683ms 2 Erropercentual:0, 41438% Lan¸camento(i) aRi m/s 2 δi 1 0,29070 0,00490 2 0,28684 0,00876 3 0,29566 0,00006 4 0,30483 0,00923 5 0,29998 0,00483 Desviorelativopercentual:3, 1225% 19
mA:1, 301kg mB :0, 05088kg Lan¸camento(i) aRi m/s 2 1 0,37739 2 0,37096 3 0,37597 4 0,36234 5 0,37363 aR obtida:0, 37206ms 2 aR te´orica:0, 36921ms 2 Erropercentual:0, 77192% Lan¸camento(i) aRi m/s 2 δi 1 0,37739 0,00533 2 0,37096 0,00110 3 0,37597 0,00391 4 0,36234 0,00972 5 0,37263 0,00057 Desviorelativopercentual:2, 6125% Grupo4 mA:1, 658kg mB :0, 07453kg Lan¸camento(i) aRi m/s 2 1 0,42201 2 0,43062 3 0,41752 4 0,42771 5 0,42705 aR obtida:0, 42498ms 2 aR te´orica:0, 42201ms 2 Erropercentual:0, 70377% Lan¸camento(i) aRi m/s 2 δi 1 0,42201 0,00297 2 0,43062 0,00564 3 0,41752 0,00746 4 0,42771 0,00273 5 0,42705 0,00207 Desviorelativopercentual:1, 7554% 20
Grupo3
Grupo5 mA:2, 000kg mB :0, 1008kg Lan¸camento(i) aRi m/s 2 1 0,47849 2 0,46611 3 0,46977 4 0,46965 5 0,46114 aR obtida:0, 46903ms 2 aR te´orica:0, 47070ms 2 Erropercentual:0, 35479% Lan¸camento(i) aRi m/s 2 δi 1 0,47849 0,00946 2 0,46611 0,00292 3 0,46977 0,00074 4 0,46965 0,00062 5 0,46114 0,00789 Desviorelativopercentual:2, 0169% Tabeladosdadosobtidospelosgrupos Grupo(i) mB grupoi mA grupoi+mB grupoi aR obtidagrupoi m/s 2 1 0,019853 0,19288 2 0,030257 0,29560 3 0,037636 0,37206 4 0,043018 0,42498 5 0,047982 0,46903 21
8Propostaderesolu¸c˜aodasquest˜oesp´os-laboratoriais
1. Retaderegress˜aolinear:
2.
Odeclivedaretarepresentaom´odulodaacelera¸c˜aograv´ıticaumavezque:
Mascomoassumimosqueoatrito´edesprez´avel(
3.
Oquenoslevaaconcluirque
Comoaregress˜aoqueobtivemosparaaretaajustefoi:
Sabemosqueovalorexperimentaldeterminadoparaom´odulodaacelera¸c˜aograv´ıtica´e:
Assimoerroobtidoser´a:
0 0.005 0.010 0.015 0.020 0.025 0.030 0.035 0.040 0.045 0.050 0.055 0.060 0.065 x 0.1 0.2 0.3 0.4 0.5 0.6 y aR =9, 898 × mB mA + mB 0, 002939(S.I.),com r 2 =0, 99956657
aR = gmB Fa mA + mB
aR = gmB mA + mB ⇔ aR = mB mA + mB × g
Fa =0)temosque:
´eodeclivedaretaajuste.
g
0, 002939(S.I.),com r 2 =0, 99956657
aR =9, 898 × mB mA + mB
gexperimental
=9, 898ms 2
Erropercentual = |aR te´orica aR obtida| aR te´orica × 100% Erropercentual = |9, 81 9, 898| 9, 81 × 100% ≈ 0, 90% 22
Vamosassumirqueofion˜aoestavanahorizontalevamoschamar θ aoˆanguloqueofiofazcomo planohorizontal.
Figura13: ˆ Anguloqueofiofazcomahorizontal
Assimconsiderandooeixodasordenadasverticaleosentidopositivodestedecimaparabaixoe oeixodasabcissasohorizontaleosentidopositivodestedaesquerdaparaadireitatemos:
aR = T cos θ Fa mA = gmB T mB mB (T cos θ Fa)= mA(gmB T ) ⇔
⇔ mB cos θT mB Fa = gmAmB mAT ⇔
⇔ mB cos θT + mAT = gmAmB + mB Fa ⇔
⇔ T (mA + mB cos θ)= mB (gmA + Fa) ⇔
⇔ T = mB (gmA + Fa) mA + mB cos θ
aR = gmB mB (gmA + Fa) mA + mB cos θ × 1 mB ⇔
⇔ aR = g gmA + Fa mA + mB cos θ ⇔
⇔ aR = gmA + gmB cos θ mA + mB cos θ gmA + Fa mA + mB cos θ ⇔
⇔ aR = gmA + gmB cos θ gmA Fa mA + mB cos θ ⇔
⇔ aR = gmB cos θ Fa mA + mB cos θ
4.
23
Mas Fa =0N,porquedeprezamostodasasfor¸casdeatrito,logo:
aR = gmB cos θ
mA + mB cos θ
Porumlado,claramente,vemosque:
aR = gmB cos θ
´eumaf´ormulamaiscomplexadoque:
mA + mB cos θ
aR = gmB mA + mB
Poroutro,tamb´em,facilmente,vemosqueamedi¸c˜aodoˆangulo θ introduziriamaisumafonte deposs´ıvelerroexperimental,porisso,conclu´ımosqueparasimplificarotratamentodedadosdesta atividadelaboratorialofiodeveestarnahorizontal.
5.
Pararesolveresteproblemavamosanalisarasfor¸casqueatuamemcadabloco.NoblocoAatuam opeso,quenaimagemfoidecompostonacomponentesegundoomovimentodocorpoA, −→ P Ax,ena componenteperpendicularaomovimentodocorpoA, −→ P Ay ,afor¸caderea¸c˜aonormaldasuperf´ıcie
N , queseanulacom −→ P Ay eatens˜ao.NocorpoBatuamapenasopesoeatens˜ao.
Sendoosentidopositivodoeixodasabcissasosentidodafor¸ca −→ T B/A,podemosescreverque:
PAx = gmA sin α
−→
Figura14:For¸casqueatuamnosistema1
24
Logo,comoaacelera¸c˜aodosdoisblocos´eamesmatemos:
Assim:
⇔ mA(gmB T )= mB (T gmA sin α) ⇔
⇔ gmB mA TmA = TmB gmAmB sin α ⇔
⇔−TmA TmB = gmAmB gmAmB sin α ⇔
⇔ TmA + TmB = gmAmB + gmAmB sin α ⇔
⇔ T (mA + mB )= gmAmB (1+sin α) ⇔
⇔ T = gmAmB (1+sin α) mA + mB
Logo:
Destaformaaacelera¸c˜aoresultantedocorpoApodesercalculadadaseguinteforma:
aR = gmB T mB = T gmA sin α mA
gmB T mB = T gmA sin α mA ⇔
aR = gmB gmAmB (1+sin α) mA + mB × 1 mB ⇔
⇔ aR = g gmA(1+sin α) mA + mB ⇔
⇔
m
⇔
m
⇔ aR = gmA + gmB mA + mB gmA + gmA sin α mA + mB
⇔ aR = gmA + gmB gmA gmA sin α
A + mB
⇔ aR = gmB gmA sin α
A + mB
a
m
a
m
m
+ mB = gmB mA + mB 25
R = gmB gmA sin α
A + mB 6. Af´ormulafuncionapara α =0,umavezque:
R = gmB gmA sin(0)
A + mB = gmB gmA × 0
A
ParaomovimentodocorpoBserdescentesabemosque:
Atendendoaodom´ıniodesin 1(x),que´e[-1,1],paraqueomovimentodocorpoBsejadescendente temosque:
7.
aR > 0 ⇒ gmB gmA sin α mA + mB > 0 gmB gmA sin α mA + mB > 0 ⇔ ⇔ gmB gmA sin α> 0 ⇔ ⇔ mB mA sin α> 0 ⇔ ⇔−mA sin α> mB ⇔ ⇔ mA sin α<mB ⇔ ⇔ sin α< mB mA ⇔ ⇔ α< sin 1 mB mA
αmax =90◦,mB >mA αmax =sin 1 mB mA ,mB ≤ mA 8. Express˜aoj´acalculadanapergunta5. T = gmAmB (1+sin α) mA + mB 9. Partindodaexpress˜aodaperguntaanterior: T = gmAmB (1+sin α) mA + mB ⇔ ⇔ 1+sin α = T (mA + mB ) gmAmB ⇔ ⇔ α =sin 1 T (mA + mB ) gmAmB 1 26
Substituindoagoraaexpress˜aoanteriorpelosvalordadosnoenunciadocalculamosqueoˆangulo α m´aximoantesdofioseromperser´a:
α =sin 1 8 × (1, 500+0, 800) 9, 81 × 1, 500 × 0, 800 1 ≈ 34, 3◦
9Testedaexatid˜aoeprecis˜aodosdadosadquiridospela aplica¸c˜aoPhysLab
Afimdetestaraextid˜aoeprecis˜aodaaplica¸c˜aoPhysLabfoirecriadaaatividadelaboratorialexemplificadaanteriormenteeestesforamosresultadosobtidos.
Massadoconjuntocarrinho+barrasmet´alicas+telem´ovel:(1, 410 ± 0, 001)kg
MassadocorpoB:(0, 02503 ± 0, 00001)kg
Figura15:Massadoconjuntocarrinho+barrasmet´alicas+telem´ovel
27
Figura16:MassadocorpoB
(obtidonoPhysLab)
28
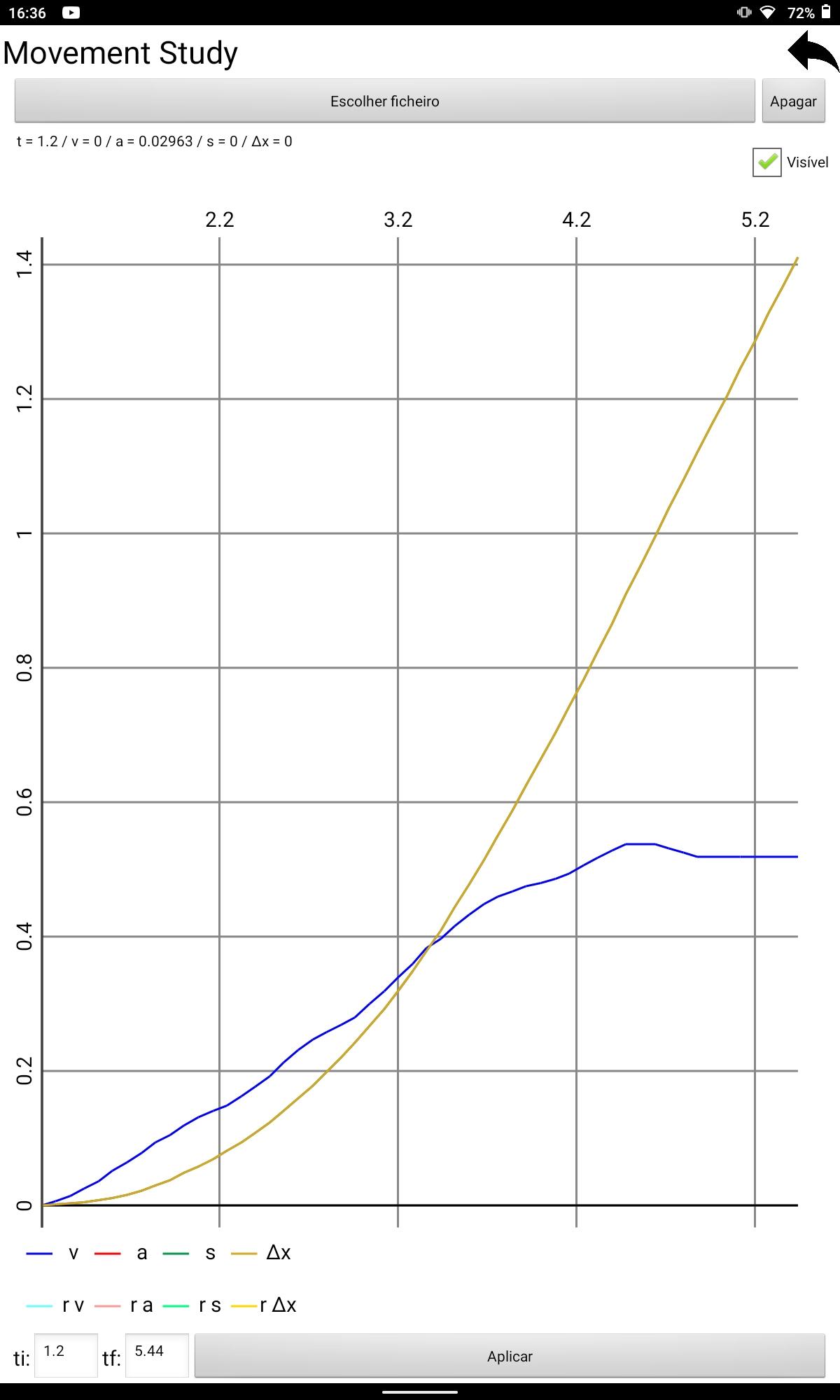
Figura17:Gr´aficodavelocidadeedeslocamentodocarrinhoemfun¸c˜aodotempo-lan¸camento1
(obtidonoPhysLab)
29
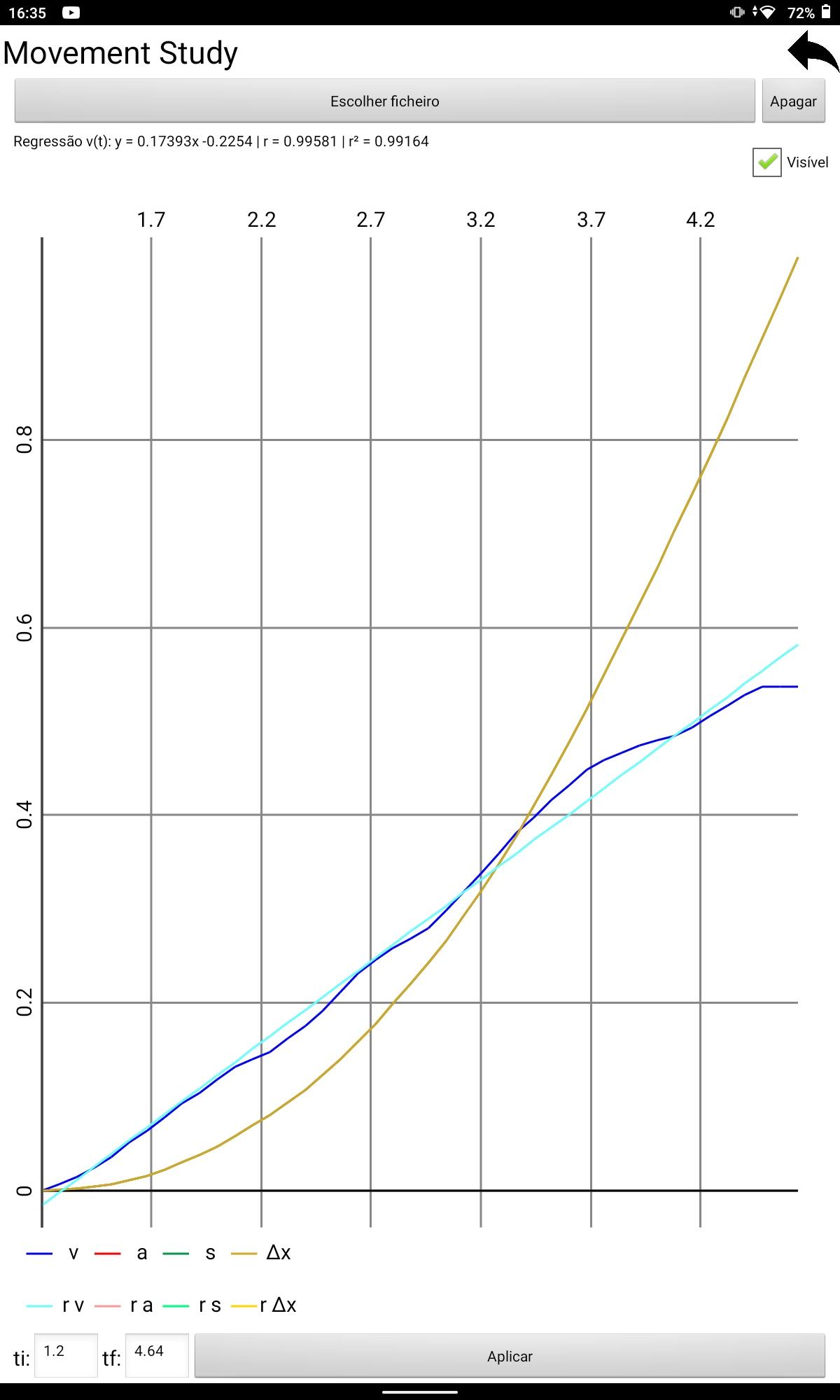
Figura18:Gr´aficodaregress˜aolineardavelocidadeantesdocorpoBalcan¸carosolo-lan¸camento1
(obtidonoPhysLab)
30
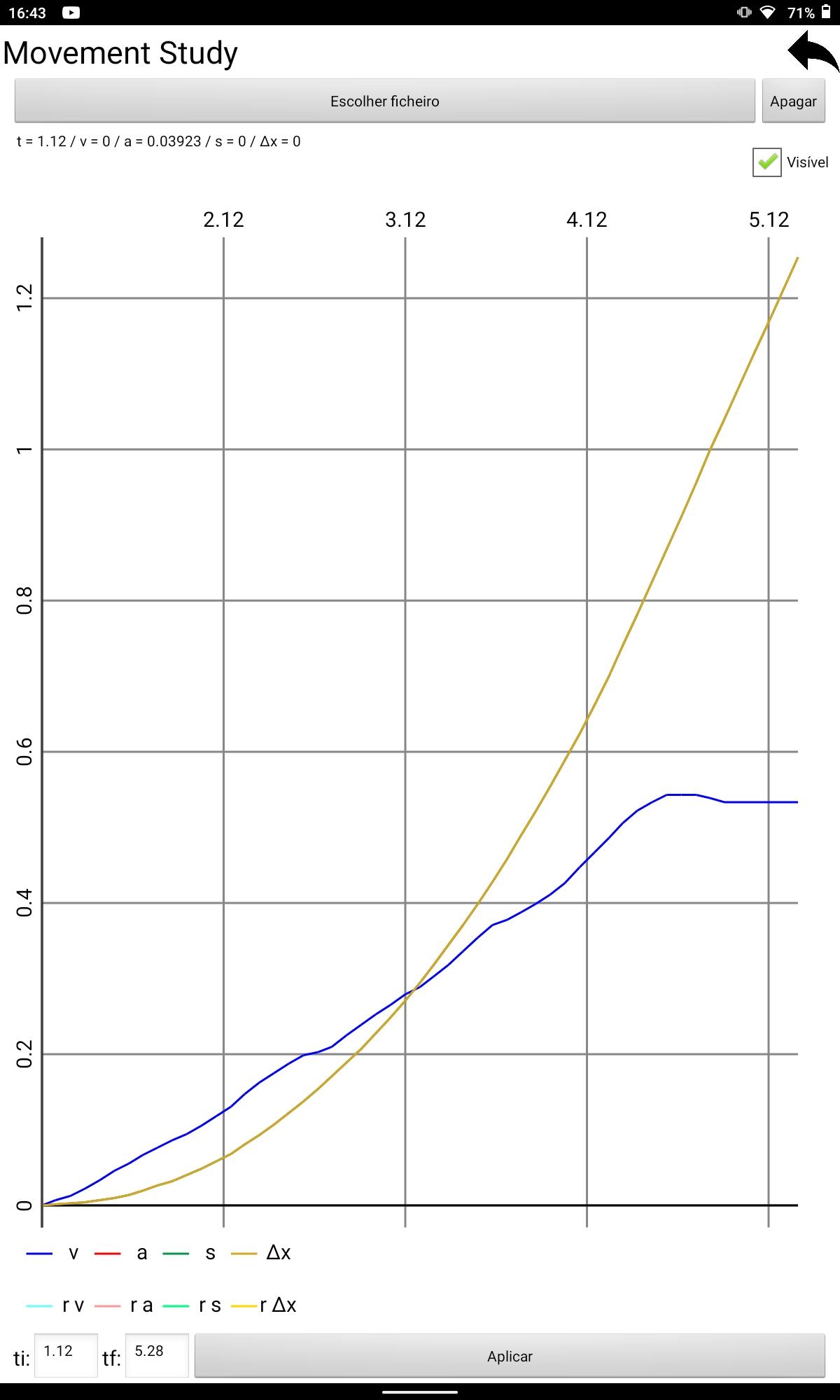
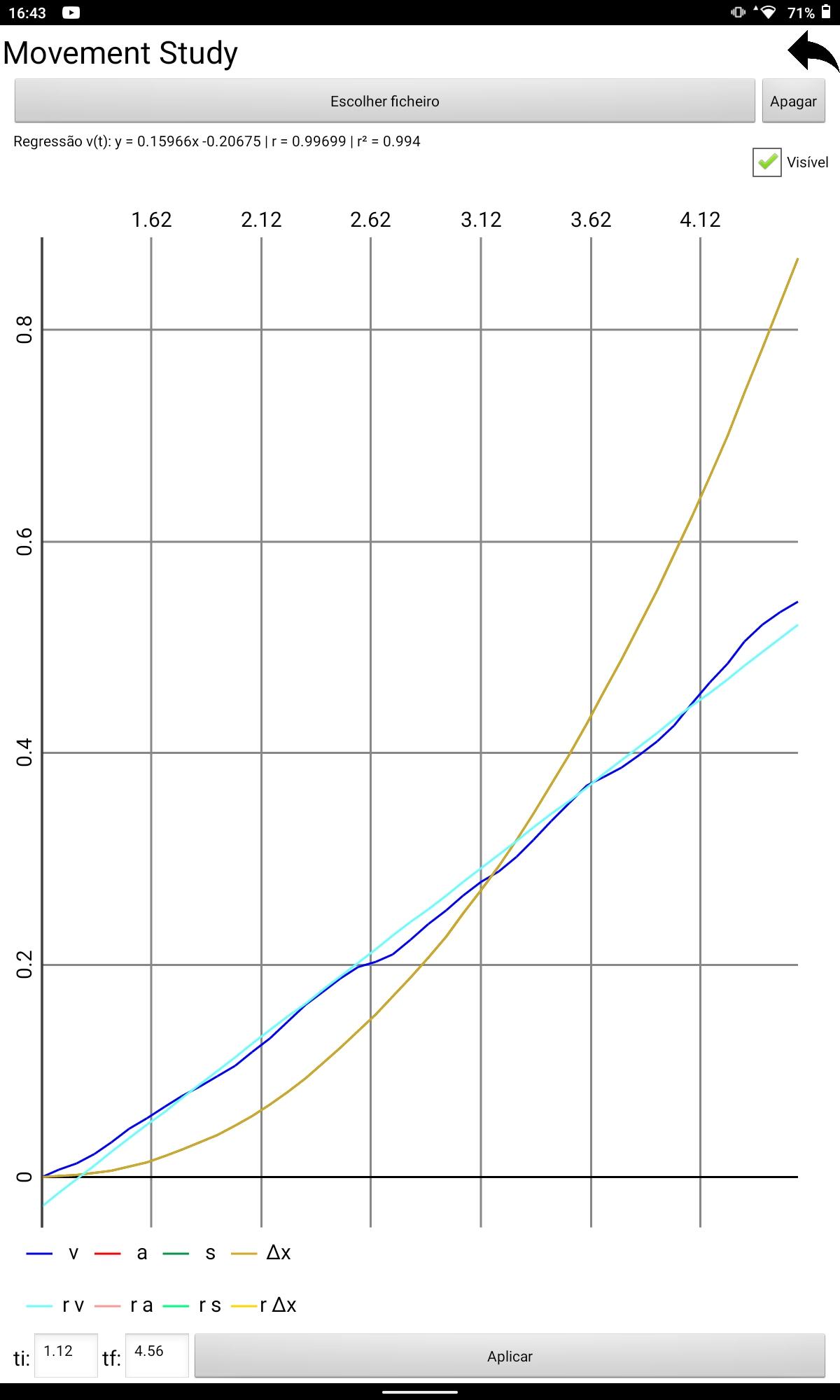
Figura19:Gr´aficodavelocidadeedeslocamentodocarrinhoemfun¸c˜aodotempo-lan¸camento2
Figura20:Gr´aficodaregress˜aolineardavelocidadeantesdocorpoBalcan¸carosolo-lan¸camento2 (obtidonoPhysLab)
31
(obtidonoPhysLab)
32
Figura21:Gr´aficodavelocidadeedeslocamentodocarrinhoemfun¸c˜aodotempo-lan¸camento3
(obtidonoPhysLab)
33
Figura22:Gr´aficodaregress˜aolineardavelocidadeantesdocorpoBalcan¸carosolo-lan¸camento3
(obtidonoPhysLab)
34
Figura23:Gr´aficodavelocidadeedeslocamentodocarrinhoemfun¸c˜aodotempo-lan¸camento4
(obtidonoPhysLab)
35
Figura24:Gr´aficodaregress˜aolineardavelocidadeantesdocorpoBalcan¸carosolo-lan¸camento4
(obtidonoPhysLab)
36
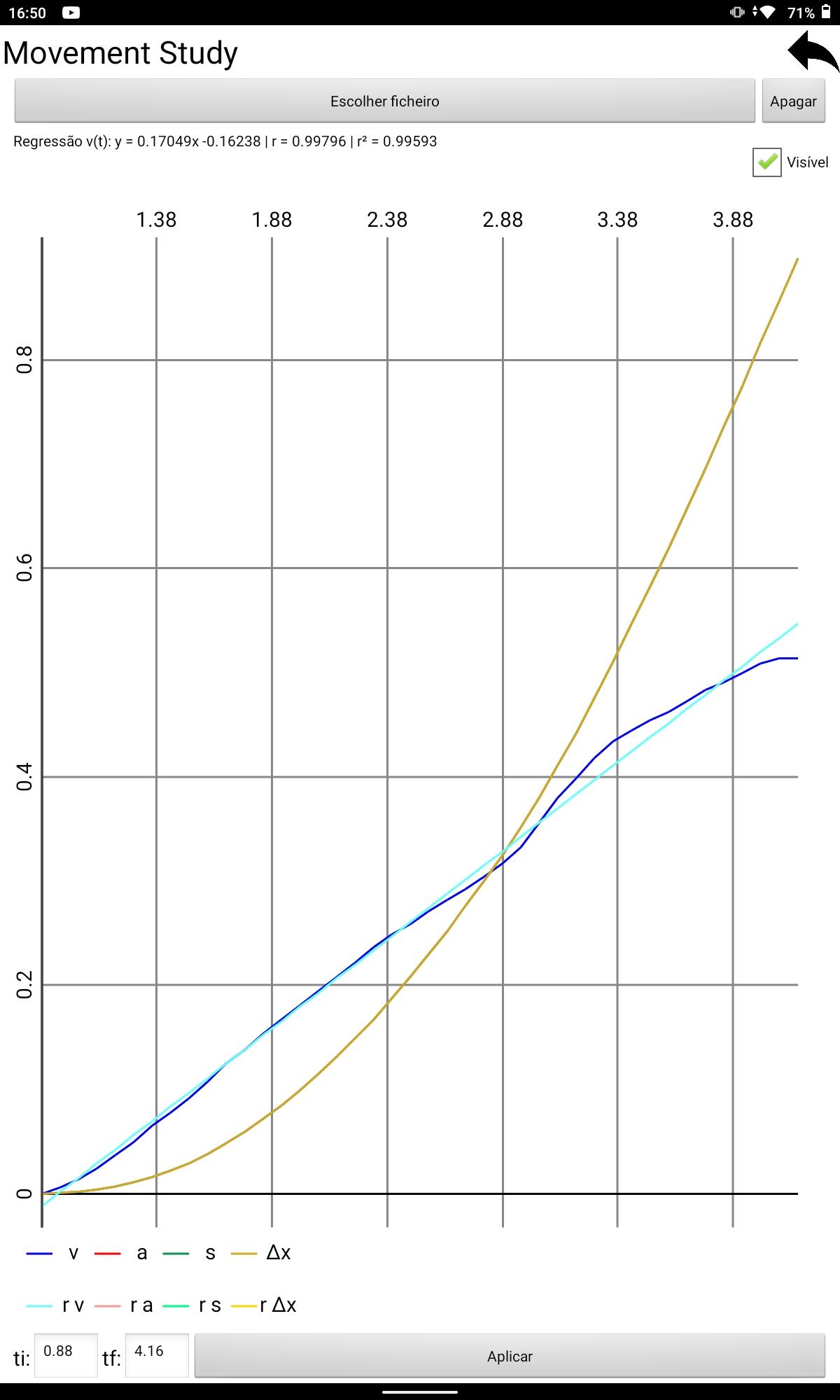
Figura25:Gr´aficodavelocidadeedeslocamentodocarrinhoemfun¸c˜aodotempo-lan¸camento5
(obtidonoPhysLab)
37
Figura26:Gr´aficodaregress˜aolineardavelocidadeantesdocorpoBalcan¸carosolo-lan¸camento5
Daquitiramosqueaacelera¸c˜aodocorpoA,nosrespetivos,lan¸camentosfoi:
umavezqueovalordaacelera¸c˜aocorrespondenumericamenteaodeclivedareta v(t).
Assimovalormaisprov´aveldaacelera¸c˜aoser´aam´ediadosvaloresobtidosanteriormente,logo:
Voltando`aequa¸c˜ao[1]sabemosqueteoricamente:
Considerandodesprez´avelafor¸cadeatrito,temosque:
Esubstituindopelasmassasmedidasanteriormenteeconsiderando(
• Lan¸camento1: v =0, 17393t 0, 22540(S.I),com r2 =0, 99164 • Lan¸camento2: v =0, 15966t 0, 20675(S.I),com r2 =0, 99400 • Lan¸camento3: v =0, 17618t 0, 13118(S.I),com r2 =0, 99462 • Lan¸camento4: v =0, 17413t 0, 11429(S.I),com r2 =0, 99048 • Lan¸camento5: v =0, 17049t 0, 16238(S.I),com r2 =0, 99593
Assimasregress˜oeslinearesobtidasforam:
• Lan¸camento1: aR1 =0, 17393ms 2 • Lan¸camento2: aR2 =0, 15966ms 2 • Lan¸camento3: aR3 =0, 17618ms 2 • Lan¸camento4: aR4 =0, 17413ms 2 • Lan¸camento5: aR5 =0, 17049ms 2
aR = 0, 17393+0, 15966+0, 17618+0, 17413+0, 17049 5 = 0, 85439 5 ms 2 Logo: aRexperimental ≈ 0, 17088ms 2
aR = gmB Fa mA + mB
aR = gmB mA + mB
g
aRte´orica = 9, 81 × 0, 02503 1, 410+0, 02503 ≈ 0, 171ms 2 38
=9, 81ms 2),temosque:
Ap´osaan´alisedosvaloresobtidos,resolvemosrepetirotratamentodedados,ignorandooensaio 2,umavezqueseafastaclaramentedosrestantes.Assim:
Assimoerropercentualobtidoser´a: Erropercentual = |Valorte´orico Valorexperimental| Valorte´orico × 100% Erropercentual = |0, 171 0, 17088| 0, 171 × 100% ≈ 0, 07% Quantoaodesviorelativo,temos: δi = |aRi aR| Lan¸camento(i) aRi m/s 2 δi 1 0,17393 0,00305 2 0,15966 0,01122 3 0,17618 0,00530 4 0,17413 0,00325 5 0,17049 0,00039
δi max =0
01122,temosqueodesviorelativoser´a: Desviorelativopercentual = δi max aR × 100% Logo: Desviorelativopercentual = 0, 01122 0, 17088 × 100% Desviorelativopercentual ≈ 6, 57%
aR = 0, 17393+0, 17618+0, 17413+0, 17049 4 = 0, 69473 4 ms 2 Logo: aRexperimental ≈ 0, 17368ms 2 Assimoerropercentualobtidoser´a: Erropercentual = |0, 171 0, 17368| 0, 171 × 100% ≈ 1, 57% 39
Ecomo
,
Quantoaonovodesviorelativo,temos:
Ecomo δi max =0, 00319,temosqueodesviorelativoser´a:
Desviorelativopercentual = 0, 00319 0, 17368 × 100%
Desviorelativopercentual ≈ 1, 84%
10Conclus˜aoean´alisecr´ıticadosresultadosexperimentais Comaaplica¸c˜aoPhysLabconseguimosestudarmovimentosuniformementeaceleradoseuniformes, comumamontagemexperimentalsimplesequerequerpoucosrecursosdispendiosos.Atrav´esdos gr´aficosgeradospelaaplica¸c˜ao´eposs´ıvelcomprovarexperimentalmentequequandoocorpoAest´a sujeitoaumafor¸cacomintensidade,dire¸c˜aoesentidoconstante:
• avelocidadedocorpoapresentaumadependˆencialinearcomotempo;
• odeclivedaretanogr´aficov(t)corresponde`aacelera¸c˜aodocorpoA.
Naan´alisemaisdetalhadaverificamosqueaacelera¸c˜aote´oricaest´abastantepr´oximadaacelera¸c˜ao experimentalcalculada.Oerropercentualencontradofoideapenas0,07%,noprimeirotratamento, ede1,57%nosegundotratamentorealizado.
Osresultadosobtidoscomprovamqueautiliza¸c˜aodaaplica¸c˜ao”PhysLab”conduzaresultados deacordocomoesperado.Oseventuaiserrosassociadosaestaatividaden˜aosedevemunicamente aimprecis˜oesdoaceler´ometrodotelem´oveloudosoftware,comotamb´em,aposs´ıveisinclina¸c˜oes vari´aveisdamesaeafor¸casdissipativasn˜aocontabilizadasequepossamsurgirduranteaexecu¸c˜ao experimental.
Tamb´ematrav´esdosgr´aficosgeradospelaaplica¸c˜aoconseguimosverque,depoisdocorpoBatingir och˜ao,avelocidadedocorposemant´empraticamenteconstante.Araz˜aoparaemalgunsdosgr´aficos avelocidadeaumentarligeiramente(verfigura16)´eaindevidainclina¸c˜aodamesa;quantoaosmotivos quejustificamquenalgunsdosgr´aficosavelocidadediminualigeiramente(verfiguras12,14,18e20) s˜ao,novamenteaindevidainclina¸c˜aodamesa,pequenosdefeitosimpercet´ıveisnosrolamentosdo carrinhoeeventuaistravagensdevidoaocarrinhopassarporcimadofio.
Nocomptogeralestaatividadeexperimentalcorreubastantebem,umavezquecompoucosrecursos conseguimosobterdadoscommuitaprecis˜aoeexatid˜ao,tendoemcontatodososerrosaleat´oriose sistem´aticosques˜aoinerentesaqualqueratividadeexperimental.
Lan¸camento(i) aRi m/s 2 δi 1 0,17393 0,00025 3 0,17618 0,00250 4 0,17413 0,00045
0,17049 0,00319
5
40
