Modeling Infectious Disease Isabelle Oliver

PARALYSIS

Paralysis affects millions of people in the world, leading to the loss of motor function to different extents. Tetraplegia is the most severe form of paralysis, not only involving the loss of movement but also sensation in all four limbs and torso. Multiple diseases lead to paralysis: traumatic stroke that damages the sensorimotor area, amyotrophiclateral sclerosis (ALS) which is resulted from the degeneration of motor neurones, spinal cord injury (SCI), and other types of severe central nervous system (CNS) injuries. As conventional therapeutic or assistive approaches exhibit limited efficacy in restoring movement in paralysed patients, researchers are developing new methods to improve their life quality. A promising direction is using a brain-computer interface (BCI).

BRAIN-COMPUTER INTERFACE (BCI)

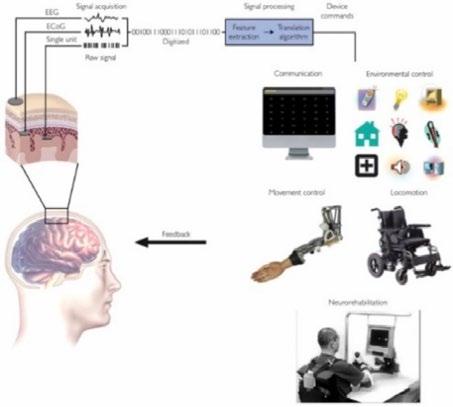
A BCI is a computer-based system that directly acquires brain signals, analyses them, and translates them into commands that are sent to an output device to carry out the desired action. Its working mechanism involves 4 sequential components. 1. Signal Acquisition: measuring brain signals using a sensor when the user is imagining themselves or perceiving a virtualisation of themselves administering a task. Equipment used to record brain signals could range in invasiveness. Overall, non-invasive sensors are the most widely used because they are cheap, safe, and easy to manipulate. More invasive sensors have a higher resolution as signals are not distorted after passing layers of tissue surrounding the brain, making it hard to accurately distinguish or locate them. However, invasive sensors suffer from low long-term stability as scars form around the implantation, interfering with signal transmission. Additionally, they pose higher risks to users due to the need for surgery.

2. Feature Extraction: distinguishing signals relevant to the desired action. Environmental artefacts such as waves produced by powerlines or magnetic field of the earth are distinguished and extracted, and the elimination of biophysiological artefacts requires machine learning. The user needs to imagine themselves conducting an action repeatedly while their brain activity is being recorded. The computer looks for similar patterns and finds the exact neural activity that relates to an action. Such a process may require repeated calibration to adapt to temporal changes in the user’s neural activity.

Type of BCI Surgery Placement Example

Non-invasive No surgery Externally or on the scalp

Invasive

Craniotomy Sitting on or embedded in the brain cortex Electroencephalogram (EEG), functional magnetic resonance imaging (fMRI)

Electrocorticography (ECoG), microelectrode array

Signal measured

Electrical or metabolic

Electrical 3. Feature Translation: using calibration acquired from machine learning, decode processed signals into appropriate commands for output devices. E.g., increased oscillation frequency produced by a certain group of neurons indicates a forward movement of the left arm.

4. Device Output: administering instructions such as robotic arm movement, cursor control, and letter selection. Feedback (usually visual) is given to the user for them to adjust movement if needed. Achieving successful movement control over a BCI can require months of practice.

THE MOTOR CORTEX

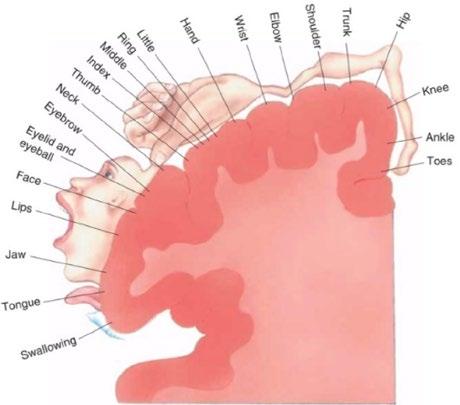
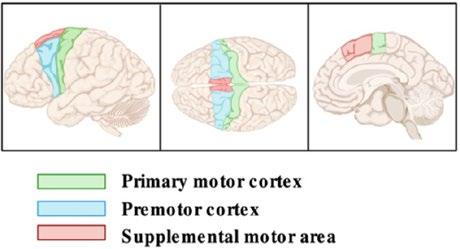
In humans, the control of voluntary movements involves the brain sending signals to muscles via the spinal cord. While multiple cortices coordinate to command a movement, the motor cortex in the frontal lobe is the most predominantly engaged region. It can be divided into three areas: the premotor cortex which plans for the movement, the supplementary motor area (SMA) which rehearses the movement, and the primary motor cortex (M1) which calculates exact vectors of the motion and sends out instructions to the spinal cord. Any disruption in this pathway, such as spinal cord injury or brain damage caused by stroke, could result in compromised movement function such as paralysis. As shown by the cortical homunculus, areas on the motor cortex are specialised in controlling the movement of individual body parts. This allows BCI sensors to be implanted or placed specifically on the desired region to acquire neural commands for moving a particular body part. Moreover, as the direction of movement changes, different groups of neurones fire (known as population coding) in synchronisation; as the strength of movement varies, neurones fire at different frequencies. The exact indication of neural activity is understood through repetitive sampling of the same movement for the machine to ‘learn’, as mentioned before.

In the motor cortex locate mirror neurones. They fire not only when executing a movement, but also when imagining a movement, known as motor imagery. Seeing or hearing someone else conducting a specific action would also trigger a mirror neurone to light up. This allows BCIs to record neural activity for a specific movement from paralyzed patients without them moving.

MOVEMENT RESTORATION

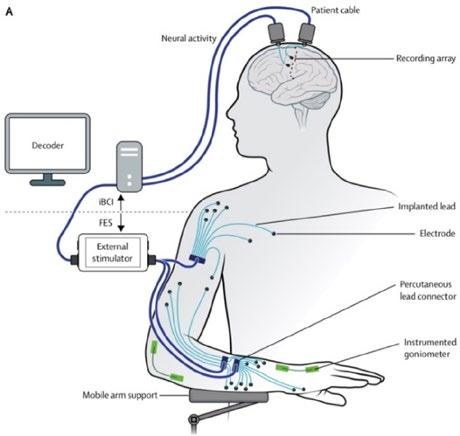
BCIs can assist movement of paralysed patients by either stimulating muscles according to acquired brain signals or using them to move a neuroprosthetic (e.g., robotic arm, exoskeleton). In a clinical trial in 2014-2016, a patient with tetraplegia received implants of intracortical microelectrodes in his brain and electrodes in his muscles. Together with another neurotechnology called functional electrical stimulus (FES), which stimulates peripheral muscles and nerves, the patient commanded functional

multi-joint movements with a success rate of 80-100%. This patient practiced target upper-limb movement by first controlling a virtual arm with brain signals, and then his own arms with a mobile arm support to overcome gravity. Eventually, he was able to reach and grasp a cup of coffee to drink after being paralysed for 8 years.

MOVEMENT REHABILITATION

Stroke is a leading cause of paralysis. Movement rehabilitation in stroke patients could be accomplished by stimulating more use of the ipsilesional (affected) brain region to increase excitatory neural activity in said region, a process known as cortical reorganisation, which could be done by FES of muscles. A controlled study involving a BCI-FES group and a pure FES group suggested that BCI is effective in patients with hemiparesis (compromised motor function on one side of the body). Usual FES gives the patient’s paretic limb an electric stimulation whenever they are instructed to move, thus stimulating the muscles to contract, attempting to reconnect motor pathways involving the ipsilesional region by this reward. However, in the BCI-FES group patients were specifically given electric stimulations when their attempt to execute a movement is recorded by the EEG, therefore providing a much more accurate reward, preventing false-positive results (when the patient didn’t attempt to move but FES is given). It was observed that the BCI-FES patients made significantly better motor recovery compared to the FES group, which is associated with increased connectivity between the premotor and primary motor cortex in the ipsilesional brain areas of BCI patients. Furthermore, the BCI group exhibit maintained functional recovery in follow-up evaluations 6-12 months after the study.

COMMUNICATION RESTORATION

In severe forms of paralysis such as tetraplegia and locked-in syndrome (LIS, where all muscles are paralysed, except for eye muscles), patients lose the ability to communicate. A study published in May 2021 demonstrated a possible assistive communication approach for these patients---brain-to-text communication via handwriting. Participant T5 had tetraplegia resulting from cervical SCI. With the implantation of 2 microelectrode arrays in his premotor area, T5 was instructed to imagine himself handwriting 26 letters and 5 punctuations with a pen for 27 repetitions in each trial, while the microelectrodes recorded his neural activity. The computer then reconstructed these characters by linearly decoding the pentip velocity from trial-averaged neural activity. During the trials, T5 ‘attempted’ to write sentences given by the researchers as the BCI decoded his handwriting in real-time and output sentences on a screen. Eventually, T5 reached a writing speed of 90 characters per minute (close to the average smartphone typing rate in his age group) with a 94.1% success rate. With the application of a language model that simulates an autocorrect mechanism retrospectively, the accuracy was increased to 99%. This study has exceeded any past BCI studies in both the speed and accuracy of communication. However, it did not enable text editing or deletion, and daily retraining of BCI was required. More studies should work on the practicality of this communication method.

THE FUTURE

BCI is still in its infancy. Only 5% of the studies in this field involve end users, and even those with one tend to be uncontrolled or case studies. Recruiting participants is particularly difficult for studies using invasive BCI due to the risks induced by surgery. Therefore, it is difficult to gain a large sample size, which is crucial for investigating the effect of variability between individual brains on the control of BCI. Although there is evidence supporting BCI’s competency in helping paralysed patients to complete functional movement or communication tasks, they are still way too basic for daily use. Moreover, the use of most BCI requires professional assistance in a lab setting, therefore more improvements should be done to the design of BCIs suitable for home use. For a user, learning to control a BCI requires good vision and cognitive function to understand instruction and receive feedback, which limits its use in some paralysed patients. In conclusion, BCI is a neurotechnology with a remarkable potential in reconnecting paralysed patients to the world through assistive and rehabilitative approaches in movement or communication restoration. However, it still lacks applicational value at the current stage. More investigations need to be conducted to generalise the long-term home-use of BCI to satisfy the large population of patients living with paralysis.

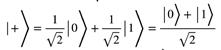
Quantum Computing

Alex Mylet

Quantum computing extends the idea of a classical computer to use quantum mechanics to its advantage, manipulating quantum bits through quantum logic gates. Richard Feynman first proposed quantum computers to simulate quantum mechanics, but it is also possible to perform mathematical calculations on them much faster than on any classical computer.

MATHEMATICS

Classical bits can either be 0 or 1 (represented as and ) but quantum bits (qubits) can be in a superposition of these two states. Superposition is often described as being in both states at once, but a better description is that when in superposition, qubits are in a combination of the states and , with a probability of being found as when measured, and a probability of being found as . In superposition, each of and (referred to as basis states) are multiplied by a complex number (a number in the form , where ) and added together, so a general qubit state . The probability of measuring is and the probability of measuring is ( means take the ‘size,’ or amplitude, of the complex number then ). Therefore . The state of the qubit is not decided in advance, and the process of measurement collapses the superposition to a single state. Alternatively, qubits can be represented using vectors, and gates by matrices, meaning linear algebra (which focuses on manipulating vectors and matrices) can be used to design quantum circuits. Doing this, is equivalent to and is equivalent to and the general state is . One of the simplest classical logic gates is the NOT gate, which turns a 0 into a 1 and vice versa. This has been extended into the quantum NOT, or X, gate, which flips the numbers in the vector of the qubit (known as a ‘bit-flip’), so . The matrix representation of the X gate is

The Hadamard gate (H) takes qubits from the basis states into and out of superposition. Applying it to gives , which has a 50% chance of being when measured and a 50% chance of being . The amplitude for each state is

therefore , and so .

The Hadamard gate takes a qubit into a superposition with the same probabilities, but there is a minus sign instead of a plus sign, hence the state is called .

The Hadamard gate is also reversible, so and .

To represent multiple qubits in a system, you can combine the qubits together to make a single vector in an operation called tensoring. The amplitude squared for each element is the probability of the whole system being measured in a particular state.

To make a universal quantum computer, you must have a set of enough one-qubit gates, as well as a twoqubit gate, such as the Controlled NOT gate (CNOT). CNOT applies NOT to one of the qubits (the target qubit), but only if the other qubit is (control qubit). CNOT can be represented as a 4x4 matrix, acting on the tensor product of the two qubits. In this form, CNOT swaps the amplitudes of and : if you have going into the gate (the first qubit being the control), the control is and so the target gets flipped, becoming (and likewise for ).

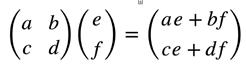
Matrix-vector multiplication Hadamard gate matrix

Tensoring of two qubits

CNOT matrix

ENTANGLEMENT

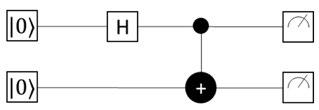
Fig. 1 Diagram of quantum circuit of making, then applying CNOT using this as the control qubit. tensored with In a two-qubit system, if you start with two qubits, apply H to the first one (getting ) and then apply CNOT with the qubit as the control and the qubit as the target, the qubits will either both be 0 or both be 1 when measured. Thus, the qubits are correlated, or entangled. The qubits will also still be correlated if you take them far apart before measuring. See the diagram for the mathematics of applying H then CNOT. Intuitively, you can understand this based on the result of the first qubit (the one that went through the H gate) retroactively determining what had to have happened to the other qubit. If the first qubit is measured in the state, then the CNOT will not have fired, so the other qubit remains in the state. However, if it is measured in the state, then the CNOT will have fired, so the other qubit is flipped to the state.

Applying CNOT: The result is a chance of being measured in each of the and the states.

ARCHITECTURE

There are three main ways of implementing qubits: using the polarisation of light, using the energy levels of charged particles (ions or electrons) trapped in magnetic fields, and using the state of a superconducting circuit, along with others still in development. In both trapped ion and superconducting architectures, different energy levels are used as the basis states of the qubit, meaning there is the potential for the system to decay back to the ground state, causing loss of the quantum superposition and causing errors.

Fig. 2 The Sycamore processor. a, layout of processor b, Photograph of the Sycamore chip. (Image: Springer nature)

A superconductor is a material where a current can keep flowing when there is no voltage and has no resistance. Electrons collect into pairs (called Cooper pairs) and a macroscopic quantum state is formed, which can be controlled with and measured by conventional electronic equipment. The qubits can be fabricated with processes adapted from integrated circuit manufacturing. However, to achieve the superconducting effect, and make a reliable qubit, metals must be cooled down below 20 mK (milli-Kelvin).

SUPREMACY

In 2019, researchers at Google AI Quantum created a 53-superconducting-qubit chip called Sycamore, which they used to achieve quantum supremacy – the completion of a task on a quantum computer that is infeasible to compute on a classical computer; in this case simulating the outputs from a random collection of quantum logic gates. Although the task has little practical application, it is still an important milestone to quantum advantage, where a quantum computer can perform a useful task that is not feasible on a classical computer. The processor uses a type of superconducting qubits called transmon qubits, which act as resonators at 5-7 GHz, where and are encoded as the lowest two energy states. Two-qubit gates are performed using coupling between neighbouring qubits, while single-qubit gates are performed by using microwave pulses while the coupling is turned off. Measurement is performed using a read-out resonator, which changes state depending on the state of the qubit.

Fig. 3 A 4-transmon-qubit circuit fabricated by IBM (Image: npj quantum information)

APPLICATIONS

Richard Feynman first proposed quantum computation to simulate quantum mechanics, as the time taken on a classical computer grows exponentially as you add more particles. This would have uses in areas such as materials science, chemistry, and physics. Quantum computers also may be useful for optimisation, machine learning, and other mathematical problems. One of these problems is factorising integers, which can be solved using Shor’s algorithm. Shor’s algorithm factorises integers using a related problem, that can be solved easily on a quantum computer (but not on a classical computer) – finding the period of the modular exponential function. Quantum computers allow us to easily measure this period, meaning it is possible to factorise numbers on a quantum computer much faster than a classical computer. This can be used to break much of modern internet cryptography, which mostly relies on the fact that factorising integers using currently known algorithms is classically ‘hard’. Another interesting quantum algorithm is Grover’s algorithm, which can be used for searching unstructured datasets. Classically, if you have items, you must check on average of them to get the item you want, and at worst all of them. However, Grover’s algorithm offers a quadratic speed-up, allowing you to find the desired item in roughly steps. The algorithm is generic, so can provide a speed-up for other classical problems, to select a single input from the domain of a function where the output is different.

ISSUES

Quantum computers have several issues that need to be solved before they will be useful at a large scale in the real world. Qubits are highly sensitive to noise from the environment (e.g., cosmic rays or random photons), and they can also randomly decay from the higher energy state ( ) to the lower energy state ( ). Therefore, robust error detection and correction are needed so that calculations can be performed at a large scale, requiring multiple physical qubits to implement one logical qubit. Some of these qubits are used to store data and others are used to detect errors in the data qubits. Another issue is the scalability of quantum computers. Currently, the largest quantum computer has 127 physical qubits, but implementing simulations of largescale quantum algorithms will require thousands of logical qubits to allow for full error correction, and tens of thousands of physical qubits. Research is ongoing into how best to scale up architectures to the desired levels, focusing on making modular designs that scale easily, and can be manufactured at scale. Quantum computers will not replace classical computers as most people use them. Instead, they will be available via the cloud, like how most large-scale computing is down currently. This is because of the need for most quantum computers to be at extremely low temperatures so that they can operate properly, which makes them unfeasible to have outside of largescale facilities.