5 minute read
Why is Euclid’s fifth postulate unproven and invalid?
Chloe
Ching ditche, UC4s the fifth postulate as she turns this fundamental mathematical rule we're all used to on its head.
Advertisement
Maths has always been a part of our society. From Euclid to Pythagoras to Archimedes to Gauss, all these people have made significant discoveries in the field of mathematics to become the famous mathematicians we know today. One person that stands out to me is Euclid.
Who was Euclid?
Euclid was most famous for his works in geometry, inventing many of the ways we conceive space, time, and shapes. He wrote one of the most famous books that is still used today to teach mathematics: "Elements" , which was well received at the time and is praised today for its thought and understanding. In school, we often memorise theorems and proofs given to us by our maths teachers, but how many of us truly understand why the theorem exists, and how the proof came about, be it the area of shapes, circle theorems or The Poincare Conjecture? I’ ve certainly never paid much attention to it. But more importantly than simply understanding it, we must keep an open mind to these mathematical formulas and be
Euclid prepared to interpret them as we learn, in order to search for absolute perfection. One controversial topic discussed largely amongst mathematicians would be Euclid’s fifth postulate seen in Euclid’s Elements, book 1.
The fifth postulate
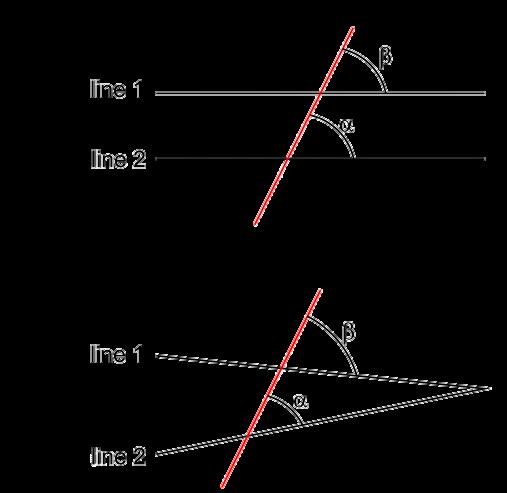
The fifth postulate, also known as the parallel postulate, states that
In easier words, this postulate says that if angle alpha and angle beta shown in the figure below do not sum to 180 degrees, then there will be a point were line 1 and 2 will eventually intersect.

The reason why some people think that the parallel postulate is wrong and thus invalid is because it cannot be drawn if you could draw and satisfy the first four postulates. However, the question is, even if it cannot be drawn, does that mean the geometry is wrong? Furthermore, if we hardly know anything about the universe, can we really understand if the parallel postulate is valid or not?

Different hypothetical forms of geometry, with non-Euclidean geometry being the hyperbolic and elliptical forms on the left and right respectively, either side of Euclidean geometry depicted in the centre.
For example, Einstein argued that the 5th postulate isn’t really true as the parallel lines that it talks about aren’t actually straight and are curved instead, causing the two parallel lines to intersect eventually, unlike what the 5th postulate states. But this is only true if we go with Einstein’s world of Non-Euclidean geometry. Even if it's wrong in our world of space-time, it doesn’t necessarily mean it’s wrong in other possibilities and universes as well. And that is something that we need to consider. Therefore, this is why the fifth postulate has confused mathematicians from Aristotle right up to Gauss and Einstein. Famously, Albert Einstein used non-Euclidean geometry as well to describe how space-time becomes warped in the presence of matter, as part of his general theory of relativity.
Due to our limited understanding on the matter of space-time as well as the different possibilities of geometry in the universe, it is safe to say that the fifth postulate is unprovable because infinite possibilities in the universe simply leads to infinite results and theorems. While the postulate may satisfy one geometry, it does not satisfy all geometries of all possibilities, with non- Euclidean geometry being an example. Therefore, Euclid’s fifth postulate is thus proven to be unprovable.
The shape of space
So what if the parallel postulate was never true all along? If the parallel postulate was not true, this would give rise to entirely new and alternative geometries, which mathematicians call NonEuclidean geometries (see figure above). The main difference between these geometries and ‘ normal’ geometry we study is that these two different geometries depend on a different curvature of the surface upon which the lines are constructed. It appears that Euclid only described one possible way to look at the universe when writing his fifth postulate. (Honestly, who can blame him? After all, people in his time still thought the Earth was flat!) So what are the different ways we could look at the universe and therefore look at his postulate? Well, flat surfaces behave one way, while positively and negatively-curved surfaces behave in a totally different way due to the different characteristics. At first these alternative geometries were found to be strange, but soon they were found to be equally adept at describing the world around us. For example, navigating our planet requires elliptical geometry while much of the art of M.C. Escher displays hyperbolic geometry.


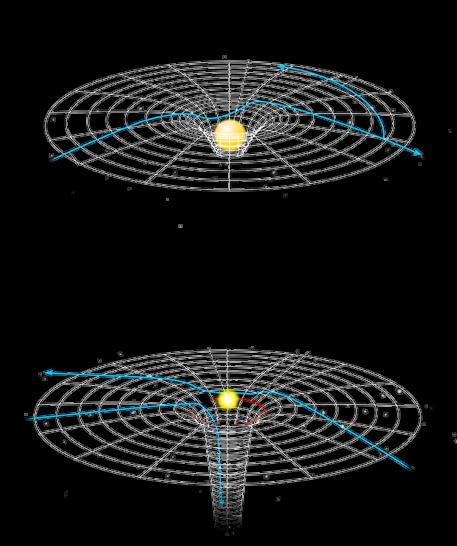
A split comparison of Escher's hyperbolic pattern Circle Limit IV, with the original on the left depicting angels (the light background) and devils (foreground) next to the analysed Circle Limit IV pattern on the right showing the underlying hyperbolic geometry. The bending of space time exhibits non-Euclidean geometry. A massive object, such as the sun, causes a deformation of the spacetime grid, while another object such as a planet or a light beam follows the shortest path (a “geodesic”) on this grid. To an observer, this looks like a deflection of the trajectory caused by gravity, shown by the blue arrow.
Consequentially, a collapsing star can form a black hole so dense and massive that it creates a region of infinite curvature (a “singularity”) so that—inside the event horizon—light cannot escape. A wormhole is formed as space time is warped, which is also an example of a non-Euclidean geometric structure. Illustration: Carin Cain










