
11 minute read
Feature: The Big Bang Theory references, explained


Advertisement





Whenever it comes to teaching the Doppler effect, physics teachers love whipping out that one scene from the Big Bang Theory. It’s Halloween and everyone is dressed as some DC or Marvel superhero, but not Sheldon. He shows up in an ambiguous suit of blackand-white stripes that resemble not those of a zebra, but wavefronts. He is the Doppler Effect. You really wouldn’t expect anything less from him. This is just one of the many physics references scattered across the show, and when I was thinking of a topic to write about, I couldn’t resist the idea of explaining a few of these references. There were many I could choose from: in one classic episode, Sheldon hysterically dives around a ball pit and models particles with peas on his plate to come to a (very loud and
public) revelation about why electrons behave as if they were massless when travelling through graphene. In another episode, upon encountering an indecisive Penny, Sheldon responds with an elusive reference to Schrödinger’s cat (you won’t know if the cat is dead or alive until you open the box i.e. give it a try because you never know!) Needless to say, Sheldon is my favourite character from the show and is involved in two other references I have chosen to explore in this article: supersymmetry and topological insulators. (I have to admit, I don’t think I’ ve ever enjoyed doing research as much as I did for this article as it obviously entailed rewatching episodes from the show and getting a little sidetracked…)
The last episode of Season 11 (spoiler alert - skip ahead if you don’t want me to spoil the show for you), “The Bow Tie Asymmetry ” , is probably my favourite episode of all time. Throughout the episode, Sheldon repeatedly notices the fact that his bow tie is askew. Minutes before their wedding (which, by the way, Mark Hamill
Meet Supersymmetry, the new DC superhero references explained
Vanessa Yip
offers explanations to the jokes and SFC1 references of everyone's favourite sitcom.
Illustrations by RosalindWignall-Torry
officiates), his lopsided bow tie leads Amy and Sheldon to a pivotal revelation about the work they ’ ve been doing on supersymmetry. The asymmetry of his bow tie serves as their eureka moment, inspiring them to invent the principle of “ superasymmetry ” .
Unfortunately, while “ superasymmetry ” is not an actual theory, supersymmetry is a fascinating principle that holds massive potential in explaining three mysteries in physics. To understand supersymmetry, we must first have a grasp of the Standard Model. Much like the physics equivalent of a Periodic Table, the Standard Model outlines the fundamental particles and forces that make up our universe. The fundamental particles include quarks (different combinations of quarks make protons and neutrons) and leptons (electrons, for example). The four fundamental forces include strong, weak, electromagnetic and gravitational, but only the first three are included in the Standard Model. These forces are a product of exchanging force-carrier particles, and the forcecarrying boson for gravity has yet to be discovered. While this model has been successful in explaining a wide range of experimental results and predicting a plethora of others, there are still gaps left by it that fail to encapsulate all phenomena in physics.





Supersymmetry is a hotly contested extension of the Standard Model that potentially fills in these gaps. It is a theoretical principle which many theories fall under, all of them sharing the common feature of equating force with matter. In other words, under this conjecture, matter and force are treated identically. All fundamental particles in our universe can be categorised as fermions or bosons, based on a property they have called spin (a particle’s intrinsic angular momentum). Fermions have half-integer spin and include electrons, quarks, neutrinos, and any particle composed of an odd number of fermions (e.g., protons and neutrons). In contrast, bosons have integer spin and include the force-carrying particles (e.g., photons and gluons), and any particle and detectable. They termed this elusive matter “dark matter” , whose existence keeps clusters of galaxies together. Among other popular dark matter candidates (including sterile neutrinos, axions, WIMPs and more), supersymmetry posits another fitting dark matter candidate: the LSP (lightest supersymmetric particle).
Lastly, if correct, supersymmetry would demonstrate the unification of the strong, weak and electromagnetic forces. Under this principle, the strengths of these forces would be equal at very high energies, a solution that demonstrates how these three forces are mere aspects of a single force which was unified in the early universe.
As exciting as supersymmetry sounds, there could be lots of explanations as to why we haven’t found a “ sneutrino” or a “ selectron” yet. It could be that superpartners predicted are too heavy to be produced with current accelerators, or that these mysterious particles surreptitiously evade detection. Interestingly, a very recent new measurement of the mass of the W boson, a particle that carries the weak force, turned out to be significantly larger than its theoretical prediction (see "Will the Standard Model break?" on p12)! While some are sceptical of the methodology, results and potential implications, others have begun to theorise the explanation behind this. It has been proposed that the existence of “ sparticles” contributed to the W boson being heavier - but, before you get too excited, this is just one of the many possible explanations, and physicists have warned against quickly interpreting this “ as a sign of new physics” .
with an even number of fermions. According to the Pauli Exclusion Principle, no two fermions can exist in the same state, whereas the same constraint does not apply to bosons. This is where it gets interesting - these two seemingly disparate families of particles can potentially
be linked together under the principle of supersymmetry. Symmetry exists everywhere in our world, especially in physics. It is relied on in the conservation of energy and momentum, in Einstein’s relativity and more. In the 1970s, string theorists looked at symmetry on a much smaller scale, spin, giving rise to supersymmetry. For every fermion in the Standard Model, they predicted a superpartner, a boson that shares its identical interactions, has an identical mass but a different spin, and vice versa. No conclusive evidence of the existence of these superpartner particles, or “ sparticles'' , has been seen. However, disproving supersymmetric theories does not necessarily mean the principle of supersymmetry is inherently wrong. Some physicists are still in favour of it because it could give an elegant solution to these three problems: the Higgs boson’s mass, dark matter and the unification of forces.
The Higgs boson, whose confirmed existence won François Englert and Peter Higgs the Nobel Prize in Physics in 2013, is a detectable particle caused by an excitation of the Higgs field, which is an energy field that gives particles mass. The fact that the Higgs boson is light has perplexed many, since its interactions with particles described in the Standard Model suggest it would be heavy. Here, supersymmetry offers an explanation. With all the new “ sparticles” predicted, they offset these interactions, yielding a light Higgs boson.
Over 80% of matter in the universe is enigmatically known as “dark matter” , matter that cannot be detected by conventional means. Their presence was hypothesised from observations made of spiral galaxies. Expecting the outer edges of galaxies to move at a slower velocity than their centres, astronomers were puzzled by their observations: both moved at the same velocity. From this, they inferred that galaxies contained more mass than what was visible

An insulator-conductor-all-inone
The episode “The Thespian Catalyst '' in season 4 opens with Sheldon delivering a condescending lecture on topological insulators. When asked if they were familiar with topological insulators, most of the doctoral candidates in the room raised their hands, only to be met by a “Don’t kid yourselves. ” What he thought was a “triumphant” lecture turned out to be badly received, which couldn't be more clearly demonstrated by “the entire lecture hall flipping him off” at the same time! Not only is this scene truly reflective of Sheldon’s character, it also perfectly illustrates how notoriously difficult it is to understand topological insulators.
The discovery of topological insulators was groundbreaking in condensed matter physics, the field that studies the physical properties of solids and liquids. While you have the standard conductors and insulators, topological insulators are naturally occurring materials that have both properties. Interestingly, the bulk of these materials are insulating, while the edges of these 2D materials or the surfaces of 3D materials are conducting. For (relative) simplicity ’s sake, this article will focus on 2D topological insulators.
“Pure mathematics and physics are becoming ever more closely connected” , said Paul Dirac at a lecture in 1939, and topological insulators are an excellent example of the amalgamation between the two subjects.
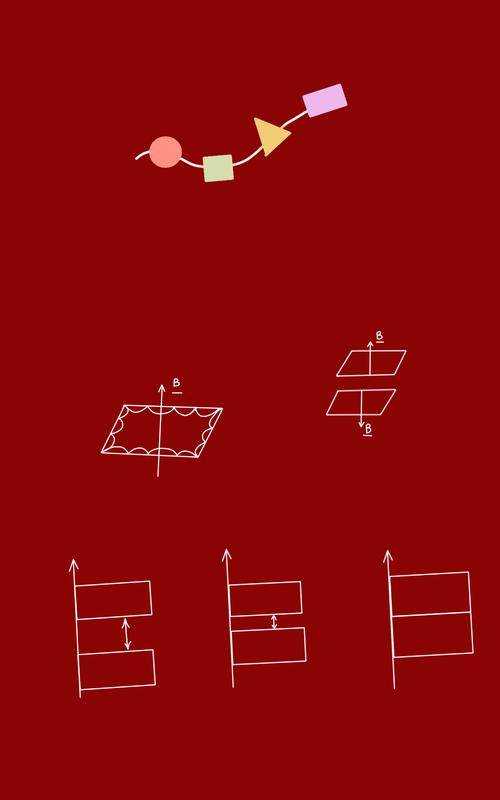
Topology is a branch of mathematics that studies properties of space preserved through continuous deformations which include twisting, stretching but not tearing. For example, you can stretch a circle into an ellipse, so these two shapes are said to be topologically equivalent. If we think in 3D, a famous example showing topological equivalence is that of a doughnut and a coffee mug. Both objects have one hole, the topological property that is preserved when a doughnut is theoretically deformed into a coffee mug. However, converting a sphere into a doughnut would require tearing a hole through it, so these two objects are not topologically equivalent. Applying topology proved useful in understanding the quantum Hall effect, which fundamentally underlies how topological insulators work. Imagine you have a 2D film of
electrons with a large magnetic field pointing upwards.
The magnetic field causes electrons to experience a perpendicular Lorentz force, which is the force exerted on a charged particle due to electric and magnetic fields. This causes electrons to travel in curved paths which quantum mechanics replaces with orbitals of quantised energies, leading to the creation of an energy gap that yields the insulating characteristic we are familiar with in the bulk of the material. However, electrons at the edges produce “ skipping orbits” that propagate in one direction and are not quantised. The lack of an energy gap therefore gives the edge states conductivity which is “topologically protected” . This property endows the edge states with perfect conduction - imperfections at the edges will not disrupt or affect the current, similar to how no matter how you deform a doughnut, its hole is retained. The edge states now propagate in opposite directions, and this is what physicists observed in 2D topological insulators. There is an even more complex reason for topological protection that arises in topological insulators: the opposite propagations at edge states are related by time-reversal symmetry. Time-reversal symmetry dictates that a system behaves the same whether time moves forwards or backwards, and it essentially yields a time-reversed partner, resulting in the counter-propagating edge states seen in topological insulators.


Scientists are excited by the multitude of potential applications endowed by topological insulators, ranging from spintronics and quantum computation to cancer diagnosis and therapy. For example, current silicon transistors in computers generate heat when turning current on and off. Replacing these with spintronics, which control whether an electron’s spin is “ up” or “down” , analogous to an “ on” or “ off” current, could theoretically yield ultralow-energy transistors. “For condensed matter physicists, this is like the Big Bang” , says physicist Yong Chen at Purdue University in West Lafayette, Indiana. You can guess why I chose this quotation!
e n e r g y conduction band
band gap
valence band
e n e r g y conduction band
band gap
valence band
e n e r g y conduction band
valence band
Insulators
Semiconductors
In topological insulators, the quantum Hall effect is invoked in a slightly different way which does not require extremely low temperatures and an external magnetic field. Instead, topological insulators rely on the quantum spin Hall effect, where the magnetic field is replaced by the interaction of an electron’s spin with its orbital motion, also known as spin-orbit coupling. Instead of one










