Trajectoires optique_3e Éd. by Les Éditions CEC

Paul Morissette

4e édition

TRAJECTOIRES

Phénomènes optiques

OFFRE ENRICHIE

Un grand nombre d’exercices et de problèmes bien gradués Des exercices interactifs autocorrectifs

Des capsules numériques qui enrichissent les concepts théoriques

Un corrigé comportant des démarches complètes

Conforme à la progression des apprentissages

Physique, 5e secondaire Cahier d’apprentissage

MATIÈRES Présentation de la collection Trajectoires V INTRODUCTION LES TECHNIQUES LIÉES AUX MESURES VIII CHAPITRE 1 LA FORMATION D’IMAGES PAR LES MIROIRS PLANS 14 APPEL R Des ondes à la lumière 15 Les ondes mécaniques 15 Les ondes électromagnétiques 16 Le spectre électromagnétique 17 La lumière visible et ses couleurs 18 APPEL R Les sources lumineuses 21 Les sources incandescentes 21 Les sources luminescentes 22 1.1 La représentation de la lumière à l’aide de rayons lumineux 24 1.2 La réflexion diffuse et la réflexion spéculaire 29 Enrichissement La vision des couleurs 30 1.3 La loi de la réflexion spéculaire 34 1.4 La formation d’images par un miroir plan 38 Les caractéristiques d’une image formée par un miroir plan 38 1.5 Le champ de vision dans un miroir plan 43 QUESTIONS DE SYNTHÈSE 47 CHAPITRE 2 LA FORMATION D’IMAGES PAR LES MIROIRS COURBES 54 2.1 La réflexion de la lumière par les miroirs courbes 55 Les miroirs cylindriques et sphériques 55 Le centre de courbure d’un miroir courbe 55 2.2 Les points principaux d’un miroir courbe 58 Le sommet et l’axe principal d’un miroir courbe 58 Le foyer d’un miroir courbe et la longueur focale 58 2.3 Les rayons principaux d’un miroir courbe 63 2.4 La formation d’images par les miroirs courbes 65 La formation d’images par les miroirs concaves 65 La formation d’images par les miroirs convexes 67 2.5 Les relations mathématiques entre les paramètres des miroirs courbes 74 La formule du grandissement d’une image 74 La formule des miroirs 75 PRÉSENT DANS CET EXTRAIT

TABLE DES

TABLE DES MATIÈRES IV © 2023, Les Éditions CEC inc. • Reproduction interdite 2.6 Une convention de signes 78 Enrichissement Les paramètres ,o et ,i 80 2.7 Une application des miroirs courbes : les télescopes 87 La formation d’images par un télescope 87 Le télescope de type Newton 88 Le télescope de type Cassegrain 88 QUESTIONS DE SYNTHÈSE 91 CHAPITRE 3 LA RÉFRACTION DE LA LUMIÈRE 98 3.1 La transmission de la lumière d’un milieu transparent à un autre 99 3.2 L’indice de réfraction et la réfringence d’un milieu 101 Les paramètres physiques caractéristiques de la réfraction 102 La compréhension qualitative de la réfraction 103 3.3 La loi de Snell-Descartes 105 Un montage expérimental fréquent 105 La loi de Snell-Descartes 106 3.4 La réflexion totale interne de la lumière (RTI) 112 L’angle d’incidence critique (θc ) 113 3.5 La dispersion chromatique 118 Enrichissement La formation de mirages 119 QUESTIONS DE SYNTHÈSE 124 CHAPITRE 4 LA FORMATION D’IMAGES PAR LES LENTILLES 134 4.1 La réfraction de la lumière par les lentilles 135 Les types de lentilles 137 La loi de la réfraction appliquée aux lentilles 138 4.2 La formation d’images par les lentilles 141 Les rayons principaux d’une lentille convergente 141 Les caractéristiques d’une image formée par une lentille convergente 144 Les rayons principaux d’une lentille divergente 144 Les caractéristiques d’une image formée par une lentille divergente 146 4.3 Les relations mathématiques entre les paramètres des lentilles 153 Enrichissement Les paramètres ,o et ,i (bis) 154 ENRICHISSEMENT Les prescriptions de lentilles correctrices 163 Le fonctionnement normal de l’œil 163 La vision de loin normale et la myopie 164 La vision de près normale et la presbytie 166 L’hypermétropie et l’astigmatisme 167 La vergence d’une lentille 168 La loi des lunettiers 168 QUESTIONS DE SYNTHÈSE 173 Index 181 Sources iconographiques 183

PRÉSENTATION DE LA COLLECTION TRAJECTOIRES

Cette collection propose une approche notionnelle par chapitre dont la séquence respecte la pratique enseignante. Elle permet une grande souplesse dans l’enseignement de la physique tout en favorisant le travail autonome des élèves.

Structure et organisation du cahier

L’introduction

Cette section présente certaines techniques liées aux mesures. On y explique les règles permettant d’exprimer les mesures et les calculs avec la précision appropriée. Les notions théoriques sont suivies d’exercices.

Les chapitres

La page d’ouverture de chaque chapitre comporte un texte d’introduction et la liste des concepts de la Progression des apprentissages abordés dans ce chapitre.

Les chapitres sont divisés en sections. Chaque section présente des notions théoriques claires appuyées par des exemples concrets. Des documents visuels variés soutiennent l’apprentissage des élèves.

La définition de certaines notions théoriques ou de formules mathématiques est mise en évidence.

Certains mots ou expressions, présentés en bleu dans le texte, sont définis dans la marge.

Des clics + sont offerts en suppléments numériques sur maZoneCEC. Ils présentent des compléments d’information variés.

Les pictogrammes Labo ou Activité indiquent qu’un laboratoire ou une activité peuvent être réalisés avec les élèves. La démarche est présentée dans le guide d’enseignement sous forme de fiches reproductibles.

À l’occasion, une section Enrichissement présente des contenus enrichis et non prescrits par la PDA.

Des capsules Pour en savoir + viennent enrichir les contenus scientifiques présentés dans le cahier. Elles précisent ou approfondissent certains aspects des sujets étudiés.

À la fin d’une section

À la fin de chaque section, des exercices permettent aux élèves de faire un retour sur les connaissances étudiées et de bien assimiler chaque notion avant de passer à la suivante. Des exercices de type défi notés par un sont parfois proposés aux élèves.

À la fin d’un chapitre

À l’aide de questions variées, les questions de synthèse permettent un retour sur l’ensemble des notions présentées dans le chapitre.

Des exercices notés par un triangle noir indiquent la présence d’un exercice portant sur un contenu d’enrichissement non prescrit par la PDA.

À la fin du cahier

L’index permet un repérage facile et rapide des connaissances présentées dans le cahier.

Des exercices notés par un triangle noir indiquent la présence d’un exercice portant sur un contenu d’enrichissement non prescrit par la PDA.

Des exercices de type défi notés par un sont parfois proposés aux élèves.

RAPPEL

Définir la fréquence d’une onde

Associer la fréquence d’une onde sonore à la hauteur du son produit

Définir la longueur d’onde

Décrire la relation entre la longueur d’onde et l’énergie qui lui est associée

Situer différents rayonnements sur le spectre électromagnétique

Décrire diverses applications des ondes électromagnétiques

PROGRESSION DES APPRENTISSAGES

Définir ce qu’est un rayon lumineux

Distinguer la réflexion diffuse de la réflexion spéculaire

Identifier les rayons incidents et les rayons réfléchis

Mesurer les angles d’incidence et de réflexion sur une représentation schématique ou expérimentalement

Expliquer des phénomènes à l’aide de la loi de la réflexion spéculaire

CHAPITRE

1LA FORMATION

D’IMAGES PAR LES

MIROIRS PLANS

Dans ce premier chapitre, nous ferons d’abord un retour sur les ondes et la lumière. Nous verrons ensuite les différents types de sources lumineuses et nous explorerons le phénomène de la vision des couleurs.

Grâce à la notion de rayon lumineux, nous distinguerons deux types de réflexion de la lumière. La notion de rayon lumineux nous servira aussi à analyser en détail la formation d’images par les miroirs plans. Nous terminerons ce chapitre par l’analyse du champ de vision d’un observateur ou d’une observatrice dans un miroir plan.

Des ondes à la lumière APPEL R

En troisième secondaire, nous avons fait la distinction entre ondes mécaniques et ondes électromagnétiques. Avant de commencer l’étude de l’optique, nous allons revenir brièvement sur ces sujets.

Les ondes mécaniques

Une onde mécanique est une perturbation qui se déplace dans un milieu matériel. Dans la figure 1.1, on observe une telle onde par la déformation de la corde qui se propage le long de celle-ci. Ce type d’ondes sont dites transversales, car la perturbation est perpendiculaire au sens de la propagation de l’onde.

La vitesse des ondes mécaniques

Une onde est caractérisée par sa longueur d’onde λ (prononcée « lambda »), sa fréquence f et sa vitesse v

• La longueur d’onde correspond à la distance entre deux crêtes successives d’une onde.

• La fréquence désigne le nombre d’oscillations de l’onde par seconde. Elle est mesurée en Hertz (Hz).

1 Hz = 1 s 1 (1 oscillation par seconde)

• Ces trois paramètres permettent d’établir la relation mathématique suivante, appelée équation des ondes :

v = λf

EXEMPLE

L’onde représentée ci-dessous se déplace à la vitesse de 1,4 m/s. Sachant que la main produit deux oscillations complètes (deux montées et deux descentes) toutes les secondes, quelle est la longueur d’onde λ de l’onde qui se propage sur la corde ?

DONNÉES

v = 1,4 m/s

f = 2 Hz = 2 s 1

λ = ?

CALCULS

v = λf λ = v f

λ = 1,4 m/s

2 s 1 ≈ 0,7 m

RÉPONSE : La longueur d’onde de cette onde est de 0,7 m.

FIGURE 1.1 Deux ondes mécaniques de fréquence différente se propageant le long d’une corde La fréquence de la première onde est supérieure à celle de la seconde, mais sa longueur d’onde λ est plus courte. Sens de propagation de l’onde

perturbation

perturbation λ λ

Sens de propagation de l’onde Sens

de la

Sens de la

Les ondes sonores, des ondes mécaniques longitudinales

Les ondes sonores émises par le haut-parleur représenté dans la figure 1.2 sont formées par des variations de la pression de l’air. Ces variations sont produites par les va-et-vient de la membrane vibrante du haut-parleur et elles se déplacent dans l’air. On dit que le son est une onde longitudinale, car la perturbation (la modification de la pression de l’air) se fait dans la même direction que la propagation de l’onde.

Les ondes électromagnétiques

À la différence des ondes mécaniques, les ondes électromagnétiques n’ont pas besoin d’un milieu matériel pour se propager.

La perturbation qui donne naissance à une onde électromagnétique est à la fois électrique et magnétique. Des ondes électromagnétiques sont formées chaque fois qu’on modifie le mouvement d’une charge électrique ou qu’on déplace un aimant. En effet, une variation d’un champ électrique s’accompagne toujours d’une variation du champ magnétique et vice-versa. Une onde électromagnétique est donc constituée de variations d’un champ magnétique et d’un champ électrique qui se déplacent en s’entraînant mutuellement (voir la figure 1.3).

FIGURE 1.2 Deux ondes sonores de fréquence différente se propageant dans l’air La fréquence de la première onde est plus grande que celle de la deuxième. Le son perçu est plus aigu.

Distance Pression Zone de compression Distance

Champ

Sensde depropagation lalumière Sensde depropagation lalumière Pression Zone de dépression

FIGURE 1.3 Deux ondes électromagnétiques de fréquence différente Champ électrique Champ électrique

magnétique

magnétique

La vitesse des ondes électromagnétiques

Les ondes électromagnétiques se déplacent dans le vide à une vitesse d’environ 3,00 × 108 m/s (299 792 458 m/s). Cette valeur est notée c Ainsi, pour une onde électromagnétique se déplaçant dans le vide, l’équation des ondes s’exprime ainsi :

c = λf, où c ≈ 3,00 × 108 m/s

Comme nous le verrons dans le chapitre 3, la vitesse des ondes électromagnétiques est pratiquement la même dans l’air que dans le vide. L’équation ci-dessus s’applique donc aussi au déplacement des ondes électromagnétiques dans l’air.

Le spectre électromagnétique

Il existe plusieurs types d’ondes électromagnétiques. On les distingue par leur fréquence. Les ondes radio et les micro-ondes sont les ondes dont la fréquence est la plus basse. Ce sont aussi les ondes les moins énergétiques. À l’autre extrémité du spectre électromagnétique (voir la figure 1.4) se trouvent les rayons X et les rayons gamma, qui possèdent la plus grande fréquence et sont donc les plus énergétiques. Entre ces deux extrêmes, on trouve les rayons infrarouges, la lumière visible et les rayons ultraviolets

Le spectre électromagnétique

Chaque type de rayonnement est caractérisé par sa fréquence. La lumière visible n’occupe qu’une toute petite portion du spectre électromagnétique.

FIGURE 1.4

Ondes radio Rayons infrarouges Microondes Rayons ultraviolets Rayons gamma Rayons X Fréquence (Hz) Longeur d’onde (m) Utilisation Lumière visible 1 109 109 10– 1 10–2 10–3 10–4 10–9 10–10 10–11 10–12 10–13 1 1010 1011 1012 4,0 × 1014 7,5 × 10–7 7,5 × 1014 4,0 × 10–7 1017 1018 1019 1020 1021 1022 1013 50

La lumière visible et ses couleurs

La lumière visible correspond aux ondes électromagnétiques que l’œil humain peut détecter. Elle comprend les ondes dont la fréquence est comprise entre 4,0 × 1014 Hz (pour la lumière rouge) et 7,5 × 1014 Hz (pour la lumière violette).

La rétine de l’œil humain perçoit les couleurs à l’aide de cellules photoréceptrices spécialisées : les cônes (voir la figure 1.5). Ces cellules transforment la lumière en impulsions électriques que notre cerveau peut ensuite analyser. Il existe trois types de cônes. Chaque type est sensible à une large gamme de couleurs, mais possède un maximum de sensibilité pour une couleur précise. Ainsi, un type de cônes est plus sensible à la lumière rouge (mais pas seulement à cette couleur), un autre à la lumière verte et un dernier à la lumière bleue. La couleur perçue par notre cerveau dépend donc de la stimulation relative des trois types de cônes.

Cônes

Bâtonnets

La rétine contient trois types de cônes (représentés en rouge, en vert et en bleu), qui sont sensibles aux couleurs, ainsi que des bâtonnets (représentés en gris), qui sont sensibles à l’intensité de la lumière.

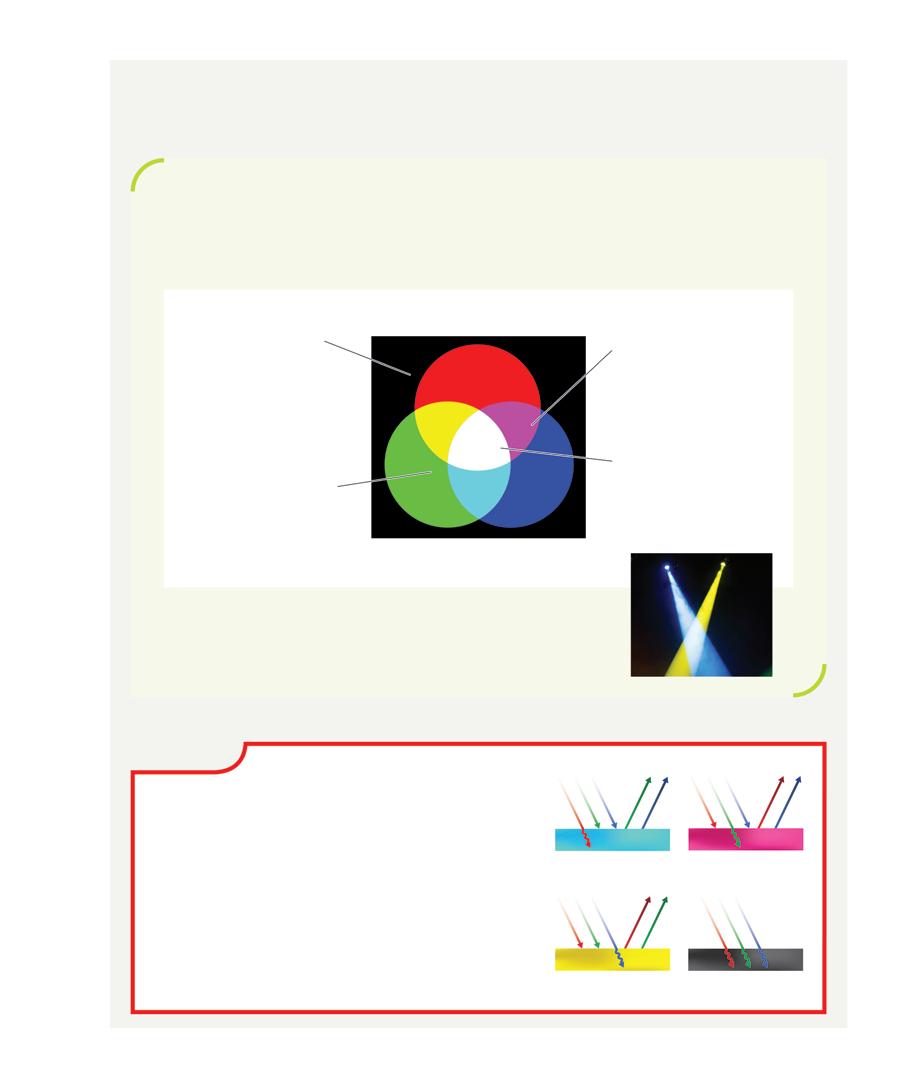
Lorsque notre œil reçoit de la lumière qui contient toutes les couleurs (la lumière solaire, par exemple), tous les types de cônes sont fortement stimulés et notre cerveau perçoit du blanc. Un éclairage composé de rouge, de vert et de bleu crée également une impression de blanc, car chacun des trois types de cônes est stimulé intensément. Nous sommes donc incapables de faire la différence entre un éclairage qui contient toutes les couleurs et un éclairage qui contient les trois couleurs de base (voir l’intersection des trois faisceaux dans la figure 1.6).

Lorsque notre œil ne reçoit que de la lumière jaune, il perçoit… du jaune. Cependant, cette couleur stimule aussi moyennement les cônes sensibles au rouge et au vert, alors que les cônes sensibles au bleu ne sont pas stimulés. Ainsi, il est possible de donner l’impression à notre cerveau qu’il regarde du jaune en utilisant une combinaison de lumière rouge et de lumière verte (comme on le voit à l’intersection du faisceau rouge et du faisceau vert, dans la figure 1.6).

FIGURE 1.6 Les couleurs primaires de la synthèse additive des couleurs sont le rouge, le bleu et le vert.

Le jaune, le cyan et le magenta sont des couleurs secondaires créées par la combinaison de deux couleurs primaires.

Conséquemment, notre cerveau est incapable de détecter la différence entre un éclairage véritablement jaune et un éclairage composé d’un mélange de vert et de rouge. C’est le principe de la synthèse additive des couleurs. Nous reviendrons sur celle-ci dans la section 1.2.

FIGURE 1.5 Les cônes et les bâtonnets

EXERCICES

1 La note la plus souvent utilisée comme référence pour accorder des instruments de musique est le la, dont la fréquence est de 440 Hz. Sachant que la longueur d’onde dans l’air d’une onde sonore de cette tonalité est de 75 cm, déterminez la vitesse du son dans l’air (en m/s).

DONNÉES CALCULS

RÉPONSE :

2 La plage de fréquence des couleurs de la lumière visible est présentée ci-dessous.

À l’aide de l’équation des ondes, déterminez la couleur d’une onde électromagnétique dont la longueur d’onde est de :

RÉPONSE : RÉPONSE : RÉPONSE :

3 Les ondes radio peuvent passer à travers les murs en béton alors que la lumière visible est bloquée par un tel mur. Cette capacité des ondes radio est en rapport avec le fait que leur longueur d’onde est très grande par rapport à la taille des atomes (qui est de l’ordre de 10 10 m). Déterminez la longueur d’onde des ondes radio d’une station qui émettrait sur une fréquence de 98 MHz (1 MHz = 1 × 106 Hz).

DONNÉES CALCULS

RÉPONSE :

Couleur Rouge Orange Jaune Vert Cyan Bleu Violet Fréquence (Hz) 4,00 × 1014 à 4,80 × 1014 4,80 × 1014 à 5,10 × 1014 5,10 × 1014 à 5,30 × 1014 5,30 × 1014 à 6,00 × 1014 6,00 × 1014 à 6,20 × 1014 6,20 × 1014 à 6,70 × 1014 6,70 × 1014 à 7,50 × 1014

a) 530 nm (5,30 × 10 7 m) b) 670 nm (6,70 × 10 7 m) c) 610 nm (6,10 × 10 7 m)

4 Vrai ou faux ?

a) La lumière est un type d’onde électromagnétique, comme les micro-ondes et les rayons gamma.

b) La lumière rouge est plus énergétique que la lumière verte.

c) Les ondes radio sont moins dangereuses que les rayons ultraviolets.

d) Les rayons X sont le type de rayonnement qui transporte le plus d’énergie.

5 À l’aide de l’illustration du spectre électromagnétique, expliquez l’usage des préfixes « infra » et « ultra » pour décrire les rayons infrarouges et ultraviolets.

6 Les yeux humains ne sont sensibles qu’à une petite partie du spectre électromagnétique. Toutefois, l’être humain a réussi à créer des appareils d’imagerie qui utilisent d’autres types d’ondes électromagnétiques. Donnez deux exemples de ces appareils et expliquez leur utilité.

7 Dans la lumière visible, il n’existe pas de lumière magenta (voir la figure 1.6, à la page 18). Lorsque notre cerveau détecte cette couleur, c’est qu’il reçoit une stimulation intense de deux types de cônes. Lesquels ?

8 Le cyan fait partie du spectre électromagnétique. Cependant, notre cerveau peut croire que nos yeux reçoivent de la lumière cyan alors qu’ils reçoivent plutôt une combinaison de lumière de deux couleurs différentes. Quelles sont ces deux couleurs ?

Lumière visible Ondes radio Rayons infrarouges Microondes Rayons ultraviolets Rayons gamma Rayons X Fréquence (Hz) Longeur d’onde (m) 1 109 109 10–1 10–2 10–3 10–4 10–9 10–10 10–11 10–12 10–13 1 1010 1011 1012 4,0 × 1014 7,5 × 10–7 7,5 × 1014 4,0 × 10–7 1017 1018 1019 1020 1021 1022 1013 50

Les sources lumineuses APPEL R

Les objets qui émettent de la lumière sont appelés des sources lumineuses. Un feu, un téléviseur ou une ampoule électrique en sont des exemples. On distingue deux types de sources lumineuses : les sources incandescentes et les sources luminescentes

Les sources incandescentes

L’incandescence est le processus par lequel une substance émet de la lumière lorsqu’elle est portée à de très hautes températures. Par exemple, le filament de tungstène d’une ampoule à incandescence est porté à une température d’environ 2500 °C (voir la figure 1.7). À cette température, les atomes de tungstène vibrent fortement et leurs électrons de valence bougent très rapidement en circulant d’un atome à l’autre (le tungstène étant un métal, il conduit l’électricité). Les électrons ralentissent et accélèrent donc fréquemment en raison de la très forte agitation thermique. Ces modifications du mouvement des électrons se traduisent par l’émission d’ondes électromagnétiques.

Une ampoule à incandescence produit beaucoup de rayons infrarouges, passablement de lumière visible et un peu de rayons ultraviolets. On dit d’une source de ce genre qu’elle est polychromatique, c’est-à-dire qu’elle contient plusieurs fréquences (plusieurs couleurs, dans le cas de la lumière visible).

La composition du rayonnement émis dépend de la température de la source. Le corps humain, dont la température est à environ 37 °C, émet lui aussi un rayonnement. Comme les charges électriques sont beaucoup moins agitées, la fréquence et l’intensité du rayonnement sont plus faibles. Il émet donc uniquement de la lumière infrarouge. La figure 1.8 montre une image prise par une caméra thermique. Ce type de caméras créent des images qui montrent une différence entre les parties chaudes ou froides d’un sujet.

Incandescence

Émission de lumière par un corps porté à haute température.

Polychromatique

Qui contient plusieurs couleurs.

FIGURE 1.7 Le filament de tungstène incandescent d’une ampoule FIGURE 1.8 Une image prise par une caméra thermique

Luminescence

Émission de lumière par un corps à la suite d’une excitation électronique autre que la chaleur.

Les sources luminescentes

La luminescence est le processus par lequel une substance émet de la lumière lorsque ses électrons se trouvent sur une couche électronique plus élevée que leur état fondamental (leur couche de base). On dit que les électrons sont alors excités. Les sources d’excitation électronique sont nombreuses et correspondent chacune à un type particulier de luminescence.

Monochromatique

Qui contient une seule couleur.

Dans tous les cas, la lumière est produite lorsque des électrons retournent à leur état fondamental en perdant le surplus d’énergie qui les avait excités. Cette énergie se propage sous la forme d’une onde électromagnétique. Lorsque tous les électrons excités ont le même niveau d’énergie, la fréquence de l’onde émise correspond à une couleur bien précise et la source lumineuse est dite monochromatique

Les sources d’excitation électronique

Source Type de luminescence

Rayonnement Fluorescence

Des lacets blancs qui émettent une lumière mauve sous une lumière noire (source de rayons ultraviolets).

Phosphorescence

Les objets qui luisent dans le noir même après que toute excitation a cessé.

Exemples

Réaction chimique ou biochimique

Chimioluminescence

Les bâtons qui luisent dans le noir lorsqu’on amorce la réaction chimique en rompant une membrane interne.

Bioluminescence

Les lucioles ou certains animaux marins qui produisent leur propre lumière.

Différence de potentiel électrique

Électroluminescence

Les diodes électroluminescentes (DEL) et les néons qui émettent de la lumière lorsqu’un courant électrique les traverse.

Fluorescence et phosphorescence

La fluorescence et la phosphorescence diffèrent par leur durée. Lorsque le rayonnement émis par une source luminescente cesse immédiatement après que l’excitation électronique a cessé, on parle de fluorescence. Lorsque le rayonnement persiste après que l’excitation a cessé, parfois pendant plusieurs heures, on parle de phosphorescence

EXERCICES

1 Pour chacune des illustrations, indiquez s’il s’agit d’incandescence ou de luminescence. Lorsqu’il s’agit de luminescence, déterminez :

1) la source de l’excitation ; 2) le type précis de luminescence qui est en jeu.

Ces deux liquides émettent de la lumière lorsqu’ils sont soumis à un rayonnement ultraviolet.

Incandescence Luminescence

1) 2)

Certaines méduses produisent de la lumière en combinant une enzyme, la luciférase, avec une molécule appelée luciférine

Incandescence Luminescence

1) 2)

Les DEL émettent de la lumière lorsqu’elles sont soumises à une différence de potentiel appropriée.

Le métal fondu émet généralement une lumière intense.

Incandescence Luminescence

1) 2)

Incandescence Luminescence

1) 2)

Ces figurines produisent de la lumière même quand aucune lumière ne les éclaire.

Incandescence Luminescence

1) 2)

La lave qui s’échappe d’un volcan produit de la lumière.

Incandescence Luminescence

Ces bracelets lumineux émettent de la lumière grâce à une réaction entre deux liquides.

Incandescence Luminescence

1) 2)

Faisceau

Quantité de lumière dont les contours peuvent être représentés par des rayons.

Source ponctuelle

Source de lumière de très petite dimension ou tellement éloignée qu’on peut l’assimiler à un point.

La représentation de la lumière à l’aide de rayons lumineux .1 1

Pour comprendre les phénomènes optiques, il faut représenter des quantités de lumière. Or, bien que la lumière soit une onde électromagnétique, il est pratique de la représenter par des faisceaux lumineux délimités par des rayons. La figure 1.9 montre la formation d’une zone de clarté sur un écran éclairé par une source de lumière minuscule que nous supposerons être une source ponctuelle de lumière.

Rayon lumineux

Construction géométrique imaginaire prenant la forme d’un segment de droite orienté (une flèche) et permettant de représenter les contours d’un faisceau lumineux. La flèche indique le sens de propagation de la lumière.

Propagation

La lumière se déplace en ligne droite, elle ne peut pas contourner les obstacles.

La représentation de la lumière sous forme d’ondes émises dans toutes les directions n’est pas utile pour expliquer la formation du cercle lumineux sur l’écran.

La délimitation à l’aide de rayons lumineux du faisceau de lumière qui passe par le trou permet d’expliquer simplement le phénomène observé sur l’écran.

Si on refait cette expérience avec une source lumineuse de plus grande dimension (voir la figure 1.10), on assiste à la formation d’une zone de pénombre (ombre partielle) entre la zone de clarté et la partie sombre de l’écran. Encore une fois, l’utilisation de rayons lumineux permet d’expliquer simplement les phénomènes observés. Cela démontre la propagation rectiligne de la lumière

L’utilisation des rayons lumineux permet d’expliquer simplement la présence de la zone de pénombre entre la zone de clarté et la zone d’ombre sur l’écran.

rectiligne de la lumière FIGURE 1.9 La formation d’un faisceau lumineux FIGURE 1.10 La formation d’une zone de pénombre lorsque l’étendue de la source lumineuse n’est pas négligeable.

LABO 1 Source étendue Zone d’ombre Zone de clarté Zone de pénombre Zone d’ombre Zone de clarté Source ponctuelle

Bien qu’on ne puisse pas isoler un rayon lumineux, il existe des quantités de lumière qui s’en approchent. Par exemple, la lumière émise par un laser est très semblable à un rayon. Elle est cependant constituée d’un très mince faisceau qui s’élargit très lentement (voir la figure 1.11). Lors de manipulations en laboratoire, on peut modéliser le comportement d’un rayon lumineux grâce à une boite à faisceaux, un appareil qui permet de diriger un ou plusieurs minces faisceaux de lumière de largeur constante (voir la figure 1.12).

Le faisceau de lumière émise par le laser est très fin et s’élargit très lentement.

En optique géométrique, on utilise les rayons pour représenter la trajectoire de la lumière et expliquer des phénomènes lumineux. Le tracé des rayons lumineux permet souvent de former des triangles semblables. Lorsque c’est le cas, on peut déterminer des valeurs inconnues à l’aide des proportions des côtes homologues de ces triangles.

EXEMPLE

Pour déterminer la hauteur H d’un arbre, Nader se positionne à l’endroit qui lui permet tout juste de voir cet objet à l’intérieur d’un tuyau d’une longueur L de 70,0 cm et dont l’ouverture a un diamètre D de 5,0 cm. Lorsqu’il se situe à une distance d de 112 m d’un arbre, il voit cet arbre en entier à l’intérieur du tuyau. Quelle est la hauteur H de cet arbre ?

Les rayons issus du haut et du bas de l’arbre, et les pointillés représentant le diamètre D du tuyau et la hauteur H de l’arbre forment deux triangles semblables imbriqués l’un dans l’autre. Ils ont chacun un angle droit et partagent un angle (cas de similitude Angle-Angle).

DONNÉES

D = 5,0 cm = 0,050 m

L = 70,0 cm = 0,700 m

d = 112 m

H = ?

Les côtés :

• D et H sont homologues entre eux ;

• L et d sont homologues entre eux.

RÉPONSE : L’arbre a une hauteur d’environ 8,0 m.

CALCULS

Par comparaison des côtés homologues :

H D = d L

H = D d L

H = 0,050 m × 112 m 0,700 m

H ≈ 8,0 m

FIGURE 1.11 Un faisceau laser FIGURE 1.12 La modélisation du comportement d’un rayon lumineux au moyen d’une boite à faisceaux

D d L H = ?

EXERCICES

Le corrigé du cahier est montré dans cette section.

1 Le schéma ci-dessous montre la formation d’une zone de clarté sur un écran éclairé par une source de lumière ponctuelle.

a) Sur ce schéma, indiquez par un point la source lumineuse et tracez le faisceau lumineux qui forme la zone de clarté. N’oubliez pas de représenter le sens de propagation de la lumière.

b) Si le diamètre du trou dans la planche est de 12,0 cm, que celui de la zone de clarté est de 21,0 cm et que l’écran se trouve à 28,0 cm de la source lumineuse, quelle distance sépare la source lumineuse de la planche trouée ? Indice : Tracez les diamètres verticaux du trou et du cercle de clarté et repérez deux triangles semblables (cas Angle-Angle).

Source lumineuse ?

DONNÉES CALCULS

dsource-écran = 28,0 cm

Dclarté = 21,0 cm

Dtrou = 12,0 cm

dsource-planche = ?

Les côtés :

• dsource-planche et dsource-écran sont homologues entre eux ;

• Dtrou et Dclarté sont homologues entre eux.

28,0 cm

12,0 cm

21,0 cm

Planche trouée Écran

dsource-planche

dsource-écran = Dtrou Dclarté

dsource-planche = dsource-écran × Dtrou Dclarté

dsource-planche = 28,0 cm × 12,0 cm 21,0 cm

dsource-planche ≈ 16,0 cm

RÉPONSE : La distance qui sépare la source lumineuse de la planche trouée est d’environ 16,0 cm.

2 Un obstacle de 40,0 cm de diamètre bloque l’éclairage d’une source lumineuse ponctuelle située à 2,50 m de cet obstacle. Quel est le diamètre de l’ombre projetée sur l’écran si celui-ci est placé à 1,25 m de l’obstacle ?

40,0 cm ?

125 cm 250 cm

Obstacle Source lumineuse Écran

DONNÉES CALCULS

dsource-obstacle = 2,50 m = 250 cm

Dobstacle = 40,0 cm

dobstacle-écran = 1,25 m = 125 cm

Dombre = ?

Les côtés :

• dsource-écran et dsource-obstacle sont homologues entre eux ;

• Dombre et Dobstacle sont homologues entre eux.

dsource-écran = 250 cm + 125 cm = 375 cm

Dombre

Dobstacle = dsource-écran dsource-obstacle

Dombre = Dobstacle × dsource-écran

dsource-obstacle

Dombre = 40,0 cm × 375 cm 250 cm

Dombre ≈ 60,0 cm

RÉPONSE : Le diamètre de l’ombre projetée sur l’écran est d’environ 60,0 cm (ou 0,600 m).

3 Par une nuit sans lune, Émilio est éclairé par un lampadaire dont l’ampoule est située à 5,00 m du sol. Sachant que l’ombre d’Émilio mesure 3,00 m, déterminez la distance horizontale qui sépare Émilio du lampadaire.

DONNÉES CALCULS

HÉmilio = 1,66 m

Hlampadaire = 5,00 m

Lombre = 3,00 m x = ?

Les côtés :

• HÉmilio et Hlampadaire sont homologues entre eux ;

• Lombre et Ltotale sont homologues entre eux.

Ltotale = Lombre + x

Ltotale = 3,00 m + x HÉmilio Hlampadaire =

RÉPONSE : La distance entre Émilio et le lampadaire est d’environ 6,02 m (6,04 m si on n’arrondit qu’à la fin)

4 Une éclipse de Soleil est représentée ci-dessous. Le schéma n’est pas à l’échelle.

Lors d’une éclipse solaire, la tache d’ombre est en réalité beaucoup plus petite que ce qu’on voit ici.

a) Tracez les rayons qui permettent d’expliquer les zones d’éclipse totale (zone d’ombre) et d’éclipse partielle (zone de pénombre).

1,66 m 5,00 m = 3,00 m 3,00 m + x 4,98 m + 1,66x = 15,0 m 1,66x ≈ 10,0 m x ≈ 6,02 m

ombre

totale

x = ? 5,00

1,66

Terre Lune

3,00 m

m Soleil

b) Tout au long de l’année, la distance entre le Soleil et la Terre fluctue. Si la distance entre la Terre et la Lune pendant une éclipse solaire est de 3,82 × 108 m, quelle doit être la distance entre le Soleil et la Terre pour que la pointe du cône d’ombre touche la Terre ? Le diamètre de la Lune est de 3,475 × 106 m, celui du Soleil est de 1,391 × 109 m et le rayon de la Terre est de 6,37 × 106 m.

Note : Les distances sont mesurées centre à centre.

DONNÉES CALCULS

DSoleil = 1,391 × 109 m

DLune = 3,475 × 106 m

dTerre-Lune = 3,82 × 108 m

RTerre = 6,37 × 106 m

dTerre-Soleil = ?

Les côtés DSoleil et DLune sont homologues entre eux, dS et dL également.

1. dL = dTerre-Lune RTerre

dL = 3,82 × 108 m 6,37 × 106 m

dL ≈ 3,76 × 108 m

2. dS dL = DSoleil DLune dS = dL × DSoleil

DLune

dS ≈ 1,51 × 1011 m

3. dTerre-Soleil = dS + RTerre

dTerre-Soleil = 1,51 × 1011 m + 6,37 × 106 m

dTerre-Soleil ≈ 1,51 × 1011 m

dS = 3,76 × 108 m × 1,391 × 109 m 3,475 × 106 m

RÉPONSE : La distance entre la Terre et le Soleil doit être d’environ 1,51 × 1011 m.

on ne considère pas le rayon de la Terre dans le premier calcul, la réponse obtenue est 1,53 × 1011 m.

5 Une camera obscura (« chambre noire » en latin) est une pièce sombre, sans autre éclairage qu’une minuscule ouverture. La lumière qui entre dans la pièce éclaire le mur qui fait face à l’ouverture, où une image inversée apparait. De nombreux artistes se sont servis d’une camera obscura comme aide au dessin.

a) Sur l’illustration, tracez les rayons issus du haut et du bas du personnage et traversant l’ouverture de la chambre noire pour former l’image sur la toile.

b) Un artiste veut faire le portrait d’une femme mesurant 1,62 m. Il souhaite que le portrait occupe les trois quarts de la hauteur de sa toile. Il utilisera une camera obscura de 1,40 m de longueur et la toile qu’il compte peindre a une hauteur de 96,0 cm. À quelle distance du trou la femme devra-t-elle se placer pour que son image ait les dimensions désirées ?

DONNÉES CALCULS

Hfemme = 1,62 m

Htoile = 96,0 cm

Lcamera obscura = 1,40 m

Himage = ?

d = ?

C d = ? 0,720 m 1,40 m 1,62 m Pointe du cône d’ombre 1,391 × 109 m 3,475 × 106 m 3,82 × 108 m 6,37 × 106 m ? dS dL

image = 0,75 × 96,0 cm = 72,0 cm = 0,720 m

d Lcamera

= H

d = Lcamera

Les côtés Hfemme et Himage sont homologues entre eux, d et Lcamera obscura également. Himage d = 1,40 m × 1,62 m 0,720 m d ≈ 3,15 m

obscura

femme

image

obscura ×

femme

RÉPONSE : La femme devra se placer à environ 3,15 m du trou.

Note

: Si

La réflexion diffuse et la réflexion spéculaire .2 1

Dans le dernier exercice de la section précédente, vous avez tracé des rayons issus de la tête et des pieds d’une personne. Pourtant, celle-ci n’est pas une source de lumière. D’où proviennent de tels rayons ? L’explication réside dans la distinction entre deux types de réflexion de la lumière : la réflexion spéculaire et la réflexion diffuse

La réflexion spéculaire de la lumière

La réflexion spéculaire se produit lorsque de la lumière rebondit sur une surface plane, comme un miroir, un morceau de métal poli ou la surface d’un lac calme. La lumière incidente (qui frappe le miroir) est alors réfléchie dans une seule direction.

La réflexion diffuse de la lumière

La réflexion diffuse se produit lorsque de la lumière rebondit sur une surface inégale, qui présente des imperfections. Ces imperfections réfléchissent alors la lumière incidente dans toutes les directions.

Grâce à la réflexion spéculaire, il est possible de former des images et de contrôler la trajectoire d’un faisceau de lumière.

La réflexion diffuse nous permet de voir les objets qui n’émettent pas de lumière. En effet, ces objets réfléchissent la lumière dans toutes les directions, ce qui explique qu’on peut les voir de tous les angles.

Absorption sélective Phénomène par lequel une substance absorbe la lumière de certaines couleurs et réfléchit les autres couleurs. L’absorption sélective explique le comportement des pigments qui colorent les objets.

La vision des couleurs

Le Soleil et la majorité des sources d’éclairage domestiques (ampoules, néons, etc.) émettent de la lumière blanche. Comme le montre la figure 1.13, la lumière blanche est composée de toutes les couleurs de la lumière visible. Mais si nous voyons les objets qui nous entourent grâce à la réflexion diffuse, pourquoi les objets éclairés par le Soleil ne sont-ils pas tous blancs ? Ce phénomène s’explique par l’absorption sélective de la lumière par les pigments qui colorent les objets. Prenons un pigment bien connu : la chlorophylle. Ce pigment colore les feuilles des végétaux en vert : il absorbe une grande partie de la lumière rouge, orange, bleue et violette, mais il réfléchit la majeure partie de la lumière verte et une bonne partie de la lumière jaune (voir la figure 1.14). Ces couleurs réfléchies vers notre œil sont interprétées comme une teinte de vert par notre cerveau.

La lumière bleue et la lumière rouge sont majoritairement absorbées.

La lumière verte et la lumière jaune sont majoritairement ré échies.

La lumière verte et la lumière jaune sont majoritairement absorbées.

La lumière bleue et la lumière rouge sont majoritairement ré échies.

On dit souvent qu’un objet vert absorbe toutes les couleurs de la lumière sauf la lumière verte. La figure 1.14 nous montre que la réalité est plus complexe. D’ailleurs, si ce modèle était bon, comment expliquer le magenta ? Cette couleur ne correspond à aucune fréquence de la lumière visible. Il s’agit d’une impression de notre cerveau lorsqu’il est soumis à une combinaison de lumière rouge et de lumière bleue. Un pigment magenta comme la mauvéine opère donc de façon contraire à la chlorophylle (voir la figure 1.15). La mauvéine est le premier colorant synthétique. On l’utilisait pour colorer les tissus. Ce pigment réfléchit le bleu et le rouge, et absorbe la majorité de la lumière verte et de la lumière jaune.

FIGURE 1.13 La décomposition de la lumière blanche par un prisme de verre FIGURE 1.14 L’absorbance de la lumière par la chlorophylle selon la couleur

0 400 450 500 600 700 550 650

FIGURE 1.15 L’absorbance de la lumière par la mauvéine selon la couleur

Longueur d’onde (nm) Absorbance 1,2 1 0,8 0,6 0,4 0,2 0 400 450 500 600 700 550 650

Longueur d’onde (nm) Absorbance 1,2 1 0,8 0,6 0,4 0,2

ENRICHISSEMENT

La couleur perçue par notre cerveau dépend de la stimulation relative des trois types de cônes qui se trouvent à la surface de notre rétine par le contenu spectral de la lumière (les différentes couleurs de lumière) qui arrive jusqu’à notre œil. L’explication complète de la vision en couleurs est très complexe, mais peut se résumer ainsi.

La synthèse additive des couleurs

Notre œil perçoit les différentes couleurs par l’addition des lumières de différentes couleurs qui l’atteignent. Les règles de cette addition de lumière sont données par le cercle de la synthèse additive des couleurs. Les couleurs primaires de la synthèse additive sont le rouge, le bleu et le vert, car ce sont ces couleurs qui sont le mieux détectées par les cônes de la rétine.

L’œil qui regarde un objet qui parait noir ne reçoit aucune lumière en provenance de cet objet.

L’œil qui regarde un objet qui parait vert ne reçoit pas (ou très peu) de lumière bleue et de lumière rouge (absorption sélective du rouge et du bleu).

Le vert et le magenta sont des couleurs complémentaires. En mode lumière, leur addition donne une impression de blanc.

De la même façon, le bleu et le jaune, ainsi que le rouge et le cyan, sont complémentaires. Leur superposition donne une impression de blanc.

POUR EN SAVOIR

L’imprimerie

Les imprimantes produisent des images en couleurs grâce à la synthèse soustractive des couleurs. En effet, en impression, on soustrait des couleurs, car la feuille sur laquelle on imprime est blanche et réfléchit donc toutes les couleurs. On doit par conséquent faire en sorte que la lumière qui atteint notre œil ne comporte que les couleurs voulues. Pour produire des impressions de qualité, on n’a besoin que de quatre pigments : le cyan, le magenta, le jaune et le noir. Chaque pigment soustrait certaines couleurs. Par exemple, pour imprimer un mot en rouge, l’imprimante doit superposer des gouttelettes de magenta et de jaune, car un mélange de ces deux pigments permet de réfléchir le rouge, mais absorbe les autres couleurs.

L’œil qui regarde un objet qui parait magenta ne reçoit pas (ou très peu) de lumière verte (absorption sélective du vert).

L’œil qui regarde un objet qui parait blanc reçoit de la lumière qui stimule suffisamment les trois types de cônes (sensibles au rouge, au bleu et au vert).

Cyan

Noir

Magenta

Jaune

EXERCICES

1 Pourquoi pouvons-nous voir une multitude d’objets qui n’émettent pas de lumière ?

2 Pourquoi peut-on tracer des rayons issus d’une personne qui se tient devant une camera obscura même si cette personne ne produit pas de lumière ?

3 La lumière d’un laser se déplace en ligne droite. On ne peut donc la voir directement qu’en dirigeant le faisceau vers nos yeux. Toutefois, la lumière émise par un laser est très dangereuse pour nos yeux (à ne tenter en aucune circonstance !). Sur la photo, des particules en suspension devant le trajet de la lumière nous la rendent visible, et ce, sans danger pour nos yeux, car seule une infime quantité de lumière est ainsi diffusée.

a) Quel type de réflexion est illustré par le changement de direction de la lumière qu’on observe ci-contre ?

b) Quel type de réflexion est illustré par les particules en suspension dans la pièce qui réfléchissent la lumière verte ?

c) Bien qu’elle portait des lunettes de protection, pourquoi la personne qui a pris la photographie pouvait-elle regarder en direction du montage sans danger ?

La lumière de chacun de ces trois projecteurs est produite par une ampoule à incandescence qui émet de la lumière blanche.

a) Pour obtenir le faisceau qui parait rouge, on a placé un filtre coloré rouge devant le projecteur. Puisque le filtre lui-même parait rouge, quelles sont les deux couleurs qu’il doit absolument absorber ? Quelle couleur doit-il absolument laisser passer ?

b) De la même façon, le projecteur du centre est muni d’un filtre vert. Quelles sont les deux couleurs qu’il doit absolument absorber pour paraitre de cette couleur ? Quelle couleur doit-il absolument laisser passer ?

c) Pourquoi l’intersection du faisceau rouge et du faisceau vert parait-elle jaune ? Votre explication doit mentionner le rôle des cônes de notre œil.

d) Pourquoi y a-t-il une zone qui parait blanche à l’intersection des trois faisceaux ? Votre explication doit mentionner le rôle des cônes de notre œil.

5 Les otorhinolaryngologistes utilisent souvent une source lumineuse qui pointe vers un réflecteur métallique. Le réflecteur est percé afin de leur permettre d’observer leurs patients.

a) La lumière réfléchie par le réflecteur subit-elle une réflexion spéculaire ou une réflexion diffuse ?

b) La lumière qui éclaire le patient est réfléchie vers l’œil du médecin S’agit-il d’un exemple de réflexion spéculaire ou diffuse ?

c) À l’aide des mots en gras dans cette question, complétez le schéma suivant, qui illustre le trajet suivi par la lumière. Réflexion spéculaire Réflexion diffuse Détection de la lumière

On peut créer des images qui semblent en trois dimensions par anaglyphe, c’est-àdire en superposant deux vues légèrement décalées d’une même scène, chaque vue étant colorée d’une teinte différente. Par exemple, l’image ci-contre montre deux vues du même panier, l’une cyan et l’autre rouge. On observe ensuite cette image à l’aide de deux filtres colorés en cyan et en rouge. Chaque œil ne perçoit alors qu’une seule des deux vues. Le cerveau les interprète comme provenant de deux points de vue différents, ce qui crée une impression de tridimensionnalité.

a) Parmi les trois couleurs primaires de la synthèse additive des couleurs (le rouge, le bleu et le vert) :

1) quelle est celle qui est réfléchie par l’encre rouge qui a servi à imprimer l’une des vues du panier ? Expliquez votre réponse.

2) quelles sont celles qui passent à travers le filtre cyan des lunettes ? quelle est celle qui est absorbée par ce filtre ?

b) L’œil qui porte le filtre cyan voit-il l’image cyan ou l’image rouge ? Expliquez votre réponse.

La loi de la réflexion spéculaire .3 1

On représente la trajectoire d’un faisceau de lumière se dirigeant vers un miroir plan puis étant réfléchi par celui-ci à l’aide de rayons (voir la figure 1.16). Les rayons de lumière qui se dirigent vers le miroir sont appelés rayons incidents. Ceux qui sont réfléchis par le miroir se nomment rayons réfléchis

Rayons incidents

FIGURE 1.16 Une réflexion spéculaire

À gauche, un faisceau incident est réfléchi par un miroir plan. À droite, la trajectoire de la lumière est représentée à l’aide de deux rayons incidents et de deux rayons réfléchis qui délimitent le faisceau de lumière. Notez au passage la façon dont le miroir est représenté.

Pour tracer le rayon réfléchi qui correspond à un rayon incident, on utilise deux angles particuliers : l’angle d’incidence et l’angle de réflexion

Les angles d’incidence (/ i ) et de réflexion (/ r)

Lorsqu’on représente la trajectoire d’un seul rayon de lumière réfléchi par un miroir plan, on exprime son orientation à l’aide d’un angle, comme le montre le schéma ci-dessous. Par convention, on mesure cet angle par rapport à la normale du miroir.

Légende

1 Normale : Droite perpendiculaire au miroir et passant par le point d’incidence.

2 Point d’incidence : Point de rencontre entre le rayon incident et la surface du miroir.

3 Angle d’incidence (/ i) : Angle formé par le rayon incident et la normale du miroir.

4 Angle de réflexion (/ r) : Angle formé par le rayon réfléchi et la normale du miroir.

LABO 2 2 1 3 4 / i / r

échis

Rayons ré

Miroir

dessus) Miroir

(vue de

À l’aide de la définition des angles d’incidence et de réflexion, il est possible d’énoncer la loi de la réflexion spéculaire.

La loi de la réflexion spéculaire

Lorsqu’un rayon de lumière est réfléchi par une surface plane, la mesure de son angle d’incidence est égale à la mesure de son angle de réflexion. m / i = m / r

Une infinité de réflexions

Lorsque deux miroirs plans parallèles se font face, on peut voir dans chacun des miroirs des images répétées des objets qui sont placés entre eux. En effet, l’image du premier miroir est réfléchie dans le second et agit elle-même comme un miroir qui crée une autre image un peu plus loin. Si les deux miroirs sont parfaitement parallèles, ce processus se répète à l’infini !

EXERCICES

1 Sur le schéma ci-contre, quelle lettre correspond :

a) au miroir ?

c) à la normale ?

e) au rayon incident ?

g) à l’angle de réflexion ?

b) au point d’incidence ?

d) au rayon réfléchi ?

f) à l’angle d’incidence ?

2 La surface d’un miroir plan est éclairée par une boite à faisceaux. Le faisceau lumineux incident forme un angle de 37° avec la surface du miroir. Quelle est la mesure de l’angle de réflexion ?

RÉPONSE :

3 Un rayon lumineux frappe un miroir selon l’angle illustré ci-dessous. Déterminez la mesure de l’angle d’incidence et celle de l’angle de réflexion de ce rayon, puis tracez le rayon réfléchi. Utilisez un rapporteur d’angle.

POUR

SAVOIR

A E C G I H F B D

4 Une source lumineuse envoie une partie d’un faisceau lumineux sur un miroir plan. Les objets O1 et O2 seront-ils éclairés ? Si oui, le seront-ils par la lumière incidente ou par la lumière réfléchie ? Tracez les rayons nécessaires, puis leur réflexion.

RÉPONSE :

5 Le schéma ci-dessous montre la trajectoire d’un rayon réfléchi par un miroir plan. Représentez le miroir avec précision, puis décrivez les étapes qui vous ont permis de le faire.

6 Sur le schéma ci-contre, trouvez, par essais et erreurs, la trajectoire du rayon qui est émis au point A et qui se dirige vers le miroir avant d’atteindre le point B. Dans la section 1.4, vous découvrirez une méthode qui permet de résoudre ce problème de façon efficace. Essayez toutefois de la trouver par vous-même ! Indice : la réflexion, c’est aussi une transformation géométrique d’un point P en un point P', ou d’un point B en un point B'

7 Tracez la trajectoire du rayon lumineux. Vous devrez tracer quatre réflexions. Mesurez les angles d’incidence et de réflexion de chacune des réflexions, puis reportez ces mesures dans le tableau.

Mesures des angles d’incidence et de réflexion

Réflexion m / i m / r

1 2 3 4

A B O2 Source O1

8 Les miroirs pivotants Lorsqu’on fait pivoter un miroir plan sans changer le point d’incidence d’un rayon, le rayon réfléchi pivote du double de l’angle selon lequel le miroir a pivoté. Cela est dû au fait qu’en faisant pivoter le miroir, la normale pivote elle aussi selon le même angle, modifiant l’angle d’incidence et l’angle de réflexion selon une même quantité. Cette situation est illustrée ci-dessous.

SITUATION 1 : Le miroir est incliné à 45,0° par rapport à l’horizontale et la normale est inclinée selon le même angle par rapport à la verticale.

SITUATION 2 : On fait pivoter le miroir de 5,0°. Il est alors incliné à 40,0° par rapport à l’horizontale et la normale est inclinée selon le même angle par rapport à la verticale.

a) Montrez qu’après que le miroir a pivoté de 5,0° (entre la situation 1 et la situation 2), le rayon réfléchi a pivoté de 10° par rapport à la situation 1.

b) Cette propriété des miroirs pivotants est mise à profit dans certains appareils d’imagerie comme le télémètre. Cet appareil permet de déterminer la distance d’un objet en superposant deux images de cet objet grâce à des miroirs plans.

Sur l’illustration ci-contre, le miroir de gauche est fixe et est orienté à 45,0° par rapport à l’axe de l’appareil. L’autre miroir est pivotant et doit être ajusté par l’utilisateur. Lorsque les deux images se superposent dans la lunette d’approche, la lumière provenant de l’objet suit deux trajets qui permettent de délimiter un triangle rectangle (le triangle ABC).

Déterminez la distance séparant l’observateur de l’objet A sachant que les deux miroirs sont distants de 70,0 cm et que le schéma n’est pas à l’échelle.

SCHÉMA CALCULS RÉPONSE : 45,0˚ 45,0˚ 40,0˚ 40,0˚ 44,5˚ 90˚ 44,5˚ 45,0˚ Lunette d’approche Position de l’observateur Objet B C A

La formation d’images par un miroir plan .4 1

Comme la chambre noire, les miroirs plans produisent une image des objets placés devant eux. Cependant, la nature de cette image est différente. Une chambre noire forme une image réelle, tandis qu’un miroir plan forme une image virtuelle

La distinction entre une image réelle et une image virtuelle

Une image réelle est une image formée par la convergence de rayons lumineux sur un écran.

Une image virtuelle est une image qui ne peut pas être captée sur un écran. Pour voir cette image, on doit regarder en direction de l’objet qui la forme (un miroir ou une lentille).

Les caractéristiques d’une image formée par un miroir plan

L’application de la loi de la réflexion spéculaire à la lumière issue d’un objet permet de déduire où se forme l’image virtuelle de cet objet. En effet, l’image n’est pas formée à la surface du miroir, mais bien à une certaine profondeur derrière celui-ci (voir la figure 1.17). C’est d’ailleurs cette propriété que les décorateurs utilisent pour donner une illusion de grandeur à une pièce (voir la figure 1.18).

La réflexion des rayons issus du haut et du bas de l’objet BH semble provenir de l’image virtuelle B'H'.

FIGURE 1.17 L’observation d’une image virtuelle

LABO 3 ACTIVITÉ 1

FIGURE 1.18 Une illusion bien connue Un miroir sur un mur donne l’impression de doubler l’espace d’une pièce. Image virtuelle

B H H' B' 4,00 cm 4,00 cm 1 cm 1 cm

Image réelle Exemple : L’image formée par un miroir plan ou celle formée par une loupe. Exemple : L’image qui se forme au fond d’une chambre noire ou celle sur un écran de cinéma.

Comme on peut le constater sur la figure 1.17, l’image formée par un miroir plan constitue bel et bien une réflexion au sens géométrique du terme. L’image du point B, notée B', est symétrique à B par rapport au miroir, qui agit comme un axe de réflexion. La taille de la flèche image B'H' est identique à celle de la flèche objet BH. Ces observations nous permettent d’énoncer les caractéristiques d’une image formée par un miroir plan.

Les caractéristiques d’une image formée par un miroir plan

Caractéristique Résultat

Nature (réelle ou virtuelle) L’image est virtuelle.

Sens (droite ou inversée) L’image est droite*.

Grandeur par rapport à l’objet L’image est de la même grandeur que l’objet.

Position par rapport à l’axe L’image est symétrique à l’objet par rapport au miroir.

* Ce qui est en haut sur l’objet reste en haut sur l’image. Ce qui est à gauche sur l’objet reste à gauche sur l’image. Voilà pourquoi on dit qu’un miroir forme une image droite. Par opposition, l’image formée par une chambre noire est inversée (bas-haut et gauche-droite).

Ces caractéristiques peuvent être mises à profit pour résoudre un problème de géométrie optique. Par exemple, le fait de savoir qu’un objet et son image sont symétriques par rapport au miroir permet de tracer efficacement les rayons incidents et réfléchis.

EXEMPLE

Rose (R) regarde l’image de son chien Puffy (P) dans un miroir. Tracez la trajectoire d’un rayon qui part de Puffy et qui se rend à Rose après avoir frappé le miroir.

ÉTAPE 1 : Positionner l’image de Puffy (P') dans le miroir en effectuant une réflexion du point P par rapport au miroir.

ÉTAPE 2 : Tracer le rayon réfléchi comme s’il provenait de l’image de Puffy. Le prolongement du rayon derrière le miroir est tracé en pointillé pour indiquer qu’il n’y a pas de lumière derrière le miroir.

ÉTAPE 3 : Tracer le rayon incident pour compléter la trajectoire de la lumière.

La trajectoire du rayon lumineux obtenu respecte nécessairement la loi de la réflexion spéculaire : m / i = m / r.

Note : On aurait pu trouver la trajectoire du rayon incident jusqu’au miroir en traçant plutôt le rayon qui part du point P vers le point R'.

P P' R P R P' P R P'

EXERCICES

1 Sur chaque illustration :

1) tracez le point image P', puis le rayon réfléchi par le miroir ;

2) mesurez l’angle d’incidence et l’angle de réflexion (n’oubliez pas la normale).

a) 1) b) 1)

2) m / i = m / r ≈

c) 1) d) 1)

2) m / i = m / r ≈

2 Effectuez la réflexion de chacun des rayons incidents illustrés ci-dessous.

P P P P P

3 Le schéma ci-contre montre un faisceau de lumière provenant d’une source S et se dirigeant vers un miroir plan. Tracez le faisceau de lumière réfléchi par le miroir sans vous servir de votre rapporteur d’angle.

4 Dans l’illustration ci-dessous, on observe non seulement des images de la girafe, mais aussi une image de chacun des deux miroirs M1 et M2

a) Représentez cette situation vue du dessus. Pour plus de simplicité, on n’a représenté que les deux pattes (P1 et P2) de la girafe qui se trouvent le plus à l’avant-plan.

b) En observant l’image ci-dessus, complétez la phrase suivante.

L’image d’un agit également comme un axe de

5 Maïka (M) et Clarisse (C) se regardent dans un miroir plan. Elles sont éloignées l’une de l’autre de 1,75 m, et toutes deux se trouvent à 1,00 m du miroir. Faites un schéma de cette situation et calculez la mesure de l’angle d’incidence d’un rayon partant de Maïka et se rendant jusqu’à l’œil de Clarisse. Indice : Vous devez faire appel à un rapport trigonométrique.

RÉPONSE :

S P1 M1 M2 P2 P1 P2 M1 M2

6 Marc (M) mesure 1,80 m et il désire se procurer un miroir plan qui lui permettra de se voir en entier.

a) Complétez le schéma en traçant les rayons appropriés, puis positionnez le miroir sur l’axe de réflexion. Déterminez ensuite la hauteur minimale que doit avoir le miroir. Indice : Dans des triangles semblables, on peut non seulement comparer les côtés homologues, mais également la hauteur des deux triangles.

DONNÉES CALCULS

RÉPONSE :

b) La distance qui sépare Marc du miroir a-t-elle une influence sur la taille minimale que doit avoir le miroir ? Comparez le tracé de rayons ci-dessous et celui réalisé en a)

RÉPONSE :

7 Virginie (V) et son frère Pierre (P) (absent du schéma) sont placés devant les deux miroirs plans M1 et M2 illustrés ci-contre. Virginie voit trois images d’elle-même dans les miroirs. Elle voit aussi trois images de son frère. Les trois rayons tracés correspondent à la lumière qui est issue de Pierre et qui atteint l’œil de Virginie après avoir subi une ou deux réflexions spéculaires.

a) Tracez sur le schéma les trois images de Virginie. Au besoin, représentez aussi l’image des miroirs.

M1 Axe de réflexion y y y y

b) Tracez les rayons appropriés permettant de déterminer la position de Pierre.

c) Complétez la trajectoire des trois rayons issus de Pierre et se dirigeant vers Virginie. M2 V

Le champ de vision dans un miroir plan .5 1

Le champ de vision est souvent mesuré en degrés. Le champ de vision binoculaire, c’est-à-dire le champ de vision lorsque nous utilisons nos deux yeux simultanément, est d’environ 160°. Cependant, lorsque nous regardons par une fenêtre (ou dans un miroir), notre champ de vision est considérablement réduit (voir la figure 1.19). Il est délimité par les rayons qui passent aux extrémités de la fenêtre et se dirigent vers l’œil de l’observateur (O).

Champ de vision

Portion d’espace vue par l’œil d’une personne lorsque cet œil regarde droit devant et est immobile.

FIGURE 1.19 Le champ de vision d’un observateur regardant par une fenêtre

À gauche, l’observateur (O) est loin de la fenêtre et son champ de vision extérieur est plus petit (16° et il ne voit que deux objets). À droite, lorsque l’observateur s’approche de la fenêtre, son champ de vision dans la fenêtre est plus grand (35° et il voit quatre objets).

Le champ de vision dans un miroir plan

Pour déterminer le champ de vision d’un observateur O dans un miroir plan, il faut tracer des rayons passant par les extrémités du miroir. On peut tracer la réflexion de ces rayons à partir de l’image (O') de l’observateur dans le miroir.

Ibn al-Haytham

La formation d’images par les miroirs n’a pu être expliquée qu’après qu’on a établi que l’œil est un organe de réception de la lumière. Bien qu’elle nous paraisse évidente, cette idée n’a pas toujours fait l’unanimité. Les pythagoriciens (une école de pensée fondée par Pythagore) croyaient plutôt que l’œil agissait comme un émetteur, un peu comme si nos yeux palpaient le monde qui nous entoure afin d’en former une image ! C’est au scientifique Ibn al-Haytham (965-1040) qu’on doit les premiers travaux sérieux sur la lumière et la réflexion de celle-ci dans toutes les directions (incluant vers nos yeux). Ce brillant mathématicien et physicien arabe est à juste titre considéré comme le précurseur de l’optique moderne.

POUR EN SAVOIR ACTIVITÉ 2 Champ de vision visible dans le miroir O O' • O 1 2 3 4 5 6 8 7 • O 1 2 3 16° 4 5 6 35° 8 7

EXEMPLE

Un observateur O1 se tient devant un miroir plan. Déterminez quels objets il peut voir dans le miroir. Pour effectuer un tel exercice, il convient de tracer le champ de vision de l’observateur O1 dans le miroir. Les objets qui sont visibles dans le miroir sont ceux qui sont compris dans son champ de vision.

D’abord, on positionne l’image de l’observateur (O1') symétriquement par rapport au miroir.

On trace ensuite les rayons venant de la pièce, frappant les extrémités du miroir et se dirigeant vers le point O1'. On trace cette dernière partie en pointillés pour indiquer que la lumière ne se rend pas de ce côté du miroir.

Attention au sens des flèches : L’observateur reçoit la lumière, les flèches se dirigent donc vers lui.

La mesure du champ de vision de l’observateur peut être prise devant ou derrière le miroir. Dans le présent exemple, son champ de vision est d’environ 24°.

On complète la trajectoire de la lumière en reliant les extrémités du miroir à l’observateur.

RÉPONSE : L’observateur O1 peut voir l’image des objets 2 , 3 et 4 , car ces objets sont compris dans son champ de vision.

1. 2. 3.

O1' O1 2 3 4 6 7 8 5 1 2 3 4 6 7 8 5 1 O1 O1 O1' 2 3 4 6 7 8 5 1 O1 24° O1' 2 3 4 6 7 8 5 1

EXERCICES

1 a) Tracez les rayons qui circonscrivent le champ de vision de l’observatrice O2 lorsqu’elle regarde dans le miroir représenté ci-contre.

b) Parmi les objets numérotés de 1 à 8 , lesquels sont visibles pour l’observatrice O2 ?

c) Combien mesure le champ de vision de l’observatrice O2 ?

d) Pourquoi l’étendue du champ de vision de l’observatrice O2 est-elle supérieure à celle de l’observateur O1 dans l’exemple de la page précédente ?

2 a) Tracez les rayons qui circonscrivent le champ de vision de l’observatrice O3 lorsqu’elle regarde dans le miroir représenté ci-contre.

b) Parmi les objets numérotés de 1 à 8 , lesquels sont visibles pour l’observatrice O3 ?

c) Pourquoi l’étendue du champ de vision de l’observatrice O3 est-elle supérieure à celle de l’observatrice O2 ?

3 a) À l’aide d’une couleur différente pour chaque œil (OD et OG), tracez les rayons qui délimitent le champ de vision de chacun des deux yeux d’un observateur.

b) Quels sont les objets visibles tant par l’œil droit que par l’œil gauche de l’observateur ?

3 4 5

c) Y a-t-il un ou des objets qui ne sont visibles que par l’œil gauche de l’observateur ? Si oui, lequel ou lesquels ?

d) Y a-t-il un ou des objets qui ne sont visibles que par l’œil droit de l’observateur ? Si oui, lequel ou lesquels ?

1 2 3 4 5 6

6 7

1 2 OD OG • • • • • • • • 2 3 4 6 7 8 5 1 2 3 4 6 7 8 5 1 • O2 • O3 2 3 4 6 7 8 5 1

a) Montrez, en traçant le champ de vision binoculaire du conducteur de la voiture illustrée ci-dessous, qu’il peut voir toute la lunette arrière.

Angle mort

b) Montrez, en traçant ci-dessus le champ de vision du conducteur dans le rétroviseur gauche, qu’il existe un angle mort, c’est-à-dire une portion d’espace qui n’est visible dans aucun des rétroviseurs. Pour le rétroviseur gauche, il n’est pas nécessaire de tracer le champ de vision de l’œil gauche : c’est l’œil droit qui délimite le champ de vision du côté gauche de la voiture.

Lunette arrière

QUESTIONS DE SYNTHÈSE

1 Lors de séances photo, les photographes utilisent souvent des réflecteurs en forme de parapluie pour éclairer leur sujet.

a) Ces réflecteurs utilisent-ils la réflexion spéculaire ou la réflexion diffuse ?

b) L’intérieur de ces parapluies est blanc. Expliquez pourquoi.

2 Parfois, les lacs reflètent le paysage qui les entoure. Pourquoi n’est-ce pas toujours le cas ?

3 Quelles sont les quatre caractéristiques d’une image formée par un miroir plan ?

4 a) Jacques (J) et Caroline (C) sont debout côte à côte devant un grand miroir plan. Ils sont placés à 1,6 m de celui-ci. Jacques se trouve à 2,4 m de Caroline. Illustrez cette situation vue de dessus à l’aide d’un schéma montrant Jacques, Caroline et l’image de Caroline, puis calculez la distance qui semble séparer Jacques de l’image de Caroline.

SCHÉMA CALCULS RÉPONSE

J C 2,4 m

b) Sur le schéma de la page précédente, tracez la trajectoire du rayon qui part de Caroline pour atteindre l’œil de Jacques. Calculez ensuite la mesure de l’angle d’incidence et de l’angle de réflexion de ce rayon.

CALCULS

RÉPONSE :

5 Une observatrice O regarde successivement dans les miroirs M1 et M2 qui se trouvent devant elle. Tracez son champ de vision dans chacun des deux miroirs, puis indiquez quels objets elle peut y voir.

RÉPONSE : 2 3 6 7 M1 M2 O • • • • • • • • 8 7 6 5 4 3 2 1

6 On tente d’éclairer indirectement quatre objets à l’aide d’un miroir. Complétez le schéma ci-dessous, puis déterminez quel objet sera éclairé par la lumière du pointeur laser si on fait pivoter le miroir de 20° dans le sens horaire, et ce, sans changer le point d’incidence sur le miroir.

SCHÉMA CALCULS

RÉPONSE : 4

7 Deux miroirs plans M1 et M2 forment un angle de 70°. Un rayon lumineux frappe le premier miroir selon un angle de 45°. Complétez le schéma ci-dessous afin de déterminer la mesure de l’angle de réflexion du rayon lumineux sur le deuxième miroir. Appuyez vos calculs sur la loi de la réflexion spéculaire ainsi que les propriétés des triangles.

CALCULS RÉPONSE : Pointeur laser 1 2 3 4 20˚ M2 M1

SCHÉMA

8 Deux miroirs plans parallèles M1 et M2 se faisant face forment une infinité d’images d’un objet placé entre eux. Dans le schéma ci-dessous, représentez les deux premières images de l’objet A dans le miroir de gauche et dans le miroir de droite. Indice : Voir l’encadré Pour en savoir + de la page 35.

9 Le schéma ci-dessous représente une source S qui émet un très mince faisceau de lumière et un détecteur de lumière D, tous deux situés à 4,00 cm du miroir M1. Sachant que le schéma n’est pas à l’échelle, déterminez la mesure de l’angle d’incidence formé sur le miroir M1 lorsqu’un rayon émis par la source S se rend jusqu’au détecteur D après avoir subi deux réflexions. Indice : Tracez l’image du détecteur dans le miroir M2.

SCHÉMA CALCULS RÉPONSE : M1 M2 D S 4,00 cm 2,00 cm 8,00 cm 15 cm 5 cm 10 cm M1 M2 A

10 Le schéma ci-contre représente un observateur P regardant un objet dans un miroir plan. Sachant que le schéma n’est pas à l’échelle, déterminez à quelle distance du miroir doit être placé cet observateur pour que l’objet occupe exactement tout son champ de vision verticalement.

DONNÉES CALCULS

RÉPONSE :

11 Carl (C) est le propriétaire d’un restaurant. Il en est également le chef cuisinier. Pour avoir un œil sur sa salle à manger, il a fait installer un miroir sur un des murs. En traçant les rayons appropriés, déterminez la ou les tables que Carl ne peut pas du tout voir de l’endroit où il se trouve.

RÉPONSE :

P Objet 4,00 m d 2,40

60,0 cm

Table 6 Table 3 Miroir Cuisine Salle à manger Table 1

Table 2 Table 4 Table 7 Table 5 Table 8

12 Julia (J) et Nadine (N) sont dans une pièce dont deux des murs sont couverts d’un miroir plan. Julia regarde l’une des trois images de Nadine qu’elle peut voir. Le schéma ci-dessous illustre une vue de dessus de cette situation et montre un rayon de lumière qui se rend à l’œil de Julia en provenance du corps de Nadine.

a) Sachant que le schéma n’est pas à l’échelle, indiquez l’emplacement de chacune des trois images de Nadine qui sont formées par les miroirs M1 et M2

b) Déterminez la distance qui semble séparer Julia de l’image de Nadine qu’elle est en train de regarder. Des constructions géométriques supplémentaires seront nécessaires pour tracer le schéma qui vous permettra de faire les calculs.

CALCULS

RÉPONSE :

c) Tracez la trajectoire complète du rayon de lumière qui quitte le corps de Nadine pour se rendre à l’œil de Julia.

d) Déterminez la mesure de l’angle de réflexion représenté sur la figure.

CALCULS RÉPONSE :

J M2 M1 N m / r 3,6 m 1,2 m 3,6 m 2,8 m

13 Si je te vois, tu me vois aussi. En traçant les rayons appropriés, montrez que deux personnes peuvent mutuellement se voir en regardant dans ce miroir, et ce, malgré le fait que chacune est placée derrière un obstacle.

RÉPONSE :

14 Une boite contient deux miroirs plans positionnés à des endroits inconnus. Une ouverture sur le dessus de la boite permet de visualiser le trajet de la lumière à l’intérieur de la boite. Avec une boite à faisceaux, on envoie le faisceau de lumière illustré en vert dans la boite. Celui-ci ressort de la boite à l’endroit indiqué après n’avoir subi qu’une seule réflexion.

a) Analysez la trajectoire du faisceau vert afin de déterminer la position de l’un des deux miroirs plans. Utilisez votre rapporteur d’angle. Notez la mesure de l’angle d’incidence (i1) et de l’angle de réflexion (r1) obtenus.

b) On envoie un deuxième faisceau (illustré en orange) à l’intérieur de la boite. Cette fois, ce faisceau subit deux réflexions. Complétez la trajectoire de ce faisceau et déterminez la position du deuxième miroir plan. Utilisez votre rapporteur d’angle. Notez la mesure des angles d’incidence et des angles de réflexion obtenus.

Mesures des angles obtenus

d’incidence

de réflexion r2

d’incidence i3

de réflexion r3

Angle d’incidence i1 Angle de réflexion r1 O1 O2 O3 O4

Angle

i2 Angle

Angle

Mesures des angles obtenus

Phénomènes optiques

Destinée à l’enseignement du cours de Physique de 5e secondaire, la collection Trajectoires couvre l’ensemble des concepts prescrits par le Programme de formation du ministère de l’Éducation. Cette collection propose une approche notionnelle par chapitre dont la séquence respecte la pratique enseignante. Elle permet une grande souplesse dans l’enseignement de la physique tout en favorisant le travail autonome des élèves.

LA 4e ÉDITION DE LA COLLECTION PROPOSE :

une organisation simple et une présentation visuelle attrayante facilitant le repérage par les élèves ;

des encadrés théoriques revus et conformes à la PDA accompagnés d’exemples de résolution de problèmes ;

des rubriques de connaissances générales ou à caractère historique qui enrichissent les notions théoriques ;

une nouvelle section Enrichissement qui présente des contenus pertinents et intéressants pour les élèves ;

un plus grand nombre d’exercices et de problèmes bien gradués ;

des espaces-réponses suffisamment grands pour des démarches complètes ;

des exercices de synthèse à la fin de chacun des chapitres ;

pour les enseignants, une foule de documents reproductibles (incluant un nouveau corrigé en vrac du cahier et de nombreux exercices et problèmes) et un corrigé en couleurs du cahier présentant des démarches complètes

UN CONTENU NUMÉRIQUE RICHE ET VARIÉ

Sur maZoneCEC, accédez aux cahiers et aux guides en format numérique (PC, Mac, Chromebook et iPad) ainsi qu’à de nombreux enrichissements, dont :

300 nouveaux exercices interactifs autocorrectifs ;

des nouvelles capsules numériques (clics +) qui présentent des compléments d’information variés ;

des hyperliens permettant d’accéder à des contenus multimédias ;

des images interactives

Pour en savoir plus, consultez notre site : www.editionscec.com

4e édition