Cap a 3r d’ESO
Refresca el que has ap r è s a 2n
d’ESO


Refresca el que has ap r è s a 2n

Refresca els teus coneixements de càlcul, àlgebra, geometria, mesura, estadística i probabilitat d’una manera pràctica i amena per començar el pròxim curs amb bon peu. 1.
Els continguts s’agrupen en sis setmane s de cinc dies . Per facilitar-te la gestió del temps , cada setmana s’especifiquen les pàgines que pots fer diàriament.
Cada setmana comença amb un enigma . El sabràs resoldre?





I, per saber com vas de matemàtiques, resol les activitats de les pàgines següents.
I, a més a més, practica una mica més amb les seccions El Repte i Sense calculadora .

I, si algun contingut et costa una mica, no et preocupis: et donem pistes !
Experimenta cada setmana el desafiament de noves situacions d’aprenentatge!

2.
3.



DISSENYEM UN EDIFICI El disseny del Burj Khalifa es basa en la forma geomètrica d’una flor, l’hemerocal·lis

I, quan et vingui de gust, fes els passatemps que trobaràs en el Calaix de sastre .
El solucionari és al final del quadern. Utilitza’l correctament i procura de no mirar-lo fins que no hagis fet les activitats.
març. c) La diferència de temperatures és de 13 °C. d) La diferència de temperatures és d’11 °C. e) L’oscil·lació tèrmica a Bjørnøya és de 14 °C. 3. Ens faltaran 474,95 m per arribar al cim. 4DIA Pàgines 12 i 13 1. Respostes correctes a) i b). Ha estalviat 643,10 €, prou per fer el curs. 2. b) –5,60102 < 5,6005 < 5,602 < 5,6005 c) –1,05 < –0,025 < 0,02 < 0,07 < 0,12 < 0,8 d) 0,507 < 0,57 < 0,705 < 0,75 e) 0,05 < 0,102 < 0,105 < 0,251 < 0,501 3. a) La mida de la pantalla d’un televisor, és la longitud diagonal de la pantalla. 27 polzades = 68,58 cm; 24 polzades = 60,96 cm; 45,725 cm = 18 polzades b) És una mesura de superfície. 100 km = 10.000 ha c) 3,781855 km; 0,96558
2 4 5 3
DHRQRZ N
YRF FRG ÇRE
NANE N YN
ÇVFOVAN

HO RESOLS?
Quin missatge ha enviat la Jana a l’Oriol?
T’atreveixes a enviar un missatge secret a un amic? No t’oblidis de donar-li la clau. QUEDEM ...

NOMBRES ENTERS
1. Omple els buits amb el nombre enter que correspongui:
a) |+7| = | | = 7
b) | | = | | = 5 c) |–4| = | | = d) | | = |+2| =

2. Troba el resultat de les operacions següents. Tingues en compte els valors absoluts i fixa’t en els exemples: |+10| = 10 |+4| = 4 |–10|= 10 |–4| = 4
a) –2 + |– 5| – 1 = c) –2 · |–5| = b) |18 : (–3)|= d) |10 – 19 + 3| =
3. Ordena els nombres següents del més petit al més gran: 8 3 +7 –4 –11
4. Descompon els nombres següents com a suma de dos enters de signe diferent:
a) –7 = b) 8 = c) –2 = d) 11 =
5. La resta de dos nombres és –4. Si un dels nombres és –1, quin és l’altre? –3 –2 –1 0 1 2 3 valor absolut: |–3| = |+3| = 3

6. El producte de dos nombres enters és –285. Si l’un és l’oposat de 15, quin ha de ser l’altre nombre?
7. Per quin nombre cal dividir –350 per obtenir –7?
L’oposat de 4 és –4.

Resol mentalment aquestes operacions i anota el temps que has trigat a fer-ho (posa el cronòmetre en marxa abans de començar).
a) En una base científica de l’Antàrtida, fa una hora el termòmetre marcava –5 °C i ara marca –13 °C. La temperatura, ha augmentat o ha disminuït? De quant ha variat?
b) A les 5 h, un termòmetre marcava –3 °C. La temperatura ha augmentat 10 °C al llarg del matí. Quina temperatura marca el termòmetre al migdia?
c) Una persona viu a la planta 4 d’un edifici, i la seva plaça de pàrquing és al soterrani 5. Quantes plantes hi ha entre el seu habitatge i la seva plaça de pàrquing?

d) Ahir l’Helena tenia 35 € en el seu compte i avui està en nombres vermells, ja que té un deute de 25 €. Des d’ahir, ha ingressat diners o n’ha gastats? Quina quantitat?
e) Euclides va néixer l’any 325 aC i Pitàgores, 247 anys abans. Quin any va néixer Pitàgores?

1. Endevina, en cada cas, de quin nombre es tracta:

2. Resol les operacions combinades següents:
a) Soc negatiu, imparell, més petit que –12 i més gran que –15.
b) Soc més gran que –7 i el triple del meu valor és –18.
c) Soc l’oposat del nombre anterior.
d) Soc positiu, el meu valor absolut és més petit que 9 i el meu oposat és un nombre negatiu més gran que –2.
a) –5 – [+5 – (–5) · (–3) + (–8)] + (–9) : (–3) = –5 – [+5 – 15 – 8] + (–9) : (–3) = –5 – (–18) + 3 = +16
b) (+4) + (–7) – (+2) + (+6) =
c) (+2) – (+8) + (–5) – (–13) – (+1) =
d) –5 + (+1) · (–4) =
e) (+10) : (–2) – (–3) =
f) [–13 + 6 + (–3)] : (–2) =
g) –6 – (–8) · (–7 + 4 – 2) =
1 2 4 5 3
(–7)2 = 49
(–7)3 = –343
3. Resol aquestes operacions combinades:
a) –14 – (+24) : (+1 – 9) – (–2 – 3) =
b) –5 · (–2 + 4) · (–2 – 4) : 2 =
c) +4 + [+2 – (+8) · (–5) – (–7 + 6)] =
d) +2 – (2 · 2)² – [+3 – (+2) · (–2 – 5)] =
e) 5 · [11 – 4 · (11 – 7)]=
f) (–4) · [12 + 3 · (5 – 8)] =
g) 4 – (–2) · [8 – 3 · (5 – 7)] =
4. Resol aquestes operacions amb potències:
a) 42 + (–42) =
b) (–4)2 – (–40) =
c) –5 · (52)3 =
Omple les caselles buides. Tingues en compte que el valor de cada casella és la suma dels dos valors de les caselles inferiors.

MULTIPLICACIÓ I DIVISIÓ AMB DECIMALS
1,5 · 2,5 15 · 25 = 375 1,5 · 2,5 = 3,75 4,5678 : 3,5 = 45,678 : 35 = 1,305
MULTIPLICACIÓ I DIVISIÓ PER LA UNITAT SEGUIDA DE ZEROS
·
5. Fes les operacions següents:

a) 1,5 · 2,5 = 3,75 d) 12,25 : 1.000 g) 288,1 : 18,73
b) 134,5678 · 10.000 e) 13,4 · 7,08 h) 54 : 0,02 c) 4,5675 : 3,5 f)
6. Fes les operacions indicades i completa la taula:
Multiplica’l per 100.
Divideix el resultat anterior per 1.000.
Suma 3,4 al resultat anterior.
Multiplica el resultat anterior per 2,3.

1. Els nois i les noies del poble on estiuejo hem organitzat una lligueta de voleibol entre quatre equips. Si un equip guanya un partit, aconsegueix 3 punts; si empata, aconsegueix 0 punts, i si perd, –1,5 punts. Cada equip ha jugat 6 partits.
Els resultats es mostren en la taula adjunta.

a) Completa la taula amb les expressions numèriques corresponents:
b) Quin equip ha guanyat la competició?
c) Quants punts sumen entre els quatre equips?

d) Quina és la diferència de punts entre l’equip guanyador i l’últim equip en la classificació?
2. Observa el gràfic, que correspon a les temperatures i les pluges registrades durant un any a Bjørnøya, una illa de Noruega situada al mar de Barentsz, a prop del cap Nord. Després, respon a les preguntes.
CLIMA POLAR
Temperatures (ºC)
Illa de l’Os (20 m)

a) Quin ha estat el mes amb les precipitacions màximes?
b) Quina és la temperatura més baixa registrada?
c) Quina diferència de temperatura hi ha hagut entre el gener i el juliol?
d) I entre el juliol i el desembre?
e) S’entén per oscil·lació tèrmica la diferència entre la temperatura anual més alta i la més baixa. Calcula el valor registrat a l’illa de Bjørnøya.
3. Hem preparat una excursió al Pedraforca. La ruta comença a 850 m sobre el nivell del mar, s’enfila 850,75 m, després baixa 220,5 m i, finalment, torna a pujar 550,8 m més. Arribats a aquest punt, encara som lluny del cim, que es troba a 2.506 m sobre el nivell del mar. Calcula els metres de pujada que ens falten per arribar al cim.

2
1. Aquest estiu, en Sergi vol estalviar per poder fer un curs de submarinisme al setembre.
Ha començat a treballar la segona quinzena de juny. Ha cobrat 38,45 € cada setmana i ha pogut estalviar tots els diners que ha guanyat.
Durant el mes de juliol cobrarà 74,5 € setmanals.
A l’agost treballarà només tres setmanes i cobrarà setmanalment un 20 % més que al juliol.
4
Vol calcular quants diners haurà estalviat a finals d’agost. Quina o quines de les expressions següents serien les adequades per fer aquests càlculs?
a)

Quant ha estalviat? Si el curs té un cost de 500 €, haurà estalviat prou per fer-lo?
2. Ordena de més petit a més gran els nombres decimals següents:
a) 6,1; 4,22; 4,02; 6,11; 3,99; 3,9 3,9 < 3,99 < 4,02 < 4,22 < 6,1 < 6,11
b) 5,602; 5,611; 5,6005; –5,60102
c) 0,02; –1,05; 0,8; 0,12; –0,025; 0,07
d) 0,75; 0,57; 0,507; 0,705
e) 0,102; 0,05; 0,105; 0,501; 0,251
3. Descobreix equivalències entre mesures!
Respon a aquestes preguntes i tingues en compte els decimals:
a) En un televisor, què mesurem en polzades?
Quant mesura en centímetres un televisor de 27 polzades?
I un de 24 polzades? Quantes polzades són 45,725 cm?
b) Què mesuraries en hectàrees?
Quantes hectàrees són 100 km2?
Una polzada equival a 2,54 cm.
Una hectàrea (ha) són 10.000 m2.
Una milla terrestre són 1,6093 km.
c) Quants quilòmetres son 2,35 milles?
I 0,6 milles?
d) Els elefants són els animals terrestres més grossos que existeixen. En néixer, una cria d’elefant pesa aproximadament 120 kg, però l’elefant més gros que s’ha vist mai pesava 11.000 kg. Quantes tones feia?

1 2 4 5 3
La Judit i la Paula han fet un viatge a Londres aquest estiu per millorar el seu anglès. Allà han conegut en Carlos, de Bogotà, i en Huang, de Pequín. Ara que cada un tornarà al seu país, volen continuar estant en contacte a través del xat, però han d’anar amb compte amb les diferències horàries entre els seus països.
1. Les dues noies tornen a Barcelona el 15 d’agost a les 21 h. Quina hora i quin dia serà a la ciutat de cadascun dels seus amics?
Tingues en compte que la franja horària de Catalunya a l’estiu és l’UTC+2.
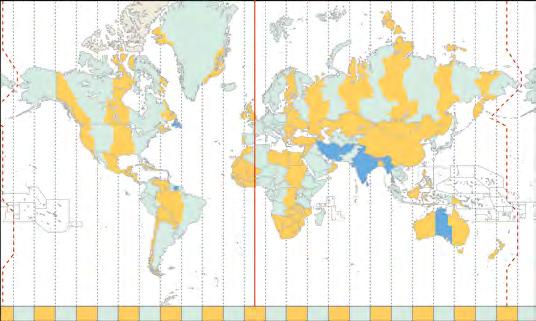
-11-10-9-8-7-6-5-4-3-2-10+1+2+3+4+5+6+7+8+9+10+11+12--11
2. Observa aquesta taula que ha fet la Paula amb els horaris dels vols dels seus amics i completa-la:
Hora de sortida de Londres Durada prevista
Carlos 11 h 12 h 15’
Huang 13 h 14 h 30’
Arribada (hora de Londres)
Arribada (hora de Barcelona)
Arribada (hora de la ciutat de destinació)
3. En quina franja horària, segons l’hora de Barcelona, es podran comunicar la Judit i la Paula amb els seus amics?
Aquests són els horaris de connexió de cada un:




En acabar el cicle formatiu de producció agropecuària, tres amics van muntar una empresa de cultiu de bolets. Es van especialitzar en el cultiu de xiitake, gírgola i gírgola groga.

1. Van fundar l’empresa al març i cada un va aportar-hi 3.500 €. Les primeres despeses van ser de 650 € en concepte de fiança pel lloguer del local, 235 € per l’adquisició de mobiliari per al magatzem i 2.045,50 € per la compra de cambres frigorífiques. De quants diners disposaven després de fer tots aquests pagaments?
2. A l’abril van començar a portar els comptes en un full de càlcul. Van pagar 325,50 € pel lloguer mensual del local i 1.750,75 € per la matèria primera, i van vendre 10 safates de xiitakes a 30,25 € cadascuna, 12 safates de gírgoles a 20,75 € cadascuna i 18 safates de gírgoles grogues per a 25,50 € cadascuna. Completa la taula amb els ingressos i el saldo corresponent: Concepte
Diners inicials
Lloguer local
Compra matèria primera
Venda xiitakes
Venda gírgoles
Venda gírgoles grogues
3. Durant el mes de maig, van veure que les despeses havien augmentat en 200 € respecte a les despeses del mes d’abril i que els ingressos per les vendes s’havien multiplicat per 3,2. Calcula el saldo final el mes de maig i valora si l’activitat els va ser rendible.
Completa totes les files. Cada casella s’omple amb la suma dels dos nombres que té just a sobre.
Què passa si sumes tots els nombres d’una fila?
Pinta les caselles amb nombres imparells i obtindràs un trosset del fractal de Sierpinski!
I, parlant de fractals, busca una mica de fresca enmig de l’estiu. Dibuixa un floc de neu.
1. Dibuixa un triangle equilàter.
4. Els fractals no tenen fi! 2 3 1 1 2 1 1 1 1
2. Divideix cada costat del triangle en tres parts iguals i dibuixa un altre triangle equilàter més petit en cadascun dels costats.
3. Repeteix aquest procediment fins que… Aquest procés és infinit!
Fes camins perquè cada emoticona trobi la seva parella.
Dissenya una ciutat!
Material
• Tauler quadriculat 4 x 4
• 16 edificis de diferents altures construïts amb cubs encaixables, daus, llaunes...
Objectiu
Col·locar els 16 edificis, tenint en compte que en cada fila i en cada columna només hi pot haver un gratacel de cada altura. Els nombres del voltant del tauler indiquen els edificis que es veuen des de cada punt de vista.
Compte! Els camins no es poden creuar. 1
Dissenya una ciutat!
Com queda aquesta ciutat?
Refresca el que has après a 2n

En aquest quadern trobaràs activitats ben diverses que et serviran per practicar, repassar i millorar tot allò que has après i preparar - te per al curs vinent.
Altres propostes per continuar repassant:

