MATEMÀTQUES IMATEMÀ
DOSSIER 1 ESO
Programa

Programa


Una passejada per la història de la numeració, l’àlgebra, les funcions, la geometria i l’atzar i la probabilitat.

















D’APRENENTATGE
Proposta de situació d'aprenentatge.
Idees per encetar el debat i fer aflorar els coneixements previs.




Conceptes explicats de manera amena amb exemples i exercicis resolts.






Unitats del bloc.



Itinerari de la unitat.
Proposta d’activitats per resoldre.
Activitats que donen peu a reflexionar sobre els objectius de desenvolupament sostenible de l’ONU.
Exercicis i problemes per treballar el que has après al llarg de la unitat.

Exercicis per practicar tot allò que has après.

Problemes que donen pistes de com resoldre la situació d’aprenentatge.
Activitats de lògica, enginy i cultura matemàtica.

Proposta per treballar els sabers i les competències matemàtiques dins un context social i cultural per analitzar i mirar de comprendre el món.
ANEM PAS A PAS
Treball pas a pas i en grups cooperatius de la situació d’aprenentatge plantejada a l’inici.
AMB ULLS DE DONA
Articles, entrevistes i relats en què científiques de diversos àmbits transmeten la passió que senten per la seva professió.


POSA'T A PROVA
Activitats per comprovar què has après.




RESOLEM










Resolució de la situació proposada i altres de similars.
PENSEM-HI
Activitats per debatre i reflexionar sobre la situació d’aprenentatge.
Reflexió sobre l’ODS relacionat amb la situació plantejada.





Una resposta global per a un entorn educatiu divers
La proposta digital de Barcanova és EDUDYNAMIC , un projecte digital complet que dona una resposta global a un entorn educatiu divers i dinàmic. A partir d’una proposta senzilla i intuïtiva, EDUDYNAMIC és un projecte digital multidispositiu i multisuport que s’adapta i es visualitza en totes les plataformes i en tots els entorns virtuals d’aprenentatge (BlinkLearning, Moodle, Alexia, Google Classroom, Clickedu, Office 365…).
La diversitat i riquesa de recursos, des d’activitats interactives traçables a vídeos, presentacions i jocs, fan d’EDUDYNAMIC un projecte digital actualitzat i complet pensat per canviar amb tu.
Integració a totes les plataformes i entorns EVA.
Gestió en línia de les activitats i tasques assignades als alumnes.

Compatibilitat i sincronització amb qualsevol dispositiu.











Totes les civilitzacions han fet servir un sistema de numeració per representar quantitats. Ja des de la prehistòria, els pobles egipci, babiloni, grec, romà, xinès, indi, àrab, maia… van utilitzar sistemes de numeració molt diversos, que van passar d’uns pobles a uns altres i van evolucionar al llarg del temps.

Inicialment, els nombres s’utilitzaven per comptar quantitats naturals (ramats, fruits, monedes…), i els sistemes de numeració eren molt rudimentaris: es feien osques en un gaiato, es dibuixaven dits i mans… Però el progrés de les civilitzacions va comportar la introducció de símbols i normes que els van fer més complexos i pràctics.
Els sistemes de numeració són útils per escriure nombres, recordar-los i transmetre’ls. Però han de servir, també, per fer operacions. Pensem en el sistema de numeració romà (que ja coneixem) i imaginem com se les devien apanyar per fer sumes. Per exemple:
MCCCXLVI + DCCCXXXIV
Complicat, oi? Doncs multiplicar encara havia de ser més difícil.
Els antics matemàtics hindús, al segle vi, van fer un gran pas endavant amb la invenció del sistema de numeració decimal posicional.
Des de l’Índia es va propagar cap al Mediterrani a través del poble àrab i va arribar a Europa als segles ix i x. Els avantatges d’aquest sistema van permetre el desenvolupament de noves estratègies de càlcul, precursores de les que fem servir actualment.
Amb els nombres i les seves operacions, calculem i obtenim dades noves útils que podem fer servir en situacions quotidianes, però en cal interpretar i resoldre l’expressió escrita.

Encara que avui fem servir els nombres negatius amb naturalitat, va haver de passar molt de temps perquè aquests nombres fossin acceptats en el món de les matemàtiques.
Curiosament, ja al segle negatives. Utilitzaven dos conjunts de varetes, unes de vermelles per a les quantitats positives i unes altres de negres per a les negatives, amb les quals feien càlculs amb una destresa extraordinària.
Van haver de passar encara uns mil anys fins que, al segle generalitzés l’ús dels nombres negatius associant-los a la categoria de deute. De l’Índia, i gràcies als àrabs, aquests conceptes van arribar a Europa cap al segle ix . No obstant això, fins al segle nes + i –; primer, per designar quantitats positives i negatives i, després, per a les operacions de suma i resta. El signe = es va inventar l’any 1557.

Els nombres naturals 1

Divisibilitat 2
Des de l’antiguitat, les matemàtiques sempre van ser una eina per resoldre problemes quotidians. Quant mesura aquest terreny? Com hem de repartir-nos la collita? Com hem d’interpretar les estrelles per orientar-nos?
Fins al segle vi aC no van aparèixer els primers matemà tics teòrics, estudiosos interessats per la investigació i el desenvolupament de la ciència, independentment de la seva utilitat pràctica. Amb aquest esperit, Pitàgores, gran matemàtic de l’antiguitat, va fundar, a Siracusa, una secta misticocientífica que retia culte a l’astronomia i que va ser un dels primers centres del saber que va acceptar dones entre els seus membres, la més coneguda de les quals va ser Teano.
Els pitagòrics van estudiar les propietats teòriques dels nom bres i les van relacionar amb la geometria. A ells els devem
Els nombres enters 3

al qual deu el seu nom, va esdevenir al segle iii aC el centre cultural (científic i artístic) més influent i prestigiós del món hel·lenístic.
, savi grec del segle iii aC, va viure a Alexandria, on va fundar l’escola més important de l’antiga Grècia, en la qual va exercir de professor i científic amb un extraordinari prestigi. Va recopilar i sistematitzar tot el coneixement matemàtic de la seva època, però no es va limitar només a això: va ser, a més, un gran matemàtic que va aportar importants descobriments.
Euclides és l’autor de l’obra Elements, composta per tretze llibres. La major part d’aquests estan dedicats a la geometria i només quatre, a l’aritmètica. En aquesta obra va olupar, entre molts altres conceptes, la teoria de la divisibilitat: nombres primers i compostos, divisors, múl-
Els elements d’Euclides han estat estudiats i admirats en totes les èpoques.


Diuen que l’economia és el que mou el món. Les revolucions socials i culturals, els canvis polítics, els desastres naturals… trastoquen l’economia i es veuen afectats per aquesta. La planificació de la despesa i el consum responsable ens afecten significativament. El govern vetlla pels pressupostos de sanitat, educació, pensions… A casa, la família té cura dels sous, el cost de les vacances… I tu, no pares de pensar en què gastaràs els estalvis.
Cal analitzar, predir, pressupostar. I aquestes decisions, des d’un punt de vista tècnic, recolzen en eines matemàtiques que ajuden a valorar resultats i predir-ne les conseqüències.
La Laia sempre ha somiat ser astronauta i viatjar a l’espai. Per començar, aquest estiu vol visitar algunes de les seus de l’Agència Espacial Europea (European Space Agency, ESA) i, per aconseguir els diners que li calen, s’ha proposat estalviar amb un mètode que li sembla infal·lible.
El primer dia posarà a la guardiola una moneda d’1 €.
El segon dia, dues monedes d’1 €.
El tercer dia, quatre monedes d’1 €.
El quart dia, vuit monedes d’1 €.
I, així, successivament, cada dia posarà a la guardiola el doble que el dia anterior.
• S i estalvia durant 10 dies, quantes seus de l’ESA creieu que podrà visitar?
• Què us sembla aquesta manera d’estalviar?

Sistemes de numeració
Tècniques de comptatge
Nombres grans

Aproximació de nombres naturals
Operacions bàsiques amb nombres naturals
Potències
Potències

Arrel quadrada
• Sistema de numeració. És el conjunt de símbols que fem servir per representar els comptatges i les normes d’ús corresponents.
• El sistema de numeració egipci. És un sistema additiu, perquè, per escriure un nombre, es van afegint els símbols necessaris fins a completar la quantitat.





• El sistema de numeració maia. Pel que fa als nombres més petits que 20, el sistema és additiu. Per escriure nombres més grans de 20, s’utilitzen els mateixos símbols, però el seu valor canvia segons la posició (sistema posicional). Aquí apareix escrit el nombre 1.333.331.
solament tres símbols: (0)(1) (5) (0) (0)(1) (5) (1) (0)(1) (5) (5)
1. Escriu d’acord amb el sistema de numeració egipci els nombres següents:
19 →
65 →
3.412 →
2. En un sistema additiu s’utilitzen aquests símbols:
1 5 10 100
• Escriu, seguint aquest sistema, els nombres següents:
7 →
→
→
3. Tradueix al sistema decimal aquests nombres del sistema maia:
4. Afegeix dos elements per la dreta i dos més per l’esquerra a aquesta sèrie de nombres del sistema maia:
Segon nivell →
Primer nivell →
Esquerra:
Dreta:
• Sistema de numeració decimal. El sistema de numeració que utilitzem actualment és el decimal. Consta de deu símbols o xifres (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) i es regeix per aquestes normes:
‒ Es defineixen ordres d’unitats: unitats, desenes, centenes…
‒ Deu unitats d’un ordre fan una unitat de l’ordre immediat superior.
‒ El valor d’una xifra depèn del lloc que ocupi (sistema de tipus posicional).
F1. Seguint el sistema de numeració decimal:
a) Quantes desenes fan 3 milers?
Exemple:
b) Quantes centenes fan una desena de miler?
c) Quantes centenes hi ha en 5 unitats de milió?
5. Completa:
a) 500 D = C = UM
b) 3.000 C = UM = DM
c) 6 UM = C = D
d) 8 CM = DM = D
6. Cert (C) o fals (F)?
a) Si canvies de lloc les xifres, canvia el valor del nombre.
b) Si afegeixes un zero a la dreta d’un nombre, el seu valor es multiplica per 10.
c) Si afegeixes un zero a l’esquerra d’un nombre, el valor es divideix entre 10.
d) Mig miler equival a 5 desenes.
e) Mil milers fan un milió.
7. Un nombre té cinc xifres que sumen 5. Si intercanvies les unitats amb les unitats de miler, augmenta 999 unitats. Quin nombre és?
8. Un nombre es pot descompondre segons els seus ordres d’unitats i segons el valor de posició de cada xifra. Observa l’esquema i completa’l:
Fem servir els nombres naturals per comptar. Però sabem que els comptatges només es fan, d’un en un, en situacions molt senzilles. Quan aquestes es compliquen, fem servir estratègies que els fan més ràpids i eficaços. Repassemne algunes:
Recomptes de dades
Exemple
A l’esquerra tens els resultats de la votació per a l’elecció de delegat en una classe de 1r d’ESO. Fixa’t que:
• A la classe, entre noies i nois, són 28 alumnes.
• La Cèlia ha obtingut 4 vots més que en Martí.
Taules i operacions
Exemple
La taula recull dades referents a la distribució de dos grups de 1r d’ESO i de dos grups de 2n d’ESO en un centre de secundària.

Fixa’t que:
• A primer hi ha 52 alumnes i a segon també 52.
• En total hi ha 49 noies, 54 nois i una persona que no vol ser comptabilitzada en cap d’aquests dos grups.
9. La Marta s’ha col·locat a la finestra de casa seva i ha anat anotant el color dels cotxes que hi han passat per davant durant mitja hora. Però, sense voler, el seu germà petit li ha esborrat algunes dades.
Completa les dades que falten en la taula.
10. De cada branca d’un arbre cada any en surten dues i de cada una en surt una flor.
• Quantes flors noves sortiran al sisè any? I al desè?
Exemple
En una urna hi ha tres boles de diferents colors (vermell, blau i groc) i ens proposen que fem l’experiència «treure successivament dues boles».
• Suposa que fem l’experiència sis vegades. En quantes, teòricament, hauria de quedar la vermella a l’urna? I si fem l’experiència 30 vegades?
Fem servir un diagrama d’arbre en el qual s’estudien totes les possibilitats.
Veiem que, teòricament, la bola vermella quedarà a l’urna dues de les sis vegades.
I si fem l’experiència 30 = 6 · 5 vegades, teòricament la vermella quedarà a l’urna, 2 · 5 vegades.
11. En Lluís se’n va d’excursió i a la motxilla hi porta unes vambes, unes sabates, dos pantalons, tres camises i una samarreta.
De quantes maneres es podrà vestir demà amb les peces de roba que porta a la motxilla?
12. Tenim una urna amb quatre boles, tres de blaves i una de vermella, i ens proposen que fem l’experiència «treure successivament dues boles».
a) Quina possibilitat hi ha que quedin a l’urna dues boles de diferent color?
b) I que les dues boles que hi quedin siguin del mateix color?
Per ajudarte a resoldre’l, pots fer un diagrama en arbre com el de l’activitat anterior.
c) I si en lloc de treure dues boles en traiem tres, quina possibilitat creus que hi ha que totes tres siguin blaves?
• El sistema de numeració decimal permet representar quantitats tan grans com desitgem.
– Un milió ↔ Un 1 seguit de 6 zeros.
– Un bilió ↔ Un milió de milions ↔ Un 1 seguit de 12 zeros.
– Un trilió ↔ Un milió de bilions ↔ Un 1 seguit de 18 zeros.
Exemple:
Temps de vida de l’univers →
Nombre de neurones en un cervell →
Volum de la Terra en km3 →
13. Escriu com es llegeixen:
a) El nombre d’habitants de la Terra, 7.000.000.000.
b) El nombre de segons d’un segle, 3.153.600.000.
c) El nombre de quilometres que té un any llum, 9.460.800.000.000.
e) Un bilió i mig.
f) Quinze bilions trescents cinquanta mil milions.
15. Completa:
a) Mil milers fan un
b) Mil milions fan un
c) Un milió de milers fan un
d) Un milió de milions és un
14. Escriu amb xifres:
a) Vintivuit milions trescents cinquanta mil.
b) Cent quarantatres milions.
c) Dos mil setcents milions.
d) Setze gigues.
16. El cos humà té entre deu i setanta milions de milions de cèl·lules. Expressa aquesta quantitat en bilions.
17. Com llegiries el nombre expressat per un 1 seguit de setze 0?
18. Les científiques i els científics calculen que els mars i oceans de la Terra contenen tres quadrilions de quilograms d’aigua. Què creus que és un quadrilió?
• Quan un nombre té moltes xifres, l’acostumem a substituir per un altre, més manejable, de valor aproximat, acabat en zeros. Aquest procediment s’anomena aproximació, i la manera més freqüent i pràctica d’aproximar és mitjançant l’arrodoniment.
• Per arrodonir un nombre a un determinat ordre d’unitats:
– Se substitueixen per zeros totes les xifres a la dreta d’aquest ordre.
– Si la primera xifra substituïda és igual a 5 o més gran, se suma una unitat a la xifra anterior.
Exemple: 35.326.000 són, aproximadament, trentacinc milions.
» FIXA IDEES
F2. Completa per aproximar el nombre 384.523 a les centenes de miler, a les desenes de miler i als milers.
19. Arrodoneix als milers aquests nombres:
a) 24.963 →
b) 7.280 →
c) 99.834 →
20. Aproxima a les centenes i a les desenes de miler:
a) 530.298 CM:
DM:
b) 359.481 CM:
DM:
c) 29.935.236 CM:
DM:
21. Aproxima als milions per arrodoniment:
a) 24.356.000 →
b) 36.905.000 →
c) 274.825.048 →
Aproximació del nombre 52.722:
– A les desenes de miler → 50.000
– Als milers → 53.000 AJUDA
22. Llegeix aquesta notícia i aproxima el nombre de turistes als milions i la despesa als milers de milions:
L’any 2022 van visitar Catalunya14.803.187 turistes que van gastar 16.461 milions d’euros.

Turistes:
Despesa:
23. Fixa’t en les diverses aproximacions al preu d’un pis en venda:
138290 € 138.290 €
a) Quina és més propera al preu real?
138.000 €
138.300 €
140.000 €
b) Quina et sembla més adequada per a una informació col·loquial, si no es recorda la quantitat exacta?
• La suma i les seves propietats. Sumar és unir, ajuntar, afegir.
Exemple: 308 + 258 = 566
La suma compleix les propietats següents:
– Propietat commutativa: El resultat de la suma no varia encara que canviem l’ordre dels sumands.
a + b = b + a
– Propietat associativa: El resultat de la suma és independent de la forma com s’agrupen els sumands.
(a + b) + c = a + (b + c)
• La resta i les seves relacions amb la suma. Restar és treure, suprimir, trobar el que falta o el que sobra; és a dir, calcular la diferència. M
Exemple: 590 – 566 = 24
24. Calcula:
a) 254 + 78 + 136 =
b) 340 + 255 – 429 =
c) 1.350 – 1.107 – 58 =
34 + 16 = 16 + 34
50 50
(18 + 3) + 17 = 18 + (3 + 17)
21 + 17 18 + 20
38 38
590 ← Minuend (M )
– 566 ← Subtrahend (S )
24 ← Diferència (D )
26. Transforma:
a) Aquesta suma en una resta: 48 + 12 = 60
b) Aquesta resta en una suma: 22 – 2 – 6 = 14
27. Si l’Albert tingués 15 anys més, encara seria 18 anys més jove que el seu oncle Tomàs, que té 51 anys. Quants anys té l’Albert?
25. Estima la resposta i comprovala després:
La Carme compra una bossa de 167 €, una gavardina de 235 € i un mocador de 32 €. Quant s’ha gastat?
a) S’ha gastat al voltant de 350 €.
b) S’ha gastat, més o menys, 450 €
c) S’ha gastat al voltant de 550 €.
28. Si comprés només una rentadora, em sobrarien 246 €, però si comprés també un televisor, em faltarien 204 €. Pots dir el preu d’algun d’aquests articles?
• La multiplicació i les seves propietats. Multiplicar és una manera abreujada de fer una suma repetida de sumands iguals.
Exemple: 15 + 15 + 15 + 15 + 15 + 15 + 15 = 15 · 7 = 105
La multiplicació compleix les propietats següents:
– Propietat commutativa: El producte no varia en canviar l’ordre dels factors.
a · b = b · a
– Propietat associativa: El resultat d’una multiplicació és independent de la forma com s’agrupin els factors.
(a · b) · c = a · (b · c)
– Propietat distributiva: El producte d’un nombre per una suma (o resta) és igual a la suma (o resta) dels productes del nombre per cada sumand.
a · (b + c) = a · b + a · c a · (b – c) = a · b – a · c
29. Completa:
a)
33. Quantes voltes fa en un quart d’hora una roda que gira a 1.500 revolucions per minut? I en una hora? I en una hora i mitja?
30. Recorda que per multiplicar per 10, per 100, per 1.000… s’afegeixen un, dos, tres… zeros. Calcula:
a) 19 · 10 = b) 12 · 100 =
c) 15 · 1.000 = d) 140 · 10 =
e) 230 · 100 = f) 460 · 1.000 =
31. Expressa amb una igualtat aritmètica:
Multiplicar un nombre per 8 és el mateix que multiplicar-lo primer per 10 i després restar-n’hi el doble.
Quina propietat s’aplica en aquesta igualtat?
32. Fixa’t en els exemples i multiplica mentalment per 9 i per 11:
• 23 · 9 = 23 · 10 – 23 = 230 – 23 = 207
• 23 · 11 = 23 · 10 + 23 = 230 + 23 = 253
a) 12 · 9 = b) 25 · 9 =
c) 33 · 9 = d) 12 · 11 =
e) 25 · 11 = f) 33 · 11 =
34. Una agricultora té un hort amb 200 presseguers. Calcula que amb cada arbre omplirà set caixes de cinc quilos de préssecs. Quin benefici obtindrà si ven tota la producció a 2 € el quilo?
35. Al viver d’una horta es preparen 50 safates amb 100 llavors cada una. En cada safata es fan malbé, de mitjana, 20 llavors. Quants plançons obtindrà el pagès?
• La divisió. Dividir és repartir un tot en parts iguals per esbrinar quantes en toquen a cada un. Dividir també és partir un tot en porcions iguals d’una determinada mida per esbrinar quantes porcions s’obtenen.
– Una divisió pot ser exacta o entera depenent del valor del residu.
– Divisió exacta (el residu és zero).
D d
0 q
⎯→ El dividend és igual al divisor multiplicat pel quocient.
D = d · q
– Divisió entera (el residu és diferent de zero).
D d
r q ⎯→ El dividend és igual al divisor multiplicat pel quocient més el residu.
D = d · q + r
– Si en una divisió es multipliquen el dividend i el divisor pel mateix nombre, el quocient no varia.
36. Esbrina el quocient i el residu de cada divisió:
a) 96 : 13 b) 713 : 31
37. Un granger recull 1.274 ous, els envasa en safates de 30 i empaqueta les safates en capses de 10. Quants ous queden sense completar una safata? Quantes safates queden sense completar una capsa?
c) 5.309 : 7 d) 7.029 : 26
e) 49.896 : 162 f ) 80.391 : 629
38. En una indústria de conserves es preparen 250 kg de melmelada de pruna, que s’envasen en pots de 200 g. Durant el procés es rebutgen 17 pots perquè s’han trencat o perquè són defectuosos. Quants pots vàlids s’obtenen?
• Ordre en què han de ferse les operacions. En les expressions amb operacions combinades, hem de resoldre: primer, els parèntesis; després, les multiplicacions i les divisions; i, finalment, les sumes i les restes.
Exemple:
48 : 3 + 5 – 2 · 3
16 + 5 – 6
21 – 6 15
48 : (3 + 5) – 2 · 3
48 : 8 – 6
6 – 6 0
48 : 3 + (5 – 2) · 3
16 + 3 · 3
16 + 9
• Amb calculadora. No totes les calculadores tenen la mateixa lògica interna, i quan inclous una seqüència d’operacions, es poden obtenir resultats diferents. Això passa perquè no totes realitzen les operacions amb el mateix ordre.
Exemple: Si introduïm a la calculadora aquesta seqüència 2 + 3 * 4 = la calculadora pot obtenir 20 o 14 com a solució.
39. Fixa’t en els exemples i fes les operacions:
• 12 – 2 · 4 = 12 – 8 = 4
• (17 – 5) : 3 = 12 : 3 = 4
a) 8 + 5 · 2 =
b) 15 – 10 : 5 =
c) 4 · 6 – 13 =
d) (15 – 3) : 4 =
40. Resol mentalment i compara els resultats:
a) 2 + 3 · 4 = (2 + 3) · 4 =
b) 6 – 2 · 3 = (6 – 2) · 3 =
41. Resol, indicant els passos seguits, i comprova la solució que es dona a la dreta. Si no coincideix, revisa l’exercici.
a) 6 · 4 – 2 · (12 – 7) ⎯→ 14
c) 26 – 5 · (2 + 3) + 6 ⎯→ 7
d) (14 + 12) : 2 – 4 · 3 ⎯→ 1
e) 2 · (6 + 4) – 3 · (5 – 2) ⎯→ 11
b) 3 · 8 – 8 : 4 – 4 · 5 ⎯→ 2
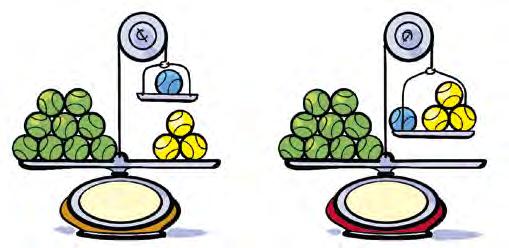
42. Escriu una expressió amb els nombres 9, 3 i 1 el resultat de la qual sigui el pes que marca cada balança: A
• Potència. És una manera abreujada d’escriure un producte de factors iguals: a · a · a · a · a = a5 .
Exemple: 3 · 3 · 3 · 3 = 34 → Tres elevat a quatre o tres elevat a la quarta potència.
2 · 2 · 2 · 2 · 2 = 25 → Dos elevat a cinc o dos elevat a la cinquena potència.
– En les potències, el factor repetit es diu base i el nombre de vegades que es repeteix, exponent
F3. Completa per calcular, amb llapis i paper, el valor de 75.
75 = 7 · 7 · 7 · 7 · 7 = (7 · 7) · (7 · 7) · 7 = 49 · 49 · 7 = · 7 =
F4. Quin és el valor de x en cada cas?
a) x3 = 125 8 x =
b) 5x = 3.125 8 x =
F5. Calcula i completa amb la quantitat que correspongui:
2 · (112 – 92) – 62 = 2 · (121 – ) – 62 = = 2 · – = – =
43. Expressa amb una potència:
a) 6 · 6 =
b) 7 · 7 · 7 =
c) 3 · 3 · 3 · 3 · 3 · 3 =
44. Llegeix aquestes potències i expressales en forma de producte:
a) 27 =
b) 93 =
c) 152 =
d) 106 =
45. Completa la taula:
F3. Completa:
52 = 5 · 5 = 25
53 = (5 · 5) · 5 = 25 · 5 =
54 = (5 · 5) · (5 · 5) =
F4. 7x = 2.401 8 Quant val x ?
Amb la calculadora senzilla:
7*7=== {∫∫∫∫“¢≠‘}
46. Calcula l’exponent en cada cas:
a) 2x = 256 =
b) 10x = 10.000 =
c) 7x = 2.401 =
d) 13x = 2.197 =
47. Un pelegrí arriba molt cansat a un alberg i paga una moneda per passarhi la nit. Com que van arribant més viatgers, l’hostaler dobla el preu, i el pelegrí paga dues monedes per la segona nit. La tercera nit l’hostaler torna a doblar el preu i la quarta, també. Finalment, un cop totalment recuperat, el pelegrí abandona l’allotjament.
a) Expressa amb potències el total pagat pel pelegrí.
b) Calcula el valor d’aquesta expressió.
• Potència de base 10. És igual a la unitat seguida de tants zeros com indica l’exponent.
Exemple: 109 = 1.000.000.000 105 = 100.000
9 zeros
5 zeros
• Expressió abreujada de nombres grans. Els nombres acabats en zeros poden expressarse com a producte d’un nombre per una potència de base 10.
Exemple: 400.000 = 4 · 100.000 = 4 · 105
• Descomposició polinòmica d’un nombre. Es tracta d’expressar un nombre com una suma de nombres naturals multiplicats per potències de base 10.
Exemple:
800.000
836.279 =
48. Escriu com a potències de base 10:
a) Un miler =
b) Un milió =
c) Mil milions =
d) Un bilió =
49. Expressa amb totes les xifres:
a) 4 · 105 =
b) 15 · 109 =
c) 86 · 1014 =
50. Escriu el valor de x en cada cas:
a) 2.936.428 ≈ 29 · 10 x →
b) 3.601.294.835 ≈ 36 · 10 x →
c) 19.570.000.000.000 ≈ 20 · 10 x →
51. Escriu la descomposició polinòmica dels nombres següents:
a) 74.238 =
b) 680.290 =
c) 4.528.926 =
52. Escriu en forma abreujada les dades següents:
a) El nombre de molècules elementals en un litre d’aigua és 334.326.000.000.000.000.000.000.
b) L’estrella Alfa Centauri està a uns quaranta bilions de quilòmetres del Sol.
53. Transforma com en l’exemple:
• 180.000 = 18 · 104
a) 5.000 =
b) 1.700.000 =
c) 4.000.000.000 =
54. Arrodoneix a la centena de miler i escriu de manera abreujada amb el suport d’una potència de base 10 el nombre d’habitants de cada ciutat:
casablanca: 5.899.000 parís: 10.858.000
san francisco: 5.929.000
• Potència d’un producte (producte de potències amb el mateix exponent). La potència d’un producte és igual al producte de les potències dels factors.
(a · b)n = an · bn
(2 · 3)3 = 63 = 6 · 6 · 6 = 216
23 · 33 = (2 · 2 · 2) · (3 · 3 · 3) = 8 · 27 = 216
→ (2 · 3)3 = 23 · 33
• Potència d’un quocient (quocient de potències amb el mateix exponent). La potència d’un quocient és igual al quocient de les potències del dividend i del divisor.
(a : b)n = an : bn
(6 : 3)3 = 23 = 2 · 2 · 2 = 8
63 : 33 = (6 · 6 · 6) : (3 · 3 · 3) = 216 : 27 = 8
→ (6 : 3)3 = 63 : 33
• No et confonguis! La potència d’una suma (o una resta) no és igual a la suma de les potències dels sumands.
(a + b)n ≠ an + bn (2 + 3)4 ≠ 24 + 34
(a – b)n ≠ an – bn
Exemple: Exemple: Exemple:
F6. Fixa’t en els exemples resolts a la dreta i, seguint els mateixos procediments, completa:
a) 25 · 55 = ( · )5 = 5 =
b) 184 : 94 = ( : )4 = 4 =
c) 63 · 53 = ( · )3 = 3 = ( · 10)3 = 3 · 103 =
= · 1.000 =
d) (85 · 65) : 245 = ( · )5 : 245 = 5 : 245 = ( : 24)5 =
= 5 =
55. Reflexiona i calcula de la forma més senzilla:
a) 53 · 23 =
b) 42 · 52 =
c) 252 · 42 =
d) 352 : 52 =
e) 183 : 63 =
f) 214 : 74 =
g) 1003 : 503 =
• 56 · 26 = (5 · 2)6 = 106 = 1.000.000
• 123 : 43 = (12 : 4)3 = 33 = 27
• 54 · 44 = (5 · 4)4 = 204 = (2 · 10)4 = = 24 · 104 = 16 · 10.000 = 160.000
• (66 · 56) : 156 = (6 · 5)6 : 156 = = 306 : 156 = (30 : 15)6 = 26 = 64
56. Calcula i observa que els resultats no coincideixen: (5 + 2)3 = 53 + 23 =
57. Calcula:
a) (10 – 6)2 – (10 – 8)3 =
b) (13 – 3)2 · (7 + 3)2 + (15 – 5)2 · 10 =
• Producte de potències amb la mateixa base. Per multiplicar dues potències amb la mateixa base, es deixa la base i es sumen els exponents.
am · an = am + n
Exemple:
• Quocient de potències amb la mateixa base. Per dividir dues potències de la mateixa base, es deixa la base i es resten els exponents.
am : an = am – n
• Potència d’una altra potència. Per elevar una potència
una altra potència, es deixa la mateixa base i es multipliquen els exponents.
(an)m = an m
Exemple: Exemple:
Tingues en compte. La potència zero d’un
58. Expressa amb una única potència:
a) 54 · 53 = b) 86 · 23 =
c) 32 · 64 = d) 44 · 53 =
e) 26 : 22 = f ) 38 : 35 =
g) 107 : 106 = h) a10 : a6 =
59. Redueix a una única potència:
a) (52)3 = b) (25)2 =
c) (103)3 = d) (a5)3 =
e) (m2)6 = f) (x4)4 =
60. Substitueix cada asterisc per l’exponent que correspongui:
a) 64 · 63 = 6* = b) a5 · a3 = a* =
c) m3 · m* = m9 = d) 26 : 24 = 2* =
e) a9 : a8 = a* = f) m8 : m* = m6 =
g) (42)3 = 4* = h) (a2)2 = a* =
i) (m4)* = m12 = j) (x*)2 = x12 =
61. Calcula:
a) 184 : (24 · 34) =
b) (35 · 33) : 36 =
c) (45)2 : (47 : 43) =
d) (62 · 65) : (63 · 64) =
e) (407 : 57) : (25 · 45) =
62. Escriu els exponents i calcula:
a) La Montse té una capsa amb molts cubs de goma d’1 cm d’aresta. Construeix tres cubs iguals de 3 cm d’aresta.
Nombre de cubs utilitzats: 3 =
b) Un pagès planta enciams al seu hort. Els distribueix en 25 solcs i en cada solc hi posa 25 enciams.
Nombre d’enciams: 25 =
c) Un camió de repartiment porta 6 palets de caixes de llet. En cada palet hi ha 36 caixes i en cada caixa, 6 brics de litre.
Nombre de litres: 6 =



• Arrel quadrada. És l’operació inversa d’elevar al quadrat.
b2 = a
ba ab 2 ) ==
Exemple: 42 = 16 → 16 16 = 4
√— a = b
⎯→ Es llegeix: L’arrel quadrada de a és igual a b.
• Arrels exactes i arrels enteres. Els quadrats dels nombres naturals s’anomenen quadrats perfectes. L’arrel quadrada d’un quadrat perfecte és una arrel exacta.
Exemple:
93==1211140020 = 9 = 3 121 = 11
• L’arrel de la majoria de nombres no coincideix amb una quantitat exacta d’unitats senceres. En aquest cas, al nombre natural que més s’aproxima, per sota, a l’arrel, l’anomenem arrel entera.
Exemple:
62 = 36 < 40
72 = 49 < 40
Exemple: 3.900 = 62 →
L’arrel entera de 3.900 és 62.
622 = 3.844 < 3.900 = 40 40 → 6 < < 7 →
L’arrel quadrada de 40 és un nombre comprès entre 6 i 7. ≈ 6 →
L’arrel entera de 40 és 6.
• Càlcul de l’arrel quadrada per tempteig. Es tracta de trobar el nombre natural el quadrat del qual és igual o s’aproxima més al radicand.
602 = 3.600 < 3.900
632 = 3.969 < 3.900
63. Observa l’exemple i completa:
• →
a) 49 7… " = →
b) 64 " = →
c) 81 " = →
65. Encercla els quadrats perfectes:
66. Una finca quadrada té 900 metres quadrats de superfície. Quants metres lineals de xarxa metàl·lica caldria comprar per tancarla? de 25 s’arrelé iguala 25 5L 5. " = de 25 s’arrelé iguala 25 5L 5. " =
64. Calcula, per tempteig, l’arrel exacta o l’entera:
b) 121 =
c) 1.785 =

Els passos per calcular una arrel quadrada són els següents:
Exemple
Calculem . 105674 :
1 Separem de dos en dos, des de la dreta, les xifres del radicand i calculem l’arrel del paquet de l’esquerra `j
√10 . 56 . 74
3 · 3 → –9
3 ← A A = 10 = 3 i queda 1 de residu.
6 ← B B: Escrivim el doble de A. 1
2 Baixem el paquet següent (56) i busquem la xifra c , de manera que 6 c × c sigui tan proper a 156 com sigui possible, sense sobrepassarlo.
√10 . 56 . 74 3
–9 ↓↓ 6 c × c
1 56
√10 . 56 . 74 3
–9 62 × 2 = 124
c = 2 156
6 2
3 Pugem el valor c = 2 al camp de la solució, baixem el paquet següent (74) i repetim el procés.
√10 . 56 . 74 32
–9 62 × 2 = 124
156 64 d × d
–124
4 Pugem el valor d = 5 al camp de la solució.
Solució:
.105674325=
Prova: 3252 + 49 = 105.674
√10 . 56 . 74 32
62 × 2 = 124
• En algunes calculadores, la successió de tecles per calcular .105674 és la següent:
105.674 $ → {«“∞…≠|∞………}
• En d’altres, és la següent:
$ 105.674 = → {«“∞…≠|∞………}
67. Completa les arrels següents resoltes mitjançant l’algorisme:
1. Tradueix al sistema decimal aquests nombres de l’antic Egipte:
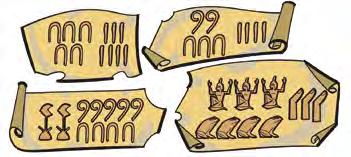
2. Escriu segons el sistema additiu egipci cada un d’aquests nombres:
a) 48:
b) 235:
c) 2.130:
3. Expressa en xifres romanes:
a) 87:
b) 425:
c) 2.600:
4. Cert o fals?
a) Un milió equival a mil centenes.
b) Mil vegades un milió fan un giga.
c) Un bilió té un milió de milions. Aproximacions
5. Completa la taula:
6. Segons va publicar un diari, la població de la capital d’Egipte, el juny de 2022, era de 21.750.020 habitants. Si et preguntessin per aquesta xifra i no recordessis la quantitat exacta, què respondries?
7. Llegeixes, en un anunci, que un habitatge es ven per 293.528 €. Uns quants dies després ho comentes amb una amiga, però no recordes exactament el preu. Quina de les expressions següents triaries per transmetre la informació? Explica per què.
a) Costa gairebé trescents mil euros.
b) Costa doscents mil euros i escaig.
c) Costa doscents noranta mil euros.
8. Aquests són els números de diverses habitacions en un hotel de platja: 401; 235; 724; 231.
a) Una de les habitacions és al final del passadís. Quina és?
b) Una altra és a l’última planta. Quin número té?
c) Quines habitacions són al mateix pis?
Operacions
Suma i resta
9. Calcula mentalment:
a) 5 + 7 – 3 – 4 =
b) 10 – 6 + 3 – 7 =
c) 12 + 13 + 8 – 23 =
10. Calcula:
a) 47 – (35 – 28) =
b) 52 – (36 – 27) =
c) 128 – (86 – 45 – 12) =
11. Calcula i comprova el resultat amb les solucions que hi ha a sota:
a) 5 – [7 – (2 + 3)] =
b) 3 + [8 – (4 + 3)] =
c) 2 + [6 + (13 – 7)] =
d) 7 – [12 – (2 + 5)] =
Solucions: a) 3; b) 4; c) 14; d) 2.
Multiplicació i divisió
12. Multiplica:
a) 128 · 10 =
b) 85 · 100 =
c) 134 · 1.000 =
13. Calcula el quocient i el residu en cada cas:
a) 2.647 : 8 =
b) 1.345 : 29 =
c) 7.482 : 174 =
14. En Raül té 65 € i està estalviant per comprarse un monopatí que costa 105 €.
a) Quant de temps trigarà a poderse’l comprar, si estalvia 5 € a la setmana? I si estalvia 6 €?
b) Quin ha de ser l’estalvi setmanal si vol aconseguir el seu objectiu en quatre setmanes?
c) Aconseguirà comprarse’l en tres setmanes si estalvia 13 € cada setmana?
Operacions combinades
15. Fes els càlculs següents:
a) 2 · (4 + 6) =
b) 2 · 4 + 6 =
c) 8 : (7 – 5) =
d) 5 · 7 – 5 =
e) (5 + 6) · 4 =
f) 5 + 6 : 3 =
16. Calcula:
a) 8 + 7 – 3 · 4 =
b) 8 : 4 + 7 – 3 =
c) 15 – 2 · 3 – 5 =
d) 10 – 12 : 6 – 4 =
e) 4 · 7 – 13 – 2 · 6 =
f) 15 : 3 + 7 + 4 : 2 =
g) 5 · 6 – 4 · 7 + 2 · 5 =
17. Calcula i comprova el resultat amb les solucions:
a) 30 – 4 · (5 + 2) =
b) 5 + 3 · (8 – 6) =
c) 3 · (2 + 5) – 13 =
d) 2 · (7 + 5) – 3 · (9 – 4) =
e) 4 · (7 – 5) + 3 · (9 – 7) =
f) 3 · 5 – 3 · (10 – 4 · 2) =
g) 2 · 3 + 5 · (13 – 4 · 3) =
18. Relaciona cada enunciat amb dues de les expressions de sota:
I. En un autobús urbà hi anaven 50 passatgers. A la primera parada en baixen 16 i en pugen 4.
II. La classe de música té 50 estudiants matriculats, però avui n’han faltat 4 i 16 han anat a un concert.
III. L’Ernest va comprar una samarreta de 16 € i una gorra de 4 € i va pagar amb un bitllet de 50 €.
IV. A l’hotel hi ha 50 clients. Avui n’entren 16 de nous i en surten 4.
a) 50 – 16 – 4 b) 50 – 16 + 4 c) 50 – (16 + 4)
d) 50 – (16 – 4) e) 50 + (16 – 4) f) 50 + 16 – 4
Solucions: a) 2; b) 11; c) 8; d) 9; e) 14; f) 9; g) 11
19. Quina o quines de les expressions aritmètiques responen a la solució d’aquest problema?
En un supermercat s’han venut aquest matí 24 kg de pomes a 2 €/kg, 12 melons a 4 € la peça i 13 pinyes a 2 € cada una. Quant s’ha ingressat a la caixa per la venda d’aquestes fruites?
a) 24 · 12 + 4 · 13 + 2 b) 24 · 2 + 12 · 4 + 13 · 2
c) (24 + 13) · 2 + 12 · 4 d) (24 + 13 + 2) · (2 + 4)
Càlcul de potències
20. Calcula mentalment:
a) 24 = b) 35 =
c) 204 = d) 300 =
21. Resol amb la calculadora:
a) 412 = b) 510 =
c) 453 = d) 993 =
22. Escriu tots els quadrats perfectes compresos entre 1.000 i 1.500.
23. Completa:
Potències de base 10. Expressió abreujada de nombres grans
24. Escriu amb totes les xifres:
a) 102 =
b) 106 =
c) 1010 =
25. Escriu amb potències de base 10:
a) Cent = b) Cent milions =
c) Cent bilions = d) Cent mil bilions =
26. Ordena, de la més petita a la més gran, aquestes quantitats:
8 · 109 17 · 107 98 · 106 1010 16 · 108 9 · 109
27. Calcula de la manera més senzilla:
a) 82 · 52 = b) 26 · 56 =
c) 253 · 43 = d) 65 : 35 =
e) 153 : 53 = f) 204 : 54 =
28. Redueix aquestes expressions:
a) x8 : x3 = b) m4 · m2 =
c) (k2)4 = d) x5 · x5 =
29. Redueix a una sola potència:
a) (a7 : a) · a3 =
b) (x9 : x4) : x3 =
c) (x3 · x7) : (x · x6) =
30. Substitueix cada asterisc pel nombre adequat i, finalment, calcula:
a) 212 : 45 = 212 : (2*)5 = 212 : 2* = 2* =
b) 36 : 92 = 36 : (3*)2 = 36 : 3* = 3* =
c) 253 : 54 = (5*)3 : 54 = 5* : 54 = 5* =
d) 164 : 45 = (4*)4 : 45 = 4* : 45 = 4* =
31. Resol amb la calculadora:
a) 655 = b) .1024 =
c) .1369 = d) .4225 =
e) .12664 = f) .33856 =
32. Escriu el signe = o el signe ≠ segons correspongui:
a) 2 · 9 36 b) 3 · 4 12
c) 5 · 16 20 d) 4 · 25 10
e) 9 · 9 18 f) 4 · 4
Deixa clar el significat de cada pas, de cada operació i de cada resultat.
Un majorista compra 150 sacs de patates de 30 kg per 2.000 €. Després, en seleccionar la mercaderia, en llença 300 kg i n’envasa la resta en bosses de 5 kg, que ven a 4 € la bossa. Quin benefici obté?

– Quilos comprats (150 sacs de 30 kg): 150 · 30 = 4.500 kg
– Quilos envasats (en llença 300 kg): 4.500 – 300 = 4.200 kg
– Bosses de 5 kg obtingudes: 4.200 : 5 = 840 bosses
– Ingressos, en euros, per la venda de 840 bosses a 4 € cada una: 840 · 4 = 3.360 €
– Beneficis (ingressos, 3.360€, menys despeses, 2.000 €): 3.360 – 2.000 = 1.360 €
Solució: Guanya 1.360 €
34. En una granja hi ha el doble de vaques que de cavalls i en total són 36 caps de bestiar. Quantes vaques i quants cavalls hi ha?

36. Un autobús amb 54 turistes a bord pateix una avaria camí de l’aeroport. El responsable del grup decideix acomodar les viatgeres i els viatgers en taxis de quatre places. Quants taxis necessiten?

37. En una escola que té 450 estudiants, dos de cada cinc estudien un segon idioma i, d’aquests, un de cada tres ha triat l’alemany. Quants estudien un segon idioma? Quants estudien alemany?
35. La Rosa té dos anys més que el seu germà petit, en Julià, i dos menys que l’Albert, el seu germà gran. Si entre tots tres igualen l’edat de la seva mare, la Marta, que acaba de fer 42 anys, quants anys té cada un dels germans?
38. PROBLEMA RESOLT
Decideix els passos intermedis. Quines dades encara no coneixes, però necessites, per arribar a la solució?
La Marta ha comprat cinc paquets amb quaranta adhesius cada un i ha decorat el cub petit. Li queden prou adhesius per decorar de la mateixa manera el cub gran?

• Quants adhesius ha comprat?
Ha comprat 5 · 40 = 200 adhesius.
• Quants n’ha utilitzat per al cub petit?
Per al cub petit ha utilitzat 6 · 32 = adhesius.
• Quants adhesius li queden?
Li queden 200 – = adhesius.
• Quants en necessita per al cub gran?
Per al cub gran necessita
Escriu la solució en cada cas.
39. Un cotxe triga 78 segons a travessar un tram de 2 km amb la velocitat limitada a 90 km/h. Creus que ha superat el límit permès? Per què?
43. Escriu les preguntes dels dos apartats del problema tenint en compte la seva resolució:
En Raül vol completar un àlbum de cromos d’una lliga de futbol de 20 equips i 25 jugadors per equip. L’àlbum li costa 5 € i cada paquet de 10 cromos, 1 €. Resolució:
a) (20 · 25) : 10 = 50
40. Quines són les dimensions del terra quadrat més gran que es pot cobrir amb 200 rajoles quadrades de 20 cm de costat, sense partirne cap? Quantes rajoles sobren?
41. En Marc té una bossa amb 50 daus de fusta d’1 cm d’aresta. Quina és l’aresta del cub més gran que pot construir amb els daus? Quants daus sobren?
b) [(20 · 25) : 10] · 1 + 5 = 55
42. Imagina’t que col·loques un granet d’arròs a la primera casella d’un tauler d’escacs, dos a la segona, quatre a la tercera, etc., i continues doblant el nombre de granets escac a escac. Expressa amb potències:
a) El nombre de grans que necessitaries per completar la primera fila.
44. Planteja un problema i escriu l’enunciat i les preguntes a partir de la informació i les operacions següents:
– Consola de 8 gigabytes de memòria RAM
– Un videojoc A ocupa 3,68 gigabytes
– Un videojoc B ocupa 3,75 gigabytes
– Un videojoc C ocupa 2,48 gigabytes
– 3,68 + 3,75 + 2,48 = 9,91 gigabytes
– 9,91 – 8 = 1,91 gigabytes
– 3,68 + 3,75 = 7,43 gigabytes
– 3,68 + 2,48 = 6,16 gigabytes
– 3,75 + 2,48 = 6,23 gigabytes

b) El nombre de grans que hauries de col·locar a l’últim escac de la segona fila.
c) Compara els resultats obtinguts en els dos apartats anteriors.
Nombres en els ordinadors
Ja saps que nosaltres, per escriure els nombres, fem servir el sistema decimal, amb deu signes, del 0 al 9. Els ordinadors i les calculadores, en el seu llenguatge intern, escriuen els nombres en el sistema binari; és a dir, utilitzant només dos signes: el 0 i l’1
• Estudia i completa les taules, seguint la lògica de les primeres files.
Quan hagis acabat, hauràs traduït al sistema binari els primers quinze nombres naturals.
La computació i, en general, les noves tecnologies, són un àmbit d’aplicació de les matemàtiquess amb molta diversitat de sortides professionals.
Nombres imparells, quadrats i cubs
El món dels nombres presenta múltiples relacions, algunes de tan sorprenents que semblen màgia. Fixa’t en l’exemple següent:
• Segons això, calcula la suma dels set primers nombres imparells S
1. Omple els buits:
a) 18 · = 180
b) · 100 = 27.000
c) 4.000 : = 40
d) : 10 = 38
2. Calcula els termes que falten:
a) 154 · = 462
b) : 27 = 98
c) 30.275 : = 35
d) 1.508 = · 125 + 8
3. Fes les operacions combinades següents:
a) 12 + 3 · 5 – 2 =
b) 19 – 5 · (10 – 7) + 4 · 7=
c) 7 · 3 – 4 · 2 + 2 =
d) 10 · [7 · 5 – (4 + 6 · 3)] =
4. Llegeix:
• L’extensió del Brasil és de vuit milions cinccents catorze mil vuitcents setantaset quilòmetres quadrats.
• La població mundial a finals de l’any 2022 era de 7.975.105.155 habitants.
a) Expressa amb xifres la primera quantitat i amb lletres, la segona.
5. En una cafeteria hi ha 60 seients. Si hi ha el triple de cadires que de banquetes, quantes n’hi ha de cada classe?
b) Arrodoneixles a les desenes de miler.
6. Calcula:
a) 26 =
b) 53 =
c) 72 =
d) 106 =
7. Redueix a una sola potència:
a) a3 · a2 =
b) x5 : x4 =
c) (a3)4 =
8. Quants daus de fusta, d’1 cm d’aresta, hi ha en 10 paquets com el que veus en la il·lustració?

10 cm 10cm 10cm
9. Copia i completa:
a) 36= b) 400=
c) .10000= d) = 3
e) = 8 f) = 30
La Laia sempre ha somniat ser astronauta i viatjar a l’espai. Per començar, aquest estiu vol visitar algunes de les seus de l’Agència Espacial Europea (European Space Agency, ESA) i, per aconseguir els diners que li calen, s’ha proposat estalviar amb un mètode que li sembla infal·lible.
El primer dia posarà a la guardiola una moneda d’1 €, el segon dia dues monedes d’1 €, el tercer dia quatre monedes d’1 €... i, així, successivament, cada dia posarà a la guardiola el doble que el dia anterior.
Si estalvia durant 10 dies, quantes seus de l’ESA creieu que podrà visitar?
Què us sembla aquesta manera d’estalviar?


1. Quina quantitat haurà de posar, la Laia, a la guardiola el quart dia? I quina quantitat tindrà acumulada després de fer-ho? Completa:
2. Observeu i completeu l’evolució de la quantitat de diners que posa cada dia a la guardiola i l’estalvi que acumula:
3. Expresseu les dades de l’activitat anterior amb potències:
4. Quants dies han de passar fins que hagi de posar més de 100 € a la guardiola? I més de 200 €?
6. Feu-vos les dues preguntes anteriors, però en cas que hi hagi de posar més de 1.000 €.
5. Quant haurà estalviat en aquell moment, comptant el que hi ha posat aquell dia?

9. Si estalvia durant 10 dies, quantes seus de l’ESA creieu que podrà visitar?
10. Què us sembla aquest mètode d’estalvi?
7. Us atreviu a respondre les preguntes anteriors per a quantitats més grans? Quant trigaria a estalviar 1.000.000 €?
8. I si, en lloc de posar a la guardiola cada dia el doble de diners que el dia anterior, n’hi posés el triple, quant trigaria a estalviar 1.000.000 €?

Reflexioneu sobre l’ODS 8: Treball digne i creixement econòmic. Què heu Penseu-hi!après?
Treballeu en equip.

Vivim en societat i la majoria de les nostres accions, de les decisions que prenem, dels interessos que perseguim i de les emocions que sentim tenen a veure amb les persones amb qui ens relacionem. Això es reflecteix en els diferents grups del nostre dia a dia dels quals formem part: la família, la classe, els amics, les extraescolars, les activitats d’oci…
Durant la nostra vida conviurem amb grups de persones diferents i la qualitat d’aquesta convivència dependrà del nostre comportament individual. L’empatia, la inclusió, la igualtat, la tolerància, etc. definiran la societat en la qual volem viure. La Mariona i en Marc observen les dinàmiques de grup de diferents activitats extraescolars que es duen a terme a l’institut. Han apreciat que els grups es conformen segons les edats i el gènere dels companys i les companyes. Les monitores sempre intenten fer grups tenint en compte la inclusió i la igualtat de gènere. Busquen totes les maneres de distribuir els participants en grups equilibrats, sense que ningú en quedi exclòs.
La Mariona i en Marc decideixen fer un estudi per mirar d’establir la millor manera de distribuir els equips.
PENSEU-HI!
• Quina creieu que és la millor manera d’agrupar?
• Els resultats de l’equip dependran de com estan fets els grups?

La relació de divisibilitat
Múltiples i divisors d’un nombre

Nombres primers i nombres compostos
Descomposició d’un nombre en factors primers
Mínim comú múltiple
Màxim comú divisor
• Dos nombres compleixen la relació de divisibilitat quan un cap en l’altre una quantitat exacta de vegades; és a dir, quan el seu quocient és exacte
• Ser múltiple de..., ser divisor de... Quan dos nombres compleixen la relació de divisibilitat: el més gran és múltiple del més petit i el més petit és divisor del més gran.
a és múltiple de b
o, dit d’una altra manera, si la divisió a : b és exacta.
b és divisor de a
a b 0 c ↓ divisió exacta
a és divisible per b. a és múltiple de b. b és divisor de a.
• Els divisors van per parelles. Cada divisor d’un nombre en té un altre de relacionat.
Exemple:
40 8 0 5
8 és divisor de 40. 5 és divisor de
F1. Fixa’t en aquestes divisions i completa:
a) 35 5 0 7
35 és divisible per
35 és múltiple de
5 és divisor de
b) 86 12 02 7
divisible per
múltiple de
divisor de
F2. Comprova si els nombres de cada parella compleixen la relació de divisibilitat. Després, completa:
a) 63 i 9
63 divisible per
63 és de
9 és de
b) 78 i 13
per
múltiple de
divisor de
F3. Una escola contracta autobusos de 45 places per portar 294 alumnes d’excursió.
a) Quants autobusos necessita? Aniran tots plens?
b) I si els autobusos fossin de 42 places?
c) 45 és divisor de 294? I 42?
5
F1 i F2. Observa els exemples:
560 40 160 14 0 És exacta.
560 és divisible per 40.
560 és múltiple de 40.
40 és divisor de 560.
47 7 5 6
47 no és divisible per 7.
47 no és múltiple de 7.
7 no és divisor de 47.
F3. Comprova si les divisions següents són exactes: 294 : 45 294 : 42
1. Pensa i contesta de manera raonada:
a) Es pot dividir una classe de 30 alumnes en grups de 7, sense que en sobri cap?
b) La Marta fa passos de 60 cm. Pot recórrer 100 metres en un nombre exacte de passos?
4. Busca tots els nombres que estan continguts una quantitat exacta de vegades en 24.
c) Pot buidar-se una tina d’oli de 1.500 litres en un nombre exacte de garrafes de 5 litres?
5. Encercla de color vermell els divisors de 90 i de color blau els múltiples de 3:
6. Respon de manera raonada:
a) Per què 522 és múltiple de 29?
d) Algun mes té un nombre exacte de setmanes?
b) Per què 17 és divisor de 544?
2. Digues si els nombres de cada parella compleixen la relació de divisibilitat:
a) 224 i 16 →
b) 420 i 35 →
c) 613 i 13 →
d) 513 i 19 →
e) 688 i 44 →
f) 2.070 i 46 →
3. Digues si les afirmacions següents són certes o falses:
a) 15 està contingut exactament 4 vegades en 60.
b) 75 està contingut exactament 3 vegades en 225.
c) 42 és divisible per 7.
d) 54 és divisible per 8.
e) 13 està contingut un nombre exacte de vegades en 65.
7. Encercla de color vermell els múltiples de 4 i de color blau els múltiples de 10:
8. En el grup de bàsquet d’extraescolars, s’hi han inscrit gairebé 60 nois i noies de 1r i 2n d’ESO. Per organitzar un torneig, havien pensat fer equips mixtos de cinc. S’adonen, però, que fent-ho així algú es quedaria sense equip, i decideixen fer equips de sis, incloent-hi dos reserves per equip. Quants alumnes hi ha inscrits?
• Càlcul dels múltiples d’un nombre. Has de tenir en compte que:
– Els múltiples d’un nombre natural, a, s’obtenen en multiplicar a per qualsevol altre nombre natural k. a · k → múltiple de a
– Qualsevol nombre natural, a, és múltiple d’ell mateix i de la unitat. → a · 1 = a
– Un nombre diferent de zero té una quantitat infinita de múltiples.
– Per referir-nos a un múltiple d’un nombre, el podem escriure amb un punt a sobre: • 7 → múltiple de 7
• Càlcul dels divisors d’un nombre. Has de tenir en compte que:
– Per obtenir tots els divisors d’un nombre, a, busquem les divisions exactes:
a : b = c a : c = b → a = b · c → Per tant, b i c són divisors de a.
– Qualsevol nombre és divisor d’ell mateix. → a : a = 1
– L’1 és divisor de qualsevol nombre. → a : 1 = a
F4. Escriu:
a) Tres múltiples de 5.
b) Tres múltiples de 12.
c) Tres múltiples de 19.
d) Tres múltiples de 30.
F5. Escriu els deu primers múltiples de 25.
F6. Quin és el primer múltiple de 8 més gran que 100?
F7. Troba, mentalment, els divisors de cada un d’aquests nombres:
a) 8 b) 12 c) 15 d) 20 e) 28
F8. Quin és el nombre els divisors del qual són els següents?
Els divisors de 18 són aquests: 1 2 3 18 9 6
F4. Múltiples de 13:
13 · 3 = 39
13 · 5 = 65
13 · 11 = 143
13 · =
F5. Quin és el primer múltiple de 13 més gran que 150?
·
= 143 < 150 13 · 12 = 156 > 150
F7 i F8. Divisors de 14:
2 7 14
• Criteris de divisibilitat. Són regles que serveixen per descobrir si un nombre és divisible per 2, 3, 5 o altres nombres senzills.
– Un nombre és divisible per 2 (és múltiple de 2) si acaba en una xifra parell: 0 - 2 - 4 - 6 - 8.
Exemple: 516 → xifra parell → 516 és múltiple de 2. 371 → xifra senar 371 no és múltiple de 2.
– Un nombre és divisible per 5 (és múltiple de 5) si acaba en 0 o en 5. Un nombre és divisible per 10 (és múltiple de 10) si acaba en 0.
Exemple: 325 → és múltiple de 5. 560 → és múltiple de 5 i de 10. 703 → no és múltiple ni de 5 ni de 10.
– Un nombre és divisible per 3 (és múltiple de 3) si la suma de les seves xifres és múltiple de 3. Un nombre és divisible per 9 (és múltiple de 9) si la suma de les seves xifres és múltiple de 9.
Exemple: 411 → 4 + 1 + 1 = 6 411 és múltiple de 3, però no de 9.
– Un nombre és divisible per 11 si la suma de les xifres de lloc parell menys la suma de les xifres de lloc senar és 0 o un múltiple d’11.
Exemple: 418 → (4 + 8) – (1) = 11 → És múltiple d’11. 1.543 → (5 + 3) – (1 + 4) = 3 → No és múltiple d’11.
F9. Quins d’aquests nombres són parells? I divisibles per 2?
21 - 28 - 45 - 59 - 80 - 88 - 146 - 255 - 270 - 299
Parells:
Divisibles per 2:
F10. Subratlla els que siguin múltiples de 5:
60 - 72 - 80 - 85 - 100 - 103 - 130 - 155 - 210
Quins dels nombres que has subratllat són també múltiples de 10?
F11. Quins d’aquests nombres són divisibles per 3? I per 9?
19 - 45 - 63 - 83 - 105 - 145 - 209 - 513 - 666 - 909
Divisibles per 3:
Divisibles per 9:
F12. Recorda el criteri de divisibilitat per 11 i identifica quins dels nombres següents són múltiples d’11: a b c 8 a + c – b = 0 o 11
110 - 111 - 155 - 187 - 209 - 398 - 759 - 606
F9. 516 → Acaba en xifra parell. És múltiple de 2.
F10. 325 → Acaba en 5. És múltiple de 5, però no de 10.
560 → Acaba en 0. És múltiple de 5 i de 10.
F11. 411 → 4 + 1 + 1 = 6 → És múltiple de 3 però no de 9.
990 → 9 + 9 + 0 = 18 → És múltiple de 3 i de 9.
• Nombres compostos. Són els nombres que es poden descompondre en factors més senzills.
Exemple: El nombre 18 és un nombre compost perquè es pot descompondre.
• Nombres primers. Són els nombres que no es poden descompondre en factors més senzills.
Exemple: El nombre 13 és primer perquè només es pot dividir per 13 i 1.
• El nombre 1, com que només té un divisor, no es considera primer. Qualsevol altre nombre o bé és primer o bé és compost. →
9. Classifica en nombres primers i nombres compostos:
5 8
11 15 21 28
31 33
Nombres primers:
Nombres compostos:
10. Entre aquests nombres, busca els dos que són primers i expressa els compostos com un producte de dos factors:
67 57 87 47 77
11. Busca tots els nombres primers més petits que 60. Són disset en total.
12. Cert (C) o fals (F)?
a) El nombre 1 no és ni primer ni compost.
b) Un nombre, si és senar, és primer.
c) Tots els nombres primers, excepte el 2, són senars.
13. Descompon el nombre 100:
a) En dos factors.
b) En tres factors.
c) En tants factors com sigui possible.
14. Indica quins nombres són primers i quins són com-
Nombres primers:
Nombres compostos:
15. Esbrina si el nombre 203 és primer o compost. Justifica la teva resposta.
• Un nombre, si no és primer, es pot descompondre en factors (factoritzar), i aquests, al seu torn, en altres factors, fins que tots siguin primers.
Exemple: La descomposició de 36 en factors primers és:
36 = 4 · 9 = 2 · 2 · 3 · 3 = 22 · 32
– Per descompondre un nombre en factors primers, el dividim entre els seus factors primers: primer, entre 2 tantes vegades com sigui possible; després, entre 3, entre 5…, i així, successivament, fins a obtenir 1 en el quocient.
16. Calcula mentalment i completa la descomposició en factors d’aquests nombres:
17. Descompon com en l’exemple:
• 24 = 6 · 4 = 2 · 3 · 2 · 2 = 23 · 3
a) 18 =
b) 20 =
c) 40 =
d) 72 =
e) 150 =
f ) 240 =
18. A quins nombres corresponen aquestes descomposicions factorials?
a) 22 · 32 · 5 =
b) 2 · 5 · 13 =
c) 2 · 52 · 7 =
quocients factors parcials primers
792 2
792 : 2 → 396 2
396 : 2 → 198 2
198 : 2 → 99 3
99 : 3 → 33 3
33 : 3 → 11 11
11 : 11 → 1
792 = 23 · 32 · 11
19. Completa i descompon en factors primers:
42 =
90 = 126 =
20. Descompon en factors primers:
a) 45 b) 76 c) 88
21. Escriu com a producte de nombres primers:
a) 170 =
b) 350 =
c) 580 = d) 888 = e) 1.024 =
f) 1.296 =
• Quina és la relació entre la descomposició d’un nombre i la descomposició dels seus múltiples?
En la descomposició de qualsevol dels múltiples d’un nombre apareixen tots els factors primers del nombre (i, generalment, alguns més).
• Quina és la relació entre la descomposició d’un nombre i la descomposició dels seus divisors?
• En la descomposició de qualsevol dels divisors d’un nombre apareixen alguns factors primers del nombre (generalment, no tots) i no apareix cap factor més.
• Per obtenir els divisors d’un nombre es pot seguir un altre procediment: amb el nombre descompost en factors, busquem tots els productes possibles entre si.
Exemple: Calculem tots els factors primers de 40:
40 = 2 · 2 · 2 · 5
Els divisors de 40 són aquests:
1, 2, 4, 5, 8, 10, 20 i 40
F13. Contesta, sense fer cap operació, i raona les respostes:
a) 8 = 2 · 2 · 2
36 = 2 · 2 · 3 · 3
8 és divisor de 36?
b) 15 = 3 · 5
90 = 2 · 3 · 3 ·
15 és divisor de 90?
F14. Tenint en compte la descomposició en factors de 126, esbrina, a simple vista, quins dels nombres següents són divisors de 126, quins són múltiples de 126 i quins no són ni divisors ni múltiples:
126 = 2 · 3 · 3 · 7 = 2 · 32 · 7
a) 4 = 22
b) 14 = 2 · 7 c) 18 = 2 · 32
d) 21 = 3 · 7 e) 28 = 22 · 7 f ) 42 = 2 · 3 · 7
g) 252 = 22 · 32 · 7 h) 180 = 22 · 32 · 5 i) 882 = 2 · 32 · 72
Divisors de 126:
Múltiples de 126:
Ni múltiples ni divisors:
F15. Escriu factoritzats, sense fer operacions:
a) Tres divisors de 72 = 23 · 32.
b) Tres múltiples de 45 = 32 · 5.
1 = 1
2 = 2
5 = 5
2 · 2 = 4
2 · 5 = 10
2 · 2 · 2 = 8
2 · 2 · 5 = 20
2 · 2 · 2 · 5 = 40
F13 i F14.
• 18 és divisor de 90, perquè tots els factors primers de 18 apareixen en 90.
18 = 2 · 3 · 3
90 = 2 · 3 · 3 · 5
• 210 és múltiple de 15 perquè conté tots els factors primers de 15.
210 = 2 · 3 · 5 · 7
15 = 3 · 5
F15.
• Dos múltiples de 28 = 2 · 2 · 7 2 · 2 · 2 · 7 3 · 2 · 2 · 7
56 84
• Dos divisors de 84 = 2 · 2 · 3 · 7 2 · 2 · 3 · 7 2 · 2 · 3 · 7 4 6
• Mínim comú múltiple, MCM (a, b, c…). És el més petit dels múltiples comuns de dos o més nombres, a, b, c…
– Càlcul del mínim comú múltiple (mètode artesanal). És apropiat per a nombres senzills. Per obtenir el mínim comú múltiple de dos nombres:
1r Escrivim els múltiples de cada un.
2n Agafem els nombres comuns.
3r Ens quedem amb el més petit.
→ 20 40 60 80 … múltiples de 20
→ 30 60 90 120 … múltiples de 30
MCM (20, 30) = 60
– Càlcul del mínim comú múltiple (mètode òptim). S’utilitza per a nombres grans. El procediment és el següent:
1r Es descomponen els nombres en factors primers.
2n Se n’agafen tots els factors primers (comuns i no comuns) elevats a l’exponent més gran.
3r Es multipliquen els factors escollits.
F16. Observa i completa a primer cop d’ull:
MCM (6, 8) =
F17. Calcula el MCM (12, 15) com en l’activitat anterior: Múltiples de :
Múltiples de :
MCM ( , ) =
F18. Completa:
20 = 22 · 5 i 30 = 2 · 3 · 5
MCM (20, 30) = 22 · 3 · 5
MCM (20, 30) = 60
F19. Completa per calcular el mínim comú múltiple de 30 i 45:
Càlcul del mínim comú múltiple de 10 i de 15.
• 10 → 10
•
Múltiples comuns → 30, 60, 90… El més petit dels múltiples comuns de 10 i 15 és 30.
MCM (10, 15) = 30
Càlcul del mínim comú múltiple de 28 i 42.
22. Observa i completa a primer cop d’ull:
• 15 → 15 30 45 60 75 90 105
• 25 → 25 50 75 100 125 150
MCM (15, 25) =
23. Calcula com en l’activitat anterior:
a) MCM (20, 25)
b) MCM (12, 24)
c) MCM (50, 75)
24. Calcula mentalment:
a) MCM (6, 9) =
b) MCM (6, 12) =
c) MCM (5, 10) =
25. Observa, completa i calcula:
=
= = _ ` a b b b
MCM (30, 40) =
MCM (40, 54) =
(30,40)… (40,54)…
26. Calcula el MCM (a, b) en cada cas:
a) a = 2 5 11
b = 3 5 11
b) a = 24 5
b = 22 52
27. Una fàbrica envia mercaderia a Castelló cada 6 dies i a Eivissa cada 8 dies. Avui han coincidit tots dos enviaments. Quan tornaran a coincidir?
28. L’autobús de la línia vermella passa per la parada de davant de casa meva cada 20 minuts i el de la línia verda, cada 30 minuts. Si tots dos passen a les dues de la tarda, a quina hora tornaran a coincidir?

29. En Juli compta de 4 en 4, l’Anna de 6 en 6 i la Sofia de 10 en 10. Quins són els tres primers nombres en els quals coincideixen?
• Màxim comú divisor, MCD (a, b, c…). És el més gran dels divisors comuns de dos o més nombres, a, b, c…
– Càlcul del màxim comú divisor (mètode artesanal). És apropiat per a nombres senzills. Per obtenir el màxim comú divisor de dos nombres:
1r Escrivim els divisors de cada nombre.
2n Agafem els nombres comuns.
3r Ens quedem amb el més gran.
→ 1 2 4 8 divisors de 8
→ 1 2 3 4 6 12 divisors de 12 comuns divisors 4→ 1 - 2 - 4
MCD (8, 12) = 4
– Càlcul del màxim comú divisor (mètode òptim). S’utilitza per a nombres grans. El procediment és el següent:
1r Es descomponen els nombres en factors primers.
2n Agafem només els factors primers comuns elevats a l’exponent més petit.
3r Es multipliquen els factors escollits.
F20. Observa i completa a primer cop d’ull:
Divisors de 12 → 1 2 3 4 6 12
Divisors de 16 → 1 2 4 8 16
MCD (12, 16) =
F21. Calcula com en l’activitat anterior:
MCD (8, 20) =
40 = 22 · 5 i 60 = 22 · 3 · 5
MCD (40, 60) = 22 · 5
MCD (40, 60) = 22 · 5 = 20
Càlcul del màxim comú divisor de 20 i 30.
Divisors de 20
Divisors de 30
Divisors comuns → 1 - 2 - 5 - 10
El més gran dels divisors comuns és 10. MCD (20, 30) = 10
F22. Completa:
40 2225
50 25 5 = = 3
90 25
(40, 50) = ·
F23. Completa per calcular el màxim comú divisor de 90 i 315:
315
MCD (90, 315) =
Càlcul del màxim comú divisor de 60 i 72:
MCD
30. Observa i completa a primer cop d’ull:
Div. de 24 → 1 2 3 4 6 8 12 24
Div. de 30 → 1 2 3 5 6 10 15 30
MCD (24, 30) =
31. Calcula seguint el criteri de l’activitat anterior:
a) MCD (10, 15)
Divisors de :
Divisors de :
MCD ( , ) =
b) MCD (12, 18)
Divisors de :
Divisors de :
MCD ( , ) =
32. Calcula mentalment:
a) MCD (30, 40) =
b) MCD (50, 75) =
33. Completa i calcula:
35. Calcula:
a) MCD (120, 144)
Divisors de :
Divisors de : MCD ( , ) =
b) MCD (140, 180)
Divisors de :
Divisors de : MCD ( , ) =
36. Calcula el MCD (a, b) en cada cas:
a) a = 4 b = 8
b) a = 5 b = 10
37. L’Anna ha tret del forn dues safates: una amb 18 brioixos i l’altra amb 24 ulleres. Encapsa el mateix nombre d’unitats de brioixos i d’ulleres, però no els barreja en la mateixa capsa. Quantes capses creus que ha omplert?
60 = 2 ·
90 = 2 ·
100 = 2 ·
MCD (60, 90) =
MCD (60, 100) =
MCD (90, 100) = →
34. Calcula el MCD (a, b) en cada cas:
a) a = 3 5 11
b = 2 5 11
b) a = 23 52
b = 22 52 7
38. La propietària d’un restaurant compra un bidó de 80 litres d’oli d’oliva i un altre de 60 litres d’oli de gira-sol i vol envasar-los en garrafes iguals, tan grosses com sigui possible, i sense barrejar-los. Quina serà la capacitat de les garrafes?
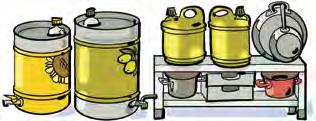
1. Escriu:
a) Els múltiples de 20 compresos entre 150 i 210.
b) Tots els parells de nombres el producte dels quals és 80.
5. Substitueix cada lletra per una xifra, perquè el nombre resultant sigui divisible per 3:
A51 2B8
32C 52D 1E8
A = B = C = D = E =
6. Busca, en cada cas, tots els valors possibles de a per tal que el nombre resultant sigui, al mateix temps, múltiple de 2 i de 3.
4 a 3 2 a 2 4 a
2. Busca tots els divisors dels nombres següents:
a) 18:
b) 20:
c) 28:
d) 39:
e) 50:
3. Busca totes les formes possibles de fer grups iguals amb 72 terrossos de sucre.

4. Escriu:
a) Un nombre de tres xifres que sigui divisible per 3.
b) Un nombre de quatre xifres que sigui divisible per 5.
c) Un nombre de cinc xifres que sigui divisible per 9.
7. El nombre 899 només té quatre divisors; un és el nombre 31. Expressa el nombre 899 com a producte de dos factors diferents d’ell mateix i de la unitat.
8. Descompon en factors primers aquests nombres:
a) 54 =
b) 140 =
c) 200 =
d) 380 =
9. Busca el primer nombre, més gran que 160, que no es pugui expressar com el producte de dos factors diferents d’ell mateix i de la unitat.
10. El mínim comú múltiple de dos nombres és 15. Quins poden ser aquests nombres?
11. Calcula el MCM i el MCD:
a) 25 i 75
b) 12, 18 i 24
12. El producte de tres nombres diferents de la unitat és 75. Quina és la seva suma?
14. En una fruiteria de Lleida envasen sucs de taronja i de poma en caixes amb el mateix nombre d’ampolles. Quantes ampolles hi ha en cada caixa si un client ha rebut 15 ampolles de suc de taronja i 12 de suc de poma?
13. Busca el nombre més petit que en dividir-lo entre 10 i entre 12 té un residu de 5.
15. PROBLEMA RESOLT
Estudia els casos possibles i comprova quins compleixen les condicions del problema.
Una fornada de magdalenes s’envasa en bosses de 6 unitats i una altra d’igual, en bosses de 10 unitats, sense que en sobri cap en tots dos casos. Quantes magdalenes surten en cada fornada si s’han omplert gairebé 50 bosses?

El nombre de magdalenes de cada fornada és un múltiple comú de 6 i de 10 i, per tant, del seu mínim comú múltiple:
MCM (6, 10) = 30
Els múltiples comuns de 6 i 10 són aquests:
30 - 60 - 90 - 120 - 150Completa la taula i acaba el problema:
16. En una classe de 1r d’ESO, es poden fer grups mixtos de 8 nois i noies, sense que en sobri ni en falti cap. D’altra banda, el nombre de nois és una mica més baix que el nombre de noies, encara que ambdós estan equilibrats, i ni ells ni elles no es poden dividir en grups més petits. Què en pots dir si, en total, són menys de 30 alumnes?
20. En l’activitat anterior has completat un problema matemàtic a partir d’unes pistes. Ara et plantegem el repte d’escriure un problema matemàtic sobre múltiples i divisors des d’un inici. Segueix els passos següents:
1. En primer lloc, tingues en compte l’entorn on es desenvoluparà el problema. En aquest cas hem escollit unes classes extraescolars de bàsquet amb 18 esportistes.
17. Volem tallar una cartolina de 48 cm × 60 cm en targetes quadrades que tinguin entre 5 i 10 cm de costat. Quina ha de ser la mida de les targetes per no desaprofitar la cartolina?

2. A continuació, pensa el context del problema per a definir la pregunta que vols fer. Per exemple: a partir d’un nombre conegut d’esportistes, formar grups de manera que es compleixi una condició determinada (que no quedi cap persona sense grup, que quedi un esportista sense grup, que els grups siguin parells, etc.).
18. Els trens a Vall de Dalt surten cada 18 min i els que vam a Vall de Baix, cada 24 min. Si són les 15 h 45 min i surten alhora, quan tornaran a coincidir?
3. Anota les dades que faràs ser vir per definir el problema i pensa la pregunta que vols fer.
Nombre de participants: 18
Pregunta:
4. Tot seguit, resol numèricament el problema.
19. Completa l’enunciat i la resolució del problema amb la informació que falta:
Per anar a treballar, en Marcel pot agafar dos autobusos, un passa cada … minuts i l’altre, cada 10 minuts. Si avui els dos autobusos han coincidit a les … del matí, quan tornaran a coincidir?
15 = 3 · = 2 · 5
MC (15, 10) = · 3 · 5 = 30
Tornaran a coincidir al cap de minuts, és a dir, a les 9.30 h.
5. Finalment, escriu l’enunciat:
En una classe extraescolar de bàsquet amb 18 participants, el monitor vol fer grups de
Els primers valen diners
Els nombres primers s’utilitzen per a la construcció de les claus que protegeixen els comptes bancaris, els ordinadors, els telèfons mòbils, la informació que circula per internet, etc. De fet, per elaborar una clau, es necessiten dos nombres primers secrets. Els fàcils ja s’han descobert i els nous són molt difícils de trobar.
• Busca el primer nombre primer més gran que 1.000.
El 101 és el protagonista
• Què li passa a un nombre de dues xifres si el multipliquem per 101?
29 × 101 =
Fixa’t en altres casos i verifica que sempre passa el mateix.
• Què tenen en comú tots els nombres de quatre xifres que es formen repetint alternativament dues xifres?
Divisibilitat i geometria
Ja has vist en altres ocasions com les característiques i les propietats dels nombres es reflecteixen en relacions i propietats geomètriques. Observa, ara, com la descomposició factorial d’un nombre, per exemple el 24, està relacionada amb les possibilitats de construir prismes amb un conjunt de 24 daus (cubs unitaris):
• Quants prismes diferents es poden construir amb 12 daus unitaris?
• I amb un conjunt de 60 daus?
1. Busca, entre els nombres següents, quatre parells de nombres que compleixin la relació de divisibilitat:
6 15 35 80 90 240
2. Indica si les afirmacions següents són certes o falses:
a) 60 és divisible per 15.
b) 7 és múltiple de 21.
c) 12 és divisor de 120.
d) 162 és múltiple de 8.
3. Escriu:
a) Els múltiples de 12 compresos entre 50 i 100.
b) Tots els divisors de 90.
4. Troba aquests nombres:
a) El primer múltiple de 13 després de 1.000.
b) L’últim múltiple d’11 abans de 1.000.
5. Completa:
a) Un nombre és múltiple de 3 quan
b) Un nombre és divisible per 5 quan
c) Un nombre és múltiple de 9 quan
6. Escriu, ordenats, tots els nombres primers més petits que 50.
7. Descompon en factors primers:
a) 36 =
b) 48 =
c) 396 =
8. Calcula:
a) MCM (36, 48)
b) MCM (10, 15, 25)
9. De quantes maneres diferents es pot dividir una classe de 28 alumnes en equips amb el mateix nombre de membres, sense que en sobri cap?
10. Quin és el costat del quadrat més petit que es pot formar si unim rajoles rectangulars de 15 cm de llargada per 6 cm d’amplada?
La Mariona i en Marc observen les dinàmiques de grup de diferents activitats extraescolars que es duen a terme a l’institut. Han apreciat que els grups es conformen segons les edats i el gènere dels companys i les companyes.
Les monitores sempre intenten fer grups tenint en compte la inclusió i la igualtat de gènere. Busquen totes les maneres de distribuir els participants en grups equilibrats, sense que ningú en quedi exclòs.
La Mariona i en Marc decideixen fer un estudi per mirar d’establir la millor manera de distribuir els equips.
Quina creieu que és la millor manera d’agrupar?
Els resultats de l’equip dependran de com estan fets els grups?


1. A l’extraescolar de patinatge de 1r d’ESO hi ha 28 inscrits, 12 noies i 16 nois. Busqueu totes les formes possibles de distribuir els inscrits en grups del mateix nombre, sense que ningú en quedi exclòs.
2. Es poden fer grups amb el mateix nombre d’alumnes, de manera que en tots hi hagi el mateix nombre de noies? I el mateix nombre de nois? Quins?


La Mariona i en Marc amplien el seu estudi als alumnes de 2n d’ESO inscrits a patinatge i creen la taula següent:


3. Com s’hauran de distribuir els inscrits perquè els grups siguin inclusius, és a dir, perquè ningú no quedi exclòs i tots els grups tinguin el mateix nombre de patinadors?
4. Es poden fer grups inclusius si els inscrits de 1r i de 2n d’ESO no entrenen junts?
5. Es poden fer grups amb el mateix nombre de noies i el mateix nombre de nois? Com ho faran per incloure tots els participants?

6. Quina creieu que és la millor manera d’agrupar?
7. Els resultats de l’equip dependran de com estan fets els grups?

Quan era petita i feia primària no m’agradava anar a l’escola. M’agradava jugar, veure dibuixos o no fer res. Confesso que fins i tot, alguna vegada, m’havia fet la malalta per no haver d’anar a l’escola.
El pitjor de tot eren les classes de «mates». Com a gairebé tothom, a mi tampoc m’agradaven les «mates». No entenia res, em feia mandra aprendre les taules de multiplicar, m’avorrien els problemes… i pensava que a mi de què em servia tot allò.
Quan preguntava als més grans per què havia d’estudiar «mates», a part de respondre’m que perquè eren al temari, les respostes eren poc convincents. I em sembla que la majoria no en tenien ni idea, i molts deixaven anar un «uf!, quin pal això de les “mates”». Fins i tot, als anuncis de medicaments per al mal de cap sortia un noi que estava estudiant «mates» per a un examen, i no es feia estrany
Així vaig passar tota la primària. I quan em preguntaven què volia ser de gran, responia: «Només sé el que no vull ser.» I ja us ho podeu imaginar, oi?
Vaig fer dotze anys i vaig entrar a l’institut a fer l’ESO. Em feia il·lusió canviar d’escola, conèixer gent, anar amb els grans, però també em feia molta por. Segur que les «mates» serien molt més difícils, els tenia pànic, em veia passant vergonya a classe quan el mestre em preguntés, repetint curs… Buf!, quin drama.




Primera classe de «mates del curs»: som-hi! La mestra va entrar i es va presentar: «Soc la Carla, m’apassionen les “mates”, m’encanta explicar “mates” i vosaltres m’agradeu molt.» Òbviament vaig pensar que aquella noia no estava bé del cap. Després de presentar-se i de dir aquestes bajanades, va projectar a la pissarra unes fotos. Us ho explico. La primera era d’una noia a casa fent una videotrucada amb una amiga que era en un vaixell a l’Antàrtida. La segona era d’un hort «intel·ligent» amb plantes que «parlaven» i deien que els faltava aigua o nutrients. Una altra era d’un bebè dins la panxa de la mare, a qui estaven operant. La quarta era d’un grup de noies instal·lant una xarxa de connexions en un poblat del Senegal… I així fins a deu fotos com aquestes. Llavors la Carla es va girar i amb un somriure ens va preguntar: «Què tenen en comú totes aquestes fotos? Com s’han pogut fer totes aquestes coses? Doncs GRÀCIES A LES “MATES”!»



Ara sí que ja no en tenia cap dubte, la mestra de «mates» estava com un llum.
Al final de la classe tothom parlava de la Carla, del que havia dit, de les fotos, de la mare d’un com- pany que era enginyera de «telecos» i que havia anat de voluntària al Senegal per fer arribar el wifi a una escola, de la cosina d’una alumna que era informàti- ca i treballava en una empresa que dissenyava exoes- quelets (m’havia de recordar quan arribés a casa de buscar què era això) i veïna de l’escala que treballava a Hewlett Packard, on fabricava impressores 3D.
Me’n vaig anar cap a casa rumiant una mica tot plegat, semblava tot bastant xulo, però… llàstima, des de petita m’havia quedat molt clar que jo no servia per a les «mates», així que valia més que deixés de pensar en els bebès operats a la panxa de la mare, els vaixells a l’Antàrtida o els ordinadors de les escoles d’Àfrica.
Segon dia de classe de «mates». La Carla va arri- bar, somrient, va saludar a tothom, perquè ja s’havia après els nostre noms i, tot seguit, va dir: «Marta, ens pots explicar què és el que més t’ha agradat de



les “mates” que has estudiat?» Em volia morir, vo- lia desaparèixer, desmaiar-me, fondre’m… Però no va passar res de tot això. Amb un fil de veu vaig aconseguir dir alguna cosa semblant a «res». Ella no ho va sentir i va insistir, així que vaig respondre, amb el mateix filet de veu, evidentment: «És que jo no serveixo per a les “mates”.» La Carla em va mirar sorpresa, amb cara de no entendre’m, i amb un gran somriure em va dir: «No sé qui t’ha ficat aquesta idea al cap, però això és una gran mentida. I tant que serveixes, és més, et prometo que aquest curs aprendràs “mates”, hi jugaràs i t’agradaran.» Crec que ja us he dit que a aquesta noia li faltava un cargol.
Jo no sé explicar què va passar, però aquesta mestra, amb el seu entusiasme, amb la seva alegria, amb les seves respostes quan li preguntàvem qualsevol dubte i amb els ànims que ens donava va aconseguir que les de «mates» fossin les classes més divertides de tot el curs i, tatxan!, vaig treure un 8! Ara sí que flipeu, oi?
Doncs encara al·lucinareu més quan us digui que vaig triar el batxillerat científic i… acabo de començar la carrera d’Enginyeria de telecomuni- cacions. És difícil, em costa, he d’estudiar molt, però m’agrada molt. De gran vull treballar fent aplicacions de mòbil per a temes relacionats amb la salut. I ara sé que sí que serveixo.
Paz Morillo Bosch és llicenciada en Matemàtiques per la UB i doctora per la UPC. Des que va acabar la carrera treballa com a professora a l’Escola Tècnica Superior d’Enginyeria de Telecomunicacions de Barce- lona, on ha fet classes de totes les assignatures de matemàtiques. Ha dirigit diversos treballs de fi de grau, de màster i tesis doctorals. L’any 1992 va crear el grup de recerca de Matemàtica Aplicada a la Criptografia. Ha estat responsable d’igualtat a l’ETSETB durant quatre anys i, des de l’any 2018, dirigeix el projecte «Una enginyera a cada escola», que té per objectiu trencar estereotips de gènere.