M M A e à t es tiQU -

coneixements
Autoria:
F. Xavier Alegria
Lucia Cabello
4
Programa Raona EDUCACIÓ PRIMÀRIA
Aquest projecte editorial de l’àrea de Matemàtiques ha estat elaborat d’acord amb el marc competencial i normatiu descrit en el Decret d’ordenació dels ensenyaments de l’educació bàsica publicat pel Departament d’Educació de la Generalitat de Catalunya l’any 2022.
Equip editorial:
Cap del projecte editorial: Montse Ballaró
Coordinació editorial i edició: Mario Suárez
Edició: Núria Riera i Fernández
Correcció: Immaculada Riera i M. Mercè Estévez
Documentalista: Cristina Boj
Coordinació artística i disseny: Laura R. Dengra
Coordinació tècnica: Mercedes F. Bravo
Maquetació: Moelmo, SCP
Coordinació tècnica digital: Montse Cascales i Yuli Rivero
Edició digital: Núria Algarra
Il·lustració de la coberta: Martuka
Il lustracions: Marta Montañá i Jordi Fenosa
Cartografia: www.marcopolo.systems
Fotografies: Agència Efe, Arxiu Anaya (Cosano, P.; Martín, J.A.), Dreamstime/ Quickimage, Getty Images, iStock/Getty Images, Ll. Valcàrcel, Photoaisa, Shutterstock.com (a_v_d; chanchai howharn; Nerthuz; Tanya Lapidus), 123RF i col·laboradors, Arxiu Barcanova
© 2023, Francesc Xavier Alegria Folch, Lucia Cabello Rimbau
© 2023 d’aquesta edició: Editorial Barcanova, SA
Rosa Sensat, 9-11, 4a planta. 08005 Barcelona
Telèfon 932 172 054
barcanova@barcanova.cat
www.barcanova.cat
Primera edició: abril de 2023
ISBN: 978-84-489-6070-4
DL B 7623-2023
Printed in Spain
Reservats tots els drets. El contingut d’aquesta obra està protegit per la llei, que estableix penes de presó i multes, a més de les indemnitzacions corresponents per danys i perjudicis, per a aquells que reproduïssin, plagiessin o comuniquessin públicament, totalment o parcialment, una obra literària, artística o científica, o la seva transformació, interpretació o execució artística fixada en qualsevol tipus de suport o comunicada per qualsevol mitjà, sense l’autorització preceptiva.
com és el llibre?
El Programa Raona de Matemàtiques de 4t d’Educació Primària està format per un llibre de Coneixements i un Dossier d’aprenentatge.




M M A
e à t

Coneixements essencials

Continguts clars per visibilitzar els coneixements bàsics i reforçar-los d’una manera adequada a l’aula.









El llibre s’estructura de la manera següent:
Doble pàgina inicial que serveix per situar l’alumne en el tema que es tractarà, a partir de les imatges.



Ciclicitat L’aprenentatge en espiral ajuda a consolidar i reforçar els coneixements, ja que l’alumnat recorda el que ja ha après i amplia els continguts a mesura que va avançant.
Pàg. 121





Aquesta icona remet a la pàgina del Dossier d’aprenentatge on hi ha les activitats corresponents.
Activitats digitals per treballar a l’aula amb la pissarra digital interactiva (PDI), disponibles en l’espai personal del web www.barcanova.cat.
es
INCLOU LLICÈNCIA DIGITAL EDUCACIÓ PRIMÀRIA
El llibre de Coneixements inclou tot el contingut curricular de l’àrea i està estructurat en 9 unitats didàctiques en què es treballen de manera competencial els diferents continguts. dossier
tQU i
4
d’aprenentatge
estQU
INCLOU LLICÈNCIA DIGITAL EDUCACIÓ PRIMÀRIA
Programa Raona M M A e à t
i
4 coneixements
6 ÉS CLAR! PERQUÈ EN TÉ MÉS. PARTS IGUALS DE LA UNITAT DE LA MEVA MARGARIDA SÓN MÉS PETITS. 92 UNITAT 6 Si pintem els pètals de les margarides fent servir només dos colors, quina tindrà el mateix nombre de pètals d’un color i de l’altre? Per què? Quins tipus de triangles coneixes? Saps què és una figura còncava? UNITAT
Programa Raona
REPRESENTEM NOMBRES DECIMALS
Fixa’t com ho fem per representar nombres decimals amb els cubs encaixables.

Així representem el nombre 1,25:

Una unitat Dues dècimes Cinc centèsimes
Una unitat té 10 dècimes 100 centèsimes.
• Si desfem una dècima, quantes centèsimes tindrem?

La Nàdia ha representat aquests dos nombres decimals:




Quin dels dos nombres és més gran?
Per què? En Miró diu que, per representar el nombre decimal 0,54, no necessitarà una planxa de 100 cubs. Què en penses tu? Com el representaries?
Per què la part entera d’aquest nombre decimal és zero?
Ús del material manipulable.
Els nombres decimals tenen dues parts: la part entera, que s’escriu a l’esquerra de la coma, la part decimal, que s’escriu a la dreta de la
N5
Compta i pensa. Activitats de càlcul mental i lògica matemàtica.
Ens preparem per resoldre problemes
Taller d’espai i forma
CONSTRUCCIÓ I REPRESENTACIÓ
Activitats exemplificades i informacions per ajudar a la comprensió dels continguts.
Estratègies de càlcul
Activitat per resoldre amb la calculadora.
Problemes
Estratègies de càlcul























amb la calculadora per trobar el nombre que falta en cada una d’aquestes multiplicacions divisions?


2,03 HEM REPRESENTAT LA UNITAT AMB UNA PLANXA DE 100 CUBS, LES DÈCIMES AMB DUES TIRES DE 10 CUBS I LES CENTÈSIMES AMB 5 CUBS.
2,13
14 UT 7 Pàg. 129 4 9 2 1 5 4 7 8 6 0 3 8 TROBEM NOMBRES DESCONEGUTS EN MULTIPLICACIONS I DIVISIONS Podem resoldre
amb
senzills mentalment. Però per
amb
grans, és millor fer‐ho en un full o amb la calculadora. Quina operació faries
120 10 10 × 120 12 4 60 4 × : 60 15 60 5 60 5 : 12 3 15 15 3 × 45 26 54 × 364 76 156 32 × 832 26 SI EN UNA DIVISIÓ FALTA EL DIVIDEND, PUC TROBAR-LO MULTIPLICANT ELS ALTRES DOS NOMBRES. PERÒ SI EL NOMBRE QUE FALTA ÉS EL DIVISOR, HE DE DIVIDIR ELS ALTRES DOS NOMBRES. SI EN UNA MULTIPLICACIÓ FALTA UN NOMBRE PERÒ SÉ QUIN ÉS EL RESULTAT, PUC TROBAR-LO FENT UNA MULTIPLICACIÓ. 15 UT 7
coma.
operacions
nombres
resoldre operacions
nombres
Pàg. 138
DE QUADRILÀTERS Fixeu-vos en aquests polígons: • Què tenen en comú la figura groga la figura blava? • I de diferent? • De totes les figures, només una és còncava. Quina és? • Quines figures tenen angles obtusos? Construïu amb geotires les cinc figures anteriors. Penseu quina mida han de tenir per tal que les pugueu construir. • Heu fet servir les geotires iguals, però les dues fi- gures no són iguals. En què es diferencien? Tots tenen 4 costats; són quadrilàters. 90º 30º 90º 60º 90º JO FARÉ UN QUADRAT I UN ROMBE. NECESSITARÉ QUE LES QUATRE GEOTIRES MESURIN IGUAL. 20 TALLER D ’ ESPAI I FORMA 18 UT 7 TALLER D ’ ESPAI I FORMA Pàg. 132
Activitat que serveix per parlar sobre els objectius de desenvolupament sostenible (ODS) de les Nacions Unides.
MULTIPLICACIONS PER NOMBRES DE DUES XIFRES


Hi ha algunes multiplicacions per nombres de dues xifres que pots fer tan ràpid com la calculadora.
Són les multiplicacions en què les xifres de les unitats dels dos nombres sumen en què les xifres de les desenes són iguals
MULTIPLICA EL NOMBRE DE LES DESENES PEL SEGÜENT, DESPRÉS MULTIPLICA ELS NOMBRES DE LES UNITATS ENTRE ELLS ESCRIU ELS RESULTATS SEGUITS. Resol aquestes multiplicacions amb la calculadora. Què observes?
• Prova-ho amb aquestes altres multiplicacions comprova el resultat amb la calculadora:
× 33 = 3 × 99 = 9 × 333 = 3 × 999 = Quin resultat creus que obtindràs si resols aquestes multiplicacions sense fer servir la calculadora?






9 × 3.333 = 3 × 9.999 = • Què creus que passarà si canvies el 3 per un 6 en totes les multiplicacions anteriors? Prova-ho amb altres multiplicacions i comprova si passa al mateix.

Proposem activitats perquè s’avaluïn per competències.











Situació d’aprenentatge / Treball cooperatiu. Al final de cada trimestre, es planteja una situació d’aprenentatge per fer en grup (de recerca, sobre els ODS o de caire matemàtic) en què l’equip ha de resoldre una sèrie d’activitats relacionades amb els continguts treballats.
EL CAMÍ DE SANT JAUME
SITUACIÓ D’APRENENTATGE
Us heu plantejat mai fer el camí de Sant Jaume? Una proposta molt interessant per a les vacances d’estiu és fer una part del camí de Sant Jaume en família. El podeu fer a peu o en bicicleta. Hi ha diferents rutes per arribar a Santiago de Compostel·la des de diversos punts d’Europa. En el mapa podeu observar alguns camins que travessen Catalunya.
CONSTRUÏM ANGLES Podem construir un angle recte combinant angles diferents.





• Són

El camí català comença al Port de la Selva o a la Jonquera passa per diferents pobles i ciutats cata- lanes. Si sou d’alguna d’aquestes localitats o hi heu passat a prop, potser haureu vist un símbol sem- blant a aquest. L’heu vist mai?
• Feu una llista del material que us recomanen agafar, segons les per- sones que fareu la ruta. Calculeu quina és la distància total de la proposta escollida.
de Tarragona a Santes Creus
32,9 km Mitjana 8 h 35 10


Trams alternatius per a ciclistes


Entreu en aquesta web de turisme de Catalunya: https://www.catalunya.com/cami-de-sant-jaume-24-1-61?language=ca Us ofereix una guia per a cinc rutes: Del Port de la Selva a Montserrat De Montserrat a Alcarràs De Barcelona a Montserrat De Tarragona a Lleida De Tortosa a Batea Hi trobareu consells, la distància a recórrer, la dificultat i la durada de cada etapa. Escolliu la que més us agradi i entreu al seu enllaç. Prepareu aquesta ruta per si algun dia la voleu fer.

Penseu quants dies necessitareu per fer-la quantes hores haureu de caminar cada dia. Si ho preferiu, també podeu fer la ruta en bicicleta Compartiu amb la resta de la classe la preparació de la vostra ruta tota aquella in- formació que us sembli interessant.
L’última etapa del camí de Sant Jaume sempre acaba a la ciutat de Santiago de Compostel·la Aquest és el perfil d’alçada de l’últim tram del camí francès
Sarria Portomarín Palas de Rei O Pino Santiago de Compostel·la Arzúa

Quina creieu que és l’etapa més llarga? la més curta? la que té més pendent? Parleu de com ho heu pensat.

14 TL CRU
15 TL CRU
10 58 × 52 3 0 1 6 5 × 6 8 × 2 45 × 45 = 76
9
9
× 74
× 3 = 27 3 × 9 = 27
106
descobrim
UNITAT 6
correctes els angles que han construït en Joan la Tura? Com ho sabeu? Podríeu fer una altra proposta d’angle de 90° fent servir el joc d’angles del material manipulable d’aula? Ara, construïu, amb els jocs d’angles les geotires, un angle de 120°, un de 60°, un de 135° i un de 150°. Podeu fer més d’una combinació per construir cada angle? 45º 45º 30º 30º 30º DONCS JO HE REPETIT TRES VEGADES L’ANGLE DE 30°. JO HO HE FET AIXÍ! HE REPETIT DUES VEGADES L’ANGLE DE 45°. 30º 90º TALLER DE MESURA 10 UT 7 TALLER D e mesur A Pàg. 133 Descobrim Taller de mesura El repte He après
una resposta global per a un entorn educatiu divers
La proposta digital de Barcanova és EDUDYNAMIC , un projecte digital complet que dona una resposta global a un model educatiu divers i dinàmic.
A partir d’una proposta senzilla i intuïtiva, EDUDYNAMIC és un projecte digital multidispositiu i multisuport que s’adapta i es visualitza en totes les plataformes i en tots els entorns d’aprenentatge virtual (Blink Learning, Moodle, Alexia, Google Classroom, Clickedu, Office 365…).
La diversitat i riquesa de recursos, des d’activitats interactives traçables a vídeos, presentacions i ludificació, fan d’EDUDYNAMIC un projecte digital actualitzat i complet pensat per canviar amb tu.

Programa competencial
Enfocat al treball competencial, conté recursos molt diversos, rics i significatius com:
• Activitats interactives
• Gamificació
• Metacognició
Un model adaptable i versàtil
Aplicable a diferents enfocaments i necessitats, tant si es prefereix completar el treball del material en paper com si es vol treballar únicament en digital.
Traçabilitat integral
Es poden visualitzar les qualificacions de les activitats així com accedir a les respostes completes.
Interactivitat total
• Vídeos
• Animacions
Compatibilitat
Compatible amb els entorns virtuals d’aprenentatge (EVA)
i les plataformes educatives (LMS) més utilitzades en els centres educatius gràcies a l’ús dels estàndards tecnològics: HTML, Marsupial, LTI i SCORM
Tots els recursos addicionals disponibles els trobaràs al web de BARCANOVA: www.barcanova.cat
Facilita la inclusió i la personalització de l’aprenentatge
L’atomització dels continguts permet assignar les tasques segons les necessitats de l’alumne.
projecte digital
MULTISUPORT
S’adapta i es visualitza en qualsevol tipus de dispositiu (ordinador, tauleta, smartphone...).
DESCARREGABLE
Permet treballar sense connexió a internet i es pot descarregar en més d’un dispositiu.
UNIVERSAL
És compatible tecnològicament amb tots els sistemes operatius.
ESPAI PERSONAL
En registrar-se en el web, es poden visualitzar els llibres en línia i descarregar els recursos personalitzats.
SENZILL I INTUÏTIU
Té un disseny d’entorn accessible adaptat a cada etapa educativa per facilitar la navegació a alumnes i docents.


SINCRONITZACIÓ
Els canvis fets per l’usuari són sincronitzats automàticament en connectar qualsevol dels dispositius amb els quals es treballi.
les claus del projecte digital

Nombres de cinc i de sis xifres 12 Utilitzem la recta numèrica 14 La recta del temps 15 Aproximacions 16 ESTRATÈGIES DE CÀLCUL Busquem el nombre que falta en una suma 17 Els cossos geomètrics 18 TALLER D’ESPAI I FORMA Construcció de cossos geomètrics ..................................... 19 Representem dades en taules i gràfics 20 ENS PREPAREM PER RESOLDRE PROBLEMES 22 PROBLEMES 23 EL REPTE Busquem totes les restes possibles ....................................... 24 HE APRÉS 25 Reconeixem i representem fraccions 62 Comparem fraccions 63 La fracció d’un nombre 64 ESTRATÈGIES DE CÀLCUL Multiplicar per 5 65 TALLER D’ESPAI I FORMA La circumferència i el cercle 66 Cossos rodons 68 PROBLEMES Hores, minuts i segons 70 Unitats de massa ........................... 72 EL REPTE Safates de fruites 74 HE APRÉS 75 La propietat distributiva de la multiplicació 44 Multipliquem per dues xifres ........... 45 TALLER D’ESPAI I FORMA Desenvolupaments plans. El cub 46 TALLER DE MESURA Mesures de longitud 48 Perímetres iguals amb formes diferents 49 Què és la mitjana aritmètica? 50 ESTRATÈGIES DE CÀLCUL Multiplicacions per nombres propers a desenes exactes 52 ENS PREPAREM PER RESOLDRE PROBLEMES 53 PROBLEMES 54 DESCOBRIM Com multiplicaven els egipcis 55 EL REPTE Embolicant capses 56 HE APRÉS 57 Situació d’aprenentatge / TREBALL COOPERATIU El gran recapte d’aliments 58 Situacions de multiplicació 28 Taules de multiplicar. La taula pitagòrica ......................... 30 Multipliquem per una xifra 31 Situacions de divisió 32 Euros i cèntims d’euro 34 ESTRATÈGIES DE CÀLCUL Sumar i restar nombres propers a desenes exactes 36 Mapes i itineraris 37 Vista des de diferents punts 38 PROBLEMES 39 EL REPTE Representem nombres amb cubets encaixables 40 HE APRÉS 41 Situacions d’estimació en el càlcul 78 Dividim per dues xifres 80 Nombres romans 81 TALLER DE MESURA Relació entre les superfícies del triangle i del rectangle 82 TALLER D’ESPAI I FORMA Transformem prismes en piràmides 84 Lectura i representació de dades en intervals ..................................... 86 ESTRATÈGIES DE CÀLCUL Dividir nombres acabats en zero entre 10, 100 i 1.000 87 ENS PREPAREM PER RESOLDRE PROBLEMES 88 PROBLEMES 89 EL REPTE Retallem triangles ........................... 90 HE APRÉS 91 NOMBRES I MÉS NOMBRES 1 COSSOS QUE RODOLEN 4 EL PERÍMETRE
MAPES I PLÀNOLS
ARRODONIM 5 índex
3
2

Fraccions i forma 94 Representem fraccions en la recta i les comparem ................................ 95 Fraccions més grans que la unitat 96 Investiguem patrons en sèries 97 Inventem instruccions 98 ESTRATÈGIES DE CÀLCUL Trobem nombres desconeguts en sumes i restes 99 TALLER D’ESPAI I FORMA Classificació de triangles 100 Composició i descomposició de figures. Polígons còncaus i convexos 102 TALLER DE MESURA Relació perímetre-superfície 103 PROBLEMES 104 EL REPTE Fem camins 105 DESCOBRIM Multiplicacions per nombres de dues xifres 106 HE APRÉS 107 SITUACIÓ D’APRENENTATGE / TREBALL COOPERATIU Els nombres a la natura 108 Comparació i ordenació de nombres decimals 148 Situem nombres decimals en la recta 149 Estimacions en multiplicacions 150 Estimacions en decimals 151 TALLER DE MESURA Estimació de magnituds usant referents comuns 152 TALLER D’ESPAI I FORMA Identificació de vistes parcials en una figura 154 Ús i anàlisi de dades 156 PROBLEMES 158 ESTRATÈGIES DE CÀLCUL Relacions entre fraccions de 100 i de 1.000 160 EL REPTE Un somni monstruós 161 DESCOBRIM Màgia matemàtica 162 HE APRÉS 163 Situació d’aprenentatge / TREBALL COOPERATIU El camí de Sant Jaume 164 Nombres decimals i mesures de longitud 130 Relacions entre fraccions i decimals 132 Significat del quocient i del residu de les divisions 134 ESTRATÈGIES DE CÀLCUL Dividir entre 4 135 TALLER D’ESPAI I FORMA Simetries 136 Girs 137 TALLER DE MESURA Magnituds mesurables 138 Posició de dues rectes 140 Camins i xarxes 141 Gràfic lineal 142 PROBLEMES 143 EL REPTE Nombres amagats 144 HE APRÉS 145 Fraccions equivalents 112 Fracció d’un nombre 113 Representem nombres decimals 114 Comprensió d’instruccions condicionals 115 L’euro i els nombres decimals 116 TALLER D’ESPAI I FORMA Construcció i representació de quadrilàters 118 TALLER DE MESURA Construïm angles 120 Unitats de capacitat: litre (L) i mil·lilitre (mL) 121 ENS PREPAREM PER RESOLDRE PROBLEMES 122 PROBLEMES 123 Exploració de la probabilitat 124 ESTRATÈGIES DE CÀLCUL Trobem nombres desconeguts en multiplicacions i divisions 125 EL REPTE Les cares amagades d’un dau 126 HE APRÉS 127 PARTS IGUALS DE LA UNITAT 6 TOT DEPÈN DEL PUNT DE VISTA 9 TRANSFORMACIONS GEOMÈTRIQUES 8 QUADRILÀTERS 7 sabers de l’àrea 166
NOMBRES I MÉS NOMBRES

1
180.000 160.000 140.000 120.000 100.000 80.000 60.000 40.000 20.000 0 Quilograms
Tonyina Gamba Lluç Galera Pop Sardina Orada
Ametlla de Mar Cambrils
10 UNITAT 1
EN UNA DE LES ESPÈCIES, HI HA MOLTA DIFERÈNCIA ENTRE

LES CAPTURES QUE S’HAN FET

EN UN PORT I LES QUE S’HAN FET EN UN ALTRE.
• Saps quants habitants té el teu municipi?
• Pensa per què t’ha estat útil fer servir la recta numèrica fins ara?
• En què s’assemblen i en què es
EN LA RESTA D’ESPÈCIES LES DIFERÈNCIES SÓN MÉS PETITES.
11 UNITAT 1
NOMBRES DE CINC I DE SIS XIFRES
Aquest estiu, en Pau, al càmping, ha conegut alguns nois i noies; en total, sis. Cada un d’aquests nois i noies ha nascut en una d’aquestes poblacions, amb un nombre d’habitants diferent.
En Pau és d’Olot: 36.299 habitants

La Cristina és de Vic: 47.319 habitants
La Sandra és de Granollers: 62.475 habitants
L’Oriol és de Lleida: 140.080 habitants
La Noemí és de Saragossa: 675.301 habitants



En Xavier és de València: 805.224 habitants


• D’aquestes poblacions, quina s’acosta més als 50.000 habitants?
• Quantes xifres fem servir per escriure la població d’Olot ? I la de Lleida?
Per què?
12 UNITAT 1 Pàg. 9
Fixa’t en el nombre d’habitants d’aquestes dues poblacions:

Observa el valor que té la xifra 6 en cadascuna de les
6 60.000
EL VALOR DEL 6 ÉS DIFERENT PERQUÈ OCUPA LLOCS DIFERENTS. CADA XIFRA TÉ UN VALOR SEGONS EL LLOC QUE OCUPA.
Amb nombres de cinc xifres podem escriure quantitats que tenen desenes de mil. Per escriure quantitats que tenen centenes de mil necessitem nombres de sis xifres.
Busqueu altres situacions en què fem servir nombres de sis xifres.
QUIN ÉS EL NÚMERO MÉS GRAN DE CINC XIFRES QUE PODEM ESCRIURE?
I EL DE SIS XIFRES?
QUÈ PASSA AMB LES SEVES XIFRES?

Una unitat de mil (UM) són 1.000 unitats
• Quantes unitats són una desena de mil (DM) ? I una centena de mil (CM)?
POBLACIÓ DE GRANOLLERS
Desenes de mil Unitats de mil Centenes Desenes Unitats 6 2 4 7 5 POBLACIÓ DE SARAGOSSA Centenes de mil Desenes de mil Unitats de mil Centenes Desenes Unitats 6 7 5 3 0 1
Centenes de mil
poblacions: Granollers
Saragossa 6 600.000
CM DM UM C D U 1 1 0 1 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0
!!
13 UNITAT 1
UTILITZEM LA RECTA NUMÈRICA
Fixa’t en aquests dos trams de la recta numèrica. La separació entre els punts és diferent en cada tram.
• Com podem saber a quin nombre correspon, en cada tram, el punt assenyalat amb la fletxa?
• Expliqueu l’estratègia que heu seguit per trobar-lo.
• Amb quin creus que està relacionat? Per què?
• Quant representa cada divisió? Com ho has sabut?
• Quin nombre representa la fletxa?

• On estaria situat el 6.000? Parleu-ne.
El fet de relacionar trams de la recta numèrica amb altres de semblants i més senzills ajuda a situar bé els nombres.
AQUEST ALTRE TRAM DE RECTA ESTÀ RELACIONAT AMB UN DELS DOS DE DALT. 350 470 350 650 3500 6500
W1 14 UNITAT 1 Pàg. 11
LA RECTA DEL TEMPS


Aquests esports van ser olímpics en diferents anys:
Bàdminton: 1992
Fixa’t en aquesta recta del temps:
• Quants anys fa que el bàsquet és un esport olímpic?
• Quants anys han passat entre dos punts consecutius de la recta? I entre una creu i un punt?
L’escalada esportiva va debutar als Jocs Olímpics de Tòquio 2020.

La recta numèrica m’ajuda a situar esdeveniments i a calcular els anys que han passat.


I
Bàsquet:
Futbol:
Natació sincronitzada: 1984 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 2000 2010 2020 2030 Bàdminton:
Futbol:
Escalada esportiva: 2020 Natació sincronitzada: 1984
1936
1900
1992
1900
Bàsquet: 1936
15 UNITAT 1 Pàg. 12
APROXIMACIONS

Aquesta és la informació relacionada amb l’observatori del Parc Astronòmic del Montsec en relació als visitants d’aquests anys

La recta numèrica ens permet veure de quin número és més a prop una determinada quantitat per expressar-la de forma aproximada.
• A quin número aproximaries els visitants de l’any 2020? I els del 2021? Explica com ho has fet.
• Per què penses que l’any 2020 els visitants van ser menys de la meitat que els de l’any 2019?

DEL MONTSEC Any Visitants 2017 32.936 2018 34.808 2019 35.219 2020 14.773 2021 24.103
PARC ASTRONÒMIC
32.250 32.000 32.500 33.000 32.936 32.750 L’ANY
34.250 34.000 34.500 35.000 34.808 34.750 16 UNITAT 1 Pàg. 13
L’ANY 2017 VAN VISITAR EL PARC UNES 33.000 PERSONES APROXIMADAMENT.
2018 VAN VISITAR EL PARC UNES 35.000 PERSONES.
BUSQUEM EL NOMBRE QUE FALTA EN UNA SUMA
Relacionem la suma i la resta buscant els nombres que falten en una suma. Hem de decidir quin dels nombres del requadre necessitem per fer aquesta suma. Podem fer proves amb la calculadora.
Si restem 312 – 136, trobarem, a la primera, el nombre que ens falta.
PODEM DESCARTAR EL 184 I EL 174. HA DE SER UN NÚMERO ACABAT EN 6, PERQUÈ 6 I 6 FAN 12, I EL RESULTAT
ACABA EN 2.
Fixa’t com trobem els números que falten en aquestes sumes; fem una resta:


• Quina operació faràs per trobar el número que falta en aquestes sumes?
PER TROBAR EL NÚMERO QUE FALTA EN LA SUMA 127 + ……… = 142, NO EM CAL FER UNA RESTA, PERQUÈ, COM QUE SÉ QUE 127 + 5 = 132, PUC
QUE ÉS EL 15.

4
8
9 2 1 5 4 7
6 0 3 8
166 206 184 174 186 176 136 312 = +
N La suma i la resta estan relacionades. 175 + … = 326 326 – 175 = 151 … + 234 = 1.010 1.010 – 234 = 776
DEDUIR
127 142 = + 118 504 = + 17 UNITAT 1 Estratègies de càlcul Pàg. 18
ELS COSSOS GEOMÈTRICS
Observa aquests objectes, que tenen forma de cos geomètric:





• Com els agruparíem si féssim el que pensa l’Andreu?
• Els prismes i els cilindres, tenen el mateix nombre de bases? I les piràmides i els cons?





• Hi ha cap cos que no tingui cap base?
• De quines altres maneres els podríem agrupar?
JO ELS AGRUPARIA SEGONS EL NOMBRE DE BASES QUE TENEN.
2 18
1 Pàg. 14
UNITAT
CONSTRUCCIÓ DE COSSOS GEOMÈTRICS

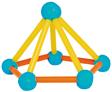
Fent servir palletes de refresc i boles de plastilina, podem construir cossos geomètrics.
QUIN ÉS EL MÍNIM NOMBRE DE PALLETES DE REFRESC QUE CALEN PER CONSTRUIR UN COS GEOMÈTRIC TANCAT? QUINA FORMA TÉ EL COS?

La Marta ha agafat palletes de refresc i plastilina, i ha anat construint cossos geomètrics. Ha fet aquests:

Amb 6 palletes de refresc
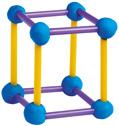
Amb 8 palletes de refresc
Amb 10 palletes de refresc
Amb 9 palletes de refresc
Amb 12 palletes de refresc
• En Jordi diu que, amb 12 palletes de refresc, també es pot fer una piràmide. Saps quina?

• Quantes palletes de refresc necessitem per construir un prisma de base hexagonal?
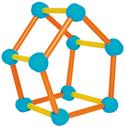
Amb 15 palletes de refresc
En aquests cossos geomètrics, les palletes de refresc representen les arestes, i les boletes de plastilina els vèrtexs.
M
TALLER D ’ ESPAI I FORMA 19 UNITAT 1 TALLER D ’ ESPAI I FORMA Pàg. 15
REPRESENTEM DADES EN TAULES I GRÀFICS
Aquest curs s’han posat molt de moda els retoladors per fer cal·ligrafia creativa. A la llibreria del poble han decidit fer un estudi estadístic per saber quins són els colors que més demanda tenen.


Aquests són els resultats de l’enquesta que es va fer als clients de la llibreria.
El valor que es repeteix més vegades, en un estudi estadístic, s’anomena moda
QUINA ÉS LA MODA
PEL QUE FA AL COLOR DELS RETOLADORS?
Color del retolador Comprats Groc 10 Vermell 40 Verd 20 Blau 60 Lila 25 Rosa 30 Marró 10 Negre 80 Groc
90 80 70 60 50 40 30 20 10 0 Nombre de retoladors
Vermell Verd Blau Lila Rosa Marró Negre Colors retoladors
20 UNITAT 1 Pàg. 16
Durant la primera setmana de setembre s’ha pres nota dels retoladors de color blau i negre venuts cada dia a la pàgina web. Aquesta és la representació gràfica:

• Quin dia van vendre més retoladors blaus? I negres?
• Hi va haver algun dia que van vendre més retoladors blaus que negres?
• Quants retoladors negres van vendre durant el cap de setmana (dissabte i diumenge)?
• Quina relació trobes entre l’enquesta que van fer a la llibreria i les vendes de la primera setmana de setembre?
• Per què diries que els servirà, a la llibreria, una enquesta d’aquesta mena?
Dies 60 50 40 30 20 10 0 Nombre
Blau Negre 21 UNITAT 1
Dilluns Dimarts Dimecres Dijous Divendres Dissabte Diumenge
de retoladors venuts
Estem preparant una ruta per descobrir petits pobles amb encant de la comarca de la Garrotxa. Ens han passat aquesta informació. Com ho podem fer per conèixer la distància entre els pobles 2 i 3? I entre els pobles 3 i 5?



1 38 km 23 km ? km 2 3 4 5 1 22 km 23 km 60 km ? 2 3 4 5
HO PODEM
UTILITZANT LA RECTA NUMÈRICA. PODEM UTILITZAR LES BARRES ADDITIVES PER TROBAR LES DISTÀNCIES MÉS FÀCILMENT. ? km 23 km 38 km 60 km 22 km ? km 23 km 60 km 1 2 3 4 5 23 km ?km 22km 38km 3 22 UNITAT 1 ENS PREPAREM PER RESOLDRE PROBLEMES Pàg. 19
TAMBÉ
FER
PROBLEMES
Mirant aquests itineraris, saps dir quants quilòmetres hi ha d’Artés a Manresa?
I de Sabadell a Terrassa?
SI SÉ ELS QUILÒMETRES QUE HI HA


DE SABADELL A MANRESA, I ELS QUE HI HA DE TERRASSA A MANRESA, PUC SABER ELS QUE HI HA DE SABADELL A TERRASSA.
PRIMER CAL SABER QUANTS
QUILÒMETRES FAN CADA DIA
ENTRE EL TRAJECTE D’ANADA
I EL DE TORNADA.
• La mare de la Jana és comercial i 3 dies a la setmana fa el trajecte Berga-Sabadell-Berga. Quants quilòmetres fa?
• El pare del Marçal és repartidor. Si fa el trajecte Vic-Manresa-Vic 5 dies a la setmana, quants quilòmetres fa?
• Quin dels dos fa més quilòmetres? Quants més?
• El Joan és un pagès de Sallent i cada dissabte porta verdura al mercat de Calaf, on té una parada. Quants quilòmetres farà el mes d’octubre?
44 km
BERGA ARTÉS VIC CALAF SALLENT 35 km 39 km ? km ? km 20 km 31 km 32 km MANRESA TERRASSA SABADELL 23 UNITAT 1 Pàg. 20
58 km MANRESA
MANRESA
e p t e l
BUSQUEM TOTES LES RESTES POSSIBLES
Amb les xifres següents, puc fer diverses restes. 6 3 9 8

r
Com ara aquesta:
e• Quantes restes diferents podem plantejar? Confeccioneu cartes de nombres i utilitzeu-les per fer proves.
• Quina estratègia podem fer servir per no deixar-nos-en cap?
–6 2 9 3 8 6
24 UNITAT 1
Cossos geomètrics
Els cossos geomètrics es poden agrupar seguint diferent criteris, com ara el nombre de bases, el nombre d’arestes, la forma de les bases…






En les piràmides, el nombre d’arestes és el doble que el de costats de la base i, en els prismes, és el triple.

Gràfics de barres. La moda
El valor més repetit en un estudi
moda UNITAT 1
Nombres de cinc i sis xifres Desenes de mil Unitats de mil Centenes Desenes Unitats 7 5 2 3 9 Centenes de mil Desenes de mil Unitats de mil Centenes Desenes Unitats 5 8 4 0 6 3 75.239 584.063 he après…
Cos geomètric Polígon de la base Nombre d’arestes de la piràmide Nombre d’arestes del prisma 6 9 8 12 10 15
estadístic s’anomena moda. 25
EL GRAN RECAPTE D’ALIMENTS
SITUACIÓ D’APRENENTATGE
A Catalunya s’organitza cada any un gran recapte d’aliments bàsics per a les persones necessitades.
Cerqueu informació sobre El gran recapte d’aliments i contesteu les preguntes:
• Des de quin any s’està portant a terme aquest projecte?
• Quins són els aliments bàsics que es recullen?
• Quins dies tindrà lloc la recollida d’aliments per part dels voluntaris?

Organitzeu-vos en grups:
• Plantegeu-vos què cal fer i com.
• Repartiu-vos les tasques.
• Respecteu-vos i ajudeu-vos.
Durant la campanya pots donar aliments o fer un donatiu a www.granrecapte.com


Imagineu-vos que participeu com a voluntaris en aquesta campanya. Us ha tocat recollir aliments en un supermercat i heu de posar tots els paquets de farina que us donin en capses de cartó.
• Les capses de cartó tenen forma de cub de 0,5 metres d’aresta.

• Les dimensions d’un paquet de farina són les de la imatge.
Penseu si convé posar els paquets ajaguts o drets per tal que en càpiga el màxim nombre en cada capsa.
• Quina serà la vostra proposta? Quants quilograms cabran en cada capsa?
Trobareu informació sobre aquest projecte solidari en l'espai personal del web www.barcanova.cat 15 cm 10 cm 5 cm
58 TREBALL COOPERATIU
Fixa’t en aquestes informacions recollides de diferents fonts en relació amb el consum alimentari a Catalunya:
1 3 malbaratat
262.471 tones
A Catalunya es llencen
262.471 tones d’aliments cada any.
35 kg 112 €
A Catalunya, cada any es malbaraten 35 kg de menjar per habitant. =
2 3 aprofitats
Això equival a 112 € per persona cada any.
• Què vol dir que 1 3 del menjar va a les escombraries? De quina manera penseu que malbaratem els aliments?
• Quants quilograms d’aliments es malbaraten a Catalunya cada any?
• Pregunteu a la cuina de la vostra escola quants quilograms dels productes indicats en la taula compren i completeu-la:
Arròs
• Si de tots aquests aliments se’n llencés un terç, quants quilograms es llençarien a les escombraries en una setmana? I en un mes? I en tot un curs?
• Què proposaríeu per tal d’evitar aquest malbaratament d’aliments?
Trobareu informació sobre el malbaratament d’aliments en l'espai personal del web www.barcanova.cat

A LA SETMANA AL MES EN TOT UN CURS Pa
Fruita
Patates
59 TREBALL COOPERATIU
Un terç del menjar que comprem va a les escombraries
COMUNICACIÓ I REPRESENTACIÓ
RESOLUCIÓ DE PROBLEMES
SENTITS
• Representació de la circumferència i del cercle.
• La fracció com a part d’una col·lecció: fracció d’un nombre.
• Comparació de fraccions.
• Reconeixement de fraccions.
• La fracció com a part d’una col·lecció: fracció d’un nombre.
NUMÈRIC
• Estratègies de càlcul: multiplicar per 5.
• Transformació de prismes en piràmides.
• Lectura i representació de dades en intervals.
• Representació de fraccions sobre la recta.
• Unitats de temps: hores, minuts i segons.
• Unitats de massa. Equivalències.
• Cossos rodons: característiques.
• Elements i característiques de la circumferència i del cercle.
• Estimació en el càlcul.
• Comparació de fraccions.
• Transformació de prismes en piràmides.
• Representació de triangles en el geoplà.
• Composició i descomposició de polígons.
• Representació de patrons en les sèries.
• Comparació i ordenació de masses.
• Representació de fraccions. DE LA MESURA
• Elements de la circumferència i del cercle. El diàmetre i el radi.
• Cossos rodons: característiques.
• Estimació en el càlcul.
• Divisió per dues xifres.
• Càlculs amb el temps.
• Lectura i interpretació de l’hora. ESPACIAL
Unitat 4. Cossos que rodolen
• Estimació en el càlcul.
• Arrodoniment.
• Nombres romans.
• Estratègies de càlcul: dividir nombres acabats en zero entre 10, 100 o 1.000.
NUMÈRIC
• Lectura i representació de dades en intervals.
• La fracció com a part de la unitat: fraccions i forma.
• Comparació de fraccions.
• Fraccions igual a la unitat i fraccions més grans que la unitat.
• Relació perímetre-superfície en un rectangle.
• Polígons còncaus i polígons convexos.
• Comparació de superfícies amb unitats no convencionals.
• Característiques dels prismes i de les pirámides.
• Situació de les fraccions en la recta numèrica.
• Perímetre superfície.
• Descobriment i descripció de patrons en les sèries.
• Ús d’estratègies que incorporen processos seqüencials.
• Utilització d’eines i estratègies de resolució.
• Mesura i càlcul de superfícies.
• Relació entre la superfície del triangle i el rectangle. ESPACIAL
DE LA MESURA
• Lectura i representació de dades en intervals.
• La fracció com a part de la unitat: fraccions i forma.
• Classificació de triangles.
• Estratègies de càlcul: trobem nombres desconeguts en sumes i restes.
• Composició i descomposició de figures.
• Representació de triangles en el geoplà.
• Composició i descomposició de figures.
• Polígons còncaus i polígons convexos.
• Patrons en les sèries.
• Comprensió d’instruccions utilitzant operadors.
• Interpretació de la informació.
ESTOCÀSTIC
DE LA MESURA
• Patrons en les sèries.
Treball cooperatiu / Situació d’aprenentatge: Els nombres a la natura:
ESPACIAL
ALGEBRAIC
RAONAMENT I PROVA CONNEXIONS
Unitat 5. Arrodonim
Unitat 6. Parts iguals de la unitat NUMÈRIC
167
L’ÀREA
SABERS DE
















































































