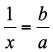1.3 Oszthatóság a természetes számok halmazában
1. l. Ismétlés és kiegészítés
Emlékeztető
Az a természetes számot osztja a b természetes szám, vagy osztható a b természetes számmal, ha van olyan c természetes szám, hogy a = b · c. Így írjuk: a ⋮ b vagy b|a.
Megjegyzés.
Példa Így írjuk Így olvassuk
6-ot osztja a 2;
6 osztható 2-vel;
6-ot osztja a 3;
6 = 3 · 2;
1. 0 ⋮ b, bármely b természetes szám esetén. (0 = b · 0)
2. a ⋮ 1 és a ⋮ a bármely a természetes szám esetén. (a = 1 · a)
6 osztható 3-mal;
2 osztja a 6-ot;
3 osztja a 6-ot.
3. Ha a ≠ 0, akkor a ⋮ ⟋0 (0 egyetlen nullától különböző természetes számnak sem osztója).
Módszertani megjegyzés: A félreértés elkerülése érdekében VI. osztályban osztóknak csak nemnulla természetes számokat tekintünk.
A fenti relációban az a számot a b szám többszörösének, b-t pedig az a szám osztójának nevezzük.
Ha a ≥ 2, akkor a-nak legalább két osztója van: az 1 és az a szám, amelyeket az a szám nem valódi osztóinak nevezünk.
Ha a-nak más osztói is vannak, akkor ezeket az a szám valódi osztóinak nevezzük.
A 6-os szám a 2 és a 3 többszöröse.
A 2 és a 3 számok a 6 osztói.
A 6-os szám esetén:
1 és 6 a nem valódi osztók;
2 és 3 a valódi osztók
A p ≥ 2 természetes számot, amelynek pontosan két osztója van (1 és p), prímszámnak nevezzük. Minden olyan n ≥ 2 természetes számot, amely nem prímszám, összetett számnak nevezzük.
Megjegyzés.
1. A 2-es az egyetlen olyan páros szám, amely prímszám is.
2. A 0 és az 1 prímszám sem, összetett szám sem.
3. Ha p prímszám, akkor p nem négyzetszám.
Fedezzük fel, értsük meg!
1. Legyen D n az n természetes szám osztóinak halmaza, M n pedig az n természetes szám többszöröseinek halmaza.
A 7, 12, 15 számok esetében írjuk fel a D n, majd az M n halmazt, kiemelve a négy legkisebb elemét.
D7 = {1, 7};
D12 = {1, 2, 3, 4, 6, 12};
D15 = {1, 3, 5, 15}.
4. A prímszámnak csak nem valódi osztója van.
5. Az összetett számnak van legalább egy valódi osztója.
M7 = {0, 7, 14, 21, …};
M12 = {0, 12, 24, 36, …};
M15 = {0, 15, 30, 45, …}.
Megjegyzés. A D n véges halmaz, bármely n nullától különböző természetes szám esetén.
Az M n végtelen halmaz, bármely n nullától különböző természetes szám esetén.
23 1. fejezet • Halmazok. A természetes számok halmaza
6 ⋮ 2 vagy
6 ⋮ 3 vagy
6.
2 | 6 vagy 3 |
2. Adott az A = {16, 19, 26, 29, 36, 39, 46, 49, 56, 59, 66, 69, 76, 79, 86, 89, 96, 99} halmaz.
a) Írd le azt a B ⊂ A részhalmazt, melynek elemei 2-vel osztható természetes számok!
b) Írd le azt a C ⊂ A részhalmazt melynek elemei 3-mal osztható természetes számok!
c) Az a) és b) alpont eredményeit használva írd le azt a D ⊂ A részhalmazt, amelynek elemei 6-tal osztható természetes számok!
d) Az a) és b) alpont eredményeit használva írd le azt az E részhalmazt, amelynek elemei a 2 vagy 3 számok közül legalább egyikkel osztható természetes számok.
Alkalmazás
Tulajdonság
Megoldás.
a) A 2-vel osztható természetes számok a 2 többszöröseinek halmazát képezik, és jele M2.
B = A ⋂ M2 = {16, 26, 36, 46, 56, 66, 76, 86, 96}.
b) A 3-mal osztható természetes számok a 3 többszöröseinek halmazát képezik, és jele M3.
C = A ⋂ M3 = {36, 39, 66, 69, 96, 99}.
c) Egy természetes szám osztható 6-tal, ha osztható 2-vel és 3-mal is, vagyis M6 = M2 ⋂ M3.
Tehát D = B ⋂ C = {36, 66, 96}.
d) Egy természetes szám csak akkor osztható legalább a 2 és a 3 számok egyikével, ha az M2⋃M3 halmaz eleme.
Akkor E = A ⋂ (M2 ⋃ M3) vagy
E = B ⋃ C = {16, 26, 36, 39, 46, 56, 66, 69, 76, 86, 96}.
1. Ha p ≥ 2 természetes szám prímszám, akkor csak nem valódi osztói vannak.
Ha p ≥ 2 természetes számnak csak nem valódi osztói vannak, akkor p prímszám.
Példa: p = 11 prímszám és D p = D11 = {1, 11}.
2. A 2-n kívül minden páros szám osztható 2-vel, tehát van legalább egy valódi osztójuk.
Halmazelméleti leírás
1. Ha p ≥ 2 prímszám, akkor
D p = {1, p}.
Ha p ≥ 2 és D p = {1, p}, akkor p prímszám.
2. Bármely k ≥ 2 esetén {1, 2, 2k} ⊂ D2k.
Példa: 62 = 2 · 31 páros szám és D62 = {1, 2, 31, 62}, tehát {1, 2, 62} ⊂ D62.
3. Bármely 0-tól és 1-től különböző négyzetszámnak van legalább 3 osztója.
Példa: 16 = 42 és D16 = {1, 2, 4, 8, 16}, tehát {1, 4, 42} ⊂ D16.
4. Ha egy természetes szám osztható két prímszámmal, akkor a prímszámok szorzatával is osztható.
Ha egy természetes szám osztható két prímszám szorzatával, akkor ezen prímszámok mindegyikével osztható.
3. Ha p ∈ ℕ , p ≥ 2, akkor {1, p, p2} ⊂D p 2.
4. Ha p és q prímszámok, akkor
M p ⋂ M q ⊂ M pq és M pq ⊂ M p ⋂ M q, tehát
M p ⋂ M q = M pq .
Példa: Ha a ⋮ 2 és a ⋮ 3, akkor a ⋮ 6, vagyis a ⋮ (2 · 3), tehát M2 ⋂ M3 ⊂ M6. Másrészt, ha a ⋮ 6, akkor a ⋮ 3 és a ⋮ 2, tehát M6 ⊂ M2 ⋂ M3. Következésképpen, M2 ⋂ M3 = M6.
5. Ha p prímszám, p | a és négyzetszám, akkor p 2 | a.
Példa: 5 100 és 100 négyzetszám. 52 = 25 és 25 100.
6. Ha a természetes szám, p pedig egy olyan prímszám, amelyre p ∣ a és p2 ∤ a akkor az a nem négyzetszám.
5. Ha p prímszám, p ∈ D a és a négyzetszám, akkor p2 ∈ D a .
6. Ha a ∈ ℕ, p egy olyan prímszám, amelyre p ∈ D a és p 2 ∤ a, akkor a nem négyzetszám.
Példa: Ha a = 300 és p = 3, akkor 3 300, 32 ∤ 300, tehát 300 nem négyzetszám, amit bizonyít a 172 < 300 <182 reláció is.
24 Matematika • Tankönyv a VI. osztály számára
1. Bizonyítsd be, hogy:
a) 68 osztható 7-tel.
b) 92 nem osztható 8-cal.
c) 6 osztja a 132-t.
d) 12 nem osztja a 146-ot.
e) 76 a 19 többszöröse.
f) 30 a 210 osztója.
2. Másold a füzetedbe, és tölts ki minden egyes szabad négyzetet a „⋮“, „ ⋮ ⟋“, „|“, „∤“ szimbólumok egyikével úgy, hogy igaz állításokat kapj:
a) 40 2;
b) 162 3;
c) 94 5;
d) 1001 10; e) 9 567; f) 103 700;
g) 2 1ab8; h) 5 152.
3. Adott az M = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} halmaz. Írd le azt a halmazt, melynek elemei:
a) az M halmaz elemei és a 10-es osztói.
b) az M halmaz elemei és a 2-es többszörösei.
c) az M halmaz elemei és a 3-nak nem többszörösei.
4. Határozd meg az n természetes számot az alábbi esetekben:
a) n a 34 valódi osztója;
b) n + 5 a 10 többszöröse és n < 20;
c) n2 + 1 a 82 nem valódi osztója.
Miniteszt
20 p 1. A 18-as osztóinak halmaza:
A. {2, 3, 4, 6, 9, 18}; B. {1, 2, 3, 6, 9, 18};
20 p 2. A 33 természetes számnak:
A. 2 osztója van; B. 3 osztója van;
20 p 3. A 18-as kétjegyű többszörseinek halmaza:
A. {18, 36, 54, 72};
B. {18, 32, 54, 76, 90};
5. Vizsgáld meg és indokolod a válaszod!
a) El lehet-e osztani három gyereknek egyenlő módon 59 narancsot?
b) Hány gyereknek lehet egyenlő módon 58 narancsot elosztani?
6. Adott az
M = {2, 4, 5, 9, 13, 20, 29, 35, 49, 77, 97} halmaz.
a) Írd fel az elemek felsorolásával az M halmazhoz tartozó prímek P halmazát!
b) Írd fel az elemek felsorolásával az M halmazhoz tartozó összetett számok C halmazát!
7. a) Határozd meg azt a két prímszámot, melynek összege 91!
b) Határozd meg azt a két prímszámot, melynek összege 42. Tárgyald az összes estetet!
8. Legyen P a természetes prímszámok és M2 a páros természetes számok halmaza. Határozd meg a P ∩ M2 halmazt!
9. Bizonyítsd be, hogy az a = 23 · 54 + 1 összetett szám!
10. Határozd meg az összes olyan prímszámot, amely b = 7 + 72 + 73 szám osztója!
C. {1, 3, 6, 9, 18};
C. 4 osztója van;
C. {0, 18, 36, 54, 90};
30 p 4. A 12-es szám 100-nál kisebb többszöröseinek száma:
A. 7; B. 8;
C. 9;
D. {1, 2, 6, 9, 18}.
D. 5 osztója van.
D. {18, 36, 54, 72, 90}.
D. 10.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
25 1. fejezet • Halmazok. A természetes számok halmaza
Gyakorlatok és feladatok
2. l. Természetes számok felbontása prímtényezők szorzatára
Emlékeztető
Bármely n ≥ 2 természetes szám felírható egy prímszám hatványaként vagy különböző prímszám alapú hatványok szorzataként.
A fenti írásmód neve: az n szám felbontása prímtényezők szorzatára.
Megjegyzés. Egy természetes számnak prímtényezők szorzatára való felbontása egyedi eltekintve a tényezők sorrendjétől.
Fedezzük fel, értsük meg!
2 = 21; 3 = 31; 5 = 51; 7 = 71;
10 = 21 51; 100 = 22 52; 1000 = 23 53;
12 = 22 31; 16 = 24; 15 = 31 51;
40 = 23 · 51; 75 = 31 · 52
40 = 23 51 = 51 23;
1000 = 23 · 53 = 53 · 23.
A gyakorlatban előnyös a prímtényezők szorzatára való felbontás algoritmusának használata. Az alábbiakban ennek lépéseit a 98-as számra fogalmaztuk meg.
Algoritmus
A folyamat lépésről lépésre
1. lépés. Megadjuk az adott szám egyik prím osztóját.
2. lépés. Megadjuk az 1’ lépésnél kapott hányados egyik prím osztóját.
3. lépés. Megadjuk az 2’ lépésnél kapott hányados egyik prím osztóját.
1’. lépés. Kiszámoljuk a szám és az adott osztó hányadosát.
2’. lépés. Kiszámoljuk az 1’ lépésnél kapott hányados és az újonnan adott osztó hányadosát.
3’ . lépés. Kiszámoljuk az 2’ lépésnél kapott hányados és az újonnan adott osztó hányadosát.
4. lépés. … . Addig folytatjuk a lépéseket, amíg a kapott hányados 1, majd a számot felírjuk prímszámok hatványainak szorzataként.
szorzatára a 78 és 210 számokat!
Prímosztó
2
7
Magyarázat összeszorozva elosztva
Megjegyzés. Ha a felbontandó szám osztható 10 egy hatványával, akkor előnyős a 10n = 2n · 5n alakú felírás. Így megkapjuk a felbontás két tényezőjét.
26 Matematika • Tankönyv a VI. osztály számára
98
= 2 · 49 98 : 2 = 49
98
7 ·
49
7
49 49 =
7
: 7 =
7 7 7 = 7 · 1 7 : 7 = 1
98
2
72 A leírt algoritmust az
bemutatott sémák egyikének formájában
Példa: Bontsd
78 = 2 · 3 · 13 78 2 3 39 13 78 39 13 1 2 3 13 78 = 2 · 39; 39 = 3 · 13; 13 = 13 · 1 Tehát 78 = 2 · 3 · 13. 210 = 2 ·3 · 5 · 7 210 2 3 5 105 35 7 210 105 35 7 1 2 3 5 7 210 21 7 1 2 · 5 3 7 210 = 2 · 105; 105 = 3 · 35; 35 = 5 · 7; 7 = 7 · 1, vagy 210 = 2 · 5 · 21; 21 = 3 · 7; 7 = 7 · 1. 210 = 2 · 3 · 5 · 7.
=
·
alábbiakban
használják.
fel prímtényezők
700
7 · 100 = = 7 · (22 · 52) = = 22 52 7.
=
Alkalmazás
1. alkalmazás Határozd meg az a + b összeget tudva, hogy a és b természetes szám, a prímszám és a · b = 52.
Megoldás. Mivel 52 = 22 · 13 és figyelembe véve, hogy a prímszám, az alábbi eseteket kapjuk:
a) a = 2 és b = 26, tehát a + b = 28; b) a = 13 és b = 4, tehát a + b = 17.
Következésképpen, a + b = 28 vagy a + b = 17.
Megjegyzés
1. Ha az a természetes szám négyzetszám, akkor a prímtényezőkre való felbontásában minden hatványkitevő páros szám.
2. Ha egy természetes szám prímtényezőkre való bontásában az összes hatványkitevő páros szám, akkor az egy négyzetszám.
3. Ha az a természetes szám prímtényezős felbontásában legalább egy olyan tényező van, amelynek hatványkitevője páratlan, akkor az a nem négyzetszám.
Gyakorlatok és feladatok
1. Ha a = 22 · 34 · 72 – n négyzetszám, akkor
2 – n páros természetes szám, vagyis n ∈{0, 2}.
2. A b = 2202 · 3404 · 54 · 1720 szám prímtényezőkre való felbontásában az összes hatványkitevő páros szám. Tehát a b négyzetszám.
3. A c = 32022 114044 54 173 szám nem négyzetszám, mert a prímtényezős felbontásában 173 található, melynek hatványkitevője páratlan.
1. Másold a füzetedbe, és töltsd ki az alábbi táblázatot a 30-as és 36-os számoknál látható minta alapján! Szám Prímtényezők szorzatára bontva
2. Írd fel príszámok szorzataként: 15, 21, 22, 39, 51, 65.
3. Bontsd fel prímtényezők szorzatára a 4, 6, 7, 10, 15, 20, 24, 45, 54, 63, 72, 88, 125, 169, 240, 576, 605, 1000, 105, 10n természetes számokat, n ∈ ℕ
4. Határozd meg:
a) a legkisebb természetes számot, amely két különböző prímtényező szorzataként írható fel; b) a legkisebb természetes számot, amely három különböző prímtényező szorzataként írható fel.
5. Írd fel prímszámok hatványainak szorzataként az alábbi számokat:
a) 125, 169, 240, 576, 605, 1000, 105, 10n , n ∈ ℕ ;
b) 252, 42 · 94, 283, (8 · 15)5.
6. a) Határozd meg a b − a különbséget tudva, hogy a2 · b = 28, a, b ∈ ℕ.
b) Határozd meg a + b + c összeget tudva, hogy a2 · b · c = 225 és a > b ≥ c > 1, a, b, c ∈ ℕ.
7. a) Bontsd fel prímtényezők szorzatára az A = 54 · p, számot tudva, hogy p prímszám és p > 3.
b) Bontsd fel prímtényezők szorzatára az A = 54 · p, számot a p ∈ {2, 3} értékei esetén.
8. Határozd meg az a, b és c prímszámot tudva, hogy a · b + a · c = 25.
27 1. fejezet • Halmazok. A természetes számok halmaza
szorzatára bontva 30 30 = 2 · 3 · 5 36 36 = 22 · 32 42 56 70 126 210 168
Szám Prímtényezők
Miniteszt
Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
15 p 1. Az A = {2, 23, 23 + 3, 32 + 2 · 3, 123} halmaz n prímszámot tartalmaz. Az n értéke:
A. 2; B. 3; C. 1; D. 4.
15 p 2. A 42-es prímtényezők szorzatára bontva:
A. 2 · 21; B. 3 · 14; C. 1 · 2 · 3 · 7; D. 2 · 3 · 7.
20 p 3. Az a szám, amelynek tényezők szorzatára bontott alakja 2·33·7 nem más, mint:
A. 378; B. 576; C. 376; D. 678.
20 p 4. Ha x és x + 11 prímszámok, akkor az x értéke:
A. 2; B. 0; C. 6; D. 11. 20 p 5. Az a legnagyobb aa alakú szám, amelynek négy osztója van:
A. 99; B. 88; C. 77; D. 66.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
3. l. A legnagyobb közös osztó meghatározása. Relatív prímszámok
Emlékeztető
Ha az a, b és d természetes számok teljesítik a d | a és d | b, relációkat, akkor a d szám az a és b szám közös osztója.
Halmazelméleti leírás
Az a és b természetes számok közös osztóinak halmaza a D a ⋂ Db metszet.
Példa: 7 a 14 és 28 természetes számok közös osztója, mert 7 | 14 és 7 | 21.
A 14 és 28 közös osztóinak halmaza a D14 ⋂ D21 = {1, 2, 7, 14} ⋂ {1, 3, 7, 21} = {1, 7}.
Megjegyzés.
1. Az 1-es az összes természetes szám közös osztója. Így írhatjuk: 1 | n vagy 1 ∈ D n bármely n természetes szám esetén.
2. Ha d a nullától különböző a és b természetes számok közös osztója, akkor d ≤ a és d ≤ b.
Indoklás
Bármely n természetes szám esetén n = 1 · n írható, vagyis 1 | n.
Mivel d|a, akkor a = d · x; x ≥1, azaz d ≤ a.
Mivel d|b, akkor b = d · y; y ≥1, azaz d ≤ b.
Azt a d természetes számot, amely az a és b számok közös osztója, és amely az a és b számok összes többi közös osztójának többszöröse, legnagyobb közös osztójuknak nevezzük.
Megegyezés szerint a és b természetes szám, és legalább az egyik nullától különböző.
Az a és b számok legnagyobb közös osztója az a legnagyobb nullától különböző d természetes szám, amely az a és b közös osztója.
Így írjuk: ln.k.o.(a, b) = d vagy (a, b) = d.
Megjegyzés. Több természetes szám legnagyobb közös osztója az a legnagyobb természetes szám, amely ezen összes szám közös osztója.
Ha a nullától különböző a és b természetes szám legnagyobb közös osztója az 1, akkor az a és b számot relatív prímeknek nevezzük.
Példa:
A 8 és 12 közös osztói: 1, 2, 4, ahol 1 < 2 < 4, tehát a 8 és 12 legnagyobb közös osztója a 4.
Így írjuk: ln.k.o.(8, 12) = 4 vagy (8, 12) = 4.
Példa: A 6, 12 és 51 legnagyobb közös osztója a 3, mert a 6, 12, 51 számok közös osztói az 1 és 3, melyek közül a legnagyobb a 3.
Így írjuk (6, 12, 51) = 3.
Példák: (1, 7) = 1; (8, 1) = 1; (2, 7) = 1; (2, 3) = 1; (7, 11) = 1; (3, 16) = 1; (6, 35) = 1; (21, 10) =1.
28 Matematika • Tankönyv a VI. osztály számára
Fedezzük fel, értsük meg!
Azonnali eredmények, hasznosak a feladatok megoldásában
Ha n nullától különböző természetes szám, akkor a 0 és n számok legnagyobb közös osztója épp az n szám.
Ha az a és b nullától különböző természetes szám és a | b, akkor a legnagyobb közös osztó az a szám.
Ha n nullától különböző természetes szám, akkor az 1 és n legnagyobb közös osztója az 1.
Bármely két különböző prímszám relatív prímek.
Alkalmazás
Páros tevékenység
Hogyan kell írni a megoldás során Példák
ln.k.o.(0, n) = n, bármely n ∈ ℕ * esetén.
(0, n) = n, bármely n ∈ ℕ * esetén.
Mivel a ∈ ℕ * , b ∈ ℕ * és a | b, akkor (a, b) = a.
(1, n) = 1, bármely n ∈ ℕ * esetén.
Mivel p1 és p2 prímszám és p1 ≠ p2, akkor (p1, p2) = 1.
(0, 1) = 1; (0, 2) = 2; (7, 0) = 7;
(0, 3) = 3; (0, 4) = 4; (9, 0) = 9;
(0, 5) = 5; (0, 6) = 6; (0, 12) = 12;
(2, 4) = 2; (3, 9) = 3; (6, 12) = 6; (9, 27) = 9; (5, 10) = 5; (8, 4) = 4;
(6, 2) = 2; (3, 1) = 1; (6, 3) = 3.
(1, 2) = 1; (1, 3) = 1; (1, 6) = 1; (1, 5) = 1; (1, 9) = 1; (1, 8) = 1; (10, 1) = 1; (11, 1) = 1; (12, 1) = 1.
(2, 3) = 1; (2, 5) = 1; (2, 7) = 1; (3, 7) = 1; (5, 11) = 1; (7, 13) = 1.
Csoportosítsuk az osztály diákjait párokba. A párok egyik tagja az S1, a másik pedig az S2 feladatot végzi.
A tevékenység utolsó részét megosztva végezik.
S1: Végezd el a 1, 2, 3, 4 lépéseket, majd a csapattársaddal együtt a 4’ lépést.
S2: Végezd el a 1, 3’ lépéseket, majd a csapattársaddal együtt a 4’ lépést.
1. lépés. Tényezők szorzatára bontjuk a 84-et és a 90-et.
2. lépés. Írd fel a 84 és 90 számok osztóinak halmazát!
3. lépés. Írd fel a 84 és 90 számok közös osztóinak halmazát!
4. lépés. Válaszd ki a 84 és 90 legnagyobb közös osztóját. Indokold meg!
3’. lépés. Írd fel az 1. lépés felbontásaiban szereplő közös prímtényezők legkisebb hatványon levő szorzatát, és számítsd ki e szorzatot!
4’. lépés. Hasonlítsd össze a 3’. és 4. lépésnél kapott eredményeket!
Állapítsd meg a kapcsolatot a legnagyobb közös osztó és a bontásokban előforduló közös prímszámok legkisebb kitevőjű hatványainak szorzata között.
1. lépés. 84 = 22 · 3 · 7; 90 = 2 · 32 · 5.
2. lépés. D84 = {1, 2, 3, 7, 4, 6, 12, 14, 21, 28, 42, 84}; D90 = {1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90}.
3. lépés. D84 ⋂ D90 ={1, 2, 3, 6}.
4. lépés. 1 < 2 < 3 < 6, (84, 90) = 6.
3’. lépés. 84 = 22 · 31 · 71; 90 = 21 · 32 · 51
Kiszámoljuk a 21 · 31 = 6 szorzatot.
2 → 3 → 4, illetve 1 → 3’ ugyanazon eredményhez vezetnek. Tehát (84, 90) = 6 vagy
(84, 90) = (22 · 31 · 71, 21 · 32 · 51) = 21 · 31= 6.
29 1. fejezet • Halmazok. A természetes számok halmaza
Jegyezd meg!
Több nem nulla természetes szám ln.k.o.-jának a meghatározása a számok prímtényezőkre való felbontásának segítségével történik, amelyet a következőképpen végzünk el:
1. Bontsd fel a számokat különböző prímszámok hatványainak szorzatára.
2. Az adott számok ln.k.o.-ja a közös prímtényezők szorzata, egyszer leírva, azzal a legkisebb hatványkitevővel, amellyel a megfelelő tényező megjelenik a számok felbontásában.
Gyakorlatok és feladatok
180 = 22 · 32 · 51
168 = 23 · 31 · 71
180 = 22 · 32 · 51
168 = 23 31 71 (180, 168) = 22 · 31 = 12
1. Másold a füzetedbe és egészítsd ki az alábbi táblázatot a minta alapján tudva, hogy D x az x természetes szám osztóinak halmaza, D y az y természetes szám osztóinak halmaza, valamint (x, y) az x és y számok legnagyobb közös osztója.
2. Írd fel az x és y számok osztóinak halmazát, közös osztóik halmazát, és határozd meg mindegyik esetben a legnagyobb közös osztójukat!
a) x = 16; y = 24; b) x = 28; y = 42.
3. Határozd meg a ln.k.o.-t az alábbi számpárok esetén!
a) 6 és 8;
b) 12 és 16;
c) 15 és 20;
d) 12 és 17;
e) 24 és 30;
f) 25 és 35.
4. A számok prímtényezős felbontása segítségével határozd meg a következő számpárok ln.k.o.-ját:
a) 36 és 48;
b) 27 és 63;
c) 105 és 45;
d) 66 és 110;
e) 27 és 135;
f) 2 · 22 · 23 · 24 és 512.
5. Határozd meg a következő számcsoportok ln.k.o.-
ját:
a) 24, 36 és 60; b) 28, 35 és 210.
6. Írj fel egy olyan természetes számpárt, amelynek legnagyobb közös osztója:
a) 6; b) 9; c) 10; d) 100.
7. Vizsgáld meg, és indokold válaszod, hogy az alábbi számpárok relatív prímszámok-e:
a) 4 és 15;
b) 8 és 9;
c) 12 és 16;
d) 21 és 40; e) 45 és 56.
f) 5 és 53.
8. Határozd meg az ab számot tudva, hogy az 54 és 81 legnagyobb közös osztója!
9. Határozd meg a 100-nál kisebb természetes számok számát, amelyek relatív prímek 100-zal.
10. Ha a 125 és a 189 számot elosztjuk ugyanazzal a természetes számmal, akkor a maradék 5, illetve 9 lesz. Keresd meg az osztót, tudva, hogy ez a lehető legnagyobb!
30 Matematika • Tankönyv a VI. osztály számára
y D x D y D x ∩ D y (x, y) 10 15 D10 = {1,
5, 10} D15 ={1, 3, 5, 15} D10 ∩ D15 ={1, 5} (10, 15) = 5
54
x
2,
30
100 75
Miniteszt
1. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
20 p a) A 18 és 27 számok egyik közös osztója:
A. 2; B. 3; C. 6; D. 12.
20 p b) A 18 és 27 számok legnagyobb közös osztója:
A. 3; B. 6; C. 9; D. 18.
20 p 2. Sorold fel az alábbi számok közös osztóit!
a) 28 és 35; b) 75 és 100; c) 36 és 49; d) 20, 30 és 40.
15 p 3. Határozd meg a cd prímszámot tudva, hogy a 460 és 138 közös osztója!
15 p 4. Határozd meg az a és b természetes számokat tudva, hogy a + b = 63 és (a, b) = 7.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
4. l. A legkisebb közös többszörös meghatározása
Emlékeztető
Ha az m, a és b természetes számok az m ⋮ a és m ⋮ b, relációt is teljesítik, akkor az m számot az a és b szám közös többszörösének nevezzük.
Halmazelméleti leírás
Az a és b természetes számok közös többszöröseinek halmaza az M a ⋂ Mb metszet.
Példa: 24 a 8 és a 6 természetes számok közös többszöröse, mert 24 ⋮ 8 és 24 ⋮ 6.
A 6 és a 8 közös többszöröseinek halmaza az
M6 ⋂ M8 = {0, 6, 12, 18, 24, …} ⋂ {0, 8, 16, 24, …} = {0, 24, 48, …}.
Megjegyzés A 0 az összes természetes szám közös többszöröse. Így írjuk: 0 ⋮ n vagy 0∈M n, bármely n természetes szám esetén.
Azt az m természetes számot, amely az a és b számok közös többszöröse, és amely az a és b számok összes többi közös többszörösének osztója, a legkisebb közös többszörösüknek nevezzük.
Az ln.k.o-hoz hasonlóan a gyakorlatban a fenti kijelentés átfogalmazásait vagy alkalmazásait fogjuk használni.
Az a és b számok legkisebb közös többszöröse az a legkisebb nullától különböző m természetes szám, amely az a és b közös többszöröse.
Így írjuk: lk.k.t[a, b] = m vagy [a, b] = m.
Megjegyzés. Több szám legkisebb közös többszöröse az a legkisebb természetes szám, amely az összes ezen szám közös többszöröse.
Példa: A 4 és 14 számok nullától különböző közös többszörösei: 28, 56, 84, 112, …, ahol a legkisebb a 28. Tehát, a 4 és 14 számok legkisebb közös többszöröse 28. Így írjuk: lk.k.t.[4, 14] = 28 vagy [4, 14] = 28.
Példa: A 15, 9 és 10 számok legkisebb közös többszöröse 90, mert:
M15 = {0, 15, 30, 45, 60, 90, ....}
M9 = {0, 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, ....}
M10 = {0, 10, 20, 30, 40, 50, 60, 70, 80, 90, ....}
M15 ⋂ M9 ⋂ M90 = {0, 90, 180, …}
A 15, 9 és 10 számok nullától különböző többszörösei közül a legkisebb 90, tehát [15, 9, 10] = 90.
31 1. fejezet • Halmazok. A természetes számok halmaza
Fedezzük fel, értsük meg!
Azonnali eredmények, hasznosak a feladatok megoldásában
Ha n természetes szám, akkor a 0 és n számok legkisebb közös többszöröse épp a 0.
Ha az a és b nullától különböző természetes számok és a | b, akkor az a és b számok legkisebb közös többszöröse a b szám.
Ha n nullától különböző természetes szám, akkor az 1 és n számok legkisebb közös többszöröse az n.
Ha p1 és p2 relatív prímek, akkor a legkisebb közös többszörösük a szorzatuk.
Alkalmazás
Hogyan kell írni a megoldás során
lk.k.t.[0, n] = 0, bármely a n ∈ ℕ esetén.
[0, n] = 0, bármely n ∈ ℕ esetén.
Ha a ∈ ℕ * , b ∈ ℕ * és a | b, akkor [a, b] = b
[1, n] = n, bármely n ∈ ℕ * esetén.
Ha p1 és p2 természetes számok
és (p1, p2) = 1, akkor
[p1, p2] = p1 · p2
Példák
[0, 1] = 0; [0, 2] = 0; [7, 0] = 0
[0, 3] = 0; [0, 4] = 0; [9, 0] = 0
[2, 4] = 4; [3, 9] = 9; [6, 12] = 12
[9, 27] = 27; [5, 10] = 10; [8, 4] = 8
[6, 2] = 6; [3, 1] = 3; [6, 3] = 6
[1, 2] = 2; [1, 3] = 3; [1, 6] = 6
[1, 5] = 5; [1, 9] = 9; [1, 8] = 8
[10, 1] = 10; [11, 1] = 11
[2, 3] = 6; [2, 5] = 10
[2, 7] = 14; [3, 7] = 21
[5, 12] = 60; [7, 8] = 56
Nézd meg a digitális tankönyvet, hogy párban végzett gyakorlati tevékenység során fedezd fel az lk.k.t. meghatározásának algoritmusát!
Jegyezd meg!
Több természetes szám lk.k.t.-ének meghatározása a számok prímtényezőkre való felbontásának segítségével történik, amelyet a következőképpen végzünk el:
1. Bontsd fel a számokat különböző prímszámok hatványainak szorzatára!
2. Az adott számok lk.k.t.-je a közös és nem közös prímtényezők szorzata, egyszer leírva, azzal a legnagyobb hatványkitevővel, amelyen az adott tényező a számok felbontásaiban előfordul.
Gyakorlatok és feladatok
180 = 22 · 32 · 51
168 = 23 · 31 · 71
180 = 22 · 32 · 51
168 = 23 · 31 · 71
[180, 168] = 23 · 32 · 51 · 71 = 2520
1. Másold a füzetedbe és töltsd ki az alábbi táblázatot, tudva, hogy M x az x természetes szám többszöröseinek halmaza, M y az y természetes szám többszöröseinek halmaza, és [x, y] az x és y számok legkisebb közös többszöröse. Az M x, M y és M x ∩ M y, halmazok esetében, a mintának megfelelően írjátok fel az első négy elemet!
32 Matematika • Tankönyv a VI. osztály számára
x y M x M y M x ∩ M y [x, y] 10 15 M10 = {0, 10, 20, 30, …} M15 = {0, 15, 30, 45, …} M10 ∩ M15 = {0, 30, 60, 90, …} [10, 15] = 30 36 54
75
100
2. Határozd meg a számok legkisebb közös többszörösét az alábbi számpárok esetén!
a) 2 és 3;
b) 4 és 6;
c) 10 és 15;
d) 9 és 12;
e) 20 és 30;
f) 25 és 50.
3. Határozz meg egy természetes számot, tudva, hogy az 500-nál kisebb, és a 12, 15 és 18 számokkal osztva a kapott maradék 0!
4. Számítsd ki az alábbi számpárok legkisebb közös többszörösét, használva a számok prímtényezők szorzatára való bontását!
a) 8 és 12;
b) 18 és 24;
c) 21 és 14;
d) 16 és 36;
e) 24 és 25;
f) 3 · 32 · 33 · 34 és 2 · 243.
5. Ugyanolyan teherbírású autókkal szállítják a kavicsot a kőbányából az építkezés helyszínére. A fuvarozó cégnek háromféle teherautója van, a terhelhetőség alapján. A teherautók maximális terhelhetősége 8 tonna, 9 tonna vagy 12 tonna. Ha maximálisan terhelnénk bármelyik teherautó-típust a három közül, az utolsó szállításra akkor is ugyanannyi kavics maradna. Határozd meg a legnagyobb szállított kavicsmennyiséget, tudva, hogy ez tonnában kifejezve egy háromjegyű természetes szám!
6. Számítsd ki az alábbi számok legkisebb közös többszörösét!
a) 4; 6 és 8; b) 20; 25 és 45.
7. Írj fel egy olyan természetes számpárt, amelynek a legkisebb közös többszöröse:
a) 10; b) 18; c) 47; d) 200.
8. Adott az x = 28 és y = 42 természetes szám. Az ln.k.o. és lk.k.t. jelöléseit használva a) számold ki (x, y) + [x, y].
Miniteszt
b) ellenőrizd, hogy az „x · y = (x, y) · [x, y]” kijelentés igaz-e bármely x és y két természetes szám esetén!
9. Határozd meg azt a legkisebb természetes számot, amelyet elosztva 15-tel, a kapott maradék 13, osztva 12-vel, a maradék 10, osztva 9-cel, a maradék 7!
10. Határozd meg az n természetes szám összes lehetséges értékét tudva, hogy (n, 36) = 12 és [n, 36] = 252.
11. Határozd meg a sportolók legkisebb számát tudva, hogy az összes sportolót 4 fős, vagy 6 fős, vagy 9 fős csapatokba is lehet szervezni!
12. Három tanuló rendezgeti a könyveket a matematikai szakterem könyvtárában. Megállapítják, hogy ha minden polcon 8 könyvet helyeznek el, vagy minden polcon 12 könyvet, vagy minden polcon 15 könyvet, akkor minden alkalommal 7 könyv marad rendezetlen. Határozd meg a lehető legkisebb számú könyvet, amely a könyvtárban lehet!
13. Szörény egy O kezdőpontú félegyenesen, a kezdőponttól kiindulva kék színű pontokat ábrázol, egymástól 12 cm távolságra. Rezső ugyanezen a félegyenesen, annak O origójából kiindulva, sárga színű pontokat ábrázol, egymástól 15 cm távolságra. Határozd meg az O pont és a következő, mindkét színnel színezett pont távolságát!
1. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
20 p a) 12 és 18 egy közös többszöröse:
A. 18; B. 24; C. 72; D. 90.
20 p b) 12 és 18 legkisebb közös többszöröse:
A. 72; B. 48; C. 1; D. 36.
20 p 2. Írj három-három közös többszöröst az alábbi számok esetén!
a) 8 és 6; b) 15 és 20; c) 7 és 11; d) 12, 18 és 36.
15 p 3. Határozd meg az ab alakú természetes számot tudva, hogy az 12 és 15 közös többszöröse!
15 p 4. Határozz meg két olyan c és d természetes számot, amelyre c · d = 864 és [c, d] = 72.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
33 1. fejezet • Halmazok. A természetes számok halmaza
Emlékeztető
Az a természetes szám osztható a b természetes számmal, ha van olyan c természetes szám, melyre a = b · c.
Fedezzük fel, értsük meg!
A tulajdonság Matematikai nyelven Példák
Bármely a természetes szám osztható saját magával. a⋮a, bármely a ∈ ℕ* esetén. 1⋮1; 2⋮2; 3⋮3; … .
Ha a és b természetes számok esetén a osztható b-vel, és b is osztható a-val, akkor a két szám megegyezik.
Ha a, b, c természetes számok esetén a osztható b-vel és b osztható c-vel, akkor a osztható c-vel.
Alkalmazás
Ha a ∈ ℕ, b ∈ ℕ a⋮b és b⋮a, akkor a = b
Ha a ∈ ℕ, b ∈ ℕ, c ∈ ℕ, a⋮b és b⋮c, akkor a⋮c.
Ha 7⋮p és p⋮7, akkor p = 7.
Ha 1⋮p és p ∈ ℕ, akkor p = 1.
Ha p⋮6 és 6⋮3, akkor p⋮3.
Ha p⋮6 és 6⋮2, akkor p⋮2.
Az oszthatósági relációnak a fenti táblázatban leírt sajátos tulajdonságai más eredményekhez, úgynevezett tulajdonságokhoz is vezetnek, amelyek megkönnyítik a természetes számokkal kapcsolatos feladatok megértését és megoldását.
1. Ha a d természetes szám az a és b természetes számok közös osztója, ahol b ≤ a, akkor d az a + b és a – b osztója is.
a) Ha a d természetes szám osztja az a és b természetes számok összegét, és d az összeg egyik tagjának osztója, akkor d a másik tagnak is osztója.
Ha d | a és d | b, ahol a, b, d ∈ℕ , b ≤ a, akkor d | (a + b) és d | (a – b).
Ha d | (a + b) és d | a, ahol a, b, d ∈ℕ , akkor d | b.
Ha d | (a + b) és d | b, ahol a, b, d ∈ℕ , akkor d | a.
b) Ha a d természetes szám osztja az a és b természetes számok különbségét, és d a különbség egyik tagjának osztója, akkor d a másik tagnak is osztója.
2. a) Ha az a természetes szám a b · c szorzat osztója, és a és b relatív prímek, akkor az a a c szám osztója.
Ha d | (a – b) és d | b, ahol a, b, d ∈ℕ , b ≤ a, akkor d | a.
Ha d | (a – b) és d | a, ahol a, b, d ∈ℕ , b ≤ a, akkor d | b.
Ha a, b, c ∈ ℕ, a | b · c és (a, b) = 1, akkor a | c.
b) Bizonyítsd be példával az a) pontban szereplő állítás érvényességét! 2 | 3 · x, x ∈ ℕ, (2, 3) = 1 akkor 2 | x
A fenti állítások indoklását lásd a digitális tankönyvben!
34 Matematika • Tankönyv a VI. osztály számára
5. l. Az oszthatóság tulajdonságai ℕ-ben
Megoldott feladatok
1. a) Számold ki 120 és 180 ln.k.o.-ját!
b) Hasonlítsd össze a 3120 és 2180 számokat! Használd az a) alpont eredményét!
2. a) Ellenőrizd az m · n = (m, n) · [m, n] egyenlőséget m = 28 és n = 21 esetén!
b) Használva az m · n = (m, n) · [m, n] kijelentést, ahol m és n tetszőleges természetes szám, indokold meg a következő kijelentést: „Az m és n relatív prímszámok legkisebb közös többszöröse ezen természetes számok szorzata.”
Megoldás. a) 120 = 23 · 3 · 5, 180 = 22 · 32 · 5
(120, 180) = 22 · 3 · 5 = 60
b) 3120 = (32)60 = 960 és 2180 = (23)60 = 860.
Mivel 9 > 8, akkor 960 > 860, azaz 3120 > 2180.
Megoldás.
a) (28, 21) = (22 · 7, 3 · 7) = 7; [28, 21] = 84; (28, 21) · [28, 21] = 7 · 84 = 588 = 28 · 21.
b) Ha m és n relatív prímek, akkor (m, n) = 1.
Mivel m · n = (m, n) · [m, n], akkor m · n = 1· [m, n], vagyis
[m, n] = m · n.
Ha m, n ∈ℕ és (m, n) = 1, akkor [m, n] = m · n.
3. Határozd meg az n, 4 · n + 3 és 5 · n + 7 természetes számokat tudva, hogy mindegyik prímszám!
Megoldás. Ha 5 · n + 7 prímszám, akkor páratlan szám. Mivel 7 páratlan, ezért 5 · n páros, tehát n páros. Az egyetlen páros prímszám az n = 2. A kapott prímszámok a következők: 2, 11, 17.
Gyakorlatok és feladatok
1. Egy természetes szám osztható 33-mal. Határozd meg ennek a számnak 3-mal való osztási maradékát!
2. Egy busz 36 férőhelyes.
a) Ha mindegyik utas csak egy helyet foglalhat, akkor határozd meg, hogy legkevesebb hány utat kell a busz megtegyen ahhoz, hogy 144 személyt szállítson el!
b) Ha mindegyik utas csak egy helyet foglalhat, akkor határozd meg, hogy legkevesebb hány utat kell a busz megtegyen ahhoz, hogy 444 személyt szállítson el!
3. Bizonyítsd be, hogy:
a) a 2 · 123 + 2 · 456 szám osztható 2-vel;
b) az 5 · 13 + 15 · 57 + 25 · 99 szám 5-nek többszöröse;
c) 4 osztja a 4 · 123 + 44 · n számot, bármely n természetes szám esetén!
4. Határozd meg:
a) a 4x3y alakú természetes számokat, ha 3-mal és 5-tel is osztható!
b) a 1x2y3x alakú természetes számokat, ha 4-gyel és 9-cel is osztható!
5. a) Bizonyítsd be, hogy a 10-es számrendszerben felírt A = 12x + 3x4 + x56, szám osztható 3-mal, bármely x számjegy esetén!
b) Határozd meg az x azon legnagyobb értékét, amelyre az A szám osztható 6-tal!
6. Bizonyítsd be, hogy nincs olyan természetes szám, amelyet 4-gyel osztva a maradék 3, 6-tal osztva pedig a maradék 4.
7. Egy osztály tanulói számára 127 füzetet és 110 ceruzát vásároltak, és egyenlően osztották szét a tanulók között. Tudva, hogy az osztályban több mint 10 tanuló van, és hogy a kiosztás után 2 ceruza és 1 füzet maradt, határozd meg az osztály tanulóinak számát!
8. Az iskolába, ahová Ilona jár kevesebb, mint 200 tanuló van, a tanulókat 18 vagy 24 fős csoportokra lehet osztani. Számítsd ki az iskolába beíratkozott tanulók szamat!
9. Határozd meg azt a legkisebb természetes számot, amely 25-tel, 45-tel és 50-nel osztva a kapott maradék 7!
35 1. fejezet • Halmazok. A természetes számok halmaza
10. Az M = {3, 4, 8, a, b, c} halmaznak az a tulajdonsága, hogy a halmaz elemei között található a halmaz
bármely két elemének ln.k.o-ja és lk.k.t.-je is. Határozd meg az M halmaz ismeretlen elemeit!
11. Számold ki az a = 425 + 1287 és b = 917 2711 számok
ln.k.o-ját és lk.k.t.-jét!
Miniteszt
12. Határozd meg azokat az a, b, c prímszámokat, melyekre 2 · a + 3 · b + 4 · c = 30.
13. Egy kozmetikai terméket 6 cm-es, 4 cm-es és 3 cm-es dobozokba csomagolnak, majd ezeket egy kocka alakú dobozba helyeznek. Határozd meg a kocka élének hosszát, tudva, hogy a kocka belseje teljesen tele van, és hogy a dobozok száma legfeljebb 50 darab!
Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
30 p 1. 780-nak tényezők szorzatára bontott alakja:
A. 22 · 32 · 5 · 7; B. 22 · 3 · 5 · 11; C. 22 · 3 · 5 · 13; D. 22 · 32 · 5 · 13.
30 p 2. 280 és 392 számok ln.k.o.-nak es lk.k.t.-nek összege:
A. 2024; B. 2016; C. 2026; D. 2014.
30 p 3. Adott a prímszámok P halmaza és A = {7, 25, 47, 64, 91}. Határozd meg az A \ P halmazt!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
ISMERETFELMÉRŐ
I. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
5 p 1. Az alábbi halmazok közül a véges halmaz az
A. {1, 10, 100, …}; B. {20, 21, 22, …}; C. D1000; D. M100.
5 p 2. Az 52 és 25 közötti természetes számok halmazának kardinálisa:
A. 7; B. 6; C. 8; D. 32.
5 p 3. Az {m, a, t, e} halmaz kételemű részhalmazainak száma:
A. 6; B. 12; C. 8; D. 10.
5 p 4. A 15 valódi osztóinak összege:
A. 24; B. 16; C. 13; D. 8.
5 p 5. A legnagyobb 1ab alakú és 9-cel osztható szám a
A. 199; B. 189; C. 999; D. 198.
5 p 6. A 4; 40; 44; 400; 404; 440; 444 számsorozat 8-cal osztható tagjainak száma
A. 6; B. 3; C. 4; D. 5. II. Írd le a teljes megoldást!
1. Adott az A = {1, 3, 4, 5}, B = {2, 4, 6} valamint a C, amely a 3-mal osztható számjegyek halmaza.
5 p
10 p 5 p
10 p 10 p
15 p 5 p
2.
a) Határozd meg a C halmazt!
b) Számítsd ki: A ⋃ B, B ⋂ C, C \ A
c) Határozd meg az a számot tudva, hogy (A ⋂ B) ⋃ {a, 5} = {3, 4, 5}.
a) Határozd meg az a0b alakú és 2-vel osztható számok számát! Válaszod indokold!
b) Írd le a 98-as szám osztóinak halmazát!
3. Adott az a = 24 és b = 45 szám.
a) Számold ki az a és a b számok legnagyobb közös osztóját és a legkisebb közös többszörösét!
b) Határozd meg azokat a prímszámokat, amelyek az a + b szám osztói!
Megjegyzés: Munkaidő: 50 perc
Hivatalból: 10 pont
36 Matematika • Tankönyv a VI. osztály számára
2. ARÁNYOK. ARÁNYPÁROK
2.1. Arányok. Aránypárok. Az egyszerű hármasszabály
1. l. Arányok
A mindennapi életben, valamint a különböző tudományos jelenségek tanulmányozása során egy mennyiség mértékegységeit más mennyiségek mértékegységeivel hasonlítjuk össze. A fizikai mennyiségek, amelyekkel számolunk, lehetnek azonos típusúak, de különbözőek is. Ebben az értelemben gyakran hasznos, ha ismerjük két azonos típusú mennyiség mértékének hányadosát (arányát), vagy két különböző, egymástól függő mennyiség mértékének hányadosát (arányát).
Oldjuk meg figyelmesen!
1. feladat
Radu több 15 cm oldalhosszúságú, négyzet alakú keretet készít a grafikai versenyre, amelyen indul. Ezek oldalhossza cm-ben van kifejezve. Ezekhez Radu fából készült léceket vásárol, amelyek 120 cm hosszúak. Hány keretet lehet készíteni egy lécből?
Megoldás. Mivel a keretek 15 cm-es oldalú négyzet alakúak, ebből következik, hogy minden kerethez egy 60 cm hosszú lécre van szükség (a négyzet kerületével megegyező hosszúságú), amelyből a 4 oldalt levágjuk.
A feladatot a következőképpen fogalmazzuk meg:
Határozd meg, hogy egy 120 cm-es léc hossza hányszor nagyobb, mint a 15 cm-es négyzet kerülete!
H = 15 cm, akkor K = 60 cm, Legyen x annyi, hogy K · x = 120 (cm). Mivel a K-et ugyanabban a mértékegységben fejezzük ki, mint a léc hosszát, x = 120 : 60, azaz x = 2. Egy léc hossza tehát a négyzet kerületének kétszerese, azaz minden lécből pontosan két keretet lehet készíteni.
A fenti feladatban minden méret azonos típusú (szakaszok hossza), ugyanabban a mértékegységben kifejezve. Annak meghatározásához, hogy az egyik mennyiség mértéke hányszor nagyobb vagy kisebb, mint egy másik mennyiség mértéke, elosztjuk a két mennyiség mértékének megfelelő számokat.
A 120 : 60 osztást 120 60 alakba írjuk és azt mondjuk, hogy leírtuk a léc hosszának és a keret kerületének arányát.
Természetesen, megfordítva a keret kerülete és a léc hosszának aránya 60 120 .
2. feladat
Egy kerékpáros 3,5 óra alatt tesz meg egy 70 km-es távot. Számítsd ki, hogy a kerékpáros milyen átlagsebességgel halad!
Megoldás.
A jármű átlagos haladási sebessége km/h-ban (km/óra) kifejezve a jármű által egy óra alatt megtett távolság kilométerben kifejezve.
Ha 3,5 óra alatt 70 km-t tesz meg, akkor egy óra alatt 3,5-ször kisebb távolságot, azaz 70 : 3,5 kilométert tesz meg.
Következésképpen a kerékpáros átlagsebességét a 70 35 , arány adja meg.
A teljes választ az osztás eredménye adja meg, amelyet az arány értékének nevezünk, azaz v = 70 35 20 , = (km/h).
Sajátos kompetenciák: 1.2; 2.2; 3.2; 4.2; 5.2; 6.2
37 2. fejezet • Arányok. Aránypárok
A fenti feladatban a mértékegységek különbözőek: a távolságot kilométerben, az időt pedig órában mérjük. E fizikai mennyiségek (távolság és idő) értékeinek hányadosa egy új fizikai mennyiséget (sebesség) eredményez, amelynek mértékegysége az adott mennyiségek mértékegységeihez viszonyítva határozható meg.
Amikor egy jármű egy d km távolságot t óra alatt tesz meg, akkor az átlagsebessége v = d t (km/h).
Amikor egy jármű egy d m távolságot t másodperc alatt tesz meg, akkor a jármű átlagsebessége v = d t m/s (méter per másodperc).
Fedezzük fel, értsük meg!
Mindkét feladat esetében két szám arányát kapjuk meg matematikai modellként.
Az a és b szám arányát a b -vel jelöljük, ahol b ≠ 0 és
az a : b hányadosát jelenti, azaz a b ab = : .
9 és 3 aránya 9 3 .
1 és 5 aránya 1 5 .
Az a és b számot az arány tagjainak nevezzük. A 9 3 arány tagjai 9 és 3, az 1 5 arány tagjai pedig 1 és 5.
Az a : b hányadosát az arány értékének nevezzük, ahol b ≠ 0.
Egy p 100 alakú arányt százalékos aránynak nevezünk.
Egy százalékos arányt a p% szimbólummal jelöljük és így olvassuk: „p század” vagy „p százalék”.
A 9 3 arány értéke 3, az 1 5 arány értéke pedig 0,2.
Bővítéssel és egyszerűsítéssel minden arányt felírhatunk százalékos arányként.
Például 50 1
2 50 100 ) = .
50 100 50 jel %.
Jegyezd meg!
Két fizikai mennyiség aránya a mennyiségek mértékének megfelelő számok aránya. A két fizikai mennyiség lehet azonos típusú, de különböző fizikai mennyiség is.
Megjegyzés.
a) Ha a két fizikai mennyiség azonos típusú, akkor méréseiket ugyanabban a mértékegységben kell kifejezni, az arány pedig egy szám.
b) Két különböző fizikai mennyiség aránya egy harmadik fizikai mennyiséghez vezet, amelynek mértékegysége az eredeti fizikai mennyiségek mértékegységétől függ.
c) Egy arány értéke nem változik, ha a törtet, amellyel ábrázoljuk, bővítjük vagy egyszerűsítjük egy nullától különböző számmal.
38 Matematika • Tankönyv a VI. osztály számára
Megoldott feladat
Szimóna egy d távolságot tesz meg kerékpárral, 12 km/h átlagsebességgel haladva, és 30 perc alatt éri el a célját. Viktor ugyanezt a távolságot 6 perc alatt teszi meg motorkerékpárjával.
a) Számítsd ki a Szimóna által megtett távolságot!
b) Számítsd ki, hogy Viktor milyen átlagsebességgel halad a motorkerékpárjával!
c) Számítsd ki, hogy a motorkerékpár sebessége hányszor nagyobb, mint a kerékpár sebessége! Használd a motorkerékpár sebességének és a kerékpár sebességének arányát!
Megoldás.
a) Jelöljük vb-vel a Szimóna haladási átlagsebességét. Ha v d bt = , akkor d = vb · t. Mivel a sebességet km/h-ban van kifejezve, arra következtetünk, hogy a távolságot kilométerben, az időt pedig órában kell kifejezni.
Mivel 30 min = 0,5 h, akkor d = 12 · 0, 5 = 6 (km).
b) Jelöljük v m-mel a motorkerékpár haladási átlagsebességét. Tehát d = 6 km, és t = 6 min = 6 60 1 10 01 hh h == , . Akkor v m = 10 6 01 60 , (km/h).
c) A két sebesség azonos típusú, azonos mértékegységben kifejezett mennyiség. Akkor v v m b == 60 12 5 , tehát Viktor 5-ször gyorsabban halad, mint Szimóna. Alkalmazás
Gyakorlatok
és feladatok
1. A mellékelt ábra egy négyzetrácsra készült. Válaszd ki a helyes választ!
Csak egy válasz helyes.
a) A színes négyzetek száma:
A. 24; B. 16; C. 12; D. 18.
b) A színezetlen négyzetek száma:
A. 24; B. 18; C. 16; D. 12.
c) A színes négyzetek számának és a színezetlen négyzetek számának aránya:
A. 1 3 ; B. 1 2 ; C. 1 4 ; D. 2 3 .
d) A színes négyzetek számának és a nagy négyzetet alkotó összes négyzet számának aránya:
A. 3 4 ; B. 2 3 ; C. 1 2 ; D. 1 3 .
2. Írd fel az a és b számok arányát, majd számítsd ki ennek az aránynak az értékét minden egyes számpárra:
a) a = 180 és b = 240;
b) a = 27,5 és b = 5,5;
c) a = 4 3 és b = 2 9 .
3. A következő táblázatban x és y gyümölcsök tonnában kifejezett mennyiségét jelöli. Másold a táblázatot a füzetedbe, és töltsd ki az üres részeket úgy, hogy az x és y arányának értéke 4 legyen.
x 12 3,6 200
y 5 24
4. Az egyik stadion befogadóképessége 36 000 férőhely. Egy labdarúgó-mérkőzésre 24 000 néző látogat el.
a) Határozd meg a foglalt és az összes ülőhely számának arányát!
b) Állapítsd meg az szabadon maradt és az elfoglalt helyek számának arányát!
5. Szerkeszd meg az AB és CD 12,5 cm és 250 mm hosszúságú szakaszokat! Döntsd el, melyik szakasz nagyobb és hányszor!
39 2. fejezet • Arányok. Aránypárok
6. Határozd meg a következő arányok értékét:
a) egy óra és egy perc;
b) egy gramm és egy kilogramm;
c) egy hektár és egy négyzetméter.
Miniteszt
1.
7. Adottak az a b = 3, b c = 12 arányok.
Számítsd ki az a c , 2 3 ⋅ a b , 5 6 ⋅ b c arányok értékét!
10 p a) Írj egy olyan számpárt, amelynek az aránya 10!
20 p b) Írj két olyan számpárt, amelyeknek az aránya 1,25!
2. Az m n arány értéke 6. Töltsd ki az üres részeket úgy, hogy igazak legyenek az állítások!
15 p a) Az m szám … mint az n szám, azaz … -szerese.
15 p b) Ha m-et és n-t megszorozzuk 3-mal, akkor az új arány értéke ….
3. Vencel hátizsákja üresen 300 g és benne van a 400 g súlyú tolltartója, a 300 g súlyú vízfestéke, az 1,6 kg súlyú füzetei és a 3,4 kg súlyú tankönyvei.
10 p a) Számítsd ki a teli hátizsák súlyát!
10 p b) Számítsd ki a teli hátizsák tömegének és a tolltartó tömegének arányát!
10 p c) Számítsd ki a vízfesték tömegének és a teljes hátizsák tömegének arányát!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
2. l. ARÁNYPÁROK
Oldjuk meg figyelmesen!
1. feladat Egy kereskedő ugyanolyan minőségű epret árul 3 kg-os vagy 5 kg-os ládákba csomagolva. Az eper ára az egyes ládákon az alábbi táblázatban szerepel. Emma nagymamája és Szonja nagymamája egyenként két láda epret vásárolt.
Az ládában levő eper mennyisége
3 kg 5 kg
Egy láda ára 27 lej 45 lej
a) Ha tudjuk, hogy Emma nagymamája 8 kg epret, Szonja nagymamája pedig 10 kg epret vásárolt, számítsd ki, hogy melyikük mennyit fizetett!
b) Számítsd ki, hogy a két nagymama fejenként milyen átlagáron vásárolt epret!
c) Számítsd ki az egyes ládákban lévő eper árát!
Megoldás. a) A 8 kg-os mennyiség csak egy 3 kg-os és egy 5 kg-os doboz megvásárlásával érhető el. Ekkor Emma nagymamája 27 + 45 = 72 (lejt) fizet. Hasonló érveléssel Szonja nagymamája két darab 5 kg-os dobozt vásárolt, és 90 lejt fizetett érte.
b) Emma nagymamája által vásárolt eper ára P1 = 72 8 9 = (lej/kg), a Szonja nagymamája által vásárolt eper ára pedig P2 = 90 10 9 = (lej/kg).
c) A 3 kg-os ládákban levő eper ára P3 = 27 3 9 = (lej/kg), az 5 kg-os ládákban levő eper ára pedig
P4 = 45 5 9 = (lej/kg).
40 Matematika • Tankönyv a VI. osztály számára
Fedezzük fel, értsük meg!
A fenti feladatból láthatjuk, hogy az eper árát több, azonos értékű aránynyal is ki lehet fejezni. Ezeket egyenlő arányoknak nevezzük.
Két arány egyenlőségét aránypárnak
Ha az a b ab , 0, 0 ≠≠ és c d cd,, 0 ≠≠ 0 arányok értéke egyenlő, akkor az a b c d = aránypárt írjuk. a d b c = kültag kültag beltag beltag
A nullától különböző a, b, c, d természetes számok az aránypár tagjai: a és d neve kültag, a b és c neve beltag.
Az aránypár alaptulajdonsága
Mindegyik aránypár esetén a beltagok szorzata egyenlő a kültagok szorzatával.
Matematikai nyelven Példák
Ha a ≠ 0, b ≠ 0, c ≠ 0, d ≠ 0 és a b c d = , akkor a · d = b · c.
A gyakorlatban hasznos, ha egy aránypárt a tagjai közötti kapcsolat alapján hozunk létre.
Ha a ≠ 0, b ≠ 0, c ≠ 0, d ≠ 0 és a · d = b · c, akkor az a, b, c, d egy aránypár tagjai.
Például az a b c d = aránypárt alkothatjuk. Mivel 2 · 18 = 12·3, akkor a
A fenti két állítás egyetlen állításként a következőképpen fogalmazható meg:
Bármely a, b, c, d természetes szám esetén a · d = b · c akkor és csakis akkor ha a b c d .
Alkalmazás
Ha a ≠ 0, b ≠ 0, c ≠ 0, d ≠ 0, akkor adbca b c d = . 2 · 18 = 12 · 3
Attól függően, hogy milyen gyakorlati összefüggésben azonosítunk egy aránypárt, az aránypár egyik tagját a másik három tag alapján határozhatjuk meg. Az a ≠ 0, b ≠ 0, c ≠ 0, d ≠ 0 a b c d = esetén azt kapjuk, hogy:
41 2. fejezet • Arányok. Aránypárok
72 8 90 10 = ; 90 10 27 3 = ; 27 3 45 5 = ; 45 5 72 8 = ; 27 3 72 8 = aránypárok.
nevezzük.
2 12 3
18 = és 2 · 18 = 12 · 3.
2 12 3 18 = aránypár
alkotható.
⇔ 2 12 3 18 = .
Képlet Számítási
Példák egy kültag beltagok szorzata másik kültag a = b c d d = b c a Mivel x 9 25 3 = , , akkor x 92 5 3 75 , , ; Mivel 4 9 5 = y , akkor y 95 4 11 25 , . egy beltag = kültagok szorzata másik beltag b = a d c c = a d b Mivel 12 3 7 m = , akkor m 12 7 3 28 ; Mivel 15 11 33 = p , akkor p 15 33 11 45 .
mód
A nullától különböző racionális számokkal végzett műveletek tulajdonságai lehetővé teszik, hogy a nullától különböző a, b, c, d számokból és az a b c d = , aránypárból kiindulva más aránypárokat képezzünk, akár ugyanazokat a tagokat használva, más szerepben, akár úgy, hogy bizonyos szabályok szerint módosítjuk a tagokat
a) Azonos tagú származtatott aránypárok a b c d =
A folyamat
A matematikai jelölések nyelvén Példák
aránypárok, ahol a tagokat megváltoztattuk:
Gyakorlatok és feladatok
1. Keresd meg az arányokat, amelyek aránypárokat alkotnak:
a) 2 3 és
9 ; b) 5 4 és 25 20 ; c)
05 , és 8 4 ; d)
. 2. Töltsd ki az üres helyeket számokkal úgy, hogy aránypárokat kapj:
. 3. Írj aránypárokat a következő számok segítségével:
a) 4; 6; 8; 12; b) 9; 3; 6; 4,5.
4. Írd fel az arányokból képezhető aránypárokat!
3 5 , 6 10 , 2 3 , 33 55 , 51 85 .
5. Másold a füzetedbe, és írj számokat az üres helyekre úgy, hogy az 5 9 = 25 45 , , aránypárból azonos tagú származtatott aránypárokat kapj!
a) ... 9 = 25 , ; b) 5 ... = ... , 45 ; c) 9 = 45 , .
6. Másold a füzetedbe, és írj számokat az üres helyekre úgy, hogy az 5 9 = 25 45 , , aránypárból megváltoztatott tagú származtatott aránypárokat kapj!
a) 5 ... = 25 , ... ; c) 5 9 = ... ... ; e) 5 9 = 10 ...
b) ... 9 = ... , 45 ; d) 30 9 = ... , 45 ;
42 Matematika • Tankönyv a VI. osztály számára
Kicseréljük a beltagokat. a b c d = ⇔ a c b d = 2 4 3 6 = ⇔ 2 3 4 6 = Kicseréljük a kültagokat. a b c d = ⇔ d b c a = 2 4 3 6 = ⇔ 6 4 3 2 = Megfordítjuk mindkét arányt. a b c d = ⇔ b a d c = 2 4 3 6 = ⇔ 4 2 6 3 =
Az a b c d = aránypárból származtatott
A kapott aránypár Példák ab b cd d ab b cd d , a > b, c > d. 4 2 6 3 = ⇔ 42 2 63 3 és 4 2 6 3 = ⇔ 42 2 63 3 a ab c cd a ab c cd , a > b, c > d. 4 2 6 3 = ⇔ 4 42 6 63 és 4 2 6 3 = ⇔ 4 42 6 63 a b mc md m ,0 ma mb c d m ,0 2 4 3 6 = ⇔ 2 4 05 3 05 6 , , és 2 4 3 6 = ⇔ 52 54 3 6 a mb c md m ,0 ma b mc d m ,0 2 4 3 6 = ⇔ 2 54 3 56 és 2 4 3 6 = ⇔ 52 4 53 6 a b ac bd a b ac bd , a > c, b > d. 6 3 4 2 = ⇔ 6 3 64 32 és 6 3 4 2 = ⇔ 6 3 64 32 .
b)
1
9 2 és 14 3
e) 25 35
, és 2 3
f) 15 3
3 6
6
;
,
;
, és
4
a) 5 28 = ; b) 05 6 ,,15 = ; c) 6
7. Határozd meg az ab természetes számot tudva, hogy a 4; 12; 13 és ab egy aránypár tagjai!
8. Határozd meg az alábbi aránypárok ismeretlen tagjait!
a) 3 735 = x ; c) 03 , y = 09 21 , ;
b) y 2 9 45 = , ; d) x 4 = 25 x .
9. Egy toll és egy golyóstoll árának aránya 22 3 . Tudva, hogy a golyóstoll ára 7,50 lei, számold ki a toll árát!
10. Egy aránypár kültagjai 2 · n + 7 és 10, illetve a beltagjai 6 és 25. Határozd meg az n értékét!
11. Írd a füzetedbe, és töltsd ki az üres helyeket úgy, hogy igaz állításokat kapj!
a) Ha a b 3 5 = , akkor a · b = ..., valamint 30 − 150 ab = …;
b) Ha a 4 = 8 b és 2 c = d 16 , akkor a · b − c · d = ….
12. Két szám aránya 2 9
a) Számítsd ki e számok összegét, tudva, hogy a kisebbik szám 10!
b) Számítsd ki e számok szorzatát, tudva, hogy a nagyobbik szám 4,5!
13. Tudva, hogy x y = 3 10 , x ≠ 0, y ≠ 0, számítsd ki:
a) xy y + ; b) x yx ; c) x y 10 ⋅ ; d) 10 3 9 xy y .
14. Két szám aránya 0,1.
a) Határozd meg a számokat, tudva, hogy összegük 44!
b) Határozd meg a számokat, tudva, hogy a különbségük 27!
Miniteszt
Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
20 p 1. Az a) 1 4 és 6 20 ; b) 7 3 és 21 9 ; c) 5 2 és 15 8 ; d) 9 10 és 27 40 arányok közül aránypárt alkotnak az
A. az a)pont arányai; B. a b)pont arányai ; C. a c) pont arányai; D. d) pont arányai.
20 p 2. Ha a 6 = 05 , b , akkor az a · b szorzat egyenlő
A. 1; B. 2; C. 3; D. 4.
20 p 3. Az 12 5 = 36 x aránypár x tagjának értéke:
A. 15;
B. 18; C. 6; D. 9.
30 p 4. Ha a 12 = 3 a , akkor az a természetes szám:
A. 15; B. 6; C. 36; D. 4.
Megjegyzés: Munkaidő: 20 perc Hivatalból: 10 pont
43 2. fejezet • Arányok. Aránypárok
Fedezzük fel, értsük meg!
1. feladat
Szonja egy 98 oldalas könyvet olvas, naponta 14 oldalt, Delila egy 147 oldalas könyből, naponta 21 oldalt, Irénke pedig egy 84 oldalas könyvből, naponta 12 oldalt. Mutasd ki, hogy a három barátnő ugyanannyi nap alatt végez az olvasással. Viktor, Irénke édesapja arra törekszik, hogy mindhárom könyvet elolvassa, és naponta annyi oldalt olvasson el, amennyit a három lány együtt olvas el egy nap alatt. Mutasd ki, hogy Viktor ugyanannyi nap alatt fejezi be az olvasást, mint a lánya. Megoldás. Az, hogy hány nap alatt fejezi be valaki egy könyv elolvasását, az összes elolvasott oldal és az egy nap alatt elolvasott oldalak számának aránya.
1. feladat egy példán keresztül bizonyítja az aránysorok egy tulajdonságát:
2
a b a b a b n n 1 1 2 2 === ... b1 ≠ 0, b2 ≠ 0, … b n ≠ 0 és b1 + b2 + … + b n ≠ 0 akkor a b a b a b n n 1
=== ... aaa bbb n n 12 12 ... .
2. feladat Határozd meg az x 2 = y 12 = z 6 , feltételt teljesítő x, y és z számot tudva, hogy x + y + z = 220.
Használva az x 2 = y 12 = z 6 = xyz ++ ++ 2126 tulajdonságot azt kapjuk, hogy x 2 = y 12 = z 6 == 220 20 11 .
Akkor, x 2 = 11, y 12 = 11, z 6 = 11, tehát x = 22, y = 132, z = 66.
3. feladat Két szám különbsége 20. Határozd meg a számokat, tudva, hogy azok egyenesen arányosak a 4-gyel és a 9-cel!
Megoldás. Legyen a, b a két szám. A kijelentés alapján abk 49 == . Mivel ak 4 = és bk 9 = , akkor a = 4 · k, illetve b = 9 · k. Mivel b > a, tehát b – a = 20, azaz 9 · k – 4 · k = 20 ⇒ 5 · k = 20, akkor az eredmény k = 4. A keresett számok a = 4 · 4 és b = 9 · 4, vagyis a = 16, b = 36.
44 Matematika • Tankönyv a VI. osztály számára
l. Aránysorok
3.
2 ≠
Így írjuk: a b a b a b a b n n 1 1 1 2 3 3 ==== . Példák 1 2 2 4 3 6 100 200 === ; 05 2 1 4 2 8 6 24 3 12 , ==== .
Három vagy több olyan a b 1 1 , a b 2 2 , a b 3 3 , …, a b n n egyenlő értékű arány, ahol b1 ≠ 0, b
0, b3 ≠ 0, …, b n ≠ 0, aránysort alkot.
Alkalmazás
Szonja Delila Irénke Viktor Oldalak száma összesen 98 147 84 98 + 147 + 84 = 329 Oldalak száma / nap 14 21 12 14 + 21 + 12 = 47 A könyv befejezéséhez szükséges napok száma 98 14 7 = 147 21 7 = 84 12 7 = 329 47 7 = A fenti táblázat alapján a következő aránysort
fel: 98 14 147 21 84 12 329 47 === , ahol mindegyik arány értéke 7. Mivel
az aránysor 98 14 147 21 84 12 98 147 84 14 21 12 .
írhatjuk
329 = 98 + 147 + 84, valamint 47 = 14 + 21 + 12, akkor
Az
Ha
1
2
Gyakorlatok és feladatok
1. A 3 5 , 2 3 , 6 10 , 10 15 , 9 15 , 2 12 , 21 35 arányok közül
kiválasztva írj:
a) három egyenlő arányból álló aránysort;
b) egy lehető legtöbb egyenlő arányból álló aránysort!
2. a) Írj egy 3 2 -del egyenlő négy arányból álló aránysort!
b) Írj egy 1 3 -dal egyenlő öt arányból álló aránysort!
3. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
a) Adott az a 2 = b 3 = c 4 = d 5 aránysor. Az a, b, c számok közül a nagyobbik:
A. a; B. b; C. c; D. d.
b) Ha a 5 = b 6 = 1 2 , akkor az a és b számok összege:
A. 1; B. 1,5; C. 5; D. 5,5.
c) Ha a m = b n = c p = 1 3 , akkor abc mnp ++ ++ értéke:
Miniteszt
A. 1 3 ; B. 2 3 ; C. 3 3 ; D. 3 1 3 .
4. Számítsd ki az alábbi aránysor ismeretlen tagjait!
1 5 = x 10 = 3 y = 4 z
5. Az a, b és c számok összege 72. Számítsd ki az a, b és c számot tudva, hogy a 3 = b 5 = c 10 .
6. Az a és b számok különbsége 12. Számítsd ki az a és b számot tudva, hogy 7 a = 3 b .
7. János 5600 lejért vett egy laptopot, egy hangrendszert és egy vetítővásznat. Számold ki az egyes termékek árát tudva, hogy a laptop árának az egynyolcada a hangrendszer arának egynegyede és a vetítővászon arának pedig a fele. Oldd meg a feladatot aránysorok segítségével!
8. Az a, b, c ∈ℕ* számok esetén a 3 = b 4 = c 5 .
a) Bizonyítsd be, hogy a2 + b2 = c2 .
b) Határozd meg azokat az (a, b, c) természetes számhármasokat, amelyekre teljesül az a + b + c < 77 feltétel!
1. Írd a füzetedbe, és töltsd ki a pontozott helyeket úgy, hogy igaz állításokat kapj!
20 p a) Az 2 5 , 4 10 , 6 15 arányokkal egyenlő egyik arány az … .
20 p b) Ha 4 36 8 == a b , akkor a + b = … .
20 p c) Ha 1 5 = c 10 = 4 3 d , akkor d − c = … .
30 p 2. Határozd meg az x, y és z számot tudva, hogy x 3 = y 4 = z 6 és x + y = 49.
Megjegyzés: Munkaidő: 20 perc Hivatalból: 10 pont
45 2. fejezet • Arányok. Aránypárok
4. l. Egyenesen arányos mennyiségek. Fordítottan arányos mennyiségek
Oldjuk meg figyelmesen!
Feladat
240 kg almát ládákban tárolnak. A raktárban 4 kg-os, 8 kg-os, 12 kg-os és 24 kg-os ládák állnak rendelkezésre.
a) Határozd meg, hogy a teljes mennyiség tárolható-e, tudva, hogy minden típusból 5 ládát használnak!
b) Hasonlítsd össze a négyféle ládában tárolt alma mennyiségét, és figyeld meg, mi történik a tárolt mennyiséggel, ha az egyes ládákban lévő almák mennyisége többszörösére nő vagy csökken!
c) Határozd meg a tárolásra használt ládák számát, ha azonos típusú ládákat használunk!
d) Figyeld meg, mi történik a felhasznált ládák számával, ha az egyes ládákban lévő alma mennyisége többszörösére nő vagy csökken!
Megoldás
a) Az adott típusú 5 ládában tárolt alma mennyisége az adott típusú ládában tárolt mennyiség és a felhasznált ládák számának, azaz az 5 számnak a szorzata.
Egy ládában tárolt mennyiség 4 kg
5 ládában tárolt mennyiség 4 · 5 = 20 (kg)
8 kg
8 · 5 = 40 (kg)
12 kg 24 kg
12 · 5 = 60 (kg) 24 · 5 = 120 (kg)
Az 5 azonos típusú ládában tárolható mennyiség 20 + 40 + 60 + 120 = 240 (kg), azaz a teljes mennyiség.
b) A táblázat adatai azt mutatják, hogy ha az egyforma ládában levő alma mennyisége többszörösére nő, akkor a tárolt alma mennyisége ugyanannyiszorosára nő a felhasznált ládák számának megváltozása nélkül.
A fenti relációkat aránysor segítségével is felírhatjuk:
8 kg = 4 kg · 2 és 40 kg = 20 kg · 2;
12 kg = 4 kg · 3 és 60 kg = 20 kg · 3;
24 kg = 4 kg · 6 és 120 kg = 20 kg ·
40 60 120 .
Azt mondjuk, hogy a két mennyiség (egy ládában lévő gyümölcs mennyisége és az állandó számú ládában tárolt gyümölcs mennyisége) egyenesen arányos.
c) A felhasznált ládák száma, a teljes almamennyiség és az egy ládában lévő alma mennyiségének aránya az alábbi táblázatból adódik:
d) A táblázat adatai azt mutatják, hogy ha az egyforma ládában lévő alma mennyisége többszörösére nő, akkor az azonos mennyiségű gyümölcshöz felhasznált ládák száma ugyanannyiszorosára csökken, azaz: Megfigyelhetjük, hogy a 8 kg-os ládákban kétszer annyi alma van, mint a 4 kg-os ládákban, és az azonos menynyiségű alma tárolásához szükséges ládák száma kétszer kisebb. Hasonlóan gondolkodva a többi ládapárnál is megállapíthatjuk: Ha az egyféle ládában lévő alma mennyiségét a többszörösére növeljük, akkor a szükséges ládák száma ugyanannyiszor csökken.
Ezt igazolják a c) táblázatban szereplő összefüggések is: c): 8 kg = 4 kg· 2 és 30 láda = 60 láda : 2; 12 kg = 4 kg · 3 és 20 láda = 60 láda : 3; 24 kg = 4 kg · 6 és 10 láda = 60 láda : 6.
Ezek az összefüggések átírhatók egyenlő szorzatok sorává is: 4 · 60 = 8 · 30 = 12 · 20 = 24 · 10.
Azt fogjuk mondani, hogy a két mennyiség (a ládában lévő gyümölcs mennyisége és az állandó tárolt mennyiséghez felhasznált ládák száma) fordítottan arányos
46 Matematika • Tankönyv a VI. osztály számára
6
48
20
12 24
Egy ládában tárolt mennyiség 4 kg 8 kg 12 kg 24 kg A használt ládák száma 240 4 60 = 240 8 30 = 240 12 20 = 240 24 10 =
Fedezzük fel, értsük meg!
Két olyan mennyiséget, amely egyidejűleg ugyanannyiszor növekszik vagy csökken, egyenesen arányos mennyiségnek nevezünk.
Az {a1, a2, a3, …, a n } és {b1, b2, b3, …, b n} rendezett véges számhalmaz
elemei egyenesen arányosak, ha felírhatjuk az a b a b a b a b n n 1 1 2 2 3 3 ==== ... aránysort.
Például az a sebesség, amellyel egy
jármű halad, és az adott idő alatt megtett távolság.
Az {5; 7,5; 12} és {10; 15; 24} halmaz elemei egyenesen arányosak, mert 5 10 75 15 12 24 == , Az arányok közös, nem nulla értékét arányossági tényezőnek vagy arányossági együtthatónak nevezzük, és általában k-val jelöljük.
A fenti rendezett halmazok arányossági tényezője k = 0,5. Két mennyiséget fordítottan arányos mennyiségnek nevezünk abban az esetben, amikor az egyik mennyiség többszörösére nő, a másik mennyiség ugyanannyiszorosára csökken.
Az {a1, a2, a3, …, a n } és {b1, b2, b3, …, b n} rendezett véges számhalmaz elemei fordítottan arányosak, ha felírhatjuk ababababnn 11 22 33 ... szorzatok sorát.
Pl. az a sebesség, amellyel egy jármű halad, és az az idő, amely alatt egy adott távolságot megtesz.
Az {3, 6, 15} és {10, 5, 2} halmazok elemei fordítottan arányosak, mert 3 · 10 = 6 · 5 = 15 · 2.
Számos számtani feladat megoldásánál alapvető fontosságú az az információ, hogy két mennyiség egyenesen arányos vagy fordítottan arányos.
Alkalmazás
Megoldott feladat.
Rendezett halmaz = olyan halmaz, melynek elemeit adott sorrendben soroltuk fel.
Az a és b természetes számok egyenesen arányosak 2-vel és 3-mal, a b és c számok pedig fordítottan arányosak 2-vel és 3-mal.
a) Bizonyítsd be, hogy a = c.
b) Határozd meg azt a három számot, amelyről tudod, hogy a + 2 · b + 3 · c = 140.
Megoldás
a) {a, b} és {2, 3} a) {a, b} és {2, 3} között egyenes arányosság áll fenn, tehát ab 23 =⇔ 3 · a = 2 · b. (1)
{b, c} és {2, 3} között fordított arányosság áll fenn, tehát 2 · b = 3 · c. (2) (1) és (2) alapján megállapítjuk, hogy 3 · a = 3 · c, vagyis a = c.
b) Ha a + 2 · b + 3 · c = 140 és a = c, akkor az (1)-et használva kapjuk, hogy a + 3 · a + 3 · a = 140, azaz 7 · a = 140. Azt kapjuk, hogy a = 20, c = 20, majd 2b = 60, vagyis b = 30.
Gyakorlatok és feladatok
1. Az alábbi táblázatok mindegyikében az A és B mennyiségek értékei szerepelnek.
Tanulmányozd, hogy ezek egyenesen arányos mennyiségek-e. Indokold válaszodat! a)
47 2. fejezet • Arányok. Aránypárok
A 1 3 6 10 12,5 B 2 6 12 20 25
A 2 4 5 15 20 B 6 12 15 40 60 Szótár
b)
2. Bogdán 24 darab egyforma matematikafüzetet vásárol, amelyekért 180 lejt fizet.
a) Számítsd ki:
a1) egy matematikafüzet árát;
a2) azt az összeget, amit Bogdán fizetett volna, ha hat ugyanilyen matekfüzetet vásárolt volna.
b) Másold a füzetedbe, majd töltsd ki a következő táblázatot, tudva, hogy n a Bogdán által vásárolt füzetek száma, s pedig az n füzetért fizetett összeg lejben.
s n 1 2 6 24 s n
3. Az x és y egyenesen arányos 2-vel és 3-mal.
a) Bizonyítsd be, hogy x < y.
b) Számold ki az x értékét, ha y = 9.
4. Határozz meg három, a 3, 7 és 5 számokkal egyenesen arányos számot, ha tudjuk, hogy a legkisebb az 21!
5. Máriusz, Dani, László és Radu lövészversenyen vesznek részt. A lövészet végén a négy gyerek által elért pontszámok egyenesen arányosak az 1,5; 2,5; 1,75 és 2 számokkal.
a) Írd fel a versenyzőket a verseny végén elért pontszámok csökkenő sorrendjében!
b) Határozd meg az egyes versenyzők által kapott pontok számát, ha együttesen 620 pontot szereztek!
Miniteszt
6. Egy személyvonat 240 km-t tesz meg. Számítsd ki, hogy a vonatnak milyen átlagsebességgel kell haladnia ahhoz, hogy a távolságot 2 óra, 3 óra, 4 óra és 6 óra alatt tegye meg!
Másold a füzetedbe és töltsd ki az alábbi táblázatot, tudva, hogy t a távolság megtételéhez szükséges idő, v pedig a vonat sebessége km/h-ban.
t 2 h 3 h 4 h 6 h v t · v
7. Az alábbi táblázatokban az A és B mennyiségek szerepelnek.
a)
b)
Tanulmányozd, hogy ezek fordítottan arányos mennyiségek-e! Indokold válaszod!
8. Az x és y szám fordítottan arányos 7-tel és 10-zel.
a) Mutasd ki, hogy x > y.
b) Határozd meg az y számot tudva, hogy x = 20.
9. Határozd meg a 4, 15, 9 számokkal fordítottan arányos számokat tudva, hogy közülük a legnagyobb a 45!
10. Az a és b számok fordítottan arányosak a 0,5 és 2,4 számokkal. Határozd meg a számokat, tudva, hogy összegük 58!
1. Töltsd ki a pontozott helyeket úgy, hogy igaz legyen az állítás!
15 p a) Ha a 4 = b 7 , akkor az a és b egyenesen arányos a következő számokkal: … .
15 p b) Ha c ·3= d ·5, akkor a c és d fordítottan arányos a következő számokkal:
20 p c) Ha a P2 négyzet oldala háromszorosa a P1 négyzet oldalának, akkor a P1 négyzet kerülete a P2 négyzet kerületénél … -szor … .
40 p 2. Egy háromszög kerülete 80 cm. Számítsd ki a háromszög oldalainak hosszát tudva, hogy azok egyenesen arányosak a 4, 5 és 7 számokkal!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
48 Matematika • Tankönyv a VI. osztály számára
A 1 3 4 10 18 B 24 8 6 2,4 1,5
A 2 3 4 5 60 B 15 10 7,5 6 0,5
5. l. Az egyszerű hármasszabály
Oldjuk meg figyelmesen!
1. feladat Péter 2 kg őszibarackot vásárolt 16 lejért. Mennyibe kerül 15 kg ugyanilyen barack?
I. módszer
Egy kilogramm őszibarack ára a 16 2 arány
értéke, azaz 8 lej/kg.
Akkor 15 kg őszibarack 15-ször többe kerül, tehát 15 · 8 = 120 lej.
II. módszer
x-szel jelöljük 15 kg őszibarack árát.
A vásárolt mennyiség és a költsége egyenesen arányos
mennyiségek, így felírhatjuk a 2 16 15 = x arányt.
Az aránypár ismeretlen tagja az x 15 16 2 120 (lej).
Tehát 15 kg őszibarack ára 120 lej.
2. feladat. Mihály 4 óra alatt tette meg a távot 60 km/h sebességgel. Mennyi idő alatt tenné meg Mihály ugyanezt a távolságot 80 km/h átlagsebességgel?
I. módszer
A Mihály által megtett út d = v · t, ahol
v = 60 km/h és t = 4 h. Azt kapjuk, hogy d = 240 km. Ha átlagsebessége 80 km/h lenne, akkor a szükséges idő t d v = lenne, ahol d = 240 km, valamint
v = 80 km/h. Tehát t == 240 80 3 (h).
II. módszer
x-szel jelöljük azt az időt, amely alatt a távolságot 80 km/h átlagsebességgel megtehetjük. A haladási sebesség és az adott távolság megtételéhez szükséges idő fordítottan arányos. Ezért felírhatjuk az 60 · 4 = 80 · x egyenletet, azaz x = 60 4 80 3 . Tehát a távolságot 3 óra alatt tenné meg.
Mindkét fent megoldott feladat esetében a második megoldás azt a lehetőséget szemlélteti, hogy egy menynyiség értékét egy másik mennyiséggel való egyenes vagy fordított arányossági kapcsolaton alapuló egyszerű számítással lehet meghatározni.
Fedezzük fel, értsük meg!
Az egyszerű hármasszabály egy olyan módszer, amellyel kiszámítható egy fizikai mennyiség értéke, ha tudjuk, hogy az egyenesen arányos vagy fordítottan arányos egy másik fizikai mennyiséggel.
Az egyszerű hármasszabály alkalmazásához a két mennyiség értékének arányosságát kell megállapítani. Ezután az ismert adatokból az értékek arányosságából kapott összefüggések segítségével meghatározzuk az ismeretlen tagot.
Ha vázlatosan felírjuk a feladat által megadott mennyiségek és ismert értékeik összefüggését, az elégséges ahhoz, hogy a feladatot egyszerű hármasszabállyal meg tudjuk oldani. Az ismeretlen érték meghatározásához elvégzendő műveletek attól függnek, hogy a feladat az arányosság két típusának melyikébe tartozik.
Ha az első mennyiség értékei a1 és a2, a másik mennyiség értékei pedig b1 és x, akkor a feladat adatai vázlatosan a következőképpen írhatók fel:
a1 b1
a
49 2. fejezet • Arányok. Aránypárok
2 ………………… x
Az ismeretlen érték meghatározásához a következő két esetet tárgyalhatjuk:
1. Ha a mennyiségek egyenesen arányosak, akkor az {a1, a2} és {b1, b2} halmaz elemei egyenesen arányosak, vagyis a b a x 1 1 2 = . Az ismeretlen tag x ab a 21 1 .
Vázlatosan, ha egyenesen arányosak, akkor a1 .............................. b1 a2 .............................. x x ab a 21 1
Alkalmazás
2. Ha a mennyiségek fordítottan arányosak, akkor az {a1, a2} és {b1, b2} halmaz elemei fordítottan arányosak, vagyis a1 · b1 = a2 · x. Az ismeretlen tag x ab a 11 2
Vázlatosan, ha fordítottan arányosak, akkor a1 .............................. .b1
a2 .............................. x x ab a 11 2
Az egyszerű hármasszabályt a mindennapi életben, a kémiában, a fizikában, a földrajzban és más területeken is gyakran használják.
Megoldott feladat. Egy úszómedencét három ugyanolyan hozamú szivattyú 45 perc alatt tudna megtölteni. Miután 30 percig együtt működtek, a szivattyúk közül kettőt kikapcsolnak. Számítsd ki, mennyi idő alatt tölti meg a medencét a megmaradt szivattyú!
Megoldás A szivattyú működési ideje és a medence töltöttségi szintje egyenesen arányos. Ezért az egyszerű hármasszabályt alkalmazva megtudhatjuk, hogy a 30 perc alatt mennyire telt meg a medence.
Tudjuk, hogy a 3 szivattyú együttesen 45 perc alatt megtölti a tartályt. A felhasznált szivattyúk száma és a töltési idő fordítottan arányos, így a hármasszabály segítségével kiszámíthatjuk, hogy mennyi idő alatt töltené meg egyetlen szivattyú a tartályt.
Ha a tartály kétharmada 30 percen belül megtelik, akkor a fennmaradó szivattyúnak egyedül kell megtöltenie a tartály egyharmadát.
45 min .............................. 1 (az egész medence)
30 min .............................. x (a medence egy része)
Azt
A működési idő és a töltési szint egyenesen arányos. Az egyszerű hármasszabályt alkalmazzuk annak megállapítására, hogy mennyi idő alatt tölti meg a maradék szivattyú a medence egyharmadát. 1
Végezetül a fennmaradó szivattyúnak még 45 percig kell működnie.
Gyakorlatok és feladatok
1. 20 kg sárgabarackból 12 kg lekvárt készítünk. Számítsd ki, hogy 25 kg sárgabarackból mennyi lekvár készül!
2. Egy 20 fős munkáscsapat 15 nap alatt tud elvégezni egy munkát. Számítsd ki:
a) hány nap alatt tudja 15 munkás befejezni a munkát;
b) hány munkás szükséges ahhoz, hogy a munkát 10 nap alatt befejezzék!
3. János családja kirándulni megy. Az 500 km megtételéhez az autó 35 liter benzint fogyasztana.
a) Határozd meg, hogy mennyi benzinre lenne szükség, ha János családja 100 km-rel csökkentené a megtett távolságot!
b) Számítsd ki a megtakarított pénzösszeget, tudva, hogy egy liter benzin 7 lejbe kerül!
4. Egy 54 oldalas dokumentum nyomtatásához 9 percig dolgozik egy nyomtató. Számítsd ki, hogy
50 Matematika • Tankönyv a VI. osztály számára
kapjuk, hogy 45 1 30 = x , tehát x 30 1 45 2 3 .
szivattyú .............................. 45 perc 1 szivattyú .............................. y Tehát 3 · 45 = 1 · y, azaz y 345 1 135 (perc).
3
medence .............................. 135 perc 1 3 medence .............................. z 1 135 1 3 = z , tehát z 135 1 3 1 135 3 45 (perc).
ugyanez a nyomtató hány perc alatt nyomtat ki egy 270 oldalas dokumentumot!
5. Egy vállalatnak öt új autót kell vásárolnia, amelyek mindegyike 12 000 euróba kerül. Határozd meg, hány autót tudna a vállalat vásárolni, ha egy autó ára 15 000 euró lenne!
6. Egy gazdaságnak szőlőszedő emberekre van szüksége. Tudva, hogy 36 ember 6 nap alatt szedné le a szőlőt, határozd meg, hány emberre van szüksége a gazdaságnak ahhoz, hogy legfeljebb 4 nap alatt befejezze a szőlőszedést!
7. Egy iskolai projekthez 4 diákra van szükség, akik mindegyike 5 órát dolgozik. Határozd meg, hogy mennyi időt kell dolgozzanak az egyes tanulók a projekten, ha a 4 tanulóhoz 2 másik tanuló is csatlakozna!
8. Dani segít beállítani a számítógépes labort, és 6 órán át cipeli a szükséges felszerelést. Sanyi ugyanezt 10 óra alatt tenné meg. Határozd meg, hogy a két diáknak együtt dolgozva mennyi időbe telne a felszerelés elszállítása!
9. Egy háromfős nyomdászcsapat egy szórólap elkészítésére készül. Az első és a második együtt 6 óra alatt, a második és a harmadik együtt 12 óra alatt, az első és a harmadik együtt 8 óra alatt készítené el a szórólapot.
a) Határozd meg, hogy az egyes nyomdászok egyedül dolgozva mennyi idő alatt tudnák elkészíteni a szórólapot!
b) Határozd meg, hogy a három nyomdász együtt dolgozva mennyi idő alatt készítené el a szórólapot!
10. Két azonos típusú lekvárosüvegbe 800 gramm lekvár fér. Hány lekváros üveget kell vásároljon a háziasszony ahhoz, hogy 2 kg lekvár legyen az üvegekben?
11. Sára és Dóra ugyanolyan sampont vásárol, Sára 30 lejt fizet egy 800 ml-es dobozért, Dóra pedig 18 lejt egy 500 ml-es dobozért. Döntsd el, hogy a két lány közül melyik vásárolta olcsóbban a sampont!
12. Számítsd ki, hány ruha készülhet 88 m2 anyagból, tudva, hogy 33 m2 anyagból 15 ugyanolyan ruha készült!
13. Egy munkáscsapat 8 nap alatt befejezné egy épület egyötödének építését.
a) Határozd meg, hogy ugyanez a csapat hány nap alatt építené fel az épület negyedét!
b) Határozd meg, hány nap alatt fejezné be ugyanaz a csapat az egész épületet!
14. Ha egy kerékpáros 24 km/h átlagsebességgel haladna, akkor 3 óra alatt érne célba. Számítsd ki:
a) mekkora átlagsebességgel kellene a kerékpárosnak haladnia ahhoz, hogy két és fél óra alatt elérje a célját;
b) mennyi idő alatt érné el a kerékpáros a célállomást percekben kifejezve, ha a kerékpáros 30 km/h átlagsebességgel haladna!
15. János 18 fényképalbumot vásárol, amelyek mindegyike 24 lejbe kerül. Számítsd ki, hány albumot vásárolna Péter ugyanennyiért, ha egy album 27 lejbe kerülne!
Miniteszt
1. Töltsd ki a pontozott helyeket úgy, hogy igaz legyen az állítás.
30 p a) Ha 8 füzet 60 lejbe kerül, akkor 9 ugyanolyan típusú füzet ára … lej.
30 p b) Ha egy munkát 16 munkás 20 nap alatt végez el, akkor 40 munkás el fogja végezni a munkát … nap alatt.
30 p 2. Egy kerékpáros 2 óra alatt éri el célját, 30 km/h átlagsebességgel haladva. Határozd meg, mekkora átlagsebességgel kellene a kerékpárosnak haladnia ahhoz, hogy másfél óra alatt elérje úti célját!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
51 2. fejezet • Arányok. Aránypárok
6. l. Százalékok. Arányok a mindennapi életben
Emlékeztető
Egy p 100 alakú arányt százalékos aránynak nevezünk. A százalékos arány jele p% és p századként vagy p százalékként olvassuk.
Következésképpen, egy a szám p %-a papapa100 100 % , szorzat, az a n , p%-a pedig a pa n pa
gyakorlatban, a b szám az a-nak p%-a, akkor így írjuk pab 100 vagy pb a 100 = .
A fenti arányban szereplő p, a, b számok bármelyike kifejezhető a másik kettővel a következőképpen: p b a 100 ; a b p 100 ; bpa 100 .
Fedezzük fel, értsük meg!
Egy anyag vízben való feloldása vizes oldatot eredményez.
1. feladat
Ferenc 50 g cukrot 150 g vízzel kever össze, és oldatot kap.
a) Számítsd ki a kapott oldat tömegét.
b) Számítsd ki a cukor tömegének és az oldat tömegének arányát. Fejezd ki a kapott arányt százalékos arányban. Megoldás. Jelölés: m o az oldat tömege, mvíz a víz tömege és m c a cukor tömege.
a) Akkor, m o = m c + mvíz = 50 g + 150 g, tehát m o = 200 g.
b) m m c o 50 200 25 100 , azaz m m c o 25%.
Írjuk azt, hogy c = 25%, és azt mondjuk, hogy a kapott cukor-víz oldat koncentrációja 25%.
Egy oldat koncentrációja azonos a 100 g oldat előállításához feloldott anyag mennyiségével.
Matematikailag az oldat koncentrációja az oldódó anyag tömegének és az oldat tömegének aránya.
Egy oldat koncentrációját általában százalékos arányban fejezik ki.
Ha 500 g oldat 30 g sót tartalmaz, akkor az oldat koncentrációját az egyszerű hármasszabály alapján határozzuk meg, vagy a 30 500 aránnyal fejezzük ki.
500 g oldat …………. 30 g só
100 g oldat …………. x g só ⇒ x =
100 30 500 6 .
Tehát az oldat koncentrációja c = 6 100 vagy c = 6%.
Hasonlóképpen, két fém összeolvasztásából ötvözet keletkezik. Számos ötvözetet használnak különböző területeken. Például az építőiparban használt acél a vas (Fe) és a szén (C) ötvözete.
A nemesfémeket tartalmazó ötvözeteket általában az orvostudományban, az elektronikában, az ékszeriparban stb. használják. Az ötvözet tulajdonságai és értéke a tisztaságától függ.
52 Matematika • Tankönyv a VI. osztály számára
25 100 25 jel %
25 1 4 25 100
Bármilyen arányt ki lehet fejezni százalékos arányként bővítésekkel vagy egyszerűsítésekkel. Például
500-nak 25%-a 25 100 500 12500 100 125 100 . 2 5 -nek 25 %-a 25 100 2 5 10 100 1 10 .
n pan pan 100 100 100 : :% szorzat, ahol n ≠ 0.
A
Az ötvözet tisztasága azonos a hozzáadott fém (nemesfém) tömegével 100 g ötvözetben.
Matematikailag az ötvözet tisztasága a nemesfém tömegének és az ötvözet tömegének aránya.
Az ötvözet tisztaságát általában százalékos arányban fejezik ki.
Ha 2 g aranyat és 8 g rezet összeolvasztunk, 10 g ötvözetet kapunk.
mAu-val jelöljük az arany tömegét, mCu-val a réz tömegét és m-mel az ötvözet tömegét. Ekkor, m = mAu + mCu, és az ötvözet tisztaságát vagy egyenesen arányos mennyiségekre vonatkozó egyszerű hármasszabállyal, vagy a T = m m Au = 2 10 1 5 02 20 ===,% arány kiszámításával határozzuk meg.
Az ötvözet tisztasága T = 20 %, azaz 100 g ötvözetben 20 g arany van.
A térképek a számunkra ismeretlen terekben való tájékozódás szükségességéből erednek. A térképek a pontok közötti távolságok arányos csökkentésével őrzik meg a részleteket.
Ha a térképen két tetszőleges A és B pontot és a földön A1 és B1 pontoknak megfelelő pontokat veszünk, akkor az AB AB11 arány állandó. (Az arány az A és B pontpártól függetlenül ugyanaz.) A fent leírt arányt, amelyet általában 1-es számlálójú törtként fejeznek ki, térképi méretaránynak (léptéknek) nevezzük.
A térkép léptéke a térképen mért távolság és a terepen mért megfelelő távolság aránya.
Ha az A és B helyszín közötti távolság a valóságban 5 000 000 cm, a térképen pedig 5 cm, akkor a térképet a következő léptékkel készítették el: 5 5 000 000 1 1000 000 = vagy 1: 1 000 000.
Megjegyzés. A térkép léptéke azt mutatja meg, hogy a térképen szereplő távolságok hányszor kisebbek, mint ugyanazok a távolságok a valóságban.
Vizsgálat: Fibonacci és az aranymetszés
Alkossatok három munkacsoportot! Olvassátok el figyelmesen az alábbi szövegeket, majd használjátok a digitális tankönyvet! Itt találjátok az egyes csoportok kutatási feladatainak részleteit, írásban is, dinamikusan is. A mindennapi életben lépten-nyomon arányokkal és arányossággal találkozunk.
1. Az aranymetszés nevű híres arány mindenben jelen van körülöttünk: a természetben, a művészetben, az építészetben, sőt még az emberi DNS-ben is. Az értékét ϕ-vel jelöljük, és megközelítőleg 1,618-nak felel meg.
2. Az aranymetszés során egy szakaszt a következő arányban osztunk fel: meghatározzuk az AB szakaszon található M pont helyzetét úgy, hogy MB MA AB MB = = ϕ.

AB MB MB MA
1 618 , A M
B
Ha MA = a és MB = b, akkor AB = a + b, és MB MA AB MB = pedig b a ab b alakban írható, melynek neve aranymetszés.
3. A természetes számok 1, 1, 2, 3, 5, 8, 13, ... sorozatát Fibonacci-sorozatnak nevezzük. Ebben a sorozatban minden egyes tag, a harmadikkal kezdve, az előző két tag összege: 2 = 1 + 1; 3 = 2 + 1; 5 = 3 + 2; 8 = 5 + 3 …
A fenti sorozatban szereplő számokat a természetben megfigyelték, és az emberi tevékenységben már ősidők óta használják.
Portfólió téma
1. Mutasd be a vizsgálatod eredményeit az osztálytársaidnak!
2. Találj kapcsolatot a csoportod eredményei és a más csoportokban lévő társaid eredményei között, és töltsd ki a személyes portfóliódat az illető adatokkal!
53 2. fejezet • Arányok. Aránypárok
Alkalmazás
Megoldott feladat
1. Sót oldunk fel vízben, és 8%-os oldatot kaptunk. Számítsd ki az 500 g oldat előállításához
feloldott só mennyiségét!
Megoldás. Jelöljük: m s a feloldott só tömege és m az oldat tömege. c = m m s , tehát 8 100 500 = ms , azaz ms 8 500 100 40 (g). Felelet: 40 g sót oldunk fel 460 g vízben.
2. 400 g arany-réz ötvözet tisztasága 0,825. Határozd meg, hogy mennyi aranyat kell hozzáadni ahhoz, hogy 0,875-ös tisztaságú ötvözetet kapjunk.
Megoldás. Legyen m1 az első ötvözethez felhasznált arany tömege. Akkor, m1 400 0 825 = , , tehát m1 = 400 · 0,825 = 330 (g). Az új ötvözet x mennyiségű arany hozzáadásával jön létre. Ekkor az új ötvözet aranyának tömege 330 + x, az ötvözet tömege pedig 400 + x. Mivel az ötvözet tisztasága 0,875, a 330 400 875 1000 125 x x arányt kapjuk, amely ekvivalens 330 400 7 8 x x -dal. Származtatott aránypárok alkalmazásával 330 70 7 1 x . Az aránypárok alaptulajdonságából adódik, hogy 330 + x = 490, tehát x = 490 – 330 = 160 (g). Felelet: 160 g aranyat adunk hozzá.
3. A térkép léptéke 1: 400 000. Számítsd ki a két hely közötti távolságot a földön, tudva, hogy a térképen ez a távolság 16 cm.
I. Nyilvánvaló, hogy a távolság a terepen és a távolság a térképen egyenesen arányos. Az egyszerű hármasszabályt alkalmazva a következőt kapjuk:
1 cm ……………. 400 000 cm 16 cm ………………… x cm x = 16 · 400 000 = 6 400 000 (cm)
II. Az értelmezést használva írhatjuk, hogy 1 400 000 16 = x .
Az arány ismeretlen tagja
x = 16 · 400 000 = 6 400 000 (cm).
Felelet: d = 6 400 000 cm = 64 km.
Megjegyzés. Sok gyakorlati helyzetben az egyszerű hármasszabály nagyobb biztonságot nyújt az érvelésben.
Gyakorlatok és feladatok
1. Fejezd ki százalékos arányok alakjában: 27 100 ; 71 100 ; 13 50 ; 1 20 ; 11 10 ; 0,2; 1,75.
2. Írd irreducibilis közönséges tört alakú arányként: 50%, 80%, 17,5%, 120%.
3. Számítsd ki:
a) 225 lej 20 %-át;
b) 440 liter 35 %-át;
c) 500 kg 12,5 %-át.
4. Határozd meg a 300-nál 25%-kal nagyobb számot!
5. Júliának 300 leje volt, aminek 20%-át elköltötte.
a) Számítsd ki a Júlia által elköltött összeget!
b) Fejezd ki százalékos arányban azt az összeget, amely Júliának maradt!
6. Miután egy színházi előadásra a jegyek 40%-át eladták, 120 jegy maradt eladatlanul. Határozd meg, hogy hány jegyet állítottak ki eladásra!
7. Számítsd ki a kapott oldat koncentrációját, ha:
a) 25 g sót 175 g vízben oldunk fel;
b) 20 g sót oldunk fel 140 g vízben.
8. Töltsd ki az üres részeket, hogy igaz mondatokat kapj!
a) 45 g cukrot vízben feloldva 450 g oldatot kaptunk. Ennek az oldatnak a koncentrációja … %.
b) 450 g vízben 50 g cukrot oldottunk fel. A kapott oldat koncentrációja … %.
9. Töltsd ki az üres részeket úgy, hogy igazak legyenek az állítások!
a) 63 a 90-nek … %-a.
54 Matematika • Tankönyv a VI. osztály számára
b) 100000 a 9250000-nek …%-a.
c) Ha egy szám 125%-a 1800, akkor az eredeti szám … .
d) 2500 kg gyümölcsöt osztanak szét 3 menzán. Az egyik menza a mennyiség 30%-át kapja, egy másik étkezde pedig a fennmaradó menynyiség 24%-át. A harmadik menza által kapott mennyiség … kg gyümölcs.
10. Olvasszunk össze 800 g 0,35 tisztaságú ezüst és alumíniumötvözetet, valamint 200 g tiszta ezüstöt.
a) Számítsd ki az új ötvözet tisztaságát!
b) Számítsd ki az új ötvözetben lévő tiszta ezüst mennyiségét!
11. Számítsd ki egy réz-arany ötvözet tisztaságát, tudva, hogy:
a) 240 g aranyat és 960 g rezet tartalmaz.
b) 100 g arany és 300 g réz összeolvasztásával jön létre.

12. Határozd meg 1800 g 0,125-ös tisztaságú ötvözetben levő ezüst mennyiségét!
Miniteszt
13. Az 1:1 000 000 léptékű térképen két város közötti távolság 12 cm.
a) Számítsd ki a két város közötti távolságot a valóságban!
b) Határozd meg ugyanezen városok közötti távolságot a térképen, ha a térképet 1:1 500 000 léptékkel rajzolták volna meg!
14. Johanna a térképen Temesvár és Nagyvárad városainak megfelelő pontokat egy 3 cm hosszú szakasszal köti össze.
Nagyvárad Arad
Temesvár
Szatmárnémeti
Nagybánya
Szamos
Duna Dés
Kolozsvár Torda
Maros
Vajdahunyad Nagyszeben
Marosvásárhely
a) Ha tudjuk, hogy a két város közötti távolság a valóságban körülbelül 150 km, számítsd ki a térkép léptékét.
b) Határozd meg a Temesvár és Kolozsvár közötti távolságot a valóságban, tudva, hogy ugyanazon a térképen a városokat egy 4,5 cm-es szakasz köti össze.
c) Számítsd ki kétféleképpen a Nagyvárad és Temesvár közötti távolságot egy 1:200 000 léptékű térképen.
1. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
15 p a) 350 kg 50%-a:
A. 125 kg; B. 225 kg; C. 175 kg; D. 225 kg.
15 p b) Johanna a nála lévő 400 lej 35%-át költötte el. A megmaradt pénzösszege:
A. 260 lej; B. 140 lej; C. 160 lej; D. 240 lej;
15 p c) Ha a b szám 25%-a 18, akkor a b szám értéke
A. 36; B. 54; C. 63; D. 72.
15 p d) A 24 000 szám 45%-nak 27%-át kiszámítva a következő eredményt kapjuk:
A. 2196; B. 2691; C. 2916; D. 2961
10 p 2. Számítsd ki egy 50 g aranyat és 250 g rezet tartalmazó ötvözet tisztaságát!
20 p 3. Számítsd ki, hogy mennyi sót kell hozzáadni 600 g 15%-os koncentrációjú oldathoz, hogy a koncentráció 25%-ra emelkedjen!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
55 2. fejezet • Arányok. Aránypárok
1. l. Adatok ábrázolása grafikonokkal az arányosság figyelembevételével.
Adatok ábrázolása matematikai szoftverek segítségével
Emlékeztető
A statisztikai vizsgálatot egy jelenség megértése, értelmezése, értékelése és szabályozása céljából végzik.
A jelenséget, amelyre a vizsgálat vonatkozik, jellemzőnek vagy változónak nevezzük, és a statisztikai sokaságot alkotó elemek (személyek, személyek csoportja, bizonyos típusú tárgyak) számát írja le. Az elemek összességét a statisztikai sokaság teljes létszámának nevezzük.
A vizsgált jellemző (változó) kifejezhető számértékekkel vagy jellemzőkkel.
A változónak megfelelő számokat vagy jellemzőket a változó értékeinek nevezzük.
Oldjuk meg figyelmesen!
A következő két példában nézd meg figyelmesen az információ háromféle bemutatási módját, majd fogalmazd meg és indokold a választ a következő kérdésekre:
1. Melyik megjelenítés látványosabb? (könnyebben megfigyelhető)
2. Melyik bemutatásban választhatjuk ki gyorsabban a legtöbbször előforduló értéket? (domináns érték)? Hát a legkevesebbszer előforduló értéket?
3. Az egyik ábrázolásból kiindulva újra elkészíthetjük-e a másik kettőt?
1. példa A VI. A osztály tanulóinak szemszínét illetően a következő információkkal rendelkezünk:
a) A hatodik osztály 24 diákjának szeme színe: barna, fekete, barna, kék, zöld, fekete, barna, fekete, kék, kék, zöld, barna, fekete, fekete, barna, barna, fekete, kék, barna, kék, fekete, kék, barna, barna.
b) A VI. A osztály diákjainak szeme színe:
A szem színe fekete barna kék zöld
Tanulók száma 7 9 6 2
Minden változatban azonosítjuk:
– Változó: szemszín;
– A változó értékei: fekete, barna, kék, zöld.
– Statisztikai sokaság: VI. A osztály tanulói.
– Statisztikai sokaság mérete: 24.
c) Grafikus ábrázolás: T anulók száma
2. példa A VI. B osztályos tanulók által a matematika tesztben elért eredményeikkel kapcsolatban a következő információkkal rendelkezünk:
a) A matematika teszten a VI. B osztály tanulói az alábbi jegyeket kapták: 8, 9, 5, 3, 4, 7, 8, 7, 6, 6, 10, 5, 6, 7, 4, 9, 10, 9, 6, 7, 8, 7.
b) A matematika teszten a VI. B osztály tanulói a következő eredményeket érték el:
Jegy
Minden változatban azonosítjuk:
– Változó: jegy;
– A változó értékei: 3, 4, 5, 6, 7, 8, 9, 10.
– Statisztikai sokaság: a VI. B osztály tanulói
– Statisztikai sokaság mérete: 22.
c) A VI. B osztályos tanulók teszteredményei:
T anulók száma
56 Matematika • Tankönyv a VI. osztály számára
2.2. Adatszervezés
Fekete Barna Kék Zöld Szemek színe
3 4 5 6 7 8 9 10
száma 1 2 2 4 5 3 3 2
Tanulók
Jegy
Megoldás
1. Minden példában hasznosabb vizuálisan, diagramokon keresztül ábrázolni.
2. Az adattáblázatból vagy a diagram ábrázolásából gyorsan kiválaszthatjuk a legnagyobb vagy a legkisebb előfordulási számmal rendelkező értéket. Ha az értékek száma nagy lenne, akkor előnyös lenne diagramokkal dolgozni.
3. A három változat ugyanazt az információt adja, így az egyik alapján rekonstruálható.
Fedezzük fel, értsük meg!
Az azonos információk bemutatásának három módja közötti összehasonlítás eredménye igazolja a rendezés szükségességét, a statisztikai adatok adattáblákba rendezését és a grafikonok vagy diagramok formájában történő ábrázolás hasznosságát.
Értelmezés. A statisztikai sokaságban a változó egyik előfordulási számát az érték abszolút gyakoriságának nevezzük.
Példák: Az 1. példában a barna érték gyakorisága 9, a zöld érték gyakorisága 2. A 2. példában a 7-es érték gyakorisága 5.
A gyakorisági táblázatok a változó minden egyes értékéhez hozzárendelik annak gyakoriságát. A gyakorisági táblázatok oszlopdiagramok (függőleges vagy vízszintes), kördiagramok, grafikonok és egyéb diagramok készítésére szolgálnak.
Az ábrázolt sávok hossza és a változó értékek abszolút gyakorisága egyenesen arányos mennyiségek, azaz a sávhosszúságok halmazának elemei és a megfelelő abszolút gyakoriság halmazának elemei egyenesen arányosak.
Így, a 2. példában használt jelölések esetén igazak az
ABCDEFGHIJKLMNQP
12 24 53 32 ======= egyenlőségek, az 1. példában
ABCDEFGH
79 62 === .
Most már minden kétséget kizáróan kijelenthetjük, hogy a legtöbb tanuló által kapott jegy a leghosszabb sávnak felel meg, azaz 7, a legkevesebb tanuló által kapott jegy pedig a legrövidebb sávnak felel meg, azaz 3.
A 2. példában szereplő diagramot tekintve megbecsülhetjük, hogy az osztály átlaga 7 körül van. Ez csak becslés, a pontos eredményt az összes kapott osztályzat számtani közepének kiszámításával kapjuk meg.
A „Jegy” adattáblában található információk alapján kiszámíthatjuk az osztály által ezen teszt során elért átlagot, amelyet a számszerű adathalmaz átlagának nevezünk.
A „Jegy” statisztikai adathalmaz esetében az adathalmaz átlaga a következő szám:
m a = 34 45 5 6666 77777 888999 10 10 22 +++++++++++++++++++++
= 34 25 26 47 58 39 3102 22
68 63
Két tizedes pontossággal m a = 6,86, ami azt mutatja, hogy a becslés nagyon jó volt.
Megjegyzés. Vannak olyan helyzetek is, amikor nehéz a számítással kapott átlaghoz ennyire közeli becsléseket készíteni.
Jegyezd meg!
Egy számszerű adathalmaz átlaga a változó összes értékének számtani közepe.
Ezt általában két tizedes pontossággal számoljuk ki.
Megjegyzés. Ha a változó nem numerikus (értékei jellemzőként vannak kifejezve), akkor a megfelelő adathalmaznak nincs átlaga.
57 2. fejezet • Arányok. Aránypárok
=
,( ) .
Alkalmazás
Alkalmazás: Az első teszten a VI. osztály 24 tanulója a következő jegyeket kapta: 4, 5, 5, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10.
a) Rendezd és szervezd a fenti adatokat gyakorisági táblázatba.
b) Készíts diagramot vízszintes sávok segítségével.
Megoldás.
b) Két, közös origóval rendelkező félegyenest tekintünk, az egyiket vízszintes helyzetben, amelyet Ox-szel, a másikat függőleges helyzetben, amelyet Oy-nal jelölünk. Az Oy tengelyre írjuk a változó értékeit, az Ox tengelyre pedig az ezeknek az értékeknek megfelelő gyakoriságot. Ezután vízszintes sávokat ábrázolunk, amelyek egyik vége az Oy tengelyen van, a változó értékeinek megfelelő pontokban, és amelyek hossza arányos az adott érték gyakoriságával.
A sávok hossza és a változó értékek abszolút gyakorisága egyenesen arányos mennyiségek, azaz a sávok hosszának halmaza egyenesen arányos a megfelelő abszolút gyakoriság halmazával.
Kezde teszt pontszáma sordiagrammal ábrázolva









Egyes tanulmányokban az értékek abszolút gyakorisága nem ad egyértelmű képet a jelenségről. Ilyenkor előnyös ismerni egy érték súlyát a teljes vizsgált sokasághoz viszonyítva.
Az érték abszolút gyakoriságának és a statisztikai sokaság méretének arányát nevezzük az érték relatív gyakoriságának.
Példa:
A kezdeti tesztpontszámok gyakorisági táblázatában a 6-os relatív gyakorisága 3
A relatív gyakoriságot általában százalékos arányban fejezik ki, ami lehetővé teszi a változó értékek viselkedésének összehasonlító értelmezését.
Példa. A 4-es gyakorisága 1, az osztály létszáma pedig 24. A 4-es jegy relatív gyakorisága 1 24 41 6 = ,( )% .
Hasonlóképpen megkapjuk a többi jegy gyakoriságát is: 8,(3)%, 12,5%, 20,8(3)%, 25%, 8,(3)%,
A százalékos arányokat használva, a diagramokkal való ábrázoláshoz a tizedes törteket egész számokhoz közelíthetjük, ügyelve arra, hogy a teljes összeg száz százalék, tehát egész legyen.
Relatív gyakoriság százalékos arányban kifejezve
A kördiagram lehetővé teszi az értékek gyakoriságának százalékban kifejezett értelmezését.
A kördiagram egy körcikkekbe osztott korong.
58 Matematika • Tankönyv a VI. osztály számára
Jegy 4 5 6 7 8 9 10 Gyakoriság/ a tanulók száma 1 2 3 5 6 5 2
a)
2468 2 3 4 5 6 7 8 9 10 tanulókszáma jegy
y 0 x
24 1 8 0 125
,
6 24 1 4 025
==
, a 8-as relatív gyakorisága pedig
== ,.
Jegy 4 5 6 7 8 9 10
4% 8% 13% 21% 25% 21% 8%
Fedezzük fel, értsük meg!
Tekintsük a következő gyakorlati helyzeteket:
1. Egy kockát, amelynek oldalai 1-től 6-ig vannak számozva, vízszintes felületen gurítunk. A dobás eredményeként egyetlen oldal jelenik meg vízszintes helyzetben, és az erre az oldalra írt szám látható.
2. Egy urnában 4 zöld, 3 rózsaszín, 2 kék és 1 piros golyó van. Csak a színükben különböznek. Ha egy golyót húzol anélkül, hogy ránéznél, akkor olyan golyót kapsz, amelyik a négy szín valamelyikét tartalmazza.
3. Az érmének két különböző oldala van. Az érme vízszintes felületre dobása azt eredményezi, hogy a két oldal közül csak az egyik jelenik meg.
A fent leírt helyzetek mindegyike tetszőlegesen sokszor és azonos feltételek mellett megismételhető.
Ezeket véletlenszerű kísérleteknek nevezik.
A kísérlet minden egyes ismétlését mintának nevezzük.
Egy kísérlet kapcsán több esemény is megfogalmazható.
1. kísérlet: A kocka dobása; Események: A1: az 1-es oldalt kapjuk; A2: a 2-es oldalt kapjuk;... A6: A 6-os oldalt kapjuk. B1: Páros számot kapunk; B2: Páratlan számot kapunk; B3: 7-nél kisebb számot kapunk; B4: A 7-est kapjuk.
2. kísérlet: A urnából való kihúzás 4 zöld, 3 rózsaszín, 2 kék és 1 piros golyó van az urnában.
Események: A: Egy piros golyót húzunk; B: Egy rózsaszín golyót húzunk; C: Egy zöld vagy rózsaszín golyót húzunk; D: Egy kék golyót húzunk.
A fenti példákban láthatjuk, hogy egyes események mindig bekövetkeznek (B3), egyesek soha nem következnek be (B4), és egyesek előfordulhatnak vagy nem (A1, ..., B2, A, B, C, D).
A kísérlet minden egyes ismétlésénél bekövetkező eseményt biztos eseménynek nevezzük.
Az olyan eseményt, amely soha nem következik be, lehetetlen eseménynek nevezzük.
Az olyan eseményt, amely sem nem biztos, sem nem lehetetlen, véletlen eseménynek nevezzük. Előfordulása a véletlennek van kitéve.
Megállapították, hogy kellően nagy számú minta esetén egy esemény megvalósulásai számának és a minták számának aránya megközelítőleg megegyezik a kedvező esetek számának és a lehetséges esetek számának arányával.
Példa: A kockadobás eredménye legalább 1 és legfeljebb 6 értékű természetes szám.
Példa: A kockadobás a 7-es szám természetes többszörösét eredményezi.
Példák: 1. A kockadobás eredménye 4-es.
2. A kockadobás páratlan számot eredményez.
Példa: A kocka dobásakor 6 helyzet lehetséges: 1. lap, 2. lap, 3. lap, 4. lap, 5. lap, 6. lap.
Ezek a kísérlet lehetséges esetei.
Az 1., 3. és 5. lap a B2-es esemény kedvező esetei.
A 6. lap az A6-os esemény egyetlen kedvező esete.
Egy esemény előfordulási gyakoriságát az esemény kedvező eseteinek és a kísérlet lehetséges esetei számának aránya adja meg. Ezt az arányt nevezzük az esemény bekövetkezése valószínűségének vagy az esemény valószínűségének
61 2. fejezet • Arányok. Aránypárok
Az M esemény bekövetkezésének valószínűségét P(M)-mel jelöljük és értéke az M esemény bekövetkezésének kedvező esetei nf számának és a kísérlet lehetséges esetei n számának aránya.
PM()
kedvező esetek száma
lehetséges esetek száma
PM n n f () = .
Példa. Egy dobozban 10 fehér és 5 fekete golyó van. Egy golyót kihúzunk. Tekintsük az eseményeket: A: Egy fehér golyót húzunk ki; B: Egy fekete golyót húzunk ki; C: Egy fehér vagy egy fekete golyót húzunk ki.
A lehetséges esetek száma a dobozban lévő golyók száma, tehát 15. Az A eseményre 10, a B eseményre 5 és a C eseményre 15 kedvező eset (golyó) van. Következésképpen
PA() ,( ) === 10 15 2 3 06 , PB() ,( ) === 5 15 1 3 03 , PC() == 15 15 1.
Könnyen belátható, hogy bármely kísérletben a lehetséges esetek száma legfeljebb a kísérlet valamely eseményének kedvező esetei számával egyenlő természetes szám. P(M) ≥ 0, P(M) ≤ 1, bármely M esemény esetén.
Alkalmazás
1. példa Pénzfeldobás
Esemény
A: Az írás jelenik meg
B: A fej jelenik meg.
C: Az írás és fej is egyidőben jelenik meg
D: Az írás vagy a fej jelenik meg.
2. példa Egy golyó kihúzása a 4 zöld, 3 rózsaszín, 2 kék és 1 piros golyót tartalmazó urnából.
Esemény
A: Zöld golyót húzunk
B: Rózsaszín golyót húzunk C: Kék golyót húzunk ki. D: Piros golyót húzunk E. Fehér golyót húzunk
Gyakorlatok és feladatok
1. Töltsd ki az üres részeket úgy, hogy igaz mondatokat kapj!
a) Annak a valószínűsége, hogy egy kockadobáskor 6-os számot dobjunk, … .
b) Annak a valószínűsége, hogy egy kockadobáskor 3-nál nagyobb számot kapjunk … .
c) Annak valószínűsége, hogy két kockával dobva a megjelenő számok összege nagyobb, mint 9, … .
2. Mária felír a táblára egy 30-nál kisebb nem nulla természetes számot.
a) Számítsd ki annak a valószínűségét, hogy a leírt szám osztható 3-mal!
F. Zöld vagy piros golyót húzunk
b) Számítsd ki annak a valószínűségét, hogy a leírt szám osztható 5-tel!
3. Egy 12 fehér, 15 piros és 18 fekete golyót tartalmazó urnából kihúzunk egy golyót. Határozd meg a következő események bekövetkezésének valószínűségét:
a) a kihúzott golyó piros;
b) a kihúzott golyó nem fekete;
c) a kihúzott golyó fehér vagy fekete.
4. Egy urnában 3, 6, 9, 12, ... , 93 számozott golyó van. Számítsd ki annak a valószínűségét, hogy egy véletlenszerűen kihúzott golyón levő szám:
a) 50-nél kisebb;
b) négyzetszám;
c) páros;
d) páratlan.
62 Matematika • Tankönyv a VI. osztály számára
Kedvező esetek száma 1 1 0 2 Valószínűség 1 2 = 0,5 1 2 = 0,5 0 2 = 0 2 2 = 1
ki. Kedvező esetek száma 4 3 2 1 0 4 + 1 + 5 Valószínűség 4 10 = 0,4 3 10 = 0,3 2 10 = 0,2 1 10 = 0,1 0 10 = 0 5 10 = 0,5
5. A kártyákra a következő számok vannak írva: 510, 85, 163, 64, 46, 15, 125. Számítsd ki annak a valószínűségét, hogy egy véletlenszerűen kiválasztott kártyán levő szám:
a) páros; b) páratlan;
ISMERETFELMÉRŐ
c) négyzetszám; d) köbszám.
6. Egy kosárban 10 alma, 15 körte és 3 narancs van. Anya ad Mihálynak egy gyümölcsöt ebből a kosárból. Számítsd ki annak valószínűségét, hogy:
a) az adott gyümölcs alma;
b) az adott gyümölcs körte;
c) az adott gyümölcs narancs.
I. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
5 p 1. A 0,4 dm és 12 cm hosszúságok aránya:
A. 1 8 ; B. 1 3 ; C. 1 2 ; D. 1 4 .
5 p 2. Ha x y = 5 és y = 2, akkor az x értéke:
A. 2,5; B. 7; C. 10; D. 3.
5 p 3. A 7 3 = x 6 aránypár x tagjának értéke:
A. 14; B. 12; C. 18; D. 21.
5 p 4. Kiszámolva 40-nek 4%-át a kapott eredmény:
A. 16; B. 8; C. 0,8; D. 1,6.
5 p 5. Hat toll 162 lejbe kerül. 54 lejért ennyi ugyanolyan tollat lehet vásárolni:
A. 1; B. 2; C. 3; D. 4. 5 p 6. Két város közötti távolság 650 km. Az 1:2000000 léptékű térképen a két város közötti távolság:
A. 130 cm; B. 65 cm; C. 32,5 cm; D. 37,5 cm.
II. Írd le a teljes megoldást!
10 p
10 p
10 p
10 p
1. a) A 240 kg lisztmennyiséget az 5, 9 és 10 számokkal egyenesen arányos részekre osztjuk. Határozd meg a kapott mennyiségek közül a legkisebbet.
b) Egy urnában 1-től 20-ig számozott golyók vannak. Számítsd ki annak a valószínűségét, hogy egy golyó véletlenszerű kivételével a golyóra írt szám a 30 osztója legyen.
2. Egy árucikk eredeti ára 700 lej, a drágítás után pedig 784 lejbe kerül.
a) Hány százalékkal nőtt a termék ára?
b) Vizsgáld meg, hogy az új ár 12%-os csökkentése magasabb vagy alacsonyabb árat eredményez-e, mint az eredeti ár!
3. Az a és b szám fordítottan arányos az 1 2 -del illetve 1 4 -del.
10 p
10 p
a) Mutasd ki, hogy b = 2 a.
b) Tudva, hogy n = a + 2 b és m = 3 a + b, számítsd ki az n nm + arány értékét.
Megjegyzés: Munkaidő: 50 perc
Hivatalból: 10 pont
63 2. fejezet • Arányok. Aránypárok
Sajátos kompetenciák: 1.3; 2.3; 3.3; 4.3; 5.3; 6.3
3. AZ EGÉSZ SZÁMOK HALMAZA
3.1. Az egész számok halmaza. A számtengelyen való ábrázolás.
Összehasonlítás és rendezés
1. l. Az egész számok halmaza. Az egész számok ábrázolása a számtengelyen
Emlékeztető
Számos konkrét helyzetben egyes fizikai mennyiségek értékeinek haladási iránya nem feltétlenül pozitív a viszonyítási ponthoz képest, így ezek az értékek nem fejezhetők ki természetes számokkal. Ez vezetett a negatív számoknak nevezett számok megjelenéséhez. Interdiszciplináris háttér:
A hőmérséklet olyan fizikai mennyiség, amely úgy mérhető, hogy egy test minden egyes melegedési állapotához számértéket rendelünk.
A környezeti hőmérséklet vagy bizonyos környezetek hőmérsékletének ismerete és szabályozása nagyon fontos a kényelem vagy a végzett tevékenység kedvező feltételeinek megteremtése szempontjából.
A hőmérő olyan eszköz, amellyel mérhetjük a levegő hőmérsékletét, a víz hőmérsékletét, a testhőmérsékletet, más közegek hőmérsékletét. Az általunk általában használt mértékegység a Celsius-fok (°C).
A hőmérőben használhatunk higanyt, alkoholt, nitrogént, hidrogént, amelyek mindegyike rendelkezik azzal a tulajdonsággal, hogy térfogatuk egyenesen arányos a hőmérséklettel.

A 0° C érték a víz fagypontját jelzi, azaz azt a szintet, amelyen a higany áll, amikor a víz megfagy. A 100° C érték a forráspontot jelzi, azaz azt a szintet, amelyen a higany jelen van, amikor a tiszta víz forr. Ez az érték csak a különleges laboratóriumokban használt hőmérőkön alakul így. Amikor a higany 0 alá csökken, a hőmérő negatív hőmérsékletet jelez: –1, –2, –3, .... (mínusz 1, mínusz 2, mínusz 3, ...).
Minél lejjebb megy, annál alacsonyabb hőmérsékletet mutat.
Tudod-e?
Az időjárási és kommunikációs műholdakat föld körüli pályán, mintegy 36000 km magasságban helyezik el.
Vannak turisztikai célú mini-tengeralattjárók, amelyek –200 méterig, azaz 200 méter mélyre süllyednek.
A tengerekben és az óceánokban akár –2000 méteren is van élet, azaz 2000 méteres mélységben.
A tengerszint feletti magasság az a magasság, amelyen a Föld felszínének egy pontja egy referenciaszint, általában a 0-nak megfelelő tengerszint felett van. Románia területén a legmagasabb pont a Moldoveanu hegycsúcs (2544 m).
A Föld felszínének legmélyebb pontja a Csendes-óceánban, a Mariana-árokban található (–11 022 m).
Fedezzük fel, értsük meg!
Tekintsük a számtengelyt, amelynek origója
O(0) és mértékegysége u, a pozitív irányt pedig balról jobbra állítottuk be.


64 Matematika • Tankönyv a VI. osztály számára
u O –n M’ 0 M n
Minden n nullától különböző természetes számot a tengelyen az M(n) ponttal jelölünk, amely pontosan n egységre van az origótól, ettől jobbra.
Az n természetes számot + n-nel jelöljük, és pozitív egész számnak nevezzük.
Az M’ pont , amely az M(n) ponttal szimmetrikus az O-ra nézve, az origótól pontosan n egységre van, de attól balra. A M’ pontnak megfelelő számot – n-nel jelöljük, és az n szám ellentettjének nevezzük.
A – n szám negatív egész szám. Azt mondjuk, hogy az M’ koordinátája–n és így írjuk M’(–n).
Ily módon a nem nulla természetes számok halmazát a pozitív egész számok halmazával azonosítjuk, amelyet ℤ + -szal jelölünk, az összes nem nulla természetes szám ellentettjeiből képzett halmazt pedig a negatív egész számok halmazának nevezzük, és ℤ – -szal jelöljük.
Tehát ℤ + = {+1, +2, +3, …, + n , +( n +1), …} ={1, 2, 3, …, n , ( n + 1), …} = ℕ * . ℤ –= {…, – (n + 1), –n, …, –3, –2, – 1}.
Az összes pozitív egész szám, az összes negatív egész szám és a 0 szám halmazát az egész számok halmazának nevezzük, és ℤ-vel jelöljük.
Következésképpen, ℤ = ℤ + ⋃ ℤ –⋃ {0} = {…, –(n + 1), –n, …, –3, –2, –1, 0, 1, 2, 3, …, n , ( n + 1), …}
Megjegyzések. A 0 szám se nem pozitív, se nem negatív. Megegyezés szerint + 0 = –0 = 0. ℕ ⊂ ℤ és ℕ* = ℤ + .
A gyakorlatban a pozitív számokat gyakran előjel nélkül használjuk, a + 1-t 1-nek, a + 2-t 2-nek és így tovább. Amikor egy a egész számról beszélünk, akkor lehet pozitív, és a > 0-t írunk, lehet negatív, és a < 0-t írunk, vagy lehet 0, és a = 0-t írunk.
Alkalmazás
Példák.
Az ábrán, a számtengelyen több egész szám látható.
A tengelyen két, az origótól szimmetrikusan elhelyezkedő pontnak a koordinátái ellentett egész számok.
Ha a nullától különböző egész szám, akkor a és – a ellentett számok.
Az a szám a – a szám ellentettje, a – a szám pedig az a szám ellentettje.
–4 –3 –2–1 0 12 3 4
Az origóra szimmetrikus pontok:
A(1) és A′(–1); B(2) és B′(–2);
C(3) és C′(–3); D(4) és D’(–4).
Ellentétes egész számok:
1 és –1; 2 és –2; 3 és –3; 4 és –4.
–1 az 1 ellentettje és 1 a – 1 ellentettje;
–2 az 2 ellentettje és 2 a – 2 ellentettje;
–3 az 3 ellentettje és 3 a – 3 ellentettje;
–4 az 4 ellentettje és 4 a – 4 ellentettje.
Megjegyzés. A 0 egész szám ellentettje szintén 0. Az a szám ellentettjét –a-val jelöljük.
Ha a pozitív, akkor –a negatív, ha a pedig negatív, akkor a –a szám pozitív.
Gyakorlatok és feladatok
1. Töltsd ki az üres cellákat az I betűvel, ha a kijelentés igaz, és a H betűvel, ha hamis!
2. Adott az
M = 24 3 2 025256 2 12 4 ;; ;; ;; ,; halmaz.
a) Írd le az M halmaz negatív egész elemeiből álló halmazt!
b) Írd le az M halmaz pozitív egész elemeiből álló halmazt!
c) Határozd meg az M ∩ ℤ halmazt!
65 3. fejezet • Az egész számok halmaza
u D’C’B’A’OABCD
ℤ 2,75 ∈ ℤ
{
⊂
Kijelentés I/H Kijelentés I/H 13 ∈
7 ∈ ℤ
4; 0; 11}
ℤ
6 ∉ ℕ { 3; 1; +3}⊂ ℕ
24∈ℤ33∉ ℤ +
3. Töltsd ki a következő táblázat üres mezőit a megfelelő egész számokkal!
Szám 5 2 0 55 z
A szám
ellentettje
7 10 +17 a
4. a) Ábrázold a számtengelyen a következő
számokat: 3; 1; 0; 4; 5; 3.
b) Ábrázold a számtengelyen a 10; +20; 0; +30; 20; 50 számokat! Válassz egy megfelelő mértékegységet!
c) Ábrázold a számtengelyen a 100; 200; +200; 0; +300; −400 számokat! Válassz egy megfelelő mértékegységet!
Miniteszt
5. Adott A = 11 2 3 02 34 39 13 7 2 ;; ;; ;, ; halmaz
Határozd meg az: A ∩ ℕ, A ∩ ℤ, A ∩ ℤ –, A \ ℤ. halmazokat!
6. a) Add meg a számtengelyen a tengely origójától 4 egységnyi távolságra levő pontok számát! Írd le ezeknek a pontoknak az abszcisszáit, és ábrázold őket a számtengelyen úgy, hogy mértékegységként a centimétert használd!
b) Legyen n egy természetes szám. Add meg a számtengelyen a tengely origójától n egységnyi távolságra lévő pontok számát! Írd le ezeknek a pontoknak a koordinátáit!
1. Töltsd ki a pontozott helyeket úgy, hogy igaz állításokat kapj!
10 p a) A –7 szám ellentettje ….
10 p b) A számtengely origójától a –23 szám ábrázolási pontjáig mért távolság … .
2.
40 p a) Ábrázold a számtengelyen a +3, 4, +2, 1, 0 koordinátájú A, B, C, D, O pontokat!
30 p b) Töltsd ki az üres cellákat az I betűvel, ha a kijelentés igaz, és a H betűvel, ha hamis!
Kijelentés I/H
p1: A C pont az AD szakaszon helyezkedik el.
p2: A B pont a CO félegyenesen helyezkedik el.
p3: A BD és AC szakasznak nincs közös pontja.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
2. l. Egy egész szám abszolút értéke.
Egész számok összehasonlítása és rendezése
Emlékeztető
Bármely n nullától különböző természetes szám esetén a számtengelyen pontosan két pont van az origótól n távolságra (az origóra szimmetrikusan): az A(– n) és B(n) pont.
Bármely pozitív a egész számot a számtengelyen az origótól jobbra ábrázolunk, és a > 0-t írunk.
Bármely negatív a egész számot a számtengelyen az origótól balra ábrázolunk, és a < 0-t írunk.
A 0 egész számot a számtengelyen az origónál ábrázoljuk.
Fedezzük fel, értsük meg!
Az a egész szám modulusa vagy abszolút értéke a számtengely origójától az a számnak a tengelyen való ábrázolási pontjáig mért távolság.
Az a egész szám modulusát | a |-val jelöljük.
66 Matematika • Tankönyv a VI. osztály számára
A számtengelyen a következő pontokat ábrázoljuk O(0), A(1), A′(– 1), B(a), B′(– a), ahol a pozitív egész szám és C(b), C′(– b), ahol b negatív egész szám.
–1 01 u b
CB’ –a
Megjegyzések.
A’OABC’ a–b
Akkor: | 0 | = 0 (az O távolsága saját magától 0).
Mivel OA′ = OA = 1, akkor | –1| = | 1 | = OA = 1;
Mivel OB′ = OB = a, akkor | –a| = | a | = OB = a;
Mivel OC = OC′ = –b, akkor | –b| = | b | = OC′ = –b.
1. Az a és – a egész számok modulusa azonos, mivel a tengelyen az origótól azonos távolságra vannak ábrázolva.
2. Bármely távolságot pozitív számmal fejezünk ki, vagy 0-val, tehát bármely egész szám modulusa pozitív szám, vagy 0.
Következtetés. 1. | x | > 0, bármely x ∈ℤ * esetén, és | x | = 0, akkor és csakis akkor, ha x = 0.
2. | x | = x, akkor és csakis akkor, ha x ≥ 0 és | x | = –x, akkor és csakis akkor, ha x ≤ 0.
3. | –x | = | x |, bármely x ∈ℤ esetén.
Bármely két egész a és b szám esetén csak az egyik összefüggés fordul elő: a < b, a = b, a > b. Az a és b egész számok összehasonlítása azt jelenti, hogy eldöntjük, hogy a fenti három összefüggés közül melyik igaz.
Ha a∈ℤ és b∈ℤ és ha az a szám ábrázolása a tengelyen az A pont, a b szám ábrázolása pedig a B pont, akkor: a < b akkor és csakis akkor, ha az A(a) pont a B(b) ponttól balra helyezkedik el.
a = b akkor és csakis akkor, ha az A(a), B(b) pontok egybeesők.
a > b akkor és csakis akkor, ha az A(a) pont a B(b) ponttól jobbra helyezkedik el.
Az a és b nem nulla számok esetén, ahol a < b, az alábbi esetek lehetségesek:
A tengelyen való ábrázolás Magyarázat
0 a OA
0 a AO
0 ab OAB
O(0) az A(a)-tól balra található, ezért
0 kisebb, mint a.
Így írjuk: 0 < a vagy a > 0.
A(a) az O(0)-tól balra található, ezért
a kisebb, mint 0.
Így írjuk: a < 0 vagy 0 > a.
a > 0, b > 0.
OA < OB, tehát | a | < | b |.
A(a) a B(b), -től balra van, azaz a < b.
Következtetés
a ∈ℤ + ⇔ a ∈ℤ és a > 0.
1; 2; 3; 10; 11 ∈ ℤ +
1 > 0; 2 > 0; 3 > 0; 10 > 0; 11 > 0.
a ∈ℤ –⇔ a ∈ℤ és a < 0.
–1; –2; –3; –10 ∈ ℤ –
–1 < 0; –2 < 0; –3 < 0; –10 < 0.
Ha a ∈ℤ + és b∈ℤ + , akkor:
a < b akkor és csakis akkor, ha | a | < | b |.
30 ∈ ℤ + és 47 ∈ ℤ +
30 < 47 és | 30 | < | 47 |.
0 ab ABO
0 ab
AOB
a < 0, b < 0.
OA > OB, tehát | a | > | b |.
A(a) a B(b)-től balra van, azaz a < b
a < 0, b > 0.
Ha OA < OB, akkor | a | < | b |.
A(a) a B(b)-től balra van, azaz a < b.
Ha a ∈ℤ –és b∈ℤ –, akkor: a < b akkor és csakis akkor, ha | a | > | b |.
–30 ∈ ℤ –és –47 ∈ ℤ ––47 < –30 és | –47 | > | –30 |.
Ha a ∈ℤ –és b∈ℤ+, akkor a < b.
Mindegyik negatív szám kisebb, mint bármely pozitív szám.
–30∈ℤ –és 47∈ℤ + akkor –30 < 47
–47∈ℤ –és 30 ∈ℤ + akkor –47 < 30.
67 3. fejezet • Az egész számok halmaza
Alkalmazás
Egész számok összehasonlítására és rendezésére gyakran használjuk a ≤ vagy ≥ összefüggések egyikét.
Az a ∈ℤ és b ∈ℤ esetén a ≤ b akkor és csakis akkor, ha a < b vagy a = b. Igazak az alábbi tulajdonságok:
Tulajdonság a ≤ a, bármely a egész szám esetén.
Ha a ∈ ℤ , b∈ℤ és ha a ≤ b és b ≤ a, akkor a = b.
Ha a ∈ ℤ , b∈ℤ és ha a ≤ b és b ≤ c, akkor a ≤ c.
Példák 0 ≤ 0; –1 ≤ –1; 2 ≤ 2;… 3 ≤ x és x ≤ 3, akkor x = 3. –2 ≤ 5 és 5 ≤ p, p∈ℤ, akkor –2 ≤ p.
Megjegyzés. A < és > relációk tranzitívak: Ha a < b és b < c, akkor a < c; Ha a > b és b > c, akkor a > c.
A < , >, ≤, ≥ relációk segítségével két vagy több egész számot tudunk növekvő vagy csökkenő sorrendbe rendezni.
Két vagy több egész szám növekvő sorrendbe rendezése azt jelenti, hogy úgy rendezzük őket, hogy mindegyik kisebb vagy egyenlő legyen az utána következőnél.
Két vagy több egész szám csökkenő sorrendbe rendezése azt jelenti, hogy a sorrendjüket úgy állítjuk be, hogy mindegyik nagyobb vagy egyenlő legyen, mint az utána következő.
Jegyezd meg!
A –32, 0, 20, –21, 5 egész számok növekvő sorrendben: –32, –21, 0, 5, 20 mert–32 ≤ –21 ≤ 0 ≤ 5 ≤ 20.
A –32, 0, 20, –21, 5 egész számok csökkenő sorrendben: 20, 5, 0, –21, –32 mert 20 ≥ 5 ≥ 0 ≥ –21 ≥ –32.
Bármely pozitív egész szám nagyobb, mint bármely negatív egész szám és a 0. Bármely negatív egész szám kisebb bármely pozitív egész számnál és a 0-nál.
Két pozitív egész szám közül a nagyobb modulusú a nagyobb. Két negatív egész szám közül a kisebb modulusú a nagyobb.
Gyakorlatok és feladatok
1. Másold a füzetedbe, és töltsd ki az alábbi táblázat üres mezőit a megfelelő egész számokkal!
a 5 2 8 0 55 10 | a |
2. Másold a füzetedbe, és töltsd ki az alábbi táblázat üres mezőit a megfelelő egész számokkal!
| a | 5 2 8 0 55 10 a
3. Határozd meg a k egész számot, az alábbi
esetekben:
a) k = 5;
b) k = + 19;
c) | k | = 10 és k ∈ ℤ;
d) | k | = 77 és k ∈ ℤ + ;
e) | k | = 0;
f) | k 2 | = 0.
4. Adott az M = { 7; 4; 2; 0; 4; 100; 2; 9} halmaz. Írd le az M halmaz A, B, C részhalmazait, ha tudjuk, hogy:
a) az A halmaz összes elemének abszolút értéke legfeljebb 3;
b) | x | = x, ahol az x a B halmaz tetszőleges eleme;
c) | x | = x, ahol x a C halmaz tetszőleges eleme.
5. Írd a következő számpárokat a füzetedbe, és húzd alá a kisebb számot mindegyik párban:
a) 7 és 4;
b) 3, és 1;
c) 6 és 16;
d) 0 és 10.
6. Írd a következő számpárokat a füzetedbe, és húzd alá a nagyobb számot mindegyik párban:
a) 4 és 6;
b) 304 és 403;
c) 72 és 70;
d) 410 és 0.
68 Matematika • Tankönyv a VI. osztály számára
7. Írj:
a) 7-nél kisebb három egész számot;
b) 2-nél nagyobb négy egész számot;
c) 14 és 4 közötti öt egész számot.
8. Töltsd ki az üres helyeket egész számokkal úgy, hogy igazak legyenek az állítások!
a) 6 < …;
b) … > 1;
c) 10 ≤ …;
d) … ≥ 3;
e) … ≤ 0;
f) 10 ≥ …;
g) 8 > …;
h 40 < … .
9. Töltsd ki az üres helyeket a <, =, > szimbólumok egyikével úgy, hogy igazak legyenek az állítások!
a) 3 … 9; e) 7 … 7;
b) 23 … 17; f) 109 … 111;
c) 8 … 23; g) 0 … 2023;
d) 40 … 3; h) Ha x ∈ ℤ , akkor x … 2.
10. Ábrázolj a számtengelyen:
a) négy olyan egymás utáni egész számot, ahol a legkisebb a 10;
b) öt olyan egymás utáni egész számot, ahol a legnagyobb az 1;
c) hat olyan egymás utáni egész számot, ahol kettő közülük pozitív.
11. Adott az A = { 12; 6; 10; 0; 3; 11; 2; 33; 9; 3} halmaz.
a) Határozd meg az x szám értékeit, ha x ∈ A és x < 4.
b) Határozd meg az y értékeit, ha y ∈ A és y > 1.
Miniteszt
c) Határozd meg az z szám értékeit, ha z ∈ A és 3 ≤ z ≤ 4.
12. a) Rendezd növekvő sorrendbe a 5; 7; 11; 0; 6; 11; 4; 13; 8; 1 számokat!
b) Rendezd csökkenő sorrendbe a 4; 1; 21; 8; 7; | 37 |; 23; 103; 18; 2 számokat!
13. Határozd meg az (x, y) egész számokat tudva, hogy a 15; 13; x; 11; y; 7 számok növekvő sorrendben vannak.
14. Az alábbi táblázat több európai fővárosban ugyanazon a napon mért minimális és maximális hőmérsékletet mutatja.
Város Minimális hőmérséklet Maximális hőmérsékelt
Athén 3 °C 10 °C
Bukarest 0 °C 8 °C
Koppenhága 2 °C 5 °C
Helsinki 7 °C 1 °C
London 3 °C +1 °C
Madrid 4 °C 11 °C
Párizs 1 °C 6 °C
Melyik az a város, ahol:
a) a legmagasabb hőmérsékletet mérték;
b) a legalacsonyabb hőmérsékletet mérték;
c) csak negatív hőmérsékletet mértek;
d) csak pozitív hőmérsékletet mértek?
1. Másold a füzetedbe és töltsd ki a pontozott helyeket úgy, hogy igazak legyenek az állítások!
10 p a) A −15 és 14 számok közül a nagyobb a … .
10 p b) A 0 és −7számok közül a nagyobb a … .
15 p c) Az 5, −9, 13, −10, −3, 0, −15 számok növekvő sorrendben: ….
10 p d) A legkisebb olyan x egész szám, amelyre | x | ≤ 3 a ….
2. Határozd meg:
15 p a) az a egész számot, ha | a | = 6 és a > 3;
15 p b) a b és c egész számot, ha | b | = 5, | c | = 4 és b < c;
15 p c) az x számjegyet, ha –2x7 < −27x.
Megjegyzés:
Munkaidő: 20 perc
Hivatalból: 10 pont
69 3. fejezet • Az egész számok halmaza
1. l. Az egész számok összeadása és kivonása. Tulajdonságok
A természetes számok összeadásából kiindulva és az egész számok számtengelyen való ábrázolásának segítségével értelmezzük az egész számok összeadását.
Oldjuk meg figyelmesen!
1. feladat Rudi a vakáció egy részét a nagyszüleinél töltötte a hegyekben. Gyönyörű hely minden évszakban. Nyomon követte a hőmérő által reggel és este mért hőmérsékletet, és készített néhány feljegyzést. Rudi alább leírt megfigyelései alapján számítsd ki a hétfőtől péntekig esténként mért hőmérsékletet!
A hőmérséklet alakulására vonatkozó megfigyelések
1. Hétfő reggel a hőmérő +3°C-ot mutatott. Hétfő este +2°C-kal volt melegebb.
2. Kedd reggel a hőmérő –3°C-ot mutatott. Kedd este hidegebb volt, a hőmérő 2°C-kal hűvösebbet mutatott.
3. Szerda reggel –6°C-ot mutatott a hőmérő, de estére 7°C-ot emelkedett a hőmérséklet.
4. Csütörtök reggel +4°C-ot mutatott a hőmérő, de estére a hőmérséklet 4°C-kal csökkent.
5. Ha a szerda esti hőmérséklethez hozzáadjuk a –12°C-ot, megkapjuk a péntek este mért hőmérsékletet.
Megoldás
1. Ha a +2°C-ot hozzáadjuk a +3°C-hoz, akkor 5°Cot kapunk. Azt írjuk, hogy +3 + (+2) = +5 vagy 3 + 2 = 5.
2. Ha –3°C-hoz hozzáadjuk –2°C-ot, akkor –5°C-ot kapunk. Azt írjuk, hogy –3 + (–2) = –5
3. Ha –6°C-hoz hozzáadjuk +7°C-ot, akkor +1°C-ot kapunk. Azt írjuk, hogy–6 + (+7) = +1.
4. Ha a hőmérséklet 4°C-kal csökkent, akkor 0°C lesz. Azt írjuk, hogy +4 + (–4) = 0 vagy +4 – (+4) = 0.
5. Ha 1°C-hoz hozzáadjuk a –12°C-ot, akkor11°C-ot kapunk +1 + (–12) = –11.
Fedezzük fel, értsük meg!
Két tetszőleges a és b egész szám esetén értelmezzük az a + b-vel jelölt egyetlen egész számot, amelyet a és b számok összegének nevezünk.
Azt a műveletet, amely során az a és b számpár mindegyik tagjához hozzárendeljük az összegüket, összeadási műveletnek nevezzük, az a és b számokat pedig az összeadás tagjainak nevezzük.
Ha a ≥ 0 és b ≥ 0, akkor a ∈ ℕ , b ∈ ℕ és alkalmazzuk az előző osztályokból ismert tulajdonságokat. Hogy könnyen megérthessük azt a technikát, amellyel az egész számok összeadásának műveletét végezzük, képzeljünk el egy sétát a számtengelyen pozitív irányban, ha pozitív számot adunk össze, és negatív irányban, ha negatív számot adunk össze.
1. Az összeg minden pozitív tagja annyi egységgel mozog a számtengelyen jobbra (pozitív irányba), amennyit a szám modulusa jelez;
A (+2) + (+3) kiszámításához a tengely origójából indulunk ki, és jobbra haladunk, először 2 egységet, majd a pontból, ahová érkeztünk, további 3 egységet haladunk jobbra, tehát összesen 5 egységet haladunk jobbra.
70 Matematika • Tankönyv a VI. osztály számára
3.2. Egész számokkal végzett műveletek
0+2 +(+3) +5 OAB +2 + (+3) = +5; | +2 | + | +3| = +2 + 3 = +5 +2 + (+3) = | +2 | + | +3|
2. Az összeg minden egyes negatív tagja annyi egységgel mozog a számtengelyen balra (negatív irányba), amennyit a szám modulusa jelez.
A (–2) + (–3) kiszámításához a tengely origójából indulunk, és balra mozdulunk, először 2 egységet, majd onnan, ahová érkeztünk, újabb 3 egységet mozdulunk balra, tehát összesen 5 egységet mozdulunk balra.
3. Ha az összeg pozitív és negatív tagokat is tartalmaz, akkor az összeg lehet pozitív vagy negatív szám, attól függően, hogy melyik irányba mozgatunk több egységet, azaz melyik szám modulusa a nagyobb.
A +2 + (–3) kiszámításához a tengely origójából indulva 2 egységet haladunk jobbra, elérjük a +2 számnak megfelelő pontot, majd ebből a pontból 3 egységet haladunk balra, és elérjük a –1 egész számnak megfelelő pontot.
Az összeg előjele megegyezik a nagyobb modulussal rendelkező tag előjelével.
–5 (–3)+ (–2) 0
BAO
(–2) + (–3) = –5;
| –2 | + | –3| = 2 + 3 = 5 (–2) + (–3) = – (| –2 | + | –3|)
(–3)
(+2) BOA
(–1) 0
(+2) + (–3) = –1; | –3 | > | +2|
|
–3 | – | +2 | = 3 – 2 = 1
(+2) + (–3) = – (| –3 | – | +2 |)
(–2)
Összefoglalva:
(+3)
OBA
(1) 0
(+3) + (–2) = +1; | +3 | > | –2|
|+3 | – | –2 | = 3 – 2 = 1
(+3) + (–2) = | +3 | – | –2 |.
Eset a ≥ 0 és b ≥ 0 a ≤ 0 és b ≤ 0 a > 0, b < 0 és | a | >| b | a > 0 és b < 0 és | a | <
| b |
Számítási mód a + b ≥ 0 és a + b = | a | + | b | a + b ≤ 0 és a + b = – (| a | + | b |) a + b > 0 és a + b = | a | – | b | a + b < 0 és a + b = – (| b | – | a |).
Mértani
Alkalmazás
Az egész számok összeadásának művelete megőrzi a természetes számok összeadásának tulajdonságait.
Az összeadás asszociatív:
(a + b) + c = a + (b + c), bármely a, b, c egész szám esetén.
Az összeadás kommutatív:
a + b = b + a, bármely a, b egész szám esetén.
A 0 szám az összeadás semleges eleme:
a + 0 = 0 + a = a, bármely a egész szám esetén.
Továbbá, bármely a egész szám esetén létezik a –a egész szám (az ellentettje), amelyre a + (– a) = (– a) + a = 0.
[(+1) + (–2)] + (+3) = (–1) + (+3) = +2;
(+1) + [(–2) + (+3)] = (+1) + (+1) = +2, tehát
(+1) + [(–2) + (+3)] = [(+1) + (–2)] + (+3).
(–5) + (–1) = –6 és (–1) + (–5) = –6, tehát
(–5) + (–1) = (–1) + (–5).
(+7) + 0 = 0 + (+7) = +7.
(–9) + 0 = 0 + (–9) = –9.
(+7) + (–7) = (–7) + (+7) = 0.
Az előző tanévek óta tudjuk, hogy ha a és b természetes szám, a ≥ b, akkor az a – b különbsége egy természetes szám.
A ℤ halmazban bármely két egész szám a – b különbségét egész számként értelmezzük.
71 3. fejezet • Az egész számok halmaza
értelmezés 0 Oab a+b 0 ba a+b O 0 b Oa a+b 0 b a a+b O
Bármely két a és b egész szám esetén az a – b különbség az a számnak és a b szám ellentettjének összege.
Gyakorlatok és feladatok
Matematikai nyelven:
a – b = a + (– b), bármely a, b ∈ ℤ esetén.
1. Másold a táblázatot a füzetedbe, és töltsd ki a megfelelő egész számokkal!
a)
b)
2. Végezd el az összeadásokat!
a) 2 + ( 8);
b) 16 + ( 9);
c) 42 + (+18);
d) ( 1) + ( 2) + ( 3);
e) 31 + (+13);
f) 26 + ( 19);
g) 100 + (+200);
h) 50 + (+25) + ( 45).
3. Válaszd ki a helyes választ! Csak egy válasz helyes.
a) A ( 35) + ( 65) számítás eredménye:
A. 100; B. 100; C. 30; D. 30.
b) A 97 és 86 számok összege:
A. 183; B. 183; C. 11; D. 11.
c) A legkisebb kétjegyű egész szám és 100 összege:
A. 1; B. 1; C. 109; D. 199.
d) Összeadva az összes olyan számot, amelynek abszolút értéke legfeljebb 3, a kapott eredmény:
A. 6; B. 0; C. 6; D. 12.
4. Írd le:
a) a 10-et, mint negatív egész számok összegét;
b) a 20-at, mint két különböző előjelű egész szám összegét;
c) a 0-t mint két egész szám összegét.
5. Párosítsd össze az A oszlopba írt összeget jelölő betűket a B oszlopba írt helyes válasznak megfelelő számmal!
a. 20 + (+74)
b. +39 + ( 93)
c. 22 + ( 33)
d. +19 + (+36)
e. 12 + ( 34) + (+104)
+59
+ 3 – (+ 7) = + 3 + (– 7) = – 4;
– 3 – (+ 7) = – 3 + (– 7) = – 10;
+ 3 – (– 7) = + 3 + (+ 7) = + 10;
– 3 – (– 7) = – 3 + (+ 7) = + 4.
6. Határozd meg az a, b és a + b számot tudva, hogy
a = 1 + ( 11) + ( 111) és
b = 102 + (+203) + ( 302) + (+201).
7. Oldd meg az összeadás tulajdonságait felhasználva:
a) 44 + ( 38) + (38);
b) ( 3) + ( 25) + ( 17) + ( 75);
c) 1 + ( 2) + (+99) + ( 88);
d) ( 103) + (+205) + ( 2023) + ( 205) + (+103);
8. Írd a számokat növekvő sorrendbe:
n = | 35 | + ( 72) + | 41 19 |,
m = | 100 + (+67) | + ( 68) + |1 + ( 19)|,
p = ( 5) + ( 4) + ( 3) + … + (+2) + (+3).
9. Végezd el az összegzést, és mondd meg, hogy az
S = ( 1) + (+2) + ( 3) + (+4) + … + ( 19) + (+20) + + ( 21) szám pozitív, negatív vagy nulla!
10. Másold a táblázatokat a füzetedbe, és töltsd ki a megfelelő egész számokkal!
a) x +4 3 12 +20 32 +41 92 x (+8)
b) y 7 4 +7 +19 38 +46 94 y ( 6)
11. Végezd el a kivonásokat!
a) 7 ( 3);
b) 14 ( 4);
c) +32 (+15);
d) 71 ( 71);
e) 0 (+13);
f) 0 ( 29);
g) 300 (+300);
h) 25 (+50) ( 75).
12. Válaszd ki a helyes választ! Csak egy válasz helyes.
a) Kiszámolva, hogy ( 15) ( 45) az eredmény:
A. 100; B. 100; C. 30; D. 30.
b) A –79 és +44 számok különbsége:
A. 123; B. 123; C. 35; D. 35.
c) Ha a legnagyobb kétjegyű egész számból kivonjuk az 1000-et, akkor a kapott eredmény:
A. 901; B. 901; C. 1010; D. 1010.
72 Matematika • Tankönyv a VI. osztály számára
x +3 4 5 +12 10 +27 35 x + (+5)
y 1 12 +5 +9 10 +36 41 y
+ ( 9)
A B
1. 58 2. 55 3. 54 4. 55 5. +54 6. –59 7.
13. Végezd el a műveleteket!
a) 41 ( 27) ( 18);
b) 7 ( 77) ( 777);
c) +22 (35) ( 48);
d) 10 ( 20) ( 30) + ( 40);
e) 1 ( 102) [ 20 + (+78)];
f) 1 ( 11) ( 111).
14. Töltsd ki az üres helyeket egész számokkal úgy, hogy egyenlőséget kapj!
a) 10 … = 20; c) … ( 20) = 8;
b) +25 … = 2; d) 203 … = 203;
Miniteszt
8 × 5 p 1. Végezd el:
a) ( 33) + (+22);
b) (+57) + ( 100) + (+23);
c) | 64 | + | +46 | + ( 101);
d) 17 + ( 71) + (+39).
2. Számítsd ki:
15. Ha |b c| = 404, számítsd ki 202 (b c).
16. a) Ha x = 13 ( 35) (+57) ( 79) és
y = 24 + ( 46) ( 68) + ( 80), számítsd ki x y.
b) Ha z = 11 ( 33) (+55) és
t = 77 + ( 999), számítsd ki 13579 z t.
17. Számítsd ki:
a) 64 + ( 45) ( 27); d) 52 [47 (–85)];
b) 38 (+63) ( 100); e) 1 [ 2 ( 3) + ( 4)];
c) 50 (+43) + ( 72); f) 7 { 8 + [ 9 (+10)]}.
e) ( 5) ( 3);
f) 18 ( 12);
g) | 37 | | 29 | (+13);
h) 17 ( 27) (+37).
15 p a) a legfeljebb +2 abszolút értékű egész számok összegét;
15 p b) a két különböző számjegyű legnagyobb negatív egész szám és a három különböző számjegyű legkisebb természetes szám ellentettjének összegét!
20 p 3. Az a és b egész számok esetén | a | = 5 és | b | = 8. Határozd meg a lehető legkisebb a + b összeget és a lehető legkisebb a b különbséget!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
2. l. Az egész számok szorzása. Tulajdonságok
Fedezzük fel, értsük meg!
Célunk, hogy megértsük az egész számok szorzásának műveletét. A természetes számok szorzását már ismerjük, tehát tudjuk, hogyan lehet nem negatív egész számokat szorozni. A nem negatív egész számok esetében a szorzás művelete megőrzi a természetes számok esetében tanult módszert és tulajdonságokat.
Ha a > 0 és b > 0, akkor a · b > 0 és a · b = = b · a.
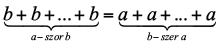
Szótár
Nem negatív szám = olyan szám, amely nem negatív; pozitív vagy nulla; 0-nál nagyobb vagy azzal egyenlő szám.
+2 = 2; +3 = 3; +6 = 6; +1 = 1; +7 = 7; tehát, (+2) · (+3) = 2 · 3 = 3 + 3 = 6; (+3) · (+2) = 3 · 2 = 2 + 2 + 2 = 6; (+1) · (+7) = 1 · 7 = 7 · 1 = 7.
0 · a = a · 0 = 0, bármely nem negatív a szám esetén. 0 · (+3) = (+3) · 0 = 0.
Külön elemezzük azt az esetet, amikor az egyik szám negatív, és azt az esetet, amikor mindkét szám negatív.
73 3. fejezet • Az egész számok halmaza
Oldjuk meg figyelmesen!
1. Ha a szorzást az egyik tényező ismételt összeadásának tekintjük, mint a természetes számoknál, akkor a (+2) · (–3) szorzatának kiszámításához azt írjuk: (+2) · (–3) = (–3) + (–3) = –6. De, –6 a 6 ellentéte, és 6 = 2 · 3, azaz (+2) · (–3) = – (2 · 3) = – (| +2 | · | –3 |).
Hasonlóan, (+3) · (–2) = (–2) + (–2) + (–2) = –6 és | (+3) · (–2) | = +6, tehát (+3) · (–2) = – (| +3 | · |–2|).
A szorzás kommutativitását követve, a (–3) · (+2), szorzat esetén (–3) · (+2) = (+2) · (–3) = –6. Hasonlóan, (–2) · (+3) = (+3) · (–2) = –6.
Ha az egyik tényező negatív, a másik pedig pozitív, akkor a szorzat negatív szám.
2. Számítsuk ki két negatív szám szorzatát! Például (–2) · (–3).
A fenti megfigyelések alapján bármely a egész szám felírható –a = (–1) · a vagy –a = a · (–1) alakban.
Akkor (–2) · (–3) = (–2) · (+3) · (–1) = ((–2) · (+3)) · (–1) = (–6) · (–1) = +6.
Akkor, (–2) · (–3) = | –2 | · | –3 | = +6.
Ha mindkét tényező negatív, akkor a szorzat pozitív szám
Ha a > 0 és b < 0, akkor a · b < 0, a · b = bbbaaa a-szorb–b-szer–a ... () () ... () = (–b) · (–a) és a · b = –(| a | · | b |).
(–12) · (+2) = –(|–12 | · | +2 |) = –(12 · 2) = –24. (+12) · (–2) = –(| +12 | · | –2|) = –(12 · 2) = –24.
0 · a = a · 0 = 0, bármely a egész szám esetén. 0 · (+3) = 0; 0 · (–3) = 0.
Ha a < 0 és b < 0, akkor a · b > 0, a · b = –[(–a) · b] = –[a · (–b)] = (–a) · (–b) és a
b = | a |
| b |.
Jegyezd meg!
Az előjelszabály szorzásnál
(–4) · (–7) = +(| –4 | · | –7|) = +( 4 · 7) = 28.
(–11) · (–2) = +(|–11| · |–2|) = +(11 · 2) = 22.
1. Két pozitív szám szorzata pozitív szám. Két negatív szám szorzata pozitív szám.
2. Egy pozitív és egy negatív szám szorzata negatív szám.
Alkalmazás
Az egész számok szorzási művelete megőrzi a természetes számok szorzásának minden tulajdonságát.
Tulajdonság A matematikai jelek nyelvén Példák
Az egész számok szorzása asszociatív.
(a · b) · c = a · (b · c), bármely a, b, c ∈ℤ esetén.
Az egész számok szorzása kommutatív. a · b = b · a, bármely a, b ∈ ℤ esetén.
[(–2) · (+7)] · (–3) = (–14) · (–3) = +(14 · 3) = +42.
(–2) · [(+7) · (–3)] = (–2) · (–21) = +(2 · 21) = +42.
(–2) · (+7) = –14 és (+ 7) · (– 2) = – 14.
74 Matematika • Tankönyv a VI. osztály számára
·
·
Az 1-es szám az egész számok szorzásának semleges eleme.
Az egész számok szorzása disztributív az öszszeadásra és a kivonásra nézve.
1 · a = a · 1 = a, bármely a ∈ ℤ esetén.
Bármely a, b, c ∈ℤ esetén, a · (b + c) = a · b + a · c; a · (b – c) = a · b – a · c.
Gyakorlatok és feladatok
1. Írd le a következő műveleteket a füzetedbe!
A szorzás elvégzése nélkül húzd alá azokat a betűket, amelyeknél a szorzás eredménye negatív egész szám! Ellenőrizd a válaszod helyességét a számítások elvégzésével!
a) 2 · ( 8);
b) 6 · ( 9);
c) +4 · (+7);
d) (+10) · 5;
e) 3 · (+5);
f) 12 · ( 1);
g) 100 · (3);
h) +9 · ( 2).
2. Írd le a következő műveleteket a füzetedbe!
A szorzás elvégzése nélkül húzd alá azokat a betűket, amelyeknél a szorzás eredménye pozitív egész szám! Ellenőrizd a válaszod helyességét a számítások elvégzésével!
a) 3 · ( 7);
b) 4 · ( 5);
c) 6 · (+8);
d) (1) · 5;
3. Végezd el a szorzásokat!
a) 4 · ( 8);
b) 3 · ( 9);
c) +2 · (+10);
d) ( 5) · 7;
4. Írj:
e) 4 · (+9);
f) 12 · ( 1);
g) 100 · (+2);
h) 9 · ( 3).
e) 6 · (+11);
f) 4 · ( 12);
g) 25 · (+2);
h) 50 · 0.
a) két olyan egész számot, amelyek szorzata pozitív egész szám;
b) két olyan egész számot, amelyek szorzata negatív egész szám;
c) két olyan egész számot, amelyek szorzata a 0;
d) három olyan egész számot, melyek szorzata –17.
5. Írd fel a –65-ös számot négy különböző egész szám szorzataként! Elemezd az összes lehetséges esetet!
1 · (+7) = (+7) · 1 = +7;
1 · (–7) = (–7) · 1 = –7.
(–2) · [(+7) + (–3)] = (–2) · (+4) = –(2 · 4) = –8; (–2) · (+7) + (–2) · (–3) = (–14) + (+6) = –8.
(–2) · [(+7) – (–3)] = (–2) · (+10) = –(2 · 10) = –20;
(–2) · (+7) – (–2) · (–3) = (–14) – (+6) = –20.
6. Párosítsd az A oszlopban levő szorzatot jelölő betűket a B oszlopban levő helyes válasznak megfelelő számjeggyel!
a. 20 · (+3)
b. 13 · ( 5)
c. 7 · ( 9)
d. | 2| · ( 4) · ( 8)
7. A szorzás asszociativitásának és kommutativitásának felhasználásával végezd el:
a) 7 · ( 5) · ( 2);
b) 4 · (+3) · ( 25);
c) 50 · ( 6) · ( 2);
d) 8 · (+9) · ( 5) · ( 1);
e) 2 · (+19) · ( 500);
f) 4 · ( 3) · ( 25) · 0.
8. A szorzás az összeadásra és kivonásra nézve disztributív. Ezt a tulajdonságot használva végezd el:
a) 5 · [( 10) + ( 100)];
b) +8 · [(+6) ( 9)];
c) 3 · [+17 + ( 12)];
d) 9 · [( 8) + ( 7)].
9. Adott az a és b két egész szám.
a) Ha a · b = 15, akkor számítsd ki a · b.
b) Ha a · b = 20, akkor számítsd ki a · ( 3) · ( 33) · b.
c) Ha a + b = 25, akkor számítsd ki ( 4) · a + ( 4) · b.
d) Ha a b = 30, akkor számítsd ki ( 5) · a ( 5) · b.
10. Az M halmaz az összes olyan egész számot tartalmazza, amely rendelkezik 10 < x ≤ 10. tulajdonsággal. Írd fel az M halmaz minden olyan részhalmazát, amely elemeinek szorzata egyenlő 10.
11. Számítsd ki az a1, a2, a3, …, a11 egész számok összegét, tudva, hogy szorzatuk -1, és hogy hárommal több negatív szám van, mint pozitív!
75 3. fejezet • Az egész számok halmaza
A B
1. +65 2. 63 3. 60 4. 64 5. –63 6. +64
1. Végezd el a szorzásokat!
10 p a) 7 · ( 12);
10 p b) 13 · ( 9);
10 p c) ( 8 + 5) · ( 2 16).
2. Számítsd ki:
15 p a) x · y + x · z, tudva, hogy x = 12 és y + z = 3.
15 p b) x · (y z), tudva, hogy x · y = 25 és x · z = 41.
30 p 3. Határozd meg az a, b, c számokat figyelve az alábbi ábrát, majd számold ki az a · b · c szorzatot!
= c –2 = b = a –22 –5 + 9 · · 12 – 21
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
3. l. Az egész számok osztása, ha az osztandó az osztó többszöröse
Emlékeztető
A b természetes szám az a természetes szám osztója, ha van olyan c természetes szám, hogy a = b · c.
Ha a, b, c nem nulla természetes számok, akkor az a = b · c, b = a : c és c = a : b egyenlőségek egyszerre igazak, azaz ha az egyik igaz, akkor a másik kettő is. Azt mondjuk, hogy a három összefüggés ekvivalens, és azt írjuk: Ha a, b, c ∈ ℕ * , akkor a = b · c ⇔ b = a : c ⇔ c = a : b.
Ha b = a : c vagy c = a : b, akkor a b az a szám és a c nem nulla szám hányadosa, c pedig az a szám és a b nem nulla szám hányadosa.
Oldjuk meg figyelmesen!
Határozd meg azt az a és b számot, amelyre 15 = (–3) · a, illetve –15 = b · (–5).
Megoldás. 15 = 3 · 5 = (–3) · (–5), tehát a = –5. Hasonlóan, –15 = 3 · (–5), tehát b = 3. Írhatjuk, hogy 15 : (–3) = –5; –15 : (–5) = +3.
Hasonlóképpen: 15 : (–5) = –3; –15 : (–3) = +5; –15 : (+5) = –3; –15: (+3) = –5.
Megjegyezzük, hogy ha | b | nem nulla természetes szám osztója, akkor az a egész szám osztható a b nem nulla számmal, és ennek az osztásnak a hányadosa a c egész szám, amelyre a = b · c.
Ha a és b egyaránt pozitív vagy negatív, akkor a : b pozitív szám.
Ha az egyik szám pozitív, a másik pedig negatív, akkor a : b negatív szám.
76 Matematika • Tankönyv a VI. osztály számára Miniteszt
Fedezzük fel, értsük meg!
A fenti példákból és az egész számok szorzására vonatkozó előjelszabályból a következő eredményekre következtethetünk:
Ha a, b, c nullától különböző egész számok, valamint | b | és | c | az | a | osztói, akkor egyidejűleg igazak az a = b · c ⇔ b = a : c ⇔ c = a : b egyenlőségek.
0 : a = 0; a : 1 = a; a : (–1) = –a; a : a = 1; a : (– a) = –1, bármely nullától különböző a egész szám esetén.
A 0-val való osztás értelmetlen!
Ha a > 0, b > 0 és b | a, akkor a : b ∈ ℤ + és a : b = | a | : | b |. (+24) : (+3) = 24 : 3 = 8
Ha a < 0, b < 0 és | b | osztja az | a |-t, akkor a : b ∈ ℤ + és a : b = | a | : | b |. (–9) : (–3) = |–9| : |–3| = 9 : 3 = 3
Ha a > 0, b < 0 és | b | osztja az | a |-t, akkor a : b ∈ ℤ _ és a : b = – (| a | : | b |). (+21) : (–7) = –(| +21 | : | –3 |) = = –(21 : 3) = –7
Ha a < 0, b > 0 és | b | osztja az | a |-t, akkor a : b ∈ ℤ és a : b = – (| a | : | b |). (–42) : (+2) = – (|–42| : | +2|) = = –(42 : 2) = –21.
Alkalmazás
a) Az a = 9 és b = –21, nem nulla egész számok esetében határozzuk meg azt a c egész számot, amelynek tulajdonsága, hogy | c | az | a | és | b | számok közös osztója!
b) Az a) alpontban kapott minden c egész szám esetén számítsd ki: a : c; b : c; a : b + a : c; a + b; (a + b) : c !
c) Az a) alpontban kapott c értékekre bizonyítsuk be az (a + b) : c = a : c + b : c egyenlőséget, amelyet a természetes számok osztásából ismerünk.
Megoldás. a) | a | = 9 és D9 = {1, 3, 9}; | b | = 21 és D21 = {1, 3, 7, 21}. A 9 és 21 számok közös osztói 1 és 3, tehát
| c | ∈ {1, 3}, azaz c ∈ {– 3, – 1, 1, 3}.
b) c 9 : c –21: c 9 : c + (–21: c) 9 + (–21) [9 + (–21)] : c
–3 –3 +7 (–3) + (7) = +4 –12 (–12) : (–3) = +4
–1 –9 +21 (–9) + (21) = +12 –12 (–12) : (–1) = +12
+1 +9 –21 (+9) + (–21) = –12 –12 (–12) : (+1) = –12
+3 +3 –7 (+3) + (–7) = –4 –12 (–12) : (+3) = –4
c) A táblázatból következik, hogy minden olyan c egész számra, amelyre a : c és b : c egész számok, igaz az
(a + b) : c = a : c + b : c egyenlőség.
Jegyezd meg!
Ha a, b, c, c ≠ 0 olyan egész számok, amelyekre a : c és b : c egész számok és a = b, akkor
a : c = b : c.
Ha a, b, c, c ≠ 0 olyan egész számok, amelyekre a : c és b : c egész számok, akkor
(a + b) : c = a : c + b : c és (a – b ) : c = a : c – b : c.
Ha a, b, c, d, c ≠ 0 és d ≠ 0 olyan egész számok, amelyekre a : c és b : d egész számok, akkor
(a · b ) : (c · d) = (a : c) · (b : d).
77 3. fejezet • Az egész számok
halmaza
Gyakorlatok és feladatok
1. Írd a negatív egész számot eredményező osztásokat jelölő betűket a füzetedbe, majd végezd el az osztásokat!
a) 32 : ( 8);
b) 27 : (9);
c) 24 : ( 3);
d) (44) : 4;
e) 30 : (5);
f) 12 : ( 1);
g) 18 : ( 6);
h) 72 : ( 12).
2. Írd a pozitív egész számot eredményező osztásokat jelölő betűket a füzetedbe, majd végezd el az osztásokat!
a) 49 : (7);
b) 42 : ( 6);
c) 18 : 9;
d) 200 : ( 4);
3. Végezd el a számításokat!
a) 48 : ( 8);
b) 63 : (+9);
c) 144 : ( 12);
d) (200) : ( 25);
4. Számold ki:
5. Párosítsd az első oszlopban szereplő számításnak megfelelő betűket a második oszlopban szereplő helyes eredményt jelentő számmal!
63
a. 512 : 8
b. 240 : ( 4)
c. 900 : 15 : ( 1)
d. 189 : ( 1 2)
60
60
64
e) 0 : ( 10);
f) 56 : ( 8);
g) 88 : ( 11);
h) 25 : ( 1) : ( 5).
e) 120 : (+5);
f) 156 : ( 13);
g) 108 : ( 9) : ( 2);
h) 400 : | 4 | : ( 2).
a) 1000 és a 25 legkisebb osztójának hányadosát;
b) a ( 33 + 99) ellentettje és a ( 11 22) szám hányadosát;
c) a nem nulla n egész szám és ellentettje hányadosát!
Miniteszt
1. Végezd el!
5 p a) 60 : ( 5);
5 p b) 100 : ( 4);
5 p c) ( 432) : ( 6) : ( 9);
5 p d) ( 23 + 58):( 2 5).
6. Határozd meg:
a) az m egész számot, ha 12 · m = 84;
b) az n egész számot, ha 5 · (n + 17) = +85;
c) a p egész számot, ha (p 9) · ( 3 + 5) = 86.
7. Számold ki:
a) 500 : ( 19 + 32);
b) 108 : [ 6 ( 29) 5];
c) [+ 47 + ( 175)] : ( 3 · 4 4 · 5).
8. Határozd meg:
a) az a egész számot, ha a · b + a · c = 225
és b + c = 15;
b) a b egész számot, ha a · b b · c = 342 és
a c = 19;
c) a c egész számot, ha a · c + b · c + c = 441
és |a + b| = 8.
30 p 2. A {9; 1; +1; 7; 72; 96; 8; 56}, halmaz elemei közül olyan számpárokat válassz, amelyek hányadosa 8.
3.
20 p a) Ha a · x + a · y = 108 és a = 18, akkor mennyi: x + y .
20 p b) Ha b · x b · y = 11 és x y = 1, akkor mennyi: b.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
78 Matematika • Tankönyv a VI. osztály számára
2.
3.
4.
1.
5. –63 6. +64
4. l. Egy nullától különböző egész szám természetes kitevőjű hatványa. Hatványokkal végzett számítási szabályok
Emlékeztető
Bármely a és n természetes szám esetén, ahol n ≥ 2, az szorzatot an-nel jelöljük és az a szám n-dik hatványának nevezzük.

Példák. A 2-es második hatványa 22 = 2 ⋅ 2.
A 2-es harmadik hatványa 23 = 2 ⋅ 2 ⋅ 2.
Az 1-es n-dik hatványa 1n =
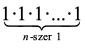
a1 = a, bármely a természetes szám esetén; a0 = 1, bármely a nem nulla természetes szám esetén.
Figyelem! 00 értelmetlen!
Fedezzük fel, értsük meg!
Adott az a ∈ ℤ, n ∈ ℕ, n ≥ 2. Az szorzatot an-nel jelöljük és az a egész szám n-dik hatványának nevezzük.

A fenti leírásban az a számot a hatvány alapjának nevezzük, az n számot pedig a hatvány kitevőjének.
A fenti információkat a következő táblázatban részletezzük.
szorzat (–2) (–2) (–1) (–1) (–1)

jelölés (–2) 2 (–1) 3 an olvasd –2 a másodikon –1a harmadikon a az n-diken magyarázat –2-nek a második hatványa –1-nek a harmadik hatványa az a szám n-dik hatványa alap –2 –1 a
kitevő 2 3 n
A természetes számoknál ismert szabályok továbbra is érvényesek:: a1 = a, bármely a egész szám esetén. a0 = 1, bármely a nem nulla egész szám esetén. 0n = 0, bármely n nem nulla egész szám esetén.
Meghatároztuk azokat a szabályokat, amelyek segítségével bizonyos számításokat végezhetünk a hatványokkal. Ezek mindegyike egész számokra is érvényes.
A szabály neve
A szabály és alkalmazásának feltétele
két azonos alapú hatvány szorzata am ⋅ an = am + n , bármely a ∈ ℤ * és m, n ∈ ℕ esetén. két azonos alapú hatvány hányadosa am : an = am – n, bármely a ∈ ℤ * és m, n∈ ℕ , ahol m ≥ n. hatvány hatványa (am)n = am n, bármely a ∈ ℤ * és bármely m, n∈ ℕ . egy szorzat hatványa
(a ⋅ b)m = am ⋅ bm, bármely a, b ∈ ℤ * és bármely m∈ ℕ . egy hányados hatványa
(a : b)m = am : bm, bármely a, b ∈ ℤ * és bármely m∈ ℕ . Emlékeztetünk, hogy 00 értelmetlen. Alkalmazás
79 3. fejezet • Az egész számok halmaza
an
1. megoldott feladat
a) Írd fel a (–3)10 : [(–3)2 · (–3)2]2 számot a –3 egyetlen hatványaként!
b) Végezd el a számításokat [(–2)12 · 510] : [(–2)9 · 57] és írd az eredményt 1-nél nagyobb kitevőjű hatványként!
c) Adott az
x = (–2)11 · 810 és y = 341 : (–3)27 egész szám. Határozd meg az a és b természetes számot tudva, hogy (x · y) : (2a · 3b) = 25 · 33.
Megoldás.
a) (–3)10 : [(–3)2 · (–3)2]2 = (–3)10 : [(–3)2 + 2]2 = = (–3)10 : [(–3)4]2 = (–3)10 : (–3)4 · 2 = (–3)10 : (–3)8 = (–3)2.
b) [(–2)12 · 510] : [(–2)9 · 57] = [(–2)12 : (–2)9]· (510 : 57) = = (–2)12 – 9 · 510 – 7 = (–2)3 · 53= [(–2) · 5]3 = (–10)3.
c) x = (–2)11 · 810 = (–2)11 · (23)10 = –211 · 23 · 10 = = –(211 · 230) = –211 + 30 = –241; y = 341 : (–3)27 = 341 : (–327) = –341 – 27 = –314.
Akkor, (x · y) : (2a · 3b) = ((–241) · (–314)) : (2a · 3b) = = (241 · 314) : (2a · 3b). Az a ≤ 41 és b ≤ 14, esetén a kijelentésben levő egyenlőség 241 – a · 314 – b = 25 · 33 lesz.
Ezért 41 – a = 5 és 14 – b = 3, vagyis a = 36 és b = 11.
Két x és y egész szám összehasonlítása azt jelenti, hogy meg kell határozni, hogy az x < y, x = y, x > y relációk közül melyik igaz.
Javasoljuk, hogy hasonlítsunk össze két hatványként írt egész számot. Könnyen felismerhetjük, hogy két olyan hatvány, amelynek ugyanaz az alapja és ugyanaz a kitevője, két egyenlő szám.
Két egész szám hatványainak összehasonlításához ajánlatos meghatározni az egyes hatványok előjelét. Ha a két hatványnak ugyanaz az előjele, akkor először hasonlítsuk össze a modulusaikat.
Ha a számok felírhatók két azonos kitevőjű, vagy két azonos alapú hatványként, akkor a természetes számok hatványainak összehasonlítására szolgáló szabályokat alkalmazva és az összehasonlított egész számok előjelét helyesen felhasználva a következő eredményeket kapjuk:
Ha a ∈ ℤ, a ≥ 2, m∈ℕ és n ∈ℕ, akkor an < am ⇔ n < m. 23 < 25; 7100 < 7101
Ha a ∈ ℤ+, b ∈ ℤ + és n ∈ℕ, akkor an < bn ⇔ a < b. 23 < 33; 7100 < 8100
Ha a ∈ ℤ_, b ∈ ℤ és n ∈ℕ páros szám, akkor an < bn ⇔ a > b. (–2)4 < (–3)4 és –2 > –3
Ha a ∈ ℤ_, b ∈ ℤ és n ∈ℕ páratlan szám, akkor an < bn ⇔ a < b. (–7)5 < (–3)5 és –7 < –3
Ha a ∈ ℤ, b ∈ ℤ és n páratlan, akkor an < bn ⇔ a < b. (–2)3 < 33 és –2 < 3
2. megoldott feladat
a) Egészítsd ki a –1, 1, –2, 2 számok hatványait a mellékelt táblázatban.
b) Az a negatív értékei esetén határozd meg a páratlan kitevőjű hatványok előjelét!
c) Mit gondolsz, milyen reláció van (–a)n és –an között, a ∈ ℤ * .
Megoldás. b) A táblázatból megállapítható, hogy a negatív számok minden páratlan kitevőjű hatványa is negatív szám. Megjegyezzük továbbá, hogy
(–1)1 = (–1)3 = (–1)5 = –1 < 0; (–1)0 = (–1)2 = (–1)4 = (–1)6 = +1 > 0;
c) (–a)n = [(–1) · a]n = (–1)n · an. Ha n páros szám, akkor (–a)n = (+1) · an = an , ha n pedig páratlan, akkor (–a)n = (–1) · an = – an.
Jegyezd meg!
1n = 1, bármely n ∈; (–1)n = 1, bármely n ∈, n páros; (–1)n = –1, bármely n ∈, n páratlan.
Ha n páros természetes szám, n ≠ 0, akkor (–a)n = an, bármely a ∈ .
Ha n páratlan természetes szám, akkor (–a)n = –an, bármely a ∈ .
80 Matematika • Tankönyv a VI. osztály számára
a a0 a1 a2 a3 a4 a5 a6 –1 +1 –1 +1 –1 +1 –1 +1 +1 +1 +1 +1 +1 +1 +1 +1 –2 +1 –2 +4 –8 +16 –32 +64 +2 +1 +2 +4 +8 +16 +32 +64
1. Írd fel természetes kitevőjű hatványként:
a) −3 · (−3); d) (−2) · (−2) · (−2) · (–2) · (–2);
b) 5 · 5 · 5; e) (–6) · (–6) · (–6) · (–6);
c) −10; f) 7 · 7 · 7 · 7 · 7 · 7.
2. Számold ki a hatványokat!
a) (–2)3; b) (–5)4; c) (–1)7; d) (–8)1; e) (10)2; f) (–3)5
3. Másold a füzetbe, végezd el a szükséges számításokat, és töltsd ki a következő táblázatot:
(–7)2 = … (–5)3 = … (–3)4 = …
(+7)2 = … (+5)3 = … (+3)4 = …
(–1)5 = … (–10)6 = … (–2)7 = …
(+1)5 = … 106 = … (+2)7 = …
4. Adott a (–1)3, 17, (–2)4, 09, (–3)5, 23, (–5)1, (–4)0, (–6)2, (–7)3,− 82 hatványok sorozata.
a) Írd le a sorozat pozitív tagjait tartalmazó halmazt!
b) Írd le a sorozat negatív tagjait tartalmazó halmazt!
c) Indokold meg, hogy igaz-e a következő kijelentés: „Az adott sorozat tartalmaz olyan egész számot, amely nem is negatív, nem is pozitív”
5. Számold ki: (–15)1, (–3)3, −24, (–13)2, −17, (–4)0, 20231
6. Írd fel a) –2 alapú hatványként a −2, 4, −8, 16, −128 számokat;
Miniteszt
1. Számítsd ki:
b) −10 alapú hatványként az 1, −10, +100, −1000, −10 000 000 számokat!
c) 3 kitevőjű hatványként az 1, −1, −27, −125, 1000 számokat!
7. Másold át a táblázatot a füzetedbe, és töltsd ki az üres helyeket egy-egy hatvánnyal úgy, hogy egyenlőségek jöjjenek létre:
23 · 24 = … ( 3)2 · (–3)4 = …
45 : 42 = … (–2)8 : (–2)3 = …
[(–2)2]3 = … [(–1)4]5 = …
(–10)3 : (–10) = … (–7)9 : (–7)3 : (–7)2 = …
[(–9)6]0 = … [(–2)2 · 23]4 = …
8. Használd a hatványokkal végzett számítási szabályokat és végezd el:
a) (2 · 32)3 ;
b) [23 · (–3)2]4 ; c) [(–4)2 · 53]5; d) [(–6)4 · (–7)2]6.
9. Végezd el a számításokat!
a) (−2)6 · 24; d) [(–3)3 ]4 : (–3)9;
b) 81 · (–3)7 : (−3)10; e) (–4)14 : (–4)12 · (−4);
c) 5 · (–52) : (–125); f) (–2)2 · (–2)6 : (–2)7.
10. Bizonyítsd be az egyenlőségeket!
a) 66 = 26 · 36;
b) (–30)5 = (–2)5 · (–3)5 · (–5)5;
c) (–10)11 = (–2)11 · 511 = 211 · (–5)11
4 × 5 p a) 23 – ( 3)2; b) ( 1)21 – ( 1)12; c) ( 2)2 ∙ ( 2)3; d) ( 5)7 : ( 5)5.
30 p 2. Határozd meg az n számot tudva, hogy igaz az [(–7)2]4 : (–7)n = (–7)3 egyenlőség!
40 p 3. Hasonlítsd össze az a = ( 8 + 1)7 : ( 6 1)4 és b = ( 2)9 számot!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
5. l. Összeadással és kivonással kapcsolatos számítások elvégzése a ℤ-beli műveletek tulajdonságainak felhasználásával
Oldjuk meg figyelmesen!
Tekintsük az a és b egész számot, célunk, hogy megsaccoljuk összegük ellentétét.
Ehhez kitöltjük és megfigyeljük az alábbi táblázatot. Mind a négy esetben az a és b számok összegének ellentéte megegyezik e számok ellentétének összegével.
a b a + b –a –b –(
81 3. fejezet • Az egész számok halmaza
Gyakorlatok és feladatok
a + b) –a + (–b) +2 +1 +3 –2 –1 –3 –3 –2 +1 –1 +2 –1 +1 +1 +2 –1 +1 –2 +1 –1 –1 –2 –1 –3 +2 +1 +3 +3
Alkalmazás
Bármely egész számmal végzett számítás eredményének helyessége az elvégzendő műveletek tulajdonságainak tiszteletben tartásától függ. Felhasználjuk a különbség értelmezését, az összeadás tulajdonságait és a szorzás disztributivitását az összeadásra nézve, és igazoljuk a fenti feltevést. Ezekből új, a számítások elvégzéséhez hasznos tulajdonságokat vezetünk le.
Tulajdonság Indoklás
1.
–(a + b) = (–a) + (–b) = –a – b, bármely a, b ∈ℤ esetén.
– (a + b) = (–1) · (a + b) = = (–1) · a + (–1) · b = = (–a) + (–b) = – a – b.
Használt tulajdonságok
Egy szám ellentettje a –1 és az adott szám szorzata.
A szorzás disztributív az összeadásra nézve. Egy összeg ellentettje egyenlő a tagok ellentettjeinek összegével.
Tulajdonság Indoklás
2.
a – (b + c) = a – b – c, bármely a, b, c egész szám esetén.
a – (b + c) = a + [–(b + c)] = = a + (–b – c) = a + [(–b) + (–c)] = = a + (–b) + (–c) = a – b – c.
Használt tulajdonságok
Egy összeg ellentettje egyenlő a tagok ellentettjeinek összegével.
Egész számok összeadásának asszociativitása.
A zárójel előtt lévő „–" jel megváltoztatja a zárójelben lévő összes tag előjelét.
Gyakorlatok és feladatok
1. Számítsd ki a zárójelek eltávolításával:
a) 35 + ( 37) (+28);
b) 27 (+52) ( 68) (+44);
c) 17 ( 71) + ( 62);
d) 307 (+82) ( 134) (+89).
2. Adott az
a = 10 + 20 ( 30 + 40 50) + ( 60) és
b = 78 + 90 + ( 55 77 + 121) szám. Másold a táblázatot a füzetedbe, majd határozd meg a kijelentések logikai értékét!
Kijelentés I/H
Az a negatív egész szám.
A b pozitív egész szám.
A a ( b) természetes szám.
a ( 102) > b ( 201)
Miniteszt
3. Végezd el a számításokat!
a) 53 + 42 67 + 81;
b) 123 87 + 59 72 23;
c) 7 ( 51 + 46 32) ( 48 + 27);
d) 321 [ 93 + ( 136 + 204) ( 64)].
4. Számold ki az összegeket!
a) 1 2 + 3 4 + … + 89 90;
b) (2 + 4 + 6 + … + 100) + ( 1 3 5 … 99).
5. Számold ki és rendezd növekvő sorrendbe a számokat!
a = 100 + [ 105 + ( 35 + 79 4) ( 35 ) + 127],
b = [ 39 + ( 23 + 9 + 20) ( 31 + 16 87) + 32] ( 71 2),
c = [( 17 + 29) + ( 14 + 32 18)] ( 104 + 120).
6. Határozd meg a x + ( y) ( z) 2024, számot tudva, hogy:
|x + ( 23)| = 0, | 32 y| = 23 x és z 33 = ( 207).
1. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
20 p a) Az x – (y + z) számításban elhagyva a zárójeleket az eredmény a következő:
A. x – y – z; B. x – y + z; C. x + y + z; D. x + y – z.
20 p b) Az x + (– y + z) számításban elhagyva a zárójeleket az eredmény:
A. x + y – z; B. x – y + z; C. x + y + z; D. x – y – z.
20 p c) A 4 – (17 – 25) szám egyenlő:
A. 8; B. –8; C. –12; D. 12.
15 p 2. Számold ki a = 25 – [–13 + (–5 + 11 – 17) + (–15)] és vizsgáld meg, hogy pozitív, negatív vagy nulla.
15 p 3. Számold ki –(−b + c), tudva, hogy b = −[−(−5)] és c = −{+ [−(+7)]}.
Megjegyzés: Munkaidő: 20 perc Hivatalból: 10 pont
82 Matematika • Tankönyv a VI. osztály számára
6. l. A műveletek elvégzésének sorrendje és a zárójelek használata
Emlékeztető
1. Ha a feladat csak azonos rendű műveleteket tartalmaz, akkor azokat a leírt sorrendben, balról jobbra haladva végezzük el.
2. Ha a feladat különböző rendű műveleteket tartalmaz, de nem tartalmaz zárójeleket, akkor végezzük el a harmad-, majd a másod- és végül az elsőrendű műveleteket az 1-nél írt sorrendben, azaz:
1. lépés. A hatványokkal végzett számításokat és a hatványozásokat végezzük el.
2. lépés. Szorozzunk és osszunk az előző lépés eredményeinek felhasználásával az 1-nél írt sorrendben.
3. lépés. Adjuk össze és vonjuk ki az előző lépés eredményeit az 1-nél írt sorrendben.
Megjegyzés: A hatványokkal végzett műveleteket elvégezhetjük az előkészítő szakaszban vagy a megoldás során, amikor bizonyos számokat olyan formában akarunk leírni, amely egyszerűsíti a számításokat.
3. Ha a feladat zárójeleket tartalmaz, akkor:
1. lépés. Elvégezzük a kerek zárójelben lévő számításokat a 2. pontban leírt sorrendben.
2. lépés. A szögletes zárójeleket kerek zárójelekké, a kapcsos zárójeleket szögletes zárójelekké alakítjuk.
3. lépés. Elvégezzük az új kerek zárójelekben levő számításokat a 2. pontban leírt sorrendet követve.
4. lépés. Így folytatjuk, amíg az összes zárójelet el nem távolítjuk, majd a számításokat zárójelek nélkül végezzük el.
Fedezzük fel, értsük meg!
Az egész számokkal végzett műveletek sorrendje ugyanaz, mint a természetes számokkal végzett műveleteké. A különlegességet a negatív számokkal végzett műveletek jelentik. Ezt fogjuk megvizsgálni:
1. gyakorlat. Végezd el a számításokat: 3 · [5 – 6 · (4 – 68 : 4 +17)].
Lépések
1. lépés. A kerek zárójelben levő szorzást és osztást végezzük el.
Megoldás
2. lépés. A kerek zárójelben levő öszszeadást és kivonást végezzük el.
2’. lépés. A szögletes zárójelet kerekké alakítjuk. […] → (…)
Számítás
4 – 68 : 4 + 17 = 4 – 17 + 17
3 · [5 – 6 · (4 – 17 + 17)]
4 − 17 + 17 = 4
3 · [5 – 6 · (+4)]
3 · (5 – 6 · 4)
3. lépés. Az új kerek zárójelben levő műveleteket végezzük el. 5 – 6 · 4 = 5 – 24 = –19
3 · (–19 )
4. lépés. Elvégezzük a számításokat. 3 · (–19) = –57.
Alkalmazás
2. gyakorlat Végezd el a számításokat: 3 · 53 − 42 − 511 · 20.
Lépések
Megoldás
2. lépés. Az eredményeket felhasználva szorzunk és osztunk, majd összeadunk és kivonunk.
Számítás
3 · 125 – 16 – 51 · 20 = = 375 – 16 – 1020 = = 359 – 1020 = – 661.
Kidolgozás
A feladat megoldása a következőképpen írható/dolgozható ki:
3 · [5 – 6 · (4 – 68 : 4 +17)] = = 3 · [5 – 6 · (4 – 17 + 17)] = = 3 · (5 – 6 · 4) = = 3 · (5 – 24) = = 3 · (–19) = = –57.
Kidolgozás
1. lépés. A hatványozást végezzük el. 53 = 125; 42 = 16; 511 = 51. 3 · 53 − 42 − 511 · 20 = = 3 · 125 – 16 – 51 · 20 = = 375 – 16 – 1020 = = 359 – 1020 = = –661.
83 3. fejezet • Az egész számok halmaza
A hatványokkal végzett műveleteket elvégezhetjük az előkészítő szakaszban vagy a megoldás során, amikor bizonyos számokat olyan formában akarunk leírni, amely egyszerűsíti a számításokat.
Gyakorlatok és feladatok
Példa.
[(− 4)6 : 211 − 2]8 − 372 + 31 · 37 = (212 : 211 − 2)8 − 372 + 31 · 37 = = (2 − 2)8 − 372 + 31 · 37 = 37 · (−37 + 31) = 37 · (−6) = −222.
1. Válaszd ki a helyes válasz betűjelét! Csak egy
válasz helyes.
a) −100 és a −3 és −33 szorzatának összege:
A. 1; B. −1; C. −3; D. 3.
b) A 196 : (–7) hányadosa és –30 különbsége:
A. 3; B. −3; C. 2; D. −2.
c) A legkisebb – ab alakú egész szám és az 5-ös köbének összege:
A. 26; B. −27; C. 27; D. −26.
2. Számold ki!
a) –29 + (15 – 36 + 79) – 144;
b) –32 – [– 60 + (– 35 + 77) – 83];
c) 45 – |–7 + 5| + | –16 + 33 – 25 |.
3. Végezd el a számításokat!
a) 1 + 2 · (– 3);
b) –4 – 5 · (–6);
c) 7 + 8 · (–9) + (–10)2;
d) –350 : (– 14) + 5 · (– 3);
e) –4 · [–10 + (–3)2] – (–23 + 25);
f) 512 : (–4)3 – (–71– 17) · (–1)6.
4. Fogalmazz meg egy olyan számítási feladatot, amelynek eredménye – 10, és amely tartalmazzon:
a) egy összeadást;
b) egy összeadást és egy kivonást;
c) egy összeadást, egy kivonást, egy szorzást és egy osztást.
5. Adott a = 2 · {–1 + [(–2)3– (–2)3 : (–2)2] : (–3) · (–1)} + 3.
a) Számold ki az a számot!
b) Határozd meg azon b egész számokat, amelyekre b3 < a < b.
Miniteszt
6. Az a = –4 és b = | –2 | esetén számold ki: A = (–a)3 + b2 – a2 · (–b)3.
7. Adott az
m = | –888 : (–4) – 84 | : (–23),
n = –14 + 3 · [–2 · (19 – 23) – 10],
p = 17 – (–4) · (–6) – (–3)3 szám. Másold a táblázatot a füzetedbe, végezd el a számításokat, majd töltsd ki a szabad négyzetet az I betűvel, ha a kijelentés igaz, és a H betűvel, ha hamis.
Kijelentés I/H
Az m negatív egész szám.
Az n nem negatív egész szám.
A p az n szám ellentettje.
Az m · (n + p + 1) számítás eredménye 6.
8. Végezd el a számításokat!
a) (–11) · [(–3)3 + (–2)4 + (–4032) : (–84)];
b) (–2)73 : (–2)69 – 3 · {–2 – 2 · [(–3)7 : (–3)5 – 14)]};
c) [(–7)7]2 : [(–7)7 · (–7)4] + (27 · 72) : (–26 · 7);
d) –4 – 4 · [(–3)5 : 81 – 2] + (–8)1 : (–8)0;
e) (–1)4 · (–5)2 · (–2)3 – (–3)5 · (2)5 : (–6)3.
9. Igazold, hogy az
x = (–3)2 · 93: (–3)7 – (–5) · (–5)4 : (–125) + 1 szám
egy egész szám köbe!
10. Adott az a = –1 + (–1)2 + (–1)3 + 4 · (–1)5, b = –22 + (–2)9 : 64 – (–5)0 és
c = [(–2)3 · (–3)4] : [(–2)2 · (–3)3] + (–7)4 : (–49) szám.
a) Írd a három számot növekvő sorrendbe!
b) Vizsgáld meg, hogy igaz vagy hamis a következő kijelentés: a3 + b2 + c < 0.
Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
20 p 1. Az 5 · (–2) + 4 : (–1) + 3 számítás eredménye:
A. 11; B. −11; C. 18; D. −18.
30 p 2. A (–132) : [23 + (–7) · 4 – (3 – 11)] számnál 14-gyel nagyobb szám:
A. 19; B. 20; C. 100; D. 25.
40 p 3. A (–18 + 21)3 · [–63 : (–9) – (–2)4]2 : ( –243) számítások elvégzése után kapott eredmény:
A. 8; B. −8; C. −9; D. 12.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
84 Matematika • Tankönyv a VI. osztály számára
3.3. Egyenletek, egyenlőtlenségek, feladatok megoldása ℤ-beli egyenletek/egyenlőtlenségek segítségével
1. l. Egyenletek az egész számok halmazán
Emlékeztető
Két egész szám, x és y akkor és csak akkor egyenlő, ha a számtengelyen azonos pontokban ábrázolhatjuk. Így írjuk: x = y.
Az egész számok halmazán levő egyenlőségi reláció a következő tulajdonságokkal rendelkezik:
a) reflexív: Bármely egész szám egyenlő saját magával, azaz x = x, bármely x egész szám esetén.
b) szimmetrikus: Ha x = y, akkor y = x.
c) tranzitív: Ha x = y és y = z, akkor x = z.
Az algebrában az egyenlőségi relációt egy vagy több változóval rendelkező állítás megfogalmazására vagy egyenletek felírására is használják.
Egy egyenlőségben az = jel bal oldalára írt kifejezést az egyenlőség bal tagjának, az = jel jobb oldalára írt kifejezést pedig az egyenlőség jobb tagjának nevezzük.
Oldjuk meg figyelmesen!
A mindennapi élet egyes problémái jól illeszkednek az általános matematikai modellekbe. Felhívószöveg Magyarázat
1. feladat Félix két évvel fiatalabb a nővérénél és öt évvel idősebb az öccsénél.
A három testvér együtt 21 éves. Határozd meg Félix korát!
A feladat adatai a következőképpen értelmezhetők: Félix életkorát x-szel jelöljük. Akkor a nővére x + 2 éves, az öccse pedig x – 5 éves. Együtt x + (x + 2 ) + (x – 5) évesek.
A fenti értelmezés alapján azt a feladatot kell megoldanunk, hogy meghatározzuk azokat az x egész számokat, amelyek esetében x + (x + 2 ) + (x – 5) = 21.
Ez a feladat a következőképpen fogalmazható meg: Oldd meg az x + (x + 2 ) + (x – 5) = 21 egyenletet a természetes számok halmazán.
Az egyenlet megoldása
Az összeadás tulajdonságait felhasználva, a fordított út módszerével az egyenlet a következő lesz: x + x + 2 + x – 5 = 21 ⇔ 3x – 3 = 21 + 3
3x = 24 : 3
x = 8.
Fedezzük fel, értsük meg!
Az a feladat, ahol olyan x ∈ E számokat kell meghatározni, amelyek egy adott egyenlőséget teljesítenek az egy E halmazon adott, az x-et tartalmazó egyenlet.
A E halmazt az egyenlet értelmezési tartományának is nevezzük.
Visszatérve az eredeti feladathoz, megállapíthatjuk, hogy Félix 8 éves.
Valóban, ha Félix 8 éves, akkor a nővére 8 + 2 = 10 (éves), az öccse 8 – 5 = 3 (éves), együtt 8 + 10 + 3 = 21 (évesek).
Feladat. Határozd meg az E = {–5, 0, 2, 5} halmaz azon egész elemeit, amelyek tulajdonsága, hogy x3 = 25 · x.
Átfogalmazás
„Oldd meg E = {–5, 0, 2, 5}-ben az x3 = 25 · x egyenletet” vagy
„Oldd meg az x3 = 25 · x egyenletet, x ∈{–5, 0, 2, 5}.”
85 3. fejezet • Az egész számok halmaza
Az összes olyan x ∈ E szám, amely teljesíti az egyenletet (az adott egyenlőséget), az egyenlet megoldása. Megoldani az egyenletet azt jelenti, hogy meg kell határozni az összes megoldását tartalmazó, általában M-mel jelölt megoldáshalmazát.
Az E mindenik elemére ellenőrizzük, hogy az egyenlet megoldása-e. Az egyenletbe helyettesítjük az x = –5-öt, és azt kapjuk, hogy –125 = –125, ami igaz kijelentés.
Az egyenletbe helyettesítjük az x = 0-t, és azt kapjuk, hogy 0 = 0, ami igaz kijelentés. Az egyenletbe helyettesítjük az x = 2-t, és azt kapjuk, hogy 8 = 50, ami hamis kijelentés. Az egyenletbe helyettesítjük az x = 5-öt, és azt kapjuk, hogy 125 = 125, ami igaz kijelentés. Következésképpen a –5, 0, +5 számok az egyenlet megoldásai, és írhatjuk, hogy M = {–5, 0, +5}
A 2 · x = –4, x ∈ ℤ és –4 · x – 8 = 0, x ∈ ℤ egyenletek ekvivalensek, mivel mindkettő ismeretlen tagja ℤ halmazbeli és ugyanaz a megoldáshalmazuk, M = {–2}.
Két egyenlet akkor ekvivalens, ha ugyanaz az értelmezési tartományuk és ugyanaz a megoldásuk.
2 · x = –4 : 2, x = –4 : 2
x = –2.
–4 · x – 8 = 0 +8 –4 · x = 8 : (–4)
x = –2.
ℤ-ben mindkét egyenlet megoldása x = –2.
Megjegyzés: Egy egyenlet megoldásainak halmaza az egyenlet értelmezési tartományának egy részhalmaza.
Egy egyenlőségből kiindulva ekvivalens egyenlőségeket kaphatunk a következő transzformációkkal:
Transzformáció
Hozzáadjuk vagy kivonjuk ugyanazt az egész számot az egyenlőség mindkét tagjából.
A matematikai jelek nyelvén
x = y ⇔ x + a = y + a , bármely a ∈ ℤ ;
x = y ⇔ x a = y a , bármely a ∈ ℤ . aa y ++ x x+ay+a
Ha x ∈ ℤ , y ∈ ℤ , akkor x = y ⇔ x + 7 = y + 7. x–ay–a aa y ––x
Szorozzuk meg vagy osszuk el az egyenlőség mindkét tagját ugyanazzal az egész nem nulla számmal.
x·a a 0 y·a aa y · · x
Ha x ∈ ℤ , y ∈ ℤ , akkor x = y ⇔ x 7 = y 7.
x = y ⇔ x · a = y · a, bármely a ∈ ℤ * ;
x = y ⇔ x : a = y : a, bármely a ∈ ℤ *
Ha x ∈ ℤ , y ∈ ℤ , akkor x = y ⇔ x · 2 = y · 2. a 0 x : ay : a aa y : : x
Ha az egyenlőség két tagja nem negatív szám, akkor egyenértékű egyenlőségeket kaphatunk akkor is, ha az egyenlőség mindkét tagját az n-dik hatványra emeljük, ahol az n nullától különböző természetes szám.
Ha | x | ⋮ 2 és | y | ⋮ 2, akkor x = y ⇔ x : 2 = y : 2.
Ha x ∈ ℤ , y ∈ ℤ , x ≥ 0 és y ≥ 0, akkor x = y ⇔ xn = yn, bármely n ∈ ℕ * .
Az alábbiakban az egyenlőség ekvivalens transzformációinak írására találunk példákat.
86 Matematika • Tankönyv a VI. osztály számára
a) xy xy xy 3 33 1 31 31 b) xy xy xy 2 22 7 72 72 c) xy xy xy 5 55 2 22 22 xy00 , esetén d) 34 34 4 33 3 xy xy xy :( )
Alkalmazás
1. Oldd meg az ( x 1)(2 x 3)(2 x + 8) = 0 egyenletet az ℕ és ℤ halmazon!
Megoldás. Az egyenlet megoldásához a következő matematikai ismeretet használjuk:
Ha két vagy több egész szám szorzata 0, akkor a tényezők közül legalább az egyik 0.
Ha a és b egész számok és a ⋅ b = 0, akkor
a = 0 vagy b = 0.
Akkor, ( x 1)(2 x 3)(2 x + 8) = 0 ⇔ x – 1 = 0 vagy 2 x – 3 = 0 vagy 2x + 8 = 0.
x – 1 = 0 | + 1
x = 1
1 ∈ ℕ és 1 ∈ ℤ
x = 1 megoldás ℕ-ben és ℤ-ben is.
2x – 3 = 0 | + 3
2x = 3 és 3 ⋮ ⟋2
Az egyenletnek nincs megoldása sem ℕ-ben, sem ℤ-ben.
2x + 8 = 0 | – 8
2x = –8 | : 2
x = –4
–4 ∉ ℕ, de –4 ∈ ℤ
x = –4 csak ℤ-ben megoldás.
Következtetés. ℕ -ben a megoldáshalmaz az M= {1}, ℤ -ben pedig a megoldáshalmaz M = { 1, – 4}.
Tehát, ha egy egyenlet értelmezési tartományát kicseréljük, akkor a megoldáshalmaz is változhat.
A legkönnyebben megoldható egyenletek az ax = b alakú egyenletek vagy az ilyen alakú egyenletekre viszszavezethető egyenletek (ekvivalens transzformációkkal), ahol a egy nullától különböző egész szám és b egy egész szám. Nyilvánvaló, hogy az egyenletnek csak akkor van megoldása ℤ-ben, ha | b | ⋮ | a |, a megoldások halmaza ebben az esetben az M = {b : a}.
2. Oldd meg a | 3x | = 12 egyenletet, x ∈ ℤ .
Megoldás. A modulus értelmezéséből tudjuk, hogy két olyan egész szám van, amelynek modulusa 12, mégpedig azoknak, amelyek a számtengelyen az origótól 12-es távolságban helyezkednek el. Ekkor 3x = 12 vagy 3x = –12. Mivel 12 ⋮ 3, akkor az x1 = 12 : 3 = 4 és x2 = (–12) : 3 = –4, megoldást kapjuk. A megoldáshalmaz M = {–4, + 4} lesz.
Gyakorlatok és feladatok
1. Másold át a füzetedbe, és töltsd ki az üres helyeket egész számokkal úgy, hogy egyenlőségeket kapj!
a) 8 + … = 3;
b) 10 … = 4;
c) 4 · … = 56;
d) 48 : … = 12;
e) … : 9 = 108;
f) (…)3 = 27.
2. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
a) A 4 ennek az egyenletnek a megoldása:
A. x + 1 = 5;
B. x + 1 = 5;
C. 3 x = 7;
D. 3 + x = 7.
b) A 3 ezeknek az egyenleteknek a közös megoldása:
A. x + 3 = 0 és x 6 = 2;
B. x 3 = 0 és 5 x = 2;
C. 3 x = 0 és x + 8 = 12;
D. 3 + x = 6 és 30 : x = 10.
c) Az egyenlet, amelynek van megoldása az egész számok halmazán, az:
A. 2 · x + 1 = 22;
B. 3 · x 4 = 16;
C. 13 2·x = 4;
D. 4·x 1 = 5.
3. Oldd meg az egész számok halmazán az alábbi
egyenleteket:
a) 6 + x = 2; d) 124 : x = 31;
b) x 5 = 8; e) x : (1 9) = 72;
c) 12 · x = 156; f) x2 = 100.
4. Oldd meg az egész számok halmazán az alábbi egyenleteket:
a) 3 · x 6 = 3; d) 11 · x + 22 = 33;
b) 2 · x + 24 = 0; e) x + ( 2)3 = 13;
c) 50 2 · x = 10; f) 100 : ( 5) + 4 · x = 12.
5. Oldd meg az egész számok halmazán az alábbi
egyenleteket:
a) 9 · (x 7) = 63;
b) (x + 4) : ( 2)2 = 207 : 23;
c) 3 · x + 11 = x 4;
d) 4 · x + 6 = x + 1;
e) 52 7 · x = 4;
f) 10 (8 x) = 13;
g) ( 6 x) + 5 = ( 2)3;
h) 1 2 · [ 3 (4 x)] = 5.
6. Határozd meg azon x egész számokat, amelyekre:
a) | x | = 5;
b) | x | = 7;
c) | x 3 | = 0;
d) | 2 x | = 1;
e) 6 + | x 4 | = 2;
f) | 4 · x | +1 = 9.
87 3. fejezet • Az egész számok halmaza
Miniteszt
1. Töltsd ki az üres részeket úgy, hogy igaz legyen az állítás!
10 p a) A 3 · x + 4 = 43 egyenlet megoldása … .
15 p b) A | 1 2 · x | = 7 egyenlet megoldáshalmaza {…}.
2. Oldd meg az egyenleteket az egész számok halmazán:
15 p a) 2 · x + 7 = 28 x;
15 p b) 5 · (x + 4) = 2 · (x + 1) 11;
15 p c) (4 · x 6) : ( 2) + 9 = 8 · x;
20 p d) [ 24 + 24 : ( 8) + 25] · ( 10)2 3 · x = 101.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
2. l. Egyenlőtlenségek az egész számok halmazán
Emlékeztető
Két egész szám, a és b összehasonlításához használjuk a számtengelyen való ábrázolásukat, valamint az egyenlőségi és a ≤, ≥, <, > egyenlőtlenségi relációk tulajdonságait.
Az egész számok halmazán a ≤ reláció tulajdonságai:
a ≤ a, bármely a ∈ ℤ Ha a ≤ b és b ≤ a, akkor a = b. Ha a ≤ b és b ≤ c, akkor a ≤ c.
A ≤ reláció tulajdonságai ≥ reláció esetén is igazak.
Az egész számok halmazán a < és > relációk tranzitívak. Ha a < b és b < c, akkor a < c. Ha a > b és b > c, akkor a > c.
Bármely két a és b egész szám esetén csak az egyik reláció igaz: a < b, a = b, a > b.
Bármely pozitív egész szám nagyobb, mint bármely negatív egész szám és nagyobb, mint 0 is.
Minden negatív egész szám kisebb, mint bármely pozitív egész szám és kisebb, mint 0 is.
Két pozitív egész szám közül a kisebb modulusú a kisebb.
A pozitív egész számokat a tengely origójától jobbra, növekvő sorrendben ábrázoljuk.
Két negatív egész szám közül a nagyobb modulusú a kisebb.
A negatív egész számokat a tengely origójától balra, csökkenő sorrendben ábrázoljuk.
Két ellentétes előjelű (az egyik pozitív, a másik negatív) egész szám szorzata negatív egész szám.
Két azonos előjelű (mindkettő pozitív vagy negatív) egész szám szorzata pozitív egész szám.
Ha a ∈ℤ + és b∈ ℤ –, akkor a > b és a > 0.
Ha a ∈ ℤ –és b∈ ℤ+, akkor a < b és a < 0.
Adott a ∈ ℤ + és b∈ ℤ + :
Ha a < b, akkor | a | < | b |.
Ha | a | < | b |, akkor a < b.
0 < 1 < 2 < 3 < 4 < 5 < 6 < 7 < 8 < …
Adott a ∈ℤ –és b∈ℤ –:
Ha a < b, akkor | a | > | b |.
Ha | a | > | b |, akkor a < b.
0 > –1 > –2 > –3 > –4 > –5 > –6 >
Ha a > 0 és b < 0 vagy a < 0 és b > 0, akkor a · b < 0 és a · b = – (| a | · | b |).
Ha a < 0 és b < 0 vagy a > 0 és b >0, akkor a · b > 0 és a · b = | a | · | b |.
88 Matematika • Tankönyv a VI. osztály számára
Oldjuk meg figyelmesen!
1. feladat Értelmezés
Határozd meg azokat az x egész számokat, amelyeknek az a tulajdonsága, hogy ha az x szám duplájához hozzáadjuk a –12-őt, akkor negatív egész számot kapunk.
Határozd meg azt az x egész számot, amelyre 2 · x + (–12) < 0.
Az olyan x egész számok meghatározásának feladata, amelyek esetében2 · x + (–12) < 0, a következőképpen fogalmazható meg: „Oldd meg ℤ-ben a 2 · x + (–12) < 0 egyenlőtlenséget!” vagy „Oldd meg a 2 · x + (–12) < 0 egyenlőtlenséget, x ∈ ℤ.”
Megoldjuk az egyenlőtlenséget: 2 · x + (– 12) < 0 ⇔
2 · x – 12 < 0 | +12
2 · x < + 12 | : 2 és 2 > 0
x < 6.
1. Mindkét oldalhoz hozzáadunk 12-őt.
2. Mindkét oldalt osztjuk 2-vel, 2 > 0.
3. Meghatározzuk a megoldásokat.
Az egyenlőtlenség megoldásai az összes 6-nál kisebb egész szám, tehát M = { …, – 1, 0, 1, 2, 3, 4, 5}.
Fedezzük fel, értsük meg!
A feladatot, amely során egy egyenlőtlenséget teljesítő x ∈ E számokat határozunk meg egyenlőtlenségnek nevezzük, ahol x ismeretlen az E halmazból. Az E halmaz az egyenlőtlenség értelmezési tartománya.
Az összes olyan x ∈ E szám, amely teljesíti az egyenlőtlenséget az egyenlőtlenség megoldása.
Megoldani az egyenlőtlenséget azt jelenti, hogy meg kell határozni az öszszes elemet, amely a megoldás része. A megoldáshalmazt általában M-mel jelöljük.
Feladat. Határozd meg az E = {–5, 0, 2, 5} halmaz azon egész elemeit, amelyekre x2 ≥ 20.
Átfogalmazás.
„Oldd meg az E = {– 5, 0, 2, 6} halmazon az x2 ≥ 20 egyenlőtlenséget!” vagy „Oldd meg az x2 ≥ 25 egyenlőtlenséget, x ∈ {–5, 0, 2, 6}”.
Az E mindenik elemére ellenőrizzük, hogy az egyenlőtlenség megoldása-e. Az egyenlőtlenségbe helyettesítjük az x = –5-öt, és azt kapjuk, hogy 25 ≥ 20, ami igaz kijelentés. Az egyenlőtlenségbe helyettesítjük az x = 0-t, és azt kapjuk, hogy 0 ≥ 20, ami hamis kijelentés. Az egyenlőtlenségbe helyettesítjük az x = 2-t, és azt kapjuk, hogy 4 ≥ 20, ami hamis kijelentés. Az egyenlőtlenségbe helyettesítjük az x = 5-öt, és azt kapjuk, hogy 36 ≥ 20, ami igaz kijelentés. Következésképpen, –5, és + 6 egyenlőtlenség megoldásai és írhatjuk, hogy M = {–5, 6}.
A 2 · x ≥ –4, x ∈ ℤ és –4 · x – 8 ≤ 0, x ∈ ℤ egyenlőtlenségek ekvivalensek, mert mindkettő ismeretlen tagja ℤ és halmazbeli és megoldáshalmazuk megegyezik, azaz a – 2-nél nagyobb vagy egyenlő összes egész szám halmaza.
Két egyenlőtlenség akkor ekvivalens, ha ugyanaz az értelmezési tartományuk és ugyanaz a megoldásuk is.
2 · x ≥ –4 : 2 és 2 > 0
x ≥ –4 : 2
x ≥ –2.
–4 · x – 8 ≤ 0 +8
–4 · x ≤ 8 : (–4), –4 < 0 x ≥ – 2.
Minden – 2-nél kisebb vagy azzal egyenlő egész szám az egyenlőtlenség megoldása.
Az egyenlőtlenségek megoldásához nagyon hasznos, ha olyan transzformációkat használunk, amelyekkel más, könynyebben megoldható egyenlőtlenségeket kapunk, amelyekkel megtalálhatjuk az eredeti egyenlőtlenség megoldásait.
Hozzáadjuk vagy kivonjuk az egyenlőtlenség mindkét tagjából ugyanazt az egész számot.
Ha a és b egész számok, ahol a ≤ b, akkor
a + c ≤ b + c és a – c ≤ b – c, bármely c ∈ ℤ. Összeadunk tagonként két azonos típusú egyenlőtlenséget.
Megszorozzuk vagy elosztjuk az egyenlőtlenség mindkét tagját ugyanazzal a pozitív egész számmal.
Megszorozzuk vagy elosztjuk az egyenlőtlenség mindkét tagját ugyanazzal a negatív egész számmal, és megfordítjuk az egyenlőtlenségi relációt.
Ha a, b, c és d egész számok, ahol a ≤ b és c ≤ d, akkor a + c ≤ b + d.
Ha a és b egész számok, ahol a < b és c ∈ ℤ+, akkor a · c < b · c, és ha c | a és c | b, akkor a : c < b : c.
Ha a és b egész szám, ahol a < b, és c ∈ ℤ –, akkor a · c > b · c, c | a és c | b, akkor a : c > b : c.
Megjegyzés A fentihez hasonló tulajdonságok fordulnak elő >, ≤, ≥ relációk esetében is.
89 3. fejezet • Az egész számok halmaza
Alkalmazás
1. feladat. Az x negatív egész szám és a –5 szám szorzata legfeljebb 20. Határozd meg az x szám értékeit.
Megoldás.
A feladat visszavezethető –5 · x ≤ 20, egyenlőtlenség megoldására a ℤ_-ban.
Az egyenlőtlenség megoldásai olyan egész számok, amelyeket az origótól balra lévő tengelyen ábrázolunk –4-ig bezárólag.
–5 · x ≤ 20 | : (–5 ) és –5 < 0 x ≥ –4.
ℤ_-ben a megoldások halmaza M = {–4, –3, –2, –1}. x ≥ –4 x < 0
–5 –4 –3 –2 –1 01 2
Megjegyzés. Ha ℤ-ben kellene megoldani, akkor az egyenlőtlenségnek minden nem negatív egész szám is megoldása lenne.
2. feladat.
Határozd meg azokat az egész számokat, amelyekre 6 · x 14 > 4 · x 18 és amelyek modulusa kisebb, mint 4! Megoldás.
6 · x 14 > 4 · x 18 | +14
6 · x > 4 · x 4 | −(4 · x)
2 · x > 4 | : 2 x > 2
1. Az egyenlőtlenség mindkét tagjához 14-et adtunk.
2. Az egyenlőtlenség mindkét tagjából kivontuk a 4 · x értéket.
3. Mindkét tagot elosztottuk a 2 pozitív számmal.
Tudjuk, hogy a megoldások a –2-nél nagyobb egész számok.
De csak azok a –2-nél nagyobb számok a feladat megoldásai, amelyek modulusa kisebb, mint 4.
–3 –2 –1 01 23 4
| x | < 4 ⇔ –4 < x < 4 x > –2
Gyakorlatok és feladatok
1. Írd le
Azok a –2-nél nagyobb számok, amelyek 4 és 4 között
vannak a –1, 0, 1, 2 és 3, tehát
M = { 1, 0, 1, 2, 3}.
a) a 5-nél nagyobb összes negatív egész számot;
b) a legfeljebb 4-gyel egyenlő nem negatív egész számokat;
c) azokat az egész számokat, amelyeknek abszolút értéke kisebb, mint 3!
2. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
a) A x + 3 < –2 egyenlőtlenséget teljesítő egyik negatív egész szám:
A. –4; B. –6; C. –2; D. –5.
b) A 4 – x > 1 egyenlőtlenséget teljesítő egyik po -
zitív egész szám:
A. 5; B. 4; C. 2; D. 3.
c) Az a legnagyobb x egész szám, amelyre
3 · x + 2 ≤ 17 az:
A. –5; B. 5; C. 4; D. 18.
d) Az a legkisebb y egész szám, amelyre
2 · y ≥ –30 az:
A. –28; B. –15; C. –32; D. –16.
3. Határozd meg az összes olyan x egész számot, amelyre:
a) x ≥ –12 és x < –8; c) x ≥ –1 és x < 1;
b) x > –2 és x ≤ 1; d) x > –6 és x∈ ℤ –.
4. Oldd meg az egyenlőtlenségeket!
a) x – 7 < –4 és x ∈ ℕ;
b) x + 5 > 13 és x ∈ ℤ;
c) 4 · x ≥ –12 és x ∈ ℤ –;
d) 3 · x + 8 ≤ x – 4 és x ∈ ℤ;
e) | x | – 6 < –2 és x ∈ ℤ;
f) 19 – 2 · x + 8 > 3 · x + 2 és x ∈ ℤ.
5. a) Az a és b egész számokról tudjuk, hogy a + b < 0, a · b > 0 és | a | < | b |. Írd az a, b és 0 számokat növekvő sorrendbe!
b) Az c és d egész számokról tudjuk, hogy c + d > 0, c2 · d < 0. Írd a c, d és 0 számokat csökkenő sorrendbe!
90 Matematika • Tankönyv a VI. osztály számára
Miniteszt
1. Töltsd ki az üres részeket úgy, hogy igaz kijelentéseket kapj!
10 p a) A –3-nál nagyobb és legfeljebb 2-vel egyenlő egész számok halmaza {…}.
15 p b) Az x2 ≤ 0 egyenlőtlenség megoldáshalmaza ….
15 p c) Az a legkisebb x egész szám, amelyre x 7 ≤ 2 · x + 3 az … .
2. Oldd meg az egyenlőtlenségeket!
2 × 15 p a) 2 · x 3 < 7, x ∈ ℕ; b) 3 · x 7 < 2 · x 5, x∈ℤ
3. Három egymás utáni egész szám összege 71 és 67 között van.
10 p a) Jelöld x-szel a három szám közül a legkisebbet, és írd le egyenlőtlenségek formájában a feladat feltételeit!
10 p b) Határozd meg az x egész számot, tudva, hogy az a) alpontnál levő egyenlőtlenségek közös megoldása!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
3. l. Egyenletek/egyenlőtlenségek segítségével megoldható feladatok az egész számokkal összefüggésben
Oldjuk meg figyelmesen!
1. feladat. Az MNPQ és RNST téglalapok méreteit ugyanabban a mértékegységben (m.e.) fejeztük ki.
a) Fogalmazz meg egy olyan x ismeretlent tartalmazó egyenletet, amely visszavezethető az a x + b = 0, alakú egyenletre, ahol a, b ∈ ℤ . Használjuk a mellékelt ábrát.
b) Oldd meg az a) alpontban kapott egyenletet!
c) Határozd meg a TS, TR és MR szakasz hosszát! Q
Megoldás a) A RNST teglalapban SN = RT = x –10. Az MNPQ téglalapban NP = MQ = 30.
De, SN + SP = NP, vagyis (x –10) + 15 = 30.
b) Használva az összeadás asszociativitását, az egyenlet x –10 + 15 = 30 lesz, majd x + 5 = 30 ⇔ x = 25.
c) TS = x = 25 (m.e.); TR = x – 10 = 25 – 10 = 15 (m.e.); MR = MN – x = PQ – x = 40 – 25 = 15 (m.e.)
Fedezzük fel, értsük meg!
A gyakorlatban felmerülő kérdések közül sok matematikailag megoldható.
A feladathoz kapcsolódó matematikai modell algebrai fogalmakhoz és megoldási módszerekhez vezethet.
Ha a feladat átfogalmazható egy egyenletté vagy egész megoldással rendelkező egyenlőtlenséggé, a feladat megoldásához a mellékelt algoritmust kell követni.
1. lépés. Az ismeretlen megállapítása, a jelölések elkészítése, a megjelenő mennyiségek közötti összefüggések matematikai nyelven történő leírása.
2. lépés. Az egyenlet vagy egyenlőtlenség felírása. 3. lépés. Az egyenlet vagy egyenlőtlenség megoldása.
4. lépés. Az egyenlet vagy egyenlőtlenség megoldásainak értelmezése, figyelembe véve azt a területet, amelyben a feladat megoldását keressük.
5. lépés. A következtetés megfogalmazása.
Megjegyzés. A kapott megoldás(ok) ellenőrzése hasznos az esetleges hibák kijavítása érdekében.
91 3. fejezet • Az egész számok halmaza
40 P 15 S MRN 30 x –10 Tx
Alkalmazás
1. feladat. Máriusznak és Mihálynak együttesen 200 leje van. Ha Máriusz 14 lejt kér kölcsön Mihálytól, akkor Mihálynak háromszor kevesebb pénze lesz, mint Máriusznak. Határozd meg, hogy mennyi pénze volt mindkettőjüknek az elején! Megoldás
1. lépés. Megállapítjuk az ismeretlent. Jelöljük a-val Mihály eredeti pénzösszegét. a 200 – a a – 14 214 – a II I Mihály Máriusz
A megjelenő mennyiségek közötti összefüggések matematikai nyelven történő leírása.
Akkor Máriusz eredeti pénze 200 – a (lej). Miután Máriusz 14 lejt kér kölcsön Mihálytól Máriusznak (200 – a) + 14 (lej) pénze lesz, Mihálynak pedig a – 14 (lej) marad.
2. lépés. Felírjuk az egyenletet. Mivel Mihály pénzösszege háromszor kevesebb, mint a Máriusz pénze, akkor a 14 = [(200 – a) + 14] : 3.
a 14 = [(200 – a) + 14] : 3 | · 3
3. lépés. Megoldjuk az egyenletet.
4. lépés. Értelmezzük a megoldást és megfogalmazzuk az eredményt.
3a – 42 = 214 – a | + (a + 42)
4a = 256 | : 4 a = 64
Az egyenlet mindkét tagját megszorozzuk 3-mal.
Mindkét taghoz hozzáadjuk az a + 42 összeget.
Az egyenlet mindkét tagját elosztjuk 4-gyel.
Ebből arra következtetünk, hogy Mihály kezdetben 64 lejjel rendelkezett, Máriusz pedig 200 – 64 = 136 (lej).
A biztonság kedvéért ellenőrizzük az eredményt.
Ha ugyanis Máriusz kölcsönkér Mihálytól 14 lejt, akkor Mihály csak 50 lejjel rendelkezik, ami Máriusz 150 lejének egyharmada.
Felelet: Mihálynak 64 leje volt, Máriusznak pedig 136 leje.
2. feladat
Johanna már 50 lejt megtakarított, de 250 lej adóssága van. Ezt szeretné visszafizetni. Az 50 lejen kívül még három hónapon keresztül egyenlő összegeket takarít meg.
Határozd meg azt a legkisebb egész összeget, amelyet Johannának mindhárom hónapban meg kell takarítania!
Megoldás x-szel jelöljük Johanna havonta megtakarított pénzét. Akkor három hónap múlva 3x lejt fog megtakarítani. Mivel Johanna ezt az összeget megtakarítva és az 50 lejből viszszafizeti a tartozását, ez azt jelenti, hogy 3x + 50 ≥ 250, azaz 3x ≥ 200. Mivel x egész szám, ebből következik, hogy 3x a 3 többszöröse és nagyobb vagy egyenlő 200-nál. Akkor 3x ∈ {201, 204, 207, …}. A legkisebb x összeg 3x = 201 esetén valósul meg, azaz x = 201: 3, tehát x = 67.
Felelet: Johannának havonta legalább 67 lejt kell megtakarítania.
Gyakorlatok és feladatok
1. Határozd meg azt az egész számot, amelyről tudod, hogy megszorozva a –3-mal, ugyanazt az eredményt kapod, mintha összeadnád a 20-szal!
2. Keress egy egész számot, tudva, hogy ha elosztod 4-gyel, akkor 155-tel kisebb számot kapsz, mint az ellentettje!
3. Egy egész szám és az ellentettjének 5-tel való szorzata közötti különbség: –96. Határozd meg a számot!
4. Öt egymást követő egész szám összege –45. Határozd meg a számok közül a legkisebbet és a legnagyobbat!
5. Három különböző negatív egész számot írunk egy papírlapra. Ha mindegyik számból kivonjuk a 13-at, és az eredményeket összeadjuk, akkor –45-öt kapunk. Határozd meg ezt a három számot!
6. Tíz egymást követő egész szám összege –25. Számítsd ki e számok szorzatát!
92 Matematika • Tankönyv a VI. osztály számára
7. Határozd meg azokat a negatív egész számokat, amelyekhez ha –5-öt hozzáadsz, akkor legalább ( 2)3 lesz az eredmény!
8. Határozz meg egy egész számot, tudva, hogy ha csökkentjük 10-zel, akkor egy 3-nál kisebb pozitív egész számot kapunk!
9. Daninak 60 lejjel kevesebb pénze van, mint Lucának. Ha kapna tőle 45 lejt, akkor 7 lejjel több lenne, mint Luca maradék pénzének kétszerese. Számítsd ki, hogy mennyi pénzük van mindkettőjüknek!
ISMERETFELMÉRŐ
10. Határozd meg az összes olyan természetes számot, amelyet ha megszorzunk 2-vel, és az eredményhez hozzáadjuk –24-et, akkor negatív egész számot kapunk!
11. A 2 · x − 1, 3 · x + 2, 4 · x − 3, 5 · x + 5 egész számok szorzata 0.
a) Határozd meg a négy számot!
b) Számold ki a kapott számok összegét!
12. A négyzet oldalhossza centiméterben kifejezett természetes szám, területe pedig legfeljebb 10 cm2. Számítsd ki a négyzet oldalhosszát és kerületét, tudva, hogy ez a lehető legnagyobb!
I. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
5 p 1. Ha A 20 5 2 5 2 5 ; ;;; , akkor az A ⋂ ℤ halmaz:
A. {−2, 0, 5}; B. 5 2 5 1 ; ; C. 20 5 1 5 ;; ; ; D. {−2, 5}.
5 p 2. A | 7 + 1 | + | 8 | szám egyenlő:
A. 0; B. 16; C. 16; D. 1.
5 p 3. Ha |x| = 4 és x < 0, akkor x + 44 egyenlő:
A. 48; B. 48; C. 40; D. 40.
5 p 4. Az a = 32 + 23, b = 7 (+8), c = 3 · (+4), d = 56 : ( 4), számok közül a legkisebb:
A. a; B. b; C. c; D. d.
5 p 5. Ha ( 3)n = 27, akkor ( 2)n egyenlő:
A. 2; B. 4; C. 8; D. 16.
5 p 6. A ( 2)1 ·( 1) + ( 2)2·( 2) + ( 2)3 · ( 3) számítás eredménye:
A. 18; B. 16; C. 18; D. 8. II. Írd le a teljes megoldást!
10 p
10 p
10 p
10 p
10 p 10 p
1. Adott az a = 2 ( 4) + 6, b = | 28 32 | |+42 |, c = [( 2)3 · ( 2)4] : [( 2)7 : ( 2)2] szám.
a) Számítsd ki az a, b, c számokat!
b) Vizsgáld meg, hogy a 9 · (a – c) + b szám pozitív, negatív, vagy nulla.
2. a) Ha x · y + x · z = 5, akkor számítsd ki 2 · x · (y + z).
b) Ha x · (y + z) = 63 és x = –7, akkor számítsd ki y + z.
3. Három különböző negatív egész számot írunk egy papírlapra. Ha mindegyik számból kivonjuk a 17-et, és az eredményt összeadjuk, akkor –57-et kapunk.
a) Számítsd ki a három szám összegét!
b) Határozd meg a három számot!
Megjegyzés: Munkaidő: 50 perc
Hivatalból: 10 pont
93 3. fejezet • Az egész számok halmaza
Sajátos kompetenciák: 1.4; 2.4; 3.4; 4.4; 5.4; 6.4
4. A RACIONÁLIS SZÁMOK HALMAZA
4.1. Racionális szám. A racionális számok halmaza
1. l. Racionális szám
Emlékeztető
Az összes a b -vel egyenértékű közönséges tört az a b pozitív racionális szám, ahol a és b nullától különböző természetes szám.
Egy racionális számot bármelyik ábrázolási módjával meg lehet adni.
Az alábbi törtek ugyanannak a pozitív racionális számnak a képviselői: 1 3 2 6 3 9 4 12 5 15 100 300 ,,, ,, ..., , ...
Bármely pozitív racionális szám egyértelműen felírható közönséges irreducibilis a b törtként, ahol a és b természetes szám, a ≠ 0 és b ≠ 0.
A fenti pozitív racionális szám az 1 3 irreducibilis formájában írható fel egyértelműen.
Megjegyzés. 1. A nullától különböző természetes számok pozitív racionális számok.
2. A 0 b törtek a 0 racionális számot jelentik, ahol b ≠ 0.
Bármely pozitív racionális szám egyértelműen felírható tizedes törtként.
Egy véges tizedes törtet közönséges törtté úgy alakítunk át, hogy a számlálóba a tizedesvessző eltávolításával kapott természetes számot írjuk, majd a nevezőbe 10k-t írunk, ahol k a tizedesjegyek száma.
Egy tiszta szakaszos tizedes törtet úgy alakítunk át közönséges törtté, hogy a számlálóba a tizedesvessző eltávolítása után kapott természetes szám és a tizedesvessző előtt szereplő természetes szám különbségét írjuk, majd a nevezőbe k darab 9-es számjegyből álló számot írunk, ahol k a szakaszban levő tizedes jegyek száma.
aapp aappaa nk nkn k 11 11 1
99 9 .... , .... .... .... .... .... számjegy 131 131 1 99 130 99 , ;
0,(932) = 931 0 999 931 999 .
Egy vegyes szakaszos tizedes törtet úgy alakítunk át közönséges törtté, hogy a számlálóba a tizedesvessző eltávolítása után kapott természetes szám és a nem szakaszban szereplő számjegyekből álló természetes szám különbségét írjuk, majd a nevezőbe k darab 9-es és m darab 0 számjegyből álló számot írunk, ahol k a szakaszban levő tizedes jegyek száma, m pedig a nem szakaszban levő tizedes számjegyek száma.
aabbppaabbppa nmk nmk 11 1 11 11 , .... .... abbnm 1 99 9000 k számjegy
94 Matematika • Tankönyv a VI. osztály számára
nk nk k 11 11 10 .... , .... = 02 2 10 , = ; 0
625 10 3 , =
aabbaabb
625
3107 3107 310 900 2797 900 , 0,328(32)
328 99000
32504 99000
m számjegy
= 32832
=
.
Oldjuk meg figyelmesen!
Nagyszüleim kertjében nyáron gyakran élvezzük a sok évvel ezelőtt ültetett diófa árnyékát.
Ez egy fenséges fa. Megkérdezem nagyapát, milyen mélyre nyúlnak a gyökerei a földbe, hogy ekkora koronát bírjon el. Nagyapa válaszol: Lássuk, mit tudunk a diófáról.
Tudod-e?
A diófa, a termése és fája miatt egyaránt nagyra becsült gyümölcsfa. Az ember által ismert és termesztett egyik legrégebbi gyümölcsfa (a diófa fosszilis leletei 9000 évre nyúlnak vissza).
A diófa magassága elérheti a 20-25 métert, koronaátmérője pedig a 10 métert.
A gyökerek általában 0,2-0,8 m mélyre nyúlnak. Csak a nagyon homokos talajokon érik el az 1,4 métert.
Vízszintes síkban a kifejlett diófa gyökere 4-7-szeresen meghaladja a korona sugarát. Az aktív gyökerek maximális sűrűsége azonban 3-4 m-re van a diófa törzsétől.

A diófa magányos. A fenti kép nem jellemző rá. Tájékozódj és indokold meg ezt az állítást!
Most pedig oldjunk meg egy gyönyörű feladatot. Képzeljük el a függőleges tengelyt, amelyen a fa nő, pozitív irányban felfelé. Tekintsük úgy, hogy a törzs egy O pontban, e tengely origójában lép be a földbe.
Ha tudjuk, hogy ez a diófa körülbelül 5,3 m magas, és hogy a gyökerei körülbelül 0,6 m mélyre nyúlnak le, ábrázoljuk a csúcsnak (a korona legmagasabb pontjának) és a gyökér legmélyebb pontjának megfelelő pontot a tengelyen, 1 m-es egységgel. Határozd meg, hogy melyik pont felel meg pozitív számnak, és melyik negatív számnak. Megoldás.
A csúcs a tengely pozitív irányába mutat, tehát a +5,3 pozitív racionális számnak felel meg. A gyökér végpontja az ellenkező irányba van tájolva, tehát az origótól számított 0,6 egységnyi negatív számnak felel meg. Ezt a – 0,6-os számmal jegyezzük.
Fedezzük fel, értsük meg!
Minden (a, b) nullától különböző természetes számpár meghatároz egy a b pozitív racionális számot! A pozitív racionális számok halmazát ℚ + -val jelöljük. 7
Tekintsük a számtengelyt, amelynek origója O(0) és mértékegysége u, amelyen a pozitív irányt balról jobbra állítottuk be.
Mindegyik a b pozitív racionális számot egyetlen M a b ponttal
ábrázoljuk a számtengelyen, az origótól a b távolságra, jobbra. a
95 4. fejezet • A racionális számok halmaza
+5,3 +5 +4 +3 +2 +1 1m 0 O Gy –0,6 –1 Cs
3 2 5 1 33 9 3 7 1 4 4 ;; ;; ;
pozitív racionális számok.
b a b u M’M O 0
Az M a b pontnak az O szerinti M’ szimmetrikusa az origótól
ugyanakkora távolságra, de tőle balra helyezkedik el.
Az M’-nek megfelelő számot a b -vel jelöljük és az a b szám
ellentettjének nevezzük. A a b negatív racionális szám.
Példák: 1 2 és
Ha a negatív egész szám, b pedig nullától különböző természetes szám, akkor az (a, b) számpár meghatározza az a b negatív racionális számot.
A negatív racionális számok halmazát ℚ –-val jelöljük.
Az egész számok osztásának előjelszabályát használva azt kapjuk, hogy:
Bármely egész számpár meghatároz egy pozitív racionális számot, ha mindkettő pozitív vagy mindkettő negatív.
Minden olyan egész számpár, amelyből az egyik pozitív, a másik negatív, negatív racionális számot határoz meg.
Negatív racionális számok:
Bármely (a, b) egész számpár, ahol b ≠ 0 meghatározza az a b racionális számot.
Megjegyzés. A (0, b) számpár, ahol b ∈ ℤ* , a 0 b = 0 racionális számot határozza meg.
Az összes pozitív racionális szám és az összes negatív racionális szám halmazát, amelyhez hozzáadjuk a 0 racionális számot is, a racionális számok halmazának nevezzük, és ℚ -val jelöljük.
Megjegyzés. 1. A 0 nem is pozitív, nem is negatív szám.
2. A nullától különböző racionális számok halmzát ℚ*-gal jelöljük, azaz ℚ* = ℚ+⋃ ℚ–vagy ℚ* = ℚ \ {0}.
Alkalmazás
1. feladat Írj példát az alábbi esetek mindegyikére:
1. Egész szám, amely természetes szám.
1’ . Egész szám, amely nem természetes szám.
2. Racionális szám, amely egész szám.
2’ . Racionális szám, amely nem egész szám.
3. Racionális szám, amely természetes szám.
3’ . Racionális szám, amely nem természetes szám.
Megoldás
1. 7 ∈ ℤ és 7 ∈ ℕ .
1’ . –3 ∈ ℤ és – 3 ∉ ℕ .
2. –7 ∈ ℚ és –7 ∈ ℤ .
2’ . 7 2 ∈ ℚ és 7 2 ∉ ℤ .
3. 2 ∈ ℚ és 2 ∈ ℕ .
3′. 0,5 ∈ ℚ és 0,5 ∉ ℕ .
96 Matematika • Tankönyv a VI. osztály számára
1 3 1 3 ; 2 5 2 5 ; 7 1 7 1
1 3 1 3 1 3 ; 2 5 2 5 2 5
0 3 0 3 0 13 0 1 ;;
;
ℚ = ℚ + ⋃ ℚ –⋃ {0}.
1 2
1 2 = 0,5,
1 2 = –0,5.
1 2
1 2
ellentett számok. Mivel
akkor
Tizedes tört alakjában fejeztük ki az
és
ellentett racionális számokat
7 3 2 5 1 33 9 3 7 1 4 4 ;; ;; ; .
Jegyezd meg!
ℕ ⊂ ℤ⊂ ℚ , vagyis:
1. Bármely természetes szám egész szám: ℕ ⊂ ℤ . 1’. Létezik olyan egész szám, amely nem természetes: ℤ ⊄ ℕ.
2. Bármely egész szám racionális szám: ℤ ⊂ ℚ 2’. Létezik olyan racionális szám, amely nem egész: ℚ ⊄ ℤ
3. Bármely természetes szám racionális szám: ℕ⊂ ℚ. 3’. Létezik olyan racionális szám, amely nem természetes: ℚ ⊄ ℕ.
A gyakorlatban a racionális számokat a kontextustól függően irreducibilis közönséges törtként, reducibilis közönséges törtként vagy tizedes törtként fejezik ki. Az egyik formából a másikba való átalakítás módszerei hasonlóak a fent említett pozitív törtszámok esetében alkalmazott módszerekhez.
2. feladat
a) Fejezd ki tizedes tört alakban az alábbi racionális számokat:
1 2 1 2 7 3 7 3 9 22 9 22 ;; ;; ; .
b) Fejezd ki irreducibilis közönséges tört alakban az alábbi racionális számokat:
0,2; –0,2; 2,(2); –2,(2); 0,1(5); –0,1(5).
Gyakorlatok és feladatok
Megoldás
a) Elvégezve az osztásokat, azt kapjuk, hogy:
1
1. Töltsd ki az üres mezőket az I betűvel, ha az állítás igaz, és a H betűvel, ha hamis. Kövesd a mintát!
4. Írj fel három megfelelő közönséges törtet az alábbi racionális számok esetén:
a) 5 3 ; b) 1 2 ; c) 1; d) 2,3.
∈ ℕ I
∈ ℤ I
a ∈ ℤ \ ℕ H
a ∈ ℚ I
a ∈ ℚ H
a ∈ ℚ \ ℤ H
2. Sorold fel az alábbi halmazok öt-öt elemét!
a) ℚ ;
b) ℚ + ; c) ℚ \ ℕ ; d) ℚ \ ℤ ; e) ℤ \ ℕ ; f) ℚ _.
3. Adott az A = { 3, 2, 0, 2, 6} és B = { 2, 1, 1, 3} halmaz.
a) Írd le az a b racionális számokat tartalmazó C halmazt, ahol a ∈ A és b ∈ B
b) Határozd meg a C ∩ ℚ _ és C ∩ ℚ * halmazt!
5. Adott az r = 10 n szám, ahol, n ∈ ℤ* .
Határozd meg az n értéket a következő esetekben:
a) r ∈ ℕ ; b) r ∈ ℤ .
6. Töltsd ki az üres mezőket az I betűvel, ha az állítás igaz, és a H betűvel, ha hamis!
Kijelentés I/H
Kijelentés I/H
a) 3 5 = 3 5 ; d) 0 2 = 0 2 ;
b) 7 4 = 7 4 ; e) 5 9 = 10 16 ;
c) 8 3 = 8 3 ; f) 6 2 = 3.
97 4. fejezet • A racionális számok halmaza
2 05 = ,
1 2 05 ,
7 3 23 7 3 23
)
9 22 04 09 9 22 04 09 ,( ); ,( ) . b) 0,2 = 2 10 1 5 2 ( = ; –0,2 = 1 5 ; 2,(2) = 22 2 9 20 9 ; –2,(2) = 20 9 ; 0,1(5) = 15 1 90 14 90 7 45 2 ( ; –0,1(5) = 7 45 .
;
;
,( ); ,(
;
a kijelentés 2 3 5 2 4 3 0 + + 15 3 12 6
a
a
7. Írd a következő racionális számokat tizedes tört alakba:
; b)
; c)
8 × 5 p
Miniteszt
;
25 p
25 p
8. Írd a következő racionális számokat irreducibilis közönséges tört alakba:
a) 0,3;
b) 2,5; c) 1,25; d) 3,625; e) 0,(6); f) 1,(12);
g) 3,1(2); h) 4,(009); i) –2,(1).
9. Bizonyítsd be, hogy nn 2 2 és 26 4 2 nn természetes számok, bármely n természetes szám esetén!
1. Másold le a füzetedbe, és töltsd ki az üres mezőket az I betűvel, ha a kijelentés igaz, és a H betűvel, ha hamis!
Kijelentés I/H
Kijelentés I/H
a) 3 5 ∈ ℚ; e) 4,2∉ℚ;
b) 4 ∉ ℚ; f) ℕ ⊂ ℤ ⊂ ℚ;
c) 9 4 ∈ ℚ \ ℤ; g) ℕ ⊄ ℚ
d) 0,(6) ∈ ℚ ; h) A ℚ végtelen halmaz.
2. Határozd meg az n szám azon értékeit, amelyekre:
a) n∈ℕ és 7 n ∈ ℤ ;
b) n ∈ ℤ , 5 < n < 0 és 8 1 n ∈ ℚ \ ℤ .
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
2. l. A racionális számok ábrázolása a számtengelyen.
A racionális szám modulusa
Emlékeztető
A racionális számok ℚ halmaza tartalmazza az összes pozitív racionális számot, amelyek a ℚ+ halmazt alkotják, az összes negatív racionális számot, amelyek a ℚ– halmazt alkotják, és a 0 számot.
Az ℚ–és ℚ+ halmazok diszjunktak (nincsenek közös elemeik). ℚ = ℚ –⋃ {0} ⋃ ℚ + . ℚ –⋂ ℚ + = ∅. 0 ∈ℚ , de 0 ∉ ℚ –és 0 ∉ ℚ + . Bármely x pozitív racionális számot a számtengelyen az origótól jobbra ábrázoljuk, és azt írjuk, hogy x > 0. A 0 racionális számot a számtengelyen az origónál ábrázoljuk.
98 Matematika • Tankönyv a VI. osztály számára
9 4
7 8
3 5
e) 2 3
f) 17 6
g) 43 100
h) 333 10 3
i) 33 10
a) 5 2
; d)
;
;
;
;
Fedezzük fel, értsük meg!
A negatív racionális számok értelmezéséből következik, hogy minden negatív x racionális számot a számtengelyen az origótól balra, az origótól ugyanolyan távolságra ábrázolunk, mint az ellentettjét. Azt írjuk, hogy x < 0. Minden x racionális számnak megfelel a számtengelyen egyetlen egy M pont, amelyet az x szám számtengelyen ábrázolt képének nevezünk.
M1 a 3 4 racionális szám képe a számtengelyen;
Ha M az x számnak a számtengelyen ábrázolt képe, akkor az x neve az M pont abszcisszája vagy koordinátája
Így írjuk: M(x). Olvasd: „M abszcisszája x” vagy „M koordinátája x”.
A mellékelt ábrán levő számtengelyen több racionális szám látható.
M2 a 3 2 racionális szám képe a számtengelyen.
Az ábrázolt pontok a tengelyen kettesével helyezkednek el, annak origójára nézve szimmetrikusan, tehát koordinátáik ellentétes racionális számok.
Ha x nullától különböző racionális szám, akkor az x és –x ellentett racionális számok.
Az x szám a –x szám ellentettje, valamint –x az x szám ellentettje.
Megjegyzések. 1. A 0 egész szám ellentettje szintén 0.
–0,5 a 0,5 ellentettje és 0,5 a –0,5 ellentettje; –2 a 2 ellentettje és 2 a –2 ellentettje;
3
ellentettje;
2. Bármely két nullától különböző ellentett racionális szám közül az egyik pozitív, a másik negatív.
Az egész számokhoz hasonlóan, bármi is legyen az x racionális szám, annak a –x ellentettje a számtengelyen az origótól ugyanolyan távolságra helyezkedik el, mint az x racionális szám.
Az x racionális számnak a modulusa vagy abszolút értéke az x számnak a számtengelyen való ábrázolási pontja, és a tengely origója közötti távolsággal egyenlő
Az x szám modulusát | x |-szel jelöljük.
Megjegyzés. Az x és –x racionális számok modulusa egyenlő, mivel a tengelyen az origótól azonos távolságra vannak ábrázolva.
Ábrázoljuk a számtengelyen a következő pontokat: O(0), A(1), A′(–1), B(x), B′(–x), ahol x pozitív racionális szám és C(y), C′(–y), ahol y negatív racionális szám.
Mivel OA′ = OA = 1, akkor| –1 | = | +1 | = OA = 1.
Mivel OB′ = OB = x, akkor| –x | = | +x | = OB = x.
Mivel OC = OC′ = –y, akkor| –y | = | +y | = OC′ = –y.
| 0 | = 0 (az O távolsága önmagától 0).
99 4. fejezet • A racionális számok halmaza
–1 01 2 M1 3 4 M2 3 2 O
4 az M1 pont koordinátája vagy abszcisszája. 3 2 az M2 pont koordinátája vagy abszcisszája.
3
7 3 DB’C’A’OACBD’ –2 –1 –0,5 0 0,5 1 2 3 2 3 2 7 3 Az origóhoz képest szimmetrikus pontok: A(0,5)
A′(–0,5); B(2) és B′(–2); CC 3 2 3 2 ,’ ; DD 7 3 7 3 și ’ Ellentett racionális számok: 0,5 és –0,5; 2 és –2; 3 2 és 3 2 ; 7 3 és 7 3 .
és
2
2
2
3 2
a 3
ellentettje és 3
a
O
Jegyezd meg!
1. | x | > 0, bármely x ∈ ℚ * és | x | = 0, akkor és csakis akkor, ha x = 0.
2. | x | = x, akkor és csakis akkor, ha x ≥ 0 és | x | = –x, akkor és csakis akkor, ha x ≤ 0.
3. | –x| = | x |, bármely x ∈ℚ.
Alkalmazás
Vannak olyan helyzetek, amikor nagyon nehéz, sőt lehetetlen megtalálni a számtengelyen a racionális számnak megfelelő pontot. Ilyenkor megfelelőbb módszereket alkalmazunk a keresett pont becslésére.
1. Ha lehetséges, és ha a feladat kontextusa megengedi, a mértékegységet előnyösen választjuk meg, mivel a szám irreducibilis közönséges törtként van felírva.
1. példa: Mértékegységnek azt a szakaszt választottuk, amelynek hossza a négyzet oldalának háromszorosa.
2. példa: Mértékegységnek azt a szakaszt választottuk, amelynek hossza a négyzet oldalának ötszöröse.
2. A racionális számot tizedes törtként írjuk fel, a racionális számot egész számokra vagy tizedekre közelítjük, és a közelítések segítségével megbecsüljük a pont helyzetét a tengelyen.
1. példa: A –0,8 tizedes törtnek a tengelyen való ábrázolásakor figyelembe vesszük, hogy –1 és 0 között van, közelebb van –1-hez, mint 0-hoz. Tehát –1 és –0,5 között van.
2. példa: A 0,67-es tizedes törtnek a tengelyen való ábrázolásakor figyelembe vesszük, hogy 0,6 és 0,7 között van, közelebb van a 0,7-hez. Választunk egy elég nagy mértékegységet, az egységet tizedekre osztjuk, majd elvégezzük az ábrázolást.
1. Ábrázold a számtengelyen azokat a pontokat, amelyek koordinátái:
a) 4,2; 3; 0,6; 5;
b) 1,5; 1; 2,5; 1,7; 2;
c) 1 2 ; 1; 2,4; 5; 3,5; 7 10 ; 20 5 .
2. A mellékelt ábrán határozd meg a számtengelyen ábrázolt pontok koordinátáit! –3
3. Ábrázold az O origójú és 1 cm mértékegységű számtengelyen az A(1,6), B(4,4), C(–3,2) pontokat, valamint az OA szakasz M felezőpontját, illetve az AB szakasz N felezőpontját! Határozd meg az M és N pontok koordinátáit!
4. Írd le a 3 4 ; 3 2 ; 1,3; 2,4; 7; + 4,5; 5 1 3 .
5. Írd le a 3 4 ; + 9 5 ; 1,25; 2 7 ; 4; 32; 2,(5) racionális számok abszolút értékeit!.
100 Matematika • Tankönyv a VI. osztály számára
–2 –1 01 2 3 ABCODE
1 3 2 3 –1 +1 0 O BA
4 5 1 5 3 5 CBA –1 0 O +1
–0,8 0+1 –1 –0,5 O 0,67 0,6 0,7 0 O 1
Gyakorlatok és feladatok
6. Másold át a táblázatot a füzetedbe, és írd a megfelelő racionális számokat az üres mezőkbe:
a 0,4 2,1
a 1 3 3,2
| a | | a | = 5 és a∈ℚ –0
Miniteszt
7. Másold a füzetedbe, és töltsd ki az üres részeket, hogy igaz legyen az állítás!
a) A 0,123 szám ellentettje ….
b) A … szám ellentettje 4,5.
c) A 5 6 szám abszolút értéke ….
d) A … és … racionális számok modulusa 7.
e) Ha a ∈ ℤ* és 8 a természetes szám, akkor a ∈ {…}.
30 p 1. Ábrázold a számtengelyen: 4; 9 2 ; 0; 1,5; 35 7 ; 3,5; 25 10 .
2. Másold le a füzetedbe, és töltsd ki az üres mezőket az I betűvel, ha a kijelentés igaz, és a H betűvel, ha hamis!
Kijelentés I/H
10 p a) A 3 5 szám ellentettje a 3 5 .
10 p b) A 4,2 szám modulusa 2,4.
10 p c) Az egyetlen olyan racionális szám, amely egyenlő az ellentettjével az a 0.
10 p d) Az r racionális szám abszolút értéke a –r racionális szám.
10 p e) | 6,3 | = 6,3.
10 p f)
12 5 12 5 .
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
3. l. Racionális számok összehasonlítása és rendezése
Emlékeztető
Minden racionális szám pozitív, negatív vagy nulla. Bármely r ∈ℚ , esetén csak az egyik reláció igaz az r > 0, r < 0, r = 0 közül.
Fedezzük fel, értsük meg!
A racionális számoknak a számtengelyen való ábrázolása, a racionális számok összehasonlítása és a racionális számok rendezése szorosan összefügg egymással. A számtengelyen való ábrázolás gyakran hasznos a törtek összehasonlításakor és növekvő vagy csökkenő sorrendjük meghatározásakor. Másrészt két vagy több racionális számot a számtengelyen balról jobbra növekvő sorrendben ábrázolunk. Így a pontok elhelyezkedése és sorrendjük a tengelyen támpontokat ad az ábrázolt számokról és a köztük lévő kapcsolatokról.
Bármely két racionális x és y szám esetén az x < y, x = y, x > y. összefüggések közül csak egyik igaz. Az x és y racionális számok összehasonlítása azt jelenti, hogy megállapítjuk, hogy a fenti három összefüggés közül melyik igaz.
101 4. fejezet • A racionális számok halmaza
Ha x ∈ ℚ és y ∈ ℚ , és ha a számtengelyen az x szám képe az A pont, az y szám képe pedig a B pont, akkor:
x < y akkor és csakis akkor, ha az A(x) pont a B(y) ponttól balra helyezkedik el.
x > y akkor és csakis akkor, ha az A(x) pont a B(y) ponttól jobbra helyezkedik el.
x = y akkor és csakis akkor, ha az A(x) és B(y) egybeesők.
A következő esetek lehetségesek:
A tengelyen való ábrázolás Leírás
0 x OA
0 x AO
0 xy OA B
xy ABO 0
x 0 y AOB
O(0) az A(x)-től balra található, tehát 0 kisebb, mint x.
Így írjuk: 0 < x vagy x > 0.
A(x) az O(0)-tól balra található, tehát x kisebb, mint 0.
Így írjuk: x < 0 vagy 0 > x
x > 0, y > 0.
OA < OB, tehát | x | < | y |.
A(x) a B(y)-tól balra található, tehát x < y.
x < 0, y < 0.
OA > OB, tehát | x | > | y |.
A(x) a B(y)-tól balra található, tehát x < y
x < 0, y > 0.
A(x) aB(y)-tól balra található, tehát x < y.
Alkalmazás
Következtetés
x ∈ ℚ+ ⇔ x ∈ ℚ és x > 0.
1; 2,3; 3,(1); 11,25 ∈ ℚ+
1 > 0; 2,3 > 0; 3,(1) > 0; 11,25 > 0.
x ∈ ℚ_ ⇔ x ∈ ℚ és x < 0.
–1; –2,3; –3,(1); –11,25 ∈ ℚ_
– 1 < 0; –2,3 < 0; –3,(1) < 0; –11,25 < 0.
Ha x ∈ ℚ+ és y ∈ ℚ+, akkor:
x < y akkor és csakis akkor, ha | x | < | y |.
3,75 ∈ ℚ+ és 4,95 ∈ ℚ+
| 3,75 | < | 4,95 | akkor3,75 < 4,95.
Ha x ∈ ℚ_ és y ∈ ℚ_, akkor: x < y akkor és csakis akkor, ha | x | > | y |.
– 3,75 ∈ ℚ_ és – 4,95 ∈ ℚ_
| – 4,95 | > | – 3,75 | akkor – 4,95 < – 3,75.
Ha x ∈ ℚ és y ∈ ℚ+, akkor x < y.
Bármely negatív szám kisebb, mint bármely pozitív szám.
–3,72∈ℚ_, 4,83∈ℚ+, akkor–3,72< 4,83; –4,83∈ℚ_, 3,72∈ℚ+, akkor–4,83< 3,73.
Az egész számok összehasonlítására és rendezésére gyakran használjuk a ≤ vagy ≥, relációk egyikét, valamint a < és >, relációkat, amelyek megőrzik az egész számoktól ismert tulajdonságokat.
Két vagy több racionális számot növekvő sorrendbe rendezni azt jelenti, hogy a sorrendjüket úgy állítjuk be, hogy mindegyik kisebb vagy egyenlő legyen, mint az utána következő.
Két vagy több racionális számot csökkenő sorrendbe rendezni azt jelenti, hogy a sorrendjüket úgy állítjuk be, hogy mindegyik nagyobb vagy egyenlő legyen az utána következőnél.
A –32,5; 0; 20,3; –21,5 racionális számok növekvő sorrendje:
–32,5; –21, 5; 0; 20,3 mert –32,5 ≤ –21,5 ≤ 0 ≤ 20,3.
A –32, 5; 0; 20,3; –21, 5 racionális számok csökkenő sorrendje:
20,3; 0; –21, 5; –32,5 mert 20,3 ≥ 0 ≥ –21,5 ≥ –32,5.
102 Matematika • Tankönyv a VI. osztály számára
Jegyezd meg!
Minden pozitív racionális szám nagyobb, mint bármely negatív racionális szám, és nagyobb, mint 0.
Bármely negatív racionális szám kisebb, mint bármely pozitív racionális szám, és kisebb, mint 0.
Két pozitív racionális szám közül a nagyobb modulusú a nagyobb.
Két negatív racionális szám közül a kisebb modulusú a nagyobb.
1. Írj:
Gyakorlatok és feladatok
a) 2-nél kisebb három racionális számot;
b) 3,5-nél nagyobb racionális számot;
c) 2 és 3,5 közötti három racionális számot.
2. Másold át a füzetedbe, és töltsd ki a pontozott helyeket a < , > , = szimbólumok valamelyikével úgy, hogy igaz állításokat kapj!
a) 1 4 … 1 3 ;
b) 1 5 … 1 6 ;
3. Írd növekvő sorrendbe a
c) 2,4 … 8 3 ; d) 1 3 … 1 2 .
2,3; 0,9; 2 3 8 ; 2; 0; 3 számokat!
4. Írd csökkenő sorrendbe a
3,2; 3,1; 3 3 10 ; 3; 0; 3,(4) számokat!
5. Határozd meg a 2,34 és 10 3 közötti összes egész számot!
6. Határozd meg
a) 77-nél kisebb legnagyobb egész számot;
b) 4,56-nál nagyobb legkisebb egész számot!
7. Határozd meg az n egész számot az alábbi esetekben:
a) n < 7 2 < n + 1;
b) n < 13 5 < n + 1;
c) n 2 < ( 2)22 : 221 < n.
8. Írd le
a) a 3-nál kisebb abszolút értékű egész számok halmazát;
b) azt a három racionális számot, amelyek abszolút értéke 1,5 és 4 között van!
Miniteszt
30 p 1. Adott az x = 22 22 2 01 23 2 +++ szám. Igazold, hogy 4 < x < 3.
2. A b és c egész számok tulajdonsága, hogy | b | ≤ 2 és | c | = 3.
20 p a) Határozd meg azokat a b és c számokat, amelyekre igazak az állításban szereplő egyenlőtlenségek!
20 p b) Írd le az összes b c alakú racionális számot használva az a) alpontban meghatározott értékeket!
20 p c) Rendezd növekvő sorrendbe a b) alpontban írt racionális számokat!
Megjegyzés:
Munkaidő: 20 perc
Hivatalból: 10 pont
103 4. fejezet • A racionális számok halmaza
1. l. Racionális számok összeadása. Racionális számok kivonása
A racionális számokkal végzett műveletek vagy úgy végezhetők el, hogy a számokat közönséges törtként írjuk fel, vagy úgy, hogy véges tizedes törtként írjuk fel.
Szakaszos tizedes törtekkel nem végzünk számításokat. Ezeket közönséges törtekként kell kifejezni.
Emlékeztető
Ahhoz, hogy két pozitív racionális számot közönséges törtként kifejezve adjunk össze vagy vonjunk ki, ugyanazzal a nevezővel kell rendelkezniük.
Ha a törteknek nem ugyanaz a nevezőjük, akkor határozzuk meg a nevezők legkisebb közös többszörösét, és ennek megfelelően bővítsük a törteket, hogy azonos nevezőre hozzuk ezeket.
Két pozitív racionális szám véges tizedes törtekkel kifejezett összeadásához vagy kivonásához helyezzük a törteket egymás alá, a tizedesvesszőt a tizedesvessző alá.
Az azonos rendű számjegyek egymás alatt lesznek. Ha egy tört nem tartalmaz egy bizonyos rendű számjegyet, akkor ez a számjegy 0. Összeadunk vagy kivonunk, mint a természetes számok esetében.
Az eredményben lévő vesszőt a két tört vesszői alá írjuk.
Fedezzük fel, értsük meg!
A racionális számok összeadása a pozitív racionális számok összeadásán és az egész számok összeadásán alapul. Két tetszőleges x és y racionális szám esetén értelmezzük az x + y-nal jelölt egyetlen racionális számot, amelyet az x és y számok összegének nevezünk. Azt a műveletet, amellyel minden x és y számpárt az összegükkel társítunk, összeadási műveletnek nevezzük, az x és y számokat pedig az összeadás tagjainak.
Két racionális szám összegének kiszámításához hasonlóan járunk el, mint az egész számokkal végzett műveletnél, a törtekkel végzett műveletek módszereit követve. Eset
104 Matematika • Tankönyv a VI. osztály számára
4.2. Műveletek racionális számokkal
Példák 1. 3 5 7 5 37 5 ; 2. 3 5 2 5 32 5 .
Példák 1. 35 3 5 7 3 9 15 35 15 44 15 )) . 2. 32 9 4 5 6 27 12 10 12 17 12 )) .
példa 123,75 + 99,1 = 222,85; 123,75 + 99,10 222,85 2. példa 123,75 – 99,1 = 24,65. 123,75 –99,10 24,65
1.
x ≥ 0 és y ≥ 0 x ≤ 0 és y ≤ 0 x > 0, y < 0 és | x | >| y | x > 0 és y < 0 és | x | < | y | Számítási mód x + y ≥ 0 és x + y = | x | + | y | x + y ≤ 0 és x + y = – (| x | + | y |) x + y > 0 és x + y = | x | – | y | x + y < 0 és x + y = – (| y | – | x |). Mértani jelentés Oxy 0 x+y yxO x+y 0 y Ox 0 x+y y Ox x+y 0
Alkalmazás
A racionális számok összeadásának művelete megőrzi az egész számok összeadásának tulajdonságait.
Az összeadás asszociatív: (x + y) + z = x + (y + z), bármely x, y, z racionális szám esetén.
Az összeadás kommutatív: x + y = y + x, bármely x és y racionális szám esetén.
Az összeadás semleges eleme a 0 : x + 0 = 0 + x = x, bármely x racionális szám esetén.
Bármely x racionális számnak létezik ellentettje, azaz a –x racionális szám úgy, hogy x + (–x) = (–x) + x = 0. A ℚ halmazban bármely két racionális szám esetén értelmezzük azt az x – y = x + (– y) racionális számot, amelyet az x és y számok különbségének nevezünk.
Bármely két x és y racionális szám esetén az x – y különbség az x számnak és az y szám ellentettjének összege.
feladatok
Matematikai nyelven:
x – y = x + (–y), bármely x, y ∈ ℚ .
+3,7 – (+7,3) = +3,7 + (–7,3) = = –(7,3 – 3,7) = –3,6;
–3,7 – (+7,3) = –3,7 + (–7,3) = = –(3,7 + 7,3) = –11.
1. A számítások elvégzése nélkül becsüld meg a kapott eredmények nagyságrendjét, és határozd meg, hogy az állítások igazak lehetnek-e! Megoldás
a) 13,9 + 48,5 = 76,4;
b) 900 – 596,9 = 294,1.
a) 13,9 < 20 és 48,5 < 50 ⇒ 13,9 + 48,5 < 70, és nem igaz az egyenlőség.
b) 596,9 < 600 ⇒ 900 – 596,9 > 300, és nem igaz az egyenlőség.
2. Végezd el a számításokat, esetleg az összeadás tulajdonságainak felhasználásával:
Gyakorlatok és feladatok
1. Végezd el az összeadásokat!
a) 4 9 + 7 9 ; d) 3 10 + ( 1,2);
b) 7 10 + 1 10 ; e) 0,25 + 1 8 ;
c) 4 5 + 11 10 ; f) 2 + 5 3 + [ 1,(2)].
2. Végezd el a kivonásokat!
a) 5 6 1 6 ; d) 1,7 3 5 ;
b) 1 4 3 4 ; e) 0,75 1 1 8 ;
c) 1 3 5 6 ; f) –3 – [– 0,(3)].
3. Számítsd ki alkalmazva a racionális számok öszszeadásának kommutativitását és asszociativitását:
a) 4 3 3 + 5 3 ; c) 4 + 1 2 3 2 + ( 3);
b) 7 5 1 15 4 5 ; d) 2,15 1,(6) + ( 2,65).
4. Számítsd ki az a szám és a b szám ellentettjének összegét!
a) a = 2 3 5 és b = + 2,2;
b) a = 1 7 22 77 333 777 és b = 5 7 + 3
.
5. Számold ki a c szám és a d szám ellentettjének különbségét!
a) c = 3 2 5 és d = 3,3;
105 4. fejezet • A racionális számok halmaza
a) 12 2 9 ,( ) ; a) 12 2 9 12 1 9 2 9 9 9 1 ,( ) ; b) 1 3 29 13 4 3 16 13 1 3 29 13 4 3 16 13 b) 1 3 29 13 4 3 16 13 . 1 3 4 3 29 13 16 13 1 3 4 3 29 13 16 1 13 14 3 29 16 13 11 0.
Megoldott
14 1 21
6. Tekintsük az alábbi számokat:
Számold ki
a) x, y és z; b) x − y és x + z.
7. Végezd el a számításokat! a)
.
b)
8. Három biológus egy rezervátumban környezeti megfigyeléseket végez a következők szerint: az
első a rezervátum 1 6 -od területén, a második a rezervátum 4 15 -öd területén, a harmadik pedig a rezervátum 2 9 -ed részét.
a) Számítsd ki, hogy a biológusok munkájának befejezése után mekkora területet kell még felmérni. b) Ellenőrizd, hogy a felmérésre maradt terület
meghaladja-e a rezervátum 2 3 -ad területét.
30 p 1. Másold le a füzetedbe, és töltsd ki az üres mezőket az I betűvel, ha a kijelentés igaz, és a H betűvel, ha hamis!
2. l. Racionális számok szorzása. Racionális számok osztása
Emlékeztető
Az a n és b p közönséges törtek szorzata az
ab np ⋅ ⋅ közönséges tört, ahol n ≠ 0 és p ≠ 0 Így írjuk: a n b p ab np
Megjegyzés. A b természetes számot 1-es nevezőjű közönséges tört alakba írhatjuk, vagyis b 1 . A b szám és az a n tört szorzata b 1 · a n = ba n ba n 1 lesz.
Fedezzük fel, értsük meg!
A racionális számok szorzása az a művelet, amelynek során az x és y racionális számok minden egyes párjának megfelel a szorzatuk, azaz az egyetlen x · y racionális szám.
106 Matematika • Tankönyv a VI. osztály számára
Kijelentés I/H Kijelentés I/H p1: 4 2 5 = 4 + 2 5 . p2: 1 3 4 2 1 4 > 0,3.
p 2. Rendezd növekvő sorrendbe az a = 11 2 + 1 6 ; b = 11 2 3 20 ; c = 11 2 7 60 számokat!
Munkaidő:
Hivatalból: 10
c
1 25 2 75
d
2 25 1 75
60
Megjegyzés:
20 perc
pont Miniteszt b)
=
és
=
x = 1,5 3 4 + | 1 | 5 8 ; y = 5 4 + 1 5 8 és z = 8 9 + 11 18 + 17 36 .
6 7 + 7 6 67 42 ; c) 1 2 9 2 1 6 7 3 0,1(6);
4 5 5 4 11 20 ; d) 7 8 2 1 9 91 72 1
.
A számítás módja az egész számok szorzásánál és a pozitív racionális számok szorzásánál elsajátított ismereteinkből következik.
Eset / számítási mód
Példák
Ha x > 0 és y > 0, akkor x · y > 0 és x · y = | x | · | y |. (+3,5) · (+0,2) = +0,75. Általában így írjuk:, 3,5 · 0,2 = 0,75.
Ha x > 0 és y < 0, vagy x < 0 és y > 0, akkor
x · y < 0 és x · y = –(| x | · | y |).
(+12) · (–0,2) = –(| +12| · | –0,2 |) = –(12 · 0,2) = –2,4.
(–1,2) · (+2) = –(| –1,2| · | +2 |) = –(1,2 · 2) = –2,4.
0 · x = x · 0 = 0, bármely x racionális számra. 0 · (+3,7) = (+3,7) · 0 = 0; 0 · (–3,5) = (–3,5) · 0 = 0.
Ha x < 0 és y < 0, akkor x · y > 0 és x · y = | x | · | y |. (–4,2) · (–7,5) = | –4,2 | · | –7,5| = 4,2 · 7,5 = 31,5.
(–2) · (–1,9) = | –2 | · | –1,9| = 2 · 1,9 = 3,8.
Jegyezd meg!
1. Bármely két pozitív vagy negatív racionális szám szorzata pozitív racionális szám. Ha x > 0 és y > 0 vagy x < 0 és y < 0, akkor x · y > 0.
2. Két olyan racionális szám szorzata, amelyek közül az egyik pozitív, a másik negatív, negatív racionális szám. Ha x > 0 és y < 0, vagy x < 0 és y > 0, akkor x · y < 0.
3. Két racionális szám szorzatának modulusa egyenlő modulusaik szorzatával, azaz | x · y | = | x | · | y |, bármely x és y racionális szám esetén.
Alkalmazás
Ha az egyik tényező egy szakaszos tizedes tört, akkor mindkét tényezőt írjuk fel közönséges törtként, majd szorozzuk meg figyelembe véve a szorzás előjelszabályát. Ilyen helyzetekben ajánlott a szorzás eredményét irreducibilis törtként megadni. A számítás megkönnyítése érdekében a közbeeső törtek egyszerűsítése vagy az eredmény egyszerűsítése is elvégezhető. A racionális számok szorzása megőrzi az egész számok szorzásának minden tulajdonságát. Ráadásul a nem nulla racionális számok invertálhatók (ahogy azt a pozitív racionális számokról már 5. osztály óta tudjuk).
Tulajdonság
A matematikai jelek nyelvén
A racionális számok szorzása asszociatív. (x · y) · z = x · (y · z), bármely x, y, z ∈ℚ .
A racionális számok szorzása kommutatív. x · y = y · x, bármely x, y ∈ ℚ .
Az 1-es szám a racionális számok szorzásának semleges eleme. 1 · x = x · 1 = x, bármely x ∈ ℚ .
Minden nem nulla racionális számnak van inverze.
Figyelem! A 0 nem invertálható.
A racionális számok szorzása disztributív az összeadásra és a kivonásra nézve.
Bármely x ∈ ℚ, x ≠ 0 esetén létezik az 1 x racionális szám úgy, hogy x · 1 x = 1 x · x = 1.
Bármely x, y, z ∈ ℚ esetén x · (y + z) = x · y + x · z és x · (y – z) = x · y – x · z.
A racionális számok összehasonlításához és rendezéséhez a monotonitási tulajdonság is hasznos, azaz:
Ha x és y racionális számok, x < y, és z pozitív racionális, akkor x · z < y · z.
Ha x és y racionális számok, x < y, és z negatív racionális, akkor x · z > y · z.
Ha x < 2,5, akkor 2 · x < 2 · 2,5, vagyis 2 · x < 5.
Ha x < –0,5, akkor (–3) · x > (–3) · (–0,5), vagyis –(3 · x) > +1,5.
107 4. fejezet • A racionális számok halmaza
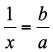
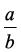
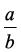
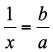
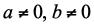
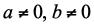
Általában az nullától különböző x szám inverzét x –1 szimbólummal
A 0-val való osztás értelmetlen!
Matematikai nyelven:
x : y = x · y – 1, bármely x ∈ℚ és y ∈ℚ * esetén.
Megjegyzés. Ha x ∈ ℚ, y∈ ℚ, y ≠ 0, akkor az x : y osztást gyakran arányként írjuk: .
2. Végezd el az osztásokat és írd fel az eredményeket irreducibilis
Gyakorlatok és feladatok
1. Írd le racionális számok szorzataként:
a) 2 + ( 2) + ( 2); b)
2. Számold ki
a) a 2 9 -nél négyszer nagyobb racionális számot;
b) a 2,25 racionális szám háromszorosát;
c) a 3 szám és a 5 9 ellentettjének szorzatát!
108 Matematika • Tankönyv a VI. osztály számára
x
a
1
b
Az szám az x = szám inverze, ahol ; Az x = szám az szám inverze, ahol
Tehát 1 1 x x jel , x ≠ 0. xx x 2 3 13 2 1 , . Írhatjuk, hogy: 2 3 3 2 1 és 3 2 2 3 1 ; 2 3 3 2 3 2 1 ; 2 3 3 2 3 2 1 . Tehát 2 3 2 3 2 3 3 2 11 1 . Bármely két racionális
és
szám esetén, ahol y ≠ 0, az x : y hányados az
szám és az y szám inverzének
Ha
=
b abab,, ,, 00 , akkor
x
a = .
;
jelöljük.
x
y
x
szorzata.
= 2: 1 2 2 2 1 4 ; 3 2 9 4 3 2 4 9 3 2 4 9 2 3 1 1 2 3 :.
(+2) : (–0,5)
Megoldott feladatok
racionális számot,
y · z = 2 7 és x · y
z = 16 49 . A szorzás asszociativitását használva az x · y · z = 16 49 így írható x · (y · z) = 16 49 . De y · z = 2 7 , tehát x 2 7 16 49 , vagyis x 16 49 2 7 16 49 7 2 16 49 7 2 8 7 :
a) 1 2 1 4 ; b) 1 3 1 9 . a) 1 2 1 4 1 2 1 4 1 2 4 1 2 1 2 : ; b) 1 3 1 9 1 3 1 9 1 3 9 1 3 1 3 : .
1. Határozd meg a x
ha
·
törtként!
3
3 1 3 1 3
3
3
3
1
1
; c)
4
4
4 10 ... tag .
3. Végezd el a szorzásokat!
a) 4 · 3 5 ; c) 11 16 · ( 8);
b) 3 8 · 10; d) 12 · ( 0,25).
4. Végezd el a szorzásokat és az eredményt írd irreducibilis tört alakjába! a)
;
;
;
.
5. Felhasználva esetleg a szorzás kommutatív és asszociatív tulajdonságát, végezd el:
a) 0,2 · 5 4 · ( 10); c) 3 11 ·0,121·( 1000);
b) 0,45 · 7 27 · 100; d) –9,8 · 17,92 · 0 · 9.
6. Írd le a 3 8 ; 1 4 ; 5; 2 1 3 ; 0,7 számok inverzét!
7. Másold a táblázatot a füzetedbe, és írd be a megfelelő eredményeket az üres mezőkbe!
9. Végezd el az osztásokat!
a) 5
: ;
: ; b)
: ;
10. Végezd el a számításokat és az eredményt írd irreducibilis tört alakjába!
a)
11. Végezd el a számításokat! a)
12. Felhasználva, hogy a szorzás disztributív az öszszeadásra és a kivonásra nézve, számold ki! a)
8. Végezd el az osztásokat!
a) 2,4 : 1,2; c) 33 : 22 3 ;
b) 6,3 : ( 0,9); d) 5,(5) : 2,(2).
Miniteszt
a) Számold ki: 2 · a 22 · b.
b) Bizonyítsd be, hogy a = 11 · b.
1. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
20 p a) A 1 3 5 és 3,75 számok szorzata:
A. 1; B. +3; C. 6; D. 8.
20 p b) A 3 4 : 9 16 : [ 1,(3)] számítás eredménye:
A. 0,5; B. 1; C. 1,5; D. 3.
50 p 2. Ha m = 0,4 · 25 8 és n = 5 2 2 2 : ( 2,5), akkor számold ki: m · n és m : n. Megjegyzés: Munkaidő: 20 perc Hivatalból: 10 pont
109 4. fejezet • A racionális számok halmaza
6 5 2 9
c) 10 3 7 20
b) 3 10 5 6
d) 1 2 3 27 5
x 3 2 1 7 1 1,2 1 x 4 5 2 1 3 x x ⋅ 1
4
3
d) 1 2 3 2 2 9
8 9 5 18
e) 10 3
3 16 15 8 : ; f) 0 23 9
25
: 20; c)
:
1 2 1 4
b) 1 3 1 9
c) 48 16
d) 17 10 01 ,
;
;
, , ;
2 9 8 3 4 ⋅ : ; c) −5 : 5 2 15 4 45 4 : ;
3
10 27 : 25 36 ; d) –13
(–12
b)
·
:
: 0,(3)).
2 3 3 2 2 ; c) 7 8 8 7 8 ;
10 9 5 6 · ( 18); d) 2 3 3 5 · 15 4 .
az a 1 2 1 4 1 6 és
1 22 1 44 1 66 szám.
b)
13. Adott
b
3. l. Egy nullától különböző racionális szám egész számú kitevőjű hatványa. Számítási szabályok hatványokkal
Fedezzük fel, értsük meg!
Bármely nullától különböző x racionális szám és bármely n ≥ 2, természetes szám esetén az x szám n-dik hatványát xn-nel jelöljük és így értelmezzük: xxxxx n n-szer ... .
Ha x egy nullától különböző racionális szám és n egy nullától különböző természetes szám, akkor az x –1 racionális szám n-dik hatványát x –n-nel jelöljük és az x szám –n-dik hatványának nevezzük.
Bármely x ∈ ℚ , x ≠ 0 és bármely n ∈ ℕ * , xx n n 1 vagy x x n n 1
Ha x a b abxa b a b x a b b a n nn n ,, ,; ** akkor 1 1 , valamint x a b b a b a n nnn n .
Megegyezés szerint: x0 = 1 és x1 = x, bármely x racionális szám esetén, ahol x ≠ 0. 0n = 0, bármely n, n ≠ 0 szám esetén. 00 értelmetlen Példák.
A racionális számok egész számú kitevőjű hatványaival való számolás szabályai hasonlóak a pozitív racionális számok természetes kitevőjű hatványaival való számolás szabályaihoz.
A szabály megnevezése A szabály és alkalmazásának feltétele
1. két azonos alapú hatvány szorzata xm xn = xm + n , bármely x ∈ ℚ * és bármely m, n ∈ ℤ esetén.
2. két azonos alapú hatvány hányadosa xm : xn = xm – n, bármely x ∈ ℚ * és bármely m, n∈ ℤ esetén.
3. hatvány hatványa
(xm)n = xm n, bármely x ∈ ℚ * és bármely m, n∈ ℤ esetén.
4. egy szorzat hatványa (x y)m = xm ym, bármely x ∈ ℚ * , y ∈ ℚ * és m∈ ℤ esetén.
Következmény: Ha x ∈ ℚ * és n∈ ℤ , akkor (–x )n = (–1)n ⋅ xn; (–x )n = xn, ha n páros és (–x )n = –xn, ha n este páratlan.
5. hányados hatványa
Megoldott feladatok
(x : y)m = xm : ym, bármely x, y ∈ ℚ * és bármely m∈ ℤ esetén.
110 Matematika • Tankönyv a VI. osztály számára
1. 1 1 1 1 1 ; 2. 11 11 41 4 4 ; 3. 11 11 31 3 3 ; 4. 2 5 2 5 8 125 3 3 3 ; 5. 22 1 2 1 16 41 4 4 ; 6. 1 3 1 3 3 1 39 21 2 2 2 ; 7. 3 5 3 5 5 3 625 81 41 4 4 . Alkalmazás
Számold ki kétféleképpen: a) 2 3 2 ; b) 2 3 .
Megoldás
a) xx xxx n n nn nn 1 11 1 , bármely x ∈ ℚ, x ≠ 0 és bármely n∈ ℤ
1. Írd fel hatványként, minden esetben megadva a hatvány alapját és a hatvány kitevőjét! a)
Másold a táblázatot a füzetedbe, és írd az üres mezőkbe az I betűt, ha a kijelentés igaz, és a H betűt, ha hamis!
111 4. fejezet • A racionális számok halmaza a) 2 3 2 3 3 2 3 2 9 4 21 2 2 2 2 . 2 3 2 3 2 1 3 1 1 2 1 3 2 2 2 2 2 2 2 1 4 1 9 1 4 9 1 9 4 :. b) 22 1 2 1 2 1 8 1 8 31 3 3 3 3 . 22 1 2 1 2 1 8 31 3 33 .
2. a) Bizonyítsd be, hogy x – n = 1 xn bármely x ∈ ℚ, x ≠ 0 és bármely n∈ ℤ esetén.
2
b) Az a) pontban megadott összefüggés alapján számítsd ki: 3 – 4; 10 – 3; (0,1) – 3;
9–
.
3 1 3 1 81 4 4 ; 10 1 10 1 1000 0 001 3 3 , ; 01 1 01 1 0 001 1000 3 3 1000 , , , ; ) 9 1 9 1 81 2 2
esetén.
b)
1 3 1 3 ⋅ ; b) 1 2 1 2 1 2 ; c) 2,5 · 2,5 · 2,5 · 2,5; d) 5 3 5 3 5 3 5 3 5 3 . 2.
43; d) ( 0,1)6;
1 2 4 ; e) 7 10 0 ; c) 4 3 3 ; f) 4 9 1 . 3. Végezd el a számításokat! a) 1 2 1 2 32 ; e) 1 3 2 3 ; b) 0,23 · 0,22; f) 04 1 4 , ; c) 1 4 6 : 1 4 4 ; g) 2 3 · 2 3 2 · 2 3 3 ; d) (–0,3)8 : (–0,3)5; h) 7 2 3 · 7 2 5 : 7 2 7 . 4. Írd fel racionális alapú hatványként: 9; 8; 1 4 ; 0,01; 0,027; 3 2 5 10 . 5.
Kijelentés I/H 0,42 · 0,45 = 0,42 + 5 2 3 7 : 2 3 4 = 2 3 74 05 2 3 , = (,05)23 2 7 3 egy negatív racionális szám. 0,62 · 0,63 = 0,62 · 3 3 2 10 : 3 2 8 = 3 2 10 8 Gyakorlatok és feladatok
Végezd el a számításokat! a)
b)
6. Számold ki!
a) 2 3 4 5 · 3 4 6
· 2 3 ; b)
:
+ 7 1 .
7. Másold át a füzetedbe, és töltsd ki a táblázatot
az x – n = 1 xn reláció segítségével, ahol bármely az
x ∈ ℚ, x ≠ 0 és bármely az n∈ ℤ
a 1 2 –0,5 –2 3 4 –1
a–1
a–2
a–3
8. Végezd el a számításokat!
a) 2 5 1 ; e) (–0,2)– 5;
b) [0,(3)]–3; f) 1– 7;
c) 4 3 2 ; g) 1 2 6 ;
d) (–1)– 4; h) (–0,1)8.
9. Adott az
a = 2 3 4 · 2 3 2 , b = 4 5 8 · 4 5 6 és
c = 3 2
· 3
, szám.
Bizonyítsd be, hogy a · b · c < 1.
10. Határozd meg azt
a) az n természetes számot, amelyre 5 3 1 1 n ;
b) az m egész számot, amelyre 2 7 35 m , ;
c) a 10-es alapú számrendszerbeli p számjegyet, amelyre 12 1 4 2 , p = . 1.
112 Matematika • Tankönyv a VI. osztály számára
6 6
4
3
5 7
5 7
5
2 2
15 2
:
p a) Az a = 1 2 3 , b = 2 3 4 , c = 3 4 5 és d = (1 – 2 + 3 – 4)5 számok közül a pozitív szám: A. a; B. b; C. c; D. d. 20 p b) A 1 2 2 racionális szám egyenlő A. 2; B. – 2; C. – 4; D. 4. 20 p c) Az 5 2 2 · 5 2 3 : 5 2 4 számítás eredménye: A. 5 2 ; B. 5 2 ; C. 25 4 ; D. 25 4 . 15 p 2. a) Számold ki 3 2 n , az n∈{ 1, 0, 1, 2, 3} esetén! 15
b) Határozd
1 ≤ 3 2 n ≤ 3.
Munkaidő: 20 perc
10 pont
Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes. 20
p
meg az n természetes számok azon értékeit, amelyekre
Megjegyzés:
Hivatalból:
Miniteszt
4. l. A műveletek elvégzésének sorrendje és a zárójelek használata
Az összeadás és kivonás elsőrendű művelet, a szorzás és osztás másodrendű művelet, a hatványokkal végzett műveletek pedig harmadrendű műveletek.
Az előző leckékből az alábbi számítási szabályokra is következtetünk:
x ⋅ 0 = 0 ⋅ x = 0, bármely x ∈ ℚ . x ⋅ (–1) = (–1) ⋅ x = – x, bármely x ∈ ℚ .
(– x) ⋅ (– y) = x ⋅ y, bármely x ∈ ℚ és y ∈ ℚ. x xx n n n 11 , bármely x ∈ ℚ, x ≠ 0 és bármely n ∈ ℤ.
– (x + y) = (– x) + (– y) = – x – y, bármely x, y ∈ℚ . x – (y + z) = x – y – z, bármely x, y, z ∈ ℚ .
Megjegyzés. A zárójelek eltávolításakor a zárójel előtt lévő – jel megváltoztatja a zárójelben lévő összes tag előjelét.
Fedezzük fel, értsük meg!
A racionális számokkal végzett műveletek sorrendje hasonló az 5. osztályban tanult pozitív racionális számokkal végzett műveletek sorrendjéhez.
Jegyezd meg!
1. Ha a feladat csak azonos rendű műveleteket tartalmaz, akkor azokat a leírt sorrendben, balról jobbra haladva végezzük el.
2. Ha a feladat különböző rendű műveleteket tartalmaz, de nem tartalmaz zárójeleket, akkor végezzük el a harmad-, majd a másod- és végül az elsőrendű műveleteket az 1.-nél leírt sorrendben. Tehát:
1. lépés. Elvégezzük a hatványokkal végzett műveleteket és a hatványozást.
2. lépés. Szorzunk és osztunk az előző lépés eredményeinek felhasználásával, az 1.-nél leírt sorrendben.
3. lépés. Összeadunk és kivonunk a 2. lépés eredményeinek felhasználásával és az az 1.-nél leírt sorrendben.
Megjegyzés: A hatványokkal végzett műveleteket elvégezhetjük az előkészítő szakaszban vagy a megoldás során, amikor bizonyos számokat olyan formában akarunk leírni, amely egyszerűsíti a számításokat.
3. Ha a feladat zárójeleket is tartalmaz, akkor:
1. lépés. Végezzük el a kerek zárójelben lévő számításokat a 2. pontban leírt sorrendben.
2. lépés. A szögletes zárójeleket alakítsuk át kerek zárójelekké, a kapcsos zárójeleket szögletes zárójelekké.
3. lépés. Számoljunk az új kerek zárójelekben, a 2. pontban leírt sorrendben.
4. lépés. Folytassuk így, amíg az összes zárójelet el nem távolítjuk, majd végezzük el a számításokat zárójelek nélkül.
Ügyeljünk arra, hogy a számításokból származó törtek irreducibilisek legyenek.
113 4. fejezet • A racionális számok halmaza
1. Számítsd ki betartva a műveletek sorrendjét!
a)
+
:
b) 0,(8) +
:
; d) 05
2. Adott az a = 0,(3) és b = 13 39 szám.
Számold ki a c = (a − b) · (a + b) számot és döntsd el, hogy negatív, pozitív vagy nulla! 3.
4. Végezd el a számításokat, és fejezd ki az eredményeket irreducibilis közönséges törtként!
a) 0,(7) · 1 21 + 2,(3) · 3–2;
b) 13
c) (6 : 1,5 + 1 : 0,2) · (–0,1)–3;
114 Matematika • Tankönyv a VI. osztály számára Alkalmazás
feladat Írd a 7 15 14 5 1 3 2 9 2 : : 1 1 3 155 93 számot irreducibilis közönséges tört alakjába!
Megoldott
Elvégezzük: Számítás a hatványokkal végzett műveleteket, és a hatványozást 7 15 14 5 1 3 2 9 2 : = 7 15 14 5 1 3 2 9 2 = 7 15 14 5 1 9 2 9 a kerek zárójelben levő szorzást 7 15 14 5 1 9 2 9 = 7 15 14 45 2 9 a kerek zárójelekben levő összeadásokat és kivonásokat 7 15 14 45 2 9 = 35 7 15 14 45 2 9 )) = 21 45 14 45 10 45 = 45 45 = –1 1 1 3 155 93 = 1 1 3 155 93 31 ( = 1 1 3 5 3 = 1 6 3 = (1 + 2) = 3. az osztást a kapott eredmények felhasználásával (–1) : 3 = 1 1 3 1 3 . Megoldási minta 7 15 14 5 1 3 2 9 2 : : 1 1 3 155 93 = 7 15 14 5 1 3 2 9 2 : 1 1 3 155 93 31 ( = = 7 15 14 5 1 9 2 9 : 1 1 3 5 3 = 35 7 15 14 45 2 9 )) :(1 + 2) = 21 45 14 45 10 45 : 3 = 45 45 : 3 = 1 3 .
Megoldás
5
7 2
1 2
9 10 5 6 27 8 9 2
; c)
: ;
4 3 2
2 3
2
1 6 2 2 () .
, :
1 3 1 3 3 45 9
Bizonyítsd be, hogy
természetes szám!
1 3 2 3 1 5 18 22 ,:
;
d) 2 5 2 5 1 32 : · 15 14 + 1,5; e) 2 2 3 11 12 3 4 12 265 11 15 2 :, , .
Gyakorlatok és feladatok
5. Adottak az alábbi számok:
a = 8 · 7 32
3 + 0,25 és b = 3,(6) + 7 3 1 2 5 : .
a) Számold ki az a és b racionális számot!
b) Határozd meg az m és n természetes számot, ha m · a + n · b = 9.
6. Adottak az alábbi számok:
7. Végezd el a számításokat!
Végezd el a számításokat, és határozd meg az alábbi kijelentések logikai értékét:
p1: 17 · c + 5 = 25 · d;
p2: c > d;
p3: c < d.
8. Számold ki az alábbi számok számtani közepét!
Miniteszt
30 p 1. Párosítsd össze az A oszlopban található számítást jelölő számokat a B oszlopban található megfelelő választ jelölő betűvel.
50 p a) Határozd meg az a, b és c számot!
10 p b) Bizonyítsd be, hogy 2 · (a · b · c) egy racionális szám négyzete!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
115 4. fejezet • A racionális számok halmaza
A B 1. 1 + 1 2 : 0,25 = 2. 33 44 32 43 : 4 2 3 = 3. 2 21 3 3 · 3 31 3 2 2,3 = a. 7 10 b. 1 c. 3 2 d. –2 e. 3 2 2. Adott az a 11 3 7 2 5 14 : , b 2 1 21 5 42 6 35 15 1 : és c 5 24 10 72 15 144 12 1 :, racionális szám.
3 8 4
c = 2 1 2 1 3 2 1 2 1 3 és d = 3 1 2 2 3 3 4 1 1 2 1 3 1 4
a) 7 15 14 5 1 3 2 9 1 1 3 155 93 2 : ; b) 1 1 2 13 1 1 4 15 1 1 6 11 ; c) 1 2 1 1 2 2 5 4 ; d) 4 3 1 1 3 1 16 2 9 43 43 100 24 : .
22 22 22 12 34 56 : és y 1 2 1 2 1 2 1 2 1 2 01 24 : 56 1 2 .
x
4.3. x + a = b; x · a = b; x : a = b, (a ≠ 0); a · x + b = c alakú egyenletek, ahol a, b, c ∈ ℚ. Ilyen egyenletekkel megoldható feladatok
1. l. x + a = b; x · a = b; x : a = b; (a ≠ 0); a · x + b = c alakú egyenletek, ahol a, b, c ∈ ℚ
Emlékeztető
A racionális számok halmazán az egyenlőségi reláció:
a) reflexív: Bármely racionális szám egyenlő önmagával, azaz a = a, bármely a ∈ ℚ esetén.
b) szimmetrikus: Ha a, b ∈ ℚ és a = b, akkor b = a.
c) tranzitív: Ha a, b, c ∈ ℚ, a = b és b = c, akkor a = c.
Egy egyenlőségből kiindulva a racionális számok összeadási, kivonási, szorzási vagy osztási műveletét használva a következő ekvivalens átalakításokat kapjuk:
Ha a, b ∈ ℚ és a = b, akkor a + c = b + c és a – c = b – c, bármely c ∈ ℚ.
Ha a, b ∈ ℚ és a = b, akkor a · c = b · c, bármely c ∈ ℚ és a : c = b : c, bármely c ∈ ℚ, c ≠ 0.
Ne feledd! A 0-val való osztás értelmetlen!
Oldjuk meg figyelmesen!
Krisztián szenvedélyesen szeret desszerteket készíteni. A nővérének születésnapjára egy csokoládétortát készít. A csokoládé a torta 20%-át teszi ki, és 250 grammot nyom.
a) Számítsd ki a szükséges csokoládé mennyiségét g-ban kifejezve, tudva, hogy már van 0,150 kg csokoládéja.
b) Számítsd ki a Krisztián által készített torta tömegét kg-ban!
Megoldás.

a) Legyen x a szükséges csokoládé tömege. Ekkor, mivel 0, 150 kg = 150 g, a 150 + x = 250 egyenletet kapjuk, ahol x az ismeretlen, s melynek megoldása x = 250 – 150, tehát x = 100 (g).
b) Legyen t a torta tömege kg-ban. Ekkor a csokoládé tömege a t 20%-a. Mivel 250 g = 0,25 kg, a 20 100 025 t , egyenletet kapjuk, ahol t az ismeretlen. Az egyenlet mindkét tagját 20 100 -dal osztjuk, és a
Felelet: a) Krisztiánnak 100 grammal több csokoládéra van szüksége. b) A nővére születésnapi tortája 1,250 kg súlyú.
Fedezzük fel, értsük meg!
A fenti feladat megoldása a racionális számok halmazán megfogalmazott és megoldott két egyenlethez vezetett.
Javasoljuk, hogy a ℚ halmazban vagy a ℚ halmaz részhalmazaiban olyan egyenleteket oldjunk meg, amelyek x + a = b; x · a = b; x : a = b; a ≠ 0 vagy a · x + b = c alakban írhatók fel, ahol a, b, c ∈ ℚ . Az ismeretlent x-szel jelöltük, de a feladatokban bármilyen más jelölést is használhatunk. Az a, b, c számok ismertek, és ezeket az egyenlet együtthatóinak nevezzük.
Az összes ilyen típusú egyenletet a fordított út módszerével oldjuk meg felhasználva a racionális számokkal végzett műveletek és az egyenlőségek ekvivalens transzformációinak fent említett tulajdonságait.
116 Matematika • Tankönyv a VI. osztály számára
t = 025 20 100 ,: kapjuk. Mivel 025 20 100 25 100 100 20 5 4 1 250 5 1 1 4 ,: , , az eredmény t = 1,250 (kg).
1. x + a = b; a, b ∈ ℚ
x + a = b | – a
x = b – a.
M = {b – a}
Példa
x + 2,9 = 1,2 | – 2,9
x = – 1,7.
M = {– 1,7}
2. x · a = b; a, b ∈ ℚ Példa
a) Ha a = 0, az egyenlet: x · 0 = b lesz.
Az egyenlőség csak b = 0 esetén igaz. Tehát
M = ∅, ha b ≠ 0 és M = ℚ, ha b = 0.
b) Ha a ≠ 0, x · a = b | : a
x = b : a.
i) x · 0 = 1, lehetetlen és M = ∅.
ii) x · 0 = – 1 + 2 : 2 ⇔ x · 0 = 0, igaz bármely x ∈ℚ esetén, azaz M = ℚ.
3. x : a = b; a, b ∈ ℚ, a ≠ 0 Példa
x : a = b | · a
x = b · a.
M = {b · a}.
4. a · x + b = c; a, b ∈ ℚ Példa
a) Ha a = 0, akkor x · 0 + b = c.
Az egyenlőség csak b = c esetén igaz. Így
M = ∅, ha b ≠ c és M = ℚ, ha b = c.
b) Ha a ≠ 0, a · x + b = c | –b
a · x = c – b | : a
x = (c – b) : a.
M = {(c – b) : a}.
Alkalmazás
x : 3,5 = –2
i) 0 · x + 3 = 5 ⇔ 0 · x = –2, lehetetlen, azaz M = ∅.
ii) 0 · x + 3 = 5 – 2 ⇔ 0 · x = 0, igaz bármely x ∈ ℚ esetén, azaz M = ℚ.
–1,2 · x + 3 = 5 | – 3
–1,2 · x = –2 | : (–1,2 ) x
Gyakran előfordul, hogy a megoldandó egyenleteket a racionális számokkal végzett műveletek tulajdonságai segítségével a fenti alakok valamelyikébe hozhatjuk.
Jegyezd meg!
Egy egyenlet megoldása a következőkből áll:
1. az egyenlet ismert alakba hozása a racionális számokkal végzett műveletek tulajdonságai alapján;
2. az így kapott egyenlet megoldása az ismert algoritmus segítségével;
3. a megoldáshalmaz felírása annak a tartománynak megfelelően, amelyben a megoldást kell megadni.
117 4. fejezet • A racionális számok halmaza
M =
b : a}. x xxxM 2 3 2 5 2 3 2 5 2 3 2 5 3 2 3 5 1 |: , 3 5
{
· 3,5 x =
3,5 x
|
–2 ·
= –7 és M = {–7}.
2
10
⇔ x
2 12 10 : . De, 2 12 10 2 10 12 2 5 6 5 3 2 1 3 : ( , tehát x = 5 3 és M = 5 3 .
12
:
=
Megoldott feladat
Oldd meg az x 2 + x 3 7 = 75 14 x egyenletet
Megoldás. Mivel nem adták meg, hogy milyen halmazban keressük a megoldásokat, ezért az egyenletet ℚ-ban oldjuk meg.
Gyakorlatok és feladatok
1. Válaszd ki azt az egyenletet jelölő betűt, ahol az egyenlet megoldása a –3 szám!
A. x + 2,5 = 1,5; C. x + 7 2 = 1 2 ;
B. x + ( 2)2 = 1; D. x + 3,(3) = 0,3.
2. Oldd meg az x + 1 2 1 3 = egyenletet és válaszd ki az egyenlet megoldáshalmazát jelölő betűt!
A. M = 1
B. M = 1
6 ; C. M = 1 5 ;
6 ; D. M = 5 6 .
3. Adott az 1 2 · x 1 4 = 0,25egyenlet. Indokolva döntsd el, hogy az egyenletnek van-e megoldása az A 20 1 2 ;; halmazban!.
4. Oldd meg a racionális számok halmazán az alábbi egyenleteket!
a) x + 3,4 = 0,15; d) x + 3,(3) = 0,3;
b) 3 · x + 2 = 10; e) 2,3 · x 4,6 = 6,9;
c) 5 · x + 2 5 = 5,4; f) x : 5 8 + 4 = 12.
5. Oldd meg a 9 2 · x = 0 egyenletet az
a) ℕ; b) ℤ; c) ℚ halmazon.
6. a) Határozd meg az a racionális számot tudva, hogy–2 az a · x + 5 = 8 a egyenlet megoldása!
b) Határozd meg a b racionális számot tud-
va, hogy 1 2 a 2 3 · x + b = 1 + b 3 egyenlet megoldása!
7. Oldd meg az egyenleteket!
a) 4 · x + 3 = x + 18;
b) 2 · (x + 1) = 4 · x + 2;
c) x 4 + 1 = x 0,5;
d) 2 3 1 2 · x = 1;
e) x + 1 2 + 3 4 = x 8 ;
f) 3 · x 1 3 = 2 · x 1 2 ;
g) 1 2 · 1 3 1 4 x = 1 24 ;
h) 1 9 ·
i)
j) x 3 4 = 1 8 ;
k) 07 1 5 , x = 0;
l) 2 + x 3 1 =1.
8. Határozd meg az ab alakú természetes számot, ha igaz az abababab 3 33 120 23 egyenlőség!
118 Matematika • Tankönyv a VI. osztály számára
1
0;
8 11 x =
2
09 06 , , x 3
x = x 27 03 , , ;
xxx 2 3 7 75 14 ⇔ 72 2 3 7 75 14 ))xxx ⇔ 7 14 26 14 75 14 xxx ⇔ 96 14 75 14 xx ⇔ 96 75 xx ⇔ ⇔ 95 76 xx ⇔ 14x = 13 tehát x = 13 14 ; M 13 14 .
Miniteszt
1. Válaszd ki a helyes választ! Csak egy válasz helyes.
25 p a) A x 1 3 = 2,(3) 3 5 x egyenlet megoldása:
A. 3 5 ; B. 1 3 ; C. 5 3 ; D. 5 3 .
25 p b) Az x 2 1 = 3 2 egyenlettel ekvivalens egyenlet az:
A. x 5 = 0; B. 1 + x = 0; C. 1 x = 0; D. x + 5 = 0.
2. Oldd meg az egyenleteket!
4 × 10 p a) x + 3,5 = 1,75; b) x :, () 22 5 13 2 2 ; c) x 3 2 15 2 (, ) ; d) 7 4 17 35 x , .
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
2. l. Egyenletekkel megoldható feladatok
A gyakorlatban felmerülő feladatok közül soknak a matematikai modellje egyenletekből áll. A feladat megoldása magában foglalja a megfelelő egyenlet megoldását abban a halmazban, amelyet a felmerülő feladat szövegkörnyezete ír elő.
Fedezzük fel, értsük meg!
Ha a feladatot át lehet fogalmazni egy olyan egyenletre, amelynek megoldásai a kívánt halmazban vannak, akkor a feladat megoldása a következő lépésekből áll: 1. lépés. Az ismeretlen megállapítása, a jelölések elkészítése, az előforduló mennyiségek közötti összefüggéseknek matematikai nyelven történő leírása. → 2. lépés. Az egyenlet felírása. → 3. lépés. Az egyenlet megoldása. → 4. lépés. Az egyenlet megoldásainak értelmezése, figyelembe véve azt a halmazt, amelyben a feladat megoldását keressük.→ 5. lépés. A következtetés megfogalmazása.
Megjegyzés. A kapott megoldás(ok) ellenőrzése hasznos az esetleges hibák kijavítása érdekében.
Alkalmazás
Megoldott feladat
Szonja szülei egyidősek (években kifejezve). Szonja kora édesanyja korának az egyötöde. Két év múlva a három családtag életkorának összege 94 év lesz. Határozd meg Szonja és édesanyja jelenlegi életkorát!
Megoldás
I módszer. Először is meghatározzuk Szonja életkorát. Ismeretlen lesz Szonja jelenlegi életkora.
1. lépés. Legyen x Szonja kora. Akkor az anya életkora egyenlő az apa életkorával, azaz 5 · x. Szonja életkora két év múlva x + 2 lesz, és mindkét szülő életkora 5 · x + 2 lesz.
2. lépés. (x + 2) + 2 · (5 · x + 2) = 94.
119 4. fejezet • A racionális számok halmaza
3. lépés. (x + 2) + 2 · (5 · x + 2) = 94 ⇔ x + 2 + 10 · x + 4 = 94 ⇔
⇔(1 + 10) · x + 6 = 94
11 · x = 88 |:11 x = 8.
11
x + 6 = 94 | –6
5. lépés. Szonja 8 éves, édesanyja pedig 40 éves.
4. lépés. Az életkort természetes számokkal fejezzük ki. A 8 egy természetes szám, az 5·8 = 40 szintén egy természetes szám. Így a feladatnak egyetlen megoldása van.
II. módszer. Először az anya életkorát határozzuk meg. Ismeretlen lesz az anya jelenlegi életkora.
1. lépés. Legyen x az anya kora. Akkor Szonja kora 1 5 x , és az
apja kora x. Két év múlva az anya x + 2 éves lesz, akárcsak az apa, és Szonja 1 5 2 x éves lesz.
2. lépés. () () xxx 22 1 5 294
22 1
3. lépés. () () xxx
294
4. lépés. Az életkort természetes számokban fejezzük ki. A 40 egy természetes szám, 40 : 5 = 8 szintén természetes szám. Tehát a feladatnak egyetlen megoldása van.
5. lépés. Az anya 40 éves, Szonja pedig 8 éves.
Megjegyzés. Az ismeretlenek megválasztása eltérő lehet, ami eltérő egyenleteket eredményez, de az egyenletek megoldása és az eredmények helyes értelmezése bizonyítja a feladat helyes megoldását.
Gyakorlatok és feladatok
1. Az a szám kétszerese 1,2-vel nagyobb, mint 1 2 . Hasonlítsd össze az a és 0,85 számot!
2. Határozd meg r ∈ ℚ , értékét, tudva, hogy megszorozva 4 5 -del a kapott eredmény ugyanaz, mint ha 10-et vontunk volna ki belőle!
3. Anna és Mária összesen 72 matematikai feladatot oldott meg a nyári szünetben. Tudva, hogy Mária 20%-kal kevesebb feladatot oldott meg, mint Anna, határozd meg a két diák által külön-külön megoldott feladatok számát!
4. Számítsd ki két pótszög mértékét az alábbi esetekben:
a) A szögek mértékének különbsége 18°.
b) A szögek mértékének aránya 7 3 .
5. A város lakosainak 32%-a tanuló, ebből 1009 óvodás, 2018 általános iskolai és 1563 középiskolai tanuló.
a) Írj egy egyenletet a feladat adatainak felhasználásával.
b) Oldd meg az a) alpontban szereplő egyenletet, és határozd meg a város lakosainak számát!
6. Egy osztályban 24 diák van, fiúk és lányok. Ha még 3 lány jönne, akkor a fiúk száma feleannyi lenne, mint a lányoké. Határozd meg az osztályban levő lányok számát!
7. Határozd meg az x racionális számot tudva, hogy a 12, 9 + x, 15 és 3 · x számok számtani közepe 16.
120 Matematika • Tankönyv a VI. osztály számára
⇔
·
xxx x
5
22 1 5 294 11 1 5 6 94 2 1 5 694 11 5 6946 11 5 88 11 5 88 5 8 ) | |: x x x x 5 11 40 1 x .
I. Válaszd ki a helyes válasz betűjelét! Csak egy válasz helyes.
5 p 1. Az 1,75 racionális szám irreducibilis közönséges tört alakba írva:
A. 7 4 ; B. 17 5 ; C. 7 5 ; D. 11 4 .
5 p 2. A 1,5 + 0,25 · 5 szám ellentettje:
A. 0; B. 0,25; C. 0,25; D. 0,5.
5 p 3. Ha |a + 3 2 | = 0, akkor az a értéke:
A. 1 3 ; B. 3 2 ; C. 3 2 ; D. 2 3 .
5 p 4. A 2,5; 11 5 ; b 10 ; 4 2 számok akkor vannak növekvő sorrendben, ha a b értéke:
A. 24; B. 19; C. 23; D. 21.
5 p 5. Az n egész szám azon értéke, amelyre n < 31 10 < n + 1 egyenlő:
A. 2; B. 4; C. 3; D. 1.
5 p 6. A 2 5 2 5 52 : számítás eredménye:
A. 6 15 ; B. + 8 25 ; C. 8 125 ; D. + 8 125 .
II. Írd le a teljes megoldást!
15 p 5 p
15 p
5 p 5 p
5 p 10
a) Vizsgáld meg, hogy a három szám között van-e olyan racionális szám, amely nem egész szám!
b) Mutasd ki, hogy a d = abc 7 természetes szám!
2. Oldd meg az x 2 5
3. András telefont akar venni. Az ajánlatokat tanulmányozva rájön, hogy csak fele annyi pénze van, mint amennyire szüksége lenne. Andrea, András nővére, a telefon árának egyharmadát adja, a nagymamájuk pedig a maradék 150 lejt. A telefon árát p-vel jelöljük!
a) Fejezd ki p függvényében, hogy András mennyi pénzzel járul hozzá!
b) Fejezd ki p függvényében, hogy Andrea mennyi pénzzel járul hozzá!
c) Írj egy egyenletet, amelyben az ismeretlen p a telefon ára, és megfelel a feladat adatainak!
d) Oldd meg az egyenletet, és határozd meg az András által kívánt telefon árát!
Megjegyzés: Munkaidő: 50 perc
Hivatalból: 10 pont
122 Matematika • Tankönyv a VI. osztály számára ISMERETFELMÉRŐ
Adott az a
1 5 1 , b = 1 4 8 3 5 5 3 és c = 24
(−32)
p 1.
=
:
− 2,75 szám.
1
3 10
2 egyenletet!
5. MÉRTANI ALAPFOGALMAK
5.1. Szögek a síkban
1. l. Ismétlés és kiegészítések
Emlékeztető
Szögnek nevezzük azt a mértani alakzatot, amelyet két közös kezdőpontú félegyenes alkot.
A két félegyenest a szög szárainak nevezzük, a közös kezdőpontot pedig a szög csúcsának.
A padtársaddal azonosíts a mellékelt ábrán három különböző méretű szöget, megfigyelve a szögek szárait és csúcsát!
Szögmérő segítségével mérd meg a kiválasztott szögeket! A mértani felszerelésedet használva rajzolj a füzetedbe ezekkel kongruens szögeket és határozd meg ezek fajtáját (hegyesszög, derékszög és tompaszög)!
A követelmények megválaszolásához használd az V. osztályban tanult, az alábbiakban említett és példákkal illusztrált ismereteket!
♦ Az OA és OB félegyenesek által alkotott szög jelölésére a következő jelöléseket használhatjuk:
AOB∢ vagy ˆ AOB vagy BOA∢ vagy ˆ BOA .
♦ Ha nincs több O csúcsú szög, akkor jelölhetjük így
O∢ vagy ˆ O .
Sajátos kompetenciák: 1.5; 2.5; 3.5; 4.5; 5.5; 6.5
O
♦ Ha az M pont a szög OA szárán van, az N pont pedig a szög OB szárán, akkor az AOB∢ szög azonos az MON∢ szöggel. O
Ábra Jelölés
A B AOB∢ vagy ˆ AOB
M A B N
Az ABC szög belseje az összes olyan pontból áll, amely az AB félegyenes által határolt és a C pontot tartalmazó félsíkban, valamint a BC félegyenes által határolt és az A pontot tartalmazó félsíkban helyezkedik el (a két félsík közös pontjaiból áll).
A szög külső tartományát alkotja az összes olyan pont, amely a C pontot tartalmazó AB félegyenes által határolt félsík és az A pontot tartalmazó BC félegyenes által határolt félsík közül legfeljebb az egyikben helyezkedik el.
BOA∢ vagy ˆ BOA
O∢ vagy ˆ O
AOB∢, BOA∢, MON∢, NOM∢, MOB∢, BOM∢, AON∢, NOA∢ ugyanazt a szöget jelöli.
A B C
A szög mértékének kifejezésére a fokot és annak törtrészeit: a percet és a másodpercet használjuk. Az egyfokos szög olyan szöget jelöl, amelynek nyílása a kör 360-ad része.
A perc a foknak a 60-ad része, egy olyan szög, melynek nyílása a kör 21600-ad része. 1° = 60’ , 360° = (360 · 60)′ = 21 600′ .
A másodperc a percnek a 60-ad része, tehát a foknak a 3600-ad része, azaz egy olyan szög nyílása mely a kör 1296000-ed részével egyenlő. 1’ = 60’’, 1° = 3600’’, 360° = (360 · 3600)′′ = 1 296 000′′ . Fedezzük fel, értsük meg!
123 5. fejezet • Mértani alapfogalmak
Int(ABC∢)
Ext(ABC∢)
A B C
Megjegyzés. Egy szög mértékét egy α valós számmal fejezzük ki fokokban, ahol 0° ≤α ° ≤ 180°.
A szögek mértékének megfelelően így osztályozhatjuk a szögeket: hegyesszögek, derékszögek, tompaszögek, nullszögek és egyenesszögek.
1. Ha egy szög szárai különböző félegyenesek melyek különböző egyenesek részei úgy, hogy a három pont mellyel a szöget megnevezzük, nem kollineáris pontok, akkor a következő esetek lehetségesek:
Hegyesszög
Azt a szöget, melynek mértéke kisebb, mint 90° hegyesszögnek nevezzük.

Derékszög
Azt a szöget, melynek mértéke egyenlő 90°-kal, derékszögnek nevezzük.

Tompaszög
Azt a szöget, melynek mértéke nagyobb, mint 90° és kisebb, mint 180° tompaszögnek nevezzük.

2. Ha egy szög két szárát alkotó félegyenesek ugyanannak az egyenesnek a részei, azaz a szöget megnevező három pont kollineáris, akkor a következő esetek lehetségesek:
Egy 0°-os szöget nullszögnek nevezünk.
A nullszög szárai azonos félegyenesek.

Egy 180°-os szöget egyenesszögnek nevezünk.
Az egyenesszög szárai ellentétes félegyenesek. O

Megjegyzés. 1. A hegyesszögeket, a derékszögeket és a tompaszögeket tulajdonképpeni szögeknek nevezzük. 2. A nullszöget és az egyenesszöget nem tulajdonképpeni szögeknek nevezzük.
Két szöget, ABC és DEF, amelyek átfedéssel egybeesnek, kongruens szögeknek nevezünk.
Két szög ABC és DEF akkor és csakis akkor kongruens, ha mértékük ugyanakkora.
Matematikailag:
Ha ABC∢ ≡ DEF∢, akkor ABC∢ = DEF∢.
Ha ABC∢ = DEF∢, akkor ABC∢ ≡ DEF∢. B A
Jegyezd meg!
A∢ ≡ A∢, bármely A∢ esetén. (Bármely szög kongruens saját magával.)
Ha A∢ ≡ B∢, akkor B∢ ≡ A∢. Ha A∢ ≡ B∢ és B∢
Alkalmazás
Ha ismert az A és a B szögek mértéke, akkor kiszámíthatjuk ezek összegét (A∢ + B∢).
Megoldásminta két szög mértéke összegének kiszámításához: Legyen MNP∢ = 57°56′20′′ , QRS∢ = 41°37′2′′

124 Matematika • Tankönyv a VI. osztály számára
O A B O A B O A B 0° < AOB∢ < 90° AOB∢ = 90°
< AOB∢ < 180°
90°
A B O A B AOB∢ = 0° AOB∢ = 180°
.
∢ +
∢
20
+ 41°37′2′′= (57 + 41)°+ + (56 + 37)′ + (20′′ + 2′′) = 98°93′22′′ = 98°+
= 98° + 1° + 33′ 22′′ = 99°33′22′′ .
Akkor MNP
QRS
= 57°56′
′′
(1 · 60 + 33)′22′′
≡ C∢, akkor
∢ ≡ C∢.
A
C E D F
Ha B∢ > A∢, akkor kiszámítható a két szög mértékének különbsége (B∢ – A∢).
Megoldásminta két szög mértékbeli különbségének kiszámításához:
1. Legyen ∢MNP∢ = 57°56′20′′ , QRS∢ = 41°37′2′′. Mivel MNP∢ > QRS∢, következik, hogy kiszámítható a különbségük MNP∢ – QRS∢ = 57°56′20′′– 41°37′2′′= (57 – 41)°+ (56 – 37)′ + (20 – 2)′′ = 16°19′18′′ .
2. Legyen MNP∢ = 54°18′21′′, QRS∢ = 42°37′35′′. Mivel MNP∢ > QRS∢, következik, hogy kiszámítható a különbségük MNP∢ – QRS∢ = 54°18′21′′ – 42°37′35′′ = 53°77′81′′ – 42°37′35′′ = (53 – 42)°+ (77 – 37)′ + (81 – 35)′′ = 11°40′46′′ .
Ha ismert az A∢ szög mértéke, akkor kiszámítható az (A∢) · n szorzat, ahol n egy természetes szám.
Megoldásminta: Legyen MPQ∢ = 33°45′12′′. Akkor, (MPQ∢) · 5 = (33°45′12′′) · 5 = 33° · 5 + 45′ · 5 + 12′′ · 5 = = 165°225′60′′ = 165°+ (3 · 60 + 45)′ + 60′′ = (165 + 3)° + (45 + 1)′, tehát (MPQ∢) · 5 = 168°46′
Ha ismert az A∢ szög mértéke, akkor kiszámítható az (A∢) : n, ahol n egy természetes szám.
Megoldásminta: Legyen MPQ∢ = 122°43′, akkor
(MPQ∢) : 5 = (122°43′) : 5 = [(24 · 5 + 2)° + (43)′] : 5 = [(24 · 5)° + (2 · 60 + 43)′] : 5 = [(24 · 5)° + (32 · 5 + 3)′] : 5 = = [(24 5)° + (32 5)′ + (3 60)′′] : 5 = [(24 5)° + (32 5)′ + (36 5)′′] : 5 = 24° + 32′ + 36′′ = 24°32′36′′ , azaz (MPQ∢) : 5 = 24°32′36′′ .
Megjegyzés. Ha az utolsó lépésben a másodpercek száma nem osztható az osztóval, akkor a másodpercek osztásának eredményét kerekítjük.
Gyakorlatok és feladatok
1. a) Írd le a mellékelt ábrán azonosított szögeket!
b) Határozd meg az a) alpontban talált szögek elemeit (szárait és csúcsát)!
2. A mértani felszerelésed segítségével rajzolj:
a) egy nullszöget; d) egy tompaszöget;
b) egy hegyesszöget; e) egy egyenesszöget;
c) egy derékszöget; f) két kongruens szöget.
3. A mellékelt ábrán az ABC szög mértéke 30°. 30°
A C D B
a) Készítsd el az ábrát a füzetedbe, tudva, hogy CBD∢ = 90°. Határozd meg a szögmérőd segítségével az ABD ∢ szög mértékét!
b) Hasonlítsd össze az ABD∢ szög mértékét a CBD∢ és CBA∢ szögek összegével!
4. A mértani felszerelésed segítségével rajzold le az
ABC szöget, melynek mértéke 23°. Másold le a füzetedbe és egészítsd ki a következő kijelentéseket úgy, hogy igaz kijelentéseket kapj!
a) A B pont az ABC szög … .
b) Az ABC szög szárai az … és az … félegyenesek.
c) Az ABC szög mértéke percben kifejezve egyenlő … ' .
5. Rajzold le az OA, OB, OC félegyeneseket úgy, hogy AOB∢ = 47°, BOC∢= 43°. Határozd meg a szögmérőd segítségével az AOC∢ szög mértékét! Vegyél figyelembe minden esetet!
6. Az OA és az OB félegyenesek ellentétes félegyenesek, az M, N pont az AB egyenes ugyanazon oldalán vannak és AOM∢, MON∢, NOB∢ szögek kongruensek.
a) Készíts az adatoknak megfelelő rajzot!
b) Ellenőrizd a szögmérő segítségével, hogy
AON∢ ≡ BOM∢.
c) Határozd meg a szögmérő segítségével az
AOM∢ és BOM∢ szögek mértékét!
125 5. fejezet • Mértani alapfogalmak
A B C D O
2. l. Kiegészítő szögek. Pótszögek
Emlékeztető
Azt a szöget, melynek mértéke 90°, derékszögnek nevezzük.
Azt a szöget, melynek mértéke 180°, egyenesszögnek nevezzük.
Azt a szöget, melynek mértéke 0°, nullszögnek nevezzük.
Azonosíts szögeket a mellékelt ábrán. Szemmérték alapján azonosíts két derékszöget, két nullszöget és két egyenesszöget!
Az ABC∢ jelölést használjuk az ABC szög megnevezésére is, és az ABC mértékére is.
Oldjuk meg figyelmesen!
1. A következő táblázatban szögpárok találhatók. Figyeld meg a megjelölt szögek mértékét és számítsd ki ezek összegét minden esetben!
∢ = 54°, DAC∢ = 126°, BAC∢ + DAC∢ = 180°. MNP∢ = 126°, QRS∢ = 54°, MNP∢ + QRS∢ = 180°.
BAC∢ = 50°, DEF∢ = 130°, BAC∢ + DEF∢ = 180°.
2. A következő táblázatban szögpárok találhatók. Figyeld meg a megjelölt szögek mértékét és számítsd ki ezek összegét minden esetben!
BOA∢ = 60°, COB∢ = 30°, BOA∢ + COB∢ = 90°.
MNP∢ = 60°, QRS∢ = 30°, MNP∢ + QRS∢ = 90°.
CBA∢ = 75°, DEF∢ = 15°, CBA∢ + DEF∢ = 90°. Fedezzük fel, értsük meg!
1. Két szöget kiegészítő szögeknek nevezünk, ha mértékük összege180°.
Ha A∢ és B∢ szög kiegészítő szögek, akkor az A∢ szöget a B∢ kiegészítő szögének nevezzük, a B∢ szöget pedig az A∢ kiegészítő szögének.
Ha A∢ = 100° és B∢ = 80°, akkor A∢ + B∢ = 180°, tehát az A∢ és B∢ szögek kiegészítő szögek.
A 100°-os szög a 80°-os szög kiegészítő szöge.
A 80°-os szög a 100°-os szög kiegészítő szöge.
126 Matematika • Tankönyv a VI. osztály számára
A B C D 54° 126° 126° M N P R Q S 54° A 50° 130° C B F E D
BAC
30° 60° A B C O 60° M P N 30° Q S R A 15° 75° C B F E D
2. Két szöget pótszögeknek nevezünk, ha mértékük összege 90°.
Ha az A∢ és a B∢ szög pótszögek, akkor az A∢ szöget a B∢ pótszögének nevezzük, a B∢ szöget pedig az A∢ pótszögének nevezzük.
Megjegyzések.
Ha A∢ = 40°15′ és B∢ = 49°45′ , akkor
A∢ + B∢ = 90°, tehát az A∢ és B∢ szög pótszögek.
A 40°15′ mértékű szög a 49°45′ mértékű szög pótszöge.
A 49°45′ mértékű szög a 40°15′ mértékű szög pótszöge
1. Ha az M és N szög kiegészítő szögek és M∢ = a°, ahol 0 ≤ a ≤ 180, akkor ∢N = 180° – a ° .
2. Ha az M és N szög pótszögek és M = b°, ahol 0 ≤ b ≤ 90, akkor ∢N = 90° – b° .
Alkalmazás
1. alkalmazás:
a) Ha két szög kongruens, akkor azok kiegészítő szögei is kongruensek.
b) Ha két szög kiegészítő szögei kongruensek, akkor a szögek is kongruensek.
2. alkalmazás:
a) Ha két hegyesszög kongruens, akkor pótszögeik is kongruensek.
b) Ha két szög pótszögei kongruensek, akkor a szögek is kongruensek.
Bizonyítás
a) Legyen A∢ ≡ B∢. Akkor az A és B szögek mértéke egyenlő, azaz A∢ = B∢ = a°, ahol 0 ≤ a ≤ 180. Az A szög kiegészítő szögének mértéke 180° – a°, ahogy a B szög kiegészítő szögének mértéke is. Írhatjuk: Ha A∢ ≡ B∢, akkor 180° – A∢ = 180° – B∢.
b) Ugyanúgy, ha 180° – A∢ = 180° – B∢, következik, hogy A∢ = B∢, tehát A∢ ≡ B∢.
Bizonyítás
a) Legyen A∢ ≡ B∢. Akkor, az A és B szögek mértéke egyenlő, azaz
A∢ = B∢ = b°, ahol 0 ≤ b ≤ 90. Az A szög pótszögének mértéke 90° – b°, ahogy a B szög pótszögének mértéke is.
Írhatjuk: Ha A∢ ≡ B∢, akkor 90° – ∢A = 90° – ∢B.
b) Ugyanúgy, ha 90° – A∢ = 90° – B∢, következik, hogy A∢ = B∢, tehát A∢ ≡ B∢.
Jegyezd meg!
Bizonyíthatjuk, hogy két szög kongruens, kimutatva, hogy kiegészítő szögeik megegyeznek vagy pótszögeik megegyeznek.
Gyakorlatok és feladatok
1. Mérd meg szögmérővel a szögeket az egyes ábrákon, és indokold meg, hogy ezen ábrák közül melyiken azonosítasz kiegészítő szögpárokat!
127 5. fejezet • Mértani alapfogalmak
A B E D F C I L K J G H M N P O R S U V T Q W Z1 Z2 Z3 X Y a) b) c) d) e)
2. Mérd meg szögmérővel a szögeket az egyes ábrákon, és indokold meg, hogy ezen ábrák közül melyiken azonosítasz pótszögpárokat!
3. Egy szög mértéke 67°. Számítsd ki: a) pótszögének mértékét; b) kiegészítő szögének mértékét.
4. Adottak az A∢ = 40°, B∢ = 60°, C∢ = 54°, D∢ = 30°, E∢ = 50°, F∢ = 26° szögek. Írd fel a pótszögpárokat, indokolva válaszod!
5. Adottak az M∢ = 140°, N∢ = 55°, P∢ = 100°30′ , Q∢ = 40°, R∢ = 125°, S∢ = 79°30′ szögek. Írd fel a kiegészítő szögpárokat, indokolva válaszod!
6. Másold le a füzetedbe és egészítsd ki a következő táblázatot:
A szög mértéke A szög pótszögének mértéke A szög kiegészítő szögének mértéke
7. Igazold, hogy:
a) Ha két szög pótszög, akkor a két szög hegyesszög.
b) Ha két szög kiegészítő szög, akkor az egyik szög tompaszög vagy derékszög.
8. Két pótszög mértékének különbsége 34°. Számítsd ki a két szög mértékét!
9. Két kiegészítő szög mértékének különbsége 72°. Számítsd ki a két szög mértékét!
Miniteszt
Másold le a füzetedbe a következő kijelentéseket és egészítsd ki, hogy igaz állításokat kapj!
20 p 1. Ha két szög kongruens és pótszögek, akkor mindegyik szög mértéke … ° .
Indoklás
20 p 2. Ha két szög kongruens és kiegészítő szögek, akkor mindegyik szög mértéke … ° .
20 p 3. Az A és a B szög pótszögek és A∢ = 72°. Akkor a B szög mértéke … °
30 p 4. A C és a D szög kiegészítő szögek, a C szög mértéke 20°-kal nagyobb, mint a D szög mértéke.
Akkor C∢ = … ° és D∢ = … °
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
128 Matematika • Tankönyv a VI. osztály számára
A B E D F C L K N M O R P S G H I J V X Z T U Y a) b) c) d) e)
27° 63° 153° 90° – 27°
180° – 27° = 153°. 80°20′ 103° 55° 101° 90°
= 63°;
3. l. Csúcsszögek. Egy pont körüli szögek
Oldjuk meg figyelmesen!
1. gyakorlati alkalmazás:
Rajzold le a d1 és a d2 egyenest, melyek az O pontban metszik egymást. Rajzoljuk az A és B pontokat a d1 egyenesre úgy, hogy az O pont az AB szakaszon legyen, majd a C és D pontot a d2 egyenesre úgy, hogy az O pont a CD szakasz egyik pontja legyen.
a) Határozd meg az AOB és a COD szög mértékét! Válaszod indokold!
b) Méréssel ellenőrizd, hogy az AOC és a BOD szögek kongruensek-e!
c) Méréssel ellenőrizd, hogy az COB és a DOA szögek kongruensek-e!
Fedezzük fel, értsük meg!
A fenti alkalmazásban:
Megoldás. a) Az AOB szög szárai ellentétes félegyenesek, tehát az AOB∢ egyenesszög. A COD∢ szög szárai ellentétes félegyenesek, tehát a COD∢ egyenesszög. Akkor∢AOB∢ = ∢COD∢ = 180°.
b) Az ábránkon AOC∢ = BOD∢ = 30°.
c) Az ábránkon COB∢ = DOA∢ = 150°.
1. Az OA és az OB félegyenesek ellentétes félegyenesek; az OC és az OD félegyenesek ellentétes félegyenesek.
2. Az AOC szög szárai az OA és az OC félegyenesek, a BOD szög szárai pedig az OB és az OD félegyenesek.
Átfogalmazások: R1: Az AOC és a BOD szögek szárai ellentétes félegyenesek.
R2: Az AOC és a BOD szögek szárai egymás meghosszabbításai.
3. Az AOD szög szárai az OA és az OD, félegyenesek, a BOC szög szárai pedig az OB és OC félegyenesek. Átfogalmazások: R1: Az AOD és a BOC szögek szárai ellentétes félegyenesek
R2: Az AOD és a BOC szögek szárai egymás meghosszabbításai.
Jegyezd meg!
Két szöget csúcsszögeknek nevezünk, ha száraik ellentétes félegyenespárok.
Bármelyik két metsző egyenes két pár csúcsszöget alkot. P M ON Q
Az OP és az OQ ellentétes félegyenesek.
Az OM és az ON ellentétes félegyenesek.
A POM∢ és QON∢ csúcsszögek.
A QOM∢ és PON∢ csúcsszögek.
Az 1. gyakorlati alkalmazásban méréssel megállapítottuk, hogy a csúcsszögek kongruensek. Ezt a tulajdonságot érveléssel fogjuk bizonyítani, bármely két csúcsszög esetén. Az érvelés lényeges a matematikában. A geometriai alakzatok néhány általános tulajdonságát különböző típusú érveléssel azonosítják és bizonyítják, mivel a mérés nem elegendő.
Szótár
Érvelés = olyan módszer, amelynek során az ismert információk összekapcsolásával új következtetéseket lehet levonni.
129 5. fejezet • Mértani alapfogalmak
A B D O d1 d2 C
1. alkalmazás:
Ha két szög csúcsszög, akkor ezek kongruensek. A B
2. gyakorlati alkalmazás
Bizonyítás. Az AOC és BOD szögek csúcsszögek. Akkor az OA és az OB ellentétes félegyenesek, tehát AOB∢ egyenesszög. Hasonlóképpen, COD∢ is egyenesszög. Következik, hogy az AOD∢ kiegészítő szöge úgy az AOC∢, mint a BOD∢ szögeknek, tehát az AOC∢ és BOD∢ szögeknek megegyezik a kiegészítő szögük, következésképpen AOB∢ ≡ COD∢ Hasonlóan, az AOD∢ és a BOC∢ szögek is csúcsszögek és ugyanaz a kiegészítő szögük, az AOC∢, tehát AOD∢ ≡ BOC∢
1. a) Rajzold le az MN egyenest és vegyél fel az MN szakaszon egy O pontot!
b) Határozd meg az MN egyenes egyik és másik oldalán keletkezett MON szögek mértékét, indokold válaszod!
c) Számítsd ki az MN egyenes egyik és másik oldalán keletkezett O szögek mértékének összegét! Megoldás.
b) A két MON szög egyenesszög, tehát mindegyik szög mértéke 180°.
c) A két szög mértékének összege 360° .
2. A mellékelt ábrán, az O pont az OA, OB, OC, OD, OE félegyenesek közös kezdőpontja. Így az O pont körül keletkeznek az AOB∢, BOC∢, COD∢, DOE∢, EOA∢, szögek, melyek belső tartományai diszjunkt halmazok .
A sík minden egyes pontja vagy egy szög belsejében, vagy egy szög egyik szárán helyezkedik el.
a) Mérd meg szögmérővel az öt megjelölt szöget!
b) Számítsd ki az AOB, BOC, COD, DOE, EOA szögek mértékének összegét! Megoldás.
a) AOB∢ = 30°; BOC∢ = 45°; COD∢ = 65°; DOE∢ = 90°; EOA∢ = 130°.
b) AOB∢ + BOC∢ + COD∢ + DOE∢ + EOA∢ = 30° + 45° + 65°+ 90° + 130°= 360°.
Jegyezd meg!
Három vagy több szöget egy pont körüli szögeknek nevezünk, ha közös csúcsuk van, belső tartományuk diszjunkt, és a sík minden egyes pontja vagy az egyik szög belsejében, vagy az egyik félegyenesen helyezkedik el.
Tétel: Egy pont körüli szögek mértékének összege 360°
Alkalmazás
1. alkalmazás: Figyeld meg az alábbi ábrákat, és állapítsd meg, hogy a megjelölt szögek csúcsszögek-e! Indokold!
130 Matematika • Tankönyv a VI. osztály számára
D C O
D E A B C O R P M N O T Z X Y O M N A B C D E O
Az A, E és C pontok nem kollineárisak, tehát az EA és az EC félegyenesek nem ellentétesek.
Következtetés: A CED∢ és az AEB∢ szögek nem csúcsszögek.
A POR∢ és PON∢ szögeknek van egy közös száruk, tehát nem lehet mindkét száruk ellentétes félegyenespár.
Következtetés: A POR∢ és a PON∢ szögek nem csúcsszögek.
Az XOT szög szárai az OX és az OT félegyenesek. Az YOZ szög egyik szára az OZ félegyenes (ellentétes az OX-szel) és az OY félegyenes (ellentétes az OT-vel).
Következtetés: Az XOT∢ és a ZOY∢ szögek csúcsszögek
Az AEB, CED és DEA szögek vannak megjelölve. Ezeknek közös a csúcsuk közös és belső tartományuk diszjunkt, de a síkban vannak olyan pontok, amelyek nem tartoznak sem a három szög egyikének belső tartományához, sem az egyik szárához.
Következtetés: AEB∢, CED∢ és DEA∢ nem az E pont körüli szögek.
Az XOY, YOZ, ZOT és TOX szögek vannak megjelölve. Ezeknek közös a csúcsuk, belső tartományuk diszjunkt, és a sík minden pontja hozzátartozik vagy a négy szög egyikének belső tartományához, vagy a szárához.
Következtetés: XOY∢, YOZ∢, ZOT∢ és TOX∢ az O pont körüli szögek.
Az AMB, BMC, CMD, DME és EMB szögek vannak megjelölve.
Az AMB∢ és EMB ∢ szögek belseje nem diszjunkt (IntAMB∢ ⊂ IntEMB∢).
Következtetés: ∢AMB∢, ∢BMC∢, ∢CMD∢, ∢DME∢ és ∢EMB∢ nem az M pont körüli szögek. A B
Az AMB, AMC és BMC szögek vannak megjelölve.
Az AMB∢ és BMC∢ szögek belseje nem diszjunkt. Az AMC ∢és BMC∢ szögek belseje sem diszjunkt.
(IntAMB∢ ⊂ IntBMC∢ és IntAMC∢ ⊂ IntBMC∢.)
A síkban vannak olyan pontok, amelyek nem tartoznak a három szög egyikének belső tartományához sem, sem az egyik szárhoz.
Következtetés: AMB∢, BMC∢, AMC∢ nem az M pont körüli szögek.
Megoldott feladat: Az AD, BE és CF egyenesek az O pontban metszik egymást.
Tudva azt, hogy COD∢ = 30° és AOB∢ = 90°, határozd meg a FOA, DOE, BOC, EOF szögek mértékét!
Megoldás. A COD∢ és FOA∢ szögek csúcsszögek, tehát COD∢ ≡ FOA∢, következik, hogy FOA∢ = 30°.
Másfelől, AOB∢ és DOE∢ csúcsszögek, tehát AOB∢ ≡ ∢DOE∢, következik, hogy DOE∢ = 90°.
BOC∢ és EOF∢ csúcsszögek, tehát BOC∢ ≡ EOF∢.
2. alkalmazás: Figyeld meg az alábbi ábrákat, határozd meg és indokold, hogy a megjelölt szögek egy pont körüli szögek-e! D E A B C
Legyen x = BOC∢ = EOF∢. Mivel egy pont körüli szögek mértékének összege 360°, következik, hogy 2 · x + 2 · 30° + 2 · 90° = 360°.
Akkor 2 · x + 240° = 360°. Visszafele út módszerét használva következik, hogy x = 60°, azaz BOC∢ = EOF∢ = 60°. Bizonyítás.
131 5. fejezet • Mértani alapfogalmak
O
T Z X Y
A B C D E M
C M
O A B 90° 30° C D F E
Gyakorlatok és feladatok
1. A mellékelt ábrán az AB és a CD egyenesek az E pontban metszik egymást. Határozd meg és nevezd meg az ábrán látható csúcsszögpárokat, és indokold meg válaszod!
2. A mértani felszerelésed segítségével szerkeszd meg:
a) az ABC és DBE csúcsszögeket;
b) az FGH és IGJ csúcsszögeket, ahol FGH∢ = 60°;
c) az MON és POQ kiegészítő és csúcsszögeket.
3. Rajzold le a AOB és COD csúcsszögeket!
a) Ha AOB∢ = 100°, számítsd ki a COD szög mértékét!
b) Ha AOB∢ + COD∢ = 170°, számítsd ki az AOB szög mértékét!
c) Ha AOB∢ = 2 · BOC∢, számítsd ki az AOD szög mértékét!
4. A mellékelt ábrán az OA, OD, illetve OB, OC ellentétes félegyenespárok és P, O, Q kollineáris pontok láthatók.
a) Bizonyítsd be, hogy AOP és DOQ csúcsszögek!
b) Ha BOP∢ = 33°, számítsd ki a COQ∢ mértékét!
c) Ha AOP∢ ≡ BOP∢ és DOQ∢ = 40°, számítsd ki a COQ szög mértékét!
5. A mellékelt ábrán az AB, CD és EF egyenesek a P pontban metszik egymást, APC∢ = BPE∢ = 28°.
A B C D P F E
a) Számítsd ki az APF, BPD szögek mértékét!
b) Felhasználva egy pont körül keletkező szögek mértékének összegét, számítsd ki CPE∢ + DPF∢.
c) Számítsd ki a CPE, DPF szögek mértékét!
6. Az AOB és COD szögek csúcsszögek és pótszögek, O ∈ AC. Számítsd ki a AOB és BOC szögek mértékét!
7. Felhasználva az ábrákon látható adatokat és jelöléseket, számítsd ki az x szám értékét és az AOB szög mértékét!
a) x° + 18°
72° A B C D O b) A B C
c) A B C
D O x° + 24° 2x°
13x° + 25°
D O 25x° + 13°
8. Számítsd ki két metsző egyenes által alkotott szögek mértékét tudva, hogy közülük két szög mértékének különbsége 56°.
9. Öt egy pont körüli szögnek ugyanaz a mértéke.
a) Határozd meg mindegyik mértékét!
b) Készíts a feladat adatainak megfelelő rajzot!
10. Adott négy egy pont körüli szög, melyek mértéke egymás utáni természetes számokkal van kifejezve fokokban. Határozd meg ezen szögek mértékét, és állapítsd meg, hogy ezek közül hány hegyesszög!
11. A következő ábrán
AOB∢ = 37°, BOC∢ = x°,
COD∢ = 2 · x°,
DOE∢ = 3 · x° és
EOA∢ = 53°.
a) Határozd meg az x szám értékét és a BOC, COD, DOE szögek mértékét!
b) Igazold, hogy az öt szög között van legalább egy kiegészítő szögpár!
12. Adott n szög az M pont körül, egyesek mértéke 30°, mások mértéke pedig 70°.
a) Határozd meg az n természetes számot!
b) Készíts a feladat adatainak megfelelő rajzot!
c) Bizonyítsd be, hogy bárhogy is rajzolnánk ezeket a szögeket, a száraik között nem lesz két ellentétes félegyenes sem!
132 Matematika • Tankönyv a VI. osztály számára
A B C D E A B C D Q P O A 37° 53° x° 2 · x° 3 · x° B C O D E
Miniteszt
45 p 1. Figyeld meg a következő ábrát, másold le a táblázatot a füzetedbe, és jelöld I betűvel, ha az állítás igaz, és H betűvel, ha az állítás hamis!
Állítás I/H
a) Az 1∢ csúcsszög a 10∢-el.
b) A 3∢ csúcsszög a 11∢-el.
c) A 12∢ és 7∢ csúcsszögek.
d) Ha 2∢ = 130°, akkor 9∢ = 50°.
e) Ha 6∢ + 8∢ = 116°, akkor 7∢ = 121°.
f) 1∢ + 2∢ + 9∢ + 10∢ = 360°.
45 p 2. Figyeld meg a következő ábrát, másold le a táblázatot a füzetedbe, és jelöld I betűvel, ha az állítás igaz, és H betűvel, ha az állítás hamis! B C D E A O
Állítás I/H
a) Az AOB, BOC, COD, DOE, EOA szögek az O pont körüli szögek.
b) Az AOB, BOC, COD, DOE szögek az O pont körüli szögek.
c) Az AOB, BOC, COD és AOD szögek az O pont körüli szögek.
d) Az AOB, BOC, COA szögek nem az O pont körüli szögek.
e) Az AOE, EOC, COA szögek az O pont körüli szögek.
Megjegyzés: Munkaidő: 20 perc Hivatalból: 10 pont
4. l. Egymás melletti szögek
Emlékeztető
A FÉLSÍK
A sík azon M pontjainak halmazát, amelyek a d egyenesnek az A ponttal azonos oldalán helyezkednek el, a d egyenes által határolt és az A pontot tartalmazó félsíknak nevezzük.
A sík azon P pontjainak halmazát, amelyek a d egyenesnek a D ponttal azonos oldalán helyezkednek el, a d egyenes által határolt és a D pontot tartalmazó félsíknak nevezzük.
Megjegyzés. A d egyenes által határolt két félsík diszjunkt (nincs egyetlen közös pontjuk sem).
α
A d egyenes által határolt és az A pontot tartalmazó félsík
A D P M d
A d egyenes által határolt és a D pontot tartalmazó félsík
Azt a szöget, mely nem nullszög és nem egyenesszög, tulajdonképpeni szögnek nevezzük. A nullszög és az egyenesszög nem tulajdonképpeni szögek.
133 5. fejezet • Mértani alapfogalmak
4 6 7 8 3 1 2 9 10 11 12 5
Oldjuk meg figyelmesen!
1. a) Írd fel az ABC és a DBC szögek közös elemeit!
b) Állapítsd meg, hogy az ABC és a CBD szögek belső tartományának vannak-e közös pontjai?
2. a) Írd fek az A′B′C′ és C′B′D′ szögek közös elemeit!
b) Állapítsd meg, hogy az A′B′C′ és a C′B′D′ szögek belső tartományainak vannak-e közös pontjaik?
Jegyezd meg!
Megoldás. A B C D a) A B pont az ABC∢ és a DBC∢ csúcsa is, tehát B közös csúcs.
A BC félegyenes közös szára az ABC∢ szögnek is, a DBC∢ szögnek is, tehát BC közös szár.
b) Az ABC∢ és DBC∢ szög belső tartománya ellentétes félsíkokhoz tartozik, tehát nincs közös pontjuk.
Azt mondjuk, hogy az ABC∢ és a DBC∢ szögek egymás melletti szögek.
Megoldás. A’ B’ C’ D’ a) A B′ pont csúcsa az A′B′C′ és a D′B′C′∢ szögnek is és a D′B′C′∢ szögnek is, tehát B∢ a két szög közös csúcsa.
A B′C′ félegyenes szára az A′B′C′∢ szögnek, és a ∢D′B′C′ szögnek is, tehát B′C′ közös szár.
b) Az A′B′C′∢ és D′B′C′∢ szögek belső tartományai ellentétes félsíkokhoz tartoznak, tehát nincs közös pontjuk. Azt mondjuk, hogy A′B′C′∢ és D′B′C′∢ szögek egymás melletti szögek.
Két tulajdonképpeni szöget egymás melletti szögeknek nevezünk ha csúcsuk közös, van egy közös száruk és belső tartományaik diszjunkt halmazok.
Fedezzük fel, értsük meg!
A fenti példa mindkét egymás melletti szögével kapcsolatosan, megfigyelhetjük, hogy:
1. A BC, félegyenes közös szára az ABC és a CBD szögeknek, és az ABD szög belső tartományában van.
2. A B′C′, félegyenes közös szára az A′B′C′ és a C′B′D′ egymás melletti szögeknek, és az A′B′D′ szög külső tartományában van.
Levezetünk egy számítási eljárást a két egymás melletti szög nem egybeeső oldalai által alkotott szög mértékének kiszámítására.
1. alkalmazás: Legyenek az AOB és a BOC egymás melletti szögek.
1. Azonosítjuk az AOC szöget, amelyet az egymás melletti szögek nem közös oldalai alkotnak.
2. Meghatározzuk az egymás melletti szögek közös oldalának helyzetét az AOC szög belső tartományához képest.
3. Kiszámítjuk az AOC szög mértékét:
a) Ha az OB félegyenes az AOC szög belső tartományában van, akkor
b) Ha az OB félegyenes az AOC szög külső tartományában van, akkor
Megjegyzés.
Ha az AOB, BOC egymás melletti szögek és B ∈ Int(AOC∢), akkor AOC∢ = AOB∢ + BOC∢.
Ha az AOB, BOC egymás melletti szögek és B ∈ Ext(AOC∢), akkor AOC∢ = 360° – (AOB∢ + BOC∢).
134 Matematika • Tankönyv a VI. osztály számára
AOC∢ =
. O A B C 75° 42° AOC∢ = AOB∢ + BOC∢; AOC∢ = 75° + 42°
AOB∢ + BOC∢
= 117°.
AOC∢ =
+ BOC
O A B C 105° 138° AOB∢, BOC∢ és
az
AOB∢ +BOC∢ + AOC∢
AOC∢ =
360° – (AOB∢
∢).
AOC∢
O pont körüli szögek, tehát
= 360°.
360° – (105° + 138°) = 117°.
A mellékelt ábrán a BM félegyenes az ABC tulajdonképpeni szög belső tartományához tartozik és ABM∢ ≡ MBC∢.
A BM félegyenest az ABC szög szögfelezőjének nevezzük.
Értelmezés. Egy tulajdonképpeni szög szögfelezőjének nevezzük azt a félegyenest, amelynek kezdőpontja a szög csúcsa, és a szög száraival kongruens szögeket alkot.
Minden tulajdonképpeni szögnek egyetlen szögfelezője van. Megjegyzés.
Ha ABC∢ egy tulajdonképpeni szög és M ∈ Int(ABC∢) úgy, hogy ABM∢ ≡ MBC∢, akkor BM félegyenes az ABC szög szögfelezője.
Ha az ABC∢ egy tulajdonképpeni szög és BM az ABC szög szögfelezője, akkor M ∈ Int(ABC∢) és ABM∢ ≡ MBC∢.
Alkalmazás
1. Szögfelező szerkesztése vonalzó és szögmérő segítségével:
1. lépés. Egy A4-es lapra rajzolj egy MON tulajdonképpeni szöget!
2. lépés. Mérd meg a lerajzolt szöget és számítsd ki MON∢ : 2.


Gyakorlati alkalmazás: Egy tulajdonképpeni szög szögfelezőjének megszerkesztése: Szükséges eszközök: egy A4-es lap, egy átlátszó fólia, ceruza, vonalzó, szögmérő, körző.
3. lépés. Szerkeszd meg a szögmérő és a vonalzó segítségével az MOP szöget, ahol P∈ Int(MON∢ ) és
MOP∢ = MON∢ : 2.
4. lépés. Határozd meg a PON szög mértékét, egymás melletti szögeket használva, vagyis
PON∢ = MON∢ – MOP∢.
Következtetés. PON∢ = MOP∢ = MON∢ : 2, tehát PON∢ ≡ MOP∢.
Vonalzó és szögmérő segítségével megrajzoltad a MON szög OP szögfelezőjét!
2. A szögfelező megszerkesztése vonalzó és körző segítségével:
1. lépés. Egy átlátszó fóliára rajzold meg az AOB tulajdonképpeni szöget.
2. lépés. Rögzítsd a körző tűjét a szög csúcsába és húzz egy körívet, mely metszi a szög mindkét szárát. Jelöld C-vel a körív és a szög OA szárának metszéspontját és D-vel a körív metszéspontját a szög OB szárával.
3. lépés. Rögzítsd a körző tűjét a C pontba és rajzolj egy körívet az AOB szög belsejében, melynek sugara nagyobb a CO távolság felénél.
4. lépés. A körző tűjét a D pontba rögzítve, ugyanakkora körzőnyílással, mint a 3. lépésben, rajzolj még egy körívet az AOB szög belső tartományában. Ez a 3. lépésben rajzolt körívet az M pontban fogja metszeni.
5. lépés. Vonalzóval húzd meg az OM félegyenest!
6. lépés. Hajtsd be a fóliát az OM félegyenes mentén!
Következtetés. Az MOA és az MOB szögek átfedéssel egybeesnek, tehát kongruensek.
Vonalzó és körző segítségével megszerkesztetted az SQR szög QT szögfelezőjét!
A szögfelező megszerkesztésének két módját lásd a digitális tankönyvben!
135 5. fejezet • Mértani alapfogalmak
M A B C
C A M B
A C D B O A B O M
B A M O
Megoldott feladatok
1. feladat
A mellékelt ábrán AOB∢ = 100°, BOC∢ = 52°, AOD∢ = 84°. Határozd meg az AOC és a BOD szögek mértékét, ha lehetséges, használj egymás melletti szögeket!
Megoldás. Könnyedén észrevesszük, hogy B∈ Int(AOC∢), tehát AOC∢ = AOB∢ + BOC∢, tehát AOC∢ = 100° + 52° = 152°.
Egymás melletti szögek segítségével a BOD tulajdonképpeni szög mértékének kiszámításához két lehetőségünk van:
1. C ∈ Int(BOD∢) és BOD∢ = BOC∢ + COD∢. Felhasználva az egy pont körüli szögek mértékének összegét, kapjuk: COD∢= 124°, és BOD∢ = 52° + 124°= 176°.
2. A ∈ Ext(BOD∢) és BOD∢ = 360° – (AOD∢ + AOB∢) = 360° – (84° + 100°) = 176°.
2. feladat
a) Számítsd ki az AOB és a BOC egymás melletti szögek szögfelezői által alkotott szöget, tudva azt, hogy AOB∢ = 70°, BOC∢ = 110°.
b) Igazold, hogy két egymás melletti kiegészítő szög szögfelezői derékszöget alkotnak!
Megoldás.
a) Legyen OM az AOB szög szögfelezője, és legyen ON a BOC szög szögfelezője. Akkor, AOM∢ = MOB∢ = AOB∢ : 2 = 70° : 2 = 35°, és
BON∢ = NOC∢ = BOC∢ : 2 = 110° : 2 = 55°.
Mivel MOB∢ és BON∢ egymás melletti szögek, következik, hogy
MON∢ = MOB∢ + BON∢ = 35° + 55° = 90°.
b) Legyen OM az AOB szög szögfelezője, és legyen ON a BOC szög szögfelezője. Ha AOB∢ = x°, akkor, BOC∢ = 180°– x°. Mivel MOB∢ és BON∢ egymás melletti szögek és MOB∢ = x° : 2, BON∢ = (180°– x°) : 2, amiből következik, hogy
MON∢ = MOB∢ + BON∢ = [x° + (180°– x° )] : 2 = 90°.
Következtetés: Két egymás melletti kiegészítő szög szögfelezői derékszöget alkotnak.
Átfogalmazás: Két egymás melletti kiegészítő szög szögfelezői a két szög közös szárával pótszögeket alkotnak.
Gyakorlatok és feladatok
1. A mellékelt ábrán több szög van ábrázolva.
Másold le a táblázatot a füzetedbe, és töltsd ki I betűvel, ha az állítás igaz, és H betűvel, ha az állítás hamis!
Állítás I/H
Az AOB és a BOC egymás melletti szögek.
Az AOC és a COD nem egymás melletti szögek.
Az AOB és a BOD egymás melletti szögek.
Az AOC és a BOD egymás melletti szögek.
Az AOD és a BOC nem egymás melletti szögek.
136 Matematika • Tankönyv a VI. osztály számára
A B B’ C D D’ O 52° 84° 100°
A B N M C O 55° 55° 35° 35°
A B N M C O x° 2 x° 2 180° – x° 2 180° – x° 2
A B C D O
2. Határozd meg, melyik esetben szögfelezője az AM félegyenes a BAC szögnek!
a) b) c) d)
3. Rajzold le az ABC és az ABD egymás melletti szögeket, majd minden esetben számítsd ki a CBD szög mértékét!
a) ABC∢ = 35°, ABD∢ = 45°;
b) ABC∢ = 137°, ABD∢ = 73°.
4. Rajzold le az AOB és a BOC egymás melletti szögeket úgy, hogy:
a) pótszögek és AOB∢ = 50°;
b) kiegészítő szögek és BOC∢ = 30° + AOB∢.
5. Az OM félegyenes az AOB szög szögfelezője.
Határozd meg:
a) az AOM és a BOM szögek mértékét úgy, hogy
AOB∢ = 100°;
b) az AOB, szög mértékét úgy, hogy
AOM∢ = 44°30′ .
6. Adottak az AOB és a COD csúcsszögek. Az M pont az AOD szög belsejében helyezkedik el úgy, hogy
AOB∢ = DOM∢ = 60°.
a) Számítsd ki a COD és az AOD szögek mértékét!
b) Igazold, hogy az OM félegyenes az AOD szög szögfelezője!
7. Bizonyítsd be, hogy ha az AOM∢ és BON∢ szögek kongruensek, az OA és az OB félegyenesek pedig ellentétesek, és az OM és az ON félegyenesek az AB egyenes különböző oldalán helyezkednek el, akkor az OM és az ON félegyenesek is ellentétes
Miniteszt
félegyenesek!
8. Az APB, BPC, CPD, DPA szögek a P pont körüli szögek, PC a BPD szög szögfelezője, PE pedig a PB félegyenes ellentétes félegyenese. Felhasználva a rajzon látható adatokat, számítsd ki a BPE, BPD, BPC, CPD és DPA szögek mértékét!
68° B A
C D E P
36°
9. a) Rajzold le a mellékelt kép vázlatát, minden utat egy félegyenes jelöl, melyek kezdőpontja az A pont! Így az AB, AC, AD, AE, AF félegyeneseket láthatjuk.
A D C F B E














b) Tudva, hogy a DAC derékszög, BAC∢= DAE∢ = = 30° és az AF félegyenes ellentétes félegyenese a CAD szög szögfelezője, számítsd ki az A pont körül keletkezett szögek mértékét!
50 p 1. Állapítsd meg, a mellékelt ábrákon látható szögpárok közül melyek egymás melletti szögek, és melyek nem egymás melletti szögek! Válaszod minden esetben indokold! a)
40 p 2. Az MON szög mértéke 120° az OA félegyenes a szög belsejében helyezkedik el, úgy, hogy AOM∢ = 10° + AON∢. Határozd meg az AOM és az AON szögek mértékét!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
137 5. fejezet • Mértani alapfogalmak
B C M 45° 45° A B C M 41° 39° A A B C M 135° 135° B A C M 46° 92°
b) c) d) e) 1 2 3 4 5 6 7 8 9 10
5.2. Párhuzamos egyenesek
1. l. Párhuzamos egyenesek. A párhuzamosok axiómája
Emlékeztető
Két különböző egyenes kölcsönös helyzetét a két egyenes közös pontjainak száma adja meg.
Egy síkban két különböző egyenes esetén a következő helyzetek lehetségesek:
A két egyenes kölcsönös helyzete
Párhuzamos egyenesek
Metsző vagy összefutó egyenesek
Megjegyzések.
Leírás/értelmezés Ábrázolás Matematikai szimbólumokkal
Egy síkban lévő két egyenest, amelyeknek nincs közös pontjuk, párhuzamos egyeneseknek nevezünk. d2 d1 d1 ∥ d2 d1 ⋂ d2 = ∅
Két egyenest, melyeknek egyetlen közös pontjuk van, metsző vagy öszszefutó egyeneseknek nevezzük. A a b a ∦ b a ⋂ b = {A}
1. A síkban két különböző egyenes vagy párhuzamos vagy összefutó.
2. Egy szakasz vagy egy félegyenes párhuzamos egy másik szakasszal vagy félegyenessel, ha tartóegyeneseik párhuzamosak.
Fedezzük fel, értsük meg!
Szótár
Egy szakasz, illetve egy félegyenes tartóegyenese egy olyan egyenes, amely tartalmazza a szakasz, illetve a félegyenes minden pontját.
Példa: az AB egyenes az AB szakasz tartóegyenese, de az AB és a BA félegyeneseké is.
Néha a tapasztalat és a környezetükben lévő tárgyak alapján felmérjük, hogy egy síkban két különböző egyenes párhuzamos vagy öszszefutó. Hátránya az, hogy az optikai csalódások vagy más tényezők befolyásolhatják az érzékelésünket.







Mindennapjainkban gyakran viszonyítjuk egymáshoz két egyenes helyzetét.


Az első képen egyértelműen látszik, hogy a vágányok, amelyeken a két kocsi halad, párhuzamosak. A második kép esetében, ha nem tudnánk tapasztalatból, hogy a vasúti sínek párhuzamos egyenes vonalakon haladnak, hajlamosak lennénk azt mondani, hogy a két sín nem is olyan messze, egy pontban találkozik.
A valóságban létező párhuzamos egyeneseket mértani eszközökkel geometriai ábrákká alakítjuk.
Megjegyzés. A matematika munkafüzetben az oldal négyzethálóját használhatjuk arra, hogy párhuzamos egyeneseket rajzoljunk.
A mértan feladatok megoldásában két egyenes párhuzamosságát úgy ellenőrizzük, vagy úgy szerkesztünk két párhuzamos egyenest vonalzó és derékszögű vonalzó segítségével, ahogy azt a következő alkalmazásban leírjuk (eltolás segítségével).
138 Matematika • Tankönyv a VI. osztály számára
1. gyakorlati alkalmazás: A d egyenesen kívül fekvő A ponton áthaladó és a d egyenessel párhuzamos egyenes megszerkesztésének eljárása.
Szükséges eszközök: matematika füzet, vonalzó, derékszögű vonalzó, egy hegyes ceruza.
1. lépés
A szerkesztés
menetének
szakaszai
A derékszögű vonalzó egyik oldalát a d egyenesre helyezzük.
2. lépés
A vonalzót a derékszögű vonalzó egy másik oldalához illesztjük, úgy, hogy mikor eltoljuk a derékszögű vonalzót a rögzített vonalzó mentén, az az A ponton haladjon át.
3. lépés
A derékszögű vonalzó mentén meghúzzuk a párhuzamost, amely áthalad az A ponton.
4. lépés
Jelöljük d’-tel, a d egyenessel párhuzamos egyenest, mely áthalad az A ponton, amely nincs a d egyenesen.
Végső
ábrázolás
Tanulmányozd a digitális tankönyvet, hogy élőben lásd a d egyenesen kívül fekvő A ponton áthaladó és a d egyenessel párhuzamos egyenes megszerkesztésének eljárását vonalzó és derékszögű vonalzó segítségével. A fenti szerkesztés intuitív módon bizonyít egy alapigazságot, az úgynevezett párhuzamossági axiómát.
Párhuzamossági axióma (Euklidész axiómája)
Egy egyenesen kívül fekvő ponton keresztül az adott egyeneshez egyetlen párhuzamos egyenes húzható.
Alkalmazás
Szótár
axióma = egy alapigazság, amely elemi fogalmakra épül, és elfogadjuk bizonyítás nélkül.
A párhuzamossági axiómából kiindulva érvekkel bizonyíthatunk más fontos eredményt is.
1. tétel (a párhuzamossági reláció tranzitivitása): Két különböző egyenes, melyek párhuzamosak egy harmadik egyenessel, egymással is párhuzamosak. a c b
Átfogalmazás matematikai szimbólumokkal: Legyenek a, b és c különböző egyenesek. Ha a ∥ b és b ∥ c, akkor a ∥ c
Egy bizonyításban fontos azonosítani a feladat vagy a tétel feltevését (az ismert adatokat) és a következtetést (amit bizonyítani kell).
Ekkor a bizonyítani való állítást átfogalmazhatjuk: „Ha, feltevés, akkor, következtetés” alakba.
Ebből a szempontból a fenti tétel a következőképpen értelmezhető:
Szótár
Tétel = Olyan állítás, amelyet logikus érvekkel bizonyítunk.
Bizonyítás = a kiindulási adatok és a már ismert egyéb eredmények által szolgáltatott információk alapján hozott érvek sorozata, amelyek alapján a következtetésre jutunk.
Feltevés Következtetés Bizonyítás. Tudjuk, hogy a ∥ b, b ∥ c, a ≠ c és szeretnénk igazolni, hogy a ∥ c. Az 1. megjegyzés alapján, az a és a c egyenes vagy metszi egymást, vagy párhuzamosak. Tételezzük fel, hogy a ∦ c. Akkor, a és c egyenesek egy M pontban metszik egymást, a b egyenesen kívül.
a ∥ b
Következik a ∥ b, ahol M ∈ a, és c ∥ b, ahol M ∈ c, vagyis az M ponton keresztül, létezik két különböző párhuzamos egyenes a b egyenessel, ami ellentmond a párhuzamossági axiómának. Következésképpen, az a ∦ c kijelentés hamis, vagyis az a ∥ c kijelentés igaz.
139 5. fejezet • Mértani alapfogalmak
A d A d A d A d A d d’ d′ ∥ d, A ∈ d′ és A ∉ d
b ∥ c a ≠ c a ∥ c
1. megjegyzés: Az 1. tétel két egyenes párhuzamosságának az egyik bizonyítási módszere.
2. tétel Adottak az A, B, C pontok, ha az AB, AC, BC szakaszok közül kettő párhuzamos d egyenessel, akkor az A, B, C pontok kollineárisak.
Bizonyítás. Legyenek A, B, C különböző pontok úgy, hogy AB ∥ d és AC ∥ d. A párhuzamossági axiómából következik, hogy az AB és a CD egyenesek egybeesnek, vagyis az A, B és C pontok kollineárisak.
2. megjegyzés: A 2. tétel három pont kollineáritásának az egyik bizonyítási módszere.
Gyakorlatok és feladatok
1. a) Azonosítsd a padtársaddal közösen az alábbi képeken azokat az éleket, amelyek párhuzamos egyenesek részét képezik:

b) Azonosíts metsző egyeneseket és párhuzamos egyeneseket, a képen levő helyiségnek a fala, a mennyezete és a padlója metszésvonalainak segítségével!
2. Anna több egyenest rajzol a matematikafüzetébe.
Figyeld meg Anna rajzát, használj esetleg mértani felszerelést vagy a füzet négyzethálóját, és határozz meg: a) párhuzamos egyenespárokat; b) metsző egyenespárokat.
3. Figyeld meg a mellékelt ábrát, másold le a füzetedbe a táblázatot és a pontozott helyeket töltsd ki a ∥ vagy ∦, szimbólumokkal úgy, hogy igaz állításokat kapj!
a b b c c d d e
a … c b … d c … e
a … d b … e
a … e
4. Adott az a egyenes és az A pont, mely nincs az a egyenesen.
a) Szerkeszd meg az A ponton keresztül azt a b egyenest, mely párhuzamos az a egyenessel!
b) Szerkeszd meg az A ponton keresztül azt a c egyenest, mely nem párhuzamos az a egyenessel!
5. Karikázd be a helyes válasznak megfelelő betűt!
Csak egy helyes válasz van.
a) Egy egyenesen kívül levő ponton keresztül húzható:
A. bármilyen sok párhuzamos egyenes az adott egyenessel;
B. két különböző egyenes, melyek párhuzamosak az adott egyenessel;
C. egyetlen egyenes, mely párhuzamos az adott egyenessel.
b) Egy egyenesen kívül levő ponton keresztül húzható:
A. bármilyen sok metsző egyenes az adott egyenessel;
B. két különböző egyenes, melyek összefutnak az adott egyenessel;
C. egyetlen egyenes, mely összefutó az adott egyenessel.
6. A d egyenes egyik és másik oldalán felvesszük az A, illetve B pontokat. Szerkeszd meg az A ponton keresztül az a egyenest, mely párhuzamos a d egyenessel, majd a B ponton keresztül a b egyenest, mely párhuzamos a d egyenessel. Határozd meg az a és a b egyenes kölcsönös helyzetét, indokold válaszod!
7. Az A és E pontok az ABCD téglalap BC oldalának egyik és másik felén helyezkednek el úgy, hogy BE ∥ CD és BE ≡ CD. Igazold, hogy B az AE szakasz felezőpontja.
140 Matematika • Tankönyv a VI. osztály számára
d e a b c a c b d B A C d
Miniteszt
45 p 1. Adottak az A, B, C különböző pontok és a d egyenes. Ha AB ∥ d és AC ∥ d, bizonyítsd be, hogy az A, B, C pontok kollineárisak!
45 p 2. ABCD és CDMN téglalapok úgy, hogy A, D, M pontok és a B, C, N pontok is kollineárisak. Másold le a füzetedbe a táblázatot és az
üres helyekre írj I betűt, ha az állítás igaz, és H betűt, ha az állítás hamis.
A D
M B C N Állítás I/H
AB ∥ CD
BC ∦ MN
AM ∥ BN
AB ∦ MN
CD ∦ BN
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
2. l. Két különböző egyenes és egy szelő által alkotott szögek
A mellékelt ábrán több egyenest tüntettünk fel. Figyeld meg a következő egyenes-hármasokat (b, c, d); (c, e, f); (a, b, f); (b, c, f).
A síkban három különböző egyenes a következőképpen helyezkedhet el:
1. kettesével párhuzamosak: Például, b ∥ c ∥ d.
2. összefutó egyenesek (van egy közös pontjuk): A c, e, f egyenesek az M pontban metszik egymást; c ⋂ e ⋂ f = {M}.

3. egyik egyenes metszi a másik két egyenest (különböző pontokban metszi az egyeneseket): a b c d e Q P f M
Az f egyenes metszi az a és a b egyenest, úgy, hogy a ⋂ f = {Q}, b ⋂ f = {P} és Q ≠ P. Azonosíts az ábrán és a valóságban más egyenes-hármasokat, melyeket egy szelő metsz!
Fedezzük fel, értsük meg!
Adottak az a és b különböző egyenesek, melyeket a c szelő az A és B pontokban metsz. Az A pont körül keletkeznek az A1∢, A2∢, A3∢, A4∢ szögek, a B pont körül pedig B1∢, B2∢, B3∢, B4∢ szögek.
Figyelembe véve a nyolc szög helyzetét a c szelőhöz és az a és b egyenesekhez képest, szögpárokba csoportosítjuk őket, amelyek közül az egyik az A csúcsban, a másik pedig B csúcsban van, és mindegyiknek külön elnevezése van. a
A szelőhöz viszonyított helyzetük alapján: a szelő egyik és másik oldalán helyezkednek el, vagy a szelő ugyanazon oldalán helyezkednek el. Azokat a szögeket, melyek a szelő egyik és másik oldalán helyezkednek el, váltószögeknek nevezzük.
141 5. fejezet • Mértani alapfogalmak
Oldjuk meg figyelmesen!
N
4
B
1 3 3 1 2 2
4 c b A
Az a és b egyenesekhez képest lehetnek: belső szögek, vagyis az a és b egyenesek között helyezkednek el, illetve külső szögek, ha az a és b egyenesek által alkotott sávon kívül helyezkednek el. Így jönnek létre a: belső váltószögek, külső váltószögek, megfelelő szögek, a szelő ugyanazon oldalán lévő belső szögek, a szelő ugyanazon oldalán levő külső szögek, ahogy a következő táblázatban is látható: belső
váltószögek külső váltószögek megfelelő szögek
A3∢ és B1∢;
A4∢ és B2∢
A1∢ és B3∢;
A2∢ és B4∢
A1∢ és B1∢; A2∢ és B2∢;
A3∢ és B3∢; A4∢ és B4∢
a szelő ugyanazon oldalán levő belső szögek
A3∢ és B2∢;
A4∢ és B1∢
a szelő ugyanazon oldalán levő külső szögek
A1∢ és B4∢;
A2∢ és B3∢
Megjegyzés. A megfelelő szögek a szelő ugyanazon oldalán helyezkednek el, az egyik belső, a másik külső szög.
Alkalmazás
Megoldott feladat:
A d egyenes metszi az a, b, c egyeneseket és ezekkel a mellékelt ábrán látható szögeket alkotja.
Tudva, hogy 1∢ = 8∢ = 115°
és 7∢ = 10∢, számítsd ki:
a) 2∢, 3∢, 4∢;
b) 5∢, 6∢, 7∢;
c) 9∢, 10∢, 11∢ és 12∢.
Gyakorlatok és feladatok
1. Tanulmányozd és elemezd a mellékelt ábrát. Másold le a szöveget a füzetedbe és töltsd ki a pontozott helyeket úgy, hogy igazak legyenek az állítások!
a c b d
a) Az a egyenes szelője a … és … egyeneseknek.
b) A b egyenes szelője a … és … egyeneseknek.
c) A c egyenes nem szelője a … és a …, illetve a … és a … egyenespároknak.
Megoldás.
a) 1∢ és 3∢ csúcsszögek.
Mivel 1∢ = 115°, következik, hogy 3∢ = 115°.
1∢ és 2∢ kiegészítő szögek. Akkor , 2∢ = 65°.
2∢ és 4∢ csúcsszögek, tehát 4∢ = 65°.
b) Hasonló gondolatmenettel kapjuk, hogy: 6∢ = 115°, 5∢ = 65°, 7∢ = 65°.
c) Mivel 7∢ = 10∢ és 7∢ = 65°, következik: hogy 10∢ = 65°.
Akkor, 9∢ = 115°, 11∢ = 115°, 12∢ = 65°.
2. Az AOB hegyesszög OA, illetve OB szárán vedd fel az M, illetve N pontokat, rajzold meg az MN egyenest. Másold le a füzetedbe a táblázatot és írj I betűt, ha az állítás igaz, illetve H betűt, ha az állítás hamis.
Állítás I/H
p1: Az AM és BN egyenes metsző egyenesek.
p2: Az MN egyenes szelője az OA és az OB egyeneseknek.
p3: Az OMN és az ONM szögek megfelelő szögek, melyeket az OA és az OB egyenes alkot az MN szelővel.
142 Matematika • Tankönyv a VI. osztály számára
a d b c 1 2 3 4 5 6 7 8 9 10 11 12
3. A mellékelt ábrán az 1, 2, 3, …, 7, 8 szögek láthatók, melyeket a d1 és a d2 egyenesek alkotnak az s szelővel. Másold le a szöveget a füzetedbe és töltsd ki a pontozott helyeket, úgy, hogy igazak legyenek az állítások!
d) A 3 és a 6 szögek … .
e) A 2 és a 7 szögek … .
4. A 3-as feladat ábráját használva:
a) Számítsd ki a 3 és a 4 szögek mértékét, tudva, hogy 1∢ = 54°.
b) Számítsd ki a 6 és a 8 szögek mértékét, tudva, hogy 5∢ + 7∢ = 72°.
5. Az a és a b egyenesek a c szelővel az ábrán látható szögeket alkotják.
Tudva, hogy 4∢ = 6∢, igazold, hogy:
a) Az 1 és 5 szögek … .
b) A 4 és a 6 szögek … .
c) A 2 és a 8 szögek … .
Miniteszt
a) 3∢ ≡ 5∢;
b) 2∢ ≡ 8∢;
c) 4∢ + 5∢ = 180°.
A következő ábrán számjegyekkel jelöltük az a és b egyenesek és a d szelő által alkotott szögeket.
Válaszd ki a helyes válasznak megfelelő betűjelet! Csak egy helyes válasz van.
18 p 1. Egy belső váltószögpár:
A. 2∢ és 4∢
B. 1∢ és 6∢
18 p 2. Egy külső váltószögpár:
C. 1∢ és 7∢; D. 3∢ és 5∢.
A. 2∢ és 5∢; B. 1∢ és 8∢; C. 2∢ és 8∢; D. 4∢ és 7∢.
18 p 3. Az ábrán látható megfelelő szögpárok száma:
A. 2; B. 4; C. 3; D. 1.
18 p 4. Egy a szelő ugyanazon oldalán fekvő belső szögpár:
A. 1∢ és 7∢; B. 3∢ és 5∢; C. 3∢ és 6∢; D. 4∢ és 7∢
18 p 5. Egy a szelő ugyanazon oldalán fekvő külső szögpár:
A. 2∢ és 7∢; B. 2∢ és 6∢; C. 3∢ és 8∢; D. 2∢ és 8∢.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
3. l. Két párhuzamos egyenes és egy szelő által alkotott szögek. Párhuzamossági kritériumok
Fedezzük fel, értsük meg!
Két egyenesnek egy szelővel alkotott szögpárjai nagyon hasznosnak bizonyulnak az a ∥ b sajátos esetben. Legynek MN ∥ PQ egyenesek és az AB szelő, A ∈ MN és B ∈ PQ. Mérd meg a két belső váltószögpár szögeinek mértékét! Hasonlítsd össze az MAB és a QBA szögek mértékét, majd hasonlítsd össze az NAB és a PBA szögek mértékét!
Az AB szelő az MN és PQ egyenesekkel kongruens belső váltószögpárokat alkot: MAB∢ ≡ QBA∢ és NAB∢ ≡ PBA∢.
143 5. fejezet • Mértani alapfogalmak a 1 2 3 4 5 6 7 8 b s
d1 s d2 4 2 1 5 6 7 8 3
a 1 2 3 4 5 6 7 8
d
;
b
;
M B P Q N A
1. tétel (belső váltószögek tétele): Ha két egyenes párhuzamos, akkor bármely szelővel kongruens belső váltószögeket alkotnak.
Az 1. tétel alapján más eredményekre is következtethetünk két párhuzamos egyenes és egy szelő által alkotott szögek esetén.
2. tétel (külső váltószögek tétele): Ha két egyenes párhuzamos, akkor bármely szelővel kongruens külső váltószögeket alkotnak.
Bizonyítás. Legyen MN ∥ PQ és CD szelő, úgy, hogy CD ⋂ MN = {A} és CD ⋂ PQ = {B}. A CAM és QBD szögek külső váltószögek.
M B C D P Q N A
Az 1. tétel alapján MAB∢ ≡ QBA∢ (belső váltószögek).
De MAB∢ és az MAC∢ kiegészítő szögek, QBA∢ és az QBD∢ kiegészítő szögek, tehát MAC∢ és QBD∢ kiegészítő szögek kongruensek, következik, hogy MAC∢ ≡ QBD∢.
Feladat a portfólióba. Alkalmazd a fenti gondolatmenetet, és igazold, hogy: CAN∢ ≡ DBP∢.
Kongruens külső váltószögpárok: MAC∢ ≡ QBD∢ és CAN∢ ≡ DBP∢.
3. tétel (a megfelelő szögek tétele): Ha két egyenes párhuzamos, akkor bármely szelővel kongruens megfelelő szögeket alkotnak.
Bizonyítás. NAB∢ kiegészítő szög az MAB∢ szöggel, a DBQ∢ pedig kiegészítő szöge a QBA∢ szögnek. Az 1. tételből következik, hogy MAB∢ ≡ QBA∢ (belső váltószögek), tehát NAB∢ és DBQ∢ szögeknek a kiegészítő szögei kongruensek, vagyis NAB∢ ≡ DBQ∢.
Feladat a portfólióba. Alkalmazd a fenti gondolatmenetet, és igazold, hogy: CAM∢ ≡ ABP∢; CAN∢ ≡ ABQ∢; BAM∢ ≡ DBP∢.
Kongruens megfelelő szögpárok: CAM∢ ≡ ABP∢, CAN∢ ≡ ABQ∢, DBP∢ ≡ BAM∢, NAB∢ ≡ DBQ∢.
4. tétel (a szelő ugyanazon oldalán fekvő belső szögek tétele): Ha két egyenes párhuzamos, akkor bármely szelővel a szelő ugyanazon oldalán található belső szögek, kiegészítő szögek.
C P Q N A
M B
D
Bizonyítás. NAB∢ kiegészítő szöge az MAB∢ szögnek, az 1. tétel alapján, MAB∢ ≡ QBA∢ (belső váltószögek). Ekkor NAB∢ kiegészítő szöge a QBA∢ szögnek, azaz NAB∢ + QBA∢ = 180°.
Feladat a portfólióba. Alkalmazd a fenti gondolatmenetet, és igazold, hogy: MAB∢ + PBA∢ = 180°.
Kiegészítő, a szelő ugyanazon oldalán fekvő belső szögpárok: NAB∢ kiegészítő szöge a QBA∢ szögnek, az MAB∢ pedig kiegészítő szöge a PBA∢ szögnek.
144 Matematika • Tankönyv a VI. osztály számára
B
P Q N A
M
C D
5. tétel (a szelő ugyanazon oldalán fekvő belső szögek tétele): Ha két egyenes párhuzamos, akkor bármely szelővel a szelő ugyanazon oldalán található külső szögek, kiegészítő szögek.
D C P Q
Bizonyítás. NAC∢ kiegészítő szöge az NAB∢ szögnek, a 3. tétel alapján, NAB∢ ≡ QBD∢ (megfelelő szögek). Ekkor QBD∢ kiegészítő szöge az NAC∢ szögnek, vagyis NAC∢ + QBD∢ = 180°.
Feladat a portfólióba. Alkalmazd a fenti gondolatmenetet, és igazold, hogy: MAC∢ + PBD∢ = 180°.
Kiegészítő, a szelő ugyanazon oldalán fekvő külső szögpárok: NAC∢ kiegészítő szöge a QBD∢ szögnek és MAC∢ kiegészítő szöge a PBD∢ szögnek.
Megjegyzés. A mértan feladatok megoldása során gyakran szükséges igazolni, hogy két szög kongruens vagy azt, hogy kiegészítő szög. Ilyenkor olyan alakzatot keresünk, amely két párhuzamos egyenesből áll, amelyeket egy szelő metsz, és amely során kongruens vagy kiegészítő szögpár keletkezik.
Alkalmazás
Ha felcseréljük egy tétel feltevését a következtetésével, és igaz állítást kapunk, akkor azt az eredeti tétel fordított (reciprok) tételének nevezzük.
Adottak az MN és PQ különböző egyenesek, melyeket a CD szelő metsz úgy, hogy CD ⋂ MN = {A} és CD ⋂ PQ = {B}.
A fenti tételek fordítottjai igazak, és elégséges feltételeket nyújtanak, hogy két egyenes párhuzamos legyen. Ezeket a tételeket párhuzamossági kritériumoknak nevezzük.
Szótár
Párhuzamossági kritérium = egy olyan tétel, amelynek segítségével bizonyítjuk két egyenes párhuzamosságát
Az MN és PQ különböző egyenesek esetén, melyeket a CD szelő metsz, ahol CD ⋂ MN = {A} és CD ⋂ PQ = {B}, alkalmazva a fenti ábrázolást, megfogalmazzuk az 1-5. tétel fordított tételeit és a következő párhuzamossági kritériumokhoz jutunk.
Párhuzamossági kritériumok: Matematikai szimbólumokkal:
K1: Ha két egyenes egy szelővel kongruens belső váltószögszögpárokat alkot, akkor a két egyenes párhuzamos.
K2: Ha két egyenes egy szelővel kongruens külső váltószögszögpárokat alkot, akkor a két egyenes párhuzamos.
K3: Ha két egyenes egy szelővel kongruens megfelelő szögpárokat alkot, akkor a két egyenes párhuzamos.
K4: Ha két egyenes egy szelővel a szelő ugyanazon oldalán fekvő kiegészítő belső szögpárokat alkot, akkor a két egyenes párhuzamos.
K5: Ha két egyenes egy szelővel a szelő ugyanazon oldalán fekvő kiegészítő külső szögpárokat alkot, akkor a két egyenes párhuzamos.
Ha MAB∢ ≡ QBA∢, akkor MN ∥ PQ.
Ha NAB∢ ≡ PBA∢, akkor MN ∥ PQ.
Ha CAN∢ ≡ PBD∢, akkor MN ∥ PQ
Ha CAM∢ ≡ QBD∢, akkor MN ∥ PQ.
Ha CAN∢ ≡ ABQ∢, akkor MN ∥ PQ.
Ha CAM∢ ≡ ABP∢, akkor MN ∥ PQ.
Ha MAB∢ ≡ PBD∢, akkor MN ∥ PQ.
Ha NAB∢ ≡ QBD∢, akkor MN ∥ PQ.
Ha MAB∢ + PBA∢ = 180°, akkor MN ∥ PQ
Ha NAB∢ + QBA∢ = 180°, akkor MN ∥ PQ.
Ha CAM∢ + PBD∢ = 180°, akkor MN ∥ PQ.
Ha CAN∢ + QBD∢ = 180°, akkor MN ∥ PQ.
Megjegyzés. A párhuzamossági kritériumok számos egyszerű és hatékony eszközt biztosítanak számunkra két egyenes párhuzamosságának bizonyítására.
145 5. fejezet • Mértani alapfogalmak
C A B M P Q D N
N M A B
Gyakorlatok és feladatok
1. Jelöljük úgy mint a mellékelt ábrán az a és b párhuzamos egyenesek és az s szelő által alkotott szögeket. Keress az ábrán az alábbi szögekre példát, és indokold választásodat!
a) az 1∢ szöggel kongruens szöget;
b) a 6∢ szöggel kongruens szöget;
c) a 3∢ szöggel kiegészítő szöget.
2. A mellékelt ábrán, az a és b egyenesek párhuzamosak, a 7∢ szög mértéke 65°. Számítsd ki a 3∢ és a 6∢ mértékét!
3. A mellékelt ábrán, az AB és CD egyenesek párhuzamosak. Az MN szelő az AB egyenest az E pontban, a CD egyenest pedig az F pontban metszi.
a) Tudva, hogy AEF∢ = 126°, számítsd ki az EFD és a CFN szögek mértékét!
b) Ha NFD∢ = 77°, számítsd ki az AEM, MEB és BEF szögek mértékét!
4. A d szelő az a, b illetve b, c párhuzamos egyenes párokat metszi, ahogy a mellékelt ábrán látszik. Tudva, hogy 4∢ = 111°, számítsd ki a 6∢ és 12∢ szögek mértékét!
5. Ábrázold az 54° mértékű AOB szöget, a BC egyenest, mely párhuzamos az OA egyenessel. A C pont az AOB szög belsejében van.
a) Számítsd ki az OBC szög mértékét!
b) Ha BA az OBC szög szögfelezője, számítsd ki a BAO szög mértékét!
6. Az ABC, CBD szögek egymás melletti szögek. Az ABD szög belsejében legyenek az AM és DN félegyenesek, melyek a BC egyenessel párhuzamos egyenesek részei.
a) Bizonyítsd be, hogy AM ∥ DN.
b) Ha BAM∢ = 134° és BDN∢ = 122°, számítsd ki az ABD szög mértékét!
7. A következő ábrák mindegyikén az a és b egyenesek párhuzamosak, c pedig szelő.
a) b a c (2x + 5)° 113°
b) b a c (x + 25)° (2x + 5)°
c) a c b x° x°
Határozd meg mindenik esetben az x szám értékét!
8. Másold le a füzetedbe és töltsd ki a pontozott helyeket a ∥ vagy ∦ jelekkel, úgy, hogy igaz kijelentéseket kapj!
a b s 4
8 1 5 2 6 3 7
a) Ha 4∢ = 64° és 6∢ = 64°, akkor a ... b.
b) Ha 2∢ = 60° és 5∢ = 130°, akkor a ... b.
c) Ha 1∢ = 119° és 8∢ = 61°, akkor a ... b.
9. Legyen ABC egy derékszög és a D pont a szög külső tartományában. Tudjuk, hogy BAC∢ = 55° és CBD∢ = 35°.
a) Készíts a feladatnak megfelelő ábrát!
b) Számítsd ki az ABD szög mértékét!
c) Igazold, hogy AC és BD egyenesek párhuzamosak!
d) Számítsd ki az ACB szög mértékét!
10. Tekintsünk két párhuzamos egyenest és egy tetszőleges szelőt.
a) Bizonyítsd be, hogy két belső váltószögpár szögfelezői párhuzamosak!
b) Bizonyítsd be, hogy a szelő ugyanazon oldalán fekvő két belső szög szögfelezői merőlegesek egymásra!
146 Matematika • Tankönyv a VI. osztály számára
a d b 4 8 1 5 2 6 3 7 M A B D C N F E a c b d 1 3 5 8 10 11 12 2 4 6 7 9 a b s 4 8 1 5 2 6 3 7
Miniteszt
1. Az a és b egyeneseket az AC és BC szelők metszik (lásd a mellékelt ábrát). x° 43°
15 p a) Határozd meg az x értékét úgy, hogy az a és b egyenesek párhuzamosak legyenek!
15 p b) Az a) alpont feltételei mellett számítsd ki az ACB szög mértékét!
70°
2. Jelöljük 1, 2, 3, … , 7, 8-cal a mellékelt ábrán keletkező szögeket, melyeket a d szelővel alkotnak.
20 p a) Ha 1∢ = 75°, számítsd ki a 4∢ és 5∢ szögek mértékét!
20 p b) Ha 2∢ = 105°, számítsd ki a 6∢ és 3∢ szögek mértékét!
20 p c) Ha 1∢ + 2∢ + 3∢ = 240°, számítsd ki a 4∢ és 7∢ szögek mértékét!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
4. l. Gyakorlati alkalmazások sokszögek és mértani testek esetén
Bármely test leegyszerűsíthető, elvonatkoztatható, felosztható több elemi mértani testre, vagy elemi mértani alakzatokra. Minden ilyen elem esetében elemezhetjük a formákat, méreteket, helyzeteket, kapcsolatokat, amelyeket aztán a gyakorlatban használhatunk.
Emlékeztető
sokszög háromszög paralelogramma téglalap négyzet
Geometriai
ábrázolás
csúcsok
A B C B C
A, B, C
oldalak AB, BC, CA
BAC∢, A∢
szögek
ABC∢, B∢
ACB∢, C∢
Mértani test
A téglatest vagy derékszögű paralelepipedon
Leírás:
• 8 csúcs: A, B, C, D, E, F, G, H
• 6 lap: ABCD, EFGH, ABFE, DCGH, BCGF, ADHE
• A téglatest minden lapja téglalap.
A, B, C, D M, N, P, Q M, N, P, Q
AB, BC, CD, DA MN, NP, PQ, QM MN, NP, PQ, QM
DAB∢, A∢
ABC∢, B∢
BCD∢, C∢
CDA∢, D∢
Geometriai ábrázolás
QMN∢, M∢
MNP∢, N∢
NPQ∢, P∢
PQM∢, Q∢
QMN∢, M∢
MNP∢, N∢
NPQ∢, P∢
PQM∢, Q∢
Testháló – egy olyan síkbeli ábrázolás, amit hajtogatással az illető mértani testté alakíthatunk
147 5. fejezet • Mértani alapfogalmak
C b
a A B
a
4 7 1 6 2 5 3 8
b
s
A
M
D
N
M
Q P N
Q P
A E F G H B C D E G H A B C B1 F1 D A2 A1 E1 E2 F
A kocka
Leírás:
• 8 csúcs; A, B, C, D, E, F, G, H
• 6 lap: ABCD, EFGH, ABFE, DCGH, BCGF, ADHE
• A kocka minden lapja négyzet.
Alkalmazások
1. alkalmazás
A d egyenes az ABC háromszög AB illetve AC oldalait az M, illetve N pontokban metszi. Tudva, hogy d ∥ BC, igazold, hogy AMN∢ ≡ ABC∢ és ANM∢ ≡ ACB∢.
Teljes megoldás
Az AB egyenes a d és a BC egyenesek szelője és AB ⋂ d = {M}. Ekkor az AMN∢ és ABC∢ szögek megfelelő szögek. Mivel MN ∥ BC, következik, hogy AMN∢ ≡ ABC∢.
Az AC egyenes a d és a BC párhuzamos egyenesek szelője, és AC ⋂ d = {N}. Akkor az ANM és ACB szögek megfelelő szögek. Mivel MN ∥ BC, következik, hogy ANM∢ ≡ ACB∢.
2. alkalmazás
A paralelogrammának két pár szemben fekvő párhuzamos oldala van.
a) Igazold, hogy a paralelogramma egymás melletti szögei kiegészítő szögek!
b) Igazold, hogy a paralelogramma szemben fekvő szögei kongruensek!
Teljes megoldás.
Legyen MNPQ paralelogramma. Akkor: MN ∥ PQ és MQ ∥ NP.
a) Van négy pár egymás melletti szög: M∢ és N∢, N∢ és P∢, P∢ és Q∢, M∢ és Q∢.
Minta. Az MQ egyenes szelő az MN és PQ párhuzamos egyenesek számára. Ekkor az M∢ és N∢ szögek a szelő ugyanazon oldalán fekvő belső szögek és kiegészítő szögek, tehát M∢ + Q∢ = 180°.
A fenti minta alapján igazold, hogy:
M∢ + N∢ = N∢ + P∢ = P∢ + Q∢ = 180°.
b) A paralelogrammának két pár szemben fekvő szöge van:
M ∢ és P∢; N∢ és Q∢; Az a) alpontból következik, hogy
M∢ + N∢ = 180° (a paralelogramma egymás melletti szögei) és
N∢ + P∢ = 180° (a paralelogramma egymás melletti szögei) . Következik, hogy az M∢ és P∢ szögeknek ugyanaz a kiegészítő szöge, tehát kongruensek, vagyis ∢M ≡ ∢P.
A fenti minta alapján igazold, hogy N∢ ≡ Q∢.
Rövid megoldás:
d ∥ BC
AB szelő
⇒ AMN∢ és ABC∢
kongruens megfelelő szögek
⇒ AMN∢ ≡ ABC∢
Bizonyítsd be, hogy ANM∢ ≡ ACB∢.
Rövid megoldás
MNPQ paralelogramma ⇒ MN ∥ PQ
és MQ ∥ NP.
a) MN ∥ PQ
MQ szelő ⇒ M∢ és Q∢
a szelő ugyanazon oldalán fekvő belső kiegészítő szögek
⇒ M∢ + Q∢= 180°.
b)
MNPQ paralelogramma
M∢, N∢ egymás melletti szögek ⇒
N∢, Q∢ egymás melletti szögek
M∢ + N∢ = 180° és
⇒ N∢ + P∢ = 180°, tehát M∢ ≡ P∢.
148 Matematika • Tankönyv a VI. osztály számára
E G H A B C D F E G H A B C B1 F1 D A2 A1 E1 E2 F
d A B C N M
N P Q
M
3. alkalmazás
A mellékelt ábrán a d1 és a d2 egyenesek párhuzamosak az ABC szög
AB, illetve BC oldalaival.
A mértani ábrázolás jelöléseit használva:
a) Azonosíts a rajzon két pár párhuzamos egyenest, melyeket egy-egy szelő metsz!
b) Igazold, hogy DMP∢ ≡ ABC∢.
c) Igazold, hogy DMQ∢ kiegészítő szöge az ABC∢ szögnek.
Megoldás
a) AB ∥ DM ahol BC szelő; BC ∥ PQ ahol DM szelő
b) A BC szelő az AB és DM párhuzamos egyenesekkel az ABC∢ és BDM∢ belső váltószögeket alkotja, tehát tehát ABC∢ ≡ BDM∢.
A DM szelő a BC és a PQ párhuzamos egyenesekkel a BDM∢ és DMP∢, belső váltószögeket alkotja, tehát BDM∢ ≡ DMP∢ Következik, hogy ABC∢ ≡ BDM∢ és BDM∢ ≡ DMP∢, tehát ABC∢ ≡ DMP∢
c) A BC szelő az AB és DM párhuzamos egyenesekkel az ABC∢ és BDF∢ a szelő ugyanazon oldalán fekvő kiegészítő belső szögeket alkotja, tehát ABC∢ + BDF∢ = 180°.
A DM szelő a BC és PQ párhuzamos egyenesekkel a BDF∢ és QMD∢ megfelelő szögeket alkotja, tehát BDF∢ ≡ QMD∢. Ekkor, ABC∢ + QMD∢ = ABC∢ + BDF∢ = 180°.
Bebizonyítottuk a következő kijelentést:
Fontos megjegyzés. Bármely két szög, melynek szárai párhuzamosak, kongruensek vagy kiegészítő szögek.
4. alkalmazás
Ismertnek tekintjük, hogy a téglalapnak van egy derékszöge. Ellenőrizd a derékszögű vonalzó segítségével az állítás érvényességét! Azt is ismertnek tekintjük, hogy a téglalap szemközti oldalai párhuzamosak. Bizonyítsuk be, hogy a téglalap minden szöge derékszög!
Bizonyítás.
Rövid megoldás:
b) AB ∥ DM
BC szelő ⇒ ABC∢ és BDM∢ (belső váltószögek) (1)
BC ∥ PQ
DM szelő ⇒ BDM∢ és PMD∢ (belső váltószögek) (2)
(1) és (2), ⇒ ABC∢ ≡ PMD∢.
c) AB ∥ DM
BC szelő
BC ∥ PQ
⇒ ABC∢ + BDF∢ = 180° (a szelő ugyanazon oldalán fekvő belső szögek) (3)
DM szelő ⇒ BDF∢ ≡ QMD∢ (megfelelő szögek) (4)
(3) és (4) ⇒ ABC∢ + QMD∢ = 180°.
Legyen A∢ = 90°. Mivel BC ∥ AD, az AB szelővel az A∢ és B∢ szögek a szelő ugyanazon oldalán levő kiegészítő belső szögek, tehát B∢ = 180° – A∢ = 90°. Mivel AB ∥ CD az AD szelővel az A∢ és D∢ a szelő ugyanazon oldalán levő kiegészítő belső szögek, tehát D∢ = 180° – A∢ = 90°. Ugyanazon párhuzamosok és a BC szelő esetén a B∢ és C∢ szögek a szelő ugyanazon oldalán levő kiegészítő belső szögek, vagyis C∢ = 180° – B∢ = 90°.
Kihívás! Oldd meg ezt a feladatot felhasználva 2. alkalmazást és azt, hogy bármely téglalap paralelogramma!
5. alkalmazás
A mellékelt ábrán egy kocka látható és a BP félegyenes. Tudva azt, hogy az A, B, és P pontok kollineárisak, igazold, hogy PBC∢ = 90° és PBF∢ = 90°.
Bizonyítás.
Mivel AB ∥ CD, a BC szelő a DCB∢ és PBC∢ belső váltószögeket alkotja, tehát PBC∢ = DCB∢ = 90°.
Hasonlóan az AE ∥ BF, egyenesek, az AB szelővel az EAB∢ és FBP∢ megfelelő szögeket alkotja, tehát PBF∢ =EAB∢ = 90°.
149 5. fejezet • Mértani alapfogalmak
M B D C P Q F d1 d2 A
D C A B
E F G H A B C D P
6. alkalmazás
A szomszédos ábra egy téglatest síkbeli lefejtését ábrázolja. Az ábrán szereplő jelölésekkel bizonyítsd be, hogy:
a) az A, B, C pontok kollineárisak;
b) az E, F, G pontok kollineárisak;
c) AE ∥ CG;
d) GAC∢ = AGE∢.
Teljes megoldás:
a) Minta: ABFE és BCGF a téglatest lapjai, tehát téglalapok és minden szögük derékszög. Ekkor az ABF∢ és CBF∢ szögek egymás melletti kiegészítő szögek, tehát ABC∢ = 180° és az A, B, C pontok kollineárisak.
b) Az a) alpont mintájára alkoss egy hasonló bizonyítást a b) alpontnak.
c) Mivel AE ∥ BF és BF ∥ CG, következik, hogy AE ∥ CG
d) Az a) és b) alpontok alapján ACGE téglalap. Tekintsük az AG szelőt és az AC és EG párhuzamos egyeneseket. Ekkor a GAC∢ és AGE∢ szögek kongruens belső váltószögek, tehát ∢GAC∢ = AGE∢
7. alkalmazás
ABCDEF egy szabályos hatszög (hat oldalú sokszög). Minden szöge kongruens, mértékük 120°, és AO, BO, CO, DO, EO, FO a hatszög szögeinek szögfelezői. Igazold, hogy:
a) Az OC és AB egyenesek párhuzamosak;
b) C, O, F pontok kollineárisak;
c) A DE és AB egyenesek párhuzamosak.
Teljes megoldás:
a) A feltevésből az ABC és BCD szögek kongruensek és mértékük 120°. A CO félegyenes a BCD szög szögfelezője, tehát az OCB és az OCD szögek kongruensek, mindenik mértéke egyenlő 60°kal. Az AB és OC egyenesek és a BC szelő az OCB és ABC szögeket alkotják, melyek a szelő ugyanazon oldalán fekvő kiegészítő belső szögek (OCB∢ + ABC∢ = 180°). Következik, hogy AB ∥ OC.
b) Hasonlóan, az AB és OF egyenesek és az AF szelő esetén az OFA és BAF szögek keletkezne, a szelő ugyanazon oldalán fekvő kiegészítő, belső szögek (OFA∢ + BAF∢ = 180°). Következik, hogy AB ∥ OF. Így OC ∥ AB ∥ OF, azaz O, F, C kollineárisak
c) Hasonló gondolatmenettel bizonyítható, hogy DE ∥ OF. Akkor, DE ∥ OF és AB ∥ OF, következik, hogy DE ∥ AB.
Rövid megoldás:
a) ABFE és BCGF téglalap
⇒ ABF∢ = CBF∢ = 90°.
ABF∢ és CBF∢ egymás melletti és ABF∢ + CBF∢ = 180°, következik hogy ABC∢ = 180°, tehát A, B, C kollineáris pontok.
c) AE ∥ BF
BF ∥ CG ⇒ AE ∥ CG.
d) AC ∥ EG
AG szelő ⇒ GAC∢ ≡ AGE∢ (belső váltószögek), tehát GAC∢ = AGE∢
Rövid megoldás:
ABC∢ = BCD∢ =120° és CO szögfelező ⇒ OCB∢ ≡ OCD∢ és OCB∢ = OCD∢ = 60°.
a) OCB∢ és ABC∢ szelő ugyanazon oldalán fekvő belső szögek a BC szelő és az AB és OC egyenesek esetén. (1)
De ABC∢ + OCB∢ =180°, (1) ⇒ AB ∥ OC
b) BOCB∢ és ABC∢ a szelő ugyanazon oldalán fekvő belső szögek, ahol AF szelő, AB és OF egyenesek. (2)
De, BAF∢ + OFA∢ = 180°. (2) ⇒ AB ∥ OF
c) Hasonlóan, ED ∥ OF. ED ∥ OF és AB ∥ OF, következik ED ∥ AB
150 Matematika • Tankönyv a VI. osztály számára
E G H A B C B1 F1 D A2 A1 E1 E2 F
A B C F E D O
5.3.
Merőleges egyenesek a síkban
1. l. Merőleges egyenesek a síkban. Egy pont távolsága egy egyenestől
Oldjuk meg figyelmesen!
A mellékelt ábrán az a és b egyenesek a fémrudak tartóegyenesei, amelyekre a négy szélmalomlapátot építették.
Mivel tudjuk, hogy bármely két szomszédos lapát kongruens szögeket zár be, határozzuk meg az a és b egyenesek által bezárt szöget.
Megoldás. Legyen {O} = a ⋂ b. Az O kezdőpontú félegyenesek az O pont körül négy kongruens szöget alkotnak. Mivel egy pont körüli szögek mértékeinek összege 360°, következik, hogy a négy szög derékszög, tehát az a és b egyenesek derékszöget zárnak be. Azt mondjuk, hogy az a és b egyenesek merőlegesek.
Fedezzük fel, értsük meg!
Értelmezés Írás /Olvasás:

Ábrázolás Az a és b egyenesek merőlegesek, ha ezek derékszöget alkotnak.
• a ⊥ b vagy b ⊥ a
• a merőleges b-re, illetve b merőleges a-ra
Ha a c és d egyenes nem alkot derékszöget, akkor mindenik egyenes ferde a másik egyeneshez képest.
• c ⊥ d vagy d ⊥ c
• c nem merőleges d-re vagy c ferde d-hez képest, illetve d nem merőleges c-re vagy d ferde c-hez képest
Tétel: A síknak egy pontján keresztül egyetlen merőleges húzható egy adott egyenesre. Bizonyítás.
1. Tekintsük azt az esetet, mikor az M pont a d egyeneshez tartozik. Ekkor, egyetlen olyan egyenes létezik, mely átmegy az M ponton, az M pontból kiinduló félegyenesek az M kezdőpontú d egyenesen lévő ellentétes félegyenesekkel 90°-os szöget alkotnak.
2. Abban az esetben, mikor az M pont a d egyenesen kívül van, feltételezzük, hogy megszerkesztjük az MA és az MB merőlegeseket (A ≠ B). Ekkor az MA és az MB egyenesek az AB szelővel kongruens megfelelő (derék)szögeket alkotnak. Következik, hogy MA és MB párhuzamosak, ami ellentmond annak, hogy M közös pontjuk. A feltevés hamis, tehát egyetlen merőleges létezik.
1. M d 90°
2. M A B d
Ahhoz, hogy az M ponton keresztül szerkesszünk egy d’ merőleges egyenest a d egyenesre, használhatjuk a derékszögű vonalzónk derékszögét vagy a körzőt.
151 5. fejezet • Mértani alapfogalmak
a b
90°
≠ 90°
c
α
d
b a
Adott a d egyenes és az M pont a síkban. Két esetünk van: M ∈ d vagy M ∉ d. 1. alkalmazás Adott pontból adott egyenesre merőleges egyenes szerkesztése derékszögű vonalzó segítségével.
a) Ha M ∈ d, megszerkesztjük az M pontban a merőlegest a d egyenesre. d d ' M Szótár
1. lépés. Rögzítsd a derékszögű vonalzód derékszögének csúcsát az M pontba, úgy, hogy a derékszögének egyik oldala a d egyenesen legyen.
egy szakasz tartóegyenese = az az egyenes amelyen van az illető szakasz.
2. lépés. Meghúzzuk a d’ egyenest, amely a vonalzó derékszöge másik oldalának tartóegyenese. Megszerkesztettük az M ponton áthaladó d egyenesre merőleges egyenest. Írhatjuk: d'⊥ d és d’ ⋂ d = {M}.
b) Ha M ∉ d, szerkesszük meg az M pontból húzott merőlegest a d egyenesre. d M d d ' M
1. lépés. Helyezzük a derékszögű vonalzónkat a d egyeneshez képest az M ponttal azonos oldalra úgy, hogy a derékszöget alkotó oldalak egyike átfedje a d egyenest.
2. lépés. Mozgassuk az derékszögű vonalzónkat a d egyenes mentén addig, amíg az M pont az derékszögű vonalzó derékszögének második oldalán helyezkedik el.
3. lépés. Meghúzzuk a d’ egyenest, a derékszög másik oldalának tartóegyenesét, amely az M pontot tartalmazza. Megszerkesztettük az M ponton áthaladó d egyenesre merőleges egyenest. Írhatjuk: d’⊥ d és M ∈d’.
2. alkalmazás: Adott pontból adott egyenesre merőleges egyenes szerkesztése, körző segítségével
a) Ha M ∈ d, megszerkesztjük az M pontban a d egyenesre merőleges egyenest.
1. lépés. Rögzítsd a körző tűjét az M pontban és rajzolj egy kört! Jelöld az A és a B pontokat, melyekben a kör metszi a d egyenest!
2. lépés. Növeld meg a körzőnyílást, majd rajzolj egy A középpontú kört, majd egy B középpontú, ugyanakkora sugarú kört. Jelöld P és Q betűkkel a két kör metszéspontjait!
3.lépés. Rajzold meg a PQ egyenest! A P, M, Q pontok kollineárisak és PQ ⊥ d, tehát d’ = PQ. Megszerkesztettük az M ponton áthaladó d egyenesre merőleges egyenest. Írhatjuk: d’ ⊥ d és d’ ⋂ d = {M}.
b) Ha M ∉ d, megszerkesztjük az M pontban a d egyenesre merőleges egyenest. d M R S
1. lépés. Rögzítsd a körző tűjét az M pontba és rajzolj egy tetszőleges sugarú kört, úgy, hogy a kör a d egyenest két pontban messe, ezeket jelöljük R-rel és S-sel!
M R S U d T
2. lépés. A körző tűjét az R pontban rögzítve, rajzolj egy kört, melynek sugara nagyobb legyen, mint az RS távolság fele! Ugyanakkora körzőnyílással, rajzolj egy S középpontú kört!
3. lépés. Jelöld T-vel és U-val a két kör metszéspontjait!
4. lépés. Húzd meg a TM egyenest! A T, M, U pontok kollineárisak és TU ⊥ d, tehát d’ = TM.
Megszerkesztettük az M ponton áthaladó d egyenesre merőleges egyenest. Írhatjuk: d’ ⊥ d és M ∈ d’.
152 Matematika • Tankönyv a VI. osztály számára
M A B d A M B Q P d
Pont távolsága egyenestől
Legyen M a d egyenes egy külső pontja. Megszerkesztjük az M ponton keresztül a merőlegest a d egyenesre és jelöljük d’-tel. Legyen {P} = d’ ⋂ d
A fenti leírásban megjelölt P pontot az M pontból a d egyenesre bocsátott merőleges talppontjának nevezzük.
Értelmezés Legyen M a d egyenesen kívül fekvő pont. Az M pont távolságán a d egyenestől az MP szakasz hosszát értjük, ahol P az M pontból a d egyenesre bocsátott merőleges talppontja.
Ha M ∈ d, az M pont távolsága d-től 0.
Példa. Ha ABCD egy téglalap, bármely két oldala merőleges egyeneseken helyezkedik el. Az A pontból a BC-re húzott merőleges talppontja éppen a B pont, tehát az A pont távolsága BC-től az AB oldal hosszával egyenlő.
d ' d
MP = az M pont távolsága d-től
P M Az M pontból a d egyenesre húzott merőleges talppontja
AD = az A pont távolsága DC-től
Hasonlóan, az A pontból a CD-re húzott merőleges talppontja a D pont, tehát az A pont távolsága a CD egyenestől egyenlő az AD oldal hosszával. A D
Alkalmazások
1. alkalmazás
Két különböző egyenes, mely merőleges egy harmadik egyenesre, egymással párhuzamos.
Feltevés a ≠ b, a ⊥ c és b ⊥ c
Következtetés. a ∥ b
Matematikai nyelvezettel:
B C
AB = az A pont távolsága BC-től
c b
Ha a, b, c három egyenes és a ≠ b, a ⊥ c és b ⊥ c, akkor a ∥ b. a
Bizonyítás. Az a ⊥ c és b ⊥ c, összefüggésekből következik, hogy az a és b egyenesek a c szelővel négy derékszöget alkotnak, tehát kongruens megfelelő szögek keletkeznek, amiből következik, hogy a ∥ b.
Fontos megjegyzés. A fenti eredmény tulajdonképpen egy újabb párhuzamossági kritérium, azaz egy lehetőség két egyenes párhuzamosságának bizonyítására.
Megoldott feladat: Az a és b egyenesek merőlegesek és a ⋂ b = {O}. Az A és a B pontok az a egyenesen vannak úgy, hogy OA = 2 cm és OB = 5 cm. A C és a D pontok a b egyenesen vannak úgy, hogy OC = OD = 4 cm.
Számítsd ki a következő távolságokat:
a) A-tól b-ig; c) B-től a-ig; e) C-től a-ig;
b) B-től b-ig; d) D-től a-ig; f) D-től b-ig.
Megoldás.
a ⊥ b, a ⋂ b = {O}, A ∈ a, B ∈ a. Ekkor: a) az A pont távolsága a b egyenestől AO = 2 cm;
b) a B pont távolsága a b egyenestől BO = 5 cm;
c) a B pont távolsága az a egyenestől 0 cm.
b ⊥ a, a ⋂ b = {O}, C ∈ b, D ∈ b. Ekkor: d) a D pont távolsága az a egyenestől DO = 4 cm;
e) a C pont távolsága az a egyenestől CO = 4 cm;
f) a D pont távolsága a b egyenestől 0 cm.
153 5. fejezet • Mértani alapfogalmak
O D
a C
A B b
1. Mérd meg szögmérővel a mellékelt ábrán levő szögeket, majd válaszd ki a helyes válasznak megfelelő betűt! Csak egy helyes válasz van. c a d b
a) Azok az egyenesek, melyek derékszöget alkotnak:
A. a és b; B. b és c; C. c és d; D. d és a.
b) Két merőleges egyenes:
A. a és d;
B. d és c;
C. c és b; D. b és a.
2. Legyen a egy tetszőleges egyenes és A egy külső pont.
a) Rajzold meg a derékszögű vonalzó segítségével a b egyenest, mely átmegy az A ponton és merőleges az a egyenesre! Írd fel matematikai szimbólumokkal a két egyenes közötti összefüggést!
b) Rajzolj a vonalzó segítségével az A ponton keresztül egy c egyenest, mely ferde az a egyeneshez képest! Írd fel matematikai szimbólumokkal a két egyenes közötti összefüggést!
3. Legyen b egy tetszőleges egyenes és B egy pont a b egyenesen.
a) Rajzold meg a derékszögű vonalzó segítségével a d egyenest, amely a B pontban merőleges a b egyenesre! Írd fel matematikai szimbólumokkal a két egyenes közötti összefüggést!
b) Rajzolj a vonalzó segítségével egy e egyenest, mely ferde a b egyeneshez képest, és tartalmazza a B pontot! Írd fel matematikai szimbólumokkal a két egyenes közötti összefüggést!
4. Legyen d egy tetszőleges egyenes és M és N tetszőleges pontok, legalább egyik a d egyenesen kívül legyen.
a) Készíts egy rajzot úgy, hogy MN ⊥ d.
b) Készíts egy rajzot úgy, hogy MN ⊥ d.
5. Rajzolj egy ABCD négyzetet! Alkoss a négyzet oldalaiból olyan párokat, melyek tartóegyenesei merőlegesek egymásra, és
írd az első oszlopba! Majd alkoss olyan párokat a négyzet oldalaiból, amelyek tartóegyenesei nem merőlegesek egymásra, és írd a második oszlopba a minta alapján!
... ⊥ ... ⊥ AB ⊥ BC AB ⊥ CD
6. Az AOB, BOC, COD, DOA szögek az O pont körüli kongruens szögek. Igazold, hogyAC ⊥ BD.
7. Az ABC és CBD szögek egymás melletti kiegészítő szögek, ABC∢ = 120°, OE az ABC szög szögfelezője és OF a CBE szög szögfelezője.
a) Szerkessz a feladat adatainak megfelelő ábrát!
b) Igazold, hogy az AD és a BF egyenesek merőlegesek!
8. Legyenek APB, BPC, CPD, DPA a P pont körüli szögek. Figyelembe véve a mellékelt ábrát, határozd meg az x értékét úgy, hogy az AP és DP egyenesek merőlegesek legyenek.
115° x° P A B C D
80°
9. Rajzolj egy tetszőleges a egyenest és egy A pontot, amely nincs az egyenesen!
a) Rajzold meg a derékszögű vonalzó segítségével az AB szakaszt úgy, hogy AB ⊥ a és B ∈ a.
b) Mérd meg beosztásos vonalzó segjtségével az AB szakasz hosszát!
c) Az előző alpontokban kapott eredményeket felhasználva töltsd ki a pontozott helyeket úgy, hogy igaz állításokat kapj!
p1: A B pontot az … pontból az … egyenesre húzott … … nevezzük.
p2: Az A pont távolsága az a egyenestől … cm.
10. Rajzolj egy tetszőleges d egyenest és az A, B, C, D pontokat úgy, hogy A ∉ d, B ∉ d, C ∉ d, D ∈ d.
154 Matematika • Tankönyv a VI. osztály számára
Gyakorlatok és feladatok
a) Szerkeszd meg: MA ⊥ d, NB ⊥ d, PC ⊥ d, QD ⊥ d, ahol M ∈ d, N ∈ d, P ∈ d.
b) Beosztásos vonalzóval mérd meg az MA, NB, PC, QD szakaszok hosszát.
c) Másold le a füzetedbe a következő mondatokat és a fenti adatok alapján töltsd ki a pontozott helyeket úgy, hogy igazak legyenek a kijelentések!
p1: Az M pontot az … pontból a … egyenesre húzott … … nevezzük.
p2: A D pontot az … pontból a … egyenesre húzott … … nevezzük
p3: A B pont távolsága a d egyenestől … cm.
p4: A C pont távolsága a d egyenestől … cm.
p5: A D pont távolsága a d egyenestől… cm.
11. Adott a d egyenes és egy rajta kívül fekvő P pont Ábrázold PA ⊥ d, A ∈ d és a B pontot a egyenesen úgy, hogy B ≠ A.
a) Beosztásos vonalzóval mérd meg a PA és PB szakaszok hosszát! A kapott értékek alapján válaszd ki az igaz kijelentésnek megfelelő betűt!
A. PA < PB; B. PA = PB; C. PA > PB.
b) Szögmérővel mérd meg a PAB és a PBA szögek mértékét! A kapott értékek alapján válaszd ki az igaz kijelentésnek megfelelő betűt!
Miniteszt
A. PAB∢ < PBA∢; B. PAB∢ = PBA∢;
C. PAB∢ > PBA∢.
12. Rajzold le az a egyenest és az M, N, P pontokat, melyek 2 cm; 3,5 cm illetve 5 cm távolságra vannak az adott egynestől!
13. Legyen ABCD egy téglalap, AB = 8 cm, BC = 6 cm, M az AB oldal felezőpontja és az N pont a BC oldalon úgy, hogy BN = 2 · CN
a) Határozd meg az AM, BM, BN, CN szakaszok hosszát!
b) Számítsd ki az M pont távolságát az AD és a BC egyenesektől!
c) Számítsd ki az N pont távolságát az AB és a CD egyenesektől!
14. Az A, B, C, D ebben a sorrendben megadott kollineáris pontok, AB = 1,5 cm, BC = 3 cm, CD = 4,5 cm.
Megszerkesztjük az AM, BN, CP, DQ egyeneseket, melyek merőlegesek az AB egyenesre. Számítsd ki:
a) az A pont távolságát az AM, BN, CP, DQ egyenesektől!
b) a C pont távolságát az AM egynestől és a C pont távolságát a DQ egyenestől!
1. Az AOB és a BOC szögek egymás melletti pótszögek. Másold le a füzetedbe a táblázatot, és felhasználva a mellékelt ábrát írj I betűt az üres négyzetbe, ha az állítás igaz és H betűt , ha az állítás hamis! 3 cm
Állítás
15 p Az AOC szög mértéke 90°.
15 p Az O pont az A pontból az OC egyenesre bocsátott merőleges talppontja.
15 p OB ⊥ OC.
15 p A C pont távolsága az AO egyenestől 3 cm.
15 p A B pont távolsága a CO egyenestől 5 cm.
15 p 2. A mellékelt ábrán OA ⊥ OD, OB ⊥ OC és AOC∢ + BOD∢ = 240°.
Számítsd ki a COD∢ szög mértékét!
155 5. fejezet • Mértani alapfogalmak
A O B C
I/H
5cm
A B C D O
Megjegyzés: Munkaidő: 20 perc Hivatalból: 10 pont
Emlékeztető
A síkban két pont közötti távolságon az AB szakasz hosszát értjük.
Ha A, B és C az adott sorrendben kollineáris pontok, akkor az AB, BC, AC szakaszok között a következő összefüggés áll fenn: AC = AB + BC
Ha az AB, BC, AC szakaszok között fennáll az: AC = AB + BC összefüggés, akkor az A, B és C az adott sorrendben, kollineáris pontok.
Két mértani alakzatot kongruenseknek nevezünk, ha átfedéssel egybeesnek.
Két, AB és CD szakaszt, melyek átfedéssel egybeesnek, kongruens szakaszoknak nevezzük.
A B C
A kongruencia reláció egyik tulajdonsága a tranzitivitás:
1. Ha AB ≡ CD és CD ≡ EF, akkor AB ≡ EF. Így írjuk: AB ≡ CD és így olvassuk: az AB szakasz kongruens a CD szakasszal (vagy egyszerűen: AB kongruens CD-vel).
Két ABC és DEF szöget, melyek átfedéssel egybeesnek, kongruens szögeknek nevezzük.
ABC∢ ≡ DEF∢ și DEF∢ ≡ MNP∢, akkor ABC∢ ≡ MNP∢. Így írjuk: ABC∢ ≡ DEF∢ és így olvassuk: az ABC szög kongruens a DEF szöggel.
Tétel:
1. Ha két szakasz kongruens, akkor hosszuk egyenlő.
2. Ha két szakasz hossza egyenlő, akkor a két szakasz kongruens.
3. Ha két szög kongruens, akkor mértékük egyenlő.
4. Ha két szög mértéke egyenlő, akkor a két szög kongruens.
Az AB szakasz felezőpontja az M pont, mely az AB szakaszon van, és egyenlő távolságra van a szakasz végpontjaitól. (AM = MB).
Az AB szakaszon lévő M pont akkor és csakis akkor a szakasz felezőpontja, ha MA ≡ MB.
B A M
Legyen C az AB szakasz felezőpontja. Akkor, az A, C, B pontok kollineárisak és AC = CB.
Ha AB = 12 cm és M az AB szakasz felezőpontja, akkor AM = MB = 6 cm.
Ha AB = 12 cm és AM = MB = 6 cm, akkor M az AB szakasz felezőpontja.
Azt mondjuk, hogy:
• A B pont az A pont szimmetrikusa a C pontra nézve.
• Az A pont a B pont szimmetrikusa a C pontra nézve.
• Az A és a B pontok szimmetrikusak a C pontra nézve.
156 Matematika • Tankönyv a VI. osztály számára 2. l. Egy szakasz felezőmerőlegese
A C D B
A D E F C B 2.
Ha
A B C
Fedezzük fel, értsük meg!
Értelmezés. Az AB szakasz felezőmerőlegesének nevezzük, azt az egyenest, mely merőleges az AB szakaszra és tartalmazza a szakasz felezőpontját.
Egy szakasz felezőmerőlegesének helyes megszerkesztése egy fontos lépés a feladatok megoldásában. Ez megvalósítható beosztásos vonalzó és derékszögű vonalzó segítségével, vagy a körző és beosztás nélküli vonalzó segítségével.
Szerkesztés beosztásos vonalzó és derékszögű vonalzó segítségével
Ha beosztásos és derékszögű vonalzót használunk, akkor az AB szakasz hosszának ismeretére alapozunk és arra, hogy M a szakasz felezőpontja, ahol AM = MB = AB : 2.
1. lépés. Kimérünk az egyik végponttól a szakaszon egy AB:2 hosszúságú szakaszt, és megjelöljük az M pontot. 2. lépés. A derékszögű vonalzó derékszögét használva megszerkesztjük a d egyenest, mely áthalad az M ponton és merőleges az AB szakaszra. A d egyenes az AB szakasz felezőmerőlegese.
Szerkesztés beosztás nélküli vonalzó és körző segítségével
Ha körzőt és beosztás nélküli vonalzót használunk, a szerkesztést úgy végezzük, hogy nem ismerjük a szakasz hosszát
Gyakorlati munka: Egy AB szakasz felezőmerőlegesének megszerkesztése vonalzó és körző segítségével
Szükséges anyagok: a matematikafüzet, körző, egy beosztás nélküli vonalzó, egy hegyes ceruza.
A szerkesztés szakaszai:
1. lépés. A körzőt kinyitjuk és rögzítjük úgy, hogy a körzőnyílás nagyobb legyen, mint az AB szakasz felbecsült hosszának a fele.
2. lépés. A körző tűjét rögzítjük az A pontban és rajzolunk egy kört. Ugyanakkora körzőnyílással rajzolunk egy B középpontú kört is.
3. lépés. Jelöljük D, illetve E pontokkal a 2. lépésben megszerkesztett körök metszéspontjait.
4. lépés. Meghúzzuk a DE egyenest, mely az AB szakasz felezőmerőlegese.
Gyakorlati alkalmazás:
Mértani ábrázolás:
Rajzolj egy 6 cm hosszúságú AB szakaszt! Körző segítségével szerkeszd meg az AB szakasz d felezőmerőlegesét! Legyen {M} = d ∩ AB és N ∈ d, N ≠ M. Beosztásos vonalzóval mérd meg az MA, MB illetve NA, NB szakaszok hosszát! Felhasználva a lemért adatokat, döntsd el, hogy melyik állítás igaz:
MA > MB, MA = MB, MA < MB, NA > NB, NA = NB, NA < NB.
Megoldás. Bármely AB szakasz esetén és bármely N pont esetén igaz, hogy MA = MB és NA = NB.
Egy szakasz felezőmerőlegesének megszerkesztése és a fenti alkalmazás a következő nagyon fontos eredményre enged következtetni:
Ha d az AB szakasz felezőmerőlegese és M ∈ d, akkor MA ≡ MB.
Ha d az AB szakasz felezőmerőlegese és MA ≡ MB, akkor M ∈ d.
A fenti két kijelentés helyettesíthető a következő állítással, amely a felezőmerőlegesen lévő pontokat jellemzi:
Tétel:
Egy szakasz felezőmerőlegese azon pontok halmaza a síkban, melyek egyenlő távolságra vannak a szakasz végpontjaitól.
157 5. fejezet • Mértani alapfogalmak
E D
A B
Alkalmazások
1. alkalmazás:
a) Ha az A, B és C pontok kollineárisak, akkor az AB és BC szakaszok felezőmerőlegesei párhuzamosak.
b) Ha az AB és BC szakaszok felezőmerőlegesei párhuzamosak, akkor az A, B és C pontok kollineárisak. Megoldás. Jelöljük d1-gyel az AB szakasz felezőmerőlegesét és d2-vel a BC szakasz felezőmerőlegesét.
a) A B pont az AC szakaszon van, ebből következik, hogy az AB, AC, BC egyenesek egybeesnek. Legyen d ez az egyenes. A d1 és d2 egyenesek felezőmerőlegesek, tehát d1 ⊥ AB és d2 ⊥ BC, azaz d1 és d2 merőlegesek ugyanarra a d egyenesre. Az AB és BC szakaszok felezőpontjai a B pont egyik és másik oldalán helyezkednek el, tehát különbözőek.
Ekkor, d1 és d2 merőlegesek ugyanarra az egyenesre két különböző pontban, tehát d1 ∥ d2.
A B C d1 d2 d
b) Feltételezzük, hogy A, B, C nem kollineáris pontok. Ekkor meghosszabbíthatjuk az AB szakaszt, mely a d2 egyenest a D pontban metszi. A d1 és d2 párhuzamos egyenesek, a BD szelővel kongruens belső váltószögeket alkotnak, tehát BD ⊥ d2. De BC ⊥ d2, mivel a B ponton keresztül, egyetlen merőlegest húzhatunk a d2 egyenesre, következik, hogy a BD és a BC egyenesek egybeesnek, tehát az A, B és C pontok kollineárisak.
2. alkalmazás
Rajzolj a füzetedbe három nem kollineáris A, B, C pontot!
a) Szerkeszd meg a d3 egyenest, mely az AB szakasz felezőmerőlegese és a d4 egyenest, mely a BC szakasz felezőmerőlegese!
b) Igazold, hogy d3 és d4 egyenesek metszik egymást egy pontban! Jelöld O-val ezt a pontot!
c) Mutasd ki, hogy az O pont hozzátartozik az AC szakasz felezőmerőlegeséhez! A B C O d3 d4 Megoldás.
b) Feltételezzük, hogy a d3 és d4 egyenesek nem metszik egymást, tehát d3 ∥ d4. Ekkor az 1. b) Alkalmazás alapján következik, hogy az A, B, C pontok kollineárisak, ami ellentmond a feltevésnek. A d3 ∥ d4 feltevés hamis, tehát a d3 és d4 egyenesek metszik egymást. Tehát létezik egy O pont úgy, hogy d3 ∩ d4 = {O}.
c) Mivel O ∈ d3, és d3 az AB szakasz felezőmerőlegese, következik, hogy OA ≡ OB. És az O ∈ d4 alapján, mivel d4 a BC szakasz felezőmerőlegese, következik, hogy OB ≡ OC; tehát OA ≡ OC, ami azt jelenti, hogy az O pont az AC szakasz felezőmerőlegesén van.
Gyakorlatok és feladatok
1. Ábrázold a 6 cm hosszúságú AB szakaszt és az M pontot, amely az AB szakasz belsejében van úgy, hogy MA = 3 cm! Szerkeszd meg a d egyenest, mely merőleges az M pontban az AB egyenesre! Másold le a füzetedbe a következő mondatokat, és töltsd ki a pontozott helyeket úgy, hogy igaz kijelentéseket kapj!
a) Az M pont az … szakasz … .
b) A d egyenes az AB egyenessel …° mértékű szöget alkot.
c) A d egyenes az … szakasz … .
2. Az AB egyenes a CD szakasz felezőmerőlegese és
AB ∩ CD = {M}. A táblázatba írj I betűt, ha az állítás igaz és H betűt, ha az állítás hamis.
Állítás I/H
AB ⊥ CD.
CM = MD.
AMB∢ = 90°.
CMA∢ = 90°
3. Rajzold le az A, B, C kollineáris pontokat úgy, hogy
AB = 2 cm és BC = 6 cm.
a) Szerkeszd meg az m1 és m2 egyeneseket, melyek az AB, illetve BC szakaszok felezőmerőlegesei.
b) Ha m1 ∩ AB = {M} és m2 ∩ BC = {N}, számítsd ki az MN szakasz hosszát! Tanulmányozz minden esetet!
158 Matematika • Tankönyv a VI. osztály számára
4. Rajzold le az A, B, C nem kollineáris pontokat! Szerkeszd meg az m1, m2 és m3 egyeneseket, melyek az AB, BC, illetve AC szakaszok felező merőlegesei!
5. Az a és a b egyenesek az MN, illetve PQ szakaszok felezőmerőlegesei. Bizonyítsd be, hogy:
a) Ha a és b párhuzamosak, akkor MN és PQ is párhuzamos vagy egybeesik.
Miniteszt
b) Ha az MN és PQ egyenesek párhuzamosak, akkor a és b is párhuzamos vagy egybeesik.
6. Legyen d az MN szakasz felezőmerőlegese, d ∩ MN = {O}, MO = 3 cm és A egy pont a d egyenesen úgy, hogy AN = 5 cm. Számítsd ki:
a) az MN és AM szakaszok hosszát;
b) az AM + MN + AN összeget!
20 p 1. Ha az A, B, C különböző kollineáris pontok és AB = BC, akkor a B pont az AC szakasz felezőmerőlegeséhez tartozik.
a) igaz; b) hamis.
20 p 2. Ha AB és d egyenesek a C pontban metszik egymást és AC = BC, akkor a d egyenes az AB szakasz felezőmerőlegese.
a) igaz; b) hamis.
20 p 3. Ha d ⊥ AB, C ∈ d és AC = BC, akkor a d egyenes az AB szakasz felezőmerőlegese.
a) igaz; b) hamis.
30 p 4. Ha az A, B, C, D pontok ebben a sorrendben megadott kollineáris pontok, AB = 2 cm, AC = 5 cm, AD = 7 cm, akkor az Ad és BC szakaszoknak ugyanaz a felezőmerőlegesük.
a) igaz; b) hamis.
3. l. Egyenes szerinti szimmetria
Emlékeztető
Megjegyzés: Munkaidő: 20 perc Hivatalból: 10 pont
Egy mértani alakzatnak szimmetriatengelye van, ha létezik egy olyan egyenes, amely mentén a síkot úgy tudjuk meghajlítani képzeletben, hogy az alakzat két része, amelyek az egyenes által határolt két félsíkban helyezkednek el, kongruensek, átfedéssel egybeesnek.
Azt az egyenest, amely mentén a hajlítást végezzük az alakzat szimmetriatengelyének nevezzük.
A mellékelt ábrán az MN egyenes az ABCD négyzet szimmetriatengelye
A D pont az A pont szimmetrikusa az MN egyenesre nézve. Azonosítsd a B, C, D, M, N pontok szimmetrikusait az MN egyenesre nézve!
Megjegyzés. M a szimmetriatengelyen helyezkedik el, tehát az ő szimmetrikusa a szimmetriatengelyhez képest saját maga.
A lap négyzethálója segít észrevenni, hogy:
• A négyzet minden pontjának szimmetrikusa az MN egyenesre nézve szintén pontja a négyzetnek. Ez azt bizonyítja, hogy MN a négyzet szimmetriatengelye.
• A négyzet egy pontjának távolsága az MN szimmetriatengelytől egyenlő a pont szimmetrikusának szimmetriatengelytől való távolságával. Például az A és a D pontok szimmetrikusak az MN egyenesre nézve; az A pont távolsága az MN egyenestől AM, a D pont távolsága az MN egyenestől DM és AM = DM.
• Az MN egyenes minden olyan szakasznak felezőmerőlegese, amelyek végpontjai szimmetrikus pontok a tengelyhez képest.
159 5. fejezet • Mértani alapfogalmak
C
B D M N
A
Fedezzük fel, értsük meg!
Alkalmazva a merőleges egyenesek tulajdonságait és a fenti megjegyzéseket, erre a következtetésre jutunk:
Legyen P a d egyenes egy külső pontja. A P pont szimmetrikusa a d egyenesre nézve az a P’ pont, amelyre a d egyenes a PP’ szakasz felezőmerőlegese.
A d egyenes a {P, P’} ponthalmaznak a szimmetriatengelye.
Megjegyzés. Ha P’ a P pont szimmetrikusa a d egyenesre nézve, akkor a P pont a P’ pont szimmetrikusa a d egyenesre nézve.
P P’
Megállapítottuk, hogy a P pont szimmetrikusa a d egyenesre nézve a P’ pont, ahol PP’ ⊥ d, illetve P és P’ egyenlő távolságra vannak a d egyenestől. Ez a megközelítés egy olyan módszert nyújt, amellyel könnyen ábrázolhatjuk egy pont szimmetrikusát egy egyenesre nézve.
1. lépés.
Ábrázoljuk a d egyenest és a P pontot.
2. lépés.
Megszerkesztjük a PM ⊥ d egyenest, M ∈ d.
3. lépés.
Megjelöljük a P’ pontot a PM egyenesen úgy, hogy M a PP’ szakasz felezőpontja legyen.
Alkalmazások
A gyakorlatban könnyen észrevehetjük, hogy egy mértani alakzat szimmetrikusa egy egyeneshez képest az eredeti alakzattal kongruens mértani alakzat, amelyet az adott alakzat pontjainak az adott tengelyre vonatkoztatott szimmetrikusai alkotnak.
Célunk az egyszerű mértani alakzatok szimmetrikusainak meghatározása egy adott egyeneshez képest.
1. alkalmazás:
Az AB szakasz szimmetrikusa a d egyenesre nézve az A1B1 szakasz, ahol A1 az
A pont szimmetrikusa a d egyenesre nézve, B1 pedig a B pont szimmetrikusa a d egyenesre nézve.
a) Készítsd el a füzetedbe a a mellékelt ábra mintájára a rajzot!
b) Ellenőrizd a körző segítségével az AB ≡ A1B1 kongruenciát! Q
Az A1B1 szakasz az AB szimmetrikusa a d egyenesre nézve, az AB szakasz pedig az A1B1 szakasz szimmetrikusa a d egyenesre nézve. A d egyenes az AB és A1B1 szakaszok egyesítésének a szimmetriatengelye.
2. alkalmazás:
Egy tetszőleges AOB szög szimmetrikusa a d egyenesre nézve az A1O1B1, szög, ahol A1 az A pont szimmetrikusa a d egyenesre nézve; O1 az O pont szimmetrikusa a d egyenesre nézve és B1 pedig a B pont szimmetrikusa a d egyenesre nézve.
a) Készíts a füzetedbe egy rajzot a mellékelt ábra szerint!
b) Ellenőrizd a szögmérőddel az AOB∢ ≡ A1O1B1 kongruenciát!
Az A1O1B1 szög az AOB szög szimmetrikusa a d egyeneshez képest, az AOB szög pedig az A1O1B1 szimmetrikusa a d egyenesre nézve.
A d egyenes a két szög pontjai halmazának szimmetriatengelye
160 Matematika • Tankönyv a VI. osztály számára
d
d P d P M d P M P’
d R A B B1 A1
d A B O O
1 B1
1 A
Következtetés.
1. Egy szakasz szimmetrikusa egy egyenesre nézve az eredeti szakasszal kongruens szakasz.
2. Egy szög szimmetrikusa egy egyenesre nézve az eredeti szöggel kongruens szög.
Feladat a portfólióba.
1. a) Ábrázolj egy átlátszó rugalmas fóliára egy AOB szöget és a szög OC szögfelezőjét!
b) Ellenőrizd behajtással és átfedéssel, hogy a szög szögfelezője a szög szimmetriatengelye!
2. a) Ábrázolj egy átlátszó rugalmas fóliára egy AB szakaszt és ennek a d felezőmerőlegesét!
b) Igazold, behajtással és átfedéssel, hogy egy szakasz felezőmerőlegese az illető szakasz szimmetriatengelye!
Gyakorlatok és feladatok
1. a) Ábrázold a d egyenesen ebben a sorrendben az A, B, C, D, E, F pontokat, AB = BC = EF = 2 cm, CD = DE = 3 cm és a BM, CN, DP egyeneseket, melyek merőlegesek a d egyenesre!
b) Másold le a füzetedbe a következő mondatokat és töltsd ki a pontozott helyeket úgy, hogy az állítások igazak legyenek!
p1: A BM egyenes az … szakasz felezőmerőlegese.
p2: Az E pont a … pont szimmetrikusa a DP egyenesre nézve.
2. Az S pont az A pont szimmetrikusa a d egyenesre nézve és AS ∩ d = {B}.
Ha AS = 8 cm, számítsd ki az AB és SB szakaszok hosszát!
3. Legyen ABCD egy négyzet az E pont pedig a B pont szimmetrikusa az AD egyenesre nézve.
a) Igazold, hogy az A, B, E pontok kollineárisak!
b) Igazold, hogy AD a BE szakasz felezőmerőlegese!
Miniteszt
4. Ábrázold az A, O, B pontokat úgy, hogy az AOB szög derékszög legyen, AO = 2,5 cm és OB = 4 cm. Szerkeszd meg a C pontot, mely az A pont szimmetrikusa az O pontra nézve, és a D pontot, mely a B pont szimmetrikusa az O pontra nézve!
Bizonyítsd be, hogy:
a) AOC∢ = BOD∢ = 180°;
b) OB az AC szakasz felezőmerőlegese;
c) a C pont az A pont szimmetrikusa az OB egyenesre nézve;
d) a B pont a D pont szimmetrikusa az AC egyenesre nézve!
5. Az A, B, C, D pontok kollineárisak, a B pont az A pont szimmetrikusa a d egyenesre nézve, a D pont pedig a C pont szimmetrikusa a d egyenesre nézve.
a) Készíts a feladat adatainak megfelelő rajzot!
b) Igazold, hogy AC ≡ BD!
1. A mellékelt ábrán az a egyenes az AA1 és BB1 szakaszok felezőmerőlegese. Másold le a füzetedbe a következő mondatokat és töltsd ki a pontozott helyeket úgy, hogy igaz állításokat kapj!
15 p a) Az a egyenes a kék ábra … .
15 p b) Az A1B1 szakasz az AB szakasz … az a egyenesre nézve.
B1 B
2. A 10 cm hosszúságú AB szakaszon felvesszük a C, D, E pontokat úgy, hogy AC = CB, AD = 2,5 cm, BE = 1,5. A D pontok keresztül megszerkesztjük a d egyenest, mely merőleges az AB egyenesre.
20 p a) Készíts a feladat adatainak megfelelő rajzot!
20 p b) Igazold, hogy a C pont az A pont szimmetrikusa a d egyenesre nézve!
20 p c) Számítsd ki a B és az E pontok távolságát a d egyenestől!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
161 5. fejezet • Mértani alapfogalmak
a A A1
5.4. A kör
1. l. A kör. A kör elemei
Fedezzük fel, értsük meg!
A „kör” szó számos jelentése ennek a geometriai alakzatnak a tökéletes formáján alapul. Határozd meg a szótár segítségével a „kör” szó négy különböző jelentését!
A kör geometriai értelemben a mindennapi életben számos tárgy vagy tevékenység matematikai modellje. Nevezz meg négy olyan tevékenységet, amelyekben kör alakú tárgyakat használnak, vagy amelyekben a kör szervezési formaként szerepel! M
Értelmezés. Legyen O egy tetszőleges rögzített pont a síkban és r egy pozitív szám. O középpontú és r sugarú körnek nevezzük a sík azon pontjainak halmazát, amelyek r távolságra helyezkednek el az O ponttól.
Jelölése C(O, r) és így olvassuk: O középpontú és r sugarú kör.
középpontja. OM a kör sugara.
M ∈ C(O, r) és OM = r
Megjegyzés. Ha M ∈ C(O, r), a kör sugarának fogjuk nevezni az OM szakaszt is, és a szakasz r hosszát is.
A C(O, r), körhöz képest a sík egy pontja lehet: a körön vagy a kör belső tartományában vagy a kör külső tartományában. M
• Ha az M kör C(O, r) egy tetszőleges pontja, akkor MO = r.
Ha M a sík egy pontja, és MO = r, akkor M a C(O, r) kör egy pontja.
• Ha a P pont a C(O, r), kör belső tartományának egy pontja, akkor PO < r.
Ha P a sík egy pontja, és PO < r, akkor P pont a C(O, r) kör belső tartományában van.
• Ha az S pont a C(O, r) kör külső tartományának egy pontja, akkor SO > r.
Ha S a sík egy pontja, és SO > r, akkor S a C(O, r) kör külső tartományában van.
A O P r
A fenti ábrán:
Matematikai szimbólumokkal:
• Ha M ∈ C(O, r), akkor MO = r
B S
• M ∈ C(O, r); A ∈ C(O, r);
B ∈ C(O, r) és
OM = OA = OB = r
• OP < OA és OA = r, tehát
OP < r és P∈ IntC(O, r)
• OS > OB és OB = r, tehát
OS > r és S∈ ExtC(O, r).
Ha MO = r, akkor M ∈ C(O, r).
• Ha P∈ IntC(O, r), akkor PO < r.
Ha PO < r, akkor P∈ IntC(O, r).
• Ha S∈ ExtC(O, r), akkor SO > r.
Ha SO > r, akkor S∈ ExtC(O, r).
Az r = OM sugarú kör szerkesztése körzővel
1. lépés. Rögzítjük az O pontot, a kör középpontját.
2. lépés. Körzőnyílásba veszünk r egységet és a körző tűjét az O pontba szúrjuk.
3. lépés. Jelöljük M-mel azt a pontot, ahol a ceruza a papírt érinti.
4. lépés. A körző tűjét az O pontba rögzítve, megforgatjuk a körző ceruzás végét, amíg újból az
M pontba kerül.
Megszerkesztettük az O középpontú és r sugarú kört. Ha megváltoztatjuk a kör középpontját, de a sugara r marad, akkor az eredeti körrel kongruens kört kapunk (átfedéssel egybeesnek).
162 Matematika • Tankönyv a VI. osztály számára
O C(O, r) r O a kör
M r O
Következik, hogy a C1(O1, r1) és C2(O2, r2) körök kongruensek, ha r1 = r2.
Legyen M és N két különböző pont a C(O, r) körön.
• Az MN szakaszt a C(O, r) kör egy húrjának nevezzük.
• A kör bármely húrját, mely tartalmazza a kör középpontját, a kör átmérőjének nevezzük.
• Ha MN egy átmérő, akkor az M és az N pontok átmérősen ellentett pontok.
• M kör azon pontjainak halmazát, amelyek az MN húr ugyanazon oldalán vannak, és tartalmazzák az M és az N pontokat is, az ⏜ MN körívnek nevezzük.
N P O MP átmérő
MN húr MN nagykörív MN kiskörív A B
M
A kör bármely két különböző pontja két körívet határoz meg a körön, melyeket hárombetűs jelöléssel különböztetünk meg egymástól.
Matematikai szimbólumokkal:
• M ∈ C(O, r), N ∈ C(O, r) és M ≠ N.
Az MN szakasz egy húr.
• Az MP szakasz húr és O ∈ MP.
Az MP húr a kör egy átmérője.
• Az M és a P pontok átmérősen ellentett pontok.
• Az MN kiskörívet ⏜ MAN -nel jelöljük.
Az MN nagykörívet ⏜ MBN -nel jelöljük.
A kör nagykörívének nevezzük azt a körívet, amely az őt meghatározó húrhoz képest a kör középpontjával azonos oldalon helyezkedik el. A húr másik oldalán levő körívet pedig a kör kiskörívének nevezzük.
Megjegyzés. Az átmérő a legnagyobb húr. Ha MN átmérő és r a kör sugara, akkor MN = 2r
Az átmérő által meghatározott köríveket félköröknek nevezzük.
CD átmérő, tehát ⏜
DAC és ⏜ DBC félkörök.
CBD félkör
A B C D O Állapítsd meg hány átmérőt lehet szerkeszteni egy C(O, r) körnek!
Rajzolj egy kört egy lapra, és húzd meg egy átmérőjét! Hajtsd be a lapot az átmérő tartóegyenese mentén! Találj indoklást arra, hogy az átmérő által meghatározott íveket miért nevezzük félköröknek!
Alkalmazás
Alkalmazás.
DAC félkör
Legyen egy O középpontú kör, melynek sugara r = 3 cm. A síkban adottak az A, B, C, D pontok úgy, hogy AO = 5 cm, BO = 1 cm, C, O, D ebben a sorrendben megadott kollineáris pontok, CO = 3 cm és CD = 6 cm.
a) Készíts körző és beosztásos vonalzó segítségével a feladat adatainak megfelelő ábrát!
b) Másold le a füzetedbe a táblázatot, az üres mezőbe írj I betűt, ha az állítás igaz, és H betűt, ha az állítás hamis.
Állítás
A1: Az A pont a kör belső tartományában van.
A2: A C és D pontok átmérősen ellentett pontok.
A3: A B pont a kör középpontja.
A4: Az O és a B pontok a kör belső tartományában vannak.
A5: Az A pont a kör külső tartományában van.
A6: A kör végtelen sok pont halmaza.
A7: A kör belső tartománya véges számú pont halmaza.
I/H
163 5. fejezet • Mértani alapfogalmak
Megoldás.
Gyakorlatok és feladatok
1. A A, B, C, D különböző pontok kollineárisak és
AB = BC = CD = 2 cm. Figyeld meg a következő ábrát, másold le a szöveget a füzetedbe, és a pontozott helyeket pótold ki, úgy, hogy igazak legyenek a kijelentések!
A B C D
Az ábrán lévő kör középpontja … sugarának hossza pedig … cm.
A B pont a kör … tartományában van.
A D pont a kör … tartományában van. A C pont … tartozik.
2. Készíts rajzot, rendre megszerkesztve:
a) az O középpontú, 3 cm sugarú kört;
b) az OA sugarát ennek a körnek;
c) a kör BC átmérőjét;
d) a körnek egy DE húrját!
3. Az AB szakasz hossza 12 cm, a P pont a szakasz egy pontja.
a) Rajzold meg az AP átmérőjű C1, illetve a BP átmérőjű C2 köröket!
b) Számítsd ki az a) alpontban szereplő körök középpontjai közötti távolságot!
4. A O, A, B, C, D, E különböző pontok és OA = 3 cm, OB = 30 mm, OC = 0,03 dm, OD = 0,3 m,
b) O a kör középpontja és OA >3, tehát
A ∈ ExtC(O, 3).
OC = OD = 3 cm és r = 3 cm, iar O, C, D pontok kollineárisak, tehát CD átmérő, azaz C és D átmérősen ellentett pontok.
O a kör középpontja és B ≠ O, tehát B nem a kör középpontja.
OB = 1 < 3 = r, és OO = 0 < 3 = r, tehát
OB < r és OO < r, azaz B ∈ IntC(O, 3) és
O ∈ IntC(O, 3).
OA = 5 > 3 = r, tehát OA > r, azaz A ∈ ExtC(O, 3).
Tehát: (A1 → F); (A2 → A); (A3 → F);
(A4 → A); (A5 → A); (A6 → A);
(A7 → F).
OE = 0,(3) dm, az F pont az A pont szimmetrikusa az O pontra nézve. Rajzold meg a C kört, melynek középpontja O és sugara 3 cm, majd határozd
meg:
a) a C körön ábrázolt pontokat;
b) a C kör belső tartományában lévő pontokat;
c) a C kör külső tartományban lévő pontokat!
5. Rajzolj egy O középpontú és r sugarú kört, majd ábrázold az A pontot a kör belső tartományában, a B és C pontokat a körön, az O pontot a BC szakaszon, a D pontot pedig a kör külső tartományában. Másold le a füzetedbe és töltsd ki a pontozott helyeket a <, =, >, jelek egyikével úgy, hogy igazak legyenek a kijelentések!
a) AO … r
b) BO … r c) CO … r d) DO … r e) BC … 2 · r f) AB … BC.
6. Az O középpontú és 5 cm sugarú körön felveszszük az M, N és P pontokat és O ∈ MN.
Másold le a táblázatot a füzetedbe, és töltsd ki az üres mezőket I betűvel, ha az állítás igaz, és H betűvel, ha az állítás hamis!
Állítás I/H
ON = 5 cm.
MP < 10 cm.
MN = 10 cm.
Az MOP háromszög kerülete legalább 20 cm.
164 Matematika • Tankönyv a VI. osztály számára
D O A
a) B C
Miniteszt
Válaszd ki a helyes válasznak megfelelő betűt! Csak egyetlen helyes válasz van.
20 p 1. Az a szakasz, amely a kör középpontját összeköti a kör egy pontjával, a kör:
A. húrja; B. átmérője; C. sugara; D. köríve
20 p 2. Az a szakasz, amely a kör két különböző pontját köti össze, a kör:
A. húrja; B. sugara; C. félköre; D. köríve.
20 p 3. Ha az A és a B pont átmérősen ellentett pontok egy 3,5 cm sugarú körön, akkor az AB szakasz hossza:
A. 3,5 cm; B. 4,5 cm; C. 6 cm; D. 7 cm.
30 p 4. Ha egy kör leghosszabb húrja 10 cm hosszúságú, akkor a kör sugara:
A. 20 cm; B. 5 cm; C. 10 cm; D. 40 cm.
2. l. Középponti szög. A középponti szög mértéke
Emlékeztető
Egy pont körüli szögek mértékeinek összege 360°.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
Egy egyenesszög mértéke 180°. Egy derékszög mértéke 90°.
Oldjuk meg figyelmesen!
1. a) Rajzolj egy lapra egy C(O, r) kört! Szerkeszd meg a kör AB és CD merőleges átmérőit!
b) Határozd meg az AOB, AOC, AOD, BOC, BOD, COD szögek mértékét! És indokold meg a válaszod!
c) A szögmérő segítségével kövessük a b) alpontban szereplő szögek mértéke és a szögmérő ívének beosztása közötti megfelelést és következtessünk a szögeknek megfelelő ívek mértékére!
d) Tűrd be a lapot az egyik átmérő mentén, és határozd meg, hogy az ⌢ AC, ⌢ CB, ⌢ BD, ⌢ DA ívek páronként átfedéssel egybeesnek-e!
Megoldás a) A mellékelt ábra.
b) AB ⊥ CD, következik, hogy az OA, OB, OC, OD félegyenesek az O pont körül négy derékszöget alkotnak: AOC∢ = AOD∢ = BOD∢ = BOC∢ = 90°. Ugyanakkor az A, O, B pont ebben a sorrendben kollineáris pontok, illetve a C, O, D pont is ebben a sorrendben kollineáris pontok. Ekkor AOB∢ = COD∢ = 180°.
c) Jelöljük a kisköríveket két betűvel, a nagyköríveket három betűvel, hogy meg tudjuk különböztetni őket.
Ekkor, ⌢ AC = ⌢ BC = ⌢ BD = ⌢ DA = 90°, ⏜ ADC = ⏜ BDC = ⏜ BCD = ⏜ DBA = 360°– 90° = 270°.
És ⏜ ACB = ⏜ BDA = ⏜ CBD = ⏜ CAD = 180°.
d) Ha az AB mentén behajtjuk a lapot, akkor ⌢ AC egybeesik ⌢ CB-vel, illetve ⌢ BD egybeesik ⌢ DA-val.
165 5. fejezet • Mértani alapfogalmak
A B C D O
C D
B O 85° 50° 90° 135° 90° + 50 ° + 85°
E F G ∢EFG
∢MNP
A
+ 135° = 360°
∢ = 180° M P N
∢ = 90°
Fedezzük fel, értsük meg!
Értelmezés. Azt a szöget, melynek csúcsa a kör középpontjában van, középponti szögnek nevezzük.
A középponti szög szárainak és a körnek metszéspontjai által meghatározott kis körívet a középponti szög szárai közé eső körívnek nevezzük. Azt a középponti szöget, amelynek szárai között kiskörív van, az adott ívnek megfelelő középponti szögnek nevezzük.
Egy kiskörív mértéke egyenlő az adott ívnek megfelelő középponti szög mértékével.
A kör mértéke egyenlő egy pont körüli szögek mértékének összegével, azaz 360°-kal.
Egy nagykörív mértéke egyenlő 360° és a kiskörív mértékének különbségével.
Alkalmazás
Emlékezzünk, hogy két C1(O1, r1) és C2(O2, r2) kör kongruens, ha r1 = r2.
Ha ∢MON∢ = α°, akkor ⏜ MN= α ° , és ⏜ MBN= 360° – α ° .
Ha ⏜ MN= α°, akkor ∢MON∢ = α ° , és ⏜ MBN= 360° – α ° .
Értelmezés. Egy körben, vagy kongruens körökben két körív kongruens, ha mértékük egyenlő. Az ⌢ AB és ⌢ CD kongruens körívek esetében, így írjuk: ⌢ AB ≡ ⌢ CD.
Megjegyzés: Nem elégséges, hogy a köríveknek ugyanakkora legyen a mértékük ahhoz, hogy kongruensek legyenek. Lényeges, hogy ezek a körívek ugyanannak a körnek, vagy kongruens köröknek legyenek az ívei.
A mellékelt ábrán ⌢
AB = 90° és ⌢ CD = 90°, tehát a köríveknek ugyanakkora a mértékük. Mégis a körívek nem kongruensek, mert átfedéssel nem esnek egybe.
Alkalmazás. Ha az A, B, C pontok a C(O, r) körön vannak, C ∈ ⌢ AB, ahol ⌢ AB kiskörív, akkor ⌢ AB = ⌢ AC + ⌢ CB.
Megoldás. Azonosítjuk az AOC, COB, AOB középponti szögeket. Észrevesszük, hogy az AOC∢ és a COB∢ egymás melletti szögek az OC közös szárral az AOB∢ belső tartományában, tehát AOB∢ = AOC∢ + COB∢ Kiindulva abból, hogy egy kiskörív mértéke egyenlő a neki megfelelő középponti szög mértékével, következik, hogy ⌢ AB = ⌢ AC + ⌢ CB. A
Feladat a portfólióba. Igazold a fenti kijelentést az ⌢ AB nagykörív esetén is!
166 Matematika • Tankönyv a VI. osztály számára
M N O
nagykörív MN kiskörív B α°
MN
O1 O2 A C D B M N R
C B O
Tétel: Ha az A, B, C pontok a C(O, r) körhöz tartoznak és C ∈ ⌢ AB, akkor ⌢ AB = ⌢ AC + ⌢ CB.
A gyakorlatban hasznosak a következő eredmények:
AB egy szakasz és C ∈ AB OC ∈ Int(AOB∢) A, B, C ugyanazon a körön vannak és C ∈ ⌢ AB
AB = AC + CB AOB∢ = AOC∢ + COB∢ ⌢ AB = ⌢ AC + ⌢ CB
Gyakorlatok és feladatok
1. Az A, B, C, D pontok ugyanazon az O középpontú körön helyezkednek el.
B C D
A mellékelt ábra alapján határozd meg:
a) a körnek egy sugarát;
b) két átmérősen ellentett pontot;
c) a körnek egy húrját, mely nem átmérő;
d) egy középponti szöget;
e) egy félkört;
f) a kör egy kiskörívét;
g) a körnek egy nagykörívét;
h) egy 180° -os körívet!
2. Egy O középpontú körön mértani felszerelés segítségével ábrázolj és jelölj:
a) egy 50°-os középponti szöget;
b) egy 50°-os körívet;
c) egy 90°-os körívet!
3. a) Rajzolj egy kört, majd ábrázold a 60°-os AB körívet és a 120°-os CD körívet!
b) Rajzold meg az a) alpontban lévő körívekhez tartozó húrokat!
c) Beosztásos vonalzóval határozd meg a húrok hosszát és állapítsd meg, hogy melyik hosszabb!
4. Az A, B, C pontok az O középpontú körön van úgy, hogy A, O és C kollineáris pontok, és BO ⊥ AC. Határozd meg az ⌢ AC, ⌢ AB, ⏜ ABC körívek mértékét!
5. Az A középpontú körön felvesszük az M, N, P különböző pontokat úgy, hogy MAN∢ ≡ NAP∢ ≡ PAM∢.
a) Határozd meg az MN, NP, PM körívek mértékét!
b) Ha MQ a kör átmérője, határozd meg a PQ kiskörív és nagykörív mértékét!
6. Az O, középpontú körön felvesszük az A, B, C, D különböző pontokat úgy, hogy az AB, BC, CD, DA körívek kongruensek legyenek.
a) Határozd meg a négy körív mértékét!
b) Igazold, hogy AC és BD a kör átmérői!
c) Igazold, hogy AC ⊥ BD.
7. Adott egy O középpontú kör és az A, B, C pont a körön úgy, hogy AOB∢ = 35° és OC ⊥ OB.
a) Ha a B pont az AOC szög belső tartományában van, számítsd ki az AB, BC, AC kiskörívek mértékét!
b) Ha a B pont az AOC szög külső tartományában van, számítsd ki az AB, BC, AC nagykörívek mértékét!
8. Az M, N, P, Q pontok egy O középpontú körön vannak. Az ábrán látható jelöléseket használva, határozd meg:
a) az MOQ szög mértékét;
b) az MQ kiskörív mértékét és az NMQ körív mértékét!
167 5. fejezet • Mértani alapfogalmak
O A
M N P 100° 45° 82° O Q
ACB O A C B O A C B
Miniteszt
Válaszd ki a helyes válasznak megfelelő betűt! Csak egy helyes válasz van.
30 p 1. Egy kör mértéke:
A. 90°; B. 180°; C. 0°; D. 360°.
30 p 2. Ha a C és a D pontok egy kör átmérősen ellentett pontjai, akkor a CD körív mértéke:
A. 180°; B. 90°; C. 60°; D. 360°
30 p 3. Az E és az F pont egy O középpontú körön van és EOF∢ = 90°. Az EF nagykörív mértéke:
A. 180°; B. 90°; C. 270°; D. 360°.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
3. l. Egy egyenes és egy kör kölcsönös helyzete. Két kör kölcsönös helyzete
Emlékeztető
Legyen C(O, r) az O középpontú és r sugarú kör. Egy tetszőleges P pont a síkból lehet a kör belső tartományában, a körön vagy a kör külső tartományában.
P ∈ IntC(O, r), OP < r P ∈ C(O, r), OP = r P ∈ ExtC(O, r), OP > r
Fedezzük fel, értsük meg!
Tekintsük a C(O, r) kört és egy tetszőleges d egyenest. Meg szeretnénk határozni, hogy az egyenesnek és a körnek hány közös pontjuk lehet. Értelemszerűen a következő három helyzetet azonosíthatjuk:
A d egyenes helyzete a C(O, r) körhöz képest d külső egyenese a körnek
Az egyenesnek és a körnek nincs egy közös pontja sem.
A közös pontok száma
C(O, r) ⋂ d = ∅
d a kör érintője
A T pont az érintési pont
Az egyenesnek és a körnek pontosan egy közös pontja van.
C(O, r) ⋂ d = {T}
d a kör szelője
Az A és a B pontban metszi a d egyenes a kört.
Az egyenesnek és a körnek pontosan két közös pontja van.
C(O, r) ⋂ d = {A, B}
Az O pont d egyenestől mért távolsága és a kör sugara közötti kapcsolat
168 Matematika • Tankönyv a VI. osztály számára
O P
C
)) r r P r O P
C(O, r))
Int(
(O, r
Ext(
S M r d d ⊂ ExtC(O, r) O P T r d (d \ {T}) ⊂ ExtC(O, r) O A B M r d d ⋂ IntC(O, r) = AB
Mértani ábrázolás O P
⊥ d és OM > r.
∈ d OT ⊥ d és OT = r OM ⊥ d és OM < r.
∈ d
OM
M
M
Megjegyzések.
1. Egy egyenesnek és egy körnek nem lehet három különböző közös pontja. Következésképpen egy kör bármely három pontja nem kollineáris
2. A kör érintője merőleges az érintési pontba húzott sugárra.
Gyakorlati alkalmazás: Két kör kölcsönös helyzete
Szükséges kellékek: két C1(O1, r1), C2(O2, r2) körré hajlított drót, r1 < r2 amelyek sugarainak hosszúsága 5 cm-nél kisebb legyen, egy beosztásos vonalzó, egy A4-es lap.
1. lépés. Jelöld az O1 pontot az A4-es lapon, majd helyezd a lapra és rögzítsd a C1(O1, r1) kört is!
2. lépés. Mozgasd a C2(O2, r3) kört a lap síkján, változtatva az O1O2 távolságot és minden esetben állapítsd meg a két kör közös pontjainak számát!
3. lépés. Szerkeszd meg körző segítségével a füzetedbe a tanulmányozott esetekhez tartozó ábrákat!
A fenti tevékenység segít megfigyelni a következő eredményeket:
A közös pontok száma és a két kör kölcsönös helyzete
0 közös pont
Diszjunkt körök
C1(O1 , r1) ⋂ C2(O2 , r2) = ∅
1 közös pont
Érintő körök
C1(O1, r1) ⋂ C2(O2, r2) = {T}
2 közös pont
Metsző körök
C1(O1 , r1) ⋂ C2(O2, r2) = {A, B}
Mértani ábrázolás
1. Mindkét kör a másik kör külső tartományához tartozik.
C2(O2, r2) ⊂ ExtC1(O1, r1) és
C1(O1, r1) ⊂ ExtC2(O2, r2)
N
M O1 r1 r2 O2
O1O2 > r 1 + r2
1. Külső érintő körök: egyik kör minden pontja (az érintési pontot kivéve) a másik kör külső tartományában van.
(C2(O2, r2) \ {T}) ⊂ ExtC1(O1, r1) és
(C1(O1, r1) \ {T}) ⊂ ExtC2(O2, r2)
2. A kisebb sugarú kör a másik kör belső tartományában van.
C1(O1, r1) ⊂ IntC2(O2, r2)
N
M O1 r1 r2 O2
0 ≤ O1O2 < r 2 – r1
Ha O1 és O2 egybeesik, a köröket koncentrikus köröknek hívjuk.
2. Belső érintő körök: a kisebb sugarú kör minden pontja (az érintési ponton kívül) a másik kör belső tartományában van.
(C1(O1, r1) \ {T}) ⊂ IntC2(O2, r2)
169 5. fejezet • Mértani alapfogalmak
O2 T O1
2
1O2 = r 1 + r2
r1 r
O
O2 T O1 r1 r2 O1O2 = r 2 – r1
A B O2 O1 r2 r1 O1O2 > r2 – r1 és O1O2 < r1 + r2
Alkalmazás
Egy érdekes sajátos eset, amikor két kongruens kör kölcsönös helyzetét tanulmányozzuk, éspedig:
kongruens külső körök
kongruens külső érintő körök
kongruens metsző körök
kongruens koncentrikus körök (azonosak)
Alkalmazás. A mellékelt kép az olimpiai zászló kicsinyített másolata. Figyeljük
meg az öt olimpiai kört: K, F, P, S, Z a színük szerint.
a) Azonosítsd az ábrán a külső körpárokat, és határozd meg ezek számát!
b) Azonosítsd az ábrán a metsző körpárokat és határozd meg ezek számát!
c) Állapítsd meg, hogy az öt kör között léteznek-e érintő körök!
Megoldás. a) Hat pár külső kör van: K ⋂ F = K ⋂ P = K ⋂ Z = F ⋂ P = S ⋂ Z = S ⋂ P = ∅.
b) Négy pár metsző kör van: card (K ⋂ S) = card (S ⋂ F) = card (F ⋂ Z) = card (Z ⋂ P) = 2.
c) A képen nincs két olyan kör, amelyeknek pontosan egy közös pontjuk lenne, így az olimpiai zászló nem tartalmaz érintő köröket.
Kis történelem. Pierre de Coubertin szimbolikus olimpiai zászlóterve 1913-ban készült el, de először 1920ban, az antwerpeni olimpiai játékokon lobogtatták. Az olimpiai zászló öt különböző színű, egybevágó körből áll, amelyek egymásba vannak kapcsolva. Az öt színt, valamint a fehér hátteret azóta is használják az olimpiai játékokon részt vevő országok zászlóiban.
Gyakorlatok és feladatok
1. Figyeld meg a mellékelt ábrát, majd karikázd be a helyes választ! c a b
Csak egy helyes válasz van.
a) A kört metsző egyenes:
A. a; B. b; C. c.
b) A kört érintő egyenes:
A. a; B. b; C. c.
c) A kör külső egyenese:
A. a; B. b; C. c.
2. Írd fel matematikai szimbólumokkal a 2. feladat minden egyes esetében a kapcsolatot a kör sugara és a kör középpontjának az egyenestől való távolsága között!
3. A P ponton keresztül rajzolj egy C(O, r) kört és ábrázold:
a) a d1 egyenest, amely a kör külső egyenese;
b) a d2 egyenest, amely a kör érintője;
c) a d3 egyenest, amely metszi a kört.
4. Adott egy O középpontú, 8,4 cm átmérőjű kör. Rögzíts egy A pontot a körön, majd rajzold meg
a kör BA érintőjét, és határozd meg:
a) a OAB szög mértékét;
b) a kör középpontjának távolságát a BA egyenestől!
5. Rajzold le a C1 és C2 metsző köröket, melyek középpontja O1, O2 sugaraik pedig r, R, ahol r < R. Igazold, hogy:
a) O1 O2 > R − r ; b) O1O2 < R + r.
170 Matematika • Tankönyv a VI. osztály számára
c) Ismételd meg az a) és a b) alpontokat, az r = 1,5 cm, R = 3,5 cm adatokkal.
6. A mellékelt ábrán az AB egyenes a T pontban érinti az O középpontú kört.
a) Határozd meg a szögmérő segítségével az ATO és a BTO szögek mértékét!
b) Másold le a füzetedbe, és töltsd ki a pontozott helyeket, hogy igaz kijelentéseket kapj!
b1) ATO∢ = … °; b2) BTO∢ = … °; b3) Az „ATO∢ = BTO∢ = 90°” egy … kijelentés.
7. Egy kör középpontja A és sugara 3,5 cm. Ábrázold az a, b, c egyeneseket és állapítsd meg mindegyik egyenes körhöz viszonyított helyzetét, ha:
a) az A pont távolsága az a egyenestől 5 cm;
b) az A pont távolsága a b egyenestől 35 mm;
c) az A pont távolsága a c egyenestől 0,2 dm.
8. Rajzolj két kört, amelyek:
a) koncentrikus körök; d) metsző körök;
b) belső körök; e) külső érintő körök;
c) belső érintő körök; f) külső körök.
9. Rajzolj két kört, melyek sugarai 2 cm, illetve 7 cm. Számítsd ki a középpontjaik közötti távolságot, mikor ezek:
a) belső érintő körök;
b) külső érintő körök.
10. Adott két O, illetve Q középpontú kör, melyek sugara 4 cm, illetve R cm, R nem nulla természetes
szám. Határozd meg az R értékét, hogy a két kör külső kör legyen és OQ = 9 cm.
11. Egy vidámparkban két kisvonat közlekedik körbe-körbe, az egyik 72 m, a másik 48 m átmérőjű kör alakú pályán. Az O1 illetve az O2 pont a körök középpontja, A és B a két kör közös pontjai, az
O1A, O1B, O2A, O2B a park sétányai.
a) Számítsd ki mekkora távolságot tesz meg Andris testvére, ha több fényképet is készít, és az O1 A O2 B O1 útvonalon halad.
b) Igazold, hogy O1O2 < 60 m.
O2 O1
12. Legyen C1 (O1, r) és C2(O2, R) két kör. Számítsd ki az AB szakasz hosszát a következő esetekben.
a)
O1 O2 A B
r = 4 cm, R = 6 cm, O1O2 = 8 cm
b) O1 O2 A B r = 2 cm, R = 6 cm
c) O2 O1 A B
r = 2 cm, R = 7 cm, O1O2 = 12 cm
Miniteszt
Válaszd ki a helyes válasznak megfelelő betűt! Csak egy helyes válasz van.
30 p 1. A kört metsző egyenes a kört:
A. egyetlen pontban metszi;
B. két különböző pontban metszi;
30 p 2. A kör érintője és az érintési pontba húzott sugár:
A. merőlegesek;
B. párhuzamosak;
C. három különböző pontban metszi;
D. végtelen sok pontban metszi.
C. egybeesők;
D. ellentétes félegyenesek.
30 p 3. Adottak a C1 (O1, r1) és C2(O2, r2) körök, r1 = 4 cm, r2 = 9 cm és O1O2 = 13 cm, ekkor a körök:
A. metsző körök;
B. belső érintő körök;
C. külső érintő körök;
D. külső körök .
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
171 5. fejezet • Mértani alapfogalmak
B
A
O A T B
I. Válaszd ki a helyes választ! Csak egyetlen helyes válasz van.
5 p 1. Az AOB∢ = 130°-os szög belső tartományában legyen a C és a D pont úgy, hogy
AOC∢ = BOD∢ = 83°. A COD szög mértéke egyenlő:
A. 30°; B. 36°; C. 34°; D. 32°.
5 p 2. AOB, BOC, COA az O pont körüli szögek, AOB∢ = BOC∢ = 135°. Akkor:
A. AO⊥OB; B. BO⊥OC; C. AO⊥OC; D. CO ∥ AB.
5 p 3. Az AB egyenes egyik és másik oldalán felvesszük a C és a D pontokat úgy, hogy CA ⊥ AB , DB ⊥ AB.
A következő állítások közül az igaz:
A. AC ∥ BD; B. AC ⊥ BD; C. AB ∥ CD; D. AB ⊥ CD.
5 p 4. Két párhuzamos egyenes egy szelővel (3 · x)° és 102° mértékű megfelelő szögeket alkot. Az x szám értéke:
A. 24; B. 32; C. 42; D. 34.
5 p 5. Az A pont a B pont szimmetrikusa a g egyeneshez viszonyítva és AB = 7,2 cm. Az A pont távolsága a g egyenestől egyenlő:
A. 2,7 cm; B. 3,6 cm; C. 4,8 cm; D. 14,4 cm.
5 p 6. Legyen adott az AB = 16 cm szakasz, az r = 6,9 cm és R = 9,6 cm számok. A C(A, r) és a C(B, R) körök:
A. metsző körök; B. külső körök; C. belső érintő körök; D. külső érintő körök.
II. Írd le a teljes megoldást!
1. Figyeld meg a mellékelt ábrát. Az ábrán lévő adatok alapján:
cd a
130°
10 p
10 p
15 p
10 p
5 p 5 p
5 p
a) állapítsd meg, hogy az a és b egyenesek párhuzamosak-e;
b) határozd meg az x szám értékét!
b 50°
(2x + 40)°
(3x + 25)°
2. Az AOB és a BOC szögek egymás melletti szögek, OM illetve ON a szögek szögfelezői. Tudjuk, hogy
AOB∢ = 30°+ BOC∢ és MON∢ = 75°.
a) Számítsd ki az AOB és BOC szögek mértékét!
b) Igazold, hogy a CON szög szögfelezője merőleges az OM egyenesre!
3. Adott egy O középpontú kör, melynek sugara r = 4 cm és egy a egyenes. Az O pont távolsága az a egyenestől d cm, d ∈ {2, 4, 6, 8}. Határozd meg a d értékét, úgy, hogy az a egyenes:
a) a kör szelője legyen;
b) a kör érintője legyen;
c) a kör külső egyenese legyen!
Megjegyzés: Munkadidő: 50 perc
Hivatalból: 10 pont
172 Matematika • Tankönyv a VI. osztály számára
ISMERETFELMÉRŐ
6. A HÁROMSZÖG
6.1 A háromszög. Háromszög szerkesztése
1. l. A háromszög. Osztályozás. Kerület
Emlékeztető
Bármely A és B különböző pontok esetében AB szakasznak (vagy BA szakasznak) nevezzük azoknak az AB egyenesen lévő M pontoknak a halmazát, melyek az A és B pontok között van. Az A és a B pont az AB szakasz végpontjai. Egy mértani ábra kerülete egyenlő az oldalak hosszának összegével.
Az ABC szög belseje az AB egyenes által határolt, C pontot tartalmazó félsík és a BC egyenes által határolt, A pontot tartalmazó félsík metszéspontjainak halmaza.
Oldjuk meg figyelmesen!
A háromszög életünk számos tárgyának motívuma. Kiskorunktól kezdve felismerjük a háromszög alakú tárgyakat, azonosítjuk elemeiket (csúcsok, oldalak, szögek).
Példa.
a) Add meg az első képen látható kirakóshoz használt háromszög alakú darabok számát!
b) Azonosíts háromszögeket a második ábrán!


Ha adottak az A, B, C nem kollineáris pontok, akkor az AB, AC és BC szakaszok keletkeznek.
Értelmezés és jelölés Mértani ábrázolás A háromszög elemei és ezek száma
Az AB, BC és CA szakaszok összes pontjainak halmaza, a végpontokkal együtt alkotják az ABC háromszöget.
Így jelöljük: ABC∆ vagy ACB∆ vagy BAC∆ és így olvassuk: az ABC háromszög vagy ACB háromszög vagy BCA háromszög.
A B
C
3 csúcs: A, B, C pontok;
3 oldal: AB, AC, BC szakaszok;
3 szög: BAC∢, ABC∢, ACB∢
vagy A∢, B∢, C∢.
Átfogalmazás, matematikai szimbólumokkal: ABC∆ = AB ⋃ BC ⋃ AC ⋃ {A, B, C}.
Az ABC háromszög összes szögének belsejébe tartozó pontokat a háromszög belső tartományának nevezzük, jelölése Int(ABC∆).
Azok a pontok, amelyek nem tartoznak a háromszöghöz vagy annak belső tartományához, a háromszög külső tartományát képezik.
A háromszög kerülete
A C B P M
Int(ABC∆) = Int(A∢) ⋂ Int(B∢) ⋂ Int(C∢)
Ha P ∉ ABC∆ és P ∉ Int(ABC∆), akkor
P ∈ Ext(ABC∆).
M ∈ Int(A∢), M ∈ Int(B∢) és M ∈ Int(C∢), tehát M ∈ Int(ABC∆).
P ∈ Ext(ABC∆).
Ha az ABC háromszög oldalainak hossza AB = c, BC = a, AC = b, akkor az ABC háromszög kerülete egyenlő az a + b + c összeggel. Jelöljük: KABC∆ = a + b + c.
Megjegyzés A gyakorlatban, olyan feladatokkal is találkozunk, amelyekben a háromszög félkerületét használjuk, vagyis .
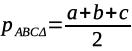
Sajátos kompetenciák: 1.6; 2.6; 3.6; 4.6; 5.6; 6.6
173 6. fejezet • A háromszög
Jegyezd meg!
A háromszögek osztályozása a szögek mértéke szerint
Szögeinek mértéke szerint egy háromszög lehet:
♦ hegyesszögű, ha mindhárom szöge hegyesszög;
♦ derékszögű, ha egyik szöge derékszög;
♦ tompaszögű, ha egyik szöge tompaszög.
Matematikai szimbólumokkal
A szögei függvényében az ABC∆ lehet:
♦ hegyesszögű, ha A∢ < 90°, B∢ < 90° és C∢ < 90°;
♦ derékszögű, ha A∢ = 90°, vagy B∢ = 90° vagy C∢ =90°;
♦ tompaszögű, ha A∢ > 90°, vagy B∢ > 90° vagy C∢ >90°.
Megjegyzés. Egy derékszögű háromszögben a derékszöggel szemben fekvő oldalt átfogónak nevezzük, a derékszög szárait pedig befogóknak.
2. feladat Mérd meg beosztásos vonalzó segítségével az MNP, QRS, TUV háromszögek oldalainak hoszszát, majd töltsd ki a táblázatot!
MNP∆ QRS∆ TUV∆
NP = 2 cm QR = 4 cm TU = 4 cm
PM = 4 cm RS = 2 cm UV = 4 cm
MN = 5 cm QS = 4 cm TV = 4 cm
Jegyezd meg!
A háromszögek osztályozása az oldalak hossza szerint:
Oldalainak hossza szerint egy háromszög lehet:
♦ általános, ha oldalainak hossza páronként különbözik;
♦ egyenlő szárú, ha az oldalai közül kettő kongruens;
♦ egyenlő oldalú, ha mindhárom oldala kongruens.
Megjegyzés
Ha a DEF derékszögű E∢ = 90°, akkor: DF átfogó, ED és EF befogók.
Matematikai szimbólumokkal:
Oldalainak hossza szerint az ABC∆ lehet:
♦ általános, ha AB ≠ BC, BC ≠ AC és AC ≠ BC.
♦ egyenlő szárú, ha AB ≡ BC vagy BC ≡ AC vagy AC ≡ AB.
♦ egyenlő oldalú, ha AB ≡ BC ≡ AC. M
1. Ha az ABC∆ egyenlő szárú, AB = BC, akkor az AC oldal a háromszög alapja.
2. Bármely egyenlő oldalú háromszög egyenlő szárú is.
174 Matematika • Tankönyv a VI. osztály számára 1. feladat Mérd meg szögmérővel az ABC, DEF, GHL háromszögek szögeit, majd töltsd ki a táblázatot! A B C D E F G H L ABC∆ DEF∆ GHL∆ A∢ = 60° D∢ = 60° G∢ = 50° B∢ = 75° E∢ = 90° H∢ = 100° C∢ = 45° F∢ = 30° L∢ = 30°
N P Q R S T U V
Alkalmazások
A 2. feladat mérései alapján, miután kitöltöttük a táblázatot, észrevesszük, hogy:
♦ Az ABC∆-ben A∢ = 60°, B ∢= 75° és C∢ = 45°, tehát az ABC∆ hegyesszögű háromszög.
♦ Az DEF∆-ben E∢ = 90°, tehát DEF∆ derékszögű háromszög.
♦ A GHL∆-ben H∢ = 100°, tehát GHL∆ tompaszögű háromszög.
♦ Az MNP∆-ben NP = 2 cm, PM = 4 cm, MN = 5 cm, tehát MN ≠ NP, NP ≠ MP és MN ≠ MP, tehát az MNP∆ általános háromszög.
♦ A QRS∆-ben QR = 4 cm, RS = 2 cm, QS = 4 cm, azaz QR = QS, tehát QRS∆ egyenlő szárú háromszög, melynek alapja RS.
♦ A TUV∆-ben TU = 4 cm, UV = 4 cm, TV = 4 cm, azaz TU = UV = TV, tehát a TUV∆ egyenlő oldalú háromszög.
Az MNP, QRS, TUV háromszögek kerülete, illetve félkerülete:
PMNP∆ = 2 cm + 4 cm + 5 cm = 11 cm, PQRS∆ = 4 cm + 4 cm + 2 cm = 10 cm, PTUV∆ = 4 cm + 4 cm + 4 cm = 12 cm.
p P MNP MNP = 2 = 5,5 cm; p P AQRS QRS == 2 5 cm; p P TUV TUV = 2 = 6 cm.
Gyakorlatok és feladatok
1. Adottak az A, B, C, D különböző pontok. Ábrázold és jelöld a keletkező háromszögeket a következő esetekben:
a) az A, B, C pontok kollineárisak és D ∉ AB;
b) bármelyik három az A, B, C, D pontok közül nem kollineáris.
2. A megadott jelöléseket használva figyeld meg a mellékelt mértani alakzatot:
a) határozd meg az ábrán látható háromszögek számát;
b) sorold fel azokat a háromszögeket, melyeknek a CD szakasz az egyik oldala;
c) sorold fel azokat a háromszögeket, melyeknek egyik szögük a DAF∢.
3. Ábrázold a DEF háromszöget és sorold fel:
a) a háromszög minden jelölési módját;
b) a háromszög csúcsait, oldalait és szögeit;
c) az EF oldalon fekvő szögeket;
d) a DEF szöggel szemben fekvő oldalt.
4. Figyeld meg a következő ábrán a háromszögeket, esetleg mérd meg a szögeiket, aztán válaszd ki a helyes válasznak megfelelő betűt! Csak egy helyes válasz van.
a) b) c)
d) e) f)
4.1. Hegyesszögű háromszögek láthatóak a következő ábrákon:
A. a), c) és d);
B. b) és f);
C. a) és f);
D. c) és e).
4.2. Tompaszögű háromszögek láthatóak a következő ábrákon:
A. c) és e);
B. b) és d);
C. a), b) és f);
D. b) és e).
4.3. Derékszögű háromszögek láthatóak a következő ábrákon:
A. c) és d);
B. a), c) és e);
C. a) és c);
D. c) és e). A B
175 6. fejezet • A háromszög
F G
C D E
5. Rajzolj minden esetben két-két háromszöget:
a) van egy közös csúcsuk, amit jelölj M-mel;
b) van egy közös oldaluk, amit jelölj NP-vel;
c) egyik háromszög belseje benne van a másik háromszög belsejében.
d) van egy ABC közös szögük; e) belső tartományuk diszjunktak.
6. Állapítsd meg az ABC háromszög természetét (egyenlő szárú, egyenlő oldalú, általános, hegyesszögű, derékszögű, tompaszögű), a következő esetekben:
a) AB = 3 cm, BC = 4 cm, AC = 3 cm;
b) AB = 5 cm, BC = 0,5 dm, AC = 50 mm;
c) AB = 6 cm, BC = 6,6 cm, AC = 6,(6) cm;
d) BAC∢ = 90°;
e) A∢ = 33°, A∢ + B∢ = 122°, C∢ = 58°;
f) ACB∢ = 6000’.
Miniteszt
7. Számítsd ki az MNP háromszög kerületét tudva, hogy:
a) MN = 8 cm, NP = 5 cm, NP = 10 cm;
b) MN = 20 cm, NP = 2,5 dm, NP = 0,15 m;
c) MN = NP = NP = 0,01 km;
d) a háromszög félkerülete 40 cm.
8. Egy egyenlő szárú háromszög kongruens oldalai 14 cm hosszúak, a háromszög kerülete pedig 35 cm. Számítsd ki a háromszög harmadik oldalának hosszát!
9. Egy egyenlő oldalú háromszög félkerülete 21 cm. Számítsd ki a háromszög egyik oldalának a hosszát!
10. Az M pont az ABC háromszög BC oldalán van. Tudjuk, hogy az ABM háromszög kerülete 40 cm, az ACM háromszög kerülete 54 cm és az ABC háromszög kerülete pedig 60 cm. Számítsd ki az AM szakasz hosszát!
1. A mellékelt ábrán az A, E, C illetve B, E, D pontok kollineárisak.
15 p a) Írd le az ábrán látható összes háromszöget!
15 p b) Írd le azokat a háromszögeket, melyeknek a BC szakasz az egyik oldala!
15 p c) Írd le azokat a háromszögeket, melyeknek egyik szöge az ABD!
30 p 2. Egy egyenlő szárú háromszög kerülete 20 cm, és egyik oldalának hossza 9 cm. Számítsd ki a háromszög többi oldalának hosszát! Tanulmányozz minden lehetséges esetet!
15 p 3. Állapítsd meg az FGH háromszög természetét, ha F∢ = 68°, F∢ + G∢ = 158°, G∢ + H∢ = 112°.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
2. l.
Háromszög külső szöge
Emlékeztető
Két párhuzamos egyenes egy szelővel kongruens belső váltószögeket, kongruens külső váltószögeket, kongruens megfelelő szögeket, a szelő ugyanazon oldalán fekvő kiegészítő belső szögeket és a szelő ugyanazon oldalán fekvő kiegészítő külső szögeket alkot.
176 Matematika • Tankönyv a VI. osztály számára
A B M C
A B
D E
C
Egy háromszög szögei mértékének összege.
Fedezzük fel, értsük meg!
1. feladat. Adott az ABC háromszög és DE az A ponton áthaladó BC-vel párhuzamos egyenes, ahol D és E az A pont különböző oldalain fekvő pontok úgy, ahogy a mellékelt ábrán látható.
a) Bizonyítsd be, hogy az EAC és az ACB szögek kongruensek!
b) Bizonyítsd be, hogy a DAB és az ABC szögek kongruensek!
c) Számítsd ki a BAC, ABC, BCA szögek mértékeinek összegét, felhasználva az a) és b) alpontokban igazolt kongruenciákat!
Bizonyítás.
a) A DE és a BC párhuzamos egyenesek az AB szelővel kongruens belső váltószögeket alkotnak, tehát DAB∢ ≡ ABC∢.
b) Ugyanazok a párhuzamosok az AC szelővel is kongruens belső váltószögeket alkotnak, tehát EAC∢ ≡ BCA∢.
c) Az E, A, D pontok kollineárisak, vagyis DAE∢ = 180°. Az EAC és a CAB illetve a CAB és a DAB szögek egymás melletti szögek, ebből következik, hogy EAC∢ + CAB∢ + DAB∢ = DAE∢ = 180°.
Az a) és a b) alpontok alapján BAC∢ + ABC∢ + BCA∢ = DAB∢ + CAB∢ + EAC∢. A c) alpontból következik, hogy BAC∢ + ABC∢ + BCA∢ = 180° vagy A∢ + B + C = 180°, ahol A∢, B∢, C∢ az ABC háromszög szögeinek mértéke.
A fenti alkalmazással bizonyítottuk a következő fontos eredményt:
Tétel
Bármely háromszög szögei mértékének összege 180°.
2. feladat. Legyen ABC egy háromszög.
Matematikai szimbólumokkal:
Az ABC háromszögben A∢ + B∢ + C∢ = 180°.
a) Ábrázold a CD félegyenest, mely a CB félegyenes ellentétes félegyenese és a CE félegyenest, mely a CA félegyenes ellentétes félegyenese.
b) Jelöld meg az ACB szöggel (a háromszög C szöge) egymás melletti kiegészítő szögeket!
c) Ismételd meg az a) és b) alpontok követelményeit az ABC háromszög A és B szögeire. Jelöld így a keletkezett félegyeneseket: AM az AB ellentétes félegyenese, AN az AC ellentétes félegyenese, illetve BP a BA ellentétes félegyenese, BQ pedig a BC ellentétes félegyenese.
d) Határozd meg a megjelölt szögek közötti összefüggést, indokolva válaszodat!
Rezolvare
és
d) B, C, D kollineárisak, A, C, E kollineárisak, azaz ACD és BCE csúcsszögek, tehát ACD∢ ≡ BCE∢. A megjelölt szögeket az ABC háromszög külső szögeinek nevezzük. Fennállnak a következő kongruenciák: ACD∢ ≡ BCE∢, CBP∢ ≡ ABQ∢, BAN∢ ≡ CAM∢.
Értelmezés. A háromszög valamelyik szögével kiegészítő egymás melletti szöget a háromszög külső szögének nevezzük. Jegyezd meg!
Minden háromszögnek három pár külső szöge van. Ugyanahhoz a csúcshoz tartozó külső szögek kongruensek.
Alkalmazások
1. alkalmazás: A mellékelt ábrán az ABC háromszög látható. A D pont a BC egyenesen található a B és a D pont között. Hasonlítsd össze az ACD szög mértékét az A∢ + B∢ összeggel.
Megoldás. A BCA és az ACD szögek egymás melletti kiegészítő szögek, tehát BCA∢ + ACD∢ = 180°.
177 6. fejezet • A háromszög
E A D B C
E
M D C E P B
N
a)
b) A B C D
c) A
Q
A B C D
De a háromszög szögei mértékének összege 180°, tehát A∢ + B∢ + BCA∢ = 180°
Következik, hogy ACD∢ = A∢ + B∢.
A fenti alkalmazással bizonyítottuk a következő fontos eredményt:
A háromszög külső szögének tétele:
Egy háromszög külső szögének mértéke egyenlő a nem mellette fekvő belső szögek mértékének összegével.
Matematikai szimbólumokkal:
Ha ACD az ABC háromszög külső szöge, akkor ACD∢ = A∢ + B∢.
2. alkalmazás: Bármely háromszögnek van legalább két hegyesszöge.
Bizonyítás. Legyen az ABC∆. Feltételezzük, hogy a háromszögnek kevesebb mint két hegyesszöge van. Akkor, legalább két szöge tompaszög vagy derékszög. Legyen A∢ ≥ 90° és B∢ ≥ 90°. Ekkor A∢ + B∢ ≥ 180° ami ellentmond az A∢ + B∢ + C∢ = 180° és C∢ > 0°. bizonyított összefüggésnek. Következik, hogy a feltételezés hamis, tehát igaz a kijelentés, amely szerint: Egy háromszögnek legalább két szöge hegyesszög.
3. alkalmazás: Egy derékszögű háromszög hegyesszögei pótszögek.
Bizonyítás Legyen az ABC∆ derékszögű háromszög, ahol A∢ = 90°. Mivel A∢ + B∢ + C∢ = 180°, következik, hogy B∢ + C∢ = 180° – 90°= 90°, ami igazolja, hogy a B∢ és a C∢ pótszögek. Gyakorlatok
1. Jelöljük az ABC háromszög szögeit A∢, B∢, C∢ Határozd meg az ismeretlen szögek mértékét a következő esetekben:
a) A∢ = 50°, B∢ = 60°;
b) B∢ = 67°, C∢ = 76°;
c) B∢ = 100°, A∢ ≡ C∢;
d) C∢ = 34°20’, B∢ = 2 · C∢;
e) A∢ ≡ B∢ ≡ C∢;
f) A∢ = 2 · B∢ = 6 · C∢.
2. Határozd meg a háromszög természetét az 1. feladat minden alpontja esetében. (hegyesszögű, derékszögű, tompaszögű).
3. Sándor lerajzolta a DEF háromszöget, melynek D szöge 48°-os. Andris azt mondja, hogy a másik két szög 70° illetve 72°-os lehet. Péter azt mondja, hogy a másik két szög 64° illetve 68°-os lehet. Állapítsd meg érvekkel alátámasztva, hogy melyiküknek van igaza!
4. Legyen az MNP háromszög. Töltsd ki a táblázatot a szögeknek megfelelő értékekkel!
M∢ N∢ P∢
75° 46°
90°
M∢
45°
5. Másold le a füzetedbe a táblázatot, és írj az üres mezőbe I betűt, ha az állítás igaz, illetve H betűt, ha az állítás hamis!
Állítás I/H
Ha A∢ + B∢ = 90°, akkor C∢ = 90°.
Ha B∢ + C∢ > 90°, akkor A∢ < 90°.
Ha C∢ + A∢ < 90°, akkor B∢ < 90°.
Ha A∢ ≥ 60°, B∢ ≥ 60°, C∢ ≥ 60°, akkor A∢ = B∢ = C∢.
6. Határozd meg minden esetben, hogy a háromszög hegyesszögű, derékszögű vagy tompaszögű:
a) A∢ = 45°, A∢ ≡ B∢;
b) B∢ = 25°, C∢ = 62°;
c) C∢ = 30°, A∢ = 24° + B∢!
7. A következő ábrán
ABE∢ = CBD∢ = 90°, a B, E, D pontok kollineárisak és
A∢ ≡ D∢.
a) Igazold, hogy C∢ ≡ AEB∢.
AC D B E
b) Ha C∢ = 60°, számítsd ki az A∢ szög mértékét!
8. Legyen az ABC háromszög A∢ = 56°, B∢ = 78°. Számítsd ki a háromszög külső szögeinek mértékét!
178 Matematika • Tankönyv a VI. osztály számára
+ 12° N∢ + 24°
és feladatok
9. Határozd meg egy háromszög szögeinek mértékét tudva, hogy fokokban mérve ezek három különböző, 18-cal osztható természetes számmal vannak kifejezve!
10. Az AOB és a COD szögek csúcsszögek, O ∈ AD, AOB∢ = 50°, OCD∢ = 80° és AB ∥ CD.
a) Készíts a feladat adatainak megfelelő rajzot!
b) Határozd meg az ADC szög mértékét!
c) Igazold, hogy AOC∢ = BAO∢ + ABO∢.
11. A mellékelt ábrán a B egy pont az ADE szög szögfelezőjén. Az ACD háromszög CD oldalának meghosszabbításán felvesszük az E pontot, amelyre DBE∢ = 40°. Tudjuk, hogyCAD∢ = 32° és ADC∢ =70°.
a) Számítsd ki a CDE, ACD és BEC szögek mértékét!
b) Határozd meg, indokolva válaszod, hogy az AD és a BE egyenesek párhuzamosak vagy metszők!
Miniteszt
12. Egy háromszög két külső szögének mértéke 99°, illetve 137°. Számítsd ki a háromszög szögeinek mértékét!
13. Határozd meg a DEF háromszög szögeinek mértékét, tudva, hogy D∢ = E∢, az F csúcsban lévő külső szög mértéke pedig 100°!
14. A BD félegyenes az ABC szög szögfelezője, az A ponton keresztül a BD egyeneshez húzott párhuzamos a BC egyenest az E pontban metszi.
a) Készíts a feladat adatainak megfelelő rajzot!
b) Igazold, hogy BAE∢ ≡ AEB∢.
c) Ha BAE∢ = 78°, számítsd ki az ABE háromszög szögeinek mértékét!
15. Az ABC háromszög AB oldalán felvesszük a P pontot úgy, hogy BCP∢ = 2 · ACP∢, APC∢ = 116° és
B∢ = 56°.
a) Számítsd ki a BCP és a CAP szögek mértékét!
b) Igazold, hogy a B pontban a BC egyenesre húzott merőleges párhuzamos az AC egyenessel!
1. Az M és N pontok az ABC háromszög BC oldalán vannak, BAC∢ = 100°, AMB∢ = 90° és MAN∢ = CAN∢ = 20°. Másold le a füzetedbe és töltsd ki a pontozott helyeket úgy, hogy igazak legyenek a kijelentések!
20 p a) Az ABC szög mértéke egyenlő … ° .
20 p b) Az ABN háromszög egyik külső szögének mértéke … . A
20 p c) Az ANC szög mértéke … ° .
30 p 2. A BC közös oldala az ABC és a DBC háromszögeknek. A mellékelt ábra jelölései segítségével számítsd ki az ACD szög mértékét!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
Fedezzük fel, értsük meg!
Adott az ABC háromszög. Mértani felszerelés segítségével megmérhetjük a három oldalának hosszúságát és három szögének mértékét.
Célunk, hogy kiderítsük, hány elemre van szükségünk a hatból a háromszög megszerkesztéséhez.
Tudjuk, hogy egy háromszög szögei mértékének összege 180°, tehát elégséges, hogy két szöget ismerjünk, hogy a harmadikat is kiszámítsuk.
179 6. fejezet • A háromszög
3. l. Háromszögek szerkesztése
B C D 110° 45° 44° 88°
B A C D E
1. feladat. a) Felhasználva azt a tényt, hogy a kör olyan pontokat tartalmaz, amelyek egy rögzített ponttól állandó távolságra vannak, ellenőrizd, hogy létezik-e olyan MNP háromszög, melynek oldalai MN = 1 cm, NP = 2 cm, MP = 4 cm.
b) Ellenőrizd, hogy létezik-e olyan QRS háromszög, melynek oldalai QR = 1 cm, RS = 2 cm, QS = 3 cm.
c) Ellenőrizd, hogy létezik-e olyan DEF háromszög, melynek oldalai DE = 3 cm, DF = 2 cm, EF = 1,5 cm.
d) Számítsd ki a DE + EF, DF + EF, DE + DF összegeket!
e) Hasonlítsd össze a DE + EF összeget DF-fel, a DF + EF összeget DE-vel, majd a DE + DF összeget EF-fel.
Megoldás. a) Megszerkesztjük az MP = 4 cm szakaszt. Ha létezik az MNP háromszög, akkor az N pont 1 cm-re van az M ponttól és 2 cm-re a P ponttól. Következésképpen N mivel az M középpontú és 2 cm sugarú körön, mind a P középpontú és 1 cm sugarú körön rajta lenne. Megszerkesztjük a két kört és észrevesszük, hogy ezeknek nincs közös pontjuk. Következik, hogy a síkban nem létezik olyan pont, mely mindkét körön rajta lenne, tehát nem létezik olyan háromszög, amelyre MN + NP < MP.
b) Megrajzolva az S középpontú és 2 cm sugarú kört, és a Q középpontú és 1 cm sugarú kört, ezek az R pontban metszik egymást, mely az SQ egyenesen van, azaz nem létezik olyan háromszög, melybenSR + RQ = SQ.
QR = 1 cm, RS = 2 cm, QS = 3 cm, tehát QS = QR + RS, ahonnan a Q, R, S pontok kollineárisak, tehát nem lehetnek egy háromszög csúcsai.
c) 1. lépés Megszerkesztjük a DE = 3 cm szakaszt és a C1(D, 2 cm) és a C2(E, 1,5 cm) köröket.
2. lépés Jelöljük F1-gyel és F2-vel a két kör metszéspontjait.
3. lépés Megrajzoljuk a DEF1 vagy DEF2 háromszögek oldalait. A DEF1 és DEF2 háromszögek bármelyikének oldalai megfelelnek a feladat követelményeinek. Következtetés: meg lehet szerkeszteni az adott feltételeknek megfelelő DEF1 és DEF2 háromszögeket.
d) DE + EF = 4,5 cm; DF + EF = 3,5 cm; DE + DF = 5 cm.
e) Felhasználva a d) alpont számításait, következik, hogy DE + EF > DF; DF + EF > DE; DE + DF > EF.
Tétel (A háromszög egyenlőtlenségei) Egy háromszögben, bármely két oldala hosszának összege nagyobb, mint a harmadik oldal hossza.
Ha létezik az ABC háromszög, akkor AB + BC > AC; AB + AC > BC; AC + BC > AB.
Ha a, b, c pozitív szám úgy, hogy a + b > c; a + c > b; b + c > a, akkor létezik egy háromszög, amely oldalainak hossza a, b, c, ugyanabban a mértékegységben kifejezve.
Megjegyzés. Ahozz, hogy létezik olyan háromszög, amelynek oldalai a < b < c pozitív számok ugyanabban a mértékegységben kifejezve, elégséges igazolni, hogy a + b > c.
2. feladat: a) Szerkeszd meg az ABC háromszöget, melyben BC = 3 cm, ABC∢ = 60° és ACB∢ = 50°.
b) Szerkeszd meg az MNP háromszöget, melyben MN = 3 cm, NMP∢ = 30° és MP = 2 cm.
Megoldás.
a) 1. lépés. Megszerkesztjük a BC = 3 cm szakaszt.
2. lépés. A BC, szakasz ugyanazon oldalán megszerkesztjük a BX és a CY félegyeneseket úgy, hogy CBX∢ = 60° és BCY∢ = 50°.
3. lépés. Jelöljük A-val azt a pontot, ahol a BX és a CY félegyenesek metszik egymást. Ez a pont létezik, mert a szögek mértékeinek összege kisebb, mint 180°.
4. lépés. Megrajzoljuk az AB és az AC oldalakat.
180 Matematika • Tankönyv a VI. osztály számára
Y A X B C
b) 1. lépés. Rögzítjük az M pontot és rajzolunk egy 30°-os szöget, melynek csúcsa az M pontban legyen.
2. lépés. A szög egyik szárán felvesszük az N pontot úgy, hogy MN = 3 cm legyen, a másik szárán pedig a P pontot úgy, hogy MP = 2 cm legyen. Ábrázoltuk a háromszög MN és MP oldalait.
3. lépés. Meghúzzuk az NP szakaszt, ami a háromszög harmadik oldala lesz. Az 1. és 2. feladat megoldása során három különböző helyzetet fedeztünk fel, amikor a háromszöget meg lehetett szerkeszteni, hat eleméből csak hármat ismerve.
Jegyezd meg!
A következő három esetben lehet megszerkeszteni egy háromszöget:
1. Ha ismerjük a háromszög mindhárom oldalának hosszát, melyek teljesítik a háromszög egyenlőtlenségeit. (O.O.O. eset)
2. Ha ismerjük a háromszög két oldalának hosszát és a közre zárt szög mértékét. (O.Sz.O. eset)
3. Ha ismerjük két szög mértékét, melyek összege kisebb, mint 180° és a csúcsaik által meghatározott oldal hosszát. (Sz.O.Sz. eset)
Megjegyzések.
1. Az O.O.O. esetben lényeges, hogy teljesüljenek a háromszög egyenlőtlenségei.
2. Egy háromszög létezését a Sz.O.Sz. esetben az a feltétel biztosítja, hogy a két ismert szög mértékének összege kisebb legyen, mint 180°, és a harmadik szög mértéke ezen összeg kiegészítő szöge legyen.
Alkalmazások
1. megoldott feladat: András és Krisztián ugyanabban a városban lakik és ugyanabba az iskolába jár. András lakása és az iskola közötti távolság 1500 m, a Krisztián háza és az iskola közötti távolság pedig 1100 m. Andris azt mondja, hogy Krisztiántól legfeljebb 400 méterre lakik.
a) Határozd meg, hogy a két tanuló lakása közötti távolság lehet-e kisebb, mint 400 m! Válaszodat indokold!
b) Határozd meg milyen esetben lakik Andris 400 méterre Krisztiántól! Megoldás.
a) A helység térképén feleltessük meg az A, K, I pontokat a két iskolatárs házának, illetve az iskolának. Ekkor AI = 1500 m és KI = 1100 m. Ha az A, K, I pontok nem kollineárisak, akkor AK + KI > AI, vagyis AK + 1100 > 1500, tehát AK > 400. A két iskolatárs nagyobb távolságra lakik egymástól, mint 400 m, azaz Andris nem lakik legfeljebb 400 méterre Krisztiántól.
b) Ha az A, K, I pontok kollineárisak, akkor három rendezési eset lehetséges, amelyek közül a feladatunk szempontjából az az eset áll fenn, hogy K az A és I pontok között van, vagyis AK + KI = AI, tehát AK = 400 m. 2. megoldott feladat:
a) Szerkessz egy ABC háromszöget, amelyben AB = 4 cm, ABC∢ = 75°, BC = 5 cm.
b) Mérd meg a szerkesztett háromszög másik három elemét!
c) Írd fel a háromszög szögeit, mértékeik csökkenő sorrendjében!
d) Írd fel a háromszög oldalait, hosszuk csökkenő sorrendjében!
Megoldás a) Megszerkesztjük a 75°-os B szöget. A szög szárain felvesszük az A és a C pontokat úgy, hogy AB = 4 cm és AC = 5 cm. Meghúzzuk az AC oldalt.
b) Szögmérővel megmérjük az A és a C szögeket, majd beosztásos vonalzóval megmérjük az AC szakasz hosszát. Azt tapasztaljuk, hogy: BAC∢ mértéke körülbelül 61°, az ACB∢ mértéke körülbelül 44°, az AC hossza pedig 5,5 cm.
c) B∢ > A∢ > C∢.
d) AC > BC > AB. C
75°
181 6. fejezet • A háromszög
P M N
B A 5 cm 4 cm
Következmény. Bármely háromszögben nagyobb szöggel szemben nagyobb oldal fekszik, kisebb szöggel szemben pedig kisebb oldal.
Bármely háromszögben nagyobb oldallal szemben nagyobb szög fekszik, kisebb oldallal szemben pedig kisebb szög.
Gyakorlatok és feladatok
1. Ábrázold a nem kollineáris A, B, C pontokat úgy, hogy AB = 3 cm, ABC∢ = 50°, BC = 4 cm.
2. Mértani felszereléssel szerkeszd meg az ABC háromszöget a következő esetekben:
a) AB = 4 cm, ABC∢ = 75°, BC = 5 cm;
b) ABC∢ = 50°, BC = 6 cm, ACB∢ = 60°;
c) AB = 7 cm, BC = 9 cm, AC = 12 cm.
3. Legyenek DE = 5 cm és EF = 8 cm szakaszok. Ábrázold a DEF háromszöget, ha DEF∢ ∈ {30°, 90°, 120°}.
4. Az MN szakasz hossza 6 cm. Szerkeszd meg az MNP háromszöget, ha MNP∢ = 80° és NMP∢ = 65°.
5. Egy egyenlő szárú háromszög egyik oldalának hossza 4 cm, egy másik oldala pedig 7 cm hoszszúságú. Szerkeszd meg a háromszöget, tanulmányozva minden lehetséges esetet!
6. Szerkessz egy egyenlő oldalú háromszöget, melynek kerülete 0,24 m legyen!
7. Két szög mértéke 87°, illetve 63°. Számítsd ki a harmadik szög mértékét úgy, hogy szerkeszthető legyen egy háromszög, mely szögeinek mértéke ekkora legyen!
Miniteszt
8. Szerkessz egy háromszöget, mely szögeinek mértéke 40°, 75° és 65°.
9. Határozd meg melyik esetben nem szerkeszthető meg az ABC háromszög! Választásod indokold!
a) A∢ = 120°, AB = 5 cm, B∢ = 60°;
b) B∢ = 88°, BC = 7 cm, C∢ = 77°;
c) AB = 11 cm, BC = 11 cm, AC = 22 cm;
d) AB = BC = 0,5 dm, AC = 9 cm.
10. Legyenek az AB = 5 cm, CD = 7 cm, EF = n cm, n ∈ ℕ szakaszok. Határozd meg az n legnagyobb, illetve legkisebb értékét úgy, hogy ezekkel a szakaszokkal szerkeszthető legyen egy háromszög!
11. Szerkessz egy BC alapú egyenlő szárú háromszöget melyben, A∢ = 90° és AB = 4,5 cm.
12. a) Legyen MNP egy háromszög, melyben MN = 6 cm, NP = 10 cm, MP = 8 cm. Írd fel a háromszög szögeit a szögek mértéke szerint növekvő sorrendbe!
b) Legyen DEF egy háromszög, melyben D∢ = 72°, E∢ = 48°. Írd fel a háromszög oldalait hosszúságuk szerint csökkenő sorrendben!
20 p 1. Szerkeszd meg az ABC háromszöget, melyben AB = 3 cm, A∢ = 105°, AC = 5 cm.
30 p 2. Szerkeszd meg a DEF egyenlő szárú háromszöget, melyben DE = 4 cm és EF = 10 cm.
40 p 3. Az ABC háromszögben ismert: A∢ = 50°, B∢ = 88°, AB = 15 cm. A táblázatban az üres mezőbe írj I betűt, ha az állítás igaz, illetve H betűt, ha az állítás hamis!
Kijelentés I/H
Kijelentés I/H
C∢ = 31° AC < 15 cm
AC > BC PABC > 45 cm
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
182 Matematika • Tankönyv a VI. osztály számára
6.2 A háromszög nevezetes vonalai
1. l. Egy háromszög szögeinek szögfelezői. A szögfelezők metszéspontja
Emlékeztető
Ha ABC egy tulajdonképpeni szög és M ∈ Int(ABC) úgy, hogy ABM ≡ MBC, akkor a BM félegyenes az ABC szög szögfelezője.
Ha ABC egy tulajdonképpeni szög BM az ABC szög szögfelezője, akkor M ∈ Int(ABC) és ABM ≡ MBC.
A d egyenes a C(O, r) kör érintője a T pontban, ha d C(O, r) = {T}.
Ha d a kör érintője a T pontban, akkor OT ⊥ d.
A kör középpontjának távolsága a kör egyik érintőjétől egyenlő a kör sugarával.
Fedezzük fel, értsük meg!
1. alkalmazás: Rajzolj egy ABC háromszöget!
a) Szerkeszd meg a BAC szög AA1 szögfelezőjét A1 ∈ BC és az ABC szög BB1 szögfelezőjét, B1 ∈ AC
b) Jelöld az AA1 és BB1 félegyenesek metszéspontját I betűvel!
c) Szerkeszd meg a CI félegyenest és jelöld C1 -gyel az AB oldallal való metszéspontját!
d) Mérd meg az ACI és a BCI szögek mértékét, határozd meg a mértékeik közötti viszonyt!
Megoldás.
a) és b)
d) Méréssel következtetjük, hogy ha AA1 és BB1 az ABC háromszög A illetve B szögeinek szögfelezői, akkor ACI∢ = BCI∢, vagyis a CI félegyenes a C szög szögfelezője.
Jegyezd meg!
Bármely ABC háromszögben a szögek szögfelezői egy pontban összefutó egyenesek. Ezt a pontot általában I-vel jelöljü
Alkalmazások
Ha AA1, BB1, CC1 az ABC háromszög A, B illetve C szögeinek szögfelezői, akkor létezik egy I pont, amelyre
AA1 ⋂ BB1 ⋂ CC1 = {I}.
2. alkalmazás: a) Rajzolj egy ABC háromszöget, majd szerkeszd meg az AA1, BB1, CC1 szögfelezőit! Jelöld I-vel azt a pontot, ahol a szögfelezők metszik egymást!
b) Szerkeszd meg az IM ⊥ BC, IN ⊥ AC, IP ⊥ AB egyeneseket, ahol M ∈ BC, N ∈ AC, P ∈ AB.
c) Mérd meg az IM, IN, IP szakaszokat és állapítsd meg, hogy az I pont ugyanakkora távolságra van-e a háromszög három oldalától!
d) Szerkeszd meg az I középpontú és IM sugarú kört!
183 6. fejezet • A háromszög
d T r O A M C B
c) A B1 C A1 B I A B1 C A1 B C1 I
a) és b)
c) Megmérve a szakaszokat kapjuk, hogy:
IM = IN = IP, tehát az M, N, P pontok egyenlő távolságra vannak az
I ponttól. Akkor a C(I, IM) kör tartalmazza az N és a P pontokat.
Az ABC háromszög oldalai a C(I, IM) kör érintői.
d)
Jegyezd meg!
Bármely ABC háromszögben, a szögfelezők metszéspontja, melyet I-vel jelölünk, egyenlő távolságra van a háromszög oldalaitól.
A C(I, r), kört az ABC háromszögbe beírt körnek nevezzük, ahol r az I pont távolsága a háromszög egy oldalától.
A háromszög három oldala a C(I, r) kör érintői.
Gyakorlatok és feladatok
1. Rajzold le az ABC háromszöget, majd húzd meg szögeinek szögfelezőit, ha az ABC háromszög:
a) hegyesszögű háromszög;
b) derékszögű háromszög;
c) tompaszögű háromszög.
2. Ábrázold a DEF háromszöget, majd húzd meg a szögeinek szögfelezőit, tudva, hogy a DEF háromszög:
a) egyenlő szárú háromszög;
b) egyenlő oldalú háromszög;
c) általános háromszög.
3. Legyen MNP egy háromszög és MS az NMP szög szögfelezője, ahol S ∈ NP.
a) Ha NMP∢ = 100°, számítsd ki az NMS és a PMS szögek mértékét!
b) Ha SMN∢ = 40°30’, számítsd ki az SMP és az NMP szögek mértékét!
4. Legyen ABC egy háromszög és I egy pont a háromszög belső tartományában. Másold le a füzetedbe a következő mondatokat és pótold a pontozott helyeket, hogy igazak legyenek a kijelentések!
a) Ha AI a BAC szög szögfelezője, BI az ABC szög szögfelezője, akkor CI … .
b) Ha BAI∢ ≡ CAI∢ és ABC∢ = 2 · ABI∢, akkor , ACI∢ … BCI∢.
5. Adott a DEF háromszög, amelyben D∢ = 68°, E∢ = 86° és FM a DFE szög szögfelezője, M∈DE.
a) Számítsd ki a DFE, DFM és EFM szögek mértékét!
b) Igazold, hogy a DMF háromszög tompaszögű!
6. Az ABC háromszög BC oldalán felvesszük a D pontot úgy, hogy BAD∢ ≡ CAD∢. Tudva azt, hogy BAD∢ = 44°, ADC∢ = 117°, számítsd ki az ABC háromszög szögeinek mértékét!
7. Az ABC és a DBC háromszögek A és D csúcsai a BC egyenes különböző oldalain helyezkednek el. Tudva, hogy ABC∢ ≡ ACB∢, DBC∢ ≡ DCB∢ és AD a BAC szög szögfelezője, igazold, hogy DA a BDC szög szögfelezője.
8. Legyen I az MNP háromszög szögfelezőinek metszéspontja.
a) Ha IMP∢ = 31°, INM∢ = 29°, számítsd ki az MNP háromszög szögeinek mértékét!
b) Ha MNP∢ = 80°, IMP∢ = 34°, számítsd ki az MPN és MIP szögek mértékét!
9. Az ABC háromszög derékszögű BAC∢ = 90°. Számítsd ki az ABC és az ACB szög szögfelezői által bezárt tompaszög mértékét!
10. a) Szerkeszd meg az ABC háromszöget, amelyben A∢ = 30°, B∢ = 60°, AB = 8 cm.
b) Szerkeszd meg az ABC háromszög szögeinek szögfelezőit, jelöld meg a háromszögbe beírt kör középpontját, és rajzold meg ezt a kört!
184 Matematika • Tankönyv a VI. osztály számára
A N B1 C C1 I P A1 M B A N B1 C C1 I P A1 M B
Megoldás.
5 × 6 p
Miniteszt
1. Figyeld meg a következő ábrát, majd írj I betűt az üres mezőbe, ha a kijelentés igaz és H betűt, ha a kijelentés hamis!
Kijelentés I/H
a) AD az ABC háromszög BAC szögének szögfelezője.
b) I az ABC háromszögbe írt kör középpontja.
c) Az ABC szög szögfelezője tartalmazza az I pontot.
d) Az ABC háromszög szögeinek szögfelezői nem összefutó egyenesek.
e) IT az ABC háromszögbe írt kör sugara.
f) BAC∢ = 2 · BIC∢
2. A mellékelt ábrán egy ABCD telek vázlata látható. A DE félegyenes az ADB szög szögfelezője, a BF félegyenes a CBD szög szögfelezője, DAB∢ = 56°, ABD∢ = 54°. Az ADB és BDC szögek kongruensek, és a DE és BF egyenesek párhuzamosok.
30 p a) Határozd meg az ADB, BDE és BCD szögek mértékét!
30 p b) Állapítsd meg, majd indokold válaszod, hogy BD az ABC szög szögfelezője-e!
2. l. Egy háromszög oldalainak felezőmerőlegesei. Az oldalfelező merőlegesek metszéspontja
Emlékeztető
C
AEB DF
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
Értelmezés. Az AB szakasz felezőmerőlegesének nevezzük azt az egyenest, mely merőleges az AB szakaszra és tartalmazza a szakasz felezőpontját.
Méréssel meggyőződtünk, hogy egy szakasz felezőmerőlegese a sík azon pontjait tartalmazza, melyek egyenlő távolságra vannak a szakasz végpontjaitól.
Alkalmazások
1. alkalmazás: Ábrázolj egy általános ABC háromszöget!
a) Szerkeszd meg a BC oldal d1 felezőmerőlegesét és az AC oldal d2 felezőmerőlegesét!
Legyen {M} = d1 ⋂ BC és {N} = d2 ⋂ AC.
b) Jelöld O-val a d1 és a d2 egyenesek metszéspontját!
c) Szerkeszd meg a d3, egyenest, mely az O pontból az AB egyenesre húzott merőleges és { {P} = d3 ⋂ AB
d) A BC illetve AC oldalak felezőmerőlegesei a d1 és a d2 egyenesek az O pontban metszik egymást (ha párhuzamosak lennének, akkor az A, B és C pontok kollineárisak lennének).
Méréssel ellenőrizzük, hogy az O pontból az AB-re húzott merőleges tartalmazza az AB szakasz felezőpontját, tehát d3 az AB oldal felezőmerőlegese.
185 6. fejezet • A háromszög
M
B A C
A F B D T C E I
d2 d1 A B C N OM a) és b) df 2 d3 d1 A B C P N OM c) Megoldás.
Jegyezd meg!
Bármely ABC háromszög esetén, az oldalfelező merőlegesek egy pontban futnak össze, melyet általában O-val jelölünk.
Ha d1, d2, d3 AC, AB oldalak felezőmerőlegesei, akkor létezik egy O pont úgy, hogy d1 ⋂ d2 ⋂ d3 = {O}.
2. alkalmazás: a) Ábrázolj egy ABC hegyesszögű háromszöget, majd a d1, d2, d3 oldalfelező merőlegeseket! Jelöld O-val azt a pontot, amelyben az oldalfelező merőlegesek metszik egymást!
b) Mérd meg az OA, OB, OC távolságokat, és állapítsd meg, hogy az O pont ugyanakkora távolságra van-e az ABC háromszög három csúcsától!.
c) Szerkeszd meg az O középpontú kört, melynek sugara OA, melyet az ABC háromszög köré írt körnek nevezünk. Rendszerint, R-rel jelöljük egy háromszög köré írt kör sugarát.
d) Mit gondolsz, ABC háromszög belső tartományához tartozik-e az O pont, a háromszög köré írt kör középpontja?
Megoldás a) b) c) f d1 d3 d2
OA = OB = OC, tehát az A, B, C pontok egyenlő távolságra vannak az O ponttól.
Ekkor, a C(O, OA) kör tartalmazza a B és a C pontokat.
Az ABC háromszög oldalai a C(O, OA) kör húrjai.
d) A hegyesszögű ABC háromszög köré írt körnek középpontja a háromszög belső tartományában van: O ∈ Int(ABC∆).
Jegyezd meg!
Bármely ABC háromszögben az oldalfelező merőlegesek metszéspontja (melyet O-val jelölünk) egyenlő távolságra van a háromszög csúcsaitól.
A C(O, R) kört az ABC háromszög köré írt körének nevezzük, ahol R az O pont távolsága a háromszög egy csúcsától. A háromszög oldalai a köréje írt kör húrjai.
3. alkalmazás:
a) Szerkeszd meg a DEF derékszögű háromszög oldalfelező merőlegeseit, ahol D = 90°.
b) Mit gondolsz, hol helyezkedik el az oldalfelező merőlegesek O metszéspontja!
Vezesd le, hogy O az EF szakasz felezőpontja, vagyis az átfogó felezőpontja!
c) Szerkeszd meg a DEF háromszög köré írt kört!
186 Matematika • Tankönyv a VI. osztály számára
PB
N
O
A
M
C
O M
A P B d1 C d3 d2 N
Megoldás. FD E O
4. alkalmazás:
a) Szerkeszd meg az MNP tompaszögű háromszög oldalfelező merőlegeseit, ahol M > 90°.
b) Szerinted hol helyezkedik el az oldalfelező merőlegesek O metszéspontja? Vezesd le, hogy O az MNP háromszög külső tartományában van!
c) Szerkeszd meg az MNP háromszög köré írt kört!
Következmény.
1. Ha ABC egy hegyesszögű háromszög, akkor az ABC háromszög köré írt kör középpontja a háromszög belső tartományában van.
2. Ha ABC egy derékszögű háromszög, akkor az ABC háromszög köré írt kör középpontja egybeesik az átfogó felezőpontjával.
3. Ha ABC egy tompaszögű háromszög, akkor az ABC háromszög köré írt kör középpontja a háromszög külső tartományában van.
Gyakorlatok és feladatok
1. a) Ábrázold a 4 cm hosszúságú AB szakaszt, és rajzold meg beosztásos vonalzó és derékszögű vonalzó segítségével a szakasz felezőmerőlegesét!
b) Rajzolj egy CD szakaszt, és szerkeszd meg beosztás nélküli vonalzó és körző segítségével a szakasz felezőmerőlegesét!
2. Szerkeszd meg az ABC háromszög oldalfelező merőlegeseit a következő esetekben:
a) az ABC háromszög hegyesszögű;
b) az ABC háromszög derékszögű;
c) az ABC háromszög tompaszögű.
3. Szerkeszd meg egy DEF háromszög oldalfelező merőlegeseit, ha:
a) a háromszög egyenlő szárú;
b) a háromszög egyenlő oldalú;
c) a háromszög általános.
4. Szerkeszd meg az ABC háromszöget, az oldalfelező merőlegeseit és a köréje írt kört a következő
esetekben:
a) AB = 5 cm, AC = 4 cm, A∢ = 60°;
b) BC = 6 cm, B = 50°, C∢ = 100°;
c) AB = BC = AC = 10 cm.
5. A DEF háromszögben, DE = 5 cm, DM az EF oldal felezőmerőlegese, M ∈ EF, FM = 3 cm.
a) Mérd meg a DF oldal hosszát!
b) Számítsd ki a DEF háromszög kerületét!
6. Legyen ABC egy derékszögű háromszög, A∢= 90° és a P pont a B pontnak a szimmetrikusa az AC egyenesre nézve. Ellenőrizd, hogy AC a BCP háromszög BP oldalának felezőmerőlegese-e!
7. Az ABC háromszögben az AB és a BC oldalak felezőmerőlegesei az O pontban metszik egymást, a BOC háromszög pedig egyenlő oldalú, és kerülete 30 cm. Számítsd ki az AO szakasz hosszát!
8. Szerkeszd meg az ABC háromszöget, melyben AB = 5 cm, a C pont az AB oldal felezőmerőlegesén van, 6 cm távolságra az AB egyenestől.
9. Az MNP háromszög MN oldalának oldalfelező merőlegese az MP oldalt az A pontban, az NP oldalt pedig a B pontban metszi.
a) Méréssel ellenőrizd, hogy az AMN és a BMN háromszögek egyenlő szárúak-e!
b) Ha PAMN = 24 cm és PBMN = 28 cm, igazold, hogy AB > 2 cm.
187 6. fejezet • A háromszög
Megoldás. N PM O
Miniteszt
1. Töltsd ki a pontozott helyeket, hogy igazak legyenek az állítások!
10 p p1: Bármely pont, amely egy szakasz felezőmerőlegesén van, … van a szakasz végpontjaitól.
10 p p2: Egy háromszög oldalfelező merőlegesei … egyenesek.
10 p p3: Egy háromszög oldalfelező merőlegeseinek metszéspontja … és … van a háromszög csúcsaitól.
10 p p4: A kört, mely tartalmazza a háromszög csúcsait, … nevezzük.
2. Legyen xOy egy szög és A, B két pont, A∈Ox, B∈Oy. Az OA és az OB szakaszok felezőmerőlegesei a C pontban metszik egymást. Indokold a következő állításokat:
25 p a) Az ACO háromszög egyenlő szárú;
25 p b) A C pont az ABO háromszög köré írt kör középpontja.
Megjegyzés: Munkaidő: 20 perc
3. l. A háromszög magasságai. A magasságok metszéspontja
Emlékeztető
Két egyenes merőleges, ha derékszöget zárnak be.
Ha M a d egyenesnek egy külső pontja, akkor az M pont távolsága a d egyenestől az MP szakasz hosszával egyenlő, ahol P az M pontból a d egyenesre bocsátott merőleges talppontja.
Ha M ∈ d, akkor az M pont távolsága a d egyenestől 0.
Fedezzük fel, értsük meg!
d' M d P
Az ábrán látható házikó eleje függőleges síkban háromszög alakú. Ha szeretnénk tudni, hogy milyen magas a házikó, megmérhetjük a háromszög csúcsának távolságát az alapjáig, vagyis megkapjuk a háromszög magasságát. Értelmezés. Az ABC háromszög magasságának nevezzük azt a pozitív számot, amely egyenlő a háromszög egyik csúcsának a szemben fekvő oldaltól mért távolságával.
Alkalmazva egy pont egyenestől való távolságának értelmezését a fenti kijelentést átfogalmazhatjuk, így:
Egy háromszög magasságának nevezzük a háromszög egyik csúcsa és az adott csúcsból a szemközti oldalra bocsátott merőleges talppontja által meghatározott szakasz hosszát.
Hivatalból: 10 pont
MP = az M távolsága d-től
Az M pontból a d egyenesre bocsátott merőleges talppontja

Megjegyzés. A háromszög magasságának fogjuk nevezni azt a szakaszt, amelyet a háromszög csúcsa és a szemközti oldalra bocsátott merőleges talppontja határoz meg, és ennek a szakasznak a hosszát is. A szövegösszefüggés sugallja, hogy a magasságnak nevezett szakaszról vagy a szakasz hosszának megfelelő pozitív számról van-e szó.
A mellékelt ábrán AA1 ⊥ BC, tehát a háromszög egyik magassága az AA1 szakasz, de a szakasz hossza is AA1, vagyis az A pont távolsága a szemközti BC oldaltól. Egy háromszög magasságainak megszerkesztéséhez a sík egy adott pontján átmenő merőleges szerkesztésének valamelyik módszerét alkalmazzuk. Derékszögű vonalzóval, vagy körzővel és beosztás nélküli vonalzóval dolgozunk.
188 Matematika • Tankönyv a VI. osztály számára
A B A1 C
Alkalmazások
1. alkalmazás:
Legyen ABC egy általános háromszög.
a) Szerkeszd meg derékszögű vonalzóval az AA1 ⊥ BC szakaszt A1 ∈ BC, majd a BB1 ⊥ AC, szakaszt B1 ∈ AC. Jelöljük H -val az AA1 és BB1 szakaszok metszéspontját!
b) Szerkeszd meg a CH egyenest és jelöld C1 -gyel azt a pontot, amelyben az AB oldalt metszi!
c) Mérd meg a CC1A vagy a CC1B szöget és állapítsd meg, hogy a CC1 ⊥ AB igaz-e!
Megoldás. c) CC1A∢ = BC1C∢ = 90°, tehát CC1 ⊥ AB, azaz CC1 a háromszög magassága.
Jegyezd meg!
Bármely ABC háromszög esetén a magasságok összefutó egyenesek, melyek metszéspontját a háromszög ortocentrumának (magasságpontjának) nevezzük, és rendszerint H-val jelöljük.
Ha AA1, BB1, CC1 a háromszög magasságai, akkor létezik egy H pont úgy, hogy AA1 ⋂ BB1 ⋂ CC1 = {H}.
Figyeld meg az ABC hegyesszögű háromszög magasságainak geometriai ábrázolását, H1, -gyel jelöltük a háromszög ortocentrumát és állapítsd meg, hogy az ortocentrum az ABC háromszög belső tartományában van, azaz:
Ha ABC∆ hegyesszögű, H1 pedig a háromszög ortocentruma, akkor H1 ∈ Int(ABC∆).
2. alkalmazás:
a) Szerkeszd meg a DEF derékszögű háromszög magasságait, ahol D∢ = 90°. Jelöld H2-vel a háromszög ortocentrumát!
b) Szerinted hol helyezkedhet el a H2 pont? Vedd észre, hogy a háromszög ortocentruma egybeesik a DEF háromszög derékszögének csúcsával!
Megoldás.
a) ED az E csúcsból húzott magasság, FD pedig az F csúcsból, DD1 ⋂ ED ⋂ FD = {H2} = {D}.
b) H2 egybeesik D-vel.
3. alkalmazás :
a) Szerkeszd meg az MNP tompaszögű háromszög magasságait, M∢ > 90°. Jelöld H-val a háromszög ortocentrumát.
b) Szerinted hol helyezkedhet el a H3 pont? Figyeld meg, hogy a háromszög ortocentruma a háromszög külső tartományában van!
Megoldás.
a) Az N, P és M csúcsokból húzott magasságok az NN1, PP1 illetve az MM1, egyenesek és MM1 ⋂ NN1 ⋂ PP1 = {H3}.
b) Észrevesszük, hogy H3 ∈ Ext(ABC∆).
Jegyezd meg!
1. Egy hegyesszögű háromszög esetében az ortocentrum a háromszög belső tartományában van.
2. Egy derékszögű háromszög esetében az ortocentrum egybeesik a háromszög derékszögének csúcsával.
3. Egy tompaszögű háromszög esetében az ortocentrum a háromszög külső tartományában van.
189 6. fejezet • A háromszög
A B1 AC 1 B C1 H1 E D=H2 D1 F N M1 P P1 H3 N1 M
A B1 AC 1 B H A B1 AC 1 B C1 H
Gyakorlatok és feladatok
1. Mértani felszereléssel rajzolj minden esetben egy háromszöget és húzd meg a magasságot:
a) egy hegyesszögű háromszögben;
b) egy derékszögű háromszögben;
c) egy tompaszögű háromszögben.
2. Másold le a füzetedbe és töltsd ki a pontozott helyeket úgy, hogy igaz kijelentéseket kapj!
p1: Egy hegyesszögű háromszög ortocentruma a háromszög … van.
p2: Egy derékszögű háromszög ortocentruma egybeesik a … .
p3: Egy tompaszögű háromszög ortocentruma a háromszög … van.
3. a) Szerkeszd meg az ABC háromszöget, melyben AB = 6 cm, ABC∢ = 55°, BC = 7 cm.
b) Szerkeszd meg derékszögű vonalzó segítségével az ABC háromszög AM, BN és CP magasságait és jelöld H-val az ortocentrumát!
c) Másold le a füzetbe a táblázatot, és az üres mezőbe írj I betűt, ha az állítás igaz, illetve H betűt, ha az állítás hamis!
Állítás I/H
Az M pont az A csúcsból a BC oldalra bocsátott merőleges talppontja.
AN ⊥ BC.
CPA∢ = 90°.
AM ⋂ BN ⋂ CP = {H}.
4. A DEF háromszög EF oldalán felvesszük az L pontot úgy, hogy EDL∢ = 25° és DEF∢ = 65°. Igazold, hogy DL a DEF háromszög magassága!
5. Szerkessz egy ABC tompaszögű háromszöget, melyben BAC∢ > 90°. Szerkeszd meg a három-
szög BM és CN magasságait és jelöld H-val ezek metszéspontját. Igazold, hogy:
a) AH ⊥ BC;
b) ABM∢ ≡ ACN∢.
6. Az MNP háromszög derékszögű, MNP∢ = 90° és
A egy pont az MN oldalon. Az A pontból az MP egyenesre bocsátott merőleges az NP egyenest a B pontban metszi. Igazold, hogy az A pont a BMP háromszög ortocentruma!
7. Legyen ABC egy háromszög, BAC∢ = 90° és AD a háromszög magassága, D ∈ BC
a) Igazold, hogy az ABD és CAD szögek kongruensek!
b) ha CAD∢ = 28°, számítsd ki az ABD háromszög szögeinek mértékét!
8. Rajzolj egy DEF háromszöget, melyben D ∢= 57° és
E∢ = 75°.
a) Számítsd ki a háromszög oldalai és a DM magasság által bezárt szögek mértékét!
b) Számítsd ki az EN és FP magasságok által bezárt hegyesszög mértékét!
9. Az ABC tompaszögű háromszögben: ACB∢ = 120°, AD a háromszög magassága, D ∈ BC,
BAC∢ ≡ CAD∢.
a) Készíts a feladat adatainak megfelelő ábrát!
b) Igazold, hogy az ABC háromszög egyenlő szárú!
10. Adott az ABC háromszög, melyben B∢ = 45°, C∢ = 60° és AD a háromszög magassága, D ∈ BC.
a) Számítsd ki a BAD és a CAD szögek mértékét!
b) Szerkeszd meg az ABC háromszöget tudva, hogy AD = 5 cm. Írd le a szerkesztés összes lépését!
30 p 1. A kék szakasz nem az ABC háromszög magassága a következő ábrán:
A. a); B. b); C. c); D. b) és c)
60 p 2. Az ABC háromszögben
ABC∢ = 50°, ACB∢ = 70°, AD a háromszög magassága, E ∈ BC és AE a BAC szög szögfelezője, E ∈ BC. Határozd meg a DAE szög mértékét!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
190 Matematika • Tankönyv a VI. osztály számára
A BC a) A BC b) BA C c)
Miniteszt
4. l. A háromszög oldalfelezői. Az oldalfelezők metszéspontja
Emlékeztető
Az AB szakasz felezőpontja az M pont, mely az AB szakaszon van, egyenlő távolságra a szakasz végpontjaitól (AM = MB).
Ha M az AB szakasz egy pontja és MA ≡ MB, akkor M a szakasz felezőpontja.
Ha AB = 20 cm és M az AB szakasz felezőpontja, akkor AM = MB = 10 cm.
Ha AB = 20 cm és AM = MB = 10 cm, akkor M az AB szakasz felezőpontja.
Ha M az AB szakasz felezőpontja, akkor A és B szimmetrikusak az M pontra nézve.
Fedezzük fel, értsük meg!
Értelmezés. Egy háromszög oldalfelezőjének nevezzük azt a szakaszt, melyet a háromszög egyik csúcsa és a szemben fekvő oldal felezőpontja határoz meg.
1. alkalmazás: a) Rajzolj egy ABC háromszöget és húzd meg az AM és a BN oldalfelezőket! Jelöld G-vel ezek metszéspontját!
b) Rajzold meg a CG félegyenest és jelöld P-vel az AB oldallal való metszéspontját!
c) Beosztásos vonalzó segítségével mérd meg a PA és a PB szakaszok hosszát és állapítsd meg, hogy CP a háromszög oldalfelezője-e!
Megoldás. c) PA = PB, tehát CP a háromszög oldalfelezője.
Jegyezd meg!
Bármely háromszögben az oldalfelezők egy pontban futnak össze, ezt a pontot a háromszög súlypontjának nevezzük, és általában G-vel jelöljük.
Alkalmazások
2. alkalmazás:
a) Vágj ki kartonból egy MNP háromszöget. Rajzold meg a háromszög MM1, NN1, PP1 oldalfelezőit és jelöld G-vel a háromszög súlypontját!
b) Próbáld egyedül a G pontra támasztva vízszintes helyzetben tartani a kivágott háromszöget, ahogy a képen látható!
Tapasztalatunk szerint egy lap súlypontja az a pont, ahol a lapot úgy lehet megtámasztani, hogy vízszintes helyzetben egyensúlyban maradjon.
A gyakorlatban egy homogén test súlypontjának ismerete alapvető fontosságú az egyensúlya megtalálásához.

Gyakorlatok és feladatok
1. Rajzolj mértani felszerelés segítségével egy-egy háromszöget az alábbiak szerint, és húzd meg az oldalfelezőket:
a) ha a háromszög hegyesszögű;
b) ha a háromszög derékszögű;
c) ha a háromszög tompaszögű.
2. Adott az ABC háromszög, AD és BE a háromszög
oldalfelezői és AD ⋂ BE = {G}. Másold le a füzetbe és a pontozott helyekre töltsd ki, hogy igaz legyen minden állítás!
p1: A D pont a BC oldal … .
p2: Ha AC = n · AE, akkor n egyenlő … .
p3: a G pontot az ABC háromszög … nevezzük.
191 6. fejezet • A háromszög
A N MC B P G
N M G P M1 N1 P1
3. Rajzolj egy ABC háromszöget, az AD, BE, CF oldalfelezőit és jelöld G-vel a háromszög súlypontját!
a) Mérd meg beosztásos vonalzóval, és fejezd ki milliméterben az AD, AG, GD szakaszok hoszszát! Töltsd ki a következő táblázatot a mérésekből kapott adatokkal:
AD AG GD AG AD GD AD
b) Mérd meg beosztásos vonalzó segítségével a BD, BG, GE, illetve a CF, CG, GF szakaszokat! Töltsd ki a következő táblázatot a kapott adatokkal:
BE BG GE
CF CG GF
BG
BE GE BE
CG
GF CF GF
c) A mérési eredmények felhasználásával írj I betűt az üres mezőbe, ha az állítás igaz, illetve H betűt, ha az állítás hamis!
Állítás I/H Állítás I/H
p1: AG = 2 3 · AD p3: AG AD BG BE CG CF === 2 3
p2: BE = 2 · GE p4: CF = 3 · GF
Megjegyzés. A 3. feladat méréssel igazolja a következő fontos eredményt, melyet később bizonyítunk: Bármely háromszögben a háromszög súlypontja mindhárom oldalfelezőn a csúcstól kétharmad részre van, az oldaltól pedig egyharmad részre található.
Miniteszt
4. Az AM, BN, CP szakaszok oldalfelezők az ABC háromszögben, a G pont pedig a háromszög súlypontja. A fenti megjegyzés alapján, számítsd ki:
a) az AG és a GM szakaszok hosszát, ha AM = 24 cm.
b) a BN szakasz hosszát, ha BG = 12 cm.
c) a CG és a CP szakaszok hosszát, ha GP = 4 cm.
5. a) Rajzold meg a DEF derékszögű háromszöget, melyben EDF∢ = 90°, DE = 6 cm, DF = 8 cm.
b) Szerkeszd meg az EF átfogóhoz tartozó DM oldalfelezőt, és beosztásos vonalzó segítségével mérd meg a DM és az EF szakaszok hosszát!
c) Jelöld meg a következő állítások közül melyik igaz:
A. DM = EF;
B. DM = EF 2 ;
C. DM = EF 3 ;
D. DM = 2EF.
6. Rajzolj egy O középpontú kört és vedd fel rajta az
A, B, C pontokat úgy, hogy BC átmérő legyen!
a) Határozd meg szögmérő segítségével a BAC szög mértékét!
b) Az 5. és 6.a) feladatban kapott eredmények alapján következtess arra, hogy igazak-e a következő állítások:
• „Bármely derékszögű háromszögben, az átfogóhoz tartozó oldalfelező hossza egyenlő az átfogó hosszának a felével.”
• „Ha egy háromszögben egy oldalhoz tartozó oldalfelező egyenlő az illető oldal hosszának a felével, akkor a háromszög derékszögű.”
7. Az ABP és az ABQ háromszögek derékszögűek, APB∢ = AQB∢ = 90°, a C pont pedig az AB szakasz felezőpontja. Igazold, hogy CP ≡ CQ
1. Adott az ABC háromszög. Másold le a füzetbe és töltsd ki a pontozott helyeket, hogy igaz legyen az összes kijelentés!
10 p a) Ha az M pont a BC oldal felezőpontja, akkor AM a háromszög … oldalához tartozó … .
10 p b) Ha BN az ABC háromszög egyik oldalfelezője, akkor az N pont a … oldal … .
10 p c) Ha AM és BN az ABC háromszög oldalfelezői és AM ⋂ BN = {G}, akkor G az … háromszög … .
10 p d) Ha AM az ABC háromszög oldalfelezője, BM = 3·x cm és CM = (x + 8) cm, akkor x = … .
2. Legyenek MA és NB oldalfelezők az MNP háromszögben, G pedig a háromszög súlypontja. Tudjuk, hogy MG = 7 cm és BG = 14 cm.
25 p a) Számítsd ki az MA és az NB szakaszok hosszát!
25 p b) Igazold, hogy az ABG és az MNG háromszögek egyenlő szárúak!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
192 Matematika • Tankönyv a VI. osztály számára
6.3 Kongruens háromszögek
1. l. Az általános háromszögek kongruenciája
Emlékeztető
Két geometriai alakzat kongruens, ha átfedéssel egybeesnek.
Kijelentés
Két AB és CD szakasz kongruens, akkor és csakis akkor, ha hosszúságuk egyenlő.
Matematikai szimbólumokkal kifejezve
Mértani ábrázolás
A
Ha AB ≡ CD, akkor AB = CD
Ha AB = CD, akkor AB ≡ CD.
Két ABC és DEF szög kongruens, akkor és csakis akkor, ha mértékük egyenlő.
Ha ABC∢ ≡ DEF∢, akkor ABC∢ = DEF∢.
Ha ABC∢ = DEF∢, akkor ABC∢ ≡ DEF∢.
Oldjuk meg figyelmesen!
B D C

AB ≡ CD AD BC

AB=CD= 6 cm




Azt szeretnénk megtudni, hogy mi jellemző két kongruens háromszögre, azaz két olyan háromszögre, amelyek átfedéssel egybeesnek.
1. gyakorlati alkalmazás: Szükséges eszközök: két átlátszó fólia, filctoll, ceruza.
1. lépés. Egy átlátszó fóliára rajzolj egy általános ABC háromszöget.
2. lépés. Helyezd a második fóliát az elsőre és „másold le” az ábrázolt háromszöget. Jelöld az új háromszöget A1 B1C1-gyel úgy, hogy az A csúcs egybeesik A1-gyel, a B csúcs egybeesik a B1-gyel, és a C csúcs egybeesik a C1-gyel. Mit gondolsz, a két háromszög kongruens-e?
3. lépés.Válaszd szét a két lapot, figyeld meg és írd fel a háromszögek elemei közötti megfelelést!
4. lépés.Határozd meg egymásra helyezéssel, hogy a két háromszög megfelelő elemei kongruensek-e!
5. lépés. Forgasd el az egyik lapot úgy, hogy A lefedje B1-et, és az AB félegyenes lefedje a B1C1 félegyenest.
6. lépés.Határozd meg, hogy az ABC háromszög átfedéssel egybeesik-e a B1C1A1 háromszöggel. Megoldás.
1. lépés
2. lépés
3. lépés
Megfelelő elemek
193 6. fejezet • A háromszög
C B A C1 B1 A1 A BB1 C1 C A1 ABC∆ A1B1C1∆ A∢ A1∢ B∢ B1∢ C∢ C1∢ AB A1B1 AC A1C1 BC B1C1
4. lépés 5. lépés 6. lépés
A∢ ≡ A1∢, B∢ ≡ B1∢, C∢ ≡ C1∢
AB ≡ A1B1,
AC ≡ A1C1,
BC ≡ B1C1
B1 =A
A1
Fedezzük fel, értsük meg!
Értelmezés.
Két ABC∆ és A1B1C1∆ háromszög kongruens, ha megfelelő elemeik kongruensek.
Jelölés: ABC∆ ≡ A1B1C1∆
C B
C1
ABC∆ és B1C1A1∆ nem esnek egybe átfedéssel.
Matematikai szimbólumokkal
Ha ABC∆ ≡ A1B1C1∆, akkor A∢ ≡ A1∢, B∢ ≡ B1∢, C∢ ≡ C1∢, AB ≡ A1B1, AC ≡ A1C1, BC ≡ B1C1.
Ha A∢ ≡ A1∢, B∢ ≡ B1∢, C∢ ≡ C1∢, AB ≡ A1B1, AC ≡ A1C1, BC ≡ B1C1, akkor ABC∆ ≡ A1B1C1∆.
1. gyakorlati alkalmazás: Igazold, hogy lehetséges, hogy ABC∆ ≡ A1B1C1, de ABC∆ ≢ B1C1A1∆, azaz mielőtt felírnánk két kongruens háromszög kapcsolatát, azonosítanunk kell a megfelelő elemeket.
Jegyezd meg!
1. Ha egy háromszögre hivatkozunk, nem lényeges, hogy milyen sorrendben olvassuk a csúcsokat. Így egy háromszög, melynek csúcsai A, B, C, felírható bármilyen formában: ABC∆, CBA∆, ACB∆, BCA∆, BAC∆, CAB∆.
2. Ha a háromszögek kongruenciájáról beszélünk, nagyon fontos, hogy a háromszögek felírásásánál betartsuk a megfelelő elemek sorrendjét.
Alkalmazások
Megoldott feladat
Adottak az ABC és az MNP kongruens háromszögek.
a) Ha AB = 10 cm, MP = 8 cm, BC = 9 cm, számítsd ki az MNP háromszög kerületét!
b) Ha A∢ = 74° és N∢ ≡ P∢, számítsd ki a B szög mértékét!
Megoldás Bizonyítás
a) Feltevés: ABC∆ ≡ MNP∆, AB = 10 cm, MP = 8 cm, BC = 9 cm
Következtetés: KMNP∆
b) Feltevés: ABC∆ ≡ MNP∆, A∢ = 74° és N∢ ≡ P∢
Következmény: B∢
Az ABC∆ ≡ MNP∆, következik, hogy AB ≡ MN, AC ≡ MP, BC ≡ NP, tehát MN = 10 cm, NP = 9 cm, MP = 8 cm és
KMNP∆ = MN + NP + MP = 27 cm.
Az ABC∆ ≡ MNP∆, következik A∢ ≡ M∢, B∢ ≡ N∢, C∢ ≡ P∢
Tehát M∢ = A∢ = 74°
Akkor N∢ + P∢ = 180°– 74° = 106°. Az N∢ ≡ P∢, következik, hogy N∢ = P∢ = 53°
De, B∢ ≡ N∢, tehát B∢ = 53°
194 Matematika • Tankönyv a VI. osztály számára
Gyakorlatok és feladatok
1. Az ABC és DEF háromszögek kongruensek. Másold le a füzetbe és töltsd ki a pontozott helyeket úgy, hogy igaz kijelentéseket kapj:
a) AB ≡ …;
b) A∢ ≡ …; c) ≡ DF; d) ≡ DFE∢
2. Az ABC és az MNP háromszögek kongruensek.
a) Indokold meg, hogy az ABC∆ ≡ MNP∆ írásmód egyenértékű az ACB∆ ≡ MPN∆ írásmóddal!
b) Azonosíts és írj még két helyes írásmódot a két háromszög kongruenciájára!
3. Az ABC háromszögre fennáll, hogy ABC∆ ≡ ACB∆. a) Írd fel a megfelelő oldalak kongruenciáját!
b) Az a) alpont eredményei alapján igazold, hogy az ABC háromszög egyenlő szárú!
c) Ha az ABC háromszög kerülete 40 cm és BC = 18 cm, számítsd ki az AB és az AC oldalak hosszát!
4. Másold le a füzetbe és írj I betűt az üres mezőbe, ha az állítás igaz, illetve H betűt, ha az állítás hamis!
Állítás
p1: Ha ABC∆ ≡ DEF∆, akkor KABC∆ = KDEF∆
p2: Ha KABC∆ = KDEF∆, akkor ABC∆ ≡ DEF∆
p3: Ha két háromszög kongruens, akkor megfelelő szögeik kongruensek.
p4: Ha két háromszög megfelelő szögei kongruensek, akkor a háromszögek kongruensek.
I/H
b) Az a) alpont eredményei alapján határozd
meg a DEF háromszög természetét!
c) Határozd meg a DFE szög mértékét!
6. a) Az alábbi ábrán két kongruens háromszög látható, a kongruens oldalpárok ugyanazzal a színnel vannak jelölve.
5. A DEF háromszögben fennáll a DEF∆ ≡ EFD∆ öszszefüggés.
a) Írd fel a megfelelő oldalak és megfelelő szögek kongruenciáját!
Miniteszt
Válaszd ki a helyes írásmódot a két háromszög
kongruenciájára!
A. ABC∆ ≡ DEF∆; B. ABC∆ ≡ DFE∆; C. FDE∆ ≡ CBA∆.
b) A következő ábrán két kongruens háromszög látható a kongruens megfelelő szögpárok ugyanolyan színnel vannak jelölve.
HP G M IN
Válaszd ki a helyes írásmódot a két háromszög kongruenciájára!
A. GHI∆ ≡ MNP∆; B. GIH∆ ≡ MNP∆; C. PMN∆ ≡ IHG∆.
7. Az ABC háromszög C∢ derékszög és B∢ = 36°. Ha ABC∆ ≡ DEF∆, határozd meg a D és az F szögek mértékét!
1. Rajzolj egy papírlapra egy ABCD négyzetet és húzd meg az AC szakaszt! Vágd ki az ABCD négyzetet és hajtsd be az AC egyenes mentén!
15 p a) Állapítsd meg, hogy a B pont rátevődik-e a D pontra!
15 p b) Mit gondolsz, az ABC és az ADC háromszögek kongruensek-e?
15 p c) Írd fel a két háromszög megfelelő elemeinek kongruenciáját!
2. Az ABC háromszögben tudjuk, hogy ABC∆ ≡ BCA∆.
15 p a) Írd fel a megfelelő kongruens oldalakat!
30 p b) Ha AB BCAC 23 11 cm, számítsd ki az ABC háromszög kerületét!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
195 6. fejezet • A háromszög
B AC E F D
Emlékeztető
A gyakorlatban jól használhatjuk azokat a matematikai tulajdonságokat, amelyekkel a kongruens alakzatok rendelkeznek, valamint néhány elégséges feltételt, amelyekkel a geometriai alakzatok kongruenciáját bizonyítani lehet.
Ha adottak az a, b, c pozitív számok, a + b > c, a + c > b és b + c > a, akkor egyetlen ABC háromszög létezik, amelyre BC = a, AC = b, AB = c. (O.O.O. szerkesztési eset)
Ha adott két a és b pozitív szám és egy α°-os szög, akkor egyetlen ABC háromszög létezik, amelyre BC = a, AC = b, ACB∢ = α°. (O.Sz.O. szerkesztési eset)
Ha adott α° és β° két szög mértéke, α° + β° < 180° és az a pozitív szám, akkor egyetlen ABC háromszög létezik, amelyre BC = a, ABC∢ = α° és ACB∢ = β°. (Sz.O.Sz. szerkesztési eset)
Fedezzük fel, értsük meg!
Ha két háromszög kongruens, az értelmezés alapján hat kongruens elempárt írhatunk fel, melyeket megfelelő oldalaknak, illetve megfelelő szögeknek nevezzük. Szeretnénk megtudni, hogy hány megfelelő elempár elégséges, hogy a két háromszög kongruens legyen.
A fent említett szerkesztési esetek arra utalnak, hogy a szerkesztett háromszög a síkban elfoglalt helyétől függetlenül egyértelműen meghatározott. A kongruens háromszögek olyan háromszögek, amelyeknek a megfelelő elemei pontosan azonos mértékűek, de a síkban különböző helyzetűek lehetnek.
Következésképpen, levezetjük, hogy két háromszög kongruenciájának bizonyításához elegendő, ha azok azonos módon szerkeszthetők, és a szerkesztésben használt elemek mértéke megegyezik.
Ezzel az érveléssel a háromszögek kongruenciájának a következő kritériumait (eseteit) kapjuk:
Kritérium
1. O.O.O. kongruencia eset
Ha két háromszögben az összes megfelelő oldalak kongruensek, akkor a két háromszög kongruens.
2. Sz.O.Sz. kongruencia eset
Mértani ábrázolás
Ha AB ≡ MN, BC ≡ NP és AC ≡ MP, akkor ABC∆ ≡ MNP∆ ABMN CP
Ha két háromszögnek egy-egy megfelelő oldala és a rajta fekvő megfelelő két-két szög kongruens, akkor a két háromszög kongruens.
Matematikai szimbólumokkal:
Ha A∢ ≡ M∢, B∢ ≡ N∢ és AB ≡ MN, akkor ABC∆ ≡ MNP∆.
Ha A∢ ≡ M∢, C∢ ≡ P∢ és AC ≡ MP, akkor ABC∆ ≡ MNP∆.
Ha B∢ ≡ N∢, C∢ ≡ P∢ és BC ≡ NP, akkor ABC∆ ≡ MNP∆.
196 Matematika • Tankönyv a VI. osztály számára
2. l. A háromszögek kongruencia- (egybevágósági) esetei (kritériumai)
CP ABMN
CP ABMN
CP ABMN
3. O.Sz.O. kongruencia eset
Ha két háromszögnek két-két megfelelő oldala és a közrezárt szögpár kongruens, akkor a két háromszög kongruens.
Matematikai szimbólumokkal:
Ha A∢≡M∢, AB≡MN és AC≡MP, akkor ABC∆≡MNP∆
Ha B∢≡N∢, BC≡NP és AB≡MN, akkor ABC∆≡MNP∆.
Ha C∢≡P∢, AC≡MP és BC≡NP, akkor ABC∆≡MNP∆.
Alkalmazás
Megoldott feladat:. Az AB és CD szakaszoknak ugyanaz az M felezőpontjuk, a C pont pedig az AB egyenes egy külső pontja.
a) Igazold, hogy MAC∆ ≡ MBD∆ és MAD∆ ≡ MBC∆
b) Az a) alpont eredménye alapján vezesd le, hogy AD ≡ BC és AC ≡ BD
c) Bizonyítsd be, hogy a CAD és a DBC háromszögek kongruensek!
d) A fenti eredményeket felhasználva indokold a következő párhuzamosságokat: AD ∥ CB és AC ∥ BD
Feltevés:
AB ⋂ CD = {M},
MA ≡ MB és
MC ≡ MD.
Bizonyítás
a) A feltevésből MA ≡ MB. (1)
Következtetés:
a) MAC∆ ≡ MBD∆ és MAD∆ ≡ MBC∆.
b) AC ≡ BD és AD ≡ BC.
c) CAD∆ ≡ DBC∆.
d) AD ∥ CB és AC ∥ BD
Az AMC és a BMD szögek csúcsszögek, tehát AMC∢ ≡ BMD∢. (2)
A feltevésből MC ≡ MD. (3)
Az (1), (2) és (3) összefüggésekbő, az O.Sz.O. kongruencia eset alapján következik, hogy MAC∆ ≡ MBD∆
A feltevésből MA ≡ MB. (4)
Az AMD és a BMC szögek csúcsszögek, tehát AMD∢ ≡ BMC∢. (5)
A feltevésből MD ≡ MC (6)
A (4), (5) és (6) összefüggésekből az O. Sz.O. kongruencia eset alapján következik, hogy MAD∆ ≡ MBC∆.
b) MAC∆ ≡ MBD∆, következik, hogy AC ≡ BD, és MAD∆ ≡ MBC∆ következik, hogy AD ≡ BC.
c) A b) alpont alapján AC ≡ BD és AD ≡ BC. De CD ≡ CD (közös oldal). Az O.O.O. kongruencia eset alapján következik, hogy CAD∆ ≡ DBC∆
d) A c) alpontban bizonyított kongruencia alapján ACD∢ ≡ CDB∢ és ADC∢ ≡ DCB∢. Az AC és a DB egyenesek a CD szelővel kongruens belső váltószögeket alkotnak, vagyis AC ∥ BD. Ugyanez a helyzet az AD és a CB egyeneseknek a CD szelővel, következik, hogyAD ∥ CB.
Feladat a portfólióba.
Az AC és BD szakaszok az M pontban metszik egymást. Tudva, hogy AB ≡ CD és AB ∥ CD, bizonyítsd be, hogy
a) az M pont az AC és BD szakaszok felezőpontja;
b) az AD és a BC egyenesek párhuzamosak.
197 6. fejezet • A háromszög
CP
CP ABMN CP ABMN
ABMN
A MD C B
Gyakorlatok és feladatok
1. A mellékelt ábrán azonos szimbólumok jelölik a háromszögek kongruens elemeit.
LEA ODN
a) Írd fel az ábrának megfelelő kongruenciákat! b) Állapítsd meg, hogy a háromszögek kongruensek-e az alkalmazott kongruenciakritérium (eset) megnevezésével, és írd fel a köztük levő kapcsolatot!
2. Az alábbi alakzatok mindegyikében két egybevágó (kongruens) háromszög látható. Azonos szimbólumokkal jelöltük a két háromszög megfelelő elemeit (oldalak és szögek), amelyekről tudjuk, hogy egybevágóak.
a) b) c)
3. Olga és Petra be kell bizonyítsa, hogy az ABC és a DEF háromszögek kongruensek. Ők bizonyították már, hogy AB ≡ DE és A ≡ D.
a) Ha Olga a O.Sz.O. kritériumot szeretné alkalmazni, állapítsd meg milyen kongruenciát kell még bizonyítania!
b) Ha Petra a Sz.O.Sz. kongruenciaesetet szeretné alkalmazni, állapítsd meg milyen kongruenciát kell még bizonyítson!
AB C D E F
4. András szeretné igazolni, hogy az ABC és az MNPháromszögek kongruensek . Ő már igazolta, hogy AB ≡ MN és BC ≡ NP. Észreveszi, hogy nincs elég feltétele, hogy igazolni tudja, hogy AC ≡ MP. Állapítsd meg, hogy milyen kongruenciaesetet tudna alkalmazni, és milyen feltételt kéne igazolnia még, hogy alkalmazhassa az illető esetet! M
d) e) f)
A rajzok jelöléseit használva minden egyes alpontnál, a minta alapján töltsd ki az ×-et abba a mezőbe, amely kritérium alapján a háromszögek kongruensek!
a) b) c) d) e) f)
O.O.O. ×
O.Sz.O.
Sz.O.Sz.
5. Adottak az ABC∆ ≡ DEF∆ és DEF∆ ≡ PQR∆ kongruenciák. Határozd meg az ABC háromszög szögeinek mértékét tudva, hogy F∢ = 54° és Q∢ = 72°.
6. a) Két egyenlő szárú háromszög alapja kongruens és kerületük egyenlő. Bizonyítsd be, hogy a háromszögek kongruensek!
b) Két egyenlő oldalú háromszög kerülete egyenlő. Bizonyítsd be, hogy a háromszögek kongruensek!
7. Az ABC háromszög egyenlő szárú, az M pont pedig a BC alap felezőpontja. Állapítsd meg, hogy az ABM és az ACM háromszögek kongruensek-e?
198 Matematika • Tankönyv a VI. osztály számára
C AB DE F C AB DE FAB E DC
E L F I H P A T M A D B C
N P AB C
Ha ez így van, határozd meg az alkalmazott kongruenciaesetet!
8. A C(A, r1) és C(B, r2) körök a C és a D pontban metszik egymást.
Bizonyítsd be, hogy az ABC és az ABD háromszögek kongruensek!
C (A,r1)
C (B,r 2) AB C D
9. A DEF általános háromszögben az A a DE oldal felezőpontja. Az A pontban a DE egyenesre bocsátott merőleges a DF oldalt az M pontban metszi, az EF egyenest pedig az N pontban.
a) Szerkessz a feladat adatainak megfelelő ábrát!
b) Igazold, hogy: ADM∆ ≡ AEM∆; ADN∆ ≡ AEN∆; DMN∆ ≡ EMN∆
10. Legyen D az ABC háromszög AB oldalának felezőpontja, Q pedig az MNP háromszög MN oldalának felezőpontja.
Bizonyítsd be, hogy ha BCD∆ ≡ NPQ∆, akkor ABC∆ ≡ MNP∆.
11. A mellékelt ábrán ABC∆ ≡ DEF∆, M egy pont a BC oldalon, N pedig egy pont az EF oldalon. Ha AM a
BAC szög szögfelezője, és DN az EDF szög szögfelezője, bizonyítsd be, hogy ABM∆ ≡ DEN∆. A BM C E N FD
12. Az M pont a ABC háromszög BC oldalának felezőpontja, N pedig a DEF háromszög EF oldalának felezőpontja. Bizonyítsd be, hogy ha
DABC ≡ DDEF, akkor DACM ≡ DDFN
13. Az O pont az ABC háromszög belső tartományában van, és ABC és AOB∆ ≡ BOC∆ ≡ COA∆.
a) Bizonyítsd be, hogy az ABC háromszög egyenlő oldalú!
b) Számítsd ki az AOB szög mértékét!
14. A mellékelt ábrán a szakaszok hossza centiméterben van kifejezve. Bizonyítsd be, hogy a háromszögek kongruensek!
15. Az ABC háromszög AB és AC oldalainak meghoszszabbításain felvesszük a P, illetve a Q pontot úgy, hogy AP ≡ AB és AQ ≡ AC. Bizonyítsd be, hogy ABC∆ ≡ APQ∆.
Miniteszt
30 p 1. A következő ábrán egyformán vannak megjelölve a kongruens szakaszok, illetve a kongruens szögek.
Bizonyítsd be, hogy ABC∆ ≡ DEF∆.
2. Rajzolj egy xOy hegyesszöget és a szög szárain vedd fel az A, B∈Ox, illetve C, D∈Oy pontokat úgy, hogy: OA = 2,5 cm, AB = 5,5 cm, OD = 8 cm, OB > OA, OC < OD és OBC∢ ≡ ODA∢
30 p a) Igazold, hogy ADO∆ ≡ BCO∆.
30 p b) Számítsd ki az OC szakasz hosszát!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
199 6. fejezet • A háromszög
AB C D E 3 cm 4 cm 4 cm 70° 70° 7cm
P N AE MB C FQ D
Emlékeztető
Derékszögű háromszögnek nevezzük azt a háromszöget, melynek van egy derékszöge.
ABC∆ derékszögű, ha A∢ = 90°, vagy B∢ = 90°, vagy C∢ = 90°.
Egy derékszögű háromszög hegyesszögei pótszögek. Ha az ABC∆ derékszögű és A∢ = 90°, akkor B∢ + C∢ = 90°.
Egy derékszögű háromszögben a derékszöggel szemben fekvő oldalt átfogónak nevezzük, a derékszög szárait pedig befogóknak.
Fedezzük fel, értsük meg!
Ha az ABC∆ derékszögű, és A∢ = 90°, akkor BC átfogó, AB és AC a háromszög befogói.
Ha két derékszögű háromszögről beszélünk, akkor már megvan a megfelelő elemek egyik kongruenciaviszonya, nevezetesen a derékszögek kongruenciája. Ezután visszatérünk a háromszögek O.Sz.O. és Sz.O.Sz. kongruencia kritériumaira.
Tekintsük az ABC és MNP derékszögű háromszögeket A∢ = M∢= 90°. Akkor az AB és AC oldalak befogók, BC pedig az ABC háromszög átfogója, MN és MP befogók, az NP pedig az MNP háromszögben átfogó.
Ha ismerjük az egyik hegyesszöget, akkor a másik hegyesszög az előző pótszöge, tehát ismert.
Az O.Sz.O. kongruenciaeset B.B. esetté alakul (befogó - befogó), és így fogalmazhatjuk meg: (B.B.)
Ha két derékszögű háromszögben a befogók páronként kongruensek, akkor a két háromszög kongruens. AB CP MN
A SZ.O.Sz kongruenciakritérium két különböző esethez vezet.
Ha AB ≡ MN és AC ≡ MP, akkor ABC∆ ≡ MNP∆
1. Ha a szóban forgó oldal befogó, akkor B.Sz. eset lesz (befogó – hegyesszög), és így fogalmazható meg: (B.Sz.)
Ha B∢ ≡ N∢ és AB ≡ MN, akkor
ABC∆ ≡ MNP∆.
Ha C∢ ≡ P∢ és AC ≡ MP, akkor ABC∆ ≡ MNP∆.
a) Ha két derékszögű háromszög egy-egy befogója és a mellette lévő hegyesszögük kongruens, akkor a háromszögek kongruensek.
b) Ha két derékszögű háromszög egy-egy befogója és a szemben fekvő hegyesszögük kongruens, akkor a háromszögek kongruensek.
Ha B∢ ≡ N ∢és AC ≡ MP, akkor
ABC∆ ≡ MNP∆.
Ha C∢ ≡ P∢ és AB ≡ MN, akkor ABC∆ ≡ MNP∆. C
200 Matematika • Tankönyv a VI. osztály számára 3. l. A derékszögű háromszögek kongruenciaesetei
C ABMN P
C AB P MN
C AB P MN
AB P MN
Ha a kongruens oldalpár átfogó, akkor Á.Sz. eset lesz (átfogó - hegyesszög), és így fogalmazható meg:
(Á.Sz.)
Ha két derékszögű háromszög átfogója és egy-egy hegyesszögük kongruens, akkor a háromszögek kongruensek.
Gyakorlati alkalmazás
1. lépés. Szerkessz egy xAy derékszöget!
y x A
Ha B∢ ≡ N∢ és BC ≡ NP, akkor
ABC∆ ≡ MNP∆.
C AB P MN
2. lépés. Az Ax szárán vedd fel a B pontot úgy, hogy AB = 4 cm. y ABx 4 cm
Ha C∢ ≡ P∢ és BC ≡ NP, akkor
ABC∆ ≡ MNP∆.
C AB P MN
3. lépés. Rajzold meg a B középpontú és 5 cm sugarú kört, és legyen
{C} = C(B, 5 cm) ⋂ Ay y Bx A C 5cm 4 cm
Szerkesztettél egy egyértelműen meghatározott derékszögű háromszöget, melynek egyik befogója 4 cm és átfogója 5 cm.
A fenti szerkesztés egy újabb kongruenciakritériumot szolgáltat a derékszögű háromszögek esetében, Á.B. eset (átfogó - befogó), amit így fogalmazhatunk meg:
(Á.B.)
Ha két derékszögű háromszögben az átfogók és egy -egy befogó kongruens, akkor a két háromszög kongruens.
Ha BC ≡ NP és AB ≡ MN, akkor ABC∆ ≡ MNP∆.
Ha BC ≡ NP és AC ≡ MP, akkor
ABC∆ ≡ MNP∆. AB
Megjegyzés Minden kritériumot az A∢ = M∢ = 90° feltevéssel fogalmaztunk meg.
Gyakorlatok és feladatok
1. A következő geometriai ábrákon két kongruens derékszögű háromszög látható.
201 6. fejezet • A háromszög
AB C
MN P
CP MN
a) b) 5 cm 5 cm 7 cm 7 cm 60° 60°9cm 9 cm c) d) 6 cm 6cm 9cm 9cm 40° 40° 3cm 3cm
A rajzok jelöléseit használva minden egyes alpontnál minta alapján jelöld x-el azt a mezőt, amely megadja a kritériumot, amely szerint a háromszögek kongruensek!
Eset a) b) c) d)
IU
CU x IC CC
2. A melléklet ábrán a háromszögek azon elemeit, melyek kongruensek, azonos szimbólumokkal jelöltük. Másold le a füzetbe, és a pontozott helyeket töltsd ki úgy, hogy a kijelentések igazak legyenek!
a) BA C S RM
A két háromszög kongruens a … kongruenciakritérium alapján, és írhatjuk: ABC∆ ≡ … .
b) C AB D E F
A két háromszög kongruens a … kongruenciakritérium alapján, és írjuk: ABC∆ ≡ … .
3. A mellékelt ábrán az ABC
és az ANM háromszögek kongruensek, a szakaszok hossza centiméterben van kifejezve.
a) Fennáll a következő
kongruencia:
A. ABC∆ ≡ AMN∆; B. ACB∆ ≡ NAM∆; C. BCA∆ ≡ MAN∆; D. ABC∆ ≡ ANM∆.
b) Az a) alpontban a következő kongruenciakritériumot alkalmaztuk:
A. Á.B. B. B.B. C. Á.Sz. D. B.Sz.
4. Az A, B, C pontok ebben a sorrendben megadott kollineáris pontok, és AC = 2·BC. Az A és a C pontokban az AC egyenesre emelt merőlegeseken felvesszük az M, illetve N pontot úgy, hogy AM ≡ CN. Igazold, hogy:
a) MAB∆ ≡ NCB∆;
b) ACN∆ ≡ CAM∆.
5. Adott egy P pont az xOy tulajdonképpeni szög szögfelezőjén. Tudva, hogy a P pont távolsága az Ox egyenestől 4,5 cm, számítsd ki a P pont távolságát az Oy egyenestől!
6. Az ABC és a DEF háromszögek kongruensek, AM és DN magasságok.
a) Bizonyítsd be, hogy ACM∆ ≡ DFN∆;
b) Ha P az A pont szimmetrikusa a BC egyenesre nézve, a Q pont pedig a D pont szimmetrikusa az EF egyenesre nézve, bizonyítsd be, hogy ABP∆ ≡ DEQ∆.
7. Legyen ABC egy háromszög, AB ≠ AC és M a BC oldal felezőpontja. Megszerkesztjük a BD ⊥ AM, D ∈ AM és CE ⊥ AM, E ∈ AM. egyeneseket. Bizonyítsd be, hogy BDM∆ ≡ CEM∆.
8. Az MNP derékszögű háromszögben MNP∢ ≡ ≡ MPN∢. Az N pontban az NP egyenesre bocsátott merőleges az MP egyenest az A pontban metszi, a P pontban az NP egyenesre húzott merőleges pedig az MN egyenest a B pontban metszi.
a) Készíts mértani felszereléssel a feladat adatainak megfelelő ábrát!
b) Számítsd ki az MNP és az MPN szögek mértékét!
c) Bizonyítsd be, hogy ANP∆ ≡ BPN∆.
9. Az ABC szög derékszög, a D pont az AC szakasz egy pontja. Jelöljük M-mel a D pontból az AB egyenesre húzott merőleges talppontját, és N-nel a D pontból a BC egyenesre húzott merőleges talppontját. Igazold, hogy:
a) DM ∥ BC és DN ∥ AB;
b) BDM∆ ≡ DBN∆.
202 Matematika • Tankönyv a VI. osztály számára
C N ABM 8 7 7 8
Miniteszt
4 × 10 p 1. Az ABC és az MNP háromszögek derékszögűek, BAC∢ = 90° és NMP∢ = 90°.
Az A oszlopban lévő betűhöz, amely a megfelelő elemek kongruenciáját jelöli, társíts a B oszlopból egy számot, amely az ABC és MNP háromszögek kongruenciakritériumát jelöli!
A
a. AB ≡ MN, AC ≡ MP
b. AC ≡ MP, ABC∢ ≡ MNP∢
c. BC ≡ NP, AB ≡ MN
d. BC ≡ NP, ACB∢ ≡ MPN∢
25 p
25 p
B
1. Á.B.
2. Á.Sz.
3. B.B.
4. B.Sz.
2. Legyen ABC egy háromszög és CD a C szög szögfelezője, D ∈ AB. Az A pontból a CD egyenesre húzott merőleges a CD egyenest a P pontban, a BC egyenest pedig az E pontban metszi.
a) Bizonyítsd be, hogy ACP∆ ≡ ECP∆ .
b) Állapítsd meg, hogy a DAC és a CED szögek kongruensek-e, majd indokold válaszod!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
4. l. A kongruens háromszögek módszere
Emlékeztető
A bizonyításon alapuló geometria matematikai állításokkal, meghatározásokkal, axiómákkal, tételekkel dolgozik.
Egy matematikai állítás egy olyan kijelentés, amely vagy igaz, vagy hamis.
Az axiómák olyan igaznak elfogadott állítások, melyek nem igényelnek bizonyítást.
A tételek igaz állítások, amelyeket axiómák és más, már bizonyított állítások alapján fogalmaznak meg és bizonyítanak.
Általában a tételek alakja: „Ha feltevés, akkor következtetés“ .
A következtetés és a feltevés vagy a feltevés egy része felcserélésével reciprok (fordított) állítást kapunk. Ha a fordított állítás igaz, akkor tétel lesz, és a tétel fordított tételének nevezzük. Az eredeti tételt pedig direkt tételnek hívjuk.
Fedezzük fel, értsük meg!
Ha a direkt tétel is, a fordított tétel is igaz, akkor egyetlen állításban is megfogalmazhatók:
1. állítás akkor és csakis akkor, ha 2. állítás
Ez a megfogalmazás feltételezi, hogy a következő állítások is igazak:
Ha 1. állítás, akkor 2. állítás és
Ha 2. állítás, akkor 1. állítás
Egy „...akkor és csakis akkor …” típusú tétel bizonyításakor mindkét tételt bizonyítani kell (a direkt tételt is, a fordított vagy reciprok tételt is)
Példa:
Legyen d az AB szakasz felezőmerőlegese, és M egy pont a síkban. Igazak a következő tételek:
a) Ha M ∈ d, akkor MA ≡ MB.
b) Ha MA ≡ MB, akkor M ∈ d.
A két kijelentés helyettesíthető egyetlen kijelentéssel:
M ∈ d akkor és csakis akkor, ha MA ≡ MB.
203 6. fejezet • A háromszög
Megjegyzés. A fenti példa egy szakasz felezőmerőlegesén levő pontok tulajdonságát adja meg, amit egy következő leckében fogunk bizonyítani.
Egy szakasz felezőmerőlegese a sík azon pontjainak halmaza, melyek egyenlő távolságra helyezkednek el egy szakasz végpontjaitól.
A kongruens háromszögek módszere jól használható szakaszok vagy szögek kongruenciájának igazolásához vagy más fontos tételek bizonyításához.
Szakaszok, illetve szögek kongruenciáját bizonyíthatjuk a kongruens háromszögek módszerével a következő lépésekben:
1. lépés. Keresünk két háromszöget úgy, hogy a két szakasz közül az egyik az egyik háromszögnek az oldala, a másik pedig a másik háromszögé. A két szög közül az egyik az egyik háromszögnek a szöge, a másik pedig a másik háromszögé.
2. lépés. Az egyik kongruenciakritérium segítségével bizonyítjuk, hogy a két háromszög kongruens.
3. lépés. Levezetjük, hogy a két háromszög megfelelő oldalai és szögei kongruensek, és ebből következik az érintett szakaszok és szögek kongruenciája.
Alkalmazások
A kongruens háromszögek módszerének felhasználásához hasznos eredményt ad az 1. alkalmazás.
1. alkalmazás: Kongruens háromszögekben kongruens oldalakkal szemben kongruens szögek vannak.
Megoldás. Legyenek adottak az ABC és az MNP kongruens háromszögek.
Feltevés: ABC∆ ≡ MNP∆
Következtetés: kongruens oldalakkal szemben kongruens szögek vannak
A
BC M NP
Bizonyítás: Ha ABC∆ ≡ MNP∆, az értelmezés alapján a következő kongruenciákat kapjuk: AB ≡ MN, AC ≡ MP,
BC ≡ NP, A ≡ M, B ≡ N, C ≡ P. Az alábbi táblázatban kiemeljük az érintett kongruenciákat.
ABC∆ ≡ MNP∆
ABC∆ oldala A szemben fekvő szög Az MNP∆ oldala A szemben fekvő szög
A megfelelő oldalak kongruensek akkor és csakis akkor, ha az oldalakkal szemben fekvő szögek kongruensek.
AB C∢ MN P∢ AB ≡ MN akkor és csakis akkor, ha C∢ ≡ P∢
AC B∢ MP N∢ AC ≡ MP akkor és csakis akkor, ha B∢ ≡ N∢
BC A∢ NP M∢ BC ≡ NP akkor és csakis akkor, ha A∢ ≡ M∢
Megjegyzés. A fenti következtetések csak kongruens háromszögekben érvényesek!
2. alkalmazás: Az MNP háromszögben, NA ⊥ MP, A ∈ MP, PB ⊥ MN, B ∈MN és NA ≡ PB.
Bizonyítsd be, hogy MN ≡ MP. M
Feltvés: MNP∆, NA ⊥ MP, A ∈ MP, PB ⊥ MN, B ∈MN és NA ≡ PB.
Következtetés: MN ≡ MP.
Bizonyítás. Legyenek az MAN∆ és MBP∆ derékszögű háromszögek. (a feltevésből) (közös szög) BSz. MAN∆ ≡ MBP∆. MAN∢ ≡ MBP∢, következik MN ≡ MP.
204 Matematika • Tankönyv a VI. osztály számára
BA NP
Gyakorlatok és feladatok
1. Másold le a füzetbe és töltsd ki a pontozott helyeket úgy, hogy igazak legyenek a következő kijelentések!
a) Kongruens háromszögekben kongruens oldalakkal szemben kongruens … vannak.
b) Kongruens háromszögekben kongruens szögekkel szemben kongruens … vannak.
c) Ha CDS∆ ≡ EFT∆, akkor DS ≡ ... és ... ≡ TFE∢.
2. Egy O középpontú kör AB és BC húrjai kongruensek. Igazold, hogy AOB∢ ≡ BOC∢.
3. Az A, B, C pontok ebben a sorrendben megadott kollineáris pontok, a D és az E pontok az AC egyenes által határolt különböző félsíkokban helyezkednek el úgy, hogy ABD∆ ≡ ABE∆. Bizonyítsd be, hogy CD ≡ CE
4. Legyenek az ABC és DEF háromszögek úgy, hogy
A∢ ≡ D∢, B∢ ≡ E∢, AB = DE = 8 cm, AC = 10 cm, EF = 6 cm. Számítsd ki az ABC háromszög kerületét!
5. Az ABC háromszög AB és AC oldalait meghoszszabbítjuk az AD ≡ AB és AE ≡ AC szakaszokkal. Bizonyítsd be, hogy:
a) ABC∆ ≡ ADE∆; b) DE ∥ BC.
6. Az ABC hegyesszögű háromszög A csúcsából meghúzzuk az AD ⊥ AB, AD ≡ AB és AE ⊥ AC egyeneseket AE ≡ AC, úgy, hogy D és C az AB különböző oldalain legyen, B és E pedig AC különböző oldalain legyen. Bizonyítsd be, hogy ABE∆ ≡ ADC∆
Miniteszt
7. A mellékelt ábrán az a és a b egyenesek párhuzamosak, a c és a d egyenesek pedig szelők. A rajzon található jelöléseket használva és tudva, hogy AB ≡ CD, bizonyítsd be, hogy az O pont a BD szakasz felezőpontja!
cOD abd
8. Az AB szakasz M felezőpontján keresztül húzunk egy d egyenest. Az A és B pontokból az AB egyenesre húzott merőlegesek a d egyenest a P, illetve Q pontban metszik, az M pontból a d egyenesre húzott merőleges a BQ egyenest a C pontban metszi. Bizonyítsd be, hogy:
a) PM ≡ QM;
b) BCM∢ ≡ PCM∢.
9. Legyenek A, B, C ebben a sorrendben megadott kollineáris pontok. Az AC egyenes ugyanazon oldalán tekintsük az AM és CN párhuzamos félegyeneseket úgy, hogy ABM∆ ≡ CNB∆.
a) Igazold, hogy AM ⊥ BC
b) Számítsd ki az MBN szög mértékét!
10. A DEF általános háromszög csúcsain keresztül párhuzamosokat húzunk a szemben fekvő oldalakkal és keletkezik az ABC háromszög D∈BC, E∈AC, F∈AB. Bizonyítsd be, hogy:
a) AEF∆ ≡ DFE∆;
b) a D pont a BC szakasz felezőpontja;
30 p 1. Az ABC háromszögben a D pont a háromszög AB oldalán található, az E pont pedig a háromszög AC oldalán. A BE és a CD egyenesek az F pontban metszik egymást, BF ≡ CF és DF ≡ EF. Bizonyítsd be, hogy BD ≡ CE.
2. Az A, B, C, D ebben a sorrendben megadott kollineáris pontok, AB ≡ CD, az E pont az AD egyenesen kívül helyezkedik el úgy, hogy EAD∢ ≡ EDA∢ és EBC∢ ≡ ECB∢. Igazold, hogy:
30 p a) EAB∆ ≡ EDC∆;
30 p b) EAC∆ ≡ EDB∆
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
205 6. fejezet • A háromszög
A B C
6.4. A kongruens háromszögek módszere. Alkalmazások
1. l. A szögfelezőn levő pontok tulajdonsága.
Egy szakasz felezőmerőlegesén levő pontok tulajdonsága
A kongruens háromszögek módszerét alkalmazva, bizonyítani fogjuk egy szög szögfelezőjén és egy szakasz felezőmerőlegesén levő pontok fontos matematikai tulajdonságait.
Fedezzük fel, értsük meg!
1. alkalmazás
a) Egy szög szögfelezőjén lévő bármely pont egyenlő távolságra helyezkedik el a szög száraitól.
b) Egy szög belső tartományában levő pont, mely egyenlő távolságra helyezkedik el a szög száraitól, a szög szögfelezőjén van.
Matematikai szimbólumokkal Mértani ábrázolás
Legyen b az AOB szög szögfelezője, M egy pont a szög belső tartományában és MP ⊥ Ox, P ∈ Ox, MQ ⊥ Oy, Q ∈Oy.
a) Ha M ∈ b, akkor MP ≡ MQ.
b) Ha MP ≡ MQ, akkor M ∈ b.
a) Feltevés: b az AOB szög szögfelezője és M ∈ b Következtetés: MP ≡ MQ
Részletes bizonyítás:
Az MPO∆ és MQO∆ , derékszögű háromszögekben: MO ≡ MO (közös átfogó). (1) Mivel b az AOB szög szögfelezője és M ∈ b, következik hogy POM∢ ≡ QOM∢. (2) (1) és (2) összefüggésekből az Á.Sz. kongruenciaeset alapján következik, hogy MPO∆ ≡ MQO∆, tehát a háromszögek megfelelő elemei kongruensek. Az MP és MQ befogók egymással megfelelő oldalak a két háromszögben, tehát MP ≡ MQ.
b) Feltevés: b az xOy szög szögfelezője, M∈Int(xOy∢) és MP ≡ MQ.
Részletes bizonyítás:
Az MPO és MQO derékszögű háromszögekben: MO ≡ MO (közös átfogó). (1) MP ≡ MQ (a feltevésből) (2)
Az (1) és (2) összefüggésekből az Á.B. kongruenciaeset alapján következik, hogy MPO∆ ≡ MQO∆, tehát a megfelelő elemek kongruensek. Az MP és MQ kongruens befogókkal szemben fekvő szögek a POM∢ és QOM∢. Következik, hogy POM∢ ≡ QOM∢, tehát M ∈ b.
A két bizonyított kijelentés alapján kijelenthetjük
Egy szög szögfelezőjén levő pontok tulajdonságának tételét:
Egy szög belső tartományában levő pont a szög szögfelezőjéhez tartozik akkor és csakis akkor, ha a szög száraitól egyenlő távolságra van.
Matematikai szimbólumokkal leírt bizonyítás
Az MPO és MQO derékszögű háromszögekben: (közös oldal) (b szögfelező)
A.Sz MPO∆ ≡ MQO∆.
MPO∆ ≡ MQO∆ ⇒ MP ≡ MQ.
Következtetés: M ∈ b
Matematikai szimbólumokkal leírt bizonyítás
Az MPO és MQO derékszögű háromszögekben:
Á.B. (közös oldal)
MPO∆ ≡ MQO∆.
(a feltevésből)
MPO∆ ≡ MQO∆ ⇒ POM∢ ≡ QOM∢, tehát M ∈ b.
Matematikai szimbólumokkal kifejezve: Legyen b az AOB szög szögfelezője, M a szög belső tartományában lévő pont és MP ⊥ OA, P ∈ OA, MQ ⊥ OB, Q ∈ OB.
Az M ∈ b akkor és csakis akkor, ha MP ≡ MQ.
206 Matematika • Tankönyv a VI. osztály számára
x b y P M OQ
Jegyezd meg!
Egy szög szögfelezője a sík azon pontjainak halmaza, amelyek a szög belső tartományában egyenlő távolságra vannak a szög száraitól.
2. alkalmazás:
a) Bármely pont egy szakasz felezőmerőlegesén egyenlő távolságra van a szakasz végpontjaitól.
b) A sík bármely pontja, mely egyenlő távolságra van egy szakasz végpontjaitól, a szakasz felezőmerőlegesén található.
Matematikai szimbólumokkal
kifejezve:
Legyen d az AB szakasz felezőmerőlegese és M a sík egy pontja.
a) Ha M ∈ d, akkor MA ≡ MB.
b) Ha MA ≡ MB, akkor M ∈ d.
a) Feltevés: d az AB szakasz felezőmerőlegese és M ∈ d. Következtetés: MA ≡ MB
Részletes bizonyítás: Matematikai szimbólumokkal leírt bizonyítás
Ha A, B, M kollineáris pontok, akkor M az AB szakasz felezőpontja, tehát MA ≡ MB.
Ha az A, B, M nem kollineáris pontok, legyen {M0} = AB ⋂ d
Ekkor M0 az AB szakasz felezőpontja és MM0 ⊥ AB.
Az MAM0 és MBM0 háromszögekben
MM0A∢ = MM0B∢ = 90°, M0A ≡ M0B (M0 felezőpont) és MM0 ≡ MM0 (közös oldal).
A B.B. kongruenciaeset alapján MAM∆0 ≡ MBM∆0. A két háromszög kongruenciájából következik a háromszögek többi három megfelelő elempárjának kongruenciája. Következik, hogy MA ≡ MB.
Ha A, B, M kollineáris pontok, akkor M az AB szakasz felezőpontja, tehát MA ≡ MB
Ha A, B, M nem kollineáris pontok, legyen
{M0} = AB ⋂ d. Ekkor MM0 ⊥ AB és M0A ≡ M0B.
MAM0∆ és MBM0∆ háromszögekben
MM0A∢ = MM0B∢ = 90° fennáll: B.B.
(közös oldal)
⇒∆MAM0∆ ≡ MBM0∆.
MAM0∆ ≡ MBM0∆ ⇒ MA ≡ MB.
b) Feltevés: d az AB szakasz felezőmerőlegese és MA ≡ MB. Következtetés: M ∈ d
Részletes bizonyítás Matematikai szimbólumokkal leírt bizonyítás
Ha A, B, M kollineáris pontok, akkor M az AB szakasz felezőpontja, tehát M ∈ d.
Ha A, B, M nem kollineáris pontok, legyen M0 az AB szakasz felezőpontja, és tekintsük az MAM0 és MBM0, háromszögeket, melyekben: MA ≡ MB (a feltevésből),
M0A ≡ M0B (M0 felezőpont) és MM0 ≡ MM0 (közös oldal).
Az O.O.O. kongruenciaeset alapján MAM0∆ ≡ MBM0∆. A két háromszög kongruenciájából következik a háromszög többi három megfelelő elempárjának kongruenciája. Tehát MM0A ≡ MM0B. (1)
MM0A és MM0B egymás melletti kiegészítő szögek. (2)
Az (1) és (2), összefüggésekből következik, hogy
MM0A = MM0B = 90°, tehát MM0 ⊥ AB, tehát M ∈ d.
A két bizonyított kijelentés alapján kijelenthetjük egy szakasz felezőmerőlegesén levő pontok tulajdonságának tételét: A sík egy pontja egy szakasz felezőmerőlegeséhez tartozik akkor és csakis akkor, ha egyenlő távolságra helyezkedik el a szakasz végpontjaitól.
Ha A, B, M kollineáris pontok, akkor M az AB szakasz felezőpontja, tehát M ∈ d.
Ha A, B, M nem kollineáris pontok, legyenM0 ∈ AB, M0A ≡ M0B. Ekkor,
(közös oldal)
(a feltevésből)
O.O.O
MAM0∆ ≡ MBM0∆.
MAM0∆ ≡ MBM0∆ ⇒MM0A ≡ MM0B.
Mivel AM0B= 180° és
AM0B = MM0A + MM0B,, következik, hogy
MM0A = MM0B = 90°, tehát MM0 ⊥ AB, tehát M ∈ d
Matematikai szimbólumokkal kifejezve
Legyen d az AB szakasz felezőmerőlegese és M a sík egy pontja.
M ∈ d akkor és csakis akkor, ha MA ≡ MB.
207 6. fejezet • A háromszög
AM
B M d
0
Jegyezd meg!
Egy szakasz felezőmerőlegese a sík azon pontjainak halmaza, melyek egyenlő távolságra vannak a szakasz végpontjaitól.
Alkalmazások
Az előző leckékben bemutatott két következtetést most már tudjuk bizonyítani geometriai eszközökkel méréssel és szerkesztéssel.
3. alkalmazás
Egy háromszög szögfelezői összefutó egyenesek.
4. alkalmazás
A háromszög oldalfelező merőlegesei összefutó egyenesek.
Legyen I a BAC és az ABC szögfelezőjének metszéspontja.
IA’ ⊥ BC, IB’ ⊥ AC, IC’ ⊥ AB
Mivel I rajta van a BAC szögfelezőjén, következik, hogy IB′≡ IC′ .
Mivel I rajta van az ABC szögfelezőjén, következik, hogy IA′≡ IC′ .
IB′≡ IC′ és IA′≡ IC′, összefüggésekből következik, hogy IB′≡ IA′ , tehát I az ACB szögfelezőjén van.
Legyen O a BC és az AB oldalfelező merőlegeseinek metszéspontja.
Mivel OA’ a BC oldalfelező merőlegese, következik, hogy OB ≡ OC.
Mivel OC′ az AB oldalfelező merőlegese, következik, hogy OB ≡ OA.
Az OB ≡ OC és OB ≡ OA összefüggésekből következik, hogy OA ≡ OC , vagyis O az AC oldalfelező merőlegesén van.
Gyakorlatok és feladatok
1. Az AMN derékszögű háromszögben MAN∢ = 90°
és MB az AMN∢ szög szögfelezője, B ∈ AN. Legyen C a B pontból az MN egyenesre bocsátott merőleges talppontja. Bizonyítsd be, hogy az ABC háromszög egyenlő szárú!
2. Az A, B, P nem kollineáris pontok. Az A pontban az AP egyenesre emelt merőleges a B pontban a PB egyenesre emelt merőlegest az I pontban metszi. a) Bizonyítsd be, hogy API∢ ≡ BPI∢, akkor AI ≡ BI. b) Tudva, hogy AIP∢≡BIP∢, bizonyítsd be, hogy AP ≡ BP.
3. Legyen O az AB és CD szakaszok közös pontja. M egy pont az AOC∢ szög belső tartományában, mely egyenlő távolságra van az AOC∢ szög száraitól, a BOD∢ szög belső tartományában tekintsük az N pontot, mely a BOD∢ szög száraitól van egyenlő távolságra. Igazold, hogy az M, O és N pontok kollineárisak!
4. Legyen ABC egy háromszög, ABC∢ = 90° és D a C pont szimmetrikusa a B pontra nézve. Bizonyítsd be, hogy AC ≡ AD.
5. Az ABC háromszögben az AD egyenes a BC oldalfelező merőlegese, D∈BC. Az AD szakaszon felvesszük az M és az N különböző pontokat. Igazold, hogy MBN∢ ≡ MCN∢.
6. Legyen O egy pont az AB oldal felezőmerőlegesén.
a) Rajzold le a C(O, AO) kört!
b) Igazold, hogy a B pont az O középpontú és OA sugarú körön van!
7. A DEF háromszög DE oldalának felezőmerőlegese a DF szakaszt a P pontban metszi, O pedig a háromszög oldalfelező merőlegeseinek metszéspontja. Bizonyítsd be, hogy:
a) DF = PF + PE;
b) a DOP és EOP háromszögeknek ugyanakkora a kerületük.
8. Az ABC háromszögben A∢ = 2·B∢, az AB oldal felezőmerőlegese az AB oldalt D-ben a BC oldalt pedig E-ben metszi. Igazold, hogy:
a) ADE∆ ≡ BDE∆;
b) AE a BAC∢ szög szögfelezője.
208 Matematika • Tankönyv a VI. osztály számára
A B' C' A' I B C
B' C' BA' C O
A
Miniteszt
Az ABC háromszög tompaszögű, ACB∢ > 90° és D a BC oldal felezőpontja. Az ACB szög szögfelezője a BC oldal felezőmerőlegesét az E pontban metszi, F pedig az E pont szimmetrikusa az AC egyenesre nézve, AC, EF ∩ AC = {P}.
30 p a) Készíts a feladat adatainak megfelelő ábrát!
30 p b) Bizonyítsd be, hogy a BDE, CDE, CPE és CPF háromszögek kongruensek!
30 p c) Ha a B, C, F pontok kollineárisak, számítsd ki az ACB∢ szög mértékét!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
2. l. Az egyenlő szárú háromszög tulajdonságai
Emlékeztető
A háromszög nevezetes vonalai: a szögek szögfelezői, az oldalak felezőmerőlegesei, a háromszög magasságai és a háromszög oldalfelezői.
Alkalmazások
1. alkalmazás
a) Igazold, hogy egy egyenlő szárú háromszögben az alapon fekvő szögek kongruensek!
b) Fogalmazz meg az a) alpontban bizonyított kijelentésnek egy reciprok (fordított) kijelentését és bizonyítsd be, hogy igaz.
a) Feltevés: ABC∆-ben AB ≡ AC. Következtetés: B∢ ≡ C∢.
Bizonyítás.
Tekintsük az ABC és az ACB háromszögeket:
(a feltevésből)
(a feltevésből)
O.O.O
ABC∆ ≡ ACB∆ ⇒ B∢ ≡ C∢.
(közös oldal)
b) Ha egy háromszög két szöge kongruens, akkor a háromszög egyenlő szárú, az alapja pedig a két kongruens szög csúcsa által meghatározott oldal lesz.
Feltevés: ABC∆-ben B∢ ≡ C∢ Következtetés: AB ≡ AC.
Bizonyítás.
Tekintsük az ABC és az ACB háromszögeket: (közös szög (közös oldal) (a feltevésből) Sz.O.Sz.
ABC∆ ≡ ACB∆ ⇒ AB ≡ AC.
Jegyezd meg!
Egy háromszög egyenlő szárú akkor és csakis akkor, ha van két kongruens szöge.
2. alkalmazás
Egy egyenlő szárú háromszögben az alaphoz tartozó nevezetes vonalak
Feltevés: ABC∆-ben AB ≡ AC.
egybeesnek. A BMC
Következtetés: Az A szög szögfelezője a BC oldal felezőmerőlegese, az A csúcsból húzott oldalfelező és az A csúcsból húzott magasság egy egyenesen helyezkednek el.
209 6. fejezet • A háromszög
A BC
Bizonyítás: Legyen M a BC oldal felezőpontja. Akkor, AM az A csúcsból húzott oldalfelező. (1)
Tekintsük az AMB és az AMC háromszögeket: ABAC MBMCM felezőpont)
AMAM (a feltevésből) ( (közös oldal) O.O.O AMB∆ ≡ AMC∆.
Következik, hogy: MAB∢ ≡ MAC∢, azaz AM az A szög szögfelezője. (2)
AMB∢ ≡ AMC∢. De AMB∢ és AMC∢ egymás melletti kiegészítő szögek, tehát AMB∢ = AMC∢ = 90°.
Ekkor, AM ⊥ BC, vagyis AM a háromszög magassága. (3)
AM ⊥ BC és M oldal felezőpontja, következik, hogy AM a BC oldal felezőmerőlegese. (4)
Feladat a portfólióba: Bizonyítsd be a kongruens háromszögek módszerével, hogy: ha az (1), (2), (3), (4) feltételek közül bármelyik kettő teljesül, akkor az ABC háromszög egyenlő szárú és alapja BC .
Jegyezd meg!
Ahhoz, hogy bebizonyítsuk, hogy egy háromszög egyenlő szárú, elegendő, ha a háromszög két nevezetes vonala átfedéssel egybeesik. (az oldalfelező és az oldalfelező merőleges vagy az oldalfelező és a szögfelező vagy az oldalfelező és a magasság vagy az oldalfelező merőleges és a szögfelező vagy az oldalfelező merőleges és a magasság vagy a szögfelező és a magasság).
A háromszög alapja az egybeeső nevezetes vonalakhoz tartozó oldal.
Gyakorlatok és feladatok
1. Szerkeszd meg az ABC egyenlő szárú háromszöget, melynek alapja BC, a következő esetekben:
a) BC = 5 cm és B∢ = 75°;
b) AB = 6 cm és A∢ = 50°.
2. Legyen ABC egy háromszög, melyben AB = 5 cm, BC = 7 cm és a háromszög kerülete 19 cm. Bizonyítsd be, hogy a háromszög egyenlő szárú! Határozd meg a háromszög alapját!
3. A DEF háromszögben D∢ = 65° és F∢ = 50°. Igazold, hogy a háromszög egyenlő szárú! Határozd meg a háromszög alapját!
4. Számítsd ki egy egyenlő szárú háromszög szögeinek mértékét tudva, hogy a háromszög egyik szögének mértéke:
a) 48°; b) 90°; c) 125°.
5. Az ABC háromszög egyenlő szárú, AB ≡ AC, D pedig egy pont a BC oldalon. Másold le a füzetbe és töltsd ki a pontozott helyeket úgy, hogy igaz
kijelentéseket kapj:
a) Ha BAD∢ ≡ CAD∢ és BC = 10 cm, akkor
CD = … cm.
b) Ha BD ≡ CD és BAD∢ = 20°, akkor BAC∢ = … °.
c) Ha AD ⊥ BC és BD = 3,5 cm, akkor
CD = … cm és BC = … cm.
d) Ha AD ⊥ BC és B∢ = 52°, akkor CAD∢ = …°.
e) Ha BAD∢ ≡ CAD∢, akkor ADB∢ = …°.
f) Ha ADC∢ = 90° és BAC∢ = 130°, akkor BAD∢ = …°.
6. BC alapú ABC egyenlő szárú háromszög belső tartományában felveszünk egy P pontot.
a) Tudva, hogy BP ≡ CP, igazold, hogy AP ⊥ BC.
b) Tudva, hogy BAP∢ ≡ CAP∢, igazold, hogy BP ≡ CP.
c) Bizonyítsd be, hogy ha AP a BAC szög szögfelezője, akkor a PD félegyenes a BPC szög szögfelezője!
7. Bizonyítsd be, hogy bármely egyenlő szárú háromszögben igazak a következő kijelentések:
a) Egy egyenlő szárú háromszögben a kongruens oldalakhoz tartozó oldalfelezők kongruensek.
b) Egy egyenlő szárú háromszögben a kongruens oldalakhoz tartozó magasságok kongruensek.
8. Bizonyítsd be, hogy egy egyenlő szárú háromszög alapján fekvő szögek hegyesszögek!
9. A DEF háromszögben, DE ≡ DF és EDF∢ = 36°. A DEF szög szögfelezője a DF oldalt az M pontban metszi. Igazold, hogy a DEM és az EFM háromszögek egyenlő szárúak!
210 Matematika • Tankönyv a VI. osztály számára
10. Az APQ háromszög egyenlő szárú. Számítsd ki a PQ oldal hosszát, tanulmányozva minden lehetséges esetet!
a) AP = 13 cm, AQ = 17,5 cm;
b) AP = 50 mm, AQ = 10 cm.
11. Az ABC háromszög egyenlő szárú, D egy pont a háromszög BC lapján. Megszerkesztjük a DE ⊥ AB, E ∈ AB és DF ⊥ AC, F ∈ AC egyeneseket. Tudva, hogy DE = DF, bizonyítsd be, hogy:
a) ADE∆ ≡ ADF∆
b) DEF∆ háromszög egyenlő szárú.
12. Az MNP háromszög M csúcsához tartozó külső szög mértéke 135° és N∢ = 2 · P∢. Bizonyítsd be, hogy az MNP háromszög egyenlő szárú!
13. A d egyenes párhuzamos az ABC egyenlő szárú háromszög AC alapjával és az AB és BC oldalakat a P, illetve Q pontban metszi. Igazold, hogy:
a) APQ∢ ≡ CQP∢; b) AP ≡ CQ.
Miniteszt
14. Az ABC egyenlő szárú háromszögben AB = AC. Az AD félegyenes a háromszög egyik külső szögének szögfelezője.
a) Bizonyítsd be, hogy AD ∥ BC.
b) Számítsd ki a háromszög szögeinek mértékét tudva, hogy CAD∢ = 100°.
15. Az ABC háromszög A és B szögeinek szögfelezői az I pontban metszik egymást. Az I ponton keresztül az AB egyenessel párhuzamos egyenes a BC oldalt az M pontban, az AC oldalt pedig az N pontban metszi.
a) Bizonyítsd be, hogy az ANI és a BMI háromszögek egyenlő szárúak!
b) Állapítsd meg, hogy igaz-e BM + AN = MN egyenlőség! Válaszod indokold!
1. Válaszd ki a helyes válasznak megfelelő betűt! Csak egy helyes válasz van.
15 p a) Egy egyenlő szárú háromszög alapjának hossza 13 cm, háromszög kerülete pedig 34 cm. Akkor a szárainak hossza:
A. 105 mm; B. 11 cm; C. 102 mm; D. 15 cm.
15 p b) Az AD szakasz az ABC háromszög magassága, melyben AB = AC. Ha BAD∢ = 35°, akkor az ACD∢ szög mértéke:
A. 35°; B. 55°; C. 70°; D. 90°.
30 p 2. Bizonyítsd be, hogy egy egyenlő szárú háromszögben az alaphoz tartozó oldalfelező merőleges tartalmazza a háromszög alapjával szemben fekvő csúcsát!
30 p 3. Számítsd ki az ABC egyenlő szárú háromszög szögeinek mértékét, tudva, hogy A∢ + B∢ = 136°. Tanulmányozz minden lehetséges esetet!
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
3. l. Az egyenlő oldalú háromszög tulajdonságai
Emlékeztető
Egy háromszöget egyenlő oldalú háromszögnek nevezünk, ha minden oldala kongruens.
ABC∆ egyenlő oldalú, ha AB ≡ AC ≡ BC.
Minden egyenlő oldalú háromszög egyenlő szárú is. Ha ABC∆ egyenlő oldalú, akkor ABC∆ egyenlő szárú.
A háromszögbe beírt kör középpontja a háromszög szögfelezőinek metszéspontja.
A háromszög köré írt kör középpontja a háromszög oldalfelező merőlegeseinek metszéspontja.
A háromszög súlypontja a háromszög oldalfelezőinek metszéspontja.
A háromszög ortocentruma az a pont, amelyben a magasságok tartóegyenesei futnak össze.
211 6. fejezet • A háromszög
Fedezzük fel, értsük meg!
1. alkalmazás
a) Egy egyenlő oldalú háromszög minden szöge kongruens és mértékük 60°.
b) Egy háromszög, melyben minden szög kongruens, egyenlő oldalú háromszög.
a) Feltevés:
ABC∆-ben AB ≡ AC ≡ BC.
Következtetés: A∢ = B∢ = C∢ = 60°.
Bizonyítás:
AB ≡ AC ⇒ B∢ ≡ C∢ (az egyenlő szárú háromszög alapon fekvő szögei kongruensek) (1)
BA ≡ BC ⇒ A∢ ≡ C∢ (az egyenlő szárú háromszög alapon fekvő szögei kongruensek) (2)
Az (1) és (2) összefüggésekből következik, hogy A∢ ≡ B∢ ≡ C∢.
De, A∢ + B∢ + C∢ = 180°, tehát A∢ = B∢ = C∢ = 60°.
b) Feltevés:
ABC∆-ben A∢ = B∢ = C∢.
Következtetés: AB ≡ AC ≡ BC.
Bizonyítás:
A∢ = B∢ ⇒ ABC∆ egyenlő szárú, alapja AB, azaz CA ≡ CB. (1)
B∢ = C∢ ⇒ ABC∆ egyenlő szárú, alapja BC, azaz AB ≡ AC. (2)
Az (1) és (2) összefüggések alapján AB ≡ AC ≡ BC, tehát ABC∆ egyenlő oldalú.
Az a háromszög, melynek minden szöge kongruens, egyenlő oldalú. Jegyezd meg!
Az egyenlő oldalú háromszög szögei kongruensek és mértékük 60°.
2. alkalmazás: Egy egyenlő szárú háromszög, melynek van egy 60°-os szöge, egyenlő oldalú.
A kijelentés értelmezése:
Legyen ABC∆, melynek alapja BC.
Két eset lehetséges:
1. A 60° -os szög az alappal szembeni szög;
2. A 60° -os szög az alapon fekvő szög.
1. eset
Feltevés: ABC∆-ben AB ≡ AC és A∢ = 60°
Következtetés: ABC∆ egyenlő oldalú.
2. eset
Feltevés: În ABC∆, AB ≡ AC és B = 60°
Következmény: ABC∆ egyenlő oldalú.
Alkalmazások
Bizonyítás: AB ≡ AC ⇒ B∢ ≡ C∢ (alapon fekvő szögek) (1)
De A∢ + B∢ + C∢ = 180°, tehát B∢ + C∢= 120°. Az (1) összefüggés alapján B∢ = C∢ = 60°. Az 1. alkalmazás alapján az ABC∆ egyenlő oldalú.
Bizonyítás: AB ≡ AC ⇒ B∢ ≡ C∢ (alapon fekvő szögek), tehát C = 60°. Mivel, A∢ + B∢ + C∢ = 180°, azaz A∢ + 120° = 180°, tehát A∢ = 60°. Az 1. alkalmazás alapján az ABC∆ egyenlő oldalú.
3. alkalmazás Egy egyenlő oldalú háromszögben a háromszög bármely csúcsához tartozó nevezetes vonalak ugyanazon az egyenesen vannak.
Feltevés: ABC∆ egyenlő oldalú..
Következtetés: Bármely csúcshoz tartozó szögfelező, a szemben fekvő oldalhoz tartozó oldalfelező és oldalfelező merőleges, valamint az illető csúcsból húzott magasság ugyanazon az egyenesen helyezkedik el.
212 Matematika • Tankönyv a VI. osztály számára
A
60° A BC 60°
BC
A P B M C N
Bizonyítás: Az ABC egyenlő oldalú háromszöget rendre BC, AC illetve AB alapú egyenlő szárú háromszögnek tekintjük.
Legyenek M, N, P a BC, AC, illetve AB oldalak felezőpontjai.
Az ABC∆ egyenlő szárú, melynek alapja BC, következik, hogy az AM félegyenes szögfelező, az AM egyenes oldalfelező merőleges, az AM szakasz oldalfelező és magasság is. (1)
Az ABC∆ egyenlő szárú, melynek alapja AC, következik, hogy a BN félegyenes szögfelező, a BN egyenes oldalfelező merőleges, az BN szakasz oldalfelező és magasság is. (2)
Az ABC∆ egyenlő szárú, melynek alapja AB, következik, hogy a CP félegyenes szögfelező, a CP egyenes oldalfelező merőleges, a CP szakasz oldalfelező és magasság is. (3)
Feladat a portfólióba. Bizonyítsd be, hogy: ha egy háromszög két csúcsához tartozó nevezetes vonalak közül kettő egybeesik, akkor a háromszög egyenlő oldalú.
Jegyezd meg!
Annak bizonyításához, hogy egy háromszög egyenlő oldalú, elegendő, ha két csúcs esetében a háromszög két nevezetes vonala fedi egymást. (oldalfelező és oldalfelező merőleges, vagy oldalfelező és szögfelező, vagy oldalfelező és magasság, vagy oldalfelező merőleges és szögfelező, vagy oldalfelező merőleges és magasság, vagy szögfelező és magasság).
A 3. alkalmazás a következő fontos kijelentéshez vezet:
Egy egyenlő oldalú háromszögben a háromszögbe beírt kör középpontja, a háromszög köré írt kör középpontja a háromszög súlypontja és a háromszög ortocentruma vagy magasságpontja egybeesik.
Gyakorlatok és feladatok
1. Szerkessz:
a) egy 4 cm oldalhosszúságú ABC egyenlő oldalú háromszöget;
b) egy 3 cm magasságú PQR egyenlő oldalú háromszöget!
2. Legyen DEF egy egyenlő oldalú háromszög. Az EF oldallal párhuzamos egyenes a DE és a DF egyeneseket az M, illetve N pontokban metszi. Igazold, hogy a DMN háromszög egyenlő oldalú!
3. Az ABC háromszögben AB = AC = 37 cm, a háromszög kerülete 111cm. Igazold, hogy az ABC háromszög egyenlő oldalú.
4. Anna és Dalma a mellékelt táblázatban levő háromszögek oldalainak hosszát és szögeinek mértékét tanulmányozza. Anna azt mondja, hogy három háromszög egyenlő oldalú. Dalma azt állítja, hogy mindegyik háromszög egyenlő oldalú. Állapítsd meg, indokolva válaszod, hogy ki válaszolt helyesen!
ABC∆ AB = 3 cm, BC = 30 mm, CA = 0,3 dm
DEF∆ D∢ = E = 2 · F∢
GHI∆ GH = GI = 4,5 cm és KGHI∆ = 13,5 cm
LMN∆ L∢ = M∢ és MN = LM
5. Igazold, hogy az a háromszög, melyben minden oldal hossza a másik két oldal hosszának a számtani középarányosával egyenlő, egy egyenlő oldalú háromszög!
6. Legyen ABC egy egyenlő oldalú háromszög és a BC oldalon az M és N pont úgy, hogy BAM∢ ≡ MAN∢ ≡ NAC∢. Számítsd ki az AMN szög mértékét!
7. Legyen MNP egy háromszög, melyben M∢≡ N∢ ≡ P∢. Az MN, NP, PM oldalakon felvesszük az A, B, illetve C pontokat úgy, hogy MA ≡ NB ≡ PC. Bizonyítsd be, hogy az ABC háromszög egyenlő oldalú!
8. A DEF és a DPQ háromszögek egyenlő oldalúak , P ∈ DE és Q ∈ DF. Bizonyítsd be, hogy PQ ∥ EF
9. Az ABC egyenlő oldalú háromszögben, BD magasság, CE oldalfelező és BD ∩ CE = {O}. Bizonyítsd be, hogy:
a) az ADE háromszög egyenlő oldalú;
b) AO ⊥ DE;
c) az A, O pontok és a BC oldal felezőpontja kollineárisak!
213 6. fejezet • A háromszög
A B MN C
10. Jelöljük K-val az ABC egyenlő oldalú háromszög kerületét és p-vel az ABC háromszög oldalainak felezőpontjai által alkotott háromszög kerületét. Igazold, hogy K = 2 · p
11. Az A pont a BC szakaszon helyezkedik el. A BC egyenes egyik és másik oldalán figyeljük meg az ABD és az ACE egyenlő oldalú háromszögeket.
a) Szerkeszd meg a feladat adatainak megfelelő ábrát!
b) Bizonyítsd be, hogy az A, D, E pontok kollineárisak!
c) Igazold, hogy ABE∆ ≡ ADC∆.
Miniteszt
12. Az ABC és a CDE háromszögek egyenlő oldalú háromszögek, az E és F pontok a BC, illetve AB oldalak felezőpontjai.
a) Igazold, hogy CD ∥ AB.
b) Bizonyítsd be, hogy BD ≡ CF.
13. A G pont az MNP egyenlő oldalú háromszög súlypontja, az L és a K pontok az NG, illetve a PG szakaszok felezőpontjai.
a) Igazold, hogyMGL∆ ≡ MGK∆.
b) Számítsd ki a GLK háromszög szögeinek mértékét!
1. Másold le a füzetbe és a táblázat üres mezőjébe I betűt írj, ha az állítás igaz és H betűt, ha az állítás hamis!
4 × 10 p Állítás
p1: Ha egy háromszög egyik csúcsához tartozó oldalfelező és magasság egybeesik, akkor a háromszög egyenlő oldalú.
p2: Ha egy háromszög két csúcshoz tartozó oldalfelező és magasság egybeesik, akkor a háromszög egyenlő oldalú.
p3: Ha az ABC háromszögben, AD a BAC szög szögfelezője, D∈BC és BD = DC = 2 cm, akkor az ABC háromszög kerülete 12 cm.
p4: Ha egy háromszög minden oldala kongruens, akkor a háromszög minden szöge is kongruens.
2. Az A, B, C ebben a sorrendben megadott kollineáris pontok.
I/H
10 p a) Szerkeszd meg az AC egyenes ugyanazon oldalán az ABD és a BCE egyenlő oldalú háromszögeket!
20 p b) Bizonyítsd be, hogy a BD és a CE egyenesek párhuzamosak!
20 p c) Bizonyítsd be, hogy ABE∆ ≡ DBC∆.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
4. l. A derékszögű háromszög tulajdonságai. Pitágorász tétele
Fedezzük fel, értsük meg!
1. alkalmazás
1. lépés: Rajzolj a füzetbe egy ABC derékszögű háromszöget, melyben A∢ = 90°, AC = 4 cm, B∢ = 30°
2. lépés: Ábrázold a D pontot, mely a C pont szimmetrikusa az AB egyenesre nézve!
3. lépés: Állapítsd meg és indokold az ABD háromszög természetét!
4. lépés: Állapítsd meg és indokold a BCD háromszög természetét!
5. lépés: Állapítsd meg igaz-e, hogy AC = BC 2 ! Indokold meg válaszod!
Megoldás.
1. lépés
2. lépés
214 Matematika • Tankönyv a VI. osztály számára
A F B CD E
B
30°
C AB 4 cm 30° C A D
4 cm
3. lépés: Ha D a C pont szimmetrikusa az AB egyenesre nézve, akkor CD ⊥ AB. Mivel CA ⊥ AB, következik, hogy C, A, D kollineáris pontok, A pedig a C pontból az AB egyenesre húzott merőleges talppontja. A szimmetriából következik, hogy AC ≡ AD. Tekintsük az ABC∆ és ABD∆ derékszögű háromszögeket. AB ≡ AB és AC ≡ AD. A B.B. kongruenciaeset alapján következik, hogy ABC∆ ≡ ABD∆. Következik, hogy ABD∢ = ABC∢ = 30°, vagyis az ABD∆ derékszögű A-ban és ABD∢ = 30°
4. lépés: Az ABC∆ ≡ ABD∆ kongruenciából következik, hogy BC ≡ BD, tehát BCD∆ egyenlő szárú. Mivel ABC∢ és ABD∢ egymás melletti szögek ABC∢= 30° és ABD∢ = 30°, tehát CBD∢ = 60°. A BCD háromszög egyenlő szárú és van legalább egy 60°-os szöge, azaz egyenlő oldalú.
5. lépés: A BCD egyenlő oldalú háromszögben: BC = CD = BD, az A pont pedig a CD oldal felezőpontja. Következik, hogy AC = CD 2 = BC 2 .
1. tétel: Egy derékszögű háromszögben a 30°-os szöggel szemben fekvő befogó hossza egyenlő az átfogó hosszának felével.
2. tétel: (1. tétel fordítottja) Ha egy háromszögben egy oldal a 30°-os szöggel szemben fekszik és hossza egyenlő egy másik oldal hosszának felével, akkor a háromszög derékszögű.
Ha az ABC∆-ben A∢ = 90° és B∢ = 30°, akkor AC = BC 2 .
Ha az ABC∆-ben A∢ = 90° és C∢ = 30°, akkor AB = BC 2 .
Ha az ABC∆-ben, B∢= 30° és AC = BC 2 , akkor A = 90°.
Ha az ABC∆-ben, B∢ = 30° és AC = AB 2 , akkor C = 90°
Feladat a portfólióba: Fogalmazz meg és oldj meg egy gyakorlati alkalmazást a 2. tétel bizonyítására!
2. alkalmazás
1. lépés: Ábrázolj a füzetben egy ABC derékszögű háromszöget, melyben A∢ = 90° és jelöld O-val a BC oldal felezőpontját!
2. lépés: Ábrázold a D pontot, az A pontnak az O pont szerinti szimmetrikusát!
3. lépés: Bizonyítsd be, hogy CD ∥ AB.
4. lépés: Igazold, hogy a BAC és a DCA háromszögek kongruensek!
5. lépés: Vezesd le és indokold, hogy AO ≡ AD 2 = BC 2 .
Megoldás.
1. lépés
2. lépés A BOC A
3. lépés: A szerkesztésből következik, hogy az A, O, D és a B, O, C pontok kollineárisak, tehát AOB∢ és DOC∢ csúcsszögek.
Az AOB és DOC háromszögekben: Az O pont a BC szakasz felezőpontja, tehát OB ≡ OC
Az O pont az AD szakasz felezőpontja, tehát OA ≡ OD
(1)
(2) AOB∢ és DOC∢ csúcsszögek, tehát AOB∢ ≡ DOC∢
(3) Az (1), (2) és (3) összefüggésekből, az O.Sz.O. kongruenciakritérium alapján következik, hogy AOB∆ ≡ DOC∆, tehát BAO∢ = CDO∢. Ekkor a CD és az AB egyenesek az AD szelővel kongruens belső váltószögpárokat alkotnak, tehát CD ∥ AB.
4. lépés: CD ∥ AB, következik, hogy a CD és az AB egyenesek az AC szelő ugyanazon oldalán fekvő belső szögek a BAC és DCA szögek kiegészítő szögek. Mivel BAC∢ = 90°, következik, hogy DCA∢ = 90°, azaz DCA∆ derékszögű C-ben.
A BAC∆ és DCA∆ derékszögű háromszögekben: AB ≡ CD (mert AOB∆ ≡ DOC∆); AC ≡ CA (közös befogó).
A B.B. kongruenciaeset alapján következik, hogy BAC∆ ≡ DCA∆.
5. lépés: BAC∆ ≡ DCA∆, következik, hogy BC ≡ DA. Mivel O az AD szakasz felezőpontja, tehát AO = AD 2 = BC 2 .
3. tétel: Bármely derékszögű háromszögben az átfogóhoz tartozó oldalfelező hossza egyenlő az átfogó hosszának a felével.
4. tétel: (3. tétel fordított tétele) Ha egy háromszögben az egyik oldalhoz tartozó oldalfelező hossza egyenlő az illető oldal hosszának a felével, akkor a háromszög derékszögű.
Ha az ABC∆-ben A∢ = 90° és AM oldalfelező, akkor AM = BC 2 .
Ha az ABC∆-ben AM oldalfelező és AM = BC 2 , akkor A∢ = 90°
Feladat a portfólióba: Fogalmazz meg és oldj meg egy gyakorlati alkalmazást a 4. tétel bizonyítására!
215 6. fejezet • A háromszög
BO D C
Kis történelem
Pitágorász nagy görög matematikus és filozófus volt, aki a nevét viselő tétel révén maradt fenn a történelemben. Íme két híres aforizmája:
„Ne mondj keveset sok szóval, hanem mondj sokat kevés szóval.”
„Gondolkozz, kutass, elmélkedj mielőtt dolgoznál.”
Oldjuk meg figyelmesen!
Megoldott feladat:

Pitagora
a) Rajzolj egy derékszögű háromszöget, amely befogóinak hossza 3 cm, illetve 4 cm!
b) Mérd meg beosztásos vonalzó segítségével az átfogó hosszát, és számítsd ki az illető természetes szám négyzetét!
c) Hasonlítsd össze a befogók hossza négyzeteinek összegét az átfogó hosszának négyzetével!
Megoldás. a) b) c)
AC B 3 cm 4 cm
5. tétel: (Pitágorász tétele)
BC = 5 cm
BC2 = 52 = 25 (cm2).
AB2 + AC2 = 32 + 42 = 25 (cm2).
BC2 = 25 (cm2).
Megjegyzés: A 3, 4, 5 számokat pitágorászi számoknak nevezzük.
Bármely derékszögű háromszögben az átfogó hosszának négyzete egyenlő a befogók hosszának négyzetösszegével.
6. tétel: (Pitágorász tételének fordított tétele)
Ha egy háromszögben egy oldal hosszának négyzete egyenlő a másik két oldal hosszának négyzetösszegével akkor a háromszög derékszögű.
Megoldott feladat
Matematikai szimbólumokkal:
Ha ABC∆ derékszögű háromszög, BAC∢ = 90°, akkor
BC2 = AB2 + AC2 .
Ha a háromszög oldalait jelöljük: AB = c, AC = b, BC = a, akkor a fenti összefüggés: a2 = b2 + c2 .
Matematikai szimbólumokkal:
Ha az ABC∆ -ben fennáll a BC2 = AB2 + AC2, akkor az
ABC∆ derékszögű és BAC∢ = 90°.
Ha a háromszög oldalait jelöljük: AB = c, AC = b, BC = a, akkor a kijelentés így alakul:
Ha az ABC∆-ben fennáll az a2 = b2 + c2, akkor
ABC∆ derékszögű és A∢ = 90°.
a) Egy földterület derékszögű háromszög alakú, melynek befogói a = 8 m és b = 6 m. Számítsd ki az átfogó hosszát!
b) Állapítsd meg, hogy lehetne-e egy olyan derékszögű háromszög alakú virágágyást berendezni, melynek oldalai a = 5 m, b = 12 m, illetve c = 13 m hosszúságúak legyenek?
c) Az a) és a b) alpontokban lévő példákból azonosíts két pitágorászi számhármast!
Megoldás

a) Pitágorász tétele alapján c2 = a2 + b2, azaz c2 = 64 + 36 = 100 = 102, tehát c = 10 m.
b) 52 + 122= 25 + 144 = 169 = 132. Pitágorász fordított tételének értelmében a háromszög derékszögű.
c) (6, 8, 10); (5, 12, 13) pitágorászi számhármasok, mert 62 + 82 = 102 és 52 + 122= 132
216 Matematika • Tankönyv a VI. osztály számára
Következésképpen, BC2 = AB2 + AC2 .
1. Szerkeszd meg az ABC derékszögű háromszöget a következő esetekben:
a) A∢ = 90°, AB = 8 cm, AC = 6 cm;
b) A∢ = 90°, BC = 6 cm, C∢ = 40°.
2. Legyen ABC egy egyenlő szárú háromszög és M a BC alap felezőpontja. Igazold, hogy az ABM és az ACM háromszögek derékszögűek!
3. A DEF háromszög derékszögű, melyben D∢ = 90°. Számítsd ki:
a) az F szög mértékét, ha E∢ = 33°;
b) az E és F szögek mértékét, ha F∢ = E∢ + 20°.
4. Számítsd ki egy derékszögű háromszög szögeinek mértékét, tudva, hogy a háromszög egyik külső szögének mértéke 132°!
5. Egy háromszög szögeinek mértéke egyenesen arányosak az 1, 2 és 3 számokkal. Bizonyítsd be, hogy a háromszög derékszögű!
6. Adott egy ABC∆, melyben A∢= 90°. Másold le a füzetbe és töltsd ki a pontozott helyeket úgy, hogy igaz kijelentéseket kapj:
a) Ha BC = 20 cm és B∢ = 30°, akkor AC = ... cm.
b) Ha AB = 7 cm és C∢ = 30°, akkor BC = ... cm.
c) Ha BC = 32 cm és B∢ = 60°, akkor AB = ... cm.
d) Ha AC = 8 cm és C∢ = 2 · B, akkor BC = ... cm.
7. Az ABC egyenlő oldalú háromszög BC oldalát meghosszabbítjuk a CD ≡ BC szakasszal.
a) Számítsd ki az ADB∢ szög mértékét!
b) Bizonyítsd be, hogy az ABD∆ derékszögű!
8. Legyen a DEF derékszögű háromszög átfogójához tartozó magasság DM. Bizonyítsd be, hogy: DEM∢ ≡ FDM∢ és EDM∢ ≡ DFE∢.
9. Az ABC derékszögű háromszög BC átfogójához tartozó oldalfelező az AD szakasz. Másold le a füzetbe és töltsd ki a pontozott helyeket úgy, hogy igaz kijelentéseket kapj:
a) Ha BC = 12 cm, akkor AD = ... cm.
b) Ha AD = 8,5 cm, akkor BC = ... cm.
c) Ha BD = 4 cm, akkor AD = ... cm.
d) Ha AC = 15 cm és B∢ = 30°, akkor az ACD háromszög ... és AD = ... cm.
10. Az ABC háromszögben M a BC oldal felezőpontja
és AM ≡ BM ≡ CM. Bizonyítsd be, hogy A∢ = 90°
11. Az LMN háromszög egyenlő oldalú, G pedig a háromszög súlypontja. legyen P a G pont szimmetrikusa az MN egyenesre nézve.
a) Számítsd ki a GMP szög mértékét!
b) Bizonyítsd be, hogy az LMP háromszög derékszögű!
12. Ábrázolj egy derékszögű háromszöget, melynek befogói 5 cm, illetve 12 cm hosszúságúak!
a) Beosztásos vonalzó segítségével határozd meg az átfogó hosszát!
b) Határozd meg az átfogó hosszát Pitágorász tételének segítségével!
c) Számítsd ki a háromszög köré írt kör sugarát és körzővel rajzold meg ezt a kört!
13. Adott az ABP háromszög, melyben AP⊥ PB
a) Ha AP = 9 cm, BP = 12 cm, számítsd ki az AB szakasz hosszát!
b) Ha AB = 20 cm, AP = 16 cm, számítsd ki a BP szakasz hosszát!
c) Ha AP = x cm, BP = 5 cm, AB = 11 cm, igazold, hogy 9 < x < 10.
14. ABCD egy négyzet, az M és N pontok a CD, illetve DA oldalak felezőpontjai. Bizonyítsd be, hogy:
a) ∆ABN∆ ≡ DAM∆; b) AM ⊥ BN.
15. Rajzold le az ABC derékszögű háromszöget, melyben A∢ = 90°, az átfogóhoz tartozó oldalfelező hossza pedig 5 cm!
16. Az A, B, C, D városok a mellékelt ábrán bemutatott hálózaton keresztül közlekednek.
A BAD∢ = CBD∢ = 90°, E a BD szakasz felezőpontja, F a CD szakasz felezőpontja, AD = 4 km, AE = 2,5 km, BC = 12 km.
a) Számítsd ki a B és a D város közötti és a C és a D város közötti távolságot!
b) Válaszd ki, melyik a legrövidebb út A városból C városba, és indokold!
217 6. fejezet • A háromszög
A B C F D E 2,5km4km 12 km Gyakorlatok és feladatok
Miniteszt
Válaszd ki a helyes válasznak megfelelő betűt! Csak egy válasz helyes.
30 p a) Egy derékszögű háromszög hegyesszögeinek mértéke egyenesen arányos a 4 és az 5 számmal. Ezen szögek mértéke:
A. 30° és 60°; B. 20° és 70°; C. 40° és 50°; D. 15° és 75°.
30 p b) Az ABC derékszögű egyenlő szárú háromszög, A∢ = 90°, AD magasság és AD = 5 cm. A háromszög átfogójának hossza:
A. 5 cm; B. 10 cm; C. 2,5 cm; D. 7,5 cm.
30 p c) Ha BC az ABC háromszög átfogója, akkor:
A. BC = AB + AC; B. BC2 = AB2 + AC2; C. AB2 = BC2 + AC2; D. AC2 = AB2 + BC2 .
ISMERETFELMÉRŐ
I. Válaszd ki a helyes válasznak megfelelő betűt! Csak egy helyes válasz van.
Megjegyzés: Munkaidő: 20 perc
Hivatalból: 10 pont
5 p 1. Ha ABC∆ ≡ DEF∆, AB = 3 cm, EF = 5 cm és KDEF = 15 cm, akkor az AC szakasz hossza:
A. 3 cm; B. 5 cm; C. 7 cm; D. 8 cm.
5 p 2. A DEF háromszög egyenlő szárú, DE ≡ DF, EM a DEF szög szögfelezője és FEM∢ = 25°
Az EDF szög mértéke:
A. 50°; B. 80°; C. 75°; D. 110°.
5 p 3. A P pont az AMN derékszögű háromszög MN átfogóján található, AP = 7,5 cm, az M és N pontok szimmetrikusak az AP egyenesre nézve. Az MN szakasz hossza:
A. 7,5 cm; B. 5 cm; C. 10 cm; D. 15 cm.
5 p 4. Az ABC háromszög egyenlő szárú, AB ≡ AC, AD⊥BC, D∈BC, AD = 4 cm. Ha az ABD háromszög kerülete 12 cm, akkor az ABC háromszög kerülete:
A. 16 cm; B. 18 cm; C. 24 cm; D. 20 cm.
5 p 5. Az ABC háromszögben ABC∢ = 40°, az AD magasság és az ABC szög BE szögfelezője az M pontban metszik egymást. Az AME szög mértéke:
A. 60°; B. 75°; C. 80°; D. 70°.
5 p 6. A következő számhármasok közül az, amelyik egy derékszögű háromszög oldalainak hosszát fejezi ki ugyanabban a mértékegységben:
A. (3; 4; 7);
II. Írd le a teljes megoldást!
10 p
10 p
B. (5; 11; 13); C. (8; 15; 17); D. (20; 30; 40).
1. A BM és CN szakaszok oldalfelezők az ABC egyenlő oldalú háromszögben, M∈AC, N∈AB és BM ⋂ CN ={G}.
a) Bizonyítsd be, hogy a BGC háromszög egyenlő szárú!
b) Ha BG = 12 cm, számítsd ki a CN oldalfelező hosszát!
10 p 2. Legyen a DEF háromszög, melyben DEF∢ = 120°. A DEF szög szögfelezőjén felvesszük az L pontot úgy, hogy EL ≡ DE. Bizonyítsd be, hogy a DEL háromszög egyenlő oldalú háromszög!
10 p
10 p
10 p 3. Az ABC derékszögű háromszögben A∢ = 90°, C∢ = 15°, pedig a BC oldal felezőpontja. A BD szakasz az ABO háromszög magassága, D ∈ AO
a) Bizonyítsd be, hogy az ACO háromszög egyenlő szárú!
b) Számítsd ki az AOB szög mértékét!
c) Ha BD = 8 cm, igazold, hogy BC = 32 cm.
Megjegyzés: Munkaidő 50 perc Hivatalból: 10 pont
218 Matematika • Tankönyv a VI. osztály számára
A
C O B
D
I ÖSSZEFOGLALÓ FELADATOK
1. Az M = {1, 2, 3, 4, …, 49, 50} halmaz elemeivel az A, B, C, D részhalmazokat képezzük a következőképpen: A tartalmazza a 2-vel osztható számokat, melyek nem oszthatók 3-mal; B azokat a 3-mal osztható számokat tartalmazza, melyek nem oszthatók 2-vel; C a 2-vel és a 3-mal is osztható számokat tartalmazza; D pedig azokat a számokat, melyek sem 2-vel, sem 3-mal nem oszthatók. Határozd meg mindegyik részhalmaz kardinálisát és állapítsd meg, hogy melyiknek van a legtöbb eleme!
2. a) Határozd meg az x egész számot, tudva, hogy (2 · x + 1) osztja a 6-ot! b) Igazold, hogy az xy + 7 · y szám páros, bármely x, y számjegyek esetén és x, y, x ≠ 0.
3. Számítsd ki az ismeretlen számot:
a) x x 25 25 7 2 , , ; b) 21 28 x x .
4. Számítsd ki a 45 és a 75 számok legnagyobb közös osztóját és a legkisebb közös többszörösét!
5. Egy 10 munkásból álló csapat egy munkát 12 nap alatt végez el. Határozd meg hány nap alatt fejezné be a munkát egy 15 munkásból álló csapat, ha ugyanolyan feltételek között dolgoznak, mint az első csapat!
6. Számítsd ki:
a) −10 − 13 − 4 + 27;
b) [4 · (− 16) − (− 5) · (− 12)] : (13 − 32);
c) –3 · [13 − (−4 · 5 + 12) : (−4)];
d) 96 : {− 5 · [1− 4 · (2 · 34 − 65)] − 67}.
7. Adottak az
a = 21 + ( 2)2 + 23 és
b = ( 3)3 + 32 + ( 3)1. számok. Hasonlítsd össze az
a 20 és b + 10 számokat!
8. Az x, y, z egész számok egyenesen arányosak a 2, 3, illetve 6 számokkal.
a) Bizonyítsd be, hogy az A = x · y + y · z + z · x szám egy négyzetszám!
b) Határozd meg a három számot tudva, hogy x · y · z > 0 és xyyzzx 23 76 .
9. Az a és b számok fordítottan arányosak az
1 3 és 1 6 , számokkal és c = ab + 2 .
Határozd meg az a, b, c számokat tudva, hogy összegük 13,5!
10. Egy 10%-os árleszállítás után egy labda 45 lejbe kerül. Számítsd ki a labda árleszállítás előtti árát!
11. 140 nápolyiszeletet kellene két csoport gyereknek elosztani úgy, hogy az első csoportnak kiosztott nápolyiszeletek számának 40%-a 8-cal több legyen, mint a második csoportban kiosztott nápolyiszeletek számának 24%-a!
12. Számítsd ki az
E = (−1)22 · (−2) + (−3) · (−1)33 + (− 1)44 · (− 4) értékét!
13. Edvin és Róbert önállóan kiszámítják az a, b, c, d, számokat: a
Miután befejezték számításaikat, így társalognak: Emil: – Egyik szám sem természetes szám.
Róbert: – Én találtam két ellentétes racionális számot.
Végezd el a számításokat és állapítsd meg hogy a két fiú állításai igazak-e! Indokold meg válaszod!
14. Számítsd ki:
a) az x racionális számok összegét, melyek teljesítik az | 3 · x – 2 | − 1 = 4 egyenlőséget;
b) az y egész számok szorzatát, melyek teljesítik a −13 ≤ 2 · y – 7 < 1 egyenlőtlenséget!
219 • Év végi ismétlés és ismeretfelmérés
= 2 3 03 05 3 4 8 9 2 ,( ), :: , b = 1 2 1 3 2 1 1 4 2 1 5 1 6 , c = 3 2 1 323 232 2 3 és d = 3 4 3 4 5 64 001 52 :: , .
ÉV VÉGI ISMÉTLÉS ÉS ISMERETFELMÉRÉS
15. Az alábbi táblázat egy iskola röplabdacsapatának létszámát és a tanulók életkorát tartalmazza.
Életkor (év)
11 12 13 14
Tanulók száma 4 6 6 4
a) Határozd meg a röplabdacsapatban részt vevő tanulók számát és átlagéletkorát!
b) Határozd meg, hány 14 éves játékost kellene felvenni a csapatba, hogy az átlagéletkor 13 év legyen!
16. Tekla nem emlékszik jelszavának utolsó két számjegyére, de tudja, hogy jelszava 2023ab alakú, és osztható 25-tel. Határozd meg, hány különböző próbálkozásra van szükség ahhoz, hogy Tekla helyesen írja le jelszavát! Indokold válaszod!
17. József b a alakú arányokat képez az a és b egész számokkal, ahol 11 < a < 6 és 0 ≤ b < 15 . Állapítsd meg, hogy hány olyan arányt képezett József, melyek értéke nagyobb, mint 2!
18. Laci háza az a utcában, az A pontban található. Laci el szeretne jutni barátjához, Vincéhez, aki a b utcában, a B pontban lakik. Laci az A – C – D – B útvonalon halad. Az ábra adatai alapján, számítsd ki az x szám értékét, ha a ∥ b és AC ∥ BD!
19. Számítsd ki az ismeretlen számok értékét a következő esetekben:
a)
b)
c)
20. Az OM és ON félegyenesek az AOB, illetve AOC nem egymás melletti szögek szögfelezői, AOB∢ = x°< 90° és OB ⊥ OC.
a) Számítsd ki x függvényében az AOM és a BON szögek mértékét!
b) Igazold, hogy az MON szög mértéke nem függ az AOM és a BON szögek mértékétől!
21. Az ABC háromszögben A∢ = 60°, AB = 2,5 cm. Számítsd ki:
a) a háromszög kerületét, ha AB = BC.
b) az AC szakasz hosszát tudva, hogy az ABC háromszög A és C szögei pótszögek!
22. Az A és B pontok a CD egyenes ugyanazon oldalán levő pontok, AD ⊥ CD, BC ⊥ DC és AD ≡ BC. Bizonyítsd be, hogy:
a) AC ≡ BD;
b) a C pont távolsága a BD egyenestől egyenlő a D pont távolságával az AC egyenestől!
23. Az MNP háromszögben MN ≡ MP, NMP∢ = 44°, a H pont pedig a háromszög ortocentruma. Számítsd ki az NHP szög mértékét!
24. Az AMN és BMN egyenlő oldalú háromszögek az MN egyeneshez képest különböző félsíkokban vannak. Bizonyítsd be, hogy:
a) az AB félegyenes az MAN szög szögfelezője;
b) az MN egyenes az AB szakasz felezőmerőlegese!
25. Az ABC háromszög egyenlő szárú, A∢ − B∢ = 105°.
a) Állapítsd meg, melyek a kongruens oldalak!
b) Számítsd ki a háromszög B és C csúcsaihoz tartozó szögfelezők által bezárt tompaszög mértékét!
26. Legyen a DEF háromszög, melyben D ∢= 90°, DE = 6 cm, DK ⊥ EF, K ∈ EF és EK = 3 cm.
a) Számítsd ki a DEF háromszög szögeinek mértékét!
b) Bizonyítsd be, hogy FK = 9 cm!
c) Ha M az EF oldal felezőpontja, számítsd ki a KM szakasz hosszát!
220 Matematika • Tankönyv a VI. osztály számára
E K M DF
A C D bB a x° 100°
27. Az ABC háromszög egyenlő szárú, alapja pedig BC és E ∈ AB, D ∈ AC,F ∈ AC úgy, hogy AD = DE = EF = FB = BC.
a) Számítsd ki a BAC szög mértékét!
b) Bizonyítsd be, hogy a BEF háromszög egyenlő oldalú!
28. Az AB és a CD szakaszok a C(O, r) kör átmérői, AB = 8 cm, az AD kiskörív mértéke 120°.
a) Bizonyítsd be, hogy az AOC háromszög egyenlő oldalú, és számítsd ki a kerületét!
b) Igazold, hogy AC ∥ BD.
II ISMERETFELMÉRŐ
1. TESZT
AC DB O
29. A DEF egyenlő oldalú háromszög kerülete 24 cm. Meghosszabbítjuk a DM és az EN oldalfelezőket az MP ≡ DM illetve azNQ ≡ EN szakaszokkal.
a) Bizonyítsd be, hogy a P, F, Q pontok kollineárisak!
b) Számítsd ki a PQ szakasz hosszát!
30. Az ABC háromszög szögfelezőinek I metszéspontján keresztül meghúzzuk a BC egyenessel párhuzamos d egyenest, d ⋂ AB = {D}, d ⋂ AC = {E}.
a) Bizonyítsd be, hogy a BDI∆ egyenlő szárú!
b) Ha I a DE szakasz felezőpontja, igazold, hogy AB ≡ AC.
31. Legyen ABC derékszögű háromszög, melynek átfogója BC, D pedig a B pont szimmetrikusa az AC egyenesre nézve és E a CD szakasz felezőpontja úgy, hogy AC ⋂ BE = { G }, AB = 4 cm, AG = 3 cm.
a) Számítsd ki a BG, CG és BE szakaszok hosszát;
b) Bizonyítsd be, hogy BC < 10 cm.
I. Karikázd be a helyes válasznak megfelelő betűt! Csak egy helyes válasz van.
5 p 1. A ( 95) : ( 19) + ( 2)3 számítás eredménye:
A. 3; B. 3; C. 13; D. 13.
5 p 2. Ha | x 0,(3) | = 0, akkor 6 · x egyenlő:
A. 2; B. 1; C. 2; D. 3.
5 p 3. 125 lejnek a 40%-a egyenlő:
A. 50; B. 55; C. 60; D. 75.
5 p 4. Ha a = 1 2 1 2 3 akkor a 10 1 a szorzat értéke egyenlő:
A. 8; B. 16; C. 8; D. 16.
5 p 5. Egy osztály 24 tanulója közül 18 tanuló 8-asnál nagyobb jegyet kapott egy teszten. Százalékban kifejezve a 8-asnál nagyobb jegyet elérő tanulók száma:
A. 80%; B. 60%; C. 75%; D. 18%.
5 p 6. Ha egy szög kiegészítő szögének mértéke 53°, akkor a szög mértéke:
A. 37°; B. 137°; C. 57°; D. 127°
5 p 7. Az AB és a CD egyenesek az O pontban metszik egymást és AOB∢ = 2· BOC∢. Akkor az AOD∢ mértéke:
A. 60°; B. 90°; C. 120°; D. 180°.
5 p 8. Az ABC háromszög kerülete 22 cm, A∢ = B ∢és AB = 6 cm. A BC oldal hossza:
A. 6 cm; B. 8 cm; C. 16 cm; D. 10 cm.
221 • Év végi ismétlés és ismeretfelmérés
10 p 15 p
1. Egy könyv 27 lejbe kerül és egy toll árának 54%-át képezi.
a) Számítsd ki a toll árát!
b) Levente vásárol egy könyvet és egy tollat, így meglévő pénzének 33%-át költi el. Számítsd ki mennyi pénze marad Leventének!
2. Az ABC háromszög egyenlő szárú, AB = AC a háromszög egyik külső szögének mértéke pedig 50°.
A D és az E pontok a háromszög BC oldalán helyezkednek el úgy, hogy BAD∢ = 35°, AEC∢ = 120°.
10 p 15 p
a) Számítsd ki az ABC háromszög szögeinek mértékét!
b) Bizonyítsd be, hogy az ADE háromszög egyenlő oldalú!
2. TESZT
I. Karikázd be a helyes válasznak megfelelő betűt! Csak egy helyes válasz van.
Megjegyzés: Munkaidő: 90 perc
Hivatalból: 10 pont
5 p 1. Annak a valószínűsége, hogy találomra kiválasztunk az {1, 2, 3, … , 30} halmazból egy elemet és ez egy prímszám legyen:
A. 1 4 ; B. 7 30 ; C. 9 20 ; D. 1 3 .
5 p 2. A 1 2 1 4 5 : számítás eredménye:
A. 3; B. 7; C. 3; D. 5.
5 p 3. Az x és y egész számok, x < 0, y > 0, x2 = 100, y2 = 400. Akkor, x : y egyenlő lesz:
A. 2; B. 0,5; C. 0,2; D. 0,2.
5 p 4. Az a és 2 számok egyenesen arányosak a 7 és 1,75 számokkal. Az a szám egyenlő:
A. 4; B. 14; C. 8; D. 3,5.
5 p 5. Ha x x 1 5 7 15 , akkor x egyenlő:
A. 2,5; B. 11; C. 3,5. D. 15;
5 p 6. AD és BE az ABC háromszög oldalfelezői, AD⋂BE ={ G}, AG = 6 cm, GE = 3 cm. Az AD – BE különbség:
A. 3 cm; B. 2 cm; C. 1 cm; D. 0 cm.
5 p 7. Az ABC derékszögű háromszögben a C szög szögfelezője a BC átfogóval 24°-os szöget alkot. Akkor a B szög mértéke:
A. 24° ; B. 42° ; C. 56°; D. 66°.
5 p 8. Legyen D az ABC egyenlő oldalú háromszög BC oldalának felezőpontja, a háromszög külső tartományában megszerkesztjük a BDE egyenlő oldalú háromszöget. A BE egyenessel párhuzamos egyenes:
A. AD; B. CD; C. AC; D. BC.
II. Írd le a teljes megoldást!
20 p 1. Határozd meg az x, y, z számokat tudva, hogy összegük 80, az x, y – 1, z – 2 számok pedig egyenesen arányosak a 2, 3 illetve 4 számokkal!
15 p 2. Az ABC egyenlő szárú háromszögben A∢ = 120° és M az AB oldal felezőpontja. Az M pontból a BC egyenesre húzott merőleges az AC egyenest a D pontban metszi. Bizonyítsd be, hogy:
a) BCD háromszög derékszögű;
15 p b) AB = 2 · DM.
Megjegyzés: Munkaidő: 90 perc
Hivatalból: 10 pont
222 Matematika • Tankönyv a VI. osztály számára II. Írd le a teljes megoldást!