PERCORSO INVALSI MATEMATICA Primo biennio - Sample

R. Gobattoni • M. Massantini • C. Pacini

PERCORSO INVALSI MATEMATICA

Per il primo biennio della scuola secondaria di secondo grado

Esercizi guidati di preparazione alla prova nazionale

EDIZIONE 2020 | COMPUTER BASED

In linea con le nuove indicazioni INVALSI

R. Gobattoni, M. Massantini, C. Pacini

PERCORSI INVALSI MATEMATICA

Coordinamento editoriale: Beatrice Loreti

Redazione e grafica: Michele Lombari

Copertina: Curvilinee

Si ringrazia Monia Cardella per il contributo al volume.

Stampato in Italia presso Tecnostampa Pigini Group Printing Division, Loreto -Trevi !9.83.540.0

ISBN 978-88-468-4052-3

Le fotocopie non autorizzate sono illegali. Tutti i diritti riservati. È vietata lariproduzione totale o parziale così come la sua trasmissione sotto qualsiasi forma o con qualunque mezzo senza previa autorizzazione scritta da parte dell’editore.

PRESENTAZIONE

Il presente testo, come suggerisce il titolo, è strutturato essenzialmente come un percorso atto a favorire nell’alunno un approccio graduale alle prove INVALSI, in modo da fargli acquisire una crescente familiarità con la tipologia dei quesiti proposti, in vista della prova ufficiale. Non meno importante è la sua organizzazione come percorso verso l’autonomia dello studente, il quale, come rivela la struttura delle prove, prima vede e impara, poi viene guidato per mano e infine è pronto per lavorare da solo, fino a volare più in alto lanciandosi nella sfida. Il testo si compone di diverse sezioni:

• La prima, SCHEDE DI RICHIAMO, propone un rapido riepilogo di Aritmetica, diAlgebra e di Geometria, con cenni di Statistica e di Probabilità.

• La seconda, PROVE UFFICIALI GUIDATE, riporta tre verifiche ufficiali Invalsi effettivamente somministrate.

- Nella PROVA 1, sviluppata come ESERCITAZIONE DI PROVA, ciascun quesito è spiegato fino alla sua completa risoluzione, in modo da fornire ai ragazzi un esempio del metodo da seguire.

- Nelle due successive, PROVA 2 e PROVA 3, i quesiti sono accompagnati da un percorso ragionato che conduce l’alunno a trovare da solo la soluzione cercata.

• La terza, PROVE SIMULATE, propone tre esercitazioni inedite, denominate PROVA 4, PROVA 5 e PROVA 6 che riportano quesiti, in parte a risposta aperta, in parte chiusa, formulati con la stessa tipologia delle verifiche ministeriali recentemente proposte e articolati secondo i nuclei contenutistici indicati dall’INVALSI: Numeri (NU), Spazio e Figure (SF), Relazioni e Funzioni (RF), Dati e Previsioni (DP). La varietà degli argomenti toccati e la vasta gamma di difficoltà previste dai quesiti garantiscono la pertinenza delle prove stesse e la loro completezza in relazione ai programmi svolti dai vari ordini di scuole.

• La quarta sezione propone una PROVA 7, dall’eloquente titolo “LA SFIDA”, che presenta quesiti più complessi ed articolati e vuole essere un ulteriore stimolo per l’alunno a mettere in gioco, oltre ad una buona dote di intuito, l’abilità raggiunta e le competenze acquisite, ma anche un’occasione per i più appassionati della materia di cimentarsi con prove a più alto livello di difficoltà.

• Un fascicolo separato, GUIDA PER L’INSEGNANTE, contiene le soluzioni ragionate dei quesiti, insieme alle griglie di correzione di tutte le prove.

Gli autori

SCHEDE DI RICHIAMO

• Aritmetica e Algebra pag. 5

• Elementi di Statistica « 19

• Elementi di Probabilità « 20

• Geometria « 22

PROVE UFFICIALI GUIDATE

Prova n. 1 « 33

Prova n. 2 « 51

Prova n. 3 « 67

PROVE SIMULATE

• Prova n. 4 « 83

• Prova n. 5 « 94

• Prova n. 6 « 106

LA SFIDA

• Prova n. 7 « 119

Schede di richiamo

Aritmetica e algebra

INSIEMI NUMERICI

naturali (N), numeri interi positivi più lo zero; interi (Z), numeri interi relativi, cioè positivi, negativi e lo zero; razionali (Q), numeri esprimibili con una frazione: interi, decimali finiti, decimali periodici, positivi, negativi e lo 0; irrazionali, numeri decimali illimitati non periodici; reali (R), unione dei numeri razionali e dei numeri irrazionali;

POTENZE

Dati a (base) e n (esponente), an = a a a  (n volte). Es.: 24 = 2 2 2 2

= 16.

Casi particolari: - 1n = 1; - 0n = 0; - a 1 = a; - 10n = 1 seguito da n zeri; - a 0 = 1 (an : a n vedi sotto la proprietà); - 00 = indeterminato. .

Proprietà delle potenze: si applicano al prodotto e al quoziente di potenze di ugual base o di ugual esponente:

Operazioni inverse dell’elevamento a potenza

Poiché la potenza non gode della proprietà commutativa (23 2), le operazioni inverse sono due:

1) Radice: serve a calcolare la base incognita di una potenza.

Esempi: x3= 8 x = 3 8 = 2 (verifica:82 3  ); x2= 9 x= 9 = ±3 (verifica: 2 3 = 9);

2) Logaritmo: serve a calcolare l’esponente incognito di una potenza.

Esempio: 2x = 64 x = 64 log 2 = 6 (verifica: 26 = 64).

Notazione scientifica di un numero: è il prodotto di una potenza di 10 per un numero decimale limitato, con 1 ≤ < 10.

Esempio 1 Il numero 163,16 viene scritto in notazione scientifica come , 02 , oppure come , 02 se si decide di approssimare il numero con un numero decimale che ha due sole cifre dopo la virgola, oppure come 02 se si decide di approssimare il numero con un numero intero.

Esempio 2 Il numero 0,0 viene scritto in notazione scientifica come , 0-2

Ordine di grandezza di un numero: è la potenza di 10 (con esponente intero) più vicina ad esso.

Se il numero è scritto in notazione scientifica n 10a  , il suo ordine di grandezza è:

 n 10 se a ≤ 5

 101n  se a > 5

Esempio: l’ordine di grandezza di 56 = ,56 103 è 103, di 705 = ,705 103 è

NUMERI PRIMI

Un numero è detto primo se ha solo due divisori, 1 e se stesso; esempi: 2, 3, 5, 7, 101, 1151, ecc.

Due numeri si dicono primi tra loro se non hanno divisori comuni tranne 1 (es. 15 e 28).

I numeri non primi si dicono composti. Essi possono esprimersi come prodotto di numeri primi.

Per determinare il massimo comune divisore (M.C.D.) tra due o più numeri:

 si scompongono i numeri in fattori primi

250 = 2∙5�

 il M.C.D. è il prodotto dei fattori comuni, presi una sola volta, con il minimo esponente.

Per determinare il minimo comune multiplo (m.c.m.) tra due o più numeri:

 si scompongono i numeri in fattori primi

Esempio: c c 00

 il m.c.m. è il prodotto dei fattori comuni e non comuni, presi una sola volta, con il massimo esponente. .

Scomponendo i due numeri, otteniamo che 4200 = 753223 e 1764 = 732222

Pertanto, M.C.D. = 732 2  = 84;

m.c.m. = 2223 7532 = 88.200.

RAPPORTI

Rapporto tra due numeri a e b è il loro quoziente b a . Può essere espresso come: a) frazione b) numero decimale c) percentuale

Come trovare la frazione generatrice di un numero decimale finito o periodico

Numeri decimali finiti

Numeri decimali periodici semplici

Al numeratore si scrive il numero senza la virgola; al denominatore si scrive 1 seguito da tanti 0 quante sono le cifre dopo la virgola

Numeri decimali periodici semplici

Al numeratore si scrive il numero senza la virgola e si sottrae la parte non periodica; al denominatore si scrivono tanti 9 quante sono le cifre del periodo, seguiti da tanti 0 quante sono le cifre dell’antiperiodo

La frazione decimale con denominatore 100 può essere espressa con il simbolo % (es.: 100 5 = 5%), così come quella con denominatore 1000 con il simbolo ‰ (es.: 1000 8 = 8‰).

La frazione decimale con denominatore 100 può essere espressa con il simbolo % (es.: 100 5 = 5%),

così come quella con denominatore 1000 con il simbolo ‰ (es.: 1000 8 = 8‰).

Come trasformare una frazione in percentuale e viceversa

Rapporto tra due grandezze: è il quoziente tra le loro misure. Le grandezze possono essere:

Omogenee (2 lunghezze, 2 pesi, ecc.): in questo caso il rapporto è un numero puro, privo di unità di misura, e indica quante volte una grandezza è contenuta in un’altra della stessa specie.

Eterogenee (con diverse unità di misura): in questo caso il rapporto è una nuova grandezza, diversa da entrambe, avente come unità di misura il rapporto tra le due unità di misura.

Esempio: Se un’auto percorre 240 km in 3 ore, ha una velocità media di h km 80 h 3 km 240  .

PROPORZIONI

Proporzione: è l’uguaglianza di due rapporti. a : b = c : d .

Proporzione:

Proporzione: è l’uguaglianza di due rapporti. a : b = c : d .

Esempio: 15 : 5 = 12 : 4

Schede di richiamo

Proprietà delle proporzioni (riferite alla proporzione 15 : 5 = 12 : 4)

 Fondamentale: 60415125  (il prodotto dei medi è uguale al prodotto degli estremi).

Essa serve a:

a. verificare se quattro numeri formano una proporzione. Es. 2, 6, 3, 9 formano la proporzione 9:36:2  , perché ,183692  mentre 3, 4, 5, 6 non la formano, perché .5463

b. calcolare il termine incognito in una proporzione (vedi più avanti).

 Permutare dei medi: 4:5 :12 15  (scambiando i medi tra loro si ottiene una nuova proporzione).

 Permutare degli estremi: 4 : 5 = 12 : 15 (scambiando gli estremi tra loro si ottiene una nuova proporzione).

 Invertire: 5 : 15 = 4 : 12 (scambiando ogni antecedente con il proprio conseguente si ottiene una nuova proporzione).

 Comporre: (15 + 5) : 15 = (12 + 4) : 12 o (15 + 5) : 5 = (12 + 4) : 4

 Scomporre: (15 – 5) : 15 = (12 – 4) : 12 o (15 – 5) : 5 = (12 – 4) : 4

Si dice:

 quarto proporzionale dopo a, b, c, il numero x che soddisfa la proporzione a : b = c : x;

 terzo proporzionale dopo a e b, il numero x che soddisfa la proporzione continua (ossia con i medi, o gli estremi, uguali) a : b = b : x;

 medio proporzionale (o media geometrica) tra a e b, il numero x che soddisfa la proporzione continua a : x = x : b.

Calcolo del termine incognito x di una proporzione

l’incognita è un estremo l’incognita è un medio la proporzione è continua noto estremo medio medio x  noto medio estremo estremo x  estremo x 

Esempi di problemi sulle percentuali risolubili con le proporzioni

Basta impostare la proporzione risolutiva:

Esempi:

a. Quanto costa un impermeabile da 320,00 € se viene venduto con lo sconto del 15%? rezzo di vendita = 100% 15% = 5%, per cui: 5 : 100 = : 0 , da cui = 7 .

b. Se l’impermeabile da 320,00 € viene venduto a 240,00 €, quale tasso di sconto è stato praticato?

Lo sconto è di ( 0 – 0) = 0 . ertanto: : 100 = 0 : 0, da cui = 5.

c. Se un cappotto, scontato del 10%, costa 270,00 €, qual è il prezzo intero?

La spesa di 70,00 costituisce il (100% 10%), cioè il 0%, del prezzo intero. ertanto: 0 : 100 = 70 : , da cui = 00 . tasso : 100 = parte percentuale : totale ;

Esempi di problemi sulla riduzione in scala

Basta impostare la proporzione risolutiva: .

1 : entità della scala = lunghezza su carta : lunghezza reale

a. A quanti centimetri corrisponde una distanza reale di 3,6 km (= 360.000 cm) su una carta topografica di scala 1 : 30.000? (1 cm su carta = 30.000 cm reali = 0,3 km)

Risoluzione: 1: 30.000 = x : 360.000, da cui x = 12 cm.

b. Qual è la distanza reale tra due punti che distano 5 cm su una carta geografica di scala 1 : 1.000.000? (1 cm su carta = 1.000.000 cm reali = 10 km)

Risoluzione: 1 : 1.000.000 = 5 : x, da cui x = 5.000.000 cm = 50 km.

MONOMI E POLINOMI

Monomio: espressione letterale in cui compaiono solo moltiplicazioni ed elevamenti a potenze.

Polinomio: somma algebrica di due o più monomi.

PRODOTTI NOTEVOLI

 Prodotto della somma di due monomi per la loro differenza: (A + B)(A − B) = A2 – B2 Il prodotto della somma di due monomi per la loro differenza è uguale alla differenza dei quadrati dei due monomi.

Esempio: (2x + y)(2x – y) = (2x)2 – (y)2 = 4x2 – y 2 

di un binomio:

Il quadrato di un binomio è uguale al trinomio formato dal quadrato del primo termine + il doppio prodotto del primo termine per il secondo + il quadrato del secondo termine. (N.B.: i quadrati sono sempre positivi, per il doppio prodotto si tiene conto della regola dei segni).

Il quadrato di un polinomio è uguale alla somma del quadrato di tutti i monomi + il doppio prodotto di ogni monomio per ciascuno dei monomi che lo seguono. (N.B.: i quadrati sono sempre positivi, per i doppi prodotti si tiene conto della regola dei segni).

Il cubo di un binomio è uguale al quadrinomio formato da: cubo del primo termine + triplo prodotto del quadrato del primo per il secondo + triplo prodotto del primo per il quadrato del secondo + cubo del secondo termine.

SCOMPOSIZIONE DI UN POLINOMIO

1. Raccoglimento totale (si raccoglie il M.C.D. dei monomi che compongono il polinomio):

2. Raccoglimento parziale:

3. Si osserva il numero dei termini del polinomio

 Un binomio può essere:

Differenza di due quadrati

Somma di cubi

Differenza di cubi

 Un trinomio può essere: Quadrato di un binomio

 Un quadrinomio può essere:

di un binomio

Differenza di due quadrati di cui uno è il quadrato di un binomio

Un polinomio con sei termini

Differenza dei quadrati di due binomi

4. Scomposizione mediante la regola di Ruffini:

Esempio: 8x4x23

. I divisori del termine noto −8 sono

Dal momento che P(−2) = 0, per il teorema di Ruffini il polinomio è divisibile per (x+2).

Dividendo il polinomio per (x+2) tramite la regola di Ruffini si ottiene come quoziente 4 x 2 x 2

Per determinare il massimo comune divisore (M.C.D.) tra due o più polinomi:

 si scompongono i polinomi in fattori irriducibili

 il M.C.D. è il prodotto dei fattori comuni, presi una sola volta, con il minimo esponente.

Per determinare il minimo comune multiplo (m.c.m.) tra due o più polinomi:

 si scompongono i polinomi in fattori irriducibili

 il m.c.m. è il prodotto dei fattori comuni e non comuni, presi una sola volta, con il massimo esponente

Esempio. Calcolare il M.C.D. e il m.c.m. tra i polinomi 12a 3a 3 e 4a4aa23 .

:

Scomponendo, otteniamo che 2a2aa3a 12 3  e 2 2aaa4a4a23

Pertanto, M.C.D. = 2aa , m.c.m. = 2 2a2aa3 .

EQUAZIONI

Identità: uguaglianza tra due espressioni letterali, verificata per qualsiasi valore attribuito alle lettere che compaiono.

Equazione: uguaglianza tra due espressioni letterali, verificata per particolari valori attribuiti alle lettere che compaiono.

Due equazioni si dicono equivalenti se hanno le stesse soluzioni.

Primo principio di equivalenza: aggiungendo o sottraendo ad entrambi i membri di una equazione uno stesso valore o una stessa espressione, si ottiene un’equazione equivalente alla data.

Principio del trasporto: in un’equazione un termine può essere trasportato da un membro all’altro col segno cambiato.

Secondo principio di equivalenza: moltiplicando o dividendo entrambi i membri di un’equazione per uno stesso valore, purché diverso da 0, si ottiene un’equazione equivalente alla data.

Legge di annullamento del prodotto: il prodotto di due numeri è uguale a 0 se e solo se almeno uno di essi è 0. In simboli, 0q0p0qp

Equazioni di primo grado ax = b:

 e a 0 e b 0, l’e uazione è determinata ed ammette una soluzione: a b x  .

 e a 0 e b = 0, l’e uazione è determinata ed ammette una soluzione: = 0.

 e a = 0 e b 0, l’e uazione è impossibile; non ammette cioè nessuna soluzione.

 e a = 0 e b = 0, l’e uazione è indeterminata; cioè ualsiasi numero è soluzione.

DISEQUAZIONI

Primo principio di equivalenza per le disequazioni: aggiungendo o sottraendo ad entrambi i membri di una disequazione uno stesso numero o una stessa espressione, si ottiene una disequazione equivalente alla data.

Secondo principio di equivalenza per le disequazioni: moltiplicando o dividendo entrambi i membri di una disequazione per uno stesso numero diverso da zero, si ottiene una disequazione equivalente, a patto

 di mantenere lo stesso verso, se il numero per cui si moltiplica o si divide è positivo;

 di invertire il verso, se il numero per cui si moltiplica o si divide è negativo.

RADICALI

 Se n è un numero naturale dispari e a è un numero reale, la radice aritmetica n-esima di a è quel numero b che, elevato ad n, restituisce a. In simboli, abba n n  , con Rb,a 

 Se n è un numero naturale positivo pari e a è un numero reale non negativo, la radice aritmetica n-esima di a è quel numero non negativo b che, elevato ad n, restituisce a. In simboli: abba n n  , con a ≥ 0, b ≥ 0.

Perciò il radicale n a esiste: ▪ per ogni valore di a, se n è dispari; ▪ solo per a ≥ 0, se n è pari.

Valgono le seguenti relazioni: se n è pari,aann  ; se n è dispari,aa nn 

Proprietà invariantiva dei radicali: pn pm nm aa  per ogni a ≥ 0 e m, n, p naturali positivi.

Operazioni tra radicali (supponiamo che a e b siano maggiori o uguali a 0)

 Moltiplicazione:

Divisione (per b>0):

 Radice:

Trasporto fuori dalla radice:

!

 Addizione e sottrazione: Attenzione:nnnbaba , nnn baba (ad es., 9 16 9 16  . Infatti, il primo membro dà 4+3 = 7, il secondo membro dà 5). L’addizione e la sottrazione si possono semplificare quando i radicali sono simili (stesso indice e stesso radicando): Es.

4 4

Invece le somme323  e 5254 3 non si possono semplificare ulteriormente.

Razionalizzazione (consiste nel trasformare una frazione in una equivalente, senza più radicali al denominatore).

a) Al denominatore c’è un radicale:

b) Al denominatore c’è la somma o la differenza di due radici quadrate:

PIANO CARTESIANO

Coordinate del punto medio M di un segmento AB:

Coordinate del punto medio M di un segmento AB

x

Coordinate del punto medio M di un segmento AB: 2

; 2 yy y BA M

Distanza di due punti A e B (lunghezza del segmento AB):

 se il segmento è parallelo all’asse x (costituito da punti di uguale ordinata): ABxxBA .

se il segmento è parallelo all’asse x (costituito da punti di uguale ordinata): ABxxBA .

 se il segmento è parallelo all’asse y (costituito da punti di uguale ascissa): AByyBA

se il segmento è parallelo all’asse x (costituito da punti di uguale ordinata): ABxxBA .  se il segmento è parallelo all’asse y (costituito da punti di uguale ascissa): AByyBA

nel caso generale:

Es.: Calcola la lunghezza del segmento AB coordinate del suo punto medio , sapendo che A ( 1), B ( , ).

Es.: Calcola la lunghezza del segmento AB e le coordinate del suo punto medio M, sapendo che A (−4, −1), B (4, 3).

Es.: Calcola la lunghezza del segmento AB e le coordinate del suo punto medio , sapendo che A ( , 1), B ( , ).

AB 2

ertanto il punto medio del segmento AB è (0, 1).

Pertanto il punto medio del segmento AB è M (0, 1).

ertanto il punto medio del segmento AB è (0, 1).

LA RETTA

La funzione lineare y = mx + q ha per grafico una retta. m è detto coefficiente angolare (o pendenza); determina l’inclinazione della retta.

La funzione lineare y = mx + q ha per grafico una retta. m è detto coefficiente angolare (o pendenza); esso determina l’inclinazione della retta.

 Se m è positivo, la retta forma un angolo acuto con l’asse x (la retta è crescente);

 se m è negativo, la retta forma un angolo ottuso con l’asse x (la retta è decrescente);

 se m = 0, la retta è parallela all’asse x retta è orizzontale).

 se m = 0, la retta è parallela all’asse x (la retta è orizzontale).

q è detto intercetta (o ordinata all’origine); rappresenta l’ordinata del punto in cui la retta interseca l’asse y.

Se q = 0, la retta passa per l’origine degli assi. In questo caso x e y sono direttamente proporzionali. Per questo la funzione y = mx è detta funzione della proporzionalità diretta.

Se q = 0, la retta passa per l’origine degli assi. In questo caso x e y sono direttamente proporzionali. Per questo la funzione y = mx detta funzione della proporzionalità diretta.

Se q = 0, la retta passa per l’origine degli assi. In questo caso x e y sono direttamente proporzionali. Per questo la funzione y = mx è detta funzione della proporzionalità diretta.

L’equazione della retta

Retta parallela all’asse x y = k

Retta parallela all’asse y x = h

Retta passante per l’origine y = mx

asse y : x = 0

Retta in posizione generica y = mx + q

Retta in posizione generica y = mx + q y = k x = h

Equazione implicita della retta: ax + by + c 0.

Equazione implicita della retta: ax + by + c = 0.

Due rette sono parallele se e solo se hanno lo stesso coefficiente angolare ( mm21  ).

Due rette sono parallele se e solo se hanno lo stesso coefficiente angolare ( 2 1 mm  ).

Due rette sono perpendicolari se e solo se il coefficiente angolare dell’una è l’antireciproco (ossia l’opposto dell’inverso) del coefficiente angolare

Due rette sono perpendicolari se e solo il coefficiente angolare dell’una è l’antireciproco (ossia l’opposto dell’inverso) del coefficiente angolare

Due rette sono perpendicolari se e solo se il coefficiente angolare dell’una è l’antireciproco (ossia l’opposto dell’inverso) del coefficiente angolare

dell’altra

dell’altra  2 1 m 1 m .

2 1 m 1 m

asse x : y = 0 = h

Schede di richiamo

Per trovare l’equazione di una retta:

 Retta passante per un punto P y,x00 , con coefficiente angolare m assegnato: 0 0 xxmyy  .

 Retta passante per due punti A e B assegnati:

coefficiente angolare =

Le coordinate del punto di intersezione di due rette soddisfano entrambe le equazioni delle due rette. Quindi tali coordinate sono la soluzione del sistema costituito dalle equazioni delle due rette. Se le due rette hanno equazionecbyax  e 'cy'bx'a  , il loro punto di intersezione avrà

per coordinate la soluzione del sistema   'cy'bx'a cbyax . i hanno tre casi (supponiamo a’, b’, c’ 0):

b ' a a sistema determinato (una e una sola soluzione)

b'

c b' b ' a a  sistema indeterminato (infinite soluzioni)

c'

b ' a a  sistema impossibile (non esistono soluzioni)

c'

c b'

le due rette sono incidenti (hanno un solo punto di intersezione)

le due rette sono coincidenti (hanno infiniti punti di intersezione)

le due rette sono parallele distinte (non hanno nessun punto di intersezione)

Intersezione di una retta con gli assi cartesiani:

Esempio:

3yx 8y4x

Esempio:

24y12x3 8y4x

2y4x 8y4x

Esempio: 

 per avere l’intersezione con l’asse x, basta porre y = 0 nell’equazione della retta;

 per avere l’intersezione con l’asse y, basta porre x = 0 nell’equazione della retta.

EQUAZIONI DI SECONDO GRADO ax 2 + bx + c = 0 (con a 0)

Eq. monomie (b = c = 0): 0ax 2  L’equazione ha due soluzioni reali coincidenti0xx21  . ;

Eq. spurie (c = 0, b ≠ 0): 0bxax 2  Fattorizzando il primo membro, ax0b x  .

Per la legge di annullamento del prodotto, 0x  oppure ax0b . Si ottengono le due soluzioni a b x,0x 2 1 

Eq. pure (b = 0, c ≠ 0): 0cax 2  . Ricavando x2, si ottiene a c x 2  , da cui:

a) se a e c sono discordi, a c risulta positivo, quindi si ottengono le due soluzioni a c x2,1  .

b) se a e c sono concordi, a c risulta negativo, quindi l’equazione non ha soluzioni reali.

Schede di

aritmetica e algebra

Caso generale Si applica la formula risolutiva dell’equazione di secondo grado:

 Si calcola il discriminante ac4b 2 

Caso generale Si applica la formula risolutiva dell’equazione di secondo grado:  Si calcola il discriminante ac4b 2 

a) Se Δ > 0, l’equazione ha due soluzioni reali distinte 1 x e 2 x , con 2a ac4bb x 2 2 ,1  

b) Se Δ = 0, l’equazione ha due soluzioni reali coincidenti: a2 b xx21 .

c) Se Δ < 0, l’equazione non ha soluzioni reali.

Formula risolutiva ridotta dell’equazione di secondo grado: è una formula alternativa, nel caso in cui b sia pari (per risparmiare calcoli). Ponendo 2 b k  , le soluzioni sono a ackk x 2 2 ,1   .

Relazioni tra soluzioni e coefficienti di un’equazione di secondo grado (con Δ ≥ 0): la somma delle soluzioni è: a b xx21  ; il prodotto delle soluzioni è: a c xx21

Regola di Cartesio. Nell’equazione ax2 + bx + c = 0 (con a, b, c ≠ 0 e Δ ≥ 0),

 ad ogni variazione nei segni dei coefficienti corrisponde una soluzione positiva;  ad ogni permanenza nei segni dei coefficienti corrisponde una soluzione negativa.

Fattorizzazione di un trinomio di secondo grado (con Δ ≥ 0):

Fattorizzazione di un trinomio di secondo grado (con Δ ≥ 0):  2 1 2 xxxxac bx ax  .

.

Condizioni in un’equazione parametrica ax2 + bx + c = 0 (con a, b, c dipendenti da un parametro)

Condizione richiesta dall’esercizio

L’equazione ha soluzioni reali

L’equazione ha soluzioni reali distinte

L’equazione ha soluzioni reali coincidenti (x1 = x2)

Condizione da imporre

Si impone che b2 − 4ac ≥ 0 (ossia che Δ ≥ 0)

Si impone che b2 − 4ac > 0 (ossia che Δ > 0)

Si impone che b2 − 4ac = 0 (ossia che Δ = 0)

Una soluzione è un numero α (dato) Si sostituisce α al posto di x

Una soluzione è un numero α (dato)

La somma delle soluzioni è s (dato)

Il prodotto delle soluzioni è p (dato)

Si sostituisce α al posto di x

Si impone che s a b  e Δ ≥ 0

Si impone che p a c  e Δ ≥ 0

1. La funzione x k y  , con k costante diversa da 0, è detta funzione della proporzionalità inversa.

A pag. 12 del file pdf sostituire i cinque disegni con questi.

Il suo grafico è un’iperbole equilatera. Esso è costituito da due rami simmetrici rispetto all’origine degli assi, giacenti nei uadranti: ▪ primo e terzo se 0, ▪ secondo e uarto se 0.

A pag. 12 i cinque disegni con questi.

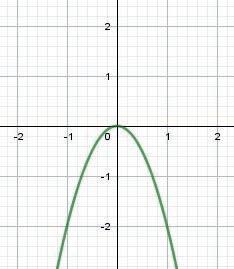
2. La funzione y = ax2 (per a 0) ha per grafico una parabola con vertice nell’origine. Tale parabola è simmetrica rispetto all’asse . e a 0, la parabola ha la concavità verso l’alto; se a 0, essa ha la concavità verso il basso.

3. La funzione y = ax2 + bx + c ha (per a 0) per grafico una parabola con asse di simmetria parallelo all’asse y. Il vertice è il punto , b V , dove ac4b 2  . Vale ancora che se a 0, la parabola ha la concavità verso l’alto; se a 0, essa ha la concavità verso il basso.

ax x k

1

, 6

Intersezioni della parabola y = ax2 + bx + c con una retta

In fondo a pag. 19 del file pdf sostituire il disegno al centro con il seguente. Non alterare le dimensioni.

A pag. 19 del file pdf (a pag. 2 del formulario geometria corretto), accanto al secondo disegno, sostituire la riga che inizia con “(In pratica” con la seguente (sono cambiati gli spazi tra i segni di punteggiatura): (In pratica, 7

Per trovare i punti di intersezione di una parabola con una retta, si mettono a sistema le loro equazioni. Le soluzioni del sistema (se esistono) saranno le coordinate di tali punti.

A pag. 19 del file pdf (a pag. 2 del formulario geometria corretto), accanto al secondo disegno, sostituire la riga che inizia con “(In pratica” con la seguente (sono cambiati gli spazi tra i segni di punteggiatura): (In pratica, 7

In particolare:

≅ , 8

 Per conoscere il punto di intersezione con l’asse y, basta porre x = 0 nell’equazione della parabola. i scopre che essa interseca l’asse nel punto di coordinate (0; c).

In fondo a pag. 19 del file pdf sostituire il disegno al centro con il seguente. Non alterare le dimensioni.

 er conoscere in uali punti la parabola interseca l’asse (se esistono), basta porre = 0; si ottiene l’equazione 0cbxax 2  ; le sue soluzioni saranno le ascisse dei punti cercati.

A pag. 20 del file pdf, a proposito dei trapezi, sostituire la figura al centro e quella a destra con le seguenti. Non alterare le dimensioni, altrimenti i quadratini all’interno si scombinano:

In pratica, se ac4b 2  è positivo, la parabola interseca l’asse in due punti distinti;

se ac4b 2  vale 0, la parabola interseca l’asse in un solo punto (il vertice); se ac4b 2  è negativo, la parabola non interseca l’asse x.

A pag. 20 del file pdf, a proposito dei trapezi, sostituire la figura al centro e quella a destra con le seguenti. Non alterare le dimensioni, altrimenti i quadratini all’interno si scombinano:

DISEQUAZIONI DI SECONDO GRADO (METODO GRAFICO)

Per risolvere una disequazione di secondo grado ax 2 + bx + c > 0,

 si disegna la parabola y = ax2 + bx + c ,

 si cercano gli eventuali punti di intersezione della parabola con l’asse x (cioè si risolve l’equazione ax2 + bx + c = 0),

 si considerano tutti i punti della parabola che si trovano nel semipiano y > 0,

 le soluzioni della disequazione sono le ascisse di tali punti.

Per risolvere una disequazione di secondo grado ax 2 + bx + c < 0,

 si disegna la parabola y = ax2 + bx + c ,

 si cercano gli eventuali punti di intersezione della parabola con l’asse x (cioè si risolve l’equazione ax2 + bx + c = 0),

 si considerano tutti i punti della parabola che si trovano nel semipiano y < 0,

 le soluzioni della disequazione sono le ascisse di tali punti.

EQUAZIONI DI GRADO SUPERIORE AL SECONDO

Teorema fondamentale dell’algebra: qualsiasi equazione di grado n ha al massimo n soluzioni reali, ciascuna contata con la propria molteplicità.

Equazioni monomie: ax n = 0 (a ≠ 0) l’unica soluzione è 0 (con molteplicità n).

Equazioni binomie: ax n + b = 0 (a, b ≠ 0)

 se n è dispari, l’equazione ha una e una sola soluzione: n a b x

;

 se n è pari e 0 a b  , l’equazione ha due soluzioni: n a b x  ;

 se n è pari e 0 a b  , l’equazione non ha soluzioni reali. 08x 3

09x 4

9x 4 

01x 6  1 x 6  l’equazione è impossibile in R

Equazioni trinomie: ax 2n + bxn + c = 0 (a ≠ 0).

Ponendo xn = t (da cui x2n = t2), l’equazione diventa 0cbtat 2  ; se questa ha due soluzioni reali 1 t e 2 t , poi si risolvono le due equazioni binomie 1 n tx  e 2 n tx  .

04x3x36

018x3x24

Poniamotx 3  04t3t 2  da cui

1t 1  , 4t 2 

Quindi, 1 x 3  11x 3  , 4 x 3  3 4x  . Le soluzioni sono, pertanto: −1, 3 4 .

Poniamotx 2  018t3t 2  da cui 3t 1  , 6t 2 

Quindi,3x 2  impossibile in R, 6x 2 6x 

Le soluzioni sono, pertanto: 6  .

Equazioni risolvibili mediante fattorizzazione

 Si portano tutti i termini dell’equazione al primo membro, lasciando 0 al secondo membro.

 Si fattorizza il polinomio al primo membro, giungendo ad una situazione del tipo

 Si applica la legge di annullamento del prodotto, ottenendo  0xP0xP0xP k

 Infine si risolve ciascuna delle equazioni  0xP i  trovate.

Applichiamo la legge di annullamento del prodotto:

*0x 5  ha per soluzione 0, con molteplicità 5,

* 04x 3  ha per soluzione 4, con molteplicità 3,

* 03x 2  non ha soluzioni reali

* 02x 2  ha per soluzioni 2x  , Quindi, le soluzioni sono 0 (molt. 5), 4 (molt. 3), 2 (molt. 1), 2 (molt. 1).

0x4x3x34

Scomponendo il polinomio al primo membro (raccoglimento totale e con la regola di Ruffini), otteniamo:  04x4x1xx 2  . Applicando ora la legge di annullamento del prodotto, ricaviamo le soluzioni 0 (molt. 1), 1 (molt. 1), −2 (molt. 2).

ELEMENTI DI STATISTICA

La statistica è la scienza che studia per mezzo di metodi matematici i fenomeni collettivi, cioè quei fenomeni che interessano un gran numero di persone o di cose. Il fenomeno studiato può essere:

La è scienza che studia mezzo metodi matematici fenomeni fenomeni interessano numero persone Il

La statistica è la scienza che studia per mezzo di metodi matematici i fenomeni collettivi, cioè quei fenomeni che interessano un gran numero di persone o di cose. Il fenomeno studiato può essere:

La statistica è la scienza che studia per mezzo di metodi matematici i fenomeni collettivi, cioè fenomeni che interessano un gran numero di persone o di cose. Il fenomeno studiato può essere:

 qualitativo, cioè espresso da qualità e non da valori numerici (professione, cittadinanza, ecc.)

 quantitativo, cioè espresso da numeri (statura, peso, numero di abitanti, ecc.)

 espresso (professione, , cioè espresso da numeri (statura, peso, numero di abitanti, ecc.)

 qualitativo, cioè espresso da qualità e non da valori numerici (professione, cittadinanza, ecc.)

 quantitativo, cioè espresso da numeri (statura, peso, numero di abitanti, ecc.)

Un’indagine statistica può essere fatta:

fatta:

 analizzando tutti gli elementi di una popolazione, detta popolazione statistica o universo statistico (rilevazione completa)

analizzando tutti gli elementi di una popolazione, detta popolazione statistica o universo statistico (rilevazione completa)

 analizzando tutti gli elementi di una popolazione, detta popolazione statistica o universo statistico (rilevazione completa)

 analizzando parte della popolazione (rilevazione incompleta o a campione) e rielaborando i dati.

 analizzando parte della popolazione (rilevazione incompleta o a campione) e rielaborando i

 analizzando parte della popolazione (rilevazione incompleta o a campione) e rielaborando i dati.

 analizzando parte della popolazione (rilevazione incompleta o a campione) e rielaborando dati.

La frequenza assoluta fa di un dato rappresenta il numero di volte in cui quel dato si presenta.

assoluta di un dato rappresenta il numero di volte in cui quel dato si presenta. frequenza relativa fr è, invece, tra e il

La frequenza assoluta fa di un dato rappresenta il numero di volte in cui quel dato si presenta.

La frequenza relativa fr è, invece, il rapporto tra la frequenza assoluta e il numero totale dei dati:

La frequenza relativa fr è, invece, il rapporto tra la frequenza assoluta e il numero totale dati:

dati dei totale n.

dei totale n.

La frequenza percentuale f% è la frequenza relativa espressa in percentuale. Essa si può calcolare con la relazione:

frequenza percentuale f% espressa in si può con relazione:

La frequenza percentuale f% è la frequenza relativa espressa in percentuale. Essa si può calcolare con la relazione:

f% = fr 100%

Sono indici statistici:

f% = fr 100%

f% = fr 100% ( )

fr 100%

 la moda, cioè il dato che si presenta con maggior frequenza;

la cioè dato presenta maggior

 la moda, cioè il dato che si presenta con maggior frequenza;

 la media aritmetica, ossia il rapporto tra la somma di tutti i dati e il numero totale dei dati stessi.

la media aritmetica, ossia il rapporto tra la somma di tutti i dati e il numero totale dei dati stessi.

La frequenza cumulata associata ad una modalità è uguale alla somma della sua frequenza assoluta e delle frequenze assolute delle modalità che la precedono. dati dei totale n.

La frequenza percentuale f% è la frequenza relativa espressa in percentuale. Essa si calcolare con la relazione:

 la media aritmetica, ossia il rapporto tra la somma di tutti i dati e il numero totale dei dati stessi.

 la media aritmetica, ossia il rapporto tra la somma di tutti i dati e il numero totale dei stessi.

 la mediana, cioè, dopo aver disposto i dati in ordine crescente,

la mediana disposto in ordine

 la mediana, cioè, dopo aver disposto i dati in ordine crescente,

 il valore che occupa la posizione centrale della sequenza (se il numero dei dati è dispari),

 il che la della sequenza il dei dati è dispari),

 il valore che occupa la posizione centrale della sequenza (se il numero dei dati è dispari),

 la media aritmetica dei due termini centrali (se il numero dei dati è pari).

La frequenza cumulata associata ad una modalità è uguale alla somma della sua frequenza assoluta e delle frequenze assolute delle modalità che la precedono. dati dei totale n.

 il valore che occupa la posizione centrale della sequenza (se il numero dei dati è dispari),

 la media aritmetica dei due termini centrali (se il numero dei dati è pari).

La frequenza cumulata associata ad una modalità è uguale alla somma della sua frequenza assoluta e delle frequenze assolute delle modalità che la precedono.

modalità è somma della sua e frequenze modalità la precedono.

La frequenza cumulata associata ad una modalità è uguale alla somma della sua frequenza assoluta e delle frequenze assolute delle modalità che la precedono. dati dei totale n.

Schede di richiamo

ELEMENTI DI PROBABILITÀ

La probabilità di un evento casuale E è definito come il rapporto tra il numero dei casi favorevoli all’evento e il numero dei casi possibili:

possibili casin.

Ovviamente sarà sempre 0 ≤ p(E) ≤ 1.

La probabilità si può esprimere come frazione, come numero decimale o come percentuale.

Esempio. Nel lancio di un dado i casi possibili sono 6, per cui:

▪ la probabilità che esca il 5 è 6 1 (come frazione) 17 (numero decimale) = 17% (percentuale);

▪ la probabilità che esca un numero pari è 2 1 6 3  (come frazione) = 0,5 (numero decimale) = 50%.

▪ la probabilità che esca il 7 è 0 6 0  (evento impossibile);

▪ la probabilità che esca un numero da 0 a 6 è 6 6 = 1 (evento certo).

Probabilità dell’evento contrario

Dato l’evento A, si definisce evento contrario l’evento A che si verifica se e solo se non si verifica A. La probabilità dell’evento contrario è il complementare a 1 della probabilità di A: .

Esempio. Calcoliamo la probabilità che, estraendo dal sacchetto uno dei 90 numeri della tombola in esso presenti, esso non termini con lo 0.

Chiamiamo A l’evento che il numero estratto termini con lo 0. Ovviamente p(A) 10 1 90 9  .

La probabilità cercata, cioè che il numero non termini con lo 0, è p( A ) = 1 – p(A)

Probabilità composta

Dati due eventi A, B, si indica con “A e B” l’evento che si verifica se e solo se si verificano sia A che B (probabilità che si verifichino insieme l’uno e l’altro evento).

 Se gli eventi sono indipendenti, ossia se il verificarsi di uno dei due eventi non influisce sulla probabilità che si verifichi l’altro, la probabilità composta è data dal prodotto delle singole probabilità: p(A e B) = p(A) p(B).

Esempio. Calcoliamo la probabilità che da un’urna con 10 palline numerate da 1 a 10 si estragga una pallina con un numero maggiore di 6 (evento A) e che si ottenga testa lanciando una moneta (evento B).

favorevoli casin. ) E ( p  p( A ) = 1 – p(A) :

I due eventi sono ovviamente indipendenti. p(A e B) = 5 1 2 1 10 4  .

 Se gli eventi sono dipendenti , ossia se il verificarsi di uno dei due eventi influisce sulla probabilità che si verifichi l’altro, la probabilità composta è data dal prodotto delle singole probabilità calcolate nell’ipotesi che gli eventi precedenti si siano verificati: p(A e B) = p(A) p(B|A), dove p(B|A) è la probabilità che si verifichi l’evento B nell’ipotesi che si sia verificato A.

Esempio. Calcolare la probabilità che da un pacchetto contenente 15 caramelle al limone e 10 all’arancia si tirino fuori a caso, una dopo l’altra, due caramelle entrambe all’arancia. I due eventi sono dipendenti, dal momento che se la prima caramella è all’arancia (evento A), varia la probabilità che anche la seconda lo sia (evento B). La probabilità che si verifichi l’evento A è p(A) = 25 10 . A questo punto, supponendo che la prima caramella sia

effettivamente all’arancia, nel pacchetto rimangono 15 caramelle al limone e 9 all’arancia, quindi la probabilità che anche la seconda sia del tipo cercato è p(B|A) = 24 9 .

In definitiva, la probabilità che entrambe siano all’arancia è p(A e B) = 20 3 24 9

.

Probabilità totale.

Dati due eventi A, B, si indica con “A o B” l’evento che si verifica se e solo se si verifica A ma non B, oppure B ma non A, oppure si verificano entrambi.

 Se gli eventi sono incompatibili, la probabilità totale è uguale alla somma delle singole probabilità: p(A o B) = p(A) + p(B).

Esempio. Calcoliamo la probabilità che, estraendo una carta da un mazzo di 40 carte, essa sia un asso (evento A) o un re (evento B). Gli eventi A, B sono ovviamente incompatibili, quindi:

p(A o B) = 5 1 40 8 40 4 40 4

.

 Se gli eventi sono compatibili, la probabilità totale è data dalla somma delle singole probabilità, diminuita della probabilità che si verifichino insieme: p(A o B) = p(A) + p(B) – p(A e B).

Esempio. Calcoliamo la probabilità di estrarre da un mazzo di 40 carte un asso (evento A) o una carta di spade (evento B). Gli eventi A, B sono compatibili, poiché può essere estratto l’asso di spade, comune a entrambi gli eventi A e B. Quindi:

p(A o B) = 40 13 40 1 40 10 40 4  .

Schede di richiamo

TRIANGOLI

Primo criterio di congruenza dei triangoli:

Se

ˆ A ˆ 'C'A AC 'B'A AB , allora ABC'C'B'A

Secondo criterio di congruenza dei triangoli: Se

ˆ C ˆ ˆ B ˆ 'C'B BC , allora ABC'C'B'A

Terzo criterio di congruenza dei triangoli:

Se  

'C'B BC 'C'A AC 'B'A AB , allora ABC'C'B'A

Classificazione dei triangoli rispetto ai lati isoscele equilatero scaleno in sintesi: se almeno due lati se i tre lati sono se tutti e tre i lati T sono congruenti congruenti sono disuguali

T = triangoli

Ti = triangoli isosceli

Te = triangoli equilateri (in questo caso, AC BC) (AB AC BC) (in questo caso, AC<AB<BC) Ts = triangoli scaleni

Proprietà del triangolo isoscele

n un triangolo isoscele gli angoli alla base sono congruenti, bisettrice, altezza e ediana coincidono Geometria

Schede di richiamo

del file pdf sostituire i cinque disegni con questi.

A pag. 19 del file pdf (a pag. 2 del formulario geometria corretto), accanto al secondo disegno, sostituire la riga che inizia con “(In pratica” con la seguente (sono cambiati gli spazi tra i segni di punteggiatura):

(In pratica,

(In pratica, 7 ˆ 1

,

;

In fondo a pag. 19 del file pdf sostituire il disegno al centro con il seguente. Non alterare le dimensioni.

A pag. 20 del file pdf, a proposito dei trapezi, sostituire la figura al centro e quella a destra con le seguenti. Non alterare le dimensioni, altrimenti i quadratini all’interno si scombinano:

del file pdf (a pag. 2 del formulario geometria corretto), accanto al secondo disegno, sostituire la inizia con “(In pratica” con la seguente (sono cambiati gli spazi tra i segni di punteggiatura):

pratica, 7

pag. 19 del file pdf sostituire il disegno al centro con il seguente. Non alterare le dimensioni.

del file pdf, a proposito dei trapezi, sostituire la figura al centro e quella a destra con le seguenti. alterare le dimensioni, altrimenti i quadratini all’interno si scombinano:

Schede di richiamo

Punti notevoli di un triangolo

Ortocentro: punto di intersezione delle altezze o dei loro prolungamenti. Se il triangolo è acutangolo, l’ortocentro è interno ad esso; se il triangolo è ottusangolo, è esterno; se il triangolo è rettangolo, l’ortocentro coincide con il vertice dell’angolo retto.

A pag. 19 del file pdf (a pag. 2 del formulario geometria corretto), accanto al secondo disegno, sostituire la riga che inizia con “(In pratica” con la seguente (sono cambiati gli spazi tra i segni di punteggiatura): (In pratica, 7 ˆ 1 ˆ ≅ , 6 ˆ 4 ˆ ≅ ;

A pag. 19 del file pdf (a pag. 2 del formulario geometria corretto), accanto al secondo disegno, sostituire la riga che inizia con “(In pratica” con la seguente (sono cambiati gli spazi tra i segni di punteggiatura):

Baricentro: punto di intersezione delle mediane. Esso è sempre interno al triangolo e divide ciascuna mediana in due parti, delle quali quella contenente il vertice è doppia dell’altra.

1

(In pratica, 7

≅ , 6

4

≅ ; 5

3

Incentro: punto di intersezione delle bisettrici. È sempre interno al triangolo. Essendo equidistante dai tre lati, l’incentro è il centro della circonferenza inscritta nel triangolo.

Circocentro: punto di intersezione degli assi dei lati. Se il triangolo è acutangolo, il circocentro è interno ad esso; se il triangolo è ottusangolo, è esterno; se il triangolo è rettangolo, il circocentro coincide con il punto medio dell’ipotenusa. Essendo equidistante dai tre vertici, il circocentro è il centro della circonferenza circoscritta al triangolo.

In fondo a pag. 19 del file pdf sostituire il disegno al centro con il seguente. Non alterare le dimensioni.

QUADRILATERI

TRAPEZIO: è un quadrilatero che ha due lati opposti paralleli

A pag. 20 del file pdf, a proposito dei trapezi, sostituire la figura al centro e quella a destra con le seguenti. Non alterare le dimensioni, altrimenti i quadratini all’interno si scombinano:

A pag. 20 del file pdf, a proposito dei trapezi, sostituire la figura al centro e quella a destra con le seguenti.

Non alterare le dimensioni, altrimenti i quadratini all’interno si scombinano:

trapezio scaleno trapezio rettangolo trapezio isoscele AB//DC, AD≠BC (AB//DC, AD DC) (AB//DC, AD BC)

Proprietà del trapezio qualunque:

A

D

 gli angoli adiacenti a ciascun lato obliquo sono supplementari ( 180C ˆ B

Proprietà del trapezio isoscele:

 le proiezioni dei lati obliqui sulla base maggiore sono congruenti (AH KB)

 gli angoli adiacenti a ciascuna base sono congruenti ( B ˆ A ˆ , C ˆ D ˆ )

 le diagonali sono congruenti (AC BD)

PARALLELOGRAMMA: è un quadrilatero con i lati opposti paralleli (AB//DC e AD//BC)

)

Proprietà del parallelogramma:

 i lati opposti sono congruenti ( DCAB , BC AD )

 gli angoli opposti sono congruenti ( ˆ DBA ˆ D , ˆ ACD ˆ A )

 gli angoli adiacenti ad uno stesso lato sono supplementari (ad es., 180CB ˆ ABA ˆ D )

 le diagonali si dividono scambievolmente per metà ( OCAO , OBDO )

Turn static files into dynamic content formats.

Create a flipbook